Página sessenta e seis

Parte 3

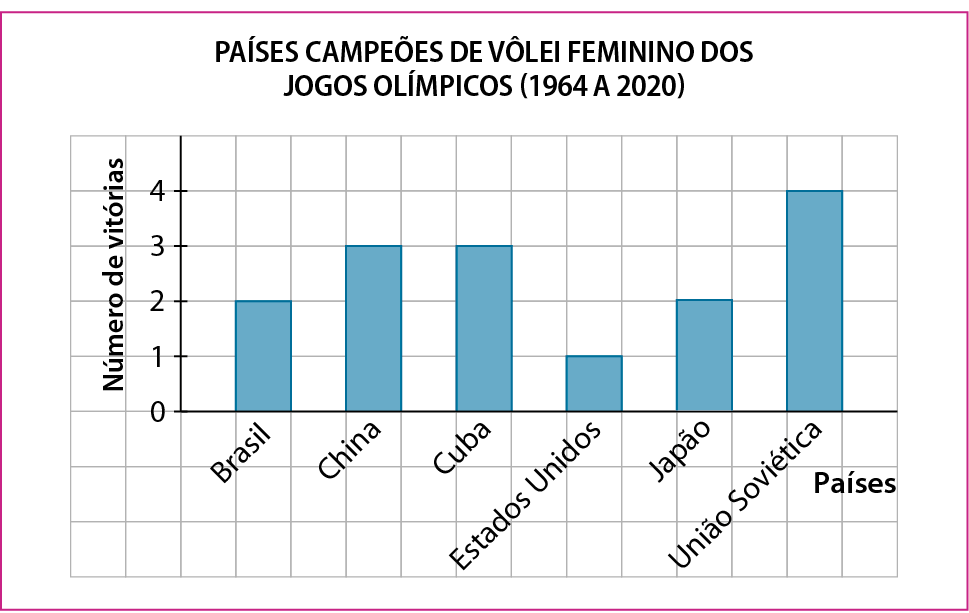
Gráfico. Gráfico de barras simples verticais. Título do gráfico: Países campeões de vôlei feminino dos jogos olímpicos abre parênteses 1 mil 964 a 2 mil e 20 fecha parênteses. Eixo horizontal perpendicular a um eixo vertical. O eixo vertical tem 5 tracinhos igualmente espaçados e nele estão indicados, de baixo para cima, os números 0, 1, 2, 3 e 4. Ele está rotulado como Número de vitórias. No eixo horizontal estão indicados os países, da esquerda para direita, Brasil, China, Cuba, Estados Unidos, Japão e União Soviética. Ele está rotulado como Países. Saindo do eixo horizontal há 6 barras azuis com a mesma largura, indicando que o Brasil teve 2 vitórias, China teve 3, Cuba teve 3, Estados Unidos teve 1, Japão teve 3 e União Soviética teve 4. Para representar a barra correspondente ao Brasil, foram preenchidos 2 quadradinhos: 1 coluna com 2 quadradinhos. Para representar a barra correspondente ao China, foram preenchidos 3 quadradinhos: 1 coluna com 3 quadradinhos. Para representar a barra correspondente ao Cuba, foram preenchidos 3 quadradinhos: 1 coluna com 3 quadradinhos. Para representar a barra correspondente aos Estados Unidos, foram preenchidos 1 quadradinhos: 1 coluna com 1 quadradinhos. Para representar a barra correspondente ao Japão, foram preenchidos 2 quadradinhos: 1 coluna com 2 quadradinhos. Para representar a barra correspondente ao União Soviética, foram preenchidos 4 quadradinhos: 1 coluna com 4 quadradinhos.

Pesquisa feita pela professora Juliana.

c) Na linha vertical, foi representado o número de vitórias. Na linha horizontal, os países vitoriosos.

d) Na linha vertical, foi representado os países vitoriosos. Na linha horizontal, o número de vitórias.

e) União Soviética.

EDUCAÇÃO FINANCEIRA

▶ Páginas 94 e 95

Resoluções e comentários em Orientações.

ATIVIDADES DE REVISÃO

▶ Página 96

1. a) cilindro

b) triângulo

c) retângulo

d) esfera

2. a) quadrados

b) retângulos

c) triângulos e quadrado

3. a) 30 cubinhos

Figura geométrica. 16 quadradinhos, em azul, dispostos em 4 fileiras com 4 quadradinhos cada.

b) 92 cubinhos

Figura geométrica. 23 quadradinhos, alaranjados, dispostos em 4 fileiras. As 3 fileiras de cima para baixo tem 7 quadradinhos. A quarta fileira tem 2 quadradinhos, sendo um na primeira coluna e outro na sétima coluna.

c) 70 cubinhos

Figura geométrica. 28 quadradinhos, em vermelho, dispostos em 4 fileiras com 7 quadradinhos cada.

PARA FINALIZAR

▶ Páginas 97 e 98

Resoluções e comentários em Orientações.

Unidade 2

Capítulo 4

ATIVIDADES

▶ Páginas 105 e 106

1. Sabemos que as bolinhas devem ser divididas entre 9 pessoas (Tiago e seus 8 primos). Entre os números 105, 117 e 130, temos que:

• 105 não é divisível por 9, pois 1 + 0 + 5 = 6 e 6 não é divisível por 9;

• 117 é divisível por 9, pois 1 + 1 + 7 = 9 e 9 é divisível por 9;

• 130 não é divisível por 9, pois 1 + 3 + 0 = 4 e 4 não é divisível por 9.

Logo, Tiago comprou 117 bolinhas de tamanho médio para distribuir igualmente entre seus primos.

2. a) Qualquer número natural terminado em 0 ou 5 sempre é divisível por 5.

b) Os números naturais ímpares nunca são divisíveis por 2, pois os números múltiplos de 2 sempre serão números pares.

3. a) O número já é divisível por 5, pois termina em 0. Para ser divisível por 3, a soma dos seus algarismos deve ser divisível por 3. Assim, temos 2 + 5 + 1 + 0 = 8. Adicionando o resultado a cada um dos possíveis algarismos, temos:

Esquema. Quadro composto por 2 linhas e 5 colunas. Na primeira coluna, sentença matemática 8 mais 0 é igual a 8. Abaixo, 8 mais 1 é igual a 9. Na segunda coluna, sentença matemática 8 mais 2 é igual a 10. Abaixo, 8 mais 3 é igual a 11. Na terceira coluna, sentença matemática 8 mais 4 é igual a 12. Abaixo, 8 mais 5 é igual a 13. Na quarta coluna, sentença matemática 8 mais 6 é igual a 14. Abaixo, 8 mais 7 é igual a 15. Na quinta coluna, sentença matemática 8 mais 8 é igual a 16. Abaixo, 8 mais 9 é igual a 17.

Dentre os resultados das adições, apenas o 9, 12 e 15 são divisíveis por 3. Portanto, os algarismos 1, 4 ou 7 podem ser colocados no lugar de ◼ para que o número seja divisível por 5 e por 3.

b) O último algarismo deve ser divisível por 2, mas não pode ser 0, pois o número dado não é divisível por 10. Os múltiplos de 2 terminam sempre em 0, 2, 4, 6 e 8. Assim, as possibilidades nesse caso são apenas 2, 4, 6 e 8.

O primeiro algarismo não interfere no número ser divisível por 2, mas não ser divisível por 10.

Portanto, o ♣ pode ser qualquer número e o ◼ pode ser 2, 4, 6 ou 8.

4. a) Verdadeira, pois os números divisíveis por 9 têm a soma dos algarismos múltiplos de 9 e, consequentemente, múltiplos de 3. Então, também são divisíveis por 3.

b) Falsa. Por exemplo, 12 é divisível por 6, mas não é por 5.

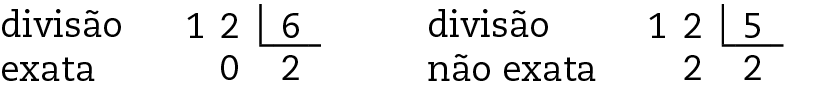
Algoritmo da divisão. 12 dividido por 6 igual a 2 com resto zero. Divisão exata. A esquerda o número 12. A direita na chave o número 6. Abaixo da chave o número 2. Abaixo do 12 o número 0, alinhado ordem a ordem com o 12. Algoritmo da divisão. 12 dividido por 5 igual a 2 com resto 2. Divisão não exata. A esquerda o número 12. A direita na chave o número 5. Abaixo da chave o número 2. Abaixo do 12 o número 2, alinhado ordem a ordem com o 12.

c) Falsa. Por exemplo, 6 é divisível por 2, mas não é por 4.

Algoritmo da divisão. 6 dividido por 2 igual a 3 com resto zero. Divisão exata. A esquerda o número 6. A direita na chave o número 2. Abaixo da chave o número 3. Abaixo do 6 o número 0, alinhado ordem a ordem com o 6. Algoritmo da divisão. 6 dividido por 4 igual a 1 com resto 2. Divisão não exata. A esquerda o número 6. A direita na chave o número 4. Abaixo da chave o número 1. Abaixo do 6 o número 2, alinhado ordem a ordem com o 6.

d) Verdadeira. Um número divisível por 10 termina em 0. Logo, também é divisível por 5.

5. a) O maior número natural de 2 algarismos é 99. Para que seja divisível por 2, deve ser par, e para ser divisível por 3, a soma de seus algarismos deve ser divisível por 3. Assim:

• 98 é par, mas não é divisível por 3, pois 9 + 8 = 17;

• 96 é par e é divisível por 3, pois 9 + 6 = 15.

Portanto, o número procurado é o 96.

b) Para que seja divisível por 6, tem de ser divisível por 2 e por 3. Assim:

• 41 não é divisível por 2, pois não é par;

• 42 é divisível por 2, pois é par; e também é divisível por 3, pois 4 + 2 = 6.

Portanto, o número procurado é o 42.

c) Para ser divisível por 5, o número deve terminar em 0 ou 5, e, para ser divisível por 2, o número deve ser par. Assim, o número procurado termina em 0. Logo:

Página sessenta e sete

• 10 não é divisível por 3, pois 1 + 0 = 1;

• 20 não é divisível por 3, pois 2 + 0 = 2;

• 30 é divisível por 3, pois 3 + 0 = 3.

Portanto, o número procurado é o 30.

d) Para ser divisível por 5, o número deve terminar em 0 ou 5. Além disso:

• .1005 não é divisível por 9, pois 1 + 0 + 0 + 5 = 6;

• .1010 não é divisível por 9, pois 1 + 0 + 1 + 0 = 2;

• .1015 não é divisível por 9, pois 1 + 0 + 1 + 5 = 7;

• .1020 não é divisível por 9, pois 1 + 0 + 2 + 0 = 3;

• .1025 não é divisível por 9, pois 1 + 0 + 2 + 5 = 8;

• .1030 não é divisível por 9, pois 1 + 0 + 3 + 0 = 4;

• .1035 é divisível por 9, pois 1 + 0 + 3 + 5 = 9.

Portanto, o número procurado é .1035.

6. Espera-se que os estudantes percebam que, para que um número seja divisível por 2, ele precisa ser par; para ser divisível por 3, a soma dos seus algarismos precisa ser um número divisível por 3; e para ser divisível por 5, precisa terminar em 0 ou 5. Com isso, espera-se que eles criem uma situação-problema em que o resultado atenda a esses três critérios, como o número 30 e seus múltiplos.

7. Iniciando a coleta dos dados dos dois recipientes em um mesmo dia, as próximas coletas serão feitas, durante 30 dias, após:

• 1º recipiente: 4, 8, 12, 16, 20, 24 e 28 dias;

• 2º recipiente: 6, 12, 18 e 24 dias.

Logo, Juliana não escolheu certo o período para trabalhar com os recipientes, pois, após 12 dias e após 24 dias do início, terá de trabalhar com os dois recipientes ao mesmo tempo, o que ela não queria.

ATIVIDADES

▶ Páginas 108 e 109

1. Exemplos de respostas:

a) 0, 9, 18 e 27

b) 0, 20, 40 e 60

c) 0, 35, 70 e 105

d) 0, 56, 112 e 168

2. a) Divisores de 24:

24 : 1 = 24

24 : 2 = 12

24 : 3 = 8

24 : 4 = 6

24 : 6 = 4

24 : 8 = 3

24 : 12 = 2

24 : 24 = 1

Os divisores de 24 são 1, 2, 3, 4, 6, 8, 12 e 24.

b) Divisores de 40:

40 : 1 = 40

40 : 2 = 20

40 : 4 = 10

40 : 5 = 8

40 : 8 = 5

40 : 10 = 4

40 : 20 = 2

40 : 40 = 1

Os divisores de 40 são 1, 2, 4, 5, 8, 10, 20 e 40.

c) Divisores de 45:

45 : 1 = 45

45 : 3 = 15

45 : 5 = 9

45 : 9 = 5

45 : 15 = 3

45 : 45 = 1

Os divisores de 45 são 1, 3, 5, 9, 15 e 45.

d) Divisores de 60:

60 : 1 = 60

60 : 2 = 30

60 : 3 = 20

60 : 4 = 15

60 : 5 = 12

60 : 6 = 10

60 : 10 = 6

60 : 12 = 5

60 : 15 = 4

60 : 20 = 3

60 : 30 = 2

60 : 60 = 1

Os divisores de 60 são 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60.

3. O número aproximado de cada tipo de veículo é dado pela divisão entre a extensão do congestionamento e a medida de comprimento aproximado do tipo de veículo considerado (mais a distância de segurança), ambos na mesma unidade de medida.

a) 400 : 5 = 80

Logo, estando presentes apenas carros, serão 80 carros.

b) 400 : 8 = 50

Logo, estando presentes apenas vans, serão 50 vans.

c) 400 : 10 = 40

Logo, estando presentes apenas ônibus, serão 40 ônibus.

4. Às 11 horas ficou verde, pois a cada 5 minutos o semáforo fica verde. Logo, ficará verde às 10 horas, 10 horas 05 minutos, 10 horas 10 minutos, reticências, 10 horas 55 minutos, 11 horas.

5. a) Espera-se que os estudantes percebam que precisam verificar se o ano no qual nasceram é múltiplo de 4 e, portanto, se são divisíveis por 4. Um número é divisível por 4 quando os seus dois últimos algarismos formam um número divisível por 4.

b) Nesse caso, como não há anos terminados em 00, devemos verificar se os números que representam os anos entre 2017 e 2027 são múltiplos de 4 e, portanto, se são divisíveis por 4. Um número é divisível por 4 quando os seus dois últimos algarismos formam um número divisível por 4. Portanto:

Esquema. Lista com os anos de 2018 até 2026 um abaixo do outro. Cota abaixo das dezenas de cada ano destacando os números 18, 19, 21, 22, 23, 25 e 26. Cota A direita da lista com o texto: Não são bissextos, pois 18, 19, 21, 22, 23, 25 e 26 não são divisíveis por 4.

2020 e 2024 são bissextos, pois 20 e 24 são divisíveis por 4. Logo, há dois anos bissextos entre 2017 e 2027. São eles: 2020 e 2024.

c) Os dois últimos algarismos de 1889 formam o número 89, que não é divisível por 4. Logo, o ano da Proclamação da República não foi bissexto.

6. Se houvesse 3 carros a mais, a quantidade de carros seria um número múltiplo de 6. Como 6 = 2 ⋅ 3, esse número seria divisível por 2 e por 3. Procurando primeiro os múltiplos de 2 entre 115 e 120, temos: 116, 118 e 120. Entre esses números, o único múltiplo de 3 é 120. Como há 3 carros a menos, concluímos que estavam no estacionamento 117 carros.

Página sessenta e oito

7. Como nas pilhas de 12, 15 ou 20 Cê dês sempre sobram 3, se ela tivesse 3 Cê dês a menos do que tem, a quantidade de Cê dês seria um número múltiplo de 12, de 15 e de 20. Vamos procurar primeiro os múltiplos de 12, 15 e 20.

• múltiplos de 12:

Algoritmo da divisão. 150 dividido por 12 igual a 12 com resto 6. A esquerda, o número 150. A direita na chave o número 12. Abaixo da chave o número 12, com seta indicando número de gavetas. Abaixo do 150, o número 30, alinhado ordem a ordem com o 150. Abaixo do 30, o número 6 alinhado ordem a ordem e com seta indicando divisão não exata.

Como 6 + 6 = 12, então 150 + 6 = 156 é divisível por 12.

Logo, os múltiplos de 12 no intervalo entre 150 e 200 são: 156, 168, 180, 192

• múltiplos de 15:

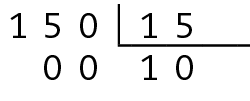
Algoritmo da divisão. 150 dividido por 15 igual a 10 com resto 0. A esquerda o número 150. A direita na chave o número 15. Abaixo da chave o número 10. Abaixo do 150, o número 00.

Logo, os múltiplos de 15 no intervalo entre 150 e 200 são: 150, 165, 180, 195

• múltiplos de 20:

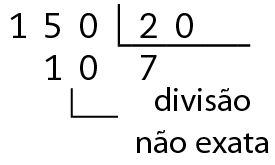
Algoritmo da divisão. 150 dividido por 20 igual a 7 com resto 10. A esquerda o número 150. A direita na chave o número 20. Abaixo da chave o número 7. Abaixo do 150, o número 10, alinhado ordem a ordem com o 150. Fio preto do 10 para o texto divisão não exata.

Como 10 + 10 = 20, então 150 + 10 = 160 é divisível por 20.

Logo, os múltiplos de 20 no intervalo entre 150 e 200 são:

160, 180, 200

O único número que é múltiplo de 12, 15 e 20 ao mesmo tempo que está entre 150 e 200 é o 180. Logo, como Gabriela tem 3 Cê dês a mais, ela tem 183 Cê dês.

8. Espera-se que os estudantes elaborem um problema em que seja preciso verificar os critérios de divisibilidade e que sua solução possa refletir que entre 2, 5, 8 e 10, apenas o 8 não é divisor de 30, pois:

• 30 é par. Portanto, é divisível por 2;

• a soma dos seus algarismos (3 + 0 = 3) é divisível por 3. Portanto, 30 é divisível por 3;

• termina em 0. Então, é divisível por 5 e por 10.

O único número dentre os propostos pela atividade que não se enquadra aos critérios é o 8.

9. Espera-se que os estudantes escolham um número natural qualquer e o multiplique por 2, por 3, por 4, e assim sucessivamente. Isso demonstrará que ele entendeu o conceito de múltiplo de um número natural.

ATIVIDADES

▶ Páginas 110 e 111

Esquema. Quadro composto por 15 quadrados divididos em 2 linhas. A primeira com 8 quadradinhos com os números: 2, 3, 5, 7, 11, 13, 17 e 19. A segunda com 7 quadradinhos com os números: 23, 29, 31, 37, 41, 43 e 47.

2. Um número primo tem apenas dois divisores naturais distintos: o número 1 e o próprio número. Para classificar um número como composto, verificamos se esse número é divisível por, pelo menos, um número primo menor que ele.

a) Podemos dividir 237 por 3; o resultado é igual a 79. Portanto, ele é um número composto.

b) Podemos dividir 505 por 5; o resultado é igual a 101. Portanto, ele é um número composto.

c) Podemos dividir .1024 por 2; o resultado é igual a 512. Portanto, ele é um número composto.

d) O número 103 tem apenas dois divisores naturais distintos: o número 1 e ele mesmo. Portanto, ele é um número primo.

e) O número 67 tem apenas dois divisores naturais distintos: o número 1 e ele mesmo. Portanto, ele é um número primo.

f) O número 307 tem apenas dois divisores naturais distintos: o número 1 e ele mesmo. Portanto, ele é um número primo.

g) Podemos dividir 247 por 13; o resultado é igual a 19. Portanto, ele é um número composto.

h) Podemos dividir 715 por 5; o resultado é igual a 143. Portanto, ele é um número composto.

3. Os números 13 e 17 são primos consecutivos e 13 + 17 = 30. Como Joana é mais velha que Ígor, então Joana tem 17 anos e Ígor tem 13 anos.

4. Os itens b e d apresentam números primos, pois os números 101 e 103 possuem apenas dois divisores: 1 e eles mesmos.

5. Só uma vez, que seria 23 + 2 = 25.

alternativa b

6. a) O menor número primo de dois algarismos é o 11.

b) Escrevendo os números de dois algarismos em ordem decrescente, temos: 99, 98, 97, reticências, 12, 11, 10. Entre eles, 99 não é primo, pois é divisível por 3; 98 não é primo, pois é divisível por 2. Aplicando os critérios de divisibilidade, observamos que 97 não é divisível por 2, nem por 3, nem por 5. Verificando os demais primos, temos:

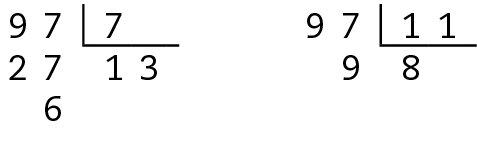
Algoritmo da divisão. 97 dividido por 7 igual a 13 com resto 6. A esquerda o número 97. A direita na chave o número 7. Abaixo da chave o número 13. Abaixo do 97, o número 27, alinhado ordem a ordem com o 97. Abaixo do 27, o número 6.Algoritmo da divisão. 97 dividido por 11 igual a 8 com resto 9. A esquerda o número 97. A direita na chave o número 11. Abaixo da chave o número 8. Abaixo do 97, o número 9, alinhado ordem a ordem com o 97.

Como as divisões não são exatas e a partir da divisão por 7 os quocientes ficarão cada vez menores que os números primos do divisor, então podemos concluir que 97 é primo.

Logo, o maior número primo de dois algarismos é o 97.

c) Escrevendo os números maiores que 300, temos: 301, 302, 303, 304, 305, 306, 307, 308, reticências

Aplicando os critérios de divisibilidade, observamos que 301 é divisível por 7, 302 é par, então é número composto; 303 é divisível por 3 (pois 3 + 0 + 3 = 6), então é número composto; 304 é par, então é número composto; 305 é divisível por 5, pois termina em 5; 306 é par, então é número composto; 307 não é divisível por nenhum número primo.

Portanto, o menor número primo maior que 300 é 307.

d) O menor número de três algarismos é o 100, que pelo fato de ser um número par já é classificado como composto. Passando para o 101, verificamos que não conseguimos aplicar a ele nenhum critério de divisibilidade. Portanto, o menor número primo de três algarismos é o 101.

ATIVIDADES

▶ Página 112

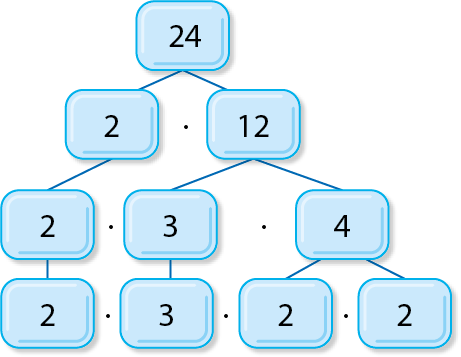
1. a) Utilizando a operação inversa, temos 24 : 2 = 12.

Logo, 2 ⋅ 12 = 24. Ao final das fatorações sucessivas, temos apenas fatores primos.

Página sessenta e nove

Qual é o número primo que, multiplicado por ele mesmo, é igual a 4? 2 ⋅ 2 = 4

Portanto, os números procurados, de cima para baixo, da esquerda para a direita, são 12, 2 e 2.

Esquema. Primeira linha: Bloco com número 24 ligado aos dois blocos da linha de baixo. Segunda linha: Bloco com 2 vezes bloco com 12. O bloco com 2 está ligado ao primeiro bloco na linha de baixo e o bloco com 12 está ligado aos outros dois blocos. Terceira linha: bloco com o 2 vezes o bloco com o 3 vezes bloco com o 4. Bloco com o 2 está ligado com o primeiro bloco da linha de baixo, bloco com o 3 está ligado com o segundo bloco e o bloco com o 4 ligado aos outros dois blocos. Quarta linha: bloco com o 2 vezes o bloco com o 3, vezes bloco com 2 vezes outro bloco com 2.

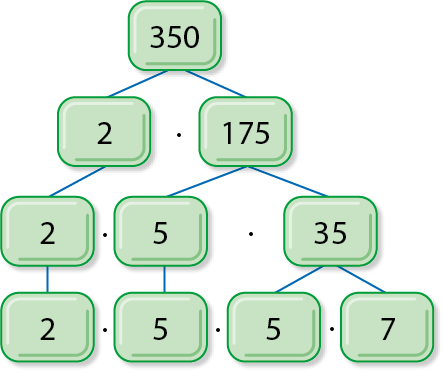
b) Para encontrar o número escondido localizado no topo do esquema, basta realizar a multiplicação 2 ⋅ 175 = 350. Utilizando a operação inversa, temos 175 : 35 = 5. Logo, 5 ⋅ 35 = 175. Ao final das fatorações sucessivas, temos apenas fatores primos.

Qual é o número primo que, multiplicado por outro número primo, é igual a 35?

5 ⋅ 7 = 35

Portanto, os números procurados, de cima para baixo, da esquerda para a direita, são 350, 5, 5, 5 e 7.

Esquema. Primeira linha: Bloco com 350 ligado aos dois blocos da linha de baixo. Segunda linha: Bloco com o 2 vezes bloco com o 175. O bloco com 2 está ligado ao primeiro bloco na linha de baixo e o bloco com o 175 está ligado aos outros dois blocos. Terceira linha: bloco com o 2 vezes o bloco com 5, vezes bloco com o 35. Bloco com o 2 está ligado com o primeiro bloco da linha de baixo, bloco com o 5 está ligado com o segundo bloco e o bloco com o 35 ligado aos outros dois blocos. Quarta linha: bloco com o 2 vezes o bloco com o 5, vezes bloco com 5, vezes bloco com 7.

2. a)

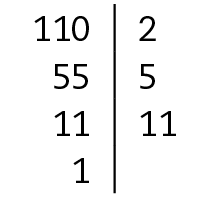
Esquema. À esquerda o número 110 e à direita, 2. Abaixo, à esquerda o 55, à direita o 5. Abaixo, à esquerda 11 e à direita 11. Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical.

Esquema. À esquerda 210 e à direita, o 2. Abaixo, à esquerda o 105, à direita, o 3. Abaixo, à esquerda 35 e à direita, o 5. Abaixo, à esquerda 7 e à direita, 7 .Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical.

3. Caio não decompôs o fator 4 em números primos (2 ⋅ 2). Não fez, portanto, uma fatoração completa.

Já Laís realizou uma fatoração completa escrevendo 60 apenas como o produto de fatores primos.

4. a) 20 = 25 ⋅ 5

b) 75 = 3 ⋅ 52

c) 32 = 25

d) 90 = 2 ⋅ 32 ⋅ 5

e) 280 = 23 ⋅ 5 ⋅ 7

f) 100 = 22 ⋅ 52

g) .1260 = 22 ⋅ 32 ⋅ 5 ⋅ 7

h) 286 = 2 ⋅ 11 ⋅ 13

i) .2431 = 11 ⋅ 13 ⋅ 17

j) 168 = 23 ⋅ 3 ⋅ 7

5. a) 3 ⋅ 5 ⋅ 7 ⋅ 11 = .1155

b) 74 = 7 ⋅ 7 ⋅ 7 ⋅ 7 = .2401

c) 22 ⋅ 3 ⋅ 29 = 2 ⋅ 2 ⋅ 3 ⋅ 29 = 348

d) 25 ⋅ 3 ⋅ 13 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 13 = .1248

6. a) Decompondo .2145 em fatores primos, temos:

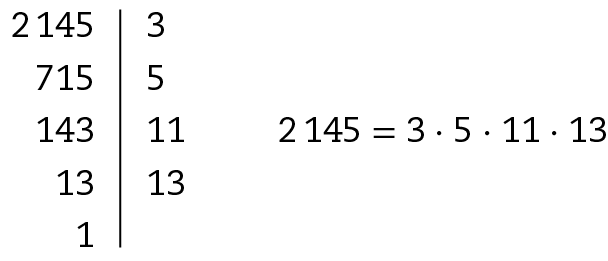
Esquema. À esquerda 2 mil 145 e à direita, o 3. Abaixo, à esquerda o 715, à direita, o 5. Abaixo, à esquerda 143 e à direita, o 11. Abaixo, à esquerda 13 e à direita, 13 .Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical. A direita do esquema, 2 mil 145 igual a 3 vezes 5 vezes 11 vezes 13.

Logo, os fatores primos de .2145 são 3, 5, 11 e 13.

b) Decompondo 322 em fatores primos, temos:

Esquema. À esquerda 322 e à direita, o 2. Abaixo, à esquerda o 161, à direita, o 7. Abaixo, à esquerda 23 e à direita, o 23. Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical. A direita do esquema, 322 igual a 2 vezes 7 vezes 23.

Logo, o maior fator primo de 322 é 23.

c) O número 67 é primo. Logo, seu menor fator primo é ele mesmo, ou seja, 67.

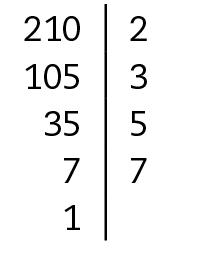
7. Para distribuir igualmente 143 moedas, precisamos encontrar números que dividam o número 143 de modo que o resto seja zero, isto é, precisamos encontrar os divisores de 143.

Esquema. À esquerda 143 e à direita, o 11. Abaixo, à esquerda o 13, à direita, o 13. Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical. A direita do esquema, 143 igual a 11 vezes 13.

Portanto, 11 e 13 são divisores de 143.

Havendo 11 jogadores, cada um ganhará 13 moedas. Se houver 13 jogadores, cada um receberá 11 moedas. Como 1 e 143 também são divisores de 143 podem participar dêsse jôgo 1, 11, 13 ou 143 pessoas.

8. O mosaico poderá ter formato retangular: 1 por 32, 2 por 16 ou 4 por 8, pois 1 ⋅ 32 = 32, 2 ⋅ 16 = 32 e 4 ⋅ 8 = 32.

9. a) Vamos decompor o número .2717 em fatores primos.

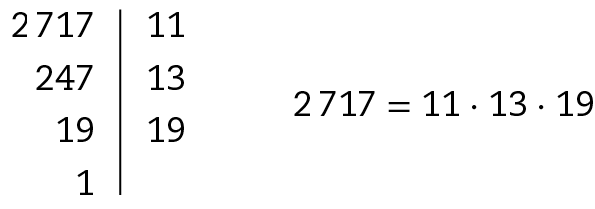
Esquema. À esquerda 2 mil 717 e à direita, o 11. Abaixo, à esquerda o 247, à direita, o 13. Abaixo, à esquerda 19 e à direita, o 19. Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical. A direita do esquema, 2 mil 717 igual a 11 vezes 13 vezes 19.

Como 11, 13 e 19 são números primos e o produto entre eles é .2717, então esses números representam as idades de Guilherme e de seus irmãos.

Portanto, Guilherme tem dois irmãos.

b) Como ele é o mais novo, ele tem 11 anos.

ESTATÍSTICA E PROBABILIDADE

▶ Páginas 114 e 115

1. Espera-se que os estudantes identifiquem os tipos de gráficos pedidos pela atividade e diferenciem suas características, consigam extrair e interpretar as informações dos gráficos escolhidos transcrevendo-as na fórma textual e elaborando questões pertinentes aos dados informados pelo gráfico.

2. a) O número de veículos lavados no primeiro trimestre de 2023.

b) março

c) 203 + 175 + 125 = 503

O total de veículos lavados no primeiro trimestre de 2023 foi 503 veículos.

3. a) Matemática, pois apresenta o maior número de livros (32).

b) História, pois a quantidade de livros de História (15) é menor que a de Geografia (20).

Página setenta

4. a) Número anual de vagas em 2019 de alguns cursos da Esalq.

b) No Jornal da úspi, em junho de 2018.

c) Engenharia Agronômica.

d) 200 + 40 + 40 + 30 = 310

No total, 310 estudantes podem ser matriculados nesses cursos.

5. a) 450 lugares.

b) Sim, os teatros Docas, Clara Nunes e Amazonas têm capacidade para mais de 400 espectadores.

c) O teatro Metrópolis da Ufes tem a menor capacidade e o teatro Amazonas tem a maior capacidade.

6. a) .1530 + .2650 + .4810 + .1120 + 370 = .10480

Foram encomendados .10480 uniformes no total.

b) 700 + 950 + .2340 = .3390

.10480 ‒ .3390 = .6490

Portanto, faltavam ser produzidos .6490 uniformes.

ATIVIDADES DE REVISÃO

▶ Página 116

1. Dividindo 150 por 12, temos:

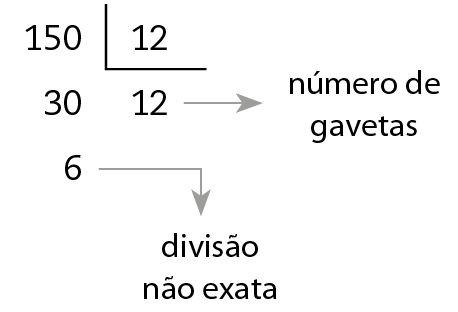
Algoritmo da divisão. 150 dividido por 12 igual a 12 com resto 6. A esquerda o número 150. A direita na chave o número 12. Abaixo da chave o número 15. Abaixo do 150, o número 30, alinhado ordem a ordem com o 150. Abaixo do 30, o número 6, alinhado ordem a ordem e com fio preto indicando divisão não exata.

Portanto, serão utilizadas 12 gavetas com 12 pastas cada uma e mais 1 gaveta que terá 6 pastas. Logo, não é possível fazer a organização pedida, pois o número 150 não é divisível por 12.

2. a) Sim. Como 560 é divisível por 20, se adicionarmos a 560 um grupo de 20, o resultado obtido continua sendo divisível por 20. Logo, 560 + 20 é divisível por 20.

b) Sim. Como 560 é divisível por 20, se subtrairmos de 560 um grupo de 20, o resultado obtido continua sendo divisível por 20. Logo, 560 ‒ 20 é divisível por 20.

c) Sim. Todo número multiplicado e, em seguida, dividido por um mesmo número resultará no número inicial. Assim, (560 ⋅ 20) : 20 = 560. Logo, 560 ⋅ 20 é divisível por 20.

d) Não. Como 560 : 20 = 28 e 28 : 20 não é uma divisão exata, pois apresenta resto igual a 8. Então, pode-se concluir que 560 : 20 não é divisível por 20.

3. a) 118 e 204

• divisores de 118: 1, 2, 59

• divisores de 204: 1, 2, 3, 17, 102

• soma dos divisores de 118: 1 + 2 + 59 = 62

• soma dos divisores de 204: 1 + 2 + 3 + 17 + 102 = 125

b) 100 e 150

• divisores de 100: 1, 2, 4, 5, 25, 50

• divisores de 150: 1, 2, 3, 5, 6, 15, 25, 50, 75

• soma dos divisores de 100: 1 + 2 + 4 + 5 + 25 + 50 = 87

• soma dos divisores de 150: 1 + 2 + 3 + 5 + 6 + 15 + 25 + 50 + 75 = 182

c) .1184 e .1210

• divisores de .1184: 1, 2, 4, 8, 16, 32, 37, 74, 148, 296, 592

• divisores de .1210: 1, 2, 5, 10, 11, 22, 55, 110, 121, 242, 605

• soma dos divisores de .1184: 1 + 2 + 4 + 8 + 16 + 32 + 37 + 74 + 148 + 296 + 592 = .1210

• soma dos divisores de .1210: 1 + 2 + 5 + 10 + 11 + 22 + 55 + 110 + 121 + 242 + 605 = .1184

d) .1020 e 142

• divisores de .1020: 1, 2, 4, 5, 10, 20, 51, 102, 255, 510

• divisores de 142: 1, 2, 71

• soma dos divisores de .1020: 1 + 2 + 4 + 5 + 10 + 20 + 51 + 102 + 255 + 510 = 960

• soma dos divisores de 142: 1 + 2 + 71 = 74

alternativa c

4. Ao trocar por cédulas de 2 reais, sobrará 1 real. Então, a quantia que Marina tem é um número ímpar entre 40 e 50. As possibilidades são, portanto, 41, 43, 45, 47 e 49. Ao trocar por cédulas de 5 reais, sobrarão 3 reais. Portanto, a quantia que ela tem não é divisível por 5, porque o resto da divisão é igual a 3.

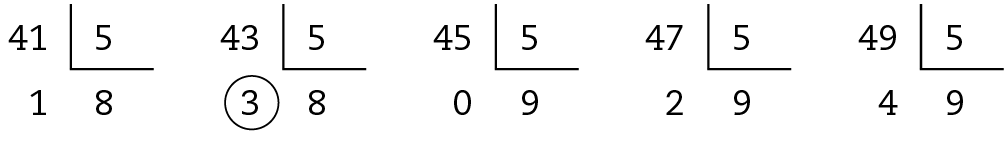
Algoritmo da divisão. 41 dividido por 5 igual a 8 com resto 1. A esquerda, o número 41. A direita na chave o número 5. Abaixo da chave o número 8, Abaixo do 41, o número 1, alinhado ordem a ordem com o 41. Algoritmo da divisão. 43 dividido por 5 igual a 8 com resto 3, que está circulado. A esquerda, o número 43. A direita na chave o número 5. Abaixo da chave o número 8, Abaixo do 43, o número 3, alinhado ordem a ordem com o 43.Algoritmo da divisão. 45 dividido por 5 igual a 9 com resto 0. A esquerda, o número 45. A direita na chave o número 5. Abaixo da chave o número 9, Abaixo do 45, o número 0, alinhado ordem a ordem com o 45.Algoritmo da divisão. 47 dividido por 5 igual a 9 com resto 2. A esquerda, o número 47. A direita na chave o número 5. Abaixo da chave o número 9, Abaixo do 47, o número 2, alinhado ordem a ordem com o 47.Algoritmo da divisão. 49 dividido por 5 igual a 9 com resto 4. A esquerda, o número 49. A direita na chave o número 5. Abaixo da chave o número 9, Abaixo do 49, o número 4, alinhado ordem a ordem com o 49.

Logo, Marina tem 43 reais.

5. O número escolhido pela professora foi 1, 2, 3, 4 ou 5. Vamos montar um quadro, indicando se o número citado pelos estudantes é ou não múltiplo desses possíveis números.

Estudantes	Falou	Múltiplo de 1	Múltiplo de 2	Múltiplo de 3	Múltiplo de 4	Múltiplo de 5
Antônio	25	sim	não	não	não	sim
Daiane	7	sim	não	não	não	não
Júlia	45	sim	não	sim	não	sim
Felipe	22	sim	sim	não	não	não
Paula	90	sim	sim	sim	não	sim

Assim, se ela tivesse escolhido o número:

• 1: todos os estudantes teriam acertado;

• 2: dois estudantes teriam acertado e três teriam errado;

• 3: dois estudantes teriam acertado e três teriam errado;

• 4: todos os estudantes teriam errado;

• 5: três estudantes teriam acertado e dois teriam errado, que foi o que a professora disse que ocorreu.

Assim:

a) Os estudantes que acertaram foram Antônio, Júlia e Paula.

b) A professora escolheu o número 5.

6. a)

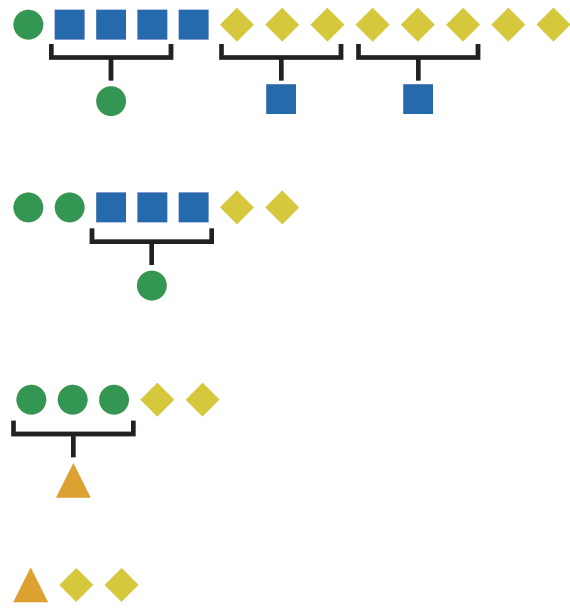
Ilustração. Sequência de figuras, da esquerda para direita: 1 círculo, 4 quadrados, 8 losangos. Cota abaixo dos 3 primeiros quadrados indicando 1 círculo. Cota abaixo dos 3 primeiros losangos indicando 1 quadrado. Cota abaixo dos três losangos seguintes indicando 1 quadrado. Abaixo, 2 círculos, 3 quadrados e 2 losangos. Cota abaixo dos 3 quadrados indicando 1 círculo. Abaixo, 3 círculos e 2 losangos. Cota abaixo dos 3 círculos indicando 1 triângulo. Abaixo, 1 triângulo e 2 losangos.

Página setenta e um

d) Cada

equivale a 3

. Cada

equivale a 3

. Então, 3

equivalem a 9

. Portanto, cada

equivale a 9

Cada

equivale a 3

. Cada

equivale a 9

. Então, 3

equivalem a 27

. Portanto, cada

equivale a 27

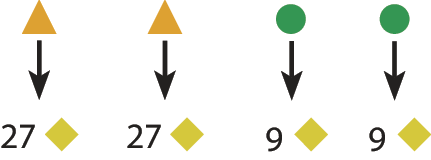
Esquema. Sequência de figuras: 2 triângulos laranjas e 2 círculos verdes. Abaixo de cada triângulo laranja, seta para baixo indicando 27 losangos amarelos. Abaixo de cada círculo verde, seta para baixo indicando 9 losangos amarelos.

Logo, são necessárias setenta e duas moedas de menor valor (27 + 27 + 9 + 9 = 72).

7. a) Para determinar a medida de comprimento de cada pedaço, com maior aproveitamento possível e de modo que cada pedaço tenha a mesma medida de comprimento, basta calcular o máximo divisor comum das medidas de comprimento correspondentes a cada cor. Decompondo as medidas correspondentes a cada cor simultaneamente, temos:

Esquema. Fatoração simultânea do 12, 18, 6 e 24. À esquerda 12, 18, 6 e 24 e à direita, o 2. Abaixo, à esquerda o 6, 9, 3, 12, à direita, o 2. Abaixo, à esquerda 3, 9, 3, 6 e à direita, o 2. Abaixo, à esquerda 3, 9, 3, 3 e à direita, 3. Abaixo, à esquerda 1, 3, 1, 1 e à direita, 3. Abaixo apenas à esquerda 4 números 1. Entre os números da esquerda e da direita há um traço vertical. Dos números à direita, de cima pra baixo, os três números 2 o primeiro número 3, cota a direita indicando fatores comuns.

Logo, o máximo divisor comum é 2 ⋅ 3 = 6.

Portanto, a medida de comprimento de cada pedaço deverá ser de 6 metros.

b) Há 24 metros de tecido vermelho para serem divididos em pedaços de 6 metros de comprimento. Assim:

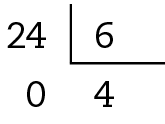
Algoritmo da divisão. 24 dividido por 6 igual a 4 com resto 0. A esquerda, o número 24. A direita na chave o número 6. Abaixo da chave o número 4, Abaixo do 24, o número 0, alinhado ordem a ordem com o 24.

Logo, haverá 4 pedaços de tecido vermelho.

c) Os divisores comuns de 12, 18, 6 e 21 são: 1, 2, 3 e 6. Logo, Maria pode ter pedaços de mesma medida de comprimento de tecido se dividi-los em pedaços com 1 metro, 2 metros ou 3 metros.

8. Vamos decompor o número 308 em fatores primos.

Esquema. À esquerda 308 e à direita, o 2. Abaixo, à esquerda o 154, à direita, o 2. Abaixo, à esquerda 77 e à direita, o 7. Abaixo, à esquerda 11 e à direita, o 11. Abaixo apenas à esquerda o 1. Entre os números da esquerda e da direita há um traço vertical. A direita do esquema, 308 igual a 2 elevado a 2 vezes 7 vezes 11.

• número da casa de Alex: 11;

• número da casa de Rosana: 7;

• número da casa de Vilma: 4.

Capítulo 5

ATIVIDADES

▶ Página 119

1. a) Três quartos de xícara.

b) Significa que o inteiro (xícara) foi dividido em 4 partes iguais.

c) Significa a quantidade de partes da xícara que será preenchida com óleo.

2. a) Um meio ou metade.

b) Significa que os estudantes da professora Márcia foram divididos em 2 grupos com o mesmo número de pessoas.

c) Significa a quantidade de grupos da sala que têm animais de estimação (um dos dois grupos).

3. a) verde:

\frac{1}{8}

laranja:

\frac{2}{8}

azul:

\frac{5}{8}

\frac{1}{8}

: um oitavo;

\frac{2}{8}

: dois oitavos;

\frac{5}{8}

: cinco oitavos

4. A torre Camélia. Espera-se que os estudantes comparem o numerador com o denominador da fração para descobrir qual representa mais da metade dos apartamentos.

5. Exemplo de respostas:

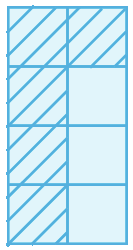
Ilustração. Retângulo dividido em 8 partes quadradas iguais, 5 delas estão hachuradas.

Ilustração. Paralelogramo dividido em 8 partes triangulares iguais, 5 delas estão hachuradas.

Ilustração. Quadrado dividido em 8 partes triangulares iguais, 5 delas estão hachuradas.

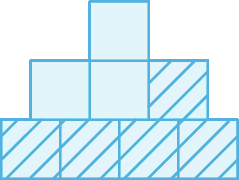
Ilustração. 8 quadrados idênticos. 5 deles estão hachurados.

6. a) bolinhas azuis:

\frac{3}{7}

; bolinhas vermelhas:

\frac{4}{7}

b) bolinha azul:

\frac{1}{10}

; bolinhas vermelhas:

\frac{9}{10}

ATIVIDADES

▶ Páginas 123 e 124

1. Exemplo de respostas:

Ilustração. Retângulo dividido em 24 partes quadradas iguais, 12 brancas e 12 azuis, que se intercalam.

Ilustração. Retângulo dividido em 24 partes quadradas iguais, dispostos em 6 colunas com 4 quadradinhos cada. Os quadradinhos da quarta fileira tem fundo azul e os demais tem fundo branco.

Ilustração. Retângulo dividido em 24 partes quadradas iguais, dispostos em 6 colunas com 4 quadradinhos cada. Os quadradinhos das duas primeiras fileiras tem fundo azul e os demais tem fundo branco.

Ilustração. Retângulo dividido em 24 partes quadradas iguais, todos azuis.

Página setenta e dois

2. Para resolver esse problema vamos calcular

\frac{1}{4}

de 120 arremessos.

120 : 4 = 30

Portanto, Oscar acertou 30 cestas.

3. a) Calculando 15 : 5 = 3. Como são dois grupos, temos 2 ⋅ 3 = 6.

Portanto,

\frac{2}{5}

de 15 bolinhas são 6 bolinhas.

b) Calculando 12 : 3 = 4. Como é apenas um grupo, temos 1 ⋅ 4 = 4.

Portanto,

\frac{1}{3}

de 12 passos são 4 passos.

c) Calculando 30 : 10 = 3. Como é apenas um grupo, temos 1 ⋅ 3 = 3.

Portanto,

\frac{1}{10}

de 30 estudantes são 3 estudantes.

4. Como uma hora tem 60 minutos, para descobrir o que é pedido, podemos dividir uma hora em partes iguais.

a) Dividindo em partes de 30 minutos, temos: 60 : 30 = 2

Logo, 30 minutos representam

\frac{1}{2}

de uma hora.

b) Dividindo em partes de 5 minutos, temos: 60 : 5 = 12

Logo, 5 minutos representam

\frac{1}{12}

de uma hora.

c) Dividindo em partes de 10 minutos, temos: 60 : 10 = 6

Logo, 10 minutos representam

\frac{1}{6}

de uma hora.

5. a) Dividindo o valor do salário pelo valor gasto no supermercado temos: .1200 : 300 = 4

Logo, 300 reais representa

\frac{1}{4}

do salário de Elton.

b) Dividindo o valor do salário pelo valor gasto para pagar as contas temos: .1200 : 200 = 6

Logo, 200 reais representa

\frac{1}{6}

do salário de Elton.

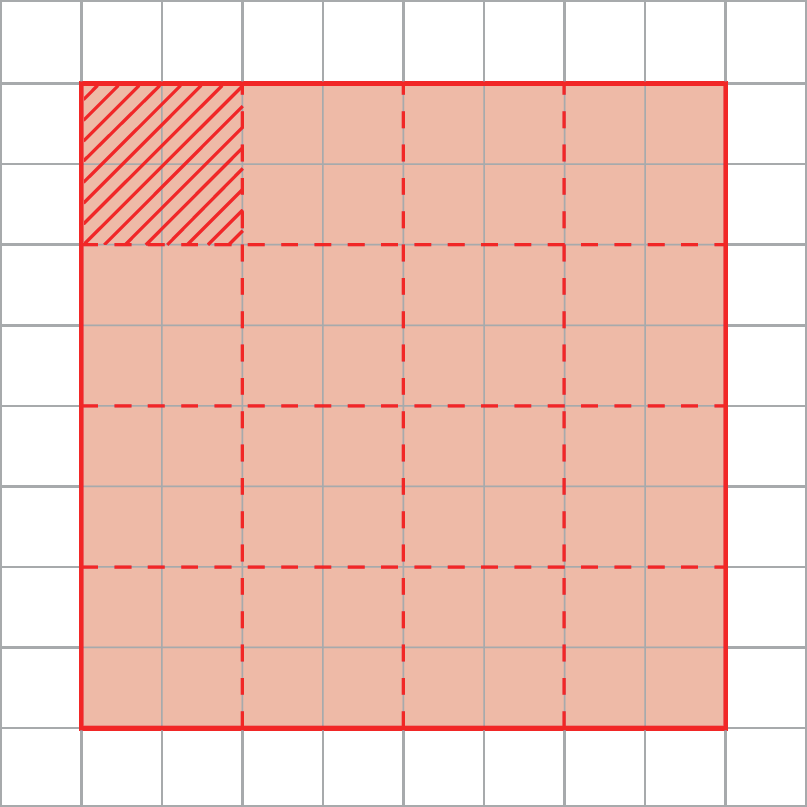
Figura geométrica, Malha quadriculada com a representação de um quadrado vermelho. O quadrado é composto por 64 quadradinhos, dispostos em 8 fileiras com 8 quadradinhos cada uma. Este quadrado vermelho foi dividido novamente em 16 partes quadradas iguais, de modo que cada parte ficou composta por 4 quadradinhos da malha. No canto superior esquerdo uma das partes está hachurada.

7. Se

\frac{2}{5}

das pessoas estão em seus lugares, então

\frac{3}{5}

das pessoas ainda não entraram. Assim: .3525 : 5 = 705

Como são 3 partes, temos 3 ⋅ 705 = .2115.

Logo, duas.115 pessoas ainda não estão em seus lugares.

8. a) Como no quadrado a cabem 4 quadrados B, temos que o quadrado B corresponde a

\frac{1}{4}

do quadrado a.

b) Como no quadrado B cabem 4 quadrados C, temos que o quadrado C corresponde a

\frac{1}{4}

do quadrado B.

c) Como no quadrado a cabem 4 quadrados B e em cada quadrado B cabem 4 quadrados C, temos que no quadrado a cabem 4 ⋅ 4 quadrados C, ou seja, 16 quadrados C. Assim, o quadrado C corresponde a

\frac{1}{16}

do quadrado a.

9. A receita indica o uso de 1 quilograma de açúcar. Como Amanda só tem

\frac{1}{2}

quilograma de açúcar, então ela deve usar metade de cada quantidade indicada para os demais ingredientes. Assim:

• gemas: 3 dúzias correspondem a 36 pois 3 ⋅ 12 = 36. Agora,

\frac{1}{2}

de 36 é igual a 18, pois 36 : 2 = 18.

• coco fresco ralado:

\frac{1}{2}

de 6 xícaras é igual a 3 xícaras, pois 6 : 2 = 3.

• manteiga:

\frac{1}{2}

de 6 colheres de chá são 3 colheres de chá, pois 6 : 2 = 3.

Portanto, Amanda deve usar 18 gemas, 3 xícaras de coco fresco ralado e 3 colheres (chá) de manteiga.

10. Espera-se que os estudantes encontrem estratégias para calcular a fração de uma quantidade. Espera-se que eles percebam que não há um único modo de fazer esse cálculo. É importante que eles possam apresentar outras maneiras de chegar à conclusão e, depois, comparar seus resultados com os de colegas e validar seus procedimentos.

ATIVIDADES

▶ Página 127

1. Para verificar se os pares de figuras representam frações equivalentes, devemos verificar se o numerador e o denominador de uma delas é resultado da multiplicação ou divisão do numerador e do denominador da outra fração por um mesmo número.

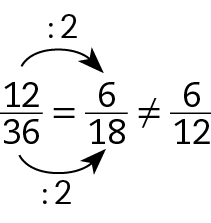
Esquema. Fração 12 sobre 36 igual a fração 6 sobre 18, diferente de fração 6 sobre 12. Seta preta de 12 para 6 com cota acima, dividido por 2. Seta preta de 36 para 18, com cota abaixo, dividido por 2.

Portanto, as frações não são equivalentes.

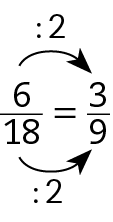
Esquema. Fração 6 sobre 18 igual a fração 3 sobre 9. Seta preta de 6 para 3 com cota acima, dividido por 2. Seta preta de 18 para 9, com cota abaixo, dividido por 2.

Portanto, as frações são equivalentes.

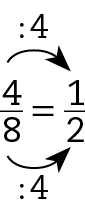
Esquema. Fração 4 sobre 8 igual a fração 1 sobre 2. Seta preta de 4 para 1 com cota acima, dividido por 4. Seta preta de 8 para 2, com cota abaixo, dividido por 4.

Portanto, as frações são equivalentes.

Página setenta e três

2. Devemos simplificar as frações para obter numerador e denominador que tenham apenas o 1 como divisor comum.

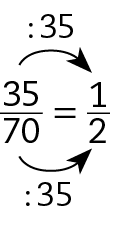
Esquema. Fração 36 sobre 70 igual a fração 1 sobre 2. Seta preta de 35 para 1 com cota acima, dividido por 35. Seta preta de 70 para 2, com cota abaixo, dividido por 35.

A fórma irredutível da fração

\frac{35}{70}

\frac{1}{2}

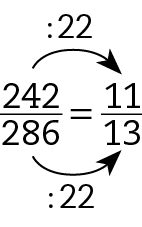
242 sobre 286 igual a 11 sobre 13. Seta preta de 242 para 11 com cota acima, dividido por 22. Seta preta de 286 para 13 com cota acima, dividido por 22.

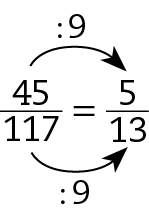
A fórma irredutível da fração

\frac{242}{286}

\frac{11}{13}

Esquema. Fração 45 sobre 117 igual a fração 5 sobre 13. Seta preta de 45 para 5 com cota acima, dividido por 9. Seta preta de 117 para 13, com cota abaixo, dividido por 9.

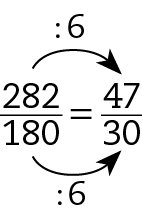
A fórma irredutível da fração

\frac{45}{117}

\frac{5}{13}

Esquema. Fração 282 sobre 180 igual a fração 47 sobre 30. Seta preta de 282 para 47 com cota acima, dividido por 6. Seta preta de 180 para 30, com cota abaixo, dividido por 6.

A fórma irredutível da fração

\frac{282}{180}

\frac{47}{30}

3. Simplificando as frações

\frac{20}{60}

\frac{100}{300}

, temos:

Esquema. Fração 20 sobre 60 igual a fração 20 sobre 60 igual a 1 sobre 3. Seta preta do segundo 20 para 1 com cota acima, dividido por 20. Seta preta do segundo 60 para 3, com cota abaixo, dividido por 20.

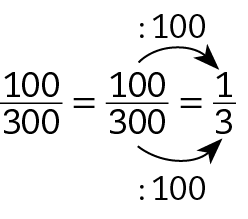
Esquema. Fração 100 sobre 300 igual a fração 100 sobre 300 igual a 1 sobre 3. Seta preta do segundo 100 para 1 com cota acima, dividido por 100. Seta preta do segundo 300 para 3, com cota abaixo, dividido por 100.

Ambas as afirmações são verdadeiras, pois as frações

\frac{20}{60}

\frac{100}{300}

\frac{1}{3}

são equivalentes.

4. Os estudantes podem resolver da seguinte maneira:

• Marília acertou 12 de 15 palavras. Logo:

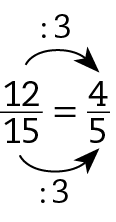
Esquema. Fração 12 sobre 15 igual a fração 4 sobre 15. Seta preta de 12 para 4 com cota acima, dividido por 3. Seta preta de 15 para 5, com cota abaixo, dividido por 3

• Luís acertou 8 de 10 palavras. Logo:

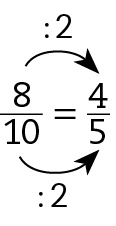
Esquema. Fração 8 sobre 10 igual a fração 4 sobre 5. Seta preta de 8 para 4 com cota acima, dividido por 2. Seta preta de 10 para 5, com cota abaixo, dividido por 2.

Observamos que ambos acertaram

\frac{4}{5}

das palavras.

Portanto, não houve vencedor, já que houve um empate na disputa, uma vez que

\frac{12}{15}

\frac{8}{10}

são frações equivalentes.

5. Analisando o que é possível ver, temos:

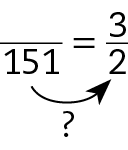
Esquema. Fração com numerador vazio sobre 151 igual a fração 3 sobre 2. Seta preta de 151 para 2, com cota abaixo, ponto de interrogação. Abaixo do esquema, 151 dividido por ponto de interrogação igual a 2

151 : ? = 2

Como não conseguimos obter 2 dividindo 151 por um número natural, concluímos que ela errou a simplificação.

6. Quando duas frações são equivalentes, o resultado obtido ao dividir o numerador de uma pelo numerador da outra é igual ao resultado obtido quando dividimos o denominador de uma pelo denominador da outra. Assim, podemos verificar se as equivalências estão corretas.

a) .1749 : 33 = 53

.1537 : 29 = 53

Como os resultados são iguais, a equivalência está correta.

b) .8624 : 98 = 88

.8876 : 102 = 87,019607reticências

Como os resultados são diferentes, a equivalência está incorreta. Corrigindo, temos:

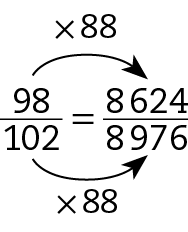
Esquema. Fração 98 sobre 102 igual a fração 8 mil 624 sobre 8 mil 976. Seta preta de 98 para 8 mil 624 com cota acima, vezes 88. Seta preta de 102 para 8 mil 976, com cota abaixo, vezes 88

c) .3390 : 30 = 113

.5085 : 45 = 113

Como os resultados são iguais, a equivalência está correta.

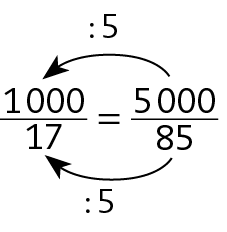
d) .5000 : .1000 = 5

85 : 34 = 2,5

Como os resultados são diferentes, a equivalência está incorreta. Podemos corrigir de dois modos:

• 1º modo:

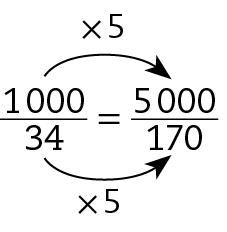
Esquema. Fração 1 mil sobre 34 igual a fração 5 mil sobre 170. Seta preta de 1 mil para 5 mil com cota acima, vezes 5. Seta preta de 34 para 170, com cota abaixo, vezes 5.

• 2º modo:

mil sobre 17 igual a 5 mil sobre 85. Seta preta de 5 mil para mil com cota acima, dividido por 5. Seta preta de 85 para 17 com cota acima, dividido por 5.

ATIVIDADES

▶ Página 130

1. a) Como as figuras estão divididas em partes iguais, as frações que as representam têm um mesmo denominador (4). Então, a figura com maior número de partes pintadas representará a maior fração. A figura da esquerda possui 3 partes pintadas, e a da direita, apenas uma parte. Portanto, representando em frações, temos que

\frac{3}{4} > \frac{1}{4}

b) As figuras estão divididas em um número diferente de partes. Como a quantidade de partes pintadas nas figuras é a mesma (1), aquela que foi dividida em um menor número de partes representará a maior fração. A figura da esquerda está dividida em 6 partes, e a da direita, em 4 partes. Portanto, representando em frações, temos que

\frac{1}{6} < \frac{1}{4}

Página setenta e quatro

c) Ambas estão divididas em 6 partes iguais e possuem 3 partes pintadas. Portanto, representando em frações, temos que

\frac{3}{6} = \frac{3}{6}

d) A quantidade de partes pintadas das figuras é a mesma (2), mas elas estão divididas em um número diferente de partes: a figura da esquerda está dividida em 4 partes iguais, e a da direita, em 8 partes iguais. Portanto, representando em frações, temos que

\frac{2}{4} > \frac{2}{8}

2. Para comparar as frações que representam as partes pintadas das figuras, os estudantes podem analisar as figuras ou encontrar frações equivalentes que tenham o mesmo denominador e, depois, compará-las.

a) Frações que representam as partes pintadas das figuras:

\frac{1}{2}

\frac{3}{4}

\frac{7}{8}

. Encontrando frações equivalentes de mesmo denominador, temos:

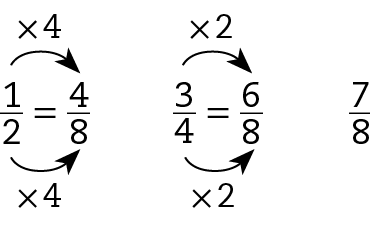
À esquerda, meio igual a 4 oitavos. Seta preta de 1 para 4 com cota cima, vezes 4. Seta preta de 2 para 8 com cota abaixo, vezes 4. À direita, 3 quartos igual a 6 oitavos. Seta preta de 3 para 6 com cota cima, vezes 2. Seta preta de 4 para 8 com cota abaixo, vezes 2. À direita, a fração 7 oitavos.

Assim, temos

\frac{7}{8} > \frac{6}{8} > \frac{4}{8}

, ou seja,

\frac{7}{8} > \frac{3}{4} > \frac{1}{2}

Portanto,

\frac{7}{8}

é a maior e

\frac{1}{2}

é a menor fração.

b) Frações que representam as partes pintadas das figuras:

\frac{3}{8}

\frac{4}{16}

. Encontrando frações equivalentes de mesmo denominador, temos:

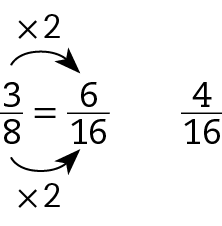
À esquerda, 3 oitavos igual a 6 dezesseis avos. Seta preta de 3 para 6 com cota cima, vezes 2. Seta preta de 8 para 16 com cota abaixo, vezes 2. À direita, a fração 4 dezesseis avos.

Assim, temos

\frac{6}{16} > \frac{4}{16}

Portanto,

\frac{3}{8}

é a maior e

\frac{4}{16}

é a menor fração.

c) Frações que representam as partes pintadas das figuras:

\frac{1}{2}

\frac{3}{4}

\frac{5}{8}

. Encontrando frações equivalentes de mesmo denominador, temos:

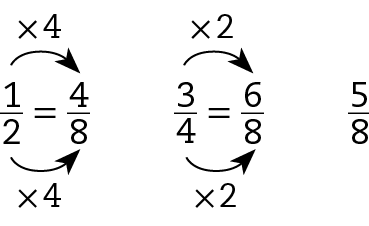
Assim, temos

\frac{6}{8} > \frac{5}{8} > \frac{4}{8}

, ou seja,

\frac{3}{4} > \frac{5}{8} > \frac{1}{2}

Portanto,

\frac{3}{4}

é a maior e

\frac{1}{2}

é a menor fração.

d) Frações que representam as partes pintadas das figuras:

\frac{4}{12}

\frac{3}{6}

. Encontrando frações equivalentes de mesmo denominador, temos:

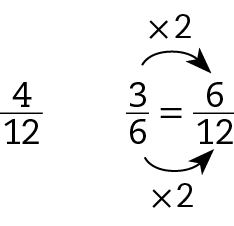
À esquerda, fração 4 doze avos. À direita, 3 sextos igual a 6 doze avos. Seta preta de 3 para 6 com cota cima, vezes 2. Seta preta de 6 para 12 com cota abaixo, vezes 2.

Assim, temos

\frac{6}{12} > \frac{4}{12}

, ou seja,

\frac{3}{6} > \frac{4}{12}

Portanto,

\frac{3}{6}

é a maior e

\frac{4}{12}

é a menor fração.

e) Frações que representam as partes pintadas das figuras:

\frac{1}{4}

\frac{1}{4}

. Podemos observar que as frações possuem o mesmo denominador e o mesmo numerador. Portanto, são iguais.

\frac{8}{18}

Existem diversas formas de chegar a essa conclusão sem a realização de cálculos. Uma das maneiras é perceber que

\frac{8}{18}

está mais próximo a metade do que

\frac{6}{15}

4. Para responder às questões, precisamos primeiro comparar as frações. Inicialmente, encontramos frações equivalentes com o mesmo denominador.

• muito satisfeitos:

\frac{2}{15} = \frac{4}{30}

• satisfeitos:

\frac{3}{10} = \frac{9}{30}

• pouco satisfeitos:

\frac{3}{15} = \frac{6}{30}

• totalmente insatisfeitos:

\frac{2}{10} = \frac{6}{30}

Percebemos que o número de clientes que responderam estar pouco satisfeitos é igual ao número de clientes que responderam estar insatisfeitos

(\frac{6}{30} dos c l i e n t e s)

. Comparando as frações, temos:

\frac{4}{30} < \frac{6}{30} < \frac{9}{30}

Assim, concluímos que:

a) a maior parte dos clientes está satisfeita, pois a maior fração é

\frac{9}{30}

, que é equivalente à fração

\frac{3}{10}

b) a menor parte dos clientes está muito satisfeita, pois a menor fração é

\frac{4}{30}

, que é equivalente à fração

\frac{2}{15}

5. Temos:

• 1ª prova: 5 acertos em 15 questões, ou seja,

\frac{5}{15} = \frac{1}{3}

• 2ª prova: 5 acertos em 10 questões, ou seja,

\frac{5}{10} = \frac{1}{2}

Portanto, ele acertou

\frac{1}{3}

das questões da primeira prova e

\frac{1}{2}

das questões da segunda prova. Além disso,

\frac{1}{2}

é maior que

\frac{1}{3}

. Logo, Jair não acertou mais da metade das questões em nenhuma das duas provas, e sua nota foi maior na segunda prova.

Página setenta e cinco

6. Para comparar as frações do total de jovens que prefere cada esporte, precisamos encontrar frações equivalentes com o mesmo denominador. Para isso, fazemos:

• futebol

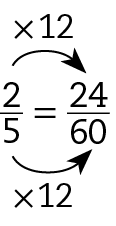
Esquema. Fração 2 sobre 5 igual a fração 24 sobre 60. Seta preta de 2 para 24 com cota acima, vezes 12. Seta preta de 5 para 60, com cota abaixo, vezes 12.

• vôlei

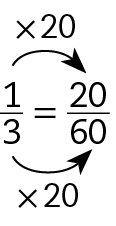
Esquema. Fração 1 sobre 3 igual a fração 20 sobre 60. Seta preta de 1 para 20 com cota acima, vezes 20. Seta preta de 3 para 60, com cota abaixo, vezes 20.

• basquete

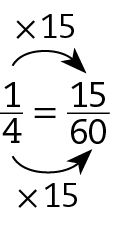
Esquema. Fração 1 sobre 4 igual a fração 15 sobre 60. Seta preta de 1 para 15 com cota acima, vezes 15. Seta preta de 4 para 60, com cota abaixo, vezes 15.

Portanto:

\frac{2}{5} > \frac{1}{3} > \frac{1}{4}

a) O futebol é o esporte preferido desses jovens.

b) O basquete é o esporte menos preferido desses jovens.

c) Para calcular o número de jovens que preferem basquete, devemos calcular

\frac{1}{4}

de 900 jovens, ou seja, 900 : 4 = 225.

Logo, 225 jovens preferem basquete.

ESTATÍSTICA E PROBABILIDADE

▶ Páginas 132 e 133

1. Espera-se que os estudantes coletem as informações com sua turma e organizem uma tabela de dupla entrada, e que nos itens a e b extraiam as informações da tabela construída.

2. a)

Tipo de filme preferido pelo público do centro cultural
Tipo de filme	Adultos	Adolescentes	Total
	Público
Suspense	84	54	138
Ficção	93	51	144
Romance	50	37	87
Terror	42	50	92
Total	269	192	461

Dados obtidos por Beatriz em julho de 2023.

b) O tipo de filme que recebeu mais votos foi o de ficção.

c) O tipo de filme mais votado pelos adolescentes foi suspense.

d) 269 + 192 = 461

Participaram da votação quatrocentas e sessenta e uma pessoas.

3. Exemplo de resposta:

Quantidade de inscrições por escola e por modalidade esportiva
Modalidade	A	B	C	D	Total
	Escola
Futebol	40	25	30	40	135
Basquete	20	35	25	25	105
Natação	10	15	10	10	45
Vôlei	35	30	50	20	135
Total	105	105	115	95	420

Dados obtidos pela organizadora do campeonato em março de 2023.

4. a)

Projeção da população no Brasil por gênero (2030 a 2060)
Ano	Homens	Mulheres	Total
	Gênero
2030	109.728.762	115.139.700	224.868.462
2040	112.962.751	118.957.171	231.919.922
2050	113.300.060	119.633.216	232.933.276
2060	110.958.642	117.327.705	228.286.347

Fonte: Instituto Brasileiro de Geografia e Estatística. Coordenação de População e Indicadores Sociais. Projeções da população: Brasil e unidades da federação: revisão 2018. segunda edição Rio de Janeiro: í bê gê É, 2018.

b) Espera-se que os estudantes percebam que, nesse caso, não faz sentido adicionar o total de homens e o de mulheres em todos os anos.

5. a)

Número de matrículas na educação básica nas redes pública e privada no Brasil
Ano	Rede pública	Rede privada	Total
2016	39.834.378	8.983.101	48.817.479
2017	39.721.032	8.887.061	48.608.093
2018	39.460.618	8.995.249	48.455.867
2019	38.739.461	9.134.785	47.874.246
2020	38.504.108	8.791.186	47.295.294

Fonte: BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Censo da Educação Básica 2020: notas estatísticas. Brasília, Distrito Federal: Inépi, 2021.

b) O ano de 2016 apresentou a maior quantidade de matrículas, com ..48817479 matrículas realizadas nesse ano.