
UNIDADE 1
Capítulo 1
Múltiplos e divisores
Capítulo 2
Números inteiros
Capítulo 3
Ângulos

UMA OLIMPÍADA HISTÓRICA
As Olimpíadas, que completaram 125 anos em 2021, são o maior evento esportivo do mundo. Desde a primeira edição da Era Moderna, que aconteceu em Atenas em 1896, os Jogos Olímpicos são realizados a cada 4 anos.
Por causa da pandemia da côvid dezenóve, houve o primeiro adiamento da história dos jogos. A edição de Tóquio, que seria realizada em 2020, ocorreu em 2021, com o Brasil tendo sua melhor performance até então. Seguindo o calendário olímpico, os próximos jogos serão sediados na cidade de Paris, na França, em 2024.
Para começar...
1. Você já assistiu aos Jogos Olímpicos? Comente.
2. De acordo com o texto, por que os jogos de Tóquio foram históricos?
3. As três próximas edições dos jogos estão previstas para quais anos? Os números que representam esses anos são múltiplos de 4? Justifique.
4. Caso os jogos sigam o calendário previsto, ocorrerá uma edição no ano de 2038? Justifique.


CAPÍTULO 1 Múltiplos e divisores
1 Divisibilidade
Observe a situação a seguir.
Karina é voluntária em uma associação e vai distribuir kits de livros infantis a crianças carentes. Ela arrecadou 624 livros e quer montar kits com 4, com 5 ou com 6 livros cada um, de modo que todos os kits tenham a mesma quantidade e não sobre nenhum livro. Como ela pode montar os kits?

Lembre-se: Escreva no caderno!
Para responder a essa questão, vamos analisar três divisões.
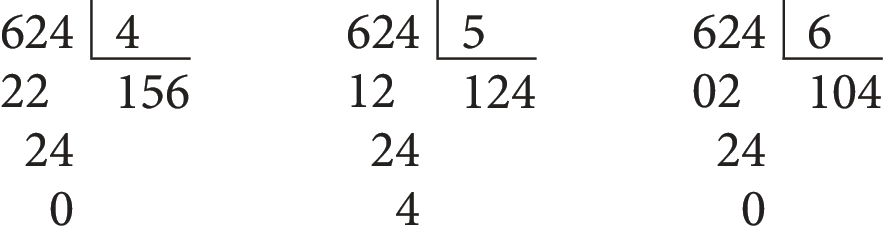
Se Karina montar kits com 4 livros, será possível distribuir 156 kits e não sobrarão livros; se montar kits com 5 livros, será possível distribuir 124 kits, mas sobrarão 4 livros; e, se montar kits com 6 livros, será possível distribuir 104 kits e não sobrarão livros. Portanto, ela deve montar kits com 4 ou com 6 livros, pois as divisões de 624 por 4 e por 6 têm resto zero.
Quando o resto de uma divisão é zero, a divisão é exata.
Um número natural a é divisível por um número natural b, diferente de zero, quando a divisão de a por b é exata. Nesse caso, também dizemos que a é múltiplo de b ou, ainda, que b é divisor de a.
Assim:
• 624 é múltiplo de 4, pois 4 ⋅ 156 = 624;
• 624 é múltiplo de 6, pois 6 ⋅ 104 = 624;
• 4 e 6 são divisores de 624;
• 624 não é múltiplo de 5, pois a divisão de 624 por 5 não é exata.
Múltiplos e divisores de um número natural
Conhecendo o conceito de múltiplo e divisor, podemos obter a sequência dos múltiplos de um número natural ou encontrar seus divisores.
Lembre-se: Escreva no caderno!
Como exemplo, vamos considerar o número 12.
Ao multiplicar esse número por qualquer número natural, obteremos um múltiplo de 12, pois a divisão do produto por 12 será exata.
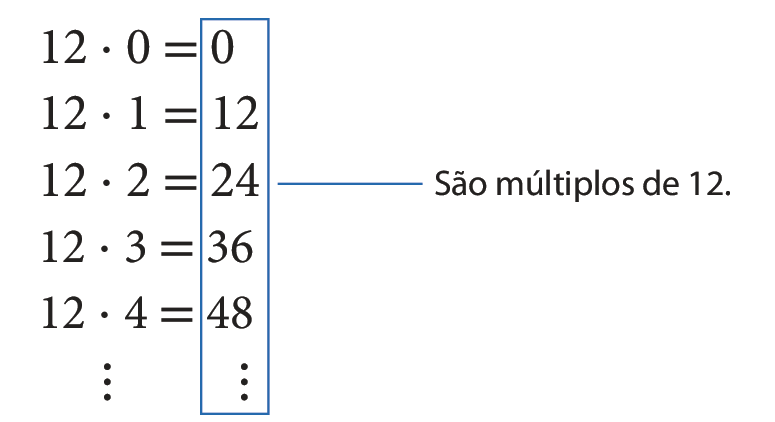
Assim, a sequência desses produtos é a sequência dos múltiplos naturais de 12:
(0, 12, 24, 36, 48, 60, 72, reticências)
Note que a sequência começa pelo zero e que o padrão é sempre adicionar 12 ao termo anterior. Da mesma fórma, podemos obter a sequência dos múltiplos de qualquer número natural.
Já para encontrar todos os divisores de 12, é necessário verificar os números naturais, diferentes de zero, pelos quais 12 é divisível.
• 12 é divisível por 1 e por 12, pois 1 ⋅ 12 = 12;
• 12 é divisível por 2 e por 6, pois 2 ⋅ 6 = 12;
• 12 é divisível por 3 e por 4, pois 3 ⋅ 4 = 12.
Como 12 não é divisível por nenhum outro número natural, os divisores de 12 são: 1, 2, 3, 4, 6 e 12.
Critérios de divisibilidade
Em alguns casos, podemos descobrir se um número é divisível por outro sem efetuar a divisão, apenas aplicando algumas regras chamadas de critérios de divisibilidade. Vamos estudar esses critérios.
Critério de divisibilidade por 2
Observe alguns números divisíveis por 2.
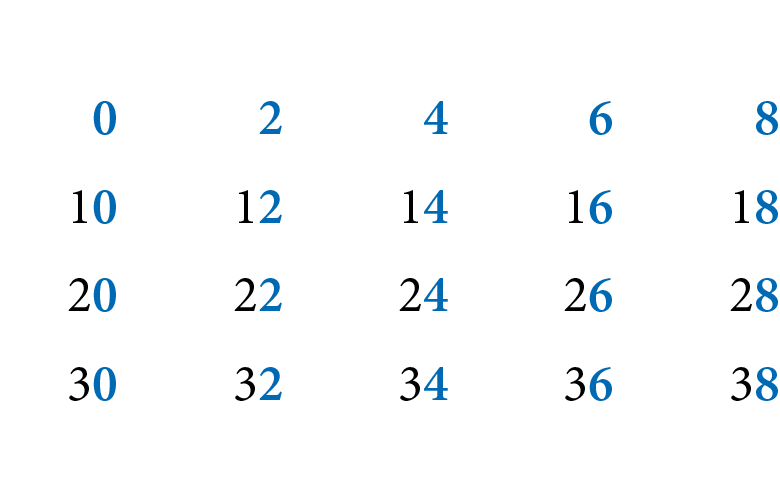
Note que esses números terminam em 0, 2, 4, 6 ou 8. Esse padrão se repete para todos os números divisíveis por 2.
Um número natural é divisível por 2 quando é par, ou seja, quando termina em 0, 2, 4, 6 ou 8.
Critério de divisibilidade por 3

Observe alguns números divisíveis por 3.
Note que, ao adicionar os algarismos de cada um desses números, obtemos um número divisível por 3.

Esse fato acontece não apenas com esses números, mas com qualquer número que seja divisível por 3.
Um número natural é divisível por 3 quando a soma de seus algarismos é divisível por 3.
Critério de divisibilidade por 6
Observe alguns números divisíveis por 6 a partir do 60.
60 66 72 78 84 90 96 102 108 114
Note que todos esses números são divisíveis por 2, pois são pares, e são divisíveis por 3, pois a soma dos algarismos de cada um deles é divisível por 3. Se isso acontece (o número é divisível por 2 e por 3), o número é divisível por 6.
Um número natural é divisível por 6 quando é divisível por 2 e por 3.
Critério de divisibilidade por 9
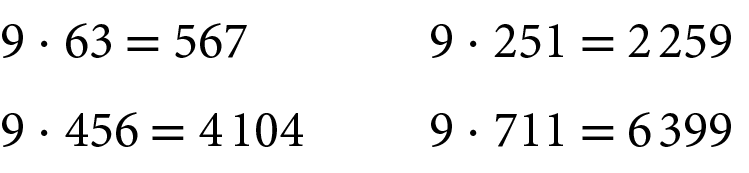
Ao multiplicar 9 por um número natural, obtemos um múltiplo de 9. Assim, 567, .2259, .4104 e .6399 são múltiplos de 9 (ou são divisíveis por 9).
Observe que a soma dos algarismos de cada um desses números é um número divisível por 9.
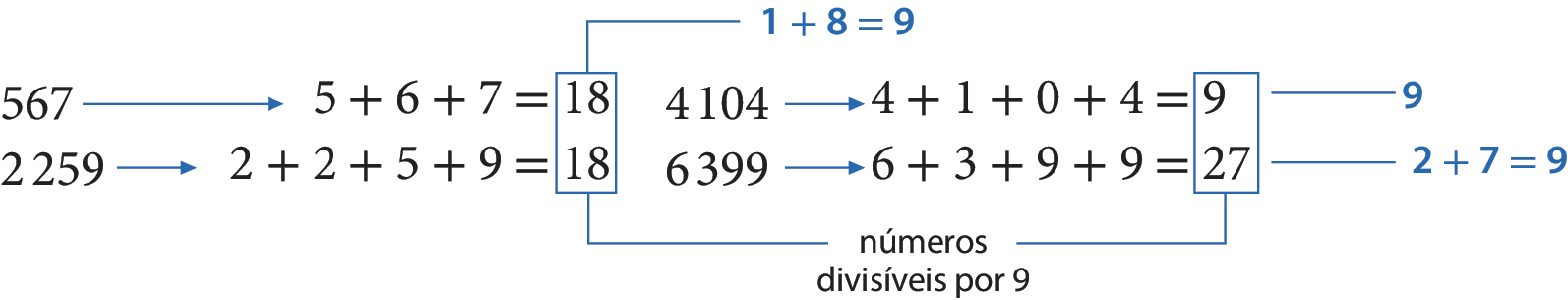
Esse fato acontece não apenas com esses números, mas com qualquer número que seja divisível por 9.
Um número natural é divisível por 9 quando a soma de seus algarismos é divisível por 9.
Lembre-se: Escreva no caderno!
Critério de divisibilidade por 4
O número .3548 é divisível por 4, assim como o número 48.
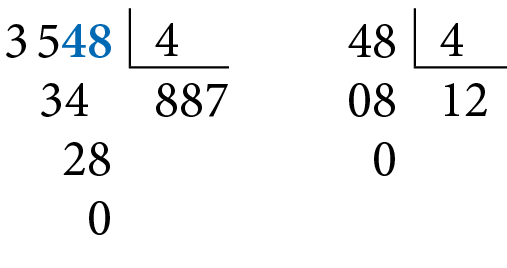
Observe o que acontece quando decompomos esse número divisível por 4.
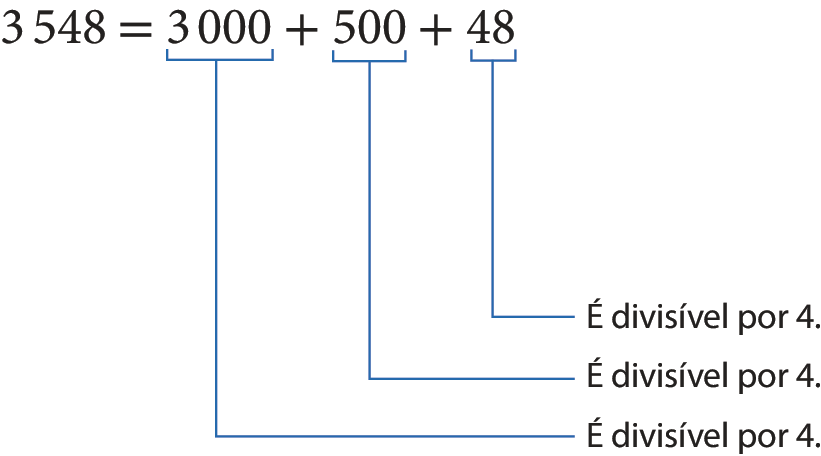
Todas as centenas inteiras, os milhares inteiros, as dezenas de milhar inteiras etcétera. são divisíveis por 4. Então, se os dois últimos algarismos de um número formam um múltiplo de 4, o número é divisível por 4.
Assim, temos o seguinte critério de divisibilidade:
Um número natural é divisível por 4 quando seus dois últimos algarismos são 00 ou formam um número divisível por 4.
Para investigar

Usando uma calculadora, verifique que 100, 200, 300, 400, 500, .1000, .2000, .20000, .30000, .50000, .100000, .200000 e ..1000000 são divisíveis por 4.
Critério de divisibilidade por 5
Observe alguns números divisíveis por 5.
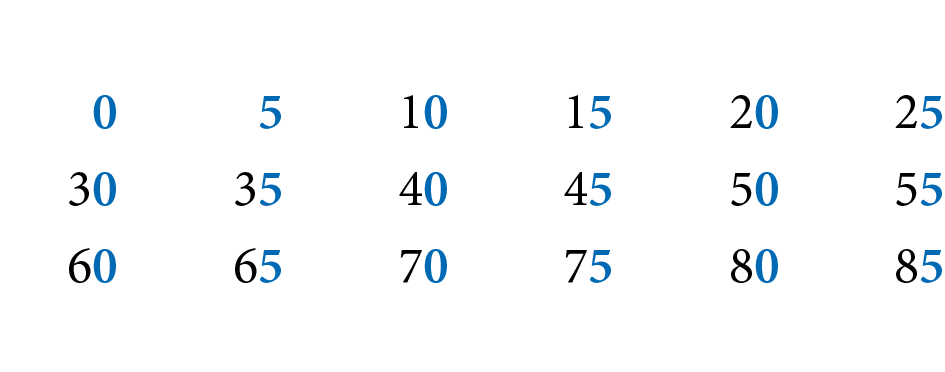
Todos esses números terminam em zero ou em 5. Esse fato acontece com todos os números divisíveis por 5.
Um número natural é divisível por 5 quando termina em zero ou em 5.
Critérios de divisibilidade por 10, por 100 e por .1000
Observe alguns números divisíveis por 10, por 100 e por .1000.
• Números divisíveis por 10:
10 20 30 40 50 60 70 80 90 100 110 reticências
• Números divisíveis por 100:
100 200 300 400 500 600 700 800 900 .1000 .1100 reticências
• Números divisíveis por .1000:
.1000 .2000 .3000 .4000 .5000 .6000 .7000 .8000 .9000 .10000 .11000 reticências
Observe o padrão na quantidade de zeros desses múltiplos. Esse padrão se repete para todos os números divisíveis por 10, por 100 e por .1000.
Um número natural é divisível:
• por 10 quando termina em 0;
• por 100 quando termina em 00;
• por .1000 quando termina em 000.
Para pensar
Pode-se dizer que qualquer número divisível por .1000 também é divisível por 100? E por 10? Justifique sua resposta.

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. No caderno, classifique as afirmações em verdadeiras ou falsas.
a) 5 é divisor de 5.
b) 5 é múltiplo de 5.
c) 1 é divisor de 5.
d) 0 é divisor de 5.
e) 0 é múltiplo de 5.
2. Jéssica faz bombons para vender. Em uma caixa cabem 6 bombons, como mostra a ilustração a seguir.

• Em um dia, ela fez 726 bombons. Quantas caixas de bombons ela poderá completar? Faltarão bombons para completar as caixas? Se faltarem, quantos?
3. Luís tem duzentas e trinta e quatro placas de vidro para colocar em janelas como a da figura a seguir. Quantas janelas Luís conseguirá envidraçar? Sobrarão placas de vidro? Se sobrarem, quantas?

4. Para fazer um trabalho em grupo, a professora precisa dividir a turma de 24 estudantes em grupos de 3 a 5 pessoas. Calcule as maneiras de dividir a turma mantendo todos os grupos com o mesmo número de estudantes.
5. Mara precisa organizar os .1567 arquivos de sua empresa em prateleiras.

• Ela tem a opção de organizá-los em 3 ou 4 prateleiras, de fórma que cada uma fique com a mesma quantidade de arquivos. Mara conseguirá realizar essa tarefa? Por quê?
6. Encontre os números naturais divisíveis por 2 e os números naturais divisíveis por 3 que estão entre 220 e 230.
• Entre os números encontrados, quais são divisíveis por 2 e por 3 ao mesmo tempo? Esses números são divisíveis por 6?
7. A professora de Matemática disse para seus estudantes:
“A minha idade é um número múltiplo de 4 e ainda é divisor de 104”.
• Sabendo que a professora tem menos de 60 anos, responda: qual é a idade dela?
8. Responda.
a) Qual é o único número natural que é divisor de qualquer outro número natural?
b) Qual é o número natural que nunca é divisor de outro?
c) Que número natural, diferente de zero, é divisor de si mesmo?
9. (ó bê mépi) O professor Samuel preencheu uma tabe la com quinhentas e sete linhas e .1007 colunas de acordo com o padrão indicado a seguir.
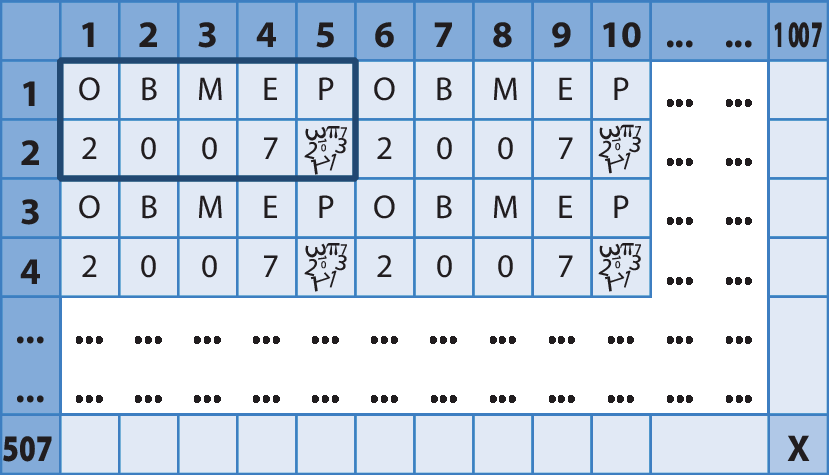
Como ele preencheu a casa marcada com o X?
a) Com o número 2.
b) Com a letra B.
c) Com a letra M.
d) Com o número 7.
e) Com o símbolo

.
10. Resolva.
a) Que algarismo podemos colocar no lugar de n em .547n, de fórma que ele seja divisível por 9 e por 10? Justifique sua resposta.
b) Que algarismo podemos colocar no lugar de m em .653m8, de fórma que ele seja divisível por 4 e por 3? Justifique sua resposta.
2 Decomposição em fatores primos
Alguns números naturais têm apenas dois divisores: o 1 e o próprio número. Esses números são chamados de números primos.
Os números primos menores que 50 são:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47
Note que todos esses números têm como divisores apenas o 1 e o próprio número.
Os números naturais maiores que 1 que não são primos são chamados de números compostos. Eles podem ser decompostos de várias fórmas, como uma multiplicação de dois ou mais fatores. Por exemplo, 140, que é um número composto, pode ser escrito como:

Quando fazemos a decomposição de modo que todos os fatores sejam números primos, realizamos a fatoração completa do número ou sua decomposição em fatores primos:
140 = 2 ⋅ 2 ⋅ 5 ⋅ 7 = 22 ⋅ 5 ⋅ 7
Há várias fórmas de obter a decomposição de um número em fatores primos.
Acompanhe como Magali e Murilo fizeram para obter a decomposição de 630 em fatores primos.


Observação
Note que, além do número 1, qualquer um dos fatores primos ou o produto de quaisquer dois ou mais fatores primos de um número é sempre divisor desse número.
Por exemplo, alguns dos divisores de 630 são:
• 1, 2, 3, 5, 7
• 2 ⋅ 3 = 6
• 2 ⋅ 5 = 10
• 3 ⋅ 7 = 21
• 2 ⋅ 3 ⋅ 3 = 18
• 3 ⋅ 5 ⋅ 7 = 105
• 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 7 = 630, reticências
3 Máximo divisor comum (mdc)
Em algumas situações, precisamos encontrar o maior dos divisores naturais comuns de dois ou mais números. Considere, por exemplo, a situação a seguir.
Haverá uma gincana da qual participarão 18 meninos e 30 meninas. A ideia é formar equipes somente de meninos ou somente de meninas. Além disso, as equipes devem ter a mesma quantidade e o maior número possível de pessoas. Qual será o número de pessoas em cada equipe?

Para resolver essa situação, precisamos encontrar um modo de distribuir os meninos e as meninas em equipes que tenham o mesmo número de pessoas.
Primeiro, vamos organizar as equipes separadamente. Observe.
• Os 18 meninos podem ser divididos em equipes de:
1, 2, 3, 6, 9 ou 18 pessoas
• As 30 meninas podem ser divididas em equipes de:
1, 2, 3, 5, 6, 10, 15 ou 30 pessoas
Comparando as divisões anteriores, percebemos que as equipes com o mesmo número de pessoas são as que têm uma, duas, 3 e 6 pessoas.
Como queremos que as equipes tenham o maior número possível de pessoas, concluímos que cada equipe deverá ter 6 pessoas.
Esse número é o máximo divisor comum (ême dê cê) de 18 e 30. Escrevemos assim: ême dê cê (18, 30) = 6
Na resolução da situação apresentada:
• primeiro, obtivemos os divisores de 18;
• depois, encontramos os divisores de 30;
• em seguida, observamos os divisores que os números 18 e 30 têm em comum;
• por último, escolhemos o maior divisor comum de 18 e 30.
Esse é um dos modos de obter o ême dê cê de dois ou mais números. Também podemos calcular o ême dê cê por meio da decomposição em fatores primos.
Observe, por exemplo, como calcular o ême dê cê de 420 e .1300.
Fazendo a decomposição de 420 e de .1300 em fatores primos, temos:
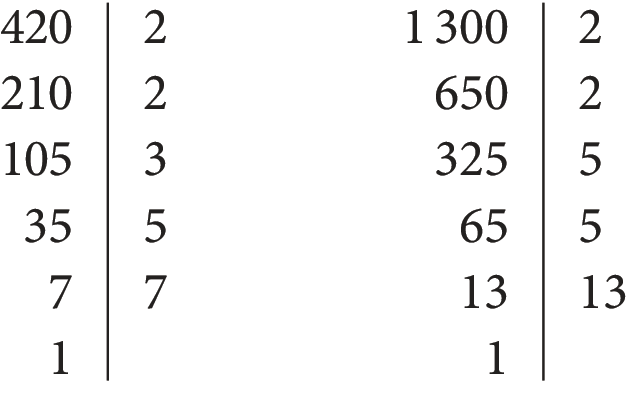

O produto dos fatores comuns dos dois números é divisor de cada um deles e é o maior divisor comum entre eles.
Assim: ême dê cê (420, .1300) = 2 ⋅ 2 ⋅ 5 = 20
Observação
Quando, entre dois ou mais números, não há fatores comuns, dizemos que esses números são primos entre si e o ême dê cê é igual a 1.
4 Mínimo múltiplo comum (mmc)
Em outras situações, precisamos encontrar o menor dos múltiplos naturais comuns, diferente de zero, de dois ou mais números. Acompanhe a situação a seguir.
Da estação de trem Esperança partem trens para as estações Felicidade e Gargalhada. Os trens com destino à estação Felicidade partem de 50 em 50 minutos e os trens com destino à estação Gargalhada partem de 60 em 60 minutos. Sabendo que dois trens, um com destino à estação Felicidade e um com destino à estação Gargalhada, partiram juntos nesse instante da estação Esperança, daqui a quanto tempo será a próxima vez que eles partirão juntos?

Para resolver esse problema, vamos listar daqui a quantos minutos os trens para cada um dos destinos partirão da estação Esperança.
• Para a estação Felicidade:
50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, reticências
• Para a estação Gargalhada:
60, 120, 180, 240, 300, 360, 420, 480, 540, 600, reticências
Os tempos comuns são: 300, 600, reticências
Assim, os trens partirão juntos novamente após 300 minutos, após 600 minutos, reticências
Portanto, a próxima vez que os trens partirão juntos será daqui a 300 minutos, ou seja, 5 horas.
Então, 300 é o mínimo múltiplo comum (ême ême cê) de 50 e 60. Escrevemos: ême ême cê (50, 60) = 300
Na resolução anterior, para encontrar o ême ême cê de 50 e 60, escrevemos os múltiplos diferentes de zero de cada um dos números e, depois, observamos o menor múltiplo comum entre eles. Esse é um modo de calcular o ême ême cê de dois ou mais números. Podemos também usar a decomposição dos números em fatores primos.
Observe, por exemplo, como calcular o ême ême cê de 30 e 84.
Decompondo os dois números em fatores primos por um dos métodos vistos, temos:
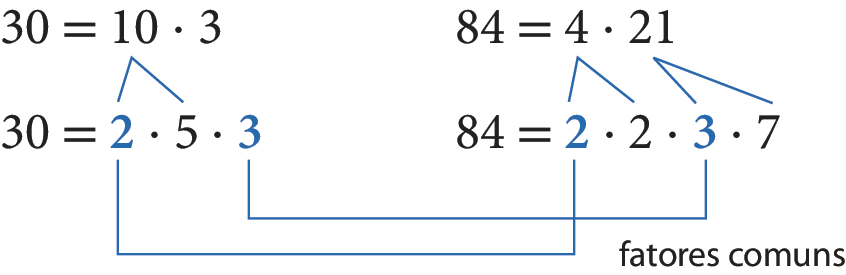
Observe o que acontece quando multiplicamos todos os fatores primos diferentes dos dois números e os fatores comuns apenas uma vez:
2 ⋅ 5 ⋅ 3 ⋅ 2 ⋅ 7 = 420
Podemos, ainda, escrever:
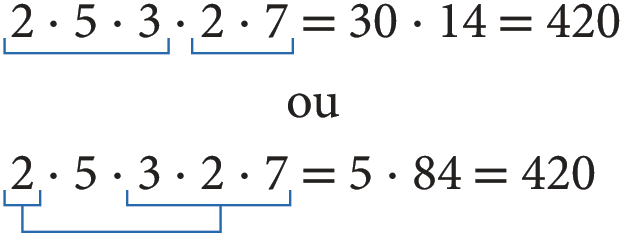
Ou seja, 420 é múltiplo de 84 e de 30, e, como 5 e 14 (2 ⋅ 7) não têm fatores primos comuns, 420 será o menor múltiplo comum de 84 e 30.
Assim, para encontrar o mmc de dois ou mais números, basta multiplicar todos os fatores primos diferentes dos números e os fatores comuns apenas uma vez:
ême ême cê (30, 84) = 2 ⋅ 5 ⋅ 3 ⋅ 2 ⋅ 7 = 420

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1.

Junte-se a um colega, analisem os problemas propostos e identifiquem os que podem ser resolvidos por meio do cálculo do ême dê cê e os que podem ser resolvidos pelo cálculo do ême ême cê.
Problema 1
Paulo tem vários livros, sendo 15 de suspense e 20 de aventura. Ele quer organizá-los em prateleiras sem misturar os gêneros e ocupando a menor quantidade de prateleiras. Cada prateleira deverá ter o mesmo número de livros. Quantos livros Paulo deverá colocar em cada prateleira?

Problema 2
Uma loja de tecidos vai promover uma semana de venda de retalhos. José ficou encarregado de montar uma banca com dois tecidos de estampas diferentes. O tecido com estampa de bolinhas mede 300 centímetros de comprimento e o tecido com estampa de listras mede 240 centímetros de comprimento. José precisa cortar os tecidos em pedaços de mesma medida de comprimento e todos os retalhos devem ter a maior metragem possível. Quantos centímetros de comprimento cada retalho medirá?
Problema 3
Júlia está fazendo um tratamento médico. Ela precisa tomar o remédio a de 4 em 4 horas e o remédio B de 6 em 6 horas. Se ela tomou os dois remédios às 8 horas, a que horas ela tomará os dois remédios juntos novamente?

• Agora, resolvam os problemas e apresentem as resoluções para os demais colegas.
2. Descubra os números que devem substituir cada ◾ nas decomposições em fatores primos e depois calcule o ême dê cê e o ême ême cê.
a) ême dê cê (.1170, .1710)

b) ême ême cê (135, 170)

3. Calcule o que se pede.
a) ême dê cê (180, 150)
b) ême dê cê (231, 825)
c) ême dê cê (340, 728)
d) ême ême cê (12, 18)
e) ême ême cê (90, 180)
f) ême ême cê (55, 121)
4. Augusto organizará apresentações artísticas com crianças de uma escola. Ao todo, serão 7 apresentações musicais e 11 apresentações teatrais. Cada criança participará somente de uma apresentação musical e de uma teatral, e em ambas as apresentações deverá haver a mesma quantidade de crianças.
• Qual é a quantidade mínima de crianças que Augusto terá de recrutar para as apresentações?
5. Um marceneiro precisa cortar três tábuas em pedaços de mesma medida de comprimento. Para melhor aproveitamento das tábuas, a medida do comprimento dos pedaços deve ser a maior possível. Uma das tábuas mede 250 centímetros de comprimento e as outras duas, 350 e 550 centímetros.

• Qual será a medida do comprimento de cada pedaço de tábua?
6. Um relógio eletrônico dispara o alarme de 40 em 40 minutos. Outro relógio soa o alarme de 30 em 30 minutos. Se os dois soaram juntos às 7 horas, a que horas isso voltará a ocorrer?
7. Três corredores largaram juntos em uma prova cujo percurso é circular. Eles correm a uma medida de velocidade constante. Bruno leva 3 minutos para completar cada volta, Henrique leva 4 minutos e Davi, 6 minutos.

• Dada a largada, depois de quanto tempo os três passarão juntos pela primeira vez por esse local?
8. Leia o texto e responda às questões.
Em uma loja, há 150 Dê vê dês de filmes de suspense, 120 de comédias, 50 de shows musicais e 250 de outros gêneros. Para que os clientes encontrem os Dê vê dês com mais facilidade, o proprietário da loja vai separá‑los em quantidades iguais nas prateleiras. Em cada uma, ele colocará a maior quantidade possível de Dê vê dês, mas sem misturar os gêneros.

a) Quantos Dê vê dês o proprietário deverá colocar em cada prateleira?
b) Quantas prateleiras serão necessárias?
9. Leia o texto e responda às questões.
Dois livros, um com 176 páginas e outro com duzentas e quarenta páginas, serão divididos em fascículos para venda semanal em bancas de jornais. Os fascículos serão montados com o maior número de páginas possível e terão o mesmo número de páginas.
a) Quantas páginas terá cada fascículo?
b) Em quantas semanas uma pessoa terá os dois livros completos, considerando que ela compre todos os fascículos e que um livro seja vendido após o outro?
10. Próximo à minha casa há um ponto de ônibus por onde passam duas linhas diferentes. Uma delas passa de 30 em 30 minutos, enquanto a outra passa de 15 em 15 minutos.
a) Se os ônibus das duas linhas passaram juntos no ponto às 13 horas e 30 minutos, a que horas eles passarão juntos novamente?
b) Se o primeiro encontro dos ônibus das duas linhas ocorre às 6 horas da manhã, a que horas deve ocorrer o décimo encontro?
11. Leia o texto e responda às questões.
A um congresso, compareceram 28 funcionários de uma empresa: 16 foram em carros particulares e 12 em carros da empresa. Cada carro transportou o maior número possível de pessoas, e todos transportaram a mesma quantidade de funcionários.
a) Quantos funcionários cada carro transportou?
b) Quantos carros foram utilizados?
12. Guilherme, Artur e Bernardo moram em São Paulo e costumam viajar a trabalho para dar palestras. Guilherme costuma viajar de 12 em 12 dias, Artur, de 15 em 15 dias e Bernardo, de 20 em 20 dias. Sabendo que os três viajaram juntos para o Rio de Janeiro, daqui a quantos dias eles viajarão juntos novamente?
13. Em uma turma existem menos de 35 estudantes. O professor de Educação Física precisa formar equipes para desenvolver uma atividade. Se o professor montar equipes de 6, 10 ou 15 pessoas, não sobrará nenhum estudante fóra das equipes. Quantos estudantes há nessa turma?
14. Leia o texto a seguir e corrija os dados incorretos.
Rafael vive no litoral em uma localidade próxima de um porto.
Ele conta que, em sua cidade, dois faróis sinalizam a entrada de um canal entre uma ilha e o continente. Um deles ilumina certo lugar de 6 em 6 minutos, e o outro ilumina o mesmo lugar de 8 em 8 minutos.
Ele também relata que às 20 horas os dois faróis iluminam juntos aquele lugar e, às 20 horas e 30 minutos, ocorre o mesmo.

15.

Resolva o problema. Se necessário, faça um esquema para ilustrar a situação.
Uma estrada mede 200 quilômetros de comprimento. Nela, a medida de distância entre um posto de combustível e outro é de 30 quilômetros, entre os telefones públicos, 8 quilômetros e entre os radares eletrônicos para contróle da medida de velocidade, 20 quilômetros. No início dessa estrada, os três estão no mesmo lugar.
a) Partindo do início, qual medida da distância, em quilômetro, é preciso percorrer para encontrar um posto de combustível, um telefone público e um radar eletrônico no mesmo local da estrada?
b) Quantas vezes ao longo de toda a estrada eles aparecerão juntos novamente?
16.


Elabore dois problemas, um que possa ser resolvido usando a ideia de ême ême cê e um usando a ideia de ême dê cê.
Passe seus problemas para um colega resolver e resolva os problemas criados por ele.

Estatística e Probabilidade
FAÇA AS ATIVIDADES NO CADERNO
Estimativa da probabilidade
Em algumas situações, para estimar a probabilidade de ocorrer determinado resultado, considera-se a ocorrência desse resultado anteriormente. Esse tipo de estudo é importante, por exemplo, para realizar previsões e planejamentos, calcular o valor de seguros, testar a eficácia de medicamentos etcétera.
Observe algumas situações.
Situação 1
Em janeiro de 2024, a Companhia de Engenharia de Tráfego da cidade Ecológica fez um levantamento do número de pessoas que utilizaram a bicicleta como meio de transporte e do número de acidentes com ciclistas nos três anos anteriores.

|
Ano |
Número de ciclistas |
Número de acidentes |
|---|---|---|
|
2021 |
1.502 |
17 |
|
2022 |
1.713 |
19 |
|
2023 |
1.988 |
20 |
Dados obtidos pela Companhia de Engenharia de Tráfego da cidade Ecológica em janeiro de 2024.
Com base nos dados da tabela, podemos calcular o percentual de ciclistas que se envolveram em acidente nos anos 2021, 2022 e 2023. Para isso, basta dividir o número de acidentes envolvendo ciclistas pelo número total de ciclistas de cada ano.
Em 2021:
Fração 17 sobre 1 mil 502
≃ 0,011 = 1,1%
Em 2022:
Fração 19 sobre 1 mil 713
≃ 0,011 = 1,1%
Em 2023:
Fração 20 sobre 1 mil 988
≃ 0,010 = 1,0%
Observe que nesses três anos aproximadamente 1% dos ciclistas se envolveu em acidente. Assim, podemos estimar que a probabilidade de um ciclista se envolver em acidente em 2024 será de aproximadamente 1%.
Repare que, nessa situação, baseamo-nos em informações estatísticas para estimar a probabilidade de um evento ocorrer, ou seja, com base na ocorrência anterior, estimamos a probabilidade de o evento ocorrer posteriormente.
Situação 2
Uma indústria farmacêutica está verificando os efeitos colaterais causados pelo uso de determinado medicamento. Para isso, realizou um experimento com .1000 pessoas. Destas, trinta e uma pessoas tiveram dores de cabeça após consumir o medicamento.
Assim,
Fração 31 sobre mil=
fração 3 vírgula 1 sobre 100.ou 3,1% das pessoas tiveram dores de cabeça.
Para obter uma estimativa melhor, a indústria realizou o experimento com mais .4000 pessoas, totalizando .5000 pessoas. Destas, cento e quarenta e duas pessoas apresentaram dores de cabeça.
Considerando o experimento todo,
Fração 142 sobre 5 mil= 0,0284 ou 2,84% das pessoas tiveram dores de cabeça.
Para melhorar ainda mais a estimativa, a indústria realizou o experimento com mais .5000 pessoas, totalizando .10000 pessoas. Destas, duzentas e noventa e três pessoas apresentaram dores de cabeça.
▶ Estatística e Probabilidade
Assim, considerando as .10000 pessoas,
Fração 293 sobre 10 mil= 0,0293 ou 2,93% das pessoas tiveram dores de cabeça.
Usando esse número, a indústria pode estimar a probabilidade de uma pessoa ter esse efeito colateral após consumir o medicamento. Para tornar ainda mais precisa a estimativa, a indústria pode realizar o experimento com mais pessoas. Quanto maior o número de repetições do experimento, mais acertada é a estimativa. Se o número de repetições é pequeno, a probabilidade estimada pode não condizer com a realidade.

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Uma conversa sobre probabilidade
Duração: 10:06min. Página: 28.
>> [LOCUTORA] Uma conversa sobre probabilidade
>> [LOCUTORA] Estatística é a ciência que se dedica a coletar, analisar e interpretar dados. Uma das áreas fundamentais dentro da Estatística é a probabilidade. Seu estudo é voltado para entender quais as chances de determinado evento ocorrer num experimento aleatório.
>> [LOCUTORA] Um dos exemplos mais básicos para se pensar em probabilidade é analisando a chance de cair cara ou coroa no lançamento de uma moeda. Podemos ainda pensar em jogos de azar que envolvem cartas, lançamentos de dados etc. No entanto, o uso da probabilidade vai muito além disso. Em experimentos aleatórios, feitos nas mais diversas áreas científicas, você precisará entender se o que ocorreu foi um simples fruto do acaso ou se foi realmente resultado de alguma intervenção. Por isso, apesar da comum associação de probabilidade com jogos, é importante notar que seu uso vai muito além.
>> [LOCUTORA] Para entendermos um pouco mais sobre probabilidade e as suas diferentes aplicações em nossa vida, convidamos o estatístico André Yukio para conversar um pouco sobre essa ciência tão presente nas mais diversas áreas do conhecimento humano.
Vinheta.
Música de fundo.
>> [LOCUTOR] Bom dia, André. Afinal de contas, o que é a Estatística?
>> [ANDRÉ YUKIO AB MOTA] Bom, Estatística é a ciência que se dedica à forma de coletar, analisar e interpretar os dados. A forma como você coleta os dados, por exemplo, numa entrevista ou quando você vai fazer uma pesquisa eleitoral, isso daí importa. A forma de você analisar esses dados e interpretar o que eles estão dizendo também. E isso é Estatística. E dentro da Estatística, uma das áreas principais é a probabilidade.
>> [ANDRÉ YUKIO AB MOTA] Que que é a probabilidade, que também tá relacionada com analisar os dados? É... O estudo da probabilidade é voltado pra entender quais as chances de um evento ocorrer em um experimento aleatório. Um exemplo é qual que é chance de cair cara ou coroa quando você joga uma moeda pra cima? Ou, então, qual que é a chance de cair determinado número numa roleta? Isso tudo é probabilidade. Esses são os exemplos mais simples, assim mais comuns também, que tão dentro de probabilidade.
>> [LOCUTOR] Mas o que é um experimento aleatório?
>> [ANDRÉ YUKIO AB MOTA] Experimentos aleatórios são os fenômenos, assim... que a gente repete inúmeras vezes, de uma forma semelhante, e eles têm resultados imprevisíveis. São os experimentos que a gente faz várias vezes e os resultados são imprevisíveis. O que acontece? A gente tem resultados conhecidos, só que eles têm um valor desconhecido, a gente não sabe qual o resultado que vai acontecer. Por exemplo, se eu jogo uma moeda pra cima, ela pode cair cara, pode cair coroa, mas eu não sei qual que vai ser a próxima face que vai cair. E ele pode ser repetido várias vezes em condições idênticas. É a mesma coisa, vamos pensar, pro mundo assim mais... mais científico mesmo. Quando a gente faz um experimento aleatório de um medicamento, o que que a gente vai fazer? A gente tem os resultados conhecidos lá, que podem ser assim: o medicamento funciona; o medicamento não funciona. E aí, a gente pode repetir várias vezes sob as mesmas condições, ou condições muito parecidas, e obviamente, como vocês sabem, a partir dos resultados que a gente obter [sic] desses experimentos a gente consegue aí determinar se o medicamento, se a droga é eficiente ou não é. Então, você vê como o experimento aleatório é o que tá presente na nossa vida todo o tempo? Diversas situações são experimentos aleatórios.
>> [LOCUTOR] E a gente usa probabilidade para quê?
>> [ANDRÉ YUKIO AB MOTA] Vamos pegar o exemplo que a gente usou agora há pouco. A gente joga uma moeda pra cima. A gente sabe que pode cair cara ou pode cair coroa. Como que a gente vai usar a probabilidade aí? Como que você usa a probabilidade, por exemplo, quando você olha para esse experimento? Aí você fala “é bem possível que caia cara, só que é bem possível que caia coroa também”. As chances são iguais. Agora, imagina que você joga várias vezes a mesma moeda e cai cara. Opa, você já ia pensar “olha, essa moeda tem alguma coisa, eu joguei cinquenta vezes e cinquenta vezes caiu cara”. Isso é muito improvável. Esse é o uso da estatística, olha que simples. Só que agora pensa nisso quando você vai aplicar um remédio. De novo voltando pro experimento do remédio. Você deu o remédio ali pra 50 pessoas, 30 delas se curaram e 20 não se curaram. Então, o remédio é eficiente? Uma pessoa pode falar “ah, é sim, se mais da metade curou…”; outra pode falar “não, mas isso daí não é suficiente pra gente afirmar que ele realmente funciona”. E a estatística vai te dar isso. Ela vai dizer, a probabilidade, né?, vai te dizer “olha, é muito improvável que o remédio não funcionando 30 pessoas se curem”. Ou ela vai dizer “pode acontecer de 30 pessoas se curarem e o remédio não ser eficiente. E a chance de isso acontecer não é baixa, não”. Então, a gente já ia ter uma cautela. E é isso que a probabilidade vai te dar. Ela vai poder te responder as perguntas: “Olha, isso daqui aconteceu, será que foi por acaso ou não? Realmente aconteceu porque esta coisa A causou essa coisa B?”. Sabe, esse remédio fez isso se curar. Essa medida aqui de política fez a educação melhorar, por exemplo. E é isso que a probabilidade vai te dar. Olha que incrível como vai muito além do lançamento de moedas ou de dados ou jogos de azar.
>> [LOCUTOR] Que tipos de eventos ou fenômenos naturais é possível prever por meio da estatística?
>> [ANDRÉ YUKIO AB MOTA] Basicamente tudo. Tudo que a gente tem hoje, que a gente tem na natureza a gente tenta modelar com estatística. Qualquer fenômeno da natureza pode ser modelado com Estatística. Se você analisar assim a grade curricular de um monte de disciplina que estuda o meio ambiente, que estuda fenômenos que ocorrem na natureza, você vai ver que eles têm Estatística. Por quê? Porque ele vai ter que olhar o histórico, vai ter que ver se aquilo é provável ou improvável, vai ter que analisar tudo que tá envolvido. “Olha, ali tá chovendo mais do que o normal.” Mas o que que mudou naquele meio ambiente? O que que tá influenciando? Qual que é a probabilidade de ter aumentado a chuva sem que tivesse alguma mudança? Qual que é a probabilidade de aumentar quando se tem tal mudança? Olha, a gente olhou pra vários ambientes e esses ambientes que tiveram essa mesma mudança, eles tiveram aumento de chuva, né?, tô usando chuva como exemplo, em 30 por cento. Então, é bem possível, me parece plausível que essa mudança aqui é o que causa esse fenômeno. Isso, óbvio, tô falando de chuva, mas eu podia tá falando de terremoto, de furacão, de qualquer outro fenômeno.
>> [ANDRÉ YUKIO AB MOTA] Então, Estatística vai estar envolvida em tudo que é tipo de modelagem que a gente esteja falando aí na natureza, em fenômenos climáticos ou o que quer que seja. Você vai ver que sempre vai tá lá uma pitadinha de probabilidade, de Estatística, ou talvez uma [riso] pitadona, né?, muito mais do que muita gente imagina.
>> [LOCUTOR] E se usa probabilidade em ciência também? Como? Não é só uma coisa de matemáticos?
Música de fundo.
>> [ANDRÉ YUKIO AB MOTA] Claro, claro que se usa. Quando a gente fala de medicamentos, tá falando de medicina, você vai ter que ter uma análise probabilística ali. Você não pode simplesmente “olha, essas pessoas vão pensar em dieta, nutrição... essas pessoas vão seguir a dieta A, essas pessoas vão seguir a dieta B, essas outras pessoas aqui vão seguir a dieta C. O grupo A ficou mais forte, o grupo B não ficou, quantas pessoas têm que ter ficado mais forte pra eu dizer que aquilo realmente é eficiente? Pra dizer que aquela dieta é realmente boa e ajuda a fortalecer?”. Olha, é isso que a probabilidade vai te dizer. Quando você tem políticas públicas, vamos ali olhar pras Ciências Sociais, pra Economia, você tem uma intervenção numa sala de aula e você vê que 50 por cento dos alunos melhoraram a nota. E aí? Isso daí ocorreu por causa dessa intervenção? O que mais tava ocorrendo antes? Qual a chance de ter ocorrido essa melhora de nota por acaso? Probabilidade, estatística. E isso a gente vai pra Psicologia, pode ir pra Biologia, pode ir pra tudo o que é área, você vai ver que tem estatística ali no meio.
>> [ANDRÉ YUKIO AB MOTA] Agora, vamos pensar em frequência de ocorrência. Vamos supor ali que você é um... você faz a análise, um estudo sobre trânsito, saindo daquela coisa matemática, você tá estudando algo social aí. De repente, você vê ali no ano inteiro quantos acidentes tiveram por dia ou por mês. Vamos pensar ali quantos acidentes tiveram por mês. No mês 1 teve 20 acidentes, no mês 2 teve 10, no mês 3 teve 5, no mês 4 teve 15. Olha como isso te diz muito. Você pode pegar essas frequências aí e olhar qual o mês que geralmente tem mais acidentes, você pode ver a média de acidentes no ano. E a gente pode pensar também em algo mais probabilístico: qual a probabilidade de você se acidentar saindo de carro em janeiro, saindo de carro em fevereiro? “Olha, janeiro tem muito mais acidente, a gente viu ali na nossa análise de frequência que tem 30 acidentes em janeiro, 20 em fevereiro e aí o resto do ano tem 10, 8 acidentes”. Se todos os meses do ano a gente tem o mesmo número de carros aí na rua, daqui eu tô supondo, é só um exemplo, então, a gente sabe que a probabilidade de a gente sofrer um acidente ali em janeiro é muito maior porque a gente tem muito mais acidentes, seja porque tem mais festas, seja porque as pessoas bebem mais. Então, isso é um exemplo bacana ali quando você usa a frequência. Você pega as frequências de um determinado evento e você sabe que onde tem... ocorre mais vezes a probabilidade é maior.
O trecho da música “Willie's Island Moped”, de The Whole Other, está disponível no YouTube.
1. A tabela a seguir mostra o número de furtos de motocicletas de 2020 a 2023 na cidade Urbana.

|
Ano |
Número de motocicletas em circulação |
Número de furtos |
|---|---|---|
|
2020 |
22.005 |
1.400 |
|
2021 |
35.158 |
2.080 |
|
2022 |
47.977 |
2.901 |
|
2023 |
62.562 |
3.510 |
Dados obtidos pela prefeitura da cidade Urbana entre 2020 e 2023.
a) Estime a probabilidade de uma motocicleta ser furtada nessa cidade.
b)

Em sua opinião, qual é a importância desse levantamento feito pela cidade Urbana? Converse com os colegas sobre isso.
2. Observe o gráfico com o tipo sanguíneo dos doadores de um hemocentro em 2022.
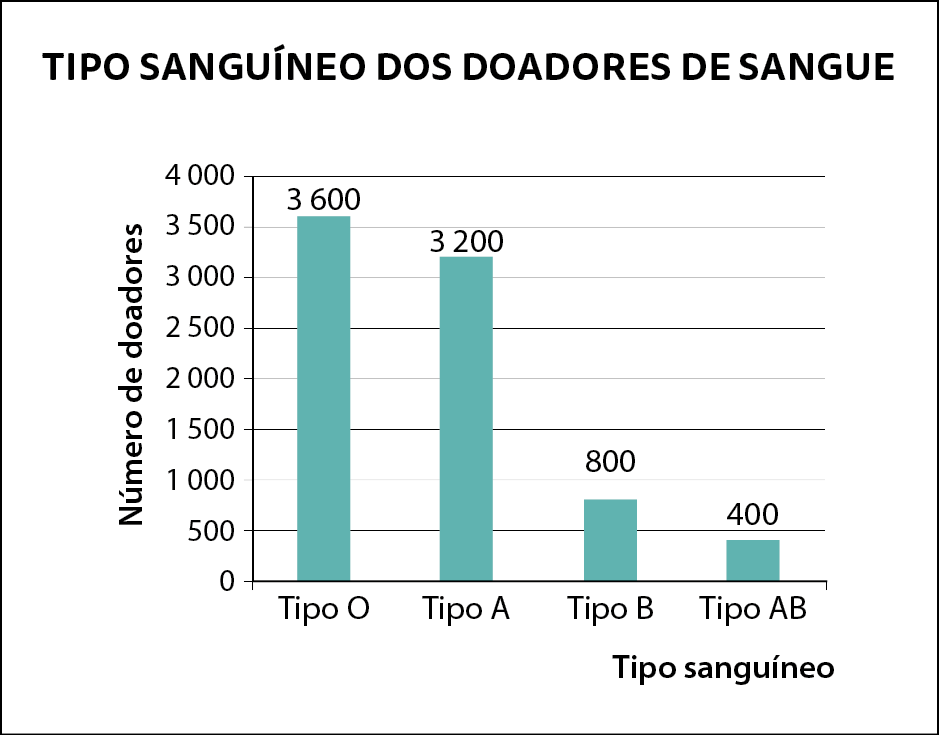
Dados obtidos pelo hemocentro em 2022.
a) Estime a probabilidade de comparecer a esse hemocentro um doador com sangue do tipo óh. E depois um doador com o sangue do tipo B.
b) A probabilidade estimada de aparecer um doador com sangue do tipo a corresponde a quantas vezes a probabilidade estimada de aparecer um doador com sangue do tipo A bê?
c)


Converse sobre as questões a seguir com os colegas e o professor.
• Qual é a importância de fazer doação de sangue?
• Alguém da sua família já doou sangue?
3. Em um jornal foi publicada a seguinte manchete:

• Estime a probabilidade de no primeiro semestre de 2023 um paciente ter dado entrada nesse posto de saúde com febre, mas não estar com gripe.
4. Carlos e Marcelo colecionam bolinhas de gude. Eles resolveram fazer o seguinte experimento:
• colocaram uma bolinha de cada cor dentro de uma caixa;
• sem olhar dentro da caixa, retiravam uma bolinha, anotavam a cor da bolinha retirada e colocavam-na de volta na caixa.
Ao final de .1000 retiradas, a frequência de ocorrência de cada uma das cores foi apresentada no quadro a seguir.
|
Cor da bolinha |
Quantidade de retiradas |
|---|---|
|
Azul |
105 |
|
Preta |
97 |
|
Verde |
95 |
|
Roxa |
99 |
|
Laranja |
103 |
|
Amarela |
98 |
|
Branca |
108 |
|
Vermelha |
96 |
|
Cinza |
98 |
|
Marrom |
101 |
a) Calcule a porcentagem de retirada de cada cor nesse experimento.
b) Estime a probabilidade de uma bolinha de cada uma dessas cores ser retirada dessa caixa.
5.

Em trios, realizem o experimento.
Parte 1: providenciem uma moeda, lápis e papel. Cada um dos integrantes do trio deverá lançar a moeda 10 vezes. Enquanto isso, um dos colegas ajudará a checar a face da moeda voltada para cima a cada lançamento e o outro anotará os resultados obtidos.
a)

Calculem a porcentagem de resultado cara e a de resultado coroa nos 30 lançamentos.
b) Com base nos resultados obtidos, estimem a probabilidade de sair cara e a probabilidade de sair coroa ao lançar essa moeda.
Parte 2: cada integrante do trio deverá lançar a moeda mais 30 vezes, e os resultados obtidos deverão ser anotados ao lado dos resultados da parte 1, totalizando 120 lançamentos.
c) Repitam os procedimentos dos itens aêbê considerando os 120 lançamentos.
Parte 3: cada integrante do trio deverá lançar a moeda mais 40 vezes, e os resultados obtidos deverão ser anotados ao lado dos resultados das partes 1 e 2, totalizando 240 lançamentos.
d) Repitam os procedimentos dos itens aêbê considerando os 240 lançamentos.
e) Comparem os resultados que vocês obtiveram com os resultados obtidos por outros trios. Os resultados são iguais?
f) O que aconteceu com a probabilidade estimada de sair cada face quando vocês aumentaram a quantidade de lançamentos? Essa probabilidade se aproximou de algum número? Se sim, de qual número?
g) Ao lançar uma moeda “honesta”, a probabilidade de sair cada face é de
um meio, ou 0,5, ou 50%. Os resultados que vocês obtiveram nesse experimento são próximos desse número? Caso não sejam, por que vocês acham que isso ocorreu?

Compreender um texto
FAÇA AS ATIVIDADES NO CADERNO


Mulheres e ciência
Se você é menina e gosta de ciência, pode pensar em qualquer profissão para o futuro. E daqui a alguns anos pode estar em um laboratório estudando vacinas; em uma floresta, rio, lago ou mar descobrindo novas espécies de plantas e animais, ou ainda, olhando para o céu com um telescópio para descobrir novas estrelas e planetas. No entanto, saiba que essa liberdade para sonhar e conquistar uma profissão na ciência, nem sempre foi igual entre meninos e meninas.


[reticências]
Embora sejam cérca de metade da população, as mulheres ainda representam apenas um terço de todos os cientistas do planeta.
São muitos os obstáculos para que uma mulher alcance o topo da carreira científica. Para começo de conversa, é comum que, em muitos lugares, os meninos sejam mais incentivados a estudar para chegar lá. A carga de trabalho em casa é bem maior para elas do que para eles. E há ainda a maternidade e o papel de cuidadoras. Quando se tornam mães ou quando precisam cuidar de alguém mais velho, muitas cientistas acabam interrompendo suas pesquisas.
Apesar disso, as mulheres têm feito alguns dos mais extraordinários trabalhos de pesquisa dos últimos anos. [reticências]
KRAPP, Juliana; BONFIM, Mel. Histórias para inspirar futuras cientistas. Rio de Janeiro: Edições Livres, 2021. página 12.

Dia Mundial das Mulheres e Meninas na Ciência
Segundo um levantamento da Unesco, apenas 30% dos cientistas no mundo são mulheres. No Brasil, a proporção é ainda menor: as mulheres ocupam apenas 14% das posições na Academia
Brasileira de Ciências. Desde que o Nobel foi criado, em 1901, o prêmio foi concedido a mais de seiscentas e vinte e duas pessoas nas áreas de ciências, mas apenas 22 dos vencedores foram mulheres. [reticências]
CARVALHO Jeziel. Dia Mundial das Mulheres e Meninas na Ciência. Disponível em: https://oeds.link/vD3WWS. Acesso em: 17 abril 2022.


ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Qual é a ideia principal do texto que você acabou de ler?
2. Qual profissão você gostaria de exercer no futuro? Comente.
3. Desde 2021, certa escola realiza uma pesquisa para saber quantas de suas estudantes do último ano do Ensino Médio almejam ser cientistas. O resultado dessas pesquisas está na tabela a seguir.
|
Ano |
Total de estudantes |
Número de estudantes que almejam ser cientistas |
|---|---|---|
|
2021 |
123 |
38 |
|
2022 |
120 |
36 |
|
2023 |
125 |
37 |
Dados obtidos pela escola de 2021 a 2023.
Estime a probabilidade de uma estudante do último ano do Ensino Médio dessa escola almejar ser cientista.
4.


Reúna-se com dois colegas, escolham uma cientista brasileira e realizem uma pesquisa sobre sua carreira e suas contribuições para a ciência.
Depois, compartilhem os resultados da pesquisa com os colegas e o professor.

Atividades de revisão
FAÇA AS ATIVIDADES NO CADERNO
1. (ó bê ême) O número 10 pode ser escrito de duas fórmas como soma de dois números primos: 10 = 5 + 5 e 10 = 7 + 3. De quantas maneiras podemos expressar o número 25 como uma soma de dois números primos?
a) 4
b) 1
c) 2
d) 3
e) nenhuma
2. Corrija as afirmações falsas.
a) Os números 35 e 55 são primos entre si, pois ême dê cê (35, 55) = 1.
b) O ême dê cê (23, 47) é igual ao ême dê cê (2, 7).
c) O ême dê cê (5, 15) é menor que o ême dê cê (3, 7).
d) Os números 42 e 147 não são primos entre si, pois ême dê cê (42, 147) = 21.
e) O maior dos divisores comuns de 7 e de 20 é menor que o maior dos divisores comuns de 2 e de 4.
3. Dois ônibus de turismo partem de uma estação com destinos diferentes. Um dos ônibus parte de 5 em 5 dias. O outro ônibus sai de 8 em 8 dias. Sabendo que, no dia 31 de março, esses dois ônibus saíram juntos, em que dia eles vão sair novamente juntos da estação?
a) 30 de abril
b) 24 de março
c) 10 de maio
d) 20 de abril
4. Renato cuida de sua orquídea de 3 em 3 dias e de seu bonsai de 14 em 14 dias. Se hoje ele cuidou dos dois, daqui a quantos dias ele voltará a cuidar deles juntos?

5. A quantidade de biscoitos que Rita comprou na padaria é menor que 200 e pode ser dividida igualmente, e sem sobras, em 8, 10 ou 15 caixas. Quantos biscoitos Rita comprou?
6. Jane, Carla e Flávia participaram de uma competição de ciclismo. Jane completava cada volta em 45 segundos, enquanto Carla levava 50 segundos e Flávia, 30 segundos. As três mantiveram suas velocidades do início ao fim da competição.
a) A cada quantos segundos as competidoras se encontram?
b) Sabendo que a competição tem 90 voltas, quando Flávia tiver completado a 90ª volta, que voltas Carla e Jane terão completado?
7. Para a gincana de uma escola serão formadas equipes de estudantes de cada curso, com a mesma quantidade e o maior número possível de estudantes. Para facilitar a montagem das equipes, os professores fizeram um quadro com a quantidade de estudantes matriculados em cada curso.
|
Curso |
Quantidade de estudantes |
|---|---|
|
A |
148 |
|
B |
160 |
|
C |
184 |
|
D |
196 |
a) Quantos estudantes haverá em cada equipe?
b) Quantas equipes serão formadas?
c) Se em cada equipe houver 8 estudantes, em quais cursos não será possível formar equipes?
8.

A seguir, está representada parte de um número natural e sua decomposição em fatores primos. Sabendo que símbolos iguais representam algarismos iguais, determine o valor de

e

.

9.

Em pequenos grupos, realizem um experimento para determinar a probabilidade de ocorrer um número múltiplo de 3 no lançamento de um dado. Registrem o planejamento (os materiais que serão necessários, a quantidade de lançamentos realizados, o modo como os resultados serão computados, o que cada integrante do grupo fará etcétera.) e os resultados do experimento.