
CAPÍTULO 2 Números inteiros
1 Números positivos e números negativos
Os números estão sempre presentes em nosso dia a dia.
Muitas medidas ou contagens que fazemos são representadas por números negativos. Eles costumam aparecer, por exemplo, em medidas de temperatura, extratos bancários e saldos de gols. Observe algumas situações a seguir.
Situação 1
Em um mesmo dia, é possível encontrar dois locais no mundo com medidas de temperatura muito diferentes. No dia 18 de janeiro de 2022, por exemplo, a medida da temperatura mínima em Salvador foi 26 graus Célsius; já em Yakutsk, na Rússia, a mínima foi ‒ 40 graus Célsius.
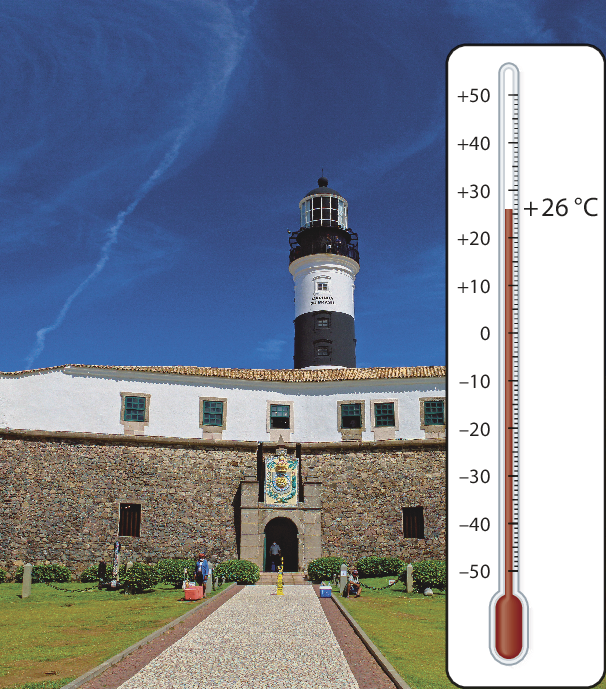
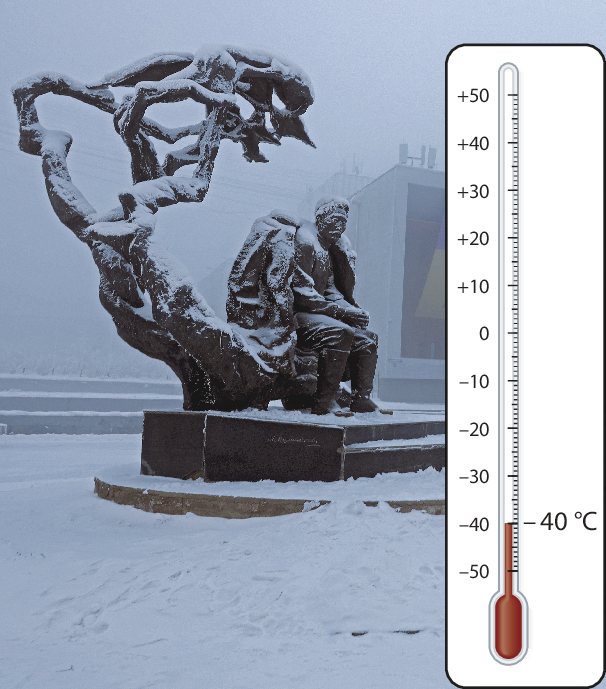
Você percebeu que, para indicar a medida da temperatura em Yakutsk, usamos o sinal negativo (‒), mas para a temperatura em Salvador, que foi positiva (acima de zero), não escrevemos o sinal positivo (+)? Isso ocorre porque, na representação de valores positivos, o uso do sinal (+) junto do número é optativo, enquanto, na representação dos valores negativos, o sinal (‒) deve, obrigatoriamente, acompanhar o número a que se refere.
Para a representação do número zero (0), não usamos nenhum dos sinais, pois ele não é positivo nem negativo.
Situação 2
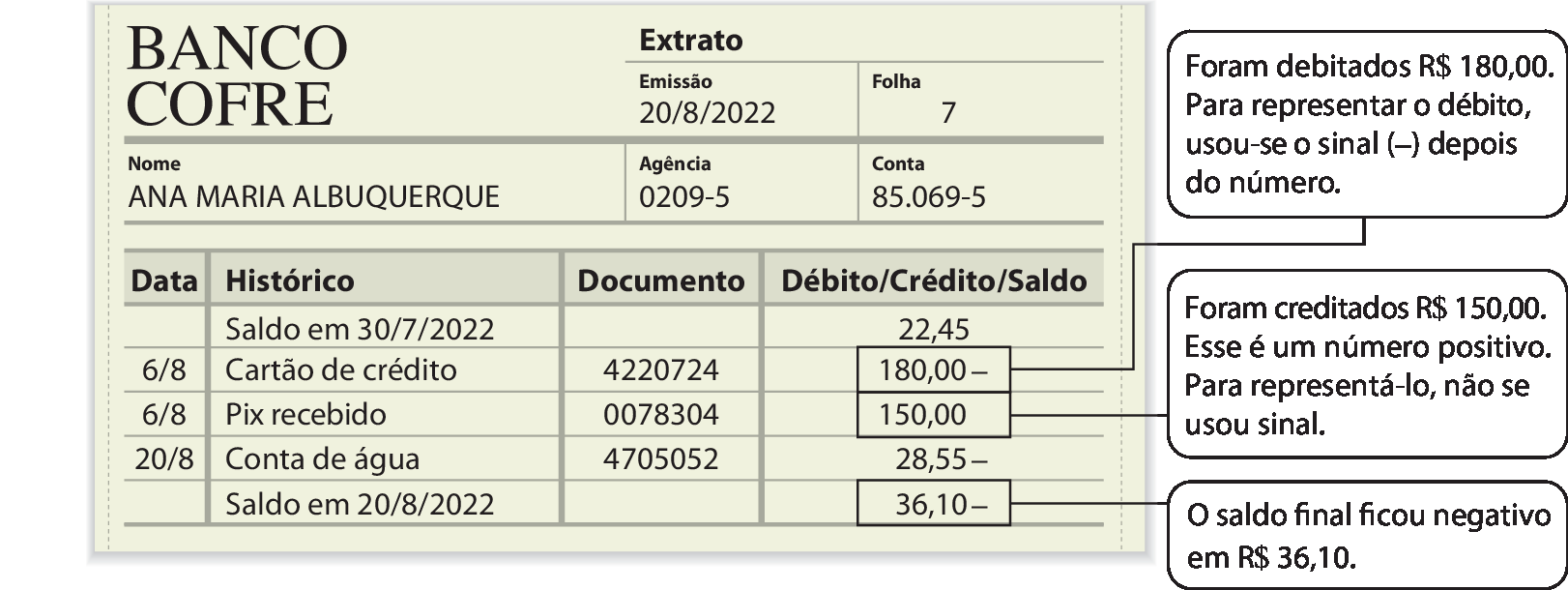
O extrato bancário a seguir apresenta alguns créditos (valores positivos) e débitos (valores negativos) em uma conta-corrente e mostra como o saldo da conta ficou negativo.
Situação 3
No Campeonato Brasileiro de Futebol, os números negativos podem aparecer no saldo de gols, ou seja, na diferença entre o número de gols marcados e o número de gols sofridos. A seguir, apresentamos a classificação final de alguns times da série a no Campeonato Brasileiro de 2021.
|
Posição |
Clube |
Gols marcados |
Gols sofridos |
Saldo de gols |
|---|---|---|---|---|
|
1º |
Atlético Mineiro (MG) |
67 |
34 |
33 |
|
12º |
Internacional (RS) |
44 |
42 |
2 |
|
15º |
Cuiabá (MT) |
34 |
37 |
−3 |
|
18º |
Bahia (BA) |
42 |
51 |
−9 |
Dados obtidos no site oficial da Confederação Brasileira de Futebol (CBF) em 8 fevereiro 2022.

Situação 4
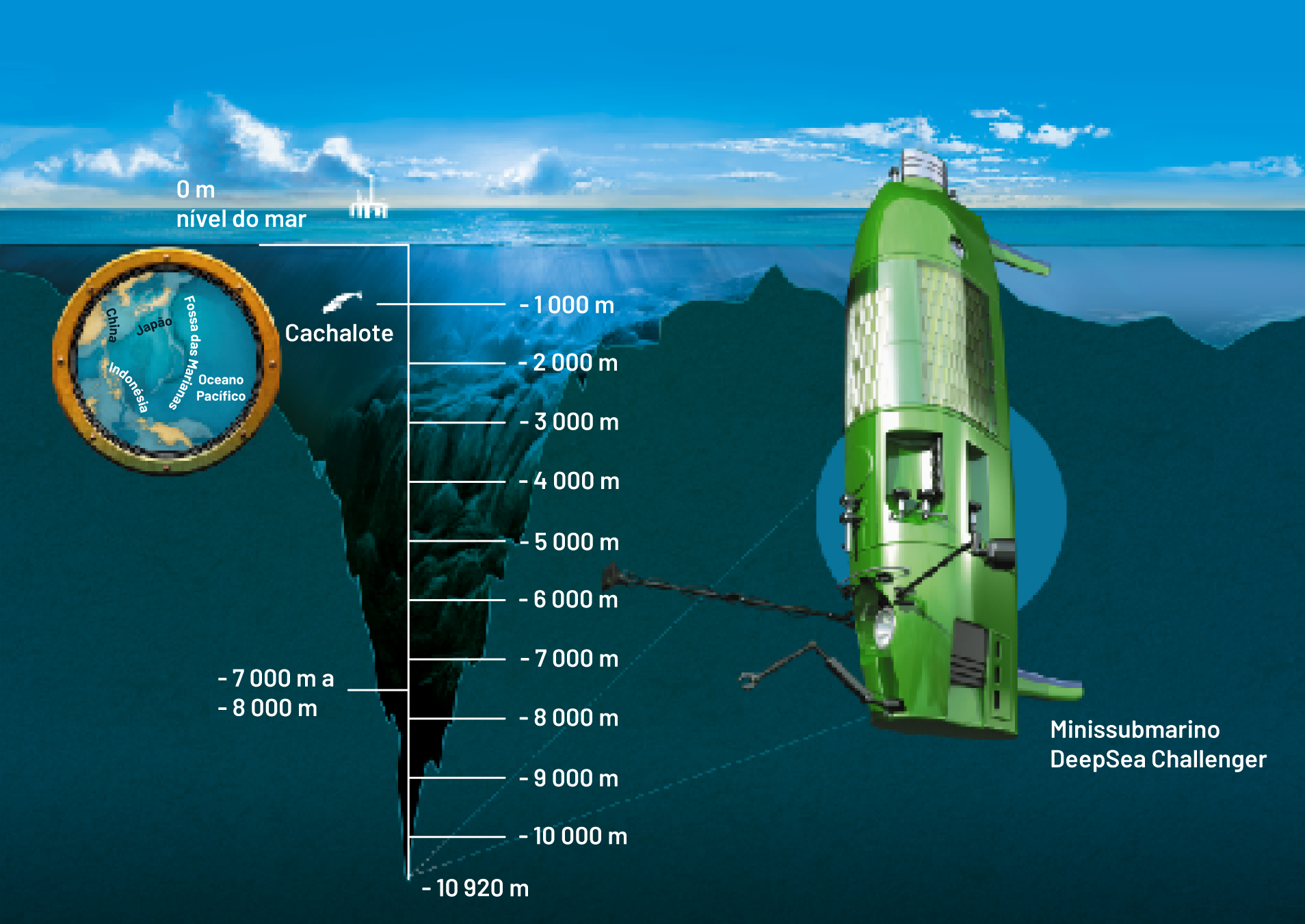
Os números negativos também são usados para indicar medidas de altitude. Nesse caso, o nível do mar é o ponto de referência, que indica a medida de zero metro; as medidas de altitude acima do nível do mar são indicadas por números positivos, e as medidas de altitude abaixo do nível do mar são indicadas por números negativos.
O ponto mais alto do mundo é o Monte Everest, que fica na fronteira entre o Nepal e o Tibete e mede + .8848 métros de altitude.
O ponto mais profundo é conhecido por "Challenger Deep", localizado na Fossa das Marianas, no Oceano Pacífico, com medida de ‒ .10924 métros de altitude (ou .10924 métros abaixo do nível do mar).

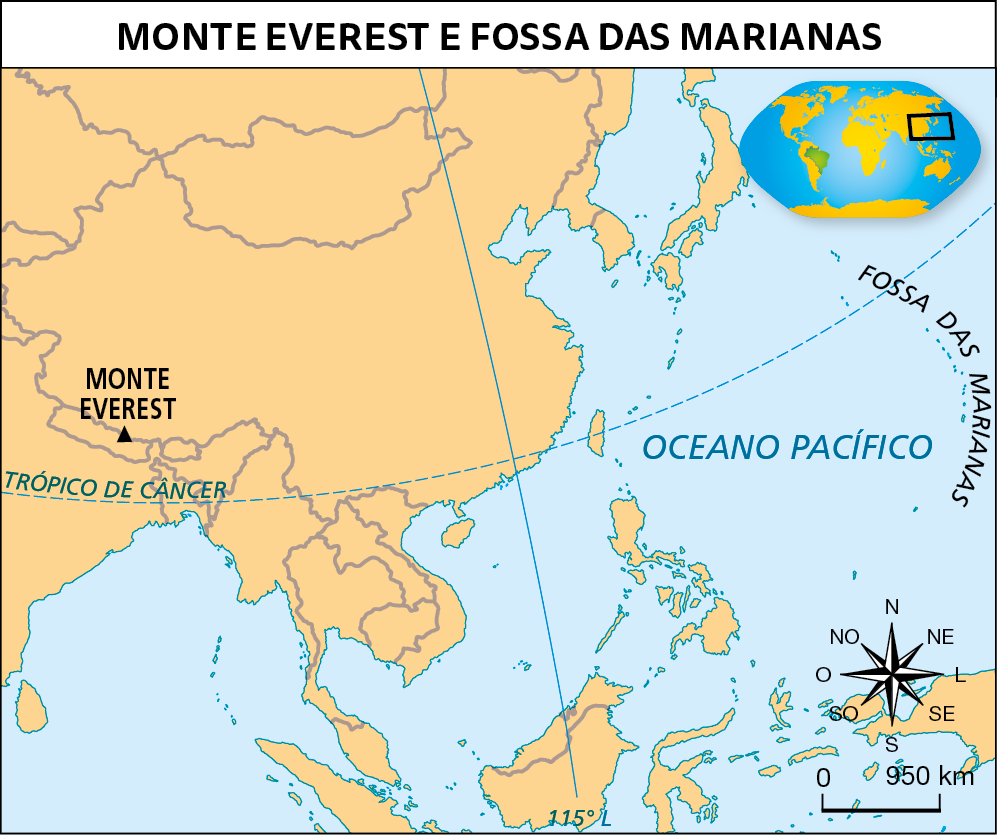
Elaborado com base em: FERREIRA, Graça Maria Lemos. Moderno atlas geográfico. sexta edição São Paulo: Moderna, 2016. página 20, 48 e 52.
Texto do Infografico

Gire o seu dispositivo para a posição vertical
Saiba mais
O número negativo
Na passagem da Idade Média para a Idade Moderna (séculos catorze a dezesseis), os países da Europa Ocidental sofreram profundas transformações. Era grande o desenvolvimento do comércio e as cidades cresciam muito. [reticências]
Paralelamente a essas mudanças econômicas, políticas e sociais, houve o florescimento da arte, da cultura e das ciências. Essa revolução cultural ficou conhecida como Renascimento.
[reticências] cada vez mais era sentida a necessidade de um novo número para enfrentar os problemas colocados pelo desenvolvimento científico do Renascimento. Discutia-se muito sobre esse novo número. Mas ele era tão difícil de se enquadrar nos números já conhecidos que os matemáticos o chamavam de número absurdo.
Que número era esse?
Vamos voltar novamente à Antiguidade. [reticências]
Segundo os matemáticos chineses da Antiguidade, os números podiam ser entendidos como excessos ou faltas.
Na resolução de problemas, os chineses realizavam todos os cálculos em tabuleiros de cálculos. Para representar os excessos, utilizavam palitos vermelhos; para as faltas, palitos pretos.
Os matemáticos da Índia também trabalharam com esses “números estranhos”.
O grande matemático Brahmagupta, nascido em 598, dizia que os números podem ser tratados como pertences ou dívidas. [reticências]
Mas este tipo de número não conseguia ir além da ideia mais concreta e primitiva: ou era um palito preto ou uma dívida.
Sem símbolos próprios para tornar compreensíveis as operações, os “números absurdos” dos chineses e dos hindus em nenhum momento conseguiram atingir a condição de verdadeiros números.
O número negativo dos comerciantes
O desenvolvimento dos conceitos matemáticos sempre esteve estreitamente ligado ao desenvolvimento dos símbolos matemáticos. [reticências]
Voltamos com isso ao Renascimento.
Nessa época, os matemáticos cada vez mais sentiam a necessidade de um novo tipo de número [reticências].
Mas, para representar o novo tipo de número a ser criado, era preciso antes encontrar um símbolo que permitisse operar com esse novo número de modo prático e eficiente.
Veja como faziam os espertos comerciantes do Renascimento.
Suponha que um deles tivesse em seu armazém duas sacas de feijão de 10 quilogramas cada.
Se esse comerciante vendesse num dia 8 quilogramas de feijão, ele escrevia o número 8 com um tracinho na frente para não esquecer de que no saco faltavam 8 quilogramas de feijão.
Mas, se ele resolvesse despejar no outro saco os 2 quilogramas que restaram, escrevia o número 2 com dois tracinhos cruzados na frente, para se lembrar de que no saco havia 2 quilogramas de feijão a mais que a quantidade inicial.
Baseando-se na solução prática adotada pelos comerciantes, os matemáticos encontraram a melhor notação para expressar um novo tipo de número que não indicasse apenas as quantidades, mas também representasse o ganho ou a perda dessas quantidades: o número com sinal, positivo ou negativo.
Demorou muito tempo para que os números negativos fossem aceitos. A representação desses números na reta numérica tornou mais clara a sua compreensão, e isso permitiu que fossem aceitos com mais facilidade pelos matemáticos.
GUELLI, Oscar. A invenção dos números. São Paulo: Ática, 1992. página cinquenta e cinco a cinquenta e oito.

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Represente o trecho destacado em cada frase por um número positivo ou por um número negativo.
a) A temperatura em Moscou mediu 12 graus Célsius abaixo de zero.
b) No Campeonato Brasileiro de Futebol de 2021, o Chapecoense (Santa Catarina) marcou 27 gols e sofreu 67. Assim, seu saldo de gols foi de 40 gols negativos.
c) Maria levou um susto ao consultar seu extrato bancário e verificar o saldo devedor de R$ 420,00quatrocentos e vinte reais.
d) O avião está a uma medida de altitude de 800 métros acima do nível do mar.
e) O submarino atingiu a medida de altitude de 150 métros abaixo do nível do mar.
2. Leia o texto e represente as medidas das temperaturas nele mencionadas com números positivos ou negativos.
A Agência Nacional de Vigilância Sanitária (Anvisa) recomenda aos comerciantes de alimentos perecíveis que os itens resfriados sejam mantidos refrigerados preferencialmente com medida de temperatura até 5 graus Célsius acima de zero e os produtos congelados, até 15 graus Célsius abaixo de zero.
3. Em um edifício, o térreo é representado pelo zero, os andares abaixo do térreo são representados com números negativos, e os andares acima do térreo, com números positivos. Registre a marcação para o 2º subsolo e para o 4º andar.
4. Leia o que disse o navegador brasileiro sobre a medida de temperatura em um verão na Antártida e faça o que se pede.
Era verão na Antártida. “A temperatura média estava agradável, entre zero e 5 graus Célsius negativos”, conta Amyr Klink.
PEGORIN, Flavia; KUTNEY, Pedro. Caçando icebergs. Náutica, São Paulo, número 105, página 24, maio 1997.

a) Transcreva a frase dita por Amyr Klink usando a notação de número negativo.
b) No município em que você mora, que medida de temperatura média é considerada agradável? Que sensação você tem quando a medida de temperatura está muito acima dessa média?
c) Se a temperatura chegasse a medir ‒ 44 graus Célsius, que sensação você teria?
2 Números inteiros
Dizemos que os números naturais correspondem aos números inteiros positivos com o zero.
Recorde
Sequência dos números naturais: (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, reticências)
Agora observe a sequência dos números inteiros negativos.
(reticências, ‒ 6, ‒ 5, ‒ 4, ‒ 3, ‒ 2, ‒ 1)
Reunindo os números naturais (números inteiros positivos e o zero) e os números inteiros negativos, obtemos a sequência dos números inteiros. Observe.
(reticências, ‒ 6, ‒ 5, ‒ 4, ‒ 3, ‒ 2, ‒ 1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, reticências)
A sequência dos números inteiros é infinita nos dois sentidos. Nessa sequência, não há um número inteiro que seja o maior de todos nem um que seja o menor de todos. Para determinar um termo seguinte qualquer, basta adicionar 1 ao termo imediatamente anterior; para determinar um termo anterior a outro, basta subtrair 1 desse termo.

Para representar o conjunto dos números naturais, usamos o símbolo

:

= {0, 1, 2, 3, 4, reticências}
Para representar o conjunto dos números inteiros, usamos o símbolo

:

= {reticências, ‒ 4, ‒ 3, ‒ 2, ‒ 1, 0, 1, 2, 3, 4, reticências}
Podemos também representar os números inteiros em uma reta numérica. Observe.

Nessa reta, o zero é associado à origem (ponto óh), e a medida de distância entre os pontos que representam dois números inteiros consecutivos é sempre a mesma. À direita de óh, com um tracinho ou com uma bolinha, marcamos pontos correspondentes aos números inteiros positivos e, à esquerda, pontos correspondentes aos números inteiros negativos.

Na reta numérica, os números inteiros estão organizados de fórma crescente, da esquerda para a direita.
Na sequência dos números naturais, o antecessor de um número natural qualquer diferente de zero é o número que vem imediatamente antes dele, e o sucessor é o número que vem imediatamente depois. O mesmo ocorre com a sequência dos números inteiros.
Observe a reta numérica a seguir com a sequência dos números inteiros representada.

Nessa reta, verificamos que o sucessor de ‒ 4 é ‒ 3 e que o antecessor de ‒ 4 é ‒ 5.
Exemplos

Lembre-se: Escreva no caderno!
Observando a sequência dos números inteiros ou a representação desses números na reta numérica, também podemos comparar números inteiros. Quanto mais à direita um número estiver, na sequência ou na reta, maior ele será.
reticências, ‒ 9, ‒ 8, ‒ 7, ‒ 6, ‒ 5, ‒ 4, ‒ 3, ‒ 2, ‒ 1, 0, + 1, + 2, + 3, + 4, + 5, + 6, + 7, + 8, + 9, + 10, + 11, + 12, reticências

Assim, percebemos, por exemplo, que:
• + 7 é maior que 0 (representamos assim: + 7 > 0 e lemos: “mais sete é maior que zero”);
• ‒ 5 é menor que ‒ 1 (representamos assim: ‒ 5 < ‒ 1 e lemos: “menos cinco é menor que menos um”);
• ‒ 9 é menor que + 3 (representamos assim: ‒ 9 < + 3 e lemos: “menos nove é menor que mais três”);
• 0 é maior que ‒ 4 (representamos assim: 0 > ‒ 4 e lemos: “zero é maior que menos quatro”).
Para pensar
Analise o que a professora Paula está dizendo.

Explique por que Paula está certa.

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Copie no caderno a reta numérica a seguir, complete-a e responda às questões.

a) Qual é o antecessor de ‒1?
b) E o sucessor de ‒1?
•


Elabore uma pergunta semelhante a essas duas. Em seguida, troque de pergunta com um colega e resolva a questão formulada por ele. Depois de resolvidas, destroquem-nas para a correção.
2. Considerando a sequência dos números inteiros, responda às questões no caderno.
a) Qual é o antecessor de ‒15?
b) Qual é o sucessor de ‒10?
c) Qual é o antecessor de 50?
d) Qual é o sucessor de 19?
3. Determine o sucessor e o antecessor dos números inteiros a seguir.
a) 99
b) + 999
c) ‒.1000
d) .1000
e) ‒ .9009
f) ‒.10000
4. Em uma sorveteria, o armazenamento dos sorvetes é feito em freezers com medida de temperatura de ‒18 graus Célsius. Qualquer temperatura acima dessa medida é inadequada e pode alterar a qualidade do produto.

a) Das medidas de temperatura a seguir, quais são adequadas e quais são inadequadas para o armazenamento de sorvetes nessa empresa?
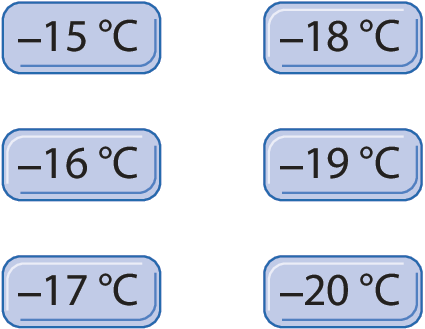
b) Por que os sorvetes precisam ser mantidos a essa medida de temperatura? Faça uma pesquisa e registre a resposta.
5. Uma universidade comprou dois freezers para o laboratório de pesquisas ambientais. Um pode armazenar materiais a medidas de temperatura de até ‒ 86 graus Célsius, e o outro, de até ‒196 graus Célsius.
a) Um funcionário desse laboratório precisa armazenar dois materiais em medidas de temperatura diferentes. Um deles deve ser armazenado a ‒100 graus Célsius, e o outro, a ‒ 80 graus Célsius. Como esse funcionário poderá armazenar esses materiais?
b) Escreva cinco medidas de temperatura maiores e cinco menores que ‒ 86 graus Célsius.
c) Escreva cinco medidas de temperatura que estejam entre ‒196 graus Célsius e ‒ 86 graus Célsius.
6. Observe os termômetros a seguir e escreva os números, positivos ou negativos, que representam as medidas de temperatura registradas por eles. Em seguida, determine o antecessor e o sucessor de cada número na sequência dos números inteiros.
a)
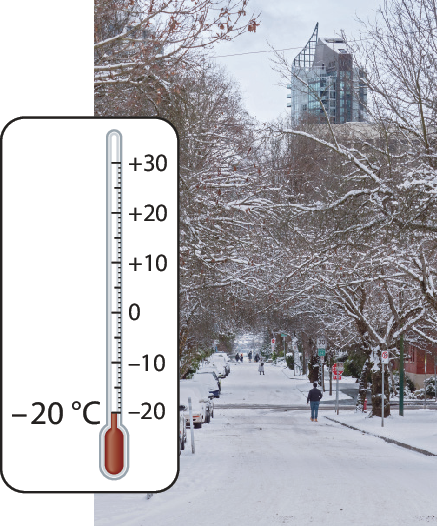
b)

c)

d)
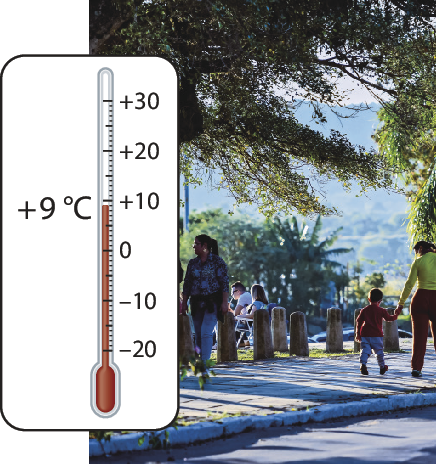
7. Leia o texto e observe os saldos de gols dos times no campeonato de futebol de salão de uma escola.
O 6º ano tem uma defesa excelente; foi o time que sofreu menos gols e obteve um saldo positivo de 13 gols. Já o 7º ano teve o melhor ataque, mas sofreu 10 gols a mais do que marcou. O 8º e o 9º ano tiveram, respectivamente, ‒ 4 e + 1 de saldo de gols.

• Agora, organize os dados em um quadro, por ordem decrescente de saldo de gols.
3 Módulo, ou valor absoluto, de um número inteiro
Podemos determinar, na reta numérica, a medida de distância entre qualquer ponto e a origem O. Observe.

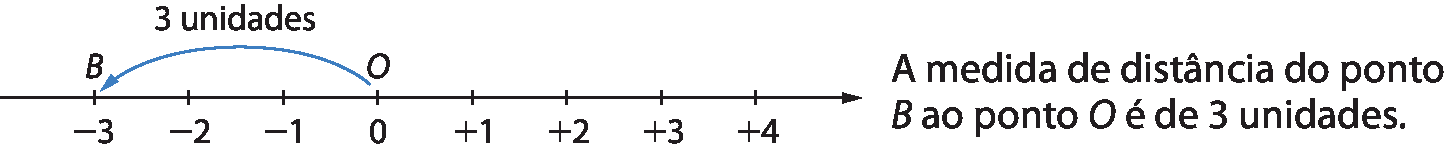
A medida de distância de um ponto da reta numérica à origem é chamada valor absoluto, ou módulo, do número associado a esse ponto.
Assim, valor absoluto, ou módulo, do número + 4 é 4 (medida de distância do ponto a à origem). Da mesma maneira, o módulo de ‒ 3 é 3 (medida de distância do ponto B à origem).
Indicamos o módulo de um número colocando esse número entre duas barras verticais paralelas. Por exemplo: o módulo de ‒ 3 é representado por ∣ ‒ 3∣.
Exemplos
• ∣+ 5∣ = 5
• ∣7∣ = 7
• ∣ ‒ 18∣ = 18
• ∣0∣ = 0
Números opostos ou simétricos
Observe a reta numérica a seguir.

Os pontos á linha e a estão associados, respectivamente, aos números inteiros ‒5 e + 5. A medida de distância do ponto á' até a origem é de 5 unidades, assim como a medida de distância do ponto a até a origem é de 5 unidades. Os pontos á linha e a estão a uma mesma medida de distância da origem, porém situados em lados opostos da reta numérica (em relação ao zero). Por isso, ‒5 e + 5 são chamados números simétricos ou números opostos.
Exemplos
• + 7 e ‒ 7 são números opostos ou simétricos.
• ‒ 4 é o oposto de 4, e 4 é o oposto de ‒ 4.

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Determine:
a) o simétrico de ‒ 23;
b) o oposto de 16;
c) o módulo do simétrico de ‒ 4;
d) o oposto do oposto de ‒ 3.
2. Copie o quadro a seguir no caderno e, depois, complete-o.

|
Número |
Oposto |
Valor absoluto |
|---|---|---|
|
7 |
||
|
23 |
||
|
50 |
• Agora, responda: existe uma única maneira de preencher o quadro? Justifique sua resposta.
3. Em nosso planeta, há muita diversidade de vegetação, de clima e de altitude.
Observe a seguir a descrição de três ambientes terrestres diferentes e, depois, responda às questões.
a) O Deserto do Atacama, no norte do Chile, é o mais seco do planeta. Nele, ocorrem grandes variações de temperatura. Em um período de 24 horas, a medida da temperatura pode cair de 40 graus Célsius, durante o dia, para ‒ 2 graus Célsius à noite! Qual dessas medidas de temperatura é a mais alta?
b) Na Antártida, no inverno, a medida da temperatura pode variar de ‒ 20 graus Célsius a ‒ 55 graus Célsius. Qual dessas medidas de temperatura é a menor?
c) A maior parte da Floresta Amazônica está localizada em território brasileiro. Seu clima é úmido e, durante o ano, não há muita variação das medidas de temperatura. As medidas de temperatura médias anuais oscilam entre 24 graus Célsius e 26 graus Célsius. Qual dessas medidas de temperatura é a mais baixa?
4. Faça o que se pede.
a) Construa no caderno uma reta numérica e localize nela os seguintes números: + 10, ‒ 4, ‒ 5, 8, ‒ 2 e 3.
b) Indique o simétrico de cada um dos números do item a.
c) Considerando apenas os números do item a, indique aqueles que têm módulo menor que 4.
5. Observe os saldos das contas-correntes de Paulo, Joana e Larissa.


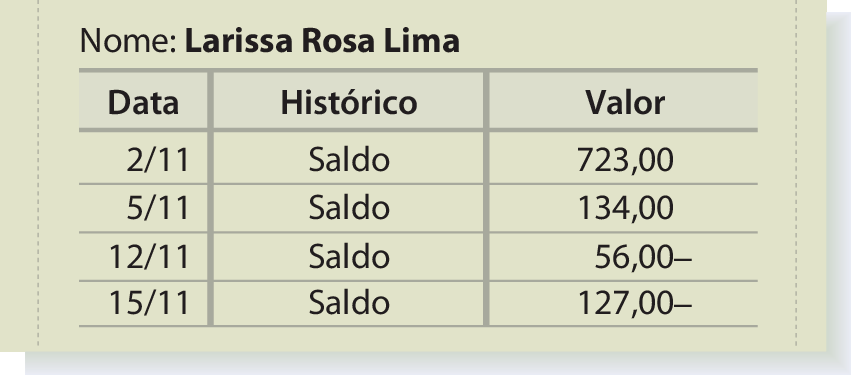
• Agora, responda às questões.
a) Os saldos das contas de Paulo, Joana e Larissa estavam positivos ou negativos em 15/11?
b) Em qual dia o saldo de cada conta estava menor? E em qual dia estava maior?
c) Como você fez para comparar os saldos de cada conta?
6. No caderno, ordene os números a seguir do menor para o maior.
‒ 5, + 3, ‒ 8, + 4, ‒ 2, + 7, ‒ 1, ‒ 10, + 11
• Agora, escreva o oposto de cada número e agrupe-os em ordem decrescente.
7. Observe o termômetro a seguir.
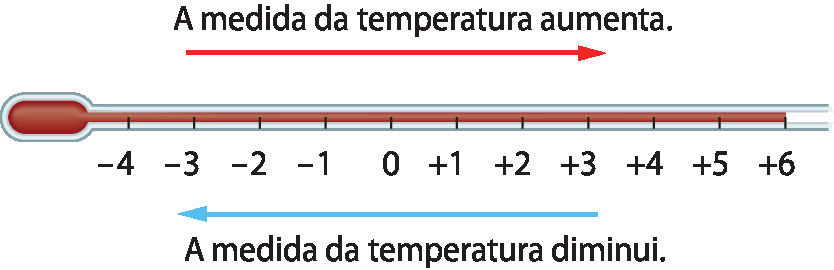
• O termômetro indicou ‒ 2 graus Célsius, depois + 6 graus Célsius e, por último, ‒ 4 graus Célsius. Escreva essas medidas de temperatura em ordem crescente.
8. Ricardo comprou um pacote de pães de queijo congelados para o lanche da tarde. Leia no quadro as instruções que havia na embalagem e, em seguida, responda às questões.
CONSERVAÇÃO
Conservar em medida de temperatura entre ‒10 graus Célsius e ‒18 graus Célsius.
PREPARO
1. Preaqueça o forno à medida de temperatura de 180 graus Célsius por 10 minutos.
2. Retire os pães de queijo da embalagem ainda congelados. Coloque‑os em uma assadeira, deixando uma distância entre eles cuja medida seja de, no mínimo, 2 centímetros de comprimento.
3. Asse-os por cêrca de 30 minutos ou até que fiquem dourados.
a) Qual é a menor medida de temperatura em que os pães de queijo devem ser conservados?
b) E a medida da maior temperatura?
c) Qual será, aproximadamente, o tempo total de preparo dos pães de queijo?
4 Adição com números inteiros
A adição com números inteiros pode ser observada em diversas situações. Acompanhe alguns exemplos.
Situação 1
Em um edifício, o 1º e o 2º subsolos são indicados por números negativos, o térreo é indicado pelo zero, e os andares acima do térreo, por números positivos. Um elevador estava parado no 2º subsolo e, em seguida, subiu 3 andares. Em que andar o elevador parou?
Se analisarmos o andar em que o elevador estava e por quais passou antes de parar, constatamos que ele partiu do ‒ 2, subiu 1 andar e chegou ao ‒ 1. Subindo mais 1 andar, chegou ao térreo e, subindo mais 1 (3 andares no total), chegou ao 1º andar.
Logo, o elevador parou no 1º andar.

Podemos representar essa situação por meio de uma adição:
(‒ 2) + (+ 3) = + 1 ou, de maneira simplificada, ‒ 2 + 3 = 1
Situação 2
Um mergulhador estava a 6 métros abaixo do nível do mar. Sabendo que poderia observar animais muito interessantes a 7 métros abaixo de onde estava, resolveu descer até lá. A qual medida de altitude, em metro, abaixo do nível do mar o mergulhador se encontrava após a descida?
Vamos representar a situação na reta numérica.
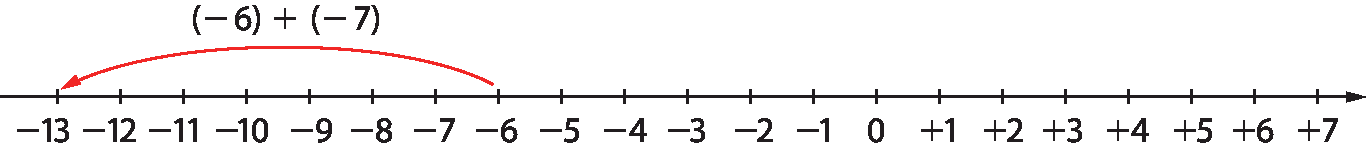
Partindo de ‒ 6, “andamos” 7 unidades para a esquerda na reta numérica e chegamos ao ponto correspondente ao número ‒13.
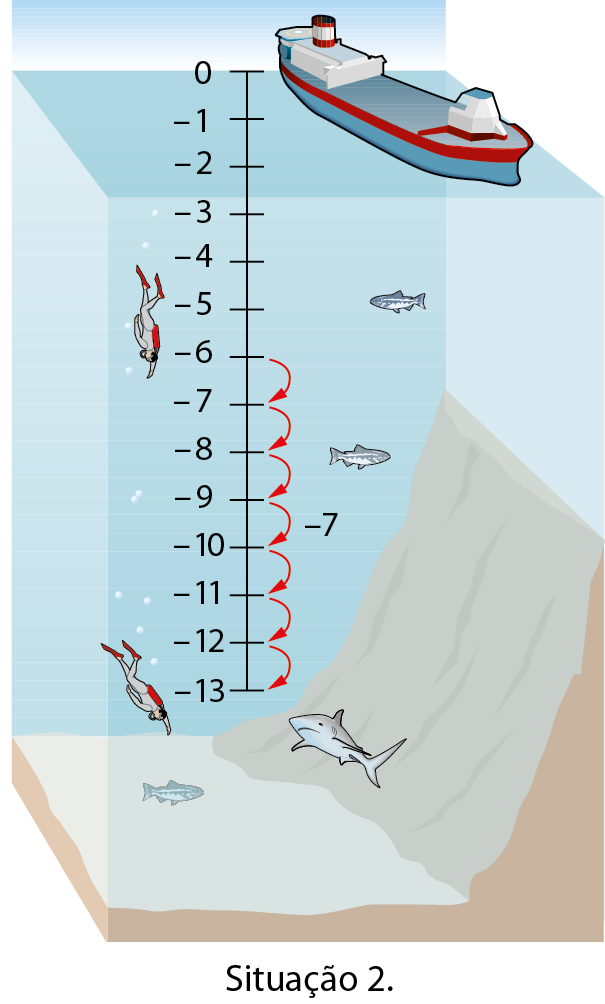
Representando essa situação por meio de uma adição, temos:
(‒ 6) + (‒ 7) = ‒ 13 ou ‒ 6 ‒ 7 = ‒ 13
Portanto, após a descida, o mergulhador se encontrava a 13 métros abaixo do nível do mar.
Situação 3
A temperatura em certa cidade media + 3 graus Célsius e sofreu uma queda de 4 graus Célsius na madrugada. Que medida de temperatura foi registrada nessa madrugada?
Partindo de + 3 na reta numérica, “andamos” 4 unidades para a esquerda e paramos no ponto correspondente ao número ‒1.

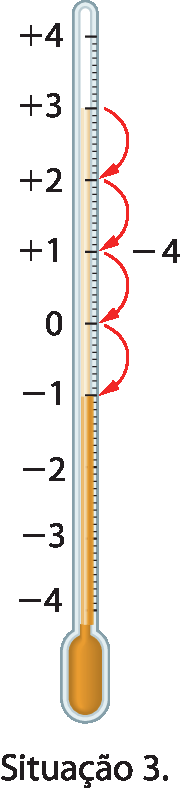
Representando essa situação por meio de uma adição, temos:
(+ 3) + (‒ 4) = ‒ 1 ou 3 ‒ 4 = ‒ 1
Então, a medida de temperatura foi de 1 grau Célsius abaixo de zero (‒1 grau Célsius) nessa madrugada.
Acompanhe agora como Diego e Mayara efetuaram as adições (‒7) + (+ 3) e (‒7) + (‒3).




Para analisar

Reúna-se com três colegas e façam o que se pede.
Cada um vai escrever, em uma folha avulsa, quatro adições com números inteiros: uma com dois números positivos; uma com dois números negativos; uma com um número positivo e outro negativo; e outra em que um dos números seja zero. Efetuem as adições e coloquem-nas em um local visível para que todos possam analisá-las. Depois, respondam às questões.
a) Os resultados das adições de números positivos foram positivos ou negativos?
b) E os resultados das adições de números negativos?
c) Os resultados das adições em que uma das parcelas é zero foram positivos ou negativos?
d) E os resultados das adições de um número positivo e um negativo?

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Calcule.
a) (+ 15) + (+ 9)
b) (‒ 22) + (+ 31)
c) (‒ 13) + (‒ 15)
d) (+ 29) + (‒ 41)
e) (‒ 36) + (+ 17)
f) + 5 + 7
g) ‒ 12 ‒ 29
h) ‒ 57 + 17
i) + 89 ‒ 21
j) ‒ 100 ‒ 10
2. Observe os movimentos da conta-corrente de Ana e responda às questões.

a) Qual era o saldo da conta-corrente de Ana ao final dos dias 11, 12 e 13?
b) Qual foi o total depositado por Ana?
3. Represente os valores a seguir com números inteiros e efetue as adições.
a) No dia 3, havia R$ 120,00cento e vinte reais em minha conta-corrente. No dia seguinte, depositei nela R$ 85,00oitenta e cinco reais. Quanto tenho agora?
b) O saldo da conta-corrente de Eva estava negativo em 95 reais. Depois de pagar uma dívida de 175 reais, que saldo Eva tem na conta-corrente?
4. Responda às questões.
a) A soma de dois números inteiros de mesmo sinal é 21. Qual é o sinal desses números?
b) A soma de dois números inteiros de mesmo sinal é ‒ 10. Qual é o sinal desses números?
c) A soma de dois números inteiros de sinais diferentes é 13. Qual é o sinal do número de maior módulo?
d) A soma de dois números inteiros de sinais diferentes é ‒ 5. Qual é o sinal do número de maior módulo?
5. Descubra a parcela desconhecida.
a) (‒12) + ◼ = ‒12
b) (+19) + ◼ = +12
c) ◼ + (‒10) = 0
d) (+ 24) + ◼ = 0
e) ◼ + (‒ 6) = ‒ 4
f) (‒ 16) + ◼ = + 9
6. Faça o que se pede.
a) Represente um prejuízo de 12 com um número inteiro.
b) Represente um lucro de 10 com um número inteiro.
c) Calcule a soma desses números inteiros.
7. Indique a operação e, a seguir, resolva-a.
a) Lucro de 14 e prejuízo de 7.
b) Prejuízo de 20 e prejuízo de 13.
c) Prejuízo de 16 e lucro de 42.
d) Lucro de 25 e prejuízo de 11.
e) Prejuízo de 29 e lucro de 47.
8. Nas operações a seguir, aêbê representam números inteiros. Encontre um possível valor para a e b em cada caso.
a) a + b = 21
b) a + b = ‒ 4
c) a + b = ‒ 1
d) a + b = 0
e) a + b = ‒ 7
f) a + b = 19
9. O termômetro eletrônico da câmara fria ilustrada estava com defeito e, por isso, sempre registrava uma medida de 4 graus acima da temperatura real.

a) Qual era a medida de temperatura real nessa câmara?
b) Qual será a medida de temperatura real se o termômetro registrar ‒ 2 graus Célsius?
Propriedades da adição
Acompanhe a situação a seguir.
Mauro é dono de uma papelaria. Ao final de cada período de quatro meses, ele faz um pequeno balanço para saber se está obtendo lucro ou prejuízo. Em janeiro, a papelaria teve lucro de R$ 12.500,00doze mil quinhentos reais, decorrente das vendas de material escolar com a volta às aulas. Em fevereiro, teve prejuízo de R$ 9.870,00nove mil oitocentos e setenta reais; em março, prejuízo de R$ 435,00quatrocentos e trinta e cinco reais; e, em abril, lucro de R$ 240,00duzentos e quarenta reais.
Mauro fez o balanço quadrimestral de duas maneiras. Observe.


Portanto, no período dos quatro meses, a papelaria teve um saldo positivo de R$ 2.435,00dois mil quatrocentos e trinta e cinco reais.
Para realizar os cálculos da segunda maneira, Mauro usou propriedades da adição de números inteiros.
Para a adição dos números naturais, são válidas a propriedade comutativa, a propriedade associativa e a existência do elemento neutro. Essas propriedades, além da existência do elemento oposto, são válidas também para a adição de números inteiros.
Propriedade comutativa
A ordem das parcelas não altera a soma. Assim, se aêbê são números inteiros, a + b = b + a.
Por exemplo:
(+ 4) + (‒ 5) = ‒1 e (‒ 5) + (+ 4) = ‒1
(+ 4) + (‒ 5) = (‒ 5) + (+ 4)
Propriedade associativa
Na adição, podemos associar as parcelas de diferentes maneiras e obter o mesmo resultado. Assim, se ei, b e c são números inteiros, (ei + b) + c = ei + (b + c).
Por exemplo:
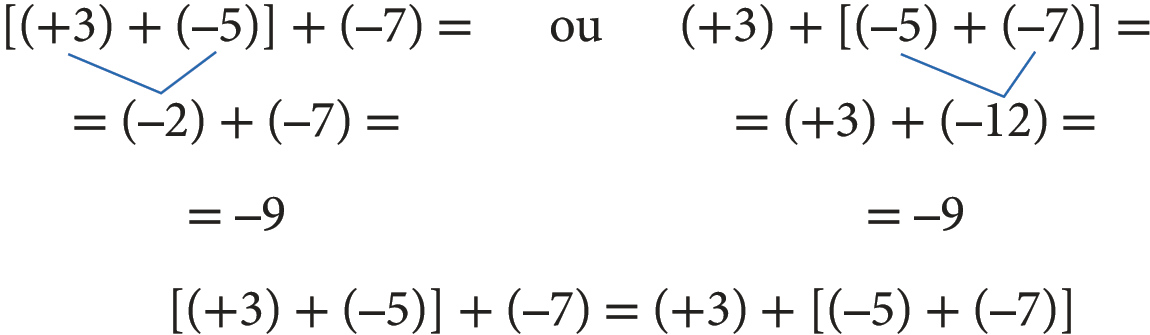
Existência do elemento neutro
O elemento neutro da adição é o zero, que, adicionado a qualquer número inteiro, resulta no próprio número. Assim, se a é um número inteiro, a + 0 = 0 + a = a.
Por exemplo:
(‒ 8) + 0 = ‒ 8 ou 0 + (‒ 8) = ‒ 8
Existência do elemento oposto
Qualquer número inteiro tem um oposto, que, adicionado a ele, resulta no elemento neutro. Assim, se a é um número inteiro, existe ‒ a, que é o oposto de a, tal que a + (‒ a) = 0.
Por exemplo:
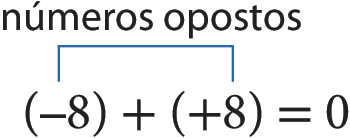
Para calcular
Calcule o valor de:
(‒ 500) + .2547 + 294 + (‒ .2547) + (‒ 394)
a) Você usou alguma das propriedades da adição de números inteiros? Se usou, qual(is)?
b)

Compare o modo como você realizou os cálculos com o de um colega e responda: vocês efetuaram as adições da mesma maneira? O resultado obtido foi o mesmo? Em qual dos modos as contas efetuadas ficaram mais simples?

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Andressa tem uma sorveteria. No início do mês, ela gastou R$ 1.100,00mil cem reais em ingredientes para a produção de sorvetes, recebeu R$ 3.500,00três mil quinhentos reais com as vendas e, no final do mês, gastou R$ 750,00setecentos e cinquenta reais com a manutenção de equipamentos.
a) Qual foi o saldo de Andressa no final do mês?
b) Ela obteve lucro ou prejuízo?

2. Efetue as adições a seguir.
a) (+ 4 ‒ 7) + (‒ 8)
b) (‒ 12) + (‒ 5 ‒ 1 + 6)
c) (‒21 + 0) + (+12 + 7) + (‒ 4 + 2)
d) (‒.1004 + 258) + (‒789)
e) (‒790 ‒ 340) + (‒130 + .1024)
f) (+ 899 ‒ 111) + (‒537 ‒ 321)
3. Rafael pediu emprestados à sua irmã R$ 30,00trinta reais para comprar uma camiseta. Depois, pediu mais R$ 40,00quarenta reais para comprar uma calça.
a) Quanto Rafael está devendo à irmã?
b) Utilizando a ideia de número negativo, represente a situação por uma expressão numérica.
4. Sílvio saiu da Vila Charmosa e está indo em direção à Vila Esperança. Neste momento, ele está no quilômetro 45 da rodovia; vai fazer a primeira parada daqui a 29 quilômetros e de lá percorrerá mais 147 quilômetros até a segunda parada.
a) Em que quilômetro da rodovia Sílvio fará a primeira parada?
b) E em que quilômetro ele fará a segunda parada?
5. Kelly e Alice fizeram uma brincadeira. Cada uma escreveu uma expressão em um pedaço de papel. Em seguida, elas dobraram os papéis, e cada uma escolheu um. Venceria quem tirasse a expressão com o maior resultado. Se Kelly tirou a expressão [(‒ .4547) + (.4547) ‒ 1] e Alice, (1 + 0), quem venceu?
6. Observe o extrato bancário de Mário.

|
Data |
Histórico |
Valor |
|---|---|---|
|
12/5 |
Saldo |
800,00 |
|
13/5 |
Cheque |
−200,00 |
|
Cheque |
−100,00 |
|
|
17/5 |
Saldo |
|
|
Depósito |
450,00 |
|
|
22/5 |
Saldo |
|
|
1/6 |
Cheque |
−1.000,00 |
|
2/6 |
Saldo |
|
|
5/6 |
Depósito |
900,00 |
|
6/6 |
Saldo |
• Agora, copie-o no caderno substituindo cada ▬ pelo valor correspondente. Depois, responda às questões.
a) Em que data a conta-corrente de Mário ficou com o maior saldo?
b) Em que data ela ficou com saldo negativo?
5 Subtração com números inteiros
No Campeonato Brasileiro de Futebol de 2021, o Palmeiras (São Paulo) obteve saldo de gols igual a 15, enquanto o Juventude (Rio Grande do Sul) obteve saldo de ‒ 8. Qual foi a diferença entre os saldos de gols do Palmeiras e do Juventude?
Localizando os números (+15) e (‒ 8) em uma reta numérica, temos:

Observando a localização dos pontos correspondentes a esses números na reta, podemos ver que a diferença entre (+15) e (‒ 8), nessa ordem, é de 23 unidades.
Também podemos encontrar a diferença entre os saldos de gols calculando o valor da expressão:
(+15) ‒ (‒ 8)
Observe que ‒ (‒ 8) é o oposto do número ‒ 8, ou seja, é igual a + 8.
Então, calculamos: (+15) ‒ (‒ 8) = +15 + 8 = + 23
Assim, verificamos que a diferença entre os saldos de gols do Palmeiras e do Juventude, no final do campeonato, foi de 23 gols.
Observe outras subtrações com números inteiros.


ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Fabrício trabalha em um frigorífico. Para manter peças de carne bovina congeladas, a medida de temperatura de uma das câmaras frigoríficas é ‒ 35 graus Célsius. Fabrício tirou uma das peças para descongelar, na geladeira, a uma medida de temperatura de 10 graus Célsius. Que variação de medida de temperatura essa peça de carne sofreu?
2. Efetue as subtrações a seguir.
a) (+17) ‒ (+ 9)
b) (‒15) ‒ (‒ 7)
c) (‒23) ‒ (‒ 4)
d) (‒ 42) ‒ (‒ 7) ‒ (‒ 8)
e) (+ 5) ‒ (‒ 21) ‒ (+ 9)
f) (‒ 71) ‒ 0
3. Encontre o valor do ◼ em cada expressão.
a) (‒14) ‒ (‒12) = ◼
b) (+ 9) ‒ (◼) = ‒ 7
c) (‒19) ‒ (◼) = ‒17
d) ◼ ‒ (‒21) = + 12
4. O quadro a seguir apresenta a medida da temperatura no interior de alguns eletrodomésticos quando em funcionamento.
|
Eletrodoméstico |
Medida da temperatura no interior (em °C) |
|---|---|
|
Forno a gás |
de +180 a +300 |
|
Refrigerador |
de +2 a +10 |
|
Freezer |
−18 |
• Em que eletrodoméstico registra-se:
a) a maior medida de temperatura?
b) a menor medida de temperatura?
c) a maior variação de medida de temperatura?
5. Considere as informações e responda.

a) Arquimedes foi um dos mais importantes matemáticos da Antiguidade. Ele nasceu no ano 287 antes de Cristo e viveu 75 anos. Em que ano Arquimedes morreu?

b) Pitágoras viveu 74 anos. Se ele morreu em 497 antes de Cristo, em que ano nasceu?

c) O primeiro matemático da Antiguidade a medir a circunferência da Terra foi Eratóstenes. Ele nasceu no ano 276 antes de Cristo e morreu em 196 antes de Cristo Quantos anos Eratóstenes viveu?
6. Em um município da Região Sul do Brasil, em um dia de inverno, às 6 horas da manhã o termômetro mediu 1 grau Célsius. Às 10 horas, a medida de temperatura havia subido 4 graus Célsius e, às 13 horas, mais 3 graus Célsius. Ao anoitecer, a medida de temperatura baixou 5 graus Célsius e, às vinte e duas horas, mais 4 graus Célsius, permanecendo a mesma até a meia-noite.
Que medida de temperatura marcava o termômetro à meia-noite?
7. Copie o quadrado mágico no caderno e complete-o, sabendo que a soma dos números de cada linha, coluna ou diagonal seja sempre 9.
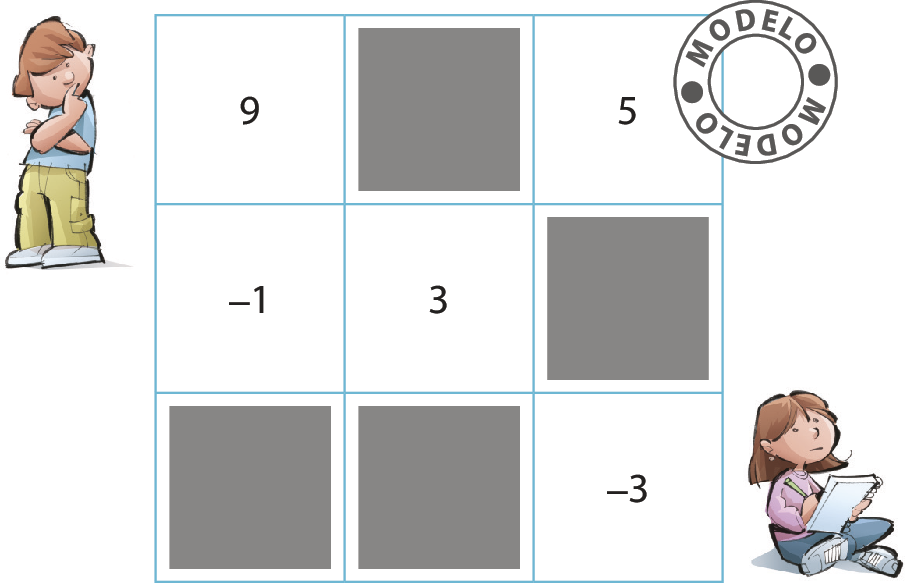
8. Copie a pilha de tijolos e complete-a seguindo o padrão indicado.


Trabalho em equipe
FAÇA AS ATIVIDADES NO CADERNO
Atenção! Cuidado ao usar a tesoura e o alfinete.
Jogo de tabuleiro
Que tal brincar um pouco para reforçar o que aprendemos até aqui? Reúna-se com alguns colegas para construir – usando cartolina ou outro papel encorpado – um tabuleiro igual ao do modelo a seguir.

JUSTIFICATIVA
Jogos de tabuleiro desse tipo, além de incentivar a socialização, propiciam o uso dos conceitos matemáticos de maneira divertida.
OBJETIVO
Estimular o cálculo mental com números inteiros.
APRESENTAÇÃO
Jogo em grupo.
MATERIAL COMPLEMENTAR
Com o mesmo tipo de papel com que fizeram o tabuleiro, elaborem e recortem as peças que usarão na hora de jogar.
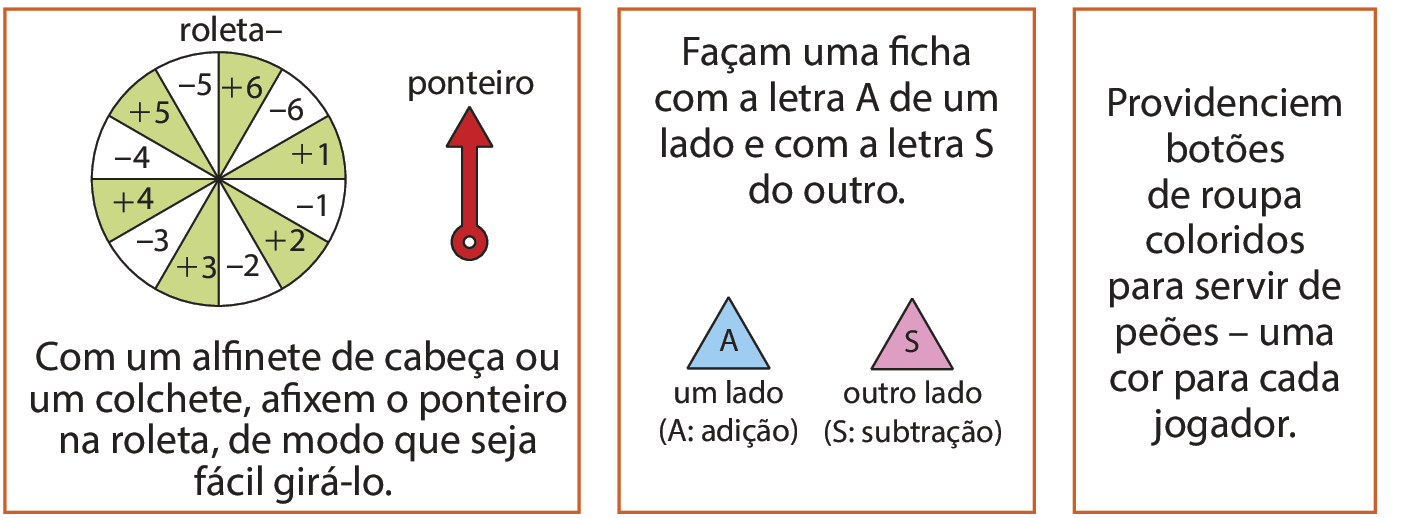
REGRAS DO JOGO
• Com os peões posicionados no zero do tabuleiro, decidam quem começa a jogar. Cada jogador, na sua vez, deve girar a roleta.
• Na sua vez de jogar, jogue a ficha. Se der:
–
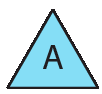
, adicione o número da roleta ao número da casa em que está e mova seu peão até a casa que tem o resultado da adição;
–
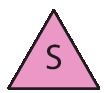
, subtraia o número da roleta do número da casa em que está e mova seu peão até a casa que tem o resultado da subtração.
• Se o peão cair em uma casa com alguma instrução, execute-a antes de passar a vez a outro jogador.
Ganhará o jogo aquele que obtiver, antes dos adversários, um número maior que +12 ou menor que ‒12.
QUESTÕES PARA PENSAR EM GRUPO
1. A instrução “vá para o oposto deste número” traz vantagem ou desvantagem para o jogador?
2. Se um jogador estiver na casa com o número ‒ 9 e tirar

, que número ele deverá tirar na roleta para ganhar o jogo? E se ele tirar

?
6 Adição algébrica
Como vimos, a subtração com dois números inteiros equivale a uma adição do primeiro número com o oposto do segundo. Por isso, a adição e a subtração com números inteiros são consideradas apenas uma operação: a adição algébrica.
A ideia de adição algébrica ajuda a simplificar uma expressão numérica que apresenta parênteses e os sinais “+” e “‒” das operações. Observe o exemplo a seguir.

Agora, basta calcular o valor da expressão do modo que preferir. Observe duas maneiras.
Lembre-se: Escreva no caderno!
1ª) Efetuando as operações na ordem em que aparecem:
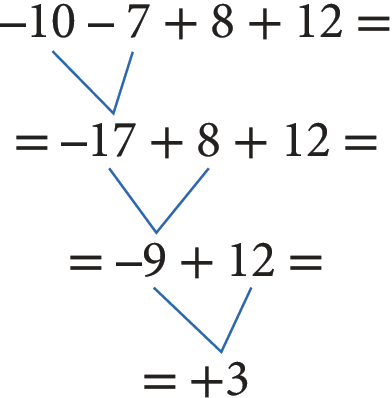
2ª) Agrupando os valores de modo conveniente:
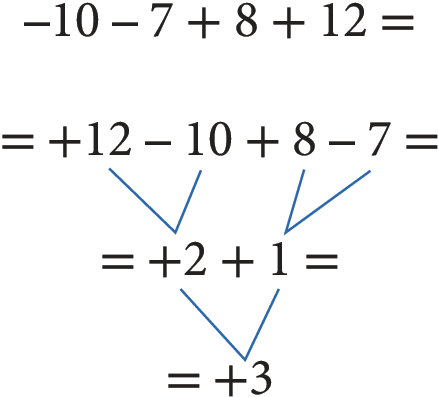
Nas expressões que apresentam adições algébricas agrupadas pelos sinais ( ), [ ] e { }, deve-se primeiro resolver as adições algébricas que estão no interior dos parênteses, depois as que estão no interior dos colchetes e, por último, as que estão no interior das chaves.
Para calcular
Calcule o valor da expressão anterior de modo diferente dos apresentados.
Exemplo


ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Calcule o valor das expressões numéricas.
a) 5 + (7 ‒ 2) ‒ (4 + 3)
b) ‒15 + [(‒12) ‒ (+ 4)] ‒ (‒7 ‒ 4)
c) 45 ‒ {51 + [(‒ 3) ‒ (+ 8)]}
d) (4 ‒ 8) ‒ {[7 + (+2 ‒ 4) ‒ (‒5 ‒ 13)] ‒ 1}
2. Encontre o erro no cálculo da expressão numérica.
(+12) + (+ 5) + (‒17) ‒ (‒ 4) =
= (+12) + (‒12) ‒ 4 =
= 0 ‒ 4 =
= ‒4
3.

Leia a explicação e faça o que se pede.
A calculadora pode ser usada para realizar operações com números inteiros.

Observe como representar e realizar operações com números inteiros usando a tecla

da calculadora.
Para representar ‒ 7, por exemplo, fazemos:

Alguns modelos apresentam:

Outros mostram na tela:

ou

Usando a calculadora, também podemos calcular o valor de expressões numéricas com números inteiros.
Para calcular ‒ 8 + (‒ 3) ‒ (‒ 6), por exemplo, digitamos:
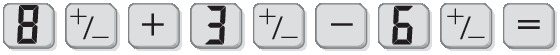
E obtemos:

a) Agora, use uma calculadora para determinar:
• 2 ‒ (+ 9) + (‒ 7)
• ‒ 46 + (‒ 53) ‒ (+ 76)
• 129 + (‒134) ‒ (‒ 289)
b) Como você calcularia a expressão numérica
‒ {16 + [‒ 27 ‒ (4 ‒ 9)]} usando a calculadora?
4.

Elabore as expressões numéricas pedidas.
a) Uma expressão numérica com 5 números inteiros cujo resultado seja zero.
b) Uma expressão numérica com 5 números e com 2 pares de colchetes.
5. Construa no caderno um quadrado mágico composto de três linhas e três colunas, como mostra a ilustração a seguir.

Depois, com os números inteiros de ‒ 4 a + 4, preencha-o de fórma que a soma dos números de cada linha, coluna ou diagonal seja zero.
6.


Elabore um problema que possa ser resolvido com adições algébricas. Dê seu problema para um colega resolver e resolva o problema criado por ele.

Educação Financeira
FAÇA AS ATIVIDADES NO CADERNO

Para onde foi meu dinheiro?
Ao pagar por uma compra, você já percebeu que tinha menos dinheiro do que imaginava? Por que isso aconteceu? Você já passou por uma situação parecida com a apresentada a seguir?

O que você faria?
O que você faria se estivesse no lugar da menina da situação anterior? Analise as alternativas a seguir e escolha uma. Você pode também criar uma resposta diferente.
a) Pediria ao amigo R$ 3,00três reais emprestados e compraria o sorvete.
b) Compraria o sorvete usando um cartão de crédito, caso tivesse um.
c) Deixaria de comprar o sorvete por não ter dinheiro suficiente.
d) Perguntaria ao sorveteiro se poderia tomar o sorvete e voltar mais tarde para pagar.
Calcule
Para evitar aquela sensação de ficar se perguntando para onde foi o dinheiro, algumas pessoas organizam seu orçamento em uma planilha eletrônica.

Jaqueline aprendeu que deve controlar seus gastos e se empenha em praticar o ensinamento recebido. Jaqueline registrou suas despesas do mês de março de 2022 em uma planilha eletrônica. Observe, a seguir, o detalhe dos registros que ela fez.
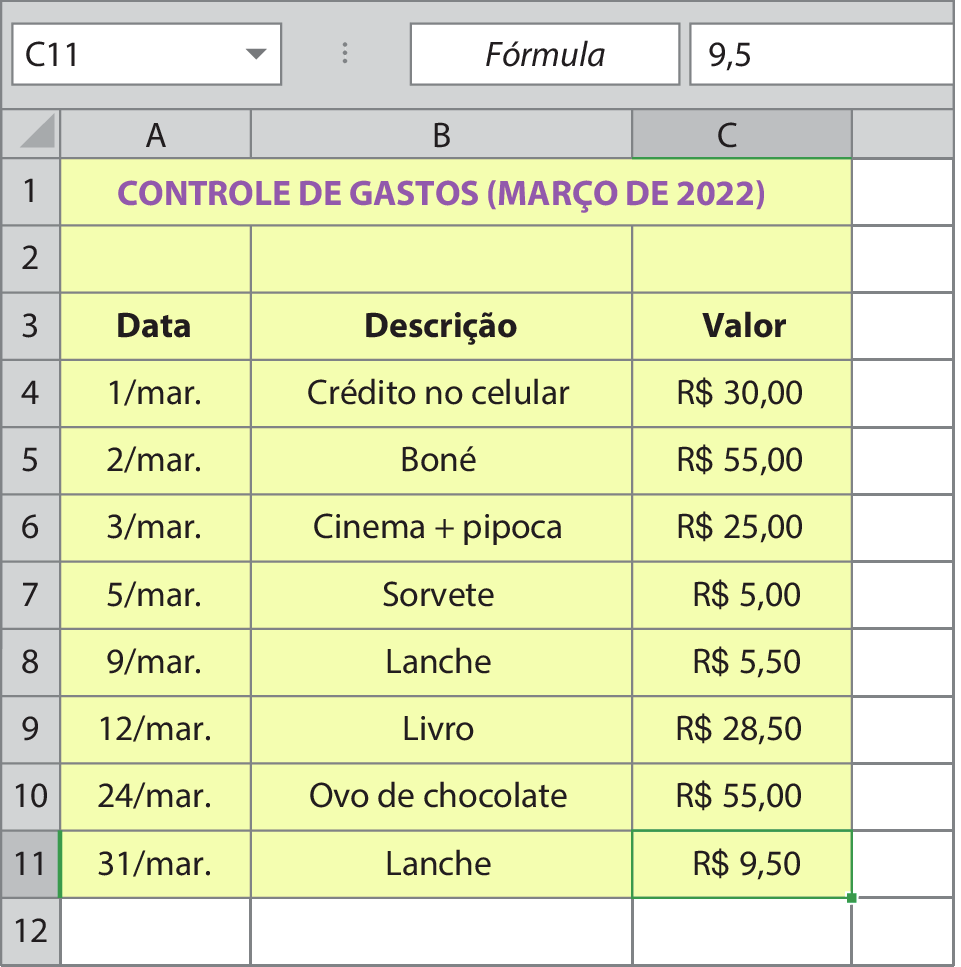
Se Jaqueline tinha R$ 250,00duzentos e cinquenta reais no início do mês, ela conseguiu economizar parte desse dinheiro? Caso tenha conseguido, o que você acha que ela deveria fazer com o dinheiro que sobrou?
Reflita

Reúna-se com alguns colegas e reflitam sobre as questões a seguir.
a) É importante controlar as despesas, mesmo as pequenas? Por quê?
b) Você tem algum sonho de consumo? Se sim, qual ou quais? Como você se planeja para realizar esse ou esses sonho(s)?
7 Multiplicação com números inteiros
Em uma caminhada matinal, nada como ouvir uma boa música.

Para isso, Clara comprou um smartwatch, que pagará em 4 prestações de R$ 65,00sessenta e cinco reais. Qual é o valor da dívida de Clara?
Para calcular o valor da dívida, podemos escrever:
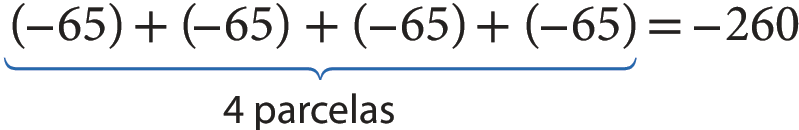
Podemos também fazer uma multiplicação:
4 ⋅ (‒ 65) = ‒ 260
Portanto, a dívida de Clara é de R$ 260,00duzentos e sessenta reais.
Esse problema foi resolvido por meio de uma multiplicação de dois números inteiros (4 e ‒ 65).
Agora, vamos analisar a multiplicação de dois números inteiros nos exemplos a seguir.
• Qual é o valor de (+ 2) ⋅ (+ 7)?
Uma das ideias da multiplicação é a adição de parcelas iguais.
Então:
(+ 2) ⋅ (+ 7) = 2 ⋅ (+ 7) = (+ 7) + (+ 7) = +14 ou apenas 14
Quando multiplicamos dois números inteiros positivos, o resultado que obtemos é positivo.
• Qual é o valor de (+ 2) ⋅ (‒ 7)?
Vamos aplicar novamente a ideia da adição de parcelas iguais.
(+ 2) ⋅ (‒ 7) = 2 ⋅ (‒ 7) = (‒ 7) + (‒ 7) = ‒ 14
Quando multiplicamos dois números inteiros, um positivo e outro negativo, o resultado que obtemos é negativo.
• Qual é o valor de (‒ 2) ⋅ (+ 7)?
(‒ 2) é o oposto de + 2. Então, podemos escrever:
(‒ 2) ⋅ (+ 7) = ‒ (+ 2) ⋅ (+ 7) = ‒ (+14) = ‒ 14
Quando multiplicamos dois números inteiros, um negativo e outro positivo, o resultado que obtemos é negativo.
• Qual é o valor de 0 ⋅ (‒ 7)?
Assim como na multiplicação de números naturais, quando um dos fatores da multiplicação de números inteiros é zero, o produto é zero.
Então:
0 ⋅ (‒ 7) = (‒ 7) ⋅ 0 = 0
• Qual é o valor de (‒ 2) ⋅ (‒ 7)?
Nesse caso, para obter o resultado, vamos nos basear em multiplicações já conhecidas. Observe a sequência de multiplicações a seguir e seus resultados.
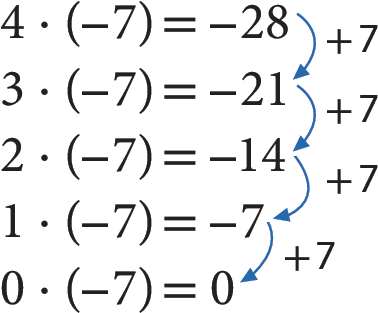
Essa sequência de multiplicações segue um padrão: o primeiro fator vem decrescendo em uma unidade (4, 3, 2, 1, 0) e o produto vem crescendo em 7 unidades (‒ 28, ‒ 21, ‒ 14, ‒ 7, 0). Seguindo esse padrão, podemos escrever:
(‒ 1) ⋅ (‒ 7) = 0 + 7 = 7
(‒ 2) ⋅ (‒ 7) = 7 + 7 = 14
(‒ 3) ⋅ (‒ 7) = 14 + 7 = 21
Observação

Quando multiplicamos dois números inteiros negativos, o resultado que obtemos é positivo.

Lembre-se: Escreva no caderno!
Cálculo mental
Observe o padrão na sequência de multiplicações a seguir.
3 ⋅ (‒ 9) = ‒ 27
2 ⋅ (‒ 9) = ‒18
1 ⋅ (‒ 9) = ‒ 9
0 ⋅ (‒ 9) = 0
Seguindo o padrão, continue a sequência e encontre o resultado de:
a) (‒1) ⋅ (‒ 9)
b) (‒ 2) ⋅ (‒ 9)
c) (‒ 6) ⋅ (‒ 9)

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Leia os dados apresentados na ilustração. Depois, escreva no caderno uma operação que associe a situação a um número inteiro.

• Agora, responda: que valor total a consumidora vai pagar pela compra no cartão de crédito?
2. Em quais das alternativas o resultado da operação é um número positivo?
a) (‒10) ⋅ (‒ 4)
b) (‒ 8) ⋅ (+ 2)
c) (+ 6) ⋅ (+1)
d) (+ 7) ⋅ (‒ 3)
3. Calcule os produtos e anote-os no caderno.
a) (+ 2) ⋅ (‒ 10)
b) (+ 3) ⋅ (‒ 5)
c) (‒ 5) ⋅ (+1)
d) (‒ 1) ⋅ (‒ 7)
e) 0 ⋅ (‒ 3)
f) (+ 12) ⋅ (‒ 5)
g) 3 ⋅ (‒ 15)
h) (+100) ⋅ (‒ 1)
4. Copie o quadro no caderno e complete-o.

|
a |
b |
Sinal de (a ⋅ b) |
(a ⋅ b) |
|---|---|---|---|
|
3 |
−7 |
||
|
−8 |
− |
−32 |
|
|
−9 |
−5 |
||
|
4 |
− |
−20 |
|
|
−2 |
+ |
+16 |
|
|
−3 |
+ |
+21 |
5. Represente cada uma das situações a seguir por meio de uma operação com números inteiros e, depois, responda às questões.
a) Um submarino estava no nível do mar quando começou a descer 100 métros de altitude a cada intervalo de meia hora. Após duas horas, a qual medida de altitude, em metro, abaixo do nível do mar o submarino se encontrava?
b) Um avião voava à altitude de 500 métros. Para escapar de uma tempestade, o piloto começou a subir 25 métros de altitude a cada minuto. Que medida de altitude o avião atingiu após 8 minutos?
c) Hugo é mergulhador. Ele estava no nível do mar e desceu 4 métros de altitude. Depois de 25 minutos, desceu 3 vezes essa medida. A que medida de altitude Hugo chegou?
d) César pratica salto ornamental. De um trampolim fixado a 1 métro acima do nível da água ele salta e consegue descer, abaixo do nível da água, até 3 vezes essa medida. A que medida de altitude César consegue descer?
Propriedades da multiplicação
Já vimos como multiplicar dois números inteiros. E para multiplicar três ou mais fatores, como fazemos?
Por exemplo, para calcular (+ 2) ⋅ (‒ 3) ⋅ (‒ 5), podemos multiplicar os fatores dois a dois. Observe duas maneiras de fazer isso.
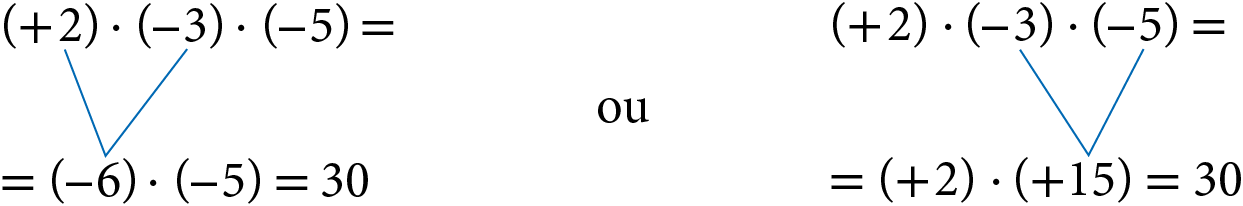
O que acabamos de fazer foi associar os fatores de diferentes maneiras e verificar que os resultados são iguais.
Para realizar os cálculos da segunda maneira, aplicamos a propriedade associativa da multiplicação, que vale para todos os números naturais e que vale também para todos os números inteiros.
Observação
Assim como a propriedade associativa, a propriedade comutativa, a propriedade distributiva e a existência do elemento neutro, válidas para a multiplicação de números naturais, também valem para a multiplicação de números inteiros.
Propriedade comutativa
Em uma multiplicação com números inteiros, a ordem dos fatores não altera o produto. Assim, se aêbê são números inteiros, a ⋅ b = b ⋅ a.
Por exemplo:
(‒ 7) ⋅ (‒ 6) = (‒ 6) ⋅ (‒ 7) = 42
Propriedade associativa
Na multiplicação com três ou mais fatores, podemos associá‑los de maneiras diferentes e obter o mesmo produto, ou seja, se a, b e c são números inteiros, (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c).
Por exemplo:
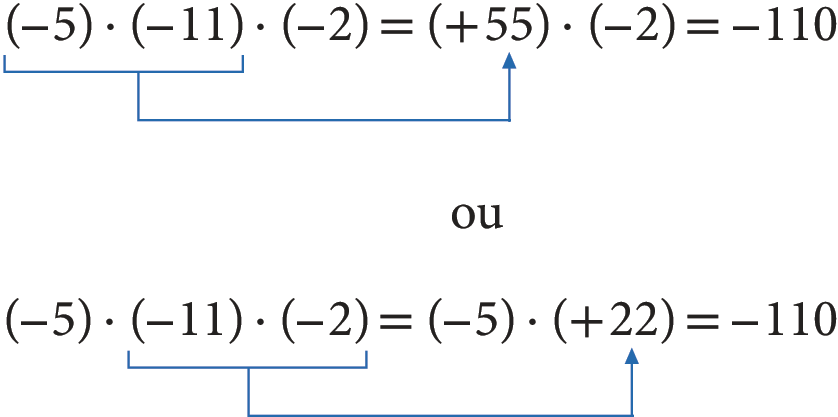
Observação
As propriedades da multiplicação, assim como as da adição, podem ser usadas para facilitar os cálculos.
Exemplo:
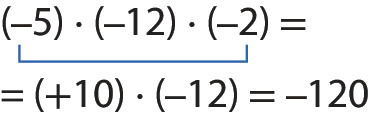
Propriedade distributiva
Em uma multiplicação de um número inteiro por outro, dado por uma adição ou por uma subtração, podemos multiplicar o primeiro número pelas parcelas e adicionar ou subtrair os resultados obtidos (propriedade distributiva da multiplicação em relação à adição ou à subtração). Assim, se a, b e c são números inteiros, a ⋅ (b + c) = a ⋅ b + a ⋅ c e a ⋅ (b ‒ c) = a ⋅ b ‒ a ⋅ c.
Por exemplo:
(‒ 2) ⋅ [(‒ 3) + (+ 4)] =
= (‒ 2) ⋅ (‒ 3) + (‒ 2) ⋅ (+ 4) =
= (+ 6) + (‒ 8) = 6 ‒ 8 = ‒2
Existência do elemento neutro
O número +1 é o elemento neutro da multiplicação, ou seja, se a é um número inteiro, temos que a ⋅ (+1) = (+1) ⋅ a = a.
Por exemplo:
(+1) ⋅ (‒ 8) = (‒ 8) ⋅ (+1) = ‒ 8

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1.

Naia está explicando como calculou mentalmente o valor da expressão: (‒ 25) ⋅ (‒ 29) ⋅ (+ 4)

• Agora, associe os fatores como preferir e calcule mentalmente os produtos a seguir.
a) (‒114) ⋅ (+ 2) ⋅ (‒ 5)
b) (+ 4) ⋅ (‒ 25) ⋅ (‒ 351)
c) (‒ 99) ⋅ (‒ 125) ⋅ (‒ 4) ⋅ (+ 2)
d) (+ 9) ⋅ (+1) ⋅ (+ 2) ⋅ (+ 5)
e) (‒ 100) ⋅ (‒ 50) ⋅ (‒ 40) ⋅ (‒10)
f) (‒12) ⋅ (‒100) ⋅ (+ 30) ⋅ (‒1)
2. Calcule, no caderno, o resultado da multiplicação de cada item.
a) (‒7) ⋅ (+11) ⋅ (‒3)
b) (‒2) ⋅ (‒14) ⋅ (‒5)
c) (‒5) ⋅ [(‒ 4) + (+ 3)]
d) (+ 8) ⋅ (‒ 9) ⋅ 0 ⋅ (‒ 16) ⋅ (+ 18)
3. Calcule os produtos a seguir e anote-os no caderno.
a) (‒12) ⋅ (+ 3) ⋅ (+1)
b) (+1) ⋅ (‒101) ⋅ (‒10)
c) (+1) ⋅ (+1) ⋅ (+1) ⋅ (+1)
d) (‒1) ⋅ (‒1) ⋅ (+ 235)
e) (‒2) ⋅ (‒5) ⋅ (+ 4)
f) (+ 6) ⋅ (‒3) ⋅ (+ 2)
g) (‒10) ⋅ (‒ 8) ⋅ (+ 5)
h) (‒12) ⋅ (‒5) ⋅ (+ 4) ⋅ (‒1)
4. Analise a afirmação a seguir.

• O menino está correto? Por quê?
8 Divisão exata com números inteiros
Observe a situação a seguir.
Um submarino está 20 métros abaixo do nível do mar. Essa posição pode ser representada por ‒ 20 métros e foi atingida em 4 etapas. Se em cada etapa o submarino submergiu a mesma medida de altitude, quantos metros ele submergiu em cada etapa?
Essa situação pode ser associada à divisão:
(‒ 20) : (4)
Você saberia dizer se o quociente dessa divisão é um número positivo ou negativo?
Para estudar o sinal do quociente entre dois números inteiros, vamos aplicar a ideia da divisão como operação inversa da multiplicação.
Quando consideramos o conjunto dos números naturais, sabemos que 15 : 3 = 5 porque 5 ⋅ 3 = 15.
Agora, faça as atividades propostas no boxe Para calcular e analise o que acontece quando o divisor e o dividendo são números inteiros.

Lembre-se: Escreva no caderno!
Para calcular
a) Qual é o resultado de (‒ 15) : (+ 3)?
Use o raciocínio da operação inversa, ou seja, comece respondendo à seguinte pergunta:
Por qual número devemos multiplicar (+ 3) para obter (‒ 15)?
◼ ⋅ (+ 3) = ‒ 15
Escreva no caderno o valor de ◼.
b) Qual é o resultado de (‒ 18) : (‒ 3)?
Ou seja, por qual número devemos multiplicar (‒ 3) para obter (‒18)?
◼ ⋅ (‒ 3) = ‒18
Registre no caderno o valor de ◼.
c) Qual é o resultado de (+ 14) : (‒2)?
Ou seja, por qual número devemos multiplicar (‒2) para obter (+ 14)?
◼ ⋅ (‒2) = + 14
Escreva no caderno o valor de ◼.
d) Qual é o resultado de 0 : (‒ 9)? E de 0 : (+11)?
Pense na operação inversa e escreva no caderno os resultados.
e)

Reúna-se com um colega e façam um resumo sobre os sinais dos quocientes de divisões de números inteiros. Depois, voltem à situação do submarino da página anterior para calcular o resultado da divisão (‒20) : (4).
Expressões numéricas
Em algumas expressões numéricas, há adições, subtrações, multiplicações e divisões. Para calculá-las, é necessário seguir esta ordem:
1º) multiplicações e divisões, na ordem em que aparecem na expressão;
2º) adições algébricas, na ordem em que aparecem na expressão.
Quando as operações estão agrupadas pelos sinais ( ), [ ] e { }, devemos efetuar primeiro as que estão entre parênteses: ( ). Em seguida, as que estão entre colchetes: [ ]. Depois, as que estão dentro das chaves: { }.
Exemplos
• 9 : {[‒ 3 ⋅ (11 ‒ 8) + 6 ] ‒ 6} =
= 9 : {[‒3 ⋅ 3 + 6 ] ‒ 6 } =
= 9 : {[‒ 9 + 6] ‒ 6} =
= 9 : {‒ 3 ‒ 6} =
= 9 : {‒ 9} = ‒ 1
• 27 + {12 + [2 ‒ (8 ‒ 6)] + 2} =
= 27 + {12 + [2 ‒ 2] + 2} =
= 27 + {12 + 0 + 2} =
= 27 + 14 =
= 41
• {40 : [(14 ‒ 2 ⋅ 5) + 1]} ⋅ 2 =
= {40 : [(14 ‒ 10) + 1]} ⋅ 2 =
= {40 : [4 + 1]} ⋅ 2 =
= {40 : 5} ⋅ 2 =
= 8 ⋅ 2 = 16
Observação
Quando uma ou mais operações aparecem dentro de um módulo, efetuamos essas operações, obtendo um número, e, em seguida, calculamos o módulo desse número. Segue um exemplo.
‒15 ‒ (‒ 8) ⋅ (+ 4) + ∣(+ 20) : (‒ 5)∣ =
= ‒ 15 ‒ (‒ 32) + ∣(‒ 4)∣ =
= ‒15 + 32 + 4 =
= +17 + 4 = + 21

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Calcule o valor de cada expressão a seguir.
a) 21 : 3 ‒ 4 ⋅ (‒ 3)
b) ∣‒10∣ ⋅ 3 + 5 ⋅ (‒ 3 + 4)
c) (‒ 5) + (‒ 3) ⋅ (‒ 4) ‒ (‒10) ⋅ (‒2)
d) [(+23) + (‒ 5)] : [12 ‒ (+ 3) ⋅ (‒ 2)]
2.

Faça mentalmente as operações e escreva no caderno aquelas que têm números inteiros como quociente.
a) (‒ 27) : (+ 3)
b) (+ 5) : (‒ 3)
c) (+ 7) : (‒ 49)
d) 0 : (‒ 9)
e) (‒ 3) : (+12)
f) (‒ 16) : (‒ 4)
3. Identifique o erro de cálculo na expressão.
‒ 25 ‒ (+ 3) ⋅ (‒ 7) ‒ 21 : (+ 3) =
= ‒ 25 ‒ (‒ 21) ‒ (+ 7) =
= ‒ 25 + 21 + 7 = ‒ 4 + 7 = + 3 = 3
• Agora, calcule-a corretamente.
4. Calcule o resultado das operações a seguir.
a) (‒ 25) : (+ 5)
b) (+ 49) : (‒ 7)
c) (‒ 81) : (‒ 1)
d) 0 : (‒ 16)
e) (‒ .2000) : (+ 200)
f) (‒ 620) : (‒ 20)
5. Agrupe as fichas numeradas em duplas, de modo que cada dupla resulte em uma divisão exata com quociente negativo.

6. Diogo precisa pagar uma conta de R$ 458,00quatrocentos e cinquenta e oito reais, mas não sabe qual é o saldo da sua conta-corrente. Ao consultar o banco, ele descobriu que:
• anteontem, seu saldo era de R$ 543,00quinhentos e quarenta e três reais;
• ontem, ele depositou R$ 273,00duzentos e setenta e três reais e emitiu um cheque de R$ 85,00oitenta e cinco reais e outro de R$ 128,00cento e vinte e oito reais.
a) O saldo bancário de Diogo é suficiente para efetuar o pagamento?
b) Vai sobrar ou vai faltar dinheiro? Quanto?
7. Calcule o que se pede e responda no caderno.
a) Um número inteiro multiplicado por ‒ 8 dá .4800. Que número é esse?
b) Qual é o número inteiro que multiplicado por 5 dá ‒ .1550?
8. Carlos vendeu sua moto, mas vai receber o pagamento em parcelas de R$ 250,00duzentos e cinquenta reais.
a) Se Carlos vendeu a moto pelo valor total de R$ 4.000,00quatro mil reais, em quantas parcelas ele receberá o pagamento?
b) Carlos quer comprar outra moto e pagá-la em 14 parcelas de R$ 260,00duzentos e sessenta reais. O dinheiro que vai receber pela venda será suficiente para pagar a nova moto?
9. Adriano e quatro amigos estão brincando com um jogo que tem as seguintes regras:
• cada jogador inicia a partida com um saldo positivo de 10 fichas e deve responder a um total de 20 questões durante o jogo;
• a cada resposta correta, o jogador recebe 3 fichas e, a cada resposta incorreta, perde uma ficha;
• será vencedor aquele que tiver o maior saldo positivo de fichas.

a) Se Adriano acertar exatamente 10 questões, qual será seu saldo ao final do jogo?
b) Se Rafael, um dos amigos de Adriano, acertar exatamente 15 questões, qual será seu saldo ao final do jogo?
c) Quantas questões um jogador deve acertar para ficar com 10 fichas ao final do jogo?
d) Qual é o maior número de fichas que um jogador pode acumular?
e) É possível que um jogador fique com um saldo devedor de fichas. Qual é o número mínimo de questões que um jogador deve acertar para que isso não aconteça?
10.

Invente uma situação que possa ser representada pela expressão:
[.2000 + (‒ 200) + 3 ⋅ (‒ 350)] : 5
9 Potenciação em que a base é um número inteiro
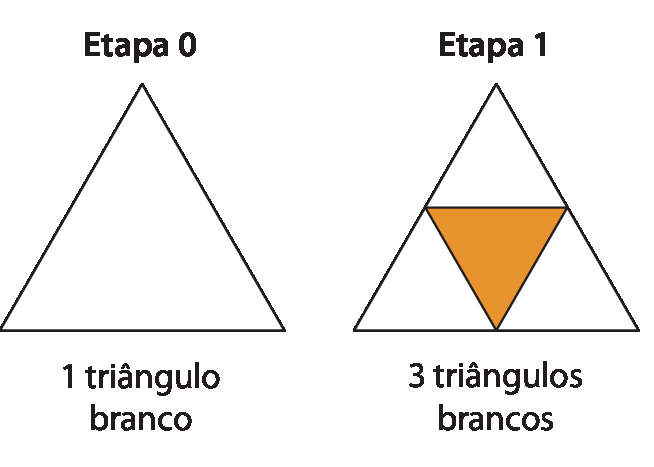
Observe a construção deste triângulo especial, criado pelo matemático polonês Waclaw Sierpiński (1882-1969).
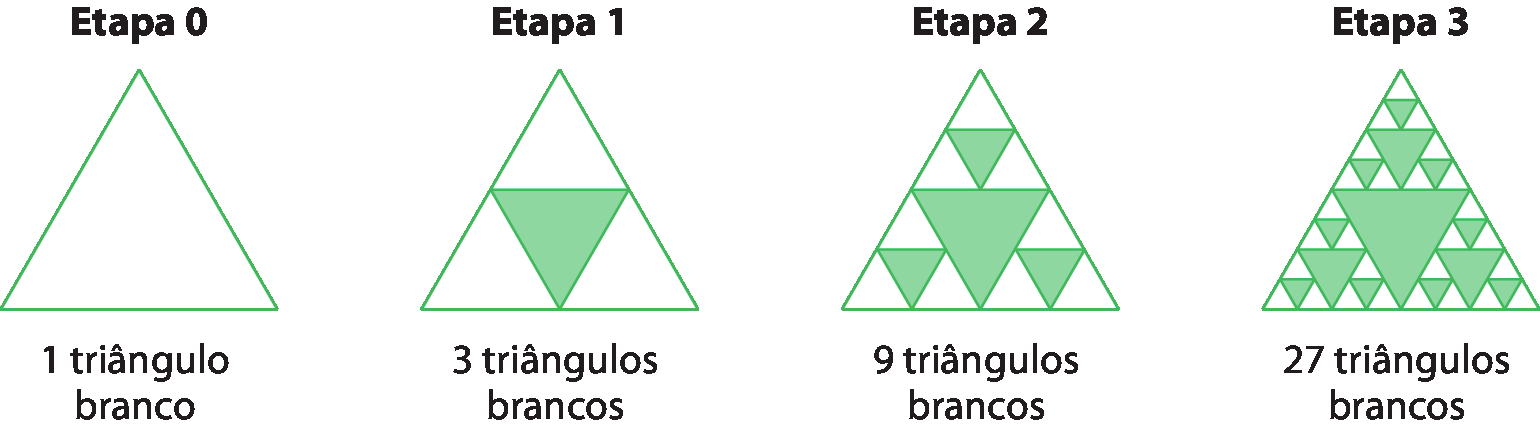
Como calcular a quantidade de triângulos brancos que haverá nas etapas 4 e 5?
A sequência formada pela quantidade de triângulos brancos (1, 3, 9, 27reticências) apresenta um padrão: a partir do segundo, cada número é o triplo do anterior. Assim, nas próximas etapas, teremos:
etapa 4

3 ⋅ 27 = 81 ou 3 ⋅ 3 ⋅ 3 ⋅ 3 = 34 = 81
etapa 5

3 ⋅ 81 = 243 ou 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 35 = 243
No caso dos números naturais, quando o expoente é maior que 1, a potenciação indica uma multiplicação de fatores iguais.

Isso também acontece quando a base da potência é um número inteiro a e o expoente é um número inteiro n maior que 1.
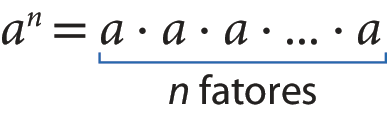
E quando o expoente é zero ou 1?
Observe o quadro a seguir, em que são relacionadas potências de base 3.
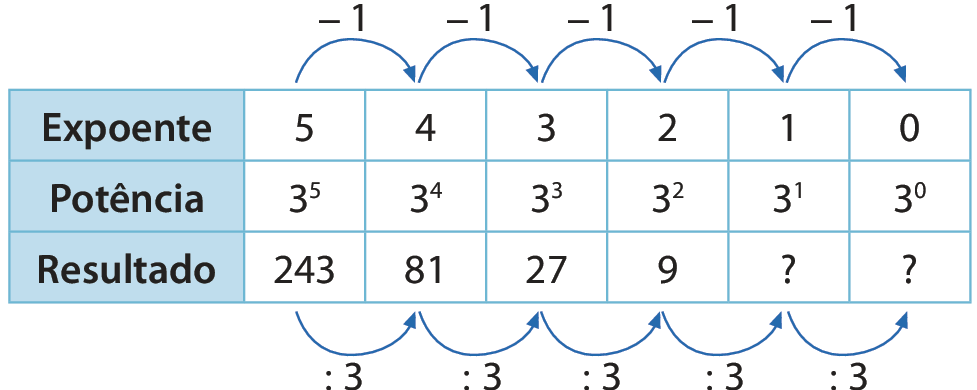
Note que, à medida que o expoente da potência 3n decresce uma unidade, o resultado é o da potência anterior dividido por 3. Assim:
31 = 9 : 3 = 3
30 = 3 : 3 = 1
Lembre-se: Escreva no caderno!
Agora, observe o quadro a seguir, em que são relacionadas potências de base (‒ 3).
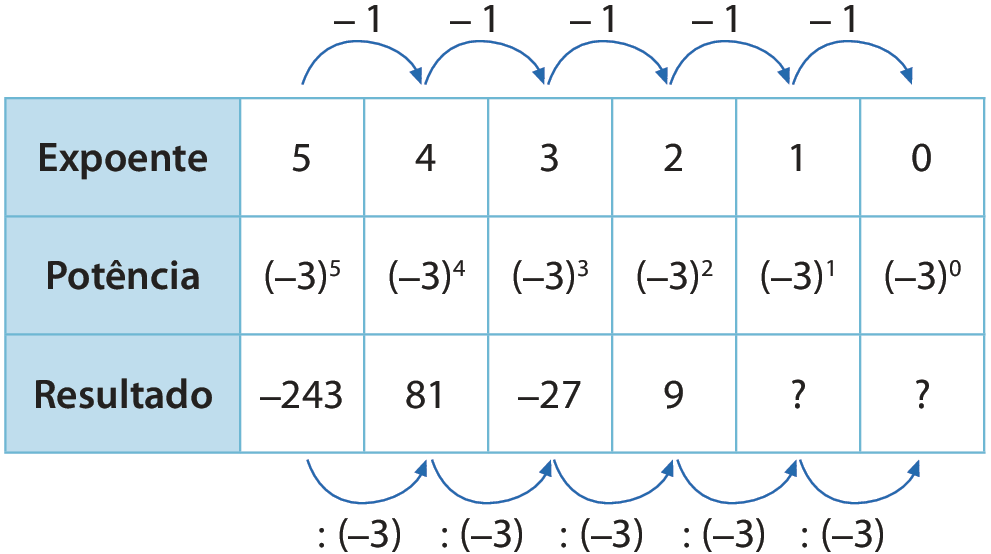
Da mesma fórma, observando a sequência de potências e seus expoentes, podemos perceber que, à medida que o expoente da potência (‒ 3)n decresce uma unidade, o resultado é o da potência anterior dividido por (‒ 3). Assim:
(‒ 3)1 = 9 : (‒ 3) = ‒ 3
(‒ 3)0 = (‒ 3) : (‒ 3) = 1
De modo geral, define-se:
• Toda potência de expoente 1 que tem como base um número inteiro é igual à própria base.
• Toda potência de expoente zero que tem como base um número inteiro não nulo é igual a 1.
Para analisar
Podemos representar a quantidade de triângulos brancos de Sierpiński das etapas 0 e 1 por meio de potências de base 3? Se pudermos, como?
Exemplos
• 26 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 64
• (+ 7)3 = (+ 7) ⋅ (+ 7) ⋅ (+ 7) = + 343
• 51 = 5
• 04 = 0 ⋅ 0 ⋅ 0 ⋅ 0 = 0
• (‒ 2)6 = (‒ 2) ⋅ (‒ 2) ⋅ (‒ 2) ⋅ (‒ 2) ⋅ (‒ 2) ⋅ (‒ 2) = 64
• (‒ 7)3 = (‒ 7) ⋅ (‒ 7) ⋅ (‒ 7) = ‒ 343
• (‒ 5)1 = ‒ 5
• (‒ 5)0 = 1
Para pensar
Calcule as potências de base negativa.
a) (‒ 5)2
b) (‒ 2)5
c) (‒1)4
d) (‒ 3)3
Os resultados foram positivos ou negativos?
•

Reúna-se com um colega e pensem em outras potências de base inteira negativa e expoente inteiro maior que 1. Em seguida, respondam: em relação ao sinal do resultado da potência de base negativa, o que sugerem os cálculos que vocês fizeram?

ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Calcule as potências a seguir.
a) (‒ 4)2
b) (‒ 2)3
c) (7)2
d) (‒ 3)4
e) 05
f) (5)0
g) (‒ 6)3
h) (‒ 100)0
i ) (‒ .1000)1
j ) (‒ 10)3
k) (‒ 5)3
l) (‒ 2)4
2. Observe a potência e responda às questões.
(‒ 4)x
a) Para que valor de x a potência é igual a ‒ 64?
b) Para que valor de x a potência é igual a + 256?
c) Substituindo x pelos números naturais 0, 1, 2 e 3, obtemos uma sequência. Analise a sequência e determine os valores de x para os quais os termos da sequência são positivos.
• Depois, determine os valores de x para os quais os termos são negativos.
3. Observe as perguntas de Jaqueline e, depois, responda-as no caderno.

4. Considere os quadrados a seguir e escreva em fórma de potência a quantidade de quadradinhos que há em cada um deles.
a)

b)

c)

d)

5. Cláudio pretende trocar o piso da garagem de sua casa. Para comprar a quantidade certa de lajotas, ele verificou que a medida da largura e a medida do comprimento da garagem eram iguais: as duas correspondiam a 16 lajotas.

a) Considerando que a nova lajota tenha o mesmo tamanho da anterior, quantas lajotas serão necessárias para que Cláudio troque todo o piso? Escreva o resultado em fórma de potência.
b) Se a medida da largura e do comprimento das lajotas novas fosse o dobro da das anteriores, quantas lajotas seriam necessárias? Escreva o resultado em fórma de potência.
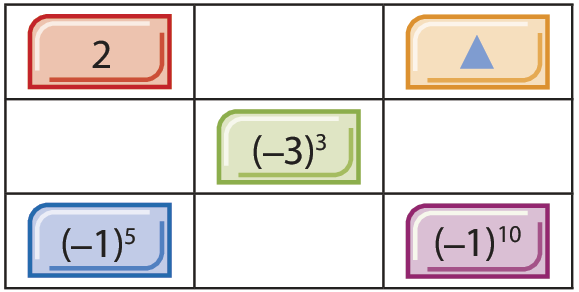
6.

Cinco fichas estão dispostas no quadro. Sabendo que os produtos dos números que estão nas diagonais são iguais, determine o número que está na ficha com o símbolo

.
10 Raiz quadrada exata de um número inteiro
Acompanhe a situação.
Neusa vai aproveitar dois muros perpendiculares de sua chácara para construir um galinheiro retangular usando uma tela que mede 6 métros de comprimento.

Observe alguns projetos para o galinheiro esquematizados por Neusa.


Neusa percebeu que o projeto de galinheiro com maior medida de área (9 métros quadrados) é o que tem formato quadrado, cujo lado mede 3 métros de comprimento.
9 = 3 ⋅ 3 = 32
Ao descobrir que o número 3 ao quadrado é igual a 9, encontramos a raiz quadrada de 9. A operação que realizamos para isso foi a radiciação. Dizemos que extraímos a raiz quadrada de 9.
O símbolo da raiz quadrada é
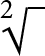
ou

.
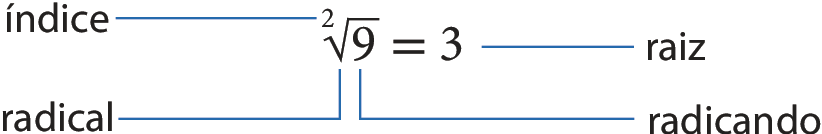
Lemos: “a raiz quadrada de 9 é igual a 3”.
Embora (+ 3)2 = 9 e (‒ 3)2 = 9, consideramos a raiz quadrada de 9 única e não negativa, ou seja, apenas o número + 3. Assim:
Raiz quadrada de 9 com número 2 no índice.= + 3
A raiz quadrada de um número inteiro a é um número não negativo b que, elevado ao quadrado, resulta em a.
Assim:
raiz quadrada de a= b se b2 = a, com b ⩾ 0.
Exemplos
•
Raiz quadrada de mais 1 igual a raiz quadrada de 1.= 1, porque 12 = 1 e 1 > 0.
•
Raiz quadrada de mais 36 igual a raiz quadrada de 36.= 6, porque 62 = 36 e 6 > 0.
•
Raiz quadrada de zero.= 0, pois 02 = 0.
Os números inteiros que podem ser escritos como potência de base inteira e expoente 2 são chamados de quadrados perfeitos. Somente esses números têm como raiz quadrada um número inteiro não negativo.
Observação
A
raiz quadrada de 8.não resulta em um número inteiro, pois 8 não é um número quadrado perfeito.
E a raiz quadrada de um número negativo?
Vamos analisar, por exemplo,
raiz quadrada de menos 25..
Sabemos que (+ 5)2 = + 25 e (‒ 5)2 = + 25 e que o quadrado de qualquer número positivo, negativo ou nulo é maior ou igual a zero. Logo, não existe número inteiro cujo quadrado seja ‒ 25. Isso ocorre com qualquer raiz quadrada de número negativo.
Observação
Preste atenção:
menos raiz quadrada de 100não é um número inteiro, mas
menos raiz quadrada de 100é um número inteiro.


ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Marta construiu três quadrados de papelão. O lado do primeiro quadrado tinha 16 de medida de comprimento, o lado do segundo tinha como medida de comprimento a raiz quadrada da medida de comprimento do lado do primeiro, e o lado do terceiro, a raiz quadrada da medida de comprimento do lado do segundo. Qual era a medida de comprimento do lado de cada quadrado construído?
2. Calcule as raízes a seguir e registre os resultados no caderno.
a)
raiz quadrada de mais 9.b)
raiz quadrada de mais 100.c)
menos raiz quadrada de mais 493. Indique no caderno as alternativas que representam números inteiros.
a)
raiz quadrada de mais 16.b)
raiz quadrada de mais 36.c)
raiz quadrada do módulo de menos 81.4. Que número(s) inteiro(s) existe(m) entre:
a)
raiz quadrada de mais 64 e raiz quadrada de mais 100.?
b)
menos raiz quadrada de 25 e menos raiz quadrada de 9.?
c)
menos raiz quadrada de mais 16 e raiz quadrada de zero.?
d)
raiz quadrada de mais 49 e raiz quadrada de mais 81.?
5. Compare, em cada triângulo, a soma dos quadrados das medidas de comprimento dos dois lados menores e o quadrado da medida de comprimento do lado maior.


Estatística e Probabilidade
FAÇA AS ATIVIDADES NO CADERNO
Construção de gráficos de barras com números inteiros
Em setembro de 2023, Rui e Lorena fizeram uma pesquisa sobre a medida de temperatura ideal para o armazenamento de alguns alimentos. Após coletar os dados, eles construíram uma tabela com os dados em uma planilha eletrônica. Observe como ela ficou.
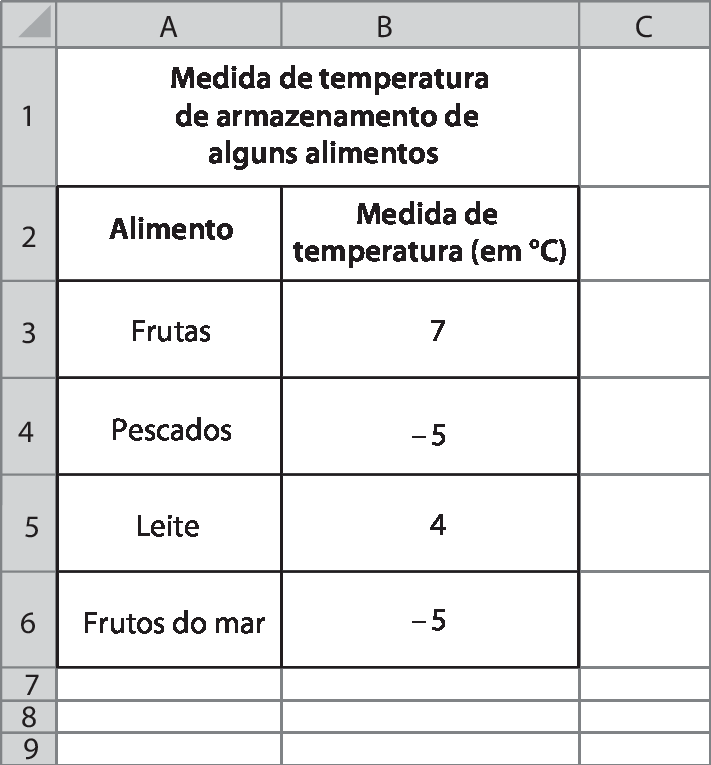
Dados obtidos em: SILVA Júnior, Eneo Alves da. Manual de contrôle higiênico-sanitário em alimentos. São Paulo: Varela, 2002. página 42.
Rui e Lorena devem apresentar essas informações para seus colegas de classe. Rui resolveu apresentá-las em um gráfico de barras horizontais, e Lorena em um gráfico de barras verticais.
Para construir cada um dos gráficos, eles selecionaram os dados da tabela, depois Rui escolheu a opção para inserir gráfico de barras horizontais, e Lorena escolheu a opção para inserir gráfico de barras verticais.
No gráfico de barras horizontais de Rui, cada barra representa um tipo de alimento.
Como as medidas de temperatura de armazenamento dos alimentos são representadas por números inteiros, a linha vertical deve apoiar, à esquerda, as barras correspondentes aos números negativos e, à direita, as barras correspondentes aos números positivos.
Para determinar a medida de comprimento de cada barra, Rui deve adotar uma escala. Como os números que representam as medidas de temperatura, em grau Celsius, são próximos de zero, ele pode usar a escala com variação de 1 grau Célsius.
Assim como a tabela feita na planilha eletrônica, o gráfico deve ter título e indicação da fonte dos dados. Dessa fórma, Rui vai obter o gráfico a seguir.
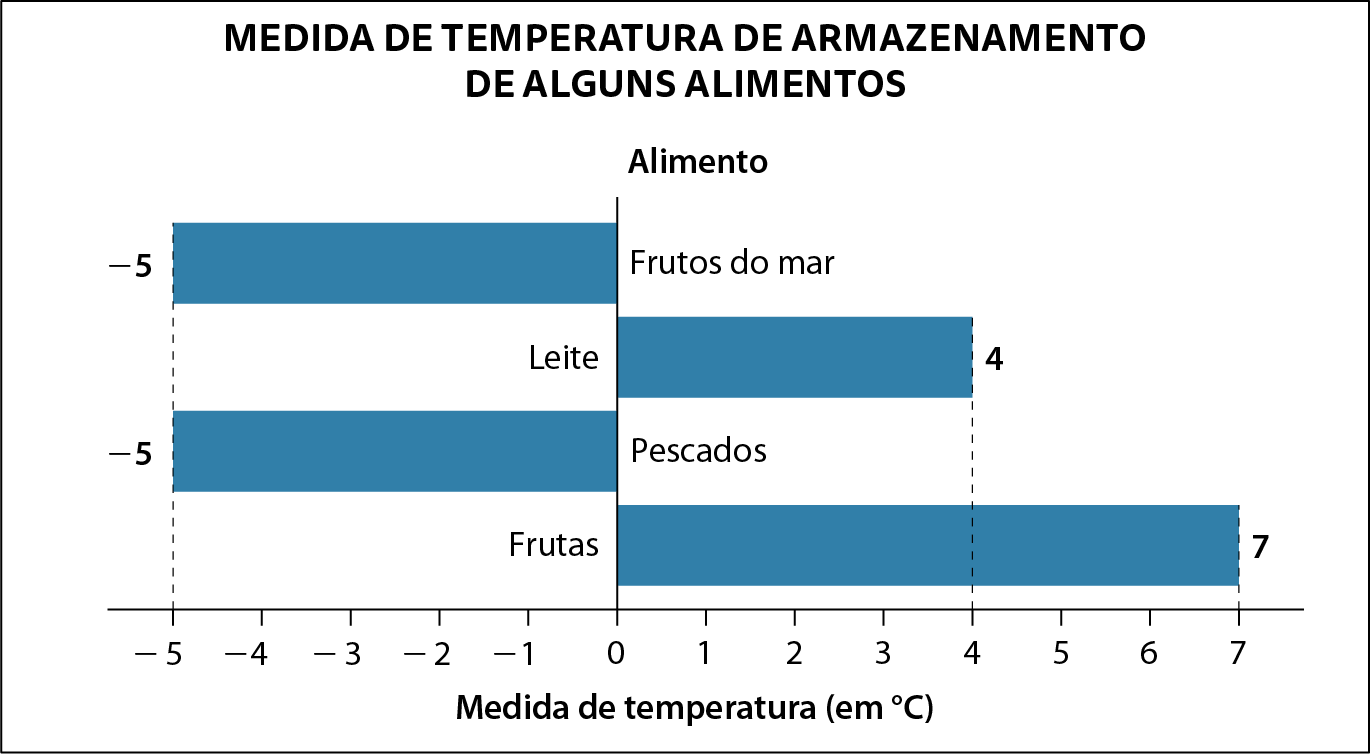
Dados obtidos em: SILVA Júnior, Eneo Alves da. Manual de contrôle higiênico-sanitário em alimentos. São Paulo: Varela, 2002. página 42.

Como Lorena decidiu construir um gráfico de barras verticais, as barras abaixo da linha horizontal que as apoia correspondem aos números negativos, e as barras acima da linha correspondem aos números positivos.
Para determinar a medida de comprimento de cada barra, Lorena deve adotar uma escala e também indicar o título e a fonte dos dados. Desse modo, Lorena vai obter o gráfico a seguir.
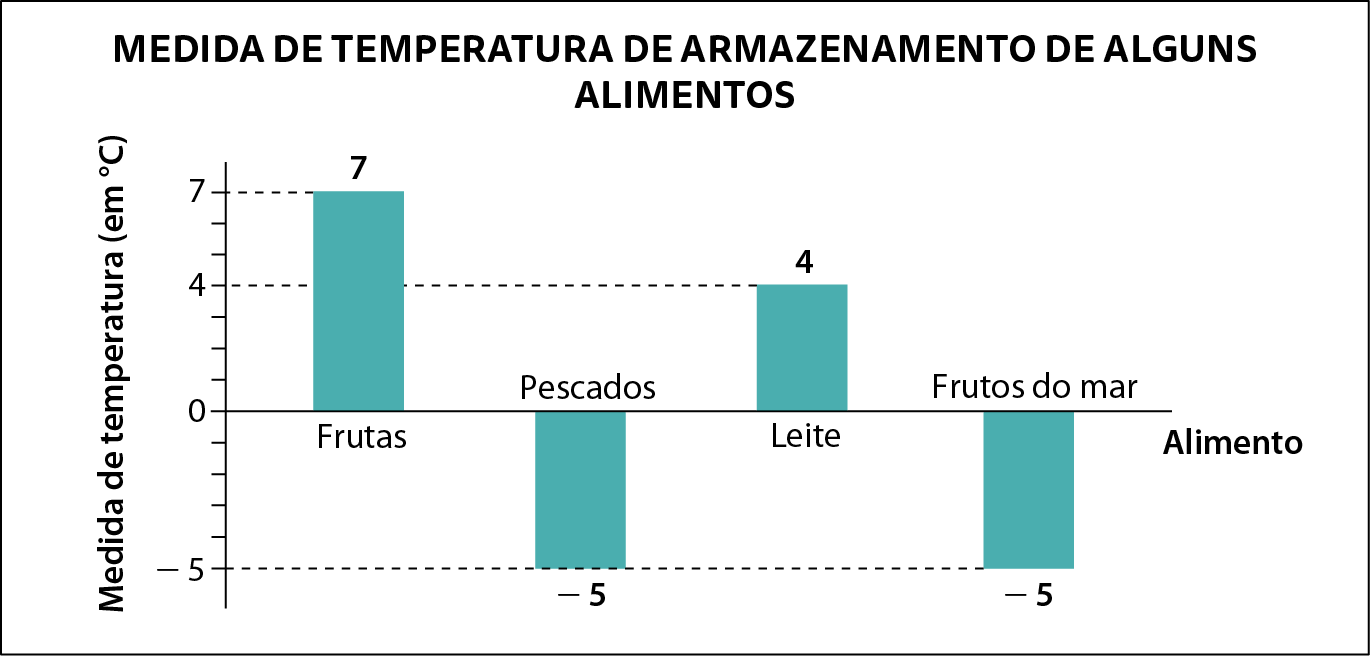
Dados obtidos em: SILVA Júnior, Eneo Alves da. Manual de contrôle higiênico-sanitário em alimentos. São Paulo: Varela, 2002. página 42.


ATIVIDADES
FAÇA AS ATIVIDADES NO CADERNO
1. Caio pesquisou na internet, em 11 de fevereiro de 2022, a previsão do tempo para o dia seguinte em diferentes cidades do mundo e as registrou na tabela a seguir.
|
Cidade |
Medida de temperatura máxima |
Medida de temperatura mínima |
|---|---|---|
|
Florianópolis (Brasil) |
28 °C |
20 °C |
|
Berlim (Alemanha) |
6 °C |
3 °C |
|
Edmonton (Canadá) |
−3 °C |
−6 °C |
|
Sapporo (Japão) |
1 °C |
−10 °C |
|
São Francisco (Estados Unidos) |
22 °C |
9 °C |
Dados obtidos por Caio em 11 fevereiro 2022.
a) Em uma planilha eletrônica, construa uma tabela com as medidas de temperatura mínima previstas para essas cidades e uma tabela com as medidas de temperatura máxima previstas.
b) Construa dois gráficos de barras verticais, um para representar as medidas de temperatura mínima e outro para representar as medidas de temperatura máxima previstas para essas cidades.
c) Em qual dessas cidades a medida de temperatura mínima prevista foi a menor? E em qual cidade a medida de temperatura mínima prevista foi a maior?
▶ Estatística e Probabilidade
2. Miguel pretende inaugurar sua lanchonete no próximo mês.

Para que os alimentos abertos e não totalmente consumidos não estraguem, em janeiro de 2023 ele pesquisou a medida de temperatura em que deverá conservá-los. Observe na tabela a seguir as informações que Miguel obteve.
|
Produto |
Medida de temperatura mínima |
Medida de temperatura máxima |
|---|---|---|
|
Margarina |
+4 °C |
+8 °C |
|
Pão de queijo |
−30 °C |
−12 °C |
|
Linguiça calabresa |
+4 °C |
+8 °C |
|
Sorvete |
−30 °C |
−18 °C |
|
Massa para pizza |
−30 °C |
−18 °C |
Dados obtidos por Miguel em janeiro de 2023.
• Com base nessas informações, faça o que se pede.
a) Calcule a diferença entre as medidas de temperatura máxima e mínima, nessa ordem, para a conservação de cada produto da tabela. Qual é a menor diferença? Qual é a maior?
b) Construa, em uma planilha eletrônica, um gráfico de barras horizontais para representar a medida de temperatura mínima de conservação desses alimentos.
c) Construa um gráfico de barras verticais para representar a medida de temperatura mínima de conservação desses alimentos.
d) Miguel comprou um freezer cuja medida de temperatura mínima é de ‒ 20 graus Célsius. Que produtos ele poderá conservar se regular o freezer na medida de temperatura mínima?
3. Andrea sempre acompanha os jogos do América Futebol Clube, time de futebol de Belo Horizonte (Minas Gerais) para o qual ela torce.

Em 2020, o time de Andrea não foi campeão e ficou em segundo lugar na classificação final. Em fevereiro de 2021, ela construiu uma tabela para mostrar a classificação final de alguns times da série B do Campeonato Brasileiro naquele ano.
|
Classificação |
Time |
Pontos ganhos |
Saldo de gols |
|---|---|---|---|
|
1º |
Chapecoense (SC) |
73 |
21 |
|
2º |
América (MG) |
73 |
20 |
|
3º |
Juventude (RS) |
61 |
10 |
|
14º |
Vitória (BA) |
48 |
0 |
|
15º |
Confiança (SE) |
46 |
−8 |
|
20º |
Oeste (SP) |
29 |
−32 |
Dados obtidos por Andrea no site oficial da Confederação Brasileira de Futebol (CBF), em 12 fevereiro 2021.
• Com base nessas informações, faça o que se pede.
a) Construa uma tabela em uma planilha eletrônica para representar a pontuação de cada time.
b) Construa um gráfico de barras horizontais para representar a pontuação de cada time.
c) Qual foi a diferença de pontos ganhos entre o Oeste e o time campeão?
d) A cada gol marcado, o time deve adicionar 1 a seu saldo de gols e, a cada gol sofrido, subtrair 1. Dos times apresentados na tabela, quais marcaram mais gols do que sofreram?

Atividades de revisão
FAÇA AS ATIVIDADES NO CADERNO
1. Construa uma reta numérica e localize nela os números ‒ 7, + 5, ‒ 3, ‒ 2, 0, +1 e + 2. Em seguida, responda às questões.
a) Qual é o maior número que você representou na reta? E o menor?
b) Qual é o sucessor de 0?
c) E o antecessor de ‒ 2?
2. Transcreva no caderno apenas as afirmações verdadeiras.
a) Na sequência dos números inteiros, o sucessor de ‒ 21 é o oposto do antecessor de 21.
b) Dois números opostos têm o mesmo módulo.
c) O módulo de um número negativo é sempre menor que o módulo de um número positivo.
3. Frederico e Gisele estavam brincando de adivinhação de cartas. Ele colocou seis cartas numeradas sobre a mesa, escondendo a numeração de uma delas.

Para que Gisele adivinhasse o número da carta virada para baixo, Frederico deu a ela as dicas a seguir.
• É o oposto de um dos números visíveis.
• É um número cujo módulo é maior que 3.
• É um número negativo.
Qual era o número da carta virada para baixo?
4. Gislaine e Marcos estavam brincando de adivinhar o número pensado. Nessa brincadeira, cada participante pensa em um número, anota-o em um papel, esconde o papel e dá dicas para que o colega adivinhe o número pensado. Gislaine deu as dicas a seguir para Marcos adivinhar o número que ela escolheu.
• É um número inteiro.
• Na sequência dos inteiros, o módulo do seu antecessor é igual ao módulo do seu sucessor.
Em que número Gislaine pensou?
5.


Pense em um número e anote-o em um papel. Escreva três dicas sobre esse número. Essas dicas devem ser suficientes para que alguém possa adivinhar o número em que você pensou. Depois, passe as dicas para um colega para que ele tente adivinhar esse número.
6. Copie as sentenças substituindo cada ◼ por > (maior que) ou < (menor que).
a) ‒ 12 ◼ +15
b) 0 ◼ ‒ 3
c) +12 ◼ ‒ 15
d) + 4 ◼ + 7
7. Amplitude térmica é a diferença entre a medida de temperatura máxima e a medida de temperatura mínima, nessa ordem, registradas em um lugar. Observe o quadro a seguir, com exemplos de medidas de temperaturas máximas e mínimas registradas em diferentes localidades.
|
Cidade |
Medida de temperatura máxima |
Medida de temperatura mínima |
|---|---|---|
|
A |
−1 °C |
−18 °C |
|
B |
2 °C |
−20 °C |
|
C |
12 °C |
−6 °C |
a) Que cidade apresentou a maior amplitude térmica? E qual apresentou a menor?
b) Em que cidade foi registrada a menor medida de temperatura?
c) Que medida de temperatura registrada ficou mais próxima de 0 grau Célsius?
8. Determine o valor desconhecido em cada caso.
a) (‒ 8) ‒ ◼ = + 4
b) (‒16) ‒ ◼ = ‒ 7
c) ◼ ‒ (‒ 8) = + 4
d) ◼ ‒ (+ 9) = ‒12
e) ◼ + ◼ = 0
9. Durante uma aula de Matemática, a professora pediu aos estudantes que adicionassem os números (‒ 5), (+ 6) e (+ 4). Flávia achou mais fácil calcular da seguinte maneira:
(‒ 5) + [(+ 6) + (+ 4)] =
= (‒ 5) + (+10) = + 5
a) Que propriedade da adição Flávia aplicou na sua resolução?
b) Resolva a mesma expressão numérica de outra maneira.
▶ Atividades de revisão
10.

Efetue mentalmente as operações a seguir e anote os resultados no caderno.
a) ‒7 + 8 ‒ 3 ‒ 8
b) + 5 ‒ 11 + 5 + 11
c) + 4 ‒ 3 + 40 ‒ 30 + 400 ‒ 300
d) ‒ 40 ‒ 7 ‒ 5 + 2 ‒ 83 + 38
e) ‒ (+ 27 ‒ 14) + (‒ 27 + 14)
11. Camila desafiou Válter a desenhar o quadrado a seguir e a completá-lo.
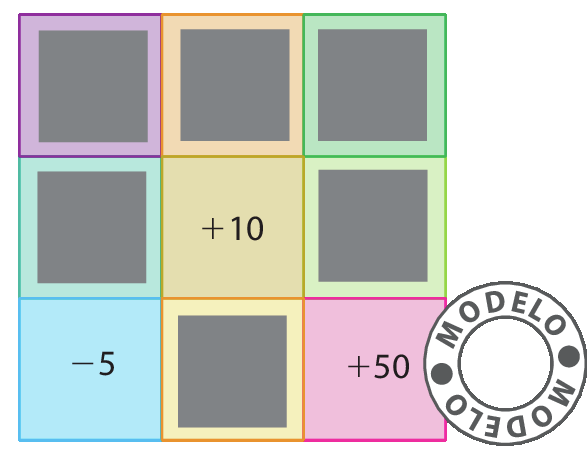
Para isso, ela deu a ele a seguinte dica:

• Ajude Válter a completar o quadrado, sabendo que nenhum número se repete.
12.

Podemos usar a calculadora para realizar operações de multiplicação e de divisão de números inteiros utilizando a tecla
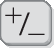
.
Observe alguns exemplos.
• Representamos ‒ 8 fazendo

.
• Para calcular o produto de ‒ 8 por 4, digitamos

e obtemos

.
• Para calcular (‒ 6) : (‒ 3), digitamos
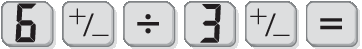
e obtemos

.
Usando a calculadora, determine:
a) 152 ⋅ (‒ 12)
b) (‒ 23) ⋅ (‒ 96)
c) .4725 : (‒ 45)
d) (‒ .1870) : (‒ 110)
13.

Copie o quadro a seguir no caderno e substitua cada ◼ por um número ou por um destes sinais de operação matemática: +, ‒ ou ×. Ao completar a cruzadinha, serão formadas quatro expressões nas linhas horizontais e mais quatro expressões nas colunas verticais. Cada número que está no quadrinho azul-claro é a soma dos quatro números que estão em seus vértices.
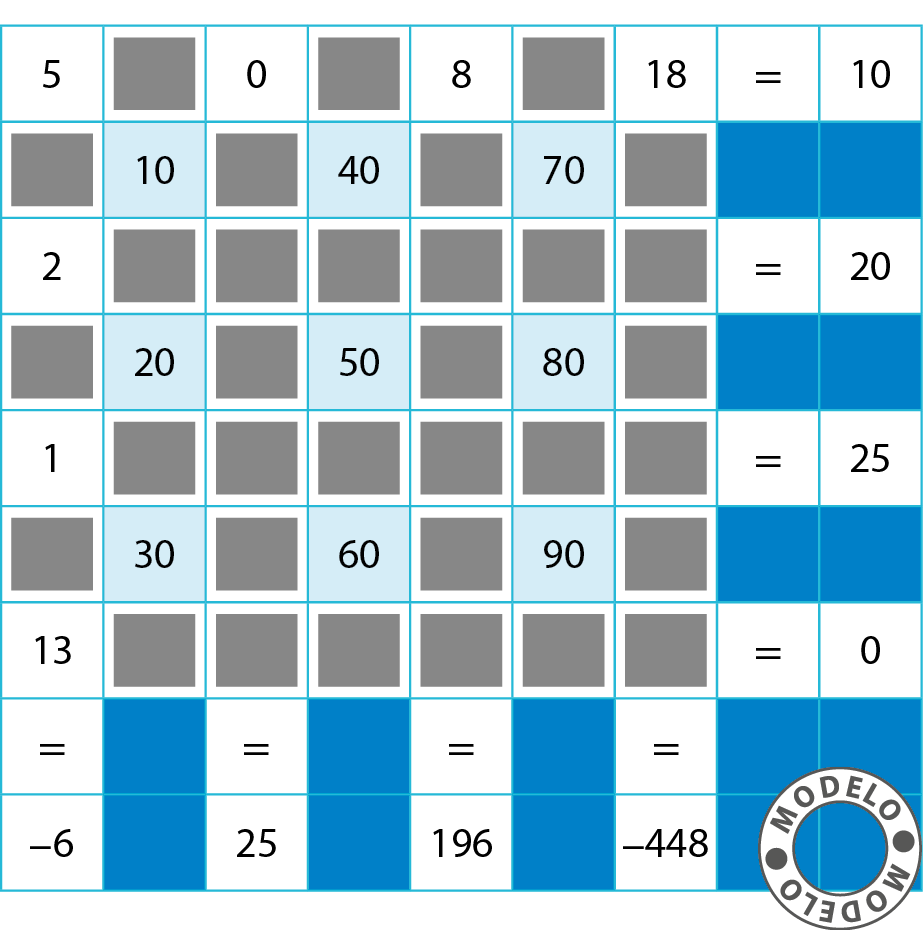
14. João trabalha dirigindo uma empilhadeira em uma fábrica de bolachas. Ele organiza o estoque guardando as caixas de bolachas em lotes que, depois, serão distribuídos para os supermercados da região. Cada lote empilhado contém 5 caixas na medida do comprimento, 5 na medida da largura e 5 na medida da altura.

a) Com uma potência de base 5, represente a quantidade de caixas de bolachas de que João precisa para montar um lote.
b) Para carregar 1 caminhão, são necessários 4 lotes. Quantas caixas de bolachas cabem em 1 caminhão?
c) Uma rede de supermercados comprou setecentas e cinquenta caixas de bolachas. De quantos lotes João precisará para montar o pedido do supermercado?
15. O cubo representado teve duas faces opostas pintadas de amarelo e as outras quatro faces pintadas de verde.
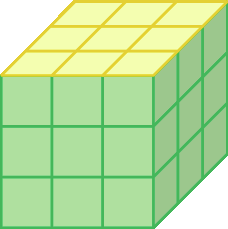
a) Represente, na fórma de potência, o número de cubinhos desse cubo.
b) Quantos cubinhos têm faces com as duas cores?
16. Observe a sequência de cubos a seguir e depois faça o que se pede.

a) De quantos

é formado cada cubo?
b) Escreva cada número obtido no item a como uma potência.
c) Determine a quantidade de cubinhos que formam: a; aêbê; a, B e C; a, B, C e D; a, B, C, D e ê; a, B, C, D, ê e F.
d) Escreva cada número obtido no item c como uma potência.
e) Calcule a soma das bases das seis potências obtidas no item b e compare essa soma com a base da sexta potência obtida no item d.
f) Repita o procedimento do item e para as cinco, as quatro, as três e as duas primeiras potências.
17. Um cientista preparou um tubo de ensaio às 11 horas. Às 14 horas do mesmo dia, colocou no tubo uma bactéria que se multiplica dobrando de quantidade a cada minuto. Às 14 horas e 20 minutos do mesmo dia, o tubo de ensaio estava cheio até a boca. Em que horário o tubo de ensaio estava com a metade da quantidade de bactérias que havia às 14 horas e 20 minutos?
18. Os números quadrados perfeitos possivelmente receberam esse nome dos pitagóricos, membros de uma comunidade grega do século seis antes de Cristo que estudavam, entre outras coisas, relações matemáticas.
O termo “quadrado perfeito” deve-se às quantidades de objetos que podem ser organizadas formando um quadrado. Observe como os pontos foram organizados.
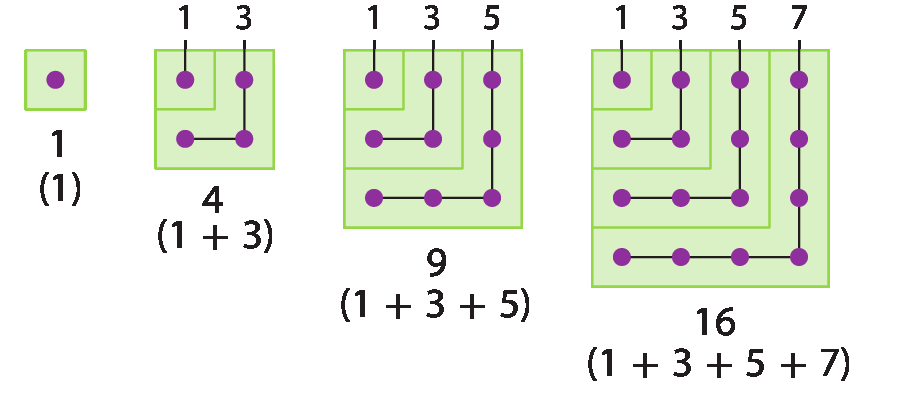
a) Qual é o próximo número dessa sequência?
b) 121 é um quadrado perfeito? Caso seja, escreva-o como soma de números ímpares.
19. Mariana está empilhando alguns cubinhos para formar cubos maiores.
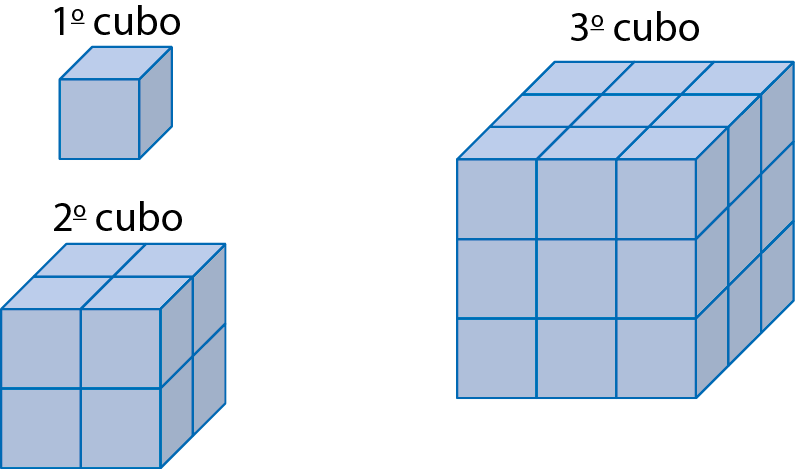
Dentro de cada cubinho há 8 bolinhas.
a) Quantas bolinhas há no segundo cubo?
b) Quantas bolinhas há no terceiro cubo?
c) Se a sequência continuar, quantas bolinhas haverá no centésimo cubo?