Página 130

CAPÍTULO 5 Grandezas e medidas

1 Unidades de medida

Leia a tirinha a seguir.

Por Rafael Silva.

História em quadrinhos. Meça suas palavras. História composta por 4 quadros, apresenta um tucano preto e amarelo com bico verde e um macaco bugio careca e pelos na cor marrom. Os animais estão conversando sentados no galho de uma árvore . Quadro 1. O tucano pergunta ao Macaco: CACO, QUAL É A SUA ALTURA? Quadro 2. O macaco responde: EU TENHO 800 milímetros! Quadro 3. O tucano fala: MUDAR A UNIDADE DE MEDIDA VAI TE DEIXAR MAIS ALTO. Quadro 4. O macaco indaga? CARA, O QUE EU FIZ PRA VOCÊ?

Para pensar

a) Qual foi a intenção do bugio Caco ao expressar a medida de sua altura em milímetro?

b) Qual é a unidade de medida de comprimento mais adequada para expressar a medida da altura de Caco?

Para medir qualquer grandeza é necessário escolher uma unidade adequada e compará-la com o que será medido.

No Sistema Internacional de Unidades (ésse Í), são atribuídas a algumas grandezas unidades de medida de base. Elas fornecem as referências que permitem definir unidades maiores (os múltiplos) e menores (os submúltiplos). Para cada caso, deve-se escolher a unidade de medida mais adequada.

Na tirinha anterior, Caco não usou a unidade de medida de comprimento adequada para expressar a medida de sua altura, com a intenção de convencer o tucano de que ele era mais alto do que realmente era. Nesse caso, Caco deveria ter expressado sua altura em centímetro.

Recorde

Grandeza	Unidade de medida
comprimento	metro (m)
tempo	segundo (s)
massa	quilograma (kg)
área	metro quadrado (m2)
volume	metro cúbico (m3)

Algumas unidades de medida

ATIVIDADES

faça as atividades no caderno

1. Escreva a unidade de medida que, em sua opinião, é adequada para medir:

a) o comprimento de uma mangueira de jardim;

b) a área de um campo de futebol;

c) a capacidade de um copo;

d) a massa de um caminhão;

e) a duração de um comercial na TV.

Página 131

2. Identifique as cenas em que a unidade de medida mencionada não foi bem empregada. Em seguida, reescreva, em seu caderno, as falas dessas cenas usando a unidade de medida adequada.

Ilustração A. Garoto de uniforme escolar sentado em um banco com um pé apoiado uma bola. À frente dele, menino de uniforme em pé diz: Meço mil e 300 milímetros de altura.

Ilustração B. Frentista de boné ao lado da bomba de combustível entrega chave do carro para mulher negra que está ao lado do carro. Ele diz: Foram abastecidos 30 litros de combustível.

Ilustração C. Dois rapazes com mochila nas costas saindo da academia. Eles estão lado a lado. O homem a esquerda diz: Ufa! Hoje fiz 45 minutos de caminhada na esteira.

Ilustração D. Senhor grisalho chega ao balcão da padaria e pede ao atendente: Eu gostaria de 0,15 de quilograma de presunto, por favor. Sobre o balcão há uma balança.

2 Unidades de medida de comprimento

O metro é a unidade de base do Sistema Internacinal de Unidades para medir comprimentos e essa unidade não é adequada, por exemplo, para medir a distância entre duas cidades ou o comprimento de um grão de arroz. Para casos como esses, devemos utilizar seus múltiplos (unidades de medida maiores que o metro) e submúltiplos (unidades de medida menores que o metro).

O submúltiplo adequado para medir o comprimento de um grão de arroz é o milímetro (ême ême) (1 milímetro equivale a 0,001 metro) e o múltiplo adequado para medir a distância entre duas cidades é o quilômetro (cá ême) (1 quilômetro equivale a .1000 metros).

Existem casos em que as medidas das distâncias são tão grandes que o quilômetro não é uma unidade de medida adequada. Para medir, por exemplo, as distâncias entre planetas e estrelas, é usada uma unidade baseada na medida da distância média da Terra ao Sol: a unidade astronômica (uma unidade astronômica, ou uma unidade astronômica, equivale a ...149597870700 metros).

Fotografia. Mão de pessoa com grãos de arroz caindo no saco com grãos de arroz. — Segundo o Instituto Agronômico (IAC) do estado de São Paulo, um grão de arroz polido mede, em média, 6,84 milímetros de comprimento.

Página 132

Há, ainda, seres ou objetos tão pequenos que podemos vê-los somente usando um microscópio. Para medi-los, existem outros submúltiplos da unidade de medida metro, como o micrômetro (1 micrômetro, ou 1 μm, equivale a 0,000001 metro) e o nanômetro (1 nanômetro, ou 1 êne ême, equivale a 0,000000001 metro). Para ter uma ideia de quão pequenas são essas medidas, basta considerar que a medida da espessura de um fio de cabelo é de aproximadamente 50 micrômetros ou .50000 nanômetros.

Ilustração. Representação artística do planeta Urano. Planeta com variações de cor azul e rosa. Ao redor do planeta tem a representação de uma circunferência representando o anel do planeta. — Os astrônomos detectaram raios X de Urano pela primeira vez no Observatório de raios X Chandra, da NASA, como mostrado nesta imagem de março de 2021. A medida da distância entre Urano e o Sol é de cérca de 18,8 unidades astronômicas.

Fotografia. Ácaro, tipo de aracnídeo. É pequeno de formato oval, cor amarelada, extremidade frontal triangular e apresenta quatro pares de pernas. — Lorryia formosa, ácaro amarelo comumente encontrado em plantas cítricas, ampliado trezentas e quarenta vezes, colorizado artificialmente. Os ácaros são visíveis apenas ao microscópio, e medem entre 140 e 170 micrômetros.

Vamos estudar agora os principais múltiplos e submúltiplos da unidade de medida metro.

Múltiplos da unidade de medida metro

Para medir grandes comprimentos, recorremos aos múltiplos da unidade de medida metro: o decâmetro (dê ah ême), o hectômetro (agá ême) e o quilômetro (cá ême).

As relações desses múltiplos com a unidade de medida metro são:

1 decâmetro = 10 ⋅ 1 métro = 10 métros

1 hectômetro = 100 ⋅ 1 métro = 100 métros

1 quilômetro = .1000 ⋅ 1 métro = .1000 métros

Ilustração. Homem de bigode, camisa verde e calça azul está em pé ao lado de um quadro de giz com esquema. Ele fala: 'A medida da distância entre Maceió e Aracaju é 605 quilômetros, que equivalem a 605 mil metros.' No quadro de giz, o esquema: 605 quilômetros. Abaixo do número 605, linha que leva para o 605. Abaixo de quilô, linha que leva para o número mil. Abaixo de metros, linha que leva para a palavra metros. Abaixo, abre parênteses, 605 vezes mil, fecha parênteses, metros. Abaixo, 605 mil metros.

Submúltiplos da unidade de medida metro

Para medir pequenos comprimentos, usamos os submúltiplos da unidade de medida metro: o decímetro (dê ême), o centímetro (cê ême) e o milímetro (ême ême).

As relações desses submúltiplos com a unidade de medida metro são:

1 decímetro =

\frac{1}{10}

⋅ 1 métro = 0,1 métro

1 centímetro =

\frac{1}{100}

⋅ 1 métro = 0,01 métro

1 milímetro =

\frac{1}{1000}

⋅ 1 métro = 0,001 métro

Ilustração. Mulher loira de casaco vermelho florido segura um caderno de espiral na horizontal e diz: Este caderno mede 28 centímetros de comprimento, que equivale a 0 vírgula 28 metros.

Página 133

Observe o quadro com a equivalência entre essas unidades de medida de comprimento e a unidade de medida metro.

	Múltiplos	Unidade de medida de base	Submúltiplos
Unidade de medida	quilômetro	hectômetro	decâmetro	metro	decímetro	centímetro	milímetro
Símbolo	km	hm	dam	m	dm	cm	mm
Relação com a unidade de medida metro	1.000 m	100 m	10 m	1 m	0,1 m	0,01 m	0,001 m

Para pensar

a) Que operação deve ser realizada para transformar uma medida de comprimento expressa em determinada unidade de medida para outra imediatamente superior? E para transformar para uma unidade de medida imediatamente inferior?

b) Como podemos expressar a medida 5 hectômetros na unidade de medida decímetro?

ATIVIDADES

faça as atividades no caderno

1. Expresse as medidas de comprimento nas unidades indicadas.

a) 15 centímetros em métro

b) 5 métros em centímetro

c) 3 quilômetros em métro

d) 3 hectômetros em decímetro

e) 70 milímetros em decâmetro

f) 0,1 quilômetro em centímetro

2. Expresse as medidas de distância em metro.

a) 9 quilômetros e 8 decâmetros

b) 18 quilômetros e 8 decâmetros

c) 2 quilômetros, 5 hectômetros e 7 decâmetros

d) 49 decímetros e 12 centímetros

e) 235 centímetros e 125 milímetros

f) 36 decímetros, 7 centímetros e 1 milímetro

3. Reescreva as frases substituindo o ◼ pela unidade de medida adequada.

a) João mede 1,76 ◼ ou 17,6 ◼ de altura.

b) Uma régua de 30 ◼ mede 300 ◼ de comprimento.

c) A medida da distância entre Belo Horizonte e Goiânia é de 884 ◼ ou .88400 ◼.

d) Carlos mede 1,8 ◼ ou 0,18 ◼ de altura.

4. Corrija as afirmações a seguir em seu caderno.

a) 2 decâmetros equivalem a 0,2 métro.

b) 1 micrômetro equivale a 0,000001 milímetro.

c) As unidades de medida quilômetro, hectômetro e decâmetro são submúltiplos da unidade de medida metro.

5.

Elabore um problema considerando as informações a seguir. Depois, entregue-o a um colega para que ele o resolva.

Trajeto medindo 720 métros de distância.

O passo de Maria mede 45 centímetros de comprimento.

6. Toda manhã, Antônio pratica corrida no parque.

Ilustração. Homem de boné, blusa e bermuda correndo em um parque com grama e árvores.

Ele costuma percorrer 130 hectômetros, mas hoje só conseguiu correr

\frac{3}{4}

dessa medida de distância. Qual foi a medida de distância, em metro, percorrida por Antônio hoje?

7. Observe a foto de uma alga, obtida por meio de um microscópio eletrônico, e faça o que se pede.

Fotografia. Alga verde com formato próximo ao circular. A largura dessa alga está destacada com uma linha branca. — Alga verde, Micrasterias, ampliada 100 vezes, colorizada artificialmente.

• Na foto, a alga foi ampliada de modo que suas medidas de comprimento, como a sua largura, destacada com uma linha branca, foram mutiplicadas por 100. Com uma régua, meça o comprimento da linha branca e calcule, em micrômetro, a medida de comprimento real aproximada da largura da alga.

Página 134

8. Responda às questões.

Fotografia. Fundo escuro com planeta vermelho. — Planeta Marte, 2020.

Fotografia. Fundo escuro com planeta amarelo e círculo ao redor representando os anéis. — Planeta Saturno, 2020.

a) A distância média entre Marte e o Sol mede 1,53 unidade astronômica. A quantos metros equivale essa medida de distância?

b) A distância de Saturno ao Sol mede aproximadamente 9,54 unidades astronômicas. A quantos quilômetros equivale essa medida de distância?

3 Unidades de medida de tempo

O segundo (ésse), o minuto (ême ih êne) e a hora (agá) são unidades de medida de tempo, sendo o segundo a unidade de medida de base do Sistema Internacinal de Unidades.

uma hora equivale a 60 minutos (uma hora = 60 minutos)

1 minuto equivale a 60 segundos (1 minuto = 60 segundos)

Agora, observe como podemos aplicar essas relações para resolver o problema a seguir.

Antônia está treinando para participar de um campeonato estadual de triatlo.

Fotografia. Atletas saindo da água, eles estão de macacão touca e óculos.

Fotografia. Vista frontal de quatro pessoas correndo de macacão.

Fotografia. Vista frontal de pessoas de capacete e roupa de natação andando de bicicletas. — Atletas em prova de triatlo nos Jogos Olímpicos de Tóquio em 2021.

No último treino, ela conseguiu a medida de tempo de 18 minutos e 37 segundos na natação, 34 minutos e 59 segundos no ciclismo e uma hora e 59 segundos na corrida. Qual foi a medida de tempo total de Antônia no treino?

Inicialmente, adicionamos as medidas de tempo obtidas por Antônia em cada modalidade.

Esquema. Medida de tempo na natação: 0 hora mais 18 minutos mais 37 segundos. Abaixo, medida de tempo no ciclismo: 0 hora mais 34 minutos mais 59 segundos. em seguida, medida de tempo na corrida: 1 hora mais 0 minutos mais 59 segundos. Traço abaixo e medida de tempo total: 1 hora mais 52 minuto mais 155 segundos.

Como 60 segundos correspondem a 1 minuto, podemos transformar a medida de tempo 155 segundos em minuto, fazendo o seguinte cálculo:

Esquema. Algoritmo da divisão. Dividendo 155. Dentro da chave, divisor 60. Abaixo de 155, número 35 (segundos). Abaixo da chave, quociente 2 (minutos).

Portanto, a medida de tempo 155 segundos corresponde a 2 minutos e 35 segundos.

Página 135

Depois, adicionamos as medidas de tempo em minuto:

52 minutos + 2 minutos = 54 minutos

Logo, a medida de tempo total de Antônia no treino foi uma hora, 54 minutos e 35 segundos, ou uma hora 54 minutos 35 segundos.

Para pensar

a) O que se deve fazer para transformar uma medida de tempo expressa em determinada unidade para outra unidade de medida imediatamente superior? E para transformar em uma unidade de medida imediatamente inferior?

b) Como podemos expressar a medida de tempo .5400 segundos em hora?

ATIVIDADES

faça as atividades no caderno

1. Responda às questões.

a) Quantos segundos tem 1 dia?

b) Quantas horas tem uma semana?

c) Quantos dias aproximadamente correspondem à medida de tempo de mil horas? E à de 1 milhão de segundos?

d) O coração de um adulto bate, em média, 70 vezes por minuto. Quantas vezes ele bate em 1 dia?

2. No vácuo, a luz percorre, aproximadamente, .300000 quilômetros em 1 segundo. A distância da Terra ao Sol mede em torno de ..150000000 quilômetros. Quantos minutos, aproximadamente, a luz do Sol demora para chegar à Terra?

3. Acionando a válvula de descarga por 6 segundos, gastam-se 10 litros de água. No banheiro de Rafael, a válvula de descarga quebrou e ficou acionada por 3 minutos, até que ele fechasse o registro de água. Quantos litros de água foram desperdiçados nesse período?

4. Nas Olimpíadas, uma das provas de ciclismo é chamada “estrada contra o relógio”. Nela, os ciclistas largam um de cada vez, em intervalos que medem 90 segundos, para percorrer .45800 métros. Quem faz a menor medida de tempo ganha a corrida.

a) Se o primeiro ciclista sair às 9 horas 45 minutos 24 segundos, a que horas sairão o segundo e o terceiro ciclista?

b) Associe a medida de tempo dos três primeiros colocados ao respectivo lugar no pódio:

• Fábio demorou uma hora, 1 minuto e 57 segundos para completar a prova.

• César demorou .3719 segundos.

• João demorou 61 minutos e 58 segundos.

5. Pedro, Nélson, Osvaldo e José participaram de uma corrida. O quadro indica a medida de tempo que cada um levou para concluir a prova.

Medida de tempo de prova
Pedro	355 s
Nélson	5 min e 40 s
Osvaldo	5 min e 35 s
José	400 s

• Associe a medida de tempo de cada um ao respectivo lugar no pódio, sabendo que eles foram os quatro primeiros colocados.

6.

Elabore um problema que envolva duas unidades de medida de tempo e a informação da legenda da foto. Depois, entregue-o a um colega para que ele o resolva.

Fotografia. Vista frontal de homem fazendo nado borboleta em uma piscina. Ele está de touca e óculos. Os braços e cabeça estão fora da água. — Na prática de natação, o gasto energético é de cérca de 6 quilocalorias (unidade de medida de energia) por minuto.

7.

Na emissora TV Piada, uma propaganda vai ao ar a cada 35 minutos. Na emissora TV Choradeira, a mesma propaganda vai ao ar a cada 40 minutos.

Às 12 horas, a propaganda foi ao ar, simultaneamente, nas duas emissoras. Descubra qual será o próximo horário em que isso ocorrerá.

Página 136

4 Unidades de medida de massa

O quilograma (cá gê), o grama (gê) e o miligrama (ême gê) são unidades de medida de massa, sendo o quilograma a unidade de base do Sistema Internacinal de Unidades.

No entanto, há outras unidades de medida de massa que são menos utilizadas. Observe a seguir.

Múltiplos da unidade de medida grama

Para medir massas maiores que 1 grama, convém usarmos os múltiplos da unidade de medida grama: o decagrama (dê ah gê), o hectograma (agá gê) e o quilograma (cá gê).

As relações desses múltiplos com a unidade de medida grama são:

1 decagrama = 10 ⋅ 1 grama = 10 gramas

1 hectograma = 100 ⋅ 1 grama = 100 gramas

1 quilograma = .1000 ⋅ 1 grama = .1000 gramas

Submúltiplos da unidade de medida grama

Para medir massas menores que 1 grama, convém usarmos os submúltiplos da unidade de medida grama: o decigrama (dê gê), o centigrama (cê gê) e o miligrama (ême gê).

As relações desses submúltiplos com a unidade de medida grama são:

1 decigrama =

\frac{1}{10}

⋅ 1 grama = 0,1 grama

1 centigrama =

\frac{1}{100}

⋅ 1 grama = 0,01 grama

1 miligrama =

\frac{1}{1000}

⋅ 1 grama = 0,001 grama

No quadro a seguir, estão indicadas as unidades de medida de massa com os símbolos e a relação de cada múltiplo e submúltiplo com a unidade de medida grama.

	Múltiplos	Unidade de medida de referência	Submúltiplos
Unidade de medida	quilograma	hectograma	decagrama	grama	decigrama	centigrama	miligrama
Símbolo	kg	hg	dag	g	dg	cg	mg
Relação com a unidade de medida grama	1.000 g	100 g	10 g	1 g	0,1 g	0,01 g	0,001 g

Ilustração. Frasco de complemento alimentar. Destaque para o rótulo: Informação nutricional. Porção de 6 gramas (12 comprimidos). Carboidratos: 27 decigrama Proteínas: 22 decigrama Gorduras totais: 2 decigrama Gorduras saturadas: 0 grama Sódio: 2 miligrama Cálcio: 44 miligrama Ferro: 0 vírgula 58 miligrama Vitamina B1: 0 vírgula 14 miligrama Fósforo: 77 miligrama Potássio: 12 centigrama — Em geral, as unidades de medida menores que 1 grama aparecem nas tabelas de informação nutricional das embalagens de alguns comprimidos.

Página 137

Para pensar

a) O que se deve fazer para transformar uma medida de massa expressa em determinada unidade para outra unidade de medida imediatamente superior? E para transformar em uma unidade de medida de massa imediatamente inferior?

b) Como podemos expressar a unidade de medida de massa .150000 miligramas em hectograma?

Observação

Também são usadas unidades de medida de massa, como:

• a tonelada (símbolo tê), que equivale a .1000 quilogramas;

• a arroba (símbolo letra á contornada por uma linha curva), que equivale a aproximadamente 15 quilogramas.

ATIVIDADES

faça as atividades no caderno

1. Responda às questões.

a) Quantos gramas há em 425 hectogramas?

b) Quantos quilogramas há em 235 vírgula 6 toneladas?

c) Quantos quilogramas há em 124 arrobas?

2. Uma distribuidora de material de construção vende sacos de cimento em dois tamanhos, com as medidas de massa e valores a seguir: um de 500 gramas que custa R$ 1,00um reais e outro de 1,5 quilogramas que custa R$ 2,00dois reais.

a) Se uma pessoa precisa de 12 quilogramas de cimento, quantos sacos de 500 gramas precisa comprar? E de 1,5 quilograma?

b) De acordo com os preços de cada saco de cimento, o que é mais vantajoso para uma pessoa que precisa comprar exatamente 10 quilogramas de cimento?

3. Complete o enunciado do problema com os valores em real e a unidade de medida de massa a seguir. Depois resolva-o.

Fichas. Três fichas com as informações: 5 reais. 18 arrobas e 52 reais e 64 centavos .

Vítor comprou

de feijão para seu armazém e pagou

por arroba. Depois, vendeu cada quilograma de feijão por

. Qual foi o lucro de Vítor nessa venda?

4. Observe a informação nutricional de uma barra de cereal.

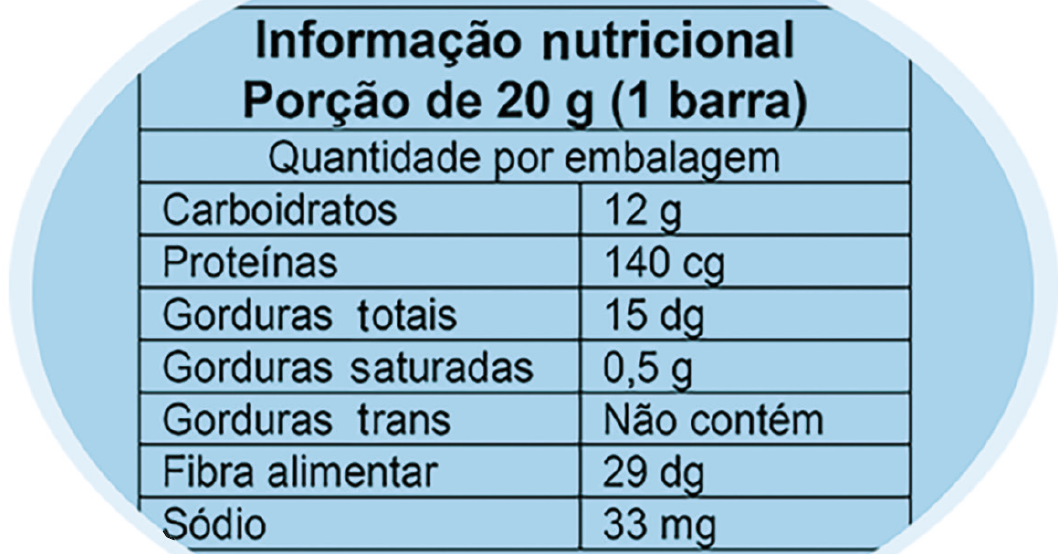
Ilustração. Destaque para o rótulo de uma barra de cereal: Informação nutricional. Porção de 20 gramas (uma barra). Quantidade por embalagem Carboidratos: 12 gramas Proteínas: 140 centigramas Gorduras totais: 15 decigramas Gorduras saturadas: 0 vírgula 5 grama Gordura Trans: não contém Fibra alimentar: 29 decigramas Sódio: 33 miligramas

• Agora, identifique as afirmações verdadeiras.

a) Uma barra de cereal contém 290 centigramas de fibra alimentar.

b) Nessa barra de cereal, há mais proteínas que carboidratos.

c) A quantidade de fibra alimentar é maior que o dobro da quantidade de proteínas.

Página 138

5 Unidades de medida de volume

Para medirmos o volume de um corpo, podemos usar o metro cúbico (ême 3 sobrescrito) como unidade de medida.

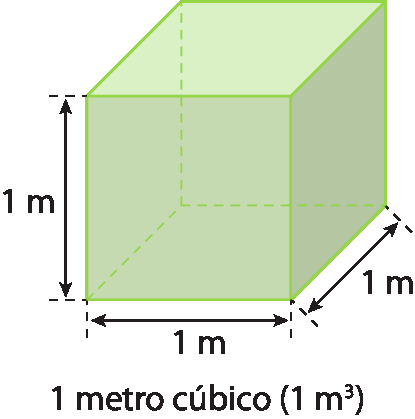
Figura geométrica. Cubo verde com indicação de medida das dimensões: 1 m por 1 m por 1 m.

Há outras unidades de medida de volume, como o centímetro cúbico (cê ême³) e o decímetro cúbico (dêême 3 sobrescrito).

Recorde

• Um metro cúbico corresponde à medida de volume de um cubo com arestas que medem 1 métro de comprimento.

• Um centímetro cúbico equivale à medida de volume de um cubo com arestas que medem 1 centímetro de comprimento.

• Um decímetro cúbico corresponde à medida de volume de um cubo com arestas que medem 1 decímetro de comprimento.

Observe o quadro com a equivalência entre algumas unidades de medida de volume e o metro cúbico.

	Múltiplos	Unidade de medida de referência	Submúltiplos
Unidade	quilômetro cúbico	hectômetro cúbico	decâmetro cúbico	metro cúbico	decímetro cúbico	centímetro cúbico	milímetro cúbico
Símbolo	km3	hm3	dam3	m3	dm3	cm3	mm3
Relação com a unidade de medida metro cúbico	1.000.000.000 m3	1.000.000 m3	1.000 m3	1 m3	0,001 m3	0,000001 m3	0,000000001 m3

Para pensar

a) O que se deve fazer para transformar uma medida de volume expressa em determinada unidade para outra unidade de medida de volume imediatamente superior? E para transformar para uma unidade de medida inferior?

b) Como podemos expressar .3000 milímetros cúbicos em metro cúbico?

Medida do volume de paralelepípedos

A medida do volume de qualquer paralelepípedo é igual ao produto da medida de seu comprimento pela medida de sua altura e de sua largura. Então, a medida do volume de um paralelepípedo, em que a representa a medida do comprimento, b a da largura e c a da altura, é dado por:

V = a ⋅ b ⋅ c

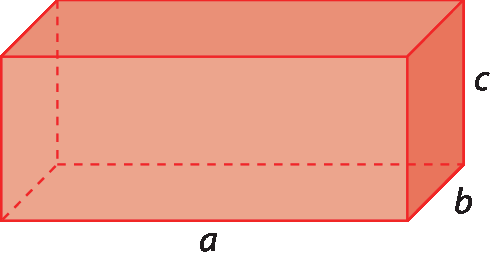
Figura geométrica. Paralelepípedo vermelho com dimensões: a por b por c.

O cubo é um caso particular de paralelepípedo cujas arestas têm a mesma medida de comprimento. Assim, a medida do volume de um cubo cujos comprimentos das arestas medem

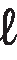
é dado por:

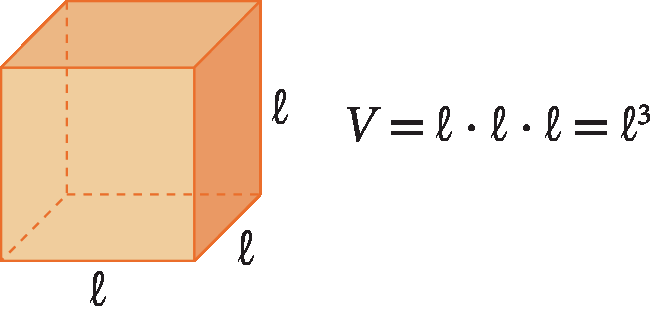
Figura geométrica. Cubo laranja medindo l por l por l. Sentença matemática. V igual a l vezes l vezes l igual a l ao cubo.

Página 139

ATIVIDADES

faça as atividades no caderno

1. Faça as transformações indicadas.

a) 0,000005 hectômetro cúbico em métro cúbico

b) .5800 milímetros cúbicos em centímetro cúbico

c) .320000 centímetros cúbicos em métro cúbico

d) 1,0258 hectômetro cúbico em decímetro cúbico

2. Calcule a medida do volume, em decímetro cúbico, dos paralelepípedos a seguir representados.

a)

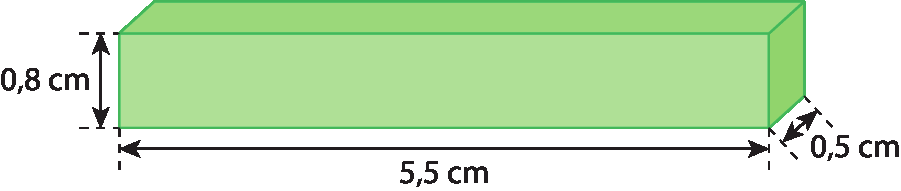
Figura geométrica. Paralelepípedo verde com indicação das dimensões: 0 vírgula 8 centímetro por 5 vírgula 5 centímetros por 0 vírgula 5 centímetro.

b)

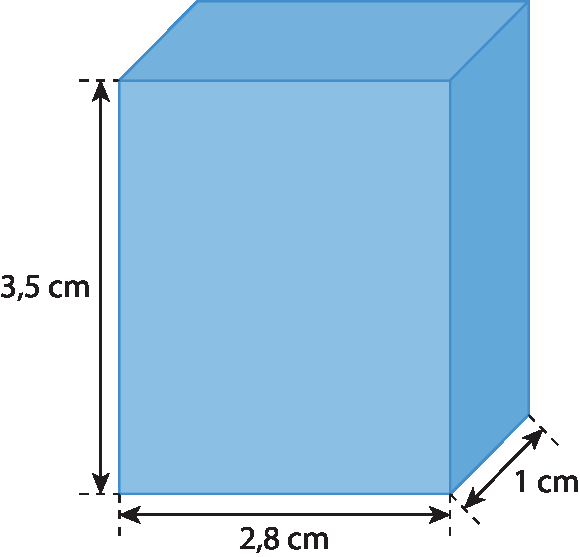
Figura geométrica. Paralelepípedo azul com indicação das dimensões: 3 vírgula 5 centímetros por 2 vírgula 8 centímetros por 1 centímetro.

3. Responda às questões.

a) Quantas vezes a medida do volume de um cubo de arestas que medem 0,2 decímetro de comprimento equivale à medida do volume de um cubo cujas arestas medem 4 centímetros de comprimento?

b) Quantas vezes a medida do volume de um paralelepípedo de arestas que medem 2 centímetros, 4 centímetros e 1 centímetro de comprimento equivale à medida do volume de um cubo cujas arestas medem 20 milímetros de comprimento?

4.

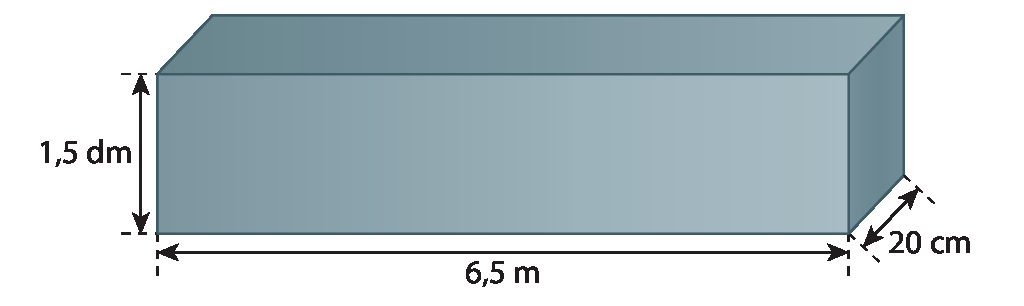
Elabore uma pergunta para a situação a seguir que envolva o cálculo da medida de volume. Depois, entregue-o a um colega para que ele a responda.

Uma empresa siderúrgica produz barras maciças de ferro que lembram paralelepípedos. Observe a representação de uma dessas peças.

Figura geométrica. Paralelepípedo cinza com indicação das dimensões: 1 vírgula 5 decímetro por 6 vírgula 5 metros por 20 centímetros.

6 Unidades de medida de capacidade

As duas unidades de medida de capacidade mais usadas no dia a dia são o litro (éle) e o mililitro (ême éle). A partir da unidade de medida litro obtemos os seus múltiplos e submúltiplos.

Múltiplos da unidade de medida litro

Os múltiplos da unidade de medida de capacidade litro são o decalitro (dê ah éle), o hectolitro (agá éle) e o quilolitro (cá éle).

1 decalitro = 10 ⋅ 1 litro = 10 litros

1 hectolitro = 100 ⋅ 1 litro = 100 litros

1 quilolitro = .1000 ⋅ 1 litro = .1000 litros

Página 140

Submúltiplos da unidade de medida litro

Os submúltiplos da unidade de medida litro são: o decilitro (dê éle), o centilitro (cê éle) e o mililitro (ême éle).

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

Fotografia. Garrafa de suco de laranja com destaque para a capacidade 380 mililitros. — Garrafa de suco com capacidade medindo 380 mililitros.

1 decilitro =

\frac{1}{10}

⋅ 1 litro = 0,1 litro

1 centilitro =

\frac{1}{100}

⋅ 1 litro = 0,01 litro

1 mililitro =

\frac{1}{1 000}

⋅ 1 litro = 0,001 litro

O quadro a seguir apresenta a equivalência entre cada múltiplo e submúltiplo com a unidade de medida litro.

	Múltiplos	Unidade de medida de referência	Submúltiplos
Unidade	quilolitro	hectolitro	decalitro	litro	decilitro	centilitro	mililitro
Símbolo	kL	hL	daL	L	dL	cL	mL
Relação com a unidade de medida litro	1.000 L	100 L	10 L	1 L	0,1 L	0,01 L	0,001 L

Ilustração. João, menino de cabelo claro, camisa e bermuda azuis. Ele em pé fala: Laura, você se lembra da relação entre medida de volume e medida de capacidade. Ao lado, Laura, menina cadeirante de cabelo castanho, camiseta cor de rosa e calça azul. Ela diz: Lembro sim, João. A medida de volume de 1 decímetro cúbico equivale à medida de capacidade de 1 litro. Laura imagina: uma jarra de 1 litro de água sendo despejada em caixa cúbica com medidas: 1 decímetro por 1 decímetro por 1 decímetro.

Para pensar

a) O que se deve fazer para transformar uma medida de capacidade expressa em determinada unidade de medida para outra unidade de medida imediatamente superior? E para transformar para uma unidade de medida inferior?

b) Como podemos expressar 75 decilitros em decalitro?

Página 141

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

ATIVIDADES

faça as atividades no caderno

1. Responda às questões em seu caderno.

a) Quantos litros são necessários para obter 3 hectolitros?

b) Quantos centilitros são necessários para obter 2,5 decalitros?

c) A quantos litros equivalem 6,3 decâmetros cúbicos?

d) Quantos mililitros são necessários para obter 5 litros?

2.

Elabore um problema utilizando as informações a seguir e que envolva a comparação de unidades de medida. Depois, entregue-o a um colega para que ele o solucione.

Um chuveiro gotejando desperdiça 46 litros de água por dia.

A capacidade da caixa-d’água de uma casa mede 500 litros.

3. A capacidade de um copo descartável usado em festas mede 250 mililitros. Quantos copos cada pessoa deverá tomar para que 35 pessoas, juntas, consumam no mínimo 20 litros de suco?

4. Um instituto de proteção ao consumidor recolheu quatro embalagens de suco (com formato de bloco retangular) para analisar. Duas delas foram reprovadas por não terem medida de capacidade suficiente para armazenar 1 litro de suco conforme indicava a embalagem.

Quadros com informações dos rótulos das embalagens. Embalagem A Medida da altura: 12 vírgula 5 centímetros Medida da largura: 10 centímetros Medida do comprimento: 7 vírgula 5 centímetros Embalagem B Medida da altura: 13 vírgula 5 centímetros Medida da largura: 11 vírgula 5 centímetros Medida do comprimento: 6 vírgula 5 centímetros Embalagem C Medida da altura: 13 centímetros Medida da largura: 9 centímetros Medida do comprimento: 8 centímetros Embalagem D Medida da altura: 18 centímetros Medida da largura: 12 centímetros Medida do comprimento: 5 centímetros

• Quais foram as embalagens reprovadas?

5. Marcela pretende encher com água um balde de 5 litros. Ao lado do balde, há os recipientes cheios de água representados na ilustração a seguir.

Ilustração. Mesa com recipientes e a indicação da capacidade de cada um deles. À esquerda, balde: 5 litros. 1. copo: 250 centímetros cúbicos. 2. Xícara: 150 decímetros cúbicos. 3. Garrafa: 1 vírgula 5 decímetros cúbicos. 4. Garrafa grande: 2 vírgula 25 decímetros cúbicos. 5. Jarra: 5 decilitros. 6. Bule: 30 centilitros. 7. Caneca: 200 centímetros cúbicos.

• Marcela deve despejar no balde o conteúdo de quais desses recipientes?

6. Associe o recipiente à medida de capacidade correspondente.

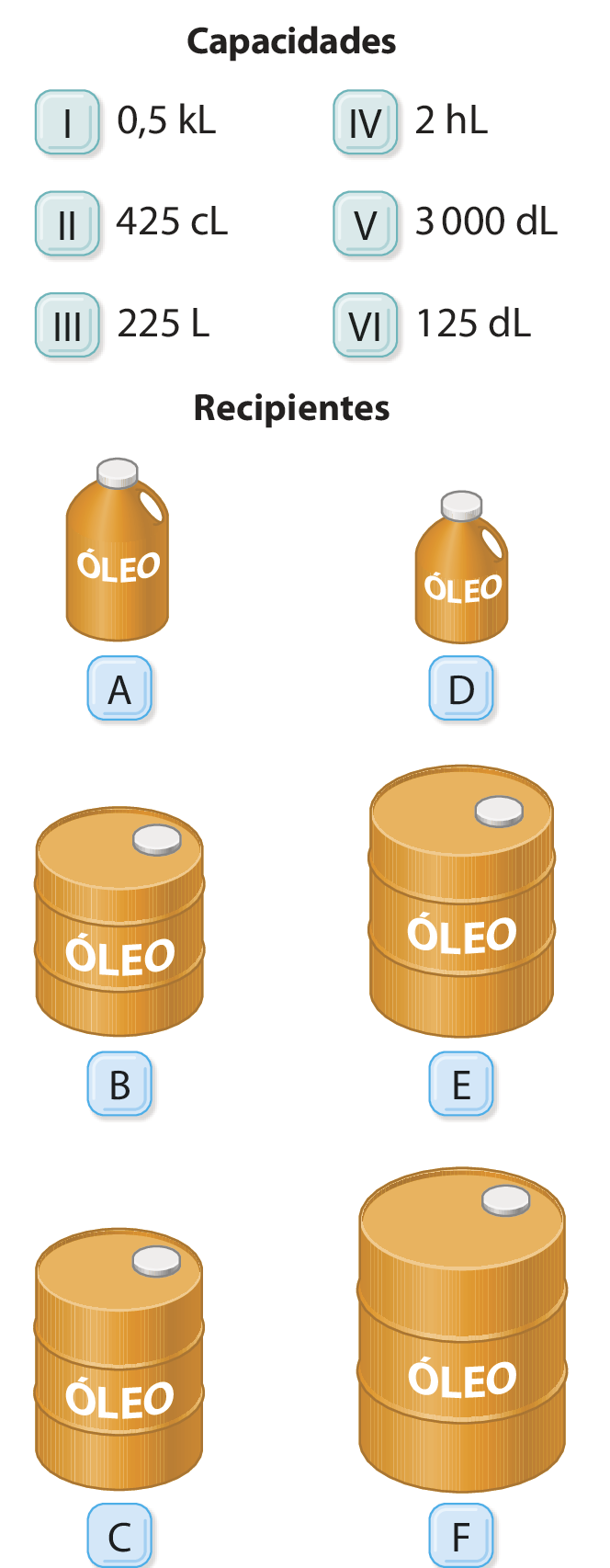
Itens. 1. 0,5 kL 2. 425 cL 3. 225 L 4. 2 hL 5. 3 mil dL 6. 125 dL. Ilustração. A. Galão de óleo grande. B. Barril de óleo pequeno. C. Barril de óleo médio. D. Galão de óleo pequeno. E. Barril de óleo grande. F. Barril de óleo muito grande.

Página 142

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

7. Augusto precisa comprar 7 litros de um produto que é vendido nas embalagens ilustradas a seguir.

Ilustração. Recipiente de 2 mil e 500 mL com preço de 20 reais. Recipiente de 5 decilitros com o preço de 5 reais. Recipiente de 200 centilitros com o preço 15 reais.

• Qual é a opção de combinação de embalagens mais econômica para Augusto?

8.

Diante de uma fonte, há dois baldes: um com medida de capacidade de 7 litros e outro com medida de capacidade de 5 litros.

Ilustração. Fonte de água com plantas ao redor. À esquerda da fonte há um balde em forma de cubo na cor azul de 7 litros e um balde em formado de vermelho de 5 litros.

• Como você faria para medir 4 litros?

7 Investigando medidas

Acompanhe a situação a seguir.

Oto e Maria mediram o comprimento de uma borracha com uma régua. Observe.

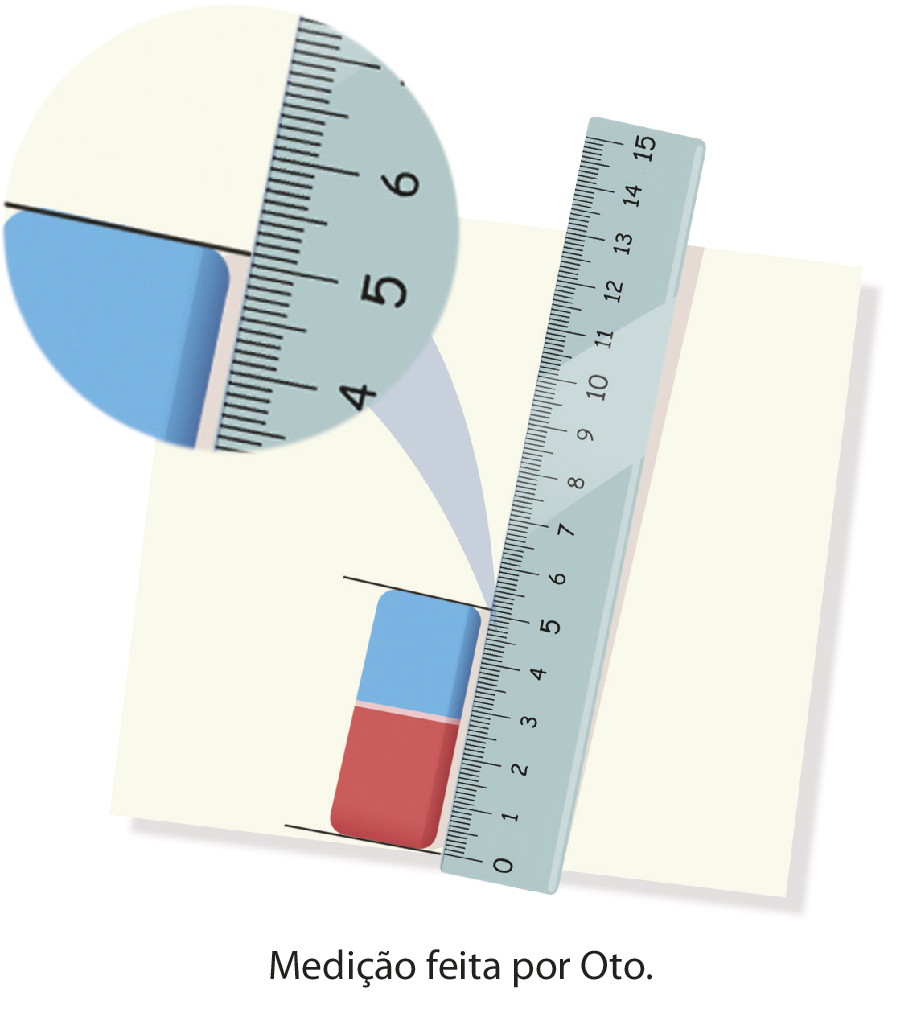
Ilustração. Borracha vermelha e azul ao lado de uma régua na cor azul. A aproximação da imagem da régua mostra que a borracha mede 5,1 centímetros.

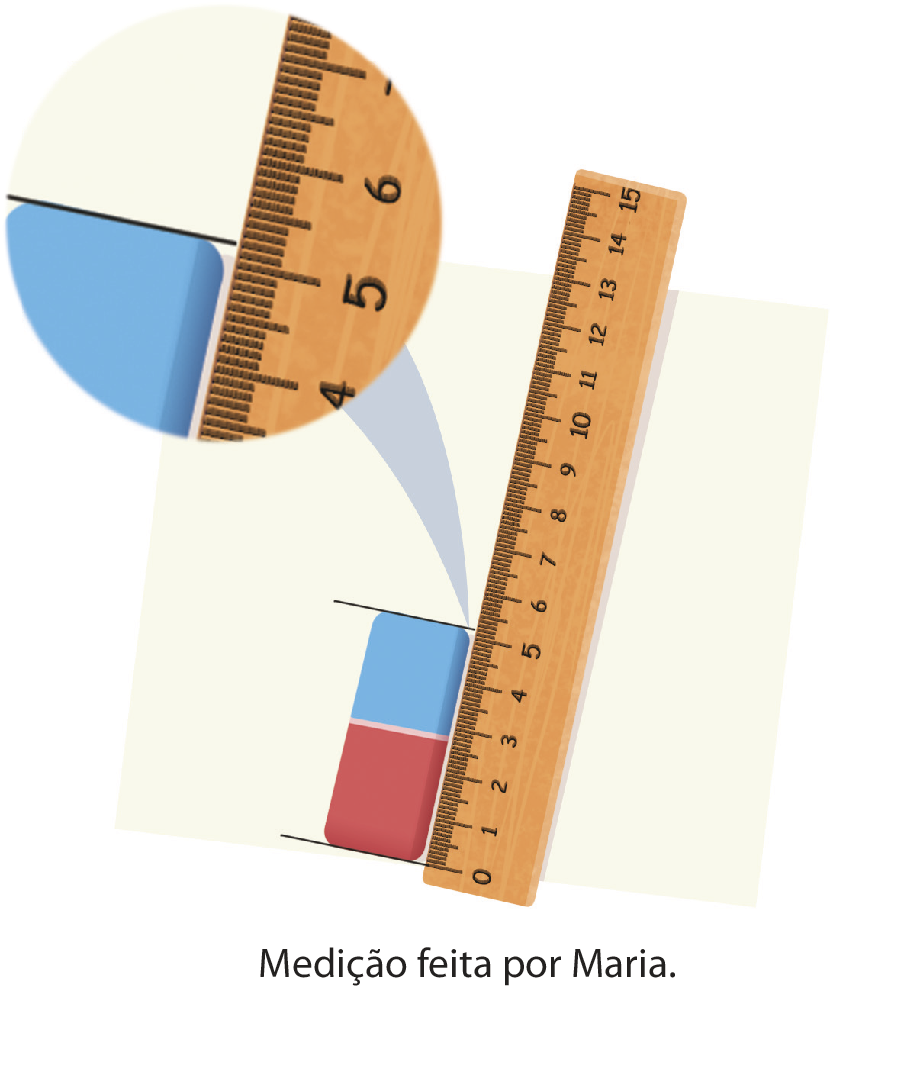
Ilustração. Borracha vermelha e azul ao lado de uma régua na cor laranja. A aproximação da imagem da régua mostra que a borracha mede 5,2 centímetros.

Note que o resultado das medições que eles fizeram foi diferente: Oto obteve a medida 5,1 centímetros, enquanto Maria obteve a medida 5,2 centímetros de comprimento. Nesse caso, a diferença ocorreu porque as réguas utilizadas por Oto e Maria não eram iguais.

Para analisar

Meça o comprimento do segmento a seguir com uma régua. Depois, compare o resultado da sua medição com o dos colegas. O que você pode perceber?

Página 143

O resultado de toda medição é aproximado. Isso acontece porque os resultados são influenciados pelos instrumentos de medida utilizados (que podem apresentar diferenças de fabricação), pelo processo de medição (manuseio e leitura do instrumento etcétera) e até mesmo pela medida da temperatura ambiente.

Ilustração. À esquerda, menina negra de cabelo enrolado segura uma régua laranja e diz: Olha só: os tracinhos da minha régua são mais grossos que os da sua. Ao lado, menino de cabelo preto segura régua azul e diz: Acho que foi por isso que o resultado das nossas medições foi diferente.

Transcrição do áudio

Um papo na medida

Duração: 3:50min. Página: 143.

>> [LOCUTORA] Um papo na medida

>> [LOCUTORA] Durante toda a nossa vida, usamos diferentes unidades pra medir cada tipo de grandeza. É essencial entender a relação entre as grandezas físicas e as unidades empregadas pra medi-las. Das várias maneiras de se medir a temperatura até os múltiplos e submúltiplos do metro que utilizamos pra calcular o comprimento, estamos cercados de situações em que a escolha de uma unidade de medida diferente da adequada pra cada circunstância pode gerar resultados imprevisíveis.

Vinheta.

Música de fundo.

>> [LOCUTORA] Para um bate-papo sobre as diferentes unidades de medidas e suas aplicações, convidamos o professor de Física, Roberto Spinelli Filho.

>> [Felipe] Bom dia, Roberto! Quais são as principais unidades de medida utilizadas no mundo?

>> [Roberto] Bom dia, Felipe. No nosso cotidiano, a gente costuma medir a distância, utilizando algumas unidades como o metro, o quilômetro; nós medimos a temperatura, pra saber se o dia está mais agradável, mais ameno, ou a temperatura está mais alta ou mais baixa, a gente utiliza graus Celsius ou graus Fahrenheit; pra medir a massa, quando você se pesa em uma balança, você normalmente utiliza o quilograma; e também pra medir o tempo, a gente usa segundos, minutos ou horas.

>> [Felipe] E quais as diferenças entre elas? Elas podem ser utilizadas em qualquer situação?

>> [Roberto] Olha, você até pode utilizar mais do que uma unidade de medida pra medir a mesma grandeza. Então, quando a gente tá falando de temperatura, você pode escolher os graus Celsius ou graus Fahrenheit... Vai depender, talvez, do lugar. Se a gente tá falando do Brasil, a gente usa Celsius, nos Estados Unidos, Fahrenheit. Agora, em algumas outras situações, a escolha é da precisão que você quer usar. Então, se você tá marcando uma reunião, você vai falar em horas, em minutos: “A reunião vai acontecer às 2 horas e 30 minutos”. Em outras situações, talvez você precise da unidade de segundos: “Ah, essa tarefa aqui levou 10 segundos pra acontecer”.

>> [Felipe] E como fazemos para saber a medida exata de algo?

>> [Roberto] Olha, Felipe, desculpa te decepcionar, mas não temos como saber a medida exata de nada, porque não existe medida exata. Sempre que a gente faz uma medida, ela utiliza algum instrumento, e esse instrumento tem alguma precisão, ou seja, sempre é uma aproximação. Toda medida vai estar limitada à precisão do instrumento que você tá usando.

>> [Felipe] E se as unidades de medida não fossem padronizadas?

>> [Roberto] Olha, aí seria realmente um problema. A gente já teria dificuldade em conversar uns com os outros; uns tão falando em metros, outros tão falando em jardas, outros tão falando em milhas... seria realmente um problema. Mas esse problema poderia ser agravado quando pessoas diferentes estão, de repente, construindo algo juntos, como já aconteceu no desenvolvimento de um satélite, alguns engenheiros tavam trabalhando nas Unidades Internacionais e outros nas Unidades Imperiais, e o satélite não funcionou, porque o software tava numa unidade e o hardware em outra e, no final, o satélite não deu certo. Isso pode ser um problema! Mas, olha só, Felipe, o mais importante é que, mesmo que a gente não possa acessar a realidade com uma medida exata, mesmo que a gente não possa conhecer a medida exata de nada, isso não é um problema, isso, de fato, não é um problema, porque, como eu disse, a gente pode sempre ter uma escala que representa o que satisfaz a nossa necessidade em cada situação. Então, tá tudo bem, você pode dormir tranquilo, porque essa coisa de medida exata não é um bicho de sete cabeças, é apenas uma limitação da nossa realidade.

>> [Felipe] Excelente, Roberto! Muito obrigado pela entrevista, muito obrigado pelas informações, aprendemos muita coisa no nosso dia de hoje.

>> [Roberto] Eu que agradeço. Bom dia!

Os trechos das músicas “Safety Net” e “Soho”, de Riot, estão disponíveis no YouTube.

ATIVIDADES

faça as atividades no caderno

1. Identifique a(s) afirmação(ões) verdadeira(s).

a) O resultado de toda medição é aproximado.

b) A medida da temperatura ambiente nunca influencia o resultado de uma medição.

c) Instrumentos de medida convencionais com unidades padronizadas nunca geram diferentes resultados de medição.

2. Acompanhe esta situação.

Ilustração. Três meninas de uniforme. Após praticar atividade física uma delas está suada, parece cansada e diz: Quantos segundos levei para dar uma volta correndo na quadra? A menina que está no centro de cabelos presos olha o cronometro e fala: Você levou 34 segundos. A menina à direita olha o cronometro na mão e comenta: O meu cronômetro está marcando 33 segundos.

• Em sua opinião, por que os cronômetros registraram medidas de tempo diferentes?

3. Diego mediu sua massa 4 vezes consecutivas na mesma balança digital. Observe as medidas que apareceram no visor.

Ilustração. Balança digital marcando 71 vírgula 2 quilogramas. Ilustração. Balança digital marcando 71 vírgula 0 quilogramas. Ilustração. Balança digital marcando 71 vírgula 3 quilogramas. Ilustração. Balança digital marcando 71 vírgula 1 quilogramas.

• Agora, responda: em sua opinião, o que provocou essas diferenças?

Página 144

Trabalho em equipe

faça as atividades no caderno

Ícone de uma árvore com seta circular da direita
para esquerda e da esquerda para direita.

Consumo de água sem desperdício

Você e seu grupo participarão de uma campanha de conscientização, na escola, com o objetivo de combater o desperdício de água, mostrando, em números, os prejuízos causados por essa prática para a economia da família e para o meio ambiente.

Justificativa

A água é um recurso natural indispensável à sobrevivência de todos. Justificar a necessidade de evitar o desperdício de água, recorrendo a dados quantitativos, é uma maneira de usar a Matemática para conscientizar as pessoas.

Fotografia. Vista superior de lavandaria, apresenta máquina de lavar roupas com abertura frontal com a mangueira soltando água dentro de um recipiente. — Uma dica para economizar água é reutilizar a água usada para lavar roupas. Essa água pode ser aproveitada, por exemplo, para lavar o quintal.

Objetivo

• Elaborar uma campanha de conscientização sobre o desperdício de água usando dados quantitativos como argumentos.

Apresentação

• Cartazes com textos explicativos, tabelas, gráficos e ilustrações.

Questões para pensar em grupo

• Todos já viram cartazes de uma campanha de conscientização?

• O que mais chama a atenção de vocês nesse tipo de cartaz?

• Serão exploradas as consequências do mau uso da água para o meio ambiente, para a economia familiar ou para ambos?

• Que dados serão usados para convencer as pessoas da importância do uso racional da água (desperdício, disponibilidade e distribuição de água no mundo etcétera)?

• Em que fontes esses dados podem ser obtidos? Será preciso efetuar uma pesquisa e fazer cálculos para obtê-los?

• Como apresentar as informações de modo claro e interessante?

• Onde os cartazes podem ser afixados para que a campanha seja eficaz?

• Que materiais serão necessários para a elaboração dos cartazes?

Não se esqueçam

• Anotem as etapas necessárias para a elaboração do trabalho. Isso facilitará a organização do trabalho.

• Verifiquem com os responsáveis e coordenadores da escola a disponibilidade de espaços adequados à exposição dos cartazes de todos os grupos da classe.

Página 145

Estatística e Probabilidade

faça as atividades no caderno

Leitura e interpretação de pictogramas

A cantina da Escola Conhecimento realizou uma pesquisa sobre as sobremesas preferidas dos estudantes. Cada entrevistado pôde votar em apenas uma sobremesa. Para apresentar os resultados da pesquisa, obtidos no primeiro bimestre de 2023, o dono da cantina fez o pictograma a seguir.

Pictograma. Título: SOBREMESAS PREFERIDAS DOS ESTUDANTES DA ESCOLA CONHECIMENTO. Ícone: pote amarelo com colher dentro. Legenda: Cada ícone equivale a 20 votos. Pudim: 5 ícones Brigadeiro: 7 ícones Fruta: 8 ícones Sorvete: 5 ícones Bolo: 3 ícones

Dados obtidos pelo dono da cantina da Escola Conhecimento no 1º bimestre de 2023.

Ilustração. Garota de cabelo castanho preso e usando uniforme da escola. Ela segura uma maçã na mão esquerda e diz: Ao ler um pictograma, é importante prestar atenção na legenda, no título e na fonte da qual os dados foram retirados.

▶ Em que sobremesas os estudantes votaram?

▶ Quantos votos recebeu cada sobremesa? Qual foi a mais votada?

▶ Quantos estudantes responderam a essa pesquisa?

Nesse pictograma, escolheu-se o ícone

Ilustração. Pote amarelo com colher dentro.

para representar o número de votos que as sobremesas receberam. Observe que cada

equivale a 20 votos e que a linha vertical do pictograma foi utilizada para apresentar as sobremesas nas quais os estudantes votaram: bolo, sorvete, fruta, brigadeiro e pudim.

Acompanhe, a seguir, a distribuição dos votos.

• Na linha que representa os votos do pudim, há 5

, ou seja, 5 ⋅ 20.

Logo, o pudim recebeu 100 votos.

• Na linha que representa os votos do brigadeiro, há 7

, ou seja, 7 ⋅ 20.

Logo, o brigadeiro recebeu 140 votos.

• Na linha que representa os votos da fruta, há 8

, ou seja, 8 ⋅ 20.

Logo, a fruta recebeu 160 votos.

• Na linha que representa os votos do sorvete, há 5

, ou seja, 5 ⋅ 20.

Logo, o sorvete recebeu 100 votos.

• Na linha que representa os votos do bolo, há 3

, ou seja, 3 ⋅ 20.

Logo, o bolo recebeu 60 votos.

Página 146

▶ Estatística e Probabilidade

Comparando o número de votos das sobremesas, concluímos que a fruta foi a sobremesa mais votada, com 160 votos.

Como cada estudante só pôde votar em uma sobremesa, para determinar o total de estudantes entrevistados nessa pesquisa basta adicionar os votos que todas as sobremesas receberam. Assim, temos:

100 + 140 + 160 + 100 + 60 = 560

Portanto, foram entrevistados 560 estudantes da Escola Conhecimento.

ATIVIDADES

faça as atividades no caderno

1. Durante uma reunião em 2022, os moradores do Condomínio São Lucas organizaram um projeto para plantar 75 árvores nos jardins do condomínio em 2023. As árvores escolhidas seriam plantadas no decorrer de seis meses, como mostra o pictograma a seguir.

Pictograma. Título: PLANEJAMENTO PARA O PLANTIO DE ÁRVORES NO CONDOMÍNIO SÃO LUCAS NO 1º SEMESTRE DE 2 mil e 23. Ícone: árvore Legenda: Cada ícone equivale a 3 árvores. Eixo vertical: Número de árvores. Eixo horizontal: Mês Janeiro: duas árvores. Fevereiro: 4 ícones. Março: 4 ícones. Abril: 6 ícones. Maio: 5 ícones. Junho: 4 ícones.

Gráfico elaborado com base na ata da reunião do Condomínio São Lucas em maio de 2022.

a) Em que mês deveriam ser plantadas mais árvores? Quantas árvores deveriam ser plantadas nesse mês?

b) Quantas árvores teriam de ser plantadas nos três primeiros meses?

c) Em que meses deveriam ser plantadas 12 árvores?

2. Observe o pictograma que representa a quantidade de medalhas de ouro conquistadas por alguns países participantes dos Jogos Paralímpicos realizados em Tóquio, em 2021. Depois, responda às questões.

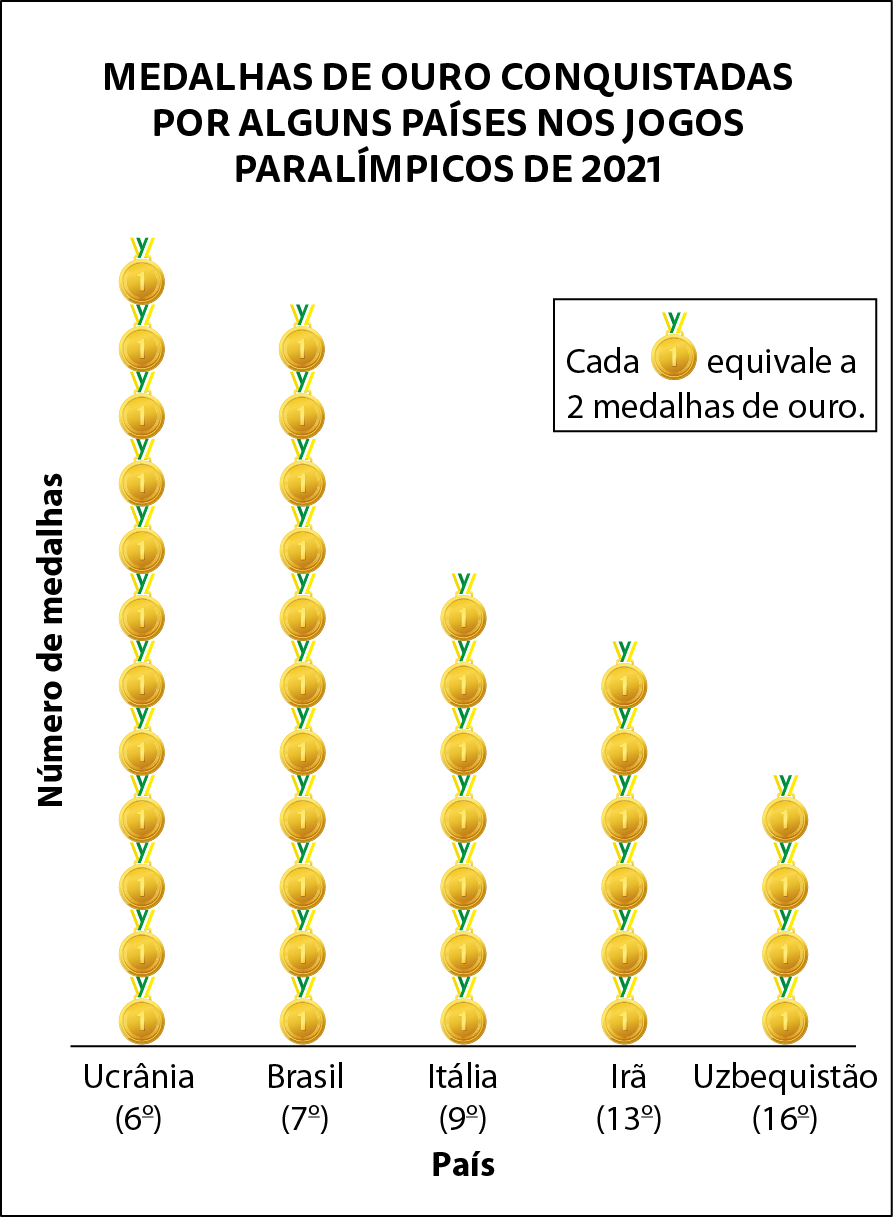
Pictograma. Título: MEDALHAS DE OURO CONQUISTADAS POR ALGUNS PAÍSES NOS JOGOS PARALÍMPICOS DE 2 mil e 21. Ícone: medalha dourada Legenda: Cada ícone equivale a duas medalhas de ouro. Ucrânia (sexto): 12 ícones. Brasil (sétimo): 11 ícones. Itália (nono): 7 ícones. Irã (décimo terceiro): 6 ícones. Uzbequistão (décimo sexto): 4 ícones.

Dados obtidos em: INTERNATIONAL PARALYMPIC COMMITTEE. Medal Standings. Disponível em: https://oeds.link/nNWMLE. Acesso em: 24 maio 2022.

a) Quantas medalhas de ouro cada país representado recebeu nos Jogos Paralímpicos de 2021?

b) Qual é a diferença no número de medalhas de ouro conquistado pelo Brasil e pelo Uzbequistão?

c) Sabendo que a Austrália recebeu vinte e uma medalhas de ouro, responda: qual foi a classificação final desse país? Explique como você descobriu.

Página 147

3. A revendedora de automóveis Auto BC fez um levantamento dos automóveis vendidos nos anos de 2019 a 2023. Para apresentar os dados aos funcionários, a empresa fez o pictograma a seguir.

Pictograma. Título: NÚMERO DE AUTOMÓVEIS VENDIDOS PELA REVENDEDORA AUTO BC DE 2 mil e 19 A 2 mil e 23. Ícone: carro vermelho Legenda: Cada ícone representa 100 automóveis. 2019: 2 ícones 2020: 3 ícones 2021: 4 ícones 2022: 4 ícones 2023: 5 ícones

Dados obtidos pela revendedora Auto BC entre 2019 e 2023.

• Agora, responda às questões de acordo com as informações apresentadas no pictograma.

a) Quantos automóveis foram vendidos em 2021?

b) Em que ano foram vendidos mais automóveis? Quantos?

c) Qual foi o total de automóveis vendidos nesses cinco anos?

4. Para montar o estoque de 2023, a loja de Cê dês Som Total fez o levantamento de vendas em 2022. Esse levantamento foi feito de acordo com o gênero de música e está representado no pictograma a seguir.

Pictograma. Título: CDS VENDIDOS PELA LOJA SOM TOTAL EM 2 mil e 22. Ícone: CD Legenda: Cada ícone equivale a mil CDs. Rock: 5 ícones Pagode: 2 ícones Axé: 2 ícones MPB: 4 ícones Forró: 5 ícones Outros: 2 ícones

Dados obtidos pela loja Som Total em 2022.

• Com base nas informações do pictograma, responda às questões.

a) Quantos Cê dês foram vendidos em 2022?

b) De quais gêneros musicais foram vendidos mais Cê dês em 2022?

5. A Secretaria de Turismo de Laranjinhas fez uma pesquisa para identificar os pontos turísticos do município mais visitados em 2023.

Ilustração. Cachoeira com uma mulher adulta vestindo maio vermelho, uma menina de cabelo preso sentada em uma pedra. Menino de sunga azul está brincando no poço da cachoeira.

Para apresentar os dados, foi publicado o seguinte pictograma em um jornal local:

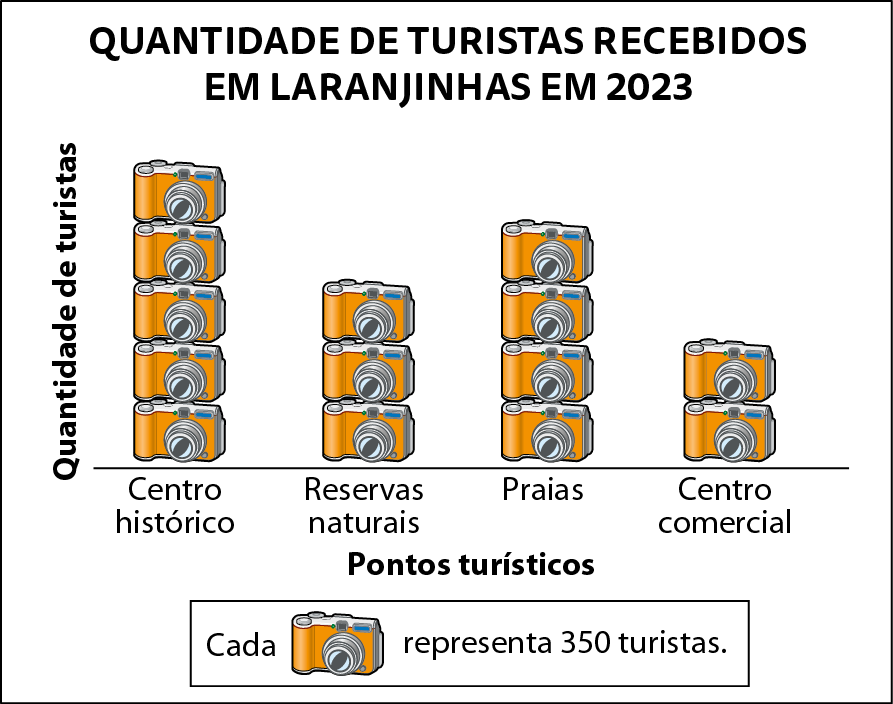
Pictograma. Título: QUANTIDADE DE TURISTAS RECEBIDOS EM LARANJINHAS EM 2 mil e 23. Ícone: máquina fotográfica. Legenda: Cada ícone representa 350 turistas. Centro histórico: 5 ícones Reservas naturais: 3 ícones Praias: 4 ícones Centro comercial: 2 ícones

Dados obtidos pela Secretaria de Turismo do município de Laranjinhas em 2023.

a) Qual foi o ponto turístico mais visitado no município de Laranjinhas em 2023? Por quantos turistas?

b) Qual foi o ponto turístico menos visitado? Por quantos turistas?

c) A prefeitura informou que vai investir no ponto turístico menos visitado a fim de dobrar a visitação ao local. Se o investimento por turista adicional for de R$ 100,00cem reais, de quanto será o novo investimento da prefeitura?

Página 148

Ilustração. Ícone. Caderno na
vertical com um lápis.

Atividades de revisão

faça as atividades no caderno

1. Dois garotos disputam uma corrida ao redor de um terreno. João parte em direção ao ponto ei, passando pelo ponto B até a chegada. Pedro parte em direção ao ponto D, passando por C até a chegada.

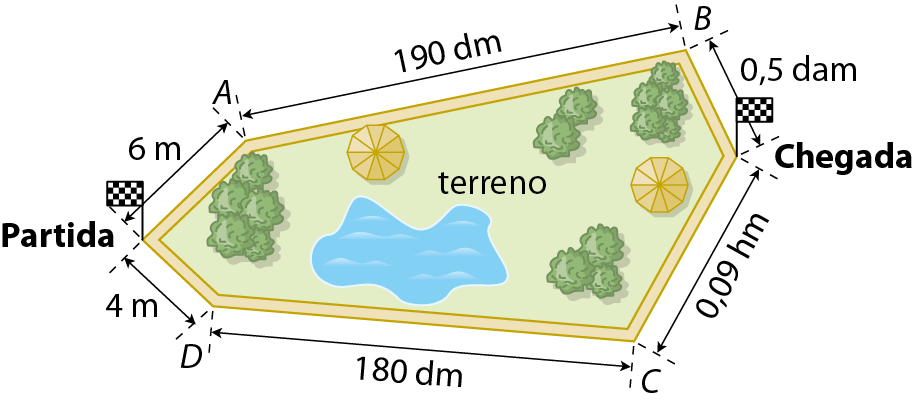
Ilustração. Terreno poligonal com 6 lados diferentes. Do ponto de partida até o ponto A o comprimento mede 6 metros. De A até B o comprimento mede 190 decímetros. De B até chegada o comprimento mede 0 vírgula 5 decâmetro. Da chegada até C o comprimento é 0 vírgula 09 hectômetros. De C até D o comprimento mede 180 decímetros. Do ponto D até o ponto de partida o comprimento mede 4 metros

a) Qual é o caminho mais curto?

b) Qual é a diferença entre as medidas de distância desses caminhos, em centímetro?

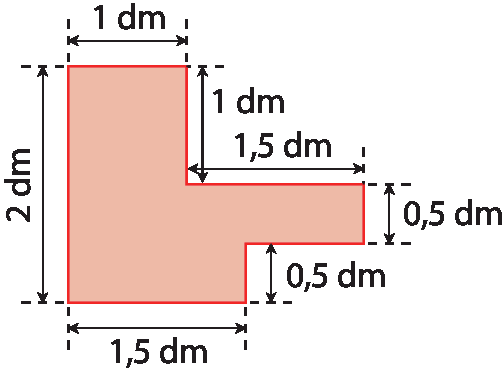
2. Determine a medida do perímetro dos polígonos em centímetro.

a)

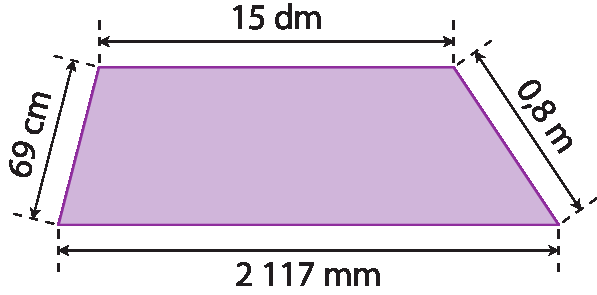
Figura geométrica. Quadrilátero com lados de comprimentos diferentes. As medidas são: 0 vírgula 8 metros, 2 mil 117 milímetros, 69 centímetros, 15 decímetros.

b)

Figura geométrica. Polígono irregular com 8 lados de comprimentos diferentes. As medidas são: 1 decímetro, 1 decímetro, 1 vírgula 5 decímetro, 0 vírgula 5 decímetro, 0 vírgula 5 decímetro, 1 vírgula 5 decímetro, 2 decímetros.

3. Gilberto vai cercar todo o contorno de seu terreno com duas voltas de arame farpado. O terreno, retangular, mede 2 decâmetros de comprimento e 5 decâmetros de largura. Que medida de comprimento, em metro, de arame farpado ele precisará comprar?

4. Observe a imagem e responda.

Fotografia. Bactérias de formado circular na cor verde unidas pela lateral. Abaixo, indicação de escala 1 micrômetro. — Bactérias Staphylococcus aureus vistas ao microscópio eletrônico, ampliadas em 19.000 vezes, colorizadas artificialmente.

• A medida de comprimento de algumas bactérias varia de 0,3 micrômetro a 10 micrômetros. Como podemos representar essas medidas de comprimento em milímetro?

5. A distância entre Júpiter e o Sol mede aproximadamente 5,2 unidades astronômicas.

Ilustração. Representação do Sistema Solar. À esquerda, Sol. Ao redor do Sol 8 elipses distintas representando o trajeto que cada planeta faz envolta do sol. Na imagem, a elipse mais próxima ao sol representa a órbita do planeta Mércurio, seguido da órbita do planeta Vênus, Terra, Marte, Júpiter, Saturno, Urano, Netuno. — Representação esquemática sem escala do Sistema Solar com cores-fantasia.

a) Qual é a medida da distância aproximada, em quilômetro, entre Júpiter e o Sol?

b) Escreva essa medida de distância usando potência de base 10.

6. Leia a explicação e interprete os dados do quadro a seguir para responder às questões.

O cubo de Rubik, também conhecido como cubo mágico, é um quebra-cabeça. Para montá-lo, deve-se movimentar as peças até que cada face do cubo fique com apenas uma cor.

Seis estudantes participaram de uma competição de montagem do cubo de Rubik, e o resultado foi o seguinte:

Medida de tempo de montagem do cubo pelos participantes na competição
Nome	Medida de tempo (em s)
Alice	1.380 (mil trezentos e oitenta)
Carlos	1.440 (mil quatrocentos e quarenta)
Daniela	1.020 (mil e vinte)
Mariana	1.980 (mil novecentos e oitenta)
Pedro	1.260 (mil duzentos e sessenta)
Ricardo	1.680 (mil seiscentos e oitenta)

Dados obtidos pela organização da competição de montagem do cubo de Rubik.

a) Quem finalizou a prova mais rápido?

b) Quem demorou mais para finalizar a prova?

c) Qual foi a diferença, em minuto, entre as medidas de tempo do primeiro e do último colocado?

7. Rubens dividiu igualmente .10000 hectogramas de soja em 200 pacotes. Que medida de massa, em quilograma, de soja ele colocou em cada pacote?