
CAPÍTULO 6 Cálculo algébrico
1 Expressões algébricas

Situação que envolve uma expressão algébrica
O Índice de Massa Corporal, conhecido pela sigla í ême cê, foi idealizado para ajudar a identificar a faixa de massa corporal mais saudável para um adulto. Para obter o í ême cê de um indivíduo adulto, calculamos o valor numérico da expressão algébrica:
Fração m sobre, a elevado ao quadrado., em que m é a medida da massa do adulto, em quilograma, e a é a medida de sua altura, em metro.
Segundo o Ministério da Saúde, a medida da massa do adulto está adequada quando o í ême cê se encontra entre 18,5 e 24,99. fóra dessa faixa, pode haver algum risco para a saúde: subnutrição, sobrepeso ou obesidade. É preciso entender, porém, que o í ême cê calculado apenas sugere uma faixa de valores indicativa de boa saúde, devendo ser considerados o sexo, o grau de atividade física do indivíduo, seu tipo físico (biótipo) e suas características hereditárias, entre outros aspectos.
Para obter o melhor rendimento possível em uma competição, muitos atletas, durante os treinamentos, são submetidos a testes físicos e ergométricos, passando por avaliações de médicos e de nutricionistas, que controlam sua alimentação e analisam suas condições físicas, como o í ême cê.


Para pensar
a) Você já havia ouvido falar em í ême cê? Se sim, em que situações?
b) Pesquise por que é calculado o í ême cê apenas de indivíduos adultos, e não o de crianças ou adolescentes.
c) Observe a foto e as informações da ginasta Rebeca Andrade. Qual é o í ême cê dela? Está na faixa adequada?
Uso de expressões algébricas
Na Matemática, muitas vezes recorremos às letras para representar números e escrever simbolicamente algumas sentenças. Esse procedimento pode ser utilizado em generalizações (fórmulas e propriedades) nas quais o valor de cada letra varia; nesse caso, as letras são chamadas variáveis.
Acompanhe o exemplo a seguir.

Também podemos usar o recurso de escrever simbolicamente algumas sentenças em situações que envolvem números desconhecidos; nesse caso, as letras são chamadas incógnitas.
Observe a balança em equilíbrio e acompanhe como Liz expressou a situação.
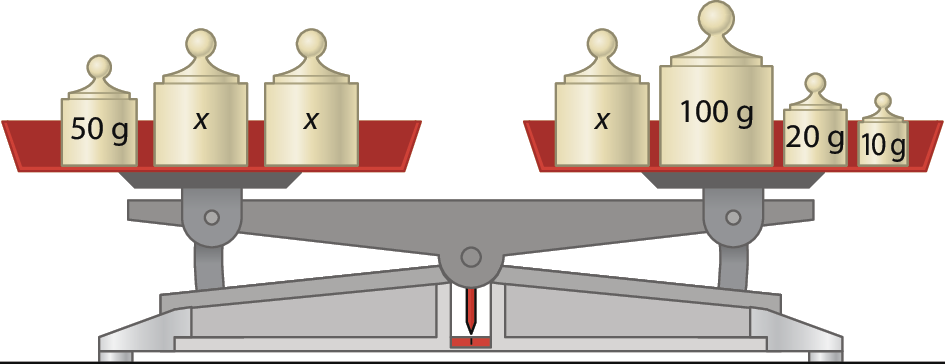

Expressões como xelevado a 2 menos yelevado a 2, abre parêntesesx + yfecha parênteses ⋅ abre parêntesesx menos yfecha parênteses, 50 + 2x e x + 130 são chamadas expressões algébricas.
Expressões algébricas são aquelas que indicam operações matemáticas e contêm números e letras ou somente letras.
Observação
As letras que aparecem nas expressões são chamadas variáveis. Uma variável pode assumir diversos valores.

ATIVIDADES
faça as atividades no caderno
1. Represente por uma expressão algébrica:
a) a adição de três números consecutivos;
b) o quadrado da soma de dois números;
c) a soma dos quadrados de dois números;
d) a terça parte de um número m adicionada ao número s.
2. Imagine que Enzo queira revestir com carpete o piso de um quarto de medidas de comprimento x e y, como mostra a figura a seguir.
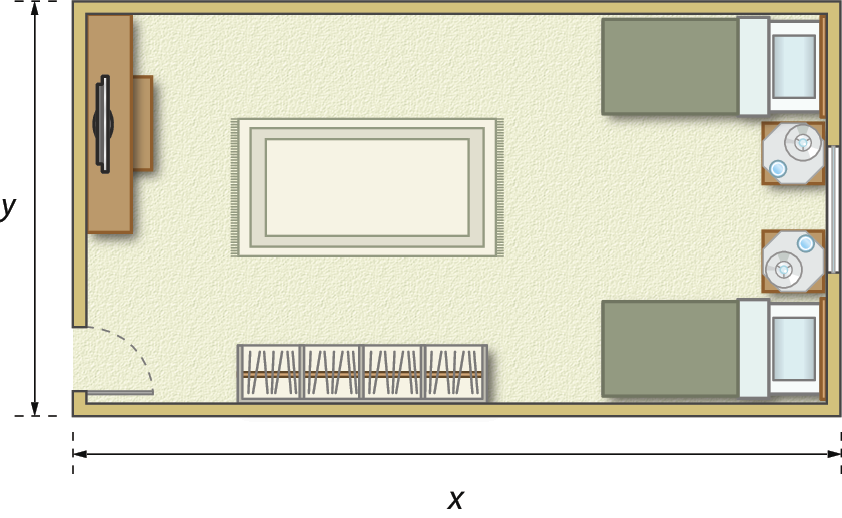
Agora, responda às questões.
a) Sabendo que o carpete é comprado por metro quadrado, como você indicaria a medida de área de carpete necessária?
b) E se Enzo decidisse colocar rodapé? Sabendo que o rodapé é comprado por metro linear, como você indicaria a medida de comprimento de rodapé necessária (não é preciso descontar o espaço da porta)?
3. Que sentença algébrica generaliza as expressões a seguir?
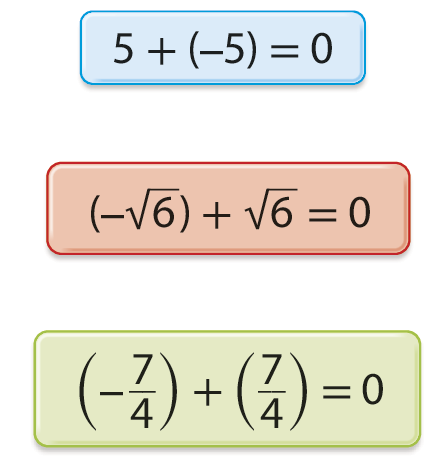
4. O elemento neutro da adição é o zero, ou seja, a soma de um número com zero é igual ao próprio número. Que sentença algébrica pode generalizar essa propriedade?
5. O elemento neutro da multiplicação é o 1. O que isso significa? Que sentença algébrica pode generalizar essa propriedade?
2 Valor numérico de expressões algébricas
Dimas precisa comprar uma camiseta e uma bermuda. Quanto ele vai pagar por essa compra?
Como não sabemos o preço das peças de roupa, vamos indicar por x o preço da camiseta e por y o preço da bermuda. Assim, podemos construir o seguinte quadro.
|
x |
y |
Valor total (x + y) |
|---|---|---|
|
10 reais |
15 reais |
25 reais |
|
12 reais |
16 reais |
28 reais |
|
18 reais |
14 reais |
32 reais |
Note que é possível escrever uma expressão algébrica para indicar o valor total, em real, da compra: x + y
Dessa fórma, para calcular, por exemplo, o valor total gasto na compra de uma camiseta de 15 reais e uma bermuda de 12 reais, basta substituir x e y na expressão por 15 e 12, respectivamente.
15 + 12 = 27 (total gasto: 27 reais)
Quando substituímos cada letra por determinado número e efetuamos as operações indicadas, obtemos o valor numérico dessa expressão para os números escolhidos.
Acompanhe outra situação.
No dia 19 de fevereiro de 2022, o buquê de rosas custava R$ 54,90cinquenta e quatro reais e noventa centavos no Mercado Vila das Flores.
Observe o quadro a seguir, que mostra o valor faturado de acordo com a quantidade de buquês de rosa vendidos.
|
Valor do buquê de rosas |
Quantidade de buquês |
Valor faturado |
|
R$ 54,90 |
2 |
R$ 109,80 (2 ⋅ R$ 54,90) |
|
4 |
R$ 219,60 (4 ⋅ R$ 54,90) |
|
|
6 |
R$ 329,40 (6 ⋅ R$ 54,90) |
|
|
9 |
R$ 494,10 (9 ⋅ R$ 54,90) |
Considerando n o número de buquês de rosas vendidos, podemos escrever a seguinte expressão algébrica para encontrar o valor faturado, em real: n ⋅ 54,90 ou 54,90n
Se foram vendidos 5 buquês de rosas, quantos reais foram faturados pela loja? Podemos calcular o valor faturado substituindo a letra n por 5 na expressão algébrica que escrevemos: 54,90 ⋅ 5 = 274,50
Encontramos, assim, o valor numérico da expressão quando n é igual a 5. Portanto, foram faturados R$ 274,50duzentos e setenta e quatro reais e cinquenta centavos pela venda de 5 buquês de rosas.
Saiba mais
Documentos históricos
Por volta de 1650 antes de Cristo, o egípcio Ahmes escreveu um texto contendo problemas matemáticos, entre eles alguns com expressões algébricas (ainda sem a linguagem algébrica usada atualmente). O papiro Rhind, como foi chamado esse texto, é considerado a principal fonte de conhecimento sobre Matemática do Egito antigo.

• Pesquise a história do papiro Rhind e por que ele recebeu esse nome.
No século três, Diofante de Alexandria começou a utilizar algumas palavras abreviadas em textos matemáticos. Seria, então, o início da linguagem (notação) algébrica.


ATIVIDADES
faça as atividades no caderno
1. Calcule o valor numérico das expressões algébricas para os números indicados.
a) menos4 ⋅ x ⋅ y, para x = 1 e y = 3.
b) 3 ⋅ a + b, para a = 5 e b = menos1.
c) 3 ⋅ x elevado a 2 + 2 ⋅ y, para x = 1 e y = 0.
d) 2 ⋅ x + z menos 9, para x = menos3 e
Sentença matemática. z = fração 1 sobre 2..
2. Observe a figura a seguir.
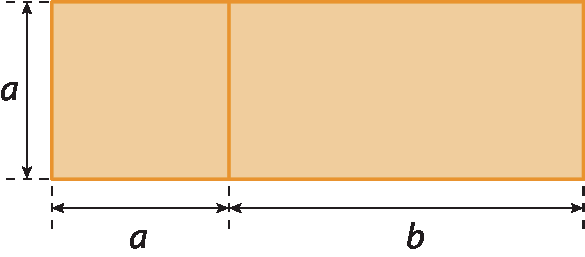
Agora, responda às questões.
a) Que expressão representa a medida do perímetro dessa figura?
b) Qual é a medida do perímetro dessa figura para a = 5 centímetros e b = 7 centímetros?
c) Que expressão representa a medida de área dessa figura?
d) Qual é a medida de área dessa figura para a = 5 centímetros e b = 7 centímetros?
3. José Carlos comprou um aparelho de som que custava x reais. Ao pagar a conta, recebeu um desconto de 20 reais. Qual das expressões algébricas a seguir corresponde à situação descrita?
a) x ⋅ 20
b) x dividido por 20
c) x + 20
d) x menos 20
4. Em uma corrida de táxi, o valor pago varia de acordo com a medida de distância x de quilômetros rodados. Considerando o valor a ser pago pela corrida representado pela expressão 2,40 ⋅ x + 5, calcule o valor a ser pago, em real, se a medida de distância for de:
a) 5 quilômetros;
b) 100 quilômetros;
c) 0,75 quilômetro;
d) .1200 quilômetros;
e) 6,3 quilômetros;
f) 10,5 quilômetros.
5. Para cada festa contratada, um bufê cobra uma taxa fixa de R$ 400,00quatrocentos reais, mais R$ 16,00dezesseis reais por criança de até 12 anos de idade e R$ 40,00quarenta reais por convidado acima dessa idade.
a) Qual é o valor fixo cobrado pelo bufê, independentemente do número de pessoas?
b) Que expressão podemos usar para calcular o orçamento de uma festa para c crianças e p pessoas acima de 12 anos?
c) Quanto esse bufê cobraria para realizar uma festa com 20 crianças e 30 pessoas acima de 12 anos?
6. Observe a figura a seguir, em que os quadrados têm lado de medida x de comprimento.
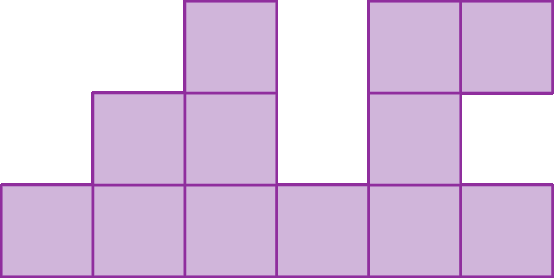
a) Qual é a expressão que representa a medida do perímetro dessa figura?
b) Qual é a medida do perímetro dessa figura para x = 3,7 centímetros?
c) Que expressão representa a medida de área da figura?
d) Qual é a medida de área dessa figura para x = 0,6 centímetro?
7.

Na malha quadriculada a seguir, considere y a medida de área de um quadradinho, em centímetro quadrado.
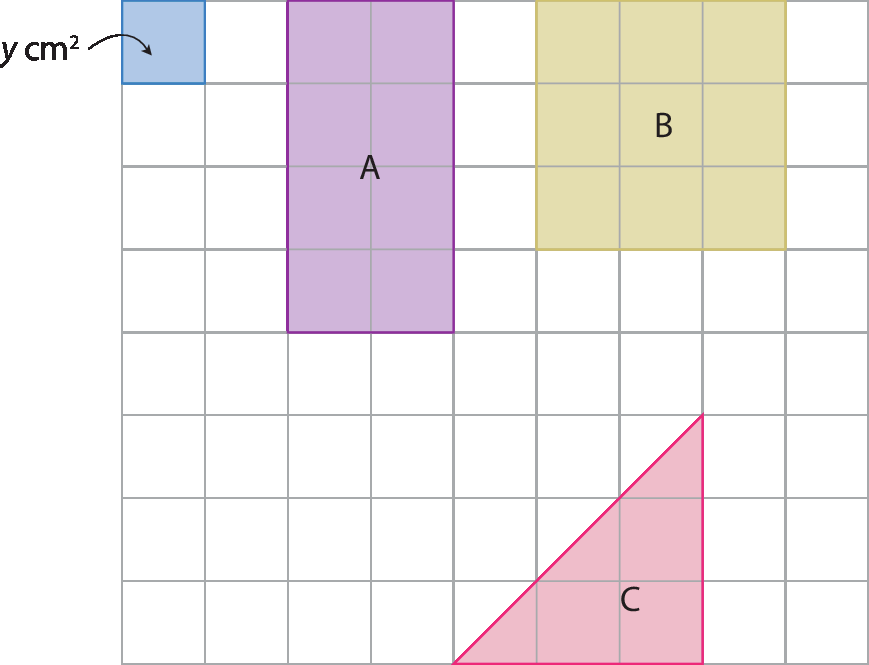
Determine:
a) a medida de área da figura a;
b) a medida de área da figura B;
c) a medida de área da figura C;
d) a metade da medida de área da figura a;
e) a terça parte da medida de área da figura B.
3 Calculando com letras
Verificamos, ao estudar as operações com números racionais, que a propriedade distributiva da multiplicação vale em relação à adição. Observe:
5 ⋅ 3 + 5 ⋅ 2 = 5abre parênteses3 + 2fecha parênteses
Como em expressões algébricas as letras representam números, podemos usar essa e outras propriedades, válidas para os números racionais, para realizar cálculos com essas expressões. Acompanhe como podemos calcular 3x + 2x.
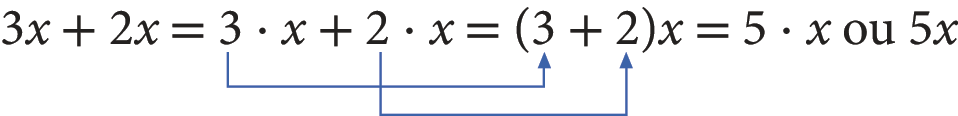
Exemplos
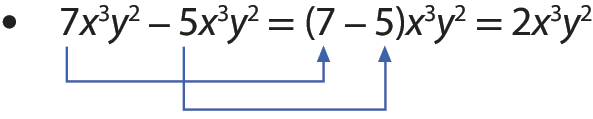
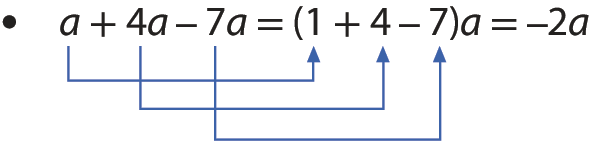
Observe, a seguir, como podemos escrever uma expressão que represente a medida do perímetro de alguns polígonos regulares cujos lados têm a medida de comprimento representada pela letra x.
Recorde
Um polígono é regular quando tem lados de mesma medida de comprimento e abertura dos ângulos internos de mesma medida.

Agora, observe como escrevemos a expressão que representa a medida do perímetro dos polígonos a seguir.

Resolvendo problemas com o uso de letras
Um motoboy recebe mensalmente um valor fixo de R$ 2.000,00dois mil reais mais R$ 10,00dez reais por entrega feita. Qual foi o valor mensal recebido por esse motoboy em um mês em que fez 80 entregas?
Representando por x o número de entregas feitas em um mês, podemos indicar o valor mensal que esse motoboy recebe, em real, pela seguinte expressão algébrica:
.2000 + 10x
Para calcular o valor mensal recebido por esse motoboy, basta substituir x por 80 na expressão algébrica acima e efetuar os cálculos:
.2000 + 10 ⋅ 80 = .2000 + 800 = .2800
Portanto, o motoboy recebeu, nesse mês, R$ 2.800,00dois mil oitocentos reais.
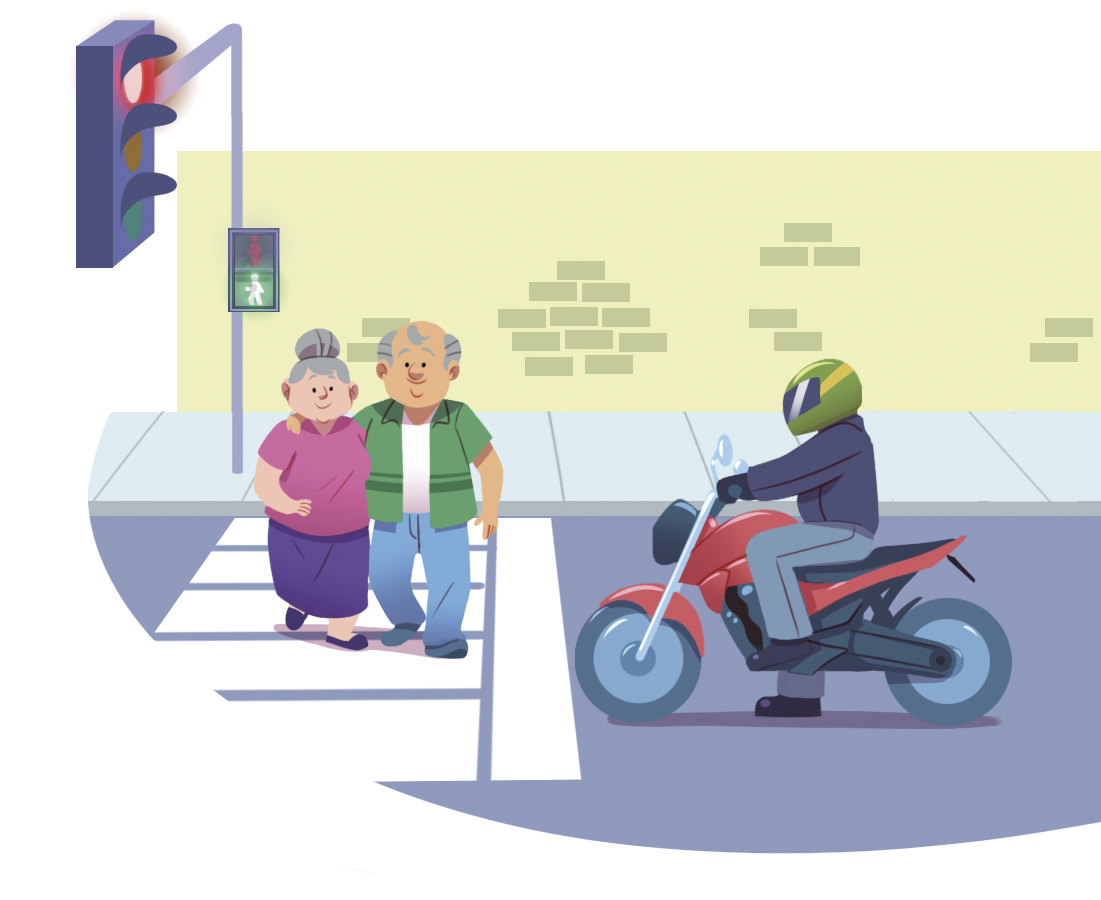
Para analisar

Qual é a importância da faixa de pedestres?

ATIVIDADES
faça as atividades no caderno
1. Calcule.
a) 29a + 4a menos 21a
b) x + 3x menos x + 5x menos x
c) 3x + 4xelevado a 3 menos 5x + xelevado a 2 + 2x
d)
Sentença matemática. 3 quartos de y, menos y sobre 5, mais 7 meios de y.e) 4a + 5b +
7 sobre 2, a.menos b
2. Identifique o erro cometido por Kevin ao calcular m + 7m + 1.
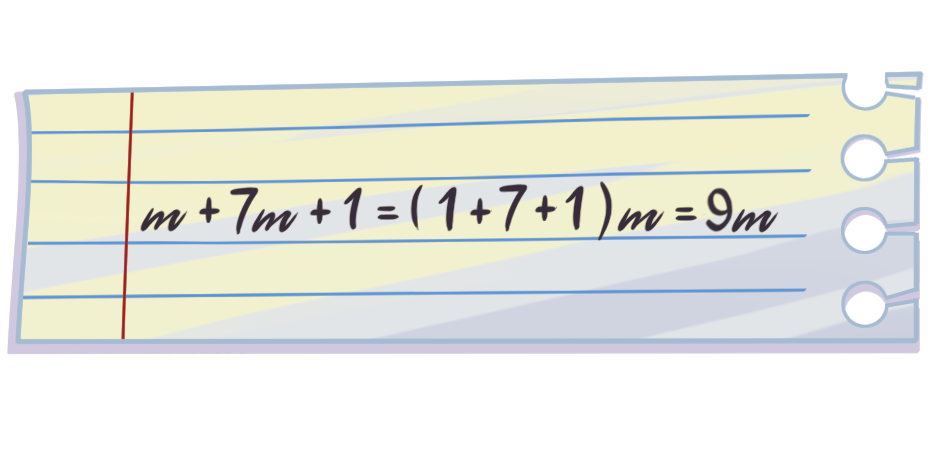
3. Observe o anúncio de uma locadora de veículos.

a) Represente, por meio de uma expressão algébrica, o custo do aluguel nesse caso.
b) Ivo alugou um carro dessa locadora por 4 dias e rodou 100 quilômetros. Quanto ele pagou?
4 Sequências numéricas
No dia a dia, nos deparamos com diversas situações em que estão presentes sequências, como as estações do ano, as fases da Lua, a classificação dos times participantes de um campeonato de futebol, a numeração das casas de uma rua, entre outros casos.

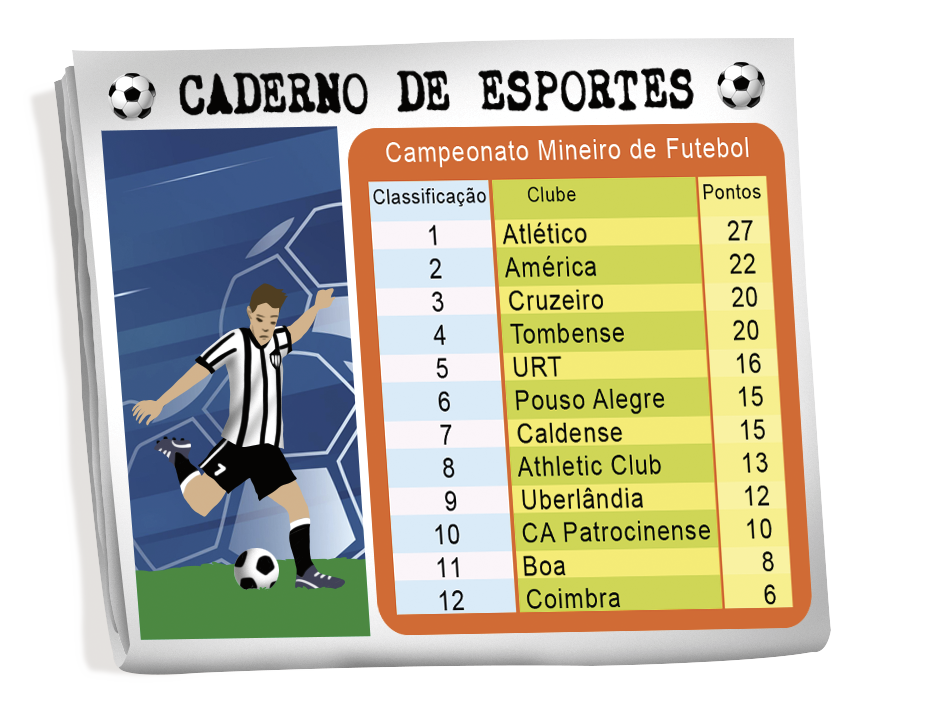
Em Matemática, estudamos as sequências numéricas. Uma sequência numérica é um conjunto de números escritos em determinada ordem.
São exemplos de sequências numéricas:
a) abre parênteses1, 6, 11, 16, 21, 26fecha parênteses
b) abre parênteses0, 2, 4, 6, 8, 10, 12, reticênciasfecha parênteses
c)
Sequência numérica. Abre parênteses 0, menos fração 1 sobre 5, menos fração 2 sobre 5, menos fração 3 sobre 5, menos fração 4 sobre 5, menos 1 fecha parênteses.d) abre parênteses1, 3, 5, 7, 9, 11, 13, reticênciasfecha parênteses

Cada elemento da sequência é chamado termo da sequência. Em uma sequência, o termo que ocupa a posição de número n é indicado pelo símbolo áíndice n, isto é:
áíndice 1 indica o primeiro termo da sequência;
áíndice 2 indica o segundo termo da sequência;
áíndice 3 indica o terceiro termo da sequência;
áíndice 4 indica o quarto termo da sequência;
⋮
án indica o enésimo termo da sequência.
Assim, indicamos uma sequência finita de n termos por abre parêntesesáíndice 1 , áíndice 2 , áíndice 3, reticências, áíndice n) e uma sequência infinita por abre parêntesesáíndice 1 , áíndice 2 , áíndice 3, reticências, áíndice n, reticênciasfecha parênteses.
Exemplos
Na sequência abre parênteses0, 4, 8, 12, 16fecha parênteses, temos: áíndice 1 = 0, áíndice 2 = 4, áíndice 3 = 8, áíndice 4 = 12 e áíndice 5 = 16.
Na sequência abre parênteses2, 7, 12, 17, ...fecha parênteses, temos: áíndice 1 = 2, áíndice 2 = 7, áíndice 3 = 12, áíndice 4 = 17, reticências
Saiba mais
No século nove, o matemático árabe al-Khowarizmi escreveu o livro Al-jabr-Wa’l muqabalah, cujo título possivelmente deu origem ao termo Álgebra.
• Pesquise o significado dos termos al-jabr e muqabalah.

No século dezesseis, François Viète contribuiu para o desenvolvimento da Álgebra simbólica, muito próxima da usada hoje em dia.

Representando os termos de sequências numéricas por meio de expressões algébricas
Acompanhe a situação a seguir.

Uma maneira possível de responder a essa pergunta é descobrir a relação existente entre os termos da sequência e calcular todos os termos até chegar ao 100º.
Por outro lado, há uma fórma de descobrir mais rapidamente o 100º termo da sequência: escrever uma expressão algébrica que expresse os termos dessa sequência numérica.
Organizando os termos da sequência em um quadro, temos:
|
1º termo |
2º termo |
3º termo |
4º termo |
... |
enésimo (nº) termo |
|---|---|---|---|---|---|
|
1 |
4 |
9 |
16 |
... |
? |
Ao analisar os termos dessa sequência, verificamos que são números quadrados perfeitos, ou seja, que podem ser escritos como um número elevado ao quadrado.

Observe que a base de cada uma dessas potências corresponde à posição de cada termo: 1o termo, base 1; 2o termo, base 2; e assim por diante.
Nesse caso, a expressão algébrica que indica o enésimo termo da sequência é nelevado a 2, em que n é um número natural maior ou igual a 1.
Com essa expressão, podemos calcular o 100º termo:
100º termo: aíndice 100 = 100elevado a 2 = .10000
Portanto, o 100º termo da sequência é .10000.
Observe como podemos representar outras sequências numéricas por meio de expressões algébricas, em que n é um número natural maior ou igual a 1.
a) A sequência dos números naturais pares é abre parênteses0, 2, 4, 6, reticênciasfecha parênteses. Podemos representar um termo qualquer dessa sequência numérica por: áíndice n = 2 ⋅ abre parêntesesn menos 1fecha parênteses ou, ainda, áíndice n = 2n menos 2
b) A sequência dos números naturais positivos múltiplos de 5 é abre parênteses5, 10, 15, 20, reticênciasfecha parênteses. Podemos representar um termo qualquer dessa sequência numérica por: áíndice n = 5n
c) A sequência dos números naturais formados usando apenas o algarismo 9, colocados em ordem crescente, é abre parênteses9, 99, 999, reticênciasfecha parênteses. Podemos representar um termo qualquer dessa sequência numérica por: áíndice n = 10elevado a n menos 1

Para pensar
A letra n nas expressões algébricas anteriores é variável ou incógnita? Por quê?
Expressões algébricas equivalentes
Leia o que Carla e Bruno falaram sobre como cada um representou a expressão de um termo qualquer da sequência: 7, 12, 17, 22, reticências

Tanto a expressão de Carla quanto a de Bruno são válidas. Isso acontece porque as duas expressões algébricas são equivalentes.
5abre parêntesesp + 1fecha parênteses menos 3 = 5p + 5 menos 3 = 5p + 2 (p é um número natural maior ou igual a 1)

ATIVIDADES
faça as atividades no caderno
1. Determine a sequência dos números:
a) naturais menores que 6;
b) inteiros que estão entre menos3 e 2;
c) primos positivos;
d) inteiros cujo módulo é menor que 2;
e) pares maiores ou iguais a 6.
2. Faça o que se pede.
a) Considere a seguinte sequência:
1º termo

2, ou seja, 2 ⋅ 1
2º termo

4, ou seja, 2 ⋅ 2
3º termo

6, ou seja, 2 ⋅ 3
• Como pode ser escrito o enésimo termo dessa sequência, ou seja, o termo de posição n?
b) Considere a sequência dos números ímpares:
1º termo

1, ou seja, 2 ⋅ 1 menos 1
2º termo

3, ou seja, 2 ⋅ 2 menos 1
3º termo

5, ou seja, 2 ⋅ 3 menos 1
• Como pode ser escrito o enésimo termo dessa sequência?
3. Escreva na fórma abre parêntesesáíndice 1 , áíndice 2 , áíndice 3, áíndice 4 , reticênciasfecha parênteses cada uma das sequências numéricas em que o enésimo termo é dado a seguir (n é número natural maior ou igual a 1).
a) áíndice n = 7n
b) áíndice n = nelevado a 3
c) áíndice n = nelevado a 2 + n
d) áíndice n = 3nelevado a 2 menos 2
4. Considere alguns termos de uma sequência numérica:

a) Determine o 5º e o 6º termos dessa sequência.
b) Escreva a expressão algébrica que indica o enésimo termo dessa sequência.
5. Observe a sequência de figuras e faça o que se pede.

a) Escreva uma expressão algébrica que relacione o número de

da figura que ocupa a enésima posição dessa sequência.
b) Calcule o número de

do 99º termo dessa sequência.
6. Observe a sequência de figuras e faça o que se pede.
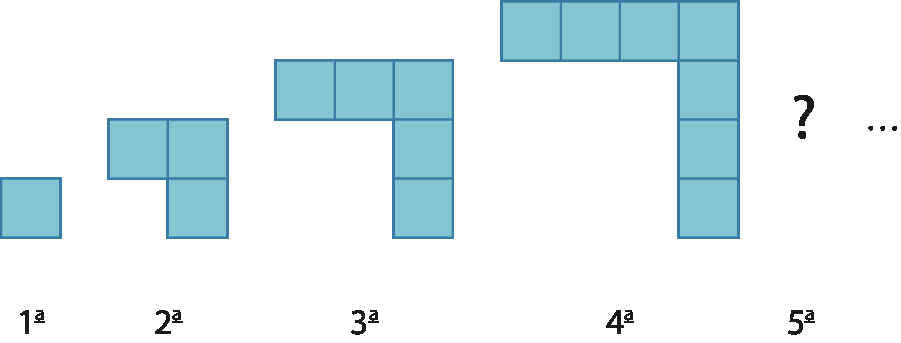
a) Quantos

a figura da 5a posição terá?
b) Utilizando a letra p para identificar a posição da figura, escreva uma expressão que determine corretamente o número de

em cada figura.
c) Calcule o número de

do 20º termo dessa sequência.
7. Observe a figura que está sendo formada com palitos de sorvete. Primeiro, formou-se um quadrado com 4 palitos; depois, acrescentaram-se 3 palitos e formou-se mais um quadrado; em seguida, com mais 3 palitos, formou-se outro quadrado; e assim por diante.

Continuando essa construção, quantos palitos serão necessários para formar:
a) 4 quadrados?
b) 5 quadrados?
c) x quadrados?
d) 15 quadrados?
Sequências numéricas recursivas
Observe a sequência numérica: abre parênteses0, 3, 6, 9, 12, 15, reticênciasfecha parênteses
Lembre-se: Escreva no caderno!
Note que o primeiro termo dessa sequência é 0 e que cada termo, a partir do segundo, é obtido adicionando-se 3 ao termo anterior. Ou seja:
áíndice 1 = 0
áíndice 2 = áíndice 1 + 3 = 0 + 3 = 3
áíndice 3 = áíndice 2 + 3 = 3 + 3 = 6
⋮
Assim, podemos representar qualquer termo dessa sequência, a partir do segundo, por:
áíndice n mais 1 = áíndice n + 3, em que n é um número natural maior ou igual a 1.
Sequências numéricas como essa, em que é possível determinar cada termo an a partir de um ou mais de seus termos anteriores abre parêntesesáíndice n menos 1, áíndice n menos 2, reticências, á₁fecha parênteses, são chamadas sequências recursivas.
Para pensar
De que outra maneira podemos representar o enésimo termo da sequência numérica abre parênteses0, 3, 6, 9, 12, 15, reticênciasfecha parênteses?
Exemplos
• abre parênteses3, 7, 15, 31, 63, reticênciasfecha parênteses
Nessa sequência, para determinar um termo, a partir do segundo, dobramos o termo anterior e adicionamos 1, ou seja:
áíndice 1 = 3
áíndice 2 = 2áíndice 1 + 1 = 2 ⋅ 3 + 1 = 7
áíndice 3 = 2áíndice 2 + 1 = 2 ⋅ 7 + 1 = 15
áíndice 4 = 2áíndice 3 + 1 = 2 ⋅ 15 + 1 = 31
áíndice 5 = 2áíndice 4 + 1 = 2 ⋅ 31 + 1 = 63
⋮
Assim, podemos representar qualquer termo dessa sequência, a partir do segundo, por:
áíndice n mais 1 = 2áíndice n + 1, em que n é um número natural maior ou igual a 1.
• abre parênteses1, 3, 4, 7, 11, 18, reticênciasfecha parênteses
Nessa sequência, para determinar um termo, a partir do terceiro, adicionamos os dois termos imediatamente anteriores, ou seja:
áíndice 1 = 1
áíndice 2 = 3
áíndice 3 = áíndice 1 + áíndice 2 = 1 + 3 = 4
áíndice 4 = áíndice 2 + áíndice 3 = 3 + 4 = 7
á₅ = á₃ + á₄ = 4 + 7 = 11
áíndice 5 = áíndice 4 + áíndice 5 = 7 + 11 = 18
⋮
Assim, podemos representar qualquer termo dessa sequência, a partir do terceiro, por:
áíndice n mais 2 = áíndice n mais 1 + áíndice n , em que n é um número natural maior ou igual a 1.
A ideia de recursão também está presente nas artes e na literatura. Observe, por exemplo, o poema “Pêndulo”, de Ernesto Manuel de Melo e Castro, reproduzido a seguir. Nesse poema, cada verso, a partir do terceiro, é idêntico ao anterior, porém acrescido de uma letra. Note que a disposição das palavras sugere o movimento de um pêndulo.
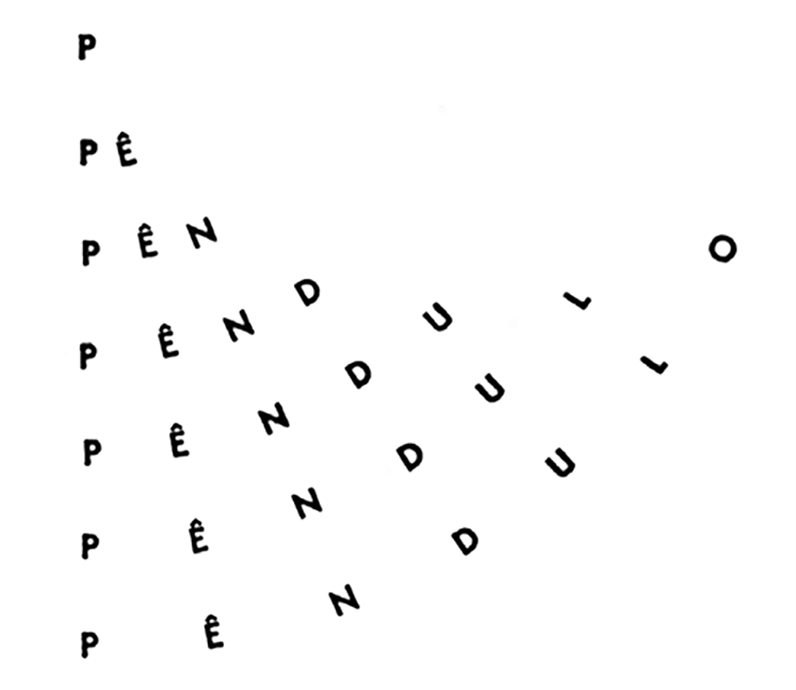
MELO E CASTRO, Ernesto Manuel de. Pêndulo. In: Antologia efémera: poemas 1950-2000. Rio de Janeiro: Lacerda, 2000. página 258.
Para investigar

Reúna-se com três colegas e pesquisem exemplos de poemas ou de obras de arte em que a ideia de recursão esteja presente.

Informática e Matemática
faça as atividades no caderno
Sequência de fibonáti na planilha eletrônica
Nesta seção, você vai utilizar uma planilha eletrônica para determinar os termos de uma sequência numérica recursiva chamada sequência de fibonáti.
Sequência de fibonáti
A sequência de fibonáti tem origem em um problema proposto pelo matemático Leonardo de Pisa, conhecido como fibonáti, no livro Liber abaci, de 1202, sobre o crescimento de uma população de coelhos.

Observe esta sequência:
abre parênteses1, 1, 2, 3, 5, 8, 13, 21, reticênciasfecha parênteses
Note que os dois primeiros termos dessa sequência são iguais a 1 e que todo termo, a partir do terceiro, é obtido adicionando-se os dois termos imediatamente anteriores.
Assim, podemos representar qualquer termo dessa sequência, a partir do terceiro, por:
áíndice n mais 2 = áíndice n mais 1 + áíndice n , em que n é um número natural maior ou igual a 1.
Planilhas eletrônicas
As planilhas eletrônicas são usadas para organizar informações e realizar cálculos.
Elas apresentam variações de formato e de ferramentas, mas, no geral, todas possuem números para indicar as linhas, letras para indicar as colunas, um campo para inserir fórmulas e um campo para indicar a célula selecionada, ou a célula em uso.
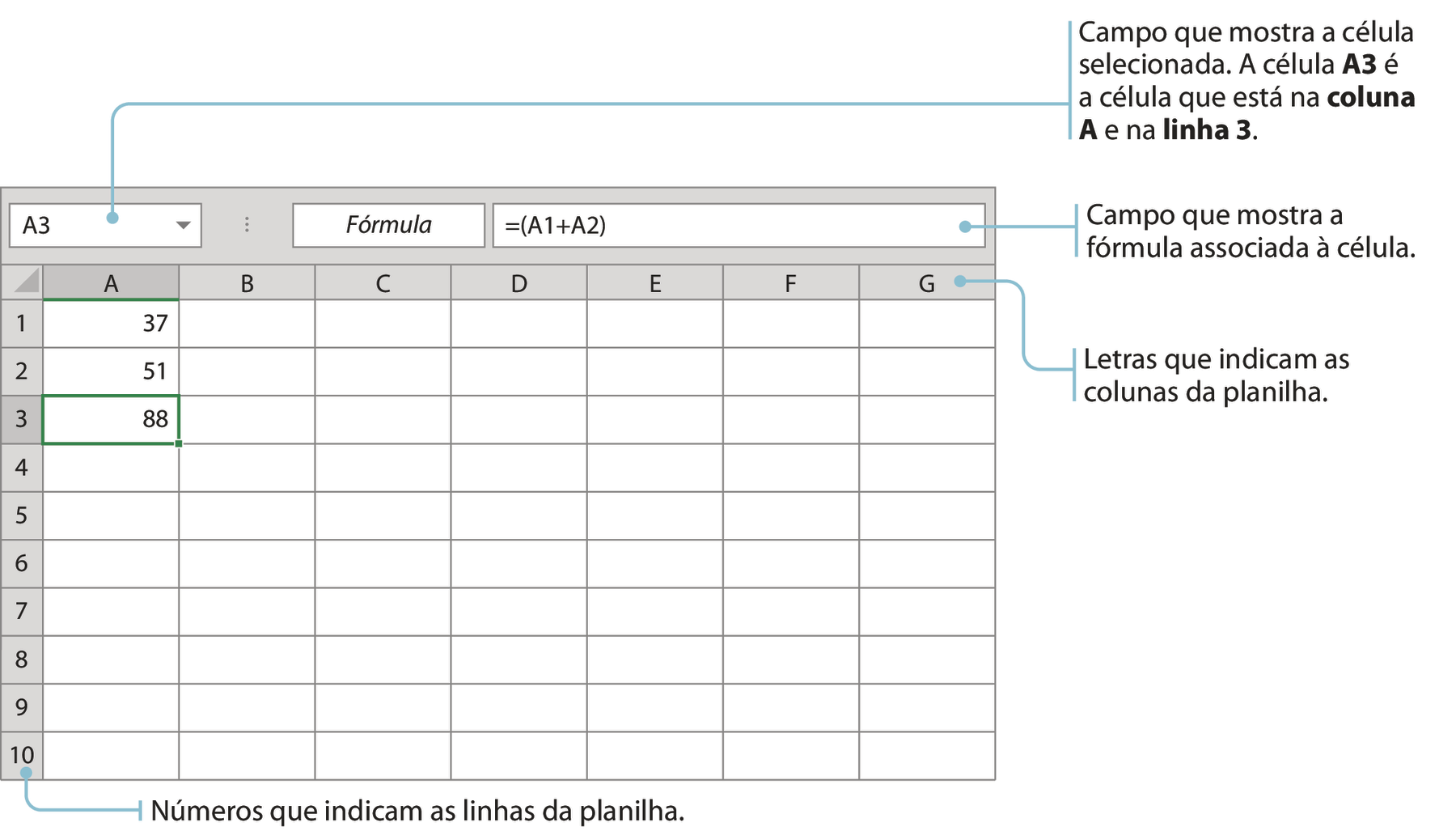
▶ Informática e Matemática
CONSTRUA
Siga os passos a seguir para gerar os termos da sequência de fibonáti em uma planilha eletrônica.
1º) Preencha a célula a um com o número 1
(primeiro termo da sequência).
2º) Preencha a célula a dois com o número 1
novamente (segundo termo da sequência).
3º) Na célula A três, digite a fórmula:
= abre parêntesesa um +a doisfecha parênteses
Dessa fórma, os valores das células a um e a dois serão adicionados. A fórmula também pode ser digitada no campo apropriado para inserir fórmulas com a célula A três selecionada.
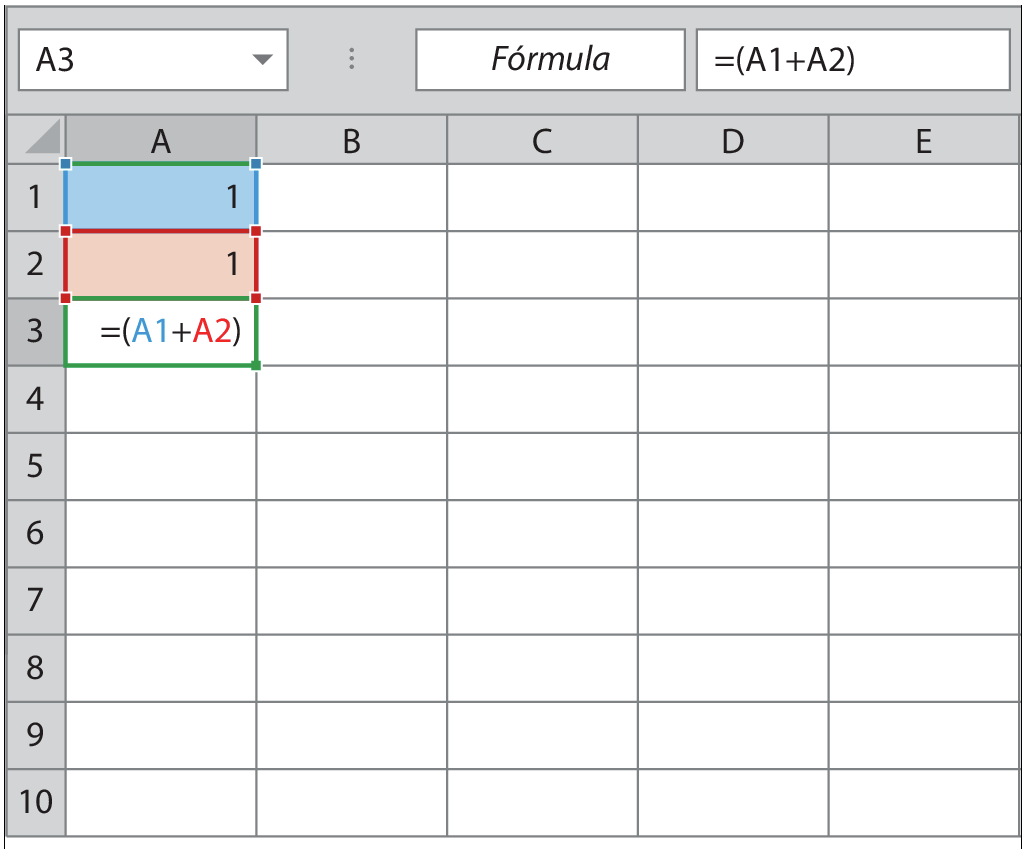
4º) Selecione a célula A três, leve o cursor até o canto inferior direito da célula e, com o botão esquerdo do mouse clicado, arraste a seleção para baixo. Assim, a fórmula será copiada para as outras células e outros termos da sequência de fibonáti serão gerados.
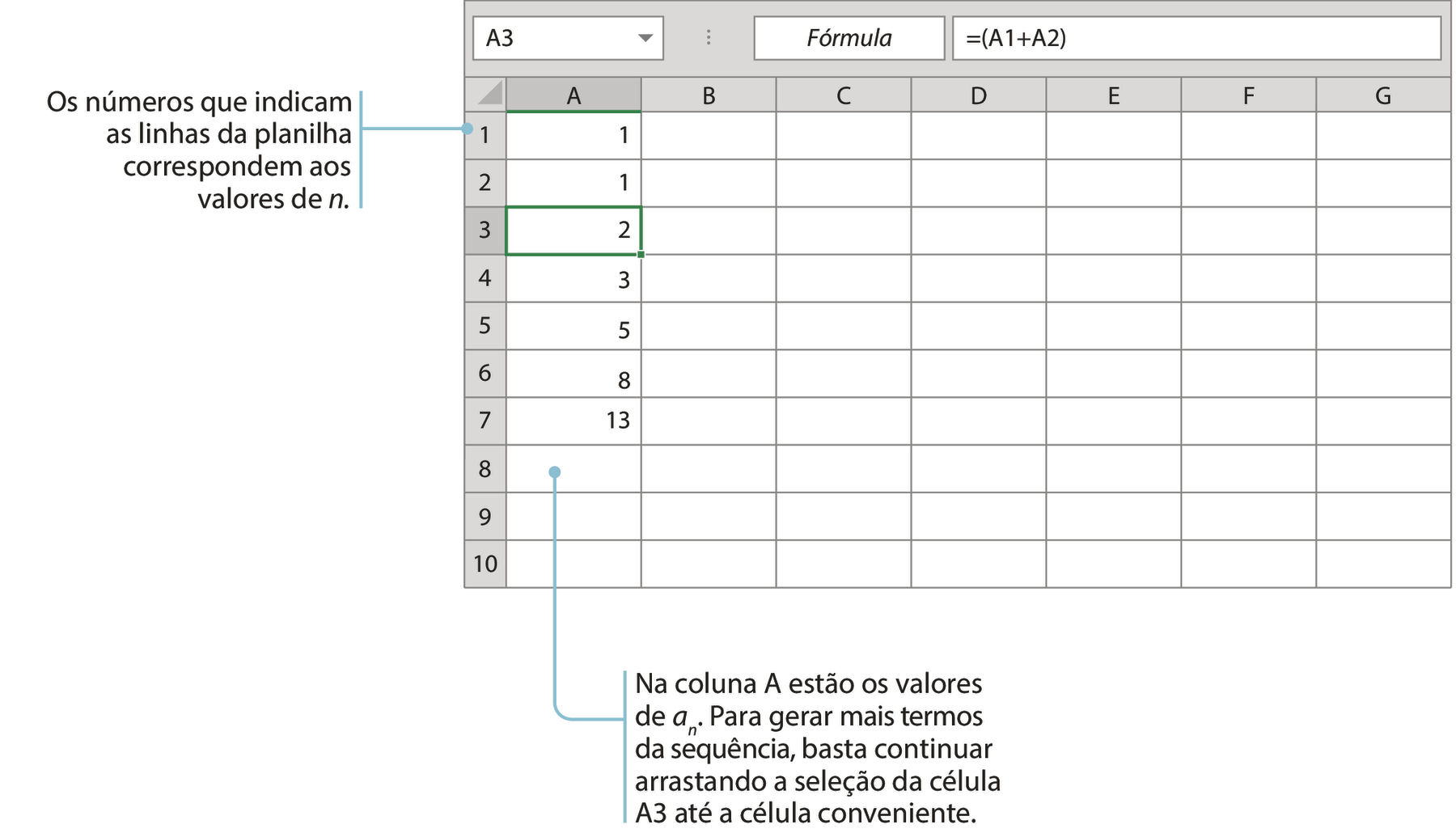
Lembre-se: Escreva no caderno!
INVESTIGUE
a) Quais são os 10 primeiros termos da sequência de fibonáti?
b) Determine o 40º termo da sequência de fibonáti. Ele é obtido com a adição de quais números?
c) ..432500302 é um termo da sequência de fibonáti? Justifique sua resposta.
d) O número ...32951280099 é um termo da sequência de fibonáti? Se for, esse número corresponde a qual termo?

ATIVIDADES
faça as atividades no caderno
1. Escreva duas sequências numéricas recursivas.
2. As sequências numéricas a seguir são recursivas. Como podemos expressar um termo qualquer de cada uma a partir do(s) termo(s) anterior(es)?
a) abre parênteses4, 8, 12, 16, 20, 24, reticênciasfecha parênteses
b) abre parênteses1, 6, 36, 216, .1296, reticênciasfecha parênteses
3. Observe como Mateus e Juliana representaram a sequência dos números naturais múltiplos de 10.

• Qual deles representou a sequência dos números naturais múltiplos de 10 corretamente?
4. No caderno, associe as representações dos termos de uma mesma sequência numérica para n natural maior ou igual a 1.


Estatística e Probabilidade
faça as atividades no caderno
Cálculo da média aritmética e da média aritmética ponderada
Média aritmética
Paulo elaborou a lista a seguir para calcular a média aritmética das idades dos participantes de um torneio de xadrez que acontecerá na escola.

Para fazer esse cálculo, ele adicionou as idades e, depois, dividiu o resultado pela quantidade de participantes. Observe.

Portanto, Paulo descobriu que a idade média dos participantes do torneio de xadrez é 12,7 anos.
Em geral, a média aritmética de um conjunto de valores numéricos representa esse conjunto.
Média aritmética ponderada
No colégio em que Everton estuda, a nota bimestral de Matemática é composta de quatro avaliações com pesos diferentes: um trabalho em grupo, um trabalho individual e duas provas individuais. Observe o peso de cada avaliação no quadro a seguir.
|
Avaliação |
Peso |
|---|---|
|
Trabalho em grupo |
1 |
|
Trabalho individual |
2 |
|
Prova individual |
3 |
Everton obteve as seguintes notas: 8 no trabalho em grupo, 7 no trabalho individual, 7 e 8,5 nas provas individuais. Qual foi a nota bimestral de Everton?
Para saber a nota bimestral de Everton, devemos calcular a média aritmética ponderada das notas obtidas nas avaliações. Como elas têm pesos diferentes, observe a seguir como deve ser feito o cálculo.

Assim, a nota bimestral de Everton foi 7,61.


ATIVIDADES
faça as atividades no caderno
1. Antes de comprar um liquidificador, Ana resolveu fazer uma pesquisa de preços. Após percorrer cinco lojas, ela organizou os dados coletados na tabela a seguir.
|
Loja |
Preço |
|---|---|
|
Casas do Brasil |
R$ 166,79 |
|
Lojas Amazonenses |
R$ 154,77 |
|
Casas do Sul |
R$ 162,74 |
|
Magazine Ceciliana |
R$ 148,25 |
|
Lojas do Silva |
R$ 149,35 |
Dados obtidos por Ana em junho 2022..
a) Quais foram o menor e o maior preços encontrados por Ana? Qual é a diferença entre eles?
b) Qual é a média aritmética dos preços do liquidificador pesquisado?
c) Em quais lojas o preço do liquidificador está acima da média? E em quais está abaixo da média?
d) Ana resolveu pesquisar o preço em uma sexta loja. Ela encontrou o mesmo liquidificador por R$ 146,30cento e quarenta e seis reais e trinta centavos. Com esse novo preço, qual é a média aritmética dos preços do liquidificador?

▶ Estatística e Probabilidade
Lembre-se: Escreva no caderno!
2. Observe o consumo de energia elétrica da família Moura em 12 meses. Depois, responda às questões.

a) Em que mês foi registrado o maior consumo? E o menor?
b) Qual foi o consumo médio de energia elétrica nesse período?
c) Em quais meses o consumo ficou acima da média? E em quais ficou abaixo da média?
3. Antes de escolher uma casa, Luiz fez uma lista das características que julgava importantes em um imóvel e atribuiu um peso a cada uma delas: quanto mais importante, maior o peso da característica. Em seguida, deu uma nota de 0 a 10 para cada característica das casas. Observe.
|
Característica |
Peso |
Nota da casa A |
Nota da casa B |
|---|---|---|---|
|
Localização |
3 |
9 |
10 |
|
Acabamento |
1 |
5 |
4 |
|
Espaço interno |
2 |
10 |
8 |
• Luiz escolheu a casa que teve a maior média aritmética ponderada das notas atribuídas às suas características. Qual das casas ele escolheu?
4. A escola de música Eustácio Amparo fez um levantamento da idade de seus estudantes no início de 2023 e organizou os dados no gráfico a seguir.
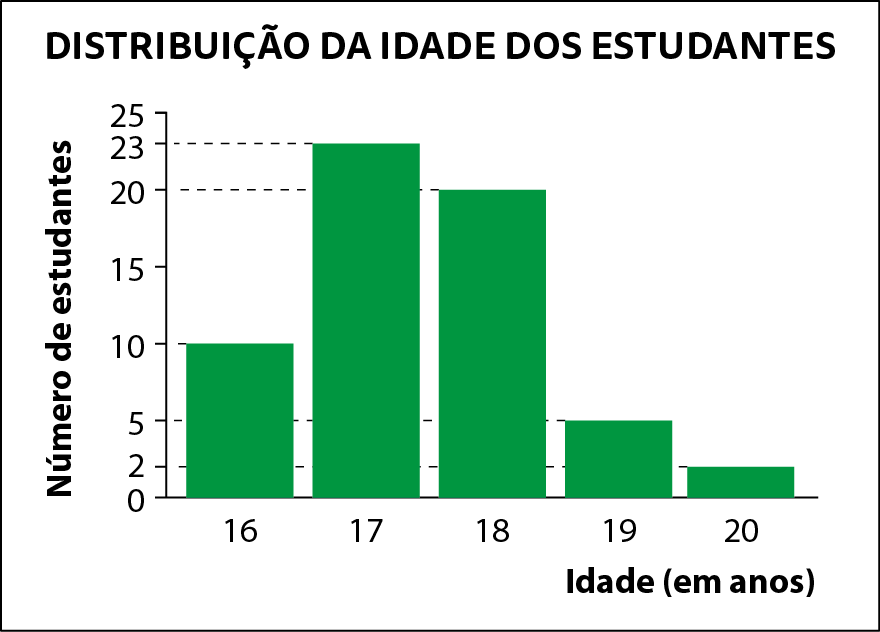
Dados obtidos pela escola Eustácio Amparo no início de 2023.
a) Indique a idade do maior e a do menor grupo de estudantes.
b) Qual é a média da idade dos estudantes?


Atividades de revisão
faça as atividades no caderno
1. Em 2020, foi plantada uma árvore que media aproximadamente 20 centímetros de altura. Em 2021, ela estava medindo 48 centímetros de altura e, em 2022, 76 centímetros de altura. Sabe‑se que a medida de altura desse tipo de árvore varia com a idade (em ano) e que sua idade limite é de 50 anos.

A fórmula que relaciona a idade da árvore t, em ano, e a medida de altura correspondente h, em centímetro, é dada por:
h = 28 ⋅ t + 20
a) Qual é a medida de altura da árvore quando t = 6 anos?
b) E quando t = 10 anos?
2. Considere S o número do sapato que uma pessoa calça. Esse número está relacionado com a medida do comprimento P, em centímetro, do pé e é dado pela seguinte sentença algébrica:
Sentença matemática. s igual a 3 meios vezes p.Qual é o número do sapato de uma pessoa de quem o pé mede 24 centímetros de comprimento?
a) 35
b) 35,5
c) 37
d) 36
e) 37,5
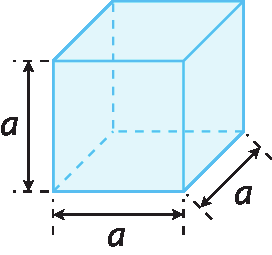
3. Observe cada figura e escreva no caderno a expressão algébrica correspondente:
a) à medida de distância entre os pontos a e cê;

b) à medida de perímetro do quadrilátero;
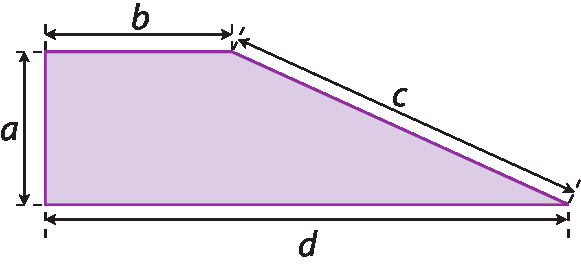
c) à medida de área do quadrado;
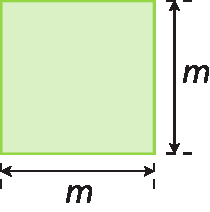
d) à medida de volume do cubo.
4. Escreva, no caderno, a expressão algébrica que representa a quantia que cada criança tem, sabendo que a quantia, em real, que João tem é x.

a) Luciana tem o dobro da quantia de João.
b) Aline tem um terço da quantia de João.
c) Janaína tem a quantia de João mais 5 reais.
d) Marta tem metade da quantia de Janaína.
5. Eduardo vai comprar corda para fazer dois varais para sua casa. Para isso, ele precisará comprar corda suficiente para a medida de comprimento x de cada varal, além de 20 centímetros a mais para prendê-lo.
a) Escreva uma expressão algébrica para indicar quantos centímetros de corda será necessário comprar para fazer cada varal.
b) Se um dos varais medir 80 centímetros de comprimento, quantos centímetros de corda Eduardo terá de comprar?
c) Para o outro varal, que medirá 1 métro de comprimento, quantos centímetros de corda Eduardo terá de comprar?
Lembre-se: Escreva no caderno!
▶ Atividades de revisão
6. Em um loteamento na área rural são vendidos terrenos retangulares cuja medida de comprimento é 25 metros maior que a medida de largura.
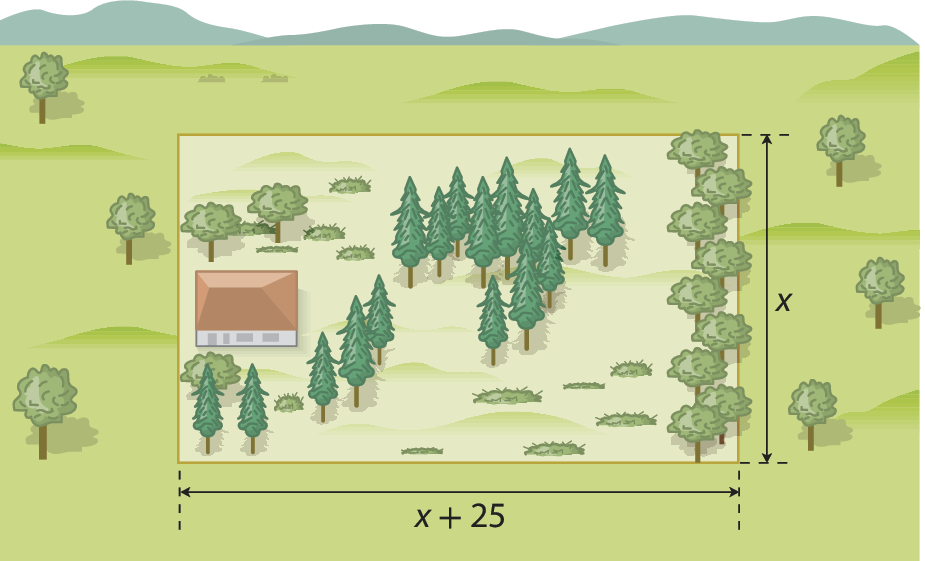
a) Qual é a medida de área do terreno?
b) Qual é a medida do perímetro desse terreno?
c) Se o terreno medir 50 metros de largura, qual será a medida de sua área? E de seu perímetro?
7. O dono de uma granja vendia uma caixa com 30 dúzias de ovos brancos por x reais. Qual era o preço da dúzia de ovos? O dono da granja precisou aumentar os preços e o valor de 30 dúzias de ovos chegou a 150 reais. Quanto passaram a custar 75 dúzias desses ovos?
8. Determine o valor numérico de cada expressão algébrica para x = 12.
a) x + 2
b) xelevado a 2 + 2x
c)
Sentença matemática. Fração, x sobre 3.9. Calcule o valor numérico das expressões para os números pedidos.
a) a + 2 ⋅ b menos 4 ⋅ celevado a 2, para a =
1 quarto, b = menos
Fração -3 meios..e c = menos1
b) a menos b + 3c, para a = menos
Fração 5 meios., b = 0,5 e c = 1
10. Determine a sequência dos números:
a) inteiros negativos maiores que menos 4;
b) primos menores ou iguais a 19;
c) naturais múltiplos de 11.
11. Escreva na fórma abre parêntesesáíndice 1 , áíndice 2 , áíndice 3, áíndice 4 , áíndice 5, reticênciasfecha parênteses cada uma das sequências numéricas a seguir, considerando n é um número natural maior ou igual a 1.
a) áíndice n = 9n
b) áíndice n = nelevado a 2 + 1
c) áíndice 1 = 1
áíndice n mais 1 = áíndice n + 10
d) áíndice 1 = 2
áíndice 2 = 8
áíndice n mais 2 = áíndice n mais 1 + áíndice n
12. A máquina a seguir associa cada número xis da coluna da esquerda a um número n da mesma linha na coluna da direita.

a) O número da direita é o dobro do número à sua esquerda?
b) Escreva com suas palavras a regra de correspondência entre os números das colunas.
c) Escreva essa regra no caderno usando a linguagem algébrica.
13. Verifique se as sequências numéricas a seguir são recursivas.
a) abre parênteses50, 51, 52, 53, 54, reticênciasfecha parênteses
b) abre parênteses10, 110, 210, 310, 410, reticênciasfecha parênteses
c) abre parênteses2elevado a 5, 2elevado a 4, 2elevado a 3, 2elevado a 2, 2elevado a 1, 2elevado a 0fecha parênteses
14. Observe a sequência de figuras.

Calcule, no caderno, o número de

da .1000a figura dessa sequência.
15.

Represente a sequência numérica a seguir de duas maneiras diferentes.
abre parênteses8, 18, 28, 38, 48, reticênciasfecha parênteses

Para finalizar
faça as atividades no caderno
organize suas ideias
Observe e responda
Considere estas imagens.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.



Com base nas imagens e também no que você aprendeu nesta Unidade, responda às questões no caderno.
1. Nas imagens anteriores, os números são empregados para representar o quê?
2. Quando realizamos medições, obtemos somente medidas inteiras? Justifique.
3.


Elabore um problema para cada caso. Em seguida, troque seus problemas com um colega e resolva-os.
a) Um problema que envolva operações com números racionais.
b) Um problema que envolva medidas de grandezas.
c) Um problema de cálculo da medida de volume de blocos retangulares.
▶ Para finalizar
Lembre-se: Escreva no caderno!
Registre

Para finalizar o estudo desta Unidade, reúna-se com um colega e façam o que se pede.
1. Que tipo de número pode ser classificado como racional? Escolham alguns exemplos e represente-os na reta numérica.
2. Vocês observam alguma relação entre números que são classificados como naturais, inteiros e racionais? Justifiquem a resposta.
3. Em que situações do dia a dia é necessário fazer a conversão de uma unidade de medida para outra?
4. Qual é a vantagem do uso de letras para representar valores desconhecidos? Justifiquem a resposta com algumas situações.
5. Na abertura desta Unidade, vocês responderam a algumas questões do boxe “Para começar...” . Comparem as respostas dadas àquelas questões com as respostas que vocês dariam agora e escrevam um texto explicando o que aprenderam nesta Unidade.
Para conhecer mais

Será o Saci?
(Matemática em mil e uma histórias)
Martins Rodrigues Teixeira
São Paulo: FTD, 2010.
Fim de semana no sítio da vó Zilá, excelente oportunidade para devorar os quitutes que ela faz e colocar em prática conhecimentos sobre perímetros e áreas. Venha compartilhar dessa aventura!

Uma raiz diferente
(A descoberta da Matemática)
Luzia Faraco Ramos
São Paulo: Ática, 2019.
Luís está largando os estudos para cuidar da roça. Mas tudo muda quando ele conhece uma turma de outra cidade. Entre outras experiências, Luís aprende as raízes quadradas e cúbicas.