Página 205

CAPÍTULO 8 Polígono, circunferência e círculo

1 Polígono e seus elementos

As asas da libélula são formadas por diversas partes que lembram polígonos. Observe.

Fotografia. Libélula em tom amarelado com as asas transparentes . Destaque para asa composta de linhas polígonais fechadas. — Libélula.

Um polígono é uma linha poligonal plana fechada e simples mais sua região interna.

Recorde

Linha poligonal plana é uma linha do plano formada apenas por segmentos de reta consecutivos (quando a extremidade de um segmento é também extremidade do outro) e não colineares.

• Linhas poligonais fechadas e simples: os segmentos não se cruzam.

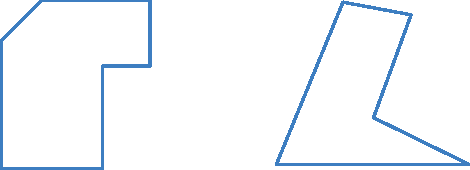
Ilustração. Uma linha poligonal fechada e simples, azul, construída com 7 segmentos de retas. Ilustração. Uma linha poligonal fechada e simples, azul, construída com 5 segmentos de retas.

• Linhas poligonais fechadas e não simples: os segmentos se cruzam.

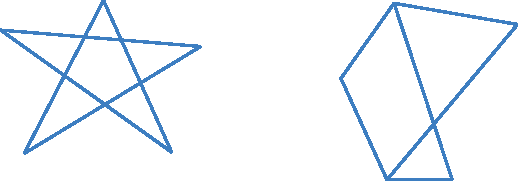
Ilustração. Linhas poligonais fechadas e não simples. azuis. A linha poligonal se parece com uma estrela construída com 5 segmentos de reta. Ilustração. Linhas poligonais fechadas e não simples, azuis, construídas por 6 segmentos de reta.

Observe exemplos de polígonos e de figuras que não são polígonos.

Ilustração. 3 linhas poligonais fechadas e simples, na cor verde. Da esquerda para a direita, a primeira linha poligonal lembra um sinal de adição, construída por 12 segmentos de reta. A segunda é construída por 6 segmentos de reta. E a terceira é construída por 8 segmentos de reta. Legenda: São polígonos. Ilustração. 3 figuras planas fechadas, na cor roxa. Da esquerda para a direita, a primeira é formada por 3 linhas curvas. A segunda é oval. E a terceira é construída 4 segmentos de reta, sendo que 2 se cruzam, dividindo a figura em 2 partes. Legenda: Não são polígonos.

A linha poligonal é o contorno do polígono e separa o plano em duas regiões: a região interna do polígono e a região externa a ele.

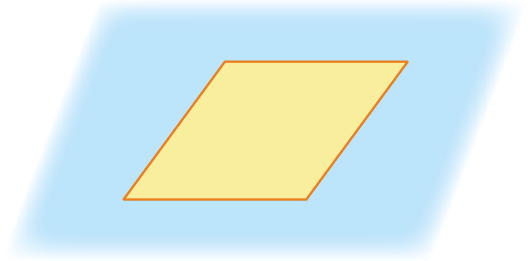
Ilustração. Uma região de cor azul em formato de paralelogramo, no centro há outro paralelogramo com a região interna de cor amarela e os lados de cor laranja. — A linha laranja é o contorno do polígono, a parte amarela é a região interna do polígono e a parte azul é a região externa ao polígono.

Página 206

Polígono convexo e polígono não convexo

Um polígono pode ser classificado em convexo ou não convexo.

Se todos os segmentos de reta com extremidades no interior de um polígono tiverem todos os seus pontos situados no interior desse polígono, ele será convexo. Observe alguns exemplos.

Ilustração. Quadrilátero com um segmento de reta na região interna do polígono. Ilustração. Triângulo obtusângulo com um segmento de reta na região interna do polígono.

Ilustração. Polígono com seis lados, com um segmento de reta na região interna do polígono. Ilustração. Polígono de cinco lados com um segmento de reta na região interna do polígono.

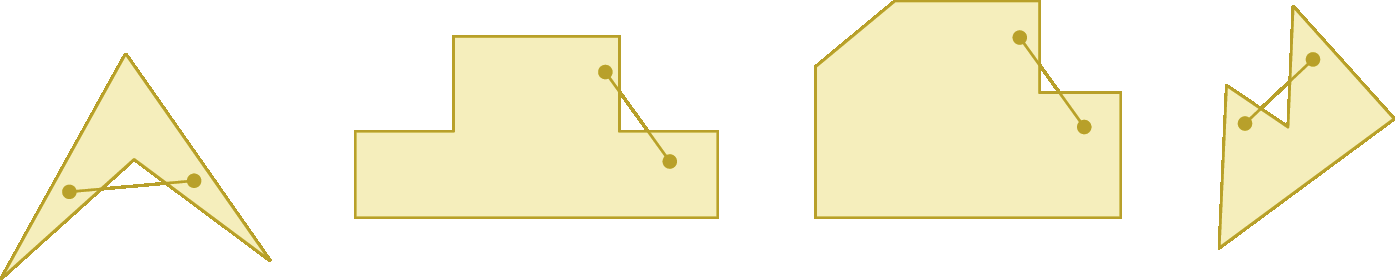
Se um segmento de reta tiver extremidades no interior de um polígono, mas nem todos os seus pontos estiverem situados no interior desse polígono, ele será não convexo. Observe alguns exemplos.

Ilustração. Quadrilátero com o formato que lembra uma seta, tendo um segmento de reta que começa no interior do polígono passa na região externa e termina novamente no interior. Ilustração. Polígono com oito lados, que lembra o formato de um pódio, com um segmento de reta que começa na região interna do polígono passa pela região externa e termina na região interna. Ilustração. Polígono com sete lados, com um segmento de reta que começa na região interna do polígono passa pela região externa e termina na região interna. Ilustração. Polígono com cinco lados, com um segmento de reta que começa na região interna do polígono passa pela região externa e termina na região interna.

Elementos de um polígono

Considere o polígono convexo representado e a indicação de seus elementos.

Ilustração. Polígono ABCDE convexo, em laranja, em seu interior foram traçadas suas diagonais formando uma estrela. Em destaque, os ângulos externos a, b, c, d e e.

• Lados são os segmentos de reta que limitam o polígono:

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} e \overline{E A}

• Vértices são os pontos que são extremidades dos lados do polígono: A, B, C, D e E

• Diagonais são segmentos de reta cujas extremidades são vértices que não pertencem a um mesmo lado do polígono:

\overline{A C}, \overline{A D}, \overline{B E}, \overline{B D} e \overline{C E}

• Ângulos internos são os ângulos formados por um par de lados consecutivos que contém a região interna do polígono:

E \hat{A} B, A \hat{B} C, B \hat{C} D, C \hat{D} E e D \hat{E} A

(também podem ser indicados por

\hat{A}, \hat{B}, \hat{C}, \hat{D} e \hat{E}

, respectivamente)

• Ângulos externos são os ângulos formados pelo prolongamento de um dos lados do polígono e por seu lado consecutivo e que não contêm a região interna do polígono:

\hat{a}, \hat{b}, \hat{c}, \hat{d} e \hat{e}

Observação

Em um polígono convexo, cada ângulo interno e o ângulo externo com vértice comum são adjacentes suplementares. Assim, a soma das medidas de suas aberturas é igual a 180graus. Então, no polígono ABCDE anterior, temos:

• medida de(

\hat{A}

) + medida de(

\hat{a}

) = 180graus

• medida de(

\hat{B}

) + medida de(

\hat{b}

) = 180graus

• medida de(

\hat{C}

) + medida de(

\hat{c}

) = 180graus

• medida de(

\hat{D}

) + medida de(

\hat{d}

) = 180graus

• medida de(

\hat{E}

) + medida de(

\hat{e}

) = 180graus

Página 207

Lembre-se: Escreva no caderno!

Nome dos polígonos

Alguns polígonos são nomeados de acordo com o número de lados. Observe.

Número de lados	Nome do polígono	Número de vértices	Número de ângulos internos
3	Triângulo	3	3
4	Quadrilátero	4	4
5	Pentágono	5	5
6	Hexágono	6	6
7	Heptágono	7	7
8	Octógono	8	8
9	Eneágono	9	9
10	Decágono	10	10
11	Undecágono	11	11
12	Dodecágono	12	12
15	Pentadecágono	15	15
20	Icoságono	20	20

Note que, para cada um desses polígonos, o número de vértices, de lados e de ângulos internos é sempre o mesmo. Isso vale para qualquer polígono.

Polígonos regulares

Os polígonos podem ser classificados segundo as medidas de comprimento dos lados ou das medidas de abertura dos ângulos.

Os polígonos que têm todos os lados de mesma medida de comprimento são denominados polígonos equiláteros. Aqueles que têm todos os ângulos internos de mesma medida de abertura são denominados polígonos equiângulos. E os polígonos que têm lados de mesma medida de comprimento e ângulos de mesma medida de abertura são denominados polígonos regulares.

Ilustração. Quadrado verde com quatro ângulos internos retos. Ilustração. Pentágono azul convexo com todos os seus lados e ângulos internos congruentes. Ilustração. octógono bege convexo com todos seus lados e ângulos internos congruentes. Legenda: Polígonos regulares.

Para pensar

Fotografia. Teia de aranha em formato circular. No centro, está uma aranha amarronzada com patas listradas de coral, verde e marrom.

Uma teia de aranha é formada por diversas partes que lembram polígonos. Esses polígonos são regulares ou não regulares?

Página 208

ATIVIDADES

faça as atividades no caderno

1. Observe o polígono e responda às questões.

Ilustração. Pentágono verde convexo ABCDE. Destaque para os ângulos externos a minúsculo, b minúsculo, c minúsculo, d minúsculo, e minúsculo.

a) Quais são seus vértices?

b) Quais são seus lados?

c) Quais são seus ângulos internos?

d) Quais são seus ângulos externos destacados na figura?

e) Quais são suas diagonais?

2. Usando régua graduada e transferidor, desenhe no caderno:

a) um quadrilátero com todos os ângulos internos com abertura medindo 90graus;

b) um polígono não equilátero e não equiângulo.

3. Observe as figuras e identifique, no caderno, a ou as afirmação ou afirmações verdadeira ou verdadeiras.

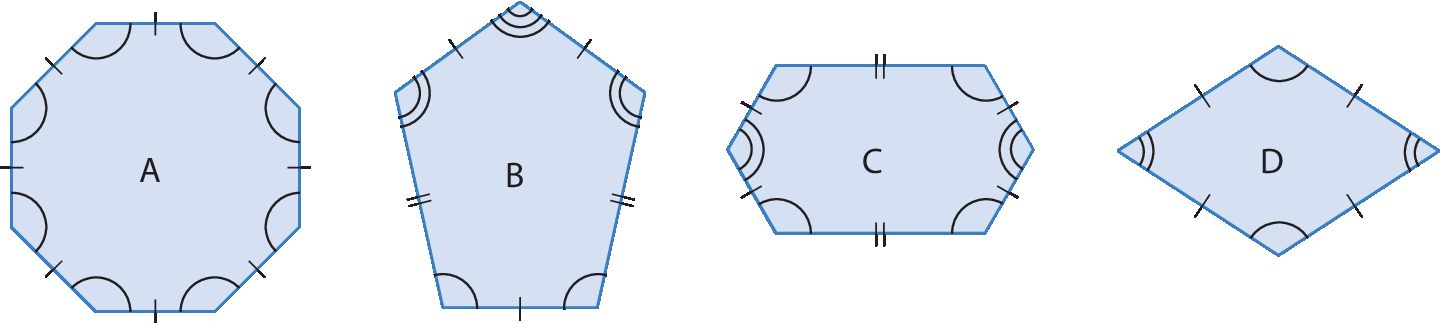
Ilustração. Polígono azul A, todos os lados são congruentes e seus ângulos internos são congruentes. Ilustração. Polígono azul B com cinco lados, dos quais dois lados são congruentes e os outros três lados são congruentes. Dos cincos ângulos internos, dois são congruentes entre si, e outros dois ângulos são congruentes entre si. Ilustração. Polígono azul C com seis lados, dos quais quatro lados são congruentes entre si e outros dois são congruentes. Dos seis ângulos internos, quatro são congruentes entre si e outros dois são congruentes entre si. Ilustração. Polígono D com quatro lados congruentes. Os ângulos internos opostos de dois a dois são congruentes.

a) O polígono a é um polígono regular.

b) O polígono C é um hexágono equiângulo.

c) O polígono D é um quadrilátero equilátero.

d) O polígono B é um pentágono equiângulo.

4. Observe a figura e, depois, responda à questão.

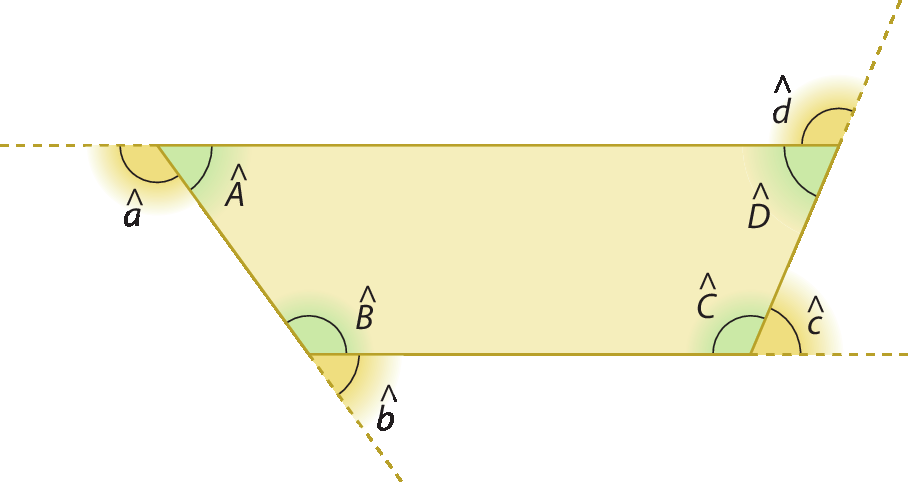
Ilustração. Trapézio bege. Destaque para os ângulos internos: A maiúsculo, B maiúsculo, C maiúsculo e D maiúsculo. ângulos externos: a minúsculo, b minúsculo, c minúsculo e d minúsculo.

• Qual é a relação entre os ângulos interno e externo que possuem o mesmo vértice?

Página 209

Informática e Matemática

faça as atividades no caderno

Mosaicos

Nessa seção, você vai utilizar um software de Geometria dinâmica para construir mosaicos usando apenas polígonos regulares. Para isso, os polígonos precisam ter pelo menos um vértice em comum e se encaixar perfeitamente, de fórma que não se sobreponham nem haja espaços entre eles.

Construa

Siga os passos para construir mosaicos com polígonos regulares. Para a construção de cada polígono, use a ferramenta própria para traçar polígonos regulares, destacada na ilustração.

Mosaico de quadrados

1º) A partir de dois pontos quaisquer, construa um quadrado.

2º) Selecione dois vértices consecutivos do quadrado construído e faça outro quadrado.

3º) Construa outros quadrados a partir de dois vértices consecutivos de um quadrado já existente até que o mosaico atinja as dimensões desejadas.

Ilustração. Software de geometria. Na parte superior, botões de comando. Destaque para o botão com um polígono: Ferramenta que traça polígonos regulares a partir de dois pontos. Na tela, figura composta de quadradinhos.

Mosaico de triângulos equiláteros

1º) A partir de dois pontos quaisquer, construa um triângulo equilátero.

2º) Selecione dois vértices consecutivos do triângulo construído e faça outro triângulo equilátero.

3º) Construa outros triângulos equiláteros a partir de dois vértices consecutivos de um triângulo já existente até formar o mosaico desejado.

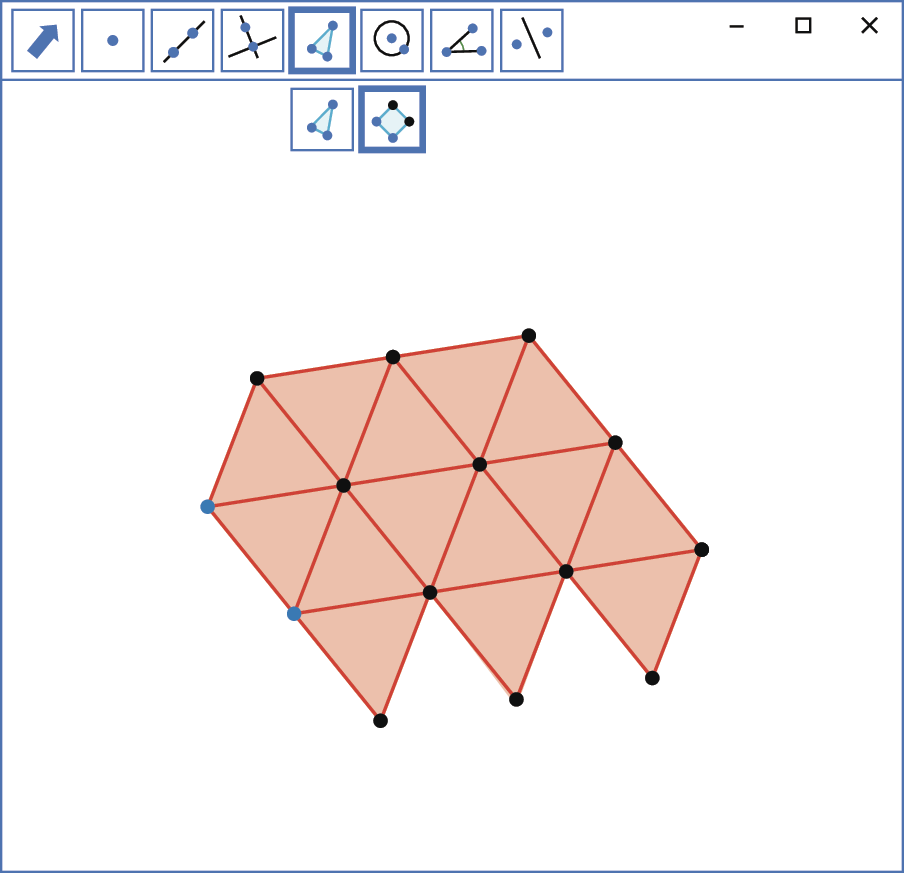
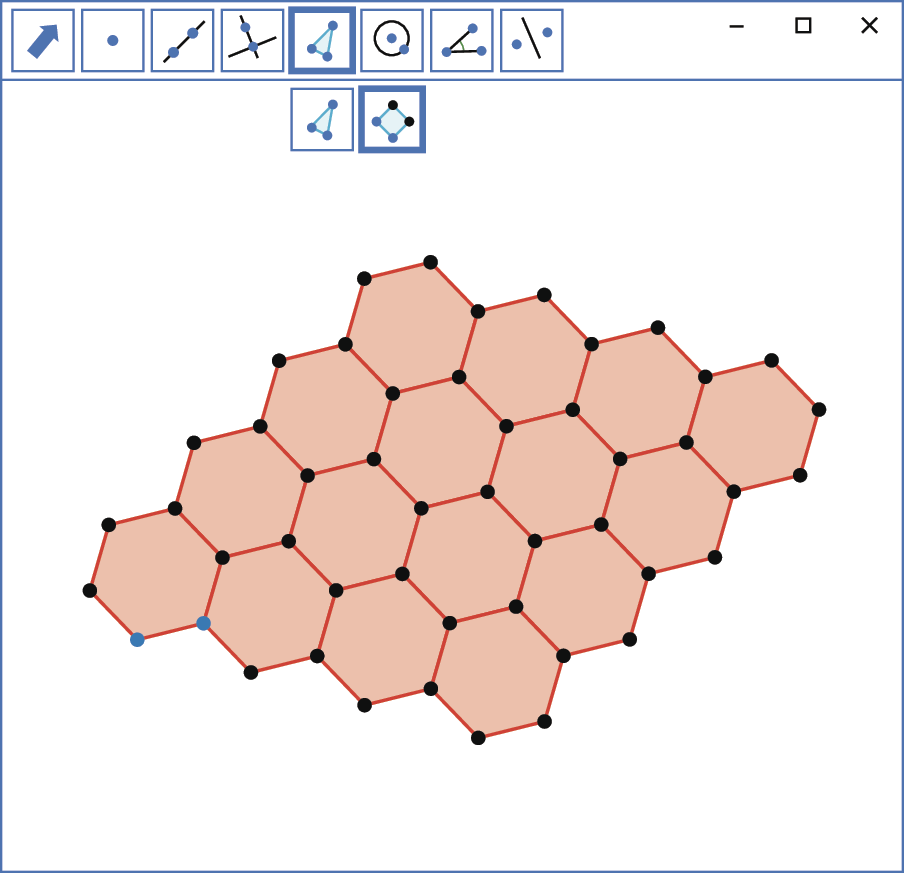
Mosaico de hexágonos regulares

1º) A partir de dois pontos quaisquer, construa um hexágono regular.

2º) Selecione dois vértices consecutivos do hexágono construído e faça outro hexágono regular.

3º) Construa outros hexágonos regulares a partir de dois vértices consecutivos de um hexágono já existente até formar o mosaico desejado.

Página 210

▶ Informática e Matemática

Mosaico composto de dois polígonos regulares diferentes

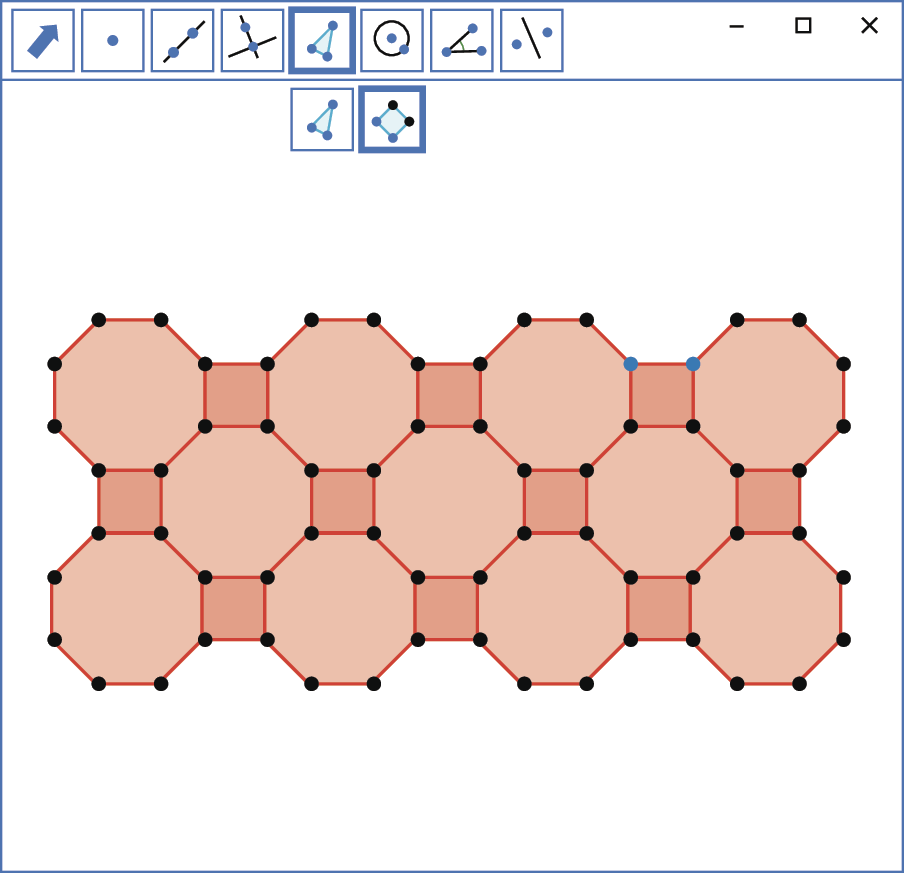
Para compor um mosaico, também podemos combinar dois ou mais polígonos regulares. Siga os passos a seguir e construa um mosaico formado por octógonos regulares e quadrados.

1º) A partir de dois pontos quaisquer, construa um octógono regular.

2º) Selecione dois vértices consecutivos do octógono regular construído e faça um quadrado.

3º) Alterne a construção de octógonos e quadrados seguindo o padrão mostrado no mosaico aqui representado até formar o mosaico desejado.

investigue

Faça o que se pede utilizando as ferramentas do software.

a) Movimente os pontos móveis dos mosaicos construídos, mudando a medida de comprimento de seus lados. O que aconteceu com as medidas de abertura dos ângulos internos dos polígonos quando modificamos as medidas de comprimento dos lados dos polígonos?

b) Se, em um dos três primeiros mosaicos construídos, escolhermos um vértice de um polígono cercado por polígonos em toda a sua volta, a soma das medidas de abertura dos ângulos internos dos polígonos ao redor desse vértice será 360graus.

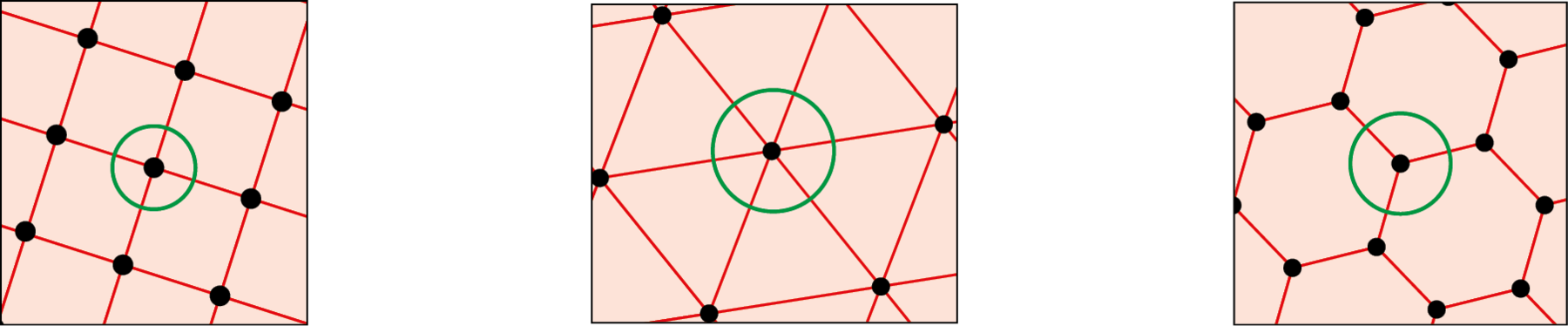
Ilustração. Quadrado maior dividido em quatro quadrados menores. No centro, nos pontos de encontro dos quadrados menores, o ponto está circulado de verde. Ilustração. Hexágono regular dividido em seis triângulos congruentes. No centro, nos pontos de encontro dos triângulos, o ponto está circulado de verde. Ilustração. Malha formada por hexágonos regulares. No centro, nos pontos de encontro dos hexágonos, o ponto está circulado de verde.

• Considerando essa informação, é possível determinar as medidas de abertura dos ângulos internos desses polígonos. Calcule a medida de abertura do ângulo interno do triângulo equilátero e do hexágono regular.

c) Observe o mosaico construído com octógonos regulares e quadrados.

Ilustração. Mosaico formado por hexágonos e quadrados.

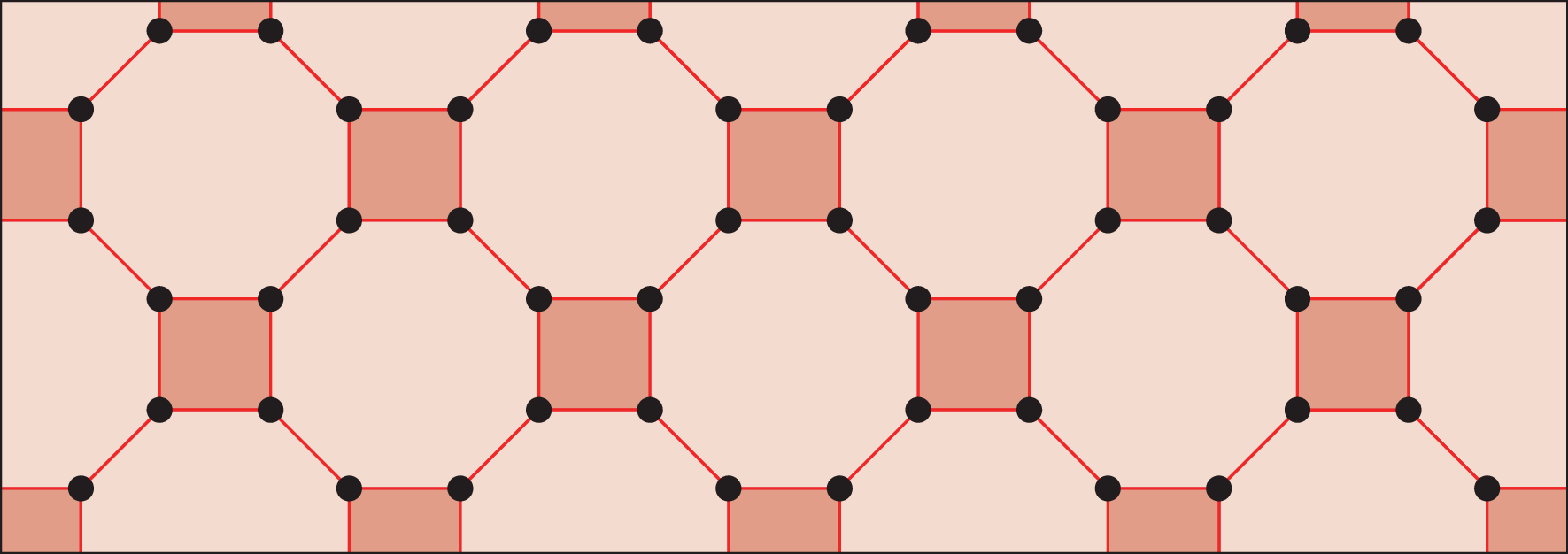
• Como podemos descobrir a medida de abertura do ângulo interno do octógono regular? Qual é essa medida?

Página 211

2 Circunferência e círculo

Observe a fotografia.

Fotografia. Atleta de ginástica rítmica de cabelo preto e roupa colorida está com os braços para o lado e o tronco abaixado para frente, a cabeça está dentro de um bambolê, apoiado em seu pescoço. — Rut Castillo, do México, durante competição de ginástica rítmica nos Jogos Olímpicos de Tóquio, Japão, 2021.

O bambolê usado pela ginasta lembra qual figura geométrica?

Em nosso dia a dia, percebemos a presença de formas circulares em vários objetos. O bambolê é um exemplo de objeto que lembra uma circunferência.

Circunferência é a figura geométrica formada por todos os pontos de um plano que estão à mesma medida de distância de um ponto fixo desse plano. O ponto fixo é chamado centro da circunferência.

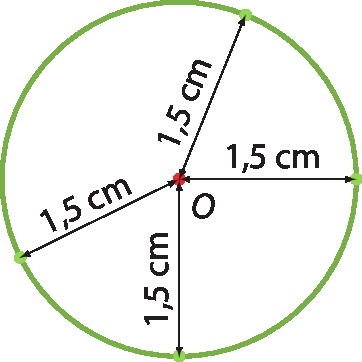
Na figura a seguir, por exemplo, a linha verde representa uma circunferência cujo centro é o ponto óh, e a distância desse ponto a qualquer ponto da circunferência mede 1,5 centímetro de comprimento.

Ilustração. Circunferência, em verde, no centro há o ponto O. Quatro segmentos traçados, cada um medindo 1,5 centímetro, começam no ponto O e tocam a circunferência.

Na foto a seguir, a parte azul da roda-gigante em que as cabines estão presas lembra uma circunferência. Note que a medida da distância entre o centro da roda e qualquer ponto dessa parte azul é a mesma.

Fotografia. Roda-gigante com cabines coloridas. Ao fundo, árvores e o céu azul. — Roda-gigante.

Para traçar uma circunferência, podemos contornar objetos circulares, utilizar fios e linhas ou usar um compasso.

Atenção! Cuidado ao usar o compasso.

Ilustração. Três garotas desenhando circunferências. Uma das meninas é loira e usa uma blusa roxa, outra é negra e usa uma blusa amarela, a última parece ser oriental e usa uma blusa verde. A garota loira está usando um pote para desenhar a circunferência. A garota negra está usando um lápis amarrado em uma haste para desenhar a circunferência. A última garota está usando um compasso para desenhar a circunferência.

Página 212

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

Raio e diâmetro de uma circunferência

Qualquer segmento de reta cujas extremidades são o centro e um ponto qualquer da circunferência chama-se raio da circunferência.

Qualquer segmento de reta que tem as duas extremidades na circunferência e que passa pelo seu centro chama-se diâmetro.

Na circunferência representada:

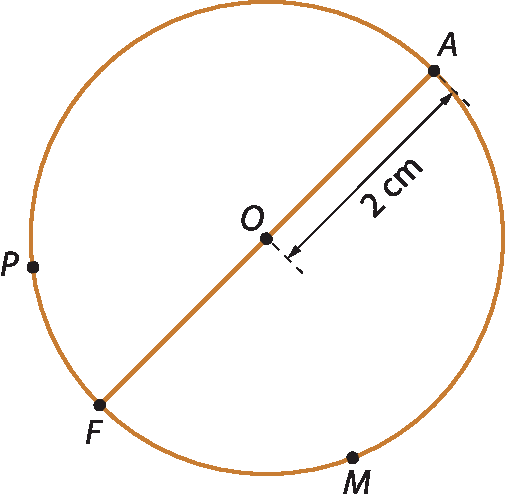
Ilustração. Circunferência de centro O, em marrom. Na circunferência, há os pontos P, F, M e A. O diâmetro traçado é FA e o raio OA mede 2 centímetros.

• óh é o centro;

• a, F, P e M são alguns pontos da circunferência;

•

\overline{A O}

é um raio;

•

\overline{F A}

é um diâmetro.

O comprimento do raio dessa circunferência mede 2 centímetros e o comprimento do diâmetro mede 4 centímetros.

Comprimento de uma circunferência

Camila desenhou três circunferências usando um compasso e indicou a medida de comprimento de seus diâmetros.

Ilustração. Circunferência, em azul. Traçado o diâmetro que mede cinco centímetros. Ilustração. Circunferência, em laranja. Traçado o diâmetro que mede dez centímetros. Ilustração. Circunferência, em verde. Traçado o diâmetro que mede quinze centímetros.

Atenção! Cuidado ao usar o compasso.

Ilustração. Garota branca de cabelo castanho e blusa azul sentada de frente para uma mesa recortando círculos com uma tesoura.

Em seguida, ela colocou uma linha sobre o contorno de cada circunferência e, depois, mediu o comprimento aproximado de cada linha.

A medida do comprimento de cada linha corresponde à medida do comprimento da circunferência. Considere as medidas aproximadas dos comprimentos das circunferências C₁, C₂ e C₃ que Camila obteve ao medir o comprimento das linhas.

C₁

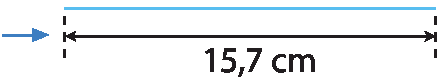
Esquema. Seta azul apontando para ilustração de um segmento de reta azul com indicação de 15,7 centímetros de medida de comprimento.

C₂

Esquema. Seta azul apontando para ilustração de um segmento de reta laranja com indicação de 31,5 centímetros de medida de comprimento.

C₃

Esquema. Seta azul apontando para ilustração de um segmento de reta verde com indicação de 47 centímetros de medida de comprimento.

Observe os valores que Camila obteve ao calcular o quociente entre a medida aproximada do comprimento de cada circunferência e a medida do diâmetro correspondente.

C₁:

\frac{15, 7}{5}

= 3,14 C₂:

\frac{31, 5}{10}

= 3,15 C₃:

\frac{47}{15}

= 3,1333reticências

Como é possível perceber, os valores obtidos por Camila nesses quocientes estão próximos de 3,14.

Página 213

Os números próximos de 3,14 que Camila obteve ao dividir as medidas dos comprimentos das circunferências pelas medidas dos comprimentos dos diâmetros correspondentes, na mesma unidade, são aproximações de um número não racional chamado pi (representado pela letra grega π).

π = 3,14159265reticências

Observação

O número π não é racional porque tem infinitas casas decimais e não tem parte periódica.

Transcrição do áudio

Uma breve história do pi

Duração: 3:04min. Página: 213.

>> [LOCUTOR] Uma breve história do pi

Música de fundo.

>> [LOCUTOR] Quando nossos antepassados começaram a observar o mundo ao seu redor com maior atenção, acabaram fazendo algumas relações entre objetos da natureza e objetos da Matemática, como as formas geométricas, por exemplo.

>> [LOCUTOR] Quando jogamos uma pedra num lago, vemos que se formam ondulações semelhantes a várias circunferências de diferentes tamanhos e com um centro em comum.

>> [LOCUTOR] Enfim, além de notarmos alguns padrões na natureza e de fazermos essas relações com círculos e circunferências, em um momento da nossa existência resolvemos estudar esses objetos.

>> [LOCUTOR] No caso da circunferência, que é a figura geométrica formada por todos os pontos de um plano que estão à mesma distância de um ponto fixo desse plano, nós nos perguntamos:

>> [LOCUTOR] Será que existe alguma relação entre o comprimento da circunferência e o seu diâmetro?

>> [LOCUTOR] Temos conhecimento, por meio de registros históricos, de que civilizações antigas, como a egípcia, por exemplo, já sabiam que o quociente entre a medida do comprimento da circunferência e a medida do seu diâmetro era constante.

>> [LOCUTOR] O mais impressionante é que, qualquer que fosse o tamanho da circunferência, o quociente era sempre o mesmo, uma constante muito próxima de 3.

>> [LOCUTOR] Por volta de 287 a.C., nascia em Siracusa, na atual Sicília, região da Itália, um dos maiores matemáticos de todos os tempos, chamado Arquimedes.

>> [LOCUTOR] Ele foi o primeiro a encontrar, matematicamente, um número muito próximo de pi, algo entre 223 71 avos e 22 sétimos.

>> [LOCUTOR] No final do século V, o chinês TsuCh’ung-Chih, chegou a um valor ainda mais preciso que o de Arquimedes, um número próximo de 3,1415926.

>> [LOCUTOR] Percebeu-se mais tarde, que o número pi não é racional porque tem infinitas casas decimais e não tem parte periódica.

>> [LOCUTOR] Mais de 1500 anos depois, em 2010, com a ajuda de um computador, um engenheiro japonês conseguiu calcular o valor de pi com 5 trilhões de casas decimais!

>> [LOCUTOR] Sua máquina demorou três meses ininterruptos para efetuar o cálculo.

>> [LOCUTOR] E, hoje, você está aqui aprendendo um pouco mais sobre a história do pi.

>> [LOCUTOR] O tempo passa, e a nossa curiosidade sobre esse número permanece.

Música de fundo.

O áudio inserido neste conteúdo é da Incompetech.

Círculo

A figura geométrica formada por uma circunferência e sua região interna chama-se círculo.

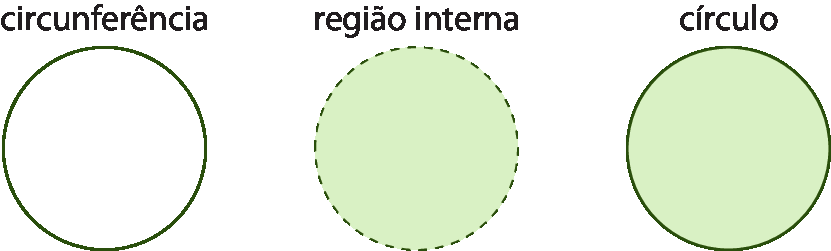
Ilustração. Circunferência, em verde. Ilustração. Circunferência tracejada em verde, a região interna esta pintada de verde. Ilustração: Circulo, em verde.

É preciso prestar atenção para não confundir circunferência com círculo.

Observe alguns objetos que lembram círculos.

As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

Fotografia. Placa de sinalização de trânsito proibindo estacionar. Placa circular com fundo branco e borda vermelha com a letra E no centro, uma linha diagonal vermelha está sobre a letra E. — Placa “proibido estacionar”.

Fotografia. Moeda de 1 real. A borda é dourada e o centro é prateado. — Moeda de 1 real.

ATIVIDADES

faça as atividades no caderno

1. No caderno, classifique os segmentos considerando que o centro da circunferência é o ponto óh.

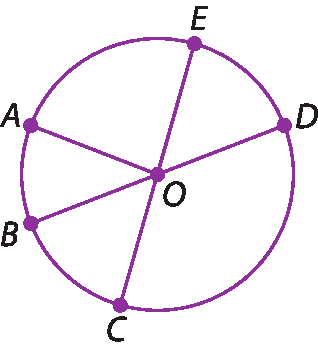
Ilustração. Circunferência, em roxo. No centro, o ponto O. Na circunferência, há os pontos A, B, C, D e E. Traçados os segmentos OA, OB, OC e OD. Traçado o segmento BD que passa pelo o ponto O.

a)

\overline{O C}

b)

\overline{O A}

c)

\overline{B D}

d)

\overline{O E}

e)

\overline{C E}

f)

\overline{O D}

Atenção! Cuidado ao usar o compasso.

2. Com um compasso, construa uma circunferência de centro óh e diâmetro com medida de comprimento igual a 4 centímetros. Depois, faça o que se pede.

a) Trace um raio

\overline{A O}

e um diâmetro

\overline{A B}

.

b) Determine a medida de comprimento dessa circunferência.

•

Converse com um colega e verifique se vocês determinaram a medida de comprimento da circunferência do mesmo modo.

Página 214

3. Considere que

\overline{C B}

é um diâmetro da circunferência a seguir e que A é um ponto qualquer dessa circunferência diferente de B e de C.

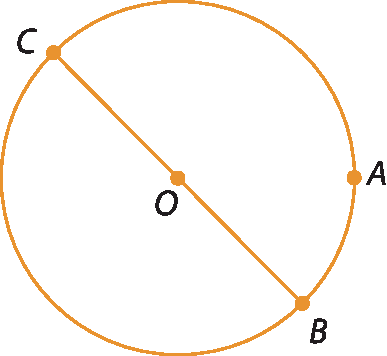
Ilustração. Circunferência, em laranja. No centro, o ponto O. Na circunferência estão os pontos A, B e C. O ponto B é oposto a C. Traçado o segmento CB

a) Podemos afirmar que os pontos a, óh e B determinam um triângulo isósceles? Por quê?

b) Podemos afirmar que os pontos a, B e C determinam um triângulo isósceles? Por quê?

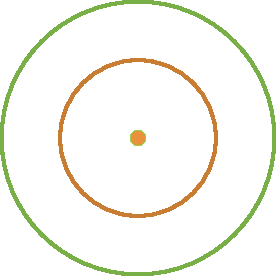
4. Observe os pares de circunferências a seguir e determine se elas têm algum ponto em comum.

a)

Ilustração. Duas circunferências com o mesmo centro. A circunferência em verde e maior que a circunferência em laranja

b)

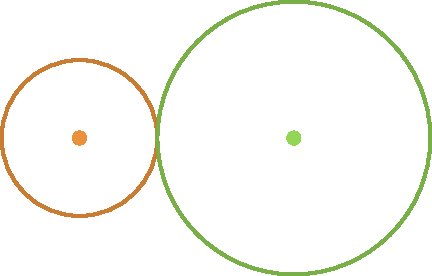
Ilustração. Uma circunferência menor laranja à esquerda encostada em uma circunferência maior verde à direita.

c)

Ilustração. Duas circunferências afastadas. Circunferência laranja menor que a circunferência verde.

d)

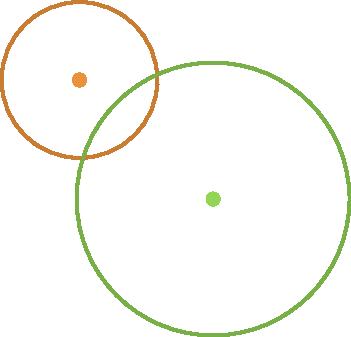
Ilustração. Duas circunferências, uma verde maior, outra laranja menor. Uma está se sobrepondo a uma parte da outra.

Versão adaptada acessível

4. Represente o que se pede em cada item.

a) Duas circunferências que não têm ponto em comum.

b) Duas circunferências que têm um ponto em comum.

c) Duas circunferências que têm dois pontos em comum.

5. Podemos dividir o círculo em partes chamadas setores circulares. Observe o círculo a seguir, de centro óh, dividido em três setores circulares.

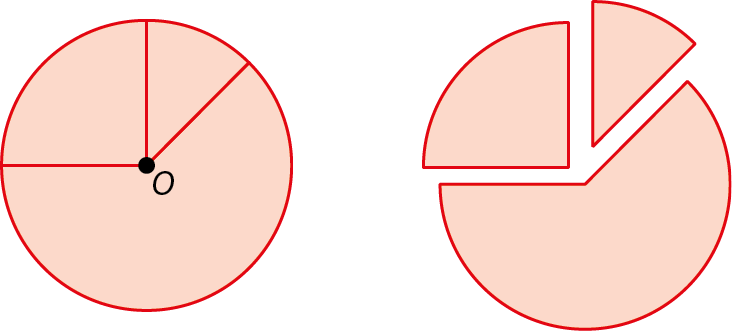
Ilustração. Círculo vermelho claro. No centro, o ponto O, traçados três segmentos que começam no ponto B e terminam na borda do circulo criando três setores circulares. O menor setor representa um oitavo do círculo, outro setor representa um quarto do círculo e o último representa o restante do círculo. Ilustração. Círculo em vermelho claro. Os três setores circulares estão separados.

Agora, observe os setores circulares destacados em cada item e associe-os a partes de giros e medidas de aberturas de ângulos.

a)

Ilustração. Círculo tracejado, um quarto do círculo está pintado de laranja.

b)

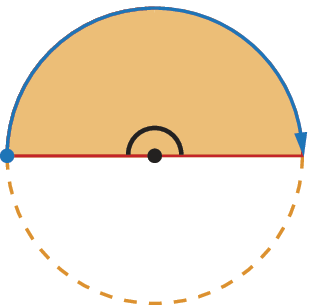
Ilustração. Círculo tracejado, a metade do círculo está pintada de laranja.

c)

Ilustração. Círculo tracejado, três quartos do círculo estão pintados de laranja.

6. Em uma fábrica de rodas para bicicletas, essas peças são embaladas em caixas.

Ilustração. Homem branco de bigode, cabelo preto e blusa azul está de frente para uma caixa segurando uma roda de bicicleta. Ao lado, carrinho com uma caixa.

Desprezando a espessura da caixa, responda às questões.

a) Se o raio de uma roda medir 17 centímetros de comprimento, qual deverá ser, no mínimo, a medida do comprimento da caixa?

b) Se o comprimento da caixa medir 62 centímetros, qual será a medida máxima do comprimento do raio da roda que a caixa comportará?

7. Míriam está fazendo uma toalha circular e quer aplicar renda em seu contorno. Qual medida de comprimento da renda, em metro, Míriam deverá usar se o diâmetro da toalha mede 1,5 métro de comprimento?

Página 215

Trabalho em equipe

faça as atividades no caderno

Atenção! Cuidado ao usar o compasso.

Criando obra de arte

Você já percebeu como a Geometria influencia a arte? Muitos artistas a estudam profundamente para criar suas obras. Agora, você vai conhecer duas pinturas do Cubismo e criar sua própria obra de arte. No Cubismo, os artistas usavam formas geométricas para mostrar que tudo o que existia no mundo real podia ser fragmentado.

Justificativa

O contato com obras de arte amplia o universo cultural.

Objetivo

Criar uma obra de arte com figuras geométricas estudadas neste capítulo.

MATERIAL NECESSÁRIO

• uma folha de cartolina;

• revistas, embalagens flexíveis ou papéis coloridos para recortar;

• tesoura com pontas arredondadas;

• cola branca;

• caneta hidrográfica preta ou outro tipo de caneta preta de ponta porosa.

Procedimento

• Reúna-se com três colegas e elaborem um trabalho de colagem. Para isso, vocês podem fazer um desenho na cartolina que será coberto com os recortes.

• Recortem diversas figuras geométricas planas nas formas e nos tamanhos que preferirem.

• Colem os recortes na cartolina preenchendo o espaço interno do desenho feito e, depois, contornem a figura com a caneta preta.

APRESENTAÇÃO

• Os trabalhos podem ser expostos na sala de aula ou em painéis na escola.

Pintura abstrata retratando jogadores de xadrez. As formas da pintura são linhas escuras e ondulações em tons de verde, bege, marrom e amarelo. — Marcel diuchomp. Retrato de jogadores de xadrez, 1911, óleo sobre tela, 100,6 centímetros × 100,5 centímetros.

Pintura abstrata representando natureza morta: a mesa.
No centro, há uma forma oval em tons de laranja e marrom. No fundo, formas retas em tom de azul. — Juan Gris. Natureza morta: a mesa, 1914, colagem e carvão sobre tela, 59,7 centímetros × 44,5 centímetros.

Página 216

Estatística e Probabilidade

faça as atividades no caderno

Construção de gráficos de setores

Uma pesquisa realizada em março de 2023 na escola de futebol Golaço revelou os times pelos quais os estudantes torcem. O resultado dessa pesquisa está apresentado na tabela a seguir.

Times pelos quais os estudantes torcem
Time	Porcentagem de estudantes
Internacional	50%
Grêmio	25%
Juventude	12,5%
Caxias	12,5%

Dados obtidos pela escola de futebol golaço em março de 2023.

Para construir o gráfico de setores referente a essa pesquisa, precisamos determinar a medida de abertura do ângulo associado a cada setor correspondente aos dados da tabela.

Como o círculo corresponde ao total de torcedores, associamos o ângulo de medida de abertura igual a 360graus a 100% dos estudantes que responderam à pesquisa. Com base nessa informação, podemos obter a medida de abertura do ângulo associado ao setor correspondente a cada dado apresentado na tabela.

Internacional

Vamos determinar 50% de 360graus:

\frac{50}{100} \cdot 360 ° = \frac{1}{2} \cdot 360 ° = 180 °

Grêmio

Vamos determinar 25% de 360graus:

\frac{25}{100} \cdot 360 ° = \frac{1}{4} \cdot 360 ° = 90 °

Juventude

Vamos determinar 12,5% de 360graus:

\frac{12, 5}{100} \cdot 360 ° = \frac{125}{1000} \cdot 360 ° = \frac{1}{8} \cdot 360 ° = 45 °

Caxias

Vamos determinar 12,5% de 360graus:

\frac{12, 5}{100} \cdot 360 ° = \frac{125}{1000} \cdot 360 ° = \frac{1}{8} \cdot 360 ° = 45 °

Ilustração. Menina branca de óculos, cabelo preto, camisa vermelha, calção branco e chuteiras. Ela está com um pé sobre uma bola de futebol e fala: Cada porcentagem está relacionada a um setor com determinada medida de abertura de ângulo do círculo. Por exemplo, a porcentagem de torcedores do Internacional está associada a um setor com ângulo de medida de abertura igual a 180°.

Página 217

Portanto, o círculo deverá ser dividido em 4 setores com as seguintes medidas de abertura: um de 180graus, um de 90graus e dois de 45graus. Depois, cada setor deve ser pintado com uma cor diferente.

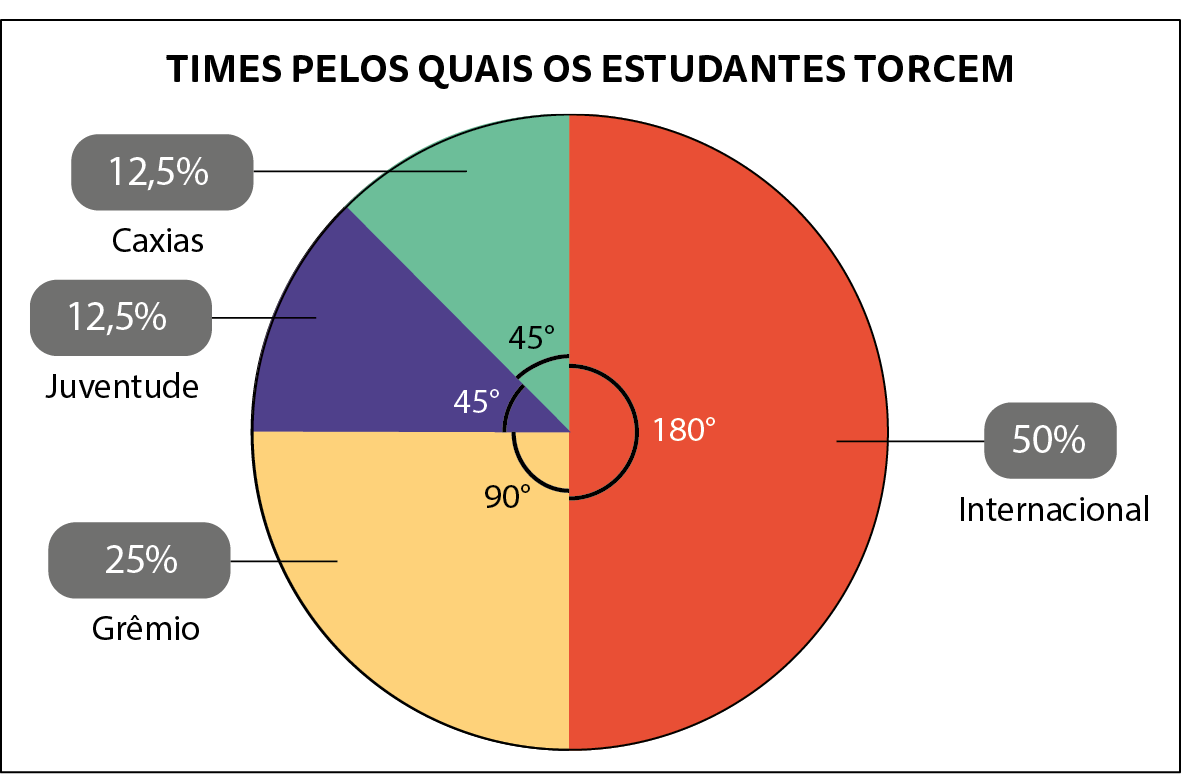
Gráfico de setores colorido. Título: Times pelos quais os estudantes torcem.
Setor vermelho, ângulo de 180 graus, representa 50% e corresponde ao Internacional. Setor amarelo, ângulo de 90 graus, representa 25% e corresponde ao Grêmio. Setor azul, ângulo de 45 graus, representa 25% e corresponde ao Juventude. Setor verde, ângulo de 45 graus, representa 25% e corresponde ao Caxias.

Dados obtidos pela escola de futebol Golaço em março de 2023.

ATIVIDADES

faça as atividades no caderno

1. Uma pesquisa realizada em 2019 pelo Ministério da Ciência, Tecnologia e Inovação analisou a opinião dos entrevistados sobre os investimentos em pesquisa científica e tecnológica no Brasil.

Observe, na tabela a seguir, os dados dessa pesquisa e, depois, faça o que se pede.

Investimentos em pesquisas científicas e tecnológicas no Brasil
Classificação	Porcentagem de entrevistados
Aumentar os investimentos	66%
Manter os investimentos	24%
Diminuir os investimentos	6%
Não sabe/não respondeu	4%

Fonte: PORTAL DA USP. Maioria dos brasileiros é otimista em relação à ciência e tecnologia. Jornal da USP, São Paulo, 23 julho. 2019. Disponível em: https://oeds.link/OIlzA0. Acesso em: 9 agosto 2022.

a) Qual é a soma das porcentagens da tabela?

b) Em um gráfico de setores construído com base nessa tabela, qual classificação representará o maior setor?

c) Com base nesses dados, construa um gráfico de setores. Não se esqueça de informar o título e a fonte dos dados.

d) Se você fizesse parte da pesquisa, qual seria a sua resposta?

Página 218

▶ Estatística e Probabilidade

Atenção! Cuidado ao usar o compasso.

2. A tabela a seguir apresenta a distribuição do consumo de água no mundo.

Consumo de água no mundo
Tipo	Porcentagem
Agrícola	69%
Industrial	19%
Outros	12%

Fonte dos dados: KONCAGÜL, E. TRAN, M. CONNOR, R. Relatório mundial das Nações Unidas sobre desenvolvimento dos recursos hídricos 2021: o valor da água; fatos e dados. [S. l.]: Unesco, 2021. Disponível em: https://oeds.link/DA5aML. Acesso em: 9 ago. 2022.

• Com base nos dados da tabela e usando compasso e transferidor, construa um gráfico de setores em uma folha de papel sulfite após responder às questões a seguir.

a) Qual será o título do gráfico? E a fonte?

b)

Qual deve ser a medida de abertura do ângulo do setor circular que representará a porcentagem do consumo agrícola? E a medida de abertura do ângulo do setor circular que representará o consumo industrial?

Ilustração. Plantação. À frente, menino de cabelo preto, blusa verde e bermuda azul fala: Calcule a medida de abertura do ângulo de cada setor circular. Lembre-se de que o círculo todo mede 360º.

c) Qual é a soma das porcentagens apresentadas na tabela?

d) Como podemos calcular a medida de abertura do ângulo do setor circular associado a outros consumos usando os resultados obtidos no item b?

3. Leia o texto e analise os dados da tabela.

Ilustração. Papel amarelo com o texto: Cuidado ao abrir os e-mails que chegam à sua caixa de entrada. Os e-mails indesejados podem ser spams publicitários, tentativas de roubar dados pessoais ou até e-mails que espalham vírus nos computadores. De acordo com uma análise feita no primeiro trimestre de 2020, quase 55% dos e-mails enviados no mundo naquele período continham spams.

De onde saem os spams que vão parar no seu e-mail
País	Porcentagem de spams
China	5,2%
Estados Unidos	9,6%
Alemanha	9,4%
França	6,3%
Rússia	20,7%
Vietnã	2,6%
Índia	2,2%

Fonte dos dados: SHCHERBAKOVA, T.; SIDORINA, T.; KULIKOVA, T. Spam and phishing in Q1 2020. SecureList, [Sulpontolesteponto], 26 may 2020. Disponível em: https://oeds.link/zhLDEF. Acesso em: 8 agosto2022.

a) A soma das porcentagens indicadas na tabela é igual a 100%? Em caso negativo, quanto falta para 100%?

b) Em uma folha de papel sulfite e usando compasso e transferidor, construa um gráfico de setores com os dados da tabela. Identifique com a palavra Outros o setor que falta para completar o círculo.

Ilustração. Quadro retangular com o texto: Para construir o gráfico, calcule, antes, as medidas de abertura aproximadas do ângulo de cada setor que representa os dados da tabela.

Página 219

Atenção! Cuidado ao usar o compasso e a tesoura.

Ilustração. Ícone. Caderno na
vertical com um lápis.

Atividades de revisão

faça as atividades no caderno

1. Calcule a medida de x e de y em cada caso.

a)

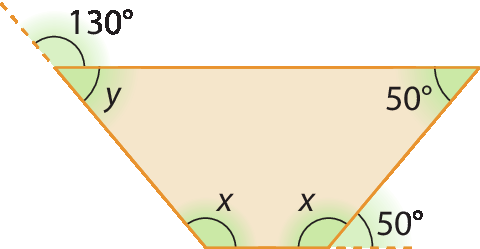
Ilustração: Trapézio. Destaque para os ângulos internos com as medidas x, x, 50 graus e y; ângulos externos 50 graus e 130 graus que são adjacente a x e y, respectivamente.

b)

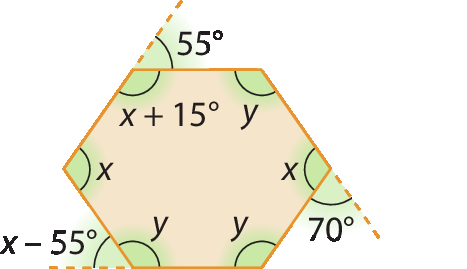
Ilustração. Hexágono convexo. Destaque para os ângulos internos: x+15 graus, y, x, y ,y, x; os ângulos externos 55 graus, 70 graus e x-55 graus são adjacentes aos ângulos x+15 graus, x e y, respectivamente.

2.

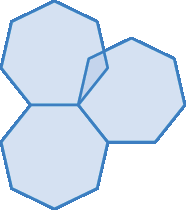
(enêm) Na construção civil, é muito comum a utilização de ladrilhos ou azulejos com a fórma de polígonos para o revestimento de pisos ou paredes. Entretanto, não são todas as combinações de polígonos que se prestam a pavimentar uma superfície plana, sem que haja falhas ou superposições de ladrilhos, como ilustram as figuras.

Ilustração. Figura composta por 4 linhas e 4 colunas de ladrilhos na cor azul. Cada ladrilho tem uma forma oval com duas retas perpendiculares. — Figura 1: Ladrilhos retangulares pavimentando o plano

Ilustração. três heptágonos iguais e um diferente com um lado sobreposto. — Figura 2: Heptágonos regulares não pavimentam o plano (há falhas ou superposição)

A tabela traz uma relação de alguns polígonos regulares, com as respectivas medidas de seus ângulos internos.

Nome	Triângulo	Quadrado	Pentágono
Figura
Ângulo interno	60°	90°	108°

Nome	Hexágono	Octógono	Eneágono
Figura
Ângulo interno	120°	135°	140°

Se um arquiteto deseja utilizar uma combinação de dois tipos diferentes de ladrilhos entre os polígonos da tabela, sendo um deles octogonal, o outro tipo escolhido deverá ter a fórma de um

a) triângulo.

b) quadrado.

c) pentágono.

d) hexágono.

e) eneágono.

3. Observe a ilustração da circunferência de centro óh. Depois, transcreva no caderno apenas as afirmações verdadeiras.

Ilustração. Circunferência, em azul. No centro, o ponto O. Na circunferência, há os ponto E e D, que são opostos, os pontos B e C que são opostos e os pontos D e F que são opostos;

traçados o segmento ED, o segmento DC e o segmento DF;

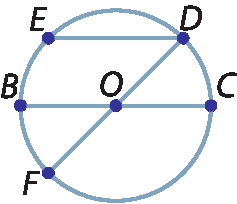
Segmento ED é paralelo ao segmento DC;

Os segmento BC e DF passam pelo ponto O.

a) O segmento

\overline{E D}

é raio da circunferência.

b) Os segmentos

\overline{B C} e \overline{F D}

são diâmetros da circunferência.

c) A medida de comprimento do diâmetro é a metade da medida de comprimento do raio.

d) O é um ponto da circunferência.

e) A medida de comprimento do raio é igual à metade da medida de comprimento do diâmetro.

4. Com um compasso ou usando objetos de formato circular, trace circunferências.

a) Marque o centro de cada circunferência.

b) Com uma régua, meça o comprimento dos raios das circunferências.

c)

Reúna-se com um colega e troquem ideias sobre como traçaram as circunferências e identificaram os raios.

5. Em uma folha de papel, desenhe uma circunferência qualquer e pinte o círculo determinado por ela. Depois, responda às questões e faça o que se pede.

a) O centro da circunferência é um ponto do círculo? É um ponto da circunferência?

b) Os pontos da circunferência fazem parte do círculo?

c) Recorte o círculo que você desenhou e faça experiências com dobras para descobrir quantos eixos de simetria ele tem.

Ilustração. À esquerda, menina branca de cabelos loiros e camiseta rosa desenha uma circunferência com um compasso em uma folha. À frente dela, menino branco de cabelo preto e blusa azul pinta um círculo em uma folha.

Página 220

▶ Atividades de revisão

Lembre-se: Escreva no caderno!

6. Se a parte livre da corda com a qual o cavalo está amarrado mede 4,35 métros de comprimento, qual é a medida de comprimento do cercado circular, em metro? (Considere: π = 3,14)

Atenção! Cuidado ao usar o compasso e a tesoura.

Ilustração. Gramado circular cercado visto de cima; No meio do cercado, há um tronco de madeira no qual um cavalo está amarrado com uma corda; O cavalo está do lado esquerdo com a corda bem esticada.

7.

Observe as pinturas a seguir. Preste atenção às cores, às formas utilizadas e à composição de cada uma.

Pintura. Formas triangulares e circulares sobrepostas em tons de amarelo, vermelho e laranja sobre fundo bege. — Wassily Kandinsky. On the Points [Nos pontos], 1928, óleo sobre tela, 140 centímetros por 140 centímetros.

Pintura. Círculos sobrepostos em tons de vermelho, amarelo, branco e azul. — Belmiro Barbosa de Almeida. Maternidade em círculos, 1908, óleo sobre tela, 46 centímetros por 61 centímetros.

a) Escreva um texto sobre o uso de formas geométricas na arte e dê sua opinião sobre as obras desta atividade.

b)

Usando régua e compasso, faça um desenho composto de círculos, circunferências e polígonos. Pinte seu desenho com as cores que preferir e apresente-o aos colegas.

8. Arquimedes, matemático grego que viveu no século três antes de Cristo, utilizou a fórma fracionária para representar, de maneira aproximada, o número irracional π.

Pintura. Retrato de homem branco de cabelos e barba grisalhos. Ele olha para baixo e está usando roupas escuras com detalhes em dourado. Na mão direita, ele segura um compasso. — Arquimedes, retratado por Giuseppe Nogari no século dezoito. Giuseppe Nogari. Archimedes, óleo sobre tela, 55 centímetros por 44,5 centímetros.

π

= 3, 141592 . . . ≃ \frac{22}{7}

a) Arredonde os números 3,141592reticências e

\frac{22}{7}

para a 2ª casa decimal e compare-os. O que você observa?

b) E se arredondá-los para a 3ª casa decimal?