CAPÍTULO 9 Triângulos e quadriláteros
1 Triângulos
Você já aprendeu que triângulo é um polígono com três lados. Na Arquitetura e na Engenharia é muito comum o uso de estruturas com formato triangular, principalmente em telhados, prédios e pontes.


Observe nas fotos anteriores que, no telhado e no edifício, há estruturas triangulares. Esse formato é muito utilizado em construções porque o triângulo é uma figura rígida, que não pode ser deformada.
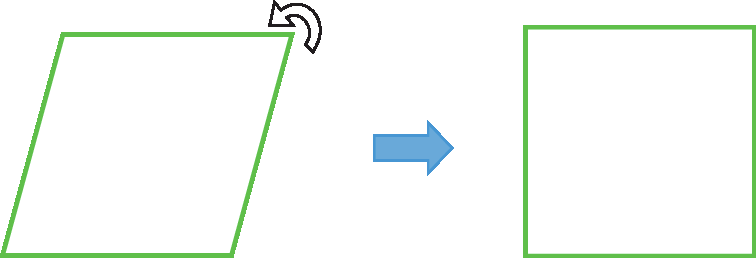
Estruturas com formato de outros polígonos podem sofrer deformações, pois é possível alterar as medidas de abertura de seus ângulos internos sem mudar a medida de comprimento de seus lados. Podemos, por exemplo, movimentar dois lados de uma estrutura com formato de um quadrilátero e transformá-la no formato de outro, com lados de mesmas medidas de comprimento e com ângulos de medidas de abertura diferentes.
Para pensar

A estante entortou!
Como isso poderia ter sido evitado? Por quê?
Lembre-se: Escreva no caderno!
Elementos de um triângulo
Considere o triângulo á bê cê a seguir. Nele, é possível identificar três vértices, três lados e três ângulos internos.
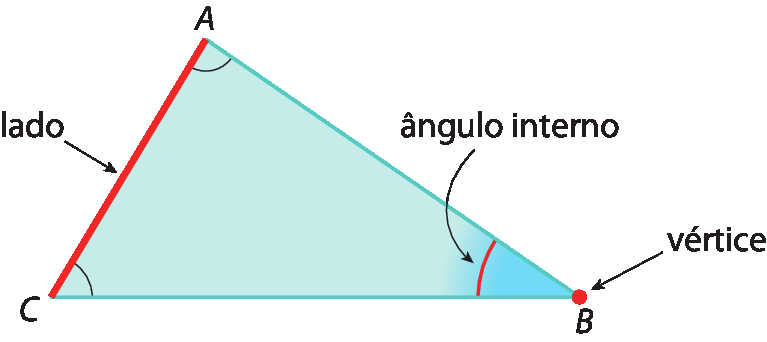
• A, B e C são os vértices;
•
Segmento de reta AB, segmento de reta AC e segmento de reta BC.são os lados;
•
Ângulo CAB, ângulo ABC e ângulo ACBsão os ângulos internos.
2 Construção de triângulos com régua e compasso
Se soubermos as medidas de comprimento dos lados de um triângulo, poderemos construí-lo usando régua e compasso.
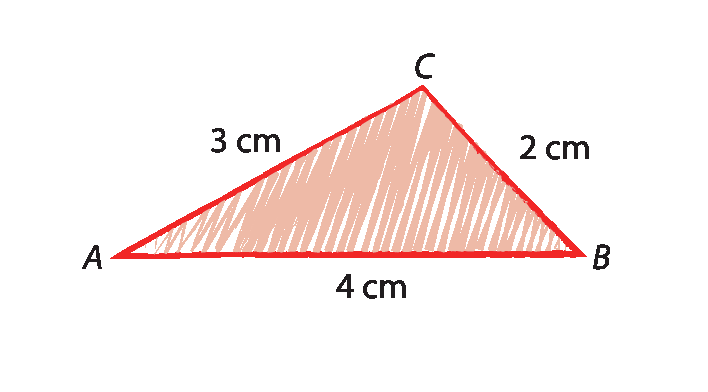
Para construir, por exemplo, um triângulo, como o representado, cujos lados medem 4 centímetros, 3 centímetros e 2 centímetros de comprimento, podemos seguir os passos a seguir.
Atenção! Cuidado ao usar o compasso.
1º) Trace uma reta r e sobre ela construa o segmento
Segmento de reta AB, medindo 4 centímetros de comprimento, que será um dos lados do triângulo.

2º) Utilize um compasso com abertura medindo 3 centímetros de comprimento e, com a ponta-seca do compasso no ponto a da reta r, trace um arco.
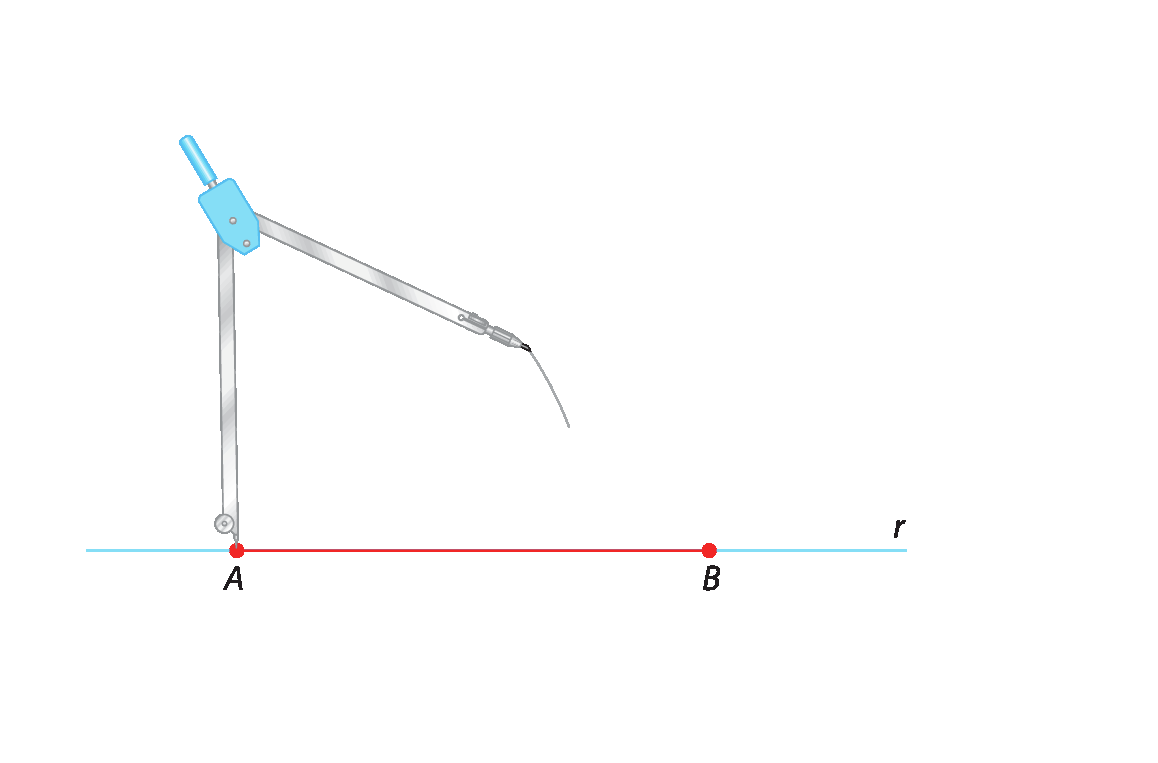
3º) Com abertura medindo 2 centímetros de comprimento e com a ponta-seca do compasso no ponto B da reta r, trace outro arco, de modo que ele cruze o anterior, obtendo o ponto C.
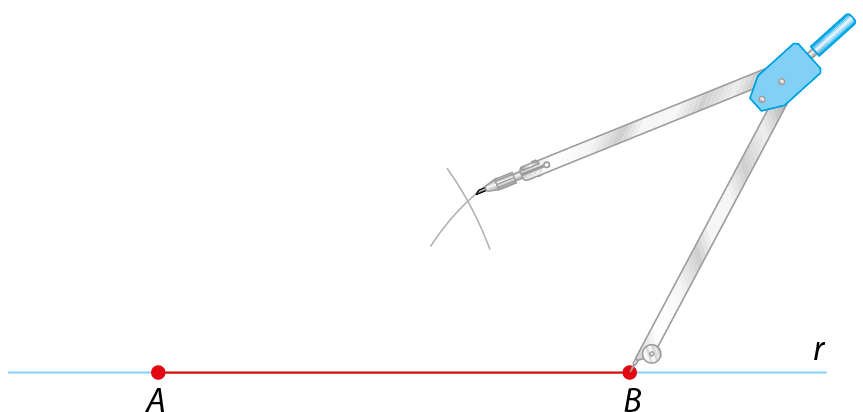
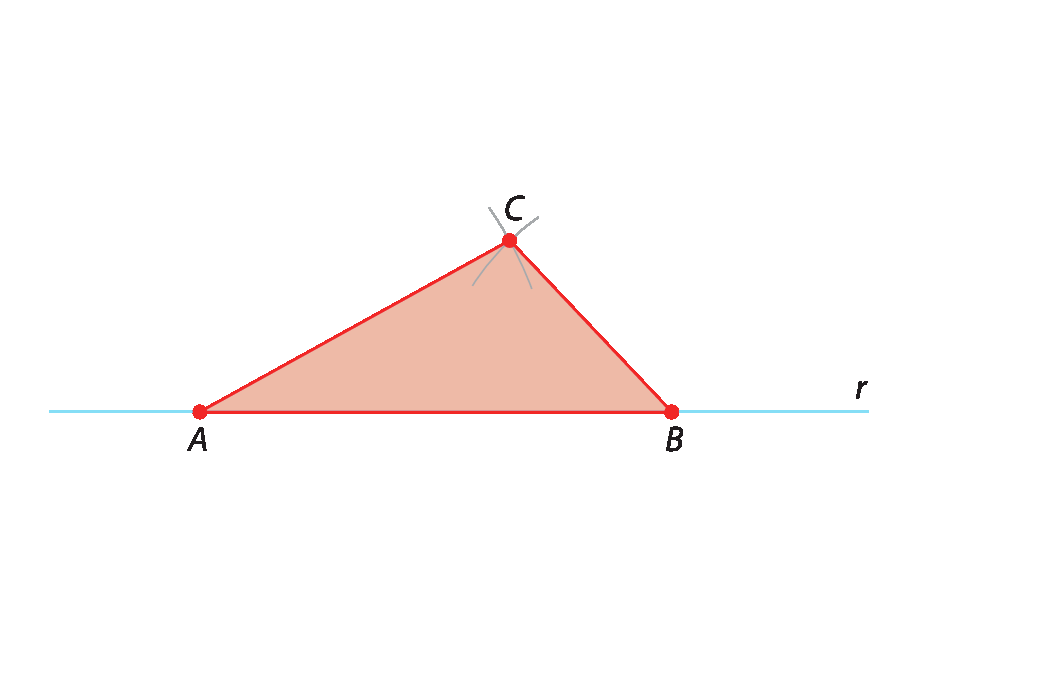
4º) Una com segmentos o ponto C aos pontos aêbê e obtenha os lados
Segmento de reta ACe
Símbolo. Segmento de reta BC. Por fim, pinte a região interna da figura e obtenha o triângulo á bê cê.
Para fazer

Descreva por meio de um fluxograma os passos para a construção de um triângulo qualquer, conhecidas as medidas de comprimento dos três lados.
Condição de existência de um triângulo
Como já sabemos, o contorno de um triângulo é formado por três segmentos, que são os seus lados. Mas devemos observar que nem sempre três segmentos podem formar o contorno de um triângulo.
Por exemplo, será que é possível construir um triângulo com lados medindo 4 centímetros, 2 centímetros e 1 centímetro de comprimento?
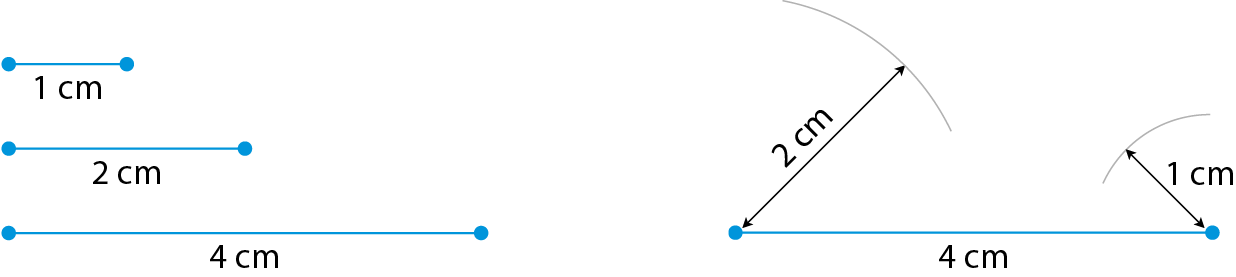
Observe que os arcos não se cruzam; portanto, não é possível construir um triângulo com essas medidas de comprimento.
Para saber se existe um triângulo com lados de determinadas medidas de comprimento, podemos aplicar a condição de existência de um triângulo, também conhecida por desigualdade triangular.
Em qualquer triângulo, a medida de comprimento de um lado deve ser menor que a soma das medidas de comprimento dos outros dois lados.
Exemplos
• Vamos verificar se é possível construir um triângulo com lados medindo 1 centímetro, 2 centímetros e 4 centímetros de comprimento.
Aplicando a condição de existência de um triângulo, temos:
1 centímetro < 2 centímetros + 4 centímetros

sentença verdadeira
2 centímetros < 1 centímetro + 4 centímetros

sentença verdadeira
4 centímetros < 1 centímetro + 2 centímetros

sentença falsa
Então, não é possível construir um triângulo com lados com essas medidas de comprimento.
• É possível construir um triângulo com lados medindo 7 centímetros, 3 centímetros e 5 centímetros de comprimento?
Novamente, vamos aplicar a condição de existência de um triângulo:
3 centímetros < 5 centímetros + 7 centímetros

sentença verdadeira
5 centímetros < 3 centímetros + 7 centímetros

sentença verdadeira
7 centímetros < 3 centímetros + 5 centímetros

sentença verdadeira
Então, é possível construir esse triângulo.
3 Soma das medidas de abertura dos ângulos internos de um triângulo
Em todo triângulo, a soma das medidas de abertura dos ângulos internos mede 180graus.
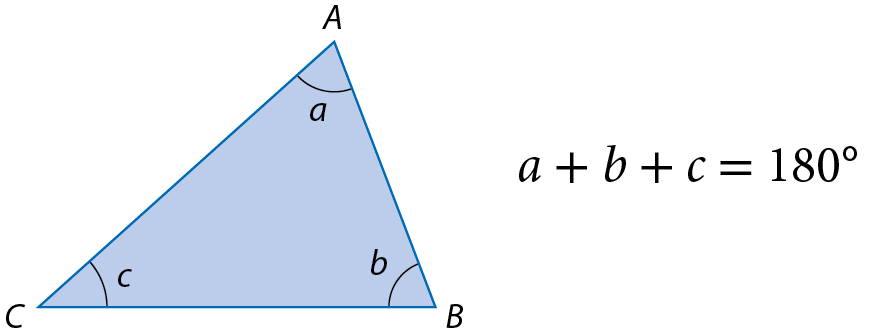
Recorde
Um ângulo cuja abertura mede 180graus corresponde ao ângulo de meia-volta.
É possível verificar essa propriedade fazendo um experimento com um modelo de triângulo de papel.
1º) Desenhe, em uma folha de papel, um triângulo qualquer e, com cuidado, recorte-o com uma tesoura sem ponta.

2º) Pinte cada ângulo interno da figura de uma cor.

3º) Recorte o triângulo em três partes de modo que cada uma contenha apenas um dos ângulos internos. Lembre-se: manuseie a tesoura com cuidado.

4º) Junte os três ângulos, formando um ângulo com abertura de medida igual a 180graus.

Assim, verificamos experimentalmente que a soma das medidas de abertura dos ângulos internos de um triângulo qualquer mede 180graus. A demonstração desse fato será feita em outro momento.

ATIVIDADES
faça as atividades no caderno
1. Você conhece alguma construção que seja sustentada por uma estrutura triangular? Em caso afirmativo, descreva-a.
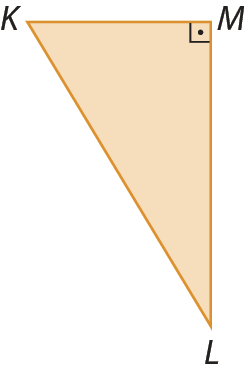
2. Identifique os lados, os vértices e os ângulos internos de cada triângulo.
a)
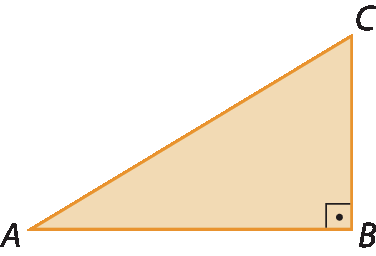
b)
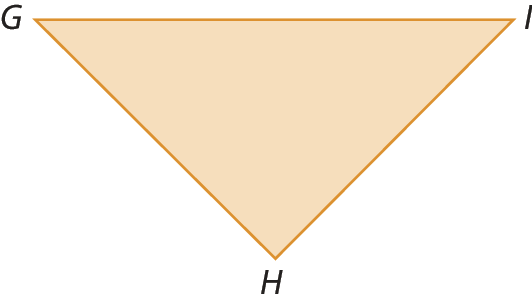
c)
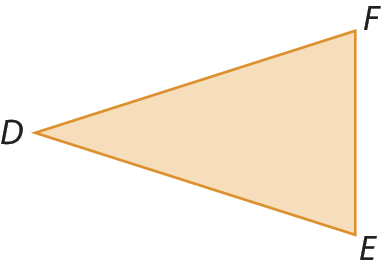
d)
3. Verifique se é possível construir triângulos cujos lados tenham as medidas de comprimento indicadas em cada caso.
a) 6 centímetros, 8 centímetros e 5 centímetros
b) 8 centímetros, 5 centímetros e 18 centímetros
c) 7 centímetros, 4 centímetros e 3 centímetros
d) 1,5 centímetro, 4 centímetros e 5 centímetros
4. Construa no caderno triângulos com as medidas de comprimento dos lados indicadas em cada item. Lembre-se: tenha cuidado ao manusear o compasso para evitar acidentes.
a) 3 centímetros, 4 centímetros e 6 centímetros
b) 7 centímetros, 8 centímetros e 4 centímetros
c) 8 centímetros, 6 centímetros e 2 centímetros
d) 16 centímetros, 10 centímetros e 4 centímetros
• Você conseguiu construir todos os triângulos?
5.

Faça o que se pede.
• Escreva no caderno um algoritmo que possa ser utilizado para verificar a condição de existência e construir os triângulos com as medidas de comprimento indicadas nas atividades 3 e 4.
Descreva por meio de um fluxograma o algoritmo que você elaborou.
•

Troque o fluxograma com um colega para que ele siga suas instruções e verifique se ele está correto.
6. Calcule a medida x em grau.
a)
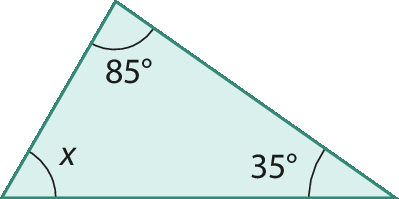
b)
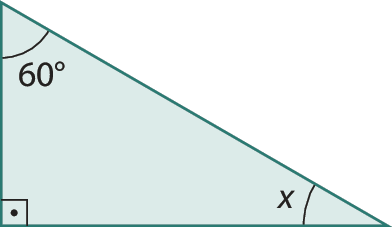
c)
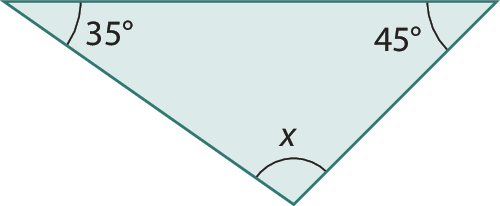
d)
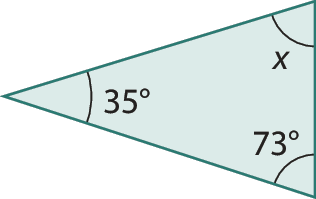
e)
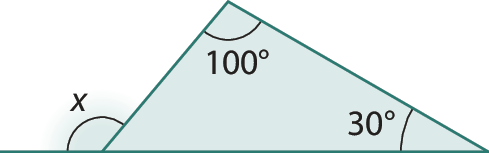
f)
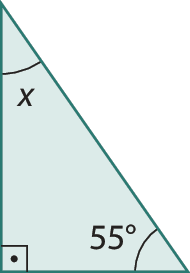
7. Responda às questões.
a) A abertura de dois ângulos internos de um triângulo mede, cada uma, 40graus. Qual é a medida de abertura do outro ângulo interno desse triângulo?
b) Um triângulo tem a abertura dos três ângulos com mesma medida. Qual é a medida de abertura de cada ângulo interno desse triângulo?
8. Responda às perguntas de Ana e João.
a)

b)

4 Classificação dos triângulos
Os triângulos recebem nomes especiais de acordo com as medidas de comprimento dos lados ou com as medidas de abertura dos ângulos internos.
Classificação dos triângulos de acordo com as medidas de comprimento dos lados
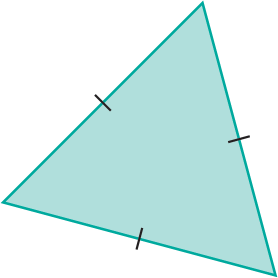
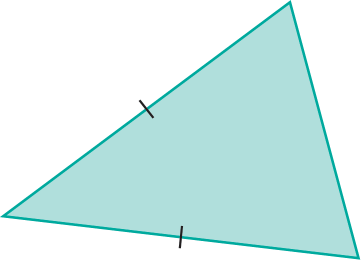
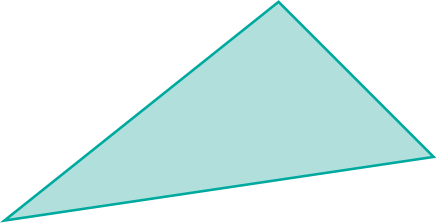
De acordo com as medidas de comprimento dos lados, os triângulos podem ser classificados em equilátero, isósceles ou escaleno.
|
Triângulo equilátero |
Triângulo isósceles |
Triângulo escaleno |
|---|---|---|
|
|
|
|
|
Um triângulo equilátero tem os três lados congruentes. |
Um triângulo isósceles tem dois lados congruentes. |
Um triângulo escaleno tem os três lados com medidas de comprimento diferentes. |
Observação
Os tracinhos indicam que os lados têm a mesma medida de comprimento.
Para fazer

Descreva com suas palavras como você construiria, usando régua e compasso, um triângulo equilátero dada a medida de comprimento de seu lado.
Classificação dos triângulos de acordo com as medidas de abertura dos ângulos
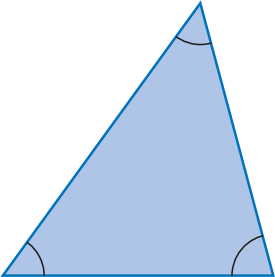
De acordo com as medidas de abertura dos ângulos, os triângulos podem ser classificados em acutângulo, retângulo ou obtusângulo.
|
Triângulo acutângulo |
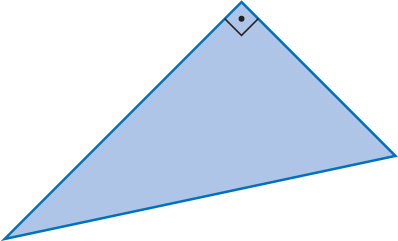
Triângulo retângulo |
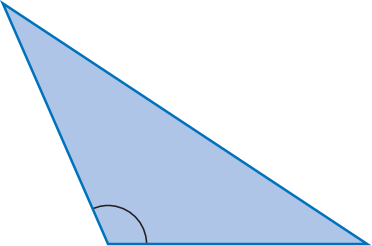
Triângulo obtusângulo |
|---|---|---|
|
|
|
|
|
Um triângulo acutângulo tem todos os ângulos internos agudos. |
Um triângulo retângulo tem um ângulo interno reto. |
Um triângulo obtusângulo tem um ângulo interno obtuso. |
Observe um exemplo do uso de triângulos retângulos na arte.

5 Relação entre lados e ângulos de um triângulo
Considere o triângulo á bê cê a seguir.
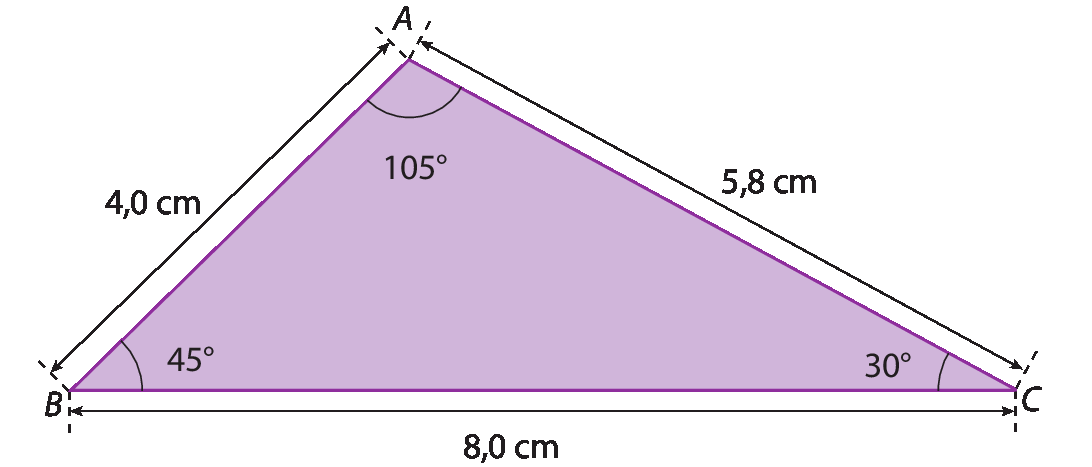
Nesse triângulo:
• o lado
Ângulo BCé oposto ao ângulo
Ângulo BAC;
• o lado
Segmento de reta ABé oposto ao ângulo
Ângulo BCA;
• o lado
Símbolo. Segmento de reta ACé oposto ao ângulo
Ângulo ABC.
Lembre-se: Escreva no caderno!
Comparando as medidas de abertura dos ângulos internos desse triângulo e relacionando-as com as medidas de comprimento dos lados opostos, temos:
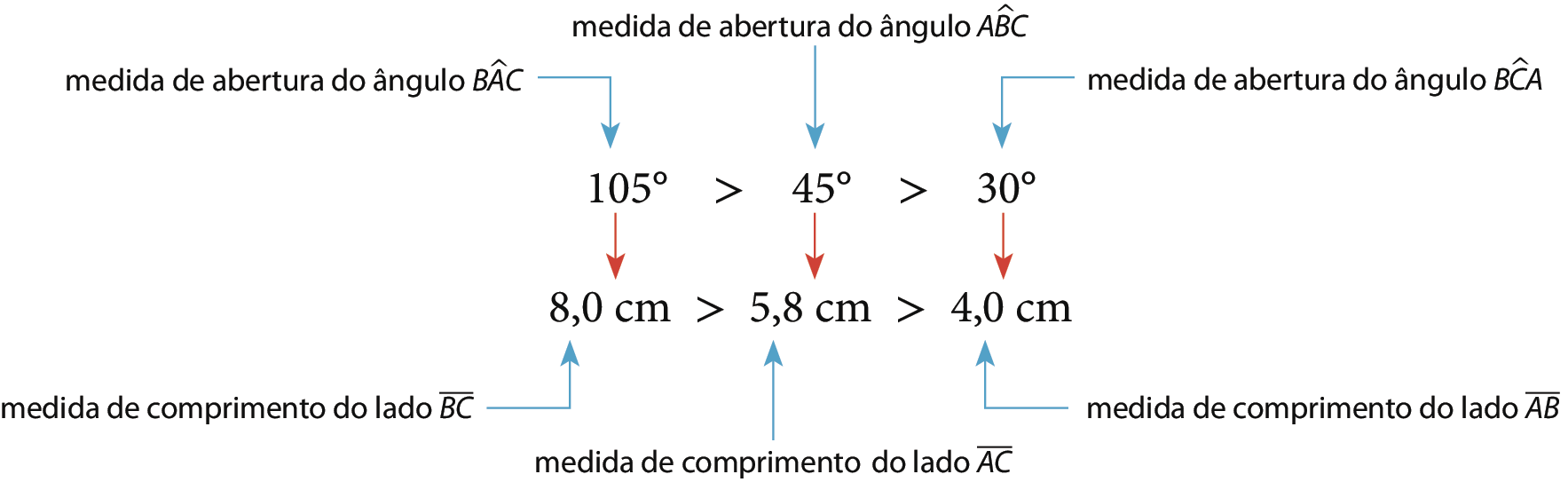
Em todo triângulo, ao ângulo com abertura de maior medida opõe-se o lado de maior medida de comprimento e, reciprocamente, ao lado de maior medida de comprimento opõe-se o ângulo com abertura de maior medida. Da mesma maneira, ao ângulo com abertura de menor medida opõe-se o lado de menor medida de comprimento.
Essa relação é válida para qualquer triângulo e será provada mais adiante, quando avançarmos no estudo da Geometria.
Podemos usar essa relação para observar que:
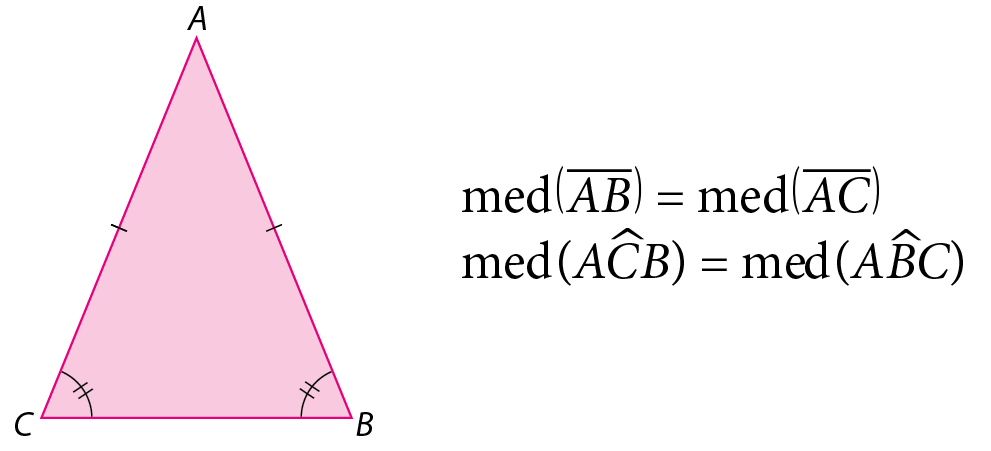
• um triângulo isósceles, que tem dois lados com mesma medida de comprimento, também tem os ângulos opostos a esses lados com abertura de mesma medida;
• um triângulo equilátero tem os três ângulos internos com abertura de mesma medida:
180graus : 3 = 60graus
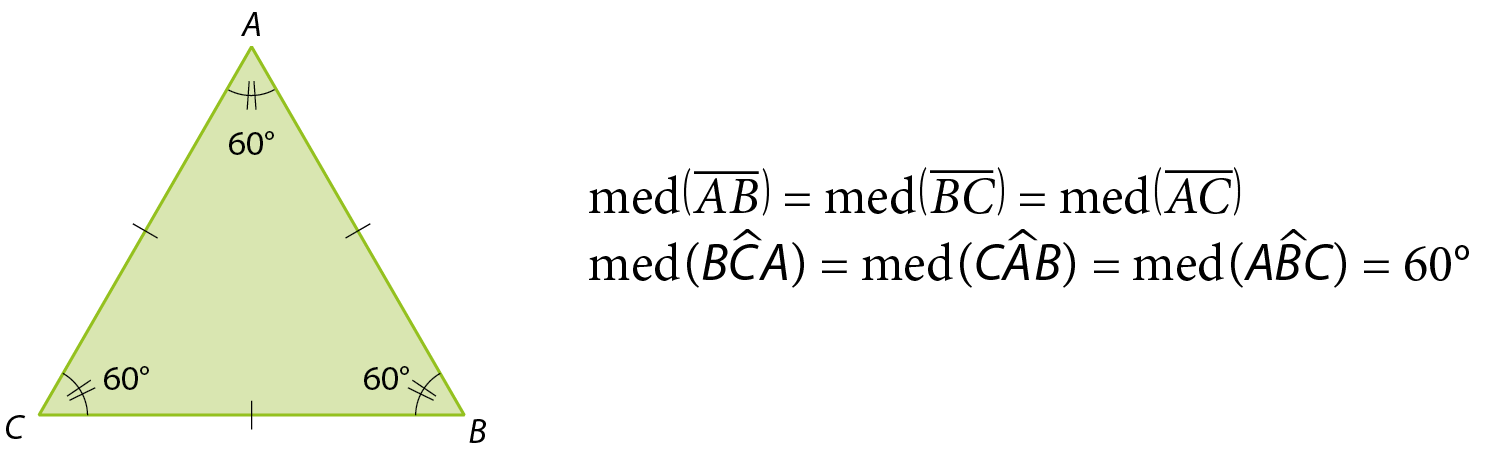
Para pensar
Todo triângulo equilátero é um polígono regular? Justifique.
Atenção! Cuidado ao usar o compasso.

ATIVIDADES
faça as atividades no caderno
1. Escreva no caderno apenas as sentenças verdadeiras.
a) Todo triângulo equilátero é isósceles.
b) Todo triângulo equilátero é acutângulo.
c) Todo triângulo retângulo é escaleno.
d) Existe triângulo escaleno isósceles.
e) Todo triângulo isósceles é acutângulo.
f ) Existe triângulo retângulo isósceles.
g) Todo triângulo isósceles é equilátero.
2. Escreva uma equação do 1º grau que represente a soma das medidas de abertura dos ângulos internos de cada triângulo. Depois, resolva as equações e determine, em cada caso, a medida x em grau.
a)
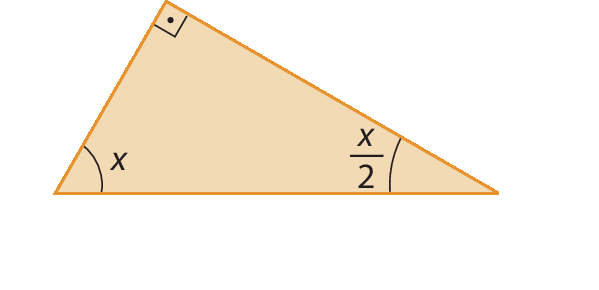
b)
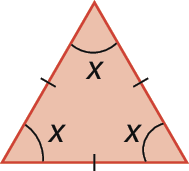
c)
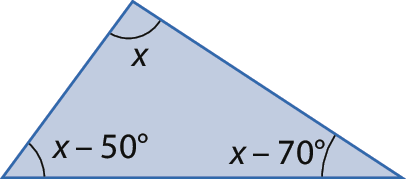
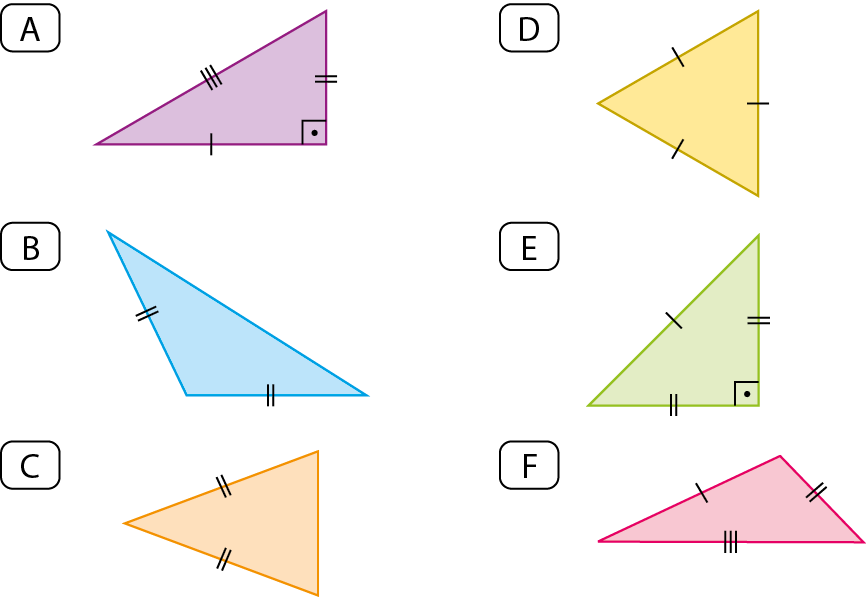
3. Sem instrumentos de medida, como régua ou transferidor, associe os triângulos às suas classificações quanto às medidas de comprimento dos lados e quanto às medidas de abertura dos ângulos.

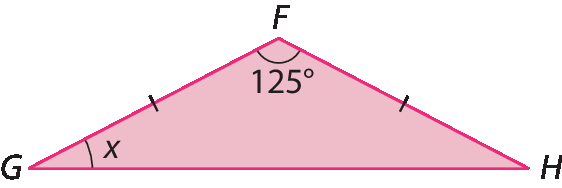
4. Calcule a medida x em grau.
5. Observe o triângulo á bê cê, em que
Símbolo. Segmento de reta BCé o lado com a maior medida de comprimento, e
Símbolo. Segmento de reta AC, com a menor.

Sabendo que as aberturas dos ângulos internos desse triângulo medem x, 3x e 5x, determine, em grau, a medida de abertura:
a) do ângulo oposto ao lado
Símbolo. Segmento de reta BC;
b) do ângulo oposto ao lado
Símbolo. Segmento de reta AC;
c) do ângulo oposto ao lado
Segmento de reta AB.
6. Se dois lados de um triângulo isósceles medem 38 centímetros e 14 centímetros de comprimento, quanto mede o comprimento do terceiro lado?
7. Construa o triângulo indicado em cada item e, depois, responda à questão.
a) Equilátero com lados que medem 3 centímetros de comprimento.
b) Isósceles com lados que medem 5 centímetros e 7 centímetros de comprimento.
c) Escaleno com lados que medem 4 centímetros, 5 centímetros e 7 centímetros de comprimento.
• Há apenas um triângulo que satisfaz cada um dos itens anteriores? Justifique.
8.

Resolva os problemas.
a) Sabendo que á bê cê é um triângulo isósceles, que
Semirreta BMé a bissetriz do ângulo
ângulo ABC e que semirreta CMé a bissetriz do ângulo
Ângulo ACB, encontre a medida x, em grau.
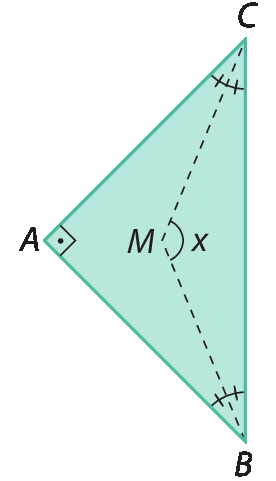
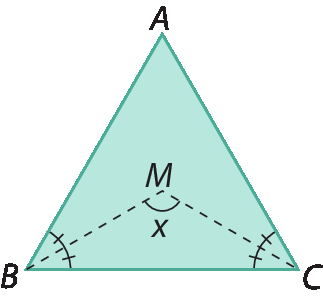
b) Se o triângulo á bê cê fosse equilátero, qual seria a medida x em grau?
6 Quadriláteros
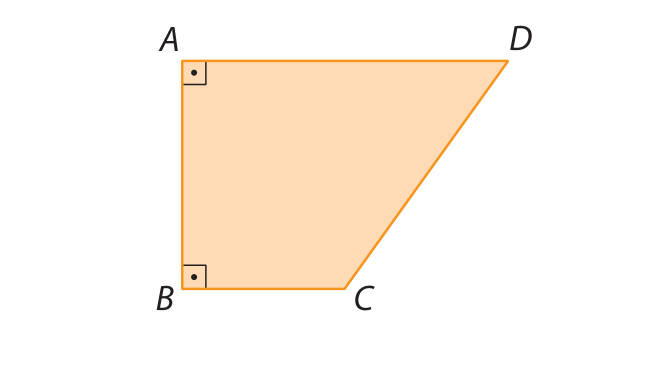
Você já aprendeu que um quadrilátero é um polígono de quatro lados. Observe na figura a seguir um exemplo de quadrilátero e seus elementos.
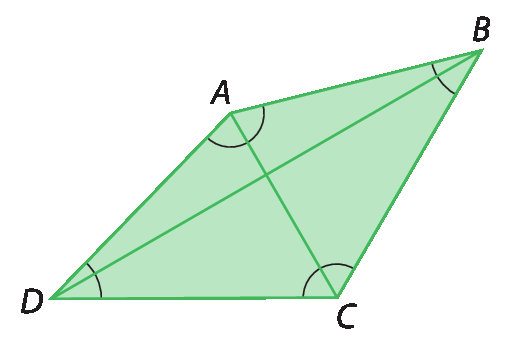
• Vértices: A, B, C e D
• Lados:
Símbolo. Segmento de reta AB, segmento de reta BC, segmento de reta CD e segmento de reta DA• Ângulos internos:
Ângulo DAB, ângulo ABC, ângulo BCD e ângulo CDA• Diagonais:
Símbolo. Segmento de reta AC e segmento de reta BDOs quadriláteros que possuem lados opostos paralelos são denominados quadriláteros notáveis. De acordo com o número de pares de lados opostos paralelos, o quadrilátero pode ser um trapézio ou um paralelogramo.
Trapézios
Os trapézios são quadriláteros que têm somente um par de lados opostos paralelos. Observe os exemplos.
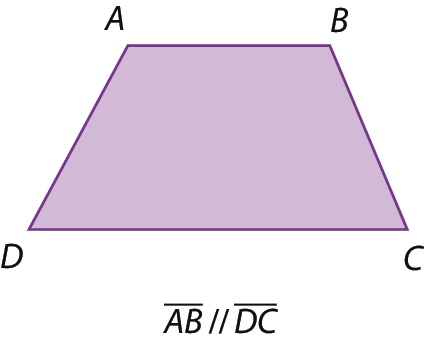
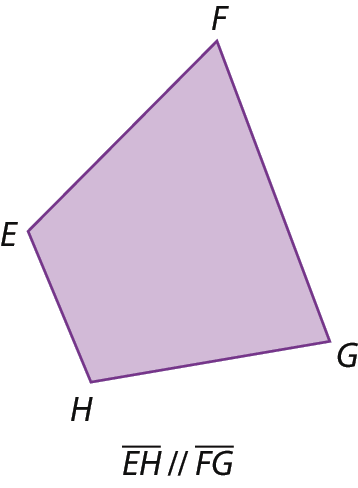
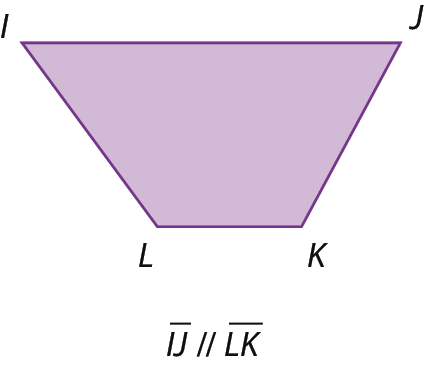
Observação
A notação // indica que duas retas ou dois segmentos são paralelos.

Paralelogramos
Os paralelogramos são quadriláteros que têm dois pares de lados opostos paralelos. Observe os exemplos.

Outros quadriláteros
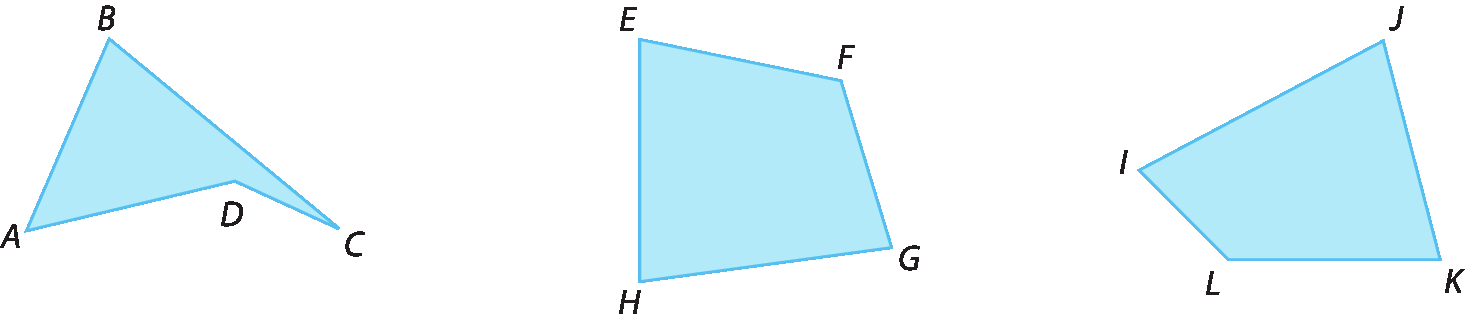
Se o quadrilátero não tem nenhum par de lados opostos paralelos, não recebe nomenclatura especial. Observe os exemplos.
7 Soma das medidas de abertura dos ângulos internos de um quadrilátero
Em um quadrilátero convexo a bê cê dê qualquer, a soma das medidas de abertura dos ângulos internos mede 360graus.
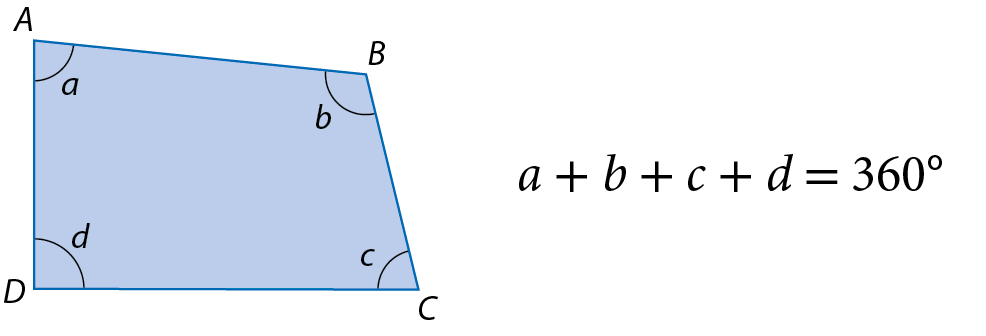
Assim como fizemos com os triângulos, é possível fazer um experimento com um modelo de quadrilátero de papel. Lembre-se: para evitar acidentes, sempre manuseie a tesoura com cuidado.
1º) Em uma folha de papel, desenhe um quadrilátero qualquer; depois, recorte-o.
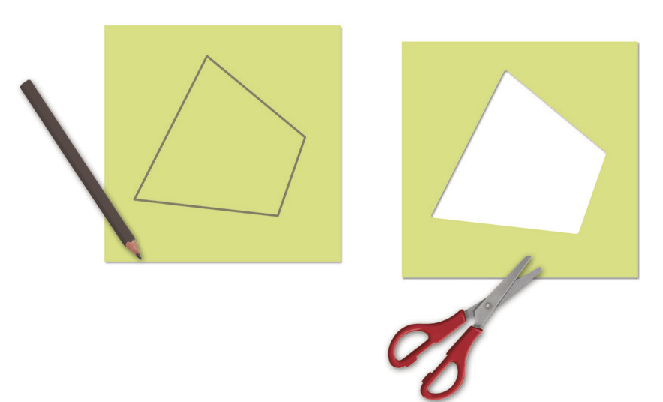
2º) Pinte cada ângulo interno da figura de uma cor.

3º) Recorte a figura em quatro partes, de modo que cada uma contenha apenas um dos ângulos internos.

4º) Reúna os pedaços recortados de modo que os quatro ângulos pintados fiquem no centro. Observe que a abertura do ângulo formado pelas quatro cores mede 360graus, ou seja, corresponde ao ângulo de uma volta completa.
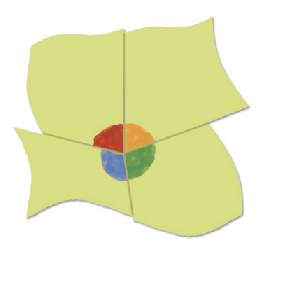
Assim, verificamos experimentalmente que a soma das medidas de abertura dos ângulos internos de um quadrilátero mede 360graus. A demonstração desse fato será feita em outro momento.
Podemos aplicar o que acabamos de verificar para calcular a medida desconhecida da abertura de um dos ângulos internos de um quadrilátero.
Observe como podemos encontrar a medida de abertura do ângulo
Ângulo ABC.
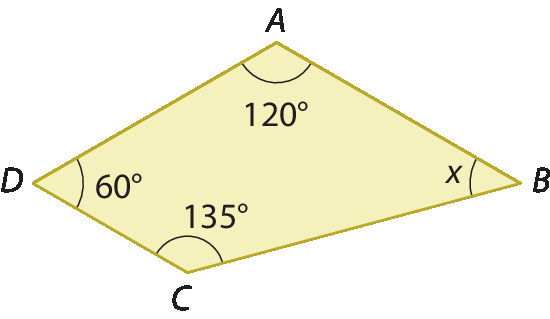
Como a bê cê dê é um quadrilátero convexo, a soma das medidas de abertura dos seus ângulos internos mede 360graus. Assim, temos:
60graus + 120graus + 135graus + x = 360graus
315graus + x = 360graus
x = 360graus ‒ 315graus
x = 45graus

ATIVIDADES
faça as atividades no caderno
1. Em cada quadrilátero, identifique os vértices, os lados, os ângulos internos e as diagonais.
a)
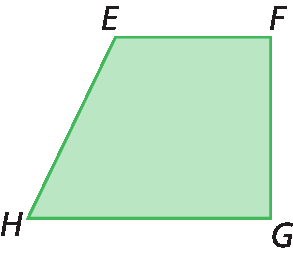
b)
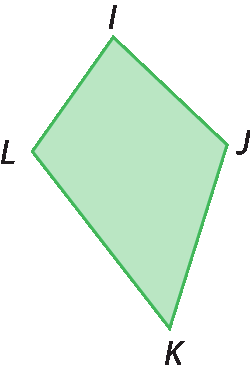
2. Observe a figura e responda: esse quadrilátero é um paralelogramo? Justifique.

Versão adaptada acessível
2. Represente dois quadriláteros. Um deles deve ser paralelogramo e outro não.
3. Classifique os quadriláteros em paralelogramo ou trapézio. Justifique sua resposta.
a)

b)

c)
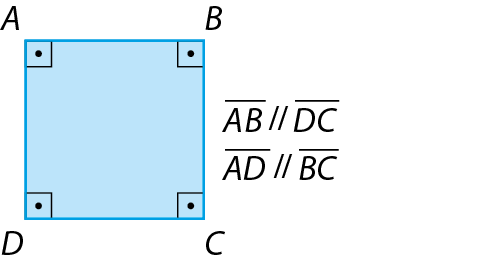
d)

e)
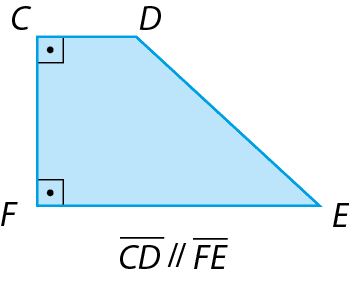
f)
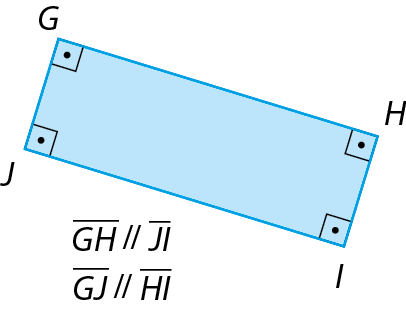
4. No caderno, classifique cada afirmação em verdadeira ou falsa.
a) Todo quadrilátero é um paralelogramo.
b) Todo paralelogramo é um trapézio.
c) Um trapézio tem somente um par de lados opostos paralelos.
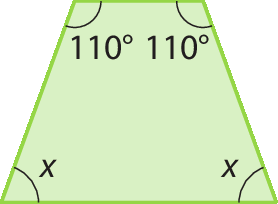
5. Em cada figura, descubra a medida x, em grau.
a)
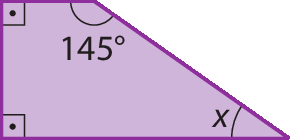
b)
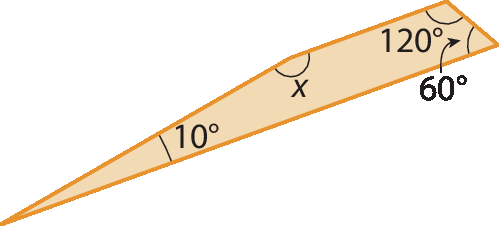
c)
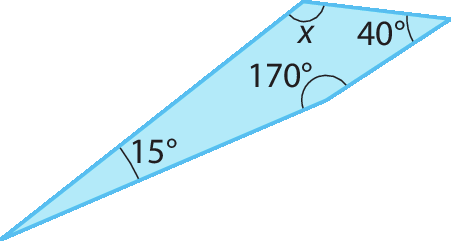
d)
6. Observe o trapézio a bê cê dê, formado pelas retas r, s, t e u. Depois, faça o que se pede.
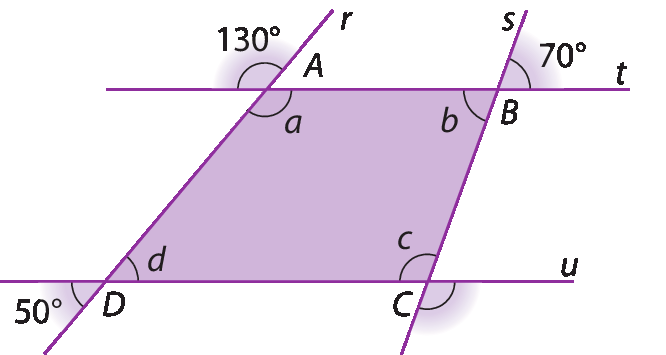
a) Indique os pares de retas concorrentes que você pode identificar na figura.
b) Determine as medidas de a, b e d e cite a propriedade que permite obter essas medidas.
c) Escreva uma equação que permita determinar a medida c. Depois, resolva-a.
7. Calcule em cada caso a medida x, em grau.
a)
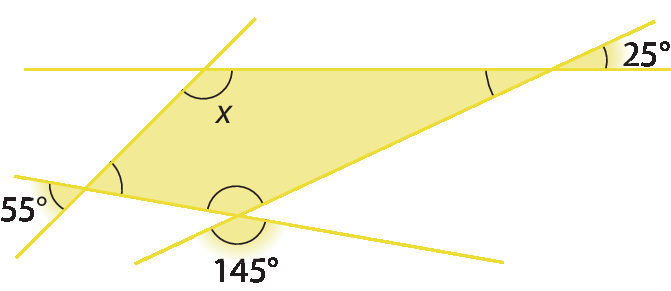
b)
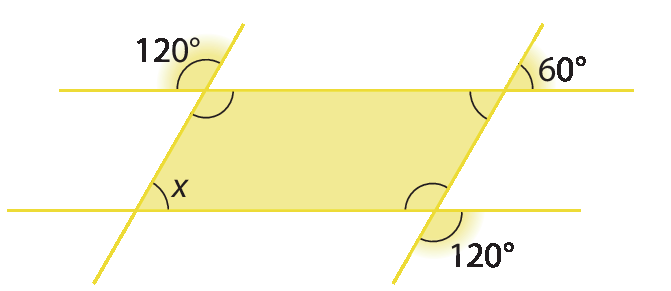
8. Observe os triângulos isósceles.
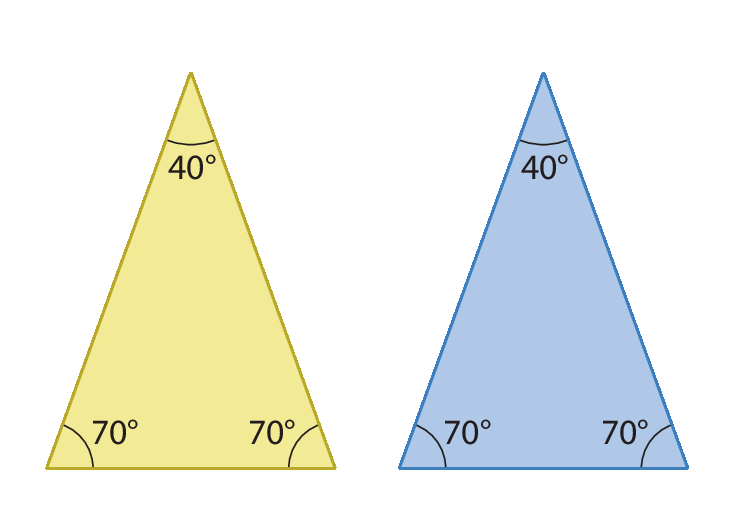
Eles foram sobrepostos de modo que foi obtida a figura a seguir.
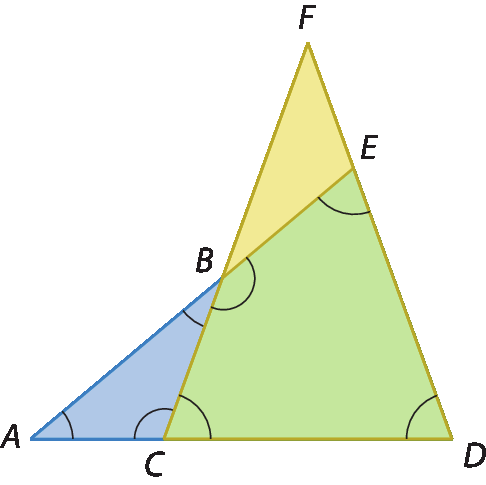
• Determine:
a) as medidas de abertura dos ângulos internos do quadrilátero BCDE;
b) as medidas de abertura dos ângulos internos do triângulo á bê cê.
9.

Em um quadrilátero a bê cê dê, o ângulo
Ângulo ABCé suplementar a um ângulo com abertura de medida 140graus.
Ângulo BCDé um ângulo reto e a abertura de
Ângulo CDAmede 70graus. Sabendo que
Semirreta APé a bissetriz do ângulo
Ângulo DAB, determine a medida de abertura do ângulo
Ângulo PAB.
8 Trapézios
Como já vimos, os trapézios são quadriláteros que têm somente um par de lados opostos paralelos.
Nos trapézios os lados paralelos são denominados bases.
Observe que o trapézio possui duas bases: a base menor e a base maior.
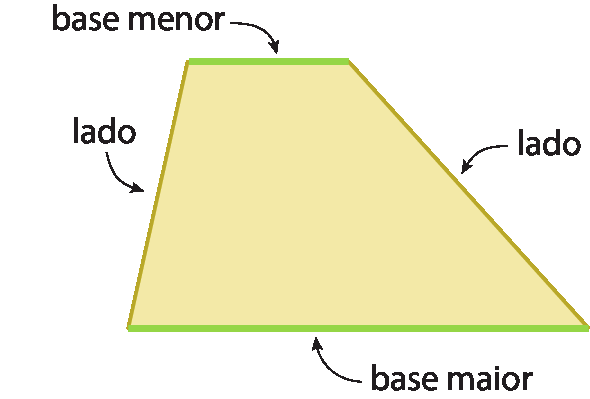
No quadro a seguir, apresentamos três modos de classificar um trapézio em relação à medida de comprimento de seus lados e à medida de abertura de seus ângulos.
|
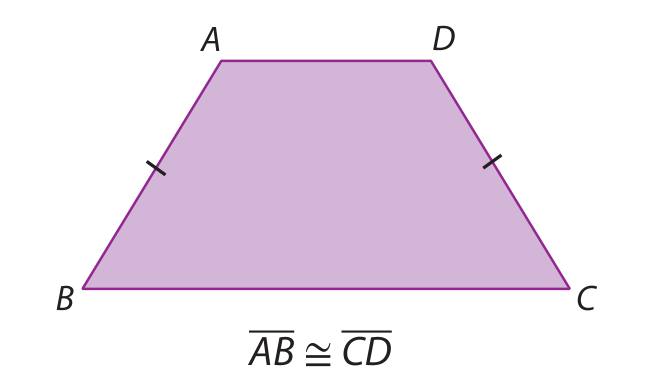
Trapézio isósceles |
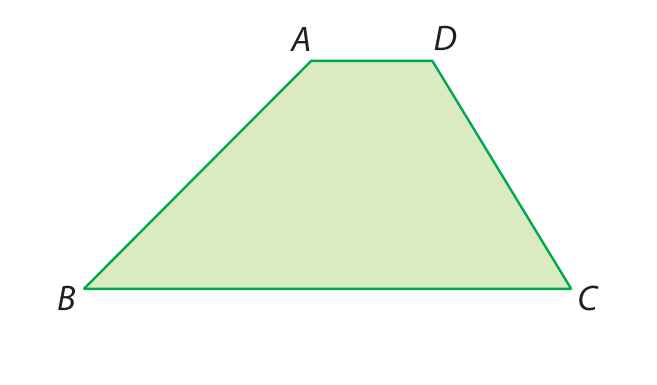
Trapézio escaleno |
Trapézio retângulo |
|---|---|---|
|
|
|
|
|
Um trapézio isósceles tem os lados não paralelos congruentes. |
Um trapézio escaleno tem os lados não paralelos com medidas de comprimento diferentes. |
Um trapézio retângulo é um trapézio escaleno que tem dois ângulos retos. |

ATIVIDADES
faça as atividades no caderno
1. Identifique a base maior e a base menor de cada trapézio.
a)
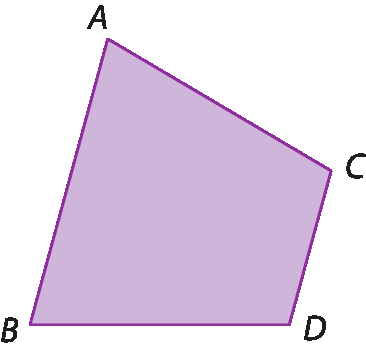
b)
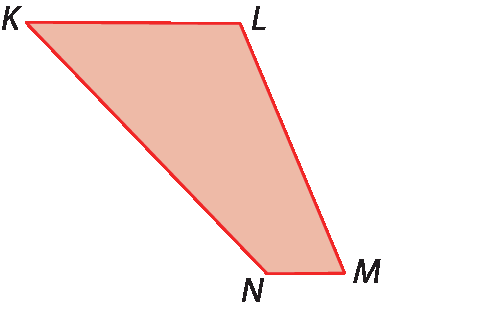
Versão adaptada acessível
1. Como você reconhece quais são as bases maior e menor em um trapézio?
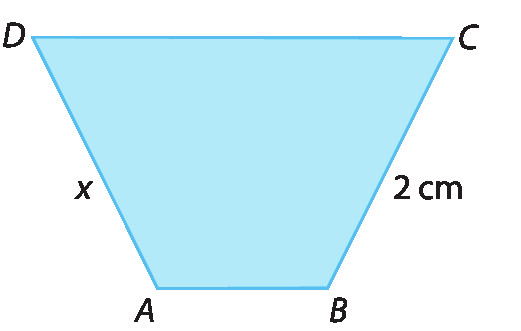
2. O trapézio a bê cê dê é isósceles. Qual é a medida de comprimento x do lado
Segmento de reta ADdesse trapézio?
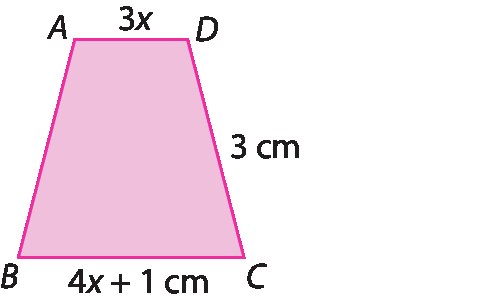
3. Escreva uma equação que represente a informação dada e determine a medida de comprimento de x.
a) A medida do perímetro do trapézio isósceles a bê cê dê é 10,5 centímetros.
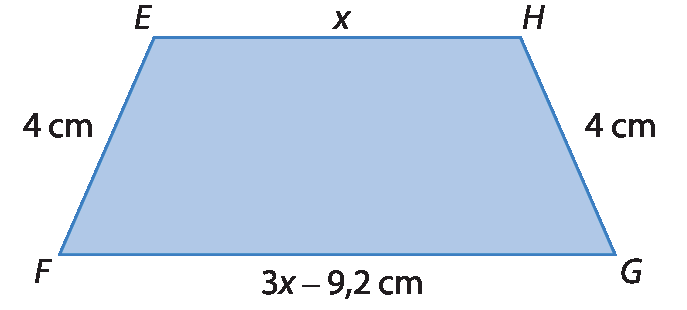
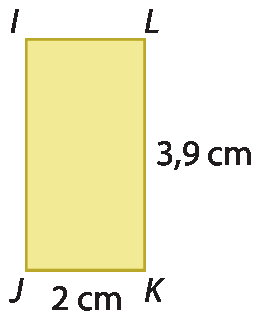
b) A medida do perímetro do trapézio isósceles ê éfe gê agá é o dobro da medida do perímetro do retângulo í jota cá éle.
9 Paralelogramos
Como já estudamos, os paralelogramos são quadriláteros que têm dois pares de lados opostos paralelos. No dia a dia, encontramos diversos objetos que lembram paralelogramos.
Observe os exemplos a seguir.


De acordo com as medidas de comprimento dos lados e de abertura dos ângulos, um paralelogramo pode ser classificado como retângulo, losango ou quadrado.
Lembre-se: Escreva no caderno!
Retângulo
Um paralelogramo com quatro ângulos retos é denominado retângulo.
Observe alguns exemplos.
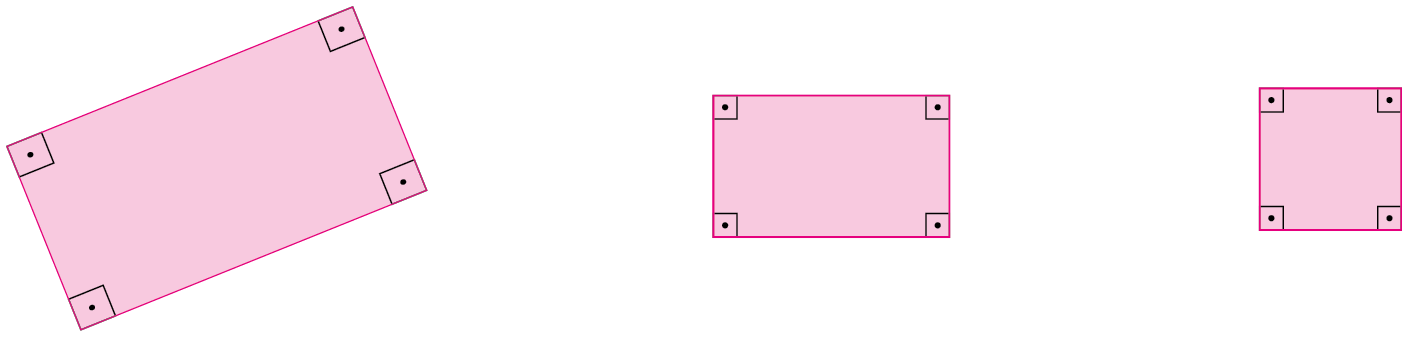
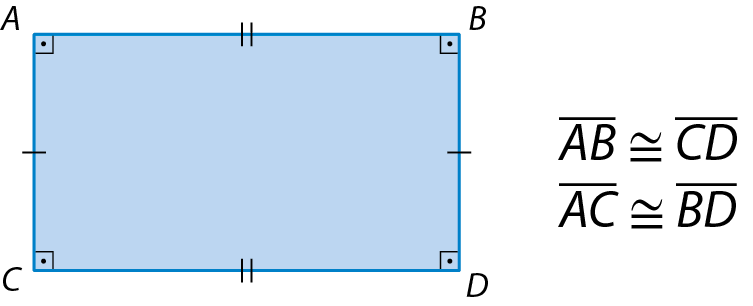
Em um retângulo, os lados opostos são congruentes.
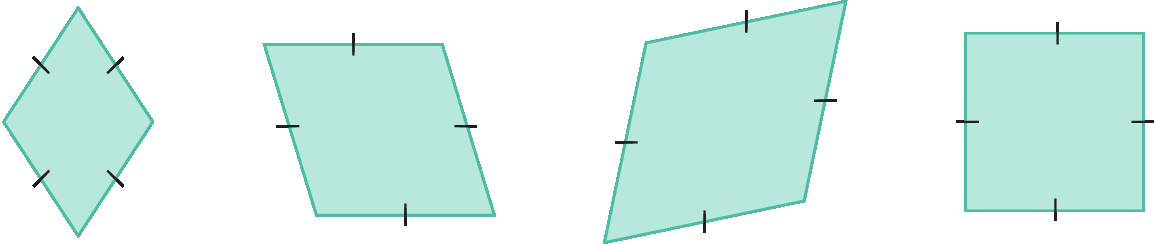
Losango
O losango é um paralelogramo com quatro lados congruentes.
Observe alguns exemplos de losango.

Quadrado
O quadrado é um paralelogramo com quatro ângulos retos e quatro lados congruentes.
Observe alguns exemplos.

Observação
Todo quadrado também é um retângulo, pois tem todos os ângulos internos retos, e também é um losango, pois tem todos os lados com a mesma medida de comprimento.

ATIVIDADES
faça as atividades no caderno
1. Classifique os paralelogramos em retângulo, losango ou quadrado.
a)
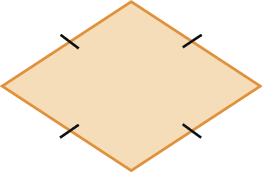
b)
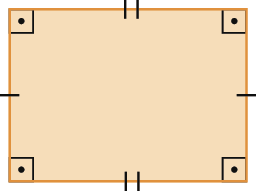
c)
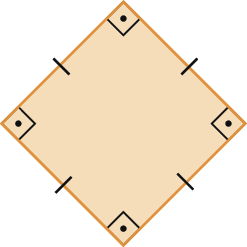
2. Para montar a bandeira do estado do Ceará, Anita fez uma composição de peças e, entre elas, há duas que lembram quadriláteros.

Olhando rapidamente, seria possível dizer que ela usou peças que lembram um retângulo e um losango. O que você faria para ter a certeza da classificação desses quadriláteros? Justifique.
3. Calcule em cada caso a medida x, em grau.
a)
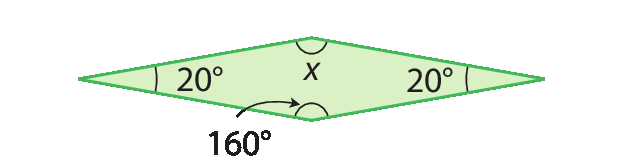
b)
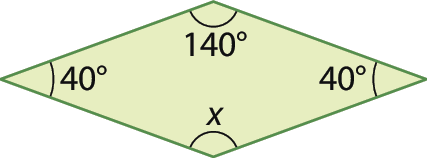
c)
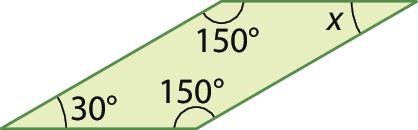
d)

• Com base nos resultados obtidos em cada item, o que você pode afirmar sobre as medidas de abertura dos ângulos opostos em cada um dos quadriláteros?
4. Determine a medida x sabendo que a medida do perímetro do losango ême êne ó pê é igual ao dobro da medida do perímetro do quadrado a bê cê dê.

5. Calcule as medidas de x e de y sabendo que:
a) a medida de y é igual ao dobro da medida de x e a medida do perímetro do retângulo a bê cê dê é igual à medida do perímetro do quadrado ê éfe gê agá;
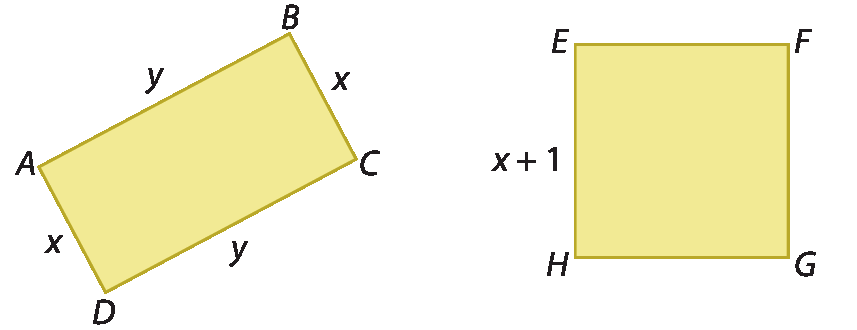
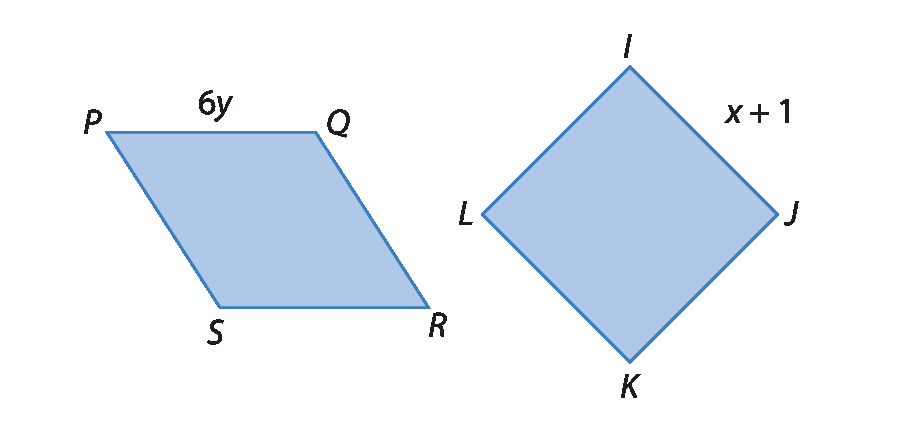
b) a medida de y é igual a um terço da medida de x e a medida do perímetro do losango PQRS é igual à medida do perímetro do quadrado í jota cá éle.
6.

Um quadrado de cartolina foi dividido e recortado, obtendo-se peças poligonais. Com algumas dessas peças, foi possível formar um octógono, conforme a figura a seguir.
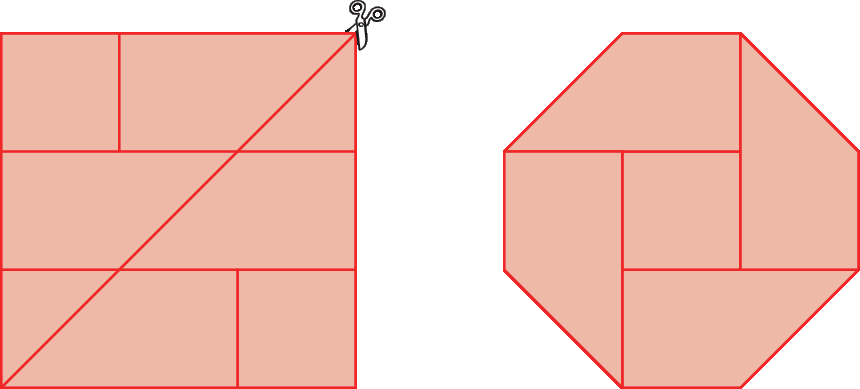
a) Qual é a medida de abertura dos ângulos internos do octógono?
b) As peças que não foram utilizadas totalizam que fração do quadrado?
Lembre-se: Escreva no caderno!
10 Construção de quadrados com régua e compasso
Vamos construir um quadrado cujo lado mede 2 centímetros de comprimento, conforme o esboço representado a seguir.
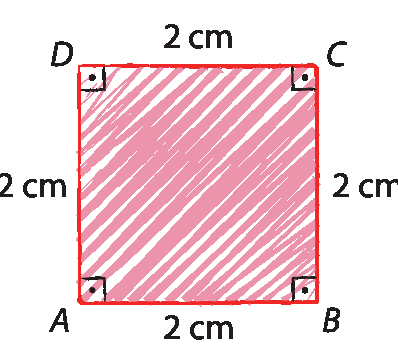
Atenção! Cuidado ao usar o compasso.
Para isso, podemos seguir os passos mostrados a seguir.
1º) Trace uma reta r e, sobre ela, construa o segmento
Segmento de reta AB, de medida de comprimento igual a 2 centímetros, que será um dos lados do quadrado.

2º) Com a ponta-seca do compasso no ponto a e com uma abertura qualquer, marque dois pontos, êêéfe, sobre r.
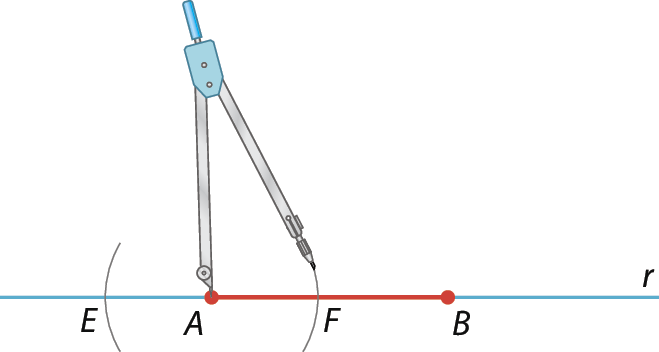
3º) Abra o compasso com uma abertura maior que a anterior e trace dois arcos: um com a ponta-seca do compasso em ê e o outro com a ponta-seca em F.
Os dois arcos se cruzarão em um ponto, que indicaremos por G.
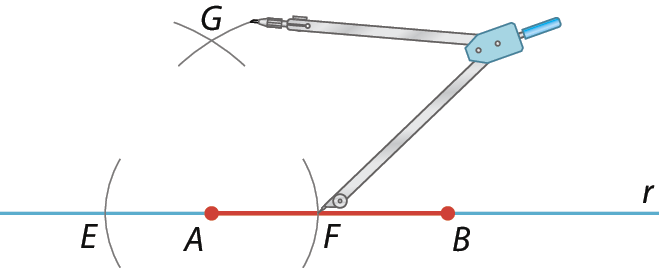
4º) Una os pontos G e a, traçando a reta s, que é perpendicular a r. Depois, com a abertura medindo 2 centímetros de comprimento e a ponta-seca do compasso em a, obtenha o ponto D sobre a reta s.
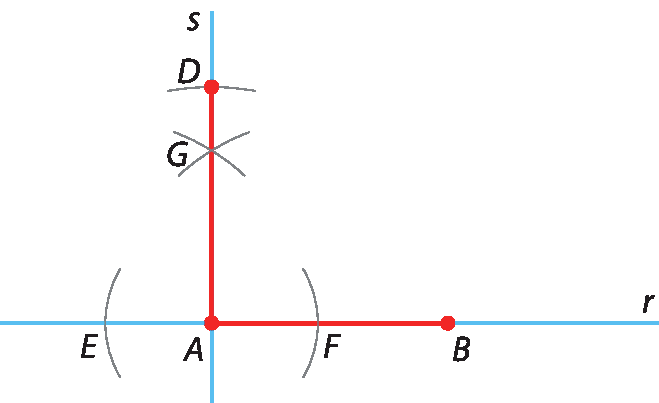
5º) Trace dois arcos utilizando o compasso com abertura medindo 2 centímetros de comprimento: um com a ponta-seca em B e o outro com a ponta-seca em D. Na intersecção desses arcos, marque o ponto C.
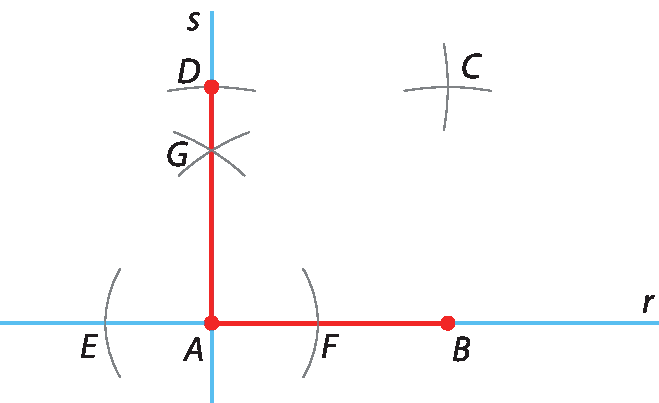
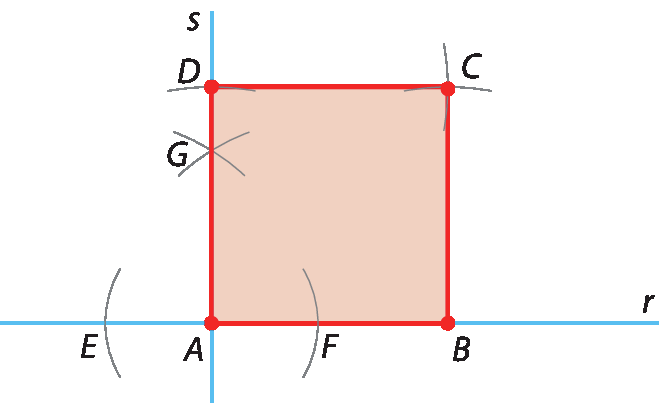
6º) Trace os segmentos
CD e CB. Por fim, pinte a região interna da figura e obtenha o quadrado a bê cê dê.
Lembre-se: Escreva no caderno!
pensamento computacional
É possível construir polígonos utilizando aplicativos de desenho. Na imagem a seguir, o triângulo equilátero na malha foi construído por meio dos comandos à esquerda.
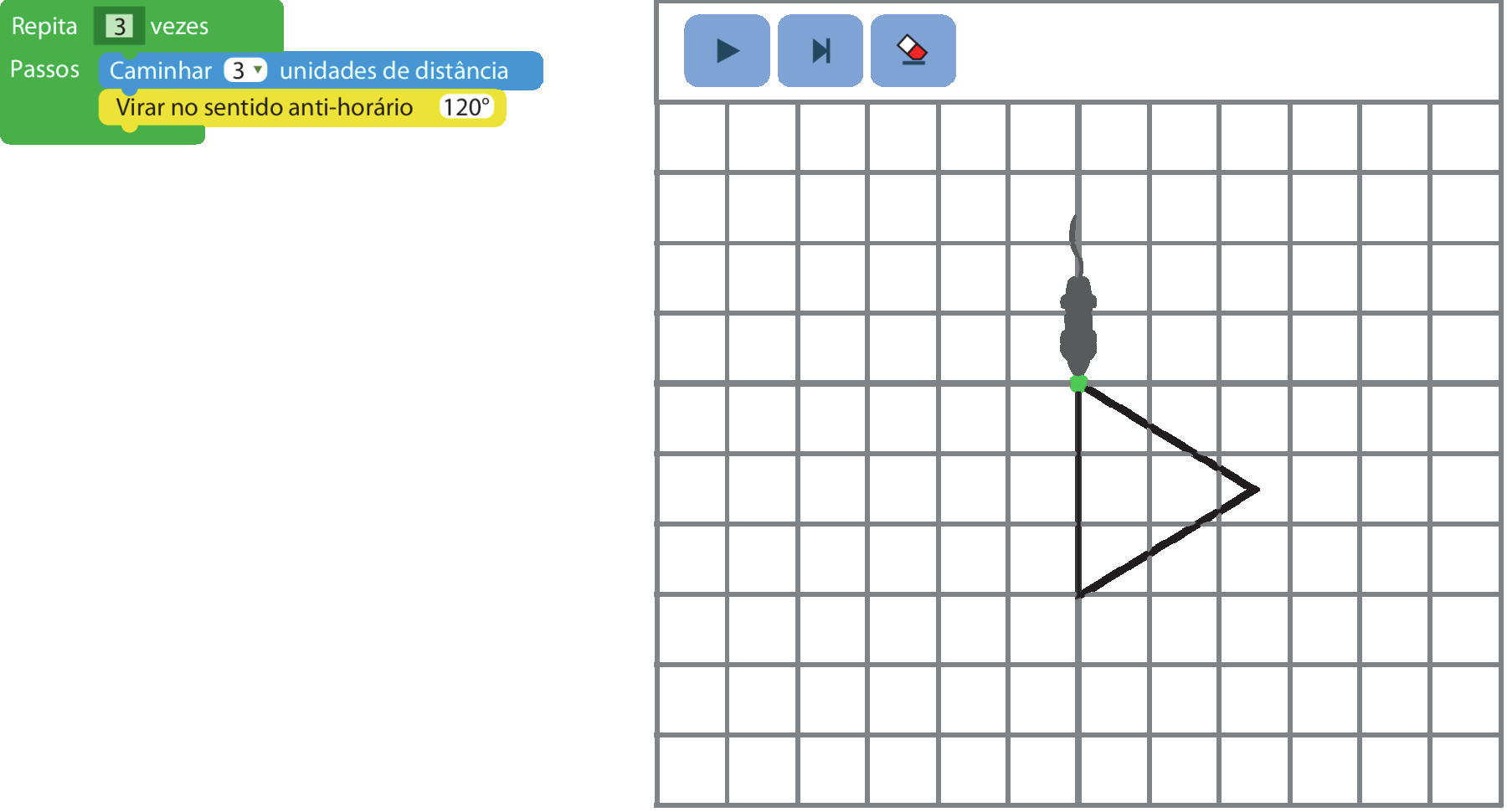
• Com base nesse exemplo, faça no caderno o que se pede.
a) Que sequência de comandos você forneceria para construir um quadrado de lado medindo duas unidades de comprimento nesse aplicativo?
b) Agora, crie um fluxograma para representar uma sequência de passos que leve à construção de um quadrado cujo lado mede 10 unidades de comprimento.
Dica: utilize as estruturas a seguir como base para a construção do fluxograma e ligue-as utilizando setas, indicando o sentido dos passos a serem seguidos.
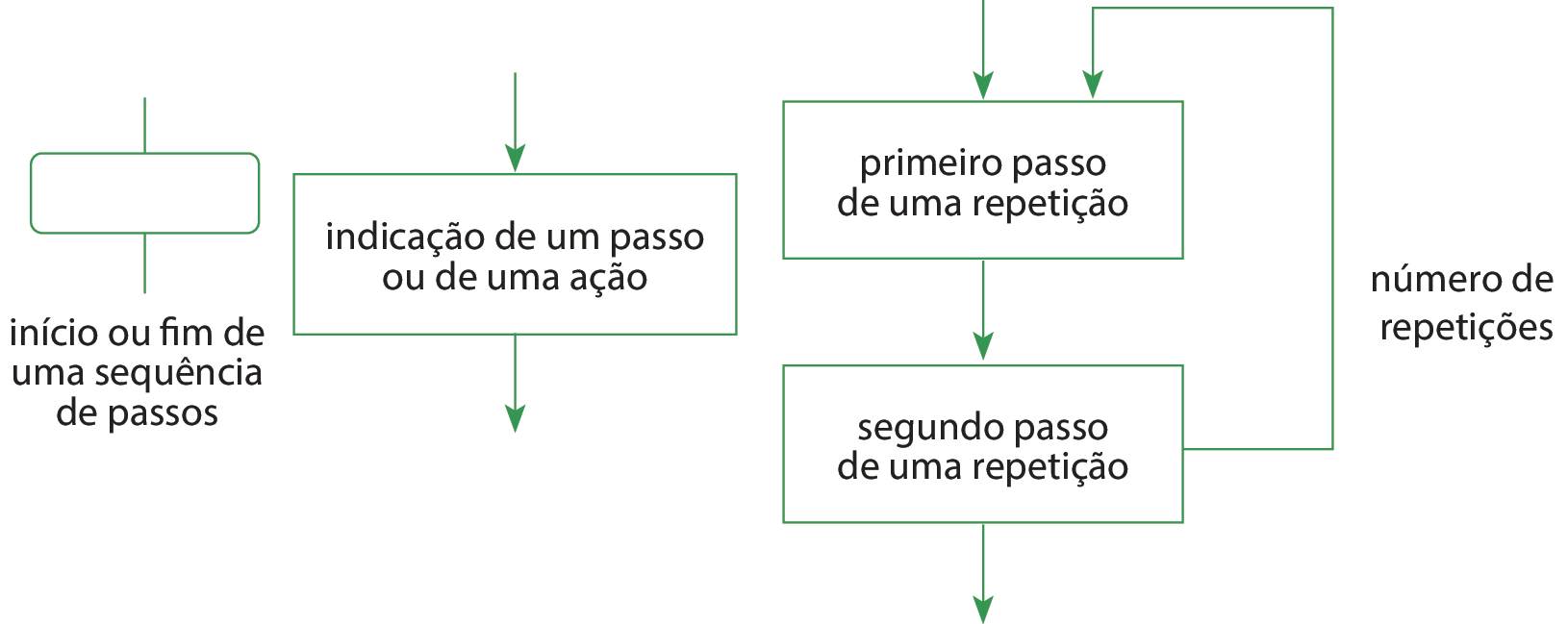

ATIVIDADES
faça as atividades no caderno
Atenção! Cuidado ao usar o compasso.
1. Construa os seguintes quadrados no caderno, usando régua e compasso e seguindo as medidas de comprimento indicadas nos esboços.
a)
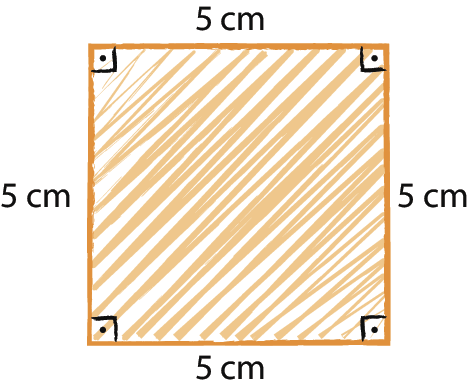
b)
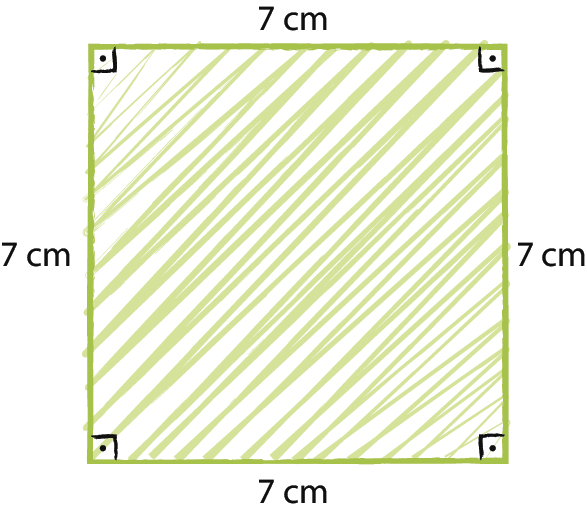
2. Responda às questões no caderno.
a) Ana construiu um paralelogramo com todos os ângulos internos congruentes. Que paralelogramo ela construiu?
b) Lucas construiu um paralelogramo com os quatro lados de medidas de comprimento iguais. Que paralelogramo ele construiu?
3. Descubra que quadrilátero Rodrigo construiu. “Primeiro, construí um segmento
PQ, de medida de comprimento igual a 5 centímetros, sobre uma reta r. Depois, tracei uma reta u, perpendicular a r, passando por P, e sobre ela construí um segmento
PSmedindo 2 centímetros de comprimento. Tracei outra reta perpendicular a r, passando por Q, e sobre ela construí um segmento
QRde medida de comprimento igual a 2 centímetros. Uni os pontos R e S e obtive um quadrilátero.”
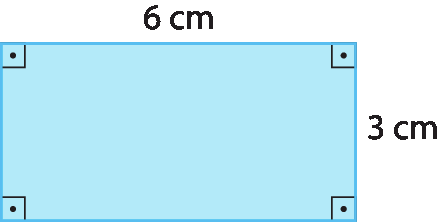
4. No caderno, descreva como você construiria o retângulo a seguir usando régua e compasso.
5. Ana construiu um trapézio retângulo. Observe como ela descreveu sua construção.
“Primeiro, construí uma reta r e, sobre ela, um segmento
AB, que media 2 centímetros de comprimento. Depois, tracei uma reta s, perpendicular a r, passando por a, e sobre ela construí um segmento
ADque media 4 centímetros de comprimento. Tracei outra reta perpendicular a r, passando por B, e sobre ela construí um segmento
BC, que media 6 centímetros de comprimento. Uni os pontos C e D e obtive um trapézio retângulo.”
• Construa esse trapézio no caderno seguindo a descrição de Ana.

Estatística e Probabilidade
faça as atividades no caderno
Leitura e interpretação de gráficos de setores
Na empresa em que trabalha, Felipe recebe R$ 1.800,00mil oitocentos reais de salário líquido. Ele utiliza esse valor para gastar com lazer, alimentação e vestuário e guarda uma parte na caderneta de poupança. Para visualizar melhor essa distribuição, Felipe construiu o gráfico de setores a seguir.
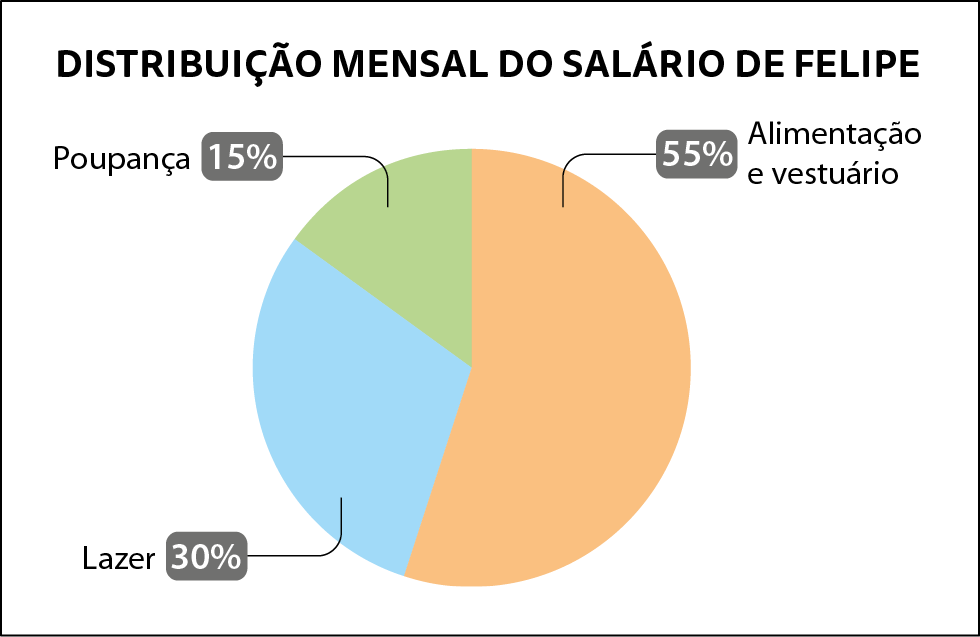
Dados obtidos por Felipe em maio de 2023.
▶ Com as informações do gráfico, é possível determinar a finalidade para a qual Felipe reserva cada parte do seu salário e calcular esses valores?
Vamos analisar alguns elementos do gráfico.
O título “Distribuição mensal do salário de Felipe” informa o que o gráfico contém.
No gráfico, cada setor (identificado com uma cor diferente) representa um tipo de gasto: alimentação e vestuário (55%), lazer (30%) e poupança (15%). Juntos, esses gastos totalizam 100% do salário mensal de Felipe.
A fonte, localizada a seguir do gráfico, informa que os dados foram obtidos por Felipe em maio de 2023.
Assim:
• Para saber a finalidade para a qual Felipe reserva a maior parte de seu salário, basta comparar as medidas de abertura dos ângulos dos setores ou as porcentagens indicadas no gráfico. Pelos dois modos, concluímos que o maior gasto de Felipe é com alimentação e vestuário (55% do salário).
Como sabemos que o salário de Felipe é de R$ 1.800,00mil oitocentos reais e que o gasto com alimentação e vestuário representa 55% desse valor, podemos calcular o valor gasto com esses itens:
55% de .1800 =
Sentença matemática. 55 centésimos⋅ .1800 = 990
Portanto, Felipe gasta mensalmente R$ 990,00novecentos e noventa reais com alimentação e vestuário.
• Analisando o gráfico, percebemos que o valor que Felipe guarda na caderneta de poupança representa 15% do salário.
Vamos calcular esse valor em real.
15% de .1800 =
Sentença matemática. 15 centésimos⋅ .1800 = 270
Logo, Felipe reserva para investir na poupança R$ 270,00duzentos e setenta reais mensais.
• Finalmente, para descobrir o valor que Felipe reserva para gastar com lazer, podemos calcular 30% de R$ 1.800,00mil oitocentos reais. Podemos, ainda, adicionar os valores reservados para investir na poupança e para gastar com alimentação e vestuário e, em seguida, subtrair essa soma de R$ 1.800,00mil oitocentos reais:
R$ 1.800,00mil oitocentos reais ‒ (R$ 990,00novecentos e noventa reais + R$ 270,00duzentos e setenta reais) = R$ 540,00quinhentos e quarenta reais
Portanto, Felipe reserva R$ 540,00quinhentos e quarenta reais para gastar com lazer.
▶ Estatística e Probabilidade

ATIVIDADES
faça as atividades no caderno
1.

A medida do volume de água no planeta Terra é de aproximadamente ...1500000000 quilômetros cúbicos (quilômetros cúbicos) de água, sendo 97% do total composto de água salgada e apenas 3% de água doce. Observe no gráfico a seguir a distribuição dessa água.
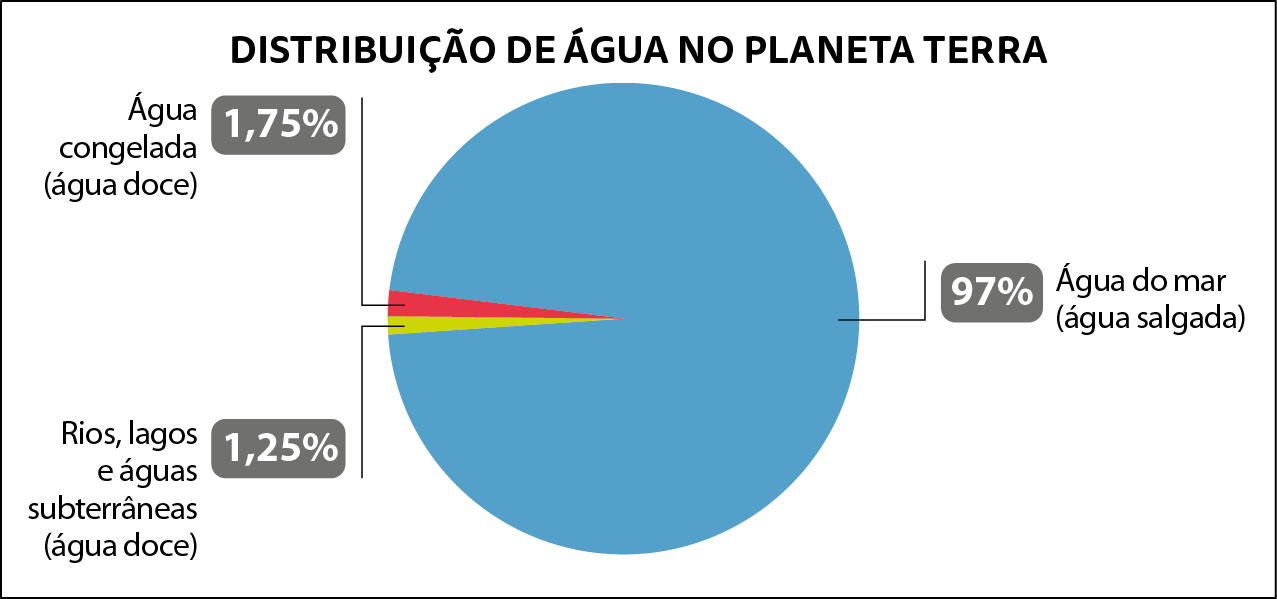
Dados obtidos em: SERVIÇO Geológico do Brasil (SGB). Coisas que Você Deve Saber sobre a Água. Disponível em: https://oeds.link/sMnrxE. Acesso em: 30 maio 2022.

• Agora, responda às questões.
a) De acordo com o gráfico, como é a divisão de água doce em nosso planeta?
b) Qual é a medida do volume, em quilômetro cúbico, de água doce não congelada?
c) E a de água salgada?
2. Em janeiro de 2023 houve eleição para presidente do grêmio estudantil de uma escola com .1100 estudantes. Concorreram nessa eleição 4 candidatos: Vinícius, Fernanda, Pedro e Daniela. Observe o gráfico feito pela coordenação da escola para divulgar o resultado da eleição.
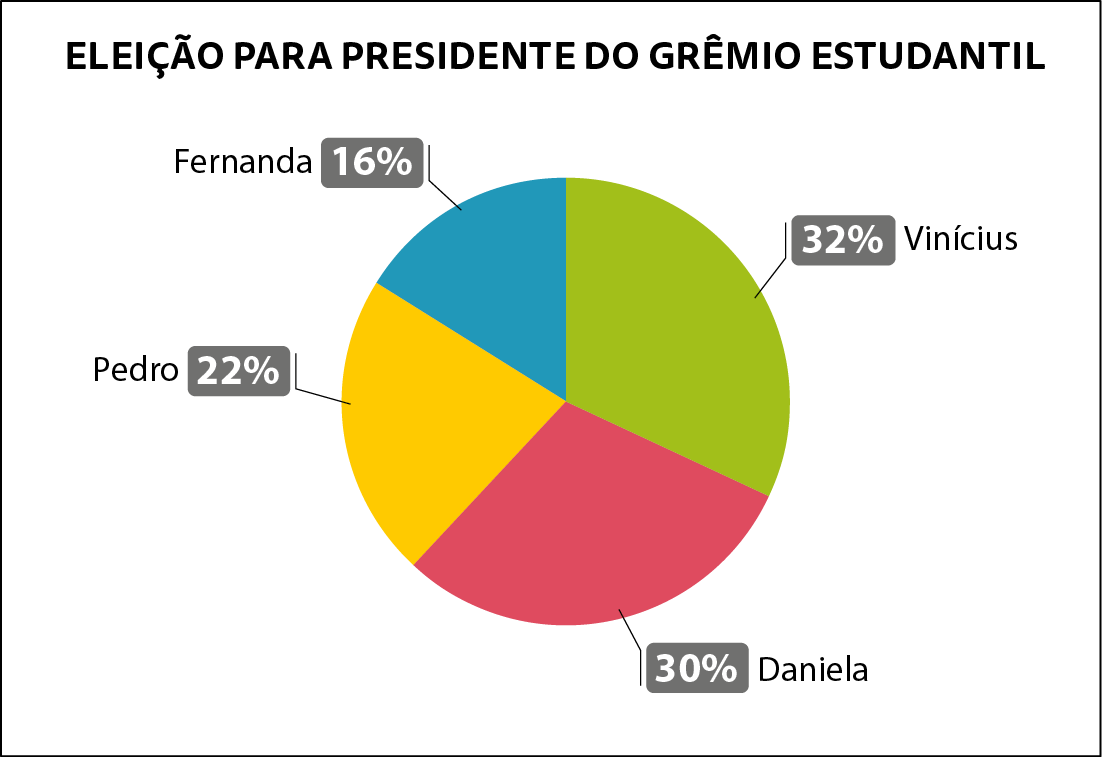
Dados obtidos pela coordenação da escola em janeiro de 2023.
• Agora, responda às questões.
a) Qual foi o candidato que recebeu a maior porcentagem dos votos? Qual foi essa porcentagem?
b) Quantos votos recebeu quem obteve menos votos?
c) Qual foi a diferença de votos entre o candidato mais votado e o menos votado?
3. Ricardo trabalha na prefeitura de sua cidade e realizou uma pesquisa entre 7 de novembro de 2023 e 8 de dezembro de 2023 para saber a medida de tempo médio de deslocamento diário que os trabalhadores entrevistados gastam de casa ao trabalho.
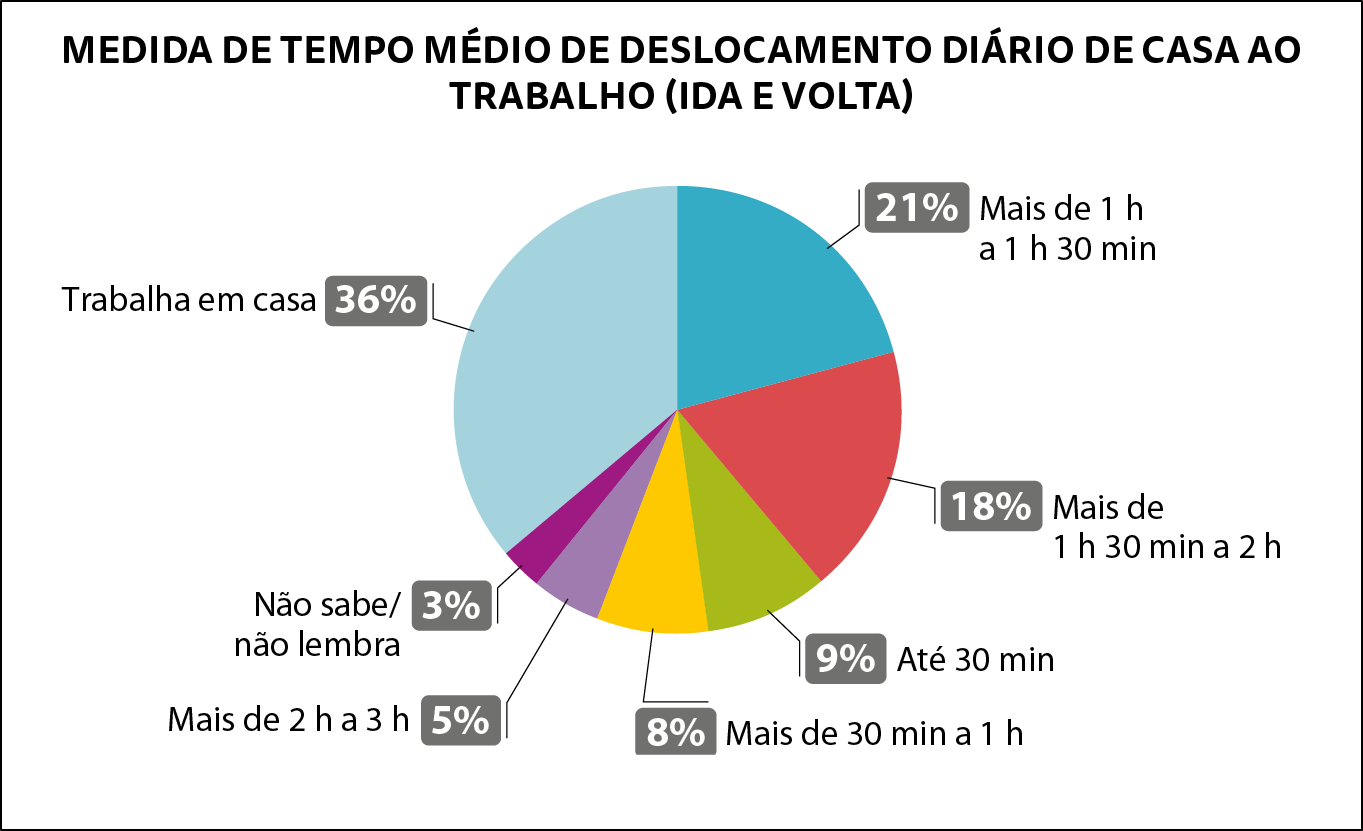
Dados obtidos por Ricardo em 2023.
a) O que respondeu a maior parte dos entrevistados?
b) Que porcentagem dos entrevistados demora até 30 minutos para se deslocar de casa ao trabalho?
c) Qual é a porcentagem dos entrevistados que demora até duas horas para se deslocar de casa ao trabalho?
d) Sabendo que .1000 pessoas foram entrevistadas, quantas demoram mais de duas horas para chegar ao trabalho?
4.

Na mesma pesquisa realizada por Ricardo, os .1000 entrevistados atribuíram notas de 1 a 10 a seu nível de satisfação com a segurança no trânsito. Observe o resultado a seguir.
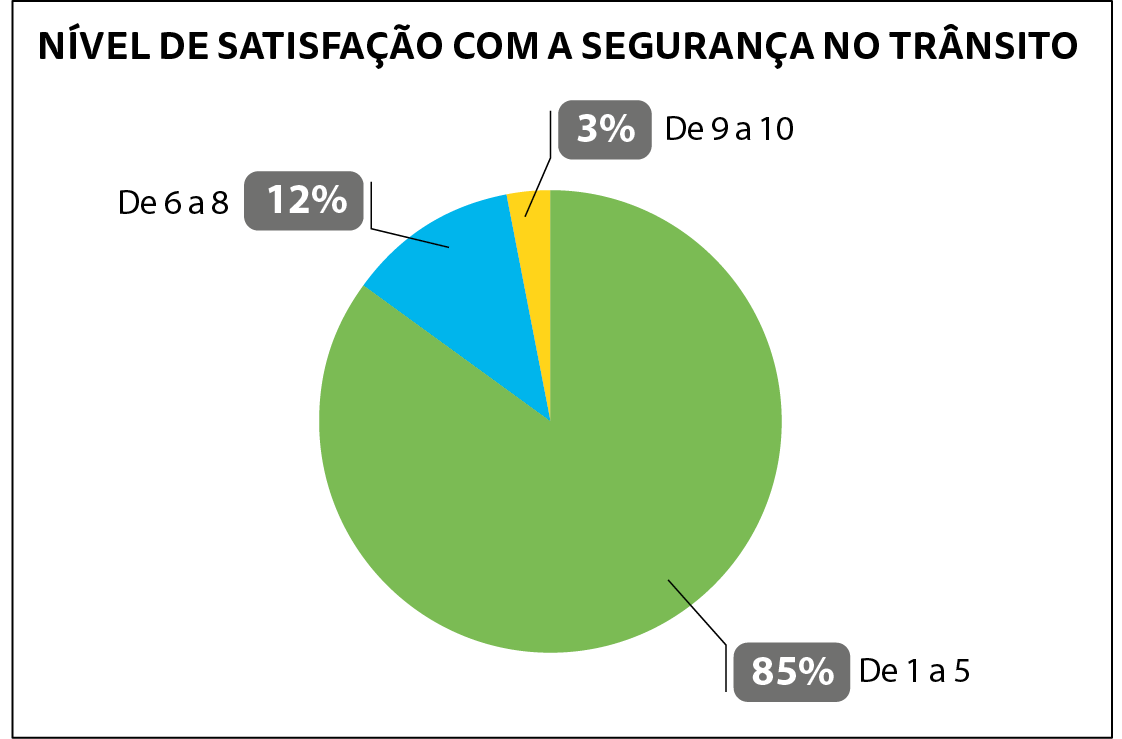
Dados obtidos por Ricardo em 2023.
a) Quantas pessoas atribuíram notas de 1 a 5 a seu nível de satisfação com a segurança no trânsito? De acordo com esses dados, os entrevistados se sentem seguros no trânsito?
b) Quantas pessoas entrevistadas estão muito satisfeitas com a segurança no trânsito?
c) O que você acha que poderia ser feito para melhorar a segurança no trânsito?

Atividades de revisão
faça as atividades no caderno
Atenção! Cuidado ao usar o compasso.
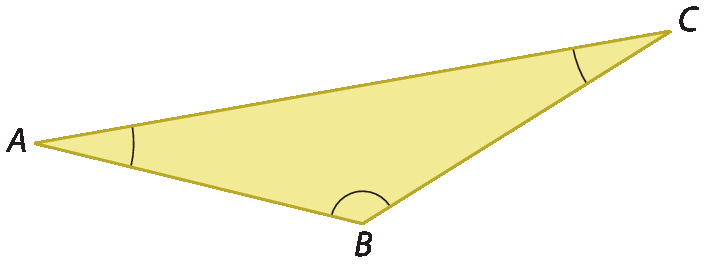
1. No triângulo a seguir, identifique os lados, os vértices e os ângulos internos.
2. (ó bê ême) Quantos triângulos há na figura a seguir?
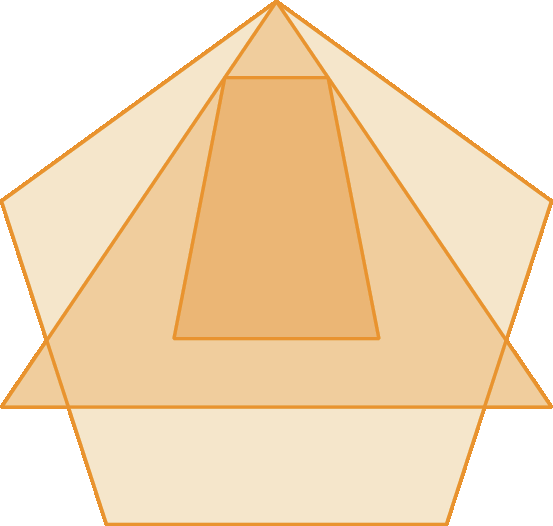
a) 3
b) 4
c) 5
d) 6
e) 7
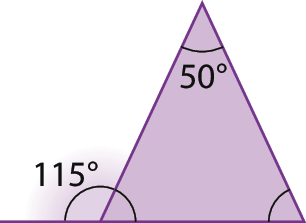
3. Em cada caso, determine a medida de abertura do ângulo desconhecida.
a)
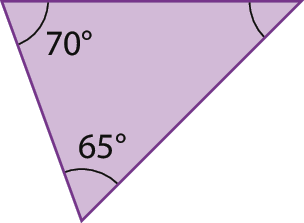
b)
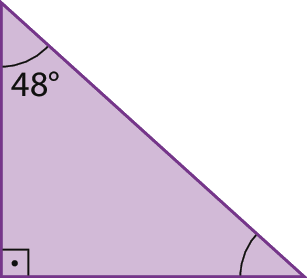
c)
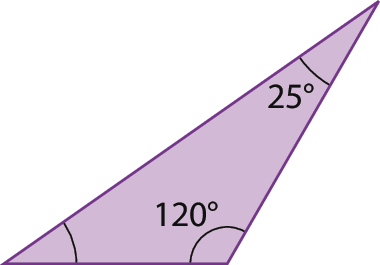
d)
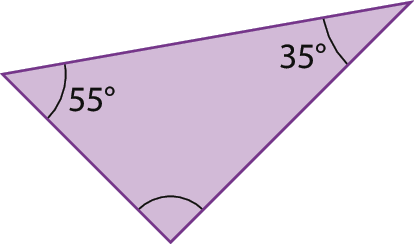
e)
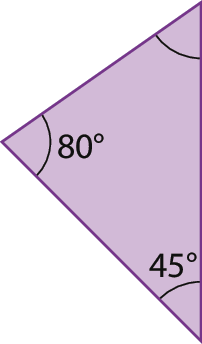
f)
4. Um triângulo isósceles tem um ângulo interno com medida de abertura igual a 20graus. Quais são as medidas de abertura dos outros dois ângulos internos desse triângulo?
5. Construa em seu caderno um triângulo:
a) equilátero de lados medindo 5 centímetros de comprimento;
b) isósceles de lados medindo 5 centímetros, 5 centímetros e 8 centímetros de comprimento;
c) escaleno de lados medindo 6 centímetros, 7 centímetros e 10 centímetros de comprimento.
6. O tangram é formado por sete peças geométricas.

Usando todas essas peças, sem que elas sejam sobrepostas, é possível formar diversas figuras, como os exemplos a seguir.
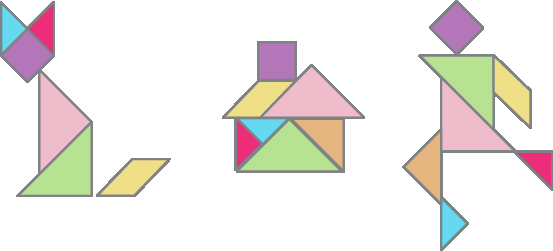
Note que cinco peças do tangram são triângulos. Observe o tangram representado na malha quadriculada e analise as medidas de comprimento dos lados e as medidas de abertura dos ângulos internos desses triângulos e faça o que se pede.
a) Classifique os triângulos de acordo com as medidas de comprimento dos lados e as medidas de abertura dos ângulos.
b) Considere que podemos classificar esses triângulos, de acordo com as medidas de comprimento de seus lados, em: pequeno, médio e grande. Quantos triângulos pequenos são necessários para formar um triângulo grande?
7. Luciana fez o esboço de alguns triângulos que vai construir. Analise as medidas de comprimento dos lados dos triângulos e responda à questão.
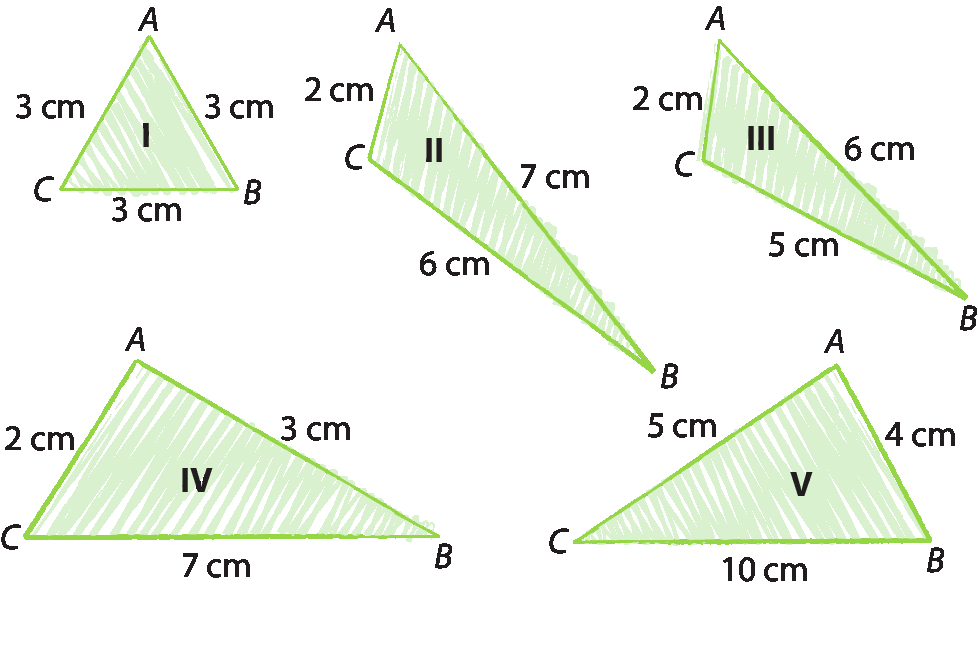
• Os esboços de Luciana estão corretos? Explique.
8. Observe os esboços e, se possível, construa os triângulos no caderno. Você pode usar régua, compasso e transferidor.
a)
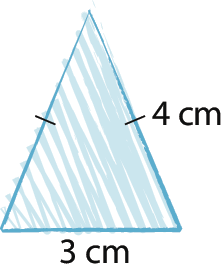
b)
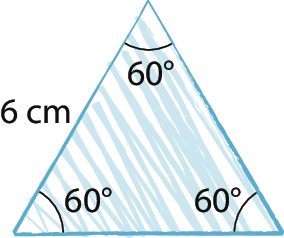
c)
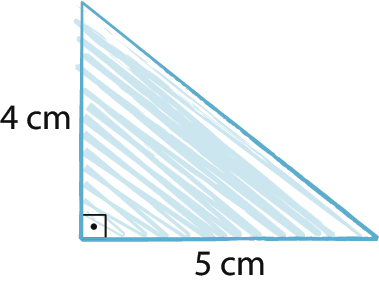
d)
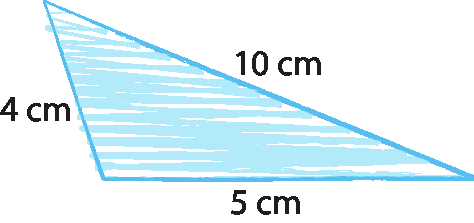
9. Laís está desenhando um triângulo. Ela desenhou o maior lado medindo 10 centímetros de comprimento e outro lado medindo 6 centímetros de comprimento. Qual deve ser a medida mínima inteira de comprimento do terceiro lado para que esse triângulo exista?
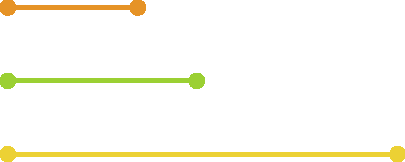
10. Usando apenas régua e compasso, verifique no caderno se é possível construir um triângulo utilizando os três segmentos fornecidos em cada item.
a)

b)
11. Observe a representação de três estruturas de metal unidas por rebites.
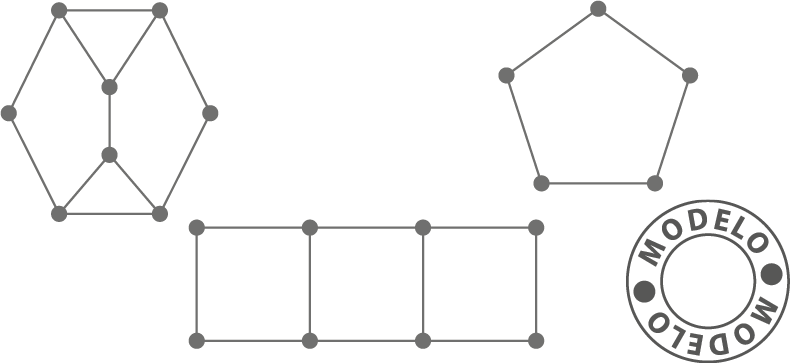
• Copie as figuras no caderno e desenhe hastes nas estruturas para que elas se tornem não deformáveis.
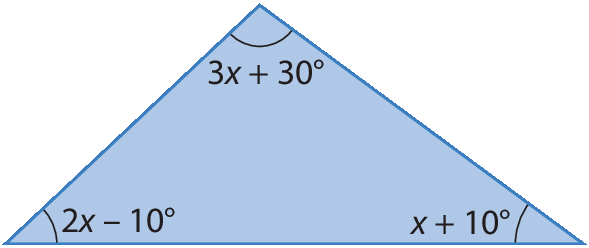
12. Escreva uma equação do 1º grau que represente a soma das medidas de abertura dos ângulos internos do triângulo a seguir e, depois, determine a medida x.
13. Classifique cada paralelogramo em retângulo ou losango.
a)

b)
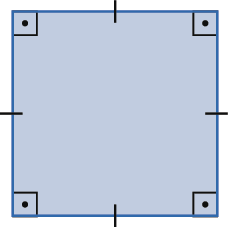
c)
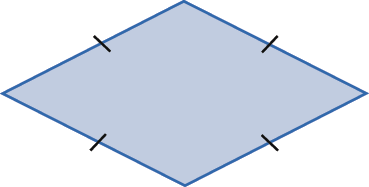
14. No caderno, associe cada trapézio a uma classificação.

15. Construa, usando régua e compasso, um quadrado de lados medindo 4 centímetros de comprimento.
16. Gabriel tinha dois triângulos isósceles de papelão com medidas de comprimento iguais e, com eles, compôs uma figura, como mostra a ilustração a seguir.

• Com o auxílio de régua e esquadro, descubra que figura ele compôs com os dois triângulos.
▶ Atividades de revisão
17. Determine a medida x considerando a medida do perímetro indicada em cada figura.
a)
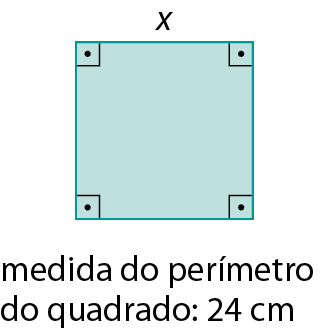
b)
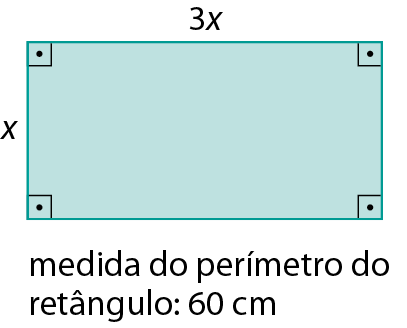
18. Calcule, em cada caso, a medida x em grau.
a)
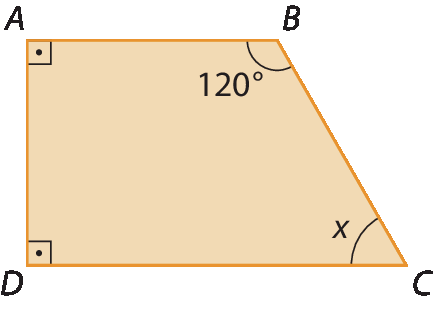
b)
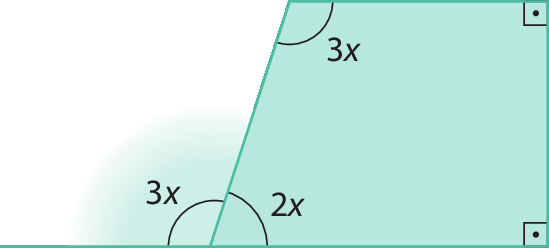
19. No caderno, classifique cada afirmação em verdadeira ou falsa.
a) Todo quadrilátero é um quadrado.
b) Todo quadrado é um quadrilátero.
c) Um retângulo é também um paralelogramo.
d) Um losango que também é um retângulo pode ser classificado como quadrado.
e) Todo quadrado é um losango.
f) Todo quadrado é um retângulo.
g) Todo quadrado é um paralelogramo.
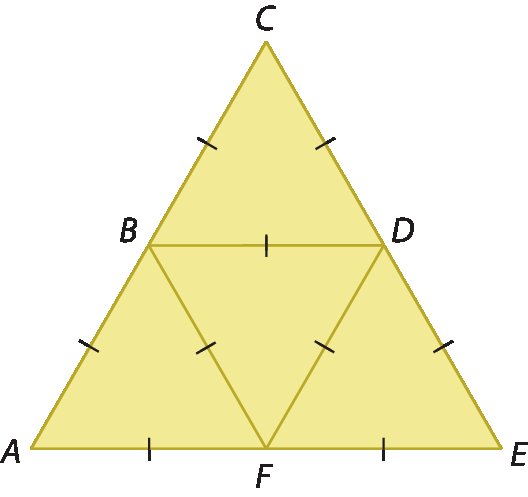
20. Sabendo que os tracinhos indicam que os segmentos têm a mesma medida de comprimento, responda às questões.
a) Quantos trapézios isósceles podemos identificar na figura?
b) E quantos losangos podemos identificar?
21. Compondo triângulos equiláteros idênticos, formamos outros triângulos equiláteros. Observe a sequência.
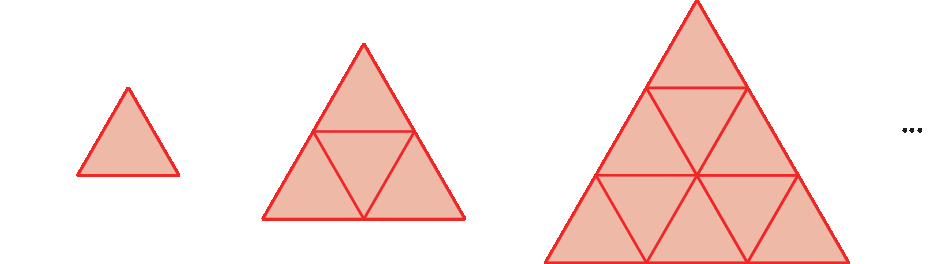
• Agora, responda: qual é a medida do perímetro de um triângulo formado por 64 triângulos equiláteros cujos lados medem 1 centímetro de comprimento?
22. Marcela desenhou quatro triângulos equiláteros, cada um com perímetro medindo 12 centímetros, justapostos a um quadrado, de modo que um dos lados de cada triângulo se apoiasse sobre um dos lados do quadrado sem que sobrasse ou faltasse nenhuma parte dos lados dos dois polígonos.
a) Que polígono Marcela formou nessa composição?
b) Qual é a medida do perímetro do polígono formado?
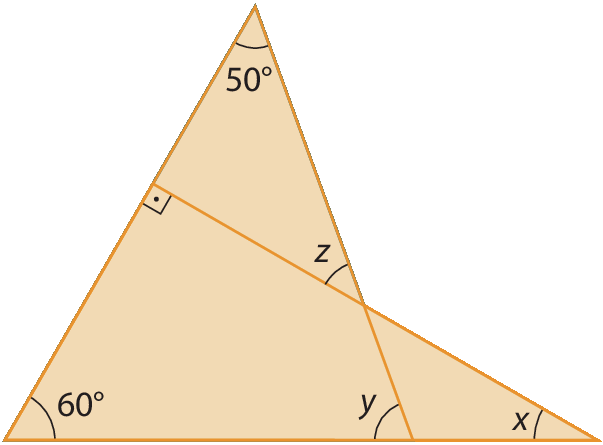
23. Determine as medidas x, y e z, em grau, na figura a seguir.
24.

Na figura, A bê = á cê , A Ê = á dê = dê ê e a abertura do ângulo
Ângulo BADmede 30graus.
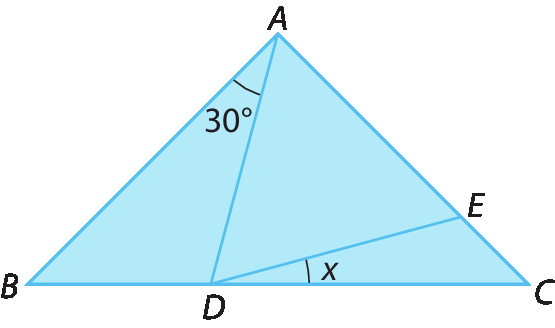
• Então, a abertura do ângulo x mede:
a) 10graus
b) 20graus
c) 15graus
d) 30graus
e) 45graus

Para finalizar
faça as atividades no caderno
organize suas ideias
Observe e responda
Analise estas imagens.



Com base nas imagens e também no que você aprendeu nesta Unidade, responda às questões no caderno.
1. A sentença matemática do quadro é uma equação ou uma inequação? Qual é o valor de x?
2. Que figuras geométricas podemos associar à bandeira do Brasil? E ao quadro de Tony Lima?
▶ Para finalizar
Registre

Para finalizar o estudo desta Unidade, reúna-se com um colega e façam o que se pede.
1. O que é uma equação? Como vocês diferenciam uma equação de uma expressão algébrica qualquer? Deem exemplos.
2. Como vocês diferenciam um círculo de uma circunferência?
3. Qual é a diferença entre os polígonos convexos e os não convexos?
4. Que características são comuns a todos os triângulos? Que características podem variar de triângulo para triângulo?
5. Quais são os quadriláteros notáveis? Deem exemplos explicando as características de cada grupo.
6. Na abertura desta Unidade, vocês responderam a algumas questões do boxe Para começar... Retomem as questões e avaliem se vocês dariam outras respostas a elas agora. Depois, escrevam um texto explicando o que vocês aprenderam nesta Unidade.
Para conhecer mais
Equação: o idioma da Álgebra
(Coleção Contando a história da Matemática)
Oscar Guelli São Paulo: Ática, 1999.
Na Antiguidade, os estudos matemáticos voltavam-se mais à Geometria do que à Álgebra. Diofante, um sábio do qual se sabe muito pouco, foi quem, possivelmente, iniciou os estudos sobre a Álgebra. Desde então, esses estudos não pararam de se desenvolver. Esse livro traz um pouco da história da Álgebra, muitas atividades desafiadoras e curiosidades sobre equações.

Calvin, o detetive
Bill Wise
São Paulo: Melhoramentos, 2013.
Uma série de crimes precisa ser resolvida pelo chefe de polícia Artur e seu ajudante mirim Calvin. A chave desses mistérios está nos números, o que exige do leitor atenção e síntese dos fatos. Os problemas desenvolvem o raciocínio lógico e as habilidades matemáticas de maneira divertida e lúdica.