
CAPÍTULO 11 Proporção e aplicações
1 Razão
Comparando por meio de uma razão
Observe o esquema com algumas informações sobre as copas do mundo de futebol de 1930 a 2018 que a professora Tânia fez e depois apresentou para a turma dela.
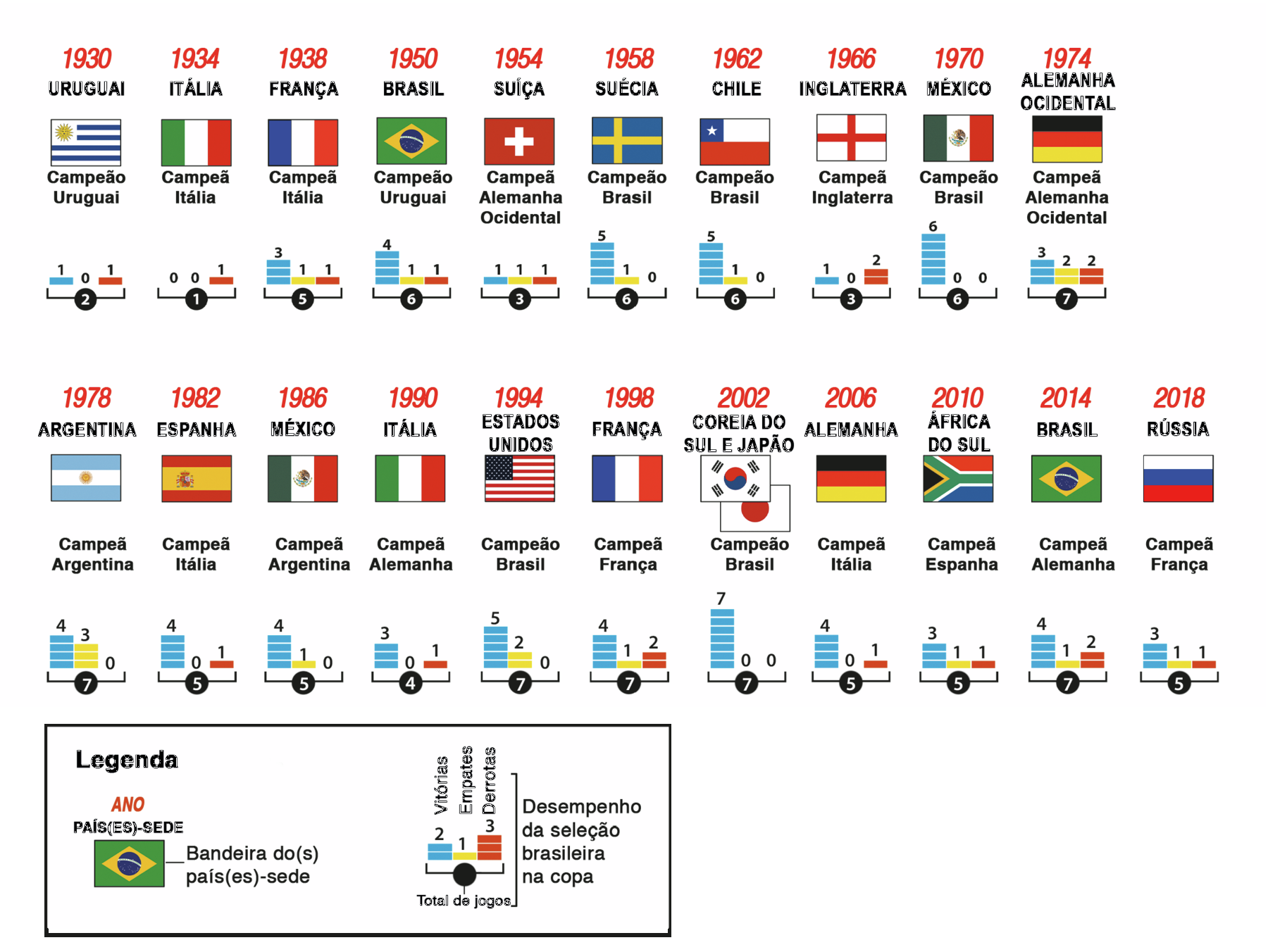
Elaborado com base nos dados publicados em: FEDERAÇÃO INTERNACIONAL DE FUTEBOL (FIFA). Disponível em: https://oeds.link/kMpsIQ. Acesso em: 14 abril 2022.
Para analisar o desempenho da seleção brasileira, a professora Tânia fez algumas comparações por meio de uma fração, que, nesse caso, chamamos de razão.

• A razão entre dois números aêbê, com b ≠ 0, nessa ordem, é dada por
fração a sobre b.
• Podemos expressar a razão na fórma de fração, de número decimal ou de porcentagem.
Lembre-se: Escreva no caderno!
Para pensar
Karina ficou pensando em uma das análises da professora Tânia.

• Responda à pergunta de Karina de acordo com o que você já estudou sobre frações e porcentagens.

ATIVIDADES
faça as atividades no caderno
1. Mariana e Lucas estão preparando um suco com a seguinte receita: para cada litro de suco concentrado, são necessários 2 litros de água.

• Como podemos comparar, por meio de uma razão, a quantidade de suco concentrado com a de água?
2. Descubra os números de acordo com cada afirmação.
a) A razão entre um número e
fração 2 sobre 3é 1.
b)
fração 1 sobre 7é a razão entre 14 e um número.
c) A razão entre 0,25 e um número é ‒ 0,5.
3. Carlos e Fernando estão no mesmo time de futebol. Na última partida, o time marcou 12 gols, dos quais 6 foram de Carlos e 4, de Fernando.

a) Escreva, na fórma de fração irredutível, a razão entre o número de gols marcados por Carlos e o número de gols marcados por Fernando.
b) Escreva, na fórma decimal, a razão entre o número de gols marcados por Fernando e o número total de gols do time.
c) Escreva, na fórma de porcentagem, a razão entre o número de gols marcados por Carlos e o número total de gols do time.
4. Em um município, há 120 dentistas para .240000 habitantes.
a) Qual é a razão entre o número de dentistas e o número de habitantes?
b) Nesse município, há quantos dentistas para cada grupo de .4000 pessoas?
•

Converse com um colega sobre como cada um encontrou a resposta do item b.
5. De trínta e duas crianças que foram acampar, 10 são meninas. Qual é a porcentagem de meninas em relação ao número total de crianças?
6. Observe a figura e responda às questões.

a) O retângulo está decomposto em quadrados. Qual é a porcentagem da medida de área do quadrado rosa em relação à medida de área do quadrado amarelo?
b) Qual é a razão entre a medida de área do quadrado verde e a medida de área do quadrado cinza?
c) Escreva, na fórma de fração irredutível, a razão entre a medida de área do quadrado amarelo e a medida de área total do retângulo.
7. O terreno que Débora pretende comprar está representado na planta por um retângulo.

• O perímetro do terreno mede 42 métros e um dos lados mede 15 métros de comprimento. Escreva, na fórma de porcentagem, a razão entre a medida de comprimento do lado maior e a do lado menor desse terreno.
8.


Reúna-se com um colega para responder à questão a seguir.
A razão entre os números negativos aêbê é 0,27. Qual desses números é o menor?
2 Proporção
Observe a situação a seguir.
Em dezembro de 2022, a agência de empregos E10 realizou uma pesquisa para comparar o número de homens e o de mulheres que trabalham em três tipos de empresa. Os dados obtidos estão representados a seguir.
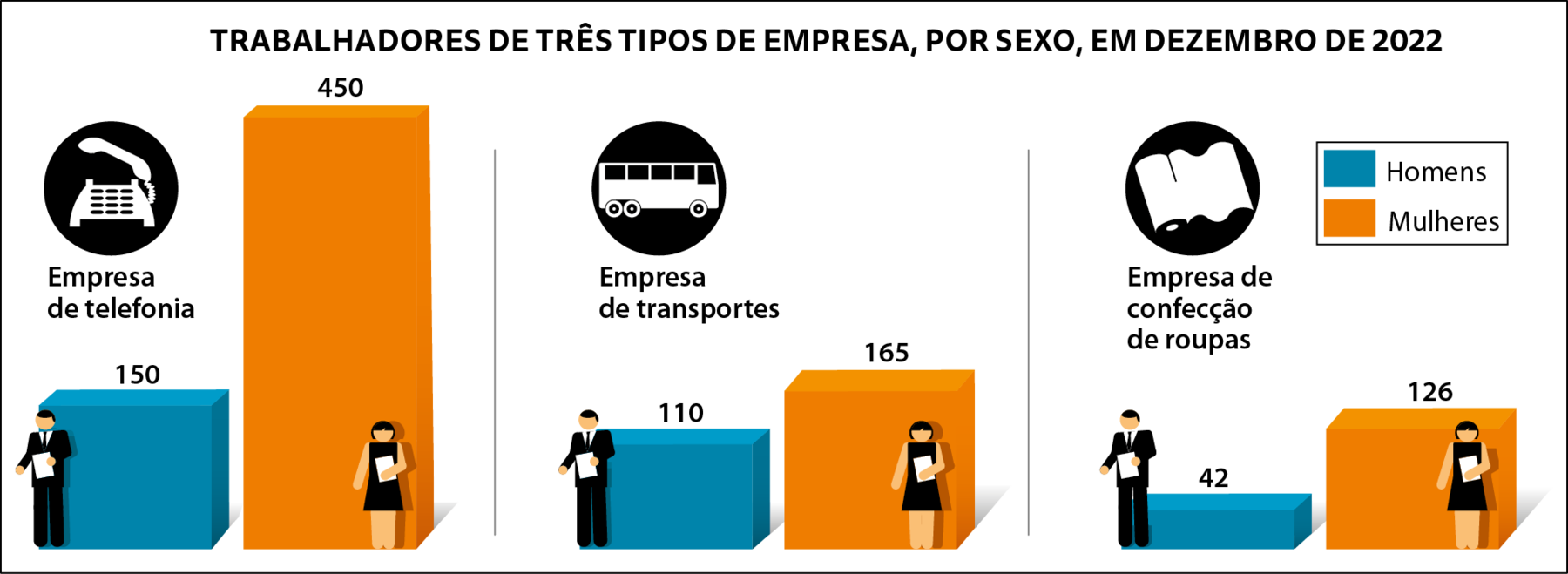
Dados obtidos pela agência E10 em dezembro de 2022.
Vamos comparar o número de homens e o de mulheres que trabalham em cada tipo de empresa por meio de uma razão.
• Em telefonia, a razão entre o número de homens e o número de mulheres é:
Fração 150 sobre 450 é igual a fração 1 sobre 3.. Isso significa que para cada homem 3 mulheres trabalham nesse tipo de empresa.
• Em transportes, a razão entre o número de homens e o número de mulheres é:
a fração 110 sobre 165 é igual a fração 2 sobre 3.. Nesse caso, para cada 2 homens, 3 mulheres trabalham nesse setor.
• Em confecção de roupas, a razão entre o número de homens e o número de mulheres é:
Fração 42 sobre 126 é igual a fração 1 sobre 3. Assim como em telefonia, para cada homem, 3 mulheres trabalham nesse setor.
Como a razão entre o número de homens e o de mulheres em telefonia é igual à razão entre o número de homens e o de mulheres em confecção de roupas, dizemos que as duas razões formam uma proporção.
Essa proporção pode ser indicada da seguinte maneira:
a fração 150 sobre 450 é igual a fração 42 sobre 126..

Quatro números não nulos, a, b, c e d, formam, nessa ordem, uma proporção quando
Fração a sobre b é igual a fração c sobre d..
Uma proporção
Fração a sobre b é igual a fração c sobre d.também pode ser representada por a : b = c : d (lemos: “a está para b, assim como c está para d ”). Os termos de uma proporção são assim denominados:

Propriedade fundamental das proporções
Acompanhe a situação a seguir.
Dois jovens vão caminhar uma distância que mede 12 quilômetros até chegar ao acampamento.

Se eles começarem a caminhar às 8 horas, a que horas chegarão ao acampamento, mantendo o mesmo ritmo de caminhada?
Considerando x a medida de tempo gasto para percorrer a distância que mede 12 quilômetros, podemos indicar a seguinte proporção, que é uma equação de incógnita x:

Logo, eles levarão 180 minutos (ou 3 horas) para percorrer uma distância que mede 12 quilômetros. Assim, eles chegarão ao acampamento às 11 horas.
Ao desenvolver os cálculos para obter o valor de x nessa proporção, podemos observar uma igualdade entre o produto dos extremos e o produto dos meios:
⇒ 1 ⋅ x = 12 ⋅ 15
Será que esse fato é válido para todas as proporções?
Com base no que já estudamos sobre operações com números racionais e resolução de equações, podemos partir de
Fração a sobre b é igual a fração c sobre d., com a, b, c e d não nulos, e obter a ⋅ d = b ⋅ c. Observe.

A igualdade obtida com base em uma proporção é conhecida como propriedade fundamental das proporções e pode ser escrita desta fórma:
Em toda proporção, o produto dos extremos é igual ao produto dos meios. Ou seja, dados os números a, b, c e d não nulos, com
Fração a sobre b é igual a fração c sobre d., temos: a ⋅ d = b ⋅ c

Usando a propriedade fundamental das proporções, podemos resolver muitos problemas.
Observação
As razões
fração 12 sobre 15 e fração 3 sobre 2 não formam uma proporção, pois: 12 ⋅ 2 ≠ 15 ⋅ 3
Desafio
Júlio tem um carro com tecnologia flex fuel (pode ser abastecido com gasolina ou etanol ou uma mistura dos dois combustíveis). No último abastecimento, Júlio abasteceu o tanque desse carro com etanol e gasolina na proporção de 1 para 4. Sabendo que a medida de capacidade do tanque é de 45 litros de combustível, responda: qual foi a quantidade máxima de gasolina colocada?


ATIVIDADES
faça as atividades no caderno
1. Copie no caderno apenas as razões que formam proporções.
a)
fração 4 sobre 10 e a fração 2 sobre 5b)
fração 8 sobre 32 e a fração 2 sobre 7c)
Fração 9 sobre 0,25 e Fração 81 sobre 2,25d)
fração 1,5 sobre 6 e 0,5 sobre 2e)
fração 35 sobre 28 e a fração 5 sobre 4f)
fração 128 sobre 93 e a fração 37 sobre 242. Descubra todas as proporções com os termos 2, 3, 10 e 15.
3. Sabendo que 42 está para x, assim como 252 está para 186, calcule o valor de x.
4. Para animar o acampamento das crianças, o cozinheiro inventou uma brincadeira. A cada 15 biscoitos, 4 seriam recheados.
Se, no final da brincadeira, a garotada encontrou 12 biscoitos recheados, quantos biscoitos foram feitos?
5. Leia atentamente o que a garota está dizendo e, depois, responda à questão.

• As razões entre a medida de distância e a de tempo, na subida e na descida, formam uma proporção? Justifique sua resposta.
6. Considerando que, em um mesmo instante do dia, as razões entre a medida da altura de um objeto e a do comprimento da sombra projetada por ele formam uma proporção, resolva o problema a seguir.
Em certo horário do dia, Eduardo, que mede 1,80 métro de altura, projeta uma sombra que mede 3 métros de comprimento. No mesmo instante, uma árvore projeta uma sombra cuja medida é igual a 7 métros de comprimento. Qual é a medida da altura da árvore?
Sequências de números diretamente proporcionais
Acompanhe a situação a seguir.
Caio é dono de uma sorveteria e produz seus próprios sorvetes. A quantidade de sorvetes produzida de cada sabor depende da preferência dos consumidores. Observe a seguir os sabores preferidos e a medida de massa de leite em pó utilizada para fabricá-los.
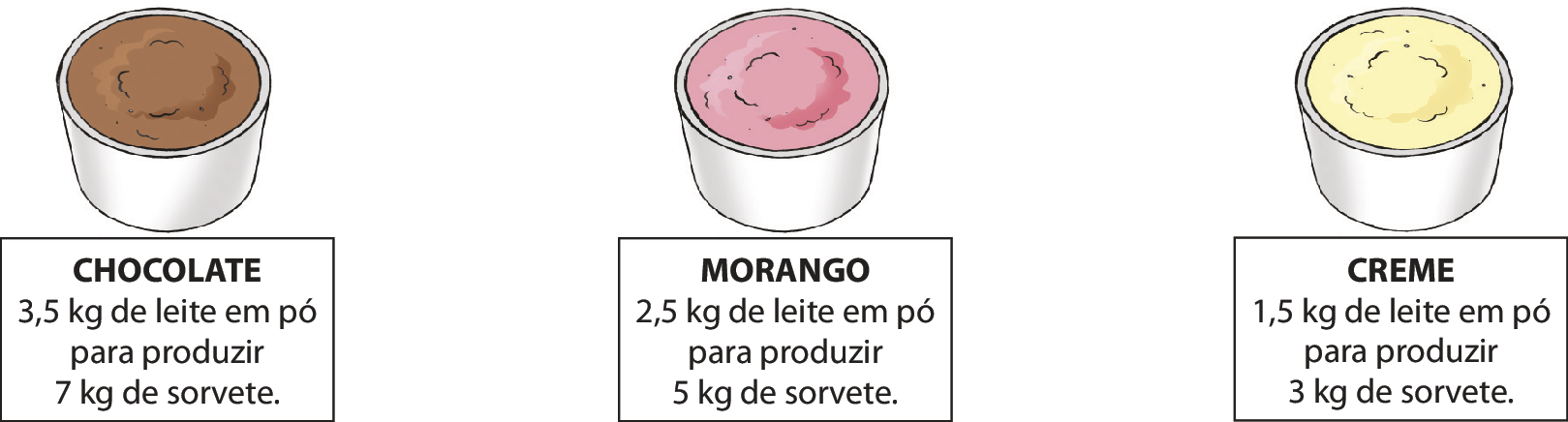
Se calcularmos as razões entre a quantidade de leite em pó, em quilograma, usada e a quantidade de quilogramas de sorvete produzida, observamos uma igualdade:
Note que o quociente de cada número da sequência (3,5; 2,5; 1,5) pelo número correspondente da sequência (7, 5, 3) resulta sempre em um mesmo número, chamado constante de proporcionalidade.
Então, dizemos que os números 3,5; 2,5 e 1,5 são diretamente proporcionais aos números 7, 5 e 3, nessa ordem.
Podemos dizer ainda que a quantidade de quilogramas de leite em pó que Caio usa é diretamente proporcional à quantidade de quilogramas de sorvete produzida.
Os números a, b, c, d, reticências são diretamente proporcionais aos números não nulos a, B, C, D, reticências, nessa ordem, quando:
Fração a minúsculo sobre A maiúsculo é igual a fração b minúsculo sobre B maiúsculo é igual a fração c minúsculo sobre C maiúsculo é igual a fração d minúsculo sobre D maiúsculo Igual reticência é igual a k
sendo cá a constante de proporcionalidade.
Sequências de números inversamente proporcionais
Observe as sequências de números a seguir.
(5, 10, 20, 40, 80)
(20; 10; 5; 2,5; 1,25)
Note que:
5 ⋅ 20 = 10 ⋅ 10 = 20 ⋅ 5 = 40 ⋅ 2,5 = 80 ⋅ 1,25 = 100
O produto de cada elemento de uma sequência pelo elemento correspondente da outra sequência resulta no mesmo número, que também é chamado constante de proporcionalidade.
Agora, observe como podemos escrever as igualdades anteriores como igualdades de razões:
Então, dizemos que os números 5, 10, 20, 40 e 80 são inversamente proporcionais aos números 20, 10, 5, 2,5 e 1,25, nessa ordem.
Repare que 5, 10, 20, 40 e 80 são diretamente proporcionais aos inversos de 20, 10, 5, 2,5 e 1,25, nessa ordem.
Os números não nulos a, b, c, d, reticências são inversamente proporcionais aos números não nulos a, B, C, D, reticências, nessa ordem, quando:
Para pensar
Identifique o item que não apresenta sequências de números diretamente proporcionais nem inversamente proporcionais.
a) (6, 9, 12, 15) e (2, 3, 4, 5)
b) (40, 38, 35) e (8, 7, 5)
c) (5, 8, 10) e (40, 25, 20)

ATIVIDADES
faça as atividades no caderno
1. Observe no quadro o número de camisetas que a empresa Ciranda Confecções produziu em determinada medida de tempo.
|
Medida de tempo (hora) |
Número de camisetas |
|---|---|
|
5 |
400 |
|
10 |
800 |
|
15 |
1.200 |
a) O que aconteceu com o número de camisetas produzido quando a medida de tempo passou de 5 para 10 horas? E de 5 para 15 horas?
b) Podemos afirmar que os números que expressam a quantidade de camisetas e a medida de tempo de produção delas são diretamente proporcionais?
2.

Observe as duas sequências de números diretamente proporcionais e descubra mentalmente os números que estão faltando.

• Agora, faça no caderno um quadro como o do modelo e complete-o com os números que estão faltando.
3. Observe as duas sequências de números diretamente proporcionais e descubra a constante de proporcionalidade.
(24, 12, 6, 3)
(4; 2; 1; 0,5)
4. A professora de Thaís pediu a ela que dividisse o número 60 em três partes diretamente proporcionais a 3, 5 e 7, nessa ordem. Observe como ela começou a resolver esse problema.

• Continue a resolução de Thaís e descubra quanto valem x, y e z.
5.

Reúna-se com um colega e descubram como dividir o número 52 em partes inversamente proporcionais a 2, 3 e 4, nessa ordem. Qual foi a resposta obtida?
3 Grandezas e medidas em nosso cotidiano
No dia a dia, deparamos com diversas grandezas (tudo que pode ser medido) e suas medidas (comparação entre a grandeza que se deseja medir e outra, de mesma espécie, tomada como unidade).
No Capítulo 5 deste livro, estudamos várias grandezas e suas unidades de medida, com múltiplos e submúltiplos. Observe a seguir algumas dessas grandezas e outras que usamos com frequência em variadas situações.
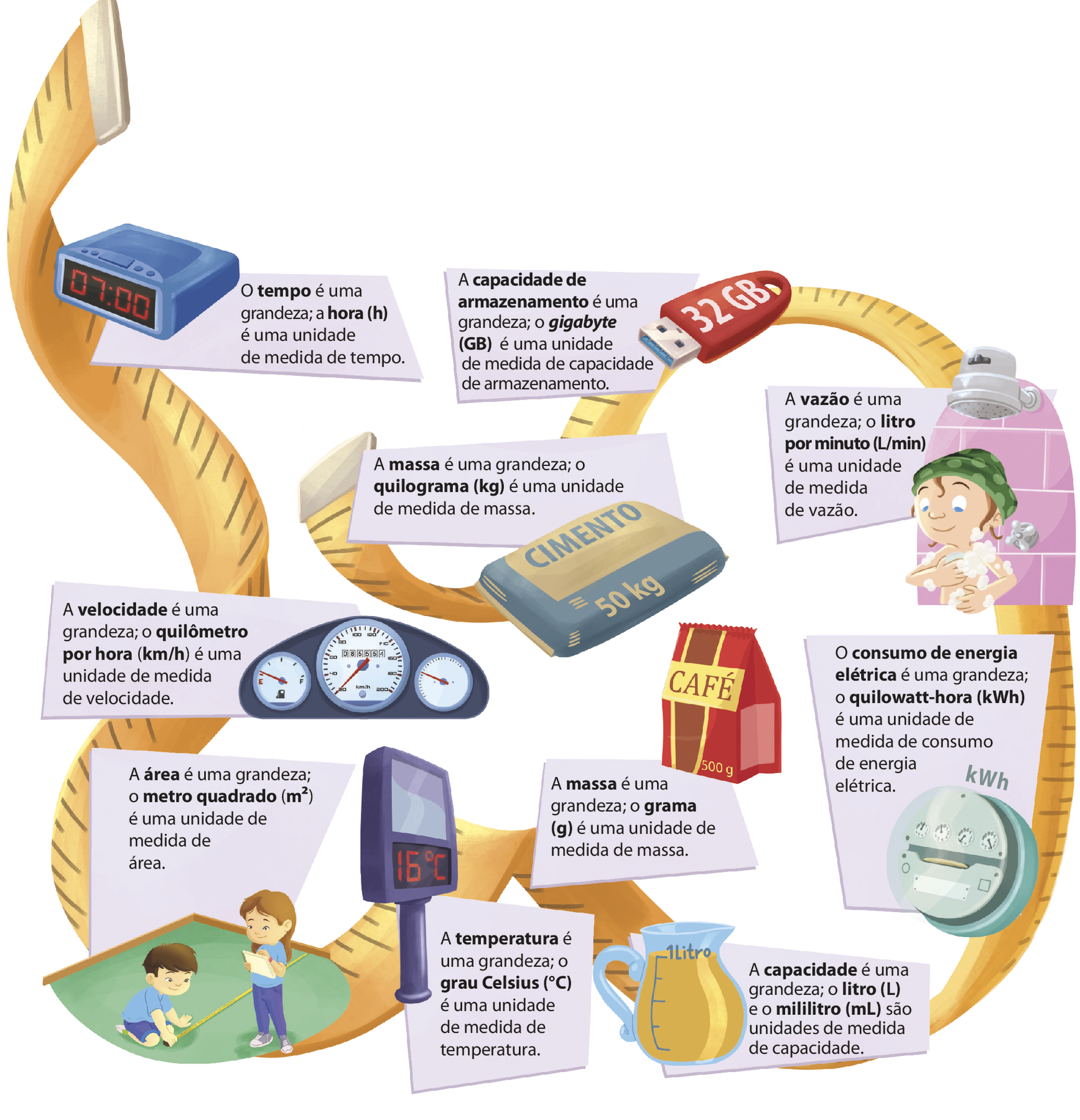
4 Grandezas diretamente proporcionais
Situação 1
Um funcionário de uma indústria automobilística decidiu testar a precisão da medida de velocidade indicada no velocímetro de um automóvel. Para isso, verificou a medida de distância percorrida pelo veículo durante 1 minuto, mantendo a mesma medida de velocidade média. Primeiro, ele manteve a medida de velocidade média do veículo em 60 quilômetros por hora e registrou a medida de distância percorrida em 1 minuto. Em seguida, testou outras medidas de velocidade. Observe os resultados do teste no quadro a seguir.
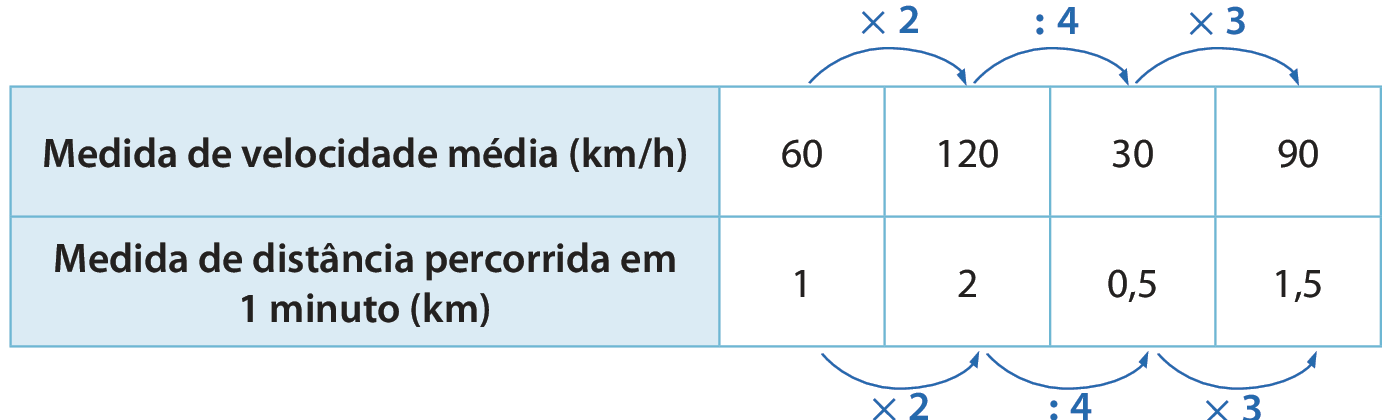
Observe que a razão entre a medida de velocidade média e a medida de distância percorrida correspondente será sempre a mesma:
Nesse caso, podemos dizer que as grandezas velocidade média e distância percorrida são diretamente proporcionais.
Observação
A razão entre a medida de distância percorrida por um corpo móvel e a medida de tempo que esse corpo gasta para percorrê-la é definida como medida de velocidade média.
Exemplo: Se a medida de distância percorrida por um carro é de 120 quilômetros em duas horas, a medida da velocidade média desse carro é
fração 120 quilômetros sobre 2 horasou
Fração 60 quilômetros sobre hora., que costumamos indicar 60 quilômetros por hora.
Duas grandezas são diretamente proporcionais quando variam sempre na mesma razão. Ou seja, duas grandezas são diretamente proporcionais quando, se a medida de uma dobra, a medida da outra também dobra; se é reduzida à metade a medida de uma, a medida da outra também se reduz à metade; e assim por diante.
Situação 2
Em uma papelaria, são cobrados 20 centavos por página copiada, como mostra o quadro a seguir.
|
Número de páginas |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
Preço total (R$) |
0,20 |
0,40 |
0,60 |
0,80 |
1,00 |
1,20 |
A razão entre o número de páginas copiadas e o preço correspondente é sempre a mesma:
O preço total é, então, diretamente proporcional ao número de páginas copiadas.
Situação 3
Observe estes quadrados:

No quadro a seguir, a medida de comprimento dos lados de cada quadrado da página anterior é relacionada à medida de seu perímetro.
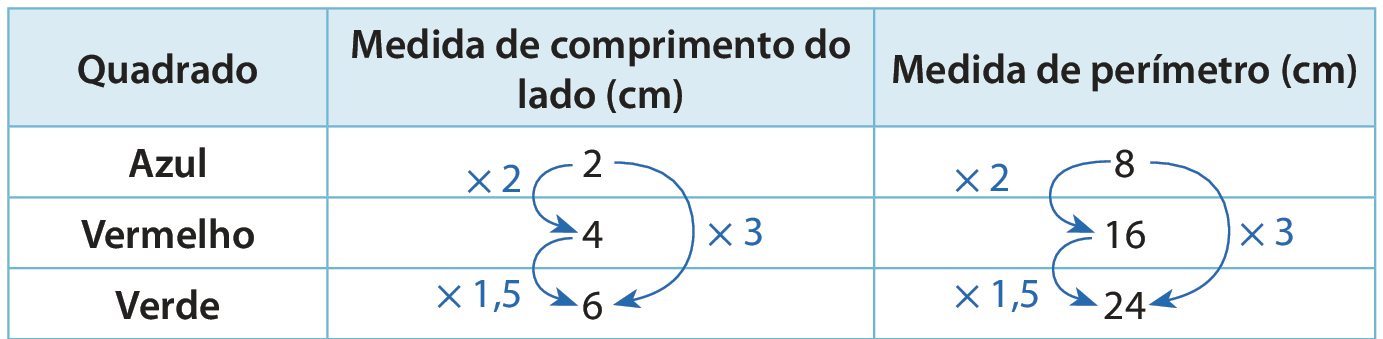
A razão entre a medida de comprimento dos lados dos quadrados e suas respectivas medidas de perímetro é sempre a mesma:
Portanto, a medida de comprimento do lado de um quadrado é diretamente proporcional à medida de seu perímetro.
Situação 4
Para verificar o desempenho de um automóvel, alguns engenheiros mecânicos mediram a distância percorrida por um veículo e a quantidade de combustível consumida durante um trajeto em que o carro manteve a medida de velocidade média constante. Observe a seguir o esquema que representa essa situação.
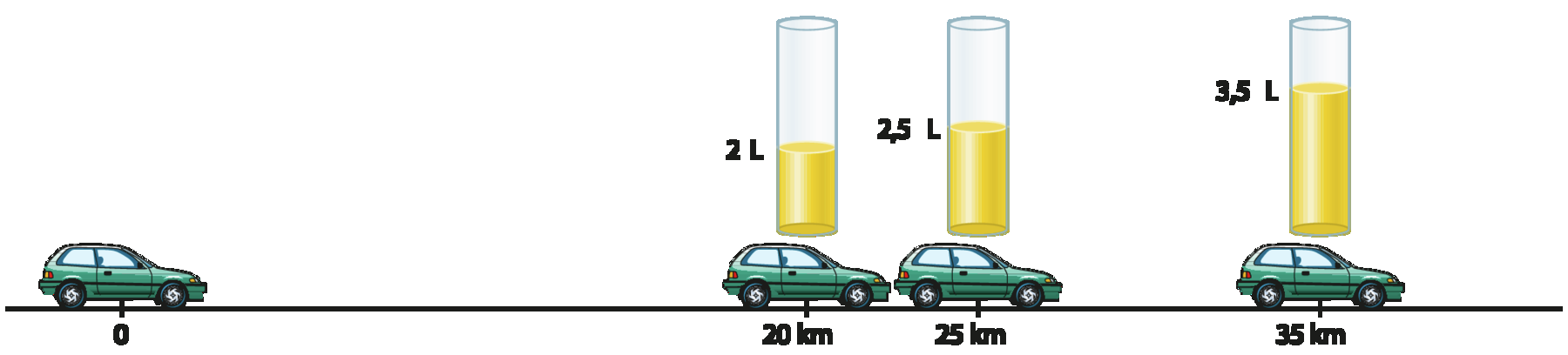
Após vários testes, os engenheiros concluíram que a medida de distância percorrida era diretamente proporcional à quantidade de combustível consumida, ou seja, a razão entre a medida de distância percorrida e a quantidade de combustível consumida era sempre a mesma:
Então, isso significa que o veículo sempre percorria 10 quilômetros por litro de combustível.

ATIVIDADES
faça as atividades no caderno
1.

Reúna-se com um colega e identifiquem o item que não apresenta grandezas diretamente proporcionais. Em seguida, escrevam uma justificativa para a resposta dada.
a) A idade e a medida de altura de uma pessoa.
b) O número de folhas e a medida de massa de um livro.
c) A quantidade de litros de água consumida em uma residência e o valor a ser pago pelo consumo.
Lembre-se: Escreva no caderno!
2. Observe o quadro com o preço do pão integral de acordo com a medida de massa em quilograma.
|
Pão (kg) |
Preço (R$) |
|---|---|
|
0,5 |
8,00 |
|
1,0 |
16,00 |
|
2,5 |
40,00 |
a) O que acontece com o preço do pão quando a medida de massa aumenta de 0,5 quilograma para 1,0 quilograma? E quando diminui de 2,5 quilogramas para 0,5 quilograma?
b) Pode-se afirmar que, nesse caso, a grandeza massa é diretamente proporcional ao preço?
3. Observe o quadro com números relacionados a duas grandezas diretamente proporcionais.
|
Grandeza A |
Grandeza B |
|---|---|
|
5 |
20 |
|
10 |
x |
|
20 |
y |
|
30 |
z |
a) Calcule os valores de x, y e z.
b) Qual é a constante de proporcionalidade entre os números relacionados à grandeza a e à grandeza B, nessa ordem?
c) Como ficaria a coluna relativa à grandeza B se a constante de proporcionalidade fosse
fração 1 sobre 2?
4. A quantia de R$ 288,00duzentos e oitenta e oito reais será repartida entre três crianças em partes diretamente proporcionais à idade delas. Quantos reais receberá a criança de 8 anos? E a de 10 anos? E a de 12 anos?

5. As frases a seguir formam um problema.

a) Ordene as frases e escreva o problema.
b) Resolva o problema que você escreveu no item anterior.
5 Grandezas inversamente proporcionais
Agora, vamos observar algumas situações que envolvem grandezas inversamente proporcionais.
Situação 1
No quadro a seguir, está representada a medida de tempo gasto por uma motocicleta para percorrer certa medida de distância variando a medida de velocidade média.
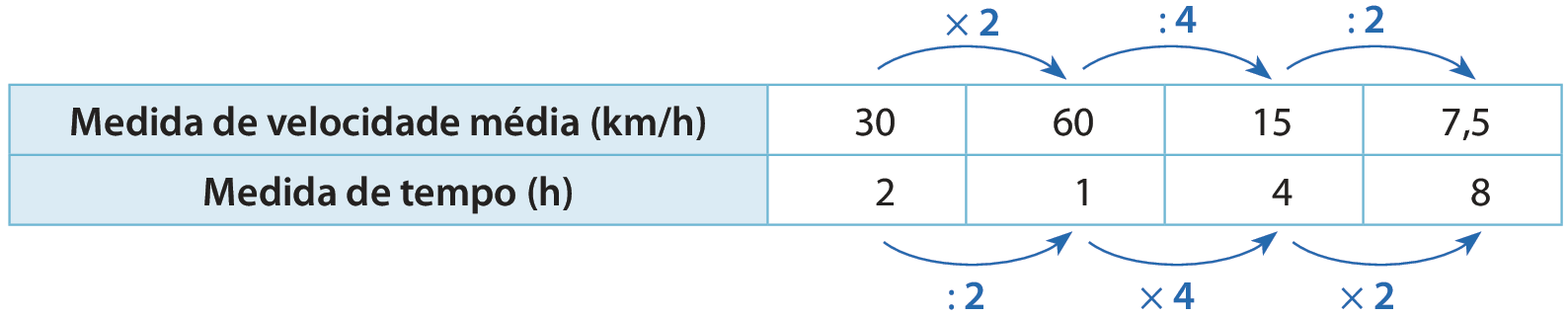
A razão entre a medida de velocidade média e o inverso do valor correspondente à medida de tempo gasto é sempre a mesma:
Nesse caso, quando a medida de velocidade dobrou, a de tempo reduziu-se à metade; quando a medida de velocidade foi dividida por 4, a de tempo foi multiplicada por 4; quando a medida de velocidade foi reduzida à metade, a de tempo dobrou. Assim, podemos concluir que as grandezas velocidade média e tempo são inversamente proporcionais.
Duas grandezas são inversamente proporcionais quando uma varia sempre na razão inversa da outra. Ou seja, duas grandezas são inversamente proporcionais se, quando a medida de uma dobra, a medida da outra se reduz à metade; se a medida de uma é dividida por 3, a medida da outra é multiplicada por 3; e assim por diante.
Situação 2
Renata comprou duzentas e quarenta figurinhas da Copa do Mundo de Futebol para dividir entre alguns de seus sobrinhos.
O número de figurinhas que cada sobrinho vai receber depende da quantidade de sobrinhos que Renata vai considerar. Observe o quadro a seguir.
|
Número de sobrinhos |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|
|
Número de figurinhas por sobrinho |
120 |
80 |
60 |
48 |
40 |
A razão entre o número de sobrinhos de Renata e o inverso do número correspondente de figurinhas por sobrinho é sempre a mesma:
Logo, o número de sobrinhos é inversamente proporcional ao número de figurinhas que cada um vai receber.
Situação 3
Há diversos retângulos cuja área mede 12 centímetros quadrados, como os dois representados a seguir.
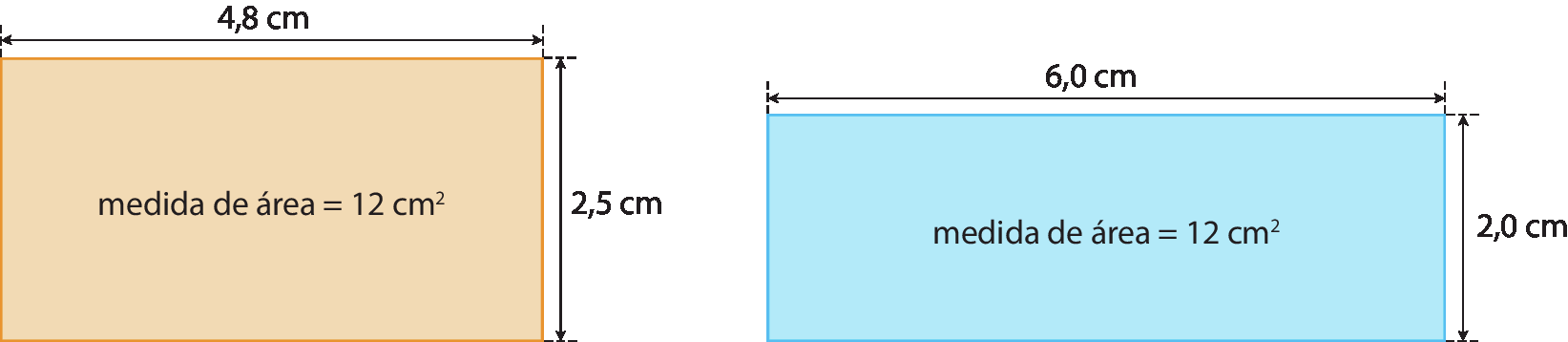
Considere algumas possíveis medidas de comprimento de lados desses retângulos.
|
Medida de comprimento (cm) |
6 |
4,8 |
3 |
2,4 |
2 |
|---|---|---|---|---|---|
|
Medida de largura (cm) |
2 |
2,5 |
4 |
5 |
6 |
A razão entre a medida de comprimento e o inverso da medida de largura é sempre a mesma:
Portanto, a medida de comprimento de cada um desses retângulos é inversamente proporcional à medida de largura.

ATIVIDADES
faça as atividades no caderno
1. Classifique as grandezas x e y, expressas pelos números em cada caso, em diretamente proporcionais ou inversamente proporcionais.
a)
|
x |
2 |
3 |
|---|---|---|
|
y |
4 |
6 |
b)
|
x |
1 |
2 |
|---|---|---|
|
y |
48 |
24 |
2. A professora Lia sempre propõe trabalhos em grupo com uma condição: todos os grupos devem ter a mesma quantidade de estudantes. Na turma de Fernanda, há 40 estudantes. Observe algumas possibilidades de formação de grupos nessa turma.
|
Número de estudantes no grupo |
10 |
8 |
4 |
|---|---|---|---|
|
Quantidade de grupos |
4 |
5 |
10 |
• Analise os números do quadro e verifique se as grandezas número de estudantes no grupo e quantidade de grupos são diretamente ou inversamente proporcionais.
•

Em seguida, converse com um colega sobre como cada um pensou para responder ao item anterior.
3. Bruno desenhou um retângulo cuja medida de comprimento era 9 centímetros e a de largura, 5 centímetros. Lúcia desenhou outro retângulo, que media 15 centímetros de comprimento e 3 centímetros de largura. Verifique se as medidas de comprimento desses retângulos são inversamente ou diretamente proporcionais à medida de largura.

4.

Com base nas ilustrações a seguir, elabore um problema envolvendo grandezas inversamente proporcionais.

6 Regra de três
Muitos problemas que envolvem duas grandezas, diretamente ou inversamente proporcionais, podem ser resolvidos de modo prático se empregarmos o procedimento chamado regra de três.
Acompanhe as situações a seguir.
Situação 1
Em um dia de sol, Janete e Paulo mediram o comprimento de suas sombras.

Janete mede 165 centímetros de altura, e Paulo, 180 centímetros. Sabendo que, em determinado horário, a medida de comprimento da sombra de Paulo é 60 centímetros, qual é a medida de comprimento da sombra de Janete? (Considere que a medida de comprimento da sombra de uma pessoa, em determinado instante, é diretamente proporcional à da sua altura.)
Para resolver esse problema, vamos montar um quadro.
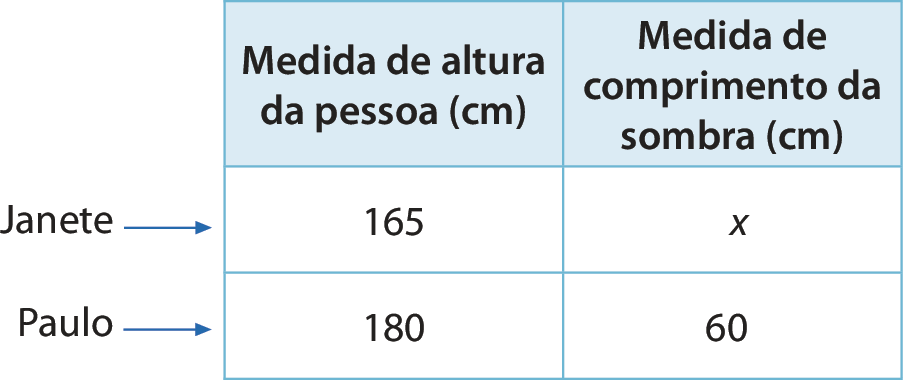
Como as grandezas são diretamente proporcionais, podemos montar a seguinte proporção:
Aplicando a propriedade fundamental das proporções e resolvendo a equação, temos:
180 ⋅ x = 165 ⋅ 60
180x = .9900
x =
fração 9900 sobre 180x = 55
Portanto, nesse horário, a medida de comprimento da sombra de Janete é 55 centímetros.
Situação 2
Uma torneira enche um barril em 20 minutos, com uma vazão medindo 15 litros por minuto.
Se a medida de vazão fosse 5 litros por minuto, quantos minutos seriam necessários para encher o barril?
Vamos organizar os dados em um quadro.
|
Medida de vazão (L/min) |
Medida de tempo (min) |
|---|---|
|
15 |
20 |
|
5 |
x |
Nesse caso, se dobrarmos a medida de vazão, a medida de tempo para encher o barril ficará reduzido à metade. Então, as grandezas são inversamente proporcionais e, por isso, montamos a seguinte proporção:
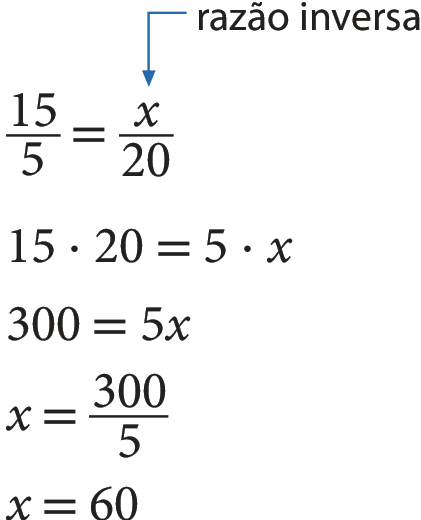
Portanto, se a medida de vazão fosse 5 litros por minuto, seriam necessários 60 minutos para encher o barril.

ATIVIDADES
faça as atividades no caderno
1. Com uma lata de leite condensado é possível fazer 50 docinhos. Se Júlia precisa fazer 300 docinhos iguais a esses, de quantas latas de leite condensado ela precisará?
2. O quadro a seguir mostra quantos quilowatts-hora (cá dáblio agá) um televisor consome, em um mês, de acordo com a medida de tempo (em hora) em que permanece ligado em um dia.
|
Medida de tempo (hora) |
2 |
4 |
6 |
8 |
y |
|---|---|---|---|---|---|
|
Consumo de energia elétrica (kWh) |
6 |
x |
18 |
24 |
30 |
• Quais são os valores de x e de y?
3. Uma indústria fornece refeições aos empregados. Um levantamento revelou que 100 funcionários, alimentados durante 10 dias, custam à empresa R$ 3.000,00três mil reais. Quanto custaria para a empresa alimentar 150 funcionários durante esse mesmo período?
4. Três mangueiras iguais, juntas, têm a medida de vazão de 12 litros de água por minuto. Qual será a medida de vazão por minuto de 7 dessas mangueiras juntas?
5. Na empresa em que Marcos trabalha, havia no banheiro torneiras que, quando abertas por 5 minutos, gastavam 80 litros de água. Para economizar, Marcos trocou 6 delas por torneiras que se fecham automaticamente depois de alguns segundos. Essas torneiras têm a mesma medida de vazão que as antigas.
Se, em média, contando os períodos de uso, cada torneira tradicional ficava aberta por 25 minutos durante 1 dia e cada torneira automática permanece aberta por 15 minutos, de quanto será a economia de água por dia?
6. Uma torneira com medida de vazão de 6 litros por minuto enche um balde em 2 minutos. Qual deverá ser a medida de vazão dessa torneira para encher o mesmo balde em 1 minuto?
7. Elisa trabalha como revisora de textos e cobra um valor fixo por página. Para revisar um livro de 127 páginas, ela cobra R$ 1.789,00mil setecentos e oitenta e nove reais. Nesta semana, ela aceitou uma proposta para revisar um livro de quinhentas e oitenta e sete páginas. Quanto ela deverá receber por esse trabalho?

8. Márcia quer ampliar uma fotografia. Na loja de revelação de fotos, a funcionária anotou as medidas da fotografia (2 centímetros de altura e 3 centímetros de comprimento) e perguntou quais deveriam ser as medidas da altura e da largura da foto ampliada. Márcia respondeu apenas que a foto deveria medir 15 centímetros de altura. Qual deverá ser a medida de comprimento da foto ampliada se as proporções forem mantidas?
9. (saréspi) As bombas de combustível dos postos de serviços têm um contador que vai acumulando o total de litros vendidos. Observe os totais acumulados por dia em cada bomba do Posto do Pedro.
|
Litros |
|
|
1ª bomba |
15.635 |
|---|---|
|
2ª bomba |
10.215 |
• Se o Posto do Pedro vender todos os dias a mesma quantidade, em quantos dias venderá .103400 litros?
a) 6 dias
b) 5 dias
c) 4 dias
d) 3 dias
10. Em uma hora, 4 torneiras despejam .1000 litros de água em um reservatório.
a) Se fossem 9 torneiras, com a mesma medida de vazão, quantos litros de água seriam despejados por hora?
b) Se a medida de capacidade do reservatório é de .18000 litros e ele está completamente vazio, quanto tempo será necessário para enchê-lo com as 9 torneiras?
11. Meire é proprietária de uma fábrica de calças. Atualmente, a fábrica produz 78 calças por dia, utilizando 260 metros de tecido. No próximo mês, Meire deverá aumentar sua produção, passando a fabricar 99 calças por dia. Considerando que os modelos das calças serão os mesmos, que medida de comprimento, em metro, de tecido será usada a mais por dia para essa nova produção?
12. Sandra vai viajar de carro para Natal, no Rio Grande do Norte.
• Com a medida de velocidade média de 60 quilômetros por hora, serão necessárias 3 horas para Sandra percorrer o trajeto de sua casa até o destino. Quanto tempo ela gastará se a medida de velocidade média for de 90 quilômetros por hora?
13. Encontre o erro que há na resolução do problema a seguir. Depois, resolva-o no caderno.
Em um posto de gasolina há uma bomba antiga e uma moderna. A bomba moderna enche o tanque de um automóvel em 3 minutos, com medida de vazão de 15 litros por minuto.
Quanto tempo a bomba antiga levará para encher o mesmo tanque se a medida de sua vazão for de 10 litros por minuto?

14. Faça o que se pede.
• Desenhe três retângulos (como os seguintes) em uma malha quadriculada, de modo que a razão entre as dimensões do primeiro retângulo para o segundo seja 1 por 2 e a razão do primeiro para o terceiro retângulo seja 1 por 3.
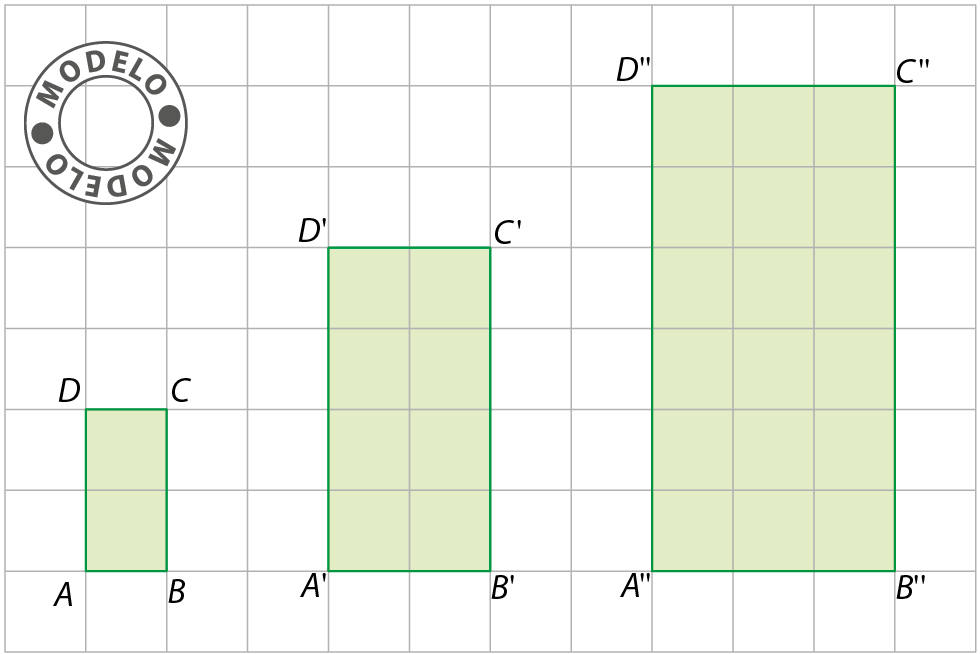
• Trace as diagonais
Segmento de reta AC Segmento de reta A linha C linha Segmento de reta A duas linhas C duas linhas• Recorte os retângulos e sobreponha-os de modo que os ângulos de vértice á, á' e á'' coincidam. Para evitar acidentes, manuseie a tesoura sem ponta com cuidado.
a) Responda: o que aconteceu com as diagonais dos três retângulos?
b) Escreva uma conclusão sobre como podemos ampliar ou reduzir um retângulo.
15.

Seis macacos comem 6 bananas em 6 minutos. Quantos minutos 3 macacos levariam para comer 3 bananas? Quantos macacos comeriam 18 bananas em 18 minutos?
7 Porcentagem
Quando fazemos compras, é muito comum encontrarmos promoções em que se oferecem descontos na aquisição de certas quantidades de produtos. Para verificar se uma promoção é vantajosa, podemos calcular a porcentagem de desconto.
Observe a situação a seguir.
Paula e Caio foram ao mercado, gostaram de uma promoção que viram e compraram 5 detergentes pelo preço de 4.

Ou seja, 1 dos 5 detergentes saiu de graça.
De quanto foi o desconto, em porcentagem, oferecido nessa promoção?
Uma maneira de raciocinar para obter o desconto em porcentagem é a seguinte: se 1 dos 5 detergentes saiu de graça, o desconto foi de
Fração 1 sobre 5sobre o valor que seria pago se não houvesse promoção.
Assim, como
Fração 1 sobre 5representa uma fração equivalente a
Fração 20 sobre 100, o desconto da promoção foi de 20%.
Taxa percentual ou porcentagem é a razão entre um número p e 100, que indicamos por
fração p sobre 100ou p%.
Observação
A expressão “por cento” vem do latim per centum, que significa “divisão por 100”.
Para pensar
Mariana quer saber qual é a porcentagem de meninas de sua turma.
Sabendo que o número total de estudantes da turma é 32 e 8 são meninos, observe os cálculos que ela fez.

a) Por que podemos dizer que 75% dos estudantes da turma de Mariana são meninas?
b)

Qual é a porcentagem de meninos na turma de Mariana? Converse com um colega sobre a estratégia que cada um usou para resolver essa questão.
c) Qual é a razão que representa o número de meninas em relação ao número total de estudantes da turma?
Diferentes modos de calcular porcentagem
Uma loja de brinquedos estabeleceu a meta de vender mais de novecentas e cinquenta bicicletas por mês. No mês passado, a loja vendeu 25% das .5100 bicicletas que estavam no estoque. A meta do mês foi atingida?
Observe como quatro pessoas resolveram esse problema.
Note que podemos utilizar diferentes estratégias para o cálculo de porcentagem.




Exemplos
• 2% de 350 =
fração 2 sobre 100⋅ 350 =
fração 700 sobre 100= 7
• 30% de 10% =
fração 30 sobre 100⋅
fração 10 sobre 100=
fração 300 sobre 10000= 0,03
• 112,5% de 70 =
fração 112 vírgula 5 sobre 100⋅ 70 = 1,125 ⋅ 70 = 78,75

ATIVIDADES
faça as atividades no caderno
1.

Usando uma calculadora, determine os valores a seguir, de acordo com a porcentagem indicada.
a) R$ 112,00cento e doze reais mais 14% de R$ 112,00cento e doze reais
b) R$ 208,50duzentos e oito reais e cinquenta centavos mais 4% de R$ 208,50duzentos e oito reais e cinquenta centavos
c) R$ 58,30cinquenta e oito reais e trinta centavos mais 26% de R$ 58,30cinquenta e oito reais e trinta centavos
d) R$ 47,80quarenta e sete reais e oitenta centavos mais 32,5% de R$ 47,80quarenta e sete reais e oitenta centavos
2. Ao reduzir R$ 99,00noventa e nove reais em 1%, qual será o valor obtido?
3. Os 78% do total de figurinhas de Mariana correspondem a 156 figurinhas. Qual é a quantidade total de figurinhas que Mariana tem?
4. Analise as promoções das duas lojas e, depois, responda à questão.
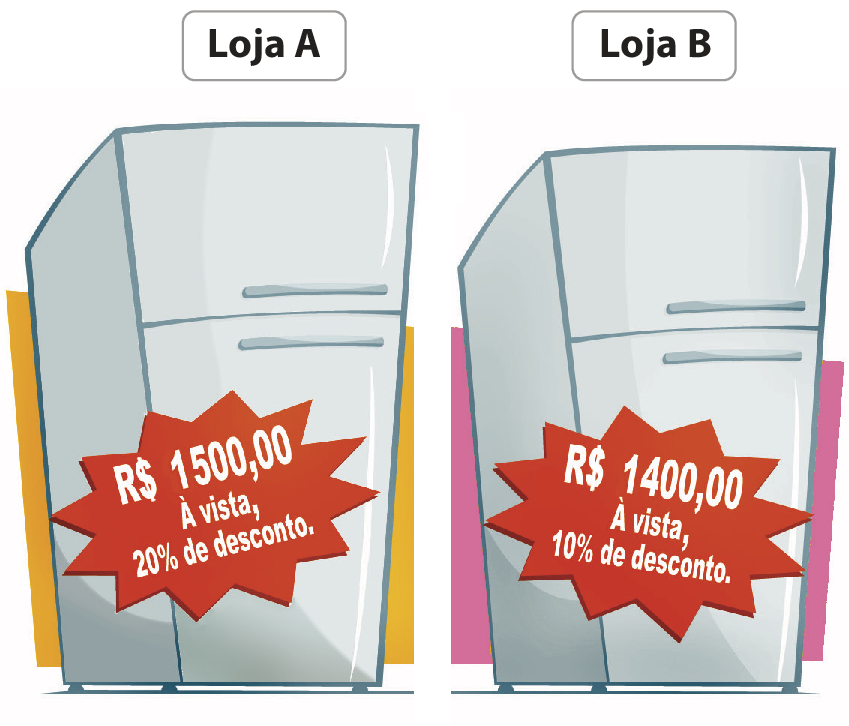
• Se comprar à vista, em qual das lojas um cliente pagará menos pela geladeira?
5. De 210 candidatos que participaram de um concurso, 70 foram aprovados. Qual foi, aproximadamente, a porcentagem dos reprovados?
6.

Márcia revendeu uma casa por R$ 460.000,00quatrocentos e sessenta mil reais, obtendo lucro de 15% sobre o preço de compra. Quanto Márcia pagou pela casa?
7.

Elabore um problema envolvendo porcentagem cujo cálculo para solucioná-lo está a seguir.

8. Uma bicicleta que custava R$ 150,00cento e cinquenta reais está sendo vendida com 40% de desconto. De quanto é o desconto? Qual é o preço atual da bicicleta? Observe como Luís e Júlia resolveram esse problema.

• Agora, resolva o problema usando uma estratégia diferente das usadas por Luís e Júlia.
9. Paulo foi jantar com sua família em um restaurante. A conta, incluindo os 10% de gorjeta da garçonete, foi de R$ 165,00cento e sessenta e cinco reais. Qual seria o valor da conta sem a gorjeta?

10. Em uma pesquisa com .1200 telespectadores, foi questionado quantas famílias assistiram às competições dos últimos Jogos Olímpicos. Concluiu-se que 65% dos telespectadores não assistiram a mais de 50% das competições. Quantos telespectadores entrevistados assistiram a mais de 50% das competições olímpicas?

Compreender um texto
faça as atividades no caderno
Lembre-se: Escreva no caderno!

Uma breve história sobre os impostos
Você já deve ter ouvido falar em impostos ou, pelo menos, alguém reclamando deles! Mas você sabe o que é isso? O próprio nome é uma dica: impostos são tributos obrigatórios cobrados pelo governo. O objetivo? custear as despesas de serviços públicos e coletivos, como educação, saúde e outros.
Atualmente, os impostos fazem parte do nosso cotidiano, mas sua história é tão antiga quanto o próprio surgimento da escrita. Leia no texto a seguir como eram cobrados os impostos na Antiguidade.
[reticências]
Peças de barro datados de 4000 antes de Cristo encontrados da Mesopotâmia são os documentos escritos mais antigos que conhecemos. E o mais antigo desses documentos faz referência aos impostos [reticências]. Além de entregar parte dos alimentos que produziam ao governo, os Sumérios, um dos povos a viver por ali, eram obrigados a passar até cinco meses por ano trabalhando para o rei.

[reticências]
Tonia Sharlach, arqueóloga da Universidade da Pensilvânia, nos Estados Unidos, afirma que [reticências] não havia garantia de contrapartida aos cidadãos. “Não sabemos quais os benefícios que as pessoas obtinham com o pagamento, mas presumimos que eles o faziam porque, caso contrário, o rei os mataria", diz.
Era assim também no antigo Egito. As evidências indicam que, em 3000 antes de Cristo, os faraós coletavam impostos em dinheiro ou em serviços pelo menos uma vez por ano. Ninguém era tão temido quanto os escribas, responsáveis por determinar a dívida de cada um [reticências]. Os impostos eram mais altos para estrangeiros, e especula-se que foi para pagar dívidas tributárias que os hebreus, por exemplo, acabaram como escravos.
O Império Romano aperfeiçoou a técnica de impor tributos a estrangeiros. [reticências] a conquista de outras terras e povos dava aos romanos acesso a mais riquezas, o que, por sua vez, permitia que conquistassem e controlassem um território ainda maior.
O censo, usado até hoje em muitos países, foi criado pelos romanos para decidir quanto deveriam cobrar de cada província. O cálculo era feito com base no número de pessoas. Até hoje, a capacidade de cobrar impostos é diretamente proporcional à quantidade de informações disponíveis sobre os contribuintes.
[reticências]
VELLOSO, Rodrigo. Uma breve história dos impostos. Superinteressante, São Paulo, 11 abril 2018. Disponível em: https://oeds.link/8HrsyC/. Acesso em: 28 fevereiro 2022.
Para se ter noção do valor monetário cobrado por impostos no Brasil, é possível acessar o portal do Impostômetro (disponível em: https://oeds.link/MTnBgo. Acesso em: 21 junho 2022). Para contabilizar o valor apresentado, são consideradas três esferas de governo: impostos, taxas e contribuições, incluindo multas, juros e correção monetária. Os levantamentos têm como fonte a base de dados oficiais, como a Receita Federal do Brasil, o Tribunal de Contas da União e o í bê gê É.

No site do Impostômetro é possível incluir filtros para personalizar uma busca por arrecadações. Alguns filtros são “Estado”, “Capitais”, “Municípios” e “Tributos”.


ATIVIDADES
faça as atividades no caderno
1. De acordo com o texto, na Antiguidade, como eram realizadas as cobranças de impostos:
a) na Mesopotâmia?
b) no Egito antigo?
c) na Roma antiga?
2.

Você sabe como os impostos são cobrados atualmente?
• Realize uma pesquisa sobre o assunto e, depois, compartilhe suas descobertas com os colegas.
3.

Marta pagou R$ 1.700,00mil setecentos reais por um smartphone. Sabendo que 15% do preço do smartphone corresponde aos impostos, calcule mentalmente e responda: quantos reais ela pagou de impostos nessa compra?
4. Um televisor custa R$ 2.570,00dois mil quinhentos e setenta reais, dos quais R$ 436,90quatrocentos e trinta e seis reais e noventa centavos são impostos. Quantos por cento do preço do televisor correspondem aos impostos?
5. Marcos comprou uma camiseta no valor de R$ 125,90cento e vinte e cinco reais e noventa centavos. Observe a seguir as porcentagens correspondentes aos impostos federais, estaduais e municipais que incidiram sobre o preço desse produto.
|
Tributo |
Federal |
Estadual |
Municipal |
|---|---|---|---|
|
Porcentagem |
9,25% |
18% |
0% |
•

Quantos reais Marcos pagou de impostos nessa compra? Utilize a calculadora para responder.
8 Juro simples
Pagamento à vista e pagamento a prazo
Acompanhe a situação.
Raul quer comprar uma televisão. A loja oferece duas fórmas de pagamento: R$ 930,00novecentos e trinta reais à vista ou em 8 parcelas de R$ 139,50cento e trinta e nove reais e cinquenta centavos.

Por que o preço a prazo (R$ 1.116,00mil cento e dezesseis reais) é maior que o preço à vista (R$ 930,00novecentos e trinta reais)?
Nessa situação, o preço a prazo é maior porque é cobrado juro (remuneração pelo parcelamento da dívida) sobre o preço à vista.
Vamos calcular o juro cobrado pelo parcelamento dessa dívida:
R$ 1.116,00mil cento e dezesseis reais ‒ R$ 930,00novecentos e trinta reais = R$ 186,00cento e oitenta e seis reais
Portanto, se Raul comprar a televisão a prazo, pagará R$ 186,00cento e oitenta e seis reais de juro.
Para encontrar a porcentagem de juro, podemos fazer:
= 0,2 = 20%
O juro (R$ 186,00cento e oitenta e seis reais) corresponde a 20% do preço à vista (R$ 930,00novecentos e trinta reais).
Dividindo 20% por 8 (número de parcelas), obtemos 2,5%, que é a taxa de juro ao mês no sistema de juro simples.
Neste capítulo, estudaremos apenas situações que envolvem o sistema de juro simples.
Aplicação financeira
Quando uma pessoa quer aplicar um valor em dinheiro, geralmente recorre a uma instituição financeira, por exemplo, um banco. Esse valor em dinheiro é chamado capital e, nesse caso, o juro é a remuneração que a pessoa vai receber do banco.
A soma do capital com o juro é chamada montante.
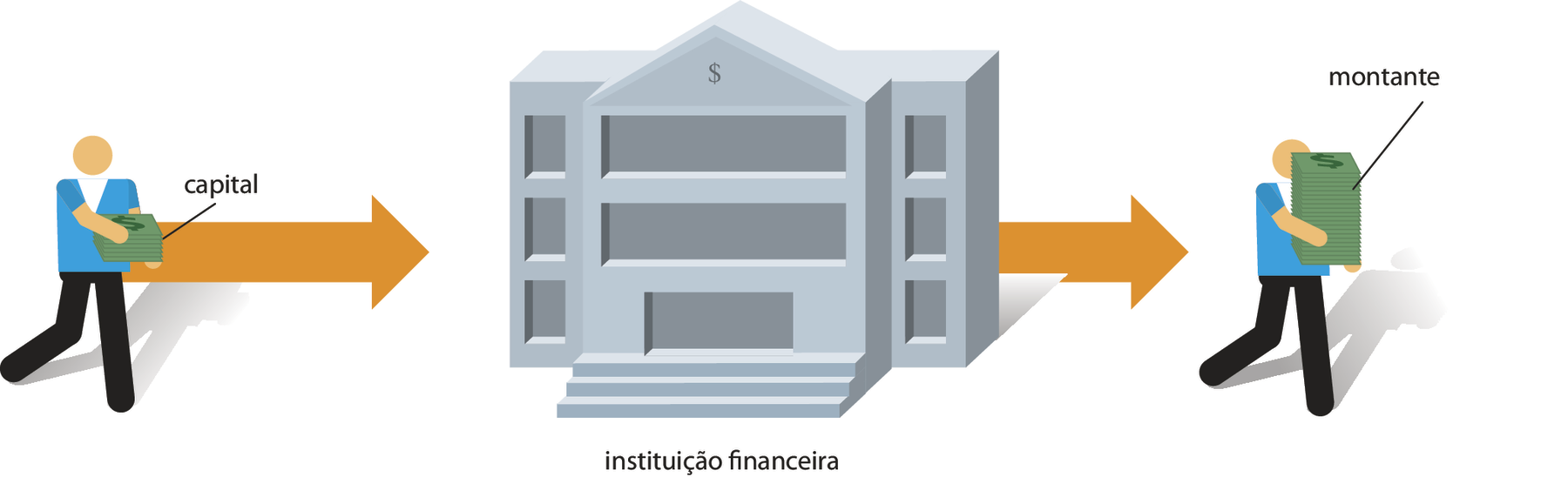
Observe uma situação de aplicação financeira.
Juliana aplicou R$ 300,00trezentos reais em um investimento à taxa de juro simples de 0,5% ao mês. Depois de 1 ano, ela tinha R$ 318,00trezentos e dezoito reais.
Nessa situação, o capital é R$ 300,00trezentos reais; a taxa de juro, 0,5% ao mês; a medida de tempo de aplicação, 1 ano ou 12 meses; o montante, R$ 318,00trezentos e dezoito reais; e o juro, R$ 18,00dezoito reais (R$ 318,00trezentos e dezoito reais ‒ R$ 300,00trezentos reais).
Empréstimo
Uma pessoa pode recorrer a uma instituição financeira para pedir dinheiro emprestado. O valor em dinheiro é chamado capital, assim como nas aplicações financeiras, e, nesse caso, o juro é a remuneração que a pessoa paga à instituição e o montante é a soma do capital com o juro.

Observe uma situação envolvendo um empréstimo.
Fábio pediu um empréstimo de R$ 1.000,00mil reais a um banco à taxa de juro simples de 2% ao mês. Depois de 3 meses, Fábio pagou R$ 1.060,00mil sessenta reais ao banco.
Nessa situação, o capital é R$ 1.000,00mil reais; a taxa de juro, 2% ao mês; a medida de tempo de empréstimo, 3 meses; o montante, R$ 1.060,00mil sessenta reais; e o juro, R$ 60,00sessenta reais (R$ 1.060,00mil sessenta reais ‒ R$ 1.000,00mil reais).
Lembre-se: Escreva no caderno!
Para pensar
Durante uma aula sobre juro simples, a professora de Rebeca fez a observação a seguir.

Pensando no futuro, Rebeca decidiu aplicar, por 6 meses, R$ 100,00cem reais em uma conta de investimento, à taxa de juro simples de 2% ao mês.
Com base no que sua professora disse, Rebeca decidiu calcular o valor que teria nessa conta após 6 meses. Observe.
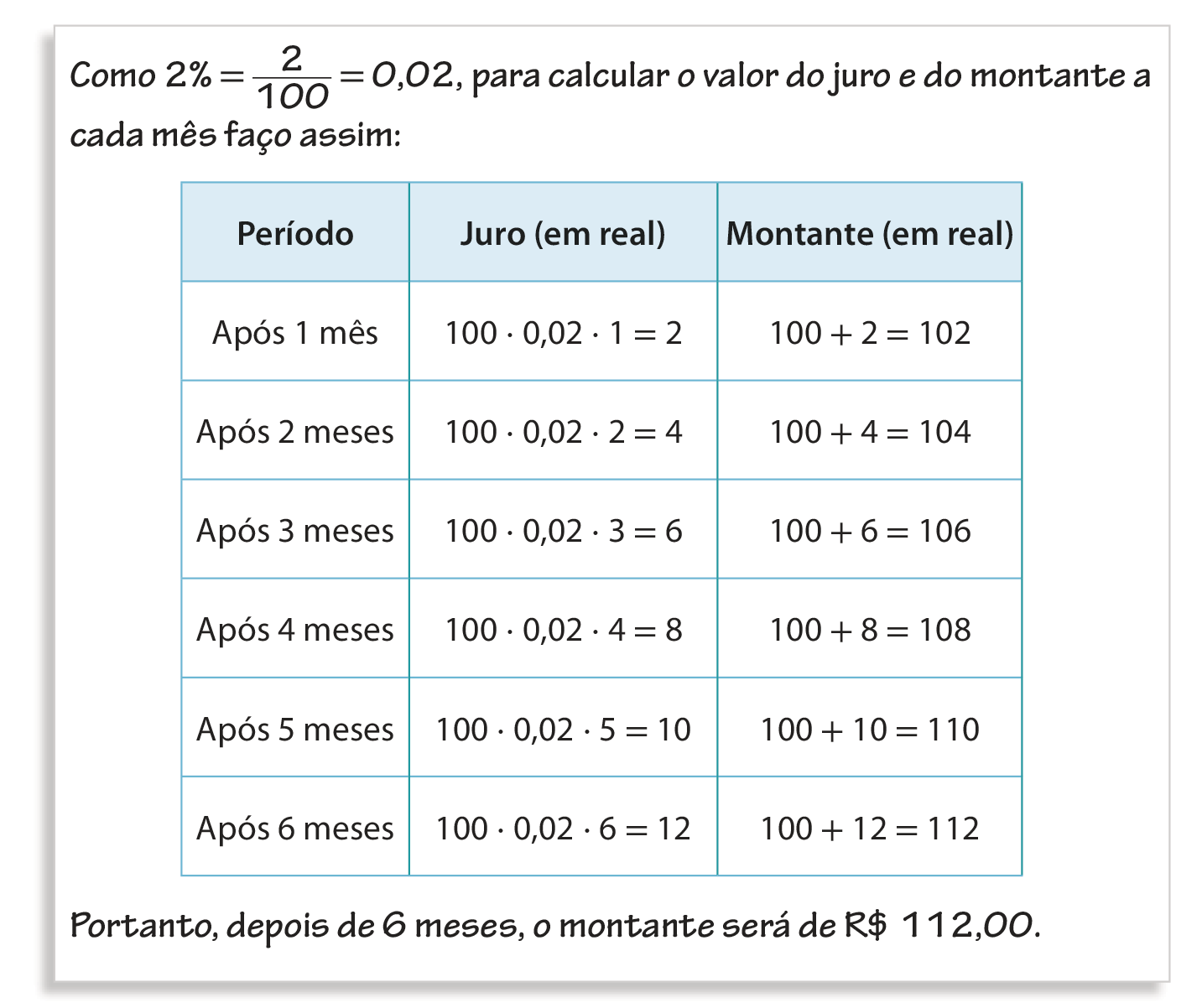
Agora, responda às questões.
a) Os cálculos de Rebeca estão corretos?
b) Qual seria o montante após 8 meses de aplicação?
c)

Determine o juro e o montante considerando 2 anos de aplicação. Em seguida, explique a um colega como você realizou os cálculos e comparem as resoluções

ATIVIDADES
faça as atividades no caderno
1. Paulo aplicou R$ 12.650,00doze mil seiscentos e cinquenta reais em um fundo de investimento à taxa de juro simples de 6% ao ano.

a) Qual será o juro obtido após 3 anos?
b) Depois de quantos anos Paulo terá um montante de R$ 16.445,00dezesseis mil quatrocentos e quarenta e cinco reais?
2.

Elabore um problema utilizando os dados a seguir.

• Agora, resolva o problema elaborado.
3. Luciano pediu um empréstimo de R$ 200,00duzentos reais à taxa de juro simples de 2% ao mês. Quanto ele deverá depois de 8 meses?
4.

Determine os valores usando uma calculadora.
a) Um capital de R$ 750,00setecentos e cinquenta reais será aplicado a juro simples de 5% ao mês durante 6 meses. Qual será o montante final dessa aplicação?
b) Um capital de R$ 700,00setecentos reais será aplicado a juro simples de 4% ao mês durante 6 meses. Qual será o montante final dessa aplicação?
c) Qual é o juro recebido sobre um capital de R$ 600,00seiscentos reais, aplicado por 7 meses a juro simples de 3% ao mês?
5. Quanto uma pessoa deve aplicar, à taxa de juro simples de 4% ao mês, para obter em 14 meses o montante de R$ 234,00duzentos e trinta e quatro reais?

6. Durante quantos meses um capital de R$ 370,00trezentos e setenta reais deve ficar aplicado, à taxa de juro simples de 2,5% ao mês, para que renda juro de R$ 83,25oitenta e três reais e vinte e cinco centavos?
7.

Uma loja vende uma Smart tíví por R$ 4.200,00quatro mil duzentos reais à vista ou em 3 parcelas iguais de R$ 1.650,00mil seiscentos e cinquenta reais.
a) Qual é a taxa de juro simples mensal cobrada pela loja?
b)

Leonardo possui um capital de R$ 4.000,00quatro mil reais e gostaria de aplicar essa quantia em uma instituição financeira à taxa de juro simples de 2,5% ao mês. Quantos meses ele precisaria aguardar para comprar a televisão à vista?
• Em sua opinião, é mais vantajoso que Leonardo pague a televisão a prazo ou à vista?

Educação Financeira
faça as atividades no caderno

Diferentes fórmas de pagamento
É fim de ano e momento de planejar alguns gastos. Paulo e Clara precisam comprar uniformes para os filhos que estão ingressando em uma nova escola.




O que você faria?
Em relação à compra de uniforme ou de qualquer outro produto com a possibilidade de mais de um modo de pagamento, é importante pensar no que é mais vantajoso e possível de acordo com a realidade de cada família.

Reúna-se com um ou dois colegas e, com base no diálogo entre Paulo e Clara, conversem sobre as questões a seguir.
a) É possível adiar essa compra ou ela deve ser feita agora?
b) Se a família tiver alguma reserva de dinheiro, qual será a fórma de pagamento mais interessante?
c) Se a família não tiver essa reserva, qual será a melhor fórma de pagamento?
d) Paulo e Clara estão lidando com algo que querem, mas que podem deixar de comprar? Explique.
Calcule
Com base nas informações apresentadas no início da seção, calcule o valor gasto por mês de acordo com cada fórma de pagamento.
Faça um quadro como este em seu caderno para registrar esses custos e compare-os.

|
Preço dos uniformes |
PIX |
1 vez no cartão |
2 vezes no cartão |
3 vezes no cartão |
|---|---|---|---|---|
|
R$ 300,00 |
||||
|
R$ 420,00 |
||||
|
R$ 540,00 |
||||
|
R$ 600,00 |


Reflita
Para concluir o tema desta seção, há algumas questões importantes que você, os colegas e o professor podem discutir e exemplificar.
• Você acha que é perigoso ou vantajoso usar o píquis?
• Quais são as taxas que um banco cobra pelo uso do cartão de crédito?
• Em que situações o uso do cartão de crédito pode fugir do controle?
• Quais são os riscos de ter vários cartões de crédito?
Agora, escreva uma frase para resumir o que você aprendeu nesta seção.
Saiba mais
Você sabia que o píquis é um meio de pagamento eletrônico instantâneo e gratuito? Ele foi lançado em novembro de 2020 pelo Banco Central do Brasil, e esse formato de pagamento existe em mais de 50 países.
O pagamento parcelado no cartão de crédito só existe no Brasil.

Estatística e Probabilidade
faça as atividades no caderno
Construção de tabelas e gráficos usando planilhas eletrônicas
O Exame Nacional do Ensino Médio (enêm) é uma maneira de avaliar o desempenho dos estudantes que concluíram o Ensino Médio. A nota obtida nesse exame pode ser utilizada pelos estudantes para ingressar em algumas universidades privadas e públicas.

No enêm, são apresentadas questões que envolvem conhecimentos de Matemática, Linguagens, Ciências Humanas e Ciências da Natureza.
A irmã de Marina vai prestar o enêm neste ano e está estudando para alcançar bons resultados na prova. Marina, que está no 7º ano, resolveu ajudar a irmã pesquisando os conteúdos que mais aparecem nas questões de Matemática, nas provas do enêm, de 2009 até 2020. Sobre isso, ela obteve as seguintes informações.
Temas mais frequentes de Matemática no enêm
Geometria: 22,5%
Escalas, razão e proporção: 14,2%
Aritmética: 11,8%
Gráficos e tabelas: 9,1%
Funções: 8,7%
Outros: 33,7%
Para facilitar a leitura das informações, Marina resolveu organizá-las em uma planilha eletrônica e, em seguida, construir um gráfico com elas.


Marina construiu alguns tipos de gráfico para avaliar qual deles era o mais adequado para representar os dados da tabela. Ela, então, selecionou os dados da tabela e escolheu a opção de inserir gráfico de barras verticais. Depois, selecionou novamente os dados e escolheu a opção de inserir gráfico de barras horizontais. Por fim, fez o mesmo procedimento, mas dessa vez escolheu a opção de gráfico de setores. Observe.
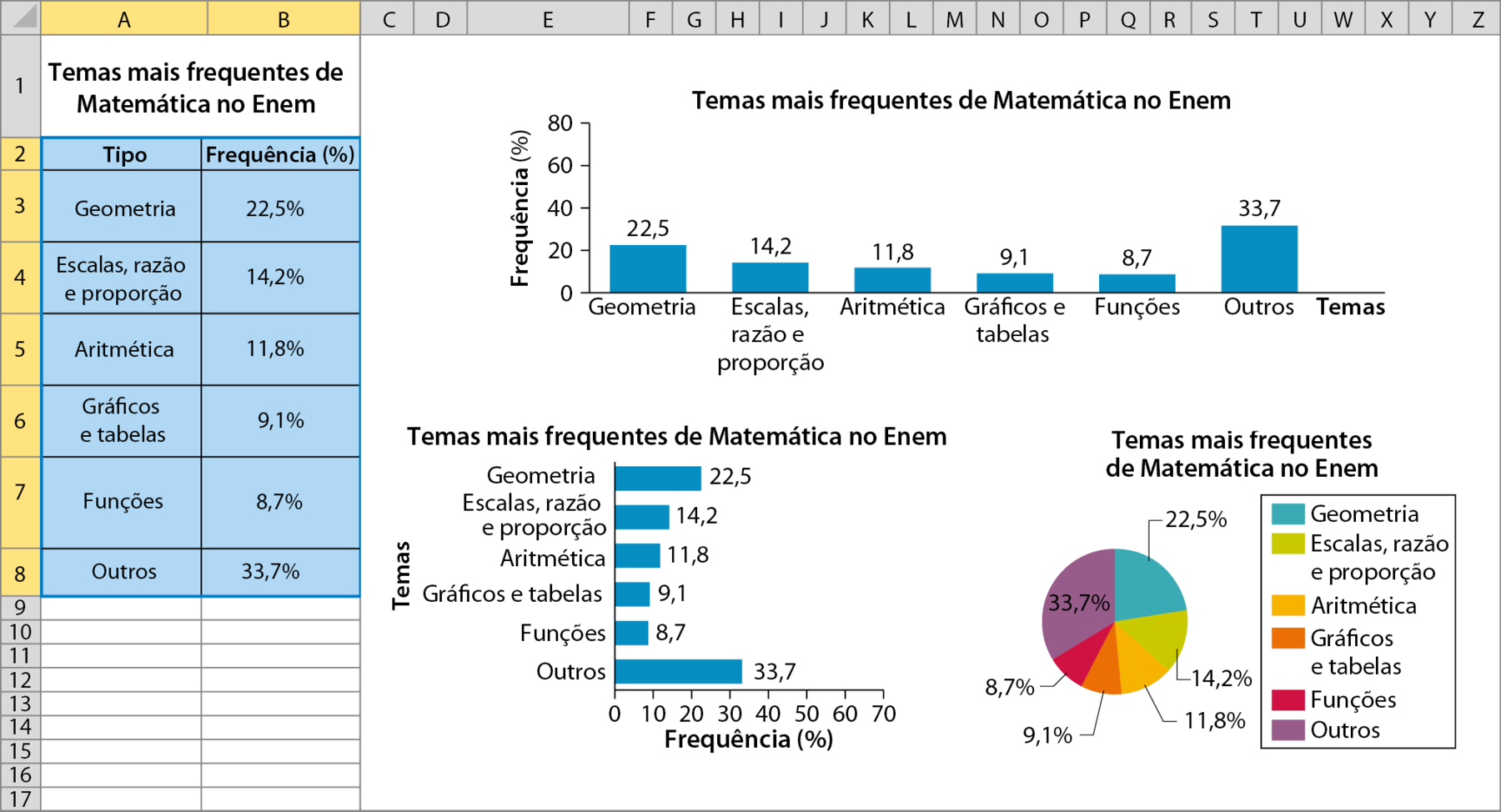
OLIVEIRA, Elida. Enem 2021: análise aponta os assuntos mais recorrentes na prova. G1, 30 junho 2021. Disponível em: https://oeds.link/eKfFYK. Acesso em: 6 janeiro 2022.
Após a construção dos gráficos, Marina considerou que o gráfico de setores foi o mais adequado para representar os dados da tabela, pois possibilita comparar cada uma das partes com o todo.

ATIVIDADES
faça as atividades no caderno
1. Reginaldo é dono de um brechó de camisas, calças e sapatos. Em janeiro de 2023, ele fez um levantamento da quantidade de peças vendidas no segundo semestre de 2022. Observe a tabela a seguir e, depois, faça o que se pede.
|
Mês |
Quantidade de peças |
|---|---|
|
Julho |
427 |
|
Agosto |
312 |
|
Setembro |
284 |
|
Outubro |
465 |
|
Novembro |
548 |
|
Dezembro |
640 |
Dados obtidos por Reginaldo em janeiro de 2023.
a) Represente esses dados em uma planilha eletrônica.
b) Qual tipo de gráfico pode representar melhor esses dados: de barras ou de setores? Por quê?
c) Construa o gráfico escolhido no item anterior.
▶ Estatística e Probabilidade
2. Juliana está fazendo uma pesquisa sobre as intenções de voto para o Grêmio Estudantil da escola em que estuda. Ela precisa apresentar os resultados em um gráfico que será colocado no jornal da escola e enviado por e-mail a todos os estudantes. Os estudantes poderão votar nas seguintes chapas: “Vamos em frente”, “A hora é agora”, “Podemos juntos” ou “É preciso agir”.
a) Em que tipos de gráfico ela pode representar os resultados dessa pesquisa? Que informações ela pode indicar em cada gráfico?
b) Há estudantes que ainda não sabem em quem votar. Como ela pode indicar essa informação no gráfico?
3. Em pesquisa realizada entre 2015 e 2019 levantaram-se alguns dados sobre os hábitos de leitura dos brasileiros de acordo com as regiões. Observe o mapa a seguir e faça o que se pede.
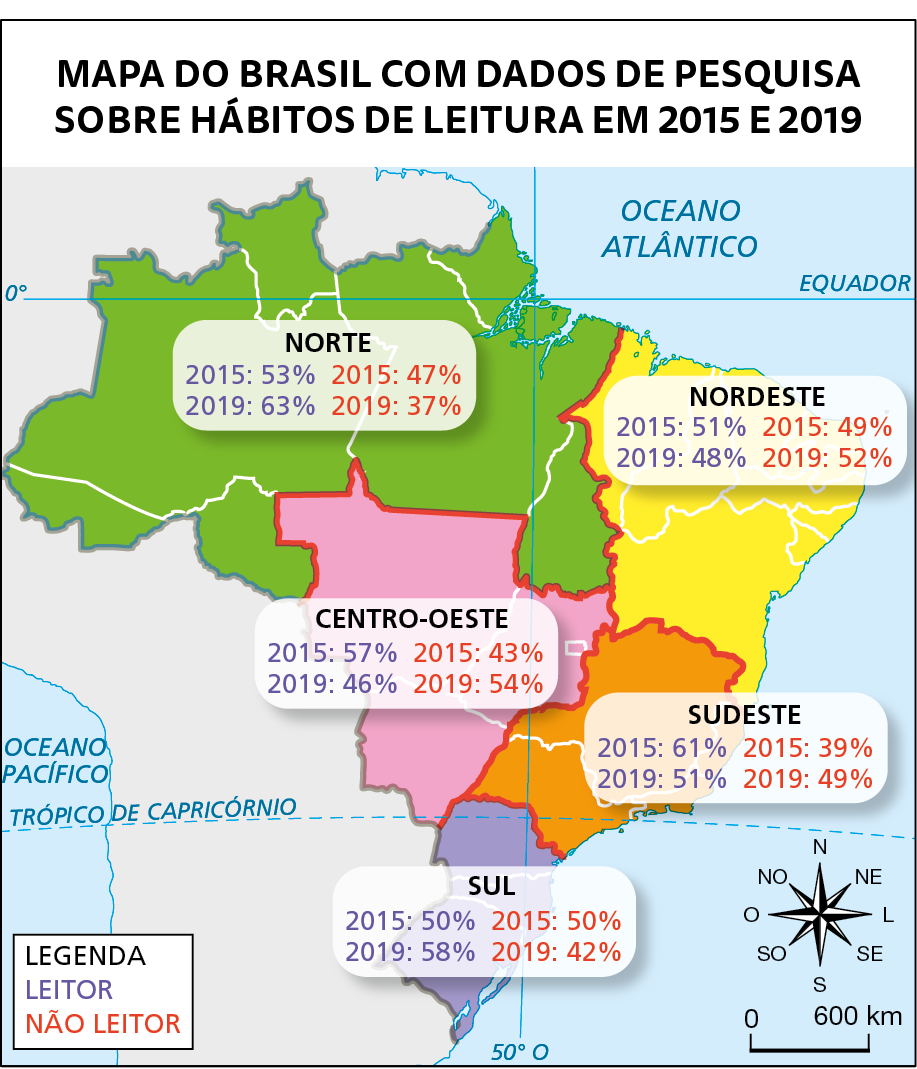
Elaborado com base em: í bê gê É. Atlas geográfico escolar. oitava edição Rio de Janeiro: í bê gê É, 2018. página 90. INSTITUTO PRÓ-LIVRO. Disponível em: https://oeds.link/WXjhJW. Acesso em: 6 fevereiro 2022.
a) Construa, em uma planilha eletrônica, uma tabela para indicar a porcentagem de leitores e não leitores das regiões brasileiras em 2015. Em seguida, construa um gráfico de barras duplas para representar esses dados.
b) Construa, em uma planilha eletrônica, uma tabela para indicar a porcentagem de leitores e não leitores das regiões brasileiras em 2019. Em seguida, construa 5 gráficos de setores, um para cada região brasileira.
c) Observe os gráficos construídos nos itens anteriores e verifique o tipo de gráfico em que é possível visualizar as informações relacionadas a todas as regiões em um ano.
4.

Para uma alimentação saudável, não devemos consumir açúcar em excesso. Observe a quantidade de açúcar presente em cada 100 gramas de algumas frutas. Em seguida, faça o que se pede.
|
Fruta |
Limão |
Morango |
Melancia |
Kiwi |
|---|---|---|---|---|
|
Quantidade de açúcar (em grama) |
2,50 |
4,60 |
5,50 |
8,99 |
MUNDO Boa fórma. 13 frutas com menos carboidratos e açúcar. Disponível em: https://oeds.link/THSvda. Acesso em: 6 fevereiro 2022.
a) Construa, em uma planilha eletrônica, uma tabela com os dados apresentados.
b) Construa, em uma planilha eletrônica, o gráfico que, para você, melhor representa esses dados.

Atividades de revisão
faça as atividades no caderno
1. Determine uma razão que forme proporção com a razão
fração 12 sobre 9.
2. Verifique se as razões formam proporções.
a)
fração 18 sobre 24e
fração 2,5 sobre 9,5
b)
fração 51 sobre 68e
fração 16,5 sobre 223. Observe a figura formada por triângulos equiláteros e, depois, responda às questões.
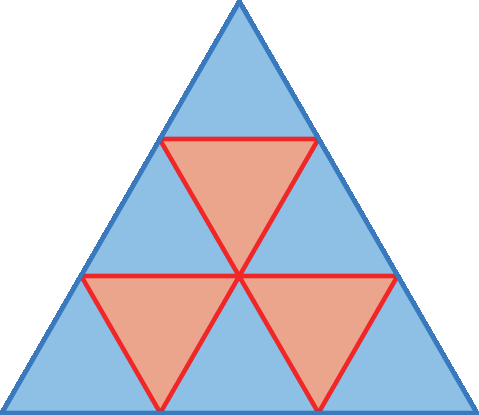
a) Qual é a razão entre a medida de área de um dos triângulos menores e a medida de área do maior triângulo?
b) Qual é a porcentagem da medida de área de um dos triângulos menores em relação à medida de área do maior triângulo?
c) Qual é a fração irredutível que representa a parte da figura que não está pintada de azul?
d) E qual é a fração irredutível que representa a parte pintada de azul?
e) Escreva, na fórma de porcentagem, as frações encontradas nos itens c e d.
4. Copie no caderno e complete os quadros de sequências de números diretamente proporcionais (a) e inversamente proporcionais (b).
a) Constante de proporcionalidade: 3

b) Constante de proporcionalidade: 20
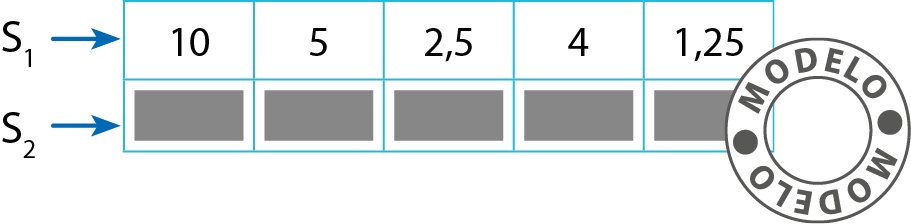
5. Bianca comprou 3 camisetas de mesmo preço por R$ 120,00cento e vinte reais. Quanto ela pagaria se comprasse 5 camisetas?
6. Um trem, deslocando-se com medida de velocidade média de 200 quilômetros por hora, demora 3 horas para completar um percurso. Que medida de tempo esse trem gastaria para fazer o mesmo percurso com velocidade média medindo 280 quilômetros por hora?
7. Três amigos montaram uma empresa de telefonia. João investiu R$ 8.000,00oito mil reais, Pedro, R$ 6.000,00seis mil reais, e Daniel, R$ 12.000,00doze mil reais. Após um ano, dividiram o lucro de R$ 91.000,00noventa e um mil reais em partes proporcionais ao capital que cada um investiu. Quanto João recebeu? E Pedro? E Daniel?
8. Para construir uma laje com medida de espessura de 7 centímetros, foram gastos 35 sacos de cimento. Cada saco tem medida de massa de 40 quilogramas. Quantos quilogramas de cimento seriam economizados se a laje tivesse sido construída com 5 centímetros de medida de espessura?
9. Bernardo consultou um mapa para saber a medida de distância entre dois municípios. Ele observou a escala e viu que a medida de 6 centímetros equivalia a 18 quilômetros da medida de distância real. Sabendo que a distância real entre os dois municípios mede 48 quilômetros, qual era a medida de distância entre esses municípios nesse mapa?
10. Jane usou uma régua e verificou em um mapa que a distância entre dois municípios media 25 centímetros. Em seguida, fez uma pesquisa e descobriu que a distância real entre os dois municípios mede .5000 quilômetros. Jane também mediu no mesmo mapa a distância entre outros dois municípios e obteve 15 centímetros. Qual é a medida de distância real entre esses dois municípios?
11.

Mauro tem uma granja com 73 galinhas. Essas galinhas botam 73 dúzias de ovos em 73 dias. Sabendo que 37 galinhas comem 37 quilogramas de milho em 37 dias, que medida de massa, em quilograma, de milho será necessária para obter uma dúzia de ovos?
12.


Elabore um problema envolvendo duas grandezas direta ou inversamente proporcionais. Passe seu problema para um colega resolver e resolva o problema criado por ele.
13. Um empresário investiu R$ 8.400,00oito mil quatrocentos reais em um projeto. Depois de um ano, seu lucro foi de R$ 1.680,00mil seiscentos e oitenta reais. Qual foi a porcentagem do lucro em relação ao investimento?
▶ Atividades de revisão
14. Observe a promoção.

Agora, responda às questões.
a) Se Cláudio comprar essa geladeira a prazo, quanto pagará?
b) Qual é a diferença, em real, entre o preço a prazo e o preço à vista?
15. Em uma rede de postos de combustível, o preço médio do litro do etanol fechou a semana com alta de 0,6% em relação à semana imediatamente anterior. Se o preço do litro era R$ 4,42quatro reais e quarenta e dois centavos, qual foi o preço cobrado por litro após o aumento?
•

Em sua opinião, é importante pesquisar os preços antes de efetuar uma compra?
16. Maria comprou uma calça e, como pagou à vista, teve desconto de 15% sobre o valor anunciado. Calcule o valor anunciado sabendo que, após obter o desconto, Maria pagou R$ 80,75oitenta reais e setenta e cinco centavos na calça.
•

Você costuma pedir desconto ao realizar uma compra? Em sua opinião, qual é a importância de obter um desconto?
17. Observe a ilustração.

Agora, responda:
a) Qual é o valor cobrado pela escola de dança em cada plano para um período de 6 meses?
b) Se uma estudante optar pelo plano semestral, qual será o percentual que ela economizará em comparação ao que pagaria pelo plano trimestral no mesmo período de 6 meses?
c) Um estudante optou pelo plano mensal por um período de 6 meses. Qual é a porcentagem que ele está pagando a mais que alguém que optou pelo plano semestral?
d)

Observe novamente os preços cobrados pela escola de dança em cada plano e responda: quais são as vantagens e as desvantagens de fazer um plano semestral?
18. Rodrigo comprou um guarda-roupa e uma cama por R$ 2.250,00dois mil duzentos e cinquenta reais. Como ele vai parcelar esse valor em 10 meses, a loja cobrará juro simples de 2% ao mês.

a) Em relação ao valor à vista, que percentual representa o juro pago após os 10 meses?
b) Qual será o valor de cada parcela?
19. Gustavo e Artur compraram uma bicicleta em sociedade e, para isso, juntaram suas economias. Gustavo investiu R$ 190,00cento e noventa reais, e Artur, R$ 110,00cento e dez reais. Depois de algum tempo, venderam a bicicleta por R$ 225,00duzentos e vinte e cinco reais e dividiram o dinheiro em partes diretamente proporcionais aos valores pagos.
a) Quanto Gustavo recebeu? E Artur?
b) Qual é a constante de proporcionalidade entre o valor que Artur pagou na compra e o valor que ele recebeu na venda da bicicleta?