Página 297

CAPÍTULO 12 Transformações geométricas

1 Localização de pontos no plano

Você já viu que determinados pontos podem ser localizados na reta numérica. Mas como podemos localizar um ponto em um plano?

Para localizar um ponto em um plano, usamos duas coordenadas: uma para indicar a localização horizontal e outra para indicar a localização vertical.

Para facilitar a localização no globo terrestre, por exemplo, foram criadas as coordenadas geográficas, duas linhas imaginárias que indicam a posição de um ponto de acordo com a localização horizontal e a vertical. Essas coordenadas são a latitude e a longitude, também utilizadas em sistemas de navegação como o Sistema de Posicionamento Global.

Ilustração. Satélite emitindo ondas dirigidas ao planeta Terra. À esquerda, mão de uma pessoa segurando aparelho GPS com coordenadas. — Representação artística do Sistema de Posicionamento Global (gê pê ésse ‒ sigla do nome em inglês Global Positioning System), que é um sistema de navegação que indica a posição de qualquer ponto no globo terrestre usando as coordenadas latitude e longitude. (Imagem sem escala; cores fantasia.)

A ideia de localização com base na latitude e na longitude é similar à de localização de pontos em um plano; por isso, antes de estudar esse assunto, vamos conhecer um pouco mais sobre latitude e longitude.

A latitude e a longitude são medidas de distância angular (em grau) empregadas para localizar qualquer ponto no globo terrestre.

A latitude toma como referência a linha do Equador e se baseia na orientação norte-sul. A longitude tem como referência o meridiano de grínitchi e se baseia na orientação leste-oeste.

Observe, a seguir, um esquema com as linhas de indicação de latitude e longitude do globo terrestre, e na página seguinte, o planisfério com a localização de algumas cidades, conforme essas coordenadas.

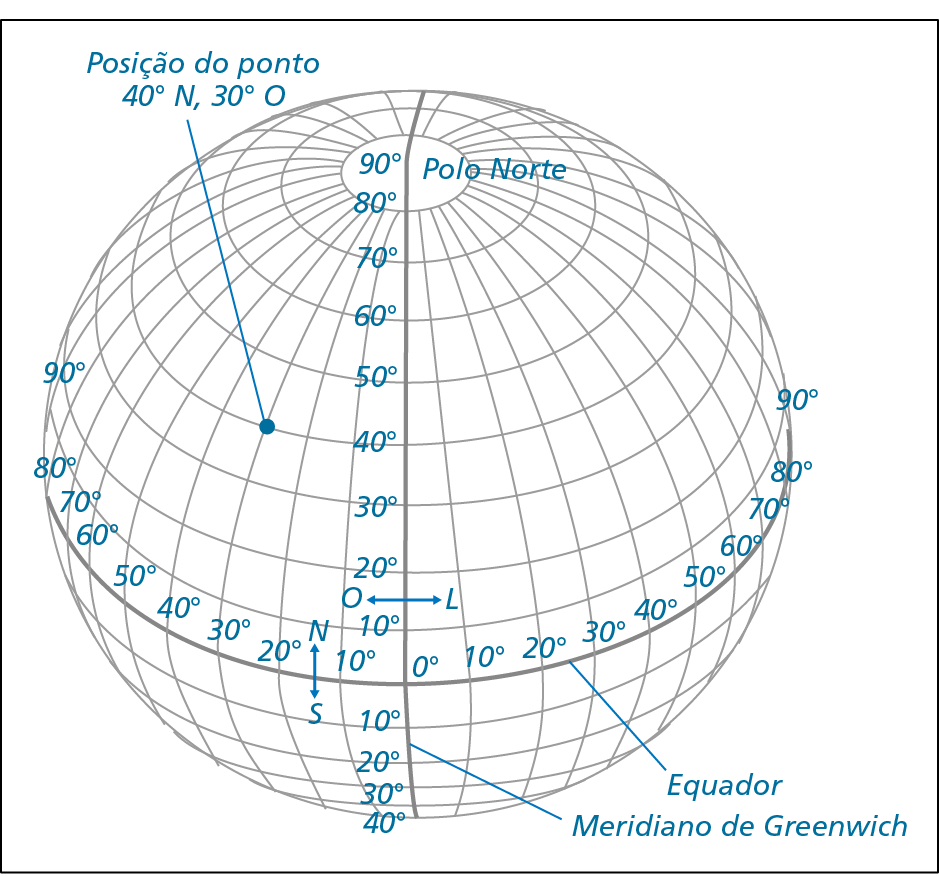
Ilustração. Globo terrestre com graus na linha do Equador e no meridiano de Greenwich. Há um ponto destacado no globo de posição 40 graus Norte, 30 graus Oeste. — Esquema das linhas de latitude e longitude.

Elaborado com base em: í bê gê É. Atlas geográfico escolar. oitava edição Rio de Janeiro: í bê gê É, 2018. página 18.

Página 298

A longitude do ponto a no planisfério, por exemplo, é 40graus leste, e a latitude é 60graus norte.

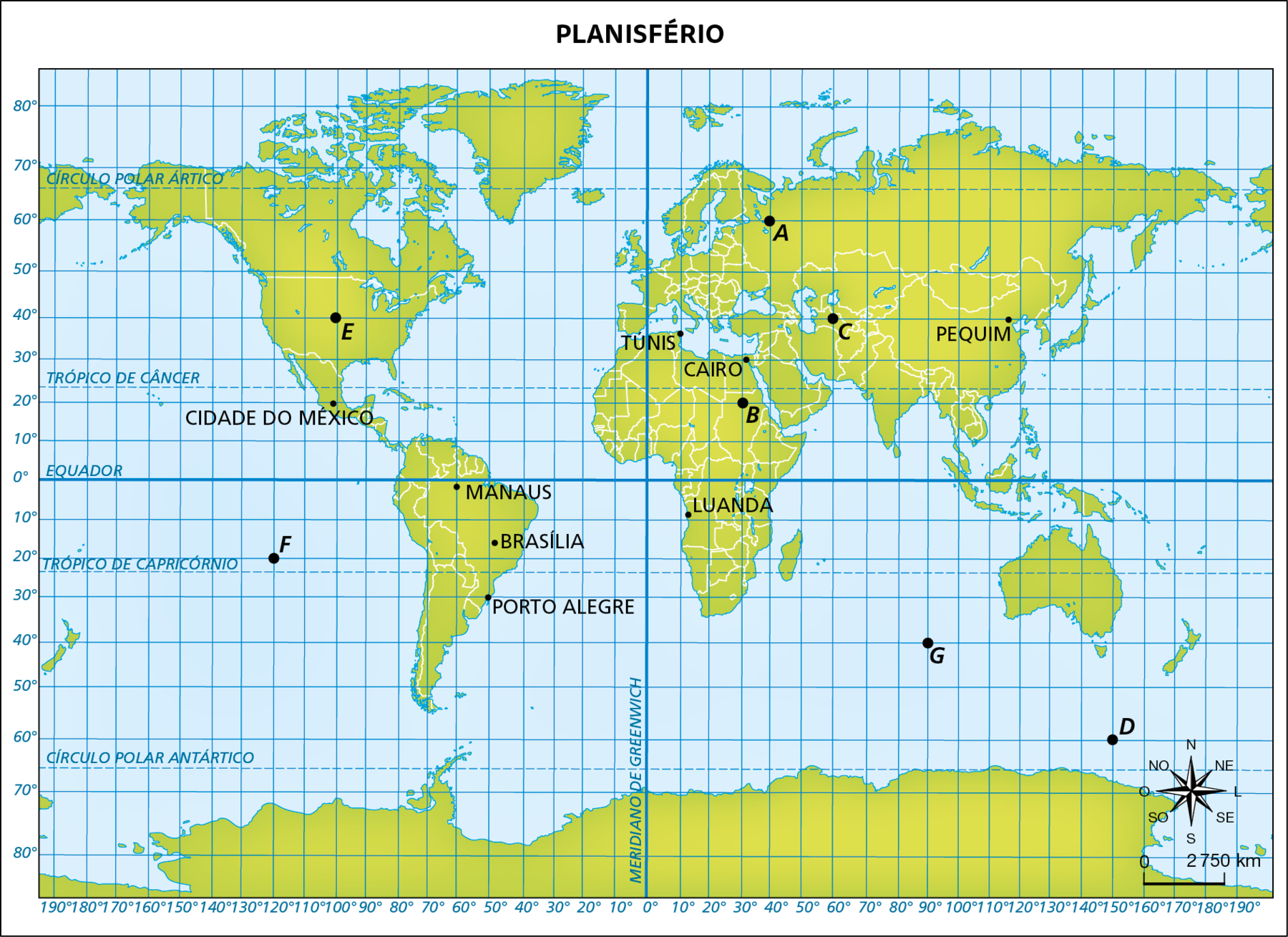
Ilustração. Planisfério. Mapa retangular com os continentes e oceanos do planeta Terra. O ponto A está em 40 graus leste e 60 graus norte. O ponto B está em 30 graus leste e 20 graus norte. O ponto C está 40 graus norte e 60 graus leste. O ponto D está 150 graus leste e 60 graus sul. O ponto E está 40 graus norte e 100 graus oeste. O ponto F está 20 graus sul 120 graus oeste. O ponto G está 40 graus sul e 90 graus leste. Estão destacadas as seguintes cidades: Cidade do México, Manaus, Brasília, Porto Alegre, Túnis, Cairo, Luanda e Pequim. No canto inferior direito há uma rosa dos ventos e a escala indicando que cada 1 centímetro do mapa corresponde a 2 mil 750 quilômetros.

Elaborado com base em: FERREIRA, Graça Maria Lemos. Moderno atlas geográfico. sexta edição São Paulo: Moderna, 2016. página 12-13.

Saiba mais

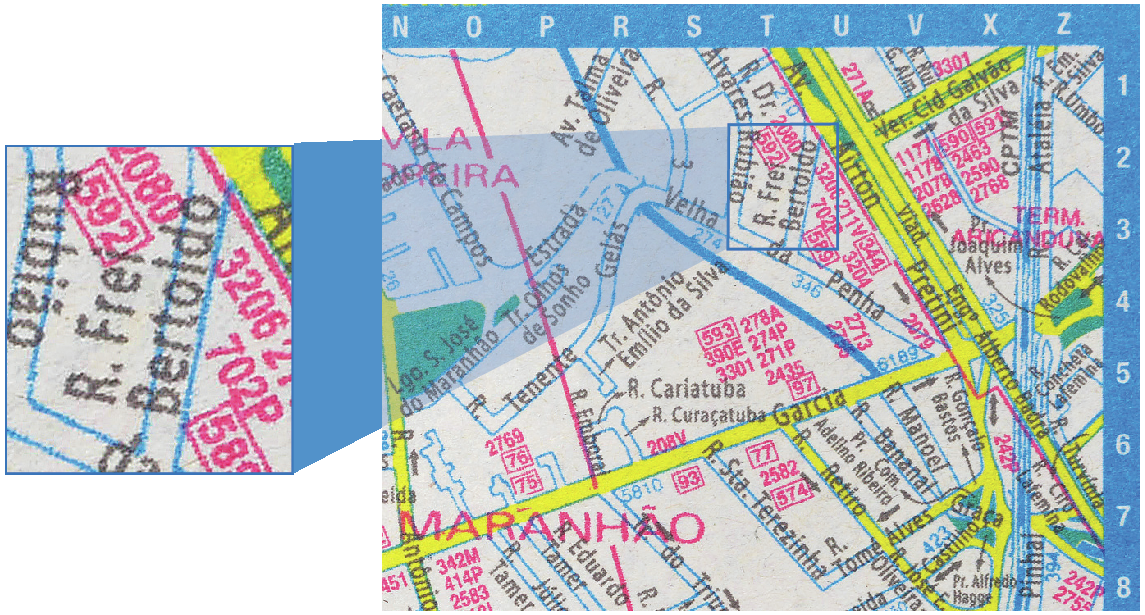
Os guias de rua impressos

Esses guias surgiram em 1970 e existem até hoje. Com o avanço da tecnologia, eles deixaram de ser a solução mais comum para se orientar no espaço urbano.

Para localizar uma rua nesse tipo de guia, além do número da página em que ela está representada, precisamos saber suas coordenadas, que, geralmente, são uma letra e um número. Observe as imagens a seguir, que indicam a localização de uma rua da cidade de São Paulo (São Paulo).

Fotografia. Guia de ruas da cidade de São Paulo com letras na parte superior e números na lateral direita, há uma parte destacada na rua Frei Bertoldo localizada no quadrante T3. — Localização da rua Frei Bertoldo no mapa. Reprodução de parte da página 128 do Guia Mapograf: ruas São Paulo e Municípios 2020/2021. São Paulo: On line Editora, 2019.

Fotografia. Ampliação da página com o CEP de ruas com a letra B, mostrando coordenadas da rua Frei Bertoldo: 03090-040 Bertoldo Frei (Maranhão) 128, T 3. As letras T3 estão circuladas em vermelho. — Reprodução de parte da página com as coordenadas da rua Frei Bertoldo do Guia Mapograf: ruas São Paulo e Municípios 2020/2021. São Paulo: On line Editora, 2019.

Página 299

Par ordenado

Como vimos, a longitude e a latitude são as coordenadas utilizadas para localizar um ponto no planisfério.

Em Matemática, a localização de pontos em um plano é feita com o auxílio de duas retas numeradas perpendiculares, denominadas eixos. Esses eixos determinam o plano cartesiano. Para localizar um ponto no plano cartesiano, usamos dois números. Esses números são expressos na fórma de um par ordenado.

Esse par de números é assim chamado porque existe uma ordem predeterminada para escrevê-lo. Considere, no plano cartesiano a seguir, o ponto P correspondente ao par ordenado abre parênteses4, 3fecha parênteses.

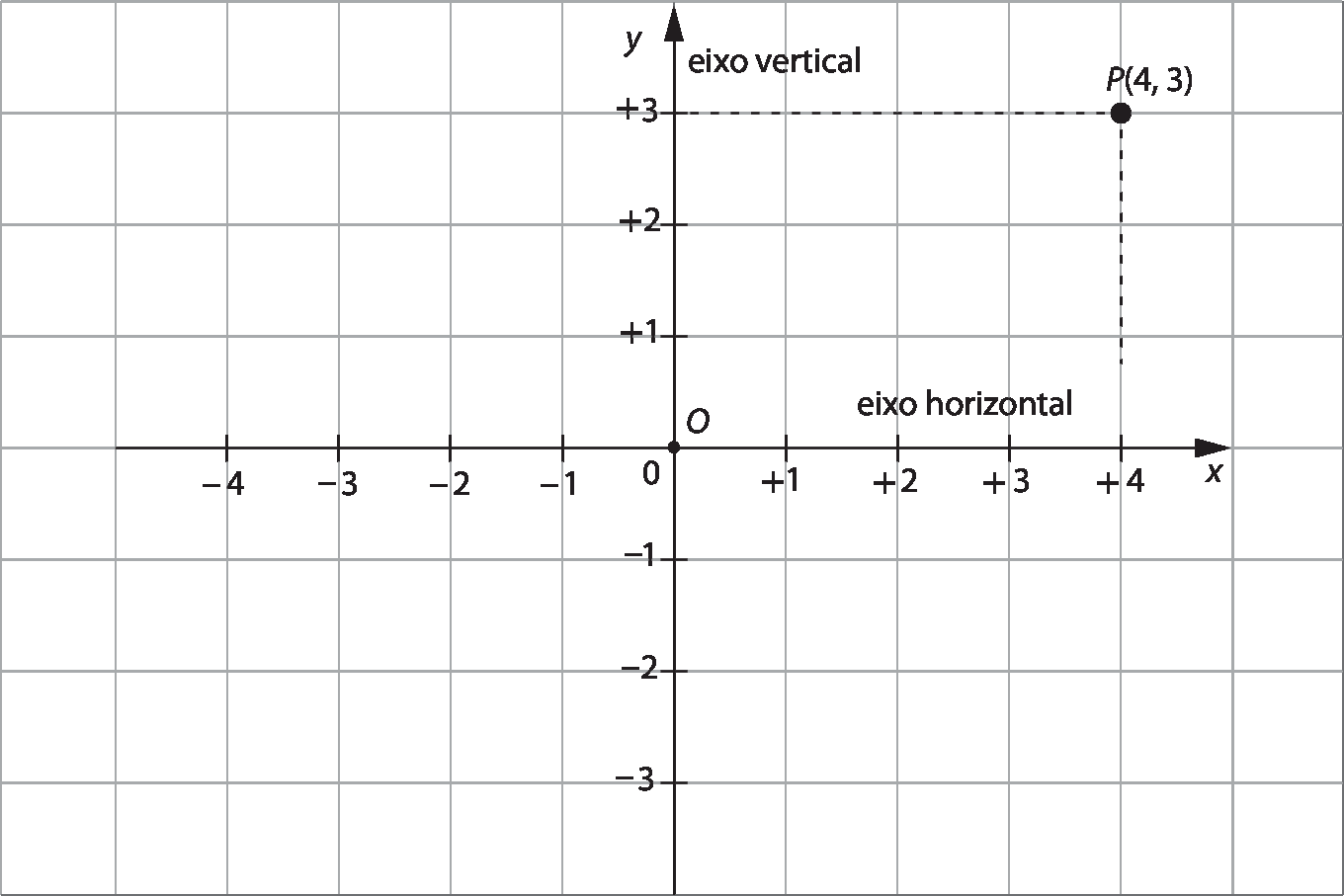
Gráfico. Malha quadriculada com plano cartesiano. Eixo x (eixo horizontal) com intervalo de menos 4 a mais 4. Eixo y (eixo vertical) com intervalo de menos 3 a mais 3. Destaque para o Ponto P correspondente ao par ordenado (4, 3).

O primeiro número do par ordenado indica a posição em relação ao eixo horizontal, e o segundo número, a posição em relação ao eixo vertical.

Observação

Representamos o ponto P de coordenadas (4, 3) por:

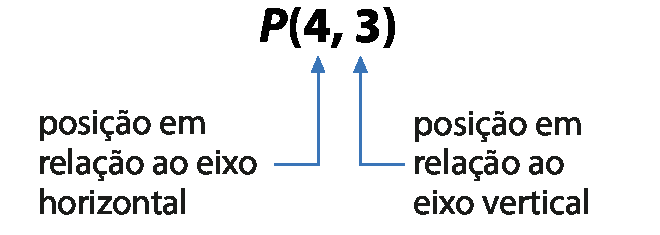
Esquema. P (4, 3) Para o número 4 há uma seta com o texto: posição em relação ao eixo horizontal Para o número 3 há uma seta com o texto: posição em relação ao eixo vertical

O ponto óh é denominado origem. No eixo horizontal, à direita de óh, estão os pontos correspondentes aos números positivos e, à esquerda, os pontos correspondentes aos números negativos. A medida de distância entre um ponto correspondente a um número inteiro e o seguinte, no eixo horizontal, é a mesma, tanto à direita quanto à esquerda da origem.

No eixo vertical, acima do ponto óh, estão os pontos correspondentes aos números positivos e, abaixo, os correspondentes aos números negativos. A medida de distância entre um ponto correspondente a um número inteiro e o seguinte, no eixo vertical, é a mesma, tanto acima quanto abaixo da origem.

Página 300

Na figura a seguir, o ponto a pode ser localizado no plano pelo par ordenado abre parênteses2, 1fecha parênteses, e o ponto B, por (‒1, 1fecha parênteses.

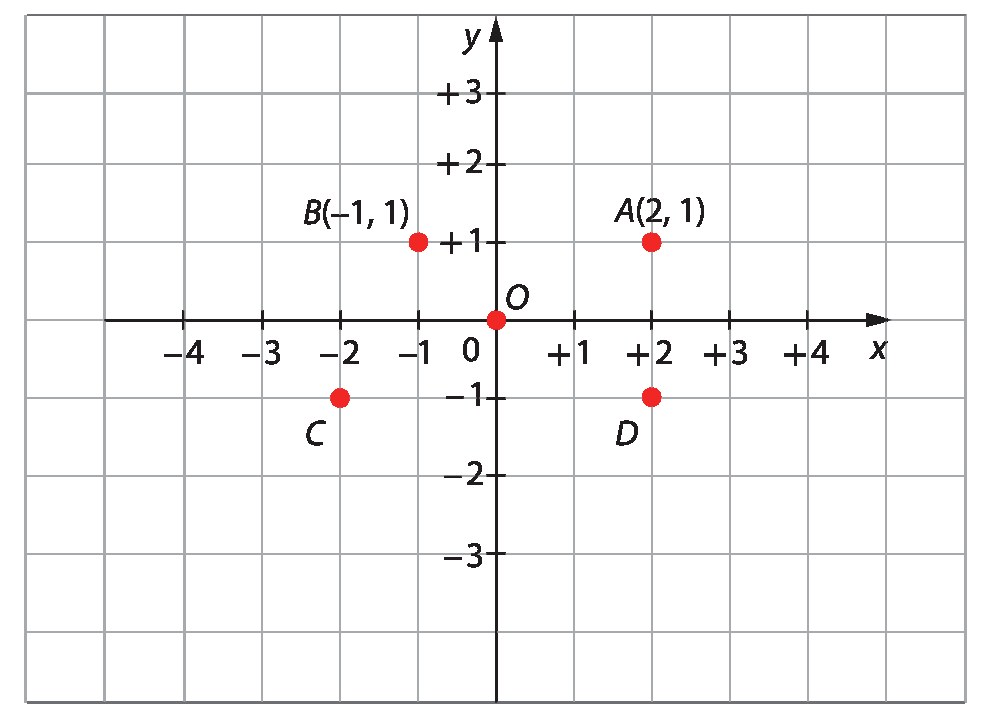
Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 4 a +4. Eixo y com intervalo de menos 3 a + 3. Estão destacados os seguintes pontos: A (2, 1); B (menos 1, 1); C (menos 2, 1); D (2, menos 1).

Para fazer

Quais são as coordenadas dos pontos C, D e óh?

Os números do par ordenado que indicam a localização de determinado ponto são as coordenadas desse ponto. A primeira coordenada é a abscissa do ponto, e a segunda, a ordenada do ponto.

ATIVIDADES

faça as atividades no caderno

1. Considere o sistema de eixos na representação a seguir e escreva, no caderno, as coordenadas dos pontos destacados.

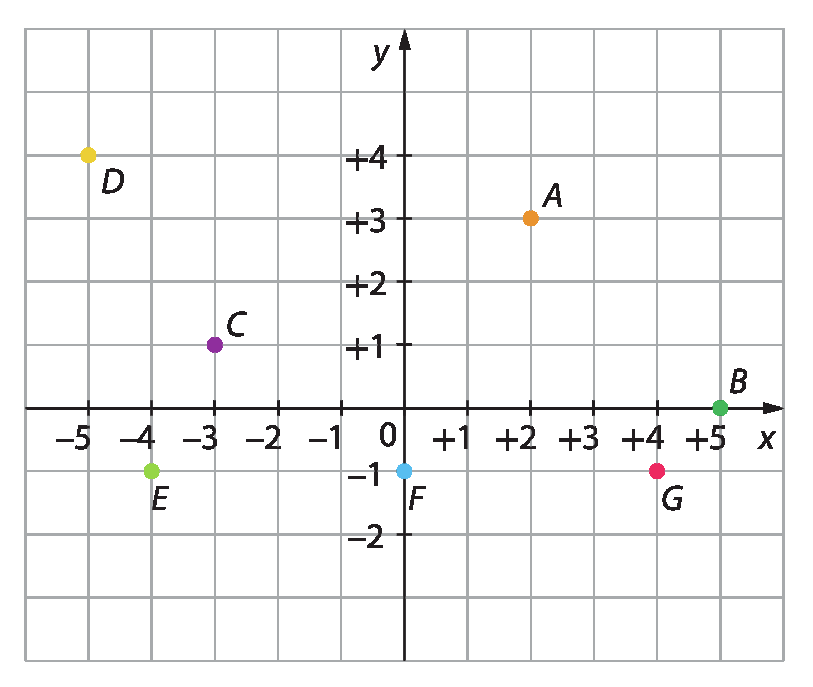
Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 5 a mais 5. Eixo y com intervalo de menos 2 a mais 4. Estão destacados os seguintes pontos: A (2, 3); B (5, 0); C (menos 3, 1); D (menos 5, 4); E (menos 4, menos 1); F (0, menos 1); G (4, menos 1).

2. Em uma folha de papel quadriculado, determine um sistema de eixos perpendiculares. Depois, trace:

a) o triângulo de vértices nos pontos aabre parênteses1, 2fecha parênteses, B(‒3, 3fecha parênteses e C(‒2, menos2fecha parênteses;

b) o quadrado de vértices nos pontos aabre parênteses2, 2fecha parênteses, B(‒2, 2fecha parênteses, C(‒2, menos2fecha parênteses e Dabre parênteses2, menos2fecha parênteses.

3. Em uma folha de papel quadriculado, determine um plano cartesiano e assinale os pontos aabre parênteses4, 1fecha parênteses, B(‒1, 3fecha parênteses e Cabre parênteses1, menos3fecha parênteses.

• Usando uma régua, ligue os pontos aêbê, B e C, C e a. Pinte a região interna da figura formada. Que figura é essa?

Página 301

4. Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente os pontos indicados a seguir. Depois, faça o que se pede.

Gráfico. Modelo. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 5 a mais 5. Eixo y com intervalo de menos 2 a mais 3. Estão destacados os seguintes pontos: A (menos 3, 3); B( 4, 1); C( 0, menos 2); D (menos 4, menos 2); E (1, 2); F (menos 2, 0).

a) Encontre o ponto cujo par ordenado é formado pelo módulo das coordenadas de cada ponto representado na malha. Por exemplo, o ponto aabre parêntesesmenos3, 3fecha parênteses será correspondente ao ponto Alinhaabre parênteses∣‒3∣, ∣3∣fecha parênteses.

b) Onde estão localizados os pontos Alinha, Blinha, Clinha, Dlinha, Elinha e Flinha? Descreva a região para os colegas.

2 Transformações geométricas no plano

Podemos fazer certos movimentos ou transformações com figuras do plano de modo que todas as suas medidas sejam preservadas. Nos exemplos a seguir, a figura 2 foi obtida com base na figura 1 por meio de uma transformação geométrica.

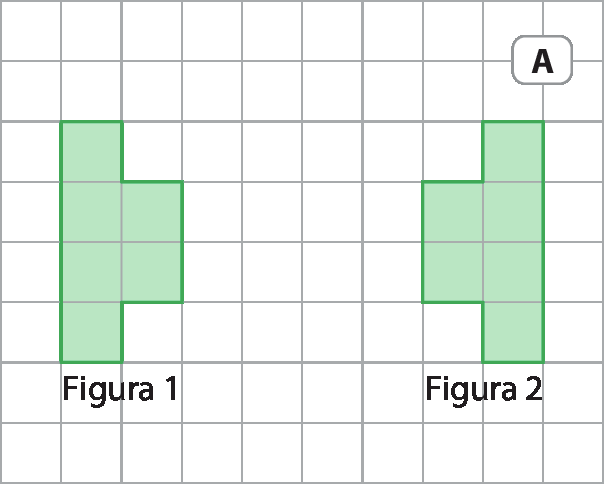
Ilustração A. Malha quadriculada. Figura 1 verde composta por 6 quadradinhos dispostos em 2 colunas, 4 quadradinhos na coluna da esquerda e 2 na coluna da direita. Figura 2 verde composta por 6 quadradinhos dispostos em 2 colunas, 2 quadradinhos na coluna da esquerda e 4 na coluna da direita. A figura 2 está disposta como se fosse um reflexo espelhado da Figura 1. As figuras 1 e 2 estão a uma distância horizontal de 4 quadradinhos uma da outra.

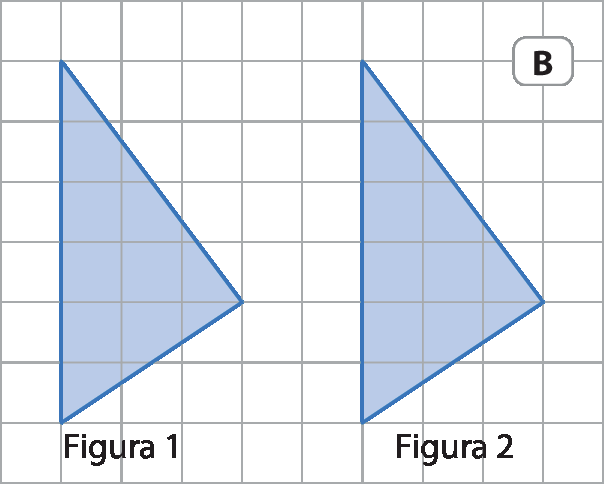
Ilustração B. Malha quadriculada. Figura 1: Triângulo azul cuja base é formada por 6 quadradinhos na vertical e altura é de 3 quadradinhos alinhada ao segundo quadradinho da base. A figura 2 é igual à figura 1, mas deslocada 5 quadradinhos para a direita.

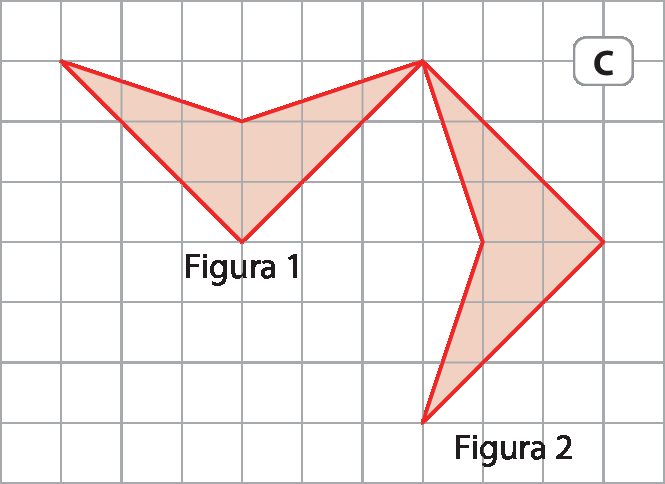
Ilustração C. Malha quadriculada. Figura 1 vermelha com 4 lados. Figura 2 igual à figura 1, mas rotacionada 90 graus para a direita no sentido anti-horário.

Como a medida de comprimento dos lados e a medida de abertura dos ângulos correspondentes das figuras 1 e 2 são iguais, essas transformações são chamadas isometrias. São exemplos de isometrias no plano: reflexão, translação e rotação.

Para investigar

Em cada exemplo, como você acha que a figura 2 foi obtida a partir da figura 1?

Página 302

3 Reflexão

Uma figura pode ser refletida em um plano de dois modos: em relação a uma reta ou a um ponto. Vamos estudar os dois casos a seguir.

Reflexão em relação a uma reta

Na figura a seguir, o triângulo AlinhaBlinhaClinha foi obtido do triângulo á bê cê por meio da reflexão em relação à reta r indicada. Dizemos que esses dois triângulos são simétricos em relação à reta r, que é o eixo de reflexão ou eixo de simetria, e que o triângulo AlinhaBlinhaClinha é a imagem do triângulo á bê cê.

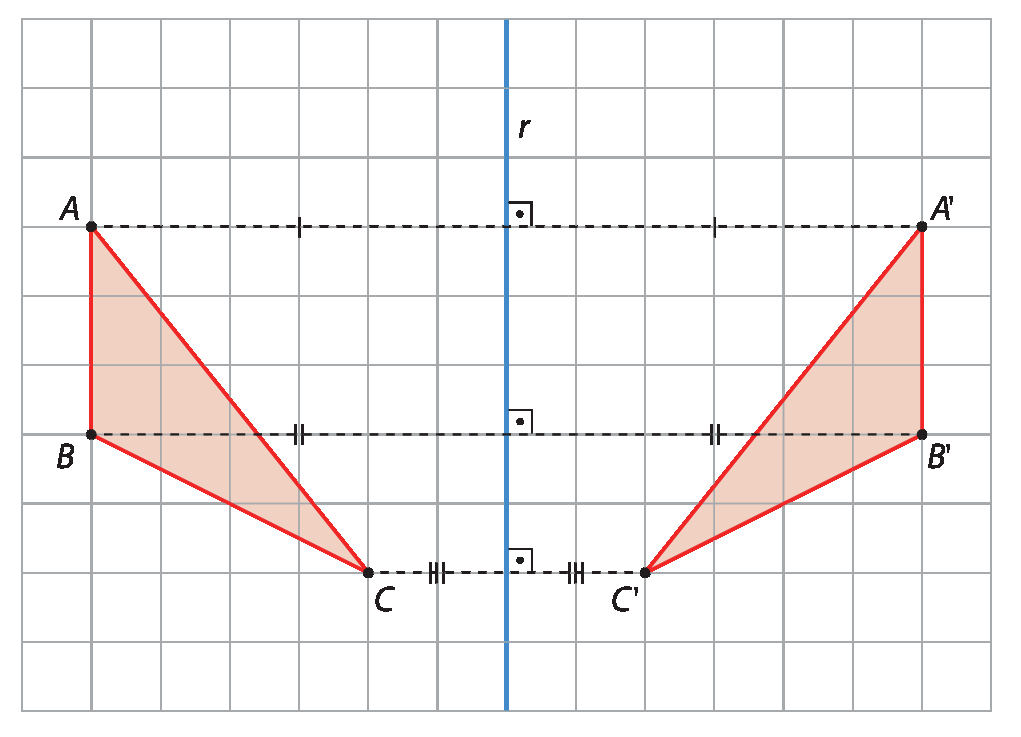
Gráfico. Malha quadriculada com triângulo ABC. Ao lado, triângulo A linha B linha C linha, igual ao triângulo ABC. Entre as figuras ha uma reta r. Os dois triângulos estão posicionados como se um fosse o reflexo do outro, com os vértices C voltados para a reta r. Os dois triângulos estão a uma distância horizontal de 4 quadradinhos um do outro.

Ilustração. Menina de cabelo castanho, preso, blusa verde claro e bermuda verde escuro. Ela está com a mão esquerda atrás das costas e a mão direita levantada com o dedo indicador esticado. Ela diz: Verifique que a medida de comprimento dos lados e a medida de abertura dos ângulos correspondentes desses triângulos são iguais.

Cada ponto do triângulo AlinhaBlinhaClinha tem um ponto correspondente no triângulo á bê cê, que é seu simétrico em relação à reta r.

Por exemplo:

• a e Alinha são simétricos em relação à reta r;

• Blinha é o simétrico de B em relação à reta r;

• Clinha é a imagem de C por meio da reta r.

Observe que dois pontos simétricos em relação à reta r estão à mesma medida de distância dessa reta, em posições opostas.

Isso sempre ocorre com duas figuras simétricas em relação a uma reta: cada ponto de uma delas é simétrico a um ponto da outra em relação à reta, e vice-versa, e os pontos simétricos estão à mesma medida de distância da reta considerada.

Observe, por exemplo, como podemos refletir o quadrilátero a bê cê dê ilustrado em relação à reta r, em uma malha quadriculada.

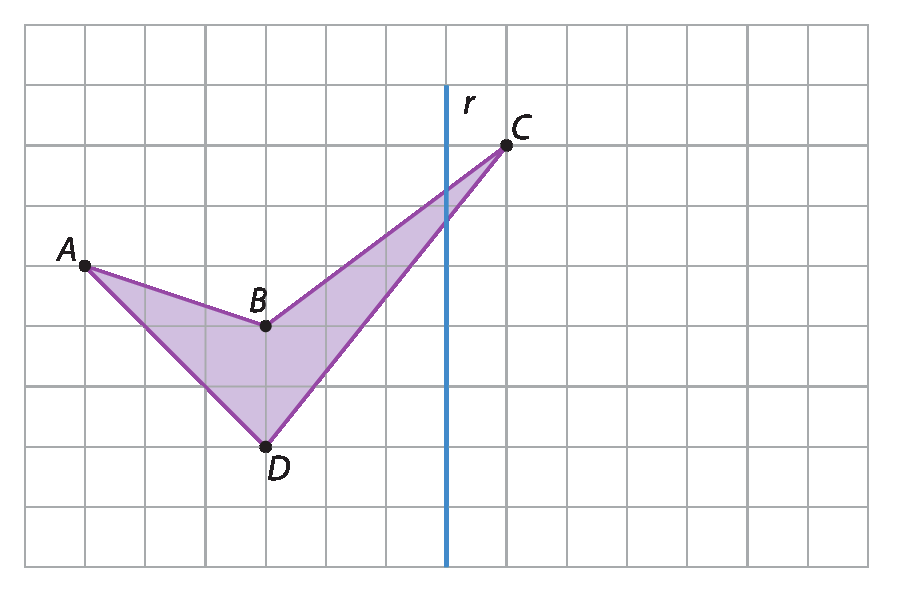
Gráfico. Malha quadriculada com figura ABCD roxa. No centro da malha há uma reta vertical r que corta parte da figura ABCD.

Página 303

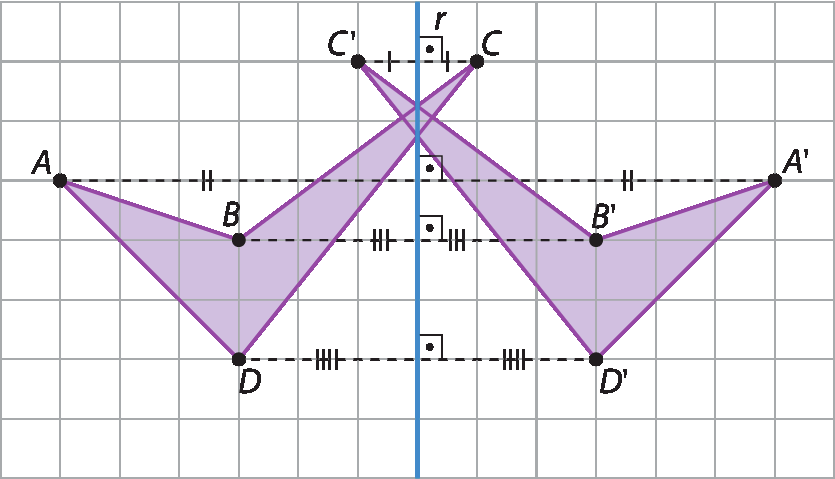
Primeiro, encontramos os simétricos dos vértices a, B, C e D do quadrilátero em relação à reta r. Vamos indicar esses pontos por Alinha, Blinha, Clinha e Dlinha, respectivamente. Em seguida, construímos o quadrilátero AlinhaBlinhaClinhaDlinha, que é simétrico do quadrilátero a bê cê dê em relação à reta r.

Note que, como o eixo de simetria corta a figura inicial, parte da figura refletida está de um lado da reta r e a outra parte está do outro lado.

Gráfico. Malha quadriculada com a mesma figura ABCD do gráfico anterior e figura A linha, B linha, C linha e D linha igual à figura ABCD, mas disposta como se fosse um reflexo da figura ABCD por meio da reta r, que corta parte das duas figuras.

Observação

• O eixo de reflexão é fixo, ou seja, não se movimenta.

• A simetria em relação a uma reta é chamada simetria axial.

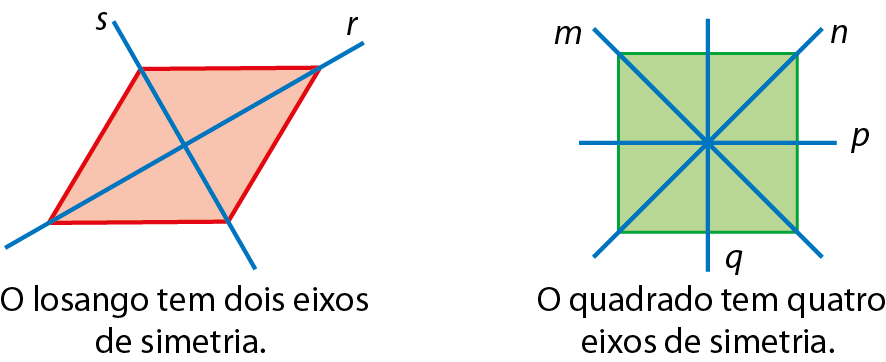
Figuras com simetria

Observe algumas figuras que apresentam simetria. Note que algumas delas têm mais de um eixo de simetria.

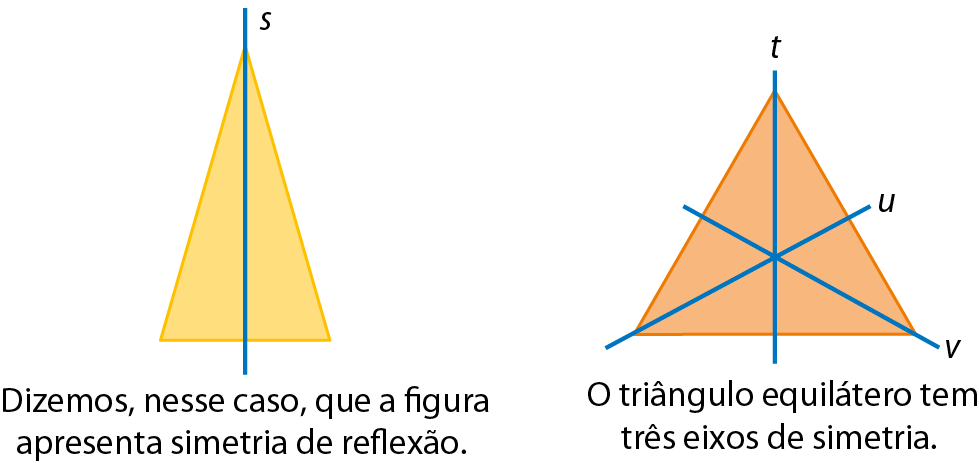
Figura geométrica. Triângulo isósceles com reta vertical s passando perpendicularmente pela metade da medida de comprimento de sua base.
Cota abaixo: Dizemos, nesse caso, que a figura apresenta simetria de reflexão.

Figura geométrica. Triângulo equilátero com retas t, u e v passando, cada uma, perpendicularmente pela metade da medida de comprimento de cada lado do triângulo.
Cota abaixo: O triângulo equilátero tem três eixos de simetria.

Figura geométrica. Losango com retas s e t, cada uma cortando dois de seus vértices ao meio.
Cota abaixo: O losango tem dois eixos de simetria.

Figura geométrica. Quadrado com retas p e q, cada uma cortando perpendicularmente dois de seus lados pelas metade da medida de comprimento, e retas m e n, cada uma cortando dois de seus vértices ao meio.
Cota abaixo: O quadrado tem quatro eixos de simetria.

Reflexão de figuras em relação aos eixos do plano cartesiano

Podemos encontrar a simétrica de qualquer figura em relação aos eixos do plano cartesiano. Vamos analisar os triângulos representados no plano cartesiano.

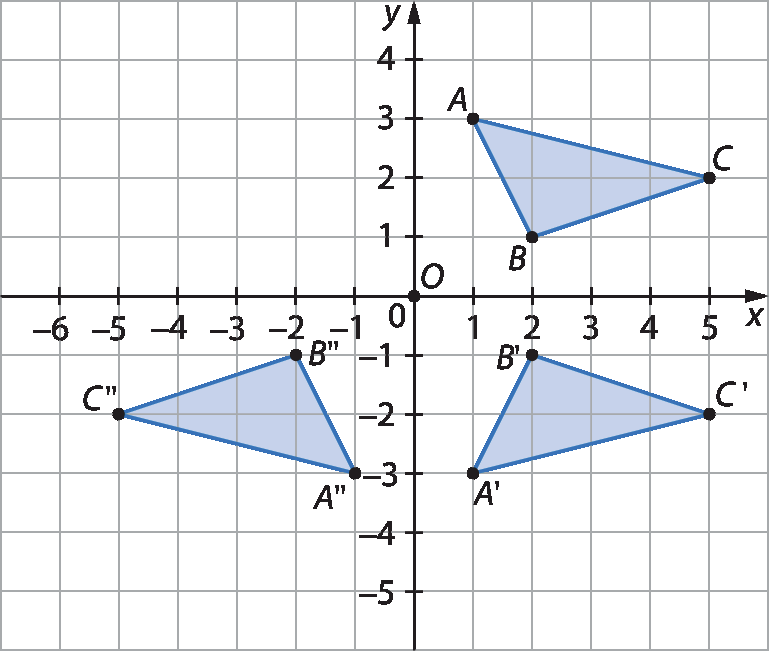
Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 6 a 5. Eixo y com intervalo de menos 5 a 4. Há três triângulos azuis iguais na malha, mas em posições diferentes. Triângulo ABC no primeiro quadrante do plano cartesiano, formado pelos pontos A (1, 3), B (2, 1) e C (5, 2). Triângulo A linha B linha e C linha no quarto quadrante do plano cartesiano, formado pelos pontos A linha (menos 3, 1), B linha (2, menos 1) e C linha (5, menos 2). Triângulo A duas linhas B duas linhas C duas linhas no terceiro quadrante do plano cartesiano, formado pelos pontos A duas linhas (menos 3, menos 2), B duas linhas (menos 2, menos 1) e C duas linhas (menos 5, menos 2).

• O triângulo AlinhaBlinhaClinha é o simétrico do triângulo á bê cê em relação ao eixo x.

Observe as coordenadas dos vértices dos triângulos á bê cê e AlinhaBlinhaClinha.

No triângulo á bê cê as coordenadas dos vértices são aabre parênteses1, 3fecha parênteses, Babre parênteses2, 1fecha parênteses e Cabre parênteses5, 2fecha parênteses enquanto as do triângulo AlinhaBlinhaClinha são Alinhaabre parênteses1, menos3fecha parênteses, Blinhaabre parênteses2, menos1fecha parênteses e Clinhaabre parênteses5, menos2fecha parênteses.

Note que as abscissas dos pontos correspondentes são iguais e que, para obter as ordenadas dos pontos Alinha, Blinha e Clinha, multiplicamos as ordenadas dos pontos correspondentes por menos1.

Página 304

• O triângulo Aduas linhasBduas linhasCduas linhas é o simétrico do triângulo AlinhaBlinhaClinha em relação ao eixo y.

Observe as coordenadas dos vértices dos triângulos AlinhaBlinhaClinha e Aduas linhasBduas linhasCduas linhas.

No triângulo AlinhaBlinhaClinha as coordenadas dos vértices são Alinhaabre parênteses1, menos3fecha parênteses, Blinhaabre parênteses2, menos1fecha parênteses e Clinhaabre parênteses5, menos2fecha parênteses e as do triângulo Aduas linhasBduas linhasCduas linhas são Aduas linhas(‒1, menos3fecha parênteses, Bduas linhas(‒2, menos1fecha parênteses e Cduas linhas(‒5, menos2fecha parênteses.

Note que as ordenadas dos pontos correspondentes são iguais e que, para obter as abscissas dos pontos Aduas linhas, Bduas linhas e Cduas linhas, multiplicamos as abscissas dos pontos correspondentes por menos1.

Para investigar

a) Que triângulo obteremos se refletirmos o triângulo á bê cê primeiro em relação ao eixo y e, depois, em relação ao eixo x?

b) Considerando que ao refletir o triângulo á bê cê em relação ao eixo y obtemos o triângulo Atrês linhasBtrês linhasCtrês linhas, quais são as coordenadas dos vértices desse novo triângulo?

ATIVIDADES

faça as atividades no caderno

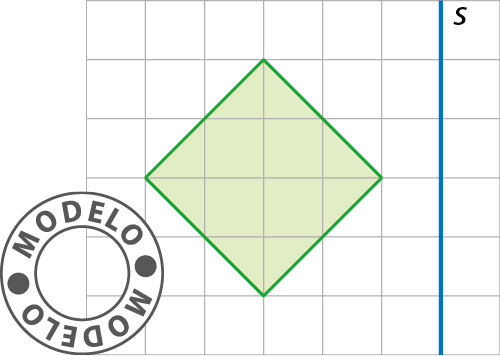
1. Copie a figura ilustrada a seguir em papel quadriculado. Em seguida, construa a figura simétrica em relação à reta s.

Gráfico. Modelo. Malha quadriculada com losango verde. À direita do losango, há uma reta vertical s.

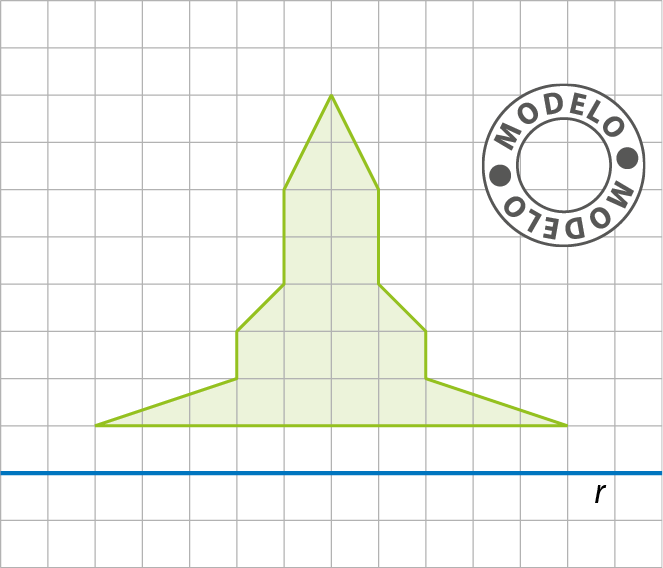
2. Copie a figura a seguir em uma folha de papel quadriculado e desenhe a figura simétrica a ela em relação à reta r.

Gráfico. Modelo. Malha quadriculada com figura geométrica verde de 11 lados. abaixo da figura há uma reta horizontal r.

3. Na imagem a seguir, o polígono AlinhaBlinhaClinhaDlinhaElinhaFlinha é o simétrico do polígono á bê cê dê é éfe em relação a uma reta r, que não está representada na figura.

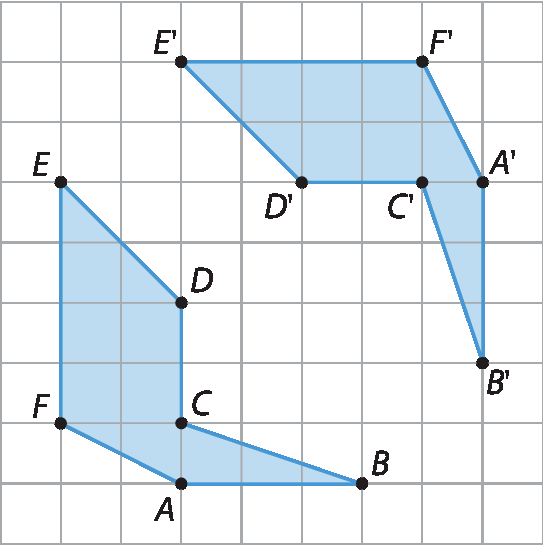
Gráfico. Malha quadriculada com duas figuras geométricas azuis de 6 lados iguais. Figura ABCDEF e figura A linha, B linha, C linha e D linha E linha e F linha igual à figura ABCDEF, mas disposta como se fosse um reflexo da figura ABCDEF.

Observe como Ana fez para representar a reta r na página seguinte.

Página 305

Ilustração. Fala de Ana: Primeiro, construí dois segmentos cujas extremidades são pontos correspondentes nos dois polígonos: os segmentos EE' e CC'.Depois, encontrei, em cada segmento, o ponto que o divide em dois segmentos de mesma medida de comprimento. Indiquei esses pontos por P e Q, respectivamente.Gráfico. Malha quadriculada com duas figuras iguais às do gráfico anterior. De E até E linha há uma linha tracejada onde foi indicado o ponto P na metade da medida de comprimento do segmento. De C até C linha há linha tracejada onde foi indicado o ponto Q na metade da medida de comprimento do segmento. Abaixo, fala de Ana: Por fim, tracei a reta que passa pelos pontos P e Q. Essa é a reta r.Gráfico. Malha quadriculada com duas figuras iguais às do gráfico anterior, mas com reta diagonal r passando pelos pontos P e Q.

• Agora, sabendo que as figuras a seguir são simétricas em relação a uma reta t, não representada, copie-as em papel quadriculado e represente a reta t.

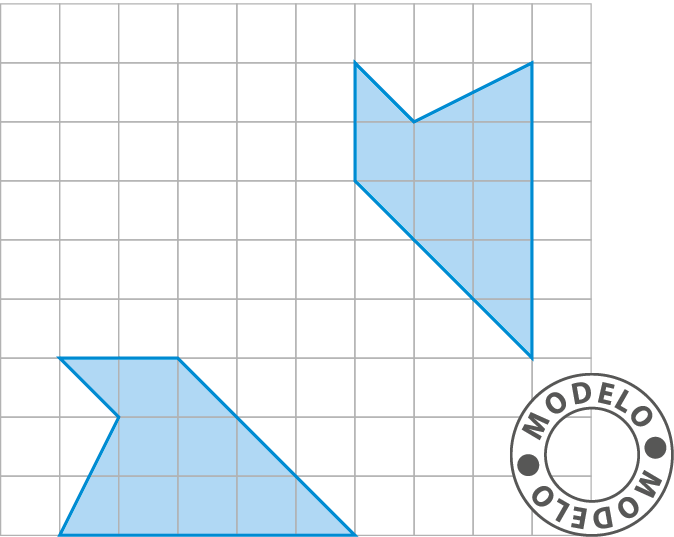
Gráfico. Modelo. Malha quadriculada com duas figuras geométricas iguais de 5 lados cada uma, como se uma fosse reflexo da outra. Uma posicionada na parte inferior esquerda e a outra na parte superior direita. As duas figuras estão a uma distância horizontal de 3 quadradinhos uma da outra.

4. Observe as coordenadas dos vértices do triângulo a seguir.

Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de 0 a 6. Eixo y com intervalo de 0 a 4. Triângulo ABC cujos vértices são formados pelos seguintes pontos: A (0, 3), B (1, 1), C (4, 2).

• Agora, responda.

a) Como é possível obter as coordenadas do triângulo AlinhaBlinhaClinha simétrico ao triângulo á bê cê em relação ao eixo x, sem que seja preciso desenhar o triângulo AlinhaBlinhaClinha?

b) Quais serão as coordenadas do triângulo AlinhaBlinhaClinha?

5. Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente nele o triângulo de vértices J(‒ 6, 2fecha parênteses, K(‒ 5, 5fecha parênteses e L(‒ 2, 2fecha parênteses e o seu simétrico em relação ao eixo x.

6. Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente nele o quadrilátero de vértices F(‒8, menos 4fecha parênteses, G(‒ 7, menos 7fecha parênteses, H(‒1, menos4fecha parênteses e ih(‒4, menos2fecha parênteses e o seu simétrico em relação ao eixo y.

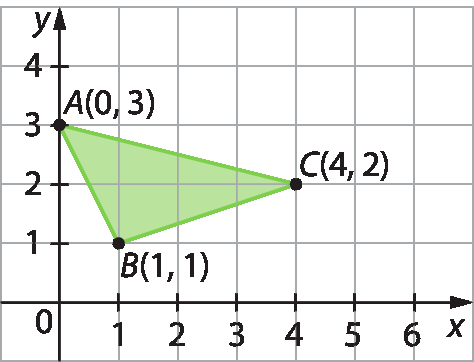
7. Observe as coordenadas dos vértices do triângulo representado no plano cartesiano a seguir.

Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 4 a 4. Eixo y com intervalo de 0 a 6. Triângulo ABC azul com os seguintes pontos: A (menos 2, 4), B (2, 5), C (1, 2).

a) Quais serão as coordenadas do vértice do triângulo AlinhaBlinhaC’ simétrico ao triângulo á bê cê em relação ao eixo y?

b) Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente o triângulo á bê cê e seu simétrico em relação ao eixo y.

Página 306

Reflexão em relação a um ponto

Observe os triângulos representados na malha quadriculada a seguir.

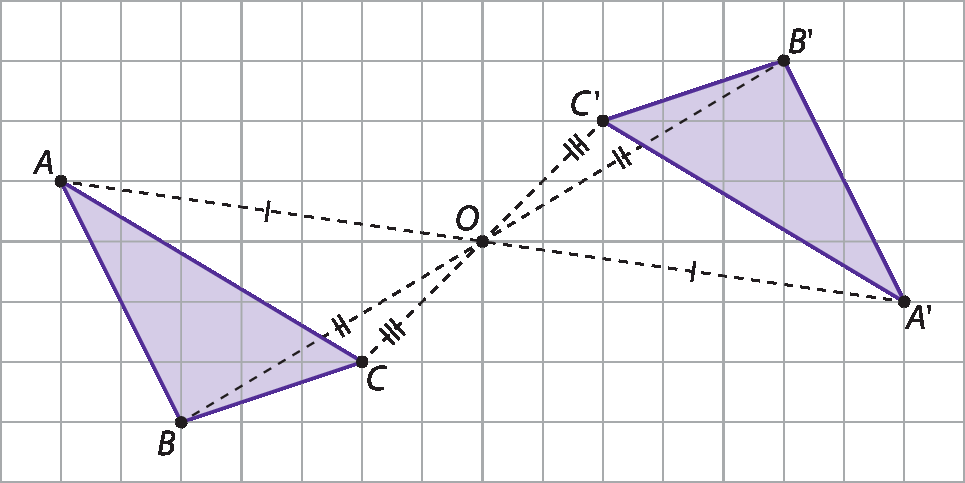
Gráfico. Malha quadriculada com dois triângulos roxos iguais, mas em posições diferentes. Triângulo ABC na parte inferior esquerda e triângulo A linha, B linha C linha na parte superior direita. De A até A linha, há uma linha tracejada. De B até B linha, há uma linha tracejada e de C até C linha, há uma linha tracejada. As linhas se cruzam no ponto O, correspondendo à metade da medida de comprimento de cada linha.

Ilustração. Menino de cabelo preto, blusa vermelha e calça azul. Está com a mão esquerda na cintura e a mão direita levantada com o dedo indicador esticado. Ele diz: O ponto O divide cada um dos segmentos, A A linha, B B linha e C C linha, em dois segmentos de mesma medida de comprimento.

O triângulo AlinhaBlinhaClinha foi obtido do triângulo á bê cê por meio da reflexão em relação ao ponto óh indicado. Dizemos que esses dois triângulos são simétricos em relação ao ponto óh, que é o centro de reflexão, e que o triângulo AlinhaBlinhaClinha é a imagem do triângulo á bê cê.

Cada ponto do triângulo AlinhaBlinhaClinha tem um ponto correspondente no triângulo á bê cê, que é seu simétrico em relação ao ponto óh.

Por exemplo:

• a e Alinha são simétricos em relação ao ponto óh;

• Blinha é o simétrico de B em relação ao ponto óh;

• Clinha é a imagem de C em relação ao ponto óh.

Isso sempre ocorre com duas figuras simétricas em relação a um ponto: cada ponto de uma delas é simétrico a um ponto da outra em relação ao centro de reflexão, e vice-versa, e os pontos simétricos estão à mesma medida de distância do centro de reflexão.

Observação

A simetria em relação a um ponto é chamada simetria central.

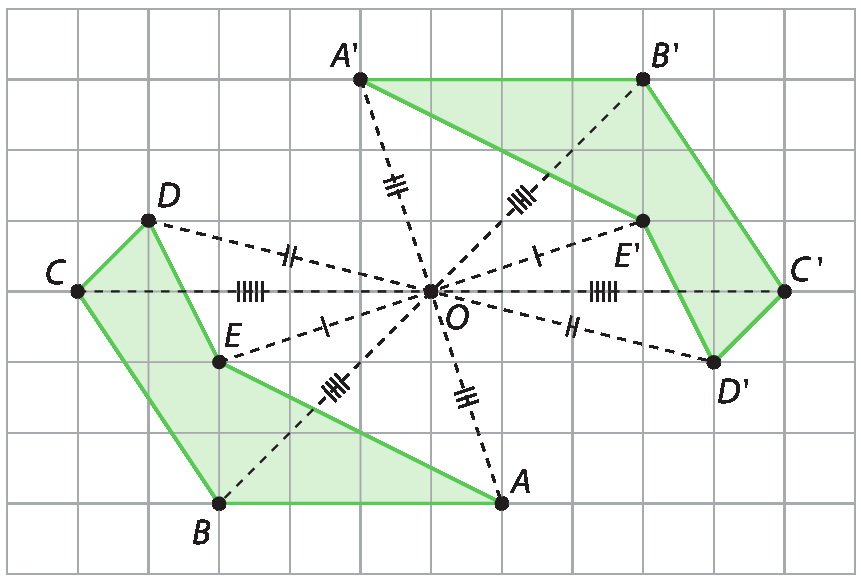
Observe, por exemplo, como podemos refletir o polígono á bê cê dê é, a seguir, em relação ao ponto óh, em uma malha quadriculada.

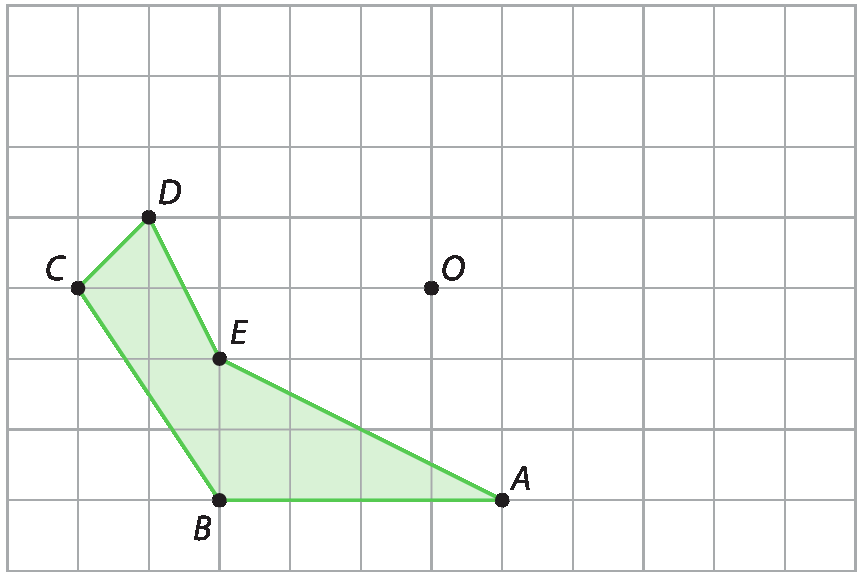
Gráfico. Malha quadriculada com figura geométrica verde de 6 lados ABCDE na parte inferior esquerda. No centro da malha, há o ponto O.

Primeiro, encontramos os simétricos dos vértices a, B, C, D e ê do polígono em relação ao ponto óh. Vamos indicar esses pontos por Alinha, Blinha, Clinha, Dlinha e Elinha, respectivamente. Em seguida, construímos o polígono AlinhaBlinhaClinhaDlinhaElinha, que é o simétrico do polígono á bê cê dê é em relação ao ponto óh.

Gráfico. Mesma malha e figura do gráfico anterior. Agora com outra figura geométrica igual a anterior, mas em posição diferente, na parte superior direita. Há linhas tracejadas entre A e A linha, B e B linha, C e C linha, D e D linha, E e E linha. As linhas se cruzam no ponto O, correspondendo à metade da medida de comprimento de cada linha.

Página 307

Reflexão de figuras em relação à origem do plano cartesiano

Podemos encontrar a simétrica de qualquer figura em relação à origem do plano cartesiano. Considere a representação a seguir.

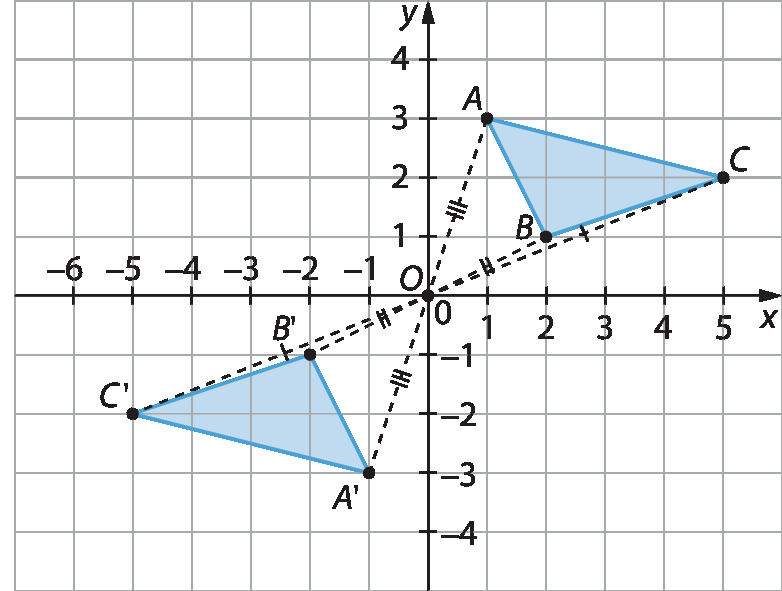
Gráfico. Malha quadriculada, com plano cartesiano e dois triângulos azuis iguais, mas em posições diferentes.
Eixo x com intervalo de menos 6 a 5. Eixo y com intervalo de menos 4 a 4.
Triângulo ABC na parte superior direita formado pelos seguintes pontos: A (1, 3), B (2, 1) e C (5, 3). Triângulo A linha B linha C linha na parte inferior esquerda formado pelos seguintes pontos: A linha (menos 1, menos 3), B linha (menos 2, menos 1) e C linha (menos 5, menos 2). Há linhas tracejadas entre A e A linha, B e B linha, C e C linha. As linhas se cruzam no ponto O, correspondendo à metade da medida de comprimento de cada linha. Além disso, o ponto O coincide com a origem do plano cartesiano.

Nesse exemplo, o triângulo AlinhaBlinhaClinha é o simétrico do triângulo á bê cê em relação à origem do plano cartesiano.

Agora, observe as coordenadas dos vértices dos triângulos á bê cê e AlinhaBlinhaClinha.

No triângulo á bê cê as coordenadas dos vértices são aabre parênteses1, 3fecha parênteses, Babre parênteses2, 1fecha parênteses e Cabre parênteses5, 2fecha parênteses, enquanto as do triângulo AlinhaBlinhaClinha são Alinhaabre parêntesesmenos1, menos3fecha parênteses, Blinhaabre parêntesesmenos2, menos1fecha parênteses e Clinhaabre parêntesesmenos5, menos2fecha parênteses.

Note que, para obter a abscissa e a ordenada dos pontos Alinha, Blinha e Clinha, multiplicamos as abscissas e as ordenadas dos pontos a, B e C por menos1, respectivamente.

ATIVIDADES

faça as atividades no caderno

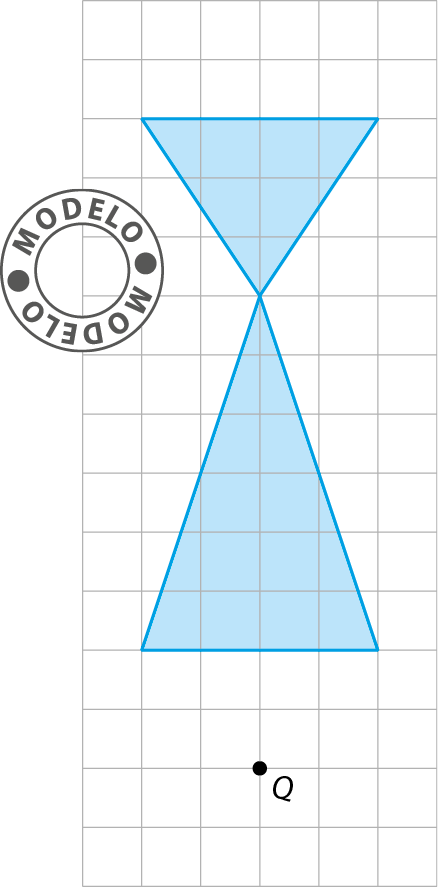
1. Copie a figura a seguir em uma folha de papel quadriculado. Depois, construa a figura simétrica a ela em relação ao ponto Q.

Gráfico. Modelo. Malha quadriculada com figura geométrica azul formada por dois triângulos que se conectam por um de seus vértices. Abaixo da figura há o ponto Q.

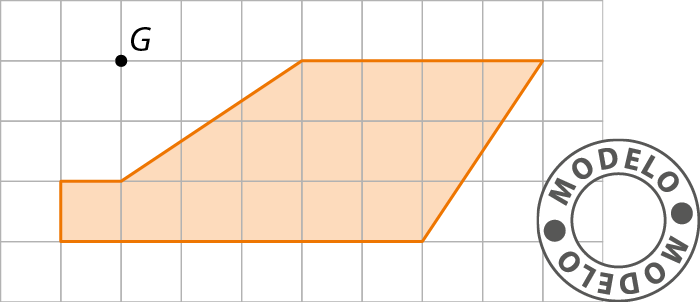
2. Copie a figura a seguir em uma folha de papel quadriculado. Depois, construa a figura simétrica a ela em relação ao ponto G.

Gráfico. Modelo. Malha quadriculada com figura geométrica laranja de seis lados. Acima e à esquerda da figura. há o ponto G.

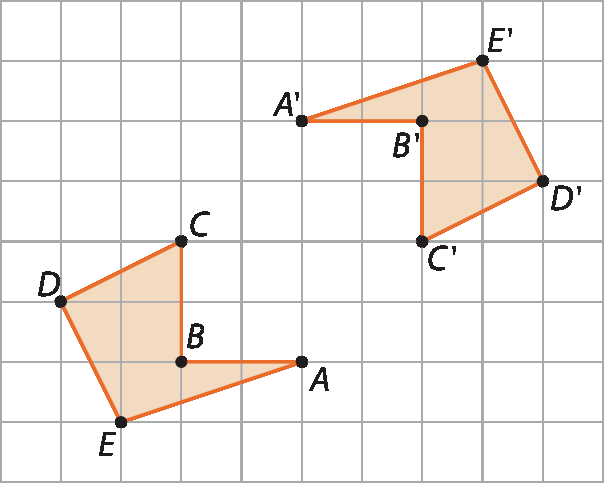
3. Na imagem a seguir, o polígono AlinhaBlinhaClinhaDlinhaElinha é o simétrico do polígono á bê cê dê é, em relação a um ponto óh, que não está representado na figura.

Gráfico. Malha quadriculada com duas figuras geométricas laranja iguais de 5 lados cada uma, como se uma fosse reflexo da outra. Figura ABCDE posicionada na parte inferior esquerda e a A linha B linha C linha D linha E linha na parte superior direita. As duas figuras estão a uma distância horizontal de 2 quadradinhos uma da outra.

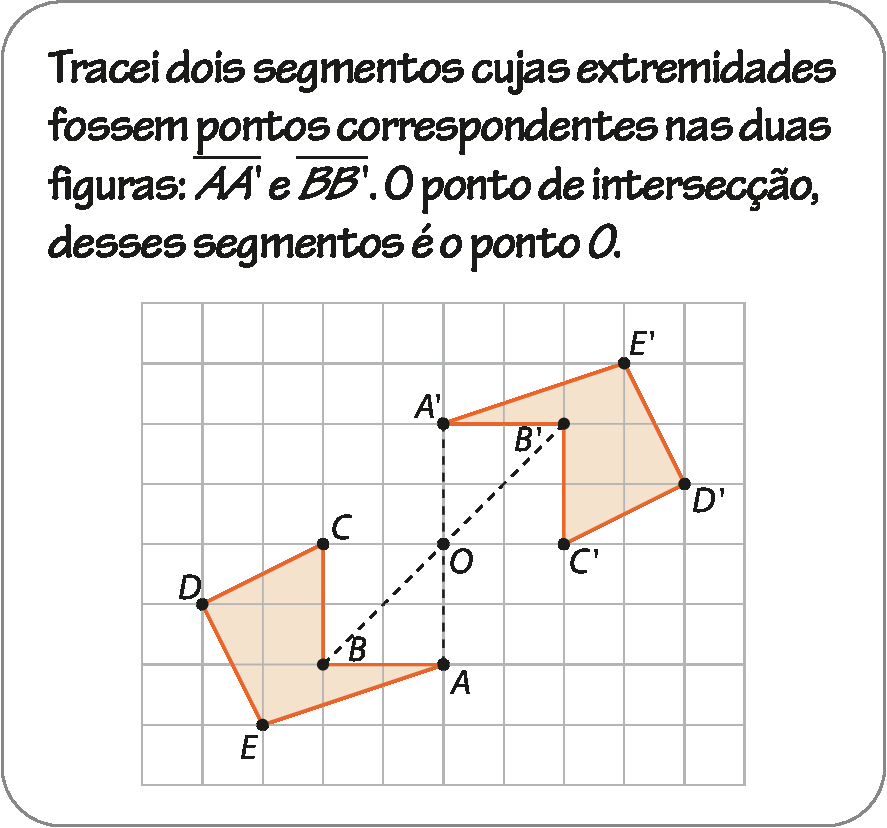
Observe como Ivo determinou a localização do ponto óh.

Ilustração. Fala de Ivo: Tracei dois segmentos cujas extremidades fossem pontos correspondentes nas duas figuras: AA' e BB'. O ponto de intersecção, desses segmentos é o ponto O.
Abaixo, mesma figura do gráfico anterior, mas agora com linhas tracejadas entre A e A linha, e entre B e B linha. As linhas se cruzam no ponto O, correspondendo à metade da medida de comprimento de cada linha.

Página 308

Lembre-se: Escreva no caderno!

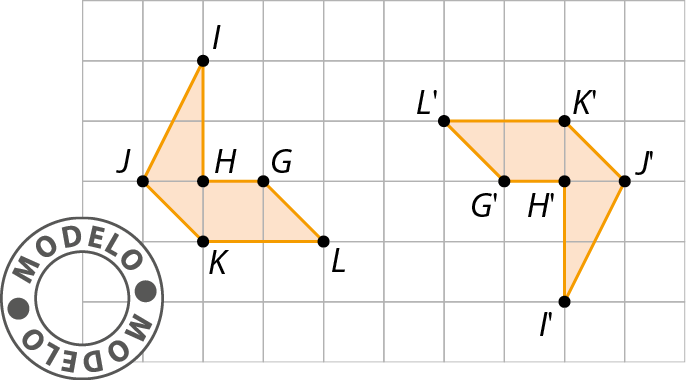
• Agora, sabendo que as figuras a seguir são simétricas em relação a um ponto T, que não está representado, copie-as em uma folha de papel quadriculado e represente o ponto T.

Gráfico. Modelo. Malha quadriculada com duas figuras geométricas iguais laranja de 6 lados cada uma. Figura GHIJKL esquerda e figura G linha, H linha I linha J linha K linha L linha na direita.
A figura à direita está posicionada como se a figura à esquerda tivesse sido rotacionada 180 graus.

4. Observe as coordenadas dos vértices do triângulo a seguir. Depois, responda às perguntas.

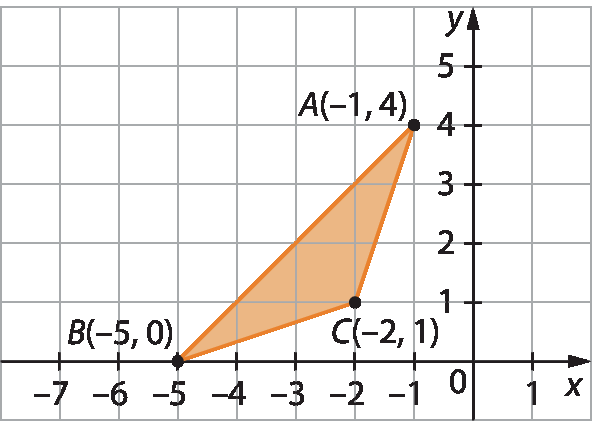
Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 7 a 1. Eixo y, intervalo de 0 a 5. Triângulo cujos vértices são formados pelos pontos: A (menos 1, 4) B (menos 5, 0) C(menos 2, 1).

a) Como é possível obter as coordenadas do triângulo AlinhaBlinhaClinha simétrico ao triângulo á bê cê em relação à origem, sem que seja preciso desenhar o triângulo AlinhaBlinhaClinha?

b) Quais serão as coordenadas do triângulo AlinhaBlinhaClinha?

5. Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente nele o pentágono de vértices Pabre parêntesesmenos 4, 2fecha parênteses, Qabre parêntesesmenos 2, 3fecha parênteses, Rabre parêntesesmenos 3, 4fecha parênteses, Sabre parêntesesmenos 5, 4fecha parênteses e Tabre parêntesesmenos 6, 3fecha parênteses e o seu simétrico em relação à origem do plano cartesiano.

4 Translação

Observe as figuras na malha quadriculada a seguir.

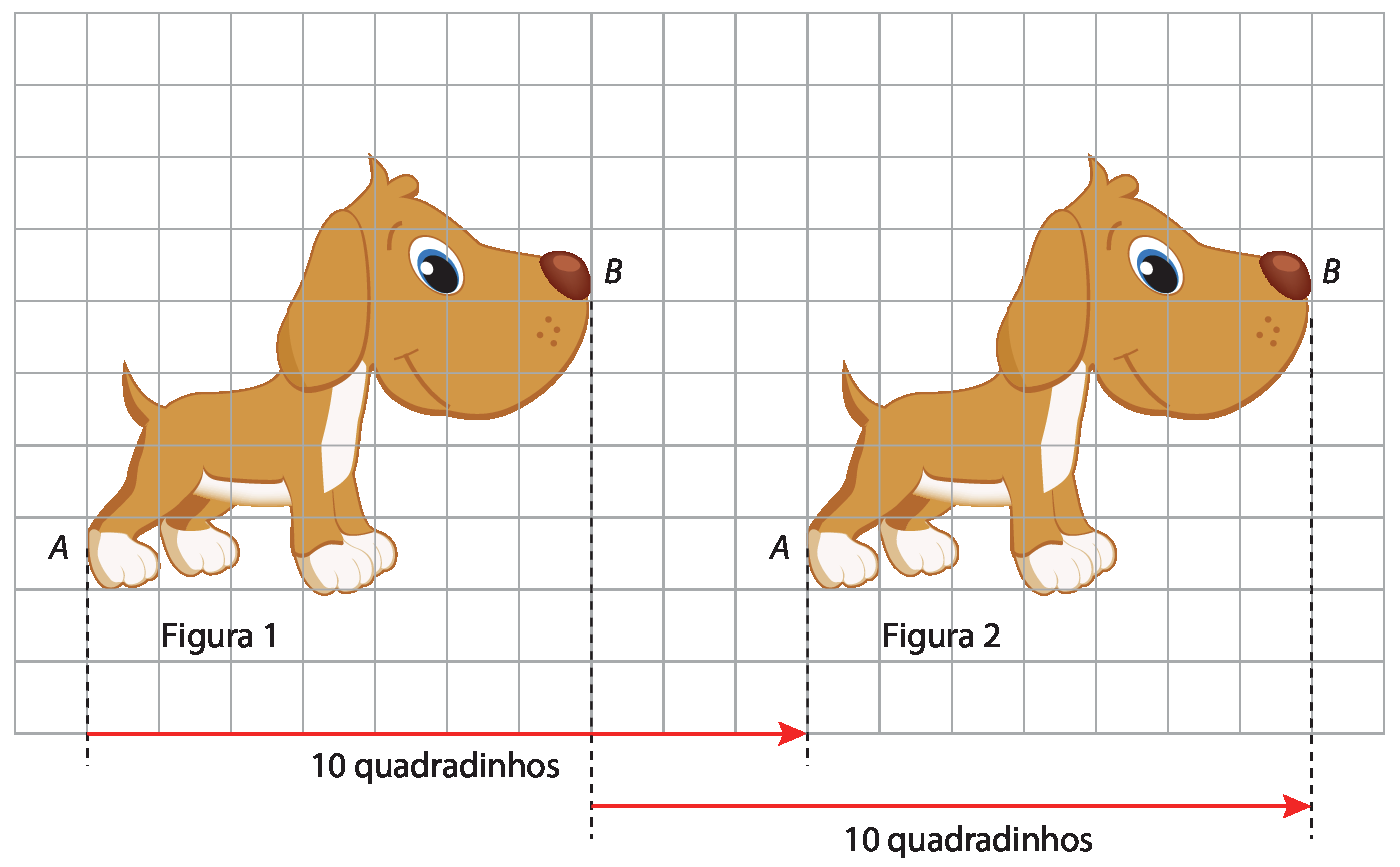
Ilustração. Malha quadriculada. Figura 1. Cachorro marrom virado para a direita. Ponto A na pata traseira direita e ponto B no focinho. À direita há a figura 2 que consiste no mesmo cachorro da figura 1, mas como se tivesse sido deslocado 10 quadradinhos para a direita.

As setas indicam que a figura 1 foi deslocada 10 quadradinhos na direção horizontal e no sentido da esquerda para a direita, gerando a figura 2.

Página 309

Considerando que esse mesmo deslocamento foi feito com todos os pontos da figura 1, dizemos que a figura 2 foi obtida por uma translação da figura 1, e que a figura 2 é a imagem da figura 1.

Observe, por exemplo, como podemos transladar o triângulo á bê cê a seguir de acordo com a medida de comprimento, a direção e o sentido da seta.

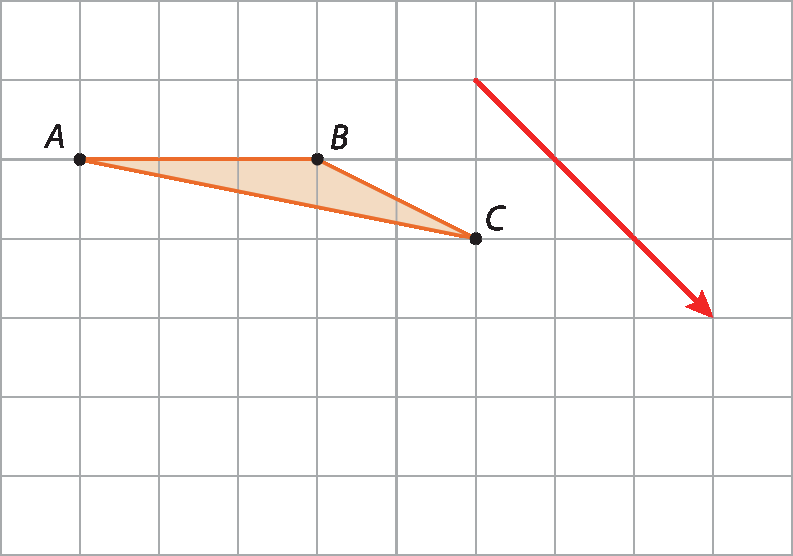
Ilustração. Malha quadriculada com triângulo laranja ABC. À direita, seta diagonal para baixo.

Ilustração. Menina de cabelo ruivo, blusa azul, tênis rosa e calça. Ela está com a mão esquerda nas costas e a mão direita levantada com o dedo indicador esticado. Ela fala: Para transladar qualquer figura, é preciso saber a direção, o sentido e a medida da distância em que ela será deslocada. Em geral, essas informações são representadas por uma seta que chamamos de vetor da translação.

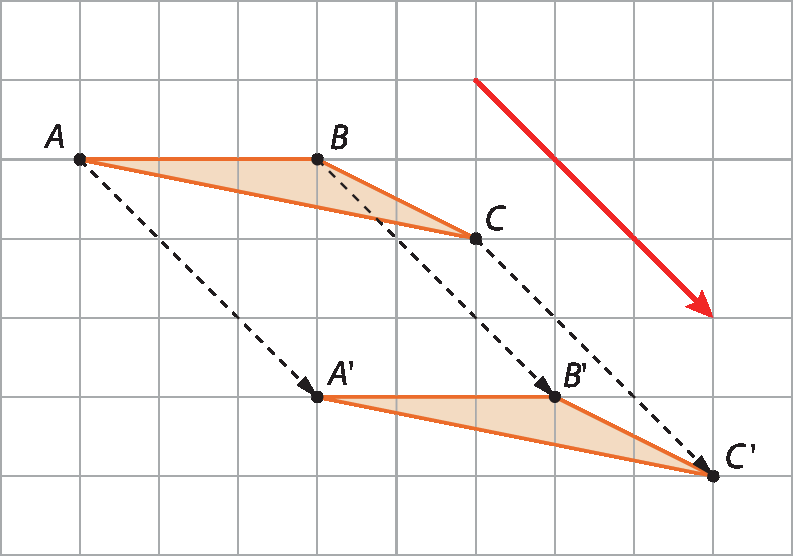
Para transladar esse triângulo, deslocamos os vértices a, B e C, 3 quadradinhos para a direita e, depois, 3 quadradinhos para baixo, obtendo os vértices Alinha, Blinha e Clinha, respectivamente. Em seguida, traçamos o triângulo AlinhaBlinhaClinha.

Gráfico. Malha quadriculada com triângulo laranja ABC na parte superior esquerda. Na parte inferior direita, triângulo laranja A linha B linha e C linha igual. Há retas tracejadas de A até A linha, de B até B linha, de C até C linha. À direita das duas figuras e das linhas tracejas há seta diagonal para baixo, com 3 diagonais de quadradinhos de comprimento, indicando que o triângulo superior direito foi transladado para a parte inferior direita.

Para analisar

O que a reflexão em relação a uma reta (ou em relação a um ponto) tem em comum com a translação? Converse com os colegas sobre isso.

ATIVIDADES

faça as atividades no caderno

1. Em cada caso, copie o polígono em uma folha de papel quadriculado. Depois, translade-o de acordo com a medida de comprimento, a direção e o sentido da seta.

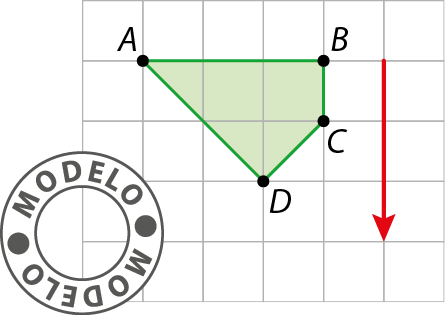
Gráfico. Modelo. Malha quadriculada com quadrilátero verde ABCD. À direita do quadrilátero, seta para baixo, com 3 quadradinhos de comprimento.

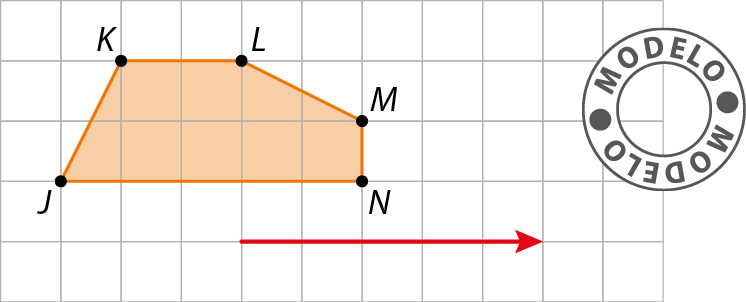
Gráfico. Modelo. Malha quadriculada com figura geométrica laranja de 5 lados JKLMN. Abaixo dele, seta para direita, com 5 quadradinhos de comprimento.

Página 310

2. Na figura a seguir, o triângulo AlinhaBlinhaClinha é imagem do triângulo á bê cê por translação. Reproduza as figuras, em uma folha de papel quadriculado, e, em seguida, desenhe o vetor dessa translação.

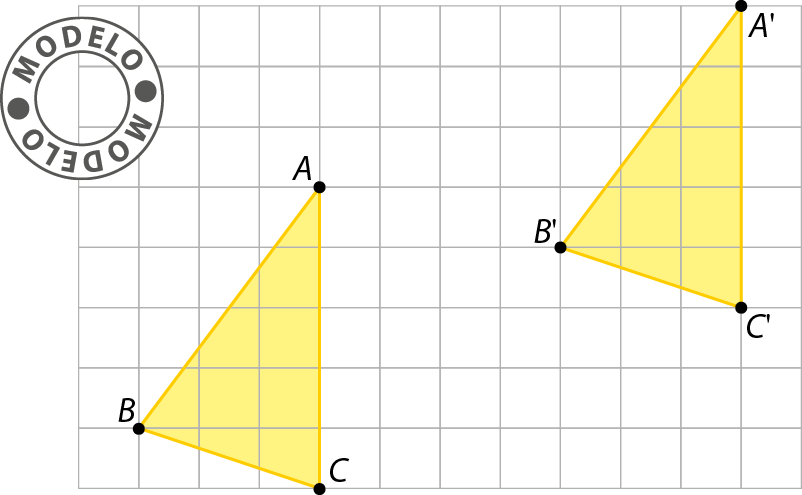
Gráfico. Modelo. Malha quadriculada com triângulo ABC amarelo no canto inferior esquerdo. No canto superior direito, triângulo A linha B linha e C linha, azul. Os dois triângulos são iguais.

3. Observe as figuras representadas na malha quadriculada a seguir. Depois, faça o que se pede.

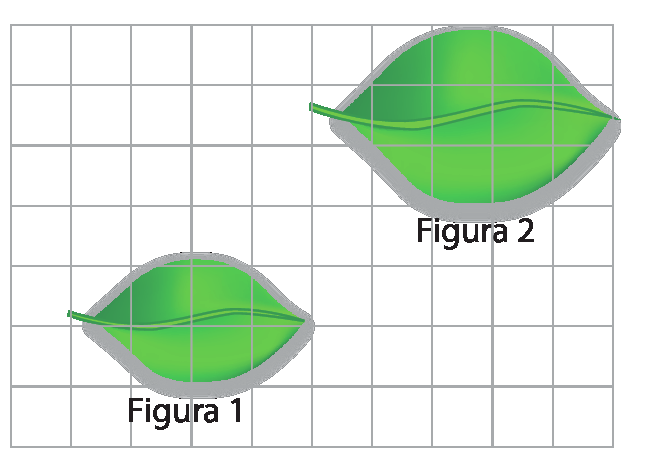
Ilustração. Malha quadriculada com figura 1: Uma folha verde no canto inferior esquerdo, com 4 quadradinhos de largura e 2 quadradinhos de altura. E figura 2: no canto superior direito, mesmo tipo de folha verde da figura 1, mas com 5 quadradinhos de largura e 3 quadradinhos de altura.

• É correto afirmar que a figura 2 foi obtida pela translação da figura 1? Justifique.

4. Observe as faixas decorativas a seguir.

Ilustração. Faixa amarela com sequência de gotas de água com rosto: rosto de olhos abertos e boca reta, olhos abertos e boca sorrindo, olhos fechados, rosto de olhos abertos e boca reta, rosto de olhos abertos e boca sorrindo, olhos fechados.

Ilustração. Faixa branca com borda vermelha com sequência de pinguins: pinguim de cachecol verde, pinguim de cachecol vermelho, coração vermelho, pinguim de cachecol verde, pinguim de cachecol vermelho, coração vermelho.

Ilustração. Faixa verde com sequência de flores: flor branca, flor amarela, flor branca, flor amarela, flor branca e flor amarela.

Ilustração. Faixa azul com sequência de flores: flor vermelha grande, flor rosa pequena, flor vermelha grande, flor rosa pequena,flor vermelha grande, flor rosa pequena,flor vermelha grande, flor rosa pequena.

• Qual é a direção da translação presente nas figuras de cada uma dessas faixas?

5 Rotação

Observe as figuras na malha quadriculada a seguir.

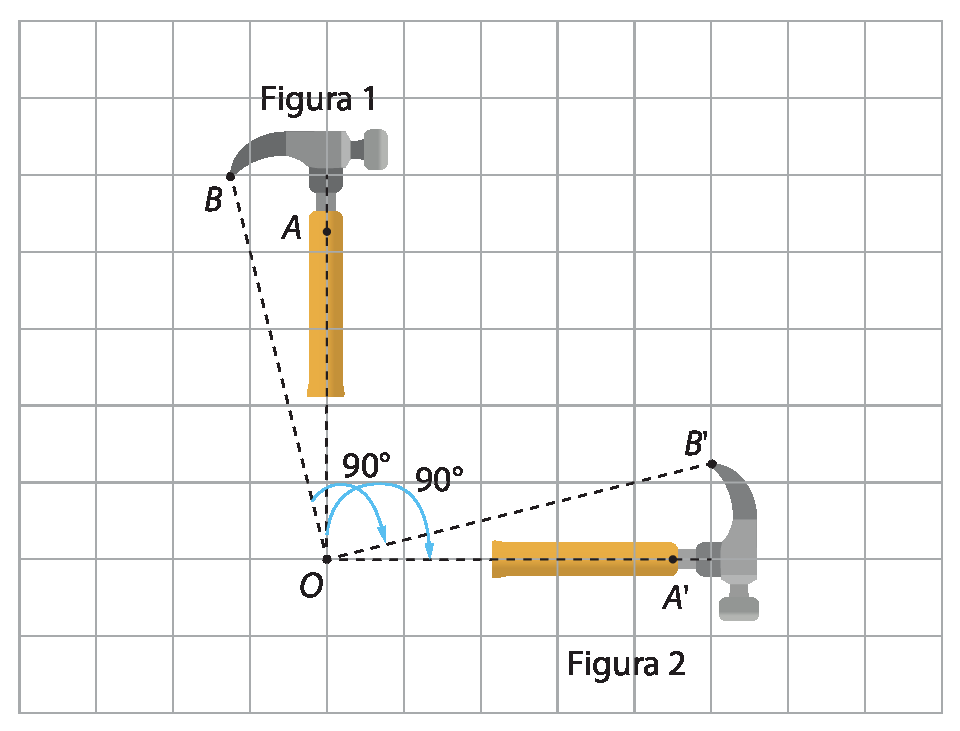
Ilustração. Malha quadriculada. Figura 1: Martelo na vertical na parte superior esquerda. Figura 2: Martelo, igual ao da figura 1, na horizontal, na parte inferior direita. Ponto A está no começo do cabo e B na extremidade, na figura 1. Ponto O na parte inferior. Ponto A linha está no começo do cabo e B linha na extremidade, na figura 2. Ponto O na parte inferior esquerda da malha. Reta tracejada de A a O e de O a B linha. Entre as duas retas tracejadas forma-se um ângulo de 90 graus.
Há uma seta azul indicando que a figura 1 foi rotacionada 90 graus no sentido horário.

Na malha quadriculada anterior, temos o desenho de dois martelos idênticos. Observe que a figura 2 foi obtida da figura 1 por meio de um giro, no sentido horário (sentido dos ponteiros do relógio), que mede 90graus ao redor do ponto óh. Assim, podemos dizer, por exemplo, que o ponto a gerou o ponto Alinha, e o ponto B gerou o ponto Blinha.

Página 311

Considerando que um giro de mesma medida foi feito com todos os pontos da figura 1, dizemos que a figura 2 foi obtida por uma rotação da figura 1 e que a figura 2 é a imagem da figura 1.

Ilustração. Dois meninos sentados lado a lado, cada um em sua mesa escolar. Os dois estão vestindo uniforme que consiste em calça e camiseta azul. O da esquerda é ruivo e usa sapatos verdes. O da direita é branco de cabelo preto, está em uma cadeira de rodas e usando tênis vermelho. O menino à direita, fala: O ponto O é chamado de centro da rotação. Para rotacionar qualquer figura, precisamos conhecer o centro da rotação, a medida de abertura do ângulo e o sentido da rotação (horário ou anti-horário).

Observe, por exemplo, como podemos construir, usando régua e transferidor, a figura obtida pela rotação do triângulo á bê cê, em torno do ponto óh, considerando um giro com medida igual a 90graus no sentido horário.

Lembre-se: Escreva no caderno!

1º) Seja o triângulo á bê cê e o ponto óh.

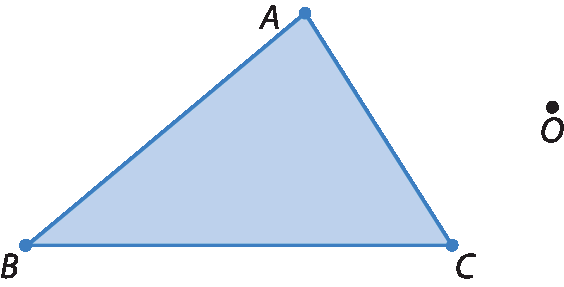
Figura geométrica. Triângulo ABC. À direita do triângulo, ponto O.

2º) Traçamos a semirreta

\vec{O A}

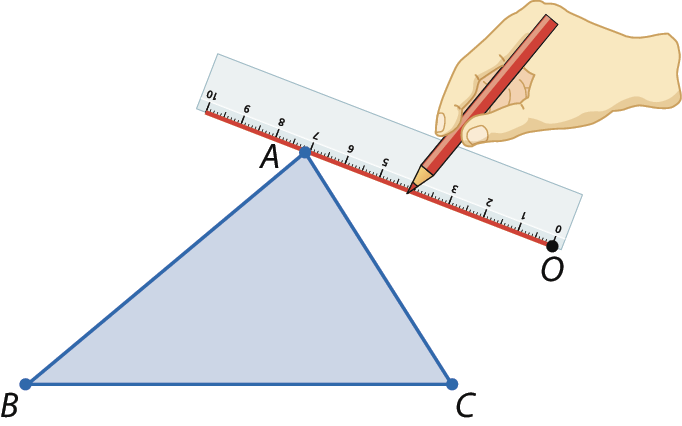
Ilustração. Mesmo triângulo ABC azul, da figura geométrica anterior. À direita, ponto O. Régua na diagonal apoiada sobre A e sobre o ponto O, com reta vermelha sendo traçada por uma mão.

3º) Usando uma régua e um transferidor, traçamos uma semirreta com origem em óh e que fórma um ângulo cuja abertura mede 90graus com

\vec{O A}

no sentido horário.

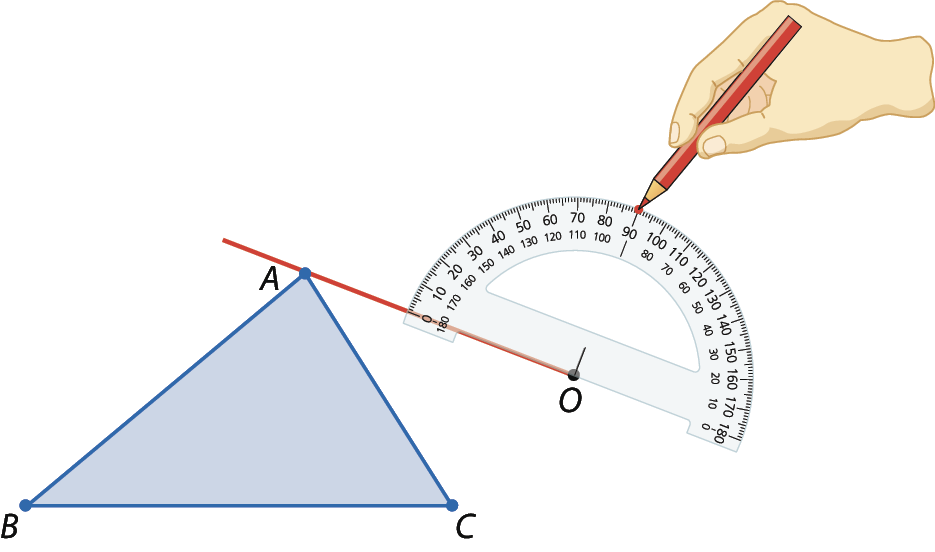
Ilustração. Mesmo triângulo ABC azul, da figura geométrica anterior. Agora com uma mão usando um lápis e um transferidor para medir e indicar um ângulo de 90 graus.

Página 312

4º) Marcamos um ponto Alinha sobre a semirreta construída, de modo que o segmento

\overline{O A'}

tenha a mesma medida de comprimento que

\overline{O A}

Lembre-se: Escreva no caderno!

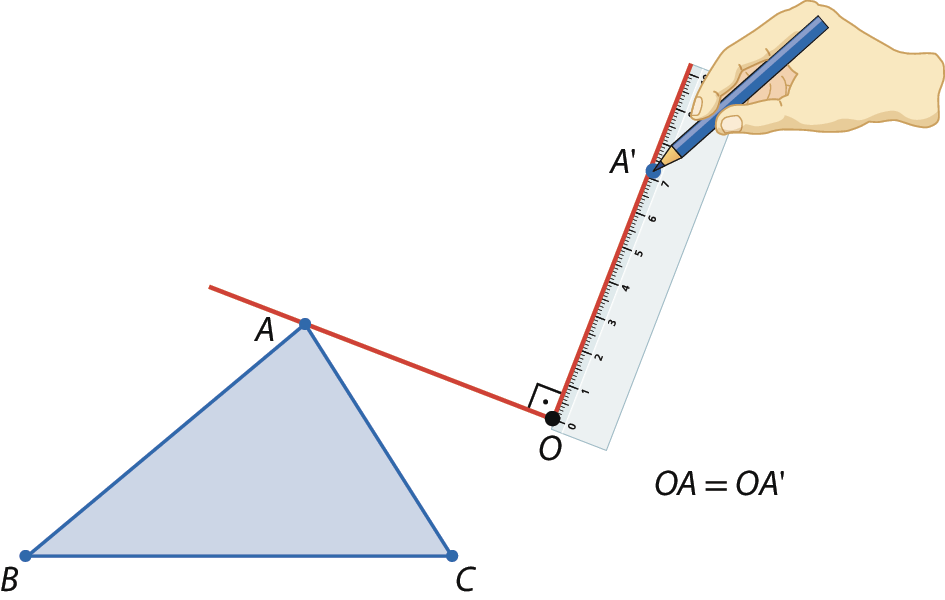
Ilustração. Mesmo triângulo ABC azul, da ilustração anterior. Agora com uma régua traçando uma reta vermelha perpendicular à reta traçada anteriormente. Há uma mão indicando o ponto A linha, com medida de comprimento de O a A linha igual à medida de comprimento de O a A do triângulo ABC. À direita da figura está a cota: OA igual a OA linha.

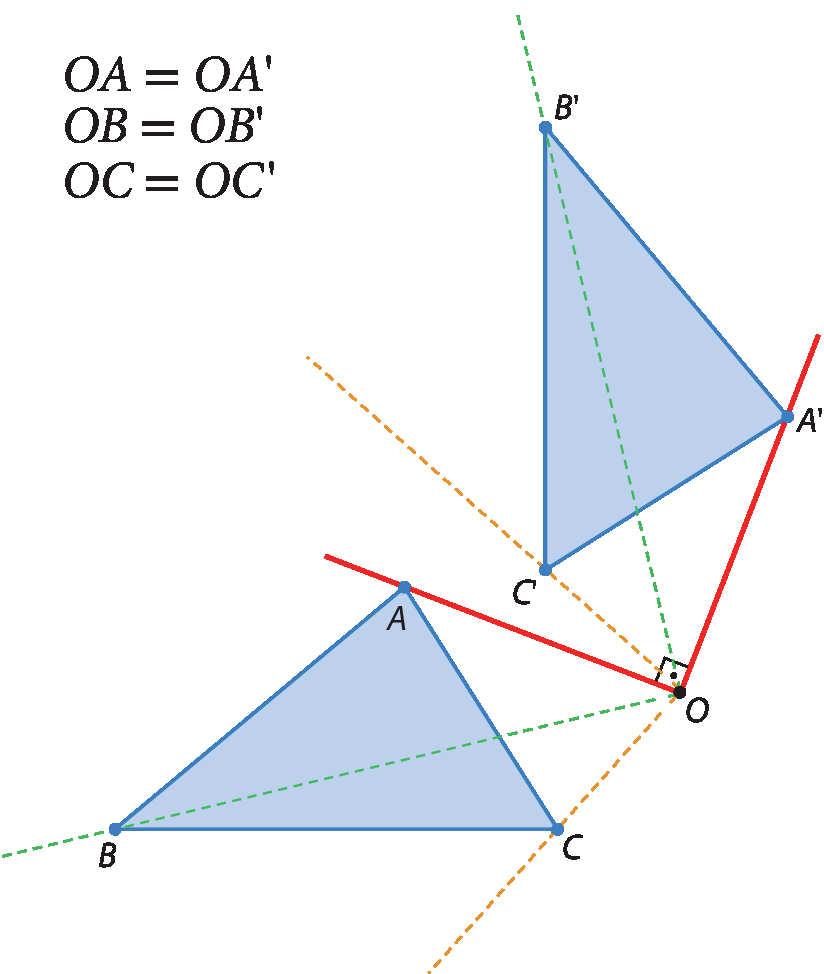
5º) Repetimos o mesmo processo com os pontos B e C para obter os pontos Blinha e Clinha, ou seja:

• traçamos

\vec{O B}

e, em seguida, uma semirreta com origem em óh e que fórma um ângulo cuja abertura mede 90graus com

\vec{O B}

no sentido horário. Depois, marcamos o ponto bit' nessa semirreta, de modo que ó bê = OB'.

• traçamos

\vec{O C}

e, depois, uma semirreta com origem em óh e que fórma um ângulo cuja abertura mede 90graus com

\vec{O C}

no sentido horário. Depois, marcamos o ponto C' nessa semirreta, de modo que ó cê = OC'.

Por fim, ligamos os pontos Alinha, Blinha e Clinha e pintamos a região interna da figura, obtendo o triângulo AlinhaBlinhaClinha.

Assim, o triângulo AlinhaBlinhaClinha foi obtido por uma rotação do triângulo á bê cê em torno do ponto óh no sentido horário e com giro medindo 90graus.

Figura geométrica. Sequência da ilustração anterior. Agora, o ponto A linha é vértice de um triângulo A linha, B linha e C linha, igual ao triângulo anterior, mas transladado 90 graus no sentido horário.
Há linhas tracejadas verdes ligando O a B linha e O a B. Há linhas tracejadas laranja ligando O a C e O a C linha.
Cota à esquerda da imagem: OA, igual, OA linha. OB, igual, OB linha. OC, linha, OC linha.

Para analisar

Compare a reflexão em relação a um ponto óh de uma figura qualquer com a rotação de centro óh e um giro com medida igual a 180graus, em qualquer sentido, dessa mesma figura. O que você pode perceber?

Página 313

ATIVIDADES

faça as atividades no caderno

1. Observe a rotação das figuras ao redor do ponto óh e responda às questões no caderno.

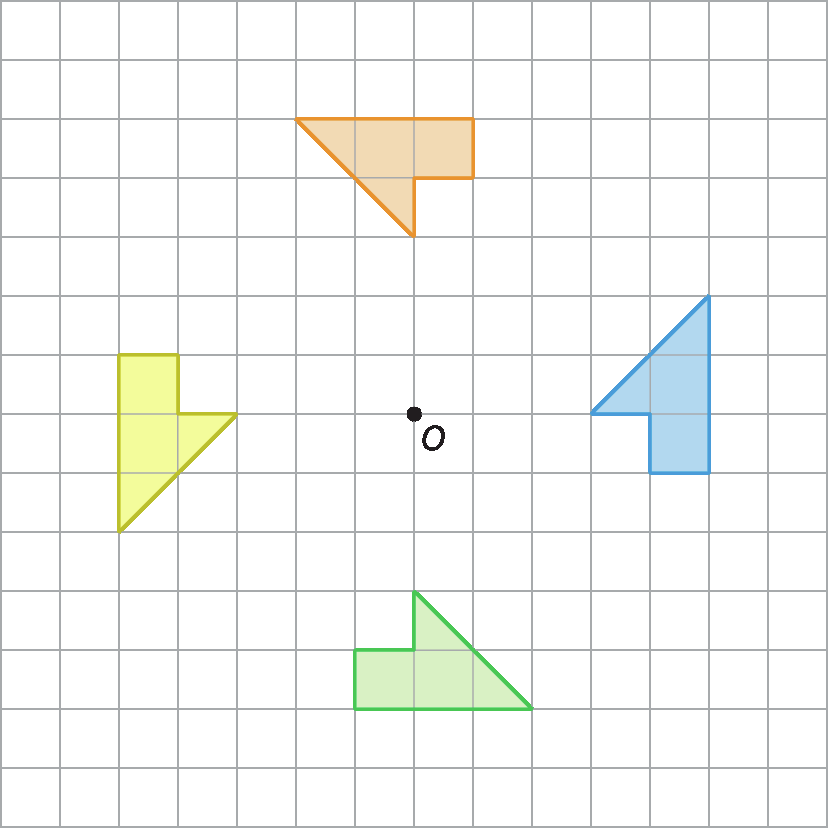
Ilustração. Malha quadriculada com 4 figuras iguais, sendo uma azul, uma verde, uma amarela e uma laranja, cada uma composta por 3 quadradinhos inteiros e um pela metade. No centro da malha, ponto O. As figuras estão ao redor do ponto O.
As 4 figuras estão posicionadas como se estivessem sendo rotacionadas ao redor de O.

a) Qual é a medida do giro de rotação no sentido anti-horário que devemos aplicar na figura azul para obter a figura laranja?

b) Ao aplicar uma rotação com giro de medida 180graus na figura laranja, obtemos qual figura?

c) Explique o sentido de rotação que devemos aplicar na figura azul para obter a figura verde.

d) Qual é a medida do giro de rotação que devemos aplicar na figura amarela para obtê-la novamente?

2. Escreva no caderno, em cada caso, a medida e o sentido da rotação realizada da figura original em torno do ponto óh.

a) Figura original: á bê cê

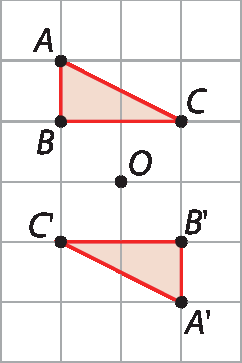
Ilustração. Malha quadriculada com dois triângulos iguais vermelhos. Triângulo ABC e triângulo A linha, B linha, C linha. Entre os dois triângulos há o ponto O. O triângulo A linha B linha C linha está posicionado como se o triângulo ABC tivesse sido rotacionado 180 graus ao redor de O.

b) Figura original: á bê cê dê é éfe

Ilustração. Malha quadriculada com duas figuras iguais vermelhas. Figura ABCDEF e figura A linha, B linha, C linha, D linha, E linha, F linha. Entre as duas figuras há o ponto O.
A figura A linha, B linha, C linha, D linha, E linha F linha é como se a figura ABCDE tivesse sido rotacionada ao redor de O 90 graus no sentido horário.

3. Construa, em seu caderno, a figura obtida pela rotação de um triângulo qualquer, em torno de um ponto óh, determinada pelo giro de medida igual a 100graus no sentido anti-horário.

4. Construa, em seu caderno, a figura obtida pela rotação de um quadrilátero qualquer, em torno de um ponto óh, determinada pelo giro de medida igual a 70graus no sentido horário.

5. Descreva a rotação que fazemos com o quadrilátero a bê cê dê a seguir quando multiplicamos as coordenadas de seus vértices por menos1.

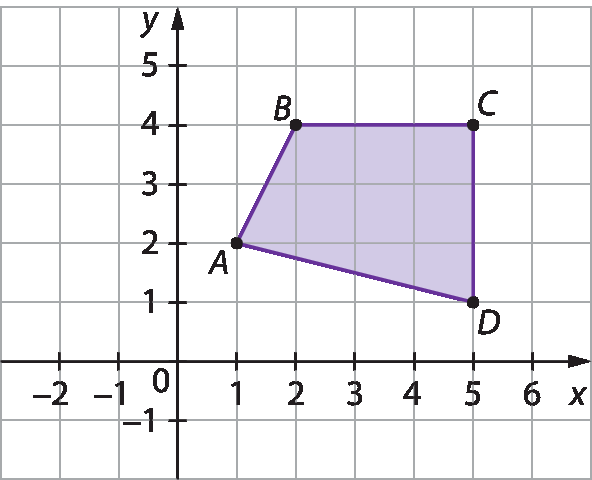
Gráfico. Malha quadriculada com gráfico. Eixo x com intervalo de menos 2 a 6. Eixo y com intervalo de menos 1 a 5. Quadrilátero no primeiro quadrante com vértices formados pelos seguintes pontos: A: (1, 2); B: (2, 4); C: (5, 4); D: (5, 1).

6. Em uma folha de papel quadriculado, represente em um plano cartesiano o triângulo de vértices Pabre parênteses2, 1fecha parênteses, Qabre parênteses3, 3fecha parênteses e Rabre parênteses4, 1fecha parênteses e o triângulo de vértices Sabre parênteses1, menos 2fecha parênteses, Tabre parênteses3, menos 3fecha parênteses e Uabre parênteses1, menos 4fecha parênteses. O que podemos afirmar sobre esses dois triângulos?

Página 314

Informática e Matemática

faça as atividades no caderno

Figuras obtidas por transformações geométricas

Nesta seção, vamos usar um software de Geometria dinâmica para refletir, transladar e rotacionar polígonos, além de investigar algumas propriedades dessas transformações geométricas.

Construa

Reflexão em relação a uma reta

Siga os passos a seguir para construir o simétrico de um polígono qualquer em relação a uma reta.

1º) Construa um polígono qualquer.

2º) Trace uma reta r qualquer. Essa reta será o eixo de reflexão.

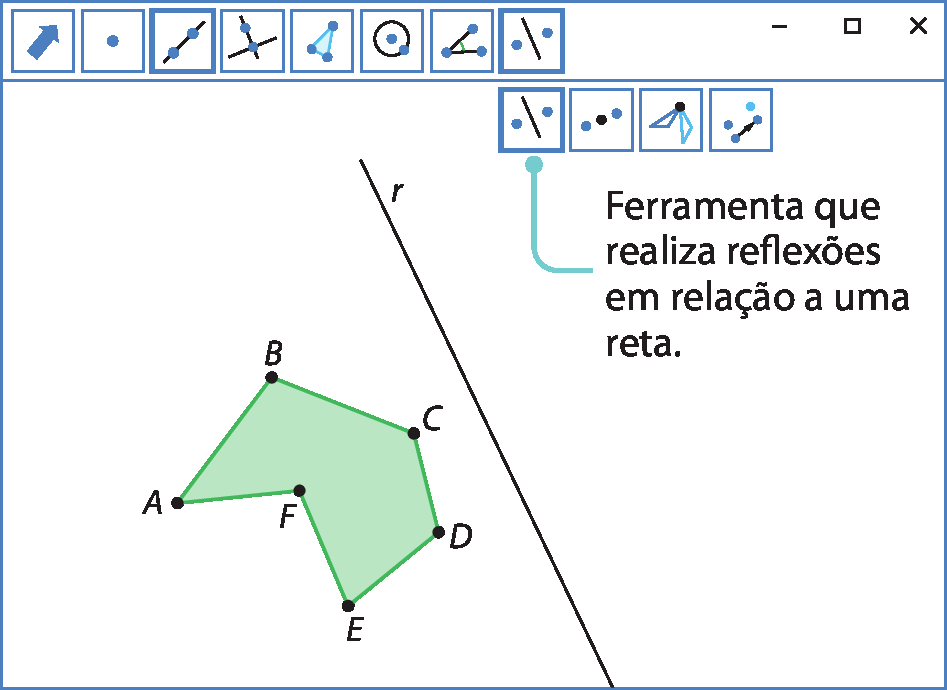
Ilustração. Software de geometria. Na parte superior, botões de comandos. Botão indicado: barra diagonal com ponto de cada lado. Ferramenta que realiza reflexões em relação a uma reta. À esquerda, polígono verde ABCDEF. À direita, reta diagonal r.

3º) Clique na ferramenta de reflexão em relação a uma reta. Depois, clique sobre o polígono e sobre a reta r. O polígono que aparecerá na tela será o simétrico do polígono inicial em relação à reta r.

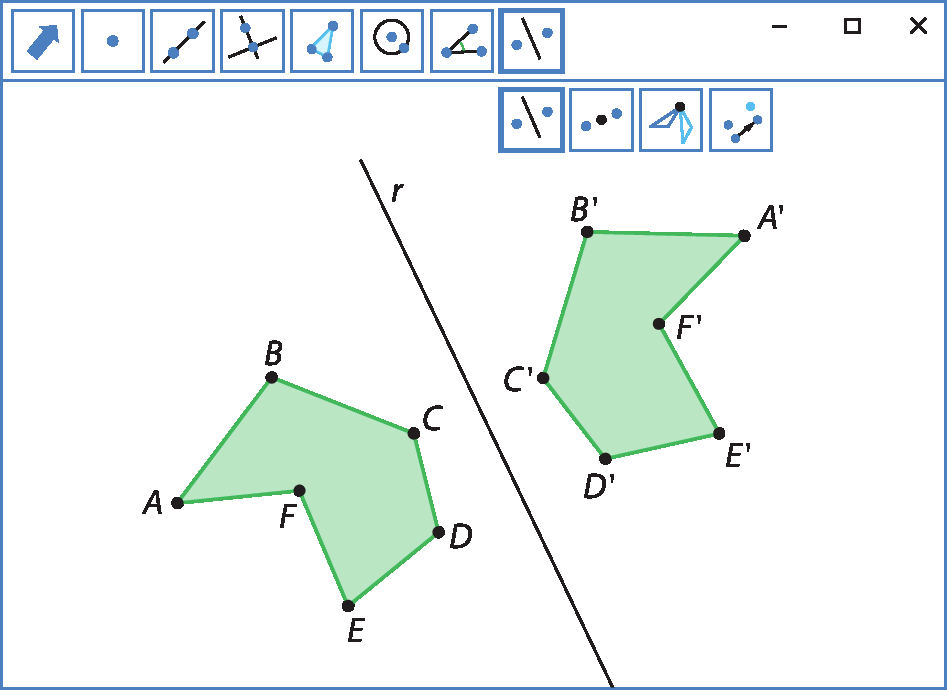
Ilustração. Software de geometria.
Sequência da ilustração anterior. Agora há um polígono verde A linha B linha C linha D linha E linha F linha à direita do ponto O. Esse polígono é uma reflexão do polígono anterior.

Reflexão em relação a um ponto

Siga os passos a seguir para construir o simétrico de um polígono qualquer em relação a um ponto.

1º) Construa um polígono qualquer.

2º) Marque um ponto óh qualquer. Esse ponto será o centro de reflexão.

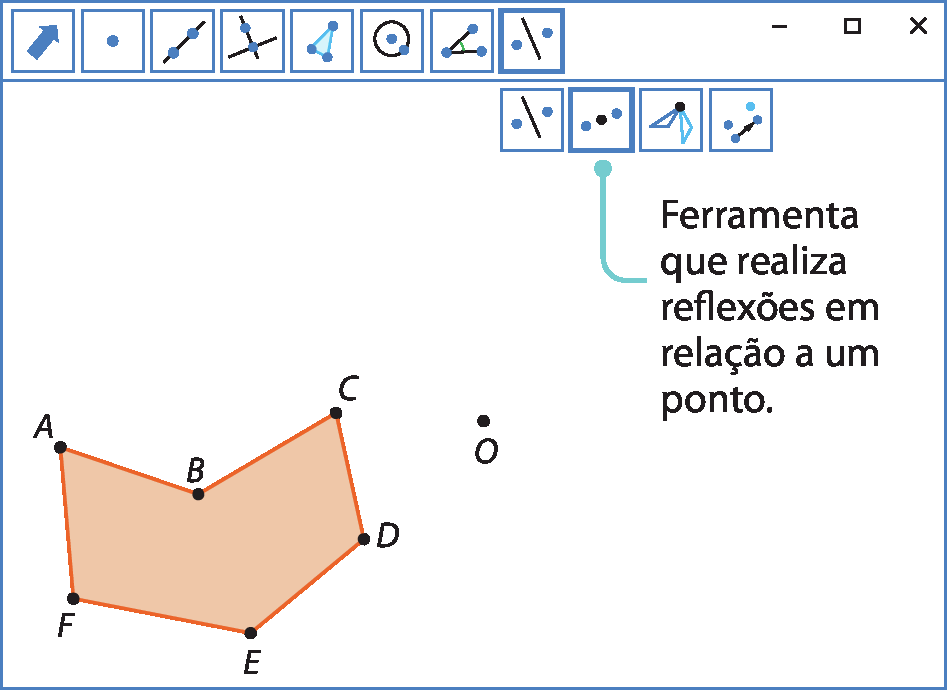
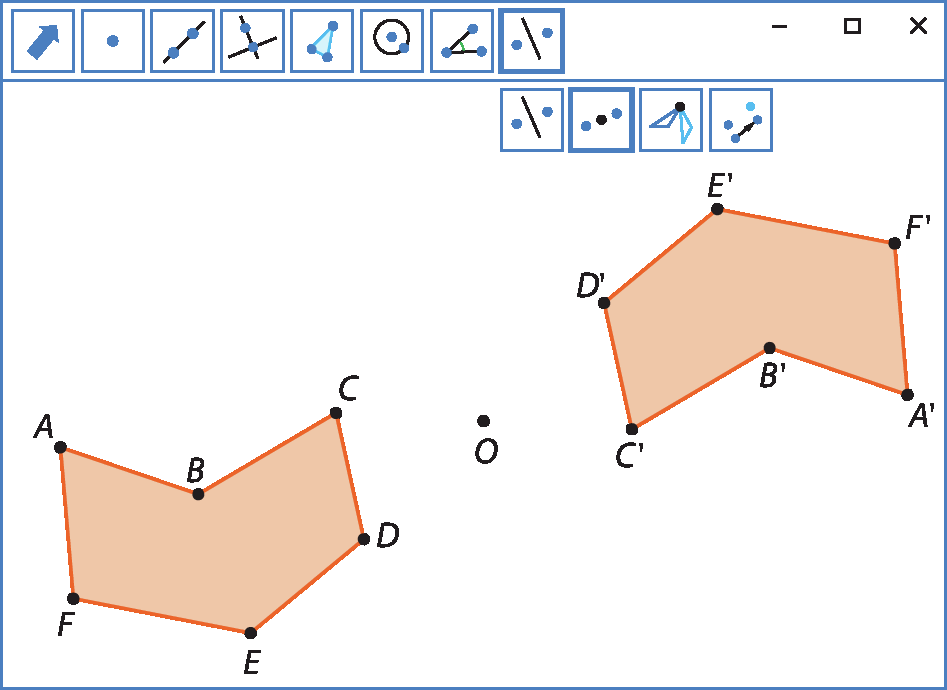
3º) Clique na ferramenta de reflexão em relação a um ponto. Depois, clique sobre o polígono e sobre o ponto óh. O polígono que aparecerá na tela será o simétrico do polígono inicial em relação ao ponto óh.

Ilustração. Software de geometria.
Sequência da ilustração anterior. Agora há um polígono laranja A linha B linha C linha D linha E linha F linha à direita da reta r. Esse polígono é uma reflexão do polígono anterior.

Página 315

Translação

Siga os passos a seguir para transladar um polígono qualquer.

1º) Construa um polígono qualquer.

2º) Clique na ferramenta para construir vetores e construa um vetor qualquer. Esse será o vetor da translação.

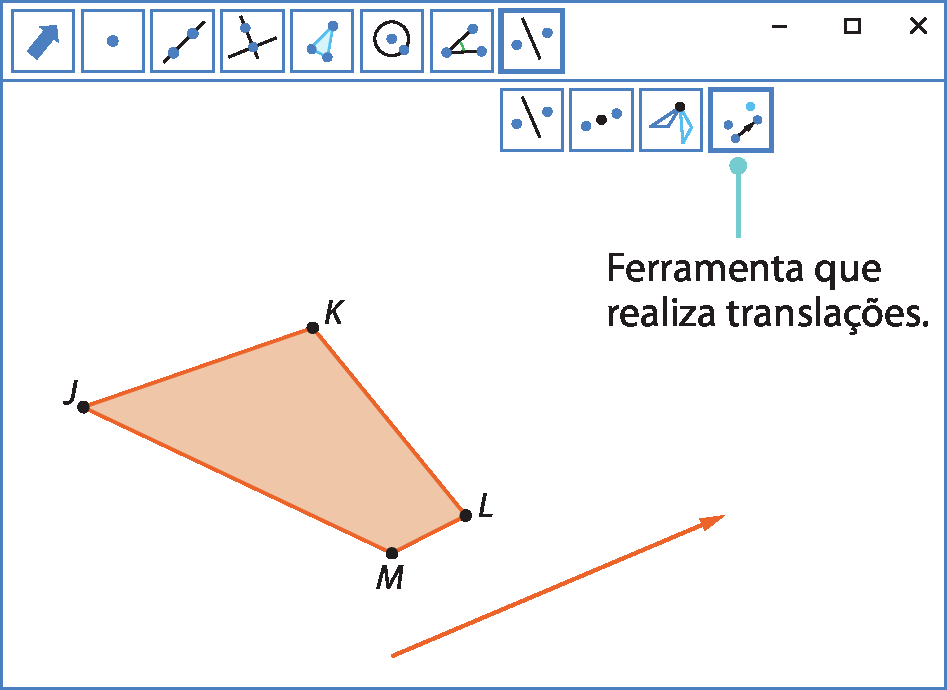
Ilustração. Software de geometria. Na parte superior, botões de comandos. Botão indicado: linha diagonal com dois pontos. Ferramenta que realiza translações. À esquerda, polígono laranja JKLM. Abaixo, seta diagonal para cima, para direita.

3º) Clique na ferramenta de translação. Depois, clique sobre o polígono e sobre o vetor. O polígono que aparecerá na tela será a imagem da translação.

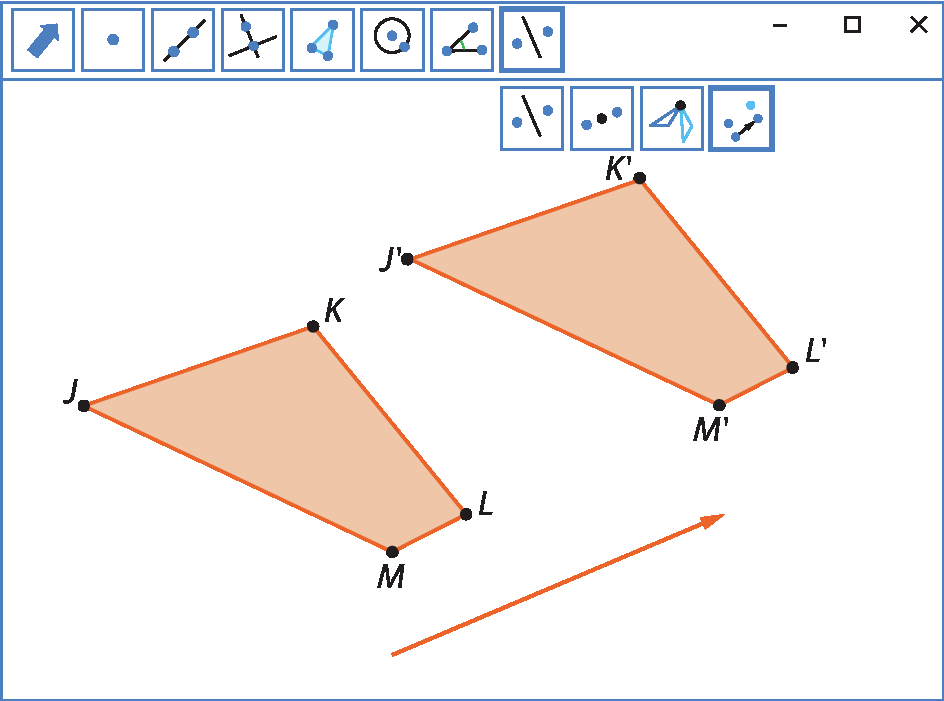
Ilustração. Software de geometria.
Sequência da ilustração anterior. Agora há um polígono laranja J linha K linha L linha M linha à direita do polígono anterior. Esse polígono é uma translação do polígono anterior.

Rotação

Siga os passos a seguir para rotacionar um polígono qualquer em torno de um ponto.

1º) Construa um polígono qualquer.

2º) Marque um ponto P qualquer. Esse ponto será o centro da rotação.

Ilustração. Software de geometria. Na parte superior, botões de comandos. Botão indicado: ponto conectando dois triângulos por um vértice. Ferramenta que realiza rotações. À esquerda, triângulo roxo ABC. À direita do triângulo, ponto P.

3º) Clique na ferramenta de rotação. Depois, clique sobre o polígono e sobre o ponto P. Por fim, escolha a medida de abertura do ângulo e o sentido da rotação. O polígono que aparecerá na tela será a imagem da rotação.

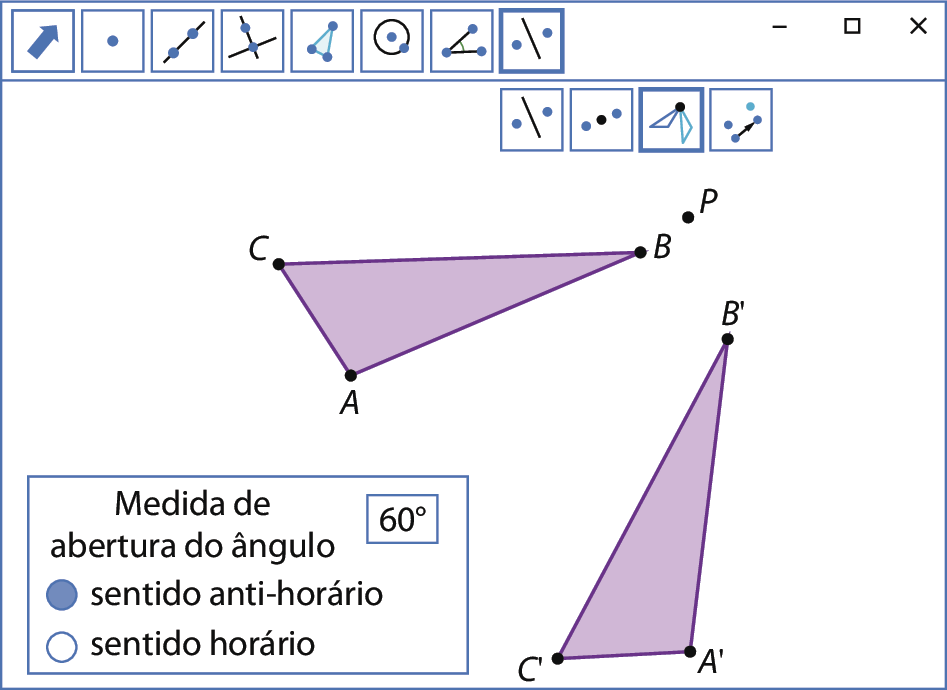
Ilustração. Software de geometria.
Sequência da ilustração anterior. Agora há um triângulo roxo A linha B linha C linha abaixo do triângulo anterior. Esse triângulo é uma rotação do triângulo anterior.
Legenda com as informações a seguir.
Medida de abertura do ângulo: 60 graus. sentido anti-horário marcado e sentido horário desmarcado.

Investigue

Em cada uma das construções que você realizou, meça o comprimento dos lados e a medida de abertura do ângulo que determinou a rotação correspondente dos polígonos. Depois, movimente-os. O que você observou?

Página 316

6 Outras transformações geométricas no plano cartesiano

Vimos que podemos fazer algumas transformações com figuras no plano cartesiano de modo que as suas medidas sejam preservadas. E, para isso, multiplicamos as abscissas e ou ou as ordenadas por menos1.

Também é possível fazer transformações geométricas que podem alterar as medidas e a fórma delas multiplicando as coordenadas por números inteiros não nulos diferentes de menos1. Acompanhe.

Multiplicando as coordenadas por números inteiros não nulos maiores que menos1

Observe as coordenadas dos vértices dos retângulos a bê cê dê e AlinhaBlinhaClinhaD linha.

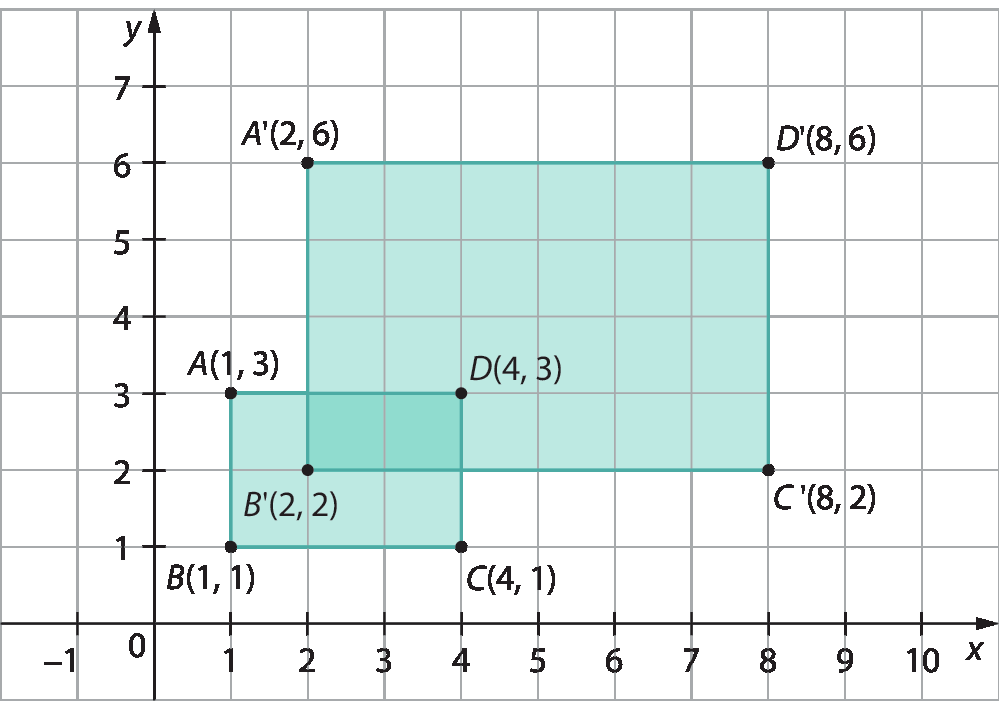
Gráfico. Malha quadriculada com gráfico. Eixo x com intervalo de menos 1 a 10. Eixo y com intervalo de 0 a 7. Retângulo verde ABCD no primeiro quadrante com vértices formados pelos pontos: A (1,3) B(1,1) C(4, 1) D(4, 3). Retângulo verde A linha B linha C linha D linha no primeiro quadrante com vértices formados pelos pontos A linha (2, 6) B linha (2, 2) C linha: 8, 2). D linha (8, 6).

O retângulo A’B’C’D’ foi obtido multiplicando as abscissas e as ordenadas de cada vértice do retângulo a bê cê dê por 2.

Note que, nesse caso, a fórma da figura original a bê cê dê foi mantida e as medidas de comprimento dos lados correspondentes foram duplicadas. Podemos dizer que o retângulo A’B’C’D’ é uma ampliação do retângulo a bê cê dê.

Multiplicando as coordenadas por números inteiros menores que menos1

Observe as coordenadas dos vértices dos retângulos a bê cê dê e A’B’C’D’.

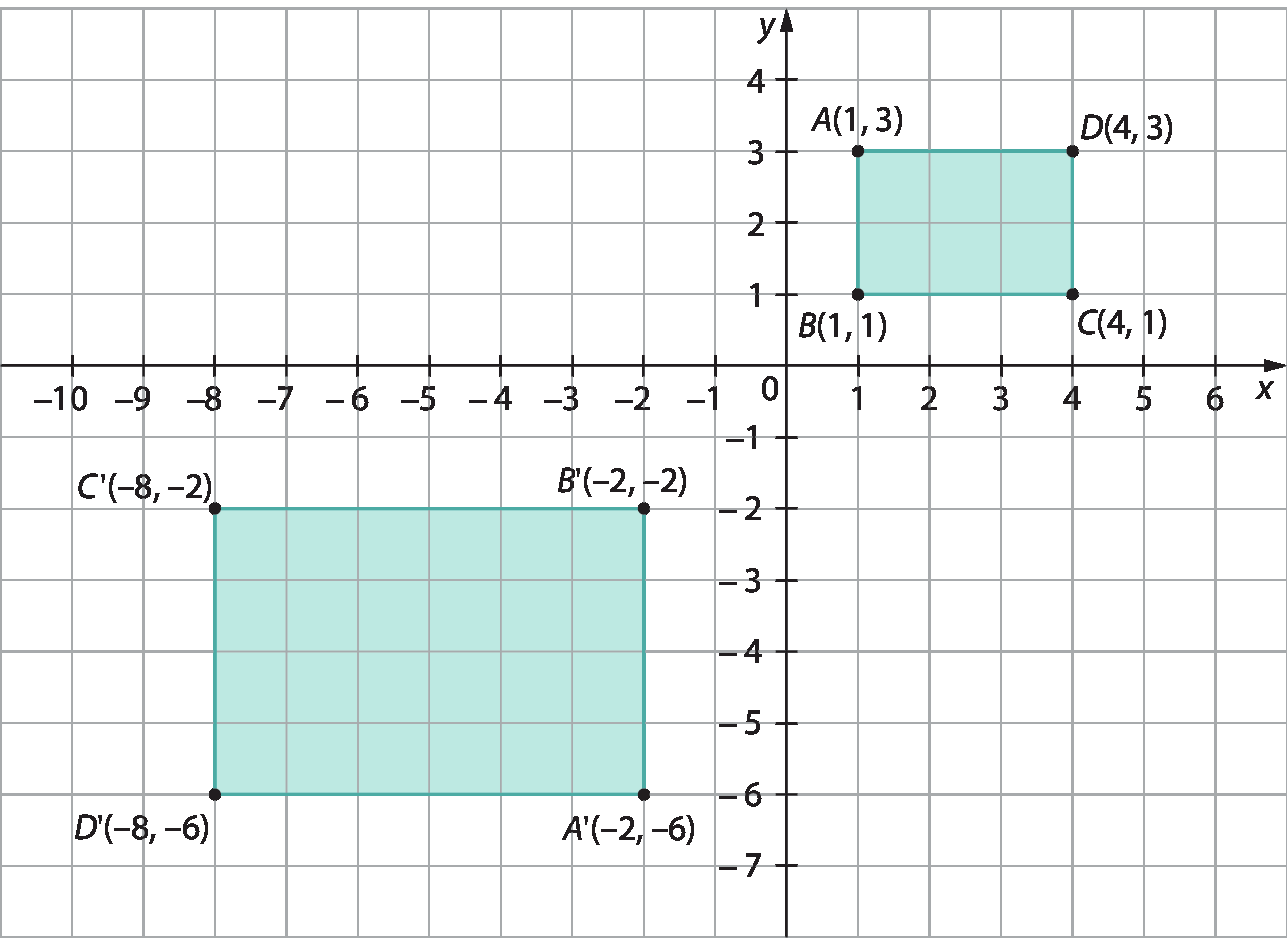
Gráfico. Malha quadriculada com gráfico. Eixo x com pontos menos 10 a 6. Eixo y com pontos menos 7 a 4. Retângulo verde ABCD no primeiro quadrante com os pontos: A (1,3) B(1,1) C(4, 1) D(4, 3). Retângulo verde A linha B linha C linha D linha no terceiro quadrante com vértices formados pelos pontos A linha (menos 2, menos 6) B linha (menos 2, menos 2) C linha (menos 8, menos 2). D linha (menos 8, menos 6).

O retângulo A’B’C’D’ foi obtido multiplicando as abscissas e as ordenadas de cada vértice do retângulo a bê cê dê por menos2.

Página 317

Note que, nesse caso, a fórma da figura original a bê cê dê foi mantida e as medidas de comprimento dos lados correspondentes também foram duplicadas, porém o retângulo AlinhaBlinhaClinhaDlinha está invertido. Podemos dizer que o retângulo AlinhaBlinhaClinhaDlinha é uma ampliação invertida do retângulo a bê cê dê.

Multiplicando uma das coordenadas por números inteiros não nulos diferentes de menos1

Observe as coordenadas dos vértices dos quadriláteros a bê cê dê e AlinhaBlinhaClinhaDlinha.

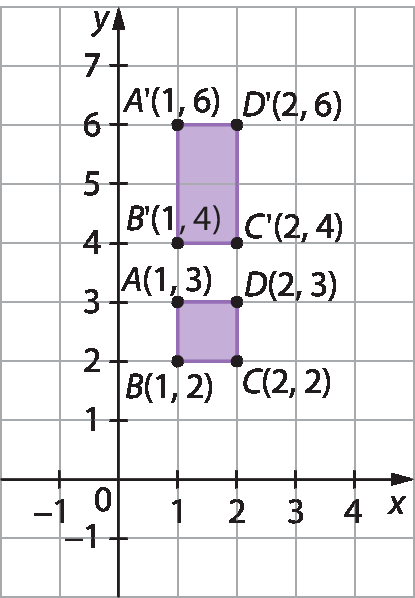
Gráfico. Malha quadriculada com gráfico. Eixo x com intervalo de menos 10 a 6. Eixo y com intervalo de menos 7 a 4. Retângulo roxo ABCD no primeiro quadrante com vértices formados pelos pontos A(1, 3) B(1, 2) C(2, 2) D(2, 3). Retângulo roxo A linha B linha C linha D linha no primeiro quadrante com vértices formados pelos pontos A linha (1, 6) B linha (1, 4) C linha (2, 4) D linha (2, 6)

O retângulo AlinhaBlinhaClinhaDlinha foi obtido multiplicando apenas as ordenadas de cada vértice do quadrado a bê cê dê por 2.

Note que o quadrado a bê cê dê teve sua fórma alterada, pois obtivemos um retângulo. Note que apenas as medidas de comprimento dos lados

\overline{A' B'}

\overline{C' D'}

são o dobro das medidas de comprimento de

\overline{A B}

\overline{C D}

e que as medidas de comprimento de

\overline{B' C'}

\overline{A' D'}

são as mesmas que as de

\overline{B C}

\overline{A D}

. Nesse caso, dizemos que houve uma deformação da figura.

Para pensar

O que aconteceria se multiplicássemos por 2 apenas as abscissas de cada vértice do quadrado a bê cê dê?

ATIVIDADES

faça as atividades no caderno

1. Observe as coordenadas dos vértices dos triângulos a seguir.

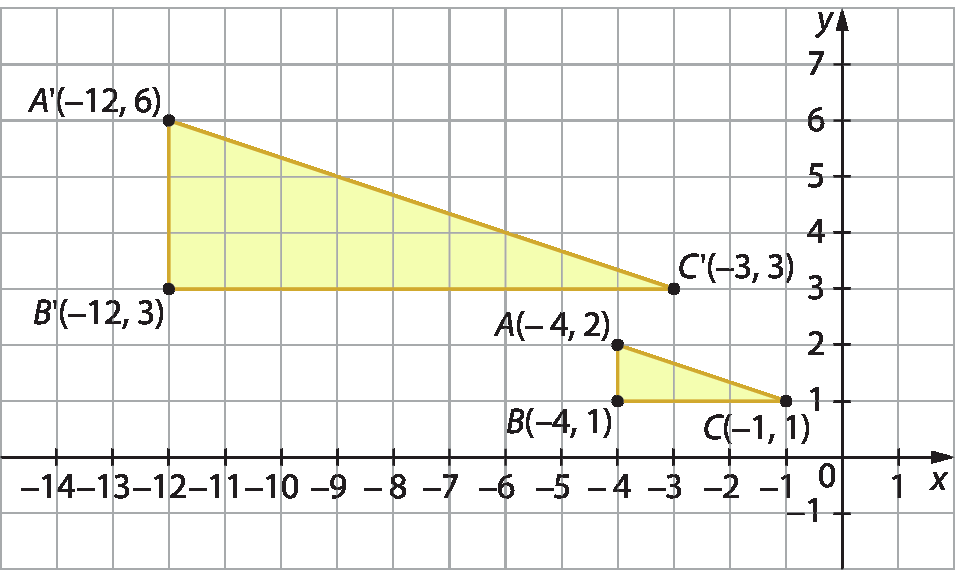
Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 14 a 1. Eixo y com intervalo de menos 1 a 7. Triângulo amarelo ABC no segundo quadrante com vértices formados pelos pontos A(menos 4, 2) B(menos 4, 1) C(menos 1, 1). Triângulo amarelo A linha B linha C linha no segundo quadrante com vértices formados pelos pontos A linha B linha C linha. A linha (menos 12, 6) B linha (menos 12, 3) C linha (menos 3, 3).

a) O que podemos afirmar sobre os triângulos á bê cê e AlinhaBlinhaClinha?

b) Como é possível obter as coordenadas dos vértices do triângulo AlinhaBlinhaClinha a partir das coordenadas dos vértices do triângulo á bê cê?

2. Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente nele o triângulo á bê cê da atividade 1.

Agora, faça o que se pede.

a) Multiplique as coordenadas do triângulo á bê cê por menos3 para obter as coordenadas Alinha, Blinha e Clinha. Determine as novas coordenadas e desenhe, no mesmo sistema de eixos cartesianos, o triângulo AlinhaBlinhaClinha.

b) O que é possível afirmar sobre o triângulo AlinhaBlinhaClinha em relação ao triângulo á bê cê?

3. Em uma folha de papel quadriculado determine um sistema de eixos cartesianos e represente nele o quadrado de vértices Pabre parêntesesmenos 4, menos 2fecha parênteses, Qabre parêntesesmenos4, menos 4fecha parênteses, Rabre parêntesesmenos2, menos 4fecha parênteses e Sabre parêntesesmenos 2, menos 2fecha parênteses.

a) Multiplique apenas as abscissas do quadrado PQRS por menos3 obtendo os pontos Plinha, Qlinha, Rlinha e S linha.

Represente o quadrilátero PlinhaQlinhaRlinhaSlinha no mesmo sistema de eixos cartesianos.

b) Multiplique apenas as ordenadas do quadrado PQRS por menos3, obtendo os pontos Pduas linhas, Qduas linhas, Rduas linhas e Sduas linhas.

Represente o quadrilátero Pduas linhasQduas linhasRduas linhasSduas linhas no mesmo sistema de eixos cartesianos.

Página 318

7 As transformações nas artes

Podemos reconhecer algumas transformações geométricas nas obras de arte, em elementos arquitetônicos e em vários outros objetos e imagens.

Ao criar uma obra de arte, muitos artistas aplicam os conceitos de simetria e repetição de padrões. O artista gráfico holandês M. C. écher (1898 a 1972), por exemplo, destaca-se pela habilidade de criar imagens com efeitos de ilusão de ótica e padrões obtidos a partir de figuras simples, como as observadas na obra reproduzida a seguir.

Fotografia. Obra de arte que lembra um mosaico composto por sequência de três peixes amarelos conectados pela boca; as caudas dos peixes se conectam com as cabeças de três lagartos na cor vermelha. No fundo azul se formam imagens de três patos em cada conjunto. — M. C. écher. Peixe/pato/lagarto, 1948, 30,5 centímetros por 32,5 centímetros.

Observe que na imagem três desenhos se repetem: peixe, pato e lagarto. Todos eles apresentam simetria em relação a uma reta.

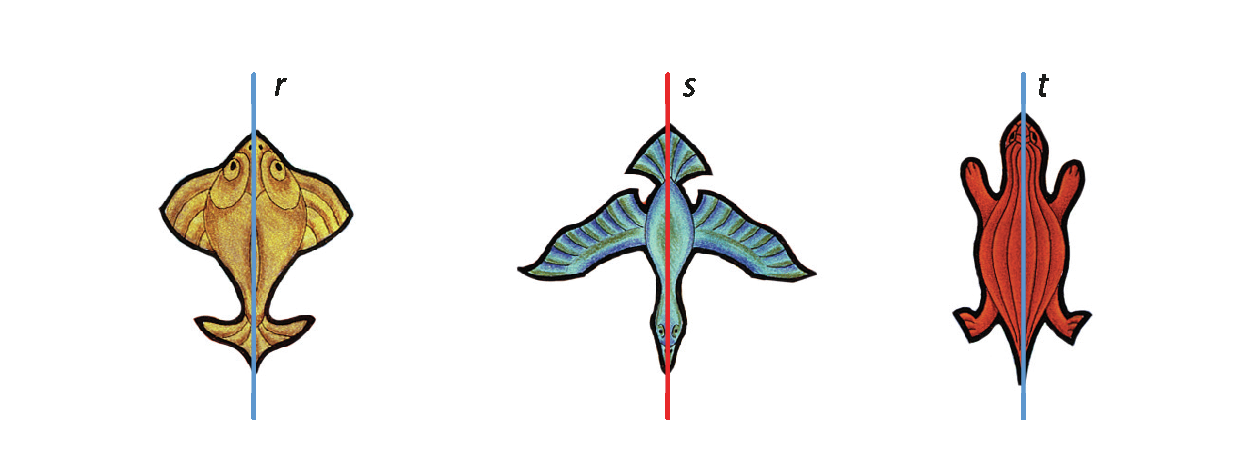
Ilustração. Peixe amarelo da fotografia anterior. Linha vertical r na metade da figura.
Ilustração. Pato azul da fotografia anterior. Linha vertical s na metade da figura.
Ilustração. Lagarto vermelho da fotografia anterior. Linha vertical t na metade da figura.

Página 319

Além disso, é possível identificar translações e rotações de figuras. Observe.

Ilustração. Corte retangular da fotografia anterior com dois peixes amarelos lado a lado em destaque. À esquerda, P1 e À direita, P2. — Nesse destaque, o peixe pê₁ foi deslocado na direção horizontal e no sentido da esquerda para a direita, resultando no peixe pê₂.

Ilustração. Corte quadrado da fotografia com três peixes amarelos organizados em círculo conectados pela boca onde se localiza um ponto amarelo. Peixe esquerdo, P1. Peixe direito: P2 e abaixo, P3. — Nesse destaque, note que o peixe pê₂ foi obtido do peixe pê₁ a partir de um giro, no sentido horário, de medida igual a 120graus ao redor do ponto amarelo. O peixe pê₃, por sua vez, foi obtido do peixe pê₂ a partir de um giro, no sentido horário, de medida igual a 120graus ao redor do ponto amarelo.

Para analisar

Observe novamente a reprodução da obra Peixe/pato/lagarto, de M. C. écher, e identifique outras translações e rotações presentes nela.

Ícone de tema contemporâneo Multiculturalismo.

As transformações geométricas também estão presentes em diferentes obras visuais indígenas, como a pintura corporal e a cestaria (técnica de produção de cestos). Uma característica comum nessas obras é a utilização de grafismos, desenhos que representam figuras geométricas ou imagens de pessoas e de animais. Observe as imagens a seguir.

Fotografia. Vista de trás de pessoas com os corpos pintados com formas geométricas na cores vermelho, preto e branco. — Indígenas da etnia Yawalapiti, no Parque Indígena do Xingu (Mato Grosso), 2012.

Fotografia. Cesto de palha com desenho de traços, linhas e triângulos. — Cesto dos povos Wayana e Apalaí. Museu do Índio, Embu das Artes (São Paulo).

Página 320

ATIVIDADES

faça as atividades no caderno

Influenciado pela cultura e pelas tradições dos povos africanos, o artista brasileiro Rubem Valentim (1922 a 1991) atribuía um caráter sagrado às suas produções. Aprecie, a seguir, a reprodução de duas de suas obras.

Fotografia. Obra de arte. Retângulo preto com círculo vermelho e desenho triangular com hastes no centro. Nas laterais, figura em formato de trapézio com traços. — Rubem Valentim, Emblemágico, 1979, 73 centímetros por 100 centímetros.

Fotografia. Obra de arte. Retângulo vermelho com círculo verde no centro com traços diagonais verdes e abaixo, figura semelhante a um tridente vermelho. — Rubem Valentim, Emblemágico 78, 1978, 75,7 centímetros por 103 centímetros.

• Agora, faça o que se pede.

a) Que transformações geométricas você reconhece na reprodução da obra Emblemágico? E na reprodução da obra Emblemágico 78?

Reúna-se com três colegas e façam uma pesquisa sobre a influência da cultura africana na formação do povo brasileiro.

2. Nas peças de cerâmica, os grafismos podem ser pintados ou feitos por incisões. Nos vasos de cerâmica marajoara reproduzidos na imagem, os grafismos foram obtidos por pequenos córtes.

Fotografia. Dois vasos cilíndricos de tamanhos diferentes. Na superfície dos vasos, desenhos geométricos. — Vasos de cerâmica marajoara. Belém (Pará).

Que transformações geométricas você reconhece nesses vasos?

3. As figuras a seguir foram criadas com base em grafismos indígenas. Observe.

Ilustração. Faixa verde com sequências de desenhos compostos por linhas dobradas. Ilustração. Faixa vermelha com sequências de quadrados com x dentro. Ilustração. Faixa verde escuro com sequências de desenhos compostos por linhas dobradas pretas.

•

Ícone de atividade com elaboração de problemas.

Inspirado pelas imagens apresentadas, crie um grafismo em uma folha de papel quadriculado.

Página 321

Ícone. Pasta azul e rosa com segmentos de reta.

Estatística e Probabilidade

faça as atividades no caderno

Pesquisa amostral e pesquisa censitária

Duas ideias muito importantes estão presentes nas pesquisas: a ideia de população e a de amostra.

População é o conjunto de todos os elementos que contêm uma característica que se quer estudar. A população pode ser formada, por exemplo, pelos habitantes de determinada cidade ou pelas peças produzidas por uma fábrica em certo período.

Ilustração. Grupo com 30 estudantes. São meninos e meninas de etnias variadas e estão todos de uniforme escolar que consiste em camisetas e bermudas azuis. Cota abaixo: População.

Amostra de uma população é uma parte da população que queremos estudar.

Ilustração. Grupo com 11 estudantes. São meninos e meninas de etnias variadas e estão todos de uniforme escolar que consiste em camisetas e bermudas azuis. Cota abaixo: Amostra da população.

Por exemplo, em uma pesquisa sobre a idade dos funcionários das 18 escolas públicas de uma cidade, temos:

• População: todos os funcionários dessas escolas.

• Amostra: funcionários de 10 das 18 escolas públicas dessa cidade.

Uma pesquisa estatística pode ser feita acessando toda a população (pesquisa censitária) ou uma parte dela (pesquisa amostral). Em geral, opta-se pelas pesquisas amostrais por razões econômicas e ou ou pela impossibilidade de acessar toda a população.

Ilustração. Homem adulto moreno, de camiseta bege e calça e sapatos azuis. Ele está segurando uma prancheta nas mãos e diz: São exemplos de pesquisas amostrais as de intenção de voto e as de opinião. Já os censos demográficos, por exemplo, são pesquisas censitárias.

Página 322

▶ Estatística e Probabilidade

ATIVIDADES

faça as atividades no caderno

1. Leia as afirmações a seguir e copie no caderno a(s) verdadeira(s).

a) Uma amostra é uma parte da população.

b) Uma pesquisa censitária é feita consultando parte da população.

c) Uma pesquisa amostral é feita consultando toda a população.

d) Se o público-alvo for pequeno, é indicado fazer uma pesquisa amostral.

2. Leia a pesquisa descrita em cada item, identifique a população e, depois, classifique-a em censitária ou amostral.

a) A dona de uma loja que vende produtos pela internet decidiu avaliar o grau de satisfação de seus clientes com o atendimento no último mês. Para isso, todo cliente que fizesse alguma compra precisava, no site, classificar o atendimento em ruim, regular ou ótimo.

b) Em um prédio com 240 moradores, foi feita uma pesquisa com 50 moradores, escolhidos aleatoriamente, para saber a intenção de voto para síndico do prédio.

c) Para fazer o recadastramento dos alunos de uma academia, foi necessário ligar para cada um e obter informações atualizadas.

Ilustração. Uma mulher branca, olhos azuis, cabelo ruivo amarrado em rabo de cavalo, está sentada atrás de uma mesa, sobre a mesa há um computador, um mouse, que está sendo usado pela mulher, e um teclado de computador. A mulher segura um microfone na outra mão, que está conectado a um fone de ouvido, e está dizendo: Alô! É o Paulo? Preciso atualizar seu cadastro.

Reúna-se com alguns colegas para realizar uma pesquisa estatística. Ao final da pesquisa, produzam um relatório escrito procurando responder às questões a seguir.

Ilustração. Folha de caderno com as informações: 1. Qual é o tema da pesquisa? Por que vocês escolheram esse tema? 2. Que perguntas serão feitas? 3. A pesquisa será censitária ou amostral? Por quê? 4. Como será feita a coleta de dados? 5. Que tipos de gráficos vocês vão construir para organizar os dados obtidos? Por que escolheram esses tipos de gráficos? 6. O que é possível concluir a partir dos gráficos construídos: 7. As questões propostas inicialmente foram respondidas? 8. Como vocês vão apresentar as conclusões da pesquisa para a turma?

Página 323

Trabalho em equipe

faça as atividades no caderno

Você e seus colegas de grupo vão realizar uma pesquisa e, para isso, precisam identificar as etapas da pesquisa, elaborar um questionário, entrevistar algumas pessoas e produzir um relatório.

Hábitos esportivos

Justificativa

A prática regular de esportes traz inúmeros benefícios para a saúde física e mental. Além disso, pode ser uma maneira divertida de passar o tempo com os amigos e com a família. Sabendo disso, você e seu grupo vão realizar uma pesquisa estatística para saber se as pessoas que moram na sua cidade têm o hábito de praticar esportes.

Com base em resultados de pesquisas estatísticas podemos tirar conclusões a respeito da população em estudo.

Ilustração. Mulher de cabelo curto e vestido verde em pé no portão de uma casa. À frente dela, três crianças, uma menina e dois meninos, uniformizadas e com mochilas. Uma delas faz anotações.

Objetivo

• Realizar uma pesquisa estatística para saber qual esporte as pessoas de sua comunidade escolar praticam e com qual frequência.

Apresentação

• Relatório escrito com gráficos e tabelas.

Questões para pensar em grupo

• Todos já participaram de uma pesquisa estatística?

• A pesquisa será censitária ou amostral? Justifique.

• Como será feita a coleta de dados?

• Quais perguntas serão feitas na entrevista?

• Quais tipos de gráficos e tabelas serão utilizados no relatório?

• Quais estratégias serão utilizadas para a construção dos gráficos e das tabelas?

• Quais informações vocês acham indispensáveis no relatório?

• O que é possível concluir analisando os dados obtidos na pesquisa?

Não se esqueçam

• Escrevam as etapas necessárias para a realização da pesquisa.

• Elaborem um questionário para ser utilizado nas entrevistas.

• Para construir os gráficos vocês podem utilizar planilhas eletrônicas.

• Agendem um horário para realizar as entrevistas.

• Organizem um cronograma para a realização de cada etapa da pesquisa.

Página 324

Ilustração. Ícone. Caderno na vertical com um lápis.

Atividades de revisão

faça as atividades no caderno

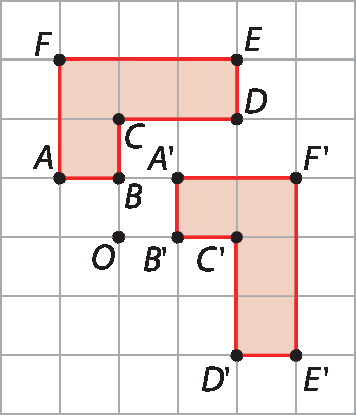
1. Com base na figura, classifique no caderno as afirmações a seguir em verdadeiras ou falsas, sabendo que o polígono AlinhaBlinhaClinhaDlinhaElinhaFlinha foi obtido a partir do polígono á bê cê dê é éfe por uma translação.

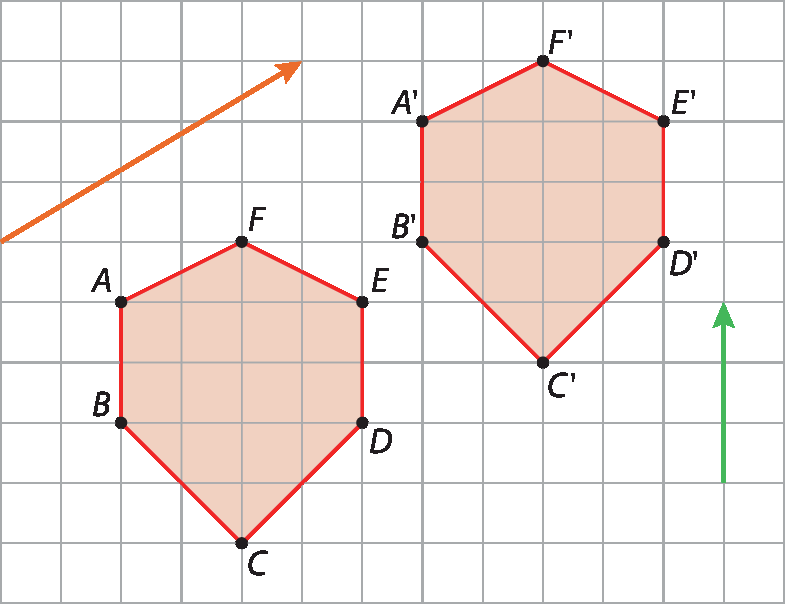
Gráfico. Malha quadriculada com figura geométrica ABCDEF vermelha no canto inferior esquerdo. Acima, seta diagonal para cima. No canto superior direito, figura geométrica vermelha igual A linha, B linha, C linha, D linha, E linha, F linha.

a) O vetor dessa translação é o de cor verde.

b) Os segmentos

\overline{BC}

\overline{B' C'}

têm mesma medida de comprimento.

c) As aberturas dos ângulos correspondentes desses polígonos não têm a mesma medida.

d) A medida de distância entre os pontos D e Dlinha é igual à medida de distância entre os pontos F e Flinha.

2. Observe como Laura descreveu a rotação representada.

Ilustração. Folha de caderno com o texto: O polígono A linha, B linha, C linha, D linha foi obtido do polígono ABCD por meio de um giro no sentido horário com medida de 285 graus ao redor do ponto O.

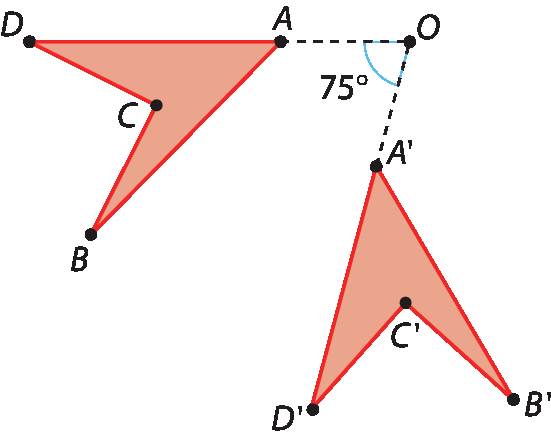
Ilustração. Polígono ABCD. À direita, ponto O. Abaixo, polígono A linha, B linha, C linha, D linha. Reta tracejada de O para A e de O para A linha. O ângulo AOA linha mede 75 graus e indica que a figura ABCD foi rotacionada 75 no sentido anti-horário ao redor do ponto O.

a) Você concorda com a descrição feita por Laura?

b) De que outra maneira ela poderia ter descrito essa rotação?

3. As transformações geométricas também estão presentes em bordados. Considere alguns exemplos de padrões de bordados.

Ilustração. Malha quadriculada composta por figura arredondada na cor verde com partes vazadas. Ilustração. Malha quadriculada composta por quadrados e traços diagonais vermelhos. Ilustração. Malha quadriculada composta por fileiras de quadrados e formas triangulares no centro.

a) Que transformações geométricas você reconhece nesses padrões?

Inspirado pelas imagens anteriores, crie um padrão de bordado em uma folha de papel quadriculado. Em seguida, compartilhe seu desenho com os colegas.

Página 325

Lembre-se: Escreva no caderno!

4. Observe o pentágono PQRST a seguir.

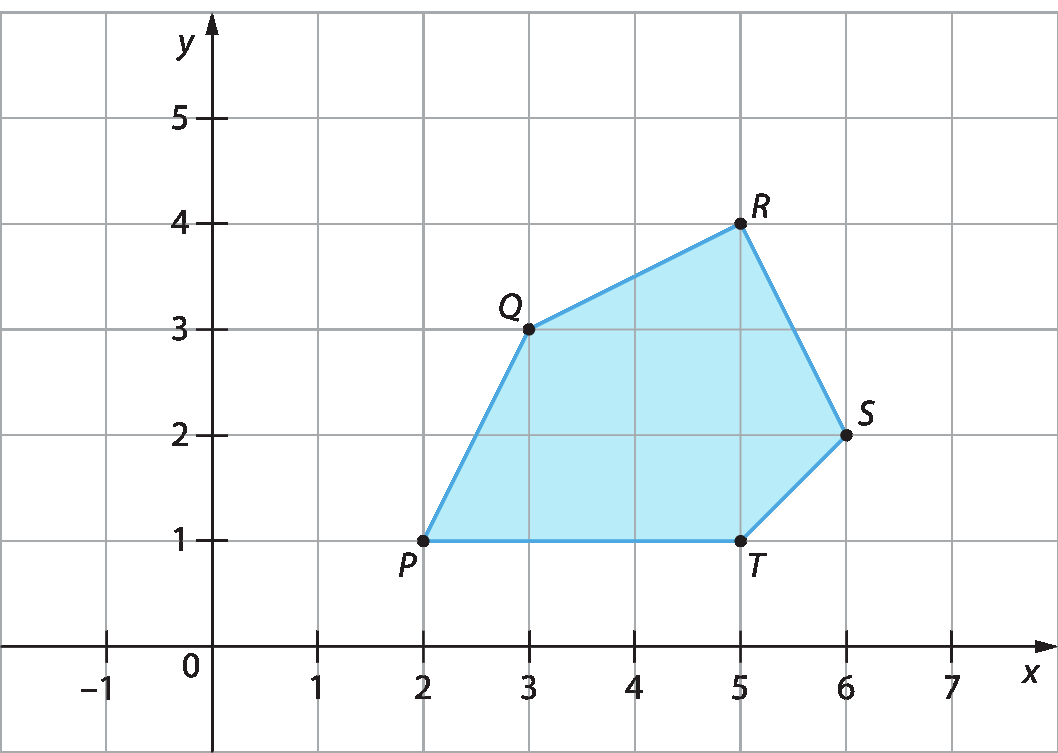
Gráfico. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 1 a 7. Eixo y com intervalo de 0 a 5. Figura geométrica azul PQRST no primeiro quadrante com vértices compostos pelos pontos: P (2, 1) Q (3, 3) R (5, 4) S (6, 2) T (5, 1).

a) Quais são as coordenadas do simétrico em relação ao eixo y deste pentágono?

b) Em uma folha de papel quadriculado, determine um sistema de eixos cartesianos e represente nele os pentágonos PQRST e PlinhaQlinhaRlinhaSlinhaTlinha.

5. Quais são as coordenadas do simétrico em relação ao eixo x do quadrilátero de vértices aabre parênteses1, 1fecha parênteses, Babre parênteses1, 3fecha parênteses, Cabre parênteses5, 5fecha parênteses e Dabre parênteses5, 2fecha parênteses?

6. Quais são as coordenadas do simétrico do quadrilátero cujos vértices são a(‒2, ‒ 6fecha parênteses, Babre parêntesesmenos3, menos 1fecha parênteses, Cabre parêntesesmenos 5, menos 3fecha parênteses e Dabre parêntesesmenos 5, menos 5fecha parênteses em relação à origem?

7. Copie a figura a seguir em uma folha de papel quadriculado.

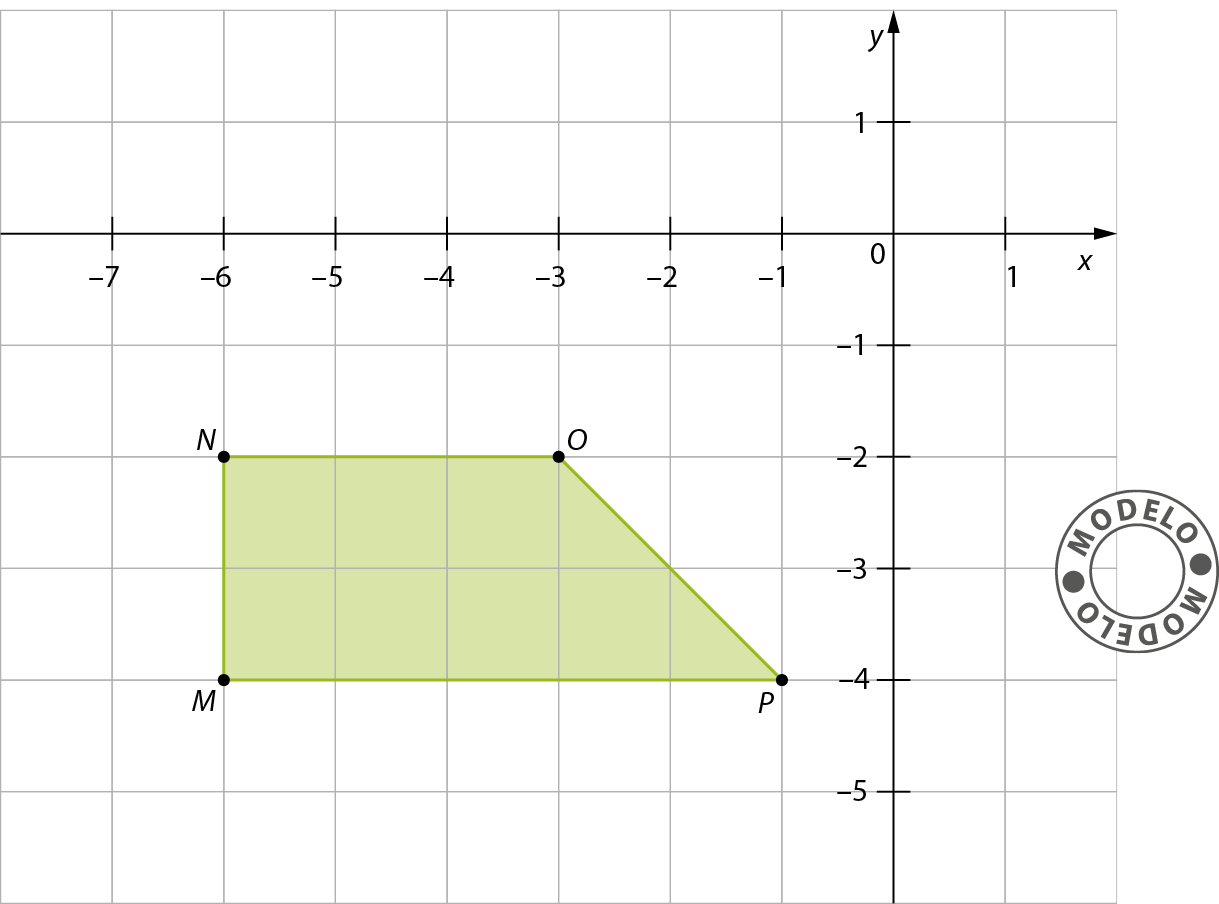
Gráfico. Modelo. Malha quadriculada com plano cartesiano. Eixo x com intervalo de menos 7 a 1. Eixo y com intervalo de menos 5 a 1. Trapézio verde M N O P no terceiro quadrante com vértices compostos pelos pontos: M (menos 6, menos 4) N (menos 6, menos 2). O (menos 3, menos 2) P (menos 1, menos 4).

a) Escreva as coordenadas dos vértices do trapézio ême êne ó pê.

b) Multiplique apenas as ordenadas dos vértices do trapézio ême êne ó pê por 2, localize no plano cartesiano as coordenadas Mlinha, Nlinha, Olinha e Plinha e desenhe o novo quadrilátero.

c) Multiplique apenas as abscissas dos vértices do quadrilátero ême êne ó pê por menos2, localize no plano cartesiano as coordenadas Mduas linhas, Nduas linhas, Oduas linhas e Pduas linhas e desenhe o novo quadrilátero.

d) Obtenha o simétrico do quadrilátero Mduas linhasNduas linhasOduas linhasPduas linhas em relação à origem.

Página 326

Para finalizar

faça as atividades no caderno

organize suas ideias

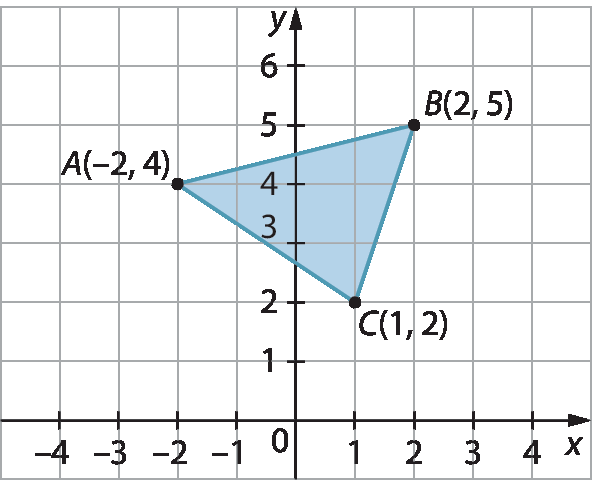
Observe e responda

Considere as imagens a seguir.

Ilustração. Vista de cima de prato com presunto, queijo e tomate, com garfo e faca do lado esquerdo. Do lado direito, cesta com pão. Na frente do prato com presunto, queijo e tomate e da cesta com o pão, está um caderno aberto com a seguinte receita: Sanduíche 10
Bauru simples 1 pão francês 2 fatias de queijo 2 fatias de presunto 2 fatias de tomate.

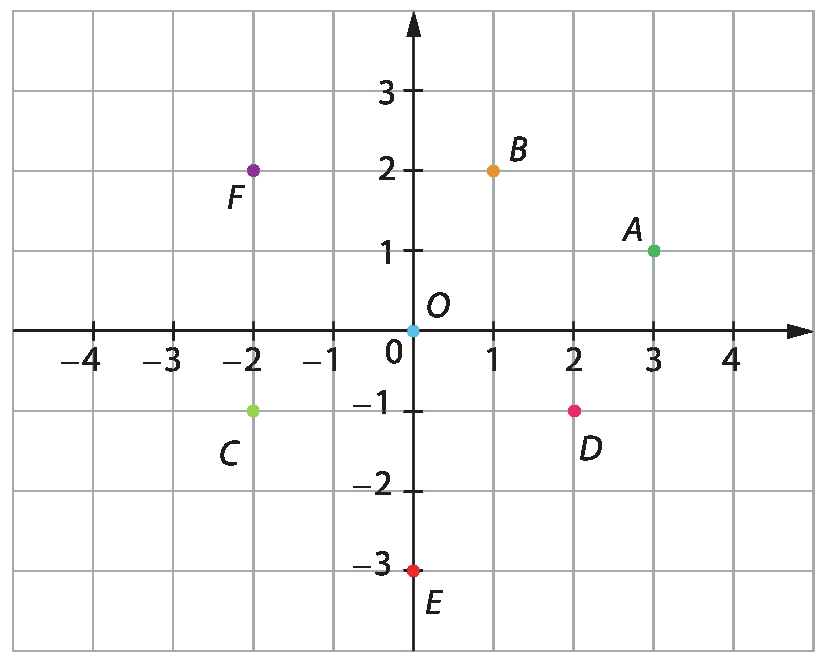
Gráfico Malha quadriculada plano cartesiano. Eixo x com intervalo de menos 4 a 4. Eixo y com intervalo de menos 3 a 3. Ponto A: 3, 1. B: 1, 2. C: menos 2, menos 1. D: 2, menos 1. E: 0, menos 3. F: menos 2, 2.

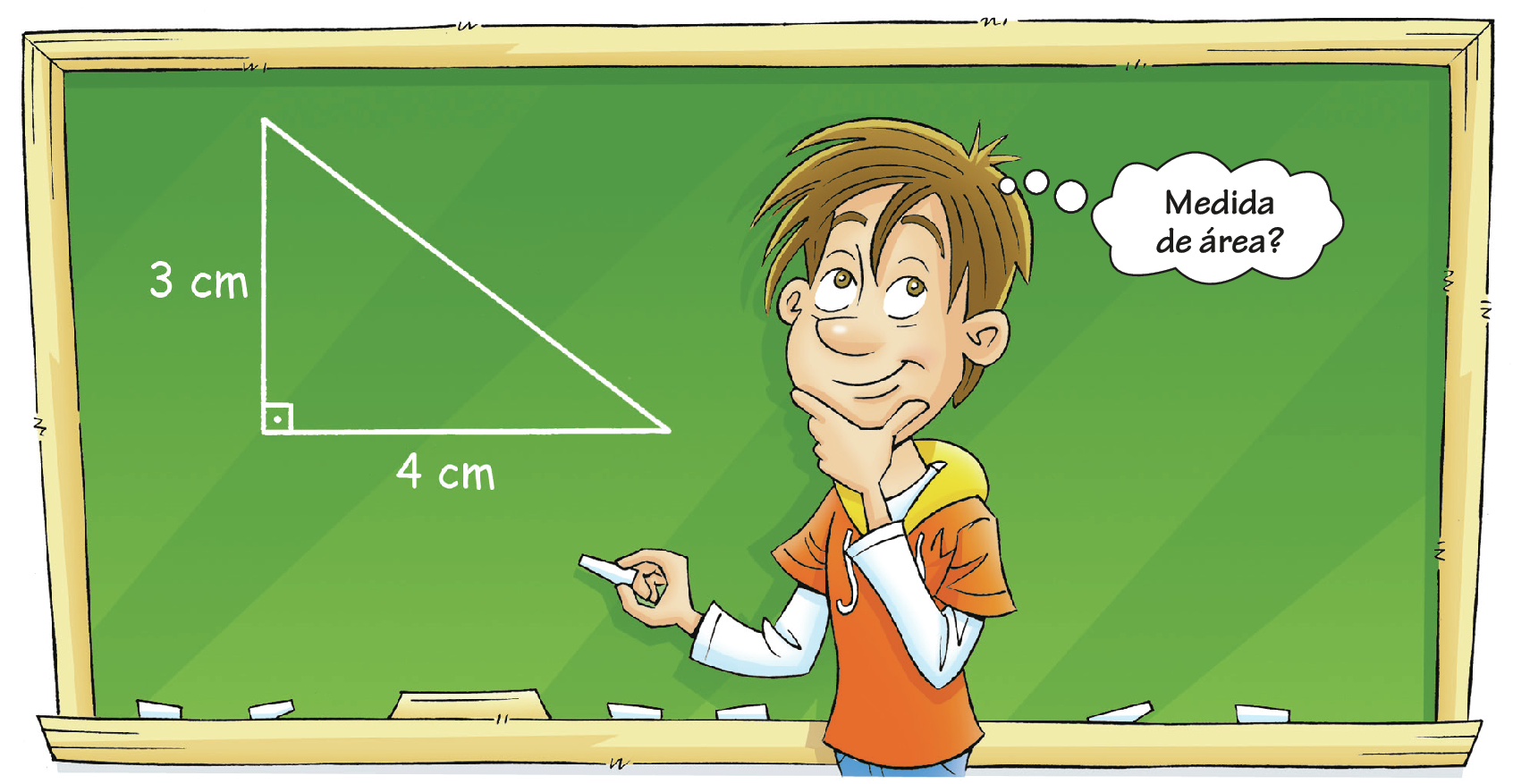
Ilustração. Rapaz de cabelo castanho e blusa laranja com gorro amarelo sobre uma camiseta de mangas compridas brancas. Ele pensa: 'medida da área?'. Atrás dele há uma lousa onde está desenhado um triângulo retângulo com catetos de medidas 3 centímetros e 4 centímetros.

Com base nas imagens e também no que você aprendeu nesta Unidade, responda às questões no caderno.

1. Qual é a medida de área do triângulo desenhado no quadro anterior?

2. De acordo com a imagem do sanduíche, para fazer um bauru simples, devem ser usadas duas fatias de queijo e duas de presunto. Quantas fatias de presunto e quantas de queijo seriam necessárias para fazer 3 desses baurus? E 4? E 5?

3. Com base no plano cartesiano, indique 4 dos pontos destacados que podem formar os vértices de um quadrado.

Página 327

Registre

Para finalizar o estudo desta Unidade, reúna-se com um colega e façam o que se pede.

1. Que polígonos vocês conhecem? Desenhem alguns exemplos e expliquem como calcular a medida de área de cada um deles.

2. O que é proporção?

3. Quantos eixos de simetria possui um quadrado? E um retângulo?

4. Na abertura desta Unidade, vocês responderam a algumas questões no boxe “Para começar...”. Retomem as questões e analisem se vocês dariam outras respostas a elas agora. Depois, escrevam um texto explicando o que aprenderam nesta Unidade.

Para conhecer mais

Geometria na Amazônia (Coleção A descoberta da Matemática)

Ernesto Rosa

São Paulo: Ática, 2002.

Assuntos importantes da Matemática do Ensino Fundamental são abordados de fórma lógica e clara nessa história dos irmãos André e Isabela. Enquanto sobrevoam a Floresta Amazônica, o avião em que estão colide com um urubu e, depois de o piloto fazer um pouso forçado, eles precisam construir um balão para deixar a floresta.

Capa de livro. Geometria na Amazônia. Na parte inferior, ilustração de uma aldeia indígena. No centro, uma fogueira.

Uma proporção ecológica

(Coleção A descoberta da Matemática)

Luzia Faraco Ramos

São Paulo: Ática, 2008.

Uma viagem para participar de um projeto de pesquisa e de divulgação sobre a importância da reciclagem do lixo leva as amigas Mari, Isabela e Lina a viver uma aventura inesperada. Qual seria a reação das pessoas à proposta de reciclar lixo? Elas entenderiam a importância desse projeto ou tentariam sabotá-lo?

Enquanto vivem essa aventura, as meninas e seus amigos aprendem razão, proporção, regra de três e porcentagem.

Capa de livro. Uma proporção ecológica. Na parte inferior, pessoas e atrás, árvore e latas de lixos recicláveis.