Página 328

Avaliação de resultado

faça as atividades no caderno

MOSTRE O QUE VOCÊ APRENDEU

1. Gabriela está fazendo uma reforma em sua casa e vai precisar pintá-la. O gerente da empresa contratada por ela informou que o tempo para finalizar a pintura dependeria da quantidade de pintores contratados e que 2 pintores realizariam o serviço em 6 dias. Se Gabriela contratar 4 pintores, em quanto tempo eles finalizarão a pintura, mantendo o mesmo ritmo de trabalho?

a) 2 dias

b) 3 dias

c) 6 dias

d) 12 dias

2. As peças a seguir fazem parte de um quebra-cabeça tridimensional. Nelas, os cubinhos possuem medida de volume igual a 1 cm³centímetros cúbicos, sendo que não há cubinhos escondidos atrás das pilhas.

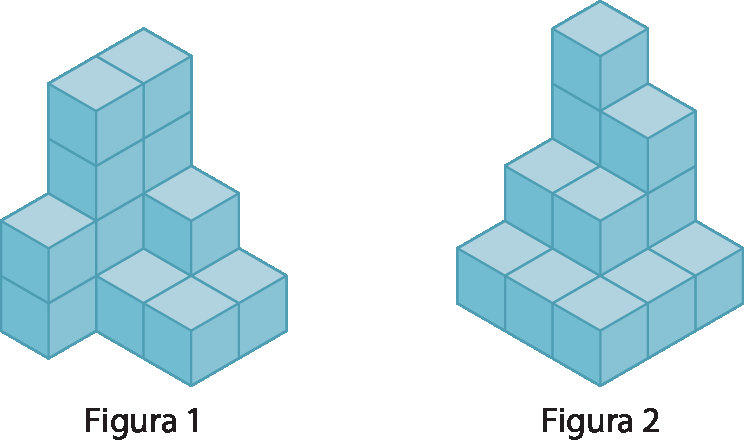
Qual alternativa indica a medida de volume da Figura 1 e a da Figura 2, nessa ordem?

a) 15 cm³centímetros cúbicos e 16 cm³centímetros cúbicos

b) 11 cm³centímetros cúbicos e 11 cm³centímetros cúbicos

c) 16 cm³centímetros cúbicos e 16 cm³centímetros cúbicos

d) 15 cm³centímetros cúbicos e 15 cm³centímetros cúbicos

3. A sequência numérica na formafórma (aá₁, aá₂, aá₃, aá₄, ...reticências) em que o enésimo termo é dado por aá_n = 7_n, em que n é um número natural maior ou igual a 1, é:

a) (71, 72, 73, 74, ...reticências)

b) (7, 14, 21, 28, ...reticências)

c) (0, 7, 14, 21, ...reticências)

d) (1, 2, 3, 4, ...reticências)

a) 1

b) 2

c) 4

d) 8

5. O gráfico a seguir representa os 30 veículos que foram vendidos no último mês em certa concessionária, segundo as quatro opções de cores disponíveis.

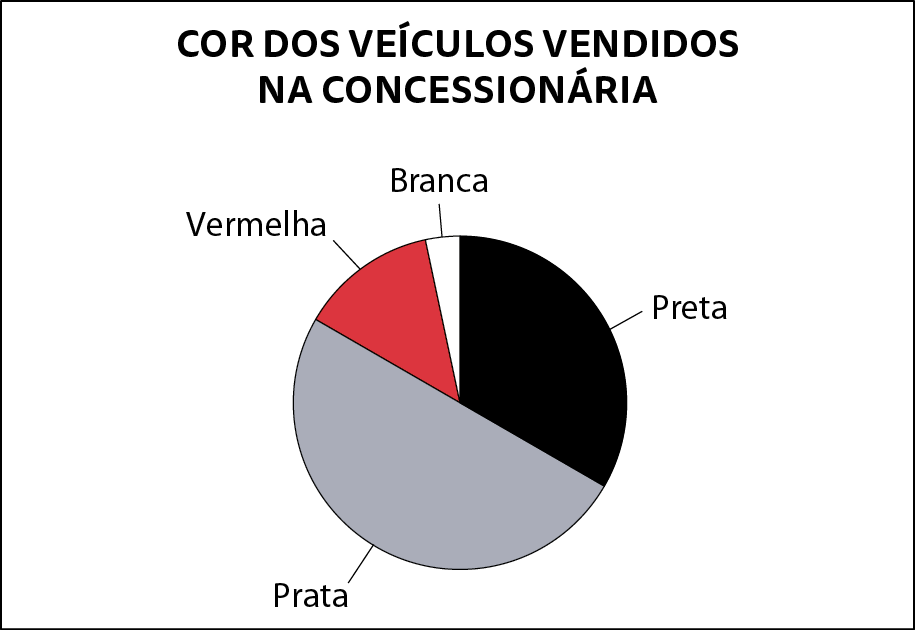
Dados obtidos pela concessionária em dezembro de 2022.

Qual alternativa indica uma possibilidade para relacionar cada setor do gráfico a uma fração da quantidade de veículos vendidos?

6. O esquema a seguir representa a medida das alturas de Sabrina e de seus pais.

Qual medida melhor representa a altura da mãe de Sabrina?

a) 0,675 mmétro

b) 1,50 mmétro

c) 1,51 mmétro

d) 1,70 mmétro

Página 329

7. A uma medida de velocidade média de 70 km/hquilômetros por hora, Felipe percorreu com seu automóvel a medida de distância entre duas cidades em 40 minutos. Quanto tempo Felipe levaria para percorrer esse mesmo trajeto a uma medida de velocidade média de 80 km/hquilômetros por hora?

a) 30 minutos

b) 35 minutos

c) 45 minutos

d) 140 minutos

8. Cada opção a seguir indica três medidas de comprimento.

Qual dessas opções pode indicar as medidas de comprimento dos lados de um triângulo?

a) A

b) B

c) C

d) D

9. O quadro a seguir mostra a quantidade de gols marcados nos cinco primeiros jogos de um campeonato de futebol.

Qual foi a média aritmética de gols marcados nesses jogos de futebol?

a) 4

b) 3

c) 3,2

d) 16

11. Em uma loja, um tênis que custava R$ 200,00duzentos reais entrou em promoção e está sendo vendido com desconto de 45%. Qual alternativa indica o preço do tênis com esse desconto?

a) R$ 90,00noventa reais

b) R$ 110,00 cento e dez reais

c) R$ 290,00 duzentos e noventa reais

d) R$ 245,00 duzentos e quarenta e cinco reais

12. Taís faz sucos naturais e bolo para vender. Ela cobra R$ 6,00seis reais pelo suco e R$ 9,00nove reais por pedaço de bolo. Qual expressão algébrica descreve o valor arrecadado por Taís com a venda de x sucos e y pedaços de bolo?

a) x + y + 15

b) x + y

c) 6x + 9y

d) 9x + 6y

13. A figura a seguir representa o formato e as dimensões internas de um aquário.

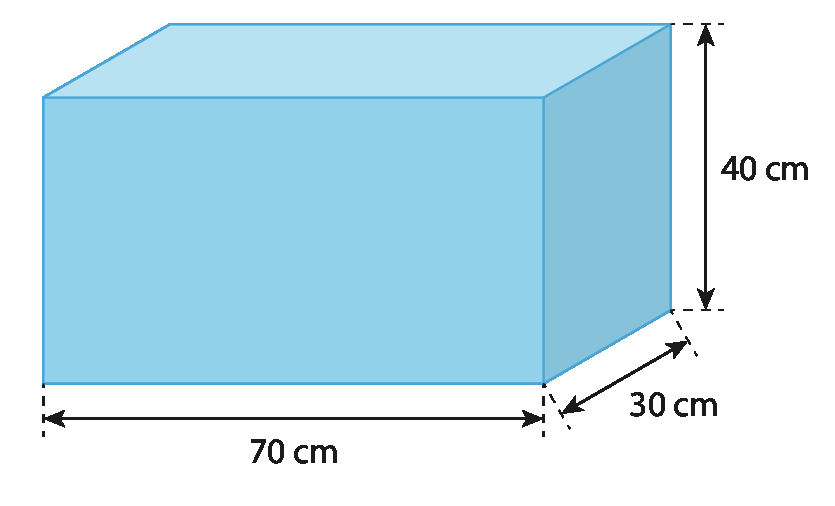
Qual item indica a medida de volume, em centímetro cúbico, desse aquário e a de sua capacidade máxima, em litro, nessa ordem?

a) 84.00084000 cm³centímetros cúbicos; 84 Llitros

b) 840 cm³centímetros cúbicos; 840 Llitros

c) 84 cm³centímetros cúbicos; 84 Llitros

d) 84.00084000 cm³centímetros cúbicos; 84.00084000 Llitros

Página 330

RESPOSTAS

CAPÍTULO 1

Página 32

1. alternativa b

2. a) Os números 35 e 55 não são primos entre si, pois mdcême dê cê (35, 55) = 5.

c) O mdcême dê cê (5, 15) é maior que o mdcême dê cê (3, 7).

3. alternativa c

4. daqui a 42 dias

5. 120 biscoitos

6. a) 450 segundos

b) Carla: 54 voltas; Jane: 60 voltas

7. a) 4 estudantes

b) 172cento e setenta e duas equipes

c) nos cursos A e D

8. 1.0501050 = 2 ⋅ 3 ⋅ 52 ⋅ 7

CAPÍTULO 2

Página 69

1. a) +5; ‒7

b) +1

c) ‒3

2. alternativas aa e êbbê

3. ‒5

4. zero

6. a) ‒12 < +15

b) 0 > ‒ 3

c) +12 > ‒15

d) + 4 < +7

7. a) a cidade B; a cidade Aa

b) na cidade B

c) ‒1 °Cgrau Célsius

8. a) ‒12

b) ‒ 9

c) ‒ 4

d) ‒ 3

e) Exemplo de resposta: 1 e (–1)

9. a) associativa

10. a) ‒10

b) +10

c) +111

d) ‒ 95

e) ‒ 26

12. a) ‒1.8241824

b) 2.2082208

c) ‒105

d) 17

14. a) 53

b) 500quinhentas caixas

c) 6 lotes

15. a) 33

b) 16 cubinhos

16. a) Aa: 1; B: 8; C: 27; D: 64; Eê: 125; F: 216

b) 13, 23, 33, 43, 53 e 63

c) 1, 9, 36, 100, 225 e 441

d) 12, 32, 62, 102, 152 e 212

e) A soma das seis bases de b é igual à sexta base de d.

f) Em cada caso, a soma das primeiras bases de b é igual à respectiva base de d.

17. às 14 horas e 19 minutos

18. a) 25

b) sim; 121 = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + + 17 + 19 + 21

19. a) 64 bolinhas

b) 216duzentas e dezesseis bolinhas

c) 8 ⋅ 1003 bolinhas

CAPÍTULO 3

Página 91

1. a) 83°graus e 143°graus

2. alternativa b

3. alternativa a

4. 160°graus

6. a) 40°graus

b) 70°graus

c) 30°graus

d) 120°graus

7. a) x = 30°graus e y = 40°graus

b) x = 110°graus e y = 30°graus

CAPÍTULO 4

Página 128

3. dormir

4. Júlia está correta, e Ricardo está errado.

Página 331

5. R$ 21,20vinte e um reais e vinte centavos

6. Exemplo de resposta: Porque o resultado de 2,25 + 3,75 é 6; portanto, esse agrupamento facilita o cálculo da operação mentalmente.

7. a) 0

b) ‒1,5

c) ‒ 0,5

d) 1,75

8. a) + 0,8

d) 0

e) ‒1,7

9. 3 kgquilogramas

13. R$ 109,35cento e nove reais e trinta e cinco centavos

14. 2,9

17. 30

18. não

CAPÍTULO 5

Página 148

1. a) o caminho de João

b) 100 cmcentímetros

2. a) 510,7 cmcentímetros

b) 90 cmcentímetros

3. 280 mmétros

4. 0,0003 mmmilímetro e 0,01 mmmilímetro

5. a) aproximadamente 780.000.000780000000 kmquilômetros

b) 7,8 ⋅ 108 kmquilômetros

6. a) Daniela

b) Mariana

c) 16 minminutos

7. 5 kgquilogramas

CAPÍTULO 6

Página 167

1. a) 188 cmcentímetros

b) 300 cmcentímetros

2. alternativa d

3. a) x + y

b) aa + b + c + d

c) m ⋅ m ou m²

d) aa ⋅ aa ⋅ aa ou a³

4. a) 2 ⋅ x

c) x + 5

5. a) x + 20

b) 100 cmcentímetros

c) 120 cmcentímetros

6. a) medida de área em metro quadrado: x(x + 25)

b) medida do perímetro em metro: 4x + 50

c) 3.7503750 m²métros quadrados; 250 mmétros

8. a) 14

b) 168

c) 4

b) 0

10. a) (‒ 3, ‒ 2, ‒1)

b) (2, 3, 5, 7, 11, 13, 17, 19)

c) (0, 11, 22, 33, 44, 55, ...reticências)

11. a) (9, 18, 27, 36, 45, ...reticências)

b) (2, 5, 10, 17, 26, ...reticências)

c) (1, 11, 21, 31, 41, ...reticências)

d) (2, 8, 10, 18, 28, ...reticências)

12. a) não

c) n = 2 ⋅ (x ‒ 1) ou n = 2x ‒ 2

13. Todas as sequências são recursivas.

14. 1.9991999

15. Exemplo de resposta:

aá_n = 10_n ‒ 2 e aá₁ = 8

aá_{n + 1} = aá_n + 10

CAPÍTULO 7

Página 203

1. a) 3x + 3 = 24; x = 7

b) 2x ‒ 25 = 7; x = 16

2. Aa – IIItrês; B – Ium; C – IVquatro; D – IIdois

Página 332

b) Não tem solução.

c) Não tem solução.

4. a) x = ‒10

c) y = 40

5. a) 12x

b) 5 cmcentímetros

c) 1.2001200 cmcentímetros

d) 2x ⋅ 4x ou 8x2

6. alternativa d

7. 2.3002300 kmquilômetros

8. R$ 18,00dezoito reais

9. aproximadamente 6.9606960 mmétros

10. R$ 24.000,00vinte e quatro mil reais

11. Jorge: 5; Ricardo: 2; Régis: 7

12. 8 filmes de ficção científica, 16 de comédia e 32 de aventura

d) Não tem solução.

14. x > 7

13. a) 2x + 4 ⩽ 12

b) 4 toneladas

16. R$ 208,00duzentos e oito reais

17. a) não

b) 18.70018700 + 12.40012400 < 34.00034000 ou 31.10031100 < 34.00034000

18. 7,5

19. O mais novo tem 7 anos e o mais velho, 28 anos.

CAPÍTULO 8

Página 219

1. a) x = 130°graus e y = 50°graus

b) x = 110°graus e y = 125°graus

2. alternativa b

3. alternativas b e eê

5. a) sim; não

b) sim

c) Há infinitos eixos de simetria.

6. aproximadamente 27,3 mmétros

CAPÍTULO 9

Página 242

vértices: Aa, B e C

2. alternativa d

3. a) 45°graus

b) 42°graus

c) 35°graus

d) 90°graus

e) 55°graus

f) 65°graus; 65°graus

4. Respostas possíveis: 80°graus e 80°graus ou 20°graus e 140°graus

6. a) Todos são triângulos retângulos isósceles.

b) 4 triângulos pequenos

7. Os esboços IVquatro e Vcinco estão errados, pois os triângulos não existem.

8. Não é possível construir um triângulo com as medidas de comprimento 4 cmcentímetros, 5 cmcentímetros e 10 cmcentímetros.

9. 5 cmcentímetros

10. a) sim

b) não

12. 3x + 30°graus + x + 10°graus + 2x ‒ 10°graus = 180°graus; x = 25°graus

13. a) retângulo

b) retângulo; losango

c) losango

14. Aa – IIItrês; B – Ium; C – IIdois

16. um paralelogramo

17. a) x = 6 cmcentímetros

b) x = 7,5 cmcentímetros

17. a) x = 60°graus

b) x = 36°graus

19. a) falsa

b) verdadeira

c) verdadeira

d) verdadeira

e) verdadeira

f) verdadeira

g) verdadeira

20. a) 3 trapézios isósceles

b) 3 losangos

21. 24 cmcentímetros

22. a) um octógono

b) 32 cmcentímetros

23. x = 30°graus; y = 70°graus; z = 40°graus

24. alternativa c

Página 333

CAPÍTULO 10

Página 263

1. a) 242 lotes

b) R$ 18.150.000,00dezoito milhões cento e cinquenta mil reais

2. a) 5 salas

b) 2,42 hahectares

3. 100 lajotas

4. 549 m²métros quadrados

5. a) 746.000746000 m²métros quadrados

b) 186.500186500 m²métros quadrados

6. 10 dm²decímetros quadrados

7. 19 cm²centímetros quadrados

8. A inclinação dos triângulos não é a mesma que a dos trapézios.

CAPÍTULO 11

Página 295

2. a) não

b) sim

b) aproximadamente 11%

e) aproximadamente 33% e 67%, respectivamente

5. R$ 200,00duzentos reais

6. aproximadamente 128 minminutos

7. R$ 28.000,00vinte e oito mil reais, R$ 21.000,00vinte e um mil reais e R$ 42.000,00quarenta e dois mil reais, respectivamente

8. 400 kgquilogramas

9. 16 cmcentímetros

10. 3.0003000 kmquilômetros

11. aproximadamente 2 kgquilogramas

13. 20%

14. a) aproximadamente R$ 1.331,48mil trezentos e trinta e um reais e quarenta e oito centavos

b) aproximadamente R$ 32,48 trinta e dois reais e quarenta e oito centavos

15. aproximadamente R$ 4,45 quatro reais e quarenta e cinco centavos

16. R$ 95,00noventa e cinco reais

17. a) plano semestral: R$ 360,00trezentos e sessenta reais; plano trimestral: R$ 420,00quatrocentos e vinte reais; plano mensal: R$ 480,00quatrocentos e oitenta reais

b) aproximadamente 14,3%

c) aproximadamente 33,33%

18. a) 20%

b) R$ 270,00 duzentos e setenta reais

19. a) R$ 142,50cento e quarenta e dois reais e cinquenta centavos; R$ 82,50oitenta e dois reais e cinquenta centavos

CAPÍTULO 12

Página 324

1. a) falsa

b) verdadeira

c) falsa

d) verdadeira

2. b) Exemplo de resposta: O polígono A'B'C'D'á linha bê linha cê linha dê linha foi obtido do polígono ABCDa bê cê dê por meio de um giro, no sentido anti-horário, com medida de 75°graus ao redor do ponto Oóh.

3. a) Exemplo de resposta: reflexão em relação à reta, reflexão em relação a um ponto, translação e rotação.

4. a) P' pê linha(‒2, 1), Q' quê linha(‒3, 3), R'érre linha (‒5, 4), S'ésse linha ícone de altura(‒ 6, 2) e T'tê linha (‒5, 1)

5. A' á linha(1, ‒1), B' bê linha(1, ‒3), C' cê linha(5, ‒5) e D' dê linha(5, ‒2)

6. A' á linha(2, 6), B' bê linha(3, 1), C' cê linha(5, 3) e D' dê linha(5, 5)

7. a) M(‒ 6, ‒ 4), N(‒ 6, ‒2), O(‒3, ‒2) e P(‒1, ‒ 4)

Página 334

REFERÊNCIAS BIBLIOGRÁFICAS COMENTADAS

ASIMOVasimóvi, Isaac. No mundo dos números. Tradução de Lauro S. Blandy. Rio de Janeiro: Francisco Alves, 1989. (Coleção Ciência).

A obra apresenta a Matemática por meio de uma linguagem simples e compreensível. Com abordagens não convencionais, solidifica as noções do significado e da aplicação dos números.

ÁVILA, Geraldo. A distribuição dos números primos. Revista do Professor de Matemática. São Paulo, n.número 19, p.página 19-26, 2º sem. semestre1991.

O artigo versa sobre a descoberta da distribuição da tabela de números primos e suas demonstrações.

BARBOSA, Ruy Madsen. Descobrindo padrões em mosaicos. 3. ed.terceira edição São Paulo: Atual, 2001.

Obra que convida a conhecer a fascinante arte de descobrir e criar padrões na Geometria plana.

BARBOSA, Ruy Madsen. Descobrindo padrões pitagóricos. 3. ed.terceira edição São Paulo: Atual, 2001.

O livro traz os conceitos que estruturam a pavimentação no plano fazendo emergir a Matemática oculta nesses padrões.

BAUMGART, John K. História da Álgebra. Tradução de Hygino H. Domingues. São Paulo: Atual, 1992. (Tópicos de história da Matemática para uso em sala de aula, v.volume 4.).

A obra traz a história da Álgebra, desde a etimologia passando da Álgebra antiga à Álgebra moderna.

BOLTIANSKI, Vladimir. G. Figuras equivalentes e equicompostas. Tradução de Seiji Hariki. São Paulo: Atual, 1996.

A obra se dedica a estudar certas questões relacionadas com a equicomposição de figuras, entre elas polígonos e poliedros.

BOYERBóiê, Carlcarl B.; MERZBACH, Uta C. História da Matemática. Tradução de Helena Castro. São Paulo: Blucher, 2012.

O livro apresenta um estudo aprofundado da história da Matemática desde o Egito antigo até as tendências mais recentes. Mostra também a fascinante relação entre o desenvolvimento dos conhecimentos sobre números, formasfórmas e padrões e a evolução da humanidade.

BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Brasil no Pisapiza 2018 [recurso eletrônico]. Brasília, DFDistrito Federal: Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira, 2020. ppágina.ponto 185.

O Pisapiza, programa internacional de avaliação de estudantes, é uma ferramenta importante para avaliar o desempenho dos estudantes que concluíram a Educação Básica, além de fornecer parâmetros que ajudam a definir o futuro da educação no país.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular – versão final. Brasília, DFDistrito Federal: MECMéqui, 2018.

Documento de caráter normativo que define o conjunto orgânico e progressivo de aprendizagens essenciais que todos os estudantes devem desenvolver ao longo das etapas e modalidades da Educação Básica.

BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCCBê êne cê cê: Contexto Histórico e Pressupostos Pedagógicos. Brasília, DFDistrito Federal: MECMéqui, 2019.

Material que apresenta a relação entre diferentes componentes curriculares de formafórma integrada, fazendo conexões com situações da realidade dos estudantes.

BRASIL. Sistema Internacional de Unidades (SIésse Í) [recurso eletrônico]. Tradução do Grupo de Trabalho luso-brasileiro do Inmetroin metro e IPQ. Brasília, DFDistrito Federal: Inmetroin metro, 2021. 842 kBquilobáites; pdfpê dê éfi.

O documento traz a revisão do Sistema Internacional de Unidades, por meio da adoção das novas definições das sete unidades de base, que entraram em vigor em 20 de maio de 2019, considerando o uso de sete constantes definidoras.

CARNEIRO, Mario; SPIRA, Michel. Oficina de dobraduras. Rio de Janeiro: IMPA/OBMEP, 2015.

O trabalho aborda a Geometria por meio de dobraduras como instrumento pedagógico, com demonstrações e atividades.

CENTURIÓN, Marília. Conteúdo e metodologia da Matemática: números e operações. São Paulo: Scipione, 1994.

A obra aborda noções fundamentais do conteúdo matemático e expressa a necessidade da construção dos conceitos de formafórma lógica.

CHI, Michelene T. H.; GLASER, Robert A. Capacidade para a solução de problemas. In: STERNBERGIstãrnberg, Robert J. As capacidades intelectuais humanas: uma abordagem em processamento de informações. Porto Alegre: Artmed, 1992.

O artigo versa sobre a competência cognitiva e sua influência na solução de problemas.

Página 335

DANTE, Luiz Roberto. Didática da resolução de problemas de Matemática. São Paulo: Ática, 1989.

A obra versa sobre a resolução de problemas como uma metodologia de ensino da Matemática; os capítulos descrevem objetivos, tipologias de problemas, abordagens, resoluções e sugestões.

DAVID, Maria Manuela M. S.; FONSECA, Maria da Conceição F. R. Sobre o conceito de número racional e a representação fracionária. Presença Pedagógica, Belo Horizonte, v.volume 3, n.número 14, mar.março/abr.abril 1997.

O artigo traz uma abordagem diferenciada para o conteúdo de números racionais, provendo o professor de elementos para compreender como o estudante assimila esse conteúdo e permitindo ao estudante perceber a intencionalidade na dinâmica da produção do conhecimento matemático.

DINIZ, Maria Ignez de Souza Vieira (coord.coordenação); SMOLE, Kátia Cristina Stocco. A construção da bissetriz de um ângulo. In: O conceito de ângulo e o ensino de Geometria. São Paulo: IMEíme-USPúspi; CAEMcaém, 1993.

O texto aborda a construção da bissetriz com o uso de régua e compasso.

DUVAL, Raymond. Registros de representações semióticas e fundamento cognitivo da compreensão em Matemática. In: MACHADO, Silvia D. A. (org.organizador). Aprendizagem em Matemática: registros de representação semiótica. Campinas: Papirus, 2003.

Trata-se de uma coletânea de pesquisas de autores nacionais com a finalidade de divulgar a teoria de Duval, que afirma que a maneira matemática de raciocinar e visualizar está intrinsecamente ligada à utilização das representações semióticas.

EVES, HowardRRAUARD. Introdução à história da Matemática. Tradução de Hygino H. Domingues. 5.quinta ed.edição Campinas: Unicampunicâmpi, 2011.

A obra abarca a história da Matemática desde a Antiguidade até os tempos modernos. O livro traz também recursos pedagógicos ao fim de cada capítulo, abordando panoramas culturais da época relatada.

FRAGOSO, Wagner da Cunha. Uma abordagem histórica da equação do 2º grau. Revista do Professor de Matemática, SBMSociedade Brasileira de Matemática, São Paulo, n.número 43, p.página 20 a 25, 2º quadrimestre 2000.

O autor tem como objetivo apresentar a história por trás da equação do 2º grau, uma perspectiva pouco abordada em sala de aula e que desperta a curiosidade dos estudantes.

GUEDJ, Denis. O teorema do papagaio. Tradução de Eduardo Brandão. São Paulo: Companhia das Letras, 2001.

O livro é um suspense matemático-policial, uma abordagem literária da história da Matemática.

HOUAISSUáis, Antonio. Minidicionário Houaiss da Língua Portuguesa. 5. ed.quinta edição São Paulo: Moderna, 2020.

Dicionário redigido seguindo o acordo ortográfico, apresenta as novas regras de acentuação, hifenização e grafia.

IBGEí bê gê É. Censo demográfico 2010. Rio de Janeiro: IBGEí bê gê É, 2011.

Constitui a principal fonte de referência para o conhecimento das condições de vida da população em todos os municípios do país e em seus recortes territoriais internos, tendo como unidade de coleta a pessoa residente, na data de referência, em domicílio do território nacional.

IFRAH, Georges. História universal dos algarismos. Tradução de Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. v.volume 2.

A obra versa sobre a história do cálculo aritmético, das escritas e notações numéricas até a informatização.

IMENES, Luiz Márcio; JAKUBOVIC, José; LELLIS, Marcelo. Equação do 2º grau. São Paulo: Atual, 1992.

Um livro repleto de exemplos de aplicações divertidas da equação do 2º grau, assim como uma viagem ao século Vcinco a.Cantes de Cristo. para conhecer o Partenon e também as resoluções usando geometria de Galileu e Isaac Newtonizáqui nílton.

IMENES, Luiz Márcio; LELLIS, Marcelo. Conversa de professor: Matemática. Brasília, DFDistrito Federal: Ministério da Educação e do Desporto, Secretaria de Educação a Distância, 1996. (Cadernos da TVtê vê Escola).

A obra desenvolve uma conversa objetiva e didática sobre o ensino da Matemática, com exemplos de aplicações que podem ser implementados em sala de aula.

LIMA, Elon Lages. Meu professor de Matemática e outras histórias. Rio de Janeiro: SBMSociedade Brasileira de Matemática, IMPAímpa, 1991. (Coleção Professor de Matemática).

O livro é composto de pequenos ensaios da matemática elementar que vão desde questões simples, como o significado da igualdade, até questões mais elaboradas, como a definição de pi.

LIMA, José Mauricio de Figueiredo. Iniciação ao conceito de fração e o desenvolvimento da conservação de quantidade. In: CARRAHER, Terezinha Nunes (org.organizador). Aprender pensando. Petrópolis: Vozes, 2008.

O texto explora uma das origens da fração, situada na divisão das terras no Egito. O autor faz a abordagem por meio da divisão de figuras enfatizando a conservação da área como pré-requisito à noção do conceito de fração.

Página 336

LINDQUIST, MaryMéri MontgomeryMomgomery ; SHULTE, Albertálbert (org.organizador). Aprendendo e ensinando Geometria. São Paulo: Atual, 2005.

A obra é uma reunião de artigos selecionados com os temas Educação Matemática e Geometria.

LINS, Romulo Campos; GIMENEZ, Joaquim. Perspectiva em Aritmética e Álgebra para o século XXIvinte e um. Campinas: Papirus, 1997.

Os autores exploram a inter-relação na aprendizagem da Álgebra e da Aritmética e analisam de que modo isso pode influenciar mudanças na educação matemática escolar.

MENDES, Iran Abreu. Números: o simbólico e o racional na história. São Paulo: Livraria da Física, 2006.

Nessa obra, o autor reorganiza a história de como os humanos inventaram e desenvolveram métodos para contar, ordenar e quantificar, com narrativa leve e diferente despertando o interesse dos estudantes.

NUNES, Terezinha; BRYANTBráian, Peterpíter. Compreendendo números racionais. In: Crianças fazendo Matemática. Porto Alegre: Artes Médicas, 1997. p.página 191-217cento e noventa e um a duzentos e dezessete.

O capítulo trata o ensino de frações a fim de evitar conduzir as crianças ao erro.

OZAMIZ, Miguel de Guzmángusmãn. Aventuras matemáticas. Tradução de João Filipe Queiró. Lisboa: Gradiva, 1991.

A obra envolve o leitor e estimula a participação ativa em diversos aspectos da criatividade matemática.

PERRENOUDPerrenôu, Phillipe et al. As competências para ensinar no século XXIvinte e um: a formação dos professores e o desafio da avaliação. Tradução de Cláudia Schillingchílin e Fátima Murad. Porto Alegre: Artmed, 2002.

Os assuntos trazidos nessa obra são de alta relevância para o professor, pois auxiliam na tomada de decisões importantes e na busca por um trabalho diferenciado e construtivo, contribuindo para o aprimoramento do ensino.

PIRES, Célia M. C.; CURI, Edda. Revendo conteúdos, propondo atividades e observando como as crianças lidam com as figuras bidimensionais. In: PIRES, Célia M. C.; CURI, Edda; CAMPOS, Tania M. M. Espaço & formafórma: a construção de noções geométricas pelas crianças das quatro séries iniciais do Ensino Fundamental. São Paulo: Proem, 2000.

As autoras, nessa obra, analisam como as crianças constroem relações espaciais e, no capítulo 4, propõem atividades com figuras bidimensionais.

POLYA, George. A arte de resolver problemas. Tradução de Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 2006.

Nessa obra o autor traz uma série de estratégias práticas que auxiliam na solução de problemas.

TAHAN, Malba. O homem que calculava. 76. ed.septuagésima sexta edição Rio de Janeiro: Recordrecór, 2009.

A obra é referência no universo dos livros paradidáticos. O objetivo da história é mostrar como a Matemática está presente em tudo, e o autor consegue envolver o leitor ao mesmo tempo que ensina Matemática.

TOLEDO, Marília; TOLEDO, Mauro. Didática de Matemática: como dois e dois – a construção da Matemática. São Paulo: FTDéfe tê dê, 1997.

Por meio de atividades diversas, os autores despertam a intuição matemática em todas as pessoas e rompem os preconceitos que cercam a disciplina. Para complementar, a obra contém textos interessantes sobre o desenvolvimento da ciência com interpretações variadas da perspectiva matemática.

ZASLAVSKY, Claudia. Jogos e atividades matemáticas do mundo inteiro: diversão multicultural para idades de 8 a 12 anos. Tradução de Pedro Theobald. Porto Alegre: Artmed, 2000.

A obra traz jogos do mundo inteiro que utilizam Geometria para desenhar tabuleiros e pensamento lógico para planejar estratégias.