
UNIDADE 3
Capítulo 7
Equações e inequações do 1º grau
Capítulo 8
Polígono, circunferência e círculo
Capítulo 9
Triângulos e quadriláteros

Os polígonos nos Grafites
O grafite é uma fórma de arte urbana caracterizada por inscrições ou desenhos que utilizam como suporte elementos da cidade: muros, equipamentos urbanos, paredes etcétera.
Para compor suas obras, os artistas utilizam sprays de tinta que são aplicadas nas superfícies a partir de diferentes técnicas. Os grafites variam em cores e formatos, a depender do estilo e do traço de cada artista.
Entre os temas abordados, destacam-se cenas do cotidiano nas cidades, homenagens a figuras públicas e eventos históricos e, principalmente, elementos de protesto, que buscam impactar os observadores e despertar reflexões sobre determinada causa.
Para começar...
1. Você já viu algum grafite na cidade em que vive? Em caso afirmativo, comente o que achou dele.
2. Você considera o grafite uma fórma de arte acessível?
3. Quais polígonos você identifica no grafite apresentado na foto?

Respostas e comentários
Os links expressos nesta coleção podem estar indisponíveis após a data de publicação deste material.
Habilidades da Bê êne cê cê trabalhadas nesta Unidade:
ê éfe zero sete ême ah um oito
ê éfe zero sete ême ah dois dois
ê éfe zero sete ême ah dois quatro
ê éfe zero sete ême ah dois cinco
ê éfe zero sete ême ah dois seis
ê éfe zero sete ême ah dois sete
ê éfe zero sete ême ah dois oito
ê éfe zero sete ême ah três três
ê éfe zero sete ême ah três cinco
ê éfe zero sete ême ah três sete
Para começar: Respostas em Orientações.
Orientações e sugestões didáticas
Abertura da Unidade 3
Objetivos
• Nesta Unidade, serão trabalhados vários conceitos relacionados às unidades temáticas Álgebra, Geometria e Probabilidade e Estatística, que, entre outros objetivos, favorecerão o desenvolvimento das habilidades da Bê êne cê cê listadas.
Orientações
• Ao abordar a página de abertura com a turma, se possível verifique se há algum tipo de expressão artística próximo da escola e realize uma pesquisa de campo ou apresente outros exemplos de grafite, para que os estudantes possam analisar suas características, comparando-os entre si. O trabalho com esse tema pode ser ampliado em conjunto com os professores de Artes e Língua Portuguesa. Algumas sugestões de artistas são: Eduardo Kobra, Simone Sapienza, Kurt Wenner e Bansky.
• Na questão 1 do boxe Para começar, incentive os estudantes a comentar se já viram um grafite e quais eram suas características (pessoa ou cena representada, formatos, cores, local em que estava etcétera). Aproveite para explorar as culturas juvenis, dando espaço aos estudantes para se posicionarem sobre o tema, questionando se o grafite é uma arte ou poluição visual, se é uma cultura urbana ou marginalizada, se podemos considerá-lo uma manifestação da linguagem etcétera. Fique atento aos comentários dos estudantes ao expressarem suas opiniões e, se necessário, ressalte a importância de respeitarmos os gostos e as preferências pessoais.
• Durante o trabalho com a questão 2, ressalte que o grafite é uma expressão artística bastante democrática por, geralmente, estar exposto de fórma gratuita em locais públicos como a rua, muros e fachadas de prédios.
• Ao trabalhar com a questão 3, explique aos estudantes que, além de apresentar polígonos em suas obras, muitos artistas utilizam perspectiva e profundidade para compor desenhos em formato tridimensional. No caso dessa foto, é possível identificar quadrados, triângulos, losangos, trapézios.
Competência geral 3: Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

CAPÍTULO 7 Equações e inequações do 1º grau
1 Igualdade
Para que uma balança de dois pratos fique equilibrada, é necessário que a medida de massa total dos objetos que estiverem em um dos pratos seja igual à medida de massa total dos objetos que estiverem no outro prato.
Nesse caso, podemos representar a medida de massa dos objetos que estão nos dois pratos com uma sentença matemática em que há o sinal de igual (=), denominada igualdade. Observe os exemplos.
• A balança a seguir está equilibrada.
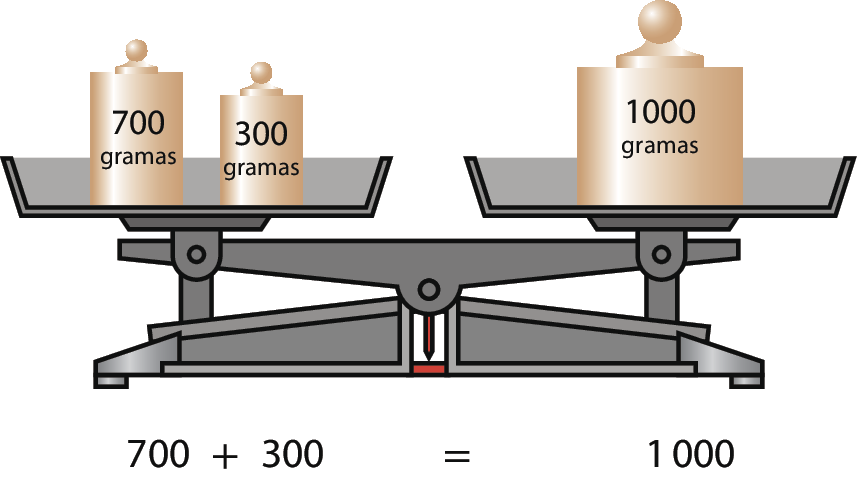
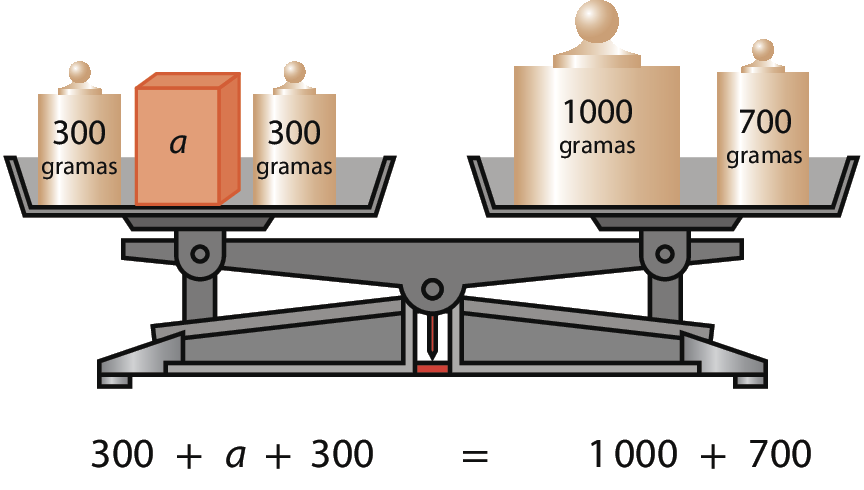
• Na balança a seguir, há um objeto com medida de massa ei desconhecida.
Lembre-se: Escreva no caderno!
Para pensar
Qual é a medida da massa a desconhecida, em grama, do objeto laranja na balança apresentada anteriormente?
Uma igualdade continuará sendo válida se:
• adicionarmos ou subtrairmos o mesmo número aos seus membros;
• multiplicarmos ou dividirmos seus membros por um mesmo número diferente de zero;
• elevarmos seus membros a um mesmo expoente.
Exemplos
• 3 + 8 = 15 menos 4
3 + 8 menos 2 = 15 menos 4 menos 2
9 = 9
• 16 menos 2 = 14
abre parênteses16 menos 2fecha parênteses dividido por 2 = 14 dividido por 2
7 = 7
• 5 menos 3 = 10 menos 9 + 1
abre parênteses5 menos 3fecha parênteseselevado a 2 = abre parênteses10 menos 9 + 1fecha parênteseselevado a 2
4 = 4
Respostas e comentários
Habilidades da Bê êne cê cê trabalhadas neste Capítulo:
ê éfe zero sete ême ah um oito
ê éfe zero sete ême ah três cinco
Para pensar: .1100 gramas
Orientações e sugestões didáticas
Igualdade
Objetivos
• Reconhecer uma igualdade.
• Reconhecer as propriedades da igualdade.
• Favorecer o desenvolvimento da habilidade da Bê êne cê cê: ê éfe zero sete ême ah um oito.
Habilidade da Bê êne cê cê
• Esse tópico favorece o desenvolvimento da habilidade ê éfe zero sete ême ah um oito ao proporcionar o estudo das propriedades da igualdade.
Orientações
• Desde os anos iniciais do Ensino Fundamental, estuda-se a relação de igualdade e suas propriedades. Então, é possível que os estudantes já tenham algum conhecimento sobre o assunto. Procure fazer um levantamento desses conhecimentos e inicie o tópico com base no que já sabem. O estudo das propriedades da igualdade se justifica porque elas serão aplicadas na resolução de equações polinomiais do 1º grau mais adiante.
• No Bócsi Para pensar, os estudantes descobrirão o valor desconhecido em uma igualdade. Incentive-os a utilizar suas estratégias pessoais para determiná-lo. Depois, peça que compartilhem com os colegas o modo como pensaram.
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à fórma ax + b = c, fazendo uso das propriedades da igualdade.
2 Equação
Observe as situações a seguir.
Situação 1

Amanda foi ao mercado comprar algumas caixas de leite e gastou, ao todo, R$ 15,00quinze reais.
Podemos indicar por x o número de caixas de leite compradas e escrever a seguinte sentença:

Situação 2
Flávia viu este recado no mural da escola:

Em seguida, ela se perguntou: quantos meninos e quantas meninas podem compor essa banda?
Como a soma do número de meninos com o de meninas é igual a 6, podemos indicar o número de meninas por x e o número de meninos por y e escrever a seguinte sentença matemática:
x + y = 6
As sentenças matemáticas 3x = 15 e x + y = 6 são exemplos de equações.
Equação é uma sentença matemática com sinal de igual (=) em que números desconhecidos são representados por letras, denominadas incógnitas.
Exemplos
• 2x = 4 é uma equação, e a incógnita dessa equação é x.
• aelevado a 2 = 4 é uma equação, e a incógnita dessa equação é a.
• 3m menos 5n = 7 é uma equação, e as incógnitas dessa equação são m e n.
Para investigar
Qual é a diferença entre variável e incógnita?
Observação
Em todas as equações há o sinal de igual (=), ou seja, todas representam uma igualdade. Em uma igualdade, a expressão à esquerda do sinal de igual é chamada de 1º membro e a expressão à direita é chamada de 2º membro da igualdade.
Respostas e comentários
Para investigar: Espera-se que os estudantes respondam, com suas palavras, que uma variável pode assumir diversos valores, enquanto uma incógnita possui um (ou mais) valor(es) determinável(eis).
Orientações e sugestões didáticas
Equação
Objetivos
• Compreender o conceito de equação.
• Traduzir um problema por meio de uma equação.
• Compreender o conceito de raiz de uma equação.
• Reconhecer o conjunto universo e o conjunto solução de uma equação.
• Resolver situações-problema com números racionais.
• Favorecer o desenvolvimento da habilidade da Bê êne cê cê: ê éfe zero sete ême ah um oito.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero sete ême ah um oito ao trabalhar os conceitos de equação e raiz de uma equação. Ambos são pré-requisitos para que o estudante, a posteriori, possa resolver e elaborar problemas representados por equações polinomiais de 1º grau.
Orientações
• É importante destacar com os estudantes que, na definição de equação, as letras passam a ter o significado de incógnita.
• Se julgar necessário, apresente outras situações e peça eles que as traduzam por meio de equações. Oriente-os a indicar no problema o que cada número e letra da equação significam.
• Nesse primeiro momento, pode-se propor aos estudantes que resolvam mentalmente as equações obtidas nas situações 1 e 2.
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à fórma á xis + b = c, fazendo uso das propriedades da igualdade.
Lembre-se: Escreva no caderno!
Nem toda sentença matemática é uma equação. As sentenças a seguir, por exemplo, não são equações.

Raiz de uma equação
A incógnita de uma equação pode assumir diversos valores, mas apenas alguns deles tornam a sentença verdadeira.
Vamos retomar a situação 1 e verificar que valor de x torna verdadeira a equação 3x = 15, em que x representa o número de caixas de leite. O número 5 torna a sentença verdadeira, pois: 3 ⋅ 5 = 15.
Dizemos, então, que o número 5 é raiz da equação 3x = 15. Assim, descobrimos que Amanda comprou 5 caixas de leite.
Raiz de uma equação é um número que, ao substituir a incógnita, torna a sentença verdadeira.
Podemos verificar se um número é raiz ou não de uma equação substituindo a incógnita por ele. Se a sentença for verdadeira, o número considerado é raiz da equação; se a sentença for falsa, o número não é raiz da equação. Observe um exemplo.
Vamos verificar se menos1 é raiz da equação 8x + 3 = menos5. Para isso, substituímos x por menos1 e efetuamos as operações indicadas:
8x + 3 = menos5
8 ⋅ abre parêntesesmenos1fecha parênteses + 3 = menos5
menos 8 + 3 = menos5
menos 5 = menos5
Como menos5 = menos5 é uma sentença verdadeira, menos1 é raiz da equação 8x + 3 = menos5.
Observação
O número 1 não é raiz da equação 8x + 3 = 5.
Ao substituir x por 1 nessa equação, obtemos:
8x + 3 = 5
8 ⋅ 1 + 3 = 5
8 + 3 = 5
11 = 5
Como a sentença 11 = 5 é falsa, o número 1 não é raiz da equação 8x + 3 = 5.
Para fazer
Verifique, no caderno, se 1 é raiz da equação 8x + 3 = menos5.
Conjunto universo e conjunto solução de uma equação
Ricardo precisa descobrir a medida de comprimento do lado de um quadrado cuja área mede 49 centímetros quadrados. Acompanhe como ele pensou para resolver a situação, considerando que o comprimento do lado do quadrado mede x.
Respostas e comentários
Para fazer: Não, pois a sentença 11 = menos5 é falsa.
Orientações e sugestões didáticas
• Proponha aos estudantes os seguintes problemas, para serem resolvidos mentalmente:
1. Qual é o número que, quando adicionado a 4, resulta em 10? (6)
2. O dobro de um número é igual a 36. Qual é esse número? (18)
3. A terça parte de um número é igual a 4. Qual é esse número? (12)
4. Descubra qual é o número cujo triplo, somado à metade do mesmo número, resulta em 21. (6)
• No boxe Para fazer, espera-se que os estudantes verifiquem se a sentença é verdadeira ou falsa substituindo o x por 1. Caso algum estudante apresente um modo diferente para verificar a veracidade da sentença, peça que compartilhe com a turma como pensou.
• É importante que fique claro para os estudantes a distinção entre os conceitos de conjunto universo e conjunto solução de uma equação. O conjunto universo corresponde ao conjunto dos números que a incógnita pode assumir; já o conjunto solução é o conjunto dos números que são raízes da equação.
Lembre-se: Escreva no caderno!

Podemos verificar que Ricardo tem razão, pois menos7 e 7 são raízes da equação x elevado a 2 = 49.
• abre parêntesesmenos7fecha parênteseselevado a 2 = 49
49 = 49
• abre parênteses7fecha parênteseselevado a 2 = 49
49 = 49
Entretanto, observe que não faz sentido a medida de comprimento do lado do quadrado ser um número negativo: menos7. Por isso, apesar de esse número ser raiz da equação, ele não é solução do problema.
Portanto, o lado de um quadrado cuja medida de área é 49 cmétros quadrados mede 7 centímetros de comprimento.
Quando resolvemos uma equação, é necessário saber seu conjunto universo, que é representado pela letra U. O conjunto universo contém todos os números que a incógnita pode assumir.
As raízes da equação que pertencem ao conjunto universo são as soluções dessa equação e formam o seu conjunto solução. Observe os exemplos.
• Vamos resolver a equação x elevado a 2 = 16, sendo conjunto universo =

.
x = 4 ou x = menos 4 são as raízes da equação, mas somente x = 4 pertence ao conjunto universo

. Assim, a solução dessa equação é somente o número 4 e seu conjunto solução é S = abre chave4fecha chave.
• Vamos resolver a equação x elevado a 2 = 16, sendo conjunto universo =

.
x = 4 e x = menos 4 são raízes da equação e ambas fazem parte do conjunto universo

. Então, menos4 e 4 são soluções da equação e seu conjunto solução é S = {‒ 4, 4fecha chave.
Agora, vamos retomar a situação 2 da página 173.
Na equação x + y = 6, x e y (que representam o número de meninas e o de meninos, respectivamente) devem ser números naturais. Então, há 7 modos diferentes de compor a banda:
|
Número de meninas (x) |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|---|
|
Número de meninos (y) |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
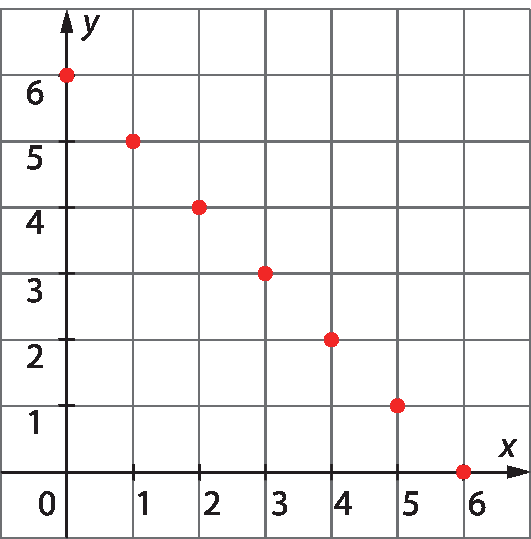
As soluções de uma equação com duas incógnitas podem ser expressas por pares ordenados abre parêntesesx, yfecha parênteses e representadas graficamente. Observe como podemos representar em um plano, que chamamos de plano cartesiano, os pares ordenados abre parênteses0, 6fecha parênteses, abre parênteses1, 5fecha parênteses, abre parênteses2, 4fecha parênteses, abre parênteses3, 3fecha parênteses, abre parênteses4, 2fecha parênteses, abre parênteses5, 1fecha parênteses e abre parênteses6, 0fecha parênteses, que são soluções da equação apresentada no problema.
Orientações e sugestões didáticas
• Comente com os estudantes que, antes de resolver uma equação, eles devem saber qual é o seu conjunto universo. Os exemplos apresentados mostram que podemos obter conjuntos soluções diferentes para uma mesma equação, dependendo do conjunto universo considerado.
• Se julgar conveniente, proponha aos estudantes que representem em um plano cartesiano alguns pares ordenados que sejam solução da equação x + y = 2, considerando x e y números naturais.
Observação
A equação x + y = 6 possui outras raízes; por exemplo:
• menos1 e 7
Verificação:
menos1 + 7 = 6
6 = 6
• 10,5 e menos 4,5
Verificação:
10,5 + (‒ 4,5fecha parênteses = 6
10,5 menos 4,5 = 6
6 = 6
Entretanto, essas raízes não podem ser solução da situação apresentada, pois xis e y representam, respectivamente, o número de meninas e o de meninos que podem compor a banda; portanto, devem ser números naturais.

ATIVIDADES
faça as atividades no caderno
1.

Observe como Rafael e Carla, calculando mentalmente, descobriram a raiz de uma equação.

a) Agora, descubra a raiz de:
Fração y sobre 3= 15
b)

Como você pensaria para encontrar o número que dividido por 3 dá 15?
Converse com um colega sobre como vocês pensaram para descobrir a raiz da equação.
2.

Encontre mentalmente a raiz de cada equação e escreva-a no caderno.
a) 10x = 15
b)
Sentença matemática. x, vezes, fração 1 meio, igual, fração 1 meio.c) x ⋅ abre parêntesesmenos1fecha parênteses = menos5
d) x ⋅
Fração 1 décimo.= 1
3. Caio foi à papelaria comprar um estojo e um caderno.

a) Escreva a equação que representa o preço x, do estojo, adicionado ao preço y, do caderno.
b) Usando a equação encontrada no item a, responda:
• Se o estojo custasse R$ 3,00três reais, qual teria sido o valor pago pelo caderno?
• Se o caderno custasse R$ 7,50sete reais e cinquenta centavos, qual teria sido o valor pago pelo estojo?
• O estojo poderia ter custado R$ 5,00cinco reais e o caderno, R$ 5,50cinco reais e cinquenta centavos? Por quê?
4. Leia e responda no caderno.
a)

b)

5. Verifique, no caderno, as equações das quais o número menos9 é raiz.

Respostas e comentários
1. a) 45
1. b) Resposta pessoal.
2. a) 1,5
2. b) 1
2. c) 5
2. d) 10
3. a) x + y = 10
3. b) R$ 7,00sete reais; R$ 2,50dois reais e cinquenta centavos; Espera-se que os estudantes respondam que não, pois a soma do preço do estojo com o preço do caderno seria R$ 10,50dez reais e cinquenta centavos, o que não corresponde ao valor pago por Caio.
4. a) 6
4. b) 5
5. alternativas a e c
Orientações e sugestões didáticas
• Coerente com o desenvolvimento teórico deste tópico, a sequência de atividades desta página mescla atividades de fixação com atividades contextualizadas. É interessante aproveitar o momento para avaliar o estágio do pensamento algébrico em que a turma se encontra. Por meio das resoluções das atividades contextualizadas, pode-se verificar quantos estudantes optaram pelos caminhos da aritmética e quantos optaram por uma estratégia algébrica. Discuta a validade e as limitações de ambos os procedimentos.
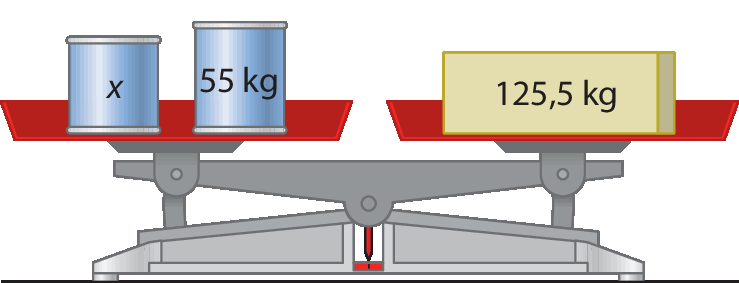
6. As balanças a seguir estão em equilíbrio. Em cada caso, descubra a medida de massa x desconhecida, em quilograma.
a)
b)
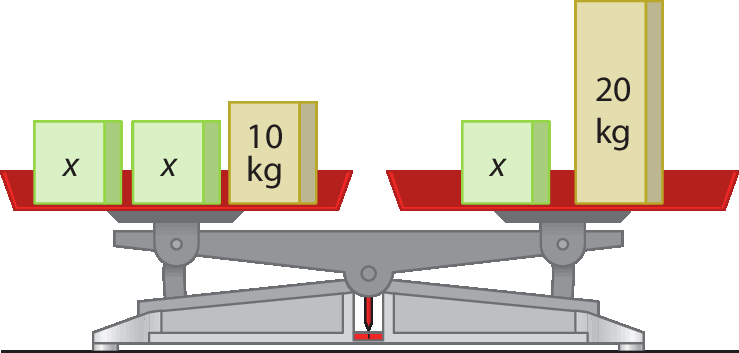
c)
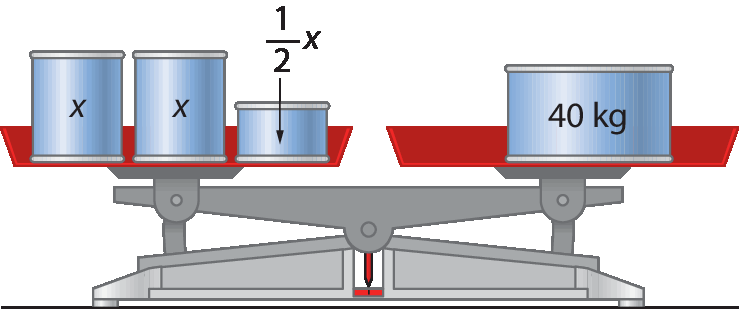
7.

Escreva no caderno uma equação para cada sentença. Depois, considerando o conjunto dos números racionais como conjunto universo, encontre a solução mentalmente.
a) O triplo de um número x é 15.
b) O quadrado de um número y é
Fração um quarto..
c) Um número n adicionado a 36 é igual a 57.
d) O quadrado de um número k é menos3.
e) O quadrado de um número a adicionado a 2 é igual a menos1.
8. Escreva no caderno uma equação que relacione os dados de cada problema e resolva-o.
a) Ana comprou uma geladeira por R$ 1.200,00mil duzentos reais. Ela deu R$ 200,00duzentos reais de entrada e pagou o restante em cinco prestações iguais. Qual foi o valor da prestação?

b) Um marceneiro cortou uma tábua que media 2 metros de comprimento em dois pedaços. A medida do comprimento de um dos pedaços é o quádruplo da medida do outro. Qual é a medida do comprimento de cada pedaço?
9. Verifique se o par ordenado abre parênteses3, 1fecha parênteses é solução das equações a seguir.
a) 2x menos y = 5
b) x + y = 4
c) x menos 2y = 3
d) x + 4y = 6
10. Márcia é professora de inglês e de espanhol e possui dicionários desses dois idiomas para trabalhar com os estudantes.

a) Usando x para indicar a quantidade de dicionários de inglês e y para indicar a quantidade de dicionários de espanhol, escreva a equação correspondente a essa situação.
b) Determine duas possíveis soluções para a equação do item a.
11. Descubra os números.

• Agora, expresse a resposta que você deu por pares ordenados e, usando papel quadriculado, represente-os em um plano cartesiano.
Respostas e comentários
6. a) 70,5 quilogramas
6. b) 10 quilogramas
6. c) 16 quilogramas
7. a) 3x = 15; 5;
7. b) y elevado a 2 =
Fração um quarto.;
Sentença matemática. Menos fração 1 meio e 1 meio.
7. c) n + 36 = 57; 21;
7. d) k elevado a 2 = menos3; não tem solução;
7. e) a elevado a 2 + 2 = menos1; não tem solução.
8. a) Exemplo de resposta: 200 + 5x = .1200; R$ 200,00duzentos reais
8. b) Exemplo de resposta: y + 4y = 2; 0,4 métro e 1,6 métro
9. a) sim
9. b) sim
9. c) não
9. d) não
10. a) x + y = 24
10. b) Exemplos de resposta: abre parênteses10, 14fecha parênteses, abre parênteses12, 12fecha parênteses
11. Resposta em Orientações.
Orientações e sugestões didáticas
• Resposta da atividade 11:
Soma de dois números naturais igual a 5: 0 e 5, 1 e 4 ou 2 e 3.
Representação por pares ordenados: abre parênteses0, 5fecha parênteses; abre parênteses1, 4fecha parênteses; abre parênteses2, 3fecha parênteses; abre parênteses3, 2fecha parênteses; abre parênteses4, 1fecha parênteses; abre parênteses5, 0fecha parênteses.
Representação no plano cartesiano:

Lembre-se: Escreva no caderno!
3 Equações equivalentes
Observe as equações.

Ao substituir x por menos3 em cada igualdade, obtemos uma sentença verdadeira. Observe.
• 8 + x = 5
8 + abre parêntesesmenos3fecha parênteses = 5
5 = 5
• x = 5 menos 8
menos3 = 5 menos 8
menos3 = menos3
• 6x = menos18
6 ⋅ abre parêntesesmenos3fecha parênteses = menos18
menos18 = menos18
Portanto, menos3 é raiz dessas três equações.
Em um mesmo conjunto universo, equações que têm as mesmas raízes são chamadas de equações equivalentes.
Em alguns casos, é necessário obter equações equivalentes para encontrar as raízes de uma equação. Vamos analisar algumas situações.
Situação 1
Em uma balança foram colocados blocos azuis de medida de massa igual a 1 quilograma cada e um bloco amarelo de medida de massa x desconhecida, em quilograma. Observe que a balança ficou equilibrada.

No prato da esquerda há um bloco de medida de massa x quilograma e 4 blocos de 1 quilograma cada. No prato da direita há 7 blocos com medida de massa igual a 1 quilograma cada. Podemos representar essa situação por meio da seguinte equação:
x + 4 = 7
Se retirarmos 4 blocos de cada prato, a balança continuará equilibrada.
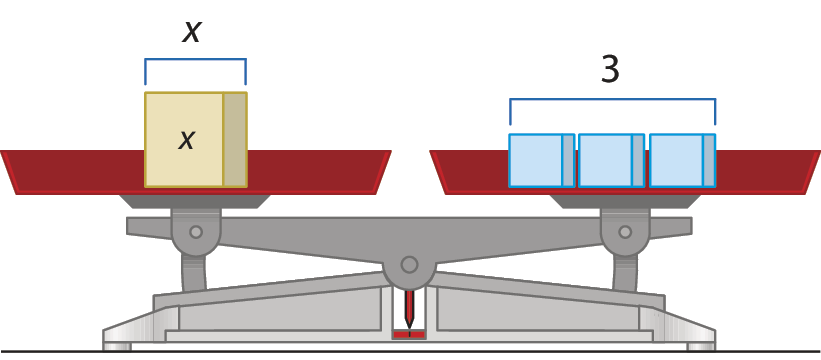
Assim, podemos concluir que o bloco que ficou no prato da esquerda tem medida de massa igual a 3 quilograma. A equação a seguir pode representar essa situação:
x = 3
Orientações e sugestões didáticas
Equações equivalentes
Objetivos
• Compreender o conceito de equações equivalentes.
• Aplicar o conceito de princípio aditivo e princípio multiplicativo das igualdades.
• Resolver problemas que possam ser representados por equações polinomiais de 1º grau.
• Favorecer o desenvolvimento da habilidade da Bê êne cê cê: ê éfe zero sete ême ah um oito.
Habilidade da Bê êne cê cê
• Esse tópico favorece o desenvolvimento da habilidade ê éfe zero sete ême ah um oito ao apresentar o conceito de equações equivalentes; importante para quando for estudada a resolução de equações polinomiais do 1º grau e para resolver e elaborar problemas.
Orientações
• Nesse estudo, foram usadas balanças para simbolizar a equação. Esse recurso é ilustrativo e permite que os estudantes visualizem as equações equivalentes no processo de resolução de uma equação com uma incógnita; é importante, no entanto, que eles também aprendam como aplicar os princípios aditivo e multiplicativo.
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à fórma ax + b = c, fazendo uso das propriedades da igualdade.
Lembre-se: Escreva no caderno!
Quando adicionamos ou subtraímos uma mesma quantidade nos dois membros de uma equação, obtemos uma equação equivalente à primeira. Esse é o princípio aditivo das igualdades.
Observe como o princípio aditivo das igualdades e o raciocínio empregado para resolver a equação da situação 1 podem ser expressos usando apenas a notação algébrica:
x + 4 = 7
Aplicando o princípio aditivo das igualdades, subtraímos 4 dos dois membros:
x + 4 menos 4 = 7 menos 4
x + 0 = 3
x = 3
Note que as equações x + 4 = 7 e x = 3 são equivalentes.
Situação 2
Em um dos pratos da balança a seguir, há 3 blocos verdes de medida de massa y desconhecida, em quilograma, e, no outro prato, há 18 blocos azuis, cada um com medida de massa de 1 quilograma.

Podemos representar essa situação por meio da equação:
3y = 18
Se deixarmos no prato da esquerda a terça parte dos blocos que havia, devemos fazer o mesmo no prato da direita para manter a balança equilibrada. A terça parte de 3 blocos iguais corresponde a 1 bloco e a terça parte de 18 blocos iguais corresponde a 6 blocos.
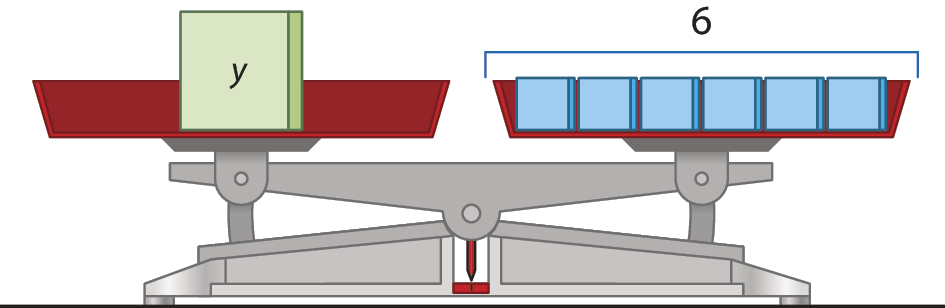
Desse modo, podemos concluir que o bloco que ficou no prato da esquerda tem medida de massa igual a 6 quilogramas. A seguinte equação representa a situação:
y = 6
Quando multiplicamos ou dividimos por um mesmo número não nulo os dois membros de uma equação, obtemos outra equação equivalente à primeira. Esse é o princípio multiplicativo das igualdades.
Orientações e sugestões didáticas
• Antes de formalizar o princípio aditivo, use exemplos para retomar com a turma o fato de uma igualdade não se alterar quando adicionamos ou subtraímos um mesmo número de ambos os seus membros.
• Ao indicar a passagem x + 0 = 3, reforce a propriedade do elemento neutro da adição. Informe aos estudantes que essa também é uma equação equivalente a x + 4 = 7.
• Antes de formalizar o princípio multiplicativo, use exemplos que reforcem o fato de uma igualdade não se alterar quando multiplicamos ou dividimos ambos os membros de uma equação por um mesmo número diferente de zero.
Observe como o princípio multiplicativo das igualdades e o raciocínio empregado para resolver a equação da situação 2 podem ser expressos usando apenas a notação algébrica.
3y = 18
Aplicando o princípio multiplicativo das igualdades, multiplicamos os dois membros por
Sentença matemática. Fração 1 terço.:
=
Fração 18 terços.
y = 6
Note que as equações 3y = 18 e y = 6 são equivalentes.

ATIVIDADES
faça as atividades no caderno
1. No caderno, associe cada equação da coluna da esquerda com a equação equivalente da coluna da direita.

2. Escreva no caderno uma equação equivalente a cada equação a seguir. Depois, encontre a raiz da equação.
a) x + 5 = 18
b) 3 + y = 2
c) 4z = 12
d) y + 9 = y + 2y
e) 2m = menos 4
f ) menos 5t = 25
g) 2x + x = 7 menos 10x
h) 12b menos 22 = 122
i) 42p + 19 = 229
3.

Márcia vai viajar e quer levar alguns gibis para ler durante a viagem. Se ela comprar gibis de R$ 3,00três reais cada um, ainda ficará com R$ 10,00dez reais. Se comprar o mesmo número de gibis, mas ao preço de R$ 7,00sete reais cada um, faltarão R$ 6,00seis reais. Quantos gibis de R$ 7,00sete reais Márcia pode comprar?
Respostas e comentários
1. A – três; B – quatro; C – um; D – cinco; E – dois
2. Exemplo de respostas:
2. a) x menos 13 = 0; x = 13
2. b) 1 + y = 0; y = menos1
2. c) 2z = 6; z = 3
2. d) 9 menos 2y = 0; y =
Fração 9 meios.2. e) 2m + 4 = 0; m = menos2
2. f) menos5t menos 25 = 0; t = menos5
2. g) 13 x menos 7 = 0; x =
Fração 7 13 avos.
2. h) 12b = 144; b = 12
2. i) 42p = 210; p = 5
3. Resposta e comentário em Orientações.
Orientações e sugestões didáticas
• Na atividade 2, incentive os estudantes a procurar a equação equivalente utilizando as propriedades estudadas. Se considerar necessário, em alguns itens, peça que justifiquem suas escolhas.
Por exemplo, no item a, eles podem fazer:
x + 5 menos 5 = 18 menos 5
x + 0 = 13
x = 13
Assim, para encontrar outra equação equivalente, poderiam fazer:
x + 0 menos 13 = 13 menos 13
x menos 13 = 0
• Peça aos estudantes que formem duplas ou trios para discutir fórmas de resolver a atividade 3 e, em seguida, registrem uma resolução completa para expor aos colegas. Dessa maneira, poderão conhecer diferentes caminhos para resolver um problema e corrigi-lo, se necessário.
Para resolver a atividade, espera-se que eles percebam que, sendo x a quantidade de gibis que serão comprados, Márcia gastará 3 ⋅ x se comprar os gibis de R$ 3,00três reais cada e gastará 7 ⋅ x se comprar os gibis de R$ 7,00sete reais cada. Assim, se no primeiro caso sobrarem R$ 10,00dez reais e no segundo caso faltarem R$ 6,00seis reais, podemos dizer que 7 ⋅ x menos 3 ⋅ x = 16. Portanto, x = 4. Desse modo, o valor que Márcia tem corresponde a 3 ⋅ 4 + 10 ou 7 ⋅ 4 menos 6, ou seja, 22 reais. Portanto, Márcia pode comprar até 3 gibis de R$ 7,00sete reais cada.
4 Equação do 1º grau com uma incógnita
Equações do 1º grau com uma incógnita são aquelas que podem ser escritas como uma equação equivalente da fórma ax + b = 0, em que a e b são números racionais conhecidos, com a diferente de zero. Nesse caso, a incógnita é x e a e b são chamados de coeficientes. Acompanhe os exemplos.
• 3x + 1 = 0 é uma equação do 1º grau com uma incógnita de coeficientes a = 3 e b = 1.
•
Sentença matemática. Menos fração x sobre 2, igual, zero.é equivalente a
Sentença matemática. Menos fração 1 meio x, mais zero, igual, zero.; portanto, é uma equação do 1º grau com uma incógnita de coeficientes
Sentença matemática. a igual a menos meio.e b = 0.
Vamos usar equações equivalentes para resolver equações do 1º grau com uma incógnita.
• Vamos resolver a equação 6x menos 2 = 16, considerando conjunto universo =

.
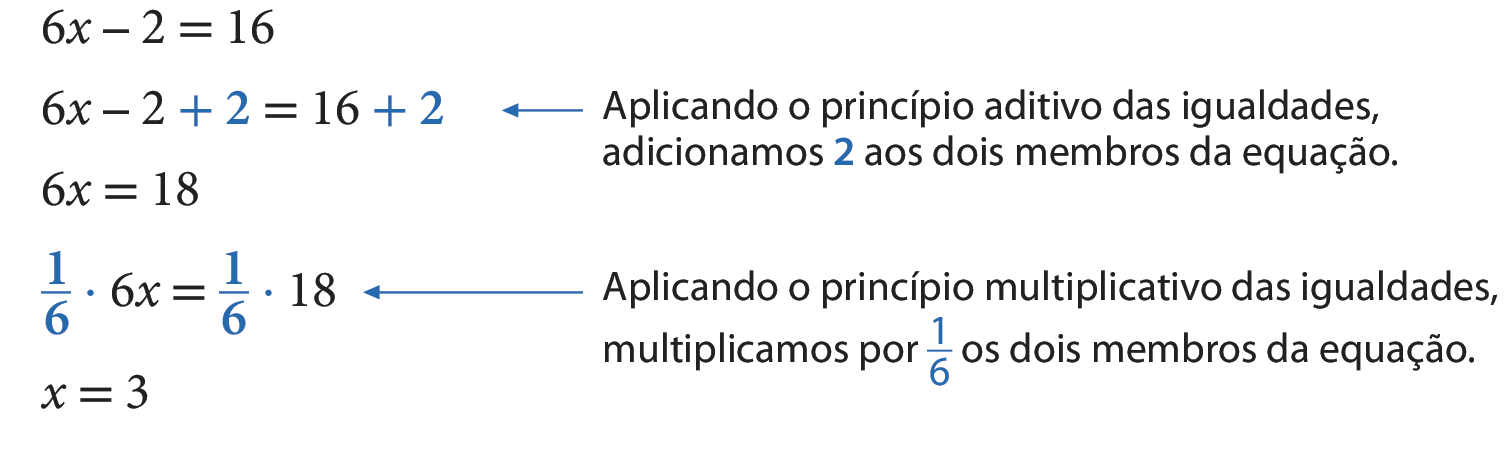
Observação
Em vez de multiplicarmos ambos os membros da equação por
fração 1 sexto, poderíamos dividi-los pelo coeficiente da incógnita x, que é 6. O resultado será o mesmo.
6x = 18
6x dividido por 6 = 18 dividido por 6
x = 3
• Agora, vamos resolver a equação 3 ⋅ abre parênteses1 menos xfecha parênteses = 5 ⋅ abre parêntesesx + 1fecha parênteses, considerando conjunto universo =

.

Como
Menos um quarto.é raiz da equação e pertence ao conjunto universo, então
S igual a, abre chaves, menos fração um quarto, fecha chaves..

Orientações e sugestões didáticas
Equação do 1º grau com uma incógnita
Objetivos
• Reconhecer uma equação polinomial de 1º grau.
• Favorecer o desenvolvimento da habilidade da Bê êne cê cê: ê éfe zero sete ême ah um oito.
Habilidade da Bê êne cê cê
• Esse tópico favorece o desenvolvimento da habilidade ê éfe zero sete ême ah um oito ao propor resolução e elaboração de problemas que possam ser representados por equações polinomiais do 1º grau.
Orientações
• As resoluções de uma equação do 1º grau com uma incógnita são apresentadas por meio dos princípios aditivo e multiplicativo das igualdades. Nesse momento, é importante empregar os princípios para que não haja mecanização das resoluções, evitando, assim, que os estudantes tenham dúvidas como “passa para o outro lado da igualdade e fica com qual sinal?”.
• Neste tópico, o estudo das equações, tanto de interpretação como de resolução, será ampliado, e os estudantes terão oportunidades de aplicar técnicas já vistas e também de utilizar conhecimentos aritméticos em situações algébricas.
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à fórma ax + b = c, fazendo uso das propriedades da igualdade.

ATIVIDADES
faça as atividades no caderno
1. Determine a solução de cada equação a seguir considerando o conjunto universo indicado.
a) x + 7 = 3, conjunto universo =

b) x menos 3 = 2x, conjunto universo =

c) 8 menos x = 2 + x, conjunto universo =

d) 17x = menos15x, conjunto universo =

e) 3x menos 7 = 17, conjunto universo =

f ) menos x = 3x + 5, conjunto universo =

g) 100 = 4x, conjunto universo =

2. Resolva as equações considerando conjunto universo =

.
a) 2x + 7x ‒ 10 = 4x + 3 menos 2x
b) 3 ⋅ abre parêntesesx + 1fecha parênteses = 8
c) 4 ⋅ abre parêntesesx menos 6fecha parênteses = menos3
d) 2 ⋅ abre parênteses3 menos xfecha parênteses = menos4 ⋅ abre parêntesesx menos 1fecha parênteses
e) menos1 ⋅ abre parêntesesx + 4fecha parênteses = 3 ⋅ abre parêntesesx + 5fecha parênteses
f ) 3 ⋅
Abre parênteses, fração 1 terço menos x, fecha parênteses.menos abre parêntesesmenos2x + 7fecha parênteses = menos3
3. Classifique cada afirmação em verdadeira ou falsa.
a) Considerando conjunto universo =

, a solução da equação 3x menos 21 = 5x é menos10.
b) Considerando conjunto universo =

, a solução da equação 7 ⋅ abre parênteses4 + 2xfecha parênteses menos 4x = 16 + 7x é menos 4.
4. Determine a solução de cada uma das equações a seguir, considerando conjunto universo =

.
a)
Sentença matemática. Fração x sobre 3, mais 2, igual, 8.
b)
Sentença matemática. Fração x sobre 2, mais, fração 3 meios x, igual, 1 menos, fração 7 décimos.
c) 2x +
Sentença matemática. Fração 2 terços.= 3x + 2
d)
Sentença matemática. Fração2 quintos.x + 3x menos 2 = x + 10
e)
Sentença matemática. Fração 2 terços x, mais, fração 1 quarto x, igual, 6.f )
Sentença matemática. Fração 1 meio x, menos 3x, menos fração 1 terço, igual, 8x mais 12.
5 Equações e resolução de problemas
Alguns problemas podem ser resolvidos por meio de equações do 1º grau com uma incógnita. Acompanhe as situações a seguir.
Situação 1
Tatiana comprou um terreno de formato retangular, cuja medida do perímetro é 68 métros e um de seus lados mede 14 métros de comprimento. Qual é a medida de área desse terreno?
Observando a figura a seguir, verificamos que falta calcular a medida de comprimento do outro lado do terreno para, posteriormente, determinar a medida de área.
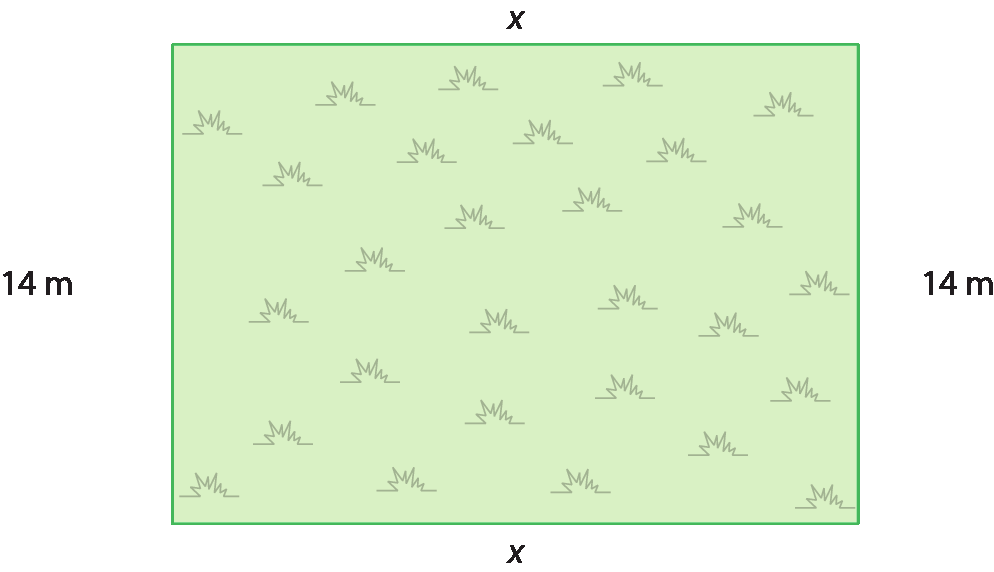
Note que a medida de comprimento desconhecida foi representada por x. Assim, podemos escrever uma equação que relaciona a medida de comprimento dos lados com a medida do perímetro desse terreno.
x + 14 + x + 14 = 68
Respostas e comentários
1. a) Não tem solução.
1. b) menos 3
1. c) 3
1. d) 0
1. e) 8
1. f)
Sentença matemática. Menos fração 5 quartos.
1. g) 25
2. a)
Sentença matemática. Fração 13 sétimos.2. b)
Sentença matemática. fração 5 terços.2. c)
Sentença matemática. Fração 21 quartos.2. d) menos1
2. e)
Sentença matemática. Menos fração 19 quartos.2. f) menos3
3. a) falsa
3. b) verdadeira
4. a) 18
4. b)
Sentença matemática. Fração 3 20 avos.
4. c)
Sentença matemática. Menos fração 4 terços.4. d) 5
4. e)
Sentença matemática. Fração 72 11 avos.
4. f)
Sentença matemática. Menos fração 74 63 avos.Orientações e sugestões didáticas
• Complemente a atividade 3 solicitando aos estudantes que reescrevam a equação do item a de modo que fique verdadeira, considerando ‒10 como raiz. Para determinar uma nova equação, eles podem substituir ‒10 na equação e verificar o que deve ser feito, como segue.
3x menos 21 = 5x ⇒
⇒ 3 ⋅ abre parêntesesmenos10fecha parênteses menos 21 = 5 ⋅ abre parêntesesmenos10fecha parênteses ⇒
⇒ menos51 = menos50 abre parêntesesfalsafecha parênteses
Assim, para que a equação tenha menos10 como raiz, basta adicionar 1 ao primeiro membro:
3x menos 21 + 1 = 5x ⇒
⇒ 3x menos 20 = 5x
Equações e resolução de problemas
Objetivo
• Favorecer o desenvolvimento da habilidade ê éfe zero sete ême ah um oito, da competência geral 9 e das competências específicas 3 e 6 da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero sete ême ah um oito por trabalhar a resolução de problemas por meio de equações polinomiais do 1º grau.
Orientações
• Neste tópico, os estudantes deverão resolver problemas em múltiplos contextos e lidar com diferentes registros, o que favorece o desenvolvimento da competência específica 6 da Bê êne cê cê.
• As equações devem ser escritas pelos estudantes com base na interpretação de cada um dos problemas propostos. É interessante que eles estejam em um ambiente que possibilite trocas e comparações, para que formulem hipóteses e questionem outras fórmas de resolução ou de representação de um mesmo problema. Dessa maneira, eles poderão exercitar a empatia, o diálogo e a cooperação, favorecendo o desenvolvimento da competência geral 9 da Bê êne cê cê.
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à fórma ax + b = c, fazendo uso das propriedades da igualdade.
Competência geral 9: Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competência específica 3: Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
Competência específica 6: Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Resolvendo essa equação:

Assim, os comprimentos dos lados do terreno medem 14 métros e 20 métros, e a medida de área desse terreno pode ser calculada da seguinte maneira:
14 ⋅ 20 = 280
Logo, a medida de área do terreno que Tatiana comprou é 280 métros quadrados.
Situação 2
Ao viajar por um dos trechos da Estrada Real, um motorista fez uma parada depois de percorrer
Sentença matemática. Fração 2 terços.do trajeto. Antes de retornar à estrada, verificou que a medida de distância que faltava para chegar ao destino era de 15 quilômetros. Quantos quilômetros mede esse trajeto?
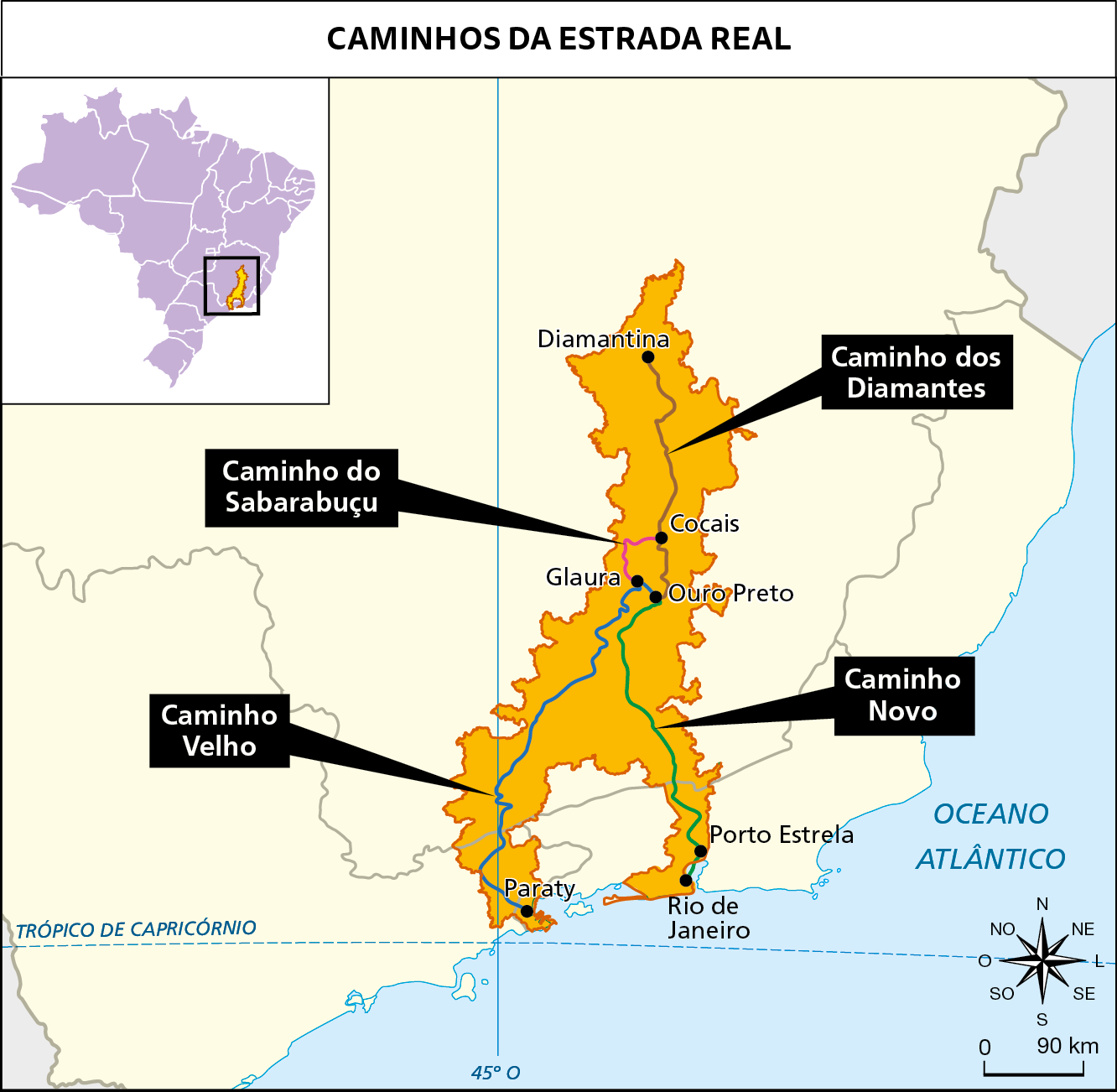
Elaborado com base em: ESTRADA REAL. Mapa da Estrada Real. Disponível em: https://oeds.link/fpDsXt. Acesso em: 5 julho 2022.
Observe que os dados do problema correspondem a duas partes do trajeto:
• a primeira, que corresponde a
Sentença matemática. Fração 2 terços.da medida do percurso;
• a segunda, que corresponde à medida de distância de 15 quilômetros.
Orientações e sugestões didáticas
• Ao analisar cada um dos problemas com os estudantes, incentive-os a identificar o conjunto universo das equações obtidas e se a raiz da equação pertence a esse conjunto.
• Se julgar conveniente, explore o mapa pedindo à turma que calcule a medida da distância em linha reta dos quatro caminhos apresentados.
Podemos fazer um esquema para representar essa situação graficamente. A medida de comprimento do segmento, indicado por x, representa todo o percurso.
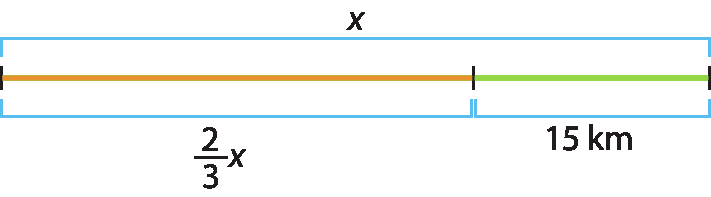
Analisando o esquema, percebemos que é possível representar o problema com a seguinte equação:
Podemos resolver essa equação do seguinte modo:

Logo: x = 45
Portanto, esse trajeto mede 45 quilômetros.
Situação 3
Bruna descobriu que mede 1,20 métro de altura e ficou curiosa para saber a medida da altura do seu pai e a da sua mãe.

Qual é a medida da altura do pai e a da mãe de Bruna?
Podemos usar a incógnita x para representar a medida da altura da mãe, em metro. Assim, temos:
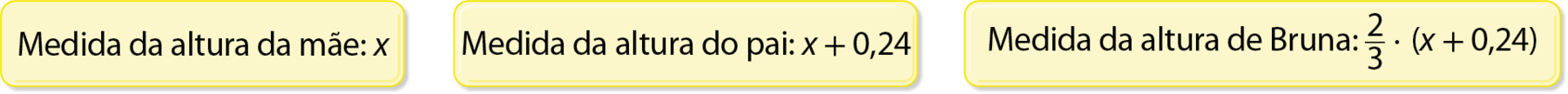
Orientações e sugestões didáticas
• Em cada uma das situações apresentadas, é possível identificar articulações entre diferentes campos da Matemática com o campo da Álgebra. Enfatize essas relações. Desse modo, a competência específica 3 da Bê êne cê cê é favorecida.
• Após apresentar a situação 3, questione os estudantes: “Como obtivemos a medida da altura do pai de Bruna?”. Espera-se que eles percebam que a medida foi obtida pela adição 1,56 + 0,24 = 1,80.
Como Bruna mede 1,20 métro de altura, podemos representar essa situação com a seguinte equação:
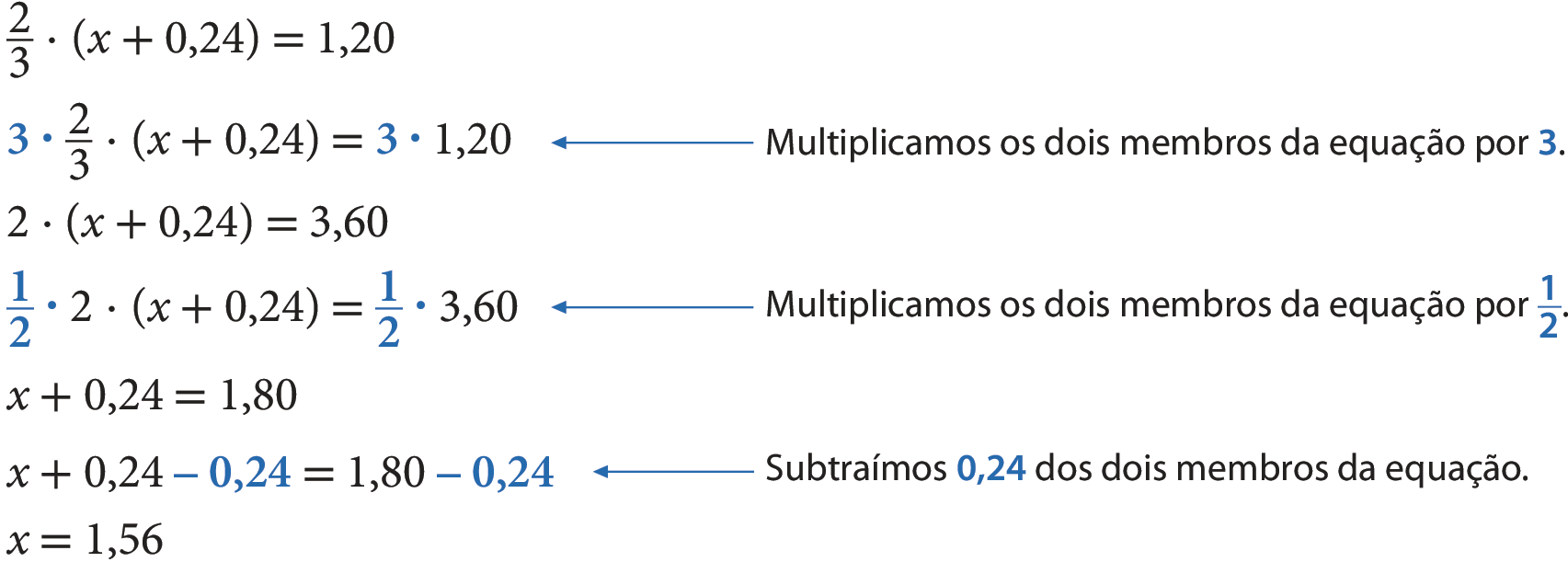
Portanto, a mãe de Bruna mede 1,56 métro de altura, e o pai, 1,80 métro.
Para pensar
Se usarmos a incógnita x para representar a medida da altura do pai de Bruna, que equação poderemos utilizar para representar essa situação? Encontre-a e resolva-a no caderno.
Situação 4
A soma de três números inteiros consecutivos é 345. Quais são esses números?
Nesse caso, que envolve números inteiros consecutivos, sabemos que a diferença entre um número e outro é de uma unidade.
Assim, se representarmos o número intermediário por x, o seu sucessor será x + 1 e o seu antecessor, x ‒ 1.

Como a soma dos três números é 345, podemos escrever a equação:

Portanto, os três números procurados são: 114, 115 e 116.
Situação 5
Uma prova era composta de 30 questões de múltipla escolha. A cada questão certa, o estudante ganhava 1 ponto, e, a cada questão errada, era descontado 0,25 ponto. Quantos pontos Mariana fez?

Se de 30 questões Mariana errou 5 e acertou 25, então o total de pontos que ela fez pode ser obtido pela seguinte expressão numérica:
25 ⋅ 1 menos 5 ⋅ 0,25 = 25 menos 1,25 = 23,75
Portanto, Mariana fez 23,75 pontos.
Joaquim, um colega de Mariana, disse que fez um total de 20 pontos. Quantas questões ele acertou?
Respostas e comentários
Para pensar:
Sentença matemática. Fração 2 terços x, igual, 1,20. Sentença matemática. x, igual, 1,80.Orientações e sugestões didáticas
• No boxe Para pensar, espera-se que os estudantes façam
Sentença matemática. Fração 2 terços.x = 1,20 para representar a medida da altura do pai de Bruna. Incentive-os a utilizar suas estratégias pessoais determinar a equação. Depois, peça que compartilhem com os colegas o modo como pensaram.
• Na situação 4, verifique se os estudantes perceberam como foram obtidos os números 114 (antecessor de 115) e 116 (sucessor de 115). Outra possibilidade é escrever x, x + 1 e x + 2 como três números consecutivos. Entretanto, o valor encontrado será o do primeiro, ou seja, nesse caso x será 114; logo, os números serão 114, 115 e 116. Os estudantes devem observar que há outras maneiras de representação e é fundamental deixar claro o que x representa em cada caso.
• Na situação 5, mostra-se como utilizar um esquema para compreender o problema. Ressalte aos estudantes que essa é uma das fórmas a que podem recorrer para resolver problemas.
Podemos recorrer ao esquema a seguir para representar essa situação.
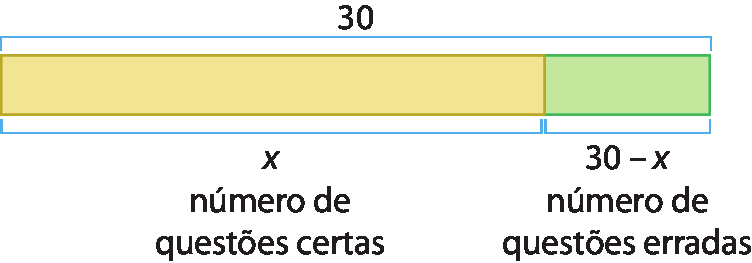
Como a cada questão certa o estudante recebe 1 ponto e a cada questão errada perde 0,25 ponto, podemos representar essa situação com a seguinte equação:
1 ⋅ x menos 0,25 ⋅ abre parênteses30 menos xfecha parênteses = 20
Observe como podemos resolver essa equação para obter o valor de x:

Portanto, Joaquim acertou 22 questões da prova.

Cálculo mental
Sofia fez essa prova e errou apenas duas questões. Quantos pontos ela obteve?

ATIVIDADES
faça as atividades no caderno
1. Um quadrado tem lado de medida de comprimento p. Se a medida do perímetro desse quadrado é 60 centímetros, qual é a medida de comprimento de p?

2. Determine a medida de comprimento dos lados de um triângulo cujo perímetro mede 24 centímetros, sabendo que essas medidas de comprimento são expressas por números naturais consecutivos.
3. As medidas dos perímetros do quadrado e do retângulo representados a seguir são iguais.
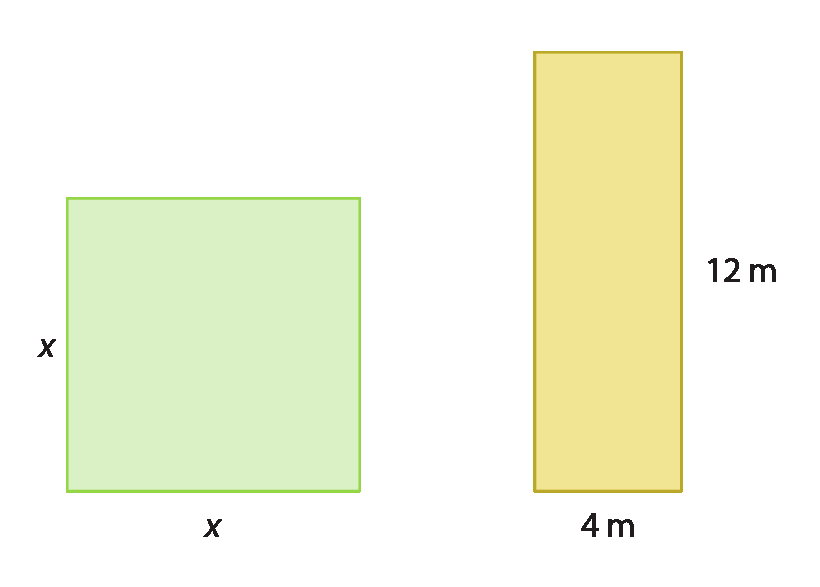
• Qual é a medida de comprimento do lado do quadrado?
4. Paulo vai construir sua casa em
Sentença matemática. Fração1 terço.da medida de área total de um terreno. Nos 160 métros quadrados restantes, ele vai construir um jardim.
a) Qual será a medida de área ocupada pela casa?
b) Qual é a medida de área total do terreno?
5. João e Pedro fizeram uma viagem de carro para Aracaju, capital de Sergipe.

• No primeiro dia, João dirigiu
Sentença matemática. Fração 1 terço.da medida de distância do percurso. No segundo dia, Pedro dirigiu
Sentença matemática. Fração 1 quinto.do percurso. Para chegar ao destino, precisaram ainda de dois dias, em que percorreram .1120 quilômetros. Quanto mede, em quilômetro, a distância percorrida em toda a viagem?
Respostas e comentários
Cálculo mental: 27,5 pontos
1. 15 centímetros
2. 7 centímetros, 8 centímetros e 9 centímetros
3. 8 métros
4. a) 80 métros quadrados
4. b) 240 métros quadrados
5. .2400 quilômetros
Orientações e sugestões didáticas
• No boxe Cálculo mental, espera-se que os estudantes percebam que Sofia ganhou 28 pontos, por ter acertado 28 questões, e perdeu 0,5 por ter errado duas (0,25 por questão). É importante que eles consigam resolver problemas que envolvam diferentes situações com números representados em diversas fórmas (decimal, fração, porcentagem). Para isso, convém que escrevam as equações com base na interpretação que fazem de cada uma das situações-problema propostas. Estimule um ambiente que possibilite trocas e comparações, para que os estudantes formulem hipóteses e questionem outras maneiras de resolução ou de representação de um problema.
6. Em uma turma do 7º ano, 30% dos estudantes devem fazer prova de recuperação, e os 28 estudantes restantes não farão. Quantos estudantes há nessa turma?
7. O prédio onde Fernanda mora tem
Sentença matemática. Fração 1 terço.da medida da altura do prédio em que Renato mora. Sabe‑se que o prédio de Fernanda tem 10 andares e que cada andar mede 2,5 métros de altura. Qual é a medida da altura do prédio em que Renato mora?
8. Em uma rodovia, Hugo percebeu que o marcador de combustível de seu carro indicava
Fração um quarto.da medida da capacidade total do tanque. Por precaução, ele abasteceu o carro com 25 litros de álcool. Depois disso, o marcador indicou
Fração 3 quartos.da medida da capacidade total. Quantos litros de combustível cabem no tanque do carro de Hugo?
9. Em uma gráfica, três impressoras funcionam diariamente para atender às encomendas. O trabalho é dividido da seguinte maneira:

• Quantas impressões são feitas diariamente nessa gráfica?
10. A professora de Matemática vai distribuir folhas quadradas para os estudantes fazerem dobraduras. Ela estimou 10 folhas para cada estudante.

• Sabendo que os estudantes fizeram uma dobradura com cada folha recebida, responda: quantas dobraduras foram feitas nessa aula?
11. Em uma sala de aula, há 20 estudantes matriculados.

Dos 20 estudantes, quantos são meninos e quantas são meninas?
•


Verifique o número de meninos e de meninas da sua sala de aula. Depois, elabore um problema indicando o número total de estudantes e uma sentença que relacione o número de meninos e o de meninas da turma. Apresente aos colegas o problema que você elaborou.
12. Em uma maratona, os três primeiros colocados foram premiados. Eles dividiram o prêmio de R$ 10.000,00dez mil reais da seguinte maneira:
✓ o 3º colocado recebeu a menor parte;
✓ o 2º colocado recebeu R$ 2.000,00dois mil reais a mais que o 3º colocado;
✓ o 1º colocado recebeu o dobro da quantia do 2º colocado.
• Quantos reais cada atleta recebeu?
13. Vitório foi à papelaria comprar canetas coloridas. Se ele comprar 7 canetas, receberá R$ 4,50quatro reais e cinquenta centavos de troco, mas, se comprar 11, faltará R$ 1,50um reais e cinquenta centavos para pagar a conta.
a) Quanto custa cada caneta?
b) Quantas canetas Vitório poderia levar sem sobrar troco nem faltar dinheiro?
14. Em um campeonato de futebol, os dois melhores jogadores são do mesmo time. Durante o campeonato, esses dois jogadores marcaram juntos 32 gols. Se um dos jogadores marcou
Sentença matemática. Fração 1 terço.do número de gols marcados pelo outro, quantos gols marcou cada jogador?
Respostas e comentários
6. 40 estudantes
7. 75 métros
8. 50 litros
9. .9000 impressões
10. trezentas dobraduras
11. 7 meninos e 13 meninas; Resposta pessoal.
12. 1º colocado: R$ 6.000,00seis mil reais; 2º colocado: R$ 3.000,00três mil reais; 3º colocado: R$ 1.000,00mil reais
13. a) R$ 1,50um reais e cinquenta centavos
13. b) 10 canetas
14. Um jogador marcou 24 gols e o outro, 8 gols.
Orientações e sugestões didáticas
• Os estudantes devem perceber que é possível resolver o problema proposto na atividade 8 por meio de estratégias diferentes. Duas dessas estratégias estão reproduzidas a seguir.
Estratégia 1:
Se o tanque do carro de Hugo estava com
Fração um quarto.da medida da capacidade e, após colocar combustível, ficou com
Fração 3 quartos.da medida da capacidade, isso significa que a quantidade de combustível utilizada no abastecimento foi correspondente à metade da medida da capacidade total, pois
Fração 3 quartos.‒
Fração um quarto.=
Fração 2 quartos.=
Sentença matemática. 1 meio. Dessa maneira, como a quantidade de combustível utilizada foi 25 litros, temos que 25 litros correspondem a meio tanque; logo, cabem 50 litros de combustível no tanque do carro de Hugo.
Estratégia 2:
Indicando por x a quantidade de litros de combustível que cabem no tanque do carro de Hugo, temos:
Fração um quarto.
x + 25 =
Fração 3 quartos.x ⇒
⇒ 25 =
Fração 3 quartos.x menos
Fração um quarto.x ⇒
⇒ 25 =
Fração 2 quartos.x ⇒ x = 50
Portanto, cabem 50 litros de combustível no tanque do carro de Hugo.
• Se julgar oportuno, apresente a seguinte questão de vestibular para que os estudantes verifiquem que é possível resolvê-la com os conhecimentos adquiridos sobre equação.
(ú éfe pê é) Em um teste de 16 questões, cada acerto adiciona 5 pontos, e cada erro subtrai 1 ponto. Se um estudante respondeu a todas as questões e obteve um total de 38 pontos, quantas questões ele errou? (alternativa d)
a) 4
b) 5
c) 6
d) 7
e) 8
15. Considere x, y e z as medidas de comprimento dos lados de um triângulo cujo perímetro mede 32 centímetros.
Se a medida de comprimento x é o dobro da de y e a medida de comprimento de z é igual a 14 centímetros, quais são as medidas de comprimento x e y?
•


Desenhe em seu caderno um triângulo e reescreva o enunciado anterior substituindo as informações de acordo com as medidas de comprimento dos lados desse triângulo. Depois, peça a um colega que descubra as medidas de comprimento de dois lados do triângulo que você desenhou.
16. (púqui-Rio de Janeiro) Um empresário possui, em sua conta, uma quantia que corresponde a
Sentença matemática. Fração 1 sexto.do valor dos equipamentos de que precisa para montar seu escritório. Se ele depositar R$ 780,00setecentos e oitenta reais na conta, passa a ter uma quantia, em reais, que corresponde a
Sentença matemática. Fração 3 quintos.do valor dos equipamentos.
a) Qual o valor total dos equipamentos?
b) Quantos reais esse empresário deverá depositar na sua conta para que possa comprar tudo de que precisa e ainda ficar com uma reserva de R$ 230,00duzentos e trinta reais?
17. Sônia foi a um supermercado e comprou uma embalagem com
Fração um quarto.de queijo. Se ela acrescentasse 630 gramas, teria uma peça inteira de queijo. Qual é a medida de massa, em grama, da peça inteira?

18. Régis e Amanda recebem juntos R$ 4.500,00quatro mil quinhentos reais por mês. Sabendo que o salário de Régis é
Sentença matemática. Fração 4 quintos.do salário de Amanda, calcule o salário de cada um.
19.

Roberto e Jorge gostam de jogar bolinha de gude. Eles foram à loja de brinquedos e cada um comprou uma quantidade de bolinhas. Observe a cena a seguir.

• Sabendo que, juntos, os meninos compraram 70 bolinhas de gude, responda às questões.
Dica: considere x o número de bolinhas verdes.
a) Quantas bolinhas Roberto comprou?
b) Quantas bolinhas verdes Jorge comprou?
20. O poço a contém 700 litros de água; o poço B contém 800 litros. Usando baldes com medidas de capacidade iguais, Paulo tirou 100 baldes cheios de água do poço a e Norberto tirou 120 baldes cheios de água do poço B.
Sabendo que os dois poços ficaram com a mesma quantidade de água, responda: qual é a medida de capacidade, em litro, de cada balde?
21.


Elabore um problema que possa ser resolvido com uma equação do 1º grau com uma incógnita. Depois, peça a um colega que resolva o seu problema e resolva o problema criado por ele.
Respostas e comentários
15. x = 12 centímetros e y = 6 centímetros; Resposta pessoal.
16. a) R$ 1.800,00mil oitocentos reais
16. b) R$ 1.730,00mil setecentos e trinta reais
17. 840 gramas
18. O salário de Amanda é R$ 2.500,00dois mil quinhentos reais, e o de Régis, R$ 2.000,00dois mil reais.
19. a) 40 bolinhas
19. b) 20 bolinhas
20. 5 litros
21. Resposta pessoal.
Orientações e sugestões didáticas
• Na atividade 15, os estudantes deverão elaborar um problema com base em um triângulo que eles terão de desenhar. É importante, no desenho, que a relação entre as medidas de comprimento dos lados do triângulo permita a elaboração de um enunciado claro. Nessa atividade, eles poderão lidar com diferentes registros: registro figural (desenho do triângulo), registro em língua materna (enunciado do problema que deverão elaborar) e registro algébrico (equação que traduz o enunciado do problema elaborado pelo colega).
• É possível que os estudantes não considerem a condição de existência do triângulo, uma vez que esse conteúdo será explorado no Capítulo 9. Assim é importante validar a elaboração considerando a condição de existência. Ao desenhar o triângulo, os estudantes podem ajustar suas hipóteses sobre como identificar as medidas de comprimento desses lados. Por exemplo, se eles desenharem um triângulo equilátero, poderão identificar a medida de comprimento de cada lado por x. Se desenharem um triângulo isósceles, poderão considerar a medida de comprimento dos dois lados congruentes como x e, então devem pensar que medida de comprimento poderá ter o outro lado verificando se pode ser, por exemplo, a metade ou o dobro de x. E assim por diante para triângulos escalenos.
• Na atividade 17, oriente os estudantes a escrever a equação:
Fração um quarto.
x + 630 = x
• Após a resolução da atividade 20, se julgar necessário, peça aos estudantes que voltem ao enunciado e confirmem a resposta obtida.
Poço A: tinha 700 litros e foram retirados 100 ⋅ 5 = 500, ou seja, ficou com apenas 200 litros.
Poço B: tinha 800 litros e foram retirados 120 ⋅ 5 = 600, ou seja, ficou com apenas 200 litros.
Portanto, os dois poços ficaram com a mesma quantidade de água, conforme o enunciado.

6 Desigualdade
Observe a medida da velocidade registrada pela lombada eletrônica em cada situação a seguir.


Podemos indicar se a medida da velocidade registrada está acima ou abaixo da medida de velocidade máxima permitida na via usando sentenças matemáticas:

Sentenças como essas são denominadas desigualdades. As desigualdades são sentenças matemáticas em que aparecem um dos sinais:
> (maior que)
< (menor que)
≠ (diferente de)
⩾ (maior que ou igual a)
⩽ (menor que ou igual a)
Assim como nas igualdades, chamamos de 1º membro a expressão que está à esquerda do sinal de desigualdade e de 2º membro a expressão que está à direita do sinal de desigualdade.
Exemplos

Para pensar
No Brasil, alguns veículos, como os de transporte escolar, são obrigados a usar um equipamento conhecido como tacógrafo. Esse aparelho registra, para efeito de fiscalização, a medida do tempo de viagem, a medida de distância percorrida e a medida da velocidade do veículo.
Você já tinha ouvido falar desse aparelho?
Respostas e comentários
Para pensar: Resposta pessoal.
Orientações e sugestões didáticas
Desigualdade
Objetivos
• Reconhecer uma desigualdade.
• Trabalhar com o Tema Contemporâneo Transversal Educação para o Trânsito, da macroárea Cidadania e Civismo.
• Compreender os princípios de equivalência das desigualdades.
Orientações
• A ideia de desigualdade pode ser introduzida usando como recurso a imagem de balanças em desequilíbrio.
• Aproveite para explorar o tema do texto inicial e comente com os estudantes que a função da lombada eletrônica é monitorar a medida da velocidade dos veículos em uma via, para que não ultrapassem a medida de velocidade máxima permitida. Dessa fórma, ajuda a melhorar a segurança no trânsito, tanto para veículos como para pedestres, em determinados locais movimentados, diminuindo os acidentes.
• Conversar com os estudantes sobre temas relacionados ao trânsito favorece a conscientização sobre o Tema Contemporâneo Transversal Educação para o Trânsito da macroárea Cidadania e Civismo.
• No boxe Para pensar, é provável que os estudantes não saibam muito sobre o tacógrafo. Explique que ele é um aparelho que registra as medidas de velocidade e de distância percorrida em um determinada medida de tempo. No vídeo disponível em https://oeds.link/57gu7K (acesso em: 31 julho 2022), há uma reportagem que traz outras informações.
• Se julgar conveniente, pode ser proposta aos estudantes uma pesquisa em que eles busquem informações a respeito do Código de Trânsito Brasileiro, com foco nas questões de medida de velocidade máxima permitida em vias urbanas, rodovias etcétera para diversos tipos de veículo. Essa proposta pode, ainda, ser ampliada em um trabalho conjunto com a área de Língua Portuguesa e/ou Arte, de modo que os estudantes organizem uma campanha de conscientização sobre a importância de respeitar as leis de trânsito. No Portal da Câmara dos Deputados (disponível em: https://oeds.link/eezDU1; acesso em: 12 agosto 2022), há a publicação do Código de trânsito brasileiro.
Lembre-se: Escreva no caderno!
Observação
Observe duas propriedades que valem para as desigualdades.
• Propriedade simétrica
Exemplo: se 12 + 4 < 25, então 25 > 12 + 4
• Propriedade transitiva
Exemplo: sendo 3 menos 2 < 8 e 8 < 11 + 5, então 3 menos 2 < 11 + 5
Princípios de equivalência das desigualdades
Antes de estudar os princípios de equivalência das desigualdades, observe o que costumamos dizer sobre os sinais que usamos para expressá-las:
< e < têm o mesmo sentido;
> e > têm o mesmo sentido;
⩽ e ⩽ têm o mesmo sentido;
⩾ e ⩾ têm o mesmo sentido;
< e > têm sentidos opostos;
> e < têm sentidos opostos;
⩽ e ⩾ têm sentidos opostos;
⩾ e ⩽ têm sentidos opostos.
Princípio aditivo da desigualdade
Acompanhe nos exemplos o que acontece quando adicionamos um mesmo número aos dois membros de uma desigualdade em que aparecem os sinais < ou > ou ⩽ ou ⩾.
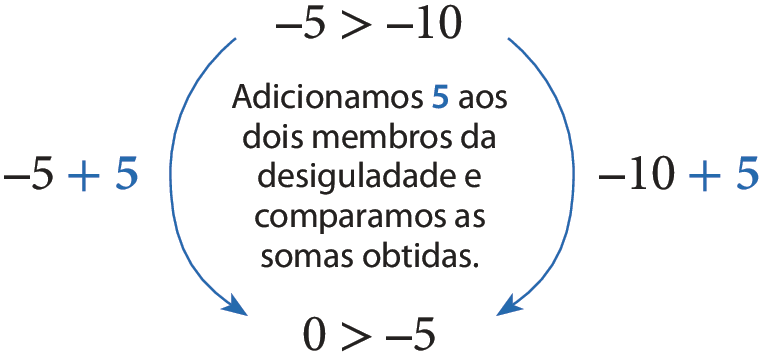
• Adicionando um número positivo aos dois membros de uma desigualdade:
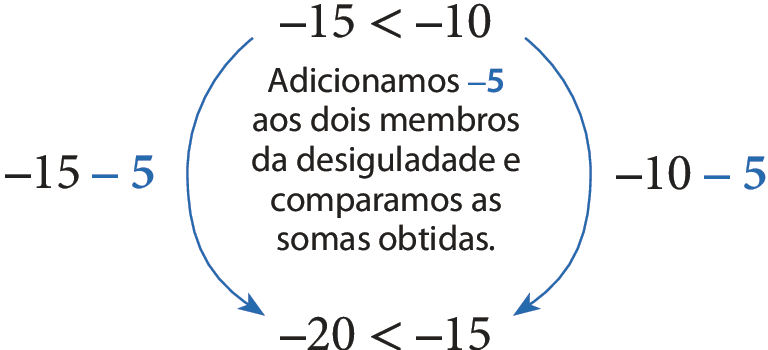
• Adicionando um número negativo aos dois membros de uma desigualdade:
• Adicionando o número zero aos dois membros de uma desigualdade:
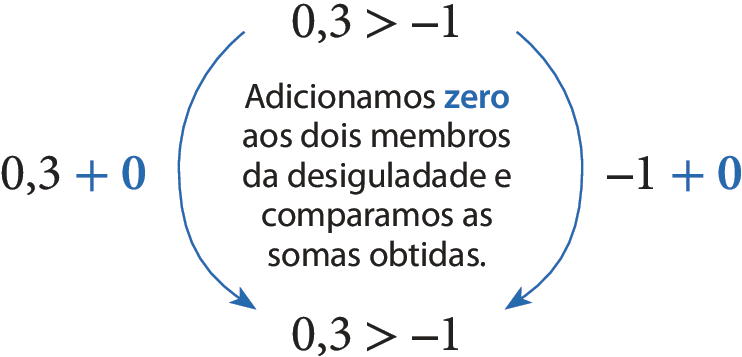
Observe que adicionar ou subtrair um mesmo número dos dois membros da desigualdade não altera o sentido da desigualdade inicial. Esse é o princípio aditivo da desigualdade.
Orientações e sugestões didáticas
• Caso seja necessário, apresente mais exemplos numéricos usando os princípios de equivalência das desigualdades. Utilizar balanças em desequilíbrio como recurso também pode contribuir para que os estudantes atribuam significado aos princípios aditivo e multiplicativo da desigualdade.
Lembre-se: Escreva no caderno!
Exemplos
• menos2 < 15
menos2 + 7 < 15 + 7
5 < 22
• 31,5 > 10
31,5 menos 20 > 10 menos 20
11,5 > menos 10
• menos7 < 1
menos7 + 0 < 1 + 0
menos7 < 1
Princípio multiplicativo da desigualdade
Acompanhe nos exemplos o que acontece quando multiplicamos os dois membros de uma desigualdade em que aparecem os sinais < ou > ou ⩽ ou ⩾ por um mesmo número:
• Multiplicando os dois membros de uma desigualdade por um número positivo.
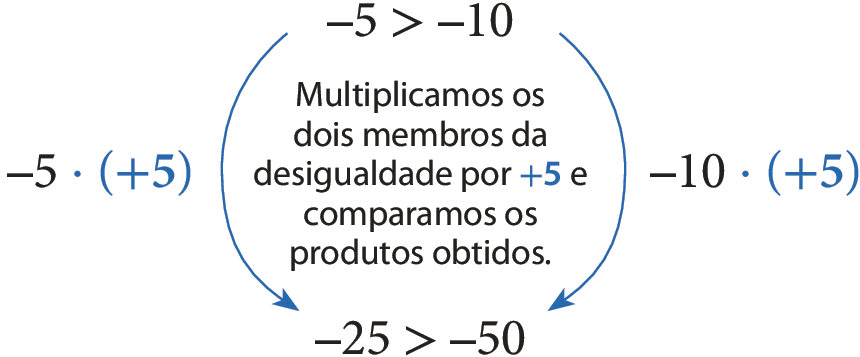
• Multiplicando os dois membros de uma desigualdade por um número negativo:
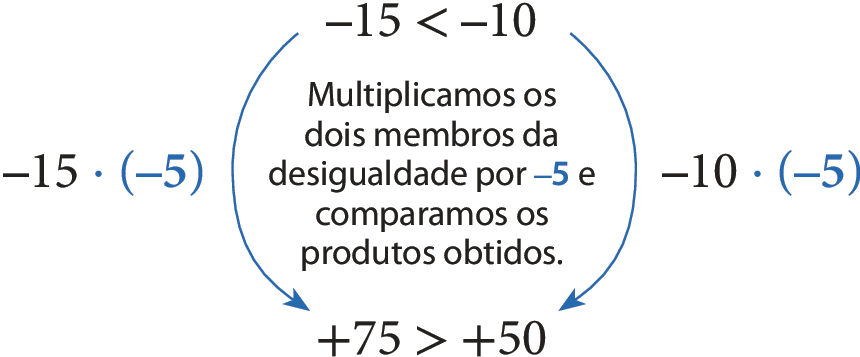
• Multiplicando os dois membros de uma desigualdade por zero:
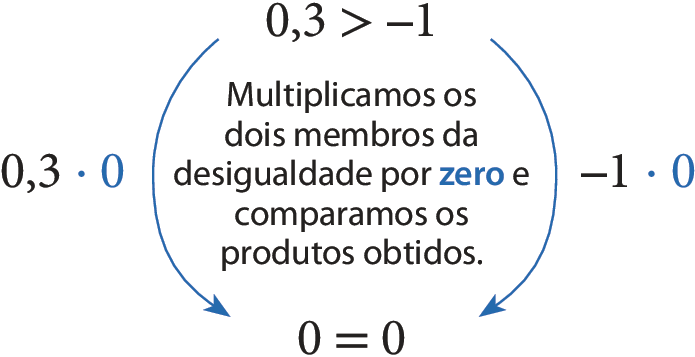
Observe que, se o número considerado é:
• positivo, obtemos outra desigualdade de mesmo sentido;
• negativo, obtemos outra desigualdade de sentido contrário;
• zero, obtemos uma igualdade abre parênteses0 = 0fecha parênteses.
Esse é o princípio multiplicativo da desigualdade.
Exemplos
• menos2 < 15
menos2 ⋅ 7 < 15 ⋅ 7
menos14 < 105
• 31,5 > 10
31,5 ⋅ abre parêntesesmenos10fecha parênteses < 10 ⋅ abre parêntesesmenos10fecha parênteses
menos315 < menos100
• menos7 < 1
menos7 ⋅ 0 = 1 ⋅ 0
0 = 0
Orientações e sugestões didáticas
• Verifique se os estudantes percebem que, nos dois últimos exemplos do princípio multiplicativo da desigualdade, o sinal foi alterado no segundo passo. É importante que compreendam o porquê de obtermos outra desigualdade de sentido contrário quando multiplicamos os seus dois membros por um número negativo. Evite que esse fato seja memorizado sem atribuição de significado por parte da turma.

ATIVIDADES
faça as atividades no caderno
1. Copie no caderno as sentenças que representam uma desigualdade.
a) 2 + 1 > menos1
b)
Sentença matemática. Abre parênteses, fração 1 terço elevado a 2, fecha parênteses, igual, fração 1 nono.c)
Fração 3 quartos.menos 1 ≠ menos1
d) 12 + 12 > 1
e) 5 menos 10 < 0
f) n menos 1 = 0
2. Copie as desigualdades a seguir identificando o 1º e o 2º membros de cada uma delas.
a) 1 menos 2 < 0
b) 2 ⩾ menos3 menos 4
c)
Sentença matemática. Menos 1, menor que, fração 1 terço.
d) 7 ⩽ 52
3. Identifique qual das desigualdades é falsa.
a) 252 dividido por 12 menos 35 > menos3 ⋅ 5
b) abre parênteses4 + 12fecha parênteses dividido por 2 < 3elevado a 2
c) 5elevado a 3 menos 25 > 10elevado a 2
d) 15 menos 3 ⋅ 4 < 36 dividido por 9
e) 98 > 256 dividido por 2elevado a 2
4. (Saresp) Observe atentamente as retas ordenadas a seguir:
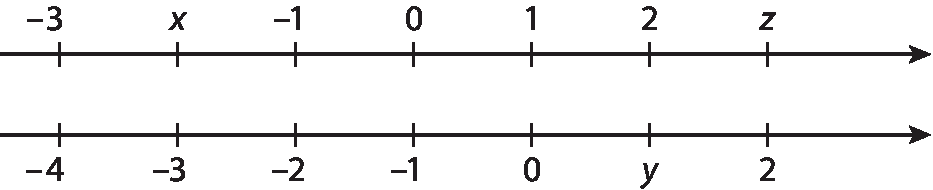
A ordenação correta entre os números representados pelas letras x, y e z é:
a) x < y < z
b) x < z < y
c) y < x < z
d) y < z < x
5. Com base no que você estudou sobre o princípio aditivo e sobre o princípio multiplicativo da desigualdade, reescreva cada sentença no caderno substituindo o ◼ pelo sinal de desigualdade adequado.
a) 10 + 1 > 2
10 + 1 menos 5 ◼ 2 menos 5
6 ◼ menos3
b) 4 ⋅ 2 < 20
4 ⋅ 2 ⋅ abre parêntesesmenos5fecha parênteses ◼ 20 ⋅ abre parêntesesmenos5fecha parênteses
menos 40 ◼ menos100
c) 7 ⩽ 10elevado a 2
7 + 10 ◼ 10elevado a 2 + 10
17 ◼ 110
d) 9elevado a 2 ⩾ 9
Sentença matemática. 9 elevado ao quadrado, vezes, abre parênteses, fração 1 terço, fecha parênteses, quadradinho cinza, 9 vezes, abre parênteses, fração 1 terço, fecha parênteses.
27 ◼ 3
6. Classifique cada afirmação a seguir em verdadeira ou falsa.
a) Se 1 + 6 < 10, então 1 + 6 + abre parêntesesmenos 6fecha parênteses > 10 + abre parêntesesmenos 6fecha parênteses.
b) Se 3 ⋅ 7 > 20, então
Sentença matemática. 3 vezes 7, vezes fração 1 terço, maior que, 20 vezes, fração 1 terço..
c) Se menos x ⩾ 8, então menos x ⋅ abre parêntesesmenos1fecha parênteses ⩽ 8 ⋅ abre parêntesesmenos1fecha parênteses.
7. Escreva uma desigualdade para representar cada situação a seguir.
a)

b)

• Agora, responda: qual é o maior número de ovos que pode haver no pote?
8. Observe as figuras representadas a seguir.
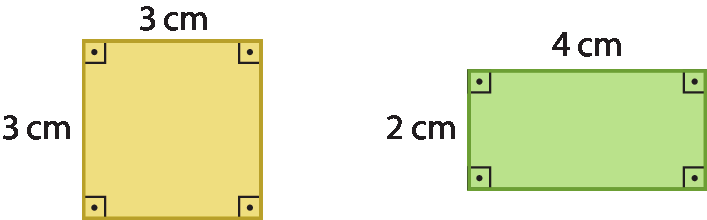
• Calcule a medida de área dessas figuras e escreva uma desigualdade para relacionar essas medidas de área.
9. (saréspi) Em um jogo de dados, Zezo tirou 3 vezes o número 6 e depois o número 12. Já Ricardo tirou o 9 na primeira jogada, o 7 na rodada seguinte e o 10 nas terceira e quarta jogadas. É correto dizer que:
a) Ricardo está 16 pontos na frente de Zezo.
b) Zezo está 4 pontos na frente de Ricardo.
c) Ricardo está 6 pontos na frente de Zezo.
d) Zezo está 1 ponto na frente de Ricardo.
Respostas e comentários
1. alternativas a, c, d, e
2. a) 1º membro: 1 menos 2; 2º membro: 0
2. b) 1º membro: 2; 2º membro: menos 3 menos 4
2. c) 1º membro: menos1; 2º membro:
Sentença matemática. 1 terço2. d) 1º membro: 7; 2º membro: 5elevado a 2
3. alternativa c
4. alternativa a
5. Respostas em Orientações.
6. a) falsa
6. b) verdadeira
6. c) verdadeira
7. Respostas em Orientações.
8. Medida de área do quadrado: 9 centímetros quadrados; Medida de área do retângulo: 8 centímetros quadrados; 8 centímetros quadrados < 9 centímetros quadrados ou 9 centímetros quadrados > 8 centímetros quadrados
9. alternativa c
Orientações e sugestões didáticas
• Na atividade 4, espera-se que os estudantes percebam que existe mais de um modo de ordenar os números representados por x, y e z. Um dos modos será observar, comparar as retas e tirar algumas conclusões.
Pela primeira reta:
menos3 < x < menos1
z > 2
Pela segunda reta:
0 < y < 2
Logo, z é o maior dos três números e x é o menor deles. Portanto, é correto afirmar que: x < y < z, o que corresponde à alternativa a.
• Resposta da atividade 5:
a) 10 + 1 > 2
10 + 1 menos 5 > 2 menos 5
6 > menos 3
b) 4 ⋅ 2 < 20
4 ⋅ 2 ⋅ (‒5fecha parênteses > 20 ⋅ (‒ 5fecha parênteses
menos 40 > menos 100
c) 7 ⩽ 10elevado a 2
7 + 10 ⩽ 10elevado a 2 + 10
17 ⩽ 110
d) 9elevado a 2 ⩾ 9
9elevado a 2 ⋅
Sentença matemática. abre parênteses 1 terço fecha parênteses⩾ 9 ⋅
Sentença matemática. abre parênteses 1 terço fecha parênteses.27 ⩾ 3
• Resposta da atividade 7:
a) 2 ⋅ 17 < 35
b) 2x < 12
No pote, pode haver no máximo 5 ovos.

Educação Financeira
faça as atividades no caderno


Comprar mais ou comprar menos?

O que você faria?
Imagine que você esteja nessa padaria diante das duas situações mostradas. Depois, copie os quadros a seguir no caderno e complete-os para descrever as circunstâncias nas quais vale ou não a pena fazer uma compra.

|
Vale a pena comprar o bolo inteiro quando... |
Vale a pena comprar o bolo em pedaços quando... |
|---|---|
Respostas e comentários
O que você faria?: Respostas pessoais.
Orientações e sugestões didáticas
Educação Financeira
Objetivos
• Refletir sobre o uso consciente de recursos financeiros.
• Trabalhar com os Temas Contemporâneos Transversais Educação para o Consumo e Educação Financeira, das macroáreas Meio Ambiente e Economia, ao propor uma reflexão sobre o consumismo.
• Favorecer o desenvolvimento das competências gerais 6 e 7 da Bê êne cê cê.
Orientações
• Fazer compras com os pais ou sozinho é um ato corriqueiro e muito propício para colocar em discussão questões de educação financeira e consumismo. Os estudantes poderão fazer uma série de questionamentos a respeito do que vale ou não a pena comprar. O consumo por impulso é tão comum que, na maioria das vezes, é visto como algo normal. No entanto, se desde criança isso for ensinado, haverá um ganho em termos financeiros e sem desperdício. Reflexões como essa contribuem para que os estudantes façam escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com consciência crítica e responsabilidade. Por isso, as competências gerais 6 e 7 têm seu desenvolvimento favorecido como também se possibilita o trabalho com os Temas Contemporâneos Transversais Educação para o Consumo e Educação Financeira das macroáreas Meio Ambiente e Economia.
• Em O que você faria?, os estudantes podem formar duplas ou trios para discutir e elaborar respostas.
• No quadro “Um dia na padaria...”, eles podem responder que vale a pena comprar o bolo inteiro quando há muitas pessoas na casa e o bolo será consumido logo, ou que é o bolo preferido deles. E responder que vale a pena comprar o bolo em pedaços quando uma só pessoa na casa gosta daquele sabor e ela ficará satisfeita com apenas um pedaço, ou que apenas 2 pedaços são suficientes.
Competência geral 6: Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
Competência geral 7: Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
▶ Educação Financeira

|
Compensa aproveitar a promoção se... |
Não compensa aproveitar a promoção se... |
|---|---|
Calcule
1. Observe na ilustração os preços dos bolos e, depois, responda às questões.

a) Quantos pedaços de bolo formam o bolo inteiro?
b) Se você comprasse 6 pedaços de bolo, quanto gastaria?
c) Quantos pedaços de bolo podem ser comprados com o preço de um bolo inteiro?
d) O preço do bolo inteiro e o preço do pedaço são proporcionais? Justifique sua resposta. Dica: serão proporcionais se o preço de 6 pedaços (equivalentes ao bolo inteiro) for igual ao preço do bolo inteiro.
e) Se você quisesse comprar 3 pedaços de bolo, o que faria: compraria o bolo inteiro ou os 3 pedaços à parte? Justifique sua resposta.
f ) Se alguém comprasse o bolo inteiro por impulso, sem de fato precisar, que problemas essa atitude acarretaria? Exemplifique com uma situação.
2. Agora, observe os preços da promoção de tortas e, depois, responda às questões.
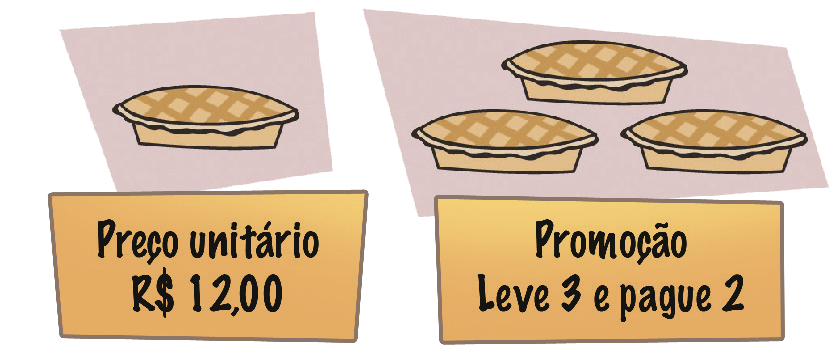
a) O preço unitário e o da promoção são proporcionais? Por quê?
b) Quais poderiam ser os preços de 1, 2 e 3 tortas para que fossem proporcionais?
c) Quanto você economizaria se aproveitasse a promoção?
d) Que problemas uma compra por impulso acarretaria? Exemplifique com uma situação.
Reflita
Nos mercados, em geral, há muitas ofertas tentadoras; por isso, precisamos pensar com responsabilidade e ter cautela para decidir o que e quanto comprar.
a) Você, ou alguém de sua família, já fez uma compra por impulso? Se a resposta for positiva, essa compra gerou desperdícios ou algum outro problema?
b) Você já ouviu falar em vendas no atacado (em grande ou média quantidade)? A que público é direcionado esse tipo de venda? Por quê?
c) Você e sua família já fizeram compras no atacado? Em caso afirmativo, em que situação?
Respostas e comentários
Calcule:
1. a) 6 pedaços
1. b) R$ 24,00vinte e quatro reais
1. c) 4 pedaços, e sobrariam R$ 2,00dois reais, pois normalmente não se vende meio pedaço.
1. d) Não, porque o bolo cortado em pedaços custaria mais caro que o bolo inteiro.
1. e) Exemplos de resposta: compraria 3 pedaços, pois gastaria somente 12 reais; compraria o bolo inteiro e daria os outros pedaços para meus amigos, pois não posso consumir todos os pedaços.
1. f) Exemplo de resposta: Se alguém comprasse um bolo inteiro para comer sozinho, consumiria mais do que o necessário ou desperdiçaria uma parte do bolo, já que tem data de validade e não pode ser guardado por muito tempo.
Calcule: 2. Respostas em Orientações.
Reflita: Respostas pessoais.
Orientações e sugestões didáticas
• No quadro “Outro dia na padaria...” do O que você faria?, os estudantes podem responder que compensa aproveitar a promoção se o tipo de torta é muito consumido em casa ou se for possível congelar as tortas para consumir depois. E responder que não compensa aproveitar a promoção se nem todas as pessoas da casa gostam de tortas ou se a quantidade total leva muito tempo para ser consumida pela família e o prazo de validade pode vencer.
• Acompanhe os cálculos dos estudantes em Calcule e não apenas dê destaque à resposta certa ou errada. Peça a eles que leiam os números encontrados para observar quanto se perde, em termos financeiros, quando são feitas compras por impulso. No item e, espera-se que os estudantes concluam que se deve comprar a quantidade necessária para evitar o desperdício. No item f, eles podem responder algo como: “Se alguém comprasse um bolo inteiro para comer sozinho, consumiria mais do que o necessário ou desperdiçaria uma parte do bolo, já que tem data de validade e não pode ser guardado por muito tempo”.
• Resposta da atividade 2 do Calcule:
a) Não; porque quando você compra apenas uma unidade paga R$ 12,00doze reais e quando compra 3 unidades paga R$ 24,00vinte e quatro reais (preço de duas unidades).
b) Exemplo de resposta: Os preços poderiam ser: uma unidade, R$ 12,00doze reais; 2 unidades, R$ 24,00vinte e quatro reais; e 3 unidades, R$ 36,00trinta e seis reais. (Nesse caso, não haveria promoção.)
c) Como seriam pagos R$ 24,00vinte e quatro reais em vez de R$ 36,00trinta e seis reais, a economia seria de R$ 12,00doze reais.
d) Exemplo de resposta: No caso de uma pessoa que foi comprar apenas uma unidade e aproveitou a promoção, o gasto total foi de R$ 24,00vinte e quatro reais, ou seja, o dobro do que ela teria gastado se comprasse apenas o que pretendia. Como nem sempre a quantidade de produto em promoção é necessária, corre-se risco de desperdiçá-lo.
• Em Reflita, as respostas são pessoais, mas é bastante oportuno conversar com os estudantes sobre momentos em que se deve escolher entre comprar em quantidades maiores ou menores, nos quais é necessário analisar a situação para ter certeza de qual é a melhor escolha. Situações em que as pessoas revendem mercadorias, têm famílias grandes, fazem festas ou viagens ou dividem compras com outras famílias são exemplos em que é adequado comprar no atacado.
7 Inequação do 1º grau com uma incógnita
Observe a seguir alguns exemplos de desigualdade.
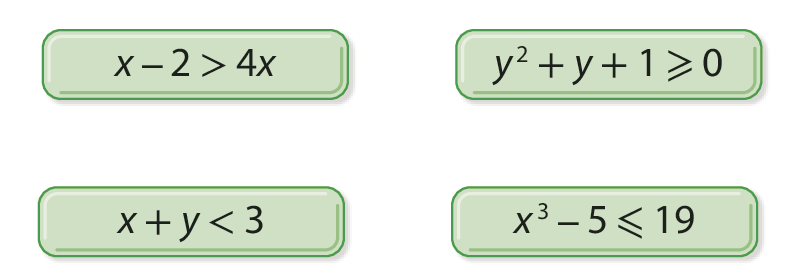
Toda desigualdade que tem uma ou mais incógnitas e cada incógnita tem expoente maior ou igual a 1 é chamada de inequação.
Entre as desigualdades apresentadas anteriormente, as inequações x menos 2 > 4x e x + y < 3 são do 1º grau. Entre elas, observe que a inequação x + y < 3 tem duas incógnitas e a inequação x menos 2 > 4x tem uma incógnita.
Toda inequação do 1º grau com uma incógnita pode ser escrita de uma das fórmas a seguir:
ax + b ≠ 0
ax + b > 0
ax + b < 0
ax + b ⩾ 0
ax + b ⩽ 0
em que ei é um número racional diferente de zero, b é um número racional qualquer e x é a incógnita.
Exemplos
Outros exemplos de inequações do 1º grau com uma incógnita.
• 2x > menos 5
•
Sentença matemática. Menos fração x sobre 2, menor que ou igual a, 7.
• x menos 1 ⩾ 0
As soluções de uma inequação são todos os números de determinado conjunto universo que ao substituírem as incógnitas tornam a sentença verdadeira.
Para resolver uma inequação, empregamos os princípios de equivalência das desigualdades. Acompanhe, por exemplo, como resolver a inequação x + 6 > 2, sendo conjunto universo =

.

Portanto, todo número inteiro maior que ‒ 4 é solução dessa inequação.
Observe como podemos representar essa solução na reta numérica.

Observação
Nessa representação feita na reta numérica, os números correspondentes aos pontos indicados com “bolinhas cheias” são algumas das infinitas soluções da inequação x + 6 > 2, sendo conjunto universo =

.
A “bolinha vazia” indica que menos 4 não é solução. A partir do menos 4, todos os números inteiros maiores que ele são soluções dessa inequação.
Orientações e sugestões didáticas
Inequação do 1º grau com uma incógnita
Objetivos
• Reconhecer uma inequação do 1º grau.
• Resolver inequações do 1º grau aplicando os princípios aditivo e multiplicativo da desigualdade.
Orientações
• Se houver dificuldade na compreensão da resolução de uma inequação do 1º grau com uma incógnita, peça aos estudantes que resolvam a equação correspondente e estudem a desigualdade, atribuindo valores aleatórios para verificar se a sentença é verdadeira ou não.
Observe agora a resolução da inequação 3 ⋅ abre parênteses1 menos xfecha parênteses ⩽ 7, sendo U =

.

Portanto, todo número racional maior ou igual a
Sentença matemática. Menos fração 4 terços.é solução dessa inequação.

ATIVIDADES
faça as atividades no caderno
1. Copie no caderno as desigualdades a seguir que são inequações do 1º grau com uma incógnita.
a) x + 3 ⩾ 3x menos 1
b) x < 0
c)
Sentença matemática. y maior que, fração 1 meio, menos 4.d) 7 menos x ⩽ x
e) x menos 5y < 12 + x elevado a 2
f ) 10y elevado a 2 ⩾ 2y menos 3
g) 9 + 2x > 5 ⋅ abre parêntesesx menos 3fecha parênteses
h) 7x menos 5 ⩽ z + 6
2. Associe cada inequação à solução correspondente, sendo conjunto universo =

.
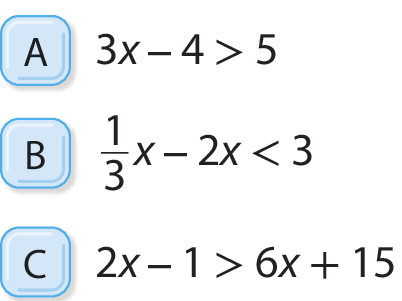
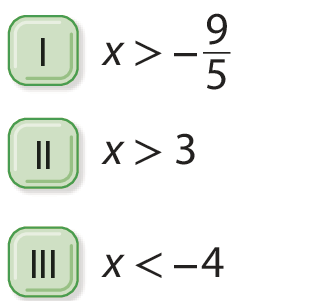
3. Considere a inequação 3x menos 4 ⋅ abre parêntesesx menos 2fecha parênteses ⩾ x + 4. Sabendo que U =

, identifique a opção em que a solução dessa inequação está representada.
a) x > 1
b) x ⩽ 2
c) x > 0
d) x ⩽ 5
4. Resolva as inequações a seguir.
a) x + 7 < 10, sendo conjunto universo =

.
b) 10x < 30, sendo conjunto universo =

.
c) 2 menos x ⩽ x + 8, sendo conjunto universo =

.
d) 12x < 4x + 5, sendo conjunto universo =

.
e) 4 ⋅ abre parêntesesx + 5fecha parênteses ⩽ 3x + 10, sendo conjunto universo =

.
5. Responda às questões a seguir.
a) Qual é o maior número inteiro que é solução da inequação 5 menos 3 ⋅ abre parêntesesx menos 2fecha parênteses > x menos 2x + 1?
b) Quais elementos do conjunto a = abre chavemenos2, 0, 1fecha chave tornam a sentença 4x + 7 < 3x + 8 verdadeira?
c) Marcelo pensou em um número natural e adicionou esse número ao seu triplo. O resultado obtido foi maior que 16. Qual é o menor número em que ele pode ter pensado?
d) O dobro de um número racional y é menor que a diferença entre o triplo desse número e 14. Que valores y pode assumir?
Respostas e comentários
1. alternativas a, b, c, d, g
2. A – dois; B – um; C – três
3. alternativa b
4. a) x < 3, com x ∈

4. b) x = 1 ou x = 2, com x ∈

4. c) x ⩾ menos 3, com x ∈

4. d)
Sentença matemática. x menor que, fração 5 oitavos., com x ∈

4. e) x ⩽ menos10, com x ∈

5. a) 4
5. b) menos2 e 0
5. c) 5
5. d) y > 14
Orientações e sugestões didáticas
• Na atividade 5, é necessário que os estudantes organizem as ideias e verifiquem a coerência de suas estratégias. No item a, precisam resolver a inequação. No item b, podem testar cada um dos números que pertencem ao conjunto A ou resolver a inequação e assim verificar quais dos números fazem parte dessa solução.
Sugestão de atividades
(UFG-GO) O menor múltiplo de 3 que satisfaz a inequação x + 5 < 2x menos 1 é: (alternativa b)
a) 12
b) 9
c) 6
d) 3
e) 0
(Fuvésti-São Paulo) Um estacionamento cobra R$ 6,00seis reais pela primeira hora de uso, R$ 3,00três reais por hora adicional e tem uma despesa diária de R$ 320,00trezentos e vinte reais. Considere-se um dia em que sejam cobradas, no total, 80 horas de estacionamento. O número mínimo de usuários necessário para que o estacionamento obtenha lucro nesse dia é: (alternativa c)
a) 25
b) 26
c) 27
d) 28
e) 29
Lembre-se: Escreva no caderno!
6. (Colégio Militar de Brasília-Distrito Federal) O produto de todas as soluções inteiras que satisfazem, simultaneamente, as desigualdades 3abre parêntesesx + 1fecha parênteses < 9 + 2x, 15x + 5 < 5x + 5 e 16 menos 2abre parêntesesx menos 2fecha parênteses > 1 menos 3abre parêntesesx menos 5fecha parênteses é:
a) 0
b) 6
c) menos6
d) 24
e) menos24
7. Observe o quadrado e o retângulo e responda à questão.
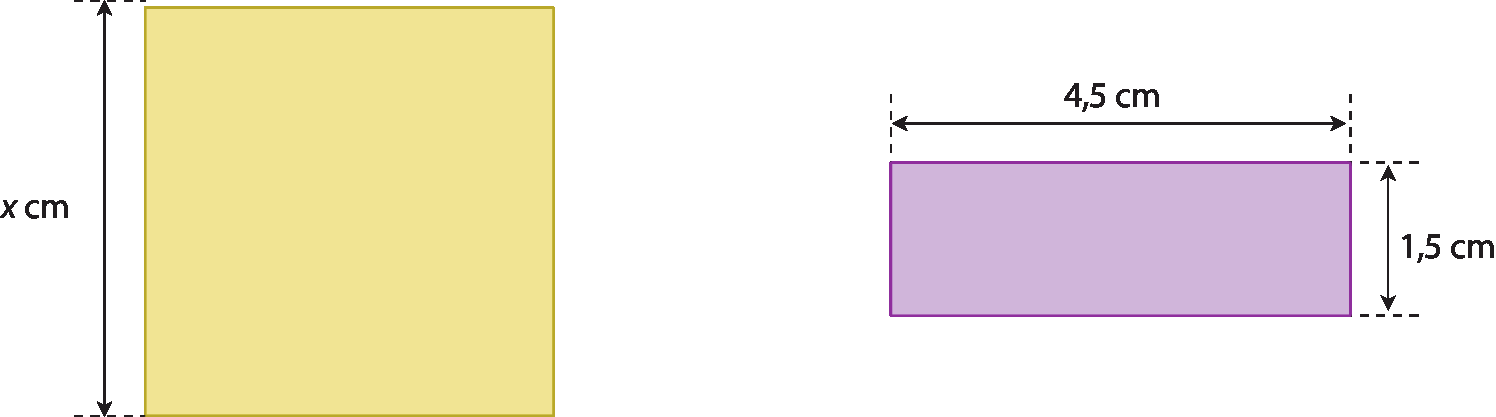
• Considerando que a medida do perímetro do quadrado é maior que a medida do perímetro do retângulo, qual é o menor número inteiro que x pode assumir?
8. Em uma concessionária, um carro popular custa o dobro do que custa uma moto.

• Considerando que o preço da moto é x reais e que o carro e a moto juntos custam mais de .45000 reais, responda às questões.
a) Que inequação relaciona as informações do enunciado?
b) O valor do carro é maior ou menor que .30000 reais? Use a inequação encontrada no item a para justificar sua resposta.
9. Uma empresa de telefonia celular oferece os dois planos descritos a seguir.
Plano a: parcela fixa de R$ 35,00trinta e cinco reais mais R$ 0,50zero reais e cinquenta centavos por minuto utilizado.
Plano B: R$ 1,20um reais e vinte centavos por minuto utilizado.
a) Qual é o plano mais vantajoso para quem utiliza 40 minutos por mês?
b) A partir de quantos minutos de uso mensal o plano a é mais vantajoso que o plano B?
Respostas e comentários
6. alternativa c
7. 4
8. a) Exemplo de resposta: x + 2x > .45000
8. b) Maior que .30000 reais, porque, resolvendo a inequação encontrada no item a, temos que x > .15000; logo, 2x > .30000.
9. a) o plano B
9. b) a partir de 51 minutos
Orientações e sugestões didáticas
• Na atividade 7, a medida do perímetro do quadrado pode ser representada por:
x + x + x + x ou 4x
Aproveite e verifique se os estudantes prestaram atenção ao enunciado e questione-os sobre qual é o conjunto universo. Espera-se que eles respondam que é o conjunto dos números inteiros. Se julgar conveniente, comente que, se o sinal da desigualdade fosse ⩾, a resposta seria 3, não 4.
• Na atividade 9, é esperado que os estudantes indiquem por x a medida do tempo, em minuto, utilizado por mês, podendo escrever a expressão que representa o gasto, em reais, de cada plano:
Plano A: 35 + 0,5x
Plano B: 1,2x
Assim, facilita-se o cálculo para responder aos itens da atividade.

Estatística e Probabilidade
faça as atividades no caderno
Média aritmética e amplitude
Na escola em que Isabela estuda será organizada uma gincana em que cada equipe deve ter 6 participantes com estudantes do 6º ao 9º ano. Isabela mede 1,61 métro de altura e quer entrar em uma equipe em que as medidas de altura dos participantes sejam próximas da dela. Por isso, o professor de Educação Física verificou as equipes que já estavam com 5 participantes e deu a Isabela duas opções.

Isabela decidiu participar da equipe Vamos Juntos, mas, ao verificar o registro da medida da altura dos participantes dessa equipe, percebeu que seus colegas não tinham a medida de altura próxima da dela.

Quando analisou o registro da medida de altura dos participantes da equipe fórça Já, notou que todos tinham a medida de altura próxima da dela.

Orientações e sugestões didáticas
Estatística e Probabilidade
Objetivo
• Favorecer o desenvolvimento da habilidade da Bê êne cê cê: ê éfe zero sete ême ah três cinco.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero sete ême ah três cinco ao calcular a média aritmética de um conjunto de dados, compreender o seu significado e relacioná-la com a amplitude desse conjunto de dados.
Orientações
• Nesta seção, os estudantes poderão estudar o conceito de amplitude e, com base nele, avaliar se a média aritmética representa bem o conjunto de dados.
• No decorrer do texto teórico e nas atividades, chame a atenção da turma para o fato de que, quanto mais próximos entre si os dados estiverem, melhor a média aritmética vai representá-los. Por outro lado, se um conjunto de dados possui um ou mais valores discrepantes, a média será muito influenciada por esse valor, tornando-a, assim, inadequada para representar o conjunto de dados em questão. Isso justifica a importância de relacionar a média com a amplitude: quanto menor a amplitude (diferença entre o maior e o menor valor do conjunto de dados), melhor a média vai representar esse conjunto.
(ê éfe zero sete ême ah três cinco) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados.
Note que analisar apenas a média das medidas de altura dos participantes das duas equipes não foi suficiente para garantir que eles teriam a medida de altura próxima da de Isabela. Para isso, seria necessário verificar a amplitude, que nesse caso corresponde à diferença entre o maior e o menor valor de um conjunto de dados.
Observe como calcular a amplitude das medidas de altura dos participantes de cada equipe:

Repare que a amplitude das medidas de altura dos participantes da equipe fórça Já é menor que a das medidas de altura dos participantes da equipe Vamos Juntos. Isso quer dizer que, na equipe fórça Já, os dados estão mais próximos um do outro, enquanto na equipe Vamos Juntos os dados estão mais dispersos.

ATIVIDADES
faça as atividades no caderno
1. Observe na tabela a medida de massa de algumas atletas da Seleção Brasileira de Judô em 2022.

|
Atleta |
Medida de massa (em kg) |
|---|---|
|
Amanda Lima |
48 |
|
Yasmim Lima |
52 |
|
Rafaela Silva |
57 |
|
Ketleyn Quadros |
63 |
|
Maria Portela |
70 |
|
Mayra Aguiar |
78 |
Dados obtidos em: CBJ Brasil. Disponível em: https://oeds.link/NW1Fz2. Acesso em: 4 abril 2022
a) Calcule a média aritmética dessas medidas de massa.
b) Determine a amplitude desse conjunto de dados.
c) Que medida de massa pode ser inserida nesse conjunto de dados de modo que sua amplitude continue a mesma?
2. A professora de pilates resolveu anotar a idade de seus alunos como mostrado a seguir.

a) Calcule a média aritmética dessas idades.
b) Qual é a menor idade? E qual é a maior idade?
c) Qual é a amplitude desse conjunto de dados?
Respostas e comentários
1. a) aproximadamente 61,33 quilogramas
1. b) 30 quilogramas
1. c) Qualquer medida de massa entre 48 quilogramas e 78 quilogramas.
2. a) 25
2. b) 20; 33
2. c) 13
Orientações e sugestões didáticas
• Antes de os estudantes iniciarem as atividades, escreva no quadro os dois conjuntos de dados a seguir:
Conjunto 1: 0, 10 e 20
Conjunto 2: 10, 10 e 10
Chame a atenção deles para o fato de esses conjuntos serem bem diferentes, apesar de terem a mesma média (10). Nesse caso, a média aritmética representa melhor o conjunto de dados 2, cuja amplitude é 0, do que o conjunto de dados 1, cuja amplitude é igual a 20.
• Espera-se que no item b da atividade 1 os estudantes percebam que, para calcular a amplitude, precisam apenas considerar o maior e o menor valor do conjunto de dados.
Aproveite a atividade para conversar com os estudantes sobre a prática de esporte. Comente que em algumas modalidades existe a divisão por categorias que são separadas de acordo com a medida da massa de cada atleta. Se julgar conveniente, pergunte se alguém pratica algum esporte ou se eles têm alguma preferência por determinado esporte. Dessa fórma é possível explorar as culturas juvenis, dando espaço para os estudantes compartilhar suas experiências. Enfatize a importância da prática do esporte para manter a saúde física e mental. Se houver possibilidade, pode ser convidado um profissional de Educação Física para ter uma conversa com os estudantes sobre o assunto.
▶ Estatística e Probabilidade
Lembre-se: Escreva no caderno!
3. A professora de Matemática do 7º ano aplicou a mesma avaliação para duas turmas. Observe as notas que os estudantes de cada turma obtiveram.

a) Qual foi a nota média de cada turma?
b) Qual é a amplitude das notas de cada turma?
c) Para ser aprovados nessa avaliação, os estudantes deveriam ter notas iguais ou superiores a 5. Qual das turmas tem mais estudantes reprovados?
4. Três pequenas empresas de uma cidade se cadastraram para um curso de capacitação oferecido pela prefeitura. Observe nas tabelas a seguir o número de funcionários de cada empresa e seus respectivos salários em dezembro de 2023.
|
Cargo |
Salário |
Número de funcionários |
|---|---|---|
|
Júnior |
R$ 1.175,00 |
8 |
|
Pleno |
R$ 1.960,00 |
2 |
|
Sênior |
R$ 2.410,00 |
1 |
Dados obtidos pela empresa ei em dezembro de 2023.
|
Cargo |
Salário |
Número de funcionários |
|---|---|---|
|
Júnior |
R$ 1.050,00 |
3 |
|
Pleno |
R$ 1.300,00 |
5 |
|
Sênior |
R$ 2.050,00 |
4 |
Dados obtidos pela empresa B em dezembro de 2023.
|
Cargo |
Salário |
Número de funcionários |
|---|---|---|
|
Júnior |
R$ 1.150,00 |
2 |
|
Pleno |
R$ 1.850,00 |
6 |
|
Sênior |
R$ 2.640,00 |
2 |
Dados obtidos pela empresa C em dezembro de 2023.
a) Qual é o salário médio dos funcionários de cada empresa?
b) A primeira empresa a participar do curso de capacitação oferecido pela prefeitura foi a que tem os funcionários cujos salários apresentam a menor amplitude. Qual é essa empresa?
Respostas e comentários
3. a) 7º ano a: aproximadamente 6,5; 7º ano B: 6,4
3. b) 7º ano a: 9; 7º ano B: 5
3. c) a turma a
4. a) empresa a: R$ 1.430,00mil quatrocentos e trinta reais; empresa B: R$ 1.487,50mil quatrocentos e oitenta e sete reais e cinquenta centavos; empresa C: R$ 1.868,00mil oitocentos e sessenta e oito reais
4. b) a empresa B
Orientações e sugestões didáticas
• Na atividade 4, verifique se os estudantes percebem que, para responder ao item a, precisam calcular a média ponderada e, para responder ao item b, basta analisar o maior e o menor salário de cada empresa.

Compreender um texto
faça as atividades no caderno

Jovens na proteção do meio ambiente
O poder dos jovens na proteção do meio ambiente
Já ouviu falar no movimento Friday [Fridays] for future (sexta [sextas] para o futuro)? Ele nasceu na Suécia, a partir da ação de Greta Túmberg, uma jovem de 16 anos. Ela estava muito preocupada com as mudanças climáticas e pensou que precisava descobrir um jeito de protestar contra o que estava acontecendo.
Greta passou a ir todas as sextas-feiras para a porta do Parlamento sueco, na cidade de Estocolmo, para exigir que fossem tomadas medidas que evitem o aquecimento global. “Como não posso votar, essa é uma das maneiras que eu posso fazer minha voz ser ouvida”, declarou durante uma entrevista.
[reticências]
Pensar global, agir local
[reticências] além da participação nas manifestações, uma boa fórma de apoiar Greta é ter consciência de que pequenas ações do dia a dia podem melhorar o meio ambiente.
É preciso, sim, estar ligado ao que acontece no mundo, mas podemos e devemos agir em nosso meio, em nossa casa e escola. O seu exemplo pode influenciar amigos, vizinhos e família, estabelecendo uma corrente do bem.

Orientações e sugestões didáticas
Compreender um texto
Objetivos
• Desenvolver a competência leitora.
• Trabalhar os Temas Contemporâneos Transversais Educação Ambiental e Educação para o Consumo da macroárea Meio Ambiente.
• Favorecer o desenvolvimento da habilidade ê éfe zero sete ême ah três cinco da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero sete ême ah três cinco ao propor que os estudantes calculem a média aritmética de um conjunto de dados e utilizem seus conhecimentos acerca da amplitude de um conjunto de dados.
Orientações
• Para iniciar o trabalho com o texto, pergunte aos estudantes o que sabem sobre o movimento Fridays for future e a atuação de Greta Túmberg. É possível que eles já tenham deparado com o assunto nas redes sociais ou assistindo aos noticiários na televisão. Nesse caso, incentive-os a compartilhar seus conhecimentos com os colegas. A troca de informações pode colaborar para a formação cidadã de cada um, como também para que compreendam os problemas atuais sobre as mudanças climáticas e o consumo consciente. Dessa maneira, os conhecimentos adquiridos sobre o cuidado com o meio ambiente ajudam os estudantes a entender e tratar as consequências do consumo em excesso e do aquecimento do planeta, incentivando-os a mudar suas condutas. Caso julgue necessário, acesse o site brasileiro do movimento Fridays for future (disponível em: https://oeds.link/S4hlZh. Acesso em: 31 maio 2021), para embasar a conversa com a turma.
• Essa abordagem possibilita o desenvolvimento de aspectos dos Temas Contemporâneos Transversais Educação Ambiental e Educação para o Consumo da macroárea Meio ambiente.
(ê éfe zero sete ême ah três cinco) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados.
▶ Compreender um texto
Recusar, Refletir, Reduzir, Reutilizar, Reciclar… e revolucionar!
As ações mais efetivas que podemos praticar em quase todos os lugares são reciclar e reutilizar materiais. A seguir, algumas dicas sobre como colocar em prática estes 5Rs que podem salvar o meio ambiente!
• Repensar o que nós consumimos: [reticências] Pense bem: será que é preciso comprar algo novo ou dá para reaproveitar algo que já temos em casa?
• Recusar produtos que prejudiquem o meio ambiente: sabe o canudinho que vem com o suco? O copinho descartável de água? A sacolinha plástica do mercado? Que tal levar seu copo reutilizável na mochila e usar sacolas de pano?
• Reduzir a produção de lixo: em vez de comprar vários pacotinhos de biscoito, que tal comprar um pacote grande e guardar em um pote?
• Reutilizar: dar utilidade a um objeto que, a princípio, foi fabricado para outro fim. É o caso do artesanato feito com garrafas péti, ou da latinha que você enfeita e usa para acomodar os seus lápis, por exemplo;
• Reciclar, que significa transformar resíduos em novos produtos, como as roupas tecidas com um fio feito a partir de garrafas péti [reticências].
BRASIL. Câmara dos Deputados. O poder dos jovens na proteção do meio ambiente. Plenarinho: o jeito criança de ser cidadão, Brasília, Distrito Federal, 26 fevereiro 2020. Disponível em: https://oeds.link/prDlOB. Acesso em: 31 maio 2022.

ATIVIDADES
faça as atividades no caderno
1. Qual é o gênero do texto apresentado? Onde e quando ele foi publicado?
2. De acordo com o texto, como surgiu o movimento Fridays for future (sexta para o futuro)?
3. Os estudantes do 7º ano da escola em que Tobias estuda organizaram uma campanha de separação e coleta de garrafas péti. A tabela apresenta a quantidade de garrafas péti coletadas mensalmente pelas turmas a e bê.
|
Mês |
Quantidade arrecadada (em quilograma) |
|
|---|---|---|
|
Turma A |
Turma B |
|
|
Março |
20 |
18 |
|
Abril |
29 |
19 |
|
Maio |
23 |
37 |
|
Junho |
28 |
15 |
|
Julho |
27 |
34 |
|
Agosto |
23 |
13 |
|
Setembro |
28 |
28 |
|
Outubro |
26 |
30 |
|
Novembro |
25 |
11 |
Dados obtidos pela escola em 2023.
a) Em média, quantos quilogramas de garrafas péti foram coletados pela turma a por mês? E pela turma B?
b) Entre as turmas a e bê, qual teve uma regularidade maior na arrecadação de garrafas? Justifique sua resposta.
4.

Você já praticou ou pratica algum dos 5Rs apresentados no texto? Reúna-se em grupo e compartilhe as experiências vivenciadas.
Respostas e comentários
1. Jornalístico. Foi publicado no site da Câmara dos Deputados, pelo programa Plenarinho, em 26 de fevereiro de 2020.
2. O movimento surgiu quando a jovem sueca Greta Trunberg passou a ir todas as sextas-feiras para a porta do Parlamento, para exigir que fossem tomadas medidas que evitem o aquecimento global.
3. a) Turma a: aproximadamente 25,44 quilogramas; turma B: aproximadamente 22,78 quilogramas.
3. b) Turma a, pois a amplitude das medidas de massa de garrafas péti coletadas por essa turma é menor do que a coletada pela turma B.
4. Resposta pessoal.
Orientações e sugestões didáticas
• O objetivo da atividade 1 é avaliar a capacidade dos estudantes de identificar diferentes gêneros textuais. Se necessário, auxilie-os, chamando a atenção para algumas características do texto relacionadas ao gênero jornalístico, como o emprego de uma linguagem clara e direta, ter como objetivo informar o leitor sobre determinado assunto, entre outras.
• Na atividade 4, incentive os estudantes a comentar ações que praticam no cotidiano com o intuito de minimizar os impactos ao meio ambiente. Caso não pratiquem nenhuma, sugira que pensem em ações que poderiam praticar no futuro. Se julgar oportuno, organize um mural para que eles possam expor suas experiências na escola.

Atividades de revisão
faça as atividades no caderno
1. Escreva a equação correspondente a cada sentença a seguir. Depois, resolva‑a.
a) O resultado da adição do triplo de um número com 3 é igual a 24. Qual é esse número?
b) A diferença entre o dobro de um número e 25 é igual a 7. Qual é esse número?
c) Metade de um número menos 1 tem como resultado 3. Que número é esse?
d) Três quartos de um número adicionados a 5 resulta em
Sentença matemática. 1 meio.. Que número é esse?
2. Associe as equações equivalentes.

3. Responda às questões.
a) Qual é a raiz da equação
Sentença matemática. Fração 3 quintos x, igual, 1.?
b) Qual é a solução dessa equação se conjunto universo =

?
c) Qual é a solução dessa equação se conjunto universo =

?
d) Qual é a solução dessa equação se conjunto universo =

?
4. Considerando conjunto universo =

, determine a solução das equações a seguir.
a) 4x + 13 = x menos 17
b)
fração numerador x mais 1, denominador 3 igual fração numerador 1 menos x denominador 2c) 3abre parêntesesy menos 5fecha parênteses = 25 + 2y
5. Observe a figura e faça o que se pede.
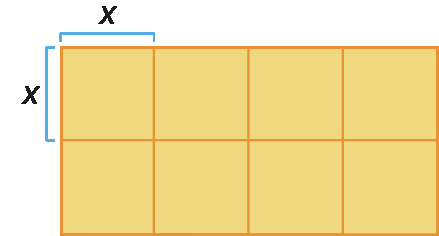
a) Escreva a expressão correspondente à medida do perímetro da figura.
b) Determine a medida de comprimento de x para que o perímetro da figura meça 60 centímetros.
c) Se x = 100 centímetros, qual será a medida do perímetro da figura?
d) Escreva a expressão correspondente à medida de área da figura.
6. (saébi) Uma prefeitura aplicou R$ 850 miloitocentos e cinquenta reais na construção de 3 creches e um parque infantil. O custo de cada creche foi de R$ 250 milduzentos e cinquenta reais. A expressão que representa o custo do parque, em mil reais, é:
a) x + 850 = 250
b) x menos 850 = 750
c) 850 = x + 250
d) 850 = x + 750
7. O entregador de uma empresa recebe mensalmente um salário fixo de R$ 1.280,00mil duzentos e oitenta reais mais R$ 0,70zero reais e setenta centavos por quilômetro percorrido.

• Qual foi a medida de distância, em quilômetro, que o entregador percorreu para receber esse salário?
8. Ari foi contratado para trocar o piso de um salão. Ele cobrou R$ 300,00trezentos reais para tirar o piso velho e mais uma quantia por metro quadrado de piso novo assentado.
Sabendo que o salão mede 57 métros quadrados e que a mão de obra total ficou em R$ 1.326,00mil trezentos e vinte e seis reais, responda: quanto Ari cobrou por metro quadrado de piso novo assentado?
9. Um alpinista aceitou o desafio de escalar o maior pico da América: o Aconcágua. Durante a subida, enfrentou uma forte tempestade e, por segurança, parou quando faltavam
Sentença matemática. Fração 3 quintosda medida da distância total. Se ele tivesse subido mais 696 metros, teria percorrido aproximadamente metade da medida da distância total. Quanto mede, aproximadamente, a altitude desse pico?
10. João colocou o carro dele à venda, e Marcos propôs pagar pelo carro R$ 16.800,00dezesseis mil oitocentos reais.
Se João vender o carro por esse valor, perderá
Sentença matemática. Fração 3 décimosdo valor de mercado. Qual é o preço de mercado do carro de João?
Respostas e comentários
1. a) 3x + 3 = 24; x = 7
1. b) 2x menos 25 = 7; x = 16
1. c)
Sentença matemática. Fração 1 meio x, menos 1, igual, 3. Sentença matemática. x, igual, 8.1. d)
Sentença matemática. Fração 3 quartos x, mais 5, igual, fração 1 meio. Sentença matemática. x, igual, menos 6.2. A – três; B – um; C – quatro; D – dois
3. a)
Sentença matemática.5 terços
3. b) Não tem solução.
3. c) Não tem solução.
3. d)
Sentença matemática.5 terços
4. a) x = menos10
4. b)
Sentença matemática. x fração igual 1 quinto4. c) y = 40
5. a) 12x
5. b) 5 centímetros
5. c) .1200 centímetros
5. d) 2x ⋅ 4x ou 8x ²
6. alternativa d
7. .2300 quilômetros
8. R$ 18,00dezoito reais
9. aproximadamente .6960 métros
10. R$ 24.000,00vinte e quatro mil reais
Orientações e sugestões didáticas
Atividades de revisão
Objetivos
• Consolidar o conhecimento adquirido no decorrer do Capítulo.
• Favorecer o desenvolvimento da habilidade da Bê êne cê cê: ê éfe zero sete ême ah um oito.
Habilidade da Bê êne cê cê
• A habilidade ê éfe zero sete ême ah um oito é desenvolvida nesta seção por meio da resolução das atividades 1 a 11.
Orientações
• Ao realizarem as atividades 1 a 8, avalie se os estudantes têm dificuldades para transitar entre o registro em língua materna e o registro algébrico. Também procure diagnosticar se calculam as raízes das equações aplicando os princípios aditivo e multiplicativo corretamente. Se necessário, repense então as estratégias didático-pedagógicas adotadas e planeje medidas que possam contribuir para que os estudantes superem suas dificuldades.
• Incentive os estudantes a identificar o conjunto universo das equações obtidas nos problemas propostos nas atividades 9, 10 e 11. Alerte-os para a possibilidade de o contexto do problema impor restrições para os possíveis valores que a incógnita pode assumir. Caso julgue necessário, apresente exemplos.
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à fórma á xis + b = c, fazendo uso das propriedades da igualdade.
▶ Atividades de revisão
11. Beatriz comprou uma caixa com 14 lápis para dividir entre seus três filhos de acordo com a quantidade que cada um precisava. Assim, Ricardo recebeu 3 lápis a menos que Jorge, e Régis ganhou 2 lápis a mais que Jorge. Quantos lápis ganhou cada um dos filhos?
12. Letícia queria organizar seus filmes em di vi di. Para isso, ela os enfileirou em uma estante, separando-os por gênero: aventura, comédia e ficção científica. Ao final, ela contou 56 dê vê dês. A quantidade de filmes de ficção científica corresponde à metade da quantidade de filmes de comédia, que, por sua vez, corresponde à metade da quantidade de filmes de aventura. Quantos filmes de cada gênero Letícia tem?
13. Resolva as inequações considerando conjunto universo =

.
a) 3abre parênteses4x menos 8fecha parênteses + 2 ⩾ 5 menos 2abre parênteses3 menos 2xfecha parênteses
b)
Sentença matemática. fração x mais 2 sobre 4 menor ou igual a fração x menos 3 sobre 6.c)
Sentença matemática. x menos, fração com numerador x mais 1 e denominador 3, menor ou igual a, fração x sobre 2.d) 2abre parêntesesx menos 1fecha parênteses menos abre parênteses1 menos xfecha parênteses ⩾ 3abre parêntesesx + 2fecha parênteses
14. Observe as figuras a seguir.
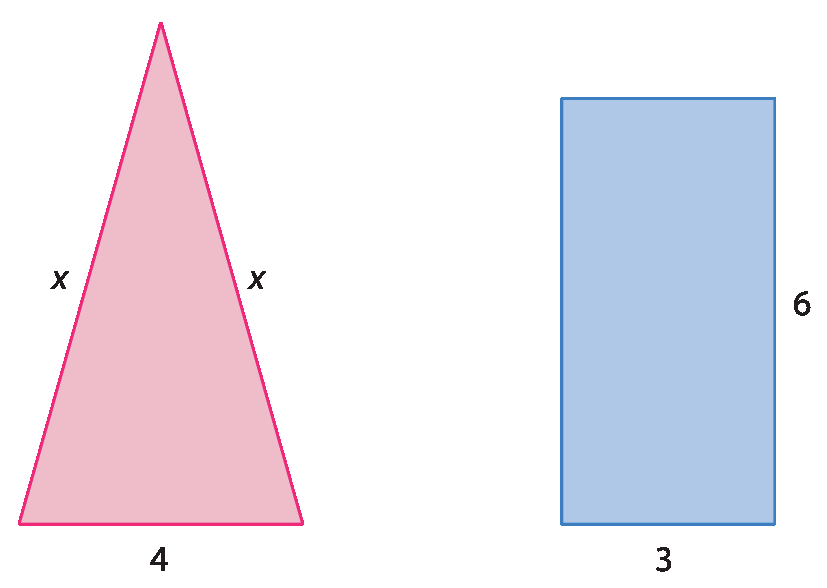
• Para que valores de x a medida do perímetro do triângulo é maior que a medida do perímetro do retângulo?
15. Certo guindaste suporta uma carga com medida máxima de 12 toneladas de massa.
Sabendo que ele vai transportar dois contêineres de mesma medida de massa x e uma caixa cuja massa mede 4 toneladas, faça o que se pede.
a) Escreva uma inequação que represente essa situação.
b) Qual é a medida de massa máxima que cada contêiner pode ter?
16. No fim do ano, uma empresa oferece aos funcionários um vale-presente e uma cesta de Natal. Para isso, é destinado um orçamento de R$ 25.000,00vinte e cinco mil reais, dos quais R$ 15.000,00quinze mil reais são gastos com as cestas e o restante determina o valor do vale-presente. Sabendo que há 48 funcionários nessa empresa, qual é o maior valor inteiro que o vale-presente pode ter para não estourar o orçamento?
17. Alexandre e Mara estão poupando uma quantia há algum tempo para comprar um carro que custa R$ 34.000,00trinta e quatro mil reais. Observe a cena e responda às questões a seguir.

a) O dinheiro que eles têm na aplicação e na poupança é suficiente para comprar o carro?
b) Que desigualdade podemos escrever para relacionar a quantia que Alexandre e Mara têm e o valor do carro?
18. Em uma escola, para um estudante ser aprovado, deve ter a média das notas dos 4 bimestres maior ou igual a 5. Observe as notas de um estudante.
|
1º bimestre |
2º bimestre |
3º bimestre |
4º bimestre |
|---|---|---|---|
|
3,0 |
5,0 |
4,5 |
? |
Qual é a nota mínima que esse estudante precisa tirar no 4º bimestre para ser aprovado?
19. Rafael e Henrique têm menos de 30 anos, mas, se adicionarmos a idade dos dois, obteremos um valor maior que 30. A idade do mais velho corresponde ao quádruplo da idade do mais novo. Qual é a idade de cada um?
Respostas e comentários
11. Jorge: 5; Ricardo: 2; Régis: 7
12. 8 filmes de ficção científica, 16 de comédia e 32 de aventura.
13. a)
Sentença matemática. x menor ou igual a, fração 21 oitavos., com x ∈

13. b) x ⩽ ‒12, com x ∈

13. c) x > 2, com x ∈

13. d) Não tem solução.
14. x > 7
15. a) 2x + 4 ⩽ 12
15. b) 4 toneladas
16. R$ 208,00duzentos e oito reais
17. a) não
17. b) .18700 + .12400 < .34000 ou .31100 < .34000
18. 7,5
19. O mais novo tem 7 anos, e o mais velho, 28 anos.
Orientações e sugestões didáticas
• Amplie as propostas das atividades desta seção pedindo aos estudantes que elaborem problemas que possam ser traduzidos por equações e inequações. Depois, oriente-os a trocar com um colega os problemas que elaboraram, para resolver os problemas propostos por ele.
• Ao final dessa seção, proponha uma autoavaliação para os estudantes. No rodapé, são sugeridas algumas questões. É importante que cada item seja analisado e adaptado à realidade da turma.
|
Eu... |
Sim |
Às vezes |
Não |
|---|---|---|---|
|
... reconheço uma equação do 1º grau com uma incógnita? |
|||
|
... compreendo o que são incógnitas? |
|||
|
... sei traduzir situações-problema por meio de equações do 1º grau com uma incógnita? |
|||
|
... sei resolver uma equação do 1º grau com uma incógnita? |
|||
|
... reconheço uma inequação do 1º grau com uma incógnita? |
|||
|
... sei traduzir situações-problema por meio de inequações do 1º grau com uma incógnita? |
|||
|
... sei resolver uma inequação do 1º grau com uma incógnita? |
|||
|
... sei utilizar letras para descrever incógnitas? |
|||
|
... sei interpretar situações-problema e traduzi-las matematicamente utilizando letras e demais símbolos? |
|||
|
... consigo reconhecer quais operações precisam ser utilizadas para representar uma situação-problema a partir de uma equação ou inequação de 1º grau? |