Resoluções
Parte 1

Avaliação diagnóstica
MOSTRE O QUE VOCÊ JÁ SABE
▶ Páginas 12 e 13
1. Para encontrar o número de triângulos brancos na etapa 3, utilizamos uma potência de base 3 da seguinte maneira:
• etapa 0:
Sentença matemática. 3 elevado a zero igual a um.• etapa 1:
Sentença matemática. Três elevado a um igual a três.• etapa 2:
Sentença matemática. Três elevado a dois igual a nove.• etapa 3:
Sentença matemática. Três elevado a três igual a vinte e sete.Portanto, na etapa 3 haverá 27 triângulos brancos.
alternativa c
2. A pizza foi dividida em 12 fatias iguais no total. Para determinar a razão entre as 4 fatias que Mateus comeu e o total de fatias da pizza, podemos fazer:
Sentença matemática: fração quatro sobre doze igual a um terço, aproximadamente, 0,33 igual a trinta e três por cento.
Portanto, a quantidade da pizza que Mateus comeu equivale a
um terçoda pizza, ou seja, aproximadamente 0,33 e aproximadamente 33%.
alternativa a
3. Vamos representar os três números consecutivos por (n ‒ 1), n e (n + 1). Como foi pedida uma expressão para representar o quadrado da soma desses três números, fazemos:
Sentença matemática: abre colchetes, abre parênteses, n menos um, fecha parênteses, mais n, mais, abre parênteses, n mais um, fecha parênteses, fecha colchetes, elevado a dois.
Portanto, a expressão algébrica é
Sentença matemática: abre colchetes, abre parênteses, n menos um, fecha parênteses, mais n, mais, abre parênteses, n mais um, fecha parênteses, fecha colchetes, elevado a dois..
alternativa c
4. Para encontrar a raiz de cada uma das equações, fazemos:
A) 3x ‒ 2 = 10
3x = 12
x = 4
Logo, A-dois.
B) 2x + 1 = 5
2x = 4
x = 2
Logo, B-três.
C) 3x = 15
x = 5
Logo, C-um.
Portanto, a associação correta entre cada equação e sua raiz é A-dois, B-três e C-um.
alternativa dê
5. A equipe de basquete de Juliana marcou 65 pontos no total, sendo 15 desses pontos marcados por ela. Para escrever a fração irredutível que representa a razão entre o número de pontos marcados por Juliana e o número total de pontos, podemos fazer:
Sentença matemática: quinze sobre sessenta e cinco, igual a fração de numerador quinze dividido por cinco e denominador sessenta e cinco dividido por cinco, igual a três sobre treze.
Portanto, a fração irredutível é
Sentença matemática. Fração: três sobre treze.alternativa b
6. De acordo com a figura apresentada, as coordenadas dos vértices do triângulo são A(2, 2), B(6, 2) e C(3, 5).
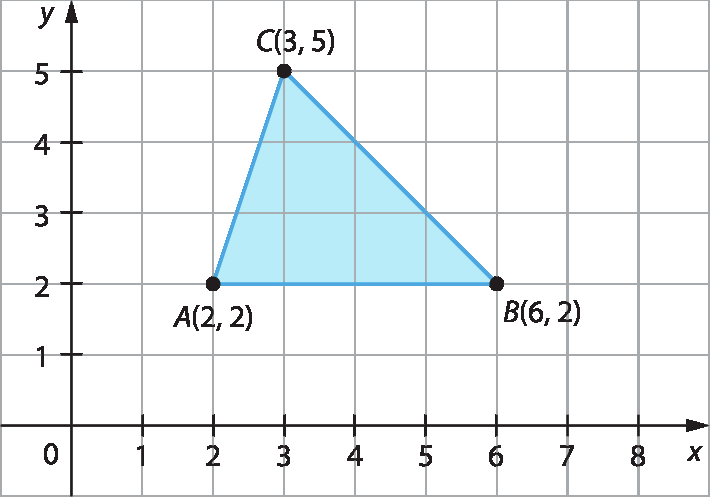
Para determinar as coordenadas do simétrico desse triângulo em relação ao eixo xis, invertemos o sinal da ordenada de cada um dos pontos, obtendo A'(2, ‒2), B'(6, ‒2) e C'(3, ‒5). Representando no plano cartesiano o triângulo original e seu simétrico em relação ao eixo xis temos:

Portanto, as coordenadas são A'(2, ‒2), B'(6, ‒2) e C'(3, ‒5).
alternativa a
7. Sabemos que uma hora equivale a 60 minutos. Se o relógio atrasa 5 minutos por dia, para encontrar a quantidade de dias necessários para ele atrasar 60 minutos (uma hora), podemos fazer:
60 : 5 = 12
Portanto, são necessários 12 dias.
alternativa c
8. Para determinar a medida da área de um paralelogramo, podemos calcular o produto entre as medidas da base (b) e da altura (h). Assim, A = b ⋅ h. Observando a figura, temos:
• medida da base: b = 2 centímetros + 3 centímetros = 5 centímetros
• medida da altura: h = 4 centímetros
Desse modo, temos:
A = 5 ⋅ 4 = 20
Portanto, a medida da área total do paralelogramo é 20 centímetros quadrados.
alternativa c
9. Para encontrar dois números naturais cuja soma é igual a 4, podemos fazer:
• 0 + 4 = 4
• 1 + 3 = 4
• 2 + 2 = 4
• 3 + 1 = 4
• 4 + 0 = 4
Escrevendo os pares de números naturais como coordenadas de pontos, temos (0, 4), (1, 3), (2, 2), (3, 1) e (4, 0). Representando esses pontos no plano cartesiano, temos:
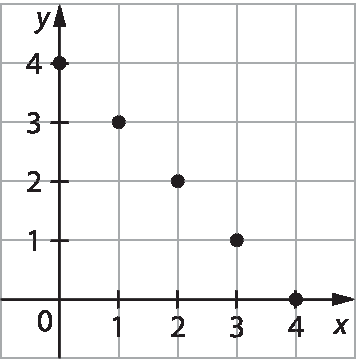
alternativa d
10. Foram entrevistadas duas. pessoas no total. De acordo com o gráfico, 25% dos entrevistados acharam ótimo o transporte público. Assim, para determinar a quantidade de pessoas que acharam o transporte público ótimo, devemos calcular 25% de duas. pessoas, ou seja:
Sentença matemática: fração 25 centésimos, vezes 2 mil, igual a fração com denominador 25 vezes 2 mil e denominador 100, igual a fração 50 mil centésimos igual a 500.
Portanto, quinhentas pessoas acharam o transporte público ótimo.
alternativa b
11. Vamos analisar cada alternativa para encontrar o polígono cuja área mede 36 centímetros quadrados.
a) Para calcular a medida da área de um quadrado cujos lados medem 6 centímetros de comprimento, fazemos:
A = ℓ = 6 = 36
Portanto, a medida da área desse quadrado é 36 centímetros quadrados.
b) Para calcular a medida da área de um triângulo cujo comprimento do lado mede 6 centímetros e a altura relativa a esse lado também mede 6 centímetros, fazemos:
Área igual a fração de numerador b vezes h e denominador dois, igual a fração de numerador seis vezes seis e denominador 2, igual a trinta e seis sobre dois, igual a dezoito.
Portanto, a medida da área desse triângulo é 18 centímetros quadrados.
c) Para calcular a medida da área de um losango cujas diagonais medem 4 centímetros e 9 centímetros de comprimento, fazemos:
Área igual a fração de numerador d minúsculo vezes D maiúsculo e denominador dois, igual a fração de numerador quatro vezes nove e denominador dois, igual a trinta e seis sobre dois, igual a dezoito.
Portanto, a medida da área desse losango é 18 centímetros quadrados.
d) Para calcular a medida da área de um quadrado cujos lados medem 9 centímetros de comprimento, fazemos:
A = ℓ = 9 = 81
Portanto, a medida da área desse quadrado é 81 centímetros quadrados.
Logo, entre as alternativas, o polígono cuja área mede 36 centímetros quadrados é o quadrado do item a.
alternativa a

Unidade 1
Capítulo 1
Atividades
▶ Páginas 16, 17 e 18
1. a) Espera-se que os estudantes identifiquem os números 2,25; 25; 1; 2022; 97; 29000-111.
b) Exemplo de resposta: 2,25 indica preço; 25, 1 e 2022 formam a data; 97 é o número da casa; 29000-111 é o código de endereçamento postal (cép).
c) Espera-se que os estudantes respondam que não, pois o número 2,25 não é um número natural.
2. Resposta pessoal. Exemplo de resposta: Os números naturais podem ser usados para fazer a contagem da quantidade de estudantes presentes na sala de aula; para compor os códigos das placas de identificação de automóveis.
3. Espera-se que os estudantes respondam que, se existisse, logo abaixo do andar –2 estaria o andar indicado pelo número –3.
4. a) A sequência dos números naturais pares pode ser representada por: 0, 2, 4, 6, 8, 10, reticências
Observe que para obter o próximo termo adiciona-se duas unidades ao termo anterior. Sendo assim, para encontrar o sucessor de um número natural n dessa sequência, podemos usar n + 2. E para o antecessor, n ‒ 2 para n ≠ 0.
b) A sequência dos números naturais ímpares pode ser representada por: 1, 3, 5, 7, 9, 11, reticências
Observe que para obter o próximo termo adiciona-se duas unidades ao termo anterior. Sendo assim, para encontrar o sucessor de um número natural n dessa sequência, podemos usar n + 2. E para o antecessor, n ‒ 2 para n ≠ 1.
5. a) Vamos representar os números naturais consecutivos por ( n ‒ 1 ),
n e ( n + 1 ).
Como a soma deles é .1233, temos:
( n ‒ 1 ) + n + ( n + 1 ) = .1233
3n = .1233
n = .1233 : 3
n = 411
Assim:
• n ‒ 1 = 411 ‒ 1 = 410
• n + 1 = 411 + 1 = 412
Logo, os números procurados são 410, 411 e 412.
b) Vamos representar dois números naturais consecutivos na sequência dos números pares por
ne ( n + 2 ). Como a soma deles é 998, temos:
n + ( n + 2 ) = 998
2n = 998 ‒ 2
Abaixo, n igual a 996 sobre 2.
n = 498
Assim:
n + 2 = 498 + 2 = 500
Logo, os números procurados são 498 e 500.
c) Vamos representar três números naturais consecutivos na sequência dos números ímpares por n, ( n + 2 ) e ( n + 4 ). Como a soma deles é 165, temos:
n + ( n + 2 ) + ( n + 4 ) = 165
3n = 165 ‒ 6
Sentença matemática. n igual a 159 sobre 3.
n = 53
Assim:
• n + 2 = 53 + 2 = 55
• n + 4 = 53 + 4 = 57
Logo, os números procurados são 53, 55 e 57.
6. a) Os termos da sequência aumentam de 15 em 15. Assim:
75 + 15 = 90
Portanto, o próximo termo dessa sequência é 90.
b) Os termos da sequência diminuem de 10 em 10. Assim:
60 ‒ 10 = 50
Portanto, o próximo termo dessa sequência é 50.
c) Os termos da sequência aumentam de 3 em 3. Assim:
15 + 3 = 18
Portanto, o próximo termo dessa sequência é 18.
d) Os termos da sequência aumentam de 8 em 8. Assim:
236 + 8 = 244
Portanto, o próximo termo dessa sequência é 244.
7. Espera-se que os estudantes percebam que se trata da sequência dos números naturais ímpares: 1, 3, 5, 7, 9, reticências
8. Exemplos de respostas:
a) n + 1, sendo n um número inteiro maior ou igual a ‒ 3.
b) ‒ 44 + 10n, sendo n um número natural.
c) 30 ‒ 6n, sendo n um número natural.
d) ‒ 300 + 100n, sendo n um número natural.
9. Espera-se que os estudantes percebam que, uma vez certo, o relógio de Pedro terá de atrasar 12 horas (ou 720 minutos) para marcar novamente a hora certa. Logo, se ele atrasa apenas 1 minuto por dia, levará 720 dias para atrasar 720 minutos. Ou seja, o relógio de Pedro estará certo, aproximadamente, uma vez a cada dois anos. Entretanto, o relógio de Daniel, por mais que esteja parado, marca a hora certa duas vezes por dia. Portanto, de acordo com a regra que eles estabeleceram, o relógio de Daniel é melhor que o de Pedro.
10. Resposta pessoal. Exemplo de sequência:
Considere a sequência (.1450, .1300, .1150, reticências). Escreva os próximos três termos dessa sequência.
Os termos da sequência diminuem de 150 em 150. Assim:
• .1150 ‒ 150 = .1000
• .1000 ‒ 150 = 850
• 850 ‒ 150 = 700
Portanto, os três termos seguintes são .1000, 850 e 700.
11. Efetuando os cálculos, para o número inteiro 9, temos:
• oposto: ‒ 9
• sucessor: 9 + 1 = 10
• antecessor: 9 ‒ 1 = 8
Efetuando os cálculos para o número oposto inteiro .1451, temos:
• número inteiro: –.1451
• sucessor: ‒ .1451 + 1 = ‒ .1450
• antecessor: ‒ .1451 ‒ 1 = ‒ .1452
Efetuando os cálculos para o número antecessor inteiro .2003, temos:
• número inteiro: .2003 + 1 = .2004
• oposto: –.2004
• sucessor: .2004 + 1 = .2005
Efetuando os cálculos para o sucessor inteiro ‒ 7, temos:
• número inteiro: ‒ 7 ‒ 1 = ‒ 8
• oposto: 8
• antecessor: ‒ 8 ‒ 1 = ‒ 9
Efetuando os cálculos para o antecessor inteiro ‒ .1999, temos:
• número inteiro: ‒ .1999 + 1 = ‒ .1998
• oposto: .1998
• sucessor: ‒ .1998 + 1 = ‒ .1997
Efetuando os cálculos para o número inteiro ‒ 125, temos:
• oposto: 125
• sucessor: ‒ 125 + 1 = ‒ 124
• antecessor: ‒ 125 ‒ 1 = ‒ 126
Efetuando os cálculos para o número inteiro 0, temos:
• oposto: 0
• sucessor: 0 + 1 = 1
• antecessor: 0 ‒ 1 = ‒ 1
Efetuando os cálculos para o sucessor inteiro ..1000000, temos:
• número inteiro: ..1000000 ‒ 1 = .999999
• oposto: ‒ .999999
• antecessor: .999999 ‒ 1 = .999998
Efetuando os cálculos para o número oposto inteiro ‒ ..1000000, temos:
• número inteiro: ..1000000
• sucessor: ..1000000 + 1 = ..1000001
• antecessor: ..1000000 ‒ 1 = .999999
Portanto, o quadro deve ser preenchido como:
|
a |
Oposto de a |
Sucessor de a |
Antecessor de a |
|---|---|---|---|
|
9 |
−9 |
10 |
8 |
|
−1.451 |
1.451 |
−1.450 |
−1.452 |
|
2.004 |
−2.004 |
2.005 |
2.003 |
|
−8 |
8 |
−7 |
−9 |
|
−1.998 |
1.998 |
−1.997 |
−1.999 |
|
−125 |
125 |
−124 |
−126 |
|
0 |
0 |
1 |
−1 |
|
999.999 |
−999.999 |
1.000.000 |
999.998 |
|
1.000.000 |
−1.000.000 |
1.000.001 |
999.999 |
12. a) Espera-se que os estudantes concluam que o oposto do oposto de 155 é o número 155, pois:
‒ [‒ ( + 155 )] = ‒[‒155] = 155
b) Espera-se que os estudantes concluam que o oposto do oposto de ‒ 155 é ‒ 155, pois:
‒ [‒ ( ‒ 155 )] = ‒[155] = ‒ 155
13. Exemplo de correções:
a) Verdadeira, pois ‒ 1 é um número inteiro, porém, por ser negativo, não é um número natural.
b) Falsa, pois 100 é um número natural, e todo número natural é um número inteiro.
c) Verdadeira, pois ‒ 9, 8 e 100 são exemplos de números inteiros.
d) Falsa, pois todo número inteiro não negativo é um número natural.
14. O termômetro marca 12 graus Célsius.
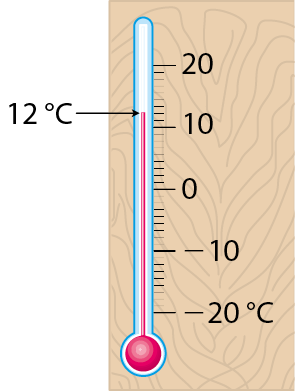
Para determinar a medida da temperatura que o termômetro marcará ao baixar 15 graus, podemos fazer:
12 graus Célsius ‒ 15 graus Célsius = ‒ 3 graus Célsius
Portanto, o termômetro marcará ‒ 3 graus Célsius.
15. A: 125 ‒ 137 = ‒ 12
B: 623 ‒ 232 = 391
C: .1040 ‒ .1100 = ‒ 60
D: 323 ‒ 402 = ‒ 79
E: 729 ‒ 701 = 28
F: 630 ‒ .1200 = ‒ 570
a) As subtrações que têm como resultado um número natural são as indicadas nos itens B e .
b) Todas as subtrações têm como resultado um número inteiro.
16. Observe os exemplos.
• O oposto de 5 é ‒ 5. Logo: 5 + ( ‒ 5 ) = 0.
• O oposto de ‒ 20 é 20. Logo: ‒ 20 + 20 = 0.
• O oposto de n é ‒ n. Logo: n + ( ‒ n ) = 0.
Portanto, a soma de dois números opostos é sempre zero.
17. Os gols sofridos são representados por números inteiros negativos e os gols marcados, por números inteiros positivos. Como o saldo de gols é ‒ 15, se o time Unidos do Bairro sofrer 3 gols e fizer 1 gol, teremos:
‒ 15 ‒ 3 + 1 = ‒ 18 + 1 = ‒ 17
Logo, o novo saldo de gols será ‒ 17 gols.
Atividades
▶ Página 22
1. a)
Fração: seis quartos.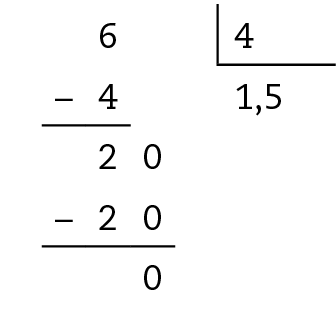
Portanto,
Fração seis quartos igual a 1 vírgula cinco..
b)
Sentença matemática. Fração um nono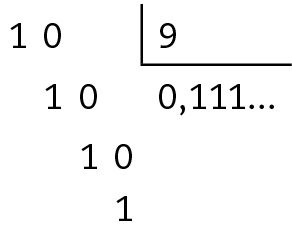
Portanto,
Sentença matemática. Fração um nono, igual a 0 vírgula um, um, um, reticências, igual a 0 vírgula um, com traço acima do um indicando dízima periódica..
c)
Sentença matemática. Fração: um terço.
Portanto,
Sentença matemática. . Fração um terço, igual a 0,333 reticências, igual a 0 vírgula 3, com traço acima do três indicando dízima periódica..
d)
Sentença matemática. Número misto 7 inteiros e três quartos, igual a fração com numerador 28 mais 3 e denominador 4, igual a fração trinta e um quartos.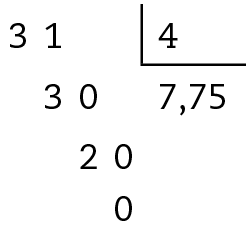
Portanto,
Sentença matemática. Número misto sete inteiros e três quartos, igual a 7 vírgula 75..
• Dos resultados obtidos, 1,5 e 7,75 são decimais exatos e
Zero vírgula um com traço acima do um indicando dízima periódica.e
e zero vírgula três com traço acima do três indicando dízima periódica.são dízimas periódicas.
2. a) Na figura um, de um total de 25 quadradinhos, 9 estão pintados inteiramente e 12 estão pintados pela metade. Como a cada duas metades obtemos um quadradinho inteiro, com 12 metades teremos 6 quadradinhos inteiros. Assim, temos 15 quadradinhos pintados de azul, pois 9 + 6 = 15. Representando em fração, temos:
Sentença matemática. Quinze sobre vinte e cinco igual a três sobre cinco.
Na figura dois, de um total de 25 quadradinhos, 13 estão pintados inteiramente e 10 estão pintados pela metade. Como a cada duas metades temos um quadradinho inteiro, teremos 5 quadradinhos inteiros. Assim, temos 18 quadradinhos pintados de azul, pois 13 + 5 = 18. Representando em fração, temos:
Sentença matemática. Fração: dezoito sobre vinte e cinco.
Logo, um número racional na fórma de fração que representa a parte colorida de azul na figura um é
Sentença matemática. Fração: três quintos.e na figura dois,
Sentença matemática. Fração: dezoito sobre vinte e cinco..
b) Pelo item a, sabemos que na figura um há 15 quadradinhos pintados de azul, ou seja, 10 quadradinhos brancos ( 25 ‒ 15 = 10 ). Para representar na fórma decimal, podemos fazer:
Sentença matemática. Dez sobre vinte e cinco igual a dois sobre cinco igual a 0,4.
Na figura dois há 18 quadradinhos pintados de azul, ou seja, 7 quadradinhos brancos ( 25 ‒ 18 = 7 ). Para representar na fórma decimal, podemos fazer:
Sentença matemática. Sete sobre vinte e cinco igual a 0,28.
Logo, um número racional na fórma decimal que representa a parte branca na figura um é 0,4 e na figura dois é 0,28.
3. Utilizando uma calculadora, obtemos os seguintes resultados:
a)
Sentença matemática. Um dividido por nove igual a zero vírgula um, um, um, reticências, igual a zero vírgula um com traço acima do um indicando dízima periódica.b)
Sentença matemática. Dois dividido por nove igual a zero vírgula dois, dois, dois, reticências, igual a zero vírgula dois com traço acima do dois indicando dízima periódica.c)
Sentença matemática. Três dividido por nove igual a zero vírgula três, três, três, reticências, igual a zero vírgula três com traço acima do três indicando dízima periódica.d)
Sentença matemática. Quatro dividido por nove igual a zero vírgula quatro, quatro, quatro, reticências, igual a zero vírgula quatro com traço acima do quatro indicando dízima periódica.Espera-se que os estudantes identifiquem o padrão existente nessas divisões por 9 e, sem usar a calculadora, determinem que o resultado de cada divisão será:
•
Sentença matemática. Cinco dividido por nove igual a zero vírgula cinco, cinco, cinco, reticências, igual a zero vírgula cinco com traço acima do cinco indicando dízima periódica.•
Sentença matemática. Seis dividido por nove igual a zero vírgula seis, seis, seis, reticências, igual a zero vírgula seis com traço acima do seis indicando dízima periódica.•
Sentença matemática. Sete dividido por nove igual a zero vírgula sete, sete, sete, reticências, igual a zero vírgula sete com traço acima do sete indicando dízima periódica.•
Sentença matemática. Oito dividido por nove igual a zero vírgula oito, oito, oito, reticências, igual a zero vírgula oito com traço acima do oito indicando dízima periódica.4. Para escrever os números em ordem crescente, podemos representar as frações como números decimais a fim de facilitar a comparação entre esses números, para, então, ordená-los do menor para o maior valor. Assim, temos:
•
Sentença matemática. Fração oito sétimos, aproximadamente um vírgula catorze.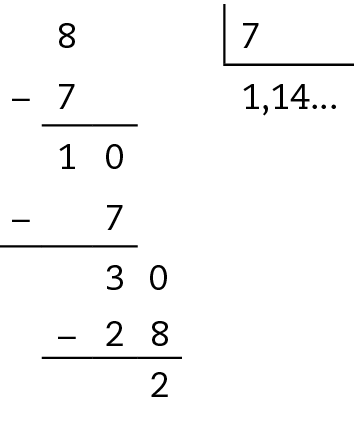
•
Sentença matemática. Fração quatro terços, igual a um vírgula três, com traço acima do três indicando dízima periódica.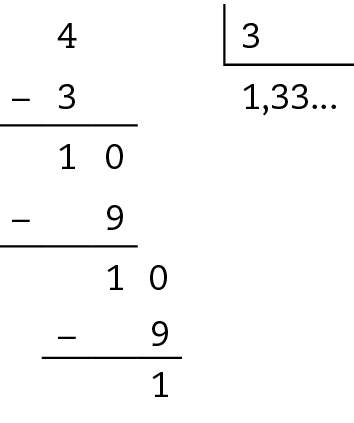
•
Sentença matemática. Fração menos três quartos, igual a menos zero vírgula setenta e cinco.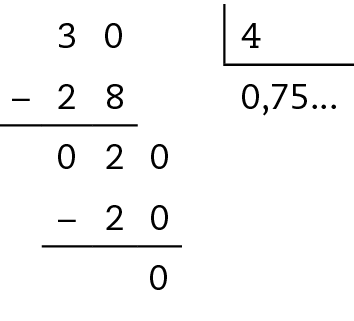
Portanto, escrevendo os números em ordem crescente, temos:
Sentença matemática. Números: menos 1,4;
Sentença matemática. Números: menos três quartos.;
Sentença matemática. Números: oito sétimos.;
Sentença matemática. Números: quatro terços;
Sentença matemática. Números: 1,916, com traço acima do 6 indicando dízima periódica..
5. a)
Zero vírgula dois, com traço acima do dois indicando dízima periódica, mais, zero vírgula cinco, com traço acima do cinco indicando dízima periódica, menos, zero vírgula sete, com traço acima do sete indicando dízima periódica, igual a zero vírgula dois, dois, dois, dois, reticências, mais, zero vírgula cinco, cinco, cinco, cinco, reticências, menos, zero vírgula sete, sete, sete, sete, reticências, igual a zero.b) Obtendo as frações geratrizes das dízimas periódicas
Zero vírgula oito, com traço acima do oito indicando dízima periódica.e
Sentença matemática. 5,6, com traço acima do seis indicando dízima periódica., temos:
x = 0,888... (um)
10x = 8,888... (dois)
9x = 8 (dois – um)
x igual a oito nonos.
y = 5,666... (três)
10y = 56,666... (quatro)
9y = 51 (quatro – três)
y igual a cinquenta e um sobre nove.
Então, podemos fazer:
0,8 com traço acima do oito indicando dízima periódica dividido por 5,6, com traço acima do seis indicando dízima periódica, igual a fração oito sobre nove, fim da fração, dividido pela fração cinquenta e um sobre nove, igual fração oito sobre nove, fim da fração, vezes fração nove sobre cinquenta e um, igual a oito sobre cinquenta e um.
c) Obtendo as frações geratrizes das dízimas periódicas
Um vírgula oitenta e três, com traço acima do três indicando dízima periódica.e
Zero vírgula quinhentos e vinte e sete, com traço acima do vinte e sete indicando dízima periódica., temos:
x = 1,8333... (um)
10x = 18,333... (dois)
100x = 183,333... (três)
90x = 165 (três – dois)
x igual a cento e sessenta e cinco sobre noventa igual a trinta e três sobre dezoito, igual a onze sobre seis.
y = 0,52727... (quatro)
10y = 5,2727... (cinco)
.1000y = 527,2727... (seis)
990y = 522 (seis – cinco)
Na décima linha, y igual a quinhentos e vinte e dois sobre novecentos e noventa igual a vinte e nove sobre cinquenta e cinco.
Então, podemos fazer:
Um vírgula oitenta e três, com traço acima do três indicando dízima periódica, vezes zero vírgula quinhentos e vinte e sete, com traço acima do vinte e sete indicando dízima periódica, igual a onze sobre seis, fim da fração, vezes vinte e nove sobre cinquenta e cinco, igual a vinte e nove sobre trinta.
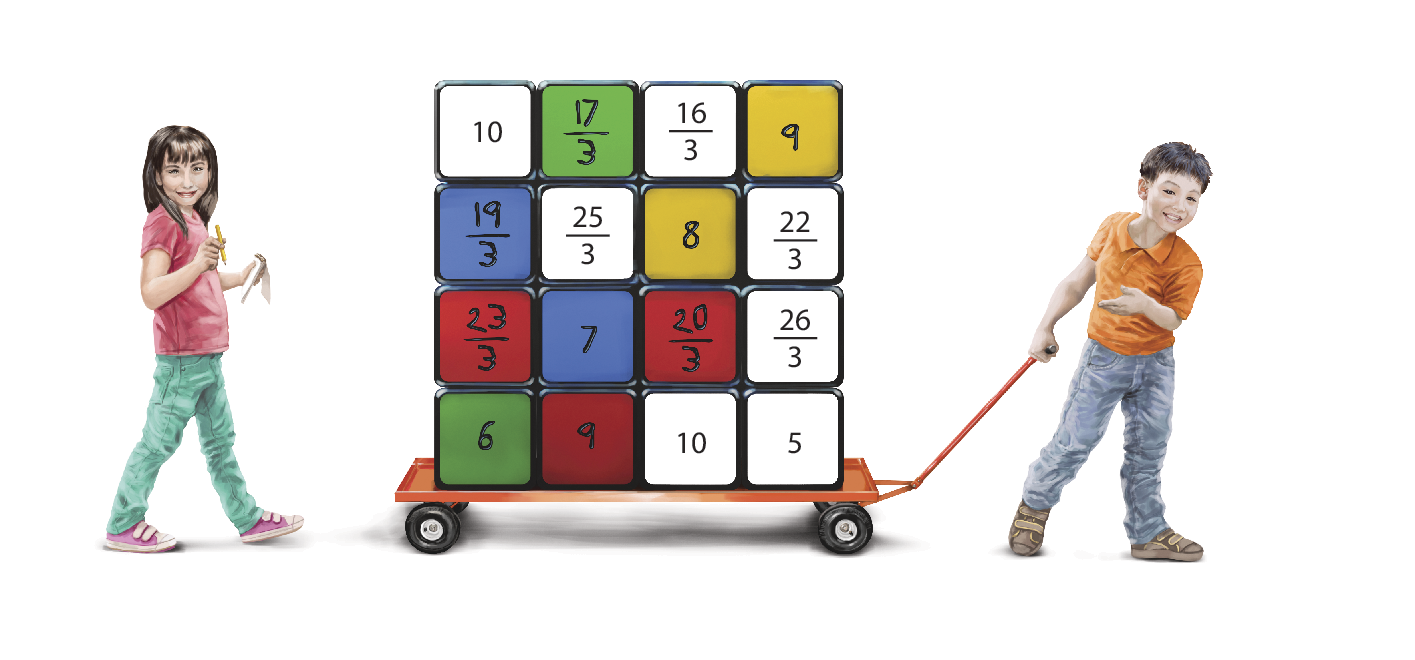
6. Podemos começar pela 1ª coluna. Para determinar o número que falta para que a soma seja igual a 30, podemos fazer:
Trinta menos, abre parênteses, dezenove sobre três, fim da fração, mais vinte e três sobre três, fim da fração, mais seis, fecha parênteses, igual a trinta menos, abre parênteses, quarenta e dois sobre três, fim da fração, mais seis, fecha parênteses, igual a trinta, menos, abre parênteses, catorze mais seis, fecha parênteses, igual a trinta menos vinte, igual a dez.
Na 3ª linha, podemos fazer:
Trinta menos, abre parênteses, vinte e três sobre três, fim da fração, mais sete mais fração vinte sobre três, fecha parênteses, igual a trinta menos, abre parênteses, fração de numerador vinte e três mais vinte e um mais vinte e denominador três, fecha parênteses, igual a trinta menos fração sessenta e quatro sobre três, igual a fração de numerador noventa menos sessenta e quatro e denominador três, igual a vinte e seis sobre três.
Assim, ficamos com o seguinte quadrado mágico:

Na 1ª linha, podemos fazer:
Trinta menos, abre parênteses, dez mais dezessete sobre três mais nove, fecha parênteses, igual a trinta menos, abre parênteses, fração de numerador trinta mais dezessete mais vinte e sete e denominador três, fecha parênteses, igual a trinta menos setenta e quatro sobre três, igual a fração de numerador noventa menos setenta e quatro e denominador três, igual a dezesseis sobre três.
Na 2ª coluna, podemos fazer:
Trinta menos, abre parênteses, dezessete sobre três mais sete mais nove, fecha parênteses, igual a trinta menos, abre parênteses, fração de numerador dezessete mais vinte e um mais vinte e sete e denominador três, fecha parênteses, igual a trinta menos sessenta e cinco sobre três, igual a fração de numerador noventa menos sessenta e cinco e denominador três, igual a vinte e cinco sobre três.
Assim, ficamos com o seguinte quadrado mágico:

Na 2ª linha, podemos fazer:
Trinta menos, abre parênteses, fração dezenove sobre três, fim da fração, mais fração vinte e cinco sobre três, fim da fração, mais oito, fecha parênteses, igual a trinta menos, abre parênteses, fração de numerador dezenove mais vinte e cinco mais vinte e quatro e denominador três, fecha parênteses, igual a trinta menos fração sessenta e oito sobre três, igual a fração de numerador noventa menos sessenta e oito e denominador três, igual a vinte e dois sobre três.
Na 3ª coluna, podemos fazer:
Trinta menos, abre parênteses, fração dezesseis sobre três, fim da fração, mais oito mais fração vinte sobre três, fecha parênteses, igual a trinta menos, abre parênteses, fração trinta e seis sobre três, fim da fração, mais oito, fecha parênteses, igual a trinta menos vinte igual a dez.
Assim, ficamos com o seguinte quadrado mágico:

Por fim, na 4ª linha, podemos fazer:
30 ‒ (6 + 9 + 10) = 30 ‒ 25 = 5
Logo:

Atividades
▶ Página 25
1. Observando a reta numérica apresentada na atividade, temos:

• ‒ 7: número negativo e não positivo
• ‒ 2: número negativo e não positivo
• 0: número natural e não positivo
• 1: número natural e positivo
• 5: número natural e positivo
Portanto, o quadro preenchido fica da seguinte maneira:
|
Número negativo |
Número natural |
Número positivo |
Número não positivo |
|
|---|---|---|---|---|
|
−7 |
X |
X |
||
|
−2 |
X |
X |
||
|
0 |
X |
X |
||
|
1 |
X |
X |
||
|
5 |
X |
X |
2. Espera-se que os estudantes localizem corretamente os números na reta numérica, de acordo com o esquema feito a seguir.

3. Espera-se que os estudantes copiem a reta numérica e indiquem os números conforme indicado a seguir:
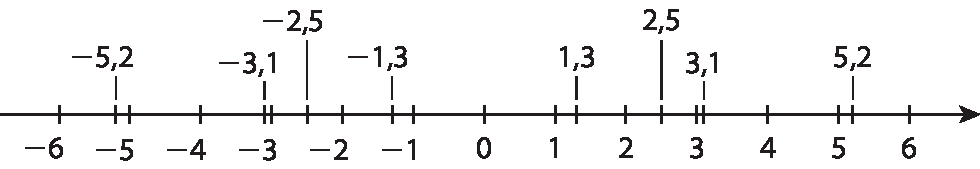
Espera-se que os estudantes escrevam os números na seguinte ordem:
‒ 5,2; ‒ 3,1; ‒ 2,5; ‒1,3; 1,3; 2,5; 3,1; 5,2
4. • Para representar
menos três oitavos.na fórma decimal, vamos efetuar a divisão de 3 por 8.

Logo,
Sentença matemática. Menos três oitavos, igual a menos zero vírgula três, sete, cinco..
• Para representar
Sentença matemática. Fração: cinco terços.na fórma decimal, vamos efetuar a divisão de 5 por 3.
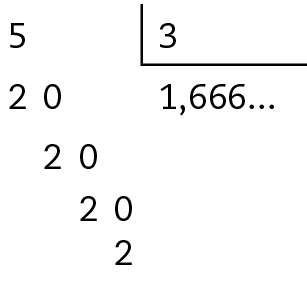
Logo,
cinco terços, igual a um vírgula seis, seis, seis, reticências.• Para representar
sete sextos.na fórma decimal, vamos efetuar a divisão de 7 por 6.
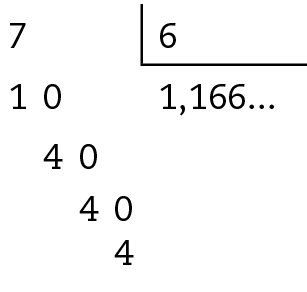
Logo,
Sentença matemática. . Sete sextos, igual a um, vírgula, um, seis, seis, reticências.• Para representar
Sentença matemática. Fração: menos sete sobre dez.na fórma decimal, vamos efetuar a divisão de 7 por 10.
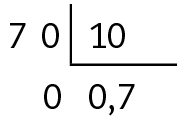
Logo,
Sentença matemática. . Menos sete sobre dez, igual a menos zero vírgula sete..
Escrevendo os números decimais na ordem decrescente, temos:
1,666reticências, 1,1666reticências; ‒ 0,375; ‒ 0,7
Portanto, os números indicados em ordem decrescente são:
Sentença matemática. Fração: cinco terços.;
Fração: sete sextos.;
menos três oitavos.;
Sentença matemática. Frações: menos sete décimos..
Portanto, a localização aproximada desses números na reta numérica é:

5. a) Falsa, pois
um terço igual a 0 vírgula 3 3 3 reticências.está entre 0 e 1, enquanto ‒
cinco oitavos= ‒ 0,625 está entre ‒ 1 e 0. Representando
um terçoe
menos cinco oitavosna reta numérica, temos:
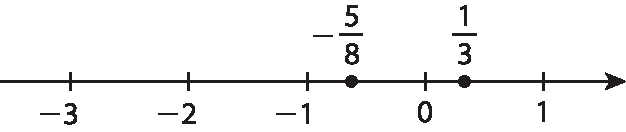
b) Falsa, pois, entre quaisquer números racionais, existem infinitos números racionais.

c) Verdadeira, pois ‒ 200 é o antecessor de ‒ 199.
6. Exemplos de respostas:
a) Número racional que esteja entre 1 e 11: 6.
b) Número racional que esteja entre ‒ 3 e 0: ‒ 2.
c) Número racional que esteja entre 1 e 2:
Fração: três sobre dois..
d) Número racional que esteja entre ‒ 3 e ‒ 2: ‒ 2,5.
7. Os estudantes podem apresentar as respostas na fórma decimal ou na fórma fracionária.
a)

b)

c)
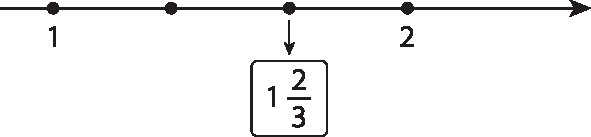
d)

e)

8. Exemplo de reta numérica que pode ser desenhada pelos estudantes:

a) Espera-se que os estudantes identifiquem que o ponto correspondente ao número
Sentença matemática. Fração: menos três quintos.na reta numérica está localizado à direita do ponto que representa ‒ 1.
b) Espera-se que os estudantes respondam que o número natural representado pelo ponto localizado entre os pontos correspondentes a ‒ 1 e 1 é o número 0.
• Resposta pessoal. Exemplo de questão: Represente na reta numérica os pontos correspondentes aos números
Sentença matemática. Fração: cinco sobre três.,
Sentença matemática. Fração: três sobre dez.e
Sentença matemática. Fração: menos três sobre dois.. Agora, responda aos itens a seguir.
a) O ponto correspondente ao número
Sentença matemática. Fração: menos três sobre dois.na reta numérica está localizado à direita ou à esquerda do ponto que representa ‒1?
b) O ponto que representa determinado número natural está localizado entre os pontos correspondentes a
Sentença matemática. Fração: três sobre dez.e
Sentença matemática. Fração: cinco sobre três.. Qual é o número natural representado por esse ponto?
Resolução: Representando os números na reta numérica, temos:
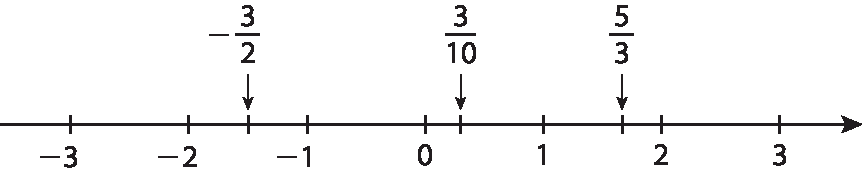
a) O ponto está localizado à esquerda.
b) O número natural representado por esse ponto é o 1.
9. Essa atividade oferece aos estudantes a oportunidade de observar o que ocorre com um número racional escrito na fórma fracionária conforme aumentamos seu denominador. Para cada uma dessas frações existe um ponto correspondente na reta numérica e, quanto maior for o denominador, mais próximo do zero ficará o número. Vale lembrar aos estudantes que eles não precisam produzir explicações escritas de maneira formal. O mais importante é que possam se expressar oralmente, de modo que expliquem o que foi observado. Nesse mesmo sentido, a representação na reta numérica poderá ser aproximada.
a) Representando os números na reta numérica, temos:
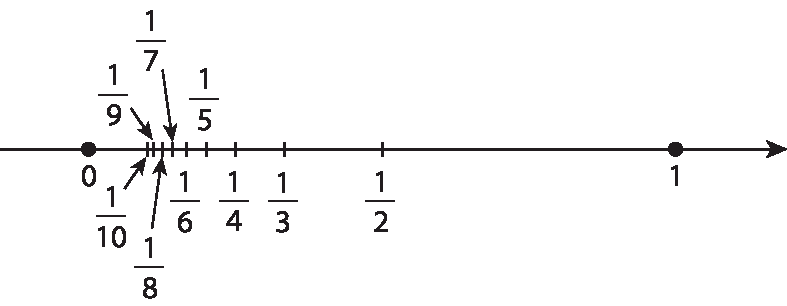
b) Exemplo de resposta: Os pontos que correspondem aos números da sequência ficam cada vez mais próximos do ponto que corresponde ao zero.
Atividades
▶ Página 27
1. Nessa atividade, são apresentadas algumas fotos com números que pertencem a diferentes conjuntos numéricos. Organize os estudantes em grupos e peça a eles que também apresentem situações do cotidiano que contenham números que correspondam a cada conjunto numérico. Pode-se organizar na lousa ou em um painel um quadro com os conjuntos numéricos e pedir a cada grupo que o preencha com a situação que identificou de cada conjunto numérico. Os estudantes poderão ter dificuldades para encontrar nas situações do cotidiano números que pertençam ao conjunto dos números irracionais. Essa conclusão é importante para que percebam que os números irracionais são utilizados em cálculos matemáticos, por exemplo na raiz quadrada.
Espera-se que os estudantes respondam que:
a) os números que aparecem na foto desse item pertencem ao conjunto dos números racionais e reais.
b) os números que aparecem na foto desse item pertencem ao conjunto dos números naturais, inteiros, racionais e reais.
c) os números que aparecem na foto desse item pertencem ao conjunto dos números racionais e reais.
d) os números que aparecem na foto desse item pertencem ao conjunto dos números naturais, inteiros, racionais e reais.
2. a) Espera-se que os estudantes respondam que não é possível identificar apenas com os algarismos visíveis na tela da calculadora. Explique que o número que aparece no visor da calculadora é parte da representação decimal de
Fração: um sobre dezenove., que é um número racional. Além disso, o período da dízima só começa a se repetir após a 19ª casa decimal.
b) Espera-se que os estudantes respondam que não, pois às vezes o período de uma dízima periódica é muito grande e em sua representação decimal expressamos um número insuficiente de casas após a vírgula para identificar esse período.
3. Exemplos de respostas:
a)
Sentença matemática. Sete igual a catorze sobre dois.b)
Sentença matemática. 0,2 igual dois sobre dez, igual a um quinto.c)
Sentença matemática. Menos sete, igual a menos sete sobre um.d)
Sentença matemática. Menos 1,32 igual a menos 132 sobre 100.e) Indicamos a dízima por x: x = 0,666... (um)
Multiplicando ambos os membros da igualdade (um) por 10, temos: 10x = 6,666... (dois)
Subtraindo membro a membro (um) de (dois), temos: 9x = 6
Logo:
x igual a fração seis nonos.Portanto,
Sentença matemática. 0,666, reticências, igual a Fração: seis nonos..
f) Indicamos a dízima por xis: x = 1,555... (um)
Multiplicando ambos os membros da igualdade (um) por 10, temos: 10x = 15,555... (dois)
Subtraindo membro a membro (um) de (dois), temos: 9x = 14
Logo:
Sentença matemática. x igual a Fração: catorze nonos.Portanto,
Sentença matemática. 1,555 reticências igual a Fração: catorze nonos..
g)
Sentença matemática. 24,3 igual a Fração: duzentos e quarenta e três sobre dez.h)
Sentença matemática. 1,05 igual Fração: cento e cinco sobre cem.4. Espera-se que os estudantes percebam que:
a)
Sentença matemática. Fração: trinta e dois sobre quatro igual a 8.pertence ao conjunto dos números naturais.
b)
Sentença matemática. Fração: trinta e dois sobre quatro igual a 8.e ‒ 27 pertencem ao conjunto dos números inteiros.
c)
Sentença matemática. Fração: trinta e dois sobre quatro igual a 8., ‒ 27,
Sentença matemática. Fração: três quintos.e
Um vírgula, trinta e cinco, com traço acima do trinta e cinco indicando dízima periódica.são números racionais.
d)
Sentença matemática. Menos raiz quadrada de dois.e π são números irracionais.
e)
Sentença matemática. Menos raiz quadrada de dois.e π são números reais e não racionais.
f)
Sentença matemática. Fração: trinta e dois sobre quatro igual a 8., ‒ 27,
Sentença matemática. Fração: três quintos.e
Um vírgula, trinta e cinco, com traço acima do trinta e cinco indicando dízima periódica.são números reais e não irracionais.
5. Exemplos de respostas:
a) Número inteiro e não natural: ‒ 15.
b) Número real e não racional: π.
c) Número racional e não inteiro: 0,5678.
d) Número inteiro e irracional: não é possível.
6. a) Todo número irracional é um número real.
b) Todo número racional é um número real.
c) Como o conjunto dos números inteiros está contido nos conjuntos dos números racionais e reais, então existem duas possibilidades para completar a frase:
• Todo número inteiro é um número racional.
• Todo número inteiro é um número real.
d) Como o conjunto dos números naturais está contido nos conjuntos dos números inteiros, racionais e reais, então existem três possibilidades de completar a frase:
• Todo número natural é um número inteiro.
• Todo número natural é um número racional.
• Todo número natural é um número real.
7. Para escrever os números em ordem crescente, podemos, primeiro, escrevê-los na fórma decimal, com aproximação de uma casa decimal. Assim, temos:

Escrevendo os números obtidos em ordem crescente, temos:
‒ 3,1; ‒ 2,4;
Menos um vírgula dois, com traço acima do dois indicando dízima periódica.;
três vírgula sessenta e dois, com traço acima do dois indicando dízima periódica.;
três vírgula sessenta e dois, com traço acima do sessenta e dois indicando dízima periódica; 5,7
Ou seja:
‒ π;
Sentença matemática. Fração: menos doze sobre cinco.;
Menos um vírgula dois, com traço acima do dois indicando dízima periódica.;
três vírgula sessenta e dois, com traço acima do dois indicando dízima periódica;
três vírgula sessenta e dois, com traço acima do sessenta e dois indicando dízima periódica;
Sentença matemática. Fração: quarenta sobre sete.8. Respostas pessoais. Exemplos de respostas:
a) Números irracionais maiores que 2,5 e menores que 3:
Sentença matemática. Raiz quadrada de sete aproximadamente dois vírgula seis.e
Sentença matemática. Raiz quadrada de oito aproximadamente dois vírgula oito.b) Números racionais maiores que
Sentença matemática. Fração: menos sete oitavos.e menores que
Sentença matemática. Fração: menos três quartos.:
Sentença matemática. Fração: menos sete oitavos igual a menos 0,875e
Sentença matemática. Fração: menos três quartos igual a menos 0,75.Sentença matemática. Fração: menos sete nonos igual a menos zero vírgula sete, com traço acima do sete indicando dízima periódica.
;
Sentença matemática. Fração: menos oito décimos igual a menos 0,8.Trabalho em equipe
▶ Página 28
Resoluções e comentários em Orientações.
Atividades
▶ Páginas 31 e 32
1. São 7 mulheres, cada mulher com 7 sacos, cada saco com 7 gatos, cada gato com 7 gatinhos. Então, temos:
Sentença matemática. Sete vezes sete, vezes sete, vezes sete, igual a sete elevado a 4, igual a 2 mil 401.
Portanto, havia /2401 gatinhos.
2. a)
Sentença matemática. Três elevado a três, igual a três vezes três, vezes três, igual a vinte e sete.b)
Sentença matemática. Abre parênteses um terço, fecha parênteses, elevado a três, igual a um terço, vezes um terço, vezes um terço, igual a um sobre vinte e sete.c)
Sentença matemática. Quatro elevado a zero igual a um.d)
Sentença matemática. Abre parênteses, menos cinco, fecha parênteses, elevado a dois, igual a abre parênteses, menos cinco, fecha parênteses, vezes, abre parênteses, menos cinco, fecha parênteses, igual a vinte e cinco.e)
Sentença matemática. Abre parênteses, menos um quinto, fecha parênteses, elevado a três, igual a, abre parênteses, menos um quinto, fecha parênteses, vezes, abre parênteses, menos um quinto, fecha parênteses, vezes, abre parênteses, menos um quinto, fecha parênteses, igual a menos um sobre cento e vinte e cinco.f)
Sentença matemática. Abre parênteses, menos sete, fecha parênteses, elevado a três, igual a, abre parênteses, menos sete, fecha parênteses, vezes, abre parênteses, menos sete, fecha parênteses, vezes, abre parênteses, menos sete, fecha parênteses, igual a menos trezentos e quarenta e três.3. a)
Sentença matemática. Dois elevado a menos um, igual a, abre parênteses, um meio, fecha parênteses, elevado a um, igual a um meio.b)
Sentença matemática. Dois elevado a menos dois, igual a, abre parênteses, um meio, fecha parênteses, elevado a dois, igual a um meio vezes um meio, igual a um quarto.c)
Sentença matemática. Dois elevado a menos dois, igual a, abre parênteses, um meio, fecha parênteses, elevado a dois, igual a um meio vezes um meio, igual a um quarto.d)
Sentença matemática. Abre parênteses, menos dois, fecha parênteses, elevado a menos três, igual a, abre parênteses, menos um meio, fecha parênteses, elevado a três, igual a, abre parênteses, menos um meio, fecha parênteses, vezes, abre parênteses, menos um meio, fecha parênteses, vezes, abre parênteses, menos um meio, fecha parênteses, igual a menos um oitavo.e)
Sentença matemática. Abre parênteses, um meio, fecha parênteses, elevado a menos um, igual a dois elevado a um, igual a dois.f)
Sentença matemática. Abre parênteses, menos um meio, fecha parênteses, elevado a menos um, igual a, abre parênteses, menos dois, fecha parênteses, elevado a um, igual a menos dois.g)
Sentença matemática. Abre parênteses, menos um meio, fecha parêntese, elevado a menos quatro, igual a, abre parênteses, menos dois, fecha parênteses, elevado a quatro, igual a, abre parênteses, menos dois, fecha parênteses, vezes abre parênteses, menos dois, fecha parênteses, vezes abre parênteses, menos dois, fecha parênteses, vezes abre parênteses, menos dois, fecha parênteses, igual a dezesseis.4. a)
Sentença matemática. Um elevado a quatro, igual a um vezes um vezes um vezes um, igual a um.b)
Sentença matemática. Um elevado a menos dois, igual a, abre parênteses, um sobre um, fecha parênteses, elevado a dois, igual a, abre parênteses, um sobre um, fecha parênteses, vezes, abre parênteses, um sobre um, fecha parênteses, igual a um sobre um, igual a um.c)
Sentença matemática. Um elevado a zero, igual a um.d)
Sentença matemática. Um elevado a cento e um, igual a um.• Exemplo de resposta: Quando a base de uma potência é 1, o resultado também é igual a 1.
5. • Na 1ª linha, basta resolver a potência:
Sentença matemática. Dois elevado a seis, igual a dois vezes, dois vezes dois, vezes dois, vezes dois vezes dois igual a sessenta e quatro.
• Fatorando o resultado da 2ª linha, temos:
Sentença matemática. Vinte e sete igual a três elevado a três.
Sabendo que o expoente é negativo, então:
Sentença matemática. Três elevado a três, igual a, abre parênteses, um terço, fecha parênteses, elevado a menos três.
• Na 3ª linha, vamos fatorar o resultado para determinar o expoente.
Sentença matemática. Quatro sobre vinte e cinco, igual a fração de numerador dois elevado a dois e denominador cinco elevado a dois, igual a, abre parênteses, dois quintos, fecha parênteses, elevado a dois.
• Fatorando o resultado da 4ª linha, temos:
Sentença matemática. Um sobre trinta e dois, igual a fração de numerador um e denominador dois elevado a cinco, igual a, abre parênteses, um meio, fecha parênteses, elevado a cinco, igual a dois elevado a menos cinco.
Portanto, há duas potências possíveis para que o resultado seja
Sentença matemática. Fração: um sobre trinta e dois..
|
Potência |
Base |
Expoente |
Resultado |
|---|---|---|---|
|
26 |
2 |
6 |
64 |
|
|
|
−3 |
27 |
|
|
|
2 |
|
|
ou (2)−5 |
ou 2 |
5 ou −5 |
|
• Espera-se que os estudantes percebam que sim, a 4ª linha.
6. Resposta pessoal. Exemplo de resposta:
•
Abre parênteses, dois quintos, fecha parênteses, elevado a dois, igual a dois quintos vezes dois quintos, igual a quatro sobre vinte e cinco.•
Abre parênteses, menos um terço, fecha parênteses, elevado a quatro, igual a abre parênteses, menos um terço, fecha parênteses, vezes, abre parênteses, menos um terço, fecha parênteses, vezes, abre parênteses, menos um terço, fecha parênteses, vezes abre parênteses, menos um terço, fecha parênteses, igual a um sobre oitenta e um.•
Dois elevado a três, igual a dois vezes dois vezes dois, igual a oito.•
Abre parênteses, menos quatro, fecha parênteses, elevado a três, igual a abre parênteses, menos quatro, fecha parênteses, vezes, abre parênteses, menos quatro, fecha parênteses, vezes, abre parênteses, menos quatro, fecha parênteses, igual a menos sessenta e quatro.•
Abre parênteses, menos dois, fecha parênteses, elevado a cinco, igual a abre parênteses, menos dois, fecha parênteses, vezes, abre parênteses, menos dois, fecha parênteses, vezes, abre parênteses, menos dois, fecha parênteses, vezes, abre parênteses, menos dois, fecha parênteses, vezes, abre parênteses, menos dois, fecha parênteses, igual a menos trinta e dois.a) Espera-se que os estudantes percebam que as potências cujas bases são positivas tiveram resultado positivo.
b) Espera-se que os estudantes percebam que as potências cujas bases são negativas tiveram resultado positivo quando os expoentes eram pares e resultado negativo quando os expoentes eram ímpares.
7. •
Dez elevado a menos um, igual a, abre parênteses, um sobre dez, fecha parênteses, elevado a um, igual a um sobre dez, igual a zero vírgula um.•
Dez elevado a menos dois, igual a, abre parênteses, um sobre dez, fecha parênteses, elevado a dois, igual a fração um sobre dez, fim da fração, vezes fração um sobre dez, igual a um sobre cem, igual a zero vírgula zero, um.•
Dez elevado a menos cinco igual a, abre parênteses, um sobre dez, fecha parênteses, elevado a cinco, igual a fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, igual a um sobre cem mil, igual a 0,00001.•
Dez elevado a menos 11, igual, abre parênteses, 1 sobre 10, fecha parênteses, elevado a 11, igual a fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez, fim da fração, vezes, fração um sobre dez.=
um sobre 100 bilhões, igual a 0,00000000001.• Resposta pessoal. Exemplo de resposta: Quanto maior for o expoente da potência, mais perto do zero eles ficam posicionados na reta numérica.
8. Observando a sequência apresentada, notamos que o número de bolinhas de cada figura é o dobro do número de bolinhas da figura anterior. Organizando os dados em um quadro, temos:

a) Logo, o número de bolinhas da figura 5 será o dobro do número de bolinhas da figura 4, ou seja, 2 ⋅ 8 = 16.
Portanto, a figura 5 terá 16 bolinhas.

b) Espera-se que os estudantes percebam que se trata de uma sequência de potências de base 2. Chamando de
n a posição de cada figura, notamos que o expoente em cada uma é ( n ‒ 1 ).
• Figura 1 → n = 1 →
dois elevado a zero.(uma bolinha)
• Figura 2 → n = 2 →
dois elevado a um(duas bolinhas)
• Figura 3 → n = 3 →
dois elevado a dois(4 bolinhas)
• Figura 4 → n = 4 →
dois elevado a três(8 bolinhas)
• Figura 5 → n = 5 →
dois elevado a quatro(16 bolinhas)
• Figura 10 → n = 10 →
ois elevado a nove(quinhentas e doze bolinhas)
Portanto, o número de bolinhas da figura 10 será igual a
Potência: dois elevado a nove., ou seja, quinhentas e doze bolinhas.
9. a) Reescrevendo a sequência, temos:
Sentença matemática. Sequência: Três elevado a três
,
três elevado a dois,
três elevado a um,reticências
Observamos que os expoentes das potências diminuem de 1 em 1. Assim, os próximos termos da sequência serão:
•
Sentença matemática. Três elevado a zero, igual a um.•
Sentença matemática. Três elevado a menos um, igual a um terço.•
Sentença matemática. Três elevado a menos dois, igual a um nono.•
Sentença matemática. Três elevado a menos três, igual a um sobre vinte e sete.•
Sentença matemática. Três elevado a menos quatro, igual a um sobre oitenta e um.b) Reescrevendo a sequência, temos:
Sentença matemática. Sequência: Cinco elevado a menos um
,
cinco elevado a menos dois,,
cinco elevado a menos três, reticências.,reticências
Observamos que os expoentes das potências diminuem de 1 em 1. Assim, os próximos termos da sequência serão:
•
Sentença matemática. Cinco elevado a menos quatro igual a um sobre seiscentos e vinte e cinco.•
Cinco elevado a menos cinco igual a um sobre três mil cento e vinte e cinco.•
Sentença matemática. Cinco elevado a menos seis, igual a um sobre quinze mil seiscentos e vinte e cinco.•
Sentença matemática. Cinco elevado a menos sete, igual a um sobre setenta e oito mil cento e vinte e cinco.•
Cinco elevado a menos oito, igual a um sobre trezentos e noventa mil seiscentos e vinte e cinco.10. a)
Cinco elevado a zero, fim do expoente, mais, abre parênteses, zero, vírgula vinte e cinco, fecha parênteses, elevado a menos dois, fim do expoente, menos, abre parênteses, zero vírgula cinco, fecha parênteses, elevado a menos dois, fim do expoente, menos dois elevado a quatro, igual.igual a um mais, abre parênteses, um quarto, fecha parênteses, elevado a menos dois, fim do expoente, menos, abre parênteses, um meio, fecha parênteses, elevado a menos dois, fim do expoente, menos dezesseis, igual.
igual a um mais quatro elevado a dois, menos dois elevado a dois, menos dezesseis, igual.
igual a um mais dezesseis menos quatro menos dezesseis, igual.
= ‒ 3
b)
Abre parênteses, um meio menos um, fecha parênteses, elevado a menos um, fim do expoente, mais, abre parênteses, menos dois, fecha parênteses, elevado a três, igual.igual a, abre parênteses, um meio menos fração dois sobre dois, fecha parênteses, elevado a menos um, fim do expoente, mais, abre parênteses, menos oito, fecha parênteses, igual.
igual a, abre parênteses, menos um meio, fecha parênteses, elevado a menos um, fim do expoente, menos oito, igual.
= ‒ 2 ‒ 8 =
= ‒ 10
11. Espera-se que os estudantes leiam e interpretem o texto para completar corretamente o quadro da seguinte maneira:
|
Horário |
Quantidade de pessoas que receberam o e-mail |
Potência |
|---|---|---|
|
13 h |
4 |
41 |
|
13 h 30 min |
4 ⋅ 4 = 16 |
42 |
|
14 h |
4 ⋅ 4 ⋅ 4 = 64 |
43 |
|
14 h 30 min |
4 ⋅ 4 ⋅ 4 ⋅ 4 = 256 |
44 |
• Para saber quantas pessoas receberam o e-mail até as 14 horas 30 minutos, adicionamos os valores da segunda coluna:
4 + 16 + 64 + 256 = 340
Portanto, trezentas e quarenta pessoas receberam o e-mail até as 14 horas 30 minutos.
Atividades
▶ Página 34
1. Para expressar os números em notação científica, fazemos:
a)
Sentença matemática. Zero vírgula zero, dois, igual a dois vezes dez elevado a menos dois.b)
Sentença matemática. Zero, vírgula zero, zero, zero, dois, igual a dois vezes dez elevado a menos quatro.c)
Sentença matemática. Duzentos mil igual a dois vezes dez elevado a cinco.d)
Sentença matemática. Mil e dois, igual a um vírgula zero, zero, dois, vezes dez elevado a três.e)
Sentença matemática. Zero, vírgula zero, zero, zero, zero, um, dois, igual a um vírgula dois vezes dez elevado a menos cinco.f)
Sentença matemática. Um bilhão e duzentos milhões, igual a um vírgula dois vezes dez elevado a nove.g)
Sentença matemática. Zero vírgula zero, zero, zero, zero, zero, zero, três, sete, um, igual a três vírgula sete, um, vezes dez elevado a menos sete.h)
Sentença matemática. Doze bilhões quinhentos e sessenta milhões, igual a um vírgula dois, cinco, seis, vezes dez elevado a dez.i)
Sentença matemática. Zero vírgula zero, zero, zero, zero, zero, zero, zero, zero, zero, sete, igual a sete vezes dez elevado a menos dez.j)
Sentença matemática. Quatrocentos e cinquenta e seis, vírgula novecentos e oitenta e sete, igual a quatro vírgula cinco, seis, nove, oito, sete vezes dez elevado a dois.2. Para resolver o problema, podemos fazer:
• 100 bilhões:
100 bilhões igual a dez elevado a onze.• número total aproximado de estrelas:
Dez elevado a onze, fim do expoente, vezes dez elevado a onze, igual a dez elevado a expoente onze mais onze, igual a dez elevado a vinte e dois.
Logo, existem no Universo, em média, 1022 estrelas.
3. As potências de base 10 cujo expoente é um inteiro negativo são menores que as potências de base 10 cujo expoente é um inteiro positivo. Além disso, considerando a relação entre o expoente e o número de algarismos zero desses números, temos:
Sentença matemática. Potências: Dez elevado a menos onze.
,
Sentença matemática. Potências: dez elevado a menos dez,
Sentença matemática. Potências: dez elevado a menos cinco.,
Sentença matemática. Potências: dez elevado a dois.,
dez elevado a cinco.,
Sentença matemática. Potências: dez elevado a sete.4. Efetuando as operações, temos:
a) 37,3 ⋅ 10–2 + 0,01 ⋅ 102 = 0,373 ⋅ 100 + 1 ⋅ 100 =
= (0,373 + 1) ⋅ 100 = 1,373 ⋅ 100
b) 0,00034 + 25,2 ⋅ 10–2 = 0,0034 ⋅ 10–1 + 2,52 ⋅ 10–1 =
= (0,0034 + 2,52) ⋅ 10–1 = 2,5234 ⋅ 10–1
c) 13 200 ⋅ 103 ‒ 5,4 ⋅ 105 = 1,32 ⋅ 107 ‒ 0,054 ⋅ 107 =
= (1,32 ‒ 0,054) ⋅ 107 = 1,266 ⋅ 107
5. Para encontrar os possíveis valores de x, fazemos:
Sentença matemática. Dois vírgula cinquenta e três, vezes dez elevado a quatro, menor que x, menor que dois, vírgula cinquenta e quatro, vezes dez elevado a quatro.
2,53 ⋅ .10000 < x < 2,54 ⋅ .10000
.25300 < x < .25400
Como x é menor que .25400, então vamos contar até .25399. Logo, .25399 ‒ .25300 = 99.
Portanto, há 99 possíveis valores para x.
6. Escrevendo os números informados em notação decimal, temos:
•
Sentença matemática. Três vírgula sessenta e seis, vezes dez elevado a oito, igual a três, vírgula sessenta e seis, vezes cem milhões, igual a trezentos e sessenta e seis milhões.•
Sentença matemática. Um vírgula trinta e nove, vezes dez elevado a nove, igual a um vírgula trinta e nove vezes um bilhão, igual a um bilhão e trezentos e noventa milhões.•
Sentença matemática. Cinco vírgula oitenta e nove, vezes dez elevado a três, igual a cinco vírgula oitenta e nove, vezes mil, igual a cinco mil oitocentos e noventa.•
Sentença matemática. Três vírgula vinte e quatro vezes dez elevado a dois, igual a três vírgula vinte e quatro vezes cem, igual a trezentos e vinte e quatro.Escrevendo os números obtidos em ordem crescente, temos:
324; .5890; ..366000000; ...1390000000
Portanto:
Sentença matemática. Números em notação científica: Três vírgula vinte e quatro vezes dez elevado a dois
;
Sentença matemática. Números em notação científica: cinco vírgula oitenta e nove vezes dez elevado a três;
três vírgula sessenta e seis vezes dez elevado a oito.;
Sentença matemática. Um vírgula trinta e nove, vezes dez elevado a nove