Página sessenta e três

Parte 4

Assim:

AE = 14,6 + 6,6 + 6,6 = 27,8

BE = 7,3 + 6,6 + 6,6 = 20,5

Portanto, BC = 7,3 centímetros; AE = 27,8 centímetros, CD = 6,6 centímetros e BE = 20,5 centímetros.

b) Como AE = 27,8 centímetros e F é ponto médio de

\overline{A E}

, então:

A F = \frac{A E}{2} = \frac{27,8}{2} = 13, 9

Portanto, AF = 13,9 centímetros.

c) Se G é ponto médio de

\overline{C D}

, então:

C G = \frac{C D}{2} = \frac{6,6}{2} = 3, 3

Então:

AG = AC = CG = 14,6 + 3,3 = 17,9

Logo, AG = 17,9 centímetros.

3. Exemplo de resposta:

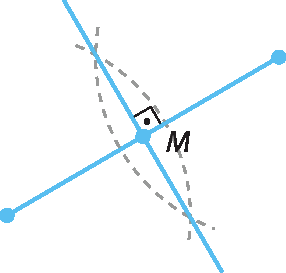
Figura geométrica: Segmento de reta e uma reta perpendiculares no ponto M. À esquerda e direita da reta, dois arcos pontilhados que se cruzam em dois pontos pertencentes à reta.

4. • Construção de M:

Esquema: segmento de reta horizontal AB. À direita, seta para a direita: o mesmo segmento AB com dois arcos que se cruzam no ponto C na região de cima e no ponto D na região abaixo. À direita, seta para a direita: mesmo segmento AB e outro segmento de reta tracejado com extremidades nos pontos C e D marcados anteriormente. Os segmentos AB e CD são perpendiculares e se cruzam no ponto M, ponto médio de AB.

• Construção de N:

Esquema: segmento de reta horizontal AB e ponto médio M. À direita, seta para a direita. À direita da seta, mesmo segmento de reta AB anterior com dois arcos tracejados entre os pontos M e B, que se cruzam em dois pontos: um na região acima de MB e outro na região embaixo. À direita, seta para a direita. À direita da seta: mesmo segmento de reta anterior. Entre os pontos M e B há um segmento de reta com extremidades no cruzamento dos arcos. Esse segmento de reta é perpendicular à AB no ponto N, que é ponto médio de MB.

Logo, teremos a figura:

Figura geométrica. Segmento de reta AB, com ponto médio M à AB e ponto médio N à MB indicados.

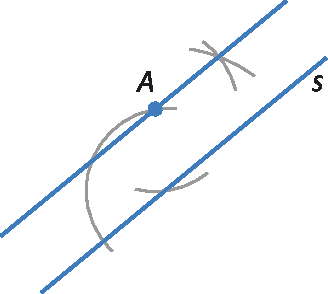
5. Exemplo de resposta:

Figura geométrica: Reta diagonal passando pelo ponto A. Abaixo, uma reta paralela. No canto superior direito inferior direito a letra s minúscula. Há um arco passando pelo ponto A e pelas duas retas.

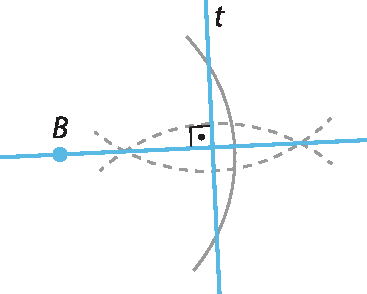
6. Exemplo de resposta:

Figura geométrica: Uma reta passando pelo ponto B. Outra reta t, perpendicular a anterior. Há dois arcos tracejados que se cruzam em dois pontos da reta que contém o ponto B e um arco contínuo que corta a reta t em dois pontos.

7. Como AC = BC, o depósito está em algum ponto da mediatriz do segmento

\overline{A B}

alternativa cê

Atividades

▶ Páginas 68 e 69

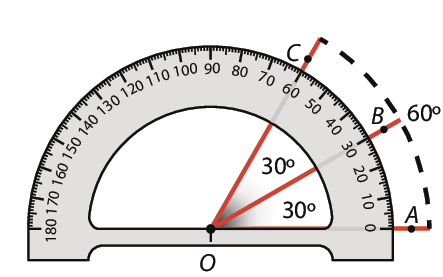
Ilustração. Ângulo AOC de 60 graus, dividido nos ângulos AOB de 30 graus e ângulo BOC de 30 graus, sendo o lado OB comum. Um transferidor de 180 graus sobrepõe estes ângulos com centro em O e linha da fé sobre o lado OA.

a) Utilizando um transferidor, temos que:

m e d (A \hat{O} B) = m e d (B \hat{O} C) = 30 °

b) Os ângulos

A \hat{O} B

B \hat{O} C

são congruentes, pois têm medidas iguais.

c) A semirreta

\vec{O B}

é a bissetriz do ângulo

A \hat{O} C

, pois os ângulos

A \hat{O} B

B \hat{O} C

são congruentes, ou seja, ambos medem 30graus.

2. a) Como

m e d (A \hat{O} B) = 120 °

\vec{O C}

é bissetriz de

A \hat{O} B

, então os ângulos

A \hat{O} C

B \hat{O} C

são congruentes, ou seja, ambos têm a mesma medida. Para determinar as medidas de abertura desses ângulos, basta calcular:

120graus : 2 = 60graus

Logo,

m e d (A \hat{O} C) = 60 °

m e d (B \hat{O} C) = 60 °

b) Como

m e d (A \hat{O} B) = 18 °

\vec{O C}

é bissetriz de

A \hat{O} B

, então os ângulos

A \hat{O} C

B \hat{O} C

são congruentes, ou seja, ambos têm a mesma medida. Para determinar as medidas de abertura desses ângulos, basta calcular:

18graus : 2 = 9graus

Logo,

m e d (A \hat{O} C) = 9 °

m e d (B \hat{O} C) = 9 °

3. Como

\vec{O R}

é bissetriz de

A \hat{O} C

, temos:

m e d (R \hat{O} C) = m e d (R \hat{O} A) = 20 °

Assim:

m e d (C \hat{O} D) = 180 ° ‒ (30 ° + 20 ° + °) = 180 ° ‒ 70 ° = 110 °

Logo, a abertura do ângulo

C \hat{O} D

mede 110graus.

4. a) O ângulo raso foi dividido em 6 ângulos de mesma medida de abertura. Logo, cada uma das medidas de abertura dos ângulos mede 180graus : 6 = 30graus. Assim, temos:

m e d (A \hat{O} B) = 3 \cdot 30 ° = 90 °

Como

\vec{O C}

é bissetriz de

A \hat{O} B

, então:

m e d (A \hat{O} C) = \frac{m e d (A \hat{O} B)}{2} = \frac{90 °}{2} = 45 °

Portanto, a abertura do ângulo

A \hat{O} C

mede 45graus.

b) Como

m e d (B \hat{O} C) = m e d (A \hat{O} C) = 45 °

m e d (B \hat{O} D) = 30 °

, então:

m e d (C \hat{O} D) = m e d (C \hat{O} B) + m e d (B \hat{O} D) = 45 ° + 30 ° = 75 °

Logo, a medida da abertura do ângulo

C \hat{O} D

mede 75graus.

5. Espera-se que os estudantes concluam que o lugar do plano formado por todos os pontos que estão à mesma medida de distância de duas semirretas de mesma origem é denominado bissetriz.

alternativa cê

Figura geométrica: Uma reta horizontal passando pelos pontos O e A. Uma reta vertical, que passa pelo ponto O, perpendicular a reta horizontal. Dois arcos pontilhados se cruzam em dois pontos da reta vertical e um arco contínuo cruza a reta OA em dois pontos.

Os ângulos formados foram dois ângulos retos.

Espera-se que os estudantes percebam que os passos são os mesmos.

Página sessenta e quatro

7. Exemplo de resposta:

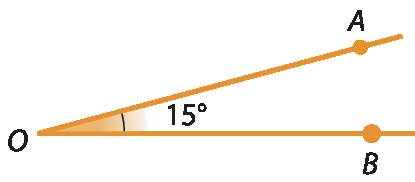
Figura geométrica: representação do ângulo BOA cuja abertura mede 15 graus.

Os estudantes podem ter traçado o ângulo por meio da bissetriz de um ângulo de 30graus.

8. a) Como

\vec{O C}

é bissetriz de

A \hat{O} B

, então:

m e d (A \hat{O} C) = m e d (C \hat{O} B)

5x ‒ 8graus = 4x + 7graus

5x ‒ 4x = 7graus + 8graus

x = 15graus

Substituindo x por 15graus na expressão que indica a medida do ângulo

A \hat{O} B

, temos:

m e d (A \hat{O} B) = (5 x ‒ 8 °) + (4 x + 7 °) = 9 x ‒ 1 ° = 9 \cdot 15 ° ‒ 1 ° = 134 °

Logo,

m e d (A \hat{O} B) = 134 °

b) Como

\vec{O C}

é bissetriz de

A \hat{O} B

, então:

m e d (A \hat{O} C) = m e d (C \hat{O} B)

3 x = (75 ° ‒ 2 x) + 30 °

3x + 2x = 105graus

5x = 105graus

x = 21graus

Substituindo x por 21graus na expressão que indica a medida do ângulo

A \hat{O} B

, temos:

m e d (A \hat{O} B) = 3 x + (75 ° ‒ 2 x) + 30 ° = x + 105 ° = 21 ° + 105 ° = 126 °

Logo,

m e d (A \hat{O} B) = 126 °

m e d (A \hat{O} B) = 68 °

. Como

\vec{O C}

é bissetriz de

A \hat{O} B

, temos:

m e d (A \hat{O} C) = m e d (C \hat{O} B) = \frac{68 °}{2} = 34 °

Como

\vec{O D}

é bissetriz de

A \hat{O} C

, temos:

m e d (C \hat{O} D) = m e d (A \hat{O} D) = \frac{34 °}{2} = 17 °

Então:

m e d (D \hat{O} B) = m e d (B \hat{O} C) + m e d (C \hat{O} D) = 34 ° + 17 ° = 51 °

Logo,

m e d (D \hat{O} B) = 51 °

10. a) Como

\vec{O C}

é bissetriz de

B \hat{O} D

, então:

m e d (B \hat{O} C) = m e d (C \hat{O} D)

6x ‒ 15graus = 2x + 25graus

6x ‒ 2x = 25graus + 15graus

4x = 40graus

x = 10graus

Logo, x = 10graus.

m e d (A \hat{O} D) = m e d (A \hat{O} B) + m e d (B \hat{O} C) + m e d (C \hat{O} D)

63 ° + (6 x ‒ 15 °) + (2 x + 25 °) = 8 x + 73 °

Substituindo x por 10graus em

8 x + 73 °

, temos:

8 x + 73 ° = 8 \cdot 10 ° + 73 ° = 153 °

Logo,

m e d (A \hat{O} D) = 153 °

11. Da fala de Gustavo, concluímos que

m e d (A \hat{O} B) = 92 °

. Portanto, a medida de abertura de

A \hat{O} B

é menor que a medida de um ângulo raso (180graus). Consequentemente,

A \hat{O} B

é um ângulo obtuso. Portanto, estão enganados Fernanda e Ricardo.

Após a resolução dessa atividade, pergunte aos estudantes como eles escolheram as falas certas e as falas erradas.

Espera-se que eles observem que não seria possível que Mariana, Ricardo e Fernanda estivessem certos simultaneamente, pois uma afirmação já torna a outra incorreta; ou seja, se um ângulo é obtuso, ele não será reto nem agudo, e o mesmo vale para as outras relações. Assim, pelo raciocínio lógico, dado que há um total de 3 afirmações corretas e duas erradas, certamente entre as duas erradas estará a de Mariana, a de Ricardo ou a de Fernanda.

INFORMÁTICA E MATEMÁTICA

▶ Páginas 70 e 71

Resoluções e comentários em Orientações.

Estatística e Probabilidade

▶ Páginas 73 e 74

1. Nessa atividade, chame a atenção dos estudantes para o fato de que a quantidade de reclamações está representada em milhares e, por isso, a quantidade indicada no gráfico, em cada semestre, deve ser multiplicada por .1000.

a) O assunto do gráfico se refere ao número de reclamações nos serviços de comunicação no Brasil.

b) O gráfico apresenta dados referentes ao período do 1º semestre de 2019 ao 1º semestre de 2021.

c) Para calcular o número de reclamações realizadas em 2020, fazemos:

• 1º semestre de 2020: .1521

• 2º semestre de 2020: .1442

.1521 + .1442 = .2963

Como os valores indicados estão em milhares, temos:

.2963 ⋅ .1000 = ..2963000

Portanto, em 2020 foram realizadas ..2963000 reclamações.

d) Espera-se que os estudantes concluam que, do 1º semestre de 2019 ao 1º semestre de 2021, a quantidade de reclamações nos serviços de comunicação diminuiu, pois no 1º semestre de 2019 foram ..1553000 reclamações e no 1º semestre de 2021 foram ..1223000 reclamações.

2. a) Espera-se que os estudantes respondam que não é possível dizer que o número de estudantes com cárie decresceu em todo o período, pois de 2017 a 2018 houve aumento nesse número.

b) O ano em que houve mais estudantes com cárie foi 2018.

c) Analisando o gráfico, é possível afirmar que em 2020 havia exatamente 217 estudantes com cárie nessa escola.

d) Espera-se que os estudantes concluam que o número de estudantes com cárie decresceu de 2018 a 2021.

3. a) Analisando o gráfico, é possível afirmar que a porcentagem de domicílios com acesso à internet aumentou a cada ano.

b) Sabemos que devemos considerar “mais da metade”, ou seja, mais que 50%. Assim, levando em conta o período apresentado no gráfico, de 2015 a 2020 mais da metade dos domicílios tinha acesso à internet.

4. a) Para calcular a quantidade de novos casos de Covid-19 registrados da 4ª para a 5ª semana de 2022, fazemos:

..26473273 ‒ ..25214622 = ..1258651

Portanto, foram registrados ..1258651 novos casos.

b) Espera-se que os estudantes respondam que entre a 3ª e a 4ª semana os casos acumulados de Covid-19 atingiram a marca de 24 milhões.

c) Não é possível, pois são valores acumulados, ou seja, o número pode permanecer o mesmo ou aumentar.

Página sessenta e cinco

EDUCAÇÃO FINANCEIRA

▶ Páginas 75 e 76

Resoluções e comentários em Orientações.

Atividades de revisão

▶ Páginas 77 e 78

1. De acordo com os dados, temos o seguinte esquema:

Figura geométrica: Reta horizontal r que passa pelos pontos: A, B, C e D. Há a indicação de que de A até C mede 50 vírgula 32 milímetros. De B até C mede 33 vírgula 73 milímetros e de B até D mede 46 vírgula 91 milímetros.

Podemos, então, fazer:

• CD = BD ‒ BC = 46,91 ‒ 33,73 = 13,18

• AD = AC + CD = 50,32 + 13,18 = 63, 5

Portanto, CD = 13,18 milímetros e AD = 63,5 milímetros.

2. Desenhamos com a régua os segmentos

\overline{A B}

\overline{C D}

. Com a ponta-seca do compasso nas extremidades do segmento, traçamos dois arcos de mesma abertura, maiores que a metade da medida do comprimento do segmento. Chamamos os pontos de encontro desses arcos de M e N. Ao traçar o segmento

\overline{M N}

, é determinado o ponto médio (L e K) do segmento inicial. Observe os esquemas.

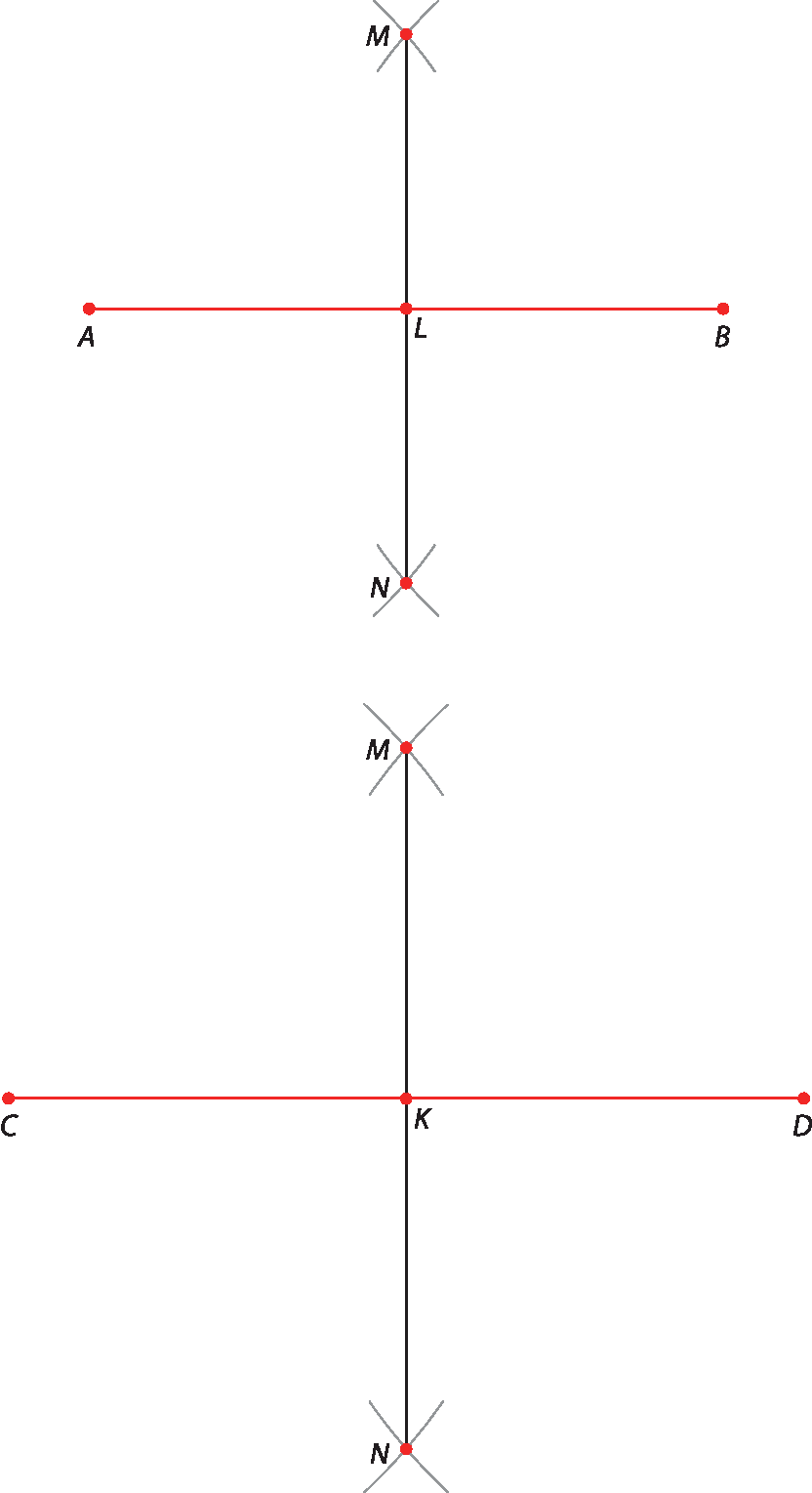
Figura geométrica: Segmento de reta horizontal AB com ponto L no centro. Segmento de reta vertical MN passando pelo ponto L, ponto médio de AB. Figura geométrica: Segmento de reta horizontal CD com ponto médio K indicado. Segmento de reta vertical MN passando pelo ponto K.

• Exemplo de resposta:

Figura geométrica: Segmento de reta horizontal AB com ponto médio L. Reta f vertical passando pelo ponto médio L. A medida AL é 2 vírgula 75 e a medida BL é 2 vírgula 75.

Figura geométrica: Segmento de reta horizontal CD com ponto médio K. Reta g vertical que passa pelo ponto K. A medida CK é 3 vírgula 45 e a medida DK é 3 vírgula 45.

L é o ponto médio de

\overline{A B}

, e K é o ponto médio de

\overline{C D}

3. a) Os ângulos obtusos, ou seja, maiores que 90graus e menores que 180graus, são

A \hat{O} C

A \hat{O} D

A \hat{O} E

B \hat{O} D

B \hat{O} E

b) Temos:

•

m e d (A \hat{O} C) = 102 °

•

m e d (A \hat{O} D) = 130 °

•

m e d (A \hat{O} E) = 155 °

•

m e d (B \hat{O} D) = m e d (A \hat{O} D) ‒ m e d (A \hat{O} B) = 130 ° ‒ 30 ° = 100 °

•

m e d (B \hat{O} E) = m e d (A \hat{O} E) ‒ m e d (A \hat{O} B) = 155 ° ‒ 30 ° = 125 °

4. a) Falsa, pois um ângulo cuja abertura mede 29graus é agudo.

b) Verdadeira, pois a abertura de um ângulo agudo é, por definição, menor que a abertura de um ângulo de 90graus.

c) Verdadeira, pois a abertura de um ângulo raso mede 180graus, que é maior que a abertura de um ângulo agudo.

d) Verdadeira, pois a abertura de todos os ângulos entre 90graus e 180graus são maiores que 85graus.

5. Como a medida de abertura do ângulo agudo é um terço da medida de abertura do ângulo reto, podemos fazer

\frac{1}{3} \cdot 90 ° = 30 °

. Como a medida de abertura do ângulo obtuso é o quíntuplo da medida de abertura do agudo, podemos fazer 5 ⋅ 30graus = 150graus. Logo, a medida de abertura do ângulo obtuso é 150graus. Portanto, a abertura do ângulo obtido pela bissetriz do ângulo obtuso mede

\frac{150 °}{2} = 75 °

6. a)

m e d (A \hat{O} C) = m e d (A \hat{O} B) + m e d (B \hat{O} C) = 40 ° + 80 ° = 120 °

b) Se

\vec{O D}

é bissetriz de

B \hat{O} C

, então:

m e d (B \hat{O} D) = m e d (D \hat{O} C) = \frac{m e d (B \hat{O} C)}{2} = \frac{80 °}{2} = 40 °

\vec{O E}

é bissetriz de

A \hat{O} B

, então:

m e d (A \hat{O} E) = m e d (E \hat{O} B) = \frac{m e d (A \hat{O} B)}{2} = \frac{40 °}{2} = 20 °

Logo, podemos fazer:

m e d (D \hat{O} E) = m e d (D \hat{O} B) + m e d (B \hat{O} E) = 40 ° + 20 ° = 60 °

Portanto,

m e d (D \hat{O} E) = 60 °

c) O ângulo formado pelas bissetrizes

\vec{O D}

\vec{O E}

é o ângulo

D \hat{O} E

, que, por ser formado por bissetrizes, é a metade da abertura de

A \hat{O} C

. Logo, se

m e d (D \hat{O} E) = 70 °

, então

m e d (A \hat{O} C) = 2 \cdot 70 °

, ou seja, 140graus.

7. Espera-se que os estudantes percebam que o monumento deve ser instalado em qualquer ponto da bissetriz do ângulo formado pelas ruas e que seja interno à região determinada pela praça. Portanto, esse local não é único.

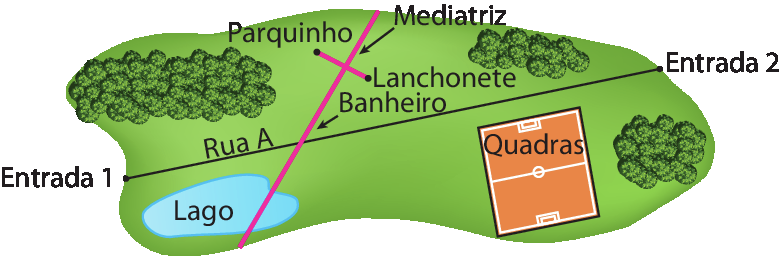
8. a) Espera‑se que os estudantes percebam que o ponto deve estar na mediatriz do segmento com extremos na lanchonete e no parquinho e que pertença ao segmento que representa a Rua a.

Página sessenta e seis

b) Nesse item, os estudantes deverão aplicar o conceito de mediatriz como lugar geométrico para resolver um problema: representar a localização de um banheiro em uma rua de modo que ele esteja à mesma medida de distância de dois pontos fixos (parquinho e lanchonete). Espera-se que eles percebam que o banheiro deve estar na intersecção do segmento de reta que representa a Rua a com a mediatriz do segmento cujas extremidades são os pontos que correspondem à localização da lanchonete e do parquinho.

Ilustração. Parque com entrada 1 à esquerda e diagonal (Rua A) até a entrada 2 à direita. Acima da diagonal, algumas árvores, parquinho e lanchonete. Abaixo, lago e quadras. Reta (Mediatriz) passa entre o Parquinho e a lanchonete e parte sobre o lago. Mediatriz e Rua A se cruzam no ponto Banheiro.

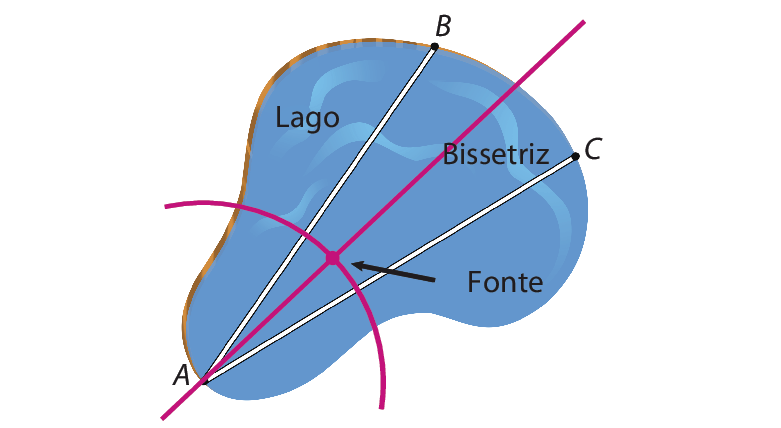
9. Nessa atividade, os estudantes vão aplicar os conceitos de circunferência e bissetriz como lugares geométricos para resolver um problema: representar a localização de uma fonte. Espera-se que eles percebam que a fonte deve estar na intersecção da bissetriz do ângulo

B \hat{A} C

com a circunferência de centro a e raio de medida de comprimento igual à do segmento

\overline{B C}

Ilustração. Lago azul de formado arredondado. Na parte inferior esquerda na borda do lago, o ponto A. Na parte superior na borda do lago os pontos B e C. Os segmentos AB e AC estão indicados. Há uma reta que divide o ângulo BAC em dois ângulos de mesma medida de abertura denominado Bissetriz. Há um arco passando pelos lados AB e AC e pela bissetriz. Na intersecção do arco com a bissetriz há indicação da palavra 'Fonte'.

alternativa dê

Unidade 2

Capítulo 3

Atividades

▶ Páginas 84 e 85

1. a) escaleno e obtusângulo, pois não tem lados congruentes e tem um ângulo interno obtuso.

b) escaleno e retângulo, pois não tem lados congruentes e tem um ângulo reto.

c) equilátero e acutângulo, pois tem três lados congruentes e tem três ângulos internos agudos.

d) escaleno e obtusângulo, pois não tem lados congruentes e tem um ângulo interno obtuso.

e) escaleno e acutângulo, pois não tem lados congruentes e tem três ângulos internos agudos.

f) isósceles e retângulo, pois tem dois lados congruentes e tem um ângulo interno reto.

2. Para que exista um triângulo com lados de determinadas medidas de comprimento, ele deve atender à condição de existência de um triângulo:

Em qualquer triângulo, a medida de comprimento de um lado é sempre menor que a soma das medidas de comprimento dos outros dois lados.

a) • 3,5 < 4,5 + 6,5

3,5 < 11 (verdadeiro)

• 4,5 < 2,5 + 6,5

4,5 < 9 (verdadeiro)

• 6,5 < 3,5 + 4,5

6,5 < 8 (verdadeiro)

Portanto, as medidas dadas neste item possibilitam a construção de um triângulo.

b) 90 < 45 + 45

90 < 90 (falso)

Portanto, as medidas dadas neste item não possibilitam a construção de um triângulo.

c) • 6 < 5,9 + 6,1

6 < 12 (verdadeiro)

• 5,9 < 6 + 6,1

5,9 < 12,1 (verdadeiro)

• 6,1 < 6 + 5,9

6,1 < 11,9 (verdadeiro)

Portanto, as medidas dadas neste item possibilitam a construção de um triângulo.

d) 10 < 2 + 3

10 < 5 (falso)

Logo, as medidas dos segmentos dos itens a e c possibilitam a construção de um triângulo.

3. A afirmação de Cátia é verdadeira, pois o triângulo tem três lados congruentes, ou seja, é equilátero. A afirmação de Lia é verdadeira, pois o triângulo tem três ângulos internos de abertura 60graus, ou seja, agudos. A afirmação de Flávia também é verdadeira, pois o triângulo é equilátero, ou seja, não é escaleno. Portanto, as três afirmações são verdadeiras.

4. a) Como o triângulo é isósceles, é necessário que tenha dois lados com a mesma medida de comprimento. Como a medida de comprimento de dois lados já foram apresentadas, 2 centímetros e 3 centímetros, é necessário que a medida de comprimento do terceiro lado seja igual a qualquer um desses dois valores. Portanto, as medidas de comprimento possíveis para o terceiro lado são 2 centímetros ou 3 centímetros.

b) Indicando por x a medida de comprimento, em centímetro, do terceiro lado do triângulo escaleno, podemos verificar a condição para a existência de um triângulo. Como dois dos lados medem 7 centímetros e 3 centímetros de comprimento, então:

x + 3 > 7

x > 4

De acordo com o enunciado, as medidas de comprimento dos lados desse triângulo correspondem a um número natural e são menores que 8 centímetros. Logo, as possibilidades são: 5 centímetros, 6 centímetros ou 7 centímetros de comprimento. Pelo fato de o triângulo ser escaleno, então desconsideramos a possibilidade de medida igual a 7 centímetros de comprimento. Portanto, as possíveis medidas de comprimento do terceiro lado desse triângulo são 5 centímetros ou 6 centímetros.

c) Indicando por x a medida de comprimento, em centímetro, do terceiro lado do triângulo escaleno, podemos verificar a condição para a existência de um triângulo. Como dois dos lados medem 6 centímetros e 9 centímetros de comprimento, então:

6 + x > 9

x > 3

De acordo com o enunciado, as medidas de comprimento dos lados desse triângulo correspondem a um número natural par e são menores que 11 centímetros. Logo, as possibilidades são: 4 centímetros, 6 centímetros, 8 centímetros e 10 centímetros. Pelo fato de o triângulo ser escaleno, então desconsideramos a possibilidade de medida igual a 6 centímetros de comprimento. Portanto, as possíveis medidas de comprimento do terceiro lado desse triângulo são 4 centímetros, 8 centímetros ou 10 centímetros.

Página sessenta e sete

5. a) Verificando a condição de existência de um triângulo para as cinco situações, temos:

2 < 3 + 6 (verdadeiro)

3 < 2 + 6 (verdadeiro)

6 < 2 + 3 (falso)

dois

3 < 1,5 + 4 (verdadeiro)

1,5 < 3 + 4 (verdadeiro)

4 < 3 + 1,5 (verdadeiro)

três

2 < 3 + 4 (verdadeiro)

3 < 2 + 4 (verdadeiro)

4 < 2 + 3 (verdadeiro)

quatro

4 < 4 + 4 (verdadeiro)

cinco

4 < 4 + 6 (verdadeiro)

6 < 4 + 4 (verdadeiro)

Logo, é possível construir o △ABC nas situações dois, três, quatro e cinco.

b) Exemplos de construções:

dois

Ilustração. Triângulo azul ABC com lados medindo 4 centímetros, 1,5 centímetros e 3 centímetros.

três

Ilustração. Triângulo verde ABC com lados medindo 4 centímetros, 2 centímetros e 3 centímetros.

quatro

Ilustração. Triângulo laranja ABC com lados medindo 4 centímetros, 4 centímetros e 4 centímetros.

cinco

Ilustração. Triângulo vermelho ABC com lados medindo 4 centímetros, 4 centímetros e 6 centímetros.

c) Para realizar este item, os estudantes deverão utilizar o transferidor a fim de encontrar as medidas de abertura dos ângulos internos de cada um dos triângulos construídos com régua e compasso no item anterior. Caminhe entre os estudantes para verificar se estão fazendo uso desse instrumento de medida de fórma adequada, pois, muitas vezes, é preciso prolongar os lados dos triângulos para conseguir medir a abertura do ângulo desejado.

As medidas aproximadas de abertura ângulos internos são:

dois:

m e d (B \hat{A} C) = 18 °

;

m e d (A \hat{B} C) = 122 °

;

m e d (B \hat{C} A) = 40 °

três:

m e d (B \hat{A} C) = 46 °

;

m e d (A \hat{B} C) = 105 °

;

m e d (B \hat{C} A) = 29 °

quatro:

m e d (B \hat{A} C) = 60 °;

m e d (A \hat{B} C) = 60 °

;

m e d (B \hat{C} A) = 60 °

cinco:

m e d (B \hat{A} C) = 41 °

;

m e d (A \hat{B} C) = 98 °

;

m e d (B \hat{C} A) = 41 °

d) Classificando os triângulos em relação às medidas de comprimento dos lados e da abertura dos ângulos, temos:

dois: escaleno e obtusângulo

três: escaleno e obtusângulo

quatro: equilátero e acutângulo

cinco: isósceles e obtusângulo

6. Indicando por x a medida de comprimento dos dois lados congruentes, em centímetro, podemos verificar a condição de existência de triângulos isósceles com lados de medidas de comprimento x, x e 6 centímetros da seguinte maneira:

x + x > 6

2x > 6

x > 3

Logo, a medida de comprimento do lado x deve ser maior que 3 centímetros. Como há infinitas medidas maiores que 3 centímetros, concluímos que é possível construir infinitos triângulos isósceles com a condição apresentada.

Atividades

▶ Página 87

1. a) x + 78graus + 50graus = 180graus

x + 128graus = 180graus

x = 180graus ‒ 128graus

x = 52graus

\frac{5 x}{2} + 3 x + 48 ° = 180 °

\frac{5 x}{2} + \frac{6 x}{2} = 180 ° ‒ 48 °

11x = 132graus ⋅ 2

x = \frac{264 °}{11}

x = 24graus

c) ( 30graus + x ) + 2x + 3x = 180graus

30graus + 6x = 180graus

6x = 180graus ‒ 30graus

6x = 150graus

x = \frac{150 °}{6}

x = 25graus

39 ° + x + 45 ° = 180 °

x + 84graus = 180graus

x = 180graus ‒ 84graus

x = 96graus

2. Como a soma das medidas de abertura dos ângulos internos de qualquer triângulo é 180graus, temos:

26graus +

(5 x + 3 °) + (4 x + 7 °)

= 180graus

9x + 36graus = 180graus

9x = 144graus

x = 16graus

Portanto, a medida de abertura de x é 16graus.

3. x +

(x + 10 °) + (x + 20 °)

= 180graus

3x + 30graus = 180graus

3x = 150

x = 50graus

Calculando a medida de abertura de cada ângulo interno desse triângulo, temos:

• x = 50graus

• x + 10graus = 50graus + 10graus = 60graus

• x + 20graus = 50graus + 20graus = 70graus

Como a medida de abertura de um ângulo externo é igual à soma das medidas de abertura dos ângulos internos não adjacentes a ele, temos:

• 50graus + 60graus = 110graus

• 50graus + 70graus = 120graus

• 60graus + 70graus = 130graus

Logo, as medidas de abertura dos ângulos externos desse triângulo são: 110graus, 120graus e 130graus.

Página sessenta e oito

4. Pela figura, temos:

a + 148graus = 180graus

a = 32graus

Do mesmo modo, temos:

b + 102graus = 180graus

b = 78graus

Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, temos:

a + b + c = 180graus

32graus + 78graus + c = 180graus

110graus + c = 180graus

c = 70graus

Assim, fazemos:

c + d = 180graus

70graus + d = 180graus

d = 110graus

Portanto, a = 32graus, b = 78graus, c = 70graus e d = 110graus.

5. a) Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus e y = 35graus (oposto pelo vértice), temos:

• 35graus + 45graus = 80graus

• 180graus ‒ 80graus = 100graus

Assim, a abertura do terceiro ângulo interno do triângulo mede 100graus. Então:

x + 100graus = 180graus

x = 80graus

Portanto, x = 80graus e y = 35graus.

b) Pela figura, temos:

y + 135graus = 180graus

y = 45graus

Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, temos:

x + y + 70graus = 180graus

x + 45graus + 70graus = 180graus

x + 115graus = 180graus

x = 65graus

Portanto, x = 65graus e y = 45graus.

c) Como x é a medida de abertura de um ângulo externo do triângulo, temos:

x = \frac{2 x}{3} + 25 °

x ‒ \frac{2 x}{3} = 25 °

\frac{x}{3} = 25 °

x = 75graus

Mas:

x + y = 180graus

75graus + y = 180graus

y = 105graus

Portanto, x = 75graus e y = 105graus.

6. Como em um triângulo a medida de abertura de um ângulo externo corresponde à medida de abertura dos dois ângulos internos não adjacentes a ele, então:

x + y = 180graus ‒ 35graus

x + y = 145graus

Esboçando esse triângulo, temos:

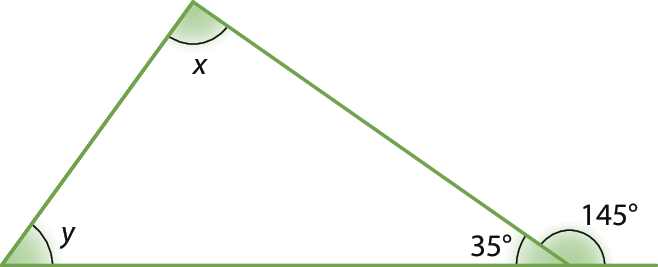
Figura geométrica: triângulo, com os ângulos internos medindo x, y e trinta e cinco graus. O ângulo que mede 35 graus tem ângulo externo que mede 145 graus.

Mas, x ‒ y = 37graus. Então:

\{\begin{cases} x + y = 145 ° \\ x ‒ y = 37 ° \end{cases}

2x = 182graus

x = 91graus

Como x = 91graus, então:

x + y = 145graus

91graus + y = 145graus

y = 54graus

Portanto, as medidas de abertura dos ângulos internos desse triângulo são 35graus, 54graus e 91graus.

INFORMÁTICA E MATEMÁTICA

▶ Página 89

Resoluções e comentários em Orientações.

Atividades

▶ Página 94

1. Espera-se que os estudantes reconheçam que o triângulo do meio fica em equilíbrio se pendurado pelo ponto indicado.

2. Representamos cada prédio como o vértice de um triângulo e encontramos o seu circuncentro. Para que o estoque esteja à mesma distância dos três prédios, ele deve estar posicionado no circuncentro do triângulo, cujos vértices representam os três prédios. O circuncentro é obtido com o encontro das mediatrizes dos vértices do triângulo.

3. a) Como

\overline{A D}

é a altura relativa ao lado

\overline{B C}

, então:

m e d (A \hat{D} C) = 90 °

Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, temos:

90 ° + 60 ° + m e d (D \hat{A} C) = 180 °

150 ° + m e d (D \hat{A} C) = 180 °

m e d (D \hat{A} C) = 30 °

Portanto, a medida de abertura do ângulo

D \hat{A} C

é 30graus.

b) Como

\overline{A D}

é mediatriz, temos BD = DC = 2 centímetros. Logo, a medida do perímetro do triângulo é dada por:

4 centímetros + 4 centímetros + 2 centímetros + 2 centímetros = 12 centímetros

4. Como

\overline{E M}

é mediana relativa ao lado

\overline{B C}

, temos:

2x ‒ 2 = x + 3

2x ‒ x = 3 + 2

x = 5

Para calcular a medida do perímetro, podemos fazer:

(2 x + 3) + (x + 1) + (x + 3) + (2 x ‒ 2)

= 6x + 5 = 6 · 5 + 5 = 35

Logo, o perímetro do triângulo BEC mede 35.

5. a) Espera-se que os estudantes concluam que o baricentro, o ortocentro e o incentro de um triângulo equilátero correspondem ao mesmo ponto, ou seja, os três pontos coincidem.

b) Espera-se que os estudantes concluam que as construções feitas por eles sugerem que nos triângulos equiláteros, o baricentro, o ortocentro e o incentro são pontos coincidentes.

6. Espera-se que os estudantes concluam que é possível traçar vários triângulos de modo que a circunferência fique inscrita neles. Por exemplo:

Figura geométrica: Triângulo azul com circunferência inscrita de centro I. Há três triângulos sobrepostos em posições diferentes circunscritos à circunferência.

Página sessenta e nove

Atividades

▶ Páginas 98 e 99

1. Espera-se que os estudantes reconheçam que os pares de triângulos congruentes são:

• a e F: éle éle éle

• B e ê: á éle á

Nos triângulos C e D, embora os três ângulos correspondentes sejam congruentes, não podemos afirmar o mesmo sobre os lados correspondentes. Se necessário, chame a atenção dos estudantes para o fato de que a a a (ângulo-ângulo-ângulo) não é um caso de congruência de triângulos.

2. a) △ABC ≅ △DCB

Os triângulos são congruentes pelo caso éle á éle.

• lado:

\overline{A B} ≅ \overline{D C}

• ângulo:

A \hat{B} C ≅ D \hat{C} B

• lado:

\overline{B C}

(lado comum)

b) △ABC ≅ △DBC

Os triângulos são congruentes pelo caso á éle á .

• ângulo:

A \hat{B} C ≅ D \hat{B} C

• lado:

\overline{B C}

(lado comum)

• ângulo:

A \hat{C} B ≅ D \hat{C} B

3. a) Falsa, pois os casos de congruência de triângulo são: éle éle éle, éle á éle, á éle á e éle á á. Logo, não há caso de congruência que envolva apenas os ângulos.

b) Verdadeira, pois a hipotenusa é a soma do quadrado dos catetos, logo tendo a medida de comprimento dos catetos é possível encontrar a medida de comprimento da hipotenusa.

c) Verdadeira, pois se os catetos são congruentes a hipotenusa também será, logo os triângulos são congruentes pelo caso éle éle éle.

alternativas bê e cê

4. a) Os triângulos são congruentes pelo caso éle á éle (lado-ângulo-lado). Logo, xis = 2.

b) Os triângulos são congruentes pelo caso (hipotenusa-cateto). Logo, xis = 4.

c) Os triângulos são congruentes pelo caso éle á éle (lado-ângulo-lado). Indicando por y a abertura do ângulo oposto ao lado de medida de comprimento 5, temos:

y + y + 90graus = 360graus

2y = 270graus

y = 135graus

Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, temos:

x + y + 15graus = 180graus

x + 135graus + 15graus = 180graus

x + 150graus = 180graus

x = 30graus

Portanto, x = 30graus.

d) Os triângulos são congruentes pelo caso éle á éle (lado-ângulo-lado). Logo, xis = 6.

5. Temos:

•

\overline{C H} ≅ \overline{D G}

(por construção)

•

\overline{H G} ≅ \overline{D C}

(por construção)

•

\overline{C G}

(lado comum)

Logo, pelo caso éle éle éle, △CHG ≅ △GDC

•

\overline{E B} ≅ \overline{C D}

(lado)

•

E \hat{B} D ≅ C \hat{D} B

(ângulos alternos internos)

•

\overline{B D}

(lado comum)

Logo, pelo caso éle á éle,

△ C D B ≅ △ E B D

•

\overline{B C} ≅ \overline{D E}

(hipotenusas congruentes)

•

\overline{A B} \neq \overline{D F}

(catetos congruentes)

Logo, pelo caso HC,

△ A B C ≅ △ F D E

Essa atividade merece uma atenção especial, pois envolve vários triângulos e exigirá que os estudantes coloquem em prática diferentes conhecimentos discutidos nas aulas. É interessante que eles possam realizar a atividade em grupos para trocar ideias e comparar caminhos de resolução. Destaque que não há medidas numéricas para as medidas de comprimento dos lados na ilustração, mas há símbolos que representam as congruências.

INFORMÁTICA E MATEMÁTICA

▶ Páginas 101 e 102

Resoluções e comentários em Orientações.

Atividades

▶ Página 105

1. Como o triângulo é isósceles, os ângulos da base são congruentes. Assim, a = 55graus.

Como a soma de abertura dos ângulos internos de um triângulo é 180graus, temos:

x + a + 55graus = 180graus

x + 55graus + 55graus = 180graus

x + 110graus = 180graus

x = 70graus

Portanto, a = 55graus e x = 70graus.

2. Como o triângulo é isósceles, então a abertura dos ângulos da base têm a mesma medida. Assim, temos:

80graus + x + x = 180graus

80graus + 2x = 180graus

2x = 100graus

x = 50graus

Portanto, a abertura dos ângulos da base medem 50graus.

3. Como AB = AC = xis, então o triângulo é isósceles.

a) Considerando

m e d (A \hat{B} C) = m e d (A \hat{C} B) = y

, temos:

m e d (A \hat{B} C) + m e d (A \hat{C} B) + m e d (B \hat{A} C) = 180 °

y + y + 90graus = 180graus

2y = 90graus

y = 45graus

Portanto,

m e d (A \hat{B} C) = 45 °

b) Pelo caso especial hipotenusa-cateto, os triângulos á bê dê e á cê dê são congruentes. Logo,

\overline{B D} ≅ \overline{D C}

. Como BC

= 28 c m

e considerando BD = DC = z, temos:

BC = 28

BD + DC = 28

z + z = 28

2z = 28

z = 14

Portanto, DC = z = 14 centímetros.

c) No triângulo ACD

, como

m e d (C \hat{A} D) = m e d (A \hat{C} D) = 45 °

, então

△ A C D

é isósceles, com

m e d (\overline{A D}) = m e d (\overline{C D})

. Do item anterior, temos

m e d (\overline{C D}) = 14 c m

. Portanto,

m e d (\overline{A D}) = 14 c m

4. Como os triângulos maiores têm todos os lados congruentes, então eles são equiláteros. Logo, a abertura de seus ângulos internos medem 60graus. Assim, a abertura de dois ângulos internos do triângulo menor medem 60graus, pois são opostos pelo vértice.

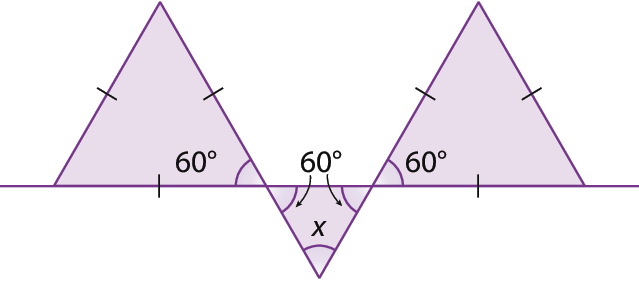
Figura geométrica: Reta horizontal. À esquerda e direita, acima da reta, triângulo de lados iguais com ângulo de 60 graus cada. Entre eles, na parte inferior da reta, triângulo com ângulo x e dois ângulos de 60 graus.

Página setenta

Como a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus, temos:

x + 60graus + 60graus = 180graus

x + 120graus = 180graus

x = 60graus

Portanto, x mede 60graus.

5. a) Sendo

\overline{A I}

a mediana do ângulo

\hat{A}

, então a base do triângulo isósceles é dividida em dois segmentos congruentes. Logo, x = 3.

b) Como o triângulo á bê cê é isósceles, então

\overline{B M}

, além de representar sua mediana, também representa a mediatriz relativa ao lado

\overline{A C}

. Logo, pela própria definição de mediatriz, x = 90graus.

6. Seja xis a medida de abertura do ângulo

\hat{A}

. Logo, a medida de abertura do ângulo

B \hat{C} A

também será xis, pois o triângulo á bê cê é isósceles. O ângulo

D \hat{B} C

é externo ao triângulo á bê cê relativo ao vértice B. Logo, a abertura de sua medida é igual à soma das aberturas das medidas dos outros dois ângulos internos, ou seja, 2x.

Como o triângulo BCD é isósceles, a abertura do ângulo

B \hat{D} C

também mede 2x.

O ângulo

E \hat{C} D

é externo ao triângulo á cê dê. Logo, a abertura de sua medida é igual à soma das aberturas das medidas dos ângulos internos não adjacentes a ele, ou seja, x + 2x = 3x.

Repetindo esse raciocínio para o ângulo

E \hat{D} F

, externo ao triângulo ê á dê, concluímos que

E \hat{D} F = 4 x

Figura geométrica: triângulo amarelo AEF com ângulos x e 4x. Dentro, triângulo isósceles ABC, com ponto B pertencente ao lado AF e ponto C pertencente ao lado AE, com ângulos de medida x na base. Triângulo isósceles BCD, com ponto D pertencente ao lado AF e pertencente ao segmento de reta BF, com ângulos de medida 2 x na base. Triângulo isósceles CDE com ângulos de medida 3 x na base. Triângulo isósceles DEF com ângulos de medida 4 x na base.

Como o triângulo

A E F

é isósceles, tendo

\overline{F E}

como base, então os ângulos

A \hat{F} E

A \hat{E} F

são congruentes, cada qual medindo 4x. Assim, nesse triângulo, temos:

x + 4x + 4x = 180graus

9x = 180graus

x = 20graus

Portanto,

\hat{A} = 20 °

Estatística e probabilidade

▶ Páginas 107 e 108

1. a) Correto. Ao observarmos o orçamento de 2020, podemos notar que o valor corresponde a .17236 milhões de reais. Portanto, ele foi menor do que .20000 milhões de reais.

b) Incorreto. Ao observar o gráfico, podemos perceber que o orçamento sofreu redução desde o ano de 2013, e não somente entre 2018 e 2020.

c) Correto. A diferença entre o investimento em 2013 e em 2020 foi de .10075 milhões de reais, pois .27311 ‒ .17236 = .10075.

d) Correto. Entre os anos apresentados, o que teve maior investimento foi 2013, com .27311 milhões de reais.

e) Correto. O orçamento em 2000 foi de .12235 milhões de reais, ou seja, menor do que .15000 milhões de reais.

alternativa bê

2. a) Verdadeiro. Em 2020 houve o menor percentual da população brasileira em segurança alimentar, com apenas 44,8%.

b) Verdadeiro. A segurança alimentar da população brasileira aumentou de 64,8% em 2004 para 69,6% em 2009, e de 69,6% em 2009 para 77,1% em 2013.

c) Verdadeiro. Se em 2020, 44,8% viviam em situação de segurança alimentar, podemos concluir, de maneira análoga, que 55,2% ( 100 % ‒ 44,8 % = 55,2% ) da população vivia uma situação de insegurança alimentar nesse ano.

d) Falso. O dado de 69,6% em 2009 refere-se à segurança alimentar, e não à insegurança alimentar.

e) Verdadeiro. De 2013 a 2020 houve uma queda de 32,3% ( 77,1% ‒ 44,8% = 32,3% ) da população brasileira em segurança alimentar.

alternativa dê

3. a) Verdadeiro, pois, observando o gráfico, podemos notar que a barra referente ao Sudeste ultrapassa a linha que indica o consumo de 150 litros de água per capita por dia.

b) Verdadeiro, pois, observando o gráfico, podemos notar que as barras referentes às regiões Sul e Centro-Oeste terminam próximo à marcação que indica o consumo de 150 litros de água per capita por dia.

c) Verdadeiro, pois, observando o gráfico, podemos notar que a barra referente ao Sudeste é a que tem a maior medida de comprimento.

d) Falso, pois, observando o gráfico, podemos notar que a medida do comprimento da barra referente à região Norte não ultrapassa a marca de consumo de 150 litros de água per capita por dia.

e) Verdadeiro, podemos notar que a medida do comprimento da barra referente à região Nordeste é a menor do gráfico.

alternativa dê

4. a) Incentive os estudantes a tirar conclusões com base no gráfico apresentado. Se julgar oportuno, peça que pesquisem em jornais, revistas ou na internet gráficos de diferentes tipos que se complementem e, depois, que escrevam um texto com base nas informações coletadas.

b) Aprofunde a proposta e peça aos estudantes que, em grupos, pesquisem em jornais, revistas ou na internet gráficos publicados pela mídia. Depois, proponha que façam a leitura e interpretação dos gráficos encontrados.

Atividades de revisão

▶ Página 109

1. Indicando por xis a medida de comprimento do outro lado desse triângulo, podemos verificar a condição de existência para triângulos.

9 < x + 6

3 < x

x < 9 + 6

x < 15

Como a medida de comprimento do lado desse triângulo deve ser maior que 3 e menor que 15, o único valor, entre as alternativas da atividade, que obedece a essa condição é 12 centímetros.

alternativa cê

2. a) Com base na medida de abertura dos ângulos externos apresentados, podemos concluir que a abertura dos ângulos internos da base do triângulo medem 45graus ( 180graus ‒ 135graus = 45graus) e 65graus ( 180graus ‒ 115graus = 65graus). Assim:

x + 45graus + 65graus = 180graus

x + 110graus = 180graus

x = 70graus

Página setenta e um

b) Como 180graus ‒ 150graus = 30graus, temos:

2x + 3x + 30graus = 180graus

5x + 30graus = 180graus

5x = 150graus

x = 30graus

3. Como o triângulo á bê cê é isósceles, então:

m e d (A \hat{B} C) = m e d (A \hat{C} B) = 22 °

A medida da abertura do ângulo externo em um triângulo é igual à soma das medidas das aberturas dos dois ângulos internos não adjacentes a ele. Logo:

x = 22graus + 22graus

x = 44graus

4. Pelo fato de o triângulo ABC ser retângulo em

\hat{A}

, temos:

x + 58graus + 90graus = 180graus

x + 148graus = 180graus

x = 32graus

Como

\overline{A D}

é bissetriz, então esse segmento divide a abertura do ângulo

\hat{A}

em dois ângulos de abertura 45graus. Ou seja:

x + y + 45graus = 180graus

32graus + y + 45graus = 180graus

y + 77graus = 180graus

y = 103graus

Portanto, x = 32graus e y = 103graus.

5. Representando o triângulo indicado no plano cartesiano, temos:

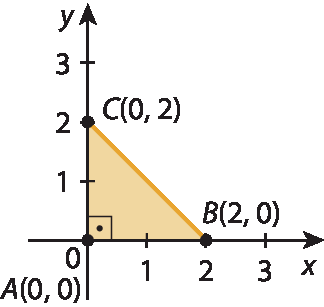
Plano cartesiano: No eixo x os números 0, 1, 2 e 3. No eixo y, os números 0, 1, 2 e 3. Há um triângulo alaranjado com os vértices nos pontos A de abscissa 0 e ordenada 0, B de abscissa 2 e ordenada 0 e C de abscissa 0 e ordenada 2.

Como o triângulo á bê cê tem dois lados de mesma medida de comprimento (

\overline{A B}

\overline{A C}

) e um ângulo reto (

\hat{A}

), então o triângulo á bê cê é retângulo e isósceles.

alternativa cê

6. Para que o poço fique à mesma distância das três casas, Reinaldo deve determinar o encontro das mediatrizes, ou seja, encontrar o circuncentro do triângulo do esquema.

7. Como

\overline{B D}

é congruente à

\overline{D C}

, temos:

a + 3 = 10

a = 7

Do mesmo modo, como

\overline{A B}

é congruente à

\overline{A C}

, então:

2b + 5 = 15

2b = 10

b = 5

Logo, a medida do perímetro do triângulo ABC é dado por:

(2 b + 5) + 15 + (a + 3) + 10 = (2 \cdot 5 + 5) + 15 + (7 + 3) + 10

= 15 + 15 + 10 + 10 = 50

Logo, a = 7, b = 5 e medida do perímetro = 50.

8. No

△ C A E

temos:

C + 90graus + 30graus = 180graus

C + 120graus = 180graus

C = 60graus

△ B D C

temos:

60 ° + 90 ° + m e d (B \hat{D} C) = 180 °

150 ° + m e d (B \hat{D} C) = 180 °

m e d (B \hat{D} C) = 30 °

Portanto, concluímos que:

m e d (B \hat{D} C) + m e d (A \hat{D} B) + 90 ° = 180 °

30 ° + m e d (A \hat{D} B) + 90 ° = 180 °

m e d (A \hat{D} B) + 120 ° = 180 °

m e d (A \hat{D} B) = 60 °

alternativa a

Capítulo 4

Atividades

▶ Página 113

1. a) Nesse quadrilátero, os ângulos internos são:

\hat{a}

\hat{b}

\hat{c}

\hat{d}

b) Nesse quadrilátero, os ângulos externos destacados são:

\hat{e}

\hat{f}

\hat{g}

\hat{h}

c) Nesse quadrilátero, os vértices são: A, B, C e D.

d) Nesse quadrilátero, os lados são:

\overline{A B}

\overline{B C}

\overline{C D}

\overline{D A}

e) Nesse quadrilátero, as diagonais são:

\overline{A C}

\overline{B D}

2. Não, um quadrilátero não pode ter os ângulos internos de medidas de abertura 123graus, 24graus, 56graus e 167graus, pois a soma das medidas de abertura desses ângulos é 370graus( 123graus +  24graus +  56graus +  167graus = 370graus ) e é maior que 360graus. Isso indica que esses ângulos não podem ser ângulos internos de um quadrilátero.

3. Indicando por x a medida de abertura do quarto ângulo, podemos escrever:

121graus + 83graus + 54graus + x = 360graus

258graus + x = 360graus

x = 102graus

Portanto, a medida de abertura do quarto ângulo desse quadrilátero é 102graus.

4. Como a soma das medidas de abertura dos ângulos internos de um quadrilátero é 360graus, temos:

x + ( x + 25graus ) + ( x + 30graus ) + ( x + 5graus ) = 360graus

4x + 60graus = 360graus

4x = 300graus

x = 75graus

Substituindo x por 75graus nas expressões que representam as medidas de abertura dos ângulos internos, temos:

• x = 75graus

• x + 25graus = 75graus + 25graus = 100graus

• x + 30graus = 75graus + 30graus = 105graus

• x + 5graus = 75graus + 5graus = 80graus

Logo, as medidas de abertura dos ângulos internos desse quadrilátero são 75graus, 100graus, 105graus e 80graus.

5. Como no vértice B os ângulos interno e externo são suplementares, ou seja, formam um ângulo de medida de abertura 180graus, podemos calcular a medida da abertura do ângulo interno desse vértice. Para isso, fazemos:

m e d (A \hat{B} C) + 22 ° = 180 °

m e d (A \hat{B} C) = 158 °

Sabemos ainda que a soma das medidas de abertura dos ângulos internos de um quadrilátero é 360graus. Logo:

x + 107graus + 43graus + 158graus = 360graus

x + 308graus = 360graus

x = 52graus