Parte 9
Substituindo x = 501 na equação y = x + 145, temos:
y = 501 + 145
y = 646
Assim, o candidato ganhador obteve 646 votos e o candidato perdedor, 501 votos.
3. Exemplo de problema: João é um ótimo jogador de basquete e em seu último treino arremessou 30 vezes e marcou um total de 66 pontos. Sabendo que esses arremessos podem valer 2 ou 3 pontos, quantos arremessos de 2 pontos e quantos de 3 pontos João acertou?
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: x mais y igual a trinta. Na segunda linha, dois x mais três y igual a sessenta e seis.
Pelo método da substituição, temos:
x + y = 30
x = 30 ‒ y
Substituindo x = 30 ‒ y na segunda equação, temos:
2x + 3y = 66
2 ⋅ ( 30 ‒ y ) + 3y = 66
60 ‒ 2y + 3y = 66
60 + y = 66
y = 66 ‒ 60
y = 6
Podemos concluir, então, que João acertou 6 arremessos de 3 pontos. Para descobrirmos quantos arremessos de 2 pontos João acertou, vamos substituir y = 6 em x + y = 30. Para isso, fazemos:
x + 6 = 30
x = 30 ‒ 6
x = 24
Portanto, João acertou 24 arremessos de 2 pontos e 6 arremessos de 3 pontos.
4. Considerando x para o copo e y para o garrafão, temos:
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: x igual a trinta e cinco y. Na segunda linha, x mais dez y igual a oito vírgula um.
Substituindo x = 35y na segunda equação x + 10y = 8,1, temos:
35y + 10y = 8,1
45y = 8,1
y igual a fração de numerador oito vírgula um e denominador quarenta e cinco.
y = 0,18
Como estamos trabalhando com a unidade de medida em litros, 0,18 litro significa que o copo tem a capacidade de 180 mililitros
abre parêntese 0,18 vezes 1000 fecha parêntese.. Substituindo y = 0,18 em x = 35y, temos:
x = 35 ⋅ 0,18
x = 6,3
O garrafão tem a capacidade de 6,3 litros.
Assim, temos que o garrafão tem capacidade para 6,3 litros, e o copo, para 180 mililitros.
5. Para a resolução, consideramos que o recipiente é representado por x, e a água, por y. Assim, temos:
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: x mais y igual a seiscentos e cinquenta. Na segunda linha: x mais um meio y igual a trezentos e sessenta.
Pelo método da substituição, isolando x na primeira equação, temos:
x + y = 650
x = 650 ‒ y
Substituindo x = 650 ‒ y na segunda equação, temos:
x mais 1 meio de y igual 360.
seiscentos e cinquenta menos y mais um meio y igual a trezentos e sessenta.
menos y mais um meio y igual a trezentos e sessenta menos seiscentos e cinquenta.
menos um meio y igual a menos duzentos e noventa.
meio y igual a duzentos e noventa.
y = 290 ⋅ 2
y = 580
Substituindo, y = 580 na primeira equação, temos:
x + y = 650
x + 580 = 650
x = 650 ‒ 580
x = 70
Assim, temos que o recipiente pesa 70 gramas.
alternativa cê
6. Nesta questão, vamos usar a propriedade que diz que a soma de dois ângulos internos de um triângulo é igual ao suplementar do terceiro ângulo. Assim, temos:
• no triângulo á cê dê:
2y + 4y = 2x + y
6y = 2x + y
6y ‒ 2x ‒ y = 0
5y ‒ 2x = 0 (um)
• no triângulo á bê cê:
y + 10graus + x = 4y
3y ‒ x = 10graus (dois)
Assim, obtemos o seguinte sistema:
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha, cinco y menos dois x igual a zero. Na segunda linha, três y menos x igual a dez graus.
Multiplicando a segunda equação por ‒ 2, temos:
3y ‒ x = 10graus ⋅ ( ‒ 2 )
‒ 6y + 2x = ‒ 20graus
Logo:
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: cinco y menos dois x igual a zero. Na segunda linha: menos seis y mais dois x igual a menos vinte graus.
Pelo método da adição, temos:
‒ y = ‒ 20graus
y = 20graus
Substituindo y = 20graus em 3y ‒ x = 10graus, temos:
3y ‒ x = 10graus
3 ⋅ 20graus ‒ x = 10graus
60graus ‒ x = 10graus
x = 60graus ‒ 10graus
x = 50graus
Assim, temos x = 50graus e y = 20graus.
7. Exemplo de resposta: A segunda equação é resultado da primeira equação multiplicada por 3.
8. Analisando o gráfico, percebemos que o par ordenado (5, 2) representa a solução do sistema. Portanto, vamos testar esse par ordenado nos sistemas das alternativas a seguir.
a)
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: dois x igual a três y igual a cinco. Abaixo, x menos y igual a dois.• Para 2x + 3y = 5, temos:
2 · 5 + 3 · 2 = 5
10 + 6 = 5
16 = 5 (falso)
Portanto, o par ordenado (5, 2) não é solução do sistema.
b)
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: x mais y igual a sete. Abaixo, x menos y igual a três• x + y = 7
5 + 2 = 7
7 = 7 (verdadeiro)
• x ‒ y = 3
5 ‒ 2 = 3
3 = 3 (verdadeiro)
Portanto, o par ordenado (5, 2) satisfaz o sistema
Esquema, de cima para baixo: à esquerda, chave. Na primeira linha: x mais y igual a sete. Abaixo, x menos y igual a três.
alternativa bê
Capítulo 10
Atividades
▶ Página 254
1. a) As grandezas são diretamente proporcionais.
b) As grandezas são inversamente proporcionais.
c) As grandezas são diretamente proporcionais.
2. a) Diretamente proporcionais. Exemplo de justificativa: Dobrando a duração, o preço também dobra. Triplicando a duração, o preço também triplica.
b) A sentença algébrica que relaciona as duas grandezas pode ser indicada por p = 75m.
c) Como 2 anos correspondem a 24 meses, substituindo m por 24 em p = 75m, temos:
p = 75m = 75 · 24 = .1800
Portanto, essa pessoa vai pagar R$ 1.800,00mil oitocentos reais por um pacote de 2 anos.
d) Substituindo p por .1500 em p = 75m, temos:
p = 75m
.1500 = 75m
mil e quinhentos sobre setenta e cinco igual a setenta e cinco m sobre setenta e cinco.
m = 20
Portanto, a duração do pacote de TV a cabo será 20 meses.
3. a) Considerando a sentença algébrica n = 2,5t, temos:
• para 10 quilômetros:
n = 2,5t
10 = 2,5t
dez sobre dois vírgula cinco igual a t.
t = 4
São necessárias 4 horas para a equipe asfaltar 10 quilômetros de estrada.
• para 20 quilômetros:
n = 2,5t
20 = 2,5t
vinte sobre dois vírgula cinco igual a t.
t = 8
São necessárias 8 horas para a equipe asfaltar 20 quilômetros de estrada.
b) Exemplo de resposta: O número de quilômetros asfaltados e o tempo são grandezas diretamente proporcionais, pois a razão entre o número de quilômetros asfaltados e a medida de tempo, em hora, é sempre a mesma.
4. a) Inversamente proporcionais. Espera-se que os estudantes justifiquem dizendo que a razão entre a medida do comprimento e o inverso da medida da largura é sempre a mesma.
Fração de numerador vinte e quatro e denominador um meio, igual a fração de numerador doze e denominador um quarto, igual a fração de numerador oito e denominador um sexto, igual a fração de numerador três e denominador um sobre dezesseis igual a quarenta e oito.
b) A sentença algébrica pode ser expressa como
y igual a quarenta e oito sobre x,.
5. a) Enquanto a engrenagem pequena dá 6 voltas completas, a engrenagem grande dá 3 voltas completas.
b) Inversamente proporcional. Exemplo de justificativa: Porque quando o número de dentes dobra o número de voltas completas que a engrenagem dá reduz pela metade.
n igual a cinco sobre d.
6. Exemplo de problema: Com medida de velocidade média de 50 quilômetros por hora, um automóvel leva duas horas para percorrer um trajeto. Quanto tempo esse automóvel levará para percorrer o mesmo trajeto caso sua velocidade média dobre?
Atividades
▶ Página 259
1. a) As grandezas são inversamente proporcionais. A sentença algébrica que expressa a relação entre elas é
y igual a dezesseis sobre x..
b) As grandezas são diretamente proporcionais. A sentença algébrica que expressa a relação entre elas é y = 12x.
c) As grandezas são não proporcionais. A sentença algébrica que expressa a relação entre elas é y = x + 1.
2. um – B, dois – C, três – A.
Estatística e Probabilidade
▶ Páginas 260 a 263
1. a) Em cada caso, a variável da pesquisa é:
um. Marca de creme dental preferida.
dois. Quantidade de vezes que os estudantes foram ao cinema no último mês.
três. Medida da altura (em metro) dos estudantes.
b) um. Organizando os dados, temos: A, A, A, A, A, B, B, B, B, B, B, B, B, B, C, C, C, C, C, C. Podemos agrupar esses dados em três classes: A, B e C.
dois. Organizando os dados, temos: 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2. Podemos agrupar esses dados em três classes: 0, 1 e 2.
III. Organizando os dados, temos: 1,40; 1,41; 1,42; 1,42; 1,43; 1,44; 1,45; 1,46; 1,49; 1,49; 1,50; 1,51; 1,52; 1,53; 1,55; 1,56; 1,56; 1,57; 1,57; 1,57. Podemos agrupar esses dados em três classes: de 1,40 a 1,47; de 1,47 a 1,54 e de 1,54 a 1,61.
c) um.
|
Marca de creme dental preferida |
Frequência absoluta |
Frequência relativa |
|---|---|---|
|
A |
5 |
0,25 |
|
B |
9 |
0,45 |
|
C |
6 |
0,30 |
dois.
|
Quantidade de vezes que foram ao cinema no último mês |
Frequência absoluta |
Frequência relativa |
|---|---|---|
|
0 |
9 |
0,45 |
|
1 |
5 |
0,25 |
|
2 |
6 |
0,30 |
três.
|
Altura (em metro) |
Frequência absoluta |
Frequência relativa |
|---|---|---|
|
1,40 ⊢ 1,47 |
8 |
0,40 |
|
1,47 ⊢ 1,54 |
6 |
0,30 |
|
1,54 ⊢ 1,61 |
6 |
0,30 |
2. Os estudantes não precisam realizar cálculos para todas as tabelas. Nesta atividade, o mais importante é que eles observem como é possível descartar algumas possibilidades. Por exemplo:
• o conjunto do item bê não está de acordo com a segunda tabela, uma vez que as frequências corretas seriam 0,6; 0,2 e 0,2, respectivamente.
• o conjunto do item cê não está de acordo com a segunda tabela, pois as frequências corretas seriam 0,3; 0,4 e 0,3, respectivamente.
Conclui-se, então, que apenas o conjunto do item a se encaixa nas duas tabelas.
alternativa a
3. a) O rol de dados pode ser crescente ou decrescente:
• rol em ordem crescente:
250, 250, 265, 270, 280, 283, 283, 290, 295, 300, 302, 304, 310, 330, 380, 385, 390, 402, 402, 407.
• rol em ordem decrescente:
407, 402, 402, 390, 385, 380, 330, 310, 304, 302, 300, 295, 290, 283, 283, 280, 270, 265, 250, 250.
b) A tabela de distribuição de frequências pode ser indicada por:
|
Área (m2) |
Frequência absoluta (número de incidências) |
Frequência relativa |
|
|---|---|---|---|
|
1ª classe |
250 ⊢ 285 |
7 |
0,35 |
|
2ª classe |
285 ⊢ 320 |
6 |
0,30 |
|
3ª classe |
320 ⊢ 355 |
1 |
0,05 |
|
4ª classe |
355 ⊢ 390 |
2 |
0,10 |
|
5ª classe |
390 ⊢ 425 |
4 |
0,20 |
Dados coletados pela prefeitura do municÍpio.
c) A maior parte das residências pesquisadas pertence à 1ª classe.
d) Uma residência de 380 métros quadrados pertence à 4ª classe. Portanto, o imposto a ser pago é R$ 1,30um reais e trinta centavos/métro quadrado. Assim, calculamos: 380 · 1,30 = 494. Logo, o imposto a ser pago é R$ 494,00quatrocentos e noventa e quatro reais.
e)
|
Área (m2) |
Classe |
Imposto (m2) |
Imposto (total) |
|---|---|---|---|
|
250 |
1ª |
R$ 1,00 |
R$ 250,00 |
|
250 |
1ª |
R$ 1,00 |
R$ 250,00 |
|
265 |
1ª |
R$ 1,00 |
R$ 265,00 |
|
270 |
1ª |
R$ 1,00 |
R$ 270,00 |
|
280 |
1ª |
R$ 1,00 |
R$ 280,00 |
|
283 |
1ª |
R$ 1,00 |
R$ 283,00 |
|
283 |
1ª |
R$ 1,00 |
R$ 283,00 |
|
290 |
2ª |
R$ 1,10 |
R$ 319,00 |
|
295 |
2ª |
R$ 1,10 |
R$ 324,50 |
|
300 |
2ª |
R$ 1,10 |
R$ 330,00 |
|
302 |
2ª |
R$ 1,10 |
R$ 332,20 |
|
304 |
2ª |
R$ 1,10 |
R$ 334,40 |
|
310 |
2ª |
R$ 1,10 |
R$ 341,00 |
|
330 |
3ª |
R$ 1,20 |
R$ 396,00 |
|
380 |
4ª |
R$ 1,30 |
R$ 494,00 |
|
385 |
4ª |
R$ 1,30 |
R$ 500,50 |
|
390 |
5ª |
R$ 1,40 |
R$ 546,00 |
|
402 |
5ª |
R$ 1,40 |
R$ 562,80 |
|
402 |
5ª |
R$ 1,40 |
R$ 562,80 |
|
407 |
5ª |
R$ 1,40 |
R$ 569,80 |
|
R$ 7.494,00 |
Logo, a prefeitura receberá R$ 7.494,00sete mil quatrocentos e noventa e quatro reais pela cobrança total do imposto dessas residências.
4. Uma alternativa para a realização dessa atividade é combinar com os estudantes o tempo para a execução, que pode também ocorrer fóra do horário de aula, e como os resultados serão apresentados à turma.
a) Estudantes do 8º ano da escola em que estudam.
b) Preferência de marca de creme dental; frequência com que foram ao cinema no último mês; medida da altura dos estudantes.
c) Verifique com os estudantes a possibilidade de realizar a pesquisa com toda a população. Caso não exista essa possibilidade, oriente-os a realizar a pesquisa a partir de uma amostra.
d) Oriente os estudantes a organizar os dados coletados em tabelas e gráficos.
EDUCAÇÃO FINANCEIRA
▶ Páginas 264 e 265
Resoluções e comentários em Orientações.
Atividades de revisão
▶ Página 266
1. a) De acordo com as informações do quadro, temos:
Cento e três vírgula cinco sobre quinze, igual a duzentos e sete sobre trinta, igual a trezentos e dez vírgula cinco, sobre quarenta e cinco, igual a quatrocentos e catorze sobre sessenta igual a seis vírgula nove.
O preço do litro da gasolina nesse posto era R$ 6,90seis reais e noventa centavos.
b) O valor pago e o número de litros de gasolina comprados são grandezas diretamente proporcionais.
c) y = 6,9x, em que x pode ser qualquer número real positivo.
2. a)
2 sobre 1,5, igual a x sobre 10,51,5x = 10,5 ⋅ 2
1,5x = 21
x igual a 21 sobre 1,5
x = 14
Portanto, a medida da altura do edifício é 14 métros.
b)
14 sobre 10,5, igual a 4,5 sobre x14 ⋅ x = 10,5 ⋅ 4,5
14x = 47,25
x igual a 47,25 sobre 14
x = 3,375
Portanto, o comprimento da sombra desse poste mede 3,375 métros.
c)
c igual a três quartos h., em que h pode ser qualquer número real maior ou igual a zero.
d) Exemplo de resposta: É uma linha reta contínua que parte do par ordenado (0, 0), passa pelos pares ordenados ( 2; 1,5 ), ( 14; 10,5 ) e ( 4,5; 3,4 ) e continua infinitamente.
3. a) A temperatura do líquido e o tempo são grandezas inversamente proporcionais.
b) A sentença algébrica que relaciona as duas grandezas é
y igual a duzentos sobre x.
c) Exemplo de resposta: É uma linha curva contínua que passa pelos pares ordenados ( 100, 2 ), ( 50, 4 ), ( 25, 8 ) e ( 12,5; 16 ).
4. Ao analisar as coordenadas dos pontos indicados no gráfico, percebemos que elas estão dobrando de valor a cada ponto: ( 1, 4 ), ( 2, 8 ), ( 4, 16 ), ( 8, 32 ). Portanto, são grandezas diretamente proporcionais.
5. a) Exemplo de resposta: y pode ser a medida do volume de um cubo, em centímetro cúbico, e x, a medida de comprimento do lado desse cubo, em centímetro.
b) As grandezas x e y são não proporcionais.
6. Exemplo de resposta: Uma loja de chocolates está colocando no mercado um novo produto. Trata-se de uma caixa com quatro trufas especiais. Chamando a caixa de y e a quantidade de trufas de x, determine a sentença matemática que determina a quantidade de trufas vendidas de acordo com a quantidade de caixas.
Capítulo 11
Atividades
▶ Páginas 268 e 269
1.
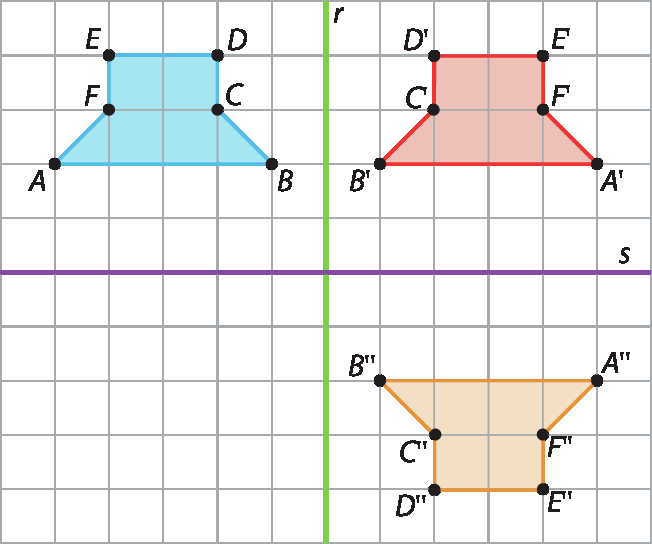
2.
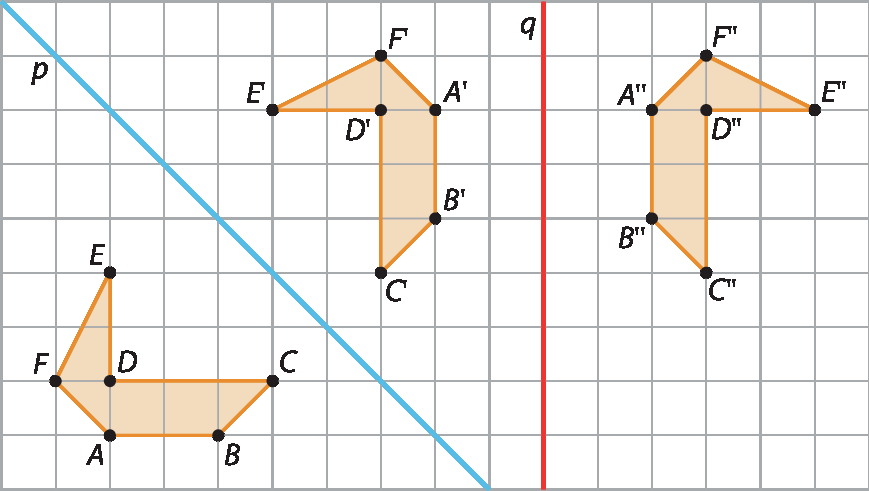
3. a)
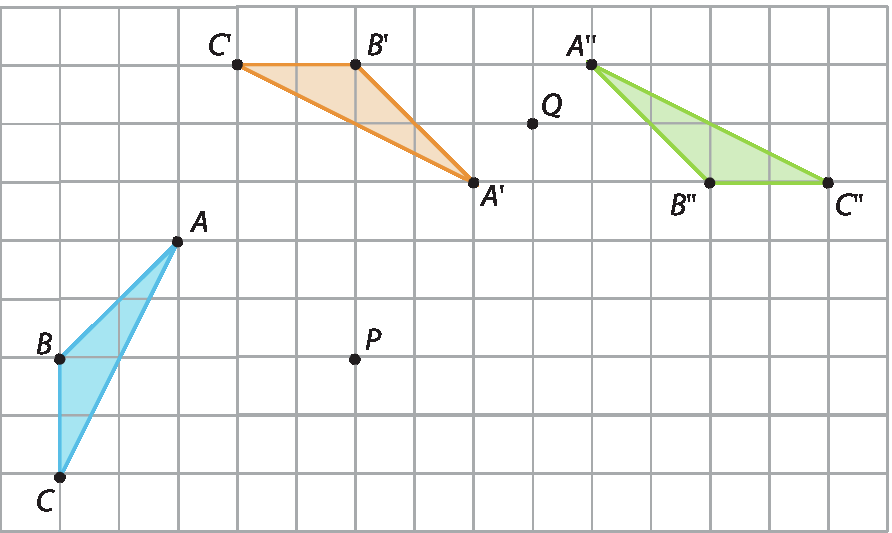
b) Exemplo de resposta: Podemos afirmar que os triângulos são congruentes.
c) A mediatriz de
Segmento ADé a reta m e a mediatriz de
Segmento EH.é a reta n.
Atividades
▶ Página 270
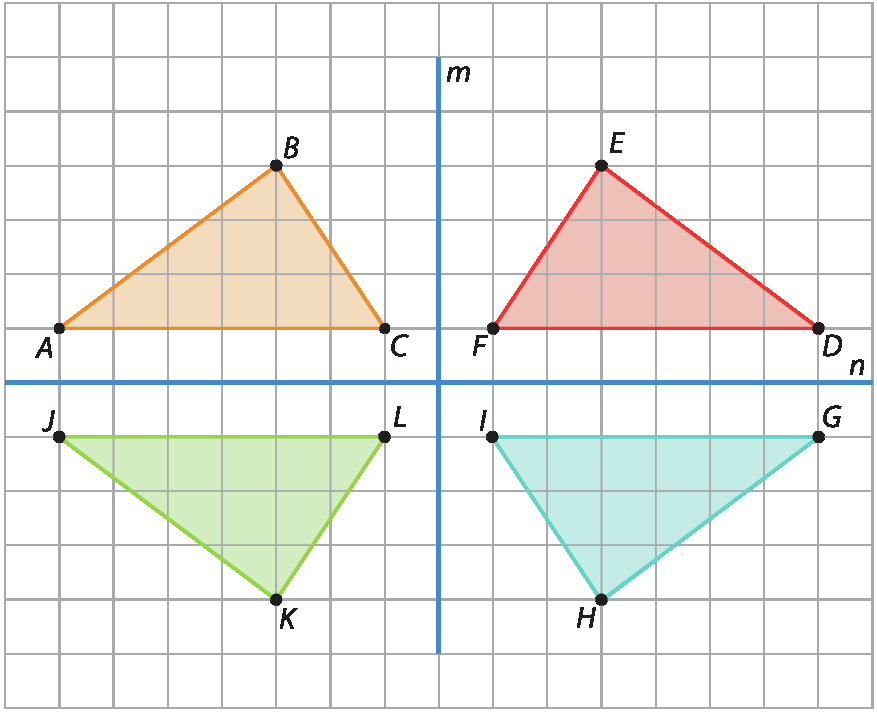
1.
a) verdadeira
b) verdadeira
c) falsa
d) falsa
2.
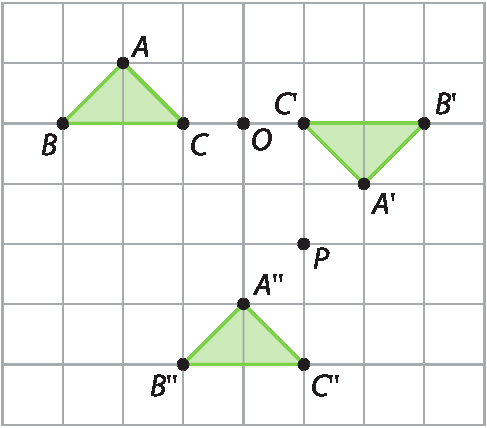
Atividade
▶ Página 271
1. a)
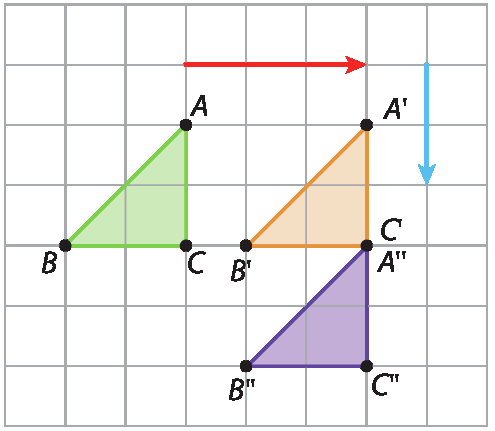
b)
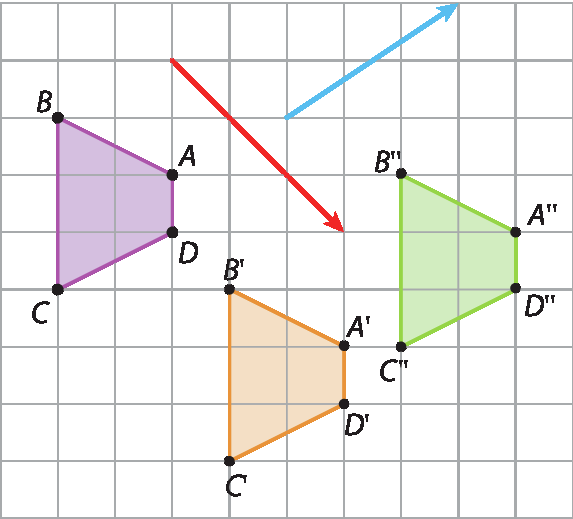
Atividades
▶ Página 273
1.
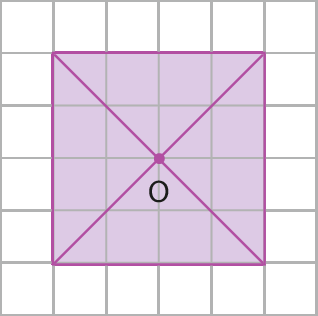
• Ao fazer as três rotações sucessivas, a figura obtida é um quadrado.
2.
Estatística e Probabilidade
▶ Páginas 274 a 276
1. A – três, B – um e C – dois.
Os estudantes deverão analisar as situações e identificar o tipo de seleção de amostra que cada uma delas exemplifica. Esse é o momento oportuno para avaliar se eles compreenderam cada tipo de seleção de amostra.
2. Resposta pessoal. Os estudantes deverão planejar e executar uma pesquisa amostral, selecionando a técnica de amostragem adequada. Em projetos como esses, eles exercitam a empatia e o diálogo (competência geral 9) e devem agir coletivamente, pautados em princípios éticos e democráticos (competência geral 10). Oriente-os a abordar questões de urgência social e a valorizar a diversidade de opiniões dos indivíduos, sem preconceitos de qualquer natureza (competência específica 7). A intenção dessa pesquisa é fazer com que os estudantes, ao interagir de fórma cooperativa com seus pares, consigam desenvolver a pesquisa para responder às indagações iniciais do grupo, discutindo temas que extrapolem os limites da escola (competência específica 8).
Combine uma parceria com o professor de Língua Portuguesa com a finalidade de ajudar os estudantes a organizar e a escrever o relatório solicitado na atividade 2.
TRABALHO EM EQUIPE
▶ Página 277
Resoluções e comentários em Orientações.
Atividades de revisão
▶ Página 278
1.
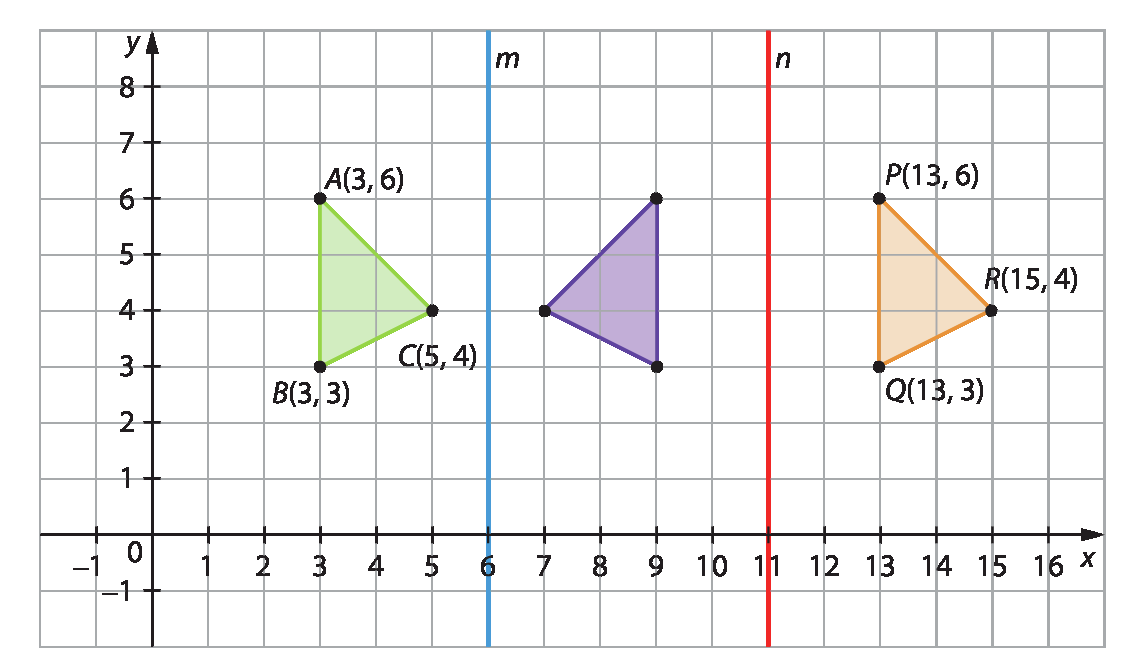
a) P( 13, 6 ), Q( 13, 3 ) e R( 15, 4 )
b) Translação na direção horizontal, da esquerda para a direita, de 10 unidades.
2. Espera-se que os estudantes percebam que a figura obtida coincide com a figura inicial.
3. a)
b)

4. Exemplo de resposta:
Para finalizar
▶ Páginas 279 e 280
Resoluções e comentários em Orientações.

Avaliação de resultado
Mostre o que você aprendeu
▶ Páginas 281 e 282
1. De acordo com os dados do enunciado, a lanchonete oferece 3 opções diferentes de sanduíches e 4 opções diferentes de sucos. Para determinar quantas são as maneiras diferentes de montar o combo, ou seja, de combinar um sanduíche e um suco natural, aplicamos o princípio fundamental da contagem, fazendo o produto dessas quantidades:
3 ⋅ 4 = 12
Portanto, são 12 maneiras diferentes de montar o combo.
alternativa cê
2. Se 1 mililitro equivale a .1000 microlitros, e em cada 1 microlitro de sangue estão presentes, em média, 5 milhões de hemácias, então, para descobrir quantas hemácias estão presentes, em média, em 1 mililitro, fazemos:
1 ⋅ .1000 ⋅ ..5000000 = ...5000000000 = 5 ⋅ 109
Portanto, estão presentes 5 ⋅ 109 hemácias, em média, em 1 mililitro de sangue.
alternativa cê
3. Do total de 800 estudantes, 15% estão matriculados em turmas de 8º ano. Para calcular quantos estudantes dessa escola estão matriculados em turmas de 8º ano, fazemos:
Sentença matemática. 15 por cento vezes 800 igual fração 15 sobre 100 vezes 800 igual 0 vírgula 15 vezes 800 igual 120
Portanto, são 120 estudantes matriculados no 8º ano, nessa escola.
alternativa bê
4. Na promoção, o aparelho que custava R$ 1.200,00mil duzentos reais passou a custar R$ 960,00novecentos e sessenta reais. Logo, houve desconto de R$ 240,00duzentos e quarenta reais (.1200 ‒ 960 = 240). Para determinar a porcentagem de desconto oferecida pela loja para o aparelho, podemos fazer a razão entre esse valor do desconto e o valor inicial do aparelho, ou seja:
Sentença matemática. Fração 240 sobre 1 200 igual 0 vírgula 20 igual 20 por cento
Portanto, a porcentagem de desconto oferecida foi de 20%.
alternativa a
5. Temos a expressão algébrica 15 ⋅ x + 30 que representa o custo para fabricar x camisetas. Para sabermos o custo para a fabricação de 18 camisetas, substituímos x por 18 nessa expressão e calculamos, ou seja:
15 ⋅ x + 30 = 15 ⋅ 18 + 30 = 300
Portanto, o custo será de R$ 300,00trezentos reais para a fabricação de 18 camisetas.
alternativa bê
6. Para traçar uma reta, é preciso, no mínimo, encontrar dois pontos. Vamos determinar alguns pontos, atribuindo valores para x na equação y = x + 1.
|
x |
y = x + 1 |
par ordenado |
|---|---|---|
|
−1 |
y = −1 + 1 = 0 |
(−1, 0) |
|
0 |
y = 0 + 1 = 1 |
(0, 1) |
|
1 |
y = 1 + 1 = 2 |
(1, 2) |
Representando esses pontos no plano cartesiano, temos:
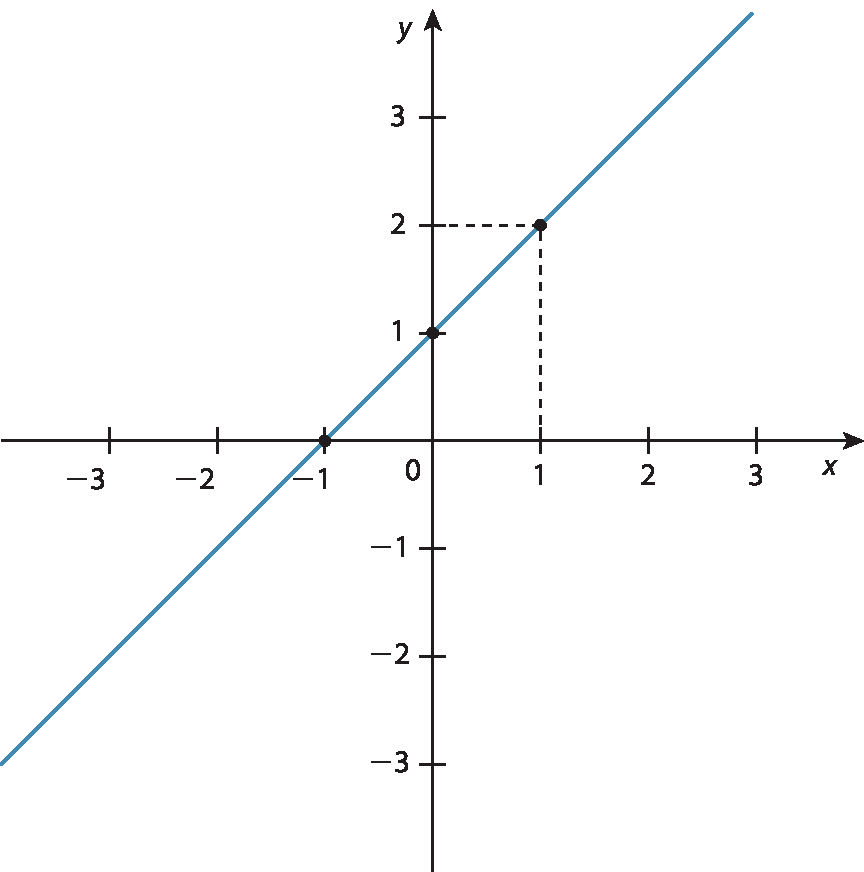
alternativa a
7. Vamos representar a idade de Luana por x. Então, a idade de Manuela será representada por 2x, pois Manuela tem o dobro da idade de Luana. Como a soma das idades de Manuela e de Luana é igual a 21, temos:
x + 2x = 21
3x = 21
3x sobre 3, igual a 21 sobre 3
x = 7
Logo, Luana tem 7 anos, e Manuela, 14 anos.
alternativa a
8. As grandezas tempo de ligações feitas em um aparelho celular e o preço pago por essas ligações são diretamente proporcionais, porque, ao dobrar uma das grandezas, a outra também dobra. Assim, a constante de proporcionalidade é:
Zero vírgula sessenta sobre cinco, igual a um vírgula vinte sobre dez, igual a dois vírgula quarenta sobre vinte igual a quatro vírgula oitenta sobre quarenta igual a zero vírgula doze.
A sentença algébrica que relaciona o preço (p), em real, com a medida de tempo da ligação (d), em minutos, nesse plano é dada por:
p sobre d igual a 0,12
p = 0,12 ⋅ d
alternativa cê
9. A piscina tem o formato de um bloco retangular, conforme a figura a seguir.
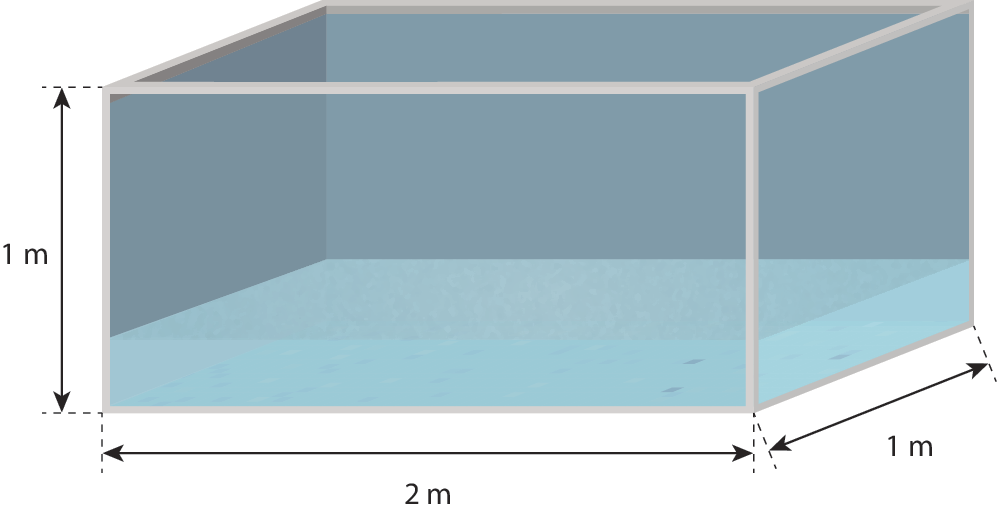
Para calcular a medida da capacidade dessa piscina, fazemos:
V = 2 métros ⋅ 1 métro ⋅ 1 métro = 2 métros cúbicos
Sabemos que 1 métro cúbico equivale a .1000 litros. Se a piscina já contém 250 litros de água, então ela já contém:
duzentos e cinquenta sobre mil igual 0 vírgula 25 metros cúbicos
de água
Para encontrar a quantidade de metros cúbicos necessários para enchê-la com água até a borda, fazemos:
2 metros cúbicos menos 0,25 metros cúbicos igual a 1,75 metros cúbicos
Portanto, é necessário 1,75 métro cúbico de água.
alternativa cê
10. A figura do quadrilátero foi decomposta em dois polígonos: um retângulo, que representa a casa e a horta, e um triângulo, que representa o pomar. Vamos calcular a medida da área de cada um deles e, depois, adicionamos as medidas obtidas para determinar a medida da área total dessa chácara.
A medida da área do retângulo pode ser obtida por meio da expressão A = b ⋅ h, em que b representa a medida de comprimento da base, e h, a medida de comprimento da altura.
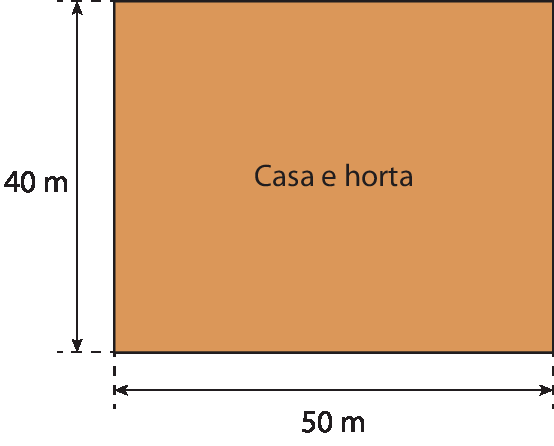
A é igual a 50 metros vezes 40 metros igual a 2 mil metros quadrados
A medida da área do triângulo pode ser obtida por meio da expressão
A maiúsculo igual a fração de numerador b vezes h minúsculos e denominador dois., em que b representa a medida de comprimento da base, e h, a medida de comprimento da altura.
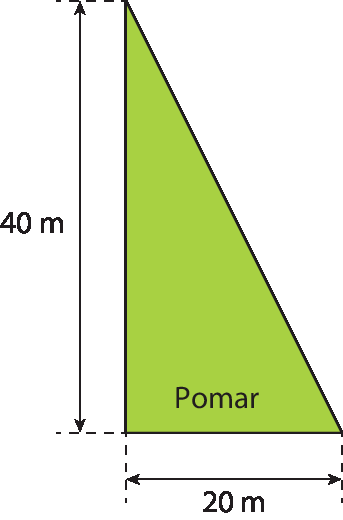
A igual a fração de numerador vinte metros vezes quarenta metros e denominador dois, igual a fração de numerador oitocentos metros quadrados e denominador dois, igual a quatrocentos metros quadrados
Logo, temos:
.2000 métros quadrados + 400 métros quadrados = .2400 métros quadrados
Portanto, a medida da área total dessa chácara é .2400 métros quadrados.
alternativa dê
11. Um baralho comum tem cinquenta e duas cartas. Essas cartas estão divididas igualmente entre os quatro naipes: ouros, paus, espadas e copas. Então, cada naipe é composto de 13 cartas, pois 52 : 4 = 13. Assim, nesse baralho temos 13 cartas de copas em um total de cinquenta e duas cartas. Para encontrar a probabilidade de Rodrigo retirar uma carta ao acaso e ela ser de copas, devemos calcular a probabilidade de retirar 13 em cinquenta e duas cartas, ou seja:
Treze sobre cinquenta e dois, igual a um quarto.
Portanto, a probabilidade é
um sobre quatroalternativa a
12. Para calcular o preço médio da venda desses quatro modelos de aparelhos, podemos fazer:
Sentença matemática. Fração 3 vezes 1200 mais 6 vezes 1500 mais 5 vezes 2150 mais 4 vezes 4200 tudo sobre 3 mais 6 mais 5 mais 4
=
=
, igual, Fração 3600 mais 9000 mais 10750 mais 16800 tudo sobre 18, igual, Fração 40150 sobre 18, aproximadamente igual, 2230 vírgula 56Portanto, o preço médio das vendas é de, aproximadamente, R$ 2.230,56dois mil duzentos e trinta reais e cinquenta e seis centavos.
alternativa cê