Página 24

Parte 3

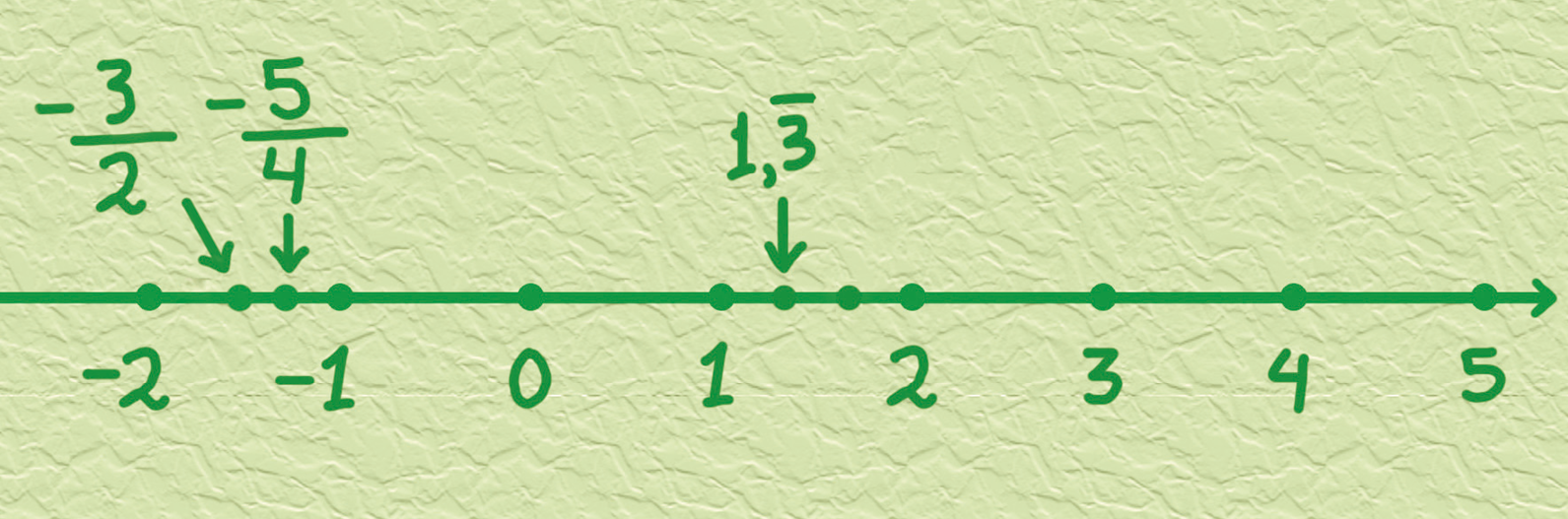
O ponto correspondente a menos1,5 está à mesma medida de distância dos pontos correspondentes a menos2 e menos1.

O número

‒ \frac{5}{4}

também está entre menos2 e menos1. Além disso, o número está entre menos1,5 e menos1, pois

‒ \frac{5}{4}

= menos1,25.

O ponto correspondente a menos1,25 está à mesma medida de distância dos pontos correspondentes aos números menos1,5 e menos1.

Já o número racional 1,

\overline{3}

está entre 1 e 2, e sua fórma fracionária é

\frac{4}{3} = 1 \frac{1}{3}

. Quando o segmento determinado pelos pontos correspondentes a 1 e 2 é dividido em três partes iguais, 1,

\overline{3}

corresponde ao primeiro ponto à direita do 1.

Gráfico: reta numérica em fundo verde, com 8 pontos equidistantes correspondentes aos números menos dois, menos um, 0, 1, 2, 3, 4 e 5. Ponto médio dos números menos dois e menos um, com indicação menos fração três sobre dois. Ponto médio dos números menos fração três sobre dois e menos um, com indicação menos fração cinco quartos. Intervalo entre os números 1 e 2 dividido em 3 partes iguais por meio de 2 pontos: no primeiro desses pontos, indicação 1 vírgula 3, com um traço horizontal acima do 3.

O que há entre dois números racionais?

Entre dois números naturais consecutivos não podemos encontrar nenhum outro número natural. Entre 3 e 4, por exemplo, não há outro número natural.

Isso também vale para os números inteiros. Entre dois números inteiros consecutivos não há nenhum outro número inteiro. Entre menos 7 e menos 6, por exemplo, não há outro número inteiro.

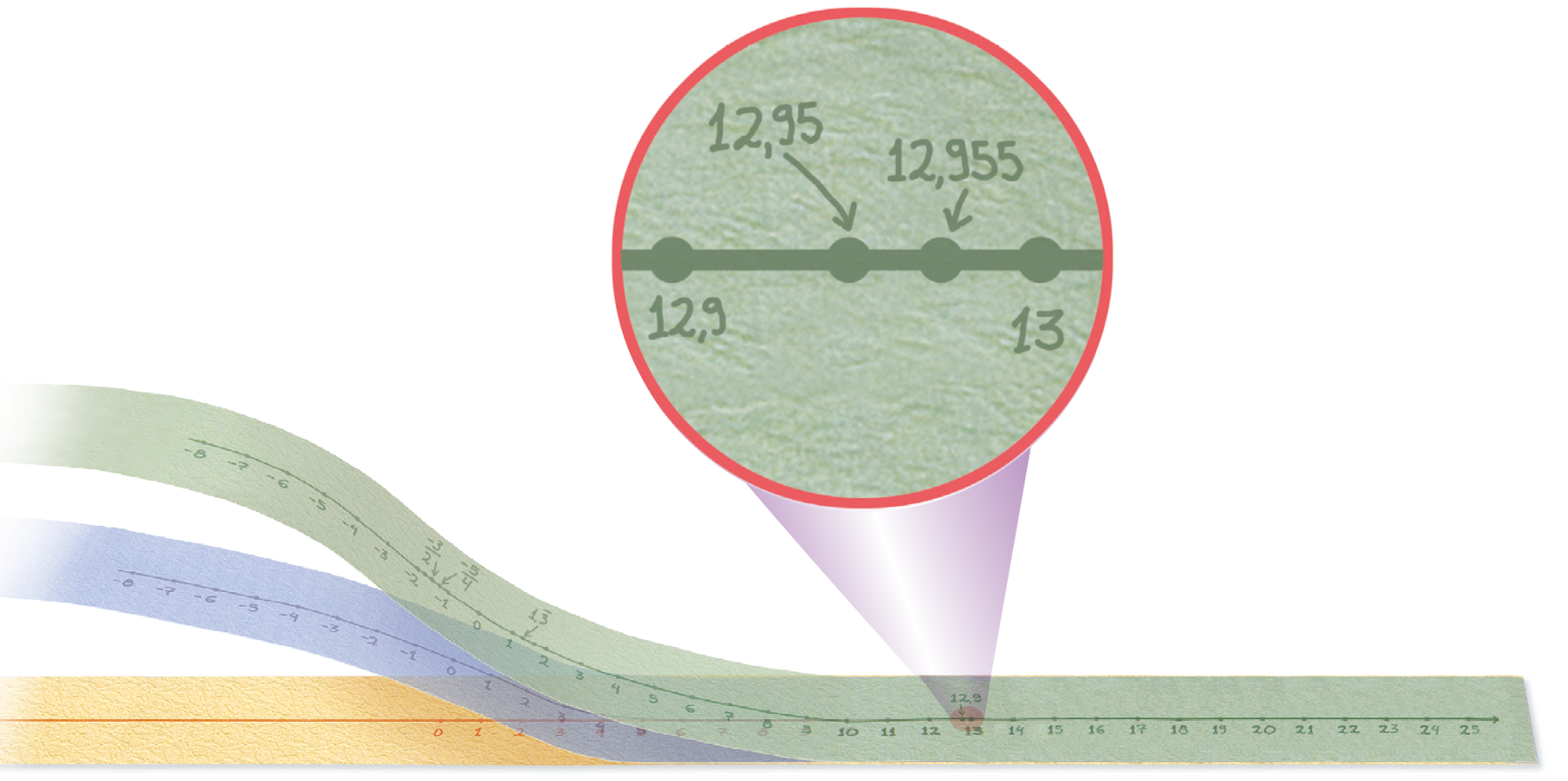
No caso dos números racionais, isso não acontece: entre dois números racionais quaisquer, sempre existe outro número racional. Por exemplo, entre 12,9 e 13 há outros números racionais, como o número 12,95. Entre 12,95 e 13 também há números racionais, como o número 12,955.

Se você continuar listando exemplos, vai verificar que pode encontrar infinitos números entre 12,9 e 13.

Ilustração: Três fitas com retas numéricas, nas cores alaranjada, azul e verde. A fita métrica verde está sobre as outras fitas. Há uma lupa fazendo zoom na fita métrica verde, com a representação de uma parte da reta numérica, com 4 pontos com os seguintes números, da esquerda para a direita: 12 vírgula 9; 12 vírgula 95; 12 vírgula 955; 13.

Orientações e sugestões didáticas

• A localização dos pontos correspondentes aos números de cada conjunto já foi explorada em anos anteriores (a de números naturais no 6º ano e a de números inteiros e racionais no 7 º ano); retome esse procedimento para ressaltar que, entre dois números racionais quaisquer, sempre existe outro número racional. Por essa ideia ser abstrata, convém associá-la a pontos de uma reta numérica. Quando os estudantes compreenderem essa ideia, provavelmente perceberão que há espaço na reta para “novos” números e, assim, a introdução de outro tipo de número – os irracionais – poderá ser mais facilmente assimilada. Como, nesse segmento, não é indicado o formalismo matemático na conceituação dos conjuntos dos números racionais e irracionais, abordaremos algumas situações em que esses números são empregados.

Página 25

ATIVIDADES

faça as atividades no caderno

1. Copie o quadro no caderno. Em seguida, consulte a reta numérica e assinale a classificação de cada número no quadro.

Reta numérica: da esquerda para a direita, números: menos sete, menos seis, menos cinco, menos quatro, menos três, menos dois, menos um, zero, um, dois, três, quatro, cinco, seis, sete.

2. Copie a reta numérica no caderno e substitua cada

pelo número inteiro correspondente a cada ponto.

Reta numérica: 17 pontos equidistantes. Da esquerda para a direita, primeiro ponto com um quadrado verde; segundo ponto com um quadrado verde; quinto ponto com um quadrado verde; oitavo ponto com um quadrado verde; nono ponto com zero; décimo ponto com um; décimo terceiro ponto com um quadrado verde; décimo sétimo ponto com um quadrado verde.

Quadro: ficha verde com o número quatro. Quadro: ficha verde com o número menos quatro. Quadro: ficha verde com o número menos oito. Quadro: ficha verde com o número menos 7. Quadro: ficha verde com o número menos 1. Quadro: ficha verde com o número 8.

3. Copie a reta numérica no caderno e represente nela os números a seguir.

Reta numérica: da esquerda para a direita, números: menos seis, menos cinco, menos quatro, menos três, menos dois, menos um, zero, um, dois, três, quatro, cinco, seis.

Quadro: ficha azul com o número 3 vírgula 1. Quadro: ficha azul com o número 1 vírgula 3. Quadro: ficha azul com o número menos 3 vírgula 1. Quadro: ficha azul com o número menos 1 vírgula 3. Quadro: ficha azul com o número 5 vírgula 2. Quadro: ficha azul com o número 2 vírgula 5. Quadro: ficha azul com o número menos 5 vírgula 2. Quadro: ficha azul com o número menos 2 vírgula 5.

• Agora, escreva esses números em ordem crescente.

4. No caderno, escreva os números a seguir em ordem decrescente e determine sua localização aproximada na reta numérica.

‒ \frac{3}{8}, \frac{5}{3}, \frac{7}{6}, ‒ \frac{7}{10}

5. Escreva no caderno a afirmação verdadeira. Mostre com uma figura que os outros itens apresentam frases incorretas.

a) Os números

\frac{1}{3} e ‒ \frac{5}{8}

estão entre os números menos3 e menos2.

b) Entre os números menos3 e menos2 há somente cinco números racionais.

c) Não existem números inteiros entre menos200 e menos199.

6. Cite um exemplo de número racional que esteja entre os números representados em cada reta numérica.

a)

Reta numérica: da esquerda para a direita, números 1 e 11.

b)

Reta numérica: da esquerda para a direita, números menos 3 e zero.

c)

Reta numérica: da esquerda para a direita, números 1 e 2.

d)

Reta numérica: da esquerda para a direita, números menos 3 e menos 2.

7. Copie cada reta numérica no caderno, divida-as em partes iguais e identifique o número correspondente a cada quadradinho.

a)

Reta numérica: com cinco pontos com mesma distância entre si. No primeiro ponto, número zero. No quarto ponto, um quadrado azul. No quinto ponto, número 1.

b)

Reta numérica: com três pontos com mesma distância entre si. No primeiro ponto, número menos cinco. No segundo ponto, um quadrado laranja. No terceiro ponto, número menos 4.

c)

Reta numérica: com quatro pontos com mesma distância entre si. No primeiro ponto, número 1. No terceiro ponto, um quadrado verde. No quarto ponto, número 2.

d)

Reta numérica: com cinco pontos com mesma distância entre si. No primeiro ponto, número menos 3. No quarto ponto, um quadrado roxo. No quinto ponto, número menos dois.

e)

Reta numérica: com onze pontos com mesma distância entre si. No primeiro ponto, número menos 1. No quarto ponto, um quadrado alaranjado. No décimo primeiro ponto, número zero.

8.

Junte-se a um colega, desenhem uma reta numérica e respondam às questões no caderno.

a) O ponto correspondente ao número

‒ \frac{3}{5}

na reta numérica está localizado à direita ou à esquerda do ponto que representa menos1?

b) O ponto que representa determinado número natural está localizado entre os pontos correspondentes a menos1 e 1. Qual é o número natural representado por esse ponto?

•

Agora, crie uma questão para seu colega resolver.

9.

Copie a reta numérica no caderno e faça o que se pede.

Reta numérica: da esquerda para a direita, números 0 e 1.

a) Represente os números da sequência a seguir na reta numérica.

1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{6}, \frac{1}{7}, \frac{1}{8}, \frac{1}{9}, \frac{1}{10}, . . .

b) O que ocorre quando representamos os termos dessa sequência na reta numérica?

Respostas e comentários

1. Resposta em Orientações.

2. menos 8, menos 7, menos 4, menos 1, 4, 8

3. Respostas em Orientações.

4. Respostas em Orientações.

5. Respostas em Orientações.

6. Exemplos de respostas: a) 6; b) menos2; c)

\frac{3}{2}

; d) menos2,5

7. a) 0,75

7. b) menos 4,5

7. c)

1 \frac{2}{3}

7. d) menos 2,25

7. e) menos 0,7

8. a) à direita

8. b) 0

8. Resposta pessoal.

9. a) Resposta e comentário em Orientações.

9. b) Os pontos que correspondem aos números dessa sequência ficam cada vez mais próximos do ponto que corresponde ao zero.

Orientações e sugestões didáticas

Resposta da atividade 1:

	Número negativo	Número natural	Número positivo	Número não positivo
−7	x			x
−2	x			x
0		x		x
1		x	x
5		x	x

Resposta da atividade 4:

\frac{5}{3}

;

\frac{7}{6}

; ‒

\frac{3}{8}

; ‒

\frac{7}{10}

;

Respostas da atividade 5:

a)

Reta numérica: da esquerda para a direita, os números: menos três, menos dois, menos um, menos fração cinco oitavos, zero, fração um terço, um.

b)

Esquema: reta numérica: da esquerda para a direita, os números: menos três, menos dois, zero. Há uma chave entre os números menos três e menos dois, com a indicação: infinitos números racionais.

c) afirmação verdadeira

• Na atividade 7, aceite respostas na fórma decimal ou na fórma fracionária.

• A atividade 9 oferece aos estudantes a oportunidade de observar o que ocorre com um número racional escrito na fórma fracionária conforme aumentamos seu denominador.

Para cada uma dessas frações existe um ponto correspondente na reta numérica, e, quanto maior o denominador, mais próximo do zero ficará o número.

Vale lembrar aos estudantes que não precisam produzir explicações escritas de maneira formal; o mais importante é que possam se expressar oralmente de modo que expliquem o que foi observado.

Nesse mesmo sentido, a representação na reta numérica poderá ser aproximada.

• Reta numérica da atividade 3:

Reta numérica: da esquerda para a direita, os números: menos 6; menos 5 vírgula 2; menos 5; menos 4; menos 3 vírgula 1; menos 3; menos 2 vírgula 5; menos 2; menos 1 vírgula 3; menos 1; zero; um; 1 vírgula 3; 2; 2 vírgula 5; 3; 3 vírgula 1; 4; 5; 5 vírgula 2; 6.

• Reta numérica da atividade 4:

Reta numérica: da esquerda para a direita, os números: menos 1; menos fração sete sobre dez; menos fração três sobre oito; zero; 1; fração sete sobre seis; 1 vírgula 5; fração cinco terços.

• Reta numérica do item a da atividade 9:

• Reta numérica da atividade 4:

Reta numérica: da esquerda para a direita, os números: zero; fração um sobre dez; fração um sobre nove; fração um sobre oito; fração um sobre sete; fração um sobre seis; fração um sobre cinco; fração um sobre quatro; fração um sobre três; fração um sobre dois; um.

Página 26

3 Conjunto dos números reais

Todo número que pode ser escrito na fórma

\frac{a}{b}

, com a e b inteiros e b ≠ 0, é um número racional. A representação decimal dos números racionais é sempre um decimal exato ou uma dízima periódica.

Quando sua representação decimal é infinita e não periódica, o número não pode ser escrito na fórma

\frac{a}{b}

, com a e b inteiros e b ≠ 0, e, portanto, não é racional. Números desse tipo são chamados de números irracionais. Observe alguns exemplos.

• No estudo das circunferências, aparece a constante π (pi), que é igual a 3,14159265reticências

Esse número tem infinitas casas decimais e não tem parte periódica; por isso, é um número irracional.

Recorde

O número obtido ao se dividir a medida de comprimento da circunferência pela medida de comprimento de seu diâmetro, na mesma unidade, é o número irracional pi (representado pela letra grega π).

•

\sqrt{5}

= 2,2360679reticências é outro exemplo de número irracional.

Já foram feitos muitos cálculos para se chegar ao valor exato de

\sqrt{5}

, mas nunca se encontrou um decimal exato ou uma dízima periódica. Os matemáticos provaram que não é possível escrever esse número como quociente de dois inteiros e, por isso,

\sqrt{5}

não pode ser expresso como um decimal exato ou uma dízima periódica.

A raiz quadrada de qualquer número que não seja quadrado perfeito é um número irracional.

• O número ϕ (), que é igual a 1,61803reticências, também conhecido como número de ouro, tem infinitas casas decimais e não tem parte periódica. Esse número é irracional.

• 0,101001000100001reticências; 1,12345678910111213reticências e menos0,252255222555reticências são números irracionais.

Se unirmos o conjunto dos números racionais (no qual estão contidos o conjunto dos números inteiros e o conjunto dos números naturais) com o conjunto dos números irracionais, obteremos outro conjunto, chamado conjunto dos números reais, que indicamos por

.

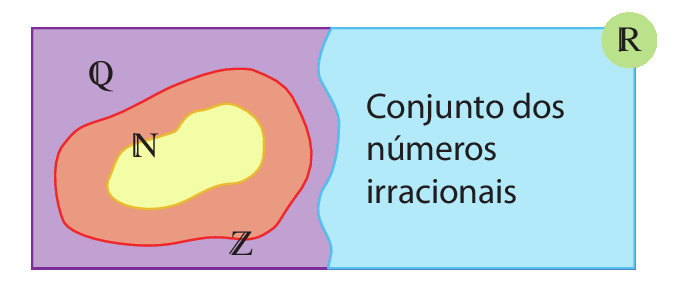
Esquema: Um retângulo representando o conjunto dos números reais. O retângulo está dividido em 2 partes maiores: na direita, fundo azul com a indicação 'conjunto dos números irracionais'; na esquerda, fundo roxo representando o conjunto dos números racionais. Dentro da parte roxa, uma parte alaranjada representando o conjunto dos números inteiros. Dentro da parte alaranjada, uma parte amarela representando o conjunto dos números naturais.

Mesmo que representássemos os infinitos números racionais na reta numérica, ainda haveria pontos da reta que não estariam associados a nenhum número racional. Já com a representação de todos os números reais, a reta numérica conterá exemplares de todos os tipos de números reais.

Todo número real tem um único ponto correspondente na reta numérica, e todo ponto da reta numérica corresponde a um único número real.

Orientações e sugestões didáticas

Conjunto dos números reais

Objetivos

• Reconhecer os números irracionais como aqueles que apresentam representação decimal infinita e não periódica.

• Introduzir o conjunto dos números reais.

Orientações

• Um dos objetivos deste tópico é mostrar aos estudantes que alguns conjuntos numéricos estão contidos em outros; os conjuntos dos números racionais e dos números irracionais não têm elementos em comum, ou seja, são conjuntos disjuntos; e o conjunto dos números reais é a reunião dos conjuntos dos números racionais e dos números irracionais.

• Algumas operações entre números reais, assim como a localização de alguns desses números na reta numérica, serão estudadas no volume 9 desta coleção.

Página 27

ATIVIDADES

1. Observe as fotos e responda à questão.

a)

Fotografia: Cartaz de supermercado. De cima para baixo, Bacalhau do porto, 45 vírgula 90 reais. Abaixo, Bacalhau Zarbo, 31 vírgula 90 reais. — Cartaz com preço.

b)

Fotografia: pista de atletismo alaranjada, com as numerações 1, 2, 3, 4 e 5. — Numeração na raia de atletismo.

c)

Fotografia: placa de trânsito com fundo amarelo, indicando que a altura máxima mede 4 vírgula 90 metros. — Placa de medida de altura máxima.

d)

Fotografia: um canhoto de um talão de cheques no valor de 120 reais, com um código de barras à esquerda. — Canhoto de talão de cheques.

• A que conjuntos numéricos pertencem os números que aparecem em cada foto?

2. Iara fez a operação 1 dividido por 19 usando uma calculadora e, no visor, apareceu o seguinte resultado:

Ilustração: visor de calculadora com o número 0 ponto 052631578.

Ilustração: menina branca, de cabelo preto, camiseta verde diz: 'como a representação decimal de fração um sobre dezenove é infinita e não periódica, ele é um número irracional'.

a) Você concorda com Iara? Por quê?

b) Podemos sempre saber se um número é racional ou irracional apenas observando sua representação decimal?

3. Escreva na fórma de fração cada número a seguir.

a) 7

b) 0,2

c) menos7

d) menos1,32

e) 0,666reticências

f) 1,555reticências

g) 24,3

h) 1,05

4. Observe os números e responda às questões.

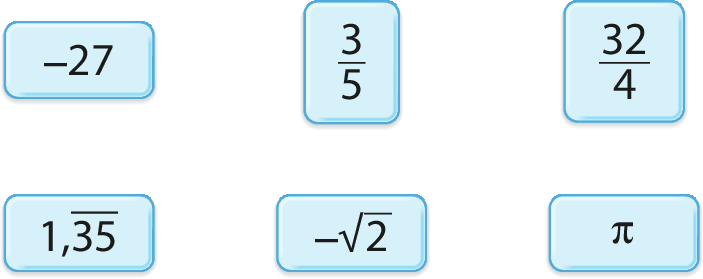
Quadro: ficha azul com o número menos 27. Quadro: ficha azul com o número fração 3 quintos. Quadro: ficha azul com o número fração 32 sobre 4. Quadro: ficha azul com o número 1 vírgula 35, com um traço horizontal acima do 35. Quadro: ficha azul com o número menos raiz de 2. Quadro: ficha azul com o número pi.

a) Qual desses números pertence ao conjunto dos números naturais?

b) Quais pertencem ao conjunto dos números inteiros?

c) Que números são racionais?

d) Que números são irracionais?

e) Que números são reais e não racionais?

f) Que números são reais e não irracionais?

5. Cite um exemplo, quando possível, de número:

a) inteiro e não natural;

b) real e não racional;

c) racional e não inteiro;

d) inteiro e irracional.

6. Copie as frases no caderno, completando-as com as palavras corretas.

a) Todo número irracional é um número ◾.

b) Todo número racional é um número ◾.

c) Todo número inteiro é um número ◾.

d) Todo número natural é um número ◾.

7. Escreva os números a seguir em ordem crescente.

Quadro: ficha azul com o número menos fração 12 quintos. Quadro: ficha azul com o número 3 vírgula 62, com um traço horizontal acima do 62. Quadro: ficha azul com o número menos 1 vírgula 2, com um traço horizontal acima do 2. Quadro: ficha azul com o número fração 40 sétimos. Quadro: ficha azul com o número menos pi. Quadro: ficha azul com o número 3 vírgula 62, com um traço horizontal acima do 2.

8. Escreva no caderno dois exemplos de números reais que obedeçam a cada uma das condições.

a) Números irracionais maiores que 2,5 e menores que 3.

b) Números racionais maiores que

‒ \frac{7}{8}

e menores que

- \frac{3}{4}

.

Respostas e comentários

1. a) racionais e reais

1. b) naturais, inteiros, racionais e reais

1. c) racionais e reais

1. d) naturais, inteiros, racionais e reais

2. a) Espera-se que os estudantes respondam que não, pois o número que aparece no visor da calculadora é parte da representação decimal de

\frac{1}{19}

, que é um número racional.

2. b) Espera-se que os estudantes respondam que não, pois às vezes o período de uma dízima periódica é muito grande e em sua representação decimal expressamos um número insuficiente de casas após a vírgula para identificar esse período.

3. a)

\frac{14}{2}

3. b)

\frac{1}{5}

3. c)

‒ \frac{7}{1}

3. d)

‒ \frac{132}{100}

3. e)

\frac{6}{9}

3. f)

\frac{14}{9}

3. g)

\frac{243}{10}

3. h)

\frac{105}{100}

4. a)

\frac{32}{4}

4. b)

\frac{32}{4}

e menos27

4. c)

\frac{32}{4}; ‒ 27; \frac{3}{5}; 1, \overline{35}

4. d)

‒ \sqrt{2}; π

4. e)

‒ \sqrt{2}; π

4. f)

\frac{32}{4}; ‒ 27; \frac{3}{5}; 1, \overline{35}

5. Exemplos de respostas: a) menos15; b) π; c) 0,5678; d) Não é possível.

6. a) real

6. b) real

6. c) Respostas possíveis: racional, real

6. d) Respostas possíveis: inteiro, racional, real

7.

‒ π; ‒ \frac{12}{5}; ‒ 1, \overline{2}; 3, 6 \overline{2}; 3, \overline{62}; \frac{40}{7}

8. Respostas pessoais.

Orientações e sugestões didáticas

• Na atividade 1, são apresentadas algumas imagens com números que pertencem a diferentes conjuntos numéricos. Organize os estudantes em grupos e peça a eles que também apresentem situações do cotidiano que contenham números que correspondam a cada conjunto numérico. Pode-se organizar no quadro ou em um painel um quadro com os conjuntos numéricos e pedir a cada grupo que o preencha com a situação que identificou de cada conjunto numérico. Os estudantes poderão ter dificuldade para encontrar nas situações do cotidiano números que pertençam ao conjunto dos números irracionais. Essa conclusão é importante para que percebam que os números irracionais são utilizados em cálculos matemáticos, por exemplo, na raiz quadrada.

• Os números na fórma de fração da atividade 3 são exemplos de respostas, já que há outras possíveis.

Página 28

Trabalho em equipe

faça as atividades no caderno

Na página 26, você conheceu o número de ouro, ϕ. Existem muitas curiosidades relacionadas com esse número, e você e seu grupo vão pesquisá-las para mostrar aos colegas.

O número de ouro

Justificativa

Alguns números repetem-se com tanta frequência na natureza que despertaram a atenção do ser humano desde tempos muito antigos. Descobrir diferentes situações associadas com um desses números é um modo de perceber a presença de curiosas relações matemáticas no mundo que nos rodeia e tentar entendê-las.

Objetivo

Pesquisar curiosidades relacionadas com a razão áurea e o número de ouro, tentando compreendê-las e relacioná-las.

Apresentação

Jornal falado, com o apoio de recursos visuais (fotos, ilustrações e cartazes).

Questões para pensar em grupo

• Onde pesquisar esse tipo de curiosidade?

• Qual será o foco da reportagem: a presença do número de ouro na natureza, nas artes ou na Matemática?

• A relação áurea aparece de modo natural ou proposital nos exemplos escolhidos?

• Como apresentar de modo claro e interessante o jornal falado?

Não se esqueçam

• Há vários outros termos relacionados ao número de ouro: razão áurea, retângulo áureo, divina proporção etcétera Pesquisem esses termos em dicionários, enciclopédias, revistas especializadas e na internet.

• Existe muito material sobre esse assunto. Pesquisem em fontes confiáveis e tenham o cuidado de escolher curiosidades adequadas ao grau de conhecimento matemático da turma.

Ilustração: um menino branco de camisa amarela e calça azul está em pé com alguns livros na mão. À direita, três crianças estão sentadas à mesa. Da esquerda para a direita, uma garota branca de cabelo preso e camiseta florida está escrevendo em um caderno. Um menino branco, de blusa vermelha, digita em um notebook. Uma menina negra, de camiseta amarela, está mexendo em alguns livros e revistas. Sobre a mesa, alguns livros, lápis e borracha.

Orientações e sugestões didáticas

Trabalho em equipe

Objetivos

• Aplicar, por meio de trabalho em grupo, os conceitos estudados.

• Favorecer o desenvolvimento das competências gerais 4 e 9 e da competência específica 2 da Bê êne cê cê.

Orientações

• O trabalho em equipe proposto consiste em uma instigante pesquisa sobre a razão áurea e o número de ouro. Livros de Matemática e a internet poderão ser de grande valia para os estudantes disporem de mais possibilidades de encontrar fatos interessantes relacionados a esse número.

• O modo de apresentação – jornal falado – será um desafio para eles e uma excelente oportunidade de se comunicarem matematicamente e também de mobilizar aspectos da competência geral 4 da Bê êne cê cê, já que precisarão recorrer a diferentes linguagens para partilhar informações.

• No site Clubes de Matemática da ó bê mépi há uma proposta de atividade relacionada à razão áurea com curiosidades, galeria de vídeos, galeria de arte e outros textos sobre o assunto. Disponível em: https://oeds.link/DGnzd9. Acesso em: 12 agosto 2022.

• O trabalho proposto também favorece o desenvolvimento da competência específica 2, ao instigar os estudantes a aprofundar os conhecimentos já trabalhados em sala de aula, por meio da busca de dados mais elaborados sobre o tema, da organização desses dados e da reflexão sobre eles, e da competência geral 9 da Bê êne cê cê na medida em que o estudante terá de interagir com seus pares, valorizando suas ideias e opiniões.

Competência geral 4: Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

Competência geral 9: Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

Competência específica 2: Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

Página 29

4 Potência com expoente inteiro

Observe o quadrado azul (índice 1), com medida de área igual a 4, que está sobreposto ao quadrado verde (índice 2), cuja área mede 4 vezes a do quadrado azul.

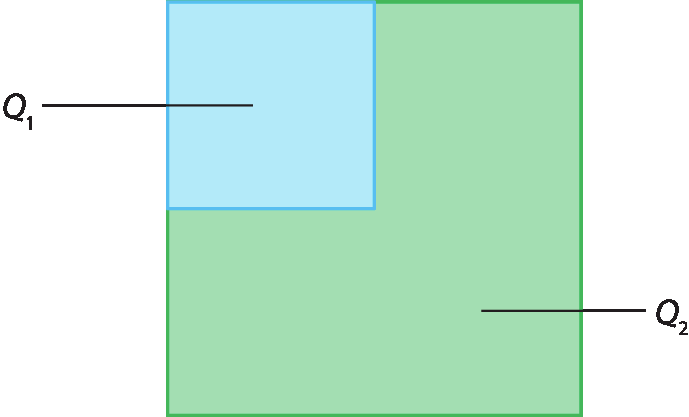
Figura geométrica: um quadrado azul sobreposto a um quadrado verde de modo que o quadrado azul corresponde a um quarto do quadrado verde. Fio no quadrado verde com a indicação Q2. Fio no quadrado azul com a indicação Q1.

As medidas de área desses quadrados formam uma sequência numérica em que cada termo é o termo anterior multiplicado por 4.

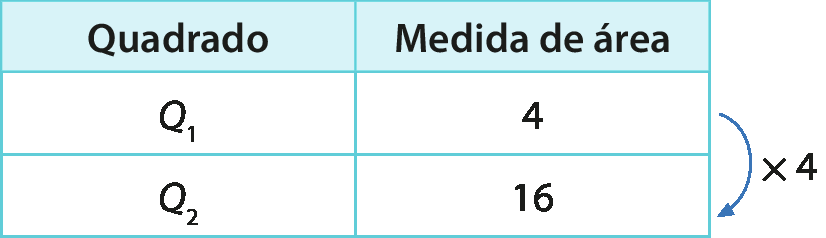
Esquema: quadro de 3 linhas e 2 colunas. Linha 1: quadrado; medida de área. Linha 2: Q1; 4. Linha 3: Q2; 16. Seta de 4 para 16 com a indicação: vezes 4.

Podemos escrever a medida de área como potência de base 4.

Quadrado	Medida de área	Medida de área escrita como potência de base 4
Q1	4	41
Q2	16	42

Se continuarmos construindo quadrados seguindo esse padrão, verificaremos que o próximo quadrado, com 4 vezes a medida de área de índice 2, medirá 4ao cubo de área.

Recorde

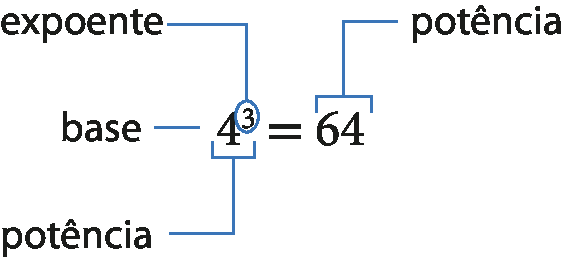
Esquema: quatro elevado a três igual a sessenta e quatro. Fio no 3 com a indicação expoente. Fio no 4 com a indicação base. Fio no quatro elevado a três com a indicação potência. Fio no 64 com a indicação potência.

Observe que usamos o termo potência para designar tanto a expressão 4ao cubo como o resultado 64.

Considere, agora, a sequência de quadrados sobrepostos a seguir, em que a área do primeiro quadrado abre parêntesesíndice 1fecha parênteses mede 4 e cada quadrado seguinte tem

\frac{1}{4}

da medida de área do quadrado anterior.

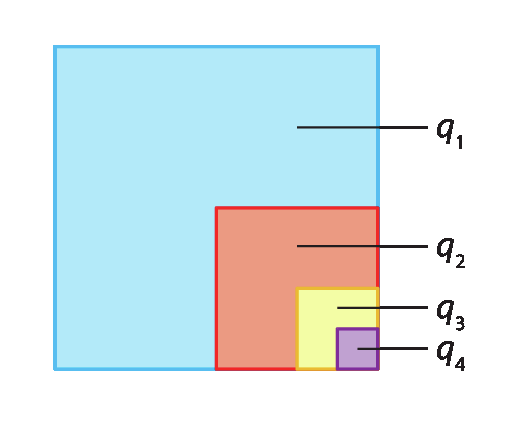
Figura geométrica: 4 quadrados: o quadrado roxo está sobreposto ao quadrado amarelo, que está sobreposto ao quadrado vermelho, que está sobreposto ao quadrado azul. Cada quadrado corresponde a um quarto do quadrado ao qual está sobreposto. Fio no quadrado azul com a indicação: q1. Fio no quadrado vermelho com a indicação: q2. Fio no quadrado amarelo com a indicação: q3. Fio no quadrado roxo com a indicação: q4.

As medidas de área dos quadrados formam uma sequência numérica em que cada termo é o termo anterior dividido por 4.

Esquema: quadro de 5 linhas e 2 colunas. Linha 1: quadrado; medida de área. Linha 2: q1; 4. Linha 3: q2; 1. Linha 4: q3; fração 1 quarto. Linha 5: q4; fração 1 sobre 16. Setas de 4 para 1, de 1 para fração 1 quarto e de fração 1 quarto para fração 1 sobre 16 com a indicação: dividido por 4.

Orientações e sugestões didáticas

Potência com expoente inteiro

Objetivos

• Ampliar e consolidar o significado da potenciação.

• Favorecer o desenvolvimento das seguintes habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero um e .

Habilidades da Bê êne cê cê

• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah zero um porque os estudantes deverão efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica. Favorece também a habilidade ê éfe zero oito ême ah um um ao propor aos estudantes que identifiquem uma regularidade em uma sequência numérica recursiva e construam um algoritmo por meio de fluxograma.

Orientações

• A intenção dessa etapa do trabalho é retomar algumas ideias sobre potenciação, além de ampliar e sistematizar os casos de potenciação cuja base é um número real e o expoente é um número inteiro.

(ê éfe zero oito ême ah zero um) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.

(ê éfe zero oito ême ah um um) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.

Página 30

Escrevendo os números como potências de base 4, temos:

Quadrado	Medida de área	Medida de área escrita como potência de base 4
q1	4	41
q2	1	40
q3	$divisão de 1 sobre 4$	4‒1
q4	$divisão de 1 sobre 16$	4‒2

Observe as potências com expoentes negativos.

• 4elevado a menos 1 =

\frac{1}{4}

• 4elevado a menos 2 =

\frac{1}{16} = \frac{1}{4^{2}}

Quando a base é um número real, as potências são definidas do mesmo modo que quando a base é um número racional.

Potência com expoente inteiro não negativo

• Qualquer potência de base real e expoente inteiro maior que 1 é produto dessa base por ela mesma tantas vezes quantas indica o expoente. Assim, sendo a um número real e n um número inteiro maior que 1, temos:

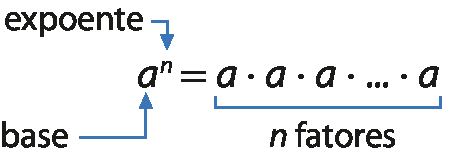
Esquema: a elevado a n, igual a vezes a, vezes a, vezes reticências, vezes a. Fio em n com a indicação expoente. Fio no a da potência com a indicação base. Fio em a vezes a, vezes a, vezes reticências, vezes a com a indicação n fatores.

• Qualquer potência de base real e expoente 1 é igual à própria base. Assim, sendo a um número real, aelevado a 1 = a.

• Qualquer potência de base real não nula e expoente zero é igual a 1. Assim, sendo a um número real não nulo, aelevado a 0 = 1.

Exemplos

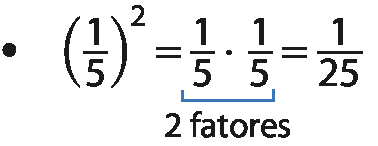
Esquema: abre parênteses, fração um quinto, fecha parênteses, elevado a dois, igual a fração um quinto vezes fração um quinto, igual a fração um sobre vinte e cinco. Fio em um quinto vezes um quinto com a indicação 'dois fatores'.

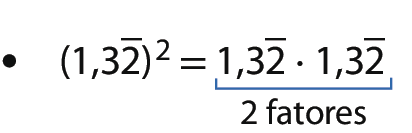
Esquema: abre parênteses, 1 vírgula 32, com um traço horizontal acima do 2, fecha parênteses, elevado a dois, igual a 1 vírgula 32, com um traço horizontal acima do 2, vezes 1 vírgula 32, com um traço horizontal acima do 2. Fio em 1 vírgula 32, com um traço horizontal acima do 2, vezes 1 vírgula 32, com um traço horizontal acima do 2, com a indicação '2 fatores'.

•

{(\frac{π}{2})}^{1} = \frac{π}{2}

•

{(\sqrt{2})}^{0} = 1

Potência com expoente inteiro negativo

Qualquer potência de base real não nula e expoente inteiro negativo é igual à potência que tem como base o inverso da base original e como expoente o oposto do expoente original. Assim, sendo a um número real não nulo e n um número inteiro,

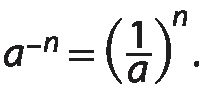
Sentença matemática: a elevado a menos n, igual a, abre parênteses, fração um sobre a, fecha parênteses, elevado a n.

Exemplos

•

{(π)}^{‒ 1} = \frac{1}{π}

•

{(\frac{2}{3})}^{‒ 2} = {(\frac{3}{2})}^{2} = \frac{3}{2} \cdot \frac{3}{2} = \frac{9}{4}

•

{(‒ 0, 01)}^{‒ 3} = {(‒ \frac{1}{100})}^{‒ 3} = {(‒ 100)}^{3} = ‒ 1 000 000

Orientações e sugestões didáticas

• Reproduza a sequência de quadrados no quadro e preencha os quadros que constam nesta página com a participação dos estudantes.

• Peça aos estudantes que observem os expoentes dos números da terceira coluna do quadro. É importante perceberem que se tratam de uma sequência que vai diminuindo uma unidade, para que compreendam de onde veio o sinal negativo.

Página 31

pensamento computacional

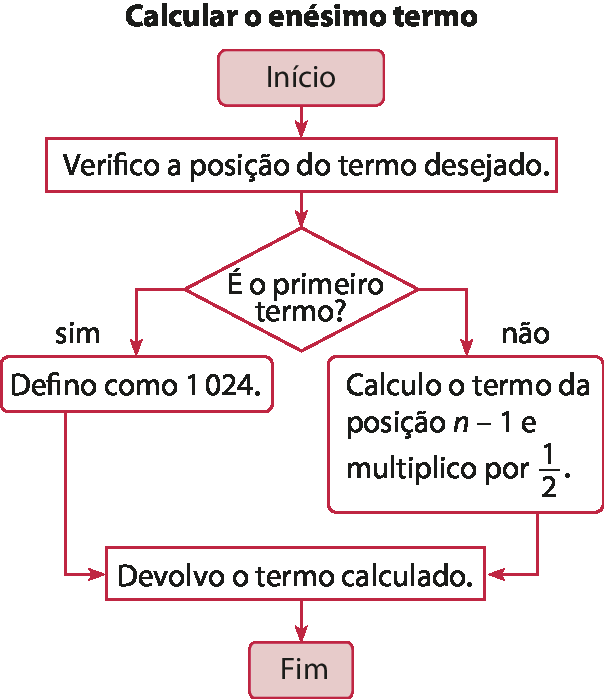
Analise a sequência recursiva:

abre parênteses.1024, 512, 256, 128, 64, reticênciasfecha parênteses

a) A partir do segundo termo, como podemos expressar um termo qualquer dessa sequência com base ?

b) Copie o fluxograma "Calcular o enésimo termo" e complete as áreas cinza de modo que ele nos permita descrever como obter o enésimo termo da sequência.

Fluxograma: CALCULAR O ENÉSIMO TERMO. Quadro Início. Seta para baixo, indicando o quadro: Verifico a posição do termo desejado. Seta para baixo, indicando o quadro: É o primeiro termo? Seta para a esquerda, com 'sim' ao lado dela e, para a direita, com 'não' ao lado dela. À esquerda e abaixo, a seta chega em um quadro com retângulo cinza. À direita e abaixo, a seta chega em outro quadro com retângulo cinza. Tanto no quadro à esquerda, quanto no quadro à direita saem setas indicando o quadro abaixo: Devolvo o termo calculado. Seta para baixo, indicando o quadro: Fim.

c)

É possível escrever o enésimo termo dessa sequência sem a necessidade de saber o termo anterior. Converse com um colega e descubram como isso pode ser feito. (Dica: Escrevam os termos da sequência como potências de base 2.)

ATIVIDADES

faça as atividades no caderno

1. Leia o texto e resolva o problema.

Quando ia a Ives,

encontrei um homem com sete mulheres,

cada mulher tinha sete sacos,

cada saco tinha sete gatos,

cada gato tinha sete gatinhos.

[reticências]

B. História da Matemática. São Paulo: Blucher, 2012. página 33.

Fotografia: sete filhotes de gato brancos.

• Quantos gatinhos havia?

2. Calcule as potências.

a) 3ao cubo

b)

{(\frac{1}{3})}^{3}

c) 4elevado a 0

d) abre parêntesesmenos5fecha parêntesesao quadrado

e)

{(‒ \frac{1}{5})}^{3}

f) abre parêntesesmenos7fecha parêntesesao cubo

3. Calcule as potências de expoente negativo.

a) 2elevado a menos 1

b) 2elevado a menos 2

c) 2fecha parênteses elevado a menos 2

d) 2fecha parênteses elevado a menos 3

e)

{(\frac{1}{2})}^{‒ 1}

f)

{(‒ \frac{1}{2})}^{‒ 1}

g)

{(‒ \frac{1}{2})}^{‒ 4}

4. Calcule as potências.

a) 1elevado a 4

b) 1elevado a menos 2

c) 10

d) 1elevado a 101

•

Agora, reúna-se com um colega e escrevam uma frase que sintetize esses resultados.

5. Reproduza o quadro no caderno, complete-o e, depois, responda à questão.

•

Há alguma linha nesse quadro que permite duas soluções? Se houver, comente com um colega os casos em que isso é possível.

Respostas e comentários

Pensamento computacional: Respostas em Orientações.

1. .2401 gatinhos

2. a) 27

2. b)

\frac{1}{27}

2. c) 1

2. d) 25

2. e)

‒ \frac{1}{125}

2. f) menos343

3. a)

\frac{1}{2}

3. b)

\frac{1}{4}

3. c)

\frac{1}{4}

3. d)

‒ \frac{1}{8}

3. e) 2

3. f) menos2

3. g) 16

4. a) 1

4. b) 1

4. c) 1

4. d) 1

4. Exemplo de resposta: quando a base de uma potência é 1, o resultado também será igual a 1.

5. Respostas em Orientações.

Orientações e sugestões didáticas

• O boxe Pensamento computacional favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um um da Bê êne cê cê porque os estudantes terão a oportunidade de completar um fluxograma que representa o processo de determinação dos números de uma sequência numérica recursiva em que cada termo, a partir do segundo, é igual ao anterior dividido por 2

(ou multiplicado por \frac{1}{2})

. Dessa fórma, temos:

\{\begin{cases} a_{1} = 1024 \\ a_{n} = \frac{1}{2} · a_{n ‒ 1} \end{cases}

No item a, o termo pode ser assim expresso:

a_{n}

=

\frac{1}{2}

⋅

a_{n ‒ 1}

b)

No item c, os estudantes deverão retomar a ideia de que a regularidade de uma mesma sequência numérica pode ser representada por duas expressões algébricas equivalentes. Caso eles tenham dificuldade, oriente-os a escrever alguns termos dessa sequência como potências de base 2. Assim:

a_{1} = 2^{10}

a_{2} = 2^{9} = 2^{10 ‒ 1}

a_{3} = 2^{8} = 2^{10 ‒ 2}

a_{n} = 2^{10 ‒ (n ‒ 1)}

• Respostas da atividade 5:

Potência	Base	Expoente	Resultado
26	2	6	64
$abre parênteses divisão de 1 sobre 3 fecha parênteses elevado a menos 3$	$divisão de 1 sobre 3$	−3	27
$abre parênteses divisão de 2 sobre 5 fecha parênteses elevado a 2$	$divisão de 2 sobre 5$	2	$divisão de 4 sobre 25$
$abre parênteses divisão de 1 sobre 2 fecha parênteses elevado a 5$	$divisão de 1 sobre 2$	5	$divisão de 1 sobre 32$

Sim. A 4ª linha.

Página 32

Lembre-se: Escreva no caderno!

6.

Escreva cinco potências cujo expoente seja um número natural e passe para seu colega calcular.

Depois que você e seu colega calcularem todas as potências, responda às questões.

a) As potências cujas bases são positivas tiveram resultado positivo ou negativo?

b) As potências cujas bases são negativas tiveram resultado positivo ou negativo?

7. Calcule as potências.

Quadro: ficha azul com a potência dez elevado a menos um. Quadro: ficha laranja com a potência dez elevado a menos dois. Quadro: ficha verde com a potência dez elevado a menos cinco. Quadro: ficha roxa com a potência dez elevado a menos onze.

• Agora, imagine a representação desses números na reta numérica. Escreva um texto relacionando os expoentes das potências às posições que os pontos correspondentes a esses números ocupam na reta.

8. Observe a sequência de figuras a seguir.

Ilustração: uma bolinha vermelha. Ilustração: duas bolinhas vermelhas. Ilustração: 4 bolinhas vermelhas, distribuídas em 2 linhas com duas bolinhas cada. Ilustração: 8 bolinhas vermelhas, distribuídas em 2 linhas com quatro bolinhas cada.

a) Desenhe a figura 5 no caderno.

b) Quantas bolinhas formarão a figura 10?

9. Escreva no caderno mais cinco termos de cada sequência:

a) 27, 9, 3, reticências

b)

\frac{1}{5}, \frac{1}{25}, \frac{1}{125},

reticências

10. Calcule o valor das expressões numéricas.

a) 5elevado a 0 + abre parênteses0,25 menos abre parênteses0,5 menos 2elevado a 4

b)

{(\frac{1}{2} ‒ 1)}^{‒ 1}

+ 2fecha parêntesesao cubo

11. Leia o texto, reproduza o quadro e complete-o.

Ilustração: uma menina branca, de cabelo castanho amarrado, camiseta listrada rosa e vermelho está sentada em frente da tela de um computador com o mouse na mão. Sobre à mesa, um porta canetas.

Como as notícias se espalham! Às 13 horas, Tina enviou um e-mail para 4 amigos contando uma novidade. Após 30 minutos, cada um desses amigos encaminhou o e-mail para outros 4 amigos, que após 30 minutos encaminharam o e-mail para outros 4 amigos, e assim sucessivamente.

• Quantas pessoas receberam o e-mail até as 14 horas 30 minutos?

Notação científica

Quando usamos números excessivamente grandes ou extremamente pequenos, podemos escrevê-los como um produto em que um dos fatores é uma potência de base 10. Isso acontece muito na área científica.

Os quadros a seguir mostram alguns exemplos de números representados em notação científica.

Alguns intervalos de tempo (aproximados) em segundo
Idade do Universo	5 ⋅ 1017
Idade da pirâmide de Quéops	1 ⋅ 1011
Período de rotação da Terra em torno de seu eixo (1 dia)	9 ⋅ 104
Intervalo entre os batimentos cardíacos de um adulto saudável	8 ⋅ 10−1
Período típico de rotação de uma molécula	2 ⋅ 10−11

Fotografia: Pirâmide antiga no deserto. Ao fundo, prédios e construções de uma cidade. — Pirâmide de Quéops, ou Grande Pirâmide, em gizé, Egito, 2021. Essa pirâmide foi construída por volta de 2500 antes de Cristo e é a única das Sete Maravilhas do Mundo Antigo que resiste ao tempo.

Respostas e comentários

6. a) positivo

6. b) Se o expoente for par, o resultado será positivo; se o expoente for ímpar, o resultado será negativo.

7. 0,1; 0,01; 0,00001 e 0,00000000001; Resposta pessoal.

8. a) A figura deverá ter 16 bolinhas.

8. b) 512 bolinhas

9. a)

1, \frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \frac{1}{81}

9. b)

\frac{1}{625}, \frac{1}{3 125}, \frac{1}{15 625}, \frac{1}{78 125}, \frac{1}{390 625}

10. a) menos3

10. b) menos10

11. Respostas em Orientações.

Orientações e sugestões didáticas

• Na atividade 8, os estudantes deverão perceber que se trata de uma sequência de potência de 2.

Chamando de n a posição de cada figura, notamos que o expoente em cada uma é abre parêntesesn menos 1fecha parênteses.

Figura 1 → n = 1 → 2elevado a 0 (1 bolinha)

Figura 2 → n = 2 → 2elevado a 1 (2 bolinhas)

Figura 3 → n = 3 → 2ao quadrado (4 bolinhas)

Figura 4 → n = 4 → 2ao cubo (8 bolinhas)

Figura 5 → n = 5 → 2elevado a 4 (16 bolinhas)

Figura 10 → n = 10 → 2elevado a 9 (512 bolinhas)

• Resolução da atividade 11:

Horário	Quantidade de pessoas que receberam o e-mail	Potência
13 h	4	41
13 h 30 min	16	42
14 h	64	43
14 h 30 min	256	44

Para saber quantas pessoas receberam o e-mail até as 14 horas 30 minutos, adicionamos os valores da segunda coluna.

4 + 16 + 64 + 256 = 340, ou seja, 340 pessoas.

Página 33

Algumas medidas de distância (aproximadas) em metro
Medida de distância da Terra à galáxia Andrômeda	2 ⋅ 1022
Medida de comprimento do raio do Sol	7 ⋅ 108
Medida da espessura da página de um livro	1 ⋅ 10−4
Medida de comprimento típico de um vírus	1 ⋅ 10−6
Medida de comprimento do raio de um átomo de hidrogênio	5 ⋅ 10−11

Algumas medidas de massa (aproximadas) em quilograma
Medida de massa de nossa galáxia	2 ⋅ 1043
Medida de massa da Terra	6 ⋅ 1024
Medida de massa de um elefante	4 ⋅ 103
Medida de massa de uma uva	3 ⋅ 10−3
Medida de massa de um grão de poeira	7 ⋅ 10−10
Medida de massa de um elétron	9 ⋅ 10−31

Resnick, róbert; ralidei, , Quênef S. Física 1. 5. edição Rio de Janeiro: éle tê cê, 2003. página 3, 5 e 6.

Essa fórma de representação facilita o uso desses números, pois escrever muitos zeros pode confundir a leitura, além de ser preciso contá-los para compreender o valor expresso. É mais fácil usar a medida de comprimento do raio do Sol, por exemplo, como 7 ⋅ 10elevado a 8 métros do que como ..700000000 métros, ou escrever a medida de massa de um grão de poeira como 7 ⋅ 10elevado a menos 10 quilogramas do que como 0,0000000007 quilogramas.

Fotografia: imagem do Sol parecendo uma esfera vermelha com vários pontinhos pretos. — Imagem do Sol obtida por equipamento do Observatório Solar da Nasa em 2018.

Um número escrito em notação científica é expresso como um produto a ⋅ 10elevado a k, em que:

• a é um número escrito na fórma decimal cuja parte inteira tem apenas um algarismo, que deve ser diferente de zero;

• k é um número inteiro.

A medida de comprimento, em metro, do raio do átomo de hidrogênio, elemento químico mais comum no Universo, é 5 ⋅ 10elevado a menos 11. Para representar essa medida com todos os seus algarismos, primeiro escrevemos 10elevado a menos 11 na fórma decimal:

10^‒¹¹ =

{(\frac{1}{10})}^{11}

=

\frac{1}{10^{11}}

=

\frac{1}{100 000 000 000}

= 0,00000000001

Depois fazemos: 5 ⋅ 0,00000000001 = 0,00000000005

Para representar a maior medida de distância da Terra até o Sol, ..152100000 quilômetros, em notação científica, temos de contar a quantidade de casas em que a vírgula será deslocada:

Esquema: número 152100000 com vírgula colocada entre o primeiro 1 e o 5. Abaixo, indicação de cada deslocamento de casa da vírgula para a esquerda, com total de 8 deslocamentos.

Deslocar a vírgula 8 casas para a esquerda significa dividir o número por ..100000000. Então, para não alterar o número, temos de multiplicá-lo por ..100000000 (que, em potência de 10, é 10elevado a 8). Assim:

..152100000 = 1,521 ⋅ 10elevado a 8

Orientações e sugestões didáticas

• Enfatize que a notação científica é um modo de representar números grandes ou pequenos na fórma de um produto em que um dos fatores é uma potência de base 10. Se achar conveniente, mostre aos estudantes na representação decimal alguns dos números presentes nos quadros. O objetivo é que eles percebam as vantagens dessa notação, como a eliminação da escrita de muitos zeros e a melhor compreensão do valor expresso.