UNIDADE 2
Capítulo 3
Congruência de triângulos
Capítulo 4
Quadriláteros
Capítulo 5
Polígonos

A geometria das abelhas
As abelhas usam cera ou fibras vegetais para construir os alvéolos das colmeias, que servem depois para armazenar alimento ou para abrigar crias em seu desenvolvimento. Elas constroem os alvéolos de fórma otimizada e econômica, ou seja, com o maior aproveitamento do espaço, reduzindo gasto de material, de modo que uns alvéolos se encaixem perfeitamente nos outros. Note que a entrada da cavidade de cada alvéolo lembra a fórma de um polígono regular; juntos, os alvéolos cobrem perfeitamente a superfície, sem deixar espaços vazios nem tendo figuras interseccionadas. É por isso que eles não são arredondados, pois a falta de “paredes” comuns entre eles deixaria uma grande quantidade de espaços não aproveitados.
Para começar...
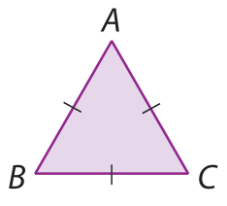
1. A entrada da cavidade de um alvéolo lembra qual polígono?
2. Quantos lados, ângulos internos e diagonais tem esse polígono?
3. Se quisermos cobrir perfeitamente um plano com um só tipo de polígono regular, sem deixar espaços vazios nem tendo figuras interseccionadas, devemos escolher um polígono tal que:
a) a quantidade de diagonais seja um número par.
b) a quantidade de ângulos internos seja igual à de vértices.
c) a quantidade de lados seja um número ímpar.
d) a medida de abertura do seu ângulo interno seja um divisor de 360graus
.

Respostas e comentários
Habilidades da Bê êne cê cê trabalhadas nesta Unidade:
ê éfe zero oito ême ah um quatro
ê éfe zero oito ême ah um cinco
ê éfe zero oito ême ah um seis
ê éfe zero oito ême ah dois três
Para começarreticências: 1. hexágono
2. 6 lados; 6 ângulos internos; 9 diagonais
3. alternativa d
Orientações e sugestões didáticas
Abertura da Unidade 2
Conteúdos
• Nesta Unidade, serão trabalhados conceitos relacionados às unidades temáticas Geometria e Probabilidade e Estatística que, entre outros objetivos, favorecerão o desenvolvimento das habilidades da Bê êne cê cê listadas.
Orientações
• A abertura relaciona natureza à Geometria ao apresentar o formato dos alvéolos das colmeias. Após a leitura individual do texto, verifique se os estudantes compreenderam o tema e solicite que respondam às questões propostas.
• Durante o trabalho com as questões 1 e 2, verifique o conhecimento prévio dos estudantes acerca da identificação dos polígonos e de seus elementos. Esse conhecimento servirá de base para o desenvolvimento de novas habilidades relacionadas à classificação de polígonos, à relação entre ângulos internos e externos e à soma das medidas de abertura dos ângulos internos, entre outras.
• Promova um momento de debate para que os estudantes justifiquem suas respostas à questão 3. A pavimentação de um plano (mosaico) consiste em cobri-lo com uma mesma figura (molde), sem deixar espaços vazios ou figuras interseccionadas. Se quisermos um mosaico formado pela propagação de um só tipo de polígono regular (lados e ângulos internos congruentes), devemos escolher tal polígono de modo que seu ângulo interno seja um divisor de 360graus (para que haja um encaixe entre os polígonos).
• A construção de mosaicos usando polígonos regulares é assunto de anos anteriores, inclusive com o apoio de softwares de Geometria dinâmica. Se julgar necessário, retome algumas atividades semelhantes, ressaltando que os polígonos precisam ter pelo menos um vértice em comum e se encaixar perfeitamente, de fórma que não se sobreponham nem haja espaços entre eles. Aproveite para exemplificar a justificativa de que a entrada da cavidade de um alvéolo não pode ser arredondada. Mostre no quadro a incompatibilidade dos círculos ao recobrir uma superfície, ressaltando que haveria muitos “buracos” entre as figuras.
• As informações desta seção foram baseadas no artigo “A geometria instintiva das abelhas” (disponível em: https://oeds.link/k5xaWg; acesso em: 4 janeiro2021).

CAPÍTULO 3 Congruência de triângulos
1 Triângulos
O formato triangular é constantemente utilizado nas mais diversas áreas, como arte, arquitetura, engenharia e computação. É comum também a utilização do formato triangular na construção de figuras não planas.
Neste Capítulo, você estudará alguns elementos e a classificação dos triângulos, e conhecerá outros conteúdos relacionados a essa figura geométrica.


Considere o triângulo á bê cê.
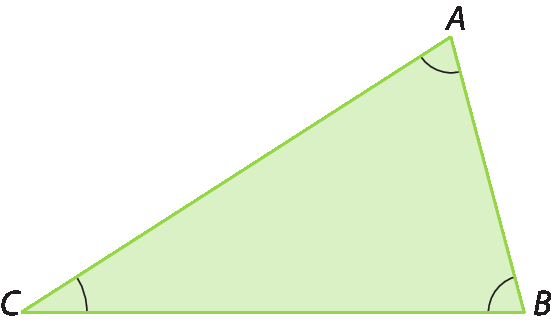
Podemos destacar alguns de seus elementos.
• Vértices: pontos A, B e C
• Lados: segmentos
AB,
BCe
CA• Ângulos internos:
ABC,
BCAe
CABEm cada vértice, vamos prolongar um dos lados do triângulo á bê cê para obter seus ângulos externos.
• Ângulos externos:
ângulo a, b e c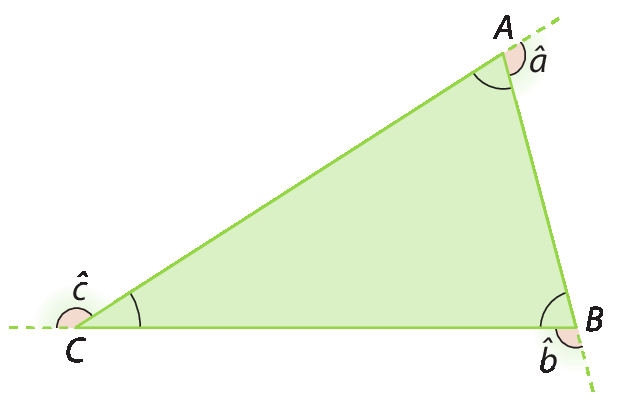
Observação
Podemos indicar um triângulo á bê cê por: △á bê cê
Respostas e comentários
Habilidade da Bê êne cê cê trabalhada neste Capítulo:
ê éfe zero oito ême ah um cinco
ê éfe zero oito ême ah dois três
Os links expressos nesta coleção podem estar indisponíveis após a data de publicação deste material.
Orientações e sugestões didáticas
Triângulos
Objetivos
• Reconhecer o formato triangular em diversas áreas do conhecimento.
• Reconhecer a condição de existência de um triângulo.
• Classificar triângulos quanto aos lados e quanto aos ângulos.
Orientações
• Neste tópico, retoma-se o estudo dos triângulos: elementos, condição de existência, soma das medidas de abertura de seus ângulos internos e classificação quanto aos lados e quanto aos ângulos. Faça essa retomada levando em consideração os conhecimentos adquiridos anteriormente pela turma.
• Destaque a importância da rigidez geométrica dos triângulos na Arquitetura e na Engenharia. Se possível, mostre ou peça aos estudantes que pesquisem outras imagens de estruturas em que o formato triangular esteja presente.
Recorde
• Se os ângulos interno e externo de um triângulo possuem o mesmo vértice, eles são adjacentes.
• Em cada vértice do triângulo, o ângulo interno e o externo são adjacentes suplementares, ou seja, a soma das medidas de abertura igual a 180graus.
Assim, no triângulo á bê cê da página anterior, temos:
Medida do ângulo a, mais medida do ângulo C A B, é igual a 180 graus.
Medida do ângulo b, mais medida do ângulo ABC, é igual a 180 graus.
Medida do ângulo c, mais medida do ângulo BCA, é igual a 180 graus.
Condição de existência de um triângulo
O contorno de todo triângulo é formado por três segmentos, que são seus lados. Porém, nem sempre três segmentos podem formar o contorno de um triângulo.
Acompanhe a construção, com régua e compasso, de um triângulo com lados de medidas de comprimento 3 centímetros, 2,5 centímetros e 2 centímetros.



Atenção! Cuidado ao usar o compasso.
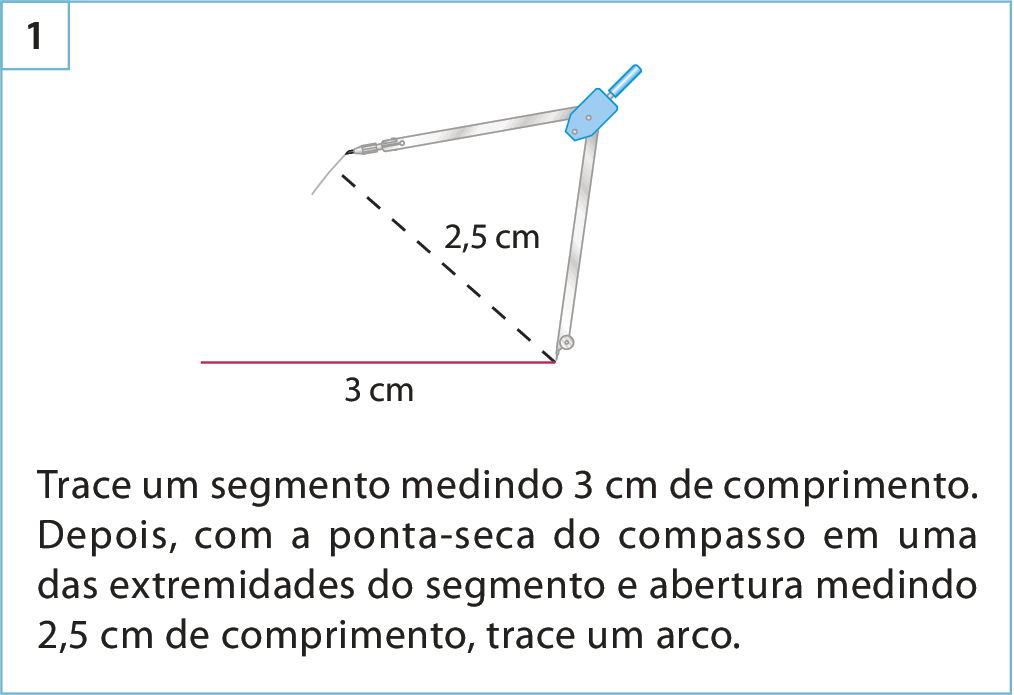
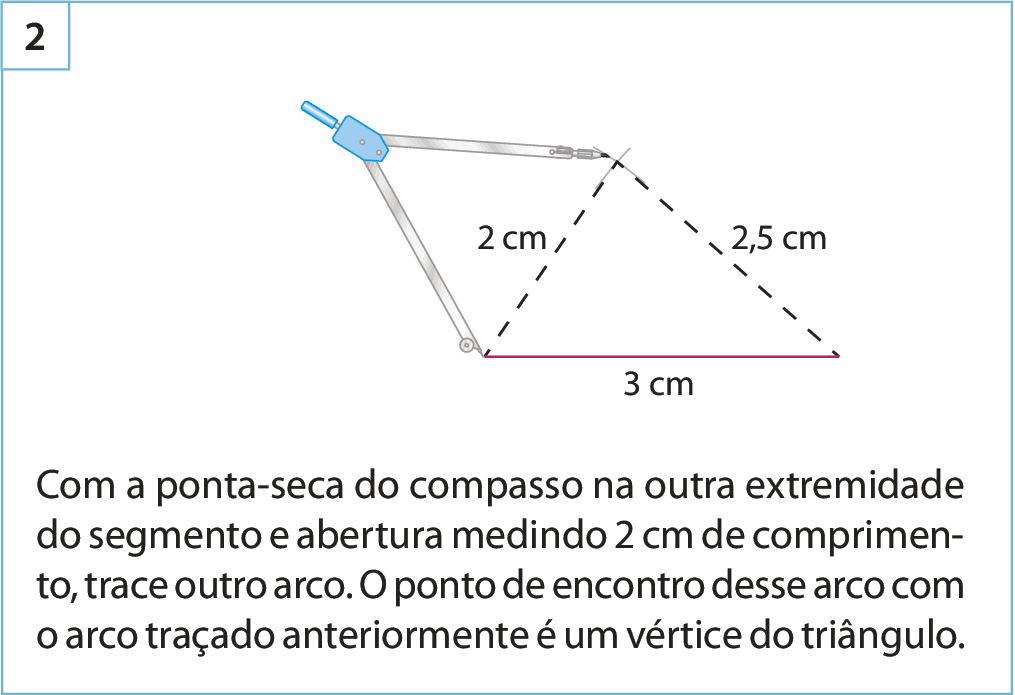
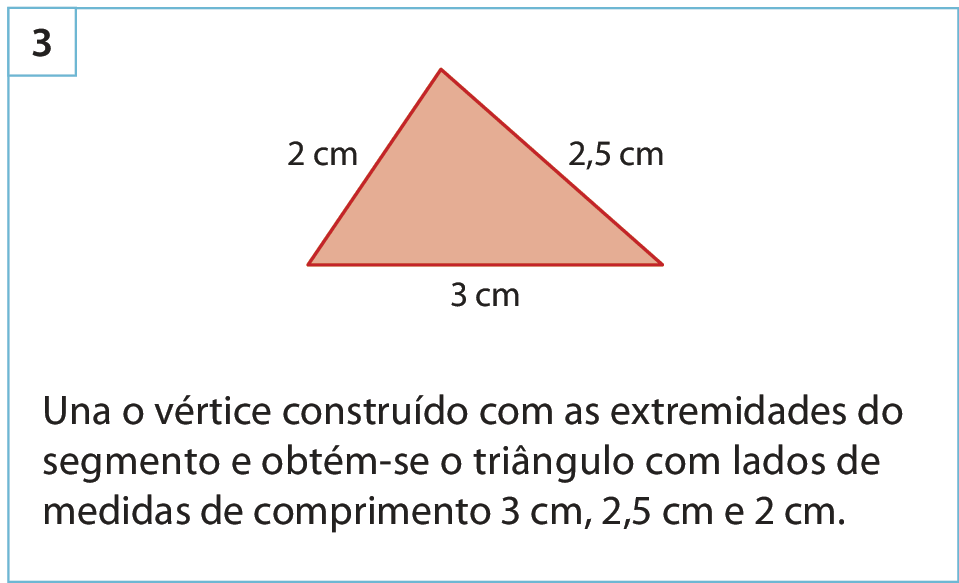
Para fazer
Tente construir no caderno um triângulo cujos lados medem 7 centímetros, 3 centímetros e 2 centímetros de comprimento.
Você conseguiu construir o triângulo? Por quê?
Para que exista um triângulo com lados de determinadas medidas de comprimento, ele deve atender à condição de existência de um triângulo.
Em qualquer triângulo, a medida de comprimento de um lado é sempre menor que a soma das medidas de comprimento dos outros dois lados.
Respostas e comentários
Para fazer: Não, porque os arcos correspondentes às aberturas do compasso com medidas 2 centímetros e 3 centímetros de comprimento não se cruzam.
Orientações e sugestões didáticas
• Antes de estudar os conceitos desta página, pode ser feito um experimento interessante a respeito da condição de existência de um triângulo. Leve para a sala de aula diversos trios de canudinhos ou palitos de madeira com medidas de comprimento variados, de modo que alguns desses trios formem triângulos e outros não. Após as tentativas de obter triângulos, peça aos estudantes que meçam o comprimento dos lados das figuras formadas e elaborem hipóteses sobre a condição de existência de um triângulo.
• No boxe Para fazer, ao tentar construir um triângulo, os estudantes vão perceber que não é possível obter um triângulo com as medidas de comprimento indicadas.
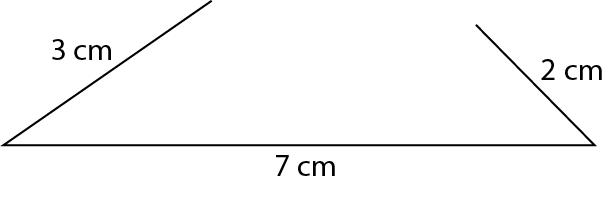
Comente com eles que, antes de tentar construir o triângulo, é possível verificar a existência dele, pois só é possível construir um triângulo quando a soma das medidas de comprimento de dois de seus lados é maior que a medida de comprimento do terceiro lado.
• Em atividades que indicam o uso do compasso, alerte os estudantes sobre o cuidado em seu manuseio, a fim de evitar acidentes.
Classificação dos triângulos
Observe, no quadro a seguir, a classificação dos triângulos de acordo com as medidas de comprimento dos lados ou com as medidas de abertura dos ângulos.

|
De acordo com as medidas de comprimento dos lados |
De acordo com as medidas de abertura dos ângulos |
||||
|---|---|---|---|---|---|
|
Equilátero |
Isósceles |
Escaleno |
Acutângulo |
Obtusângulo |
Retângulo |
|
|
|
|
|
|
|
|
Tem três lados congruentes. |
Tem dois lados congruentes. |
Não tem lados congruentes. |
Tem três ângulos internos agudos. |
Tem um dos ângulos internos obtuso. |
Tem um dos ângulos internos reto. |

ATIVIDADES
faça as atividades no caderno
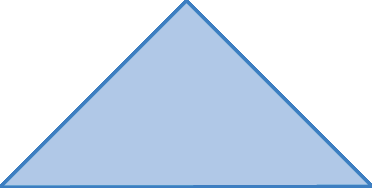
1. Usando régua e transferidor, classifique os triângulos conforme as medidas de comprimento dos lados e de abertura dos ângulos.
a)
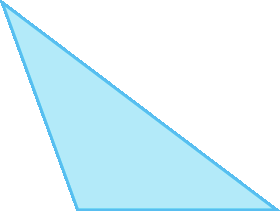
b)

c)

d)

e)

f)
Versão adaptada acessível
1. Responda às questões.
a) Explique as características dos triângulos isósceles, equiláteros e escalenos, levando em consideração as medidas do comprimento dos lados desses triângulos.
b) Agora, levando em consideração as medidas das aberturas dos ângulos, dê as características dos triângulos acutângulos, obtusângulos e retângulos.
Orientação para acessibilidade
Respostas
a) Triângulos isósceles têm dois lados congruentes, triângulos equiláteros têm três lados congruentes e triângulos escalenos não têm lados congruentes.
b) Triângulos acutângulos têm três ângulos internos agudos, triângulos obtusângulos têm um dos ângulos internos obtuso e triângulos retângulos têm um dos ângulos internos reto.
2. Que alternativas contêm medidas de comprimento de segmentos que possibilitam a construção de um triângulo?
a) 3,5 centímetros, 4,5 centímetros e 6,5 centímetros
b) 90 centímetros, 45 centímetros e 45 centímetros
c) 6 centímetros, 5,9 centímetros e 6,1 centímetros
d) 10 centímetros, 2 centímetros e 3 centímetros
3. Observe o triângulo que Jonas desenhou e analise as afirmações de Cátia, Lia e Flávia.
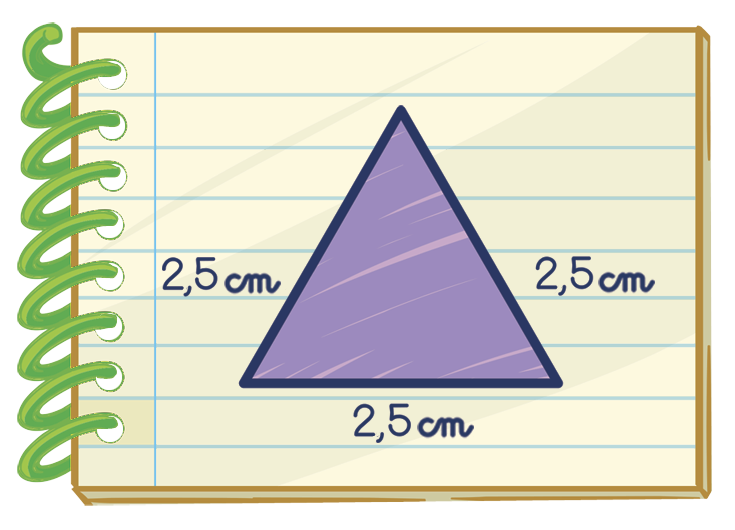

• Quais afirmações são verdadeiras?
Respostas e comentários
1. a) escaleno e obtusângulo
1. b) escaleno e retângulo
1. c) equilátero e acutângulo
1. d) escaleno e obtusângulo
1. e) escaleno e acutângulo
1. f) isósceles e retângulo
2. alternativas a e c
3. as três
Orientações e sugestões didáticas
• Ao trabalhar a classificação dos triângulos quanto à medida de comprimento dos lados, é importante comentar que os triângulos equiláteros são também equiângulos e, por isso, regulares, e, ainda, que todo triângulo equilátero é também isósceles, pois tem dois lados de mesma medida de comprimento; entretanto, nem todo triângulo isósceles é equilátero.
• Explique aos estudantes que é comum usar risquinhos para indicar medidas de comprimento dos lados ou medidas de abertura de ângulos iguais.
• Os prefixos equi e iso indicam igualdade, o que sugere o significado das palavras equilátero e isósceles. A palavra escaleno vem do grego skalēnós, que significa desigual, de tamanhos diferentes, como as medidas de comprimento dos lados do triângulo escaleno.
Atenção! Cuidado ao usar o compasso.
4. Responda às questões.
a) Se dois lados de um triângulo isósceles medem 2 centímetros e 3 centímetros de comprimento, quais são as possíveis medidas de comprimento do terceiro lado?
b) As medidas de comprimento de dois lados de um triângulo escaleno são 7 centímetros e 3 centímetros. Quais são as possíveis medidas de comprimento do outro lado, sabendo que elas são menores que 8 centímetros e correspondem a um número natural?
c) As medidas de comprimento de dois lados de um triângulo escaleno são 6 centímetros e 9 centímetros. Quais são as possíveis medidas de comprimento do terceiro lado? Sabe-se que elas são menores que 11 centímetros de comprimento e estão representadas por um número natural par.
5. No quadro a seguir são apresentadas as medidas de comprimento dos segmentos
AB, BC e AC(que indicamos por A bê, BC e á cê ), expressas em centímetro, em cinco situações abre parêntesesum, dois, três, quatro e cincofecha parênteses. Em todas elas, os pontos a, B e C não estão alinhados.
|
I |
II |
III |
IV |
V |
|
|---|---|---|---|---|---|
|
AB |
2 |
3 |
2 |
4 |
4 |
|
BC |
3 |
1,5 |
3 |
4 |
4 |
|
AC |
6 |
4 |
4 |
4 |
6 |
•

Faça o que se pede e, depois, compare suas respostas com as de um colega.
a) Verifique as situações em que é possível construir o △á bê cê.
b) Considere as situações indicadas no item anterior e construa os triângulos usando régua e compasso.
c) Meça a abertura dos ângulos internos de cada triângulo construído e escreva as medidas de abertura dos ângulos em grau.
d) Classifique os triângulos em relação às medidas de comprimento dos lados e da abertura dos ângulos.
6.

Quantos triângulos isósceles é possível construir com o lado não congruente medindo 6 centímetros de comprimento?
2 Ângulos nos triângulos
Soma das medidas de abertura dos ângulos internos
As aberturas dos ângulos internos do triângulo á bê cê medem a, b e c.
Consideremos a reta r, paralela ao lado
Segmento BC, passando pelo vértice a.
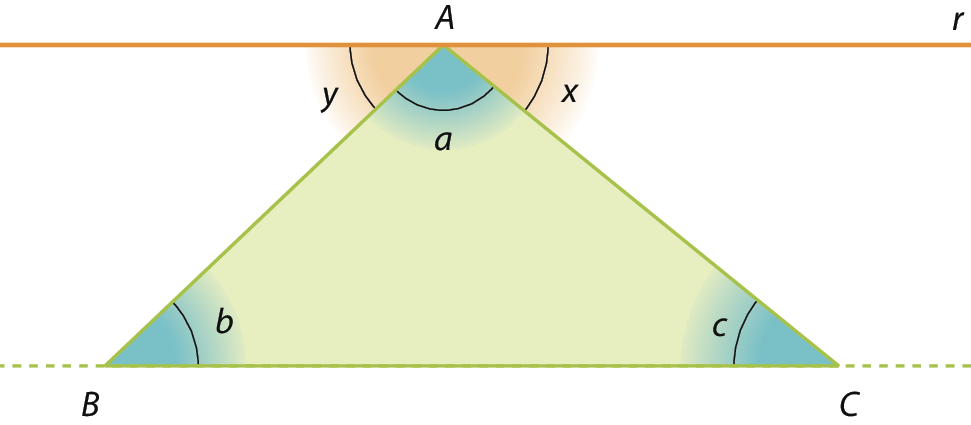
De acordo com a figura, temos:
• x = c, pois os ângulos de medidas de abertura x e c são alternos internos;
• y = b, pois os ângulos de medidas de abertura y e b são alternos internos;
• x + a + y = 180graus.
Então, temos: c + a + b = 180graus
Assim, mostramos que:
Em qualquer triângulo, a soma das medidas de abertura dos ângulos internos é 180graus.
Respostas e comentários
4. a) 2 centímetros ou 3 centímetros
4. b) 5 centímetros ou 6 centímetros
4. c) 10 centímetros, 8 centímetros ou 4 centímetros
5. Respostas na seção Resoluções neste manual.
6. infinitos
Orientações e sugestões didáticas
• A atividade 5 explora diversos conteúdos já vistos pelos estudantes e, com isso, é possível verificar se algum deles apresenta dificuldade em, por exemplo, aplicar a condição de existência de um triângulo, manusear o compasso e/ou o transferidor e classificar um triângulo em relação às medidas de comprimento dos lados e de abertura dos ângulos.
Ângulos nos triângulos
Objetivos
• Demonstrar que a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus.
• Reconhecer a relação entre um ângulo externo e dois ângulos internos não adjacentes de um triângulo qualquer.
• Favorecer o desenvolvimento da competência específica 3 da Bê êne cê cê.
Orientações
• Reproduza no quadro a demonstração de que a soma das medidas de abertura dos ângulos internos de um triângulo é 180graus e incentive a participação da turma. É importante enfatizar que, nessa demonstração, é empregada a relação entre os ângulos formados por retas paralelas cortadas por uma transversal. Se achar conveniente, retome esse assunto com a turma.
Competência específica 3: Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
Observação
Dadas duas retas paralelas cortadas por uma transversal, podemos destacar alguns pares de ângulos.
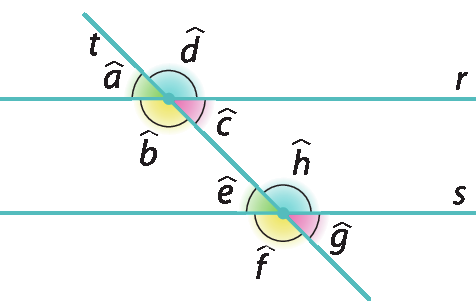
• Ângulos correspondentes:
Ângulo a e e, ângulos b e f, ângulos c e g, ângulos d e h• Ângulos alternos internos:
ângulos b e h, ângulos c e e• Ângulos alternos externos:
Ângulos a e g, ângulos d e fQuaisquer dois ângulos correspondentes são congruentes e, portanto, quaisquer dois ângulos alternos (internos ou externos) são congruentes, desde que as retas sejam paralelas.
Relação entre um ângulo externo e dois ângulos internos não adjacentes
Observe o triângulo á bê cê.
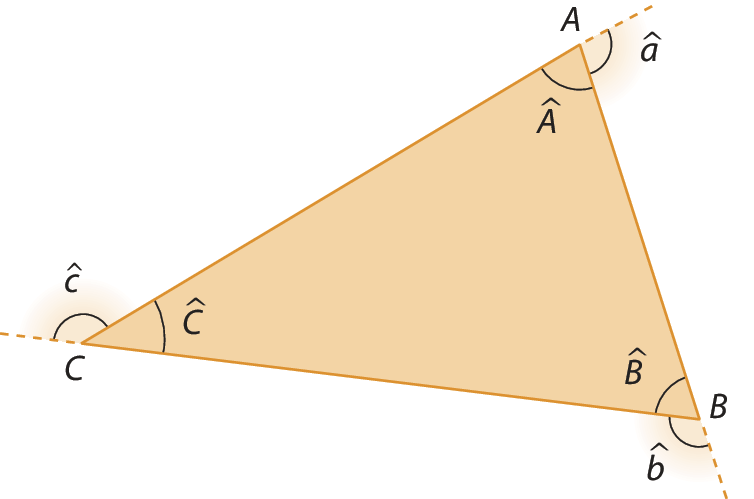
De acordo com a figura, temos:
medida de(
ângulo A interno) + medida de(
ângulo a externo) = 180graus
Então:
medida de(
ângulo A interno) = 180graus menos medida de(
ângulo a externo) (um)
Sabemos que:
medida de(
ângulo A interno) + medida de(
ângulo B interno) + medida de(
ângulo C interno) = 180graus (dois)
Substituindo um em dois, obtemos:
medida de(
ângulo A interno) + medida de(
ângulo B interno) + medida de(
ângulo C interno) = 180graus
180graus ‒ medida de(
ângulo a externo) + medida de(
ângulo B interno) + medida de(
ângulo C interno) = 180graus
medida de(
ângulo B interno) + medida de(
ângulo C interno) = 180graus menos 180graus + medida de(
ângulo a externo)
medida de(
ângulo B interno) + medida de(
ângulo C interno) = medida de(
ângulo a externo)
Considerando cada um dos outros ângulos externos da figura, chegaremos a:
medida de(
ângulo C interno) + medida de(
ângulo A interno) = medida de(
ângulo b externo)
medida de(
ângulo B interno) + medida de(
ângulo A interno) = medida de(
ângulo c externo)
Assim:
Em qualquer triângulo, a medida de abertura de um ângulo externo é igual à soma das medidas de abertura dos ângulos internos não adjacentes a ele.
Exemplo
Vamos determinar a medida x , em grau.
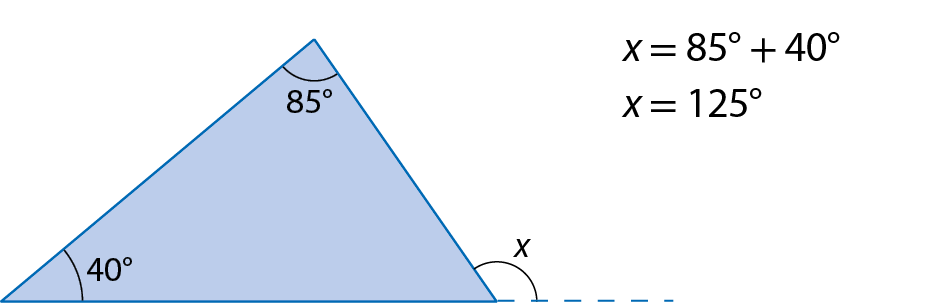
Orientações e sugestões didáticas
• Proponha aos estudantes que se reúnam com um colega e tentem descobrir, por meio de experimentações, a relação entre a medida de abertura de um ângulo externo e dois ângulos internos não adjacentes a ele em um triângulo qualquer. Essa experimentação pode ser feita com o auxílio de um transferidor ou utilizando um software de Geometria dinâmica. Depois, reproduza a demonstração no quadro com a participação da turma. A definição de ângulos suplementares e o fato de a soma das medidas de abertura dos ângulos internos de um triângulo ser 180graus são aplicados nessa demonstração.

ATIVIDADES
faça as atividades no caderno
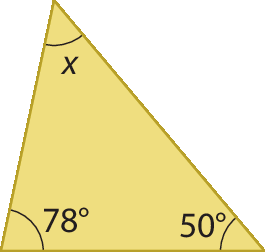
1. Encontre a medida x, em grau, em cada item.
a)
b)
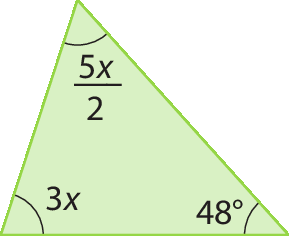
c)
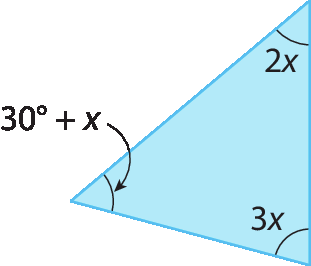
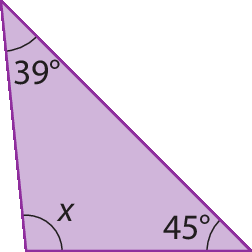
d)
2. As aberturas dos ângulos internos de um triângulo medem 26graus, 5x + 3graus e 4x + 7graus. Qual é o valor de x, em grau?
3. Quais são as medidas de abertura dos ângulos externos de um triângulo se as medidas de abertura de seus ângulos internos são x, x + 10graus e x + 20graus?
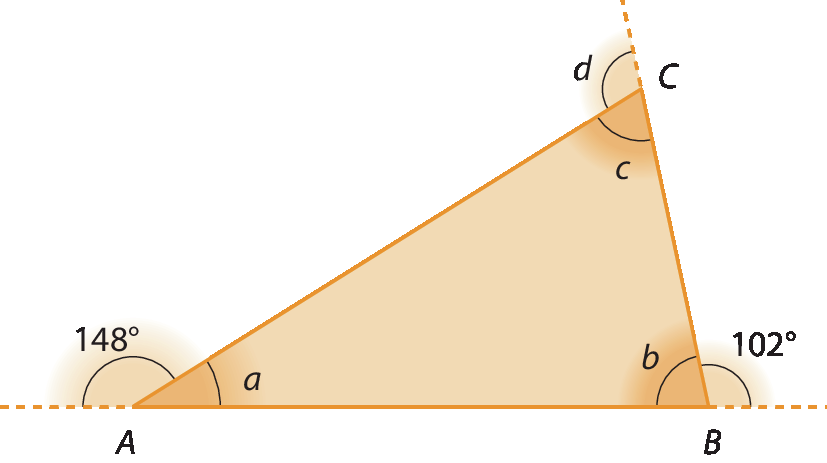
4. Determine as medidas a, b, c e d no triângulo á bê cê a seguir.
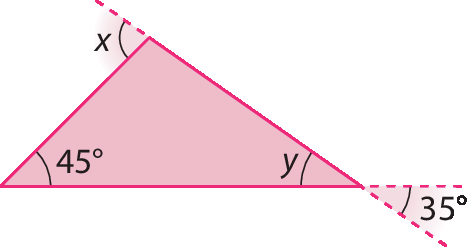
5. Determine x e y, em cada item.
a)
b)
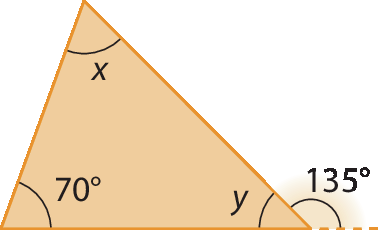
c)
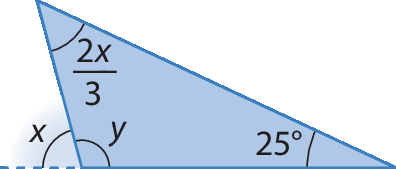
6. A abertura de um dos ângulos internos de um triângulo mede 35graus. A diferença entre as medidas de abertura dos outros dois ângulos é igual a 37graus. Quais são as medidas de abertura dos ângulos internos desse triângulo?
3 Pontos notáveis de um triângulo
Há quatro pontos em um triângulo que apresentam propriedades importantes e, por isso, são denominados pontos notáveis: baricentro, ortocentro, incentro e circuncentro. Vamos estudar um pouco sobre cada um desses pontos.
Intersecção das medianas: baricentro
As medianas de um triângulo são segmentos que têm uma extremidade em um dos vértices do triângulo e a outra extremidade no ponto médio do lado oposto a esse vértice.
Respostas e comentários
1. a) 52graus
1. b) 24graus
1. c) 25graus
1. d) 96graus
2. 16graus
3. 130graus, 120graus e 110graus
4. a = 32graus, b = 78graus, c = 70graus, d = 110graus
5. a) x = 80graus e y = 35graus
5. b) x = 65graus e y = 45graus
5. c) x = 75graus e y = 105graus
6. 54graus, 91graus e 35graus
Orientações e sugestões didáticas
• As atividades propostas requerem do estudante a mobilização dos conceitos dos campos da Geometria e da Álgebra, o que favorece o desenvolvimento da competência específica 3 da Bê êne cê cê.
• Após a resolução da atividade 6, peça aos estudantes que retomem o enunciado e confiram as respostas obtidas, ou seja, que façam os cálculos necessários com os valores encontrados para validá-los. É importante enfatizar essa validação de resultados em busca de maior autonomia do estudante.
Pontos notáveis de um triângulo
Objetivos
• Reconhecer e construir com régua e compasso os pontos notáveis de um triângulo.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco da Bê êne cê cê ao propor aos estudantes que, usando instrumentos de desenho, construam a mediana, a altura, a bissetriz e a mediatriz de um triângulo.
Orientações
• Neste tópico, serão sistematizados os conceitos de baricentro, ortocentro, incentro e circuncentro. Além de reconhecer esses pontos, os estudantes devem construí-los com o auxílio de régua e compasso, assim como resolver problemas que os envolvam.
• Antes de definir mediana, bissetriz, altura e mediatriz e suas respectivas intersecções (baricentro, incentro, ortocentro e circuncentro), pode-se identificá-las e obtê-las por meio de dobraduras em papel.
(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.
Observe como construir, usando régua e compasso, uma das medianas de um triângulo.
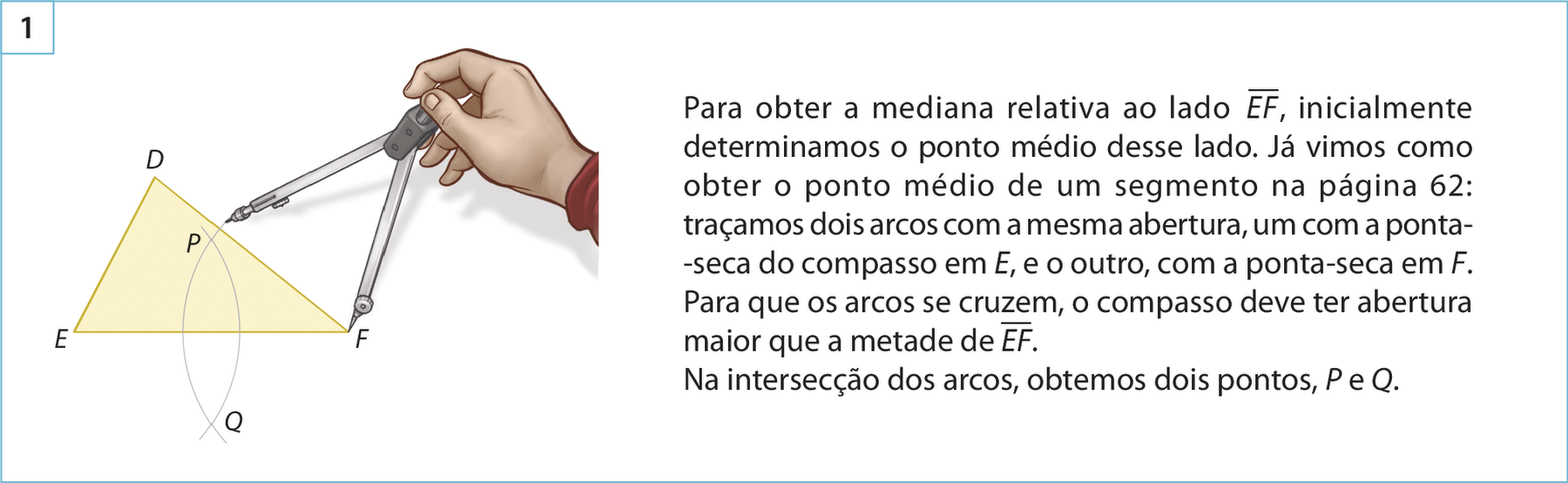
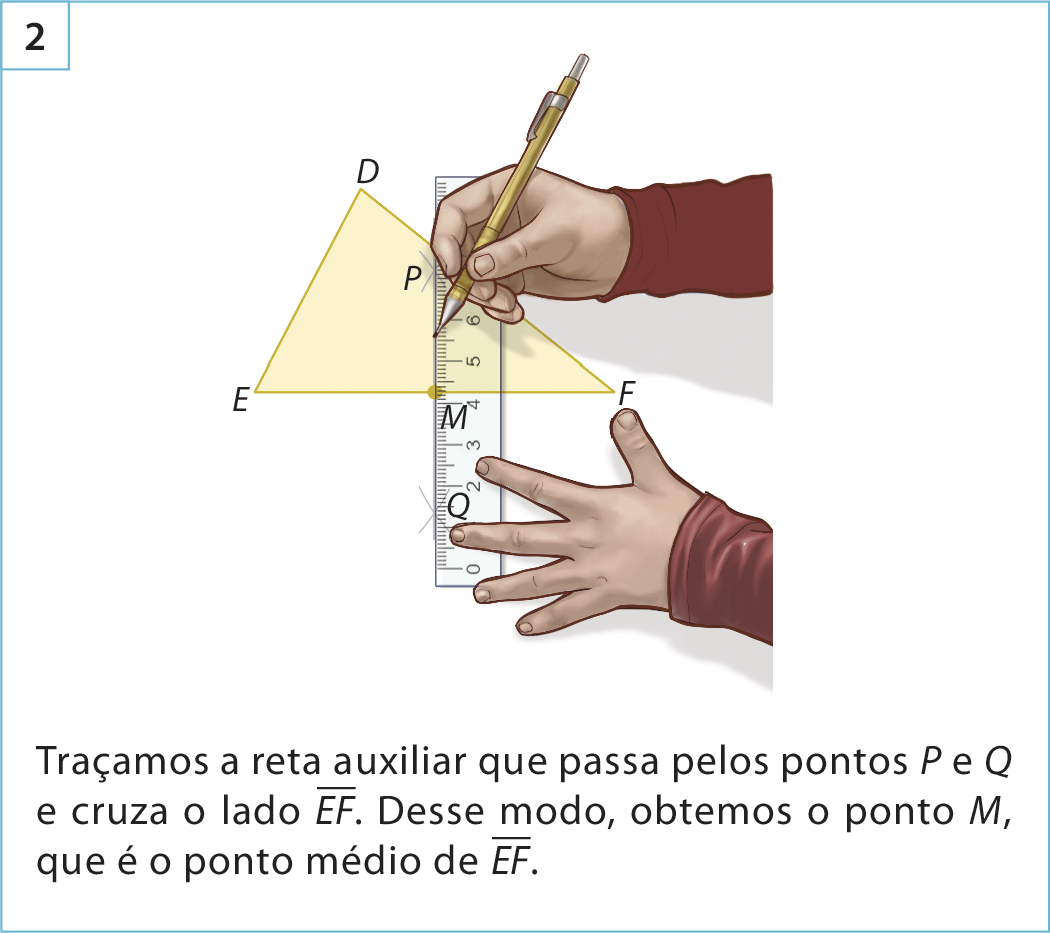
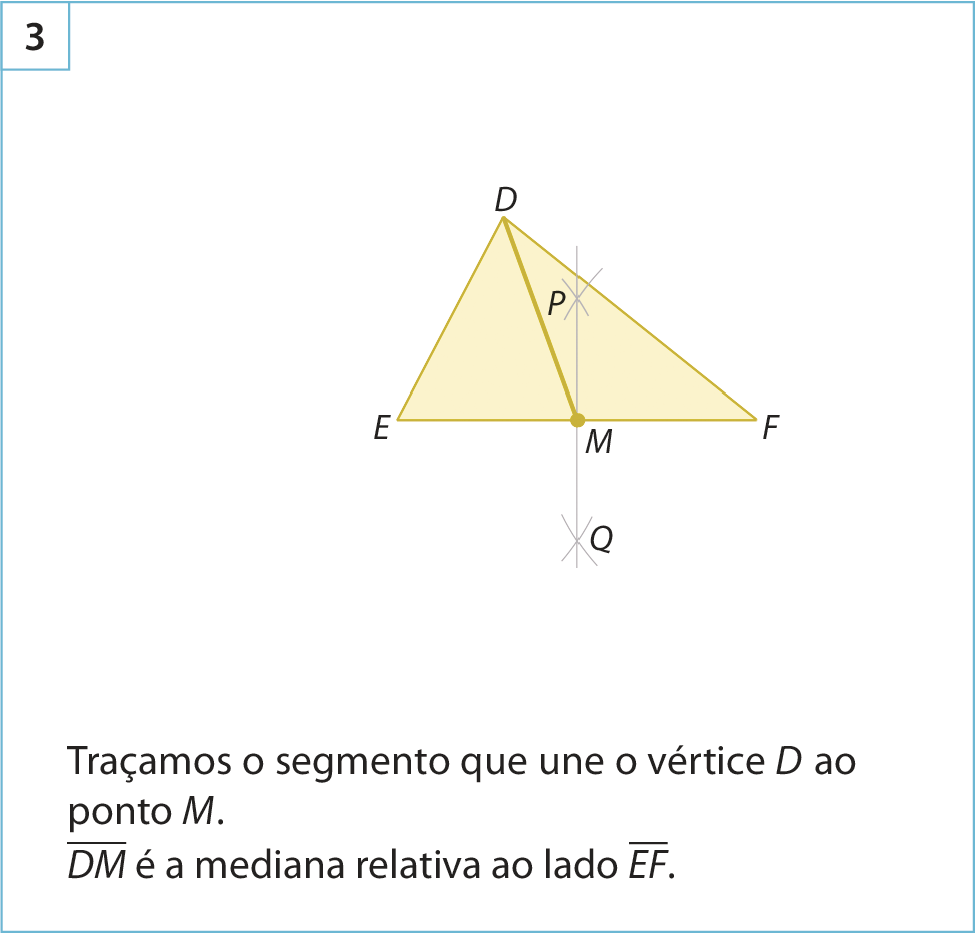
A intersecção das medianas de um triângulo determina um ponto chamado baricentro.
Observe o triângulo á bê cê .
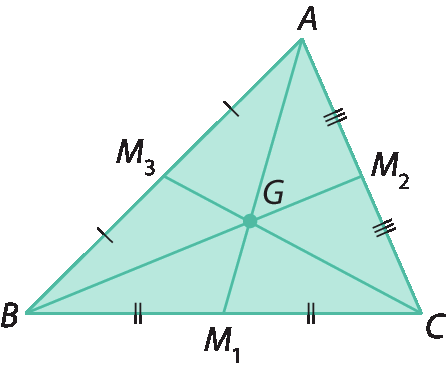
• múltiplos de é o ponto médio de
segmento BC; então,
segmento AM1é a mediana relativa ao lado
Segmento BC.
• múltiplos de é o ponto médio de
Segmento AC; então,
segmento BM2é a mediana relativa ao lado
segmento AC.
• múltiplos de é o ponto médio de
Segmento AB; então,
segmento CM3é a mediana relativa ao lado
segmento AB.
• G é o baricentro do triângulo.
Para fazer
O baricentro de um corpo qualquer é considerado seu centro de gravidade (ou centro de massa). Se apoiarmos um corpo em seu baricentro, ele ficará em equilíbrio. Vamos verificar?

a) Desenhe um triângulo em uma cartolina e determine o seu baricentro, conforme explicado anteriormente. Depois, recorte esse triângulo usando uma tesoura sem pontas.
b) Apoie o ponto que representa o baricentro do triângulo na ponta de um lápis. Então, verifique se o triângulo se manteve em equilíbrio.
Respostas e comentários
Para fazer: Resposta pessoal.
Orientações e sugestões didáticas
• Para obter as medianas e sua intersecção (baricentro) com dobraduras de papel, peça aos estudantes que recortem triângulos quaisquer (inicialmente triângulos escalenos e acutângulos) e sigam os procedimentos indicados a seguir.
1. Obter os pontos médios múltiplos de índice 1, múltiplos de índice 2 e múltiplos de índice 3 dos lados
Segmento BC,
Segmento ACe
Segmento AB
por dobradura de um lado sobre ele mesmo.
2. Traçar as medianas
Segmento AM1,
Segmento BM2e
Segmento CM3, obtendo o baricentro G.
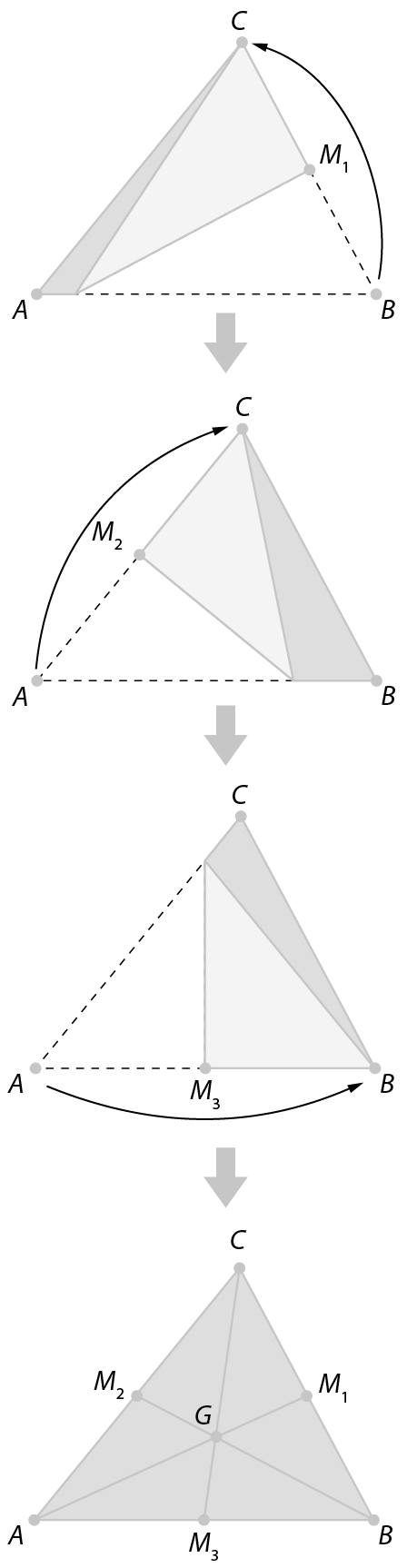
• Ao trabalhar o boxe Para fazer, os estudantes terão a oportunidade de verificar na prática que o triângulo fica em equilíbrio ao apoiar o baricentro na ponta do lápis. Caso o triângulo não fique em equilíbrio, peça aos estudantes que verifiquem se o baricentro foi obtido corretamente.

Informática e Matemática
faça as atividades no caderno
Investigando uma propriedade do baricentro
Nesta seção, vamos usar um software de Geometria dinâmica para construir e investigar uma propriedade do baricentro.
Construa
Siga os passos para construir um triângulo e obter seu baricentro.
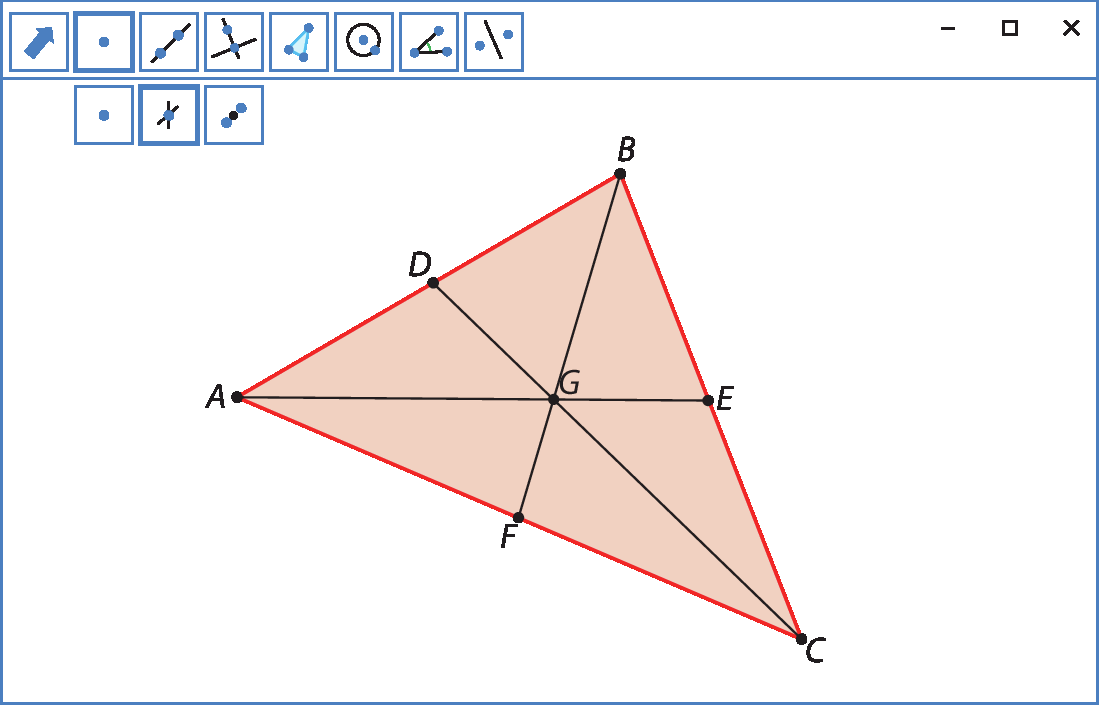
1º) Construa um triângulo á bê cê qualquer.
2º) Construa dê, ê e éfe, pontos médios dos lados
Segmento AB,
Segmento BC
e
Segmento AC, respectivamente.
3º) Trace a mediana relativa a cada lado do triângulo unindo, com um segmento de reta, o ponto médio de um lado ao vértice oposto a esse lado.
4º) Marque o ponto G, intersecção das medianas do triângulo. Esse ponto é o baricentro.
INVESTIGUE
Faça o que se pede usando as ferramentas do software.
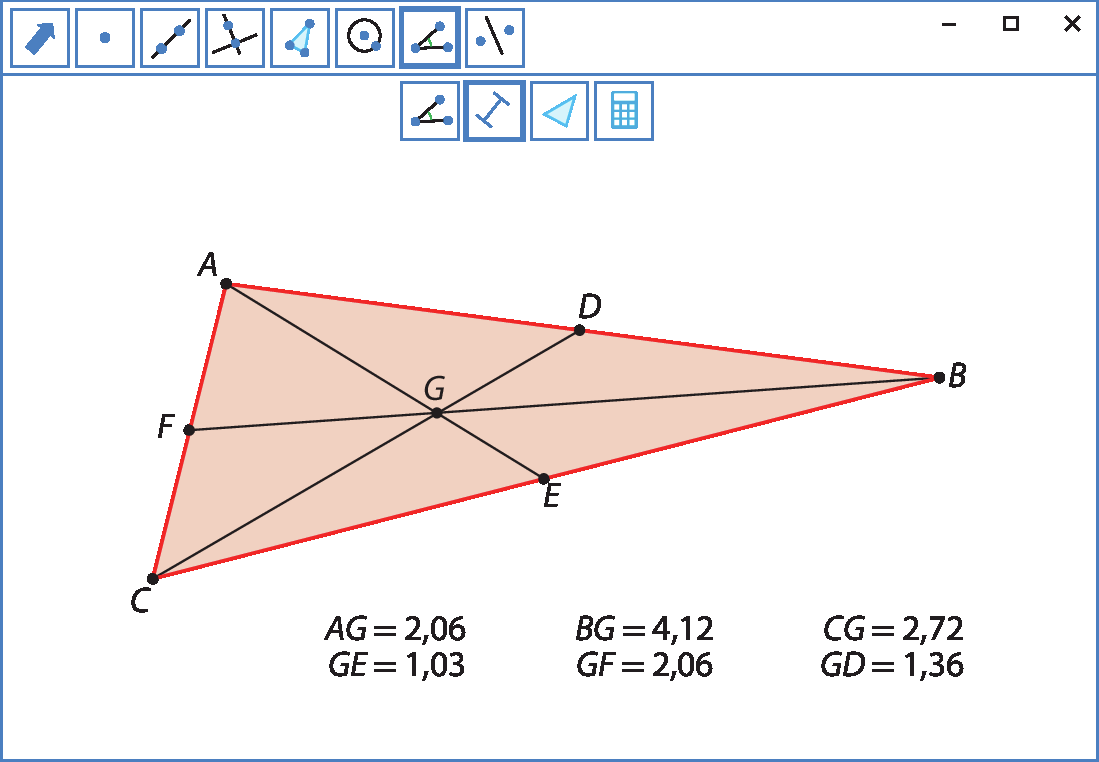
a) Meça as distâncias á gê e gê é. Você consegue perceber alguma relação entre essas medidas?
b) Meça as distâncias bê gê e e observe-as. Repita o procedimento com cê gê e gê dê. É possível perceber alguma relação entre os pares de medidas?
c)

Movimente os pontos a, B e C, mudando a configuração do triângulo, e observe se a relação entre os pares de medidas se mantém. Converse com um colega e verifique se ele observou a mesma relação que você.
Respostas e comentários
Investigue: Comentários em Orientações.
Orientações e sugestões didáticas
Informática e Matemática
Objetivos
• Investigar uma propriedade do baricentro utilizando um software de Geometria dinâmica.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco, da competência geral 5 e das competências específicas 2 e 4 da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco da Bê êne cê cê ao propor aos estudantes que construam, usando software de Geometria dinâmica, o baricentro de um triângulo qualquer.
Orientações
• Nesta seção, os estudantes deverão construir o baricentro de um triângulo qualquer e verificar, com base em observações sistemáticas, que esse ponto divide cada mediana do triângulo em duas partes, sendo que a parte que contém o vértice tem o dobro da medida de comprimento da parte que contém o ponto médio do lado, o que favorece o desenvolvimento da competência específica 4 da Bê êne cê cê.
• O uso do software promovido por esta seção contribui para que os estudantes desenvolvam a competência geral 5 e a competência específica 2 da Bê êne cê cê, uma vez que terão de assumir uma postura investigativa e produzir argumentos com base em observações sistemáticas de aspectos quantitativos (medida das partes em que o baricentro divide as medianas) fornecidos pelo software ao movimentar a construção realizada.
• No item a de Investigue, espera-se que os estudantes respondam que o comprimento de á gê mede o dobro do comprimento de gê é ou que o comprimento de gê é mede a metade do comprimento de á gê. No item b, espera-se que percebam que a medida de distância de cada vértice ao baricentro é o dobro da medida de distância entre o baricentro e o ponto médio do lado oposto. Ao responderem o item c, os estudantes devem verificar que a relação entre os pares de medidas se mantém e, depois, confirmar esta constatação com um colega.
(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.
Competência geral 5: Compreender, utilizar e criar tecnologias digitais de informação e comunicação de fórma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
Competência específica 2: Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
Competência específica 4: Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
Intersecção das alturas: ortocentro
As alturas de um triângulo são segmentos que têm uma extremidade em um dos vértices do triângulo e a outra na reta suporte do lado oposto ao vértice, formando um ângulo com abertura medindo 90graus com essa reta.
Observe como construir, usando régua e compasso, uma das alturas de um triângulo.
Atenção! Cuidado ao usar o compasso.
Recorde
Para obter a reta suporte de um segmento, basta prolongá-lo nos dois sentidos.

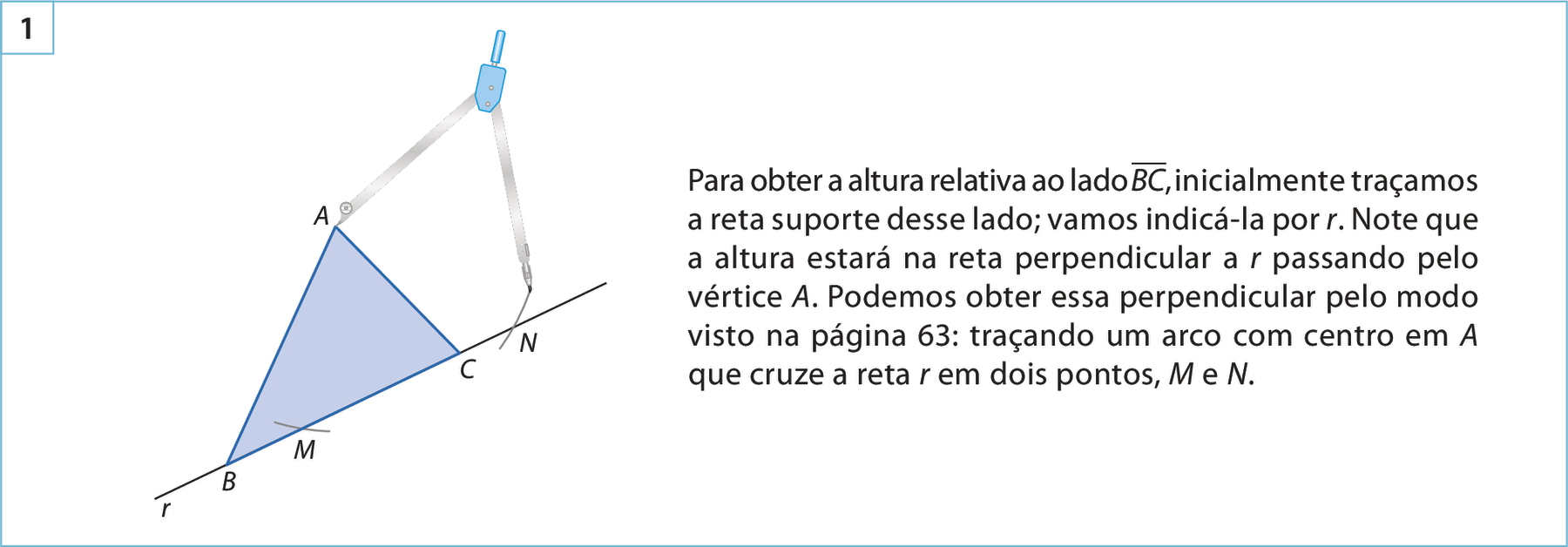
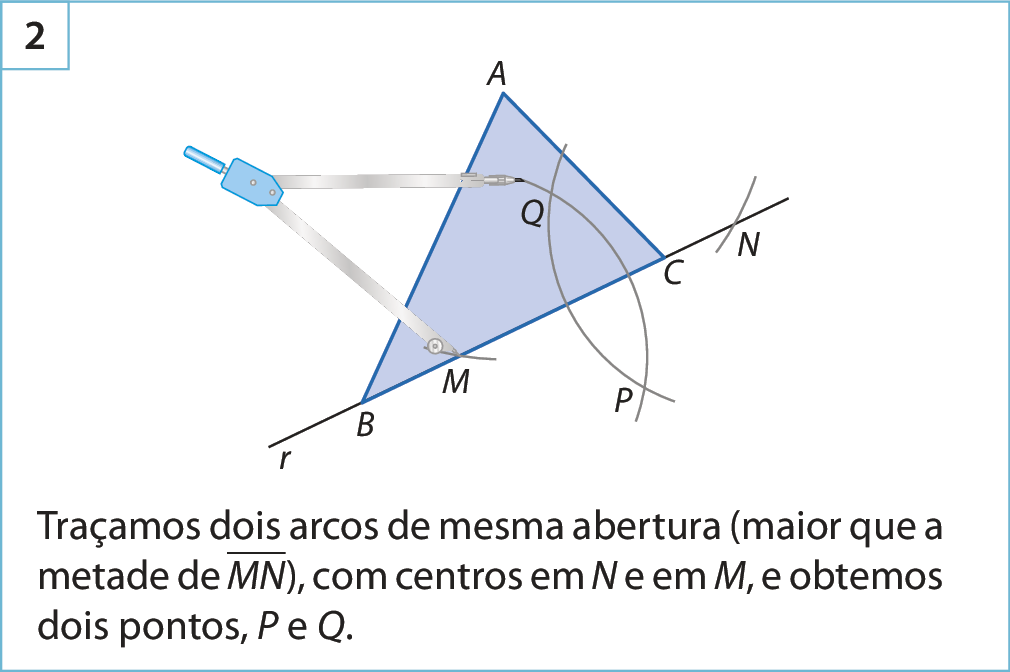
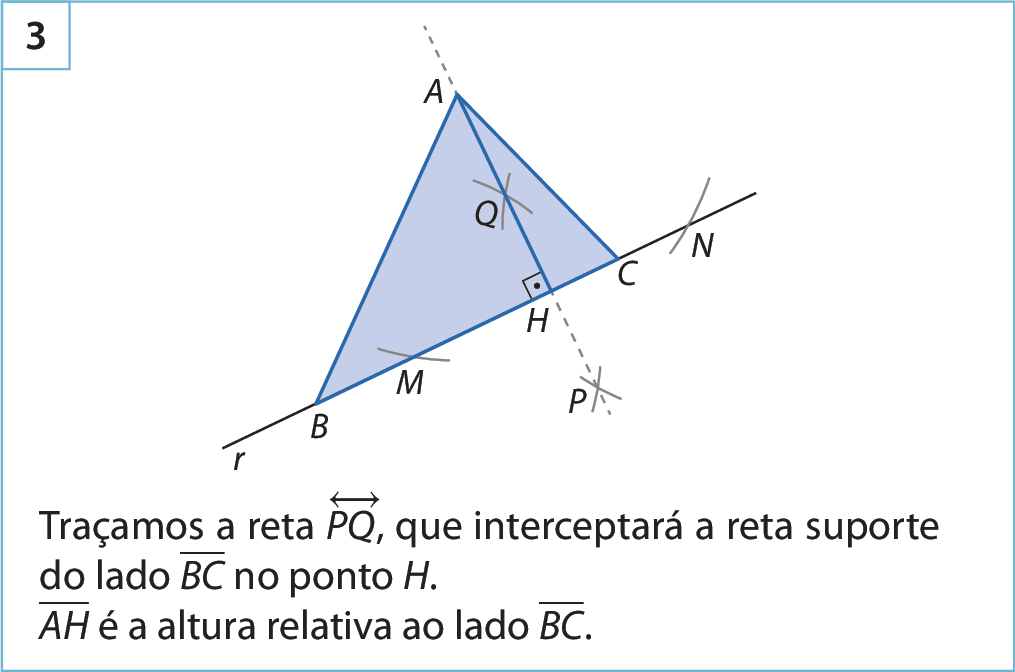
O ponto de encontro das retas suporte das alturas é denominado ortocentro.
Observe as alturas e o ortocentro de diferentes tipos de triângulo.
a) Triângulo acutângulo
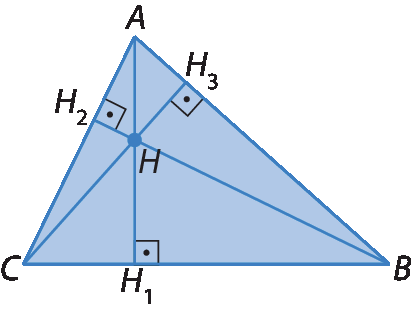
•
Segmento AH1é a altura relativa ao lado
Segmento BC.
•
Segmento BH2é a altura relativa ao lado
Segmento AC.
•
Segmento CH3é a altura relativa ao lado
Segmento AB.
• H é o ortocentro do triângulo á bê cê.
Nesse caso, as alturas encontram-se na região interna do triângulo.
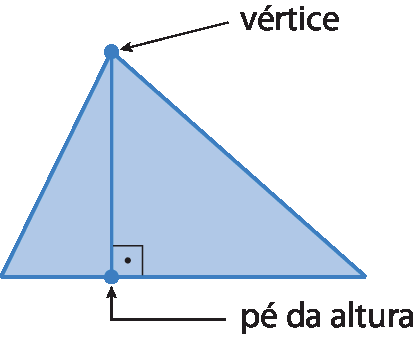
Observação
Uma das extremidades de uma altura é o vértice. A outra extremidade é um ponto denominado pé da altura.
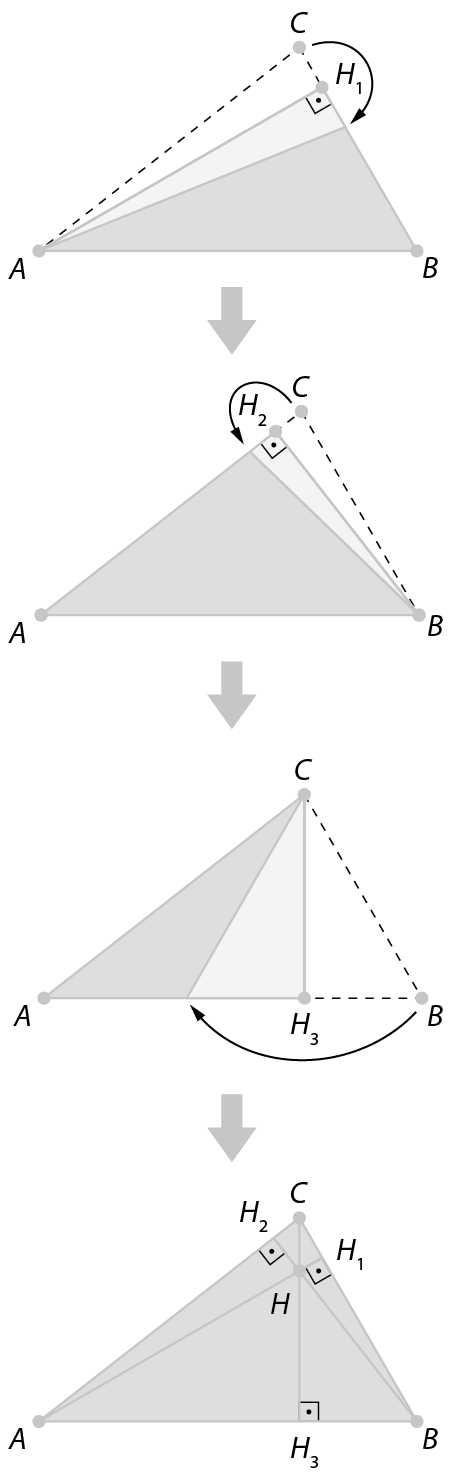
Orientações e sugestões didáticas
• Para obter as alturas e sua intersecção (ortocentro) com dobraduras de papel, peça aos estudantes que recortem triângulos quaisquer (exceto obtusângulos, pois nesse caso o ortocentro encontra-se na região externa do triângulo) e sigam os procedimentos indicados a seguir.
1. Dobrar um lado sobre ele mesmo, de modo que o vinco passe pelo vértice que não pertence a esse lado, obtendo as alturas
Segmento AH1,
Segmento BH2e
Segmento CH3.
2. As três alturas de um triângulo encontram-se em um mesmo ponto H, chamado ortocentro do triângulo.
b) Triângulo retângulo
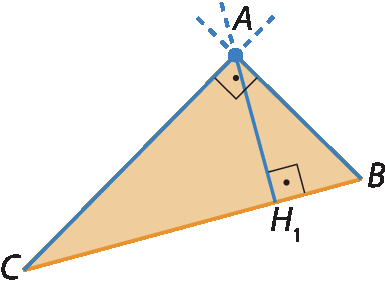
•
Segmento AH1é a altura relativa ao lado
Segmento BC.
•
Segmento BAé a altura relativa ao lado
Segmento AC.
•
Segmento CAé a altura relativa ao lado
Segmento AB.
• a é o ortocentro do triângulo á bê cê.
Nesse caso, uma das alturas coincide com o lado
Segmento AB; outra altura, com o lado
Segmento AC; e o ortocentro, com o vértice a.
c) Triângulo obtusângulo
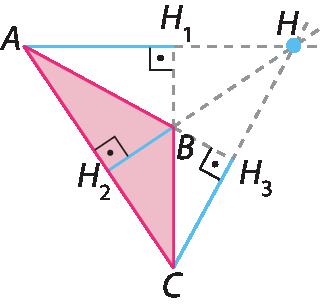
•
Segmento AH1é a altura relativa ao lado
Segmento BC.
•
Segmento BH2é a altura relativa ao lado
Segmento AC.
•
Segmento CH3é a altura relativa ao lado
Segmento AB.
• H é o ortocentro do triângulo á bê cê.
Nesse caso, as retas suporte das alturas de um triângulo obtusângulo encontram-se na região externa do triângulo.
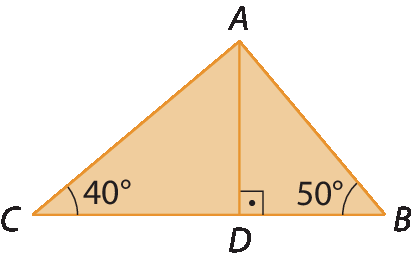
Desafio
Sabendo que
Segmento ADé a altura relativa ao lado
Segmento BCdo triângulo á bê cê, calcule a medida de abertura do ângulo
ângulo CAD.
Intersecção das bissetrizes: incentro
As bissetrizes de um triângulo são os segmentos que dividem os seus ângulos internos em dois ângulos congruentes e têm uma extremidade em um dos vértices do triângulo e a outra no lado oposto a esse vértice.
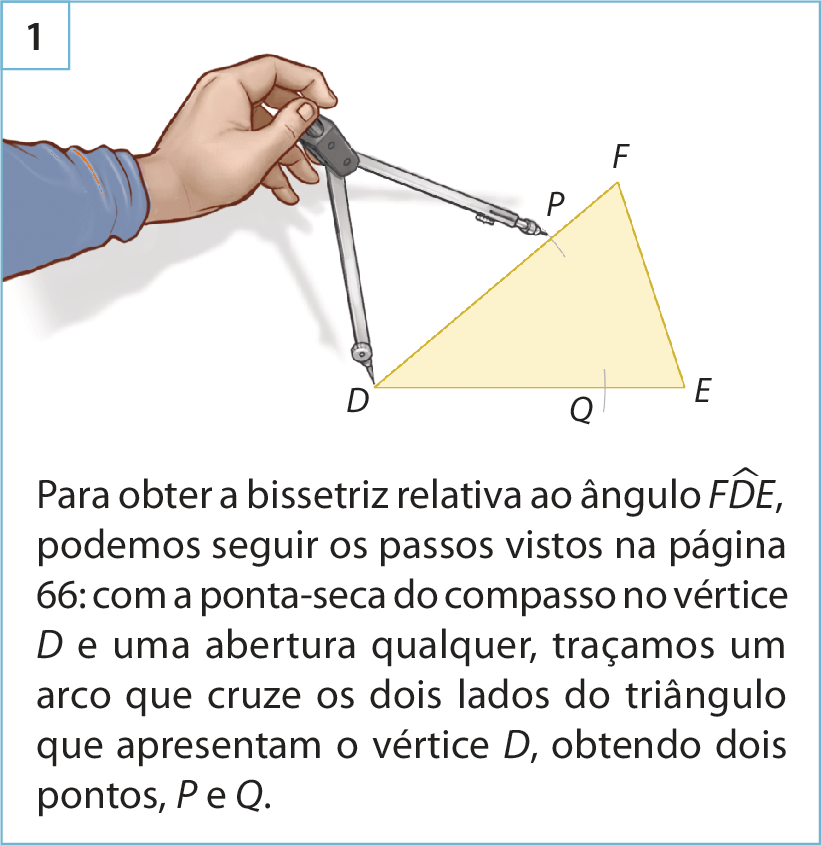
Observe como construir, usando régua e compasso, uma das bissetrizes de um triângulo.
Atenção! Cuidado ao usar o compasso.
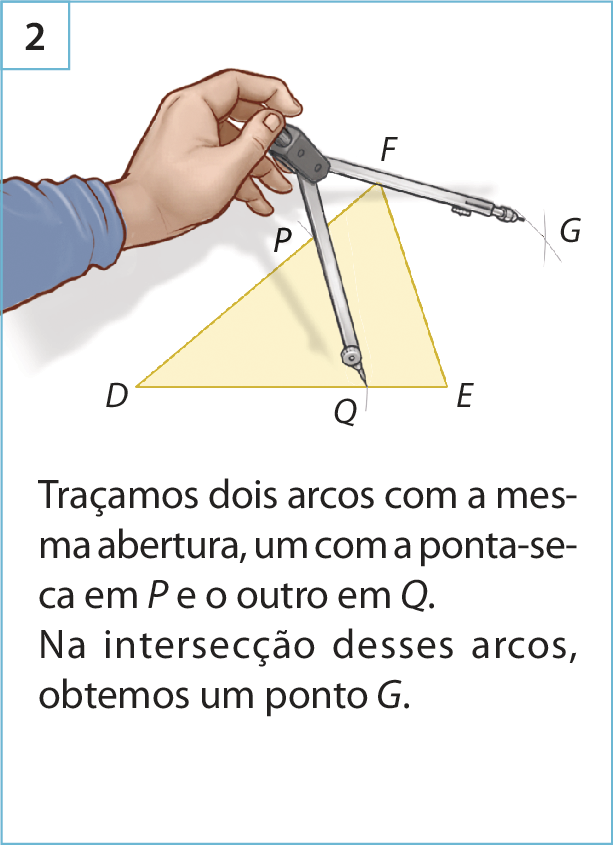
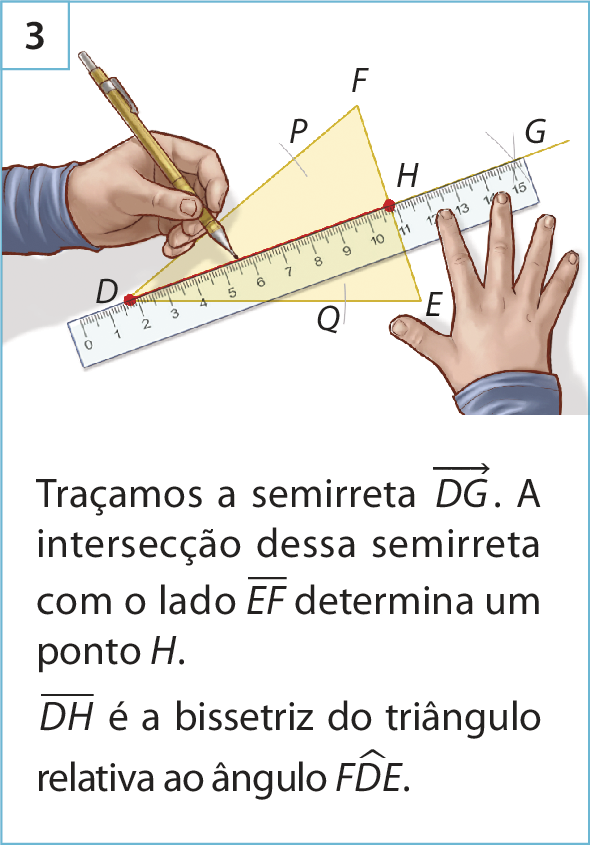
Respostas e comentários
Desafio: 50graus
Orientações e sugestões didáticas
• Resolução do boxe Desafio:
Observando o triângulo á dê cê, temos que o ângulo
Ângulo ADB.é externo a ele e sua abertura mede 90graus. Desse modo, utilizando a relação de um ângulo externo e dois ângulos internos não adjacentes, podemos fazer:
medida de(
Ângulo CAD.) + 40graus = 90graus
medida de(
Ângulo CAD.) = 50graus
Logo,
Ângulo CAD.mede 50graus.
• Para obter as bissetrizes e sua intersecção (incentro) com dobraduras de papel, peça aos estudantes que recortem triângulos quaisquer (inicialmente triângulos escalenos e acutângulos) e sigam o procedimento indicado a seguir.
Dobrar de modo que um lado fique sobreposto a outro, obtendo as bissetrizes internas
Segmento AS1,
Segmento BS2e
Segmento CS3, além do incentro I do triângulo.
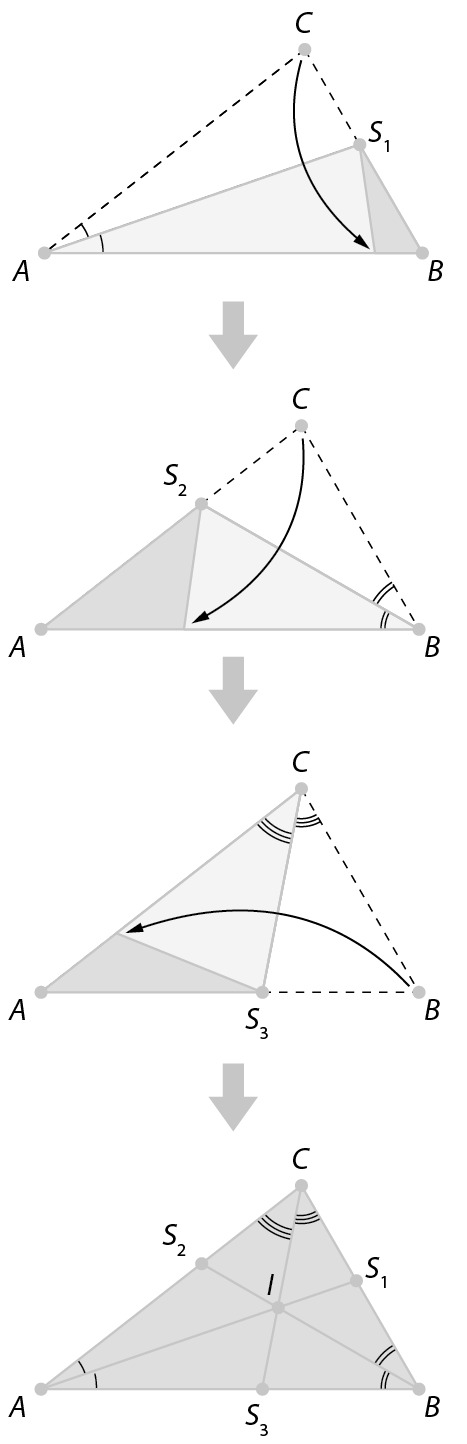
O ponto de encontro das três bissetrizes de um triângulo é denominado incentro.
No triângulo á bê cê a seguir:
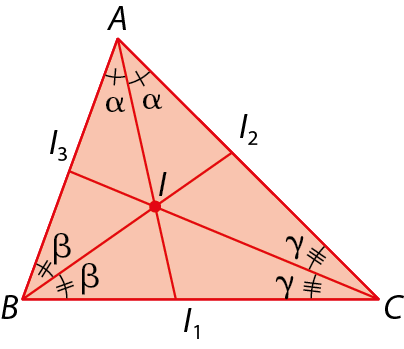
•
Segmento AI1é a bissetriz relativa ao ângulo
ângulo BAC;
•
Segmento BI2é a bissetriz relativa ao ângulo
ângulo ABC;
•
Segmento CI3é a bissetriz relativa ao ângulo
ângulo ACB;
• ih é o incentro do triângulo á bê cê.
Circunferência inscrita a um triângulo
A bissetriz equidista dos lados que formam o ângulo, e como o incentro é a intersecção das bissetrizes, esse ponto é equidistante dos três lados do triângulo. Portanto, a medida de distância é sempre a mesma entre o incentro e qualquer um dos lados do triângulo.
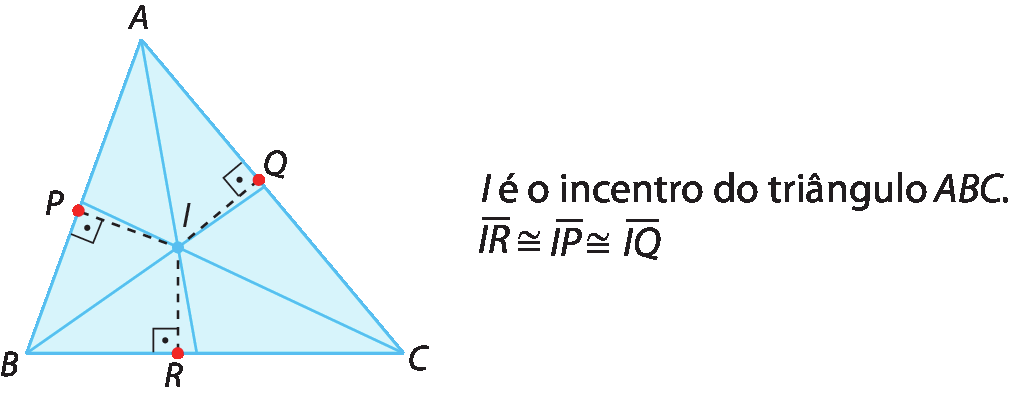
Observação
Usamos o símbolo

para indicar a congruência entre dois segmentos, entre dois ângulos ou entre dois polígonos.
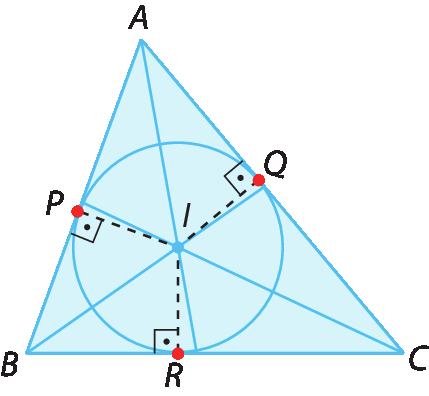
Assim, podemos traçar uma circunferência de centro ih e raio
Segmento IP, que contém apenas um ponto em comum com cada lado do triângulo. Essa circunferência é inscrita ao triângulo.
Intersecção das mediatrizes: circuncentro
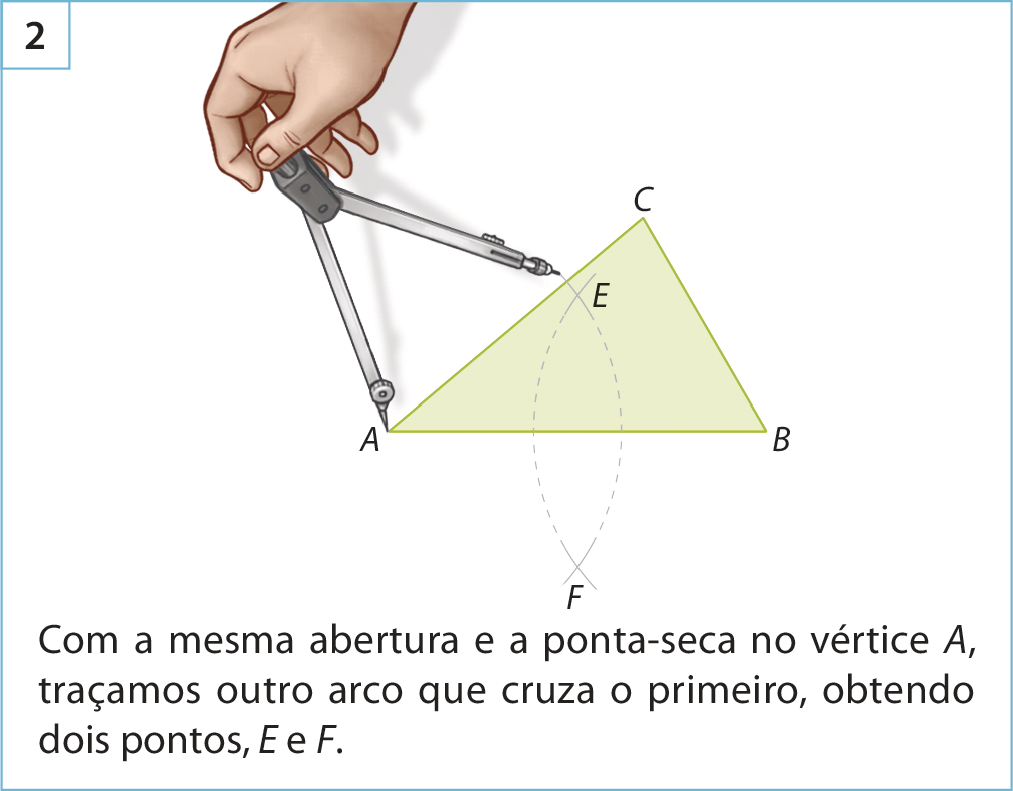
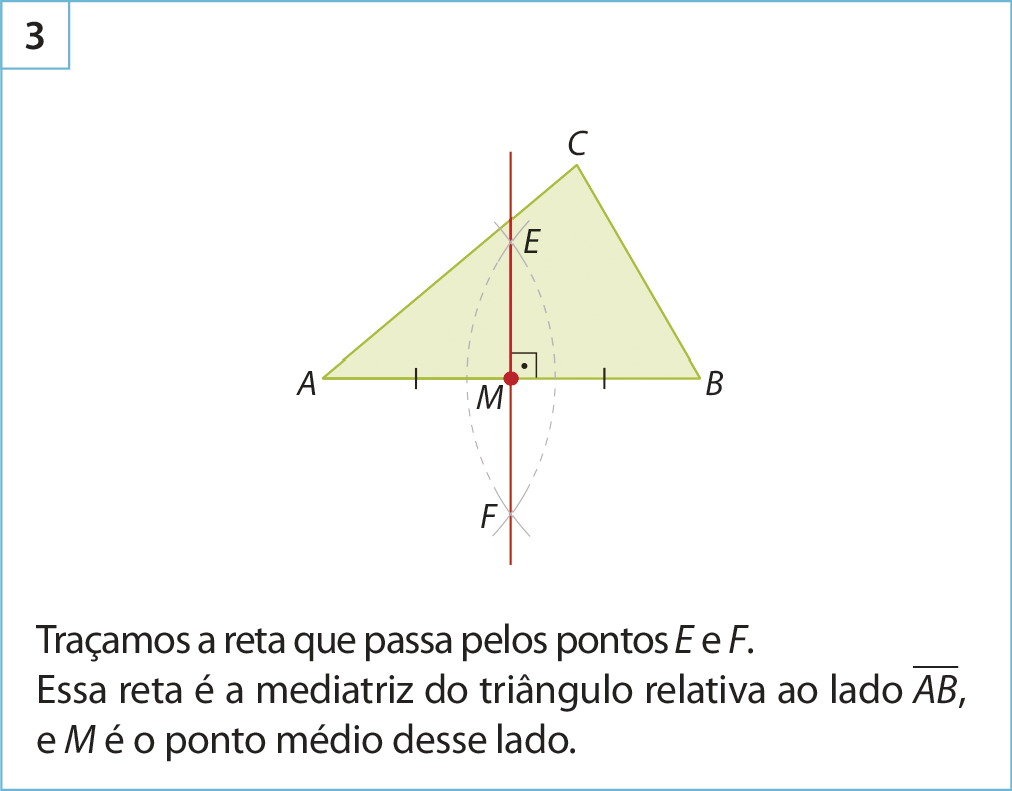
As mediatrizes de um triângulo são as mediatrizes de cada um de seus lados, ou seja, são as retas perpendiculares aos seus lados que passam pelo ponto médio do lado correspondente.
Observe como construir, usando régua e compasso, uma das mediatrizes de um triângulo.
Atenção! Cuidado ao usar o compasso.

Orientações e sugestões didáticas
• Por meio das construções feitas com papel é possível verificar experimentalmente algumas propriedades, como o fato de o incentro ser equidistante dos três lados do triângulo. Peça aos estudantes que tracem a circunferência inscrita ao triângulo que construíram.
• Oriente os estudantes para terem cuidado com o manuseio do compasso para a realização do trabalho proposto, a fim de que evitem acidentes.
• Proponha aos estudantes que obtenham as mediatrizes de triângulos quaisquer e sua intersecção (circuncentro) utilizando um software de Geometria dinâmica. Depois, oriente-os a verificar experimentalmente que esse ponto é equidistante dos três vértices dos triângulos e a construir a circunferência circunscrita a ele.
Um triângulo tem três mediatrizes. A intersecção delas determina um ponto chamado circuncentro.
No triângulo á bê cê:
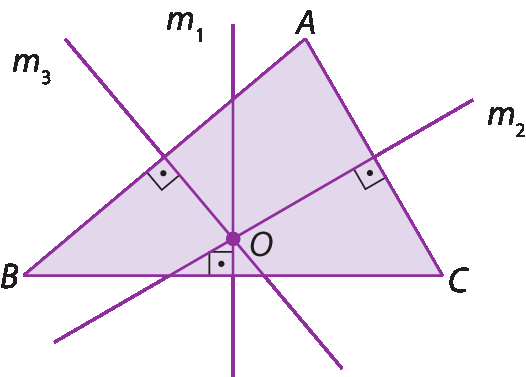
• míndice 1 é a mediatriz relativa ao lado
Segmento BC;
• míndice 2 é a mediatriz relativa ao lado
Segmento AC;
• míndice 3 é a mediatriz relativa ao lado
Segmento AB;
• óh é o circuncentro do triângulo á bê cê.
Circunferência circunscrita a um triângulo
Cada mediatriz equidista dos extremos do segmento, e como o circuncentro é a intersecção das mediatrizes, esse ponto é equidistante dos três vértices do triângulo. Portanto, a distância entre o circuncentro e qualquer um dos vértices do triângulo é sempre a mesma.
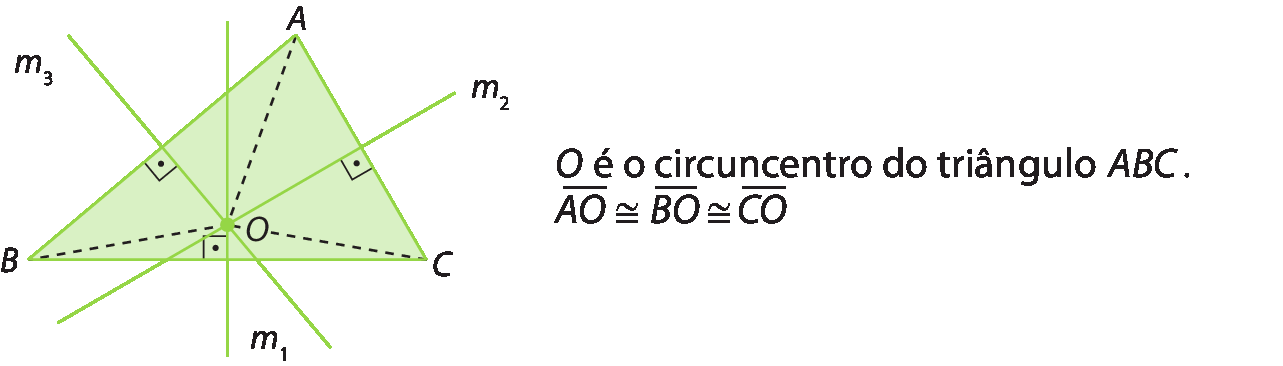
Assim, podemos traçar uma circunferência de centro óh e raio
Segmento AOque passa pelos três vértices do triângulo. Essa circunferência é circunscrita ao triângulo.
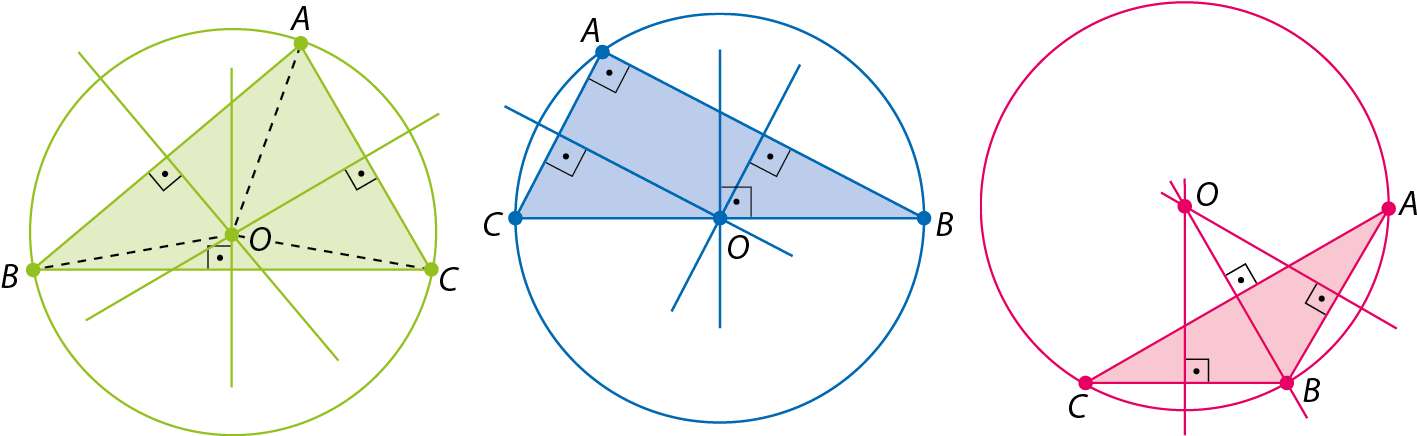

Orientações e sugestões didáticas
• Após fazer as construções em triângulos escalenos e acutângulos, oriente os estudantes a investigar esses mesmos elementos em triângulos retângulos, em triângulos obtusângulos e em triângulos isósceles e equiláteros. Eles deverão observar alguns casos curiosos, como o do triângulo obtusângulo, cujo ortocentro é um ponto externo ao triângulo, o do triângulo retângulo, cujo ortocentro é o vértice do ângulo reto, e o do triângulo equilátero, cujos baricentro, incentro, circuncentro e ortocentro coincidem.

ATIVIDADES
faça as atividades no caderno
Atenção! Cuidado ao usar o compasso.
1. Um quadro ficará em posição de equilíbrio se o ponto pelo qual for pendurado estiver na mesma linha vertical que seu centro de gravidade.
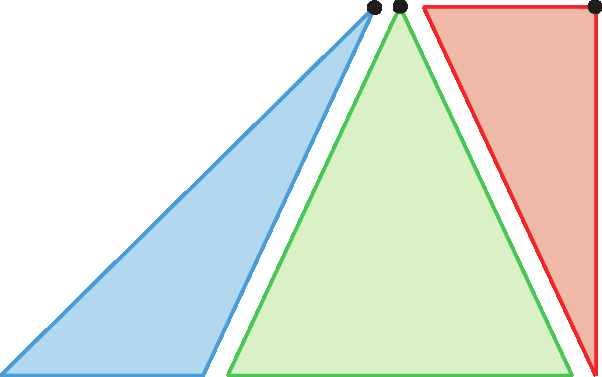
• Qual dos quadros triangulares apresentados fica em equilíbrio quando pendurado pelo ponto indicado?
2. Durante a construção de um condomínio formado por três prédios, a construtora pretende estocar os materiais em local que esteja à mesma distância dos três prédios. Sabendo que esses prédios não estarão alinhados, qual é o ponto mais próximo dos três?
3. No triângulo á bê cê,
reta ADé a mediatriz e
Segmento ADé a altura relativas ao lado
Segmento BC.
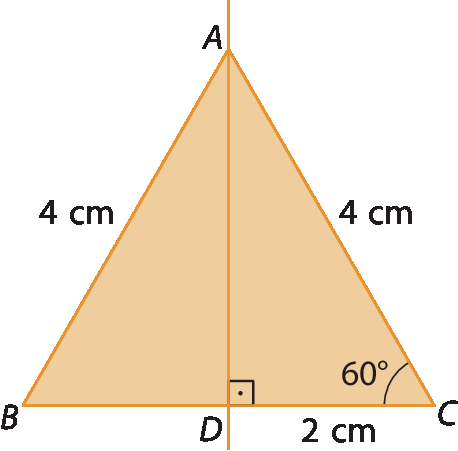
a) Qual é a medida de abertura do ângulo
DAC?
b) Qual é a medida do perímetro do triângulo á bê cê, ou seja, a soma das medidas de comprimento de seus lados?
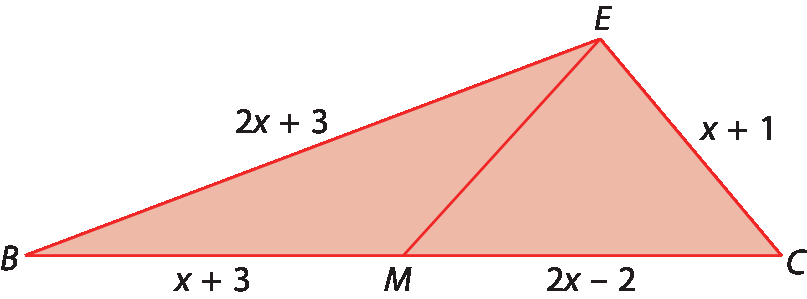
4. Calcule a medida do perímetro do triângulo sabendo que
Segmento EMé a mediana relativa ao lado
Segmento BC.
5. Construa um triângulo equilátero e encontre o baricentro, o ortocentro e o incentro dele.
a) O que você observou?
b)

Converse com um colega, e verifiquem se vocês chegaram à mesma conclusão.
6.

Reúna-se com um colega e leiam o texto.
Em um triângulo qualquer, o incentro (I) do triângulo é único.
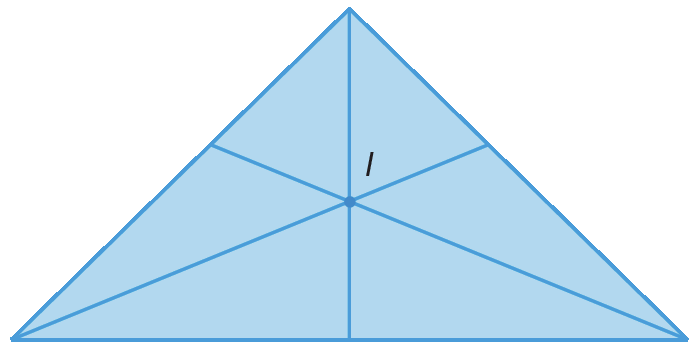
Por isso, é possível traçar apenas uma circunferência inscrita nesse triângulo.
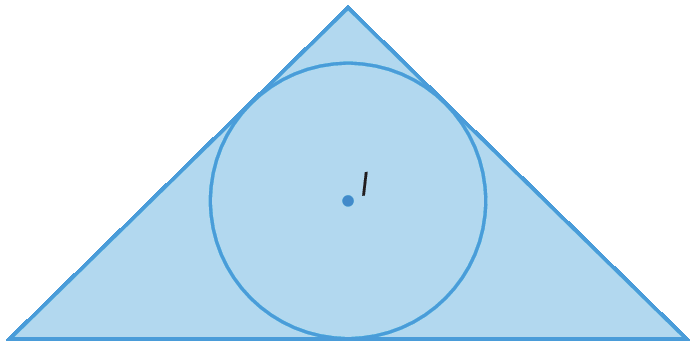
Agora, respondam no caderno.
• Dada uma circunferência, é possível traçar apenas um triângulo, de maneira que essa circunferência seja inscrita nele?
4 Congruência
Dizemos que segmentos congruentes são aqueles que têm mesma medida de comprimento, e ângulos congruentes, os que têm mesma medida de abertura. Agora, vamos ampliar o estudo sobre a congruência de duas figuras planas.
Respostas e comentários
1. o quadro verde
2. O circuncentro do triângulo com vértices nos três prédios.
3. a) 30graus
3. b) 12 centímetros
4. 35
5. a) Os três pontos coincidem.
5. b) Espera-se que os estudantes concluam que as construções feitas por eles sugerem que nos triângulos equiláteros, o baricentro, o ortocentro e o incentro são pontos coincidentes.
6. Resposta na seção Resoluções neste manual.
Orientações e sugestões didáticas
• Na atividade 2, espera-se que os estudantes tracem um triângulo pelos três pontos que representam os prédios e as respectivas mediatrizes desse triângulo. Dessa maneira, é possível obter o ponto C (circuncentro do triângulo) que é equidistante dos vértices do triângulo.
• Na atividade 4, é necessário determinar o valor de x para calcular a medida do perímetro do triângulo . Os estudantes devem estar atentos à informação de que
Segmento EMé a mediana relativa ao lado
Segmento BC. Verifique se eles já estão familiarizados com o termo “mediana” e, se necessário, retome o conceito com a turma.
Congruência
Objetivo
• Compreender o conceito de congruência de triângulos e reconhecer triângulos congruentes segundo um dos casos: éle á éle, éle éle éle, á éle á , e éle á á ó.
Orientações
• Neste tópico, são propostas diferentes situações que exploram os casos de congruência de triângulos. Os casos são: éle á éle, éle éle éle, á éle á , éle á á ó e o do triângulo retângulo.
Para entender o conceito de congruência de duas figuras, imagine que seja possível “deslocar” uma delas até que fique perfeitamente sobreposta à outra. Essa é a ideia da congruência.
Dizemos que dois polígonos são congruentes quando atendem simultaneamente a estas duas condições:
• os lados correspondentes são congruentes;
• os ângulos correspondentes são congruentes.
Observe os triângulos na malha quadriculada a seguir.
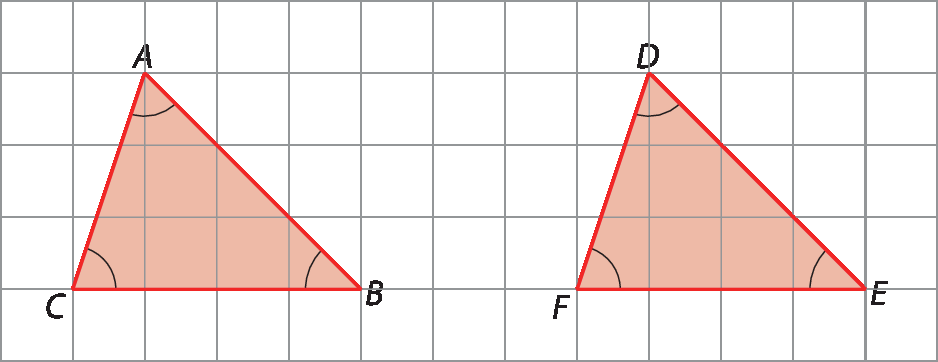
Os lados correspondentes são congruentes:
Segmento AB congruente segmento DE, segmento BC congruente segmento EF, segmento CA congruente segmento FDOs ângulos correspondentes são congruentes:
ângulo A congruente ângulo D, ângulo B congruente ângulo E, ângulo C congruente ângulo FLogo, o triângulo á bê cê é congruente ao triângulo dê ê éfe. Indicamos essa congruência assim:
△á bê cê ≅ △dê ê éfe
Note que, para concluir que os triângulos são congruentes, verificamos as congruências entre os lados correspondentes e entre os ângulos correspondentes. Porém, não é necessário checar todas essas medidas: se verificarmos a congruência de alguns elementos, escolhidos convenientemente, a congruência dos outros já estará garantida.
É importante observar que há uma ordem correta para representar a congruência. Devemos escrever os vértices na ordem em que ocorrem as correspondências dos ângulos e dos lados.
No exemplo anterior, o triângulo á bê cê não é congruente ao triângulo éfe dê é, pois os ângulos
ângulo A e ângulo F, ângulo B e ângulo D, ângulo C e ângulo Enão são congruentes, assim como não são congruentes os lados
Segmento ABe
Segmento FD,
Segmento BCe
Segmento DE, e
Segmento CAe
Segmento EF.
A seguir, veremos casos em que se relacionam condições mínimas para garantir a congruência de dois triângulos.
Casos de congruência de triângulos
Caso lado-ângulo-lado (éle á éle)
Dois triângulos são congruentes se têm um ângulo correspondente congruente e os dois lados correspondentes que formam esse ângulo também congruentes.
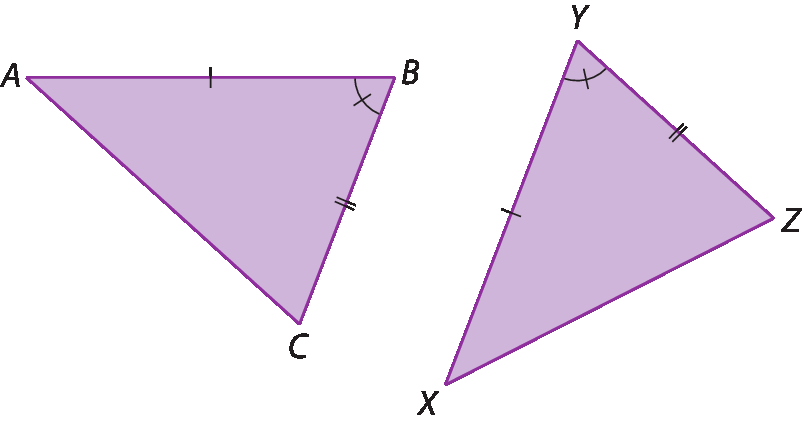
• Lado

• Ângulo

• Lado

Então: △á bê cê ≅ △XYZ
Orientações e sugestões didáticas
• Ao trabalhar o conceito de congruência de triângulos, pode-se comentar com os estudantes que o modo usual de representar que dois triângulos, á bê cê e , são congruentes (á bê cê≅ ) indica que o vértice a corresponde ao vértice á linha, o vértice bê corresponde ao vértice e o vértice cê corresponde ao vértice .
Lembre-se: Escreva no caderno!
Caso lado-lado-lado (éle éle éle)
Dois triângulos que têm os três lados correspondentes congruentes são congruentes.
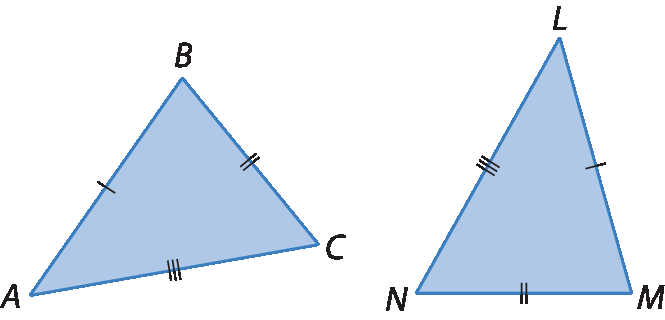
• Lado

• Lado

• Lado

Logo: △á bê cê ≅ △LMN
Exemplo
Vamos verificar se os triângulos á bê cê e cê dê á a seguir são congruentes.
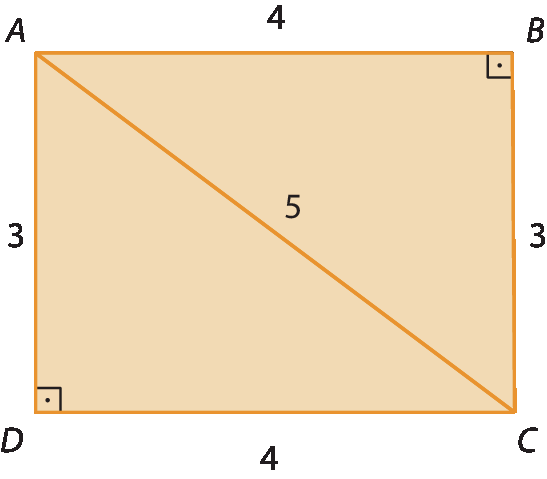
• Lado

A bê = CD = 4
• Lado

BC = dê á = 3
• Lado

á cê = 5 (
Segmento ACé comum aos dois triângulos)
Logo: △á bê cê ≅ △cê dê á
Para pensar
Observe os triângulos á bê cê e pê quê érre.
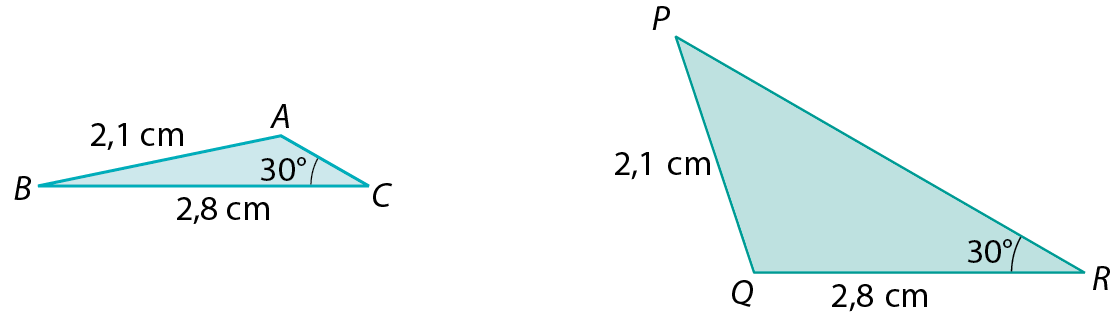
a) Os triângulos têm dois lados correspondentes congruentes?
b) Os triângulos têm um ângulo correspondente congruente?
c) Podemos dizer que esses triângulos são congruentes pelo caso éle á éle? Justifique.
Caso ângulo-lado-ângulo (á éle á )
Dois triângulos são congruentes se têm, respectivamente, um lado congruente e os dois ângulos adjacentes a esse lado também congruentes.
Observe os triângulos á bê cê e a seguir.
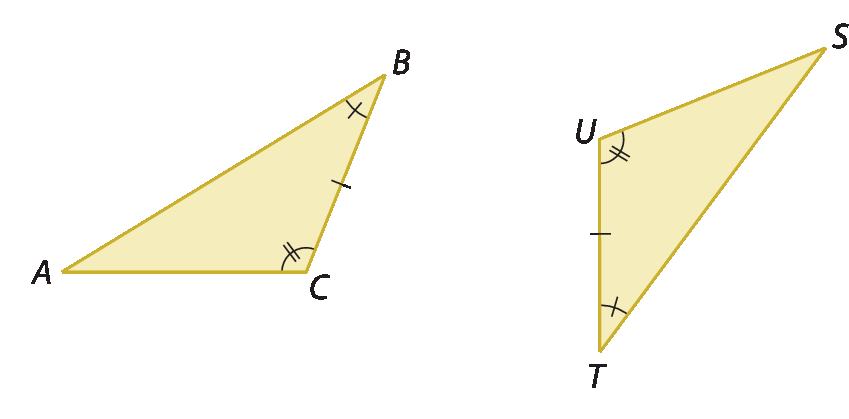
• Ângulo

• Lado

• Ângulo

Então: △á bê cê ≅ △
Respostas e comentários
Para pensar: a) sim; b) sim; c) Não, pois pelo caso éle á éle, o ângulo congruente deve estar compreendido entre os lados congruentes, o que não acontece neste caso.
Orientações e sugestões didáticas
• Comente com os estudantes que, para verificar que dois triângulos são congruentes, não é preciso verificar as seis congruências, três entre lados e três entre ângulos. Existem condições mínimas para que dois triângulos sejam congruentes. Ao apresentar os casos de congruência de triângulos, enfatize que é necessário verificar apenas a congruência de três pares de elementos correspondentes em determinada ordem.
• É interessante também comentar com os estudantes que os casos de congruência de triângulos podem ser aplicados para determinar elementos desconhecidos nos triângulos e para demonstrar algumas propriedades importantes da Geometria.
• No item c do Bócsi Para pensar, espera-se que os estudantes percebam que a ordem dos elementos congruentes deve ser respeitada para que os dois triângulos sejam congruentes. Nesse caso, para os triângulos serem congruentes, os ângulos congruentes deveriam ser aqueles formados entre os lados de medidas de comprimento 2,1 centímetros e 2,8 centímetros. Portanto, apesar de os triângulos terem dois lados congruentes e um ângulo congruente, o triângulo á bê cê não é congruente ao triângulo PQR.
Exemplo
Vamos verificar se os triângulos á bê cê e é dê cê a seguir são congruentes.
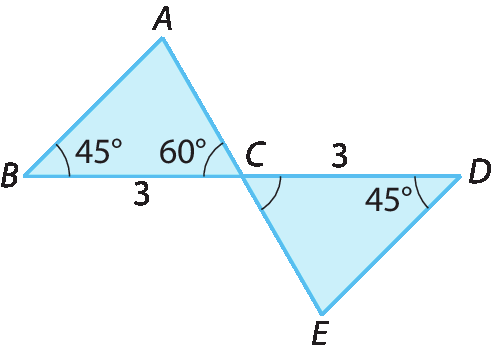
• Ângulo

medida de(
ângulo ABC) = medida de(
ângulo EDC) = 45graus
• Lado

BC = DC = 3
• Ângulo

medida de(
ângulo BCA) = medida de(
ângulo DCE) = 60graus
Então: △á bê cê ≅ △é dê cê
Recorde
Quando dois ângulos têm o vértice comum e os lados de um deles são semirretas opostas aos lados do outro, eles são denominados opostos pelo vértice (ó pê vê). Dois ângulos opostos pelo vértice são sempre congruentes.
Na figura do exemplo anterior, os ângulos
ângulo BCAe
ângulo DCEsão congruentes porque são opostos pelo vértice (ó pê vê).
Para analisar
Observe os triângulos á bê cê e dê ê éfe.
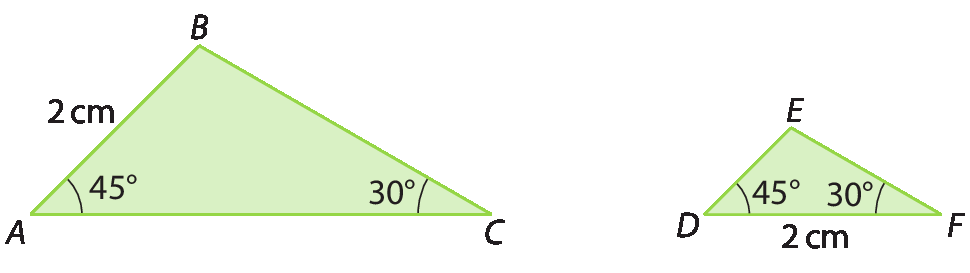
Podemos dizer que esses triângulos são congruentes pelo caso á éle á ? Justifique sua resposta no caderno.
Caso lado-ângulo-ângulo oposto (éle á á ó)
Dois triângulos são congruentes se têm um lado correspondente congruente e se um dos ângulos adjacentes a esse lado e o ângulo oposto a ele também forem congruentes aos respectivos ângulos correspondentes.
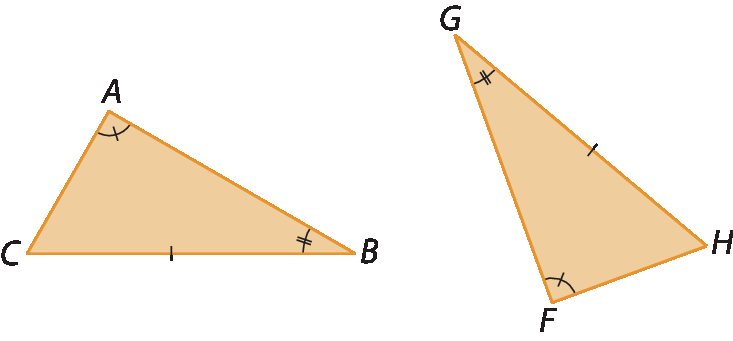
• Lado

• Ângulo

• Ângulo oposto

Então: △á bê cê ≅ △FGH
Exemplo
Vamos verificar se os triângulos á bê cê e é dê cê a seguir são congruentes.
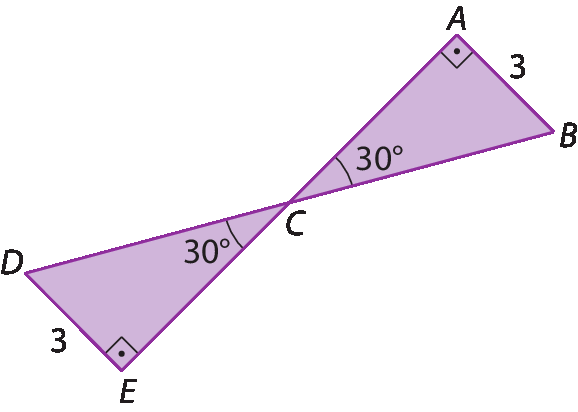
• Lado

A bê = ê de = 3
• Ângulo

• Ângulo oposto

Logo: △á bê cê ≅ △é dê cê
Respostas e comentários
Para analisar: Não, pois, pelo caso á éle á , o lado congruente deve ser o compreendido entre os ângulos congruentes correspondentes, o que não acontece nesse caso.
Orientações e sugestões didáticas
• É interessante que os estudantes observem que existem triângulos que não são congruentes, mas que têm dois ângulos correspondentes de mesma medida de abertura e um dos lados também de mesma medida de comprimento. Se julgar necessário, desenhe um exemplo no quadro.
• O boxe Para analisar permite que os estudantes observem que existem triângulos não congruentes que apresentam dois ângulos correspondentes de mesma medida de abertura e um dos lados também de mesma medida de comprimento. Enfatize que, para serem congruentes pelo caso á éle á , o comprimento do lado
Segmento ACdo triângulo á bê cê teria de medir 2 centímetros.
Caso especial do triângulo retângulo: hipotenusa-cateto ()
Sabemos que um triângulo é retângulo quando um de seus ângulos internos é reto, ou seja, tem medida de abertura igual a 90graus.
Em um triângulo retângulo, os lados recebem nomes especiais:
• os lados que determinam o ângulo reto são denominados catetos;
• o lado oposto ao ângulo reto é denominado hipotenusa.
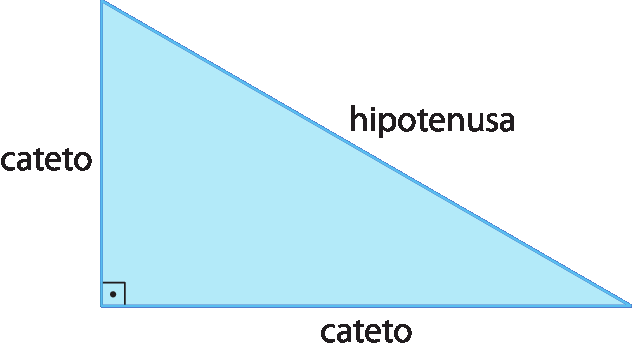
Os outros casos de congruência estudados podem ser aplicados a qualquer tipo de triângulo, mas o caso a seguir só pode ser utilizado em triângulos retângulos.
Dois triângulos retângulos são congruentes se um tem um dos catetos e a hipotenusa congruentes aos lados correspondentes do outro.
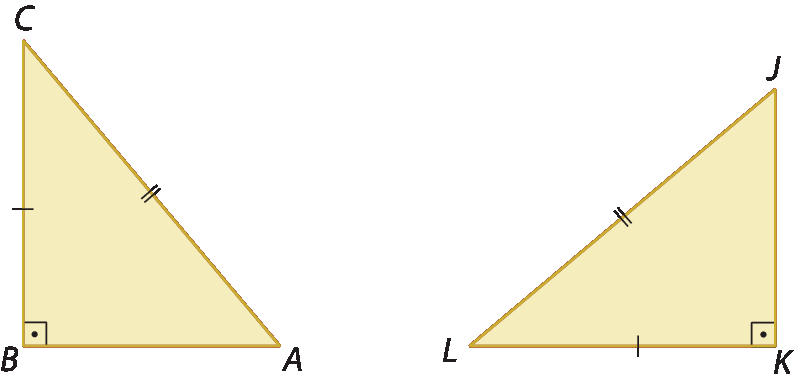
• Hipotenusa

• Cateto

Então: △á bê cê ≅ △JKL
Exemplo
Vamos verificar se os triângulos á bê cê e são congruentes.
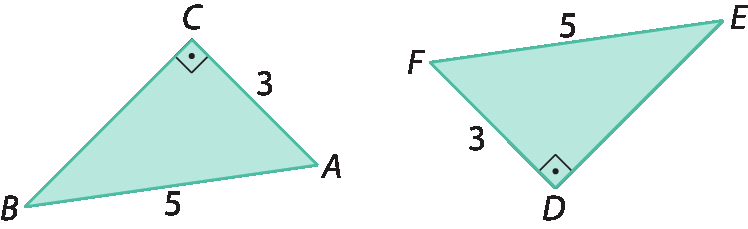
• Cateto

á cê = FD = 3
• Hipotenusa

A bê = éfe ê = 5
Logo: △á bê cê ≅ △

ATIVIDADES
faça as atividades no caderno
1. Entre as figuras a seguir, encontre os pares de triângulos congruentes e indique o caso de congruência que se aplica a eles.
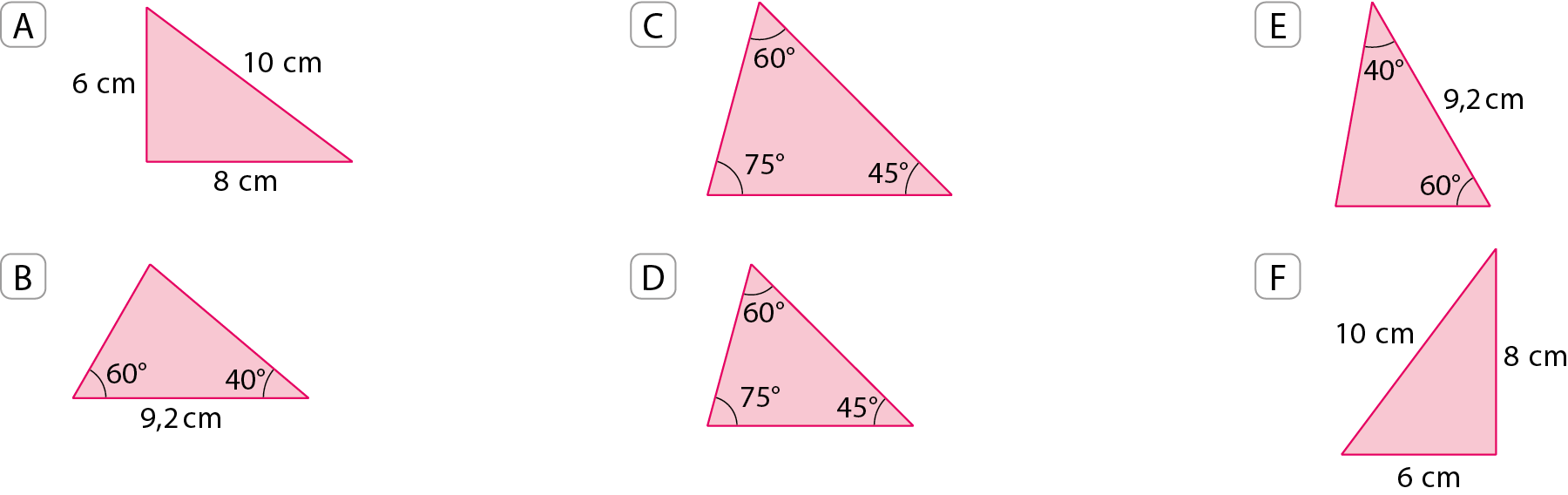
Respostas e comentários
1. a e F: éle éle éle; B e ê: á éle á
Orientações e sugestões didáticas
• Depois do estudo dos casos de congruência de triângulos, peça aos estudantes que verbalizem o que aprenderam, apresentando suas conclusões e sínteses para os colegas. Esse é um momento de avaliar o que aprenderam e o modo como se comunicam matematicamente.
• Se necessário, na atividade 1, observe com os estudantes que a a a (ângulo-ângulo-ângulo) não é um caso de congruência de triângulos.
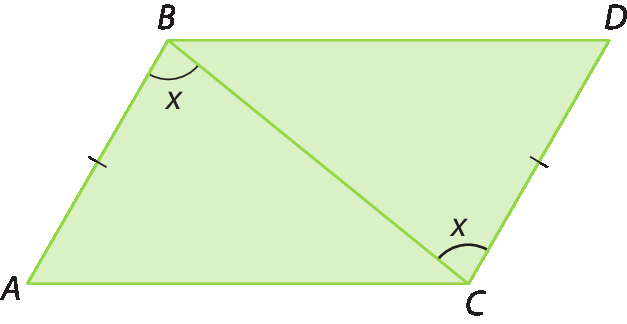
2. Em cada figura a seguir há um par de triângulos congruentes. Identifique esses triângulos e indique o caso de congruência. Justifique sua resposta.
a)
b)
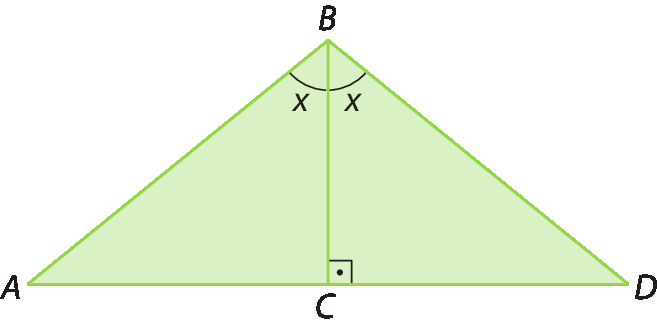
3. Copie no caderno as afirmações verdadeiras.
a) Se dois triângulos têm os três ângulos respectivamente congruentes, eles são congruentes.
b) Para construir um triângulo retângulo, basta conhecer a medida dos dois catetos.
c) Dois triângulos retângulos que têm os catetos congruentes são congruentes.
4. Determine a medida x em cada caso.
a)

b)
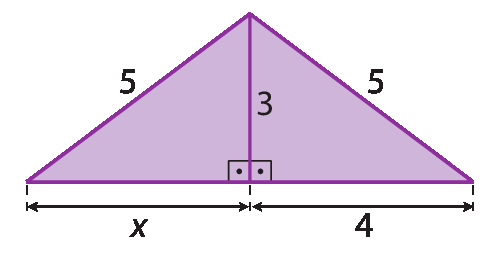
c)
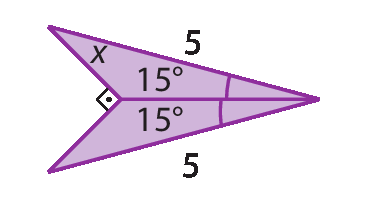
d)
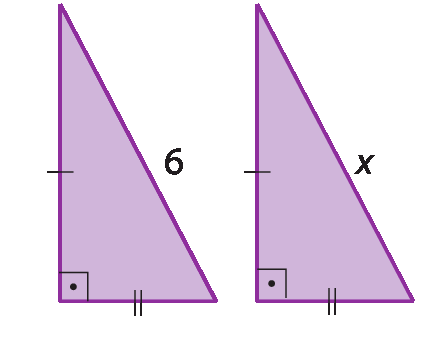
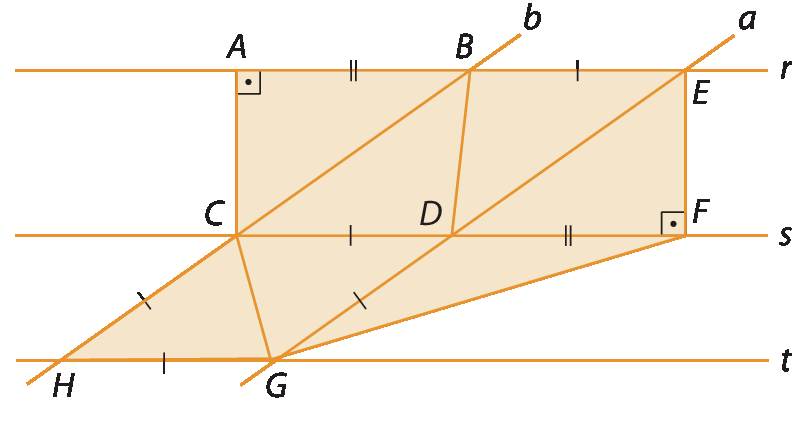
5.

Observe os triângulos formados na figura a seguir e identifique os triângulos congruentes sabendo que r // s // t e que a // b.
5 Triângulos isósceles e triângulos equiláteros
Como vimos, os triângulos podem ser classificados conforme a medida de comprimento de seus lados. Nessa classificação, o triângulo equilátero é aquele que tem todos os lados congruentes; já o triângulo isósceles é aquele que tem dois lados congruentes. Então, podemos dizer que todo triângulo equilátero também é isósceles.
No caso de um triângulo isósceles não equilátero, o lado não congruente é denominado base do triângulo. Quando o triângulo isósceles é equilátero, qualquer um dos lados pode ser considerado base.
Observe o triângulo isósceles á bê cê a seguir.
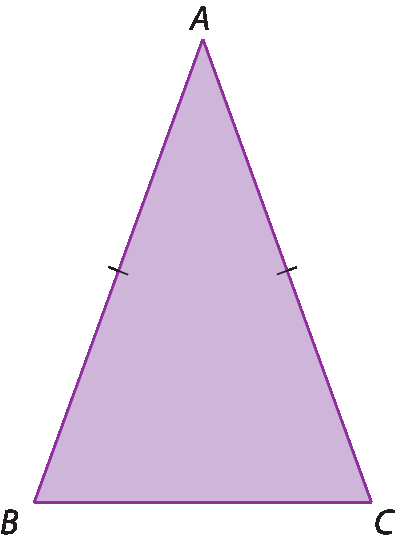
Nesse triângulo:
• os lados congruentes são
segmento AB e segmento AC;
• a base é
Segmento BC;
• os ângulos da base são
ângulo B e ângulo C.
Vamos estudar algumas propriedades dos triângulos isósceles e dos triângulos equiláteros.
Respostas e comentários
2. a) △á bê cê ≅ △DCB
caso éle á éle
• lado:
segmento AB congruente segmento DC• ângulo:
ângulo ABC congruente ângulo DCB• lado:
Segmento BC(lado comum)
2. b) △á bê cê ≅ △DBC
caso á éle á
• ângulo:
ângulo ABC congruente ângulo DBC• lado:
Segmento BC(lado comum)
• ângulo:
ângulo ACB congruente ângulo DCB
3. alternativas b e c
4. a) 2; b) 4; c) 30graus; d) 6
5. △CHG ≅ △GDC (éle éle éle); △CDB ≅ △ (éle á éle); △á bê cê ≅ △éfe dê é ()
Orientações e sugestões didáticas
• A atividade 5 merece uma atenção especial, pois envolve vários triângulos e exige que os estudantes coloquem em prática diferentes conhecimentos discutidos nas aulas. É interessante que eles possam realizar a atividade em grupos para trocar ideias e comparar caminhos de resolução. Destaque que não há medidas numéricas para as medidas de comprimento dos lados na ilustração, mas há símbolos que representam congruência.
Triângulos isósceles e triângulos equiláteros
Objetivo
• Reconhecer e demonstrar propriedades dos triângulos isósceles e equilátero.
Orientações
• Para que os estudantes aprimorem seus conhecimentos sobre triângulos e suas propriedades, nessa etapa dois tipos de triângulo ganham destaque: o isósceles e o equilátero.
Propriedade dos ângulos da base de um triângulo isósceles
Em um triângulo isósceles, os ângulos da base são congruentes.
Acompanhe a demonstração dessa propriedade.
Considere o △á bê cê, com
segmento AB congruente segmento AC, sendo
Segmento AIa bissetriz relativa ao ângulo
A.
Nos triângulos á í bê e á í cê:
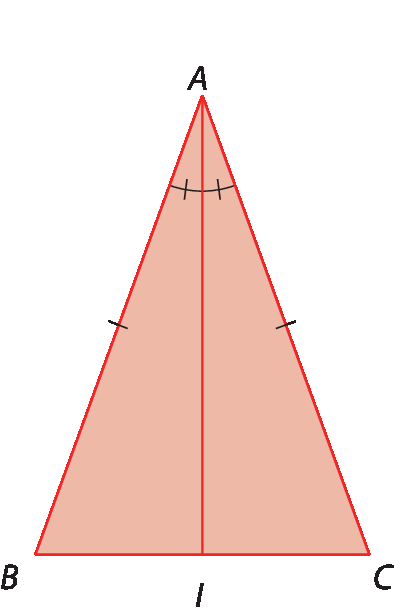
•
Segmento AI
é comum

lado;
•
ângulo IAB congruente ângulo IAC, pois
Segmento AIé bissetriz

ângulo;
•
segmento AB congruente segmento AC
, pois o triângulo é isósceles

lado.
Portanto, pelo caso éle á éle: △á í bê ≅ △á í cê
Como os triângulos á í bê e á í cê são congruentes:
ângulo B congruente ângulo CAssim, concluímos que os ângulos da base de um triângulo isósceles são congruentes.
Propriedade dos ângulos internos de um triângulo equilátero
Em qualquer triângulo equilátero, os três ângulos internos são congruentes a abertura de cada um mede 60graus.
Vamos demonstrar essa propriedade.
Observe o △á bê cê equilátero e a mediana
Segmento AMrelativa ao lado
Segmento BC.
Nos triângulos á ême bê e á ême cê:
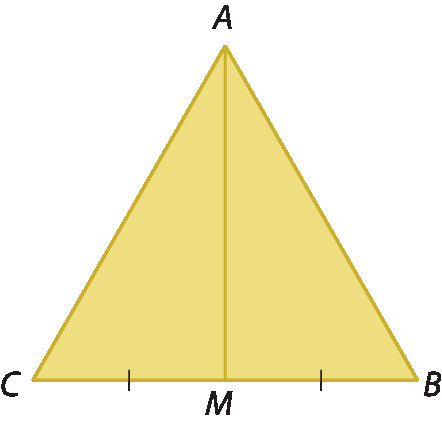
•
Segmento AMé comum

lado;
•
segmento BM congruente segmento CM, pois M é o ponto médio de
Segmento BC
lado;
•
segmento AB congruente segmento AC, pois o △á bê cê é equilátero

lado.
Portanto, pelo caso éle éle éle: △á ême bê ≅ △á ême cê
Logo:
ângulo B congruente ângulo C(um)
Vamos, agora, traçar a mediana
Segmento BNrelativa ao lado
Segmento AC.
Nos triângulos e :
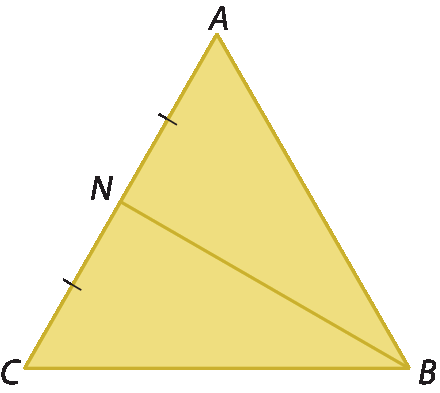
•
Segmento BNé comum

lado;
•
segmento AN congruente segmento CN, pois N é o ponto médio de
Segmento AC
lado;
•
segmento BA congruente segmento BC, pois o △á bê cê é equilátero

lado.
Portanto, pelo caso LLL: △ ≅ △BNC
Logo:
ângulo A congruente ângulo C(dois)
De um e dois vem:
ângulo A congruente ângulo B congruente ângulo CComo medida de(
ângulo A) + medida de(
ângulo B) + medida de(
ângulo C) = 180graus, então:
medida de(
ângulo A) = medida de(
ângulo B) = medida de(
ângulo C) = 60graus
Assim, demonstramos que os ângulos internos de um triângulo equilátero são congruentes e a abertura de cada um mede 60graus.
Orientações e sugestões didáticas
• Antes de apresentar a propriedade dos ângulos da base de um triângulo isósceles e a propriedade dos ângulos internos de um triângulo equilátero, proponha aos estudantes que investiguem essas propriedades utilizando um software de Geometria dinâmica. Propostas como essa colocam-nos como protagonistas de seu processo de aprendizagem e contribuem para que valorizem as demonstrações que serão feitas posteriormente.
• Demonstre cada uma dessas propriedades no quadro, incentivando a participação da turma. Em cada caso, é importante deixar claras as hipóteses e a tese. Enfatize os conceitos empregados e deixe que os estudantes identifiquem os triângulos congruentes.

Informática e Matemática
faça as atividades no caderno
Investigando os pontos notáveis em um triângulo
Antes de apresentar a próxima propriedade, vamos utilizar um software de Geometria dinâmica para fazer algumas investigações.
ConstruA
Triângulo isósceles
Inicialmente, vamos construir um triângulo isósceles.
1º) Trace um segmento
Segmento ABqualquer.
2º) Trace a circunferência de centro em a passando por B.
3º) Escolha um ponto C qualquer nessa circunferência e trace o triângulo á bê cê.
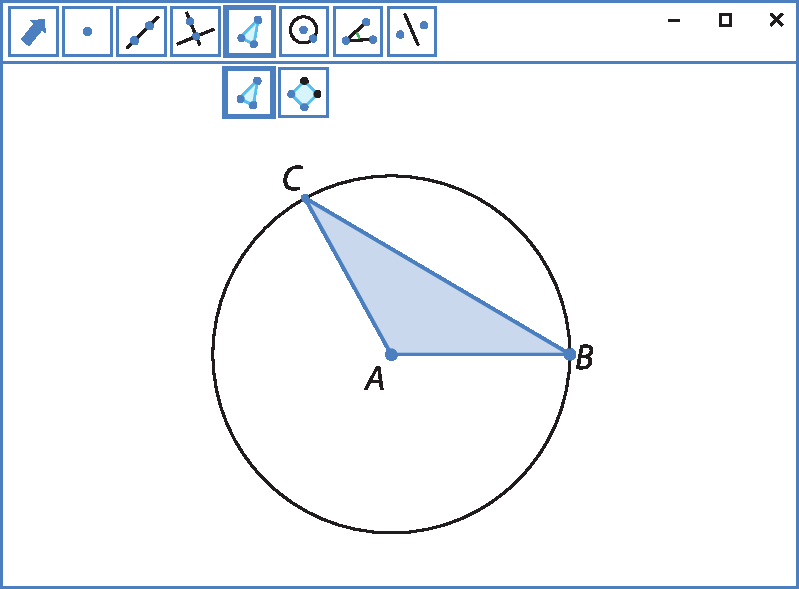
Mesmo com a movimentação dos vértices, pela construção, esse triângulo será isósceles.
Triângulo equilátero
Agora, vamos construir um triângulo equilátero.
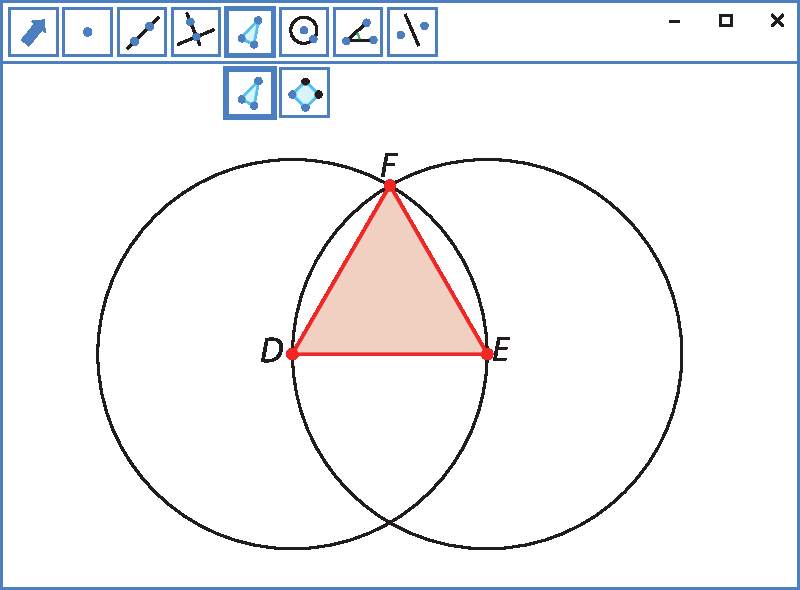
1º) Trace um segmento
Segmento DE
qualquer.
2º) Trace a circunferência de centro em D passando por ê.
3º) Trace a circunferência de centro em ê passando por D.
4º) Em uma das intersecções das circunferências marque o ponto F e trace o triângulo dê ê éfe. Mesmo com a movimentação dos vértices D e ê, pela construção, esse triângulo será equilátero.
Orientações e sugestões didáticas
Informática e Matemática
Objetivos
• Investigar a posição dos pontos notáveis em triângulos isósceles e equiláteros.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco, da competência geral 5 e da competência específica 2 da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco da Bê êne cê cê ao propor aos estudantes que construam, usando software de Geometria dinâmica, um triângulo isósceles e um triângulo equilátero e, depois, investiguem os pontos notáveis desses triângulos.
Orientações
• Nesta seção, os estudantes deverão construir um triângulo isósceles e um triângulo equilátero, suas medianas, alturas, bissetrizes e mediatrizes e seus pontos notáveis (baricentro, ortocentro, incentro e circuncentro).
(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.
Competência geral 5: Compreender, utilizar e criar tecnologias digitais de informação e comunicação de fórma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
Competência específica 2: Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
▶ Informática e Matemática
Pontos notáveis
Agora, usando o passo a passo visto neste Capítulo ou as ferramentas do software (alguns softwares contêm ferramentas que determinam pontos médios, mediatrizes, bissetrizes e retas perpendiculares), para cada um dos triângulos trace:
• as medianas do triângulo e o ponto G (baricentro), intersecção dessas medianas;
• as alturas do triângulo e o ponto H (ortocentro), intersecção dessas alturas;
• as bissetrizes do triângulo e o ponto I (incentro), intersecção dessas bissetrizes;
• as mediatrizes do triângulo e o ponto óh (circuncentro), intersecção dessas mediatrizes.
Usando uma ferramenta do software, esconda as construções auxiliares, deixando somente os triângulos e os pontos notáveis visíveis. No caso do triângulo isósceles, não esconda a mediatriz, a altura e a mediana relativas à base
Segmento BCe a bissetriz relativa ao ângulo
A.
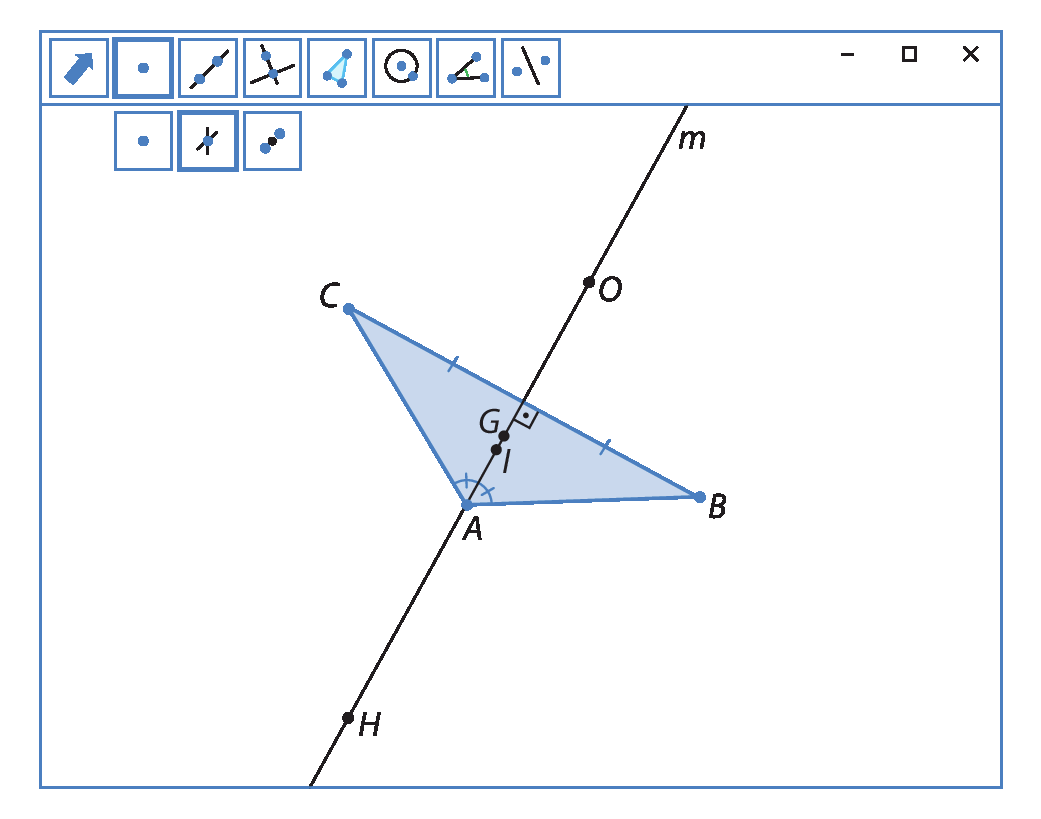
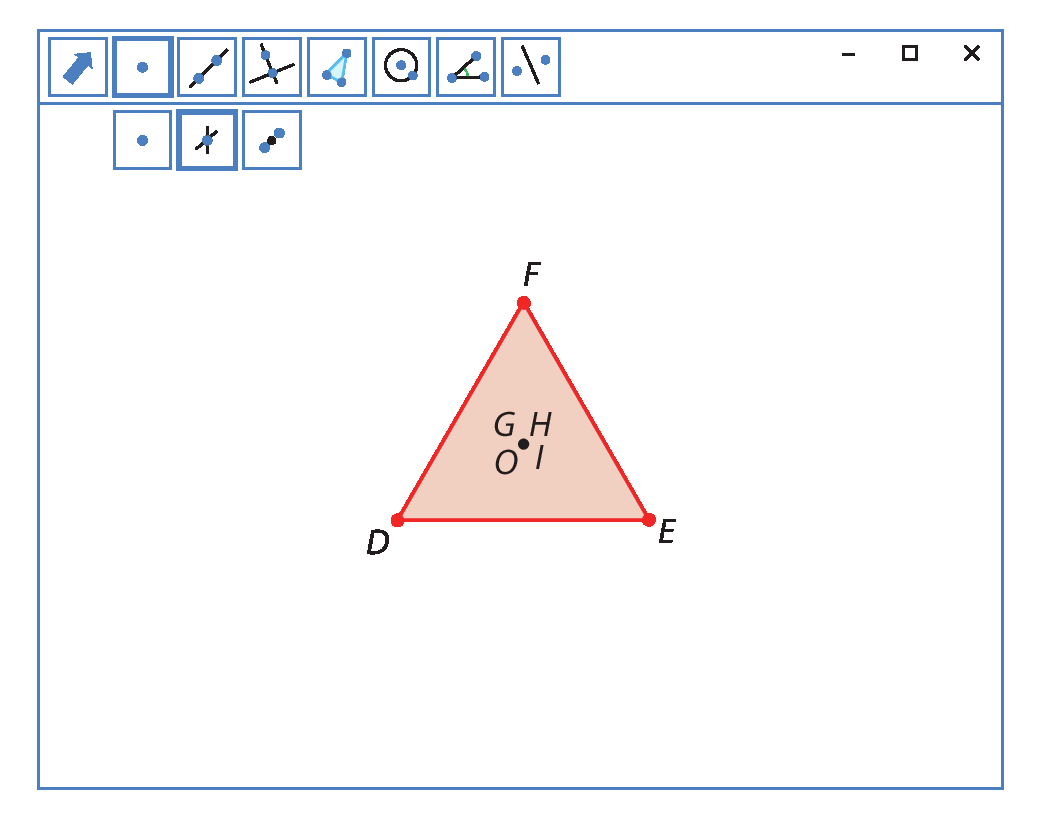
A maioria dos softwares tem uma ferramenta para esconder construções. Utilize esse recurso a cada passo para esconder os traçados auxiliares.
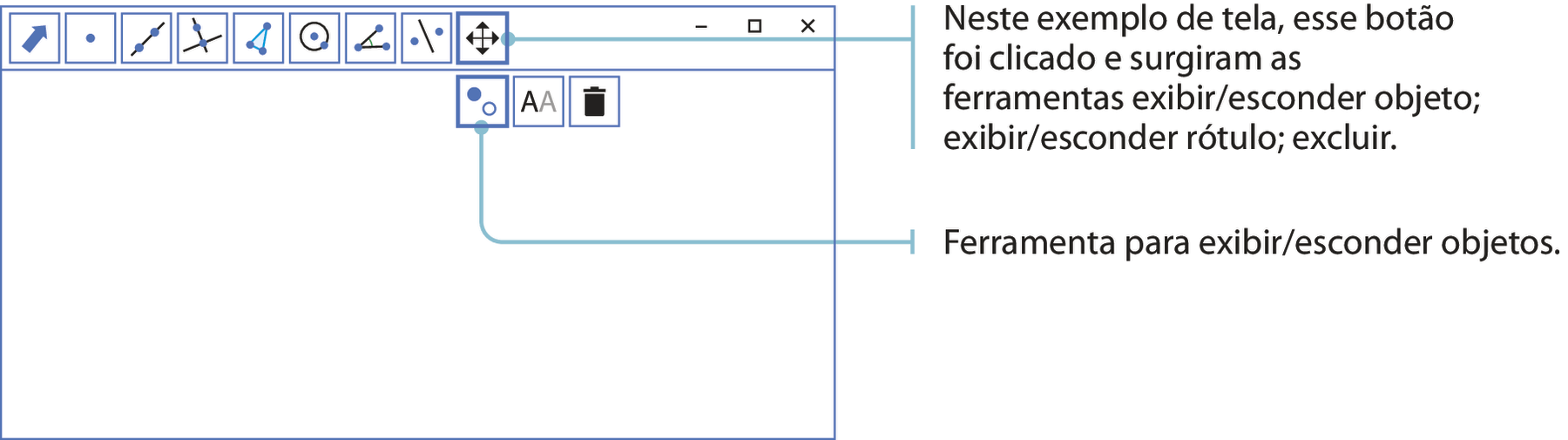
iInvestigue
a) Movimente os vértices do triângulo isósceles construído a fim de modificar sua configuração. O que acontece com a mediatriz, a altura e a mediana relativas à base
Segmento BCe a bissetriz relativa ao ângulo oposto?
b) Os pontos notáveis do triângulo isósceles estão alinhados? Isso acontece mesmo quando você movimenta o triângulo?
c) Movimente os vértices móveis do triângulo equilátero construído para modificar sua configuração. O que você observa em relação aos pontos notáveis de um triângulo equilátero?
Respostas e comentários
Investigue: a) A altura, a mediana e a bissetriz coincidem e estão contidas na reta que é a mediatriz relativa à base.
b) Espera-se que os estudantes percebam que em um triângulo isósceles os pontos notáveis estão sempre alinhados.
c) Espera-se que os estudantes percebam que os pontos notáveis coincidem.
Orientações e sugestões didáticas
• Em Investigue, os estudantes deverão movimentar os vértices dos triângulos construídos e verificar experimentalmente que a mediatriz, a altura e a mediana relativas à base e a bissetriz relativa ao ângulo oposto à base coincidem. Além disso, eles devem observar que os pontos notáveis estão alinhados no triângulo isósceles (não equiláteros), e que esses pontos coincidem no triângulo equilátero. É importante enfatizar que as investigações realizadas apenas sugerem que essas propriedades são válidas e que elas serão demonstradas nas páginas seguintes.
• O uso da tecnologia digital de fórma significativa contribui para o desenvolvimento da competência geral 5 da Bê êne cê cê. Além disso, essa atividade proporciona aos estudantes desenvolver o espírito de investigação e a capacidade de produzir argumentos convincentes, o que favorece o desenvolvimento da competência específica 2 da Bê êne cê cê.
Propriedade da mediana, da altura e da bissetriz de um triângulo isósceles
Em qualquer triângulo isósceles, a mediana relativa à base e a altura relativa à base coincidem com a bissetriz do ângulo do vértice oposto à base.
No triângulo á bê cê isósceles a seguir,
segmento AB congruente segmento ACe a mediana
Segmento AMé relativa à base
Segmento BC.
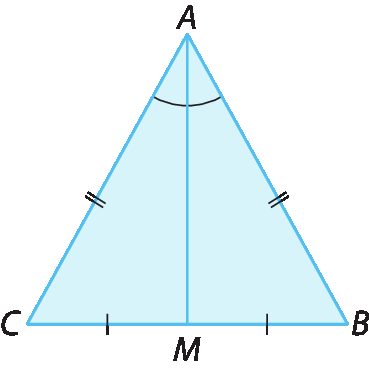
Lembre-se: Escreva no caderno!
Vamos demonstrar, inicialmente, que
Segmento AMtambém é a bissetriz relativa ao ângulo
A.
Considerando os triângulos á ême bê e á ême cê, podemos afirmar que:
•
Segmento AMé comum

lado;
•
segmento BM congruente segmento CM, pois M é o ponto médio de
Segmento BC
lado;
•
segmento AB congruente segmento AC, pois o △á bê cê é isósceles

lado.
Portanto, pelo caso LLL: △á ême bê ≅ △á ême cê
Assim:
ângulo MAB congruente ângulo MACPortanto,
Segmento AMé a bissetriz relativa ao ângulo
A.
Agora, vamos demonstrar que
Segmento AMtambém é a altura relativa à base
Segmento BC.
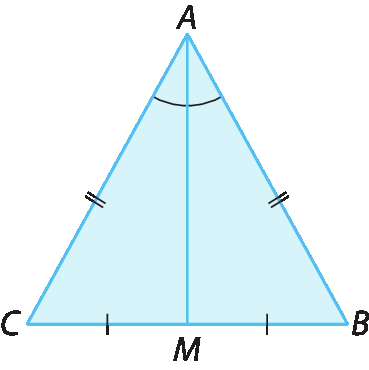
Como foi demonstrado anteriormente, os triângulos á ême bê e á ême cê são congruentes.
Portanto,
ângulo AMB congruente ângulo AMC.
Além disso,
ângulo AMB e ângulo AMCsão suplementares. Então:
medida de(
ângulo AMB) + medida de(
ângulo AMC) = 180graus
medida de(
ângulo AMB) + medida de(
ângulo AMB) = 180graus
2 ⋅ medida de(
ângulo AMB) = 180graus
medida de(
ângulo AMB) = 90graus
Portanto,
Segmento AMé a altura relativa à base
Segmento BC.
Orientações e sugestões didáticas
• A propriedade da mediana, da altura e da bissetriz de um triângulo isósceles, investigada pelos estudantes na seção Informática e Matemática, agora deve ser demonstrada. Convém demonstrá-la no quadro com a colaboração da turma. Novamente, ressalta-se a importância de deixar claras as hipóteses e a tese. A identificação dos triângulos congruentes deve ficar a cargo dos estudantes.
• As demonstrações matemáticas geralmente são feitas com vocabulário próprio, diferente do que aquele com o qual os estudantes estão acostumados. Por essa razão, às vezes eles podem ter dificuldade de compreendê-las. Tenha isso em vista ao propor as demonstrações e verifique o entendimento dos estudantes durante a explicação.
Observações
• Pela propriedade demonstrada, em um triângulo isósceles:
a) a mediatriz relativa à base é reta suporte da altura e da mediana relativas à base e da bissetriz do ângulo oposto;
b) os pontos notáveis são colineares.
Note nos triângulos a seguir a posição dos pontos óh (circuncentro), G (baricentro), ih (incentro) e H (ortocentro).
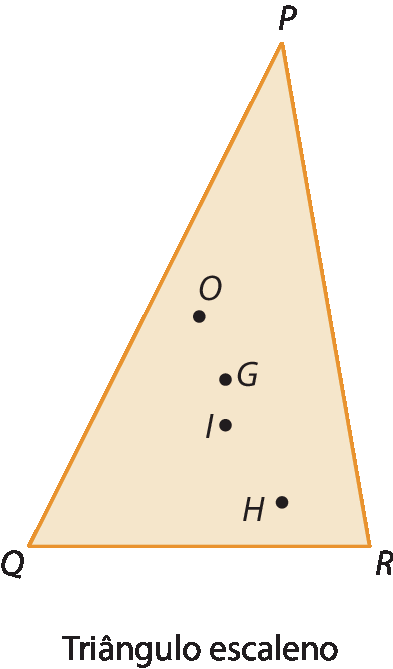
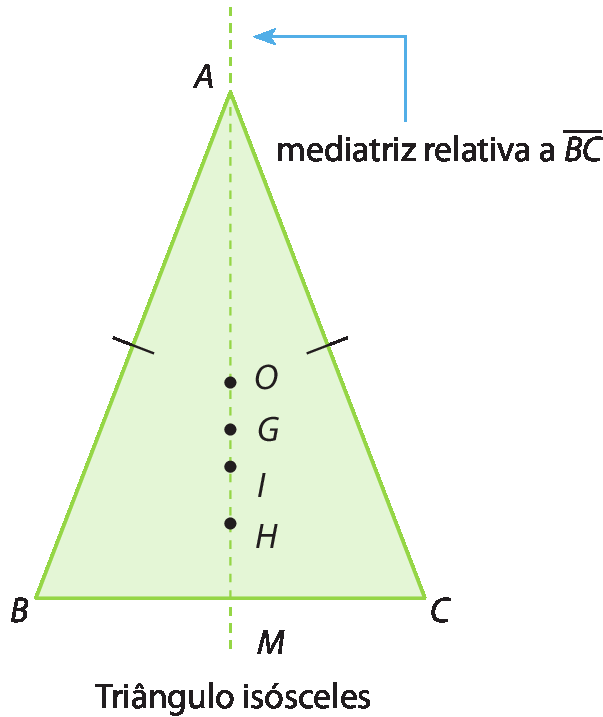
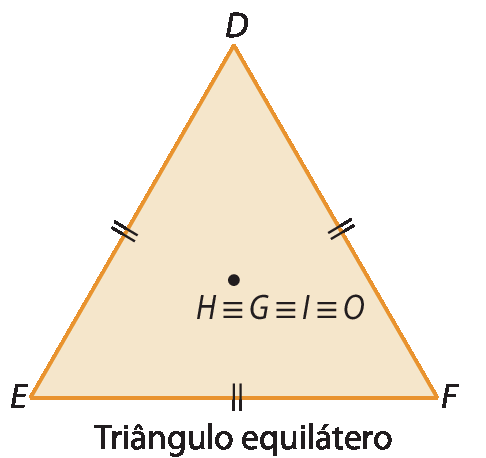
• Como um triângulo equilátero é também isósceles, a mediatriz relativa a cada lado será reta suporte de cada bissetriz, mediana e altura. Assim, os pontos notáveis de um triângulo equilátero coincidem. Indicamos: H ≡ G ≡ I ≡ O
6 Justificativa de algumas construções com régua e compasso
Bissetriz
A bissetriz do ângulo
B O Ca seguir foi construída como mostrado na página 66.
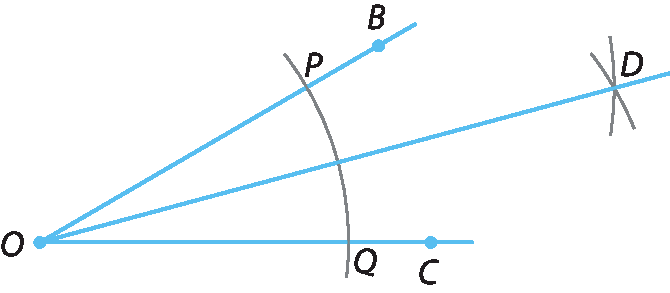
Vamos verificar que, de fato, com os passos realizados,
Semirreta ODé a bissetriz do ângulo
B O C.
Podemos considerar dois triângulos: △ e △
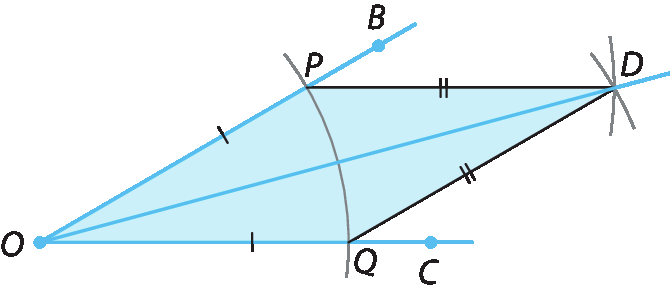
Com base na construção realizada, sabemos que
segmento OP congruente segmento OQ, segmento PD congruente segmento QD e ODé lado comum aos triângulos. Logo, pelo critério éle éle éle: △ ≅ △
Então,
ângulo BOD congruenteângulo COD
e, portanto,
Semirreta ODé a bissetriz do ângulo
B O C.
Orientações e sugestões didáticas
Justificativa de algumas construções com régua e compasso
Objetivos
• Justificar a construção com régua e compasso da bissetriz de um ângulo qualquer.
• Justificar a construção com régua e compasso de um ângulo com medida de abertura de 60graus.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco da Bê êne cê cê ao propor aos estudantes que construam, usando instrumentos de desenho, a bissetriz e o ângulo com medida de abertura de 60graus.
Orientações
• No Capítulo 2, foram estudadas algumas construções com régua e compasso, e, neste tópico, algumas delas serão demonstradas. A construção da bissetriz, por exemplo, será demonstrada por meio da identificação de triângulos congruentes.
• Ao propor o uso de compasso, enfatize aos estudantes o cuidado com seu manuseio, a fim de evitar acidentes.
(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.
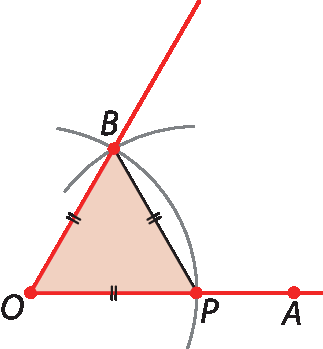
Ângulo com medida de abertura de 60graus
O ângulo cuja abertura mede 60graus da figura foi construído como mostrado na página 67.
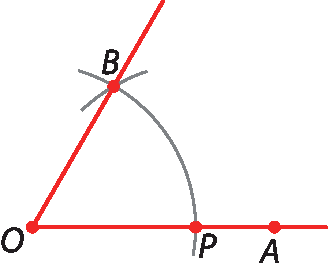
Vamos verificar que, com a construção realizada, a abertura do ângulo
ângulo AOBmede, de fato, 60graus.
Com base nos passos realizados na construção, sabemos que
segmento OB congruente segmento OP congruente segmento PBLogo, o triângulo ó pê bê é equilátero e, portanto, a abertura de seus ângulos internos mede 60graus. Então, medida de(
AOB) = 60graus.

ATIVIDADES
faça as atividades no caderno
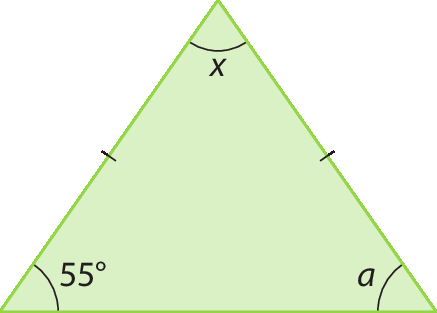
1. O triângulo a seguir é isósceles. Determine o valor de a e de x, em grau.
2. A abertura do ângulo do vértice a, oposto à base de um triângulo isósceles, mede 80graus. Quanto mede a abertura dos ângulos da base
ângulo B e ângulo C?
3. Considerando o triângulo a seguir, em que BC = 28 centímetros, calcule no caderno:
a) a medida de abertura do ângulo interno
ABC;
b) a medida de comprimento do segmento
DC;
c) a medida de comprimento do segmento
AD.
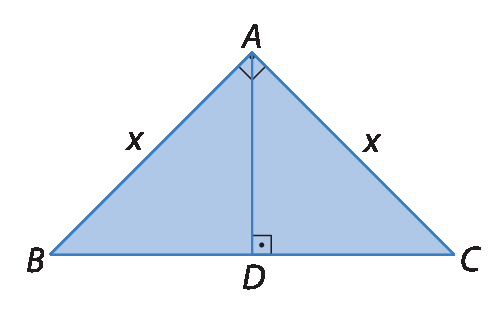
4. Determine a medida x, em grau.
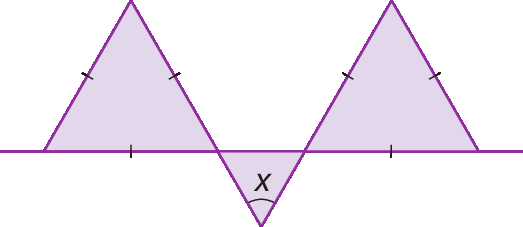
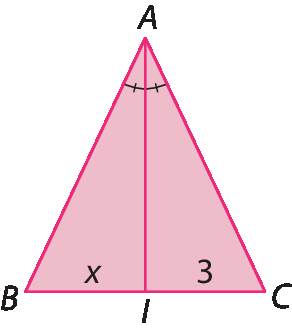
5. Determine x sabendo que o triângulo á bê cê, em cada item, é isósceles.
a)
Segmento AIé a bissetriz relativa ao vértice a.
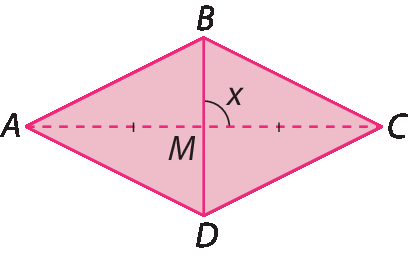
b)
Segmento BMé a mediana relativa ao lado
Segmento ACdo triângulo á bê cê.
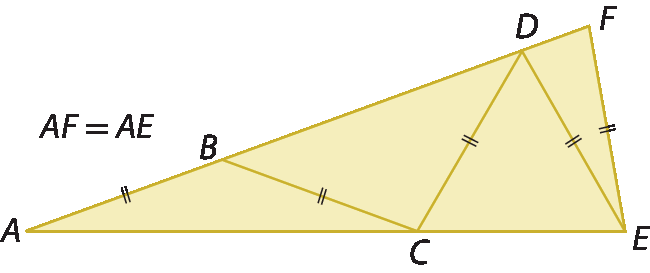
6.


Reúna-se com um colega e resolvam.
Dado um triângulo isósceles (
Segmento AF≅
Segmento AE) com um caminho de cinco segmentos congruentes A-B-C-D-E-F, ache a medida, em grau, [da abertura] do ângulo
A.
Milauskas, djêordji. Problemas de geometria criativos podem levar à resolução criativa de problemas criativos. In: (organizador). Aprendendo e ensinando geometria. tradução Hygino H. Domingues. São Paulo: Atual, 1996. página 93.
Respostas e comentários
1. a = 55graus
x = 70graus
2. 50graus
3. a) 45graus
3. b) 14 centímetros
3. c) 14 centímetros
4. 60graus
5. a) 3
5. b) 90graus
6. 20graus
Orientações e sugestões didáticas
• Na resolução dessas atividades, solicite aos estudantes que registrem de fórma sucinta as ideias ou propriedades que utilizaram. A intenção não é que a descrição fique longa ou demasiadamente formal, mas apenas deixar claro o caminho percorrido para chegar a cada uma das soluções. Nesse sentido, contribui-se para que os estudantes aprimorem sua habilidade de comunicarem-se matematicamente.
• Se julgar conveniente, peça aos estudantes que avaliem se todas as medidas encontradas estão coerentes com as ilustrações apresentadas. Assim, eles mesmos poderão identificar possíveis falhas nos cálculos ou na interpretação.

Estatística e Probabilidade
faça as atividades no caderno
Leitura e interpretação de gráficos
Em muitas situações do dia a dia você deve ter visto diversos tipos de gráfico, como os de barras, os de setores, os de linhas e os pictogramas. Para que a informação seja transmitida de maneira clara, é preciso, entre outras coisas, que o tipo de gráfico seja adequado aos dados que contém.
Para interpretar um gráfico, é importante saber analisar seus elementos e usar o que você já sabe sobre o assunto abordado.
Observe os gráficos elaborados a partir de uma pesquisa publicada pelo Instituto Brasileiro de Geografia e Estatística (í bê gê É).
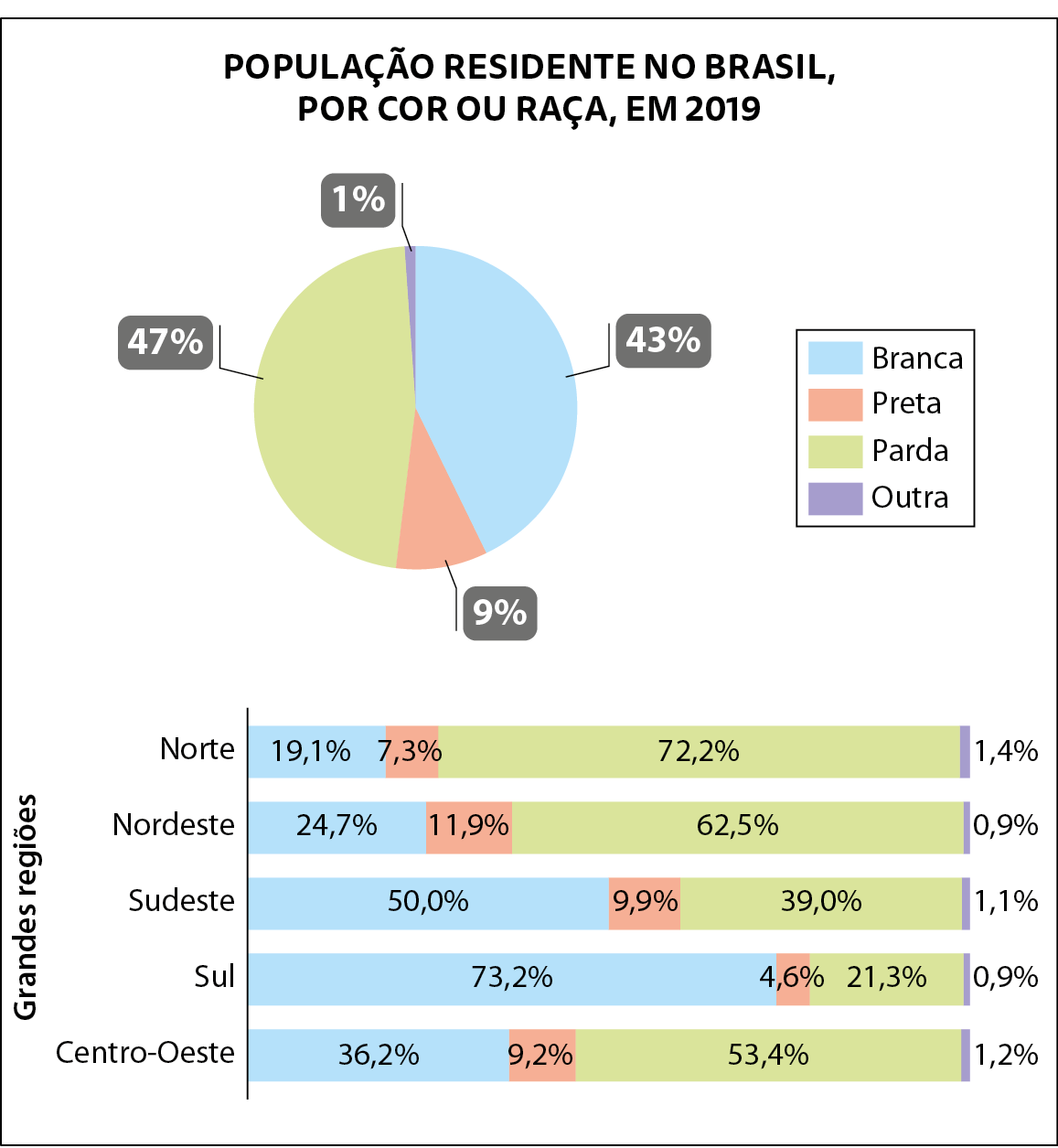
Fonte: í bê gê É. Pesquisa Nacional por Amostra de Domicílios Contínua: características gerais dos domicílios e dos moradores 2019.

Com base nos gráficos, podemos tirar várias conclusões. Leia algumas delas:
• a pesquisa foi realizada em 2019 pelo í bê gê É;
• no Brasil, 43% das pessoas se autodeclararam brancas, 9% pretas, 47% pardas e 1% de outra cor ou raça;
• a maioria dos brasileiros se autodeclarou parda;
• nas regiões Norte, Nordeste e Centro-Oeste mais da metade das pessoas se autodeclararam pardas;
• no Sul, 73,2% das pessoas se autodeclararam brancas;
• havia diferenças significativas entre as porcentagens de acordo com a cor ou a raça autodeclarada por grande região do Brasil.
Orientações e sugestões didáticas
Estatística e Probabilidade
Objetivos
• Ler e interpretar gráficos de diferentes tipos publicados pela mídia.
• Trabalhar com os Temas Contemporâneos Transversais Ciência e Tecnologia, da macroárea Ciência e Tecnologia; Educação Alimentar e Nutricional, da macroárea Saúde; e Educação para o Consumo, da macroárea Economia.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah dois três e das competências gerais 7 e 9 da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Esta seção contribui para o desenvolvimento da habilidade ê éfe zero oito ême ah dois três da Bê êne cê cê porque trabalha a leitura e a interpretação de determinado conjunto de dados representados em gráficos.
Orientações
• O acesso à informação de maneira rápida e organizada é de grande importância na sociedade atual. Para oferecer esse tipo de informação, as diferentes mídias habitualmente se utilizam de informações visuais, entre elas os gráficos, para apresentar dados que abordam temas de interesse da população, como questões econômicas, políticas e esportivas, entre outras. É com base nessas informações, veiculadas pelos diferentes meios de comunicação, que o indivíduo faz previsões, toma decisões e se mantém informado. Nesse sentido, a proposta desta seção favorece o desenvolvimento da competência geral 7 da Bê êne cê cê.
• Busca-se proporcionar aos estudantes a experiência de ler e interpretar diferentes tipos de gráfico publicados pela mídia. A intenção é que eles desenvolvam um olhar crítico sobre as informações apresentadas pela mídia de modo que possam ler dados e realizar questionamentos necessários à sua interpretação.
(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.
Competência geral 7: Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
Competência geral 9: Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

ATIVIDADES
faça as atividades no caderno
1. Observe o gráfico a seguir.
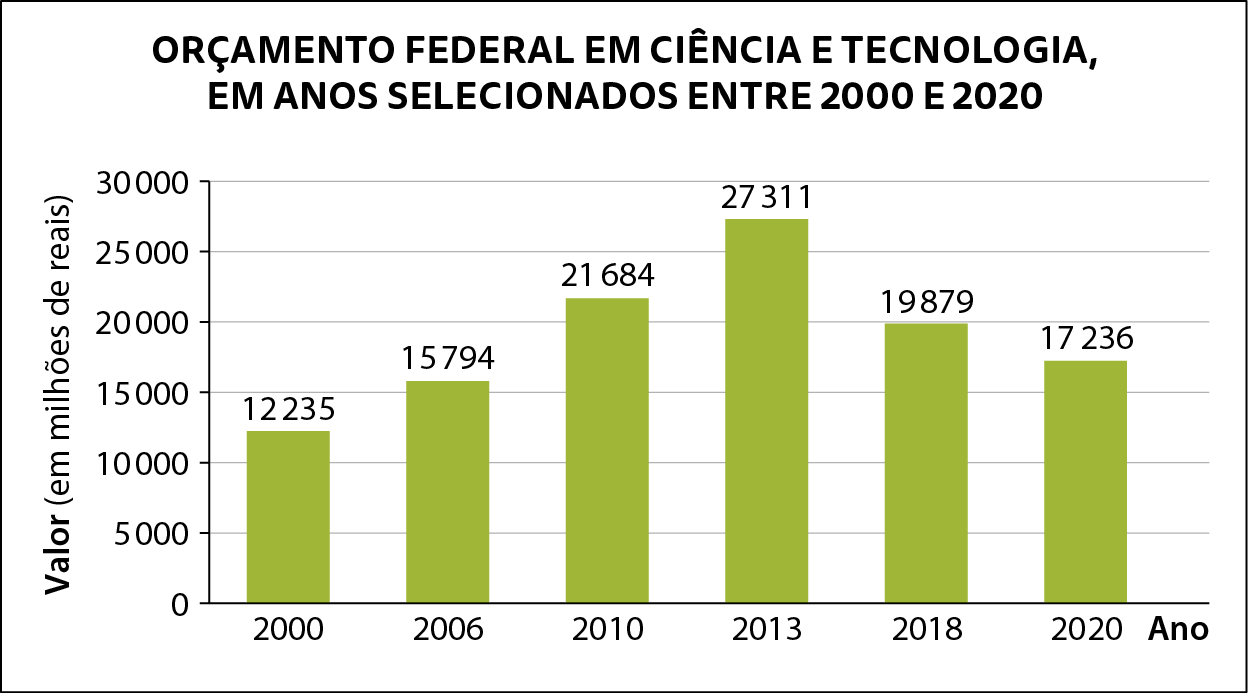
Fonte: INSTITUTO DE PESQUISA ECONÔMICA APLICADA (ipéa). Políticas Públicas para Ciência e Tecnologia: cenário e evolução recente. Disponível em: https://oeds.link/iMhO6y. Acesso em: 2 agosto 2022.
Para pensar

Você acha importante que o governo federal invista mais em ciência e tecnologia no Brasil?
De acordo com as informações do gráfico, é incorreto afirmar que:
a) o orçamento no ano de 2020 foi menor que .20000 milhões de reais.
b) entre os anos apresentados, houve redução do orçamento somente entre 2018 e 2020.
c) a diferença entre o investimento em 2013 e em 2020 foi de .10075 milhões de reais.
d) entre os anos apresentados, o que teve maior investimento foi 2013.
e) o orçamento em 2000 foi menor que .15000 milhões de reais.
2.

A segurança alimentar é a garantia de ter acesso pleno e permanente aos alimentos. Apesar de ser um direito do brasileiro assegurado por lei desde 2010, em 2020 mais da metade da população se encontrava em situação de insegurança alimentar, que pode ser classificada em leve, moderada ou grave, quando a fome passa a ser uma realidade.
Observe a seguir os dados apresentados sobre esta situação no Brasil ao longo dos anos.
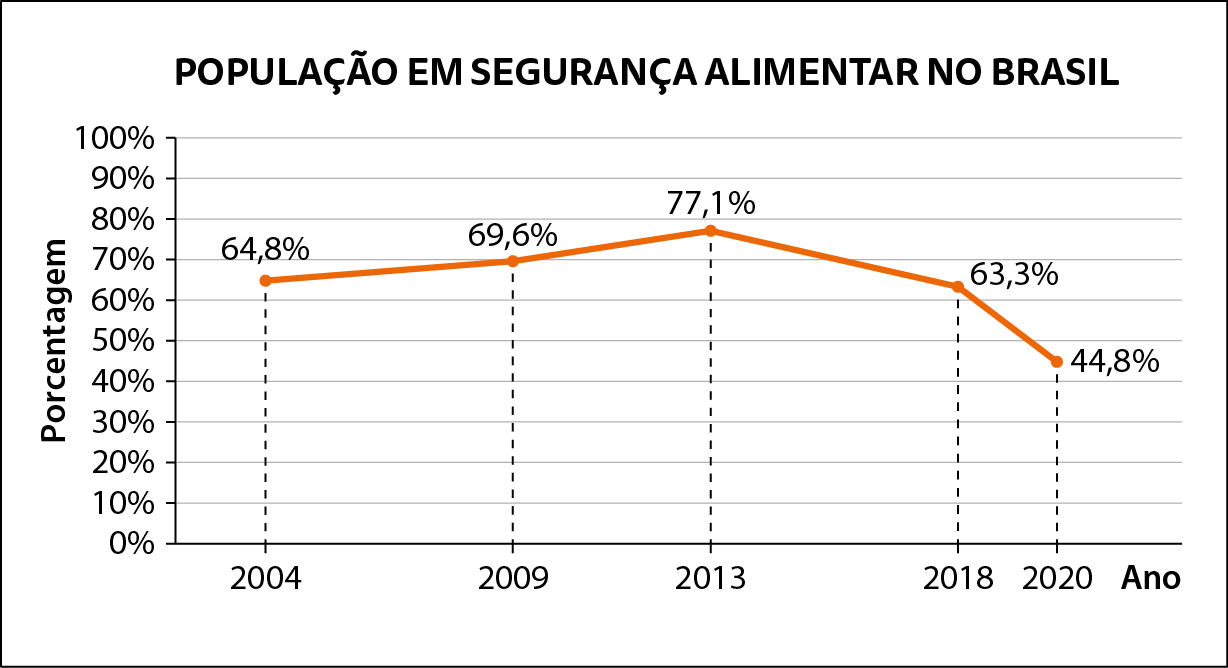
Fonte: REDE BRASILEIRA DE PESQUISA EM SOBERANIA E SEGURANÇA ALIMENTAR E NUTRICIONAL (Rede penssan). Inquérito Nacional sobre Insegurança Alimentar no Contexto da Pandemia da Covid-19 no Brasil. Disponível em: https://oeds.link/RmXi5B. Acesso em: 15 junho 2022.

Com base na análise do gráfico, não podemos afirmar que:
a) entre os anos apresentados, em 2020 houve o menor percentual da população brasileira em segurança alimentar.
b) a segurança alimentar da população brasileira aumentou de 2004 a 2009 e de 2009 a 2013.
c) em 2020 cêrca de 55,2% da população vivia algum tipo de insegurança alimentar.
d) em 2009, 69,6% da população brasileira vivia em insegurança alimentar.
e) de 2013 a 2020 houve uma queda de 32,3% da população brasileira em segurança alimentar.
Respostas e comentários
Para pensar: Resposta pessoal.
1. alternativa b
2. alternativa d
Orientações e sugestões didáticas
• Se achar conveniente, retome os tipos de gráfico estudados neste ano e em anos anteriores, enfatizando as situações em que o uso de um é mais adequado que o uso do outro. Além disso, convém retomar o conceito de porcentagem. Ao fazer essa ponte com os conhecimentos previamente adquiridos pela turma, pode-se contribuir para que realizem as atividades propostas com mais facilidade.
• Durante a realização das atividades 1 e 2, incentive os estudantes a explicar o porquê de as afirmações serem falsas ou verdadeiras.
• A temática proposta na atividade 1 possibilita desenvolver o Tema Contemporâneo Transversal Ciência e Tecnologia, da macroárea Ciência e Tecnologia. Após resolver a atividade 1, proponha aos estudantes que reflitam sobre a pergunta do Bócsi Para pensar. Em seguida, peça a alguns deles que compartilhem suas opiniões com a turma. Promova um ambiente acolhedor, de modo que os estudantes sintam-se à vontade para colocar suas ideias e ouçam a opinião do colega com empatia e respeito. Assim, promove-se a competência geral 9 da Bê êne cê cê.
• Aproveite o tema da atividade 2 e converse com os estudantes sobre o aumento da fome no país e as possíveis causas para esse aumento, possibilitando, assim, o desenvolvimento do Tema Contemporâneo Transversal Educação Alimentar e Nutricional, da macroárea Saúde.
▶ Estatística e Probabilidade
3. O gráfico de barras a seguir apresenta o consumo médio doméstico per cápita de água nas macrorregiões do Brasil em 2020.
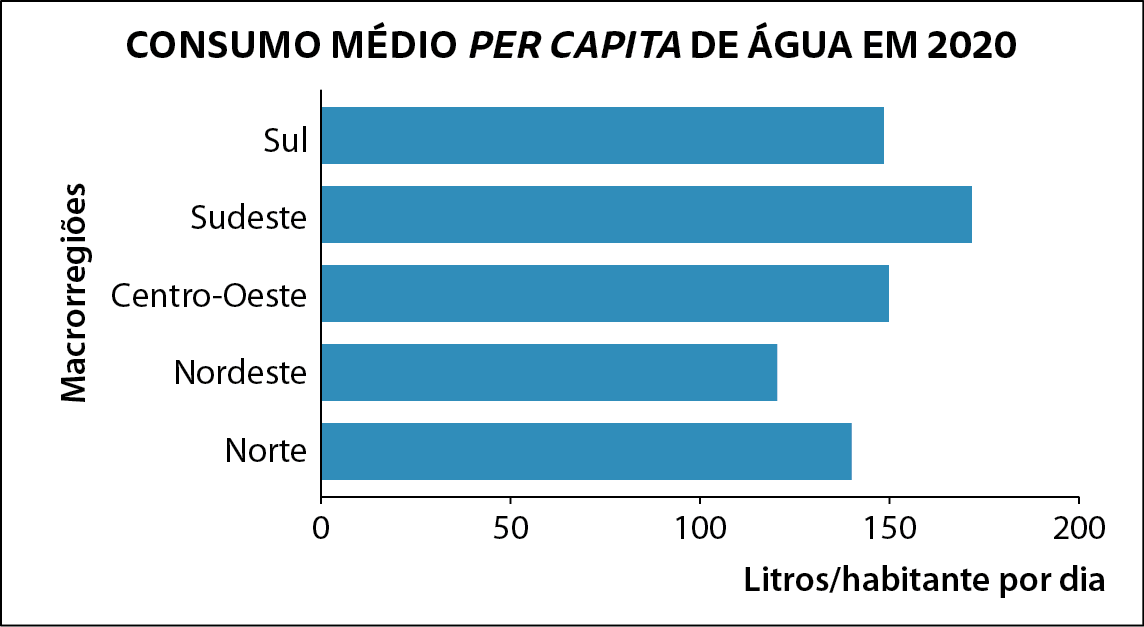
Fonte: MINISTÉRIO DO DESENVOLVIMENTO REGIONAL; SECRETARIA NACIONAL DE SANEAMENTO – ésse ene ésse. Diagnóstico Temático Serviços de Água e Esgoto dezembro/2021: visão geral – ano de referência 2020. Disponível em: https://oeds.link/0LSZ5K. Acesso em: 15 junho 2022.

Com base nas informações do gráfico, é incorreto afirmar que, em 2020:
a) o consumo de água per capita no Sudeste era de mais de 150 litros.
b) os consumos de água per capita no Sul e no Centro-Oeste eram próximos a 150 litros.
c) o Sudeste era a região em que o consumo de água per capita em 2020 era maior.
d) o consumo de água per capita no Norte era maior do que 150 litros.
e) o Nordeste era a região em que o consumo de água per capita em 2020 era menor.
Para pensar

Você tem ideia de quanto gasta de água por dia? Que ações você pode tomar para diminuir o consumo de água em sua casa?
4. Analise o gráfico a seguir.
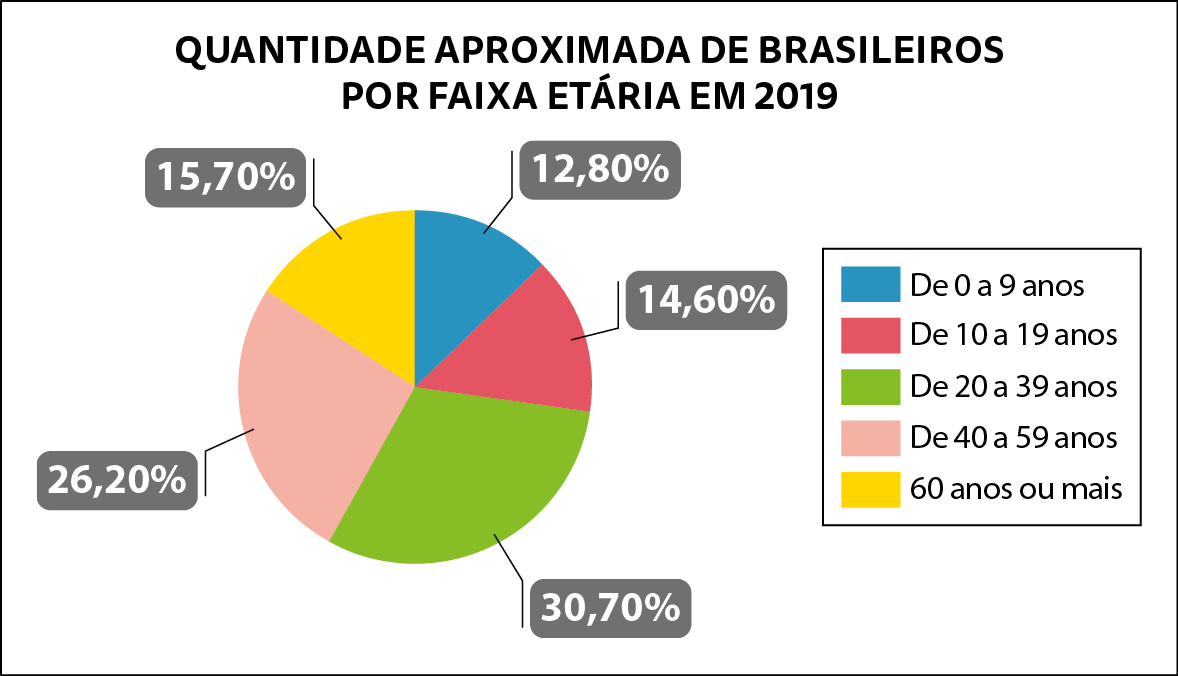
Fonte: í bê gê É. Pesquisa Nacional por Amostra de Domicílios Contínua: características gerais dos domicílios e dos moradores 2019.
a) Escreva um parágrafo com três conclusões sobre as informações contidas nesse gráfico.
b)

Converse com dois colegas e comparem as conclusões que vocês escreveram. Caso as conclusões dos colegas sejam diferentes das suas, copie-as no caderno.
Respostas e comentários
3. alternativa d
Para pensar: Respostas pessoais.
4. a) Resposta pessoal.
4. b) Resposta pessoal.
Orientações e sugestões didáticas
• Enfatize a importância de obter o título, a legenda e a fonte dos gráficos no processo de compreensão dos dados apresentados. Se achar pertinente, mostre para os estudantes os impactos da supressão dos títulos e das legendas.
• Se possível, converse com eles a respeito dos temas a que os gráficos se referem, de modo a possibilitar uma maior interação deles com os gráficos. O boxe Para pensar, por exemplo, favorece tal discussão com relação ao tema do gráfico da atividade 3. Se julgar conveniente, mostre a eles algumas ferramentas, disponíveis na internet, que estimam quantidades gastas de água com algumas atividades (por exemplo: https://oeds.link/Jj6afz; acesso em: 12 agosto 2022.). Comente com os estudantes algumas medidas que podem evitar o desperdício, como tomar banhos mais curtos, desligar o registro ao ensaboar a louça, aproveitar a água da chuva etcétera Esse assunto favorece o desenvolvimento do Tema Contemporâneo Transversal Educação para o Consumo, da macroárea Meio Ambiente.
• Amplie a proposta desta seção e peça aos estudantes que, em grupos, pesquisem em jornais, revistas ou internet gráficos publicados pela mídia. Depois, proponha que façam a leitura e a interpretação do material encontrado.

Atividades de revisão
faça as atividades no caderno
1. (-Rio de Janeiro) Dois lados de um triângulo medem 9 centímetros e 6 centímetros. Qual das seguintes medidas pode ser escolhida para o terceiro lado?
a) 2 centímetros
b) 15 centímetros
c) 12 centímetros
d) 3 centímetros
2. Calcule a medida x em cada item.
a)
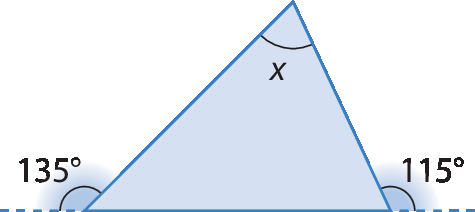
b)

3. Observe o projeto de um telhado.
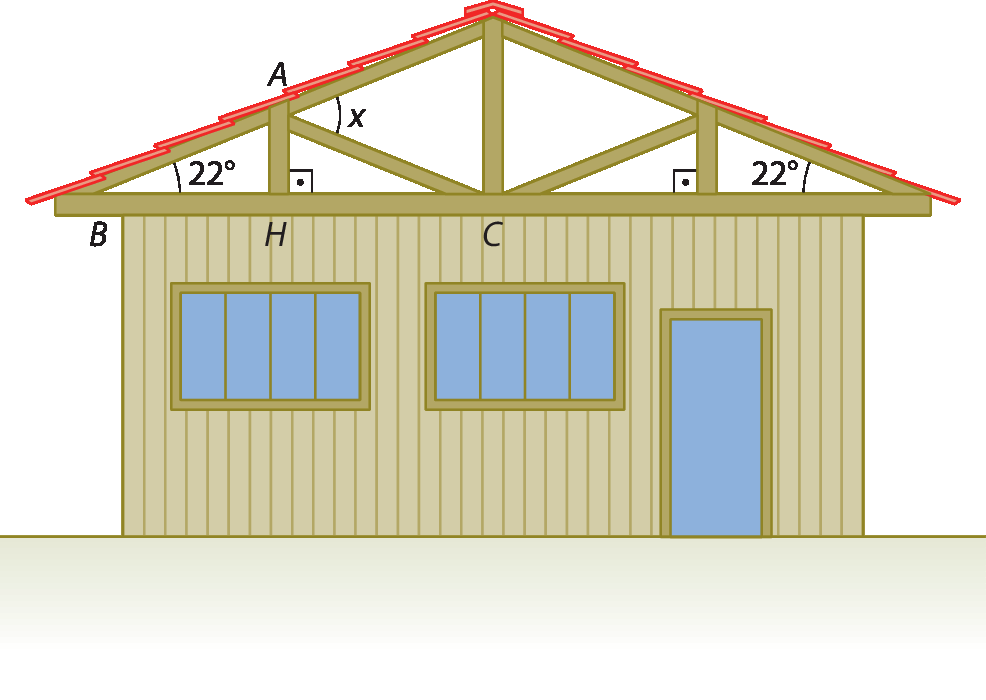
• Se o triângulo á bê cê é isósceles e
Segmento AH
é sua altura, qual é a medida x, em grau?
4. Determine as medidas x e y, em grau, sabendo que o triângulo á bê cê é retângulo, o ângulo
Aé reto e o segmento
ADé uma de suas bissetrizes.
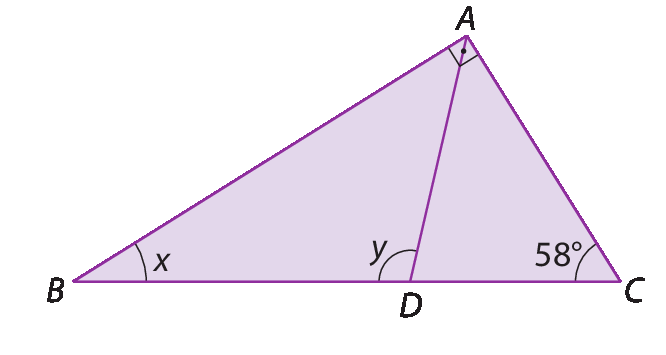
5. (-São Paulo) Se Aabre parênteses0, 0fecha parênteses, Babre parênteses2, 0fecha parênteses e Cabre parênteses0, 2fecha parênteses são os vértices de um triângulo no plano cartesiano, então esse triângulo é:
a) retângulo e não isósceles.
b) equilátero.
c) retângulo e isósceles.
d) isósceles e não retângulo.
e) escaleno e retângulo.
6. Reinaldo vai perfurar um poço em sua propriedade. Ele quer que o poço fique à mesma medida de distância de três casas. Por isso, fez um esquema representando a posição das casas nos vértices de um triângulo. Explique como Reinaldo deverá proceder para encontrar o local onde ficará o poço.
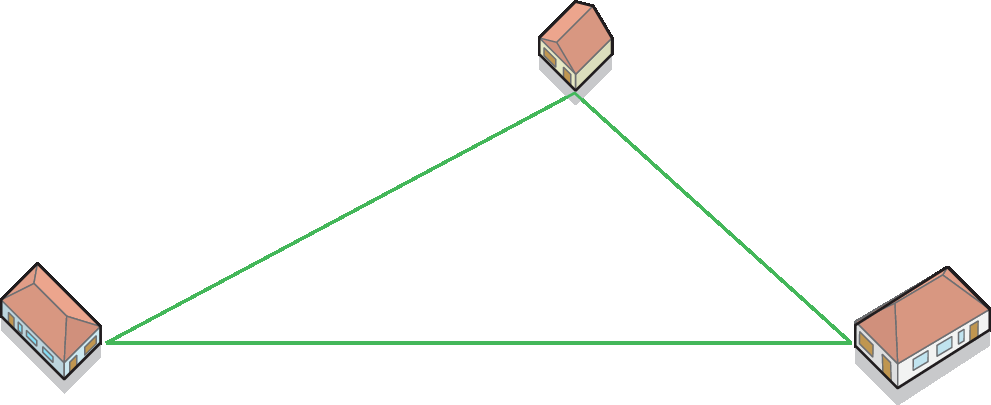
7. Determine a, b e a medida do perímetro do triângulo á bê cê.
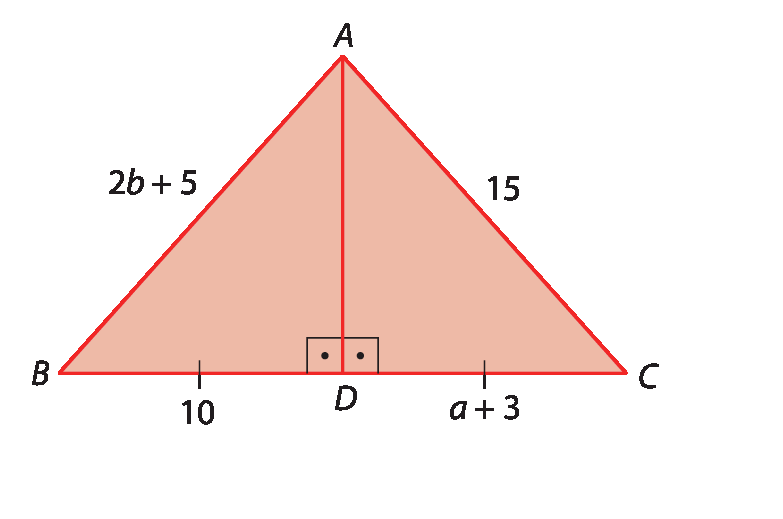
8. (faapi-São Paulo) Observe a figura:
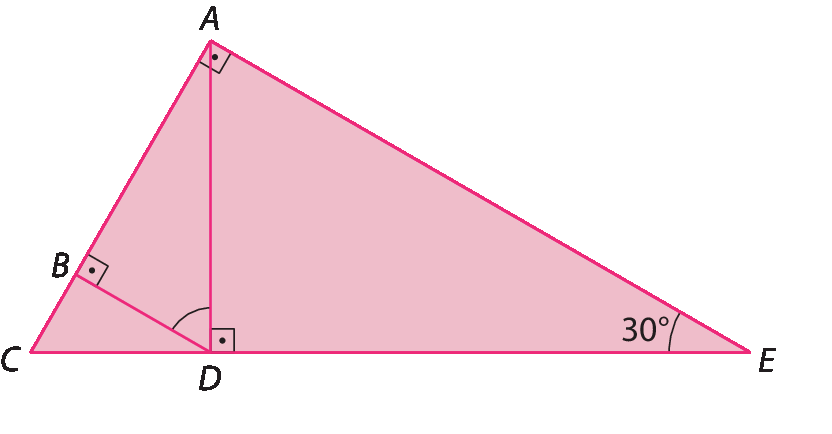
• Qual é a medida do ângulo
BDA?
a) 60graus
b) 30graus
c) 45graus
d) 90graus
e) 40graus
Respostas e comentários
1. alternativa c
2. a) 70graus
2. b) 30graus
3. 44graus
4. x = 32graus;
y = 103graus
5. alternativa c
6. Reinaldo deve determinar o encontro das mediatrizes, ou seja, o circuncentro do triângulo do esquema.
7. a = 7; b = 5; medida do perímetro = 50
8. alternativa a
Orientações e sugestões didáticas
Atividades de revisão
Objetivo
• Consolidar os conhecimentos adquiridos no decorrer do Capítulo.
Orientações
• Os estudantes serão desafiados a resolver, entre outras atividades, alguns testes de vestibulares, todos de acordo com os temas trabalhados neste Capítulo.
• Na atividade 5, eles devem retomar a representação de pontos no plano cartesiano e, com base na representação desses 3 pontos, analisar e classificar o triângulo formado.
• Sugerimos algumas questões para que os estudantes possam refletir sobre suas aprendizagens e possíveis dificuldades no estudo deste Capítulo, as quais devem ser adaptadas à realidade da turma. Oriente-os a fazer a autoavaliação, respondendo às questões no caderno com “sim”, “às vezes” ou “não”.
reticências sei classificar um triângulo com respeito à medida de comprimento de seus lados?
reticências sei classificar um triângulo com respeito à medida de abertura de seus ângulos?
reticências sei identificar os casos de congruência de triângulos?
reticências sei identificar os pontos notáveis de um triângulo?
reticências consigo construir os elementos notáveis de um triângulo com software de Geometria dinâmica?
reticências sei ler e interpretar gráficos de diferentes tipos?
reticências tenho um bom relacionamento com meus colegas de sala?
reticências consigo expor minhas ideias e opiniões em grupo?
reticências tenho facilidade para compreender os conteúdos?
Em todo caso, conforme sugerido nas Orientações Gerais deste Manual do Professor, outros aspectos, além dos conteúdos e conceitos desenvolvidos no Capítulo, devem ser avaliados.