
CAPÍTULO 8 Problemas de contagem
1 Contagem
Em muitas situações do dia a dia, temos de fazer contagens. Acompanhe algumas delas a seguir.
Lembre-se: Escreva no caderno!


Note que, nesses dois casos, os elementos foram contados um a um, mas há situações em que essa fórma de contagem é muito trabalhosa ou não é viável.
Respostas e comentários
Habilidades da Bê êne cê cê trabalhadas neste Capítulo:
ê éfe zero oito ême ah zero três
ê éfe zero oito ême ah dois dois
Orientações e sugestões didáticas
Contagem
Objetivo
• Explorar o desenvolvimento do raciocínio combinatório.
Orientações
• O assunto que é tema deste capítulo envolve um raciocínio matemático particular: o raciocínio combinatório. Contar é uma habilidade básica que se procura desenvolver desde muito cedo na formação do ser humano. Na análise combinatória, há situações nas quais os elementos a serem contados não aparecem explícitos, mas são definidos por características dadas, que permitem perceber quais são todos esses elementos, por meio do raciocínio combinatório.
Imagine, por exemplo, que uma turma de formandos de um colégio resolveu fazer uma rifa para levantar fundos para a festa de formatura. Cada bilhete será formado com duas letras, entre as cinco primeiras do nosso alfabeto, seguidas de dois algarismos. Observe alguns exemplos de bilhetes dessa rifa.

Quantos são os bilhetes dessa rifa?
Para responder a essa pergunta, poderíamos listar todas as combinações possíveis de letras e de números, e depois contá-las, mas isso seria muito trabalhoso. Entretanto, podemos utilizar um procedimento que permite contar, de fórma indireta, os bilhetes dessa rifa. Para compreender como esse método funciona, acompanhe outras situações parecidas com essa.
2 Princípio multiplicativo ou princípio fundamental da contagem
Clara está em um restaurante italiano e não sabe que combinação de massa e molho escolher. Ela tem à disposição 4 tipos diferentes de massa – espaguete, talharim, parafuso e nhoque – e 3 tipos de molho – de tomate, pesto e branco. De quantas maneiras diferentes Clara pode combinar uma massa com um molho?
Observe as combinações que podem ser feitas com um tipo de massa e um tipo de molho.

De acordo com esse quadro, há 12 maneiras diferentes de combinar uma massa com um molho.
Orientações e sugestões didáticas
• Comente com os estudantes que eles resolverão o problema da quantidade de bilhetes da rifa mais adiante neste Capítulo (atividade 6 da página 217).
Princípio multiplicativo ou princípio fundamental da contagem
Objetivos
• Definir o princípio multiplicativo ou princípio fundamental da contagem.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero três da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah zero três porque será definido o princípio multiplicativo, e os estudantes poderão aplicá-lo na resolução de problemas.
Orientações
• O raciocínio combinatório precisa ser desenvolvido pelos estudantes para que tenham a capacidade de lidar com números em situações nas quais não haviam antes pensado e que são instigantes e desafiadoras.
• Antes de iniciar este tópico, apresente aos estudantes o problema e peça a eles que, utilizando estratégias pessoais, encontrem de quantas maneiras diferentes se pode escolher uma massa e um molho. Após discutirem, mostre como solucionar esse problema listando todas as combinações em um quadro e por meio da árvore de possibilidades, conforme ilustrado no Livro do Estudante. A construção de uma representação visual da situação descrita, por exemplo, um quadro ou a árvore de possibilidades, permite que os estudantes compreendam o princípio multiplicativo, atribuindo significado ao produto que fornece o total de opções.
(ê éfe zero oito ême ah zero três) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Podemos, também, representar essas possibilidades por meio de um esquema chamado árvore de possibilidades. Observe.

Note que, como a quantidade de maneiras de combinar uma massa com um molho não é grande, foi possível listar todas as combinações. Mas como listaríamos todas as combinações se a quantidade de tipos de massa e de molho fosse bem maior que a da situação apresentada?
Em casos como esse, aplicaríamos o princípio multiplicativo ou o princípio fundamental da contagem.
Se uma decisão divisores de pode ser tomada de pê maneiras diferentes e se, uma vez tomada a decisão divisores de , a decisão divisores de puder ser tomada de pê maneiras diferentes, então o número de maneiras de tomar as decisões divisores de e divisores de é pê ⋅ pê.
Na situação anterior, duas decisões poderiam ser tomadas: divisores de (escolher o tipo de massa entre as 4 opções possíveis) e divisores de (escolher o tipo de molho entre as 3 opções possíveis). Portanto, o número de maneiras distintas de tomar as decisões divisores de e divisores de era 12, pois 4 ⋅ 3 = 12.
O princípio multiplicativo pode ser estendido para mais de duas decisões. Acompanhe a situação a seguir.
Em uma lanchonete são oferecidas diferentes opções de combo aos clientes.

De quantas maneiras diferentes uma pessoa pode montar um combo?
Nesse caso, três decisões podem ser tomadas: divisores de (escolher o lanche entre as 4 opções possíveis), divisores de ícone de altura(escolher o sabor do suco entre as duas opções possíveis) e divisores de (escolher o doce entre as duas opções possíveis). Portanto, o número de maneiras distintas de tomar as decisões divisores de , divisores de e divisores de é 16, pois 4 ⋅ 2 ⋅ 2 = 16.
Para fazer
Construa uma árvore de possibilidades para representar as diferentes maneiras de montar um combo.
Respostas e comentários
Para fazer: Resposta em Orientações.
Orientações e sugestões didáticas
• Ao lidar com problemas de contagem, os estudantes, cada um no seu tempo, começam a substituir a construção de quadros ou esquemas, completa ou parcialmente, por uma resolução aritmética. Entretanto, é importante ressaltar que essa substituição deve partir dos estudantes.
• Exemplo de resposta do boxe Para fazer:
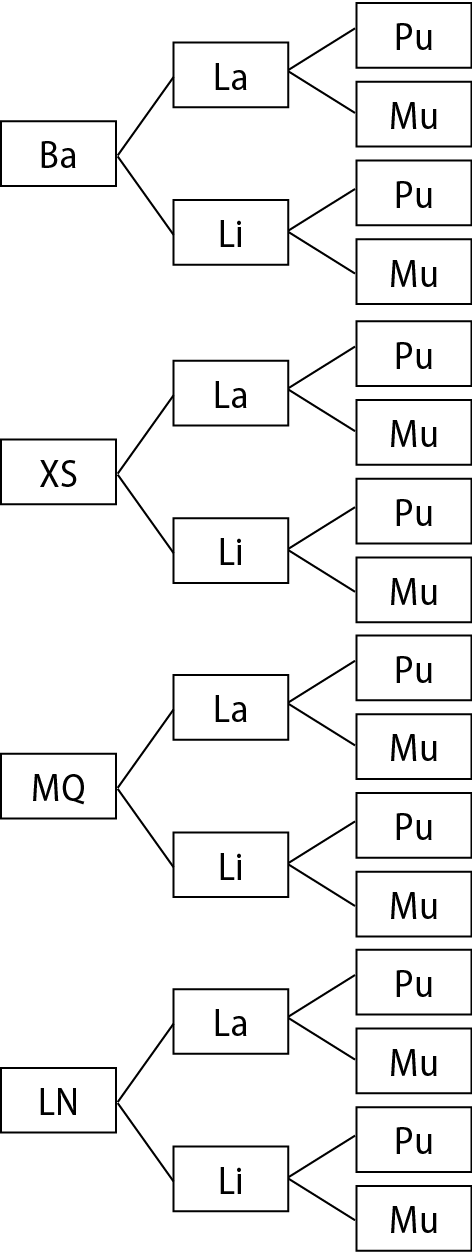
bê á – Bauru
– X-salada
– Misto-quente
– Lanche natural
– Suco de laranja
éle i – Suco de limão
– Pudim
– Mousse

ATIVIDADES
faça as atividades no caderno
1. Em uma loja são oferecidos 10 modelos de telefone, disponíveis em 4 cores. Para quem quer comprar um telefone nessa loja, quantas escolhas são possíveis?
2. Paulo possui 3 bolinhas vermelhas numeradas (quinto, quinto e quinto), 5 bolinhas azuis numeradas (á, á, á, á e á) e 4 bolinhas roxas, também numeradas (érre minúsculo, érre minúsculo, érre minúsculo e érre minúsculo). Quantos trios, escolhendo uma bolinha numerada de cada cor, Paulo pode formar?
Problemas que envolvem o princípio fundamental da contagem
Podemos usar o princípio fundamental da contagem para resolver muitos problemas. Analise alguns exemplos.
Situação 1
Quantos números de três algarismos podem ser formados?
Para responder a essa pergunta, poderíamos listar e contar todos os números de três algarismos, mas isso daria muito trabalho. Nesse caso, podemos aplicar o princípio fundamental da contagem.
Como nenhum número pode começar com o algarismo zero, o algarismo das centenas pode ser escolhido de 9 modos. O algarismo das dezenas e o das unidades podem ser escolhidos de 10 modos cada um.

Assim, podem ser formados 900 números de três algarismos, pois 9 ⋅ 10 ⋅ 10 = 900.
Para calcular
Quantos números de quatro algarismos podem ser formados?
Situação 2
Quantos números de quatro algarismos distintos podem ser formados?
Uma vez que listar todos esses números e depois contá-los não é a estratégia mais adequada, vamos aplicar o princípio fundamental da contagem. Observe o esquema.

Dessa fórma, podem ser formados .4536 números de quatro algarismos distintos, pois 9 ⋅ 9 ⋅ 8 ⋅ 7 = .4536.
Respostas e comentários
1. 40 escolhas
2. 60 trios
Para calcular: .9000 números
Orientações e sugestões didáticas
• Na atividade 1, os estudantes devem observar que para cada modelo de telefone há quatro cores. Como são 10 modelos, temos 40 escolhas possíveis, pois 10 ⋅ 4 = 40.
• Na atividade 2, como são 3 bolinhas vermelhas, 5 azuis e 4 roxas, é possível formar 60 trios, pois 3 ⋅ 5 ⋅ 4 = 60.
• Em Problemas que envolvem o princípio fundamental da contagem é apresentada a resolução de diferentes situações por meio da aplicação do princípio multiplicativo.
• No boxe Para calcular, espera-se que os estudantes empreguem raciocínio semelhante ao apresentado na Situação 1.

A quantidade de números é obtida por meio da multiplicação: 9 ⋅ 10 ⋅ 10 ⋅ 10 = .9000
Portanto, podem ser formados .9000 números de quatro algarismos.
Situação 3
De quantos modos diferentes é possível que 3 pessoas se sentem em 3 cadeiras?

Para resolver esse problema, podemos imaginar as diferentes maneiras de dispor essas pessoas nas cadeiras e depois contá-las.






Portanto, as 3 pessoas podem se sentar de 6 maneiras diferentes nas 3 cadeiras.
Também podemos resolver esse problema aplicando o princípio fundamental da contagem.

A cadeira verde pode ser ocupada de 3 modos diferentes, a azul, de 2 modos, e a laranja, somente de 1 modo.
Assim, há 6 modos diferentes de essas pessoas se sentarem em 3 cadeiras, pois 3 ⋅ 2 ⋅ 1 = 6.
Para calcular
De quantos modos diferentes é possível que 5 pessoas se sentem em 3 cadeiras?
Respostas e comentários
Para calcular: 60 modos
Orientações e sugestões didáticas
• Cada situação precisa ser examinada com cuidado, solicitando a participação dos estudantes. É importante que eles exponham suas ideias e troquem informações.
• No boxe Para calcular, espera-se que os estudantes concluam que é possível 5 pessoas sentarem-se em 3 cadeiras de 60 modos diferentes, pois 5 ⋅ 4 ⋅ 3 = 60.

ATIVIDADES
faça as atividades no caderno
1. Quantos números de dois algarismos existem?
2. Quantos números de três algarismos distintos existem?
3. Quantos números de três algarismos distintos podemos formar com os algarismos 2, 4, 6, 7, 8 e 9?
4. De quantas maneiras diferentes 7 pessoas podem ficar em fila?
5. Quantos números de três algarismos menores que 700 podem ser formados com os dígitos 4, 5, 6, 7 e 8, considerando que:
a) os algarismos podem se repetir;
b) os algarismos não podem se repetir.
6. Você se lembra do problema do início deste Capítulo? Agora, é a hora de resolvê-lo.
Uma turma de formandos do colégio resolveu fazer uma rifa para levantar fundos para a festa de formatura. Cada bilhete será formado com duas letras, entre as cinco primeiras do nosso alfabeto, seguidas de dois algarismos. Quantos bilhetes há nessa rifa?
7. Quantas palavras de 4 letras diferentes, com sentido ou não, podem ser formadas com um alfabeto de 26 letras?
8. Marília precisa criar uma senha de acesso à rede do instituto em que estuda. Ela foi informada de que a senha precisa ter 6 dígitos, sendo um deles uma letra e os demais, algarismos, que podem ser repetidos. Todas as senhas criadas por Marília começam com o algarismo 9 e terminam com uma vogal. Quantas senhas diferentes Marília pode criar com base nesse critério?

Situação 4
Chamamos de anagramas as diferentes maneiras de ordenar as letras de uma palavra para formar outra palavra, com sentido ou não.
Quantos são os anagramas da palavra MEU?
Para responder a essa pergunta, podemos listar todos os anagramas e depois contá-los:
MEU EMU UME
MUE EUM UEM
Portanto, existem 6 anagramas da palavra MEU.
Também podemos aplicar o princípio fundamental da contagem. Os anagramas da palavra MEU têm 3 letras. Para a primeira letra, temos 3 escolhas; para a segunda, duas escolhas; e, para a terceira, somente uma escolha.

Assim, o número de anagramas da palavra MEU é 6, pois 3 ⋅ 2 ⋅ 1 = 6.
Respostas e comentários
1. 90 números
2. 648 números
3. 120 números
4. .5040 maneiras
5. a) 75 números
5. b) 36 números
6. .2500 bilhetes
7. trezentas e cinquenta e oito.oitocentas palavras
8. .50000 senhas
Orientações e sugestões didáticas
• As atividades propostas nesta página pretendem mobilizar os conhecimentos e as situações exploradas neste Capítulo até o momento, contribuindo para o desenvolvimento do raciocínio combinatório.
• A atividade 6 retoma a situação apresentada no início do capítulo (página 213). Verifique se os estudantes identificam que, no enunciado do problema, não é informado que as letras precisam ser diferentes e que os algarismos devem ser distintos. Então, temos: para as letras, 25 possíveis escolhas, pois 5 ⋅ 5 = 25; e, para os algarismos, 100 possíveis escolhas, pois 10 ⋅ 10 = 100. Logo, os números da rifa são .2500, pois 25 ⋅ 100 = .2500.
• Antes de explorar a Situação 4, verifique se os estudantes conhecem o significado de anagrama e explore alguns com eles.
Situação 5
Jorge, Lucas e Iara se candidataram ao cargo de monitor da classe. Sabendo que 2 deles serão escolhidos, quantas duplas diferentes de monitores podem ser formadas?
Para resolver esse problema, vamos imaginar as duplas que podem ser formadas.






Note que há duplas formadas pelos mesmos integrantes, portanto são iguais. Por exemplo, a dupla Jorge e Lucas é igual à dupla Lucas e Jorge. Assim, observando novamente as imagens anteriores, podemos concluir que existem 3 duplas diferentes.
Também podemos usar o princípio multiplicativo para resolver esse problema. O primeiro estudante da dupla pode ser escolhido de 3 modos, e o segundo, de 2 modos, o que totalizaria 6 duplas, pois 3 ⋅ 2 = 6.

No entanto, da mesma fórma, cada dupla foi contada duas vezes. Então, é necessário dividir o total 6 por 2 para eliminar as repetições.
Portanto, podem ser formadas 3 duplas diferentes, pois 6 : 2 = 3.
Para calcular
E se fossem 4 candidatos ao cargo de monitor da classe, quantas duplas diferentes de monitores poderiam ser formadas?
Respostas e comentários
Para calcular: 6 duplas
Orientações e sugestões didáticas
• A solução de problemas de contagem exige compreensão plena da situação descrita. Muitos deles, como os apresentados nas Situações 5 e 6, não podem ser resolvidos aplicando diretamente o princípio multiplicativo. Por esse motivo, incentive os estudantes a expor o que entenderam e como acham que devem proceder para resolver determinado problema.
• Para solucionar a questão proposta no boxe Para calcular, espera-se que os estudantes concluam que, para compor a dupla de monitores, podemos escolher 1 entre os 4 candidatos, e para o segundo monitor da dupla, restam 3 estudantes para serem escolhidos. Assim, o total de duplas é calculado por: 4 ⋅ 3 = 12
Desconsiderando a quantidade de repetições, temos 12 : 2 = 6, ou seja, 6 duplas.
Situação 6
Quantos são os anagramas da palavra CARA?
Vamos listar todos os anagramas da palavra CARA, supondo que as letras a sejam “diferentes”. Para isso, vamos destacar cada letra A com uma cor.
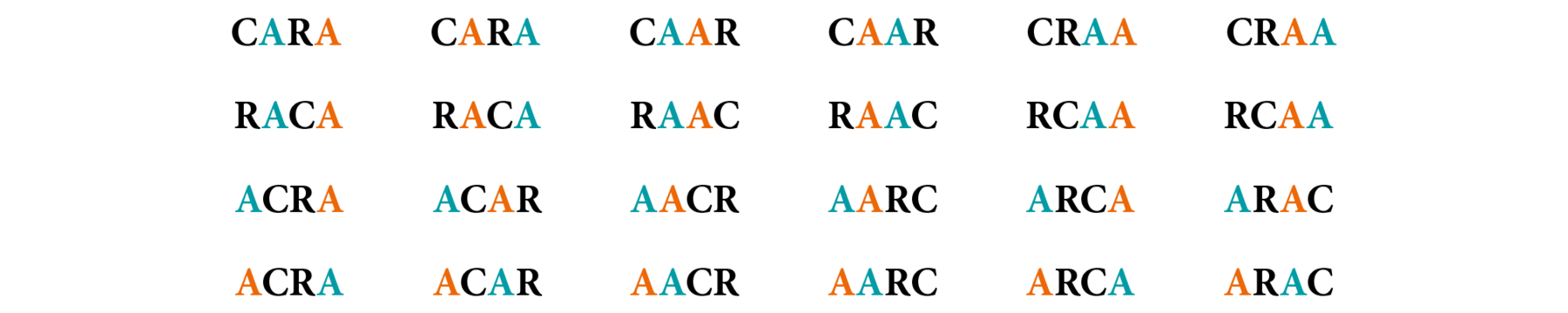
Dessa fórma, listamos 24 anagramas. No entanto, como as letras a não são diferentes, os pares de anagramas destacados a seguir são iguais.
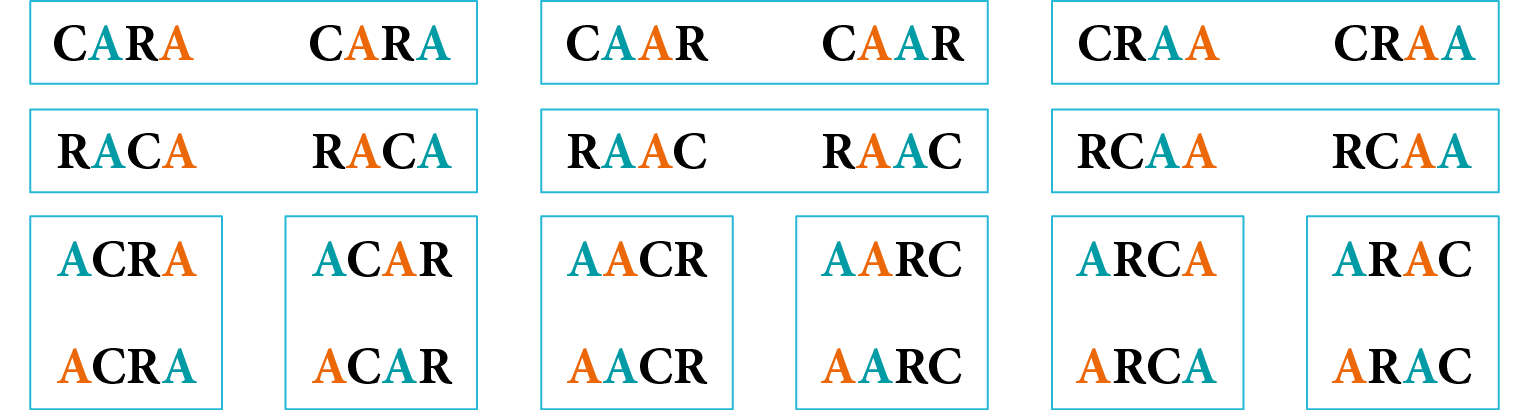
Note que metade dos anagramas apresentados anteriormente é igual. Portanto, a palavra CARA tem, na verdade, 12 anagramas.
Nesse caso, também podemos aplicar o princípio fundamental da contagem. Se todas as letras fossem diferentes, teríamos 4 escolhas para a primeira letra, 3 para a segunda, duas para a terceira e somente uma para a quarta. Isso daria 24 anagramas, pois 4 ⋅ 3 ⋅ 2 ⋅ 1 = 24. No entanto, como cada anagrama foi contado duas vezes, devemos dividir 24 por 2 para eliminar as repetições.
Portanto, a palavra CARA tem 12 anagramas, pois 24 : 2 = 12.
Para investigar

Reúna-se com um colega e calculem o número de anagramas da palavra AMADA.

ATIVIDADES
faça as atividades no caderno
1. Quantos são os anagramas da palavra LIVRO?
2. Quantos são os anagramas da palavra LIVRO que começam com I e terminam com óh?
3. Com os 5 tipos de fruta que há em uma fruteira, quantos tipos de salada, contendo 3 delas, podemos fazer?
4. Dado um conjunto de 10 pessoas, quantas comissões diferentes de 3 pessoas é possível formar?
5. Quantos são os anagramas da palavra ABACATE?
6.


Elabore um problema envolvendo o princípio fundamental da contagem. Passe seu problema para um colega resolver e resolva o problema criado por ele.
Respostas e comentários
Para investigar: 20 anagramas
1. 120 anagramas
2. 6 anagramas
3. 10 tipos de salada
4. 120 comissões
5. 840 anagramas
6. Resposta pessoal.
Orientações e sugestões didáticas
• No boxe Para investigar, espera-se que os estudantes identifiquem, a princípio, que, se todas as letras fossem diferentes, teríamos 5 escolhas para a primeira letra, 4 para a segunda, 3 para a terceira, duas para a quarta e somente uma para a quinta, o que resultaria em 120 anagramas, pois 5 ⋅ 4 ⋅ 3 ⋅ 2 ⋅ 1 = 120. Como a letra a se repete 3 vezes na palavra AMADA, devemos computar o número de anagramas repetidos, ou seja, 3 ∙ 2 ∙ 1 = 6. Assim, é preciso dividir o total de anagramas pelo número de repetições: 120 : 6 = 20.
Portanto, há 20 anagramas da palavra AMADA.
• Na resolução da atividade 3, para fazer a salada com 3 tipos de fruta, temos: para a primeira fruta, 5 escolhas; para a segunda, 4; e, para a terceira, 3. Há, portanto, 60 escolhas para os três tipos de fruta, pois 5 ⋅ 4 ⋅ 3 = 60. Mas esse não é o total de saladas, pois aquela formada pelas frutas a, B e C é a mesma daquela formada por B, C e a, por exemplo. Precisamos eliminar as repetições: cada salada foi contada 6 vezes, pois 3 ⋅ 2 ⋅ 1 = 6. Logo, o número de saladas de frutas desejado é 10, pois 60 : 6 = 10.
• Nos problemas de contagem, é possível, frequentemente, mudar um pouco o enunciado para ter outro problema. Nesses casos, pode acontecer de algum estudante sugerir “... e se fosse assim?”, o que é muito bom. Caso isso não ocorra, pode-se sugerir a alteração e colocar a nova situação em discussão.
• Após a criação de problemas, na atividade 6, é importante promover a troca dos problemas entre os estudantes. Isso pode ser feito em duplas, quando cada um propõe um problema para o colega resolver, ou em pequenos grupos, quando cada estudante propõe um problema para o grupo – cinco ou seis estudantes – discutir e resolver.

Trabalho em equipe
faça as atividades no caderno
Gincana dos problemas de contagem
Existem muitas situações envolvendo o raciocínio combinatório em que a quantidade de possibilidades não é explícita, mas deve ser calculada por meio das características dadas. Sabendo disso, você e seu grupo vão elaborar problemas de contagem com restrições e resolvê-los em uma “gincana matemática”.
Justificativa
Para resolver um problema de contagem com um número pequeno de combinações, podemos usar um diagrama de árvore ou outra representação para listar todas as possibilidades. No entanto, quando o número de combinações é muito grande, temos de usar outras estratégias, principalmente quando esses problemas trazem restrições muito específicas. Uma gincana é um meio divertido de treinar essas habilidades.
Objetivo
Elaborar problemas de contagem com restrições que possam ser resolvidos pela turma, por meio do princípio multiplicativo.
Apresentação
Gincana entre os diversos grupos da sala.
Questões para pensar em grupo
• Que tipo de problema de contagem com restrições pode ser resolvido por meio do princípio multiplicativo?
• Problemas de contagem podem envolver combinações de letras, números, senhas, anagramas, sabores de sorvete e cobertura, de sanduíches e sucos, cartas de baralho, fichas numeradas, entre outros. Quais elementos vocês escolherão?
• Antes de apresentar o problema para a turma, é importante que todos os integrantes do grupo saibam resolvê-lo. Como garantir que o problema elaborado possa ser resolvido usando apenas os conhecimentos matemáticos adquiridos até o momento?
• Quais serão as regras da gincana?
Não se esqueçam
• Cada grupo vai elaborar um problema de contagem com restrições, o qual deve ser apresentado (oralmente ou por escrito em uma folha ou no quadro) para os demais grupos, que, por sua vez, devem resolvê-lo e anotar em uma folha a resposta dos problemas.

Orientações e sugestões didáticas
Trabalho em equipe
Objetivos
• Aplicar, por meio de trabalhos em grupos, os conceitos estudados.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero três e das competências gerais 9 e 10 da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah zero três porque os estudantes deverão elaborar problemas que possam ser resolvidos pelo princípio multiplicativo.
Orientações
• Organize a turma em grupos. Após a leitura da seção, é importante verificar se os estudantes compreenderam claramente a atividade proposta. Se julgar oportuno, cite exemplos de problemas de contagem com restrições, como: “Quantos números de 9 algarismos podem ser formados, de modo que o primeiro algarismo seja maior do que 5?”, “Quantos anagramas da palavra BELO podem ser formados, tal que a última letra seja uma vogal?”.
• Antes de os grupos se apresentarem, verifique se os problemas estão adequados ao que foi estudado, se envolve apenas os conhecimentos matemáticos adquiridos até o momento e se todos os integrantes do grupo participaram da tarefa.
• Essa proposta de trabalho em equipe favorece o desenvolvimento das competências gerais 9 e 10 da Bê êne cê cê pois estimula o exercício da empatia e do diálogo, além de colocar em prática a cooperação e a competitividade entre os estudantes.
• Após todos os grupos elaborarem seus problemas e resolverem os problemas dos demais grupos, sugira que cada grupo resolva o seu problema no quadro e oriente os demais a compararem as resoluções. Verifique e valorize as diferentes estratégias.
• Se julgar conveniente, sugira uma votação para o problema de contagem com a situação mais criativa, a mais difícil e a mais fácil.
(ê éfe zero oito ême ah zero três) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.
Competência geral 9: Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competência geral 10: Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Estatística e Probabilidade
faça as atividades no caderno
Aplicação do princípio fundamental da contagem em cálculos de probabilidade
Marcos fez uma mágica com um baralho comum de cinquenta e duas cartas. Para isso, ele espalhou as cartas sobre a mesa com as faces voltadas para baixo. Em seguida, pediu a Aline que retirasse uma carta qualquer do baralho.

▶ Qual carta tinha maior probabilidade de ser retirada por Aline?
Experimento aleatório e experimento equiprovável
Retirar uma carta qualquer do baralho é um experimento cujo resultado não pode ser previsto. É chamado experimento aleatório.
Além disso, o experimento que Aline realizou ao retirar uma carta qualquer do baralho é equiprovável, ou seja, todas as cartas têm a mesma probabilidade de ser retiradas.
Cálculo de probabilidade
Para calcular a probabilidade de um evento ocorrer, basta dividir o número de casos favoráveis pelo número de elementos do espaço amostral. Para determinar esses números, quando necessário, podemos usar o princípio fundamental da contagem.
Espaço amostral é o conjunto formado por todos os resultados possíveis de um experimento.
Orientações e sugestões didáticas
Estatística e Probabilidade
Objetivo
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah dois dois da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah dois dois porque os estudantes terão a oportunidade de calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
Orientações
• Dando continuidade à resolução de problemas que envolvem combinações e contagens, esta seção propõe aos estudantes que façam aplicações do princípio multiplicativo em cálculos de probabilidades empregando uma razão.
• Aproveite a situação inicial e peça aos estudantes que calculem a probabilidade de Aline retirar uma carta 7 de determinado naipe. Espera-se que eles concluam que a probabilidade é de
fração: um cinquenta e dois avos., dado que há apenas um caso favorável (uma carta 7 para o naipe escolhido). Se julgar oportuno, proponha outros cálculos envolvendo a mesma situação, como a probabilidade de escolher carta 4 de qualquer naipe
entre parênteses, fração quatro cinquenta e dois avos., ou uma carta de determinado naipe
entre parênteses, fração treze cinquenta e dois avos..
(ê éfe zero oito ême ah dois dois) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.
▶ Estatística e Probabilidade
Lembre-se: Escreva no caderno!
Acompanhe, por exemplo, como calcular a probabilidade de uma senha de três algarismos diferentes começar com 0:
• número de senhas com três algarismos diferentes que começam com 0 (casos favoráveis):
1 ⋅ 9 ⋅ 8 = 72
• número de senhas com três algarismos diferentes (casos possíveis):
10 ⋅ 9 ⋅ 8 = 720
Ou seja, a probabilidade de a senha começar com 0 é dada por:
sentença matemática: fração 72 sobre 720 igual a um décimo.
= 0,1 ou 10%
Da mesma maneira, a probabilidade de essa senha começar com o algarismo 1 é
fração um décimo, de começar com o algarismo 2 é
fração um décimoe assim por diante.
Note que a soma de todas essas probabilidades é igual a 1:
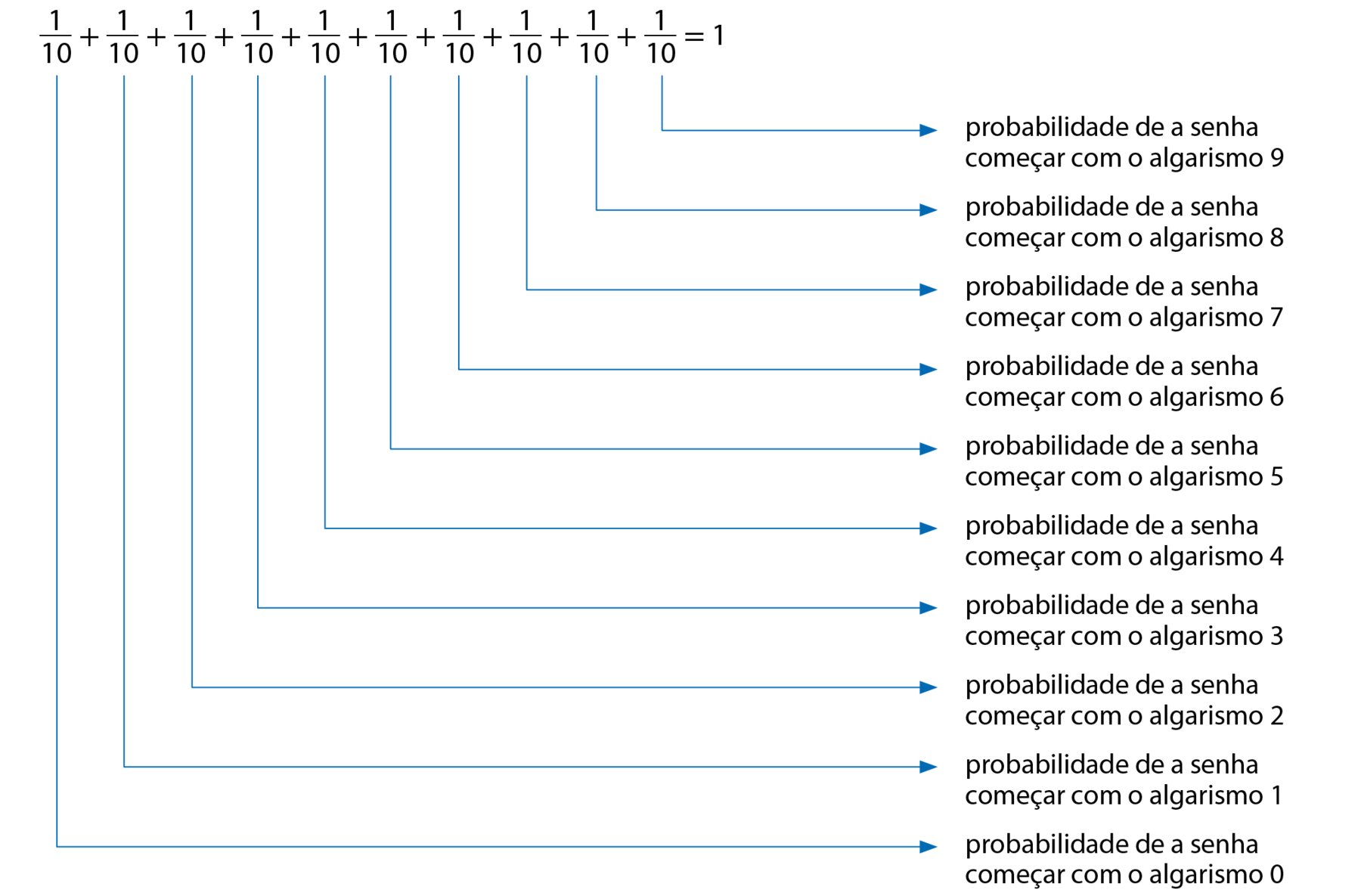
Isso ocorre com a soma das probabilidades de todos os elementos de um espaço amostral: a soma das probabilidades é sempre igual a 1.

ATIVIDADES
faça as atividades no caderno
1. Fernando, Luana, Pedro, Alexandre, Izabel, Marta e Carla estão participando de um torneio de xadrez na escola. Considerando que eles são os únicos participantes e que todos têm a mesma probabilidade de ficar em primeiro lugar, responda às questões a seguir.
a) Quantas são as possíveis combinações de colocação desses participantes no campeonato?
b) Qual é a probabilidade de Fernando ser o primeiro colocado?
Respostas e comentários
1. a) .5040 combinações
1. b) aproximadamente 14,29%
Orientações e sugestões didáticas
• Caso julgue conveniente retomar os conceitos envolvidos para o desenvolvimento da habilidade sugerimos os cadernos de exercícios do Portal da Matemática ó bê mépi, para explorar a fração como probabilidade. Disponível em: https://oeds.link/Pp9T7D. Acesso em: 7 julho 2022.
2. Ana tem conta-corrente em um banco em que recebe o salário. Para sacar o dinheiro do banco, ela recebeu uma senha composta de quatro algarismos seguidos por duas letras, os quais podem ser iguais.
a) Qual é o total de senhas que podem ser criadas nessas condições?
b) Qual é a probabilidade de a senha de Ana ter a letra a na última posição?
c) Se as letras e os algarismos não pudessem ser iguais, quantas senhas poderiam ser criadas? Nessas condições, qual seria a probabilidade de a senha de Ana ter a letra a na última posição?
3. Na sorveteria de Fábio são oferecidos sorvetes na casquinha com 6 opções de sabores: morango, limão, abacaxi, creme, flocos e chocolate.

a) De quantas maneiras é possível montar um sorvete com duas bolas de 2 sabores diferentes?
b) Qual é a probabilidade de um cliente pedir um sorvete com duas bolas de 2 sabores diferentes, das quais uma bola seja de chocolate?
c)

Você acha que, na realidade de uma sorveteria, essa probabilidade é verdadeira? Converse com um colega a respeito do assunto e formulem uma hipótese.
4. Everton resolveu pintar sua nova casa antes de se mudar. Para deixá-la com aspecto alegre, decidiu usar uma cor diferente em cada cômodo. Então, comprou 7 cores de tinta: azul, amarela, branca, lilás, verde, rosa e laranja.

Considerando que a casa tem 2 quartos, uma sala, uma cozinha, 2 banheiros e uma lavanderia, responda às questões.
a) De quantas maneiras diferentes Everton poderá pintar sua casa?
b) Qual é a probabilidade de ele pintar a cozinha de laranja?
c) Nas condições apresentadas no enunciado, se Everton tivesse 8 cores de tinta, de quantas maneiras distintas ele poderia pintar sua casa?
Respostas e comentários
2. a) .setecentas e sessenta. senhas
2. b) aproximadamente 3,85%
2. c) .duzentas e setenta e seis. senhas; aproximadamente 3,85%
3. a) 30 maneiras
3. b) aproximadamente 33,33%
3. c) Resposta pessoal.
4. a) .5040 maneiras
4. b) 14,29%
4. c) .trezentas e vinte maneiras
Orientações e sugestões didáticas
• Comente com os estudantes que, na atividade 3, é preciso levar em conta a ordem das bolas de sorvete na casquinha. Por exemplo, o sorvete com a bola de flocos embaixo e a de limão em cima é diferente do sorvete com a bola de limão embaixo e a de flocos em cima. Então, o número de possibilidades de sorvete com apenas uma bola de chocolate será a soma do número de possibilidades de sorvete com uma bola de chocolate embaixo e do número de possibilidades de sorvete com uma bola de chocolate em cima.

Atividades de revisão
faça as atividades no caderno
1. Leia a tirinha e, depois, responda às questões.

a) Qual foi o engano cometido pelo tucano?
b) A senha de Bugio é formada por cinco algarismos. Quantas senhas é possível formar com cinco algarismos?
2. Em uma empresa são fabricados cadeados que só abrem por meio de um código, dispensando o uso de chave. Os códigos são formados por sete algarismos distintos. Quantos cadeados com códigos diferentes podem ser fabricados nessa empresa?

3. Uma senha para acessar a internet é formada por uma letra do nosso alfabeto seguida de quatro algarismos, que podem ser iguais.

• Quantas senhas é possível formar?
4. De quantos modos podemos escolher 3 entre 8 pessoas?
5. Quantos são os anagramas da palavra ARARA?
Respostas e comentários
1. a) O tucano não sabia que cada bolinha preta que visualizou esconde um caractere da senha de Bugio.
1. b) .100000 senhas
2. .604800 cadeados
3. duzentas e sessenta. senhas
4. 56 modos
5. 10 anagramas
Orientações e sugestões didáticas
Atividades de revisão
Objetivos
• Consolidar o conhecimento adquirido no decorrer do capítulo.
• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero três da Bê êne cê cê.
Habilidade da Bê êne cê cê
• A habilidade ê éfe zero oito ême ah zero três é desenvolvida nesta seção por meio da resolução das atividades propostas.
Orientações
• Aproveite o tema das primeiras atividades propostas nesta seção e peça aos estudantes que pesquisem e tragam informações para a aula seguinte a respeito do uso de senhas seguras, antes da realização das atividades.
• Faça uma roda de conversa para que eles exponham o que sabem e o que pesquisaram sobre o assunto. Espera-se que eles indiquem o cuidado com a criação das senhas, evitando o uso de dados pessoais e priorizando senhas longas, com caracteres diversos e/ou aleatórios.
• Faça a mediação sobre o uso das senhas, cuidando para que não sejam expostas nem compartilhadas, tampouco usadas em computadores públicos sem conexões seguras. É possível que algum estudante traga a informação sobre phishing, que são códigos maliciosos usados para invadir computadores ou copiar senhas.
• Se julgar conveniente, oriente os estudantes a elaborarem cartazes com dicas e hábitos de segurança para o uso de senhas.
• Sugerimos algumas questões para que os estudantes possam refletir sobre suas aprendizagens e possíveis dificuldades no estudo deste Capítulo, as quais devem ser adaptadas à realidade da turma. Oriente-os a fazer a autoavaliação, respondendo às questões no caderno com “sim”, “às vezes” ou “não”.
Eu...
... compreendo o princípio multiplicativo ou princípio fundamental da contagem?
... sei resolver problemas utilizando o princípio multiplicativo ou princípio fundamental da contagem?
... compreendo o que são anagramas?
... compreendo o conceito de probabilidade?
... sei calcular a probabilidade da ocorrência de um evento?
(ê éfe zero oito ême ah zero três) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.

Para finalizar
faça as atividades no caderno
Observe e responda
Considere as imagens a seguir.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.



Orientações e sugestões didáticas
Para finalizar
Objetivo
• Analisar o que foi estudado na Unidade e avaliar o aprendizado.
Orientações
• Para fechar a Unidade de modo que fique claro para os estudantes quais conceitos foram discutidos e se possa verificar se ainda há dúvidas, essa etapa promove discussões orais sobre expressões algébricas, medida de volume e problemas de contagem.
• Com debates e registros, é possível que todos tirem suas conclusões e estejam mais seguros em relação ao conhecimento construído.
• Oriente os estudantes a reverem as atividades feitas nos capítulos e peça que:
1) Listem as atividades dos capítulos 6, 7 e 8 que eles tiverem dificuldades de resolver.
2) Relacionem as atividades que listaram na questão anterior com os conteúdos estudados.
3) Reúnam-se em grupos e resolvam juntos as atividades listadas. Se ainda tiverem dúvidas, formulem questões para o professor a fim de esclarecê-las.
▶ Para finalizar
Lembre-se: Escreva no caderno!
Com base nas imagens e também no que você aprendeu nesta Unidade, responda às questões.
1. Observe a figura da ave. Ela foi composta com as peças do quadrado. Como você faria para calcular a medida da área dessa figura?
2. Como podemos calcular a medida de volume de água necessária para encher o aquário da foto?
3. Na placa de trânsito, a medida de comprimento de cada lado do octógono está representada por a. Como você indicaria a medida do perímetro desse octógono?
4. Uma senha de 6 dígitos foi digitada na máquina retratada na página anterior. Qual é a probabilidade de adivinharmos essa senha, sabendo que ela é formada por algarismos distintos?
Registre

Para finalizar o estudo desta Unidade, reúna-se com alguns colegas e façam o que se pede.
1. Como se calcula a medida de volume de um paralelepípedo?
2. Como vocês diferenciam expressões algébricas de expressões numéricas? Deem exemplos.
3. O que são monômios? E polinômios? O que os diferencia das equações?
4. Quais operações podem ser realizadas entre os polinômios? Exemplifiquem cada uma delas.
5. O que diz o princípio fundamental da contagem?
6. Na abertura desta Unidade, vocês responderam a algumas questões no boxe “Para começar...”. Comparem as respostas dadas àquelas questões com as respostas que vocês dariam agora e escrevam um texto explicando o que vocês aprenderam nesta Unidade.
Para conhecer mais
O código polinômio (Coleção A descoberta da Matemática)
Luzia Faraco Ramos
São Paulo: Ática, 2019.
O relógio antigo do pai de Leo desaparece, e o ladrão deixa como pista desafios matemáticos. Leo pede a ajuda da professora Paula para desvendar os códigos, o que acaba por despertar o ciúme da namorada Kika. Será que a Matemática vai conseguir solucionar esse problema também?

Respostas e comentários
Observe e responda: 1. Espera-se que os estudantes percebam que basta medir o comprimento do lado e calcular a medida da área do quadrado. A medida da área da figura da ave será igual à do quadrado.
Observe e responda: 2. Multiplicando as dimensões a, b e c do aquário.
Observe e responda: 3. 8a
Observe e responda: 4.
fração 1 sobre cento e cinquenta e um mil e duzentosRegistre: 1. Multiplicando-se a medida do comprimento pelas medidas da largura e da altura.
Registre: 2. Expressões algébricas são formadas por operações com números e letras ou somente por letras. Expressões numéricas são formadas apenas por um número ou por operações entre números. Exemplos pessoais.
Registre: 3. Monômio é um número ou uma expressão algébrica formada pela multiplicação de um número por uma ou mais letras. Polinômio é um monômio ou uma soma finita de monômios. As equações expressam uma igualdade, enquanto monômios e polinômios, não.
Registre: 4. Espera-se que os estudantes façam uma breve síntese das operações e dos métodos aprendidos nesta Unidade.
Registre: 5. Se uma decisão divisores de pode ser tomada de pê maneiras diferentes e se, uma vez tomada a decisão divisores de , a decisão divisores de puder ser tomada de pê maneiras diferentes, então o número de maneiras de tomar as decisões divisores de e divisores de é pê ⋅ pê.
Registre: 6. Resposta pessoal.
Orientações e sugestões didáticas
• Na questão 3, proposta em Observe e responda, espera-se que os estudantes determinem a medida do perímetro do octógono, calculando: 8 ⋅ a
• Na questão 4, como a senha é formada por algarismos distintos, temos que: 10 ∙ 9 ⋅ 8 ⋅ 7 ⋅ 6 ⋅ 5 = .151200
Portanto, é possível formar cento e cinquenta e uma.duzentas senhas diferentes.
A probabilidade de se acertar uma senha nesse total é de
fração 1 sobre cento e cinquenta e um mil e duzentos• Em Registre, na atividade 2, exemplos de resposta:
– expressão algébrica: 5x; x + 3
– expressão numérica: (3 ⋅ 2) + 5
• Na atividade 6, espera-se que, após o estudo dos capítulos, tenha ficado mais fácil responder às questões propostas na abertura desta Unidade.
• O livro paradidático apresentado na seção Para conhecer mais pode ser usado como material complementar e também auxiliar na aprendizagem.
Verifique se ele está disponível na escola e incentive os estudantes a lê-lo. Com isso, eles não só estarão desenvolvendo a competência leitora como também poderão lidar com alguns dos conceitos estudados.