Página 227

UNIDADE 4

Capítulo 9

Equações e sistemas de equações

Capítulo 10

Proporcionalidade entre grandezas

Capítulo 11

Transformações geométricas

Fotografia. Frascos com remédios e uma seringa ao lado. Ao fundo, pessoa deitada em uma cama. — Remédios devem ser manipulados somente por adultos e utilizados só em casos de necessidade e na dosagem correta com prescrição médica.

o Cuidado com as doses pediátricas

A prescrição de medicamentos deve ser precisa, segura e eficaz, considerando tanto as informações do medicamento (doses máxima e efetiva, intervalo entre as doses etcétera) quanto as vias (oral, nasal etcétera) e as técnicas de aplicação (subcutânea, intramuscular, intravenosa etcétera). Especificamente no caso de crianças, embora não haja um consenso, a dosagem pode ser calculada com base na dosagem já estabelecida para adultos e na medida de massa ou idade da criança. Para efeito de curiosidade, considere três fórmulas que podem ser usadas para determinar a dosagem pediátrica, em que DP refere-se à dose pediátrica e dê á à dose para adultos.

Nome da regra	Característica da criança	Fórmula
Regra de Clark	Medida de massa corporal menor que 30 kg	$D P igual a divisão de abre parênteses D A vezes abre parênteses k g fecha parênteses fecha parênteses sobre abre parênteses 70 k g fecha parênteses$
Regra de Law	Idade inferior a 1 ano	$D P igual a divisão de abre parênteses D A vezes fecha parênteses sobre 150$
Regra de Young	Entre 1 e 12 anos de idade	$D P igual a divisão de abre parênteses D A vezes fecha parênteses sobre abre parênteses mais 12 fecha parênteses$

Fonte: LIBERATO, Eryck êti Fármacos em crianças. In: BRASIL. Ministério da Saúde. Secretária de Ciência, Tecnologia e Insumos Estratégicos. Departamento de Assistência Farmacêutica e Insumos Estratégicos. Formulário terapêutico nacional 2008: 2006. Brasília, Distrito Federal: Ministério da Saúde, 2008. página 22.

Para começarreticências

1. Quais são as características consideradas no cálculo da dosagem pediátrica?

2. Indique uma fórmula que pode ser usada para determinar a DP de um medicamento para cada uma das crianças a seguir.

• Lucas: 5 meses e 5 quilogramas

• Maria: 9 meses e 10 quilogramas

• Aline: 7 anos e 25 quilogramas

• João: 11 anos e 32 quilogramas

3. Calcule a DP aproximada para as crianças do item anterior, considerando que a dê á seja 200 miligramas por dia.

Respostas e comentários

Habilidades da Bê êne cê cê trabalhadas nesta Unidade:

ê éfe zero oito ême ah zero sete

ê éfe zero oito ême ah zero oito

ê éfe zero oito ême ah zero nove

ê éfe zero oito ême ah um dois

ê éfe zero oito ême ah um três

ê éfe zero oito ême ah um oito

ê éfe zero oito ême ah dois quatro

ê éfe zero oito ême ah dois cinco

ê éfe zero oito ême ah dois seis

ê éfe zero oito ême ah dois sete

Para começarreticências: 1. A medida de massa e a idade da criança.

2. Lucas: regra de Clark ou regra de ; Maria: regra de Clark ou regra de ; Aline: regra de Clark ou regra de iãng; João: regra de iãng.

3. Lucas: 17 miligramas por dia (Clark e ); Maria: 29 miligramas por dia (Clark) e 26 miligramas por dia (); Aline: 71 miligramas por dia (Clark) e 74 miligramas por dia (iãng); João: 96 miligramas por dia (iãng).

Orientações e sugestões didáticas

Abertura da Unidade 4

Conteúdos

• Nesta Unidade, serão trabalhados vários conceitos relacionados às unidades temáticas Álgebra, Geometria e Probabilidade e Estatística, que, entre outros objetivos, favorecerão o desenvolvimento das habilidades da Bê êne cê cê listadas.

Orientações

• A proposta da abertura possibilita trabalhar com o Tema Contemporâneo Transversal Saúde da macroárea Saúde, ao tratar de cuidados com a dosagem de medicação indicada para crianças e apresentar fórmulas para seu cálculo, com base na dosagem já estabelecida para adultos e na medida de massa e idade da criança.

• Estimule-os a pesquisar as palavras que não conhecem. Se julgar necessário, explique a eles que pediatria é o ramo da medicina que trata a saúde e os cuidados das crianças e adolescentes. Explique ainda os significados das palavras citadas nas técnicas de aplicação: subcutânea (sob a pele), intramuscular (interior do músculo) e intravenosa (interior da veia).

• Os links expressos nesta coleção podem estar indisponíveis após a data de publicação deste material.

• Após responderem à questão 1 do boxe Para começar, pergunte aos estudantes se a dose para adultos (dê á), a medida de massa e a idade da criança, presentes nas fórmulas são variáveis ou incógnitas. Espera-se que eles respondam que são variáveis, uma vez que podem assumir valores diferentes. Aproveite essa pergunta para verificar se está clara para eles a distinção entre variável e incógnita.

• Alerte-os de que nunca devem tomar medicamentos sem prescrição médica e acompanhamento de um adulto, pois a automedicação pode gerar consequências graves, ou até a morte.

• O trabalho com este tema permite que os estudantes conheçam algumas fórmulas matemáticas usadas na área da saúde, além de servir para a aprendizagem de conceitos relacionados ao cálculo do valor numérico de expressões algébricas, conforme solicitado na questão 3. Reforce que tais fórmulas devem guiar exclusivamente os médicos, pois eles também podem considerar outros fatores além da idade e da medida de massa da criança.

• O Formulário Terapêutico Nacional () contém informações científicas, embasadas em evidências sobre os medicamentos selecionados na Relação Nacional de Medicamentos Essenciais (), visando subsidiar os profissionais de saúde em prescrição, dispensação e uso dos medicamentos essenciais. Disponível em: https://oeds.link/koyzC9. Acesso em: 24 julho 2022.

Página 228

CAPÍTULO 9 Equações e sistemas de equações

1 Equação do 1º grau com duas incógnitas

As equações do 1º grau também são chamadas equações polinomiais do 1º grau. Vamos analisar algumas situações em que aparecem equações do 1º grau com duas incógnitas.

Situação 1

No mercado Ver-o-Peso, Benedito tem uma banca de camarão e Izabel, uma banca de farinhas. Observe os preços a seguir.

Fotografia. Recipiente com camarões vermelhos e a informação: quilograma: 32,00 reais

Fotografia. Sacos com farinha e a informação: FARINHA BRANCA 4 reais e 50 centavos por quilograma. — O camarão seco e a farinha branca são ingredientes típicos da cozinha paraense. O camarão seco é usado no preparo de um prato de origem indígena: o tacacá, um mingau feito da goma da mandioca com jambu (erva da região). Já a farinha branca é usada pura ou para engrossar o pirão servido com peixes.

Como podemos expressar o gasto de R$ 20,00vinte reais na compra de certa quantidade de farinha branca e de outro tanto de camarão seco por meio de uma sentença algébrica?

Indicando por x e y, respectivamente, a quantidade de farinha branca e a quantidade de camarão seco, em quilograma, podemos escrever:

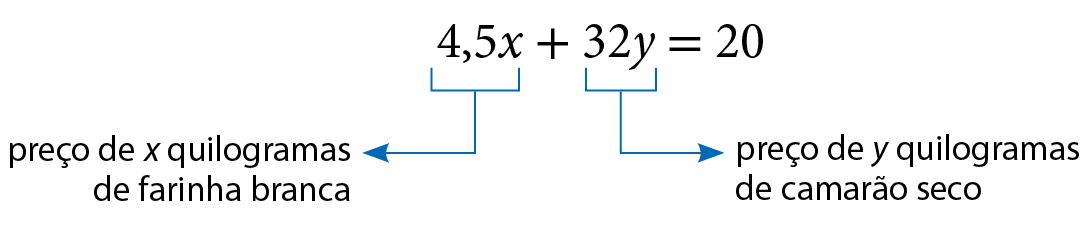
Esquema. 4 vírgula 5x mais 32y é igual a 20. Destaque em 4 vírgula 5x que representa o preço de x quilogramas de farinha branca e em 32y que representa o preço de y quilogramas de camarão seco.

Esse é um exemplo de equação do 1º grau com duas incógnitas.

Fotografia. Vista do alto de construção com torres. Ao redor, barcos. Ao fundo, prédios. — Mercado Ver-o-Peso (no centro da imagem), em Belém (Pará), 2020. O conjunto arquitetônico e paisagístico do Mercado Ver-o-Peso foi tombado pelo Instituto do Patrimônio Histórico e Artístico Nacional (ifãn) em 1977.

Lembre-se: Escreva no caderno!

Respostas e comentários

Habilidades da Bê êne cê cê trabalhadas neste Capítulo:

ê éfe zero oito ême ah zero sete

ê éfe zero oito ême ah zero oito

ê éfe zero oito ême ah zero nove

ê éfe zero oito ême ah dois cinco

Orientações e sugestões didáticas

Equação do 1º grau com duas incógnitas

Objetivos

• Introduzir o conceito de equação do 1º grau com duas incógnitas.

• Verificar se um par ordenado é solução de uma equação do 1º grau com duas incógnitas.

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero sete da Bê êne cê cê.

Habilidade da Bê êne cê cê

• Este tópico contribui para o desenvolvimento da habilidade ê éfe zero oito ême ah zero sete da Bê êne cê cê ao promover a associação entre uma equação linear de 1º grau com duas incógnitas e uma reta no plano cartesiano.

Orientações

• Aproveite o contexto da Situação 1 e proponha aos estudantes que conversem sobre as seguintes questões: “Você costuma ir a feiras ou mercados como o Ver-o-Peso?”; “Que outros tipos de feira você conhece?”; “O que mais chama sua atenção nesses ambientes?”; ”Como os alimentos são comercializados em uma feira livre?”. É possível que os estudantes respondam que conhecem feiras de objetos antigos, de mostruário, de livros e revistas etcétera Os alimentos, em geral, são comercializados por unidade, baciada, pedaço ou quilograma.

• Neste tópico, o foco do trabalho está voltado para a equação do 1º grau com duas incógnitas, envolvendo definição, solução e representação gráfica da solução. Verifique inicialmente se os estudantes compreenderam como a equação 4,5x + 32y = 20 se relaciona com a situação-problema apresentada. Se possível, verifique se eles conseguem prever valores para x e y que satisfaçam essa equação.

(ê éfe zero oito ême ah zero sete) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano.

Página 229

Situação 2

Irineu cortou fios coloridos com medida de 20 centímetros de comprimento para construir modelos do contorno de figuras retangulares. Se ele usou um fio inteiro para cada modelo, quais medidas de comprimentos dos lados esses modelos podem ter?

Considere alguns exemplos de modelos construídos por Irineu.

Ilustração. Rapaz branco, de cabelos castanho, usando camiseta clara sentado de frente a uma mesa com figuras com formatos retangulares compostas de fios coloridos.

Figura geométrica. Retângulo roxo sendo com comprimento igual a 8 centímetros e altura igual a 2 centímetros. Figura geométrica. Retângulo verde com comprimento igual a 4 centímetros e a altura igual a 6 centímetros. Figura geométrica. Quadrado laranja com comprimento do lado igual a 5 centímetros.

A medida do perímetro de todos os modelos construídos é 20 centímetros; logo, a medida do semiperímetro é 10 centímetros.

Indicando por x e y, respectivamente, a medida da largura e a medida do comprimento em centímetro dessas figuras, podemos escrever: x + y = 10.

Esse é outro exemplo de equação do 1º grau com duas incógnitas.

Os pares ordenados abre parêntesesx, yfecha parênteses, correspondentes às medidas da largura e do comprimento das figuras feitas por Irineu, abre parênteses2, 8fecha parênteses, abre parênteses4, 6fecha parênteses e abre parênteses5, 5fecha parênteses, são soluções da equação x + y = 10, porque 2 + 8 = 10, 4 + 6 = 10 e 5 + 5 = 10. Observe a seguir mais alguns pares ordenados que são soluções dessa equação.

• abre parênteses1, 9fecha parênteses, porque 1 + 9 = 10;

• abre parênteses3,8; 6,2fecha parênteses, porque 3,8 + 6,2 = 10;

•

(\frac{13}{2}, \frac{7}{2})

, porque

\frac{13}{2} + \frac{7}{2}

= 10.

Para pensar

A equação x + y = 10 tem infinitas soluções, mas a situação 2 descrita nesta página impõe algumas condições para os valores de x e de y. Quais são essas condições?

Equação do 1º grau com duas incógnitas, x e y, é uma sentença matemática que pode ser reduzida a uma sentença do tipo ax + by = c, sendo a, b e c números reais, em que a e b são não nulos.

São equações do 1º grau com duas incógnitas:

•

\frac{1}{2} x ‒ \sqrt{3} y = 4

• 1,65x + 22y =

\sqrt{7}

•

8 x + \frac{7}{2} = ‒ \frac{y}{3}

Não são equações do 1º grau com duas incógnitas:

• x ao quadrado + y = 2

•

\sqrt{x}

+ y = 1

• 5x menos abre parênteses2yfecha parêntesesao quadrado = 6

Observação

Podemos verificar se um par ordenado abre parêntesesx, yfecha parênteses é solução de uma equação do 1º grau com duas incógnitas substituindo as incógnitas pelos valores numéricos correspondentes. Se a sentença obtida for verdadeira, o par ordenado é solução da equação. Caso contrário, não é solução. No exemplo, o par ordenado abre parênteses1, menos7fecha parênteses é solução da equação 3x menos y = 10.

Ilustração. Quadro com o cálculo:
3x menos y é igual a 10,
Substituímos o valor de x por 1 e de y por -7 do par ordenado.
3 vezes 1 abre parênteses menos 7 fecha parênteses igual a 10, abaixo,
3 mais 7 é igual a 10, abaixo,
10 é igual a 10 abre parêntese sentença verdadeira fecha parênteses

Respostas e comentários

Para pensar: Nenhuma das medidas x e y pode ser negativa, nula, igual a 10 ou maior que 10.

Orientações e sugestões didáticas

• Se achar pertinente, apresente a Situação 2 e proponha aos estudantes que a representem por meio de uma equação do 1º grau com duas incógnitas. Incentive-os a verbalizar o que indica cada uma das incógnitas da equação que obtiveram. Depois, formalize o conceito de equação do 1º grau com duas incógnitas e o compare com o conceito de equação do 1º grau com uma incógnita. Estabelecer essa ponte entre o que já estudaram e o que estão estudando contribui para que eles atribuam significado ao novo conceito.

• Converse com eles sobre as soluções da equação x + y = 10. O boxe Para pensar contribui para que notem que a situação-problema impõe restrições aos valores que x e y podem assumir. Por representar medidas, x e y não podem ser negativos; também não podem ser iguais a 0, pois dessa fórma não teríamos uma figura retangular; e, por fim, não podem ser iguais ou maiores que 10, porque, em uma adição de números positivos não nulos, qualquer uma das parcelas não pode ser igual ou maior que a soma.

• Após abordar o conteúdo destas páginas, explique aos estudantes o porquê de as equações apresentadas também receberem o nome de “equações polinomiais do 1º grau”. Explique que uma equação polinomial é dada por Pabre parêntesesxfecha parênteses = 0, em que Pabre parêntesesxfecha parênteses é um polinômio qualquer. Logo, como as equações apresentadas podem ser expressas dessa fórma abre parêntesespor exemplo, na situação 1, 4,5x + 32y menos 10 = 0fecha parênteses, são chamadas de polinomiais.

Página 230

Representação gráfica das soluções

Cada par ordenado abre parêntesesx, yfecha parênteses, em que x e y são números reais, é representado por um ponto P do plano cartesiano. Os números x (abscissa de P) e y (ordenada de P) são as coordenadas do ponto P.

Ilustração. Homem branco de cabelo escuro na altura dos ombros, roupa escura com gola branca grande. — O matemático e filósofo francês Renê Decarte (1596-1650) foi o primeiro a usar o método de representação de coordenadas como o conhecemos hoje. O sistema de coordenadas cartesianas recebeu esse nome em sua homenagem.

Agora, vamos considerar a equação x + y = 10 sem levar em conta a situação-problema que a originou, ampliando o significado de x e de y para além de medidas de comprimento dos lados de uma figura e, assim, superando as restrições aos valores das incógnitas. Vamos pensar em dois números reais quaisquer cuja soma seja 10.

É possível representar no plano cartesiano as soluções (pares ordenados) da equação x + y = 10. Observe como Rubens fez.

Valor atribuído a x	Equacão em y	Valor de y	Par ordenado (x, y)
−1	−1 + y = 10	11	(−1, 11)
5	5 + y = 10	5	(5, 5)
7	7 + y = 10	3	(7, 3)
12	12 + y = 10	−2	(12, −2)

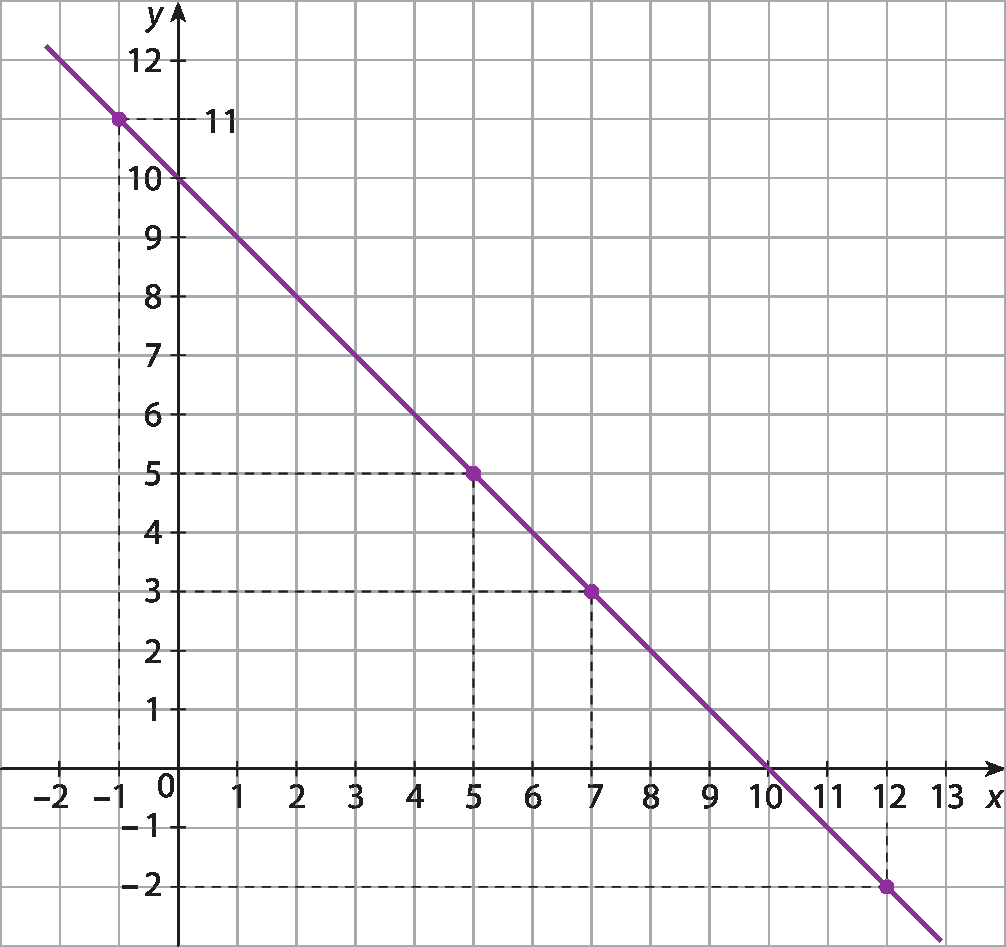
Gráfico. Eixo x com pontos de menos 2 a 13. Eixo y com pontos de menos 2 a 12. Pares ordenados: abre parêntese menos 1 vírgula 11 fecha parêntese. abre parêntese 5 vírgula 5 fecha parêntese. abre parêntese 7 vírgula 3 fecha parêntese. abre parêntese 12 vírgula menos 2 fecha parêntese. Por esses pares ordenados passa uma reta de cor roxa.

Ilustração. Menino branco de cabelo escuro e camisa azul escreve em uma folha. Ele fala: Atribuí alguns valores a x, calculei os correspondentes valores de y e escrevi os pares ordenados formados. Depois, localizei no plano cartesiano os pontos que representam os pares e tracei a reta que passa por eles.

Note que os pontos que representam os pares listados estão alinhados. Podemos demonstrar que o conjunto de todas as soluções de x + y = 10, em que x e y são números reais, é representado por uma reta. O mesmo ocorre com o conjunto das soluções de qualquer equação do 1º grau com duas incógnitas que possam ser qualquer número real.

O conjunto das soluções de uma equação do 1º grau com duas incógnitas pode ter nenhum, finitos ou infinitos elementos, dependendo da equação e dos números que as incógnitas podem assumir.

Para fazer

a) Determine quatro soluções da equação x + y = 2, sendo x e y números reais.

b) Agora, represente por meio de pares ordenados as soluções que você encontrou no item anterior.

Respostas e comentários

Para fazer: a) Exemplos de resposta: x = menos2,5 e y = 4,5; x = menos1 e y = 3; x = 0 e y = 2; x = 1 e y = 1

b) Exemplos de resposta: abre parêntesesmenos2,5; 4,5fecha parênteses; abre parêntesesmenos1, 3fecha parênteses; abre parênteses0, 2fecha parênteses; abre parênteses1, 1fecha parênteses

Orientações e sugestões didáticas

• Se julgar oportuno, para fazer uma retomada do assunto, proponha uma atividade em que os estudantes tenham de representar pontos em um plano cartesiano.

• Comente com eles que uma equação do 1º grau com duas incógnitas, quando desvinculada de um contexto, tem infinitas soluções, uma vez que, para cada valor atribuído a uma das incógnitas (podemos atribuir um número infinito de valores), encontramos um valor correspondente para a segunda incógnita. O fato de a reta ser a representante do conjunto de todas as soluções de uma equação do 1º grau com duas incógnitas, considerando que as incógnitas possam ser qualquer número real, reforça a ideia de que essas equações têm infinitas soluções, uma vez que uma reta tem infinitos pontos.

• No boxe Para fazer, após os estudantes resolverem as questões, peça a eles que comparem as respostas entre si e discutam possíveis divergências. Essa troca favorece a autonomia, uma vez que precisarão, eles mesmos, conferir o que fizeram e compreender o motivo de possíveis divergências. Essa troca de ideias desenvolve, ainda, a capacidade de argumentação dos estudantes, pois eles têm de se expressar por meio de textos orais e escritos.

Página 231

ATIVIDADES

faça as atividades no caderno

1. Represente cada situação por uma equação.

a) O preço z reais de um lápis adicionado ao preço y reais de uma borracha é R$ 3,00três reais.

b) Diva tem x reais e Reginaldo tem y reais. A diferença entre o triplo do valor que Diva tem e o dobro do valor que Reginaldo tem é 14.

2. Analise as equações e identifique qual delas é uma equação do 1º grau com duas incógnitas.

a) 4xy = 15

b) 2x menos y ao cubo = 7

c) .2008 = x menos y

d) x + 4y = z

e) x + 3 = 8

f) 2x + x ao quadrado = 10

3. Verifique se o par ordenado abre parênteses4, menos1fecha parênteses é solução das equações a seguir.

a) x + 4y = 15

b) x menos 4y = 0

c) 4x menos 4y = 12

d) 4x + y = 15

e) 3x + 2y = menos10

f) 2x +

\frac{y}{2}

= 7,5

4. Faça o que se pede.

a) Determine duas soluções para a equação 2x menos y =

\frac{1}{2}

.

b) Invente uma equação do 1º grau com duas incógnitas que tenha como solução os números menos3 e 12.

5. Faça um plano cartesiano em uma folha de papel quadriculado e localize os pontos representados pelos pares ordenados: Aabre parênteses3, menos1fecha parênteses, Babre parênteses0, 5fecha parênteses, Cabre parênteses4, menos3fecha parênteses, Dabre parênteses7, menos1fecha parênteses e Eabre parênteses1, 3fecha parênteses. Depois, verifique se esses pontos pertencem à mesma reta.

6. Escreva no caderno uma equação do 1º grau com duas incógnitas que tenha uma das soluções representada pelo ponto no plano cartesiano a seguir.

Gráfico. Eixo x com pontos de menos 2 a 5. Eixo y com pontos de 0 a 6. Pares ordenados: abre parêntese 0 vírgula 5 vírgula 4 vírgula 5 fecha parêntese e abre parêntese a fração 3 sobre 2 vírgula fração 9 sobre 2 fecha parêntese.

7.

Enrico propôs um desafio para sua amiga Juliana. Ele pediu a ela que encontrasse um número natural que, multiplicado por 5, acrescentando 5 unidades ao produto, dividindo o resultado por 2 e, depois de extrair a raiz quadrada, acrescentando 10 unidades, resultasse em 15. Qual era esse número?

8. Entre as representações gráficas a seguir, qual corresponde às soluções da equação 2x menos y = 4, em que x e y são números reais?

a)

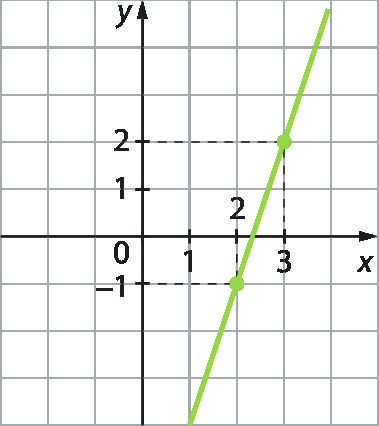
Gráfico. Eixo x com pontos de menos 1 a 3. Eixo y com pontos de menos 1 a 2. Pares ordenados: abre parêntese 3 vírgula 2 fecha parêntese e abre parêntese 2, menos 1 fecha parêntese. Reta verde passa pelos pares ordenados.

b)

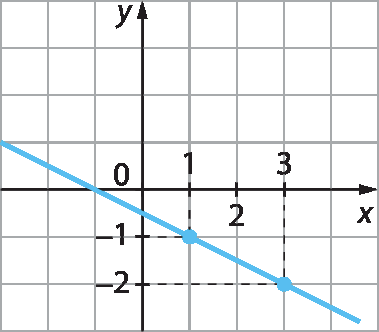
Gráfico. Eixo x com pontos de 0 a 3. Eixo y com pontos de menos 2 a 0. Pares ordenados: abre parêntese 3 vírgula menos 2 fecha parêntese e abre parêntese 1 vírgula 1 fecha parêntese. Reta azul passa pelos pares ordenados.

c)

Gráfico. Eixo x com pontos de 0 a 3. Eixo y com pontos de menos 4 a 2. Pares ordenados: abre parêntese 3 vírgula 2 fecha parêntese e o abre parêntese 2 vírgula menos 4 fecha parêntese. Reta laranja passa pelos pares ordenados

•

Explique a um colega como você fez para identificar a representação gráfica correta.

9. Leia e faça o que se pede.

a) Um par ordenado cuja abscissa vale 3 é solução da equação 3x menos 4y = 7. Determine a ordenada desse par ordenado.

b) Uma das soluções da equação 2x menos y = 5 é o par ordenado cuja ordenada vale menos5. Determine a abscissa desse par ordenado.

10. Represente em um mesmo plano cartesiano as soluções de cada uma das equações e depois responda à questão.

(um) x + y = 5

(dois) y = 3x menos 3

• Que par ordenado é solução das duas equações?

Respostas e comentários

1. a) z + y = 3

1. b) 3x menos 2y = 14

2. alternativa c

3. a) não

3. b) não

3. c) não

3. d) sim

3. e) não

3. f) sim

4. a) Exemplo de resposta:

(0, ‒ \frac{1}{2}) e (1, \frac{3}{2})

4. b) Exemplo de resposta: menosx + y = 15

5. Resposta em Orientações.

6. Exemplo de resposta: 2x + 2y = 12

7. 9

8. alternativa c

Exemplo de explicação: Substituí as incógnitas pelas coordenadas de dois pontos de cada gráfico, verificando se as igualdades obtidas eram verdadeiras.

9. a)

\frac{1}{2}

9. b) 0

10. Resposta em Orientações.

Orientações e sugestões didáticas

• Resposta da atividade 5:

Ilustração. Malha quadriculada com gráfico. Eixo x, pontos menos 1, 0, 3, 4 e 7. Eixo y, pontos menos 3, menos 1, 0, 3, 5. Pares ordenados: A abre parêntese 3 vírgula menos 1 fecha parêntese. B abre parêntese 0 vírgula 5 fecha parêntese. C: abre parêntese 4 vírgula menos 3 fecha parêntese. D: abre parêntese 7 vírgula menos 1 fecha parêntese. E: abre parêntese 1 vírgula 3 fecha parêntese.

Logo, os pontos não pertencem a uma mesma reta.

• Na atividade 7, Enrico propôs a Juliana que encontrasse um número. Verifique se eles usam a estratégia de montar uma equação do primeiro graus com uma incógnita para obter o número desconhecido.

• Na atividade 10, oriente os estudantes a montar um quadro para identificar pares ordenados que são soluções de cada uma das equações até obter o par ordenado que é solução das duas equações. A representação em um mesmo plano cartesiano pode ser observada na figura a seguir, entretanto, verifique se os estudantes percebem que para a representação das soluções de cada equação seja de fato uma reta, é necessário considerar que x e y podem ser qualquer número real.

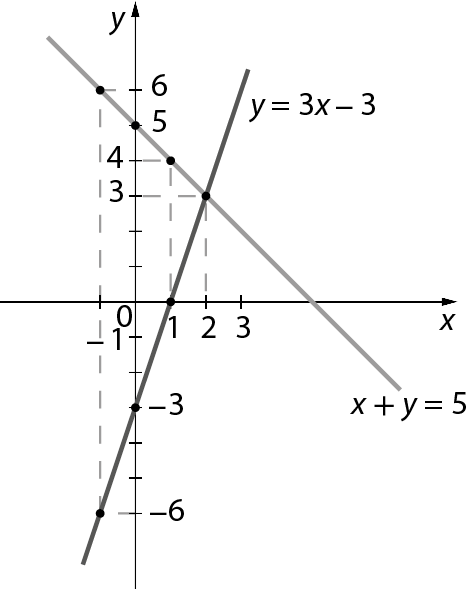
Gráfico. Eixo x com pontos 0, 1, 2 e 3. Eixo y, pontos de menos 6 a 6. Reta y é igual a 3x menos 3 passa pelos pares: abre parêntese 2 vírgula 3 fecha parêntese, abre parêntese 1 vírgula 0 fecha parêntese, abre parêntese 0, menos 3 fecha parêntese, abre parêntese menos 1, menos 6 fecha parêntese. Reta x mais y é igual a 5 passa pelos pares: parêntese vírgula 3 fecha parêntese, abre parêntese 1 vírgula 4 fecha parêntese, abre parêntese 6 vírgula menos 6 fecha parêntese.

O par ordenado que é solução das duas equações é abre parênteses2, 3fecha parênteses.

Página 232

2 Sistemas de duas equações do 1º grau com duas incógnitas

Analise as situações a seguir.

Situação 1

Leia o diálogo a seguir.

Fotomontagem. À esquerda, menino branco de cabelo preto e camiseta branca. Ele fala: Luísa, eu descobri que tenho 12 figurinhas a mais que você.
Ao lado, menina branca de cabelo claro e camisa estampada diz: E eu sei que, juntos, temos 52 figurinhas. Eles estão de frente a uma mesa com álbuns abertos e figurinhas.

Vamos escrever equações que representam a situação apresentada.

Indicando por x o número de figurinhas de Jorge e por y o número de figurinhas de Luísa, temos:

• A diferença entre o número de figurinhas de Jorge e de Luísa é 12

x menos y = 12

• Jorge e Luísa têm, juntos, 52 figurinhas

x + y = 52

Essas equações formam um sistema de duas equações do 1º grau com duas incógnitas.

Costumamos dispor as equações de um sistema em uma chave.

\{\begin{cases} x ‒ y = 12 \\ x + y = 52 \end{cases}

, em que x e y são números naturais.

Situação 2

Em um parque de diversões há dois preços para a entrada:

Esquema. Pessoas com idade até 12 anos seta à direita 18,00 reais Pessoas com mais de 12 anos seta à direita 25,00 reais

Joana foi com alguns familiares a esse parque. No total, compraram 5 ingressos e gastaram R$ 111,00cento e onze reais. Nessa situação, quantas pessoas com idade até 12 anos e quantas pessoas com mais de 12 anos participaram do passeio familiar?

Esse problema pode ser traduzido para a linguagem algébrica. Ao indicar por x o número de pessoas com mais de 12 anos e por y o número de pessoas com idade até 12 anos, temos:

Informações do enunciado	Linguagem algébrica
“compraram 5 ingressos”	x + y = 5
“gastaram R$ 111,00”	25x + 18y = 111

Orientações e sugestões didáticas

Sistemas de duas equações do 1º grau com duas incógnitas

Objetivos

• Introduzir o conceito de sistema de duas equações do 1º grau com duas incógnitas.

• Resolver sistemas de equações do 1º grau com duas incógnitas utilizando diferentes estratégias.

• Interpretar graficamente as soluções de sistemas de duas equações do 1º grau com duas incógnitas.

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero oito e da competência específica 6 da Bê êne cê cê.

Habilidade da Bê êne cê cê

• Este tópico contribui para o desenvolvimento da habilidade ê éfe zero oito ême ah zero oito da Bê êne cê cê porque os estudantes terão a oportunidade de resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas, e de interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.

Orientações

• O estudo prossegue com a introdução dos sistemas de duas equações do 1º grau com duas incógnitas, relacionando um problema a um sistema. É importante destacar que as duas equações que compõem um sistema expressam duas condições que devem ser verificadas ao mesmo tempo. Assim, não se pode considerar as equações do sistema desconectadas uma da outra.

(ê éfe zero oito ême ah zero oito) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.

Competência específica 6: Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

Página 233

Nesse caso, podemos também montar um sistema de equações, considerando que x e y são números naturais.

\{\begin{cases} x + y = 5 \\ 25 x + 18 y = 111 \end{cases}

Para pensar

a) Como você faria para resolver o problema?

b) Qual é a solução do problema?

Assim como as equações do 1º grau com duas incógnitas, o sistema de equações do 1º grau com duas incógnitas pode ter nenhuma, uma ou infinitas soluções. Se tiver solução, cada uma das soluções será um par ordenado abre parêntesesx, yfecha parênteses.

A seguir, vamos estudar métodos de resolução de sistemas de equações do 1º grau com duas incógnitas.

Resolução de um sistema de duas equações do 1º grau com duas incógnitas por tentativa e erro

No jogo de basquete, há cestas que valem 3 e 2 pontos. Durante uma partida, Robson converteu 10 cestas e marcou 22 pontos. Quantas cestas de 3 pontos e quantas de 2 pontos Robson converteu nessa partida?

Indicando por x o número de cestas de 3 pontos e por y o número de cestas de 2 pontos, podemos traduzir o problema por meio de um sistema de equações do 1º grau com duas incógnitas, em que x e y representam números naturais. Assim:

• Robson converteu 10 cestas: x + y = 10

• Robson marcou 22 pontos: 3x + 2y = 22

\{\begin{cases} x + y = 10 \\ 3 x + 2 y = 22 \end{cases}

Para resolver esse sistema, Robson usou o método de tentativa e erro, ou seja, testou alguns valores para x e para y e verificou se as soluções encontradas estavam de acordo com os dados do problema.

x + y	Valor atribuído a x	Valor de y	Valor de 3x + 2y
10	5	5	3 ⋅ 5 + 2 ⋅ 5 = 25
10	4	6	3 ⋅ 4 + 2 ⋅ 6 = 24
10	3	7	3 ⋅ 3 + 2 ⋅ 7 = 23
10	2	8	3 ⋅ 2 + 2 ⋅ 8 = 22

Portanto, Robson converteu duas cestas de 3 pontos e 8 cestas de 2 pontos.

Fotografia. Menino branco e loiro de regata branca e bermuda. Ele segura uma bola de basquete com um dedo. Ele pensa: Primeiro, considerei x igual a 5. Então, y deve valer 5 para que a soma seja 10. Depois, fazendo x = 5 e y = 5, calculei o valor numérico de 3x + 2y, que nesse caso deu 25. Mas, como deveria dar 22, tive de testar outros valores menores para x.

Observação

Nas situações apresentadas, cada uma das equações do sistema tem mais de uma solução, mas o sistema formado por essas duas equações tem apenas uma solução.

Respostas e comentários

Para pensar: a) Resposta pessoal; b) 3 pessoas com mais de 12 anos e duas pessoas com idade até 12 anos.

Orientações e sugestões didáticas

• Ao resolver o item a do boxe Para pensar, os estudantes podem fazer várias conjecturas sobre como resolver esse problema. Avalie cada uma das estratégias apresentadas. Atividades desse tipo favorecem o desenvolvimento do raciocínio lógico.

• O modo de resolução discutido neste momento é o de tentativa e erro, com ênfase na verificação da solução; ou seja, depois de encontrar a solução, os estudantes são estimulados a retomar o problema original e verificar se ela faz sentido para aquela situação. Resolver um sistema por tentativa e erro é uma estratégia pouco econômica, mas pode constituir uma experiência significativa para os estudantes, pois eles poderão valorizar os métodos da substituição e da adição, que serão estudados mais adiante.

Página 234

Resolução de um sistema de duas equações do 1º grau com duas incógnitas pelo método da substituição

Vamos estudar agora outro método para obter a solução de um sistema de equações do 1º grau com duas incógnitas: o método da substituição.

Na semana passada, Augusto completou 46 anos de idade. Ele é pai de Clara e de Mateus. Observe o que as crianças pensaram a respeito da idade de cada um.

Ilustração. Homem negro de óculos, camisa verde e calça marrom sentado em uma poltrona amarela. à frente dele, menino negro de camiseta laranja e bermuda verde pensa:
O triplo da idade de Clara mais o dobro da minha idade corresponde à idade do nosso pai. Atrás, menina negra de blusa rosa e calça pensa: A soma da minha idade com a idade de Mateus é 18 anos.

Qual é a idade dos filhos de Augusto?

Indicando por c a idade de Clara e por m a idade de Mateus, o sistema a ser resolvido é:

\{\begin{cases} c + m = 18 \\ 3 c + 2 m = 46 \end{cases}

Na primeira equação, c + m = 18, isolamos uma das incógnitas:

Esquema. c mais m menos m é igual a 18 menos m. Destaque em menos m em vermelho indicando que foi aplicado o princípio aditivo das igualdades Abaixo c é igual a 18 menos m

Substituindo na equação 3c + 2m = 46 a expressão encontrada para c, obtemos:

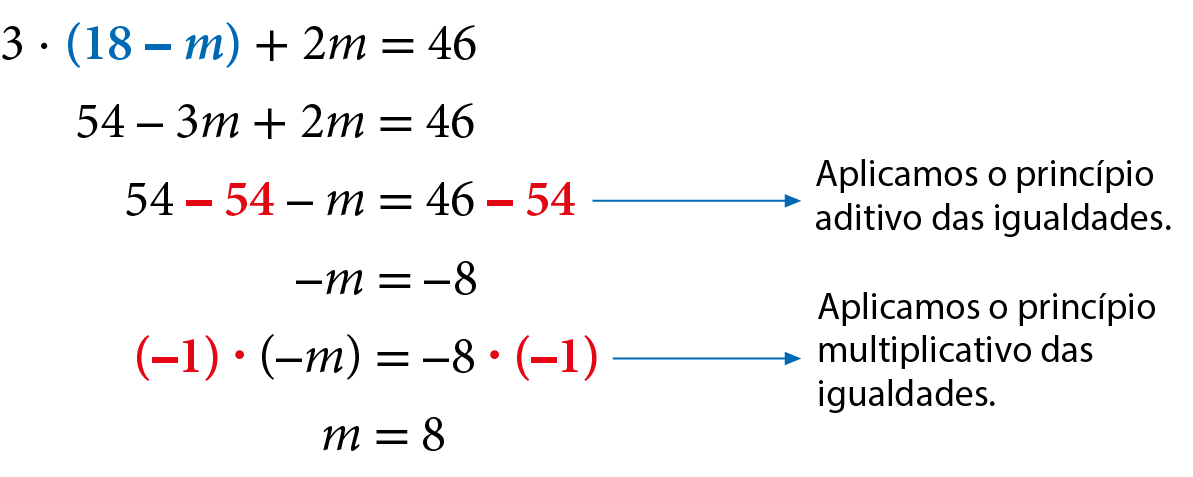
Esquema. 3 multiplicado por abre parêntese 18 menos m fecha parêntese mais 2m é igual a 46, 18 menos m destacado em azul abaixo, 54 menos 3m mais 2m igual 46 abaixo, 54 menos 54 menos m igual a 46 menos 54. Destaque em menos 54 em vermelho indicando que foi aplicado o princípio aditivo das igualdades abaixo, menos m igual a menos 8 abaixo, abre parêntese menos 1 multiplicado por abre parêntese menos m igual a menos 8 multiplicado por abre parêntese menos 1 fecha parêntese. Destaque em abre parênteses menos 1 fecha parênteses vezes indicando que foi aplicado o princípio multiplicativo das igualdades abaixo, m = 8

Agora, substituímos o valor obtido para m em uma das equações do sistema, para encontrar o valor de c.

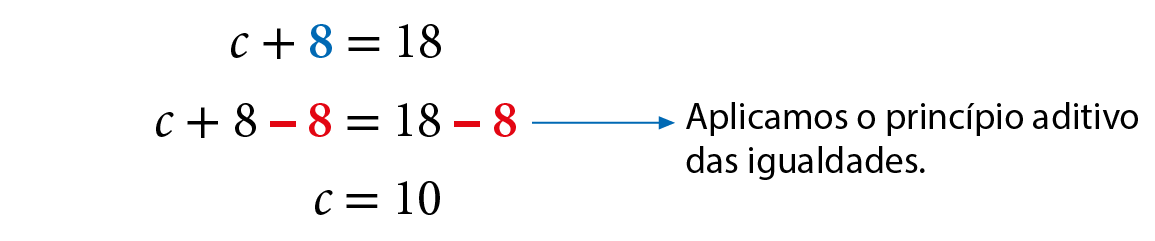
Esquema. c mais 8 é igual a 18. Destaque no 8 em azul. abaixo, c mais 8 menos 8 igual a 18 menos 8. Destaque no menos 8 em vermelho indicando que foi aplicado o princípio aditivo das igualdades abaixo, c igual a 10

Logo, a solução do sistema é o par ordenado abre parênteses10, 8fecha parênteses.

Portanto, Clara tem 10 anos e Mateus, 8 anos.

Observação

Ao resolver um sistema, podemos fazer mentalmente ou por escrito a verificação da solução obtida.

Observe o cálculo para verificar a solução obtida para o sistema da situação das idades de Clara e Mateus.

Solução obtida: abre parênteses10, 8fecha parênteses

Sistema:

\{\begin{cases} c + m = 18 \\ 3 c + 2 m = 46 \end{cases}

Verificação:

Esquema. Sistema de duas equações uma embaixo da outra, envolvidas por uma chave; 10 mais 8 é igual a 18 abre parêntese sentença verdadeira fecha parêntese 3 multiplicado por 10 mais 2 multiplicado por 8 é igual a 46 abre parêntese sentença verdadeira fecha parêntese

Para pensar

a) As incógnitas c e m no sistema de equações anterior podem assumir valores negativos? Por quê?

b) As incógnitas c e m podem assumir valores maiores que 18? Por quê?

Respostas e comentários

Para pensar: a) Não, porque c e m indicam idades e, portanto, só podem assumir valores maiores ou iguais a zero.

b) Não, porque a soma das idades de Clara e de Mateus deixaria de ser 18.

Orientações e sugestões didáticas

• Nesta e na próxima página, mostra-se como resolver sistemas de equações pelo método da substituição. Após estudarem a resolução do sistema por meio dessa estratégia, chame a atenção dos estudantes para o fato de existirem outras maneiras de resolvê-lo. Se achar pertinente, proponha a eles que resolvam esse mesmo sistema de outras maneiras e que compartilhem o modo como resolveram com os colegas.

• Após resolver um sistema de duas equações do 1º grau com duas incógnitas que traduz um problema, é imprescindível que os estudantes verifiquem se a solução encontrada satisfaz as condições do problema que deu origem ao sistema. Sempre que possível, oriente-os e lembre-os a fazer isso.

• No boxe Para pensar, espera-se que os estudantes percebam que os valores de c e m não podem ser negativos pois indicam idades como também as incógnitas não podem ser maiores ou iguais a 18 pois na situação proposta é mencionada a condição de que c + m = 18.

Página 235

Lembre-se: Escreva no caderno!

Agora, observe como Lúcia resolveu o sistema:

\{\begin{cases} 3 x + 2 y = 9 \\ 2 x + 3 y = 16 \end{cases}

Lúcia escolheu uma das equações para isolar uma das incógnitas. Ela isolou x na equação 3x + 2y = 9.

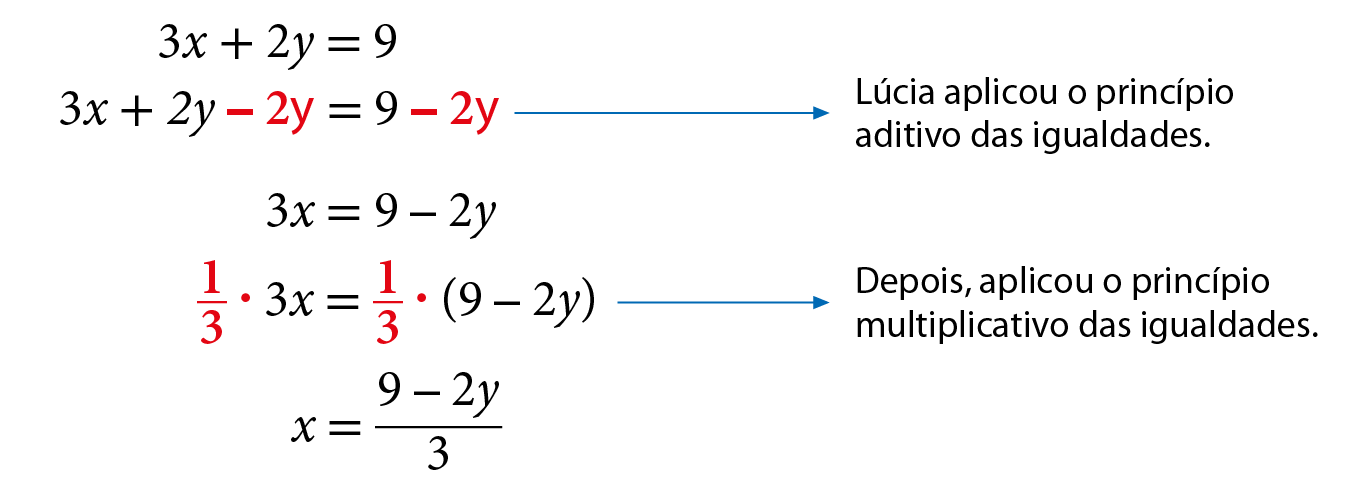
Esquema. 3x mais 2y igual a 9 abaixo, 3x mais 2y menos 2y igual a 9 menos 2y, destaque em vermelho no menos 2y nos dois membros indicando que Lúcia aplicou o princípio aditivo das igualdades. abaixo, 3x igual a 9 menos 2y abaixo, um terço vezes 3x igual a um terço, abre parênteses, 9 menos 2y, fecha parênteses, destaque em vermelho em um terço nos dois membros indicando que depois foi aplicado o princípio multiplicativo das igualdades. abaixo, x igual a 9 menos 2y, tudo sobre 3.

Em seguida, na equação 2x + 3y = 16, ela substituiu x por

\frac{9 - 2 y}{3}

e, assim, obteve uma equação com apenas uma incógnita.

Esquema. 2x mais 3y igual a 16 abaixo, 2 vezes abre parênteses, 9 menos 2y, tudo sobre 3, fecha parênteses, mais 3y igual a 16. Com destaque azul: abre parênteses, 9 menos 2y, tudo sobre 3, fecha parênteses, abaixo, 18 menos 4y, tudo sobre 3, fim da fração, mais 3y igual a 16 abaixo, 3 multiplicado abre parêntese fração 18 menos 4y sobre 3 fecha parêntese mais 3 multiplicado por 3y é igual a 3 multiplicado por 16. Destaque para o 3 que está em vermelho, indicando que a Lúcia aplicou o princípio multiplicativo das igualdades abaixo, 18 menos 4y mais 9y igual a 48 abaixo, 18 menos 18 menos 4 mais 9y é igual a 48 menos 18. Destaque para o menos 18 em vermelho, indicando que depois foi aplicado o princípio aditivo das igualdades abaixo, 5y igual a 30 abaixo, fração 1 sobre 5 multiplicado por 5y é igual a fração 1 sobre 5 multiplicado por 30 Destaque para a fração 1 sobre 5 indicando que em seguida foi aplicado o princípio multiplicativo das igualdades abaixo, y igual a 6.

Desse modo, Lúcia determinou o valor de y.

Depois, ela substituiu y por 6 na equação em que isolou x e obteve o valor de x.

x =

\frac{9 ‒ 2 y}{3}

x =

\frac{9 ‒ 2 \cdot 6}{3}

x = ‒

\frac{3}{3}

x = menos1

Logo, o par ordenado abre parêntesesmenos1, 6fecha parênteses é a solução do sistema.

Ilustração. Menina de cabelo liso castanho e blusa lilás diz: Para resolver esse sistema, usei o método da substituição, isto é, substituí uma das incógnitas, em uma das equações, por uma expressão que obtive da outra equação, que continha a outra incógnita.

Para pensar

• Você conhece uma maneira de verificar se a solução obtida por Lúcia está correta? Explique no caderno.

• Há outras maneiras de resolver o sistema anterior? Será que Lúcia chegaria ao mesmo resultado se tivesse escolhido a equação 2x + 3y = 16 para isolar uma das incógnitas? Tente resolver esse sistema de outra maneira.

Respostas e comentários

Para pensar: Respostas pessoais.

Orientações e sugestões didáticas

• O boxe Para pensar traz à tona a importância de verificar se a solução obtida após resolver um sistema de duas equações do 1º grau com duas incógnitas é ou não correta e também o fato de que há outras maneiras de aplicar o método da substituição para resolver um sistema. Deixe os estudantes à vontade para pensar sobre esses dois aspectos e, depois, incentive-os a compartilhar as conclusões a que chegaram com os colegas.

• Exemplo de resposta da primeira questão do boxe Para pensar:

Substituindo os valores encontrados nas duas equações: se as sentenças obtidas forem verdadeiras, a solução estará correta; caso contrário, haverá algum erro.

3x + 2y = 9

3 ⋅ abre parêntesesmenos1fecha parênteses + 2 ⋅ 6 = 9

menos3 + 12 = 9

(sentença verdadeira)

2x + 3y = 16

2 ⋅ abre parêntesesmenos1fecha parênteses + 3 ⋅ 6 = 16

menos2 + 18 = 16

(sentença verdadeira)

Portanto, a solução está correta.

• Exemplo de resposta da segunda questão do boxe Para pensar:

Lúcia poderia isolar y na equação 2x + 3y = 16, obtendo

y = \frac{16 - 2 x}{3}

Em seguida, substituiria y por

\frac{16 - 2 x}{3}

na equação 3x + 2y = 9, obtendo x = menos1.

Por fim, substituiria x por menos1 em

y = \frac{16 - 2 x}{3}

, obtendo y = 6.

Portanto, Lúcia chegaria à mesma solução.

Página 236

Resolução de um sistema de duas equações do 1º grau com duas incógnitas pelo método da adição

Para resolver sistemas de equações do 1º grau com duas incógnitas, podemos usar também o método da adição. Analise a situação a seguir.

Na compra de 3 mangas e 2 melões, Adriana gastou R$ 28,00vinte e oito reais. Observando o preço dessas frutas, ela percebeu que não havia diferença entre o custo de 4 mangas e o de 2 melões. Qual é o preço de cada fruta?

Ilustração. À esquerda, mulher de blusa florida e calça preta segura um carrinho de compras. Ao lado, barraca listrada de verde e branco com mangas à venda e barraca listrada de vermelho e branco com melões à venda

Indicando por x o preço da manga e por y o preço do melão, podemos escrever o seguinte sistema de equações:

\{\begin{cases} 3 x + 2 y = 28 \\ 4 x - 2 y = 0 \end{cases}

Nesse sistema, como há incógnita (y) com coeficientes opostos, adicionamos membro a membro das equações e obtemos uma equação com apenas a incógnita x. Resolvendo-a, obtemos o valor de x.

Esquema. Adição na vertical. 3x mais 2y é igual a 28. 4x menos 2y é igual a 0. Barra horizontal. 7x mais 0y é igual a 28. Ao lado da adição: 7x igual a 28. 7x sobre 7 igual 28 sobre 7. x igual a 4.

Em seguida, substituímos x por 4 em uma das equações do sistema.

Esquema. Primeira equação. 3x mais 2y igual a 28. 3 vezes 4 mais 2y igual a 28, com o número 4 destacado em azul. 12 mais 2y igual a 28. 12 menos 12 mais 2y igual a 28 menos 12. 2y igual a 16. 2y sobre 2 igual a 16 sobre 2. y igual a 8.

ou

Esquema. Segunda equação. 4x menos 2y igual a 0. 4 vezes 4 menos 2y igual a 0, com o número 4 destacado em azul. 16 menos 2y igual a 0. 16 menos 16 menos 2y igual a 0 menos 16. menos 2y igual a menos 16. menos 2y sobre menos 2 igual a menos 16 sobre menos 2. y igual a 8.

Portanto, a manga custa R$ 4,00quatro reais, e o melão, R$ 8,00oito reais.

Orientações e sugestões didáticas

• Nestas páginas, trabalha-se a resolução de sistemas de equações pelo método da adição. É importante que os estudantes percebam que convém aplicar esse método quando os coeficientes de uma mesma incógnita nas duas equações são opostos. Nos casos em que isso não ocorre, é possível preparar uma das equações multiplicando-a por um número, de modo que as equações passem a ter coeficientes opostos para uma das incógnitas.

• Peça aos estudantes que façam a verificação da solução obtida para o sistema desta página, ou seja:

3x + 2y = 28

3 ⋅ 4 + 2 ⋅ 8 = 28

(sentença verdadeira)

4x menos 2y = 0

4 ⋅ 4 menos 2 ⋅ 8 = 0

(sentença verdadeira)

Página 237

Acompanhe como Davi resolveu o sistema:

\{\begin{cases} x + 2 y = 10 \\ 2 x - y = 0 \end{cases}

Ao multiplicar a equação 2x menos y = 0 por 2, ele obteve coeficientes opostos para y.

Esquema. Sistema de duas equações uma embaixo da outra, envolvidas por uma chave; x mais 2y é igual a 10 2x menos y é igual a 0 à direita, seta azul, acima da seta: vezes 2 Esquema. Sistema de duas equações uma embaixo da outra, envolvidas por uma chave; x mais 2y é igual a 10 4x menos 2y é igual a 0

Adicionando membro a membro das duas equações, Davi obteve:

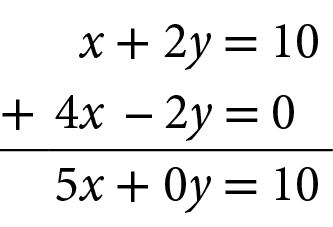
Esquema de Adição vertical. Equações uma embaixo da outra. x mais 2y é igual a 10 4x menos 2y é igual a 0 Barra horizontal 5x mais 0y é igual a 10

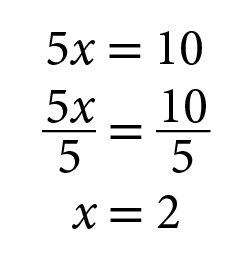
Esquema. 5x igual a 10. 5x sobre 5 igual a 10 quintos. x igual a 2

Em seguida, substituiu x por 2 em uma das equações do sistema.

2x menos y = 0

2 ⋅ 2 menos y = 0

4 menos y = 0

4 menos 4 menos y = 0 menos 4

menos y = menos 4

y = 4

Logo, o par ordenado abre parênteses2, 4fecha parênteses é a solução do sistema.

Ilustração. Menino de cabelo preto e camiseta azul fala: Para aplicar o método da adição, tive de preparar uma das equações, multiplicando-a por um número, de modo que as equações tivessem coeficientes opostos para uma das incógnitas.

Agora, observe como Davi resolveu o sistema

\{\begin{cases} 3 x + 2 y = 2 \\ ‒ 5 x + 3 y = 22 \end{cases}

Ao multiplicar a equação 3x + 2y = 2 por 5 e a equação menos5x + 3y = 22 por 3, ele obteve coeficientes opostos para x.

Esquema. Sistema de equações do primeiro grau com 2 incógnitas. A equação de cima é 3x mais 2y igual a 2 e a de baixo é menos 5x mais 3y igual a 22. da primeira equação sai um seta azul com vezes 5 acima dela da segunda equação sai uma seta azul com vezes 3 acima dela Esquema. Sistema de duas equações uma embaixo da outra, envolvidas por uma chave; 15x mais 10y é igual a 10 menos 15x mais 9y é igual a 66

Ilustração. Menino de cabelo preto e camiseta azul fala: Nesse caso, tive de preparar ambas as equações. Para isso, multipliquei cada uma por números convenientes antes de adicioná-las.

Adicionando membro a membro das duas equações, Davi obteve:

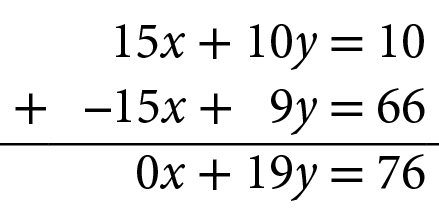
Esquema de Adição vertical. Equações uma embaixo da outra; 15x mais 10y é igual a 10 menos 15x menos 9y é igual a 66 Barra horizontal 0x mais 19y é igual a 76

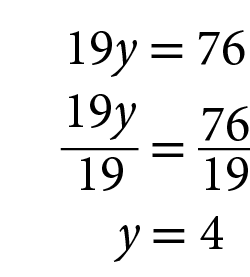
Esquema. 19y igual a 76. 19y sobre 19 igual a 76 sobre 19. y igual a 4

Depois, substituiu y por 4 em uma das equações do sistema.

3x + 2y = 2

3x + 2 ⋅ 4 = 2

3x + 8 = 2

3x + 8 menos 8 = 2 menos 8

3x = 2 menos 8

3x = menos 6

\frac{3 x}{3}

=

\frac{‒ 6}{3}

x = menos 2

Logo, o par ordenado abre parêntesesmenos 2, 4fecha parênteses é a solução do sistema.

Para pensar

Podemos preparar o sistema apresentado anteriormente de modo que obtenhamos duas novas equações, com coeficientes de y opostos. Para isso, por qual número podemos multiplicar a equação 3x + 2y = 2? E a equação menos 5x + 3y = 22?

Respostas e comentários

Para pensar: Exemplo de resposta: Multiplicamos a equação 3x + 2y = 2 por 3, e a equação menos5x + 3y = 22 por menos2.

Orientações e sugestões didáticas

• Assim como ocorre com o método da substituição, é possível aplicar de diferentes maneiras o método da adição. No primeiro exemplo apresentado nesta página, a equação 2x menos y = 0 foi preparada de modo que as equações do sistema tivessem coeficientes opostos para a incógnita y. Outra possibilidade é preparar a equação x + 2y = 10 para que as equações do sistema tenham coeficientes opostos para a incógnita x. Nesse caso, todos os membros dessa equação devem ser multiplicados por menos2. Mostre essa e outras alternativas de resolução para os estudantes. O objetivo é que aos poucos eles ampliem o repertório de cálculo.

• Reproduza o segundo exemplo desta página no quadro e enfatize o fato de que, nesse caso, houve a necessidade de preparar as duas equações. Se possível, dê um tempo para que os estudantes percebam por si sós essa necessidade e como devem proceder para fazer a preparação das equações.

• Após apresentar os exemplos desta página, peça aos estudantes que verifiquem se as soluções obtidas, ao serem substituídas nas equações dos sistemas, as tornam verdadeiras.

• No boxe Para pensar, espera-se que os estudantes percebam que precisam determinar os coeficientes para y de modo que um seja o oposto do outro.

Página 238

ATIVIDADES

faça as atividades no caderno

1.

Calcule mentalmente a solução abre parêntesesx, yfecha parênteses de cada sistema. Em seguida, compare suas respostas com as de um colega.

a)

\{\begin{cases} x = ‒ 3 \\ x - y = ‒ 7 \end{cases}

b)

\{\begin{cases} 2 x - y = 15 \\ y = ‒ 3 \end{cases}

2. Determine a solução dos sistemas aplicando os métodos da substituição e da adição. Considere que x e y podem ser qualquer número real.

a)

\{\begin{cases} x + 6 y = 5 \\ 2 x - 3 y = 5 \end{cases}

b)

\{\begin{cases} 6 x + y = 5 \\ ‒ 3 x + 2 y = 5 \end{cases}

c)

\{\begin{cases} 3 x + 5 y = 11 \\ 4 x - 5 y = 38 \end{cases}

d)

\{\begin{cases} 7 x - 3 y = 12 \\ 2 x + 3 y = 10 \end{cases}

3. Hoje, Fábio tem o triplo da idade de Lucas e, daqui a 12 anos, terá o dobro da idade dele.

Ilustração. À esquerda, menino branco ao lado de um rapaz negro. Abaixo deles, o texto: Lucas e Fábio, hoje. À direita, Adolescente branco e homem negro. Abaixo deles, o texto: Lucas e Fábio, daqui a 12 anos.

Indicando por x a idade atual de Fábio e por y a idade atual de Lucas:

a) escreva a relação entre as idades atuais deles;

b) escreva a relação entre as idades daqui a 12 anos;

c) resolva o sistema formado pelas equações dos itens a e b e descubra a idade de cada um hoje.

4.

Reúna-se a um colega e respondam à questão no caderno.

Qual é a importância de verificar a solução de problemas que são resolvidos por um sistema de equações?

5. Em um escritório trabalham 33 funcionários, entre homens e mulheres. Se forem demitidos 3 homens e admitidas 4 mulheres, o número de homens e de mulheres passará a ser igual. Quantas mulheres trabalham nesse escritório?

6. O quadro a seguir mostra o desempenho da equipe Azul em um torneio de vôlei.

Equipe Azul
Partidas	14
Pontos	32

Ilustração. Rapaz com uniforme esportivo azul rebatendo bola de vôlei

• Sabendo que a equipe vencedora da partida ganha 3 pontos e a equipe perdedora, ganha 1 ponto, determine quantas partidas a equipe Azul ganhou e quantas perdeu.

7. Ana fez uma prova que continha 50 questões. Para cada questão correta, ela ganhava 5 pontos; para cada questão errada, perdia 3 pontos. Se Ana fez um total de 130 pontos, quantas questões ela acertou?

8.

Com base no sistema a seguir, elabore um problema e dê para um colega resolver. Depois, verifique se a resposta dele está correta.

\{\begin{cases} x + y = 10 \\ x - y = 2 \end{cases}

9. A medida do perímetro de um retângulo é igual a 32 centímetros, e a medida da largura é 4 centímetros menor que a medida do comprimento. Determine a medida de área desse retângulo.

10. Uma corda de 405 centímetros de comprimento foi dividida em duas partes de tal fórma que o comprimento da parte menor media a terça parte do comprimento da parte maior mais 25 centímetros. Determine a medida de comprimento de cada parte dessa corda.

Respostas e comentários

1. a) abre parêntesesmenos3, 4fecha parênteses

1. b) abre parênteses6, menos3fecha parênteses

2. a)

(3, \frac{1}{3})

2. b)

(\frac{1}{3}, 3)

2. c) abre parênteses7, menos2fecha parênteses

2. d)

(\frac{22}{9}, \frac{46}{27})

3. a) x = 3y

3. b) x + 12 = 2abre parêntesesy + 12fecha parênteses

3. c) x = 36 e y = 12; Fábio: 36 anos e Lucas: 12 anos.

4. Exemplo de resposta: A importância está em conferir se a solução obtida satisfaz as condições do problema.

5. 13 mulheres

6. Ganhou 9 partidas e perdeu 5.

7. 35 questões

8. Resposta pessoal.

9. 60 centímetros quadrados

10. 285 centímetros e 120 centímetros

Orientações e sugestões didáticas

• Ao resolver as atividades desta página, deixe os estudantes livres para usarem o método que acharem mais adequado a cada situação. Contudo, é importante acompanhá-los para avaliar se o aplicam corretamente e questioná-los em determinadas situações se um ou outro é mais adequado.

• Um problema que pode ser elaborado pelos estudantes na atividade 8 é: “Lucas e Miguel têm juntos R$ 10,00dez reais. Sabendo que Lucas tem R$ 2,00dois reais a mais que Miguel, quantos reais cada um tem?”.

Página 239

Análise da solução por meio da representação gráfica

Já vimos que as soluções de uma equação do 1º grau com duas incógnitas, x e y, do tipo ax + by = c, em que a, b e c são números reais conhecidos (coeficientes) e a e b são não nulos, podem ser representadas por uma reta no plano cartesiano.

Recorde

Duas retas no plano podem ser:

• concorrentes, quando possuem apenas um ponto em comum;

• paralelas, quando não possuem pontos comuns;

• coincidentes, quando possuem infinitos pontos comuns.

Agora, vamos analisar graficamente a solução de alguns sistemas em que x e y são números reais.

a) Vamos analisar graficamente a solução do sistema:

\{\begin{cases} x - y = 2 \\ 2 x + y = 13 \end{cases}

Resolvendo esse sistema por qualquer um dos métodos estudados, obtemos como solução o par ordenado abre parênteses5, 3fecha parênteses. Podemos verificar graficamente essa solução. Para isso, é necessário traçar em um mesmo plano cartesiano as duas retas que representam as soluções das equações do sistema.

Lembrando que, para traçar uma reta, basta conhecer dois de seus pontos. Para isso, atribuímos dois valores a uma das incógnitas e calculamos os valores correspondentes da outra, obtendo, assim, pares ordenados que são coordenadas de dois dos pontos de cada reta.

x − y = 2
x	y	(x, y)
3	1	(3, 1)
4	2	(4, 2)

2x + y = 13
x	y	(x, y)
3	7	(3, 7)
4	5	(4, 5)

Gráfico. Eixo x com pontos 0 a 9 e eixo y com pontos menos 2 a 7. Reta x menos y é igual a 2 passa pelos pares: abre parêntese 4 vírgula 2 fecha parêntese abre parêntese 3 vírgula 1 fecha parentese. Reta 2 x mais y é igual a 13 passa pelos pares: abre parêntese 3 vírgula 7 fecha parêntese abre parêntese 4 vírgula 5 fecha parêntese. As duas retas se cruzam no ponto P abre parêntese 5 vírgula 3 fecha parêntese.

Observe que no plano cartesiano localizamos os quatro pontos obtidos e, depois, traçamos as retas correspondentes. Como o ponto P, e só ele, pertence às duas retas, suas coordenadas satisfazem as duas equações; logo, podemos verificar que o par ordenado abre parênteses5, 3fecha parênteses, intersecção das duas retas, é a solução do sistema. Esse é um exemplo de sistema possível e determinado.

Um sistema é possível e determinado quando tem apenas uma solução. As retas que representam as soluções das equações de um sistema possível e determinado são concorrentes, ou seja, interceptam-se em apenas um ponto.

b) Vamos analisar graficamente o sistema:

\{\begin{cases} x + y = 3 \\ x + y = 0 \end{cases}

Atribuindo valores a uma das incógnitas e calculando os valores correspondentes da outra, determinamos as coordenadas de dois pontos de cada reta.

x + y = 3
x	y	(x, y)
0	3	(0, 3)
3	0	(3, 0)

x + y = 0
x	y	(x, y)
0	0	(0, 0)
1	−1	(1, −1)

Orientações e sugestões didáticas

• Nesta página, o estudo dos sistemas é ampliado. Os estudantes enriquecem seu repertório aprendendo a analisar a solução por meio da representação gráfica e compreendendo o que significa obter retas paralelas (o sistema não tem solução), retas concorrentes (o ponto de interseção é a solução) e retas coincidentes (há infinitas soluções).

Página 240

Localizamos no plano cartesiano os pontos obtidos e traçamos as retas.

Ilustração. Retas x mais y igual a 3 e x mais y igual a zero representadas em um mesmo plano cartesiano. A reta x mais y igual a 3 passa pelos pontos que correspondem aos pares ordenados (0 ,3) e (3 ,0). A reta x mais y igual a zero passa pelos pontos que correspondem aos pares ordenados (0 ,0) e (1 ,menos 1). As retas são paralelas. — Se o sistema tivesse solução, existiriam dois números cuja soma seria igual a 3 e também a zero, o que seria um absurdo.

Como as retas são paralelas, não há ponto cujas coordenadas satisfaçam as duas equações. Logo, o sistema não tem solução. Esse é um exemplo de sistema impossível.

Um sistema é impossível quando não tem solução. As retas que representam as soluções das equações de um sistema impossível são distintas e paralelas; logo, não têm ponto comum.

c) Agora, vamos analisar graficamente o sistema:

\{\begin{cases} x + 2 y = 1 \\ 2 x + 4 y = 2 \end{cases}

Atribuindo valores a uma das incógnitas e calculando os valores correspondentes da outra, determinamos as coordenadas de dois pontos de cada reta.

x + 2y = 1
x	y	(x, y)
0	$1 meio$	$par ordenado zero, 1 meio$
1	0	(1, 0)

2x + 4y = 2
x	y	(x, y)
3	−1	(3, −1)
1	0	(1, 0)

Localizamos no plano cartesiano os dois pontos de cada reta e, assim, observamos que as retas são coincidentes.

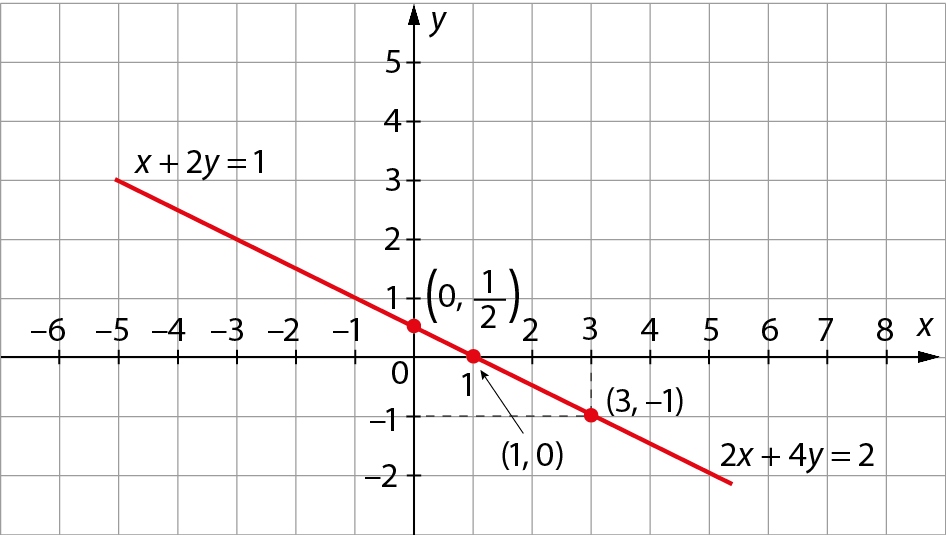
Ilustração. Retas x mais 2y igual a 1 e 2x mais 4y igual a 2 representadas em um mesmo plano cartesiano. Ambas as retas passam pelos pontos que correspondem aos pares ordenados (0, meio), (1 ,0) e (3, menos 1). As retas são coincidentes.

Ilustração. Homem branco de cabelo castanho, óculos e jaleco branco. Ele fala: Todo par ordenado que satisfaz a equação x mais 2y igual a 1 também satisfaz a equação 2x mais 4y igual a 2.

Como as retas são coincidentes, têm infinitos pontos comuns. Logo, o sistema tem infinitas soluções. Esse é um exemplo de sistema possível e indeterminado.

Um sistema é possível e indeterminado quando tem infinitas soluções. As retas que representam as soluções das equações de um sistema possível e indeterminado são coincidentes.

Observando as equações, percebemos que, ao multiplicar cada termo da primeira equação por 2, obtemos a segunda equação. Assim, as equações são equivalentes, isto é, têm as mesmas soluções.

Orientações e sugestões didáticas

• Pesquisadores em Educação Matemática enfatizam que os estudantes alcançam a apreensão conceitual quando lhes é exigida a coordenação de diferentes registros, como o algébrico, o gráfico, o figural, o registro em língua materna etcétera Isso se dá porque cada um desses registros caracteriza o conceito matemático de uma maneira e todas as maneiras se complementam. Resolver uma situação-problema e recorrer aos gráficos para a resolução de sistemas são atividades que contribuem para essa mobilização. Nesse sentido, a competência específica 6 da Bê êne cê cê tem seu desenvolvimento favorecido porque os estudantes lidam com situações-problema e expressam suas respostas ou sintetizam conclusões utilizando diferentes linguagens, como a algébrica e a gráfica.

Página 241

Informática e Matemática

faça as atividades no caderno

Análise da solução de sistemas de equações do 1º grau com duas incógnitas por meio da representação gráfica

Nesta seção, você vai utilizar um software de construção de gráficos para representar graficamente as soluções de uma equação do tipo ax + by = c. Além disso, vai utilizar esse software para verificar se um sistema apresenta uma, infinitas ou nenhuma solução.

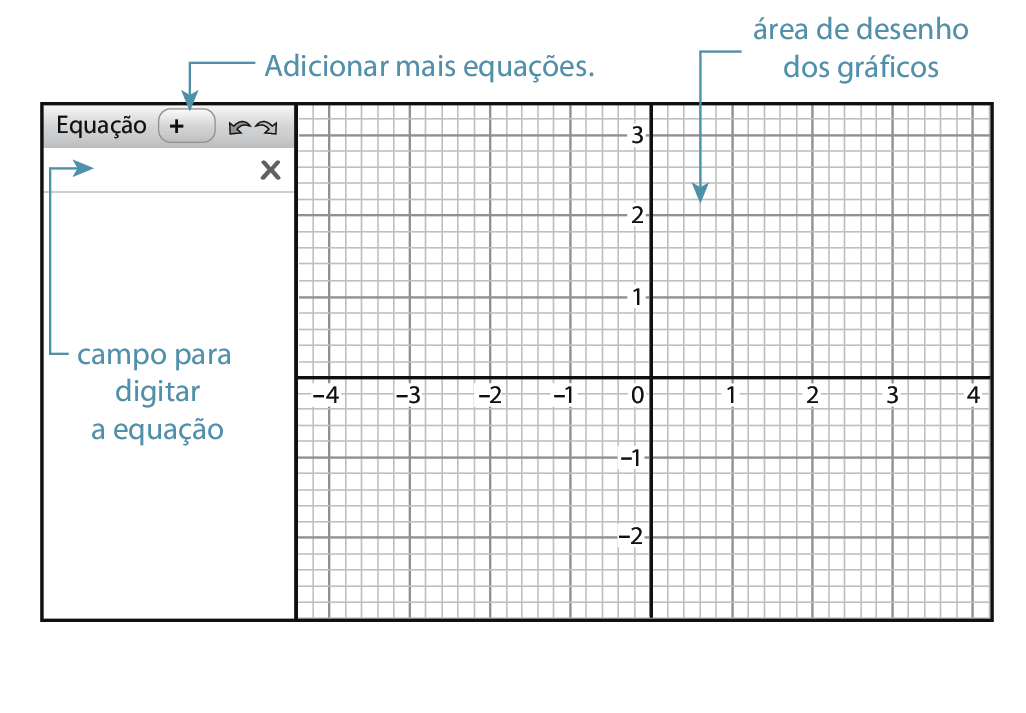
Ilustração. Software de geometria. À esquerda, campo para digitar equação e acima, sinal de mais: adicionar mais equações. À direita, área de desenho dos gráficos composto por malha quadriculada com eixo x de menos 4 a 4 e eixo y de menos 2 a 3. — Tela inicial de um softwarede construção de gráficos.

Construa

Para obter a representação gráfica das soluções de uma equação do tipo ax + by = c, basta digitar a equação no campo apropriado.

1º) Construa a representação gráfica das soluções da equação x + 2y = 2.

2º) Construa a representação gráfica das soluções da equação 2x menos y = 4.

Ilustração. Software de geometria. À esquerda, campo para digitar equação e acima, sinal de mais: amarelo: x mais 2y é igual a 2. Azul: 2 x menos y é igual a 4. À direita, malha quadriculada com eixo x de menos 4 a 4 e eixo y de menos 2 a 3. As retas se cruzam em 2 vírgula zero.

• O sistema

\{\begin{cases} x + 2 y = 2 \\ 2 x - y = 4 \end{cases}

é possível e determinado, possível e indeterminado ou impossível? Por quê?

3º) Construa a representação gráfica das soluções da equação x + y = 3.

4º) Construa a representação gráfica das soluções da equação x + y = 0.

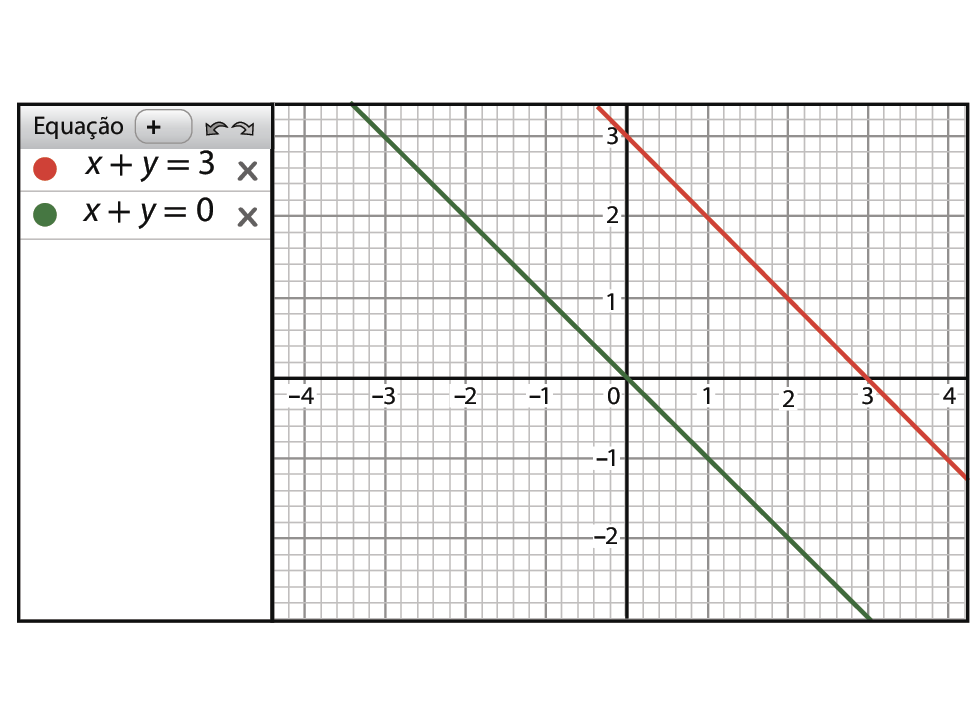
Ilustração. Software de geometria. À esquerda, campo para digitar equação e acima, sinal de mais: vermelho: x mais y é igual a 3. Verde: x mais y é igual a zero. À direita, malha quadriculada com eixo x de menos 4 a 4 e eixo y de menos 2 a 3. Reta verde passa em zero vírgula zero e reta vermelha em 3 vírgula zero.

• O sistema

\{\begin{cases} x + y = 3 \\ x + y = 0 \end{cases}

é possível e determinado, possível e indeterminado ou impossível? Por quê?

INVESTIGUE

•

Invente um sistema possível e indeterminado e, depois, construa a representação gráfica das soluções de cada uma das equações desse sistema. Como ficaram as retas que você construiu?

Respostas e comentários

Construa: Respostas em Orientações.

Investigue: Resposta em Orientações.

Orientações e sugestões didáticas

Informática e Matemática

Objetivos

• Interpretar graficamente as soluções de sistemas de duas equações do 1º grau com duas incógnitas.

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero oito e da competência geral 2 da Bê êne cê cê.

Habilidade da Bê êne cê cê

• Esta seção possibilita que os estudantes usem um software de construção de gráficos para analisar a solução de sistemas de equação do 1º grau graficamente, contribuindo assim para o desenvolvimento da habilidade ê éfe zero oito ême ah zero oito.

Orientações

• Nesta seção, os estudantes deverão representar graficamente, com o auxílio de um software de construção de gráficos, as soluções de sistemas de duas equações do 1º grau com duas incógnitas.

• Em Construa, a resposta da pergunta feita sobre o sistema de equações da primeira imagem é possível e determinado, porque as retas que representam as soluções de cada uma das equações são concorrentes. Já a resposta para o sistema referente à segunda imagem é impossível, porque as retas que representam as soluções de cada uma das equações são paralelas.

• Em Investigue, para a construção sugerida, da representação gráfica de soluções das equações de um sistema possível e indeterminado, espera-se que os estudantes obtenham retas coincidentes.

(ê éfe zero oito ême ah zero oito) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.

Competência geral 2: Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

Página 242

ATIVIDADES

faça as atividades no caderno

1. Represente graficamente cada sistema, em que x e y são números reais.

a)

\{\begin{cases} x + y = 2 \\ 2 x - y = 4 \end{cases}

b)

\{\begin{cases} x - y = 2 \\ x - y = ‒ 1 \end{cases}

c)

\{\begin{cases} x - 2 y = 3 \\ 2 x + y = 6 \end{cases}

d)

\{\begin{cases} x - y = 0 \\ ‒ x + y = ‒ 3 \end{cases}

2. (saréspi) O gráfico a seguir representa o sistema:

\{\begin{cases} x + y = 4 (r) \\ x - y = 2 (s) \end{cases}

Ilustração. Retas r e s representadas em um mesmo plano cartesiano. A reta r passa pelos pontos correspondentes aos pares ordenados (1, 3), (2 ,2), (3, 1) e 4, 0). A reta s passa pelos pontos correspondentes aos pares ordenados (0, menos 2), (1, menos 1), (2, 0), (3, 1) e (4 ,2). As retas são concorrentes.

O par ordenado abre parêntesesx, yfecha parênteses que satisfaz o sistema é:

a) abre parênteses4, 0fecha parênteses

b) abre parênteses3, 1fecha parênteses

c) abre parênteses2, 2fecha parênteses

d) abre parênteses2, 0fecha parênteses

3. Lívia representou graficamente um sistema. Considere a representação que ela fez e descubra o sistema correspondente.

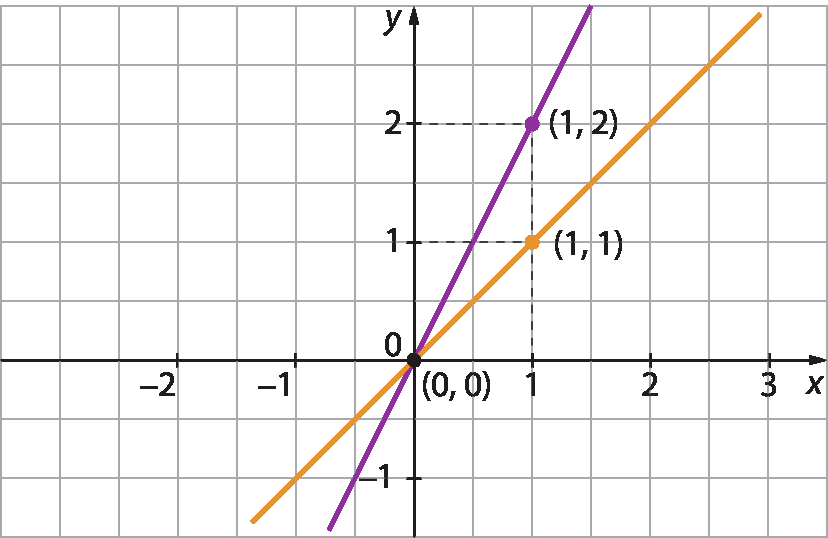
Ilustração. Duas retas representadas no mesmo plano cartesiano, ambas passando pela origem. Uma passa pelo ponto (1, 2) e a outra passa pelo ponto (1 ,1).

a)

\{\begin{cases} x - y = 0 \\ 2 x = y \end{cases}

b)

\{\begin{cases} x + y = 0 \\ x = 2 y - 1 \end{cases}

c)

\{\begin{cases} 2 x + 1 + y = 0 \\ x = ‒ 2 y \end{cases}

4. Observe a folha de caderno em que Joana derrubou café e, depois, faça o que se pede.

Ilustração. Menina branca de cabelo castanho e blusa laranja olha um caderno escrito com um sistema: abre chave, primeira linha: 3x mais y é igual menos 1. Segunda linha: mancha de café. A solução do sistema é abre parêntese 2 vírgula 7 fecha parêntese

a) Represente graficamente as soluções da equação que você pode ler no caderno de Joana.

b) Sabendo que a solução do sistema é o par ordenado abre parênteses2, 7fecha parênteses, trace no mesmo plano cartesiano uma reta que represente as soluções da segunda equação desse sistema.

c)

Compare suas respostas com as de seus colegas e verifique se todos traçaram a mesma reta.

5. Leia as afirmações a seguir e copie no caderno as verdadeiras.

a) Um sistema de duas equações do 1º grau com duas incógnitas que tem apenas uma solução é representado graficamente por retas concorrentes.

b) A representação gráfica a seguir está associada a um sistema de duas equações do 1º grau com duas incógnitas que tem infinitas soluções.

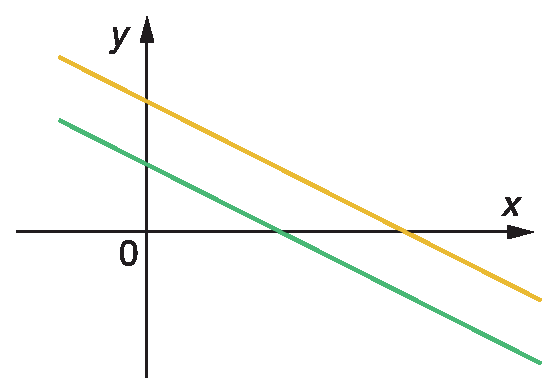
Ilustração. Duas retas paralelas representadas em um mesmo plano cartesiano.

c) Um sistema de duas equações do 1º grau com duas incógnitas que tem infinitas soluções é representado graficamente por retas coincidentes.

Respostas e comentários

1. Respostas em Orientações.

2. alternativa b

3. alternativa a

4. Respostas em Orientações.

5. alternativas a e c

Orientações e sugestões didáticas

Respostas da atividade 1:

a)

Ilustração. Retas x mais y igual a 2 e 2x menos y igual a 4 representadas em um mesmo plano cartesiano. A reta x mais y igual a 2 passa pelos pontos que correspondem aos pares ordenados (menos 1, 3), (2, 0) e (4, menos 2). A reta 2x menos y igual a 4 passa pelos pontos que correspondem aos pares ordenados (0, menos 4), (1, menos 2) e (2, 0). As retas são concorrentes.

b)

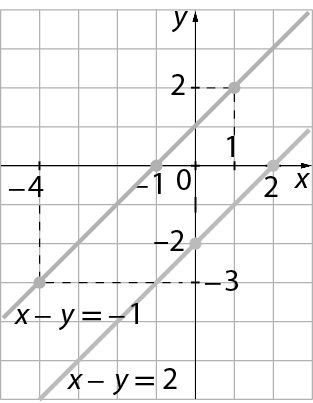
Ilustração. Retas x menos y igual a menos 1 e x menos y igual a 2 representadas em um mesmo plano cartesiano. A reta x menos y igual a menos 1 passa pelos pontos que correspondem aos pares ordenados (menos 4, menos 3), (menos 1, 0) e (1, 2). A reta x menos y igual a 2 passa pelos pontos que correspondem aos pares ordenados (menos 1, menos 3), (0, menos 2) e (2, 0). As retas são paralelas.

c)

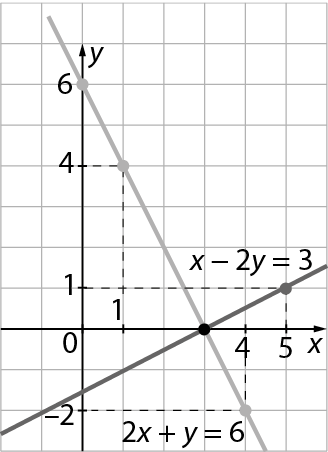
Ilustração. Retas 2x mais y igual a 6 e x menos 2y igual a 3 representadas em um mesmo plano cartesiano. A reta 2x mais y igual a 6 passa pelos pontos que correspondem aos pares ordenados (1, 4), (3, 0) e (4, menos 2). A reta x menos 2y igual a 3 passa pelos pontos que correspondem aos pares ordenados (menos 1, menos 2), (3, 0) e (5, 1). As retas são concorrentes.

d)

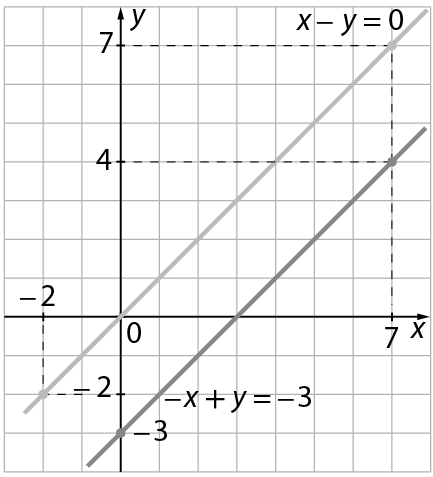
Ilustração. Retas x menos y igual a 0 e menos x mais y igual a menos 3 representadas em um mesmo plano cartesiano. A reta x menos y igual a 0 passa pelos pontos que correspondem aos pares ordenados (menos 2, menos 2), (0, 0) e (7, 7). A reta menos x mais y igual a menos 3 passa pelos pontos que correspondem aos pares ordenados (0, menos 3), (3, 0) e (7, 4). As retas são paralelas.

• No item c da atividade 4, espera-se que os estudantes percebam que há infinitas possibilidades para a reta que representa a solução da segunda equação.

• Resposta do item a da atividade 4:

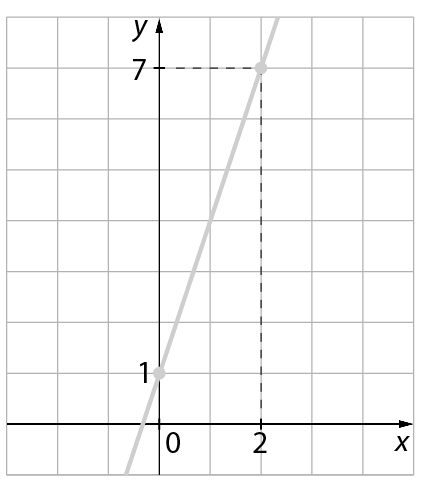
Ilustração. Malha quadriculada com gráfico. Eixo x com pontos 0 e 2. Eixo y com pontos 1 e 7. Pares ordenados: abre parêntese 2 vírgula 7 fecha parêntese, abre parêntese zero vírgula 1 fecha parêntese. Reta diagonal passa pelos pares.

• Exemplo de resposta do item b da atividade 4:

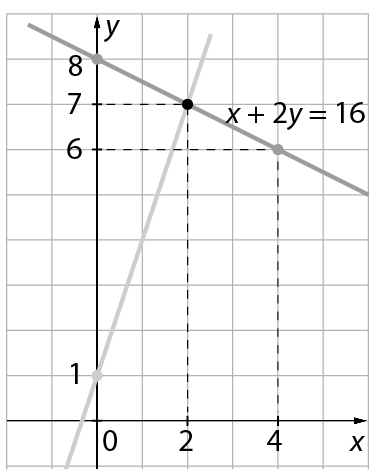
Ilustração. Malha quadriculada com gráfico. Eixo x com pontos zero, 2 e 4. Eixo y com pontos zero, 1, 6 e 7. Reta passa pelos pares: (2, 7), (zero, 1). Reta x + 2 y = 16 passa pelos pares: (4, 6), (2, 7) (zero, 8). As retas se cruzam em 2, 7.

Página 243

3 Introdução às equações do 2º grau

Miguel propôs um desafio para Alice.

Ilustração. À esquerda, rapaz de cabelo castanho, camiseta azul listrada. Ele está sentado em uma mesa escolar e diz: O dobro do quadrado de um número real é igual a 50. Que número é esse? Ao lado, garota negra de cabelo castanho e camiseta azul setada em uma mesa escolar, pensa: Posso escrever uma equação para descobrir esse número.

Observe como Alice resolveu esse desafio.

Alice indicou por x o número real desconhecido e representou o seu quadrado por xao quadrado. Como Miguel disse que o dobro do quadrado do número real é igual a 50, ela escreveu a equação:

2xao quadrado = 50

Essa equação é um exemplo de equação do 2º grau com uma incógnita (a letra x).

Para solucionar o desafio, foi preciso resolver a equação.

Alice aplicou o princípio multiplicativo das igualdades, multiplicando por

\frac{1}{2}

os dois membros da equação.

\frac{1}{2}

⋅ 2xao quadrado =

\frac{1}{2}

⋅ 50

xao quadrado = 25

Por fim, precisou descobrir os números que, quando elevados ao quadrado, resultam no número 25. Após testar alguns valores, Alice percebeu que x podia ser igual a 5 ou menos5, pois 5ao quadrado = 25 e abre parêntesesmenos5fecha parêntesesao quadrado = 25. Assim, ela descobriu duas raízes para a equação 2xao quadrado = 50, uma positiva e outra negativa.

A raiz positiva dessa equação também poderia ser encontrada usando uma calculadora.

Ilustração. Teclas de calculadora: 50 dividido por 2 = raiz quadrada. No visor, 5.

Portanto, o dobro do quadrado dos números reais 5 e menos5 é igual a 50.

Para pensar

Se o desafio fosse descobrir um número real que, elevado ao quadrado, resultasse em menos25, qual seria esse número?

Respostas e comentários

Para pensar: Espera-se que os estudantes percebam que não existe número real que, elevado ao quadrado, resulte em número negativo. Logo, esse desafio não tem solução.

Orientações e sugestões didáticas

Introdução às equações do 2º grau

Objetivos

• Introduzir o conceito de equação do 2º grau com uma incógnita.

• Resolver equações do 2º grau com uma incógnita com e sem uso de tecnologias.

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero nove da Bê êne cê cê.

Habilidade da Bê êne cê cê

• Este tópico favorece o desenvolvimento da ê éfe zero oito ême ah zero nove da Bê êne cê cê porque os estudantes poderão resolver e elaborar, com e sem uso de tecnologias, problemas que podem ser representados por equações polinomiais de 2º grau do tipo axao quadrado = b.

Orientações

• O objetivo deste tópico é ampliar o estudo das equações introduzindo o conceito de equação do 2º grau com uma incógnita. Nesse momento, vamos nos restringir às equações do tipo axao quadrado = b, em que a e b são números reais positivos.

• O objetivo do boxe Para pensar é que os estudantes, percebam que qualquer número real elevado ao quadrado não pode resultar em um número negativo.

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo axao quadrado = b.

Página 244

Informática e Matemática

faça as atividades no caderno

Solução de equações do 2º grau do tipo ax² = b

Na seção Informática e Matemática da página 241, vimos como utilizar um software de construção de gráficos para representar as soluções de uma equação do tipo

a x + b y = c

. De maneira semelhante, podemos resolver uma equação do tipo

a x^{2} = b

, utilizando apenas a janela de álgebra, sem considerar a janela de gráficos.

Construa

1º) Para resolver a equação

3 x^{2} = 9

, digite no campo apropriado Resolverabre parênteses3x^2=9fecha parênteses.

Ilustração. Software de gráficos. Acima, equação, sinal de mais e seta curvada dupla. Abaixo, bolinha amarela: resolver abre parênteses 3x circunflexo 2 é igual a 9 fecha parênteses.

2º) Ao pressionar Enter, as duas soluções da equação,

x = - \sqrt{3}

e

x = \sqrt{3}

aparecerão na próxima linha.

Note que o símbolo do acento circunflexo (^) foi utilizado para representar uma potência, ou seja, x^2 representa

x^{2}

. Geralmente, é preciso pressionar a tecla Shift do teclado junto com a tecla em que aparece esse símbolo.

3º) Clique no botão com o símbolo (

\approx

) para visualizar uma aproximação das soluções da equação, que são

- 1, 73

e

1, 73

.

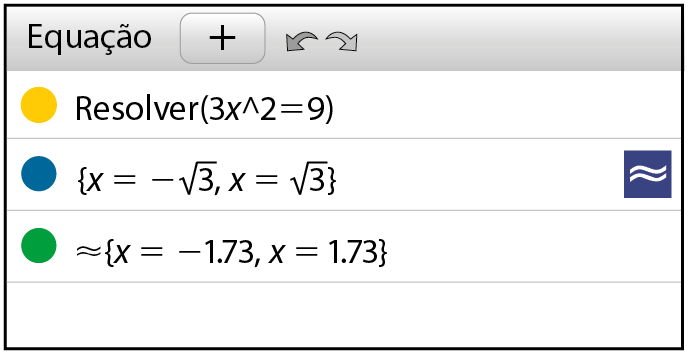
Neste caso, a aproximação ocorreu até os centésimos, porém, em geral, é possível configurar o software para exibir mais casas decimais.

INVESTIGUE

1. Determine as soluções exata e aproximada de cada equação a seguir:

a)

5 x^{2} = 10

b)

3 x^{2} = 21

c)

2 x^{2} = 10

2.

Invente uma equação e, depois, dê para um colega resolver usando o software.

Respostas e comentários

Investigue: 1. a)

x = - \sqrt{2}

e

x = \sqrt{2}

;

x = - 1, 41

e

x = 1, 41

b)

x = - \sqrt{7}

e

x = \sqrt{7}

;

x = - 2, 65

e

x = 2, 65

c)

x = - \sqrt{5}

e

x = \sqrt{5}

;

x = - 2, 24

e

x = 2, 24

Investigue: 2. Resposta pessoal.

Orientações e sugestões didáticas

Informática e Matemática

Objetivos

• Resolver equações do 2º grau do tipo axao quadrado = b.

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero nove da Bê êne cê cê.

Habilidade da Bê êne cê cê

• Esta seção propõe que os estudantes resolvam equações de 2º grau do tipo axao quadrado = b por meio de um software de construção de gráficos (ou de Geometria dinâmica), favorecendo o desenvolvimento da habilidade ê éfe zero oito ême ah zero nove.

Orientações

• Nesta seção, os estudantes deverão resolver algebricamente equações do 2º grau do tipo axao quadrado = b com o auxílio de um software de Geometria dinâmica. Eles terão a oportunidade de obter a solução exata e a solução aproximada desse tipo de equação para resolver problemas.

• Certifique-se de que os estudantes reconhecem que o símbolo do acento circunflexo (^) é utilizado para representar uma potência. Leve-os a perceber que o botão com o símbolo (≈) que aparece no passo 3 não aparece no caso de soluções inteiras.

• Sugira aos estudantes que resolvam ou verifiquem as respostas de algumas atividades da página seguinte com o auxílio de um software de Geometria dinâmica. Eles terão a oportunidade de obter a solução exata e a solução aproximada desse tipo de equação para resolver problemas.

• Um exemplo de resposta para a seção Investigue é 3xao quadrado = 42.

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo axao quadrado = b.

Página 245

ATIVIDADES

faça as atividades no caderno

1. Determine as raízes de cada equação a seguir, considerando que x pode ser qualquer número real.

a) x ao quadrado = 81

b) x ao quadrado = 144

c) 2x ao quadrado = 32

d) 2x ao quadrado = 128

• O que as raízes dessas equações sugerem?

2. Tadeu assentou 16 ladrilhos de formato quadrado em uma parede. A área revestida mede .6400 centímetros quadrados. Todos os ladrilhos têm as mesmas dimensões, e a medida de comprimento do lado de cada ladrilho é x.

Ilustração. Quatro fileiras e quatro colunas de ladrilhos coloridos e diferentes.

Veja como Ana iniciou os cálculos para saber quanto mede o comprimento do lado de cada ladrilho.

Ilustração. Folha de papel com as informações: A parede está revestida com 16 ladrilhos de mesmas dimensões e a área da parede mede 6.400 centímetros quadrados 16 x elevado ao quadrado vezes 6.400 Aplicando o princípio multiplicativo das igualdades, multiplicamos por 1 sobre 16 os dois membros da equação fração 1 sobre 16 vezes 16 x elevado ao quadrado vezes a fração 1 sobre 16 vezes 6400 x elevado ao quadrado vezes 400.

a) Para a equação 16x ao quadrado = .6400, Ana encontrou duas raízes. Ambas podem ser consideradas solução para o problema apresentado?

b) Quanto mede o comprimento do lado de cada ladrilho?

3. Paulo fará uma horta em um terreno de formato quadrado cuja área mede 169 métros quadrados. Qual é a medida de comprimento e de largura desse terreno?

Ilustração. Terreno quadrado com 3 pés de alface e 3 de couve plantados. Há uma parte do terreno vaga.

4.

Elabore um problema cuja solução possa ser encontrada resolvendo a seguinte equação:

x ao quadrado = 144

5. Teresa fez um tapete de 640 centímetros quadrados usando retalhos de formato quadrado. Observe.

Ilustração. Tapete composto por 10 retalhos quadrados diferentes dispostos em 2 fileiras com 5 retalhos cada.

• Quanto mede o comprimento do lado de cada retalho quadrado que ela utilizou?

6.

Escreva o enunciado do problema formado pelas frases a seguir. Depois, resolva-o.

Ilustração. Três papéis com as informações: A medida de comprimento desse canteiro é o dobro da medida da sua largura. Quais são as medidas de comprimento e de largura desse canteiro? Júlio construiu um canteiro de formato retangular cuja área mede 32 metros quadrados.

Respostas e comentários

1. Respostas em Orientações.

2. a) Não, pois a raiz negativa abre parêntesesmenos20fecha parênteses não pode representar medidas, já que medidas de comprimento são sempre positivas.

2. b) 20 centímetros

3. O comprimento e a largura medem 13 métros.

4. Resposta pessoal.

5. 8 centímetros.

6. Júlio construiu um canteiro de formato retangular cuja área mede 32 métros quadrados. A medida de comprimento desse canteiro é o dobro da medida de sua largura. Quais são as medidas de comprimento e de largura desse canteiro? (Resposta: 8 métros e 4 métros.)

Orientações e sugestões didáticas

• A fim de favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero nove, na seção Atividades, os estudantes são levados a resolver e a elaborar problemas que podem ser representados por equações do 2º grau do tipo axao quadrado = b, em que a e b são números reais positivos.

• Respostas da atividade 1:

a) xíndice 1 menos 9 e xíndice 2 = menos9

b) xíndice 1 menos 12 e xíndice 2 = menos12

c) xíndice 1 menos 4 e xíndice 2 = menos4

d) xíndice 1 menos 8 e xíndice 2 = menos8

Espera-se que os estudantes respondam ao item proposto dizendo que as raízes dessas equações sugerem que em uma equação do 2º grau com uma incógnita que é reduzida axao quadrado = b, em que b é um número positivo e a é diferente de zero há sempre duas raízes reais opostas.

• Chame a atenção dos estudantes para o fato de que nem sempre as duas raízes encontradas ao resolver a equação do 2º grau satisfazem o problema que a originou. Os problemas propostos nas atividades 3 e 5, por exemplo, admitem como solução apenas a raiz positiva da equação oriunda deles, uma vez que solicitam aos estudantes que determinem medidas: medida do comprimento do lado do terreno (atividade 3) e medida do comprimento do lado do retalho (atividade 5).

• A atividade 4 solicita aos estudantes que elaborem um problema. Após terminarem, proponha que o troquem com um colega e resolvam o problema criado por ele.

Página 246

Compreender um texto

faça as atividades no caderno

Qual objeto cai mais rápido: o mais leve ou o mais pesado?

Atualmente, sabemos que a medida da distância percorrida por um objeto caindo a partir do repouso, livre da resistência do ar ou com resistência desprezível, pode ser representada pela equação, conhecida por lei dos corpos em queda:

d = \frac{1}{2} g t^{2}

em que:

• d: medida da distância percorrida pelo objeto, em metro;

• t: medida do tempo de queda, em segundo;

• g: medida da aceleração da gravidade terrestre, aproximadamente 10 metros por segundo ao quadrado.

Por exemplo, para calcular a medida de tempo que uma pedra leva para atingir o chão ao ser solta da beira de um precipício medindo 125 métros de altura, efetuamos:

d = \frac{1}{2} g t^{2} \Rightarrow 125 = \frac{1}{2} \cdot 10 t^{2} \Rightarrow 125 = 5 t^{2} \Rightarrow \frac{125}{5} = \frac{5 t^{2}}{5} \Rightarrow \frac{125}{5} = t^{2} \Rightarrow t^{2} = 25

Logo: t = 5 ou t = menos5

No entanto, t não pode ser negativo, pois representa uma medida de tempo; logo, a pedra atingirá o chão após 5 segundos.

Note que a equação anterior não depende da medida de massa do objeto, mas nem sempre foi assim. Aristóteles (384-322 antes de Cristo) afirmava que corpos mais pesados caíam mais rapidamente do que corpos mais leves. Essa crença perdurou por muitos anos sem que ninguém pudesse verificar ou contestar, até que Galileu Galilei (1564-1642), ao introduzir o método experimental, chegou à conclusão de que isso não é verdade, ou seja, quando dois corpos de medidas de massas diferentes, desprezando a resistência do ar, são abandonados da mesma medida de altura, ambos alcançam o solo no mesmo instante.

Fotografia. Busto de homem de cabelo curto, barba e manto sobre os ombros.

Pintura. Homem branco de cabelo grisalho, barba e roupa escura com gola branca. Ele está sentado segurando um objeto cilíndrico. — Busto de Aristóteles (primeira imagem) e pintura retratando Galileu Galilei (segunda imagem).

Orientações e sugestões didáticas

Compreender um texto

Objetivos

• Desenvolver a competência leitora.

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah zero nove e das competências gerais 1 e 2 da Bê êne cê cê.

Habilidade da Bê êne cê cê

• O trabalho com esta seção possibilita que os estudantes desenvolvam a habilidade ê éfe zero oito ême ah zero nove, uma vez que resolvem problemas usando a lei dos corpos em queda e, consequentemente, equações do 2º grau do tipo axao quadrado = b, com e sem o uso de tecnologias.

Orientações

• Inicie lendo apenas o título e instigue os estudantes a responder à pergunta. Após a leitura, que pode ser realizada individual ou coletivamente, aproveite a atividade 1 e verifique se eles mantiveram a resposta anterior, questionando-os caso mudem de opinião. Comente com os estudantes que, no título, os termos “mais leve” e “mais pesado” referem-se a “menor medida de massa” e “maior medida de massa”, respectivamente.

• A abordagem histórica nos estudos relacionados à queda livre, comparando as teorias de Aristóteles e Galileu, contribui para o desenvolvimento da competência geral 1 da Bê êne cê cê. Além disso, despertar a curiosidade dos estudantes quanto à experimentação de investigações com o campo da Física na resolução de problemas em diferentes áreas favorece o desenvolvimento da competência geral 2 da Bê êne cê cê.

• Diga aos estudantes que alguns historiadores afirmam que o experimento na torre de Pisa não ocorreu, teria sido apenas um experimento mental de Galileu. Talvez seja por isso que muitos seguidores de Aristóteles não se convenceram e Galileu acabou sendo alvo de perseguições por causa de suas ideias revolucionárias.

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo axao quadrado = b.

Competência geral 1: Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

Competência geral 2: Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

Página 247

A ciência estudada nas universidades na época de Galileu privilegiava a teoria aristotélica e colocava a técnica ou a experiência em segundo plano, isto é, havia um desprezo do método experimental pelos professores peripatéticos – que ensinavam andando, passeando, como era o costume de Aristóteles. Nessa época, tudo o que fosse contrário à interpretação aristotélica dos fenômenos da natureza não recebia crédito perante o corpo docente das universidades.

Observe uma curiosidade acerca do experimento de Galileu na Torre de Pisa, na Itália.

Galileu demoliu facilmente a hipótese de Aristóteles sobre a queda dos corpos. Conta-se que Galileu deixou cair da torre inclinada de Pisa vários objetos com pesos [massas] diferentes e comparou suas quedas. Ao contrário da afirmativa de Aristóteles, Galileu comprovou que uma pedra duas vezes mais pesada que outra não caía realmente duas vezes mais rápido. Exceto pelo pequeno efeito da resistência do ar, ele descobriu que objetos de vários pesos, soltos ao mesmo tempo, caíam juntos e atingiam o chão ao mesmo tempo. Em certa ocasião, Galileu presumivelmente teria atraído uma grande multidão para testemunhar a queda de dois objetos com pesos [massas] diferentes do topo da torre. A lenda conta que muitos observadores desta demonstração que viram os objetos baterem juntos no chão zombaram do jovem Galileu e continuaram a sustentar os ensinamentos de Aristóteles.

, P. G. Física conceitual. décima segunda edição Porto Alegre: Bookman, 2015. página 49.

Observação

Na prática, o que influencia na queda mais lenta de uma pena, um paraquedista ou uma folha de papel em comparação à queda de uma pedra, por exemplo, é a resistência do ar, pois, se a desconsiderássemos, todos chegariam ao chão simultaneamente.

Ilustração. Retângulo azul com uma pena branca na horizontal.

ATIVIDADES

faça as atividades no caderno

1. Responda à pergunta do título (Qual objeto cai mais rápido: o mais leve ou o mais pesado?) justificando-a. Para isso, desconsidere a resistência do ar.

2. Se uma pedra leva 6 segundos para cair de certa medida de altura, quanto tempo levaria uma segunda pedra, cuja medida de massa mede duas vezes a da primeira, solta da mesma medida de altura, segundo Aristóteles? E segundo Galileu?

3. Pegue duas folhas do caderno, de modo que ambas tenham a mesma medida de massa, e amasse apenas uma delas, formando uma bolinha. Depois, solte-as, simultaneamente, da maior medida de altura que puder com seus braços esticados para cima. Qual delas chegou ao chão primeiro? Por que isso aconteceu?

4. Na seção Informática e Matemática da página 244, vimos como empregar um software de construção de gráficos para resolver uma equação do tipo

a x^{2} = b

, usando apenas a janela de álgebra, sem considerar a janela de gráficos. Utilize essa ferramenta para calcular a medida de tempo que uma pedra leva para atingir o chão ao ser solta da beira de um precipício medindo:

a) 80 métros de altura.

b) 90 métros de altura.

c) 150 métros de altura.

d) 200 métros de altura.

5.

Reúna-se com alguns colegas e façam uma pesquisa sobre o método experimental (experimentação ou experimentalismo) e o empirismo. Montem um cartaz com algumas frases e imagens listando etapas, exemplificando algumas contribuições ou ressaltando a importância desse método em diferentes áreas, como na Ciência e na Medicina, por exemplo.

Respostas e comentários

1. Os dois objetos caem juntos, pois a medida de distância percorrida por um objeto caindo a partir do repouso não depende da medida de massa do objeto.

2. 3 segundos; 6 segundos.

3. A folha amassada chegou primeiro; isso aconteceu devido à resistência do ar.

4. a) 4 segundos

4. b)

2 \sqrt{3}

segundos ou, aproximadamente, 4,25 segundos

4. c) 30 segundos

4. d)

2 \sqrt{10}

segundos ou, aproximadamente, 6,32 segundos

5. Resposta pessoal.

Orientações e sugestões didáticas

• Para responderem à atividade 2, oriente os estudantes a retomar o texto e localizar a informação necessária para a obtenção da resposta. Pela frase “Ao contrário da afirmativa de Aristóteles, Galileu comprovou que uma pedra duas vezes mais pesada (maior medida de massa) que outra não caía realmente duas vezes mais rápido.”, podemos presumir que, segundo Aristóteles, uma pedra com o dobro de medida de massa cairia na metade da medida de tempo. Alguns estudantes podem demonstrar dificuldade em reconhecer a proporção inversa e apresentar resposta com o dobro da medida de tempo em vez da metade. Nesse caso, ajude-os ou permita que um colega relate como chegou à resposta.

• Durante o trabalho com o experimento da atividade 3, certifique-se de que os estudantes concordam que a folha amassada chega primeiro ao chão devido à menor resistência do ar.

Ao realizar este experimento, certifique-se de que os estudantes o façam de fórma segura, a fim de que não haja riscos para sua integridade física.

• A atividade 4 favorece o desenvolvimento da habilidade ê éfe zero oito ême ah zero nove, pois permite ao estudante obter a solução exata e a solução aproximada de uma equação polinomial de 2º grau do tipo axao quadrado = b usando um software de Geometria dinâmica.

• Na atividade 5, espera-se que os estudantes realizem investigações sobre o tema proposto e suas etapas. Compartilhe os cartazes e promova discussões com a turma sobre as etapas do método experimental.

• Esta seção foi elaborada com base no texto O papel da experimentação no ensino de Ciências, de Marcelo Giordan, publicado nas Atas do segundo Encontro Nacional de Pesquisa em Educação em Ciências (), realizado em Valinhos/São Paulo em 1999.

Página 248

Estatística e Probabilidade

faça as atividades no caderno

Média aritmética, moda, mediana e amplitude

Nove idosos participam semanalmente do Encontro da Terceira Idade para praticar atividades físicas e se divertir. Em outubro de 2022, foi feito um levantamento da idade desses idosos, como podemos observar na tabela a seguir.

Ilustração. Grupo com 9 idosos, 4 homens e 5 mulheres. Alguns estão sentados em bolas coloridas.

Idade dos idosos do Encontro da Terceira Idade
Idoso	Idade (em ano)
Alice	68
Benedito	68
Manoela	70
Yoko	70
Chang	70
José	73
Julieta	75
Sebastião	75
Ubiratan	77

Dados obtidos pelo organizador do Encontro da Terceira Idade em outubro de 2022.

▸ Qual é a média aritmética, a moda, a mediana e a amplitude da idade desses idosos?

Média aritmética

Para calcular a média aritmética simples (ou média aritmética) de um conjunto de valores, adicionamos todos e dividimos o resultado pela quantidade de valores.

Na situação anterior, para calcular a idade média dos 9 idosos, adicionamos todas as idades e dividimos o resultado por 9.

\frac{68 + 68 + 70 + 70 + 70 + 73 + 75 + 75 + 77}{9} = \frac{646}{9} ≃ 71, 8

Assim, podemos dizer que a idade média dos idosos que participam dos encontros é aproximadamente 71,8 anos.

Para analisar

Se um idoso de 80 anos entrasse no grupo, a média de idade aumentaria ou diminuiria? Esse valor seria maior ou menor que 80 anos? Por quê?

Respostas e comentários

Para analisar: Espera-se que os estudantes respondam que a média aumentaria, pois a idade do idoso que entrou é superior à média, mas esta seria menor que 80, pois, dos 10 idosos que fazem parte do grupo, 9 têm idade inferior a 80 anos.

Orientações e sugestões didáticas

Estatística e Probabilidade

Objetivos

• Favorecer o desenvolvimento da habilidade ê éfe zero oito ême ah dois cinco da Bê êne cê cê.

• Trabalhar o Tema Contemporâneo Transversal Processo de envelhecimento, respeito e valorização do idoso, da macroárea Cidadania e Civismo, ao falar de temáticas relacionadas ao envelhecimento.

Habilidade da Bê êne cê cê

• Este tópico favorece o desenvolvimento da habilidade ê éfe zero oito ême ah dois cinco da Bê êne cê cê porque os estudantes poderão obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.

Orientações

• Provavelmente, os estudantes dessa faixa etária já vivenciaram situações em que houve necessidade de calcular a média aritmética de uma amostra de dados. Aqui, esse tema é retomado com base em uma problematização a respeito da idade dos participantes de um Encontro da Terceira Idade.

• Aproveite o contexto para trabalhar o Tema Contemporâneo Transversal Processo de envelhecimento, respeito e valorização do idoso da macroárea Cidadania e Civismo. É importante debater temáticas relacionadas ao processo de envelhecimento, natural ao longo do ciclo da vida, e à valorização do idoso, eliminando preconceitos, reconhecendo seus direitos e respeitando suas histórias e vivências.

• Além dos cálculos envolvidos na discussão, os estudantes devem compreender o significado de média e como fazer inferências.

• O objetivo do boxe Para analisar é que os estudantes percebam que a média da idade vai aumentar sem que seja preciso calcular a média aritmética novamente, bastando analisar a média de idade calculada antes da entrada do novo idoso.

(ê éfe zero oito ême ah dois cinco) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.

Página 249

Moda

Em um conjunto de dados com valores numéricos ou não, o valor ou os valores que apresentam a maior frequência, ou seja, que ocorrem mais vezes, são chamados moda do conjunto de dados.

Para organizar os dados, construímos a tabela a seguir, que indica a quantidade de vezes que cada idade apareceu.

Frequência das idades dos idosos do Encontro da Terceira Idade
Idade	Frequência
68	2
70	3
73	1
75	2
77	1

Dados obtidos pelo organizador do Encontro da Terceira Idade em outubro de 2022.

Como a idade que mais aparece, nesse conjunto de dados, é 70 anos, dizemos que a moda é 70 anos.

Mediana

Para determinar a mediana de um conjunto de dados, primeiramente é preciso escrever os valores do conjunto de dados em ordem crescente ou decrescente.

Mediana em um conjunto de dados com número ímpar de valores

Quando você tem um conjunto de dados com um número ímpar de valores e os ordena, do menor para o maior ou do maior para o menor, o valor que ocupa a posição central nessa ordenação é chamado mediana. Esse é o caso da situação apresentada, pois o conjunto de dados tem 9 idades.

Observando as idades organizadas em ordem crescente, temos:

Sequência numérica primeira posição: 68; segunda posição: 68; terceira posição:70; quarta posição 70; quinta posição 70; Sexta posição:73; sétima posição: 75 oitava posição:75; nona posição: 77; Destaque para posição central que está ocupada pelo número 70.

Com essa organização, a idade 70 anos ocupou a posição central.

Assim, dizemos que a mediana das idades é 70 anos.

Para pensar

Suponha que um idoso de 70 anos saia do grupo e um de 71 anos entre no grupo. Qual passará a ser a mediana das idades?

Mediana em um conjunto de dados com número par de valores

Quando um conjunto de dados tem um número par de valores, dois deles ocuparão a posição central. Nesse caso, a mediana será a média aritmética desses dois valores.

Imagine que, na situação apresentada, um indivíduo de 68 anos entre no grupo. Nesse caso, se organizarmos as idades em ordem crescente, teremos dois valores ocupando a posição central. Observe.

Sequência númerica primeira posição: 68; segunda posição: 68; terceira posição:68; quarta posição 70; quinta posição 70; Sexta posição:70; sétima posição: 73 oitava posição:75; nona posição: 75; decima posição:77; Destaque para os termos centrais ocupados pelos números 70 e 70 Destaque para posição central que está ocupada pelo número 70.

Respostas e comentários

Para pensar: A mediana das idades passará a ser 71 anos.

Orientações e sugestões didáticas

• Dando continuidade à exploração das medidas de tendência central de uma pesquisa, os estudantes deverão estudar os conceitos de moda e de mediana.

• A situação apresentada mostra que a moda do conjunto de dados é 70 anos. No entanto, se um idoso de 75 anos entrar nesse grupo, teremos duas modas: 70 anos e 75 anos.

• Os estudantes devem observar que, para determinar a mediana, é necessário organizar os dados apresentados para que se busque a posição central. Independentemente do número de elementos, par ou ímpar, é possível determinar a mediana.

• No boxe Para pensar, espera-se que os estudantes não apresentem dificuldades em responder a pergunta. Eles devem reordenar as idades excluindo uma de 70 e incluindo uma de 71 anos.

Página 250

▶ Estatística e Probabilidade

Em situações como essa, a mediana será a média aritmética dos dois valores centrais:

média aritmética =

\frac{70 + 70}{2} = \frac{140}{2} = 70

Assim, dizemos que 70 anos é a mediana desse conjunto de dados.

Amplitude de um conjunto de dados

A amplitude de um conjunto de dados é a diferença entre o menor e o maior valor que aparecem nesse conjunto. Nesse caso, é interessante que os dados estejam organizados em ordem crescente ou decrescente para melhor visualização desses valores.

Na situação inicial do grupo de idosos, como a menor idade é 68 anos e a maior idade é 77 anos, a amplitude será calculada assim:

77 menos 68 = 9

Perceba que, se entrarem idosos com mais de 77 anos ou menos de 68 anos, a amplitude do conjunto de dados será maior.

Assim, respondendo à pergunta sobre o grupo de idosos, obtemos média aritmética: aproximadamente 71,8; moda: 70 anos; mediana: 70 anos; e a amplitude: 9.

ATIVIDADES

faça as atividades no caderno

1. Larissa, dona de uma escola de danças de salão, abrirá um horário de aula às sextas-feiras. Para conseguir atender o maior número de estudantes possível, ela fez, em outubro de 2022, uma pesquisa para identificar as preferências de período e de tipo de dança, conforme indicado a seguir.

Período e tipo de dança preferidos
Nome	Período	Tipo de dança	Nome	Período	Tipo de dança
Camila	Manhã	Tango	Lúcia	Noite	Tango
Jéferson	Noite	Zouk	Ana Maria	Tarde	Zouk
Amanda	Tarde	Zouk	Carolina	Tarde	Zouk
Jonas	Noite	Zouk	Pedro	Manhã	Tango
Lucas	Tarde	Samba	Érica	Noite	Samba
Tamires	Noite	Tango	João Paulo	Tarde	Samba
Pablo	Tarde	Samba	Cláudio	Noite	Samba
Leandro	Noite	Zouk	Samanta	Manhã	Samba
Rubens	Manhã	Samba	Felipe	Tarde	Samba

a) Construa duas tabelas: a primeira com os tipos de dança e a quantidade de vezes que cada tipo foi citado na pesquisa; a segunda, com os períodos e a quantidade de vezes que cada um apareceu.

b) Qual foi o tipo de dança preferido pelos estudantes?

c) ?

d) Qual é a moda do conjunto de dados sobre o período e a moda do conjunto de dados sobre o tipo de dança?

Respostas e comentários

1. a) Resposta em Orientações.

1. b) samba

1. c) tarde e noite

1. d) Duas modas para o período: tarde e noite; moda para o tipo de dança: samba.

Orientações e sugestões didáticas

• Explique aos estudantes que a média aritmética, bem como a mediana e a moda, caracteriza um conjunto de valores. Convém usar a média quando o conjunto de dados não apresenta valores discrepantes, pois, caso contrário, o resultado fornecido pode desencadear conclusões falhas. A mediana representa melhor o conjunto de dados quando este apresenta valores discrepantes, pois esses dados não “contaminam” o seu valor. Mais importante do que o cálculo dessas medidas é o trabalho com a interpretação delas. Pode-se, sempre que possível, incentivar os estudantes a observar os aspectos anteriormente apontados, trabalhando o cálculo dessas medidas com base num conjunto de dados sem valores discrepantes e depois acrescentando um valor bem maior ou menor que os demais. Se houver discrepância entre os dados, torna-se interessante calcular a amplitude.

• Resposta do item a da atividade 1:

Frequência dos tipos de dança
Tipo de dança	Frequência
Tango	4
Samba	8
Zouk	6

Dados obtidos por Larissa em outubro de 2022.

Frequência dos períodos
Período	Frequência
Manhã	4
Tarde	7
Noite	7

Dados obtidos por Larissa em outubro de 2022.

Página 251

2. Paulo faz salgados para vender. Ele estipulou uma meta de vendas para o mês de junho de 28 salgados por dia, em média. A tabela a seguir mostra as vendas no mês de junho.

Número de salgados vendidos no mês de junho
Tipo	Quantidade vendida
Empada	150
Quibe	180
Croquete	250
Coxinha	320

Dados obtidos por Paulo em junho de 2022.

a) Paulo conseguiu atingir sua meta em junho?

b) No mês de julho, Paulo vendeu 10% a menos do que no mês de junho. Qual foi a média aproximada de salgados vendidos por dia no mês de julho? Lembre-se de que julho tem 31 dias.

3. Observe a tabela e responda às questões.

Medida de massa dos jogadores do clube Alegria Total
Nome	Medida de massa (em kg)	Nome	Medida de massa (em kg)
Toninho	85	Gilberto	78
Rogério	85	Luciano	80
César	82	Luisão	84
Marinho	74	Juan	73
Vevé	69	Cris	77
Carlos	67	Émerson	72
Roberto	72	Ricardinho	73
Gustavo	74	Ronaldo	90,5
Marcinho	65	Adriano	86
Will	76	Renan	75
Fabinho	75	Juninho	76

Dados obtidos pelo clube Alegria Total em outubro de 2022.

a) Qual é a mediana das medidas de massa desses jogadores?

b) Qual é a média das medidas de massa dos jogadores?

c) Qual é a moda da medida de massa desses jogadores?

d) Qual é a amplitude desse conjunto de dados?

e) Em sua opinião, para analisar a medida de massa desses jogadores, qual das informações é menos representativa: a mediana, a média ou a moda dos dados? Justifique sua resposta.

4. Vera fez uma entrevista com algumas pessoas e marcou em uma folha a idade de cada uma.

Enquanto tomava seu lanche da tarde, ela deixou cair café na folha, e a idade da última pessoa entrevistada ficou ilegível.

Ilustração. Prancheta com folha branca e as informações: Idade dos entrevistados: 27, 52, 78, 45, 89, 15, 32, 40, 43

a) Qual é a idade da última pessoa entrevistada, se a mediana para as idades dos entrevistados é igual a 42 anos?

b) Calcule no caderno a média das idades dos entrevistados após descobrir a última idade anotada.

5. Observe quantas escolas e estudantes matriculados em creches havia na rede pública e na rede privada do Brasil, de acordo com o Censo da Educação Básica 2020. Em seguida, faça o que se pede.

Números da Educação em 2020 – creches
Rede	Matrícula	Número de escolas
Pública	2.399.766	52.178
Privada	1.017.444	18.716

Dados obtidos em: BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inépi). Censo da educação básica 2020: resumo técnico. Brasília, Distrito Federal: Inépi, 2021.

a) A média aritmética do número de estudantes matriculados em creches, por tipo de rede, é ..1708605. Em que tipo de rede o total de estudantes matriculados está abaixo da média?

b) Em cada rede de ensino, qual é a média aritmética aproximada do número de estudantes por escola?

c) Com base nos dados do item b, construa um gráfico de barras horizontais indicando a quantidade média aproximada (para número inteiro) de estudantes matriculados em creches por tipo de rede de ensino em 2020.

Respostas e comentários

2. a) Sim, pois a média de vendas diárias foi de 30 salgados.

2. b) A média aproximada foi de 26 salgados vendidos por dia.

3. a) 75,5 quilogramas

3. b) 76,75 quilogramas

3. c) 72 quilogramas, 73 quilogramas, 74 quilogramas, 75 quilogramas, 76 quilogramas e 85 quilogramas

3. d) 25,5

3. e) Espera-se que os estudantes concluam que a moda é menos representativa nessa situação porque não existe apenas uma, mas várias, indicando que os dados variam bastante. Tanto a média como a mediana representam melhor a situação.

4. a) 41 anos

4. b) 46,2 anos

5. a) na rede privada

5. b) pública: 45,99 estudantes; privada: 54,36 estudantes

5. c) Resposta em Orientações.

Orientações e sugestões didáticas

• Após a resolução da atividade 3, peça aos estudantes que comparem as duas medidas de tendência central. A mediana é 75,5 quilogramas e a média é 76,75 quilogramas. Liste no quadro a medida da massa de todos os jogadores e localize as duas medidas. É interessante comentar que a maior medida de massa, 90,5 quilogramas, influiu bastante no fato de a média aritmética ter sido maior que a mediana.

• Os dados da atividade 5 foram obtidos do Censo 2020. Essa e outras informações interessantes podem ser conferidas em: https://oeds.link/qnFmhn. Acesso em: 13 agosto 2022.

• Resposta do item c da atividade 5:

Gráfico em barras horizontais. Número médio aproximado de estudantes por creche – 2020. Eixo x, número médio aproximado de estudantes. Eixo y, Tipo de rede de ensino. Os dados são: Rede pública: 46. Rede privada: 54.

Dados obtidos em: BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inépi). Censo da educação básica 2020: resumo técnico. Brasília, Distrito Federal: Inépi, 2021.

Página 252

Atividades de revisão

faça as atividades no caderno

1. Aldo e Samanta realizaram um trabalho e ganharam juntos R$ 500,00quinhentos reais. Se Aldo ganhou

\frac{1}{4}

do valor recebido por Samanta, quanto ganhou cada um?

2. Uma escola realizou eleições para o grêmio. Havia dois candidatos concorrendo ao cargo de presidente. Sabendo que .1230 estudantes votaram, que houve 83 votos brancos e nulos e que o vencedor ganhou por uma diferença de 145 votos, calcule a quantidade de votos que obteve cada candidato.

3.

Elabore e resolva um problema envolvendo cestas de 2 e de 3 pontos no basquete e que possa ser resolvido por meio de um sistema de equações do 1º grau, de maneira semelhante ao apresentado na página 233.

4. Reginaldo despejou a água de um garrafão, completamente cheio, em 35 copos iguais, enchendo-os. Se o conteúdo desse garrafão e de outros 10 copos fosse colocado em um recipiente com capacidade medindo 8,1 litros, esse recipiente ficaria cheio. Quanto mede a capacidade do garrafão? E a do copo?

Ilustração. Mesa com 35 copos com água. Ao lado da mesa, menino de cabelo castanho e camiseta branca despela água em um copo utilizando um garrafão

5. A massa de um recipiente cheio de líquido mede 650 gramas. Se retirarmos metade desse líquido, essa medida cairá para 360 gramas. Quanto mede a massa do recipiente vazio?

a) 40 gramas

b) 50 gramas

c) 70 gramas

d) 80 gramas

e) 90 gramas

6. Quais são as medidas de x e de y, em grau, na figura?

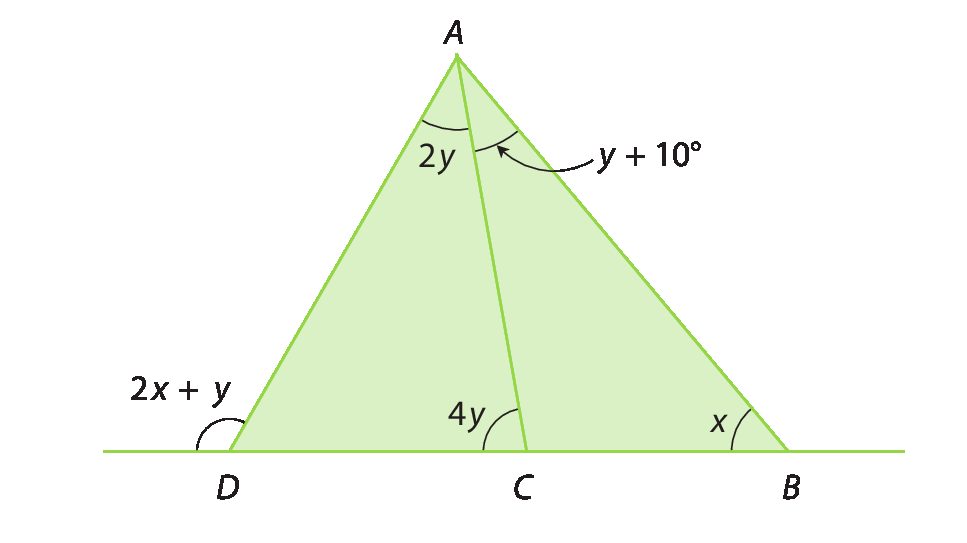
Figura geométrica. Triângulo verde dividido em dois triângulos. Do lado esquerdo, triângulo ACD com ângulos 2y, 4y e ângulo externo em D 2x mais y. Do lado direito, triângulo ABC com ângulos x e y mais 10 graus.

7. Sem resolver, explique por que o sistema a seguir é um sistema possível e indeterminado.

\{\begin{cases} 2 x + y = 8 \\ 6 x + 3 y = 24 \end{cases}

8. Analise a representação gráfica e responda à questão.

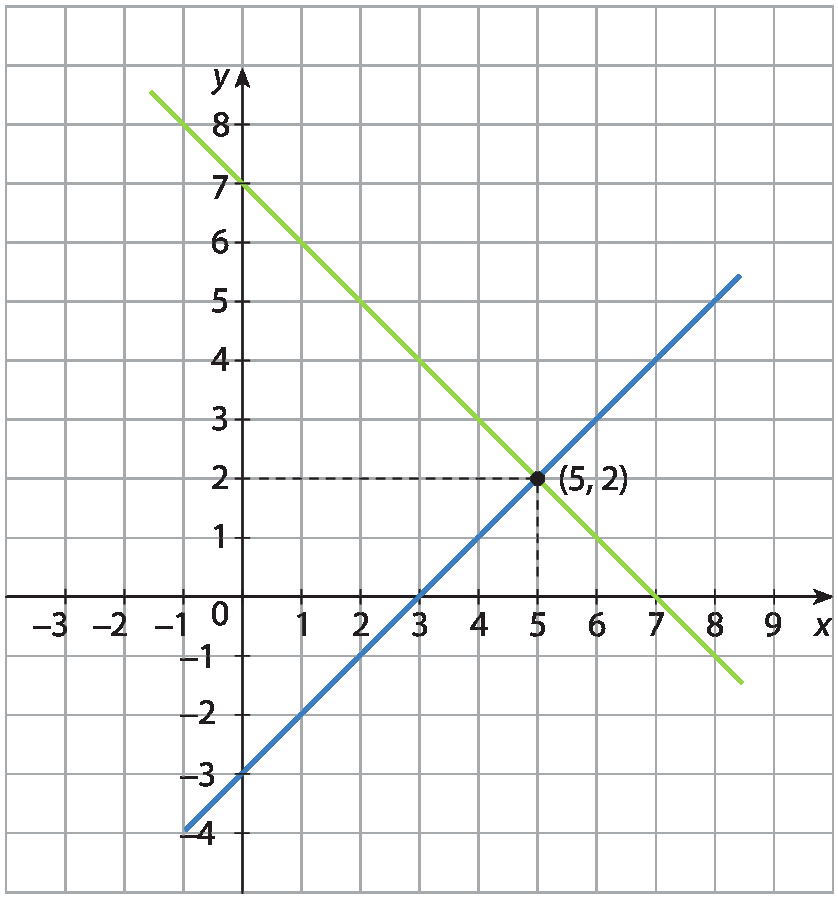
Ilustração. Duas retas concorrentes representadas em um plano cartesiano. As retas se interceptam no ponto (5, 2).

• Essa representação gráfica corresponde à solução de que sistema?

a)

\{\begin{cases} 2 x + 3 y = 5 \\ x - y = 2 \end{cases}

b)

\{\begin{cases} x + y = 7 \\ x - y = 3 \end{cases}

c)

\{\begin{cases} 2 x + y = 5 \\ x - 2 y = 7 \end{cases}

d)

\{\begin{cases} x + 2 y = 1 \\ 2 x + 3 y = 3 \end{cases}

e)

\{\begin{cases} 2 x - y = 7 \\ x - 2 y = 3 \end{cases}

Respostas e comentários

1. Aldo: R$ 100,00cem reais; Samanta: R$ 400,00quatrocentos reais

2. candidato ganhador: 646 votos; candidato perdedor: 501 votos

3. Resposta pessoal.

4. garrafão: 6,3 litros; copo: 180 mililitros

5. alternativa c

6. x = 50 e y = 20

7. Exemplo de resposta: A segunda equação é resultado da primeira equação multiplicada por 3.

8. alternativa b

Orientações e sugestões didáticas

Atividades de revisão

Objetivos

• Consolidar o conhecimento adquirido no decorrer do capítulo.

• Favorecer o desenvolvimento das habilidades ê éfe zero oito ême ah zero sete e ê éfe zero oito ême ah zero oito da Bê êne cê cê.

Habilidades da Bê êne cê cê

• Esta seção contribui para o desenvolvimento da habilidade ê éfe zero oito ême ah zero sete porque na atividade 8, ao identificar o sistema que corresponde à representação gráfica, os estudantes deverão associar uma equação do 1º grau com duas incógnitas a uma reta no plano cartesiano. Já a habilidade ê éfe zero oito ême ah zero oito tem o seu desenvolvimento favorecido porque são propostos problemas que podem ser representados por sistemas de equações do 1º grau com duas incógnitas.

Orientações

• Esse é o momento para os estudantes colocarem em prática o que estudaram no capítulo. É importante incentivá-los a justificar suas resoluções e a verificar as respostas obtidas.

• Ao realizar as atividades, incentive os estudantes a representar graficamente os sistemas de equações usados para traduzir as situações apresentadas.

• Procure identificar as dificuldades enfrentadas por eles e ajude-os a superá-las. Se achar conveniente, peça que façam uma autoavaliação do que aprenderam e do que precisam aprender.

• Sugerimos algumas questões para que os estudantes possam refletir sobre suas aprendizagens e possíveis dificuldades no estudo deste Capítulo, as quais devem ser adaptadas à realidade da turma. Oriente-os a fazer a autoavaliação, respondendo às questões no caderno com “sim”, “às vezes” ou “não”.

Eureticências

reticências sei representar situações-problema por meio de equações de 1º grau com duas incógnitas?

reticências sei avaliar soluções para equações de 1º grau com duas incógnitas?

reticências compreendo o que são sistemas de equações lineares de 1º grau?

reticências identifico as coordenadas de um ponto representado no plano cartesiano?

reticências sei determinar as medidas de tendência central associadas a um conjunto de dados?

(ê éfe zero oito ême ah zero sete) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano.

(ê éfe zero oito ême ah zero oito) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.