
CAPÍTULO 3 Circunferência
1 Circunferência e círculo
As figuras com formato arredondado são suaves e dão a impressão de movimento e leveza. Esse formato pode ser observado em partes de construções, objetos, pinturas etcétera
Aprecie as reproduções das pinturas a seguir e, em seguida, responda: elas lembram que figuras geométricas com esse formato?
Lembre-se: Escreva no caderno!


A circunferência é a figura geométrica formada por todos os pontos de um plano que estão à mesma medida de distância de um ponto fixo desse plano. Este ponto fixo é o centro da circunferência.
Considere alguns elementos da circunferência:
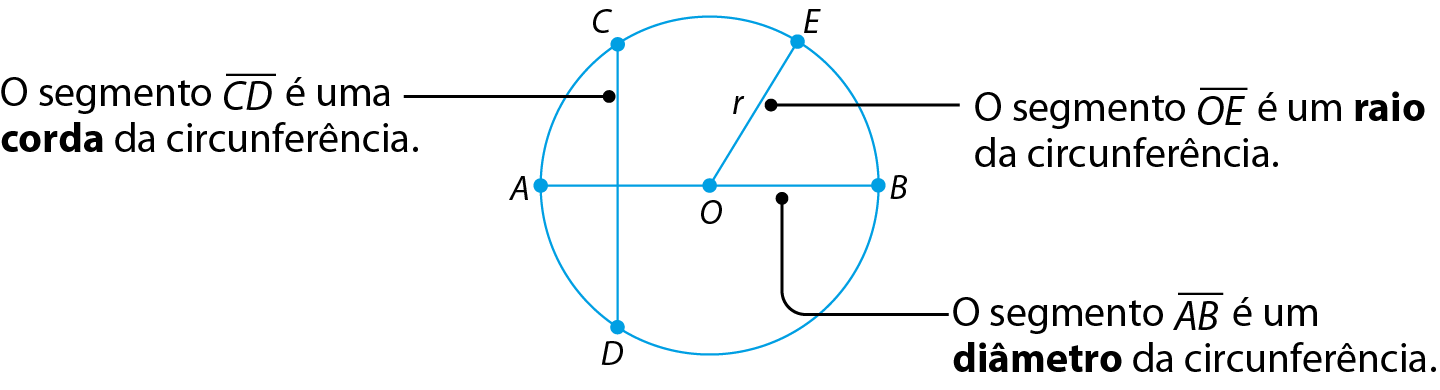
• corda é um segmento cujas extremidades são dois pontos distintos quaisquer da circunferência;
• raio é um segmento cujas extremidades são o centro e um ponto qualquer da circunferência;
• diâmetro é uma corda que passa pelo centro da circunferência.
Observe esses elementos na circunferência de centro O e raio r.
Atenção! Cuidado ao usar o compasso.
Círculo é a figura geométrica formada por uma circunferência e sua região interna.
Não confunda círculo com circunferência:

Para fazer
Observe a foto da construção Ring of life, que mede 157 metros de altura e fica na cidade de Fushun, na China.

O contôrno da parte interna dessa construção lembra uma circunferência.

Pesquise imagens de outras construções e pinturas que dão a ideia de círculos e de circunferências. Leve as imagens para a aula e compartilhe-as com os colegas.

ATIVIDADES
faça as atividades no caderno
1. Considere a circunferência a seguir, de centro O, e classifique cada um dos segmentos em raio, corda ou diâmetro.
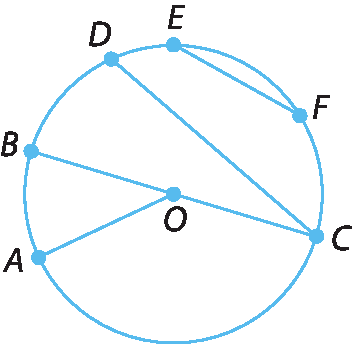
a)
Símbolo. Segmento de reta OA.b)
Símbolo. Segmento de reta BC.
c)
Segmento de reta CD.
d)
Símbolo. Segmento de reta EF.2. No caderno, construa com um compasso:
a) uma circunferência de centro O e raio de medida de comprimento igual a 3 centímetros;
b) uma circunferência de centro O e diâmetro de medida de comprimento igual a 4,5 centímetros.
3. Determine a medida de comprimento do diâmetro de uma circunferência sabendo que o comprimento de seu raio mede:
a) 17,2 centímetros;
b) 0,65 centímetro.
4. Leia atentamente as questões e responda-as.
a) Se a medida de comprimento do diâmetro de uma circunferência é igual a 34 centímetros e a do raio, (2x ‒ 13) centímetros, quanto mede x, em centímetro?
b) A medida de comprimento do diâmetro de uma circunferência é 3x + 4, e a de seu raio, x + 8. Quais são essas medidas?
5. Em seu caderno, classifique cada afirmação em verdadeira ou falsa.
a) Se a medida de comprimento do raio de um círculo é 4 centímetros, então a medida de comprimento do seu diâmetro é 2 centímetros.
b) Em um círculo, a circunferência que o limita tem o mesmo centro e as mesmas medidas de comprimento do raio e do diâmetro.
c) Todos os pontos de um círculo pertencem à circunferência que o contém.
d) Em um círculo cujo diâmetro mede 2,5 centímetros de comprimento, o raio mede 5 centímetros de comprimento.
2 Posições relativas
Posições de um ponto em relação a uma circunferência
Um professor pediu à turma que desenhasse uma circunferência de centro O, com raio que mede 1 centímetro de comprimento e um ponto P. Observe o desenho de três estudantes.

Observe que cada estudante desenhou o ponto P em uma posição diferente em relação à circunferência. No desenho de Lucas, P é externo à circunferência; no de Mariana, P é interno à circunferência; e no de Rafaela, P pertence à circunferência.
Considere uma circunferência de centro O e raio de medida de comprimento r e um ponto P, no mesmo plano, tal que a medida da distância entre P e O seja d.
• P é interno à circunferência se d for menor que r.
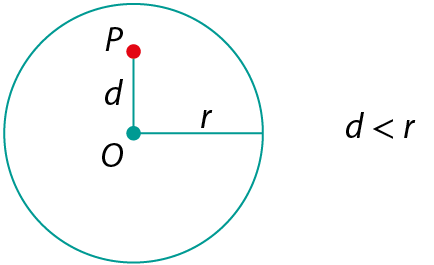
• P pertence à circunferência se d for igual a r.

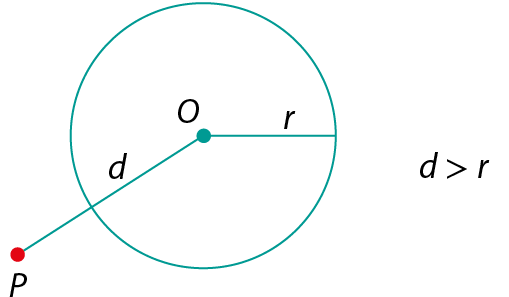
• P é externo à circunferência se d for maior que r.
Posições de uma reta em relação a uma circunferência
Uma reta e uma circunferência podem ter dois pontos comuns, um só ponto comum ou nenhum ponto comum.
Vamos ilustrar essas três situações, considerando uma circunferência de centro O e raio de medida de comprimento r e uma reta t em um mesmo plano.
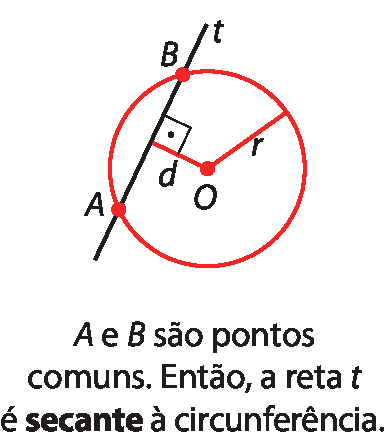

• Uma reta é secante a uma circunferência se tem dois pontos comuns com a circunferência. Nesse caso, a medida da distância d do centro O à reta t é menor que a medida de comprimento r do raio: d < r
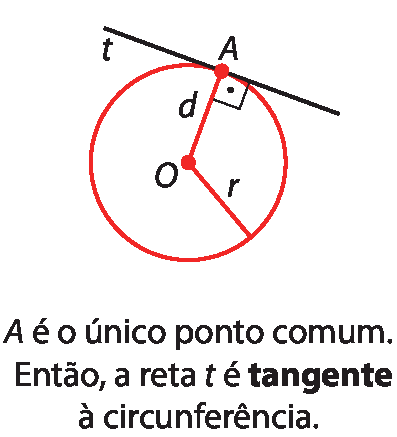
• Uma reta é tangente a uma circunferência se tem apenas um ponto comum com a circunferência. Nesse caso, a medida da distância d do centro O à reta t é igual à medida de comprimento r do raio: d = r
• Uma reta é externa ou exterior a uma circunferência se não tem ponto comum com a circunferência. Nesse caso, a medida da distância d do centro O à reta t é maior que a medida de comprimento r do raio: d > r
Observação
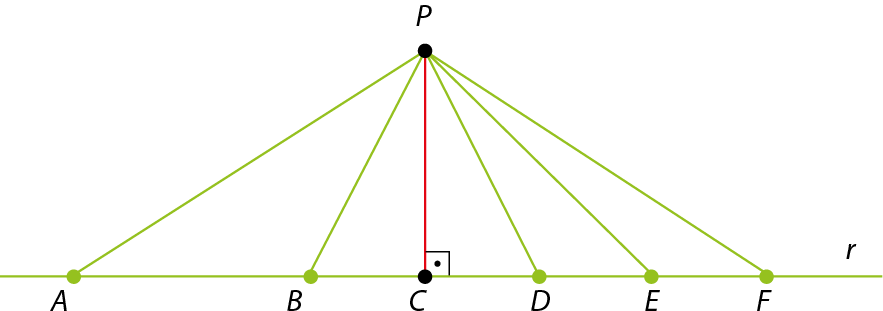
Há vários segmentos que ligam um ponto P a algum ponto da reta r. Entre eles existe apenas um segmento (
Símbolo. Segmento de reta PC.), cuja medida de comprimento é a menor possível, que é perpendicular à reta r. A medida de comprimento desse segmento é igual à da distância do ponto P à reta r.
Propriedades das retas secantes e tangentes a uma circunferência
Agora, você vai estudar propriedades das retas secantes e tangentes a uma circunferência que auxiliam na compreensão das relações entre essas retas e a circunferência.
● Propriedade da reta secante a uma circunferência
Atenção! Cuidado ao usar o compasso.
Para analisar
Com base nas orientações a seguir, construa uma figura como a mostrada.
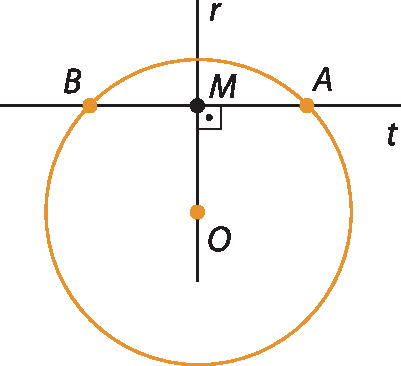
Trace uma circunferência de centro O e uma reta secante qualquer a essa circunferência. Repare que essa reta secante determina uma corda. Agora, com um esquadro, trace uma reta que passe pelo centro O e seja perpendicular à reta secante. A reta que você acabou de traçar divide a corda em seu ponto médio?
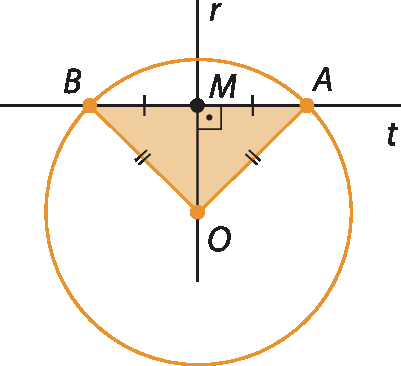
Se uma reta r passa pelo centro O de uma circunferência e é perpendicular a uma corda
Símbolo. Segmento de reta AB.dessa circunferência, então a reta r intercepta a corda em seu ponto médio M.
Vamos demonstrar essa propriedade.
Consideremos a circunferência de centro O, a reta secante e os segmentos
Símbolo. Segmento de reta OA.e
Símbolo. Segmento de reta OB. Como esses segmentos têm a mesma medida de comprimento, pois são raios da circunferência, o triângulo á ó bê é isósceles. Assim, a medida da altura
Símbolo. Segmento de reta OM.relativa à base
Símbolo. Segmento de reta AB.coincide com a medida da mediana relativa à base
Símbolo. Segmento de reta AB.. Logo, o ponto M divide a corda
Símbolo. Segmento de reta AB.em dois segmentos congruentes (AM = MB), ou seja, M é o ponto médio de
Símbolo. Segmento de reta AB..
● Propriedade da reta tangente a uma circunferência
Para analisar
Com base nas orientações a seguir, construa uma figura como a mostrada a seguir.
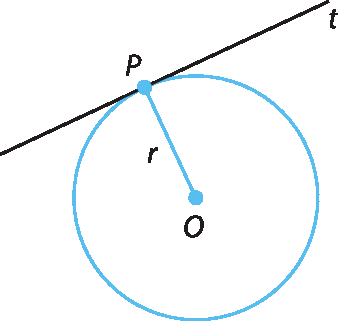
Desenhe uma circunferência e uma reta tangente a ela. Depois, trace o raio que contém o ponto de tangência. Com um transferidor, meça a abertura do ângulo determinado pelo raio e pela reta tangente. Qual foi a medida obtida?
Uma reta t, tangente à circunferência, é perpendicular ao raio da circunferência no ponto de tangência.
Essa propriedade também pode ser demonstrada.
● Propriedade de dois segmentos, com uma extremidade comum, tangentes a uma circunferência
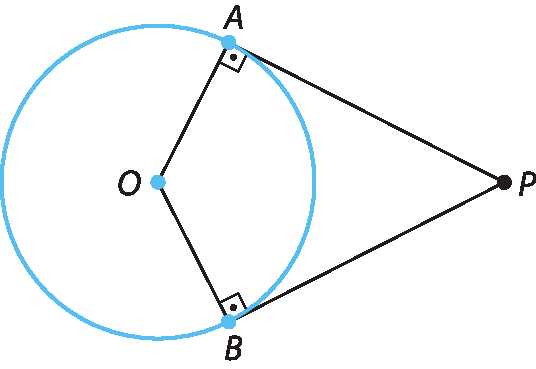
Considere uma circunferência de centro O, um ponto P externo a ela e dois segmentos,
Símbolo. Segmento de reta PA.e
Símbolo. Segmento de reta PB., tangentes a ela. Se medirmos os segmentos
Símbolo. Segmento de reta PA.e
Símbolo. Segmento de reta PB., verificaremos que eles têm a mesma medida.
Dois segmentos,
Símbolo. Segmento de reta PA.e
Símbolo. Segmento de reta PB., tangentes a uma circunferência nos pontos A e B, são congruentes.
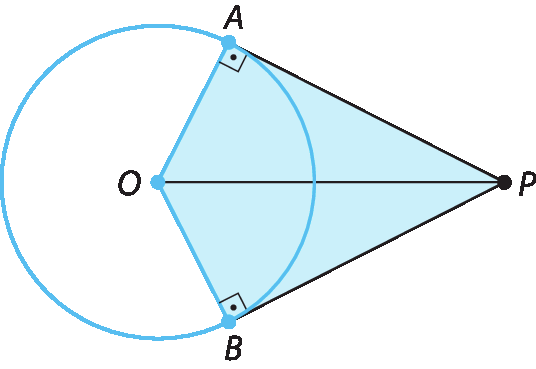
Vamos demonstrar essa propriedade.
Traçando o segmento
Símbolo. Segmento de reta OP., e considerando os triângulos AOP e BOP, temos:
•
Símbolo. Segmento de reta AO.≅
Símbolo. Segmento de reta BO.(raios);
•
Símbolo. Segmento de reta OP.(lado comum);
• medida de
Ângulo OAP.= medida de
Ângulo OBP.= 90graus (A e B são pontos de tangência).
Pelo caso de congruência do triângulo retângulo (hipotenusa-cateto), △AOP ≅ △BOP.
Portanto,
Símbolo. Segmento de reta PA.≅
Segmento de reta PB.
Aplicando essa propriedade, podemos resolver problemas de polígonos circunscritos a uma circunferência.
Vamos calcular, por exemplo, a medida x de comprimento do segmento
Símbolo. Segmento de reta AB.da figura a seguir.
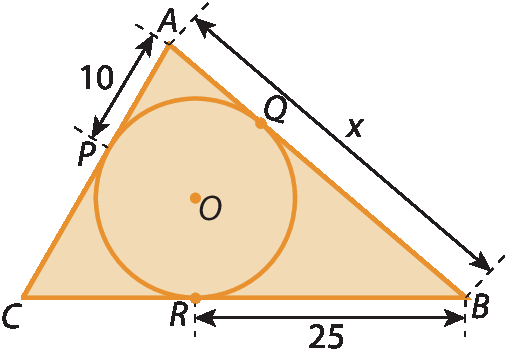

Observe que:
• x = AB = AQ + QB;
•
Símbolo. Segmento de reta AP.≅
Símbolo. Segmento de reta AQ., pois ambos são segmentos tangentes que passam pelo ponto A;
•
Símbolo. Segmento de reta BQ.≅
Símbolo. Segmento de reta BR., pois ambos são segmentos tangentes que passam pelo ponto B.
Portanto: x = A bê = 10 + 25 = 35
Para investigar
a) Considere um quadrilátero ABCD qualquer circunscrito a uma circunferência.
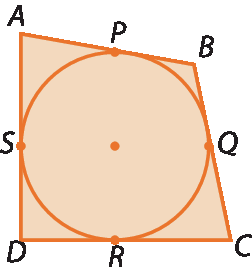
Que relação podemos estabelecer entre as somas das medidas de comprimento dos lados opostos desse quadrilátero (A bê + CD e BC + dê á)?
b) Usando a relação obtida no item anterior, calcule o valor de x na figura a seguir.
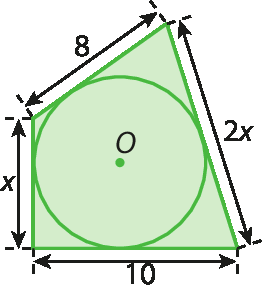
Atenção! Cuidado ao usar o compasso.

ATIVIDADES
faça as atividades no caderno
1. Com régua e compasso, faça as construções no caderno.
a) Trace uma circunferência e marque três pontos: A, interno à circunferência; B, externo; C, pertencente à circunferência.
b) Por meio de cada um dos três pontos do item a, tente traçar três retas: uma secante, uma tangente e uma externa à circunferência. Foi possível traçar todas as retas pedidas?
2. Observe a figura a seguir e indique a posição relativa dos pontos e das retas em relação à circunferência.
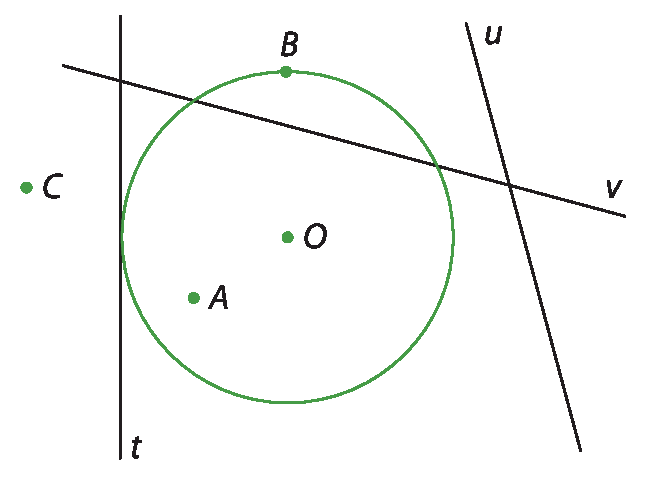
a) Ponto A
b) Ponto B
c) Ponto C
d) Reta t
e) Reta u
f) Reta v
3. Calcule a medida de comprimento de x, sabendo que a circunferência está inscrita no triângulo em cada caso.
a)
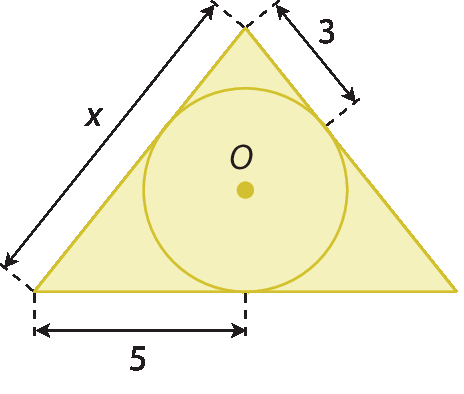
b)
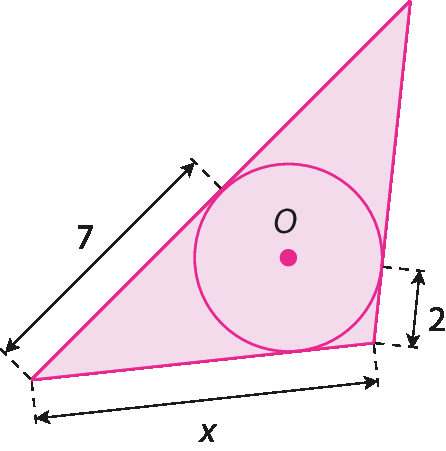
4. Calcule a medida de comprimento de x e de y, considerando que na figura o triângulo é circunscrito à circunferência.
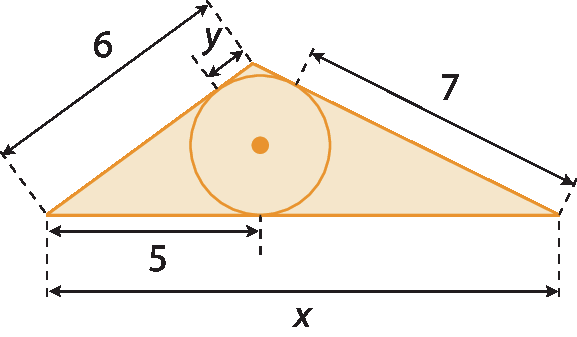
5. Observe as figuras e encontre a medida de x em cada caso.
a)

b)
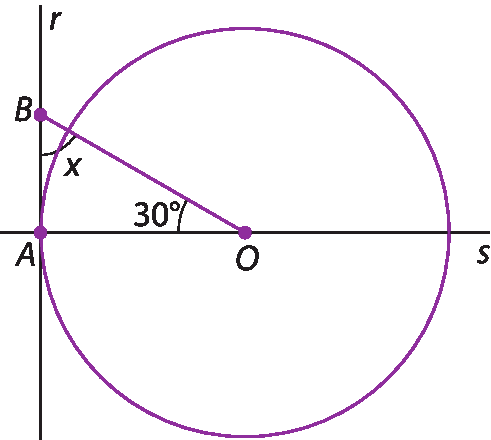
Posições relativas entre duas circunferências
Duas circunferências podem assumir diferentes posições uma em relação à outra. Observe as fotos a seguir.

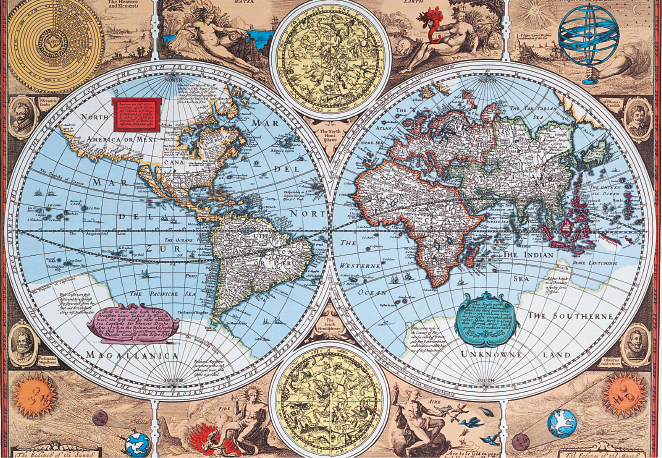

O símbolo dos Jogos Olímpicos lembra circunferências secantes. Já no mapa-múndi há detalhes que lembram circunferências tangentes exteriores. As marcas no solo vistas na foto da plantação com sistema de irrigação com pivô central, por sua vez, lembram circunferências concêntricas.
Vamos estudar as relações entre as circunferências nessas e em outras posições.
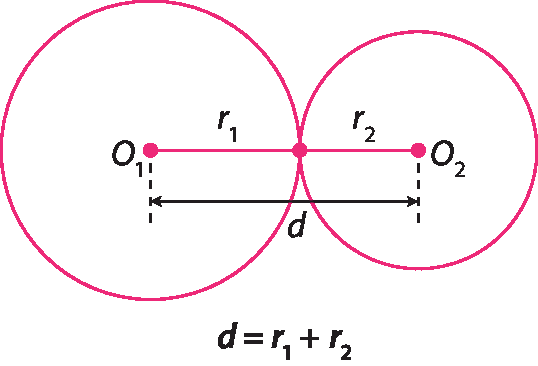
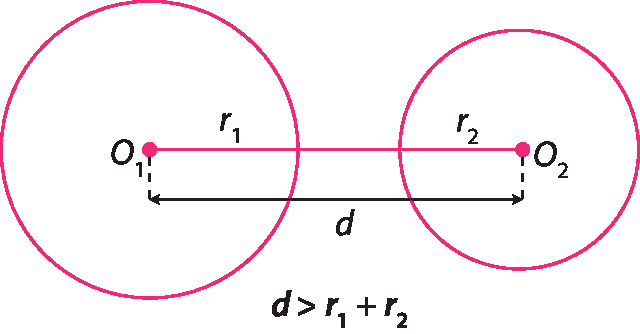
Circunferências tangentes exteriores
Duas circunferências são tangentes exteriores se têm apenas um ponto em comum e se a medida de distância entre seus centros é igual à soma das medidas de comprimento de seus raios.
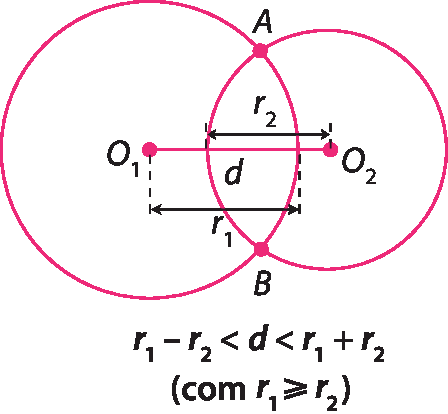
Circunferências secantes
Duas circunferências são secantes se têm exatamente dois pontos em comum.
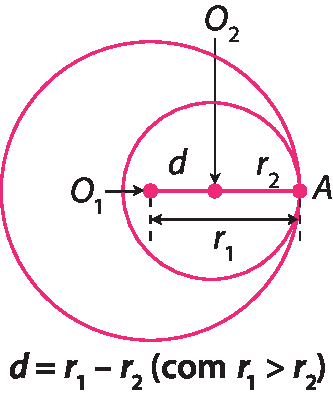
Circunferências tangentes interiores
Duas circunferências são tangentes interiores se têm apenas um ponto em comum e se a medida da distância entre seus centros é igual à diferença entre as medidas de comprimento de seus raios.
Circunferências internas
Duas circunferências são internas se não têm pontos em comum e se a medida da distância entre seus centros é menor que a diferença entre as medidas de comprimento de seus raios.
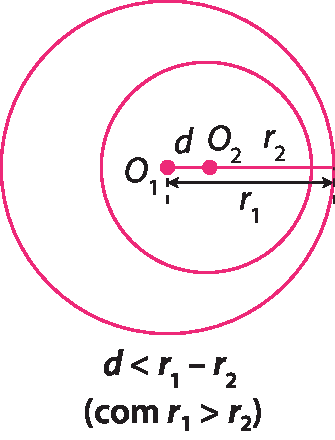
Circunferências externas
Duas circunferências são externas se não têm pontos em comum e se a medida da distância entre seus centros é maior que a soma das medidas de comprimento de seus raios.
Circunferências concêntricas
Duas circunferências são concêntricas se uma é interna à outra e se as duas têm o mesmo centro.
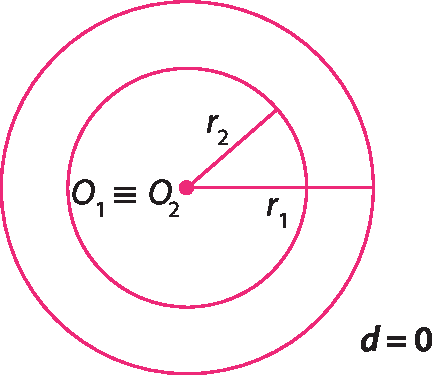
Observação
O₁ ≡ O₂ indica que os pontos O₁ e O₂ são coincidentes.

ATIVIDADES
faça as atividades no caderno
1. Considerando a posição relativa de duas circunferências, indique a posição relativa entre as circunferências a seguir.
(Os pontos O e O' são os centros das circunferências.)
a)
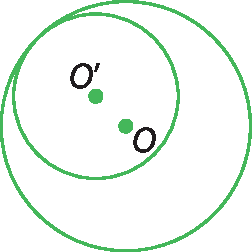
b)
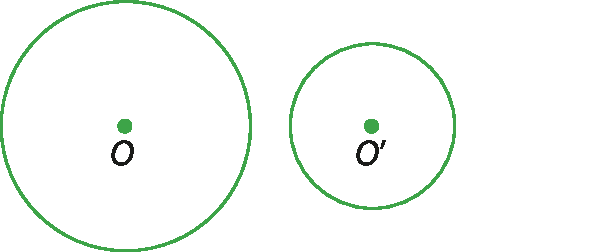
c)
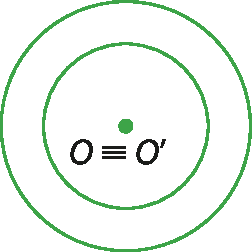
d)
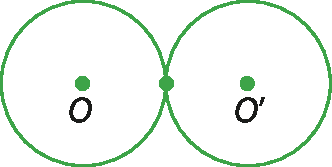
Atenção! Cuidado ao usar o compasso.
2. Faça no caderno o que se pede.
a) Construa duas circunferências que não tenham pontos em comum. Qual é a posição relativa entre elas? Há apenas uma resposta para esse problema? Se não, quais seriam as outras?
b) Construa duas circunferências que tenham apenas um ponto em comum. Qual é a posição relativa entre elas? Há apenas uma resposta para esse problema? Se não, quais seriam as outras?
3. Dadas as circunferências, seus centros e alguns segmentos, determine a maior medida inteira de comprimento que x pode assumir em cada caso, de modo que a posição relativa entre elas seja mantida.
a)
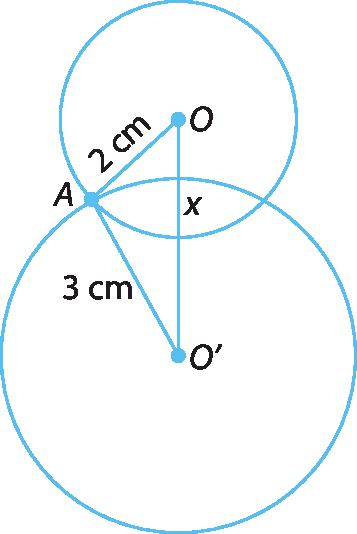
b)
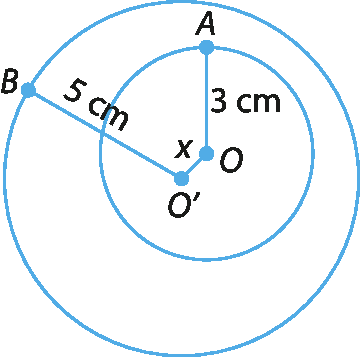
c)
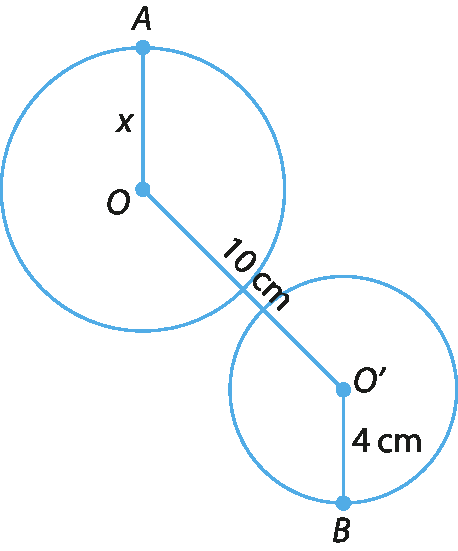
d)
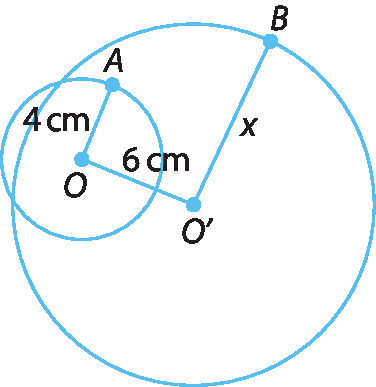
4.

Considere uma circunferência centésimo₁ cujo comprimento do raio mede 10 centímetros, uma circunferência centésimo₂ com raio de comprimento medindo 5 centímetros e a distância entre os centros de centésimo₁ e centésimo₂ mede 5 centímetros.
Indicando por x e por y, respectivamente, as medidas das distâncias de um ponto P qualquer aos centros de centésimo₁ e de centésimo₂ , determine as medidas de x e de y para que o ponto P seja:
a) externo à circunferência centésimo₁;
b) externo à circunferência centésimo₂;
c) interno à circunferência centésimo₁;
d) interno à circunferência centésimo₂.
Lembre-se: Escreva no caderno!
3 Ângulos na circunferência
Arco de circunferência
Quando ocorre um eclipse lunar em uma noite sem nuvens, podemos observar uma sombra que vai gradativamente cobrindo a Lua e, em seguida, descobrindo-a. Isso acontece quando, durante sua órbita em torno do Sol, a Terra fica por alguns minutos posicionada entre o Sol e a Lua. Como os astros têm formato arredondado, os contornos das imagens parciais da Lua, como os vistos na sequência a seguir, lembram arcos de circunferência.

Dois pontos, A e B, de uma circunferência dividem-na em duas partes. Cada uma dessas partes é denominada arco de circunferência.
Os pontos A e B são chamados extremidades do arco.
Para diferenciar o arco maior do arco menor, escolhemos um ponto qualquer do arco maior (neste caso escolhemos o X ) e indicamos:
• o arco menor por
Símbolo. Arco AB.;
• o arco maior por
Símbolo. Arco AXB..

Ângulo central
Chamamos de ângulo central de uma circunferência qualquer ângulo cujo vértice seja o centro da circunferência. Observe.
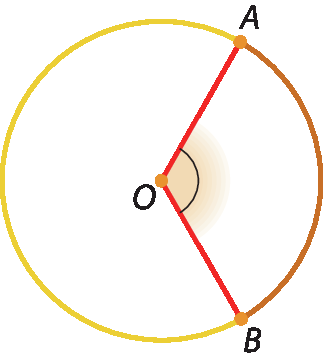
De acôrdo com a figura, temos:
•
Ângulo AOB.é um ângulo central;
•
Símbolo. Arco AB.é o arco correspondente ao ângulo central
Ângulo AOB..
Medida de arco (em grau)
A medida em grau de um arco de circunferência é a medida de abertura do ângulo central correspondente a esse arco.
Indicamos a medida de um arco
Símbolo. Arco AB.por medida de(
Símbolo. Arco AB.).
Então, nas figuras apresentadas, medida de(
Ângulo AOB.) = medida de(
Símbolo. Arco AB.).
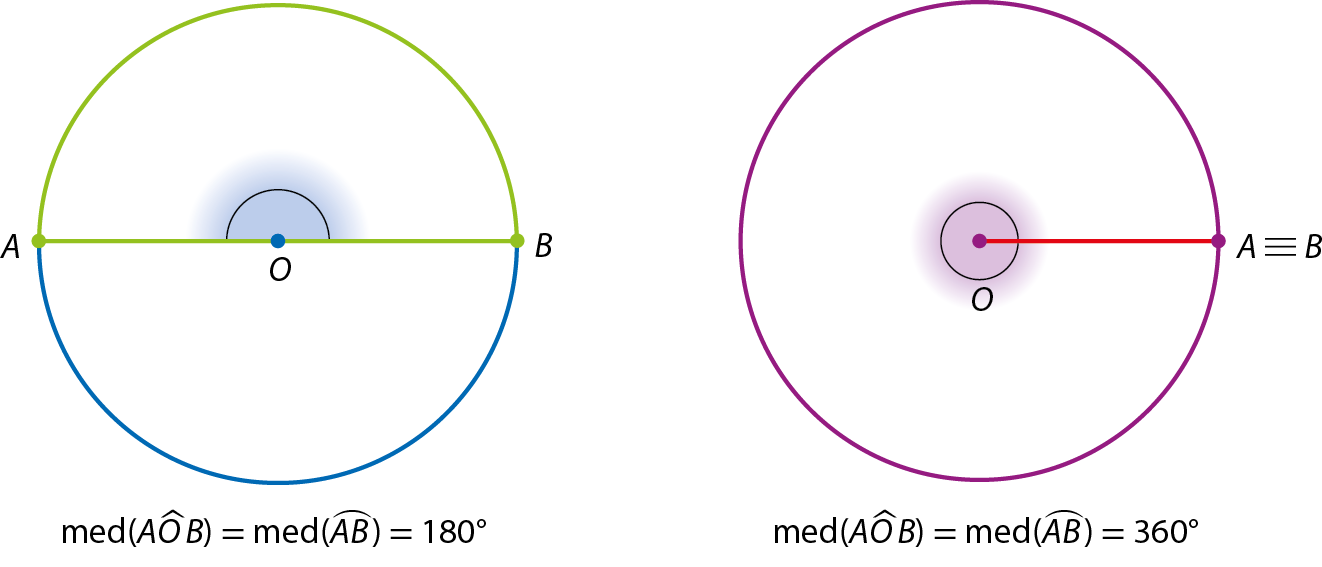
Quando a medida de abertura do ângulo central é igual a 180graus (meia-volta), o arco correspondente é uma semicircunferência.
Quando a medida de abertura do ângulo central é igual a 360graus (uma volta), o arco correspondente é a própria circunferência.
Arcos de mesma medida são denominados arcos congruentes.
Para pensar
Observe a figura.
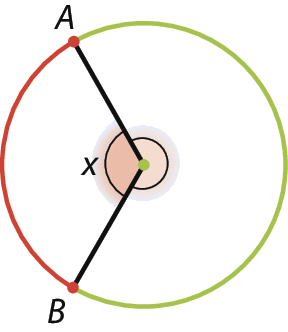
A medida de abertura do ângulo central menor é x. Como podemos indicar, com base na medida do arco menor, a medida do arco maior?

ATIVIDADES
faça as atividades no caderno
1. As extremidades de um mesmo diâmetro dividem uma circunferência em dois arcos. Qual é a medida de cada um desses arcos?
2. Determine a medida dos arcos
AB,
BCe
CDem cada caso. Considere que
Segmento de reta AC e Segmento de reta BDsão diâmetros das circunferências.
a)
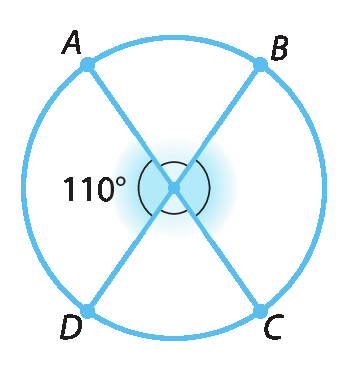
b)
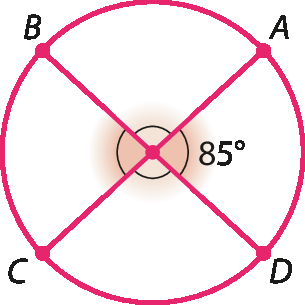
3. Calcule em cada caso a soma das medidas dos arcos
Símbolo. Arco AB.e
Símbolo. Arco CD., sabendo que os ângulos indicados são ângulos centrais.
a)
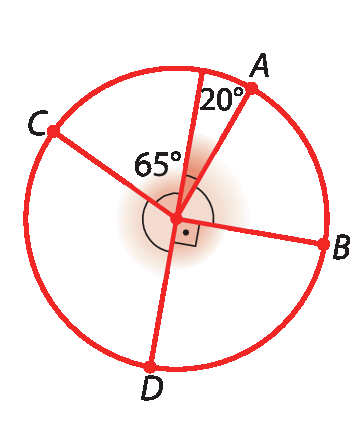
b)
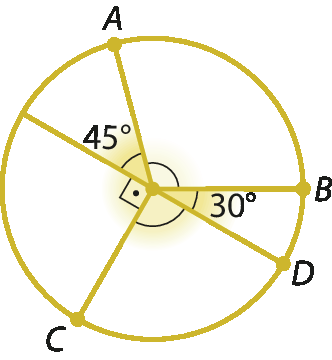
Lembre-se: Escreva no caderno!
4. Analise como Bruno construiu um hexágono regular com compasso e régua.

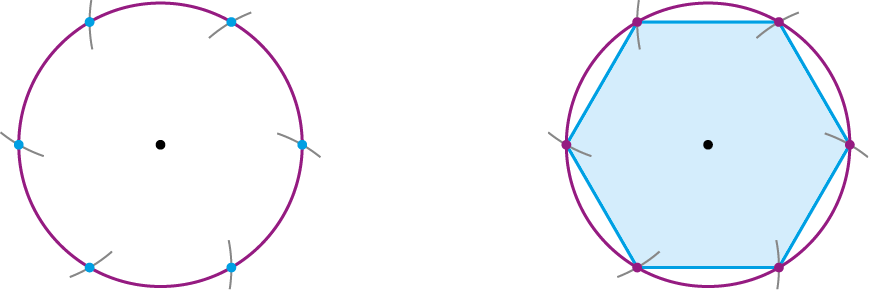
Atenção! Cuidado ao usar o compasso.
Com base no procedimento de Bruno, construa um hexágono regular no caderno e responda às questões.
a) Qual é a medida de comprimento do lado do hexágono?
b) Se ligarmos o centro da circunferência a cada um dos vértices do hexágono, que novas figuras obteremos?
c) Qual é a medida de abertura de cada ângulo central formado quando ligamos o centro da circunferência aos vértices do hexágono?
d) Se, em vez de um hexágono regular, a figura construída fosse um octógono regular, qual seria a medida de abertura de cada ângulo central?
e)

Observe o fluxograma a seguir com os passos para a construção de um octógono regular inscrito em uma circunferência cujo raio mede 4 centímetros de comprimento.
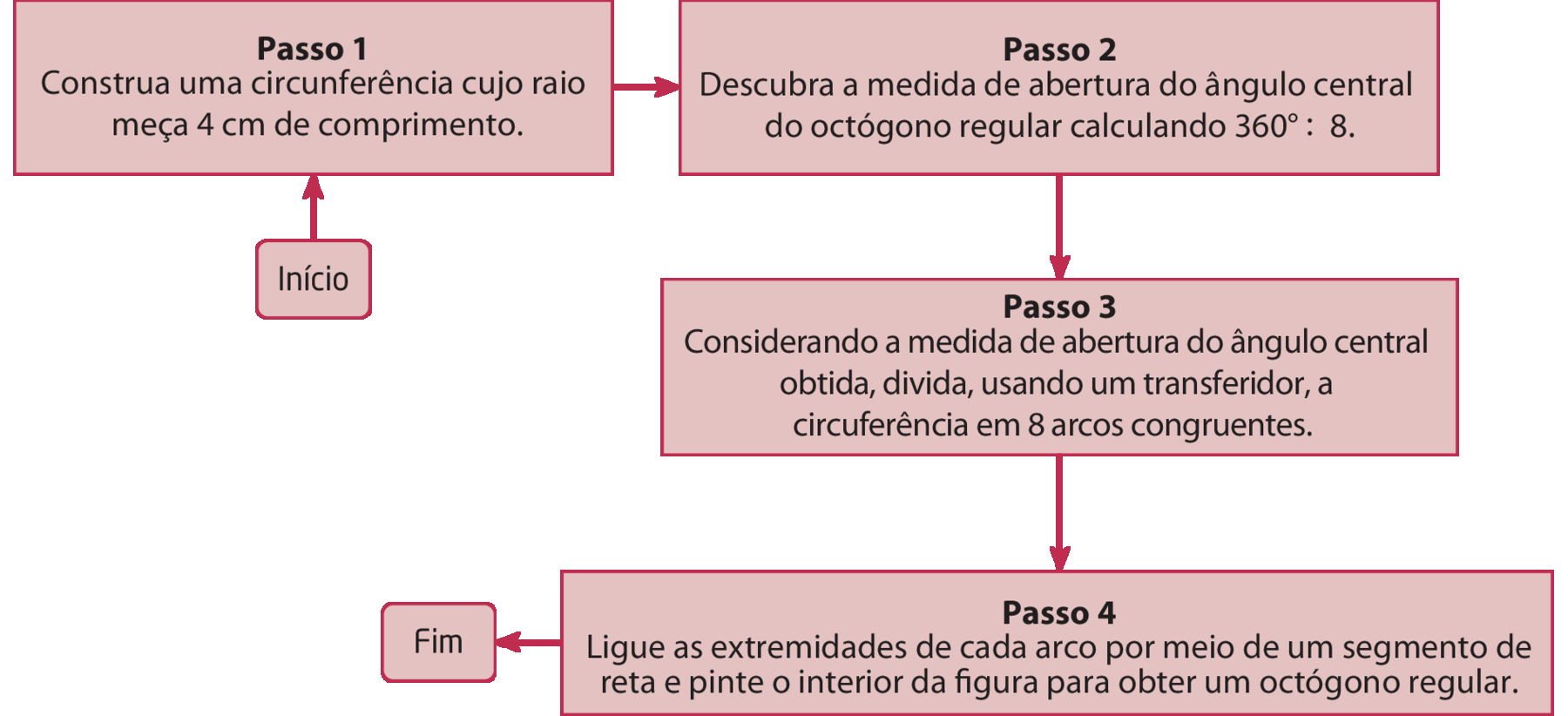
• Em seu caderno, crie um fluxograma com os passos para a construção de um polígono regular de n lados inscrito em uma circunferência cujo raio mede
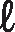
unidades de comprimento.
Ângulos inscritos
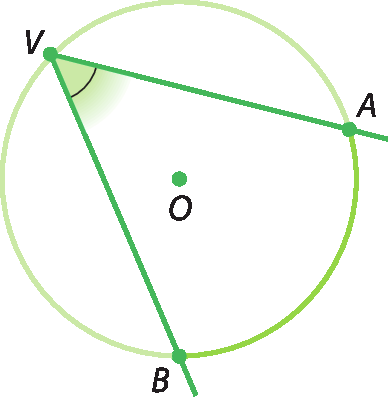
Todo ângulo cujo vértice é um ponto da circunferência e cujos lados são secantes a essa circunferência é chamado ângulo inscrito.
Observe na figura apresentada em verde que
Símbolo. Ângulo AVB.é um ângulo inscrito que determina o arco
Símbolo. Arco AB..
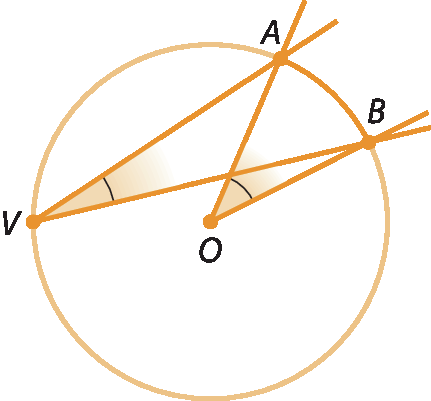
A todo ângulo inscrito corresponde um ângulo central, que determina, na circunferência, o mesmo arco.
Observe na circunferência a seguir que o ângulo inscrito
Símbolo. Ângulo AVB.e o ângulo central
Ângulo AOB.determinam o arco
Símbolo. Arco AB..

Informática e Matemática
faça as atividades no caderno
Ângulos em uma circunferência
Nesta seção, você vai utilizar um software de Geometria dinâmica para construir um ângulo inscrito em uma circunferência e o ângulo central correspondente. Depois, vai investigar a relação entre suas medidas.
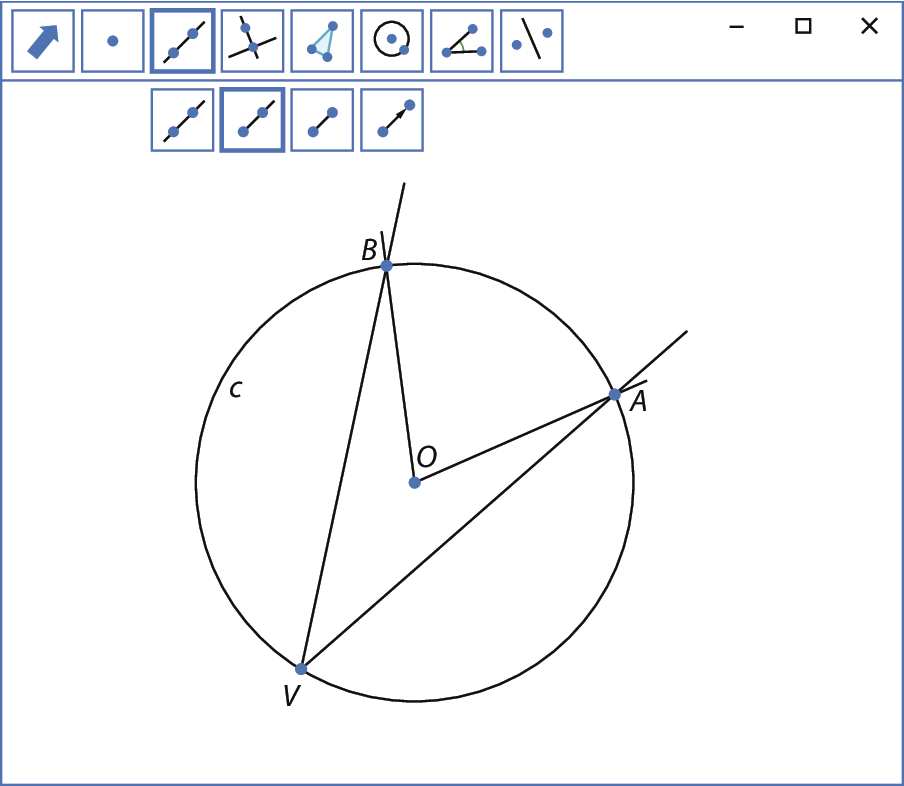
Construa
Siga os passos a seguir.
1º) Construa uma circunferência c de centro O.
2º) Marque três pontos distintos, A, B e V, na circunferência.
3º) Trace as semirretas
Símbolo. Semirreta OA.e
Símbolo. Semirreta OB..
4º) Trace as semirretas
Símbolo. Semirreta VA.e
Símbolo. Semirreta VB..
A
Símbolo. Ângulo V.B é um ângulo inscrito e
Ângulo AOB.é o ângulo central correspondente.
Investigue
Faça o que se pede usando as ferramentas do software.
a) Meça as aberturas dos ângulos
AVB.e
AOB.. É possível perceber alguma relação entre essas medidas?
b) Movimente os pontos móveis da construção, modificando a configuração inicial. A relação observada no item anterior continua válida em diferentes configurações?
Lembre-se: Escreva no caderno!
Relação entre ângulo inscrito e ângulo central
A relação que você observou na seção Informática e Matemática vale para todo ângulo inscrito e central correspondente em uma circunferência.
A medida de abertura de um ângulo inscrito é igual à metade da medida de abertura do ângulo central correspondente, ou seja, é igual à metade da medida do arco de circunferência compreendido entre seus lados.
Vamos demonstrar essa relação analisando três casos.
Caso 1: Um dos lados do ângulo inscrito contém o diâmetro
Observe a figura a seguir, em que
Símbolo. Ângulo AVB.é um ângulo inscrito e
Símbolo. Segmento de reta VB.é um diâmetro da circunferência.
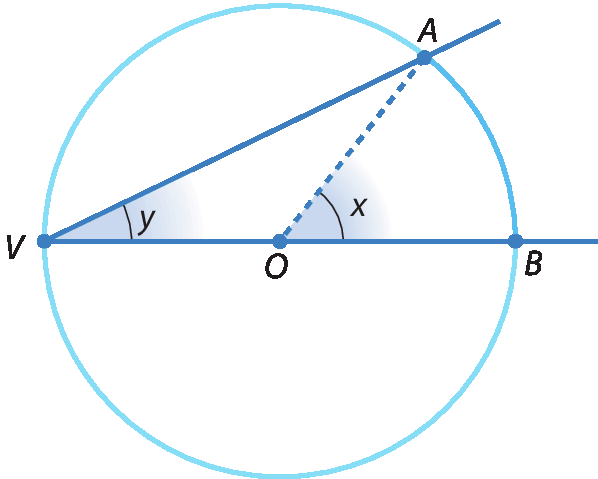
Indicamos por x a medida de abertura do ângulo central
Símbolo. Ângulo AOB.e por y a do ângulo inscrito
Símbolo. Ângulo AVB..
Observe a figura representada em azul.
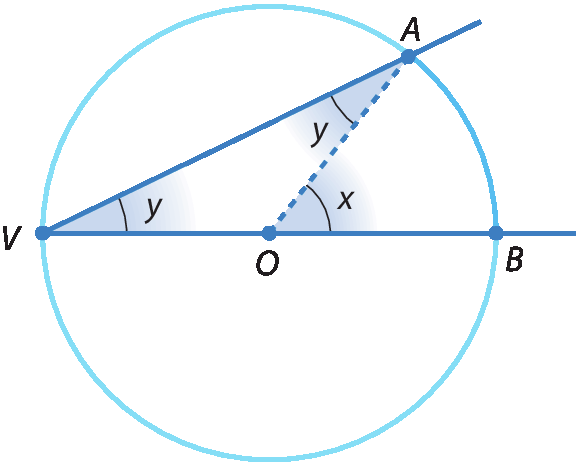
Como
Símbolo. Segmento de reta OV e OA.são raios da circunferência, o triângulo AOV é isósceles; logo, os ângulos de sua base são congruentes:
Sentença matemática. Ângulo OVA congruente ao ângulo VAO.Como
Ângulo AOB.é um ângulo externo do triângulo AOV, temos:
y + y = x
2y = x
y =
Fração de x sobre 2.Portanto, medida de(
Símbolo. Ângulo AVB.) =
Metade da medida do comprimento do arco AB., ou seja: medida de(
Símbolo. Ângulo AVB.) =
Metade da medida do comprimento do arco AB.Caso 2: O centro da circunferência é interno ao ângulo inscrito
Na figura a seguir,
AVB.é um ângulo inscrito.
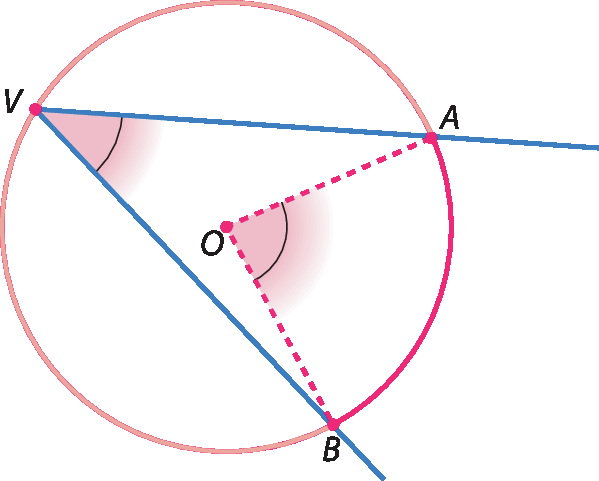
Traçando o diâmetro
VC., dividimos o ângulo
Símbolo. Ângulo AVB.em dois ângulos inscritos:
Símbolo. Ângulo BVC.e
Símbolo. Ângulo AVC.. Além disso, dividimos o ângulo central
AOB.em dois ângulos:
BOC e AOC..
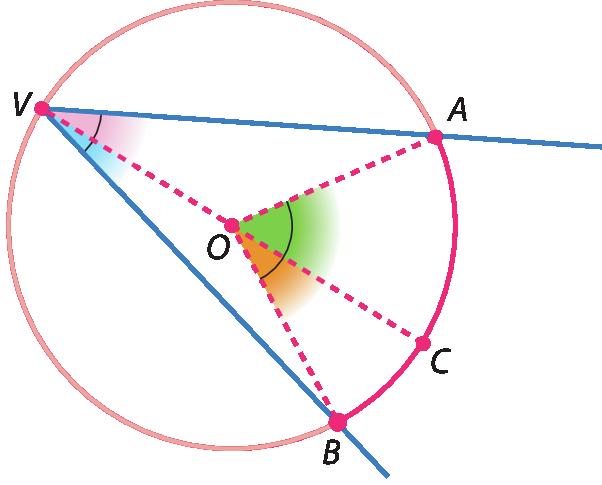
Ao analisar o ângulo inscrito
Símbolo. Ângulo BVC.pelo caso 1, temos:
medida de(
Símbolo. Ângulo BVC.) =
metade da medida da abertura do ângulo BOC.(um)
Analisando o ângulo inscrito
Símbolo. Ângulo AVC.pelo caso 1, temos:
medida de(
Símbolo. Ângulo AVC.) =
metade da medida da abertura do ângulo AOC.(dois)
Adicionando um a dois, membro a membro, temos:

Então, medida de(
Símbolo. Ângulo AVB.) =
metade da medida da abertura do ângulo AOB.e, portanto, medida de(
Símbolo. Ângulo AVB.) =
metade da medida do arco AB..
Caso 3: O centro da circunferência é externo ao ângulo inscrito
Na figura a seguir,
Símbolo. Ângulo AVB.é um ângulo inscrito.
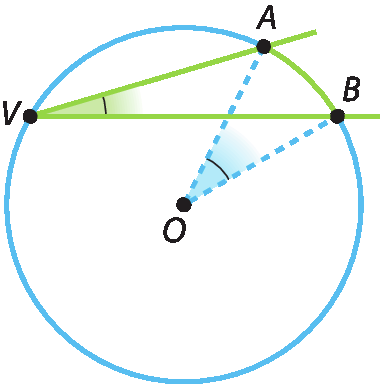
Traçamos o diâmetro
VC.. Vamos considerar os ângulos inscritos
Sentença matemática. Ângulos AVB, BVC e AVC.e seus respectivos ângulos centrais correspondentes:
Ângulo AOB.,
Sentença matemática. Ângulos BOC e AOC..
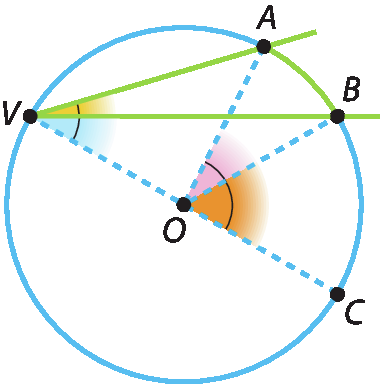
Observe que, nos ângulos inscritos, temos a seguinte relação:
medida de(
Símbolo. Ângulo AVB.) + medida de(
Símbolo. Ângulo BVC.) = medida de(
Símbolo. Ângulo AVC.)
Já nos ângulos centrais, temos esta relação:
medida de(
Ângulo AOB.) + medida de(
Símbolo. Ângulo BOC.) = medida de(
Símbolo. Ângulo AOC.)
Considerando o ângulo inscrito
Símbolo. Ângulo BVC.pelo caso 1, temos:
medida de(
Símbolo. Ângulo BVC.) =
metade da medida da abertura do ângulo BOC.(um)
E, considerando o ângulo inscrito
Símbolo. Ângulo AVC.pelo caso 1, temos:
medida de(
Símbolo. Ângulo AVC.) =
metade da medida da abertura do ângulo AOC.(dois)
Subtraindo um de dois, membro a membro, chegamos a:
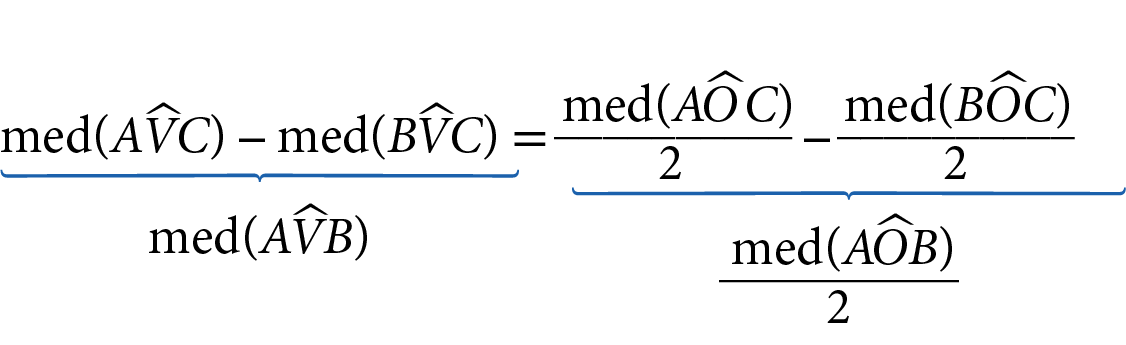
Então, medida de(
Símbolo. Ângulo AVB.) =
Metade da medida da abertura do ângulo AOB.e, portanto, medida de(
Símbolo. Ângulo AVB.) =
Metade da medida do comprimento do arco AB..
Para investigar
Um ângulo é inscrito em uma semicircunferência quando é um ângulo inscrito e seus lados contêm as extremidades de um mesmo diâmetro. Observe, por exemplo, o ângulo
Símbolo. Ângulo AVB.dado.
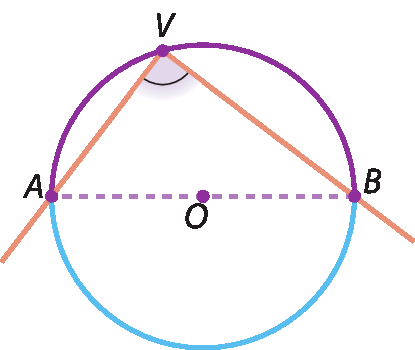
•

Analise a afirmação de Luciene na ilustração.
Em seguida, converse com um colega e discutam se Luciene está correta. Justifiquem.


ATIVIDADES
faça as atividades no caderno
1. Determine em cada caso a medida x, em grau, sendo O o centro da circunferência.
a)
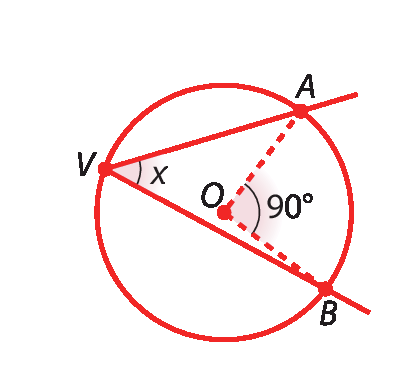
b)
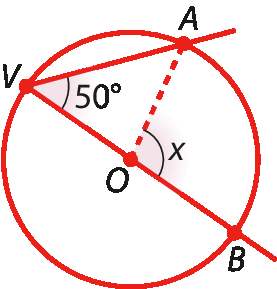
c)
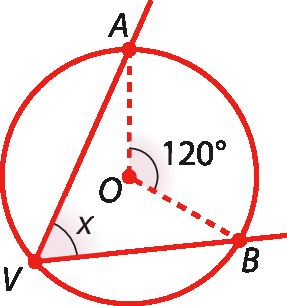
d)
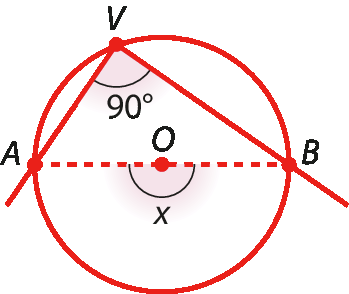
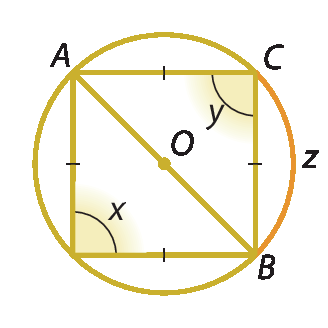
2. Calcule as medidas x, y e z, em grau, para cada caso, considerando que o ponto O é o centro da circunferência.
a)
b)
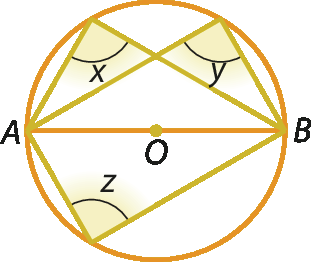
3. Responda às questões.
a) Se a medida de abertura de um ângulo inscrito em uma circunferência é 46graus, qual é a medida do arco de circunferência determinado por ele?
b) Se o arco de circunferência determinado pelo ângulo inscrito
Símbolo. Ângulo AVB.tem medida igual a 25graus, qual é a medida de
Símbolo. Ângulo AVB.?
4. Observe as figuras e responda às questões.

a) Qual é a medida x, em grau?
b) Qual é a medida y, em grau?
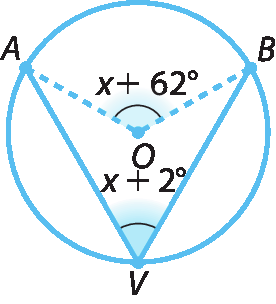
5. Observe as figuras e determine a medida de abertura do ângulo inscrito e a do ângulo central em cada caso.
a)
b)
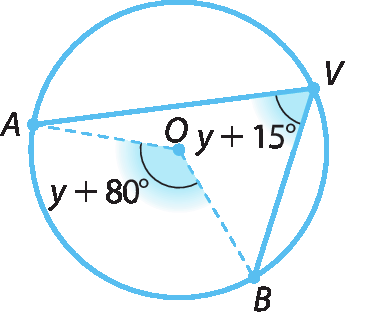

Estatística e Probabilidade
faça as atividades no caderno

Média aritmética, mediana e moda
Uma organização sem fins lucrativos promoveu uma campanha de arrecadação de alimentos que durou uma semana.

Ítalo anotou a medida de massa, em quilograma, de alimentos arrecadados em cada dia.

Para pensar

Converse com os colegas sobre a importância das campanhas de arrecadação de alimentos.
Após o fim da campanha, observando os dados registrados, Sofia, Ivo e Ítalo se reuniram para analisar o resultado de cada medida desse conjunto de dados.

Lembre-se: Escreva no caderno!


▶ Estatística e Probabilidade
Comparação entre a média aritmética, a mediana e a moda
A média aritmética (simples ou ponderada), a mediana e a moda são medidas de tendência central. Elas são usadas para representar um conjunto de dados. Em determinadas situações, uma pode ser mais conveniente que a outra.
Em geral, a moda oferece pouca informação a respeito do conjunto de dados e, por esse motivo, é a menos usada entre as medidas de tendência central estudadas. Na situação apresentada, a moda não é única e, portanto, não é a medida mais conveniente para representar o conjunto de dados.
Repare que a média aritmética foi influenciada pela medida de massa de alimentos arrecadados no sábado, que destoou do que foi arrecadado nos demais dias.
Em situações como essa, em que um ou mais valores do conjunto de dados destoam dos demais, a mediana é a medida estatística mais adequada para representar esse conjunto, pois ela não sofre influência de valores extremos. Caso contrário, a média aritmética simples ou ponderada seria a medida adequada, por levar em consideração todos os valores do conjunto.

ATIVIDADES
faça as atividades no caderno
1. Joana é professora de Educação Física e mede regularmente a massa e a altura de seus estudantes. Observe, no quadro a seguir, as medidas que ela obteve.
|
Nome |
Medida da massa (em quilograma) |
Medida da altura (em metro) |
|---|---|---|
|
Alício |
53,4 |
1,62 |
|
Bruna |
48,6 |
1,54 |
|
Diana |
45,3 |
1,59 |
|
Elisângela |
49,8 |
1,68 |
|
Josué |
51,2 |
1,58 |
|
Manuel |
48,0 |
1,54 |
|
Nilce |
47,5 |
1,62 |
|
Renan |
51,5 |
1,67 |
|
Renato |
45,6 |
1,55 |
|
Silmara |
45,6 |
1,52 |
|
Sueli |
48,9 |
1,66 |
|
Tomás |
49,0 |
1,67 |
a) Calcule a média aritmética da medida de massa desses estudantes e a média da medida de altura deles.
b) Quais dos estudantes têm medida de massa abaixo da média? E quais têm medida de altura acima da média?
c) Qual é a moda das medidas de massa desses estudantes? E a das medidas de altura?
2. A rádio FM fez uma pesquisa para saber a opinião dos ouvintes sobre um novo programa que foi ao ar, avaliando-o com uma nota de 5 a 10. Os dados coletados na pesquisa estão representados no gráfico a seguir.
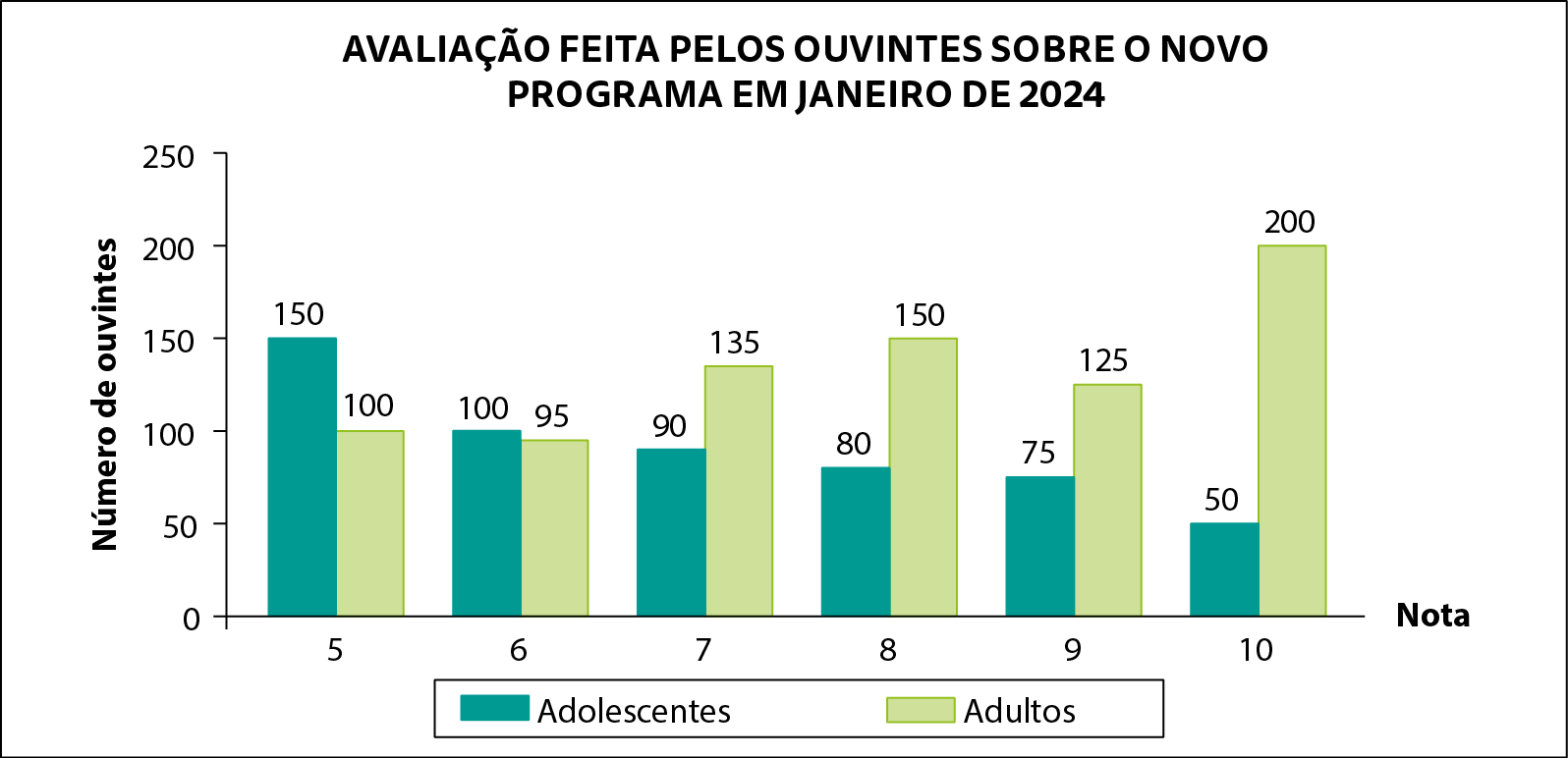
Dados obtidos pela rádio FM em janeiro de 2024.
a) Quantos ouvintes foram pesquisados?
b) Qual foi a média aritmética das notas dadas por ouvintes adolescentes? E por ouvintes adultos?
c) Qual foi a moda das notas dadas por ouvintes adultos?
d) Qual foi a mediana das notas dadas por ouvintes adolescentes?
e) Calcule a média aritmética, a moda e a mediana das notas dadas pelo total de ouvintes (adolescentes e adultos).
3. Claudete quer oferecer mais três opções de salada em seu restaurante. Para decidir os tipos de salada que começará a servir, ela fez uma pesquisa, em fevereiro de 2024, na qual os entrevistados indicavam a salada preferida, como mostrada no quadro a seguir. Nessa pesquisa, eles poderiam escolher apenas um tipo de salada.
|
Salada |
Número de pessoas |
|---|---|
|
Tropical (folhas variadas, tomate, palmito, cenoura ralada e ovo) |
50 |
|
Cozida (batata, brócolis, couve-flor e cenoura cozidos no vapor e queijo parmesão) |
10 |
|
Vegana (folhas variadas, vagem, tomate e cenoura ralada) |
20 |
|
Grãos (folhas variadas, tomate-cereja, grão-de-bico, cenoura ralada, gergelim, linhaça e semente de girassol) |
23 |
|
Salpicão (erva-doce, repolho, frango desfiado e cenoura ralada) |
32 |
a) Qual das medidas de tendência central – média, moda ou mediana – pode ser calculada para a tomada de decisão nessa pesquisa? O que essa medida indica?
b) De acôrdo com o resultado da pesquisa, que saladas Claudete incluirá no cardápio de seu restaurante?

Atividades de revisão
faça as atividades no caderno
1. Observe a circunferência de centro O e responda à questão.
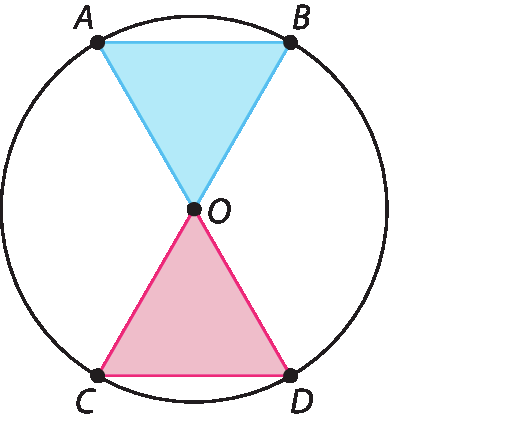
• Os triângulos ó á bê e OCD são congruentes? Justifique.
2. Calcule a medida do perímetro do quadrado de vértices A, B, C e D.
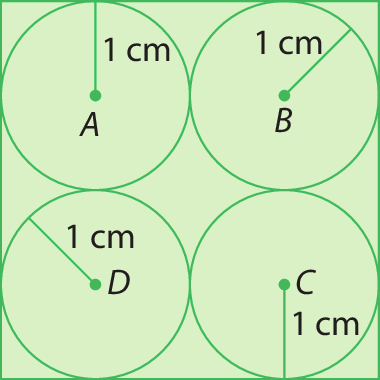
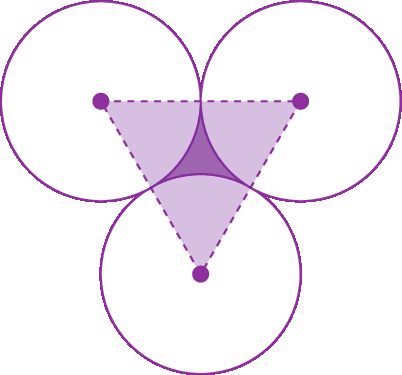
3. Calcule a medida do perímetro do triângulo cujos vértices são os centros das três circunferências, sabendo que a medida de comprimento dos raios das circunferências é 1 centímetro.
4. Traçaram-se duas circunferências, com raios que medem 7 centímetros e 4 centímetros de comprimento. Se a distância entre os centros mede 10 centímetros, qual é a posição relativa entre essas circunferências? Justifique sua resposta.
5. Observe a circunferência a seguir, de centro B, e calcule a medida do perímetro do quadrilátero ABCD.
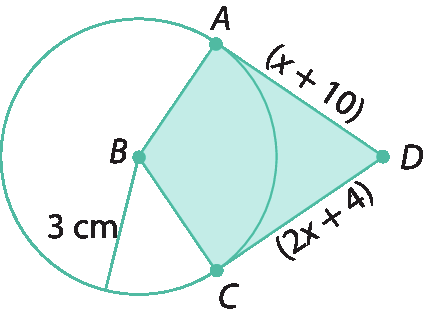
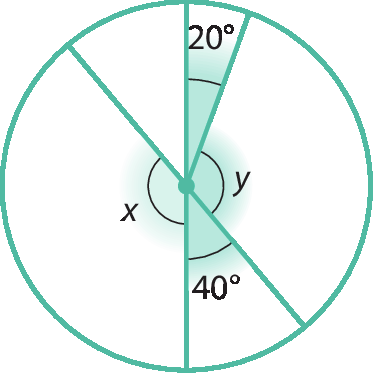
6. Determine as medidas x e y, em grau, em cada caso, sabendo que todos os ângulos indicados têm vértice no centro da circunferência.
a)
b)
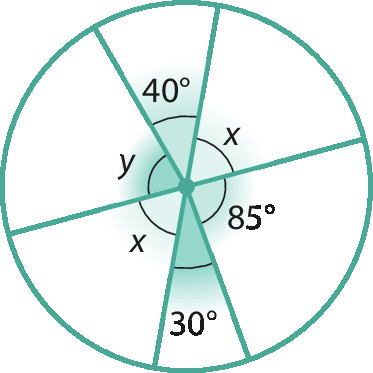
c)

d)
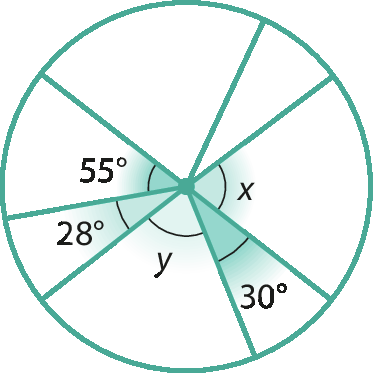
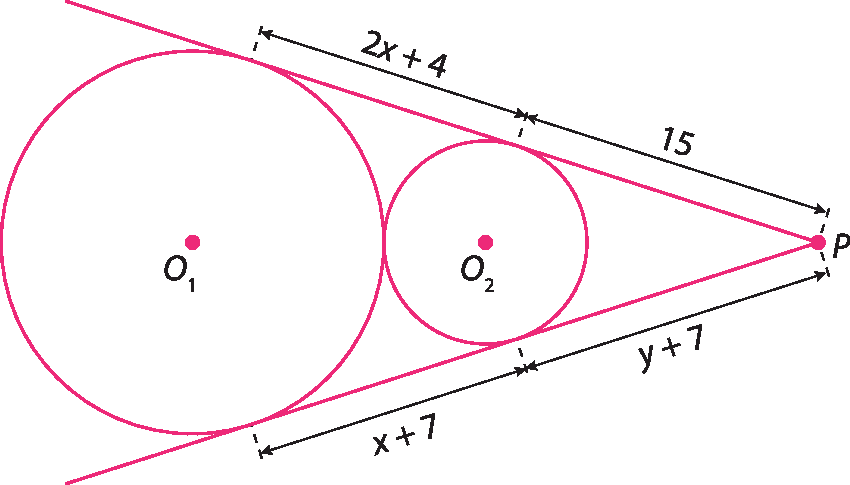
7. Observe a figura e calcule a medida de x e de y, sabendo que as circunferências (com centros O₁ e O₂) são tangentes às semirretas.
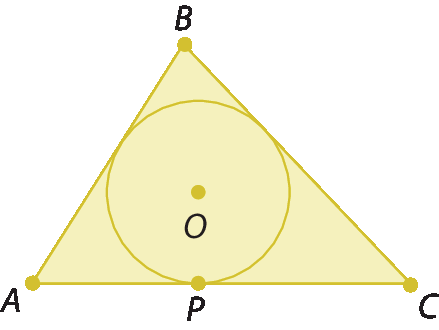
8. (Universidade Federal de Minas Gerais) O triângulo ABC, cujos lados medem A bê = 6, BC = 7 e á cê = 8, está circunscrito à circunferência de centro O. Sendo P o ponto de tangência em relação ao lado
Segmento de reta AC, a medida do segmento
Símbolo. Segmento de reta AP.é:
a) 6
b) 4,5
c) 4
d) 3,5
e) 2,5
9. Observe as circunferências a seguir, de centro O, e calcule, em cada caso, a medida do arco
Símbolo. Arco AB., em grau.
a)
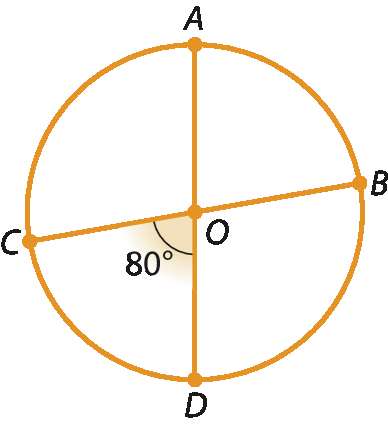
b)
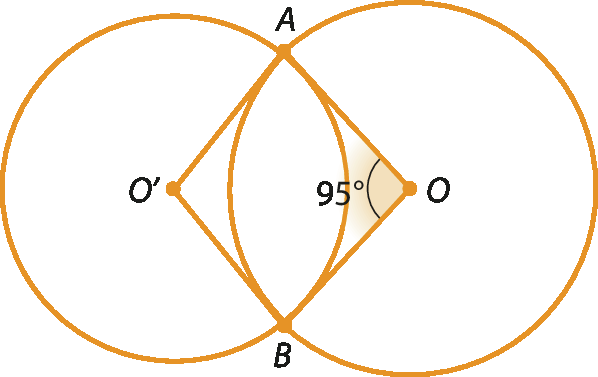
c)
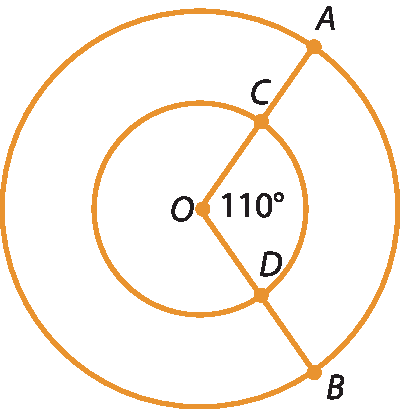
10. Os pontos a, B, C e D de uma circunferência de centro O determinam os diâmetros
Segmento de reta AC e Segmento de reta BD. Se medida de(A
OB) = 90graus, qual é a medida de abertura dos ângulos
COD, AOD e BOC?11. Para a gravação de um telejornal, uma emissora posicionou duas câmeras em pontos diferentes (A e B), conforme o esquema a seguir.
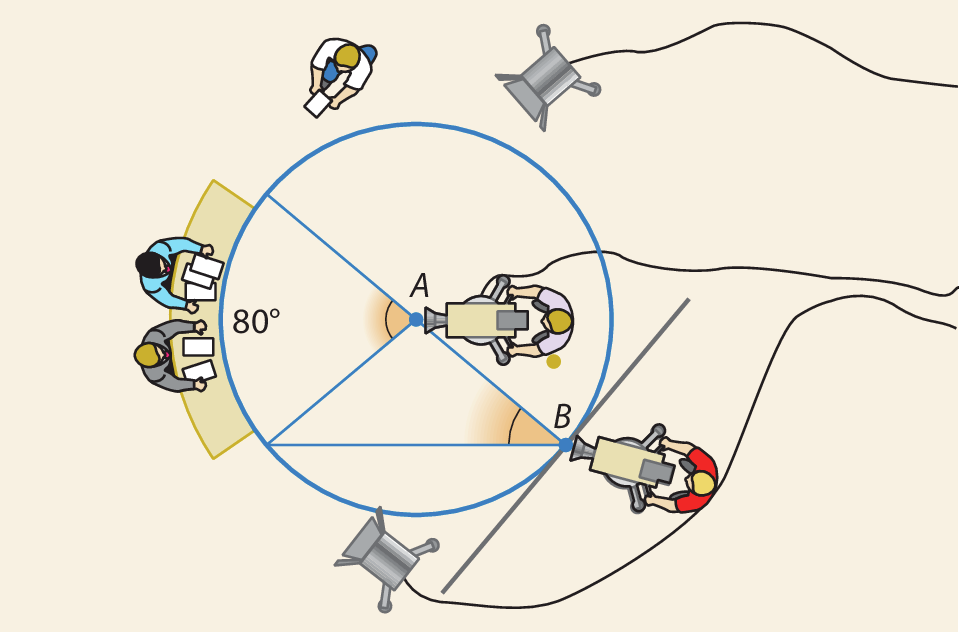
•
Qual é a medida de abertura dos ângulos
Símbolo. Ângulo A.e
Símbolo. Ângulo B., destacados na figura?
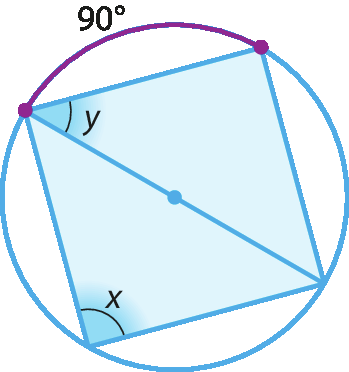
12. Calcule as medidas de x e y, em grau, em cada caso.
a)

b)
13.

Determine as medidas x e y, em grau, em cada caso, sabendo que óh é o centro das circunferências.
a)
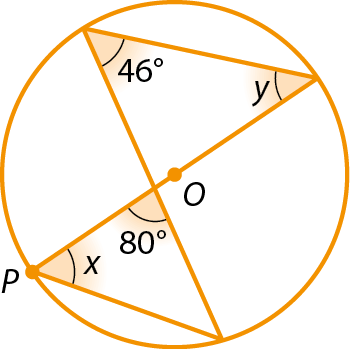
b)
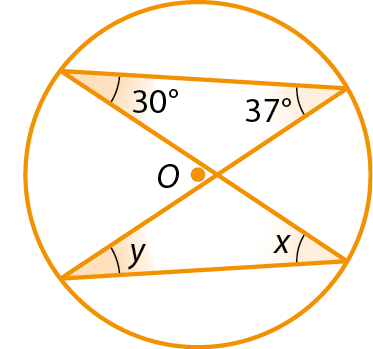

Para finalizar
faça as atividades no caderno
organize suas ideias
Observe e responda
Considere as seguintes imagens.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
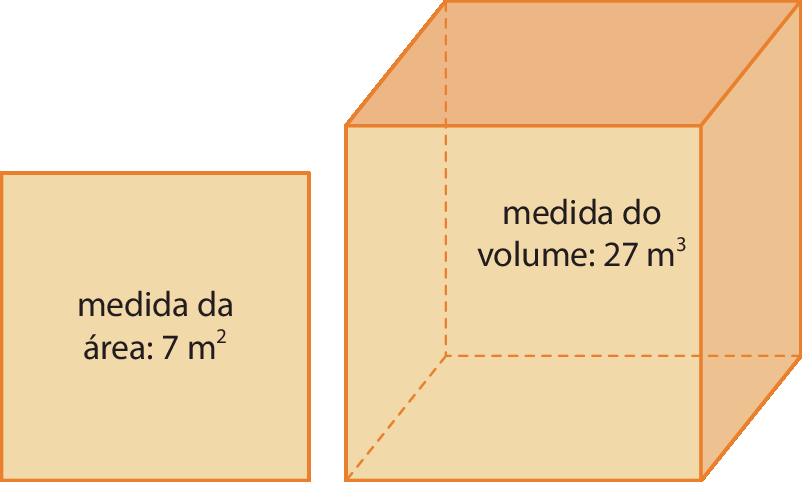



Com base nas imagens e também no que você aprendeu nesta Unidade, faça o que se pede.
1. Que operação é necessário realizar para calcular a medida de comprimento do lado do quadrado e a medida de comprimento da aresta do cubo anterior? Calcule essas medidas.
2. A medida de comprimento do lado do quadrado, em metro, é um número irracional. Dê exemplos de outros números que pertencem ao conjunto dos números irracionais.
3. Escreva a medida da massa da Lua com todos os algarismos.
4. Que maneira de escrever a medida da massa da Lua você acha mais fácil? Justifique.
5. Em que situações é usada a representação em notação científica?
6. Na imagem do campo de futebol, qual é a posição relativa entre a circunferência central e a reta determinada pela linha de meio de campo?
Lembre-se: Escreva no caderno!
Registre
Para finalizar o estudo desta Unidade, faça o que se pede.
1. Que propriedades da potenciação você conhece? Explique-as com alguns exemplos.
2. Como representamos um número em notação científica?
3. Como podemos obter a raiz quadrada ou a raiz cúbica de um número? Exemplifique com expressões que contenham raízes.
4. Qual é a relação entre a medida de abertura de um ângulo inscrito em uma circunferência e a do ângulo central correspondente?
5. Na abertura desta Unidade, você respondeu a algumas questões no boxe “Para começarreticências”. Compare as respostas dadas àquelas questões com as respostas que você daria agora e escreva um texto explicando o que você aprendeu nesta Unidade.
Para conhecer mais
Do zero ao infinito (e além)
Tudo o que você sempre quis saber sobre matemática e tinha vergonha de perguntar
Mike Goldsmith
São Paulo: Benvirá, 2016.
Alguma vez você já se perguntou "por que preciso estudar Matemática?" ou "o que vou fazer com frações no dia a dia?". Esse livro fará com que você goste e, principalmente, entenda Matemática. Nele, o autor mostra como a Matemática afeta tudo ao nosso redor, do comportamento dos animais até a maneira como escutamos música. Prepare-se para desvendar os mistérios dessa ciência e descobrir a maravilha dos números. Descubra por que o zero é tão importante nas operações matemáticas, como a música, a matemática e o espaço estão conectados e até por que as abelhas fazem suas colmeias em formato de hexágono. Você vai achar incrível e divertido aprender Matemática!

Salvo pela Matemática
Sean Connolly
São Paulo: Coquetel, 2016.
Já imaginou o que aconteceria se você ficasse sem gasolina no meio do deserto ou se você tivesse de resgatar um prisioneiro usando apenas um lençol? E como você faria para escapar de uma lâmina afiada em um pêndulo? Nesse livro, você encontra 18 desafios, com cenários e personagens inusitados, que podem ser resolvidos com conhecimentos básicos de fração, geometria, padrões e, o melhor, usando a Matemática de fórma divertida.
