Página setenta e nove

Parte 8

b) Para sabermos a medida de comprimento da diagonal

\overline{A G}

, precisamos conhecer a medida de comprimento da diagonal

\overline{E G}

da face inferior do cubo. Veja a representação dela na figura a seguir:

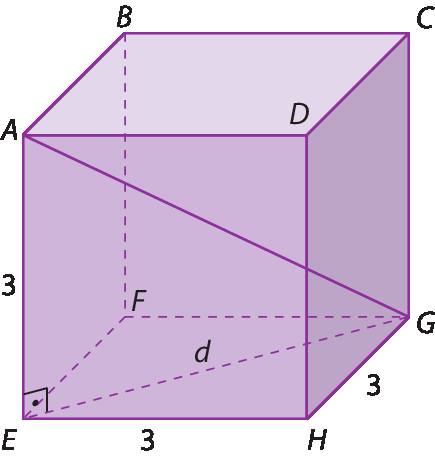
Figura geométrica. Cubo cuja medida do comprimento das arestas é igual a 3. A face superior do cubo é um quadrado ABCD e a face interior é um quadrado EFHG. Estão representadas as diagonais de EFGH que tem medida de comprimento d e a a diagonal do cubo que corresponde ao segmento de reta com extremidades nos pontos A e G.

Como a face

EFGH é um quadrado, podemos utilizar a relação

d = ℓ \sqrt{2}

. Assim:

d = 3 \sqrt{2}

Agora, vamos observar o triângulo retângulo

AEG:

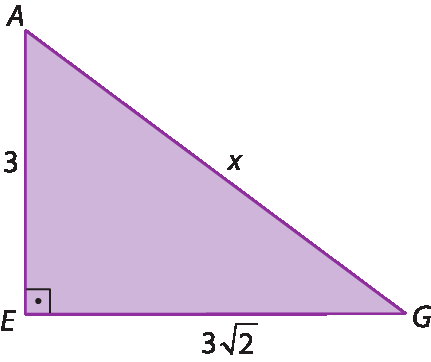
Figura geométrica. Triângulo retângulo AEG, retângulo em E. A medida do comprimento de AE é 3, a medida do comprimento de EG é 3 vezes raiz quadrada de 2 e a medida do comprimento de GA é indicada pela letra x.

Aplicando o teorema de Pitágoras, temos:

x^{2} = 3^{2} + {(3 \sqrt{2})}^{2}

x^{2} = 9 + 9 \cdot 2

x^{2} = 9 + 18

x^{2} = 27

x = \pm \sqrt{27} = \pm 3 \sqrt{3}

Como x representa uma medida, desconsideramos a solução

x = ‒ 3 \sqrt{3}

Assim,

x = 3 \sqrt{3}

Logo, a medida de

\overline{A G}

3 \sqrt{3}

14. Chamando de x a medida de comprimento do lado do quadrado, verificamos que o segmento de reta tracejado é a diagonal de um retângulo de medidas: 3x de comprimento por 1x de largura.

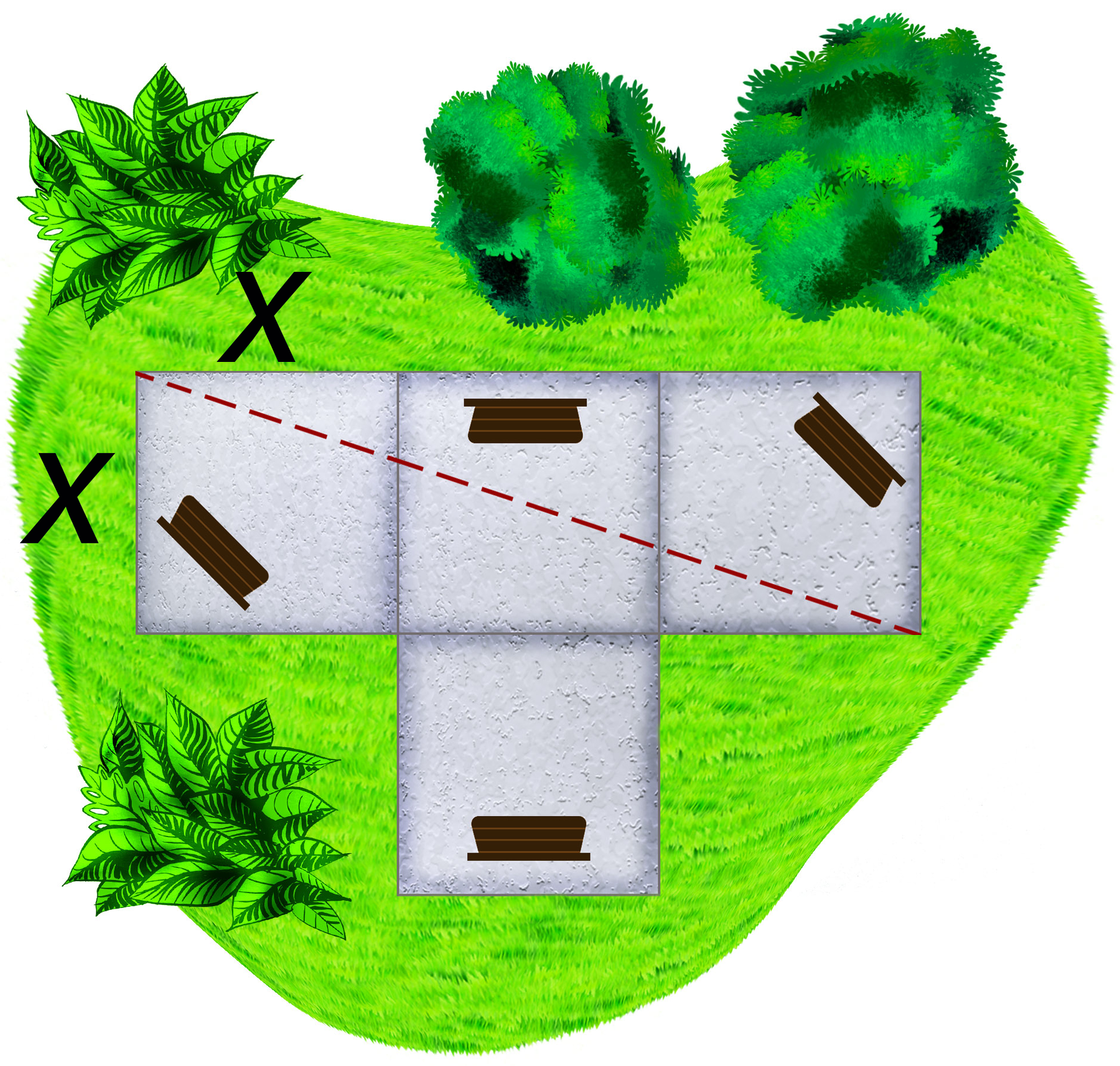
Ilustração. Gramado com quatro quadrados na cor cinza em duas fileiras. A primeira fileira tem três quadrados, com indicação de medida x no primeiro quadrado e a segunda fileira tem um quadrado, abaixo apenas do quadrado central da primeira fileira. Há uma linha vermelha destacando a diagonal do retângulo formado pelos três quadrados da primeira fileira.

Aplicando o teorema de Pitágoras no triângulo retângulo, temos:

20^{2} = x^{2} + {(3 x)}^{2}

400 = x^{2} + 9 x ²

10 x^{2} = 400

x^{2} = \frac{400}{10}

x^{2} = 40

x = \pm \sqrt{40}

Como x representa uma medida, desconsideramos a solução x =

‒ \sqrt{40}

Assim,

x = \sqrt{40}

Portanto, a medida de comprimento é

3 x = 3 \sqrt{40}

métros e da largura é

1 x = \sqrt{40}

métros.

A medida da área da praça é composta da medida da área de 4 quadrados de lado

\sqrt{40}

métros.

Portanto, a medida da área de cada quadrado é:

\sqrt{40} \cdot \sqrt{40} = \sqrt{1 600} = 40

Então, a medida da área da praça é:

4 ⋅ 40 = 160

Logo, a medida da área da praça é 160 métros quadrados.

15. O segmento de reta

\overline{B E}

é a diagonal da face

ABEF do cubo.

Sendo

d = ℓ \sqrt{2}

, então:

d = 6 \sqrt{2}

Logo, o comprimento da diagonal

\overline{B E}

mede

6 \sqrt{2}

centímetros.

Atividades

▶ Páginas 162 e 163

1. a) Para encontrar a medida do segmento de reta

\overline{A B}

, podemos usar, como auxílio, a seguinte figura.

Gráfico. Eixo horizontal perpendicular a um eixo vertical.
No eixo horizontal com sentido para a direita, estão indicados os números menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4 e 5 e ele está rotulado como x.
No eixo vertical, com sentido para cima, estão indicados os números 0, 1, 2, 3 e 4 e ele está rotulado como y.
No plano cartesiano está representado um triângulo retângulo roxo com ângulo reto no ponto C, com vértices nos pontos: A com coordenadas 1 e 3; B com coordenadas 5 e 1; C com coordenadas 1 e 1. A medida do comprimento de AC é 2, a medida do comprimento de CB é 4 e a medida do comprimento de BA é indicada pela letra x.

Aplicando o teorema de Pitágoras no triângulo

A B C

, temos:

x^{2} = 2^{2} + 4^{2}

x^{2} = 4 + 16

x^{2} = 20

x = \pm \sqrt{20}

Como x representa uma medida, desconsideramos a solução

x = ‒ \sqrt{20}

Assim,

x = \sqrt{20}

x = \sqrt{20} = \sqrt{4 \cdot 5} = 2 \sqrt{5}

Logo, a distância entre os pontos mede

2 \sqrt{5}

b) Para encontrar a medida do segmento de reta

\overline{A B}

, podemos usar, como auxílio, a seguinte figura.

Página oitenta

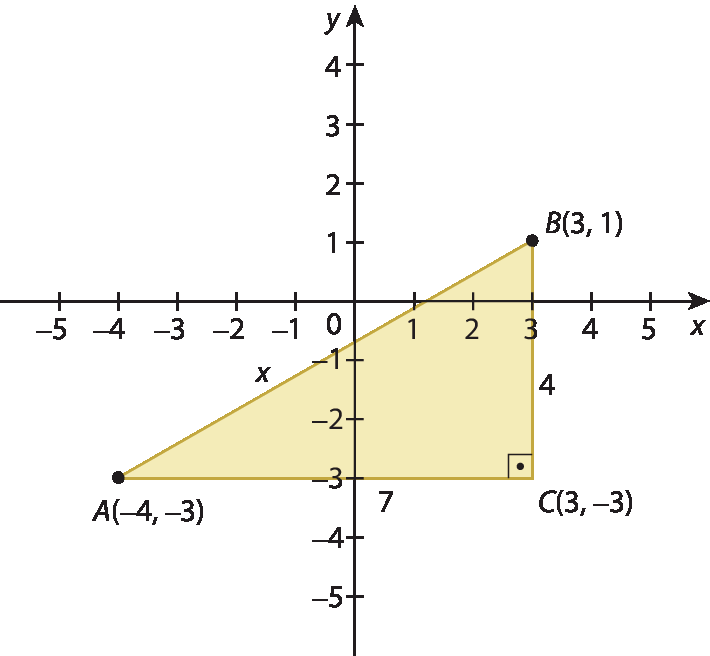
Aplicando o teorema de Pitágoras no triângulo ABC, temos:

x^{2} = 7^{2} + 4^{2}

x^{2} = 49 + 16

x^{2} = 65

x = \pm \sqrt{65}

Como x representa uma medida, desconsideramos a solução

x = ‒ \sqrt{65}

Logo, a distância entre os pontos mede

\sqrt{65}

2. a) Inicialmente, vamos construir uma figura de acordo com o que foi dado no enunciado:

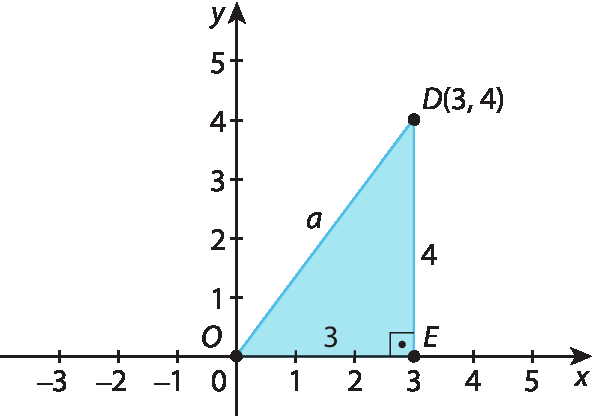
Ilustração. Eixo horizontal perpendicular a um eixo vertical.
No eixo horizontal com sentido para a direita, estão indicados os números menos 3, menos 2, menos 1, 0, 1, 2, 3, 4 e 5 e ele está rotulado como x .
No eixo vertical, com sentido para cima, estão indicados os números 0, 1, 2, 3, 4 e 5 e ele está rotulado como y.
No plano cartesiano está indicado um triângulo retângulo azul com ângulo reto no ponto E, com vértices nos pontos: O com coordenadas 0 e 0; E com coordenadas 3 e 0; D com coordenadas 3 e 4. Com indicação de medidas: no segmento de reta OE, 3, no segmento de reta ED, 4 e no segmento de reta OD, a.

Aplicando o teorema de Pitágoras no triângulo

DEO, temos:

a^{2} = 3^{2} + 4^{2}

a = 9 + 16

a^{2} = 25

a = \pm \sqrt{25}

Como a representa uma medida, desconsideramos a solução

a = ‒ \sqrt{25}

Assim:

a = \sqrt{25}

= 5

Logo, a medida da distância do ponto Dabre parênteses4, 3fecha parênteses à origem é 5.

b) Pela figura, a medida da distância do ponto Dabre parênteses4, 3fecha parênteses ao eixo das ordenadas é 3.

c) Pela figura, a medida da distância do ponto Dabre parênteses4, 3fecha parêntesesao eixo das abscissas é 4.

3. Para determinarmos as coordenadas do ponto médio de um segmento, vamos calcular as médias aritméticas das abscissas e das ordenadas das extremidades do segmento. Entretanto, elas podem ser obtidas por semelhança de triângulos.

Extremidades do segmento: Oabre parênteses1, 3fecha parênteses

e Pabre parênteses5, 1fecha parênteses

Abscissa do ponto médio:

\frac{1 + 5}{2} = \frac{6}{2} = 3

Ordenada do ponto médio:

\frac{3 + 1}{2} = \frac{4}{2} = 2

Portanto, as coordenadas do ponto médio são abre parênteses3, 2fecha parênteses.

4. a) Extremidades do segmento: Cabre parênteses1, 2fecha parênteses e Dabre parênteses5, 4fecha parênteses

Abscissa do ponto médio:

\frac{1 + 5}{2} = \frac{6}{2} = 3

Ordenada do ponto médio:

\frac{2 + 4}{2} = \frac{6}{2} = 3

Portanto, as coordenadas do ponto médio são abre parênteses3, 3fecha parênteses.

b) Extremidades do segmento: Cabre parêntesesmenos3, 2fecha parênteses

e Dabre parênteses1, menos2fecha parênteses

Abscissa do ponto médio:

\frac{‒ 3 + 1}{2} = \frac{‒ 2}{2} = ‒ 1

Ordenada do ponto médio:

\frac{2 + (‒ 2)}{2} = \frac{0}{2} = 0

Portanto, as coordenadas do ponto médio são abre parêntesesmenos1, 0fecha parênteses.

5. Do enunciado sabemos que Babre parênteses3, 1fecha parênteses e que o ponto médio de

\overline{A B}

é Mabre parênteses2, 3fecha parênteses.

Para determinar o valor x correspondente à abscissa do ponto A, podemos fazer:

\frac{x + 3}{2} = 2

x + 3 = 2 ⋅ 2

x + 3 = 4

x = 4 menos 3

x = 1

Para encontrar o valor de y correspondente à ordenada do ponto A, podemos fazer:

\frac{y + 1}{2} = 3

y + 1 = 3 ⋅ 2

y + 1 = 6

y = 6 menos 1

y = 5

Logo, Aabre parênteses1, 5fecha parênteses.

6. Observe a figura:

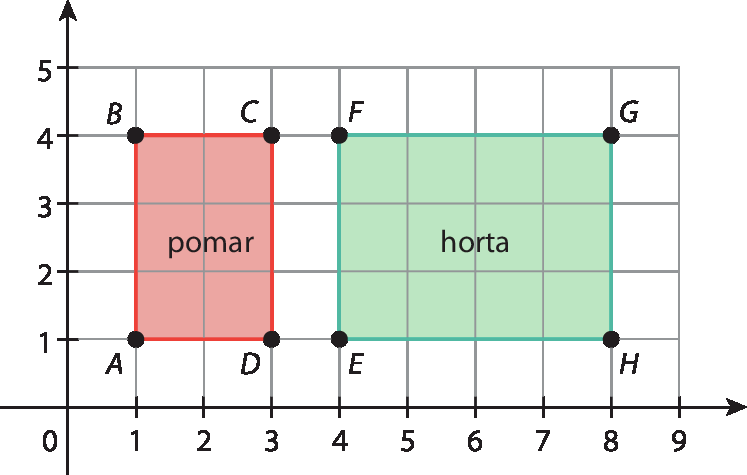
Ilustração. Malha quadriculada com eixo horizontal perpendicular a um eixo vertical.
No eixo horizontal estão indicados os números 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
No eixo vertical estão indicados os números 0, 1, 2, 3, 4 e 5 e ele está rotulado como y.
No plano cartesiano estão representados dois retângulos. Um retângulo vermelho que é formado pelos pontos A com coordenadas 1 e 1; B com coordenadas 1 e 4; C com coordenadas 3 e 4 e D com coordenadas 3 e 1. Ele está representando o pomar. O outro retângulo é verde e formado pelos pontos E com coordenadas 4 e 1; F com coordenadas 4 e 4; G com coordenadas 8 e 4 e H com coordenadas 8 e 1. Ele está representando a horta.

Como o esquema está representado em um plano cartesiano, podemos calcular a medida da distância entre os pontos para encontrar a medida desses segmentos de reta e, em seguida, calcular a medida da área dos retângulos que representam a medida da área do pomar e a medida da área da horta.

a) Para calcular a medida da área destinada ao pomar, temos:

AD = BC = 2 e AB = DC = 3

Portanto:

A = 2 ⋅ 3 = 6

Logo, a medida da área destinada ao pomar é 6 métros quadrados.

b) Para calcular a medida da área destinada à horta, temos:

EH = FG = 4 e EF = HG = 3

Portanto:

A = 4 ⋅ 3 = 12

Logo, a medida da área destinada à horta é 12 métros quadrados.

c) Diferença entre as duas medidas de área:

12 menos 6 = 6

Logo, a diferença entre as medidas de área do pomar e da horta é de 6 métros quadrados.

7. a) Aabre parênteses1, 2fecha parênteses e Babre parênteses6, 4fecha parênteses Aabre parênteses1, 2fecha parênteses e Babre parênteses6, 4fecha parênteses Aabre parênteses1, 2fecha parênteses e Babre parênteses6, 4fecha parênteses

Aabre parênteses1, 2fecha parênteses e Babre parênteses6, 4fecha parênteses

b) Abscissa do ponto médio:

\frac{1 + 6}{2} = \frac{7}{2} = 3,5

Ordenada do ponto médio:

\frac{2 + 4}{2} = \frac{6}{2} = 3

Portanto, as coordenadas do ponto médio são abre parênteses3, 5; 3fecha parênteses.

Página oitenta e um

8. Inicialmente vamos construir o triângulo ABC:

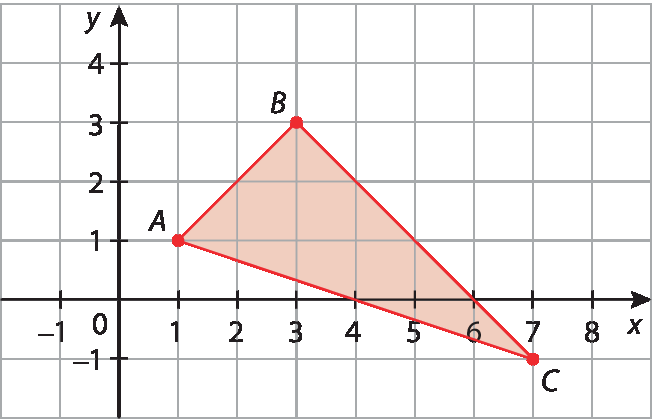
Gráfico. Malha quadriculada com eixo horizontal perpendicular a um eixo vertical.
No eixo horizontal estão indicados os números menos 1, 0, 1, 2, 3, 4, 5, 6 e 7 e 8 e ele está rotulado como x.
No eixo vertical estão indicados os números menos 1, 0, 1, 2, 3 e 4 e ele está rotulado como y.
No plano cartesiano estão indicados os pontos A com coordenadas 1 e 1; B com coordenadas 3 e 3 e C com coordenadas 7 e menos 1. Esses pontos são os vértices de um triângulo vermelho.

Para calcular a medida de comprimento dos lados

\overline{A B}

\overline{A C}

\overline{B C}

, formaremos alguns triângulos retângulos.

• Para encontrar a medida de comprimento do lado

\overline{A B},

podemos fazer:

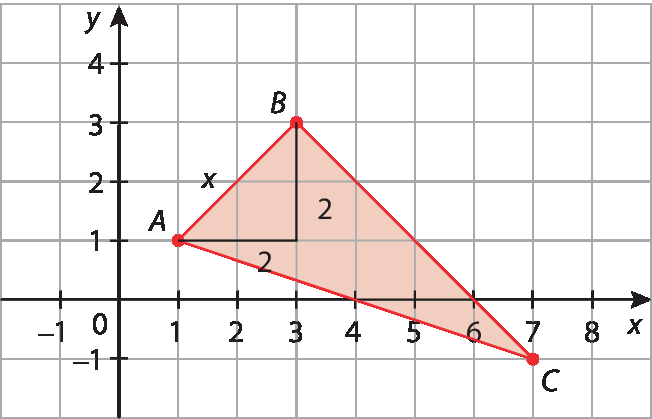
Aplicando o teorema de Pitágoras no triângulo construído, temos:

xelevado a 2 = 2elevado a 2 + 2elevado a 2 ⇒ xelevado a 2 = 4 + 4 ⇒ xelevado a 2 = 8 ⇒ x =

2 \sqrt{2}

• Para encontrar a medida de comprimento do lado

\overline{A C}

, podemos fazer:

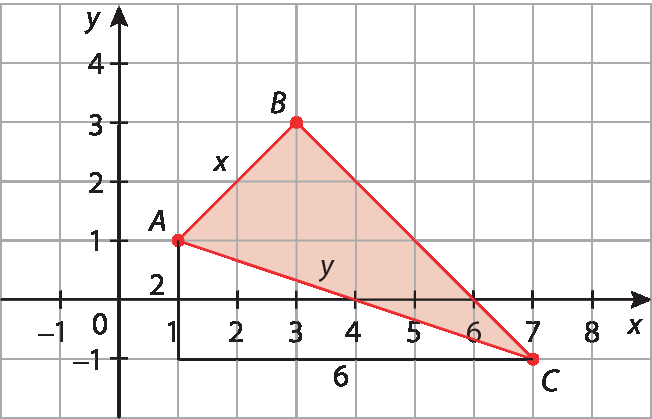
Aplicando o teorema de Pitágoras no triângulo construído, temos:

yelevado a 2 = 2elevado a 2 + 6elevado a 2 ⇒ yelevado a 2 = 4 + 36 ⇒ yelevado a 2 = 40 ⇒ y =

\sqrt{40}

⇒ y =

2 \sqrt{10}

• Para encontrar a medida de comprimento do lado

\overline{B C},

podemos fazer:

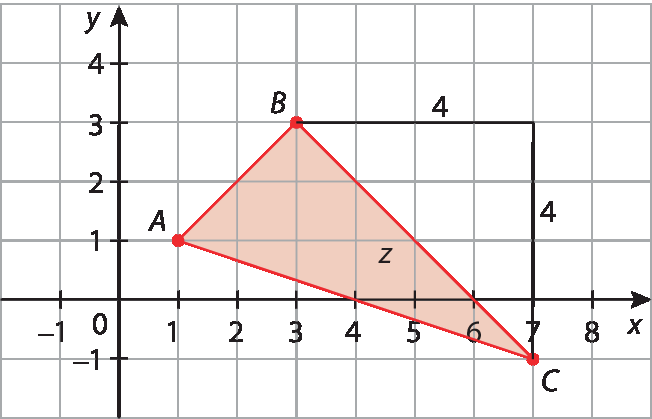
Aplicando o teorema de Pitágoras no triângulo construído, temos:

zelevado a 2 = 4elevado a 2 + 4elevado a 2 ⇒ zelevado a 2 = 16 + 16 ⇒

⇒ zelevado a 2 = 32 ⇒ z =

\sqrt{32}

⇒ z =

4 \sqrt{2}

Vamos verificar se o triângulo ABC é retângulo em

\hat{B}

{(A C)}^{2} = {(A B)}^{2} + {(B C)}^{2}

{(2 \sqrt{10})}^{2} = {(2 \sqrt{2})}^{2} + {(4 \sqrt{2})}^{2}

40 = 8 + 32

40 = 40

Como vale o teorema de Pitágoras, então o △ABC é retângulo em

\hat{B}

Logo:

P_{△ A B C} = 2 \sqrt{2} + 2 \sqrt{10} + 4 \sqrt{2} \Rightarrow 6 \sqrt{2} + 2 \sqrt{10} \Rightarrow 2 (3 \sqrt{2} + \sqrt{10})

A_{△ A B C} = \frac{2 \sqrt{2} \cdot 4 \sqrt{2}}{2} \Rightarrow \frac{8 \cdot 2}{2} \Rightarrow \frac{16}{2} \Rightarrow 8

Estatística e Probabilidade

▶ Páginas 164 a 166

1. a) Falsa. Em 2019, a Escola Ponte Feliz conquistou o mesmo número de medalhas de ouro e de prata.

b) Falsa. Em 2015, o número de medalhas de bronze e de ouro conquistadas foi o mesmo.

c) Verdadeira. Em 2023 foram conquistadas 3 medalhas de ouro e em 2014 foram conquistadas 2 medalhas no total.

d) Falsa. Em 2023, foram conquistadas 17 medalhas no total.

alternativa c

2. a) Exemplo de resposta:

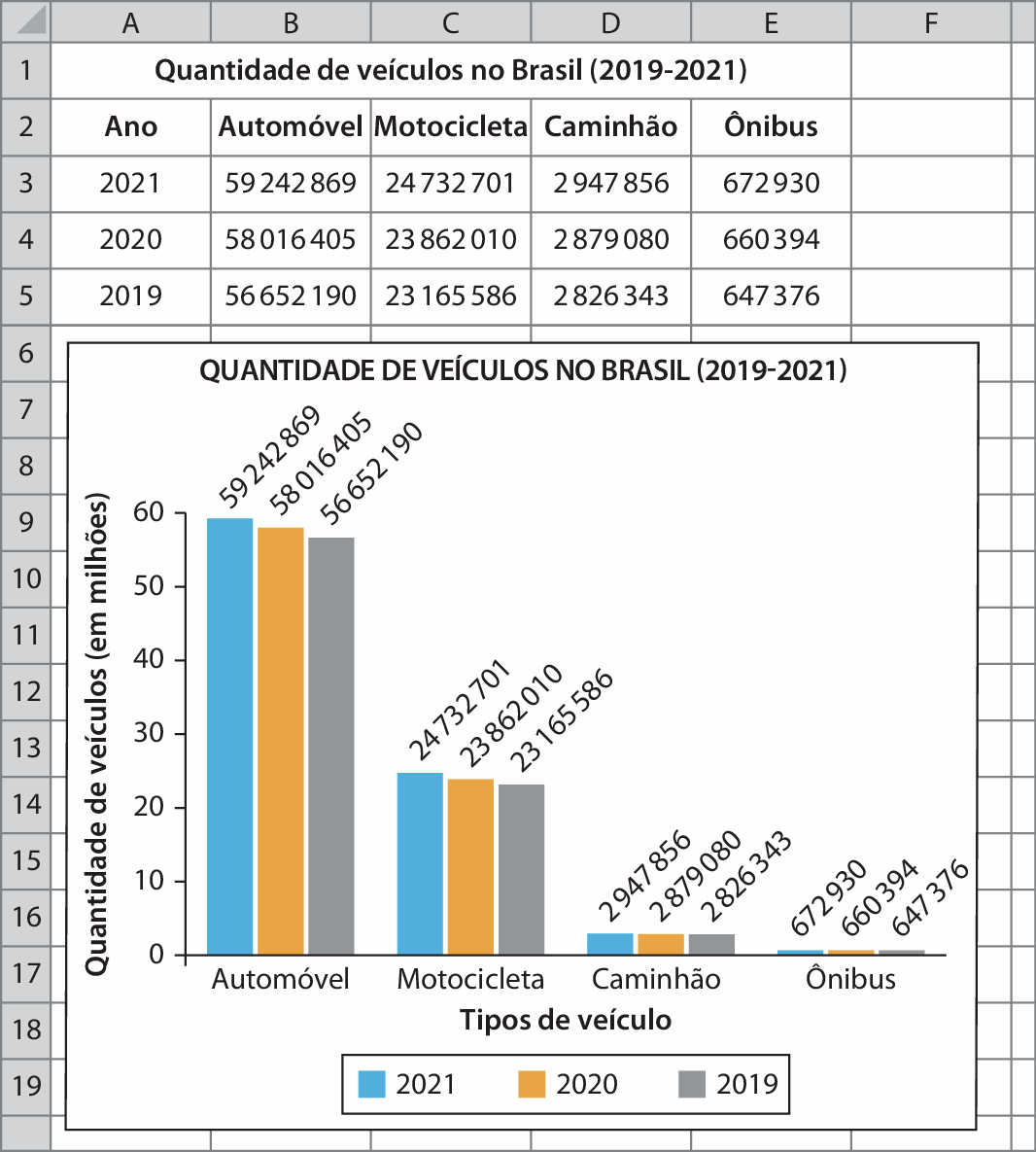
Ilustração. Planilha eletrônica com colunas A, B, C, D, E e F e linhas do 1 ao 19.
Na primeira linha o título: quantidade de veículos no Brasil (2 mil e 19 - 2 mil e 21).
Na segunda linha: coluna A, Ano; coluna B, Automóvel; coluna C, Motocicleta; coluna D, Caminhão; coluna E, Ônibus.
Na terceira linha: coluna A, 2 mil e 21; coluna B, o número 59 milhões 242 mil 869; coluna C, o número 24 milhões 732 mil 701; coluna D, o número 2 milhões 947 mil 856; coluna E, o número 672 mil 930.
Na quarta linha: coluna A, 2 mil e 20; coluna B, o número 58 milhões 16 mil 405; coluna C, o número 23 milhões 862 mil e 10; coluna D, o número 2 milhões 879 mil e 80; coluna E, o número 660 mil 394.
Na quinta linha: coluna A, 2 mil e 19; coluna B, o número 56 milhões 652 mil 190; coluna C, o número 23 milhões 165 mil 586; coluna D, o número 2 milhões 826 mil 343; coluna E, o número 647 mil 376.
Gráfico. Título do gráfico de barras verticais triplas: quantidade de veículos no Brasil (2 mil e 19 - 2 mil e 21).
Eixo horizontal perpendicular a uma eixo vertical.
O eixo vertical tem 7 tracinhos igualmente espaçados e neles estão indicados, de baixo para cima a quantidade veículos: 0, 10, 20, 30, 40, 50 e 60. Ele está rotulado como quantidade de veículos (em milhões).
No eixo horizontal estão indicados os tipos de veículos, automóvel, motocicleta, caminhão e ônibus. Ele está rotulado como tipos veículo.
Abaixo do gráfico a legenda: cor azul para o ano de 2 mil e 21, cor laranja para o ano de 2 mil e 20 e cor cinza para o ano de 2 mil e 19.
Sobre o eixo horizontal a quatro barras verticais azuis, quatro barras verticais laranjas e quatro barras verticais cinzas com a mesma largura, indicando que: o número de automóveis no Brasil em 2 mil e 21 era de 59 milhões 242 mil 869, em 2 mil e 20 era de 58 milhões 16 mil 405 e em 2 mil e 19 era de 56 milhões 652 mil 190; o número de motocicletas no Brasil em 2 mil e 21 era de 24 milhões 732 mil 701, em 2 mil e 20 era de 23 milhões 862 mil e 10 e em 2 mil e 19 era de 23 milhões 165 mil 586; o número de caminhão no Brasil em 2 mil e 21 era de 2 milhões 947 mil 856, em 2 mil e 20 era de 2 milhões 879 mil e 80 e em 2 mil e 19 era de 2 milhões 826 mil 343; o número de ônibus no Brasil em 2 mil e 21 era de 672 mil 930, em 2 mil e 20 era de 660 mil 394 e em 2 mil e 19 era de 647 mil 376.

Dados obtidos em: MINISTÉRIO DA INFRAESTRUTURA, Secretaria Nacional de Trânsito – Senatran – 2019, 2020 e 2021.

b) Exemplos de resposta:

• Em 2019, havia .647376 ônibus no Brasil.

• Em todos os anos apresentados, havia mais automóveis do que caminhões, motocicletas e ônibus.

• De 2019 a 2020, houve um aumento de mais de meio milhão de motocicletas.

• Em 2021, havia aproximadamente 88 milhões de automóveis, caminhões, motocicletas e ônibus.

c) Nesse caso, o gráfico terá quatro linhas, cada uma representando um dos tipos de veículo (automóvel, caminhão, motocicleta e ônibus).

Página oitenta e dois

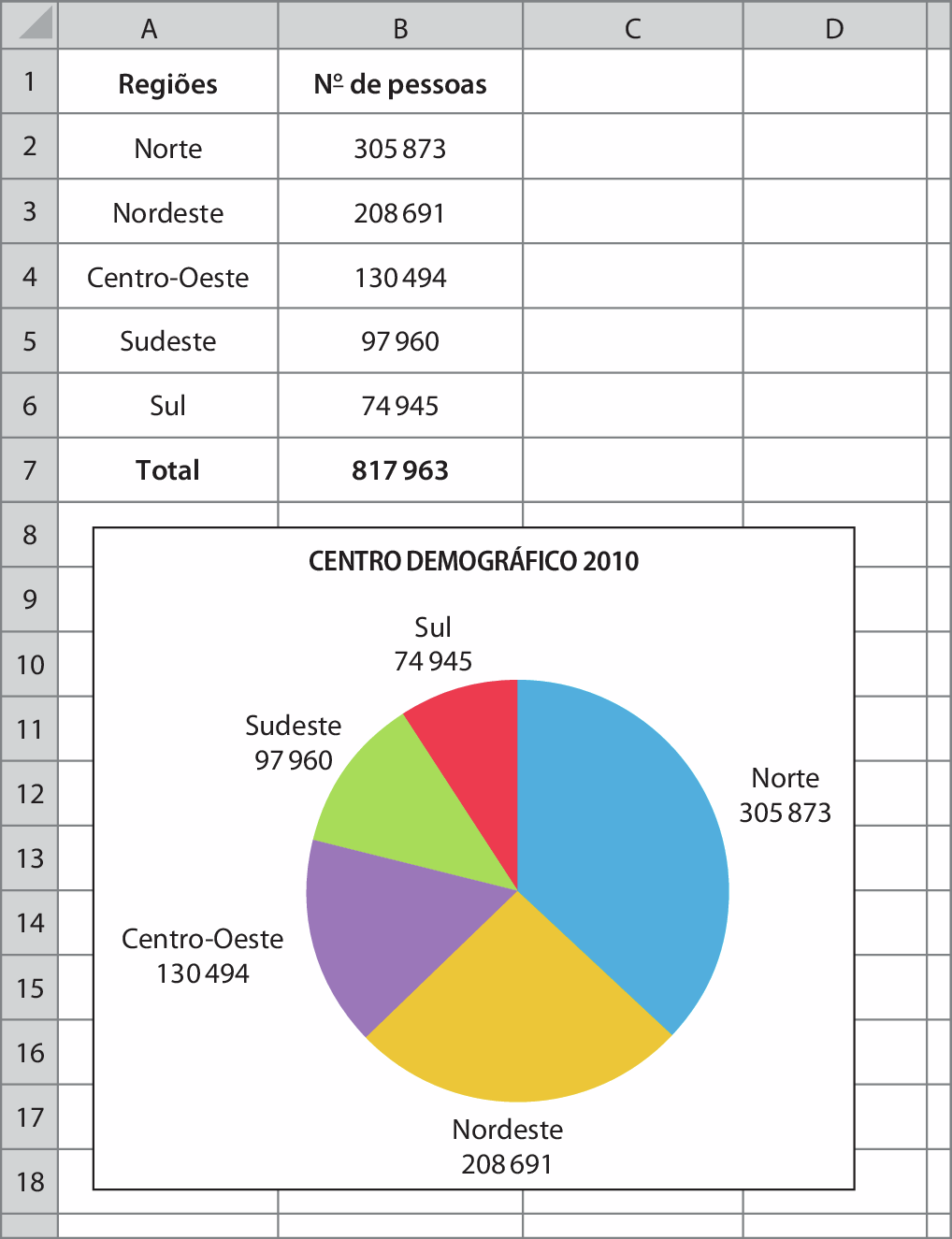
Ilustração. Planilha eletrônica aparecendo as colunas A, B, C e D e linhas do 1 ao 18. Na parte superior uma tabela e abaixo um gráfico.
Na primeira linha: coluna A, Regiões; coluna B, Número de pessoas.
Na segunda linha: coluna A, Norte; coluna B, o número 305 mil 873.
NA terceira linha: coluna A, Nordeste; coluna B, o número 208 mil 691.
Na quarta linha: coluna A, Centro-Oeste; coluna B, o número 130 mil 494.
Na quinta linha: coluna A, Sudeste; coluna B, o número 97 mil 960.
Na sexta linha: coluna A, Sul; coluna B, o número 74 mil 945.
Na sétima linha: coluna A, Total; coluna B o número 817 mil 963.
Gráfico. Título do gráfico de setores: Censo demográfico de 2 mil e 10. Abaixo, círculo dividido em cinco partes. Uma parte, na cor azul com indicação: Norte, 305 mil 873. Outra parte, em amarelo, com indicação: Nordeste, 208 mil 691. Última parte, em verde com o número 200 mil. Outra parte, em roxo, com indicação: Centro-Oeste, 130 mil 494. Outra parte, em verde, com indicação: Sudeste, 97 mil 960. Última parte, em vermelho, com indicação: Sul, 74 mil 945.

Dados obtidos em: IBGE, Censo 2010.

TRABALHO EM EQUIPE

▶ Página 167

Resoluções e comentários em Orientações.

COMPREENDER UM TEXTO

▶ Páginas 168 e 169

Resoluções e comentários em Orientações.

Atividades de revisão

▶ Páginas 170, 171 e 172

1. a) Aplicando o teorema de Pitágoras, temos:

25^{2} = 7^{2} + x^{2}

625 = 49 + x²

x^{2} = 625 ‒ 49

x^{2} = 576

x = \pm \sqrt{576}

x = ± 24

Como x representa uma medida, desconsideramos a solução x = menos24.

Medida do perímetro: 24 + 25 + 7 = 56

b) Aplicando o teorema de Pitágoras, temos:

x^{2} = {(2 \sqrt{5})}^{2} + {(4 \sqrt{5})}^{2}

x^{2} = 20 + 80

x^{2} = 100

x = \pm \sqrt{100}

x = ± 10

Como x representa uma medida, desconsideramos a solução x = menos10.

Medida do perímetro:

2 \sqrt{5} + 4 \sqrt{5} + 10 = 10 + 6 \sqrt{5}

2. A diagonal do retângulo é a hipotenusa de um triângulo retângulo e os lados do retângulo são os catetos. Chamando de x a medida de comprimento do retângulo e aplicando o teorema de Pitágoras, temos:

8^{2} = 6^{2} + x^{2}

64 = 36 + x²

x^{2} = 64 ‒ 36

x^{2} = 28

x = \pm \sqrt{28}

x = \pm 2 \sqrt{7}

Como x representa uma medida, desconsideramos a solução x = menos

2 \sqrt{7}

Portanto, a medida de comprimento de

\overline{D C}

2 \sqrt{7}

centímetros.

3. Usando a relação

d = ℓ \sqrt{2}

, temos:

8 = ℓ \sqrt{2}

ℓ = \frac{8}{\sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} = \frac{8 \sqrt{2}}{2} = 4 \sqrt{2}

Medida do perímetro:

4 \cdot 4 \sqrt{2} = 16 \sqrt{2}

Logo, a medida do perímetro do quadrado é

16 \sqrt{2}

centímetros.

4. Sendo b e c medidas de comprimento dos catetos, a da hipotenusa e h da altura, aplicamos a relação métrica b ⋅ c = a ⋅ h e obtemos:

\sqrt{5} \cdot 1 = \sqrt{6} \cdot h

h = \frac{\sqrt{5}}{\sqrt{6}} = \sqrt{\frac{5}{6}}

5. a) Aplicando a relação métrica celevado a 2 = a · m, temos:

6^{2} = 10 \cdot x

36 = 10 ⋅ x

x = \frac{36}{10}

x = 3,6

b) Aplicando a relação métrica celevado a 2 = a · m, temos:

12^{2} = x \cdot 8

144 = 8 ⋅ x

x = \frac{144}{8}

x = 18

c) Aplicando o teorema de Pitágoras, temos:

a^{2} = 12^{2} + 16^{2}

a^{2} = 144 + 256

a^{2} = 400

a = ± 20

Como x representa uma medida, desconsideramos a solução a = menos20. Portanto, a = 20.

Aplicando a relação métrica b · c = a · h, temos:

12 ⋅ 16 = 20 ⋅ x

192 = 20 ⋅ x

x =

\frac{192}{20}

x = 9,6

6. a) Aplicando o teorema de Pitágoras, temos:

x^{2} = 6^{2} + 8^{2}

x^{2} = 36 + 64

x^{2} = 100

x = \pm \sqrt{100}

x = ± 10

Página oitenta e três

Como x representa uma medida, desconsideramos a solução x = menos10.

Portanto, a hipotenusa mede 10 centímetros de comprimento.

b) Aplicando a relação métrica belevado a 2 = a · n, temos:

6elevado a 2 = 10 ⋅ n

36 = 10 ⋅ n

n = \frac{36}{10}

n = 3,6

Aplicando a relação métrica celevado a 2 = a · m, temos:

8elevado a 2 = 10 · m

64 = 10 · m

m =

\frac{64}{10}

m = 6,4

Portanto, as medidas de comprimento das projeções ortogonais de cada cateto sobre a hipotenusa são 3,6 centímetros e 6,4 centímetros.

c) Aplicando a relação métrica

h^{2} = m \cdot n

, temos:

h^{2} = 6,4 \cdot 3,6

h^{2} = 23,04

h = \pm \sqrt{23,04}

h = ± 4,8

Como h representa uma medida, desconsideramos a solução h = menos 4,8.

Portanto, a altura mede 4,8 centímetros de comprimento.

7. Um triângulo retângulo isósceles possui os dois catetos de mesma medida de comprimento. Então:

8^{2} = x^{2} + x^{2}

64 = 2xelevado a 2

x^{2} = 32

x = \pm \sqrt{32} = \pm 4 \sqrt{2}

Como x representa uma medida, desconsideramos a solução x = menos

4 \sqrt{2}

Portanto, a medida do perímetro é dada por:

4 \sqrt{2} + 4 \sqrt{2} + 8 = (8 + 8 \sqrt{2})

Logo, a medida do perímetro é

(8 + 8 \sqrt{2})

centímetros.

8. Aplicando a relação métrica

h^{2} = m \cdot n

, temos:

2^{2} = 1 \cdot n

4 = n

Logo, a medida de comprimento da projeção do cateto

\overline{A C}

é 4.

Figura geométrica. 2 triângulos retângulos ABD e BCE roxos com o ponto B em comum.
No triângulo ABD o ângulo reto está no vértice A, o lado AD está na vertical e tem medida de 6 decímetros e o lado AB está na horizontal e tem medida x decímetro, a hipotenusa BD tem medida de 10 decímetros.
No triângulo BCE o ângulo reto está no vértice C, o lado CE está na vertical e tem medida de 4 decímetros, o lado BC está na horizontal e a hipotenusa BE tem medida y decímetros.
O ângulo externo DBE é reto também e os pontos A, B e C estão alinhados e a medida do segmento de reta AC é 11 decímetros.

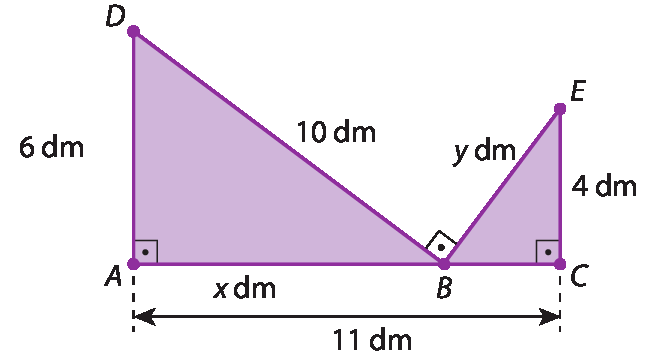
Vamos calcular primeiro a medida de comprimento AB:

10^{2} = 6^{2} + x^{2} \Rightarrow 100 = 36 + x^{2} \Rightarrow x^{2} = 100 ‒ 36 \Rightarrow x^{2}

= 64 ⇒

⇒ x = ± 8

Como x representa uma medida, desconsideramos a solução x = menos 8. Portanto, x = 8 decímetros.

Então, podemos concluir que a medida de comprimento

\overline{B C}

é igual a 3 decímetros, pois 11 decímetros menos 8 decímetros = 3 decímetros.

Calculando a medida de comprimento de

\overline{E B}

, temos:

y^{2} = 4^{2} + 3^{2} \Rightarrow y^{2} = 16 + 9 \Rightarrow y^{2} = 25 \Rightarrow y = \pm 5

Como y representa uma medida, desconsideramos a solução y = menos5. Portanto, y = 5.

Logo, a medida de comprimento de

\overline{E B}

é 5 decímetros.

alternativa d

10. Calculando c, temos:

13^{2} = 12^{2} + c^{2} \Rightarrow 169 = 144 + c^{2} \Rightarrow c^{2} = 169 ‒ 144 \Rightarrow c^{2}

= 25 ⇒ c = 5

Calculando m, temos:

c^{2} = 13 \cdot m \Rightarrow 5^{2} = 13 \cdot m \Rightarrow 25 = 13 \cdot m \Rightarrow m = \frac{25}{13} \Rightarrow m ≃ 1,92

Calculando n, temos:

a = m + n ⇒ 13 = 1,92 + n ⇒ n = 13 ‒ 1,92 ⇒ n ≃ 11,08

Calculando h, temos:

12 \cdot 5 = 13 \cdot h \Rightarrow 60 = 13 \cdot h \Rightarrow h = \frac{60}{13} \Rightarrow h ≃ 4,62

11. Calculando a medida de comprimento da projeção do cateto

\overline{B C}

, temos:

h^{2} = m \cdot n \Rightarrow 3^{2} = 4 \cdot n \Rightarrow 9 = 4 \cdot n \Rightarrow n = \frac{9}{4} \Rightarrow n = \frac{9}{4}

Somando as medidas dos comprimentos das duas projeções, temos a medida de comprimento da hipotenusa:

4 + \frac{9}{4} = \frac{25}{4}

Calculando a medida de comprimento do cateto

\overline{A B}

, temos:

x^{2} = 16 + 9 \Rightarrow x^{2} = 25 \Rightarrow x = 5

Medida do perímetro:

5 + \frac{15}{4} + \frac{25}{4} = \frac{60}{4} = 15

12. a) As diagonais do losango são perpendiculares e se encontram no ponto médio. Dessa forma, as duas diagonais formam quatro triângulos retângulos iguais de catetos com medidas de comprimento 3 centímetros e 4 centímetros. Aplicando o teorema de Pitágoras em um dos triângulos, temos:

x^{2} = 4^{2} + 3^{2} \Rightarrow x^{2} = 16 + 9 \Rightarrow x^{2} = 25 \Rightarrow x = \pm 5

Como x representa uma medida, desconsideramos a solução x = menos5.

Logo, o comprimento do lado do losango mede 5 centímetros e seu perímetro mede:

4 ⋅ 5 = 20

Portanto, a medida do perímetro é 20 centímetros.

b) A medida de comprimento da altura de um triângulo equilátero é dada por

\frac{ℓ \sqrt{3}}{2}

. Então:

h = \frac{2 x \sqrt{3}}{2} = x \sqrt{3}

c) A diagonal do retângulo é a hipotenusa do triângulo retângulo. Assim:

d^{2} = 7^{2} + 3^{2} \Rightarrow d^{2} = 49 + 9 \Rightarrow d^{2} = 58 \Rightarrow d = \pm \sqrt{58}

Como d representa uma medida, desconsideramos a solução d = menos

\sqrt{58}

Portanto, a medida de comprimento da diagonal do retângulo é

\sqrt{58}

centímetros.

13. De acordo com o enunciado, podemos fazer:

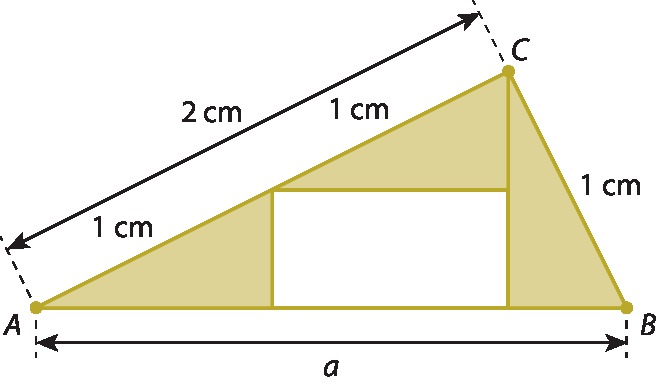
Figura geométrica. Triângulo ABC composto por 1 retângulo branco e 3 triângulos retângulos iguais. O triângulo ABC tem medida do lado AB, indicada por a, a medida do lado AC, 2 centímetros e a medida do lado BC, 1 centímetro. Os três triângulos retângulos tem a medida da hipotenusa 1 centímetro.

Página oitenta e quatro

Aplicando o teorema de Pitágoras, temos:

aelevado a 2 = 1elevado a 2 + 2elevado a 2

aelevado a 2 = 1 + 4

aelevado a 2 = 5

a = ±

\sqrt{5}

Como a representa uma medida, desconsideramos a solução a = menos

\sqrt{5}

Assim, a =

\sqrt{5}

A medida do perímetro é dada por:

\sqrt{5}

+ 1 + 2 =

\sqrt{5}

+ 3

Logo, a medida do perímetro do triângulo ABC é (

\sqrt{5}

+ 3

) centímetros.

alternativa a

14. Observando o

△

DCA, vamos calcular a medida CA.

Temos DC = 16 centímetros e DA = 20 centímetros e AC = x. Então:

20^{2} = 16^{2} + x^{2} \Rightarrow 400 = 256 + x^{2} \Rightarrow x^{2} = 400 ‒ 256 \Rightarrow x^{2}

= 144 ⇒ ⇒ x = ±12

Como x representa uma medida, desconsideramos a solução x = menos12.

Sabendo que CA = 12 centímetros, conseguimos descobrir que

\overline{A B}

mede 8 centímetros.

Agora, vamos calcular a medida de

\overline{A P}

Considerando AP = z, temos

P B = (16 - z)

. Aplicando Pitágoras, temos:

z^{2} = {(16 ‒ z)}^{2} + 8^{2} \Rightarrow z^{2} = 256 ‒ 32 z + z^{2} + 64 \Rightarrow 32 z = 320 \Rightarrow z = 10

△ D A P

, temos DA = 20 centímetros e PA = 10 centímetros, e falta calcular DP = y:

y^{2} = 20^{2} + 10^{2} \Rightarrow y^{2} = 400 + 100 \Rightarrow y^{2} = 500 \Rightarrow y = \pm \sqrt{500}

⇒

⇒ y = ±10

\sqrt{5}

Como y representa uma medida, desconsideramos a solução y = menos

10 \sqrt{5}

Logo, a medida de comprimento de

\overline{D P}

10 \sqrt{5}

centímetros.

15. O percurso do ônibus é pela Rua A e pela Rua B, ou seja, pelos catetos do triângulo. Para colocar um ponto T no meio desse caminho, temos:

– pela Rua A o ônibus percorre uma medida de distância igual a: 550 menos 30 = 520

– pela Rua B o ônibus percorre uma medida de distância igual a: 320 menos 20 = 300

No total ele percorre do ponto P até o ponto Q: 520 + 300 = 820

Metade dessa medida de distância equivale a: 820 dividido por 2 = 410

Contando essa medida de distância a partir de P temos: 30 + 410 = 440

Como essa distância ainda se encontra na ordenada 20, então o ponto T deverá estar nas coordenadas abre parênteses440, 20fecha parênteses.

alternativa ê

16.

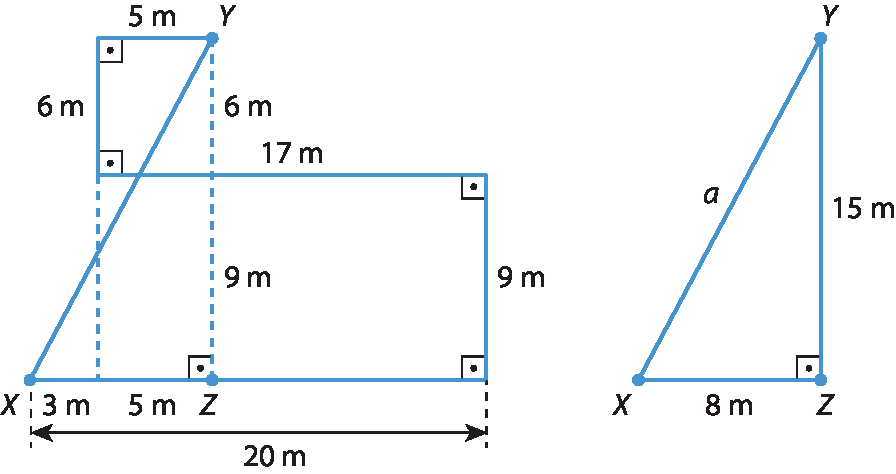
Ilustração. À esquerda, caminho em formato de S formado por linhas retas. O ponto x está no canto inferior esquerdo e a partir dele está indicado a trajetória que a pessoa percorreu até o ponto y. Partindo de x andou 20 metros para frente, girou 90 graus para esquerda, andou 9 metros para frente, girou 90 graus para esquerda, andou 17 metros para frente, girou 90 graus para a direita, andou 6 metros para frente, girou 90 graus para a direita e andou 5 metros para frente chegando no ponto y. Segmento de reta ligando o ponto x ao ponto y em linha reta, linha traceja perpendicular das extremidades do segmento de reta de 5 metros, que finalizou o percurso, ao segmento inferior que deu início ao percurso, formando um ângulo reto no ponto z, com indicação de medida de z até a linha tracejada 5 metros e da linha traceja ao ponto x, 3 metros.
À direita, triângulo retângulo que foi formado pelo caminho percorrido em linha reta do ponto inicial X até o ponto final Y. Triângulo retângulo XYZ com ângulo reto em Z, com a medida da hipotenusa, indicada por a, o segmento de reta de XZ 8 metros e o segmento de reta de YZ 15 metros.

Aplicando o teorema de Pitágoras no triângulo XZY, temos:

a^{2} = 15^{2} + 8^{2}

a^{2} = 225 + 64

a^{2} = 289

a = \pm \sqrt{289}

a = ±17

Como a representa uma medida, desconsideramos a solução a = menos17.

Portanto, o percurso em linha reta de X até Y mede 17 métros.

alternativa c

17. Medida do perímetro da região quadrada: 40 métros

Medida de comprimento do lado da região quadrada: 40 dividido por 4 = 10; assim, a medida do comprimento do lado da região quadrada é 10 métros.

A estátua se encontra na metade da medida de comprimento da diagonal desse quadrado. Vamos, então, calcular a medida de comprimento da diagonal:

x^{2} = 10^{2} + 10^{2} \Rightarrow x^{2} = 100 + 100 \Rightarrow x^{2} = 200 \Rightarrow x = \pm \sqrt{200}

⇒

⇒ x = ±10

\sqrt{2}

Como x representa uma medida, desconsideramos a solução x = menos

10 \sqrt{2}

Logo, a metade dessa medida é dada por:

\frac{10 \sqrt{2}}{2} = 5 \sqrt{2}

Portanto, a medida da distância da estátua a um dos cantos desse pátio é

5 \sqrt{2}

métros.

18. Para determinar as coordenadas do ponto médio do segmento

\overline{B C}

, vamos calcular as médias aritméticas das abscissas e das ordenadas das extremidades desse segmento.

Extremidades do segmento: Babre parênteses4, 2fecha parênteses e Cabre parêntesesmenos2, 4fecha parênteses

Abscissa do ponto médio:

\frac{4 + (‒ 2)}{2} = \frac{4 ‒ 2}{2} = \frac{2}{2} = 1

Ordenada do ponto médio:

\frac{2 + 4}{2} =

\frac{6}{2} = 3

Portanto, as coordenadas do ponto médio são abre parênteses1, 3fecha parênteses.

19. Precisamos encontrar um ponto P que esteja no eixo das ordenadas e que tenha a mesma medida de distância da origem e de Aabre parênteses0, 10fecha parênteses.

Como o ponto P pertence ao eixo das ordenadas, sua abscissa será zero: Pabre parênteses0, yfecha parênteses. Então:

y =

\frac{10 ‒ 0}{2}

= 5

Portanto, as coordenadas do ponto P são abre parênteses0, 5fecha parênteses.

20. Nessa atividade, como estamos trabalhando com medidas, vamos desconsiderar as soluções negativas.

a) Aplicando o teorema de Pitágoras nos triângulos retângulos convenientes que podemos observar, calculamos a medida de comprimento de cada um dos lados:

• lado

\overline{A B}

delevado a 2 = 2elevado a 2 + 2elevado a 2

d^{2} = 8

d = 2 \sqrt{2}