
CAPÍTULO 2 Potenciação e radiciação
Neste Capítulo, vamos estudar potenciação com números reais, radiciação, porcentagem e fazer operações com números reais na fórma de raiz.
1 Potências
Analise a situação a seguir.

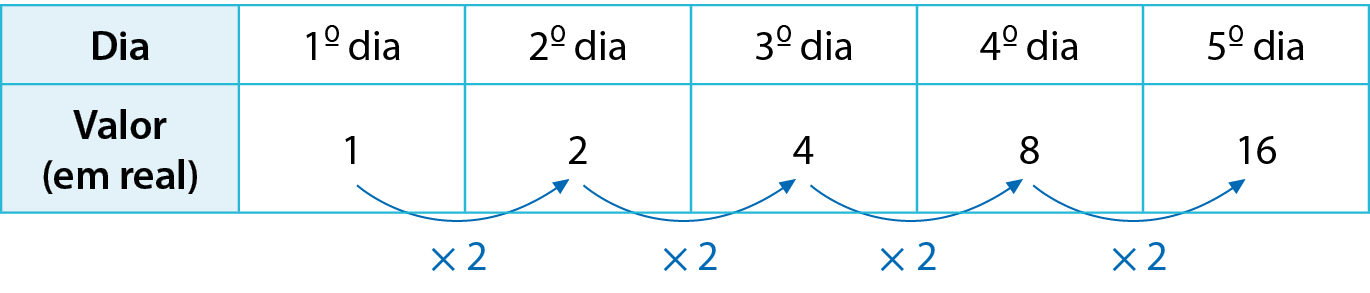
Marcela está juntando dinheiro. A cada dia de uma semana ela deposita em seu cofrinho o dobro do que havia depositado no dia anterior. No 1º dia, ela depositou R$ 1,00um reais. Quanto será poupado no 7º dia se ela cumprir com o planejado?
Podemos organizar os dados dessa situação em um quadro.
Respostas e comentários
Habilidades da Bê êne cê cê trabalhadas neste Capítulo:
ê éfe zero nove ême ah zero três
ê éfe zero nove ême ah zero quatro
ê éfe zero nove ême ah zero cinco
ê éfe zero nove ême ah um oito
ê éfe zero nove ême ah dois dois
Orientações e sugestões didáticas
Potências
Objetivos
• Retomar o estudo da potenciação com números reais das propriedades da potenciação para potências com expoentes inteiros.
• Reconhecer e empregar a escrita de números em notação científica.
• Favorecer o desenvolvimento das habilidades ê éfe zero nove ême ah zero três, ê éfe zero nove ême ah zero quatro e ê éfe zero nove ême ah um oito da Bê êne cê cê.
Habilidades da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah zero três porque os estudantes vão calcular potências com números reais. Favorece também o desenvolvimento da habilidade ê éfe zero nove ême ah zero quatro, ao propor aos estudantes que resolvam e elaborem problemas com números reais, inclusive em notação científica. Por fim, na seção Atividades, o tópico também favorece o desenvolvimento da habilidade ê éfe zero nove ême ah um oito, porque os estudantes deverão reconhecer e empregar unidades de medida muito grandes ou muito pequenas.
Orientações
• Neste tópico será explorado o cálculo de potências com expoente inteiro e com base negativa e não negativa. Além disso, desenvolve-se um trabalho com notação científica, muito usada em diversas áreas do conhecimento e nos meios de comunicação. Caso julgue oportuno, antes de iniciar a leitura desta página, faça um levantamento dos conhecimentos que os estudantes já têm sobre o assunto.
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.
(ê éfe zero nove ême ah um oito) Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.
Note que os valores formam uma sequência em que cada termo a partir do 2º é o termo anterior multiplicado por 2. Podemos escrever cada valor como uma potência de base 2.
|
Dia |
1º dia |
2º dia |
3º dia |
4º dia |
5º dia |
|---|---|---|---|---|---|
|
Valor (em real) |
2elevado a 0 |
2 = 2elevado a 1 |
2 ⋅ 2 = 2elevado a 2 |
2 ⋅ 2 ⋅ 2 = 2elevado a 3 |
2 ⋅ 2 ⋅ 2 ⋅ 2 = 2elevado a 4 |
Analisando essa sequência, deduzimos que o valor poupado no 7º dia será 2elevado a 6 reais, ou seja, R$ 64,00sessenta e quatro reais.
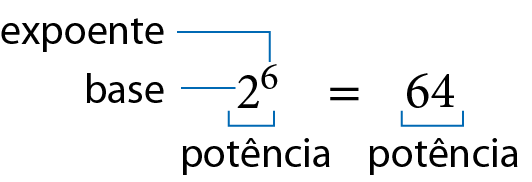
Observe que usamos o termo potência para designar tanto a expressão 2elevado a 6 como o resultado 64.
A seguir, estão algumas definições importantes acerca da potenciação.
• Qualquer potência de base real e expoente inteiro maior que 1 é produto dessa base por ela mesma tantas vezes quantas indica o expoente. Assim, sendo a um número real e n um número inteiro maior que 1, temos:

• Qualquer potência de base real e expoente 1 é igual à própria base. Assim, sendo a um número real, temos:
aelevado a 1 = a
• Qualquer potência de base real não nula e expoente zero é igual a 1. Assim, sendo a um número real, temos:
aelevado a 0 = 1, com a ≠ 0
Exemplos


• πelevado a 1 = π
•
Abre parênteses, raiz quadrada de 5, fecha parênteses, elevado a 0.= 1
A respeito de potências com expoente inteiro negativo, considere a situação a seguir.
A matrioska é um brinquedo artesanal originário da Rússia, que agrupa várias bonecas de tamanhos distintos encaixadas umas dentro das outras.

Rodrigo é artesão e, para produzir uma matrioska, confeccionou uma sequência de cinco bonecas, de modo que a primeira boneca mede 2 decímetros de altura, e cada boneca seguinte mede a metade da altura da anterior.
Orientações e sugestões didáticas
• Explore a situação inicial com os estudantes e deixe que percebam a regularidade presente na sequência formada pelos números correspondentes aos valores depositados por Marcela em cada dia. Se achar conveniente, peça que escrevam a expressão algébrica correspondente à quantia, em real, depositada no enésimo dia. abre parênteses2elevado a n ⁻ ¹)
• Mesmo considerando que os estudantes já tenham algum repertório sobre o estudo de potências com expoente natural e inteiro negativo, verifique se eles apresentam alguma dificuldade a respeito desse assunto ao explorar os exemplos desta página. Aproveite para fazer a análise da potência com base negativa e base não negativa, com expoente natural par ou ímpar.
Lembre-se: Escreva no caderno!
Assim, as medidas da altura das bonecas, em decímetro, formam uma sequência numérica em que cada termo é o termo anterior dividido por 2.
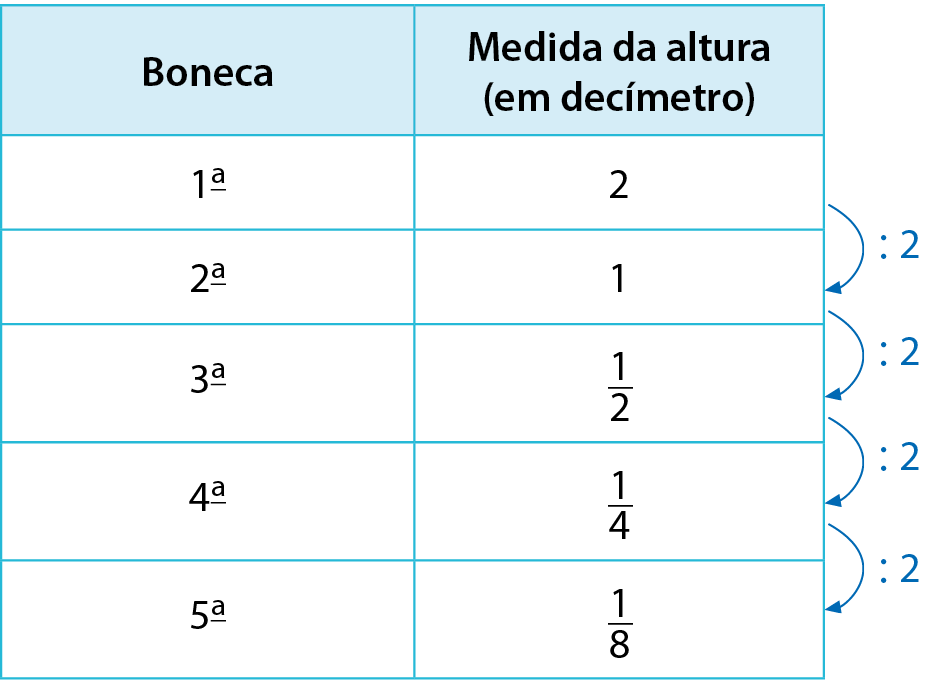
Para calcular
Expresse, em centímetro, as medidas da altura das cinco bonecas que Rodrigo confeccionou.
Podemos escrever esses números na fórma de potências de base 2. Como cada termo é o termo anterior dividido por 2, os expoentes das potências de base 2 diminuirão 1 unidade a cada termo.
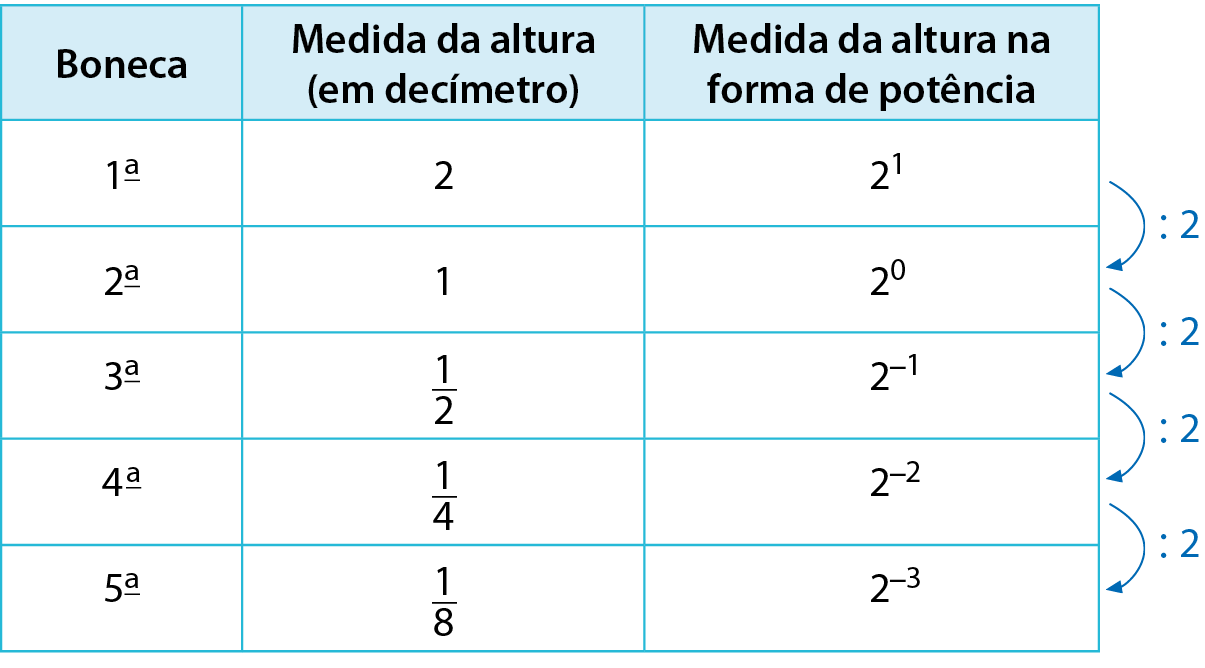
Observe as potências com expoentes negativos que obtivemos no quadro anterior.
•
Potenciação. 2 elevado a menos 1, é igual a fração 1 meio.•
Potenciação. 2 elevado a menos 2, igual a fração 1 quarto, é igual a fração 1 sobre 2 ao quadrado.•
Potenciação. 2 elevado a menos 3, igual a fração 1 oitavo, é igual a fração 1 sobre 2 ao cubo.Um número real a, não nulo, elevado a um expoente inteiro negativo menosn é igual a
Sentença matemática. Fração 1 sobre a elevado a n.:
Potenciação. a elevado a menos n, igual a fração 1 sobre a elevado a n, é igual a fração, abre parênteses, 1 sobre a, fecha parênteses, elevado a n, com a diferente de 0.
, com a ≠ 0
Exemplos
• 3elevado a menos 1 =
fração 1 terço• 5elevado a menos 2 =
fração 1 sobre 5 ao quadrado, é igual a fração, abre parênteses, 1 sobre 5, fecha parênteses, ao quadrado, é igual a fração 1 sobre 25.•
Potenciação. Abre parênteses, fração 2 sobre 3, fecha parênteses, elevado a menos 3, igual a, abre parênteses, fração 3 sobre 2, fecha parênteses, ao cubo, é igual a fração 27 sobre 8.Respostas e comentários
Para calcular: 20 centímetros, 10 centímetros, 5 centímetros, 2,5 centímetrose 1,25 centímetro
Orientações e sugestões didáticas
• A partir da situação da matrioska é gerada uma sequência formada pelas medidas das alturas das bonecas. Os estudantes devem perceber que, nessa sequência, cada número, a partir do segundo, é igual ao anterior dividido por 2. Proponha aos estudantes que tentem escrever os números dessa sequência na fórma de potências de base 2. Enfatize o fato de algumas dessas potências terem expoente inteiro negativo. Também, nesse caso, pode-se pedir a eles que encontrem a expressão algébrica correspondente à medida de altura, em decímetro, da enésima boneca. abre parênteses2⁻elevado a n ⁺ ²fecha parênteses
• No boxe Para calcular, os estudantes vão colocar em prática seus conhecimento em relação às transformações de unidades de medida de comprimento, além de realizar sucessivas divisões por 2. Eles podem apresentar alguma dificuldade em transformar decímetro em centímetro, já que o decímetro é uma unidade de medida pouco usada. Se julgar conveniente, retome brevemente o conteúdo.
Propriedades da potenciação para potências com expoentes inteiros
As propriedades a seguir podem ser úteis nos cálculos com potências.
Considere que as bases a e b são números reais não nulos e os expoentes m e n são números inteiros.
● Produto de potências de mesma base
Para calcular o produto de potências de mesma base, mantemos a base e adicionamos os expoentes.
aelevado a m ⋅ aelevado a n = aelevado a m ⁺ elevado a n
● Quociente de potências de mesma base
Para calcular o quociente de potências de mesma base, mantemos a base e subtraímos os expoentes.
aelevado a m dividido por aelevado a n = aelevado a m ⁻ elevado a n
● Potência de uma potência
Para calcular a potência de uma potência, mantemos a base e multiplicamos os expoentes.
abre parêntesesaelevado a mfecha parênteseselevado a n = aelevado a m ⋅ elevado a n
● Potência de um produto
A potência de um produto pode ser transformada em um produto de potências.
abre parêntesesa ⋅ bfecha parênteseselevado a m = aelevado a m ⋅ belevado a m
● Potência de um quociente
A potência de um quociente pode ser transformada em um quociente de potências.
abre parêntesesa dividido por bfecha parênteseselevado a m = aelevado a m dividido por belevado a m
Exemplos
•
Sentença matemática. Abre parênteses, menos 3, fecha parênteses, ao quadrado vezes, abre parênteses, menos 3, fecha parênteses, elevado a 5, igual a, abre parênteses, menos 3, fecha parênteses, elevado a 2 mais 5, é igual a, abre parênteses, menos 3, fecha parênteses, elevado a 7.•
Sentença matemática. Abre parênteses, raiz quadrada de 2, fecha parênteses, ao cubo, dividido por, abre parênteses, raiz quadrada de 2, fecha parênteses, elevado a 4, igual a, abre parênteses, raiz quadrada de 2, fecha parênteses, elevado a 3 menos 4, é igual a, abre parênteses, raiz quadrada de 2, fecha parênteses, elevado a menos 1.•
Sentença matemática. Abre parênteses, 5 vezes pi, fecha parênteses, ao cubo, é igual a, 5 ao cubo vezes pi ao cubo.•
Sentença matemática. Abre parênteses, 1 vírgula 4 dividido por 3, fecha parênteses, elevado a 10, é igual a, 1 vírgula 4 elevado a 10 dividido por 3 elevado a 10.
•
Potenciação. Abre colchetes, abre parênteses, fração 2 sobre 3, fecha parênteses, elevado a 5, fecha colchete, elevado a 7, igual a, abre parênteses, fração 2 sobre 3, fecha parênteses, elevado a 5 vezes 7, é igual, abre parênteses, fração 2 sobre 3, fecha parênteses, elevado a 35, é igual a fração 2 elevado a 35 sobre 3 elevado a 35.Lembre-se: Escreva no caderno!
Notação científica
Números excessivamente grandes ou extremamente pequenos podem ser expressos como um produto em que um dos fatores é uma potência de base 10. Isso ocorre muito na área científica. Observe os textos a seguir.
Orientações e sugestões didáticas
• Ao explorar as propriedades da potenciação para potências com expoentes inteiros, aproveite para destacar que elas são utilizadas na simplificação de cálculos e ajudam a “encurtar” o caminho em algumas resoluções. Os exemplos apresentados permitem aos estudantes a perceber a utilidade dessas propriedades. Se achar necessário, apresente mais exemplos para a turma.
• Na retomada da escrita de números em notação científica, é fundamental que os estudantes compreendam o conceito e percebam a conveniência de expressar números muito grandes ou muitos pequenos utilizando uma potência de base 10.
Os relógios atômicos são tão estáveis que, em princípio, dois relógios de césio teriam que funcionar por .6000 anos para que a diferença entre suas leituras fosse maior que 1 segundo. Mesmo assim, essa precisão não é nada em comparação com a dos relógios que estão sendo desenvolvidos atualmente, que pode chegar a uma parte em 10elevado a 18, ou seja, 1 segundo em 1 × 10elevado a 18 segundos (cêrca de 3 × 10elevado a 10 anos).
ralidei, D.; Resnick, R.; uólquer, J. Fundamentos de Física. nona edição Rio de Janeiro: éle tê cê, 2012. volume 2, página 6.

A unidade de medida de massa unidade (unificada de massa atômica), cujo símbolo é u, equivale a 1,66054 × 10elevado a menos 27 quilograma e corresponde à massa de
Fração 1 sobre 12.da massa de um átomo de carbono12.
Dados publicados pelo Instituto de Pesos e Medidas do estado de São Paulo (Ipem-ésse pê).
Os números 1 × 10elevado a 18, 3 × 10elevado a 10 e 1,66054 × 10elevado a menos 27 estão representados em notação científica. Isso facilita a leitura de números muito grandes ou muito pequenos. Por exemplo, é mais fácil escrever 1 × 10elevado a 18 segundos do que ......1000000000000000000 segundos ou 1,66054 × 10elevado a menos 27 quilograma do que 0,00000000000000000000000000166054 quilograma.
Recorde
Um número escrito em notação científica é expresso como um produto a ⋅ 10elevado a k, em que:
• a é um número escrito na fórma decimal cuja parte inteira tem um único algarismo diferente de zero;
• k é um número inteiro.
Para escrever um número em notação científica, devemos verificar quantas casas a vírgula deve ser deslocada para obter um número escrito na fórma decimal cuja parte inteira tem um único algarismo diferente de zero. Por exemplo, vamos escrever ...125060000000 em notação científica.

Deslocar a vírgula 11 casas para a esquerda significa dividir o número por ...100000000000. Então, para não alterar o número, devemos multiplicá-lo por ...100000000000 ou 10elevado a 11. Assim:
...125060000000 = 1,2506 ⋅ 10elevado a 11
Da mesma fórma, podemos escrever o número 0,000000021 em notação científica.

Deslocar a vírgula 8 casas para a direita significa multiplicar o número por ..100000000. Então, para compensar, devemos dividi-lo por ..100000000 ou 10elevado a 8:
0,000000021 = 2,1 dividido por 10elevado a 8 = 2,1 ⋅
fração 1 sobre 10 elevado a 8= 2,1 ⋅ 10elevado a menos 8
Orientações e sugestões didáticas
• Peça aos estudantes que calculem a medida de massa de um átomo de carbono 12 em unidade unificada de massa atômica e em quilograma. Espera-se que obtenham 12 unidades e 1,992648 ⋅ 10elevado a menos 26 quilograma.
• Pode-se escrever alguns números muito grandes ou muito pequenos no quadro e pedir aos estudantes que expressem esses números utilizando a notação científica. Aproveite a oportunidade para, aos poucos, explicar o procedimento para escrever um número nessa notação.
• O trabalho com números muito grandes ou muito pequenos será retomado nas seções Compreender um texto e Trabalho em equipe neste Capítulo.

ATIVIDADES
faça as atividades no caderno
1. Calcule no caderno.
a) 2elevado a 6
b)
Potência. Abre parênteses, 1 terço, fecha parênteses, elevado a menos 2.c) πelevado a 0
d)
Potência. Abre parênteses, 5 quartos, fecha parênteses, elevado a menos 3.e) 0,2elevado a 4
f)
Potência. Abre parênteses, raiz quadrada de 3, fecha parênteses, elevado a 1.2. O número de diagonais de um polígono de n lados pode ser obtido por meio da expressão:
Sentença matemática. Fração n ao quadrado menos 3n sobre 2.. Calcule o número de diagonais de um polígono de 12 lados.
3. Leia o texto a seguir.
De acôrdo com o Instituto Nacional de Pesquisas Espaciais (ínpi), é muito difícil estimar o número de estrelas e de galáxias no Universo. As estrelas não estão espalhadas ao acaso pelo Universo, mas encontram-se aglutinadas em “ilhas estelares”, denominadas galáxias. Estima-se que a nossa galáxia, a Via Láctea, possui de 200 a 400 bilhões de estrelas. As galáxias possuem em média centenas de bilhões de estrelas. E as estimativas também apontam para centenas de bilhões de galáxias no Universo. Isso resultaria na existência de mais de 10 sextilhões de estrelas.
• Escreva no caderno os números destacados em azul em notação científica.
4. Se a = 0,000001 e b = abre parênteses100elevado a 3fecha parênteseselevado a 4, calcule, expressando os valores em potências de base 10.
a) a ⋅ b
b) a : b
c) b dividido por a
5. Observe os valores de algumas potências de base 15.
15elevado a 2 = 225
15elevado a 3 = .3375
15elevado a 4 = .50625
Considerando os valores dados, calcule, expressando os resultados em notação científica.
a) 0,015elevado a 2
b) 0,000015elevado a 4
c) .15000elevado a 3
d)
Potência. Abre parênteses, 1 vírgula 5 vezes 10 elevado a 7, fecha parênteses, elevado a 4.
6. Simplifique a expressão
Sentença matemática. Fração 81 ao cubo dividido por 9 ao quadrado vezes 729 elevado a menos 2 tudo sobre 59 mil e 49.e, depois, escreva-a na fórma de uma potência.
7.

O esquema a seguir mostra um dispositivo para calcular 11elevado a 2 e 111elevado a 2.
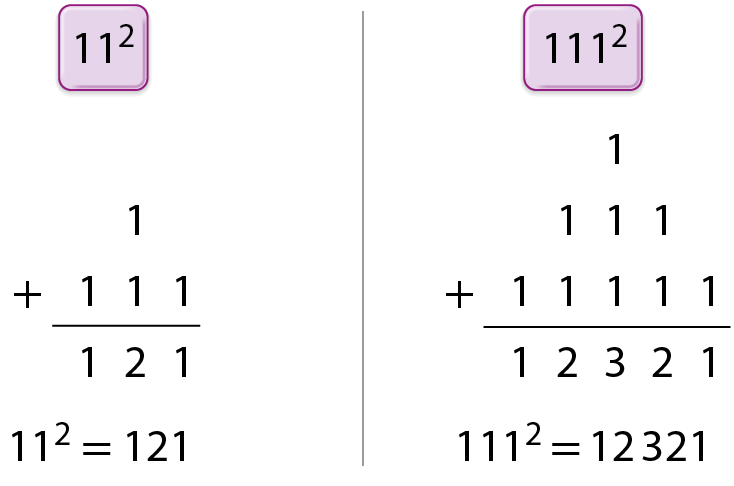
• Agora, calcule 111 111elevado a 2 e 11 111 111elevado a 2.
8.

Observe a sequência formada por quadrados:
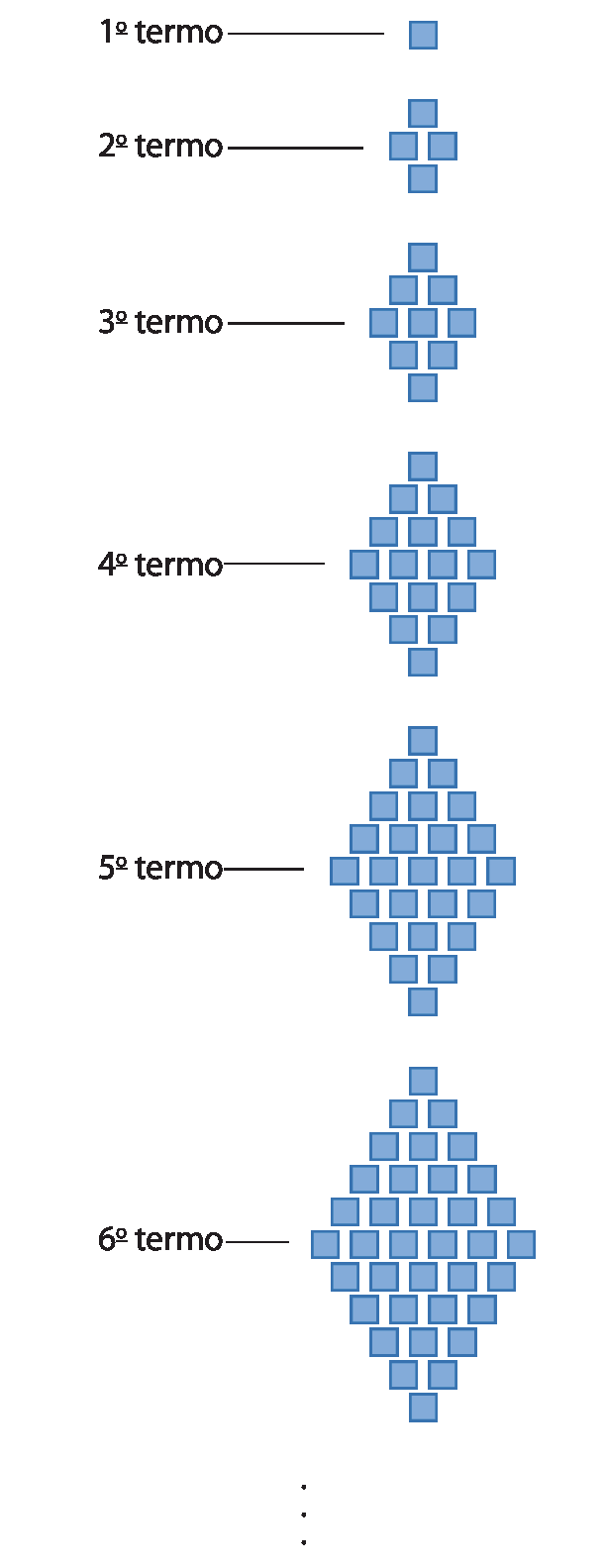
É possível escrever a quantidade de quadrados de cada termo da sequência como um número quadrado perfeito.
Descubra a quantidade de quadrados do enésimo termo abre parêntesestermo nfecha parênteses.
Respostas e comentários
1. a)
64
1. b)
9
1. c)
1
1. d)
Fração de 64 sobre 1251. e)
0,0016
1. f)
Sentença matemática. Raiz quadrada de 3.2. 54 diagonais
3. 2 ⋅ 10elevado a 11; 4 ⋅ 10elevado a 11; 1 ⋅ 10elevado a 22
4. a) 10elevado a 18
4. b) 10elevado a menos 30
4. c) 10elevado a 30
5. a)
Potência. 2 vírgula 25 vezes 10 elevado a menos 4.5. b)
Potência. 5 vírgula 0625 vezes 10 elevado a menos 20.5. c)
Potência. 3 vírgula 375 vezes 10 elevado a 12.5. d)
Potência. 5 vírgula 0625 vezes 10 elevado a 28.6. 3 elevado a menos 14
7. ...12345654321 e ....123456787654321
8. n elevado a 2
Orientações e sugestões didáticas
• Peça aos estudantes que façam as atividades propostas. Pode-se, em um primeiro momento, solicitar a eles que trabalhem por conta própria, sem qualquer intervenção inicial. Em seguida, com base nas dúvidas apresentadas por eles, retome aquilo que for necessário, destacando aspectos que, mesmo já tendo sido trabalhados, eles ainda não dominem totalmente.
• Para resolver a atividade 5, os estudantes deverão escrever os números convenientemente para usar as potências de base 15 indicadas e, depois, aplicar as propriedades da potenciação.
Veja um exemplo de resolução para o item a:
0,0152 =
abre parênteses, fração 15 sobre 1 mil, fecha parênteses, ao quadrado=
abre parênteses, fração 15 sobre 10 ao cubo, fecha parênteses, ao quadrado=
fração 15 ao quadrado sobre 10 elevado a 6.Como 15elevado a 2 = 225, temos:
Fração 225 sobre 10 elevado a 6
=
fração 2 vírgula 25 vezes 10 ao quadrado, sobre 1 vezes 10 elevado a 6= 2,25 ⋅ 10elevado a menos 4
• As atividades 7 e 8 apresentam uma regularidade, com ênfase na dedução de uma expressão que generalize essa regularidade. Incentive os estudantes a resolver os problemas com estratégias próprias.
• Resolução da atividade 7:
No primeiro caso, 11elevado a 2 é igual a 121 e 111elevado a 2 é igual a .12321.
Pede-se que calculemos as potências .111111elevado a 2 e ..11111111elevado a 2.
Analisando a regularidade para o número 11, composto de 2 algarismos, verificamos que seu quadrado abre parênteses121fecha parênteses é formado por uma sequência de números naturais que crescem a partir do número 1 até o 2 e decrescem para o 1.
O segundo número, 111, é composto de 3 algarismos, e seu quadrado abre parênteses.12321fecha parênteses segue o mesmo padrão do 11elevado a 2, ou seja, é formado por uma sequência de números naturais que crescem a partir do 1 até o 3 e decrescem para o 1.
Assim, para calcular as potências pedidas, verificamos que .111111elevado a 2 é formado por uma sequência de números naturais que crescem a partir do 1 até o 6 (.111111 é formado por 6 algarismos) e decrescem para o 1; ..11111111elevado a 2 é formado por uma sequência de números naturais que crescem a partir do 1 até o 8 e decrescem para o 1. Então:
.111111elevado a 2 = ...12345654321
..11111111elevado a 2 = ....123456787654321
• Para resolver a atividade 8, os estudantes podem observar a quantidade de quadrados para cada termo, identificando e analisando as regularidades.
|
Termo |
Quantidade de quadrados |
Padrão |
|---|---|---|
|
1º |
1 |
1elevado a 2 |
|
2º |
4 |
2elevado a 2 |
|
3º |
9 |
3elevado a 2 |
|
4º |
16 |
4elevado a 2 |
|
5º |
25 |
5elevado a 2 |
|
6º |
36 |
6elevado a 2 |
Assim, pode-se escrever o número de quadrados de cada termo como um número quadrado perfeito; logo, a quantidade de quadrados do enésimo termo é indicada por nelevado a 2.
9. Leia o texto a seguir.
Os maiores vírus descobertos até hoje no mundo vêm de dois ambientes extremos do Brasil: os lagos de água muito salgada e alcalina do Pantanal e as profundezas do litoral do Rio de Janeiro, cêrcade 3 quilômetros abaixo da superfície do mar.
Para os padrões do mundo microscópico, os dois Tupanvírus, como foram apelidados, são imensos, chegando a superar diversos tipos de bactérias. [reticências]
Vistas pelo microscópio, as partículas virais parecem pequenos microfones peludos. As maiores medem 2,3 micrômetros ou mícrons (cada mícron tem um milésimo de milímetro), e grande parte desse comprimento corresponde à cauda cilíndrica do vírus.
LOPES, R. J. Maiores vírus já descobertos são do Brasil. Folha de São Paulo, São Paulo, página B7, 28 fevereiro 2018.
De acôrdo com o texto, responda.
a) Cada micrômetro ou mícron corresponde a quantos metros?
b) Escreva a medida do comprimento, em metro, das maiores partículas virais dos Tupanvírus, expressando o valor com todas as casas decimais e, depois, em notação científica.
10. (Mackenzie-São Paulo) Considere as seguintes afirmações:
1) abre parênteses0,001)elevado a menos 3 = 10elevado a 9
2)
Menos 2 ao quadrado é igual a fração 1 quarto.3) abre parêntesesa elevado a menos 1 + b elevado a menos 1) elevado a menos 2 = aelevado a 2 + belevado a 2
Associando v ou f a cada afirmação, nesta ordem, conforme seja Verdadeiro ou Falso, tem-se:
a) V V V
b) V V F
c) V F V
d) F V F
e) V F F
11. Observe a conversa entre Schroeder e Lucy.


Junte-se a um colega e façam o que se pede.
a) Escrevam no caderno, em notação científica, o valor de 1 googol.
b) Na opinião de vocês, esse número é grande ou pequeno? Isso significa queé muito provável ou pouco provável que Xiróder e Lúci se casem um dia?
c) Vocês já haviam ouvido falar em googol? Conversem a respeito disso e pesquisem informações sobre esse número.
12. (Etec-São Paulo) Os microprocessadores usam o sistema binário de numeração para tratamento de dados.
• No sistema binário, cada dígito abre parênteses0 ou 1fecha parênteses denomina-se bit (binary digit).
• Bit é a unidade básica para armazenar dados na memória do computador.
• Cada sequência de 8 bits, chamada de byte (binary term), corresponde a um determinado caractere.
• Um kilobyte (cá bê) corresponde a 2elevado a 10 bytes.
• Um megabyte (ême bê) corresponde a 2elevado a 10 quilobáites.
• Um gigabyte (gê bê) corresponde a 2elevado a 10 mégabáites.
• Um terabyte (tê bê) corresponde a 2elevado a 10 gigabáites.
Atualmente, existem microcomputadores que permitem guardar 160 gigabáites de dados binários, isto é, são capazes de armazenar n caracteres. Nesse caso, o valor máximo de n é:
a) 160 ⋅ 2elevado a 20
b) 160 ⋅ 2elevado a 30
c) 160 ⋅ 2elevado a 40
d) 160 ⋅ 2elevado a 50
e) 160 ⋅ 2elevado a 60
13. Considerando os dados apresentados na atividade anterior, faça o que se pede.
a) Certo agá dê externo tem capacidade de armazenamento de 3 térabáites. Calcule a quantidade de caracteres, no máximo, que esse agá dê é capaz de armazenar.
b)

Elabore um problema envolvendo medidas de armazenamento de dados em um computador.
Respostas e comentários
9. a) 10elevado a menos 6 métro
9. b) 0,0000023 métro; 2,3 ⋅ 10elevado a menos 6 métro
10. alternativa ê
11. a) 1 ⋅ 10elevado a 100
11. b) Espera-se que os estudantes respondam que se trata de um número grande, o que significa ser pouco provável que as personagens se casem um dia.
11. c) Resposta pessoal.
12. alternativa b
13. a) 3 ⋅ 2elevado a 40 caracteres
13. b) Resposta pessoal.
Orientações e sugestões didáticas
• Converse com os estudantes sobre aparelhos ou objetos que estão presentes no cotidiano deles e que utilizam unidades de medida como as exploradas na atividade 12. Por exemplo: pen-drives, CDs, dê vê dês e HDs externos.
• Resolução da atividade 12:
Pelo enunciado, temos:
1 giga báite = 2elevado a 10 mégabáites
1 mega báite = 2elevado a 10 quilobáites
1 quilo báite = 2elevado a 10 bytes
Portanto:
1 giga báite = 2elevado a 10 mégabáites = 2elevado a 10 ⋅ 2elevado a 10 quilobáites = = abre parênteses2elevado a 10 ⋅ 2elevado a 10 ⋅ 2elevado a 10fecha parênteses bytes = 2elevado a 30 bytes
160 giga báite = 160 ⋅ 2elevado a 30 bytes
Como cada byte corresponde a um determinado caractere, um microcomputador que permite guardar 160 gigabáites de dados binários é capaz de guardar 160 ⋅ 2elevado a 30 caracteres.
Logo, o valor máximo de n é 160 ⋅ 2elevado a 30.
alternativa b
• No item b da atividade 13, peça aos estudantes que compartilhem o problema elaborado com um colega e que resolvam o problema proposto por ele.

Trabalho em equipe
faça as atividades no caderno
Conhecendo o mundo microscópico
Justificativa
Com os telescópios, o ser humano pôde conhecer corpos e fenômenos que estão a enormes distâncias do planeta Terra; com os microscópios, pôde conhecer organismos inacreditavelmente pequenos, que vivem dentro e fóra do corpo humano. Para ampliar nosso universo de conhecimento, ultrapassando as fronteiras do mundo visível, é igualmente importante ter noção tanto das grandes quanto das pequenas dimensões que nos cercam.

Objetivo
• Pesquisar o mundo microscópico e as unidades de medida a ele relacionadas.
Apresentação
• Painel expositivo com imagens ampliadas de organismos visíveis somente ao microscópio, acompanhadas de informações sobre suas medidas e as correspondentes unidades.
Questões para pensar em grupo
• O que é importante saber a respeito do mundo microscópico?
• Convém pesquisar a invenção e a evolução do microscópio?
• Que tipos de avanço científico o estudo de lentes microscópicas possibilitou?
• Quais unidades de medida são adequadas a tamanhos tão pequenos? Como elas se relacionam com as unidades de medida que vocês já conhecem? A notação científica é a mais útil para expressar essas relações?
• Onde vocês podem obter as imagens ampliadas? O que convém colocar nas legendas dessas imagens?
• Seria interessante acrescentar imagens de corpos grandes, visíveis a ôlho nu (do corpo humano, por exemplo), para o estabelecimento de comparações com as dimensões dos microrganismos?
• Como vão organizar as informações coletadas no painel?
NÃO SE esqueçam
• Vocês podem selecionar imagens pequenas, de revistas especializadas, por exemplo, e ampliá-las em máquinas fotocopiadoras ou computadores.
• Vocês também podem produzir desenhos ampliados com base em figuras de livros e enciclopédias.
2 Raiz enésima de um número real
Raiz quadrada
No Capítulo 1, estudamos a raiz quadrada de 2.
Para determinar a raiz quadrada de um número real a, precisamos encontrar um número não negativo b que, multiplicado por ele mesmo, resulte em a.

Recorde
Podemos indicar uma raiz quadrada usando os símbolos:
Raiz quadrada com 2 no índice ou raiz quadrada sem o 2 no índice.
.
Orientações e sugestões didáticas
Trabalho em equipe
Objetivos
• Aplicar, por meio de trabalhos em grupo, os conceitos estudados.
• Favorecer o desenvolvimento das habilidades ê éfe zero nove ême ah zero quatro e ê éfe zero nove ême ah um oito, das competências gerais 9 e 10 e das competências específicas 7 e 8 da Bê êne cê cê.
Habilidades da BNCC
• Esta seção favorece o desenvolvimento das habilidades ê éfe zero nove ême ah zero quatro e ê éfe zero nove ême ah um oito porque os estudantes deverão reconhecer o uso de unidades para expressar medidas muito pequenas do mundo microscópico.
Orientações
• Para construir um painel que aborde medidas utilizadas no mundo microscópico, os estudantes trabalharão com pesquisa, análise e interpretação de dados sobre organismos visíveis apenas por meio de microscópio. É fundamental que eles trabalhem coletivamente e saibam argumentar, escutar os colegas com atenção e empatia, o que favorece o desenvolvimento das competências gerais 9 e 10 e das competências específicas 7 e 8 da Bê êne cê cê.
• É importante acompanhar as pesquisas e fazer as interferências necessárias para que a turma atinja o objetivo do trabalho.
Raiz enésima de um número real
Objetivos
• Compreender como se calcula a raiz enésima de um número real.
• Compreender a noção de radical, suas propriedades e mobilizá-las na resolução de problemas.
• Favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah zero quatro da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah zero quatro, uma vez que propõe aos estudantes que resolvam e elaborem problemas com números reais envolvendo a radiciação.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.
(ê éfe zero nove ême ah um oito) Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.
Competência geral 9: Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competência geral 10: Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.
Competência específica 7: Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
Competência específica 8: Interagir com seus pares de fórma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Então, para determinar a
Sentença matemática. Raiz quadrada de 2., precisamos encontrar um número não negativo que, multiplicado por ele mesmo, seja igual a 2. Como já vimos, esse número, com infinitas casas decimais que não se repetem periodicamente, é irracional.
= 1,4142135623730reticências
Para indicar
Sentença matemática. Raiz quadrada de 2., podemos escrever o número com algumas casas decimais seguidas de reticências
Sentença matemática. Raiz quadrada de 2, igual a 1 vírgula 414 reticências.ou usar o símbolo de aproximação (
Sentença matemática. Raiz quadrada de 2.≃ 1,414).
Podemos dizer, ainda, que a aproximação de
Sentença matemática. Raiz quadrada de 2.até a 2ª casa decimal ou até os centésimos é 1,41 por falta ou 1,42 por excesso. Isso significa que
Sentença matemática. Raiz quadrada de 2.está entre 1,41 e 1,42:

Nem toda raiz quadrada é um número irracional. Quando um número é racional e é um quadrado perfeito, sua raiz quadrada é um número racional.
Observação

A raiz quadrada de um número real a maior que zero equivale, geometricamente, à medida de comprimento
do lado de um quadrado cuja medida de área é a.
Exemplos
•
Sentença matemática. Raiz quadrada de 25.= 5, pois 5elevado a 2 = 25 e 5 > 0.
•
Sentença matemática. Raiz quadrada de 1,21 é igual a raiz quadrada de 121 sobre 100 e é igual a 11 sobre 10.= 1,1, pois 1,1elevado a 2 = 1,21 e 1,1 > 0.
Para verificar se um número é quadrado perfeito, podemos fatorá-lo. Acompanhe.
a) Vamos verificar se 441 é quadrado perfeito.
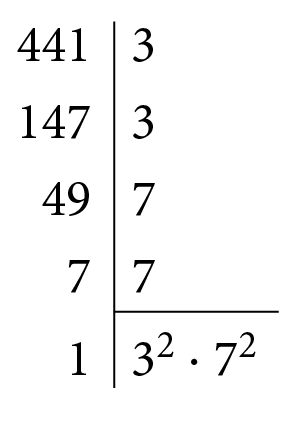
Logo: 441 = abre parênteses3 ⋅ 7fecha parênteseselevado a 2 = 21elevado a 2
Portanto, 441 é quadrado perfeito.
b) Vamos verificar se 2,25 é quadrado perfeito. Sabemos que: 2,25 =
Fração 225 sobre 100.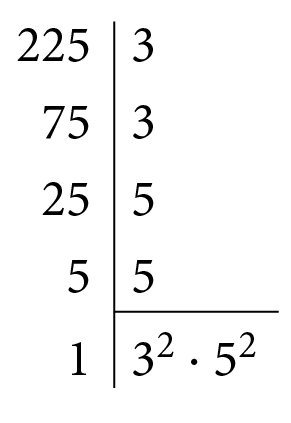
Logo:
2 vírgula 25, igual a, fração 225 sobre 100, igual a, fração abre parênteses, 3 vezes 5, fecha parênteses, ao quadrado sobre 10 ao quadrado, igual a fração, abre parênteses, 15 sobre 10, fecha parênteses, ao quadrado, é igual a, abre parênteses, 1 vírgula 5, fecha parênteses, ao quadrado.Portanto, 2,25 é quadrado perfeito.
A raiz quadrada de um número real pode ser um número racional, um número irracional ou um número que não é real.
As raízes quadradas de números reais negativos não são números reais, pois não existe número no conjunto dos números reais que, elevado ao quadrado, resulte em número negativo. Essas raízes serão estudadas no Ensino Médio.
Orientações e sugestões didáticas
Orientações
• Por definição, a raiz quadrada de um número a é um número b não negativo, tal que belevado a 2 = a.
Vale ressaltar que, quando nos deparamos com a resolução de uma equação como xelevado a 2 = 9, temos de atentar para o fato de que, para resolver a equação, ou seja, determinar o valor de x, não afirmamos que x = 3 ou x = menos3 por causa da raiz quadrada de 9, mas porque o número x que, elevado ao quadrado, resulta em 9 pode ser tanto 3 como menos3. Assim:
xelevado a 2 = 9
Sentença matemática. Raiz quadrada de x ao quadrado.
=
Sentença matemática. Raiz quadrada de 9.∣x∣ =
Sentença matemática. Raiz quadrada de 9.∣x∣ = 3
x = 3 ou x = menos3
(O número negativo, menos3, não veio da raiz de 9, mas decorre do módulo de x.)
Assim, resolver essa equação, por exemplo, significa determinar quais valores que, elevados ao quadrado, resultem em 9. E extrair a raiz quadrada de 9, por definição, é determinar o valor não negativo que, elevado ao quadrado, resulte em 9.
• Algumas vezes, quando é necessário calcular a raiz quadrada de um número decimal, ao escrevê-lo na fórma de fração, encontramos um valor grande no numerador, cuja raiz quadrada não sabemos. Então, podemos fatorar esse número para encontrar sua raiz quadrada, como feito no item b. Para calcular
Sentença matemática. Raiz quadrada de 2 vírgula 25., podemos fazer:
Raiz quadrada de fração 225 sobre 100
=
fração raiz quadrada de 15 ao quadrado sobre raiz quadrada de 10 ao quadrado=
fração 15 sobre 10= 1,5
Lembre-se: Escreva no caderno!
Raiz cúbica
Vamos analisar um cubo que mede 64 centímetros cúbicos de volume e arestas de medida de comprimento desconhecida.

Para calcular a medida a, da aresta do cubo, em centímetro, temos de encontrar um número que, quando multiplicado três vezes por ele mesmo, resulte em 64.
O número procurado é 4, pois 4 ⋅ 4 ⋅ 4 = 64.
Assim, a raiz cúbica de 64 é 4, e indicamos:
Símbolo de raiz com 3 no índice e 64 no radicando.= 4, pois 4elevado a 3 = 64.
Para determinar a raiz cúbica de um número real a, precisamos encontrar um número real b tal que belevado a 3 = a.
Exemplos
•
Sentença matemática. Raiz cúbica de 27.= 3, pois 3elevado a 3 = 27
•
Raiz cúbica de menos 64.= menos 4, pois abre parêntesesmenos 4fecha parênteseselevado a 3 = menos 64
•
Raiz cúbica de mil= 10, pois 10elevado a 3 = .1000
Há também raízes cúbicas que são números irracionais e podem ser aproximadas por falta ou por excesso. Por exemplo:
= 1,442249570307408reticências
Por falta,
Sentença matemática. Raiz cúbica de 3.é 1,442; por excesso,
Sentença matemática. Raiz cúbica de 3.é 1,443.
Observe que, em ambos os casos, há aproximação até a 3ª casa decimal ou até os milésimos:

Diferentemente do que ocorre no cálculo da raiz quadrada de um número real, a raiz cúbica de um número real é sempre um número real.
Raiz enésima
Podemos generalizar o índice e estudar raízes de índice n qualquer, ou seja, as raízes enésimas.
A raiz enésima de um número real a, que tem como índice um número natural n ⩾ 2, é assim representada:
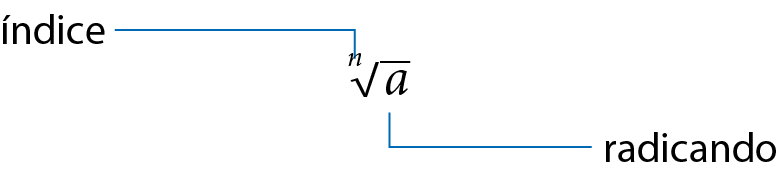
O cálculo da raiz enésima pode ser analisado considerando-se dois casos: o índice n par e o índice n ímpar.
Orientações e sugestões didáticas
• Para abordar a raiz enésima de um número real, retome com os estudantes os cálculos de raízes quadradas e cúbicas de um número real, pois eles já devem estar mais familiarizados com esse tipo de cálculo.
● Índice par
A raiz enésima de índice par de um número real a abre parêntesesa ⩾ 0fecha parênteses é o número real b abre parêntesesb ⩾ 0fecha parênteses tal que belevado a n = a.
= b se, e somente se, belevado a n = a e b ⩾ 0
Exemplos
•
Raiz quadrada da fração, 1 sobre 36, é igual a fração 1 sexto., pois
abre parênteses, fração um sexto, fecha parênteses, ao quadrado, é igual a fração 1 sobre 36e
1 sexto maior que 0.•
Raiz sexta de 729, é igual a 3, pois
3 elevado a 6, é igual a 729e 3 > 0
•
Sentença matemática. Raiz décima segunda de 1 é igual a 1., pois 1elevado a 12 = 1 e 1 > 0
Observação
Se a for um número real menor que zero, a raiz enésima de a, com n par, não será um número real, pois não existe número real que, elevado a um expoente par, resulte em um número negativo.
Exemplos:
•
Sentença matemática. Raiz quadrada de manos 81.∉
(lemos:
Sentença matemática. Raiz quadrada de menos 81.não pertence ao conjunto dos números reais)
•
Sentença matemática. Raiz quarta de menos 16.∉
(lemos:
Sentença matemática. Raiz quarta de menos 16.não pertence ao conjunto dos números reais)
Então, ∄ (não existe) no conjunto dos números reais os números
Sentença matemática. Raiz quadrada de menos 81.e
Sentença matemática. Raiz quarta de menos 16..
● Índice ímpar
A raiz enésima de índice ímpar de um número real a é o número real b tal que belevado a n = a.
= b se, e somente se, belevado a n = a
Exemplos
•
Raiz cúbica de menos 216, é igual a menos 6, pois
abre parênteses, menos 6, fecha parênteses, ao cubo, é igual a menos 216.
•
Raiz sétima de 128, é igual a 2, pois 2elevado a 7 = 128
•
Raiz quinta de 0 vírgula 00001, é igual a 0 vírgula 1, pois 0,1elevado a 5 = 0,00001

ATIVIDADES
faça as atividades no caderno
1. Determine, no caderno.
a)
Raiz cúbica de menos mil.
b)
Menos raiz quadrada de 121.
c)
Menos raiz cúbica de menos 64.d)
Raiz cúbica de 729.e)
Raiz quarta de 81.f)
Raiz cúbica da fração 1 sobre 27.
g)
Raiz quinta da fração 1 sobre 32.h)
Raiz quarta de 256.
i)
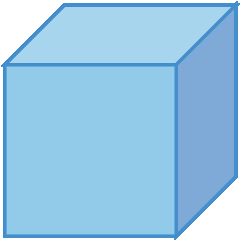
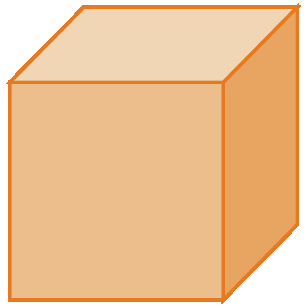
Raiz quinta de três mil cento e vinte e cinco.2. Calcule as medidas de comprimento das arestas de cada cubo.
a)
b)
3.

Determine, usando uma calculadora, a raiz aproximada até os centésimos, por falta e por excesso.
a)
Sentença matemática. Raiz quadrada de 5.b)
Sentença matemática. Raiz quadrada de 7.c)
Sentença matemática. Raiz quadrada de 10.d)
Sentença matemática. Raiz quadrada de 20.4.

Cada um dos números a seguir localiza-se entre dois números naturais consecutivos. Quais são esses números em cada caso? Calcule mentalmente e anote a resposta no caderno.
a)
Sentença matemática. Raiz quadrada de 75.b)
Sentença matemática. Raiz quadrada de 901.5.

Usando uma calculadora, determine as medidas de comprimento dos lados de cada quadrado com aproximação por falta até a 1ª casa decimal.
a)

b)

Respostas e comentários
1. a) menos10
1. b) menos11
1. c) 4
1. d) 9
1. e) 3
1. f)
Fração 1 sobre 3.1. g)
Fração 1 sobre 2.1. h) 4
1. i) 5
2. a) 9 centímetros
2. b) 0,3 métro
3. a) 2,23 e 2,24
3. b) 2,64 e 2,65
3. c) 3,16 e 3,17
3. d) 4,47 e 4,48
4. a)
Sentença matemática. Raiz quadrada de 75.está entre 8 e 9.
4. b)
Sentença matemática. Raiz quadrada de 901.está entre 30 e 31.
5. a) 18,7 métros
5. b) 31,6 centímetros
Orientações e sugestões didáticas
• Utilize os exemplos de raiz enésima de um número real para auxiliar a compreensão dos estudantes. Se possível, peça que calculem as raízes enésimas de alguns números reais utilizando uma calculadora científica e que também calculem raízes enésimas de índice par de números reais negativos para que percebam que no visor da calculadora aparecerá uma mensagem de êrro. Diante desse fato, comente que, se a for um número real menor que zero, a raiz enésima de a, com n par, não será um número real, pois não existe um número real que elevado a um número par resulte em um número negativo.
• Para obter as aproximações solicitadas na atividade 3, os estudantes podem ser agrupados em duplas ou trios e pode-se pedir a eles que realizem testes com números para encontrar, com o auxílio da calculadora, mas sem usar a tecla

, as aproximações pedidas. Para começar, eles devem encontrar entre quais números naturais estão as raízes procuradas. No item a, por exemplo,
Sentença matemática. Raiz quadrada de 5.está entre os números naturais 2 e 3; em seguida, os estudantes precisam fazer testes com números racionais com uma casa decimal e, para finalizar, com números de duas casas decimais.
Radicais
A raiz enésima
Raiz enésima de a., em que a é um número real e n é um número natural, com n ⩾ 2, é chamada também de radical.
São exemplos de radicais:
Sentença matemática. Raiz quadrada de 11, raiz quinta de 3, raiz cúbica de menos 1 vírgula 5 e raiz quarta de fração 1 16 avos..
Saiba mais
O símbolo que utilizamos para indicar a raiz
Símbolo. Raiz quadrada, o símbolo lembra o formato de uma letra r minúscula com o lado direito mais alongado com um traço horizontal na parte superior cobrindo o radicando.também é chamado de radical. Ele foi introduzido em 1525 pelo matemático alemão Christoff Rudolff, provavelmente por sua semelhança com o “r” minúsculo da palavra radix (“raiz”, em latim). Antes disso, usavam-se outros símbolos para representar a raiz de um número.
Propriedades dos radicais
As propriedades dos radicais podem ser usadas para simplificar os cálculos.
● 1ª propriedade
Observe um radical com índice ímpar.
, pois 5elevado a 3 = 125
Como 125 = 5elevado a 3, podemos escrever:
Sentença matemática. Raiz cúbica de 125, igual a raiz cúbica de 5 ao cubo, é igual a 5.Agora, considere um radical com índice par.
, pois 11elevado a 2 = 121 e 11 > 0
Como 121 = 11elevado a 2, podemos escrever:
Sentença matemática. Raiz quadrada de 121, igual a raiz quadrada de 11 ao quadrado, é igual a 11.
De modo geral:
Para todo número a real não negativo e n natural, com n ⩾ 2, temos:
= a
Exemplos
•
Sentença matemática. Raiz quadrada de 4 ao quadrado, é igual a 4.•
Sentença matemática. Raiz sexta de 7 elevado a sexta potência, é igual a 7.•
Sentença matemática. Raiz sétima de 1 vírgula 2 elevado a sétima potência, é igual a 1 vírgula 2.•
Sentença matemática. Raiz quinta de pi elevado a quinta potência, é igual a pi.Para investigar
a) Calcule o valor de
Sentença matemática. Raiz quadrada de, abre parênteses, menos 11, fecha parênteses, ao quadrado.
b) É correto afirmar que
Sentença matemática. Raiz quadrada de a ao quadrado, é igual a.?
● 2ª propriedade
Observe o que Aline percebeu.
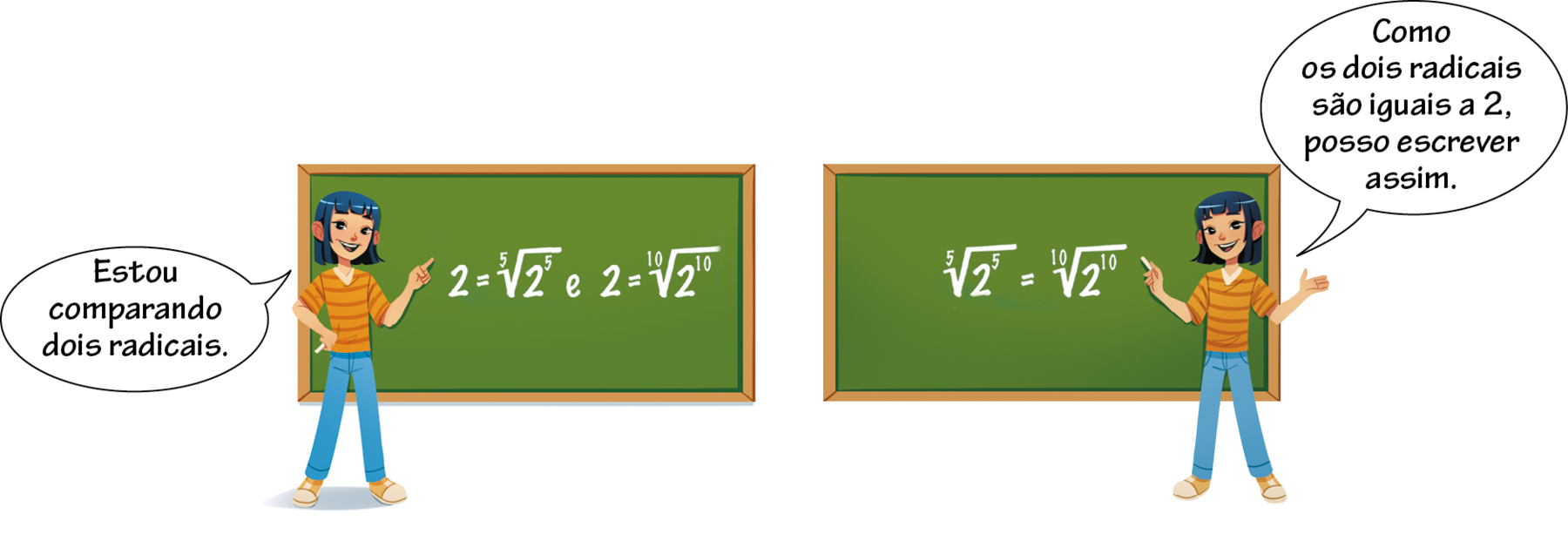
Orientações e sugestões didáticas
• A partir desta página são introduzidas as propriedades dos radicais. Conhecendo as propriedades dos radicais, os estudantes podem construir procedimentos próprios, a fim de realizar cálculos em problemas que envolvem o uso de radicais e em operações com números reais na forma de raiz. É importante que sejam propostas situações de aprendizagem que sejam desafiadoras e adequadas para que elas sejam, de fato, compreendidas e não apenas memorizadas. É a compreensão dessas propriedades, e não a memorização sem qualquer significado ou reflexão, que permitirá que elas sejam corretamente mobilizadas na resolução das atividades.
• Ao explorar o boxe Para investigar, peça aos estudantes que escolham alguns valores negativos para a e verifiquem se a igualdade é válida para os valores escolhidos. Espera-se que eles percebam que a igualdade não será válida para nenhum valor negativo de a que eles escolherem. Ressalte o fato de que a 1ª propriedade é válida somente para um número real a maior ou igual a zero.
Lembre-se: Escreva no caderno!
Observe que o radical
Sentença matemática. Raiz quinta de 2 elevado a quinta potência.pode ser obtido a partir de
Sentença matemática. Raiz décima de 2 elevado a décima potência.. Para isso basta dividir o índice e o expoente do radicando pelo divisor comum 2.
De modo geral, vale a seguinte propriedade:
Para todo número a real não negativo, m e n naturais, com n ⩾ 2, e p divisor comum de n e m com p ≠ n e p ≠ 0, temos:
Exemplos
•
Sentença matemática. Raiz décima segunda de 2 elevado a décima segunda potência, é igual a raiz cúbica de 2 elevado ao cubo.•
Sentença matemática. Raiz nona de 27 elevado ao cubo, é igual a raiz cúbica de 27 elevado a 1, é igual a 3.
•
Sentença matemática. Raiz décima quarta de 3 elevado a menos 7, é igual a raiz décima quarta de, abre parênteses, fração 1 terço, fecha parênteses, elevado a 7, é igual a, raiz quadrada de, abre parênteses, fração 1 terço, fecha parênteses.
•
Sentença matemática. Raiz índice 30 de, abre parênteses, fração 1 quinto, fecha parênteses, elevado a 25, é igual a raiz sexta de, abre parênteses, fração 1 quinto, fecha parênteses, elevado a 5.● 3ª propriedade
De modo geral, vale a seguinte propriedade:
Para a e b, números reais não negativos e n natural, com n ⩾ 2, temos:
Exemplos
•
Sentença matemática. Raiz quadrada de 4 vezes 10, é igual a raiz quadrada de 4 vezes raiz quadrada de 10.•
Sentença matemática. Raiz cúbica de, abre parênteses, fração 1 décimo, fecha parênteses, vezes 3 vírgula 43, é igual a raiz cúbica de fração 1 décimo vezes raiz cúbica de 3 vírgula 43.● 4ª propriedade
De modo geral, temos:
Para a e b, números reais não negativos, com b ≠ 0, e n natural, com n ⩾ 2, temos:
Exemplos
•
Sentença matemática. Raiz quadrada de fração 30 sobre 7, é igual a fração raiz quadrada de 30 sobre raiz quadrada de 7.•
Sentença matemática. Raiz cúbica de 0 vírgula 001, igual a raiz cúbica de fração 1 milésimo, igual a fração raiz cúbica de 1 sobre raiz cúbica de 1 mil, é igual a fração 1 décimo.Observação
Todas as propriedades apresentadas são válidas apenas para radicandos reais não negativos. As propriedades só serão válidas para radicandos negativos se os índices dos radicais forem ímpares. Exemplos:
•
Sentença matemática. Raiz cúbica de, abre parênteses, menos 2, fecha parênteses, elevado ao cubo, igual a raiz cúbica de menos 8, é igual a menos 2.•
Sentença matemática. Raiz índice 15 de, abre parênteses, menos 1, fecha parênteses, elevado ao cubo, igual a raiz índice 15 de menos 1, igual a menos 1, é igual a raiz quinta de menos 1.•
Sentença matemática. Raiz quinta de, abre parênteses, menos 1, fecha parênteses, vezes 243, igual a raiz quinta de menos 243, igual a menos 3, igual a raiz quinta de, abre parênteses, menos 1, fecha parênteses, vezes raiz quinta de 243.•
Sentença matemática. Raiz cúbica de fração menos 8 sobre 125, igual a fração menos 2 sobre 5, é igual a fração raiz cúbica de menos 8 sobre raiz cúbica de 125.Orientações e sugestões didáticas
• Se julgar conveniente, aprofunde a discussão de cada propriedade. Com relação à 4ª propriedade, em que
Raiz índice n de fração a sobre b.=
Fração: raiz índice n de a, sobre raiz índice n de b., por exemplo, se n é par, a e b devem ser números reais não negativos com b diferente de zero. Se n for ímpar, a e b podem ser quaisquer números reais, com b diferente de zero.
Lembre-se: Escreva no caderno!
Aplicação das propriedades dos radicais
● Extração de fatores do radicando
Aplicando as propriedades, podemos simplificar alguns radicais.
Exemplos
•
Raiz cúbica de 1 mil 728.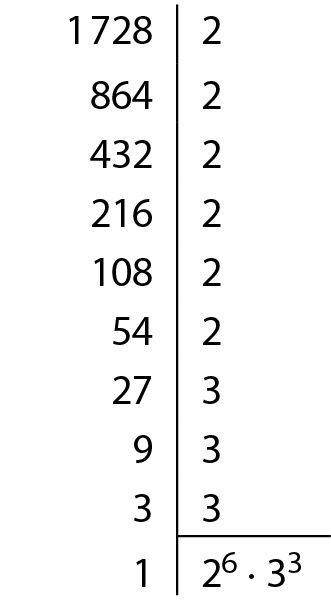
raiz cúbica de 1 mil 728, igual a raiz cúbica de 2 elevado a 6 vezes 3 ao cubo
=
raiz cúbica de 2 elevado a 6 vezes raiz cúbica de 3 ao cubo, igual a raiz cúbica de, abre parênteses, 2 ao quadrado, fecha parênteses, ao cubo vezes 3= 2elevado a 2 ⋅ 3 = 12
Nesse caso, como o radicando é um número racional e é possível extrair todos os fatores decompostos, a raiz é um número racional.
•
Raiz quadrada de 245.
Raiz quadrada de 245, igual a raiz quadrada de 7 ao quadrado vezes 5, igual a raiz quadrada de 7 ao quadrado vezes raiz quadrada de 5, é igual a 7 vezes raiz quadrada de 5.
Nesse caso, como nem todos os fatores podem ser extraídos, a raiz é um número irracional.
● Introdução de fatores externos no radicando
Assim como é possível extrair alguns ou todos os fatores de uma raiz, podemos introduzir fatores externos no radicando.
Exemplos
•
Sentença matemática. 2 vezes raiz quarta de 5, igual a raiz quarta de 2 elevado a quarta potência vezes raiz quarta de 5, igual a raiz quarta de 2 elevado a quarta potência vezes 5, igual a raiz quarta de 16 vezes 5, é igual a raiz quarta de 80.•
Sentença matemática. 3 ao quadrado vezes raiz cúbica de 2, igual a raiz cúbica de, abre parênteses, 3 ao quadrado, fecha parênteses, ao cubo vezes raiz cúbica de 2, igual a raiz cúbica de, abre parênteses, 3 ao quadrado, fecha parênteses, ao cubo vezes 2, igual a raiz cúbica de 729 vezes 2, é igual a raiz cúbica de 1 mil 458.
ATIVIDADES
faça as atividades no caderno
1. Decomponha o radicando em fatores primos e calcule o valor de cada radical.
a)
Sentença matemática. Raiz quinta de 32.
b)
Sentença matemática. Raiz cúbica de 343.
c)
Sentença matemática. Raiz cúbica de fração 729 sobre 64.
d)
Sentença matemática. Raiz quadrada de 121.
e)
Sentença matemática. Raiz quarta de fração 625 sobre 256.f)
Sentença matemática. Raiz quinta de fração 1 sobre 1 mil e 24.2. Decomponha o radicando em fatores primos e simplifique cada radical.
a)
Sentença matemática. Raiz décima quinta de 1 mil e 24.
b)
Sentença matemática. Raiz décima segunda de 256.
c)
Sentença matemática. Raiz sexta de 2 mil 187.
d)
Sentença matemática. Raiz quinta de 160.
e)
Sentença matemática. Raiz cúbica de 108.
f)
Sentença matemática. Raiz quarta de 16 mil 807.Respostas e comentários
1. a) 2
1. b) 7
1. c)
Fração 9 sobre 4.1. d) 11
1. e)
Fração 5 sobre 4.1. f)
Fração 1 sobre 4.2. a)
Sentença matemática. Raiz cúbica de 2 ao quadrado.2. b)
Sentença matemática. Raiz cúbica de 2 ao quadrado.2. c)
Sentença matemática. 3 vezes a raiz sexta de 3.2. d)
Sentença matemática. 2 vezes a raiz quinta de 5.2. e)
Sentença matemática. 3 vezes a raiz cúbica de 2 ao quadrado.2. f)
Sentença matemática. 7 vezes a raiz quarta de 7.Orientações e sugestões didáticas
• Neste tópico, mostra-se como aplicar algumas propriedades dos radicais para simplificar o cálculo de raízes enésimas de um número real. Reproduza os exemplos no quadro e enfatize as propriedades empregadas em cada passagem.
Lembre-se: Escreva no caderno!
3. Sabendo que
Sentença matemática. Raiz quadrada de 5.é aproximadamente igual a 2,24, calcule o valor aproximado de cada radical.
a)
Sentença matemática. Raiz quadrada de 125.
b)
Sentença matemática. Raiz quadrada de 20.
c)
Sentença matemática. Raiz quadrada de 500.
d)
Sentença matemática. Raiz quadrada de fração 1 quinto.
e)
Sentença matemática. Raiz quadrada de 605.
f)
Sentença matemática. Raiz quadrada de fração 45 quartos.
g)
Sentença matemática. Raiz quadrada de fração 80 sobre 81.
h)
Sentença matemática. Raiz quadrada de fração 720 sobre 441.
4. Calcule:
a)
Sentença matemática. Raiz cúbica de 512.
b)
Sentença matemática. Raiz quarta de 121 vezes raiz quarta de 121.
c)
Sentença matemática. Raiz quadrada de 2 mil 744 dividido por raiz quadrada de 14.
d)
Sentença matemática. Raiz quinta de 3 vírgula 2 vezes 10 elevado a seis.
e)
Sentença matemática. Raiz cúbica de fração 8 vezes 10 elevado a 9 sobre 27 vezes 10 elevado a 6.
5. Determine o valor de x em cada caso.
a)
Sentença matemática. Raiz décima segunda de 2 elevado a 8, é igual a raiz índice x de 2 ao quadrado.
b)
Sentença matemática. Raiz décima de 3 elevado a 15, é igual a raiz índice x de 3 ao cubo.
c)
Sentença matemática. Raiz índice 27 de 512, é igual a raiz cúbica de 2 elevado a x.
d)
Sentença matemática. Raiz décima de fração 81 sobre 625, é igual a raiz quinta de, abre parênteses, fração 3 sobre 5, fecha parênteses, elevado a x.
e)
Sentença matemática. Raiz índice x de fração 5 sobre 9, é igual a raiz sexta de fração 125 sobre 729.
f)
Sentença matemática. Raiz oitava de fração 2 mil 401 sobre 625, é igual a raiz índice x de fração 7 sobre 5.6. Luísa, Carla, Gabriel e Ricardo estavam estudando Matemática quando depararam com a sentença:
Sentença matemática. Raiz quadrada de 6, é igual a raiz quadrada de 2 vezes raiz quadrada de 3.
Então, eles concluíram que
Sentença matemática. Raiz quadrada de ab, é igual a raiz quadrada de a vezes raiz quadrada de b..
Em duplas, eles simplificaram a expressão
Sentença matemática. Raiz quadrada de menos 1 vezes raiz quadrada de menos 1..
Observe como cada dupla fez o cálculo.
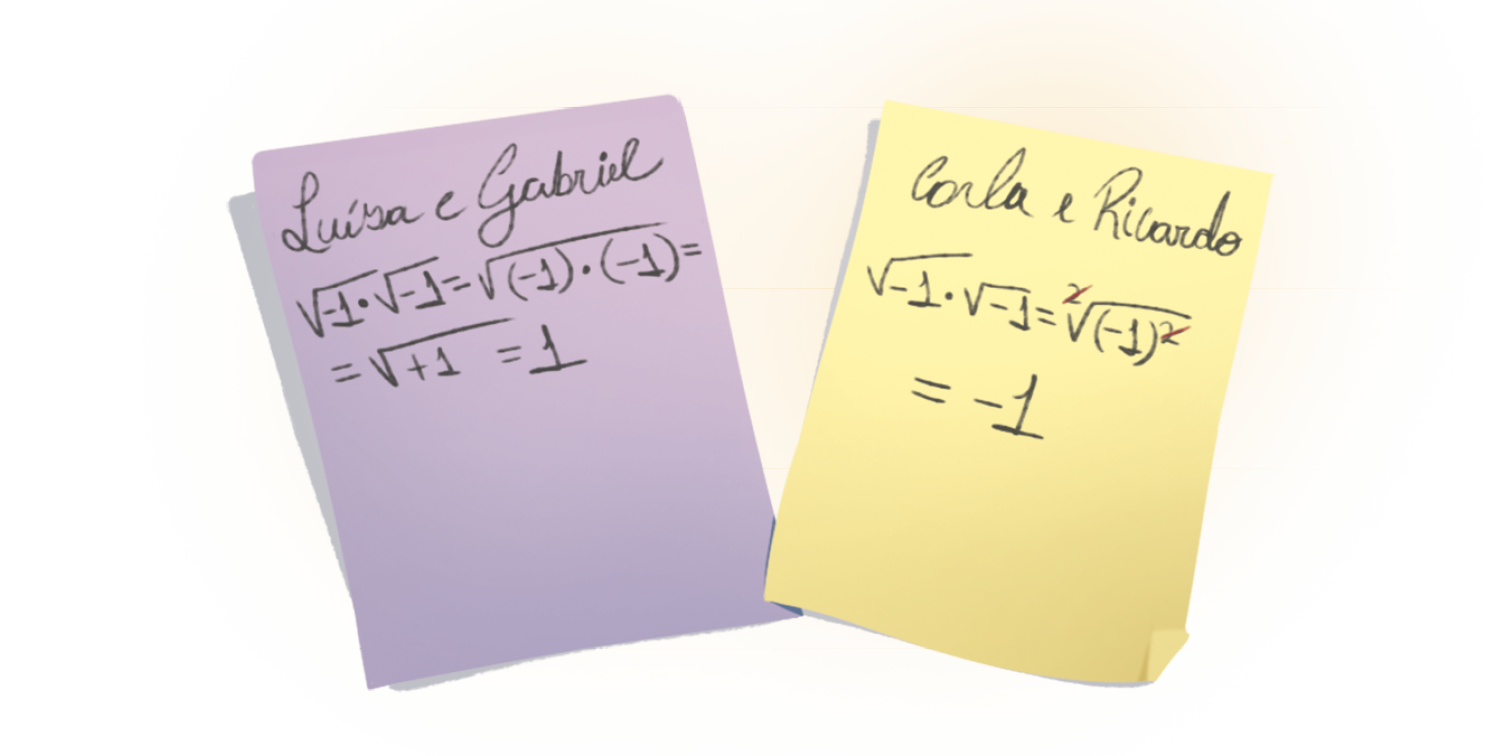
Cada dupla chegou a um resultado diferente. Em alguma etapa do raciocínio, houve um êrro.
Encontre o êrro.
7.

Resolva a expressão a seguir e escreva no caderno a alternativa correta.

a) 4elevado a 3
b) 1
c) 2elevado a 19
d) 2
Respostas e comentários
3. a) 11,2
3. b) 4,48
3. c) 22,4
3. d) 0,45
3. e) 24,6
3. f) 3,36
3. g) 1
3. h) 1,28
4. a) 8
4. b) 11
4. c) 14
4. d) 20
4. e)
Fração 20 sobre 3.5. a) 3
5. b) 2
5. c) 1
5. d) 2
5. e) 2
5. f) 2
6. A propriedade
Sentença matemática. Raiz quadrada de a vezes b é igual a raiz quadrada de a vezes a raiz quadrada de b.é válida somente para a e b reais não negativos.
Como o índice do radical é par, a propriedade
Sentença matemática. Raiz quadrada de a ao quadrado.= a também é válida somente para a real não negativo. Portanto, as duas duplas cometeram erros.
7. alternativa d
Orientações e sugestões didáticas
• Circule entre os estudantes observando, de fórma geral, os registros feitos e as atividades que exigem mais atenção para se chegar às respostas. Quando observar que a maioria dos alunos terminou, escreva as respostas no quadro para que possam conferi-las. Dessa maneira, já será possível fazer um “filtro” e saber quais questões merecem mais atenção.
• Aproveite a atividade 3 para discutir com os estudantes um outro modo de calcular uma raiz aproximada: com base no valor aproximado da raiz quadrada de 5 e com o uso da decomposição em fatores primos.

Compreender um texto
faça as atividades no caderno
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.

Saturno, um planeta colossal
Saturno é o sexto planeta a partir do Sol e o segundo maior planeta do Sistema Solar. Sua fama se dá, principalmente, por seus anéis, que são formados por bilhões de fragmentos de gêlo e rochas espaciais: alguns semelhantes a grãos de areia, outros do tamanho de uma casa. A medida da largura do sistema de anéis se estende até .282000 quilômetros de comprimento do planeta e é composto por sete anéis e lagunas.

A medida do raio de .58232 quilômetros de comprimento de Saturno é aproximadamente 9 vezes a medida do raio da Terra. Agora tente imaginar a Terra como se fosse do tamanho de uma moeda de um real. Saturno seria do tamanho de uma bola de vôlei.
Enquanto a Terra demora 365 dias para completar a volta ao redor do Sol, Saturno leva .10756 dias terrestres (29,4 anos terrestres). Em compensação, o dia em Saturno demora menos da metade do dia da Terra, isto é, o dia em Saturno é um dos mais curtos do Sistema Solar, levando apenas 10,7 horas.
Diferentemente do planeta Terra, que tem um único satélite natural, a Lua, Saturno tem 62. Mas como os planetas conseguem seus satélites? Umas das maneiras é capturando-os! Isso mesmo, capturando corpos que, até então, vagavam ao redor do Sol. Esses corpos são atraídos para a órbita do planeta e passam a ser suas luas.
Saturno, por sua vez, possui o segundo maior satélite do Sistema Solar, chamado Titã, que gira no sentido contrário ao qual o planeta gira sobre si. Tendo isso em vista, é bem provável que esse satélite seja um corpo “capturado”. Titã é maior que a lua da Terra e maior até que o planeta Mercúrio.
A medida de distância entre Titã e Saturno é de aproximadamente ..1192000 quilômetros de comprimento. Uma questão que intrigou os pesquisadores é como se formaram os satélites entre Saturno e Titã. Recentemente, foi descartada a possibilidade de que eles tenham se formado junto com o planeta, pois, por meio de estudos, concluiu-se que, assim como a Lua está se afastando da Terra, as luas de Saturno estão se afastando dele e, nesse caso, os satélites deveriam estar muito mais distantes do que estão.
Orientações e sugestões didáticas
Compreender um texto
Objetivos
• Desenvolver a competência leitora.
• Favorecer o desenvolvimento das habilidades ê éfe zero nove ême ah zero quatro e ê éfe zero nove ême ah um oito e das competências específicas 1 e 3 da Bê êne cê cê.
Habilidades da Bê êne cê cê
• Esta seção favorece o desenvolvimento das habilidades ê éfe zero nove ême ah zero quatro e ê éfe zero nove ême ah um oito ao propor problemas com números reais, em especial em notação científica, empregando unidades de medidas para expressar distâncias dentro do Sistema Solar.
Orientações
• Oriente os estudantes a realizar uma leitura silenciosa do texto. Em seguida, proponha à turma uma leitura conjunta. Caso julgue conveniente, faça pequenas pausas entre os parágrafos para que eles possam comentar os assuntos tratados em cada um deles. Por fim, incentive-os a compartilhar suas opiniões sobre o que foi lido.
• Se julgar pertinente, informe-lhes que Saturno está fortemente presente na cultura juvenil. Diga-lhes que esse planeta aparece em inúmeras histórias de ficção científica, filmes, histórias em quadrinhos e videogames.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.
(ê éfe zero nove ême ah um oito) Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.
Competência específica 1: Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
Competência específica 3: Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

Foi então que os pesquisadores levantaram a hipótese – comprovada após muitos cálculos – que todos os satélites entre Saturno e Titã são mais “jovens” e se formaram a partir dos próprios anéis do planeta, que fazem parte de um sistema ativo que gera novos corpos celestes.
Dados obtidos em: NASA SCIENCE. Solar System Exploration. Saturn. [sem local, 2022?]. Disponível em: https://oeds.link/hg0FLD. Acesso em: 18 julho 2022.

ATIVIDADES
faça as atividades no caderno
1. Qual é a ideia principal do texto que você acabou de ler?
2. Cite o nome de outros planetas que você conhece.
3. Qual é o segundo maior satélite do Sistema Solar? Quanto mede a distância, em quilômetro, entre esse satélite e Saturno? Escreva essa medida em notação científica.
4. De acôrdo com o texto, como se formaram os satélites entre Titã e Saturno?
5. Na página anterior, há uma imagem de Saturno do Telescópio Espacial Hubble da Nasa, de 20 de julho de 2019. Nesse registro, a que medida de distância Saturno estava da Terra? Escreva essa medida de distância em notação científica. (Dica: aproximar até os centésimos)
6. Para facilitar o trabalho com distâncias dentro do Sistema Solar, cientistas criaram a unidade astronômica (U A), que é a medida de distância média entre a Terra e o Sol. (Dica: aproximar até os centésimos)
uma ua = ...149597870700 quilômetros
a) Utilizando notação científica, escreva a medida de distância média, em quilômetro, entre a Terra e o Sol.
b) A medida da distância média aproximada entre alguns planetas e o Sol está no quadro a seguir. Escreva a medida de distância, em quilômetro, de cada planeta.
|
Planeta |
Medida da distância média (ua) |
|---|---|
|
Vênus |
0,7 |
|
Marte |
1,5 |
|
Júpiter |
5,2 |
|
Saturno |
9,5 |
|
Urano |
19,8 |
Respostas e comentários
1. Conhecer um pouco sobre Saturno e a formação dos seus satélites.
2. Resposta pessoal.
3. Titã. Aproximadamente 1,192 ⋅ 10elevado a 6 quilômetros
4. Todos os satélites entre Titã e Saturno se formaram a partir dos anéis do planeta, um depois do outro.
5. aproximadamente 1,36 ⋅ 10elevado a 9 quilômetros
6. a) 1,49 ⋅ 10elevado a 11 quilômetros
6. b) Respostas em Orientações.
Orientações e sugestões didáticas
• Na atividade 2, espera-se que os estudantes citem os outros planetas que compõem o Sistema Solar: Mercúrio, Vênus, Terra, Marte, Júpiter, Urano e Netuno. Caso não se recordem, oriente-os a realizar uma pesquisa em sites, livros ou revistas especializadas.
• No item b da atividade 6, verifique como os estudantes realizam a conversão solicitada. Se necessário, permita que trabalhem com a calculadora ou com um aplicativo de calculadora do smartphone. Caso opte pela segunda opção, informe-lhes que, em grande parte dos aplicativos de calculadora, é utilizado o símbolo ê (ou ê) para indicar a expressão “vezes 10 elevado a”. Resposta:
Vênus: 1,05 ⋅ 10elevado a 12
Marte: 2,24 ⋅ 10elevado a 12
Júpiter: 7,78 ⋅ 10elevado a 12
Saturno: 1,42 ⋅10elevado a 12
Urano: 2,96 ⋅ 10elevado a 12
• Se julgar conveniente, amplie o tema e peça aos estudantes que façam uma pesquisa sobre as cinco maiores luas e compartilhem com a turma. O tema proposto contribui para o desenvolvimento do Tema Contemporâneo Transversal Ciência e Tecnologia, da macroárea Ciência e Tecnologia.
3 Operações com radicais
Adição algébrica com radicais
Observe a adição algébrica:
= 2 + 3 = 5
A adição algébrica com radicais fica mais simples quando podemos extrair todas as raízes e efetuar o cálculo sem os radicais.
Exemplos
•
Raiz cúbica de 27 mais raiz cúbica de 125 menos raiz cúbica de 343.
= 3 + 5 menos 7 = 1
•
Raiz quarta de 0 vírgula 0625 menos raiz quarta de 0 vírgula 0001 menos raiz quarta de 0 vírgula 0256.= 0,5 menos 0,1 menos 0,4 = 0
Mesmo quando as raízes têm índices diferentes, devemos tentar extraí-las e, depois, efetuar os cálculos. Por exemplo:
= menos2 + 10 menos 1,3 = 6,7
Entretanto, nem sempre é possível extrair todas as raízes, pois alguma delas pode ser um número irracional. Vamos estudar outras maneiras de efetuar adições algébricas com radicais quando isso acontece.
Adição algébrica com radicais semelhantes
Chamamos de radicais semelhantes aquelas expressões que têm radicais com radicandos iguais e mesmo índice. Por exemplo:
•
Raiz cúbica de 15 e raiz cúbica de 15.são radicais semelhantes.
•
Raiz quadrada de 7 e 2 vezes a raiz quadrada de 7.são radicais semelhantes.
Quando há radicais semelhantes em uma expressão, colocamos em evidência o radical comum e efetuamos a adição algébrica indicada.
Exemplos
•
Sentença matemática. 3 raiz quadrada de 11 mais 7 raiz quadrada de 11, igual a, abre parênteses, 3 mais 7, fecha parênteses, raiz quadrada de 11, é igual a 10 raiz quadrada de 11.•
Sentença matemática. Raiz sétima de 9 menos fração raiz sétima de 9 sobre 2 mais fração raiz sétima de 9 sobre 3, igual a, abre parênteses, 1 menos 1 meio mais um terço, fecha parênteses, raiz sétima de 9, igual a fração 5 sextos raiz sétima de 9 ou fração 5 raiz sétima de 9 sobre 6.Para pensar
Observe a expressão com radicais não semelhantes:
Sentença matemática. Raiz quadrada de 2 mais raiz quadrada de 8 menos raiz quadrada de 50.•

Converse com um colega e pensem em uma maneira de efetuar essa adição. Em seguida, compartilhem a resolução com a turma.
Adição algébrica com radicais que se tornam semelhantes
Há expressões que não apresentam radicais semelhantes, mas contêm radicais que podem ser transformados em radicais semelhantes aplicando as propriedades dos radicais. Após realizar as transformações, efetuamos a adição algébrica com os radicais semelhantes.
Exemplos
•
Sentença matemática. Menos raiz cúbica de 40 menos raiz cúbica de 135 mais 2 raiz cúbica de 320, igual a menos 2 raiz cúbica de 5 menos 3 raiz cúbica de 5 mais 2 vezes 4 raiz cúbica de 5, é igual a 3 raiz cúbica de 5.•
Sentença matemática. Raiz sexta de 216 mais raiz quadrada de 24 menos raiz quarta de 576, igual a raiz sexta de 6 ao cubo mais raiz quadrada de 2 ao quadrado vezes 6 menos raiz quarta de 2 elevado a 4 vezes 6 ao quadrado, igual a.=
=
igual a raiz quadrada de 6 mais 2 raiz quadrada de 6 menos 2 raiz quadrada de 6, é igual a raiz quadrada de 6.
Respostas e comentários
Para pensar: Respostas pessoais.
Orientações e sugestões didáticas
Operações com radicais
Objetivos
• Identificar radicais semelhantes.
• Compreender como realizar adições, subtrações, multiplicações, divisões, potenciações e radiciações com radicais.
• Favorecer o desenvolvimento das habilidades ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro da Bê êne cê cê.
Habilidades da Bê êne cê cê
• Este tópico favorece o desenvolvimento das habilidades ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro porque os estudantes deverão operar com radicais para resolver e elaborar problemas.
Orientações
• Adicionar radicais é um procedimento no qual os estudantes podem enfrentar dificuldades. Por esse motivo, convém explorar o assunto de fórma cuidadosa e avaliar os enganos cometidos por eles na realização das atividades.
• Certifique-se de que os estudantes compreenderam cada uma das passagens dos exemplos apresentados.
• Na resolução da atividade proposta no boxe Para pensar, deixe que os estudantes sugiram fórmas de fazer a adição algébrica. Caso não surja a ideia de reduzir os termos a um radical semelhante, ou realizar aproximações, apresente os próximos itens e peça a eles que voltem a essa adição algébrica depois.
• Exemplo de resposta do boxe Para pensar:
Sentença matemática. Raiz quadrada de 2.
+
Sentença matemática. Raiz quadrada de 8.menos
Sentença matemática. Raiz quadrada de 50.=
=
Sentença matemática. Raiz quadrada de 2.+ 2
Sentença matemática. Raiz quadrada de 2.‒ 5
Sentença matemática. Raiz quadrada de 2.= menos 2
Sentença matemática. Raiz quadrada de 2.• No primeiro exemplo do tópico Adição algébrica com radicais que se tornam semelhantes, peça aos esudantes que fatorem 135 e 320 para que entendam por que
Sentença matemática. Raiz cúbica de 135.= 3
Sentença matemática. Raiz cúbica de 5.e
Sentença matemática. Raiz cúbica de 320.= 4
Sentença matemática. Raiz cúbica de 5..
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.
Observação
Adição algébrica com aproximações
Em algumas situações, o cálculo aproximado da adição algébrica é mais conveniente. Nesses casos, calculamos o valor aproximado de cada raiz e efetuamos a adição algébrica.
Acompanhe como Luciana efetuou a adição
Sentença matemática. Raiz quadrada de 5 mais raiz quadrada de 6..




Para analisar
Observe como Aline efetuou a adição
Raiz quadrada de 4 mais a raiz quadrada de 9..

O procedimento de Aline está correto? Por quê?

ATIVIDADES
faça as atividades no caderno
1. Calcule o valor de cada expressão.
a)
Sentença matemática. Raiz quadrada de 9 mais raiz quadrada de 16.
b)
Sentença matemática. Menos raiz quadrada de 25 mais raiz quadrada de 49.c)
Sentença matemática. Menos raiz cúbica de 8 mais raiz quadrada de 144.d)
Sentença matemática. Raiz quadrada de 100 menos raiz cúbica de 64.
e)
Sentença matemática. Menos raiz quadrada de 121 mais raiz quadrada de 196.f)
Sentença matemática. Raiz cúbica de 27 menos raiz quadrada de 9.
g)
Sentença matemática. Raiz quadrada de 169 menos raiz quadrada de 225.
h)
Sentença matemática. Raiz cúbica de 125 menos raiz cúbica de 8 mais raiz quadrada de 81.
i)
Sentença matemática. Raiz quadrada de 0 vírgula 04 menos raiz quadrada de 0 vírgula 09 mais raiz quadrada de 0 vírgula 16.j)
Sentença matemática. Raiz quadrada de fração 1 sobre 4 menos raiz quadrada de fração 1 sobre 9 mais raiz quadrada de fração 1 sobre 16.2. Calcule o valor de cada expressão considerando as aproximações:

a)
Sentença matemática. 3 raiz quadrada de 250 menos 4 raiz quadrada de 90.
b)
Sentença matemática. Raiz quadrada de 275 menos raiz quadrada de 99.
c)
Sentença matemática. 2 raiz quadrada de 99 mais 2 raiz quadrada de 44 mais 5 raiz quadrada de 7 menos raiz quadrada de 63.Respostas e comentários
Para analisar: Não. Está errado, pois:
= 2 + 3 = 5 ≠
Raiz quadrada de 13.1. a) 7
1. b) 2
1. c) 10
1. d) 6
1. e) 3
1. f) 0
1. g) menos2
1. h) 12
1. i) 0,3
1. j)
Fração 5 sobre 12.2. a) 9,48
2. b) 6,64
2. c) 38,5
Orientações e sugestões didáticas
• Mostre aos estudantes que existem situações em que, para dar mais significado ao resultado, é necessário fazer aproximações. Para isso, dê outros exemplos além do apresentado na página e mostre os cálculos necessários.
• Verifique se algum estudante tem a ideia incorreta de que
Sentença matemática. Raiz índice n de a mais b.é equivalente a
Raiz enésima de a.+
Raiz índice n de b.ou de que
Sentença matemática. Raiz índice n de a menos b.é equivalente a
Raiz enésima de a.menos
Raiz índice n de b., sendo a e b números reais maiores ou iguais a zero e n um número natural maior ou igual a 2. Trabalhe o boxe Para analisar, cuja finalidade é auxiliar os estudantes a superar essa eventual concepção equivocada.
• Na atividade 1, a maior parte dos números apresentados tem raiz quadrada exata, então ficará mais claro para os estudantes analisar o que pode e o que não pode ser feito no caso de adições algébricas com radicais.
• Na atividade 2, espera-se que os estudantes façam a decomposição dos números em fatores primos para escrevê-los da fórma mais simplificada e, assim, usar as raízes aproximadas já indicadas no enunciado. Vale lembrá-los de que todos os resultados obtidos são aproximados, uma vez que já utilizaram um valor aproximado dado.
3.


Elabore uma adição ou uma subtração de radicais cujo resultado se aproxime do número 0,2.
Passe sua expressão para um colega calcular e calcule o valor da expressão que ele elaborou.
Depois, respondam quem escreveu a expressão cujo valor é mais próximo de 0,2.
4.

Com uma calculadora, efetue as adições aproximando as raízes até a 2ª casa decimal. Escreva as adições e os resultados no caderno.
a)
Sentença matemática. Raiz quadrada de 2 mais raiz quadrada de 5.b)
Sentença matemática. Raiz quadrada de 10 mais raiz quadrada de 9.c)
Sentença matemática. Raiz quadrada de 3 mais raiz quadrada de 12.5. Efetue as adições algébricas.
a)
Sentença matemática. Raiz quadrada de 10 mais 2 raiz quadrada de 10 menos 5 raiz quadrada de 10.b)
Sentença matemática. 3 raiz quadrada de 8 menos raiz quadrada de 18 mais 2 raiz quadrada de 32.c)
Sentença matemática. Raiz cúbica de 81 mais 2 raiz cúbica de 24 menos 3 raiz cúbica de 375.d)
Sentença matemática. Raiz quadrada de 50 menos raiz quadrada de 300 menos raiz quadrada de 98 mais raiz quadrada de 363.e)
Sentença matemática. 5 raiz quadrada de 8 menos 2 raiz quadrada de 18 mais fração 1 meio raiz quadrada de 200.f)
Sentença matemática. 3x raiz quadrada de x vezes y elevado ao cubo menos xy raiz quadrada de 4xy menos 2 raiz quadrada de x ao cubo vezes y ao cubo., com x ⩾ 0 e y ⩾ 0
g)
Sentença matemática. 3 raiz quadrada de a ao cubo menos a vezes raiz quadrada de a mais fração raiz quadrada de a elevado a 5 sobre a., com a > 0
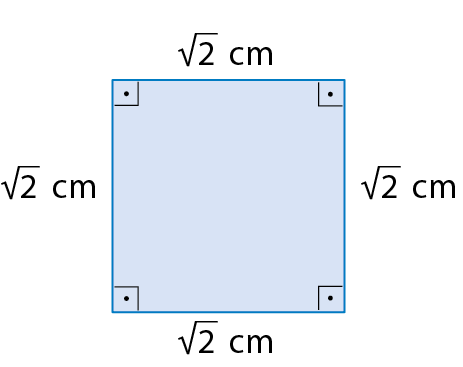
6. Determine a medida do perímetro de cada figura.
a)
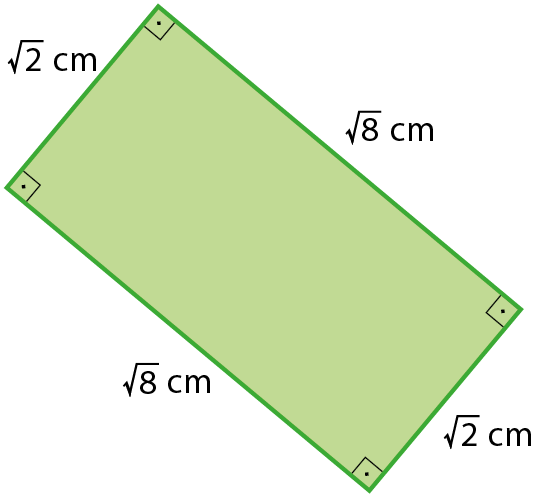
b)
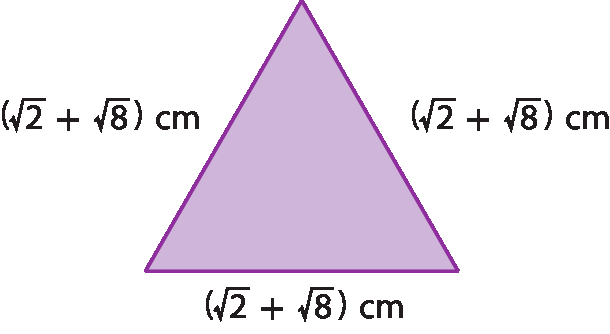
c)
d)

Multiplicação e divisão com radicais
Para multiplicar ou dividir radicais de mesmo índice, usamos a 3ª e a 4ª propriedades dos radicais. Observe os exemplos.
• Para a multiplicação de radicais, fazemos:
Sentença matemática. Raiz quinta de 4 vezes raiz quinta de 8, igual a raiz quinta de 4 vezes 8, igual a raiz quinta de 32, igual a raiz quinta de 2 elevado a quinta potência, é igual a 2.
• Para a divisão de radicais, fazemos:
Sentença matemática. Fração raiz cúbica de 9 sobre raiz cúbica de 3, igual a raiz cúbica de fração 9 sobre 3, é igual a raiz cúbica de 3.
Para pensar

Converse com um colega e pensem em uma fórma de efetuar a multiplicação de raízes com índices diferentes:
Sentença matemática. Raiz quarta de 3 vezes raiz quinta de 7.Respostas e comentários
3. Resposta pessoal.
4. a) 1,41 + 2,24 = 3,65
4. b) 3,16 + 3 = 6,16
4. c) 1,73 + 3,46 = 5,19
5. a)
Sentença matemática. Menos 2 raiz quadrada de 10.5. b)
Sentença matemática. 11 raiz quadrada de 2.5. c)
Sentença matemática. Menos 8 raiz cúbica de 3.5. d)
Sentença matemática. Raiz quadrada de 3 menos 2 raiz quadrada de 2.5. e)
Sentença matemática. 9 raiz quadrada de 2.5. f)
Sentença matemática. Menos xy raiz quadrada de xy.5. g)
Sentença matemática. 3 vezes a vezes raiz quadrada de a.6. a)
Sentença matemática. 4 raiz quadrada de 2 centímetros.6. b)
Sentença matemática. 6 raiz quadrada de 2 centímetros.6. c)
Sentença matemática. 9 raiz quadrada de 2 centímetros.6. d)
Sentença matemática. 22 raiz quadrada de 3 centímetros.Para pensar: Resposta pessoal.
Orientações e sugestões didáticas
• Na atividade 6, os números irracionais estão representando medidas (no caso, são medidas de comprimento dos lados de alguns polígonos). Aproveite para retomar com os estudantes que o aparecimento dos números irracionais ao longo da história se deu justamente por causa das medidas.
• Ao trabalhar a multiplicação e a divisão com radicais, reproduza os exemplos no quadro e enfatize as passagens em que a 3ª e a 4ª propriedades são empregadas.
• No boxe Para pensar, deixe que as duplas analisem o problema e sugiram maneiras de fazer a multiplicação de raízes com índices diferentes. Em seguida, peça que cada dupla compartilhe com o resto da turma como pensou. Espera-se que todos os estudantes percebam que é preciso reduzir os radicais ao mesmo índice e, depois, efetuar a multiplicação.
Quando os índices dos radicais são diferentes, é preciso reduzir os radicais ao mesmo índice e, depois, efetuar a multiplicação ou a divisão. Para fazer isso, podemos usar a 2ª propriedade dos radicais. Considere, por exemplo, como Henrique efetuou
Sentença matemática. Raiz quadrada de 2 vezes raiz cúbica de 2 ao quadrado..


ATIVIDADES
faça as atividades no caderno
1. Efetue as operações no caderno.
a)
Sentença matemática. Raiz quadrada de 4 vezes raiz quadrada de 16.
b)
Sentença matemática. Raiz cúbica de 5 vezes raiz cúbica de 25.
c)
Sentença matemática. Raiz cúbica de 18 vezes raiz cúbica de 6.
d)
Sentença matemática. Raiz quadrada de 2 vezes raiz quadrada de 10 vezes raiz quadrada de 15.e)
Sentença matemática. Raiz quadrada de 6 dividido por raiz quadrada de 3.f)
Sentença matemática. Fração raiz quadrada de 24 sobre raiz quadrada de 6.
g)
Sentença matemática. Raiz cúbica de 10 dividido por raiz cúbica de 2.
h)
Sentença matemática. Fração raiz quadrada de 120 sobre raiz quadrada de 3.
2. Calcule o valor de cada expressão.
a)
Expressão matemática. Raiz quadrada de 6 vezes, abre parênteses, raiz quadrada de 15 mais raiz quadrada de 60, fecha parênteses.
b)
Expressão matemática. Raiz quadrada de 3 vezes, abre parênteses, raiz quadrada de 54 menos raiz quadrada de 6, fecha parênteses.c)
Expressão matemática. Abre parênteses, raiz quadrada de 3 menos 1, fecha parênteses, vezes, abre parênteses, raiz quadrada de 3 mais 1, fecha parênteses.d)
Expressão matemática. Abre parênteses, 2 menos raiz quadrada de 2, fecha parênteses, vezes, abre parênteses, 2 mais raiz quadrada de 2, fecha parênteses.e)
Expressão matemática. Abre parênteses, raiz quadrada de 2 mais 1, fecha parênteses, vezes, abre parênteses, raiz quadrada de 2 mais 1, fecha parênteses.3. Encontre o valor aproximado das expressões.
(Considere:
Sentença matemática. Raiz quadrada de 5.≃ 2,2.)
a)
Sentença matemática. 2 raiz quadrada de 5 mais 7 raiz quadrada de 5.b)
Sentença matemática. Abre parênteses, 5 raiz quadrada de 5, fecha parênteses, vezes, abre parênteses, raiz quadrada de 5 elevado a 4, fecha parênteses.c)
Sentença matemática. Abre parênteses, 5 raiz quadrada de 5, fecha parênteses, ao quadrado menos 3 raiz quadrada de 5.d)
Sentença matemática. Raiz quadrada de 125 dividido por raiz quadrada de 625.
e)
Sentença matemática. Raiz quadrada de 45 mais raiz quadrada de 20 menos 5 raiz quadrada de 5.f)
Sentença matemática. Raiz quadrada de 5 mais 2 raiz quadrada de 25.4. Efetue as operações.
a)
Sentença matemática. Raiz quadrada de 2 dividido por raiz cúbica de 2.
b)
Sentença matemática. Raiz quarta de 3 ao cubo vezes raiz quadrada de 3 elevado a 4.
c)
Sentença matemática. Fração raiz cúbica de 3 sobre raiz quadrada de 2.
d)
Sentença matemática. Fração raiz quarta de 5 vezes raiz cúbica de 6 sobre raiz quadrada de 15.
5. Calcule a medida do perímetro e a da área dos retângulos representados a seguir.
a)

b)

Potenciação e radiciação com radicais
Observe uma potenciação com radicais.
De modo geral, para efetuar a potenciação com um radical em que o radicando é número real positivo, elevamos o radicando ao expoente dado:
Sentença matemática. Abre parênteses, raiz índice n de a, fecha parênteses, elevado a m, é igual a raiz índice n de a elevado a m., em que a > 0, n é um número natural, com n ⩾ 2, e m é um número inteiro.
Respostas e comentários
1. a) 8
1. b) 5
1. c)
Sentença matemática. 3 raiz cúbica de 4.1. d)
Sentença matemática. 10 raiz quadrada de 3.1. e)
Sentença matemática. Raiz quadrada de 2.1. f) 2
1. g)
Sentença matemática. Raiz cúbica de 5.1. h)
Sentença matemática. 2 raiz quadrada de 10.2. a)
Sentença matemática. 9 raiz quadrada de 10.2. b)
Sentença matemática. 6 raiz quadrada de 2.2. c) 2
2. d) 2
2. e)
Sentença matemática. 3 mais 2 raiz quadrada de 2.3. a) 19,8
3. b) 275
3. c) menos1,6
3. d) 0,44
3. e) 0
3. f) 12,2
4. a)
Sentença matemática. Raiz sexta de 2.4. b)
Sentença matemática. 9 raiz quarta de 3 ao cubo.4. c)
Sentença matemática. Fração raiz sexta de 9 sobre 8.4. d)
Sentença matemática. Fração raiz décima segunda de 16 sobre 1 mil 125.5. a) medida do perímetro:
Sentença matemática. 2, abre parênteses, 2 mais 3 raiz quadrada de 2, fecha parênteses, metros.métros medida da área:
Sentença matemática. 4, abre parênteses, raiz quadrada de 2 mais 1, fecha parêntesesmétros quadrados
5. b) medida do perímetro:
Sentença matemática. 4 raiz quadrada de 5 centímetros.medida da área: 4 centímetros quadrados
Orientações e sugestões didáticas
• Após realizarem as atividades propostas, incentive os estudantes a se reunir com os colegas para que possam comparar as respostas obtidas e corrigir eventuais erros. Esse é o momento em que eles podem verificar diferentes métodos e processos de resolução, justificando-os.
• No estudo da potenciação e da radiciação com radicais, pode haver uma tendência à memorização dos procedimentos sem atribuir significado a eles. Sempre que possível, faça os estudantes recorrerem à definição dessas operações.
Exemplos
•
Sentença matemática. Abre parênteses, raiz quadrada de 5, fecha parênteses, ao cubo, igual a raiz quadrada de 5 ao cubo, igual a raiz quadrada de 5 ao quadrado vezes 5, é igual a 5 raiz quadrada de 5.•
Sentença matemática. Abre parênteses, raiz cúbica de 3, fecha parênteses, elevado a menos 2, igual a raiz cúbica de 3 elevado a menos 2, igual a raiz cúbica de fração 1 sobre 3 ao quadrado, igual a fração raiz cúbica de 1 sobre raiz cúbica de 3 ao quadrado, é igual a fração 1 sobre raiz cúbica de 3 ao quadrado.•
Sentença matemática. Abre parênteses, 2 raiz cúbica de 3, fecha parênteses, elevado a 5, igual a 2 elevado a cinco vezes raiz cúbica de 3 elevado a 5, igual a 32 vezes raiz cúbica de 3 ao cubo vezes 3 ao quadrado, igual a 32 vezes 3 vezes raiz cúbica de 3 ao quadrado, é igual a 96 raiz cúbica de 3 ao quadrado.•
Sentença matemática. Abre parênteses, 6 raiz quadrada de 4 menos x, fecha parênteses, ao quadrado, igual a 6 ao quadrado vezes raiz quadrada de, abre parênteses, 4 menos x, fecha parênteses, ao quadrado, igual a 36 vezes, abre parênteses, 4 menos x, fecha parênteses.= 144 ‒ 36x, com x < 4
Para entender o procedimento da radiciação com radicais, compare as expressões:
As duas expressões são iguais a 3. Então:
Sentença matemática. Raiz quadrada de raiz cúbica de 729, é igual a raiz sexta de 729, é igual a 3.De modo geral, para efetuar a radiciação fazemos:
Sentença matemática. Raiz índice m de raiz índice n de a, é igual a raiz índice m vezes n de a.em que a ⩾ 0 e m e n são números naturais maiores ou iguais a 2.
Exemplos
•
Sentença matemática. Raiz cúbica de raiz quadrada de 2, igual a raiz índice 3 vezes 2 de 2, é igual a raiz sexta de 2.•
Sentença matemática. Raiz quadrada de raiz cúbica de fração 1 mil sobre 64, igual a raiz índice 2 vezes 3 de fração 1 mil sobre 64, igual a raiz sexta de fração 1 mil sobre 64, igual a raiz sexta de fração 10 ao cubo sobre 2 elevado a 6, igual a fração raiz sexta de 10 ao cubo sobre raiz sexta de 2 elevado a 6, é igual a fração raiz quadrada de 10 sobre 2.
ATIVIDADES
faça as atividades no caderno
1. Calcule as potências.
a)
Sentença matemática. Abre parênteses, raiz quadrada de 7, fecha parênteses, ao cubo.
b)
Sentença matemática. Abre parênteses, 3 raiz quadrada de 5, fecha parênteses, ao quadrado.
c)
Sentença matemática. Abre parênteses, raiz quadrada de fração 3 quartos, fecha parênteses, ao cubo.
d)
Sentença matemática. Abre parênteses, raiz quarta de 9, fecha parênteses, ao quadrado.
e)
Sentença matemática. Abre parênteses, 2 raiz quinta de 27, fecha parênteses, elevado a 4.
f)
Sentença matemática. Abre parênteses, 3 raiz quadrada de 2a mais 1, fecha parênteses, ao quadrado.2. Escreva, no caderno, como uma única raiz.
a)
Sentença matemática. Raiz quadrada de raiz cúbica de 64.
b)
Sentença matemática. Raiz oitava de raiz quinta de 6.
c)
Sentença matemática. Raiz quadrada de 3 de raiz quadrada de 4.
d)
Sentença matemática. 2 raiz quadrada de 2 de raiz quadrada de 2.
3. Dados a = 5 +
Sentença matemática. Raiz quadrada de 3.e b = 5 menos
Sentença matemática. Raiz quadrada de 3., determine:
a) a + b
b) a menos b
c) aelevado a 2
d) belevado a 2
e) a · b
f) b menos a
4. Classifique cada igualdade em verdadeira ou falsa.
a)
Sentença matemática. Raiz quadrada de raiz quadrada de 2, é igual a, abre parênteses, raiz quadrada de 2, fecha parênteses, ao quadrado.b)
Sentença matemática. Raiz quadrada de raiz quadrada de 9, é igual a, raiz quadrada de 3.c)
Sentença matemática. Abre parênteses, raiz cúbica de 2, fecha parênteses, elevado a 6, é igual a, 2 ao quadrado.d)
Sentença matemática. Raiz cúbica de 3 de raiz quadrada de 3, é igual a, raiz sexta de 27.5.

Faça o que se pede.
Elabore uma expressão envolvendo operações com radicais cujo valor final seja um número racional.
6. Observe o paralelepípedo a seguir e determine a medida de seu volume.
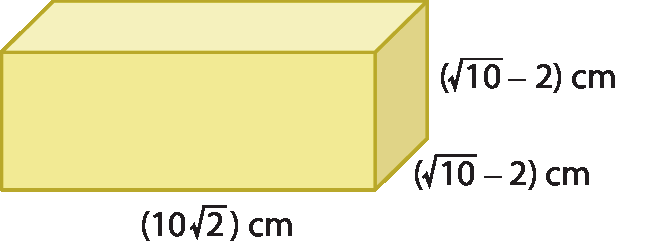
Respostas e comentários
1. a)
Sentença matemática. 7 Raiz quadrada de 7.1. b) 45
1. c)
Fração de numerador 3 raiz quadrada de 3 e denominador 8.1. d) 3
1. e)
Sentença matemática. 144 raiz quinta de 9.1. f) 18a + 9, com a >
Menos fração 1 sobre 2.2. a)
Sentença matemática. Raiz sexta de 64.2. b)
Sentença matemática. Raiz índice 40 de 6.2. c)
Sentença matemática. Raiz quarta de 36.2. d)
Sentença matemática. Raiz quarta de 128.3. a) 10
3. b)
Sentença matemática. 2 raiz quadrada de 3.3. c)
Sentença matemática. 28 mais 10 raiz quadrada de 3.3. d)
Sentença matemática. 28 menos 10 raiz quadrada de 3.3. e) 22
3. f)
Sentença matemática. Menos 2 raiz quadrada de 3.4. a) falsa
4. b) verdadeira
4. c) verdadeira
4. d) verdadeira
5. Resposta pessoal.
6.
Sentença matemática. Abre parênteses, 140 raiz quadrada de 2 menos 80 raiz quadrada de 5, fecha parênteses, centímetros cúbicos.Orientações e sugestões didáticas
• Após a realização das atividades, peça aos estudantes que se organizem em duplas. Cada membro da dupla deve perguntar ao outro sobre as atividades que considerou mais difíceis, para então compararem as resoluções e, por fim, indicarem ao professor as dúvidas que ainda persistiram.
4 Racionalização de denominadores
Algumas frações apresentam no denominador uma raiz não exata, ou seja, um número irracional. Dada uma dessas frações, podemos obter outra fração, equivalente a ela, que tenha como denominador um número racional. O procedimento usado para isso é chamado racionalização do denominador.
Esse procedimento é possível quando o denominador é um número com infinitas casas decimais não periódicas. Por exemplo, para calcular
Sentença matemática. Fração 1 sobre raiz quadrada de 2., sabemos que:
= 1,4142135623730reticências
Teríamos, então:
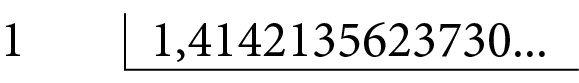
Mesmo que usássemos uma aproximação de
Sentença matemática. raiz quadrada de 2., ou seja, 1,4142135, mas a divisão seria trabalhosa. Observe.
Lembre-se: Escreva no caderno!

O processo de racionalização do denominador consiste em multiplicar a fração dada por uma fração equivalente a 1, de modo que o produto dos denominadores seja um número racional.
Então, no exemplo
Sentença matemática. Fração 1 sobre raiz quadrada de 2., temos:
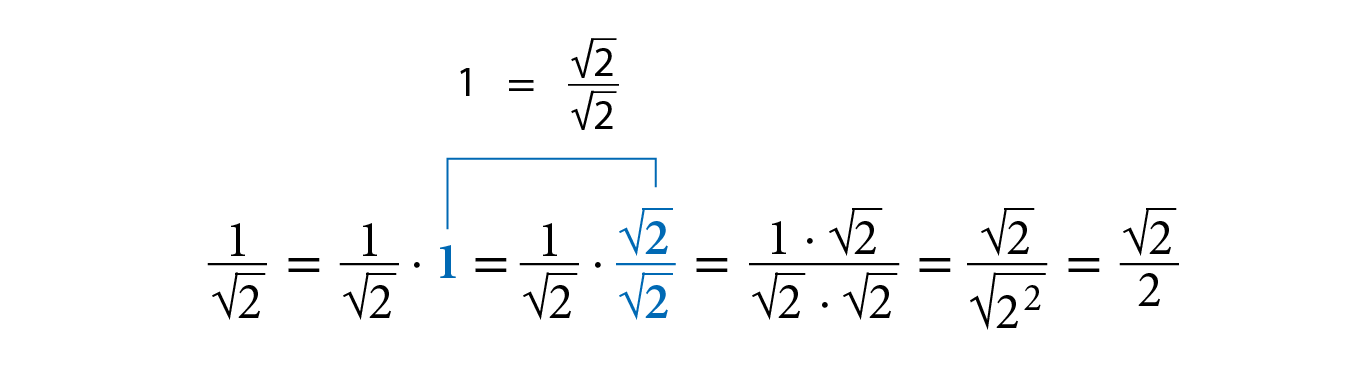
Note que, após a racionalização, obtemos uma fração equivalente à primeira, mas com denominador racional.
Calcular
Sentença matemática. Fração raiz quadrada de 2 sobre 2.é mais simples que calcular
Sentença matemática. Fração 1 sobre raiz quadrada de 2..
Orientações e sugestões didáticas
Racionalização de denominadores
Objetivos
• Racionalizar denominadores.
• Favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah zero três da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah zero três da Bê êne cê cê porque trabalha a realização de cálculos com números reais.
Orientações
• Aqui vale destacar que o termo “racionalizar” vem de “tornar racional”. Nas expressões apresentadas com denominadores irracionais, torná-los racionais facilita os cálculos. O exemplo apresentado nesta página contribui para que os estudantes percebam a vantagem da racionalização do denominador.
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
Lembre-se: Escreva no caderno!
Exemplos
• Vamos racionalizar o denominador de
Sentença matemática. Fração 2 sobre 3 raiz quadrada de 8..
Sentença matemática. Fração 2 sobre 3 raiz quadrada de 8, igual a fração 2 sobre 3 raiz quadrada de 8 vezes fração raiz quadrada de 8 sobre raiz quadrada de 8, igual a fração 2 raiz quadrada de 8 sobre 3 vezes 8, igual a fração 2 raiz quadrada de 8 sobre 24, igual a fração raiz quadrada de 8 sobre 12, igual a fração raiz quadrada de 2 ao quadrado vezes 2 sobre 12, igual a fração 2 raiz quadrada de 2 sobre 12, é igual a fração raiz quadrada de 2 sobre 6. Destaque em azul para a fração raiz quadrada de 8 sobre raiz quadrada de 8.
• Vamos racionalizar o denominador de
Sentença matemática. Fração 3 sobre raiz quarta de 3..
Sentença matemática. Fração 3 sobre raiz quarta de 3, igual a fração 3 sobre raiz quarta de 3 vezes fração raiz quarta de 3 ao cubo sobre raiz quarta de 3 ao cubo, igual a fração 3 raiz quarta de 3 ao cubo sobre raiz quarta de 3 elevado a 4, igual a fração 3 raiz quarta de 3 ao cubo sobre 3, igual a raiz quarta de 3 ao cubo. Destaque em azul para a fração raiz quarta de 3 ao cubo sobre raiz quarta de 3 ao cubo.
E quando, no denominador da fração, há uma adição algébrica em que pelo menos uma das parcelas é um número irracional?
Para entender por qual fração equivalente a 1 é necessário multiplicar as frações de modo que os denominadores sejam números racionais, observe o que ocorre quando, dados dois números reais a e b, fazemos abre parêntesesa + bfecha parênteses ⋅ abre parêntesesa menos bfecha parênteses.
Aplicamos a propriedade distributiva:
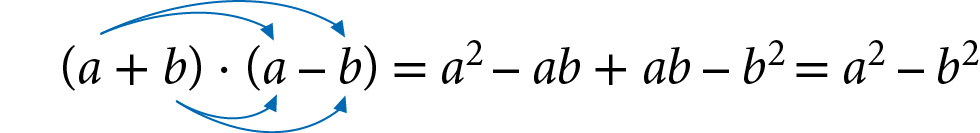
Então: abre parêntesesa + bfecha parênteses ⋅ abre parêntesesa menos bfecha parênteses = aelevado a 2 menos belevado a 2
Usando esse resultado, temos, por exemplo:
Exemplos
• Vamos racionalizar o denominador de
Sentença matemática. Fração 3 sobre raiz quadrada de 3, fim da raiz, mais 1..
Para racionalizá-lo, vamos multiplicar a fração por
Sentença matemática. Fração raiz quadrada de 3, fim da raiz, menos 1 sobre raiz quadrada de 3, fim da raiz, menos 1..
Sentença matemática. Fração 3 sobre raiz quadrada de 3, fim da raiz, mais 1, igual a fração 3 sobre raiz quadrada de 3, fim da raiz, mais 1 vezes fração raiz quadrada de 3, fim da raiz, menos 1 sobre raiz quadrada de 3, fim da raiz, menos 1, igual a fração 3 vezes, abre parênteses, raiz quadrada de 3, fim da raiz, menos 1, fecha parênteses, sobre, abre parênteses, raiz quadrada de 3, fecha parênteses, ao quadrado menos, abre parênteses, 1, fecha parênteses, ao quadrado, igual a fração 3 raiz quadrada de 3, fim da raiz, menos 3 sobre 3 menos 1, é igual a fração 3 raiz quadrada de 3, fim da raiz, menos 3 sobre 2. Destaque em azul para a fração raiz quadrada de 3, fim da raiz, menos 1 sobre raiz quadrada de 3, fim da raiz, menos 1.
• Vamos racionalizar o denominador de
Sentença matemática. Fração 2 sobre raiz quadrada de 2 mais raiz quadrada de 5..
Nesse denominador, há uma adição de dois números irracionais. Para racionalizá-lo, vamos multiplicar a fração por
Sentença matemática. Fração raiz quadrada de 2 menos raiz quadrada de 5 sobre raiz quadrada de 2 menos raiz quadrada de 5..
Sentença matemática. Fração 2 sobre raiz quadrada de 2 mais raiz quadrada de 5 vezes fração raiz quadrada de 2 menos raiz quadrada de 5 sobre raiz quadrada de 2 menos raiz quadrada de 5, igual a fração 2 vezes, abre parênteses, raiz quadrada de 2 menos raiz quadrada de 5, fecha parênteses, sobre, abre parênteses, raiz quadrada de 2, fecha parênteses, ao quadrado menos, abre parênteses, raiz quadrada de 5, fecha parênteses, ao quadrado, igual a fração 2 raiz quadrada de 2 menos 2 raiz quadrada de 5 sobre 2 menos 5, é igual a menos fração, abre parênteses, 2 raiz quadrada de 2 menos 2 raiz quadrada de 5, fecha parênteses, sobre 3. Destaque em azul para a fração raiz quadrada de 2 menos raiz quadrada de 5 sobre raiz quadrada de 2 menos raiz quadrada de 5.
Orientações e sugestões didáticas
• Nesta página são apresentados outros exemplos de racionalização dos denominadores de alguns números. Reproduza alguns desses exemplos no quadro e peça aos estudantes que completem os cálculos.
• Se julgar conveniente, comente com os estudantes que na racionalização de
Sentença matemática. Fração 2 sobre 3 raiz quadrada de 8.poderíamos multiplicar o numerador e o denominador por
Sentença matemática. Raiz quadrada de 2.. O importante é obter no denominador uma raiz que resulte em um número racional.
• Vamos racionalizar o denominador de
Sentença matemática. Fração raiz quadrada de 6 sobre 4 menos raiz quadrada de 5..
Sentença matemática. Fração raiz quadrada de 6 sobre 4 menos raiz quadrada de 5 vezes fração 4 mais raiz quadrada de 5 sobre 4 mais raiz quadrada de 5, igual a fração raiz quadrada de 6 vezes, abre parênteses, 4 mais raiz quadrada de 5, fecha parênteses, sobre 4 ao quadrado menos, abre parênteses, raiz quadrada de 5, fecha parênteses, ao quadrado, igual a fração 4 raiz quadrada de 6 mais raiz quadrada de 30 sobre 16 menos 5, é igual a fração 4 raiz quadrada de 6 mais raiz quadrada de 30 sobre 11. Destaque em azul para a fração 4 mais raiz quadrada de 5 sobre 4 mais raiz quadrada de 5.

ATIVIDADES
faça as atividades no caderno
1. Racionalize o denominador dos números a seguir.
a)
Sentença matemática. Fração 1 sobre raiz quadrada de 3.b)
Sentença matemática. Fração 3 sobre 2 raiz quadrada de 5.
c)
Sentença matemática. Fração 2 sobre raiz quadrada de 8.d)
Sentença matemática. Fração raiz quadrada de 5 menos raiz quadrada de 3 sobre raiz quadrada de 3.
e)
Sentença matemática. Fração 3 mais raiz quadrada de 3 sobre raiz quadrada de 3.
f)
Sentença matemática. Fração 10 sobre 2 menos raiz quadrada de 2.g)
Sentença matemática. Fração 3 sobre raiz quadrada de 5 mais raiz quadrada de 3.h)
Sentença matemática. Fração raiz quadrada de 2 sobre raiz quadrada de 3, fim da raiz, menos 1.
i)
Sentença matemática. Fração raiz quadrada de 11, fim da raiz, mais 1 sobre raiz quadrada de 11, fim da raiz, menos 1.
j)
Sentença matemática. Fração 7 sobre 2 mais raiz quadrada de 5.
2. Determine o número a que satisfaz a expressão a seguir.

3. Racionalize o denominador e faça o que se pede.
a) Sabendo que
Sentença matemática. Raiz quadrada de 5.é aproximadamente 2,24 (aproximação até os centésimos), determine o valor aproximado de
Sentença matemática. Fração 4 sobre raiz quadrada de 5, fim da raiz, menos 1..
b) Sabendo que
Sentença matemática. Raiz quadrada de 7.é aproximadamente 2,65 e que
Sentença matemática. Raiz quadrada de 3.é aproximadamente 1,73 (aproximações até os centésimos), determine o valor aproximado de
Sentença matemática. Fração 20 sobre raiz quadrada de 7 mais raiz quadrada de 3..
4. Simplifique as expressões.
a)
Sentença matemática. Fração raiz quadrada de 120 sobre raiz quadrada de 3.b)
Sentença matemática. Fração raiz cúbica de a elevado a 10 sobre raiz cúbica de a elevado a 4., com a ≠ 0
c)
Sentença matemática. Fração raiz quarta de 81 vezes x elevado a 7 sobre raiz quarta de x ao cubo., com x > 0
d)
Sentença matemática. Fração raiz quadrada de 5 vezes raiz quadrada de 8 sobre raiz quadrada de 10.5 Potência com expoente fracionário
Vimos como é definida uma potência de base real e expoente inteiro. O expoente de uma potência, porém, pode ser um número na fórma de fração; por exemplo:
Sentença matemática. 3 elevado a fração 1 meio,,
Sentença matemática. Abre parênteses, fração 1 quinto, fecha parênteses, elevado a fração 4 terços.e
Sentença matemática. 2 elevado a fração 2 quintos..
As propriedades de potências com expoentes inteiros vistas neste Capítulo são válidas nos casos em que o expoente é um número na fórma de fração e a base é um número real positivo. Assim, temos, por exemplo:
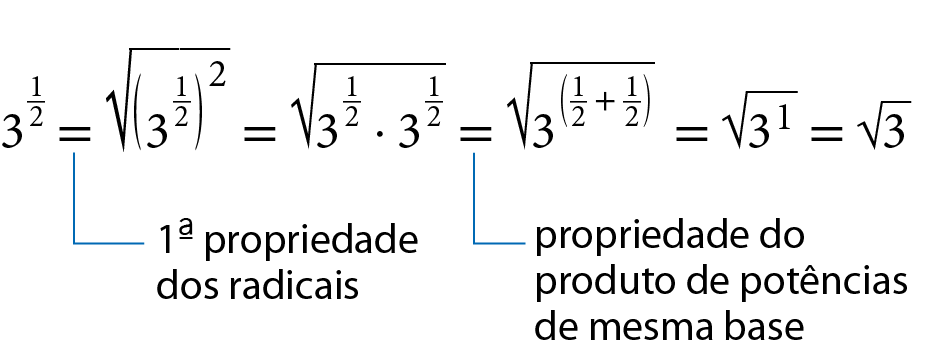
Portanto:
Sentença matemática. 3 elevado a fração 1 meio, é igual a raiz quadrada de 3.Respostas e comentários
1. a)
Sentença matemática. Fração raiz quadrada de 3 sobre 3.1. b)
Sentença matemática. Fração 3 raiz quadrada de 5 sobre 10.1. c)
Sentença matemática. Fração raiz quadrada de 2 sobre 2.1. d)
Sentença matemática. Fração raiz quadrada de 15, fim da raiz, menos sobre 3.1. e)
Sentença matemática. Raiz quadrada de 3 mais 1.1. f)
Sentença matemática. 5, abre parênteses, raiz quadrada de 2, fim da raiz, mais 2, fecha parênteses.1. g)
Sentença matemática. Fração 3, abre parênteses, raiz quadrada de 5 menos raiz quadrada de 3 sobre 2.1. h)
Sentença matemática. Fração raiz quadrada de 6 mais raiz quadrada de 2 sobre 2.1. i)
Sentença matemática. Fração 6 mais raiz quadrada de 11 sobre 5.1. j)
Sentença matemática. Menos 14 mais 7 raiz quadrada de 5.2.
Fração menos 3 sobre 283. a) 3,24
3. b) 4,60
4. a)
Sentença matemática. 2 raiz quadrada de 10.4. b) aelevado a 2
4. c) 3x
4. d) 2
Orientações e sugestões didáticas
• É importante salientar que a ideia principal, na atividade 3, é substituir as raízes pelos seus valores aproximados depois da racionalização em cada expressão.
• Na atividade 4, não é necessário racionalizar os denominadores, pois em todos os itens é possível simplificar as expressões.
Potência com expoente fracionário
Objetivos
• Calcular potências com expoente fracionário.
• Favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah zero três da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah zero três da Bê êne cê cê porque os estudantes deverão calcular potências com expoentes fracionários.
Orientações
• Inicie o tópico comentando com os estudantes que as propriedades de potências com expoentes inteiros continuam válidas quando o expoente da potência é um número na fórma de fração e a base é um número real positivo.
• Podemos estender a definição para uma potência de base negativa. Como o denominador do expoente será o índice da raiz, se ele for ímpar a base poderá ser negativa. Por exemplo:
abre parêntesesmenos27
elevado à fração 1 terço.=
Sentença matemática. Raiz cúbica de menos 27.= menos3
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
Procedendo do mesmo modo:
•
Sentença matemática. Abre parênteses, fração 1 quinto, fecha parênteses, elevado a fração 4 terços, igual a raiz cúbica de, abre colchete, abre parênteses, fração 1 quinto, fecha parênteses, elevado a fração 4 terços, fecha colchetes, elevado ao cubo, igual a raiz cúbica de, abre parênteses, fração 1 quinto, fecha parênteses, elevado a fração 4 terços vezes, abre parênteses, fração 1 quinto, fecha parênteses, elevado a fração 4 terços vezes, abre parênteses, fração 1 quinto, fecha parênteses, elevado a fração 4 terços, é igual a raiz cúbica de, abre parênteses, fração 1 quinto, fecha parênteses, elevado a 4.•
Sentença matemática. 2 elevado a fração 2 quintos, igual a raiz quinta de, abre parênteses, 2 elevado a fração 2 quintos, fecha parênteses, elevado a 5, igual a raiz quinta de 2 elevado a fração 2 quintos vezes 2 elevado a fração 2 quintos vezes 2 elevado a fração 2 quintos, vezes 2 elevado a fração 2 quintos vezes 2 elevado a fração 2 quintos, é igual a raiz quinta de 2 ao quadrado.Da mesma fórma, podemos escrever outras potências de expoente fracionário como um radical. De modo geral:
Para todo número real positivo a, m inteiro e n natural, com n ⩾ 2, temos:
Exemplos
•
Sentença matemática. 4 elevado a fração menos 1 meio, igual 4 elevado a fração menos 1 meio, igual a raiz índice 2 de 4 elevado a menos 1, igual a raiz quadrada de fração 1 quarto, é igual a fração 1 meio.•
Sentença matemática. Abre parênteses, fração 2 sétimos, fecha parênteses, elevado a fração 3 quartos, igual a raiz quarta de, abre parênteses, fração 2 sétimos, fecha parênteses, elevado ao cubo, é igual a raiz quarta de fração 8 sobre 343.•
Sentença matemática. Pi elevado a fração 2 quintos, é igual a raiz quinta de pi ao quadrado.
ATIVIDADES
faça as atividades no caderno
1. Expresse cada potência na fórma de radical.
a)
Sentença matemática. 43 elevado a fração 1 nono.b)
Sentença matemática. 7 elevado a fração menos 2 terços.c)
Sentença matemática. Abre parênteses, fração 1 quarto, fecha parênteses, elevado a fração 1 quarto.d)
Sentença matemática. Abre parênteses, 0 vírgula 25, fecha parênteses, elevado a fração 5 sobre 12.2. Calcule o valor das expressões.
a)
Sentença matemática. 81 elevado a fração 1 quarto mais 81 elevado a fração menos 1 quarto.b)
Sentença matemática. 8 elevado a fração 1 terço vezes 125 elevado a fração 2 terços.c)
Sentença matemática. 343 elevado a fração 4 terços dividido por 49 elevado a 0 vírgula 5.d)
Sentença matemática. 36 elevado a fração 3 meios menos 32 elevado a fração 2 quintos.3. Expresse as potências como radicais e os radicais como potências.
a)
Sentença matemática. Raiz quadrada de raiz quadrada de 5 ao quadrado.b)
Sentença matemática. Abre parênteses, 3 ao quadrado, fecha parênteses, elevado a fração 1 terço.c)
Sentença matemática. Raiz quinta de raiz quadrada de 3 vezes raiz quarta de 2.d)
Sentença matemática. 3 vezes raiz cúbica de 2 de raiz cúbica de 2 de raiz quadrada de 2.e)
Sentença matemática. Raiz cúbica de raiz quadrada de 18.f)
Sentença matemática. Abre parênteses, 2 elevado a fração 1 quinto, fecha parênteses, elevado a fração 2 terços.g)
Sentença matemática. Raiz quadrada de raiz quadrada de raiz quadrada de 30.h)
Sentença matemática. Raiz quadrada de 2 de raiz quadrada de 2 de raiz quadrada de 2.4. Calcule o valor de n para que:
Sentença matemática. Abre parênteses, 1 nono, fecha parênteses, elevado a n, igual a 2 mil 187.Respostas e comentários
1. a)
Sentença matemática. Raiz nona de 43.1. b)
Sentença matemática. Raiz cúbica de fração 1 sobre 7 ao quadrado.1. c)
Sentença matemática. Raiz quarta de fração 1 quarto ou raiz quadrada de fração 1 meio.1. d)
Sentença matemática. Raiz índice 12 de fração 0 vírgula 25 elevado a 5 ou raiz sexta de 0 vírgula 5 elevado a 5.2. a)
Fração 10 sobre 3.2. b) 50
2. c) 343
2. d) 212
3. a)
Sentença matemática. 5 elevado a fração 1 meio.3. b)
Sentença matemática. Raiz cúbica de 3 ao quadrado.3. c)
Sentença matemática. 3 elevado a fração 1 sobre 10 vezes 2 elevado a fração 1 sobre 20.3. d)
Sentença matemática. 3 vezes 2 elevado a fração 1 meio.3. e)
Sentença matemática. 18 elevado a fração 1 sexto.3. f)
Sentença matemática. Raiz índice 15 de 2 ao quadrado.3. g)
Sentença matemática. 30 elevado a fração 1 oitavo.3. h)
Sentença matemática. 2 elevado a fração 7 oitavos.4.
Fração menos 7 sobre 2.Orientações e sugestões didáticas
• Durante a realização das atividades, oriente os estudantes a escrever os cálculos de fórma organizada em seus cadernos. Isso contribui para que consigam desenvolver o raciocínio de maneira organizada, evitando erros de cálculo.
6 Porcentagem
Situação 1

Leia o texto a seguir.
Com base no Sistema Alarmes (Alerta de Área com Monitoramento Estimado por Satélite), do Laboratório de Aplicações de Satélites Ambientais da Universidade Federal do Rio de Janeiro (Lasa-ú éfe érre jota), o Instituto Socioambiental da Bacia do Alto Paraguai SOS Pantanal divulgou que os incêndios de 2020 no Pantanal foram os piores da história do bioma, resultando em mais de 26% de seu território consumidos pelo fogo, até então representado por ..15034903 hectares de medida de área, atingindo principalmente o Pantanal norte (Poconé, Barão de Melgaço e Cáceres) e a Serra do Amolar, no Pantanal sul.

No texto, há um dado em fórma de porcentagem: 26%
Esse valor significa “26 em cada 100” e pode ser expresso como
Fração 26 sobre 100.ou 0,26.
Segundo os dados, foram consumidos pelo fogo 26% da medida de área de ..15034903 hectares. Uma das fórmas de calcular 26% de ..15034903 é:
26% de ..15034903 =
Fração 26 sobre 100.· ..15034903 ≃ ..3909075
Então, ..3909075 dos ..15034903 hectares do território pantaneiro foram consumidos pelo fogo.
Situação 2
Em uma loja de eletrodomésticos, certo modêlo de televisor custava R$ 1.500,00mil quinhentos reais. Depois de um aumento, esse aparelho passou a custar R$ 1.620,00mil seiscentos e vinte reais. Vamos calcular o aumento em porcentagem.
O aumento no preço foi de: R$ 1.620,00mil seiscentos e vinte reais menos R$ 1.500,00mil quinhentos reais = R$ 120,00cento e vinte reais
Para calcular a taxa percentual t que esse aumento representa em relação ao valor inicial, fazemos:
Logo, o aumento no preço foi de 8%.
Situação 3
Joana comprou um jôgo cujo preço original era R$ 72,00setenta e dois reais, mas estava em promoção, com desconto de 30%. Ao passar no caixa, como tinha o cartão de fidelidade da loja, Joana conseguiu mais um desconto de 10% sobre o valor promocional. Quanto ela pagou pelo jôgo?
Vamos responder a essa pergunta calculando o preço do jôgo após cada desconto.
Calculamos o preço do jôgo após o 1º desconto:

Orientações e sugestões didáticas
Porcentagem
Objetivos
• Retomar o conceito de porcentagem.
• Calcular acréscimos e descontos.
• Favorecer o desenvolvimento das habilidades ê éfe zero nove ême ah zero cinco e ê éfe zero nove ême ah um oito e da competência específica 6 da Bê êne cê cê.
Habilidades da Bê êne cê cê
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah zero cinco, pois serão exploradas situações que envolvem o cálculo de descontos e acréscimos, bem como apresentadas situações que envolvem o cálculo de taxas percentuais sucessivas com ou sem o uso de calculadora. Também favorece a habilidade ê éfe zero nove ême ah um oito ao trabalhar e expressar medida de área muito grande como o hectare.
Orientações
• O conceito de porcentagem é retomado por meio de diferentes situações. Sempre que possível, oriente os estudantes a mobilizar as representações nas fórmas de fração e decimal de uma porcentagem, pois isso pode contribuir não somente para a apreensão desse conceito como também na otimização dos cálculos.
• A situação 1 mostra como o conceito de porcentagem está presente no cotidiano. Chame a atenção dos estudantes para a unidade de medida de área empregada no texto (hectare, representado por agá ah). Verifique o que eles já sabem sobre essa unidade de medida e então explique que é bastante empregada para medir áreas rurais e que, 1 éctare corresponde a .10000 métros quadrados. Amplie a situação proposta e informe que, em 2021, o Pantanal teve 9% de seu território incendiado; então, peça a eles que calculem quantos hectares foram queimados em 2021. (aproximadamente ..1353141 hectares)
• Conversar com os estudantes sobre assuntos como esse favorece o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental, da macroárea Meio Ambiente.
• A situação 2 expressa um aumento por meio de uma porcentagem. Converse com os estudantes sobre situações cotidianas em que devemos fazer esse tipo de cálculo. Reproduza o cálculo no quadro e tire as eventuais dúvidas da turma.
• As situações 3 e 4 mostram como calcular descontos e acréscimos sucessivos. Converse com os estudantes sobre situações cotidianas em que esse tipo de cálculo é aplicado.
(ê éfe zero nove ême ah zero cinco) Resolver e elaborar problemas que envolvam porcentagens, com a ideia de aplicação de percentuais sucessivos e a determinação das taxas percentuais, preferencialmente com o uso de tecnologias digitais, no contexto da educação financeira.
(ê éfe zero nove ême ah um oito) Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.
Competência específica 6: Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Lembre-se: Escreva no caderno!
Como o segundo desconto foi aplicado sobre o valor promocional, temos:

Portanto, após os descontos, Joana pagou R$ 45,36quarenta e cinco reais e trinta e seis centavos pelo jôgo.
Observação
Ter dois descontos sucessivos, o primeiro de 30% e o seguinte de 10%, não é equivalente a um desconto de 40%. Caso Joana tivesse recebido apenas um desconto de 40%, o preço pago pelo jôgo seria:
R$ 72,00setenta e dois reais menos 0,40 ⋅ R$ 72,00setenta e dois reais = R$ 43,20quarenta e três reais e vinte centavos
Situação 4
Paula tem uma loja de calçados. Em determinada ocasião, ela reduziu o preço de todos os calçados em 15%. Depois, com o intuito de voltar ao preço original, Paula aumentou o preço em 15%. Ela atingiu o objetivo?
Para verificar, vamos ver o que ocorre quando um valor x sofre um desconto de 15% seguido de um aumento de 15%.
•
preço após o desconto:
x menos 0,15 vezes x, igual a 0,85 x.• preço com o aumento sobre o novo valor:
0,85x mais 0,15 vezes 0,85x, igual a 0,85x mais 0,1275x, igual a 0,9775x
Assim, um produto com preço x, após um desconto de 15% seguido de um aumento de 15%, passará a custar 0,9775x ou 97,75% de x; ou seja, o preço será menor que o original. Portanto, Paula não atingiu o objetivo.
Para analisar
Antes de comprar um produto, é sempre interessante pesquisar. Nem sempre um produto anunciado em promoção está realmente mais barato que antes. Alguns lojistas aumentam o preço dos produtos para depois oferecer um desconto, o que pode não ser tão vantajoso quanto parece ao consumidor. Leia a seguinte situação.
Ana estava acompanhando o preço de certo refrigerador todos os dias no site de uma loja. Um dia, a loja anunciou que todos os refrigeradores estavam com 10% de desconto. Porém, ao checar o site, Ana percebeu que o preço do refrigerador havia aumentado 11% antes dessa oferta.
• Em sua opinião, a promoção realmente era vantajosa?
Situação 5
Alex investiu R$ 1 000,00mil reais em um fundo de investimento que rende 1% ao fim de cada mês, sempre calculado sobre o valor total que há no fundo naquele mês (valor do mês anterior mais rendimento).
Observe como Alex verificou, usando uma calculadora, o valor que terá ao fim de 4 meses, caso não mexa no dinheiro.
Respostas e comentários
Para analisar: Resposta pessoal. Espera-se que os estudantes percebam que, nesse caso, o valor do refrigerador era 99,9% do valor inicial, ou seja, o desconto foi de apenas 0,1%.
Orientações e sugestões didáticas
• Na situação 3, é importante que os estudantes compreendam que devemos calcular o primeiro desconto sobre o valor inicial e que o segundo desconto deve ser aplicado tomando como referência o valor obtido no primeiro cálculo.
• Se julgar oportuno, antes de mostrar a resolução do problema apresentado na situação 4, peça aos estudantes que o resolvam utilizando suas estratégias pessoais. Também, nesse caso, é importante que eles compreendam que o segundo cálculo terá como referência o valor que já sofreu alteração após o primeiro cálculo.
• Aproveite o boxe Para analisar e pergunte à turma quem conhece alguém que já passou pela mesma situação que Ana ou alguma situação parecida. Chame a atenção para a importância de pesquisar e/ou acompanhar o preço de determinado produto para evitar situações como essa.
• A situação 5 mostra como calcular juro composto com o auxílio de uma calculadora. A ideia não é definir juro composto nem formalizar o cálculo. Se julgar necessário, proponha aos estudantes uma pesquisa e uma breve apresentação do desenvolvimento histórico da ideia de juro e seus diferentes regimes.



Para analisar

Converse com um colega sobre a importância de fazer um investimento.

ATIVIDADES
faça as atividades no caderno
1. Calcule as porcentagens no caderno.
a) 15% de 130
b) 2% de R$ 3 450,00três mil quatrocentos e cinquenta reais
c) 25% de duas.000 pessoas
d) 12,5% de 32
e) 110% de R$ 350,00trezentos e cinquenta reais
2. Certo modêlo de celular custava R$ 850,00oitocentos e cinquenta reais à vista em uma loja. Em uma promoção, os preços de todos os produtos da loja tiveram um desconto de 2%. Porém, para pagamento a prazo, é cobrada uma taxa de 5% sobre o valor final do produto. Quanto uma pessoa pagaria por um celular desse modêlo caso optasse por comprar esse celular a prazo durante a promoção?
3. Observe a ilustração e responda.
Qual é o percentual de desconto oferecido no preço deste computador?

4.

Segundo dados do Instituto Brasileiro de Geografia e Estatística (í bê gê É), em 2010 a população brasileira era de ..190755799 pessoas. Já em 2021, a população estimada era de ..213317639 pessoas. Usando uma calculadora, obtenha a taxa de crescimento aproximada, em porcentagem.
5.

Maria aplicou R$ 12 000,00doze mil reais em um investimento que rende 0,8% ao mês. Usando uma calculadora, verifique quanto Maria terá após 5 meses.
6.

Fabio comprou um automóvel de R$ 40 000,00quarenta mil reais, que vai sofrer uma desvalorização de 10% ao ano. Usando uma calculadora, verifique quanto o automóvel vai desvalorizar, em real, após 4 anos.
7.

Elabore:
a) um problema em que seja necessário calcular o percentual de desconto ou de aumento de um produto;
b) um problema em que seja necessário calcular um valor após aumentos ou diminuições sucessivas.

• Passe seus problemas para um colega resolver e resolva os problemas criados por ele.
Respostas e comentários
Para analisar: Resposta pessoal.
1. a) 19,5
1. b) R$ 69,00sessenta e nove reais
1. c) quinhentas pessoas
1. d) 4
1. e) R$ 385,00trezentos e oitenta e cinco reais
2. R$ 874,65oitocentos e setenta e quatro reais e sessenta e cinco centavos
3. 7% de desconto
4. A taxa de crescimento aproximada foi de 11,83%.
5. aproximadamente R$ 12 487,74doze mil quatrocentos e oitenta e sete reais e setenta e quatro centavos
6. R$ 13 756,00treze mil setecentos e cinquenta e seis reais
7. Resposta pessoal.
Orientações e sugestões didáticas
• No boxe Para analisar, espera-se que os estudantes percebam que ao investir certa quantia em dinheiro obtém-se uma renda extra que pode ser gasta com bens e consumos que se deseja ou que sejam necessários sem se endividar.
• Antes de propor a realização das atividades, converse com os estudantes sobre a importância de fazer estimativas em casos de porcentagem. Usar referências como 10%, 25%, 50% e 75%, que, em geral, são mais simples de calcular, pelo menos de fórma aproximada, auxilia nas diferentes situações do dia a dia. Nessas atividades, eles podem fazer essa estimativa e depois conferir.

Educação Financeira
faça as atividades no caderno

Quando o barato sai caro
Durante um encontro entre amigos, o assunto era economizar. Eles comentavam, especificamente, situações em que a tentativa de economizar não havia dado muito certo. Observe.

O que você faria?

Reúna-se com seus colegas e leiam atentamente a conversa anterior. Depois, discutam a respeito do que compreenderam. Vocês acham que, analisando as situações apresentadas, é possível entender o significado da expressão “o barato sai caro”?
Após conversarem sobre isso, deem sua opinião sobre os acontecimentos descritos, completando as frases a seguir no caderno.
a) Quando vejo um posto de combustível oferecendo gasolina por um preço inferior ao de todos os outros da região, eureticências
b) Se decido pintar minha casa e verifico que o pintor cobra um preço muito alto, eureticências
c) Caso encontre uma roupa com preço muito baixo, eureticências
d) As ofertas dos sites de compras coletivas são incríveis; então, eureticências
Respostas e comentários
O que você faria?: a) Escolho o de menor preço, pois é importante economizar; peço ao frentista para fazer um teste de qualidade com o combustível, uma exigência que é direito do consumidor.
O que você faria?: b) Poupo dinheiro por mais um tempo; pesquiso os preços de outros profissionais; tento pintar sozinho ou chamo algum amigo que saiba fazer isso.
O que você faria?: c) Vejo se me agrada e, em caso positivo, já compro; observo para verificar a procedência da roupa; só compro se tenho alguma referência da marca.
O que você faria?: d) Vejo se há alguma promoção naquele restaurante que adoro; pesquiso sempre para verificar se é realmente uma promoção que vale a pena; avalio se preciso mesmo do produto antes de comprar.
Orientações e sugestões didáticas
Educação Financeira
Objetivos
• Refletir sobre o uso consciente de recursos financeiros.
• Trabalhar o Tema Contemporâneo Transversal Educação Financeira, da macroárea Economia.
• Favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah zero cinco, da competência geral 7 e da competência específica 8 da Bê êne cê cê.
Habilidade da Bê êne cê cê
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero nove ême ah zero cinco porque os estudantes terão de resolver problemas que envolvam porcentagens.
Orientações
• Nesta seção, são apresentadas algumas situações comuns no cotidiano, nas quais, ao pensar estar poupando, são tomadas atitudes que levam a prejuízos, uma vez que se pagou por um produto ou serviço que não pôde ser aproveitado de maneira satisfatória por ser de má qualidade ou por ter o prazo de validade expirado. Nesse sentido, o estudante discutirá situações em que é preciso avaliar e refletir sobre as consequências de suas decisões, desenvolvendo assim o Tema Contemporâneo Transversal Educação Financeira, da macroárea Economia.
• Antes de os estudantes discutirem as questões propostas em O que você faria?, verifique se compreenderam as falas de cada personagem. Por exemplo, da esquerda para a direita: 1º caso, ao verificar o custo do serviço de um pintor, a pessoa decidiu fazer a pintura por conta própria e, por falta de habilidade, o resultado foi insatisfatório. Assim, obteve prejuízo, pois, além de ter desperdiçado material, teve de contratar um pintor, arcando com mais custos. No 2º caso, a pessoa pagou mais barato ao abastecer o tanque do carro, mas teve gastos imprevistos com a troca de peças do motor, em decorrência de um combustível sem qualidade. No 3º caso, a pessoa adquiriu um produto “baratinho” e, provavelmente, de baixa qualidade. O 4º caso é um exemplo de compra por impulso sem atentar para uma série de itens, como: dias em que a promoção é válida, regras em caso de troca, prazo de entrega, data de validade de produtos etcétera Em seguida, a intenção é que os estudantes simulem cada situação e apresentem sua opinião. Não se trata de um julgamento de opiniões; a intenção é refletir sobre o que se ganha e o que se perde em cada escolha.
(ê éfe zero nove ême ah zero cinco) Resolver e elaborar problemas que envolvam porcentagens, com a ideia de aplicação de percentuais sucessivos e a determinação das taxas percentuais, preferencialmente com o uso de tecnologias digitais, no contexto da educação financeira.
Competência geral 7: Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
Competência específica 8: Interagir com seus pares de fórma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Calcule
Suponha que você esteja visitando um site de compras coletivas e encontre ofertas como estas.

Agora, responda às questões a seguir.
a) Quanto uma pessoa economizaria, em valor e em percentual, ao aproveitar cada oferta?
b) Quanto você desperdiçaria caso realizasse a compra da 1ª oferta e não conseguisse viajar (por falta de tempo, imprevistos etcétera)?
c) Qual seria o valor total, sem desconto, do tablet anunciado na 3ª oferta?
Reflita
a) Você já comprou algum produto barato que não tinha boa qualidade?
b) O produto mais caro é sempre melhor?
c) Pergunte aos seus pais, familiares e amigos se já passaram por situações em que o “barato saiu caro”.
d) Os sites de compras coletivas sempre valem a pena?
e) Procure exemplos de produtos e situações em que não compensa adquirir algo mais caro e durável.
f) Existem situações em que o mais barato, mesmo sendo descartável, é uma opção interessante?
Dica
É importante pesquisar e economizar para não desperdiçar dinheiro. Mas não se esqueça: verifique sempre as condições do produto e da oferta!

Respostas e comentários
Calcule: a) Na 1ª oferta, economizaria 40%, ou seja, R$ 879,60oitocentos e setenta e nove reais e sessenta centavos. Na 2ª oferta, 50%, ou seja, R$ 15,75quinze reais e setenta e cinco centavos. Na 3ª oferta, a economia seria de 70%, ou seja, R$ 420,00quatrocentos e vinte reais.
Calcule: b) R$ 1 319,40mil trezentos e dezenove reais e quarenta centavos
Calcule: c) R$ 600,00seiscentos reais
Reflita: Respostas pessoais.
Orientações e sugestões didáticas
• Em Calcule, o foco da discussão são os sites de compras coletivas. É importante salientar para a turma que devem ser verificadas todas as condições da oferta e a confiabilidade da loja antes de efetuar uma compra pela internet.
• Em Reflita, espera-se que os estudantes tragam exemplos reais para compartilhar com os amigos e percebam que o custo de um produto ou serviço não é o único item que deve ser considerado ao tomar decisões. Deve-se pensar se o custo é baixo porque o produto é de má qualidade, se o produto é durável, se está no prazo de validade etcétera e, principalmente, se o produto é adequado para as nossas necessidades. Por exemplo, se pensarmos em uma festa na qual vários adereços são distribuídos entre os convidados, os produtos são descartáveis, mas cumprem seu objetivo naquele momento, diferentemente de outras situações em que é importante optar por algo durável, para evitar uma nova compra. Por argumentar com base em exemplos reais, posicionando-se eticamente em relação a si mesmos e aos outros, e por ter de interagir com seus pares, a competência geral 7 e a competência específica 8 da Bê êne cê cê têm o seu desenvolvimento favorecido.

Estatística e Probabilidade
faça as atividades no caderno

Gráficos e média aritmética
Em 2019, havia no Brasil 131,2 milhões de pessoas com algum tipo de rendimento proveniente de trabalho ou de outras fontes, como aposentadoria, aluguel e programas de transferência de renda.
Observe, no gráfico a seguir, o rendimento médio mensal das pessoas residentes em cada região do Brasil. A linha vermelha está na altura correspondente ao rendimento médio mensal de todas as pessoas que declararam ter algum tipo de rendimento.
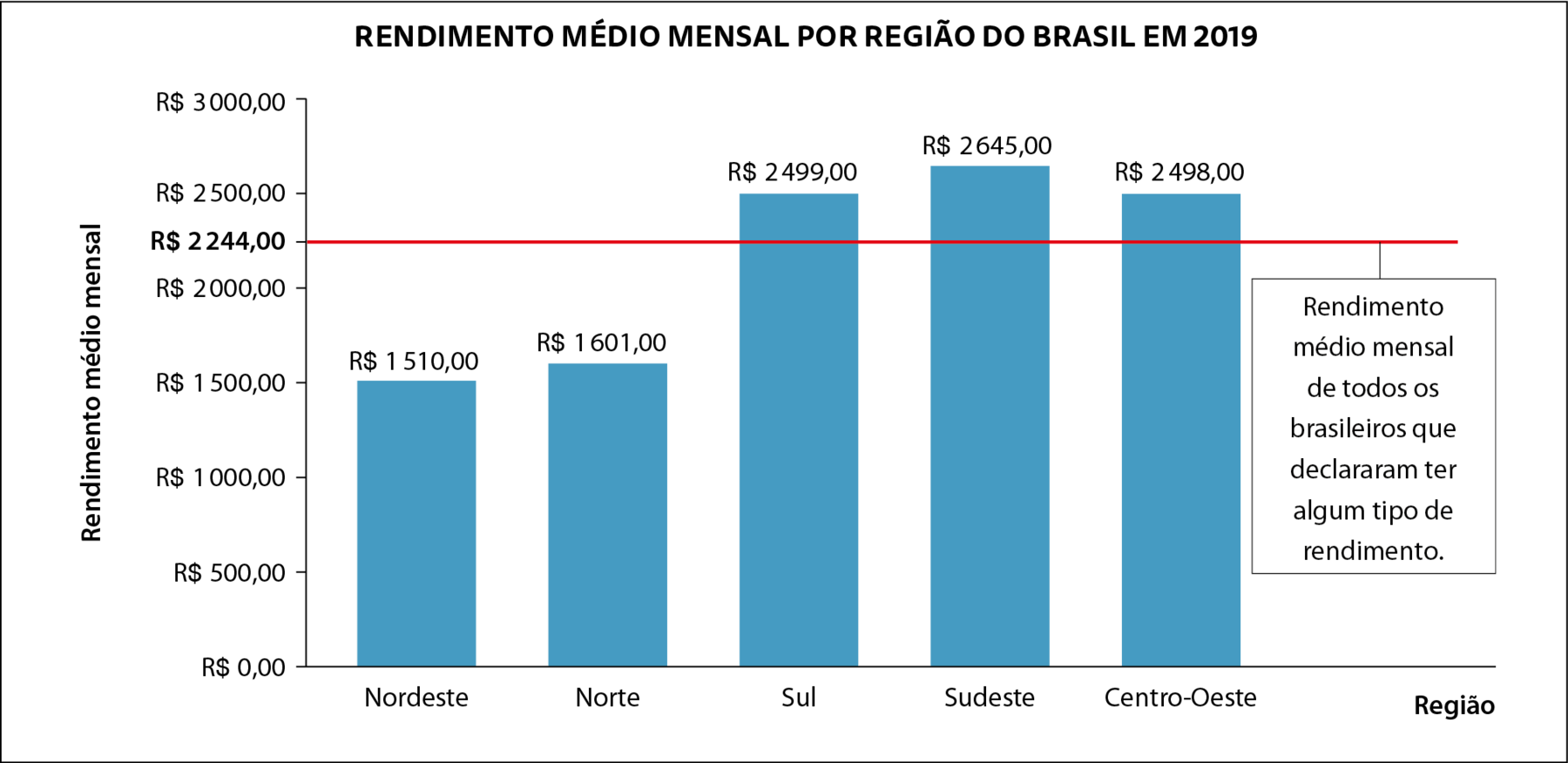
Fonte: BRASIL. Instituto Brasileiro de Geografia e Estatística (í bê gê É). Pesquisa Nacional por Amostra de Domicílios Contínua 2012-2019. Brasília, Distrito Federal: Instituto Brasileiro de Geografia e Estatística, [2020?].

Note que:
• o rendimento médio mensal das pessoas residentes nas regiões Nordeste e Norte está abaixo do rendimento médio mensal de todos os brasileiros;
• o rendimento médio mensal das pessoas residentes nas regiões Sul, Sudeste e Centro-Oeste está acima do rendimento médio mensal de todos os brasileiros;
• o rendimento médio mensal das pessoas residentes na região Sudeste é o mais alto comparando com as demais regiões;
• o rendimento médio mensal das pessoas residentes na região Nordeste é o mais baixo comparando com as demais regiões.
Para pensar
1. Faz sentido construir um gráfico de setores com base nos dados do gráfico de barras anterior? Por quê?
2. Faz sentido construir um gráfico de linha com base nos dados do gráfico de barras anterior? Por quê?
Respostas e comentários
Para pensar: 1. Espera-se que os estudantes respondam que não. Em um gráfico de setores, os dados adicionados compõem o todo de um aspecto da realidade, e isso não ocorre com os dados do gráfico de barras anterior.
Para pensar: 2. Espera-se que os estudantes respondam que não. Os gráficos de linha são usados para mostrar a evolução de um dado no decorrer do tempo, e isso não ocorre no gráfico de barras anterior.
Orientações e sugestões didáticas
Estatística e Probabilidade
Objetivos
• Reconhecer e construir o gráfico mais adequado para representar determinado conjunto de dados.
• Representar graficamente a média aritmética de um conjunto de dados.
• Trabalhar o Tema Contemporâneo Transversal Trabalho e Educação em Direitos Humanos, das macroáreas Economia e Cidadania e Civismo, respectivamente.
• Favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah dois dois e das competências gerais 7 e 9 Bê êne cê cê.
Habilidade da Bê êne cê cê
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero nove ême ah dois dois porque os estudantes terão a oportunidade de analisar o gráfico mais adequado para apresentar determinado conjunto de dados e destacar nele a média aritmética desse conjunto.
Orientações
• Nesta seção, os estudantes deverão avaliar e construir o gráfico mais adequado para apresentar determinado conjunto de dados e destacar nele a média aritmética desse conjunto por meio de uma linha.
• Esse modo de representar a média possibilita perceber os valores do conjunto de dados que são maiores e menores que a média. A ideia é que os estudantes leiam e interpretem os dados tomando a média aritmética como referência. Analise coletivamente o gráfico desta página e incentive a turma a tirar conclusões com base nas informações presentes e na representação gráfica da média aritmética (linha vermelha horizontal).
• Amplie o assunto com a turma e comente que, segundo o Instituto Brasileiro de Geografia e Estatística, no país, entre 2018 e 2019 não houve uma queda significativa no rendimento médio mensal, que passou de R$ 2 247,00dois mil duzentos e quarenta e sete reais para R$ 2 244,00dois mil duzentos e quarenta e quatro reais. Considerando o mesmo período, as regiões que tiveram um aumento no valor do rendimento médio mensal foram Nordeste e Sul, e as regiões que apresentaram queda foram Norte, Sudeste e Centro-Oeste. Esse tema contribui para o desenvolvimento do Tema Contemporâneo Transversal Trabalho, da macroárea Economia. Dados obtidos em: https://oeds.link/UNFS9x. Acesso em: 18 julho 2022.
(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.
Competência geral 7: Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
Competência geral 9: Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

ATIVIDADES
faça as atividades no caderno
1. Observe o gráfico que representa o salário médio dos homens e das mulheres acima de 14 anos de idade em 2019.
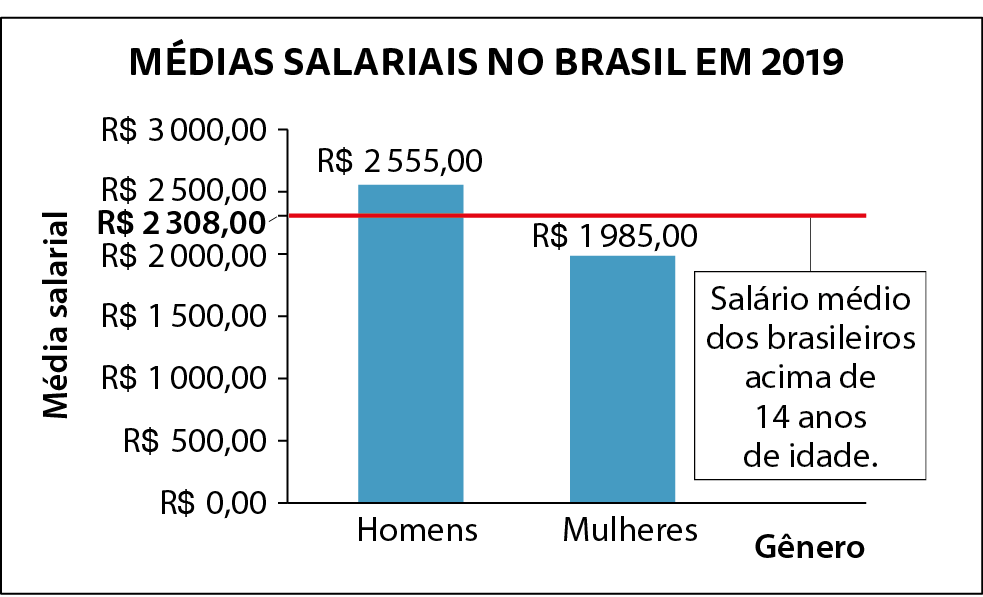
Fonte: BRASIL. Instituto Brasileiro de Geografia e Estatística (í bê gê É). Pesquisa Nacional por Amostra de Domicílios Contínua 2012-2019. Brasília, Distrito Federal: Instituto Brasileiro de Geografia e Estatística, [2020?].
a) Qual era a diferença entre a média salarial dos homens e das mulheres acima de 14 anos de idade no Brasil em 2017?
b) Leia a afirmação a seguir.

Você concorda com essa afirmação? Justifique sua resposta.
c) O salário médio dos homens estava abaixo ou acima do salário médio de todos os brasileiros acima de 14 anos de idade em 2017? E o salário médio das mulheres?
d) Em uma planilha eletrônica, construa um gráfico de barras horizontais com base nos dados do gráfico apresentado.
2. Observe os dados apresentados a seguir.
|
Cor ou raça |
Salário médio |
|---|---|
|
Brancos |
R$ 2.999,00 |
|
Pretos |
R$ 1.673,00 |
|
Pardos |
R$ 1.719,00 |
Fonte: BRASIL. Instituto Brasileiro de Geografia e Estatística (í bê gê É). Pesquisa Nacional por Amostra de Domicílios Contínua 2012-2019. Brasília, Distrito Federal: Instituto Brasileiro de Geografia e Estatística, [2020?].
a) Qual desses tipos de gráfico é o mais adequado para representar os dados da tabela: de barras, de setores ou de linhas? Construa esse gráfico em uma planilha eletrônica.
b) Sabendo que o salário médio dos brasileiros acima de 14 anos de idade era R$ 2.308,00dois mil trezentos e oito reais em 2019, represente essa média com uma linha no gráfico que você construiu no item anterior.
c) Compare os salários médios de brancos, pretos e pardos com o salário médio dos brasileiros. O que você pode concluir?
Para pensar



Em sua opinião, deveria haver essa desigualdade salarial entre brancos, pretos e pardos? E entre homens e mulheres? Por quê? Converse com os colegas sobre isso.
Respostas e comentários
1. a) R$ 570,00quinhentos e setenta reais
1. b) Espera-se que os estudantes respondam que sim, pois, ao calcular a porcentagem do salário médio dos homens que corresponde ao salário médio das mulheres, obtemos aproximadamente 77,69%.
1. c) acima; abaixo
1. d) Respostas em Orientações.
2. a) gráfico de barras
2. b) Resposta em Orientações.
2. c) Espera-se que os estudantes concluam que apenas a média salarial dos brancos estava acima do salário médio dos brasileiros com mais de 14 anos de idade em 2019.
Para pensar: Respostas pessoais.
Orientações e sugestões didáticas
• Aproveite os questionamentos do boxe Para pensar e inicie uma conversa com a turma sobre a desigualdade salarial indicada no gráfico da atividade 1 e na tabela da atividade 2. Momentos como esse exercitam o diálogo, desenvolvem a capacidade de argumentar e chamam à reflexão sobre respeito, desigualdade e cidadania. Para enriquecer a discussão, leve para a sala de aula textos com outras informações acerca dessas diferenças. Conversar com os estudantes sobre esses temas auxilia no desenvolvimento dos Temas contemporâneos Transversais Trabalho e Educação em Direitos Humanos, das macroáreas Economia e Cidadania e Civismo, respectivamente.
• Resposta do item d atividade 1:

Fonte: BRASIL. Instituto Brasileiro de Geografia e Estatística (í bê gê É). Pesquisa Nacional por Amostra de Domicílios Contínua 2012-2019. Brasília, Distrito Federal: Instituto Brasileiro de Geografia e Estatística, [2020?].
Resposta dos itens a e b da atividade 2:

Fonte: BRASIL. Instituto Brasileiro de Geografia e Estatística (í bê gê É). Pesquisa Nacional por Amostra de Domicílios Contínua 2012-2019. Brasília, Distrito Federal: Instituto Brasileiro de Geografia e Estatística, [2020?].

Atividades de revisão
faça as atividades no caderno
1. Reproduza as afirmações verdadeiras no caderno.
a) Um cubo cuja aresta mede 9 centímetros de comprimento tem o triplo da medida do volume de um cubo de aresta que mede 3 centímetros de comprimento.
b) Um cubo cuja aresta mede 6 centímetros de comprimento tem medida de volume igual a 8V, em que V é a medida do volume de um cubo de aresta que mede 3 centímetros de comprimento.
c) Um cubo cuja aresta mede 1 centímetro de comprimento tem
Fração 1 sobre 3.da medida do volume de um cubo de aresta que mede 3 centímetros de comprimento.
d) Um cubo cuja aresta mede 5 centímetros tem
Fração 1 sobre 8.da medida do volume de um cubo de aresta que mede 10 centímetros de comprimento.
2. Um aquário com formato cúbico, com medida de capacidade de .27000 mililitros de água, está cheio.
Qual é a medida da altura do aquário?
(Lembre-se de que 1 centímetros cúbicos corresponde a 1mililitro.)
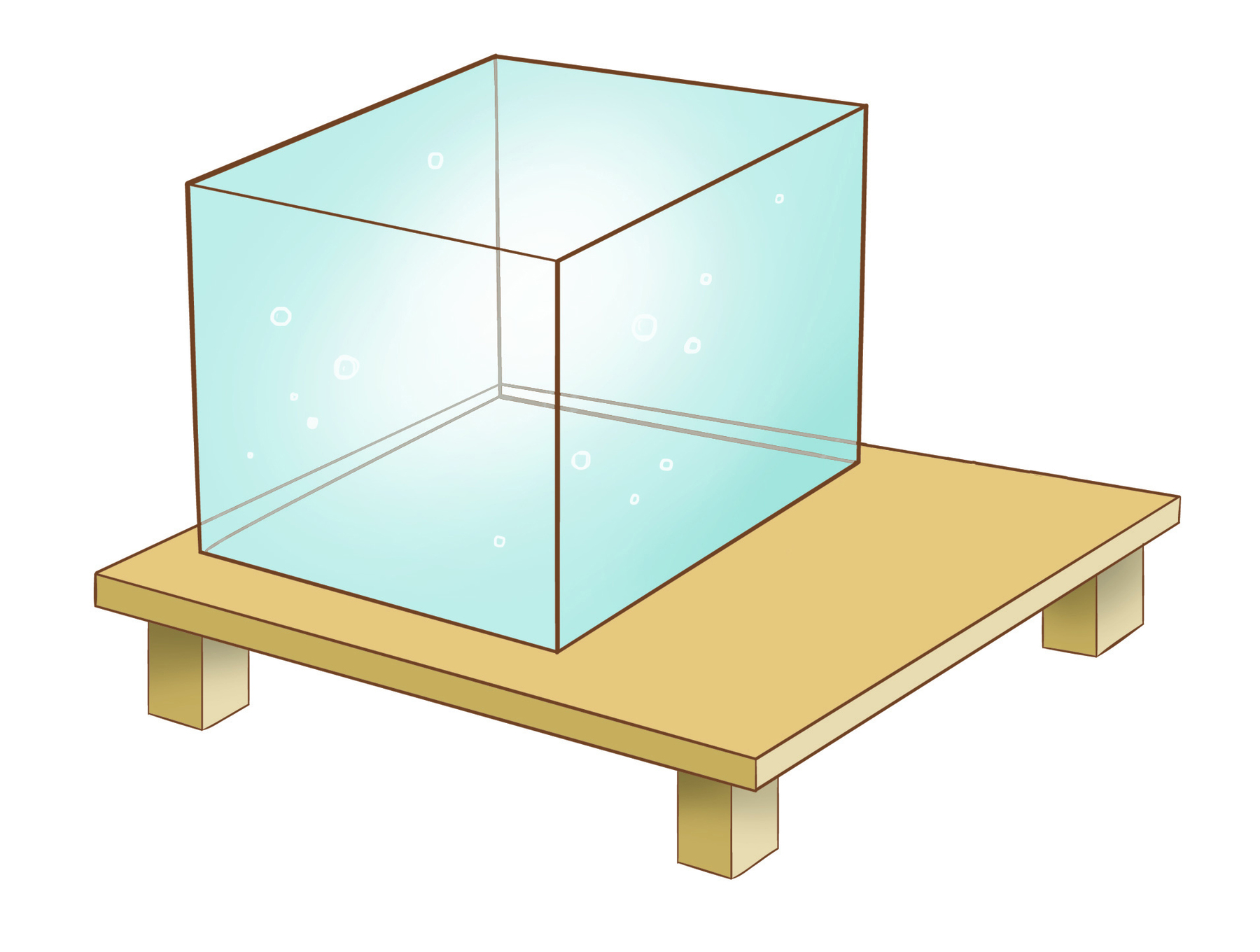
3. Certa folha de papel mede 0,074 milímetro de espessura. Converta essa medida em metro e represente-a em notação científica.
4. Observe no quadro alguns dados publicados pelo Departamento de Astronomia do Instituto de Física da Universidade Federal do Rio Grande do Sul (u éfe érre gê ésse).
|
Planeta |
Medida da massa (kg) |
Medida da distância média ao Sol (km) |
|---|---|---|
|
Mercúrio |
3,303 ⋅ 10elevado a 23 |
57.910.000 |
|
Júpiter |
1,900 ⋅ 10elevado a 27 |
778.330.000 |
|
Saturno |
5,688 ⋅ 10elevado a 26 |
1.429.400.000 |
Agora, escreva:
a) as medidas das massas dos planetas em ordem crescente;
b) a medida da distância média de cada planeta ao Sol em notação científica.
5. Calcule o preço aproximado de uma camisa que inicialmente custava R$ 45,00quarenta e cinco reais após sofrer três aumentos sucessivos de 2%.
6. Calcule e simplifique.
a)
Sentença matemática. Raiz quadrada de 2 vezes raiz quadrada de 18.
b)
Sentença matemática. Raiz quadrada de 5 vezes raiz quadrada de 10 vezes raiz quadrada de 2.c)
Sentença matemática. Raiz quadrada de fração 3 quintos vezes raiz quadrada de fração 5 terços.
d)
Sentença matemática. Abre parênteses, raiz quarta de 9, fecha parênteses, ao quadrado.e)
Sentença matemática. Fração raiz quadrada de 6 sobre raiz quarada de 3.
f)
Sentença matemática. Fração raiz cúbica de 24 sobre raiz cúbica de 3.7. Uma lata com formato cúbico tem arestas que medem
Sentença matemática. 5 raiz quadrada de 3.centímetros de comprimento.
a) Quantos centímetros quadrados de plástico serão necessários para forrar toda a lata?
b) Márcia quer saber se 1 litro de óleo cabe nessa lata. Que cálculo ela precisa fazer?
c) Depois de fazer os cálculos necessários, a que conclusão Márcia chegará?
8. Racionalize o denominador de cada fração.
a)
Sentença matemática. Fração 3 sobre raiz quadrada de 2.
b)
Sentença matemática. Fração 10 sobre 3 raiz quadrada de 5.c)
Sentença matemática. Fração 3 sobre raiz quarta de 2.
d)
Sentença matemática. Fração 1 sobre 2 mais raiz quadrada de 3.e)
Sentença matemática. Fração 1 sobre raiz quadrada de 3 menos raiz quadrada de 2f)
Sentença matemática. Fração 2 menos raiz quadrada de 2 sobre raiz quadrada de 2, fim da raiz, menos 1.9. Simplifique.
a)
Expressão matemática. Abre parênteses, raiz cúbica de menos 8, fim da raiz, mais 3, fecha parênteses, ao quadrado menos, abre chaves, 2 menos, abre colchetes, raiz quadrada de, abre parênteses, fração 1 nono, fecha parênteses, elevado a menos 1, fim da raiz, menos 12, fecha colchetes, fecha chaves.b)
Expressão numérica. 0 vírgula 25 vezes, abre parênteses, menos 3, fecha parênteses, ao quadrado dividido por, abre parênteses, fração 1 quarto, fecha parênteses, menos, abre parênteses, 3 vezes raiz cúbica de menos 8, fim da raiz, mais 11, fecha parênteses.10. Calcule o valor de
Sentença matemática. Fração raiz quadrada de, 1 mais raiz quadrada de 121, sobre raiz quadrada de, 45 mais raiz quadrada de 900..
11.

A caixa de bombons representada aseguir tem o formato que lembra um trapézio.
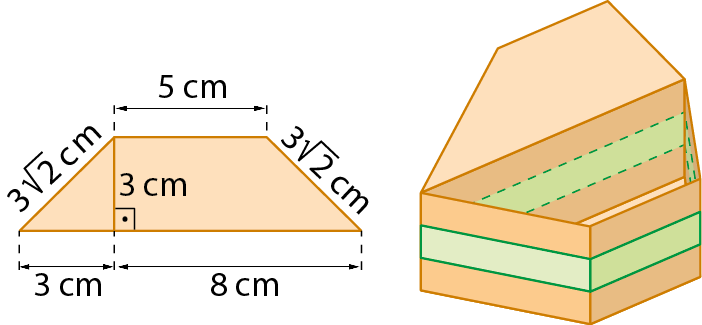
a) Quantos centímetros de fita verde são necessários para contornar uma vez a caixa?
b) Quantos centímetros quadrados de papelão são necessários para confeccionar 15 tampas para caixas como essa?
Respostas e comentários
1. alternativas b e d
2. 30 centímetros
3. 7,4 ⋅ 10elevado a menos 5 métros
4. a) 3,303 ⋅ 10elevado a 23, 5,688 ⋅ 10elevado a 26, 1,900 ⋅ 10elevado a 27
4. b) 5,791 ⋅ 10elevado a 7; 7,7833 ⋅ 10elevado a 8; 1,4294 ⋅ 10elevado a 9
5. aproximadamente R$ 47,75quarenta e sete reais e setenta e cinco centavos
6. a) 6
6. b) 10
6. c) 1
6. d) 3
6. e)
Sentença matemática. Raiz quadrada de 2.6. f) 2
7. a) 450 centímetros quadrados
7. b) o cálculo da medida do volume da lata
7. c) Não vai caber (a medida do volume é aproximadamente 650 centímetros cúbicos).
8. a)
Sentença matemática. Fração 3 raiz quadrada de 2 sobre 2.8. b)
Sentença matemática. Fração 2 raiz quadrada de 5 sobre 3.8. c)
Sentença matemática. Fração 3 raiz quarta de 8 sobre 2.8. d)
Sentença matemática. 2 menos raiz quadrada de 3.8. e)
Sentença matemática. Raiz quadrada de 3 mais raiz quadrada de 2.8. f)
Sentença matemática. Raiz quadrada de 2.9. a) menos10
9. b) 4
10.
Fração 2 sobre 5.11. a) (6
Sentença matemática. Raiz quadrada de 2.+ 16) centímetros ou aproximadamente 24,5 centímetros
11. b) 360 centímetros quadrados
Orientações e sugestões didáticas
Atividades de revisão
Objetivos
• Consolidar o conhecimento adquirido no decorrer do Capítulo.
• Favorecer o desenvolvimento das habilidades ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro da Bê êne cê cê.
Habilidades da Bê êne cê cê
• Esta seção favorece o desenvolvimento das habilidades ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro à medida que são propostos cálculos e problemas com números reais.
Orientações
• Resolução da atividade 7:
a) Um cubo tem 6 faces.
A medida de área de cada uma das faces da lata é 75 centímetros quadrados, pois:
Sentença matemática. 5 raiz quadrada de 3.
2 centímetros quadrados = 75 centímetros quadrados
Portanto, para forrar as 6 faces, serão necessários 450 centímetros quadrados de plástico, pois 6 ⋅ 75 centímetros quadrados = 450 centímetros quadrados.
b) Para saber se 1 litro de óleo cabe nessa lata, é necessário calcular seu volume:
Sentença matemática. 5 raiz quadrada de 3.
3 centímetros cúbicos = 375
Sentença matemática. Raiz quadrada de 3.centímetros cúbicos ≃ 650 centímetros cúbicos
c) A medida de capacidade aproximada da lata é de 650 mililitros; portanto, não cabe 1 litro de óleo na lata.
• Sugerimos algumas questões para que os estudantes possam refletir sobre suas aprendizagens e possíveis dificuldades no estudo deste Capítulo, as quais devem ser adaptadas à realidade da turma. Oriente-os a fazer a autoavaliação, respondendo às questões no caderno com “sim”, “às vezes” ou “não”.
Eureticências
reticências sei representar números em notação científica?
reticências sei aplicar as propriedades das potências e as dos radicais?
reticências sei identificar radicais semelhantes?
reticências sei resolver operações com números reais com potenciações e radiciações com radicais?
reticências sei racionalizar denominadores de frações?
reticências sei calcular porcentagens?
reticências sei reconhecer e construir o gráfico mais adequado para representar determinado conjunto de dados.
reticências sei representar graficamente a média aritmética de um conjunto de dados.
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.