
UNIDADE 3
Capítulo 6
Relações métricas no triângulo retângulo
Capítulo 7
Equações do 2º grau

Plante e replante
Todos os anos, milhares de quilômetros quadrados de florestas são desmatados no Brasil. Essa ação causa, entre outras consequências, alteração no microclima da região, perda da biodiversidade, erosão do solo e desertificação. As soluções para esse problema? Combate ao desmatamento e reflorestamento.

Você provavelmente já ouviu falar sobre reflorestamento. Mas você sabe qual é seu significado? Reflorestamento consiste no repovoamento de áreas desmatadas com o objetivo de recuperar florestas que foram destruídas. Essa ação pode ser feita por meio do plantio de sementes e mudas de árvores nativas ou da manutenção da vegetação já existente. Entretanto, o reflorestamento não é tão simples assim, não se trata de plantar árvores de maneira aleatória, é preciso fazer um estudo de campo sobre a área que pretende plantar como, por exemplo, analisar o solo, o clima, o tipo de espécie para plantar e o método de plantio. Todo este estudo ajuda a evitar problemas futuros.
Para começarreticências
1. Qual é a importância do combate ao desmatamento?
2. Qual é o intuito do reflorestamento?
3. Uma organização não governamental reflorestou uma região quadrada cuja área mede .1600 métros quadrados. Qual é a medida do comprimento do lado dessa região?

Respostas e comentários
Habilidades da BNCC trabalhadas nesta Unidade:
ê éfe zero nove ême ah zero um
ê éfe zero nove ême ah zero nove
ê éfe zero nove ême ah um três
ê éfe zero nove ême ah um quatro
ê éfe zero nove ême ah um seis
ê éfe zero nove ême ah dois um
ê éfe zero nove ême ah dois dois
Para começar: 1. Resposta pessoal. Exemplo de resposta: Ao combater o desmatamento evita-se, por exemplo, a alteração no microclima da região, perda da biodiversidade, erosão do solo e a desertificação.
2. Resposta pessoal. Exemplo de resposta: o intuito é repovoar áreas desmatadas com o objetivo de recuperar florestas que foram destruídas.
3. 40 métros
Orientações e sugestões didáticas
Abertura da Unidade 3
Objetivos
• Nesta unidade, serão trabalhados vários conceitos relacionados às unidades temáticas Números, Álgebra, Geometria e Probabilidade e Estatística, que, entre outros objetivos, favorecerão o desenvolvimento das habilidades da BNCC.
Orientações
• Ao trabalhar com a página de abertura, converse com os estudantes sobre as consequências do desmatamento. Explique-lhes, por exemplo, que a vegetação das florestas absorve energia solar e, ao desmatá-las, o calor se propaga com mais intensidade para a atmosfera, alterando assim, o microclima da região. O tema trabalhado na abertura contribui para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental, da macroárea Meio Ambiente.
• Se julgar conveniente, complemente o trabalho com esta página promovendo uma discussão a respeito da Agenda 2030, com ênfase para o objetivo 15, que diz
Proteger, recuperar e promover o uso sustentável dos ecossistemas terrestres, gerir de fórma sustentável as florestas, combater a desertificação, deter e reverter a degradação da terra e deter a perda de biodiversidade.
GTSCA 2030. Objetivos de desenvolvimento sustentável. Disponível em: https://oeds.link/NxQmvH. Acesso em: 10 março 2022.
• Informe aos estudantes que a Agenda 2030 é um plano de ação global criado para fortalecer a paz universal, erradicar a pobreza e promover vida digna a todos, respeitando as condições oferecidas pelo planeta, sem comprometer a qualidade de vida das próximas gerações.
• Ao trabalhar com a questão 3, os estudantes farão uso de conhecimentos sobre raiz quadrada e medidas de comprimento. Verifique se eles se recordam da expressão de cálculo da medida de área de um quadrado e se efetuam corretamente a radiciação em questão.

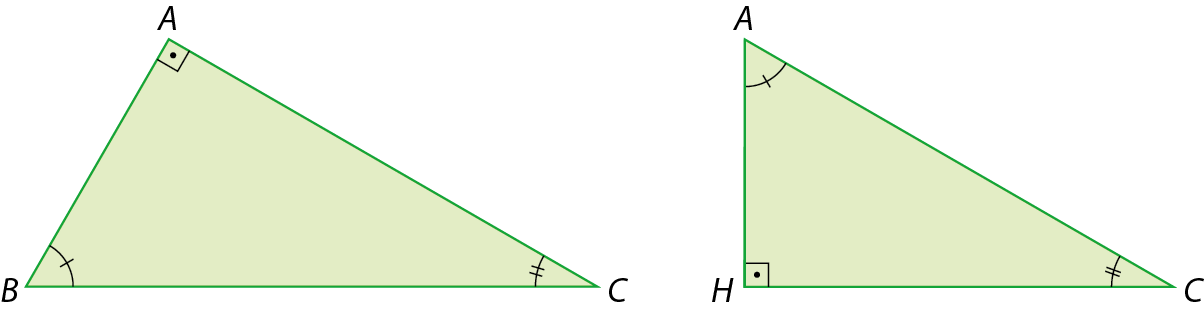
CAPÍTULO 6 Relações métricas no triângulo retângulo
1 Primeira relação métrica: teorema de Pitágoras
O filósofo e matemático grego Pitágoras nasceu na ilha grega de Samos, por volta de 572 antes de Cristo Fundou, em Crotona, a Escola Pitagórica, um centro de estudos de Filosofia, Ciências Naturais e Matemática. A escola era reservada a poucos iniciados, os estudos eram comunitários e o conhecimento produzido era creditado ao mestre. Por isso, várias descobertas foram atribuídas a Pitágoras, embora não se saiba ao certo se realmente foram realizadas por ele ou por outros membros do grupo.

Pitágoras é lembrado até hoje, principalmente, pelo teorema que leva seu nome e estabelece uma relação entre as medidas de comprimento dos lados de um triângulo retângulo.
No triângulo retângulo a seguir,
Símbolo. segmento de reta BC.é a hipotenusa e
Segmentos de reta AC e AB.são os catetos.
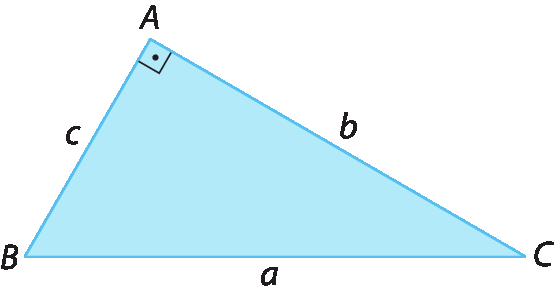
Em qualquer triângulo retângulo, o maior lado chama-se hipotenusa, e os lados que formam o ângulo reto são denominados catetos.
De acôrdo com o teorema de Pitágoras:
Em um triângulo retângulo qualquer, a soma dos quadrados das medidas de comprimento dos catetos é igual ao quadrado da medida de comprimento da hipotenusa.
Assim, na figura anterior, temos: belevado a 2 + celevado a 2 = aelevado a 2
Observe, por exemplo, como podemos determinar a medida de comprimento da hipotenusa no triângulo a seguir, em que
Segmentos de reta AB e AC.são os catetos e
Símbolo. Segmento de reta BC.é a hipotenusa.
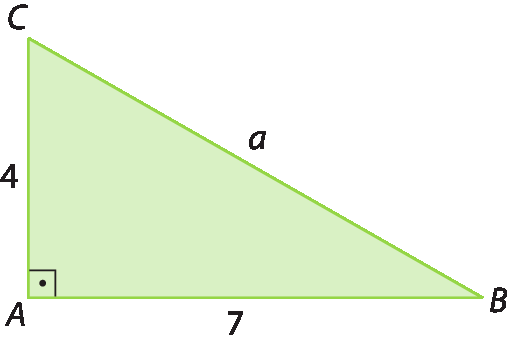
Aplicando o teorema de Pitágoras, temos:
aelevado a 2 = 7elevado a 2 + 4elevado a 2
aelevado a 2 = 49 + 16
aelevado a 2 = 65
a =
raiz quadrada de 65.a ≃ 8,06
Observação
Resolver uma equação do tipo x elevado a 2 = k, em que k é um número real, consiste em encontrar os valores de x que, elevados ao quadrado, resultam em k.
Nesse caso, como a medida de comprimento de um lado de qualquer figura sempre será um número positivo; ao resolver a equação, consideramos somente a raiz positiva.
Respostas e comentários
Os links expressos nesta coleção podem estar indisponíveis após a data de publicação deste material.
Habilidades da BNCC trabalhadas neste Capítulo:
ê éfe zero nove ême ah zero um
ê éfe zero nove ême ah um três
ê éfe zero nove ême ah um quatro
ê éfe zero nove ême ah um seis
ê éfe zero nove ême ah dois dois
Orientações e sugestões didáticas
Primeira relação métrica: teorema de Pitágoras
Objetivos
• Compreender e aplicar o teorema de Pitágoras.
• Favorecer o desenvolvimento das habilidades da BNCC: ê éfe zero nove ême ah um três e ê éfe zero nove ême ah um quatro.
Habilidades da BNCC
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah um três porque será demonstrado o teorema de Pitágoras. A habilidade ê éfe zero nove ême ah um quatro também tem o seu desenvolvimento favorecido porque os estudantes terão a oportunidade de resolver e elaborar problemas de aplicação do teorema de Pitágoras.
Orientações
• Neste tópico, apresenta-se o teorema de Pitágoras. Após verificar sua validade de modo experimental por meio de um software de Geometria dinâmica, esse teorema será, primeiramente, demonstrado com base na noção de área.
• Faça a leitura compartilhada do texto e ressalte que o teorema de Pitágoras teve grande importância para o desenvolvimento da Matemática e da Física e que é amplamente aplicado no dia a dia.
(ê éfe zero nove ême ah um três) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos.
(ê éfe zero nove ême ah um quatro) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

Informática e Matemática
faça as atividades no caderno
Verificação experimental
Nesta seção, você vai utilizar um software de Geometria dinâmica para construir um triângulo e três quadrados, sendo cada quadrado com um lado em comum com o triângulo e externo a ele, e, então, comparar a medida da área do quadrado maior com a soma das medidas das áreas dos quadrados menores.
CONSTRUA
Utilize a ferramenta para a construção de polígonos e siga os passos descritos a seguir.
1º) Construa um triângulo á bê cê qualquer.
2º) Sobre o lado
Símbolo. Segmento de reta AB., construa um quadrado á bê dê é externo ao triângulo.
3º) Do mesmo modo, construa o quadrado BCFG sobre o lado
Símbolo. Segmento de reta BC.e o quadrado á cê í agá sobre o lado
Símbolo. Segmento de reta AC..
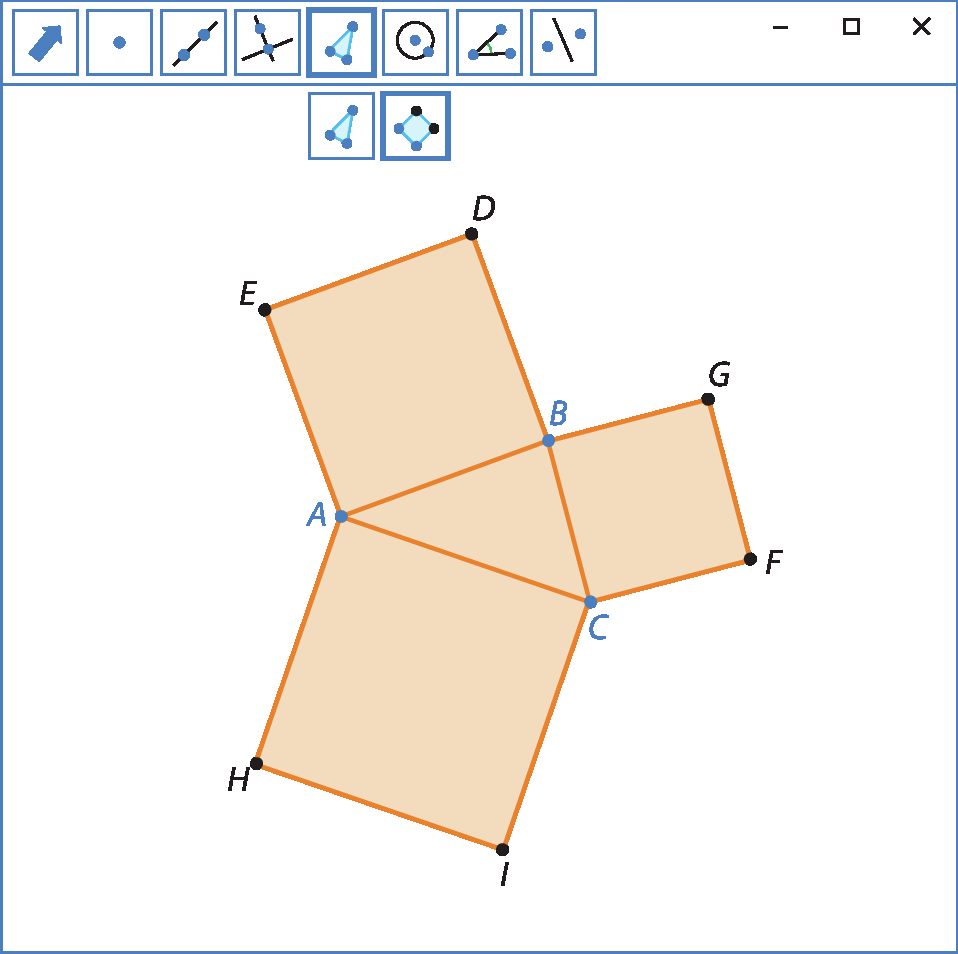
INVESTIGUE
a) Meça a abertura dos três ângulos internos do triângulo á bê cê e, usando a ferramenta de cálculo de medida de área, determine as medidas das áreas dos quadrados á bê dê é, BCFG e á cê í agá.
b) Movimente um dos vértices do triângulo construído de modo que obtenha um triângulo acutângulo. Compare a medida da área do quadrado maior com a soma das medidas das áreas dos quadrados menores. O que você observa?
c) Movimente, agora, um dos vértices do triângulo de modo que obtenha um triângulo obtusângulo. Compare a medida da área do quadrado maior com a soma das medidas das áreas dos quadrados menores. O que você observa?
d) Mais uma vez, movimente um dos vértices do triângulo de modo que a medida de abertura de um dos seus ângulos internos se aproxime de 90graus. O que você observa?
e) Repita a construção descrita anteriormente, porém desenhe um triângulo retângulo no 1º passo. Determine a medida de área dos quadrados e compare a medida da área do quadrado maior com a soma das medidas das áreas dos quadrados menores. Movimente a construção. O que você observa?
Respostas e comentários
Investigue: Respostas e comentários em Orientações.
Orientações e sugestões didáticas
Informática e Matemática
Objetivo
• Verificar experimentalmente, com o auxílio de um software de Geometria dinâmica, a validade do teorema de Pitágoras.
Orientações
• Nesta seção, os estudantes terão a oportunidade de construir quadrados cujos lados correspondem aos lados de um triângulo retângulo e verificar que a medida da área do quadrado cujo lado é a hipotenusa é igual à soma das medidas das áreas dos quadrados cujos lados são os catetos. Oriente-os quanto às ferramentas que devem utilizar na construção e, depois, na investigação que deverão realizar. Deixe-os livres para conjecturar e trocar ideias.
• Em Construa, no 2º e 3º passo, oriente os estudantes a construir os quadrados de modo que eles fiquem externos ao triângulo para facilitar a investigação.
• Para o Investigue, relembre-os de que um triângulo é acutângulo quando a abertura de seus ângulos internos é menor que 90graus, é obtusângulo quando a abertura de um de seus ângulos mede mais que 90graus e é retângulo quando a abertura de um dos seus ângulos mede 90graus. Espera-se que os estudantes percebam que:
– no item b, nos quadrados construídos sobre os lados do triângulo acutângulo, a medida da área do quadrado maior é menor que a soma das medidas das áreas dos quadrados menores;
– no item c, nos quadrados construídos sobre os lados do triângulo obtusângulo, a medida da área do quadrado maior é maior que a soma das medidas das áreas dos quadrados menores;
– no item d, quando o triângulo se aproxima de um triângulo retângulo, a medida da área do quadrado maior se aproxima da soma das medidas das áreas dos quadrados menores;
– no item ê, a medida da área do quadrado maior é igual à soma das medidas das áreas dos quadrados menores.
Demonstração do teorema de Pitágoras
Uma das primeiras demonstrações dêsse teorema foi desenvolvida por Euclides, em sua obra Os elementos, por volta de 300 antes de Cristo Além dela, são conhecidas mais de trezentas e cinquenta demonstrações.
A seguir, apresentamos uma demonstração por meio da comparação de medidas de áreas de figuras geométricas.
Observe a seguir o triângulo retângulo á bê cê.
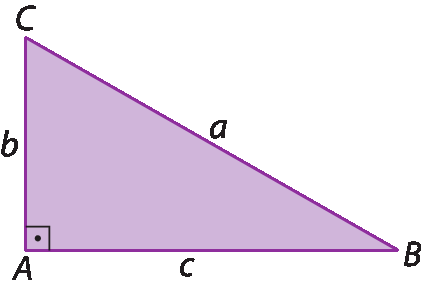
Queremos demonstrar que aelevado a 2 = belevado a 2 + celevado a 2.
Observe as figuras.
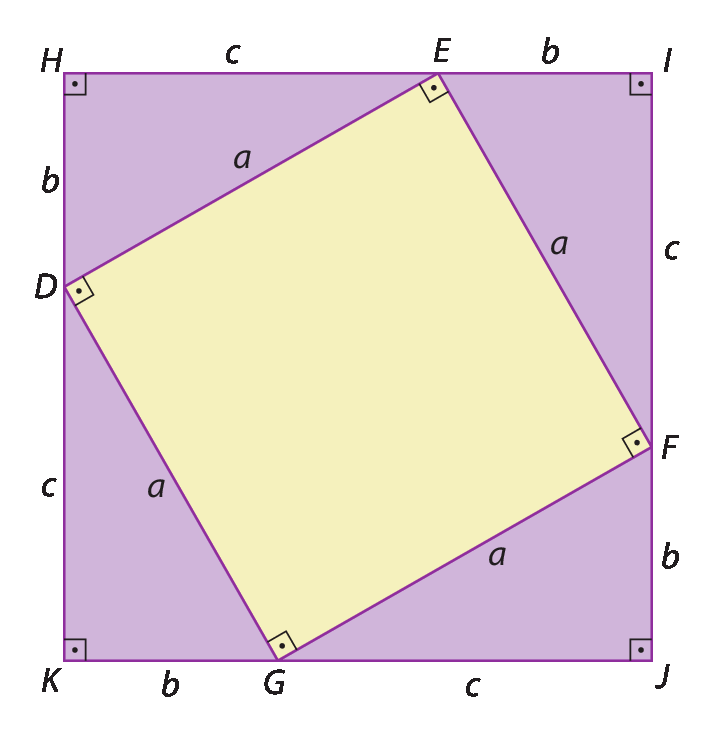
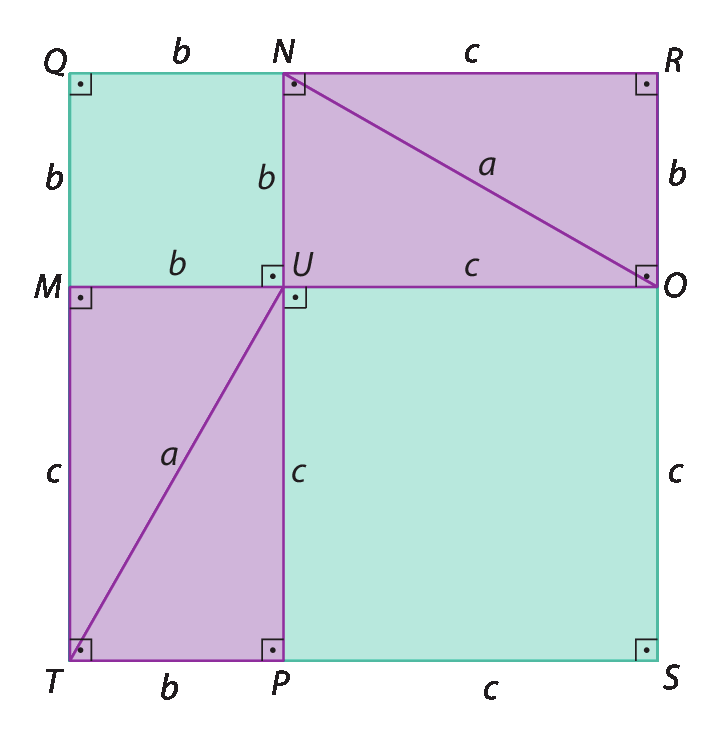
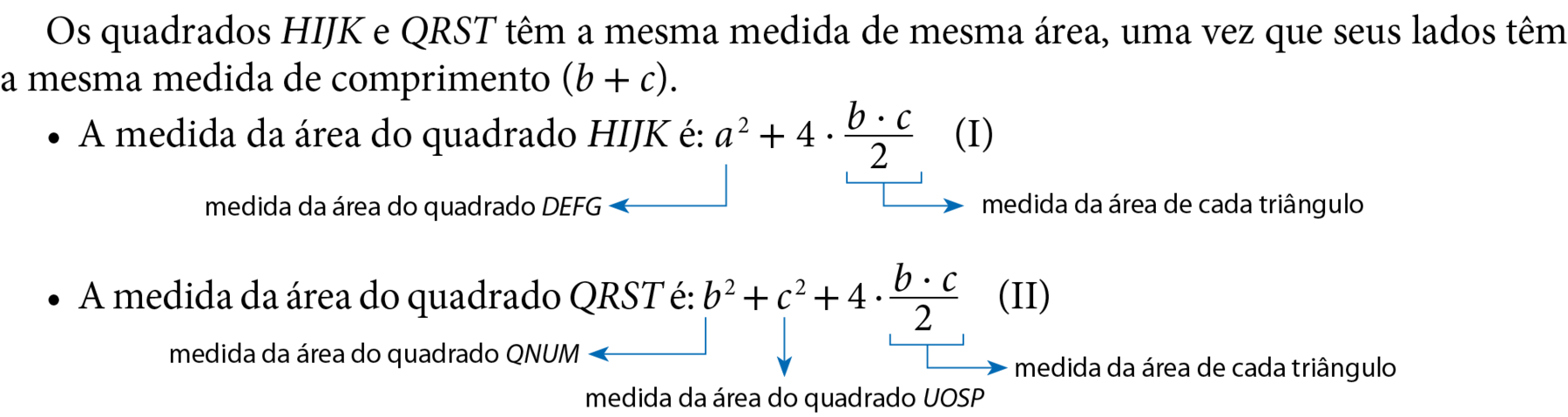
Como as medidas das áreas dos quadrados agá í jóta cá e QRST são iguais, igualamos um e dois:
Subtraindo
Sentença matemática. 4 vezes fração com numerador b vezes c e denominador 2.dos dois membros, temos:
aelevado a 2 = belevado a 2 + celevado a 2
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Trabalho com Pitágoras
Duração: 4:33min. Página: 149.
>> [Locutor] Trabalho com Pitágoras
>> [Locutora] O teorema de Pitágoras é muito importante para profissões que dependem diretamente da Matemática, como a Engenharia Civil e a Arquitetura. Em conversa com o matemático Eduardo Colli, professor do Instituto de Matemática e Estatística da Universidade de São Paulo, descobrimos como o teorema de Pitágoras aparece no dia a dia das profissões. Vamos ouvi-lo?
>> [Professor] Eu sou professor na USP, no Instituto de Matemática e Estatística. Minha área de formação como pesquisador é... tem o nome de “sistemas dinâmicos”. E eu tenho me dedicado bastante também à divulgação da Matemática, com destaque pra uma iniciativa que se chama “Matemateca”, que é um acervo de objetos matemáticos interativos, né? Qualquer um pode procurar a palavra “matemateca” ou “matemateca USP” na internet e vai achar o nosso projeto.
>> [Locutora] Cite alguns exemplos de aplicações do teorema de Pitágoras.
>> [Professor] Bom, eu entendo que a maior utilidade do teorema de Pitágoras é no cálculo de distâncias. Apenas pra começar, pra dar um exemplo, né?, imagina que você quer saber a distância entre o seu pé e o topo do prédio que está bem na tua frente, né? Então, você imagina que, do seu pé ao prédio, é um cateto, né?. Você vai imaginar um triângulo retângulo, então, você tem um cateto do seu pé até o prédio. Aí, você sobe na linha vertical até o topo, e aí você tem o outro cateto. Então, a hipotenusa desse triângulo retângulo é o segmento de reta imaginário que liga seu pé até o topo do prédio. Se você souber o tamanho dos catetos, que aqui são a distância ao prédio, né? – o primeiro cateto, e a altura do prédio, o segundo cateto – então, você vai ter o tamanho da hipotenusa, né?, que é a distância que você desejava saber aplicando o teorema de Pitágoras. Só que é bem mais do que aplicar numa situação como essa, que nem é tão comum, né? Por que as pessoas vão querer medir a distância do pé até o topo do prédio? Acontece que, nas profissões técnicas, todas as que envolvem medidas, é... cedo ou tarde, você vai colocar no espaço um sistema de coordenadas. Por exemplo, se você tá no plano, você vai pôr lá sistema cartesiano, X e Y. Então, se você souber as coordenadas de dois pontos diferentes, é o teorema de Pitágoras que vai te permitir calcular a distância entre eles. É assim que, por exemplo, os aplicativos de celular, de GPS, né?, ele pode [sic] calcular, por exemplo, a distância até o destino, até onde você quer chegar, né?, a pé ou de carro ou de ônibus... Porque ele sabe as coordenadas das esquinas das ruas e, assim, ele pode calcular o tamanho de cada rua e somar esses tamanhos e saber a distância total.
>> [Locutora] O teorema de Pitágoras está presente em algumas profissões? Quais?
>> [Professor] Em nível superior, todas as carreiras científicas de Exatas, claro! Mas também tem as carreiras práticas, como a Engenharia e a Arquitetura. Além disso, há profissões técnicas, como Agrimensura, Topografia... e diversas ligadas ao setor de construção.
>> [Locutora] Como a Matemática aparece no dia a dia dos engenheiros e arquitetos?
>> [Professor] No caso do arquiteto, o conhecimento de geometria é fundamental, principalmente, geometria espacial. Se o arquiteto não quer ficar no arroz com feijão, é... se ele conhecer os aspectos mais avançados da geometria, isso vai trazer pra ele uma grande dose de criatividade nos seus trabalhos. Pro engenheiro, além disso, né?, tem também a questão dos processos físicos, né? Ele precisa conhecer a fundo os processos físicos que embasam a engenharia, né? E aqueles que estão presentes mais em sua área de atuação, porque são várias as áreas de atuação de engenheiros, né? E esses processos físicos, né?... [reformula o raciocínio] A Física, você não faz Física sem saber Matemática, né? O maior sucesso da Matemática como aplicação no mundo real ainda é essa compreensão que ela permite sobre a realidade e a capacidade de fazer previsões. Às vezes muito precisas, né?
Studio Núcleo de Criação Produções em Áudio
Assim, demonstramos que, em um triângulo retângulo qualquer, a soma dos quadrados das medidas de comprimento dos catetos é igual ao quadrado da medida de comprimento da hipotenusa.
Orientações e sugestões didáticas
• A Geometria será abordada com caráter cada vez mais demonstrativo, pois o desenvolvimento dessa linguagem também é foco de aprendizagem. Assim, dedique tempo para as etapas da demonstração apresentada.
• A demonstração para o teorema de Pitágoras apresentada no livro é desenvolvida interativamente no link “Uma demonstração sem palavras do ‘Teorema de Pitágoras’“ (disponível em: https://oeds.link/zYSSbz; acesso em: 20 julho 2022).
• No site https://oeds.link/bOTjrY (acesso em: 20 julho 2022), há sugestões de como trabalhar o teorema de Pitágoras em sala de aula, além de apresentar um vídeo com uma verificação experimental muito interessante dêsse teorema. Se possível, apresente esse vídeo aos estudantes.

ATIVIDADES
faça as atividades no caderno
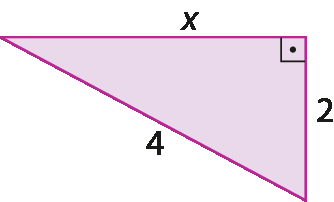
1. Em cada caso, determine a medida de comprimento x.
a)
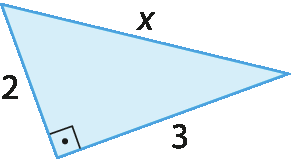
b)
2. Determine a medida de comprimento dos catetos de um triângulo retângulo isósceles cuja hipotenusa mede 10 centímetros de comprimento.
3. Uma escada está apoiada no tronco de uma árvore, conforme o esquema a seguir.
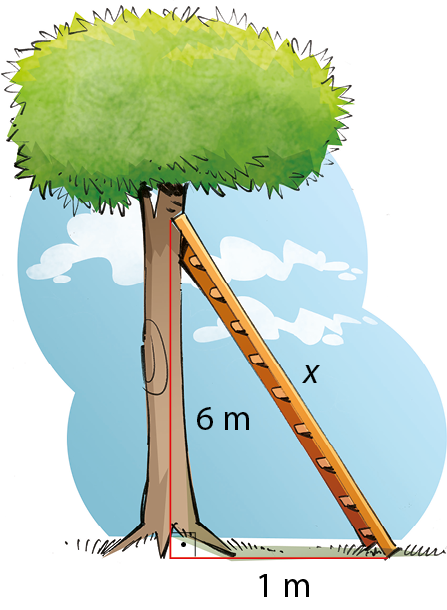
Calcule a medida de comprimento x, em metro, dessa escada.
4. Em um triângulo retângulo á bê cê, a hipotenusa mede
3 raiz quadrada de 5.centímetros de comprimento, e um cateto mede o dobro do comprimento do outro. Determine a medida de área dêsse triângulo.
5. Rui vai comprar uma ripa de madeira para fazer um reforço diagonal em uma cêrca que mede 0,8 métro de altura por 2 métros de comprimento. Qual deve ser a medida de comprimento da ripa?
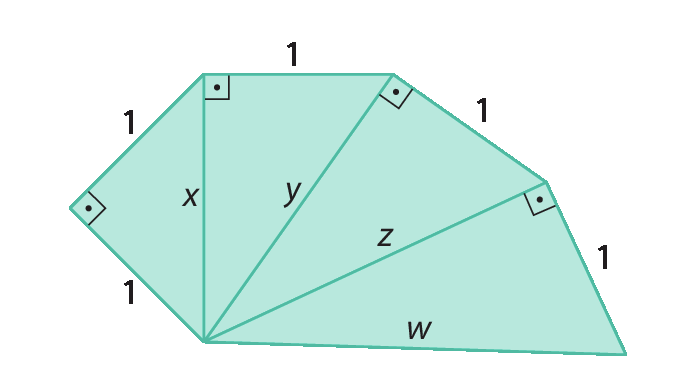
6. Determine as medidas de comprimento x, y, z e w indicadas na figura.
7. Observe a figura e faça o que se pede.
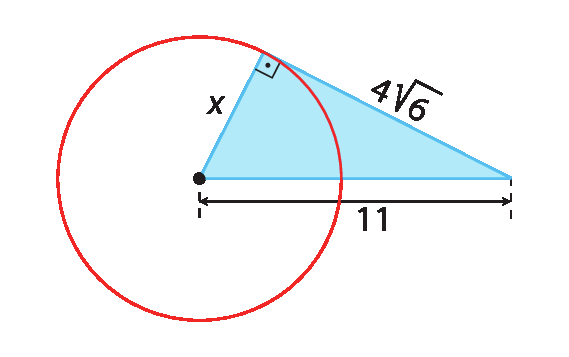
Determine:
a) a medida de comprimento x do raio da circunferência;
b) a medida do perímetro do triângulo;
c) a medida de área do triângulo.
8. (Etec-São Paulo) A pipa, também conhecida como papagaio ou quadrado, foi introduzida no Brasil pelos colonizadores portugueses no século dezesseis.
Para montar a pipa, representada na figura, foram utilizados uma vareta de 40 centímetros de comprimento, duas varetas de 32 centímetros de comprimento, tesoura, papel de seda, cola e linha.
As varetas são fixadas conforme a figura, formando a estrutura da pipa. A linha é passada em todas as pontas da estrutura, e o papel é colado de modo que a extremidade menor da estrutura da pipa fique de fóra.
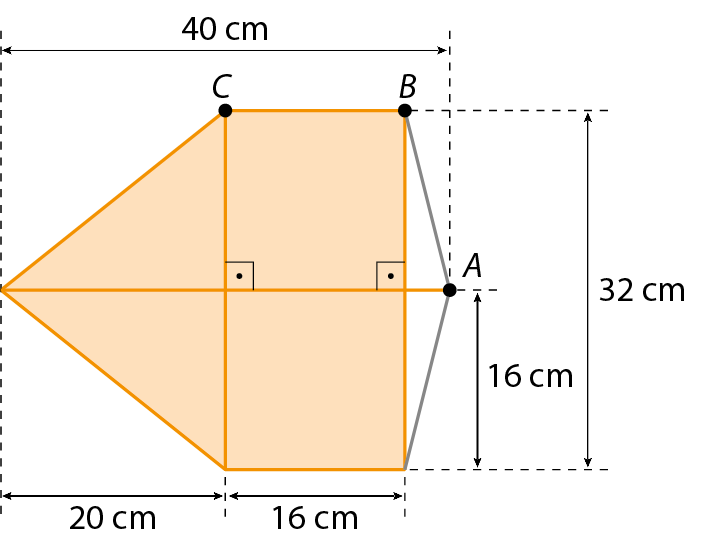
O comprimento da linha que passa pelos pontos a, B e C do contorno da estrutura da pipa, em centímetro, é:
a)
4 vezes abre parênteses 4 mais raiz quadrada de 17 fecha parênteses.b)
2 vezes abre parênteses 8 mais raiz quadrada de 19 fecha parênteses.c) 16 +
raiz quadrada de 17.d) 18 ⋅
raiz quadrada de 19.e) 20 ⋅
raiz quadrada de 17.9. Um fazendeiro caminhou do ponto a ao ponto B e depois do ponto B ao ponto C, conforme o esquema a seguir.
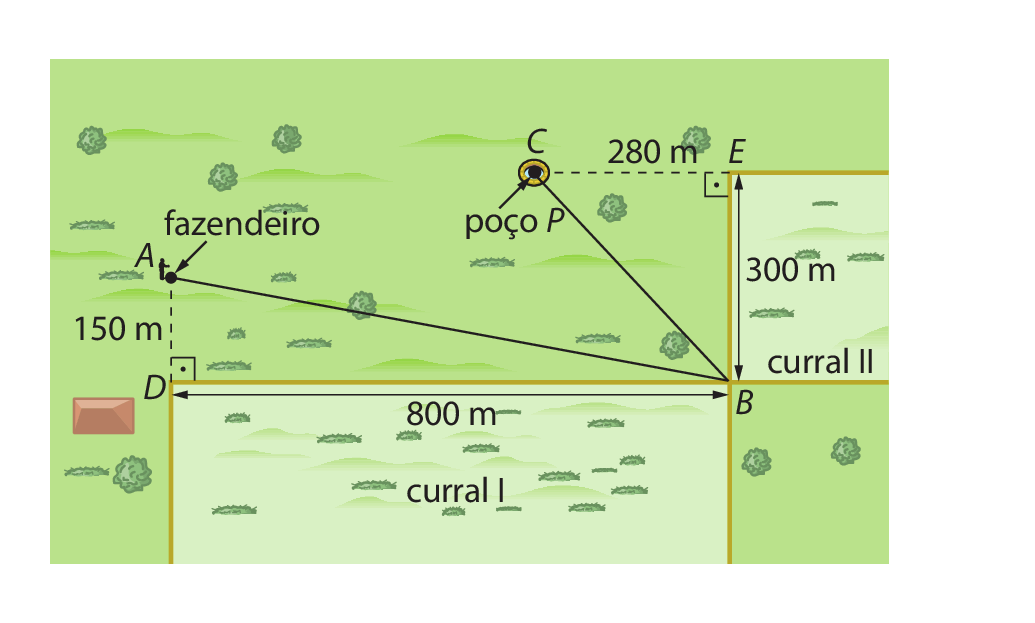
Qual é a medida da distância, em metro, que ele caminhou aproximadamente?
Respostas e comentários
1. a)
Raiz quadrada de 13.b)
Sentença matemática. 2 raiz quadrada de 3.2.
Sentença matemática. 5 raiz quadrada de 2, fim da raiz, centímetros.3.
raiz quadrada de 37.métros
4. 9 centímetros quadrados
5. aproximadamente 2,16 métros
6. x =
raiz quadrada de 2, y igual a raiz quadrada de 3, z igual a 2 e w igual a raiz quadrada de 5.7. a) 5
7. b)
Sentença matemática. 4 abre parênteses 4 mais raiz quadrada de 6 fecha parênteses.7. c)
Sentença matemática. 10 raiz quadrada de 6.8. alternativa a
9. .1224 métros
Orientações e sugestões didáticas
• Na resolução das atividades desta página, verifique se os estudantes lembram-se de que, em um triângulo retângulo, a hipotenusa é o lado oposto ao ângulo de 90graus. Identificar corretamente catetos e hipotenusa em um triângulo retângulo é fundamental para a aplicação correta do teorema de Pitágoras.
• A atividade 3 amplia o estudo sobre o teorema de Pitágoras, uma vez que os estudantes deverão utilizá-lo em situações mais complexas e sucessivas vezes, começando por encontrar o valor de x.
Sugestão de atividade
Márcia está participando de uma caça ao tesouro com um mapa de instruções e uma bússola. Ao chegar à última instrução, ela deu 120 passos para o oeste, mas deveria ter dado 50 passos para o norte. Ao perceber o erro, em vez de voltar e recomeçar, ela pensou que poderia economizar alguns passos se soubesse a direção exata do tesouro a partir daquele ponto. Se pudesse ir direto ao tesouro, quantos passos a menos Márcia daria?
Resolução: desenhando um esquema para ajudar na resolução da atividade, temos:
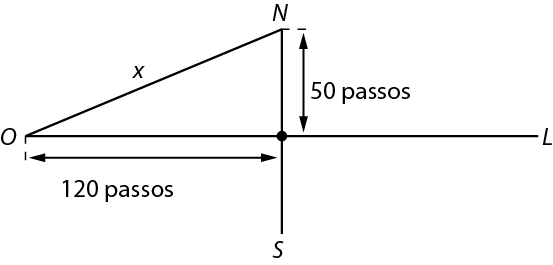
Se Márcia voltasse, daria 170 passos, pois 120 + 50 = 170. Para calcular quantos passos ela daria se fosse direto ao tesouro, consideramos o triângulo retângulo formado:
120elevado a 2 + 50elevado a 2 = xelevado a 2
xelevado a 2 = 16 900
x = 130
Portanto, se Márcia fosse direto ao tesouro, daria 40 passos a menos, pois 170 menos 130 = 40.
2 Outras relações métricas no triângulo retângulo
O teorema de Pitágoras é a primeira das relações métricas no triângulo retângulo que estudamos. Além dessa relação métrica, existem outras. Antes de estudá-las, porém, vamos ver alguns conceitos para entender os termos que serão usados.
• Projeção ortogonal de um ponto sobre uma reta
Considere um ponto P e uma reta r.
Ao traçar a reta s, perpendicular à reta r, e passando pelo ponto P, obtemos o ponto pêlinha. O ponto pêlinha é a projeção ortogonal do ponto P sobre a reta r.
Se o ponto pertence à reta, coincide com sua projeção ortogonal sobre a reta.
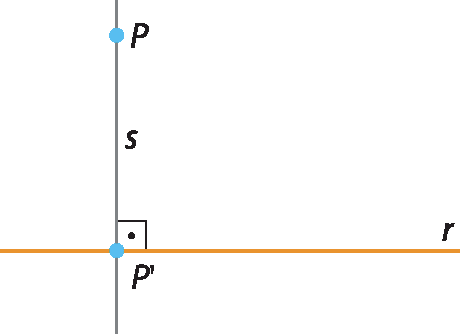
• Projeção ortogonal de um segmento sobre uma reta
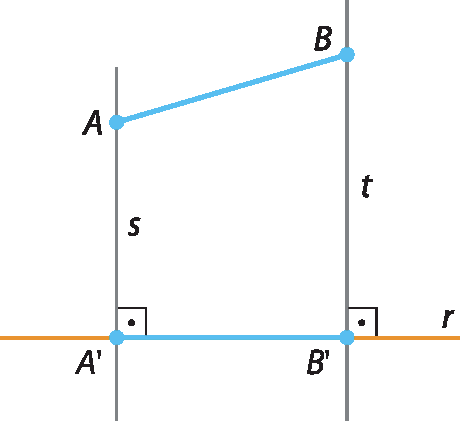
Considere um segmento
Símbolo. Segmento de reta AB.e uma reta r.
O ponto álinha é a projeção ortogonal do ponto A sobre a reta r, e o ponto bitlinha é a projeção ortogonal do ponto B sobre a reta r. Dessa fórma,
Símbolo. Segmento de reta A linha B linha.é a projeção ortogonal do segmento
Símbolo. segmento de reta AB.sobre a reta r.
Para pensar
No caso de um segmento
Símbolo. segmento de reta CD.ser perpendicular a uma reta r, que figura corresponde à projeção ortogonal do segmento sobre a reta?
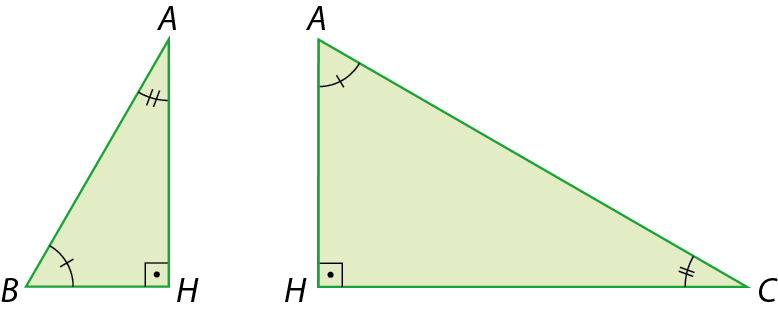
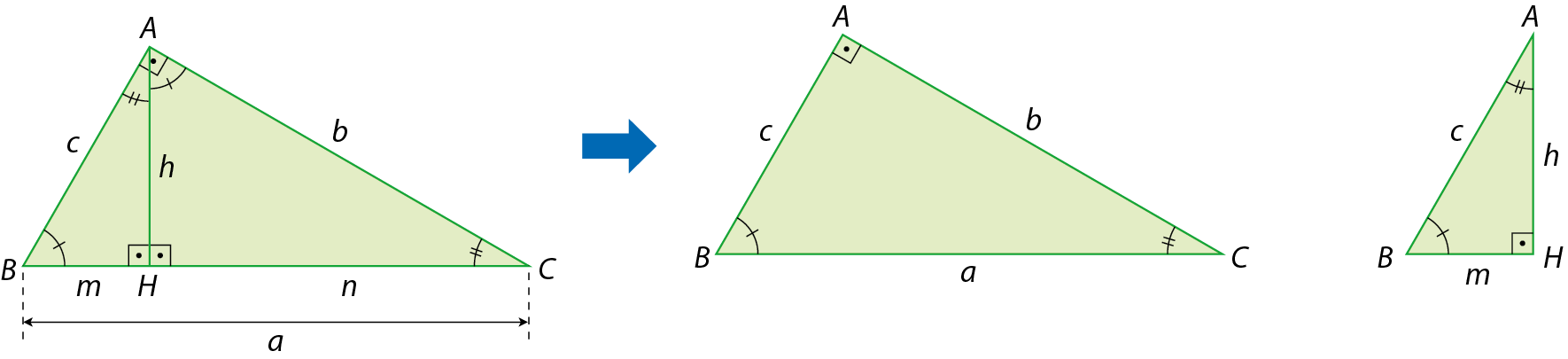
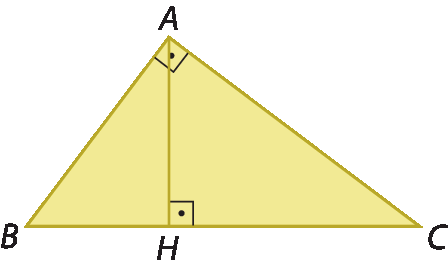
As próximas relações que estudaremos serão demonstradas com base no conceito de semelhança de triângulos. Para isso, considere o triângulo retângulo á bê cê representado a seguir.
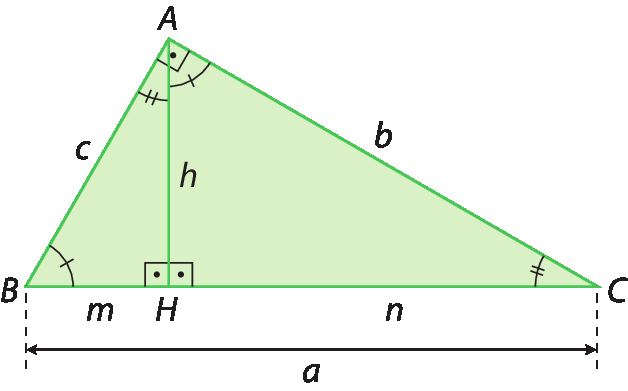
Nesse triângulo:
•
Símbolo. Segmento de reta BC.é a hipotenusa de medida de comprimento a;
•
Símbolo. Segmento de reta AB.é o cateto de medida de comprimento c;
•
Símbolo. Segmento de reta AC.é o cateto de medida de comprimento b;
•
Símbolo. segmento de reta AHé a altura relativa à hipotenusa; sua medida de comprimento é h;
•
Símbolo. segmento de reta BHé a projeção ortogonal do cateto
Símbolo. segmento de reta ABsobre a hipotenusa; sua medida de comprimento é m;
•
Símbolo. segmento de reta HCé a projeção ortogonal do cateto
Símbolo. segmento de reta ACsobre a hipotenusa; sua medida de comprimento é n.
O triângulo á bê cê pode ser decomposto em dois triângulos retângulos: △agá bê á e △agá á cê. Observando-os, notamos que:
•
Símbolo. Ângulo B e ângulo HAC.são ângulos complementares do ângulo
Símbolo. ângulo C.; logo,
Sentença matemática. ângulo HBA congruente ao ângulo HAC.;
•
Símbolo. Ângulo C e ângulo HAB.são ângulos complementares do ângulo
Símbolo. ângulo B.; logo,
Sentença matemática. ângulo HAB congruente ao ângulo HCA..
Respostas e comentários
Para pensar: um ponto
Orientações e sugestões didáticas
Outras relações métricas no triângulo retângulo
Objetivo
• Favorecer o desenvolvimento das habilidades da BNCC: ê éfe zero nove ême ah zero um e ê éfe zero nove ême ah um três.
Habilidades da BNCC
• Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah um três porque serão demonstradas as relações métricas no triângulo retângulo, entre elas o teorema de Pitágoras. Além disso, contribui para o desenvolvimento da habilidade ê éfe zero nove ême ah zero um ao identificar que existem segmentos de reta cujo comprimento não é expresso por número racional.
Orientações
• As demonstrações das relações métricas foram feitas a partir da semelhança entre os triângulos. Se julgar necessário, retome com os estudantes os casos de semelhança de triângulos.
• Nesta página, são apresentados alguns conceitos que darão subsídios para que os estudantes compreendam as demonstrações das relações métricas. Ao trabalhar as noções de projeção ortogonal de um ponto sobre uma reta e de um segmento sobre uma reta, retome a construção da perpendicular a uma reta por um ponto usando instrumentos de desenho. Alerte os estudantes para o cuidado ao manusear o compasso.
• No boxe Para pensar, espera-se que os estudantes percebam que, se o segmento de reta é perpendicular à reta, então o ponto de interseção entre eles coincide com a projeção ortogonal do segmento de reta sobre a reta.
(ê éfe zero nove ême ah zero um) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).
(ê éfe zero nove ême ah um três) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos.
Vamos analisar esses triângulos dois a dois.
• △ABC e △HBA
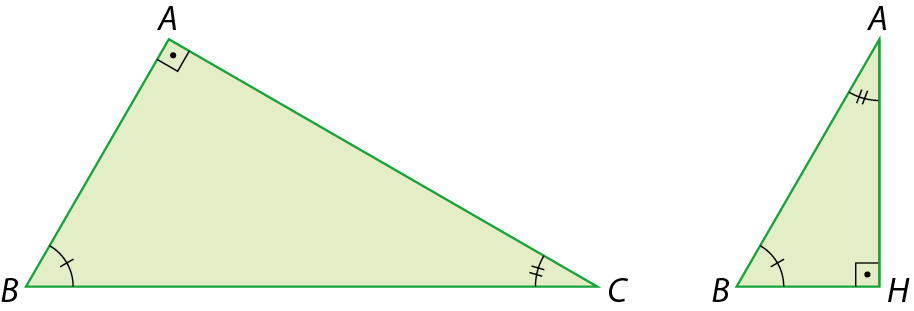
Ângulo BAC congruente a ângulo BHA.
abre parêntesesângulos retosfecha parênteses
Ângulo ABC congruente a ângulo HBA.
abre parêntesesângulo comumfecha parênteses
Então: △ABC ∼ △HBA abre parêntesescaso á áfecha parênteses
• △ABC e △HAC
Ângulo BAC congruente a ângulo AHC.
abre parêntesesângulos retosfecha parênteses
Ângulo ACB congruente a ângulo HCA.
abre parêntesesângulo comumfecha parênteses
Então: △ABC ∼ △HAC abre parêntesescaso á áfecha parênteses
• △HBA e △HAC
Ângulo BHA congruente a ângulo AHC.
abre parêntesesângulos retosfecha parênteses
Ângulo ABH congruente a ângulo CAH.
Então: △HBA ∼ △HAC abre parêntesescaso á áfecha parênteses
Usando essas semelhanças de triângulos, vamos mostrar as outras relações métricas.
Segunda relação métrica
Vamos retomar o triângulo ABC e considerar os triângulos ABC e HBA, que são semelhantes pelo caso de semelhança á á, conforme verificamos.
Podemos escrever a seguinte proporção entre as medidas de comprimento dos lados correspondentes dos triângulos:
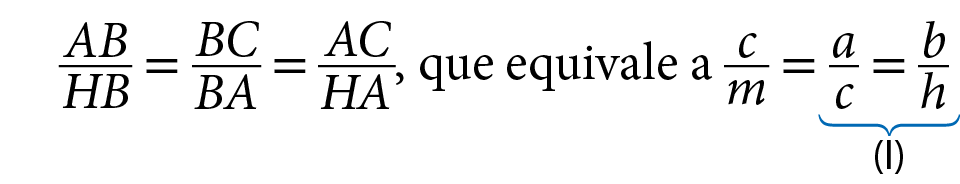
Da igualdade um, temos:
, ou seja, b · c = a · h
Orientações e sugestões didáticas
• É importante que os estudantes percebam que as relações métricas têm origem a partir do traçado da altura do triângulo retângulo em relação à hipotenusa.
• Se possível, antes de apresentar a segunda relação métrica, oriente os estudantes a verificar sua validade com o auxílio de um software de Geometria dinâmica. Com isso, eles poderão atribuir significado à demonstração que será feita na sequência.
• Faça a demonstração da segunda relação métrica com a participação da turma. Incentive os estudantes a identificar os lados e ângulos correspondentes dos triângulos semelhantes e a ditar a proporção entre as medidas de comprimento dos lados correspondentes.
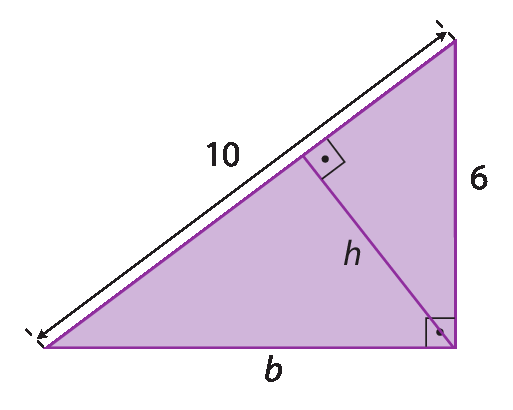
Esta é a segunda relação métrica:
Em um triângulo retângulo qualquer, o produto das medidas de comprimento dos catetos é igual ao produto da medida de comprimento da hipotenusa pela medida de comprimento da altura relativa à hipotenusa.
Observe como determinar as medidas de comprimento b e h indicadas no triângulo a seguir, aplicando o teorema de Pitágoras e a segunda relação métrica.
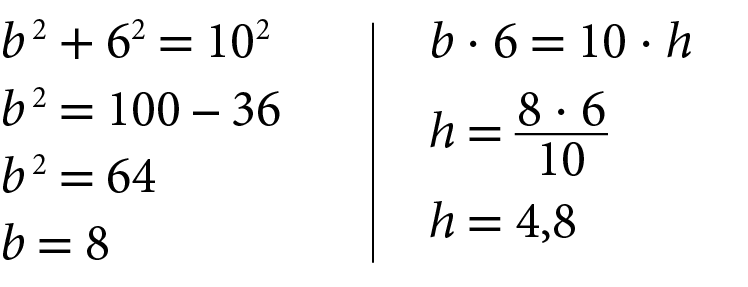
Terceira relação métrica
Vamos retomar a proporção entre as medidas de comprimento dos lados correspondentes dos triângulos semelhantes á bê cê e agá bê á:

Da igualdade dois, temos:
, ou seja, celevado a 2 = a · m
Agora, vamos considerar os triângulos á bê cê e agá á cê. Como vimos anteriormente, esses triângulos também são semelhantes.

Podemos escrever a seguinte proporção entre as medidas de comprimento dos lados correspondentes dos triângulos:
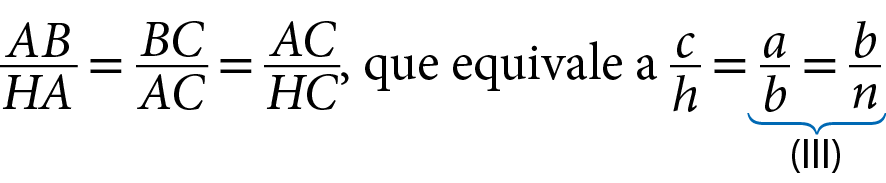
Da igualdade três, temos:
, ou seja, belevado a 2 = a · n
Assim, obtemos a terceira relação métrica:
Em um triângulo retângulo qualquer, o quadrado da medida de comprimento de um cateto é igual ao produto da medida de comprimento da hipotenusa pela medida da projeção ortogonal dêsse cateto sobre a hipotenusa.
Orientações e sugestões didáticas
• Assim como no estudo da segunda relação métrica, convém que os estudantes verifiquem experimentalmente a validade da terceira relação antes que esta seja apresentada e demonstrada para eles. Também, nesse caso, é de grande valia demonstrar essa relação no quadro com a participação da turma.
Acompanhe, por exemplo, como podemos determinar as medidas de comprimento b e c indicadas no triângulo a seguir.
Nesse triângulo, a medida de comprimento da hipotenusa
BC.é igual a 5, pois a = 3,2 + 1,8 = 5.
Então:

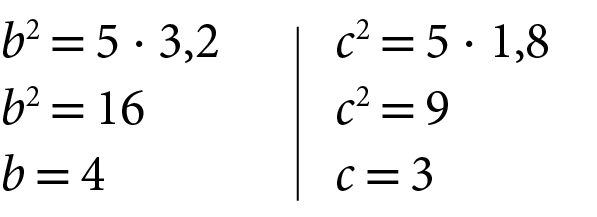
Para demonstrar

Você sabia que é possível demonstrar o teorema de Pitágoras usando a terceira relação métrica? Junte-se a um colega e façam o que se pede.
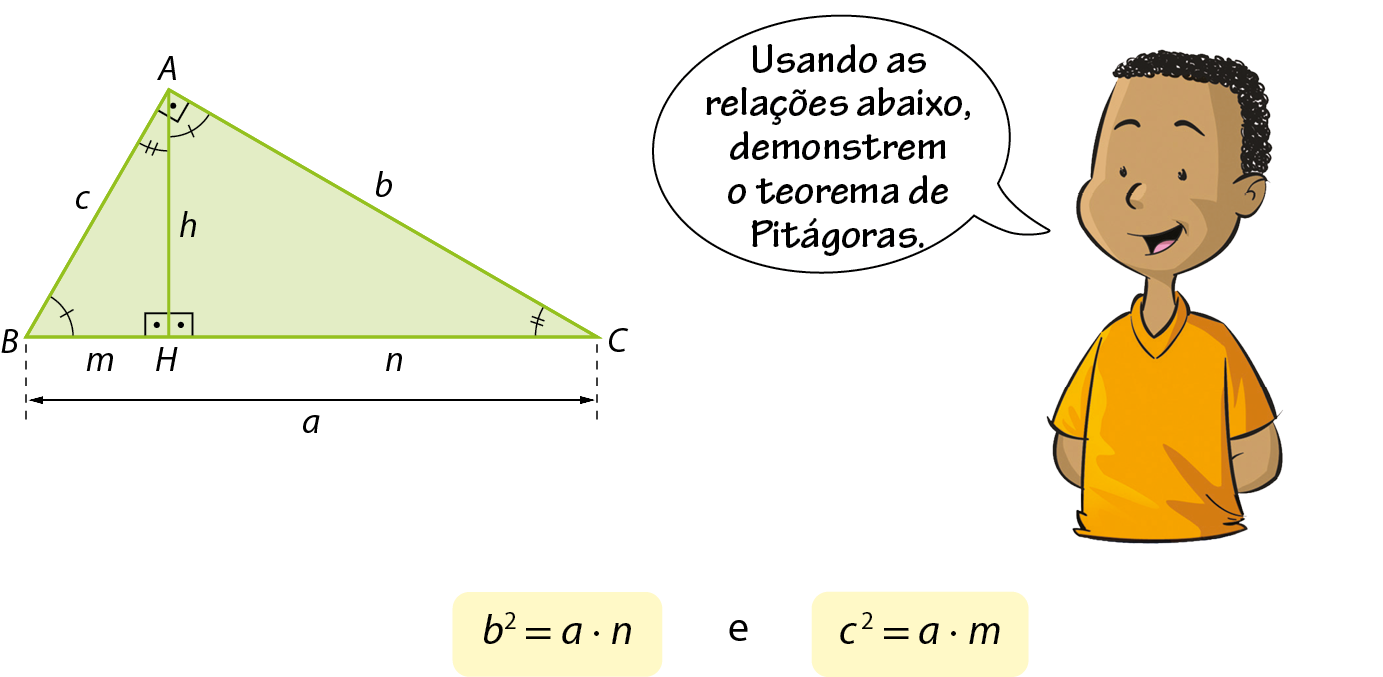
Quarta relação métrica
Vamos considerar, agora, os triângulos semelhantes agá bê á e agá á cê.
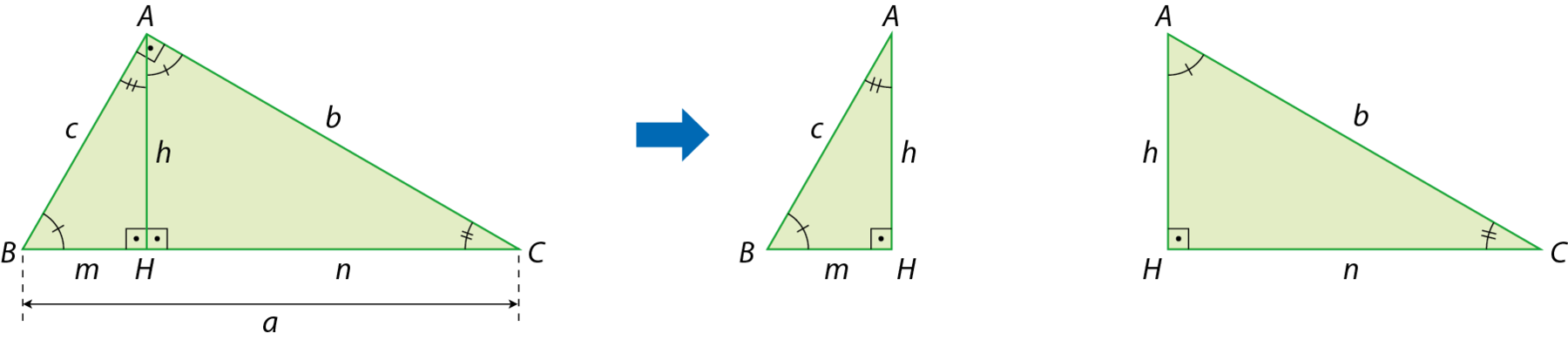
Podemos escrever a seguinte proporção entre as medidas de comprimento dos lados correspondentes:
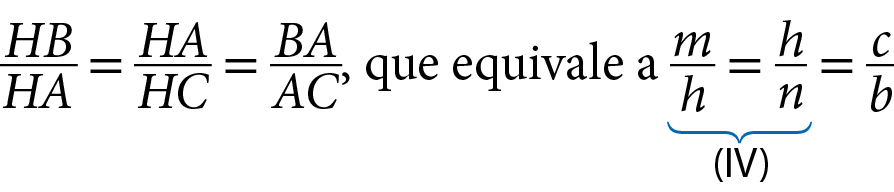
Da igualdade quatro, temos:
, ou seja, helevado a 2 = m · n
Respostas e comentários
Para demonstrar:
Adicionando membro a membro as duas igualdades, temos:
b elevado a 2 + c elevado a 2 = a ⋅ n + a ⋅ m
b elevado a 2 + c elevado a 2 = a ⋅ (n + m)
Substituindo (n + m) por a, temos:
b elevado a 2 + c elevado a 2 = a ⋅ (n + m)
b elevado a 2 + c elevado a 2 = a ⋅ a
b elevado a 2 + c elevado a 2 = aelevado a 2
Orientações e sugestões didáticas
• O teorema de Pitágoras já foi demonstrado a partir da noção de área. No boxe Para demonstrar, os estudantes poderão fazer a demonstração do teorema a partir da terceira relação métrica, que, por sua vez, decorre da semelhança de triângulos. É importante enfatizar para a turma que na Matemática há diferentes caminhos que podem conduzir ao mesmo fim. Se julgar conveniente, proponha aos estudantes que pesquisem outras demonstrações do teorema de Pitágoras e que cada um escolha uma das demonstrações, entenda seus passos e explique-a a um colega. Em seguida, oriente-os a ouvir a explicação da demonstração que o colega escolheu e, se necessário, fazer perguntas para compreender melhor. Conversem sobre qual demonstração eles acharam mais fácil e, depois, peça que compartilhem com a turma o que concluíram. A atividade de pesquisa, explicação e argumentação permite que os estudantes exercitem várias atitudes para a vida, como organizar as ideias e comunicar-se de maneira clara, além de perceber que um mesmo teorema pode ser demonstrado de diferentes maneiras.
• Trabalhe a quarta relação assim como as demais. É importante que os estudantes não sejam incentivados a memorizar essas relações, mas sim que atribuam significado a cada uma delas.
Chegamos, então, à quarta relação métrica:
Em um triângulo retângulo qualquer, o quadrado da medida de comprimento da altura relativa à hipotenusa é igual ao produto das medidas de comprimento das projeções ortogonais dos catetos sobre a hipotenusa.
Observe, por exemplo, como podemos calcular a medida de comprimento h da altura do triângulo retângulo a seguir usando a quarta relação métrica.
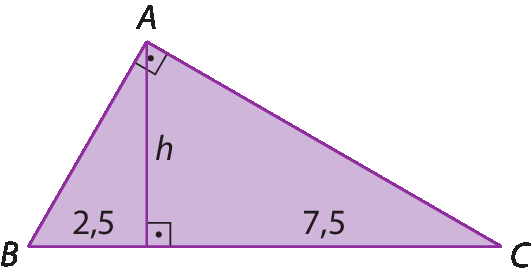
helevado a 2 = 2,5 ⋅ 7,5
helevado a 2 = 2,5 ⋅ 2,5 ⋅ 3
h = 2,5 ⋅
Sentença matemática. Raiz quadrada de 3.h ≃ 4,33

ATIVIDADES
faça as atividades no caderno
1. Observe as figuras.
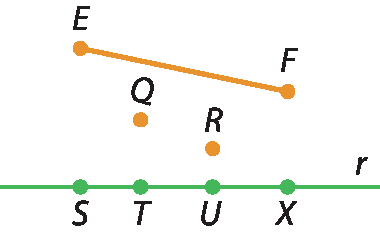
Usando um esquadro, identifique as projeções ortogonais na reta r :
a) dos pontos Q, R e u;
b) dos segmentos
Símbolo. Segmento de reta EF e segmento de reta TU..
2. Observe o triângulo e associe as colunas no caderno.

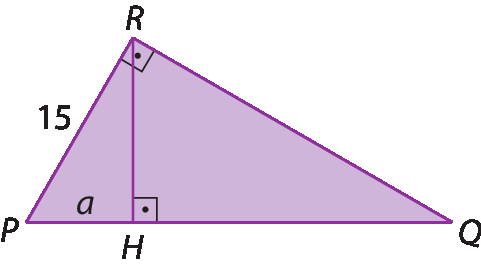
3. Determine a medida de comprimento de
Símbolo. Segmento de reta PQ.em função de a.
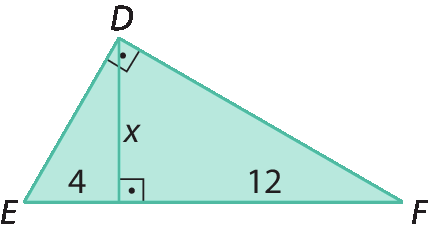
4. Em cada caso, determine a medida de comprimento x indicada no triângulo retângulo.
a)
b)
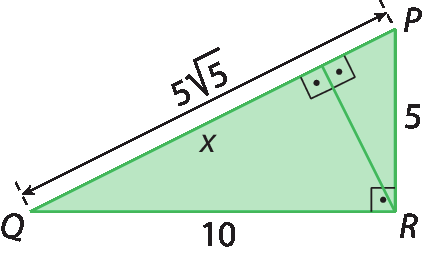
c)
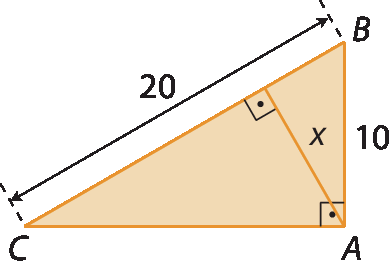
d)
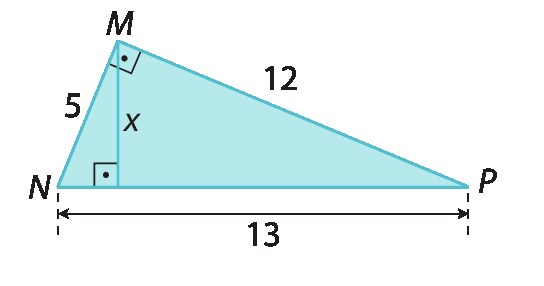
e)
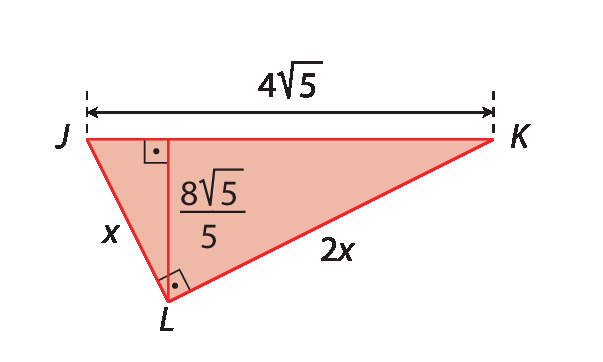
Respostas e comentários
1. a) T, u e u
1. b)
Símbolo. Segmento de reta SX e segmento de reta TU.2. A – três; B – um; C – dois
3.
Fração 225 sobre a.4. a) 4
Sentença matemática. Raiz quadrada de 3.4. b)
4 raiz quadrada de 5.4. c)
5 raiz quadrada de 3.4. d)
fração 60 sobre 13.4. e) 4
Orientações e sugestões didáticas
• As atividades desta página exigem dos estudantes a aplicação das relações métricas estudadas anteriormente. Aproveite a oportunidade para avaliar o que aprenderam e identificar as principais dificuldades.
• Aproveite as atividades 1 e 2 para verificar se os estudantes compreenderam a ideia de projeção ortogonal e os termos usados.
Lembre-se: Escreva no caderno!
5. Reproduza a afirmação verdadeira no caderno.
a) Ao traçar a altura relativa à hipotenusa de qualquer triângulo retângulo cujo comprimento da hipotenusa mede 10 centímetros, a projeção de um dos catetos sobre a hipotenusa terá medida igual a 5 centímetros de comprimento.
b) Se a altura relativa à hipotenusa de um triângulo retângulo mede 10 centímetros de comprimento, a hipotenusa dêsse triângulo também mede 10 centímetros de comprimento.
c) Se as projeções ortogonais dos catetos de um triângulo retângulo medem 5,3 centímetros e 4,5 centímetros de comprimento, a altura relativa à hipotenusa mede aproximadamente 4,88 métros de comprimento.
6. Leia e faça o que se pede.
a) Em um triângulo retângulo, a medida de comprimento da hipotenusa é igual a 10 centímetros e a dos catetos,
2 raiz de 5, fim da raiz, centímetros e 4 raiz de 5, fim da raiz.centímetros. Calcule a medida de comprimento da altura relativa à hipotenusa.
b) Determine, em um triângulo retângulo de catetos com medidas de comprimento iguais a 3 decímetros e 4 decímetros, a medida de comprimento da hipotenusa e da altura relativa à hipotenusa.
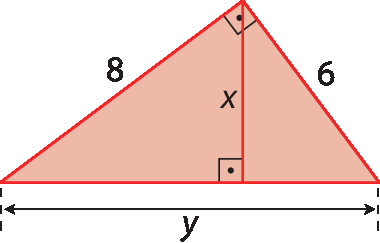
7. Determine a medida de comprimento das incógnitas em cada item.
a)
b)
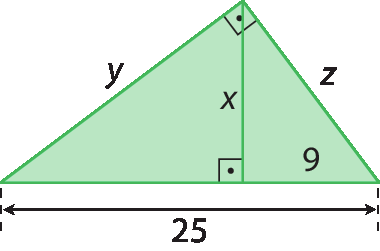
c)
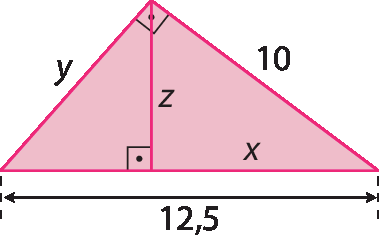
d)
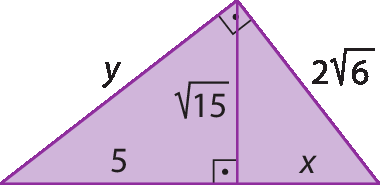
e)
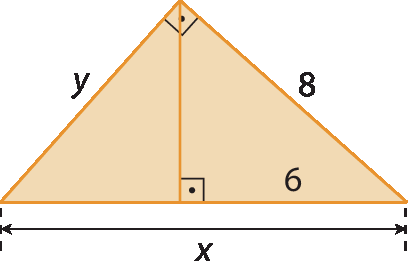
f)
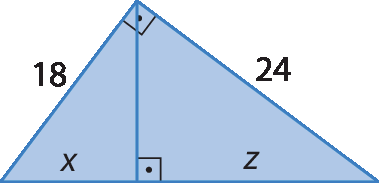
8.


Elabore uma atividade envolvendo um triângulo retângulo isósceles com, pelo menos, um dos lados medindo 16 centímetros de comprimento. Depois, em duplas, troquem as atividades e resolvam.
3 Aplicações do teorema de Pitágoras
Medida de comprimento da diagonal de um quadrado
Considere um quadrado a bê cê dê cujo comprimento do lado mede
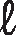
e o da diagonal mede d.
Observe que a diagonal
Símbolo. Segmento de reta AC.divide o quadrado em dois triângulos retângulos congruentes: △á bê cê e △á dê cê.
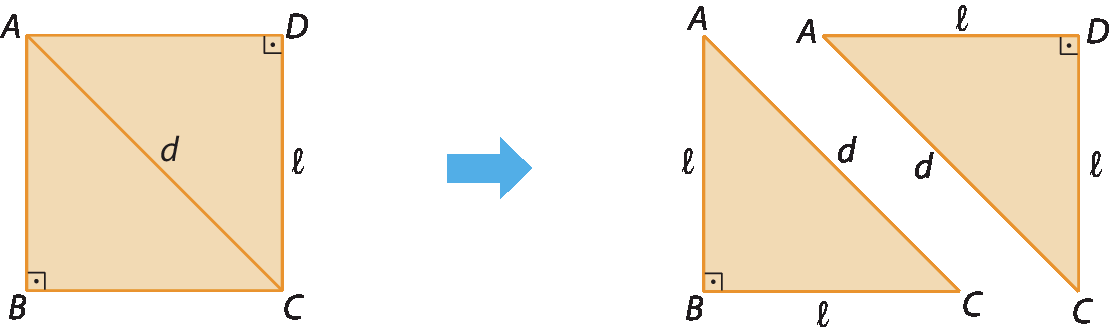
Aplicando o teorema de Pitágoras ao △á bê cê, temos:
d ² = ℓelevado a 2+ ℓelevado a 2
d ² = 2ℓelevado a 2
d =
início da raiz quadrada, 2 l elevado ao quadrado, fim da raiz=
l raiz quadrada de 2.Assim:
Em um quadrado de lado de medida de comprimento ℓ
, a medida de comprimento da diagonal é ℓ
raiz quadrada de 2.
Respostas e comentários
5. alternativa c
6. a) 4 centímetros
6. b) medida de comprimento da hipotenusa: 5 decímetros; medida de comprimento da altura: 2,4 decímetros
7. a) x = 4,8 e y = 10
7. b) x = 12, y = 20 e z = 15
7. c) x = 8, y = 7,5 e z = 6
7. d) x = 3 e y =
2 raiz quadrada de 10.7. e)
x igual a fração 32 sobre 3 e y igual a fração com numerador 8 raiz quadrada de 7 e denominador 3.
7. f) x = 10,8 e z = 19,2
8. Resposta pessoal.
Orientações e sugestões didáticas
• Na atividade 5, oriente os estudantes a fazer uma figura que represente cada uma das afirmações para ajudá-los a identificar a verdadeira.
• Ao resolver a atividade 6, peça aos estudantes que registrem a relação (ou relações) que estão aplicando: teorema de Pitágoras, segunda, terceira ou quarta relação métrica. Não é necessário fazer sempre esse registro, mas neste início dos estudos ele auxiliará a apreensão dessas ideias.
• Para fazer a atividade 7, os estudantes podem formar duplas ou trios e, assim, trocar informações. É fundamental que justifiquem a resposta apresentada.
Aplicações do teorema de Pitágoras
Objetivo
• Favorecer o desenvolvimento das habilidades da BNCC: ê éfe zero nove ême ah zero um, ê éfe zero nove ême ah um quatro e ê éfe zero nove ême ah um seis.
Habilidades da BNCC
• Este tópico favorece o desenvolvimento das habilidades ê éfe zero nove ême ah um quatro e ê éfe zero nove ême ah um seis porque os estudantes vão resolver e elaborar problemas de aplicação do teorema de Pitágoras; inclusive problemas de determinação do ponto médio de um segmento de reta e da medida de distância entre dois pontos dadas as coordenadas desses pontos no plano cartesiano. Além disso, a habilidade ê éfe zero nove ême ah zero um também é favorecida ao resgatar a ideia do número irracional na diagonal do quadrado.
Orientações
• Algumas das aplicações destacadas no texto referem-se à medida de comprimento da diagonal do quadrado e à medida de comprimento da altura de um triângulo equilátero, mas essas ideias podem ser estendidas para outras figuras planas, como o retângulo, o losango e o triângulo isósceles. Além disso, os estudantes verão como localizar alguns números reais na reta numérica e como determinar a medida da distância entre dois pontos do plano cartesiano aplicando o teorema de Pitágoras.
(ê éfe zero nove ême ah zero um) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).
(ê éfe zero nove ême ah um quatro) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
(ê éfe zero nove ême ah um seis) Determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer, dadas as coordenadas desses pontos no plano cartesiano, sem o uso de fórmulas, e utilizar esse conhecimento para calcular, por exemplo, medidas de perímetros e áreas de figuras planas construídas no plano.
Lembre-se: Escreva no caderno!
Medida de comprimento da altura de um triângulo equilátero
Considere um triângulo equilátero á bê cê cujo comprimento do lado mede
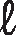
e o da altura mede h.
Observe que a altura
Símbolo. Segmento de reta AH.divide o △á bê cê em dois triângulos retângulos congruentes: △á bê agá e △á cê agá.
Aplicando o teorema de Pitágoras ao △á cê agá, temos:
=
Fração com numerador l raiz quadrada de 3 e denominador 2.Então:
Em um triângulo equilátero de lado de medida de comprimento ℓ
, a altura mede
Fração com numerador l raiz quadrada de 3 e denominador 2de comprimento.
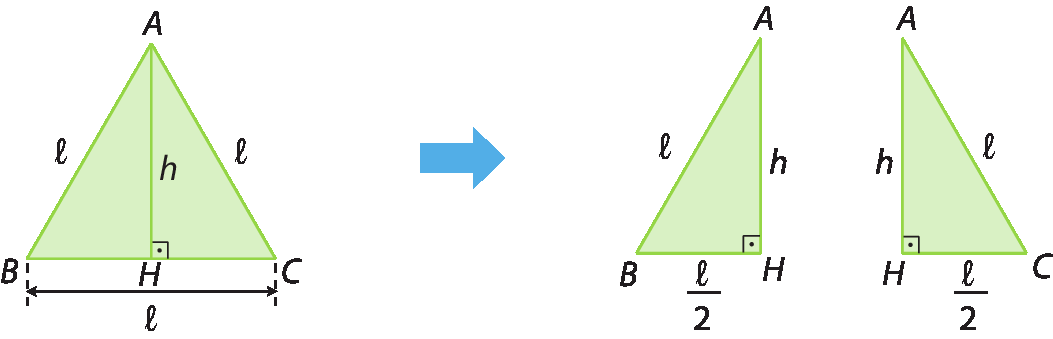
Recorde
Em um triângulo equilátero qualquer, a medida de comprimento da altura relativa a um de seus lados coincide com a da mediana relativa ao mesmo lado, formando dois triângulos retângulos congruentes.

△á bê agá ≅ △á cê agá abre parêntesespois os lados correspondentes são congruentesfecha parênteses.
Para fazer
Nas páginas 24 e 25, você viu como localizar o ponto correspondente ao número irracional
Raiz quadrada de 2.na reta numérica, transferindo com o compasso a medida de comprimento da diagonal de um quadrado com uma unidade de medida de comprimento de lado para a reta.
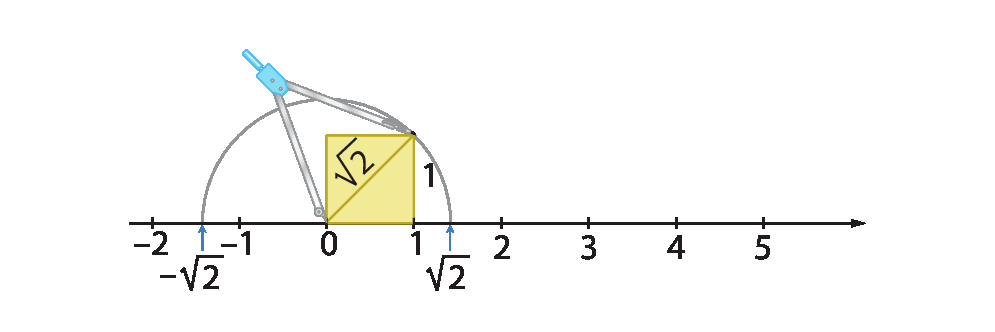
Atenção! Cuidado ao usar o compasso.
Agora, faça o que se pede.
a) Calcule a medida de comprimento da diagonal de um retângulo de lados que medem uma unidade e duas unidades de comprimento.
b) Usando régua e compasso, construa em seu caderno uma reta numérica e localize nela o ponto correspondente ao número irracional
raiz quadrada de 5.
c)

Converse com um colega sobre como vocês poderiam localizar nessa reta os pontos correspondentes aos números irracionais
Raiz quadrada de 10.e
Raiz quadrada de 13..
Respostas e comentários
Para fazer: Respostas em Orientações.
Orientações e sugestões didáticas
• É importante estimular os estudantes a não memorizar que, em um quadrado de lado
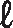
, a medida de comprimento da diagonal é
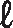
e que, em um triângulo equilátero de lado
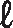
, a medida de comprimento da altura mede
Fração com numerador l raiz quadrada de 3 e denominador 2.. O objetivo é que eles compreendam como essas sentenças algébricas podem ser deduzidas a partir do teorema de Pitágoras.
• No boxe Para fazer, espera-se que os estudantes se lembrem de como localizar o número irracional
raiz quadrada de 2.na reta numérica a fim de entender os passos para resolver os itens propostos.
Resolução:
a) Para facilitar o cálculo, sugira aos estudantes que desenhem o retângulo proposto no caderno e tracem a diagonal. Depois, basta aplicar o teorema de Pitágoras para encontrar a diagonal medindo
raiz quadrada de 5unidades de comprimento.
b) Exemplos de resposta:


c) Espera-se que os estudantes percebam que basta construir dois retângulos: um de lados medindo uma e 3 unidades de comprimento (que terá diagonal medindo
Símbolo. raiz quadrada de 10.unidades de comprimento) e outro de lados com medidas de duas e 3 unidades de comprimento (que terá diagonal medindo
Símbolo. raiz quadrada de 13.unidades de comprimento). Em seguida, é preciso transferir, com o compasso, as medidas de comprimento das diagonais desses retângulos para a reta numérica. Alerte-os para os eventuais riscos ao manusear o compasso, garantindo assim a integridade física deles.
Se julgar conveniente, amplie a proposta dêsse boxe e mostre como utilizar o teorema de Pitágoras para localizar na reta numérica outros números irracionais, por exemplo
Menos raiz quadrada de 7, menos raiz quadrada de 3, raiz quadrada de 3, raiz quadrada de 7.etcétera

ATIVIDADES
faça as atividades no caderno
1. Determine a medida de comprimento x indicada em cada figura.
a)
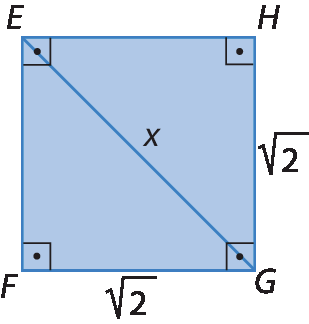
b)
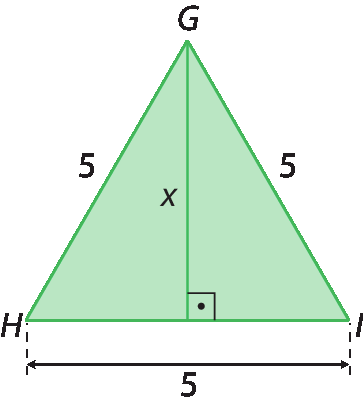
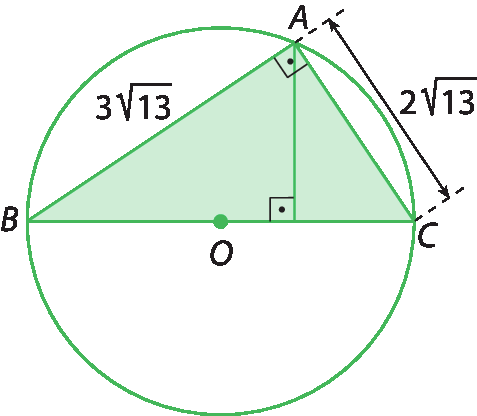
2. Em cada caso, calcule a medida de comprimento do raio de cada circunferência com centro óh.
a)
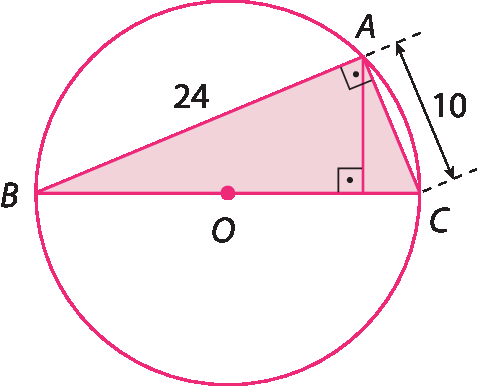
b)
3. Responda às questões.
a) Qual é a medida de comprimento da diagonal de um quadrado cujo perímetro mede 16 centímetros?
b) Qual é a medida de comprimento da altura de um triângulo equilátero cujo perímetro mede 24 centímetros?
c) Qual é a medida do perímetro de um quadrado cuja diagonal mede
3 raiz quadrada de 2.centímetros de comprimento?
d) Qual é a medida do perímetro de um triângulo equilátero cuja altura mede
7 raiz quadrada de 3.centímetros de comprimento?
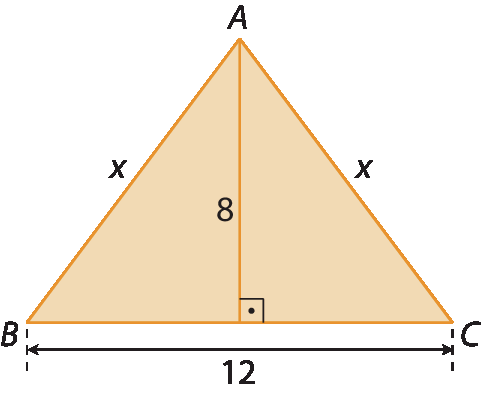
4. Calcule a medida do perímetro do triângulo isósceles á bê cê.
5. Observe o esquema a seguir.
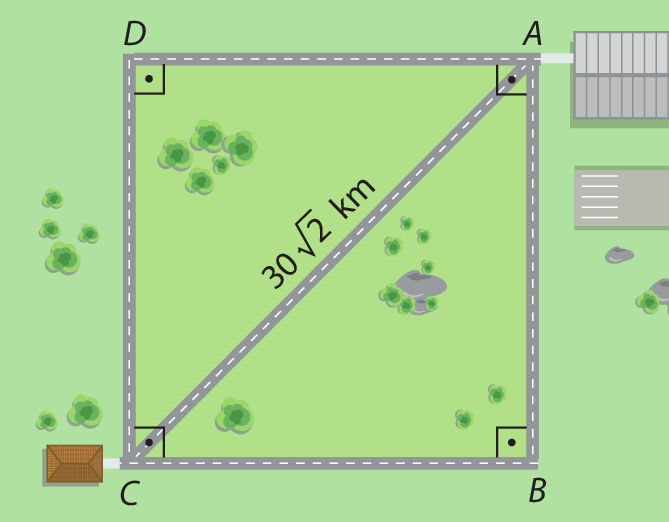
Márcia está no ponto A, que representa o aeroporto da cidade, e pretende ir até o ponto C, onde fica sua residência.
Sabendo que a representação dessas vias fórma um quadrado a bê cê dê, quantos metros de comprimento Márcia terá de percorrer para chegar até sua casa, se ela tiver de passar pelo ponto B?
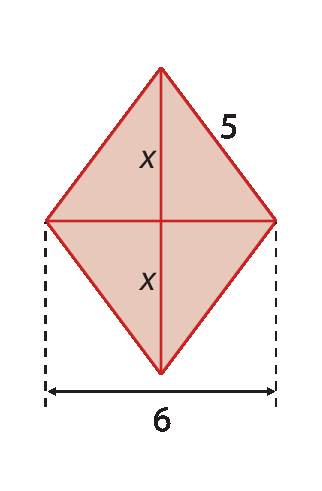
6. Determine a medida de comprimento de x nos losangos.
a)
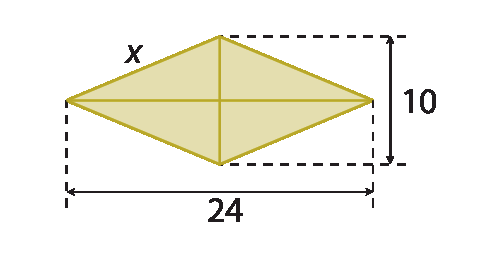
b)
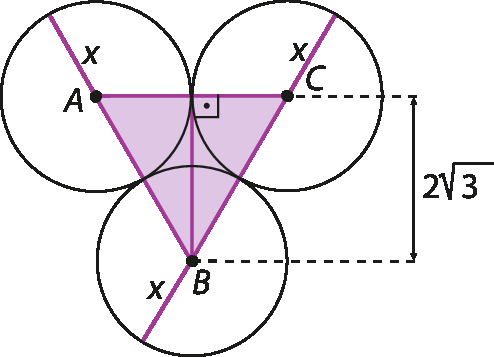
7. Calcule o que se pede.
a) Sabendo que a área de um quadrado mede 25 centímetros quadrados, calcule a medida de comprimento de sua diagonal.
b) Se um quadrado tem diagonal que mede 8 centímetros de comprimento, qual é sua medida de área?
8. Calcule a medida de comprimento x sabendo que a, B e C são os centros das circunferências e que elas são tangentes duas a duas.
Respostas e comentários
1. a) 2
1. b)
Sentença matemática. Fração com numerador 5 raiz quadrada de 3 e denominador 2.2. a) 13
2. a)
Sentença matemática. fração 13 sobre 2.3. a)
Sentença matemática. 4 raiz quadrada de 2, fim da raiz, centímetros.3. b)
Sentença matemática. 4 raiz quadrada de 3, fim da raiz, centímetros.3. c) 12 centímetros
3. d) 42 centímetros
4. 32
5. .60000 métros
6. a) 13
6. b) 4
7. a)
Sentença matemática. 5 raiz quadrada de 2, fim da raiz, centímetros.7. b) 32 centímetros quadrados
8. 2
Orientações e sugestões didáticas
• Para estas atividades, é esperado que os estudantes já utilizem, de modo mais natural, as relações métricas estudadas, mas eles podem fazer as consultas que forem necessárias a fim de resolver as atividades aqui propostas.
• Na atividade 3, os estudantes aplicarão o teorema de Pitágoras em situações que envolvem quadrados ou triângulos equiláteros. Em todas as situações há alguma relação com o perímetro do polígono em questão. Observe se os estudantes fazem adequadamente as relações de acôrdo com os dados do enunciado de cada item.
• Para ampliar a atividade 6, peça aos estudantes que calculem, em centímetro e em centímetro quadrado, a medida do perímetro e a da área dos losangos de cada item. (Respostas: item a: 52 centímetros; 120 centímetros quadrados; item b: 20 centímetros; 24 centímetros quadrados.). Se julgar necessário, relembre a eles como calcular a medida do perímetro e da área do losango. No caso da medida da área, os estudantes também podem calcular a medida da área de um dos quatro triângulos que formam o losango e depois multiplicar por 4.
9. Sabendo que a medida do perímetro do quadrado dê é éfe gê é um terço da medida do perímetro do triângulo equilátero á bê cê, determine a medida de comprimento da diagonal do quadrado.
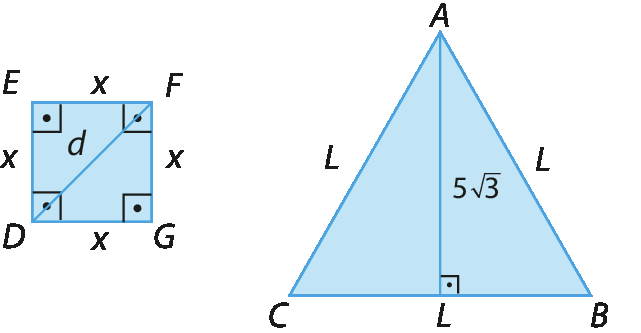
10. O triângulo á bê cê é equilátero e cada um de seus lados mede 12 centímetros de comprimento.
Sabendo que os segmentos
C D,
D Ee
E Ftêm a mesma medida de comprimento, determine quanto mede:
a) o comprimento do segmento
Símbolo. Segmento de reta DE.;
b) o perímetro do triângulo CFB.
11. Uma escada será construída para facilitar o acesso a um saguão. O desnível entre a rua e o saguão mede 2 métros de comprimento. A medida de comprimento de cada degrau será de 25 centímetros na horizontal e de 20 centímetros na vertical. Determine:
a) a quantidade de degraus que terá essa escada;
b) a medida de comprimento mínimo do corrimão para que ele ocupe toda a extensão da escada.
12. (enêm)
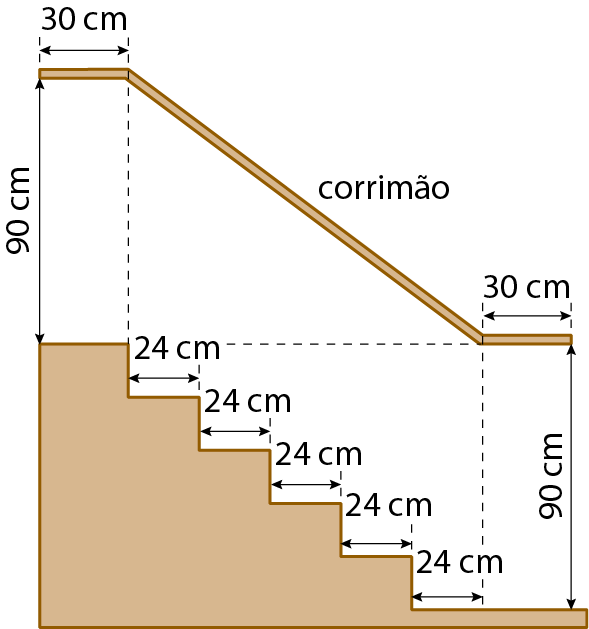
Na figura anterior, que representa o projeto de uma escada com 5 degraus de mesma altura, o comprimento total do corrimão é igual a:
a) 1,8 métros
b) 1,9 métros
c) 2,0 métros
d) 2,1 métros
e) 2,2 métros
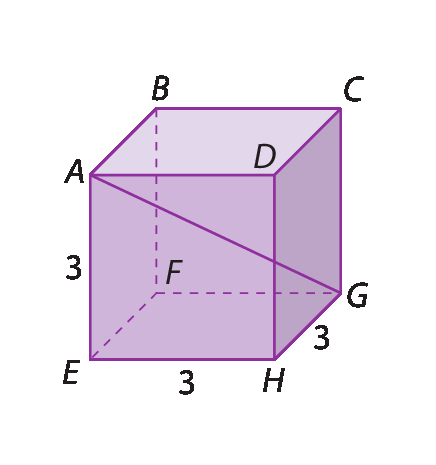
13. Calcule as medidas de comprimento solicitadas sabendo que os sólidos são paralelepípedos.
a) A medida de comprimento de
Símbolo. Segmento de reta EG..
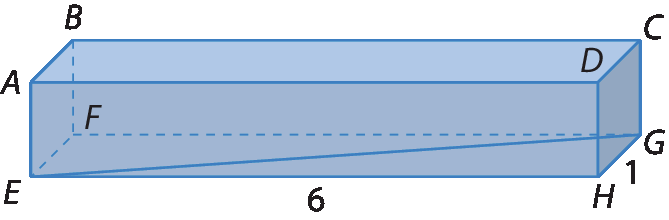
b) A medida de comprimento de
Símbolo. Segmento de reta AG..
14. O chão cimentado de uma praça tem formato de 4 quadrados congruentes, conforme a figura a seguir.

• Determine a medida da área do chão cimentado dessa praça, sabendo que a medida de comprimento destacada na figura por uma linha tracejada é 20 métros.
15. Observe o cubo representado a seguir e o segmento roxo em seu interior.
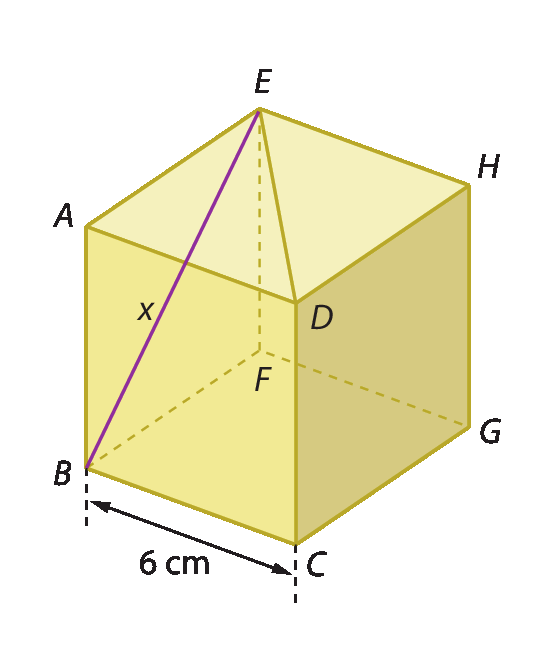
• Calcule a medida de comprimento do ponto B ao ponto ê.
Respostas e comentários
9.
Sentença matemática. Fração com numerador 5 raiz quadrada de 2 e denominador 2.10. a)
Sentença matemática. 2 raiz quadrada de 3, fim da raiz, centímetros.10. b)
Sentença matemática. Abre parênteses 18 mais 6 raiz quadrada de 3 fecha parênteses centímetros.11. a) 10 degraus
11. b)
Sentença matemática. Raiz quadrada de 10 vírgula 25, fim da raiz, metros.12. alternativa d
13. a)
Sentença matemática. Raiz quadrada de 37.13. b)
Sentença matemática. 3 raiz quadrada de 3.14. 160 métros quadrados
15. 6
Sentença matemática. Raiz quadrada de 2.centímetros
Orientações e sugestões didáticas
• Solicite aos estudantes que formem duplas ou trios para resolver as atividades 9 e 10 e sugira que, depois, comparem as resoluções com as de outras duplas. Faça as intervenções necessárias de maneira individual ou coletiva, estimulando-os a analisar e entender os erros cometidos, de acôrdo com o grupo de estudantes e suas resoluções.
• Resolução da atividade 14:
É possível destacar na figura dada um triângulo retângulo á bê cê, reto em B, com a hipotenusa
Símbolo. segmento de reta AC.de medida 20 métros, cateto
Símbolo. Segmento de reta BC.de medida ℓ
e cateto
Símbolo. Segmento de reta BA.de medida 3ℓ
.
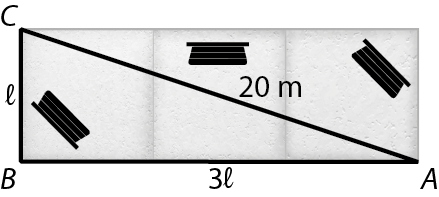
Aplicando o teorema de Pitágoras no triângulo ABC, temos:
ACelevado a 2 = ABelevado a 2 = BCelevado a 2
20elevado a 2 = (3ℓ)elevado a 2 = ℓelevado a 2
400 = 9ℓelevado a 2 = ℓelevado a 2 = 10ℓelevado a 2
ℓelevado a 2 = 40 (medida da área de um quadrado)
Calculando a medida de área:
4ℓelevado a 2 = 4 ⋅ 40 = 160
Logo, a medida da área do chão da praça é 160 métros quadrados.
• Resolução da atividade 15:
Símbolo. Segmento de reta BE.
é diagonal de uma das faces de um cubo cuja aresta mede 6 centímetros.
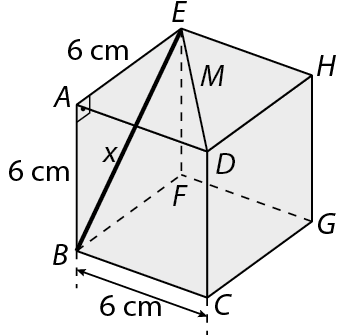
Aplicando o teorema de Pitágoras no triângulo retângulo bê á é, temos:
xelevado a 2 = 6elevado a 2 + 6elevado a 2
xelevado a 2 = 36 + 36
xelevado a 2 = 72
xelevado a 2 =
início da raiz quadrada, 2 vezes 36, fim da raiz.xelevado a 2 =
6 raiz quadrada de 2.Portanto, a distância do ponto B ao ponto E mede
6 raiz quadrada de 2.centímetros.
Lembre-se: Escreva no caderno!
Medida de distância entre dois pontos no plano cartesiano
A distância entre dois pontos é a medida de comprimento de um segmento de reta. No plano cartesiano podemos calcular a medida de distância, analisando as coordenadas dos pontos.
Recorde
Representamos o ponto P de coordenadas abre parênteses3, 5fecha parênteses por:
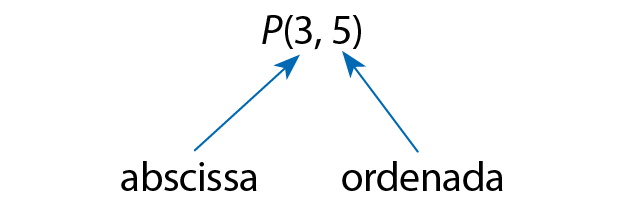
Podemos ter pontos com ordenadas iguais, pontos com abscissas iguais e pontos cujas abscissas e ordenadas são respectivamente diferentes.
Vamos determinar a medida de distância entre os pontos P e Q no plano cartesiano a seguir.
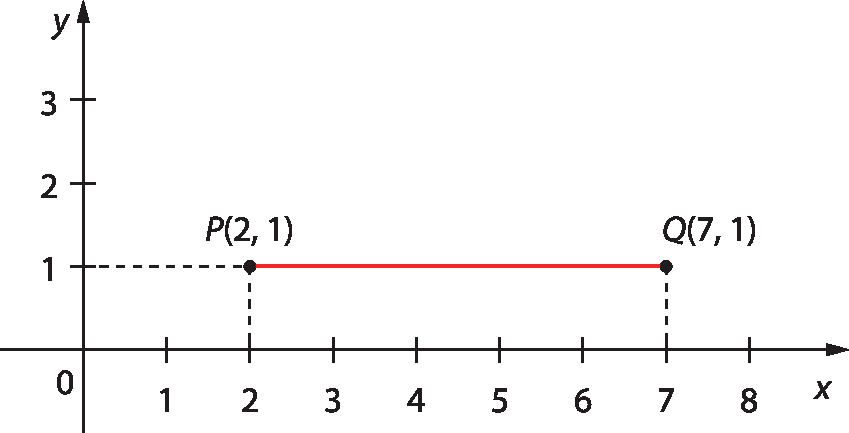
Note que as ordenadas dos pontos P e Q são iguais; então a medida de distância entre P e Q é o módulo da diferença entre as abscissas desses pontos. Assim:
PQ = |7 menos 2| = 5
Portanto, a medida de distância entre P e Q é de 5 unidades.
Vamos determinar a medida de distância entre os pontos M e N no plano cartesiano a seguir.
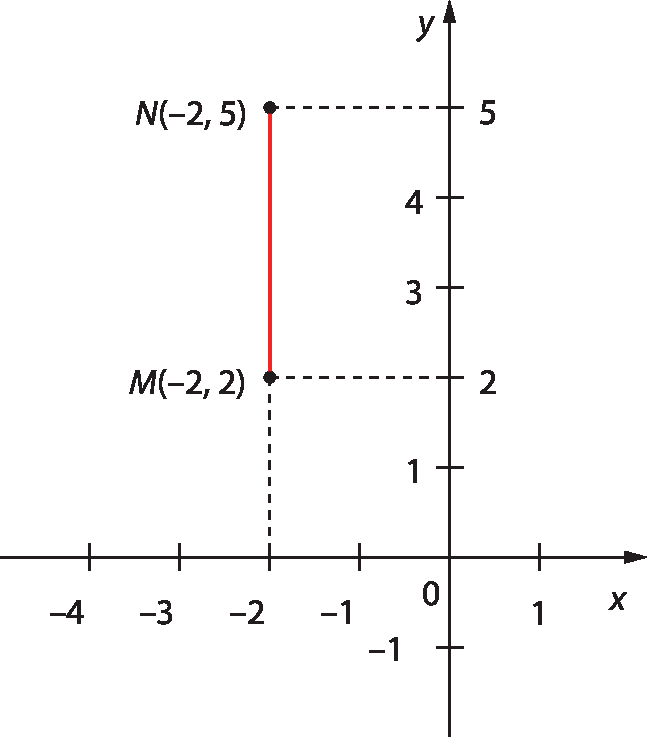
Note que as abscissas dos pontos M e N são iguais; então a medida de distância entre M e N é o módulo da diferença entre as ordenadas desses pontos. Assim:
MN = |5 menos 2| = 3
Portanto, a medida de distância entre M e N é de 3 unidades.
Orientações e sugestões didáticas
• Nesta página, mostra-se como determinar a medida de distância entre dois pontos do plano cartesiano considerando os três casos possíveis: pontos com abscissas iguais, pontos com ordenadas iguais e pontos que têm abscissas e ordenadas diferentes. Nesse último caso, o teorema de Pitágoras é utilizado como recurso, o que favorece o desenvolvimento da habilidade ê éfe zero nove ême ah um seis da BNCC.
• Antes de mostrar para os estudantes como isso pode ser feito, peça a eles que se reúnam em duplas ou em trios para conjecturar como podem encontrar a medida de distância entre dois pontos no plano cartesiano. Caso tenham dificuldade, peça a eles que desenhem o plano cartesiano em uma malha quadriculada e representem os pontos escolhidos nela. Oriente-os a testar as hipóteses e a validá-las ou não com base no que já estudaram. Propor a eles que elaborem e testem as hipóteses criadas ajuda a desenvolver as capacidades de argumentar e inferir sobre o conteúdo estudado. Se julgar pertinente, proponha que façam essa investigação com o apoio de um software de Geometria dinâmica.
• Caso julgue necessário, peça aos estudantes que, em duplas, encontrem a sentença algébrica que possibilita encontrar a medida de distância d entre dois pontos quaisquer do plano cartesiano Pabre parêntesesxíndice 1, yíndice 1fecha parênteses e Qabre parêntesesxíndice 2, yíndice 2fecha parênteses. Espera-se que eles concluam que a sentença, nesse caso, será a seguinte:
Lembre-se: Escreva no caderno!
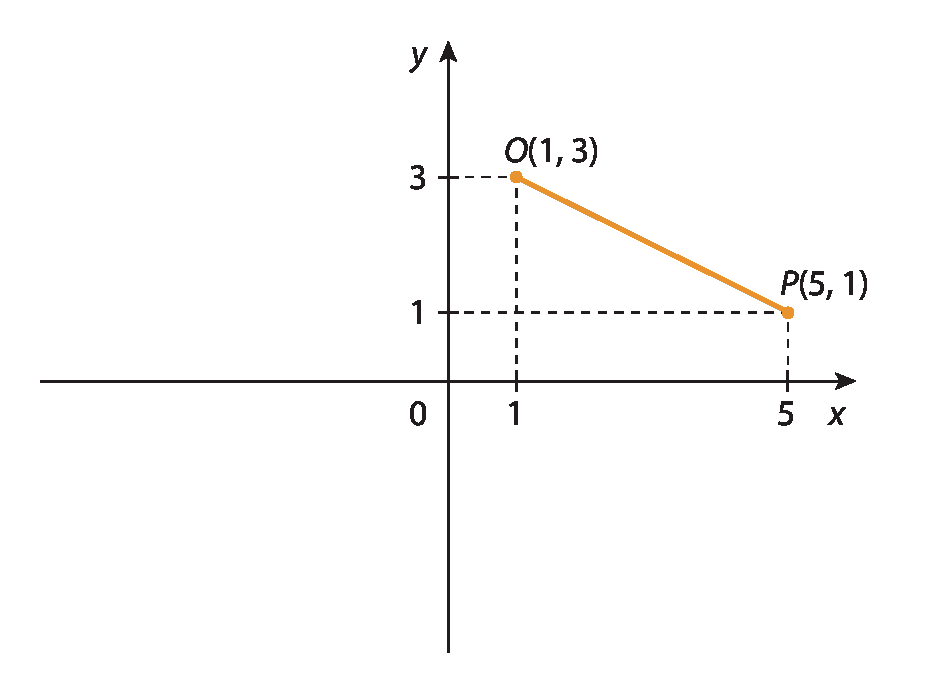
Agora, vamos determinar a medida de distância entre os pontos A e B no plano cartesiano a seguir.
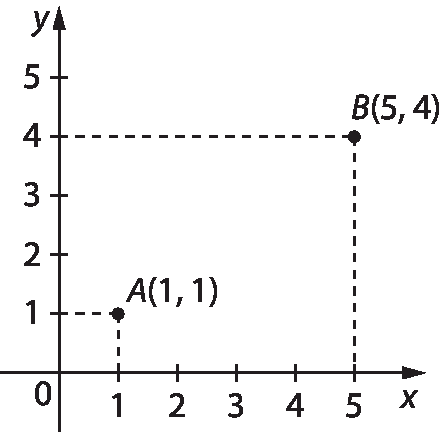
Como os eixos x e y que determinam o plano cartesiano são perpendiculares, podemos construir um triângulo retângulo cuja hipotenusa seja o segmento
Símbolo. Segmento de reta AB.. Assim, determinamos um triângulo cujos vértices são aabre parênteses1, 1fecha parênteses, Babre parênteses5, 4fecha parênteses e Cabre parênteses5, 1fecha parênteses.
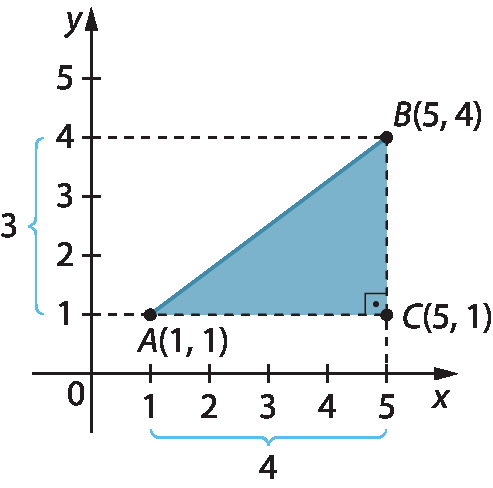
Aplicando o teorema de Pitágoras, para determinar a medida de comprimento do segmento
Símbolo. Segmento de reta AB., temos:
Assim, a medida de comprimento do segmento
Símbolo. Segmento de reta AB.é igual a 5, ou seja, a medida de distância entre a e B é de 5 unidades.
Ponto médio de um segmento
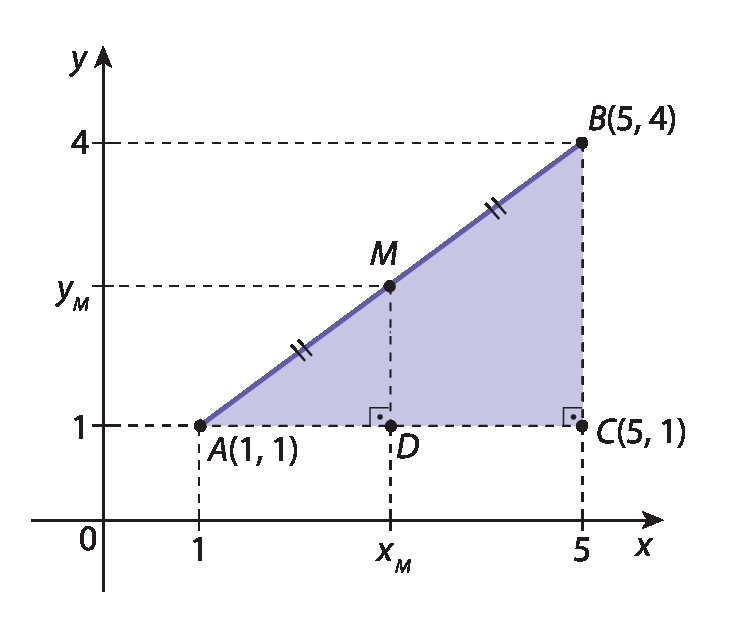
Acompanhe como podemos determinar as coordenadas do ponto médio de um segmento de reta representado no plano cartesiano.
Observe o segmento
Símbolo. Segmento de reta AB.a seguir. Vamos considerar um ponto M nesse segmento de modo que M o divida em dois segmentos congruentes, ou seja, de modo que M seja o ponto médio de
Símbolo. Segmento de reta AB..
Para determinar as coordenadas do ponto M, vamos considerar os triângulos retângulos á ême dê e á bê cê.
Orientações e sugestões didáticas
• Nesta página, mostra-se como determinar o ponto médio de um segmento de reta representado no plano cartesiano. Reproduza o exemplo apresentado no quadro e verifique se os estudantes identificam os triângulos retângulos semelhantes.
Espera-se que eles percebam que, nesses triângulos, temos:
•
ângulo BCA≅
ângulo MDA.(ângulos retos)
•
ângulo CAB≅
ângulo DAM.(ângulo comum)
Então, pelo critério á á:
△á ême dê ∼ △á bê cê.
A partir daí, incentive-os a ditar quais são os próximos passos para encontrar o ponto médio do segmento
Símbolo. Segmento de reta AB..
Este tópico favorece o desenvolvimento da habilidade ê éfe zero nove ême ah um seis da BNCC.
Como os triângulos á bê cê e á ême dê são semelhantes, podemos escrever a seguinte proporção:
=
fração AC sobre AD(um)
Como M é o ponto médio de
Símbolo. Segmento de reta AB., temos:
AB = 2 ⋅ AM (dois)
Assim, substituindo dois em um:
=
Sentença matemática. Fração AC sobre AD.AC = 2 ⋅ AD
5 menos 1 = 2 ⋅ (xíndice m menos 1)
2xíndice m = 6
xíndice m = 3
Analogamente, encontramos yíndice m:
=
fração BC sobre MD(três)
Substituindo dois em três, obtemos:
=
fração BC sobre MDBC = 2 ⋅ MD
4 menos 1 = 2 ⋅ abre parêntesesyíndice m menos 1fecha parênteses
2yíndice m = 5
yíndice m = 2,5
Concluímos, assim, que as coordenadas do ponto médio do segmento
Símbolo. Segmento de reta AB.são Mabre parênteses3; 2,5fecha parênteses.
Pode-se demonstrar, mas não o faremos nessa coleção, que para determinarmos a abscissa do ponto médio de qualquer segmento, podemos calcular a média aritmética das abscissas dos pontos que são extremidades do segmento e, ainda, que para determinarmos a ordenada do ponto médio de um segmento, podemos calcular a média aritmética das ordenadas dos pontos que são as extremidades do segmento.
Para pensar
a) Determine as coordenadas do ponto médio M do segmento cujas extremidades são os pontos Tabre parêntesesmenos1, 4fecha parênteses e Uabre parênteses3, 4fecha parênteses.
b) Determine as coordenadas do ponto médio N do segmento cujas extremidades são os pontos Rabre parênteses5, 6fecha parênteses e Sabre parênteses5, 12fecha parênteses.

ATIVIDADES
faça as atividades no caderno
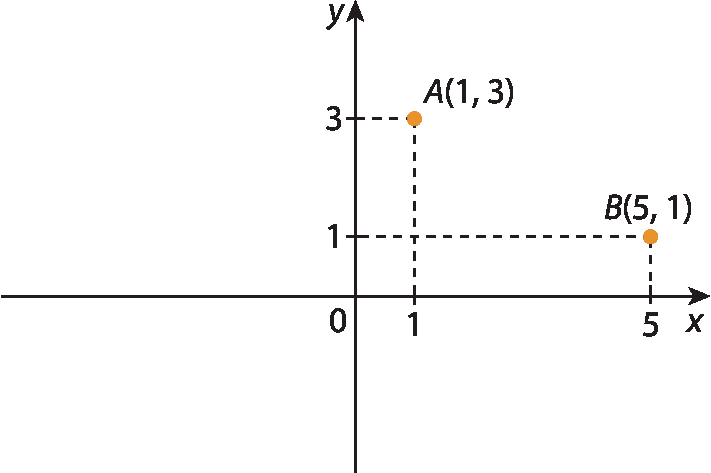
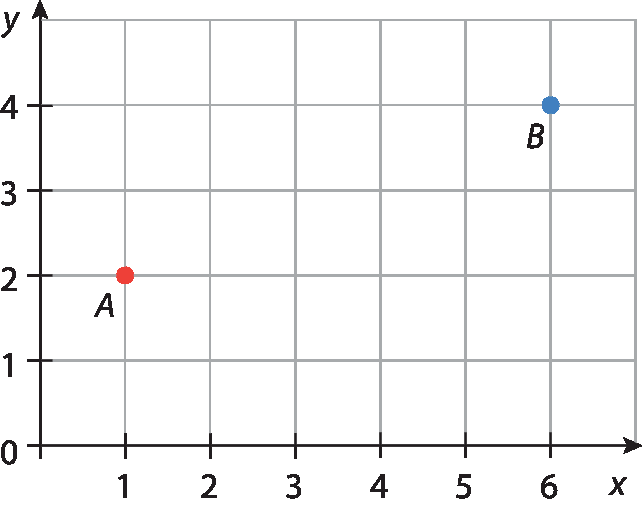
1. Calcule, no caderno, a medida de distância entre os pontos a e B em cada caso.
a)
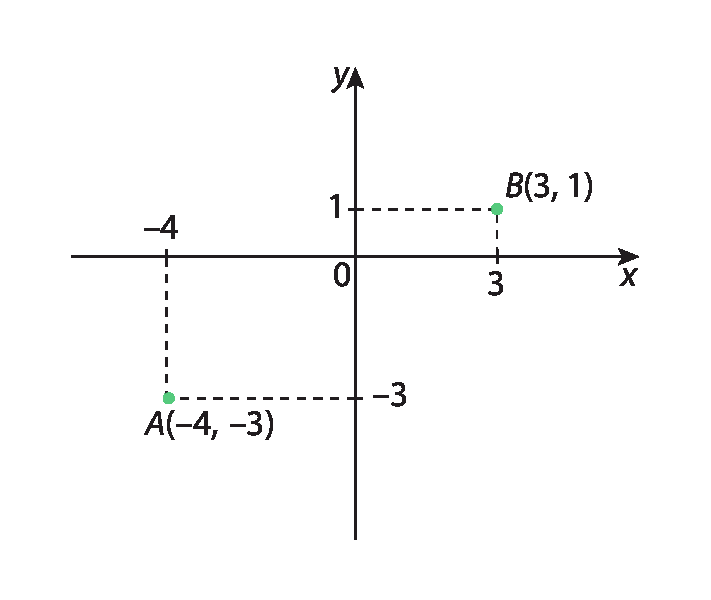
b)
Respostas e comentários
Para pensar: Respostas em Orientações.
1. a)
Sentença matemática. 2 vezes raiz quadrada de 5.1. b)
Raiz quadrada de 65.Orientações e sugestões didáticas
• Resposta do boxe Para pensar:
a) Mabre parênteses1, 4fecha parênteses. Espera-se que os estudantes percebam que, quando o segmento de reta é paralelo ao eixo x, a abscissa do seu ponto médio é a média aritmética das abscissas dos pontos que são extremidades dêsse segmento e que a ordenada do ponto médio é igual à ordenada de qualquer ponto que pertença ao segmento.
b) Nabre parênteses5, 9fecha parênteses. Espera-se que os estudantes percebam que, quando o segmento de reta é paralelo ao eixo y, a abscissa do ponto médio é igual à abscissa de qualquer ponto que pertença ao segmento e que a ordenada do ponto médio é a média aritmética das ordenadas dos pontos que são extremidades dêsse segmento.
• Diga aos alunos que eles vão aprofundar o estudo da medida de distância entre dois pontos e ponto médio de um segmento no plano cartesiano no Ensino Médio.
• Na atividade 1, se julgar conveniente, junte os estudantes em duplas ou trios para facilitar as trocas de estratégias e comparação de respostas. Incentive-os, antes de aplicar o teorema de Pitágoras, a avaliar se as medidas dos catetos estão corretas.
2. Determine a medida de distância do ponto Dabre parênteses3, 4fecha parênteses:
a) à origem do sistema cartesiano;
b) ao eixo das ordenadas;
c) ao eixo das abscissas.
3. Obtenha as coordenadas do ponto médio do segmento de reta a seguir.
4. Determine as coordenadas do ponto médio do segmento
Segmento de reta CD.em cada caso.
a) Cabre parênteses1, 2fecha parênteses e Dabre parênteses5, 4fecha parênteses
b) Cabre parêntesesmenos3, 2fecha parênteses e Dabre parênteses1, menos2fecha parênteses
5. Se o ponto médio do segmento
Segmento de reta AB.é Mabre parênteses2, 3fecha parênteses, determine as coordenadas do ponto a, sabendo que Babre parênteses3, 1fecha parênteses.
6. O esquema a seguir, feito em um plano cartesiano, representa a vista superior da área destinada à plantação no sítio de Edgar. Sabendo que cada unidade de medida de comprimento do plano cartesiano corresponde a 1 metro na realidade, faça o que se pede.

a) Determine a medida da área destinada ao pomar no sítio de Edgar.
b) Quantos metros quadrados mede a área destinada à horta?
c) Qual é a diferença entre essas medidas de área?
7. Observe os pontos representados no plano cartesiano a seguir.
Os pontos a e B representam duas árvores na praça em frente à casa de Denise. A prefeitura fará uma pista de caminhada passando pelo ponto médio entre as duas árvores.
a) Determine as coordenadas da localização de cada árvore.
b) Encontre as coordenadas do ponto médio entre as árvores representadas.
8. Em uma malha quadriculada, trace um plano cartesiano e desenhe nesse plano o triângulo de vértices nos pontos aabre parênteses1, 1fecha parênteses, Babre parênteses3, 3fecha parênteses e Cabre parênteses7, menos1fecha parênteses. Verifique no caderno se esse triângulo é retângulo e, depois, calcule a medida de seu perímetro e a de sua área.
Respostas e comentários
2. a) 5
2. b) 3
2. c) 4
3. abre parênteses3, 2fecha parênteses
4. a) abre parênteses3, 3fecha parênteses
4. b) abre parêntesesmenos1, 0fecha parênteses
5. aabre parênteses1, 5fecha parênteses
6. a) 6 métros quadrados
6. b) 12 métros quadrados
6. c) 6 métros quadrados
7. a) aabre parênteses1, 2fecha parênteses e Babre parênteses6, 4fecha parênteses
7. b) abre parênteses3,5; 3fecha parênteses
8. Resposta em Orientações.
Orientações e sugestões didáticas
• Se julgar necessário, comente com os estudantes que nas atividades 2, 3, 4 e 5 eles podem fazer a representação gráfica na malha quadriculada de maneira que os pontos sejam adequadamente indicados no plano cartesiano e, assim, buscar as relações métricas para chegar às respostas de cada atividade.
• Resposta da atividade 8:
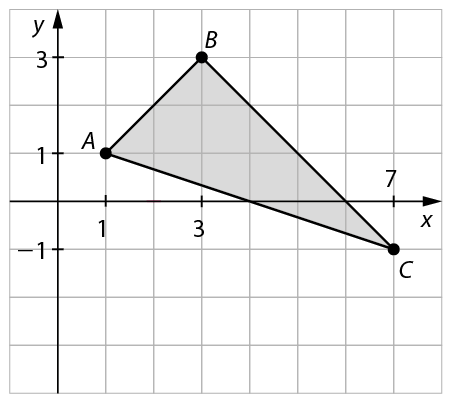
O triângulo é retângulo.
Medida do perímetro:
Sentença matemática. 6 raiz quadrada de 2, fim da raiz, mais 2 raiz quadrada de 10.Medida de área: 8
• Após os estudantes terminarem as atividades, proponha que elaborem problemas que envolvam a aplicação do teorema de Pitágoras. Após fazer isso, eles podem trocar os problemas com um colega e resolver os propostos por ele.

Estatística e Probabilidade
faça as atividades no caderno
Construção, leitura e interpretação de gráficos em planilhas eletrônicas
Leia a notícia a seguir.
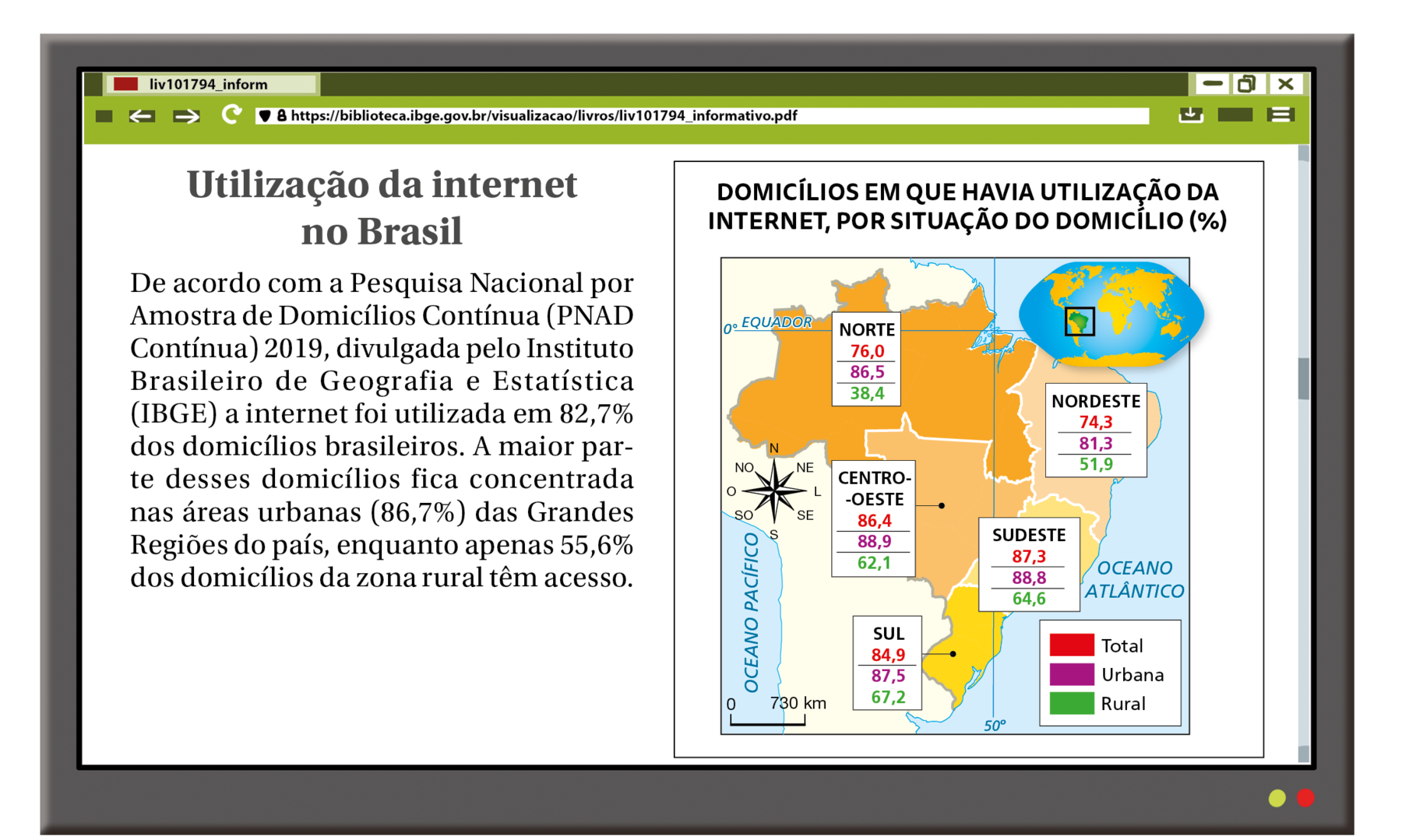
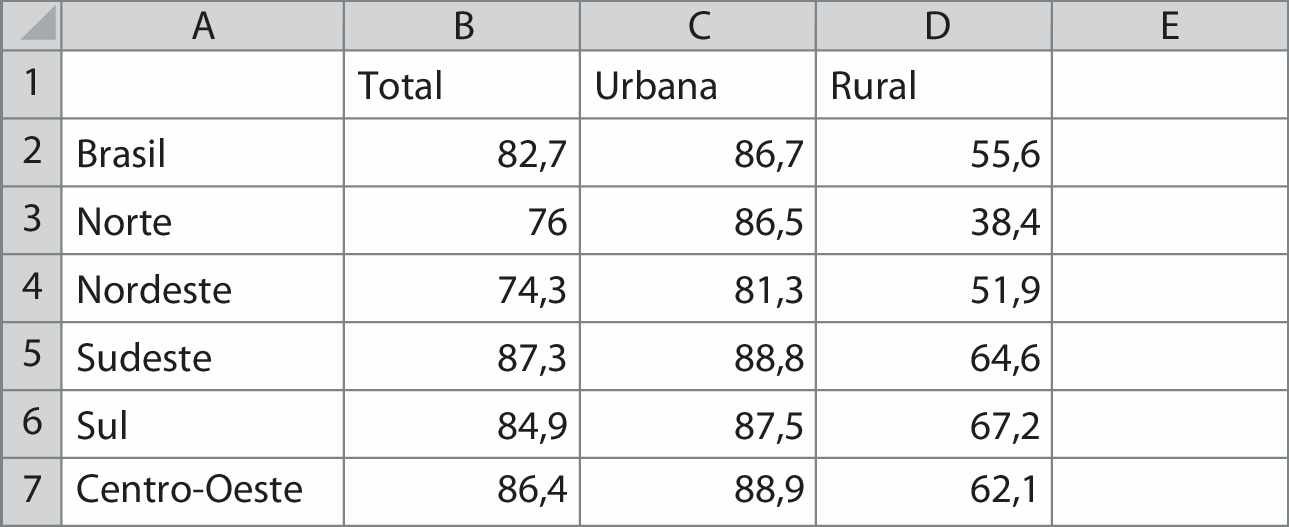
Dados obtidos em: í bê gê É, Diretoria de Pesquisas, Coordenação de Trabalho e Rendimento. Acesso à internet e à televisão e posse de telefone móvel celular para uso pessoal 2019. Pesquisa Nacional por Amostra de Domicílios Contínua 2019.Disponível em: https://oeds.link/0A3tBp. Acesso em: 15 março 2022.
A professora Rose pediu aos estudantes de uma de suas turmas que observassem a notícia. Depois, deveriam utilizar uma planilha eletrônica para construir uma tabela e um gráfico com as informações sobre o uso da internet nos domicílios no Brasil e nas grandes Regiões. O objetivo era validar se a informação apresentada retratava o mesmo cenário em todas as regiões. Observe como alguns estudantes pensaram.
Primeiro eles organizaram os dados em uma tabela.
Orientações e sugestões didáticas
Estatística e Probabilidade
Objetivos
• Construir e interpretar gráficos em planilhas eletrônicas.
• Favorecer o desenvolvimento da habilidade da BNCC: ê éfe zero nove ême ah dois dois.
Habilidade da BNCC
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero nove ême ah dois dois porque propõe aos estudantes que analisem e construam o gráfico mais adequado para um conjunto de dados com o uso de planilhas eletrônicas.
Orientações
• Nesta seção, os estudantes deverão avaliar e construir o gráfico mais adequado para apresentar determinado conjunto de dados e destacar algumas conclusões.
• Antes de iniciar o estudo, retome com os estudantes a leitura e interpretação de gráficos de barras simples e gráfico de linhas.
(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (coluna, setores ou linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.
Em seguida, os estudantes discutiram qual representação gráfica seria mais adequada para esse conjunto de dados.

Para criar o gráfico, um dos estudantes selecionou os dados, escolheu a ferramenta “Inserir gráfico” e, então, escolheu o gráfico mais adequado ao conjunto de dados.
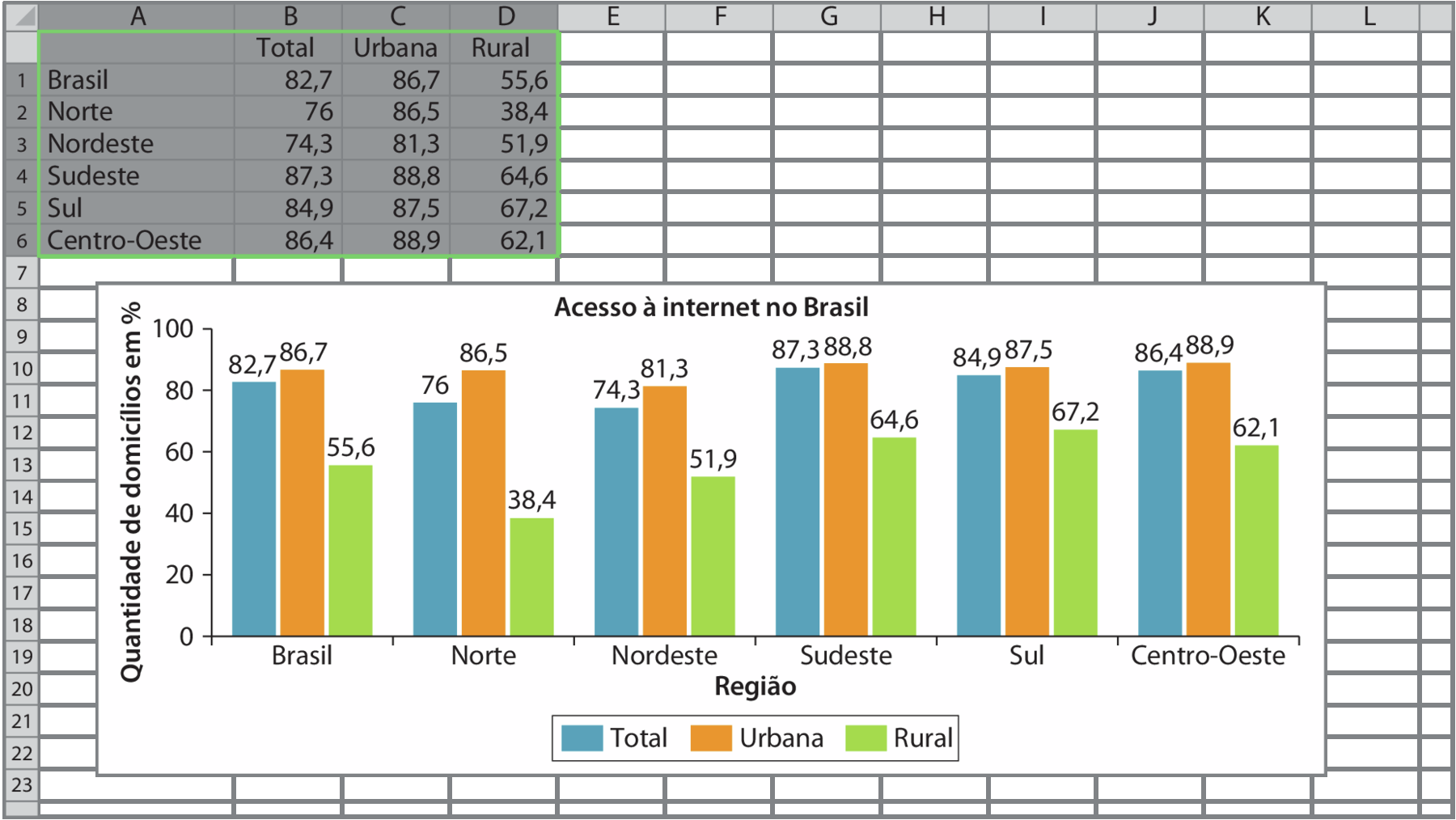
Dados obtidos em: í bê gê É, Diretoria de Pesquisas, Coordenação de Trabalho e Rendimento. Acesso à internet e à televisão e posse de telefone móvel celular para uso pessoal 2019. Pesquisa Nacional por Amostra de Domicílios Contínua 2019. Disponível em: https://oeds.link/0A3tBp. Acesso em: 15 março 2022.
A turma da professora Rose analisou os dados do gráfico e percebeu que o uso da internet na zona urbana apresenta valores parecidos nas grandes regiões; entretanto, na zona rural, é possível notar que a Região Norte apresenta a menor porcentagem (38,4%) de domicílios que utilizaram a internet em 2019.
Para fazer

Reúna-se em grupo, pesquisem os dados mais recentes sobre a utilização da internet no Brasil e construam um gráfico do mesmo jeito que os estudantes da turma da professora Rose. Personalizem-no colocando os títulos dos eixos, o título do gráfico, a legenda, a fonte de onde foram retiradas as informações, trocando as cores, entre outros detalhes que julgarem pertinentes.
Respostas e comentários
Para fazer: Espera-se que os estudantes sigam os procedimentos indicados anteriormente e obtenham um gráfico parecido com o apresentado.
Orientações e sugestões didáticas
• Convém destacar para os estudantes quando é mais adequado utilizar um ou outro tipo de gráfico. Os gráficos de barras, por exemplo, favorecem a comparação entre quantidades, e os gráficos de linhas mostram como determinado dado estatístico variou durante certo período, ou seja, mostram as evoluções e regressos de algum fenômeno.
• Comente com eles que, independentemente do tipo de gráfico, a legenda é imprescindível, porque é por meio dela que fica claro o significado de cada barra ou linha. Se achar oportuno, proponha a eles que leiam e interpretem gráficos com múltiplas barras ou com múltiplas linhas primeiro sem a legenda e, depois, com a legenda, para que percebam quanto esse elemento é importante nesse tipo de representação.
• Se possível, reserve uma aula para que os estudantes possam utilizar a sala de informática e realizar a atividade proposta no boxe Para fazer. Assim, é possível que você avalie os conhecimentos dos estudantes sobre a construção de gráficos em planilhas eletrônicas e sane qualquer dificuldade.
▶ Estatística e Probabilidade

ATIVIDADES
faça as atividades no caderno
1. Observe, no gráfico a seguir, a quantidade de medalhas obtidas pela Escola Ponte Feliz no campeonato de atividades físicas entre 2014 e 2023. Depois, copie a alternativa correta no caderno.
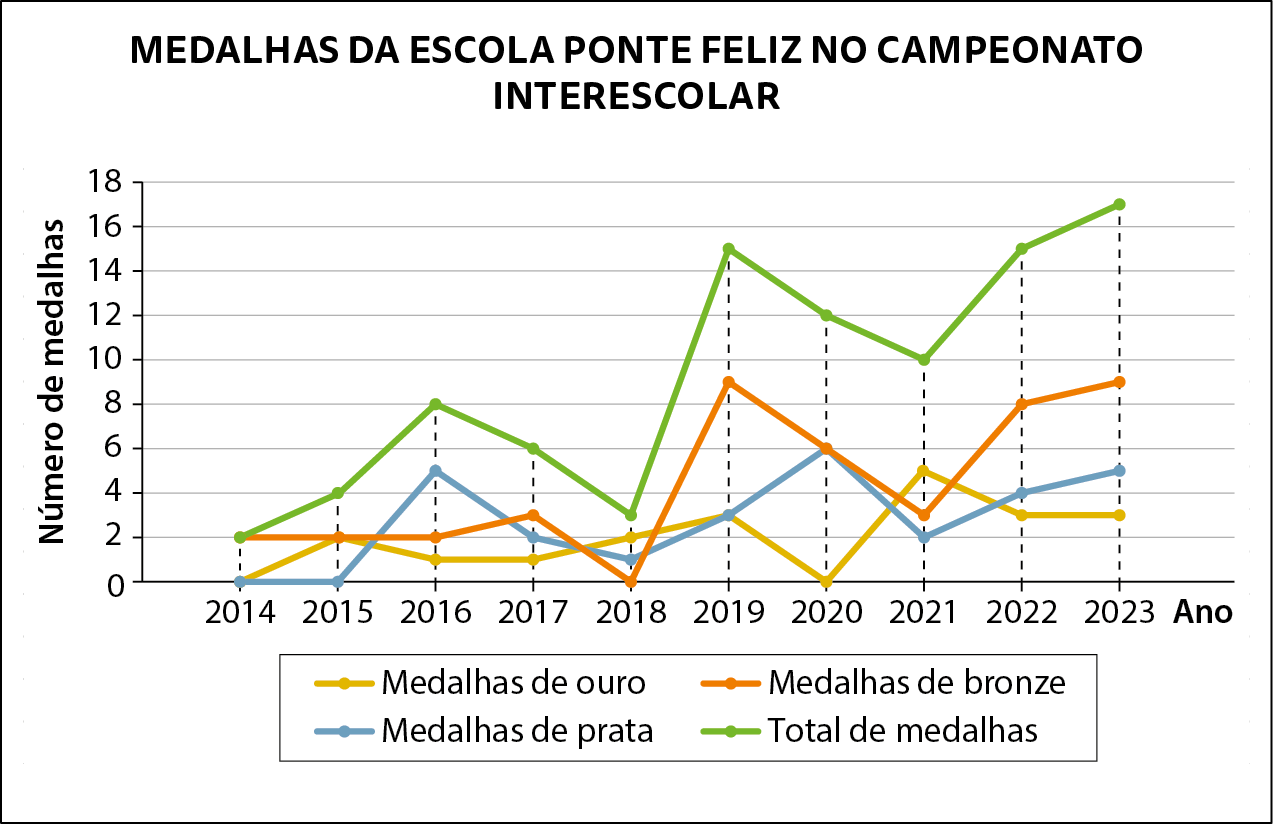
Dados obtidos pela Escola Ponte Feliz em janeiro de 2024.
a) Em 2019, a Escola Ponte Feliz conquistou mais medalhas de ouro que de prata.
b) Em 2015, o número de medalhas de bronze e de prata conquistadas foi o mesmo.
c) Essa escola conquistou mais medalhas de ouro em 2023 que o total de medalhas conquistadas em 2014.
d) Em 2023, foram conquistadas 34 medalhas no total.
2. Giovani pesquisou sobre a frota de alguns tipos de veículo no Brasil em 2019, 2020 e 2021 e construiu a tabela a seguir.
|
Ano |
Automóvel |
Motocicleta |
Caminhão |
Ônibus |
|---|---|---|---|---|
|
2021 |
59.242.869 |
24.732.701 |
2.947.856 |
672.930 |
|
2020 |
58.016.405 |
23.862.010 |
2.879.080 |
660.394 |
|
2019 |
56.652.190 |
23.165.586 |
2.826.343 |
647.376 |
Dados obtidos em: MINISTÉRIO DA INFRAESTRUTURA, Secretaria Nacional de Trânsito - Senatran – 2019, 2020 e 2021.

Reúna-se com um colega e façam o que se pede.
a) Representem os dados coletados por Giovani em uma planilha eletrônica e construam um gráfico de barras.
b) Escrevam quatro conclusões que podem identificar com base no gráfico construído. Depois, comparem as conclusões que escreveram com as de outra dupla.
c) Com as informações dessa tabela, podemos construir um gráfico de múltiplas linhas. Quantas linhas terá o gráfico e o que representa cada uma delas?
3. De acôrdo com o Censo Demográfico 2010, publicado pelo í bê gê É, a população indígena, por domicílio, no Brasil, estava distribuída assim:
• Região Norte: .305873 pessoas
• Região Nordeste: .208691 pessoas
• Região Centro-Oeste: .130494 pessoas
• Região Sudeste: .97960 pessoas
• Região Sul: .74945 pessoas
Com base nestas informações, construa um gráfico de setores em uma planilha eletrônica.
Respostas e comentários
1. alternativa c
2. a) Resposta na seção Resoluções neste manual.
2. b) Exemplos de resposta:
• Em 2019, havia .647376 ônibus no Brasil.
• Em todos os anos apresentados, havia mais automóveis do que caminhões, motocicletas e ônibus.
• De 2019 a 2020, houve um aumento de mais de meio milhão de motocicletas.
• Em 2021, havia aproximadamente 87,6 milhões de automóveis, caminhões, motocicletas e ônibus.
2. c) Nesse caso, o gráfico terá quatro linhas, cada uma representando um dos tipos de veículo (automóvel, caminhão, motocicleta e ônibus).
3. Resposta na seção Resoluções neste manual.
Orientações e sugestões didáticas
• Ao realizarem as atividades propostas, avalie como os estudantes escolhem o tipo de gráfico mais adequado para representar determinado conjunto de dados. Se julgar necessário, oriente-os na construção do gráfico usando a planilha eletrônica.
• Na atividade 1, para escolher a alternativa correta, os estudantes precisarão analisar todos os dados do gráfico, fazer comparações e eliminar as afirmações falsas. Assim, terão a oportunidade de fazer uma interpretação dos dados sem realizar nenhum cálculo.
• No item b da atividade 2, uma das conclusões pode ser o total dos tipos de veículo em determinado ano. Nesse caso, os estudantes podem utilizar calculadora, pois o foco não são os cálculos, mas sim a interpretação dos dados apresentados; é preciso identificar que dados são necessários para responder à questão e que tipo de cálculo está envolvido. Como os números envolvidos são muito grandes, o uso da calculadora é interessante e os estudantes podem fazer estimativas da frota total de veículos no Brasil em cada ano.

Trabalho em equipe
faça as atividades no caderno
Você e seu grupo vão pesquisar as normas de segurança no trânsito e, com base nessas informações, criar um folheto informativo para motoristas e pedestres.

Dados estatísticos e o trânsito
Justificativa
O Brasil está entre os campeões mundiais em acidentes de trânsito com vítimas fatais. O estudo e a compreensão dessa situação ajudam todos a perceber com mais clareza os riscos de dirigir de maneira irresponsável e imprudente e, também, a propor medidas para evitar tais riscos. Ao elaborar um folheto informativo que contenha dados estatísticos e análises especializadas, exercitamos nossa capacidade de crítica e argumentação.
Objetivo
Criar um folheto de conscientização sobre segurança no trânsito.
Saber o significado de algumas placas de trânsito é importante para motoristas e também para pedestres. As informações das placas são de fácil compreensão para todos que as observam.




Apresentação
Folheto em fórma de fôlder (uma folha de papel encorpado, dobrado uma ou mais vezes). Podem ser acrescentadas ilustrações de apoio ao texto informativo.
Questões para pensar em grupo
• Onde procurar as informações e orientações relativas ao assunto? Os sites oficiais sobre trânsito podem fornecê-las? E os jornais e revistas de grande circulação?
• Qual será o público-alvo, isto é, o perfil (idade, ocupação, nível de escolaridade etcétera) das pessoas com as quais vocês desejam se comunicar? Como isso interfere na elaboração do folheto?
• Que argumentos convencerão esse público da mensagem principal do folheto?
• Como a Matemática contribuirá para tornar a argumentação mais eficiente?
• Serão usadas figuras ou fotografias ilustrativas?
Não se esqueçam
• Embora o assunto seja muito sério, esse tipo de mensagem atinge melhor seus objetivos quando veiculado de fórma leve e bem-humorada.
Orientações e sugestões didáticas
Trabalho em equipe
Objetivos
• Aplicar, por meio de trabalhos em grupo, os conceitos estudados.
• Favorecer o desenvolvimento das competências gerais 4 e 7 e das competências específicas 7 e 8 da BNCC.
Orientação
• Para realizar o trabalho em equipe, é importante que os estudantes conversem sobre o tema, pois as discussões entre eles podem ser concluídas com várias ideias e opiniões sobre o respeito às regras de trânsito e a conduta dos motoristas, favorecendo, assim, o Tema Contemporâneo Transversal Educação para o Trânsito, da macroárea Cidadania e Civismo.
• As etapas dêsse trabalho (pesquisa, seleção de informação, decisão sobre como apresentar os dados e como os folders serão distribuídos etcétera) possibilitam o desenvolvimento de diversas competências e atitudes para a vida, entre elas imaginação, criatividade, inovação, espírito de equipe e coletividade.
• A importância dêsse trabalho se justifica pela possibilidade de abordar um tema relacionado aos direitos e deveres do cidadão e por estimular a interação de fórma cooperativa entre os estudantes, favorecendo o desenvolvimento das competências específicas 7 e 8 da BNCC. Além disso, pesquisar dados estatísticos para produzir uma argumentação consistente na elaboração do folheto favorece o desenvolvimento das competências gerais 4 e 7.
Competência geral 4: Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos as linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
Competência geral 7: Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
Competência específica 7: Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
Competência específica 8: Interagir com seus pares de fórma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Compreender um texto
faça as atividades no caderno


Cidadania digital
O que é cidadania digital
Quando estamos diante das telas dos celulares ou computadores, temos a sensação de que estamos sozinhos. E mais: de que ninguém percebe o que fazemos ou deixamos de fazer. Mas não podíamos estar mais enganados.
Na internet, somos quase 4 bilhões de pessoas conectadas e compartilhando informações em fórma de textos, emôjis, memes, fotos, vídeos e sons. [reticências]

Se somos tantos interligados, também precisamos de normas para nos relacionarmos, como acontece no mundo físico, certo? E isso é tão importante que recebeu um nome especial: cidadania digital.
Anote aí: cidadania digital é o conjunto de normas que devemos seguir para utilizarmos a internet com consciência, responsabilidade, ética e segurança. [reticências]
A cidadania digital compreende temas bem importantes. Vamos conhecer alguns deles?
Segurança digital
O bom cidadão digital precisa saber proteger os seus dados. É necessário aprender a criar senhas fortes (aquelas bem difíceis de descobrir) e a guardá-las de maneira segura. Senha com a data de aniversário? Nem pensar!
Outra medida importante é saber reconhecer e-mails mal intencionados, sites falsos e outras fórmas de golpe na internet. Elas costumam ser portas de entrada para vírus de computador e celular: basta um clique para contaminar o seu equipamento e roubar seus dados pessoais. Ah, claro, ter um bom antivírus também ajuda muito!
[reticências]
Ética e respeito
Embora a gente às vezes sinta que está falando sozinho quando emite uma opinião na internet, isso é uma ilusão: há muita gente ouvindo. [reticências]
Então, se ligue: as regras de boa convivência e de respeito ao próximo usadas no mundo físico se aplicam ao mundo virtual. Nunca se esqueça de que há pessoas de carne e osso, como você, recebendo a sua mensagem.
Orientações e sugestões didáticas
Compreender um texto
Objetivos
• Desenvolver a competência leitora.
• Favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah dois dois, da competência geral 5 e da competência específica 6 da BNCC.
Habilidade da BNCC
• Esta seção favorece o desenvolvimento da habilidade ê éfe zero nove ême ah dois dois porque os estudantes devem identificar, em algumas atividades, o gráfico mais adequado para apresentar determinado conjunto de dados e, quando conveniente, destacar nele a média aritmética dêsse conjunto.
Orientações
• Para explorar o tema da cidadania digital, peça aos estudantes que realizem uma pesquisa sobre o assunto e elaborem uma lista no caderno com os direitos e deveres de um cidadão digital. Entre os direitos, eles poderão identificar o direito à privacidade, à segurança dos dados e à autoria das criações divulgadas. Quanto aos deveres, eles poderão listar o dever de agir de fórma educada com as outras pessoas, de não expô-las ao ridículo ou ao ataque de outros internautas, de respeitar seus direitos autorais e de não compartilhar notícias falsas. O trabalho com esse tema possibilita o desenvolvimento dos Temas Contemporâneos Transversais Ciência e Tecnologia e Vida familiar e social, das macroáreas Ciência e Tecnologia e Cidadania e Civismo, respectivamente.
(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.
Competência geral 5: Compreender, utilizar e criar tecnologias digitais de informação e comunicação de fórma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
Competência específica 6: Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Responsabilidade na divulgação de informações
Há alguns anos, as fake news – notícias falsas divulgadas pela internet – entraram em evidência. Criadas para confundir as pessoas, elas podem gerar desde um simples burburinho até a destruição da reputação de alguém. Por isso, todo bom cidadão digital precisa zelar pela veracidade das informações que divulga entre os seus contatos. [reticências]
BRASIL. Câmara dos Deputados. O que é cidadania digital. Plenarinho: o jeito criança de ser cidadão, Brasília, Distrito Federalponto, 7 agosto 2020. Disponível em: https://oeds.link/7LopQS. Acesso em: 14 março 2022.


ATIVIDADES
faça as atividades no caderno
1. O que é cidadania digital?
2. Márcia sabe a importância de proteger seus dados; por isso ela usa um antivírus (software que previne, detecta e elimina vírus) em seu computador. A tabela a seguir apresenta a quantidade de vírus combatidos em alguns dias de 2022.
|
Dia |
05/02/2022 |
13/05/2022 |
07/06/2022 |
23/10/2022 |
01/11/2022 |
13/12/2022 |
|---|---|---|---|---|---|---|
|
Quantidade |
27 |
35 |
42 |
21 |
27 |
29 |
Dados obtidos por Márcia em 2022.
a) Qual tipo de gráfico é o mais adequado para representar os dados da tabela: de barras, de setores ou de linhas? Construa esse gráfico em uma planilha eletrônica.
b) Em 2022, o antivírus do computador de Márcia combateu, em média, 35 vírus por dia. Represente essa média com uma linha no gráfico que você construiu no item anterior.
c) Em sua opinião, é importante o uso de antivírus no computador?
3. Antônio checa a veracidade de todas as notícias que recebe no aplicativo de mensagens instantâneas, pois, infelizmente, algumas delas são fake news. Na primeira semana de março de 2022, 33% do total de notícias recebidas por ele eram fake news e as demais eram confiáveis.
a) Qual tipo de gráfico é o mais adequado para representar os dados apresentados: de barras, de setores ou de linhas? Construa esse gráfico em uma planilha eletrônica.
b) Ao receber uma notícia, você verifica a veracidade da mesma? Comente.
c) De acôrdo com o texto, por que é importante verificar a veracidade de uma informação antes de divulgá-la?
Respostas e comentários
1. Cidadania digital é o conjunto de normas que devemos seguir para utilizarmos a internet com consciência, responsabilidade, ética e segurança.
2. a) gráfico de barras
2. b) Resposta em Orientações.
2. c) Resposta pessoal.
3. a) gráfico de setores
3. b) Resposta pessoal.
3. c) É importante verificar a veracidade de uma informação antes de divulgá-la, porque as fêique níus podem gerar desde um simples burburinho até a destruição da reputação de alguém.
Orientações e sugestões didáticas
• O texto abordado na seção foi retirado da página Plenarinho, criada pela Câmara dos Deputados. Caso julgue oportuno, leve os estudantes ao laboratório de informática para que possam testar seus conhecimentos sobre cidadania digital na Trívia – Segurança na internet, um jôgo interativo de perguntas e respostas sobre segurança digital. Disponível em: https://oeds.link/HMu5zl. Acesso em: 24 julho 2022.
• Caso não seja possível desenvolver o trabalho com planilhas eletrônicas, oriente os estudantes a construir no caderno os gráficos solicitados nas atividades 2 e 3.
• Após os estudantes construírem os gráficos nas atividades 2 e 3, organize uma roda de conversa para que justifiquem suas escolhas e apresentem as etapas de construção. Compartilhar as estratégias usadas ajuda a desenvolver o raciocínio e a perceber as diversas maneiras de resolver um problema.
• Resposta do item a da atividade 3:
Dados obtidos por Antônio em 2022.
Resposta do item a da atividade 2:
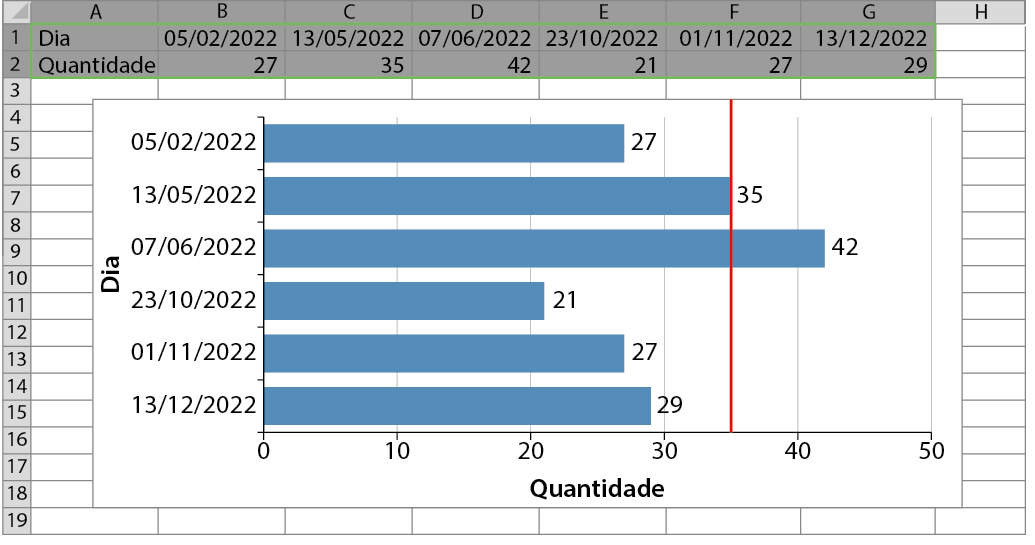
Dados obtidos por Márcia em 2022.

Atividades de revisão
faça as atividades no caderno
1. Determine a medida do perímetro dos triângulos.
a)
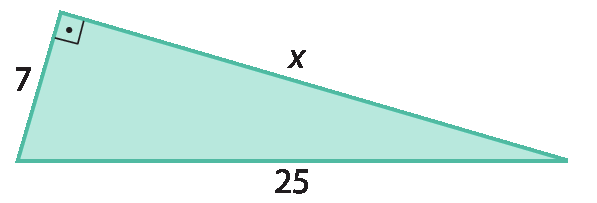
b)
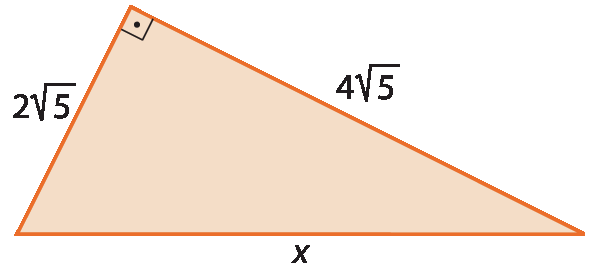
2. A diagonal do retângulo a bê cê dê mede 8 centímetros de comprimento. Determine a medida do comprimento de
Símbolo. Segmento de reta DC..

3. Calcule a medida do perímetro do quadrado.
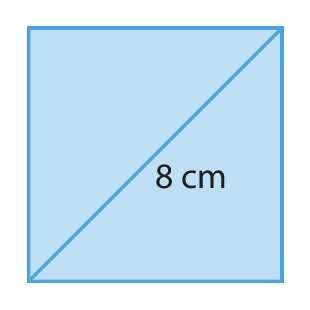
4. Determine a medida de comprimento h indicada na figura.
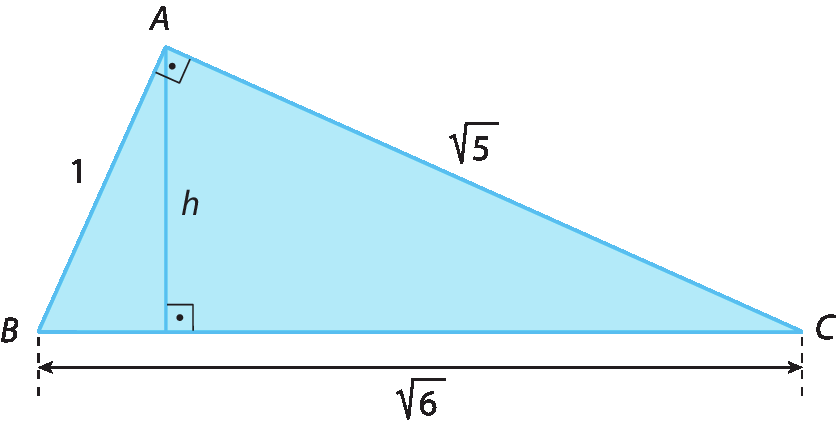
5. Determine a medida de comprimento x indicada nos triângulos.
a)
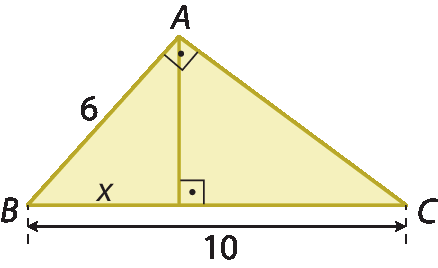
b)
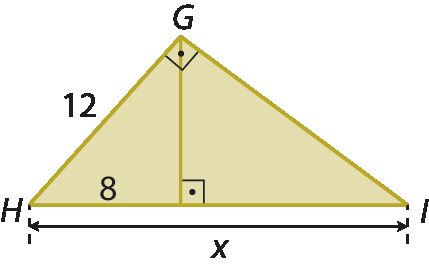
c)
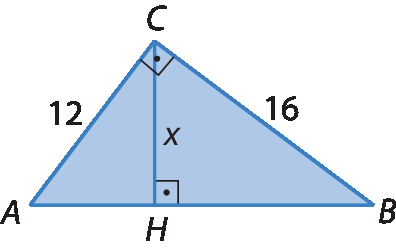
6. Em um triângulo retângulo, os catetos medem 6 centímetros e 8 centímetros de comprimento. Determine a medida de comprimento:
a) da hipotenusa;
b) das projeções ortogonais de cada cateto sobre a hipotenusa;
c) da altura relativa à hipotenusa.
7. A hipotenusa de um triângulo retângulo isósceles mede 8 centímetros de comprimento. Qual é a medida do perímetro dêsse triângulo?
8. Na figura, determine a medida de comprimento da projeção ortogonal do cateto
Símbolo. Segmento de reta AC.sobre a hipotenusa.
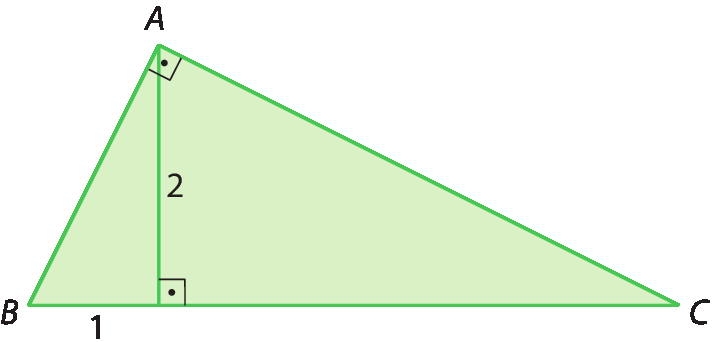
9. Na figura, B é um ponto do segmento de reta
Símbolo. Segmento de reta AC., e os ângulos
Símbolo. Ângulo DAB, ângulo DBE e ângulo BCE.são retos.
Se á dê = 6 decímetros, AC = 11 decímetros, EC = 4 decímetros e DB = 10 decímetros, a medida de comprimento de
Símbolo. Segmento de reta EB.é:
a) 4,5 decímetros
b) 8 decímetros
c) 7 decímetros
d) 5 decímetros
Respostas e comentários
1. a) 56
1. b)
Sentença matemática. 10 mais 6 raiz quadrada de 5.2.
2 raiz quadrada de 7, fim da raiz, centímetros.3.
16 raiz quadrada de 2, fim da raiz, centímetros.4.
Sentença matemática. Raiz quadrada da fração 5 sobre 6.5. a) 3,6
5. b) 18
5. c) 9,6
6. a) 10 centímetros
6. b) 3,6 centímetros e 6,4 centímetros
6. c) 4,8 centímetros
7.
Sentença matemática. Abre parênteses 8 mais 8 raiz quadrada de 2 fecha parênteses centímetros.8. 4
9. alternativa d
Orientações e sugestões didáticas
Atividades de revisão
Conteúdos
• Consolidar o conhecimento adquirido no decorrer do capítulo.
• Favorecer o desenvolvimento das habilidades da BNCC: ê éfe zero nove ême ah um quatro e ê éfe zero nove ême ah um seis.
Habilidades da BNCC
• Esta seção favorece o desenvolvimento das habilidades ê éfe zero nove ême ah um quatro e ê éfe zero nove ême ah um seis porque os estudantes resolverão problemas que envolvem a aplicação do teorema de Pitágoras; inclusive problemas de determinação do ponto médio de um segmento de reta e da medida da distância entre dois pontos dadas suas coordenadas no plano cartesiano, e de aplicação dêsse conhecimentos para calcular as medidas dos perímetros e das áreas.
Orientações
• As atividades desta seção proporcionam aos estudantes aplicar o teorema de Pitágoras e as outras relações métricas do triângulo retângulo em diferentes situações. Aproveite a oportunidade para avaliar o aprendizado deles e o modo como encaminham a resolução das atividades. Incentive-os a compartilhar com os colegas o modo como fizeram a fim de identificar os possíveis erros cometidos. Estimular os estudantes a analisar e entender os erros cometidos ajuda a desenvolver a capacidade de inferir o problema.
(ê éfe zero nove ême ah um quatro) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
(ê éfe zero nove ême ah um seis) Determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer, dadas as coordenadas desses pontos no plano cartesiano, sem o uso de fórmulas, e utilizar esse conhecimento para calcular, por exemplo, medidas de perímetros e áreas de figuras planas construídas no plano.
10. Sabendo que b = 12 centímetros e que m + n = 13 centímetros, calcule as medidas de comprimento c, h, m e n.
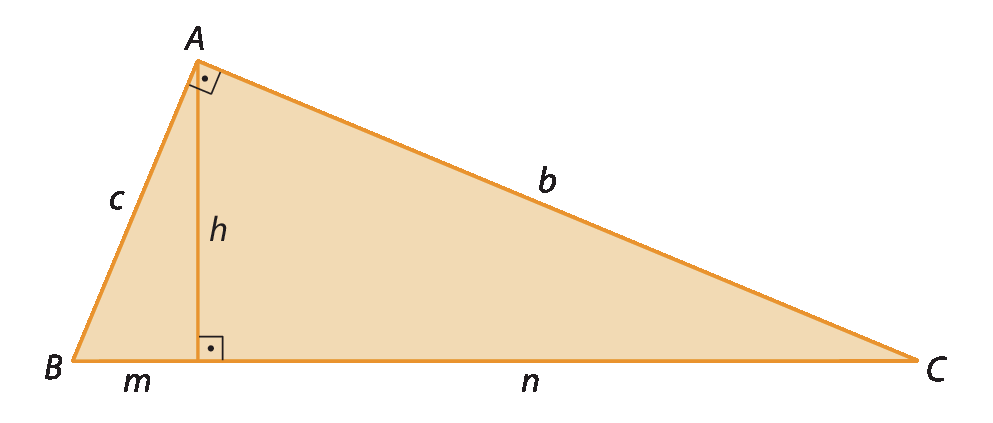
11. Determine a medida do perímetro do triângulo retângulo á bê cê, sabendo que o comprimento da projeção ortogonal do cateto
Símbolo. Segmento de reta AB.sobre a hipotenusa mede 4 centímetros, a altura em relação à hipotenusa
Símbolo. Segmento de reta AC.mede 3 centímetros e o do cateto
BC.mede
Fração 15 sobre 4centímetros.
12. Responda às questões.
a) Qual é a medida do perímetro de um losango cujas diagonais medem 6 centímetros e 8 centímetros de comprimento?
b) Qual é a medida de comprimento da altura de um triângulo equilátero cujos lados medem 2x de comprimento?
c) Qual é a medida de comprimento da diagonal de um retângulo que mede 7 centímetros de comprimento e 3 centímetros de largura?
13. (ó bê mépi) A figura mostra um triângulo retângulo á bê cê e três triângulos retângulos congruentes coloridos. O lado BC tem comprimento 1 centímetro. Qual é o perímetro do triângulo á bê cê, em centímetro?
a) 3 +
raiz quadrada de 5b) 2 +
2 raiz quadrada de 5.c) 5 menos
raiz quadrada de 5d) 5
e) 6
14. Um papel de presente de fórma retangular (figura 1) foi dobrado (figura 2). Calcule a medida de comprimento de
Símbolo. Segmento de reta DP..

15. (enêm) Devido ao aumento do fluxo de passageiros, uma empresa de transporte coletivo urbano está fazendo estudos para a implantação de um novo ponto de parada em uma determinada rota. A figura mostra o percurso, indicado pelas setas, realizado por um ônibus nessa rota e a localização de dois de seus atuais pontos de parada, representados por P e Q.
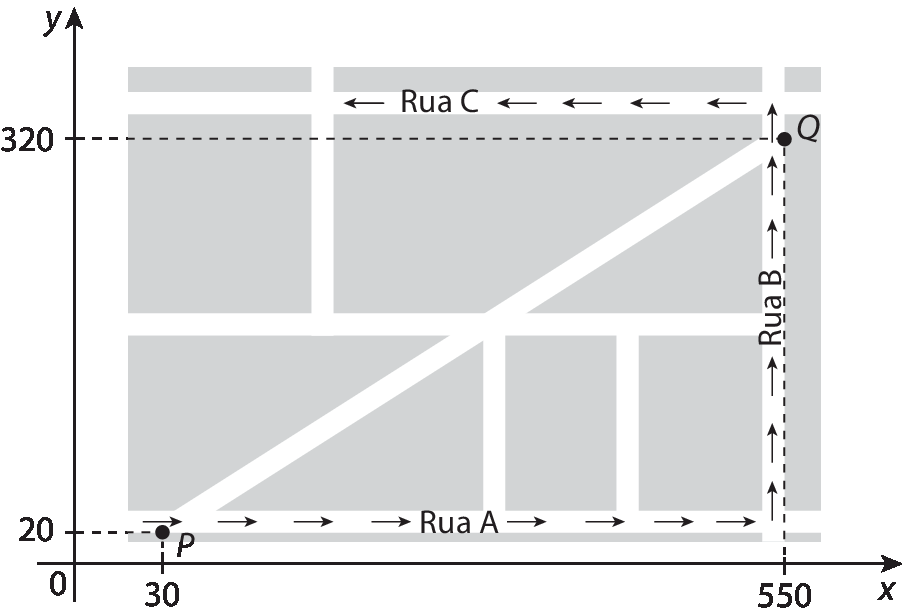
Os estudos indicam que o novo ponto T deverá ser instalado, nesse percurso, entre as paradas já existentes P e Q, de modo que as distâncias percorridas pelo ônibus entre os pontos P e T e entre os pontos T e Q sejam iguais. De acôrdo com os dados, as coordenadas do novo ponto de parada são:
a) abre parênteses290, 20fecha parênteses
b) abre parênteses410, 0fecha parênteses
c) abre parênteses410, 20fecha parênteses
d) abre parênteses440, 0fecha parênteses
e) abre parênteses440, 20fecha parênteses
Respostas e comentários
10. c = 5 centímetros
h ≃ 4,62 centímetros
m ≃ 1,92 centímetros
n ≃ 11,08 centímetros
11. 15 centímetros
12. a) 20 centímetros
12. b)
Sentença matemática. x raiz quadrada de 3.12. c)
Raiz quadrada de 58, fim da raiz, centímetros.13. alternativa a
14.
10 raiz quadrada de 5, fim da raiz, centímetros.15. alternativa ê
Orientações e sugestões didáticas
• Se for possível, faça com os estudantes a dobradura descrita na atividade 14 em uma folha de papel retangular com as medidas exatas indicadas na atividade e peça a eles que, após fazer os cálculos, meçam o papel dobrado.
• Resolução da atividade 14:
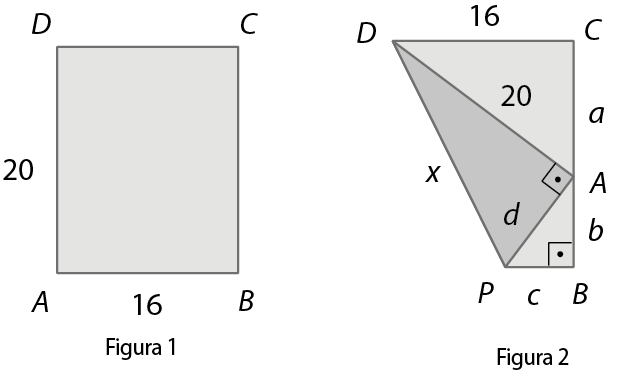
No triângulo retângulo á cê dê da figura 2, pelo teorema de Pitágoras, temos:
20elevado a 2 = 16elevado a 2 + aelevado a 2
a = 12
Como CB = 20 e CB = a + b, temos:
b = 20 menos 12 = 8
No triângulo retângulo ABP, temos:
d elevado a 2 = c elevado a 2 + 8elevado a 2
Como d + c = 16, então d = 16 menos c; assim:
delevado a 2 = celevado a 2 + 8elevado a 2
abre parênteses16 menos cfecha parênteseselevado a 2 = c elevado a 2 + 8elevado a 2
256 menos 32c + c elevado a 2 = c elevado a 2 + 64
32c = 192
c = 6
Logo: d = 16 menos c = 16 menos 6 = 10
No triângulo retângulo a dê pê, temos:
xelevado a 2 = 20elevado a 2 + 10elevado a 2
x = 10
raiz quadrada de 5Portanto, a medida de
Símbolo. Segmento de reta DP.é 10
raiz quadrada de 5centímetros.
▶ Atividades de revisão
16.

(púqui-São Paulo) A figura a seguir mostra a trajetória percorrida por uma pessoa para ir do ponto X ao ponto Y, caminhando em terreno plano e sem obstáculos.
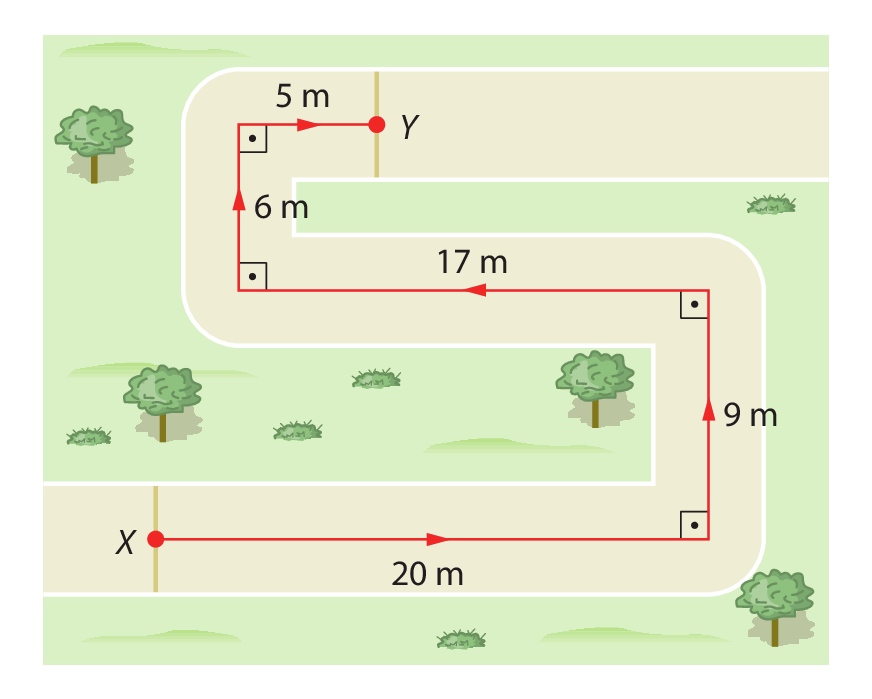
Se ela tivesse usado o caminho mais curto para ir de X a Y, teria percorrido:
a) 15 métros
b) 16 métros
c) 17 métros
d) 18 métros
e) 19 métros
17. Um mosteiro medieval foi construído em torno de um pátio de formato quadrado. No centro do pátio, encontra-se uma estátua do fundador da ordem religiosa. Se a medida do perímetro do pátio é 40 métros, qual é a medida de distância da estátua a um dos cantos dêsse pátio?

18. Determine as coordenadas do ponto médio do lado
Símbolo. Segmento de reta BC.do triângulo á bê cê.
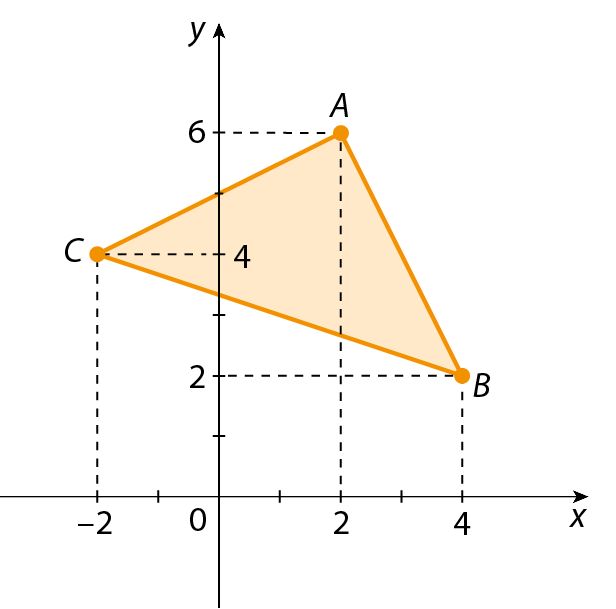
19. Obtenha as coordenadas do ponto P do eixo das ordenadas equidistante da origem e de aabre parênteses0, 10fecha parênteses.
20. Em cada item, calcule a medida do perímetro do pentágono á bê cê dê é.
a)
b)
21. Em uma malha quadriculada, trace um plano cartesiano e localize nele os vértices aabre parênteses3, 3fecha parênteses, Babre parênteses9, 3fecha parênteses, Cabre parênteses9, menos3fecha parênteses e Dabre parênteses3, menos3fecha parênteses do quadrilátero a bê cê dê. Em seguida, responda às questões.
a) Qual é a medida de área dêsse quadrilátero?
b) Qual é a medida do seu perímetro?
c) Qual é a medida de comprimento da sua diagonal?
22.

O terreno do sítio de Alexandre foi representado no plano cartesiano a seguir, de modo que cada unidade do plano cartesiano corresponde à medida de comprimento de 10 métros na realidade.

•

Junte-se a um colega, pensem em uma estratégia para calcular a medida da área dêsse terreno.
Respostas e comentários
16. alternativa c
17.
Sentença matemática. 5 raiz quadrada de 2, fim da raiz, metros.18.
par ordenado (1, 3)19. abre parênteses0, 5fecha parênteses
20. a)
Sentença matemática. 2 mais 4 raiz quadrada de 2, fim da raiz, mais 2 raiz quadrada de 10.20. b)
Sentença matemática. 5 mais raiz quadrada de 10, fim da raiz, mais 3 raiz quadrada de 13.21. a) 36 unidades da medida de área
21. b) 24 unidades de medida de comprimento
21. c)
6 raiz de 2unidades de medida de comprimento
22. Uma estratégia possível para calcular a medida de área do terreno é calcular a medida de área do retângulo de vértices êabre parêntesesmenos5, 3fecha parênteses, Fabre parêntesesmenos5, menos2fecha parênteses, Gabre parênteses3, menos2fecha parênteses, Habre parênteses3, 3fecha parênteses e, em seguida, subtrair dela as medidas das áreas dos triângulos EAB, FAD, GDC e HBC. Logo, medida de área do terreno é .2200 métros quadrados.
Orientações e sugestões didáticas
• Para resolver a atividade 16, os estudantes precisam, antes de tudo, identificar que o caminho mais curto para ir de X a Y é o segmento que liga esses dois pontos; já que não há obstáculos nesse terreno plano, bastará encontrar a medida de comprimento dêsse segmento de reta.
• Resolução da atividade 17:
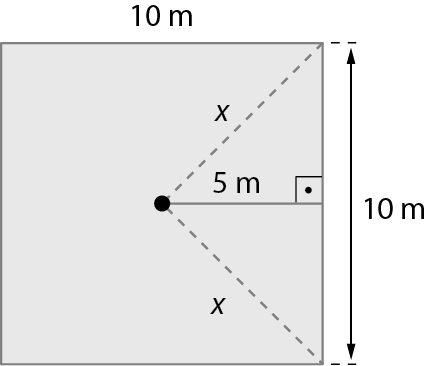
O pátio do mosteiro tem formato quadrado e perímetro medindo 40 métros de comprimento. Logo, cada um de seus lados mede 10 métros de comprimento.
Pela segunda relação métrica, temos:
x ⋅ x = 5 ⋅ 10
xelevado a 2 = 50
x =
raiz de 50= 5
raiz de 2Portanto, a medida de distância da estátua a um dos cantos do pátio é 5
raiz de 2métros.
• Sugerimos algumas questões para que os estudantes possam refletir sobre suas aprendizagens e possíveis dificuldades no estudo deste Capítulo, as quais devem ser adaptadas à realidade da turma. Oriente-os a fazer a autoavaliação, respondendo às questões no caderno com sim, às vezes ou não.
Eureticências
reticências sei identificar um triângulo retângulo a partir de seus elementos?
reticências compreendo o teorema de Pitágoras?
reticências sei aplicar o teorema de Pitágoras na resolução de problemas?
reticências compreendo as demais relações métricas envolvendo triângulos retângulos?
reticências sei empregar as relações métricas nos triângulos retângulos para a resolução de problemas?
reticências compreendo que o teorema de Pitágoras e as relações métricas podem ser aplicadas apenas em triângulos retângulos?
reticências sei construir gráficos utilizando planilhas eletrônicas?
reticências sou capaz de identificar triângulos retângulos em problemas envolvendo, por exemplo, quadriláteros, visando sua resolução utilizando as relações métricas?
reticências reconheço os tipos de gráfico mais adequados para representar um conjunto de dados?
reticências cuido do meu material escolar?
reticências tenho um bom relacionamento com meus colegas de turma?
reticências consigo expor minhas ideias e opiniões em grupo?
reticências tenho facilidade para compreender os conteúdos?
reticências realizo as tarefas propostas?