MP059
Introdução da Unidade 2
Dando continuidade ao trabalho desenvolvido na Unidade 1, as Unidades Temáticas são abordadas considerando os conhecimentos anteriores, bem como os que decorrem de sua apropriação.
A ponte entre as Unidades 1 e 2 é a abertura desta, que proporciona aos estudantes, na imagem contextualizada, o reconhecimento de números, além de efetuar várias contagens de elementos agrupados.
Assim, as atividades relativas à Unidade Temática Números ampliam os conhecimentos tratados na Unidade 1 e constituem-se como alicerces para a construção de conhecimentos futuros.
Por exemplo, contar de maneira exata ou aproximada, empregando diferentes estratégias como pareamento e outros agrupamentos, conhecimento contemplado na Unidade 1, será ampliado na Unidade 2 por meio de atividades que promovem a comparação de números, assim como o uso de números naturais como indicadores de quantidade (com as escritas literal e simbólica de números até 31), de código ou de ordem em diferentes situações.
Ao mesmo tempo, tais conhecimentos serão suporte para a comparação e a ordenação de números naturais (até a ordem das dezenas) por meio da compreensão de características do sistema de numeração decimal, conhecimentos a serem contemplados no 2º ano do Ensino Fundamental.
Os estudos referentes à Unidade Temática Álgebra estão presentes em atividades que buscam reconhecer, explicitar e descrever padrões em sequências de números naturais (crescentes/decrescentes), articulando-se, assim, com Números. Tais atividades buscam ampliar os conhecimentos que dizem respeito à organização e à ordenação de objetos familiares ou representações por meio de atributos e que foram estudados na Unidade 1. Além disso, visam oferecer suporte para que os estudantes sejam capazes de descrever padrões de sequências por meio de palavras, símbolos ou desenhos, conhecimentos a serem tratados no 2º ano do Ensino Fundamental.
Em Grandezas e medidas, os conhecimentos que envolvem valores de moedas e de cédulas do sistema monetário brasileiro para resolver situações simples do cotidiano dos estudantes serão aprofundados no ano seguinte, na perspectiva de que sejam capazes de estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro. Para isso, considera-se que a resolução de problemas, abordada desde a Educação Infantil, seja suporte para a apropriação dos conhecimentos a serem explorados nesta Unidade.
A abordagem da Unidade Temática Probabilidade e estatística considera conhecimentos previstos para o Ensino Fundamental, entre eles, o uso de gráficos básicos para expressar medidas. Assim, a proposta das atividades desta Unidade é ampliar as situações em que estejam presentes dados organizados em tabelas e em gráficos de barras simples, a fim de que, no ano seguinte, os estudantes utilizem tais conhecimentos para comparar informações de pesquisas apresentadas por meio de tabelas de dupla entrada e em gráficos de colunas ou barras simples.
Competência geral favorecida
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competência específica favorecida
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
MP060
UNIDADE 2. VAMOS CONTAR

MANUAL DO PROFESSOR
Objetivos da Unidade
Apropriar-se de procedimentos de contagem e da récita numérica.
Ler, escrever e comparar números naturais até 31.
Reconhecer a ideia de zero.
Utilizar números naturais como indicadores de quantidades ou de ordem.
Compor e decompor números de até duas ordens por meio de diferentes adições.
Reconhecer regularidades em sequências numéricas crescentes e em sequências decrescentes, e descrever elementos ausentes.
Estimar e comparar quantidades e comprimentos.
Reconhecer e relacionar dias da semana, dias e meses do ano utilizando um calendário.
Reconhecer e relacionar valores de moedas e de cédulas do sistema monetário brasileiro.
Aproximar-se dos contextos sociais de uso do sistema monetário.
Ler dados registrados em tabelas.
A cena de abertura mostra situações em que a relação entre a quantidade e o número que a representa pode ser explorada para a observação do conhecimento prévio dos estudantes. Verifique o entendimento da correspondência um a um, necessária à contagem; o conhecimento da récita numérica, em que a ordem é fundamental (um, dois, três, quatro...); o reconhecimento dos símbolos numéricos; a compreensão do aspecto cardinal (quantidade) dos números.
O uso de algum recurso material ou dos dedos para a contagem não deve ser visto como problema; a área cerebral responsável pelo controle dos dedos é a mesma cuja atividade se intensifica quando se realizam cálculos aritméticos.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA03, EF01MA04, EF01MA05, EF01MA07, EF01MA10, EF01MA15, EF01MA17, EF01MA19, EF01MA21
MP061
Página sem conteúdo.
MANUAL DO PROFESSOR
Comece a explorar a cena de abertura perguntando aos estudantes se eles já foram a um parque de diversões e de quais brinquedos mais gostaram. Depois, comente que os personagens Guilherme e Letícia foram a um parque em que os brinquedos tinham temas marinhos.
Com base na ilustração, sonde os conhecimentos prévios dos estudantes sobre contagem, correspondência um a um e reconhecimento de pequenos agrupamentos. Faça questionamentos, de modo que eles possam expor oralmente seus conhecimentos, como:
Quantas crianças estão tomando sorvete? (Uma.)
Quantos balões o menino está segurando? (Dois.)
Quantas latas a menina derrubou na barraca? (Três.)
Quantas crianças estão no brinquedo que cai na água? (Quatro.)
Quantas crianças estão no carrossel? (Cinco.) Verifique se, ao contar, os estudantes incluem as crianças que estão na fila. Discuta com eles essa situação. Espera-se que compreendam que somente as crianças que já estão no brinquedo devem ser consideradas.
Quantas crianças estão na roda-gigante? (Seis.)
Quantos funcionários do parque aparecem na cena? (Sete.)
Quantas crianças estão brincando no polvo? (Oito.)
Quantos algodões-doces aparecem na cena? (Nove.)
Quantas maçãs do amor o vendedor está carregando? (Dez.)
Quantos elefantes aparecem na cena? (Nenhum ou zero.)
Esta Unidade visa ampliar o conceito de número que os estudantes trazem da Educação Infantil, contemplando o (re)conhecimento dos números em seu aspecto cardinal (que diz respeito à quantificação). Exploram-se a identificação e a comparação de quantidades, que são tratadas até o número 31.
MP062
JOGO: BINGO DE NÚMEROS
Observação: ACOMPANHE AS INSTRUÇÕES QUE O PROFESSOR VAI LER. Fim da observação
MATERIAL: 1 CARTELA, QUE ESTÁ ABAIXO NESTA PÁGINA, E 4 MARCADORES PARA CADA JOGADOR, QUE PODEM SER TAMPINHAS, PEDAÇOS DE PAPEL AMASSADOS ETC.

JOGADORES: TODA A TURMA.
REGRAS:
- ESCREVA QUATRO NÚMEROS DE 0 A 10 NA CARTELA ABAIXO. NÃO VALE REPETIR NÚMEROS.
- OUÇA OS NÚMEROS QUE SEU PROFESSOR VAI DIZER EM VOZ ALTA.
- SE O PROFESSOR DISSER UM DOS NÚMEROS DE SUA CARTELA, COLOQUE UM MARCADOR EM CIMA DELE.
- GANHA O JOGO QUEM MARCAR PRIMEIRO TODOS OS NÚMEROS DA CARTELA.
CARTELA

MANUAL DO PROFESSOR
Objetivos
Reconhecer quantidades até dez e a ideia de zero.
Utilizar números naturais como indicadores de quantidades.
Ler e escrever números de zero a dez.
Ajude os estudantes na leitura e na compreensão das regras.
Por envolver diversas nuances, a construção do conceito de número é um processo longo, que não se completa apenas com a compreensão dos números de 0 a 10. Por isso, além de verificar conhecimentos prévios, esse trabalho permitirá reconhecer os diferentes níveis de compreensão dos estudantes, visto que o desenvolvimento não ocorre igualmente para todos.
O jogo de bingo é sempre um dos preferidos dos estudantes, principalmente porque é o fator sorte que determina o vencedor, e não a habilidade deles com jogos. Jogos desse tipo contribuem, então, para aumentar a autoestima de alguns deles. Além disso, facilitam o reconhecimento dos símbolos numéricos (algarismos).
A proposta do jogo de bingo é que os estudantes trabalhem com os números no decorrer de uma partida completa: no momento da escolha dos que serão preenchidos em sua cartela e no acompanhamento dos números sorteados.
A turma poderá trabalhar o reconhecimento dos números em suas formas oral e escrita de um modo divertido e atraente. Acompanhando a escolha dos números pelos estudantes, observe como eles os escrevem e se associam corretamente o símbolo escrito à designação do número, em cada caso.
BNCC em foco:
EF01MA01, EF01MA04; competência específica 3
Sugestão de trabalho interdisciplinar
Proponha uma atividade interligada ao componente Língua Portuguesa. Peça a cada estudante que escreva 4 palavras que representem objetos encontrados em parques. Em seguida, elabore com eles uma lista com essas palavras na lousa. Essa pode ser uma possibilidade de reflexão e construção coletiva de escrita, pois, ao elaborar a lista de palavras com os estudantes, você pode perguntar como se escreve determinada palavra e qual letra é utilizada para representar um som específico. Depois, sugira que copiem da lousa a palavra na frente da que haviam escrito no caderno e, em seguida, tentem descobrir as diferenças existentes. Incentive-os a verificar se há a mesma quantidade de letras e se as letras são iguais.
MP063
QUESTÕES SOBRE O JOGO
- OBSERVE AS CARTELAS DE CARLOS E DE FABIANA.


- SE O PROFESSOR DISSER EM VOZ ALTA O NÚMERO SETE, QUEM PODERÁ COLOCAR UM MARCADOR EM SUA CARTELA?

( )

( )
PROFESSOR
Resposta: FABIANA- OBSERVE AS CARTELAS DE OUTROS ESTUDANTES.
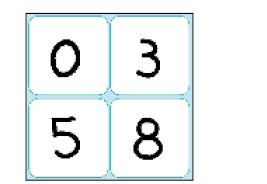
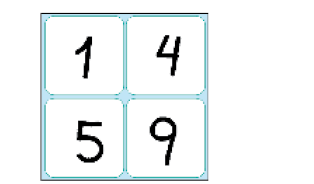
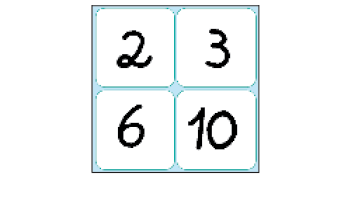
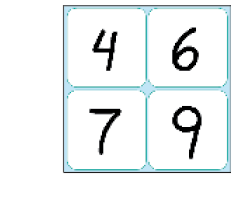
- O PROFESSOR DISSE EM VOZ ALTA O NÚMERO TRÊS.
EM QUANTAS CARTELAS APARECE ESSE NÚMERO? _____
PROFESSOR
Resposta: 2
MANUAL DO PROFESSOR
Explore novamente diferentes maneiras de a turma decidir quem começa o jogo, evitando que a decisão fique por conta de cada grupo de estudantes. Retome os modos já sugeridos, como jogar os dados (quem tira o maior número começa ou quem tira o menor número começa), entre outros. Circule entre eles enquanto jogam, fazendo comentários sobre como se organizam e ajudando quem precisar.
Questões sobre o jogo
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões.
Nelas, os estudantes terão de associar a forma por extenso dos números com sua representação simbólica (com algarismos) para responder às perguntas. Observe se algum estudante apresenta dificuldade e, se necessário, leia em voz alta os enunciados para a classe.
Variações
Caso julgue oportuno, sugira modificações nas regras para agregar outros desafios: você poderá cantar os números e mostrar sua forma escrita ou, em outro momento, somente cantar os números para que os estudantes encontrem a forma escrita. Julgando oportuno, peça que façam uma malha quadriculada formada por três fileiras com três quadrinhos cada uma e disponham nela nove números, sem repetição. O objetivo, nesse caso, é obter três números alinhados na horizontal, na vertical ou na diagonal; quem conseguir primeiro vencerá a partida.
Este jogo pode ser aproveitado em diferentes momentos e adaptado para números de dois algarismos ou de três algarismos, neste ano e em anos seguintes.
BNCC em foco:
EF01MA01, EF01MA04; competência específica 3
MP064
NÚMEROS ATÉ 10
- LIGUE CADA NÚMERO AO BOLO COM A QUANTIDADE CORRESPONDENTE DE VELAS.
COLUNA 1
5
6
4
COLUNA 2



PROFESSOR
Resposta: 5 - imagem 26 - imagem 3
4 - imagem 1
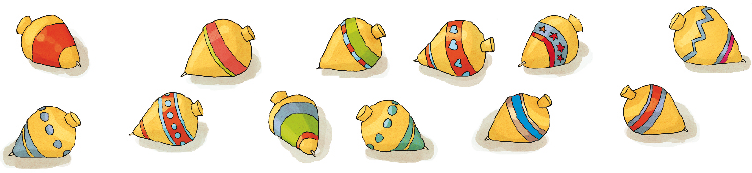
- NAS FIGURAS, QUANTOS BRINQUEDOS SÃO DE CADA TIPO?

SÃO _____ PIPA, _____ BOLAS, _____ PIÕES E _____ BONECAS.
PROFESSOR
Resposta: uma, duas, três, quatro.

- DESENHE 3 MAÇÃS. DEPOIS, PINTE-AS.
PROFESSOR
Exemplo de desenho:
MANUAL DO PROFESSOR
Objetivos
Reconhecer quantidades até dez e a ideia de zero.
Utilizar números naturais como indicadores de quantidades.
Identificar e comparar quantidades com base em uma imagem.
Ler e escrever números de zero a dez.
Atividade 1
Verifique como os estudantes procedem para escolher o número que corresponde a cada quantidade de velas.
Se julgar oportuno, comente com eles que os números 1, 2, 3, 4, 5 e 6 podem ser representados de maneira diferente da que aparece no livro. Leve recortes de jornais, revistas e folhetos para eles com esses números registrados com tipologias variadas para que possam observar.
Atividade 2
Nesta atividade, além do senso numérico, exploram-se outras habilidades, como a noção de frequência (brinquedo que aparece certa quantidade de vezes).
Explore a escrita dos números com algarismos e por extenso. Após contarem a quantidade de cada brinquedo, peça que completem a frase escrevendo os números por extenso.
Aproveite a imagem da pipa e comente que, dependendo da região do país, esse brinquedo é conhecido como papagaio, arraia, cafifa, pandorga, raia.
Atividade 3
Esta atividade pode ser ampliada pedindo aos estudantes que desenhem:
2 maçãs vermelhas e 1 maçã verde;
1 maçã vermelha e 2 maçãs verdes.
Desse modo, os estudantes tomam contato com maneiras diferentes de compor o número 3 e podem verificar que o 3 contém o 1 e o 2. Aqui também há um trabalho prévio com as ideias de adição e da sua propriedade comutativa, sem que se fale delas.
BNCC em foco:
EF01MA01, EF01MA04
MP065

- PINTE 4 BONÉS.
PROFESSOR
Exemplo de pintura:
- ESCREVA OS NÚMEROS.
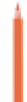
1, 1
PROFESSOR
Resposta: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1
2, 2
PROFESSOR
Resposta: 2, 2, 2, 2, 2, 2, 2, 2, 2, 2
3, 3
PROFESSOR
Resposta: 3, 3, 3, 3, 3, 3, 3, 3, 3, 3
4, 4
PROFESSOR
Resposta: 4, 4, 4, 4, 4, 4, 4, 4, 4, 4
5, 5
PROFESSOR
Resposta: 5, 5, 5, 5, 5, 5, 5, 5, 5, 5
6, 6
PROFESSOR
Resposta: 6, 6, 6, 6, 6, 6, 6, 6, 6, 6

- FAÇA A ESCRITA POR EXTENSO DESSES NÚMEROS NO CADERNO.
PROFESSOR
Resposta: Os estudantes devem escrever: um, dois, três, quatro, cinco e seis.- CERQUE COM UMA LINHA CADA ESTRELA COM 5 PONTAS.

- QUANTAS ESTRELAS VOCÊ CERCOU?
_____
PROFESSOR
Resposta: 7
MANUAL DO PROFESSOR
Atividade 4
Proponha aos estudantes que pintem um boné de cada vez, até que 4 bonés estejam pintados.
Ao pintarem o primeiro boné, pergunte: “Quantos bonés já pintaram?” (Um.). Depois de pintarem o próximo boné: “E agora, quantos bonés já pintaram?” (Dois.). Ao pintarem outro boné: “E agora, quantos bonés estão pintados?” (Três.); “Quantos falta pintar para ficarem 4 bonés pintados?” (Um.). Depois de pintados os 4 bonés, peça aos estudantes que contem os bonés pintados para verificar se já têm a quantidade pedida.
Os estudantes podem pintar quaisquer 4 bonés. Socialize as configurações que aparecerem.
Atividade 5
Enquanto os estudantes se acostumam com o traçado dos números de 1 a 6, peça a eles que citem exemplos de situações ou objetos que indiquem quantidades que podem ser registradas com esses números: 1 mesa do professor, 1 lousa, 1 professor por sala de aula, 2 traves de gol na quadra, 3 livros, 4 lápis, 5 dedos, 6 brinquedos etc.
Por se tratar de uma obra de alfabetização matemática, é importante proporcionar aos estudantes a oportunidade de expor hipóteses sobre os números e suas escritas numéricas, pois essas hipóteses constituem subsídios para a organização de atividades apresentadas posteriormente na obra e na coleção.
Atividade 6
Nesta atividade, além do senso numérico, explora-se a observação de características comuns e não comuns (se a estrela tem 5 pontas ou não, se há estrelas com mais pontas etc.).
O número 5 tem grande importância, pois é um valor intermediário em nosso sistema de numeração, servindo de apoio para representações e escritas numéricas. O fato de termos cinco dedos em cada mão certamente contribuiu para essa posição de destaque. Para auxiliar nas dificuldades que surgirem, apresente outras situações ilustradas para que os estudantes possam associar os números com as quantidades envolvidas e identificar os diferentes registros dos números.
BNCC em foco:
EF01MA01, EF01MA04
MP066

- CAMILA PRECISA PINTAR 9 BOLINHAS DE ISOPOR. ELA JÁ PINTOU 5. PINTE AS BOLINHAS QUE FALTAM PARA CHEGAR EM 9.
PROFESSOR
Exemplo de pintura:

- OS BRINQUEDOS ESTÃO ORGANIZADOS EM GRUPOS. OBSERVE-OS E FAÇA O QUE SE PEDE.

- CERQUE COM UMA LINHA AZUL O GRUPO QUE TEM 7 BRINQUEDOS.
PROFESSOR
Resposta: Grupo dos soldados. - CERQUE COM UMA LINHA VERDE O GRUPO QUE TEM 8 BRINQUEDOS.
PROFESSOR
Resposta: Grupo dos carrinhos.• QUANTOS BRINQUEDOS VOCÊ NÃO CERCOU? _____
PROFESSOR
Resposta: 10
- MARQUE COM UM X O QUADRO EM QUE HÁ 10 DEDOS LEVANTADOS.
( )
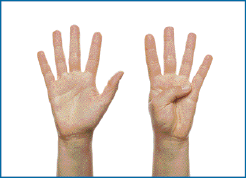
( )

PROFESSOR
Resposta: Quadro 2.

- QUANTOS DEDOS ESTÃO LEVANTADOS NO QUADRO QUE NÃO FOI ASSINALADO?
PROFESSOR
Resposta: Nove dedos.
- CERQUE COM UMA LINHA O NINHO EM QUE NÃO HÁ OVOS.


PROFESSOR
Resposta: Ninho 2.MANUAL DO PROFESSOR
Atividade 7
Depois de os estudantes pintarem, peça que contem as bolinhas pintadas para comprovar se há 9. Podem ser pintadas quaisquer 9 bolinhas. Socialize as diferentes maneiras de pintar que aparecerem.
Atividade 8
Amplie a atividade e pergunte: “Se tirarmos um brinquedo de cada grupo, quantos brinquedos ficarão em cada um?” (Ficarão 4 bolinhas, 6 soldadinhos, 7 carrinhos, 3 bonecas e nenhum urso de pelúcia.). Peça aos estudantes que socializem as estratégias que usaram para responder a essa pergunta.
Atividade 9
Os estudantes podem vivenciar a atividade antes de respondê-la, fazendo as representações que aparecem nas fotografias. Pergunte a eles se é possível obter o 9 com os dedos de uma única mão e peça que justifiquem a resposta dada.
O estabelecimento de relações entre a quantidade de dedos levantados e os símbolos numéricos é uma atividade bastante simples, uma vez que faz parte das práticas cotidianas a representação da idade da criança por meio dos dedos das mãos. Essa associação dos dedos com os símbolos numéricos possibilita o reconhecimento de que a contagem dos dedos é interessante e pode ser feita. A criança deve se sentir livre para contar nos dedos.
Outros recursos comuns para representar quantidades de 0 a 10 são aqueles feitos por meio de uma disposição geométrica que facilite seu reconhecimento, como acontece em peças de dominó ou em registros pictográficos, por exemplo:

CRÉDITO: PAULO MANZI
BNCC em foco:
EF01MA01, EF01MA02, EF01MA04
Atividade 10
Apesar de o zero não fazer parte da contagem direta, ele é importante para indicar a falta ou inexistência de algo. Pergunte: “O ninho em que não há ovos é o da esquerda ou o da direita?” (O da direita.); “Esse ninho está vazio. Quantos ovos há nesse ninho?” (Nenhum ou zero.); “Que quantidade de ovos podemos associar a esse ninho?” (Zero.).
Proponha aos estudantes outras situações que podem ser registradas com o número zero:
• A caixa de lápis de cor está vazia. Quantos lápis de cor há nessa caixa? (Nenhum ou zero.)
• Minha carteira de dinheiro está vazia. Quantos reais eu tenho na carteira? (Nenhum ou zero.)
MP067
- LIGUE CADA NÚMERO AO AQUÁRIO COM A QUANTIDADE CORRESPONDENTE DE PEIXES.
COLUNA 1
9
0
2
8
10
COLUNA 2





PROFESSOR
Resposta: 9 - aquário 30 - aquário 4
2 - aquário 2
8 - aquário 5
10- aquário 1
- ESCREVA OS NÚMEROS.

7, 7, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 7, 7, 7, 7, 7, 7, 7, 7, 7, 7.
8, 8, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 8, 8, 8, 8, 8, 8, 8, 8, 8, 8.
9, 9, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 9, 9, 9, 9, 9, 9, 9, 9, 9, 9.0, 0, _____, _____, _____, _____, _____, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.
10, _____, _____, _____, _____, _____, _____, _____
PROFESSOR
Resposta: 10, 10, 10, 10, 10, 10, 10.

- VOCÊ SABE ESCREVER ESSES NÚMEROS POR EXTENSO?
PROFESSOR
Resposta pessoal.
CONVERSE COM SEU PROFESSOR PARA FAZER ESSA ESCRITA NO CADERNO.
PROFESSOR
Resposta: Os estudantes devem escrever: sete, oito, nove, zero e dez.
MANUAL DO PROFESSOR
Atividade 11
Esta atividade proporciona uma síntese do reconhecimento dos números de 0 a 10 e pode ser ampliada com outras propostas, por exemplo:
• Marque com um X o aquário que tem menos peixes.
• Cerque com uma linha o aquário que tem mais peixes.
Atividade 12
Enquanto os estudantes se acostumam com o traçado dos números 0 (zero) e de 7 a 10, pergunte o que eles conhecem que remete à ideia desses números. É possível que se lembrem:
• dos 7 dias da semana (para o 7);
• dos 10 dedos das mãos (para o 10);
• da quantidade de irmãos que um filho único tem (para o zero).
A aprendizagem dos números ocorre paralelamente ao raciocínio aditivo, pois a construção de cada número se dá pelo acréscimo de uma unidade ao número anterior. O fato de uma criança conhecer os números até certo valor não significa que ela já abstraia a ideia de número para valores maiores, tampouco implica que ela não esteja apta a fazê-lo abstraindo a relação entre um número e o seguinte.
É importante observar se os estudantes são capazes de desvincular o registro da quantidade representada, pois a ideia de número é uma construção mental. Isso pode ser feito observando se conseguem compreender os registros numéricos sem o apoio material da quantidade que eles representam.
Também deve ser observado se compreendem o conceito de número, que não necessariamente está vinculado à leitura ou à escrita correta do símbolo, que é apenas sua representação.
Relacione cada número de 1 a 10 a outros números – como um a mais que ele ou um a menos que ele –, pois isso facilitará, entre outras coisas, o desenvolvimento do cálculo mental. Por exemplo, o número 9 é um a mais que 8 ou um a menos que 10.
Proponha também aos estudantes que indiquem, usando os dedos das mãos e de diferentes maneiras, as quantidades que representam os números de 1 a 10, a fim de que, novamente, vejam maneiras diferentes de compor o número e percebam a inclusão hierárquica. Por exemplo, o 8 contém o 3 e o 5 (3 dedos em uma mão com 5 dedos na outra compõem 8 dedos). Pergunte também: “Como podemos indicar o número zero com as duas mãos?”. Espera-se que eles percebam que podem mostrar as duas mãos fechadas.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA04
MP068
SEQUÊNCIAS
- DESCUBRA QUAIS NÚMEROS ESTÃO FALTANDO NAS BOLINHAS DE SABÃO E COMPLETE A SEQUÊNCIA DOS NÚMEROS DE 0 A 10.
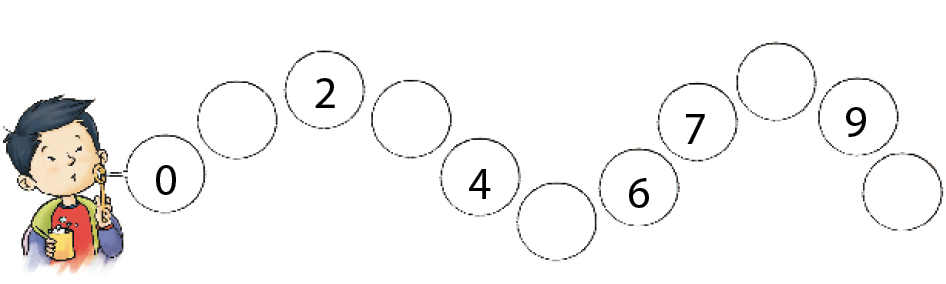
PROFESSOR
Resposta: 1, 3, 5, 8, 10.

- COMO VOCÊ DESCOBRIU OS NÚMEROS QUE ESTAVAM FALTANDO NESSA SEQUÊNCIA?
PROFESSOR
Resposta pessoal.
- OBSERVE OS NÚMEROS NOS PEIXINHOS PESCADOS POR GIOVANA NA BARRACA DA PESCARIA.
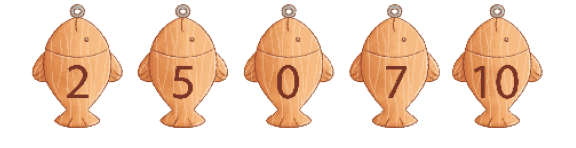
- AGORA, COMPLETE A SEQUÊNCIA FORMADA COM ESSES NÚMEROS, DO MENOR PARA O MAIOR NÚMERO.
0, _____, _____, 7, _____
PROFESSOR
Resposta: 2, 5, 10DEPOIS DE UM TEMPO, GIOVANA BRINCOU NOVAMENTE E PESCOU MAIS ESTES PEIXINHOS. VEJA OS NÚMEROS NELES.
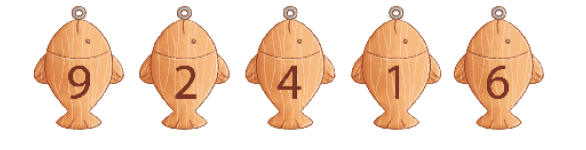
- ESCREVA A SEQUÊNCIA FORMADA COM ESSES NÚMEROS, DO MAIOR PARA O MENOR NÚMERO.
_____, _____, _____, _____, _____
PROFESSOR
Resposta: 9, 6, 4, 2, 1MANUAL DO PROFESSOR
Objetivos
Apropriar-se da récita numérica.
Reconhecer regularidades em sequências numéricas crescentes e sequências numéricas decrescentes, e descrever elementos ausentes.
Atividade 1
Depois de os estudantes completarem a sequência numérica, peça que leiam em voz alta a sequência formada. Chame a atenção deles para a ordem em que os números estão dispostos, do menor para o maior número, ou seja, do 0 ao 10, o que caracteriza a ordem crescente. Essa é uma maneira de comprovar se eles colocaram corretamente os números em seus lugares. Em seguida, peça que leiam em voz alta a mesma sequência, mas dessa vez do maior para o menor número, isto é, do 10 ao 0, o que caracteriza a ordem decrescente.
Observar, registrar e ler sequências numéricas em ordem crescente e em ordem decrescente deve fazer parte do cotidiano escolar dos estudantes.
Atividade 2
Esta atividade propicia aos estudantes observarem sequências numéricas nas quais aparecem números salteados, não contendo todos os números do 0 ao 10.
Ao término da atividade, solicite que leiam em voz alta as duas sequências formadas. Em seguida, peça que digam os números que faltam, na ordem correta, em cada sequência, para que se tenha a sequência completa do 0 ao 10.
BNCC em foco:
EF01MA01, EF01MA10
Sugestão de atividade
Parlendas
Parlendas são versos geralmente recitados para entreter, divertir ou escolher a pessoa que iniciará um jogo. Reproduza na lousa a letra da parlenda a seguir e sugira aos estudantes que a recitem todos juntos. Em seguida, peça que digam os números que aparecem nela.
1, 2, FEIJÃO COM ARROZ
3, 4, FEIJÃO NO PRATO
5, 6, FEIJÃO INGLÊS
7, 8, COMER BISCOITO
9, 10, COMER PASTÉIS
Da tradição popular.
MP069
DEZ UNIDADES OU UMA DEZENA
- CERQUE COM UMA LINHA 10 PIÕES E COMPLETE A FRASE.
PROFESSOR
Exemplo de agrupamento:
FORAM CERCADOS _____ PIÕES OU _____ DEZENA DE PIÕES.
PROFESSOR
Resposta: 10, uma.- LIGUE CADA ENGRADADO AMARELO A UM ENGRADADO VERMELHO CORRESPONDENTE PARA JUNTAR 10 GARRAFAS.
COLUNA 1




COLUNA 2




PROFESSOR
Resposta: engradado 1 (coluna 1) - engradado 1 (coluna 2)PROFESSOR
engradado 2 (coluna 1) - engradado 4 (coluna 2)PROFESSOR
engradado 3 (coluna 1) - engradado 2 (coluna 2)PROFESSOR
engradado 4 (coluna 1) - engradado 3 (coluna 2)

- DESENHE 5 FLORES EM CADA FLOREIRA.
PROFESSOR
Exemplo de desenho:PROFESSOR

- AGORA, CONTE TODAS AS FLORES. NO TOTAL, HÁ QUANTAS FLORES?
_____
PROFESSOR
Resposta: 10 flores, ou dez flores, ou uma dezena de flores.
MANUAL DO PROFESSOR
Objetivos
• Apropriar-se de procedimentos de contagem.
• Utilizar números naturais como indicadores de quantidades.
• Identificar quantidades até dez com base em uma imagem.
• Compor uma dezena por meio de diferentes adições.
Atividade 1
Para comprovar a resposta, peça aos estudantes que contem os piões que foram cercados por eles.
Atividade 2
Esta atividade favorece a compreensão do número 10 pela visualização espacial das garrafas nos engradados, compensando as quantidades, de maneira que possibilite a compreensão das composições e decomposições do número 10. Fale frases do tipo: “9 garrafas e 1 garrafa juntas são 10 garrafas; 3 garrafas e 7 garrafas juntas são 10 garrafas; 6 garrafas e 4 garrafas juntas são 10 garrafas” etc.
Conhecer a sequência oral dos números é condição necessária para contar corretamente, embora não seja suficiente. Meios eficientes para ensinar essa recitação são as parlendas e as brincadeiras com a sequência oral dos números.
Atividade 3
Esta atividade pode ser ampliada pedindo aos estudantes que façam no caderno outros desenhos de dois grupos de flores que formem no total 10 flores (por exemplo: 2 e 8 flores; 3 e 7 flores; 1 flor e 9 flores).
Desse modo, os estudantes tomam contato com várias maneiras de compor o número 10 e podem verificar que o 10 contém o 1, o 2, o 3, o 4, o 5, o 6, o 7, o 8 e o 9.
O número 10 é fundamental para a Matemática por ser a base de nosso sistema de numeração. Contamos e representamos os números por meio de agrupamentos de dez: 10 unidades formam 1 dezena, 10 dezenas formam 1 centena, 10 centenas formam 1 unidade de milhar e assim por diante.
Construa com os estudantes a sequência numérica do 0 ao 10 em um varal na sala de aula. É importante que esses símbolos estejam visíveis para eles. Para isso, use representações numéricas recortadas de jornais e revistas, de modo que sejam símbolos similares aos encontrados no cotidiano dos estudantes.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA04, EF01MA07
MP070
- OBSERVE E COMPLETE COM AS QUANTIDADES.

10 E 1
11

10 E 2
12

_____ E 3
PROFESSOR
Resposta: 1013

10 E _____
PROFESSOR
Resposta: 414

_____ E 5
PROFESSOR
Resposta: 1015

10 E _____
PROFESSOR
Resposta: 616

_____ E 7
PROFESSOR
Resposta: 10_____
PROFESSOR
Resposta: 17
10 E _____
PROFESSOR
Resposta: 8_____
PROFESSOR
Resposta: 18
_____ E 9
PROFESSOR
Resposta: 10_____
PROFESSOR
Resposta: 19
10 E _____
PROFESSOR
Resposta: 1020
MANUAL DO PROFESSOR
Objetivos
• Apropriar-se de procedimentos de contagem e da récita numérica.
• Utilizar números naturais como indicadores de quantidades.
• Reconhecer e registrar quantidades até 20.
• Reconhecer regularidades em sequências numéricas e descrever elementos ausentes.
• Compor números até 20 por meio de diferentes adições.
Atividade 1
Esta atividade apresenta uma quantidade de maçãs de dois tipos diferentes (vermelhas e verdes) e o número correspondente a elas. As dez unidades (a dezena) de cada número são representadas pelas maçãs vermelhas, e as unidades restantes pelas maçãs verdes, a fim de promover a observação das regularidades envolvidas na escrita numérica. Pergunte: “Há quantas maçãs no grupo de maçãs vermelhas? Essa quantidade aparece no número correspondente, na próxima coluna? E quanto às maçãs verdes que não formam um grupo de 10? A quantidade delas, em cada caso, aparece no número correspondente?”. Essas perguntas levam os estudantes a estabelecer uma correspondência entre o número de dezenas e o algarismo da esquerda no número, assim como entre as unidades restantes e o algarismo da direita no número.
Comente a similaridade entre a quantidade em cada caso e a forma como se escreve por extenso (com exceção do onze): doze guarda relação com dois, treze com três, catorze com quatro, quinze com cinco, e, a partir de dezesseis, essa relação é ainda mais explícita: dezesseis é formado por dez e seis, dezessete é dez e sete, dezoito é dez e oito, dezenove é dez e nove.
A representação numérica de quantidades maiores que dez não é tão óbvia para os estudantes. Nesse momento, exploramos o raciocínio aditivo.
A construção da ideia de número está relacionada às experiências adquiridas pela criança em seu meio e em atividades didaticamente organizadas que favorecem sua aprendizagem. Contar diversas quantidades, nomeá-las e relacioná-las é parte importante do processo, mas saber contar até dez e registrar esse número por meio dos algarismos 1 e 0 não significa que a criança compreende o porquê dessa forma de registro escrito.
Apesar de oferecermos várias situações de aprendizagem buscando essa compreensão, é importante ressaltar que não necessariamente, no 1º ano, os estudantes compreenderão toda a estrutura lógica do sistema de numeração decimal (o valor posicional, a ideia aditiva e o uso do zero).
BNCC em foco:
EF01MA01, EF01MA02, EF01MA07
MP071
- DESCUBRA QUAIS NÚMEROS ESTÃO FALTANDO NAS PORTAS E COMPLETE A SEQUÊNCIA DE NÚMEROS DO 11 AO 20.

PROFESSOR
Resposta: 12, 14, 15, 16, 17, 18, 20AGORA, FAÇA O QUE SE PEDE.
- QUAL NÚMERO ESTÁ ENTRE O 16 E O 18?
_____
PROFESSOR
Resposta: 17 - QUAIS NÚMEROS ESTÃO ENTRE O 14 E O 17?
_____
PROFESSOR
Resposta: 15 e 16 - QUAL NÚMERO ESTÁ ENTRE O 11 E O 13?
_____
PROFESSOR
Resposta: 12 - QUAL NÚMERO ESTÁ ENTRE O 18 E O 20?
_____
PROFESSOR
Resposta: 19
- OBSERVE AS IMAGENS ABAIXO.




- OS NÚMEROS QUE APARECEM NESSAS IMAGENS INDICAM CONTAGEM? INDICAM ORDEM?
PROFESSOR
Resposta: Não; não.
MANUAL DO PROFESSOR
Atividade 2
Promova a récita da sequência apresentada (do 11 ao 20), o que facilitará aos estudantes saberem os números faltantes nas portas. Incentive-os a perceber que os números aumentam de 1 em 1.
Se julgar oportuno, amplie o trabalho com a ordem numérica do maior para o menor número (ordem decrescente).
As questões propostas nesta atividade levam os estudantes a perceber o intervalo entre dois números. Verifique se eles necessitam consultar a sequência para responder às questões ou se já são capazes de respondê-las sem o suporte visual.
Atividade 3
Espera-se que os estudantes percebam que os números que aparecem nas imagens não indicam contagem nem ordem. Comente com eles que esses números indicam códigos de identificação.
Converse com a turma sobre situações em que os números são empregados para codificar; por exemplo, nos letreiros dos ônibus, nas placas dos carros, nos números das casas, dos telefones etc.
Sugestão de atividade
Contagem regressiva
Conte aos estudantes que, antes do lançamento de um foguete, é feita uma contagem regressiva que começa no número 10 (dez) e termina no número 0 (zero).
Apresente a sequência decrescente (do 10 ao 0) com algumas lacunas e peça aos estudantes que a completem.10, 9, 8, _____, 6 _____, _____, _____, _____, 1, 0
Resposta: 7, 5, 4, 3 e 2.
BNCC em foco:
EF01MA01, EF01MA10
MP072
NÚMEROS ATÉ 31

- DESENHE AS BOLINHAS QUE ESTÃO FALTANDO PARA COMPLETAR A QUANTIDADE INDICADA. DEPOIS, COMPLETE OS QUADRINHOS COM OS NÚMEROS REFERENTES À QUANTIDADE DE BOLINHAS EM CADA POTE.
PROFESSOR
Resposta pessoal.
PROFESSOR
Resposta: 5, 7- OBSERVE E COMPLETE COM AS QUANTIDADES DE MAÇÃS EM CADA AGRUPAMENTO.

20 E 21

20 E _____
PROFESSOR
Resposta: 424

_____ E 8
Resposta: 20
28

_____ E 0
PROFESSOR
Resposta: 30_____
PROFESSOR
Resposta: 30
_____ E _____
PROFESSOR
Resposta: 30 E 1_____
PROFESSOR
Resposta: 31MANUAL DO PROFESSOR
Objetivos
Apropriar-se de procedimentos de contagem.
Utilizar números naturais como indicadores de quantidades.
Identificar e comparar quantidades com base em uma imagem.
Reconhecer e registrar quantidades até 31.
Decompor números de até duas ordens em duas parcelas.
Reconhecer e relacionar dias da semana, dias e meses do ano utilizando um calendário.
Atividade 1
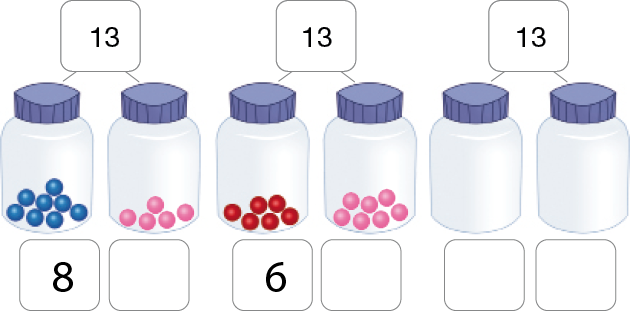
O foco desta atividade é a decomposição em duas parcelas do número 13, com duas representações: formal e não formal. Parte-se de uma representação numérica formal, atribui-se uma representação não formal (dois grupos de bolinhas) para auxiliar os estudantes a compor a solução do problema e, então, retorna-se para a representação formal.
Amplie a atividade decompondo outros números até 31.
Atividade 2
Esta atividade propicia a compreensão dos números até 31. Os estudantes terão de reconhecer os agrupamentos propostos e indicar a quantidade, como feito anteriormente no caso de 11 a 20. Aqui também se apresentam quantidades de maçãs vermelhas e de maçãs verdes. As maçãs vermelhas aparecem em grupos de 20 ou de 30 elementos. Os estudantes devem perceber que a quantidade de maçãs verdes determina quantas maçãs existem além das vermelhas (20 ou 30). Amplie o quadro mostrando a formação de todos os números de 21 a 31.
Mais uma vez, é importante destacar a similaridade entre a quantidade em cada caso e a forma como se escreve por extenso (de 21 a 29, 30 e 31).
Se julgar oportuno, explique aos estudantes que, no sistema de numeração decimal, os símbolos criados para representar qualquer número são: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9. Eles são chamados de algarismos ou dígitos. Dê alguns exemplos com esses dez símbolos, que podem ser repetidos quantas vezes forem necessárias. Você também pode fazer uma brincadeira, pedindo a eles que digam números que consideram difíceis; em seguida, escreva-os na lousa para que os estudantes percebam que os números sempre serão compostos de algarismos.
Lembre-os de que os números de 0 a 9 são escritos com um algarismo.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA07
MP073
- OS CALENDÁRIOS AJUDAM A ORGANIZAR NOSSA ROTINA, POIS APRESENTAM O REGISTRO DOS DIAS AGRUPADOS. OBSERVE O CALENDÁRIO ABAIXO E FAÇA O QUE SE PEDE.

- MARQUE COM UM
X
O DIA QUE ESTÁ ENTRE 27 E 29.
PROFESSOR
Resposta: 28 - CERQUE COM UMA LINHA O DIA 20.
PROFESSOR
Resposta: 20
- COMPLETE ESTE CALENDÁRIO DO MÊS DE MAIO.

PROFESSOR
Resposta: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31- QUAIS SÃO OS NÚMEROS QUE INDICAM OS DIAS QUE FORAM SEXTAS-FEIRAS NESSE MÊS?
_____
PROFESSOR
Resposta: 3, 10, 17, 24, 31
MANUAL DO PROFESSOR
As atividades 3 e 4 exploram a sequência numérica de 1 a 31 por meio de um calendário mensal.
Os estudantes já devem ter tido contato com os dias da semana e os meses do ano no convívio social ou na Educação Infantil.
Atividade 3
Para verificar os conhecimentos prévios dos estudantes acerca das medidas de tempo (dias da semana e meses do ano), mostre-lhes um calendário (grande) anual e peça que digam o que sabem sobre ele. Incentive-os a dizer quantos e quais são os dias da semana e os meses do ano. Podem-se fazer perguntas sobre alguns elementos do calendário apresentado na atividade (junho de 2023) antes de responder às questões propostas. Por exemplo:
Que dia da semana é o dia 2 desse mês? (Domingo.)
Quantos sábados há nesse mês de junho? (Cinco.)
Quantos dias tem o mês de junho? (Trinta.)
Depois, peça que leiam a sequência dos dias (do 1 ao 30) e proponha as questões do livro.
Para identificar o número (28) que fica entre o 27 e o 29, é importante que os estudantes retomem a récita numérica até 30 quantas vezes forem necessárias.
Enfatize para os estudantes que cada mês tem sempre o mesmo número de dias, independentemente do ano, mas que a cada ano o mês começa em um dia diferente da semana. Também é um bom momento para destacar o mês de fevereiro, único que pode ter variação no número de dias, a cada quatro anos. Se julgar conveniente, dependendo do grau de interesse e de desenvolvimento da turma, comente que o ano em que acontece essa variação é chamado de bissexto.
Atividade 4
Esta atividade amplia o trabalho feito na atividade anterior, explorando outro mês (maio de 2023). Pendure um calendário grande desse mês na lousa e peça a alguns estudantes que venham mostrar suas respostas para que os demais colegas façam a validação, sob sua orientação. Pergunte: “Quantos dias há no mês de maio?” (31 dias.).
Amplie a atividade propondo questões similares às apresentadas na atividade anterior, usando o calendário apresentado.
BNCC em foco:
EF01MA01
MP074
NÚMEROS NA FORMA ORDINAL
- DANIELA VENCEU O CAMPEONATO DE NATAÇÃO. DIANA FOI A SEGUNDA COLOCADA E RENATA, A TERCEIRA. ESCREVA O NOME DE QUEM RECEBEU CADA MEDALHA.

2ª COLOCADA
_____
PROFESSOR
Resposta: Diana
1ª COLOCADA
_____
PROFESSOR
Resposta: Daniela
3ª COLOCADA
_____
PROFESSOR
Resposta: Renata- COMPLETE O QUADRO QUE INDICA O ANDAR ONDE MORA CADA PESSOA.
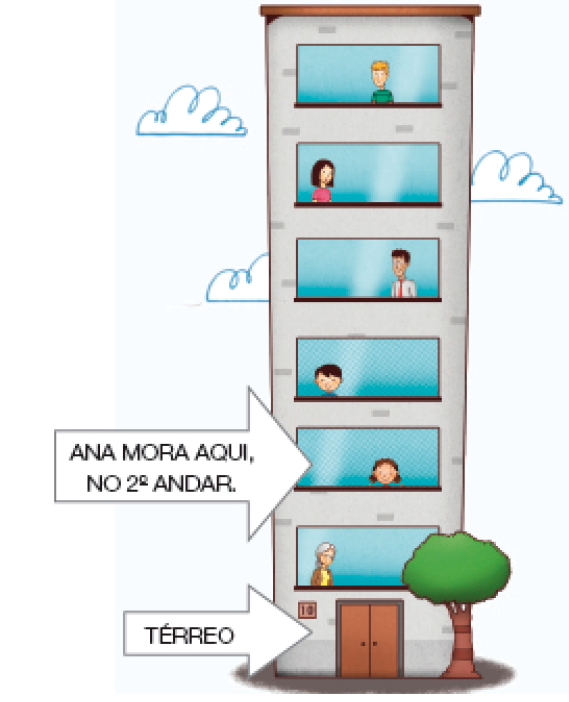
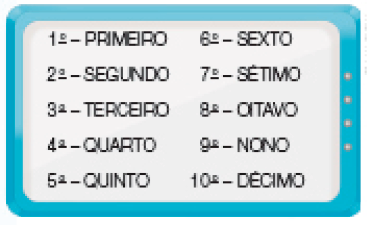
Tabela: equivalente textual a seguir.
|
|
_____ |
QUARTO |
|
|
_____ |
SEXTO |
|
|
_____ |
PRIMEIRO |
|
|
_____ |
TERCEIRO |
|
|
2º |
SEGUNDO |
|
|
_____ |
QUINTO |
PROFESSOR
Resposta: 4º, 6º, 1º, 3°, 5°.MANUAL DO PROFESSOR
Objetivo
Apresentar números naturais como indicadores de ordem.
Atividades 1 e 2
Estas atividades mostram o uso do número na forma ordinal em situações conhecidas pela maioria dos estudantes. Observe se eles associam a posição de cada esportista às medalhas correspondentes ao 1º lugar, ao 2º lugar e ao 3º lugar na atividade 1, e se conseguem identificar sem dificuldades o andar dos moradores do edifício na atividade 2.
BNCC em foco:
EF01MA01
MP075
COMPARAÇÕES
- LIGUE CADA CRIANÇA À COLEÇÃO DE FIGURINHAS DELA.
COLUNA 1



COLUNA 2



PROFESSOR
Resposta: Lucas - coleção 3PROFESSOR
Jean - coleção 1PROFESSOR
Antônio - coleção 2

- VOCÊ COLECIONA ALGUM OBJETO? CONTE A UM COLEGA.
PROFESSOR
Resposta pessoal.
- A CASTANHEIRA (BERTHOLLETIA EXCELSA) É UMA DAS ÁRVORES MAIS ALTAS DO BRASIL. OBSERVE A IMAGEM E RESPONDA À QUESTÃO.

LEGENDA: CASTANHEIRA (BERTHOLLETIA EXCELSA). FIM DA LEGENDA.
- SE EMPILHÁSSEMOS BONECOS EM PÉ, QUANTOS BONECOS VOCÊ ACHA QUE PRECISARÍAMOS PARA TER UMA PILHA COM A MESMA ALTURA QUE A CASTANHEIRA?
PROFESSOR
Atenção professor: Espera-se que os estudantes estimem mais de 20 bonecos. Fim da observação.
MANUAL DO PROFESSOR
Objetivo
Estimar e comparar quantidades e comprimentos.
Atividade 1
Incentive os estudantes a observar as informações dadas pelas crianças sobre a quantidade de figurinhas de sua coleção para que descubram a quantidade de figurinhas de cada uma.
Atividade 2
Convém dizer aos estudantes que, nesta atividade, eles estão fazendo uma estimativa.
Os estudantes devem estimar quantos bonecos em pé devem ser colocados um sobre o outro para obter uma pilha de bonecos com a mesma altura de uma das maiores castanheiras do país. Em seguida, peça que comparem as estimativas e as justifiquem, de modo a socializá-las.
BNCC em foco:
EF01MA01, EF01MA03, EF01MA15
MP076
USANDO O DINHEIRO
- OBSERVE UMA MOEDA E ALGUMAS CÉDULAS DE REAL. DEPOIS, ESCREVA O VALOR DE CADA UMA.

1 REAL

_____ REAIS
PROFESSOR
Resposta: 2
_____ REAIS
PROFESSOR
Resposta: 5
_____ REAIS
PROFESSOR
Resposta: 10
_____ REAIS
PROFESSOR
Resposta: 20AGORA, RESPONDA:
- QUAL DESSAS CÉDULAS TEM O MENOR VALOR?
_____
PROFESSOR
Resposta: A cédula de 2 reais. - QUAL DESSAS CÉDULAS TEM O MAIOR VALOR?
_____
PROFESSOR
Resposta: A cédula de 20 reais. - COM UMA CÉDULA DE 20 REAIS, É POSSÍVEL COMPRAR UM PRESENTE NO VALOR DE 19 REAIS? MARQUE COM UM
X
.
( ) SIM
( ) NÃO
PROFESSOR
Resposta correta: Sim.
- SE VOCÊ TIVESSE APENAS UMA CÉDULA DE 5 REAIS E UMA CÉDULA DE 2 REAIS, QUAL DELAS USARIA PARA PAGAR UMA COMPRA NO VALOR DE 3 REAIS?
PROFESSOR
Resposta: A cédula de 5 reais.
MANUAL DO PROFESSOR
Objetivos
Utilizar números naturais como indicadores de quantidades.
Comparar números naturais até 31.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Aproximar-se dos contextos sociais de uso do sistema monetário.
O foco das atividades destas páginas é explorar os números associados a quantias compostas de cédulas e moedas do sistema monetário brasileiro (o real). Fique atento às diferentes estratégias pessoais que os estudantes utilizarão para resolver as situações propostas. É interessante que você possibilite a socialização das diferentes estratégias na classe, para que os estudantes acompanhem o raciocínio de cada colega e possam ampliar seu repertório.
Atividade 1
Explore com os estudantes a moeda e as cédulas apresentadas. Espera-se que eles não tenham dificuldades em identificar qual cédula tem maior ou menor valor. No entanto, se ainda surgir alguma dificuldade, incentive-os a desenhar quantas moedas de 1 real compõem o valor exato de cada cédula. Comparar a quantidade de moedas facilitará o entendimento sobre o valor de cada cédula e a comparação entre essas e outras quantias.
BNCC em foco:
EF01MA01, EF01MA05, EF01MA19
MP077
- LIGUE CADA CÉDULA DE REAL À FRUTA QUE PODE SER PAGA COM ELA.
COLUNA 1




COLUNA 2




PROFESSOR
Exemplo de resposta:PROFESSOR
2 reais - laranjaPROFESSOR
10 reais - melãoPROFESSOR
5 reais - cocoPROFESSOR
20 reais - melancia

- ESSAS CÉDULAS DE REAL FORAM SUFICIENTES PARA COMPRAR TODAS AS FRUTAS?
PROFESSOR
Resposta: Sim
Boxe complementar:
DESAFIO
ACOMPANHE A LEITURA DO DIÁLOGO E DESCUBRA O NÚMERO EM QUE A MENINA PENSOU.

CRÉDITO: ILUSTRAÇÕES: ALEXANDRE MATOS
Resposta: 29.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, explore também os significados, dentro do contexto da situação, dos termos necessário (essencial, indispensável) e suficiente (o que basta, o bastante).
Desafio
Nesta atividade, há dois desafios de naturezas diferentes: um é interpretar as informações fornecidas sobre o número pensado; o outro é organizar uma estratégia para coordenar essas informações a fim de descobri-lo. Você perceberá que muitos estudantes, a princípio, terão dificuldade em considerar as informações simultaneamente.
Leia as dicas para os estudantes e sugira que façam um quadro com números até 30 e marquem os números excluídos a cada dica.
Por exemplo, ao informar que o número pensado é menor que 30 e maior que 21, pergunte: “Quais desses números vocês já sabem que não podem ser o número escolhido? Vamos marcar esses números para saber que não são esses? E agora, quais ainda podem ser?”. Espera-se que os estudantes percebam que os números de 1 a 21 e o 30 devem ser marcados, pois não podem ser escolhidos. A proposta de ir marcando no quadro os números excluídos a cada dica lida é interessante, mas precisa ser bem discutida com o grupo, de modo que seu uso faça sentido e não se torne apenas um truque.
Sugira aos estudantes que criem outras charadas do tipo “Descubra em qual número pensei”.
Um recurso que pode facilitar esse tipo de atividade é a construção de um quadro numérico com 10 unidades por linha. Com esse apoio, eles poderão utilizar outras dicas, como “Está na coluna do 9”, “Está na linha do 20”, percebendo assim regularidades no quadro numérico.
BNCC em foco:
EF01MA01, EF01MA05, EF01MA19
MP078
LER TABELAS
- VEJA O DESEMPENHO DE ALGUNS ESTUDANTES SELECIONADOS PARA UM TRABALHO ESPECIAL DE MATEMÁTICA.
TRABALHO ESPECIAL DE MATEMÁTICA EM 2023
Tabela: equivalente textual a seguir.
|
ESTUDANTE |
ANA |
JOSÉ |
LUÍS |
SÍLVIA |
SUELI |
|---|---|---|---|---|---|
|
NOTA NO TRABALHO |
8 |
7 |
8 |
7 |
7 |
FONTE: ESCOLA PESQUISADA EM MAIO DE 2023.
DE ACORDO COM AS INFORMAÇÕES DA TABELA:
- MARQUE COM UM
X
AS NOTAS OBTIDAS POR ESSES ESTUDANTES:
( ) 5
( ) 6
( ) 7
( ) 8
( ) 9
PROFESSOR
Resposta: 7, 8 - QUAL FOI A NOTA DE LUÍS?
_____
PROFESSOR
Resposta: 8 - QUAIS ESTUDANTES OBTIVERAM NOTA 7?
( ) ANA
( ) SÍLVIA
( ) JOSÉ
( ) SUELI
( ) LUÍS
PROFESSOR
Resposta: Sílvia, José, Sueli.
- OBSERVE A TABELA A SEGUIR E COMPLETE.
ESTUDANTES DO PERÍODO DA MANHÃ EM 2023
Tabela: equivalente textual a seguir.
|
IDADE DO ESTUDANTE |
6 ANOS |
7 ANOS |
8 ANOS |
9 ANOS |
10 ANOS |
|---|---|---|---|---|---|
|
QUANTIDADE DE ESTUDANTES |
10 |
22 |
18 |
20 |
15 |
FONTE: ESCOLA PESQUISADA EM FEVEREIRO DE 2023.
- NO PERÍODO DA MANHÃ DA ESCOLA PESQUISADA, HÁ
_____
ESTUDANTES COM 7 ANOS.
PROFESSOR
Resposta: 22• NESSA ESCOLA, HÁ _____ ESTUDANTES COM _____ ANOS.
- ESSE É O MENOR GRUPO DE ESTUDANTES COM A MESMA IDADE NESSE PERÍODO.
PROFESSOR
Resposta: 10, 6- SÃO
_____
ESTUDANTES COM 10 ANOS E 18 ESTUDANTES COM
_____
ANOS.
PROFESSOR
Resposta: 15, 8
- SÃO
_____
ESTUDANTES COM 10 ANOS E 18 ESTUDANTES COM
_____
ANOS.
MANUAL DO PROFESSOR
Objetivo
Ler dados registrados em tabelas.
Atividade 1
Comente que nas tabelas há um título e que elas são formadas por linhas e colunas. Na disposição em que a tabela é apresentada nesta atividade, a primeira linha mostra os nomes dos estudantes selecionados, e a segunda mostra a nota obtida por eles. Comente também que na tabela é informada a fonte dos dados: “Escola pesquisada em maio de 2023”.
Discuta as questões propostas com a turma. Destaque os fatos de que cada estudante tem uma única nota e essas notas podem ser iguais ou não às dos colegas.
Atividade 2
Antes de os estudantes responderem às questões propostas no livro, explore as informações apresentadas na tabela.
Quais são as idades dos estudantes do período da manhã? (6 anos, 7 anos, 8 anos, 9 anos e 10 anos.)
Quantos estudantes têm 7 anos? (22.) E 10 anos? (15.)
Que idade corresponde à quantidade de 20 estudantes? (9 anos.)
Para cada questão do livro, peça aos estudantes que comentem como podem obter a resposta e, junto com eles, validem os procedimentos descritos. Na primeira e na terceira, precisam localizar e relacionar os dados apresentados. Já na segunda, eles devem perceber que precisam saber qual é a menor quantidade de estudantes (10) e verificar a idade correspondente (6 anos).
Para fazer a comparação proposta na terceira questão, os estudantes podem determinar a quantidade de estudantes que têm 8 anos (18) e 10 anos (15) e comparar essas quantidades (18 é maior do que 15). Desse modo, podem identificar que há mais estudantes com 8 anos do que com 10 anos. Essa é uma questão desafiadora para eles.
BNCC em foco:
EF01MA05, EF01MA17, EF01MA21
MP079
- A TABELA A SEGUIR APRESENTA O RESULTADO DA CAMPANHA DE ARRECADAÇÃO DE BRINQUEDOS NOVOS DE UMA ESCOLA.
BRINQUEDOS MAIS ARRECADADOS
Tabela: equivalente textual a seguir.
|
TIPO DE BRINQUEDO |
|
|
|
|
|---|---|---|---|---|
|
QUANTIDADE |
15 |
20 |
20 |
25 |
FONTE: CAMPANHA DE ARRECADAÇÃO DE BRINQUEDOS EM OUTUBRO DE 2023.
DE ACORDO COM A TABELA:
- MARQUE COM UM X O TIPO DE BRINQUEDO QUE FOI O MAIS ARRECADADO.
( )

( )

( )

( )

PROFESSOR
Resposta: Jogo- LIGUE O TIPO DE BRINQUEDO AO SEU NOME.
COLUNA 1




COLUNA 2
BOLA
BONECA
JOGO
URSO
PROFESSOR
Resposta: bola ‒ imagem 2; boneca ‒ imagem 3; jogo ‒ imagem 4; urso ‒ imagem 1.- CERQUE COM UMA LINHA OS TIPOS DE BRINQUEDO APRESENTADOS NA TABELA.
BONECA, JOGO, PIÃO, URSO, BOLA, PETECA
PROFESSOR
Resposta: boneca, jogo, urso, bola• RESPONDA À QUESTÃO.
- QUAIS OS TIPOS DE BRINQUEDO QUE TIVERAM A MESMA QUANTIDADE ARRECADADA?
_____
PROFESSOR
Resposta: Bola e boneca.
MANUAL DO PROFESSOR
Atividade 3
Para ampliar esta atividade, apresente na lousa a tabela da atividade em outra disposição e destaque os mesmos elementos explorados na atividade proposta no livro (a leitura agora deve ser feita por colunas).
Tabela: equivalente textual a seguir.
|
Idade do estudante |
Quantidade de estudantes |
|---|---|
|
ESTUDANTES DO PERÍODO DA MANHÃ EM 2023 |
|
|
6 anos |
10 |
|
7 anos |
22 |
|
8 anos |
18 |
|
9 anos |
20 |
|
10 anos |
15 |
Fonte: Escola pesquisada em fevereiro de 2023.
Esta atividade pode ser feita em duplas, pois a troca de ideias entre os estudantes enriquece o aprendizado.
Peça aos estudantes que reconheçam os elementos da tabela nas duas disposições (a apresentada no livro e a da lousa). Explore os elementos da tabela para verificar dúvidas que eles ainda possam apresentar.
Em uma roda de conversa, pergunte a opinião deles sobre o propósito de fazer campanhas desse tipo.
Depois de resolver as questões, peça a alguns estudantes que comentem como fizeram. Pergunte: “Como você fez para saber o tipo de brinquedo mais arrecadado?” (Exemplo de resposta: Procurei na tabela a maior quantidade e verifiquei o brinquedo correspondente.).
Se necessário, explique a eles que os tipos de brinquedo da tabela foram os mais arrecadados, mas podem ter sido arrecadados outros tipos que não apareceram na tabela, pois estavam em menor quantidade.
A organização de dados em tabelas relaciona-se ao processo mental de classificação, que consiste em separar os elementos de um grupo de acordo com atributos, propriedades, similaridades ou diferenças entre eles.
O foco destas atividades é a leitura de dados organizados em tabelas simples. Elas possibilitam analisar uma situação de maneira mais fácil. É importante propiciar aos estudantes todas as possibilidades de observação e leitura dos dados de uma tabela simples.
BNCC em foco:
EF01MA05, EF01MA21; competência geral 9
Sugestão de trabalho voluntário
Proponha aos estudantes a produção de cartazes para sensibilizar a comunidade escolar e arrecadar brinquedos a fim de entregar a alguma instituição idônea que trabalhe com crianças carentes. Providencie imagens de brinquedos extraídas de jornais e revistas para os estudantes colarem nos cartazes.
MP080
O QUE VOCÊ APRENDEU

- PINTE 14 PIPAS.


- PARA CADA COR, CONTE OS BALÕES PENDURADOS E ESCREVA O NÚMERO QUE INDICA A QUANTIDADE DELES.

- PINTE UM QUADRINHO PARA CADA BALÃO QUE VOCÊ CONTOU.

3

_____
PROFESSOR
Resposta: 5
_____
PROFESSOR
Resposta: 6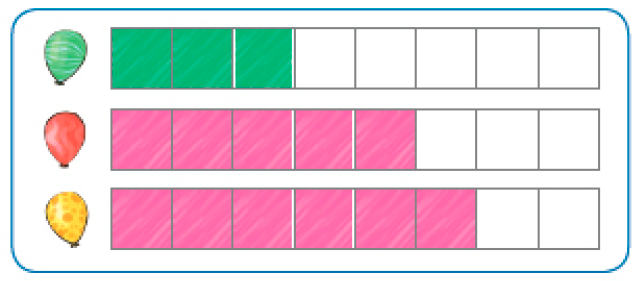
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Verifique como os estudantes procedem à contagem e socialize com a classe as diferentes maneiras que aparecerem. Explore a atividade fazendo outros questionamentos:
Quantas pipas ficaram sem pintar? (Duas.)
Quantas pipas há neste quadro? (Dezesseis.)
Atividade 2
Combine com os estudantes uma estratégia para que façam a contagem dos balões. Por exemplo, eles podem começar a contar os balões verdes, fazendo uma marca naqueles que já foram contados. Depois contam os vermelhos e, por fim, os amarelos. Deixe que os estudantes exponham suas ideias. Ao fazer a contagem por cor, pintamos quadrinhos correspondentes. No caso dos balões verdes, a contagem servirá para a confirmação dos quadrinhos já pintados.
Explore os registros feitos pelos estudantes e pergunte:
Qual é a cor do balão que aparece em maior quantidade? (Amarela.)
Como você chegou a essa conclusão? (Resposta pessoal.)
Esse tipo de questão possibilita perceber se os estudantes comparam as quantidades por meio dos números representados, da contagem (recontando) ou da visualização geométrica do maior comprimento obtido pelos quadrinhos pintados.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA04
MP081
AVALIAÇÃO PROCESSUAL
- OBSERVE ABAIXO AS MOEDAS E A CÉDULA.


- HÁ QUANTAS MOEDAS DE 1 REAL?
_____
PROFESSOR
Resposta: 10 moedas. - HÁ QUANTAS CÉDULAS DE 10 REAIS?
_____
PROFESSOR
Resposta: 1 cédula. - ACIMA, TODAS AS MOEDAS DE 1 REAL QUE VOCÊ CONTOU REPRESENTAM UMA QUANTIA MENOR, IGUAL OU MAIOR QUE 10 REAIS? MARQUE COM UM
X
.
( ) MENOR
( ) IGUAL
( ) MAIOR
PROFESSOR
Resposta: igual.
- OBSERVE A QUANTIDADE DE PEÇAS INDICADA NA CAIXA DE CADA QUEBRA-CABEÇA.



- ESCREVA, DO MENOR PARA O MAIOR, A SEQUÊNCIA FORMADA COM OS NÚMEROS INDICADOS NESSAS CAIXAS.
_____
PROFESSOR
Resposta: 29, 30, 31
AUTOAVALIAÇÃO

- CONSIGO DIZER NOMES DE NÚMEROS E SABER COMO SÃO ESCRITOS POR EXTENSO?
PROFESSOR
Resposta: Resposta pessoal.
- SEI ESCREVER O NÚMERO PARA INDICAR UMA QUANTIDADE DE OBJETOS QUE CONTEI?
PROFESSOR
Resposta: Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Se julgar oportuno, utilize as cédulas e as moedas do Material complementar para que os estudantes vivenciem a situação proposta. Esta atividade pode ser expandida comparando moedas de 1 real com cédulas de 2 reais, de 5 reais e de 20 reais.
Atividade 4
Aproveite esta atividade para verificar se os estudantes ainda apresentam alguma dificuldade na comparação de números com base na sequência numérica. Amplie a atividade perguntando: “Quantas peças há no quebra-cabeça que tem mais peças?” (31 peças.); “Qual número indica a quantidade de peças do quebra-cabeça com menos peças?” (29.).
Autoavaliação
Na primeira questão, os estudantes devem refletir sobre a relação entre o nome do número e seu símbolo numérico. Muitas vezes eles utilizam a récita de sequências numéricas para relacionar nome e símbolo.
Desse modo, as respostas podem vir acompanhadas de exemplos de números que os estudantes:
reconhecem com facilidade;
ainda precisam de ajuda por conta de dúvidas (por exemplo, em relação ao valor posicional);
não reconhecem.
Na segunda questão, o símbolo numérico deve estar associado a quantidades. Por exemplo, os estudantes devem saber que “23” corresponde a “vinte e três” e também precisam fazer a relação com a quantidade de 23 objetos quaisquer. A récita também é apoio para a contagem, entretanto os estudantes precisam fazer a relação um a um do objeto contado com o número recitado, sem contar o mesmo objeto mais de uma vez, para que a contagem seja correta.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA05, EF01MA19
MP082
Comentários para o professor
Conclusão da Unidade 2
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observações |
|---|---|---|
|
Escreve números naturais de 0 a 10, literalmente e simbolicamente (por meio de algarismos)? |
_____ |
_____ |
|
Identifica e compara, com apoio de imagens, quantidades de 0 a 31 objetos, assimilando-as enquanto números compostos de dezena(s) e unidade(s)? |
_____ |
_____ |
|
Ordena quantidades de objetos por meio de atributos comuns (ordem crescente ou decrescente), reconhecendo os aspectos cardinal e ordinal do número? |
_____ |
_____ |
|
Compara e relaciona objetos por critérios relativos às suas grandezas e medidas, por exemplo, objeto mais alto com objeto de maior altura? |
_____ |
_____ |
|
Estabelece relações entre o símbolo e o que ele representa, ou seja, entre o representante e o representado? |
_____ |
_____ |
|
Identifica e reconhece o valor de moeda (1 real) e das cédulas de 2, 5, 10 e 20 reais do sistema monetário brasileiro? |
_____ |
_____ |
|
Consegue organizar informações e registrá-las por meio de desenhos ou palavras? |
_____ |
_____ |
|
Compreende e realiza a leitura de tabela simples aplicando-a na resolução de problemas simples? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP083
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação, encenações e dramatizações, entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
AUTOAVALIAÇÃO |
|||
|---|---|---|---|
|
NOME: |
|||
|
MARQUE UM X EM SUA RESPOSTA PARA CADA PERGUNTA. |
SIM |
MAIS OU MENOS |
NÃO |
|
1. PRESTO ATENÇÃO NAS AULAS? |
_____ |
_____ |
_____ |
|
2. PERGUNTO AO PROFESSOR QUANDO NÃO ENTENDO? |
_____ |
_____ |
_____ |
|
3. SOU PARTICIPATIVO? |
_____ |
_____ |
_____ |
|
4. RESPEITO MEUS COLEGAS E PROCURO AJUDÁ-LOS? |
_____ |
_____ |
_____ |
|
5. SOU EDUCADO? |
_____ |
_____ |
_____ |
|
6. FAÇO TODAS AS ATIVIDADES COM CAPRICHO? |
_____ |
_____ |
_____ |
|
7. TRAGO O MATERIAL ESCOLAR NECESSÁRIO E CUIDO BEM DELE? |
_____ |
_____ |
_____ |
|
8. CUIDO DOS MATERIAIS E DO ESPAÇO FÍSICO DA ESCOLA? |
_____ |
_____ |
_____ |
|
9. GOSTO DE TRABALHAR EM GRUPO? |
_____ |
_____ |
_____ |
|
10. RESPEITO TODOS OS MEUS COLEGAS DE TURMA, PROFESSORES E FUNCIONÁRIOS? |
_____ |
_____ |
_____ |





