MP084
Comentários para o professor:
Introdução da Unidade 3
As páginas de abertura possibilitam diálogos a serem usados com o objetivo de diagnosticar os conhecimentos e habilidades que os estudantes trazem da Educação Infantil e, assim, constituírem-se em um bom instrumento para planejar as estratégias de ensino a serem aplicadas durante o ano letivo.
Nesta Unidade, serão aprofundados conhecimentos acerca dos números naturais, assim como conhecimentos relativos às características do sistema de numeração decimal, considerando a Unidade Temática Números. Nas atividades, ampliam-se as situações abordadas na Unidade anterior e que envolvem a utilização de números naturais como indicador de quantidade em diferentes situações. Ampliam-se, também, as situações que objetivam a comparação de números naturais de até duas ordens em situações cotidianas, com e sem suporte da reta numérica.
A diversidade de situações envolvendo tais conhecimentos tem em vista aqueles que serão explorados no 2º ano do Ensino Fundamental, entre eles, a comparação e a ordenação de números naturais até três ordens.
Ainda na Unidade Temática Números, e considerando-se que a resolução de problemas tem permeado todos os conhecimentos construídos pelos estudantes desde a Educação Infantil, os fatos fundamentais da adição serão abordados na resolução e na elaboração de problemas de adição e de subtração, envolvendo até dois algarismos, que contemplam os significados de juntar, acrescentar, retirar, comparar e completar, desenvolvidos com o suporte de imagens e/ou material manipulável, além do estímulo ao uso de estratégias e formas de registros pessoais na composição/decomposição de um número até duas ordens. A propósito, o ponto central desta Unidade é fazer os estudantes tomarem parte em situações-problema, que envolvam a adição e a subtração, nas suas particularidades diversas, para serem resolvidas por eles.
Destaca-se que esses conhecimentos se articulam com aqueles a serem desenvolvidos no ano seguinte e que, apesar de também se referirem à construção de fatos básicos da adição e da subtração, serão utilizados em estratégias de cálculo mental ou escrito.
As atividades relacionadas à Unidade Temática Álgebra articulam-se com Números, pois um dos objetivos é descrever, após o reconhecimento de um padrão (ou de uma regularidade), os elementos ausentes em sequências recursivas de números naturais, inclusive representando-os na reta numérica. Esses conhecimentos serão aprofundados no ano seguinte por meio de atividades que envolvem a descrição de um padrão (ou de uma regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos.
A Unidade Temática Grandezas e medidas é abordada por meio de atividades que conduzem os estudantes a reconhecer e a estabelecerem equivalência entre valores de moedas e de cédulas do sistema monetário brasileiro para resolver situações cotidianas. Essa abordagem considera, também, o cenário das aprendizagens no 3º ano do Ensino Fundamental, entre elas, a resolução e a elaboração de problemas que envolvem, além da equivalência, a comparação de valores do sistema monetário brasileiro em situações de compra, venda e troca. A título de complemento, a seção A Matemática me ajuda a ser... uma pessoa consciente do valor das coisas aborda a passagem histórica do escambo à utilização do dinheiro nas transações comerciais.
Classificar eventos que consideram o acaso, tais como “acontecerá com certeza”, “talvez aconteça” e “é impossível acontecer”, em situações do cotidiano, é a abordagem proposta nesta Unidade para Probabilidade e estatística. Cabe observar que tais conhecimentos já foram abordados na Unidade 1, sendo, agora, ampliados e aprofundados, na perspectiva de preparar os estudantes para, no ano seguinte, classificarem resultados de eventos cotidianos aleatórios como “pouco prováveis”, “muito prováveis”, “improváveis” ou “impossíveis”.
Competências gerais favorecidas
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
MP085
Competências específicas favorecidas
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos alguns roteiros de aula que poderão servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados pelo professor em função das características da turma e dos recursos disponíveis.
Os jogos são recursos valiosos para o desenvolvimento simultâneo de habilidades matemáticas, motoras, sociais e éticas de estudantes nessa faixa etária. Conheça um exemplo de roteiro de aula relacionado à seção Jogo desta Unidade.
Roteiro de aula – Jogo: Árvore das maçãs
1 ª parte – Tempo sugerido: 20 a 25 minutos
Organize as carteiras de modo que os estudantes possam trabalhar em duplas, trios ou quartetos. Para a composição dos grupos, sugira escolhas livres, no entanto, fique atento e auxilie aqueles que estiverem com dificuldade de encontrar colegas para realizar a atividade.
Auxilie, se necessário, o recorte (com tesoura de pontas arredondadas) e a montagem do material a ser usado no jogo: as ilustrações de maçãs e os dados amarelo e vermelho. O tabuleiro já se encontra no Livro do Estudante.
Faça a leitura coletiva das regras do jogo e certifique-se de que elas foram compreendidas por todos. Avalie a necessidade de simular, com um dos grupos, um início de procedimento que sirva como exemplo e esclareça possíveis dúvidas. Essa orientação é válida para os jogos em geral, portanto, pode ser adaptada para atividades semelhantes.
2ª parte – Tempo sugerido: 25 minutos
Anuncie o tempo programado para o jogo que se inicia. Cada grupo escolhe um participante para anotar o ganhador de cada rodada e quantas vezes esse ganhador precisou jogar os dados para ganhar. O objetivo pedagógico dessa proposta é apenas que considerem, nos trabalhos em grupo, a possibilidade de atribuições aos seus elementos. Deixe-os jogar por 15 minutos livremente, mas acompanhe as ações dos grupos para administrar impasses, caso necessário.
A seguir, peça que retomem o livro, respondam individualmente às questões propostas (5 minutos) e, depois, troquem os livros para socializarem as respostas.
Nos últimos 5 minutos, antes de recolocar as carteiras nas posições de costume, solicite a um estudante voluntário que justifique a resposta da primeira questão; faça o mesmo para a segunda questão.
MP086
UNIDADE 3. VAMOS ADICIONAR E SUBTRAIR

MANUAL DO PROFESSOR
Objetivos da Unidade
Desenvolver estratégias pessoais para resolver adições e subtrações.
Utilizar números naturais como indicadores de quantidades.
Identificar e comparar quantidades.
Compor e decompor números por meio de diferentes adições.
Representar simbolicamente as operações de adição e de subtração.
Construir fatos fundamentais da adição.
Usar estratégias próprias para resolver problemas que envolvam adição e subtração.
Reconhecer regularidades em sequências numéricas e descrever elementos ausentes.
Reconhecer e relacionar valores de moedas e de cédulas do sistema monetário brasileiro.
Localizar números na reta numérica.
Aproximar-se dos contextos sociais de uso do sistema monetário.
Fazer contagens e apresentar registros verbais e simbólicos.
Classificar eventos que envolvem o acaso.
O foco principal desta Unidade é envolver os estudantes em situações de operações matemáticas por meio de atividades que lhes possibilitem a experiência de adicionar e subtrair, tendo contato com os diferentes significados das operações: adição (juntar e acrescentar quantidades) e subtração (retirar, comparar e completar quantidades).
Alguns estudantes podem ter dificuldades em operar com os números, pois memorizar o símbolo numérico que representa determinada quantidade pode não ser tão simples, uma vez que os símbolos não representam quantidades explícitas (contáveis). Para favorecer essa memorização, podem-se usar materiais manipuláveis ou propor jogos com peças de dominó ou dados com configurações geométricas (pontos) que representem uma quantidade e possam ser reconhecidas visualmente.
BNCC em foco:
EF01MA01, EF01MA04, EF01MA05, EF01MA06, EF01MA07, EF01MA08, EF01MA10, EF01MA19, EF01MA20
MP087
Página sem conteúdo.
MANUAL DO PROFESSOR
Explore a abertura comentando que Guilherme e Letícia estão em um passeio da escola em um local muito divertido, com várias atividades, entre elas o jogo da trilha, em que os participantes são os piões que andam sobre um grande tabuleiro ao ar livre.
A situação ilustrada possibilita abordar conceitos relativos ao registro numérico (como o número de cada casa e o número de crianças ou de outros elementos na imagem) e aos significados da adição e da subtração.
Explore a ilustração com os estudantes, pedindo que observem com atenção os detalhes da cena e, principalmente, a trilha. Depois, pergunte:
Algumas crianças estão em cima das casas numeradas da trilha. Que números há nessas casas? Como você descobriu? (2, 5 e 10. Resposta pessoal.)
Em que casa se encontra a criança que está na frente do jogo da trilha? Quantas casas faltam para ela chegar ao Fim da trilha? (Na casa 10; falta 1 casa.)
Quem terminou primeiro o jogo da trilha? (O menino que está na cadeira de rodas.)
A trilha da abertura pode ser reproduzida em papel sulfite e usada como tabuleiro de um jogo. Organize os estudantes em duplas. Ambos posicionam os marcadores no Início da trilha. Cada um, em sua vez, joga o dado e movimenta seu marcador pelo número de casas correspondente. Ao cair em uma casa, o jogador deve verificar se há algum comando a ser feito. É possível que alguns estudantes contem a casa em que está seu marcador antes de movimentá-lo, deixando de andar uma casa. Para ensiná-los a contar corretamente, pergunte o que acontece quando se tira o número 1 no dado, para que observem o que está sendo contado. Outra possibilidade é levar os estudantes para o pátio ou afastar as cadeiras na sala de aula e riscar as casas da trilha no chão, para que eles a percorram. Vencerá quem primeiro alcançar o Fim da trilha.
MP088
JOGO: ÁRVORE DAS MAÇÃS
Observação ACOMPANHE AS INSTRUÇÕES QUE O PROFESSOR VAI LER. Fim da observação.

MATERIAL: TABULEIRO DA ÁRVORE ABAIXO, MAÇÃS DA PÁGINA 203 E 2 DADOS DA PÁGINA 201, QUE DEVERÃO SER MONTADOS.

JOGADORES: 2 OU MAIS.
REGRAS:
- OS JOGADORES DECIDEM QUEM VAI COMEÇAR O JOGO.
- O PRIMEIRO JOGA OS DADOS E PEGA A QUANTIDADE DE MAÇÃS CORRESPONDENTE AO TOTAL DOS VALORES INDICADOS NOS DADOS.
- EM SEGUIDA, O JOGADOR COLOCA AS MAÇÃS NA ÁRVORE DELE E PASSA OS DADOS PARA O PRÓXIMO JOGADOR.
- GANHA QUEM PREENCHER PRIMEIRO A ÁRVORE COM AS MAÇÃS.

MANUAL DO PROFESSOR
Objetivos
• Desenvolver estratégias pessoais para resolver adições.
• Utilizar números naturais como indicadores de quantidades.
• Identificar e comparar quantidades.
• Compor números por meio de diferentes adições.
Ajude os estudantes na leitura e na compreensão das regras. Auxilie-os na montagem dos dados e no recorte das peças. Oriente-os a guardar os dados para serem usados em outros jogos e a usar o próprio livro como tabuleiro.
A cada rodada, os estudantes lançam os dois dados e adicionam os números obtidos, o que pode ser realizado de várias maneiras:
• juntando as quantidades de maçãs correspondentes a cada número do dado e depois contando o total de maçãs reunidas;
• representando o número de cada dado com tracinhos e contando-os;
• contando o número em um primeiro dado e depois continuando a contagem com o número obtido no segundo dado.
Repare como os estudantes fazem a adição dos números e discuta com eles as diferentes maneiras de proceder. Observe como realizam o cálculo da quantidade de maçãs obtidas em cada rodada, a fim de subsidiar a retomada de procedimentos ou conceitos nas aulas seguintes, o que propicia a aprendizagem dos aspectos em que eles apresentam mais dificuldade. Esse procedimento propicia compreender os três princípios ligados à quantificação:
• Princípio da adequação única: saber que cada número falado deve corresponder a um objeto contado (e que está ligado ao procedimento).
• Princípio de cardinalidade: compreender que o último número falado após a contagem de determinado conjunto de objetos corresponde a todos os que foram contados.
• Princípio de indiferença da ordem: compreender que a ordem em que se contam as unidades não altera a quantidade, desde que seja respeitado o princípio da adequação única.
Para ajudar na compreensão desses princípios, proponha situações em que deverão contar, comparar, adicionar, juntar, separar e tirar, discutindo e compartilhando as ideias e os procedimentos envolvidos. No caso do jogo, é interessante mostrar os modos mais eficazes de adicionar os pontos dos dados, mas não convém insistir para que todos eles os adotem, evitando que usem um procedimento que não compreenderam.
Aproveite para perguntar: “Qual é a maior quantidade de maçãs que se pode juntar em uma única rodada? E a menor?”. Espera-se que respondam que a maior quantidade é 12 e a menor é 2.
BNCC em foco:
EF01MA01, EF01MA04, EF01MA08
MP089
QUESTÕES SOBRE O JOGO
- OBSERVE OS DADOS DE CADA CRIANÇA E MARQUE COM UM X A CRIANÇA QUE COLOCOU MAIS MAÇÃS NO TABULEIRO NESTA RODADA.


PROFESSOR
Resposta: criança 1.- OBSERVE ESTE TABULEIRO.

- AGORA, ESCREVA NOS DADOS ABAIXO DUAS POSSIBILIDADES DIFERENTES DE PONTOS PARA COMPLETAR O TABULEIRO ACIMA EM UMA ÚNICA RODADA.
_____ _____
PROFESSOR
Exemplo de resposta: 5, 2;_____ _____
PROFESSOR
Exemplo de resposta: 3, 4MANUAL DO PROFESSOR
Questões sobre o jogo
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões.
A questão 1 explora a soma dos pontos dos dados e a comparação do número de maçãs que cada criança colocou no tabuleiro na rodada.
Na questão 2, os estudantes devem descobrir combinações possíveis nos dados que levem ao número de maçãs para completar a árvore, ou seja, eles precisam descobrir composições do número 7 por meio de adições com duas parcelas. Essa questão é mais desafiadora porque as soluções não são tão evidentes. No entanto, a quantidade de maçãs que faltam na árvore (sete) facilita a resolução do problema, pois sete e seis são as quantidades com o maior número de combinações possíveis de se obter com a adição dos pontos de dois dados lançados simultaneamente.
O procedimento de contagem inclui alguns conhecimentos coordenados: conhecer a sequência oral dos números e contar cada objeto somente uma vez (ou seja, não pular nem contar duas vezes um objeto do conjunto que se deseja quantificar). Em jogos como o da trilha, essa segunda condição é facilitada, pois há um caminho organizado a ser percorrido, diferentemente da contagem de um punhado de botões, por exemplo (quando os estudantes precisam organizar os objetos para não contá-los duas vezes nem deixar de contar algum). Mesmo assim, alguns deles tenderão a falar os números sem associá-los aos passos dados entre uma casa do jogo e outra. Eles aprenderão o procedimento correto pela experiência de contar, aliada à observação dos colegas que o fazem corretamente e às suas intervenções.
BNCC em foco:
EF01MA04, EF01MA05, EF01MA07, EF01MA08
Variações
Incentive os estudantes a alterar algumas regras: por exemplo, o jogador que obtiver em um lançamento dois números iguais deverá jogar novamente.
MP090
ADIÇÃO COM NÚMEROS ATÉ 10
- A ESCOLA DE AMANDA E ÍGOR ESTÁ PARTICIPANDO DE UMA CAMPANHA DE ARRECADAÇÃO DE ALIMENTOS. VEJA O QUE CADA CRIANÇA TROUXE PARA ESSA CAMPANHA.

- QUANTOS PACOTES DE ALIMENTOS AMANDA E ÍGOR TROUXERAM NO TOTAL?
_____
PROFESSOR
Resposta: 63 PACOTES MAIS 3 PACOTES É IGUAL A _____ PACOTES.
PROFESSOR
Resposta: 6
- CONTE E COMPLETE EFETUANDO AS ADIÇÕES.
-
 _____
MAIS
_____
MAIS  _____
É IGUAL A
_____
É IGUAL A 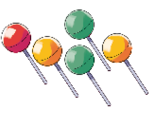 _____
_____
PROFESSOR
Resposta: 2, 3, 5-
 _____
MAIS
_____
MAIS  _____
É IGUAL A
_____
É IGUAL A  _____
_____
PROFESSOR
Resposta: 4, 1, 5MANUAL DO PROFESSOR
Objetivos
Desenvolver estratégias pessoais para resolver adições.
Representar simbolicamente a operação de adição.
Construir fatos fundamentais da adição.
As atividades destas páginas visam explorar a noção de juntar quantidades, que é um dos significados da adição no qual há dois conjuntos, cada um com sua quantidade de elementos, que passam a formar um novo todo, e a representação simbólica da adição.
À medida que os estudantes vivenciam diversas situações que envolvem adição de quantidades, alguns resultados são memorizados, e eles passam a recuperá-los diretamente da memória. Por exemplo, as adições de parcelas iguais, 2 + 2 ou 3 + 3, são facilmente memorizadas e podem auxiliar o cálculo de 2 + 3, fazendo: 2 + 3 = (2 + 2) + 1 = 4 + 1 = 5.
Atividade 1
Optamos por escrever a expressão “3 pacotes mais 3 pacotes é igual a 6 pacotes” para propiciar uma aproximação da língua materna com a sentença matemática, o que é muito importante para a apropriação da linguagem matemática pelos estudantes. Assim, o símbolo + passa por um processo de construção por meio do termo mais.
As estratégias para determinar a soma de duas quantidades conhecidas podem basear-se em contagem. Uma possibilidade é os estudantes conhecerem as quantidades, mas, ao juntá-las, passarem a contar tudo desde o início. Outra possibilidade é contarem a primeira quantidade e então continuarem a contagem com base no último elemento contado. Por exemplo, juntando as quantidades 2 e 3, contam: 1, 2 e então a contagem continua com os elementos da outra quantidade: 3, 4, 5. Deixe que os estudantes usem a estratégia que preferirem. Aproveite a atividade para conversar com a turma sobre a importância das campanhas de arrecadação de alimentos ou de outros itens, ressaltando a necessidade da proteção à vida, a fim de promover a solidariedade.
Atividade 2
Nesta atividade, também foi mantida a escrita da sentença matemática conforme a língua materna. Nesse caso, foram usadas imagens dos elementos para indicar as quantidades envolvidas, para que os estudantes percebam visualmente a ideia de juntar.
BNCC em foco na dupla de páginas:
EF01MA06, EF01MA08
MP091
- BRUNO TEM 5 BOLINHAS DE GUDE, E SEU IRMÃO TEM 3 BOLINHAS DE GUDE.
- JUNTOS, OS DOIS TÊM QUANTAS BOLINHAS DE GUDE?
 MAIS
MAIS  É IGUAL A
É IGUAL A 
5 BOLINHAS DE GUDE MAIS 3 BOLINHAS DE GUDE É IGUAL A _____ BOLINHAS DE GUDE.
PROFESSOR
Resposta: 8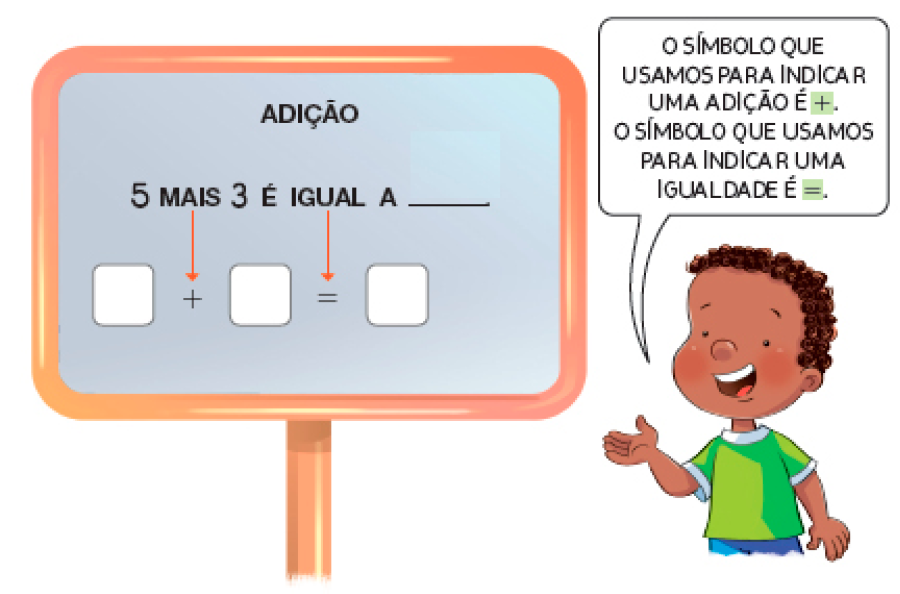
PROFESSOR
Resposta: 5 mais 3 é igual a 8.PROFESSOR
5 + 3 = 8JUNTOS, BRUNO E SEU IRMÃO TÊM _____ BOLINHAS DE GUDE.
PROFESSOR
Resposta: 8- AGORA, FAÇA UM REGISTRO DA ADIÇÃO 4 MAIS 4 É IGUAL A 8.
_____
PROFESSOR
Resposta: 4 + 4 = 8
MANUAL DO PROFESSOR
Atividade 3
Nesta atividade, os estudantes são incentivados a registrar uma operação de adição por meio dos símbolos convencionais 3,+ e 5.
A compreensão do símbolo 5 não é tão natural para os estudantes, pois na verdade ele representa uma equivalência. Escrever 5 + 3 e dizer que “é igual” (=) a 8 não é tão óbvio assim. Procure abordar o símbolo (=) usando os termos “é o mesmo que”, “tem o mesmo valor que”. Essa associação pode facilitar a compreensão.
Sugestão de atividade
As teclas da calculadora
Material necessário:
uma calculadora simples
Um modo interessante de evidenciar a necessidade do uso de uma simbologia convencional é recorrendo a uma calculadora. Para isso, peça aos estudantes que realizem a adição de 2 com 5 sem apertar a tecla + e observem o resultado que aparecer no visor. Eles devem perceber que a máquina registrará apenas 25, pois não foi dado nenhum comando que indicasse a execução de uma operação. Solicite então que apertem as teclas 2 + 5 sem apertar a tecla = e observem o que ocorre. Mais uma vez, o resultado não aparecerá no visor, pois, na calculadora, a tecla = indica que se pede o resultado da operação. O uso de símbolos para expressar uma operação aritmética surgiu após a utilização do texto escrito, geralmente em latim, durante a Idade Média (séculos V a XV). Graças ao grande trabalho envolvido em copiar textos escritos, gradativamente passaram-se a empregar abreviações para as palavras relacionadas às operações. No caso de uma adição, a palavra et (“e”) era usada para expressar a situação em que se juntavam uma e outra quantidade. Com o tempo, et foi abreviada pela letra t, cujo formato em duas linhas cruzadas deu origem ao símbolo +.
MP092
MAIS ADIÇÕES

- CALCULE E REGISTRE OS RESULTADOS.
- 3 + 7 =
_____
PROFESSOR
Resposta: 10 - 7 + 3 =
_____
PROFESSOR
Resposta: 10 - 5 + 5 =
_____
PROFESSOR
Resposta: 10 - 1 + 9 =
_____
PROFESSOR
Resposta: 10 - 9 + 1 =
_____
PROFESSOR
Resposta: 10 - 10 + 0 =
_____
PROFESSOR
Resposta: 10
- 3 + 7 =
_____
ESCREVA OUTRAS ADIÇÕES COM RESULTADO IGUAL A 10.
_____
PROFESSOR
Resposta: 2 + 8 = 10, 8 + 2 = 10, 6 + 4 = 10, 4 + 6 = 10, 0 + 10 = 10- VEJA JANAÍNA EXPLICANDO A FÁBIO COMO CALCULOU MENTALMENTE O RESULTADO DE 8 + 6.


AGORA, CALCULE E REGISTRE O RESULTADO DAS ADIÇÕES.
- 5 + 8 =
_____
PROFESSOR
Resposta: 13 - 7 + 9 =
_____
PROFESSOR
Resposta: 16 - 6 + 7 =
_____
PROFESSOR
Resposta: 13 - 8 + 9 =
_____
PROFESSOR
Resposta: 17

- VEJA O DINHEIRO DE NÁDIA E O DE JÚLIO. DEPOIS, COMPLETE.
DINHEIRO DE NÁDIA

DINHEIRO DE JÚLIO

NÁDIA E JÚLIO TÊM JUNTOS _____ REAIS.
PROFESSOR
Resposta: 27MANUAL DO PROFESSOR
Objetivos
Representar simbolicamente a operação de adição.
Usar estratégias pessoais para resolver problemas de adição.
Reconhecer regularidades em sequências numéricas e descrever elementos ausentes.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Construir fatos fundamentais da adição.
Compor números por meio de diferentes adições.
Localizar números na reta numérica.
Atividade 1
Esta atividade possibilita aos estudantes desenvolverem estratégias para compor o número 10 e construir os fatos fundamentais da adição.
Atividade 2
Observe se os estudantes compreenderam a estratégia de cálculo mental de Janaína e pergunte se alguém tem um jeito diferente de calcular mentalmente.
Atividade 3
Nesta atividade, os estudantes devem reconhecer a quantia que Nádia e Júlio têm e adicionar esses valores para obter a quantia total.
O uso social do dinheiro possibilita aos estudantes que reconheçam as quantidades envolvidas e realizem a adição. Proponha, então, cálculos de quantias com outros valores de cédulas.
Reconhecer e operar com cédulas de diferentes valores, como 2 reais e 5 reais, permite a eles desvincular a quantia do número de cédulas.
Por exemplo, ao calcular o valor total de 3 cédulas de 2 reais e 1 cédula de 5 reais, os estudantes não adicionarão a quantidade de cédulas (4), mas os valores que elas representam: 2 reais mais 2 reais mais 2 reais mais 5 reais são 11 reais.
Amplie a atividade e pergunte: “Se Nádia ganhar mais 1 real, quantos reais os dois terão juntos?” (28 reais.). Observe se os estudantes só acrescentam uma unidade ao total obtido anteriormente ou se recomeçam os cálculos.
BNCC em foco:
EF01MA06, EF01MA07, EF01MA08, EF01MA19
MP093
- MARIANA E RODRIGO JOGARAM BOLINHAS DE GUDE. MARIANA TINHA 23 BOLINHAS DE GUDE E GANHOU 8 BOLINHAS DE RODRIGO.
QUANTAS BOLINHAS DE GUDE MARIANA TEM AGORA?
- COMPLETE O CÁLCULO ABAIXO.
23 + _____ = _____
PROFESSOR
Resposta: 23 + 8 = 31AGORA, MARIANA TEM _____ BOLINHAS DE GUDE.
PROFESSOR
Resposta: 31
- COMPLETE O CÁLCULO ABAIXO.
- ESCREVA OS DOIS PRÓXIMOS NÚMEROS DE CADA SEQUÊNCIA.
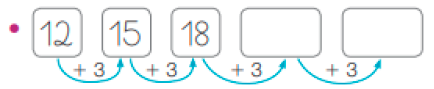
PROFESSOR
Resposta: 21, 24

PROFESSOR
Resposta: 25, 29

PROFESSOR
Resposta: 26, 31Boxe complementar:
DICA
- OBSERVE A REGULARIDADE EM CADA SEQUÊNCIA.
Fim do complemento.

- OBSERVE UMA RETA NUMÉRICA COM NÚMEROS QUE AUMENTAM DE 1 EM 1 UNIDADE.

AGORA, NESTAS OUTRAS RETAS NUMÉRICAS, ESCREVA OS NÚMEROS QUE ESTÃO FALTANDO NOS ESPAÇOS INDICADOS.
- OS NÚMEROS AUMENTAM DE 4 EM 4 UNIDADES.

PROFESSOR
Resposta: 12, 20, 24, 28- OS NÚMEROS AUMENTAM DE 5 EM 5 UNIDADES.

PROFESSOR
Resposta: 10, 15, 25MANUAL DO PROFESSOR
Atividade 4
Nesta atividade, está presente o significado de acrescentar uma quantidade a outra, outro significado associado à adição, em que, em um conjunto dado, são colocados novos elementos, também formando um novo todo.
A diferença entre essa situação e a que envolve juntar quantidades pode ser compreendida ao observarmos que nesse caso ocorre uma transformação (um estado inicial é alterado), ao passo que, no significado de juntar quantidades, dois estados são combinados para a obtenção de um estado final.
Atividade 5
Esta atividade possibilita aos estudantes observarem regularidades em sequências numéricas por meio da descoberta de padrões de formação que envolvem adição de quantidades iguais. Eles devem observar a quantidade que está sendo adicionada a cada número, o que os auxiliará a obter os dois números seguintes. Crie outras sequências e peça aos estudantes que descubram a regularidade.
Atividade 6
Nesta atividade, a reta numérica é apresentada para explorar sequências numéricas crescentes com um padrão de regularidade.
BNCC em foco:
EF01MA05, EF01MA08, EF01MA10
MP094
SUBTRAÇÃO COM NÚMEROS ATÉ 10
- CONTE OS CARRINHOS DE ARTHUR E COMPLETE.

HÁ _____ CARRINHOS SOBRE A MESA.
PROFESSOR
Resposta: 10
ARTHUR COLOCOU _____ CARRINHOS NA PRATELEIRA.
PROFESSOR
Resposta: 3- QUANTOS CARRINHOS FICARAM SOBRE A MESA?
_____
PROFESSOR
Resposta: 710 CARRINHOS MENOS 3 CARRINHOS É IGUAL A _____ CARRINHOS.
PROFESSOR
Resposta: 7
MANUAL DO PROFESSOR
Objetivos
Desenvolver estratégias pessoais para resolver subtrações.
Representar simbolicamente a operação de subtração.
Decompor números por meio de diferentes adições.
As atividades destas páginas possibilitam trabalhar a subtração com o significado relacionado à retirada de quantidades, em que se calcula quanto sobra, ou seja, o resto, e a representação simbólica da subtração.
Durante as atividades, observe as estratégias utilizadas pelos estudantes para responder à questão. É possível que alguns usem a ilustração como suporte; outros talvez contem nos dedos. É fundamental acolher todas as estratégias.
Atividade 1
Nesta atividade, os estudantes provavelmente usarão a contagem dos elementos da ilustração para preencher as lacunas.
Assim como fizemos com a adição, escrevemos a expressão “10 carrinhos menos 3 carrinhos é igual a 7 carrinhos” usando a linguagem materna, com o objetivo de aproximá-la da linguagem matemática.
Para obter a resposta desta atividade, os estudantes podem usar diferentes estratégias, como:
retirar 3 unidades e depois contar os carrinhos restantes: 1, 2, 3, 4, 5, 6, 7;
começando com 10, contar 3 unidades em ordem decrescente: 9, 8, 7.
Subtrair quantidades de dez é outro aspecto da decomposição desse número e oferece subsídios para que os estudantes realizem futuramente cálculos mentais. Por exemplo, para subtrair 13 de 30, podem decompor o número 30, como 13 + 7 + 10; subtraindo 13, eles obtêm 7 + 10 ou 17.
Peça à turma que dê outros exemplos de situações em que é necessário tirar quantidades para determinar a quantidade restante e aproveite essas situações para propor novos problemas.
Na atividade 1, proponha outras situações na lousa sem o apoio da ilustração ou variando o que se pretende descobrir, como: “Havia 8 carrinhos sobre a mesa e guardei 4. Quantos carrinhos sobraram sobre a mesa?” (4 carrinhos.); “Havia 7 carrinhos sobre a mesa, guardei alguns e ficaram 4. Quantos carrinhos eu guardei?” (3 carrinhos.).
Observe que é possível modificar o desafio utilizando exemplos similares. Por isso, é importante propor aos estudantes diversos tipos de problema para ampliar a habilidade deles em resolvê-los.
BNCC em foco:
EF01MA07, EF01MA08
MP095
- FÁTIMA TEM 5 ABÓBORAS E VAI USAR 3 PARA FAZER UM DOCE.
• QUANTAS ABÓBORAS SOBRARÃO?

5 ABÓBORAS MENOS 3 ABÓBORAS É IGUAL A _____ ABÓBORAS.
PROFESSOR
Resposta: 2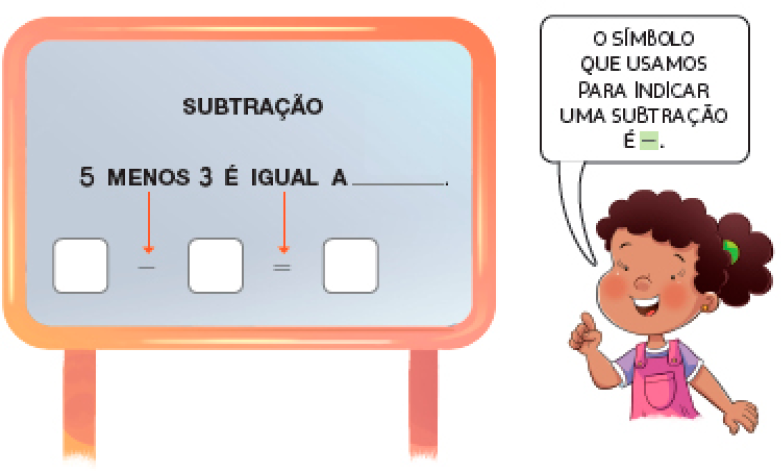
PROFESSOR
Resposta: 5 menos 3 é igual a 2.SOBRARÃO _____ ABÓBORAS.
PROFESSOR
Resposta: 2- AGORA, FAÇA UM REGISTRO DA SUBTRAÇÃO 10 MENOS 5 É IGUAL A 5.
_____
PROFESSOR
Resposta: 10 - 5 = 5
- COMPLETE.
- 7 − 1 =
_____
PROFESSOR
Resposta: 6 -
_____
= 8 − 2
PROFESSOR
Resposta: 6 - 9 − 3 =
_____
PROFESSOR
Resposta: 6 - 7 − 6 =
_____
PROFESSOR
Resposta: 1 - 8 −
_____
= 2
PROFESSOR
Resposta: 6 -
_____
= 9 − 6
PROFESSOR
Resposta: 3
- 7 − 1 =
_____
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, os estudantes realizarão subtrações e registrarão as sentenças matemáticas associadas a essas operações por meio dos símbolos convencionais 3, − e 5.
A ação de riscar as abóboras para indicar que foram usadas no doce indica uma possível estratégia para realizar subtrações. Incentive as diferentes maneiras de calcular.
Atividade 3
Esta atividade explora a relação de equivalência nas sentenças. Assim, os estudantes são levados a pensar em qual número torna a igualdade verdadeira. Após completarem a atividade, explore a leitura das sentenças, como: “Sete menos um é igual a seis” ou “Seis é igual a sete menos um”.
Sugestão de atividade
Situações de subtração associada ao significado de retirar
João tinha 8 figurinhas e deu 5 para um colega. Com quantas figurinhas João ficou? (João ficou com 3 figurinhas.)
O vendedor de sorvetes tinha 29 picolés para vender. Sabendo que ele vendeu 3 picolés, quantos sobraram? (26 picolés.)
Sempre que uma solução for apresentada, tanto correta como incorreta, convide os estudantes a conferir com você, levantando questões como: “Alguém disse que sobraram 25 picolés. Vou desenhá-los aqui. Quantos picolés ele tinha vendido? (3.) Vou desenhar os picolés que ele vendeu também. Se a resposta estiver certa, juntando os picolés que ele vendeu aos que sobraram, quantos picolés devem totalizar?”. Espera-se que os estudantes percebam o erro ao totalizar 28 picolés, em vez de 29.
Durante muito tempo, as operações matemáticas eram descritas por meio de textos, o que tornava a cópia e a leitura dos livros tarefas difíceis e trabalhosas. Por volta do século XV, a palavra minus era usada para indicar uma subtração; com o tempo, passou a ser abreviada pela letra m com um traço horizontal em cima, até que restou apenas a escrita do traço horizontal, como o sinal que conhecemos hoje.
BNCC em foco:
EF01MA06, EF01MA08
MP096
MAIS SUBTRAÇÕES
- JÚNIOR TEM 11 ANOS DE IDADE, E PÂMELA TEM 7. ELES FAZEM ANIVERSÁRIO NO MESMO DIA.
- SE, PARA CADA VELINHA QUE PÂMELA APAGOU EM SEU BOLO, JÚNIOR APAGAR UMA VELINHA NO BOLO DELE, QUANTAS VELINHAS FICARÃO ACESAS NO BOLO DE JÚNIOR?
- CALCULE QUANTOS ANOS JÚNIOR TEM A MAIS QUE PÂMELA.

JÚNIOR TEM _____ ANOS A MAIS QUE PÂMELA.
PROFESSOR
Resposta: 4

- DESCUBRA, EM CADA CASO, QUANTAS CAIXAS AMARELAS FALTAM PARA QUE A FIGURA 1 FIQUE COM A MESMA QUANTIDADE DE CAIXAS VERDES QUE A FIGURA 2. DEPOIS, COMPLETE.
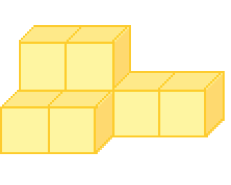
LEGENDA: FIGURA 1 FIM DA LEGENDA.
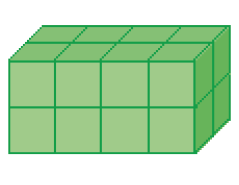
LEGENDA: FIGURA 2 FIM DA LEGENDA.
FALTAM _____ CAIXAS.
PROFESSOR
Resposta: 8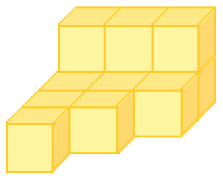
LEGENDA: FIGURA 1 FIM DA LEGENDA.
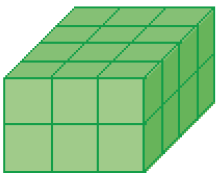
LEGENDA: FIGURA 2 FIM DA LEGENDA.
FALTAM _____ CAIXAS.
PROFESSOR
Resposta: 12Observação: NÃO HÁ CAIXAS ESCONDIDAS ATRÁS DAS PILHAS. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
Utilizar números naturais como indicadores de quantidades.
Identificar e comparar quantidades.
Usar estratégias próprias para resolver problemas que envolvam subtração.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
As atividades destas páginas possibilitam trabalhar situações em que:
se evidencia o uso dos termos “a mais” ou “a menos” relacionados ao significado de comparar quantidades e, portanto, à operação de subtração; nesse caso, o que se determina é a diferença entre duas quantidades;
o significado da subtração corresponde a completar quantidades. Os estudantes determinarão quanto falta para que certa quantidade seja igual a outra.
Atividade 1
Nesta atividade, a pergunta a respeito de quantos anos Júnior tem a mais que Pâmela não significa que se deva realizar uma adição, como alguns estudantes podem pensar, mas que é preciso calcular a diferença de idade entre eles, por meio de uma subtração. O significado envolvido na situação é o de comparação entre as idades.
Sugira aos estudantes que risquem as velas de aniversário do bolo de Júnior de acordo com as velas apagadas no bolo de Pâmela. Depois, pergunte: “Quantas velas Júnior tem a mais que Pâmela?” (4 velas.); “Quantas velas Pâmela tem a menos que Júnior?” (4 velas.).
Atividade 2
Esta atividade explora a visualização geométrica das quantidades e estimula a imaginação, pois os estudantes precisam “completar” a figura 1 e construir a 2 sem conseguir enxergar algumas caixas.
Se achar oportuno, leve para a sala de aula um conjunto de dados ou os cubinhos do Material Dourado, se houver disponibilidade, para os estudantes fazerem os empilhamentos mostrados na atividade. Essa ação é importante para que percebam as caixas que não estão visíveis. Proponha, também, que eles criem outros empilhamentos.
BNCC em foco:
EF01MA05, EF01MA08
MP097
- PARA UMA CAMPANHA DE ARRECADAÇÃO DE ALIMENTOS, FORAM DOADOS 31 PACOTES DE AÇÚCAR E 17 PACOTES DE CAFÉ. QUANTOS PACOTES DE AÇÚCAR FORAM DOADOS A MAIS QUE OS PACOTES DE CAFÉ? ABAIXO, ESCREVA O CÁLCULO QUE VOCÊ FEZ.

FORAM DOADOS _____ PACOTES DE AÇÚCAR A MAIS QUE OS PACOTES DE CAFÉ.
PROFESSOR
Resposta: 14- NA FESTA DE ANIVERSÁRIO DE ROBERTO, FORAM CONSUMIDAS 27 TAPIOCAS DOCES E 18 TAPIOCAS SALGADAS. QUANTAS TAPIOCAS DOCES FORAM CONSUMIDAS A MAIS QUE AS SALGADAS? ABAIXO, ESCREVA O CÁLCULO QUE VOCÊ FEZ.
_____
FORAM CONSUMIDAS _____ TAPIOCAS DOCES A MAIS QUE AS SALGADAS.
PROFESSOR
Resposta: 9- JOÃO TEM 1 CÉDULA DE 5 REAIS E 2 CÉDULAS DE 10 REAIS. QUANTO FALTA PARA ELE COMPLETAR 31 REAIS? ABAIXO, ESCREVA O CÁLCULO QUE VOCÊ FEZ.
_____
FALTAM _____ PARA COMPLETAR 31 REAIS.
PROFESSOR
Resposta: 6 reais.MANUAL DO PROFESSOR
Atividade 3
Verifique as estratégias utilizadas pelos estudantes na resolução da situação proposta. Se necessário, peça que representem com desenhos os pacotes de açúcar e de café para fazer a comparação. Espera-se que eles percebam que os pacotes de açúcar que não tiverem correspondência com algum pacote de café formam a quantidade a mais (14 pacotes de açúcar ficarão sem correspondência).
Atividade 4
Nesta atividade, de maneira análoga ao que foi feito na atividade 3, os estudantes podem fazer a comparação identificando os elementos um a um (para cada tapioca doce consumida, considera-se uma tapioca salgada). Desse modo, podem obter ou verificar sua resposta.
Atividade 5
O uso social do dinheiro possibilita resolver problemas por meio de estratégias diferentes das normalmente abordadas na escola. É possível que alguns estudantes, em vez de proceder à contagem sequencial das quantidades, agrupem diretamente as duas cédulas de 10 reais, totalizando 20 reais, e depois acrescentem a cédula de 5 reais, o que resulta em 25 reais. Depois, eles podem fazer: 26, 27, 28, 29, 30 e 31, obtendo 6 reais como resposta.
BNCC em foco:
EF01MA05, EF01MA08
MP098
- NA FESTA JUNINA DA ESCOLA, DANIEL BRINCOU DO JOGO DE DERRUBAR LATAS. NA SEGUNDA RODADA, ELE FEZ 14 PONTOS. AGORA, DANIEL ESTÁ COM 22 PONTOS.

- QUANTOS PONTOS DANIEL FEZ NA PRIMEIRA RODADA?
_____
PROFESSOR
Resposta: 8 - QUANTOS PONTOS DANIEL DEVERÁ FAZER NA TERCEIRA RODADA PARA COMPLETAR 30 PONTOS?
_____
PROFESSOR
Resposta: 8 pontos
- SANDRA E RENATO TAMBÉM BRINCARAM DO JOGO DE DERRUBAR LATAS. SANDRA CONSEGUIU FAZER 30 PONTOS. RENATO FEZ 16 PONTOS A MENOS QUE SANDRA. QUANTOS PONTOS RENATO FEZ?
_____
RENATO FEZ _____ PONTOS.
PROFESSOR
Resposta: 14- OS CÃES DE BEATRIZ FAZEM ANIVERSÁRIO NO MESMO DIA. AQUILES FAZ 9 ANOS E BRIDA FAZ 13 ANOS. O PRESENTE QUE BEATRIZ VAI DAR É 1 BISCOITINHO PARA CADA ANO DE IDADE DELES.

- JUNTOS, AQUILES E BRIDA TÊM
_____
ANOS.
PROFESSOR
Resposta: 22
- OS BISCOITINHOS DE UM SACO SÃO SUFICIENTES PARA PRESENTEAR OS DOIS? EXPLIQUE.
_____
PROFESSOR
Resposta: Não, pois os dois juntos têm 22 anos e o saquinho contém 20 biscoitinhos.
MANUAL DO PROFESSOR
Atividade 6
Esta atividade amplia o trabalho feito com as operações de adição e de subtração, pois envolve a noção de operação inversa. Observe que, agora, a identificação do que fazer não é tão simples, pois o que se busca não é o resultado da ação feita, e sim um elemento desconhecido que participa dessa ação.
Os estudantes podem pensar assim: “Quantos pontos devo juntar a 14 pontos para obter, ao todo, 22 pontos?”.
Nesse caso, é provável que eles resolvam por contagem (ou tentativa e erro), sem perceber a subtração embutida. Converse com eles mostrando essa relação, ou seja, que essa situação corresponde a: “Quanto falta a 14 para atingir 22?”.
Caso os estudantes tenham dificuldade, apresente outras situações similares que os ajudem a pensar na busca de outros elementos que participam de uma adição (ou subtração) que não sejam os resultados.
Atividade 7
Esta atividade explora a subtração com o significado de comparar, usando o termo “a menos” em vez de “a mais”. Verifique como os estudantes resolvem a subtração. Em uma roda de conversa, peça que expliquem como pensaram. Deixe à disposição deles material manipulável (tampinhas, botões etc.), para que utilizem, caso sintam necessidade.
Atividade 8
Os estudantes têm a oportunidade de combinar as duas operações: a adição seguida da subtração. Após adicionarem 9 biscoitinhos a 13 biscoitinhos, obtendo 22 biscoitinhos, eles podem concluir que um saco não é suficiente para os dois cachorros, uma vez que contém 20 biscoitinhos.
BNCC em foco:
EF01MA05, EF01MA08
MP099
RESOLVENDO PROBLEMAS COM ADIÇÃO E SUBTRAÇÃO
- EM UM JOGO DE BASQUETE, AO FAZER UMA CESTA DE 3 PONTOS, O TIME DE LAURA TOTALIZOU 31 PONTOS. O TIME DE BIANCA FEZ 4 PONTOS A MENOS QUE O TOTAL DE PONTOS DO TIME DE LAURA.

- QUANTOS PONTOS TINHA O TIME DE LAURA ANTES DE FAZER A CESTA DE 3 PONTOS?
_____
PROFESSOR
Resposta: 28. Exemplos de cálculo: 31 − 3 = 28 - QUAL FOI O TOTAL DE PONTOS DO TIME DE BIANCA?
_____
PROFESSOR
Resposta: 27. 31 − 4 = 27
- TAINÁ E MAURÍCIO TÊM JUNTOS 30 FIGURINHAS.

- SABENDO QUE TAINÁ TEM 17 FIGURINHAS, QUANTAS FIGURINHAS TEM MAURÍCIO?
_____
PROFESSOR
Resposta: 13 - QUANTAS FIGURINHAS TAINÁ TEM A MAIS QUE MAURÍCIO?
_____
PROFESSOR
Resposta: 4
MANUAL DO PROFESSOR
Objetivos
Usar estratégias pessoais para resolver problemas que envolvam adição e subtração.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Atividade 1
Esta atividade explora a noção de operação inversa (relacionando a adição e a subtração).
Para obter a quantidade de pontos que o time de Laura tinha antes de fazer a cesta de 3 pontos, os estudantes podem pensar assim:
Quanto se deve adicionar a 3 para obter 31 ( _____ + 3 = 31)?
Nesse caso, para obter a resposta, eles podem usar desenhos, contagem progressiva ou outro recurso. Espera-se que alguns estudantes percebam que podem pensar assim também:
Quanto falta a 3 para atingir 31?
Dessa maneira, os estudantes podem fazer desenhos para completar o 3 até o 31; se perceberem que terão de fazer 31 − 3, podem tirar 3 de 31 e obter o que sobra. Isso pode ser feito com uma contagem regressiva, por exemplo: 30, 29, 28.
Para determinar o total de pontos do time de Bianca, primeiro os estudantes devem compreender que, embora essa situação esteja ligada a uma adição, o que deve ser feito é uma subtração, uma vez que a informação dada é “o time de Bianca fez 4 pontos a menos que o total do time de Laura”.
Proponha questionamentos intermediários para que os estudantes percebam esse fato e possam verificar se sua resposta é válida:
Quantos pontos ao todo fez o time de Laura? (31 pontos.)
O time de Bianca fez quantos pontos a menos que o time de Laura? (4 pontos.)
Atividade 2
Esta atividade pode ser trabalhada de forma análoga à atividade 1. É fundamental que os estudantes aprendam a fazer perguntas sobre problemas, assim passam a analisar o tipo de informações de que dispõem para resolvê-los.
BNCC em foco:
EF01MA05, EF01MA08
MP100
- GISELE GANHOU UMA CAIXA COM 20 BOMBONS E COMEU 3 DELES. QUANTOS BOMBONS SOBRARAM NA CAIXA?

SOBRARAM _____ BOMBONS NA CAIXA.
PROFESSOR
Resposta: 17. Exemplo de cálculo: 20 − 3 = 17- ANA TINHA 9 REAIS E GANHOU MAIS 15 REAIS DE SUA TIA. ELA QUER COMPRAR UM LIVRO QUE CUSTA 30 REAIS. QUANTOS REAIS FALTAM PARA QUE ANA CONSIGA COMPRAR ESSE LIVRO?
FALTAM _____ REAIS PARA ANA COMPRAR O LIVRO.
PROFESSOR
Resposta: 6. Exemplo de cálculos: 9 + 15 = 24. 30 − 24 = 6- BRUNA FEZ UM DESENHO DE QUADRADOS COLORIDOS, E MARIANA DESENHOU CÍRCULOS COLORIDOS.
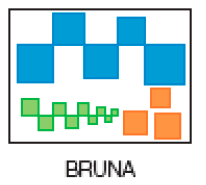

- QUANTOS QUADRADOS BRUNA DESENHOU?
_____
PROFESSOR
Resposta: 17 - QUANTOS CÍRCULOS FORAM DESENHADOS POR MARIANA?
_____
PROFESSOR
Resposta: 24
- QUANTAS FIGURAS BRUNA DESENHOU A MENOS QUE MARIANA?
_____
PROFESSOR
Resposta: 7
MANUAL DO PROFESSOR
Atividade 3
Observe as estratégias utilizadas pelos estudantes para descobrir quantos bombons sobraram na caixa. Socialize os diferentes procedimentos e, com os estudantes, faça a sua validação. Pergunte: “E se a caixa tivesse um bombom a mais, quantos sobrariam depois de Gisele comer 3 deles?”. Verifique se os estudantes acrescentam 1 bombom ao resultado que já tinham ou se realizam os mesmos passos feitos anteriormente.
Atividade 4
Nesta atividade, os estudantes se deparam com dois significados: o de acrescentar uma quantia à outra (9 + 15), obtendo 24 reais; e o de completar o total obtido para atingir os 30 reais necessários para comprar o livro, concluindo que faltam 6 reais. Incentive-os a efetuar os cálculos mentalmente, a explicar para um colega como pensaram e a registrar as operações feitas com a linguagem matemática.
Atividade 5
Explore as imagens de cada quadro com os estudantes e verifique o conhecimento que já trazem sobre as figuras apresentadas. Nesta fase, espera-se que reconheçam quadrados e círculos. Observe como eles determinam a quantidade de figuras usada por Bruna e por Mariana. Verifique também como efetuam a subtração. Socialize as diferentes estratégias com toda a turma, o que aumentará o repertório dos estudantes e auxiliará aqueles que ainda têm dificuldade em realizar essa operação.
A contagem dos círculos pode ser facilitada se eles forem classificados por cor, ou por tamanho, por exemplo, adicionando-se as quantidades de cada tipo ao final.
BNCC em foco:
EF01MA05, EF01MA08
Sugestão de atividades
Situações de adição e subtração
Juliana comprou 5 mudas de árvore para plantar no parque. Ela já plantou 2 mudas de árvore. Quantas ainda falta plantar? (3 mudas.)
Observe a quantia que Jorge e Lucas têm.
Jorge tem 3 cédulas de 2 reais.
Lucas tem 1 cédula de 2 reais.
Quantos reais os dois têm juntos? (8 reais.)
Quantos reais Jorge tem a mais que Lucas? (4 reais.)
MP101
- QUATRO AMIGOS FAZEM ANIVERSÁRIO NESTE MÊS. VAMOS DESCOBRIR EM QUAIS DIAS CADA UM FAZ ANIVERSÁRIO? REGISTRE SEUS CÁLCULOS.

ANA NASCEU NO DIA 17.

_____
LARISSA NASCEU NO DIA _____.
PROFESSOR
Resposta: 19. Exemplos de cálculo: 17 + 2 = 19
_____
O ANIVERSÁRIO DE JOÃO É NO DIA _____.
PROFESSOR
Resposta: 14. Exemplos de cálculo: 17 − 3 = 14
_____
O ANIVERSÁRIO DE CAIO É NO DIA _____.
PROFESSOR
Resposta: 27. Exemplos de cálculo: 17 + 10 = 27MANUAL DO PROFESSOR
Atividade 6
Incentive os estudantes a tentar resolver o problema primeiro fazendo uso de anotações e do cálculo mental.
Valorize a etapa de verificação do problema, pedindo que observem as afirmações de cada criança.
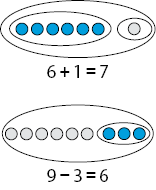
As aprendizagens da adição e da subtração estão relacionadas à compreensão da relação parte/todo, que pode ser resumida na frase: “O todo é igual à soma das partes”. Entretanto, como muitos professores observam, a subtração parece ser mais difícil que a adição. Por quê? Considerando a adição 6 + 1 e a subtração 9 − 3, associadas a seus possíveis desenhos, pode-se entender isto:
CRÉDITO: PAULO MANZI.
No caso da adição, os estudantes começam com dois “todos”, 6 e 1, e os combinam em um todo de ordem superior (7), em que ambos se tornam partes.
Na subtração 9 − 3, eles precisam lidar, simultaneamente, com o todo 9 e a parte 3, que se encontram em níveis hierárquicos diferentes, representados pelas linhas fechadas que contornam a quantidade 3 e a quantidade 9. Fazer isso é muito mais difícil para os estudantes que lidar com um único nível hierárquico.
BNCC em foco:
EF01MA05, EF01MA08
MP102
Boxe complementar:
DESAFIO

OBSERVE A BANCA DE FRUTAS E RESPONDA À QUESTÃO.

CRÉDITO: ILUSTRAÇÕES: LENINHA LACERDA
NATÁLIA VAI COMPRAR UM  E UMA
E UMA  . ELA VAI PAGAR
. ELA VAI PAGAR
SUA COMPRA COM DUAS CÉDULAS DE 10 REAIS. QUANTOS REAIS NATÁLIA RECEBERÁ DE TROCO?
Exemplo de estratégia de resolução: 
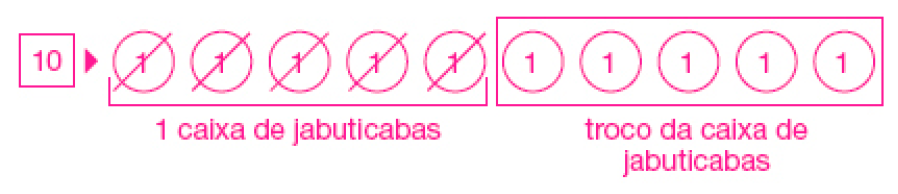
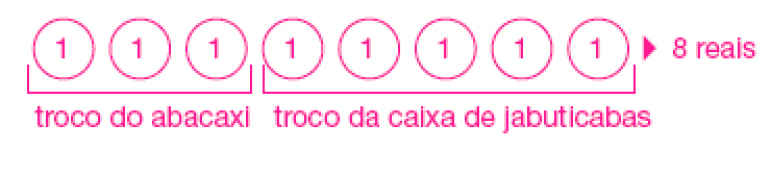
NATÁLIA RECEBERÁ _____ REAIS DE TROCO.
Resposta: 8
Fim do complemento.
MANUAL DO PROFESSOR
Desafio
A situação possibilita mais uma vez combinar as duas operações: adição e subtração.
É muito comum os estudantes resolverem parcialmente os problemas que envolvem duas operações, efetuando apenas uma delas. Desse modo, é importante repetir a pergunta do problema muitas vezes para eles: “Quanto ela receberá de troco?”.
Uma estratégia possível é adicionar os preços das duas frutas (7 reais mais 5 reais são 12 reais). Depois, fazer a subtração.
Veja algumas possíveis estratégias:
Tirar quantidades: das 20 unidades, retiram-se 12, restando 8 unidades, que podem ser obtidas por meio de contagem.

Comparar quantidades: colocam-se 12 unidades embaixo das 20 unidades; as que ficam sem par correspondem ao resultado da subtração.

Completar quantidades: desenham-se 12 unidades e, em seguida, desenham-se as unidades necessárias para chegar a 20 unidades; aquelas desenhadas após a décima segunda unidade correspondem ao resultado da subtração.

CRÉDITO: ILUSTRAÇÕES: ERICSON GUILHERME LUCIANO
Observe as estratégias comuns e faça um cartaz para socializá-las com o grupo.
Uma situação propícia para a realização de cálculos envolvendo adição e subtração é pedir aos estudantes que tragam, previamente, embalagens de diversos produtos com preços de até 30 reais para criar uma feira, na qual eles façam compras de maneira livre ou direcionada, usando cédulas do Material complementar. Pode-se, por exemplo, propor a tarefa de comprar três produtos na feira gastando menos de 20 reais, ou comprar o maior número possível de produtos com 15 reais, ou, ainda, fazer outras compras para calcular trocos, entre outras situações.
BNCC em foco:
EF01MA08, EF01MA19
MP103
A MATEMÁTICA ME AJUDA A SER
... UMA PESSOA CONSCIENTE DO VALOR DAS COISAS
Observação ACOMPANHE A LEITURA QUE O PROFESSOR VAI FAZER. Fim da observação.
HOJE EM DIA, USAMOS O DINHEIRO PARA FAZER COMPRAS, MAS NEM SEMPRE FOI ASSIM.
ANTES DE O DINHEIRO EXISTIR, AS COMPRAS ERAM FEITAS POR MEIO DA TROCA DE MERCADORIAS, COMO A TROCA DE PEIXES POR LEITE, A DE FRUTAS POR TECIDOS ETC. ESSA TROCA DE MERCADORIAS FICOU CONHECIDA COMO ESCAMBO.
COM O PASSAR DO TEMPO, HOUVE A NECESSIDADE DE SE CRIAR ALGO QUE FACILITASSE ESSAS TROCAS. ENTÃO, FOI CRIADO O DINHEIRO. PORÉM, AINDA HOJE É POSSÍVEL ENCONTRAR ESCAMBOS EM FEIRAS DE LIVROS, DE ROUPAS, DE BRINQUEDOS, ENTRE OUTRAS.

TOME NOTA
- COMO ERAM FEITOS OS ESCAMBOS?
_____
PROFESSOR
Resposta: Os escambos eram feitos por meio da troca de mercadorias.
- O QUE FOI CRIADO PARA FACILITAR AS TROCAS?
_____
PROFESSOR
Resposta: O dinheiro.
REFLITA

MARIANA TEM UM CADERNO NOVO QUE NÃO VAI USAR, E CARLOS TEM UMA BORRACHA NOVA. CARLOS PROPÔS A MARIANA QUE TROCASSE A BORRACHA PELO CADERNO. CONSIDERANDO QUE O CADERNO CUSTA 14 REAIS E A BORRACHA CUSTA QUASE 5 REAIS, VOCÊ CONSIDERA ESSA TROCA JUSTA?
PROFESSOR
Resposta pessoal.MANUAL DO PROFESSOR
Objetivo
Aproximar-se dos contextos sociais de uso do sistema monetário.
Leia o texto para os estudantes por partes, conversando com eles sobre o que diz cada uma das partes. Verifique se eles já conheciam o termo “escambo” e seu significado.
Proponha uma situação de escambo na sala. Para isso, solicite aos estudantes antecipadamente que tragam coisas que possam ser trocadas. Reúna-os em círculo, deixe que eles façam as propostas para as trocas e, com a turma, discutam sobre elas.
Tome nota
Atividades 1 e 2
Depois de os estudantes vivenciarem uma situação de escambo, reúna-os em duplas e deixe que troquem ideias sobre as questões propostas. Em seguida, peça que registrem suas respostas. Novamente com a turma disposta em círculo, peça a algumas duplas que contem o que responderam.
Espera-se que os estudantes compreendam que os escambos eram feitos por meio da troca de mercadorias e que a criação do dinheiro facilitou as trocas e as relações comerciais.
Reflita
Espera-se que os estudantes compreendam que a troca não é justa porque os objetos trocados têm valores diferentes.
Também é possível que as crianças raciocinem na base do valor de uso dos itens, concluindo que, ao final, cada um ficou com aquilo que desejava.
Discuta com os estudantes sobre o que seria uma troca que julguem justa envolvendo o caderno e a borracha. É possível que sugiram que Carlos deve oferecer mais alguns objetos além da borracha, por exemplo uma régua e um lápis.
BNCC em foco:
EF01MA19; competências gerais 1 e 9; competências específicas 4 e 6
MP104
COMPREENDER INFORMAÇÕES
O QUE VAMOS TER?
- OS DADOS SÃO MUITO USADOS EM JOGOS DE TABULEIRO. COMO MOSTRADO A SEGUIR, CADA UMA DAS 6 FACES DE UM DADO TEM PONTINHOS QUE REPRESENTAM NÚMEROS DE 1 A 6.

- OBSERVE ABAIXO O LANÇAMENTO DE ANA. PINTE O QUADRINHO COM A QUANTIDADE DE CASAS QUE ELA DEVE ANDAR.

1, 2, 3, 4, 5, 6
PROFESSOR
Resposta: 6- LUCAS JOGOU O DADO E A FACE
 FICOU PARA CIMA. ENTÃO,
FICOU PARA CIMA. ENTÃO, LUCAS DEVE ANDAR _____ CASAS NO TABULEIRO.
PROFESSOR
Resposta: 5
- DOS NÚMEROS ABAIXO, CERQUE COM UMA LINHA AQUELES QUE SÃO IMPOSSÍVEIS DE SAIR QUANDO JOGAMOS UM DADO.
1, 3, 5, 7, 9, 11, 10, 8, 6, 4, 2
PROFESSOR
Resposta: 7, 9, 11, 10, 8IMPORTANTE
NO LANÇAMENTO DE UM DADO, O RESULTADO É AO ACASO, PORQUE NÃO SABEMOS, COM CERTEZA, QUAL SERÁ.
- PODEMOS DIZER, COM CERTEZA, QUE ANA VAI TIRAR 6 NA PRÓXIMA RODADA?
( ) SIM
( ) NÃO
PROFESSOR
Resposta: não
MANUAL DO PROFESSOR
Objetivos
Classificar eventos que envolvam o acaso.
Contar e registrar simbolicamente quantidades.
As atividades destas páginas ampliam a exploração de situações que envolvem o acaso, para que os estudantes classifiquem eventos em “acontecerá com certeza”, “talvez aconteça” e “é impossível acontecer”.
Atividade 1
Embora os estudantes já tenham utilizado o dado em atividades anteriores ou mesmo no convívio social, explore novamente seus elementos. Leve um dado grande para a sala (de preferência com pontinhos, como na atividade) e mostre cada uma de suas faces, para que eles façam a identificação.
Lance o dado algumas vezes e pergunte que face ficou voltada para cima.
Em uma roda de conversa, coloque as questões propostas no livro e discuta as respostas dadas pela turma.
Amplie a atividade e faça outros questionamentos:
Se em uma jogada saiu a face com 6 pontinhos, posso andar 4 casas em um jogo de tabuleiro? Por quê? (Não, pelo fato de que os 6 pontinhos indicam a quantidade 6 para andar, e não apenas 4.)
Se há apenas um dado no jogo, qual é a maior quantidade de casas que eu posso andar? Por quê? (6 casas, porque o maior número que pode aparecer nesse dado é o 6.)
Por que é impossível sair uma face do dado com 10 pontinhos? (Porque a maior quantidade de pontinhos que pode aparecer em um dado comum é 6.)
Comente com os estudantes o fato de o lançamento de um dado comum (“honesto”) ser uma situação em que não se pode prever (antecipadamente) que face ficará voltada para cima ao lançar o dado, embora já saibamos todas as possibilidades que podem ocorrer. Peça que citem outras situações que envolvem o acaso. Espera-se que os estudantes reconheçam a situação de lançamento de uma moeda para observar a face que fica voltada para cima ou o sorteio de bolinhas numeradas (como em um bingo) como situações que envolvem o acaso.
Desse modo, eles podem perceber que não há como dizer com certeza a face que Ana tirará. Proponha que joguem um dado e verifiquem esse fato.
BNCC em foco:
EF01MA04, EF01MA20
MP105
- ANA FEZ UMA VITAMINA DE FRUTAS COM MAÇÃS E LARANJAS.
- MARQUE COM UM
X
AS FRUTAS QUE ANA COM CERTEZA COLOCOU NA VITAMINA DE FRUTAS.
( )
- MARQUE COM UM
X
AS FRUTAS QUE ANA COM CERTEZA COLOCOU NA VITAMINA DE FRUTAS.

( )

( )

PROFESSOR
Resposta: laranja, maçã.- CARLA PREPAROU TRÊS TAÇAS DE SORVETE: UMA COM SORVETE DE CREME, UMA COM SORVETE DE CHOCOLATE E OUTRA COM SORVETE DE MORANGO. A FILHA DELA PEGOU UMA DAS TAÇAS, AO ACASO, SEM NOTAR O SABOR DO SORVETE.
- MARQUE COM UM
X
A FRASE CORRETA SOBRE O SORVETE DA TAÇA QUE A FILHA DE CARLA PEGOU.
( ) O SABOR COM CERTEZA É CREME.
( ) TALVEZ O SABOR SEJA CREME.
( ) É IMPOSSÍVEL O SABOR SER CREME.
PROFESSOR
Resposta correta: Talvez o sabor seja creme.
- MARQUE COM UM
X
A FRASE CORRETA SOBRE O SORVETE DA TAÇA QUE A FILHA DE CARLA PEGOU.
- DANIEL E RUI ESTÃO BRINCANDO COM DOIS DADOS. DANIEL TIROU

 E RUI TIROU
E RUI TIROU 
 .
. - COMPLETE.
RUI TIROU 3 E 6, QUE ADICIONADOS RESULTAM EM _____ PONTOS. DANIEL TIROU _____ PONTOS AO TODO.
PROFESSOR
Resposta: 9, 9 - NA PRÓXIMA JOGADA, RUI DISSE QUE VAI FAZER 13 PONTOS JOGANDO OS DOIS DADOS. ISSO:
( ) É IMPOSSÍVEL ACONTECER.
( ) TALVEZ ACONTEÇA.
( ) ACONTECERÁ COM CERTEZA.
PROFESSOR
Resposta correta: é impossível acontecer.
- COMPLETE.
MANUAL DO PROFESSOR
Atividade 2
Peça aos estudantes que justifiquem as escolhas das frutas que Ana com certeza colocou na vitamina. Faça o mesmo com a fruta que não foi assinalada.
Atividade 3
Pergunte aos estudantes: “Por que as afirmações ‘O sabor com certeza é de creme’ e ‘É impossível o sabor ser de creme’ não estão corretas?”.
Espera-se que eles mencionem os três sabores (creme, chocolate e morango) e relacionem essa situação com o acaso.
Atividade 4
Aproveite para mostrar representações do total de pontos obtidos pelos dois meninos:

5 + 4 = 9

CRÉDITO: ILUSTRAÇÕES: ERICSON GUILHERME LUCIANO
3 + 6 = 9
Assim, os estudantes percebem várias composições de um mesmo número.
BNCC em foco:
EF01MA04, EF01MA07, EF01MA20
MP106
O QUE VOCÊ APRENDEU

- PINTE AS FICHAS COM O RESULTADO INDICADO EM CADA QUADRO.
RESULTADO 10
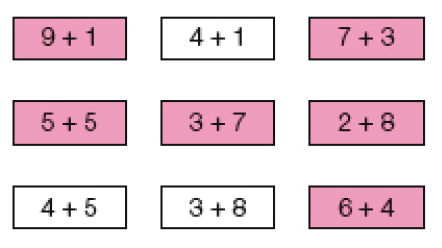
RESULTADO 14
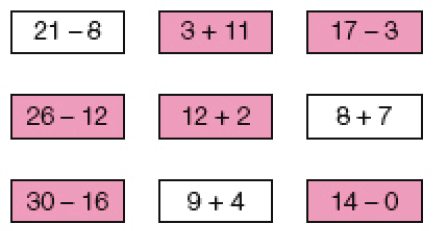
- REGINA FOI À FEIRA. ELA COMPROU 1 ABACAXI POR 7 REAIS E 1 MELANCIA POR 10 REAIS.

- QUANTOS REAIS REGINA GASTOU NO TOTAL?
_____
PROFESSOR
Resposta: 17 - REGINA USOU UMA CÉDULA DE 20 REAIS PARA PAGAR A COMPRA. QUANTOS REAIS ELA RECEBEU DE TROCO?
_____
PROFESSOR
Resposta: 3
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Proponha a atividade e peça aos estudantes que façam apenas uma marca a lápis nas fichas que acreditam que devem pintar.
Depois, faça uma correção coletiva com um levantamento de dúvidas e peça a alguns estudantes que relatem como fizeram suas escolhas. Ao final, peça que pintem as fichas.
Amplie a atividade e peça aos estudantes que listem outras quantidades que, adicionadas, resultem 10 e, depois, outras que resultem 14. Faça o registro de cada grupo, em quadros separados, na lousa. Discuta com eles os exemplos citados, validando-os ou não.
Atividade 2
Reúna os estudantes em duplas para realizar esta atividade.
Se julgar necessário, sugira a eles que utilizem as cédulas e as moedas do Material complementar.
Peça que elaborem uma questão, usando os dados da feira, troquem-na com outra dupla e, então, cada uma deve responder à questão da outra. Corrija coletivamente, socializando as questões criadas e suas resoluções.
BNCC em foco:
EF01MA06, EF01MA07, EF01MA08, EF01MA19
MP107

- CARLOS E ANDRÉ FORAM À PAPELARIA. OUÇA A LEITURA DAS INFORMAÇÕES ABAIXO E, DEPOIS, RESPONDA ÀS QUESTÕES.
- CARLOS COMPROU UM CADERNO POR 7 REAIS E UMA CARTELA DE ADESIVOS POR 7 REAIS.
- ANDRÉ COMPROU UMA LAPISEIRA POR 10 REAIS E UMA CANETA POR 7 REAIS.
- QUEM GASTOU MAIS DINHEIRO: CARLOS OU ANDRÉ?
_____
PROFESSOR
Resposta: André.QUANTOS REAIS A MAIS? _____
PROFESSOR
Resposta: 3
- DESENHE A MENOR QUANTIDADE DE CÉDULAS QUE CARLOS PODE USAR PARA PAGAR SUAS COMPRAS SEM RECEBER TROCO.
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes desenhem uma cédula de 10 reais e duas cédulas de 2 reais. Fim da observação.

- COMPLETE COM O NÚMERO QUE FALTA EM CADA CASO.
- 7 +
_____
= 10
PROFESSOR
Resposta: 3 -
_____
− 7 = 3
PROFESSOR
Resposta: 10 - 10 −
_____
= 7
PROFESSOR
Resposta: 3 - 5 + 5 =
_____
PROFESSOR
Resposta: 10 - 4 +
_____
= 9
PROFESSOR
Resposta: 5 - 5 +
_____
= 9
PROFESSOR
Resposta: 4
AUTOAVALIAÇÃO

-
CONSIGO ADICIONAR OU SUBTRAIR NAS ATIVIDADES QUE FAÇO EM CASA?
PROFESSOR
Resposta pessoal.
-
UTILIZO ADIÇÕES OU SUBTRAÇÕES EM SITUAÇÕES DO MEU DIA A DIA?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Solicite aos estudantes que permaneçam reunidos em grupo e, se necessário, incentive-os a utilizarem o Material complementar. Novamente, peça que elaborem uma questão, usando os dados da papelaria, e troquem-na com outra dupla para cada uma responder à questão da outra. Corrija coletivamente, socializando as questões criadas e suas resoluções.
Atividade 4
Proponha esta atividade individualmente, mas deixe que os estudantes troquem ideias com os colegas, caso desejem.
Se julgar necessário, proponha algumas perguntas para norteá-los:
Que quantidade deve-se adicionar a 7 para obter 10? Posso pensar de maneira diferente? Quanto falta a 7 para atingir 10?
De qual quantidade retiram-se 7 e ainda sobram 3? Quanto se obtém ao adicionar 3 a 7?
Que valor obtenho ao juntar 5 com 5?
4 adicionado a quanto resulta 9? 9 tem quantas unidades a mais que 4?
5 adicionado a quanto resulta 9? 9 tem quantas unidades a mais que 5?
Autoavaliação
Na primeira questão, é possível resgatar os procedimentos de lição de casa, estimulando os estudantes a perceber se realizam tais atividades individualmente, com a ajuda de adultos, ou se não estão fazendo as atividades em casa. Do mesmo modo, também podem indicar se adicionam e subtraem números com dificuldade, com tranquilidade ou se precisam de ajuda.
Na segunda questão, ajude os estudantes a identificar situações em que podem ter utilizado adições e subtrações, como em brincadeiras, jogos ou para organizar materiais na sala de aula ou em casa.
Ajude-os a responder de forma reflexiva, verificando, por exemplo, se identificam situações em que os conteúdos estudados são utilizados e se conseguem encontrar soluções. Assim, eles podem responder que não sentem necessidade de adicionar ou subtrair em situações do cotidiano; que sentem necessidade, mas não conseguem operar; que conseguem adicionar e subtrair números com tranquilidade ou que precisam de ajuda.
BNCC em foco:
EF01MA05, EF01MA06, EF01MA08, EF01MA19
MP108
Comentários para o professor
Conclusão da Unidade 3
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observações |
|---|---|---|
|
Reconhece números no contexto diário, fazendo indicação de quantidades, de ordem ou de código para a organização de informações? |
_____ |
_____ |
|
Efetua contagem de rotina, ordenando quantidades de objetos por meio de atributos comuns (ordem crescente ou decrescente), reconhecendo o aspecto cardinal do número? |
_____ |
_____ |
|
Lê, interpreta e identifica os elementos pertinentes a situações-problema que envolvem adições e subtrações e são apresentados em contextos do cotidiano do estudante, resolvendo-as? |
_____ |
_____ |
|
Adiciona, com o apoio de imagens, quantidades de objetos de dois conjuntos com soma até 31, mentalmente e simbolicamente aplicando os sinais “+” e “=” com os significados de juntar e acrescentar? |
_____ |
_____ |
|
Subtrai, com o apoio de imagens, quantidades de objetos de dois conjuntos com soma até 31, mentalmente e simbolicamente aplicando os sinais “−” e “=” com os significados de tirar, de comparar e de completar? |
_____ |
_____ |
|
Identifica, completa e representa na escrita e na reta numérica sequências recursivas com regras enunciadas, por exemplo, por mais 1, mais 2, menos 1, menos 2? |
_____ |
_____ |
|
Consegue organizar informações e registrá-las por meio de desenhos ou palavras? |
_____ |
_____ |
|
Compreende e realiza a leitura de imagens? |
_____ |
_____ |
|
Classifica resultados de eventos cotidianos aleatórios como acontece com certeza, talvez aconteça, impossível acontecer? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |