MP109
Introdução da Unidade 4
As páginas de abertura possibilitam diálogos que podem ser usados com o objetivo de diagnosticar os conhecimentos e habilidades que os estudantes trazem da Educação Infantil e, assim, constituírem-se em um bom instrumento para planejar as estratégias de ensino a serem aplicadas durante o ano letivo.
Em relação à Unidade Temática Álgebra, destacam-se, nesta Unidade, a retomada e a ampliação de conhecimentos relativos à organização e à ordenação de objetos ou representações por meio de figuras, considerando seus atributos. Objetiva-se, também, contemplar os conhecimentos relativos à descrição de padrões, de elementos ausentes em sequências de objetos ou figuras. Esses conhecimentos articulam-se com aqueles a serem tratados no ano seguinte e que devem conduzir os estudantes à descrição de padrão e de elementos ausentes em sequências repetitivas e de sequências recursivas de números naturais, objetos ou figuras, por meio de palavras, símbolos ou desenhos.
As atividades envolvendo a Unidade Temática Geometria são foco nesta Unidade. Consideramos duas abordagens: a primeira delas diz respeito à localização de pessoas e de objetos no espaço em relação à sua própria localização e em relação a um ponto de referência, com o uso dos termos à direita, à esquerda, entre outros. Vale ressaltar que atividades relacionadas à localização foram desenvolvidas na Unidade 1, e sua retomada pretende consolidar esse conhecimento e, ao mesmo tempo, auxiliar na apropriação de conhecimentos que serão abordados no 2º ano do Ensino Fundamental, cujos conteúdos relacionam-se à localização e aos deslocamentos de pessoas e de objetos no espaço, considerando mais de um ponto de referência e indicando as mudanças de direção e de sentido.
A segunda abordagem para Geometria insere-se nos estudos das relações entre figuras geométricas não planas (cones, cilindros, esferas, pirâmides, cubos e paralelepípedos não cúbicos) e objetos familiares do mundo físico, bem como na identificação e nomeação de figuras geométricas planas que compõem as faces de figuras geométricas não planas. Nessa abordagem, o manuseio do Tangram proporciona experiências de composição de figuras planas por justaposição, o que pode desenvolver nos estudantes a acuidade visual, capacitando-os à apreciação de obras de arte. Nesse sentido, os conhecimentos apropriados pelos estudantes serão subsídios para que, no ano seguinte, venham a reconhecer, nomear e comparar as figuras geométricas não planas. Por ser o primeiro momento em que tais conhecimentos são abordados, é importante sua articulação com os objetivos de aprendizagem e desenvolvimento previstos para a Educação Infantil e que buscam estimular os estudantes a estabelecer relações de comparação entre objetos, observando suas propriedades.
Os conhecimentos desenvolvidos sobre leitura de dados expressos em tabelas serão suporte para os estudos de Probabilidade e estatística nesta Unidade. Assim, as atividades propostas têm como objetivo levar os estudantes a organizar dados de pesquisa (apresentados em listas e textos) em tabelas simples, conhecimentos que se ampliarão no 2º ano do Ensino Fundamental, considerando-se que os dados serão organizados em tabelas simples e em gráficos de colunas simples.
Competências gerais favorecidas
3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
MP110
UNIDADE 4. GEOMETRIA

MANUAL DO PROFESSOR
Objetivos da Unidade
Associar objetos do cotidiano a figuras geométricas não planas.
Relacionar representações de figuras geométricas.
Identificar, quantificar e nomear representações de figuras geométricas planas.
Observar regularidade em sequências de representações geométricas.
Reconhecer o uso de representações de figuras geométricas planas em uma obra de arte.
Compor e decompor representações de figuras geométricas planas com o auxílio de um Tangram.
Descrever a localização de pessoas e de objetos no espaço em relação à sua própria posição.
Descrever a localização de pessoas e de objetos no espaço em relação a um dado ponto de referência.
Desenvolver interesse por explorar e observar modelos de figuras geométricas no cotidiano.
Organizar informações em listas e tabelas.
Realizar pesquisa e organizar os dados obtidos por meio de representações próprias.
Desenvolver estratégias pessoais em um jogo.
Esta Unidade trata de uma discussão acerca da Geometria, abordando alguns aspectos relacionados às figuras geométricas (reconhecimento de figuras geométricas não planas e de figuras geométricas planas, e identificação de similaridades e diferenças) e ao espaço (localização e pontos de referência).
BNCC em foco:
EF01MA04, EF01MA09, EF01MA10, EF01MA11, EF01MA12, EF01MA13, EF01MA14, EF01MA22
MP111
Página sem conteúdo.
MANUAL DO PROFESSOR
Inicialmente, comente que na aula de Arte da escola de Guilherme e Letícia os estudantes montam brinquedos com embalagens usadas, bolinhas de isopor e modelos de figuras geométricas que a professora os ajudou a fazer. Pergunte aos estudantes se já usaram embalagens usadas para produzir brinquedos.
Convide-os a realizar uma atividade parecida (montagem de brinquedos com embalagens usadas). Verifique o que sabem a respeito das figuras geométricas representadas e observe a linguagem que usam para descrevê-las ou se referir a elas.
Trabalhe a discriminação visual da representação de figuras geométricas, pedindo que observem objetos do cotidiano cuja forma lembre a das figuras geométricas não planas.
É possível que não descrevam os objetos usando o nome das figuras geométricas de maneira adequada, mas, à medida que trabalharem com as figuras nas atividades, se apropriarão gradativamente dessa nomenclatura.
Explore a cena perguntando:
Quais objetos da imagem têm forma parecida entre si? (Exemplo de resposta: A cesta dos balões e o tronco das árvores têm a forma cilíndrica.)
O telhado de vidro se parece com a copa das árvores? Por quê? (Espera-se que os estudantes digam que não, pois uma dessas figuras é arredondada e a outra não. O telhado de vidro lembra uma pirâmide, enquanto as copas das árvores lembram cones.)
Vocês têm algum objeto parecido com os objetos da cena? (É provável que pelo menos a bola deva aparecer como resposta, associada aos balões.)
Em que situações vocês reconhecem algumas das figuras apresentadas, como cones, cubos, esferas etc.? (Exemplo de resposta: no formato dos prédios, das frutas etc.)
MP112
OBJETOS AO MEU REDOR
EM MUITOS LUGARES, PODEMOS OBSERVAR OBJETOS QUE SE PARECEM COM FIGURAS GEOMÉTRICAS NÃO PLANAS.
- OBSERVE AS IMAGENS A SEGUIR.

LEGENDA: BRINQUEDOS QUE VOCÊ PODE FAZER. FIM DA LEGENDA.

LEGENDA: VASOS DECORATIVOS. FIM DA LEGENDA.

LEGENDA: REFEIÇÃO SAUDÁVEL. FIM DA LEGENDA.

- PENSE NOS AMBIENTES E NOS OBJETOS DE SUA ESCOLA. DEPOIS, DESENHE NO ESPAÇO ABAIXO OS QUE SE PARECEM COM AS FIGURAS GEOMÉTRICAS DESTACADAS NAS FOTOGRAFIAS ACIMA.
_____
PROFESSOR
Desenho pessoal.MANUAL DO PROFESSOR
Objetivos
Associar objetos do cotidiano a representações de figuras geométricas não planas.
Relacionar representações de figuras geométricas.
Desenvolver interesse por explorar e observar modelos de figuras geométricas no cotidiano.
Nestas atividades, os estudantes são incentivados a observar que alguns objetos presentes no dia a dia lembram figuras geométricas não planas e que cada uma dessas figuras tem um nome.
É importante que manipulem embalagens variadas para observar suas similaridades e diferenças. Deixamos para o 2º ano o uso de linhas tracejadas ou pontilhadas para indicar a profundidade das figuras geométricas não planas.
Atividade 1
Os estudantes são confrontados com cenas que mostram objetos do cotidiano que lembram figuras geométricas não planas. Pergunte se identificam alguma característica comum entre as latinhas e a bola (que representam um cilindro e uma esfera, respectivamente); é possível que comentem o fato de ambos serem arredondados ou terem partes curvas, ou rolarem.
Rolar não é uma propriedade geométrica, no entanto, pode ajudar na identificação de algumas figuras que, se deixadas em repouso, podem rolar quase espontaneamente em função de forças dadas, por exemplo, pela ação da gravidade em um plano inclinado ou pela ação do vento, com pequena intensidade.
Providencie embalagens vazias e limpas que não ofereçam riscos aos estudantes, como lata de leite em pó; caixa de sapato, de leite; bolinhas.
Peça que as manipulem e as separem em dois grupos, escolhendo o critério de agrupamento. É importante perceberem a diferença e a especificidade do formato de cada figura geométrica.
BNCC em foco:
EF01MA13
A discriminação visual relaciona-se aos processos mentais de:
comparação, sem o qual não é possível estabelecer as diferenças e as similaridades entre representações de figuras geométricas não planas e de figuras geométricas planas;
classificação, para separar grupos de representações de figuras em categorias distintas; no caso, figuras geométricas não planas e figuras geométricas planas;
conservação, pois é necessário compreender que as características de uma figura geométrica não dependem da orientação ou de sua disposição.
É importante ressaltar que as figuras geométricas são abstrações de nossa mente e não se encontram na realidade.
MP113

- PINTE DA MESMA COR OS OBJETOS QUE TÊM FORMAS PARECIDAS.
PROFESSOR
Exemplo de resposta: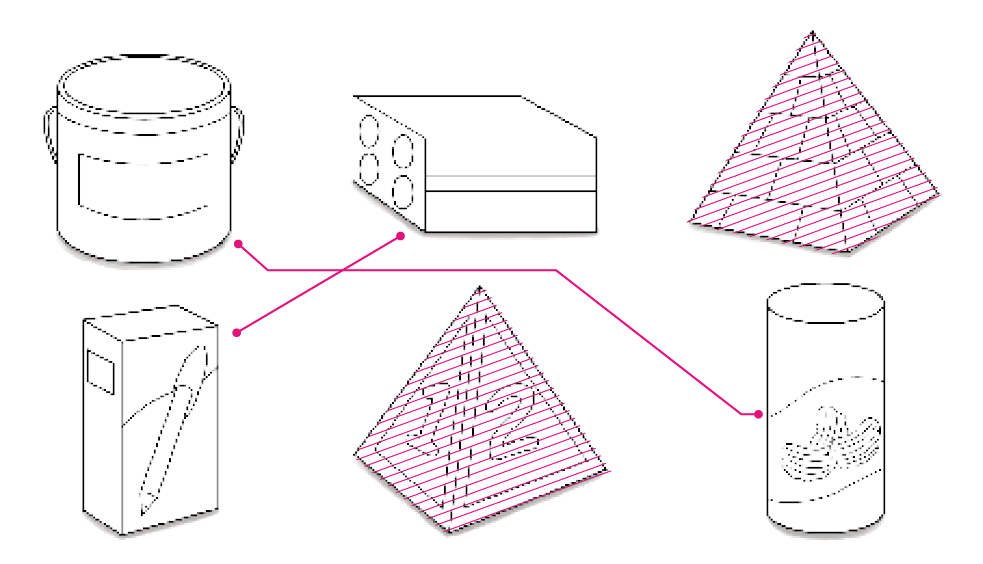
- OBSERVE OS DIFERENTES COPOS DE UMA LANCHONETE. MARQUE COM UM X O COPO QUE NÃO SE PARECE COM TODOS OS OUTROS.

- CIBELE EMBRULHOU ALGUNS PRESENTES COM PAPÉIS COLORIDOS. CERQUE COM UMA LINHA A EMBALAGEM QUE MAIS PARECE CONTER UMA BOLA DE BASQUETE.

PROFESSOR
Resposta esperada: embalagem 2.MANUAL DO PROFESSOR
Por esse motivo, muitas vezes nos referimos a alguns objetos como “representações” ou “modelos” de figuras geométricas, ou dizemos que são “parecidos com” ou “lembram” determinada figura. Como exemplo, pode ser citada uma folha de papel, que, por mais fina que seja, tem espessura; portanto, não é um retângulo.
Crianças da faixa etária de 6 anos costumam identificar figuras geométricas usando expressões como: “A porta é um retângulo. A bola é um círculo” etc. À medida que crescem e entram em contato com novas experiências, elas refinam seu vocabulário, discriminam algumas propriedades das figuras geométricas e, em vez de descrever a porta como um retângulo, passam a compreender que uma porta, considerando a espessura, tem a forma parecida com a de um paralelepípedo. Em relação a uma bola, aprenderão que não se parece com um círculo, mas com uma esfera.
Atividade 2
Aproveite o momento para ressaltar algum aspecto relacionado aos objetos físicos utilizados no dia a dia que lembre figuras geométricas não planas. Por exemplo:
A forma cilíndrica é usada em embalagens de xampu, em colunas de sustentação de prédios etc.
A forma de pirâmide é encontrada em objetos decorativos e na cúpula de alguns edifícios.
Atividade 3
A característica preponderante que os estudantes devem observar para marcar o copo diferente é a forma arredondada ou não, uma vez que entre os copos cilíndricos há variação no formato também (mais alto/mais baixo; mais fino/mais grosso etc.).
Comente com os estudantes o fato de que os copos, apesar de lembrarem cilindros ou paralelepípedos, não são sólidos geométricos, pois são ocos por dentro.
Atividade 4
Esta atividade pode ser feita em dupla, para que os estudantes possam expor ideias e argumentos ao colega.
Depois, em uma roda de conversa, peça que apresentem justificativas para as escolhas feitas.
BNCC em foco:
EF01MA13
MP114
JOGO: DOMINÓ GEOMÉTRICO
Observação ACOMPANHE AS INSTRUÇÕES QUE O PROFESSOR VAI LER. Fim da observação.

MATERIAL: 28 PEÇAS RECORTADAS DA PÁGINA 199.

JOGADORES: 2, 3 OU 4.
REGRAS:
- NO CENTRO DA MESA, COLOQUE AS PEÇAS COM AS FIGURAS VOLTADAS PARA BAIXO E EMBARALHE-AS.
- CADA JOGADOR PEGA 6 PEÇAS E NÃO DEIXA OS OUTROS COLEGAS VEREM AS FIGURAS. AS DEMAIS PEÇAS FICAM DE RESERVA.
- O JOGADOR QUE TIVER A PEÇA COM DUAS FIGURAS IDÊNTICAS (DUPLA) INICIA A PARTIDA, COLOCANDO-A SOBRE A MESA. CASO MAIS DE UM JOGADOR ESTEJA NESSA CONDIÇÃO, DEVE-SE ESCOLHER UM DELES PARA DAR INÍCIO. SE NENHUM JOGADOR TIVER UMA PEÇA DUPLA, ESCOLHE-SE ALGUÉM PARA COMEÇAR COM QUALQUER PEÇA DE SUA MÃO.
- O PRÓXIMO JOGADOR DEVE COLOCAR UMA PEÇA DELE EM UMA DAS EXTREMIDADES DA SEQUÊNCIA DE PEÇAS QUE FORMAM O JOGO QUE ESTÁ SOBRE A MESA. PELO MENOS UMA DAS FIGURAS DA PEÇA COLOCADA DEVE SER IDÊNTICA À DA EXTREMIDADE ESCOLHIDA E FICAR ENCOSTADA NESSA EXTREMIDADE.
- SE O JOGADOR DA RODADA NÃO TIVER UMA PEÇA COM UMA DAS FIGURAS IDÊNTICA PARA COLOCAR NO JOGO, DEVERÁ PEGAR UMA PEÇA DA RESERVA ATÉ CONSEGUIR UMA QUE SIRVA. CASO NÃO CONSIGA E AS PEÇAS DESSA RESERVA ACABEM, PASSARÁ A VEZ PARA O PRÓXIMO JOGADOR.
- VENCE O PRIMEIRO QUE ENCAIXAR NO JOGO TODAS AS PEÇAS QUE TIVER NAS MÃOS OU O JOGADOR QUE TIVER MENOS PEÇAS SE O JOGO TRAVAR, OU SEJA, QUANDO NÃO EXISTIREM MAIS PEÇAS DISPONÍVEIS PARA SEREM ENCAIXADAS.

MANUAL DO PROFESSOR
Objetivos
Organizar e ordenar representações de figuras geométricas não planas por meio dos atributos cor e forma.
Relacionar representações de figuras geométricas.
Desenvolver estratégias pessoais para a leitura das peças e das possibilidades de jogo.
Ajude os estudantes na leitura e na compreensão das regras.
Esta é uma variação do jogo de dominó comum, em que as peças são compostas de representações de figuras geométricas não planas e o encaixe se dá por figuras idênticas.
O dominó é um jogo tradicional, geralmente conhecido pelos estudantes. Brincar de dominó, além de possibilitar a cooperação, favorece momentos de comunicação, de construção de informações compartilhadas e de aprendizagem de conceitos matemáticos, principalmente os conceitos de igual e de diferente. Os jogos se relacionam diretamente com o pensamento matemático, uma vez que há regras, instruções, ações, deduções, desenvolvimento e aplicação de conceitos e procedimentos.
Antes de realizar o jogo, leve para a sala de aula objetos que lembrem as figuras geométricas não planas envolvidas. Por exemplo:
uma bola para representar uma esfera;
um dado para representar um cubo;
uma caixa de creme dental para representar um paralelepípedo;
uma vela piramidal para representar uma pirâmide;
uma lata de milho-verde em conserva para representar um cilindro;
um chapéu de festa de aniversário para representar um cone.
BNCC em foco:
EF01MA09, EF01MA13; competência geral 9; competências específicas 7 e 8
MP115
Boxe complementar:
VEJA SE ENTENDEU

OBSERVE ESTA PARTE DE UM JOGO.
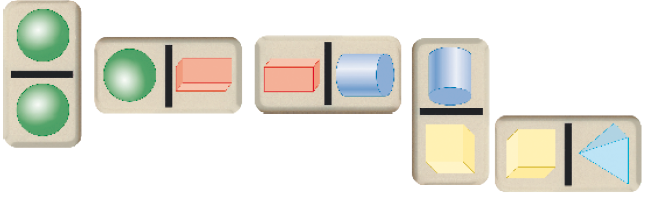
Resposta possível: Primeira peça; Última peça.
QUAL PEÇA VOCÊ ACHA QUE FOI COLOCADA PRIMEIRO? E POR ÚLTIMO?
A ÚLTIMA PEÇA FOI COLOCADA CORRETAMENTE NA SEQUÊNCIA DO JOGO?
Resposta: Sim.
Fim do complemento.
QUESTÕES SOBRE O JOGO
- VEJA COMO ESTÁ O JOGO. É A VEZ DE JOÃO JOGAR.
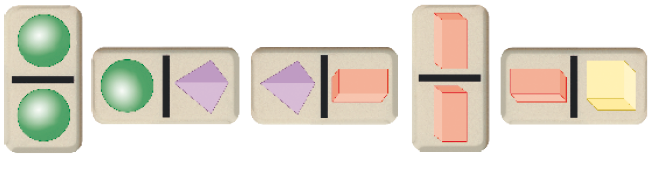
- AGORA, OBSERVE AS PEÇAS DE JOÃO E CERQUE COM UMA LINHA CADA UMA DAS PEÇAS QUE ELE PODE COLOCAR NO JOGO ACIMA.

PROFESSOR
Resposta: peças 2 e 3.- DEPOIS DE JOÃO, É A VEZ DE CARLA JOGAR. VEJA ABAIXO A PEÇA QUE ELA QUER ENCAIXAR NO JOGO DA ATIVIDADE ANTERIOR.
- É POSSÍVEL CARLA ENCAIXAR ESTA PEÇA? POR QUÊ?
_____
- É POSSÍVEL CARLA ENCAIXAR ESTA PEÇA? POR QUÊ?
PROFESSOR
Atenção professor: Espera-se que os estudantes respondam que é possível Carla encaixar essa peça, pois as figuras são idênticas às das duas extremidades antes de João fazer a sua jogada. Fim da observação.
MANUAL DO PROFESSOR
Leve uma quantidade suficiente de objetos de modo que haja um para cada estudante ou para cada dupla. Comente que esses objetos são apenas modelos, que as figuras geométricas estudadas (esfera, cubo, paralelepípedo, pirâmide, cilindro e cone) são maciças, não ocas, ou seja, possuem preenchimento.
Disponha os objetos sobre a mesa para serem observados e trabalhe o reconhecimento dessas figuras geométricas não planas: as formas e os nomes. Em seguida, realize uma atividade de fixação: diga aleatoriamente o nome de uma figura geométrica não plana e que aquele que possuir um objeto que lembre a figura dita deverá levantá-lo para os demais colegas verem.
Para realizar o jogo proposto, leia e explique as regras aos estudantes. Auxilie-os no recorte das peças. Depois, analise com eles as peças, pedindo que descrevam cada tipo de figura. Em seguida, mostre alguns encaixes possíveis entre as peças. Proponha algumas jogadas, de modo que se familiarizem com a estratégia do jogo.
Questões sobre o jogo
Após jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões. Estimule-os a simular a situação de jogo apresentada nas questões.
Verifique se eles constatam que, na questão 1, há duas peças que João pode encaixar no jogo, uma peça para cada extremidade.
Na questão 2, é importante que os estudantes percebam que, independentemente da peça colocada por João, Carla poderá encaixar sua peça na extremidade não escolhida por João, pois as figuras na peça de Carla são idênticas às das duas extremidades da situação apresentada.
BNCC em foco:
EF01MA09, EF01MA13
Sugestão de leitura para o professor
Livro
GRANDO, Regina Célia. O jogo e a Matemática no contexto da sala de aula. São Paulo: Paulus, 2004.
Discute a riqueza pedagógica que existe na utilização correta de jogos para ensinar Matemática, para desenvolver o pensamento criativo ou até mesmo para transformar o erro em sucesso.
MP116
FIGURAS GEOMÉTRICAS NÃO PLANAS
- LIGUE CADA OBJETO À FIGURA COM A QUAL ELE MAIS SE PARECE.
COLUNA 1




COLUNA 2

LEGENDA: CUBO FIM DA LEGENDA.

LEGENDA: CONE FIM DA LEGENDA.

LEGENDA: ESFERA FIM DA LEGENDA.

LEGENDA: PIRÂMIDE FIM DA LEGENDA.

LEGENDA: CILINDRO FIM DA LEGENDA.

LEGENDA: PARALELEPÍPEDO FIM DA LEGENDA.
COLUNA 3




PROFESSOR
Resposta: chapéu - cone; lata - cilindro; imagem da pirâmide - pirâmide; caixa de sabonete - paralelepípedo; dado - cubo; bolinha de gude - esfera; caixa de presente - cubo; caixa - paralelepípedo.Observação OS OBJETOS NESTA PÁGINA NÃO ESTÃO APRESENTADOS EM ESCALA DE TAMANHO. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
Associar objetos do cotidiano a figuras geométricas não planas.
Relacionar e quantificar representações de figuras geométricas.
Desenvolver interesse por explorar e observar modelos de figuras geométricas no cotidiano.
Observar regularidades em sequências de representações geométricas.
Neste nível de estudo, não é esperado que os estudantes liguem o dado e a caixa de presente com o paralelepípedo, mas, se surgir alguma dúvida a respeito, avalie a conveniência de explicar que o cubo é um caso particular de paralelepípedo.
Atividade 1
Traga modelos das figuras geométricas não planas exploradas nesta atividade. O manuseio dos modelos pelos estudantes facilita a apropriação de suas características e a percepção de que tais características independem da posição em que se encontram as figuras. Apoie cada modelo de diferentes maneiras sobre o tampo de uma mesa para que os estudantes relacionem cada um com a respectiva figura geométrica não plana apresentada no livro.
BNCC em foco:
EF01MA13
MP117
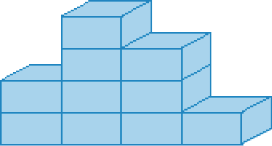
- GUSTAVO USA ALGUMAS EMBALAGENS PARA BRINCAR DE CONSTRUÇÃO.

- COMPLETE NA IMAGEM ABAIXO A QUANTIDADE DE EMBALAGENS DE CADA TIPO USADA NA CONSTRUÇÃO FEITA POR GUSTAVO.
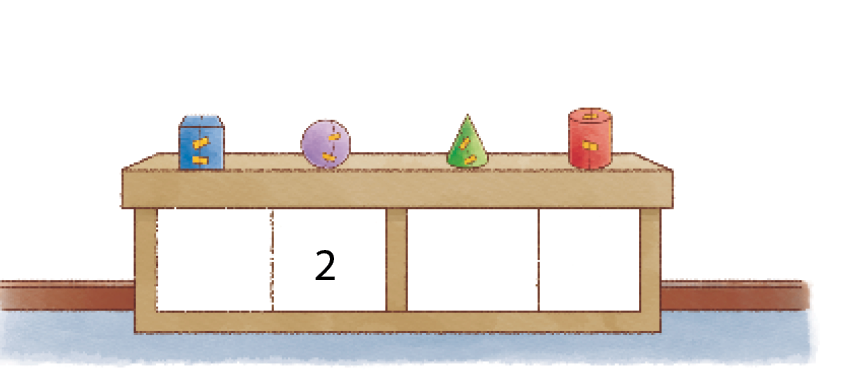
PROFESSOR
Resposta: 8, 2, 1- MARQUE COM UM X A EMBALAGEM QUE GUSTAVO USOU MAIS VEZES NA CONSTRUÇÃO.
( )

( )

( )

( )

PROFESSOR
Resposta: Embalagem 4.- QUANTAS PEÇAS É POSSÍVEL VER EM CADA PILHA?
( )

PROFESSOR
Resposta: 8( )

PROFESSOR
Resposta: 15( )
PROFESSOR
Resposta: 10MANUAL DO PROFESSOR
Atividade 2
Esta atividade trabalha o reconhecimento de peças utilizadas em uma brincadeira de construção e a quantificação delas.
Antes da atividade, apresente modelos de figuras não planas, como embalagens variadas, e realize atividades que levem os estudantes a explicitar as diferenças e similaridades entre as peças, descrevê-las por meio de linguagem não formal e observar suas características. Não é necessário dizer o nome das figuras geométricas que elas lembram, a menos que os estudantes perguntem. Por exemplo: esconda um modelo de figura não plana em uma caixa e desafie-os a dizer com qual peça da construção de Gustavo ele se parece. Supondo que seja escondido um modelo de cilindro, dê dicas como: “A figura não tem ‘bicos’” ou “Ela é arredondada”, e assim por diante, até que a turma descubra que o modelo parece a embalagem vermelha dessa construção.
Depois de realizar a atividade diversas vezes, sugira aos estudantes que façam o mesmo: escolham o modelo a ser escondido e deem dicas aos demais colegas. Desse modo, é possível explorar a oralidade e incentivar a participação de todos.
Para completar a segunda ilustração da página com a quantidade de embalagens de cada tipo, é preciso observar novamente a ilustração anterior com um novo olhar. Oriente os estudantes a contar a quantidade de embalagens de cada tipo, respeitando as estratégias pessoais, como iniciar a contagem pela embalagem azul (a primeira a aparecer na segunda ilustração) ou pela embalagem verde (a mais alta da pilha da esquerda). Após a contagem das embalagens de cada tipo, peça que registrem o número obtido.
BNCC em foco:
EF01MA04, EF01MA13
Atividade 3
Esta atividade explora a quantificação de elementos. Os estudantes podem contar uma a uma as peças de cada pilha. Eles podem vivenciar a atividade com material concreto e formar a própria pilha.
MP118
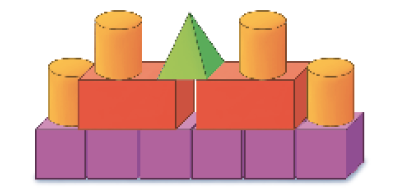
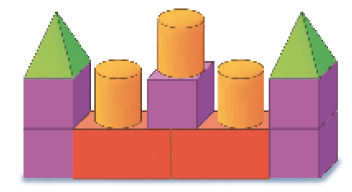
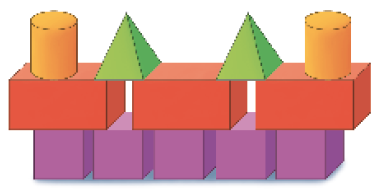
- OBSERVE AS PEÇAS DO BRINQUEDO DE CLARA.

- QUAL DOS CASTELOS ABAIXO CLARA PODE MONTAR COM TODAS AS PEÇAS DE SEU BRINQUEDO?
( )
( )
( )
( )
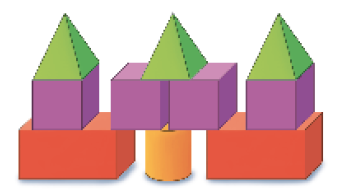
PROFESSOR
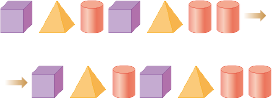
Resposta: Castelo 3.- OBSERVE ESTA SEQUÊNCIA DE FIGURAS.

- AGORA, MARQUE COM UM X A PRÓXIMA FIGURA DESSA SEQUÊNCIA.
( )

( )

( )

PROFESSOR
Exemplo de resposta: cubo.MANUAL DO PROFESSOR
Atividade 4
Providencie objetos que lembrem cada uma das peças da atividade e instigue os estudantes a descobrir com qual peça do brinquedo se parecem.
Além do trabalho com representações de figuras geométricas não planas, esta atividade trata também de quantificação, pois os estudantes devem identificar a quantidade correta de cada peça, de acordo com o brinquedo de Clara, para saber qual castelo pode ser construído.
Atividade 5
Espera-se que os estudantes marquem com um X o cubo, pois considerar que o padrão seja o trio (cubo, pirâmide, cilindro), nessa ordem, é o mais comum. Mas é possível definir outros padrões. Caso algum estudante marque o X em outra figura, peça a ele que descreva o padrão considerado na sequência para verificar se a resposta está correta.
Se a justificativa for coerente, aceite-a. Ele pode, por exemplo, dizer que a próxima figura é um cilindro e dar a justificativa desenhando o padrão que pensou.
CRÉDITO: ERICSON GUILHERME LUCIANO
BNCC em foco:
EF01MA09, EF01MA13
MP119
FIGURAS GEOMÉTRICAS PLANAS

- PINTE UM QUADRINHO PARA CADA FIGURA QUE VOCÊ VÊ NO DESENHO.

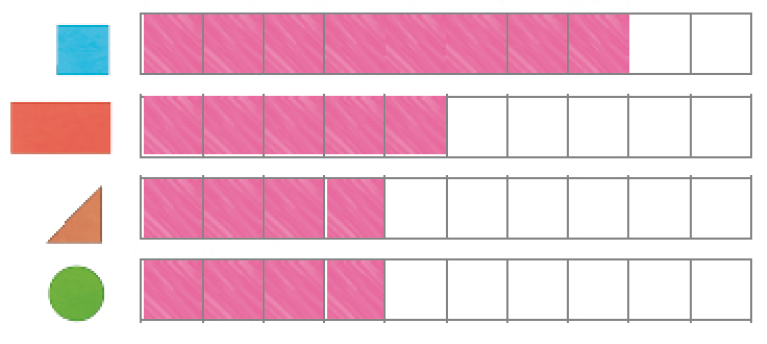
- LIGUE CADA OBJETO À FIGURA COM A QUAL ELE MAIS SE PARECE.
LINHA 1




LINHA 2

LEGENDA: QUADRADO FIM DA LEGENDA.

LEGENDA: CÍRCULO FIM DA LEGENDA.

LEGENDA: TRIÂNGULO FIM DA LEGENDA.

LEGENDA: RETÂNGULO FIM DA LEGENDA.
PROFESSOR
Resposta: objeto 1 - retângulo; objeto 2 - triângulo; objeto 3 - quadrado; objeto 4 - círculo.Observação: OS OBJETOS NESTA ATIVIDADE NÃO ESTÃO APRESENTADOS EM ESCALA DE TAMANHO. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
Identificar e quantificar representações de figuras geométricas planas.
Observar regularidades em sequências de representações geométricas.
Atividade 1
Oriente os estudantes a pintar os quadrinhos começando sempre de uma das extremidades para que as barras que formarem mostrem a ideia de um gráfico de colunas horizontais.
Verifique como os estudantes fazem a contagem das figuras do desenho. Eles podem realizar a contagem por tipo de figura, observando as de mesma representação, e pintar os quadrinhos referentes à figura escolhida, por exemplo todas as representações de triângulos. Em seguida, as representações dos círculos e assim por diante. Para não perder a contagem, sugira a eles que façam no livro uma marca nas figuras que já foram contadas.
Amplie a atividade perguntando:
Qual figura geométrica é representada em maior quantidade? (O quadrado.)
Como vocês chegaram a essa conclusão? (Resposta pessoal.)
Essa ampliação possibilita perceber se os estudantes comparam as quantidades pela contagem (recontando) ou pela visualização do maior comprimento (ou de comprimentos iguais) obtido pelos quadrinhos pintados.
Atividade 2
Nesta atividade, os estudantes devem relacionar figuras geométricas planas (quadrado, retângulo, triângulo e círculo) a objetos do cotidiano.
Faça perguntas para que os estudantes percebam algumas características comuns e também diferenças entre o quadrado e o retângulo e entre o círculo e as demais figuras, como: “O que há de parecido entre o quadrado e o retângulo? Como você explicaria a diferença entre eles?”.
Provavelmente os estudantes darão respostas como “O retângulo é maior que o quadrado”. Nesse caso, mostre que é possível desenhar um quadrado grande e um retângulo pequeno, a fim de que busquem novos recursos para responder às perguntas, apoiando-se em características geométricas, e não relacionadas a tamanho ou posição. Note que, quando mencionamos retângulo aqui, estamos nos referindo a retângulo, não a quadrado. Avalie a conveniência de esclarecer aos estudantes que o quadrado é um retângulo particular.
BNCC em foco:
EF01MA04, EF01MA14
MP120
- OBSERVE ESTAS PÁGINAS DE UM ÁLBUM DE FIGURINHAS.

- NUMERE AS FIGURINHAS A SEGUIR DE ACORDO COM O NÚMERO QUE INDICA O LOCAL EM QUE CADA FIGURINHA DEVE SER COLADA.
( )

PROFESSOR
Resposta: 7( )

PROFESSOR
Resposta: 1( )

PROFESSOR
Resposta: 9( )

PROFESSOR
Resposta: 4- MARQUE COM UM X TODOS OS NOMES DAS FIGURAS GEOMÉTRICAS PLANAS QUE ESTÃO REPRESENTADAS NO DESENHO DO ROBÔ ABAIXO.

( ) RETÂNGULO
( ) TRIÂNGULO
( ) QUADRADO
( ) CÍRCULO
PROFESSOR
Resposta: Respostas corretas: retângulo; quadrado; círculo.MANUAL DO PROFESSOR
Atividade 3
Incentive os estudantes a identificar que figuras geométricas planas lembram as figurinhas que faltam, para viabilizar a escolha do número correto.
Atividade 4
É importante apresentar as representações de figuras geométricas planas em diferentes posições (como ocorre no robô), para que os estudantes compreendam que, ao mudar a posição da figura (girando-a), sua forma não se altera, como mostrado a seguir.
Exemplos de quadrado:

Exemplos de retângulo:

Exemplos de triângulo:

CRÉDITO: ILUSTRAÇÕES: FERNANDO JOSÉ FERREIRA
Sugestão de leitura para o professor
Livro
SMOLE, Kátia S.; DINIZ, Maria Ignez S. V.; CÂNDIDO, Patrícia T. Figuras e formas. Porto Alegre: Artmed, 2014.
Esse livro proporciona uma discussão sobre o conteúdo e a maneira de ensinar Matemática, de modo que as crianças possam desenvolver e conservar a curiosidade sobre a Geometria, e, assim, adquirir diferentes maneiras de perceber a realidade.
BNCC em foco:
EF01MA04
Sugestão de atividade
Descrevendo figuras
Peça aos estudantes que tentem descrever a um colega o que é um triângulo.
Exemplo de descrição: O triângulo é uma figura que tem três “bicos”.
Atividades como esta, que propõem a descrição de alguma figura, nesse caso um triângulo, possibilitam aos estudantes buscar informações em suas vivências ou em conhecimentos anteriores, organizar essas informações e expressá-las de modo que o colega entenda. Além disso, tornam familiar aos estudantes um vocabulário específico da Matemática. Nesse momento, eles ainda não têm rigor matemático para explicar o que é um triângulo. Por isso, provavelmente usarão uma linguagem não formal ou até mesmo desenhos. Se julgar oportuno, peça que descrevam também o retângulo, o quadrado e o círculo.
MP121


- OBSERVE, NA SUPERFÍCIE DE UM CUBO E NA SUPERFÍCIE DE UM PARALELEPÍPEDO, REPRESENTAÇÕES DE FIGURAS GEOMÉTRICAS PLANAS.
CUBO
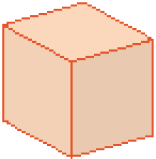
PARALELEPÍPEDO


- AGORA, DIGAM AS CARACTERÍSTICAS IGUAIS E AS DIFERENTES QUE VOCÊS PERCEBERAM.
PROFESSOR
Resposta pessoal.

- OBSERVE AS PINTINHAS NA JOANINHA REPRESENTADA ABAIXO. QUAL FIGURA GEOMÉTRICA PLANA ELAS LEMBRAM?
PROFESSOR
Resposta: Círculo.

Boxe complementar:
DESAFIO
ANALISE A SEQUÊNCIA DE FIGURAS ABAIXO.

QUAIS SÃO AS TRÊS PRÓXIMAS FIGURAS QUE PODEM CONTINUAR A SEQUÊNCIA ACIMA?
( )

( )

( )

CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Resposta: Figura 1.
Fim do complemento.
MANUAL DO PROFESSOR
Se possível, solicite antecipadamente aos estudantes que desmontem algumas embalagens de papelão que parecem paralelepípedos, cubos, pirâmides e cones, e identifiquem representações de figuras geométricas planas em suas partes. Se encontrarem dificuldade, proponha que recortem essas embalagens de modo a obter partes que pareçam representações de figuras geométricas planas.
Peça aos estudantes que passem tinta guache ou acrílica na superfície das embalagens e as carimbem no papel para verificar os desenhos de figuras geométricas planas obtidos. Cada estudante pode ficar com uma embalagem e depois socializar com a turma os desenhos de figuras geométricas obtidos.
. Atividade 5
Peça aos estudantes que levem para a aula uma caixa vazia de creme dental e retomem um dos cubos do Material complementar, montados na Unidade 3. Proponha a eles que manipulem esses objetos antes de responderem à questão.
Comente que essas figuras geométricas não planas também são conhecidas como blocos retangulares. Nesse momento, não se espera que eles reconheçam que um quadrado também é um retângulo.
Atividade 6
Se possível, leve para a sala uma joaninha de brinquedo ou algum objeto que se pareça com uma figura geométrica não plana que contenha figuras planas, a fim de que os estudantes manuseiem e percebam como as figuras planas aparecem nas figuras não planas. Vale ressaltar que as pintinhas da joaninha de verdade não são planas, mas na fotografia (imagem plana) parecem um círculo.
Desafio
A observação de padrões geométricos (além das cores) em sequências de figuras é muito rica. Peça aos estudantes que descrevam oralmente a(s) próxima(s) figura(s) que fará(ão) parte da sequência. Desse modo, pode-se verificar também que características dessas figuras já foram apreendidas por eles. Caso tenham dificuldade, peça que marquem o grupo de figuras e mostrem o padrão de repetição, a fim de comprovar suas escolhas. Proponha aos estudantes que criem outras sequências desse tipo e discuta com a turma os padrões envolvidos.
Sugestão de atividade
Observe a sequência a seguir e cerque com uma linha as peças que faltam para completá-la.
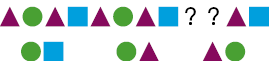
Resposta:

CRÉDITO: ADILSON SECCO
BNCC em foco:
EF01MA10, EF01MA14
MP122
FIGURAS GEOMÉTRICAS PLANAS E ARTE
- MUITOS ARTISTAS USAM FIGURAS GEOMÉTRICAS EM SUAS OBRAS. OBSERVE, POR EXEMPLO, ESTA REPRODUÇÃO DE UMA PINTURA DE PAUL KLEE.

LEGENDA: VELEIROS, DE PAUL KLEE, 1927. LÁPIS E AQUARELA SOBRE PAPELÃO, 22,8 cm × 30,2 cm. FIM DA LEGENDA.
- QUANTAS FIGURAS PARECIDAS COM
 VOCÊ VÊ?
_____
VOCÊ VÊ?
_____
PROFESSOR
Resposta pessoal.
- VEJA ABAIXO O CÍRCULO QUE JOÃO DESENHOU.
- MARQUE COM UM X QUAL DESTES OBJETOS ELE CONTORNOU PARA FAZER ESSE DESENHO.

LEGENDA: CÍRCULO. FIM DA LEGENDA.
( )

( )

( )

PROFESSOR
Resposta: moeda.Observação: OS OBJETOS NESTA ATIVIDADE NÃO ESTÃO APRESENTADOS EM ESCALA DE TAMANHO. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
Identificar, nomear e quantificar representações de figuras geométricas planas.
Reconhecer o uso de representações de figuras geométricas planas em uma obra de arte.
Desenvolver interesse por explorar modelos de figuras geométricas no cotidiano.
Atividade 1
É possível que os estudantes reconheçam todas as figuras que têm três lados como triângulos, ou que somente reconheçam as que estiverem na posição do triângulo indicado, ou as que sejam idênticas àquele triângulo. É possível, também, que não reconheçam os triângulos formados por outros triângulos ou aqueles que estão sobrepostos. Assim, para cada resposta que os estudantes apresentarem, solicite que justifiquem a contagem dos triângulos.
Vale ressaltar que, nesta atividade, não há uma resposta única, ela pode variar de acordo com a percepção do estudante.
Comente que o uso de representações de figuras geométricas planas nas composições artísticas deve-se às suas inúmeras possibilidades de composição e à facilidade de reconhecimento dessas representações nas obras, pois elas são universais.
Atividade 2
Se possível, disponibilize aos estudantes os objetos mostrados (pingente, moeda e régua) e peça que contornem cada um a fim de descobrirem qual representação de figura pode ser obtida por meio do contorno.
BNCC em foco na dupla de páginas:
EF01MA14
Sugestão de trabalho interdisciplinar
Peça aos estudantes que elaborem uma pequena composição livre usando representações de quadrados, triângulos, retângulos e círculos, colorindo-as de acordo com suas preferências.
Separe os estudantes em grupos: cada grupo deve pesquisar obras de arte que apresentam representações de figuras geométricas e selecionar uma obra para pesquisar o artista que a fez. Depois, cada grupo deve contar aos demais colegas o que mais gostou de descobrir com essa pesquisa. A seguir, sugerimos para a pesquisa alguns artistas que usaram representações de figuras geométricas em suas obras: Waldemar Cordeiro (1925-1973), Alfredo Volpi (1896-1988), Geraldo de Barros (1923-1998) e Luiz Sacilotto (1924-2003).
MP123
TANGRAM
- VOCÊ CONHECE O TANGRAM? ELE É UM QUEBRA-CABEÇA QUE FOI CRIADO NA CHINA HÁ MUITO TEMPO.

- JUNTAS, AS 7 PEÇAS DO TANGRAM AO LADO FORMAM UM:
( ) CÍRCULO
( ) QUADRADO
PROFESSOR
Resposta correta: quadrado.

- RECORTE AS PEÇAS DA PÁGINA 197 E MONTE AS FIGURAS A SEGUIR.


- USE SUAS PEÇAS PARA MONTAR UMA NOVA FIGURA. DEPOIS, MOSTRE-A A SEUS COLEGAS.
PROFESSOR
Atenção professor: A figura montada depende da imaginação de cada estudante, desde que sejam usadas todas as peças sem sobreposição. Fim da observação.MANUAL DO PROFESSOR
Objetivos
Compor e decompor representações de figuras geométricas planas com o auxílio de um Tangram.
Desenvolver interesse por explorar e observar modelos de figuras geométricas no cotidiano.
Atividade 1
Aproveite e faça o reconhecimento de todas as peças que compõem o Tangram com os estudantes, pedindo que nomeiem a figura geométrica que cada peça lembra e atentando para a nomenclatura usada por eles.
Atividade 2
As atividades de composição e decomposição de figuras planas por meio de quebra-cabeças como o Tangram promovem o desenvolvimento de diversas habilidades, como a coordenação visual e a motora, a noção de posição relativa entre as peças (em cima, à direita etc.), o reconhecimento de uma figura geométrica representada independentemente da posição, além de abordagens intuitivas de ângulos, área e simetria (que não são objeto de estudo nessa faixa etária).
Tangram é um antigo quebra-cabeça de origem chinesa, apreciado há séculos por proporcionar diversão e desafio. Contudo, pouco se sabe de sua verdadeira origem, razão pela qual há várias lendas sobre ela. O Tangram é composto de sete peças:
cinco representam triângulos de três tamanhos diferentes;
uma representa um quadrado;
uma representa um paralelogramo.
A proposta original do jogo é juntar as sete peças para representar um quadrado. Além dele, diversas outras figuras podem ser obtidas, sempre observando duas regras: todas as peças devem ser usadas e não é permitido sobrepô-las.
Amplie a atividade e peça aos estudantes que se reúnam em duplas, cada um com as peças do Tangram de seu material, para selecionar duas peças e, justapondo-as, desenhar seu contorno em uma folha de papel. Em seguida, trocarão o desenho com o colega, que deverá descobrir as peças usadas e montar novamente a figura original.
Sugestão de leitura para o professor
Livro
MACEDO, Lino de; PETTY, Ana Lúcia Sícoli; PASSOS, Norimar Christe. Os jogos e o lúdico na aprendizagem escolar. Porto Alegre: Artmed, 2005.
O livro oferece um trabalho com jogos que favorece o desenvolvimento da leitura e da escrita dos estudantes, além de subsídios de avaliação formativa.
MP124

- OBSERVE SUA SALA DE AULA E RESPONDA ÀS QUESTÕES.
- O QUE HÁ NA SUA FRENTE?
PROFESSOR
Atenção professor: A resposta vai depender da disposição da sala de aula em que esta atividade for realizada. Fim da observação. - À SUA DIREITA, O QUE VOCÊ VÊ?
PROFESSOR
Atenção professor: A resposta vai depender da disposição da sala de aula em que esta atividade for realizada. Fim da observação.
- QUANDO VOCÊ ESTÁ SENTADO NA SUA CAMA, A JANELA FICA ATRÁS DE VOCÊ OU NA SUA FRENTE?
PROFESSOR
Resposta pessoal.
- RODRIGO VAI ARRUMAR A COZINHA. NO ARMÁRIO EM CIMA DA PIA, SERÃO GUARDADOS OS PRATOS, OS COPOS E OS POTES E, NO ARMÁRIO EMBAIXO DA PIA, SERÃO GUARDADAS AS PANELAS E AS ASSADEIRAS.
- AJUDE RODRIGO RESPONDENDO ONDE ESTÁ O ARMÁRIO EM QUE CADA OBJETO A SEGUIR DEVE SER GUARDADO: EM CIMA OU EMBAIXO DA PIA?
- O QUE HÁ NA SUA FRENTE?

_____
PROFESSOR
Resposta: em cima
_____
PROFESSOR
Resposta: em cima
_____
PROFESSOR
Resposta: embaixo
_____
PROFESSOR
Resposta: embaixo
_____
PROFESSOR
Resposta: em cima
_____
PROFESSOR
Resposta: embaixoMANUAL DO PROFESSOR
Objetivos
Descrever a localização de pessoas e objetos no espaço em relação à sua própria posição.
Descrever a localização de pessoas e de objetos no espaço em relação a um dado ponto de referência.
Atividade 1
Esta atividade retoma conceitos tratados na Unidade 1 deste volume. Amplie-a propondo o uso de outros termos, como atrás e entre.
Atividade 2
O enunciado sugere que a janela estará na frente ou atrás do estudante, mas é possível que esteja de um dos lados, dependendo da configuração do cômodo. Explore essa possibilidade, possibilitando aos estudantes que falem sobre a planta de seus quartos. Nesse caso, amplie a atividade pedindo que digam se a janela está à direita ou à esquerda da posição imaginada pelo estudante. É possível ainda que a cama esteja no centro do quarto, possibilitando ao estudante que se sente ora à direita, ora à esquerda da janela.
Atividade 3
Esta atividade também propicia a retomada de conceitos já trabalhados. Aproveite o momento para observar possíveis dúvidas sobre esses conceitos. Leia o comando para os estudantes e peça que expliquem o que entenderam antes de completarem a questão.
BNCC em foco:
EF01MA11, EF01MA12
MP125

- OBSERVE UMA PARTE DO BAIRRO ONDE JOANA MORA.
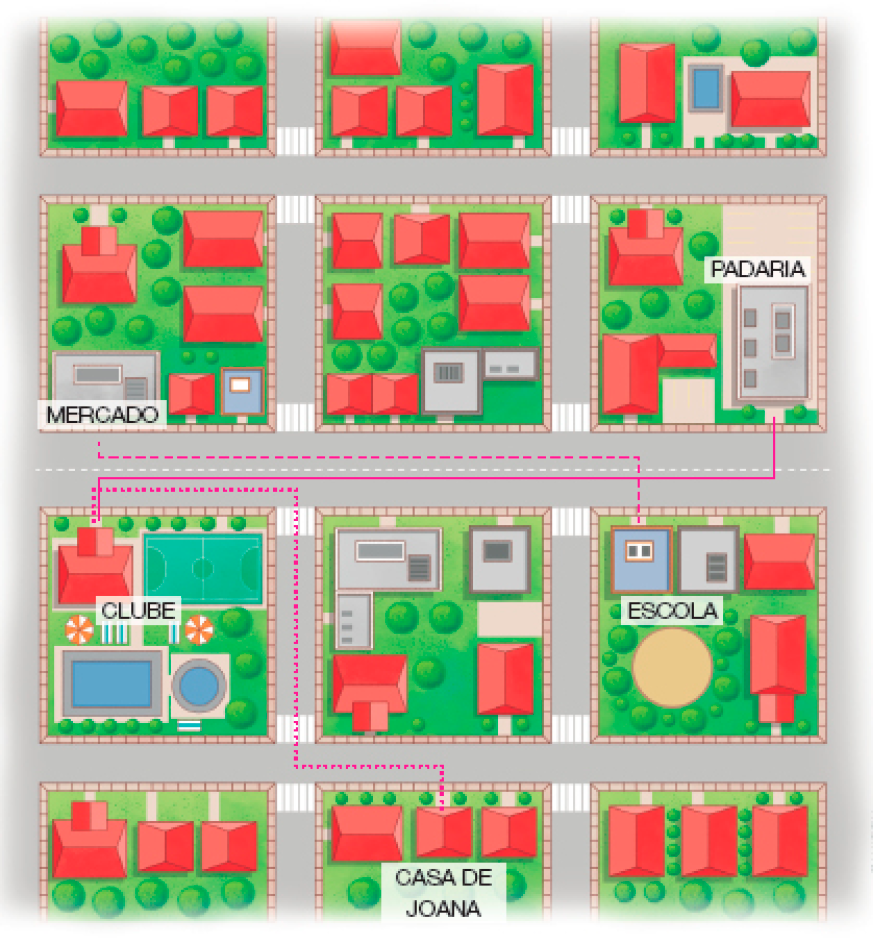
- TRACE UM CAMINHO DA CASA DE JOANA ATÉ O CLUBE.
PROFESSOR
Resposta possível indicada na linha pontilhada da ilustração. Há outros caminhos possíveis. - TRACE UM CAMINHO DO CLUBE ATÉ A PADARIA.
PROFESSOR
Resposta possível indicada na linha contínua da ilustração. Há outros caminhos possíveis. - TRACE O CAMINHO MAIS CURTO DO MERCADO ATÉ A ESCOLA.
PROFESSOR
Atenção professor: Resposta indicada na linha tracejada da ilustração. Fim da observação.
- EXISTE APENAS UM CAMINHO PARA IR DA CASA DE JOANA ATÉ O CLUBE?
PROFESSOR
Resposta: Não.
MANUAL DO PROFESSOR
Atividade 4
Antes de os estudantes realizarem esta atividade, organize as carteiras em filas (linhas e colunas) como se fossem os “quarteirões”. Peça a alguns estudantes que se desloquem de sua carteira até determinado colega (um de cada vez) e que os demais descrevam o caminho para outro estudante desenhar na lousa, usando comandos como “Ande para a frente tantas carteiras”, “Vire para a direita” etc.
Sugestões de atividades
Se você fosse um robô
Proponha à turma brincadeiras de robô em que um estudante dê comandos para um colega, que será orientado a ir de um lugar até outro. É importante que eles percebam a necessidade do ponto de referência para que o colega evite um obstáculo no caminho. Por exemplo, no caso de a brincadeira acontecer na sala de aula, no percurso da lousa até o fundo da sala, as carteiras tornam-se obstáculos. Assim, a cada comando, quando houver uma carteira no caminho, a trajetória precisará ser alterada.
Peça aos estudantes que usem comandos como: “Avance três passos para a frente.”, “Vire à esquerda.”, “Ande dois passos para trás.” etc., de modo que se familiarizem com a linguagem.
Percorrendo trajetos
Organize os estudantes em grupos. Cada grupo deverá percorrer um trajeto desejado dentro da escola e descrevê-lo em uma folha de papel, utilizando os termos já trabalhados. Depois, deverão ler seus registros para a turma, sem contar o ponto de chegada, apenas indicando a origem e o caminho percorrido para que os colegas descubram qual é o destino descrito.
É comum explicar um caminho a outra pessoa ou seguir instruções para chegar a um local. Proponha atividades de descrição de trajetos orientados, em que os estudantes se baseiem em instruções orais, sem ver o caminho por onde passarão, ou tenham à disposição um mapa no qual possam fazer o registro do trajeto. Para essa faixa etária, contudo, não é adequado oferecer mapas mais elaborados, em que os caminhos não estejam apenas na disposição retangular. Para eles, seria necessário utilizar termos que pudessem explicar movimentos mais complexos, ainda não trabalhados.
Após descreverem um caminho, incentive-os a fazer o mesmo com o caminho contrário, explorando as instruções que possibilitem retornar ao ponto de partida.
BNCC em foco:
EF01MA14
MP126
- CARLOS E LIA ESTÃO BRINCANDO DE JOGO DA VELHA. AS PEÇAS DE CARLOS LEMBRAM QUADRADOS, E AS DE LIA, TRIÂNGULOS.
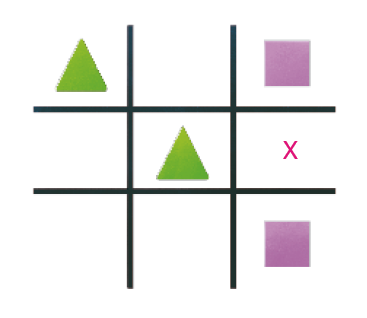
- É A VEZ DE LIA JOGAR. NO TABULEIRO AO LADO, MARQUE COM UM X O LOCAL ONDE LIA DEVE COLOCAR UMA PEÇA PARA QUE CARLOS NÃO GANHE ESSA PARTIDA.
- EM UM JOGO DE DAMAS, AS PEÇAS PODEM SER DESLOCADAS NA DIAGONAL (SENTIDO INCLINADO) PARA A FRENTE OU PARA TRÁS, PARA A DIREITA OU PARA A ESQUERDA, SE FOR PARA CAPTURAR AS PEÇAS DO ADVERSÁRIO.

- A PEÇA PRETA INDICADA PELA SETA AZUL DEVE CAPTURAR 3 PEÇAS VERMELHAS NESTA JOGADA. O PRIMEIRO MOVIMENTO JÁ ESTÁ INDICADO. INDIQUE OS OUTROS DOIS.
PROFESSOR
Exemplo de desenho:
MANUAL DO PROFESSOR
Atividade 5
Explique o jogo da velha para os estudantes. Peça que formem duplas e deixe que joguem um pouco antes de resolverem a questão.
Atividade 6
Explique o jogo de damas para os estudantes e mostre algumas jogadas possíveis. Caso julgue oportuno, providencie tabuleiros para eles jogarem antes de resolverem a questão.
Solicite aos estudantes que descrevam oralmente o trajeto que a peça preta fez nesta jogada. Espera-se que digam que a peça preta deve “andar” na diagonal para a frente pulando uma a uma as duas peças vermelhas (“comendo” essas duas peças) e, em seguida, deve “andar” na diagonal para trás pulando uma peça vermelha (“comendo” essa peça). Assim, essa peça preta “comerá” três peças vermelhas em uma única jogada.
Avalie a conveniência de explorar uma próxima jogada em que a peça preta usada na jogada anterior será comida pela peça vermelha da segunda linha, à direita, que ainda poderá comer mais duas peças pretas na mesma jogada.
Sugestão de leitura para o professor
Livro
PANIZZA, Mabel et al. Ensinar Matemática na Educação Infantil e nas séries iniciais: análise e propostas. Porto Alegre: Artmed, 2006.
No capítulo “À direita... de quem? Localização espacial na Educação Infantil e nas séries iniciais”, há sugestões de atividades para o trabalho de orientação espacial.
BNCC em foco:
EF01MA12
MP127
A MATEMÁTICA ME AJUDA A SER
... UMA PESSOA QUE VÊ GEOMETRIA NA ARTE
Observação ACOMPANHE A LEITURA QUE O PROFESSOR VAI FAZER. Fim da observação.
VAMOS CONHECER O ARTISTA NEWTON AVELINO?
ESSE ARTISTA TRANSFORMA SUAS VIVÊNCIAS EM OBRAS DE ARTE IMPRESSIONANTES. EM SUAS OBRAS, ELE COSTUMA RETRATAR A CULTURA NORDESTINA COM UM ESTILO MUITO PRÓPRIO.

LEGENDA: OS FORROZEIROS, DE NEWTON AVELINO, 2008. ACRÍLICA SOBRE TELA, 50 cm × 90 cm. FIM DA LEGENDA.
TOME NOTA
OBSERVANDO A IMAGEM ACIMA, RESPONDA ÀS QUESTÕES:
- VOCÊ VÊ INSTRUMENTOS MUSICAIS? SE SIM, QUANTOS?
_____
PROFESSOR
Respostas pessoais. Respostas esperadas: sim; três. - VOCÊ CONHECE ESSES INSTRUMENTOS? SE SIM, QUAIS SÃO OS NOMES DELES?
_____
PROFESSOR
Respostas pessoais. Respostas esperadas: sim; triângulo, sanfona e zabumba.QUAIS FIGURAS GEOMÉTRICAS PLANAS ESTÃO REPRESENTADAS?
_____
PROFESSOR
Respostas possíveis: triângulos, quadrados, retângulos e círculos.
REFLITA


AS CORES UTILIZADAS DÃO SENSAÇÃO DE TRISTEZA OU DE ALEGRIA? CONTE AOS COLEGAS.
PROFESSOR
Respostas pessoais.MANUAL DO PROFESSOR
Objetivos
Identificar e nomear representações de figuras geométricas planas.
Reconhecer o uso de representações de figuras geométricas planas em uma obra de arte.
Tome nota
Organize os estudantes em roda para conversar acerca da vida e da obra desse artista. Newton Avelino nasceu em 25 de março de 1960, em Natal, no Rio Grande do Norte. Sua família era ligada à arte, por isso, desde cedo Newton esteve habituado a conviver com poetas, escritores, cantores, pintores e artistas gráficos.
Em uma parte de sua infância, ele morou no Piauí, o que ampliou sua visão da cultura nordestina.
Movendo-se entre a arte cubista e a arte figurativa, Newton Avelino retrata, em suas obras, cirandas, pastoris, reisados, maracatus e outras manifestações da cultura nordestina.
Sua obra é inspirada na de Pablo Picasso, um dos criadores do Cubismo e, segundo Newton Avelino mesmo disse, “o artista mais completo que o mundo já conheceu”.
Suas pinturas mostram protestos contra as dificuldades no sertão, mas também mostram a alegria das cores vibrantes e dos traços inovadores de seu estilo de pintar.
As obras de Newton Avelino são divulgadas no Brasil, na Suécia, na Suíça e nos Estados Unidos.
Reflita
Peça aos estudantes que contem suas impressões sobre a obra e explore todas as representações presentes nela, como linhas, figuras geométricas planas, cores.
BNCC em foco:
EF01MA14; competência geral 3
MP128
COMPREENDER INFORMAÇÕES
ORGANIZAR INFORMAÇÕES EM TABELAS
- ADELAIDE É SÍNDICA DO PRÉDIO ONDE MORA E PRETENDE CONSTRUIR UM CANTEIRO DE FLORES NA ENTRADA DELE. PARA ISSO, ELA FEZ UMA PESQUISA PARA SABER QUAIS SÃO AS FLORES PREFERIDAS DOS MORADORES. OBSERVE AS ANOTAÇÕES DELA SOBRE A VOTAÇÃO.
MARGARIDA

AZALEIA

LÍRIO

ROSA

- AGORA, LIGUE CADA TIPO DE FLOR À QUANTIDADE DE VOTOS RECEBIDOS NA PESQUISA.
COLUNA 1




COLUNA 2
10
18
20
15
PROFESSOR
Resposta: lírio - 10; rosa - 20; margarida - 15; azaleia - 18.- COMPLETE A TABELA ABAIXO COM A QUANTIDADE DE VOTOS QUE CADA TIPO DE FLOR RECEBEU.
Tabela: equivalente textual a seguir.
FLORES PARA O CANTEIRO
|
TIPO DE FLOR |
|
|
|
|
|---|---|---|---|---|
|
QUANTIDADE DE VOTOS |
_____ |
_____ |
_____ |
_____ |
FONTE: PESQUISA DE ADELAIDE (ABR. 2023).
PROFESSOR
Resposta: 15, 20, 10, 18MANUAL DO PROFESSOR
Objetivos
Organizar informações em listas e tabelas.
Organizar os dados obtidos em pesquisa por meio de representações próprias.
As atividades destas páginas propiciam que os estudantes tenham contato com situações de pesquisa em que há a coleta de dados e a posterior organização desses dados em listas e tabelas. Aproveite o momento e proponha outras situações em que os estudantes possam eles próprios fazer o levantamento de informações e sugerir maneiras de organizá-las.
Atividade 1
Comente com os estudantes o modo de indicar a quantidade apresentada. Caso seja necessário, explique a eles que cada traço na anotação da síndica corresponde a um voto no tipo de flor contado por ela. Incentive-os a perceber que dessa maneira a contagem é facilitada, pois os traços formam grupos de 5. Peça que escrevam na frente das marcas a quantidade obtida.
Em seguida, solicite que identifiquem cada número que indica a quantidade de cada flor com a respectiva imagem da flor.
Peça aos estudantes que identifiquem o título da tabela: “Flores para o canteiro”. Relembre-os de que uma tabela é formada por linhas e colunas. Nesse caso, a primeira linha mostra o tipo de flor (margarida, rosa, lírio e azaleia), e a segunda linha apresenta a quantidade de votos que cada um desses tipos recebeu.
Proponha questões para que os estudantes percebam como consultar a tabela em suas respostas:
Que tipo de flor recebeu mais votos? (A rosa.)
E que tipo recebeu menos votos? (O lírio.)
Quantos votos teve a margarida? (15 votos.)
E a azaleia? (18 votos.)
BNCC em foco:
EF01MA22; competência específica 3
MP129
- LAÍS E EDU GANHARAM UM JOGO COM REPRESENTAÇÕES DE FIGURAS GEOMÉTRICAS QUE CONTÉM 10 CUBOS, 8 ESFERAS, 5 PIRÂMIDES, 20 CILINDROS, 12 CONES E 15 PARALELEPÍPEDOS.
- COMPLETE A TABELA DE ACORDO COM A QUANTIDADE DE REPRESENTAÇÕES DE CADA FIGURA GEOMÉTRICA NO JOGO.
Tabela: equivalente textual a seguir.
QUANTIDADE DE FIGURAS GEOMÉTRICAS
|
FIGURA GEOMÉTRICA |
|
|
|
|
|
|
|---|---|---|---|---|---|---|
|
QUANTIDADE |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
FONTE: CAIXA DO JOGO (ABR. 2023).
- QUAL É A COR DA FIGURA GEOMÉTRICA QUE TEM MENOS REPRESENTAÇÕES?
_____
PROFESSOR
Resposta: Roxo. - QUAL FIGURA POSSUI EXATAMENTE 1 DEZENA DE REPRESENTAÇÕES? E QUANTAS DEZENAS SÃO AS REPRESENTAÇÕES DOS CILINDROS?
_____
PROFESSOR
Resposta: Cubo; 2 dezenas.
- RAUL FEZ UMA PESQUISA NO BAIRRO SOBRE QUE BRINQUEDOS DEVEM SER COLOCADOS NA PRACINHA. O ESCORREGADOR RECEBEU 28 VOTOS, O BALANÇO FICOU COM 30 VOTOS, O GIRA-GIRA TEVE 25 VOTOS E A GANGORRA, 11 VOTOS.
- COMPLETE A TABELA DE ACORDO COM A QUANTIDADE DE VOTOS DE CADA BRINQUEDO NA PESQUISA DE RAUL.
Tabela: equivalente textual a seguir.
RESULTADO DA PESQUISA
|
BRINQUEDO |
BALANÇO |
ESCORREGADOR |
_____ |
GIRA-GIRA |
|---|---|---|---|---|
|
QUANTIDADE DE VOTOS |
_____ |
_____ |
11 |
_____ |
FONTE: PESQUISA DE RAUL (JUN. 2023).
PROFESSOR
Resposta: Brinquedo: Balanço; Quantidade de votos: 30.PROFESSOR
Brinquedo: Escorregador; Quantidade de votos: 28.PROFESSOR
Brinquedo: Gangorra; Quantidade de votos: 11.PROFESSOR
Brinquedo: Gira-gira; Quantidade de votos: 25.

- NA PRACINHA SÓ CABEM TRÊS BRINQUEDOS. QUAL DELES PODERIA SER DESCARTADO? EXPLIQUE POR QUÊ.
PROFESSOR
Resposta: A gangorra, porque foi o brinquedo menos votado.
MANUAL DO PROFESSOR
Atividade 2
Leia o comando da questão com os estudantes e peça que releiam a lista de peças do jogo. Traga modelos das figuras geométricas não planas envolvidas na questão para os estudantes reconhecerem pelos nomes quais são elas, antes de completarem a tabela. Explore os elementos da tabela com eles.
Aproveite o momento para explorar a comparação dos números envolvidos e propor situações que envolvam adição e subtração. Por exemplo:
Entre as figuras geométrica que representam cones e as que representam cilindros, qual há em maior quantidade? (As que representam cilindros.)
Reunindo as peças que representam cones e as que representam pirâmides, quantas peças são? (17 peças.)
Quantas representações de esferas há a menos que de cubos? (2 representações.)
Atividade 3
Esta atividade pode ser feita com os estudantes organizados em duplas. Deixe que discutam sobre como devem completar a tabela.
BNCC em foco:
EF01MA22; competências específicas 3 e 4
MP130
O QUE VOCÊ APRENDEU
- OBSERVE AS VELAS DECORATIVAS QUE ANDRÉ GANHOU.



- MARQUE COM UM X A ALTERNATIVA QUE APRESENTA OS NOMES DAS FIGURAS GEOMÉTRICAS NÃO PLANAS COM QUE ESSAS VELAS SE PARECEM.
( ) PIRÂMIDE; CONE; CILINDRO
( ) CILINDRO; CUBO; ESFERA
( ) CILINDRO; PIRÂMIDE; CUBO
PROFESSOR
Resposta correta: cilindro; pirâmide; cubo.

- CAROLINA FEZ ESTE PAINEL PARA ENFEITAR O QUARTO DELA.

- QUAL É A FIGURA GEOMÉTRICA PLANA QUE CAROLINA DESENHOU E PINTOU VÁRIAS VEZES NESSE PAINEL?
PROFESSOR
Resposta: Triângulo.
- CERQUE COM UMA LINHA CADA UMA DAS FIGURAS GEOMÉTRICAS NÃO PLANAS REPRESENTADAS A SEGUIR.

PROFESSOR
Resposta: círculo; paralelepípedo, pirâmide; cubo.MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Inicialmente, peça aos estudantes que identifiquem a figura geométrica não plana com a qual cada vela se parece, o que facilitará a escolha da alternativa correta.
Atividade 2
Explore o painel feito por Carolina. Peça aos estudantes que descrevam, na opinião deles, como esse painel foi formado.
Atividade 3
Traga modelos das figuras geométricas apresentadas na atividade para os estudantes fazerem a classificação delas em dois grupos: o das figuras geométricas não planas e o das figuras geométricas planas. Discuta essa classificação para que os estudantes troquem de grupo as figuras que acharem necessário. Depois disso, peça que realizem a atividade. Os estudantes podem consultar os grupos que montaram.
BNCC em foco:
EF01MA09, EF01MA13, EF01MA14
MP131
AVALIAÇÃO PROCESSUAL
- FABIANA FEZ O CONTORNO DE TRÊS FIGURAS EM UMA MALHA PONTILHADA.
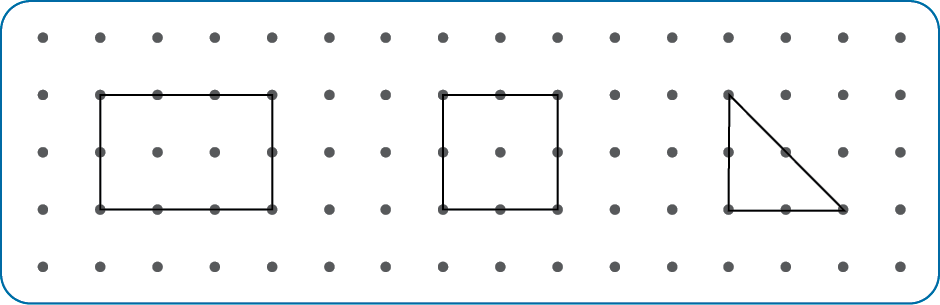

- REPRODUZA, NA MALHA PONTILHADA ABAIXO, OS CONTORNOS DAS FIGURAS QUE FABIANA FEZ. DEPOIS, PINTE CADA FIGURA COM UMA COR DIFERENTE.
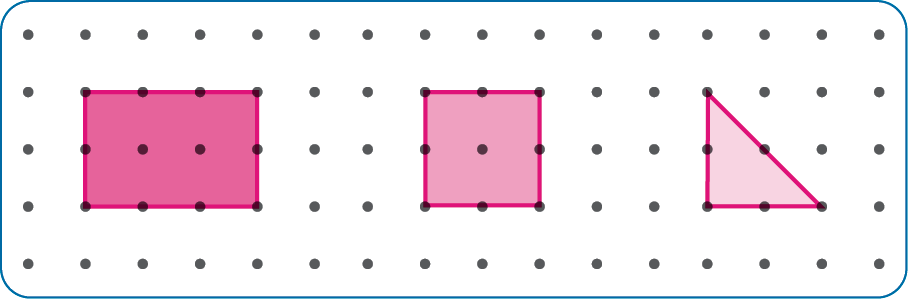

- QUAIS FIGURAS GEOMÉTRICAS PLANAS VOCÊ REPRODUZIU?
PROFESSOR
Resposta: Retângulo, quadrado e triângulo.
AUTOAVALIAÇÃO

• QUANDO OBSERVO UM OBJETO, COMO FAÇO PARA PERCEBER A FIGURA GEOMÉTRICA NÃO PLANA QUE PODE SER REPRESENTADA POR ELE?
PROFESSOR
Resposta pessoal.

- CONSIGO COMPREENDER INDICAÇÕES DE LOCALIZAÇÃO DE OBJETOS OU DE ALGUNS TRAJETOS?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Os estudantes precisam ficar atentos à medida do comprimento dos lados, percebendo quantos pontos da malha pontilhada estão no contorno da figura, quantos e quais pontos serão os vértices etc.
A representação de figuras geométricas planas em uma malha pontilhada exige o reconhecimento de diversas características da figura, como a relação entre os lados consecutivos, que podem ou não formar “cantos retos”, podem ou não ter a mesma medida de comprimento etc.
É necessário também que eles localizem os pontos que estão na mesma posição nos dois quadros. Chame a atenção para as duas direções (vertical e horizontal) em que podem contar os pontos a fim de se localizarem. Por fim, retome a nomenclatura das figuras.
Se necessário, destaque que a escala não será usada, servirá apenas de apoio para o traçado dos lados das figuras. É comum que crianças dessa faixa etária tenham dificuldades em fazer coincidir as extremidades da linha reta com os pontos da malha; oriente-as a colocar o lápis sobre um dos pontos (extremidades) e, apoiando a régua na ponta do lápis, girá-la, de modo que a façam coincidir com a outra extremidade.
Autoavaliação
Na primeira pergunta, alguns estudantes podem perceber semelhanças e diferenças entre as figuras não planas; outros podem apresentar dificuldades em relacionar as características à nomenclatura; outros, ainda, podem não identificar diferenças entre as quantidades de faces ou lados.
Alguns já podem ter desenvolvido um bom olhar geométrico e conseguem comunicar os elementos de cada objeto. Portanto, é importante que respondam às questões de forma detalhada para que sejam feitas as intervenções necessárias.
Na segunda questão, resgate a conversa realizada ao final da Unidade 1, que explora conceitos relacionados à posição. Para que os trajetos sejam compreendidos, alguns termos trabalhados anteriormente precisam estar internalizados. Espera-se que os estudantes sinalizem que não entendem descrições de trajetos por não reconhecerem certos vocábulos; outros podem precisar de ajuda com apenas alguns conceitos, como direita e esquerda; outros, além de compreender, podem comunicar outras possibilidades de trajeto para o mesmo espaço.
BNCC em foco:
EF01MA14
MP132
Comentários para o professor
Conclusão da Unidade 4
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observações |
|---|---|---|
|
Reconhece e relaciona figuras geométricas espaciais com objetos familiares do mundo físico? |
_____ |
_____ |
|
Reconhece e relaciona figuras geométricas planas com o formato das faces de figuras geométricas espaciais? |
_____ |
_____ |
|
Descreve a localização de pessoas e de objetos no espaço em relação à própria posição e também itinerários fazendo uso de termos como à direita, à esquerda, em frente, atrás, em cima, embaixo, perto, longe? |
_____ |
_____ |
|
Identifica regularidades ou padrões figurais em sequências recursivas, bem como completa-as com elementos faltantes? |
_____ |
_____ |
|
Compõe figuras planas pela justaposição de outras figuras dadas, por exemplo, com as partes do Tangram? |
_____ |
_____ |
|
Coleta informações em textos e listas e as organiza em tabelas? |
_____ |
_____ |
|
Estabelece relações entre o símbolo e o que ele representa, ou seja, entre o representante e o representado? |
_____ |
_____ |
|
Consegue organizar informações e registrá-las por meio de desenhos ou palavras? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP133
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação, encenações e dramatizações, entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
AUTOAVALIAÇÃO |
|||
|---|---|---|---|
|
NOME: _____ |
|||
|
MARQUE UM X EM SUA RESPOSTA PARA CADA PERGUNTA. |
SIM |
MAIS OU MENOS |
NÃO |
|
1. PRESTO ATENÇÃO NAS AULAS? |
_____ |
_____ |
_____ |
|
2. PERGUNTO AO PROFESSOR QUANDO NÃO ENTENDO? |
_____ |
_____ |
_____ |
|
3. SOU PARTICIPATIVO? |
_____ |
_____ |
_____ |
|
4. RESPEITO MEUS COLEGAS E PROCURO AJUDÁ-LOS? |
_____ |
_____ |
_____ |
|
5. SOU EDUCADO? |
_____ |
_____ |
_____ |
|
6. FAÇO TODAS AS ATIVIDADES COM CAPRICHO? |
_____ |
_____ |
_____ |
|
7. TRAGO O MATERIAL ESCOLAR NECESSÁRIO E CUIDO BEM DELE? |
_____ |
_____ |
_____ |
|
8. CUIDO DOS MATERIAIS E DO ESPAÇO FÍSICO DA ESCOLA? |
_____ |
_____ |
_____ |
|
9. GOSTO DE TRABALHAR EM GRUPO? |
_____ |
_____ |
_____ |
|
10. RESPEITO TODOS OS MEUS COLEGAS DE TURMA, PROFESSORES E FUNCIONÁRIOS? |
_____ |
_____ |
_____ |









