MP134
Comentários para o professor:
Introdução da Unidade 5
As páginas de abertura possibilitam diálogos a serem usados com o objetivo de diagnosticar os conhecimentos e habilidades que os estudantes trazem da Educação Infantil e, assim, constituírem-se em um bom instrumento para planejar as estratégias de ensino a serem aplicadas durante o ano letivo.
Em continuidade ao trabalho desenvolvido até aqui, em particular na Unidade 2, as Unidades Temáticas são abordadas considerando os conhecimentos anteriores, principalmente os decorrentes dessa Unidade.
Nesta Unidade, articulam-se todos os conhecimentos trabalhados nas unidades anteriores que dizem respeito à Unidade Temática Números. Assim, retomam-se atividades que envolvem: o uso de números naturais como indicador de quantidade ou de ordem; a contagem exata ou aproximada com o uso de diferentes estratégias; a contagem de objetos de coleções com até 100 unidades; a comparação entre números naturais até 100, com e sem o uso da reta numérica; e a composição e a decomposição de números.
As operações de adição e subtração também são retomadas por meio da resolução de problemas envolvendo números de até dois algarismos e os significados de juntar, acrescentar, comparar, completar e retirar com estratégias e registros pessoais.
Todos esses conhecimentos articulados constituem-se como subsídios para os estudos sobre a Unidade Temática Números, a serem desenvolvidos no 2º ano do Ensino Fundamental, entre os quais destacamos: a contagem ou estimativa da quantidade de objetos em coleções de até 1 000 unidades; a compreensão das características do sistema de numeração decimal, por meio da comparação e ordenamento de números naturais até a ordem das centenas; a composição e a decomposição de números naturais até a ordem das centenas, por meio de diferentes adições; a elaboração e resolução de problemas de adição e subtração com o uso de estratégias pessoais convencionais.
As diferentes abordagens para a Unidade Temática Números possibilitam que os conhecimentos sobre Álgebra permeiem as atividades que envolvem sequências recursivas de números naturais, suscitando, assim, o reconhecimento, a explicitação e, consequentemente, a descrição de um padrão relativo a cada sequência.
O reconhecimento e a relação entre valores de moedas e de cédulas do sistema monetário brasileiro – conhecimentos relativos a Grandezas e medidas – foram explorados nas Unidades 2 e 3 deste livro. A abordagem apresentada pretende retomar as situações que envolvem esse conhecimento, a fim de proporcionar aos estudantes saberes necessários para a resolução de problemas envolvendo a comparação e a equivalência de valores monetários do sistema brasileiro, conhecimento que será ampliado no 2º ano do Ensino Fundamental.
As Unidades Temáticas Números e Probabilidade e estatística articulam-se nas atividades apresentadas com o objetivo de ler dados expressos em gráficos de colunas simples. Esse trabalho foi iniciado nas unidades anteriores e é ampliado agora com a leitura de informações de pesquisas apresentadas por meio de gráfico de colunas simples com a introdução de legenda, para melhor compreensão de aspectos da realidade próxima.
Competência geral favorecida
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
MP135
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos alguns roteiros de aula que poderão servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados pelo professor em função das características da turma e dos recursos disponíveis.
Os jogos são recursos valiosos para o desenvolvimento simultâneo de habilidades matemáticas, motoras, sociais e éticas de estudantes nessa faixa etária. Conheça um exemplo de roteiro de aula relacionado à seção Jogo desta Unidade.
Roteiro de aula – Jogo: Desafio da selva 1 ª parte – Tempo sugerido: 15 minutos
Este é um jogo de trilha. Nele, a movimentação das peças reforça o entendimento de sequência numérica recursiva, mas também impõe atenção às ordens que quebram as regras de padrão e enriquecem o jogo. Nesse aspecto, proporcionam ao estudante um exercício de aprendizagem para lidar com tutoriais, cada dia mais importante nas mais diversas atividades humanas.
Organize as carteiras de modo que os estudantes possam trabalhar em duplas ou trios. Para a composição dos grupos, sugira escolhas livres, porém fique atento e auxilie aqueles que estiverem com dificuldade de encontrar colegas para realizar a atividade.
Auxilie, se necessário, o recorte do tabuleiro com tesoura de pontas arredondadas. Para cada grupo, basta um tabuleiro.
Faça a leitura coletiva das regras do jogo e certifique-se de que elas foram compreendidas por todos. Avalie a necessidade de simular, junto com um dos grupos, um início de procedimento que sirva como exemplo e esclareça possíveis dúvidas. Essa orientação é válida para os jogos em geral, portanto, pode ser adaptada para atividades semelhantes.
2 ª parte – Tempo sugerido: 25 minutos
Anuncie que o tempo do jogo é de 15 minutos, e, nesse tempo, deixe os estudantes jogarem livremente, mas acompanhe as ações dos grupos para administrar impasses, caso necessário.
A seguir, peça a eles que retomem o livro, respondam individualmente às questões propostas (5 minutos) e depois troquem os livros para socializarem as respostas.
Nos últimos 5 minutos, antes de recolocar as carteiras nas posições de costume, solicite a três estudantes (verifique se há voluntários) que respondam a cada questão.
MP136
UNIDADE 5. VAMOS CONTAR MAIS

MANUAL DO PROFESSOR
Objetivos da Unidade
Ampliar os procedimentos de contagem e a récita numérica.
Usar estratégias próprias para resolver problemas de adição e subtração.
Explorar adição e subtração em situação de jogo.
Reconhecer, fazer contagens e registrar quantidades até 99.
Compor e decompor números por meio de adições.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Comparar números naturais até 100.
Reconhecer regularidades em sequências numéricas e descrever elementos ausentes.
Utilizar números naturais como indicadores de quantidades.
Construir fatos fundamentais da adição.
Ler dados registrados em gráficos de colunas simples.
Esta Unidade explora e aprofunda o conteúdo relacionado à Unidade Temática Números. As quantidades são maiores e possibilitam o trabalho com a contagem e com sua representação numérica. São exploradas situações que permitem significar a manipulação de grandes quantidades.
As atividades desta Unidade permitem:
aos estudantes reconhecer agrupamentos e elaborar a escrita matemática;
ao professor identificar se os estudantes se apropriam desse modo de organização (agrupamento de 10 em 10) para completar quantidades.
BNCC em foco:
EF01MA01, EF01MA02, EF01MA04, EF01MA05, EF01MA06, EF01MA07, EF01MA08, EF01MA10, EF01MA19, EF01MA21
MP137
Página sem conteúdo.
MANUAL DO PROFESSOR
Explore a abertura e aponte para as ações dos personagens Guilherme e Letícia, que foram à casa do colega Lucas. Comente: “Sabem onde ele mora? Em um sítio! Lá há cavalos, vacas, bois, ovelhas, galinhas e um lindo cão que ajuda a tomar conta das ovelhas. Até passeio em carro de boi eles fizeram”. Incentive os estudantes a procurar os personagens na cena e pergunte: “Quem já montou em um cavalo?”; “Vocês já viram uma carroça puxada por bois, como a da cena?”. Conte que esse meio de transporte é geralmente chamado de carro de boi.
Com base na ilustração, sonde os conhecimentos prévios dos estudantes sobre os assuntos que serão explorados na Unidade, fazendo perguntas como:
Quantos animais há nessa cena? (20 animais.)
Quantas pessoas estão no carro de boi? (6 pessoas.)
No carro de boi cabem 10 pessoas. Quantas pessoas faltam para lotá-lo? (4 pessoas.)
Nesse sítio, também há galinhas. Elas botam ovos todos os dias. Somente hoje elas botaram, no total, 10 ovos. Vamos desenhar esses ovos? Se as galinhas botarem 10 ovos por dia, quantos ovos terão botado em 3 dias? (30 ovos.)
Lucas disse que havia 25 ovelhas no sítio. Foram compradas outras 4. Qual é o total de ovelhas agora? (29 ovelhas.)
Sugestão de trabalho interdisciplinar
Para um trabalho integrado com Língua Portuguesa, proponha aos estudantes a criação de uma história com base na imagem de abertura. Comece a história. Por exemplo: “Era uma vez um sítio, nesse sítio vivia uma família que criava ovelhas...”. Escreva essa introdução na lousa, convide algum estudante para continuar a história e escreva a continuação. Vá chamando diferentes estudantes e incentive-os a explorar os elementos da imagem.
MP138
JOGO: DESAFIO DA SELVA
Observação. ACOMPANHE AS INSTRUÇÕES QUE O PROFESSOR VAI LER. Fim da observação.

MATERIAL: TABULEIRO DAS PÁGINAS 193 E 195, MARCADORES (PEDRINHAS, TAMPINHAS OU OUTROS), UM PARA CADA JOGADOR, E O DADO QUE VOCÊ USOU NO JOGO ÁRVORE DAS MAÇÃS.

JOGADORES: 2 OU 3
REGRAS:
- CADA JOGADOR POSICIONA SEU MARCADOR NA CASA DE NÚMERO 1.
- OS JOGADORES DECIDEM QUEM VAI COMEÇAR.
- QUEM COMEÇA LANÇA O DADO E ANDA COM SEU MARCADOR O NÚMERO DE CASAS INDICADO NO DADO.
- CONFORME FOR PERCORRENDO A TRILHA, CADA JOGADOR DEVE LIDAR COM AS VANTAGENS E AS DESVANTAGENS DOS OBSTÁCULOS.
- GANHA QUEM CHEGAR PRIMEIRO À CASA DE NÚMERO 40.
Boxe complementar:
VEJA SE ENTENDEU
OBSERVE O MARCADOR DE TIAGO NO TABULEIRO E OS PONTOS QUE ELE ACABOU DE TIRAR NO DADO.

CRÉDITO: HÉLIO SENATORE/GEORGE TUTUMI

CRÉDITO: JOSÉ LUÍS JUHAS
EM QUAL CASA O MARCADOR DE TIAGO VAI PARAR NESSA JOGADA? _____
Resposta: 10
Fim do complemento.
MANUAL DO PROFESSOR
Objetivos
Ampliar os procedimentos de contagem e a récita numérica.
Explorar a adição e a subtração em situação de jogo.
Ajude os estudantes na leitura e na compreensão das regras. Os jogos de percurso atraem a atenção deles. De modo geral, eles apreciam jogos de tabuleiro, em que são solicitados a se movimentar com o objetivo de atingir o fim do percurso.
No contexto do jogo, a contagem e a sequência dos números são constantemente usadas em situações que se sucedem rapidamente – portanto, propícias ao cálculo mental e ao controle das ações dos colegas.
É importante definir previamente as duplas ou os trios para o jogo, levando em conta a autonomia nos procedimentos (ou seja, que “funcionem” bem) e os conhecimentos matemáticos, para que consigam mover o marcador de acordo com o número indicado no dado. Se possível, um estudante em cada dupla ou trio deve ler as armadilhas e os atalhos no tabuleiro.
Talvez alguns ainda não façam a correspondência de cada número falado com uma casa contada; será possível demonstrar esse procedimento a eles em uma situação contextualizada, como o jogo. É provável, ainda, que vários deles contem a casa da qual estão partindo ao avançar o marcador (assim, se tirarem três no dado, avançarão apenas duas casas). Caso isso aconteça, após a primeira partida, mostre no tabuleiro que se deve contar cada passo dado, de modo que não entra na conta a casa onde se está.
Em princípio, observe os estudantes jogarem livremente. Verifique se compreenderam as regras e se usam os conhecimentos numéricos para fazer previsões de resultados; por exemplo, à medida que se aproximam do fim do percurso, passam a se perguntar quantos pontos precisam tirar para vencer, quantos pontos o colega deve tirar para não vencer em determinada jogada etc.
BNCC em foco na dupla de páginas:
EF01MA02, EF01MA08; competência geral 9
Peça aos estudantes que, no fim do jogo, registrem os números das casas onde terminaram e faça perguntas como: “Quantas casas separaram o jogador que venceu (que ficou em primeiro lugar) do que estava mais próximo dele (em segundo lugar)? Seria possível você vencer (no caso de a pergunta não se dirigir ao vencedor da partida) com apenas mais um lançamento do dado?”.
Depois que todos os estudantes tiverem jogado ao menos uma vez – e nunca durante as partidas, pois é importante não interrompê-los para isso –, proponha alguns desafios orais:
MP139
QUESTÕES SOBRE O JOGO
OBSERVE ONDE ESTÃO OS MARCADORES DE CADA JOGADOR.

- O MARCADOR DE
 ESTÁ NA CASA DE NÚMERO 16. SE ELA AVANÇAR 3 CASAS, EM QUAL CASA VAI PARAR?
_____
ESTÁ NA CASA DE NÚMERO 16. SE ELA AVANÇAR 3 CASAS, EM QUAL CASA VAI PARAR?
_____
PROFESSOR
Resposta: 17 - QUANTOS PONTOS
 PRECISA TIRAR NO DADO PARA GANHAR O JOGO?
_____
PRECISA TIRAR NO DADO PARA GANHAR O JOGO?
_____
PROFESSOR
Resposta: 1, 4, 5 ou 6 - O MARCADOR DE
 ESTAVA NA CASA 14. PARA CHEGAR À CASA 17, QUANTOS PONTOS ELE TIROU NO DADO?
_____
ESTAVA NA CASA 14. PARA CHEGAR À CASA 17, QUANTOS PONTOS ELE TIROU NO DADO?
_____
PROFESSOR
Resposta: 3
MANUAL DO PROFESSOR
Meu marcador estava na casa 10 e tirei 5 no dado. Em que casa fui parar? (15, mas, como nessa casa há um comando para voltar 1 casa, parei na casa 14.)
Se você cai na casa 19, que manda voltar duas casas, em que número de casa você vai parar? (17.)
Se João está na casa 10 e Sofia, na casa 20, quantas casas ela está na frente dele? (10.)
Questão sobre o jogo
A questão proposta explora os três principais desafios presentes no jogo: compreender as informações dadas nos enunciados; contar corretamente as casas; compreender a diferença entre os números que indicam a ordem das casas (os que estão escritos em cada uma delas) e os números que indicam a quantidade de passos.
A ação de avançar no percurso corresponde a acrescentar ao número da casa em que se está os passos dados na jogada, para descobrir o número da casa a que se chegará. No entanto, é preciso observar também os atalhos e as armadilhas para saber o posicionamento correto.
Variações
Depois que os estudantes já estiverem habituados a esse jogo, pode-se propor a eles, em momentos posteriores, durante o ano, voltar ao jogo utilizando dois dados e observando se os estudantes obtêm a soma dos pontos e fazem o deslocamento ou se realizam o deslocamento relativo a cada quantidade obtida nos dados.
MP140
APRENDENDO MAIS NÚMEROS
- CARINA, JÚLIA E LUANA QUEREM COMPRAR UM QUEBRA-CABEÇA QUE CUSTA 28 REAIS. CADA UMA ECONOMIZOU 10 REAIS. SE ELAS JUNTAREM ESSAS QUANTIAS ECONOMIZADAS, CONSEGUIRÃO COMPRAR O QUEBRA-CABEÇA?

( ) SIM
( ) NÃO
PROFESSOR
Resposta correta: sim. 30 é maior que 28; então, elas conseguirão comprar.

- DESCUBRA O “SEGREDO” DE CADA SEQUÊNCIA E COMPLETE-A.

PROFESSOR
Resposta: 10, 15, 25, 30
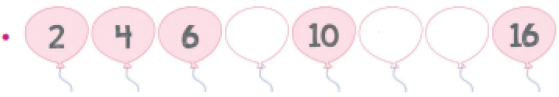
PROFESSOR
Resposta: 8, 12, 14

PROFESSOR
Resposta: 12, 10, 6

PROFESSOR
Resposta: 26, 22, 18- AUGUSTO FEZ 3 DEZENAS DE BRIGADEIROS E 12 CAJUZINHOS. QUANTOS BRIGADEIROS ELE FEZ A MAIS QUE CAJUZINHOS?

AUGUSTO FEZ _____ BRIGADEIROS A MAIS QUE CAJUZINHOS.
PROFESSOR
Resposta: 18PROFESSOR
Exemplos de cálculos:PROFESSOR
10 + 10 + 10 = 30PROFESSOR
30 − 12 = 18MANUAL DO PROFESSOR
Objetivos
Reconhecer, fazer contagens e registrar quantidades até 99.
Compor e decompor números por meio de adições.
Usar estratégias pessoais para resolver problemas de adição e subtração.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Comparar números naturais até 99.
Reconhecer regularidades em sequências numéricas e descrever elementos ausentes.
Escreva na lousa os números de 1 a 30 (registrando de 10 em 10 em cada linha) e explore: “Qual é o número dez? E o número vinte? E o vinte e oito?”. Observe como os estudantes procuram os números e se eles percebem as regularidades nessa organização numérica. Pergunte também: “Como sabem que esse número é o vinte e oito?”. Deixe que apresentem suas justificativas e ouçam as dos colegas. O objetivo é retomar a regularidade na escrita dos números.
Outras perguntas ligadas à quantidade podem ser feitas, como: “Se tivermos dez laranjas em uma cesta e colocarmos mais duas, quantas laranjas ficarão na cesta?”. Peça que registrem essa quantidade e observe como isso é feito. Alguns costumam escrever o 10 e o 2 justapostos (102).
A escrita 102 no lugar de 12 é bastante comum entre os estudantes, o que não significa que não compreendam a quantidade 12, mas ainda estão em processo de aprendizagem sobre a escrita desses números.
Atividade 1
Disponibilize material manipulável (tampinhas ou cubinhos do Material Dourado) para os estudantes usarem, se necessário, a fim de obter a quantia economizada. Espera-se que eles observem que 30 é maior que 28 e, assim, concluam que as meninas conseguirão comprar o quebra-cabeça.
Atividade 2
Os estudantes podem ser organizados em duplas para realizar esta atividade. Sugira a eles que façam a contagem um a um primeiro, para depois perceberem o “segredo” de cada sequência. Depois, em uma roda de conversa, peça que expliquem como pensaram e como completaram cada sequência.
Atividade 3
Leia o problema e peça a alguns estudantes que expliquem o que ele diz. Registre na lousa os elementos fornecidos e a pergunta. Dê um tempo para eles elaborarem uma estratégia de resolução, observando o entendimento deles sobre a dezena (agrupamento de 10 unidades).
BNCC em foco:
EF01MA02, EF01MA05, EF01MA08, EF01MA10
MP141
- VAMOS CONTAR.
- HÁ QUANTOS PALITOS?
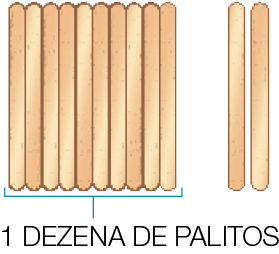
1 DEZENA MAIS _____ UNIDADES
_____ + 2 = _____
HÁ _____ (DOZE) PALITOS (OU UMA DÚZIA DE PALITOS).
PROFESSOR
Resposta: 1 DEZENA MAIS 2 UNIDADESPROFESSOR
10 + 2 = 12PROFESSOR
HÁ 12 (DOZE) PALITOS (OU UMA DÚZIA DE PALITOS).- HÁ QUANTOS COPOS?

_____ DEZENAS MAIS _____ UNIDADES.
30 + _____ = 36
HÁ _____ (TRINTA E SEIS) COPOS OU _____ DÚZIAS DE COPOS.
PROFESSOR
Resposta: 3 DEZENAS MAIS 6 UNIDADES.PROFESSOR
30 + 6 = 36PROFESSOR
HÁ 36 (TRINTA E SEIS) COPOS OU 3 DÚZIAS DE COPOS.- OBSERVE AS 4 CÉDULAS DE 10 REAIS E COMPLETE.

_____ CÉDULAS DE 10 REAIS FORMAM 40 REAIS.
PROFESSOR
Resposta: 44 DEZENAS É IGUAL A _____ (QUARENTA) UNIDADES.
PROFESSOR
Resposta: 40MANUAL DO PROFESSOR
Atividade 4
Nesta atividade, a ideia é dar pistas do princípio aditivo da formação dos números (12 = 10 + 2 e 36 = 30 + 6), mas não se espera que nessa faixa etária os estudantes se apropriem por completo desse conceito.
Atividade 5
Peça aos estudantes que manipulem cédulas e moedas do Material complementar para responder a novos questionamentos, como: “Se juntarmos quatro cédulas de 10 reais e cinco moedas de 1 real, quantos reais teremos?” (45 reais.).
BNCC em foco:
EF01MA02, EF01MA07, EF01MA19
MP142
- COMPLETE O QUADRO.
Quadro: equivalente textual a seguir.
|
41 |
QUARENTA E _____ |
45 |
QUARENTA E CINCO |
|
_____ |
QUARENTA E DOIS |
46 |
QUARENTA E _____ |
|
_____ |
QUARENTA E TRÊS |
47 |
QUARENTA E _____ |
|
44 |
QUARENTA E _____ |
48 |
QUARENTA E OITO |
PROFESSOR
Resposta: um, 42, 43, quatro, seis, sete.- EM CADA CAIXA, HÁ 10 LARANJAS.

- HÁ QUANTAS LARANJAS NO TOTAL?
_____ + _____ + _____ + _____ + _____ = 50
PROFESSOR
Resposta: 10 + 10 + 10 + 10 + 10 = 50
5 DEZENAS É IGUAL A _____ (CINQUENTA) UNIDADES.
PROFESSOR
Resposta: 50

- DESENHE OS CHAPÉUS QUE FALTAM PARA COMPLETAR 35 (TRINTA E CINCO).

PROFESSOR
Exemplo de desenho:
MANUAL DO PROFESSOR
Atividade 6
Esta atividade pode ser ampliada pedindo aos estudantes que escrevam por extenso os números de 30 a 50. Faça um cartaz com os números de 1 a 50 para ampliar também a récita numérica, a fim de que eles consultem sempre que sentirem necessidade.
Atividade 7
Nesta atividade, a quantidade 50 é composta da adição de 5 grupos de 10 (5 dezenas), ou seja, são relacionadas as diferentes quantidades entre si. Atividades de composição e decomposição de números possibilitam estabelecer relações entre as quantidades, aspecto fundamental na construção do conceito de número, pois a sequência dos números não é uma sucessão de termos desconexos.
Ao final da atividade, verifique se os estudantes abstraem o conceito de número para quantidades maiores que 50 propondo a situação: “Se tenho 2 baldes, um com 49 bolinhas e outro com 50 bolinhas, qual deles tem mais bolinhas? Quantas a mais?”. Pergunte, então: “Se eu colocar uma bolinha em cada balde, sucessivamente (para cada bolinha colocada em um balde, coloco uma bolinha no outro balde), após fazer isso muitas e muitas vezes, qual dos baldes terá mais bolinhas?”. Espera-se que eles compreendam que o balde que começou com 50 bolinhas sempre terá 1 bolinha a mais que o outro. Isso indicará que foram capazes de pensar na ausência dos objetos físicos e abstraíram a ideia de número para quantidades maiores do que as que já tiveram a oportunidade de contar.
Espera-se, também, que os estudantes compreendam que há uma regularidade na ação realizada, uma vez que a diferença na quantidade de bolinhas (1) se mantém se a mesma quantidade é adicionada nos dois baldes.
Atividade 8
A situação proposta é uma ótima oportunidade para discutir as vantagens da organização em grupos de dez. É importante que os estudantes utilizem essa estratégia, pois fazer contagens agrupando de dez em dez os prepara para os cálculos mentais.
BNCC em foco:
EF01MA04, EF01MA07
MP143
- FAÇA A CORRESPONDÊNCIA CORRETA.
COLUNA 1
41
35
50
COLUNA 2
5 DEZENAS
4 DEZENAS MAIS 1 UNIDADE
3 DEZENAS MAIS 5 UNIDADES
PROFESSOR
Resposta: 41 - 4 dezenas mais 1 unidadePROFESSOR
35 - 3 dezenas mais 5 unidadesPROFESSOR
50 - 5 dezenas- ESCREVA OS NÚMEROS QUE ESTÃO ENTRE O NÚMERO 45 E O NÚMERO 50.
_____
PROFESSOR
Resposta: 46, 47, 48, 49

- RESPONDA ÀS PERGUNTAS DE MÁRCIA.

PROFESSOR
Resposta: 35 reais; o jogo de 33 reais.MANUAL DO PROFESSOR
Atividade 9
Amplie a atividade escrevendo outros números (entre 1 e 50) na lousa e peça a alguns estudantes que façam a decomposição do mesmo modo que foi feito nesta atividade. Em seguida, escreva a decomposição de outros números, para que mais alguns estudantes venham escrever o número formado por ela. Depois, faça um ditado de números (de 1 a 50) falando suas decomposições para que eles registrem o número usando algarismos e por extenso.
Atividade 10
Comente que “entre 45 e 50” são os números que, na sequência numérica de um em um, ficam depois do 45, mas antes do 50. Por isso, nem o número 45 nem o 50 fazem parte da resposta.
Aproveite e comente que, quando falamos “de 45 a 50”, significa todos os números iniciando no 45 e finalizando no 50, contando de um em um.
Dê outros intervalos, tais como:
Escreva os números que estão entre o número 31 e o número 45. (32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43 e 44.)
Quais números são maiores que 45 e menores que 49? (46, 47 e 48.)
Escreva os números que estão entre 39 e 49. (40, 41, 42, 43, 44, 45, 46, 47 e 48.)
Atividade 11
Inicialmente, explore a imagem. Peça aos estudantes que descrevam os elementos que fazem parte dela. Pergunte:
Qual brinquedo é mais caro? (O urso.)
E qual é o mais barato? (O jogo.)
Quantos reais faltam para a menina comprar o carrinho? (3 reais.)
BNCC em foco:
EF01MA04, EF01MA05
Sugestão de leitura para o professor
Livro
PARRA, Cecília; SAIZ, Irma (org.). Didática da Matemática: reflexões psicopedagógicas. Porto Alegre: Artmed, 1996.
A obra traz reflexões sobre a Matemática a ser ensinada na Educação Básica, além de analisar a situação do ensino e da aprendizagem de conteúdos importantes do Ensino Fundamental.
MP144
DE DEZ EM DEZ

- QUAL É O ESPORTE QUE RODOLFO PRATICA? MARQUE COM UM X. PARTINDO DO 0 (ZERO), PARA SABER O PRÓXIMO NÚMERO, SEMPRE ACRESCENTE 10. PINTE OS CÍRCULOS DOS NÚMEROS QUE DESCOBRIR E CHEGUE NO ESPORTE DE RODOLFO.

( ) FUTEBOL
( ) BASQUETE
( ) VÔLEI
PROFESSOR
Resposta correta: futebol- AGORA, COMPLETE A SEQUÊNCIA DE NÚMEROS DOS CÍRCULOS QUE VOCÊ PINTOU.
Tabela: equivalente textual a seguir.
|
0 |
10 |
_____ |
_____ |
_____ |
50 |
_____ |
70 |
_____ |
90 |
100 |
PROFESSOR
Resposta: 20, 30, 40, 60, 80MANUAL DO PROFESSOR
Objetivos
Ampliar os procedimentos de contagem e a récita numérica.
Utilizar números naturais como indicadores de quantidades.
Comparar números naturais até 100.
Construir fatos fundamentais da adição.
Reconhecer regularidades em sequências numéricas e descrever elementos ausentes.
Usar estratégias próprias para resolver problemas de adição e subtração.
Compor e decompor números até 100.
As dezenas inteiras são importantes por facilitarem a contagem de quantidades, além de estarem diretamente relacionadas às características do sistema de numeração decimal. Elas servem para a localização de números em uma sequência numérica e são importantes para o desenvolvimento das habilidades de estimativa e de cálculo mental. Por exemplo, para saber quantos grupos são 37 balas, podemos avaliá-las como uma quantidade maior que três grupos de 10 balas e menor que quatro grupos de 10 balas.
É importante trabalhar com a sequência das dezenas inteiras, incentivando-os a expressá-las nas ordens crescente e decrescente: dez, vinte, trinta, quarenta etc.
Atividade 1
Aproveite para perguntar: “Conhecer a escrita dos números (com símbolos) de 1 a 10 ajuda a escrever as dezenas inteiras de 10 a 100?”. Espera-se que os estudantes observem as regularidades na escrita que há entre os números de 1 a 9 e as dezenas inteiras 10, 20, 30, 40, 50, 60, 70, 80 e 90. É importante perceberem que basta acrescentar o algarismo zero à direita do número – o que significa que o algarismo 1, por exemplo, que representa uma unidade, passa a representar uma dezena ou 10. (Não é necessário aprofundar o assunto nesse momento.)
Pergunte: “Que dezena inteira está entre trinta e cinquenta? E que dezena inteira é a primeira maior que oitenta?”. Espera-se que os estudantes respondam, respectivamente, quarenta e noventa. Perguntas desse tipo favorecem o estabelecimento de relações entre as dezenas inteiras e desenvolvem a estimativa de cálculo pelos estudantes.
BNCC em foco:
EF01MA01, EF01MA05, EF01MA06, EF01MA10
MP145

- DESENHE AS BOLAS QUE FALTAM PARA COMPLETAR 10 (DEZ UNIDADES OU 1 DEZENA) EM CADA UMA DAS PRATELEIRAS DA ESTANTE ABAIXO.
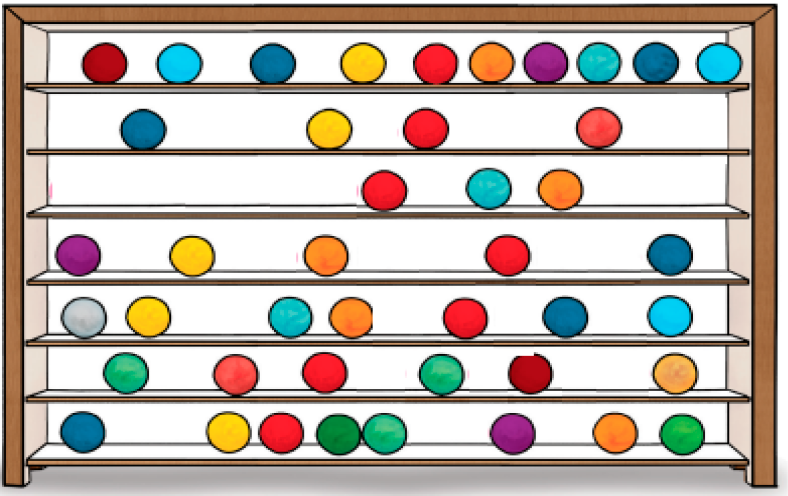
PROFESSOR
Resposta: Exemplo de desenho: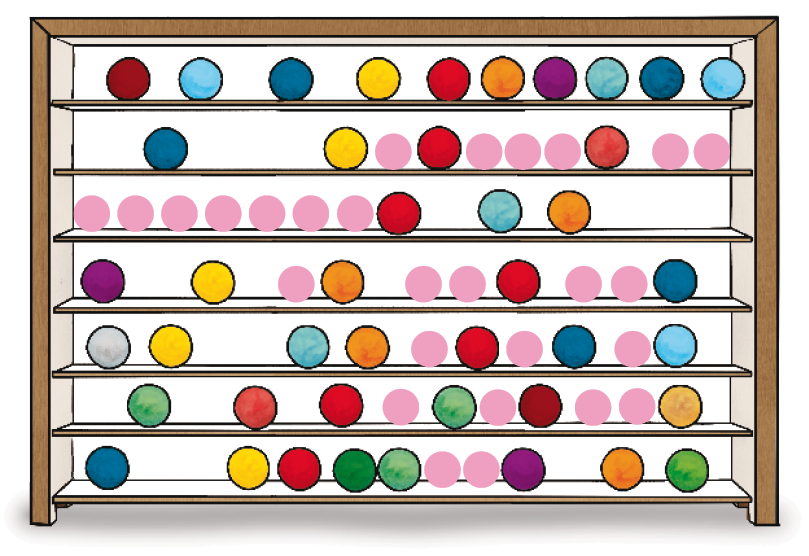
AGORA QUE VOCÊ COMPLETOU AS PRATELEIRAS, RESPONDA:
- QUANTAS BOLAS HÁ EM 2 PRATELEIRAS CHEIAS?
_____
PROFESSOR
Resposta: 20 - QUANTAS BOLAS HÁ EM 5 PRATELEIRAS CHEIAS?
_____
PROFESSOR
Resposta: 50 - QUANTAS BOLAS HÁ EM TODA A ESTANTE?
_____
PROFESSOR
Resposta: 70
- OS NÚMEROS NA LOUSA ESTÃO DESORGANIZADOS.

- ORGANIZE-OS ABAIXO, ESCREVENDO DO MAIOR PARA O MENOR.
_____, 80, _____, _____, _____, _____
PROFESSOR
Resposta: 100, 60, 50, 30, 10MANUAL DO PROFESSOR
Atividade 2
Quando os estudantes tiverem completado as prateleiras da estante, pergunte quantas bolas precisaram acrescentar para completar dez em cada prateleira, anotando todas as combinações na lousa. Ao final, terão uma lista de modos de formar 10 pela adição de duas parcelas: 4 e 6; 3 e 7; 5 e 5 etc. Podem-se também apresentar essas combinações como sentenças matemáticas:
4 + 6 = 10; 3 + 7 = 10 etc.
Composições como essas contribuem para desenvolver habilidades de cálculo mental, em que uma das estratégias mais utilizadas para a adição é o agrupamento em 10.
Atividade 3
Se perceber que os estudantes estão com dificuldade em ordenar os números do maior para o menor, peça a eles que, para cada número, desenhem tracinhos e os agrupem de 10 em 10. Assim, poderão ordenar os números comparando os grupos de 10 tracinhos.
Amplie a atividade e construa, na lousa, uma reta numérica marcando os números 10, 50 e 80. Então, peça aos estudantes que localizem os demais números que aparecem na atividade.

CRÉDITO: ADILSON SECCO
O uso de cédulas e moedas do Material complementar pode ser um bom recurso para enfatizar a relação entre unidades simples e dezenas inteiras. No caso de moedas de 1 real, a contagem da quantidade de moedas e a do valor correspondente aumentam de um em um, enquanto no caso da contagem de cédulas de 10 reais a quantidade de cédulas aumenta de um em um, e a contagem do valor correspondente aumenta de dez em dez, favorecendo a observação de “unidades de diferentes valores”.
BNCC em foco:
EF01MA05, EF01MA06, EF01MA07, EF01MA08
MP146
- CERQUE COM UMA LINHA GRUPOS DE 10 ELEMENTOS.
PROFESSOR
Exemplo de agrupamentos:
PROFESSOR
Resposta: circular 6 grupos com 10 elementos cada.- QUANTAS DEZENAS VOCÊ CERCOU?
_____
PROFESSOR
Resposta: 6 - QUANTOS ELEMENTOS HÁ AO TODO?
_____
PROFESSOR
Resposta: 60

- LORENZO FEZ COMPOTAS DE FRUTAS E COLOCOU EM POTES. PARA FAZER CADA COMPOTA, ELE USOU 10 FRUTAS.
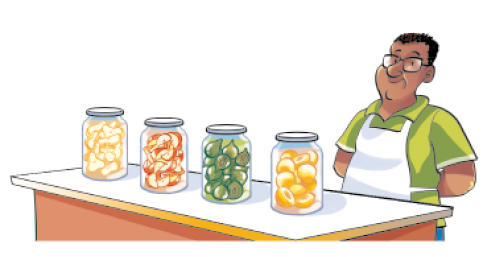
- QUANTAS COMPOTAS LORENZO FEZ?
_____
PROFESSOR
Resposta: 4 - QUANTAS DEZENAS DE FRUTAS LORENZO USOU AO TODO?
_____
PROFESSOR
Resposta: 4 - QUANTAS FRUTAS LORENZO USOU AO TODO?
_____
PROFESSOR
Resposta: 40

- COMPLETE A SEQUÊNCIA ABAIXO SABENDO QUE SEUS NÚMEROS DIMINUEM DE 10 EM 10.
100, 90, 80, _____, 60, _____, _____, _____, _____
PROFESSOR
Resposta: 70, 50, 40, 30, 20
- QUAL É O MENOR NÚMERO DESSA SEQUÊNCIA?
_____
PROFESSOR
Resposta: 20
MANUAL DO PROFESSOR
Atividade 4
Explique aos estudantes que eles devem cercar todos os grupos de 10 elementos que possam formar. Relembre-os de que 1 dezena corresponde a um agrupamento de 10 unidades.
Atividade 5
Antes de realizar esta atividade, promova uma situação similar na sala. Para isso, providencie 4 caixinhas de cores diferentes e as peças do Material Dourado (cubinhos e barrinhas).
1º) Mostre aos estudantes que 1 barrinha corresponde ao agrupamento de 10 cubinhos, ou seja, equivale a 1 dezena de cubinhos.
2º) Coloque 1 barrinha em cada caixa e pergunte:
Quantas dezenas foram colocadas em cada caixa? (Uma.)
Quantas dezenas foram colocadas ao todo nessas caixas? (Quatro.)
Quantas unidades foram colocadas ao todo nessas caixas? (Quarenta.)
3º) Para comprovar a quantidade total de unidades colocada nas caixas, troque cada barrinha por 10 cubinhos (soltos) em cada caixa e depois, com os estudantes, conte o total de cubinhos.
Em seguida, leia o comando da atividade para os estudantes e peça a eles que respondam a cada questão.
Atividade 6
Antes de realizar esta atividade, conte em voz alta com os estudantes de 10 em 10, a partir do 10 até o 100 (dez, vinte, trinta, quarenta, cinquenta, sessenta, setenta, oitenta, noventa, cem). Depois, proponha a eles que falem os mesmos números (de 10 em 10, do 10 ao 100), mas, dessa vez, do maior para o menor (cem, noventa, oitenta, ..., vinte, dez).
Em seguida, leia o comando da atividade para os estudantes e deixe que eles completem a sequência dada.
BNCC em foco:
EF01MA01, EF01MA04, EF01MA06, EF01MA07, EF01MA08
MP147
- ROBERTA GANHOU 8 PACOTES DE FIGURINHAS COM 5 FIGURINHAS EM CADA UM PARA COLAR EM SEU ÁLBUM.
- QUANTAS FIGURINHAS ROBERTA GANHOU AO TODO?

PROFESSOR
Resposta: Exemplos de cálculos: 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 40ROBERTA GANHOU AO TODO _____ FIGURINHAS.
PROFESSOR
Resposta: 40- EM CADA PÁGINA DO ÁLBUM, CABEM 10 FIGURINHAS. QUANTAS PÁGINAS ROBERTA PODE COMPLETAR COM A QUANTIDADE DE FIGURINHAS QUE GANHOU?
PROFESSOR
Resposta:
ROBERTA PODE COMPLETAR _____ PÁGINAS.
PROFESSOR
Resposta: 4- QUANTAS DEZENAS DE FIGURINHAS ROBERTA GANHOU?
PROFESSOR
Resposta:
ROBERTA GANHOU _____ DEZENAS DE FIGURINHAS.
PROFESSOR
Resposta: 4Boxe complementar:
DESAFIO

SIGAM AS DICAS PARA DESCOBRIR OS NÚMEROS PROCURADOS.

CRÉDITO: CLAUDIO CHIYO / ILUSTRAÇÕES: JOSÉ LUÍS JUHAS
Resposta: 49. Espera-se que os estudantes percebam que não há um único número como resposta. Há três possibilidades: 33, 34 ou 35.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 7
Para responder a esta atividade, os estudantes não precisam saber significados da multiplicação nem da divisão; basta aplicar o que já aprenderam sobre contagem. Eles podem acrescentar uma quantidade a outra.
Faça questionamentos sobre outras quantidades para auxiliar os estudantes a obterem a quantidade de figurinhas correspondente a 8 pacotes ao todo, sabendo que cada pacote contém 5 figurinhas. Por exemplo:
Ao todo, quantas figurinhas há em 2 pacotes? (10 figurinhas.)
E em 3 pacotes? (15 figurinhas.)
E em 4 pacotes? (20 figurinhas.)
E em 5 pacotes? (25 figurinhas.)
E em 7 pacotes? (35 figurinhas.)
Da mesma maneira, explore as demais questões da atividade.
Desafio
Organize os estudantes em duplas e oriente-os de modo que cada dupla discuta critérios e procedimentos e proponha uma única resposta. Assim eles terão de explicitar, para si mesmos e para o outro, o caminho que os levou a concluir que a resposta seria um ou mais números.
Pode-se perguntar, por exemplo: “Existe algum número ou números que não precisa(m) ser procurado(s)?”. Lembre-se também de perguntar após cada exclusão: “Ainda há algum número que pode ser o procurado?”.
BNCC em foco:
EF01MA01, EF01MA04, EF01MA05, EF01MA06, EF01MA07, EF01MA08, EF01MA10
MP148
- VOCÊ JÁ BRINCOU DE JOGO DE BAFO OU DE BATE FIGURINHAS? GANHA QUEM VIRAR MAIS FIGURINHAS AO BATER COM A PALMA DA MÃO NO MONTE DE FIGURINHAS.
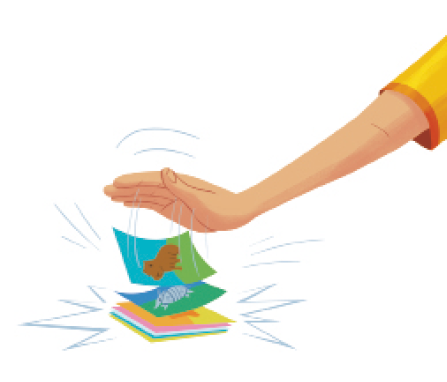
QUATRO AMIGOS JOGARAM BAFO. VAMOS DESCOBRIR QUANTAS FIGURINHAS CADA UM TEM APÓS ALGUMAS RODADAS?

ANA TEM:


ELISA TEM _____ FIGURINHAS.
PROFESSOR
Resposta: 22; Exemplo de cálculo: 12 + 10 = 22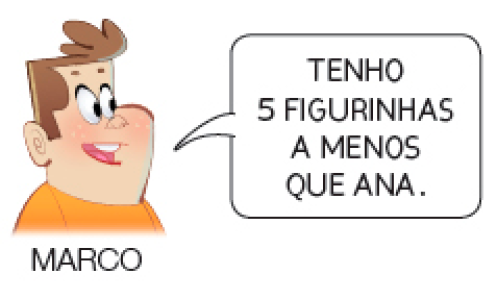
MARCO TEM _____ FIGURINHAS.
PROFESSOR
Resposta: 7; Exemplo de cálculo: 12 - 5 = 7
CAIO TEM _____ FIGURINHAS.
PROFESSOR
Resposta: 20; Exemplo de cálculo: 12 + 8 = 20MANUAL DO PROFESSOR
Objetivos
Usar estratégias próprias para resolver problemas de adição e subtração.
Comparar números naturais até 99.
Atividade 1
Incentive os estudantes a resolverem esta atividade fazendo uso do cálculo mental. Depois, se julgar conveniente, oriente-os a usar material manipulável para conferir os cálculos propostos ou dirimir as dúvidas. Valorize a etapa de verificação do problema, pedindo aos estudantes que observem, ao separar o material manipulável, se as afirmações a respeito da quantidade que cada criança tem se tornam verdadeiras pela solução encontrada por eles.
BNCC em foco:
EF01MA08
MP149

- NO JOGO DE BAFO DA ATIVIDADE ANTERIOR, APENAS ELISA TEM FIGURINHAS REPETIDAS, E SÃO 5. OS QUATRO AMIGOS TÊM UM ÚNICO ÁLBUM COM 58 ESPAÇOS PARA COLAR AS FIGURINHAS.

FAÇA ESTIMATIVAS PARA RESPONDER:
- QUANTAS FIGURINHAS, APROXIMADAMENTE, OS QUATRO AMIGOS CONSEGUIRAM JUNTAR?
PROFESSOR
Respostas pessoais.
ELES CONSEGUIRAM JUNTAR, APROXIMADAMENTE, _____ FIGURINHAS.
PROFESSOR
Resposta: 60- VÃO SOBRAR OU FALTAR FIGURINHAS PARA COMPLETAR O ÁLBUM? APROXIMADAMENTE, QUANTAS?
VÃO _____, APROXIMADAMENTE, _____ FIGURINHAS.
PROFESSOR
Resposta: Faltar.PROFESSOR
Atenção professor: Espera-se que os estudantes estimem menos de 10 figurinhas. Fim da observação.- SE JUNTAREM APENAS AS FIGURINHAS DE ANA, MARCO E CAIO, APROXIMADAMENTE, QUANTAS DEZENAS FALTARÃO PARA COMPLETAR O ÁLBUM?
FALTARÃO, APROXIMADAMENTE _____ DEZENAS.
PROFESSOR
Resposta: duas.MANUAL DO PROFESSOR
Atividade 2
Esta atividade explora uma situação-problema com várias questões envolvidas, em que cada resposta é importante para dar prosseguimento à resolução das outras questões. Pergunte aos estudantes se eles acham que a quantidade de figurinhas que os amigos têm é suficiente para preencher o álbum. Peça a eles que mostrem como pensaram para responder às questões. Somente depois deixe que façam os cálculos, usando estratégias pessoais, e socializem as diferentes estratégias. Se não surgir o assunto, lembre-os de que há 5 figurinhas repetidas, o que fará muita diferença no resultado final.
BNCC em foco:
EF01MA05, EF01MA08
MP150
- OBSERVE A LOTAÇÃO DESTES MEIOS DE TRANSPORTE E RESPONDA ÀS PERGUNTAS.
AVIÃO
LOTAÇÃO: 65 PASSAGEIROS
ÔNIBUS
LOTAÇÃO: 40 PASSAGEIROS
BARCO
LOTAÇÃO: 50 PASSAGEIROS
- QUAL DESSES MEIOS DE TRANSPORTE PODE LEVAR MAIS
PASSAGEIROS DE UMA VEZ? _____
PROFESSOR
Resposta: Avião - ESTANDO LOTADO, QUAL LEVA MENOS PASSAGEIROS?
_____
PROFESSOR
Resposta: Ônibus. - SE 60 PASSAGEIROS QUISEREM VIAJAR JUNTOS, EM QUAL DESSES MEIOS DE TRANSPORTE ELES PODERÃO VIAJAR COM CERTEZA?
_____
PROFESSOR
Resposta: No avião. - SE 35 PASSAGEIROS FOREM PARA A AMAZÔNIA DE ÔNIBUS, QUANTOS ASSENTOS FICARÃO VAZIOS DURANTE A VIAGEM?
FICARÃO VAZIOS _____ ASSENTOS.
PROFESSOR
Resposta: 5- LEIA A FRASE. DEPOIS, MARQUE COM UM X A AFIRMAÇÃO CORRETA DE ACORDO COM A LOTAÇÃO INDICADA ACIMA.
45 PASSAGEIROS VIAJARAM JUNTOS.
( ) COM CERTEZA ELES FORAM NESSE AVIÃO.
( ) COM CERTEZA ELES FORAM NESSE BARCO.
( ) É IMPOSSÍVEL QUE TENHAM IDO NESSE ÔNIBUS.
PROFESSOR
Resposta correta: é impossível que tenham ido nesse ônibus.MANUAL DO PROFESSOR
Atividade 3
Trata-se de uma situação-problema em que as respostas desencadeiam novos questionamentos. Esta atividade propõe aos estudantes que comparem números para verificar qual é o meio de transporte mais adequado para viajar, considerando a quantidade de pessoas que devem embarcar.
Em situações-problema como esta, é necessário reconhecer que não existe a melhor maneira de resolução. Todas as estratégias pessoais que os estudantes realizam devem ser valorizadas, e as estratégias que não oferecem a resposta correta necessitam ser problematizadas, permitindo que eles próprios percebam o erro e possam refletir sobre ele, a fim de encontrar uma maneira de corrigi-lo.
Observe que os significados envolvidos nesses problemas precisarão ser discutidos no grupo, pois, para os estudantes, não é simples traduzi-los em uma estratégia de resolução. Por isso, invista na interpretação e na verificação dos problemas: verificar se a resposta encontrada está de acordo com o que o problema apresenta como dado também é um jeito de avançar na compreensão do enunciado.
Na questão: “Se 35 passageiros forem para a Amazônia de ônibus, quantos assentos ficarão vazios durante a viagem?”, o significado da subtração é o de comparar quantidades; no entanto, ao resolvê-la, os estudantes podem usar a estratégia de completar quantidades, ou seja, considerando que são 35 passageiros, podem contar a partir do 36 até chegar ao 40, usando os dedos e estabelecendo relação entre a quantidade de dedos usados e a resposta. Lembre-se de discutir diferentes estratégias, validando aquelas que se mostram coerentes com o problema.
Para ampliar a atividade, proponha outras questões:
• Quantos passageiros o barco pode levar a mais que o ônibus? (10 passageiros.)
• Quantas pessoas o avião pode levar a mais que o barco? (15 pessoas.)
• Ao todo, quantos passageiros podem ser levados usando o ônibus e o barco? (90 passageiros.)
Para responder, é possível que os estudantes juntem as quantidades de passageiros por causa da palavra mais no enunciado, mas essa questão remete à comparação do número máximo de passageiros que cada meio de transporte apresentado pode levar.
Pode-se recorrer a outras atividades de comparação de quantidades para que os estudantes percebam o significado da situação. Por exemplo, recupere quais procedimentos eles usam para descobrir nos jogos quantos pontos um jogador ou time tem a mais que outro.
BNCC em foco:
EF01MA05, EF01MA08
MP151
- KAREN É COSTUREIRA E VAI FAZER UM MODELO NOVO DE BLUSA PARA A FÁBRICA EM QUE TRABALHA. PARA ISSO, FORAM COMPRADOS 3 ROLOS DE TECIDO.
VEJA A QUANTIDADE MÁXIMA DE ROUPAS DESSE MODELO NOVO QUE PODE SER FEITA COM CADA ROLO DE TECIDO.

TECIDO LISTRADO
10 BLUSAS DO MODELO NOVO

TECIDO DE BOLINHAS
12 BLUSAS DO MODELO NOVO
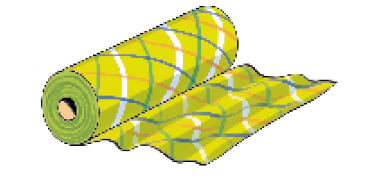
TECIDO XADREZ
18 BLUSAS DO MODELO NOVO

- EM QUAL DOS 3 ROLOS HÁ MAIS TECIDO?
PROFESSOR
Resposta: No rolo de tecido xadrez.
- EM QUAL DOS 3 ROLOS HÁ MENOS TECIDO?
PROFESSOR
Resposta: No rolo de tecido listrado.
- COMO VOCÊ PENSOU PARA RESPONDER ÀS QUESTÕES ANTERIORES?
PROFESSOR
Resposta pessoal. - NO MÁXIMO, QUANTAS BLUSAS DO MODELO NOVO PODERÃO SER PRODUZIDAS COM OS 3 ROLOS DE TECIDO?
PROFESSOR
Exemplo de cálculo: 10 + 12 + 18 = 40
PODERÃO SER PRODUZIDAS _____ BLUSAS DO MODELO NOVO COM OS 3 ROLOS DE TECIDO.
PROFESSOR
Resposta: 40MANUAL DO PROFESSOR
Atividade 4
O objetivo desta atividade é que os estudantes exercitem o que já aprenderam a respeito dos números e consigam perceber qual dos 3 rolos tem mais tecido com base na informação da quantidade de peças que podem ser feitas com cada rolo.
BNCC em foco:
EF01MA05, EF01MA08
MP152
COMPREENDER INFORMAÇÕES
LER GRÁFICOS
- EUGÊNIO FEZ UM GRÁFICO PARA MOSTRAR AS QUANTIDADES DE TRÊS TIPOS DE BRINQUEDO QUE ELE TINHA EM MAIO DE 2023.
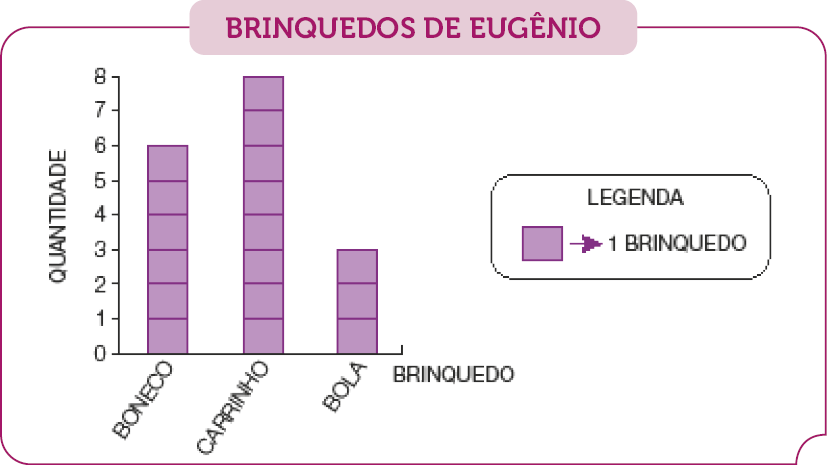
FONTE: LISTA DE BRINQUEDOS DE EUGÊNIO (MAIO 2023).
ESSE GRÁFICO É CONHECIDO COMO GRÁFICO DE COLUNAS.
NO GRÁFICO DE EUGÊNIO, CADA COLUNA É FORMADA POR QUADRINHOS, E CADA UM DELES REPRESENTA UM BRINQUEDO.
- QUAL É O BRINQUEDO QUE APRESENTA A COLUNA COM MAIS QUADRINHOS?
_____
PROFESSOR
Resposta: Carrinho. - SE A COLUNA DA BOLA TEM 3 QUADRINHOS, QUANTAS BOLAS EUGÊNIO TINHA?
_____
PROFESSOR
Resposta: 3 - PREENCHA A TABELA DE ACORDO COM O GRÁFICO.
BRINQUEDOS DE EUGÊNIO
Tabela: equivalente textual a seguir.
BRINQUEDO
BONECO
_____
_____
QUANTIDADE
6
_____
_____
FONTE: LISTA DE BRINQUEDOS DE EUGÊNIO (MAIO 2023).
PROFESSOR
Resposta: Brinquedo: carrinho. Quantidade: 8.PROFESSOR
Brinquedo: Bola. Quantidade: 3.
MANUAL DO PROFESSOR
Objetivos
Ler dados registrados em gráficos de colunas simples.
Comparar números naturais até 99.
Os gráficos estão presentes nas mais diversas situações. Saber ler, interpretar e tomar decisões com base em dados organizados em gráficos é fundamental para o exercício da cidadania.
O trabalho com gráficos baseia-se em conhecimentos prévios desenvolvidos em atividades que favorecem a classificação, a contagem e a comparação.
Comente que, assim como nas tabelas, os gráficos também devem apresentar um título e conter a informação sobre a fonte dos dados que possibilitaram sua construção.
Atividade 1
Com os estudantes, explore os elementos do gráfico, como o título, a fonte e os eixos.
Espera-se que os estudantes observem a quantidade de cada brinquedo na respectiva coluna e compreendam que cada quadrinho que compõe as colunas do gráfico corresponde a 1 brinquedo. Assim, eles podem identificar oralmente que Eugênio tem:
6 bonecos, já que a coluna correspondente a eles é composta de 6 quadrinhos;
8 carrinhos, pois a coluna correspondente a eles é composta de 8 quadrinhos;
3 bolas, pois a coluna correspondente a elas é composta de 3 quadrinhos.
Desse modo, os estudantes podem observar ainda, por exemplo, que a coluna que se refere aos carrinhos é a mais alta; portanto, indica o brinquedo que Eugênio tem em maior quantidade.
Depois, peça a eles que completem as questões e a tabela de acordo com os dados do gráfico.
BNCC em foco:
EF01MA21; competências específicas 3 e 4
MP153
- O MURO DA ESCOLA DE SUZANA SERÁ PINTADO. PARA DECIDIR A COR, OS ESTUDANTES PARTICIPARAM DE UMA VOTAÇÃO, EM FEVEREIRO DE 2023.
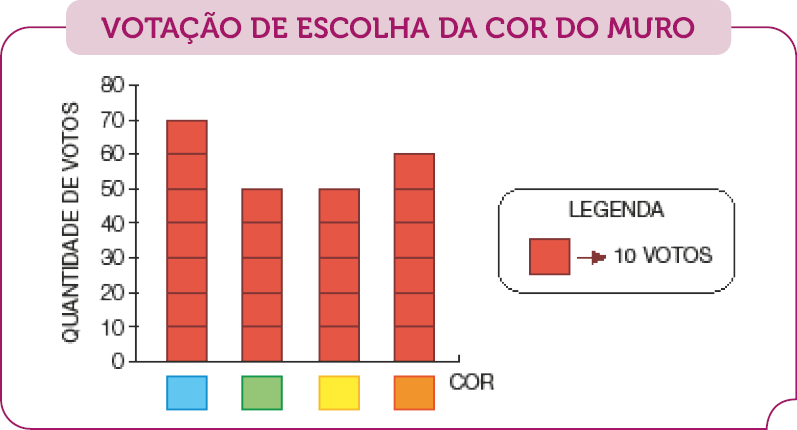
FONTE: ESCOLA PESQUISADA (FEV. 2023).
OBSERVE O GRÁFICO PARA RESPONDER ÀS QUESTÕES.
- QUANTOS VOTOS RECEBEU A COR AMARELA?
_____
PROFESSOR
Resposta: 50 - CADA QUADRINHO VERMELHO QUE COMPÕE AS COLUNAS CORRESPONDE A QUANTOS VOTOS?
_____
PROFESSOR
Resposta: 10 - QUE COR RECEBEU 60 VOTOS?
_____
PROFESSOR
Resposta: Laranja. - MARQUE COM UM X A COR MAIS VOTADA.
( )

( )

( )

( )

- QUE COR VOCÊ ESCOLHERIA PARA PINTAR O MURO?
_____
PROFESSOR
Resposta pessoal.
- COM QUAL COR O MURO PROVAVELMENTE SERÁ PINTADO? POR QUÊ?
PROFESSOR
Resposta: Azul, pois foi a cor que recebeu mais votos.
MANUAL DO PROFESSOR
Atividade 2
Da mesma maneira que na atividade 1, explore os elementos do gráfico apresentado. Verifique se eles percebem que as quantidades indicadas se referem aos votos dados pelos estudantes ao optarem pela cor preferida para pintar o muro da escola.
Essa questão apresenta uma dificuldade maior em relação à anterior, pois cada quadrinho que compõe as colunas do gráfico representa10 votos, ou seja, a simples contagem dos quadrinhos da coluna não dá o total de votos. Eles devem efetuar uma contagem de 10 em 10. Antes de continuar a atividade, verifique se todos entenderam esse fato.
Faça outros questionamentos, de modo que ora os estudantes observem as cores, ora procurem a quantidade de votos, conforme as questões propostas, para que se acostumem a buscar a informação no gráfico. Por exemplo:
Que cor teve 50 votos? (Espera-se que os estudantes percebam que foram duas: a verde e a amarela.)
Quantos votos teve a cor laranja? (60 votos.)
Por que as colunas que correspondem às cores verde e amarela têm a mesma altura? (Espera-se que os estudantes respondam que têm a mesma altura porque a quantidade de votos de cada uma dessas cores foi a mesma, ou seja, 50. Caso eles respondam que é porque têm a mesma quantidade de quadrinhos, pergunte por que isso aconteceu).
BNCC em foco:
EF01MA05, EF01MA21; competências específicas 3 e 4
MP154
O QUE VOCÊ APRENDEU
- FABIANA É PROFESSORA DE DUAS CLASSES DO 1º ANO. EM UMA CLASSE, HÁ 18 ESTUDANTES; NA OUTRA, 21 ESTUDANTES. QUANTOS ESTUDANTES DO 1º ANO FABIANA TEM AO TODO?

PROFESSOR
Exemplo de cálculo: 18 + 21 = 39FABIANA TEM _____ ESTUDANTES DO 1 º ANO.
PROFESSOR
Resposta: 39- ALEX PRECISA DE UMA DEZENA DE TAMPINHAS PARA FAZER UMA ATIVIDADE NA ESCOLA. ELE CONSEGUIU 6 TAMPINHAS. QUANTAS TAMPINHAS FALTAM PARA ALEX COMPLETAR UMA DEZENA?
PROFESSOR
Exemplo de cálculo: 10 − 6 = 4FALTAM _____ TAMPINHAS PARA ALEX COMPLETAR UMA DEZENA.
PROFESSOR
Resposta: 4

- PINTE COM A MESMA COR OS ESPAÇOS ESCRITOS COM NÚMEROS QUE, AO SEREM ADICIONADOS, FORMAM UMA DEZENA.
PROFESSOR
Resposta: 3, 2, 4, 7, 8, 6PROFESSOR
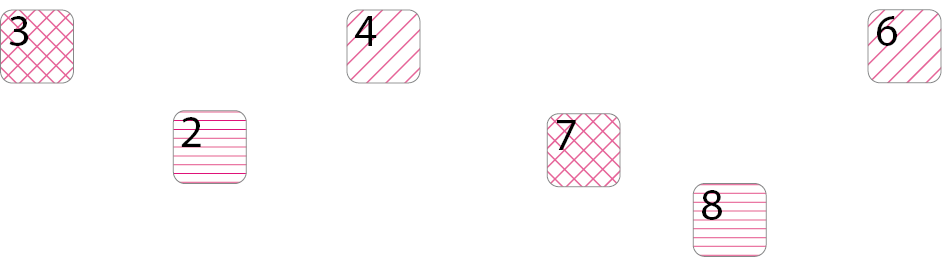
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Depois de realizar esta atividade, peça aos estudantes que modifiquem os dados do problema para que a professora Fabiana tenha, ao todo, 50 estudantes do 1 º ano.
Atividade 2
Peça aos estudantes que escrevam outras maneiras de completar 1 dezena, no caderno, com cálculo mental ou com material manipulável. Por exemplo, você pode fazer um ditado de quantidades para eles registrarem quanto falta para formar 10 unidades (e não o que foi ditado):
9 maçãs (O estudante deve registrar: 1 maçã.)
5 chaves (O estudante deve registrar: 5 chaves.)
1 caneta (O estudante deve registrar: 9 canetas.)
4 borrachas (O estudante deve registrar: 6 borrachas.)
8 cães (O estudante deve registrar: 2 cães.)
Atividade 3
Peça aos estudantes que digam os pares de números a serem pintados antes de efetuar a pintura.
BNCC em foco:
EF01MA06, EF01MA07, EF01MA08
MP155
AVALIAÇÃO PROCESSUAL
- LILIAN LEVOU 60 REAIS PARA FAZER COMPRAS NO MERCADO E VOLTOU COM 10 REAIS. QUANTOS REAIS LILIAN GASTOU?
PROFESSOR
Exemplo de cálculo: 60 − 10 = 50LILIAN GASTOU _____ REAIS.
PROFESSOR
Resposta: 50- OBSERVE A QUANTIDADE DE BRINQUEDOS EM CADA CAIXA.

- QUAL É A COR DA CAIXA EM QUE HÁ MAIOR QUANTIDADE DE BRINQUEDOS?
_____
PROFESSOR
Resposta: Amarela. - QUAL É A COR DA CAIXA EM QUE HÁ MENOR QUANTIDADE DE BRINQUEDOS?
_____
PROFESSOR
Resposta: Vermelha.
- QUANTOS BRINQUEDOS A CAIXA VERDE TEM A MAIS QUE A CAIXA VERMELHA?
_____
PROFESSOR
Resposta: 10 brinquedos.
AUTOAVALIAÇÃO

- CONSIGO LER E ESCREVER NÚMEROS DE MAIS DE UMA MANEIRA?
PROFESSOR
Resposta pessoal.
- CONSIGO IDENTIFICAR AS DEZENAS E AS UNIDADES QUE COMPÕEM UM NÚMERO?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Se necessário, deixe que os estudantes manipulem cédulas e moedas do Material complementar para auxiliar no cálculo ou para comprová-lo.
Amplie a atividade propondo:
Componha de duas maneiras a quantia que Lilian tinha. (Exemplos: 1 cédula de 50 reais e 1 cédula de 10 reais; 6 cédulas de 10 reais.)
Depois do que gastou no mercado, Lilian poderia comprar um livro de 12 reais? Por quê? (Espera-se que os estudantes percebam que faltariam 2 reais.)
Atividade 5
Esta atividade pode ser realizada em duplas ou trios para que os estudantes justifiquem suas respostas. Proponha outras questões:
Qual número é maior: 78 ou 68? Por quê? (Espera-se que percebam que 78 é maior porque contém mais grupos de 10 do que 68.)
Qual número é maior: 87 ou 68? Por quê? (Nesse caso, eles já podem ter mais dificuldade, dizendo equivocadamente que 68 é maior pelo fato de 8 ser maior do que 7. Se necessário, peça a eles que usem cubinhos do Material Dourado e façam contagens um a um.)
Qual é maior: 87 ou 78? Por quê? (O fato de os números terem os mesmos algarismos em ordem trocada pode gerar dificuldade. Construa a reta numérica na lousa e localize os dois números, de modo que observem que o 78 está mais próximo de 80 e que o 87 está mais próximo de 90. Assim, 87 é maior que 78.)
BNCC em foco:
EF01MA05, EF01MA08, EF01MA19
Autoavaliação
No primeiro item, explique que padrões são características que se repetem na construção de números ou de sequências específicas. Eles podem indicar que: só leem escritas numéricas com números até 20 ou que ainda confundem a posição dos algarismos; têm boas hipóteses de leitura de números até 99. Verifique os conhecimentos algébricos referentes aos padrões de diferentes sequências numéricas, pois a identificação desses padrões possibilita ampliar os conhecimentos sobre o sistema de numeração decimal. Os estudantes podem não encontrar padrões; conseguir encontrá-los com ajuda ou quando os números envolvidos são mais familiares ou têm mais proximidade com o sistema de numeração decimal; ou identificar padrões com tranquilidade.
A segunda questão também se refere às características do sistema de numeração decimal.
Os estudantes deverão indicar se: conseguem identificar quantas dezenas há em certos números; não conseguem identificar, e a ideia de agrupamento ainda não faz sentido; conseguem identificar essa quantidade só com dezenas inteiras ou com qualquer número familiar.
MP156
Comentários do professor
Conclusão da Unidade 5
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observações |
|---|---|---|
|
Reconhece números no contexto diário e faz indicação de quantidades, indicação de ordem ou indicação de código para a organização de informações? |
_____ |
_____ |
|
Consegue organizar informações colhidas de situações-problema e registrá-las por meio de desenhos ou palavras para as respectivas resoluções? |
_____ |
_____ |
|
Identifica e compara, com o apoio de imagens, quantidades de objetos, assimilando-as como números compostos de dezena(s) e unidade(s)? |
_____ |
_____ |
|
Ordena quantidades de objetos por meio de atributos comuns (ordem crescente ou decrescente), reconhecendo os aspectos cardinal (de 0 até 100) e ordinal do número? |
_____ |
_____ |
|
Identifica regularidades ou padrões figurais em sequências recursivas, bem como as completa com elementos faltantes? |
_____ |
_____ |
|
Identifica as grandezas variáveis cuja relação é dada por um gráfico de colunas e faz a leitura dos valores pertinentes a elas, considerando as informações das legendas? |
_____ |
_____ |
|
Estabelece relações entre o símbolo e o que ele representa, ou seja, entre o representante e o representado? |
_____ |
_____ |
|
Classifica resultados de eventos cotidianos aleatórios como acontecerá com certeza, talvez aconteça, impossível acontecer? |
_____ |
_____ |
|
Compreende e realiza a leitura de imagens? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |