MP205
Introdução da Unidade 8
As páginas de abertura possibilitam diálogos a serem usados com o objetivo de diagnosticar os conhecimentos e habilidades que os estudantes trazem das unidades anteriores. Estes diálogos estudante/professor constituem uma via de mão dupla na troca de informações. Eles formam um bom instrumento para planejar as estratégias de ensino-aprendizagem a serem aplicadas para recuperar possíveis falhas ou para fazer ampliações do que foi trabalhado no ano letivo para melhor prover o ano seguinte. Tanto a imagem rural da abertura da Unidade 5 quanto a imagem urbana da abertura desta Unidade fornecem elementos de análise para um diálogo construtivo.
Os conhecimentos abordados nas unidades anteriores relativos a Números, Grandezas e medidas, Probabilidade e estatística, Geometria e Álgebra são retomados nesta Unidade com dois objetivos: o de consolidar o conhecimento apreendido, tornando-o base de apoio para novos conhecimentos, e o de diversificar a aplicação dos conceitos em mais situações do cotidiano do estudante. Não basta, portanto, dedicar uma Unidade ao estudo de certos conceitos se estes não forem empregados para resolver problemas em diferentes contextos e não articularem as Unidades Temáticas. Assim, todos os conhecimentos necessários às atividades propostas nesta Unidade foram desenvolvidos ao longo de cada uma das Unidades que compõem este volume.
Acreditamos que este livro tenha contribuído para o desenvolvimento do letramento matemático e das competências específicas, considerando os objetos de conhecimento propostos, visando à continuidade deste trabalho no 2º ano do Ensino Fundamental.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretendem desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletiva. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.
10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.
Competências específicas favorecidas
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
MP206
UNIDADE 8. AMPLIANDO

MANUAL DO PROFESSOR
Objetivos da Unidade
Retomar processos de contagem.
Retomar comparação de números naturais.
Construir fatos fundamentais da adição.
Usar estratégias próprias para resolver problemas que envolvam adição e subtração.
Descrever a localização de pessoas e de objetos no espaço em relação à sua própria posição e em relação a um dado ponto de referência.
Relacionar objetos do cotidiano a figuras geométricas não planas.
Identificar e nomear figuras geométricas planas.
Identificar e relatar sequência de acontecimentos relativos a um dia.
Ampliar e retomar o trabalho com medidas de tempo (dias e meses).
Retomar o trabalho com medidas de comprimento e medidas de capacidade.
Reconhecer regularidades em sequências e descrever elementos ausentes.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Perceber a variação de padrão (tamanho, cor, forma) em uma sequência de figuras.
Ler dados registrados em tabelas e em gráficos de colunas simples.
Organizar informações coletadas em tabelas, em gráficos de colunas simples e por meio de representações próprias.
BNCC em foco:
EF01MA02, EF01MA05, EF01MA06, EF01MA08, EF01MA09, EF01MA10, EF01MA11, EF01MA12, EF01MA13, EF01MA14, EF01MA15, EF01MA16, EF01MA17, EF01MA19, EF01MA21, EF01MA22
MP207
Página sem conteúdo.
MANUAL DO PROFESSOR
A ilustração mostra uma parte de um bairro da cidade com ruas, prédios comerciais, casas, adultos e crianças. Nessa cena, é possível retomar alguns temas estudados ao longo deste ano.
Podem ser explorados: a descrição da localização de pessoas e de objetos no espaço em relação à sua própria posição e segundo um ponto de referência; representações de figuras geométricas; contagem, entre outros.
Incentive os estudantes a localizarem Guilherme e Letícia na cena.
Faça questionamentos, de modo que eles possam expor oralmente seus conhecimentos, como:
Quando vocês olham para a praça, a árvore está no lado direito ou no lado esquerdo da praça? (No lado direito.)
O homem que está em frente à casa de número 19 segura a pasta com qual de suas mãos? (Com a mão esquerda dele.)
Ao fazer essa pergunta, certifique-se de que os estudantes compreenderam que o referencial utilizado para respondê-la é a direita e a esquerda do homem que está segurando a mala. Se gerar dúvidas, peça a eles que se posicionem da mesma maneira que o homem que está na imagem.
Observem as casas que ficam na mesma rua que a casa de número 19. A numeração das casas nessa rua aumenta da esquerda para a direita ou da direita para a esquerda? Como vocês pensaram para responder? (Aumenta da esquerda para a direita. Espera-se que os estudantes observem a sequência crescente da numeração das casas: 17, 19, 21, 35.)
Na cena, há mais ou há menos de 1 dezena de pessoas? Como vocês fizeram para responder? (Há mais de uma dezena de pessoas. Incentive os estudantes a estimarem essa quantidade.)
Que figura geométrica não plana a bola lembra? (A esfera.)
MP208
JOGO: MARQUE 10
Observação ACOMPANHE AS INSTRUÇÕES QUE O PROFESSOR VAI LER. Fim da observação.
MATERIAL: CARTELA ABAIXO E MARCADORES (FEIJÕES, TAMPINHAS OU OUTROS).

JOGADORES: TODA A TURMA.
REGRAS:
- PREPARE SUA CARTELA PARA JOGAR. PARA ISSO, COMPLETE-A COM OS NÚMEROS QUE FALTAM.
Tabela: equivalente textual a seguir.
|
1 |
2 |
3 |
_____ |
5 |
6 |
_____ |
8 |
_____ |
10 |
|
_____ |
12 |
13 |
14 |
15 |
16 |
17 |
_____ |
19 |
_____ |
|
21 |
22 |
_____ |
24 |
25 |
_____ |
27 |
28 |
_____ |
30 |
|
31 |
32 |
33 |
_____ |
35 |
36 |
37 |
38 |
_____ |
40 |
|
_____ |
42 |
43 |
44 |
_____ |
46 |
47 |
48 |
49 |
_____ |
PROFESSOR
Resposta: 4, 7, 9, 11, 18, 20, 23, 26, 29, 34, 39, 41, 45, 50.

- DEPOIS, ESCOLHA 10 QUADRINHOS DE SUA CARTELA E PINTE-OS COM UMA COR BEM CLARINHA.
- SEU PROFESSOR VAI SORTEAR E LER EM VOZ ALTA UM NÚMERO.
- SE ELE LER UM NÚMERO QUE VOCÊ PINTOU, COLOQUE UM MARCADOR SOBRE ESSE NÚMERO.
- QUEM MARCAR PRIMEIRO OS 10 QUADRINHOS QUE PINTOU VENCE O JOGO.
MANUAL DO PROFESSOR
Objetivos
Retomar processos de contagem.
Retomar comparação de números naturais.
Reconhecer regularidades em sequências.
Descrever elementos ausentes.
Este jogo é similar ao Bingo de números (na Unidade 2), mas apresenta números organizados até 50. Ao ouvir o número sorteado, os estudantes precisam relacionar a designação dele com sua representação por meio de algarismos do sistema de numeração decimal. A observação da disposição dos números na cartela possibilita identificar regularidades: cada fileira horizontal mostra números cujo algarismo das dezenas é o mesmo, exceto pelo último, ou que os números dispostos em uma mesma fileira vertical têm o mesmo algarismo das unidades. Espera-se que observem essas regularidades, mesmo sem usar esses termos (já que ainda não foram estudados formalmente).
Peça aos estudantes que comentem as estratégias usadas para localizar os números na cartela, pois, ao compartilhá-las, todos têm a oportunidade de observar melhor a estrutura do quadro e, assim, estabelecer novas relações entre os números. Algumas estratégias que podem surgir são:
Contar a partir do número 1 apontando para cada número do quadro, em ordem crescente.
Usar números de referência próximos do número que se quer registrar, como dezenas inteiras, para assim localizá-lo.
Procurar a fileira horizontal correspondente à dezena à qual pertence o número e depois procurar a fileira vertical correspondente ao algarismo das unidades.
As diferentes estratégias empregadas pelos estudantes refletem diversos níveis de domínio da sequência numérica e do estabelecimento de relações entre os números. É esperado e desejável que todas as estratégias convivam em um mesmo grupo, por isso, estimule os estudantes a apresentá-las aos colegas. A cada partida, oriente-os a trocarem de livro com um colega diferente.
BNCC em foco:
EF01MA05, EF01MA10; competência específica 8
MP209
QUESTÕES SOBRE O JOGO
TELMA PINTOU SEIS NÚMEROS EM SUA CARTELA. DESCUBRA QUAIS SÃO.
- PARA ISSO, OUÇA AS DICAS QUE SEU PROFESSOR VAI LER E ESCREVA OS NÚMEROS.
1º NÚMERO: É MAIOR QUE DEZ E MENOR QUE DOZE._____
PROFESSOR
Resposta: 112º NÚMERO: VEM IMEDIATAMENTE ANTES DO VINTE E CINCO. _____
PROFESSOR
Resposta: 243º NÚMERO: VEM IMEDIATAMENTE DEPOIS DO QUARENTA E NOVE. _____
PROFESSOR
Resposta: 504º NÚMERO: É MAIOR QUE VINTE E MENOR QUE VINTE E DOIS. _____
PROFESSOR
Resposta: 215º NÚMERO: VEM IMEDIATAMENTE ANTES DO QUARENTA. _____
PROFESSOR
Resposta: 396º NÚMERO: ESTÁ ENTRE O NOVE E O ONZE. _____
PROFESSOR
Resposta: 10

- AGORA, PINTE NESTA OUTRA CARTELA OS NÚMEROS QUE VOCÊ DESCOBRIU.
Tabela: equivalente textual a seguir.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
PROFESSOR
Resposta: 10, 11, 21, 24, 39, 50.MANUAL DO PROFESSOR
Questões sobre o jogo
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões.
Crie outras dicas para que os estudantes descubram mais números e possam pintar na cartela da página. Veja alguns exemplos.
O número vem imediatamente depois do 19. (20.)
O número tem 3 unidades a mais que 21. (24.)
O número tem 5 unidades a menos que 37. (32.)
O número representa o dobro de 2 dezenas. (40.)
O número representa a metade de 2 dezenas. (10.)
Variações
Proponha o jogo novamente, criando charadas para os números que são sorteados, em vez de dizê-los em voz alta, como foi feito em Questões sobre o jogo.
BNCC em foco:
EF01MA05, EF01MA10; competência específica 8
MP210
LOCALIZANDO
- OBSERVE A CENA.

- O QUE HÁ EMBAIXO DA PONTE?
_____
PROFESSOR
Resposta: Uma pedra. - A TOALHA COM OS ITENS DO PIQUENIQUE ESTÁ DE QUAL LADO DO HOMEM?
_____
PROFESSOR
Resposta: Lado direito. - EM RELAÇÃO À MENINA, A TOALHA COM OS ITENS DO PIQUENIQUE ESTÁ DE QUAL LADO?
_____
PROFESSOR
Resposta: Lado esquerdo. - O PASSARINHO ESTÁ EM CIMA OU EMBAIXO DA PONTE?
_____
PROFESSOR
Resposta: Em cima.
MANUAL DO PROFESSOR
Objetivo
Descrever a localização de pessoas e de objetos no espaço em relação à sua própria posição e em relação a um dado ponto de referência.
As atividades destas páginas retomam conceitos estudados referentes à localização de pessoas e de objetos em imagens variadas. É importante proporcionar atividades similares na sala de aula ou no pátio da escola para que os estudantes possam vivenciá-las.
Atividade 1
Inicialmente, explore a imagem com os estudantes, pedindo que descrevam oralmente o que veem nela. Observe se utilizam os termos: embaixo, em cima, do lado esquerdo, do lado direito. Em seguida, leia com eles cada questão para que respondam oralmente. Faça a validação das respostas com os estudantes, mostrando na imagem a posição correta. Depois, peça que registrem no livro a conclusão obtida.
BNCC em foco:
EF01MA11, EF01MA12
MP211
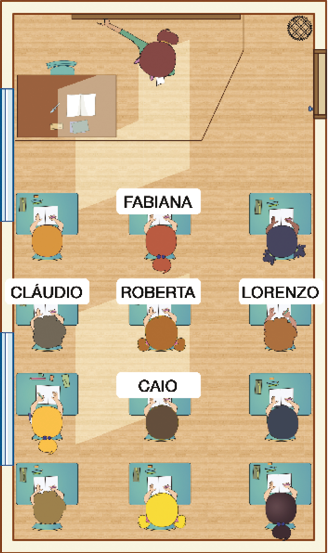
- ESTA É UMA REPRESENTAÇÃO DA SALA DE AULA DE ROBERTA.
ATRÁS
ESQUERDO
ENTRE
NA FRENTE
DIREITO
- COMPLETE COM OS TERMOS EM DESTAQUE NA COR VERDE.
ROBERTA SENTA _____ DE CAIO E _____ DE FABIANA. DO LADO _____ DE ROBERTA SENTA CLÁUDIO E DO LADO _____ DELA SENTA LORENZO. ROBERTA SENTA _____ CLÁUDIO E LORENZO.
PROFESSOR
Resposta: na frente; atrás; esquerdo; direito; entre.

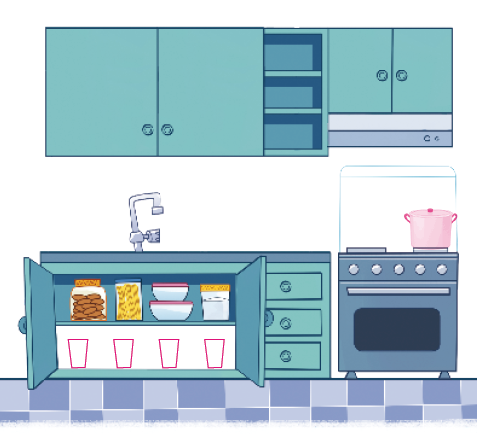
- SIGA AS DICAS PARA ORGANIZAR A COZINHA DE JOCA.
Boxe complementar:
DICAS
- DESENHE 4 COPOS NA PRATELEIRA QUE ESTÁ EMBAIXO DA PIA.
- DESENHE UMA PANELA EM CIMA DO FOGÃO, NO QUEIMADOR QUE ESTÁ DO LADO ESQUERDO DO FOGÃO.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 2
Se julgar oportuno, antes de realizar a atividade, organize as carteiras na disposição da figura e escolha o estudante que se encontra na posição de Roberta para responder aos mesmos questionamentos. Depois, escolha outro estudante e faça o mesmo.
Em seguida, proponha aos estudantes as questões da atividade e verifique as estratégias que eles utilizam.
Explore a imagem com mais alguns questionamentos:
Quem senta atrás de Caio tem cabelo claro ou escuro? (Cabelo claro.)
Na fileira de Lorenzo, há quantos estudantes? (4 estudantes.)
Fabiana, Cláudio e Caio se sentam na mesma fileira? (Não.)
Atividade 3
Inicialmente, peça a alguns estudantes que descrevam os objetos que estão em cima da mesa de um dos colegas que ficam a seu lado. Depois, peça que coloquem uma borracha embaixo da cadeira em que estão sentados.
Em seguida, proponha a eles que façam a atividade. Caso haja dúvida quanto à resposta da panela, explique que ela deve ser desenhada no queimador do lado esquerdo do fogão e à direita de quem vê o fogão. Verifique as dúvidas que ainda surgirem e sugira que os colegas expliquem como fizeram, de modo que eles próprios possam elucidá-las.
BNCC em foco:
EF01MA11, EF01MA12
MP212
FORMANDO NÚMEROS

- RECORTE AS CARTAS DA PÁGINA 185.
- SEPARE AS SEGUINTES CARTAS:

- USANDO APENAS DUAS DESSAS CARTAS POR VEZ, FORME TODOS OS NÚMEROS POSSÍVEIS. DEPOIS, ESCREVA OS NÚMEROS QUE VOCÊ FORMOU.
12
_____
_____
_____
_____
_____
_____
_____
_____
PROFESSOR
Resposta: 24, 14, 41, 21, 42.- QUAL DOS NÚMEROS FORMADOS É O MAIOR?
_____
PROFESSOR
Resposta: 42 - QUAL DOS NÚMEROS FORMADOS É O MENOR?
_____
PROFESSOR
Resposta: 12
- SEPARE AS CARTAS: 3, 5, 8 E 9.

- QUAL É O MAIOR NÚMERO QUE VOCÊ CONSEGUE FORMAR USANDO APENAS DUAS DESSAS CARTAS?
_____
PROFESSOR
Resposta: 98 - QUAL É O MENOR NÚMERO QUE VOCÊ PODE FORMAR COM DUAS DESSAS CARTAS?
_____
PROFESSOR
Resposta: 35
MANUAL DO PROFESSOR
Objetivo
Retomar a comparação de números naturais até 99.
Atividade 1
Esta atividade possibilita a escrita de números de dois algarismos com base nas cartas com os algarismos 1, 2 e 4. Peça aos estudantes que leiam o número escrito em cada caso e anote na lousa os números formados. Depois, convide-os a conferir se todas as possibilidades foram criadas. Faça perguntas como: “Colocando a carta com o algarismo 2 na frente, formamos todos os números possíveis?”; “E colocando a carta com o algarismo 1?”; “E colocando a carta com o algarismo 4?”. Assim, são dadas referências sobre combinação. É importante os estudantes perceberem que há apenas seis combinações possíveis. Como os algarismos não podem ser repetidos, três lacunas ficarão em branco.
Atividade 2
Pergunte: “Para obter o maior número possível de dois algarismos dentre as cartas com os algarismos 3, 5, 8 ou 9, qual devo colocar na frente?”; “Agora, entre as cartas que sobraram, qual devo colocar em seguida?”. Espera-se que os estudantes percebam que o número deve começar com o algarismo de maior valor (9), seguido do algarismo de maior valor que restou (8), obtendo o número 98.
De modo análogo, proceda na formação do menor número. Nesse caso, eles devem utilizar as cartas com os algarismos de menores valores (3 e 5), obtendo o número 35.
Explore a atividade perguntando: “Se fosse possível repetir os algarismos 3, 5, 8 ou 9, qual seria o maior número obtido com dois algarismos?”; “E o menor número?”. Espera-se que os estudantes respondam 99 e 33, respectivamente.
BNCC em foco:
EF01MA05; competência geral 2
Sugestão de atividade
Joana tem duas cédulas de 50 reais. Veja a sequência de compras dela.
No supermercado, ela comprou carne e ovos, gastando ao todo 35 reais.
No caixa da farmácia, Joana pagou 30 reais pelos produtos que comprou.
Antes de voltar para casa, ela passou no jornaleiro e comprou uma revista por 15 reais.
Com que quantia Joana saiu de cada estabelecimento?
Uma estratégia de resolução é realizar subtrações conforme as compras de Joana. Assim: do supermercado ela saiu com 65 reais; da farmácia ela saiu com 35 reais; do jornaleiro ela saiu com 20 reais.
MP213
PROBLEMAS
- HELENA E ROBERTO COLECIONAM SELOS. HELENA TINHA 24 SELOS E GANHOU 12. ROBERTO TINHA 12 SELOS E GANHOU 24.
• COM QUANTOS SELOS CADA UM FICOU?
PROFESSOR
Exemplos de cálculo: Helena: 24 1 12 = 36; Roberto: 12 1 24 = 36HELENA FICOU COM _____ SELOS. ROBERTO, COM _____ SELOS.
PROFESSOR
Resposta: 36, 36.

- QUEM FICOU COM A MAIOR QUANTIDADE DE SELOS: HELENA OU ROBERTO?
PROFESSOR
Resposta: Os dois ficaram com a mesma quantidade de selos.
- EM UM PRÉDIO COM 48 APARTAMENTOS, HÁ APARTAMENTOS COM DOIS OU COM TRÊS DORMITÓRIOS. NESSE PRÉDIO, HÁ, EXATAMENTE, 12 APARTAMENTOS COM TRÊS DORMITÓRIOS. QUANTOS SÃO OS APARTAMENTOS COM DOIS DORMITÓRIOS?
_____
PROFESSOR
Resposta: 36 apartamentos. Exemplo de cálculo: 48 − 12 = 36
- OBSERVE A QUANTIA DE DINHEIRO QUE VANESSA TINHA.

- DEPOIS DE VANESSA COMPRAR UMA CAMISETA POR 45 REAIS E UM LENÇO POR 15 REAIS, QUANTO SOBROU DE
_____
DINHEIRO?
PROFESSOR
Resposta: 20 reais. Exemplos de cálculo: 45 + 15 = 60; 80 − 60 = 20
MANUAL DO PROFESSOR
Objetivos
Construir fatos fundamentais da adição.
Usar estratégias próprias para resolver problemas de adição e subtração.
Reconhecer e relacionar valores de moedas e cédulas do sistema monetário brasileiro.
Atividade 1
Pretende-se explorar intuitivamente a comutatividade da adição, envolvendo o significado de acrescentar associado a essa operação. Incentive os estudantes a perceberem a propriedade comutativa da adição, sem nomeá-la, ou seja, que os números envolvidos na adição são os mesmos, mas na ordem invertida, e os resultados obtidos são iguais.
Atividade 2
Os estudantes devem perceber que só há duas possibilidades: ou o apartamento tem 2 dormitórios ou tem 3 dormitórios. Desse modo, se em 48 apartamentos há 12 de 3 dormitórios, os restantes têm 2 dormitórios cada um.
Atividade 3
Observe as estratégias usadas pelos estudantes para encontrar a solução do problema: se realizam a adição dos valores gastos na compra de Vanessa e em seguida subtraem da quantia que ela possuía, ou se subtraem um valor e em seguida o outro, para então encontrar a quantia que restou. Deixe à disposição deles as cédulas e moedas do Material complementar para que as utilizem no cálculo ou na comprovação da resposta.
Amplie a atividade e peça aos estudantes que elaborem um problema envolvendo a quantia que sobrou após a compra e o resolvam. Um exemplo é: “Vanessa quer comprar um boné que custa 26 reais. Ela pode comprá-lo com a quantia que possui?”. Espera-se que os estudantes percebam que ela não pode comprá-lo pois tem apenas 20 reais, ou seja, faltam 6 reais.
Valorize as diferentes estratégias usadas pelos estudantes. A resolução de problemas está ligada principalmente à interpretação da situação, ao reconhecimento de uma estrutura que pode ser traduzida pelo uso de uma operação aritmética, à verificação da possibilidade de resolução e da validade da resposta obtida.
Reforce que é necessário entender o problema muito bem, lendo o enunciado com atenção. Além disso, pode-se representá-lo por um desenho ou esquema que facilite a compreensão. Algumas perguntas podem ajudá-los:
Que informações são conhecidas?
O que se deseja saber?
As informações são suficientes?
Que estratégias posso usar?
A resposta encontrada faz sentido?
BNCC em foco:
EF01MA05, EF01MA06, EF01MA08, EF01MA19
MP214
FIGURAS GEOMÉTRICAS
- MARQUE COM UM
X
O OBJETO QUE SE PARECE COM

( )

( )

( )

PROFESSOR
Resposta: balde.- NA ESCOLA DE ELIS, FOI REALIZADA UMA FEIRA DOS ESTADOS BRASILEIROS. ELIS É BAIANA E APRESENTOU NA FEIRA UM MURAL COM ALGUMAS INFORMAÇÕES, FOTOGRAFIAS E A BANDEIRA DO ESTADO ONDE NASCEU.

- EM QUAL ESTADO ELIS NASCEU?
_____
PROFESSOR
Resposta: Bahia. - QUE TIPO DE FIGURAS GEOMÉTRICAS PODEMOS IDENTIFICAR NA BANDEIRA DO MURAL FEITO POR ELIS?
( ) FIGURAS GEOMÉTRICAS PLANAS
( ) FIGURAS GEOMÉTRICAS NÃO PLANAS
PROFESSOR
Resposta correta: figuras geométricas planas. - QUAIS SÃO AS FIGURAS GEOMÉTRICAS QUE PODEMOS IDENTIFICAR NA BANDEIRA DO ESTADO ONDE ELIS NASCEU?
_____
PROFESSOR
Exemplo de resposta: Quadrado, triângulo e retângulo.
MANUAL DO PROFESSOR
Objetivos
Relacionar objetos do cotidiano a figuras geométricas não planas.
Identificar e nomear figuras geométricas planas.
Atividade 1
Apresente aos estudantes vários objetos do dia a dia para que os relacionem às figuras geométricas não planas que tais objetos lembram, resgatando o que já foi visto anteriormente.
Atividade 2
Amplie a atividade apresentando as bandeiras dos estados brasileiros para que os estudantes possam encontrar a imagem da bandeira do estado em que nasceram. Proponha a eles que pesquisem, por exemplo, os principais pontos turísticos desse estado. Os estudantes podem fazer cartazes para apresentar aos colegas.
Sugestão de atividade
Peça aos estudantes que reproduzam a bandeira do estado em que nasceram.
Neste site, é possível fazer o download das bandeiras dos estados do Brasil e das bandeiras dos países. Disponível em: http://fdnc.io/eRN. Acesso em: 22 jan. 2021.
BNCC em foco:
EF01MA13, EF01MA14
MP215
MEDIDAS DE TEMPO
- COMPLETE COM OS MESES QUE FALTAM.
MARÇO
_____
OUTUBRO
_____
AGOSTO
_____
JULHO
JANEIRO
PROFESSOR
Resposta: Verde_____
_____
NOVEMBRO
_____
PROFESSOR
Resposta: Os meses que estão faltando são: fevereiro, abril, maio, junho, setembro e dezembro.

AGORA, FAÇA O QUE SE PEDE:
- PINTE DE
 O PRIMEIRO MÊS DO ANO.
O PRIMEIRO MÊS DO ANO. - PINTE DE
 O DÉCIMO SEGUNDO MÊS DO ANO.
O DÉCIMO SEGUNDO MÊS DO ANO. - PINTE DE
 O MÊS EM QUE VOCÊ FAZ ANIVERSÁRIO.
O MÊS EM QUE VOCÊ FAZ ANIVERSÁRIO.
PROFESSOR
Atenção professor: Espera-se que cada estudante pinte de azul o quadro no qual escreveu “dezembro”. Fim da observação.PROFESSOR
Resposta pessoal.- AS CENAS ESTÃO FORA DE ORDEM. NUMERE-AS NA ORDEM EM QUE ACONTECERAM.
( )

PROFESSOR
Resposta: Exemplo de resposta: 2( )

PROFESSOR
Resposta: Exemplo de resposta: 1( )

PROFESSOR
Resposta: Exemplo de resposta: 3MANUAL DO PROFESSOR
Objetivos
Identificar e relatar sequência de acontecimentos relativos a um dia.
Ampliar e retomar o trabalho com medidas de tempo (dias e meses).
Atividade 1
Se julgar oportuno, leve um calendário para a sala de aula, a fim de que a turma possa consultá-lo para resolver a atividade. Caso os estudantes tenham dificuldade em determinar o primeiro e o último mês do ano, ordene na lousa, com a ajuda deles, os meses que estão faltando (fevereiro, abril, maio, junho, setembro e dezembro), para que depois possam realizar as pinturas solicitadas.
Atividade 2
Peça aos estudantes que descrevam cada cena e proponham uma ordenação possível. Escovar os dentes, por exemplo, é uma atividade que poderia estar sendo feita após a refeição, no entanto, nesse caso, a menina ainda está de pijama e sonolenta.
Sugestão de atividade interdisciplinar
Aproveite a atividade 2 e promova uma discussão em comum com a área de Ciências, falando sobre hábitos de higiene pessoal e vida saudável.
Sugestão de atividade
Desenhe o calendário do mês de outubro (do ano corrente) e peça aos estudantes que respondam às questões.
Quantos domingos teve esse mês?
Que dia da semana foi o dia 3 de outubro neste ano?
Que dias desse mês foram quartas-feiras?
Qual é o Dia das Crianças? Em que dia da semana esse dia ocorreu neste ano?
BNCC em foco:
EF01MA16, EF01MA17; competência geral 8
MP216
OUTRAS MEDIDAS
- OBSERVE OS PEDAÇOS DE FITA DESENHADOS A SEGUIR E CERQUE COM UMA LINHA AQUELE QUE NÃO É O MAIS CURTO NEM O MAIS COMPRIDO.

PROFESSOR
Resposta: Fita 2.


- CONVERSE COM OS COLEGAS E DESENHE DUAS SITUAÇÕES: UMA EM QUE SE MEDE O COMPRIMENTO DE OBJETOS E OUTRA EM QUE SE MEDE A ALTURA DE PESSOAS.
_____
_____
PROFESSOR
Atenção professor: Desenhos pessoais. Fim da observação.

- QUAL COPO VOCÊ ESCOLHERIA PARA TOMAR SUCO? POR QUÊ?
PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR
Objetivo
Retomar o trabalho com medidas de comprimento e medidas de capacidade.
Atividade 1
Nesta atividade, os estudantes vão comparar o comprimento das fitas desenhadas. Ressalte que todas as fitas têm a mesma largura, para que eles não confundam o comprimento da fita com a largura dela.
Atividade 2
Espera-se que os estudantes lembrem situações de seu cotidiano ou outras que presenciem no dia a dia, na televisão etc., por exemplo:
No pediatra, quando será medida a sua altura.
Na sala de aula, para saber o livro mais grosso ou o lápis mais comprido.
Em casa, para saber em qual parede do quarto cabe uma cômoda ou um guarda-roupa.
Atividade 3
Verifique se os estudantes utilizam como critério de escolha a capacidade dos copos. Peça a eles que socializem suas justificativas de escolha. Supondo que o copo escolhido tenha sido o da direita, exemplificamos possíveis justificativas:
Porque é o copo mais alto.
Porque cabe mais suco.
BNCC em foco:
EF01MA15; competências específicas 6 e 8
MP217
PADRÕES
- OBSERVE A SEQUÊNCIA.

- CERQUE COM UMA LINHA O PRÓXIMO BORRÃO DA SEQUÊNCIA.

PROFESSOR
Resposta: borrão 1.- MARQUE COM UM
X
O QUE ESTÁ VARIANDO NA SEQUÊNCIA.
( ) TAMANHO
( ) COR
( ) FORMA
PROFESSOR
Resposta correta: cor.
- RICARDO COLECIONA FLORES SECAS, OU SEJA, FLORES QUE CAÍRAM DAS ÁRVORES. EM ALGUMAS DELAS, HÁ 5 PÉTALAS E, EM OUTRAS, 4 PÉTALAS. OBSERVE A ILUSTRAÇÃO A SEGUIR E RESPONDA ÀS QUESTÕES.

- QUANTAS PÉTALAS HÁ NO TOTAL?
_____
PROFESSOR
Resposta: No total, há 35 petálas.
- RICARDO DESEJA ORGANIZAR ESSAS FLORES EM DUAS CAIXAS DIFERENTES. COMO VOCÊ PODERIA SUGERIR QUE RICARDO FIZESSE ESSA ORGANIZAÇÃO?
PROFESSOR
Atenção professor: Espera-se que os estudantes sugiram o critério de separar as flores, nas duas caixas diferentes, por quantidade de pétalas para fazer essa organização. Fim da observação.
Boxe complementar:
DESAFIO

SABENDO QUE O RESULTADO DA ADIÇÃO 47 + 39 É 86, QUAL É O RESULTADO DA ADIÇÃO 39 + 47? _____
Resposta: 86
Fim do complemento.
MANUAL DO PROFESSOR
Objetivos
Construir fatos fundamentais da adição.
Reconhecer regularidades em sequências e descrever elementos ausentes.
Perceber a variação de padrão (tamanho, cor, forma) em uma sequência de figuras.
Atividade 1
Peça aos estudantes que observem a sequência de figuras e digam o que percebem. Eles devem notar que as cores se repetem de acordo com um padrão. Solicite, então, que falem em voz alta as cores na sequência em que elas aparecem. Peça a eles que identifiquem o padrão dessa sequência (amarelo, azul, azul, vermelho).
Atividade 2
Os estudantes podem utilizar estratégias de contagem por agrupamento. Valorize e valide os diferentes procedimentos de contagem que aparecerem. Incentive o cálculo mental.
Desafio
Explique para os estudantes que o desafio é descobrir o resultado da adição 39 + 47 sem efetuar cálculo algum. Promova questionamentos que os levem a observar a relação entre as duas adições:
Que números estão sendo adicionados em 47 + 39 = 86? (47 e 39.) E na adição
39 + 47 = ? (39 e 47.)
Nas duas adições anteriores, os números adicionados são os mesmos? (Sim.)
Nesse caso, o que se espera dos resultados dessas duas adições? Por quê? (Espera-se que os resultados sejam iguais, já que os números adicionados são os mesmos.)
Deixe os cubinhos do Material Dourado à disposição deles, caso queiram utilizá-los no cálculo.
BNCC em foco:
EF01MA02, EF01MA06, EF01MA09, EF01MA10; competência específica 3
MP218
NÚMEROS NA ARQUIBANCADA
- MUITAS PESSOAS COMPRARAM BILHETES NUMERADOS PARA ASSISTIR A UM JOGO DE BASQUETE, MAS ALGUMAS CADEIRAS DA ARQUIBANCADA NÃO ESTÃO NUMERADAS. VAI SER UMA CONFUSÃO NA HORA DE CADA UM ENCONTRAR O LUGAR!
- AJUDE A EVITAR ESSA CONFUSÃO, NUMERANDO OS ASSENTOS QUE ESTÃO SEM NÚMERO.

PROFESSOR
Resposta: 3, 7, 10, 11, 12, 15, 16, 18, 21, 25, 27, 30, 32, 34, 38, 43, 45, 49, 51, 60, 62, 66, 78, 80, 85, 89, 93, 97, 99.- MARQUE COM UM
X
A QUANTIDADE DE CADEIRAS QUE ESTAVAM SEM NÚMERO.
( ) MAIS DE 30 CADEIRAS
( ) MENOS DE 30 CADEIRAS
PROFESSOR
Resposta correta: menos de 30 cadeiras.
MANUAL DO PROFESSOR
Objetivos
Retomar processos de contagem.
Retomar comparação de números naturais.
Reconhecer regularidades em sequências e descrever elementos ausentes.
Esta atividade propõe a construção do quadro de números até 100, possibilitando a observação de regularidades nesses números.
Aproveitando a disposição dos números (tabela formada por dez fileiras horizontais e dez fileiras verticais), pergunte: “O que há em comum entre os números de cada fileira horizontal?”; “E entre os números de cada fileira vertical?”; “Qual é a diferença entre dois números vizinhos em uma mesma fileira horizontal?”; “E entre dois números vizinhos em uma mesma fileira vertical?”. Permita aos estudantes que explorem o quadro numérico e exponham suas hipóteses. Valide as justificativas das regularidades mencionadas por eles, de modo que a composição do número seja observada, bem como o sucessor e o antecessor de um número natural, sem fazer uso desses termos.
Antes das questões a seguir, retome o vocabulário: imediatamente antes, maior que, menor que, entre. É interessante mostrar essas sequências numéricas também na fita métrica, no calendário, no quadro de números ou em outros portadores numéricos acessíveis.
Qual desses números vem imediatamente antes de 70? (69.)
Qual deles vem imediatamente depois de 28? (29.)
Quais estão entre 23 e 29? (24, 25, 26, 27 e 28.)
Quais desses números são menores que 7? (1, 2, 3, 4, 5 e 6.)
BNCC em foco:
EF01MA02, EF01MA05, EF01MA10; competências específicas 2 e 3
MP219
A MATEMÁTICA ME AJUDA A SER
Observação ACOMPANHE AS INSTRUÇÕES QUE O PROFESSOR VAI LER. Fim da observação.
VOCÊ SABIA QUE O PEIXE-BOI-DA-AMAZÔNIA É UM DOS ANIMAIS MAIS AMEAÇADOS DE NOSSO PAÍS?
ELE ESTÁ EM EXTINÇÃO POR CAUSA DA CAÇA SEM CONTROLE, DA MORTE ACIDENTAL EM REDES DE PESCA, DO ENCALHE DE FILHOTES ÓRFÃOS E DOS ESTRAGOS AMBIENTAIS.
NO MUNDO, HÁ QUATRO ESPÉCIES DE PEIXE-BOI. O PEIXE-BOI-DA-AMAZÔNIA É UM DELES E VIVE APENAS EM ÁGUA DOCE, NA REGIÃO AMAZÔNICA, NO BRASIL.
ELE CHEGA A MEDIR MAIS DE 3 METROS. CADA GESTAÇÃO DURA 12 MESES, GERANDO APENAS 1 FILHOTE E SÓ ACONTECE DE 3 EM 3 ANOS. APÓS O NASCIMENTO, O FILHOTE PASSA PELO MENOS 2 ANOS AO LADO DA MÃE.

LEGENDA: PEIXE-BOI-DA-AMAZÔNIA (TRICHECHUS INUNGUIS). FOTOGRAFIA DE 2017. FIM DA LEGENDA.
TOME NOTA
- PESQUISE O SIGNIFICADO DA PALAVRA EXTINÇÃO.
_____
PROFESSOR
Exemplo de resposta: o desaparecimento total de algum tipo de ser vivo, animal ou vegetal, e pode ocorrer por diversas causas.
- EM QUAL REGIÃO VIVE O PEIXE-BOI-DA-AMAZÔNIA?
_____
PROFESSOR
Resposta: Na região amazônica.
- A GESTAÇÃO DO PEIXE-BOI-DA-AMAZÔNIA DURA MAIS DE 10 MESES?
_____
PROFESSOR
Resposta: Sim.
REFLITA


O QUE PODEMOS FAZER PARA PROTEGER ESSE ANIMAL?
PROFESSOR
Respostas pessoais.MANUAL DO PROFESSOR
Objetivo
Ampliar e retomar o trabalho com medidas de tempo (dias e meses).
Tome nota
Atividade 1
Explique para os estudantes que os animais e as plantas ameaçados de extinção são aqueles que, em um futuro próximo, podem não existir mais. Isso pode ocorrer por causas naturais, como mudanças no clima e na falta de capacidade de alguns seres vivos de se adaptarem a condições novas e diferentes para sobreviver na natureza.
Infelizmente, o ser humano tem contribuído para esse processo de extinção com atitudes como a destruição de ambientes naturais para expansão urbana, poluição, incêndios florestais, uso de grandes áreas para pastagem ou agricultura, diminuindo as chances de sobrevivência de muitas espécies.
Atividade 2
Incentive os estudantes a relerem o texto para buscar a informação necessária para a resposta (Região amazônica, no Brasil).
Atividade 3
De acordo com o texto, a gestação desse animal dura 12 meses; portanto, espera-se que os estudantes compreendam que 12 meses é mais que 10 meses. Esta seção possibilita um trabalho interdisciplinar com Ciências da Natureza quanto à classificação taxonômica. Comente com a turma que o peixe-boi, apesar do nome, não é um peixe, mas sim um mamífero.
Reflita
Espera-se que os estudantes listem algumas destas atitudes:
Evitar a poluição da água, o tráfico e a comercialização desse animal.
Conscientizar as pessoas do respeito ao meio ambiente.
Divulgar iniciativas contra a caça sem controle.
BNCC em foco:
EF01MA05, EF01MA17; competências gerais 6, 7 e 10;
competências específicas 2, 3, 4 e 6
Sugestão de leitura para o professor
Plano de Ação Nacional para a Conservação dos Mamíferos Aquáticos Amazônicos. O plano compreende o período de 2019-2024. Disponível em: https://www.icmbio.gov.br/portal/faunabrasileira/planos-de-acao/10193-plano-de-acao-nacional-para-a-conservacao-mamiferos-aquaticos-amazonicos . Acesso em: 22 jan. 2021.
MP220
COMPREENDER INFORMAÇÕES
- NA DANÇA DA FESTA ANUAL DAS FLORES DA ESCOLA, CADA CASAL DE ESTUDANTES ESCOLHEU UMA FLOR PARA USAR: UM CASAL ESCOLHEU MARGARIDAS, TRÊS CASAIS ESCOLHERAM CRAVOS, DOIS CASAIS, AZALEIAS, E QUATRO CASAIS, ROSAS. CADA ESTUDANTE RECEBERÁ UMA FLOR DO TIPO ESCOLHIDO.
- COMPLETE A TABELA COM A QUANTIDADE CORRESPONDENTE DE FLORES PARA ESSES CASAIS.
FLORES ESCOLHIDAS
Tabela: equivalente textual a seguir.
|
TIPO DE FLOR |
MARGARIDA |
CRAVO |
AZALEIA |
ROSA |
|---|---|---|---|---|
|
QUANTIDADE |
_____ |
6 |
_____ |
_____ |
FONTE: FESTA ANUAL DAS FLORES EM 2023.
PROFESSOR
Resposta: 2, 4, 8.

- COM BASE NOS DADOS DA TABELA, PINTE AS COLUNAS PARA COMPLETAR O GRÁFICO.
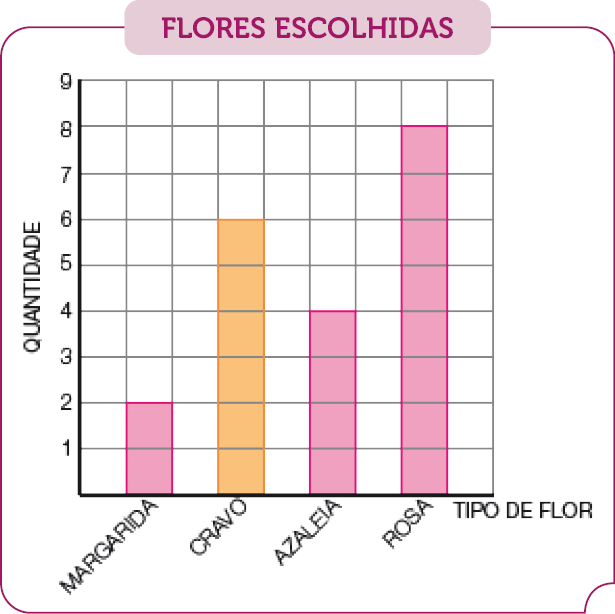
FONTE: FESTA ANUAL DAS FLORES EM 2023.
- AO TODO, QUANTAS FLORES FORAM ESCOLHIDAS?
_____
PROFESSOR
Resposta: 20 - QUAL TIPO DE FLOR FOI O MAIS ESCOLHIDO?
_____
PROFESSOR
Resposta: Rosa. - O TOTAL DE FLORES É O DOBRO DO TOTAL DE CASAIS?
_____
PROFESSOR
Resposta: Sim.
MANUAL DO PROFESSOR
Objetivos
Ler dados registrados em tabelas e em gráficos de colunas simples.
Organizar informações coletadas em tabelas, gráficos de colunas simples e por meio de representações próprias.
Atividade 1
Peça aos estudantes que expliquem como fizeram para encontrar a quantidade de cada tipo de flor para registrar na tabela. Observe se eles perceberam que o número de flores é o dobro do número de casais e que este corresponde à metade daquele.
Depois, proponha a eles que completem o gráfico de colunas de acordo com os dados da tabela.
Peça aos estudantes que, em duplas, comparem seus gráficos, levantando semelhanças e diferenças.
Depois, discuta com toda a classe o que observaram e proponha as demais questões.
Atividades com coleta de dados ajudam os estudantes a compreenderem como funcionam pesquisas estatísticas, pois possibilitam a eles perceber a necessidade da coleta de dados antes da apresentação de um resultado por meio de uma tabela ou de um gráfico.
BNCC em foco:
EF01MA21, EF01MA22; competências específicas 3, 4 e 6
Sugestão de atividade
Divida a lousa em três colunas e, no topo de cada coluna, escreva o nome de um esporte (por exemplo, futebol, voleibol e basquete). Em seguida, explique aos estudantes que será feita uma coleta de dados para descobrir qual desses três esportes é o preferido da turma.
Pergunte a cada estudante: “Qual desses esportes você prefere?”. A cada resposta, faça um risquinho na coluna do esporte escolhido. É importante deixar claro que cada estudante poderá escolher apenas um dos esportes.
Depois, peça aos estudantes que reproduzam no caderno a lista que você fez na lousa.
Oriente-os a preencher uma tabela com os dados dessa lista. Eles devem contar a quantidade de tracinhos em cada esporte e representá-la na tabela usando algarismos, por exemplo. Em seguida, peça aos estudantes que criem algumas questões que possam ser respondidas com base na observação dos dados organizados.
MP221
- OBSERVE OS DESENHOS DE FIGURAS GEOMÉTRICAS PLANAS A SEGUIR E FAÇA O QUE SE PEDE.

- CRIE E REGISTRE UMA ESTRATÉGIA PARA ORGANIZAR E QUANTIFICAR AS FIGURAS GEOMÉTRICAS PLANAS ACIMA.
PROFESSOR
Resposta: FIGURAS GEOMÉTRICAS PLANASPROFESSOR
Tabela: equivalente textual a seguir.PROFESSOR
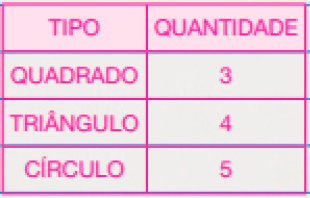
FONTE: DADOS OBTIDOS NO LIVRO DO ESTUDANTE, EM 2023.
PROFESSOR
Atenção professor: Espera-se que os estudantes identifiquem algum tipo de classificação das figuras geométricas planas, como cor ou forma. Os dados podem estar organizados em lista ou tabela, por exemplo. Fim da observação.
- A PARTIR DOS DADOS QUE VOCÊ ORGANIZOU, CONSTRUA UM GRÁFICO PARA REPRESENTÁ-LOS.
PROFESSOR
O gráfico dependerá da organização dos dados na questão anterior.PROFESSOR
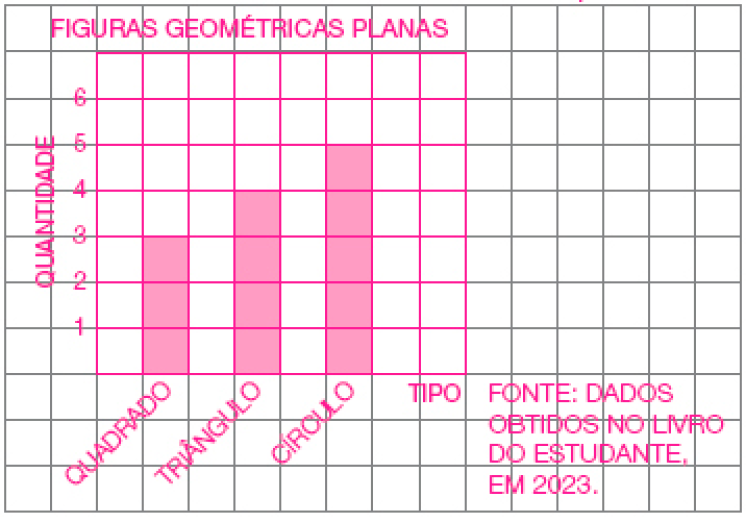
FONTE: DADOS OBTIDOS NO LIVRO DO ESTUDANTE, EM 2023.

- ELABORE UMA QUESTÃO QUE POSSA SER RESPONDIDA COM BASE NO GRÁFICO QUE VOCÊ DESENHOU.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
Depois que os estudantes observarem o quadro com os desenhos de figuras geométricas, peça a eles que expliquem como podem organizar e quantificar as figuras. Uma das estratégias é contar as figuras do quadro considerando a forma ou, então, sua cor.
Espera-se que os estudantes elaborem uma lista com os elementos e a frequência com que aparecem, ou então tabulem os dados em uma tabela.
Na resposta colocamos um exemplo de tabela considerando o tipo de figura geométrica e a quantidade. Em seguida, os estudantes devem transpor esses dados para um gráfico. Apresentamos na resposta um exemplo de gráfico de colunas, considerando a tabela elaborada.
Incentive os estudantes a coletarem dados na classe para construir outros gráficos. Sugira que escolham situações do dia a dia, como o tipo de comida preferida da turma ou as brincadeiras de que mais gostam. Auxilie-os em todo o processo, acompanhando a coleta de dados e a organização deles, seja em listas, tabelas ou gráficos.
BNCC em foco:
EF01MA21, EF01MA22; competências específicas 3, 4 e 6
MP222
O QUE VOCÊ APRENDEU
- OBSERVE OS COLEGAS QUE ESTÃO SENTADOS PERTO DE VOCÊ NA SALA DE AULA.
- QUEM ESTÁ À SUA ESQUERDA? _____
- QUEM ESTÁ NA SUA FRENTE? _____
- QUEM ESTÁ ATRÁS DE VOCÊ? _____
- QUEM ESTÁ À SUA DIREITA?
_____
PROFESSOR
Atenção professor: As respostas vão depender da localização da carteira em que o estudante estiver sentado. Fim da observação.

- EM CADA QUADRO, PINTE O RECIPIENTE EM QUE CABE MAIS LÍQUIDO.
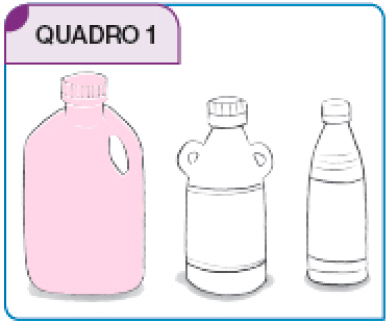
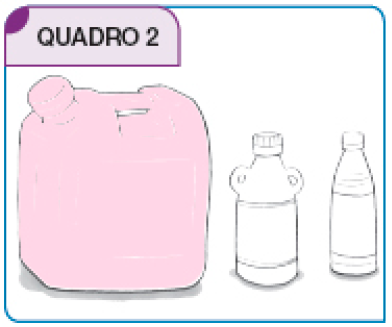
- EM QUAL DOS QUADROS ESTÁ O RECIPIENTE DE MAIOR CAPACIDADE?
_____
PROFESSOR
Resposta: No quadro 2.
- OBSERVE O DESENHO DE FIGURAS GEOMÉTRICAS NÃO PLANAS E CERQUE COM UMA LINHA AQUELAS EM QUE PODEMOS IDENTIFICAR QUADRADOS.
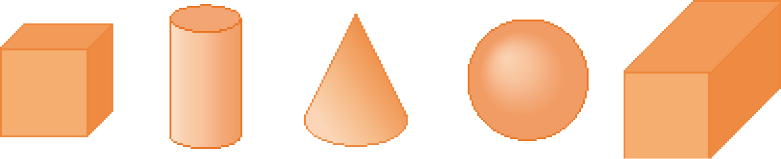
PROFESSOR
Resposta: cubo; paralelepípedo.MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Com esta atividade, pode-se verificar quais estudantes ainda sentem dificuldade com relação aos conceitos estudados. As respostas vão depender da localização da carteira em que o estudante que responder a esta atividade estiver sentado. Por exemplo: se a carteira do estudante estiver localizada na fileira do canto direito da sala de aula junto da parede, não haverá nenhum colega sentado à direita desse estudante; se a carteira do estudante estiver localizada em último na fileira, não haverá nenhum colega sentado atrás dele.
Atividade 2
Nesta atividade, o foco não é a unidade de medida, mas sim comparar os recipientes apresentados em cada um dos quadros, de modo que os estudantes possam decidir qual recipiente tem a maior capacidade. Peça a eles que socializem suas respostas e justificativas.
Atividade 3
Com esta atividade, pode-se verificar se os estudantes ainda sentem dificuldade para identificar figuras geométricas planas em figuras geométricas não planas.
BNCC em foco:
EF01MA11, EF01MA14, EF01MA15
Sugestão de atividade
Descobrindo números escondidos
Alguns números foram apagados nos cartões ao lado. Descubra quais são esses números e escreva-os nos espaços vazios.
Observação: Diga que, se precisarem, podem consultar o quadro de números até 100.
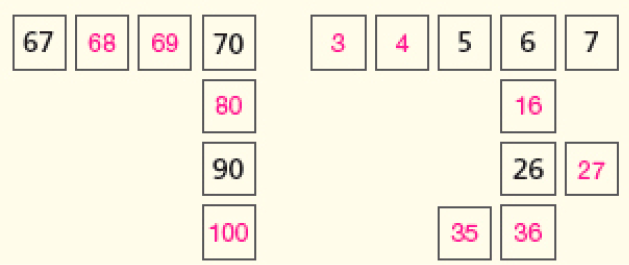
CRÉDITO: ANDERSON DE ANDRADE PIMENTEL
MP223
AVALIAÇÃO PROCESSUAL
- FLÁVIA E ALBERTO BRINCARAM DE BATER FIGURINHAS. NO INÍCIO DO JOGO, CADA UM DELES TINHA 25 FIGURINHAS. NO FIM DO JOGO, ALBERTO TINHA PERDIDO 13 FIGURINHAS PARA FLÁVIA. COM QUANTAS FIGURINHAS ALBERTO FICOU?
_____
PROFESSOR
Exemplo de cálculo: 25 − 13 = 12
ALBERTO FICOU COM _____ FIGURINHAS.
PROFESSOR
Resposta: 12- OBSERVE O CALENDÁRIO DA PÁGINA 128 DESTE LIVRO E ESCREVA O NOME DOS MESES EM QUE HÁ 31 DIAS.
_____
PROFESSOR
Resposta: Janeiro, março, maio, julho, agosto, outubro e dezembro.
- OBSERVE O QUADRO NUMÉRICO E COMPLETE COM OS NÚMEROS QUE ESTÃO FALTANDO NELE.
Quadro: equivalente textual a seguir.
|
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
|
70 |
_____ |
_____ |
73 |
74 |
75 |
_____ |
_____ |
78 |
79 |
|
80 |
_____ |
_____ |
83 |
84 |
85 |
_____ |
_____ |
88 |
89 |
|
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
PROFESSOR
Resposta: 71, 72, 76, 77, 81, 82, 86, 87.AUTOAVALIAÇÃO

- EM QUAIS ATIVIDADES TIVE MAIS DIFICULDADE DURANTE OS ESTUDOS DESTE ANO? E QUAIS FORAM MAIS FÁCEIS?
PROFESSOR
Resposta pessoal.
- O QUE EU MAIS GOSTEI DE APRENDER DE MATEMÁTICA?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Nesta atividade, não é utilizada a informação sobre a quantidade de figurinhas de Flávia. O fato de Flávia e Alberto terem a mesma quantidade de figurinhas no início do jogo é irrelevante, pois o que se quer saber é com quantas figurinhas Alberto ficou. Ao final, peça aos estudantes que reescrevam o problema sem o dado desnecessário, o que explicitará a compreensão deles sobre a situação. Em seguida, peça que escrevam um novo problema, de modo que a informação da quantidade inicial de figurinhas de Flávia seja necessária.
Atividade 5
Não é exigido que os estudantes descrevam os meses na ordem em que eles aparecem no ano, mas mostre que é importante pensar em uma organização, para não esquecer algum mês.
Atividade 6
“O uso de quadros numéricos é um excelente recurso didático para que as crianças possam fazer mais observações sobre as regularidades das escritas numéricas, além da que já percebem por seu contato cotidiano com elas. [...]
Quadros numéricos podem ser organizados em diferentes etapas da escolaridade, apresentando nível de dificuldade compatível com o grupo de estudantes a que se destinam. [...]”
PIRES, Célia Maria Carolino. Números naturais e operações. São Paulo: Melhoramentos, 2013. p. 127-129. (Coleção Como eu Ensino.)
BNCC em foco:
EF01MA05, EF01MA08, EF01MA10, EF01MA17; competências específicas 1 e 2
Autoavaliação
Para resgatar os conteúdos e habilidades trabalhadas, é interessante propor estas questões mais abertas para que os estudantes possam organizar os acontecimentos do ano e avaliar suas relações com os conceitos matemáticos. Certamente haverá conteúdos mais fáceis e outros mais difíceis para cada um, portanto a socialização neste momento pode ser interessante, para que percebam a diversidade de relações estabelecidas com a Matemática estudada neste ano.
Peça sempre que justifiquem suas escolhas. Tais justificativas podem dar indicativos de lacunas em alguns conceitos e ajudá-los a perceber o que precisarão estudar mais no ano seguinte.
MP224
Comentários para o professor
Conclusão da Unidade 8
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observações |
|---|---|---|
|
Descreve a localização de pessoas e de objetos no espaço em relação à própria posição, fazendo uso de termos como à direita, à esquerda , em frente, atrás, em cima, embaixo, perto, longe? |
_____ |
_____ |
|
Quantifica elementos de uma coleção (até 100) fazendo estimativas, contagem um a um, pareamento ou comparando com outros agrupamentos? |
_____ |
_____ |
|
Ordena quantidades de objetos por meio de atributos comuns (ordem crescente ou decrescente), reconhecendo os aspectos cardinal e ordinal do número? |
_____ |
_____ |
|
Reconhece sequência recursiva, identifica padrões figurais ou numéricos, completando os elementos faltantes? |
_____ |
_____ |
|
Identifica e organiza informações colhidas de situações-problema aditivas ou subtrativas apresentadas e registra-as por meio de palavras, tabelas ou gráficos para elaborar as respectivas resoluções? |
_____ |
_____ |
|
Compara e classifica objetos por meio de critérios relativos às suas grandezas e medidas, por exemplo: mais fino/mais grosso ; mais alto/mais baixo ; mais curto/mais comprido ; cabe mais ; mais pesado? |
_____ |
_____ |
|
Identifica em um calendário gregoriano mês, semana, dia; no dia distingue manhã, tarde e noite? |
_____ |
_____ |
|
Reconhece e classifica figuras geométricas como planas ou não planas? |
_____ |
_____ |
|
Reconhece e efetua cálculos com cédulas e moedas do sistema monetário brasileiro? |
_____ |
_____ |
|
Consegue organizar informações e registrá-las por meio de tabelas e de gráficos de colunas? |
_____ |
_____ |
MP225
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observações |
|---|---|---|
|
Compreende e realiza a leitura de tabelas e de gráficos? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação, encenações e dramatizações, entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
AUTOAVALIAÇÃO |
|||
|---|---|---|---|
|
NOME: _____ |
|||
|
MARQUE UM X EM SUA RESPOSTA PARA CADA PERGUNTA. |
SIM |
MAIS OU MENOS |
NÃO |
|
1. PRESTO ATENÇÃO NAS AULAS? |
_____ |
_____ |
_____ |
|
2. PERGUNTO AO PROFESSOR QUANDO NÃO ENTENDO? |
_____ |
_____ |
_____ |
|
3. SOU PARTICIPATIVO? |
_____ |
_____ |
_____ |
|
4. RESPEITO MEUS COLEGAS E PROCURO AJUDÁ-LOS? |
_____ |
_____ |
_____ |
|
5. SOU EDUCADO? |
_____ |
_____ |
_____ |
|
6. FAÇO TODAS AS ATIVIDADES COM CAPRICHO? |
_____ |
_____ |
_____ |
|
7. TRAGO O MATERIAL ESCOLAR NECESSÁRIO E CUIDO BEM DELE? |
_____ |
_____ |
_____ |
|
8. CUIDO DOS MATERIAIS E DO ESPAÇO FÍSICO DA ESCOLA? |
_____ |
_____ |
_____ |
|
9. GOSTO DE TRABALHAR EM GRUPO? |
_____ |
_____ |
_____ |
|
10. RESPEITO TODOS OS MEUS COLEGAS DE TURMA, PROFESSORES E FUNCIONÁRIOS? |
_____ |
_____ |
_____ |