MP059
Introdução da Unidade 2
As páginas de abertura possibilitam diálogos com o objetivo de diagnosticar os conhecimentos e habilidades que os estudantes trazem das unidades anteriores. Estes diálogos se prestam ao planejamento de estratégias a serem aplicadas para recuperar possíveis falhas anteriores de ensino-aprendizagem ou para fazer ampliações do que foi trabalhado neste ano letivo para melhor prover o ano seguinte. Assim, essa abertura revela o quão presente são os números no dia a dia do estudante, em seus diversos significados.
A abordagem dada aos números de até três ordens se fundamenta nos conhecimentos construídos ao longo do 1º ano, por exemplo, apropriação da contagem de objetos de coleções de até 100 unidades; comparação, composição e decomposição de números naturais de até duas ordens; estimativa e comparação de quantidades de objetos de dois conjuntos e, finalmente, construção de fatos fundamentais da adição para a resolução de problemas. Esses conhecimentos se articulam com outros do 3º ano do Ensino Fundamental para consolidar a identificação de características do sistema de numeração decimal, utilizando a composição e decomposição de números naturais de até quatro ordens, bem como a ordenação de números naturais por meio das relações desses com pontos da reta numérica.
Na Unidade Temática Grandezas e medidas, o estudo acerca da relação entre valores de moedas e de cédulas do sistema monetário brasileiro servirá de suporte para a apropriação de conhecimentos sobre a equivalência entre esses valores em situações de compra, venda e troca.
A abordagem proposta para a Unidade Temática Probabilidade e estatística tem, entre seus objetivos, a compreensão de aspectos da realidade próxima. Nela, consideramos tanto os conhecimentos construídos durante o 1 º ano, como leitura de dados em tabelas e gráficos de colunas simples, quanto aqueles previstos para o 3º ano: resolução de problemas com base em dados apresentados em gráficos de barras ou colunas e tabelas de dupla entrada.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo e de espaço, além de um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
MP060
UNIDADE 2. Números

MANUAL DO PROFESSOR
Objetivos da Unidade
• Compreender as ideias de dezena, de dúzia e de meia dúzia.
• Fazer contagem um a um, relacionando a contagem à adição.
• Construir fatos básicos da adição e utilizá-los no cálculo mental ou escrito.
• Comparar e ordenar números naturais pela compreensão de características do sistema de numeração decimal.
• Registrar o resultado de contagens por meio de diferentes estratégias.
• Compor e decompor números naturais de até três ordens.
• Compreender a ideia de centena.
• Construir e descrever sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.
• Representar e localizar números na reta numérica.
• Ler e comparar dados registrados em tabelas e gráficos de colunas.
• Organizar dados coletados em listas e tabelas simples.
A Unidade trata de números, explorando seus aspectos cardinais (que dizem respeito à quantidade) e ordinais (que consideram o número em uma ordem na sequência numérica). Explora também os agrupamentos em dezenas e em centenas, as composições e decomposições numéricas em centenas, dezenas e unidades, os arredondamentos e as estimativas, o uso da reta numérica, as regularidades em sequências numéricas, as cédulas e moedas do sistema monetário brasileiro. Possibilita, ainda, a compreensão da organização de dados em tabelas.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA03, EF02MA04, EF02MA05, EF02MA06, EF02MA09, EF02MA11, EF02MA20, EF02MA22, EF02MA23
MP061

Para refletir...


- • Descreva a história em quadrinhos contando a um
colega
o que a menina da primeira cena faz nas demais cenas.
PROFESSOR
Resposta pessoal. - • Procure e registre os números espalhados pela história.
_____
PROFESSOR
Resposta: 07:00; 189; 4ª; 6; 0143.

- • Converse com os colegas e o professor sobre o que cada um desses números indica.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
É sugerido o trabalho com o ábaco e o Material Dourado, para complementar a ideia de agrupamentos e as características do sistema de numeração. A tendência do uso desses tipos de material foi difundida na década de 1990, provavelmente para incentivar o trabalho com objetos concretos para o aprendizado das crianças. Entretanto, vale destacar que o uso desses materiais não garante a passagem do “concreto” para as noções matemáticas “abstratas”. Não é o uso específico do material que propiciará a construção de conceitos matemáticos, mas a maneira como ele será utilizado e a significação da situação que será proposta.
Explore a ilustração da abertura com os estudantes. Converse com eles sobre o que se passa: A colega de classe de Amélia acordou, preparou-se para tomar o café da manhã e foi para a escola. Aprendeu sobre reciclagem, teve aula de música e voltou para casa.
Para refletir...
Depois que os estudantes fizerem as descrições para um colega, em uma roda de conversa, proponha à turma que elabore uma descrição que será registrada na lousa, para depois cada estudante registrar em seu caderno.
Espera-se que os estudantes localizem o horário (07:00) no relógio digital e o número do endereço da escola (189), que indicam medidas, a indicação de uma ordenação (4ª aula), a indicação de uma quantidade (6 instrumentos) e a indicação de um código (0143) na placa do ônibus do último quadrinho. Converse com eles sobre os diferentes papéis que o número assume.
MP062
Agrupamentos
Dezena
- Cerque com uma linha 1 dezena de joaninhas. Depois, complete a frase.
PROFESSOR
Exemplo de agrupamento:
Há _____ dezena de joaninhas mais _____ joaninhas.
PROFESSOR
Resposta: 1; 5- Observe a ilustração e, em seguida, faça o que se pede.

- Quantos carros estão na fila do pedágio?
_____
PROFESSOR
Resposta: 9
- Se outro carro chegar a essa fila, sem que nenhum dos outros saia quantos carros ficarão?
_____
PROFESSOR
Resposta: 10 carrosAdição - 9 + 1 = _____
PROFESSOR
Resposta: 10Dez ‒ 10 unidades ou 1 dezena


- Em cada caso abaixo, o visor da calculadora mostra um número. Desenhe, em seu caderno, as teclas que você precisaria apertar para efetuar uma adição em que o
número
10 aparecesse em cada visor.
-

PROFESSOR
Exemplo de respostas:PROFESSOR

-

PROFESSOR
Resposta:PROFESSOR

-
MANUAL DO PROFESSOR
Objetivos
• Compreender a ideia de dezena.
• Fazer contagem um a um, relacionando a contagem à adição.
• Construir fatos básicos da adição.
Atividade 1
Na atividade, os estudantes são incentivados a reconhecer 10 unidades e agrupá-las em uma dezena, delimitando-as com uma linha.
Pergunte como se registra o total de joaninhas. É possível que, por não compreenderem totalmente o modo como se registra um número em nosso sistema de numeração, alguns estudantes escrevam 105 para representar a quantidade 15, por exemplo. Nesse caso, a ideia provavelmente teria sido juntar os números 10 e 5, mas a dezena foi escrita como 10 porque não há a compreensão de que a posição que o algarismo ocupa no número altera seu valor e de que cada ordem (unidades e dezenas) é representada por apenas um algarismo e de que levaria ao registro correto, 15.
Atividade 2
Nessa atividade, os estudantes são incentivados a reconhecer que 10 unidades são formadas por 9 unidades mais 1 unidade, e que 10 unidades equivalem a 1 dezena.
Atividade 3
A atividade permite o uso de calculadoras. Então, se possível, disponibilize-as, pois os estudantes vão completar a dezena fazendo uma composição aditiva a partir de um número dado.
As respostas apresentadas podem não ser únicas, mas, usando a adição e a menor quantidade de teclas (ou números), elas são as únicas.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA05
MP063
Uma dúzia e meia dúzia
- Quantas bananas há em cada bandeja?

Há _____ bananas ou uma dúzia de bananas.
PROFESSOR
Resposta: 12Uma dúzia = 12 unidades

Há _____ bananas ou meia dúzia de bananas.
PROFESSOR
Resposta: 6Meia dúzia = 6 unidades

- Desenhe as laranjas que faltam para completar uma dúzia.
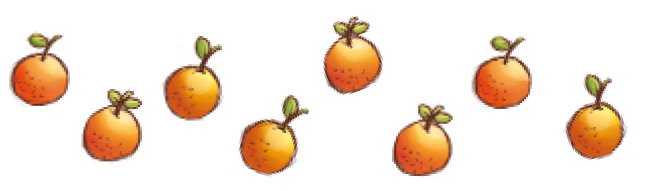
PROFESSOR
Resposta: Exemplo de desenho:
- Observe abaixo os ovos que tia Célia comprou na feira.

- Marque com um X essa quantidade de ovos.
( ) 1 dúzia
( ) 2 dúzias
( ) 1 dúzia e meia
PROFESSOR
Resposta correta: 1 dúzia e meia- Registre, sem usar a palavra dúzia, a quantidade de ovos que tia Célia comprou:
_____
ovos.
PROFESSOR
Resposta: 18 (ou dezoito)
MANUAL DO PROFESSOR
Assim, se após a contagem chegava-se a 60 unidades, isso era indicado por cinco dedos levantados da segunda mão usada, pois 5 × 12 = 60. É possível que daí venha o uso da contagem em grupos de 60 na Mesopotâmia antiga (atual Iraque), há milhares de anos. É possível considerar também que a divisão do dia em dois grupos de 12 horas, sendo cada hora dividida em 60 minutos, deva sua origem a esse hábito.
Objetivos
• Compreender as ideias de dúzia e meia dúzia.
• Registrar o resultado de contagens.
Alguns dos modos usados para agrupar quantidades são a dúzia e a meia dúzia. Pergunte: “O que vocês conhecem que é vendido em dúzia? E em meia dúzia?”.
Atividades 1 e 2
Nessas atividades, os estudantes são incentivados a reconhecer a dúzia e a meia dúzia na contagem de diversas quantidades. Comente que muitos produtos, antes vendidos por dúzia, atualmente são comercializados por quilograma.
O termo “meia” é bastante utilizado como sinônimo para o número seis. O motivo é que na linguagem oral as palavras “seis” e “três” têm pronúncias muito parecidas, de modo que o uso de “seis” pode causar confusão; com a palavra “meia”, esse problema é evitado. O termo também aparece em frases populares, como “trocar seis por meia dúzia”, as quais podem fornecer material valioso para abordar o assunto com os estudantes.
Atividade 3
Observe como os estudantes expressam a quantidade total de ovos. Caso julgue necessário, organize agrupamentos de elementos com 1 dúzia e 2 dúzias para que eles comparem as quantidades.
A origem do hábito de agrupar em 12 unidades (dúzia) é incerta, mas o contato com modos antigos de fazer o registro numérico em alguns lugares da Ásia Central fornece indícios sugestivos: trata-se do hábito de contar as quantidades apontando as falanges dos dedos de uma mão a cada unidade indicada. Como há 12 falanges nos dedos de uma mão (sem contar o polegar), uma vez atingida essa quantidade levantava-se um dedo da outra mão e prosseguia-se a contagem.
BNCC em foco:
EF02MA01, EF02MA02
MP064
Dezenas e centenas
- Observe que, no Material Dourado, cada
 (barra) é formada por 10
(barra) é formada por 10  (cubinhos). Em seguida, complete.
(cubinhos). Em seguida, complete.

ou

10 unidades ou 1 dezena
Dez

2 dezenas ou 20 unidades
Vinte

_____ dezenas ou 30 unidades
PROFESSOR
Resposta: 3Trinta

_____ dezenas ou 40 unidades
PROFESSOR
Resposta: 4Quarenta
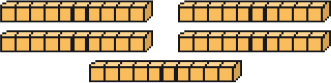
_____ dezenas ou _____ unidades
PROFESSOR
Resposta: 5; 50Cinquenta
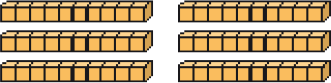
_____ dezenas ou _____ unidades
PROFESSOR
Resposta: 6; 60Sessenta
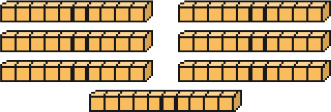
_____ dezenas ou _____ unidades
PROFESSOR
Resposta: 7; 70Setenta
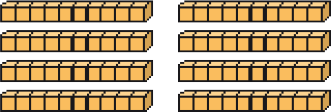
_____ dezenas ou _____ unidades
PROFESSOR
Resposta: 8; 80Oitenta
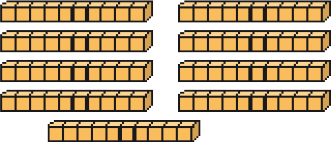
_____ dezenas ou _____ unidades
PROFESSOR
Resposta: 9; 90Noventa
MANUAL DO PROFESSOR
Objetivos
• Comparar e ordenar números naturais pela compreensão de características do sistema de numeração decimal.
• Registrar o resultado de contagens ou de estimativas.
• Compor e decompor números naturais de até três ordens.
• Construir fatos básicos da adição.
• Compreender a ideia de centena.
• Completar e descrever sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.
Atividade 1
O Material Dourado é composto de peças de quatro tipos: cubinhos (unidades), barras (dezenas), placas (centenas) e cubos (milhares). Nessa atividade, usamos apenas cubinhos e barras. Caso haja disponibilidade, leve o Material Dourado para a sala de aula, deixe os estudantes manipularem suas peças e solicite-lhes que observem o número de cubinhos que formam uma barra.
Ele foi concebido para que sua forma e estrutura remetam à ideia de que dez unidades podem ser reunidas em um grupo (dezena), facilitando a compreensão do processo de trocas entre elas. Entretanto, como a posição das peças do Material Dourado não obedece necessariamente à ordem seguida na escrita no sistema de numeração decimal, não é possível explorar com ele o fato de esse sistema ser posicional. Por exemplo, ao representar o número 14 com uma barra e quatro cubinhos, eles não precisam estar dispostos na posição correspondente aos algarismos no número 14. Assim, seu uso deve ser complementado com atividades que trabalhem a importância da posição na escrita dos números, como o uso do ábaco vertical.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA03, EF02MA04
MP065
- Ana convidou 9 amigos para sua festa de aniversário. Ela preparou 9 saquinhos com 10 balas cada um para dar como lembrancinha. Ao todo quantas balas Ana colocou nesses saquinhos?

10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 = _____
PROFESSOR
Resposta: 90- Durante a festa, Ana percebeu que havia mais uma pessoa. Então, ela preparou rapidamente um
saquinho
com 10 balas. No total, Ana colocou quantas balas nos saquinhos?
_____ + 10 = 100
PROFESSOR
Resposta: 90No total, Ana colocou 100 balas ou 1 centena de balas nos saquinhos.
1 centena ou 10 dezenas ou 100 unidades
- Complete as sequências de acordo com cada regra.
- Adicionar 2: 84,
_____,
_____,
90,
_____,
_____,
_____,
_____,
100
PROFESSOR
Resposta: 86, 88, 92, 94, 96, 98.
- Adicionar 5: 60,
_____,
70,
_____,
_____,
85,
_____,
_____,
_____
PROFESSOR
Resposta: 65, 75, 80, 90, 95, 100
- Adicionar 10: 20, ____,
_____,
_____,
_____,
70,
_____,
90,
_____
PROFESSOR
Resposta: 30, 40, 50, 60, 80, 100

- João tinha 50 reais e ganhou 60 reais. Ele ficou com mais de 100 reais ou menos de 100 reais?
_____
PROFESSOR
Resposta: Mais de 100 reais.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, o objetivo é estabelecer relações entre centena, dezenas e unidades. Os estudantes podem contar o total em agrupamentos de 10 em 10 e, a partir do 90, contar de 1 em 1. Observe os procedimentos usados por eles e socialize-os com a turma.
Atividade 3
A atividade possibilita aos estudantes explorar sequências numéricas crescentes com padrão de regularidade.
Para ampliar a atividade, pode-se pedir que elaborem outras sequências, que devem começar no:
• 70 e ir adicionando 3 unidades até chegar a 100;
• 40 e ir adicionando 6 unidades até chegar a 100;
• 60 e ir adicionando 4 unidades até chegar a 100.
Crie outras sequências e peça aos estudantes que descubram a regularidade.
Atividade 4
Alguns estudantes podem saber que duas cédulas de 50 reais totalizam 100 reais e, assim, descobrir que João tem mais de 100 reais. Outros podem raciocinar assim: “João ficou com mais de 100 porque 60 é maior que 50 e já sei que 50 mais 50 são 100”; ou, ainda: “João ficou com mais de 100 reais porque 5 dezenas mais 6 dezenas são 11 dezenas, ou seja, 110 reais”.
A fim de ampliar o repertório de procedimentos, socialize com a turma as estratégias usadas pelos estudantes.
Para facilitar a compreensão da ideia de centena, leve o Material Dourado para a sala de aula e peça que ajudem a contar de 1 a 100, representando cada unidade de contagem por 1 cubinho. Quando a contagem chegar a 10, é possível que sugiram trocar 10 cubinhos por 1 barra. Espera-se que o fim da contagem resulte em 10 barras e que os estudantes observem que as 10 barras (10 dezenas) podem ser trocadas por uma única placa (a centena).
BNCC em foco:
EF02MA01, EF02MA04, EF02MA06, EF02MA09, EF02MA11
MP066
- Veja a quantidade de peças de roupas arrecadadas em uma campanha de doação durante três dias da semana.
Tabela: equivalente textual a seguir.
|
Dia da semana |
Peças de roupas |
|---|---|
|
Quinta-feira |
30 |
|
Sexta-feira |
20 |
|
Sábado |
50 |
- Quantas peças de roupas foram arrecadadas ao todo nesses três dias?
_____
PROFESSOR
Resposta: 100 peças.

- Complete com o número de cédulas ou de moedas necessárias para obter 100 reais em cada caso.
a)

_____
PROFESSOR
Resposta: 100b)

_____
PROFESSOR
Resposta: 10c)

_____
PROFESSOR
Resposta: 2d)

_____
PROFESSOR
Resposta: 1


- O visor de uma calculadora mostra o número indicado em cada caso. Desenhe as teclas que você deve apertar para efetuar uma adição em que apareça o número 100 em cada visor.
a)

PROFESSOR
Exemplo de resposta: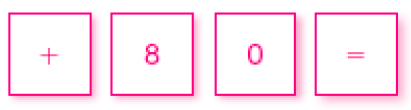
b)

PROFESSOR
Exemplo de resposta:
MANUAL DO PROFESSOR
Atividade 5
Ao indicar quantas peças de roupas foram arrecadadas nos três dias, chega-se à composição da quantidade 100 peças de roupas por meio da adição de três parcelas.
Pergunte:
• Em qual dia foram arrecadadas mais peças de roupa? (No sábado.)
• Quantas peças de roupa foram arrecadadas nesse dia? (50 peças de roupa.)
• Quantas dezenas de peças de roupas foram arrecadadas nesses três dias? (10 dezenas de peças de roupas.)
Pode-se alterar a quantidade de peças de roupas arrecadadas em um dos dias da semana – por exemplo, na sexta-feira – para 40 peças e desafiá-los a descobrir o número de peças arrecadadas no sábado para que o total de peças arrecadadas nos três dias continue sendo igual a 100. Espera-se que se obtenham 30 peças arrecadadas no sábado.
Atividade 6
Nesta atividade, os estudantes devem compor 100 reais com diferentes cédulas e moedas, o que permite relacionar a centena com outros números. Produza, antecipadamente, cédulas e moedas de real para os estudantes utilizarem quando necessário. Oriente-os a guardá-las, pois poderão ser utilizadas em outras atividades. Peça que se reúnam em grupos e, usando as cédulas produzidas, realizem a atividade e registrem a estratégia empregada. É possível que contem a quantia, como se faz nas práticas sociais. Por exemplo, para obter a quantidade de cédulas de 10 reais que formam 100 reais, podem contar: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, ou seja,10 cédulas.
Atividade 7
Os estudantes podem usar quaisquer operações para chegar ao resultado 100. Peça que socializem as respostas. Se algum deles não tiver usado o número indicado no visor da calculadora, oriente-o a usá-lo.
BNCC em foco:
EF02MA04, EF02MA06, EF02MA20; competências específicas 3 e 7
Sugestão de trabalho voluntário
Aproveite a atividade 5 para falar sobre a importância do ato de doar. Sugira aos estudantes que, se tiverem roupas que não sirvam ou que não queiram mais, em boas condições de uso, eles poderão doá-las a quem precisa.
MP067
Analisando os números
- Descubra a quantidade em cada caso.

_____ centena e _____ unidade
PROFESSOR
Resposta: 1;1100 + 1 = 101
Cento e um
1 centena e _____ unidade
PROFESSOR
Resposta: 13_____ + _____ = 113
PROFESSOR
Resposta: 100; 13Cento e treze

_____ centena e _____ unidade
PROFESSOR
Resposta: 1; 54_____ + _____ = _____
PROFESSOR
Resposta: 100 + 54 = 154Cento e cinquenta e quatro
- Complete as sequências adicionando sempre 1.
-
a) 138, 139,
_____,
_____,
_____
PROFESSOR
Resposta: 140, 141, 142
-
b) 796, 797,
_____,
_____,
_____
PROFESSOR
Resposta: 798, 799, 800
Os símbolos 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9 são chamados de algarismos. Com eles podemos representar qualquer número.
- Escreva o valor que indica o algarismo 4 em cada número.
204
4: _____ unidades
PROFESSOR
Resposta: 4240
4: _____ dezenas ou _____ unidades
PROFESSOR
Resposta: 4; 40420
4: _____ centenas ou _____ unidades
PROFESSOR
Resposta: 4; 400MANUAL DO PROFESSOR
Objetivos
• Comparar e ordenar números naturais pela compreensão de características do sistema de numeração decimal.
• Registrar o resultado de contagens.
• Compor e decompor números naturais de até três ordens.
• Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
Atividade 1
Os estudantes devem observar a regularidade na composição de números de três algarismos. Na lousa, apresente outros exemplos, como:
• 1 centena e 5 unidades é o mesmo que 100 + 5 ou 105, que lemos “cento e cinco”;
• 1 centena e 50 unidades é o mesmo que 100 + 50 ou 150, que lemos “cento e cinquenta”.
Atividade 2
Comente que sequências desse tipo, em que os números vão do menor para o maior, têm os números em ordem crescente. Depois de completar as duas sequências, peça aos estudantes que, no caderno, escrevam os números de cada sequência do maior para o menor, formando duas outras sequências, que agora têm os números em ordem decrescente.
Atividade 3
A atividade explora a noção do valor posicional de um algarismo. Faça uma roda de conversa e incentive os estudantes a exporem suas opiniões. Registre na lousa as conclusões da turma sobre as escritas dos números.
Caso os estudantes tenham dificuldades com a escrita dos números em nosso sistema de numeração, faça representações com o Material Dourado, ou com moedas de 1 real e cédulas de 10 e de 100 reais, produzidas anteriormente, além do ábaco.
É importante propiciar atividades em grupo, nas quais os estudantes tenham de observar, registrar, negociar pontos de vista e argumentar.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA04, EF02MA09
MP068
- Observe abaixo a representação com o Material Dourado. Cada placa é formada por 10 barrinhas e cada barrinha é formada por 10 cubinhos. Depois, complete os espaços a seguir.
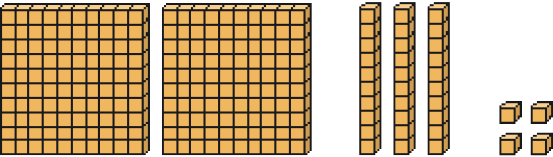
2 placas _____ barras _____ cubinhos
PROFESSOR
Resposta: 3; 4_____ centenas, _____ dezenas e _____ unidades compõem o número 234.
PROFESSOR
Resposta: 2; 3; 4200 + 30 + _____ = _____
PROFESSOR
Resposta: 4; 234234 ‒ Lemos: duzentos e trinta e quatro.
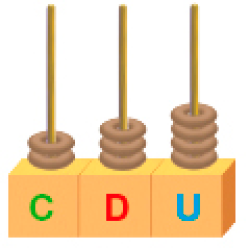
- Agora, veja outras representações do número 234.
Quadro de ordem
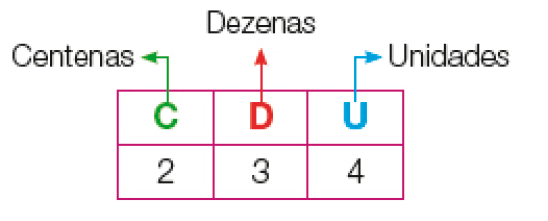
Ábaco
- Complete o quadro a seguir.
Quadro: equivalente textual a seguir.
|
Número de centenas |
Número de dezenas |
Número de unidades |
Compondo o número |
|---|---|---|---|
|
3 |
2 |
2 |
_____ + _____ + _____ = _____ |
|
5 |
_____ |
0 |
_____ + 70 + _____ = 570 |
|
_____ |
_____ |
_____ |
400 + 0 + 9 = _____ |
PROFESSOR
Resposta: Número de centenas: 4;PROFESSOR
Número de dezenas: 7; 0PROFESSOR
Número de unidades: 9PROFESSOR
Compondo o número:PROFESSOR
300 + 20 + 2 = 322PROFESSOR
500 + 70 + 0 = 570PROFESSOR
400 + 0 + 9 = 409MANUAL DO PROFESSOR
Atividade 4
A atividade apresenta a composição e a decomposição do número 234, representado de várias maneiras: com Material Dourado, no quadro valor de lugar (ou quadro de ordem) e pelo ábaco.
Atividade 5
A atividade explora a compreensão da composição numérica em centenas, dezenas e unidades.
Para ampliar a atividade, peça aos estudantes que façam outras composições dos números 322, 570 e 409. Por exemplo:
50 + 50 + 200 + 22 = 322
500 + 70 = 570
300 + 100 + 9 = 409
É importante que a turma compreenda a ideia de valor posicional, em que um mesmo algarismo pode representar diferentes quantidades, dependendo da sua posição no número.
Um modo de evidenciar essa estrutura é por meio de um ábaco, como mostram as figuras a seguir, em que se indicam as quantidades de unidades que compõem o número.

CRÉDITO: MARCOS DE MELLO
BNCC em foco:
EF02MA01, EF02MA02, EF02MA03, EF02MA04
MP069
- Escreva o número representado em cada ábaco.
a)
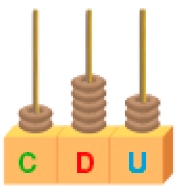
_____
PROFESSOR
Resposta: 253b)
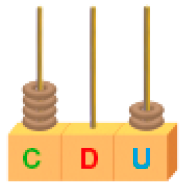
_____
PROFESSOR
Resposta: 402- Escreva o
número
em cada caso, usando algarismos.
- Cento e sete: 107
- Cento e dezenove:
_____
PROFESSOR
Resposta: 119
- Cento e quarenta:
_____
PROFESSOR
Resposta: 140
- Cento e oitenta e seis:
_____
PROFESSOR
Resposta: 186
Boxe complementar:
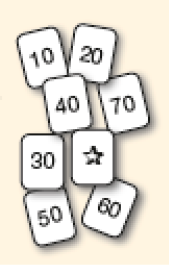
Desafio
Descubra e escreva nas placas o número da casa de cada criança.

CRÉDITO: GEORGE TUTUMI
PROFESSOR
Resposta: 340; 338; 300Fim do complemento.
MANUAL DO PROFESSOR
Atividade 6
Providencie pelo menos um ábaco para os estudantes usarem para registrar números e fazer a leitura de registros feitos por outros.
Atividade 7
Os itens a e c dessa atividade apresentam números cuja representação escrita exige o uso do algarismo zero. Nos primeiros contatos dos estudantes com números como o 107, é comum representarem 1.007 ou 17. No primeiro caso, possivelmente pensam em 100 com 7 e escrevem 100 e 7 justapostos, formando 1.007. No segundo caso, escrevem 1 para representar cem e 7 para sete unidades, sem considerar que a ordem das dezenas deveria ser representada com o algarismo zero.
Desafio
Nessa proposta, a ordem de apresentação e de leitura das informações não corresponde à ordem em que devem ser consideradas na resolução, uma vez que o número da casa de Luís e o da casa de Márcio dependem do número da casa de Pedro (300). Como o número da casa de Luís tem 4 dezenas a mais que o número da casa de Pedro, ele mora na casa de número 340. O número da casa de Márcio tem 2 unidades a menos que o número da casa de Luís, portanto ele mora na casa de número 338.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA03, EF02MA04, EF02MA05; competência geral 2
Sugestão de leitura para o professor
Livro
PIRES, Célia Maria Carolino. Educação matemática : conversas com professores dos anos iniciais. São Paulo: Zapt, 2012.
Nesse livro, sugerimos o texto “Artefatos para calcular”, que explora a composição de números de três algarismos por meio de uma adição em que uma das parcelas é 100 e a outra é um número menor ou igual a 99. Desse modo, associamos a composição com a leitura desses números.
MP070
Jogo: 100 com 4 cartas

Materiais: Tabuleiro da página 219 e 32 cartas feitas em cartolina pelos jogadores: 6 cartas com o número 10, 6 cartas com o número 20, 4 com o número 30, 4 com o número 40, 4 com o número 50, 2 com o número 60, 2 com o número 70 e 4 coringas.

Jogadores: 2, 3 ou 4
Regras:
- Embaralham-se as cartas e distribuem-se 3 a cada jogador. As demais cartas ficam viradas para baixo em um monte para compras.
- Cada jogador deixa suas cartas viradas para cima, expostas aos demais.
- Os jogadores decidem quem começará. Cada um, na sua vez, coloca uma carta em uma casa do tabuleiro com o objetivo de obter exatamente 100 ao adicionar os números de 4 cartas em uma fileira (horizontal, vertical ou diagonal). Depois, retira uma carta do monte que substitui a carta usada, ficando sempre com 3 cartas.
- Quando um jogador conseguir obter 100 com as 4 cartas, deverá recolhê-las e guardá-las com ele.
- Caso o jogador obtenha ao mesmo tempo 100 em mais de uma fileira, só poderá retirar 4 cartas de uma dessas fileiras.
- O coringa pode ser usado no lugar de qualquer carta.
- O jogo termina se não houver mais cartas no monte e um dos jogadores ficar com 2 cartas.
- Se as 16 casas do tabuleiro estiverem ocupadas, o jogador seguinte poderá tentar obter 100 trocando uma das cartas do tabuleiro por uma de suas cartas. Se ninguém conseguir, o jogo terminará e vence aquele que tiver guardado mais cartas.
MANUAL DO PROFESSOR
Objetivos
• Registrar o resultado de contagens.
• Construir fatos básicos da adição e utilizá-los no cálculo mental ou escrito.
• Compor o número 100 por meio de diferentes adições.
Ajude os estudantes na leitura e na compreensão das regras e explique termos que talvez não conheçam, como horizontal, vertical e diagonal, desenhando na lousa as casas do tabuleiro nas seguintes posições:
Horizontal
Vertical

Diagonais
CRÉDITO: ADILSON SECCO
Em seguida, ajude os estudantes a elaborarem as cartas e o tabuleiro, conforme ilustrado, em um papel mais resistente, por exemplo, uma cartolina. Explique a eles que as cartas confeccionadas devem ser um pouco menores que as casas do tabuleiro.
O jogo trabalha com a ideia de composição do número 100 por meio de quatro parcelas; o estudante vai perceber que o número 100 pode ser obtido por meio de variadas composições. A adição de dezenas inteiras pode ser facilitada pela adição das unidades que correspondem ao algarismo das dezenas inteiras. Por exemplo, saber que 3 + 2 + 1 + 4 = 10 ajuda a obter o resultado de 30 + 20 + 10 + 40 = 100.
BNCC em foco:
EF02MA02, EF02MA04, EF02MA05; competência geral 9; competências específicas 7 e 8
MP071
Questões sobre o jogo

- Por que não há cartas de número 80 no jogo?
PROFESSOR
Resposta: A menor carta do jogo é a de número 10 e, caso existisse a carta de número 80, não seria possível obter 100 com a adição dos números de 3 outras cartas desse jogo.- Veja as cartas que estão no tabuleiro abaixo e responda à pergunta de Júlia.

_____
PROFESSOR
Resposta: Com as cartas de números 10 e 50, ou 20 e 40, ou 30 e 30.- Observe a seguinte situação do jogo.

- Laís pode completar 100
nessa
jogada? Explique sua resposta.
_____
PROFESSOR
Resposta: Sim, colocando a carta de número 30 na diagonal que tem as cartas de número 40, 20 e 10.
- Se
fosse
a vez de Otávio, que carta ele deveria ter para completar 100
nessa
jogada? Explique os casos possíveis.
_____
PROFESSOR
Resposta: Uma carta de número 30, como a menina; ou uma carta de número 10, para formar 100 na fileira das cartas com os números 30, 10 e 50 ou na fileira das cartas com os números 20, 30 e 40; ou um coringa.
MANUAL DO PROFESSOR
Após o jogo, pode-se promover uma discussão na classe, anotando na lousa diversas composições possíveis para formar 100:
• 10 + 10 + 10 + 70
• 10 + 10 + 20 + 60
• 10 + 10 + 30 + 50
• 10 + 10 + 40 + 40
• 10 + 20 + 20 + 50
• 20 + 20 + 30 + 30
Questões sobre o jogo
As questões trazem uma reflexão sobre as ações realizadas nas partidas. O ideal é que sejam respondidas em dupla ou em grupo, após os estudantes jogarem algumas vezes.
Na questão 1, espera-se que os estudantes percebam que a menor carta do jogo é a de número 10 e que, se existisse a carta de número 80, para completar 100 faltariam 20, impossível de obter com a adição dos números de três outras cartas desse jogo.
A questão 2 permite mais de uma resposta. Como a soma das duas cartas que completam a fileira deve ser igual a 60, ela pode ser obtida por meio das cartas de números 10 e 50, 20 e 40, ou 30 e 30.
Na questão 3, a proposta é descobrir qual dos dois jogadores da ilustração tem as cartas necessárias para obter 100 em uma fileira nessa jogada. Há três fileiras com três cartas: duas delas com soma igual a 90 (na vertical e na horizontal), e outra com soma igual a 70 (na diagonal).
Pergunte: “Que carta completa uma das fileiras com soma 90 no tabuleiro?”. (A carta de número 10 ou o coringa.)
Variações
Uma possibilidade de variação no jogo, que aumenta o nível de dificuldade, é propor a confecção de cartas com números que não sejam formados por dezenas inteiras.
BNCC em foco:
EF02MA02, EF02MA04, EF02MA05; competência geral 9; competências específicas 7 e 8
MP072
Trocando dinheiro
Observe as moedas do dinheiro brasileiro.
Moedas

1 centavo

5 centavos

10 centavos

25 centavos

50 centavos

1 real
- Veja algumas trocas que podemos fazer e complete.
10  trocamos por 1
trocamos por 1 
10  trocamos por 1
trocamos por 1 
_____
 trocamos por 1
trocamos por 1 
PROFESSOR
Resposta: 10
_____
 trocamos por 1
trocamos por 1 
PROFESSOR
Resposta: 10
_____
 trocamos por 1
trocamos por 1 
PROFESSOR
Resposta: 1001.000  trocamos por
_____
trocamos por
_____

PROFESSOR
Resposta: 1
_____
 trocamos por 1
trocamos por 1 
PROFESSOR
Resposta: 100MANUAL DO PROFESSOR
Objetivo
• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.
Com base em situações que envolvem trocas de cédulas e moedas, é possível identificar os conhecimentos anteriores dos estudantes. Explore o assunto perguntando: “O que é possível comprar com uma moeda de 25 centavos? E com uma cédula de 10 reais? E com uma cédula de 50 reais?”. Proponha, por exemplo, que os estudantes usem cédulas (já confeccionadas) para vivenciarem situações, como realizar um pagamento de 75 reais usando cédulas de 20 reais, 10 reais e 5 reais, ou outras que envolvam a devolução de troco, observando como procedem, por exemplo, na hora de dar o troco: se completam o valor que deve ser cobrado até atingir o valor entregue em cédulas ou se realizam uma subtração.
Atividades como a realização de uma feirinha ou mercado em sala de aula, usando embalagens vazias, folhetos promocionais e cédulas (de dinheiro fantasia) também são ótimas oportunidades para observar o modo como os estudantes resolvem as situações propostas e se utilizam cálculo mental ou escrito nas operações aritméticas.
Sugestão de leitura para o estudante
Livro
ROCHA, Ruth. A galinha dos ovos de ouro e outras histórias. Ilustrações de Cláudio Martins. São Paulo: Salamandra, 2009. (Série Conte um Conto.)
A leitura do livro permite discutir temas importantes com os estudantes, como o valor do trabalho, a relação das pessoas com o dinheiro, a riqueza e a ganância.
BNCC em foco:
EF02MA20; competência específica 3
Sugestão de atividade
Jogo Formando dezenas
Providencie palitos de sorvete e peça aos estudantes que se reúnam em grupos. Em cada rodada, o estudante, na sua vez, joga um dado, recolhe a quantidade de palitos correspondente aos pontos do dado e organiza-os em montes de uma dezena. Ganha quem conseguir formar mais grupos de uma dezena de palitos após um número predeterminado de rodadas. Uma variação possível é permitir que as dezenas sejam formadas apenas quando se obtiver no dado exatamente o valor que falta para uma dezena. Por exemplo, se o jogador tiver 6 palitos, ele formará a dezena apenas quando conseguir tirar o número 4 no dado, pois 6 + 4 = 10.
MP073
Reta numérica
Faça o que se pede.
- Numere as casas desta rua com uma sequência de 10 em 10.

PROFESSOR
Resposta: 940, 960, 970, 990- Represente na reta numérica os números das casas do item anterior.

PROFESSOR
Resposta: 940, 960, 970, 980, 1.000- Observando a reta numérica, responda às questões.
- Sabrina estava parada diante da casa de
número
950. Ela andou 5 casas para a direita e depois voltou 3 casas. Qual é o
número
da casa diante da qual Sabrina parou?
_____
PROFESSOR
Resposta: 970
- Sabrina estava parada diante da casa de
número
950. Ela andou 5 casas para a direita e depois voltou 3 casas. Qual é o
número
da casa diante da qual Sabrina parou?
_____

- Felipe estava parado diante da casa de
número
990. Ele andou 4 casas para a
esquerda
e depois voltou 5 casas. Qual é o
número
da casa diante da qual Felipe parou?
_____
PROFESSOR
Resposta: 1.000

MANUAL DO PROFESSOR
Objetivos
• Comparar e ordenar números naturais pela compreensão de características do sistema de numeração decimal.
• Representar e localizar números na reta numérica.
A representação de números em uma reta numérica facilita a visualização e a comparação dos números de uma sequência numérica.
No item c, explora-se a ideia de deslocamento, além de significados associados à adição e à subtração sem o uso dos algoritmos usuais. Os estudantes devem realizar os deslocamentos diretamente sobre a reta numérica ou determinar o sentido e o número de casas andadas, para depois realizar os deslocamentos. Por exemplo, Sabrina deslocou-se 5 casas para a direita: 960, 970, 980, 990, 1 000, e depois voltou três casas: 990, 980, 970. Portanto, Sabrina parou diante da casa de número 970. Outra possibilidade seria pensar que, se Sabrina deslocou-se 5 casas para a direita e depois voltou três casas, como 5 − 3 = 2, esses deslocamentos equivalem a Sabrina ter se deslocado 2 casas para a direita: 960, 970. Peça que expliquem qual raciocínio usaram.
Os usos do número 10
Por ser tão importante no sistema de numeração decimal, o número 10 aparece nos mais variados contextos. Peça aos estudantes que tragam fotografias, desenhos, textos, entre outros, que contenham: uma lista de dez coisas importantes (músicas, personalidades, hábitos de higiene etc.); uma situação em que se faz uma contagem regressiva começando com 10; jogadores de futebol que já usaram ou usam a camisa de número 10; imagens, à escolha dos grupos, nas quais haja esse número.
Na sala de aula, eles deverão se reunir em grupo e produzir um painel com o material trazido.
BNCC em foco:
EF02MA01, EF02MA09, EF02MA11
MP074
Comparações
- No sábado, Gabriel e Leandro começaram a preparar doces. Gabriel fez 100 doces e Leandro, 140.
- Qual deles fez mais doces?
_____
PROFESSOR
Resposta: Leandro.
- A reta numérica abaixo representa essa situação. Complete-a.
- Qual deles fez mais doces?
_____

PROFESSOR
Resposta: 100, 120, 140, 160- Em uma reta numérica, o
número
maior fica à direita ou à
esquerda
do
número
menor?
_____
PROFESSOR
Resposta: À direita.
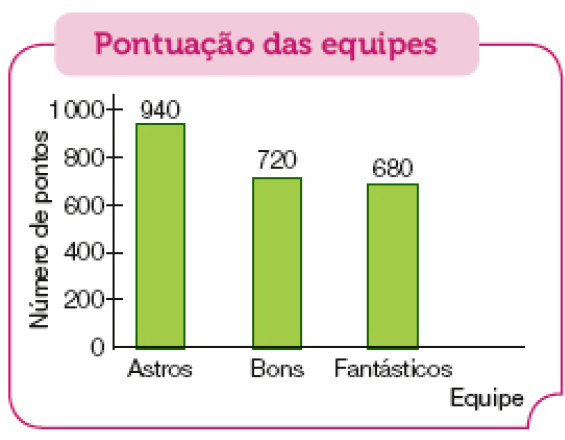
- O gráfico abaixo mostra a pontuação de três equipes de basquete em um campeonato.
Fonte: Campeonato de basquete (maio 2023).
- Qual das equipes fez o maior
número
de pontos?
_____
PROFESSOR
Resposta: Astros.
- Qual das equipes fez o
menor
número
de pontos?
_____
PROFESSOR
Resposta: Fantásticos.
- Qual foi a pontuação da equipe com maior
número
de pontos? E da equipe com
menor
número
de pontos?
_____
PROFESSOR
Resposta: 940 pontos; 680 pontos.
- A pontuação da equipe Astros está mais próxima de 800 ou de 1 000?
_____
PROFESSOR
Resposta: Mais próxima de 1.000.
MANUAL DO PROFESSOR
Objetivos
• Comparar e ordenar números naturais pela compreensão de características do sistema de numeração decimal, com suporte da reta numérica.
• Ler e comparar dados registrados em gráfico de colunas.
Atividade 1
A reta numérica oferece uma visualização da sequência dos números e permite a comparação e a identificação do maior e do menor.
Na atividade, os estudantes poderão observar que, à medida que os números aumentam, eles se localizam mais à direita em sua representação na reta numérica.
Atividade 2
A atividade propicia aos estudantes a leitura de um gráfico de colunas. Ao fazerem a interpretação das informações nele apresentadas, identificarão o maior e o menor número de pontos obtidos por três equipes de basquete, tendo como auxílio a possibilidade de comparar entre si as alturas das colunas desse gráfico, além de estimar a proximidade da altura da maior coluna com o número 1 000.
Sugestão de trabalho interdisciplinar
O uso da reta numérica pode auxiliar na compreensão de linhas do tempo, que geralmente são trabalhadas em História.
BNCC em foco:
EF02MA01, EF02MA03, EF02MA09, EF02MA22; competência específica 3
MP075
Arredondamentos e estimativas
- Henrique tem aproximadamente 40 reais. Qual destas quantias pode ser a quantia exata de Henrique?
( ) 26 reais.
( ) 39 reais.
( ) 58 reais.
PROFESSOR
Resposta correta: 39 reais.

- Observe os brinquedos a seguir.

- Se Antônio comprar os dois brinquedos para dar de presente a seus filhos, quanto, aproximadamente, ele vai pagar?
_____
PROFESSOR
Exemplo de resposta: Aproximadamente 100 reais.

- Luísa observou o preço dos dois móveis que estava comprando e estimou que pagaria 600 reais. Marque com um X os possíveis preços desses móveis.

( ) 180 reais e 930 reais.
( ) 327 reais e 135 reais.
( ) 375 reais e 192 reais.
PROFESSOR
Resposta correta: 375 reais e 192 reais.


- Reúna-se com um colega e, juntos, discutam como cada um pensou para responder à estimativa.
MANUAL DO PROFESSOR
Muito empregado no cotidiano, o arredondamento facilita a estimativa de cálculo mental. Há que se considerar que ele pode ser feito tanto para valores maiores (estimativa para mais) quanto para valores menores (estimativa para menos).
Em situações de compra não é possível arredondar “para menos”. Se um produto custa 37 reais, por exemplo, não é possível comprá-lo com 35 reais, a não ser que haja um desconto.
Objetivo
• Comparar números naturais por estimativas ou arredondamentos.
Atividade 1
Nessa atividade explora-se o arredondamento feito para um valor maior, já que 40 (que é o valor arredondado) é maior que 39 (valor exato).
Atividade 2
Esclareça aos estudantes que não há somente uma forma de arredondar um número. Nessa atividade, a aproximação possível de 100 reais sugere que os preços em reais sejam arredondados para a dezena inteira mais próxima (57 para 60 e 39 para 40). Contudo, qualquer outro valor próximo de 96 (que é o valor exato do gasto na compra dos dois brinquedos) é válido e aceitável.
Atividade 3
Nessa atividade, os estudantes são solicitados a verificar qual dos pares de quantias corresponde aos preços de cada móvel por meio de arredondamentos e de uma adição, tendo como condição o resultado aproximado dessa adição (600 reais). Espera-se que eles percebam facilmente que a primeira possibilidade é inviável, já que somente a quantia 930 já é maior que 600. Fazendo arredondamentos para a centena inteira mais próxima das outras duas possibilidades, temos:
• arredondando 327 para 300 e 135 para 100, obtemos um total de 400;
• arredondando 375 para 400 e 192 para 200, obtemos um total de 600.
Assim, os estudantes podem concluir que os preços são 375 reais e 192 reais.
Se necessário, use a reta numérica como apoio.
As atividades propostas na página exploram o cálculo mental e a estimativa, incentivando o arredondamento como estratégia. Após a realização das atividades, questione os estudantes sobre como eles pensaram para fazer a estimativa e o cálculo mental.
BNCC em foco:
EF02MA02
MP076
A Matemática me ajuda a ser
... uma criança que conhece diversas culturas
Você já usou os dedos das mãos para mostrar uma quantidade ou para fazer uma conta?
Saiba que esse recurso é mais comum do que você imagina.
Segundo pesquisadores, usar os dedos na prática de contagens ou de registros de números foi, e ainda é, um recurso valioso, presente em diferentes culturas de todo o mundo, incluindo a de vários povos indígenas do Brasil.
Veja, por exemplo, como os Kuikuro, que habitam o Parque Indígena do Xingu (Mato Grosso), associam os números com os dedos das mãos e dos pés.
Tabela: equivalente textual a seguir.
|
Nosso símbolo |
Na língua dos Kuikuro |
Significado em língua portuguesa |
|---|---|---|
|
0 |
inhalü |
não há |
|
5 |
nhatüi |
contei todos os dedos de uma mão |
|
10 |
timüho |
duas mãos |
|
12 |
takiko itühügü iheke |
dois do pé |
|
15 |
heine utapügü |
contei toda a mão e um lado do pé |
|
20 |
tatute utapügü itühügü iheke |
toda a mão e todo o pé |
|
21 |
aetsi tela inhatügü itühügü iheke |
um peguei da mão de outro |
FONTE: Informações obtidas no artigo “A numeração Karib no Alto Xingu”, de Pedro Paulo Scandiuzzi, publicado na Revista Latinoamericana de Etnomatemática, v. 1, n. 2, p. 75-87, jul. 2008. Disponível em: http://fdnc.io/eTL. Acesso em: 11 jan. 2021.
MANUAL DO PROFESSOR
Objetivo
• Registrar o resultado de contagens por meio de diferentes estratégias.
A ideia de número é algo tão presente nas mais diversas culturas que seu registro, por meio da linguagem oral e da escrita, tornou-se corriqueiro. Entretanto, a adoção quase universal do sistema de numeração decimal tende a ocultar o fato de que ele sofreu mudanças ao longo da história e que existiram, e ainda existem, outros sistemas de numeração, empregados em outras culturas.
Nesse texto, discute-se o uso dos dedos para a contagem e o registro dos números, assim como sua influência na nomenclatura numérica utilizada pelo povo indígena Kuikuro, no Brasil.
Comente com a turma que há diversos vestígios sobre a importância dos dedos no sistema de numeração decimal. Por exemplo, a palavra dígito, originada do latim, significa dedo e é usada como sinônimo de algarismo.
O sistema de numeração que usamos é decimal porque contamos em grupos de dez, que é o total dos dedos das mãos. Em outras culturas já foram usadas contagens com base em grupos de cinco (cujo resquício ainda se encontra no ábaco japonês – Soroban), que corresponde ao número de dedos de uma das mãos.
BNCC em foco na dupla de páginas:
EF02MA02; competências gerais 4 e 9
Sugestão de atividade
Jogo Borboleta
Material:
• 18 fichas (nove de cada cor);
• um tabuleiro em papel ou cartolina (figura 1).
Esse jogo, proveniente de Moçambique, na África, chama-se Borboleta. As 18 fichas são dispostas conforme mostra a figura 2 (cada cor de um lado), deixando vago apenas o ponto central.
Na sua vez, o jogador movimenta uma de suas fichas até um ponto vizinho que esteja vazio, ou salta por cima da peça do colega, capturando-a, desde que o ponto seguinte, em linha reta, esteja vazio. O jogador pode realizar mais de um salto com a mesma peça, capturando mais de uma peça do colega, se for possível. Se o jogador puder realizar um salto e não o fizer, perderá essa peça, que será retirada do tabuleiro e ficará com o colega. Caso seja possível saltar com mais de uma peça em uma jogada, o jogador pode escolher com qual delas saltará. Vence quem capturar todas as peças do adversário.
LEGENDA: Figura 1. FIM DA LEGENDA.
LEGENDA: Figura 2. FIM DA LEGENDA.
CRÉDITO: ADILSON SECCO
MP077
Tome nota
- Abaixo, vemos uma fotografia da aldeia dos Kuikuro. Onde ela está localizada?

LEGENDA: Aldeia dos Kuikuro, no Parque Indígena do Xingu, Mato Grosso, em 2019. FIM DA LEGENDA.
_____
PROFESSOR
Resposta: No Parque Indígena do Xingu, que fica no Mato Grosso.- Segundo pesquisadores, qual é a parte do corpo que foi, e ainda é, recurso valioso para fazer contagens?
_____
PROFESSOR
Resposta: Os dedos.
- Como é o 5 na língua dos Kuikuro? O que significa em nossa língua?
_____
PROFESSOR
Resposta: Nhatüi. Em nossa língua, significa: “contei todos os dedos de uma mão”.
Reflita
- Marque com um X o Kuikuro que está indicando o número 8.

( )

( )
PROFESSOR
Resposta correta: imagem 2

- Pinte os dedos da Kuikuro para representar o número 18.

PROFESSOR
Resposta: Exemplo de pintura:
MANUAL DO PROFESSOR
Tome nota
Para a realização dessas atividades, é pertinente ler com a turma cada quantidade indicada no quadro da página 48 do Livro do Estudante, estabelecendo relação com o número de dedos correspondentes, em cada caso. Chame alguns estudantes à frente da sala e peça-lhes que representem algumas quantidades da mesma maneira que os indígenas Kuikuro.
Reflita
Após a discussão das atividades, amplie a reflexão com a seguinte pergunta: “Você usa os dedos para fazer contagem ou para calcular?”. Nesse momento, pode-se abrir espaço para os estudantes dizerem como fazem contagem e cálculo: se usam ou não os dedos, se os usam com frequência ou apenas quando não sabem os cálculos de memória.
Curiosamente, pesquisas mostram que a parte do cérebro que se mantém mais ativa enquanto se realizam operações aritméticas é a mesma que controla os dedos. Pessoas que sofrem lesões nessa área do cérebro (lobo parietal esquerdo) apresentam perda de sensibilidade nos dedos e dificuldade com números, o que se conhece como síndrome de Gerstmann.
Aproveite para conversar sobre quais cálculos os estudantes já sabem de memória e quais ainda precisam aprender. Pergunte também se conhecem ou sabem algo sobre a contagem ou sobre os números na história de outros povos.
MP078
Compreender informações
Organizar dados em listas e tabelas
- Em janeiro de 2023, Elaine recebeu novos materiais para as aulas de ginástica e quis organizá-los.
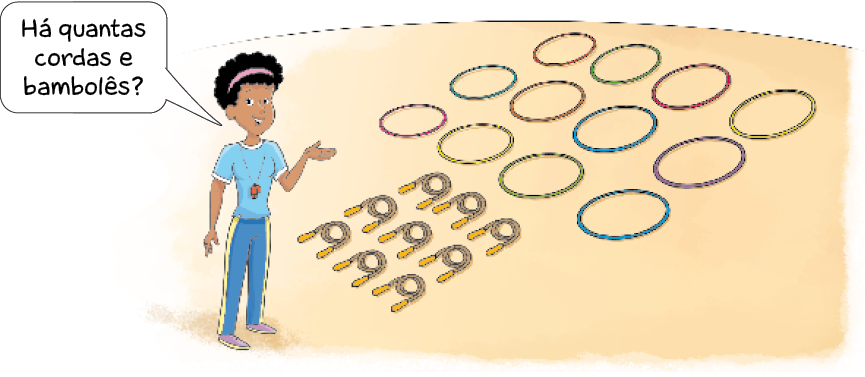
- Primeiro, ela separou os bambolês e as cordas. Depois, contou-os e montou uma lista em que fez um traço para cada unidade do material de ginástica contado por ela. Complete a lista de Elaine, conforme a imagem acima.
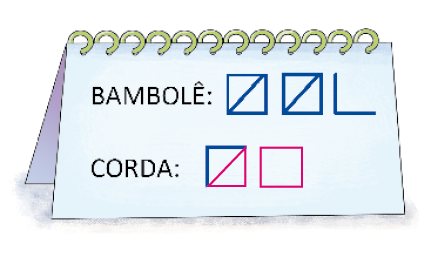
- Depois, Elaine organizou essas informações em uma tabela. Veja como ela começou a fazer e complete.
Materiais para as aulas de ginástica
Tabela: equivalente textual a seguir.
|
Material |
Quantidade |
|
|
_____ |
|
|
_____ |
Fonte: Anotações de Elaine (jan. 2023).
PROFESSOR
Resposta: 12; 9MANUAL DO PROFESSOR
Objetivos
• Organizar dados coletados em listas e tabelas.
• Ler e comparar dados expressos em tabelas.
As atividades das páginas 50 e 51 retomam e ampliam o trabalho com tabelas, explorando a coleta de dados e a organização deles em listas e tabelas. Assim, são propostas situações que envolvem a identificação de quantidades por meio da contagem, de informações do próprio problema ou a partir da coleta de dados com a turma. Em seguida, esses dados são organizados em tabelas, favorecendo a comparação de quantidades. Diferentes categorias são apresentadas nas tabelas, e a turma deve preenchê-las de acordo com a quantidade de cada elemento.
Atividade 1
Os estudantes devem observar os objetos (cordas e bambolês) e contar a quantidade correspondente a cada um. Antes de transpor esses dados para uma tabela, faça a leitura do texto com eles e peça que completem a lista de Elaine. Depois, pergunte: “Quantos são os bambolês e quantas são as cordas?”.
Em seguida, explore os elementos da tabela. Comente que toda tabela é formada por linhas e colunas, deve ter um título (Materiais para as aulas de ginástica) e a fonte de onde os dados foram retirados [Anotações de Elaine (jan. 2023)]. A tabela de Elaine tem duas colunas; uma coluna mostra o material (bambolê ou corda), e a outra, a quantidade de cada um desses materiais.
A organização de dados em listas e tabelas relaciona-se ao processo mental de classificação, que consiste em separar um grupo de elementos de acordo com atributos, propriedades, semelhanças ou diferenças entre eles.
BNCC em foco:
EF02MA23; competência geral 8; competências específicas 3 e 4
MP079
- Em fevereiro de 2023, Luara organizou os livros da brinquedoteca em uma estante. Há 4 gibis, meia dúzia de livros de passatempo, uma dezena de livros de colorir e 9 livros de recortar.
- Complete a tabela abaixo com a quantidade de cada tipo de livro.
Livros na estante
Tabela: equivalente textual a seguir.
|
Tipo de livro |
Quantidade |
|---|---|
|
|
4 |
|
|
_____ |
|
|
_____ |
|
|
_____ |
Fonte: Livros da brinquedoteca (fev. 2023).
PROFESSOR
Resposta: 6; 10; 9- Qual é o tipo de livro em maior quantidade?
_____
PROFESSOR
Resposta: Livro de colorir.
- E o tipo de livro em
menor
quantidade?
_____
PROFESSOR
Resposta: Gibi.
- Quantos livros há na brinquedoteca no total?
_____
PROFESSOR
Resposta: 29 livros.

- Com seus colegas e com o auxílio do professor, pesquise o tipo de sobremesa preferido de sua turma.



Boxe complementar:
Importante
Cada estudante deve escolher uma única opção entre sorvete, bombons e frutas.
Fim do complemento:
Observação: Os objetos nesta atividade não estão apresentados em escala de tamanho. Fim da observação.
- Faça uma lista, no caderno, com a opção de cada um. Depois, organize em uma tabela os dados coletados para mostrar a preferência dos estudantes por essas sobremesas.
- Qual é a sobremesa preferida de sua turma?
_____
PROFESSOR
Atenção professor: A resposta depende dos dados coletados pelos estudantes. Fim da observação.
MANUAL DO PROFESSOR
Atividade 2
Aproveite a atividade para perguntar: “Se fossem trocadas as informações das colunas, ainda assim a tabela ficaria adequada?”. Espera-se que os estudantes percebam que, como lemos da esquerda para a direita, fica mais “natural” que as categorias (tipo de livro) sejam apresentadas na coluna da esquerda. Se fosse o contrário, em uma primeira leitura da tabela apareceria um número que não saberíamos a que estaria se referindo. Entretanto, a ordem em que as diferentes linhas aparecem poderia ser alterada: por exemplo, colocando os tipos de livros em ordem decrescente de quantidade.
Atividade 3
Comece coletando os dados e registrando-os na lousa. Peça que sugiram o modo mais adequado de fazer esse registro.
É possível que escolham fazer tracinhos correspondentes a cada estudante que disser preferir determinado tipo de sobremesa. Após contar o número de estudantes que preferem cada tipo de sobremesa, faça uma tabela com os tipos de sobremesa e a quantidade (que dependerá das respostas). Peça também que criem um título para a tabela e indiquem a fonte. Espera-se que os estudantes percebam que a fonte deve ser a própria turma. Após responderem à última questão, sobre a sobremesa preferida da turma, pergunte: “Que sobremesa foi escolhida pelo maior número de estudantes? Que sobremesa teve a menor preferência?”.
BNCC em foco:
EF02MA23; competência geral 8; competências específicas 3, 4 e 6
MP080
O que você aprendeu
Avaliação processual
- Em cada caso, escreva com algarismos e por extenso o número representado.
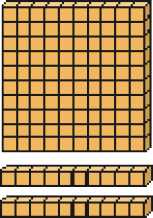
_____
PROFESSOR
Resposta: 120_____
PROFESSOR
Resposta: cento e vinte
_____
PROFESSOR
Resposta: 356_____
PROFESSOR
Resposta: trezentos e cinquenta e seis
_____
PROFESSOR
Resposta: 682_____
PROFESSOR
Resposta: seiscentos e oitenta e dois- Cerque com uma linha a única cédula que permite pagar um produto que custa 149 reais.

PROFESSOR
Resposta correta: cédula 200 reais..

- Estime e marque com um X o valor aproximado.

( ) Entre 150 e 200 reais.
( ) Entre 210 e 220 reais.
( ) Entre 300 e 320 reais.
( ) Entre 380 e 400 reais.
PROFESSOR
Resposta correta: Entre 300 e 320 reais.MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A s eção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Nessa atividade, os números são representados por meio de Material Dourado, argolas em um ábaco e decomposição. O objetivo de trabalhar com diferentes representações é ampliar a compreensão dos estudantes a respeito das ideias do campo numérico, estabelecendo relações entre elas. Na representação com Material Dourado, os algarismos das diferentes ordens (centenas, dezenas e unidades) são contados diretamente como número de placas, barras e cubinhos, enquanto no ábaco é o número de argolas em cada haste que corresponde aos algarismos escritos. Nas decomposições, a ideia é reconhecer 6 centenas, 8 dezenas e 2 unidades como 600 + 80 + 2.
Como ampliação para a atividade, peça aos estudantes que representem 23 dezenas e 4 unidades. Eles têm de reconhecer que 23 dezenas e 4 unidades podem ser transformadas em 2 centenas, 3 dezenas e 4 unidades, ou 234 (o Material Dourado pode ajudar nessa descoberta).
Atividade 2
Espera-se que os estudantes percebam que apenas com a cédula de 200 reais é possível comprar esse produto. Incentive-os a expor como pensaram.
Atividade 3
Incentive os estudantes a tentarem estimar mentalmente o total dos dois valores somados para depois escolherem a alternativa correspondente. Caso tenham dificuldade, poderão apoiar-se nas opções disponíveis para realizar as estimativas.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA04, EF02MA09
MP081
- Marque na reta numérica a localização aproximada de cada número.
210; 35; 345; 480

PROFESSOR
Resposta: Localizações aproximadas: 35; 210; 345; 480.

- Se você tivesse de aproximar o número 480, aproximaria para 450 ou para 500? Por quê?
PROFESSOR
Atenção professor: Espera-se que aproximem para 500, observando a reta numérica acima. Fim da observação.

- Calcule mentalmente da mesma maneira que as crianças calcularam e escreva o resultado.

- 200 + 100 = 300 ‒ Trezentos
- 300 − 100 =
_____
‒
_____
PROFESSOR
Resposta: 200; duzentos
- 400 + 200 =
_____
‒
_____
PROFESSOR
Resposta: 600; seiscentos
Autoavaliação

- Reconheço números maiores que 100? Quais?
PROFESSOR
Resposta pessoal.
- Consigo fazer cálculos aproximados nas atividades e no meu dia a dia?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Inicialmente, converse com os estudantes para que eles determinem o intervalo em que cada número está contido. Espera-se que eles pensem no arredondamento para saber de qual extremidade do intervalo o número está mais próximo.
Atividade 5
Os estudantes podem observar a similaridade entre o cálculo com centenas inteiras e o cálculo com unidades. Isso remete ao uso, no cálculo mental, do algoritmo realizado da esquerda para a direita, começando com as centenas em vez das unidades.
Aproveite para perguntar: “Se o cálculo de 400 + 200 fosse realizado em uma calculadora cuja tecla zero estivesse quebrada, como ele poderia ser feito?”. Uma estratégia possível seria acrescentar determinado valor a uma das quantidades e retirar esse valor da outra, evitando o uso dos zeros. Por exemplo, pode-se calcular:
411 + 189 → (400 + 11) + (200 − 11).
Autoavaliação
Na primeira questão, peça que observem alguns números trabalhados na Unidade e tentem reconhecê-los. Alguns estudantes podem apontar que reconhecem alguns, outros podem já ter compreendido o valor posicional do sistema de numeração decimal; e outros podem estar em processo de construção do conceito de número.
Na segunda questão, é retomada a ideia de arredondamentos e estimativas, destacando que não é necessário saber o resultado exato.
Alguns estudantes podem relatar que só conseguem fazer uso desses cálculos no dia a dia, ou só na escola, sem transpor experiências do cotidiano para o ambiente formal e vice-versa. Outros podem ainda sentir a necessidade de cálculos exatos, enquanto alguns já os realizam com facilidade.
BNCC em foco:
EF02MA01, EF02MA02, EF02MA03, EF02MA04, EF02MA05
MP082
Comentários para o professor
Conclusão da Unidade 2
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue comparar e ordenar números naturais até a 3ª ordem pela compreensão de características (valor posicional e função do zero) do sistema de numeração decimal? |
_____ |
_____ |
|
Faz estimativas, por meio de estratégias diversas, da quantidade de objetos (até 1 000 unidades) de coleções e registra o resultado da contagem desses objetos? |
_____ |
_____ |
|
Compõe e decompõe números naturais com até três ordens, com suporte de material manipulável, por meio de diferentes adições? |
_____ |
_____ |
|
Emprega fatos básicos da adição e da subtração, no cálculo mental ou escrito, para resolver problemas envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar? |
_____ |
_____ |
|
Descreve a regra contemplada pelos elementos em sequências repetitivas e/ou recursivas de números naturais, objetos ou figuras, e as completa com os elementos ausentes? |
_____ |
_____ |
|
Indica com precisão a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas? |
_____ |
_____ |
|
Lê, organiza e relaciona informações apresentadas por meio de tabelas de dupla entrada e gráficos de colunas simples ou barras, para compreender o contexto das situações problemas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP083
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome:_____ |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |





