MP084
Comentários para o professor:
Introdução da Unidade 3
O foco desta Unidade é a Unidade Temática Números. A sua abertura, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior, permite uma abordagem por meio de observações e de descobertas da imagem de uma festa junina, atividade comum ao calendário de escolas brasileiras. Nas festas juninas escolares há interações lúdicas e de consumo que também envolvem questões em outras Unidades Temáticas.
A construção de fatos fundamentais da adição e subtração, com o objetivo de empregá-los no cálculo mental ou escrito, assim como a elaboração e resolução de problemas relativos a essas duas operações, é feita por atividades propostas que se pautam pela concepção de que os conhecimentos devem ser articulados e retomados com maior intensidade e ampliação.
No que diz respeito às estratégias de cálculo, a adição e a subtração serão exploradas tanto a partir da decomposição dos números quanto de estratégias pessoais, além de seus algoritmos usuais. Ressalta-se, nesse caso, que a decomposição de números é fonte para a compreensão do sistema de numeração decimal, o que corrobora a criação de estratégias pessoais, a fim de chegar à compreensão também dos algoritmos. Ao longo do 1º ano, a composição e a decomposição foram trabalhadas com números de até duas ordens.
Assim, sem perder de vista a resolução e a elaboração de problemas envolvendo números de até três ordens, bem como os significados de juntar, acrescentar, separar e retirar, pretende-se oferecer aos estudantes as bases para que, no 3 º ano, esses conhecimentos sejam ampliados e aprofundados.
Quanto à Unidade Temática Álgebra, serão retomados os estudos com as sequências recursivas de números naturais, objetos ou figuras com o objetivo de que os estudantes identifiquem regularidades resultantes da realização de adições ou subtrações sucessivas, por um mesmo número, descrevam uma regra de formação da sequência e determinem elementos faltantes ou seguintes.
A abordagem da Unidade Temática Probabilidade e estatística apresenta-se na proposta de atividades que conduzem os estudantes à compreensão de aspectos significativos da realidade sociocultural, por meio da leitura, interpretação e comparação de dados contidos em tabelas e gráficos.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
MP085
5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determi nada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Cálculo mental, desta Unidade.
Roteiro de aula – Cálculo mental
1 ª parte – Atividade preparatória – Tempo sugerido: 20 minutos
Advertência: inicialmente convém observar aos estudantes que o cálculo mental, em tese, ocorre sem o uso de instrumentos físicos, isto é, sem material manipulável, sem lápis/caneta e papel, sem calculadora. Porém, para desenvolver os estudos sobre cálculo mental temos que nos comunicar por meio de registros físicos. Em muitas atividades, o cálculo é mental, mas é pedido que se explique como o cálculo mental foi elaborado. Em seguida, faça a leitura coletiva da parte inicial da atividade 1 e valide a resposta com eles. Sugerimos que as atividades sejam feitas em dupla.
Para a compreensão de algumas estratégias de cálculo mental a serem aplicadas nesta aula, alguns prerrequisitos são necessários, tais como: composição e decomposição dos números, tendo em vista as características do sistema de numeração decimal; arredondamento para dezena e para centena (nesta etapa escolar), adição/subtração de “dezenas inteiras” e “centenas inteiras”. Portanto, verifique se esses conceitos estão sedimentados na compreensão e prática dos estudantes. Proponha algumas questões a serem discutidas e compartilhadas coletivamente em voz alta, como: “Se o vovô tem 48 anos e a vovó tem 42 anos, qual deles tem idade mais próxima de 40 anos? E de 50 anos?”. O objetivo é que entendam igualdades do tipo: 48 = 50 − 2; 42 = 40 + 2.
2 ª parte – Cálculo mental – Tempo sugerido: 35 minutos
Faça a leitura do restante da atividade 1 e, por alguns minutos, deixe que os estudantes a completem no livro. Porém, antes de seguir adiante, valide o resultado obtido. É importante que, para a continuidade, não haja dúvidas.
Anuncie o tempo de 8 minutos (sugestão) para a resolução da atividade 2.
Leia junto com a turma a atividade 3 e peça argumentações voluntárias de dois ou três estudantes para validar a resposta.
Adote o mesmo procedimento para a parte inicial da atividade 4. Lembrando-os de que o cálculo é mental, mas o registro da resposta deve ser feito no livro, solicite que efetuem o cálculo mental usado por Jonas para o restante da atividade.
Finalizando a aula, faça a leitura coletiva da atividade 5. Antes de efetuarem os itens a e b, peça a dois ou três estudantes que falem sobre o que entenderam das estratégias de Aline e de Cléber.
MP086
UNIDADE 3. Adição e subtração

MANUAL DO PROFESSOR
Objetivos da Unidade
• Construir fatos básicos da adição e da subtração e utilizá-los no cálculo mental ou escrito.
• Ampliar o significado de adição envolvendo mais de duas parcelas.
• Resolver e elaborar problemas envolvendo adição e subtração.
• Compor e decompor números naturais.
• Compreender os significados da adição e da subtração.
• Calcular o resultado de uma adição e de uma subtração por meio de diferentes estratégias.
• Ampliar estratégias de cálculo mental em situações de adição e de subtração.
• Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
• Descrever um padrão (ou regularidade) de sequências por meio de palavras, símbolos ou desenhos.
• Descrever elementos ausentes em sequências de números naturais.
• Ler, interpretar e comparar informações registradas em gráficos de colunas e de barras simples.
BNCC em foco:
EF02MA04, EF02MA05, EF02MA06, EF02MA09, EF02MA10, EF02MA11, EF02MA20, EF02MA22
MP087
Boxe complementar:
Para refletir...

• Vanessa comprou uma tapioca e uma água. Quantos reais ela pagou?
_____
PROFESSOR
Resposta: 7 reais.

• Jonas comprou um origami de garça e pagou com uma cédula de 10 reais. Quantos reais ele recebeu de troco?
_____
PROFESSOR
Resposta: 4 reais.



• Lilian tem 20 reais na carteira e quer comprar dois origamis, uma salada de frutas e uma água. O dinheiro dela é suficiente? Explique aos colegas e ao professor.
PROFESSOR
Resposta: Sim. Resposta pessoal.Fim do complemento.
MANUAL DO PROFESSOR
O foco desta Unidade é envolver os estudantes em situações que abrangem adição e subtração, resgatando e ampliando seus significados. O estudo dessas duas operações, aqui, envolve números de até três algarismos, e são exploradas diversas estratégias de cálculo.
Explore a ilustração das páginas de abertura com os estudantes.
Para refletir...
Em uma roda de conversa, leia as questões para os estudantes e peça que comentem as duas primeiras situações. Pergunte: “Do que elas tratam? Quais as semelhanças e diferenças entre elas?”. Espera-se que eles percebam os significados envolvidos em cada uma delas: na primeira questão, eles devem adicionar os dois preços; na segunda, da quantia que Jonas usou para pagar, eles devem retirar o valor da compra. Explore as palavras desconhecidas pelos estudantes, como pode ser o caso do termo troco. Se julgar oportuno, produza, antecipadamente, cédulas e moedas de real para os estudantes utilizarem. Oriente-os a guardá-las, pois poderão ser empregadas em outras atividades.
Na terceira questão, os estudantes devem perceber que é preciso obter o total (mesmo que aproximado) do que se quer comprar para poder avaliar se os 20 reais são suficientes.
Observe as estratégias que eles utilizam nos cálculos, a fim de levantar os conhecimentos prévios que têm sobre as operações de adição e subtração.
MP088
Jogo: Caixa completa
Material: 4 conjuntos de cartas numeradas de 0 a 9 e 2 quadros Caixa completa (um quadro para cada dupla). As cartas e os quadros devem ser confeccionados pelos jogadores, conforme modelo abaixo.


Jogadores: 4 (duas duplas).
Regras:
- Os jogadores decidem qual dupla começará o jogo.
- As 40 cartas devem ser embaralhadas e colocadas com o número voltado para baixo, formando um monte.
- Cada dupla, na sua vez, vira a primeira carta do monte. Se a dupla achar que o número dessa carta é necessário para tentar obter o número do topo de uma das colunas, por meio da adição dos 4 números anotados nessa coluna, deverá escrever esse número no quadro. Se a dupla achar que o número da carta não é necessário na sua jogada, não será obrigada a usá-lo. A seguir, passará a vez.
- As cartas viradas a cada jogada devem ser descartadas.
- Se as cartas do monte acabarem, as que foram descartadas deverão ser reembaralhadas para formar um novo monte e dar continuidade ao jogo.
- Ganha a dupla que primeiro conseguir obter o número do topo em duas colunas de seu quadro e disser: “Caixa completa”.
MANUAL DO PROFESSOR
Objetivos
• Construir fatos básicos da adição e utilizá-los no cálculo mental ou escrito.
• Ampliar a ideia de adição envolvendo mais de duas parcelas.
• Resolver e elaborar problemas envolvendo adição.
• Compor e decompor números naturais.
Ajude os estudantes na leitura e na compreensão das regras.
O jogo Caixa completa possibilita aos estudantes trabalharem o cálculo mental com a operação de adição, explorando as diferentes maneiras de obter uma quantidade predefinida. Por exemplo, para obter 19 pode-se calcular:
9 + 5 + 4 + 1, ou 8 + 6 + 4 + 1, ou 7 + 7 + 4 + 1 etc.
Verifique se os estudantes utilizam subtrações quando buscam os números que completam as colunas e socialize esse procedimento.
Durante o jogo, é importante incentivá-los a fazerem a análise da melhor jogada e a tomarem decisões em parceria com o colega da dupla, o que permite momentos ricos para a análise de possibilidades de jogadas.
Jogar em duplas incentiva o diálogo e a troca de ideias, favorecendo a socialização e o surgimento de conflitos, que devem ser resolvidos em comum pelos jogadores.
Um dos aspectos mais interessantes desse jogo é que ele não envolve apenas sorte, pois os estudantes podem escolher qual é a melhor coluna para colocar o número da carta obtida em uma jogada, desenvolvendo, assim, a estimativa e a elaboração de hipóteses. Por exemplo, ao trabalhar com mais de uma coluna simultaneamente, determinado número que ultrapassa o número do topo da coluna pode ser colocado em outra coluna, de modo que amplie as possibilidades de completar as diferentes colunas nas jogadas seguintes.
Oriente a confecção das cartas, que podem ser desenhadas em papel sulfite, e depois coladas em um papel mais resistente ou desenhadas diretamente em cartolina. Depois, leia as regras em voz alta e realize algumas jogadas para que os estudantes as compreendam. Observe as diferentes estratégias usadas pelos estudantes e, depois, socialize-as com a turma.
BNCC em foco:
EF02MA04, EF02MA05, EF02MA06
MP089
Questões sobre o jogo
- O
número
40 poderia estar no topo de uma
coluna
do quadro? Por quê?
_____
PROFESSOR
Resposta: Espera-se que os estudantes percebam que o número 40 não poderia estar no topo de uma coluna do quadro, porque o maior número possível de se obter adicionando os números de quatro cartas (numeradas de 0 a 9) é 36, que é o resultado de 9 + 9 + 9 + 9. - Leia o que Reinaldo sugeriu fazer em uma jogada.

- Você considera essa sugestão uma boa ideia? Por quê?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que a sugestão de Reinaldo não é uma boa ideia, porque 6 é um número maior que 5, que, nesse caso, é o número do topo da coluna. Fim da observação.
- Observe uma situação desse jogo.
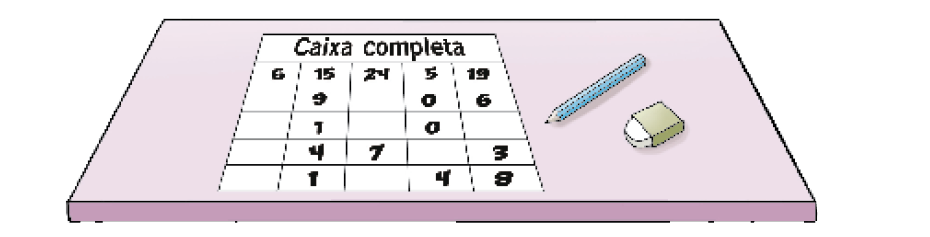

- Qual carta na próxima rodada faria a dupla que preencheu esse quadro vencer o jogo? Justifique sua resposta.
PROFESSOR
Resposta: A carta de número 1, que completaria a coluna com o número 5 no topo, ou a carta de número 2, que completaria a coluna com o número 19 no topo.MANUAL DO PROFESSOR
Questões sobre o jogo
As questões propostas possibilitam reflexões que podem não ter sido problematizadas durante a ação no jogo.
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões.
A questão 1 propõe uma reflexão sobre possíveis números que podem ser representados no topo de uma coluna. Espera-se que os estudantes percebam que o número da maior carta é 9 e que 36 representa a maior soma possível nesse jogo, pois: 9 + 9 + 9 + 9 = 36, não atingindo, portanto, o número 40. Desse modo, a turma conhece os limites impostos pelo próprio material do jogo.
Com a questão 2, os estudantes têm a oportunidade de pensar sobre quais são as possíveis cartas que completam determinada coluna. Se o número da carta for maior que o número no topo da coluna, a jogada é inviável.
A questão 3 apresenta uma situação de jogo que possibilita aos estudantes realizar análises quanto à melhor jogada, refletindo sobre os valores já obtidos e aqueles possíveis de serem retirados.
Se achar conveniente, proponha outras questões, como:
• Dê duas combinações diferentes de quatro cartas para completar a coluna do número 6. (4, 1, 1 e 0, ou 5, 1, 0 e 0, ou 6, 0, 0 e 0 etc.)
• Uma dupla de jogadores anotou os números 9 e 8 na coluna do número 24. Quais números estão faltando para completar a coluna? (0 e 7, 1 e 6, 2 e 5 ou 3 e 4.)
• Uma dupla de jogadores anotou os números 4, 5 e 6 na coluna do número 15. Qual número está faltando para completar a coluna? (Zero.)
BNCC em foco:
EF02MA04, EF02MA05, EF02MA06; competências gerais 2 e 9; competências específicas 7 e 8
Variações
É possível criar outros quadros, alterando o número do topo de cada coluna ou de linhas em cada uma, que pode aumentar ou diminuir, dependendo desses números.
Também podem ser criadas novas cartas, com valores diferentes das sugeridas nas regras. Uma sugestão é ampliar o campo numérico, trabalhando com dezenas inteiras. Dessa maneira, para compor o número 60, por exemplo, os estudantes podem calcular: 10 + 10 + 10 + 30 ou 20 + 20 + 10 + 10 etc.
MP090
Adição
- Carolina tem 5 gibis e Joaquim tem 4 gibis. Quantos gibis eles têm no total?

5 mais 4 é igual a ____.
PROFESSOR
Resposta: 9Adição: 5 + 4 = _____
PROFESSOR
Resposta: 9No total, eles têm _____ gibis.
PROFESSOR
Resposta: 9

- Veja a quantia de dinheiro de Nádia e de Júlio e complete.
Dinheiro de Nádia

Dinheiro de Júlio

FOTOS: BANCO CENTRAL DO BRASIL
Nádia e Júlio têm juntos _____ reais.
PROFESSOR
Resposta: 18- Os cachorrinhos gostam de brincar. Complete e responda: quantos filhotes participaram da brincadeira?
Antes
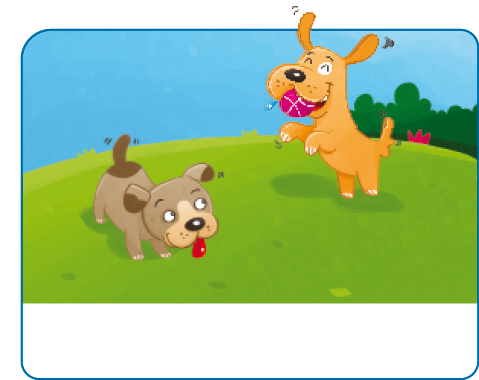
Havia _____ filhotes.
PROFESSOR
Resposta: 2Depois

Chegaram _____ filhotes.
PROFESSOR
Resposta: 32 mais 3 é igual a _____.
PROFESSOR
Resposta: 5Adição: _____ + _____ = _____
PROFESSOR
Resposta: 2 + 3 = 5Participaram da brincadeira _____ filhotes.
PROFESSOR
Resposta: 5MANUAL DO PROFESSOR
Objetivo
• Compreender os significados da adição: juntar e acrescentar quantidades.
As atividades que envolvem o significado de juntar quantidades combinam dois estados para a obtenção de um estado final, enquanto no significado de acrescentar quantidades há uma transformação – um estado inicial é alterado.
Atividade 1
O desenvolvimento das habilidades de cálculo pelos estudantes ocorre paralelamente às habilidades de contagem, de modo que é possível que eles usem a contagem para obter o resultado da adição na atividade.
As diferentes estratégias apresentadas podem ser confrontadas para que a turma construa novos significados e reelabore a maneira de pensar a situação. Por exemplo, alguns estudantes podem usar o fato de que 4 + 4 = 8 para obter o resultado de 5 + 4, que tem 1 unidade a mais que 8, ou seja, 9.
Atividade 2
Nessa atividade, a cédula de 5 reais já é uma representação da quantidade 5, de modo que, se os estudantes não observarem o valor da cédula, poderão pensar que tanto Nádia quanto Júlio têm 3 reais. Entretanto, em razão do uso social do dinheiro e do que viram no 1º ano, é provável que reconheçam o valor da cédula e não adicionem simplesmente a quantidade de cédulas e/ou moedas mostradas.
Atividade 3
Os estudantes devem observar que, na primeira cena, há 2 filhotes e, na segunda, há 5 filhotes, o que sugere que chegaram outros 3, ou seja, devem acrescentar 3 ao 2, obtendo 5.
As operações matemáticas estão associadas a diferentes significados e devem ser apresentadas por meio de problemas. Para a adição, os significados são de juntar quantidades e de acrescentar uma quantidade a outra. A diferença é bastante sutil, mas é fundamental estar atento para garantir que esses significados sejam trabalhados em situações variadas.
O emprego dos símbolos + e = deve ser incentivado, para ampliar as possibilidades de comunicação de ideias, raciocínios e estratégias.
BNCC em foco na dupla de páginas:
EF02MA05, EF02MA06
MP091
Algumas estratégias para o cálculo da adição
- Américo tem uma pequena criação de aves com 12 patos e 16 galinhas. Observe a ilustração.
- Quantas aves Américo tem no total?

Cálculo por decomposição
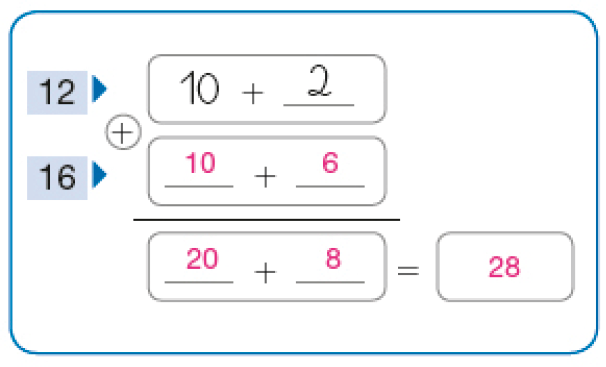

Cálculo com o algoritmo usual
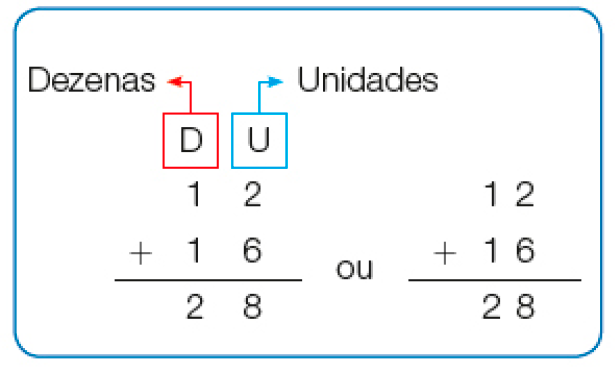
Adição: 12 + 16 = _____
PROFESSOR
Resposta: 28Américo tem _____ aves no total.
PROFESSOR
Resposta: 28- Calcule o resultado em cada caso.
- 27 + 41 =
_____
PROFESSOR
Resposta: 68
- 83 + 5 =
_____
PROFESSOR
Resposta: 88
- 54 + 45 =
_____
PROFESSOR
Resposta: 99
- 31 + 2 =
_____
PROFESSOR
Resposta: 33
- 13 + 4 + 1 =
_____
PROFESSOR
Resposta: 18
- 20 + 15 + 5 =
_____
PROFESSOR
Resposta: 40

- Você considera mais fácil adicionar usando cálculo mental, cálculo com o algoritmo usual ou cálculo por decomposição?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
• Calcular o resultado de uma adição por meio de diferentes estratégias.
• Resolver e elaborar problemas envolvendo adição.
Atividade 1
Nessa atividade, os estudantes observam o cálculo do resultado da adição 12 + 16 por decomposição e com o algoritmo usual. Eles podem fazer o cálculo e o registro de outras maneiras, o que deve ser valorizado. Por exemplo:

CRÉDITO: ADILSON SECCO
Havendo disponibilidade, o Material Dourado pode auxiliar na representação da resolução da atividade, uma vez que os estudantes podem agrupar as 2 barras (dezenas) e os 8 cubinhos (unidades).
Atividade 2
Espera-se que os estudantes percebam que há várias maneiras de obter um mesmo resultado. Verifique o tipo de resolução que eles consideram mais fácil para, assim, perceber qual é o tipo que eles acham mais difícil, procurando dar mais atenção às dúvidas relatadas por eles.
O uso do algoritmo usual da adição pode ser introduzido de maneira gradual, à medida que os estudantes trabalhem simultaneamente com outros modos de obter a soma. A vantagem desse algoritmo é o número reduzido de etapas empregadas e, portanto, o menor tempo para a obtenção da resposta. Porém, é importante considerar outras estratégias usadas pelos estudantes, desde que conduzam ao resultado correto e façam sentido para eles. Trabalhar paralelamente com o cálculo por decomposição e com o algoritmo usual apresentados nessas páginas permite aos estudantes reconhecerem a similaridade entre eles e evidencia o significado dos procedimentos executados no algoritmo usual.
MP092
Subtração
- Jonas tinha 6 balões e deu 2 deles para sua prima. Com quantos balões Jonas ficou?

6 menos 2 é igual a _____.
PROFESSOR
Resposta: 4Subtração: 6 − 2 = _____
PROFESSOR
Resposta: 4Jonas ficou com _____ balões.
PROFESSOR
Resposta: 4
- Havia 8 casacos à venda em um bazar. Tânia comprou 2 deles. Quantos casacos ainda estão à venda?
Subtração _____ − _____ = _____
PROFESSOR
Resposta: 8 − 2 = 6Ainda estão à venda _____ casacos.
PROFESSOR
Resposta: 6

- Complete com os números 1, 3, 4 e 7 para que a frase se torne verdadeira.
Pedro levou _____ morangos para o lanche na escola. Ele deu _____ morango para cada um de seus _____ amigos e ainda ficou com _____ morangos.
PROFESSOR
Exemplo de respostas: 7; 1; 4; 3PROFESSOR
Outra resposta possível seria completar com os números 7, 1, 3 e 4, nessa ordem.
MANUAL DO PROFESSOR
Objetivos
• Compreender os significados da subtração.
• Construir fatos básicos da subtração.
Atividade 1
A observação dos registros dos estudantes pode revelar diferentes estratégias: é possível que alguns contem de trás para a frente duas unidades a partir de seis, ou que desenhem seis traços no papel e risquem dois deles, ou, ainda, que usem os dedos como apoio para o registro das contagens parciais.
Atividade 2
Os estudantes precisarão completar as lacunas de modo que a subtração seja representada simbolicamente. Um modo interessante de levá-los a empregar os sinais − e = corretamente e valorizar sua importância é pedindo que tentem realizar, em uma calculadora, por exemplo, a subtração 5 − 3 = 2 sem apertar uma das teclas de sinal e observarem o resultado. Desse modo, compreenderão a importância dos sinais como parte fundamental da linguagem matemática.
Atividade 3
A atividade apresenta um problema não convencional e possibilita interpretar e escolher os valores mais adequados ao contexto proposto. Os estudantes estão habituados a trabalhar com problemas cujos dados numéricos estão postos, e a resolução significa realizar uma operação. Entretanto, nessa atividade, eles são chamados a pensar nas quantidades que tornam o problema adequado. É um problema do tipo“aberto” que admite mais do que uma solução.
Apresente problemas que podem ter nenhuma, uma, mais de uma ou infinitas soluções. Veja os exemplos.
• Nenhuma solução: Carlos tinha algumas canetas coloridas, ganhou 4 canetas verdes e ficou com mais de 10 canetas no total. Quantas canetas azuis ele tinha no início? (Não há solução.)
• Solução única: Carlos tinha algumas canetas, ganhou mais 4 e ficou com 9 canetas. Quantas canetas ele tinha no início? (5 canetas.)
• Mais de uma solução: Carlos tinha menos de 3 canetas e ganhou mais 4. Com quantas canetas ele ficou? (4, 5 ou 6 canetas.)
• Infinitas soluções: Carlos tinha mais de 3 canetas e ganhou mais 4. Com quantas canetas ele ficou? (Mais de 7 canetas, ou seja: 8, 9, 10, 11, ...)
BNCC em foco:
EF02MA05, EF02MA06
MP093
- Paula tem 9 biscoitos. Ela colocou 7 no prato amarelo e o restante colocará no prato vermelho. Quantos biscoitos Paula colocará no prato vermelho?
Paula tem _____ biscoitos.
PROFESSOR
Resposta: 9No prato amarelo, ela colocou _____.
PROFESSOR
Resposta: 7Subtração: _____ − _____ = _____
PROFESSOR
Resposta: 9 − 7 = 2Paula colocará _____ biscoitos no prato vermelho.
PROFESSOR
Resposta: 2

- Luís tem 20 reais. Usando toda essa quantia, ele consegue comprar o ingresso do cinema e um saco de pipoca. Se ele pagou 11 reais pelo ingresso, quanto custa o saco de pipoca?
PROFESSOR
Resposta: Exemplo de cálculo: 20 − 11 = 9
O saco de pipoca custa _____ reais.
PROFESSOR
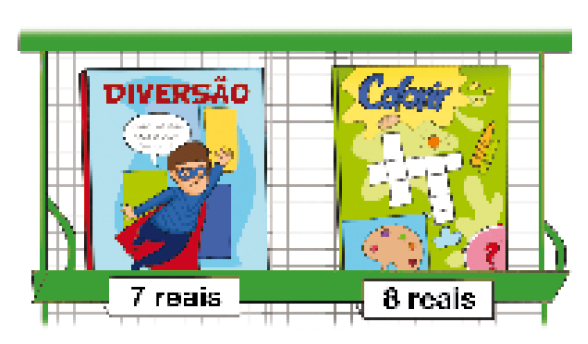
Resposta: 9- Beatriz tem 13 reais para comprar uma das revistas abaixo e para pagar um passeio que custa 5 reais. Qual revista ela pode comprar?
PROFESSOR
Resposta: Exemplo de cálculo: 13 − 5 = 8_____
PROFESSOR
Resposta: Beatriz pode pagar o passeio e comprar qualquer uma das duas revistas.MANUAL DO PROFESSOR
Atividade 4
Caso os estudantes tenham dificuldade em perceber como foi realizada a separação, desenhe os biscoitos na lousa e faça a correspondência um a um com a quantidade que já foi colocada no prato amarelo. Desse modo, eles podem verificar que os biscoitos que Paula colocará no prato vermelho são os 2 biscoitos que sobraram (depois de ela ter colocado 7 no outro prato).
Atividade 5
O uso social do dinheiro permite resolver o problema por meio de estratégias diferentes das normalmente abordadas na escola. Por exemplo, é possível que alguns estudantes continuem a contagem a partir do 11 até chegar ao 20, fazendo: 12, 13, 14, 15, 16, 17, 18, 19 e 20, obtendo a resposta 9 reais.
Atividade 6
Os estudantes podem resolver a situação adicionando o valor de cada revista (7 ou 8 reais) ao preço do passeio (5 reais) e comparando se o total obtido ultrapassa os 13 reais que Beatriz possui. Desse modo, concluem que ela pode escolher qualquer uma das duas revistas.
Valorize e socialize os diferentes procedimentos. Caso não surjam resoluções envolvendo a subtração, ressalte para os estudantes esse procedimento: dos 13 reais que Beatriz tem, ela terá de reservar 5 reais para o valor do passeio e, com o que sobra, verificar qual revista pode comprar (13 − 5 = 8).
Aproveite o contexto da atividade 6 e peça a eles que tragam, previamente, embalagens de diversos produtos com preços de até 30 reais para criar uma feira, em que façam compras de maneira livre ou direcionada, usando as cédulas e as moedas confeccionadas previamente por eles mesmos. Pode-se, por exemplo, propor a tarefa de comprar três produtos da feira gastando menos de 20 reais, ou comprar a maior quantidade possível de produtos com 15 reais, fazer outras compras para calcular trocos etc.
BNCC em foco:
EF02MA05, EF02MA06, EF02MA20
MP094
Algumas estratégias para o cálculo da subtração
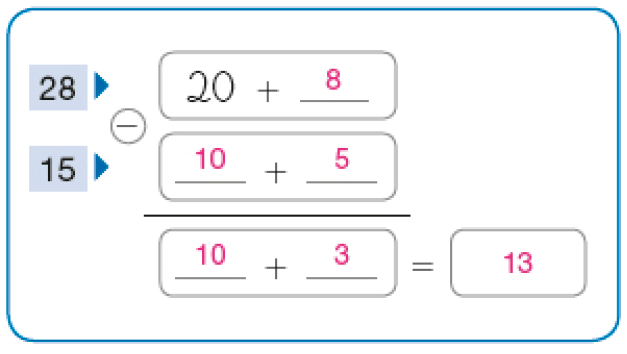
- No dia do seu aniversário, Carina levou 28 pedaços de bolo para a escola. Ela deu um pedaço para cada um dos 15 colegas da sua classe. Quantos pedaços sobraram?
Cálculo por decomposição

Cálculo com o algoritmo usual
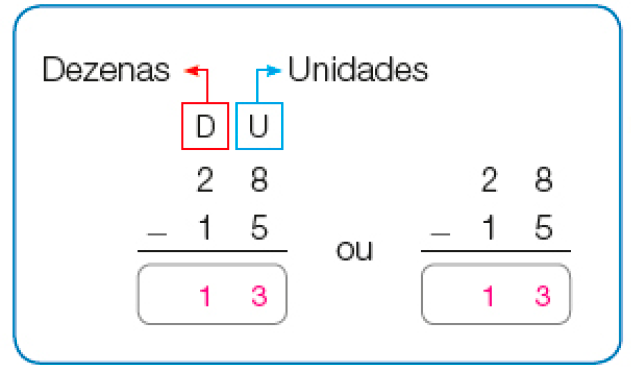
Subtração: 28 − 15 = _____
PROFESSOR
Resposta: 13Sobraram _____ pedaços.
PROFESSOR
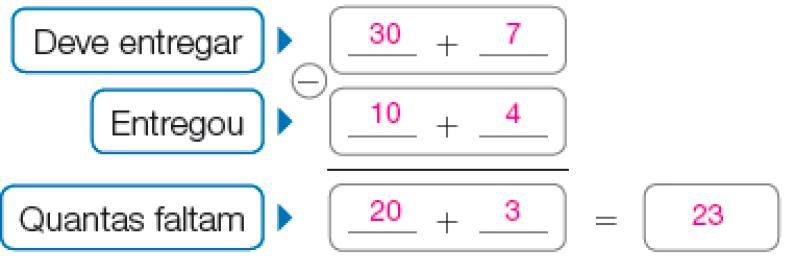
Resposta: 13- Hoje, um carteiro
deve
entregar 37 cartas. Se ele já entregou 14, quantas cartas faltam para ele entregar?
_____
PROFESSOR
Resposta: 23 cartas.
Cálculo por decomposição
MANUAL DO PROFESSOR
Objetivos
• Construir fatos básicos da subtração e utilizá-los no cálculo mental ou escrito.
• Calcular o resultado de uma subtração por meio de diferentes estratégias.
• Ampliar estratégias de cálculo mental em situações de subtração.
• Resolver e elaborar problemas envolvendo subtração.
A proposta do ensino dos algoritmos para a subtração valoriza diferentes formas de resolução do cálculo e agrega significado ao cálculo com o algoritmo usual por meio da comparação com o cálculo por decomposição.
É necessário que o contato com o algoritmo usual da subtração, da mesma maneira que com o algoritmo usual da adição, seja acompanhado por uma linguagem adequada. Assim, lembre-os sempre, pela linguagem, do valor posicional de cada algarismo no número considerado (destacando o que é dezena e o que é unidade).
É importante que sejam valorizadas outras estratégias de cálculo que eles construíram ou que estão habituados a fazer.
Atividade 1
Antes que os estudantes completem o cálculo por decomposição e observem o cálculo com o algoritmo usual, pode-se perguntar como fariam para efetuar o cálculo.
Exemplos de cálculo que podem ser apresentados são: 25 − 15 = 10, depois adicionar 10 com 3 (diferença entre 28 e 25), resultando em 13.
O Material Dourado pode auxiliar na representação das ações realizadas no cálculo. Os estudantes podem fazer: de 2 barras e 8 cubinhos, retiram-se 1 barra e 5 cubinhos, restando 1 barra (dezena) e 3 cubinhos (unidades), resultando em 13. Essa subtração tem o significado de retirar uma quantidade da outra.
Explique que essa variedade de algoritmos reflete as diferenças existentes na realização dos cálculos, em diferentes épocas e por diferentes povos, e que os algoritmos passaram por grandes transformações. Até a Idade Média, na Europa, a maior parte dos cálculos era realizada por meio de ábacos; os algoritmos escritos passaram a ser difundidos muito tempo depois de os árabes introduzirem os algarismos indo-arábicos nesse continente.
BNCC em foco:
EF02MA05, EF02MA06
MP095
- Veja como Carlos e Rui calcularam mentalmente, de maneiras diferentes, o resultado de 17 menos 8. Complete esses cálculos.

PROFESSOR
Resposta: 10; 1; 10 − 1 = 9
PROFESSOR
Resposta: 7; 2;PROFESSOR
7 + 2 = 9


- Você resolveria de uma maneira diferente? Explique aos colegas e ao professor.
PROFESSOR
Resposta pessoal.
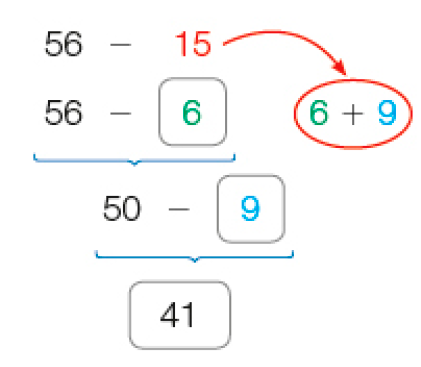
- Veja como Roberto calculou mentalmente o resultado de 25 menos 9.


- O cálculo
dele
está correto? Se não estiver, como deveria ser feito?
PROFESSOR
Resposta: Espera-se que os estudantes percebam que o cálculo de Roberto está errado. Ele precisaria, ainda, adicionar 1 a 15, obtendo 16.
- O cálculo
dele
está correto? Se não estiver, como deveria ser feito?
- Calcule e escreva o resultado de cada caso.
- 14 − 7 =
_____
PROFESSOR
Resposta: 7
- 16 − 5 =
_____
PROFESSOR
Resposta: 11
- 23 − 9 =
_____
PROFESSOR
Resposta: 14
- 26 − 8 =
_____
PROFESSOR
Resposta: 18
- 19 − 8 =
_____
PROFESSOR
Resposta: 11
- 35 − 6 =
_____
PROFESSOR
Resposta: 29
- 24 − 7 =
_____
PROFESSOR
Resposta: 17
- 43 − 9 =
_____
PROFESSOR
Resposta: 34
- 37 − 5 =
_____
PROFESSOR
Resposta: 32
MANUAL DO PROFESSOR
Atividade 2
Na atividade, a subtração está associada ao significado de completar uma quantidade (14) para atingir outra (37). Socialize os diferentes procedimentos de cálculo que aparecerem.
Atividade 3
Para subtrair 8 de 17, Carlos fez o cálculo de modo sequencial: primeiro ele subtraiu 7 e depois 1, resultando 9. Por outro lado, Rui subtraiu 10 e depois adicionou 2. Em cada caso, o cálculo mental foi realizado para atender às particularidades de cada pessoa. Entretanto, de modo geral, a ideia de trabalhar com dezenas inteiras facilita o cálculo mental.
Esses procedimentos exploram relações numéricas importantes para uma melhor compreensão pelos estudantes do sistema de numeração decimal, o que por sua vez é fundamental para o entendimento dos algoritmos da adição e da subtração.
Atividade 4
Na atividade apresenta-se um cálculo errado ou incompleto feito por Roberto para a operação 25 − 9. Espera-se que os estudantes acompanhem o que foi feito e observem que Roberto subtraiu 10 e não fez a compensação, aumentando 1 ao resultado, pois o que se queria era subtrair 9. Para terminar o cálculo, Roberto deveria adicionar 1 a 15, obtendo 16.
Atividade 5
Peça aos estudantes que exponham oralmente o procedimento que utilizaram para obter o resultado das subtrações propostas na atividade.
BNCC em foco:
EF02MA05, EF02MA06
Sugestão de atividade
A subtração “intrometida”
Calcule mentalmente o resultado de cada operação e assinale aquela que tem resultado diferente em cada quadro.Quadro: equivalente textual a seguir.
|
48 − 18 = 30 |
|
37 − 7 = 30 |
|
59 − 29 = 30 |
|
45 − 10 = 35 X |
|
33 − 3 = 30 |
Quadro: equivalente textual a seguir.
|
27 − 7 = 20 X |
|
35 − 20 = 15 |
|
45 − 30 = 15 |
|
25 − 10 = 15 |
|
29 − 14 = 15 |
Quadro: equivalente textual a seguir.
|
37 − 36 = 1 |
|
45 − 43 = 2 X |
|
56 − 55 = 1 |
|
18 − 17 = 1 |
|
12 − 11 = 1 |
MP096
Adição e subtração com dezenas inteiras
- No mercado, são vendidos pacotes de pregadores de roupa, como mostra a imagem abaixo. Cada pacote contém 10 pregadores.
- Vânia comprou 3 pacotes de pregadores vermelhos e 6 pacotes de pregadores azuis. Complete abaixo com a quantidade de pregadores que ela comprou.
 _____
dezenas
de pregadores vermelhos
_____
dezenas
de pregadores vermelhos
PROFESSOR
Resposta: 3
 _____
dezenas
de pregadores azuis
_____
dezenas
de pregadores azuis
PROFESSOR
Resposta: 6- Quantos pregadores de
roupa
Vânia comprou no total?
_____ + _____ = _____
PROFESSOR
Resposta: 30 + 60 = 90Vânia comprou _____ pregadores de roupa no total.
PROFESSOR
Resposta: 90
- Quantos pregadores azuis Vânia comprou a mais que vermelhos?
_____ − _____ = _____
PROFESSOR
Resposta: 60 ‒ 30 = 30Vânia comprou _____ pregadores azuis a mais que vermelhos.
PROFESSOR
Resposta: 30

- Cláudio e Renato têm juntos 70 bolinhas de gude.
- Cláudio tem 20 bolinhas; então, quantas
bolinhas
Renato tem?
_____
PROFESSOR
Resposta: Renato tem 50 bolinhas.
- Quantas
bolinhas
Cláudio tem a menos que Renato?
_____
PROFESSOR
Resposta: Cláudio tem 30 bolinhas a menos que Renato.
MANUAL DO PROFESSOR
Objetivo
• Construir fatos básicos de adição e subtração e utilizá-los no cálculo mental ou escrito.
Ao trabalhar adição e subtração com dezenas inteiras, faça questionamentos como: “Será que saber o resultado da adição 2 + 3 ajuda a descobrir o resultado da adição 20 + 30? Por quê? Quantas unidades tem o resultado da adição 10 + 20? Esse número corresponde a quantas dezenas?”, permitindo que relacionem os cálculos de adição e de subtração com unidades simples àqueles que envolvem dezenas inteiras.
Atividade 1
Pergunte: “Em quais outras situações do cotidiano pode ser necessário adicionar dezenas inteiras?”.
É possível que observem que há muitos produtos comercializados em embalagens com 10 unidades, como pratos descartáveis. Assim, quando se compra mais de uma embalagem, basta adicionar dezenas inteiras para saber o total.
Atividade 2
Os estudantes já se depararam com situações similares à do item a no contexto de adição. Agora, podem observar que, ao pensarem um número que adicionado a 20 resulta 70, eles podem resolver a questão descobrindo o número que falta a 20 para atingir 70, ou seja, efetuar a subtração 70 − 20 e, assim, encontrar 50. Já no item b, explora-se a subtração associada ao significado de comparação.
BNCC em foco:
EF02MA05, EF02MA06
Sugestão de leitura para o estudante
Livro
LOBATO, Monteiro. Aritmética da Emília. São Paulo: Globo, 2009.
Nesse clássico de Monteiro Lobato, a turma do Sítio do Picapau Amarelo participa de uma aventura envolvendo os números e as operações aritméticas. Assim, o País da Aritmética chega ao Sítio e se apresenta num circo organizado pelo Visconde de Sabugosa. Em meio a divertidas situações, os artistas mostram a Emília, Narizinho e toda a turma que a Matemática pode ser bem divertida!
MP097
Cálculo mental
- Alice não tem lápis, papel
nem
calculadora. Como ela pode descobrir o resultado da adição? Marque com um
X
a sua resposta.
( ) Mentalmente.
( ) Contando nos dedos.
( ) Com algum material concreto.
PROFESSOR
Resposta pessoal.


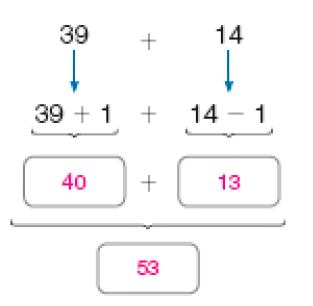
- Existem algumas estratégias de cálculo mental que ajudam em casos como o de Alice. Leia e complete com os números que faltam.
Para facilitar o cálculo mental, Alice adicionou 1 ao número 39 para formar dezena inteira, e subtraiu 1 do número 14.
E depois, calculou o resultado.

- Descubra cada resultado utilizando a estratégia de cálculo mental apresentada na atividade anterior.
- 59 + 35 =
_____
PROFESSOR
Resposta: 94
- 186 + 9 = ____
PROFESSOR
Resposta: 195
- 89 + 13 =
_____
PROFESSOR
Resposta: 102
- 49 + 53 =
_____
PROFESSOR
Resposta: 102
- 209 + 4 =
_____
PROFESSOR
Resposta: 213
- 35 + 79 =
_____
PROFESSOR
Resposta: 114
- 59 + 35 =
_____


- Depois de observar a estratégia de cálculo mental apresentada na atividade 1, Ricardo fez 49 + 15 e obteve o resultado 65. O resultado encontrado por Ricardo está correto? Se não estiver, o que ele pode ter feito de errado?
PROFESSOR
Resposta: Não.PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que Ricardo pode ter feito apenas a primeira parte da estratégia, adicionando 1 ao 49, mas ter se esquecido de subtrair 1 de 15. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
• Construir fatos básicos da adição e da subtração e utilizá-los no cálculo mental.
• Ampliar estratégias de cálculo mental.
Atividade 1
Em uma roda de conversa, antes de apresentar a estratégia sugerida no livro, incentive os estudantes a exporem suas opiniões e comentarem como fariam 39 + 14. Observe se eles apresentam justificativas e como o fazem. Em seguida, valide os diferentes procedimentos que aparecerem. Aproveite o momento para comentar a importância de respeitar a opinião do outro.
Na lousa, reproduza o procedimento apresentado no livro e, ao ler cada passo com os estudantes, mostre onde isso ocorre.
Atividade 2
A atividade pode ser feita em duplas. Procure organizar as duplas de modo que um estudante que tenha mais facilidade faça par com outro que ainda tenha alguma dúvida sobre o procedimento, para enriquecer a troca de ideias.
Apresentamos a seguir exemplos de resoluções para os itens b e f.
• 186 + 9 = 186 − 1 + 9 + 1 = 185 + 10 = 195
• 35 + 79 = 35 − 1 + 79 + 1 = 34 + 80 = 114
Verifique como os estudantes fazem o cálculo de 34 + 80. Caso julgue oportuno, deixe à disposição material manipulável (Material Dourado, por exemplo).
Atividade 3
Nessa atividade apresenta-se o resultado errado de 49 + 15 obtido por Ricardo. O possível erro dele pode ter sido realizar apenas parte do procedimento de cálculo mental apresentado na atividade 1.
BNCC em foco:
EF02MA05
Sugestão de leitura para o professor
Livro
CURY, Helena Noronha. Análise de erros: o que podemos aprender com as respostas dos estudantes. Belo Horizonte: Autêntica, 2007. (Coleção Tendências em Educação Matemática.)
A autora apresenta a análise de erros como uma metodologia de ensino cujo objetivo é fazer os educandos refletirem a respeito de seus erros, que devem ser vistos como elemento importante da aprendizagem, e não como indicativo de fracasso.
MP098
- Como você faria para descobrir mentalmente o resultado da subtração em que Jonas está pensando? Explique.
_____
PROFESSOR
Resposta pessoal.

- Veja a estratégia que Jonas usou.

- Agora, aplique a estratégia de Jonas para descobrir os resultados em cada caso.
- 75 − 55 =
_____
PROFESSOR
Resposta: 20
- 97 − 56 =
_____
PROFESSOR
Resposta: 41
- 85 − 36 =
_____
PROFESSOR
Resposta: 49
- 125 − 14 =
_____
PROFESSOR
Resposta: 111
- Observe como Aline e Cléber calcularam o resultado de 14 − 8.
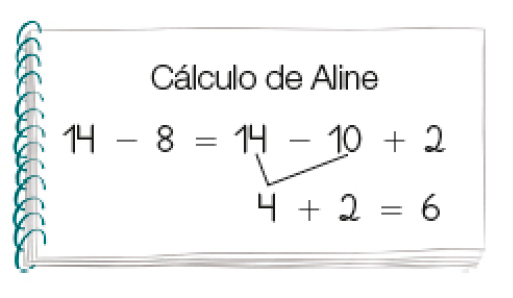
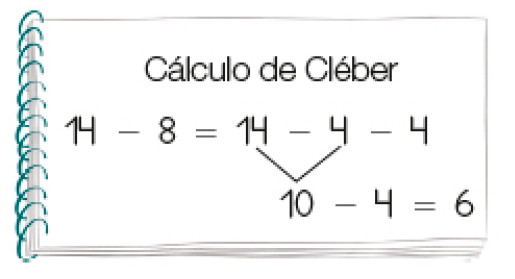

- Explique a um
colega
como Aline e Cléber pensaram.
PROFESSOR
Resposta pessoal.

- Agora, descubra os resultados, utilizando essas estratégias de cálculo.
- 17 − 8 =
_____
PROFESSOR
Resposta: 9
- 25 − 7 =
_____
PROFESSOR
Resposta: 18
MANUAL DO PROFESSOR
Atividade 4
Pode-se proceder de maneira similar à atividade 1. Valorize as estratégias apresentadas, socialize-as e valide-as com eles.
Atividade 5
Antes de propor esta atividade, pode-se usar lançamentos de três dados para que os estudantes realizem duas operações (adições e/ou subtrações) com os números das faces voltadas para cima. Registre na lousa a sentença relativa a cada cálculo proposto por eles. Por exemplo, se os números forem 2, 3 e 6, podem fazer:
• 2 + 3 + 6 = 11
• 3 − 2 + 6 = 7
• 6 − 3 − 2 = 1
• 6 − 3 + 2 = 5
• 6 − 2 + 3 = 7
Sugestão de atividade
Roletas da subtração
Material necessário:
• 2 roletas grandes de cartolina, repartidas em 10 regiões iguais, e 2 setas, como mostram as figuras a seguir.
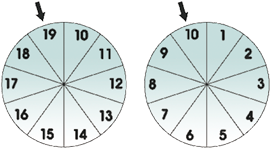
CRÉDITO: GEORGE TUTUMI
Fixe cada roleta a um papelão ou placa de isopor, colocando um percevejo em seu centro, de modo que a roleta possa girar livremente, e cole ou desenhe uma seta, como ilustrado. Com um pedaço de fita adesiva, prenda o conjunto na lousa.
Peça a um estudante que gire as roletas. Outro estudante deverá subtrair o número tirado na roleta da direita do número tirado na roleta da esquerda. Peça, então, que mostrem como chegaram ao resultado, socializando as diferentes estratégias de resolução.
BNCC em foco:
EF02MA05
MP099
Sequências
- Represente a sequência com números.

2

_____
PROFESSOR
Resposta: 3
_____
PROFESSOR
Resposta: 4
_____
PROFESSOR
Resposta: 5
_____
PROFESSOR
Resposta: 6
_____
PROFESSOR
Resposta: 7- Observe as sequências e escreva o padrão de cada uma delas.
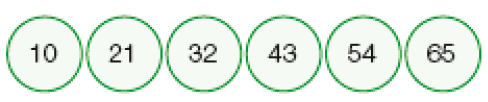
_____
PROFESSOR
Resposta: Adicionar 11.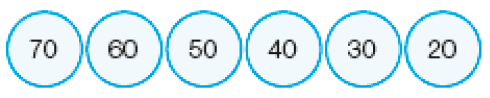
_____
PROFESSOR
Resposta: Subtrair 10.- Descubra o padrão de cada sequência e complete-a.
- 33, 30, 27,
_____,
_____,
_____,
_____
PROFESSOR
Resposta: 24, 21, 18, 15
- 75, 65,
_____,
45,
_____,
_____,
_____
PROFESSOR
Resposta: 55, 35, 25, 15
- 20,
_____,
44, 56,
_____,
_____,
_____
PROFESSOR
Resposta: 32, 66, 80, 92
- 33, 30, 27,
_____,
_____,
_____,
_____
Boxe complementar:
Desafio
André ganhou 30 sementes de girassol. Se a cada dia ele plantar a quantidade de sementes que tem na mão, quantos dias serão necessários para plantar todas as sementes? _____
PROFESSOR
Resposta: 6 dias.

CRÉDITO: VANESSA ALEXANDRE
Fim do complemento.
MANUAL DO PROFESSOR
Objetivos
• Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
• Descrever um padrão (ou regularidade) de sequências por meio de palavras, símbolos ou desenhos.
• Descrever elementos ausentes em sequências de números naturais.
Atividade 1
O trabalho com sequências geométricas propicia aos estudantes observar padrões numéricos mais facilmente. Peça a eles que observem cada sequência de figuras (uma de cada vez). Converse sobre o que observaram e pergunte que números devem associar a cada figura. Espera-se como resposta a associação a cada figura do número de cubinhos que há nela. Verifique se observam também que o padrão da sequência de figuras permanece na sequência numérica correspondente: acrescenta-se 1 unidade (1 cubinho) ao elemento anterior.
Comente que a sequência numérica obtida é crescente, pois os números vão aumentando (do menor número para o maior, ordem crescente).
Atividades 2 e 3
Para enriquecer a exploração dessas atividades e ampliar o repertório dos estudantes, sugerimos que elas sejam feitas em duplas.
Observe as estratégias utilizadas pelos estudantes na obtenção e descrição do padrão das sequências. O fato de faltarem elementos nas sequências da atividade 3 pode gerar maior dificuldade. Incentive-os a observar os números apresentados e, se for o caso, proponha que pensem em números que poderiam completar cada sequência segundo o padrão observado, mesmo que seja por tentativa e erro.
BNCC em foco:
EF02MA09, EF02MA10, EF02MA11
Desafio
Leia o comando para os estudantes e peça que expliquem o que entenderam. Verifique se eles percebem que precisam observar também a ilustração, que fornece a quantidade de sementes a serem plantadas diariamente.
Incentive os estudantes a escreverem uma sequência que traduza a situação para resolver o problema.
MP100
Compreender problemas
Para resolver
Problema 1

Para criar um problema, considere a situação ou o contexto, o tipo de problema, os dados e a pergunta, para depois escrevê-lo.
Qual é o contexto? → Frutas nos cestos.
Qual poderia ser o problema? → Juntar quantidades.
Quais seriam os dados do problema? → Quantidade de frutas em cada cesto.
Que pergunta você faria? → Quantas frutas há no total?
Problema 2

Para refletir
- Complete a redação do problema com base nas informações do Problema 1.
Márcia tem dois cestos com frutas. Em um cesto, há _____ maçãs e, no outro, há _____ peras. Quantas frutas Márcia tem ao todo?
PROFESSOR
Resposta: 15; 12
MANUAL DO PROFESSOR
Objetivo
• Elaborar problemas envolvendo adição e subtração.
O objetivo dessas páginas é que os estudantes consigam elaborar um problema com base em um contexto. Atente às diferentes estratégias pessoais que utilizarão para resolver as questões propostas. Possibilite a socialização dessas estratégias para que acompanhem o raciocínio de cada colega, ampliando seu repertório.
Para resolver
Problema 1
Explore a imagem com os estudantes, incentivando-os a perceberem o contexto envolvido e qual seria um possível problema.
Problema 2
Proponha que observem a ilustração e, em duplas, descrevam o que veem, discutam sobre o contexto envolvido e pensem em que problema pode ser criado.
Para refletir
Atividades 1 e 2
Reforce que, para resolver as atividades, os estudantes terão de rever as informações do Problema 1. Na atividade 1, terão de completar o texto e, na atividade 2, terão de usar as informações do Problema 1 para escrever um novo problema. Exemplo de elaboração para a atividade 2:
• Contexto: Tipos de frutas nos cestos.
• Tipo de problema: Comparar quantidades.
• Dados do problema: 15 maçãs e 12 peras.
• Pergunta: Quantas maçãs há a mais do que peras?
• Redação do problema: Em um cesto, há 15 maçãs e em outro há 12 peras. Quantas maçãs há a mais do que peras?
BNCC em foco:
EF02MA06; competência geral 2; competências específicas 1, 3 e 5
MP101
- Elabore outro problema com as informações do Problema 1.
_____
PROFESSOR
Resposta pessoal.
- Planeje a criação de um problema com base na ilustração do Problema 2.
PROFESSOR
Resposta pessoal.Qual é o contexto? → _____
Qual poderia ser o problema? → _____
Quais seriam os dados do problema? → _____
Que pergunta você faria? → _____
- Redija seu problema com base nas informações da atividade 3.
_____
PROFESSOR
Resposta pessoal.
- Troque o problema que você fez na atividade 4 com um
colega
e peça a ele que o
resolva
no caderno. Em seguida, você
deve
resolver o dele.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividades 3 e 4
Os estudantes terão de resolver a atividade 3 com base nas conclusões que tiraram quando observaram a ilustração do Problema 2.
Exemplo de elaboração para a atividade 3:
• Contexto: Itens de cozinha.
• Tipo de problema: Descobrir o valor gasto na compra dos itens.
• Dados do problema: O valor de cada item de cozinha.
• Pergunta: Quantos reais seriam gastos se fossem comprados os dois itens de cozinha?
Na atividade 4, peça que escrevam o problema em que o estudante ou a dupla pensou. Exemplo de redação: Ana quer comprar os dois itens de cozinha que está observando na vitrine. Quantos reais ela gastará comprando os dois itens?
Atividade 5
Para essa troca de problemas, peça aos estudantes que escolham um colega diferente daquele com quem se reuniram em dupla anteriormente.
BNCC em foco:
EF02MA06; competência geral 2; competências específicas 1, 3 e 5
MP102
A Matemática me ajuda a ser
... um passageiro responsável
O uso do cinto de segurança no banco traseiro é tão importante quanto no banco dianteiro
Se os motoristas não respeitam as leis de trânsito, eles são punidos com uma multa e alguns pontos na carteira de acordo com a gravidade da infração.
Por exemplo, não usar cinto de segurança é considerado uma infração grave e o valor da multa é cobrado por passageiro sem cinto de segurança. Além disso, o condutor do veículo é penalizado com 5 pontos na carteira. Caso não conste nenhuma infração gravíssima, atingindo 40 pontos no período de um ano, ele perde o direito de dirigir até que cumpra o prazo de penalidade e faça o curso de reciclagem.
O uso do cinto de segurança é obrigatório não só nas estradas como também em todas as cidades brasileiras. Essa regra vale para todos os ocupantes de um veículo, com exceção de ônibus, em percursos que seja permitido viajar em pé.
Não esqueça que essas regras valem também para quem usa transporte escolar, pois o uso do cinto de segurança é obrigatório para todos os passageiros. Faça a sua parte: ao entrar no veículo, não deixe de colocar o cinto e peça a todos os passageiros que o usem também.
Atenção, crianças, vocês também têm algumas responsabilidades!
- Permanecer sentado enquanto o veículo estiver em movimento.
- Afivelar o cinto de segurança durante todo o percurso.
- Não falar com o motorista enquanto ele estiver dirigindo.
- Nunca descer do veículo em movimento.

LEGENDA: Placa que indica uso obrigatório de cinto de segurança. FIM DA LEGENDA.
Tome nota
- 1. Quantos pontos na carteira o motorista recebe por não usar o cinto de segurança?
_____
PROFESSOR
Resposta: 5 pontos.
- 2. Se um motorista tiver 14 pontos na carteira e não tiver nenhuma infração gravíssima nos últimos 12 meses, quantos pontos faltarão para ele perder o direito de dirigir? Justifique.
_____
PROFESSOR
Resposta: Faltam 26 pontos, pois 40 − 14 = 26.
MANUAL DO PROFESSOR
Objetivos
• Resolver problemas envolvendo adição e subtração.
• Interpretar dados numéricos apresentados em texto referente ao trânsito.
O texto trata de um assunto importante que deve ser discutido com as crianças desde cedo: a educação no trânsito. A seção destaca o uso do cinto de segurança nos veículos, tanto por crianças quanto por adultos.
Aproveite a situação e liste com os estudantes outras ações (ou regras) que devemos ter (ou seguir), como pedestres, para um trânsito mais seguro a todos.
Tome nota
Atividades 1 e 2
Comente com os estudantes que a pontuação das infrações depende da gravidade da infração. Informe-os de que essas infrações podem ser consideradas leves, médias, graves ou gravíssimas, e a pontuação é respectivamente: 3, 4, 5 e 7 pontos.
Sugira aos estudantes que grifem no texto as informações numéricas e identifiquem qual é referente à pontuação em que se perde o direito de dirigir. É possível ampliar a discussão fazendo perguntas similares, como: “Se um motorista que tiver 23 pontos na carteira, nenhum resultante de infração gravíssima, cometer duas infrações gravíssimas e uma infração leve, ele perderá o direito de dirigir? E se forem duas infrações graves e uma média?”.
(Sim, pois 23 + 7 + 7 + 3 = 40; não, pois 23 + 5 + 5 + 4 = 37.)
BNCC em foco:
EF02MA06; competência específica 1
MP103
Reflita

- 1. Leia os quadrinhos e responda às questões.
TURMA DA MÔNICA
Mauricio de Sousa

- a) Você sempre usa o cinto de segurança?
-
b) A Magali acha que o pai
dela
está exagerando. E você, o que acha? Explique.
PROFESSOR
Respostas pessoais.

- 2. Reúna-se com seus colegas e escrevam o que pensam sobre a importância do uso do cinto de segurança.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Reflita
Atividade 1
Explore os quadrinhos com os estudantes. Aproveite a atividade para incentivá-los a discutirem sobre a responsabilidade de cada um quanto ao uso do cinto de segurança.
Enfatize a fala do pai de Magali sobre o respeito à lei. Depois, proponha uma discussão sobre o motivo da existência dessa lei. Comente que as leis são criadas para estabelecer ordem e para facilitar o convívio social. Elas podem ser questionadas, mas para isso é preciso entendê-las. Com os estudantes, levante os motivos da existência da lei do cinto de segurança também no banco traseiro. Questione-os sobre o que poderia acontecer em um acidente em que os passageiros estivessem sem cinto. É importante que eles percebam a necessidade de cumprir a lei por questão de segurança.
Atividade 2
A produção de texto também é um modo de organizar informações. Na atividade, a produção poderá ser feita em pequenos grupos ou de maneira coletiva pela sala, tendo um dos estudantes como escriba. A escolha dependerá da disponibilidade da sua turma. Uma possibilidade é organizar em tópicos as principais discussões das atividades anteriores e depois redigir o texto.
BNCC em foco:
EF02MA06; competência específica 1
MP104
Compreender informações
Ler e interpretar gráficos
- 1. Observe o gráfico de colunas que mostra a preferência de passatempo das crianças do bairro onde Cláudio mora e faça o que se pede.
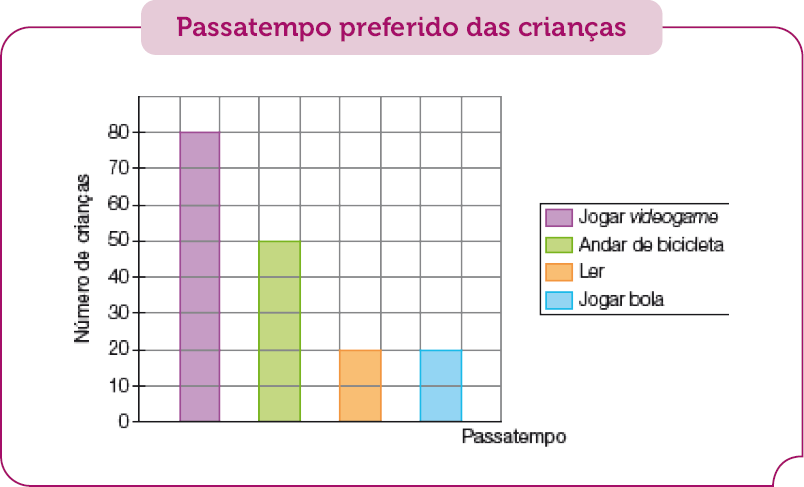
Fonte: Associação do bairro (jul. 2023).

-
a) Nesse gráfico, podemos observar que cada quadrinho que compõe as colunas corresponde ao voto de quantas crianças?
_____
PROFESSOR
Resposta: Corresponde a 10 crianças, ou seja, a 10 votos.
-
b) Qual passatempo teve mais votos? Como você fez para saber?
_____
PROFESSOR
Resposta: Jogar videogame .PROFESSOR
Resposta pessoal.
- c) Há passatempos que tiveram a mesma quantidade de votos?
- Em caso positivo, escreva quais são.
_____
PROFESSOR
Resposta: Sim; Ler e jogar bola.
-
d) Qual é a diferença de votos entre o passatempo “Andar de bicicleta” e o passatempo “Jogar bola”?
_____
PROFESSOR
Resposta: 30 votos.
-
e) Quantos votos a mais o passatempo “Jogar
videogame
” teve em relação ao passatempo “Ler”?
_____
PROFESSOR
Resposta: 60 votos.
-
f) Seu passatempo preferido apareceu nesse gráfico?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivo
• Ler, interpretar e comparar informações registradas em gráficos de colunas e de barras simples.
Atividade 1
Explore o gráfico e a legenda de cores com os estudantes. Peça a eles que observem o gráfico e que identifiquem cada coluna de acordo com a legenda. Discuta as questões com os estudantes em uma roda de conversa, antes de fazerem o registro no livro. Comente que cada criança escolheu um passatempo como preferido, ou seja, deu seu voto. Assim, o número de crianças que escolheu certo passatempo (entre os quatro apresentados) determina o número de votos que esse passatempo recebeu.
Para o item a, espera-se que os estudantes identifiquem que cada quadrinho que compõe as colunas corresponde a 10 votos.
Para o item b, espera-se que os estudantes identifiquem a maior preferência pela coluna de maior altura. No entanto, eles podem apenas comparar os números 80, 50 e 20 e verificar que 80 é o maior deles. Valorize as estratégias dos estudantes, mas comente a possibilidade de observar as colunas do gráfico para identificar o elemento mais escolhido (relativo à coluna de maior altura) ou o elemento menos escolhido (relativo à coluna de menor altura).
Aproveite o momento de encerrar a atividade para ampliar a discussão com os estudantes sobre pluralidade, diversidade e diferença.
BNCC em foco:
EF02MA22; competências específicas 3 e 4
MP105
- 2. Observe o gráfico de barras que a professora Ana fez depois de uma pesquisa com estudantes de suas duas classes e faça o que se pede.
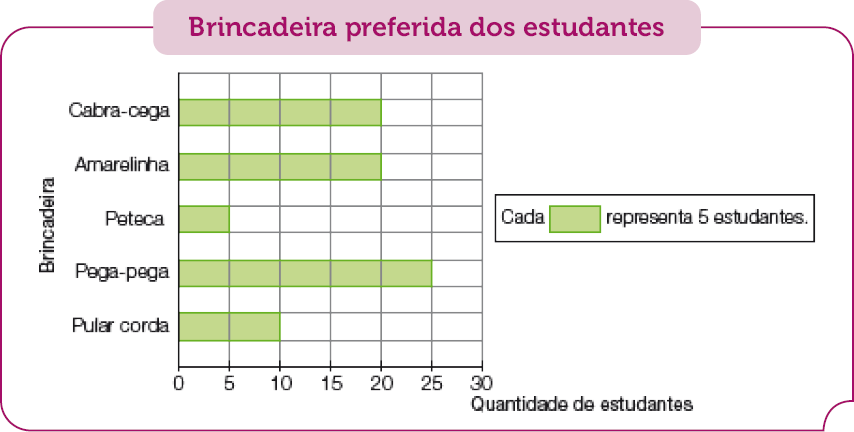
Fonte: Pesquisa da professora Ana (fev. 2023).
- a) Complete a tabela com as informações do gráfico acima.
Brincadeira preferida dos estudantes
Tabela: equivalente textual a seguir.
|
Brincadeira |
Quantidade de estudantes |
|---|---|
|
Cabra-cega |
20 |
|
Amarelinha |
_____ |
|
Peteca |
_____ |
|
Pega-pega |
_____ |
|
Pular corda |
_____ |
Fonte: Pesquisa da professora Ana (fev. 2023).
PROFESSOR
Resposta: 20; 5; 25; 10-
b) Qual foi a brincadeira mais escolhida pelos estudantes da professora Ana?
_____
PROFESSOR
Resposta: Pega-pega.
-
c) Das brincadeiras escolhidas, qual recebeu menos votos?
_____
PROFESSOR
Resposta: Peteca.
-
d) A brincadeira “esconde-esconde” apareceu nas preferências dos estudantes da professora Ana? Como você pensou para saber?
_____
PROFESSOR
Resposta: Não.PROFESSOR
Resposta pessoal.
-
e) Quantos estudantes, no total, responderam à pesquisa da professora Ana?
_____
PROFESSOR
Resposta: 80 estudantes.
MANUAL DO PROFESSOR
Atividade 2
Ao observar o gráfico de barras com os estudantes, peça que escrevam na frente das barras o número de estudantes que escolheu cada brincadeira; por exemplo, espera-se que eles identifiquem que pular corda é a brincadeira preferida de 10 crianças. Depois da leitura do gráfico, verifique se os estudantes têm alguma dificuldade ao completar a tabela. Peça que comparem sua tabela com a de um colega e discutam as diferenças encontradas.
Discuta as questões propostas no livro com os estudantes e observe onde eles buscam as informações (no gráfico ou na tabela). Incentive-os a contar como pensaram ao responder às questões.
BNCC em foco:
EF02MA22; competências específicas 3 e 4
MP106
O que você aprendeu
Avaliação processual
- 1. Gil tinha algumas figurinhas. Ao jogar com seus amigos, ele perdeu 25 dessas figurinhas e sobraram 13. Quantas figurinhas Gil tinha antes de jogar com os amigos?
PROFESSOR
Resposta: Exemplo de cálculo:PROFESSOR
25 + 13 = 38Gil tinha _____ figurinhas antes de jogar com os amigos.
PROFESSOR
Resposta: 38

- 2. Calcule o resultado das operações e ligue cada tampa a seu pote.
Linha 1
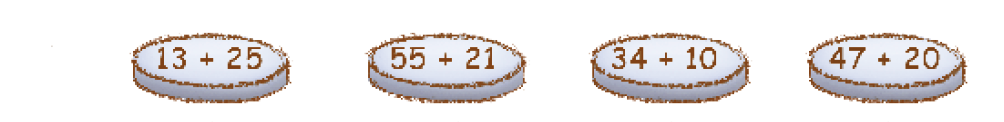
Linha 2

PROFESSOR
Resposta: 13 + 25; 38PROFESSOR
55 + 21; 76PROFESSOR
34 + 10; 44PROFESSOR
47 + 20; 67

- 3. Com a quantia que Paula tinha, ela comprou uma bolsa.
Ela gastou 

 e ainda sobraram
e ainda sobraram 
 . Quantos reais Paula tinha antes de comprar a bolsa?
_____
. Quantos reais Paula tinha antes de comprar a bolsa?
_____
PROFESSOR
Resposta: 96 reais.MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Peça que representem a situação com material concreto (pedaços de papel para representar as figurinhas) ou que desenhem a situação (um tracinho para representar cada figurinha).
Como Gil perdeu 25 figurinhas, é possível que alguns estudantes pensem, de maneira equivocada, que se trata de um cálculo de subtração. Entretanto, a atividade faz referência a uma transformação na quantidade inicial a fim de obter as 13 figurinhas finais. Portanto, é necessário calcular 13 + 25 = 38, obtendo-se assim o número de figurinhas iniciais.
Solicite aos estudantes que criem outras questões, que, para serem solucionadas, necessitem de uma adição e nas quais apareçam termos como perdeu, a menos, entre outros.
Atividade 2
É interessante observar os procedimentos que usarão para realizar a atividade. Talvez não encontrem os valores exatos, mas sejam capazes de estimar os resultados. No caso de 13 + 25, por exemplo, se pensarmos em adicionar 1 dezena com 2 dezenas obteremos 30, e o número mais próximo desse resultado que se encontra na atividade é 38 (a resposta). Estimativas desse tipo possibilitam aos estudantes “ganhar tempo” e contribuem para as situações cotidianas que exigem estimativas e não o cálculo exato.
Atividade 3
O uso de dinheiro confeccionado previamente favorece a compreensão da atividade. Socialize as estratégias que os estudantes usaram para resolver a atividade.
BNCC em foco:
EF02MA06
Sugestão de leitura para o professor
Livro
• CARRAHER, Terezinha Nunes; CARRAHER, David; SCHLIEMANN, Analúcia. Na vida dez, na escola zero. 16ª ed. São Paulo: Cortez, 2015.
Os autores mostram que a aritmética escolar formal é apenas uma face do saber matemático. Alertam para o fato de que esse saber pode ser desenvolvido tanto nas atividades sociais quanto nas atividades informais de crianças trabalhadoras nas grandes cidades do país, que ganham a vida em ruas e esquinas realizando pequenos trabalhos informais.
MP107

- 4. Mário e José
colhem
pés de alface. Ao todo, eles colheram 86 pés de alface. Sabendo que Mário colheu 45 pés de alface, quantos pés de alface José colheu?
_____
PROFESSOR
Resposta: 41 pés de alface.

- 5. Lucas tem 20 reais e quer comprar 2 brinquedos para seus sobrinhos. Observe o preço dos brinquedos e complete as frases.

-
a) Se Lucas comprar o carrinho e a bola, ele pagará
_____
reais e sobrarão
_____
reais.
PROFESSOR
Resposta: 15; 5
-
b) Se Lucas comprar o ursinho e a bola, ele pagará
_____
reais e sobrarão
_____
reais.
PROFESSOR
Resposta: 18; 2
-
c) Se Lucas comprasse o ursinho e o carrinho, ele pagaria
_____
reais e faltaria
_____
real.
PROFESSOR
Resposta: 21; 1
- 6. Escolha um
número
para ser o primeiro termo, determine um padrão e crie uma sequência.
PROFESSOR
Resposta: A sequência depende do número e padrão escolhidos.
Autoavaliação

- • Consigo pensar em uma estratégia para resolver um problema?
PROFESSOR
Resposta pessoal.
- • Utilizo diferentes estratégias de cálculo para adicionar ou subtrair quantidades?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Atividades como esta mostram aos estudantes a ligação entre a adição e a subtração, possibilitando o desenvolvimento da noção de operação inversa.
Atividade 5
Nessa atividade, os estudantes experimentam algumas possibilidades de compras. Em nossas práticas cotidianas, muitas vezes a realização do cálculo mental oferece a praticidade na hora de decidir uma compra ou calcular um troco a ser recebido. Socialize com a turma os diferentes procedimentos que aparecerem.
Atividade 6
Proponha aos estudantes que troquem o livro com um colega para que cada um descubra o padrão da sequência criada pelo outro. Faça uma correção coletiva, validando com os estudantes as sequências criadas e os padrões descritos.
Autoavaliação
Na primeira questão, é importante solicitar aos estudantes que destaquem quais tipos de problemas são mais fáceis ou difíceis. As respostas podem dar indicativos tanto nas lacunas de interpretação das situações apresentadas como nas dificuldades relacionadas aos significados da adição e da subtração.
Na segunda questão, é interessante perguntar quais estratégias eles têm utilizado, a fim de saber se estão ou não diversificando suas escolhas. Os estudantes podem utilizar cálculo mental, decomposição, cálculos aproximados, entre outras estratégias para encontrar resultados. Desse modo, para responder à questão além do “sim”, “não” ou “mais ou menos”, peça que indiquem de quais estratégias já se apropriaram e quais não compreendem, ou, ainda, desconhecem.
BNCC em foco:
EF02MA06, EF02MA09, EF02MA10
MP108
Comentários para o professor:
Conclusão da Unidade 3
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue compor e decompor números naturais de até três ordens, com ou sem suporte de material manipulável, por meio de diferentes adições? |
_____ |
_____ |
|
Constrói fatos básicos da adição e da subtração e utiliza-os no cálculo mental ou escrito? |
_____ |
_____ |
|
Compreende o contexto enunciado pelos problemas relacionados a adição e subtração, envolvendo números de até três ordens, com os significados de juntar, acrescentar, separar, retirar, e resolve-os utilizando estratégias pessoais? |
_____ |
_____ |
|
Constrói sequências numéricas crescentes ou decrescentes, iniciando de diferentes números e aplicando uma regularidade estabelecida? |
_____ |
_____ |
|
Descreve um padrão (ou regularidade) de sequências repetitivas e de sequências recursivas, por meio de palavras, símbolos ou desenhos, e completa com os elementos faltantes? |
_____ |
_____ |
|
Indica com precisão a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas? |
_____ |
_____ |
|
Lê, interpreta e compara informações registradas em gráficos de colunas ou de barras simples? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |