MP109
Introdução da Unidade 4
Nesta Unidade, a Unidade Temática Geometria receberá maior atenção. Pretende-se, assim, criar possibilidades para a abordagem de dois aspectos relativos a ela, quais sejam, as figuras geométricas não planas e as figuras geométricas planas. Apesar de predominarem os estudos sobre Geometria, habilidades de outras Unidades Temáticas permeiam as atividades propostas, como Números e Probabilidade e estatística, demonstrando, assim, a articulação entre esses conhecimentos.
A abertura da Unidade, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior, permite uma abordagem de observações e de descobertas por meio de uma imagem que apresenta o seu objeto de estudo: representações de figuras geométricas em um acampamento estilizado. Essa abertura contempla, e assim podem ser exploradas, tanto as figuras espaciais representadas por barracas prismáticas ou piramidais, árvores de troncos cilíndricos e copas cônicas ou esféricas, quanto as figuras planas representadas pelas projeções das sombras no chão.
As atividades propostas pretendem oferecer aos estudantes o reconhecimento, a nomeação e a comparação de figuras geométricas espaciais, já citadas, sem perder de vista a relação de objetos do mundo físico com essas figuras geométricas. Destaca-se que tais conhecimentos ampliam e aprofundam aqueles construídos pelos estudantes no 1º ano, quando relacionaram objetos do mundo físico com as figuras geométricas não planas.
O tratamento dado à Geometria, ao longo desta Unidade, vislumbra também a apropriação de conhecimentos previstos para o 3º ano: descrever características de algumas figuras geométricas espaciais (prismas retos, pirâmides, cilindros, cones), relacionando-as com suas planificações, que dizem respeito à relação entre prismas retos, pirâmides, cilindros e cones com suas planificações, além de nomear e associar essas figuras a objetos do mundo físico.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
Competências específicas favorecidas
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
MP110
UNIDADE 4. Geometria

MANUAL DO PROFESSOR
Objetivos da Unidade
• Identificar figuras geométricas não planas com superfície arredondada e com superfície não arredondada.
• Reconhecer, nomear e comparar figuras geométricas não planas: cubo, paralelepípedo, pirâmide, cone, cilindro e esfera.
• Registrar o resultado de estimativas.
• Relacionar figuras geométricas planas à superfície de figuras geométricas não planas.
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
• Comparar informações registradas em tabelas de dupla entrada.
Esta é a primeira Unidade que explora o conteúdo de Geometria neste livro. No início dela, há a discussão sobre figuras geométricas não planas com superfície arredondada ou não, a apresentação de algumas figuras não planas, com destaque para o atributo forma, e a introdução da noção de planicidade (que será ampliada na Unidade 8). Ainda nesta Unidade, há uma exploração das figuras geométricas planas básicas: quadrado, retângulo, triângulo e círculo. A proposta é que, ao trabalhar as atividades desta Unidade, os estudantes sejam capazes de identificar figuras geométricas não planas e figuras geométricas planas básicas.
BNCC em foco:
EF02MA02, EF02MA03, EF02MA06, EF02MA11, EF02MA12, EF02MA14, EF02MA15, EF02MA22
MP111
Para refletir...


Observe a imagem e converse com os colegas.
• O que as pessoas estão fazendo?
PROFESSOR
Respostas pessoais.• Em que lugar elas estão?

Agora fale de você.
PROFESSOR
Respostas pessoais.• Como você costuma se divertir?
• Você frequenta parques ou acampamentos?
MANUAL DO PROFESSOR
É importante ter em mente que os estudantes estão trabalhando com representações e não com as próprias figuras. Em toda representação há perda de informação, pois nem todos os atributos das figuras tornam-se perceptíveis na imagem ou no objeto “concreto”. A perda de informação é maior ainda quando a representação de uma figura tridimensional é proposta no plano bidimensional, pois mais atributos ficam imperceptíveis nesses casos.
Para refletir...
Para explorar a ilustração de abertura, solicite aos estudantes que observem a cena e descrevam o local, o que percebem nele e o que as pessoas estão fazendo. Se necessário, comente que Daniel e Amélia foram acampar com os colegas, sob supervisão de adultos, e que algumas crianças estão brincando de esconde-esconde, e outras, jogando. Pergunte:
• Como são as árvores?
• Todas as barracas estão representadas da mesma maneira?
Espera-se que os estudantes façam uma correlação com as figuras geométricas não planas: a copa das árvores ilustradas lembra esferas, e o tronco, cilindros; há barracas que lembram cone, cubo, paralelepípedo e pirâmide.
Depois, peça que localizem as personagens deste livro, Daniel e Amélia.
Proponha uma roda de conversa coletiva para que uma discussão sobre as questões apresentadas enriqueça e amplie o repertório dos estudantes.
MP112
Algumas figuras geométricas não planas
Estudo de superfícies

- Cole os moldes de algumas figuras geométricas que estão nas páginas 209 a 217 em um papel mais resistente. Depois, recorte-os com uma tesoura de pontas arredondadas e monte-os usando fita adesiva.

- Veja como Camila separou alguns objetos em dois grupos. Observe esses objetos e ligue cada grupo a uma etiqueta.
Linha 1


Linha 2


PROFESSOR
Resposta: Grupo: Objetos com superfícies arredondadasPROFESSOR
Grupo 2: Objetos com superfícies não arredondadas

- Agora, dê exemplos de objetos encontrados em sua casa ou na escola que
tenham
superfícies arredondadas e de objetos que não
tenham
superfícies arredondadas.
PROFESSOR
Exemplos de resposta: Superfícies arredondadas ‒ lixeira, copo etc.PROFESSOR
Superfícies não arredondadas − mesa, caixa de sapatos etc.
MANUAL DO PROFESSOR
Objetivo
• Identificar figuras geométricas não planas com superfície arredondada e com superfície não arredondada.
A apropriação dos conhecimentos geométricos por parte dos estudantes não é imediata; cabe ao professor propor situações para que isso aconteça e eles construam gradativamente seu pensamento geométrico.
Para estas atividades, os estudantes devem montar os modelos de cone, cilindro, pirâmide, paralelepípedo e cubo, cujos moldes estão no Material complementar.
Atividade 1
Antes de realizar a atividade, providencie papel mais resistente, fita adesiva e cola, para que os estudantes montem os modelos das figuras geométricas não planas. É importante que esses modelos sejam guardados para serem usados ao longo dos estudos desta Unidade ou no restante do ano letivo.
Atividade 2
Peça aos estudantes que deem alguns exemplos de objetos de seu dia a dia que tenham superfície arredondada e de outros que apresentem superfície não arredondada.
Classificar figuras geométricas em duas categorias, com superfície arredondada ou com superfície não arredondada, contribui para o posterior reconhecimento das figuras geométricas não planas e não arredondadas, como os poliedros. Com essas classificações, é possível estudar propriedades comuns a um grande número de figuras geométricas, generalizando resultados.
É importante destacar que figuras geométricas, planas ou não planas, são conceitos abstratos. Os materiais manipuláveis ou as ilustrações apresentadas nos livros são apenas representações de figuras geométricas, mas auxiliam na construção de sua imagem mental.
Evite falar de figuras com superfície arredondada como sendo aquelas que “rolam”, pois essa não é uma característica geométrica – além disso, um objeto que representa uma figura com superfície não arredondada pode ser arremessado com força suficiente para rolar, apesar de sua superfície ser imprópria para isso. É mais conveniente dizer que a “rolagem” de um objeto é uma aplicação prática decorrente da forma das figuras geométricas com superfície arredondada, propícia a tais usos.
BNCC em foco na dupla de páginas:
EF02MA14
MP113
- Cerque com uma linha o objeto “intrometido” em cada quadro.

PROFESSOR
Exemplo de respostas: Pirâmide
PROFESSOR
Resposta: Cilindro
PROFESSOR
Resposta: Caixa de leiteObservação: As figuras nesta atividade não foram apresentadas em escala de tamanho. Fim da observação.
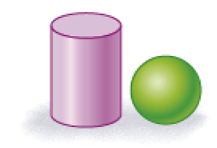
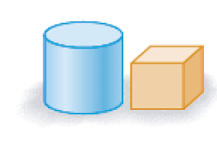
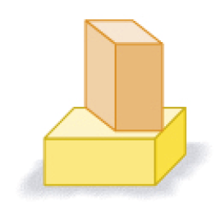
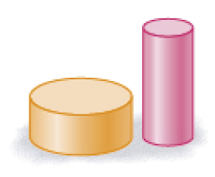
- Marque com um X apenas os pares de figuras com superfícies arredondadas.
( )

( )
( )
( )
( )

( )
PROFESSOR
Resposta: pares de figuras com superfícies arredondadas: cilindro e esfera. Cone e esfera. Cilindros. Cones.

- Pinte as figuras de acordo com a legenda a seguir.
 figuras com superfície arredondada
figuras com superfície arredondada
 figuras com superfície não arredondada
figuras com superfície não arredondada
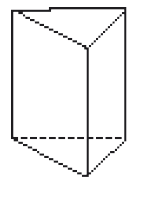
PROFESSOR
Resposta: azul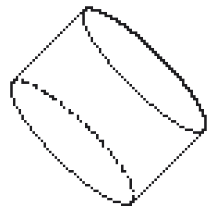
PROFESSOR
Resposta: vermelho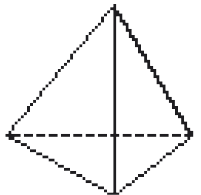
PROFESSOR
Resposta: azul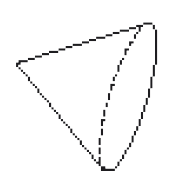
PROFESSOR
Resposta: vermelho
PROFESSOR
Resposta: azulMANUAL DO PROFESSOR
Atividade 3
A atividade tem por objetivo fazer os estudantes observarem as características comuns a cada grupo de objetos, trabalhando a formação do conceito por meio de exemplos e de contraexemplos. No caso do 1º quadro talvez eles digam que a pirâmide é a figura intrometida por ser a única com “pontas”.
No 3º quadro, eles podem marcar o balão e justificar dizendo que é a única figura que não tem “bico”, ou marcar a caixa de leite e justificar dizendo que é a única figura que não apresenta superfície arredondada.
Aproveite para introduzir, informalmente, o vocabulário matemático correto: as “pontas” são vértices; os “lados” nas figuras com superfície não arredondada são faces. Nas figuras com superfície não arredondada, destacamos ainda que as arestas são os segmentos de reta que unem dois vértices.
Se julgar necessário, esclareça que se denomina “intrometido” o objeto que difere dos outros três objetos do quadro quanto a ter ou não partes de superfície arredondadas.
Atividades 4 e 5
Se possível, leve modelos de figuras geométricas para que os estudantes as manuseiem. Na atividade 5, aproveite para perguntar: “Quais desses desenhos representam figuras com superfície arredondada e quais representam figuras que não têm superfície arredondada? Por que essas representações de figuras geométricas apresentam pontilhado ou tracejado?”.
Sua intervenção é importante para promover questionamentos que levem os estudantes a observarem novas relações, a argumentarem, a defenderem pontos de vista e a conhecerem determinadas convenções – como o uso da linha pontilhada ou tracejada, que indica que a figura representada não é plana.
Por sua importância para o desenvolvimento do pensamento geométrico, atualmente a Geometria é ensinada desde os anos iniciais do Ensino Fundamental, permitindo aos estudantes descreverem e representarem alguns aspectos do mundo que os cerca.
Pesquisas destacam as etapas do pensamento geométrico, apontando um nível inicial em que a compreensão dos estudantes parte da realidade. O enfoque dado à Geometria nesta Unidade vincula-se a essa fase. Os objetos de estudo são representados por materiais concretos, que podem ser manipulados. Por isso, leve para a classe modelos de algumas figuras geométricas não planas.
MP114
Cubos, paralelepípedos e pirâmides

- Cíntia e Caio estão observando as peças.

- O que as peças de Cíntia e de Caio têm de parecido?
PROFESSOR
Resposta pessoal.
- O que elas têm de diferente?
PROFESSOR
Exemplo de resposta: A peça de Cíntia tem todas as “partes” iguais; a de Caio, não (referindo-se às faces).
- Janaína precisa guardar as peças azuis abaixo nas caixas de papelão.
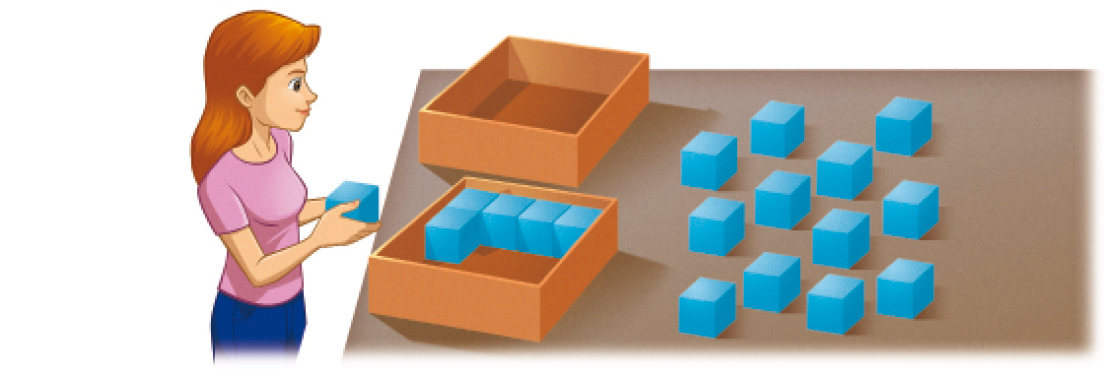

- Cada peça azul parece qual figura geométrica?
PROFESSOR
Resposta: Um cubo ou um paralelepípedo.
- Sabendo que as duas caixas de papelão são iguais, todas as peças azuis caberão nelas?
_____
PROFESSOR
Resposta: Sim, pois podemos estimar que em cada caixa de papelão caberão 12 peças. Nas duas caixas, caberão 24 peças, e Janaína precisa guardar 18 peças ao todo.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas: cubo, paralelepípedo e pirâmide.
• Registrar o resultado de estimativas.
Durante a realização das atividades desta página e das páginas 81, 82 e 83, proponha aos estudantes que manipulem os modelos de figuras geométricas que montaram na atividade 1 da página 78 para auxiliá-los.
Atividade 1
O objetivo da atividade é que os estudantes comecem a perceber as diferenças e as características comuns entre o cubo e o paralelepípedo.
Avalie a conveniência de esclarecer os estudantes sobre o fato de o cubo ser um caso particular de paralelepípedo.
Inicialmente, podem ser levadas para a classe algumas embalagens que lembrem essas figuras, para que a turma as recorte e possa perceber que um cubo tem todas as faces quadradas, o que não ocorre com um paralelepípedo (não cúbico).
É importante permitir aos estudantes que se expressem de maneira não formal, usando sua própria linguagem. Por exemplo, eles podem falar “bicos”, em vez de vértices, ou “partes”, referindo-se às faces.
É possível que alguns estudantes percebam que o cubo é um caso particular de paralelepípedo. Nesse momento, não é necessário chamar a atenção para esse fato.
LEGENDA: Cubo FIM DA LEGENDA.
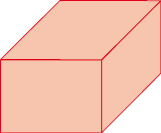
LEGENDA: Paralelepípedo FIM DA LEGENDA.
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF02MA02, EF02MA14
Aprender a nomenclatura correta de figuras geométricas e observar características que as identifiquem são ações que exigem intervenção do professor, que deve exercer o papel de provocador e incentivador de questionamentos e troca de pontos de vista entre os estudantes.
A manipulação dos modelos de figuras geométricas não planas é importante como apoio na observação das características de cada figura. Aproveite para fazer perguntas que instiguem a turma a refletir sobre algumas propriedades das figuras. Por exemplo: “Quantos vértices (pontas) tem um cubo? E uma pirâmide?” (Cubo: 8; pirâmide: depende do formato da base, no mínimo 4.).
MP115
- Quantas peças há em cada empilhamento?
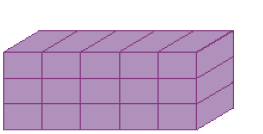
_____
PROFESSOR
Resposta: 15 peças.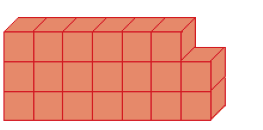
_____
PROFESSOR
Resposta: 20 peças.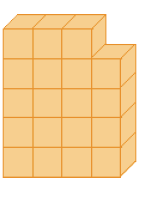
_____
PROFESSOR
Resposta: 19 peças.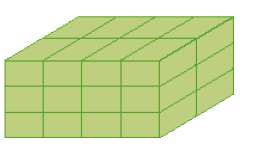
_____
PROFESSOR
Resposta: 24 peças.


- Observando todas as peças dos empilhamentos, faça uma estimativa: quantas peças há no total?
PROFESSOR
Atenção professor: Espera-se uma estimativa em torno de 80 peças. Fim da observação.
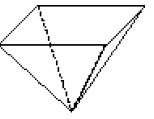
- A barraca que Luciana montou no quintal parece uma figura geométrica chamada pirâmide.

- Pinte de
 os paralelepípedos e de
os paralelepípedos e de  as pirâmides.
as pirâmides.
- Pinte de

PROFESSOR
Resposta: verde
PROFESSOR
Resposta: amarelo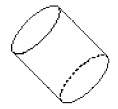
PROFESSOR
Resposta: amarelo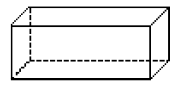
PROFESSOR
Resposta: verde

- Alguma figura não pode ser pintada? Por quê?
PROFESSOR
Resposta: Sim; o cilindro, pois não é um paralelepípedo nem uma pirâmide.
Boxe complementar:
Desafio
Estime a quantidade de peças cúbicas de cor laranja que cabem no recipiente transparente abaixo.
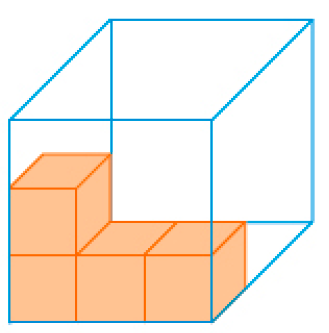
CRÉDITO: ADILSON SECCO
Cabem _____ peças cúbicas de cor laranja nesse recipiente.
PROFESSOR
Resposta: 27

• Conte a seus colegas como você pensou para chegar à resposta.
PROFESSOR
Resposta pessoal.Fim do complemento.
MANUAL DO PROFESSOR
Atividade 2
Aproveite para explorar situações de contagem:
• Quantas peças azuis há na caixa? (5)
• Quantas peças sobre a mesa há a mais que as da caixa? (12)
• Além desses locais, aparece mais alguma peça? (Sim, há uma na mão da mulher.)
• Faça uma estimativa: todas as peças azuis que aparecem na ilustração cabem em uma única caixa? Por quê? (Espera-se que os estudantes percebam que em uma caixa não cabem todas as peças azuis.)
• Você sabe quantas peças preenchem uma dessas caixas? (Espera-se que os estudantes percebam que cabem exatamente 12 peças em uma caixa.)
Atividade 3
Verifique as estratégias utilizadas pelos estudantes. Valorize-as e aceite, desde que façam sentido. Em uma roda de conversa, peça a eles que exponham suas respostas e digam como fizeram. Depois, proponha que contem as peças de cada empilhamento para comprovar sua resposta e validar a estimativa.
Atividade 4
Espera-se que os estudantes percebam que o cilindro não deve ser pintado de cor alguma, pois não se encaixa no grupo dos paralelepípedos nem no das pirâmides.
Desafio
Espera-se que os estudantes percebam que é possível colocar 3 peças cúbicas no comprimento, 3 na altura e 3 na profundidade do recipiente, totalizando 27 peças cúbicas. Incentive-os a socializarem a estratégia que utilizaram para fazer a estimativa.
BNCC em foco:
EF02MA02, EF02MA14; competência geral 2
Sugestão de leitura para o professor
Livro
CROWLEY, Mary L. Aprendendo e ensinando geometria. In: LINDQUIST, Mary M.; SHULTE, Albert P. (orgs.). O modelo Van Hiele de desenvolvimento do pensamento geométrico. São Paulo: Atual, 2012.
O texto discute o modelo Van Hiele de desenvolvimento do pensamento geométrico, oferecendo importantes contribuições para identificar e compreender o processo do pensamento geométrico.
MP116
Cones, cilindros e esferas
- O chapéu de festa parece uma figura geométrica chamada cone.

- Observe abaixo e cerque com uma linha a fotografia do objeto que parece um cone.




PROFESSOR
Resposta: vela.Observação: Os objetos nesta atividade não estão apresentados em escala de tamanho. Fim da observação.
- Com argila, Gabriela fez uma escultura que parece uma pirâmide e, depois, a transformou em outra escultura que parece um cone.


- Observe as duas esculturas feitas por Gabriela e escreva o que as figuras geométricas com que elas se parecem têm em comum.
PROFESSOR
Resposta esperada: Essas duas figuras geométricas têm uma “pontinha” e estão apoiadas na mesa por uma parte “achatada”.
- Analise as bolinhas e a embalagem mostradas abaixo.
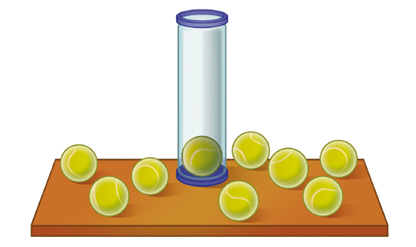

- Até quantas
bolinhas
você acha que podem ser colocadas na embalagem?
_____
PROFESSOR
Resposta: Até 4 bolinhas.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas: cone, cilindro e esfera.
• Registrar o resultado de estimativas.
• Relacionar figuras geométricas planas à superfície de figuras geométricas não planas.
As atividades destas páginas exploram as figuras não planas convencionais com superfície arredondada: o cilindro, o cone e a esfera, nomeando-as e identificando algumas de suas características.
Retome a manipulação dos modelos de figuras geométricas não planas e as características de cada figura e faça perguntas que instiguem a turma a fazer novas reflexões acerca das propriedades das figuras. Por exemplo: “Se uma figura tem uma ‘ponta’ (vértice), pode-se afirmar que ela é um cone? O que há de parecido entre uma esfera e um cilindro?”.
Sugerimos que, ao realizar essas perguntas, seja apresentada a nomenclatura adequada das figuras geométricas e de alguns de seus elementos, de modo que os estudantes se acostumem com essa nomenclatura ( esfera em vez de bola ; cone em vez de chapéu de aniversário ; vértice em vez de ponta etc.).
Atividade 1
Explore as imagens apresentadas. Pergunte, por exemplo: “O dado lembra qual figura geométrica? E a caixa verde?”. (Cubo; paralelepípedo.)
Atividade 2
Uma possível resposta dos estudantes é: Essas duas figuras geométricas têm uma “pontinha”e estão apoiadas na mesa por uma parte achatada.
Peça aos estudantes que descrevam diferenças entre as figuras geométricas representadas pelas duas esculturas. Espera-se que eles associem a forma arredondada apenas à escultura que lembra um cone.
BNCC em foco:
EF02MA02, EF02MA14; competência geral 2
Atividade 3
Espera-se que os estudantes consigam perceber que cabem até 4 bolinhas na embalagem que lembra um cilindro. As bolinhas não podem ultrapassar o limite da embalagem porque, do contrário, não seria possível tampá-la.
MP117
- Observando os objetos mostrados abaixo, podemos verificar que a lata parece uma figura geométrica chamada cilindro. E a bola parece uma figura geométrica chamada esfera .



Observação: Os objetos nesta atividade não estão apresentados em escala de tamanho. Fim da observação.
- Agora, escreva nomes de objetos que se parecem com:
- cilindro:
_____
PROFESSOR
Exemplo de respostas: Copo e lata de suco.
- esfera:
_____
PROFESSOR
Resposta: Bola de futebol, bola de pingue-pongue e ervilha.
- O molde de um dado é formado por 6 partes. Cada parte parece um quadrado.
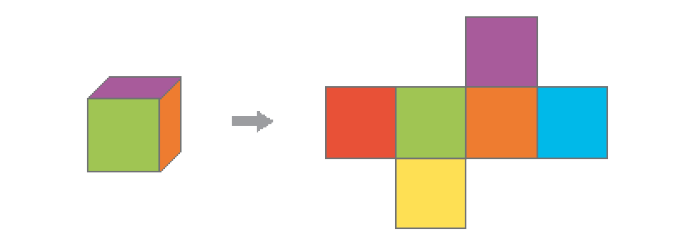
- Cerque com uma linha o molde que pode formar um cilindro.

PROFESSOR
Resposta: Figura 3.- Quais figuras planas podem ser reconhecidas no
molde
do cilindro?
( ) Retângulo e círculo.
( ) Triângulo e círculo.
PROFESSOR
Resposta correta: Retângulo e círculo.
MANUAL DO PROFESSOR
Atividade 4
Peça aos estudantes que deem alguns exemplos de objetos de seu dia a dia que tenham forma arredondada e que lembrem um cilindro. Depois, faça o mesmo em relação à esfera.
Para ampliar, peça que identifiquem semelhanças e diferenças entre o cilindro e a esfera. Uma semelhança que podem observar é a forma arredondada, e uma diferença é que o cilindro tem partes achatadas, mas a esfera não.
Atividade 5
Providencie um modelo de cubo (pode ser um dado que não tenha pontas arredondadas) e um modelo de cilindro (pode ser uma vela ornamental) para os estudantes poderem manusear.
Explore o modelo de cubo e pergunte:“Que partes planas aparecem nesse objeto? Vocês sabiam que cada uma dessas partes planas é chamada de face?”. Espera-se que os estudantes percebam também que o cubo tem 6 faces.
Explore o modelo de cilindro e identifique cada base, para que eles percebam que essas partes “achatadas” também são figuras planas.
Observando o modelo de cilindro e os moldes apresentados no item a, os estudantes poderão perceber mais facilmente aquele que corresponde ao molde do cilindro.
Comente que, no caso do cilindro e do cone, as partes “achatadas” (planas), pelas quais eles podem ser apoiados sobre um tampo de mesa sem rolar, são chamadas de bases. Esclareça que, para as figuras geométricas com superfície arredondada, as partes planas não são chamadas de faces.
Peça aos estudantes que justifiquem o porquê de os demais moldes não poderem ser o de um cilindro. Ao observar o que “não é”, eles ampliam o conceito do “que é”, apropriando-se das características da figura estudada.
BNCC em foco:
EF02MA014, EF02MA15
MP118
O que as figuras geométricas não planas têm de parecido?
- Observe as figuras geométricas não planas representadas abaixo.
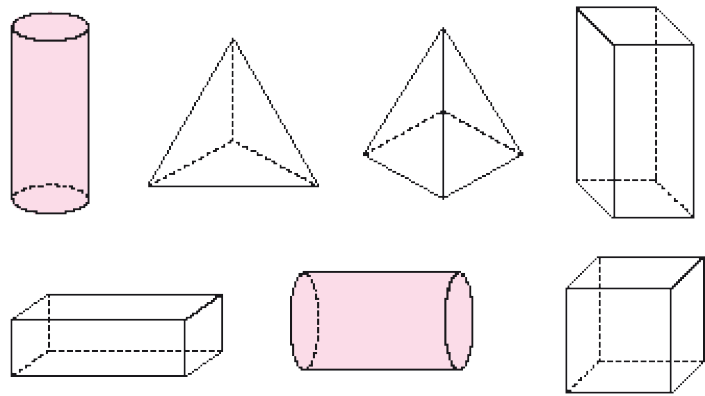

- Pinte de
 as figuras geométricas que não têm pontas.
as figuras geométricas que não têm pontas.
- Qual é o nome das figuras geométricas não planas que você pintou de
 ? E o das figuras geométricas não planas que não foram pintadas?
? E o das figuras geométricas não planas que não foram pintadas? _____
PROFESSOR
Resposta: Cilindro; cubo, paralelepípedo e pirâmide.
- Qual é o nome de outra figura geométrica não plana que não tem ponta?
_____
PROFESSOR
Resposta: Esfera.
- Marque com um X a dupla de figuras geométricas não planas que têm mais características em comum.
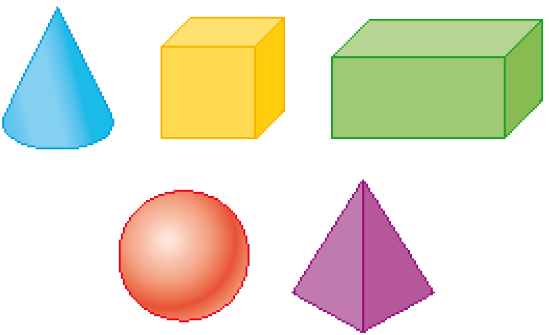
( ) Esfera e pirâmide.
( ) Esfera e cubo.
( ) Cubo e paralelepípedo.
( ) Cubo e cone.
PROFESSOR
Resposta correta: Cubo e paralelepípedo.MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas: cubo, paralelepípedo, pirâmide, cone, cilindro e esfera.
• Identificar características similares e diferenças entre as figuras geométricas não planas estudadas.
A ideia matemática de plano não encontra respaldo no mundo físico, no sentido de que mesmo uma folha de papel, por mais fina que seja, sempre terá espessura e será uma figura não plana. É por isso que se fala em “parecer” figuras planas.
Atividade 1
Explique novamente o significado das linhas tracejadas: elas dão ideia de profundidade e indicam partes que não podemos ver no objeto real. Aproveite também e reforce a nomenclatura correta, sem, no entanto, exigir dos estudantes que a usem. Assim, comente com eles que essas pontas são chamadas de vértices da figura geométrica.
Atividade 2
Em uma roda de conversa, peça aos estudantes que elenquem diferenças e semelhanças de cada dupla de figuras e registre as respostas na lousa identificando a que dupla de figuras se referem. Depois, ajude os estudantes a procurarem as duas figuras geométricas que têm mais semelhanças.
BNCC em foco:
EF02MA14
MP119
Algumas figuras geométricas planas
- Augusto usou um envelope para colocar um cartão de aniversário que fez para sua mãe.


O envelope visto deste modo parece uma figura geométrica plana chamada retângulo.
Para embrulhar o presente, Augusto usou uma folha de papel florida.

O papel de presente visto desta maneira parece uma figura geométrica plana chamada quadrado.
Observação: Os objetos nesta atividade não estão apresentados em escala de tamanho. Fim da observação.
- Pinte apenas as figuras que são representações de quadrados e retângulos.
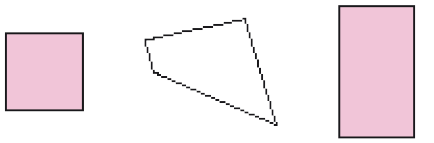
- Nas ruas, há várias placas de trânsito que parecem figuras geométricas planas.


- Cerque com uma linha as imagens que parecem um círculo e um triângulo.

PROFESSOR
Resposta: círculo e triângulo..MANUAL DO PROFESSOR
Objetivo
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
Atividade 1
Nesse momento, não se espera que os estudantes percebam propriedades mais refinadas dessas figuras geométricas planas, mas, sempre que possível, incentive-os a observar as características comuns entre o quadrado e um retângulo qualquer. O reconhecimento de que o quadrado também é um retângulo será concretizado nos anos finais do Ensino Fundamental.
Atividade 2
Verifique se os estudantes se atêm às figuras geométricas planas ou se confundem com as figuras não planas, considerando, por exemplo, a pirâmide como um triângulo. Nesse caso, volte a mostrar a diferença que existe quando colocamos tais modelos de figuras sobre a mesa, retomando a noção de planificação.
Sugestão de atividade
Recortando embalagens
Providencie embalagens cujas partes planas lembrem figuras geométricas planas estudadas. Peça, então, aos estudantes que recortem as partes dessas embalagens e as colem em uma folha de papel. Em seguida, discuta com eles as diferenças entre as embalagens e as partes delas que foram recortadas e coladas no papel. Peça que identifiquem que figura plana cada parte colada lembra.
BNCC em foco:
EF02MA15
MP120
O que há de comum e o que há de diferente entre figuras geométricas planas?
- Observe as figuras geométricas planas representadas abaixo.

- Quais são as duas figuras geométricas planas que apresentam mais características em comum?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes respondam que são o quadrado e o retângulo. Fim da observação.

- Agora, explique a um
colega
como você chegou a essa conclusão.
PROFESSOR
Resposta pessoal.

- Recorte as peças verdes da página 207 e faça o que se pede.
- Escolha dois triângulos e forme um quadrado.
_____
PROFESSOR
Resposta:
- Com os outros dois triângulos, obtenha um retângulo.
_____
PROFESSOR
Resposta:
- Agora, cole as figuras planas formadas nos respectivos espaços.

- O que você notou entre os triângulos usados para
obter
cada figura plana acima?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que os triângulos têm as mesmas características, uma das quais é ter um ângulo reto. Não importa que eles não verbalizem, basta que reconheçam o ângulo relacionando-o com um “canto da porta”, por exemplo. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
• Identificar características similares e diferenças entre as figuras geométricas planas estudadas.
Atividade 1
Espera-se que os estudantes percebam as semelhanças entre o quadrado e o retângulo: o número de lados, 4 “bicos”, dois a dois lados de mesmo comprimento, por exemplo.
Atividade 2
Espera-se que os estudantes percebam que os triângulos que formam o quadrado são idênticos entre si, assim como os que formam o retângulo; porém os que formam o quadrado são diferentes daqueles que formam o retângulo. Os estudantes podem verificar isso sobrepondo os triângulos de modo que coincidam, quando forem idênticos. Mesmo as duas figuras (quadrado e retângulo) sendo formadas por triângulos, é preciso atentar para a forma de cada triângulo.
Para ampliar a atividade, apresente triângulos variados em tamanho, forma e posição para os estudantes perceberem que, embora todos tenham a forma triangular (ligada à quantidade de lados), há diferentes tipos de triângulo.
BNCC em foco:
EF02MA15; competência específica 6
MP121


- Para formar o retângulo da atividade 2, juntamos dois triângulos diferentes dos usados para
obter
o quadrado. Agora,
recorte
as peças azuis da página 207 e observe-as.
- É possível formar um retângulo com todas as peças azuis? Explique sua resposta.
PROFESSOR
Resposta: Sim. Exemplo de resposta: formar dois quadrados e justapô-los.
- É possível representar com essas peças uma figura geométrica plana diferente do retângulo? Se for possível, qual é o
número
de peças usadas? E qual é a figura geométrica representada?
PROFESSOR
Resposta: Sim. Exemplo de resposta: justapor dois triângulos pelos seus catetos formando um outro triângulo retângulo e isósceles ou formando um paralelogramo (que eles ainda não conhecem).
- O que podemos concluir com a atividade 2 e os itens a e b desta atividade?
PROFESSOR
Resposta pessoal.
- É possível formar um retângulo com todas as peças azuis? Explique sua resposta.
- Observe as figuras geométricas planas representadas abaixo.

- Marque com um X a figura geométrica plana que tem menos características comuns com as demais.
PROFESSOR
Resposta: círculo

- Recorte e monte o molde da página 205. Analise atentamente a figura geométrica com que o seu modelo montado parece.

LEGENDA: Museu do Louvre em Paris, França, em 2019. FIM DA LEGENDA.
- Com qual figura geométrica não plana esse
modelo
parece?
_____
PROFESSOR
Resposta: Pirâmide.
- Quais figuras geométricas planas podem ser reconhecidas na figura geométrica não plana representada pelo
modelo
que você montou?
_____
PROFESSOR
Resposta: Triângulo e quadrado.
MANUAL DO PROFESSOR
Atividade 3
No item a, espera-se que os estudantes percebam que, ao juntar as peças triangulares, é possível obter um retângulo. Uma explicação possível no item b: podemos juntar dois triângulos, formando um quadrado; depois juntar os outros dois, obtendo outro quadrado; e, por fim, juntar os dois quadrados, formando um retângulo. Também podemos justapor dois triângulos, retângulos e isósceles pelos seus catetos e formar outro triângulo retângulo e isósceles, ou ainda formar um paralelogramo (que eles ainda não conhecem). Não convém aplicar essa nomenclatura para eles, apenas sugira possibilidades ou deixe que eles experimentem o prazer das descobertas.
Uma conclusão plausível no item c: é possível obter algumas figuras planas por meio de composições com outras figuras planas.
Atividade 4
Em uma roda de conversa, incentive os estudantes a explorarem as características das figuras planas estudadas.
Atividade 5
Se julgar conveniente, amplie a atividade e explore outras representações de pirâmides, destacando que a base da pirâmide aceita outras figuras geométricas planas além do quadrado, como o triângulo, o pentágono e o hexágono; entretanto, suas outras faces sempre serão triangulares.
BNCC em foco:
EF02MA14, EF02MA15
MP122
A Matemática me ajuda de ser
... um observador do cotidiano
No cotidiano, nas atividades escolares, nas brincadeiras, estamos sempre rodeados de objetos, construções, alimentos, brinquedos que nos lembram alguma figura geométrica não plana.

LEGENDA: Oca na aldeia pataxó Jaqueira, município de Porto Seguro, Bahia, em 2019. FIM DA LEGENDA.

LEGENDA: Farol da Barra, no município de Salvador, Bahia, em 2018. FIM DA LEGENDA.

LEGENDA: Menina brincando com bolas de sabão. FIM DA LEGENDA.

LEGENDA: Embalagens de presentes. FIM DA LEGENDA.
Observação: As imagens nesta página não estão apresentadas em escala de tamanho. Fim da observação.
Tome nota
Observe as imagens acima e faça uma lista de figuras geométricas não planas que você identifica representadas nelas.
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes identifiquem: paralelepípedos, cilindro, cone e esferas. Fim da observação.


- Depois, compare a lista que você fez com a de um
colega
e responda: elas são diferentes?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas.
• Identificar características similares e diferenças entre as figuras geométricas não planas estudadas.
A discussão de assuntos de relevância social e cultural favorece uma educação matemática crítica. As imagens apresentadas nessa seção representam objetos e arquiteturas que lembram figuras geométricas não planas.
Tome nota
As imagens e o texto oferecem aos estudantes subsídios para que observem elementos de seu dia a dia e de outros lugares do mundo e percebam a presença constante da Matemática e, em particular, da Geometria.
A atividade possibilita discutir com os estudantes alguns aspectos relacionados à observação da arquitetura.
Sugerimos que a discussão seja encaminhada de modo que os leve a perceber a importância das construções na sociedade, como o formato se modificou ao longo da história e como a cultura de um país interfere nelas. Se julgar oportuno, proponha aos estudantes que pesquisem sobre a construção da roda na Antiguidade, das pirâmides no Egito etc. Traga imagens de outras edificações famosas para os estudantes observarem, como Pirâmide do Museu do Louvre, Torre Eiffel, Torre de Pisa, Auditório do Ibirapuera, Instituto Inhotim etc.
A segunda parte da atividade proporciona um momento de compartilhamento de informações entre os estudantes. Esses momentos são muito importantes para que eles observem as estratégias utilizadas pelos colegas, desenvolvam a autocrítica e ampliem seu repertório acerca do tema estudado.
Explore com os estudantes as imagens apresentadas nessas páginas. Verifique se eles identificam algumas delas ou já viram outras figuras parecidas. Uma ampliação possível é os estudantes percorrerem a escola (ou arredores dela), observando objetos e construções que lembrem essas figuras. Depois, em uma roda de conversa, eles podem expor o que observaram.
Incentive os estudantes a buscarem nas imagens todas as figuras geométricas não planas que o colega listou e ele não.
BNCC em foco:
EF02MA14; competências gerais 1 e 6; competência específica 1
MP123
Reflita

- Observe a imagem com as caixas de presente da página anterior.
- Qual dessas embalagens é mais adequada para guardar uma bola?
PROFESSOR
Resposta pessoal.
- E para guardar um par de sapatos?
PROFESSOR
Resposta pessoal.
- Qual dessas embalagens é mais adequada para guardar uma bola?
- Observe as embalagens abaixo.
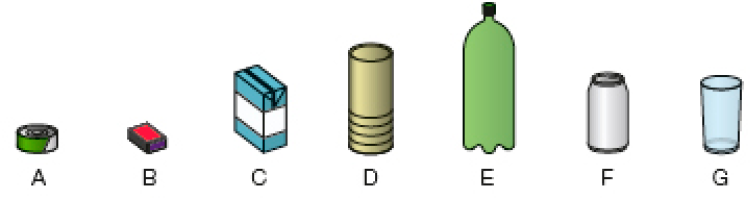
- Agora, complete o quadro.
Quadro: equivalente textual a seguir.
|
Embalagem |
Nome da figura geométrica que ela lembra |
|---|---|
|
A |
_____ |
|
B |
_____ |
|
C |
_____ |
|
D |
_____ |
|
E |
_____ |
|
F |
_____ |
|
G |
_____ |
PROFESSOR
Resposta: Exemplos de resposta: Cilindro, Paralelepípedo, Paralelepípedo, Cilindro, Cilindro, Cilindro, Cilindro.


- Depois, classifique as figuras das embalagens em grupos. Conte aos colegas e ao professor o que você considerou para organizar esses grupos e quantos grupos você criou.
PROFESSOR
Exemplo de resposta: 2 grupos. Grupo 1: B, C; Grupo 2: A, D, E, F e G. As embalagens do Grupo 1 têm superfície externa não arredondada; as do Grupo 2 têm superfície externa arredondada.
MANUAL DO PROFESSOR
Reflita
Atividade 1
No item a, os estudantes podem dizer que a embalagem de presente mais adequada depende do tamanho da bola e das caixas. Discuta com eles, caso surjam outras respostas, validando-as.
Atividade 2
Se possível, traga para a sala de aula embalagens como as envolvidas na atividade e deixe que os estudantes as manuseiem e observem similaridades e diferenças entre elas.
Organize uma roda de conversa, mostre cada embalagem ou aponte-a no livro e peça que identifiquem a figura geométrica não plana que pode ser representada por ela. Depois que todos concordarem com a nomeação da figura, peça que registrem a resposta no quadro apresentado no livro.
Para finalizar, proponha aos estudantes que busquem um critério para classificar esses modelos (embalagens) de figuras geométricas não planas em apenas 2 grupos. Eles podem se reunir em pequenos grupos para a escolha do critério e, depois, discutir coletivamente, para definirem um único critério para a turma.
Um critério possível é se a embalagem tem ou não superfície arredondada. Com esse critério, formamos:
• o Grupo 1, das embalagens que têm superfície não arredondada: B e C;
• o Grupo 2, das embalagens que têm superfície arredondada: A, D, E, F e G.
BNCC em foco:
EF02MA14; competências gerais 1 e 6; competência específica 1
Sugestão de trabalho interdisciplinar
O conteúdo desta seção pode também ser trabalhado e ampliado nas aulas de:
• Arte: estudando a mudança de estilo e representação artística ao longo do tempo;
• Educação Física e Ciências da Natureza: estudando a importância da prática de esportes e brincadeiras ao ar livre;
• Língua Portuguesa: elaborando textos relacionados às imagens apresentadas ou inspirados nelas.
MP124
Compreender informações
Ler e interpretar tabelas de dupla entrada
- Glória tem um brinquedo cujas peças parecem figuras geométricas não planas. Observe as peças desse brinquedo.
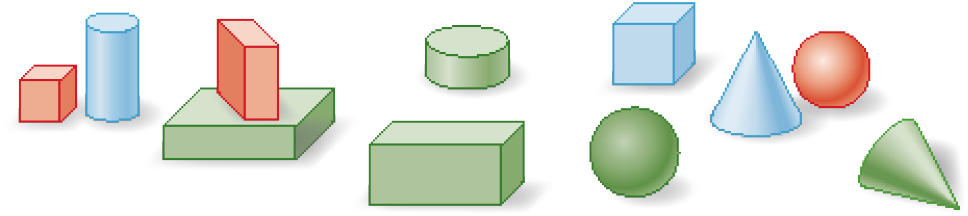
Ela organizou essas peças pelas suas características. Depois, contou e registrou as quantidades em uma tabela. Veja.
Características das peças
Tabela: equivalente textual a seguir.
|
Cor Tipo de superfície |
Azul
|
Vermelha
|
Verde
|
|---|---|---|---|
|
Com superfície arredondada |
2 |
1 |
3 |
|
Sem superfície arredondada |
1 |
2 |
2 |
Fonte: Anotações de Glória (mar. 2023).
- Agora, de acordo com a tabela, responda.
- Quantas características Glória observou nas peças do brinquedo?
Quais são elas? _____
PROFESSOR
Resposta: 2 características: tipo de superfície e cor.
- Quantas peças verdes há no brinquedo de Glória?
_____
PROFESSOR
Resposta: 5 peças.
- Quantas peças com superfície arredondada há nesse brinquedo?
_____
PROFESSOR
Resposta: 6 peças.
- Há mais peças verdes ou azuis?
_____
PROFESSOR
Resposta: Verdes.
- Quantas peças há nesse brinquedo?
_____
PROFESSOR
Resposta: 11 peças.
MANUAL DO PROFESSOR
Objetivo
• Comparar informações registradas em tabela de dupla entrada.
Atividade 1
A atividade apresenta dados que podem ser classificados por dois critérios: tipo de figura e cor. Situações como essa podem ser organizadas em uma tabela de dupla entrada, cuja leitura exige o cruzamento das informações provenientes de uma linha (fileira horizontal) e de uma coluna (fileira vertical). Por exemplo, relacionando uma figura com superfície arredondada de cor vermelha, pode-se verificar que, no brinquedo de Glória, há apenas 1 peça vermelha cuja superfície é arredondada.
Explique a maneira de ler os dados nesse tipo de tabela: para cada figura, há uma cor. Aproveite o momento e peça aos estudantes que nomeiem as peças do brinquedo de Glória. Retome as figuras que gerarem dificuldade.
Proponha perguntas que sugiram a busca de informação nesse tipo de tabela:
• “Quantas peças com superfície arredondada são azuis? E quantas são vermelhas? E verdes?” (2 são azuis, 1 é vermelha e 3 são verdes.)
Observe como eles buscam esses dados. Caso eles contem as peças do brinquedo, incentive-os, questionando: “E como podemos obter essas informações olhando para a tabela que Glória construiu?”.
• “Quantas peças azuis não têm superfície arredondada? E vermelhas? E verdes?” (1 peça azul, 2 vermelhas e 2 verdes.)
Nesse caso, os estudantes devem buscar a característica cor na coluna, e, depois, o tipo de figura na linha correspondente. É importante que eles percebam que podem iniciar pela linha ou pela coluna, dependendo da característica a ser procurada.
Em uma roda de conversa, discuta com os estudantes as questões propostas no livro.
BNCC em foco:
EF02MA03, EF02MA06, EF02MA22; competências específicas 3 e 4
MP125
- Paulo e Flávio moram em sítios e criam vacas e porcos.
Observe a tabela que mostra a quantidade de animais que cada um deles criava em maio de 2023.
Animais criados
Tabela: equivalente textual a seguir.
|
Animal Criador |
|
|
|---|---|---|
|
Paulo |
13 |
25 |
|
Flávio |
32 |
14 |
Fonte: Anotações de Paulo e de Flávio (maio 2023).
- De acordo com a tabela, responda.
- Quantas vacas Paulo cria?
_____
PROFESSOR
Resposta: 13 vacas.
- Quantos
porcos
Flávio cria?
_____
PROFESSOR
Resposta: 14 porcos.
- Quantos animais Flávio cria no total? E Paulo?
_____
PROFESSOR
Resposta: 46 animais; 38 animais.
- Quem cria mais porcos? Quantos a mais?
_____
PROFESSOR
Resposta: Paulo; 11 porcos a mais.
- Quem cria menos vacas? Quantas vacas faltam para que esse criador fique com a mesma quantidade de vacas que o outro criador?
_____
PROFESSOR
Resposta: Paulo; ele precisa de mais 19 vacas.
- Juntando as vacas de Paulo e as de Flávio e juntando os
porcos
desses dois criadores, pode-se perceber que há menos
porcos
que vacas. Quantos
porcos
faltam para termos a mesma quantidade total de vacas?
_____
PROFESSOR
Resposta: Faltam 6 porcos.PROFESSOR
Exemplos de cálculo:PROFESSOR
13 + 32 = 45PROFESSOR
25 + 14 = 39PROFESSOR
45 − 39 = 6
- Quantos animais há ao todo, juntando as criações de Paulo e as de Flávio?
_____
PROFESSOR
Resposta: 84 animais.PROFESSOR
Exemplo de cálculo:PROFESSOR
45 + 39 = 84
MANUAL DO PROFESSOR
Atividade 2
Os estudantes devem relacionar a informação da linha com a da coluna correspondente em cada caso para responder às perguntas. Proponha a eles que resolvam as questões individualmente para que você possa, em uma avaliação formativa, se inteirar do quanto cada estudante assimilou da leitura desse tipo de tabela e das reflexões feitas na atividade 1.
No item a, por exemplo, é preciso localizar a posição da tabela que relaciona a linha correspondente a Paulo com a coluna correspondente à vaca, obtendo assim o valor 13.
No item c, para calcular o número de animais criados por Flávio (e por Paulo), basta adicionar os números de uma única linha. No caso de Paulo: 13 + 25 = 38; no caso de Flávio: 32 + 14 = 46.
Sugestão de atividade
Providencie modelos de figuras planas feitos de cartolinas de duas cores: um grupo de retângulos e quadrados e outro de triângulos variados.
Peça aos estudantes que organizem essa coleção de modelos de figuras planas em uma tabela envolvendo dois critérios: quantidade de vértices (pontas) e cor. Desse modo, eles deverão montar uma tabela de dupla entrada, sob sua orientação. Eles podem, por exemplo, colocar nas linhas o tipo de figura: que têm 3 “pontas” (ao todo) e que têm 4 “pontas”, e, nas colunas, as cores: verde e vermelha (ou podem pôr as cores nas linhas e pôr nas colunas as outras características das figuras).
BNCC em foco:
EF02MA03, EF02MA06, EF02MA22; competências específicas 3 e 4
MP126
O que você aprendeu
Avaliação processual
- Observe a reprodução da obra e responda às questões.
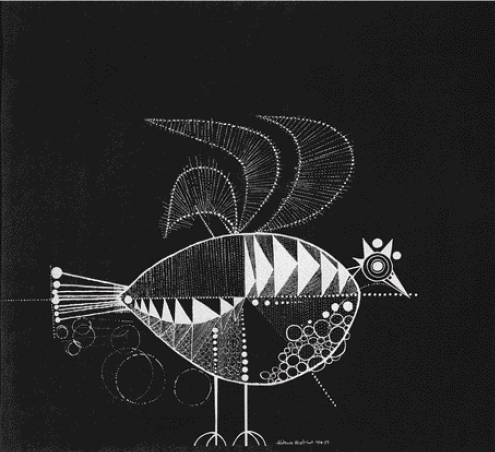
LEGENDA: Pássaro, de Aldemir Martins, 1958/1959. Estudo para painel – nanquim branco sobre papel preto, 55 cm × 60 cm. FIM DA LEGENDA.
- Nessa obra, o artista desenhou figuras geométricas planas ou figuras geométricas não planas?
_____
PROFESSOR
Resposta: Figuras geométricas planas.
- Descreva essa imagem para um colega.
PROFESSOR
Resposta pessoal.

- Veja estas representações de pirâmides e responda às questões.
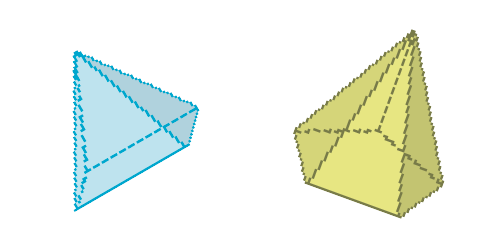
- O que elas têm de parecido?
PROFESSOR
Exemplo de respostas: As duas têm partes triangulares.
- O que elas têm de diferente?
PROFESSOR
Resposta: A parte que não é triangular da pirâmide azul é diferente da parte não triangular da pirâmide verde.

- Siga os comandos das setas azuis abaixo e construa uma figura a partir do ponto verde na malha. Depois, pinte a parte interna da sua figura.
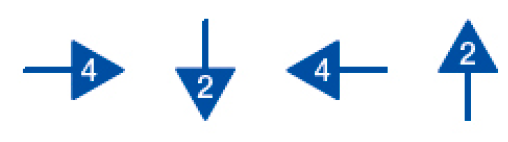
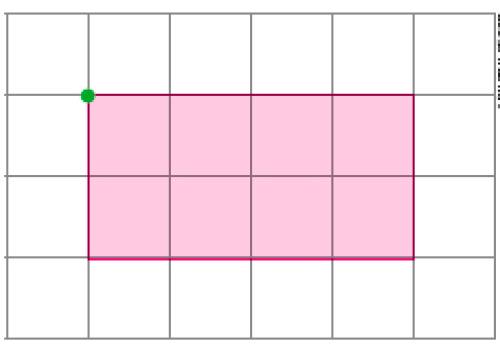
- A figura pintada é uma representação de qual figura geométrica plana?
PROFESSOR
Resposta esperada: retângulo.
MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
Observando a obra, espera-se que os estudantes percebam representações de triângulos e de círculos de diferentes tamanhos, dispostos de modo não convencional, concluindo que as figuras, apesar de dispostas desse modo, mantêm suas características.
No item b, uma descrição do todo exigiria uma interpretação subjetiva do significado da obra ou da possível intenção do artista ao fazê-la. Assim, é possível que a descrevam como uma figura que lembra uma ave, com triângulos e círculos de tamanhos diferentes.
Atividade 2
Espera-se que os estudantes identifiquem como parecido o fato de ambas as pirâmides terem partes triangulares (faces laterais). Como diferente, podem notar que a parte não triangular de cada pirâmide (base) é formada por figuras diferentes.
Se julgar oportuno, amplie a atividade pedindo aos estudantes que comparem uma pirâmide e um cone. Embora as duas figuras sejam não planas, elas têm diferenças significativas. A pirâmide é uma figura com superfície não arredondada e tem faces em forma de polígonos, enquanto o cone tem a forma arredondada e sua base é um círculo.
A ação de desmontar seus modelos auxilia a visualização dessas diferenças.
Atividade 3
Retome com os estudantes o código de setas que indica os comandos para formar a figura na malha. Para ampliar, pergunte como deveriam ser os comandos para que a figura representada fosse um quadrado.
BNCC em foco:
EF02MA12, EF02MA14, EF02MA15
MP127
- Observe a legenda abaixo.
P: Parece figura geométrica plana.
N: Parece figura geométrica não plana.
- Agora, coloque a letra correspondente no quadrinho de cada objeto, de acordo com o tipo de figura com que ele se parece.

_____
PROFESSOR
Exemplo de respostas: P.
_____
PROFESSOR
Resposta: N.
_____
PROFESSOR
Resposta: N.
_____
PROFESSOR
Resposta: N.
_____
PROFESSOR
Resposta: N.
_____
PROFESSOR
Resposta: N.Observação: As imagens nesta página não foram apresentadas em escala de tamanho. Fim da observação.

- Observe a sequência e marque com um X a figura “escondida” pelas bandeiras.


( )

( )

( )
PROFESSOR
Resposta correta: cuboAutoavaliação

- Consigo perceber diferenças entre figuras geométricas planas e figuras geométricas não planas?
PROFESSOR
Resposta pessoal.
- Percebo o que há em comum entre algumas figuras geométricas não planas? E entre algumas figuras planas?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Certifique-se de que os estudantes entenderam o código para indicar se o objeto lembra uma figura geométrica plana ou uma figura geométrica não plana. Incentive-os a explicarem o que caracteriza cada uma dessas figuras.
Atividade 5
Nessa atividade, o estudante precisa, em cada caso, descobrir a regularidade da sequência para então identificar qual é a figura geométrica não plana que completa essa sequência.
Na primeira questão, os estudantes precisam verificar se já conseguem diferenciar figuras geométricas planas de figuras geométricas não planas. Mostre objetos que as representem para os estudantes citarem as diferenças que conseguem perceber.
Para responder às questões do segundo item, eles devem refletir sobre semelhanças e diferenças em cada tipo de figura. Os estudantes poderão aproveitar para citar a diferença entre corpos arredondados e as demais representações de figuras não planas. Vale ressaltar que a percepção sobre semelhanças e diferenças de atributos geométricos é um caminho para levantarem propriedades e definições de figuras geométricas.
BNCC em foco:
EF02MA11, EF02MA14, EF02MA15
MP128
Comentários para o professor:
Conclusão da Unidade 4
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue identificar figuras geométricas não planas com superfícies arredondadas e figuras geométricas não planas com superfícies não arredondadas? |
_____ |
_____ |
|
Reconhece, nomeia e compara figuras geométricas não planas: paralelepípedo, cubo, pirâmide, cone, cilindro e esfera? |
_____ |
_____ |
|
Reconhece, compara e nomeia figuras planas (círculo, quadrado, retângulo e triângulo), por meio de características comuns, em desenhos apresentados em diferentes disposições ou em sólidos geométricos? |
_____ |
_____ |
|
Lê e compara informações registradas em tabelas de dupla entrada? |
_____ |
_____ |
|
Compreende e realiza a leitura de imagens? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP129
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: _____ |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |




