MP130

Comentários para o professor:

Introdução da Unidade 5

Esta unidade trabalha enfaticamente a Unidade Temática Números, porém aborda também Álgebra e Probabilidade e estatística. Nessas três Unidades Temáticas, as atividades propostas consideram os conhecimentos construídos no 1º ano, ao mesmo tempo em que se articulam com aqueles a serem desenvolvidos no 3º ano.

Quanto a Números, apresentam-se duas das ideias relacionadas à multiplicação: adição de parcelas iguais, nas multiplicações por 2, 3, 4 e 5, e proporcionalidade, abrangendo dobro e triplo. Ambas têm como objetivo a construção de conhecimentos relativos à resolução e elaboração de problemas, com recurso às estratégias pessoais. Embora este seja o primeiro contato dos estudantes com conceitos específicos de multiplicação, os conhecimentos relativos aos fatos básicos da adição e da subtração, tal como abordados nas Unidades 2 e 3, alicerçam a construção dos novos conhecimentos, presentes nesta Unidade. Destacam-se, ainda, os estudos a serem desenvolvidos no 3º ano, cuja abordagem amplia ideias envolvidas na multiplicação para a disposição retangular em situações que envolvam multiplicações por 10.

As atividades que exploram Probabilidade e estatística buscam ampliar conhecimentos construídos no 1º ano, passando da classificação de eventos que abrangem o acaso, como acontecerá com certeza, talvez aconteça e é impossível acontecer, para a classificação de resultados de eventos aleatórios, como em pouco prováveis, muito prováveis, improváveis e impossíveis.

A abordagem de Álgebra, ao longo do 1º ano, possibilitou aos estudantes a apropriação de conhecimentos relativos à organização e à ordenação de objetos do cotidiano ou a representações figurais, considerando os atributos cor, forma e medida; assim como descrever os elementos ausentes em sequências recursivas de números naturais, objetos ou figuras, após o reconhecimento e a explicitação de uma regra padrão.

Nesta Unidade, na perspectiva de ampliar e aprofundar esses conhecimentos, destacam-se atividades que favorecem o desenvolvimento da habilidade de os próprios estudantes descreverem o padrão da sequência recursiva, seja ela numérica, de objetos ou de figuras. Espera-se que tal abordagem contribua para que os estudantes, quando no 3º ano, desenvolvam as habilidades de identificar regularidades em sequências ordenadas de números naturais resultantes da realização de adições ou de subtrações sucessivas, por um mesmo número, de descrever uma regra de formação da sequência e de determinar elementos faltantes ou seguintes.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.

Competências gerais favorecidas

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

Competências específicas favorecidas

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

MP131

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Sugestão de roteiro de aula

Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.

Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas, de acordo com as atividades propostas, e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item 2 vezes ou o dobro, desta Unidade.

Roteiro de aula – 2 vezes ou o dobro

1 ª parte – Introdução – Tempo sugerido: 10 minutos

Espera-se que os estudantes já tenham consolidado o conhecimento trabalhado nos itens anteriores, referente à ideia da multiplicação significando uma adição reiterada, pois aqui temos um objetivo que amplia essa concepção para a ideia de a multiplicação significar também proporcionalidade. Iniciamos com o fator 2, que é bem simples e mais presente no cotidiano dos estudantes dessa faixa escolar. No item seguinte será dado o prosseguimento com o fator 3 ou o triplo.

A proporcionalidade é um conceito matemático essencial e será replicado e ampliado ao longo do Ensino Fundamental.

Antes de abordar a atividade 1, sugerimos uma conversa dialogada com a turma sobre situações usuais em que o dobro se manifesta. Por exemplo, pode-se tratar do corpo humano, questionando: “Quantos dedos temos em uma das mãos? E em duas mãos?”. Ou tratar da grandeza tempo: “Quantos dias há em uma semana? E em duas semanas?”. Ou teatralizar: andar contando quantos passos regulares há de um lado ao outro da lousa e depois fazer o mesmo percurso, com passos iguais, porém, indo e voltando.

Abrindo o diálogo, peça que apresentem outros exemplos e verifique, junto com a turma, a adequação ou não desses exemplos.

2 ª parte – 2 vezes ou o dobro – Tempo sugerido: 40 minutos

Solicite aos estudantes que façam a leitura silenciosa da atividade 1 e que completem o que é pedido. Faça o mesmo com a atividade 2, percorrendo a sala para dirimir possíveis dúvidas. Depois questione: “Na flor dada (item A), quantas folhas há? E quantas folhas você pintou?”; “Ainda na flor dada, quantas pétalas (verifique se entendem o que é pétala) há? E quantas pétalas você pintou?”.

Prossiga orientando a execução individual da atividade 3.

Na atividade 4, faça a leitura coletiva e, após alguns minutos para a resolução, destaque que as expressões “dobro” e “2 vezes” têm o mesmo significado: as sentenças “Valéria tem o dobro da idade de Maria” e “Maria tem a metade da idade de Valéria” são equivalentes, têm o mesmo significado. Por ora, não se espera que os estudantes relacionem metade com divisão por 2, mas este é um primeiro contato com um fato básico da divisão.

Na atividade 5, após a leitura coletiva do enunciado do problema, oriente-os a: identificar e registrar as informações dadas; identificar o que é pedido para calcular; adotar uma estratégia de, a partir das informações, obter o que é pedido.

Por fim, na atividade 6, após a leitura e a resolução, faça uma enquete e exponha na lousa o resultado sobre a estratégia mais usada pela turma.

MP132

UNIDADE 5. Multiplicação

Imagem: Ilustração. Jogo de tabuleiro. À esquerda, na parte superior, um hexágono verde com a letra I. Ao lado, um quadro com um jovem ruivo escovando os dentes (+20). Abaixo há uma menina com cabelo castanho e curto sobre um hexágono amarelo. Em seguida, hexágono amarelo e ao lado, quadro com o jovem ruivo jogando lixo em cestos recicláveis (x3). Abaixo, quatro quadrados amarelos e ao lado do quarto há um quadro com o jovem ruivo jogando uma garrafa dentro de um cesto de lixo, que está pendurado em um poste (x2). À direita, um hexágono amarelo e ao lado, um quadro com uma pessoa dentro de um carro e jogando uma garrafa na rua (-10) (Resposta: Há um X neste hexágono). Acima, um hexágono amarelo e ao lado, quadro do jovem ruivo tomando banho (x3). Em seguida, um menino loiro com boné azul está sobre um hexágono amarelo e depois, mais três hexágonos amarelos. Ao lado do segundo há um quadro com o jovem ruivo segurando uma mangueira e jorrando água na calçada (-10) (Resposta: Há um X neste hexágono). Em seguida, uma menina com cabelo preso está em pé, sobre um hexágono amarelo. Abaixo dela há um hexágono amarelo e ao lado, um quadro com um carrinho feito de garrafa PET. Na garrafa há quatro furos com dois palitos atravessando e quatro tampinhas nas pontas, formando rodinhas (x2). Ao lado, um hexágono verde com a letra F. Ao redor do tabuleiro, Daniel, Amélia, Bizi e outras crianças estão observando e sorrindo (Resposta: Amélia, Daniel e Bizi estão aqui). Fim da imagem.
MANUAL DO PROFESSOR

Objetivos da Unidade

• Compreender situações de multiplicação com a ideia de adição de parcelas iguais.

• Usar estratégias próprias para resolver problemas que envolvem multiplicação.

• Registrar uma multiplicação por meio da sentença matemática usual.

• Resolver problemas envolvendo noções de dobro, metade e triplo.

• Calcular e observar regularidades envolvendo o dobro e o triplo de um número.

• Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

• Reconhecer regularidades em sequências numéricas ou de figuras e descrever elementos ausentes.

• Ler, interpretar e comparar preços anunciados em folhetos de propaganda.

• Classificar resultados de eventos aleatórios.

A Unidade trata de situações que envolvem a multiplicação, explorando a ideia de adição de parcelas iguais em variadas situações, a representação da multiplicação por meio da expressão matemática, bem como a resolução de problemas envolvendo dobro e triplo.

BNCC em foco:

EF02MA07, EF02MA08, EF02MA09, EF02MA10, EF02MA11, EF02MA21

MP133

Para refletir...

Na trilha, o dado indica quanto cada um anda na sua vez.

Imagem: Ícone: Oral. Fim da imagem.

• Quantos pontos tem a menina que acabou de sair da casa I?

PROFESSOR Resposta: 20 pontos.

• Em quais casas os jogadores podem perder pontos? Marque com um X.

Imagem: Ícone: Oral. Fim da imagem.

• O que acontece com a pontuação do menino de boné azul se o dado jogado indicar que ele deve andar duas casas? Por quê?

PROFESSOR Resposta esperada: Perde 10 pontos porque não devemos desperdiçar água potável.
MANUAL DO PROFESSOR

Em uma roda de conversa, deixe que os estudantes exponham suas impressões sobre o que veem na ilustração da abertura desta Unidade, bem como suas hipóteses quanto ao que as pessoas estão fazendo.

Depois dessa exploração inicial, comente que as crianças estão brincando em um jogo de trilha em que os peões são elas mesmas. Explique aos estudantes que as imagens em destaque estão associadas às casas e indicam a pontuação recebida. Se a ação mostrada na imagem é um bom hábito, ganham-se pontos de acordo com a operação indicada; se é um mau hábito, perdem-se pontos. Por exemplo, ao cair na casa cuja imagem mostra uma pessoa jogando papel para fora do carro, que é um hábito ruim, perdem-se 10 pontos (indicado por −10). Se cair na casa cuja imagem mostra o menino jogando papel na lixeira, que é um bom hábito, dobra-se a pontuação (indicado por ×2). Caso os estudantes não reconheçam esse símbolo, explique o que significa e diga que a multiplicação será estudada nesta Unidade.

Para refletir...

Verifique se os estudantes fizeram alguma menção sobre o significado das casas com as letras I e F. Explique a eles que a letra I indica o início da trilha, e a F, o fim da trilha. Peça, então, que digam o que aparece na imagem associada à casa com a letra I e qual é o seu significado. Espera-se que reconheçam um bom hábito (escovar os dentes) e, por isso, os jogadores ganham 10 pontos (indicado por +10).

Aproveite e pergunte aos estudantes como um jogador poderia se tornar o vencedor nesse jogo. Eles podem indicar o que primeiro atingir a casa com a letra F ou o que conseguir mais pontos durante a trilha.

Na segunda questão, espera-se que os estudantes marquem com um X as casas associadas aos maus hábitos, ou seja, as ações que não devem ser praticadas.

MP134

Adição com parcelas iguais

  1. Quantos ossos os três cachorros têm juntos?
Imagem: Ilustração. Três cachorros estão sorrindo. Na frente de cada um há dois ossos. Fim da imagem.

Juntos, os três cachorros têm _____ ossos.

PROFESSOR Resposta: 6
  1. Laura e seus amigos estão brincando com um jogo de cartas em que cada jogador recebe 3 cartas numeradas. Pelo menos quantas cartas serão necessárias, se esse jogo tiver 5 participantes?
Imagem: Ilustração. Cinco pessoas estão sentadas em volta de uma mesa redonda e cada uma está segurando três cartas. Fim da imagem.

Com 5 participantes, serão necessárias, no mínimo, _____ cartas.

PROFESSOR Resposta: 15
  1. Na produção de 1 urso de brinquedo, são usados pedaços de tecido da seguinte maneira: 4 da cor azul, 1 da amarela, 2 da laranja e 2 da verde.
Imagem: Ilustração. Um urso de pelúcia com orelhas verdes, cabeça amarela, braços e pernas azuis e barriga laranja. Fim da imagem.

LEGENDA: Urso de brinquedo FIM DA LEGENDA.

  1. Para produzir 2 ursos de brinquedo, são necessários os seguintes pedaços de tecido: _____ da cor azul, _____ da amarela, _____ da laranja e _____ da verde.
    PROFESSOR Resposta: 8; 2; 4; 4
  1. Para produzir 3 ursos de brinquedo, são necessários os seguintes pedaços de tecido: _____ da cor azul, _____ da amarela, _____ da laranja e _____ da verde.
    PROFESSOR Resposta: 12; 3; 6; 6
MANUAL DO PROFESSOR

Objetivos

• Compreender situações de multiplicação com a ideia de adição de parcelas iguais.

• Usar estratégias próprias para resolver problemas que envolvem multiplicação.

Para que uma situação seja caracterizada como um problema, é necessário que ela proponha desafios a serem solucionados. Quando lhes faltam meios, os estudantes precisam buscar novos recursos para encontrar a solução, o que gera novas aprendizagens. Portanto, mesmo que ainda não conheçam a técnica operatória da multiplicação ou o símbolo que a representa, é importante que busquem novas estratégias, apoiando-se em conhecimentos que já possuem.

As atividades destas páginas iniciam a exploração da multiplicação associada ao conceito de adição de quantidades iguais, uma das ideias relacionadas à multiplicação.

Atividade 1

Explore o problema mudando os dados, de modo que os estudantes não possam utilizar a imagem como recurso para efetuar a contagem. Por exemplo, você pode problematizar da seguinte maneira: “Chegaram outros dois cachorros, cada um deles com dois ossos. Agora, quantos ossos terão todos os cachorros juntos?”.

Observe como eles interagem com a nova situação e deixe que troquem ideias, usem materiais de apoio ou esquemas no papel para chegar à solução. É possível que desenhem, por exemplo, cinco cachorros e dois riscos diante de cada um deles. A obtenção do resultado (10) pode ser feita por meio da contagem direta do número de riscos feitos no papel.

Do ponto de vista cognitivo, o processo que leva a essa formulação aditiva passa pela compreensão do raciocínio multiplicativo relacionado à correspondência um para muitos. A diferença é que o raciocínio aditivo incorpora a relação parte/todo: “O todo é igual à soma das partes”. Já a correspondência um para muitos está relacionada à existência de duas variáveis e de uma relação fixa entre elas. Por exemplo, na atividade 2, as variáveis são as quantidades de cartas e de jogadores, e a relação entre elas é de 3 cartas por jogador. A expressão aritmética equivalente é 3 + 3 + 3 + 3 + 3, mas o percurso cognitivo necessário à compreensão do conceito de multiplicação é a correspondência um para muitos.

BNCC em foco:

EF02MA07; competência geral 2

MP135

  1. Observe os 3 enfeites de porta que Verusca fez para dar às suas amigas. Em cada um dos enfeites, ela colocou 2 passarinhos.
Imagem: Ilustração. À esquerda, dois pássaros estão um de frente para o outro e atrás deles há uma faixa com a informação: BEM-VINDO. No centro, dois pássaros estão um de frente para o outro e atrás deles há uma faixa com o texto: CASA FELIZ. À direita, dois pássaros estão um de frente para o outro e atrás deles há uma faixa com a informação: DOCE LAR. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

  1. Veja na imagem as frutas que Maria vende em sua barraca.
Imagem: Ilustração. Maria, mulher loira com cabelo preso, boné verde e avental branco. Ao seu lado há uma barraca com frutas e placas com as informações: MELANCIA – 15 REAIS CADA; ABACAXI – 5 REAIS CADA; MAÇÃ – 1 REAL CADA; MAMÃO – 2 REAIS CADA; GOIABA – 1 REAL CADA. Fim da imagem.
  1. Pela manhã, Maria vendeu 6 maçãs. Quantos reais ela recebeu pelas maçãs?
  1. Maria recebeu _____ reais pelas maçãs.
    PROFESSOR Resposta: 6
  1. Mais tarde, ela vendeu 2 abacaxis. Quantos reais ela recebeu pelos 2 abacaxis?
  1. Pelos 2 abacaxis, Maria recebeu _____ reais.
    PROFESSOR Resposta: 10
  1. Quantos reais Maria recebeu pelas 8 frutas vendidas?
  1. Maria recebeu _____ reais pelas frutas vendidas.
    PROFESSOR Resposta: 16
MANUAL DO PROFESSOR

Atividade 2

Espera-se que eles entendam que 15 cartas é a menor quantidade possível para esse jogo, pois cada jogador precisa de 3 cartas. No entanto, pode-se ter mais cartas. Observe as estratégias dos estudantes para obter o total e socialize-as para a turma. Explore com os estudantes o significado da expressão “pelo menos”, que equivale à expressão “no mínimo”.

Atividade 3

Nessa atividade, os estudantes podem fazer registros para ajudar nos cálculos. Em cada caso (produção de 2 ursos e produção de 3 ursos), pergunte: “Como você obteve o total de pedaços de tecido da cor azul?”. Observe se fazem a contagem um a um (com auxílio de material manipulável ou de desenhos) ou se já conseguem acrescentar mentalmente 4 à quantidade de tecido azul, como ao recitar a sequência numérica: 4, 8, 12.

Atividade 4

Proponha questionamentos que possam facilitar o cálculo:

• Quantas vezes são colocados os 2 passarinhos? (3 vezes.)

• 3 vezes 2 passarinhos são quantos passarinhos? (6 passarinhos.)

Atividade 5

Pergunte aos estudantes que operações eles usaram na resolução da atividade. Espera-se que grande parte deles tenha usado a adição. Socialize os procedimentos utilizados para que percebam também o uso da multiplicação.

BNCC em foco:

EF02MA07; competência geral 2; competência específica 3

MP136

Situações comuns

  1. João trabalha em uma fábrica de tapetes em 2 períodos: de manhã e à tarde.

    João sempre fabrica 3 tapetes por período.

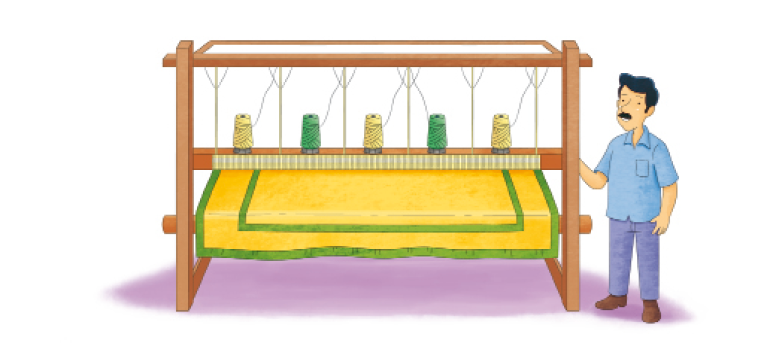
Imagem: Ilustração. João, homem com cabelo preto e bigode está ao lado de uma máquina de tear. Na máquina há três rolos de linha amarela e dois rolos de linha verde. No centro, um tapete amarelo e verde. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Desenhe os tapetes fabricados por João no período da tarde.

Manhã

_____

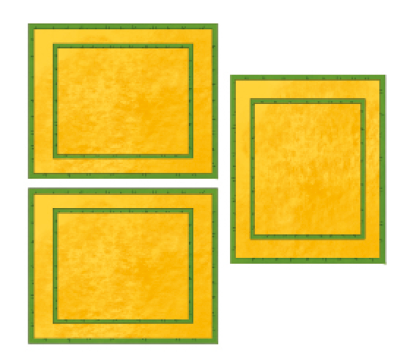
Imagem: Ilustração. Três tapetes amarelos e verdes. Fim da imagem.

Tarde

_____

PROFESSOR Exemplos de desenho: Resposta: Ilustração. Três tapetes.
  1. Quantos tapetes João fabrica em um dia de trabalho? _____
    PROFESSOR Resposta: 6
  1. Quantos tapetes João fabrica em 2 dias de trabalho? _____
    PROFESSOR Resposta: 12
    PROFESSOR Atenção professor: Pode-se sugerir aos estudantes que desenhem os tapetes que João fabrica como estratégia para responder a essas questões. Fim da observação.
  1. Em 3 dias, quantos tapetes João fabrica? _____
    PROFESSOR Resposta: 18
MANUAL DO PROFESSOR

Objetivo

• Usar estratégias próprias para resolver problemas de multiplicação.

Nesses problemas, o desafio é adicionar sucessivamente a mesma quantidade. Trata-se de um dos significados da multiplicação. Os estudantes poderão recorrer a diferentes estratégias, como desenhos, que deverão ser valorizadas e socializadas entre eles.

Nesse momento, ainda não é necessário cobrar dos estudantes que realizem cálculos com o algoritmo usual da multiplicação.

Atividade 1

Para saber quantos tapetes João fabrica em um dia de trabalho, os estudantes podem fazer a contagem direta, com base na imagem, depois de desenharem os tapetes feitos no período da tarde.

Para responder às demais questões, os estudantes também podem desenhar os tapetes que João fabrica, mas espera-se que eles percebam que, conforme aumentam os dias, esse procedimento fica mais trabalhoso e lento. Incentive-os a buscarem novas estratégias. Para simplificar, eles podem fazer risquinhos ou bolinhas em vez dos desenhos dos tapetes; por exemplo, para representar os tapetes feitos por João em dois dias de trabalho podemos fazer:

Imagem: Ilustração. Doze bolinhas azuis lado a lado. Fim da imagem.

ou

Imagem: Ilustração. Quatro grupos com três bolinhas cada. Fim da imagem.

ou

Imagem: Ilustração. Dois grupos com seis risquinhos cada. Fim da imagem.

CRÉDITO: PAULO MANZI

Amplie a atividade 1 e construa uma tabela na lousa para registrar a quantidade de tapetes que João consegue fazer em um dia, em dois dias e em três dias. Depois, questione: “Olhando para a tabela, vocês saberiam me dizer quantos tapetes João consegue fazer em quatro dias?”.

É possível que alguns estudantes percebam a relação observando a tabela, enquanto outros necessitarão fazer a contagem. O importante é organizar os resultados de modo que seja possível estabelecer relações numéricas diretas.

BNCC em foco:

EF02MA07; competência geral 2

MP137

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Observe no quadro a quantidade de frutas que Analice vendeu durante a manhã.
    1. Quantas maçãs Arnaldo comprou?
Imagem: Ilustração. Quadro com a informação: VENDAS DA MANHÃ. ARNALDO COMPROU: Duas caixas com seis maçãs cada. LAURA COMPROU: três caixas com cinco peras cada. JULIANA COMPROU: três caixas com quatro mamões cada. Fim da imagem.

Boxe complementar:

Dica

Faça desenhos para descobrir as respostas das questões a seguir.

Fim do complemento.

Arnaldo comprou _____ maçãs.

PROFESSOR Resposta: 12
  1. Quantas peras Laura comprou?

Laura comprou _____ peras.

PROFESSOR Resposta: 15
  1. Quantos mamões Juliana comprou?

Juliana comprou _____ mamões.

PROFESSOR Resposta: 12

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Observe abaixo as vendas de Analice no período da tarde. Depois, responda à questão.
    • Quantos mamões Analice vendeu à tarde?
Imagem: Ilustração. Quadro com a informação: VENDAS DA TARDE. Em seguida há nove caixas com quatro mamões cada. Fim da imagem.

No período da tarde, Analice vendeu _____ mamões.

PROFESSOR Resposta: 36

Imagem: Ícone: Grupo. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Diga aos colegas e ao professor como você descobriu as respostas das atividades 2 e 3.
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 2

Incentive os estudantes a socializar os registros e os procedimentos. É importante perceber se a ideia na contagem que eles fizeram para chegar à resposta é de uma adição (no item a, 6 + 6; no item b, 5 + 5 + 5) ou de uma multiplicação (no item a, 2 grupos de 6; no item b, 3 grupos de 5). Do mesmo modo, no item c poderão somar 4 + 4 + 4 ou pensar em 3 grupos de 4 mamões.

Atividade 3

Peça aos estudantes que estimem a quantidade total de mamões vendidos. Eles podem fazer o cálculo mentalmente, mas é importante incentivá-los a descreverem o processo que fizeram.

Atividade 4

Aproveite o momento de conversa para incentivar os estudantes a compartilharem as estratégias que usaram.

BNCC em foco:

EF02MA07; competência geral 2

Sugestão de leitura para o professor

Livro

PINTO, Luciane da Silva. A educação matemática e a construção do cálculo na confecção de sapatos: perspectivas socioculturais. Porto Alegre: Premier, [s.d.].

A autora apresenta uma pesquisa realizada com crianças em seu percurso de aprendizagem da Matemática. As reflexões que o livro suscita permitem um novo olhar sobre os encaminhamentos pedagógicos nas aulas de Matemática e o uso do contexto sociocultural dos estudantes, considerando as famílias, as experiências de vida, os conhecimentos e as necessidades deles.

MP138

Registro da multiplicação

  1. Observe abaixo os estudantes de uma turma de capoeira.
Imagem: Ilustração. Seis jovens com roupas brancas. No centro, dois jovens estão dançando e atrás deles, quatro estão batendo palmas ao lado de instrumentos musicais. Fim da imagem.
Imagem: Ilustração. Uma menina com cabelo comprido e roupa branca está apontando para o lado e falando: O símbolo que usamos para indicar uma multiplicação é x. Ao seu lado, lousa com a informação: Multiplicação. 3 vezes 6 é igual a espaço para resposta. 3 x 6 = 18. Fim da imagem.
PROFESSOR Resposta: 18

Em 3 turmas de capoeira com 6 estudantes cada uma, há _____ estudantes.

PROFESSOR Resposta: 18
  1. Observe as jogadoras de uma equipe de basquete e, depois, responda.
Imagem: Ilustração. Cinco meninas com uniforme verde estão sorrindo. Na frente delas há uma bola de basquete e ao fundo, uma cesta. Fim da imagem.

Quantas jogadoras há em:

  1. duas equipes de basquete como esta?

    São 2 equipes de basquete com 5 jogadoras em cada equipe.

    Multiplicação: _____ × _____ = _____

    PROFESSOR Resposta: 2 × 5 = 10

    Há _____ jogadoras em duas equipes de basquete como essa.

    PROFESSOR Resposta: 10
  1. quatro equipes de basquete como essa?

    Multiplicação: _____ × _____ = _____

    PROFESSOR Resposta: 4 × 5 = 20

    Há _____ jogadoras em quatro equipes de basquete como essa.

    PROFESSOR Resposta: 20
MANUAL DO PROFESSOR

Objetivos

• Registrar uma multiplicação por meio da sentença matemática usual.

• Usar estratégias próprias para resolver problemas que envolvem multiplicação.

• Compreender situações de multiplicação com a ideia de adição de parcelas iguais.

Nestas páginas, apresentamos a escrita multiplicativa equivalente à escrita aditiva de parcelas iguais.

Atividade 1

Espera-se que os estudantes compreendam que: a situação “3 turmas com 6 estudantes” equivale a adicionar “6 estudantes com 6 estudantes com 6 estudantes”, ou seja: 3 × 6 = 6 + 6 + 6 = 18.

Disponibilize para os estudantes material manipulável, caso eles sintam necessidade de usá-lo em seus cálculos, ou, ainda, deixe que façam desenhos.

Atividade 2

Amplie a atividade e faça perguntas do tipo:

• “Alguém sabe quantos jogadores participam de um jogo de futebol?” (22 jogadores, 11 em cada equipe.)

• “E de vôlei?” (12 jogadores, 6 em cada equipe.)

• “Se cada equipe de handebol tem 7 jogadores, quantos jogadores há em 4 equipes de handebol?” (28 jogadores, são 4 grupos de 7.)

Sugestão de atividade interdisciplinar

Aproveite a atividade 2 para conversar com os estudantes a respeito da importância da prática de esportes. Pode-se propor um trabalho em conjunto com o professor de Educação Física.

BNCC em foco:

EF02MA07

Sugestão de atividades

Mais problemas

Peça aos estudantes que escrevam duas sentenças matemáticas (aditiva e multiplicativa) para cada problema.

1. Em certa rua há 4 casas. Em cada casa moram 4 crianças. No total, quantas crianças moram nessas 4 casas? (16 crianças; 4 + 4 + 4 + 4 = 16; 4 × 4 = 16)

2. Cada jarra cheia de suco que Marlene costuma fazer enche 4 copos. Se ela fizer 3 dessas jarras de suco, poderá encher no máximo quantos copos de suco?

(12 copos; 4 + 4 + 4 = 12; 3 × 4 = 12)

MP139

  1. Adílson e Flávio querem descobrir quantos carrinhos há na estante.
Imagem: Ilustração. No centro há uma estante com três prateleiras e em cada uma há quatro carros coloridos. À esquerda, Adílson, menino com cabelo castanho fala: Nesta estante há 3 prateleiras. À direita, Flávio, menino com cabelo encaracolado diz: Em cada prateleira, há 4 carrinhos. Fim da imagem.
  1. Ao todo, quantos carrinhos há na estante?

    _____

    PROFESSOR Resposta: 12 carrinhos.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Como você calculou esse total?
    PROFESSOR Resposta pessoal.
  1. Vamos representar o total de carrinhos de duas maneiras. Complete.

    Adição: 4 + 4 + 4 = _____

    PROFESSOR Resposta: 12

    Multiplicação: 3 vezes 4 é igual a _____

    PROFESSOR Resposta: 12

    Multiplicação: 3 × 4 = _____

    PROFESSOR Resposta: 12
  1. Complete as duas maneiras de calcular o total de mangas.
Imagem: Fotografia. Quatro pratos com duas mangas cada. Fim da imagem.

2 + _____ + _____ + _____ = _____

PROFESSOR Resposta: 2 + 2 + 2 + 2 = 8

4 × _____ = _____

PROFESSOR Resposta: 4 × 2 = 8

No total, há _____ mangas

PROFESSOR Resposta: 8
  1. Complete as adições e as multiplicações para calcular o total de pontos dos dados em cada caso.
Imagem: Ilustração. Quatro dados com o número 5 para cima. Fim da imagem.

_____ + _____ + _____ + _____ = _____

PROFESSOR Resposta: 5 + 5 + 5 + 5 = 20

_____ × _____ = _____

PROFESSOR Resposta: 4 × 5 = 20
Imagem: Ilustração. Cinco dados com o número 6 para cima. Fim da imagem.

_____ + _____ + _____ + _____ + _____ = _____

PROFESSOR Resposta: 6 + 6 + 6 + 6 + 6 = 30

_____ × _____ = _____

PROFESSOR Resposta: 5 × 6 = 30
MANUAL DO PROFESSOR

Atividade 3

Primeiro, peça aos estudantes que observem a imagem e respondam:“Quantos carrinhos há ao todo na estante? Como vocês encontraram esse resultado?”. É provável que contem os carrinhos um a um.

É importante chamar a atenção para a quantidade de prateleiras e de carrinhos em cada prateleira. Pode-se perguntar: “Se fossem quatro prateleiras com quatro carrinhos, quantos carrinhos haveria?” (16 carrinhos.); “E se fossem cinco prateleiras?” (20 carrinhos.).

Ressalte as escritas aditiva e multiplicativa.

Atividade 4

Nesta atividade, os estudantes são incentivados a relacionar a situação apresentada na imagem à sua expressão na forma aditiva e na forma multiplicativa.

Faça perguntas que evidenciem a relação entre as variáveis. Pergunte: “Há quantos pratos? Quantas frutas em cada prato? E quantas frutas ao todo?” (Há 4 pratos; há 2 frutas em cada prato; ao todo há 8 frutas.).

É importante que os estudantes sejam incentivados a registrar a resolução por meio das escritas aditiva e multiplicativa. Incentive-os a usar representações, como desenhos ou esquemas, pois talvez disponham de uma estratégia correta que não empregue símbolos ou registros numéricos.

Atividade 5

Comente com os estudantes que a atividade poderá ajudá-los em situações de jogos que utilizem mais de um dado. Além de retomar as escritas aditiva e multiplicativa, os estudantes podem ampliar o repertório para o cálculo mental.

BNCC em foco:

EF02MA07; competência geral 2; competência específica 5

Sugestão de atividade

Calculadora

Usando uma calculadora comum, peça aos estudantes que apertem as teclas: Ilustração. Teclas: 3, x, 4, =.

Em seguida, solicite a eles que observem o resultado obtido (12).

Depois, combine com eles que a tecla Ilustração. Tecla x. está quebrada.

Desse modo, pergunte como é possível obter o mesmo resultado com outra operação. Um exemplo de resposta seria apertar as teclas:

Imagem: Ilustração. Teclas: 4, +, 4, +, 4, =. Fim da imagem.

CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO

MP140

2 vezes ou o dobro

  1. Observe as crianças juntando materiais recicláveis.
Imagem: Ilustração. Paulo, menino loiro aponta para quatro latinhas sobre uma mesa e fala: Eu juntei 4 latinhas de suco. Ao lado, Marina, menina ruiva aponta para oito latinhas sobre uma mesa e diz: Eu juntei o dobro de 4 latinhas. Fim da imagem.

Calcular duas vezes um número é o mesmo que encontrar o dobro desse número.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Desenhe em cada quadro o dobro da quantidade de figuras em cada caso. Depois, responda.

A

Imagem: Ilustração. Uma flor rosa. Fim da imagem.
PROFESSOR Exemplo de desenhos: Ilustração. Duas flores.

B

Imagem: Ilustração. Duas esferas azuis. Fim da imagem.
PROFESSOR Resposta: Ilustração. Quatro esferas.

C

Imagem: Ilustração. Três lápis verdes. Fim da imagem.
PROFESSOR Resposta: Ilustração. Seis lápis.

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

• Registrar uma multiplicação por meio da sentença matemática usual.

• Resolver problemas envolvendo dobro e metade.

Atividade 1

Pergunte aos estudantes se eles sabem o que significa o dobro de uma quantidade e peça que deem alguns exemplos. Espera-se que relacionem a expressão dobro com 2 vezes ou com adicionar um número a ele mesmo.

Atividade 2

Para enriquecer o aprendizado, pode-se ampliar a atividade com a exploração de dobro de uma quantidade, que pode ser obtido juntando-a a uma quantidade igual a ela. Incentive os estudantes a representarem visualmente números obtidos como o dobro de outras quantidades:

Imagem: Ilustração. Duas bolinhas. Fim da imagem.

Dobro de 1

Imagem: Ilustração. Quatro bolinhas. Fim da imagem.

Dobro de 2

Imagem: Ilustração. Seis bolinhas. Fim da imagem.

Dobro de 3

Imagem: Ilustração. Oito bolinhas. Fim da imagem.

Dobro de 4

CRÉDITO: ILUSTRAÇÕES: PAULO MANZI

A relação inversa entre multiplicação e divisão é muito importante do ponto de vista cognitivo, pois está relacionada ao raciocínio multiplicativo, que deve considerar esses dois aspectos mutuamente integrados. Isso pode ser percebido quando observamos o esquema a seguir.

Imagem: Ilustração. Na parte superior, silhueta de três pessoas. Na parte inferior há três papéis embaixo de cada um. Fim da imagem.

CRÉDITO: ADILSON SECCO

BNCC em foco:

EF02MA07, EF02MA08; competências gerais 2 e 7

Sugestão de atividade interdisciplinar

Se julgar oportuno, aproveite a atividade 1 e converse com a turma a respeito da importância da reciclagem, tanto para o meio ambiente como para as pessoas que sobrevivem com o dinheiro recebido com a coleta e a venda dos materiais que serão reciclados.

MP141

  1. Conte as penas das petecas e as bolas dentro das caixas e, depois, complete.
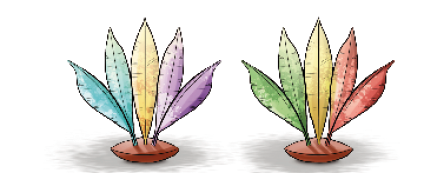
Imagem: Ilustração. Duas petecas coloridas. Fim da imagem.

5 + 5 = _____

PROFESSOR Resposta: 10

_____ × _____ = _____

PROFESSOR Resposta: 2 × 5 = 10

_____ é o dobro de 5.

PROFESSOR Resposta: 10

Há _____ penas nas 2 petecas.

PROFESSOR Resposta: 10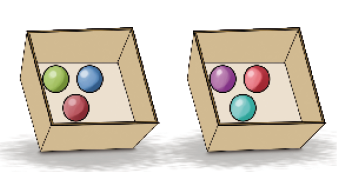
Imagem: Ilustração. Duas caixas e dentro de cada uma há três bolinhas coloridas. Fim da imagem.

_____ + _____ = _____

PROFESSOR Resposta: 3 + 3 = 6

_____ × _____ = _____

PROFESSOR Resposta: 2 × 3 = 6

_____ é o dobro de _____.

PROFESSOR Resposta: 6; 3

Há _____ bolas nas 2 caixas.

PROFESSOR Resposta: 6

Imagem: Ícone: mental. Fim da imagem.

  1. Leia as frases abaixo e marque com um X as corretas.

    Sabendo que Maria tem 7 anos de idade e Valéria tem 14, então:

    ( ) Valéria tem o dobro da idade de Maria.

    ( ) Maria tem o dobro da idade de Valéria.

    ( ) Valéria tem 2 vezes a idade de Maria.

    ( ) Maria tem a metade da idade de Valéria.

    PROFESSOR Respostas corretas:
    PROFESSOR Valéria tem o dobro da idade de Maria.
    PROFESSOR Valéria tem 2 vezes a idade de Maria.
    PROFESSOR Maria tem a metade da idade de Valéria.
Imagem: Ilustração. Uma jovem loira está sorrindo com a mão esquerda na cintura. Ao seu lado, uma menina sorri e olha para cima. Fim da imagem.
  1. Elaine foi à feira com seu primo Pedro e comprou meia dúzia de bananas, enquanto Pedro comprou o dobro dessa quantidade. Quantas bananas, no total, eles compraram?

    _____

    PROFESSOR Exemplos de cálculo:
    PROFESSOR 2 × 6 = 12
    PROFESSOR 6 + 12 = 18

    Eles compraram, no total, _____ bananas.

    PROFESSOR Resposta: 18
  1. Registre como você calcularia o dobro de 13.

    Imagem: Ícone: Dupla. Fim da imagem.

    Imagem: Ícone: Oral. Fim da imagem.

    • Converse com os colegas para descobrir a maneira que vocês acham mais fácil de obter esse resultado.
      PROFESSOR Exemplo de resposta: Fazendo uma multiplicação (2 × 13 = 26) ou uma adição (13 + 13 = 26).
MANUAL DO PROFESSOR

Atividade 3

Nesta atividade são solicitados os resultados de multiplicações do tipo 2 vezes, os quais podem ser obtidos por meio de contagem direta dos elementos das ilustrações, por cálculo mental ou pelo uso da correspondência um para dois.

Aproveite para pedir aos estudantes que calculem o dobro de números entre 5 e 10, de modo que seja possível observar como eles realizam o cálculo sem um recurso visual disponível.

Atividade 4

A atividade explora as diversas maneiras de expressar que uma quantidade é o dobro de outra.

Além disso, a afirmação “Maria tem a metade da idade de Valéria” relaciona as ideias de metade e dobro. Verifique os conhecimentos prévios da noção de metade que os estudantes têm.

Atividade 5

Na atividade, a turma pode verificar de modo exploratório a relação entre “dobro’ e “metade”, pois, ao calcular o dobro de meia dúzia, obtém-se a dúzia inteira, ou seja, o dobro de uma metade é igual ao todo, no caso a dúzia.

Atividade 6

Os estudantes podem apontar como procedimento de cálculo a adição 13 +13 = 26, a utilização de desenhos e contagem dos elementos (por exemplo, desenhar 2 grupos de 13 bolinhas e contar o total de bolinhas), entre outros.

Propicie um momento de conversa entre os estudantes para que eles socializem os métodos de cálculo utilizados e incentive o cálculo mental. O esquema permite duas interpretações:

• Multiplicação: foram distribuídas três folhas de papel para cada pessoa; quantas folhas foram distribuídas ao todo para as três pessoas? (9 folhas.)

• Divisão: nove folhas de papel foram distribuídas igualmente entre três pessoas; quantas folhas cada pessoa recebeu? (3 folhas.)

Essa relação será ampliada na Unidade 7 (Operando com números naturais), quando trataremos das noções de metade e terça parte.

BNCC em foco:

EF02MA07, EF02MA08; competência geral 2

MP142

3 vezes ou o triplo

  1. Observe a cena a seguir e, depois, complete os cálculos.

    Carlos é técnico de aparelhos elétricos.

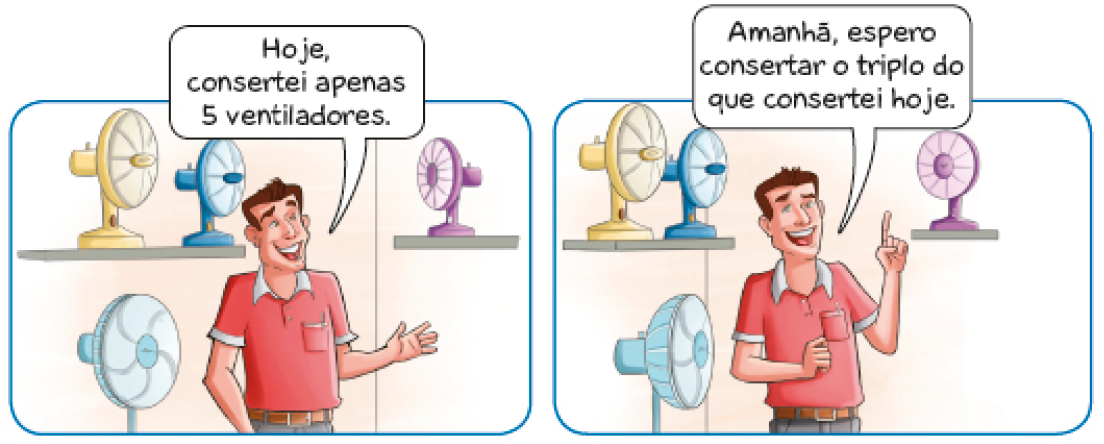
Imagem: Ilustração. À esquerda, Carlos, homem com cabelo castanho-escuro e camiseta vermelha, olha para o lado e fala: Hoje, consertei apenas 5 ventiladores. Atrás dele há cinco ventiladores. À direita, Carlos sorri com o dedo indicador levantado e diz: Amanhã, espero consertar o triplo do que consertei hoje. Fim da imagem.

Calcular três vezes um número é o mesmo que encontrar o triplo desse número.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Pinte o triplo da quantidade indicada em cada caso.

a)

Imagem: Ilustração. Dois lanches. Fim da imagem.
PROFESSOR Exemplos de pintura:

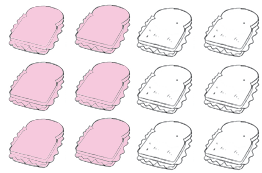
Imagem: Ilustração em preto e branco. Doze lanches. Seis lanches estão pintados de rosa. Fim da imagem.

b)

Imagem: Ilustração. Quatro maçãs. Fim da imagem.
PROFESSOR Resposta:

Imagem: Ilustração em preto e branco. Dezoito maçãs. Doze maçãs estão pintadas de rosa. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

• Registrar uma multiplicação por meio da sentença matemática usual.

• Resolver problemas envolvendo triplo.

Atividade 1

Pergunte aos estudantes se eles sabem o que significa o triplo de uma quantidade e peça que deem alguns exemplos. Comente que calcular o triplo de um número corresponde a calcular 3 vezes esse número ou fazer uma adição de três quantidades iguais a esse número.

Pergunte: “Se Carlos tivesse consertado 7 ventiladores hoje, quantos ventiladores ele pretenderia consertar amanhã?” (21 ventiladores, que é o triplo de 7). Os estudantes podem representar com desenhos a quantidade de ventiladores que Carlos consertou e o triplo dessa quantidade.

Atividade 2

Na atividade, os estudantes precisam observar a imagem para saber quantos sanduíches e quantas maçãs devem pintar para obter o triplo da quantidade de cada um. Espera-se que percebam que devem pintar 3 grupos de 2 sanduíches (6 sanduíches), no item a, e 3 grupos de 4 maçãs (12 maçãs), no item b.

Por que a memorização das listas de multiplicações (tabuadas) não é rápida e fácil? Alguns estudos sugerem que os impulsos nervosos em nossas redes neurais “se confundem” quando há repetição dos mesmos números. É o mesmo processo que ocorre com nossa linguagem. Experimente memorizar as frases abaixo:

• Bruno Carlos é amigo de Daniel Emílio.

• Carlos Daniel é amigo de Emílio Bruno.

• Emílio Carlos é amigo de Daniel Bruno.

Observe que, com apenas três frases combinando os nomes apresentados, temos dificuldade de memorizá-las. Isso também acontece com as listas de multiplicações, que apresentam resultados de multiplicações entre diversos números.

BNCC em foco:

EF02MA07, EF02MA08

MP143

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Veja como podemos calcular o resultado de 3 × 5 com o auxílio de uma calculadora.
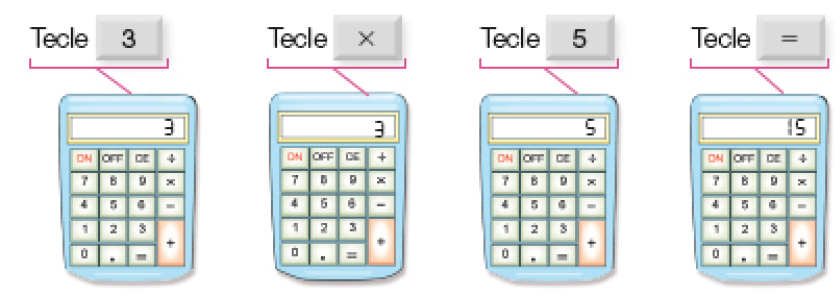
Imagem: Ilustração. Na parte inferior, quatro calculadoras com os números na tela: 3, 3, 5, 15. Na parte superior, as informações em cada uma delas: tecle 3, tecle x, tecle 5, tecle =. Fim da imagem.
  1. Lucas apertou as teclas: Ilustração. Teclas: 3, x, 9, =.

    Que resultado apareceu no visor da calculadora? _____

    PROFESSOR Resposta: 27

    Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Ana multiplicou dois números com a calculadora.

    Uma das teclas apertadas foi Ilustração. Tecla: 3. , e o resultado foi 24.

    Desenhe as teclas que Ana apertou.

    PROFESSOR Exemplos de desenhos:
    PROFESSOR Ilustração. Teclas: 8, x, 3, =. ou Ilustração. Teclas: 3, x, 8, =.

Boxe complementar:

Desafio

Um cachorro pegou 3 sacos com o mesmo número de bolinhas de ração em cada um. Para cada bolinha de ração que comeu, ele deu um latido. Após ter comido todas as bolinhas de ração dos 3 sacos, o cachorro havia dado 27 latidos.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

• Pinte os 3 sacos que o cachorro pegou.

Imagem: Ilustração. Um cachorro está abanando o rabo. Na frente dele há nove sacos com os números: 7, 7, 9, 9, 8, 8, 9, 8, 7. Sacos pintados de rosa: 9, 9, 9. Fim da imagem.

CRÉDITO: DANILO SOUZA

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 3

Se possível, reúna a turma em grupos e distribua algumas calculadoras para realizarem a atividade.

Depois, explore um pouco mais a atividade: peça aos estudantes que façam outras multiplicações usando a calculadora e registrem os resultados.

Pode-se perguntar: “Como você faria para obter o resultado da multiplicação 5 × 7 sem apertar a tecla da multiplicação?”. Um exemplo de resposta seria apertar as teclas:

Imagem: lustração. Teclas: 7, +, 7, +, 7, +, 7, +, 7, =. Fim da imagem.

CRÉDITO: ADILSON SECCO

Desafio

Explique aos estudantes que o número escrito em cada saco indica o número de bolinhas de ração que há dentro dele. Depois da resolução, é interessante perguntar: “Se o cachorro tivesse pegado os 3 sacos com 7 bolinhas de ração cada um, quantos latidos ele teria dado? E se tivesse pegado os 3 sacos com 8 bolinhas de ração cada um?” (21 latidos; 24 latidos).

Observe que as atividades de exploração de dobro e de triplo (assim como seriam as de 4 vezes e de 5 vezes) não representam o que costumamos denominar de “tabuada do 2, do 3, do 4 e do 5”, porque o fator a ser multiplicado não é ele mesmo, mas o número que será transformado. Assim, achar o dobro de 7 é o mesmo que fazer 2 × 7 = 14, que é diferente de fazer 7 × 2. Embora o resultado seja 14, esta última expressão não representa o dobro de 7. Observe que:

2 × 7 = 7 + 7 = 14

7 × 2 = 2 + 2 + 2 + 2 + 2 + 2 + 2 = 14

BNCC em foco:

EF02MA07, EF02MA08; competência geral 2; competência específica 5

MP144

Jogo: Encontre o dobro ou o triplo

Imagem: Ícone: Material complementar. Fim da imagem.

Material: Cartela e dado da página 203 e 20 marcadores (10 para cada jogador), que podem ser feijões, tampinhas ou outros.

Imagem: Ilustração. À esquerda, uma menina loira com cabelo preso está ajoelhada e segurando um dado. À direita, um menino com cabelo preto e curto está ajoelhado e com as mãos sobre as pernas. Entre eles há dois tabuleiros sobre uma mesa. Nos tabuleiros, os números: 2, 3, 4, 6, 8, 9, 10, 12, 15, 18. Ao lado de cada um há feijões. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Jogadores: 2

Regras:

MANUAL DO PROFESSOR

Objetivos

• Calcular e observar regularidades envolvendo o dobro e o triplo de um número.

• Resolver problemas envolvendo dobro e triplo.

Ajude os estudantes na leitura e na compreensão das regras.

O objetivo do jogo é retomar a ideia de dobro e de triplo de um número e permitir que os estudantes, ao jogar, calculem mentalmente os resultados dessas multiplicações.

Os estudantes devem recortar a cartela disponível no Material complementar e colá-la em um papel mais resistente, como cartolina. Auxilie-os nesse processo.

A memorização de resultados de cálculos aritméticos, de modo geral, é um processo longo, que pode ser facilitado por meio do uso de jogos como o proposto aqui. Por sua natureza dinâmica, o jogo permite que a realização dos cálculos ou sua memorização ocorra de modo natural, pois os erros e os acertos se sucedem rapidamente, não deixando marcas negativas, além de manter a atenção dos estudantes na realização de todos os cálculos, os de sua própria jogada e os das jogadas dos colegas, para acompanhamento.

É importante ler as regras e discuti-las com a turma, tirando eventuais dúvidas. Observe as diferentes estratégias de cálculo usadas pelos estudantes e, depois, socialize-as com a classe.

BNCC em foco:

EF02MA07, EF02MA08; competências gerais 2 e 9; competências específicas 7 e 8

MP145

Questões sobre o jogo

Imagem: Ícone: Oral. Fim da imagem.
  1. Um jogador obteve o número 4 no dado e quer cobrir o número 9 em sua cartela. Ele poderá fazer isso? Justifique sua resposta.
    PROFESSOR Resposta: Não, pois o número 9 não é o dobro nem o triplo do número 4.
  1. Observe esta situação do jogo e descubra qual é o número que Renata poderá cobrir em sua cartela.

    _____

    PROFESSOR Resposta: O número 15, que é o triplo de 5, pois o número 10, que é o dobro de 5, já está coberto.
Imagem: Ilustração. A menina loira está sentada e de costas. Na frente dela, o tabuleiro com um feijão sobre o número 10. Ao lado, um dado com o número 5 para cima. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Reúna-se com um colega para responder à Helena e ao Miguel.
Imagem: Ilustração. Helena, menina ruiva com tiara verde está ajoelhada e sorrindo. Ela pergunta: Será que o número 11 poderia estar na cartela? Por quê? Na frente dela, Miguel, menino com cabelo castanho está sentado com as pernas cruzadas. Ele pergunta: Por que o maior número da cartela é o 18? Fim da imagem.
PROFESSOR Resposta: Helena: Não, pois o número 11 não é o dobro nem o triplo de nenhum número do dado.
PROFESSOR Miguel: Porque o maior número possível de obter no dado é o 6, e o triplo de 6 é igual a 18.

Imagem: Ícone: Oral. Fim da imagem.

  1. Um jogador precisa cobrir o número 3 da cartela. Que número ele precisa obter no dado? Por quê?
    PROFESSOR Resposta: O número 1, pois o triplo de 1 é igual a 3.
  1. Há algum número na cartela que é o dobro de um número do dado e, ao mesmo tempo, o triplo de outro número do dado? Se houver, quais são?

    _____

    PROFESSOR Resposta: Sim; são os números 6 e 12.
    PROFESSOR 6 é o dobro de 3 e é o triplo de 2; e 12 é o dobro de 6 e é o triplo de 4.
MANUAL DO PROFESSOR

Questões sobre o jogo

Depois de os estudantes jogarem algumas vezes, proponha que resolvam, individualmente ou em duplas, se julgar oportuno, as questões propostas.

Na questão 1, espera-se que os estudantes percebam que, obtendo o número 4 no dado, não é possível cobrir o número 9, pois 9 não é o dobro nem o triplo de 4. Pode-se perguntar: “Se o jogador tirar o número 6 no dado, quais números da cartela ele poderá cobrir?”. Espera-se que respondam 12 e 18.

Na questão 2, espera-se que os estudantes percebam que a única possibilidade é fazer o triplo de 5 para cobrir o número 15, pois o número 10, que é o dobro de 5, já está coberto.

Na questão 3, peça à turma que dê outros exemplos de números que não poderiam estar na cartela.

Outros exemplos são: 1, 5, 7, 13...

Na questão 4, pergunte: “É possível obter 3 usando o dobro de algum número no dado? Por quê?”.

Espera-se que os estudantes respondam que não, pois não há número no dado cujo dobro seja 3.

Na questão 5, se julgar oportuno, peça aos estudantes que calculem o dobro e o triplo de todos os números do dado.

Variações

Uma variação para o jogo é utilizar dois dados e confeccionar novas cartelas com dobros e triplos de números obtidos pela adição dos pontos obtidos nos dois dados.

BNCC em foco:

EF02MA08; competências gerais 2 e 9; competências específicas 7 e 8

MP146

Completando sequências

  1. Complete as sequências e, depois, descubra multiplicações cujos resultados sejam os números da sequência.
    1. 2, 4, 6, 8, _____, _____, _____, _____, _____, _____
      PROFESSOR Resposta: 10, 12, 14, 16, 18, 20

      2 × 1; 2 × 2; 2 × 3; 2 × 4; _____

      PROFESSOR Resposta: 2 × 5

      _____, _____, _____, _____, _____

      PROFESSOR Resposta: 2 × 6; 2 × 7; 2 × 8; 2 × 9; 2 × 10.
    1. 3, 6, 9, _____, _____, _____, _____, _____, _____, _____
      PROFESSOR Resposta: 12, 15, 18, 21, 24, 27, 30

      3 × 1; 3 × 2; 3 × 3; _____; _____

      PROFESSOR Resposta: 3 × 4; 3 × 5

      _____, _____, _____, _____, _____

      PROFESSOR Resposta: 3 × 6; 3 × 7; 3 × 8; 3 × 9; 3 × 10.
  1. Agora é a sua vez de construir uma sequência e registrar multiplicações cujos resultados sejam os números da sequência.

    _____, _____, _____, _____, _____, _____, _____, _____, _____, _____

    ×, ×, _____, _____, _____

    _____, _____, _____, _____, _____

    PROFESSOR Resposta pessoal.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Estes cinco quadros devem formar uma sequência. Pinte os quadradinhos de acordo com o padrão da sequência.
PROFESSOR Exemplo de pintura:
Imagem: Ilustração. Cinco quadros e cada um há cinco colunas e cinco fileiras. No primeiro quadro, o quadradinho da coluna um e fileira um está pintado de preto. No segundo quadro, os quadradinhos da coluna um e fileira um e coluna dois, fileira dois estão pintados de preto. Em seguida, os quadros estão em branco. Resposta: No terceiro quadro há três quadradinhos pintados de rosa (coluna um, fileira um; coluna dois, fileira dois; coluna três, fileira três). No quarto quadro há quatro quadradinhos pintados de rosa (coluna um, fileira um; coluna dois, fileira dois; coluna três, fileira três; coluna quatro, fileira quatro). E no quinto quadro, cinco quadradinhos pintados de rosa, formando uma linha diagonal (coluna um, fileira um; coluna dois, fileira dois; coluna três, fileira três; coluna quatro, fileira quatro; coluna cinco, fileira cinco). Fim da imagem.
MANUAL DO PROFESSOR

Objetivos

• Construir e completar sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.

• Reconhecer regularidades em sequências numéricas ou de figuras e descrever elementos ausentes.

Atividade 1

Essas duas atividades exploram a observação e a criação de padrões em sequências numéricas associados à multiplicação.

Antes de os estudantes fazerem os registros no livro, em uma roda de conversa, proponha a primeira sequência na lousa. Peça aos estudantes que conversem sobre como ela é formada.

Espera-se que eles percebam que os números aumentam de 2 em 2 unidades. Em seguida, chame alguns estudantes para que completem os próximos seis números dessa sequência (cada estudante escreve um número seguindo o padrão), e valide as respostas com toda a classe.

Comente que nesse tipo de sequência, que vai do número menor para o maior, os números estão em ordem crescente.

Proceda do mesmo modo com a segunda sequência. Nesse caso, espera-se que os estudantes percebam que os números aumentam de 3 em 3 unidades.

Atividade 2

Peça que observem novamente cada uma das sequências da atividade 1 e incentive-os a perceberem que a primeira é formada pelo dobro dos números de 1 a 10 e a segunda, pelo triplo desses mesmos números. Então, oriente-os a escreverem multiplicações cujos resultados sejam os números da sequência, pensando no dobro e no triplo.

BNCC em foco:

EF02MA09, EF02MA10, EF02MA11; competências específicas 1 e 3

MP147

  1. 4. Observe os cálculos indicados nos quadrinhos a seguir.

    1 × 10

    2 × 10

    3 × 10

    4 × 10

    5 × 10

    1 × 1

    2 × 1

    3 × 1

    4 × 1

    5 × 1

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Pinte no quadro abaixo apenas os números que correspondem aos resultados desses cálculos.

    Tabela: equivalente textual a seguir.

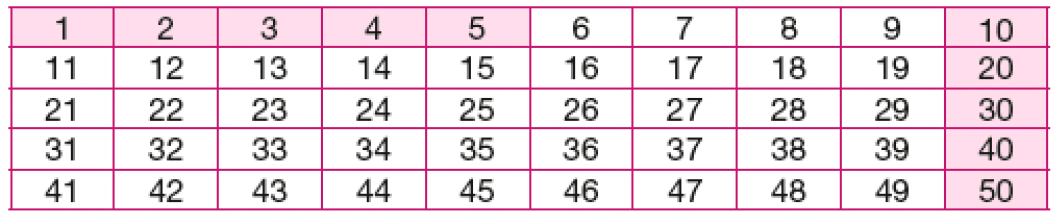
Imagem: Quadro com 5 linhas e 10 colunas. Cada quadradinho tem um número que vai de 1 a 50. Estão pintados de rosa os seguintes números: 1, 2, 3, 4, 5, 10 20, 30, 40, 50. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Converse com seus colegas sobre o que vocês podem observar em relação aos números que foram pintados.
    PROFESSOR Resposta pessoal.
  1. Observe as casas ilustradas abaixo.
Imagem: Ilustração. Casas coloridas lado a lado com números. Da esquerda para direita: casa roxa (25), casa verde (23), casa azul (31), casa amarela (29) e casa laranja (27). Fim da imagem.
  1. Na ordem em que estão apresentados, os números dessas casas formam uma sequência que segue algum padrão? Caso sigam, qual?

    _____

    PROFESSOR Resposta: Não seguem padrão.
  1. Escreva os números dessas casas em ordem crescente.

    _____

    PROFESSOR Resposta: 23, 25, 27, 29 e 31.
  1. A sequência formada por esses números em ordem crescente possui algum padrão? Se possuir, escreva qual.

    _____

    PROFESSOR Exemplo de resposta: Aumenta de 2 em 2.
  1. Observe a sequência com a representação de figuras geométricas planas.
Imagem: Ilustração. Figuras geométricas laranja: triângulo, losango, pentágono e hexágono. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 3

Trabalhos com padrões geométricos são mais motivadores e ampliam a habilidade de percepção de regularidades. Na sequência de figuras apresentada, os estudantes podem observar outro padrão e pintar de maneira diferente daquela apresentada como sugestão de resposta. Nesse caso, peça a eles que descrevam como pensaram. Caso faça sentido, aceite a resposta dada. Socialize todas as maneiras que aparecerem.

Atividade 4

Organize a turma em pequenos grupos e deixe que troquem ideias sobre que quadrinhos pintar, incentivando-os a justificar suas opiniões. Proponha a cada grupo que escreva uma conclusão. Em seguida, peça a um representante de cada grupo que exponha o que o grupo pensou. Os demais estudantes, sob sua orientação, devem comentar a conclusão de cada grupo.

Atividade 5

Amplie a atividade e proponha uma pesquisa com os estudantes e seus familiares para que indiquem:

• o número da casa em que moram;

• o número das casas vizinhas.

Em seguida, peça que respondam se os números das casas da rua onde moram seguem algum padrão.

Atividade 6

Explore as figuras com os estudantes e socialize as respostas, validando-as com eles. Para ampliar, pode-se pedir que criem outra sequência com figuras planas. Lembre-os de que, para criar uma sequência, precisam pensar no padrão de formação dela.

Sugestão de leitura para o estudante

Livro

ROCHA, Ruth. Almanaque Ruth Rocha. São Paulo: Editora Salamandra, 2011.

Esse almanaque contém histórias, brincadeiras, charadas, provérbios, adivinhas, piadas, entre outros, para a diversão. Um livro para ler durante o ano inteiro!

BNCC em foco:

EF02MA10; competência específica 3

MP148

A Matemática me ajuda a ser

... um consumidor atento

Observe o folheto com as ofertas de um supermercado.

Imagem: Ilustração. Folheto com a informação: SUPERMERCADO. LEVE MAIS POR MENOS. Em seguida, uma embalagem de balas com 10 unidades – BALAS 3 REAIS. Ao lado, embalagem de balas com 40 unidades – EMBALAGEM ECONÔMICA 10 REAIS. Abaixo, uma embalagem de chocolates com 100g – CHOCOLATE 2 REAIS. Ao lado, embalagem de chocolate com 12 tabletes – EMBALAGEM ECONÔMICA COM 12 TABLETES 26 REAIS. Fim da imagem.

As pessoas que moram com você costumam comprar produtos em oferta ou em embalagens econômicas?

Imagem: Fotografia. Uma mulher com cabelo preso, óculos e regata preta está sentada com a mão direita virada para cima. Ela fala: Propaganda enganosa é crime! O anúncio enganador é aquele que conduz o consumidor ao erro, garantindo algo que, de fato, não vai acontecer. Fim da imagem.

É preciso estar sempre atento! Há ofertas e embalagens econômicas que não são realmente vantajosas para o consumidor.

MANUAL DO PROFESSOR

Objetivos

• Usar estratégias próprias para resolver problemas que envolvem multiplicação.

• Ler, interpretar e comparar preços anunciados em folhetos de propaganda.

Tome nota

Atividades 1, 2 e 3

Espera-se que os estudantes percebam que a oferta de chocolate não é vantajosa, já que 12 tabletes vendidos separadamente custam menos que uma embalagem (caixa) com 12, supostamente mais vantajosa.

Observe as estratégias utilizadas pelos estudantes para responder às questões. Espera-se que eles percebam que precisam obter o quanto pagariam comprando a mesma quantidade da embalagem maior usando o preço da unidade ou da embalagem menor. No caso do chocolate, por exemplo, os estudantes precisam calcular o preço total de 12 tabletes de chocolate (quantidade correspondente a uma caixa), sabendo que 1 tablete custa 2 reais, ou seja, eles precisam saber que quantia é formada com 12 grupos de 2 reais.

Para calcular 12 × 2, os estudantes podem usar estratégias próprias, com base em imagens, cálculo mental ou uso de material manipulável para contagem. Disponibilize cédulas de 2 reais ou moedas de 1 real de dinheiro produzido previamente para que utilizem, se necessário. Desse modo, os estudantes podem concluir que, no caso do tablete de chocolate, é mais vantajoso comprar 12 unidades individuais em vez da embalagem com 12.

Converse com os estudantes sobre o consumo desnecessário. Não é porque há uma oferta, mesmo que realmente vantajosa, que precisamos comprar o produto.

É preciso avaliar a real necessidade que temos desse produto e se, naquele momento, devemos “empatar” uma quantia maior de dinheiro; por exemplo, será que necessitamos comprar 12 tabletes de chocolate de uma única vez? Um ou dois tabletes podem perfeitamente satisfazer a vontade de comer chocolate por alguns dias, pois não devemos comer tudo de uma vez.

Além disso, muitas ofertas são feitas por causa da validade dos produtos; dessa forma, é necessário avaliar se vamos consumir todo o produto antes da data de vencimento.

BNCC em foco:

EF02MA07; competência geral 7; competências específicas 2, 3, 4 e 7

MP149

Tome nota

Imagem: Ícone: Oral. Fim da imagem.
  1. Você acha que as duas ofertas do folheto são vantajosas?
    PROFESSOR Resposta pessoal.
  1. É mais vantajoso comprar a embalagem econômica com 12 tabletes de chocolate ou comprar 12 tabletes separadamente? Explique.

    _____

    PROFESSOR Resposta: 12 tabletes separadamente, com preço de 24 reais, menor do que 26 reais.
  1. Se comprar a embalagem econômica de balas, você vai economizar? Explique.

    _____

    PROFESSOR Resposta: Sim, pois cada pacote com 10 balas custa 3 reais, e 4 desses custariam 12 reais.
  1. A propaganda “LEVE MAIS POR MENOS” do folheto é verdadeira?

    _____

    PROFESSOR Resposta: No caso da embalagem econômica de chocolate, não é verdadeira.

Reflita

  1. Quais deveriam ser os preços das embalagens econômicas do folheto para que o consumidor realmente tivesse vantagem?

    _____

    PROFESSOR Exemplo de resposta: Balas: preço menor que 12 reais; chocolate: preço menor que 24 reais.

Imagem: Ícone: Oral. Fim da imagem.

  1. Marque com um X as ofertas vantajosas.
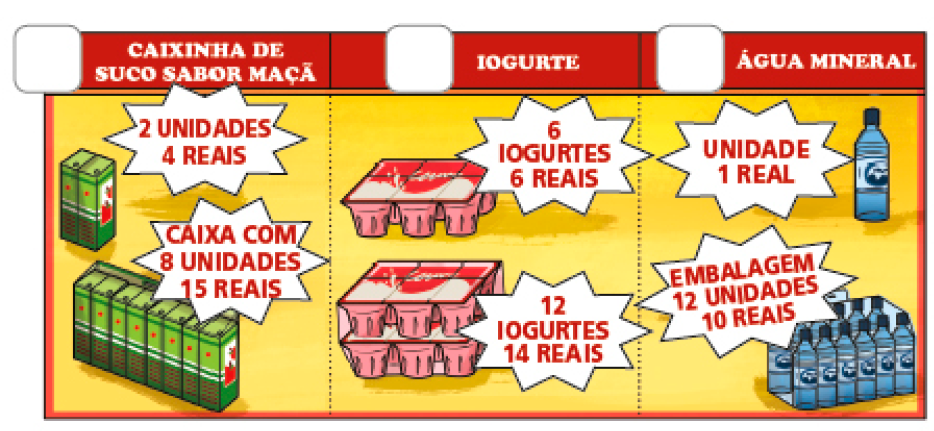
Imagem: Ilustração. Três ofertas. 1) CAIXINHA DE SUCO SABOR MAÇÃ. Duas caixinhas de suco - 2 UNIDADES 4 REAIS. Oito caixinhas de suco - CAIXA COM 8 UNIDADES 15 REAIS. 2) IOGURTE. Embalagem com seis unidades – 6 IOGURTES 6 REAIS. Duas embalagens com seis unidades – 12 IOGURTES 14 REAIS. 3) ÁGUA MINERAL. Uma garrafa – UNIDADE 1 REAL. Embalagem com doze garrafas – EMBALAGEM 12 UNIDADES 10 REAIS. Fim da imagem.
PROFESSOR Resposta: caixinha de suco sabor maçã e água mineral.
MANUAL DO PROFESSOR

Atividade 4

Espera-se que os estudantes percebam que essa propaganda é enganosa, pois, no caso do chocolate, a embalagem com 12 custa mais do que 12 tabletes vendidos separadamente.

Reflita

Atividade 1

Espera-se que os estudantes respondam que a embalagem econômica de biscoito deveria custar qualquer preço menor que 12 reais e a embalagem econômica de chocolate deveria custar qualquer preço menor que 24 reais. Para chegar a essa conclusão, os estudantes podem lançar mão de uma multiplicação ou da adição de parcelas iguais.

Atividade 2

Pergunte aos estudantes: “Na atividade 2, para que todas as ofertas sejam realmente vantajosas, quanto deveriam custar, no máximo?”. Espera-se que os estudantes respondam que a caixa com 8 unidades de suco sabor maçã deveria custar menos de 16 reais; a bandeja de 12 iogurtes, menos de 12 reais; e a embalagem com 12 unidades de água mineral, menos de 12 reais. A “oferta” de iogurtes, portanto, não é vantajosa.

BNCC em foco:

EF02MA07; competência geral 7; competências específicas 2, 3, 4 e 7

MP150

Compreender informações

Classificar e analisar situações prováveis ou impossíveis

  1. Tábata gosta de brincar com dados. Hoje ela resolveu observar o total obtido ao adicionar os números das partes que ficam voltadas para cima no lançamento de dois dados comuns: um branco e um verde.
Imagem: Fotografia. Um dado verde com o número 4 para cima. Ao lado, um dado branco com o número 5 para cima. Fim da imagem.
  1. Tábata obteve 11 em dois lançamentos dos dois dados. Veja:
Imagem: Fotografia. Um dado verde com o número 6 para cima. Ao lado, um dado branco com o número 5 para cima. À direita, fotografia. Um dado verde com o número 5 para cima. Ao lado, um dado branco com o número 6 para cima. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Que total Tábata obteve na situação mostrada acima? _____
    PROFESSOR Resposta: 5

    Imagem: Ícone: Desenho ou pintura. Fim da imagem.

    • Desenhe todas as maneiras de obter esse total no lançamento de um dado branco e outro verde.
      PROFESSOR Resposta: O estudante deve desenhar os seguintes pares de faces (sendo uma verde e outra branca, nessa ordem): 1 e 4; 4 e 1; 2 e 3; 3 e 2.

Imagem: Ícone: Oral. Fim da imagem.

  1. É pouco provável ou muito provável Tábata obter total 12 em um desses lançamentos? Por quê?
    PROFESSOR Resposta: Pouco provável, porque há apenas uma possibilidade de isso ocorrer: saírem 6 pontos nos dois dados.

    Imagem: Ícone: mental. Fim da imagem.

  1. Tábata ficou pensando em todas as possibilidades de obter total 7 em um lançamento desses dois dados. Marque com um X para responder. Obter total 7 é:

    ( ) impossível.

    ( ) pouco provável.

    ( ) muito provável.

    PROFESSOR Resposta correta: muito provável
MANUAL DO PROFESSOR

Objetivo

• Classificar resultados de eventos aleatórios.

As atividades ampliam a exploração de situações que envolvem a noção de aleatório (acaso), para que os estudantes classifiquem os resultados em pouco prováveis, muito prováveis, improváveis e impossíveis.

Atividade 1

Providencie dois dados grandes, se possível com cores diferentes, com pontinhos nas faces, e mostre cada uma das faces de um deles para os estudantes identificarem. Lance os dados algumas vezes e pergunte que face ficou voltada para cima em cada dado.

Em uma roda de conversa, peça que listem todos os totais possíveis de se obter ao adicionar os pontos de cada face que fica voltada para cima, em cada lançamento, e todas as maneiras possíveis de compor esses totais com os dois dados (verde e branco). Registre na lousa esses resultados para que os estudantes possam consultá-los ao realizar a atividade. Chame a atenção para a quantidade de possibilidades de cada resultado.

Espera-se que identifiquem essas somas, considerando dado verde e dado branco, respectivamente:

• soma 2 → 1 e 1 (uma única possibilidade)

• soma 3 → 1 e 2; 2 e 1 (2 possibilidades)

• soma 4 → 1 e 3; 3 e 1; 2 e 2 (3 possibilidades)

• soma 5 → 1 e 4; 4 e 1; 2 e 3; 3 e 2 (4 possibilidades)

• soma 6 → 1 e 5; 5 e 1; 2 e 4; 4 e 2; 3 e 3 (5 possibilidades)

• soma 7 → 1 e 6; 6 e 1; 2 e 5; 5 e 2; 3 e 4; 4 e 3 (6 possibilidades)

• soma 8 → 2 e 6; 6 e 2; 3 e 5; 5 e 3; 4 e 4 (5 possibilidades)

• soma 9 → 3 e 6; 6 e 3; 4 e 5; 5 e 4 (4 possibilidades)

• soma 10 → 4 e 6; 6 e 4; 5 e 5 (3 possibilidades)

• soma 11 → 5 e 6; 6 e 5 (2 possibilidades)

• soma 12 → 6 e 6 (uma única possibilidade)

Proponha aos estudantes que formem duplas para responder às questões do livro. Pergunte algumas somas impossíveis: “Como posso obter total 1?”. Espera-se que os estudantes percebam que não é possível saírem faces cujos pontos adicionados totalizem 1.

BNCC em foco:

EF02MA21; competências específicas 3 e 4

MP151

  1. Carla tem 2 gizes de cera verdes, o triplo dessa quantidade de gizes na cor azul e o dobro da quantidade de gizes azuis na cor vermelha.
Imagem: Fotografia. Um giz de cera azul e um giz verde. Fim da imagem.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Desenhe com Ilustração. Lápis azul. os gizes de cera azuis e com Ilustração. Lápis vermelho.os gizes de cera vermelhos de Carla.

    _____

    PROFESSOR Atenção professor: Espera-se que o estudante desenhe 6 gizes de cera azuis e 12 gizes de cera vermelhos. Fim da observação.
  1. Carla colocou todos esses gizes em uma sacola e sorteou um deles.
    • Que cor de giz é muito provável de ser sorteada? _____
      PROFESSOR Resposta: Vermelha
    • Sortear um giz cor de laranja é impossível ou improvável? _____
      PROFESSOR Resposta: Impossível.

      Imagem: Ícone: Oral. Fim da imagem.

    • O que se deve fazer para ser possível sortear um giz de cera amarelo?
      PROFESSOR Atenção professor: Espera-se que o estudante perceba que precisam ser colocados na sacola gizes amarelos. Fim da observação.
    1. Um jogo tem 52 cartas: 13 vermelhas, 13 verdes, 13 amarelas e 13 azuis. As cartas de cada cor são numeradas de 1 a 13.
      • Agora, responda:
      1. Quantas cartas verdes com o número 7 há nesse jogo? _____
        PROFESSOR Resposta: 1 carta.
      1. Quantas cartas com o número 7 há ao todo? _____
        PROFESSOR Resposta: 4 cartas.
      1. Retirando uma carta qualquer desse jogo (sem olhar), é impossível sair uma carta com o número 7?

        _____

        PROFESSOR Resposta: Não. É possível sair uma carta com o número 7.
      1. Sair uma carta verde com o número 7 é pouco provável ou muito provável? E sair uma carta numerada de 1 a 10?

        _____

        PROFESSOR Resposta: Pouco provável; muito provável.

        Imagem: Ícone: Dupla. Fim da imagem.

      1. Troque ideias com um colega sobre como vocês pensaram para responder às questões desta atividade.
        PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 2

Explique a situação proposta e retome as noções de dobro e triplo, fazendo questionamentos acerca dessa situação:

• Quantos gizes verdes Carla tem? (2 gizes.)

• Quantos gizes azuis ela tem? (Espera-se que os estudantes obtenham o triplo de 2 e respondam 6 gizes.)

• Quantos gizes vermelhos Carla tem? (Espera-se que os estudantes obtenham o dobro de 6 e respondam 12 gizes.)

• Quantos gizes Carla colocou na sacola? (Espera-se que os estudantes percebam que devem calcular o total de gizes que Carla tem, 2 + 6 + 12 = 20.)

• Que cores de gizes há na sacola? (Verde, azul e vermelha.)

• Sorteando um giz da sacola, de que cor pode sair? (Verde, azul ou vermelha.)

Se julgar necessário, peça aos estudantes que desenhem os gizes de cada cor para que possam contá-los.

Ressalte para os estudantes a quantidade de cada cor de giz em relação ao total:

• Há 2 gizes verdes em 20.

• Há 6 gizes azuis em 20.

• Há 12 gizes vermelhos em 20.

Proponha as questões do livro e discuta, oralmente, com os estudantes as respostas, validando-as com eles.

Atividade 3

Amplie os questionamentos sobre quantidades de cartas:

• “Quantas cartas com o número 1 há nesse jogo de 52 cartas? Quais são elas?” (4 cartas; 1 vermelha, 1 verde, 1 amarela e 1 azul.)

• “Quantas cartas com números maiores que 10?” (12 cartas.)

Proponha as questões do livro aos estudantes para que respondam oralmente.

Incentive-os a justificarem as respostas. Depois, peça que registrem no livro. Caminhe entre os estudantes e verifique se ainda há alguém com alguma dificuldade e retome o que julgar necessário.

BNCC em foco:

EF02MA08, EF02MA21

MP152

O que você aprendeu

Avaliação processual

  1. Calcule o número de livros das três prateleiras.
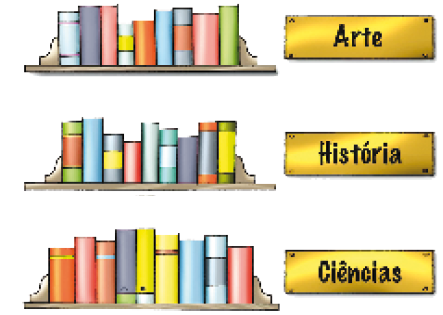
Imagem: Ilustração. Três prateleiras com nove livros cada. Ao lado, placas com as informações: Arte, História e Ciências. Fim da imagem.

9 + _____ + _____ = _____

PROFESSOR Resposta: 9 + 9 + 9 = 27

_____ × _____ = _____

PROFESSOR Resposta: 3 × 9 = 27

Há _____ livros nas prateleiras.

PROFESSOR Resposta: 27
  1. Complete o quadro de multiplicações.

Quadro: equivalente textual a seguir.

Imagem: Ilustração. Sinal de multiplicação. Fim da imagem.

1

2

3

4

5

6

7

8

9

10

1

1

2

_____

_____

_____

_____

_____

_____

9

_____

2

_____

_____

_____

_____

10

_____

_____

_____

_____

_____

3

_____

6

_____

12

_____

_____

_____

24

_____

_____

4

_____

_____

_____

_____

_____

_____

_____

_____

_____

_____

5

_____

10

_____

_____

_____

_____

_____

_____

45

_____

PROFESSOR Resposta: 3, 4, 5, 6, 7, 8, 10
PROFESSOR 2, 4, 6 ,8, 12, 14, 16, 18, 20
PROFESSOR 3, 9, 15, 18, 21, 27, 30
PROFESSOR 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
PROFESSOR 5, 15, 20, 25, 30, 35, 40, 50

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Fotografia. Quatro pães. Fim da imagem.
  1. Com 1 pacote de farinha de trigo, Adelson faz 4 pães. Na próxima semana, ele fará 12 desses pães para a família.
    • De quantos desses pacotes de farinha de trigo Adelson precisará para fazer os pães?

      _____

      PROFESSOR Resposta: Adelson precisará de 3 desses pacotes de farinha de trigo.
MANUAL DO PROFESSOR

Objetivo

• Retomar os conceitos estudados.

A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.

Atividade 1

A atividade retoma o registro da escrita aditiva e da escrita multiplicativa, explorando a ideia de adição de parcelas iguais associada à multiplicação.

Atividade 2

Os estudantes devem completar o quadro com os resultados das multiplicações e observar regularidades.

Eles podem perceber que, na primeira fileira (horizontal ou vertical), os números aumentam de 1 em 1 unidade; na segunda fileira (horizontal ou vertical), de 2 em 2 unidades; na terceira fileira (horizontal ou vertical), de 3 em 3 unidades; na quarta fileira (horizontal ou vertical), de 4 em 4 unidades etc.

Os estudantes também podem explorar regularidades ao comparar a fileira (horizontal ou vertical) do 2 com a do 4, do 3 com a do 6, do 5 com a do 10, entre outras em que há a relação de dobro. Relações de triplo, metade e outras identificadas pelos estudantes também podem ser levantadas e discutidas.

Sempre que necessário, incentive-os a consultar esse quadro de multiplicações.

Atividade 3

Peça aos estudantes que comparem seus cálculos e discuta as diferentes estratégias usadas.

Uma estratégia é desenhar 3 agrupamentos de 4 pães para identificar a necessidade de 3 pacotes de farinha de trigo.

BNCC em foco:

EF02MA07, EF02MA10

Sugestão de atividade

Quadro do dobro ou 2 vezes

Prepare quadros como estes e proponha aos estudantes que os preencham. Depois, reúna-os em duplas para compararem os resultados e discutirem as estratégias usadas.

Quadro: equivalente textual a seguir.

Número

Dobro ou 2 vezes

1

2 (2 × 1 = 2)

2

4 (2 × 2 = 4)

3

6 (2 × 3 = 6)

4

8 (2 × 4 = 8)

5

10 (2 × 5 = 10)

6

12 (2 × 6 = 12)

7

14 (2 × 7 = 14)

8

16 (2 × 8 = 16)

9

18 (2 × 9 = 18)

10

20 (2 × 10 = 20)

MP153

  1. Resolva os problemas a seguir.
    1. Ana foi à padaria e comprou 3 sorvetes, como o da imagem abaixo.

      Imagem: Fotografia. Placa com a informação: Picolé 3 reais cada. Ao lado, foto de três picolés vermelhos. Fim da imagem.

      Quantos reais ela gastou?

      _____ × _____ = _____

      PROFESSOR Resposta: 3 × 3 = 9

      Ana gastou _____ reais.

      PROFESSOR Resposta: 9
    1. Cristina comprou um bolo como este abaixo e gastou o triplo do que Ana gastou com os sorvetes. Quantos reais Cristina gastou?

      Imagem: Fotografia. Bolo de chocolate com raspas de chocolate em cima. Fim da imagem.

      _____ × _____ = _____

      PROFESSOR Resposta: 3 × 9 = 27

      Cristina gastou _____ reais.

      PROFESSOR Resposta: 27

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Pedro estava utilizando uma calculadora para fazer multiplicações. Ele apertou a tecla Ilustração. Tecla 7. , depois a tecla Ilustração. Tecla x. e se esqueceu da tecla que apertou em seguida. Mas, quando apertou a tecla Ilustração. Tecla =. , o resultado da multiplicação foi 21. Qual foi a tecla que Pedro apertou e de que não se lembra? _____
    PROFESSOR Resposta: 3
  1. Calcule os resultados para formar uma sequência numérica.

    1 × 6; 2 × 6; 3 × 6; 4 × 6; 5 × 6

    _____, _____, _____, _____, _____

    PROFESSOR Resposta: 6, 12, 18, 24, 30

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 4

Peça aos estudantes que façam desenhos ou esquemas que evidenciem a correspondência “um sorvete pelo preço de 3 reais”. Eles podem trabalhar com a representação do valor 3 reais desenhando 3 moedas de 1 real (ou 1 cédula de 2 reais e 1 moeda de 1 real) para cada sorvete comprado.

Verifique, no item b, como procedem para determinar o triplo da quantia que Ana gastou com os sorvetes, socializando e validando com os estudantes.

Atividade 5

Espera-se que os estudantes percebam a seguinte situação: 7 vezes “certo número” resulta 21. Pergunte: “Como Pedro pode pensar para descobrir o número esquecido?”. Uma possível maneira é: “7 vezes que número resulta 21?”. Os estudantes podem fazer desenhos para indicar as possibilidades ou registrá-las em um quadro, como segue. Assim, eles podem concluir que o número que Pedro apertou e esqueceu é o 3.

Tabela: equivalente textual a seguir.

7 × 1 = 7

7 é diferente de 21

7 × 2 = 14

14 é diferente de 21

7 × 3 = 21

21 é igual a 21

Atividade 6

Observe como os estudantes procedem para obter os resultados dessas multiplicações.

Autoavaliação

Na primeira questão, incentive os estudantes a exemplificarem os problemas que, segundo eles, envolvem multiplicações. Alguns podem relatar que resolvem a mesma situação realizando adições. Nesse caso, é importante destacar que as adições de parcelas iguais estão relacionadas ao campo multiplicativo.

Na segunda questão, o foco está no sinal de multiplicação e na escrita de sentenças matemáticas. Vale destacar a importância da escrita matemática quando nos referimos às diferenças entre 3 × 2 e 2 × 3, por exemplo. Essas duas multiplicações têm o mesmo resultado, mas podem não refletir a mesma situação.

Alguns estudantes podem ter dificuldade no reconhecimento da escrita matemática, e outros, em representar situações por meio dela.

BNCC em foco:

EF02MA07, EF02MA08, EF02MA11

MP154

Comentários para o professor:

Conclusão da Unidade 5

Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Compreende e emprega, por meio de estratégias e formas de registro pessoais, a ideia da multiplicação enquanto adição de parcelas iguais?

_____

_____

Identifica o que é informado e o que é pedido no enunciado de um problema?

_____

_____

Resolve problemas que envolvem dobro, metade e triplo, com o suporte de imagens ou material manipulável, utilizando estratégias pessoais?

_____

_____

Reconhece e constrói sequências numéricas crescentes e decrescentes, recursivas ou não?

_____

_____

Descreve o padrão e, por este, os elementos faltantes em sequências repetitivas e em sequências recursivas de números naturais, de objetos ou de figuras?

_____

_____

Estabelece relacões entre o símbolo e o que ele representa, ou seja, entre o representante com o representado?

_____

_____

Classifica resultados de eventos familiares aleatórios como pouco prováveis, muito prováveis, improváveis e impossíveis?

_____

_____

Compreende e realiza a leitura de imagens utilizando-as na resolução de problemas?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____