MP155
Introdução da Unidade 6
A abertura da Unidade, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior e de oferecer suporte e prerrequisitos para o ano seguinte, propõe uma abordagem por meio de observações e de descobertas em uma imagem representativa do cotidiano urbano do estudante do 2º ano do Ensino Fundamental, em que diversas aplicações dos conteúdos da Unidade Temática Grandezas e medidas se fazem presentes.
Nesta Unidade, a abordagem de Grandezas e medidas busca contemplar diferentes conhecimentos, tais como: estimativa, medida e comparação de comprimentos, de capacidade e de massa; indicação da duração de intervalos referentes aos dias da semana e meses do ano; medida da duração de intervalos de tempo, por meio de relógio digital; equivalência de valores e cédulas do sistema monetário brasileiro.
As atividades propostas envolvem majoritariamente Grandezas e medidas, mas há articulação delas com outras Unidades Temáticas. Por exemplo, em Geometria, são abordados aspectos relativos a plantas de ambientes familiares a partir de problemas relacionados às medidas de comprimento.
Como nas outras unidades, nesta se observa a relação com conhecimentos já adquiridos pelos estudantes no 1º ano e com aqueles a serem construídos no 3º ano. Assim, espera-se que os conhecimentos aqui desenvolvidos sejam aporte àqueles que serão objetos de estudo no 3º ano, entre eles: o reconhecimento de que o resultado de uma medida depende da unidade de medida empregada; a escolha da unidade de medida mais apropriada; a estimativa, medição e comparação de comprimentos, de capacidades e massas, recorrendo às unidades de medidas padronizadas e não padronizadas.
Ainda sobre a Unidade Temática Grandezas e medidas, destaca-se a articulação com os estudos desenvolvidos no 1º ano acerca do reconhecimento e da relação entre períodos do dia, dias da semana e meses do ano, além da escrita de datas. Tais conhecimentos conduzirão os estudantes a, neste ano, indicar intervalos relativos aos dias da semana e meses do ano, assim como a determinar a duração de intervalos de tempo em relógios digitais. Assim, na perspectiva de ampliação e aprofundamento no 3º ano, espera-se que os estudantes se apropriem da leitura e do registro de medidas de intervalos de tempo, utilizando o relógio analógico, e do reconhecimento da relação entre hora e minutos, e entre minuto e segundos.
Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro é mais uma abordagem desta unidade, que pretende conduzir os estudantes a indicar equivalência entre esses mesmos valores. Além disso, oferece condições a eles para que, no 3º ano, se instrumentalizem na resolução e elaboração de problemas envolvendo comparação e equivalência em situações de compra, venda e troca.
Quanto à Probabilidade e estatística, as atividades estimulam os estudantes a compararem informações organizadas em tabelas de dupla entrada, incluindo as que são resultantes de pesquisa que envolve o universo de até 30 elementos, o que significa uma ampliação do que foi tratado no 1º ano. Ao mesmo tempo, oferecem as bases para a resolução de problemas cujos dados são apresentados em tabelas de dupla entrada, a serem desenvolvidas no 3º ano. Essa abordagem pretende sistematizar os conhecimentos adquiridos no 1º ano, em que as atividades propostas indicavam a organização por meio de representações pessoais. Simultaneamente, pretende-se possibilitar o desenvolvimento da leitura, interpretação e comparação de dados envolvendo resultados de pesquisas significativas e dispostos em tabelas de dupla entrada, gráficos de barras ou de colunas, fazendo uso de termos como maior e menor frequência, e assim incorporando esse tipo de linguagem para compreender aspectos significativos da realidade sociocultural.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
MP156
UNIDADE 6. Grandezas e medidas

MANUAL DO PROFESSOR
Objetivos da Unidade
• Estimar, medir e comparar comprimento, massa e capacidade, utilizando unidades de medida não padronizadas.
• Identificar, estimar, medir, usar e comparar medidas de comprimento, utilizando unidades de medida padronizadas: centímetro, metro e milímetro.
• Identificar, estimar e comparar medidas de massa, utilizando unidades de medida padronizadas: grama e quilograma.
• Identificar, estimar e comparar medidas de capacidade, utilizando unidades de medida padronizadas: litro e mililitro.
• Medir a duração de um intervalo de tempo por meio de relógio digital.
• Ler horas em relógios digitais.
• Identificar e relacionar as unidades de medida de tempo, horas, dias, dias da semana, meses e anos.
• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.
• Resolver problemas de adição, de subtração e de multiplicação, por meio de estratégias pessoais.
• Elaborar problemas de adição e de subtração.
• Resolver problemas com dados apresentados em plantas e esquemas envolvendo medidas de comprimento.
• Ler, interpretar e organizar dados coletados em tabelas simples e de dupla entrada.
BNCC em foco:
EF02MA06, EF02MA07, EF02MA16, EF02MA17, EF02MA18, EF02MA19, EF02MA20, EF02MA23
MP157
Para refletir...

Amélia e Daniel estão passeando pela rua.
• O relógio na loja de sucos está marcando 10 horas da manhã ou 10 horas da noite?
PROFESSOR
Resposta: 10 horas da manhã.• Você é mais alto ou mais baixo que as varas de pescar à venda?
PROFESSOR
Resposta esperada: Mais baixo.• Quais produtos da cena costumam ser pesados para a venda?
PROFESSOR
Resposta: Peixes e frutas.• Quais produtos costumam ser vendidos em litros?
PROFESSOR
Resposta: Água e sucos.MANUAL DO PROFESSOR
A Unidade explora diferentes unidades de medida de comprimento, de massa, de capacidade, de medida de tempo, bem como o sistema monetário. As situações-problema propostas possibilitam aos estudantes estimar e fazer comparações entre as medidas de grandezas indicadas.
Na abertura, apresentam-se diversas situações do dia a dia em que é possível observar os elementos básicos da ideia de medição. Explore a ilustração para que os estudantes reconheçam a presença da grandeza, da unidade empregada e da medida obtida (não é necessário definir esses termos, apenas evidenciar sua presença nas situações mostradas). Por exemplo, na situação mostrada na placa “Temos varas de pescar de 2 m” a grandeza medida é o comprimento, a unidade de medida é o metro e o número 2 indica quantas vezes a unidade metro cabe no comprimento da vara. Sugerimos que esse processo de evidenciar os elementos envolvidos em uma medição seja obtido por meio de perguntas, como: “O que o vendedor da loja de peixe está medindo com a balança?” (A massa dos peixes.).
Para refletir...
Ao questionar se são 10 horas da manhã ou da noite, incentiva-se a leitura da imagem e a relação do horário com os ciclos diários de luz. É claro que essa conclusão se refere ao contexto de nosso país, uma vez que, se a cena ocorresse no verão europeu, por exemplo, seria possível estar claro às 10 horas da noite.
A segunda pergunta explora a capacidade que os estudantes têm de estimar e comparar. Providencie alguns pedaços de barbante com 1 metro de comprimento para que visualizem o comprimento referente à unidade de medida metro e possam fazer novas comparações.
Espera-se que os estudantes percebam que existem diferentes grandezas para medir: massa e capacidade, além de comprimento e tempo já tratadas. Peça a eles que mencionem outras situações em que é necessário fazer medições.
MP158
Medindo comprimentos
- Complete as frases de acordo com as ilustrações abaixo.
Antônio e João estão construindo paredes.
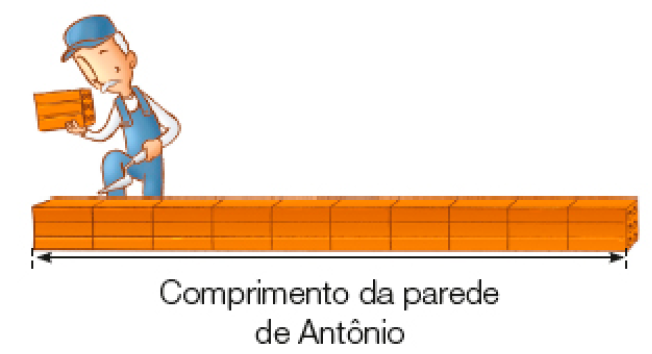

- A medida do comprimento da parede de Antônio corresponde à medida do comprimento de
_____
tijolos.
PROFESSOR
Resposta: 10
- A medida do comprimento da parede de João corresponde à medida do comprimento de
_____
tijolos.
PROFESSOR
Resposta: 8
- Os garotos vão jogar futebol. Para construir cada gol, eles decidiram usar duas latas separadas pelo comprimento de medida igual à de 6 pés.


- Quem tem o pé maior: Marcos ou Abel?
_____
PROFESSOR
Resposta: Abel.
- Você acha
certo
que os gols de Marcos e de Abel fiquem com comprimentos diferentes?
PROFESSOR
Resposta pessoal.
- O que poderia ter sido feito para que esses gols não ficassem com comprimentos diferentes?
PROFESSOR
Exemplo de resposta: Apenas um deles (Marcos ou Abel) poderia ter construído os dois gols, usando a medida do próprio pé.
MANUAL DO PROFESSOR
Objetivo
• Estimar, medir e comparar comprimentos, utilizando unidades de medida não padronizadas.
Antes de realizar as atividades, pergunte: “Como vocês mediriam o comprimento de uma parede?”. Depois, discuta com a classe as diferentes respostas obtidas, aproveitando para verificar se elas envolvem o uso de uma unidade de medida, se essa unidade de medida se mantém durante o processo de medição (por exemplo, quando dizem que a medida de comprimento da parede é igual a 8 passos e 2 palmos).
Atividade 1
Peça aos estudantes que, em duplas, estimem o comprimento de certa parede da escola, deixando livre a unidade de medida. Espera-se que eles percebam a importância da unidade de medida, uma vez que as medições apresentadas expressam unidades diferentes.
Para indicar o comprimento de cada uma das paredes, o comprimento do tijolo foi usado como unidade de medida.
Atividade 2
A atividade apresenta uma situação em que se obtêm valores iguais, mas com unidades de medida diferentes (pé do Marcos e pé do Abel), para expressar o que supostamente teria um mesmo comprimento. Em uma roda de conversa, discuta as soluções propostas com os estudantes.
Para ampliar, desafie os estudantes a medir a largura da sala utilizando o passo e, depois, o polegar como unidades de medida. Em seguida, pergunte em que situação tiveram mais dificuldade.
Avalie a conveniência de conversar com os estudantes sobre a importância da unidade de medida padronizada.
BNCC em foco:
EF02MA16
MP159
O centímetro
- Os desenhos a seguir podem ser medidos com uma régua graduada em centímetro.
Indique a quantidade de centímetros que corresponde à medida do comprimento de cada brinquedo.
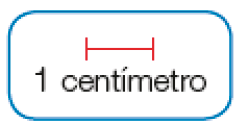

A medida do comprimento do desenho da motocicleta é igual a _____ centímetros.
PROFESSOR
Resposta: 4
O desenho desse trem mede _____ centímetros de comprimento.
PROFESSOR
Resposta: 8Indicamos 1 centímetro por: 1 cm
- Escolha o instrumento de medida – régua, fita métrica ou trena – que você usaria para medir o comprimento em cada caso.

LEGENDA: Régua. FIM DA LEGENDA.

LEGENDA: Fita métrica. FIM DA LEGENDA.

LEGENDA: Trena. FIM DA LEGENDA.
Observação: As imagens não estão apresentadas em escala de tamanho. Fim da observação.
- Comprimento de uma lapiseira: _____
- Comprimento de uma corda: _____
- Comprimento do
contorno
do pulso:
_____
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Objetivo
• Medir e comparar comprimento, utilizando centímetro como unidade de medida.
Atividade 1
Peça aos estudantes que observem que, na medição do comprimento, tanto no desenho da motocicleta quanto do trem, o início do desenho coincide com a marca zero da régua. Isso facilita a leitura, pois a medida será o número correspondente à marca da outra extremidade do desenho na régua.
Ao usar uma régua, é comum alguns estudantes colocarem o início do desenho na marca 1 centímetro; nesse caso, eles devem compreender que a medida será o número correspondente à marca da outra extremidade do desenho subtraída de uma unidade.
Atividade 2
Os estudantes devem identificar a situação em que o uso de cada instrumento de medida de comprimento é, na opinião deles, mais adequado. Por exemplo, peça a eles que tentem medir o contorno do punho com uma régua, de modo que verifiquem que o resultado obtido é impreciso.
Havendo possibilidade, disponibilize os instrumentos de medida apresentados na atividade para a classe e verifique se a turma conhece outras situações de uso social para eles.
O trabalho com unidades de medida tem grande importância para o desenvolvimento do pensamento matemático, pois, além de relacionar-se com muitos momentos do cotidiano, pode articular diferentes campos matemáticos, como Aritmética, Geometria e Álgebra.
A construção do conceito de medida é complexa e envolve o reconhecimento de grandezas, a escolha de uma unidade adequada para sua medida e a expressão da relação entre a grandeza e sua unidade, por meio de um número que indica quantas vezes a grandeza contém a unidade.
MP160
O metro
- Estime as medidas e complete com mais de ou menos de.
- Meu braço
mede
_____
1 metro de comprimento.
PROFESSOR
Resposta: menos de
- A porta da sala de aula
mede
_____
1 metro de altura.
PROFESSOR
Resposta: mais de
- Minha carteira escolar
mede
_____
1 metro de altura.
PROFESSOR
Resposta: menos de
- Meu braço
mede
_____
1 metro de comprimento.
- Para expressar as medidas da altura de uma pessoa e do comprimento de muitas outras coisas, podemos usar a unidade de medida metro. Observe a cena.


- Agora, responda às questões.
- Quem tem menos de 1 metro de medida de altura
nessa
cena?
PROFESSOR
Resposta: A criança de fralda e o cachorro.
- Quem tem entre 1 metro e 2 metros de medida de altura?
PROFESSOR
Resposta: A mulher.
- O muro verde-claro da cena tem cerca de quantos metros a mais de medida de altura que o garoto de camiseta azul?
PROFESSOR
Resposta: Cerca de 2 metros.
Indicamos 1 metro por: 1 m
- Cite três animais que têm mais de 1 metro de medida de altura.
_____
PROFESSOR
Exemplos de resposta: Girafa, elefante, camelo.
MANUAL DO PROFESSOR
Objetivo
• Identificar, estimar e comparar comprimento, utilizando o metro como unidade de medida.
Atividade 1
Leve para a sala de aula barbantes com 1 metro de comprimento e distribua-os entre os estudantes para que possam utilizá-los para medir vários objetos. Essa experiência os ajudará no momento de realizar as estimativas pedidas na atividade.
Pode-se perguntar: “A lousa tem mais de 1 metro ou menos de 1 metro de comprimento?”. Espera-se que os estudantes estimem mais de 1 metro.
Depois que os estudantes fizerem a atividade, peça a eles que, com os pedaços de barbante de 1 metro de comprimento, validem as estimativas feitas.
Atividade 2
Amplie os questionamentos e pergunte:
• “A bananeira tem quantos metros de altura a menos que a altura do muro?” (1 metro.)
• “Qual é o elemento mais alto na cena? E o mais baixo?” (O mais alto é o muro, e o mais baixo, o cachorro.)
Atividade 3
Primeiro, elabore uma lista com alguns animais que têm menos de 1 metro de altura e outros que têm mais de 1 metro de altura. Organize uma roda de conversa para apresentar a lista aos estudantes. Depois, peça a eles que estimem a medida da altura de cada um dos animais da lista. Eles podem utilizar os pedaços de barbante de 1 metro para auxiliar nessas estimativas.
BNCC em foco na dupla de páginas:
EF02MA16
MP161
O milímetro
- Marcos tentou
medir
o comprimento da ponta de seu lápis.
Ele percebeu que a ponta era muito pequena, menor do que 1 centímetro. Então, escolheu o milímetro para expressar a medição.

- Qual é a medida do comprimento da ponta do lápis de Marcos em milímetro?
_____
PROFESSOR
Resposta: 4 milímetros.
- Cerque com uma linha os objetos em que o milímetro é a unidade de medida mais adequada para expressar a medida do comprimento.

LEGENDA: Caderno. FIM DA LEGENDA.

LEGENDA: Botão. FIM DA LEGENDA.

LEGENDA: Grão de arroz. FIM DA LEGENDA.

LEGENDA: Lantejoula. FIM DA LEGENDA.

LEGENDA: Prédio. FIM DA LEGENDA.
PROFESSOR
Respostas esperadas:Grão de arroz; Lantejoula.Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.
- Em quais outros objetos você
expressaria
medidas de comprimento em milímetro?
_____
PROFESSOR
Resposta pessoal.
- Os milímetros também podem ser muito utilizados para expressar medidas de pequenas espessuras.

LEGENDA: Folha de papel. FIM DA LEGENDA.

LEGENDA: Moeda. FIM DA LEGENDA.

LEGENDA: Azulejo. FIM DA LEGENDA.
- Qual desses objetos você acha que tem
menor
espessura?
_____
PROFESSOR
Resposta: Folha de papel.
MANUAL DO PROFESSOR
Objetivo
• Medir, estimar e comparar comprimentos, utilizando o milímetro como unidade de medida.
Avalie a conveniência de informar que massa e peso são conceitos diferentes. Quanto maior a massa de um corpo, maior é o seu peso. Massa: grandeza cuja medida dá a quantidade de matéria de um corpo. Peso: força exercida sobre um corpo pela atração gravitacional.
Atividade 1
Explore a régua com os estudantes, mostrando o comprimento correspondente a 1 milímetro e a 1 centímetro.
Antes de realizar a atividade, sugira a eles que meçam alguns objetos (borracha, apontador, giz etc.) com uma régua utilizando o milímetro para expressar essa medição.
Atividade 2
Os estudantes devem identificar a situação em que, para expressar medições de comprimento, o uso do milímetro é mais adequado. Peça a eles que meçam comprimentos de objetos maiores, como a altura da mesa do professor, utilizando como unidade de medida o milímetro, a fim de que observem que, com comprimentos maiores, a unidade milímetro não é a mais adequada para ser empregada. Por outro lado, peça a eles que tentem medir o comprimento de um grão de arroz utilizando como unidade de medida o metro e o centímetro, para observarem que, nesse caso, o milímetro seria a unidade mais apropriada.
Atividade 3
Os estudantes dessa faixa etária provavelmente já conhecem o termo espessura (“grossura”), porém é pertinente explicar o significado antes da atividade. Isso pode ser feito por meio da comparação entre dois objetos com espessuras diferentes, por exemplo, dois livros. Então, pergunte: “Qual livro é mais grosso, ou seja, tem espessura maior? Qual é mais fino, ou seja, tem espessura menor?”.
Sugestão de leitura para o professor
Livro
CARRAHER, Terezinha Nunes; CARRAHER, David; SCHLIEMANN, Analúcia. Na vida dez, na escola zero. 16. ed. São Paulo: Cortez, 2015.
O livro possibilita compreender as diferenças regionais de produção de medidas e a articulação entre a Matemática escolar e a não escolar.
MP162
Medindo massas
- Observe a imagem e marque com um X a frase correta.
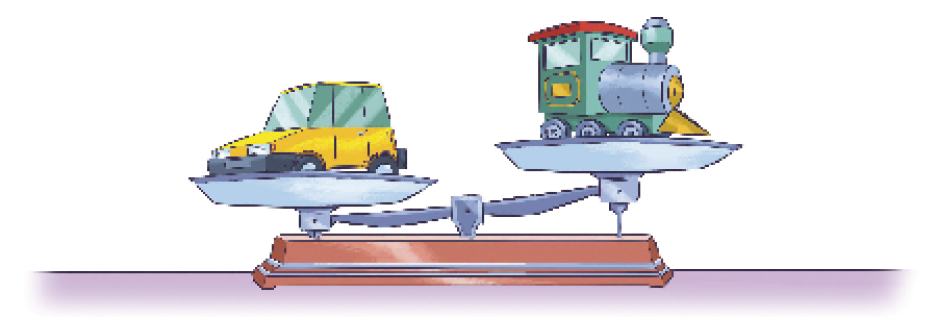
( ) O carrinho é mais pesado que o trenzinho.
( ) O trenzinho é mais pesado que o carrinho.
( ) O carrinho é mais leve que o trenzinho.
PROFESSOR
Resposta correta: O carrinho é mais pesado que o trenzinho.


- Explique para um
colega
como você pensou para marcar a frase correta e ouça a explicação dele.
PROFESSOR
Resposta pessoal.
- Observe a melancia, a maçã e a jabuticaba nas balanças e faça o que se pede.

- Qual das três frutas tem a
menor
massa?
_____
PROFESSOR
Resposta: Jabuticaba.
- A maior massa pertence a qual fruta?
_____
PROFESSOR
Resposta: À melancia.
MANUAL DO PROFESSOR
Objetivo
• Estimar e comparar massas, utilizando estratégias pessoais e unidades de medida não padronizadas.
Comente com os estudantes que, na linguagem popular, os termos massa e peso são usados com o mesmo significado, mas que conceitualmente está errado, pois essas duas grandezas, embora relacionadas, são diferentes. Procuramos evitar o uso da palavra peso, pois o que pretendemos dizer é massa, mesmo quando usamos o verbo pesar. Vale salientar que a compreensão dessa diferença costuma ser complexa para estudantes dessa faixa etária. Então, sugerimos que empregue o vocabulário correto, mas deixe os estudantes se apropriarem dele com o tempo.
Atividade 1
Caso os estudantes apresentem dificuldade em compreender o funcionamento desse tipo de balança, retome o significado da altura dos pratos. Espera-se que eles percebam que o prato com o carrinho está mais baixo em relação ao prato com o trenzinho; logo, o carrinho é mais pesado que o trenzinho.
Atividade 2
Na atividade, pode-se explorar a propriedade transitiva: se a jabuticaba é mais leve que a maçã e esta é mais leve que a melancia, conclui-se que a jabuticaba é a mais leve de todas essas frutas e, assim, a melancia é a mais pesada de todas, ou seja, é a que tem a maior massa.
BNCC em foco:
EF02MA17, EF02MA18
MP163
O grama e o quilograma
- Observe as imagens abaixo e responda às questões.




- Quantos quilogramas tem o pacote de açúcar?
_____
PROFESSOR
Resposta: 1 quilograma.
- O pacote de arroz tem mais de 1 quilograma ou menos de 1 quilograma?
_____
PROFESSOR
Resposta: Mais de 1 quilograma.
- Quantos gramas tem o pacote de amendoim?
_____
PROFESSOR
Resposta: 400 gramas.
- O pacote de orégano tem mais de 500 gramas ou menos de 500 g?
_____
PROFESSOR
Resposta: Menos de 500 gramas.
Indicamos 1 quilograma por: 1 kg
Indicamos 1 grama por: 1 g
- Fábio foi à feira para comprar temperos. Comprou 10 g de pimenta-do-reino moída, 20 g de alecrim e 15 g de colorau. Qual foi a medida da massa total de temperos comprados por Fábio?
_____
PROFESSOR
Resposta: 45 gPROFESSOR
Exemplo de cálculo:PROFESSOR
10 + 20 + 15 = 45

- Calcule mentalmente e complete a frase.

O filho de Karina nasceu com 3 kg. Depois de dois meses, quando foi ao pediatra, ele já estava com 5 kg.
A massa do bebê aumentou _____ kg.
PROFESSOR
Resposta: 2MANUAL DO PROFESSOR
Objetivo
• Identificar, estimar e comparar medidas de massa, utilizando unidades de medida padronizadas: grama e quilograma.
Atividade 1
Antes de iniciar a atividade, pergunte: “O que vocês conhecem que tem 1 quilograma de massa? Um lápis tem mais de 1 quilograma ou menos de 1 quilograma? E uma geladeira? Que produtos são vendidos de acordo com sua massa?”. Para a última pergunta, as respostas podem variar segundo as experiências dos estudantes e da região onde moram; por exemplo, há lugares em que a jabuticaba também é vendida em litro.
Explique que quilograma e grama são unidades de medida de massa, sendo o quilograma mais adequado para expressar medidas de massa de objetos maiores.
Atividade 2
Peça aos estudantes que expressem as medidas de massa apresentadas, a fim de verificar se eles compreenderam o símbolo de grama. Observe as estratégias utilizadas e os respectivos registros. Os estudantes podem efetuar os cálculos apenas dos números e apresentar a unidade de medida somente na resposta, ou podem expressar todos os elementos da adição com a respectiva unidade de medida. Convém observar que
20 + 10 + 15 = 45 e 20 g + 10 g + 15 g = 45 g.
Caso tenham dificuldade com o cálculo da adição, organize os estudantes em trios e peça a eles que compartilhem as técnicas utilizadas na resolução da atividade.
Atividade 3
Verifique a estratégia utilizada pelos estudantes e se associam a situação apresentada a outras que envolvem operações do campo aditivo.
BNCC em foco:
EF02MA17; competência específica 3
Sugestão de leitura para o estudante
Livro
MIRANDA, Alda de. Tem planta que virou bicho! 2. ed. Ilustrações de Cacio Murilo. São Paulo: Escrituras, 2009.
A obesidade é um problema que já atinge muitas crianças brasileiras, ganho de massa relacionado, entre outros fatores, aos hábitos alimentares. O livro incentiva a adoção de hábitos saudáveis e aborda as coisas da natureza enquanto passeia pelo universo lúdico.
MP164
Medindo capacidades
- Observe os recipientes abaixo e, em seguida, faça o que se pede.

- Qual recipiente tem
menor
capacidade? Cerque-o com uma linha.
PROFESSOR
Resposta: xícara

- Explique para um
colega
como você chegou à resposta da pergunta anterior.
PROFESSOR
Resposta pessoal.
- Daniel e Eduardo compraram garrafas iguais de suco de uva. Cada um despejou todo o conteúdo de sua garrafa em alguns copos. Observe e responda.
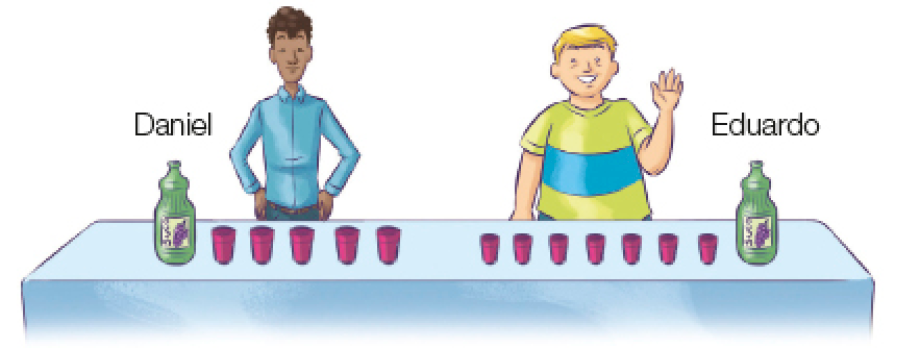
- Quantos copos cada um encheu com suco?
_____
PROFESSOR
Resposta: Daniel: 5 copos; Eduardo: 7 copos.
- Apesar de a quantidade de suco ser igual nas duas garrafas, por que o
número
de copos enchidos por Daniel e por Eduardo foi diferente?
_____
PROFESSOR
Resposta esperada: Porque as capacidades dos copos são diferentes.
MANUAL DO PROFESSOR
Objetivo
• Estimar, medir e comparar capacidades, utilizando estratégias pessoais e unidades de medida não padronizadas.
A ideia de capacidade relaciona-se à possibilidade de um objeto ser preenchido ou ocupado completamente em seu interior. Não se pode falar em capacidade de uma bola de bilhar, por exemplo, pois ela é maciça. Nesse caso, empregamos o termo volume. Portanto, as ideias de capacidade e de volume estão relacionadas, mas não são equivalentes.
Atividade 1
Explore a imagem com os estudantes, fazendo alguns questionamentos:
• É possível colocar todo o líquido da jarra cheia na xícara? E na caneca? Por quê? (Não é possível. Espera-se que os estudantes reconheçam que, na jarra, haverá mais líquido do que cabe na xícara e na caneca.)
• É possível encher a caneca com algumas xícaras de água? (Sim. Nesse caso, espera-se que os estudantes percebam que, como cabe menos água na xícara do que na caneca, é possível encher a caneca com a água da xícara, repetindo o procedimento algumas vezes.)
Atividade 2
Espera-se que os estudantes percebam que a quantidade de suco de uva que cabe em cada copo que Daniel usou é maior que a quantidade de suco que cabe em cada copo que Eduardo usou; então, os copos de Daniel têm capacidade maior que os copos de Eduardo. Como os copos de Daniel têm maior capacidade, Daniel precisa de menos copos que Eduardo para acomodar a mesma quantidade de suco.
Durante os anos de estudo, os estudantes desenvolvem diversos processos mentais que permitem a aprendizagem matemática, entre eles a conservação. No caso da grandeza capacidade, trata-se de compreenderem que a transferência de uma quantidade de líquido de um recipiente para outro, de formato diferente, não alterará a quantidade de líquido. É essa noção que lhes possibilita comparar capacidades.
BNCC em foco:
EF02MA17
MP165
O litro e o mililitro

- Observe e pinte os recipientes de acordo com a legenda.
 recipientes com menos de 1 litro de capacidade
recipientes com menos de 1 litro de capacidade
 recipientes com mais de 1 litro de capacidade
recipientes com mais de 1 litro de capacidade
1

2
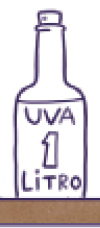
3

4

5

PROFESSOR
Resposta: az: azul: 1, 3PROFESSOR
am: amarelo 4, 5Indicamos 1 litro por: 1 L
- Mililitro é uma unidade de medida usada para representar medidas de capacidade menores que 1 litro. Marque com um X os produtos que costumam ser vendidos em mililitro.

PROFESSOR
Resposta: Todos os produtos.Indicamos 1 mililitro por: 1 mL
Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.
Boxe complementar:
Desafio
Luana quer colocar os 2 litros de leite de um recipiente em garrafinhas de meio litro. Quantas dessas garrafinhas ela pode encher com o conteúdo desse recipiente? _____
PROFESSOR
Resposta: 4 garrafinhas.


• Compare sua resposta com a de um colega e conversem sobre como cada um pensou para resolver o problema.
Resposta pessoal.

CRÉDITO: ARTUR FUJITA
Fim do complemento.
MANUAL DO PROFESSOR
Objetivo
• Identificar, estimar e comparar medidas de capacidade, utilizando unidades de medida padronizadas: litro e mililitro.
Atividade 1
A imagem facilita a estimativa dos estudantes, pois as capacidades dos recipientes são bem distintas. Explique a eles que litro é uma unidade de medida de capacidade bastante utilizada no nosso dia a dia. Peça que exemplifiquem produtos vendidos em litros. Possíveis respostas: água, leite, suco etc.
Atividade 2
Peça aos estudantes que pesquisem produtos (em folhetos de supermercado, por exemplo) cuja embalagem indique uma quantidade menor que 1 litro. Espera-se que indiquem: caixa de suco, garrafinhas de água etc. Comente também sobre os remédios em gotas. Explique a eles que, para esses recipientes de menor capacidade, o mililitro é unidade de medida mais adequada do que o litro.
Desafio
É importante que os estudantes percebam as relações entre a metade e o inteiro. Faça perguntas, como: “Se repartirmos 1 litro de leite igualmente entre dois recipientes de mesma capacidade, que quantidade de leite haverá em cada recipiente?”. (Meio litro de leite.) “E quantos recipientes de meio litro são necessários para encher uma garrafa de 1 litro?” (2 recipientes.)
A situação proposta envolve a comparação entre garrafinhas de meio litro e um recipiente de 2 litros. Para resolvê-la, é provável que a turma estabeleça um raciocínio de correspondência, como mostra a figura abaixo.
Portanto, Luana pode encher quatro garrafinhas de meio litro com o conteúdo do recipiente de 2 litros.
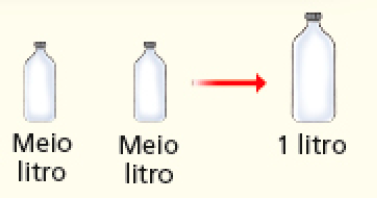
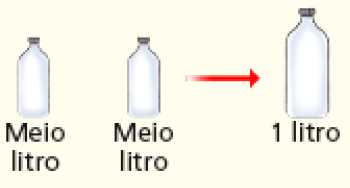
CRÉDITO: ILUSTRAÇÕES: GEORGE TUTUMI
BNCC em foco:
EF02MA17; competência específica 3
MP166
Medindo tempo
Horas
- Complete com mais ou com menos em cada caso.
- Lavar as mãos demora
_____
de 1 hora.
PROFESSOR
Resposta: menos
- Uma partida de futebol dura
_____
de 1 hora.
PROFESSOR
Resposta: mais
- Escovar os dentes leva
_____
de 1 hora.
PROFESSOR
Resposta: menos
- Lavar as mãos demora
_____
de 1 hora.

- Observe o relógio que fica na sala da casa de Cláudio e responda: quanto tempo durou o filme a que ele assistiu?
PROFESSOR
Resposta: 1 hora.
No começo do filme, o relógio marcava:

No fim do filme, o relógio marcava:

Indicamos 1 hora por: 1 h
- Leia e complete.

Às 12 horas, dizemos que é meio-dia. Após o meio-dia, de hora em hora, o relógio digital marca: 13 h, 14 h, _____, _____, _____, _____, _____, _____, _____, _____, _____, 0 h.
PROFESSOR
Resposta: 15 h, 16 h, 17 h, 18 h, 19 h, 20 h, 21 h, 22 h, 23 h.MANUAL DO PROFESSOR
Objetivos
• Medir a duração de um intervalo de tempo por meio de relógio digital.
• Ler horas em relógios digitais.
O tempo é um conceito complexo, porque é possível perceber sua passagem, registrá-lo, organizar-se em função dele, mas defini-lo não é tão simples.
Atividade 1
Uma opção para iniciar o estudo da grandeza tempo é pedir aos estudantes que deem exemplos de termos que envolvam seu uso, como enquanto (ideia de simultaneidade), antes, depois, em seguida (ideia de sequência).
Comente que, para expressarmos a medida de um intervalo de tempo, é necessária uma unidade de medida, e uma das que têm maior uso social é a hora. É possível, porém, que muitos estudantes não saibam estimar adequadamente a duração de algumas atividades; por isso, discuta as questões com eles.
Atividade 2
Acompanhe os estudantes na realização da atividade, que possibilita verificar os conhecimentos prévios que eles têm acerca da leitura da indicação de horários em um relógio digital. Peça aos estudantes que observem como as horas são indicadas nesse tipo de relógio.
BNCC em foco:
EF02MA19
Atividade 3
Pergunte se já perceberam que alguns relógios digitais marcam as horas cheias da 1 hora às 12 horas; nesse caso, para não haver confusão na leitura e saber se a hora indicada refere-se ao período antes do meio-dia ou após o meio-dia, há as indicações am (abreviação de ante meridiem, em latim, que significa antes do meio-dia) e pm (abreviação de post meridiem, em latim, que significa após o meio-dia). Explique aos estudantes que a indicação mostrada no relógio digital é utilizada aqui no Brasil.
É possível que muitos estudantes ainda não saibam fazer a leitura das horas, por isso é importante explorá-la em sala de aula. Diga que há dois tipos de relógio, um que tem ponteiros e outro que não tem, chamado relógio digital.
MP167
Dias
- Em cada situação, escreva se o período de tempo indicado é maior que 1 dia ou
menor
que 1 dia.
- Renata ficou em jejum por 12 horas para fazer exame de sangue.
_____
PROFESSOR
Resposta: Período menor que 1 dia.
- Marina comprou uma cama em uma loja e foi informada de que a entrega ocorreria em 36 horas.
_____
PROFESSOR
Resposta: Período maior que 1 dia.
- Renata ficou em jejum por 12 horas para fazer exame de sangue.
- Leia o que os policiais Marcelo e Renato estão dizendo e responda às questões.

- O plantão de Marcelo durará quantas horas?
_____
PROFESSOR
Resposta: 24 horas.
Um período de 24 horas corresponde a 1 dia.
-
Quantas horas Marcelo terá de folga após o plantão?
_____
PROFESSOR
Resposta: 48 horas.
- Escreva 4 atividades que você sempre faz nas 24 horas de um dia.
_____
PROFESSOR
Exemplos de resposta: escovar os dentes, comer, beber água, respirar, andar, dormir e tomar banho.
MANUAL DO PROFESSOR
Objetivo
• Identificar e relacionar as unidades de medida de tempo horas e dias.
Atividade 1
Nesta atividade, os estudantes devem identificar em quais situações o período de tempo é maior ou menor que um dia. Para isso, eles devem mobilizar seus conhecimentos prévios, sendo uma boa oportunidade para observar a compreensão que têm do assunto.
A noção de dia relaciona-se à ideia de alternância cíclica dos períodos de luz solar e rege o ritmo das atividades humanas, como o trabalho, o período de descanso etc.
Pergunte aos estudantes: “Que situações envolvem períodos de tempo maiores que 1 dia? E menores que 1 dia?”. Exemplos de situação:
• períodos maiores que 1 dia: crescimento de uma árvore, vida de um gato;
• períodos menores que 1 dia: tempo de aula, passeio com os amigos, tempo do almoço.
Atividade 2
O conceito de tempo resulta de construções lógicas originadas não apenas das experiências que desenvolvem a noção de dia, mas também da ação, estando relacionado ao domínio da linguagem. Por meio da linguagem, os estudantes traduzem sua experiência com o tempo, atribuindo significados aos termos a ele relacionados, como as ideias de ontem, hoje e amanhã. Crianças pequenas podem dizer frases como“ontem eu vou”, o que mostra que elas passam a relacionar o uso da linguagem com a percepção da duração e continuidade do tempo de forma gradativa, sendo uma construção mental de longo prazo.
BNCC em foco:
EF02MA18
Atividade 3
Diversas situações da rotina escolar podem contribuir para a percepção temporal e para a relação entre horas e dias, como o uso do calendário, o agendamento de tarefas e eventos escolares.
Aproveite a situação proposta na atividade 2 para comentar alguns contextos em que usamos a palavra dia:
• Período de 24 horas: “Vai demorar um dia para acabar isto”.
• Período claro do dia: “Ele trabalha durante o dia e descansa à noite”.
• Sentido de data: “O aniversário dela é dia 17”.
MP168
Semanas
- Veja os pratos especiais do dia que Raquel serve em seu restaurante semanalmente. Depois, complete, considerando que hoje seria quarta-feira.

- Se hoje é quarta-feira, o prato do dia é
_____.
PROFESSOR
Resposta: feijoada
- O prato do dia servido ontem foi
_____
e o de amanhã será
_____.
PROFESSOR
macarronada; moqueca
- Cada prato do dia é servido novamente após
_____.
PROFESSOR
Resposta: 7 dias
Um período de 7 dias é chamado semana.
- Complete.
- 2 semanas são
_____
dias.
PROFESSOR
Resposta: 14
- 3 semanas são
_____
dias.
PROFESSOR
Resposta: 21
- 4 semanas são
_____
dias.
PROFESSOR
Resposta: 28
- 2 semanas são
_____
dias.
- Guilherme
pratica
natação às terças-feiras e às quintas-feiras. Na semana passada, a terça-feira foi dia 21. Que dia foi a quinta-feira da semana passada?
_____
PROFESSOR
Resposta: Dia 23.
MANUAL DO PROFESSOR
Objetivo
• Identificar e relacionar as unidades de medida de tempo dias da semana.
Atividade 1
Explore a leitura dos dias no calendário. Pergunte: “Que dia da semana é hoje? Após quantos dias será novamente o mesmo dia da semana?”. Espera-se que os estudantes percebam que, a cada 7 dias, os dias da semana se repetem.
A organização dos dias em semanas ocorre de modo simultâneo à numeração dos dias do mês, de modo que podemos nos referir a determinado dia por seu número ou pelo dia da semana. Por exemplo, é comum dizer: “A consulta médica está marcada para a próxima quinta-feira”.
Atividade 2
Pergunte aos estudantes:
• Se hoje é quarta-feira, daqui a uma semana será que dia? (Quarta-feira.)
• Se hoje é quinta-feira, daqui a duas semanas será que dia? (Quinta-feira.)
• Se hoje é sexta-feira, daqui a três dias será que dia? (Segunda-feira.)
Atividade 3
Se julgar necessário, utilize um calendário para que os estudantes percebam que a quinta-feira é dois dias depois da terça-feira.
BNCC em foco:
EF02MA18
Sugestão de atividades
1. Sabendo que as borboletas vivem, em média, 14 dias, quantas semanas, aproximadamente, vivem as borboletas? (2 semanas.)
2. De quanto em quanto tempo é sábado? (Exemplos de respostas: A cada 7 dias; de uma em uma semana; de duas em duas semanas etc.)
3. Complete o quadro.
Quadro: equivalente textual a seguir.
|
Ontem |
Hoje |
Amanhã |
|---|---|---|
|
Quinta-feira, 24 |
Sexta-feira, 25 |
Sábado, 26 |
|
Terça-feira, 8 |
Quarta-feira, 9 |
Quinta-feira, 10 |
|
Domingo, 14 |
Segunda-feira, 15 |
Terça-feira, 16 |
MP169
Meses e anos

- Responda às questões.
- Qual é sua idade em anos?
- Já se passaram quantos meses desde seu último aniversário?
PROFESSOR
Respostas pessoais.
- Observe o calendário e faça o que se pede.
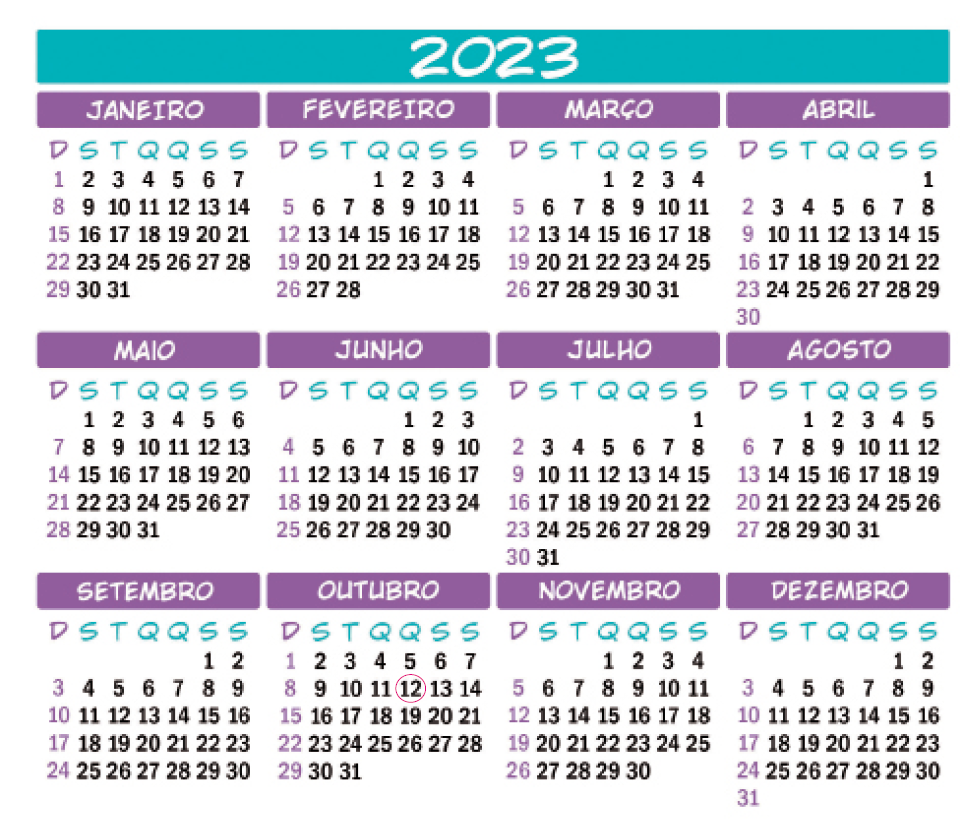
- No calendário, cerque com uma linha o Dia das Crianças.
PROFESSOR
Resposta: 12 de outubro.

- Reúna-se com um
colega
e, juntos, descubram quantos meses inteiros faltam para o primeiro dia do próximo ano.
PROFESSOR
Atenção professor: A resposta dependerá do mês em que a atividade for realizada. Fim da observação.
Um período de 12 meses é chamado ano.
- Quantos anos há em um período de 36 meses?
_____
PROFESSOR
Resposta: 3 anos.
MANUAL DO PROFESSOR
Objetivo
• Identificar e relacionar as unidades de medida de tempo dias, meses e anos.
As atividades buscam relacionar as medidas de tempo em meses e em anos.
A intervenção do professor é importante para ajudar os estudantes a estimar intervalos de tempo mais longos, como um mês ou um ano, pois é comum não terem uma boa percepção desses períodos. Relacionar tais períodos de tempo à ocorrência de eventos significativos para o estudante ajuda-o a estimá-los, assim como perguntar a respeito de eventos futuros, como: “Quanto tempo falta para que cheguem as férias?”.
Atividade 1
Pergunte aos estudantes: “Quantos meses separam 2 aniversários seguidos de uma pessoa?”. Espera-se que os estudantes respondam 12 meses, que correspondem a 1 ano. “Que situações envolvem períodos de tempo medidos em anos? E em meses?”. Exemplos de resposta em anos: idade, há quanto tempo uma pessoa mora em determinado local etc; em meses: idade, tempo de gestação, quanto tempo (meses) falta para acabar o ano etc.
Atividade 2
Sugerimos o uso diário do calendário para marcar datas e agendar acontecimentos importantes para o grupo. Para isso, providencie um calendário anual para cada estudante. Esse é um modo significativo de promover a aproximação dos estudantes a esse importante instrumento de registro do tempo, possibilitando a organização do tempo semanal e mensal do estudante. Se julgar oportuno, faça um cartaz com os aniversariantes de cada mês do ano.
Considere solicitar aos estudantes que marquem com um X o dia do aniversário deles.
BNCC em foco:
EF02MA18; competência específica 3
Atividade 3
Uma estratégia para resolver a atividade é considerar que, se em 1 ano há 12 meses, então em 3 anos há 12 + 12 + 12 meses, ou seja, 36 meses.
As atividades desenvolvidas nessas páginas possibilitam aprofundar a compreensão e o registro do calendário, de modo que os estudantes compreendam como o tempo está organizado em dias, meses e semanas, reconhecendo que existe o dia que é do mês (representado por um número), o dia que é da semana (representado por um nome: segunda-feira, terça-feira etc.) e que o dia do mês e o dia da semana podem ser diferentes do ano anterior. Por exemplo, dia 12 de outubro de 2023 é uma quinta-feira e, em 2024, sexta-feira.
MP170
Jogo: Competição animal

Material: 12 cartas com informações de animais da página 201.

Jogadores: 2, 3 ou 4.
Regras:
- As 12 cartas são embaralhadas e repartidas igualmente entre os jogadores.
- Cada um coloca as cartas em sua frente voltadas para baixo, formando um monte.
- Os jogadores decidem quem começará a partida.
- A cada rodada, todos os jogadores pegam a carta de cima de seu monte.
- Cada jogador, na sua vez, escolhe uma das três medidas (de comprimento, de massa ou de tempo de gestação) do animal representado na carta e lê a informação em voz alta.
- Os outros jogadores
devem
dizer, em voz alta, qual animal está na sua carta e qual é a medida correspondente. Quem tiver o animal com a maior medida vencerá a rodada e ficará com todas as cartas da rodada, que deverão ser colocadas embaixo de seu monte.
Veja um exemplo de uma rodada:

- O jogo prossegue com o próximo jogador à esquerda, que escolherá uma das medidas do animal da primeira carta de seu monte.
- Quando um jogador ficar sem cartas, sairá do jogo.
- Vence o jogador que ficar com todas as cartas.
MANUAL DO PROFESSOR
Objetivos
• Identificar, estimar e comparar medidas de comprimento, utilizando o centímetro como unidade de medida.
• Identificar, estimar e comparar medidas de massa, utilizando o quilograma como unidade de medida.
• Ler e comparar períodos de tempo em dias.
Ajude os estudantes na leitura e na compreensão das regras. Eles devem colar as cartas do Material complementar em um papel mais resistente, como cartolina, antes de recortá-las.
O objetivo do jogo é que os estudantes reconheçam medidas de comprimento, de massa e de tempo associadas a alguns animais e comparem determinada grandeza a cada rodada de uma partida. Assim, os estudantes têm a oportunidade de se familiarizarem com as unidades de medida empregadas e passam a reconhecer quais medidas em cada animal têm mais chances de serem maiores que as dos outros animais. É importante incentivar as comparações, sem preocupação com a formalização da linguagem.
Observe as estratégias usadas pelos estudantes para fazer a comparação entre os números; verifique se comparam a quantidade de algarismos ou, no caso de terem a mesma quantidade de algarismos, se comparam os algarismos da ordem correspondente (centenas, dezenas e unidades, nessa sequência).
BNCC em foco:
EF02MA16, EF02MA17, EF02MA18; competências gerais 2 e 9; competências específicas 3, 4 e 8
Sugestão de atividade interdisciplinar
O jogo apresenta particularidades de alguns animais, possibilitando a interdisciplinaridade com Ciências. Se julgar oportuno, peça aos estudantes que comparem as medidas de comprimento, massa e tempo de gestação de alguns animais das cartas com as medidas correspondentes de animais domésticos, como gatos e cachorros.
MP171
Questões sobre o jogo
- Qual é o animal das cartas do jogo que tem a maior massa? E o que tem a
menor
massa?
_____
PROFESSOR
Resposta: O animal de maior massa é o peixe-boi; o de menor massa é o gambá.

- Qual é a diferença entre a massa, em quilograma, do animal que tem a maior massa e a do que tem a
menor
massa?
_____
PROFESSOR
Resposta: 477 quilogramas.
- Imagine que você tenha a carta com a lontra. Escolha uma grandeza que lhe permita ganhar do jogador que tenha a carta com o bugio.

LEGENDA: Lontra. FIM DA LEGENDA.
Medidas
Massa 5 kg
Tempo de gestação 56 dias
Comprimento 66 cm (sem a cauda)

LEGENDA: Bugio. FIM DA LEGENDA.
Medidas
Massa 7 kg
Tempo de gestação 187 dias
Comprimento 63 cm (sem a cauda)
_____
PROFESSOR
Resposta: Comprimento (sem a cauda) ou massa.- Em quais medidas a onça-pintada vence o jupará?
_____
PROFESSOR
Resposta: A onça-pintada vence na medida da massa e na medida do comprimento (sem a cauda).
- Nesta rodada, o menino escolhe uma medida do animal de sua carta. Por que você acha que ele está comemorando?

_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que é porque o menino sabe que, se escolher a medida do tempo de gestação, ele ganhará de qualquer animal de outra carta. Fim da observação.MANUAL DO PROFESSOR
Questões sobre o jogo
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões propostas.
Na questão 1, pode-se perguntar: “A medida da massa do peixe-boi é maior do que a medida da massa de uma pessoa adulta? E a medida da massa do gambá?”. Espera-se que os estudantes digam que a medida da massa do peixe-boi é maior do que a medida da massa de uma pessoa adulta e que a medida da massa do gambá é menor.
Avalie a conveniência de observar aos estudantes que muitas vezes, para simplificar a comunicação, podemos omitir a expressão “a medida da/do” nas comparações entre as medidas de uma mesma grandeza. Por exemplo, no parágrafo anterior, a pergunta poderia ser “A massa do peixe-boi é maior do que a massa de uma pessoa adulta? E a massa do gambá?”.
Nas demais questões, espera-se que os estudantes observem que, nas rodadas, eles devem considerar que alguns animais têm duas ou mais medidas pequenas em relação a essas mesmas medidas da maioria dos animais das outras cartas; portanto, a escolha deve recair sobre a medida com a maior chance de vitória, que dependerá também da sorte.
Podem ser propostas mais questões sobre o jogo. Por exemplo:
• “Quais animais das cartas têm menos de 1 metro de comprimento sem a cauda?” (Jaguatirica, quati, gambá, lontra e bugio.)
• “Qual é o comprimento da capivara, expresso em metro e centímetro?” (1 metro e 34 centímetros.)
• “Qual desses animais tem tempo de gestação menor que o de um mês?” (Gambá.)
• Quais desses animais têm tempo de gestação de aproximadamente 2 meses? (Lontra; lobo-guará.)
BNCC em foco:
EF02MA16, EF02MA17, EF02MA18; competências gerais 2 e 9; competências específicas 3, 4 e 8
Variação
Uma possibilidade de variação do jogo é propor a confecção de novas cartas com informações de outros animais.
MP172
Trabalhando com o nosso dinheiro
- Observe os brinquedos e o preço de cada um deles.

LEGENDA: Boneca. FIM DA LEGENDA.

LEGENDA: Trem. FIM DA LEGENDA.

LEGENDA: Peteca. FIM DA LEGENDA.
Observação: As imagens nesta página não estão apresentadas em escala de tamanho. Fim da observação.
- Qual é o brinquedo mais caro?
_____
PROFESSOR
Resposta: Trem.
- Com 100 reais, seria possível comprar os 3 brinquedos?
_____
PROFESSOR
Resposta: Não.
- Cerque com uma linha a menor quantidade de cédulas necessárias para formar 174 reais.

PROFESSOR
Exemplo de resposta: cédula de 100 reais, cédula de 50 reais, cédula de 20 reais, duas cédulas de 2 reais.

- Flaviana faz bolachas decoradas para vender. Ela vende caixinhas com 10 bolachas cada uma por 25 reais.
- Nesta semana, ela vendeu 4 caixinhas de bolachas. Quantos reais ela recebeu pelas caixinhas vendidas?
_____
PROFESSOR
Resposta: 100 reais.
- Nesta semana, ela vendeu 4 caixinhas de bolachas. Quantos reais ela recebeu pelas caixinhas vendidas?
_____
MANUAL DO PROFESSOR
Objetivos
• Estabelecer a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro.
• Resolver problemas de adição e multiplicação por meio de estratégias pessoais.
Atividade 1
Explore o valor de cada cédula e a moeda de 1 real. Componha quantias com as cédulas e a moeda de 1 real com os estudantes. Use dinheiro fantasia para eles fazerem essas composições.
Em seguida, proponha as questões da atividade. Se necessário, deixe que utilizem as cédulas de dinheiro fantasia para realizar a atividade.
Atividade 2
Enfatize para os estudantes que há diversas maneiras de compor 174 reais com essas cédulas. Porém, como eles precisam utilizar a menor quantidade de cédulas, se julgar oportuno, dê uma dica dizendo que devem começar escolhendo a cédula com o maior valor, mas menor do que 174 reais; no caso, a cédula de 100 reais.
Atividade 3
Verifique as estratégias de cálculo utilizadas pelos estudantes e socialize-as com toda a turma.
BNCC em foco:
EF02MA06, EF02MA07, EF02MA20; competência específica 3
MP173
- Gregório foi ao cinema com seus 3 sobrinhos. Antes de entrarem na sala do cinema, ele comprou 3 pacotes de pipoca.

- Quantos reais custaram os 3 pacotes de pipoca?
_____
PROFESSOR
Resposta: 15 reais.PROFESSOR
Exemplo de cálculo:PROFESSOR
3 × 5 = 15
- Qual foi a quantia gasta por Gregório com os ingressos
dele
e de seus sobrinhos?
_____
PROFESSOR
Resposta: 50 reais.PROFESSOR
Exemplos de cálculo:PROFESSOR
3 × 10 = 30PROFESSOR
30 + 20 = 50
- Ao todo, quantos reais Gregório gastou com os pacotes de pipoca e com os ingressos?
_____
PROFESSOR
Resposta: 65 reais.PROFESSOR
Exemplo de cálculo:PROFESSOR
15 + 50 = 65
- Gabriel tem 1 cédula de 50 reais e Clara tem 2 cédulas de 20 reais.
- Quem possui mais cédulas?
_____
PROFESSOR
Resposta: Clara.
- Quem tem a maior quantia em reais?
_____
PROFESSOR
Resposta: Gabriel.
- O que você pode concluir com as respostas dos itens a e b?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que ter mais cédulas não implica ter uma quantia maior. Fim da observação.
- Quem possui mais cédulas?
_____
MANUAL DO PROFESSOR
Atividade 4
Incentive os estudantes a fazerem os cálculos mentalmente. Para auxiliar, faça questionamentos:
• “Qual é o preço de cada pacote de pipoca?” (5 reais.)
• “E quanto se paga por 2 desses pacotes de pipoca?” (10 reais.)
• “E por 3 deles?” (15 reais.)
• “Quanto custa o ingresso de uma criança?” (10 reais.) Se necessário, explique o que é meia-entrada.
• “Quanto se gasta ao comprar 3 ingressos para 3 crianças?” (30 reais.)
• “Quanto é o ingresso de um adulto não idoso?” (20 reais.)
• “Quantos reais são gastos ao comprar 3 ingressos de crianças e 1 ingresso de adulto não idoso?” (50 reais.)
Atividade 5
Espera-se que os estudantes consigam estabelecer relação entre a quantidade de cédulas e a quantia total em reais, percebendo que não é condição obrigatória ter mais cédulas para ter uma quantia maior.
BNCC em foco:
EF02MA06, EF02MA07, EF02MA20; competência específica 3
MP174
Compreender problemas
Para resolver
Leia e resolva os problemas considerando a planta da cozinha e o esquema.

Problema 1
A planta a seguir representa a cozinha da casa de Leonardo. Qual é a medida da largura da porta dessa cozinha?
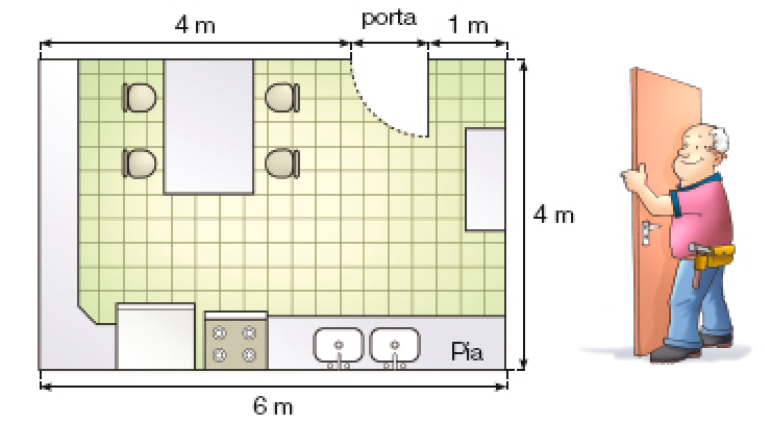
A porta da cozinha tem _____ metro de medida de largura.
PROFESSOR
Resposta: 1Problema 2
Andreza, Juliana e Wílliam estão caminhando em uma pista. De acordo com os dados do esquema abaixo, qual é a distância entre Wílliam e Juliana?
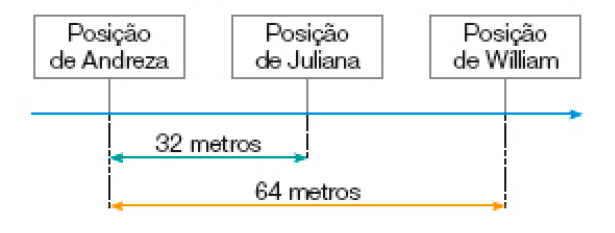
A distância entre Wílliam e Juliana é de _____ metros.
PROFESSOR
Resposta: 32MANUAL DO PROFESSOR
Objetivos
• Identificar, estimar e comparar medidas de comprimento, utilizando o metro como unidade de medida.
• Resolver problemas com dados apresentados em plantas e esquemas envolvendo medidas de comprimento.
• Resolver e elaborar problemas de adição e subtração.
Nos problemas desta página, os dados são apresentados em uma planta e em um esquema, explorando as unidades de medidas de comprimento.
Para resolver
Problema 1
Espera-se que os estudantes reconheçam que a cozinha representada é retangular e, portanto, as paredes opostas têm o mesmo comprimento. Devem observar também que a parede na qual está a porta tem seu comprimento obtido pela adição das medidas: 4 metros mais a largura da porta mais 1 metro.
Desse modo, tem-se:
4 metros + largura da porta + 1 metro = 6 metros
Logo, falta apenas 1 metro para completar os 6 metros, isto é, a largura da porta é 1 metro.
Problema 2
Os estudantes devem observar que, no problema, é dada a distância entre Andreza e Wílliam (o todo) e a distância entre Andreza e Juliana (uma das partes), de modo que é preciso determinar a distância entre Juliana e Wílliam (a outra parte). Assim, eles podem chegar à resolução calculando: 64 − 32 = 32.
BNCC em foco:
EF02MA06, EF02MA16
MP175
Para refletir
- No Problema 1, a parede à direita da pia
mede
4 metros de comprimento. Se essa medida
fosse
diferente, a resposta do problema mudaria? Por quê?
_____
PROFESSOR
Resposta: Não, pois esse dado não é usado na resolução do problema.
- Leia abaixo como Caio pensou para resolver o Problema 1.

- Essa resolução está correta? Por quê?
_____
PROFESSOR
Resposta: Não.PROFESSOR
Exemplo de justificativa: Caio subtraiu 1 metro de 4 metros quando deveria ter adicionado essas medidas e subtraído o resultado de 6 metros.
- Observando apenas as informações do esquema do Problema 2, o que você pode saber sem fazer cálculos?
( ) A distância total da caminhada.
( ) A distância já percorrida por Andreza.
( ) Quantos metros separam Andreza de Juliana e Andreza de Wílliam.
PROFESSOR
Resposta correta: Quantos metros separam Andreza de Juliana e Andreza de Wílliam.
- No esquema do Problema 2, se Wílliam estivesse posicionado mais à direita, o que aconteceria com a distância entre Andreza e Juliana?
_____
PROFESSOR
Resposta: Essa distância não se alteraria.

- Modifique as informações do Problema 2 para que a resposta
dele
seja 30 metros.
Distância entre Andreza e Juliana: _____ metros.
PROFESSOR
Exemplo de resposta: 34Distância entre Andreza e Wílliam: _____ metros.
PROFESSOR
Exemplo de resposta: 64
MANUAL DO PROFESSOR
Para refletir
Atividade 1
Perguntas como a feita nessa atividade são importantes para verificar se os estudantes compreendem quais dados do problema são relevantes para a obtenção da resposta. No caso, o comprimento da parede à direita da pia (4 metros) não é um dado que deve ser considerado na resolução do Problema 1.
Explique que eles devem usar o próprio corpo como referencial para localizar a parede à direita da pia, considerando o ponto de vista do leitor.
Atividade 2
O modo como Caio resolveu o Problema 1 não está correto porque ele subtraiu 1 metro de 4 metros, quando deveria ter adicionado essas medidas. Sugira aos estudantes que façam a verificação da resposta obtida por Caio por meio do cálculo da adição: 4 m + 3 m + 1 m = 8 m, cujo resultado é diferente da medida esperada para o comprimento da parede, que é de 6 metros.
Atividade 3
Explique que o modo de não fazer cálculos é utilizando as informações que o problema fornece. Caso haja dificuldade, sugira a eles que troquem ideias com um colega e compartilhem as estratégias utilizadas.
Atividade 4
Atividades como essa são importantes para os estudantes perceberem que a posição de um terceiro objeto não influencia na distância dos dois primeiros objetos, caso eles não se locomovam. Se houver dificuldade, simule as duas situações (antes e depois de mudar a posição de Wílliam) e determine as distâncias de Andreza e Juliana, confirmando que as distâncias não se alteram.
BNCC em foco:
EF02MA06, EF02MA16
Atividade 5
Espera-se que os estudantes percebam que a distância de 32 metros, que separava Wílliam de Juliana, seria diminuída para 30 metros (nova resposta), ou seja, 2 metros a menos. Portanto, para que haja diminuição de 2 metros nessa distância, é necessário que a distância entre Andreza e Juliana aumente em 2 metros, passando a ser de 34 metros. Contudo, esse é apenas um exemplo de resposta.
Outro exemplo de resposta:
• Distância entre Andreza e Juliana: 50 metros.
• Distância entre Andreza e Wílliam: 80 metros.
MP176
Matemática em textos
Leia
Período de gestação de alguns animais
Alguns animais nascem de ovos, e o período que eles passam crescendo dentro dos ovos é chamado incubação. Outros animais crescem dentro da barriga da mãe, período que é denominado gestação. Os períodos de gestação variam de espécie para espécie. Vamos conhecer o período de gestação de alguns animais.
Observação: As imagens nesta página não estão apresentadas em escala de tamanho. Fim da observação.

LEGENDA: hipopótamo - 240 dias. FIM DA LEGENDA.

LEGENDA: vaca - 284 dias. FIM DA LEGENDA.

LEGENDA: urso-polar - 240 dias. FIM DA LEGENDA.

LEGENDA: leão - 100 dias. FIM DA LEGENDA.

LEGENDA: cavalo - 330 dias. FIM DA LEGENDA

LEGENDA: gato - 63 dias. FIM DA LEGENDA.

LEGENDA: cachorro - 63 dias. FIM DA LEGENDA.

LEGENDA: elefante indiano - 624 dias. FIM DA LEGENDA.

LEGENDA: lobo - 63 dias. FIM DA LEGENDA.

LEGENDA: tigre - 105 dias. FIM DA LEGENDA.

LEGENDA: coelho - 30 dias. FIM DA LEGENDA.

LEGENDA: porco - 112 dias. FIM DA LEGENDA

LEGENDA: leão-marinho - 350 dias. FIM DA LEGENDA.
FONTE: Dados obtidos em: DUARTE, Marcelo. O guia dos curiosos. São Paulo: Panda Books, 2006. p. 60.
MANUAL DO PROFESSOR
Objetivo
• Identificar, comparar e relacionar as unidades de medida de tempo dias e meses.
Nestas páginas, os estudantes trabalharão com as unidades de medida de tempo, dia e mês no contexto de tempo de gestação de alguns animais.
Leia
Caso julgue oportuno, realize uma atividade com Ciências. Peça aos estudantes que pesquisem em livros, revistas ou na internet sobre os hábitos alimentares dos animais citados no texto. Depois, podem ser feitos cartazes com fotografias dos animais e os dados obtidos na pesquisa para apresentar aos colegas de classe ou fixar em um mural.
BNCC em foco: EF02MA18
MP177
Responda
- Alguns animais nascem de ovos. Como é chamado o período que esses animais passam crescendo dentro dos ovos?
_____
PROFESSOR
Resposta: Incubação.
- Gestação é o período em que os animais crescem dentro da barriga da mãe. Qual é o tempo de gestação do leão? E o do gato?
_____
PROFESSOR
Resposta: 100 dias; 63 dias.
Analise
- Qual dos animais mostrados na página anterior tem maior tempo de gestação? E qual tem
menor
tempo de gestação?
_____
PROFESSOR
Resposta: Maior: elefante; menor: coelho.

- Quais desses animais têm o tempo de gestação igual a aproximadamente duas vezes o tempo de gestação do coelho?
_____
PROFESSOR
Resposta: Gato, cachorro e lobo.

- Qual é a diferença entre o tempo de gestação do leão-marinho e o do cavalo?
_____
PROFESSOR
Resposta: 20 dias.
- Quais desses animais têm o tempo de gestação entre 6 meses e 9 meses?
_____
PROFESSOR
Resposta: Hipopótamo e urso-polar.
Aplique
- O tempo de gestação do ser humano é de aproximadamente 270 dias. Esse tempo é mais próximo do tempo de gestação de qual desses animais?
_____
PROFESSOR
Resposta: Da vaca.

- Os coelhos vivem, em média, de 5 a 6 anos. O que você acha que aconteceria com a população de coelhos se o tempo de gestação deles
fosse
igual ao dos elefantes indianos?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Responda
Atividades 1 e 2
Peça aos estudantes que busquem no texto as informações necessárias para registrarem as respostas.
Analise
Atividades de 1 a 4
Com base na leitura e na interpretação do texto e das imagens, os estudantes podem observar a diferença entre os tempos de gestação de vários animais. Esse contexto possibilita a comparação e o estabelecimento de relações entre esses tempos.
Os dados do texto são apresentados em número de dias, o que em alguns casos pode dificultar a estimativa de quanto tempo isso representa em relação a meses ou anos. Incentive a turma a transformar alguns dados em meses, considerando cada mês como 30 dias. Faça algumas dessas transformações na lousa, se julgar necessário.
Aplique
Atividades 1 e 2
Na atividade 1, verifique como os estudantes fazem a comparação dos dados.
Na atividade 2, é importante que eles percebam que o tempo de gestação do elefante indiano, que é de 624 dias, corresponde a aproximadamente 20 meses, ou a cerca de 1 ano e 8 meses. Observe as estratégias usadas pelos estudantes nessa transformação. Se o tempo de gestação dos coelhos fosse igual ao dos elefantes, os coelhos reproduziriam bem menos, já que vivem somente 5 ou 6 anos.
BNCC em foco:
EF02MA18
MP178
Compreender informações
Organizar dados em tabelas
- Veja a remessa de violões, pandeiros, flautas e violinos que uma loja de instrumentos musicais recebeu em janeiro de 2023.

O gerente da loja começou a anotar as quantidades em uma lista para depois organizar uma tabela.

- Termine de completar a lista com a quantidade de cada tipo de instrumento.
PROFESSOR
Resposta: 8; 4- Agora, complete a tabela.
Instrumentos musicais recebidos
Tabela: equivalente textual a seguir.
|
Instrumento |
Violino |
Flauta |
_____ |
Pandeiro |
|---|---|---|---|---|
|
Quantidade |
_____ |
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Violino: 2; Flauta: 4; Violão: 8; Pandeiro: 3.Fonte: Loja de instrumentos musicais (jan. 2023).
- Nessa remessa, que tipo de instrumento foi comprado pela loja em maior quantidade?
_____
PROFESSOR
Resposta: O violão.
- Quantos violinos falta comprar para atingir a quantidade de violões dessa remessa?
_____
PROFESSOR
Resposta: 6 violinos.
- Há instrumentos cuja quantidade é o dobro da quantidade de outro
nessa
remessa? Quais?
_____
PROFESSOR
Resposta: Sim. O violão e a flauta; a flauta e o violino.PROFESSOR
A quantidade de violões (8) é o dobro da de flautas (4) e a quantidade de flautas (4) é o dobro da quantidade de violinos (2).
MANUAL DO PROFESSOR
Objetivos
• Organizar dados coletados em tabelas simples e de dupla entrada.
• Ler e interpretar dados apresentados em tabelas simples e de dupla entrada.
Atividade 1
Caso julgue necessário, explore o nome e a imagem dos instrumentos musicais com os estudantes antes de realizarem a atividade.
Pergunte: “Onde devemos buscar as informações para completar a lista de instrumentos?”. Espera-se que os estudantes percebam que os dados estão na ilustração.
Explore a imagem com os estudantes de modo que eles identifiquem os instrumentos e possam contá-los.
Proponha que completem a tabela com base nas informações da lista. Verifique se eles percebem que, na primeira linha, devem completar com o nome do instrumento que falta (em relação aos apresentados na lista).
Discuta as demais questões com os estudantes, observando se procuram os dados na tabela, na lista ou na ilustração.
No item e, espera-se que os estudantes reconheçam que a quantidade de violões (8) é o dobro da de flautas (4), que por sua vez é o dobro da quantidade de violinos (2).
BNCC em foco:
EF02MA23
MP179
- Doze de agosto é o Dia Nacional das Artes. A professora de Marta organizou uma semana no mês de agosto dedicada às artes.
- Leia o que diz Marta e complete a tabela com a distribuição das aulas nessa semana.

Aulas na semana dedicadas às artes
Tabela: equivalente textual a seguir.
|
Dia da semana Tipo de aula |
Seg. |
Ter. |
Qua. |
Qui. |
Sex. |
|---|---|---|---|---|---|
|
Dança e música |
_____ |
2 |
2 |
_____ |
3 |
|
Pintura e desenho |
2 |
_____ |
_____ |
1 |
2 |
|
Teatro e cinema |
2 |
0 |
_____ |
2 |
_____ |
Fonte: Professora de Marta (ago. 2023).
PROFESSOR
Resposta: 1; 2; 3; 0; 3; 0- Quantas aulas de dança e música Marta teve na segunda-feira?
- E de teatro e cinema?
_____
PROFESSOR
Resposta: 1 aula; 2 aulas.
- Marta teve quantas aulas de pintura e desenho na terça-feira?
- E na sexta-feira?
_____
PROFESSOR
Resposta: 3 aulas; 2 aulas.
- Houve algum dia da semana em que ela não teve aula de teatro e cinema? Se houve, qual foi esse dia?
_____
PROFESSOR
Resposta: Sim, na terça-feira e na sexta-feira.
- Que modalidade teve mais aulas
nessa
semana?
_____
PROFESSOR
Resposta: Dança e música.
- Faça uma pesquisa e colete o mês do aniversário dos estudantes de sua turma, incluindo o seu. Depois,
organize
as informações em uma tabela que mostre quantos estudantes da turma fazem aniversário em cada mês.
PROFESSOR
Atenção professor: Resposta de acordo com os dados levantados pelo estudante. Fim da observação.
MANUAL DO PROFESSOR
Atividade 2
A atividade explora a tabela de dupla entrada. Se necessário, retome a leitura dos dados nesse tipo de tabela.
Discuta com os estudantes as informações dadas por Marta:
• Se todos os dias têm 5 aulas, cada coluna deve totalizar 5. Assim, podemos preencher as quantidades de aulas que faltam na primeira, segunda, quarta e quinta coluna, respectivamente, com 1 (aula de dança e música), 3 (aulas de pintura e desenho), 2 (aulas de dança e música) e 0 (aula de teatro e cinema).
• Se para cada tipo de aula há um único dia com 3 aulas, observando as linhas, vamos verificar que na linha correspondente a teatro e cinema falta esse dia com 3 aulas. Sendo assim, na quarta-feira deve haver 3 aulas de teatro e cinema.
• Por fim, podemos completar a coluna relativa à quarta-feira, colocando 0 aula para pintura e desenho.
Em seguida, discuta as questões com os estudantes, incentivando-os a buscar os dados na tabela que completaram.
Atividade 3
Depois de listarem o mês de aniversário de cada estudante da sala na lousa, auxilie-os na organização dos dados em uma tabela. Eles podem montar a tabela horizontalmente, indicando na primeira linha o mês e na segunda, a quantidade de estudantes. Como o espaço nas folhas de caderno é maior na vertical, considere a possibilidade de montar a tabela em colunas em vez de em linhas. Depois, com os dados da lousa completam a tabela com a quantidade respectiva a cada mês. Lembre-os de escolher um título para a tabela. Explique a eles que a fonte dos dados pode ser “Estudantes da turma do 2º ano de (ano corrente)”.
Em seguida, peça que se reúnam em duplas e formulem questões sobre a tabela. Depois, que troquem com outra dupla: uma responde às questões que a outra fez. Socialize as questões e as respostas, em uma correção coletiva.
BNCC em foco:
EF02MA23
MP180
O que você aprendeu
Avaliação processual
- Complete com a unidade de medida adequada: metro ou centímetro.
- A altura de um prédio pode ser 25
_____.
PROFESSOR
Resposta: metros
- A gaveta do meu armário tem largura de 40
_____.
PROFESSOR
Resposta: centímetros
- Priscila tem 1
_____
e 52
_____
de altura.
PROFESSOR
Resposta: metro; centímetros
- A altura de um prédio pode ser 25
_____.
- Escreva os horários nos relógios digitais abaixo. Depois, responda às questões.

PROFESSOR
Exemplos de respostas:PROFESSOR
2: 7:00; 3: 11:00; 4: 12:00; 5: 15:00; 6: 21:00.

- Se no dia seguinte Isabela acordou no mesmo horário, quantas horas ela dormiu?
_____
PROFESSOR
Resposta: 9 horas.
- Se Isabela dormir esse mesmo
número
de horas por 3 noites, ela terá dormido mais ou menos de 24 horas?
_____
PROFESSOR
Resposta: Mais de 24 horas.
MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividade 1
A atividade retoma as medidas de comprimento metro e centímetro. Então, sugerimos que, antes de sua realização, você escreva na lousa essas medidas e peça aos estudantes que deem exemplos do que seria adequado medir, utilizando essas unidades para expressar a medida.
Atividade 2
Depois de os estudantes resolverem as questões, pergunte: “O número de horas que Isabela dormiria por três noites corresponde a mais ou a menos de 1 dia?”. (Dormindo 9 horas por noite, em 3 dias dormiria ao todo 27 horas, o que corresponde a 1 dia e 3 horas, ou seja, ela dormiria mais de 1 dia.)
Pergunte: “A rotina de Isabela é igual à de vocês? Vocês seguem uma rotina? Comente alguma atividade que vocês já tiveram de fazer fora de sua rotina”. Ou ainda: “Quais são suas principais atividades no período da manhã? E no período da tarde? E à noite?”.
BNCC em foco:
EF02MA16, EF02MA19
MP181

- Observe o que Luís está dizendo e responda à questão.

- Lucas e Viviane chegaram atrasados e perderam o ônibus da manhã. Quanto tempo falta para o próximo ônibus partir?
_____
PROFESSOR
Resposta: Faltam 4 horas.
- Observe as balanças em equilíbrio e responda à questão.

Observação: As figuras nesta página não estão apresentadas em escala de tamanho. Fim da observação.
- Sabendo que as caixas verdes têm medidas de massa iguais, quantos quilogramas tem a bola roxa?
_____
PROFESSOR
Resposta: 24 quilogramas.
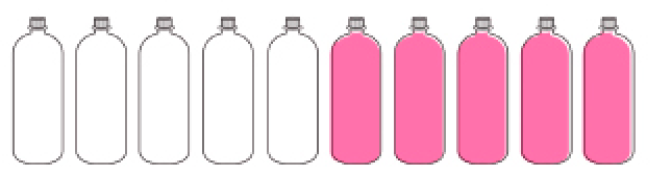
- Bruna fez 5 litros de suco para distribuir entre seus amigos.


- Pinte a quantidade de garrafas de 1 litro que ela conseguirá encher.
PROFESSOR
Exemplo de pintura:
Autoavaliação

- Utilizo unidades de medida padronizadas para expressar medidas de comprimento, massa e capacidade?
PROFESSOR
Resposta pessoal.
- Utilizo unidades de medida de tempo para organizar minhas atividades?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
A atividade incentivará os estudantes a revisarem a leitura de horários no relógio e também a realizarem o cálculo mentalmente. Peça a eles que compartilhem suas estratégias com alguns colegas e observem as deles.
Atividade 4
Na atividade, os estudantes devem relacionar as informações obtidas em duas situações em que as balanças estão em equilíbrio e com os pratos nivelados. Observando a balança da esquerda, pode-se concluir que a massa de uma caixinha é igual a 8 quilogramas; como há três caixas em um dos pratos da balança da direita, pode-se concluir que a bola tem massa igual ao triplo de 8 quilogramas, ou seja, 24 quilogramas.
Atividade 5
Nesta atividade, o estudante deve pintar 5 garrafas quaisquer dentre as 10 apresentadas. Socialize as diferentes maneiras de escolher 5 garrafas que surgirem.
Autoavaliação
Explore e diferencie o uso de medidas padronizadas e de não padronizadas no cotidiano, como o uso de palmos para comparar o comprimento de dois objetos.
Na primeira questão, é importante que os estudantes verifiquem se conseguem relacionar cada unidade de medida à sua respectiva grandeza, não confundindo metro com litro, por exemplo. Na segunda questão, explore o uso de horas, dias, semanas e meses na organização de atividades. Os estudantes podem apontar que conseguem identificar as unidades de medida de tempo, mas que ainda precisam de ajuda de adultos para utilizá-las no dia a dia. Também podem revelar que, embora reconheçam as unidades de medida, ainda não organizam o tempo com autonomia, ou podem apresentar facilidade para lidar com medidas de tempo.
BNCC em foco:
EF02MA17, EF02MA19
MP182
Comentários para o professor:
Conclusão da Unidade 6
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue fazer estimativas, comparar e medir, empregando unidades de medida não padronizadas, nas grandezas comprimento, massa e capacidade? |
_____ |
_____ |
|
Consegue fazer estimativa, comparar e medir comprimentos utilizando como unidade de medida o metro, o centímetro e o milímetro? |
_____ |
_____ |
|
Resolve problemas que envolvem medidas de comprimento a partir de esquemas e plantas? |
_____ |
_____ |
|
Identifica, faz uso, faz estimativa e comparação de medidas de massa, por meio de unidades de medida padronizadas: grama e quilograma? |
_____ |
_____ |
|
Identifica, faz uso, faz estimativa e comparação de medidas de capacidade, por meio de unidades de medida padronizadas: litro e mililitro? |
_____ |
_____ |
|
Estabelece relações entre o símbolo e o que ele representa, ou seja, entre o representante com o representado? |
_____ |
_____ |
|
Identifica e relaciona as unidades de medida de tempo: horas, dias, dias da semana, meses e anos? |
_____ |
_____ |
|
Registra e aplica em problemas períodos de tempo em dias, semanas e meses? |
_____ |
_____ |
|
Mede, registra e aplica intervalos de tempo por meio de relógio digital? |
_____ |
_____ |
|
Faz corretamente a leitura de horas em relógios digitais? |
_____ |
_____ |
|
Estabelece corretamente a equivalência de valores entre moedas e cédulas do sistema monetário brasileiro para resolver situações cotidianas? |
_____ |
_____ |
|
Lê, interpreta e organiza dados coletados em tabelas simples e de dupla entrada? |
_____ |
_____ |
Continua
MP183
Continuação
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Realiza pesquisa escolhendo variáveis categóricas de seu interesse, organizando os dados coletados em listas e tabelas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: _____ |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |