MP184
Comentários para o professor:
Introdução da Unidade 7
A abertura desta Unidade, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior, por meio de observações em sua imagem, permite uma abordagem que leva a um diagnóstico dos conhecimentos já adquiridos, assim como a descobertas do que está por ser tratado ao longo deste 2º ano do Ensino Fundamental.
Nesta Unidade, o foco está em duas Unidades Temáticas: Números e Álgebra. Assim como foi feito nas Unidades anteriores, a ênfase está na abordagem de tais Unidades Temáticas, mas outras permeiam as atividades propostas; é o caso de Grandezas e medidas, mediante conhecimentos relativos às medidas de comprimento, de massa e de tempo, e Probabilidade e estatística, presentes nas atividades com tabelas de dupla entrada.
Espera-se que os estudantes construam conhecimentos relativos a Números na perspectiva da compreensão de fatos básicos da adição e subtração, além da resolução e da elaboração de problemas de adição, subtração, multiplicação, dobro, metade, triplo e terça parte.
Vale observar que esses conhecimentos se pautam naqueles abordados durante o 1º ano e vislumbram outros a serem estudados no 3º ano.
Dessa forma, os estudos sobre adição envolvem os significados já abordados, destacando o uso de estratégias pessoais ou convencionais e dando suporte às estratégias de cálculo mental e estimativa. Em relação à multiplicação, as atividades propostas possibilitam a resolução e elaboração de problemas que abrangem a ideia de adição de parcelas iguais ou reiterada, incluindo conhecimentos como dobro, metade, triplo e terça parte de um número – todos já abordados em Unidades anteriores. Assim, constroem-se possibilidades para a resolução e elaboração de problemas que envolvem, além do significado de parcelas iguais, a disposição retangular – conhecimentos previstos para o 3º ano.
As atividades relativas à Álgebra que abordam a descrição de regularidades em sequências repetitivas e recursivas e, ainda, a descrição dos elementos ausentes de números naturais, objetos ou figuras consolidam os conhecimentos construídos pelos estudantes ao longo do 1º ano. Além disso, observa-se a articulação com conhecimentos a serem desenvolvidos no 3º ano, entre eles, a identificação de regularidades em sequências ordenadas de números naturais, que resultam de operações de adição e de subtração, assim como a descrição da regra de formação e a identificação de elementos faltantes ou dos próximos elementos das sequências.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.
7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
MP185
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção Compreender problemas, desta Unidade.
Roteiro de aula – Compreender problemas
1 ª parte – Introdução – Tempo sugerido: 5 a 10 minutos
Inicie a aula dizendo que esta lição é simples, mas que ela tem um desafio: “Quando é dado um problema, o que é preciso para resolvê-lo?”.
Apresente o desafio na lousa para marcar o foco da aula. Peça aos estudantes que reflitam sobre a pergunta e reserve um tempo para isso. Talvez alguém diga: mas qual é o problema?
Mesmo que isso não aconteça, continue dizendo que para resolver um problema é necessário inicialmente saber qual é o problema, isto é, compreender o problema.
Então anote na lousa (sempre pronunciando em voz alta o que escreve, dado que pode haver estudantes com dificuldade de leitur a) algumas perguntas que podem ajudar a compreender um problema dado:
- Quais são as informações que o problema dá?
- O que o problema pede para obtermos?
Diga então que vamos ler as atividades propostas neste item do livro, tentando sempre responder a essas duas perguntas.
2 ª parte – Atividades – Tempo sugerido: 25 minutos
Problema 1. Leia com os estudantes o enunciado do problema 1. Peça a ajuda da turma para escrever na lousa as respostas às duas perguntas anteriores.
- As galinhas botaram, ao todo, 28 ovos.
Cada galinha botou 2 ovos.
- Quantas são as galinhas?
Esclareça que agora vem a segunda parte da resolução do problema, que é também muito importante: montar uma estratégia de resolução usando as informações para responder à pergunta.
Consulte-os sugerindo se podemos desenhar os 28 ovos e desenhe na lousa 28 ovos.
Peça que desenhem no livro (entre o enunciado e a ilustração) 28 ovos.
Diga que, como temos a informação de que cada galinha botou 2 ovos, vamos então cercar com uma linha grupos de 2 ovos desenhados. Depois que cercarem as duplas de ovos, peça a eles que contem quantos grupos de 2 ovos eles conseguiram cercar. Devem contar 14 duplas de ovos.
Pergunte: qual é o número de galinhas do sítio? Espera-se que concluam que são 14 galinhas.
Esclareça que ainda há uma terceira parte da resolução do problema, que é verificar se 14 é a resposta válida. Para isso, devemos confirmar se as 14 duplas de ovos equivalem ao total de ovos botados. Confirmamos calculando 14 × 2 = 28.
Assim, podemos dizer que resolvemos o problema.
Problema 2. Faça a leitura coletiva do enunciado do problema 2.
Oriente-os a escreverem no caderno:
- Quais são as informações que o problema dá?
- O que o problema pede para obtermos?
Percorra a sala e verifique se eles conseguiram responder as questões a e b acima. Verifique que estratégias estão usando para a resolução ou se é necessário induzi-los, formulando algumas perguntas que os encaminhem à resolução.
3 ª parte – Para refletir – Tempo sugerido: 25 minutos
Sugerimos que esta parte seja feita em duplas. Faça a leitura coletiva das questões da página e valide as respostas com a turma.
Destaque a questão 3, indagando se eles tinham percebido a informação desnecessária (48).
Pergunte se essa informação dificultou o entendimento do problema. Convém alertar que sempre devemos estar atentos e rejeitar as informações que nos desviem do objetivo do problema, assim como verificar se as informações são suficientes, isto é, se não faltam informações que nos permitam resolver o problema.
Na questão 5, verifique se os estudantes percebem que os números da coluna pontos são, respectivamente, o dobro dos números da coluna cestas.
MP186
UNIDADE 7. Operando com números naturais

MANUAL DO PROFESSOR
Objetivos da Unidade
• Construir fatos básicos da adição e da subtração e utilizá-los no cálculo mental ou escrito.
• Perceber a relação inversa entre as operações de adição e de subtração.
• Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
• Descrever um padrão (ou regularidade) de sequências por meio de palavras, símbolos ou desenhos.
• Descrever elementos ausentes em sequências de números naturais.
• Resolver problemas envolvendo adição e subtração.
• Resolver e elaborar problemas de multiplicação.
• Resolver problemas envolvendo o significado da distribuição em partes iguais.
• Resolver problemas envolvendo as noções de dobro, metade, triplo e terça parte.
• Identificar, estimar, usar e comparar medidas de comprimento, utilizando unidades de medida padronizadas: centímetro e metro.
• Ler, interpretar e comparar informações registradas em tabelas simples e em gráficos de colunas simples.
A Unidade retoma as operações de adição, subtração e multiplicação, ampliando as estratégias de cálculo com essas operações, e explora o significado da repartição em partes iguais e as noções de metade e terça parte.
Explore a cena com os estudantes. Em uma roda de conversa, deixe que eles exponham as opiniões sobre o que veem na imagem e as hipóteses quanto ao que as pessoas estão fazendo. Depois, comente que Daniel, Amélia e Bizi compareceram a uma feira beneficente cujo objetivo era doar artigos para cães.
BNCC em foco:
EF02MA05, EF02MA06, EF02MA07, EF02MA08, EF02MA09, EF02MA10, EF02MA11, EF02MA16, EF02MA22
MP187
Para refletir...


Observe a imagem e converse com os colegas.
PROFESSOR
Respostas pessoais.• Você conhece os produtos que estão disponíveis nas mesas?
• Quais produtos você acha que são necessários para cuidar de um cachorro?
• Em cada kit que será doado cabem 2 sacos de ração. Quantos kits são necessários para guardar os 40 sacos de ração que estão em uma das mesas?
PROFESSOR
Resposta: 20 kits.MANUAL DO PROFESSOR
Explique aos estudantes que um evento beneficente pode ser uma alternativa para instituições arrecadarem recursos financeiros a fim de ajudar quem precisa, juntando dinheiro com a venda de produtos ou doando algo a quem não tem condições de comprar.
Verifique se os estudantes observam os diversos estandes expondo alimentos para cães, petiscos, caminhas e kits utilizados para cuidar de cachorros.
Para refletir...
Discuta as questões com os estudantes, incentivando que exponham oralmente as opiniões. Faça outras perguntas, como: “Alguém tem cachorro em casa? O que ele come? Você já comprou ração ou outro produto para o seu cachorro?”, e deixe que os estudantes se expressem livremente.
Peça a eles que determinem a quantidade de latas de alimento para cães e a quantidade de sacos de ração que há na cena. Observe as estratégias utilizadas por eles e incentive-os a contar ou calcular de maneiras diferentes. É possível que contem um a um, mas espera-se que percebam que podem usar adição ou multiplicação, favorecida pela disposição retangular.
Por exemplo:
• Latas de alimentos para cães:
5 × 5 = 5 + 5 + 5 + 5 + 5 = 25
• Sacos de ração Saborosa:
5 × 8 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 40
Ao propor a última questão, deixe que os estudantes discutam entre si uma possível estratégia. Incentive-os a representar a situação com desenhos ou a formar os kits na própria ilustração da cena.
MP188
Adição e subtração
- Calcule o resultado de cada operação e, em seguida, faça o que se pede.
21 + 9 = _____
PROFESSOR
Resposta: 3053 + 7 = _____
PROFESSOR
Resposta: 6034 + 6 = _____
PROFESSOR
Resposta: 4065 + 5 = _____
PROFESSOR
Resposta: 7042 + 8 = _____
PROFESSOR
Resposta: 5076 + 4 = _____
PROFESSOR
Resposta: 80

- Converse com seus colegas sobre os resultados das adições e as estratégias utilizadas para resolver cada operação.
PROFESSOR
Resposta pessoal.
- Converse com seus colegas sobre os resultados das adições e as estratégias utilizadas para resolver cada operação.
- Complete o quadro com os números que estão faltando.
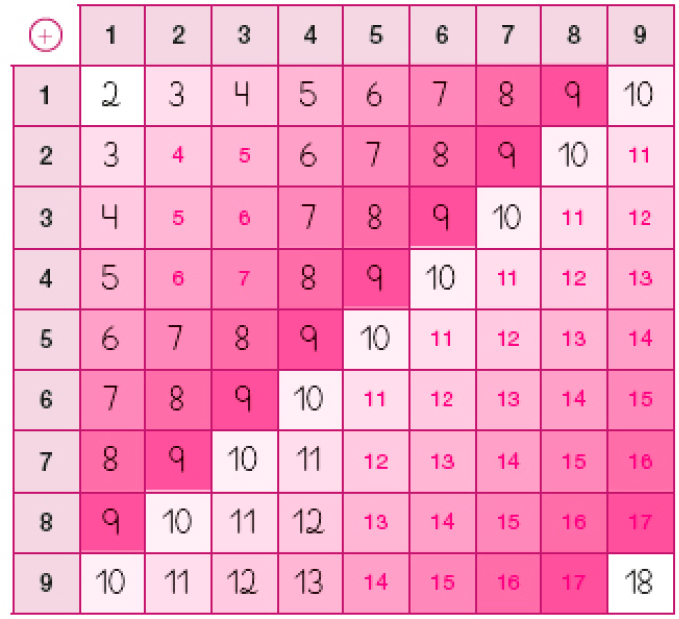

- Agora, pinte os números iguais com a mesma cor.


- Converse com seus colegas sobre o que vocês observaram no quadro.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
• Construir fatos básicos da adição e da subtração e utilizá-los no cálculo mental ou escrito.
• Perceber a relação inversa entre as operações de adição e de subtração.
• Construir sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
• Descrever um padrão (ou regularidade) de sequência por meio de palavras, símbolos ou desenhos.
• Descrever elementos ausentes em sequências de números naturais.
Atividade 1
Antes de propor as adições desta atividade, explore a composição das unidades para formar uma dezena: 1 e 9, 2 e 8, 3 e 7, 4 e 6, 5 e 5.
Espera-se que os estudantes observem que todos os resultados são dezenas inteiras e que utilizem a formação da dezena no cálculo mental, como:
• 21 + 9 = 1 + 9 + 20 = 10 + 20 = 30
• 76 + 4 = 6 + 4 + 70 = 10 + 70 = 80
Atividade 2
Na atividade, os estudantes devem completar um quadro aditivo. Inicialmente, certifique-se de que entenderam como devem proceder: adicionar cada número da linha azul com cada número da coluna azul. Observe se algum deles inicia pelos números da coluna para adicionar aos da linha, o que no caso também é válido pela comutatividade da adição. Se julgar oportuno, explore essa situação. Em uma roda de conversa, discuta com os estudantes o que observaram no quadro. Uma possibilidade: traçando linhas transversais (iniciando da parte superior do quadro, à direit a), todos os números dessas linhas são iguais.
BNCC em foco:
EF02MA05, EF02MA09, EF02MA10; competência geral 2
MP189
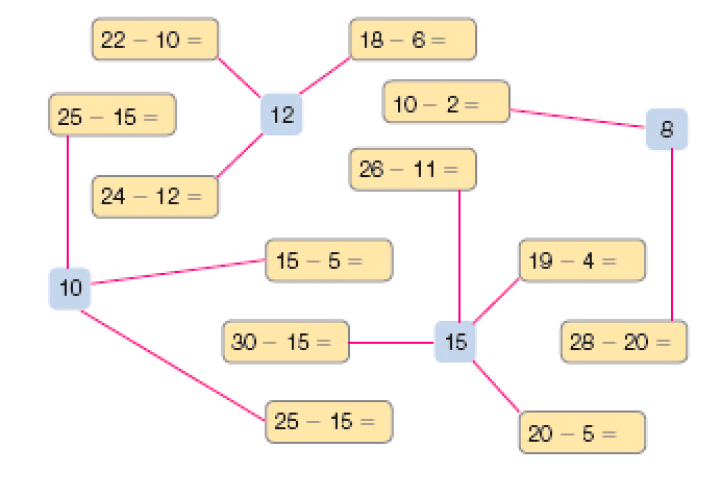
- Ligue cada quadrinho amarelo ao resultado da operação contida nele.
- Complete os quadros com as operações ou os resultados que faltam.
Quadro: equivalente textual a seguir.
|
_____ |
30 |
|
47 − 5 |
_____ |
|
110 − 10 |
_____ |
|
178 − 177 |
_____ |
PROFESSOR
Exemplos de respostas: 54 − 24; 42; 100; 1Quadro: equivalente textual a seguir.
|
317 - 115 |
_____ |
|
_____ |
6 |
|
_____ |
7 |
|
16 - 14 |
_____ |
PROFESSOR
Resposta: 202; 87 − 81; 107 − 100; 2- Complete com os números que estão faltando nas adições e subtrações a seguir.
- 14 +
_____
= 21
PROFESSOR
Resposta: 7
-
_____+
13 = 23
PROFESSOR
Resposta: 10
- 129 +
_____
= 140
PROFESSOR
Resposta: 11
- 132 − 8 =
_____
PROFESSOR
Resposta: 124
- 188 −
_____
= 187
PROFESSOR
Resposta: 1
-
_____
− 5 = 232
PROFESSOR
Resposta: 237
- 14 +
_____
= 21
MANUAL DO PROFESSOR
Atividade 3
A atividade propicia aos estudantes verificar que há subtrações diferentes que produzem o mesmo resultado.
Atividade 4
Peça aos estudantes que compartilhem as respostas com os colegas, a fim de que percebam que, em alguns casos, há mais de uma opção para completar o quadro corretamente.
Atividade 5
Observe como os estudantes procedem para obter os números que faltam.
Por exemplo, na primeira adição, é possível que resolvam o problema adicionando unidades ao 14, uma a uma, até totalizar 21. Incentive os estudantes a perceberem a relação existente entre a adição e a subtração: 21 − 14 = 7. Enfatize que as duas maneiras são estratégias válidas, porém a primeira pode ser mais trabalhosa, caso o número seja maior.
BNCC em foco:
EF02MA05; competência geral 2
MP190
- Complete a sequência com os números que estão faltando.
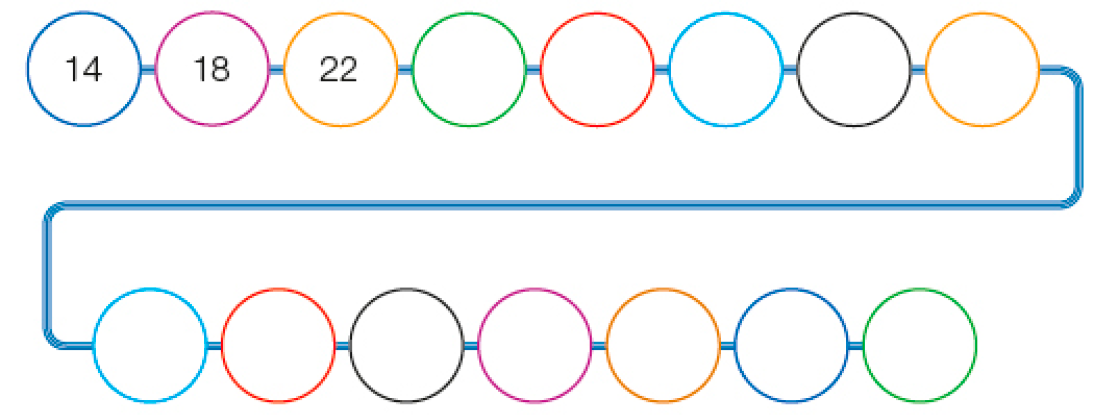
PROFESSOR
Resposta: 26, 30, 34, 38, 42, 46, 50, 54, 58, 62, 66, 70- Qual é a regularidade dessa sequência?
_____
PROFESSOR
Resposta: Os números estão aumentando de 4 em 4.
- Observe a sequência de flores e faça o que se pede.

- Qual seria a cor da próxima flor?
_____
PROFESSOR
Exemplos de resposta: Rosa; amarela.

- Converse com seus colegas sobre duas maneiras diferentes de compor essa sequência de flores.
PROFESSOR
Resposta pessoal.
- Calcule o resultado de cada operação para completar a sequência.

PROFESSOR
Resposta: 4; 6; 1; 4; 6; 1

- Converse com seus colegas sobre a sequência que foi construída com o resultado de cada operação. O que vocês perceberam?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 6
Amplie a atividade e apresente outras sequências que contenham padrões numéricos envolvendo adição ou subtração. Peça que observem os números da sequência e identifiquem alguma regularidade, a fim de obter os demais elementos. Socialize as estratégias utilizadas.
Atividade 7
Os estudantes podem responder rosa, repetindo a sequência de três cores, ou podem dizer amarela, considerando a seguinte sequência: amarela-rosa-vermelha-amarela-amarela-rosa-vermelha-amarela-amarela...
Atividade 8
Verifique se os estudantes percebem que, ao adicionar 3 e depois 2, estão adicionando 5; por isso, ao retirar 5, voltam ao número inicial e a sequência se repete.
BNCC em foco:
EF02MA09, EF02MA10, EF02MA11; competência geral 2
Sugestão de atividade
Números e letras
No quadro, os números em cada fileira (horizontal ou vertical) foram escritos sequencialmente, mas alguns deles estão representados por letras. A que número corresponde cada letra?
Quadro: equivalente textual a seguir.
|
950 |
951 |
952 |
A (953) |
954 |
B (955) |
C (956) |
|
D (960) |
961 |
E (962) |
963 |
F (964) |
965 |
G (966) |
|
970 |
H (971) |
972 |
973 |
974 |
I (975) |
976 |
|
980 |
981 |
982 |
J (983) |
984 |
K (985) |
986 |
|
L (990) |
991 |
992 |
993 |
M (994) |
995 |
996 |
MP191
- Agora é a sua vez. Escolha uma regra e crie uma sequência de números no espaço abaixo.
_____
PROFESSOR
Resposta pessoal.
- Qual seria o próximo
número
da sua sequência? ( )
PROFESSOR
Resposta pessoal.
- Qual é a regra da sequência que você criou?
_____
PROFESSOR
Resposta pessoal.
- Observe a sequência criada por seus colegas e tente descobrir quais foram as regras escolhidas por eles.

- Calcule os resultados das operações.
- 27 − 13 =
_____
PROFESSOR
Resposta: 14
- 14 + 13 =
_____
PROFESSOR
Resposta: 27
- 38 − 16 =
_____
PROFESSOR
Resposta: 22
- 38 − 22 =
_____
PROFESSOR
Resposta: 16
- 21 + 11 =
_____
PROFESSOR
Resposta: 32
- 32 − 11 =
_____
PROFESSOR
Resposta: 21
- 14 + 25 =
_____
PROFESSOR
Resposta: 39
- 39 − 14 =
_____
PROFESSOR
Resposta: 25
- 27 − 14 =
_____
PROFESSOR
Resposta: 13
- 32 − 21 =
_____
PROFESSOR
Resposta: 11
- 16 + 22 =
_____
PROFESSOR
Resposta: 38
- 39 − 25 =
_____
PROFESSOR
Resposta: 14- Observe os números das operações e os respectivos resultados. O que você percebeu?
_____
PROFESSOR
Resposta pessoal.
- Observe os números das operações e os respectivos resultados. O que você percebeu?
- 27 − 13 =
_____
MANUAL DO PROFESSOR
Atividade 9
O objetivo da atividade é que os estudantes apliquem os conhecimentos construídos sobre sequências numéricas. Observe se eles usam uma regularidade na formação de sua sequência. Se julgar necessário, monte uma sequência na lousa com a ajuda da turma. Por exemplo, peça a um estudante que escolha o número com o qual a sequência se iniciará; depois, outro escolhe o padrão de formação a fim de obter os demais números. Então, juntos, construam essa sequência na lousa.
Atividade 10
O objetivo dessa atividade é que os estudantes percebam que a subtração e a adição são operações que se relacionam. Se julgar adequado, comente que a adição e a subtração são chamadas operações inversas . Incentive-os a observar cada grupo de operações. Depois, proponha uma nova subtração para eles escreverem as outras duas operações relacionadas (uma adição e outra subtração).
Sugestão de atividade
Quadrado mágico
Os quadrados mágicos são malhas quadriculadas com três fileiras horizontais e três fileiras verticais, ou quatro fileiras de cada tipo, ou ainda cinco, e assim por diante.
Adicionando os números em cada fileira horizontal, vertical ou diagonal, o resultado obtido é sempre o mesmo. O desafio é completá-las com os números faltantes. Complete o quadrado mágico a seguir apenas com dezenas inteiras: 10, 20, 30, ..., 90, de modo que o resultado das adições em qualquer fileira (horizontal, vertical ou diagonal) seja sempre igual a 150. Não vale repetir números.
Quadro: equivalente textual a seguir.
|
20 |
70 |
60 |
|
90 |
50 |
10 |
|
40 |
30 |
80 |
BNCC em foco:
EF02MA09, EF02MA10; competência geral 2; competência específica 3
MP192
Multiplicação

- Leia e complete.
Marcos comprará _____ bandejas com _____ ovos cada uma.
Quantos ovos ele comprará?
PROFESSOR
Resposta: 4; 6
Adição: 6 + 6 + _____ + _____ = _____
PROFESSOR
Resposta: 6 + 6 + 6 + 6 = 24Multiplicação: _____ × _____ = _____
PROFESSOR
Resposta: 4 × 6 = 24Marcos comprará _____ ovos.
PROFESSOR
Resposta: 24- Sandra produz 2 tipos de espelho em sua empresa: arredondados e retangulares. Leia as falas de Sandra e, em seguida, faça o que se pede.
a)

3 + _____ + _____ + _____ = _____
PROFESSOR
Resposta: 3 + 3 + 3 + 3 = 12_____ × _____ = _____
PROFESSOR
Resposta: 4 × 3 = 12Sandra produzirá _____ espelhos arredondados em 4 dias.
PROFESSOR
Resposta: 12b)

2 + _____ + _____ + _____ = _____
PROFESSOR
Resposta: 2 + 2 + 2 + 2 = 8_____ × _____ = _____
PROFESSOR
Resposta: 4 × 2 = 8Sandra produzirá _____ espelhos retangulares em 4 dias.
PROFESSOR
Resposta: 8MANUAL DO PROFESSOR
Objetivos
• Resolver e elaborar problemas de multiplicação.
• Completar sequências de números naturais em ordem crescente ou decrescente a partir de um número qualquer, utilizando uma regularidade estabelecida.
Atividade 1
Amplie a atividade e pergunte: “Se Marcos comprasse 4 bandejas com 12 ovos cada uma, quantos ovos ele compraria?”. Os estudantes podem obter a resposta calculando o resultado de 12 + 12 + 12 + 12 ou calculando o dobro da resposta obtida no caso das bandejas com 6 ovos.
O estudo das regularidades dos números obtidos como resultado de uma multiplicação do tipo 4 vezes pode ser feito comparando-os com os de uma multiplicação do tipo 2 vezes ou o dobro. Como 4 = 2 × 2, os números do quadro da multiplicação 4 vezes correspondem aos números do quadro de 2 vezes multiplicados por 2.
Atividade 2
Comente que, nesse contexto, não é adequado escrever 3 × 4 = 12 e 2 × 4 = 8, apesar de os resultados serem iguais aos das multiplicações 4 × 3 = 12 e 4 × 2 = 8, respectivamente. Afinal, fabricar 3 espelhos arredondados por dia durante 4 dias é diferente de fabricar 4 espelhos arredondados por dia durante 3 dias, e fazer 2 espelhos retangulares por dia durante 4 dias é diferente de fabricar 4 espelhos retangulares por dia durante 2 dias.
BNCC em foco:
EF02MA07; competência geral 2
Sugestão de atividades
Completando multiplicações
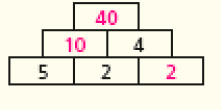
1. Proponha aos estudantes que completem o quadro de multiplicações.
2. Em cada bloco, o número é o resultado da multiplicação dos dois números abaixo dele. Complete com os números que faltam.
Quadro: equivalente textual a seguir.
|
× |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
2 |
2 |
4 |
6 |
8 |
10 |
12 |
|
4 |
4 |
8 |
12 |
16 |
20 |
24 |
CRÉDITO: ADILSON SECCO
MP193
- Veja como Tadeu calculou o resultado de 5 × 1 com a ajuda da reta numérica.

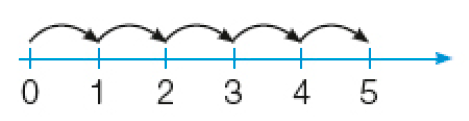
5 × 1 = _____
PROFESSOR
Resposta: 5- Agora, faça como Tadeu, complete e calcule o resultado das seguintes multiplicações nas retas numéricas abaixo.

5 × 2 = _____
PROFESSOR
Resposta: 10
5 × 3 = _____
PROFESSOR
Resposta: 15- Calcule o total de figos das imagens abaixo.

_____ × _____ = _____
PROFESSOR
Resposta: 5 × 8 = 40No total, há _____ figos.
PROFESSOR
Resposta: 40

- Complete a sequência utilizando uma calculadora.

PROFESSOR
Resposta: 27; 81; 243- Quais teclas você apertou?
_____
PROFESSOR
Exemplo de resposta: As teclas: 1, ×, 3 e =.


- Complete o quadro com a massa em grama.
Quadro: equivalente textual a seguir.
|
Quantidade de balas |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|---|---|---|---|---|---|---|---|---|---|---|
|
Massa em grama |
5 |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
MANUAL DO PROFESSOR
Atividade 3
Nessa atividade, mostra-se o uso da reta numérica como recurso para a obtenção do resultado de uma multiplicação do tipo 5 vezes. No caso da multiplicação 5 vezes o número 2, partindo do zero, devemos avançar na reta numérica 2 unidades para a direita por 5 vezes. De modo análogo efetuamos 5 vezes o número 3.
Explore um pouco mais a atividade perguntando: “Se
fosse
necessário
obter
o resultado de uma multiplicação como 5 × 2 com uma calculadora, sem apertar a tecla  , como isso poderia ser feito?”. Uma opção seria apertar as seguintes teclas:
, como isso poderia ser feito?”. Uma opção seria apertar as seguintes teclas:

CRÉDITO: ILUSTRAÇÕES; ADILSON SECCO
Atividade 4
Amplie a atividade perguntando:
• Qual seria o total de figos se houvesse mais uma dessas caixas? Como vocês calculariam esse total?
• É possível descobrir esse total usando o resultado obtido com as 5 caixas de figos?
Espera-se que os estudantes percebam que podemos calcular o resultado de 6 × 8 adicionando 8 ao resultado de 5 × 8, que é igual a 40, e obtendo 48. Essa estratégia pode ser aplicada na realização de cálculo mental, pois eles podem memorizar os resultados de algumas multiplicações e depois usá-los para obter outros resultados.
Atividade 5
Pergunte aos estudantes outra maneira de obter os números usando a calculadora.
Espera-se que eles percebam que é possível obter o número seguinte adicionando o anterior 3 vezes, a partir do segundo número. Por exemplo, para obter 3 fazemos 1 + 1 + 1, para obter 9 fazemos 3 + 3 + 3, para obter o próximo, que é 27, fazemos 9 + 9 + 9, depois fazemos 27 + 27 + 27 obtendo 81 e, por fim, fazemos 81 + 81 + 81 obtendo 243. Também é possível que os estudantes utilizem a multiplicação de cada número por 3 para obter o número seguinte.
Atividade 6
Se necessário, explique aos estudantes que a primeira linha (horizontal) apresenta a quantidade de balas (1, 2, 3, 4, ...) e, abaixo, em correspondência a cada um desses números, há o resultado das multiplicações: 1 × 5, 2 × 5, 3 × 5, 4 × 5 etc.
Sugira aos estudantes que façam no caderno desenhos para auxiliar no preenchimento do quadro. Um exemplo de desenho seria:
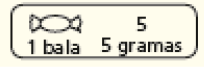

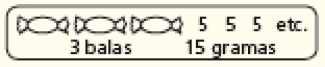
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF02MA07, EF02MA09, EF02MA10; competência geral 2
MP194
Distribuição
- Fábio pediu ajuda a Bruno para distribuir sua coleção de brinquedos antigos entre seus primos.


- Quantos brinquedos antigos sobrarão se cada primo receber 2 brinquedos?
_____
PROFESSOR
Resposta: 8 brinquedos.


- Quantos brinquedos Fábio poderá distribuir para cada primo de modo que não sobre nenhum brinquedo?
_____
PROFESSOR
Resposta: 3 brinquedos.
- Camila entregou 4 pacotes de figurinhas para cada uma de suas 6 amigas. Quantos pacotes de figurinhas, no mínimo, ela tinha para distribuir entre suas amigas?
_____
PROFESSOR
Resposta: 24 pacotes de figurinhas.PROFESSOR
Exemplo de cálculo:PROFESSOR
4 × 6 = 24
MANUAL DO PROFESSOR
Objetivo
• Resolver problemas que envolvem o significado da distribuição em partes iguais.
Os problemas apresentados estão relacionados à ideia de repartir (ou distribuir) em quantidades iguais.
Atividade 1
Os estudantes devem fazer a distribuição dos 24 brinquedos entre 8 primos.
Talvez alguns necessitem fazer desenhos e ligar os brinquedos aos primos, mas outros resolvam agrupando as quantidades de brinquedos para depois distribuí-los. É importante socializar as diferentes estratégias de resolução do problema para que todos possam conhecê-las e discuti-las.
Atividade 2
Comente com os estudantes que a atividade poderá ajudá-los em situações do dia a dia, como em jogos e distribuição de doces ou de figurinhas. Observe quais estratégias de resolução os estudantes utilizam. Depois, compartilhe esses procedimentos e retome as escritas aditiva e multiplicativa.
BNCC em foco:
EF02MA08; competência geral 2
MP195
- De que modo você distribuiria 18 balas para 4 pessoas?
_____
PROFESSOR
Resposta pessoal.
- Se cada pessoa precisasse receber a mesma quantidade de balas, como você faria a distribuição?
_____
PROFESSOR
Resposta: Cada pessoa receberia 4 balas e sobrariam 2 balas.
- Roberto distribuiu igualmente 6 canetas entre seus 3 netos. Com quantas canetas cada
neto
ficou?
A distribuição das canetas foi realizada em 2 etapas, conforme mostrado a seguir.
1ª etapa
Roberto distribuiu uma caneta para cada um de seus netos.

Roberto tinha 6 canetas.
Ele distribuiu 3 canetas.
Restaram _____ canetas.
PROFESSOR
Resposta: 32ª etapa
Novamente, Roberto distribuiu uma caneta para cada um de seus netos.

Roberto ainda tinha 3 canetas.
Ele distribuiu as 3 canetas.
Restou _____ caneta.
PROFESSOR
Resposta: 0Cada neto ficou com _____ canetas.
PROFESSOR
Resposta: 2MANUAL DO PROFESSOR
Atividade 3
Como na proposta inicial nada se fala da distribuição equitativa, é possível que alguns estudantes apresentem uma distribuição não equitativa. Outros podem utilizar o desenho, entre outras estratégias. Incentive também o cálculo mental e a estimativa. Discuta com os estudantes todas essas questões.
Atividade 4
Nesta atividade, Roberto distribuiu em etapas, uma a uma, as canetas entre os três netos. O registro das ações realizadas na forma de subtração possibilita aos estudantes perceber que a distribuição em partes iguais (divisão) pode ser realizada por meio de subtrações sucessivas. Assim, calcular o resultado da distribuição equitativa de 6 canetas para os 3 netos equivale a efetuar 6 − 3 = 3 e 3 − 3 = 0, subtraindo por duas vezes o número 3 do número 6 (que corresponde a quantas vezes a distribuição das canetas foi repetid a) ; por isso o resultado é igual a 2 (duas canetas para cada neto).
Se julgar oportuno, apresente outras situações e peça aos estudantes que as resolvam por meio de subtrações sucessivas, podendo ser representadas por esquemas ou desenhos.
BNCC em foco:
EF02MA08
Sugestão de atividade
Repartindo materiais
Peça a cada estudante que leve para a sala de aula um conjunto de materiais, como palitos de fósforo usados, tampinhas de garrafa, clipes etc. Cada estudante deverá contar a quantidade de unidades do seu material e, depois, reparti-lo igualmente entre os componentes de seu grupo. Se houver sobra, ela deve ser retirada e a repartição refeita com o número que sobrou.
Solicite que registrem no caderno como pensaram.
Aproveite a oportunidade e discuta com os estudantes a respeito do egoísmo e da importância de reconhecer que, em muitas situações da vida, é justo repartir algo em partes iguais, favorecendo, assim, a conscientização sobre esses valores.
MP196
Metade
- Sobre a mesa havia 10 potes de iogurte. Os filhos de Cícera comeram metade dessa quantidade.

- Quantos iogurtes eles comeram?
Havia 10 potes de iogurte sobre a mesa.
Eles comeram _____ potes.
PROFESSOR
Resposta: 5
10 é o dobro de _____.
PROFESSOR
Resposta: 55 é a metade de _____.
PROFESSOR
Resposta: 10

- Dirceu foi à feira e comprou 12 maçãs. Metade da quantidade das maçãs era verde, a outra metade era vermelha. Pinte as maçãs de Dirceu com
 e
e  . Depois, responda às questões.
. Depois, responda às questões.

PROFESSOR
Exemplo de pintura:PROFESSOR
6 maçãs vermelhas; 6 maçãs verdes.- Quantas maçãs vermelhas Dirceu comprou?
_____
PROFESSOR
Resposta: 6 maçãs vermelhas.
- Quantas maçãs verdes Dirceu comprou?
_____
PROFESSOR
Resposta: 6 maçãs verdes.

- Desenhe a metade do dobro de 8 ovos.
_____
PROFESSOR
Resposta: O estudante deve desenhar 8 ovos.
MANUAL DO PROFESSOR
Objetivo
• Resolver problemas envolvendo as noções de dobro e metade.
Provavelmente a ideia de metade é familiar a estudantes dessa faixa etária, em razão de seu uso social. Desse modo, pode-se fazer uma discussão prévia a respeito da palavra metade para verificar o que eles sabem sobre o assunto, pedindo a eles que deem exemplos de situações em que essa ideia aparece.
É comum, entretanto, que reconheçam metade como uma distribuição em duas partes, não necessariamente em partes iguais. Por isso, as atividades dessas páginas possibilitam conceituar metade como uma distribuição em duas partes iguais.
Para calcular a metade de uma quantidade contável, basta repartir essa quantidade em dois grupos de quantidades iguais entre si. Se a metade referir-se a uma figura, como um quadrado ou um círculo, será necessário dividi-la em duas partes de mesmo tamanho (mesma áre a).
Atividades 1 e 2
Nessas atividades, os estudantes devem obter a metade de quantidades em diferentes situações (quantidade de potes de iogurte e quantidade de maçãs). Para explorar mais as atividades, pode-se pedir a eles que completem as frases a seguir com os termos o dobro ou a metade :
• 5 é ________ de 10. (a metade)
• 10 é ________ de 5. (o dobro)
• 12 é ________ de 6. (o dobro)
• 6 é ________ de 12. (a metade)
Atividade 3
Proponha aos estudantes que realizem a atividade em duplas. Observe as estratégias utilizadas e valide-as com eles, socializando os diferentes procedimentos.
Espera-se que os estudantes percebam que, para obter a metade, deverão primeiro saber de que quantidade devem obter essa metade. Incentive-os a fazer desenhos para representar a situação.
Explore a relação entre dobro e metade:
• 10 é o dobro de 5, então 5 é metade de 10.
• 30 é o dobro de 15, então 15 é metade de 30.
• 25 é metade de 50, então 50 é o dobro de 25.
• 20 é a metade de 40, então 40 é o dobro de 20.
Exemplifique essa relação com desenhos na lousa.
BNCC em foco:
EF02MA08
MP197
- Marque com um
X
a resposta correta.
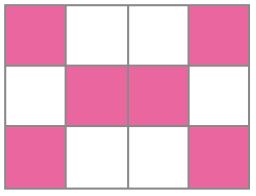
- • Em qual das figuras abaixo a quantidade de quadrinhos pintados não corresponde exatamente à metade da quantidade total de quadrinhos?

( )
( )
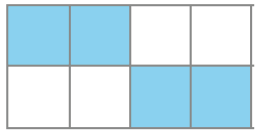
( )
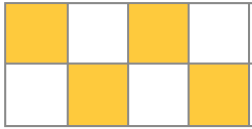
( )
PROFESSOR
Resposta: figura 1.- Veja os ingredientes da receita e escreva a quantidade necessária de cada ingrediente para fazer 20 hambúrgueres.

_____
PROFESSOR
Resposta: • 2 quilogramas de carne moída• 1 cebola pequena picada
• 2 ovos inteiros
• 1 colher (de chá) de azeite
• 4 colheres (de sopa) de farinha de trigo
• sal a gosto
• pão para acompanhar
Boxe complementar:
Desafio
Rafael tem 5 anos de idade, e sua amiga Cláudia tem 12 anos. Os dois fazem aniversário no mesmo dia.
a) Daqui a quantos anos a idade de Rafael corresponderá à metade da idade de Cláudia? _____
PROFESSOR
Resposta: Daqui a 2 anos.b) Qual será a idade de Rafael e de Cláudia quando isso ocorrer?
_____
PROFESSOR
Resposta: Rafael: 7 anos; Cláudia: 14 anos.Fim do complemento.
MANUAL DO PROFESSOR
Atividade 4
Nessa atividade, os estudantes podem comparar a quantidade de quadrinhos pintados e não pintados e verificar que apenas no caso da primeira figura, da esquerda para a direita, essas quantidades não são iguais. Caso haja dúvida, explique que quadradinho pintado é aquele cuja cor difere da cor de fundo da página.
Atividade 5
A atividade propõe uma situação que envolve unidades de medida muito comuns no dia a dia. Para resolvê-la, é necessário que os estudantes percebam que devem encontrar a metade de cada ingrediente da receita apresentada, pelo fato de que o rendimento da receita apresentada é igual a 40 hambúrgueres, e o que se deseja é a metade desse rendimento, ou seja, 20 hambúrgueres.
Desafio
Provavelmente, os estudantes resolverão esse problema por tentativas, aumentando a idade de Rafael e Cláudia de um em um ano, até que a idade de Rafael seja igual à metade da idade de Cláudia. Sugira que organizem as tentativas em um quadro como este:
Quadro: equivalente textual a seguir.
|
Idade de Rafael |
Idade de Cláudia |
|---|---|
|
5 anos |
12 anos |
|
6 anos |
13 anos |
|
7 anos |
14 anos |
Como 7 é a metade de 14, conclui-se que em 2 anos a idade de Rafael corresponderá à metade da idade de Cláudia, o que ocorrerá quando Rafael estiver com 7 anos e Cláudia com 14 anos.
BNCC em foco:
EF02MA08; competência geral 2; competência específica 3
MP198
Terça parte
- Há muitas crianças na fila querendo brincar no gira-gira do parque.
Um terço delas poderá entrar na próxima vez.
- Quantas crianças brincarão na próxima vez?

Há _____ crianças na fila.
PROFESSOR
Resposta: 12Na próxima vez, brincarão 4 crianças.
12 é o triplo de _____.
PROFESSOR
Resposta: 44 é um terço de _____.
PROFESSOR
Resposta: 12

- Pinte um terço das figuras em cada caso e complete.
a)
PROFESSOR
Exemplos de pinturas:
_____ é um terço de _____.
PROFESSOR
Resposta: 3, 9Um terço de 9 camisetas são _____ camisetas.
PROFESSOR
Resposta: 3b)
PROFESSOR
Exemplos de pinturas:
_____ é um terço de _____.
PROFESSOR
Resposta: 10; 30Um terço de 30 bolinhas são _____ bolinhas.
PROFESSOR
Resposta: 10

- Aline tinha 24 peras na fruteira e usou a terça parte dessas peras para fazer um doce. Quantas peras Aline usou?
_____
PROFESSOR
Resposta: 8 peras.
MANUAL DO PROFESSOR
Objetivo
• Resolver problemas envolvendo as noções de triplo e terça parte.
O objetivo das atividades propostas nas páginas é apresentar a ideia de terço. Ao contrário da ideia de metade, encontrar a terça parte ou um terço de uma quantidade não é uma tarefa corriqueira nas práticas sociais. Esse termo não surge com frequência na linguagem cotidiana, o que faz com que sua aprendizagem exija intervenção.
É importante os estudantes compreenderem que calcular um terço de uma quantidade exige repartir essa quantidade em três grupos de quantidades iguais entre si. Obter o terço de uma figura (quadrado ou um círculo) pode exigir o conhecimento de ângulos, o que não é trabalhado com estudantes dessa faixa etária; por isso não há situações com figuras planas.
Atividade 1
A atividade propicia aos estudantes desenvolver a noção de terço ao propor uma situação em que é necessário fazer uma distribuição em três partes iguais. Retome a noção de triplo e explore a relação entre triplo e terça parte, assim como foi feito com dobro e metade.
Atividade 2
Na atividade, os estudantes devem pintar um terço da quantidade apresentada em cada caso.
Uma estratégia possível é, antes de pintar, separar as camisetas (ou bolinhas) em três grupos de mesma quantidade, o que é fácil fazer em razão da disposição retangular das figuras, e, depois, contar quantas camisetas (ou bolinhas) há em cada grupo separado. Esse número é a quantidade de quaisquer camisetas (ou bolinhas) que devem ser pintadas.
Socialize as pinturas para que os estudantes percebam que há maneiras diferentes de pintar, mas que a quantidade que compõe a terça parte é sempre a mesma.
Depois, pode-se pedir a eles que completem frases com um terço ou o triplo. Por exemplo:
• 2 é __________ de 6. (um terço)
• 12 é __________ de 4. (o triplo)
• 15 é __________ de 5. (o triplo)
• 5 é __________ de 15. (um terço)
Atividade 3
Observe as diferentes formas de resolução propostas pelos estudantes e valide-as. Socialize as que julgar importantes para a aprendizagem da turma.
BNCC em foco:
EF02MA08
MP199
- Observe a ilustração e complete.

Há _____ pulseiras para repartir igualmente entre as _____ crianças.
PROFESSOR
Resposta: 15; 3_____ é um terço de _____.
PROFESSOR
Resposta: 5; 15Um terço de _____ pulseiras são _____ pulseiras.
PROFESSOR
Resposta: 15; 5Cada criança ficará com _____ pulseiras.
PROFESSOR
Resposta: 5- Calcule e escreva por extenso cada resultado.
- Um terço de seis.
_____
PROFESSOR
Resposta: Dois.
- Um terço de dezoito.
_____
PROFESSOR
Resposta: Seis.
- Um terço de vinte e um.
_____
PROFESSOR
Resposta: Sete.
- Um terço de três.
_____
PROFESSOR
Resposta: Um.
- Um terço de seis.
_____
Boxe complementar:
Dicas
- Mole percorreu 6 metros.
- Vagaroso andou 3 metros a mais que Mole.
- Lento andou um terço da distância percorrida por Vagaroso.
Fim do complemento.
- Os jabutis Mole, Lento e Vagaroso estavam dando voltas na praça.
- De acordo com as dicas acima, quantos metros andou o jabuti Lento?
Lento andou _____ metros.
PROFESSOR
Resposta: 3- No dia seguinte, Mole percorreu 12 metros e Vagaroso, um terço da distância percorrida por Mole. Quantos metros Vagaroso percorreu?
_____
PROFESSOR
Resposta: 4 metros.
MANUAL DO PROFESSOR
Atividade 4
A atividade pode ser utilizada para reforçar a ideia de que alguns cálculos podem ser úteis em questões do dia a dia deles. Observe a técnica que os estudantes vão utilizar para realizar a repartição das pulseiras entre as crianças. Depois, peça a eles que a compartilhem com os colegas.
Atividade 5
A atividade propõe calcular a terça parte de algumas quantidades.
Atividade 6
A atividade propõe a análise de uma situação de comparação entre as distâncias percorridas pelos jabutis.
Para resolver a primeira questão, é necessário observar as informações no boxe Dicas. Com base no que andou o jabuti Mole (6 metros), deve-se calcular quantos metros o jabuti Vagaroso andou (6 metros mais 3 metros, ou seja, 9 metros) e, depois, calcular um terço dessa distância, relativo ao que o jabuti Lento andou (um terço de 9 metros são 3 metros). Assim, Lento andou 3 metros.
Na segunda questão, sabe-se que o jabuti Vagaroso percorreu um terço do que andou o jabuti Mole, ou seja, deve-se calcular um terço de 12 metros, que é igual a 4 metros.
BNCC em foco:
EF02MA08; competência geral 2
MP200
Jogo: Trilha da diversão

Material: Tabuleiro da página 197, marcadores (um para cada jogador) e 12 cartas da página 199. Depois de recortar o tabuleiro, os marcadores e as cartas, cole-os em papel mais resistente, como cartolina.
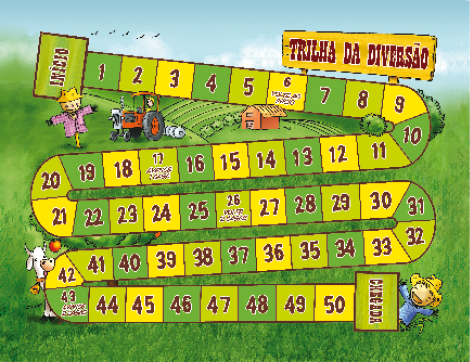

Jogadores: 2, 3 ou 4.
Regras:
- As 12 cartas devem ser embaralhadas e colocadas com as faces voltadas para baixo, formando um monte.
- Os jogadores decidem quem começará a partida.
- Na sua vez, cada jogador pega uma carta de cima do monte e, com seu marcador no tabuleiro, avança o número de casas correspondente ao número representado pela expressão da carta. Se houver alguma instrução na casa em que o marcador parar, o jogador deverá segui-la.
- As cartas com os números 6, 12 e 18 possibilitam que o jogador escolha entre a metade ou um terço do respectivo número.
- Depois de usada, a carta deve ser colocada ao lado do jogador.
- Quando acabarem as cartas do monte, os jogadores devem juntar as cartas usadas, embaralhá-las novamente e fazer um novo monte para continuar a partida.
- Vencerá quem chegar primeiro ao fim da trilha.
MANUAL DO PROFESSOR
Objetivo
• Calcular a metade e a terça parte utilizando cálculo mental e estratégias pessoais em situação de jogo.
Ajude os estudantes na leitura e na compreensão das regras.
Nesse jogo, para movimentar o marcador em cada rodada, os estudantes devem obter o número indicado na carta por meio do cálculo da metade ou de um terço de alguns números e, assim, avançar a quantidade de casas correspondentes ao número obtido.
Jogos como esse geralmente são apreciados pelos estudantes dessa faixa etária, que se sentem motivados a percorrer o caminho mais rapidamente que seus colegas. É importante ler as regras do jogo com eles e ajudá-los a compreendê-las.
Além disso, é fundamental que se familiarizem com as cartas e discutam as opções que têm, porque algumas delas apresentam dois cálculos possíveis (metade ou terça parte). Nesses casos, os estudantes precisam reconhecer que ao repartirem mais partes iguais obtém-se um número menor, ou seja, quando se calculam a metade e um terço de uma mesma quantidade, o maior número é obtido no cálculo da metade.
BNCC em foco:
EF02MA08; competências gerais 2 e 9; competências específicas 7 e 8
MP201
Questões sobre o jogo

- Observe a situação do jogo acima. Cláudia está com seu marcador na casa de
número
23. Ela tirou a carta 6. Ela pode escolher entre a metade de 6 e um terço de 6.
- Qual é a melhor jogada que Cláudia pode fazer?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que a melhor jogada que Cláudia poderá fazer é escolher um terço de 6 e ir até a casa de número 25; se ela escolher a metade de 6, seu marcador cairá na casa de número 26, que a obrigará a voltar 2 casas, ficando na casa de número 24. Fim da observação.
- Qual é a melhor jogada que Cláudia pode fazer?
- O marcador de Rodrigo está na casa de número 31. Ele calculou em seu caderno o número que sua carta indica.

- Qual é a carta de Rodrigo?
_____
PROFESSOR
Resposta: A carta com “A metade de 10”.
- A qual casa seu marcador chegará?
_____
PROFESSOR
Resposta: Chegará à casa de número 36.
- Se o marcador de um jogador estiver na casa de
número
35, que carta o fará avançar 10 casas? Explique sua resposta.
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que é a carta com “A metade de 16”, pois essa carta o fará avançar inicialmente 8 casas, chegando à casa de número 43, que lhe possibilitará avançar mais 2 casas. Fim da observação.
MANUAL DO PROFESSOR
Questões sobre o jogo
Após algumas jogadas, proponha aos estudantes que resolvam, individualmente ou em duplas, as questões propostas. Sugira que tenham o tabuleiro e as cartas à disposição para simular as jogadas.
A questão 1 possibilita a decisão de fazer o cálculo da metade ou de um terço. Para saber qual é a melhor jogada, devem pensar nos dois casos:
• Se Cláudia fizer a metade de 6, ela avançará 3 casas, chegando à casa de número 26.
• Se escolher calcular um terço de 6, ela avançará 2 casas com seu marcador, chegando à casa de número 25.
Observando esses resultados, poderíamos concluir que a melhor jogada seria o cálculo da metade, mas nesse caso o marcador de Cláudia chegaria à casa de número 26, o que a obrigaria a voltar 2 casas e parar na casa de número 24. Complete essa análise perguntando: “Fazer o cálculo cujo número obtido seja o maior é sempre a melhor jogada? Por quê?”.
Na questão 2, os estudantes precisam reconhecer que os agrupamentos realizados por Rodrigo no caderno (2 grupos de 5 palitos) correspondem a obter a metade de 10, que é 5. Para responder ao item b, devem avançar 5 casas a partir da casa de número 31 ou calcular: 31 + 5 = 36.
Na questão 3, os estudantes devem perceber que não é possível avançar 10 casas somente com os números indicados pelas cartas; precisam também observar o tabuleiro. Nele, na casa de número 43 há uma instrução para avançar 2 casas; então, pela carta, basta avançar 8 casas, chegando à casa de número 43, que fará avançar mais 2 casas – o que possibilita avançar 10 casas de uma só vez. Espera-se que os estudantes percebam que a carta com “A metade de 16” possibilita isso.
BNCC em foco:
EF02MA08; competências gerais 2 e 9; competências específicas 1 e 7
Variações
Uma sugestão é confeccionar outras cartas mantendo a mesma ideia, ou seja, algumas cartas com números que são divisíveis por 2 e por 3 (por exemplo, 24 e 36), cartas com números que são divisíveis por 2 e não por 3 (por exemplo, 20 e 22) e outras cartas cujos números são divisíveis por 3 e não por 2 (por exemplo, 21 e 27).
MP202
Compreender problemas
Para resolver
Problema 1
No sítio do vovô João, as galinhas botaram, ao todo, 28 ovos em um só dia. Cada galinha botou 2 ovos. Quantas galinhas há no sítio do vovô João?

No sítio do vovô João, há _____ galinhas.
PROFESSOR
Resposta: 14Problema 2
Em um jogo de basquete, o time de Lucas, Cássio e Adriano marcou 48 pontos, e os três juntos marcaram 36 pontos ao todo. Eles fizeram a mesma quantidade de cestas e todas elas valiam 2 pontos cada uma.

- Quantos pontos fez cada um dos três amigos?
_____
PROFESSOR
Resposta: 12 pontos.
- Quantas cestas fez cada um dos três amigos?
_____
PROFESSOR
Resposta: 6 cestas.
MANUAL DO PROFESSOR
Objetivo
• Resolver problemas envolvendo dobro, metade, triplo e terça parte.
Para resolver
Problema 1
Nessa situação, os estudantes devem identificar os dados relevantes para a resolução do problema: total de 28 ovos, cada galinha botou 2 ovos e a pergunta “Quantas galinhas há no sítio do vovô João?”. Uma estratégia de resolução é fazer agrupamentos de 2 em 2 ovos até obter os 28 ovos, e a quantidade de galinhas é determinada pela quantidade de agrupamentos que conseguirem formar. Se necessário, incentive-os a fazer desenhos para exemplificar a situação.
Problema 2
Espera-se que os estudantes percebam que a informação “o time marcou 48 pontos” não é necessária para a resolução das questões propostas. No item a, os estudantes devem perceber que, se os três amigos fizeram a mesma quantidade de cestas de mesmo valor, o que acarreta mesma pontuação, e ao todo fizeram 36 pontos, basta distribuir igualmente essa quantidade de pontos entre os três para obter a pontuação de cada um.
No item b, espera-se que os estudantes percebam que, se cada cesta feita valia 2 pontos e cada um fez 12 pontos, basta descobrir quantos grupos de 2 pontos podemos formar com esses 12 pontos, ou seja, que número vezes 2 resulta 12 e, assim, obter a quantidade de cestas que cada um fez.
BNCC em foco:
EF02MA08; competência geral 2; competência específica 3
MP203
Para refletir
- Qual foi o cálculo necessário para resolver o Problema 1?
_____
PROFESSOR
Exemplo de resposta: Metade de 28 são 14.
- No Problema 1, se as galinhas botassem ao todo os 28 ovos em 2 dias e cada galinha botasse apenas 1 ovo por dia, mudaria a quantidade de galinhas que há no sítio?
_____
PROFESSOR
Resposta: Não.

- Converse com um
colega
sobre como cada um pensou para responder a essa questão.
PROFESSOR
Resposta pessoal.
- No Problema 2, existe alguma informação desnecessária para sua resolução?
PROFESSOR
Resposta: Sim, a de que o time marcou 48 pontos.
- Quais foram os cálculos necessários para resolver o Problema 2?
_____
PROFESSOR
Exemplos de resposta: a) Um terço de 36 são 12. b) Metade de 12 são 6.
- Um time de basquete tem 5 jogadores em quadra durante um jogo. Considere a ilustração do Problema 2 e responda.
- Quantos jogadores faltavam na cena para completar o time de camiseta verde em quadra?
_____
PROFESSOR
Resposta: 2 jogadores.
- O outro time de basquete marcou 24 pontos, sendo que todas as cestas também valiam 2 pontos. Preencha o quadro com uma possibilidade de quantidade de cestas e de pontos para cada jogador.
- Quantos jogadores faltavam na cena para completar o time de camiseta verde em quadra?
_____
- Converse com um
colega
sobre como cada um pensou para responder a essa questão.
Quadro: equivalente textual a seguir.
|
Jogadores |
Cestas |
Pontos |
|---|---|---|
|
Jogador 1 |
0 |
0 |
|
Jogador 2 |
1 |
2 |
|
Jogador 3 |
_____ |
_____ |
|
Jogador 4 |
_____ |
_____ |
|
Jogador 5 |
_____ |
_____ |
PROFESSOR
Exemplo de respostas: Jogador 3: 4; 8PROFESSOR
Jogador 4: 6; 12PROFESSOR
Jogador 5: 1; 2MANUAL DO PROFESSOR
Para refletir
Atividade 1
Incentive os estudantes a explicarem para os colegas como resolveram o Problema 1, o que aumentará o repertório de estratégias de cada um deles.
Atividade 2
Como cada galinha bota apenas 1 ovo por dia, o total de ovos botados por dia é sempre o mesmo e indica a quantidade de galinhas. Como os 28 ovos são o total dos ovos botados em 2 dias, de acordo com as conclusões anteriores em cada dia foram botados 14 ovos, ou seja, há 14 galinhas. Logo, a quantidade de galinhas não mudaria.
Atividade 3
Peça aos estudantes que façam uma lista ou sublinhem todas as informações dadas no Problema 2 e, depois, que localizem quais dessas informações foram utilizadas na resolução das questões desse problema. Espera-se que os estudantes observem que o total de pontos (48) que o time fez é uma informação que não foi usada.
Atividade 4
Valorize as estratégias pessoais dos estudantes, socialize e comprove-as com a turma.
Atividade 5
Explore a ilustração do Problema 2 com os estudantes. Peça a eles que identifiquem na imagem os jogadores que estão em um mesmo time. Espera-se que percebam esse fato pelas camisetas. Assim, poderão concluir que há 3 jogadores do time verde e que, portanto, faltam 2 jogadores (resposta para o item a).
No item b, há diferentes maneiras de compor 24 pontos. O quadro pode ter várias respostas corretas. Socialize e comprove-as com os estudantes.
BNCC em foco:
EF02MA08; competência geral 2; competência específica 3
MP204
Matemática em textos
Leia
Recordes
Você sabe o que é um recorde? Recorde é algo extraordinário que ultrapassa o que havia sido feito antes ou supera outro de seu tipo ou gênero.
As pessoas batem recordes por diversos motivos: por exemplo, para chamar a atenção sobre uma situação importante, por realização pessoal ou só por diversão.
Conheça alguns recordes.
Maior medalhista olímpico brasileiro
O velejador Robert Scheidt é o maior medalhista do Brasil nos jogos olímpicos, com um total de 5 medalhas, sendo 2 de ouro, 2 de prata e 1 de bronze.
Fonte: http://fdnc.io/eTM. Acesso em: 20 jan. 2021.

LEGENDA: Robert Scheidt nas Olimpíadas do Rio de Janeiro, em 2016. FIM DA LEGENDA.
Pernas mais compridas
A estadunidense Maci Curran tem as pernas mais compridas do mundo. Sua perna direita tem 1 metro e 34 centímetros e a esquerda tem 1 metro e 35 centímetros.

LEGENDA: Maci Curran, Estados Unidos, em 2019. FIM DA LEGENDA.
Cachoeira mais alta do Brasil
A Cachoeira da Fumaça, localizada na Chapada Diamantina (BA), é a cachoeira mais alta do Brasil, com 380 metros.

LEGENDA: Cachoeira da Fumaça, na Chapada Diamantina, Bahia, em 2018. FIM DA LEGENDA.
MANUAL DO PROFESSOR
Objetivos
• Resolver problemas envolvendo adição e subtração.
• Identificar, estimar, usar e comparar medidas de comprimento, utilizando unidades de medida padronizadas: centímetro e metro.
Questione os estudantes sobre alguns recordes que eles possam conhecer e pergunte o que pensam a respeito dos recordes mostrados no texto: “Eles são relevantes, em algum aspecto, para a sociedade? Algum desses recordes ajudou a divulgar alguma causa importante? Que recordes vocês gostariam de superar?”.
Os recordes, no sentido esportivo, adquirem um significado especial por nos inspirarem com histórias de perseverança, determinação, luta diante das dificuldades. No caso de atletas com deficiência, essas qualidades envolvem também a dimensão da inclusão social.
Sugestão de atividade interdisciplinar
Aproveite para discutir valores como respeito ao próximo, aceitação de diferenças, solidariedade e outros. Pode-se complementar esse trabalho, em conjunto com o professor de Educação Física, com uma pesquisa a respeito das estratégias que as pessoas com deficiência desenvolveram para realizar as ações exigidas em cada esporte. Por exemplo: “Como os jogadores de futebol de cinco (para deficientes visuais) localizam-se em quadra? Como eles estimam a distância entre si e o goleiro adversário?”. Selecione um estudante e oriente-o a ficar alguns minutos, por exemplo, com uma venda nos olhos. Em seguida, peça a ele que conte aos colegas as dificuldades encontradas.
BNCC em foco:
EF02MA16
Sugestão de atividade
Pernas mais compridas da turma
Com sua ajuda, um estudante de cada vez mede as pernas de um colega (do quadril até os pés) com uma fita métrica. Então, faça uma tabela com as medidas, em centímetro, na lousa. Depois de anotar todas as medidas, pergunte como fazer para descobrir quem tem as pernas mais compridas. Observe como eles comparam os valores da tabela e ajude-os, se for necessário.
Explore mais o tema sugerindo outras categorias para os estudantes descobrirem quem é o recordista da turma: quem tem os avós mais idosos, quem tem o nome mais comprido etc.
MP205
Maior medalhista brasileiro em paraolimpíadas
Daniel Dias, nadador brasileiro, é recordista paraolímpico com 24 medalhas, sendo 14 de ouro, sete de prata e três de bronze.
Fonte: http://fdnc.io/eTN. Acesso em: 20 jan. 2021.

LEGENDA: Daniel Dias, nas Paraolimpíadas do Rio de Janeiro, em 2016. FIM DA LEGENDA.
Responda
- Quantas medalhas olímpicas o velejador Robert Scheidt já conquistou?
_____
PROFESSOR
Resposta: 5 medalhas.
- Quantos metros tem a cachoeira mais alta do Brasil?
_____
PROFESSOR
Resposta: 380 metros.
- Quantas medalhas de ouro o nadador Daniel Dias conquistou em Paraolimpíadas?
_____
PROFESSOR
Resposta: 14 medalhas.
Analise
- Cada uma das pernas de Maci Curran tem mais de 1 metro ou menos de 1 metro de comprimento?
_____
PROFESSOR
Resposta: Mais de 1 metro de comprimento.
- No Havaí, há uma cachoeira que possui 520 metros a mais do que a cachoeira da Fumaça. Qual é a altura dessa cachoeira localizada no Havaí?
_____
PROFESSOR
Resposta: 900 metros.
Aplique

Faça uma estimativa para descobrir quantas crianças de sua altura teriam de ser colocadas uma em cima da outra para atingir a altura da cachoeira da Fumaça: mais de 100 ou menos de 100? _____
PROFESSOR
Resposta: Mais de 100.MANUAL DO PROFESSOR
Responda
Atividades 1 a 3
Incentive os estudantes a reler o texto, interpretar as perguntas e retirar os dados numéricos para responder às questões.
Analise
Atividade 1
Talvez os estudantes já saibam que 1 metro corresponde a 100 centímetros. Inicialmente, deixe que discutam a questão entre eles, para que você perceba os conhecimentos que já têm sobre isso. Depois, com o auxílio de uma fita métrica ou trena, peça aos estudantes que observem e descubram o comprimento correspondente a 100 centímetros. Mostre a eles que, nesses instrumentos, também há a indicação dos comprimentos em metro. Peça a eles que observem novamente e mostrem comprimentos de 1 metro e de 2 metros. Em seguida, solicite a eles que verifiquem na fita métrica (ou tren a) quantos centímetros correspondem ao comprimento de 1 metro. Se necessário, auxilie-os nessa pesquisa. Espera-se que os estudantes percebam a equivalência entre 1 metro e 100 centímetros.
Após essas explorações, proponha a atividade 1. Com esse novo conhecimento, espera-se que os estudantes consigam comparar 100 cm com 132 cm e, assim, concluir que cada uma das pernas da estadunidense Maci Curran tem mais que1 metro de comprimento.
Atividade 2
Incentive os estudantes a buscarem, no texto, dados que não foram apresentados no enunciado da atividade (a altura da cachoeira da Fumaça: 380 metros). Socialize as diferentes estratégias de resolução.
BNCC em foco:
EF02MA06, EF02MA16; competências gerais 1, 2, 3 e 7; competências específicas 2, 6 e 7
Aplique
Se julgar conveniente, após a estimativa feita na atividade, talvez seja interessante que alguns estudantes meçam a altura de um colega para perceber que seriam necessárias mais de 100 vezes a altura de um estudante para atingir os 380 metros da cachoeira da Fumaça.
MP206
Compreender informações
Ler, interpretar e comparar informações em tabelas e gráficos
- Uma distribuidora vende água mineral em 4 recipientes de capacidades diferentes. Veja na tabela a medida de capacidade de cada recipiente e seu preço. Depois, responda às questões.
Venda de água mineral
Tabela: equivalente textual a seguir.
|
Capacidade do recipiente |
1 litro |
2 litros |
5 litros |
20 litros |
|---|---|---|---|---|
|
Preço de venda |
3 reais |
4 reais |
10 reais |
20 reais |
Fonte: Distribuidora pesquisada (out. 2023).
- Quanto custa cada litro de água mineral no recipiente de 20 litros? E no de 5 litros?
_____
PROFESSOR
Resposta: Cada litro de água mineral custa 1 real no recipiente de 20 litros e 2 reais no de 5 litros.
- Levando em consideração os valores obtidos no item a, seria mais vantajoso comprar água no recipiente de 20 litros ou de 5 litros? Explique.
_____
PROFESSOR
Resposta: Espera-se que o estudante responda que seria mais vantajoso comprar água no recipiente de 20 litros, pois o preço de cada litro de água mineral sai 1 real mais barato.
- Cerque com uma linha a menor quantidade de cédulas suficiente para pagar três recipientes de 2 litros de água mineral.

PROFESSOR
Resposta: cédula de 20 reais.

- Considerando sua resposta no item c, haverá troco ou não ao fazer esse pagamento? Caso haja, de quanto será o troco?
PROFESSOR
Resposta: Haverá troco de 8 reais.
MANUAL DO PROFESSOR
Objetivo
• Ler, interpretar e comparar informações registradas em tabelas simples e em gráficos de colunas simples.
Existe uma grande variedade de tipos de gráfico. Entretanto, nos anos iniciais, os gráficos de colunas e os de barras são os mais explorados, devido ao modo de organização da informação, que se aproxima das situações indicadas para essa faixa etária.
Nesta Unidade e na próxima, os estudantes ampliarão os conhecimentos analisando e construindo gráficos de colunas.
Atividade 1
Retome com os estudantes a leitura de uma tabela e, se julgar necessário, antes de propor a atividade, propicie uma situação em que eles possam montar uma tabela com informações fornecidas por você, na lousa.
Peça a eles que expliquem do que trata a tabela apresentada nesta atividade e que descrevam os dados organizados. Eles devem observar que, na primeira linha, aparecem as capacidades dos recipientes comercializados pela distribuidora e, na segunda linha, o preço de venda de cada um desses recipientes.
Discuta as questões propostas com os estudantes, pedindo a eles que justifiquem as respostas.
No item a, espera-se que percebam que:
• se o recipiente tem capacidade de 20 litros e custa 20 reais, então, nesse caso, cada litro custa 1 real (distribuindo igualmente os reais para cada litro);
• se o recipiente tem capacidade de 5 litros e custa 10 reais, cada litro, nesse caso, custa 2 reais.
No item b, espera-se que o estudante responda que seria mais vantajoso comprar água no recipiente de 20 litros, pois o preço de cada litro de água mineral é a metade do custo na embalagem de 5 litros.
Contudo, no nosso dia a dia, precisamos avaliar a real necessidade de comprar e mesmo de transportar essa quantidade de água mineral, dependendo da situação.
Em uma roda de conversa, incentive os estudantes a exporem as opiniões acerca das questões c e d. Se necessário, relembre o que é troco. Convide aqueles que já sabem para explicar aos demais colegas.
BNCC em foco:
EF02MA22; competências específicas 3 e 4
MP207
- A professora Jurema construiu um gráfico indicando a quantidade de estudantes que obteve cada pontuação na gincana junina.
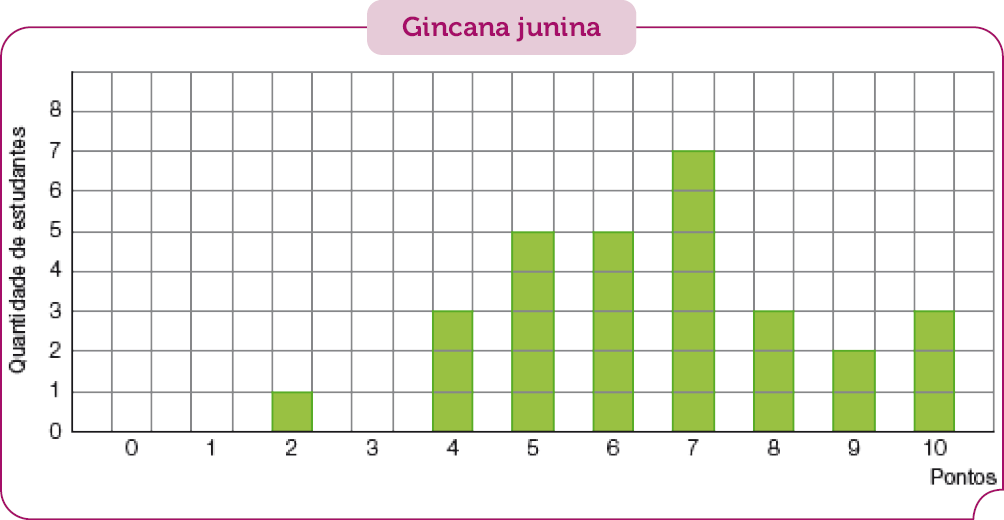
Fonte: Anotações da professora Jurema (jun. 2023).
- Complete a tabela com os dados do gráfico acima.
Gincana junina
Tabela: equivalente textual a seguir.
|
Pontos |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Quantidade de estudantes |
_____ |
0 |
1 |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
Fonte: Anotações da professora Jurema (jun. 2023).
PROFESSOR
Resposta: 0; 0; 3; 5; 5; 7; 3; 2; 3- Quantos estudantes obtiveram a maior pontuação?
_____
PROFESSOR
Resposta: 3 estudantes.
- Qual foi a pontuação mais
obtida
pelos estudantes?
_____
PROFESSOR
Resposta: 7 pontos.
- Existe alguma pontuação que ninguém obteve? Quais?
_____
PROFESSOR
Resposta: Sim: 0, 1 e 3 pontos.
- Houve mais estudantes que obtiveram menos de 5 pontos ou mais de 5 pontos?
_____
PROFESSOR
Resposta: Mais de 5 pontos.

- Explique para um
colega
como você pensou para responder ao item anterior.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, os estudantes são motivados a produzir uma tabela com base nas observações que fazem sobre os dados apresentados em um gráfico de colunas. Retome e explore com eles a leitura do gráfico.
Depois, proponha que resolvam as questões individualmente e, em seguida, em uma roda de conversa, peça a eles que exponham as respostas e digam como pensaram para obtê-las. Verifique se buscaram as informações no gráfico ou na tabela e discuta com os estudantes em qual deles é mais fácil obter os dados.
Para os itens e e f, organize os estudantes em duplas. Um exemplo de explicação é: Observei no gráfico que há mais quadrinhos pintados para pontuações maiores que 5 pontos do que menores que 5 pontos.
BNCC em foco:
EF02MA22; competências específicas 3 e 4
Sugestão de leitura para o professor
Artigo
SELVA, Ana Coelho Vieira. Crianças da educação infantil explorando gráficos de barras. Disponível em: http://fdnc.io/eTP. Acesso em: 2 fev. 2021.
O artigo apresenta uma pesquisa exploratória realizada com crianças de Educação Infantil a respeito da compreensão de gráficos de barras, por meio de atividades de resolução de problemas aditivos com blocos de encaixe e por meio da representação convencional do gráfico de barras.
MP208
O que você aprendeu
Avaliação processual
- Roberto tinha algumas
bolinhas
de gude para jogar. Durante o jogo, ganhou 8
bolinhas
de gude de Paola e 9 de Juliana. Depois de jogar, Roberto ficou com 29
bolinhas
de gude. Quantas
bolinhas
de gude Roberto tinha no início do jogo?
_____
PROFESSOR
Exemplos de cálculo:PROFESSOR
8 + 9 = 17PROFESSOR
29 − 17 = 12
Roberto tinha _____
PROFESSOR
Resposta: 12 bolinhas de gude.- Em um ônibus, havia 12 passageiros. Na primeira parada entraram outros 5. Na segunda parada, alguns passageiros saíram. Ficaram 14 passageiros no ônibus. Quantos passageiros saíram na segunda parada?
PROFESSOR
Exemplos de cálculo:PROFESSOR
12 + 5 = 17PROFESSOR
17 − 14 = 3
Na segunda parada saíram _____
PROFESSOR
Resposta: 3 passageiros.- Observe a multiplicação representada na reta numérica.
4 × 2 = 8:

- Agora, complete a reta numérica e calcule.
3 × 3 = _____:

PROFESSOR
Resposta: 9
- Sônia tinha uma caixa de bombons e os distribuiu igualmente entre seus 4 sobrinhos. Não sobrou nenhum bombom, e cada sobrinho recebeu apenas bombons inteiros. Quantos bombons havia na caixa? Apenas uma alternativa é correta. Marque-a com um
X
.
( ) 9 bombons.
( ) 11 bombons.
( ) 16 bombons.
PROFESSOR
Resposta correta: 16 bombons.
MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Atividades 1 e 2
Nestas atividades, os estudantes devem mobilizar seus conhecimentos para resolver problemas de adição e subtração. Verifique as estratégias utilizadas por eles, que podem, por exemplo, adicionar os dois números que já têm e subtrair da quantidade final apresentada. Socialize as diferentes maneiras que surgirem e valide-as com os estudantes.
Atividade 3
A atividade retoma a representação da multiplicação na reta numérica.
Atividade 4
A atividade tem solução única entre as alternativas apresentadas, mas, se elas não fossem colocadas, haveria outras soluções possíveis. Como os bombons são distribuídos igualmente entre os quatro sobrinhos, o número de bombons poderia ser: 4, 8, 12, 16, 20, 24, ...
BNCC em foco:
EF02MA06, EF02MA07, EF02MA08
MP209
- Marina tem 18 peixes e colocará 6 peixes em cada aquário. De quantos aquários Marina vai precisar?
Marina vai precisar de _____ aquários.
PROFESSOR
Resposta: 3- Descubra a regra de cada sequência numérica e complete-as com os números que faltam. Depois, complete as frases.
a)

PROFESSOR
Resposta: 205 é a metade de _____.
PROFESSOR
Resposta: 1020 é o dobro de _____.
PROFESSOR
Resposta: 10b)

PROFESSOR
Resposta: 271 é um terço de _____.
PROFESSOR
Resposta: 39 é o triplo de _____.
PROFESSOR
Resposta: 3- Leia as dicas, observe as balanças e complete as frases.
Boxe complementar:
Dicas
- As balanças estão em equilíbrio.
- As bolas têm massas iguais.
- As caixas têm massas iguais.
Fim do complemento.
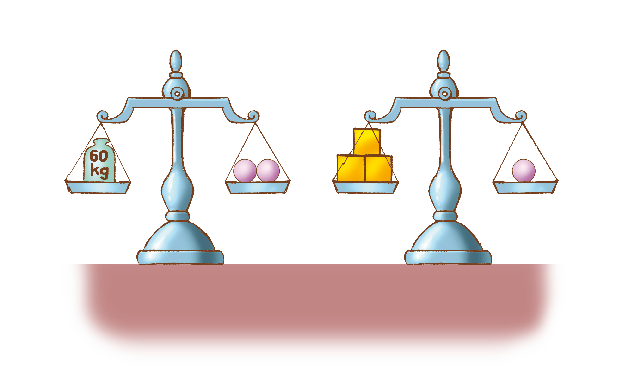
- Cada bola tem
_____
kg.
PROFESSOR
Resposta: 30
- Cada caixa tem
_____
kg.
PROFESSOR
Resposta: 10
Autoavaliação

- Consigo identificar os padrões em sequências numéricas e completá-las com os números que faltam?
PROFESSOR
Resposta pessoal.
- Consigo resolver problemas que envolvem o dobro ou a metade? E problemas que envolvem o triplo ou a terça parte?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 5
Observe as estratégias utilizadas: fazer desenhos dos peixes, indicar os agrupamentos com tracinhos ou separar 6 peixes a cada etapa para formar um aquário e repetir o procedimento até acabarem os peixes (usando subtrações sucessivas).
Atividade 6
Analise e complete na lousa, com os estudantes, as duas sequências apresentadas, explorando suas regularidades. No caso do item a, uma sequência decrescente, eles podem dizer que “o número seguinte é metade do anterior”; no item b, uma sequência crescente, eles podem dizer que “o número seguinte é o triplo do anterior”.
Atividade 7
Na atividade, combina-se o cálculo da metade e da terça parte de quantidades em um mesmo problema.
Na primeira balança, os estudantes devem calcular a metade de 60 quilogramas para saber a massa de cada bola; na outra balança, 3 caixas se equilibram com uma das bolas, que tem 30 quilogramas, e a turma deve calcular sua terça parte, já que as caixas têm massas iguais, obtendo como resultado a massa de cada caixa (10 quilogramas).
Autoavaliação
Na primeira questão, os estudantes podem destacar sequências em que tenham mais facilidade (como as que apresentam relações com dobros, triplos ou adições) e outras em que encontram dificuldade pelo fato de os intervalos não fazerem parte de seus repertórios. Sempre incentive os estudantes a justificarem suas respostas, de modo que possam refletir sobre lacunas no aprendizado e potencialidades para avançar.
Na segunda questão, espera-se que os estudantes reflitam sobre como lidam com os problemas que envolvem dobro, metade, triplo e terça parte, resgatando as estratégias utilizadas.
É provável que já tenham entrado em contato com esses termos em diferentes situações do cotidiano; assim, neste momento de reflexão, é importante buscarem relações de tais experiências com os estudos em sala de aula.
BNCC em foco:
EF02MA07, EF02MA08, EF02MA11
MP210
Comentários para o professor:
Conclusão da Unidade 7
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue resolver e elaborar problemas de adição e de subtração com os significados de juntar, acrescentar, separar e retirar, empregando estratégias pessoais? |
_____ |
_____ |
|
Resolve e elabora problemas de multiplicação (por 2, 3, 4 e 5) com a ideia de adição reiterada mediante estratégias e formas de registro pessoais, usando ou não imagens, reta numérica e/ou material manipulável? |
_____ |
_____ |
|
Resolve e elabora problemas envolvendo as ideias de distribuição, de dobro, metade, triplo e terça parte, com o apoio ou não de imagens ou de material manipulável, usando estratégias pessoais? |
_____ |
_____ |
|
Constrói sequências de números naturais em ordem crescente/decrescente a partir de um número qualquer, por meio de uma regularidade dada? |
_____ |
_____ |
|
Identifica regularidades e descreve os elementos ausentes em sequências recursivas numéricas e figurais? |
_____ |
_____ |
|
Consegue estimar, medir e comparar comprimentos empregando unidades de medida não padronizadas e padronizadas (metro, centímetro e milímetro) e instrumentos adequados? |
_____ |
_____ |
|
Lê, interpreta e compara informações registradas em tabelas e em gráficos de colunas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |