MP211
Introdução da Unidade 8
A abertura da Unidade, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior, propõe uma abordagem de observações e de descobertas por meio de uma imagem com a qual crianças na faixa etária dos estudantes do 2º ano do Ensino Fundamental se identificam.
A Unidade 8, com foco na Unidade Temática Geometria, encerra os estudos deste volume. Nela serão retomados os conhecimentos relativos às figuras geométricas planas e figuras geométricas não planas já abordados na Unidade 1.
Em relação às figuras geométricas não planas (cubo, bloco retangular, pirâmide, cone, cilindro e esfera), as atividades propostas evidenciam suas relações com objetos do mundo físico.
Sobre as figuras planas (círculo, quadrado, retângulo e triângulo), as atividades buscam o reconhecimento, a comparação e sua nomeação por meio da identificação de características comuns em desenhos. Também procuram efetivar a relação destas com as superfícies de representações de figuras geométricas não planas, por meio das planificações.
Assim, esses conhecimentos constituem-se aportes a outros a serem desenvolvidos no 3º ano, os quais envolvem a nomeação das figuras geométricas não planas e a relação de algumas dessas figuras com suas planificações. Serão aporte, também, aos estudos acerca das figuras geométricas planas, notadamente a classificação e comparação de triângulos, quadrados, retângulos, trapézios e paralelogramos, em relação a seus lados (quantidade, posições relativas e comprimento) e vértices.
A seção Compreender problemas contribui com o aspecto lúdico do Tangram e com a perspectiva de desenvolver no estudante, além do olhar crítico assentado na aplicação da simetria, a composição de figuras.
A seção Matemática em textos também contribui com o aspecto lúdico, retoma o tema da abertura da Unidade e traz outras informações em um contexto familiar ao estudante do Ensino Fundamental.
Por fim, a Unidade Temática Probabilidade e estatística é contemplada na seção Compreender informações com a leitura e interpretação de tabelas e de gráficos e pretende ser esteio para aprofundamento e ampliação no 3º ano da resolução de problemas com dados apresentados em tabelas de dupla entrada e gráficos de barras e de colunas.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.
7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
Competências específicas favorecidas
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
MP212
UNIDADE 8. Conhecendo as figuras

MANUAL DO PROFESSOR
Objetivos da Unidade
• Reconhecer, nomear e comparar figuras geométricas não planas: cubo, paralelepípedo, pirâmide, cone, cilindro e esfera.
• Relacionar figuras geométricas planas com as partes planas da superfície de figuras geométricas não planas.
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
• Explorar a composição de figuras geométricas planas usando o Tangram.
• Organizar dados coletados em tabelas e em gráficos de colunas simples.
No início do Ensino Fundamental, às vezes, os estudantes classificam figuras geométricas com base em atributos não relevantes, como cor, textura ou material. É provável que, nesse momento da aprendizagem, os estudantes já tenham superado essa fase, mas observe se ainda apresentam dificuldade.
Observe também se os estudantes fazem descrições misturando designações de figuras geométricas não planas com figuras geométricas planas. Por exemplo, um cubo ser descrito como um quadrado, uma pirâmide como um triângulo, uma esfera como um círculo etc. Isso não implica que eles considerem que o quadrado é a mesma figura geométrica que o cubo; pode apenas ser o uso inapropriado da linguagem matemática.
Oriente os estudantes a observarem nas imagens as nuances das cores aplicadas nas figuras não planas que representam os objetos tridimensionais. Assim, eles terão mais facilidade em reconhecê-las e diferenciá-las das figuras planas.
BNCC em foco:
EF02MA14, EF02MA15, EF02MA22, EF02MA23
MP213
Para refletir...

• Quais figuras geométricas planas ou não planas você identifica nessa cena?
PROFESSOR
Resposta pessoal.

Observe os objetos abaixo e, depois, responda às questões.
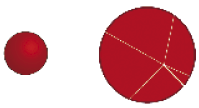
PROFESSOR
Respostas pessoais.• O que eles têm de parecido?
• O que eles têm de diferente?
MANUAL DO PROFESSOR
Como uma figura geométrica não plana está representada em uma página que é plana, leve para a sala de aula, sempre que possível, modelos de figuras geométricas não planas para se assegurar de que os estudantes relembrem essa representação. Pelo contato com essa representação ao longo das atividades, ela se tornará comum, e gradativamente os estudantes se apropriarão dela.
Estudar formas e relações entre elementos de figuras planas e espaciais associadas aos objetos que nos cercam, além de desenvolver o pensamento geométrico do estudante, dá a ele ferramentas e autonomia para a resolução de diversos problemas do mundo físico.
Para refletir...
Explore a cena com os estudantes, incentivando-os a falar sobre a imagem, que apresenta crianças e adultos aproveitando um dia ensolarado em um parque, crianças produzindo e empinando pipas, uma família lanchando. Espera-se que os estudantes observem que as pipas e embalagens sobre a mesa lembram figuras geométricas.
Exemplos de resposta para a primeira questão proposta: cubo, paralelepípedo, cilindro, pirâmide, esfera, quadrado, triângulo, retângulo.
Na busca de semelhanças e diferenças entre os objetos mostrados, espera-se que os estudantes identifiquem:
• como possíveis semelhanças: a cor vermelha e a forma arredondada;
• como possíveis diferenças: a bola é redonda e a pipa é achatada.
MP214
Objetos que parecem figuras geométricas
- Observe a cena abaixo e responda às questões.

- Escreva o nome de pelo menos um elemento presente na imagem da cozinha que parece uma figura geométrica não plana.
_____
PROFESSOR
Exemplo de resposta: relógio.
- Qual figura geométrica plana pode ser identificada na figura geométrica não plana respondida na questão anterior?
_____
PROFESSOR
Exemplo de resposta: círculo.
- Observe as imagens abaixo e, em seguida, responda.




Observação: Os objetos nesta página não estão apresentados em escala de tamanho. Fim da observação.
- Com quais figuras geométricas não planas os objetos representados se parecem?
_____
PROFESSOR
Resposta: Cone, esfera, paralelepípedo e cilindro.
- Quais figuras geométricas planas podemos identificar nas figuras geométricas não planas citadas na questão anterior?
_____
PROFESSOR
Resposta: Círculo e retângulo.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas: cubo, paralelepípedo, pirâmide, cone, cilindro e esfera.
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
Atividade 1
Amplie a atividade e peça aos estudantes que, em grupos, confeccionem um cartaz com desenhos das figuras planas estudadas e os respectivos nomes. Deixe os cartazes em um lugar visível para que os estudantes possam recorrer a eles sempre que necessário. Esse tipo de exposição também auxilia a memorizar o nome das figuras relacionando-o às imagens.
Atividade 2
Espera-se que os estudantes consigam identificar as figuras geométricas planas. Além disso, eles devem identificar as figuras geométricas não planas nos sólidos que correspondem aos objetos fotografados. Incentive-os a nomear as figuras geométricas que já conhecem e a trocar ideias com os colegas para ampliar seus conhecimentos acerca delas. Comente com os estudantes que os objetos fotografados são modelos de figuras geométricas.
Observe alguns critérios empregados pelos estudantes para diferenciar uma figura de outra, de acordo com certas características – que podem se referir ao fato de ela ser plana ou não plana, apresentar “pontas” (vértices), ter superfície arredondada ou não etc. Verifique a compreensão dos critérios utilizados para identificar, comparar e classificar as figuras, orientando os estudantes, se necessário.
BNCC em foco:
EF02MA14, EF02MA15
MP215
Planificando superfícies
- Dora gosta de montar e de desmontar modelos.

- Ao desmontar o
modelo
de paralelepípedo, Dora obteve quantas partes?
_____
PROFESSOR
Resposta: 6 partes.
- Qual é o nome da figura geométrica com que cada uma dessas partes parece?
_____
PROFESSOR
Resposta: Retângulo.

- Ao desmontar o
modelo
de cubo, Dora obteve quantas partes?
_____
PROFESSOR
Resposta: 6 partes.
- Cada uma dessas partes parece uma figura geométrica plana. Qual é o nome dela?
_____
PROFESSOR
Resposta: Quadrado.
MANUAL DO PROFESSOR
Objetivos
• Relacionar figuras geométricas planas com as partes planas da superfície de figuras geométricas não planas.
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
As atividades destas páginas exploram as figuras geométricas planas quadrado e retângulo a partir da desmontagem de um modelo de paralelepípedo e de um modelo de cubo.
É importante que os estudantes não confundam a nomenclatura e saibam as diferenças entre um quadrado e um cubo. Por exemplo, o quadrado é uma figura plana, já o cubo é uma figura não plana, cujas faces são quadradas.
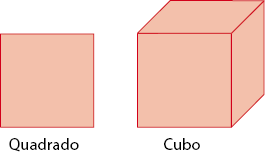
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Atividade 1
A situação propõe abordar as figuras geométricas planas – quadrados e retângulos (não quadrados) – relacionando-as às faces de figuras geométricas não planas – cubos e paralelepípedos (não cúbicos). Se possível, peça antecipadamente aos estudantes que separem em casa algumas embalagens de papelão que lembrem cubos e outras que lembrem paralelepípedos e as levem para a sala de aula, de modo que possam desmontá-las e reconhecer as figuras geométricas planas em suas partes, como fez Dora.
Faça perguntas para que a turma perceba características comuns e características diferentes entre os quadrados e os retângulos (não quadrados). Por exemplo: “O que há de parecido entre essas duas figuras geométricas? Como você explicaria a diferença entre elas?”.
Quando os estudantes observam figuras desenhadas, e não seus modelos concretos, e mostram-se capazes de compreender algumas de suas características, isso indica que atingiram um nível em que a justificativa de propriedades é feita por meio da produção de imagens mentais e não mais por manipulação. Entretanto, quando o estudante trabalhou primeiro no concreto, geralmente tem mais facilidade de visualizar as características das figuras quando desenhadas no papel.
BNCC em foco:
EF02MA15; competência geral 2; competência específica 6
MP216
- Observando sua sala de aula e seu material escolar, você vê algo que parece um retângulo? Identifica algo que parece um quadrado? O quê?
_____
PROFESSOR
Exemplos de respostas: Parecem um retângulo: lousa, capa do livro, porta, tampos da carteira e da mesa do professor. Parece um quadrado: folha de papel para fazer dobradura.
- Observe a embalagem abaixo.


- Se ela for desmontada, quais das partes abaixo vamos obter? Pinte-as.
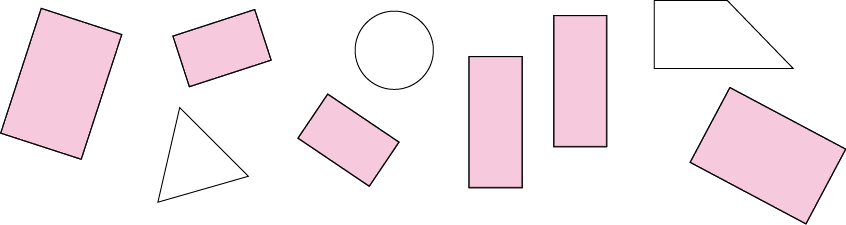
- As partes que você pintou parecem que figura geométrica plana?
_____
PROFESSOR
Resposta: Retângulo.
- Observe o que Carlos fez e, depois, responda às questões.

- Quantas peças Carlos usou para montar o
modelo
de pirâmide?
_____
PROFESSOR
Resposta: 4 peças.
- No
modelo
de pirâmide, foram usadas peças que parecem uma figura geométrica. Qual é o nome dessa figura?
_____
PROFESSOR
Resposta: Triângulo.
MANUAL DO PROFESSOR
Atividade 2
É natural que os estudantes dessa faixa etária não percebam que o quadrado é um tipo de retângulo. Se eles questionarem, isso pode ser mencionado.
Atividade 3
Caso os estudantes tenham dificuldade em considerar as faces “não visíveis” da caixa, utilize uma caixa real para ilustrar a situação e depois a desmonte para que eles vejam as partes que a compõem.
Atividade 4
A atividade possibilita identificar o triângulo a partir da montagem de um modelo de pirâmide.
Se possível, leve para a sala de aula um modelo planificado de pirâmide de base quadrada, pentagonal ou hexagonal, para que a turma observe que as faces laterais das pirâmides têm sempre formato triangular.
É importante também apresentar diferentes triângulos, em posições variadas.
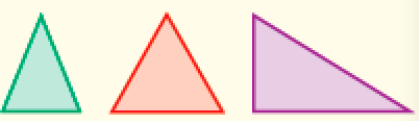
LEGENDA: Imagens clássicas de triângulos. FIM DA LEGENDA.
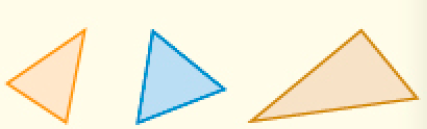
LEGENDA: Outras imagens de triângulos. FIM DA LEGENDA.
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Amplie as observações das propriedades dos triângulos pelos estudantes com perguntas que os levem a notar que eles podem ser definidos como tendo três lados, três vértices ou mesmo três aberturas (ângulos).
Da mesma maneira que um cubo é um caso particular de paralelepípedo, um quadrado é um caso particular de retângulo. Por isso, é possível que alguns estudantes citem um objeto que lembre um quadrado ao se referirem a objetos que lembrem um retângulo.
Estudantes dessa faixa etária, de modo geral, identificam algumas propriedades das figuras geométricas, por exemplo, o fato de todo quadrado ter os quatro lados de mesma medida. Às vezes, porém, eles podem não observar todas as condições que uma figura deve satisfazer para ser um quadrado, como a necessidade de também ter os quatro “cantos”(ângulos) retos.
BNCC em foco:
EF02MA15
MP217

- Faça, no espaço abaixo, o que Melissa está pedindo.

PROFESSOR
Resposta: Exemplos de desenhos:


- Agora, compare seu desenho com o de seu colega. Eles são iguais ou apenas parecidos?
PROFESSOR
Resposta pessoal.
Boxe complementar:
Desafio
Antonela recortou algumas peças como as que estão representadas a seguir.
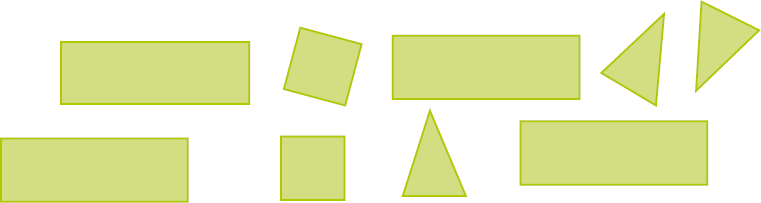
CRÉDITO: RLIMA
a) Com essas peças, é possível formar uma figura que pareça uma pirâmide, em que uma das peças é um quadrado? Por quê?
_____
PROFESSOR
Resposta: Não; pois, para formar uma pirâmide em que uma das peças fosse um quadrado, precisaríamos de 4 triângulos iguais aos que foram recortados, mas só há 3.b) É possível representar uma figura geométrica não plana com as peças acima? Qual?
_____
PROFESSOR
Resposta: Sim; paralelepípedo.Fim do complemento.
MANUAL DO PROFESSOR
Atividade 5
É possível que os estudantes desenhem triângulos e retângulos semelhantes às imagens clássicas. Por isso, a questão proposta para ser discutida oralmente auxilia na percepção da variedade de representações dessas figuras geométricas planas. Se possível, peça a eles que desenhem representações diferentes entre si para fixar no mural da sala de aula, possibilitando a ampliação de repertório geométrico.
É importante que os estudantes percebam que é possível representar diferentes triângulos e retângulos.
Promova com os estudantes uma discussão sobre o que eles acham dos significados das palavras igual e parecido. Avalie a possível comparação: duas pessoas podem ser parecidas (semelhantes), mas não são iguais.
Desafio
Se julgar necessário, reproduza as peças e, com a turma, junte-as para mostrar que não é possível obter uma figura geométrica que lembre uma pirâmide, mas que é possível representar um paralelepípedo.
BNCC em foco:
EF02MA15; competência geral 2; competência específica 6
MP218
O círculo e a esfera
- Laís fez um trabalho usando modelos de figuras geométricas, cartolina e tinta guache.

- Quantas figuras carimbadas apareceram no trabalho de Laís?
_____
PROFESSOR
Resposta: 5 figuras.
- Essas figuras carimbadas parecem qual figura geométrica plana?
_____
PROFESSOR
Resposta: Círculo.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas: cone, cilindro e esfera.
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
As atividades destas páginas possibilitam não somente o reconhecimento do círculo por meio das figuras geométricas não planas cilindro e cone, como também a classificação e a discriminação das outras figuras geométricas planas trabalhadas anteriormente: retângulo, triângulo e quadrado.
Atividade 1
Nessa situação, as representações de círculos, que são figuras planas, foram obtidas a partir da base de um modelo de cone e de cilindro, que são figuras geométricas não planas.
É importante os estudantes observarem que um círculo inclui a região interior, para que nos anos posteriores não se confunda círculo com circunferência, que é a figura geométrica formada apenas pelo contorno do círculo.
Se possível, leve para a sala de aula alguns modelos de cones e de cilindros e peça aos estudantes que, com tinta guache e folhas de papel, façam como Laís. Assim, vivenciando a experiência, poderão se apropriar do conhecimento estudado.
BNCC em foco:
EF02MA15
MP219
- Observe as cenas. Depois, responda à questão.
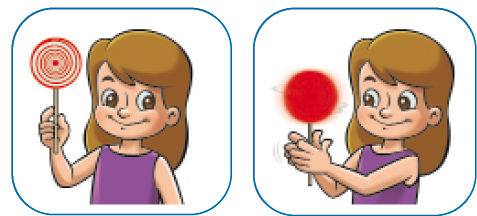
- Ao girar o palito que está fixado ao pirulito, que parece um círculo, a menina obtém uma imagem que parece qual figura geométrica não plana?
_____
PROFESSOR
Resposta: Esfera.
- Marque os desenhos: com C, o que parece um círculo; com R, o que parece um retângulo; com T, o que parece um triângulo.

( )
PROFESSOR
Resposta: C
( )
PROFESSOR
Resposta: R
( )
PROFESSOR
Resposta: TObservação: Os objetos nesta página não foram apresentados em escala de tamanho. Fim da observação.

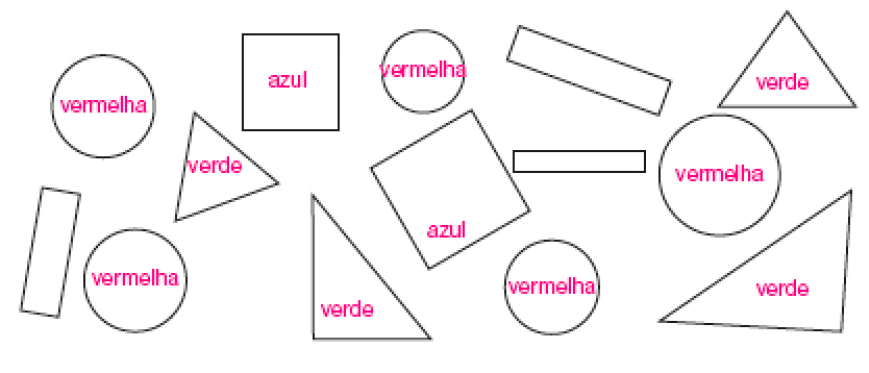
- Pinte com
 as figuras geométricas que representam círculos, com
as figuras geométricas que representam círculos, com  as que representam quadrados e com
as que representam quadrados e com  as que representam triângulos.
as que representam triângulos.
MANUAL DO PROFESSOR
Atividade 2
A atividade possibilita o reconhecimento da esfera, de modo que ela seja identificada como um círculo em movimento.
Se houver possibilidade, peça aos estudantes que, usando palito e papelão, reproduzam a atividade, para visualizar a imagem da esfera.
Atividades 3 e 4
A elaboração dos conceitos geométricos envolve atividades de identificação, comparação e classificação, geralmente inter-relacionadas. Essas atividades envolvem a identificação de círculos, quadrados e triângulos, mas para sua resolução os estudantes podem comparar essas figuras.
Na atividade 3, certifique-se de que os estudantes compreenderam o código para a classificação (C, R e T).
Na atividade 4, pergunte aos estudantes: “Quantas figuras ficaram sem pintar? Com que figura geométrica elas se parecem?” (Três; retângulos.).
Caso algum estudante pinte também as figuras que lembram retângulos, considerando-os quadrados, retome as diferenças entre essas duas figuras geométricas.
BNCC em foco:
EF02MA14, EF02MA15
Sugestão de atividade
Desenhando círculos
Peça aos estudantes que representem círculos com desenhos. Depois, sugira que socializem suas estratégias. É possível que eles comentem sobre suas dificuldades em desenhar círculos e apontem como estratégia a utilização de objetos que lembrem cones e cilindros para contornar as bases. Apresente outra estratégia para traçar o contorno do círculo: pegar um pedaço de barbante e amarrar um lápis em uma das extremidades; segurar a outra extremidade em cima de um papel, sem mover; girar o lápis sobre o papel sempre com o barbante esticado até completar uma volta, depois pintar a região interior.
MP220
Comparações
- Observe a representação de alguns quadrados e, em seguida, responda.
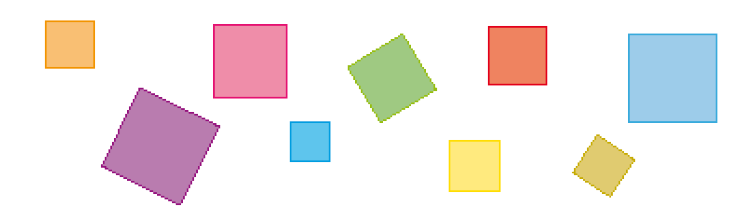
- Qual das figuras geométricas citadas abaixo tem mais características em comum com um quadrado?
( ) Retângulo.
( ) Triângulo.
( ) Círculo.
PROFESSOR
Resposta correta: Retângulo

- Explique a um
colega
como você chegou a essa conclusão.
PROFESSOR
Resposta pessoal.
- Na aula de Arte, a professora pediu a cada estudante que representasse com desenhos duas figuras geométricas planas parecidas.
Observe as figuras representadas por Leandro e Vânia.
Leandro

Vânia

- Quem representou corretamente figuras geométricas planas parecidas: Leandro ou Vânia?
_____
PROFESSOR
Resposta: Leandro.
- Cite uma diferença entre as figuras geométricas planas representadas pelo estudante que não entendeu o pedido da professora.
_____
PROFESSOR
Resposta: As figuras de Vânia parecem um círculo e um retângulo. O círculo não possui “bicos”, já o retângulo possui quatro “bicos”.
MANUAL DO PROFESSOR
Objetivo
• Reconhecer, nomear e comparar figuras geométricas planas: retângulo, quadrado, triângulo e círculo.
Atividade 1
Provavelmente em aulas e atividades anteriores, os estudantes já perceberam que o retângulo e o quadrado se assemelham. Caso apresentem dificuldade, faça perguntas para que eles comparem essas figuras geométricas planas, por exemplo: “Quantos vértices (pontas) tem o quadrado? Qual outra figura também tem 4 vértices?”.
Atividade 2
Nesta atividade, os estudantes devem comparar a dupla de figuras de cada criança, identificando se há alguma semelhança entre elas. As figuras representadas por Vânia não se assemelham, pois uma delas tem vértices (pontas) e a outra não.
Sugestão de atividade
Providencie duas folhas de papel com forma retangular para cada dupla de estudantes.
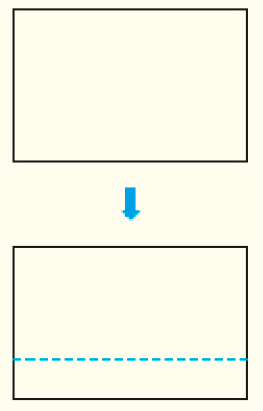
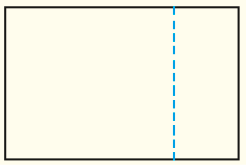
• Peça a eles que dobrem uma das folhas de maneira que, com a dobra, apareçam dois retângulos.
ou
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Não se espera que o estudante, ao fazer esta atividade, saiba que traçou linhas paralelas ou perpendiculares aos lados do retângulo.
• Peça aos estudantes que dobrem a outra folha de maneira que, com a dobra, apareçam dois triângulos.
Não se espera que o estudante, ao fazer esta atividade, saiba que traçou as diagonais do retângulo.
ou
BNCC em foco:
EF02MA15
MP221
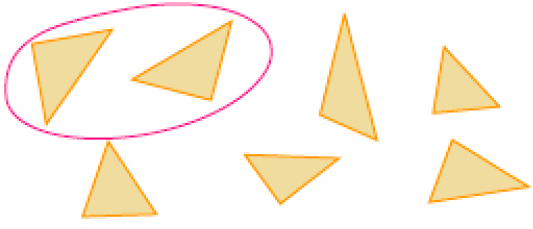
- Em cada caso, escolha e cerque com uma linha duas peças triangulares que, juntas, formam a figura em destaque.

Quadrado

Retângulo
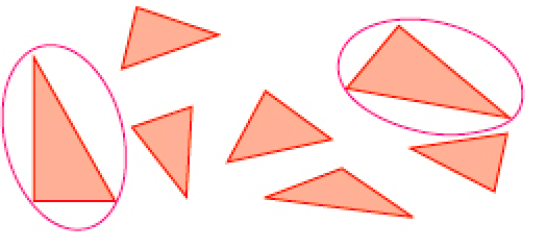

Círculo

PROFESSOR
Nenhuma peça deve ser cercada.
Triângulo
- Das quatro figuras em destaque, há alguma que não pode ser formada juntando duas peças triangulares? Qual?
_____
PROFESSOR
Resposta: Sim; círculo.
- Por que não é possível formar essa figura juntando duas peças triangulares?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Espera-se que os estudantes reconheçam que, no caso do círculo, não existem triângulos que, justapostos, possam formá-lo. Espera-se que eles percebam que isso ocorre porque o círculo tem características diferentes das do triângulo, por não ter um contorno retilíneo.
Sugestão de atividade
Palitos
Material necessário: 20 palitos de sorvete
Proponha problemas que envolvam a visualização de figuras, como:
• A figura abaixo é formada por 12 palitos; retire 2 palitos de modo que fiquem apenas 2 quadrados.

Exemplo de resposta:

• Forme um retângulo com 12 palitos inteiros.
Respostas possíveis:
CRÉDITO: ILUSTRAÇÕES: PAULO MANZI
BNCC em foco:
EF02MA15; competência específica 3
Sugestão de atividade
Ainda com palitos de sorvete, peça aos estudantes que formem um quadrado com 10 palitos de sorvete. Não vale quebrar palito.
Resposta: Não é possível formar um quadrado com 10 palitos inteiros.
MP222
Jogo: De olho na figura

Material: Tabuleiro da página 193, 12 marcadores (3 para cada jogador) e 30 cartas com figuras da página 195 e 1 saco não transparente para guardar e sortear as cartas.
Jogadores: 3 ou 4
Regras:
- Os jogadores decidem quem começará o jogo.
- As 30 cartas com figuras são misturadas dentro do saco, e o primeiro a jogar retira uma delas sem deixar que os outros a vejam. Os outros jogadores têm de descobrir a figura dessa carta. Para isso, cada um na sua vez faz uma pergunta sobre as características da figura, sem falar o nome dela. Por exemplo:

- A cada pergunta respondida, o jogador que quiser poderá apostar, no tabuleiro, posicionando um marcador na figura que julgar correta. Atenção: dois jogadores não podem apostar na mesma figura.
- Quem acertar a figura fica com todos os marcadores das apostas e a carta dessa figura é deixada de lado. Se ninguém acertar, quem sorteou a carta responde a novas perguntas, e os outros mudam suas apostas até que alguém acerte.
- O jogador à direita daquele que acabou de sortear uma carta sorteia outra.
- O jogo termina quando não houver mais marcadores para apostar ou cartas para retirar do saco.
- O jogador que ficar com mais marcadores no fim do jogo é o vencedor.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas não planas.
• Reconhecer, nomear e comparar figuras geométricas planas.
A finalidade desse jogo é permitir aos estudantes que reconheçam as diversas características das figuras e verbalizem suas impressões.
Oriente os estudantes na confecção do material. Eles devem colar o tabuleiro, as fichas e as cartas disponíveis no Material complementar em um papel mais resistente, como cartolina, depois, recortá-los. Providencie sacos para a turma guardar o material.
É importante ler e explicar as regras do jogo aos estudantes. O aspecto do jogo de falar sobre as características de uma figura geométrica exige que os estudantes verbalizem e reconheçam essas características em determinada figura, fazendo com que todos se habituem à linguagem matemática.
Os jogadores devem combinar antes do jogo a ordem em que serão feitas as apostas.
BNCC em foco:
EF02MA14, EF02MA15; competências gerais 2 e 9; competências específicas 7 e 8
MP223
Questões sobre o jogo
- Lina, Fausto, Marisa e César estavam jogando. Marisa foi a primeira a retirar uma carta.
Veja abaixo as apostas que eles fizeram.

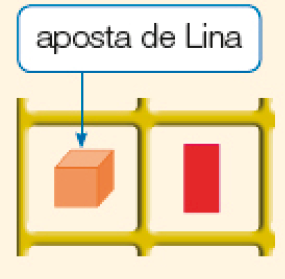
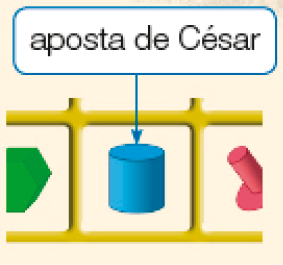
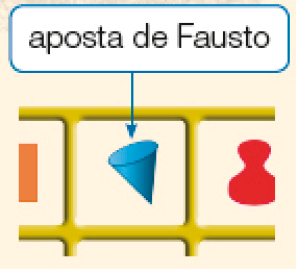

- Agora, reúna-se com um colega e, juntos, respondam às questões a seguir.
- Quem pode ter acertado a figura sorteada?
_____
PROFESSOR
Resposta: Lina.
- Com certeza, quem não acertou a figura sorteada?
_____
PROFESSOR
Resposta: César e Fausto.
- Em cada caso, marque com um X a figura “intrometida”.

( )

( )

( )

( )
PROFESSOR
Resposta: cilindro.
( )

( )

( )

( )
PROFESSOR
Resposta: cubo.

- Agora, justifique suas respostas descrevendo as figuras “intrometidas”.
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Questões sobre o jogo
Faça uma rodada do jogo com a classe e peça que anotem quem é o vencedor de cada grupo. Depois de comentar o jogo, sugira que resolvam, individualmente ou em duplas, as questões propostas.
Na questão 1, peça aos estudantes que oralmente justifiquem suas respostas. Espera-se que eles percebam que Lina pode ter acertado porque a figura que ela escolheu não tem superfície arredondada. César e Fausto certamente não acertaram porque escolheram figuras com superfície arredondada.
A questão 2 propicia a descrição das figuras “intrometidas” e também a ampliação da linguagem relativa às características de figuras geométricas. Certamente, os estudantes justificarão suas respostas descrevendo as figuras “intrometidas” com uma linguagem não formal. Exemplo de justificativas, caso o estudante tenha identificado como figuras “intrometidas”o cilindro no item a e o cubo no item b :
a) “É a única figura com superfície arredondada.”
b) “É a única figura não achatada.”
Variações
Uma possível variação é limitar a quantidade de perguntas que cada jogador pode fazer; no caso de não acertarem a figura com essa quantidade de perguntas, quem ganha a ficha é o jogador que sorteou a carta.
BNCC em foco:
EF02MA14, EF02MA15; competências gerais 2 e 9; competências específicas 7 e 8
MP224
Compreender problemas
Para resolver

Use o Tangram da página 191 para resolver estes problemas.
O Tangram é um quebra-cabeça que contém 7 peças. Com essas peças, podemos formar muitas figuras, mas para montá-las é preciso ficar atentos a duas regras:


Problema 1
Monte estas figuras com seu Tangram.

b)
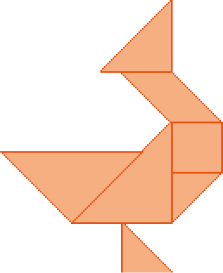
Problema 2
- Construa um quadrado com 2 peças do Tangram.
PROFESSOR
Exemplo de construção:
- Agora, construa um triângulo com 2 peças do Tangram.
PROFESSOR
Exemplo de construção:
MANUAL DO PROFESSOR
Objetivos
• Reconhecer, nomear e comparar figuras geométricas planas.
• Explorar a composição de figuras geométricas planas usando o Tangram.
Para resolver
Problema 1
Inicialmente, pode-se propor aos estudantes que realizem montagens livres com as peças do Tangram, lembrando-os de que devem usar todas as sete peças sem sobrepô-las.
Se surgir dúvida, esclareça que neste problema não estamos montando um quebra-cabeça com o Tangram, mas apenas compondo figuras com parte de suas peças.
Problema 2
A atividade possibilita explorar relações entre as peças do Tangram. Os estudantes podem perceber no item a que, ao juntar os dois triângulos maiores ou os dois triângulos menores, obtém-se um quadrado e que, reposicionando apenas um triângulo de cada um desses quadrados, é possível obter os triângulos sugeridos no item b.
Respostas possíveis:
a) Quadrado formado pelos dois triângulos maiores:

b) Quadrado formado pelos dois triângulos menores:

c) Triângulo formado pelos dois triângulos maiores:
d) Triângulo formado pelos dois triângulos menores:
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
O Tangram é um dos quebra-cabeças mais tradicionais no ensino de Geometria. As sete peças que o compõem proporcionam aos estudantes dessa faixa etária o reconhecimento de algumas figuras geométricas, como o triângulo, o quadrado e o paralelogramo, assim como o uso em atividades de composição de figuras.
Muitos quebra-cabeças exploram a composição e a decomposição de figuras planas, mas o Tangram merece destaque por apresentar uma particularidade: suas peças são proporcionais, o que contribui para o reconhecimento de propriedades das figuras planas e a comparação entre elas (congruência nas medidas dos lados, equivalência entre áreas, ampliação e redução de figuras etc.).
BNCC em foco:
EF02MA15; competência específica 3
MP225
Para refletir
- Sandra e Ademir fizeram uma montagem diferente da figura do item a do Problema 1.
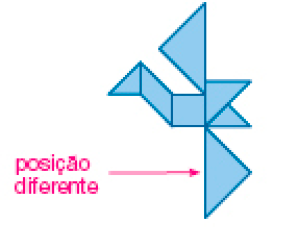
LEGENDA: Figura de Sandra. FIM DA LEGENDA.
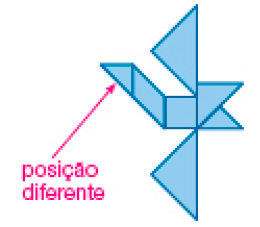
LEGENDA: Figura de Ademir. FIM DA LEGENDA.

- Descubra onde está a diferença da montagem de cada um.
PROFESSOR
Resposta: Sandra fez diferente ao posicionar o triângulo maior da parte inferior da figura. Ademir fez diferente ao posicionar o triângulo pequeno da lateral esquerda da figura.- Veja o que Betina descobriu ao resolver o Problema 2.

PROFESSOR
Resposta:


- Converse com um
colega
sobre a descoberta de Betina. Ela está certa ou não?
PROFESSOR
Resposta pessoal.
- Leia o que Camila está dizendo e faça o que se pede.

PROFESSOR
Resposta: Exemplo de construção:
- Assim como Camila fez, monte um quadrado com 3 peças de seu Tangram.
MANUAL DO PROFESSOR
Para refletir
Atividade 1
O objetivo dessa atividade é que os estudantes observem uma pequena alteração na disposição de uma peça na montagem da figura, o que exige o reconhecimento das formas e da relação que cada peça estabelece com as demais na figura. É possível que a turma tenha familiaridade com esse tipo de atividade, em razão de brincadeiras como o “Jogo dos sete erros”, encontrado em jornais e revistas infantis.
Se houver disponibilidade, leve para a sala de aula outras figuras que possam ser formadas com as peças do Tangram, para que os estudantes as montem.
Algumas figuras que podem ser sugeridas são:
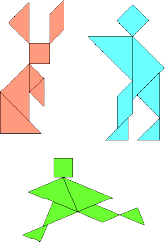
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Atividade 2
Espera-se que os estudantes percebam que a descoberta de Betina está certa, pois é possível, sim, montar um quadrado ou um triângulo com os 2 triângulos menores ou com os 2 triângulos maiores.
Atividade 3
Na resolução, os estudantes podem aproveitar o que aprenderam na atividade anterior; se os dois triângulos forem posicionados para montar um quadrado, não haverá uma terceira peça do Tangram que, acrescentada a esse quadrado, resulte em outro quadrado maior.
Portanto, os dois triângulos menores devem ser posicionados de modo que formem um triângulo maior, que corresponderá à metade do quadrado. A terceira peça, então, só pode ser o triângulo maior do Tangram.
Amplie a exploração do Tangram fazendo outros questionamentos. Por exemplo: “Como obter o triângulo grande usando três peças?”. Exemplos de respostas:
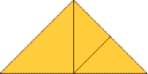
LEGENDA: Dois triângulos menores e um triângulo médio. FIM DA LEGENDA.

LEGENDA: Dois triângulos menores e um quadrado. FIM DA LEGENDA.
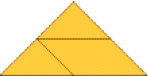
LEGENDA: Dois triângulos menores e um paralelogramo. FIM DA LEGENDA.
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
BNCC em foco:
EF02MA15; competência geral 2; competência específica 3
MP226
Matemática em textos
Leia
Papagaio, pipa, pandorga, jamanta, maranhão...
Papagaio, pipa, pandorga, jamanta, maranhão são exemplos de como esse brinquedo é conhecido no Brasil.

LEGENDA: Festival de pipas na Austrália, em 2018. FIM DA LEGENDA.
O nome pode variar, mas a diversão fica garantida desde o momento da produção com varetas de madeira ou de taquara, linha, papel fininho colorido e cola, até o momento em que colore o céu!
Apesar de ser um brinquedo popular, é preciso ficar atento e evitar riscos de acidentes ao empinar uma pipa. Veja algumas dicas:
- Não solte pipas perto de fios ou antenas para evitar choques elétricos;
- procure locais abertos, como parques, praças ou campos de futebol;
- não solte pipa em lajes ou telhados, para evitar quedas;
- olhe bem onde pisa, especialmente quando andar para trás, para não cair;
- nunca use linha com algum tipo de cortante.
MANUAL DO PROFESSOR
Objetivos
• Reconhecer e nomear figuras geométricas não planas.
• Reconhecer e nomear figuras geométricas planas.
Essa seção amplia a exploração do tema da abertura da Unidade que envolve brincadeiras com pipas. É mais um momento para verificar os conhecimentos que os estudantes já construíram acerca desse assunto.
BNCC em foco:
EF02MA15; competência geral 7
MP227
Responda
- Dê alguns exemplos de como o papagaio é conhecido no Brasil.
_____
PROFESSOR
Resposta: Papagaio, pipa, pandorga, jamanta, maranhão.
- Quais são os materiais necessários para fazer uma pipa?
_____
PROFESSOR
Resposta: Varetas de madeira ou de taquara, linha, papel fininho colorido e cola.
- Por que não devemos soltar pipas perto de fios ou antenas?
_____
PROFESSOR
Resposta: Para evitar choques elétricos.
Analise
Muitas pipas parecem figuras geométricas planas. Qual é a figura geométrica plana que normalmente é a mais representada nas pipas?
_____
PROFESSOR
Exemplo de resposta: Quadrado.Aplique

Que tal fazer algumas pipas que representem figuras geométricas planas?
Combine com os colegas e o professor, providenciem os materiais e mãos à obra!
- Quais figuras planas estão representadas nas pipas que vocês fizeram?
_____
PROFESSOR
Resposta variável.
MANUAL DO PROFESSOR
Responda
Atividades 1, 2 e 3
Pergunte aos estudantes se eles já empinaram e se já fizeram alguma pipa.
Converse sobre os perigos de se empinar pipas em locais inadequados, explorando as dicas fornecidas no texto.
Peça aos estudantes que busquem no texto as informações necessárias para responderem às questões propostas. Comente que eles devem sempre reler o texto na busca dessas informações.
Analise
Os estudantes devem observar as partes que formam as pipas que aparecem na imagem e identificar que figuras geométricas não planas essas partes lembram. Pergunte a eles também se alguma dessas partes lembra alguma figura geométrica plana.
Aplique
Caso os estudantes já tenham construído pipas, peça a eles que observem se essas pipas têm partes que representam figuras geométricas planas.
Sugira aos estudantes que confeccionem pipas que contenham representações de figuras planas em alguma parte da pipa, procurando variar a figura geométrica representada. Depois, eles devem identificar as figuras geométricas planas representadas nas pipas. Por fim, faça uma exposição das pipas construídas pelos estudantes.
BNCC em foco:
EF02MA15; competência geral 7; competência específica 3
MP228
Compreender informações
Ler e interpretar tabelas e gráficos
- Em julho de 2023, Eduardo fez um gráfico de colunas sobre a quantidade de estudantes que têm maior facilidade em aprender determinado tipo de figura geométrica.
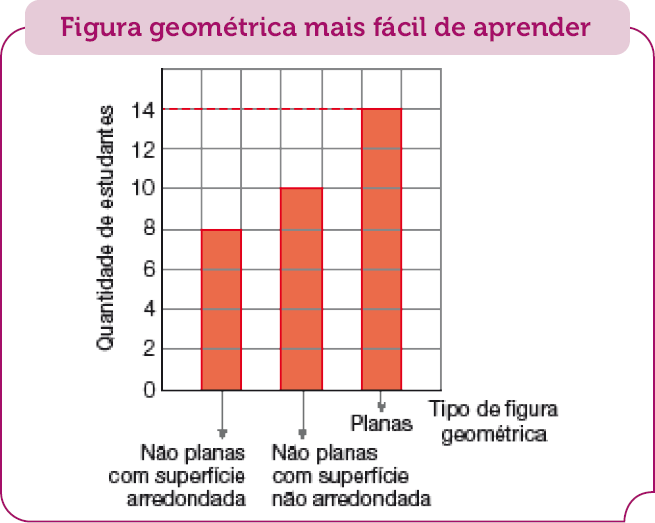
Fonte: Anotações de Eduardo (jul. 2023).
Boxe complementar:
Importante
Observe que a linha vermelha tracejada liga a coluna que se refere às figuras geométricas planas ao número 14 para indicar a quantidade de estudantes com facilidade em aprender sobre esse tipo de figura geométrica.
Fim do complemento.
- Registre, na tabela abaixo, a quantidade de estudantes que têm mais facilidade em aprender cada tipo de figura geométrica.
Figura geométrica mais fácil de aprender
Tabela: equivalente textual a seguir.
|
Tipo de figura geométrica |
Não plana com superfície arredondada |
Não plana com superfície não arredondada |
Plana |
|---|---|---|---|
|
Quantidade de estudantes |
_____ |
_____ |
_____ |
Fonte: Anotações de Eduardo (jul. 2023).
PROFESSOR
Resposta: 8; 10; 14- Quantos estudantes têm mais facilidade em aprender figuras geométricas planas?
_____
PROFESSOR
Resposta: 14
- Considerando os dois tipos de figuras geométricas não planas, quantos estudantes têm mais facilidade em aprendê-las?
_____
PROFESSOR
Resposta: 18
MANUAL DO PROFESSOR
Objetivo
• Organizar dados coletados em tabelas e em gráficos de colunas simples.
Atividade 1
A atividade propicia aos estudantes verificar como se faz a leitura dos dados indicados no eixo vertical de um gráfico de colunas simples. Peça a eles que, com o uso de uma régua, tracem no gráfico as linhas tracejadas relativas à indicação dos valores das demais colunas.
Explore o gráfico com os estudantes, incentivando-os a perceberem que cada quadrinho que compõe as colunas vale 2 unidades.
Em uma roda de conversa, proponha questionamentos para serem respondidos apenas com a observação do gráfico, como os abaixo.
• “Com que tipo de figura os estudantes têm mais facilidade?” (Figuras geométricas planas.) Explique como você pensou.
(Os estudantes podem: contar o número de quadrinhos, observar os valores relativos a cada coluna e fazer a comparação ou observar qual é a coluna mais alta.)
• “Quantas unidades faltam para que a preferência por figuras planas tenha a mesma quantidade de todas as figuras não planas?” (4 unidades.)
Verifique as estratégias utilizadas. Espera-se que eles percebam que devem adicionar as quantidades das duas colunas relativas às figuras não planas e depois subtrair a quantidade da coluna relativa às figuras planas.
Em seguida, proponha que completem a tabela utilizando as informações do gráfico e discutam as questões dos itens b e c com base na tabela.
Aproveite a atividade para discutir com os estudantes os motivos pelos quais se representam dados coletados em gráficos e tabelas: eles permitem a visualização organizada das informações. Pergunte onde acharam mais fácil buscar os dados: na tabela ou no gráfico?
BNCC em foco:
EF02MA14, EF02MA15, EF02MA22; competências específicas 3 e 4
MP229
- Todos os anos, em maio, Marisa e seus amigos participam de diversas atividades sociais. Veja a turma toda reunida em maio de 2023.

- Registre na tabela a quantidade de crianças envolvidas em cada atividade.
Participação das crianças em atividades sociais
Tabela: equivalente textual a seguir.
|
Atividades sociais |
Organização de torneios esportivos |
Arrecadação de agasalhos |
Participação no clube de leitura |
Campanha de reciclagem |
|---|---|---|---|---|
|
Quantidade de crianças |
2 |
_____ |
_____ |
_____ |
Fonte: Anotações de Marisa (maio 2023).
PROFESSOR
Resposta: 5; 3; 1- Represente as informações da tabela no gráfico abaixo.
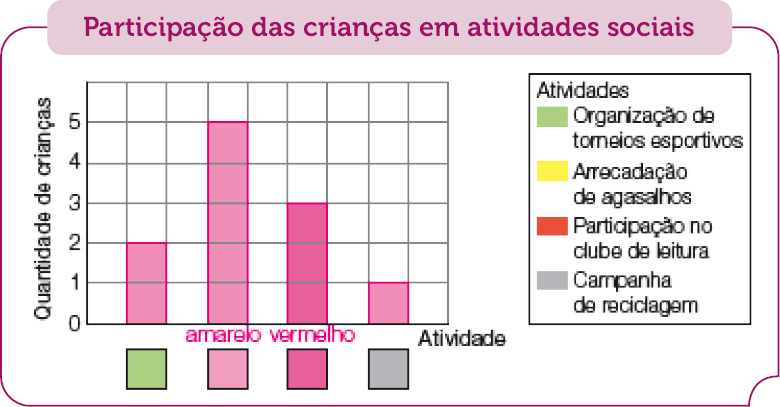
Fonte: Anotações de Marisa (maio 2023).

- Faça uma pesquisa com os colegas para saber de qual dessas atividades gostariam de participar e organizem os dados em um gráfico.
PROFESSOR
Resposta: O gráfico depende das respostas dos estudantes.
MANUAL DO PROFESSOR
Atividade 2
Peça aos estudantes que contem a quantidade de crianças que participam de cada atividade social e anotem essa quantidade abaixo de cada figura. Depois, solicite a eles que transfiram essa informação para a tabela.
Se julgar oportuno, no item b, faça o gráfico na lousa em conjunto com a sala. Explique a legenda no gráfico.
Para o item c, oriente os estudantes na coleta e na organização dos dados. Lembre-os de que devem atribuir um título para a tabela e para o gráfico, devem também informar, além da data da coleta, qual é a fonte das informações.
BNCC em foco:
EF02MA22, EF02MA23; competências gerais 2 e 7; competências específicas 3, 4 e 6
MP230
O que você aprendeu
Avaliação processual
- Observe os quadros feitos por Angélica e Silvano.

LEGENDA: Quadro de Angélica. FIM DA LEGENDA.

LEGENDA: Quadro de Silvano. FIM DA LEGENDA.
- O que os dois quadros têm em comum?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que em ambos há representações de figuras geométricas. Fim da observação.
- Cite uma diferença entre os quadros de Angélica e de Silvano.
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que Angélica usou apenas representações de figuras geométricas planas, enquanto Silvano usou apenas representações de figuras geométricas não planas. Fim da observação.
- Abaixo, foram representadas algumas figuras não planas.
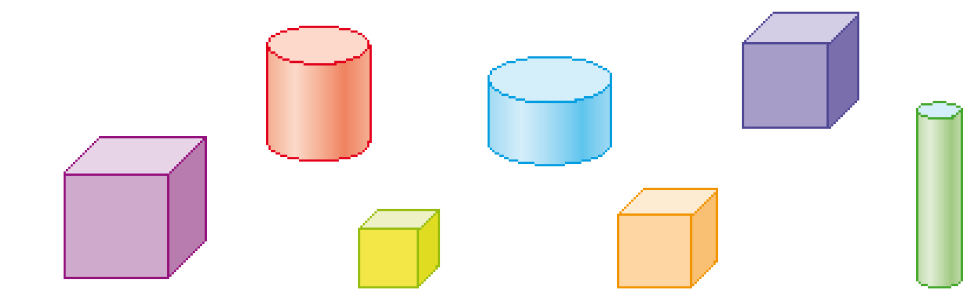
- Quais figuras geométricas não planas estão representadas?
_____
PROFESSOR
Resposta: Cubos e cilindros.
MANUAL DO PROFESSOR
Objetivo
• Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, promovendo um momento de avaliação processual sob a perspectiva da avaliação formativa.
Se necessário, reforce a orientação para os estudantes observarem, nas figuras, as nuances das cores aplicadas nas figuras não planas que representam os objetos tridimensionais. Assim eles terão mais facilidade em reconhecê-las e diferenciá-las das figuras planas.
Atividade 1
A atividade retoma as figuras que os estudantes conheceram e observaram ao longo da Unidade.
Explore as imagens dos quadros com os estudantes, solicitando que descrevam o que observam e que figuras conhecem.
Espera-se que eles percebam que, em ambos os quadros, há representações de figuras geométricas planas. Mas que, no quadro de Silvano, as figuras geométricas planas estão representadas nos desenhos de figuras geométricas não planas.
Em seguida, explore o tipo de figura geométrica apresentado em cada quadro. Analise com os estudantes o quadro de Angélica: “Vocês conhecem os tipos de figura geométrica representados aqui? Diga uma característica comum a todas elas. Você sabe nomeá-las?”. Espera-se que os estudantes percebam que Angélica usou apenas representações de figuras geométricas planas, enquanto Silvano usou representações não planas.
Para facilitar a visualização, traga modelos de cilindros e cubos para que os estudantes manuseiem e observem as partes planas que compõem sua superfície. Providencie também modelos de círculos e quadrados que se sobreponham exatamente nessas partes planas, e modelos de triângulos e retângulos (não quadrados). Entregue os modelos de figuras planas aos estudantes e peça que verifiquem quais deles se sobrepõem às partes planas dos modelos de cilindros e cubos.
BNCC em foco:
EF02MA14, EF02MA15; competência geral 3
MP231
- Veja alguns carimbos e responda.
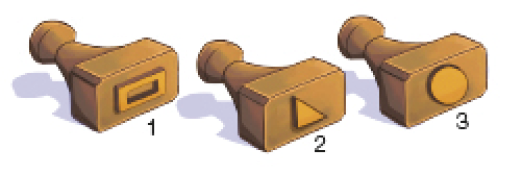
- Qual carimbo
deve
ser escolhido para
obter
uma figura que represente um círculo?
_____
PROFESSOR
Resposta: O carimbo 3.
- Para
obter
uma figura que represente um quadrado, é preciso usar um dos carimbos duas vezes, carimbando uma figura ao lado da outra. Qual carimbo
deve
ser escolhido para isso?
_____
PROFESSOR
Resposta: O carimbo 2.

- Usando o Tangram, podemos representar algumas figuras planas, por exemplo, o quadrado.
- Das figuras planas estudadas nesta unidade, qual delas não é possível representar usando as 7 peças do Tangram?
_____
PROFESSOR
Resposta: Círculo.
- E quais podem ser representadas pelo Tangram?
_____
PROFESSOR
Resposta: Quadrado, retângulo e triângulo.
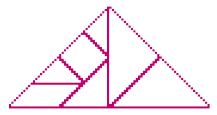
- Agora, com todas as peças do seu Tangram usado nas páginas 178 e 179, monte as representações de um retângulo e de um triângulo.
- Das figuras planas estudadas nesta unidade, qual delas não é possível representar usando as 7 peças do Tangram?
PROFESSOR
Resposta: Exemplo de construção:PROFESSOR
PROFESSOR
Autoavaliação

- Consigo relacionar a planificação da superfície de uma figura geométrica à respectiva figura geométrica não plana?
PROFESSOR
Resposta pessoal.
- Relembre o que estudou ao longo deste ano. Quais atividades foram mais fáceis e quais foram mais difíceis?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Se possível, traga as imagens apresentadas nos carimbos feitas em cartolina para que os estudantes possam manuseá-las e explorar a composição de outras figuras planas.
Atividade 4
Nesta atividade, espera-se que os estudantes identifiquem as figuras geométricas planas que podem ser representadas com as peças do Tangram e percebam que apenas o círculo não pode ser representado com elas.
Organize os estudantes em duplas para fazer o item c, a fim de que compartilhem estratégias e discutam possíveis representações que possam ser feitas.
Autoavaliação
A primeira questão traz a relação entre as figuras geométricas planas e as figuras geométricas não planas por meio das planificações. Espera-se que os estudantes percebam se reconhecem as faces de figuras geométricas não planas e as identificam nas respectivas planificações. Incentive-os a indicar quais são as figuras geométricas não planas cujas planificações sentem mais dificuldade em identificar e quais eles reconhecem com mais facilidade.
Na segunda questão é importante propiciar um momento de resgate dos principais objetos de conhecimento estudados durante o ano letivo. Também é importante resgatar as potencialidades, valorizando as conquistas e as construções de conhecimentos ao longo do ano letivo.
BNCC em foco:
EF02MA15; competência geral 3
MP232
Comentários para o professor:
Conclusão da Unidade 8
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Reconhece, nomeia e compara figuras geométricas não planas: paralelepípedo, cubo, pirâmide, cone, cilindro e esfera, associando-as com objetos do mundo físico? |
_____ |
_____ |
|
Reconhece e nomeia figuras planas (círculo, quadrado, retângulo e triângulo)? Compara-as por meio de características comuns, representadas em diferentes disposições ou na superfície de sólidos geométricos? |
_____ |
_____ |
|
Faz composição de figuras planas usando peças do Tangram? |
_____ |
_____ |
|
Organiza e compara dados coletados em textos, e constrói, a partir deles, tabelas e gráficos de colunas ou de barras simples? |
_____ |
_____ |
|
Faz pesquisa, definidas as variáveis categóricas, organizando os dados coletados em listas, tabelas e gráficos de colunas ou de barras simples? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP233
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |
