MP036
Comentários para o professor
Introdução da Unidade 1
A abertura da primeira Unidade, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior, propõe uma abordagem de observações e de descobertas por meio de uma imagem na qual números de até 3ª ordem expressam códigos que são utilizados em uma atividade social e cultural. O contexto que a imagem descreve proporciona a descoberta da regra de uma sequência numérica e de alguns de seus elementos faltantes. Assim, a abertura retoma abordagens feitas no ano anterior para serem aprofundadas neste volume.
Com foco no desenvolvimento das habilidades da Unidade Temática Números, as atividades desta Unidade têm por objetivo desenvolver a leitura, a escrita e a comparação de números naturais até a ordem de unidade de milhar, estabelecendo relações entre os registros numéricos e em língua materna. Nessa perspectiva, destaca-se a relação entre os conhecimentos construídos no 2º ano e aqueles a serem abordados nos anos seguintes. Por exemplo, a composição e a decomposição de números naturais de até três ordens são ampliadas para os números naturais de até quatro ordens. Essa ampliação servirá de base para, no 4º ano, os estudantes sedimentarem seu conhecimento do sistema de numeração decimal e compreenderem a composição e a decomposição de números naturais de até cinco ordens, por meio de adições e multiplicações por potências de 10.
Também são destaque as atividades que ajudam a construir e aplicar fatos básicos da adição, que estabelecem relação entre números naturais e pontos da reta numérica. Note a articulação a se fazer aqui com a Unidade Temática Álgebra, que pode ser empregada tanto na ordenação de tais números (em sequências recursivas, por exemplo) quanto na construção de fatos básicos da adição e da subtração.
A Unidade Temática Álgebra também é contemplada por meio de atividades que ampliam os conhecimentos construídos no ano anterior acerca da identificação e descrição de elementos ausentes em sequências de números naturais, bem como da descrição de padrões dessas sequências. Assim, as atividades promovem a identificação de regularidades em sequências ordenadas de números naturais, que resultam da realização de adições ou subtrações sucessivas por um mesmo número, além da descrição de regras de formação de sequências. Vale destacar que tais conhecimentos ajudarão os estudantes a identificarem, no ano seguinte, regularidades em sequências numéricas compostas por múltiplos de um número natural.
Quanto à Unidade Temática Grandezas e medidas, são propostos problemas em que os estudantes trabalham a comparação e a equivalência de valores monetários do sistema brasileiro. Os conhecimentos adquiridos nessa etapa serão fundamentais para que, ao longo do 4º ano, os estudantes sejam capazes de resolver e elaborar problemas envolvendo situações de compra, venda e formas de pagamento.
Contemplando a Unidade Temática Probabilidade e estatística, ao longo da Unidade também há problemas cujos dados estão apresentados em tabelas de dupla entrada e em gráficos de barras e de colunas para o desenvolvimento das habilidades de leitura, interpretação e comparação destes, apropriando-se desse tipo de linguagem para compreender aspectos significativos da realidade sociocultural.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. As variáveis são muitas: dos conteúdos às habilidades e aos objetivos de aprendizagem.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.
Competências específicas favorecidas
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.
MP037
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção A Matemática me ajuda a ser... desta Unidade.
Roteiro de aula – A Matemática me ajuda a ser... uma pessoa que se preocupa com o meio ambiente 1 ª parte – Introdução – Tempo sugerido: 10 minutos
Inicie uma conversa com a turma comentando que o meio ambiente é sempre o lugar onde estamos ou onde poderemos estar e, por isso, ao cuidarmos dele, estamos cuidando de nós também. E quem é que não gosta de cuidar de si?
Esclareça que essa seção trata apenas de um dos muitos assuntos que dizem respeito ao meio ambiente: o plástico.
Peça que deem exemplos de objetos da sala de aula feitos com plástico. Depois pergunte se sabem de outros exemplos de uso de plástico em geral. Liste-os na lousa.
A seguir, peça que conversem em dupla, em tom baixo para que todos ouçam o companheiro, sobre o que acham que se deve fazer com os objetos de plástico quando eles não são mais úteis. Sugestão: 2 ou 3 minutos devem ser suficientes, pois o objetivo é despertar a atenção sobre o problema do plástico no meio ambiente.
2 ª parte – Leitura e interpretação de texto – Tempo sugerido: 50 minutos
Inicie lendo o 1 º parágrafo e solicitando que observem as ilustrações da página dupla identificando os objetos de plástico listados na lousa. Dê um tempo para que explorem o infográfico e descubram alguns desses objetos.
Solicite voluntários para ler os pequenos trechos informativos – um estudante por trecho. Ao término de cada um deles, verifique se houve entendimento das palavras e das sentenças. Esclareça as possíveis dúvidas.
Depois da leitura, pergunte se perceberam a diferença entre a reciclagem, que transforma o produto para um novo uso, e a reutilização, que dá outros usos ao mesmo objeto. Pergunte também se, além desses dois “erres” – de R eciclagem e de R eutilização – eles conhecem o terceiro “erre”, o da R edução. Explique que a redução acontece quando diminuímos a quantidade de plástico (e de outros materiais nocivos ao meio ambiente) ao mínimo necessário.
Para terminar esta parte, solicite que deem sugestões de como as pessoas podem reutilizar e reciclar alguns dos objetos de plástico mais usados. Peça também que respondam à questão proposta no Tome nota.
3 ª parte – Pesquisa proposta no Reflita – Tempo sugerido: 30 minutos
A apresentação do resultado da pesquisa deve ser feita em outro dia.
Sugestão: 1 ou 2 semanas após a 2ª parte.
Forme com a turma grupos de 3 a 5 estudantes. Oriente-os a definir as perguntas que irão compor o questionário da pesquisa, comum a todos os grupos, para tornar possível a posterior tabulação e as conclusões. Oriente-os a se organizarem no grupo e distribuírem as tarefas necessárias à realização: reprodução do questionário (um para cada elemento), organização (tabulação) das respostas dadas pelos pesquisados, elaboração de um painel com o resultado organizado da pesquisa (texto, quadro/tabela, gráfico), apresentação em aula do trabalho.
MP038
UNIDADE 1. Sistema de numeração decimal

MANUAL DO PROFESSOR
Objetivos da Unidade
- Ler e escrever números naturais de até 4 algarismos.
- Estabelecer relações entre os registros numéricos e em língua materna de números de até 4 algarismos.
- Comparar números naturais de até 4 algarismos.
- Identificar características do sistema de numeração decimal, utilizando composição e decomposição de número natural de até 4 ordens.
- Resolver problemas que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro.
- Representar números naturais de até 4 algarismos com o Material Dourado, no ábaco e no quadro valor de lugar.
- Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
- Representar números naturais na reta numérica.
- Utilizar a reta numérica para a ordenação dos números naturais e também na construção de fatos da adição e da subtração.
- Identificar regularidades em sequências ordenadas de números naturais, resultantes da realização de adições ou subtrações sucessivas, por um mesmo número.
- Reconhecer e descrever uma regra de formação de uma sequência numérica e determinar elementos faltantes ou seguintes.
- Desenvolver a noção de antecessor e sucessor de um número natural, explorando sequências numéricas.
- Interpretar texto e identificar medidas de tempo contidas nele.
- Resolver problemas cujos dados estão apresentados em tabela de dupla entrada, gráficos de barras ou de colunas.
BNCC em foco:
EF03MA01, EF03MA02, EF03MA03, EF03MA04, EF03MA10, EF03MA24, EF03MA26
MP039
Boxe complementar
Fim do complemento
MANUAL DO PROFESSOR
Para refletir...
Antes de iniciar a atividade, peça aos estudantes que observem a cena ilustrada na abertura e identifiquem os números que estão relacionados ao sorteio da bicicleta (789, 798, 799 e 768). Em seguida, eles devem comparar os números dos convites recebidos por Antonieta e pelo pai de Caio e responder à primeira questão proposta.
Algumas perguntas podem ser feitas para ajudar os estudantes na organização dos dados apresentados na ilustração:
Quantas duplas estão participando do concurso de dança? (8 duplas.)
Quais são os números que identificam as duplas? (60, 30, 70, 100, 10, 20, 40 e 90.)
Verifique se os estudantes conseguem encontrar todos os números e colocá-los em ordem crescente: 10, 20, 30, 40, 60, 70, 90, 100.
Espera-se que eles percebam que é possível completar a sequência com os números 50 e 80, obtendo: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100.
Assim, a regra para obter o próximo termo da sequência, a partir do 10, seria adicionar 10.
Para refletir...
Após o concurso de dança, haverá o sorteio de uma bicicleta. O pai de Caio recebeu o convite de número 768 e Antonieta, o de número 789. O número do convite dela é maior ou menor que o número do convite do pai de Caio? _____
PROFESSOR
Resposta: Maior.Se ordenarmos de modo crescente os números até 100, usados para identificar cada dupla do concurso de dança, poderemos obter uma sequência. Descubra a regra dessa sequência.
_____
PROFESSOR
Resposta: A regra é adicionar 10.MP040
O número 1.000 – o milhar
- Conheça a coleção de
bolinhas
de gude de João.
João guarda sua coleção de bolinhas de gude em 10 caixas. Em cada caixa, cabem 100 ou 1 centena de bolinhas.

- Quantas
bolinhas
João tem?
_____
PROFESSOR
Resposta: 999 bolinhas.
- Se João ganhar 1 bolinha, ele ficará com quantas centenas de bolinhas?
_____
PROFESSOR
Resposta: 10 centenas.
- Se João ganhar 1 bolinha, com quantas
bolinhas
ele ficará?
999 + _____ = 1.000
PROFESSOR
Resposta: 1João ficará com mil bolinhas ou 1 milhar de bolinhas.
1 milhar ou mil ou 1.000 unidades
1 milhar ou 10 centenas ou 100 dezenas ou 1.000 unidades
MANUAL DO PROFESSOR
Objetivos
Ler e escrever números naturais de até 4 algarismos.
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Resolver problemas que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro.
Nesse momento, os estudantes estenderão os agrupamentos de nosso sistema de numeração estabelecendo a ordem da unidade de milhar. Contar até 1.000 exige o conhecimento do padrão de escrita e de nomeação dos números de três algarismos e do número 1.000. Compreender a lógica que determina a escrita do número 1.000 e sua relação com as demais ordens é algo complexo e exige que os estudantes mobilizem diversos níveis hierárquicos, bem como que compreendam o valor posicional dos algarismos em um número.
É importante que a noção de milhar também seja construída a partir dos agrupamentos de dez.
Atividade 1
As questões propostas possibilitam reconhecer o milhar e compará-lo a 10 centenas, 100 dezenas ou 1.000 unidades. Se possível, disponibilize o Material Dourado e recorde com os estudantes:
10 cubinhos (10 unidades) formam 1 barra (1 dezena);
10 barras (10 dezenas) formam 1 placa (1 centena);
10 placas (10 centenas) formam 1 cubo grande (1 unidade de milhar).
BNCC em foco:
EF03MA01
MP041
- Marcos separou seu dinheiro em três partes. Conte a quantia de dinheiro em cada parte e responda às questões.



- Quantos reais há em cada parte?
_____
PROFESSOR
Resposta: Parte 1: 900 reais; Parte 2: 90 reais; Parte 3: 3 reais.
- No total, quantos reais Marcos tem?
_____
PROFESSOR
Resposta: Marcos tem 993 reais.
- Quantos reais faltam para Marcos completar 1.000 reais?
_____
PROFESSOR
Resposta: 7 reais.
- Leia e complete.
André produziu 10 pacotes de chaveiros em sua fábrica.

- André produziu
_____
chaveiros ou
_____
milhar de chaveiros.
PROFESSOR
Resposta: 1.000; 1.
- André tirou 10 chaveiros com defeito de um desses pacotes.
No total, sobraram _____ chaveiros de sua produção.
PROFESSOR
Resposta: 990.

- Em cada caso, complete com a quantidade que falta para formar mil.
999 + _____
PROFESSOR
Resposta: 1990 + _____
PROFESSOR
Resposta: 10900 + _____
PROFESSOR
Resposta: 100200 + _____
PROFESSOR
Resposta: 800
MANUAL DO PROFESSOR
Atividade 2
Nessa atividade, os estudantes devem relacionar o número 1.000 à quantidade 1.000 reais. Conte com eles a quantia de reais em cada parte, agrupando as cédulas e as moedas de mesmo valor:
100, 200, 300, ..., 900, 910, 920, ..., 990, 991, 992, 993.
Para saber quanto falta para Marcos completar a quantia de 1.000 reais, os estudantes podem continuar a contagem oralmente: 994, 995, 996, 997, 998, 999, 1.000 (7 unidades), ou seja, faltam 7 reais.
Atividade 3
Na atividade, aproveite para trabalhar a composição de quantidades a fim de obter o milhar.
Atividade 4
Verifique se os estudantes articulam adequadamente as diferentes quantidades envolvidas na composição do número 1.000 (unidades, dezenas e centenas).
Observe se não escrevem os números desconsiderando o valor posicional dos algarismos, erro comum quando os números representados envolvem zeros. Por exemplo, é comum estudantes dessa idade escreverem 9 009 para o número “novecentos e nove”, pois, em vez de usarem a ideia de valor posicional dos algarismos, empregam a justaposição de 900 com 9, lado a lado.
BNCC em foco:
EF03MA03, EF03MA24
Sugestão de leitura para o estudante
Livro
ROCHA, Ruth. Uma história com mil macacos. Ilustrações de Cláudio Martins. São Paulo: Salamandra, 2009. (Série Vou te contar!)
O livro conta a história de uma cidade invadida por macacos. Um cientista encomenda um ou dois macacos para seus estudos, mas, por um erro de interpretação da mensagem enviada, entregam 1.000 macacos.
Aproveite e pergunte: “Que erro na mensagem pode ter causado tamanha confusão? Como podem ser evitados erros na escrita de números com muitos zeros? Vocês se lembram de alguma confusão causada por interpretações erradas de números?”.
MP042
Milhares inteiros
- Veja a quantidade que cada peça do Material Dourado representa e complete.
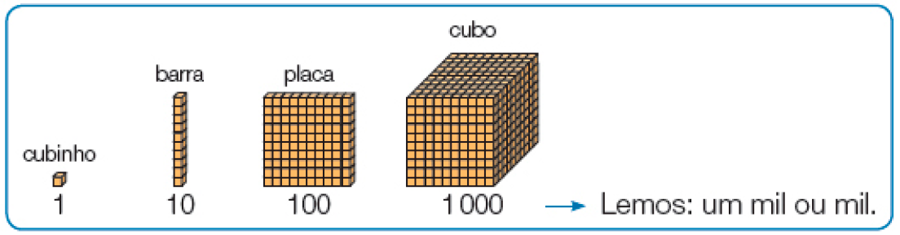
- 10
 formam 1
formam 1 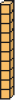
_____ unidades ou _____ dezena
PROFESSOR
Resposta: 10, 1- 10
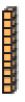 formam 1
formam 1 
_____ dezenas ou _____ centena
PROFESSOR
Resposta: 10, 1- 10
 formam 1
formam 1 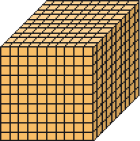
_____ centenas ou _____ milhar
PROFESSOR
Resposta: 10, 1- Complete.
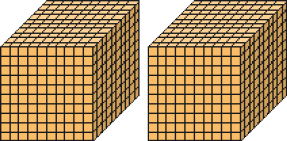
Número: 2.000
Lemos: dois mil
b)
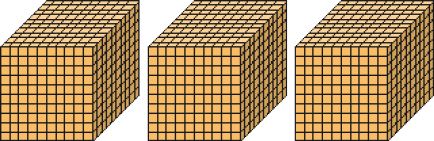
Número: _____
PROFESSOR
Resposta: 3.000Lemos: _____
PROFESSOR
Resposta: três milc)
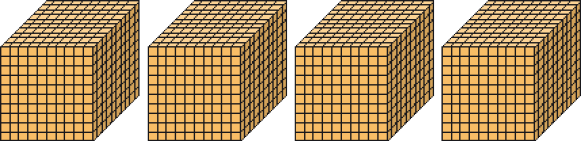
Número: _____
PROFESSOR
Resposta: 4.000Lemos: _____
PROFESSOR
Resposta: quatro milMANUAL DO PROFESSOR
Objetivos
Ler e escrever números naturais de até 4 algarismos.
Estabelecer relações entre os registros numéricos e em língua materna de números de até 4 algarismos.
Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural de até quatro ordens.
Resolver problemas que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro.
Representar números naturais de até 4 algarismos com o Material Dourado.
É importante observar se os estudantes conseguem se apropriar de algumas das características principais do nosso sistema de numeração.
Essas atividades possibilitam aos estudantes a composição do milhar e as operações com quantidades relativas a ele, com o auxílio do Material Dourado na resolução de situações-problema. O Material Dourado é composto de 4 tipos de peças, em geral de madeira: cubinhos, barras, placas e cubo. Se houver disponibilidade, leve o Material Dourado à sala de aula para que os estudantes manipulem suas peças.
Atividade 1
A apresentação da atividade é muito útil no trabalho com os agrupamentos do nosso sistema de numeração.
Porém, é importante lembrar que, com o Material Dourado, não é possível explorar o valor que os algarismos assumem conforme sua posição no número. Saliente aos estudantes que 10 unidades formam 1 dezena, 10 dezenas formam 1 centena e 10 centenas formam 1 milhar.
Atividade 2
Para a realização da atividade, pode-se também utilizar o Material Dourado como ferramenta auxiliar. Enfatize que, apesar de o cubo grande representar 1 milhar, lemos esse número como 1 mil.
BNCC em foco:
EF03MA01, EF03MA02
O trabalho com milhares inteiros pode ser precedido de uma observação dos padrões na escrita de dezenas inteiras e centenas inteiras. Pergunte: “O que há em comum na escrita das dezenas inteiras, das centenas inteiras e dos milhares inteiros? E de diferente?”. Espera-se que os estudantes observem que a similaridade é a modificação apenas do algarismo na posição inicial do número, em cada caso, à medida que as quantidades inteiras aumentam: 10, 20, 30, ..., 100, 200, 300, ..., 1.000, 2.000, 3.000 etc. A diferença entre essas quantidades está no algarismo das dezenas nas dezenas inteiras, no das centenas nas centenas inteiras e no dos milhares nos milhares inteiros. Reforce a diferença na quantidade de zeros quando se muda de ordem.
MP043
- Em um teatro, a peça Os três porquinhos ficou em cartaz por 4 meses.
Nos dois primeiros meses, compareceram ao teatro 500 pessoas por mês. Em cada um dos dois meses seguintes, o movimento foi o dobro do registrado no primeiro mês. Quantas pessoas assistiram a essa peça nesses 4 meses?

Nesses 4 meses _____ pessoas assistiram a essa peça.
PROFESSOR
Resposta: 3.000

- Alfredo trabalha em um supermercado. No fim de um dia, ele sempre conta o dinheiro do caixa. Em um desses dias, a quantia que havia no caixa era:
- 100 cédulas de

- 20 cédulas de

- 20 cédulas de

- 20 cédulas de

- Esse dinheiro corresponde a quantos reais?
_____
PROFESSOR
Resposta: 8.000 reais.
- Em outro dia de trabalho, Alfredo contou 2.000 reais no caixa. Quantas cédulas de cada quantia ele pode ter contado?
_____
PROFESSOR
Exemplos de resposta: 40 cédulas de 50 reais; 20 cédulas de 50 reais e 10 cédulas de 100 reais.
- Escreva como se lê cada um dos números a seguir.
- 5.000:
_____
PROFESSOR
Resposta: cinco mil
- 8.000:
_____
PROFESSOR
Resposta: oito mil
- 9.000:
_____
PROFESSOR
Resposta: nove mil
- 5.000:
_____
MANUAL DO PROFESSOR
Atividade 3
Explore a atividade perguntando: “Supondo que cada ingresso para essa peça tenha custado 1 real mais 1 quilograma de alimento não perecível, quantos reais teriam sido obtidos e quantos quilogramas de alimento teriam sido arrecadados nos 4 meses de apresentação?”. (3.000 reais e 3.000 quilogramas de alimento.)
Atividade 4
Para obter o total de reais com a quantidade de cédulas de 10 reais e de 100 reais, os estudantes podem fazer agrupamentos de 10 em 10. Por exemplo, eles podem observar que 10 cédulas de 10 reais formam 100 reais e que 10 cédulas de 100 reais formam 1.000 reais. A atividade amplia o raciocínio introduzindo as cédulas de 50 e de 200 reais, cujas composições exigem cálculos mais elaborados.
Peça aos estudantes que realizem o item b individualmente e que exponham suas respostas, depois, valide-as com eles. Comente que há diferentes maneiras de compor determinadas quantias. Proponha a eles que formem, por exemplo, 2.000 reais usando duas composições de cédulas diferentes. Depois, peça que compartilhem com a classe para que possam ser feitas eventuais correções e os estudantes percebam a grande variedade de respostas possíveis.
Apresentamos alguns exemplos de respostas:
5 cédulas de 200 reais e 10 cédulas de 100 reais;
50 cédulas de 20 reais e 100 cédulas de 10 reais.
Atividade 5
Espera-se que os estudantes reconheçam que se trata de unidades de milhar. Amplie a atividade colocando outros números (de até 3 algarismos e milhares inteiros) na lousa para que eles escrevam por extenso. Você pode realizar um ditado; peça que registrem no caderno a escrita numérica dos números que você falar.
BNCC em foco:
EF03MA01, EF03MA02, EF03MA24
MP044
Números de quatro algarismos
- No domingo passado, 1 356 pessoas visitaram uma feira de livros.
- Veja a representação do número 1 356, que tem quatro algarismos, no quadro valor de lugar e no ábaco.
Quadro valor de lugar
Quadro: equivalente tectual a seguir.
|
UM |
C |
D |
U |
|---|---|---|---|
|
1 |
3 |
5 |
6 |
Ábaco
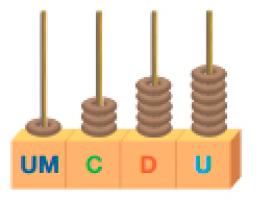
- Complete o valor de cada um dos algarismos desse número.
1356
6: _____ unidades
PROFESSOR
Resposta: 65: 5 dezenas ou _____ unidades
PROFESSOR
Resposta: 503: _____ centenas ou _____ dezenas ou _____ unidades
PROFESSOR
Resposta: 3, 30, 3001: 1 unidade de milhar ou _____ centenas ou _____ dezenas ou _____ unidades
PROFESSOR
Resposta: 10, 100, 1.000- Agora, complete a decomposição desse
número
considerando o valor de cada algarismo.
1.356 = _____ + _____ + _____ + _____
PROFESSOR
Resposta: 1.000 + 300 + 50 + 6
Lemos: mil trezentos e cinquenta e seis.
- Decomponha os números considerando o valor de cada algarismo.
- 4.320 =
_____
+
_____
+
_____
+
_____
PROFESSOR
Resposta: 4.000 + 300 + 20 + 0
- 7.023 =
_____
+
_____
+
_____
+
_____
PROFESSOR
Resposta: 7.000 + 0 + 20 + 300
- 4.320 =
_____
+
_____
+
_____
+
_____
MANUAL DO PROFESSOR
Objetivos
Ler e escrever números naturais de até 4 algarismos.
Estabelecer relações entre os registros numéricos e em língua materna de números de até 4 algarismos.
Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural de até 4 ordens.
Representar números naturais de até 4 algarismos no ábaco e no quadro valor de lugar.
As páginas exploram a composição e a decomposição do milhar, com números maiores que 1.000 e menores que 10.000.
Atividade 1
Na resolução do item a, certifique-se de que os estudantes compreenderam a representação no ábaco fazendo perguntas como: “Se tirarmos uma argola da posição UM (unidades de milhar), que número estará representado?” (356). Peça que decomponham o número 1 356 considerando as dezenas inteiras e as unidades. São possíveis várias decomposições. Em seguida, solicite que reconheçam qual é a decomposição com o maior número de dezenas inteiras, ou seja, 135 dezenas.
Atividade 2
Incentive-os a decompor outros números e a compartilhar com os colegas. Quando comparam suas escritas numéricas, estabelecem relações, refletem sobre as respostas possíveis e os procedimentos empregados e validam ou não determinadas escritas.
Surge, assim, a percepção das regularidades do nosso sistema de numeração.
As hipóteses sobre as escritas numéricas podem levar a conclusões contraditórias.
Estudos revelam que, quando uma criança escreve, por exemplo, 3.000 300 40 5 para indicar “três mil trezentos e quarenta e cinco” usando mais algarismos do que para escrever 4.000, ela conclui que “três mil trezentos e quarenta e cinco” é maior que 4.000, pois imagina que, quanto mais algarismos, maior é o número.
Porém, ao comparar 3.000 com 4.000, ela afirma que 4.000 é maior que 3.000, pois pensa: “O primeiro número é o que manda”.
BNCC em foco:
EF03MA01, EF03MA02
MP045
- Observe os números nos cartazes e responda às questões.
- Qual é o valor do algarismo 4 nestes números?

4.675
_____
PROFESSOR
Resposta: 4.0006.740
_____
PROFESSOR
Resposta: 40- E o valor do algarismo 7 nestes números?
4.675
_____
PROFESSOR
Resposta: 706.740
_____
PROFESSOR
Resposta: 700

- Comparando a quantidade de pessoas que assistiram a cada um desses filmes, podemos dizer que o filme A Terra em 2030 foi visto por aproximadamente 2.000 pessoas a mais que o filme O Guloso?
_____
PROFESSOR
Resposta: Sim.
- Escreva como você pensou para responder à questão anterior.
_____
PROFESSOR
Resposta pessoal.
Boxe complementar:
Desafio
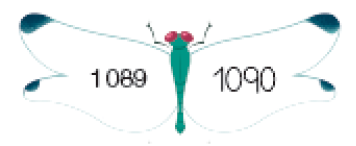
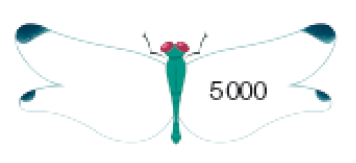
De qual número as crianças estão falando?

CRÉDITO: GEORGE TUTUMI
Respostas possíveis: 1.189, 1.198
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 3
A atividade possibilita o reconhecimento do valor posicional que os algarismos assumem em números naturais e a comparação entre as quantidades formadas por números de 4 algarismos, tarefas que não são tão simples para estudantes dessa idade. Por isso, o ábaco é um ótimo instrumento para a decomposição de um número, pois nele se representam as quantidades referentes a cada ordem (unidades, dezenas, centenas e unidades de milhar).
Para responder às questões a e b, os estudantes devem observar o valor posicional dos algarismos em cada número. Na questão c, eles podem arredondar os números para a unidade de milhar mais próxima ou para a centena mais próxima.
Desafio
O desafio explora o valor numérico dos algarismos em uma situação de adivinha, de que os estudantes geralmente gostam. Espera-se que eles percebam que necessitam organizar as informações dadas pelas crianças para descobrir os algarismos e formar o número procurado.
Se “o número tem 4 algarismos e é menor que 2.000”, os estudantes podem concluir que o algarismo das unidades de milhar só pode ser 1; se fosse zero, teria 3 algarismos, o que contraria a informação. Como “o algarismo das centenas é igual ao das unidades de milhar”, eles podem deduzir que o das centenas também é 1 (soma igual a 2) e o que falta para a soma 19, ou seja, 17, só pode ser obtido por 8 + 9 ou 9 + 8. Portanto, o número pode ser 1.189 ou 1.198.
BNCC em foco:
EF03MA01, EF03MA02; competência geral 2; competência específica 2
MP046
- As quantidades de pessoas que assistiram, em dois dias, a apresentação do mágico foram representadas com o Material Dourado. Compare-as.
Quantidade de espectadores no 1º dia: 1.645
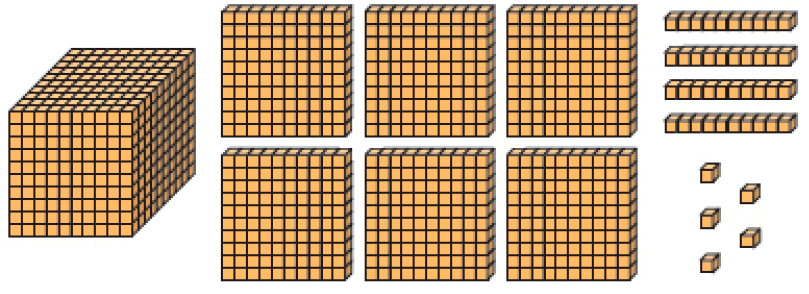
Quantidade de espectadores no 2º dia: 1.329
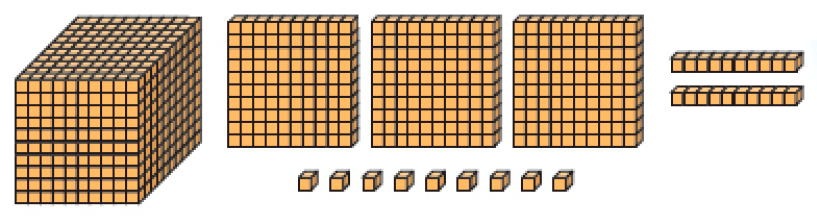

- Em qual dos dias havia mais espectadores? Escreva como você descobriu.
_____
PROFESSOR
Resposta: No 1º dia. Exemplo de explicação: Comparei as unidades de milhar e vi que havia uma em cada número. Depois, comparei as centenas e vi que havia mais centenas em 1.645 que em 1.329.
- Se no 2º dia houvesse 1.684 espectadores, em qual dos dias o público teria sido maior? Justifique sua resposta.
_____
PROFESSOR
Resposta: No 2ᵒ dia. Exemplo de justificativa: Comparei as unidades de milhar e vi que havia uma em cada número. Depois, comparei as centenas e vi que havia seis em cada número. Então, comparei as dezenas e vi que havia mais dezenas em 1.684 que em 1.645.
MANUAL DO PROFESSOR
Objetivos
Comparar números naturais de até 4 algarismos representados com o Material Dourado.
Comparar números naturais de até 4 algarismos.
Resolver problemas cujos dados estão apresentados em tabela de dupla entrada.
Atividade 1
Como os números têm a mesma quantidade de algarismos, ou seja, têm a mesma ordem de grandeza, os estudantes devem comparar os algarismos de cada ordem. Assim, primeiro analisam os algarismos da unidade de milhar e verificam que são iguais (1 .645 e 1 .329); em seguida, comparam os algarismos das centenas e observam que 6 é maior que 3 (. 6 45 e1. 3 29); então já podem concluir que 1.645 é maior que 1.329. É possível, porém, que os estudantes ainda não tenham compreendido que essa conclusão se deve ao fato de que o 6 representa 6 centenas e o 3 representa 3 centenas.
Se no 2º dia 1.684 espectadores tivessem assistido à apresentação, então nesse dia teria havido a maior quantidade de espectadores, pois 1.684 é maior que 1.645:
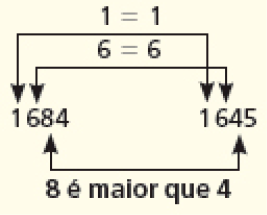
É importante que os próprios estudantes percebam isso por meio das comparações: primeiro as unidades de milhar, depois as centenas, depois as dezenas e por último as unidades.
BNCC em foco:
EF03MA01, EF03MA02
MP047
- Observe a tabela e responda às questões.
Pontuação dos jogadores em cada fase de um jogo de videogame
Tabela: equivalente textual a seguir.
|
Fase Jogador |
Primeira |
Segunda |
Terceira |
|---|---|---|---|
|
Jair |
968 |
1.249 |
3.257 |
|
Laura |
2.257 |
3.458 |
3.450 |
Fonte: Dados fornecidos pelos jogadores. (fev. 2023)
- Em qual fase do jogo Jair fez mais pontos? E Laura?
_____
PROFESSOR
Resposta: Na terceira fase; na segunda fase.
- Na 3ª fase quem fez mais pontos: Jair ou Laura?
_____
PROFESSOR
Resposta: Laura.
- Observe o
número
que Amanda
escreveu
e responda.

- Se ela trocar de posição o algarismo das
dezenas
com o algarismo das unidades de milhar, qual
número
será formado?
_____
PROFESSOR
Resposta: 4.720
- O
número
que ela encontrará é maior ou
menor
que o
número
que ela
escreveu
inicialmente?
_____
PROFESSOR
Resposta: Maior.
- Se ela trocar de posição o algarismo das
dezenas
com o algarismo das unidades de milhar, qual
número
será formado?
_____
- Observe as informações das placas e faça o que se pede.

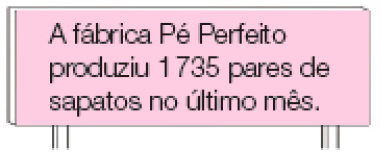
PROFESSOR
Resposta: placa 2

- Pinte a placa que indica a maior produção no último mês.
- Complete as sentenças usando maior que ou menor que.
1.728 é _____ 1.735
1.728 < 1.735
PROFESSOR
Resposta: menor que1.735 é _____ 1.728
1.735 > 1.728
PROFESSOR
Resposta: maior queO símbolo que usamos para indicar menor que é , e para indicar maior que é >.
MANUAL DO PROFESSOR
Atividade 2
Os estudantes devem mobilizar seus conhecimentos sobre os conceitos de maior que ou menor que e a leitura de dados apresentados em uma tabela de dupla entrada para responder às questões. Se julgar necessário, retome com eles como fazer essa leitura.
Atividade 3
Peça aos estudantes que leiam o novo número formado após a troca da posição dos algarismos. Pergunte a eles: “Qual é o valor posicional que o algarismo 2 tem em cada um dos números?”. (No número 2.740, o valor posicional do algarismo 2 é 2.000, e no número 4.720 é 20.) Sugira que tentem escrever outros números alterando a posição dos algarismos, organizando-os depois em ordem crescente.
Atividade 4
Explore as informações dos quadros com os estudantes, antes que escolham o quadro que devem pintar. Peça que expliquem o raciocínio usado para descobrir o maior número. Ressalte os sinais < (menor que) e > (maior que), mas deixe que os estudantes os assimilem aos poucos.
Se julgar oportuno, amplie a atividade pedindo que se organizem em duplas. Cada estudante deve ficar com papel e lápis em mãos. Um da dupla (o desafiante) escreve na sua folha de papel, em segredo, um número de 4 algarismos. O colega (o descobridor) anuncia como “palpite” um número de 4 algarismos e o registra em sua folha.
No caso de o palpite ser maior que o número a ser descoberto, o desafiante diz sobre o número oculto: é menor ; sendo menor, ele diz é maior.
O procedimento se repete até que o número em segredo seja descoberto.
BNCC em foco:
EF03MA01, EF03MA02, EF03MA26
MP048
Sequências
- As meninas estão na fila da roda-gigante. Elas serão chamadas de acordo com o
número
que receberam.
Ana será a próxima. Depois de Ana, será a vez de Cida. Em seguida, Célia andará na roda-gigante.

- Complete com o antecessor e o sucessor em cada caso.
a) _____ 10 _____
PROFESSOR
Resposta: 9, 11b) _____ 86 _____
PROFESSOR
Resposta: 85, 87c) _____ 19 _____
PROFESSOR
Resposta: 18, 20d) _____ 43 _____
PROFESSOR
Resposta: 42, 44
- Escreva os números que faltam na sequência de acordo com a regra indicada.

PROFESSOR
Resposta: 4.000, 5.000, 6.000, 7.000, 8.000, 9.000.MANUAL DO PROFESSOR
Objetivos
Desenvolver a noção de antecessor e sucessor de um número natural, explorando sequências numéricas.
Identificar regularidades em sequências ordenadas de números naturais, resultantes da realização de adições ou subtrações sucessivas por um mesmo número.
Reconhecer e descrever uma regra de formação de uma sequência numérica e determinar elementos faltantes ou seguintes.
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Representar números naturais na reta numérica.
A sequência dos números naturais (0, 1, 2, ...) não é uma lista qualquer, na qual um elemento não tem relação com os outros. Pelo contrário, cada número diferente de zero dessa sequência é obtido pela adição de 1 unidade ao número anterior. Portanto, a relação “estar entre” é fundamental para caracterizar um número natural de forma inequívoca (com exceção do número zero). Por exemplo, o número natural que está entre o 7 e o 9 é o número 8.
Atividade 1
Verifique se os estudantes reconhecem as regularidades na escrita do antecessor e do sucessor de um número, propondo questões como: “O sucessor de um número tem o algarismo das unidades igual a 3. Qual é esse número?”. (Espera-se que concluam que há mais de uma possibilidade de resposta para essa questão, como: 2, 12, 22, 32, 42, 52, ...)
Atividade 2
Os estudantes reconhecerão e completarão sequências de números formadas por milhares inteiros. Como o padrão de adicionar 1.000 a cada elemento já está indicado, espera-se que consigam completar o restante da sequência sozinhos. Caso contrário, peça que troquem ideias com um colega e compartilhem as técnicas utilizadas.
O conceito de “estar entre” é explorado por meio da ideia de antecessor e sucessor de um número natural. Esse conceito assume relevância no reconhecimento de um número em uma sequência numérica qualquer e na comparação entre os números de determinada sequência. Por exemplo: 99 é o antecessor de 100, portanto 100 é maior que 99, embora este seja formado por algarismos 9. A exploração de um calendário também é significativa, porque sempre lidamos com o conceito de sucessor e antecessor como medida de tempo. Por exemplo, se hoje é dia 16, ontem foi dia 15 (antecessor) e amanhã será dia 17 (sucessor).
BNCC em foco:
EF03MA10
MP049
- Dê "saltos" nas retas de acordo com o padrão indicado e escreva os números que faltam nas sequências.
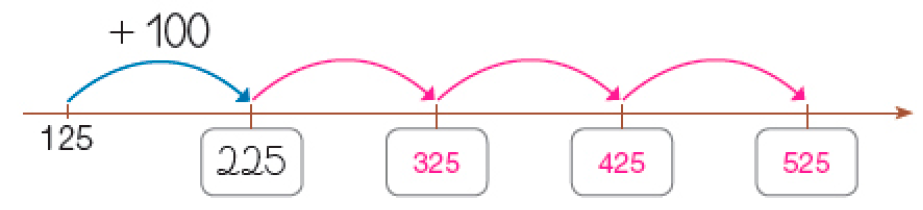
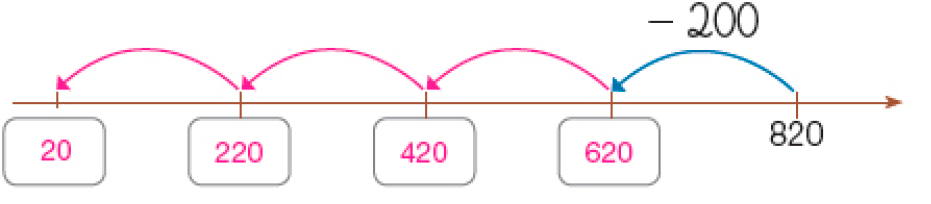
- Descubra o padrão de cada sequência representada na reta numérica. Depois, complete as sequências com os números que estão faltando.

PROFESSOR
Resposta: 160, 170, 180, 190
PROFESSOR
Resposta: 200, 350, 400, 450
PROFESSOR
Resposta: 342, 442, 542, 642, 742- Escreva uma sequência em ordem decrescente com números entre 10 e 190. Depois, peça a um colega que descubra a regra usada nessa sequência e registre-a.
PROFESSOR
Exemplo de resposta: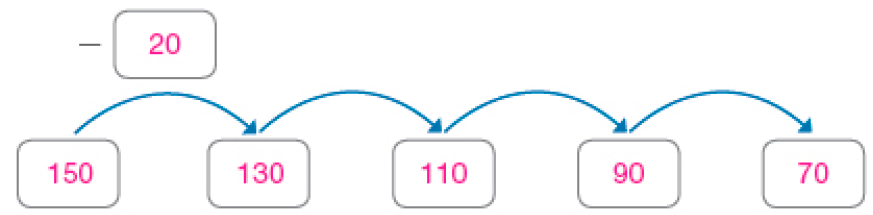
MANUAL DO PROFESSOR
Atividade 3
A atividade retoma a representação de números na reta numérica e as estratégias de adicionar “saltando para a direita” e de retirar “saltando para a esquerda” certa quantidade indicada.
No item a, como a quantidade adicionada é sempre 100, os estudantes devem completar a sequência com facilidade. Pergunte: “O que ocorre se a quantidade adicionada for 200 e o primeiro número da sequência for 346?”. Peça que retratem essa situação em uma reta numérica. Espera-se que os estudantes façam a seguinte representação:
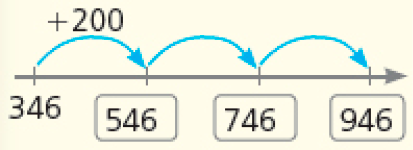
CRÉDITO: ADILSON SECCO
No item b, espera-se que os estudantes percebam que devem proceder do mesmo modo, só que com “saltos” para a esquerda, efetuando subtrações sucessivas.
Atividade 4
Nessa atividade, para que os estudantes determinem os números faltantes em cada sequência representada na reta numérica, eles devem identificar o padrão de formação. Peça, em seguida, que expliquem como pensaram.
Atividade 5
Verifique se os estudantes compreendem o que são sequências decrescentes. Se necessário, exemplifique para que eles percebam que essas sequências são organizadas do maior para o menor número e, para essa classificação, sempre devem ser lidas da esquerda para a direita, que é o caso da sequência do item b da questão 3.
Depois que realizarem a troca com o colega, em uma roda de conversa peça que apresentem suas sequências e expliquem a regra de formação, validando-as com os estudantes.
BNCC em foco:
EF03MA03, EF03MA04, EF03MA10
MP050
Jogo: Maior de todos
Material: 4 conjuntos de 9 cartas numeradas de 1 a 9.
Jogadores: 2
Regras:
- As cartas devem ser embaralhadas e empilhadas no centro da mesa, com os números voltados para baixo.
- Cada jogador deverá retirar quatro cartas dessa pilha.
- A cada rodada, ao retirar as cartas da pilha, o jogador deve formar com elas o maior número possível composto de quatro algarismos e anotar no quadro abaixo.
- A partida termina após quatro rodadas.
- Vence o jogo quem formar o maior número de quatro algarismos em mais rodadas.
Tabela: equivalente textual a seguir.
|
Jogador |
1ª rodada |
2ª rodada |
3ª rodada |
4ª rodada |
Maior número |
|---|---|---|---|---|---|
|
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |
|
_____ |
_____ |
_____ |
_____ |
_____ |
_____ |

MANUAL DO PROFESSOR
Objetivos
Escrever números naturais de até 4 algarismos.
Comparar números naturais de até 4 algarismos.
Identificar características do sistema de numeração decimal, utilizando a composição de número natural de até quatro ordens.
O objetivo do jogo é que os estudantes formem números de 4 algarismos, ampliando a compreensão sobre a unidade de milhar, e percebam de que modo podem compor o maior número.
Antes de iniciar o jogo, ajude-os na leitura e na compreensão das regras. As cartas podem ser confeccionadas pelos jogadores ou podem ser usadas as cartas numeradas de 2 a 9 e o ás de um baralho comum. Nesse caso, a carta ás substitui a carta de número 1.
A cada rodada, os jogadores devem avaliar de que modo podem obter o maior número de 4 algarismos com suas cartas, o que os levará à compreensão da estratégia de comparação dos números naturais (pela comparação dos algarismos de mesma ordem).
Observe as estratégias dos estudantes para a escolha dos números que devem ser formados; verifique se eles comparam os algarismos da ordem correspondente (das unidades de milhar, das centenas, das dezenas e das unidades, nessa sequência), já que todos os números deverão ter 4 algarismos. Verifique também se formaram o maior número possível com as cartas que retiraram da pilha e qual foi o raciocínio utilizado para essa formação.
BNCC em foco:
EF03MA01, EF03MA02
Variações
Uma possibilidade de variação do jogo é propor a confecção de uma carta com o zero, o que modifica e dificulta o jogo. Discuta com os estudantes o que ocorreria se uma das cartas retiradas fosse a do número zero. Outra opção é inserir uma carta coringa, que, ao ser retirada, o estudante pode escolher o algarismo correspondente.
MP051
Questões sobre o jogo
- Responda de acordo com a partida que você e seu
colega
jogaram e com o que preencheram no quadro.
- Quais cartas você retirou na 1ª rodada? _____
- Qual
número
você formou com essas cartas?
_____

- Esse número era o maior número que você poderia formar com essas cartas? Por quê?
- Seu colega formou qual número na 1ª rodada? _____
- Esse número é maior ou menor que o número que você formou?
- _____
- Quem formou o maior número de todas as rodadas? Qual foi esse número? _____
- Coloque em ordem crescente os números que você e seu colega formaram em todas as rodadas.
- _____
- Quem venceu a partida?
_____
PROFESSOR
Respostas pessoais.
- Veja uma rodada da partida de Marina e Rafael e responda.

- Com essas cartas, qual é o maior
número
que:
- Marina pode formar?
_____
PROFESSOR
Resposta: 9.842 - Rafael pode formar?
_____
PROFESSOR
Resposta: 9.731
- Quem ganha essa rodada se formar o maior
número
possível?
_____
PROFESSOR
Resposta: Marina.
- Marina pode formar?
_____
MANUAL DO PROFESSOR
Questões sobre o jogo
Incentive os estudantes a jogarem várias partidas para que se familiarizem com as cartas, antes de responderem às questões. Proponha que respondam às questões individualmente ou em duplas.
Na questão 1, as respostas dependerão dos resultados obtidos durante o jogo. Se julgar oportuno, no item g, proponha que o estudante ou a dupla escreva todos os números da rodada em uma folha de papel avulsa, o que facilitará a montagem da sequência com esses números em ordem crescente. No item c, verifique se os estudantes formaram o maior número possível com as cartas que retiraram da pilha e qual foi o raciocínio utilizado para a formação.
Para ampliar a questão 2, pergunte: “Qual seria o menor número possível que Marina poderia formar? E Rafael?”. (Marina: 2.489; Rafael: 1.379.) Peça que observem o maior e o menor número que Marina e Rafael poderiam formar e verifique se observam o que ocorreu com a posição dos algarismos.
BNCC em foco:
EF03MA01, EF03MA02
MP052
A Matemática me ajuda a ser
... uma pessoa que se preocupa com o meio ambiente

FONTE: Infográfico elaborado com base nos dados obtidos em: Plástico: história, composição, tipos, produção e reciclagem. Disponível em: http://fdnc.io/eTR. Acesso em: 4 ago. 2021.
MANUAL DO PROFESSOR
Objetivo
Interpretar texto e identificar medidas de tempo contidas nele.
Explore o infográfico com os estudantes, desde os pequenos trechos informativos até as ilustrações. Para ampliar a discussão, pergunte quais objetos e produtos utilizados por eles no dia a dia são feitos de plástico e faça uma lista na lousa para que percebam a variedade de produtos. Enfatize a diferença entre reutilizar e reciclar o plástico, pois alguns estudantes podem usar essas palavras como sinônimos. É importante perceberem que a reciclagem transforma o produto para um novo uso, enquanto a reutilização dá outros usos para o mesmo objeto. Verifique se eles já ouviram falar sobre o petróleo e sua retirada do ambiente. Se julgar conveniente, proponha uma pesquisa a respeito dessa substância oleosa muito utilizada como matéria-prima. Por fim, explore o tempo de decomposição do plástico resgatando as noções relacionadas à medida tempo. Se possível, apresente o tempo de decomposição de outros materiais, como o náilon (de 30 a 40 anos), o fósforo (2 anos) e as latas de alumínio (100 a 500 anos).
Avalie a conveniência de acrescentar mais um “R” aos dois “R” de Reciclar e Reutilizar, que é o “R” de Reduzir, ou seja, de diminuir ao que é estritamente necessário o uso do plástico e de outros materiais que podem ser nocivos ao meio ambiente. Assim completam-se os “3 R”: Reduzir, Reciclar e Reutilizar.
BNCC em foco:
competência geral 10; competência específica 7
MP053
Tome nota
Quanto tempo uma embalagem de plástico demora para se decompor na natureza?
_____
PROFESSOR
Resposta: De 100 a 450 anos.Reflita


Façam uma pesquisa para descrever como sua comunidade se preocupa com o meio ambiente em relação à reciclagem e à reutilização do plástico.
MANUAL DO PROFESSOR
Tome nota
Aproveite a atividade para ampliar a noção de tempo construída pelos estudantes. Após identificarem o tempo de decomposição das embalagens de plástico, proponha a comparação com o tempo médio de vida das pessoas ou de alguns animais para que percebam que 450 anos é um tempo muito longo.
Reflita
Oriente os estudantes na elaboração da estratégia de pesquisa: delimitação do público a ser pesquisado, elaboração do questionário e tabulação das respostas.
A distribuição de equipamentos apropriados para descarte seletivo na comunidade é um bom item para pesquisa, assim como dias e horários de coleta desse material, dados que podem ser obtidos com a própria comunidade ou na prefeitura da cidade.
Uma maneira de ampliar a visão dos estudantes sobre a importância da reciclagem é o convite a um funcionário de cooperativa de reciclagem ou da prefeitura para uma conversa. Nesse caso, peça aos estudantes que formulem com antecedência algumas questões para essa conversa.
BNCC em foco:
competências específicas 7 e 8
Sugestão de atividade
Como diminuir o consumo do plástico
Proponha aos estudantes que façam uma pesquisa sobre alternativas de materiais para diminuição do uso do plástico, por exemplo, o uso de embalagens de papel reciclado, canudinhos de papel, escovas dentais feitas com bambu ou sacolas de compras reutilizáveis.
Comente também que existem estudos sobre a fabricação de plásticos menos prejudiciais ao meio ambiente.
MP054
Compreender informações
Interpretar gráfico de barras
- Em um supermercado, as garrafas de água são vendidas em três tipos de embalagem. O gráfico abaixo apresenta a quantidade de copos (250 mililitros cada um) necessária para encher cada tipo de embalagem. Cada 4 copos correspondem a 1 litro, ou seja, 1 litro tem 1.000 mililitros.
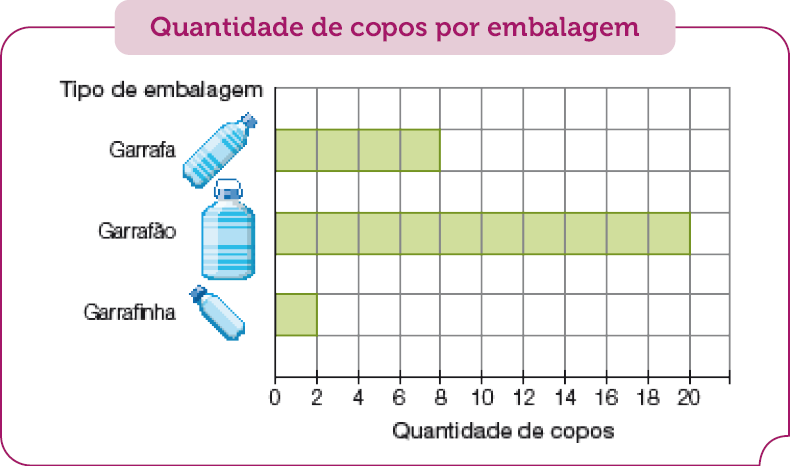
Fonte: Supermercado pesquisado. (fev. 2023)
- Complete a frase abaixo de acordo com o gráfico.
Para encher o garrafão são necessários _____ copos.
PROFESSOR
Resposta: 20
- Quantos mililitros de água cabem, no máximo, em cada tipo de embalagem?
Garrafa: _____
PROFESSOR
Resposta: 2.000 mililitros.Garrafão: _____
PROFESSOR
Resposta: 5.000 mililitros.Garrafinha: _____
PROFESSOR
Resposta: 500 mililitros.
- Complete a tabela abaixo com a quantidade necessária de litros para encher cada embalagem.
Litros por embalagem
Tabela: equivalente textual a seguir.
|
Tipo de embalagem |
Litros de água |
|---|---|
|
|
_____ |
|
|
_____ |
|
|
_____ |
Fonte: Supermercado pesquisado. (fev. 2023)
PROFESSOR
Resposta: 2 litros; 5 litros; meio litro.MANUAL DO PROFESSOR
Objetivo
Resolver problemas cujos dados estão apresentados em gráficos de barras.
Comente que, na sociedade atual, que tem acesso a uma grande quantidade de informações, alguns recursos visuais são usados constantemente, como gráficos e tabelas, e a leitura correta desses recursos é importante para a compreensão de informações que chegam até nós pelos meios de comunicação.
Atividade 1
Comente com os estudantes que esse tipo de gráfico é denominado gráfico de barras. É importante esclarecer que a opção por um gráfico de barras (horizontais), em vez de um gráfico de colunas (verticais), não obedece a nenhum critério de adequação matemática; trata-se de uma escolha pessoal ou, em alguns casos, de uma melhor ocupação do espaço disponível na página. Peça que levem para a sala de aula reportagens que apresentem dados em gráficos de barras. Desse modo, eles poderão se reunir em grupo e discutir as informações apresentadas nesse material.
Explore os elementos do gráfico mostrado na atividade: do que trata (quantidade de copos por embalagem), o que aparece no eixo horizontal (quantidade de copos), o que aparece no eixo vertical (tipo de embalagem).
Faça outros questionamentos que facilitem a leitura e a interpretação do gráfico pelos estudantes, como: “A quantos copos equivale cada quadradinho que compõe as barras?” (2 copos), “Quantos mililitros representa cada quadradinho?”(500 mililitros).
Discuta com os estudantes as questões propostas no livro, socializando e validando as respostas com eles.
BNCC em foco:
EF03MA26; competência específica 4
MP055
- No gráfico a seguir, o professor registrou as alturas dos estudantes que fazem parte do time de futebol da escola.
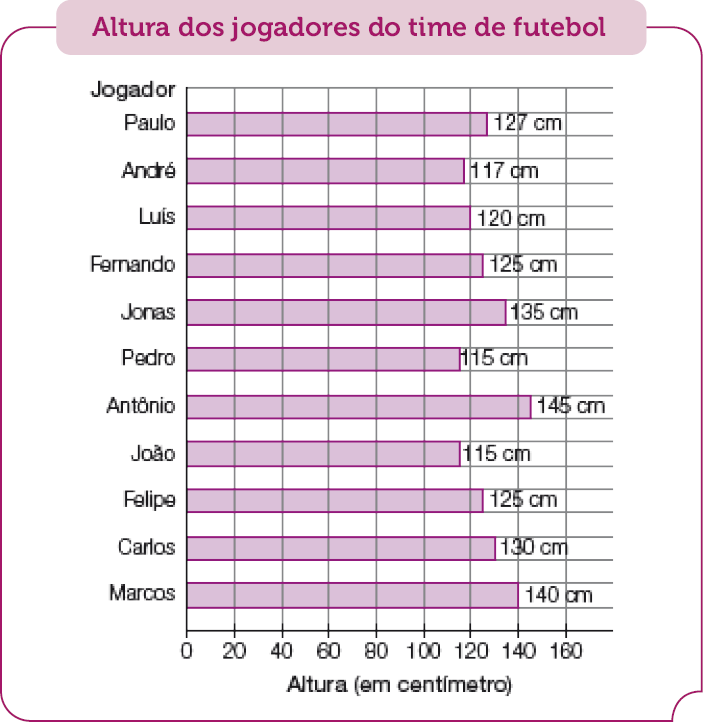
Fonte: Estudantes do time da escola. (fev. 2023)
- Qual é o jogador mais alto? Qual é a altura dele?
_____
PROFESSOR
Resposta: Antônio; a altura dele é 145 cm.
- Existem jogadores que têm a mesma altura? Quem são?
_____
PROFESSOR
Resposta: Sim; Fernando e Felipe (a altura de cada um deles é 125 cm) e Pedro e João (a altura de cada um deles é 115 cm).
- Quantos centímetros o jogador mais alto tem a mais que cada um dos jogadores mais baixos?
_____
PROFESSOR
Resposta: 30 centímetros.
- Elabore mais uma pergunta com base nos dados desse gráfico. Converse com seus colegas e professor sobre a resposta.
_____
PROFESSOR
Resposta: Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
Se julgar necessário, retome com os estudantes que cm é o símbolo de centímetro, unidade de medida de comprimento que eles já estudaram no 2º ano.
Observe as estratégias utilizadas pelos estudantes ao responderem às questões, verificando os pontos de maior dificuldade.
Em seguida, em uma roda de conversa, peça que exponham suas respostas e digam como pensaram. Aproveite esse momento para ampliar a exploração dos itens em que eles tiveram dificuldades. Proponha a cada estudante que leia a questão elaborada no item d e peça aos demais que lhe respondam.
BNCC em foco:
EF03MA26; competência específica 4
MP056
O que você aprendeu
- Complete a sequência numérica.
Boxe complementar:
Dica
Atenção! Para descobrir a regra da sequência, observe os primeiros números.
Fim do complemento.

PROFESSOR
Resposta: 6.000, 7.000, 7.500.

- Patrícia recebeu por um trabalho 15 cédulas de
 e 3 cédulas de
e 3 cédulas de  . Quantos reais ela recebeu?
_____
. Quantos reais ela recebeu?
_____
PROFESSOR
Resposta: 1.530 reais.
- Associe as quantidades iguais.
Linha 1
1.000 + 800 + 90 + 5; 8.095; 1.805; 89 dezenas e 5 unidades.
Linha 2
8.000 + 90 + 5; 1.895; 895; 18 centenas e 5 unidades.
PROFESSOR
Resposta: 1.000 + 800 + 90 + 5 - 1.895;PROFESSOR
8.095 - 8.000 + 90 + 5;PROFESSOR
1.805 - 18 centenas e 5 unidades;PROFESSOR
89 dezenas e 5 unidades - 895.- Complete com o antecessor ou o sucessor em cada caso.
PROFESSOR
Resposta: 4.999
PROFESSOR
Resposta: 3.000
PROFESSOR
Resposta: 4.029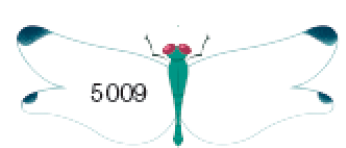
PROFESSOR
Resposta: 5.010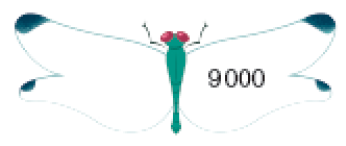
PROFESSOR
Resposta: 8.999MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Propicie conversas entre os estudantes sobre as estratégias que usaram para resolver as atividades.
Atividade 1
Aqui, eles precisam completar a sequência crescente, em que o número seguinte aumenta 500 unidades.
Aproveite para fazer perguntas como: “Qual será o 10º número dessa sequência?”. Os estudantes podem usar diversas estratégias:
Observar que, do primeiro ao décimo número, aumentam-se nove quantidades iguais a 500 unidades, ou seja, 4 500 unidades. Como o primeiro número é igual a 4.500, então: 4.500 + 4.500 = 9.000.
O número 7 500 é o sétimo número da sequência; então, basta aumentar três quantidades iguais a 500, ou seja: 7.500 + 500 + 500 + + 500 = 9.000.
Atividade 2
Incentive os estudantes a desenvolverem estratégias próprias, valorizando-as. Eles podem usar o conhecimento de que 10 centenas formam 1.000.Assim, verificarão que 15 cédulas de 100 reais compõem 1.500 reais, que, junto com os 30 reais (3 cédulas de 10 reais), resulta em 1 530 reais.
Atividade 3
A atividade explora as diferentes maneiras de registrar uma quantidade. Se o estudante apresentar dificuldade, peça que se reúna com um colega para discutirem juntos, o que aumentará o seu repertório e enriquecerá o aprendizado de ambos.
Atividade 4
Faça a leitura dos números com os estudantes, pois isso pode ser objeto de dificuldade para alguns, o que pode impedir de obter o sucessor ou o antecessor de um número, mas eles podem usar como estratégia ler o número em voz alta. Por exemplo, para chegar ao sucessor de 5.009 podem ler: cinco mil e nove, cinco mil e dez, e então escrever esse número com algarismos.
BNCC em foco:
EF03MA01, EF03MA02, EF03MA03, EF03MA10, EF03MA24
MP057
Avaliação processual
- Escreva seis números de quatro algarismos, em ordem decrescente, da
esquerda
para a direita.
_____, _____, _____, _____, _____, _____.
PROFESSOR
Exemplo de resposta: 5.836, 5.835, 5.834, 5.833, 5.832, 5.831.

- Uma fábrica de papel reflorestou uma área desmatada. Veja no gráfico a quantidade de árvores plantadas em um trimestre de 2022 e responda às questões abaixo.
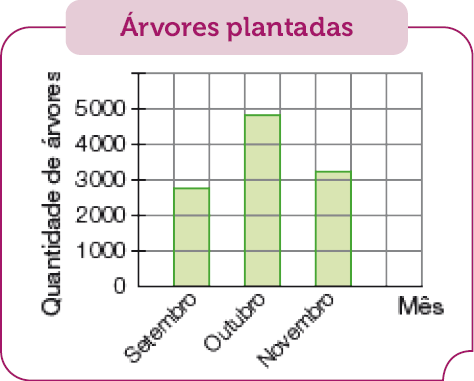
Fonte: Dados fornecidos pela fábrica de papel. (nov. 2022)
- Quantas árvores ao todo foram plantadas, aproximadamente, nesses três meses?
_____
PROFESSOR
Resposta: Exemplo de aproximação: 11.000 árvores.
- Componha cada
número
e escreva como se lê.
- 1 unidade de milhar, 7 centenas, 9
dezenas
e 5 unidades -
_____
PROFESSOR
Resposta: 1.795Lemos: _____
PROFESSOR
Resposta: mil setecentos e noventa e cinco.
- 7 unidades de milhar, 8
dezenas
e 4 unidades -
_____
PROFESSOR
Resposta: 7.084Lemos: _____
PROFESSOR
Resposta: sete mil e oitenta e quatro.
- 1 unidade de milhar, 7 centenas, 9
dezenas
e 5 unidades -
_____
Autoavaliação

- Reconheço números com quatro algarismos?
PROFESSOR
Resposta pessoal.
- Consigo comparar números com quatro algarismos?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 5
Inicialmente, os estudantes devem escolher os seis números. Oriente-os a escrever no caderno os números escolhidos, sem se importar com a ordem. Verifique se todos os números têm 4 algarismos. Em seguida, peça que os organizem em ordem decrescente (do maior para o menor) formando uma sequência.
Nessa atividade, como os números têm a mesma quantidade de algarismos, espera-se que os estudantes comparem ordem a ordem. Socialize com a turma as respostas e discuta com os estudantes os procedimentos utilizados.
Atividade 6
Na atividade, os estudantes devem observar um gráfico de colunas para fazer arredondamentos. Isso pode ser feito pela observação das linhas do gráfico. Por exemplo, no mês de setembro, a altura da coluna é um valor próximo de 3.000, de modo que o arredondamento será feito para 3.000 árvores plantadas nesse mês. Nos outros meses, os arredondamentos esperados são 5.000 árvores plantadas em outubro e 3.000 árvores plantadas em novembro.
Atividade 7
Para ampliar a proposta, você pode elaborar e aplicar um ditado para que os estudantes escrevam a decomposição de cada número falado por você, da mesma maneira que foi feito nessa atividade.
BNCC em foco:
EF03MA01, EF03MA02, EF03MA03, EF03MA26
Autoavaliação
Para finalizar a primeira Unidade do livro, explique aos estudantes que essas duas questões serão utilizadas para que eles analisem o trabalho realizado e como seus conhecimentos foram construídos.
É importante que percebam a diferença entre as duas perguntas, sendo a primeira relacionada à leitura e escrita de números, e a segunda, ao estabelecimento de relações por meio da comparação para perceber, por exemplo, qual número é maior que outro.
Por meio das perguntas, os estudantes poderão perceber quanto avançaram ou não no reconhecimento de números e na compreensão do funcionamento do sistema de numeração.
MP058
Comentários para o professor
Conclusão da Unidade 1
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue ler, escrever e comparar números naturais até a quarta ordem, e estabelecer relações entre os registros numéricos (escritos ou com material manipulável) e a língua materna? |
_____ |
_____ |
|
Identifica características do sistema de numeração decimal, empregando a composição e a decomposição de número natural de até quatro ordens? |
_____ |
_____ |
|
Constrói fatos básicos da adição e da subtração e utiliza-os no cálculo mental ou escrito? |
_____ |
_____ |
|
Estabelece a relação entre números naturais e pontos da reta numérica, ordenando-os, e também na construção de fatos da adição e da subtração, relacionando-os com deslocamentos? |
_____ |
_____ |
|
Identifica regularidades em sequências numéricas resultantes de adições ou subtrações sucessivas? |
_____ |
_____ |
|
Reconhece e descreve regras de formação de sequências numéricas e identifica elementos ausentes ou seguintes? |
_____ |
_____ |
|
Resolve problemas que envolvem a comparação e a equivalência de valores monetários do sistema brasileiro? |
_____ |
_____ |
|
Resolve problemas cujos dados são apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |


