MP059
Introdução da Unidade 2
Esta Unidade tem como foco tratar os conhecimentos a serem desenvolvidos na Unidade Temática Números. Assim, a abertura traz, em página dupla, uma imagem próxima do cotidiano da criança na faixa etária do estudante do 3º ano do Ensino Fundamental, com informações a serem exploradas em Para refletir ...
Nesta Unidade, além de reforçar nos estudantes o desenvolvimento das habilidades de identificação das características do sistema de numeração decimal, por meio da composição e da decomposição de número natural de até quatro ordens; de construção e aplicação, com estratégias pessoais, dos fatos básicos da adição e da multiplicação para o cálculo mental ou escrito e de relacionar os números naturais com pontos da reta numérica na construção de fatos da adição e da subtração, mediante deslocamentos para a direita ou para a esquerda, e também a ordenação dos números naturais, já trabalhadas na Unidade 1, explora-se o uso de diferentes procedimentos de cálculo mental e cálculo escrito (exato ou aproximado; por decomposição ou por algoritmo) na resolução de problemas significativos que envolvam adição e subtração com números naturais e seus diferentes significados: juntar, acrescentar, separar, retirar, comparar e completar quantidades, ampliando os objetos de conhecimento da Unidade Temática Números. Destacam-se também as atividades que propõem que os estudantes elaborem questões com base nos dados apresentados por maneiras diversas, seja por texto, por tabelas e gráficos, por imagens ilustrativas ou fotográficas, ou ainda por esquemas.
A Unidade Temática Probabilidade e estatística é contemplada em atividades propositivas de problemas que exploram a habilidade dos estudantes de mobilizar os conhecimentos necessários ao desenvolvimento da leitura, da interpretação, bem como da aplicação e comparação de dados apresentados em tabelas e gráficos de barras envolvendo resultados de pesquisas com o objetivo de compreender aspectos da realidade sociocultural significativos. Essas atividades ampliam os conhecimentos desenvolvidos no 2º ano do Ensino Fundamental e preparam para os que serão trabalhados no 4º ano.
Competência geral favorecida
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
Competências específicas favorecidas
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
MP060
UNIDADE 2. Adição e subtração

MANUAL DO PROFESSOR
Objetivos da Unidade
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Identificar características do sistema de numeração decimal, utilizando composição e decomposição de números naturais (de até 4 algarismos).
Representar números naturais na reta numérica para utilizá-la na construção de fatos da adição e da subtração, relacionando-os com deslocamentos para a direita ou para a esquerda.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada ou gráficos de colunas.
Organizar dados coletados em pesquisa utilizando tabelas e gráficos de barras.
Para explorar a ilustração da abertura, é importante reservar um tempo para que os estudantes observem a cena e conversem entre si sobre os espaços e objetos presentes na sorveteria. Comente com eles que Melissa e Caio estão na sorveteria e peça que os localizem.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA04, EF03MA05, EF03MA06, EF03MA11, EF03MA26, EF03MA27
MP061
Para refletir...
Os sabores dos picolés são: morango, limão e maracujá. Luís está separando quatro picolés de cada sabor para levar a seus amigos. Quantos picolés no total ele vai levar? _____
Resposta: 12 picolés.
Cada pote de sorvete de massa serve vinte bolas caprichadas. Melissa pediu três casquinhas com duas bolas de sorvete do mesmo sabor em cada uma. Quantas bolas ainda é possível servir com esse pote?
_____
Resposta: 14 bolas.
MANUAL DO PROFESSOR
Para refletir...
Na primeira questão, espera-se que os estudantes utilizem a adição reiterada, ou seja, a adição de parcelas iguais com a qual já devem ter tido contato no ano anterior. Como há 3 sabores de picolé e ele vai levar 4 picolés de cada sabor, o total é 12 picolés. Ao comentar a abertura, registre na lousa:
4 + 4 + 4 = 12.
Já na segunda questão, espera-se que os estudantes identifiquem que essa é uma situação que envolve a adição e a subtração. Incentive-os a elaborarem uma estratégia de resolução e, depois de aplicá-la, fazerem a verificação do resultado obtido, observando sua adequação à situação proposta.
MP062
Jogo: Fazendo quinze
Material: Para cada jogador, 1 conjunto de cartas numeradas de 1 a 10 e 10 feijões para fazer a contagem dos pontos. As cartas podem ser confeccionadas pelos jogadores ou podem ser usadas as cartas numeradas de 2 a 10 e o ás de um baralho comum. Nesse caso, a carta ás substitui a carta de número 1.

Jogadores: 2, 3 ou 4
Regras:
- Inicialmente, escolhe-se o carteador, ou seja, quem vai distribuir as cartas e determinar o número de rodadas a serem jogadas, que deverá ser entre 5 e 10.
- O carteador embaralha as cartas e distribui duas para cada jogador, incluindo ele mesmo. As cartas restantes ficam no centro da mesa, voltadas para baixo.
- Cada jogador olha suas cartas sem deixar que os demais as vejam.
- O primeiro a jogar é quem está à esquerda do carteador, e assim por diante.
- Cada jogador, na sua vez, pode pedir mais uma carta ao carteador, verificando seu valor sem mostrá-la a ninguém. Isso se repete até que o jogador diga que não quer mais cartas ou até que ele obtenha soma maior que 15 com a adição dos números de suas cartas. Nesse último caso, o jogador deve mostrar suas cartas aos outros jogadores e não participar mais dessa rodada.
- Quando nenhum jogador quiser mais cartas, faz-se a verificação: aquele que conseguir obter, com a adição dos números de suas cartas, a soma igual a 15 (ou, se ninguém conseguir a soma igual a 15, aquele que alcançar a soma mais próxima de 15) ganha um feijão de cada jogador. Em caso de empate, ninguém ganha.
• Após cada rodada, embaralham-se novamente as cartas.
• Vence o jogo quem tiver mais feijões no fim de todas as rodadas.
MANUAL DO PROFESSOR
Objetivo
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Auxilie os estudantes na leitura e na compreensão das regras do jogo, que envolve o cálculo mental com adição de várias parcelas. O aspecto mais interessante é a necessidade de descobrir, a cada rodada, quais cartas podem levar à soma 15 ou a uma quantidade aproximada, porém inferior. A habilidade de tomar decisões em situações como essa (pegar mais cartas ou não, e quantas pegar) exige rapidez para estimar resultados possíveis. Espera-se que os estudantes considerem que, se tiverem cartas cuja soma seja próxima de 15, não devem pedir mais cartas, se desejarem permanecer no jogo; se a soma for abaixo de 6, devem pedir ao menos mais uma carta. Deixe-os jogar algumas partidas para se familiarizarem com as regras e com as estimativas de resultados possíveis em diversas jogadas. Observe as estratégias empregadas durante o jogo: se fazem alguma análise sofisticada em relação aos números ou se jogam aleatoriamente.
Variações
À medida que explorarem o jogo, é possível que os estudantes queiram buscar novos desafios. Por exemplo, alterar a soma a ser obtida ou os valores e a quantidade de cartas disponíveis aos jogadores etc. Eles também podem modificar algumas regras, como eliminar a regra de que, passando de 15, o jogador sai do jogo; assim, tomarão decisões também pela proximidade dos sucessores de 15. No decorrer das aulas, pode ainda ser alterada a operação para multiplicação, mas nesse caso o valor 15 deve ser mudado para um número maior.
BNCC em foco:
EF03MA03
MP063
Questões sobre o jogo
- Qual é a
menor
soma possível que um jogador pode
obter
ao receber as duas primeiras cartas? E a maior?
_____
PROFESSOR
Resposta: Menor soma: 2; maior soma: 20.
- É possível um jogador
obter
soma 15 nas duas primeiras cartas distribuídas no jogo? No caso de ser possível, com quais números?
_____
PROFESSOR
Resposta: Sim; com os números 8 e 7 (8 + 7 = 15), ou com os números 9 e 6 (9 + 6 = 15), ou com os números 10 e 5 (10 + 5 = 15).
- Veja as cartas de Adriana em uma das rodadas.

Se ela solicitasse mais uma carta, qual ela poderia receber de modo que não fosse excluída da rodada?
_____
PROFESSOR
Resposta: A carta de número 4, 3, 2 ou 1.

- Se você estivesse jogando e suas cartas tivessem soma 13, você se arriscaria a pedir mais cartas? Por quê?
PROFESSOR
Respostas pessoais.
- Carlos, Vanessa e Ricardo estavam jogando. Observe as cartas de cada um deles.
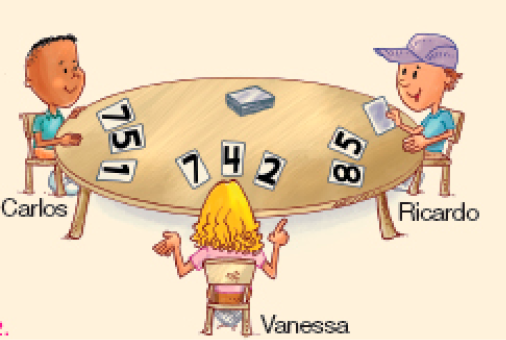
Sabendo que Ricardo venceu a rodada, qual poderia ser sua terceira carta? Leve em consideração que cada jogador encerrou a rodada com 3 cartas.
PROFESSOR
Resposta: A de número 1 ou 2.MANUAL DO PROFESSOR
Questões sobre o jogo
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões de 1 a 5, que auxiliam na compreensão de escolhas de possibilidades, na análise de riscos e na tomada de decisões.
Na questão 2, espera-se que os estudantes percebam que é possível obter soma 15 com os números 8 e 7, ou com 9 e 6, ou ainda com 10 e 5.
Na questão 4, espera-se que o estudante perceba que ele já tem 13, o que está muito próximo de 15, ou seja, não é uma boa estratégia pedir outra carta, pois, para que ele não saia do jogo, as únicas cartas que lhe servem são as de número 1 ou de número 2.
Na questão 5, espera-se que os estudantes percebam que a terceira carta de Ricardo poderia ser a de número 1 ou 2, pois, no primeiro caso, ele teria soma igual a 14 e, no segundo, soma igual a 15, enquanto Vanessa e Carlos pararam de pedir cartas quando alcançaram a soma igual a 13.
Após a resolução das questões, proponha aos estudantes que joguem novamente. Observe se eles mudaram de postura durante o jogo: se as análises estão mais profundas e cuidadosas do que anteriormente.
Esse retorno ao jogo pode representar um momento de, na perspectiva de uma avaliação formativa, diagnóstico do quanto os estudantes se apropriaram das técnicas de análise propiciadas pela resolução das questões.
BNCC em foco:
EF03MA03
MP064
Situações de adição e de subtração
- Mariana colheu várias frutas de seu pomar: 44 laranjas, 23 mangas e 12 abacates.
- Quantas frutas foram colhidas no total?
_____
PROFESSOR
Resposta: 79 frutas.
- Mariana precisa colher, no total, 2 dúzias de abacates. Quantos abacates ela ainda precisa colher?
_____
PROFESSOR
Resposta: 12 abacates.
- Quantas frutas foram colhidas no total?
- Há 32 anos, Miguel tinha 14 anos de idade. Quantos anos Miguel tem agora?
_____
PROFESSOR
Resposta: 46 anos.
- Amélia tinha algumas figurinhas e ganhou outras 12 de seu pai. Ela passou a ter 48 figurinhas. Quantas figurinhas Amélia tinha antes de ganhar outras de seu pai?
_____
PROFESSOR
Resposta: 36 figurinhas.
- Em uma escola, houve apresentação musical feita por alguns estudantes. Na plateia, estavam 232 pais e 105 estudantes. Quantas pessoas assistiram à apresentação?
_____
PROFESSOR
Resposta: 337 pessoas.5. No site de uma loja, Marília viu a propaganda dos produtos abaixo.
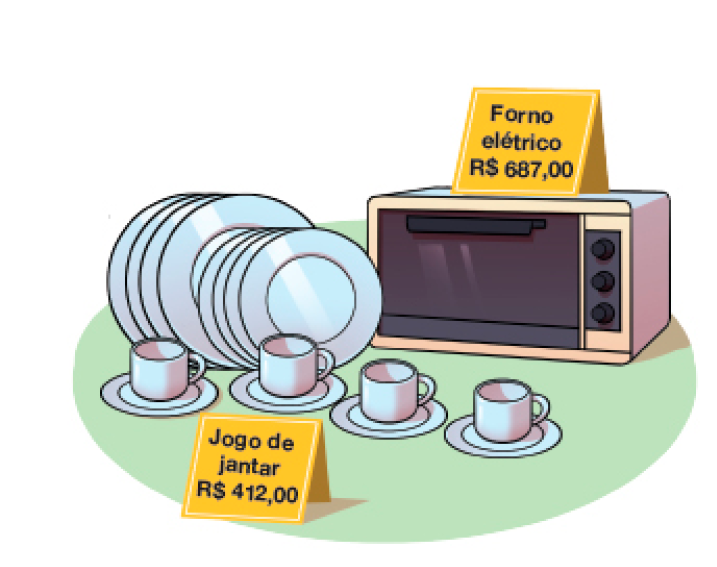
- Faça uma estimativa de qual é o valor aproximado da diferença entre os preços dos produtos divulgados.
_____
PROFESSOR
Resposta: Exemplo de estimativa: 300 reais.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e de subtração, utilizando diferentes estratégias de cálculo, incluindo o cálculo mental e a estimativa.
Resolver problemas cujos dados estão apresentados em gráficos de colunas.
Atividade 1
Nessa atividade, os estudantes precisam buscar informações no texto e interpretá-las, juntar mais de duas quantidades, ter noção de dúzia e completar uma quantidade para atingir outra. É interessante propor a socialização das estratégias utilizadas por eles.
Incentive os estudantes a utilizarem o espaço ao lado das atividades para realizar seus cálculos, por algoritmo ou por meio de registros pessoais. Se possível, ofereça a eles algum tipo de material manipulável para ajudar nas resoluções.
Atividades 2, 3 e 4
Disponibilize para os estudantes materiais manipuláveis (fichas, palitos, Material Dourado) que os auxiliem nessas atividades. Escolha alguns estudantes para explicar, oralmente ou por escrito, como resolveram cada cálculo.
Atividade 5
Produza, antecipadamente, cédulas e moedas de real para os estudantes vivenciarem a situação e utilizarem como apoio para o cálculo. Oriente-os a guardá-las, pois poderão ser utilizadas em outras atividades.
Observe se os estudantes apresentam alguma dificuldade para estimar os valores aproximados (se julgar necessário, exemplifique na lousa e retome a representação na reta numérica). Eles podem, por exemplo, arredondar os números para a dezena mais próxima e, depois, subtraí-los: 690 − 410 = 280; ou arredondar para a centena mais próxima e efetuar a subtração: 700 − 400 = 300.
Após a resolução, peça aos estudantes que calculem o valor exato e comparem com os resultados obtidos nos arredondamentos.
A abordagem em sala de aula deve levar em conta as dificuldades de cada tipo de problema e os procedimentos de resolução que fazem parte do repertório dos estudantes. As operações podem ser feitas pelos algoritmos tradicionais, por estimativas ou com o auxílio de instrumentos manipuláveis, como o Material Dourado e o ábaco.
BNCC em foco:
EF03MA06
MP065
- Observe no monitor abaixo a quantidade de livros de uma biblioteca e responda às questões.

- Quantos livros de contos há a mais que livros de arte?
Há _____ livros de contos a mais que livros de arte.
PROFESSOR
Resposta: 141
- Quantos livros de poemas há a menos que livros de contos?
Há _____ livros de poemas a menos que livros de contos.
PROFESSOR
Resposta: 211

- Invente um problema usando os dados da ilustração e escreva-o nas linhas. Depois, peça a um
colega
que o resolva.
_____
PROFESSOR
Resposta pessoal.


- Em uma exposição, há fotografias de diferentes animais. Observe o gráfico ao lado para responder às questões.
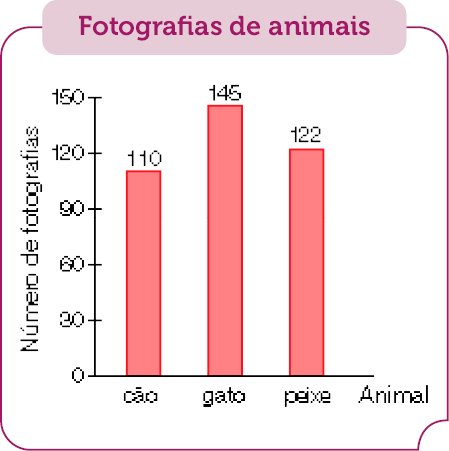
Fonte: Acervo da exposição. (fev. 2023)
- Quantas fotografias estão expostas ao todo?
_____
PROFESSOR
Resposta: 377 fotografias.
- Quantas fotografias de gatos há a mais que fotografias de cães?
_____
PROFESSOR
Resposta: 35 fotografias.
MANUAL DO PROFESSOR
Atividade 6
Espera-se que os estudantes identifiquem nas questões propostas o significado de comparação de quantidades da subtração. Incentive-os a propor estratégias próprias para efetuar os cálculos com ou sem apoio de material manipulável. Socialize os diferentes procedimentos e valide-os com os estudantes.
Atividade 7
Os estudantes devem elaborar um problema com base na ilustração, que fornece dados numéricos. Em propostas desse tipo são comuns problemas que envolvam muitos cálculos, com “números grandes”, pois os estudantes acreditam que, dessa maneira, tornam maior o desafio para os colegas. Incentive-os a pensar em problemas com cálculos simples, porém criativos.
Atividade 8
Atividades desse tipo possibilitam relacionar as operações aritméticas à exploração de um gráfico. Observe se, para responder às questões, os estudantes leem e compreendem as informações do gráfico. Pergunte: “Quantas fotografias de cães faltam para chegar à mesma quantidade de fotografias de peixes?”. Espera-se que respondam 12 fotografias de cães.
Os diferentes procedimentos de cálculo se relacionam e se complementam: o cálculo escrito, para ser compreendido, apoia-se no cálculo mental, nas estimativas e nas aproximações. Ao organizar o trabalho com cálculos, é importante privilegiar uma abordagem que explore concomitantemente procedimentos de cálculos mental e escrito, para que os estudantes percebam gradativamente as relações existentes entre eles e, com isso, aperfeiçoem seus procedimentos pessoais, tornando-os cada vez mais práticos e próximos das técnicas usuais.
BNCC em foco:
EF03MA06, EF03MA26
MP066
- O esquema abaixo mostra os caminhos possíveis entre a casa de Carla e a escola onde ela estuda.
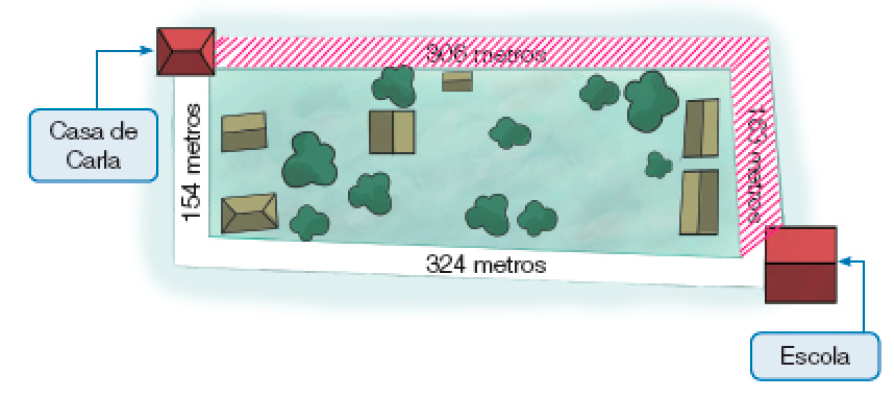

- Pinte o caminho mais curto entre a casa de Carla e a escola.
- Qual é a medida do comprimento, em metro, do caminho mais curto?
_____
PROFESSOR
Resposta: 469 metros.
- Observe o painel que mostra o número de participantes de uma meia maratona e responda às questões.
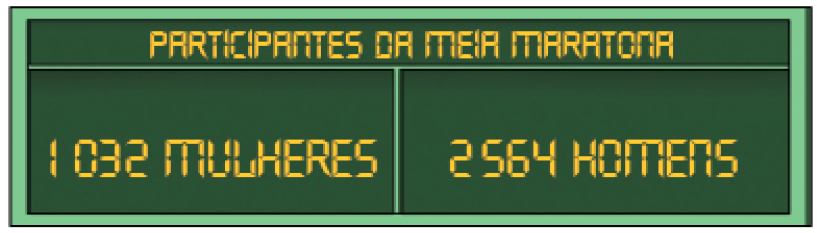
- Quantas pessoas participaram dessa meia maratona?
_____
PROFESSOR
Resposta: 3.596 pessoas.
- Quantos homens participaram a mais que mulheres?
_____
PROFESSOR
Resposta: 1.532 homens.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada.
As atividades propostas nestas páginas apresentam situações que articulam as operações de adição e subtração com outras Unidades Temáticas da Matemática (Geometria, Grandezas e medidas e Probabilidade e estatístic a); retomam conceitos já trabalhados, como movimentação no espaço, representação de trajetos, noções de medidas de comprimento e interpretação de dados registrados em tabela de dupla entrada. O aspecto importante é a necessidade que os estudantes terão de decidir quais operações conduzem à resolução do problema.
Atividades 9 e 10
Explore com a turma as ilustrações e as informações contidas nelas. Se julgar oportuno, reúna os estudantes em duplas para discutirem as estratégias a serem usadas. Verifique como eles procedem no caso das quantidades expressas por números de 4 algarismos. Disponibilize o Material Dourado como apoio para a realização desses cálculos. Depois, as duplas podem compartilhar suas estratégias com toda a turma, em uma roda de conversa.
BNCC em foco:
EF03MA06
Sugestão de leitura para o professor
Artigo
RIZZARDO, Juliana C. Corbanezi. A adição no processo de tomada de consciência: um estudo de caso. Disponível em: http://fdnc.io/eU1. Acesso em: 21 maio 2021.
Nesse artigo, a autora discute um estudo de caso que envolve um estudante de 8 anos em atividades de adição em uma escola pública. Constam do artigo a fundamentação, o método de trabalho, os diálogos e as intervenções da pesquisadora no processo de aprendizagem.
MP067
- Meire tem uma floricultura. Veja na tabela abaixo a quantidade de flores que ela usou durante um mês para fazer arranjos. Em seguida, complete-a.
Quantidade de flores
Tabela: equivalente textual a seguir.
|
Flor Cor |
Gérbera |
Rosa |
|---|---|---|
|
Branca |
1 202 |
1 490 |
|
Vermelha |
2 314 |
2 308 |
|
Total |
_____ |
_____ |
Fonte: Controle da floricultura da Meire. (jan. 2023)
PROFESSOR
Resposta: Gérbera: 3.516; Total Rosa: 3.796.- Quantas flores brancas e quantas flores vermelhas Meire usou para fazer os arranjos nesse mês?
_____
PROFESSOR
Resposta: Meire usou 2.692 flores brancas e 4.622 flores vermelhas.
- Quantas rosas foram usadas a mais que gérberas?
_____
PROFESSOR
Resposta: Foram usadas 282 rosas a mais.
- Agora, invente outra questão que possa ser respondida com os dados da tabela e peça a um
colega
que a responda.
_____
PROFESSOR
Exemplo de questão: “Quantas flores Meire usou nesse mês?”. (7.314 flores.)
- O Teatro Castro Alves, no município de Salvador (Bahia), tem capacidade para 1.554 pessoas. Se em uma apresentação foram 1.342 pessoas, quantos assentos ficaram vazios?

LEGENDA: Interior do Teatro Castro Alves, município de Salvador, Bahia, em 2018. FIM DA LEGENDA.
Ficaram vazios _____ assentos.
PROFESSOR
Resposta: 212MANUAL DO PROFESSOR
Atividade 11
A atividade possibilita que os estudantes reconheçam o cálculo a ser feito pela análise dos dados registrados em uma tabela de dupla entrada e proponham novos problemas com base nesses dados. Auxilie-os na leitura da tabela de dupla entrada, esclarecendo que cada tipo de flor (gérbera e rosa) pode aparecer com duas cores diferentes (branca e vermelha). Faça questionamentos que promovam o entendimento desse tipo de tabela. Por exemplo:
Há quantas rosas brancas? (1.490)
Quantas gérberas são vermelhas? (2.314)
Há mais rosas brancas ou vermelhas? (Vermelhas, pois 2.308 > 1.490.)
Que tipo de flor há mais na cor vermelha: gérbera ou rosa? Por quê? (Gérbera, porque há 2.314 gérberas vermelhas e 2.308 rosas vermelhas, e 2.314 > 2.308.)
Que tipo de flor há em maior quantidade? (Rosas.)
Atividade 12
Organize os estudantes em grupos, distribua um kit de Material Dourado para cada grupo e proponha que representem 1.554 e 1.342 com as peças desse material. Se julgar necessário, relembre com eles as seguintes equivalências:
1 cubinho corresponde a 1 unidade;
1 barra corresponde a 10 unidades ou 1 dezena;
1 placa corresponde a 100 unidades ou 1 centena;
1 cubo grande corresponde a 1.000 unidades ou 1 unidadede milhar.
Peça aos estudantes que registrem no caderno essas representações com desenhos. Depois, eles devem discutir estratégias para o cálculo usando as representações feitas e registrar no caderno os procedimentos e o resultado obtido.
Para finalizar, cada grupo apresenta para a turma seu cálculo usando as representações feitas com o Material Dourado.
BNCC em foco:
EF03MA06, EF03MA26
MP068
Algumas estratégias de cálculo
Cálculo mental e estimativas
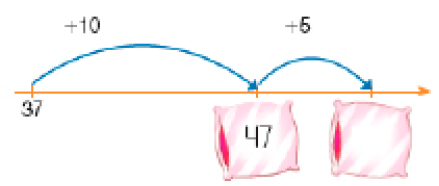
- Calcule o resultado em cada caso dando “saltos duplos” na reta numérica.
- Sabendo que:
15 = 10 + _____
PROFESSOR
Resposta: 537 + 15 = _____
PROFESSOR
Resposta: 52
PROFESSOR
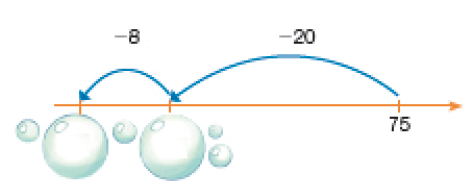
Resposta: 52- Sabendo que:
28 = _____ + 8
PROFESSOR
Resposta: 2075 − 28 = _____
PROFESSOR
Resposta: 47
PROFESSOR
Resposta: 47, 55- Um ciclista percorreu uma trilha do quilômetro 28 até o quilômetro 49. Usando a reta numérica, Adriana e Cláudio decidiram calcular quantos quilômetros o ciclista percorreu nessa trilha. Verifique a estratégia usada pelas crianças e complete.
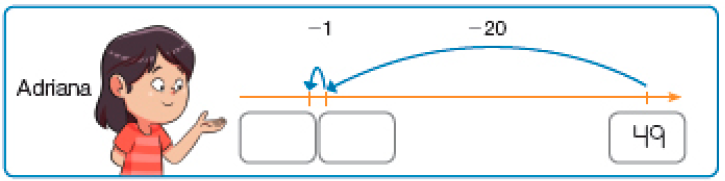
PROFESSOR
Resposta: 28, 29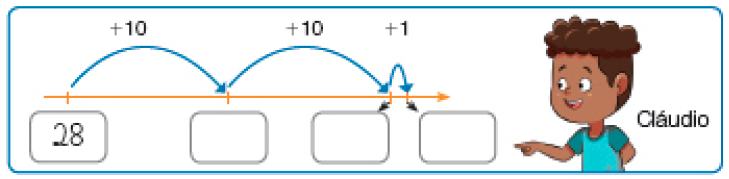
PROFESSOR
Resposta: 38, 48, 49O ciclista percorreu _____ quilômetros.
PROFESSOR
Resposta: 21MANUAL DO PROFESSOR
Objetivos
Representar números naturais na reta numérica para utilizá-la na construção de fatos da adição e da subtração, relacionando-os com deslocamentos para a direita ou para a esquerda.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Atividade 1
A atividade propicia aos estudantes conhecerem estratégias de cálculo como apoio da reta numérica para efetuar adições e subtrações. Espera-se que eles se apropriem desse conhecimento e o apliquem ao fazer cálculos mentais.
Atividade 2
Peça aos estudantes que observem as estratégias das duas crianças para descobrir a distância percorrida pelo ciclista, que partiu do quilômetro 28 e chegou ao quilômetro 49.
Adriana fez a subtração 49 − 28, com o recurso da reta numérica. Dando dois “saltos” para trás, um de 20 e outro de 1, ela encontrou o resultado 28, concluindo que o ciclista percorreu 21 quilômetros.
Cláudio calculou de outra maneira: realizou dois “saltos” de 10 e um “salto” de 1 para a frente, a fim de chegar ao número 49. Nesse caso, ao adicionar os “saltos” 10 + 10 + 1, ele chegou ao resultado de 21, ou seja, 21 quilômetros.
Proponha aos estudantes que desenhem uma reta numérica e marquem nela o ponto 28, para representar o quilômetro de onde partiu o ciclista. A partir desse ponto, darão “saltos” (quantos quiserem) até atingirem o ponto 49, que representa o quilômetro da chegada. Outra possibilidade é marcarem o quilômetro 49 e realizarem o movimento contrário até atingir a marca do quilômetro 28. Em ambos os casos, para saber a distância percorrida basta adicionar as distâncias realizadas em cada “salto”.
BNCC em foco:
EF03MA04, EF03MA05
MP069
- Sandra tem 780 gramas de farinha de trigo e quer fazer 2 bolos: um de abacaxi e outro de chocolate.
Quantidade de farinha de trigo necessária
Tabela: equivalente textual a seguir.
|
Tipo de bolo |
Quantidade de farinha |
|---|---|
|
Chocolate |
360 gramas |
|
Abacaxi |
310 gramas |
Fonte: Receitas de Sandra. (jan. 2023)
- Fazendo uma estimativa, é possível dizer que a quantidade de farinha de trigo que Sandra tem é suficiente para fazer os 2 bolos?
_____
PROFESSOR
Resposta: Sim.
- Quantos gramas de farinha de trigo sobrariam ou faltariam para Sandra fazer os dois bolos?
_____
PROFESSOR
Resposta: 110 gramas.

- Isabela leu dois livros: um com 313 páginas e o outro com 189 páginas. Descubra a quantidade, aproximada, de páginas lidas por Isabela.
- O
número
313 está mais próximo de 300 ou de 400?
_____
PROFESSOR
Resposta: De 300.
- O
número
189 está mais próximo de 100 ou de 200?
_____
PROFESSOR
Resposta: De 200.
- Quantas páginas, aproximadamente, Isabela leu ao todo?
_____
PROFESSOR
Resposta: Exemplo de estimativa: Aproximadamente, 500 páginas.
- O
número
313 está mais próximo de 300 ou de 400?
_____


- Qual é, aproximadamente, o
preço
da geladeira e da TV juntas?

_____
PROFESSOR
Resposta: Exemplo de estimativa: Aproximadamente, 2.400 reais.
MANUAL DO PROFESSOR
Atividade 3
Espera-se que os estudantes respondam que sim. No entanto, como se trata de uma estimativa, pode ser que algum deles empregue um critério de arredondamento para cima em relação às centenas (400 gramas para os dois bolos). Desse modo, a resposta será não.
É importante salientar que isso não é um erro. Mais do que isso, é uma oportunidade de discussão a respeito dos critérios aplicados pelos estudantes durante a estimativa.
Atividade 4
Depois que os estudantes responderem às questões, pergunte a eles: “Qual é o resultado exato da adição 313 + 189?” (502). É importante eles perceberem que, nesse caso, o cálculo exato apresenta uma diferença pequena em relação à estimativa feita (500), pois o arredondamento de 313 para 300 diminui o número em 13 unidades, enquanto o arredondamento de 189 para 200 o aumenta em 11 unidades. Portanto, o resultado será 2 unidades (13 − 11) a menos que o resultado exato. A atividade pode ser ampliada fazendo-se perguntas como: “Que resultado seria obtido se o arredondamento dessa adição fosse para a dezena mais próxima? Qual é o resultado exato da adição 313 + 189?”.(310 + 190 = 500; 502)
Atividade 5
Os estudantes podem resolver a atividade em duplas. Verifique se primeiro fazem o arredondamento dos valores para depois efetuarem a adição.
Após a resolução, sugira a eles adições similares, para que calculem os resultados por meio de estimativas.
Para verificar se o resultado obtido estava correto, costumava-se fazer a “prova real” (operação inversa) ou a “prova dos noves”, que não dá garantia absoluta da comprovação. Hoje, essas técnicas de verificação de resultados têm sido substituídas pelas estimativas, sobretudo por se reconhecer sua grande contribuição para o cálculo mental, mais práticas nas situações cotidianas. Por isso, oferecer aos estudantes situações em que as aproximações e estimativas de resultados sejam mais importantes que o cálculo exato contribui de modo significativo para o desempenho deles em situações do dia a dia e para a compreensão dos resultados obtidos por meio de algoritmos ou de calculadora. Saber estimar resultados possibilita reconhecer erros de digitação, ao deparar com um resultado “absurdo” na calculadora.
BNCC em foco:
EF03MA05
MP070
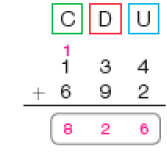
Decomposição e algoritmo usual
- Os estudantes do 3º ano foram a um zoológico que acomoda 142 mamíferos e 253 aves. Quantos mamíferos e aves há ao todo nesse zoológico?
Para descobrir, vamos adicionar 142 com 253.
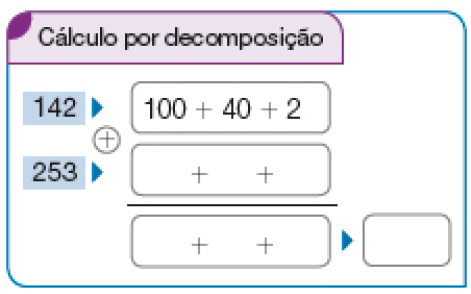
PROFESSOR
Resposta: 200 + 50 + 3PROFESSOR
300 + 90 + 5PROFESSOR
395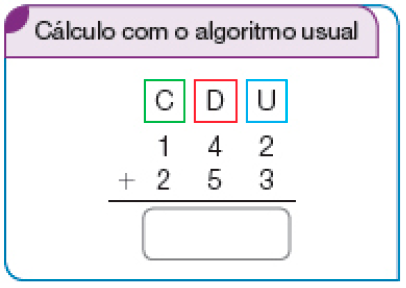
PROFESSOR
Resposta: 395
PROFESSOR
Resposta: 5, 9, 3Adição 142 + 253 = _____
PROFESSOR
Resposta: 395Ao todo, nesse zoológico, há _____ mamíferos e aves.
PROFESSOR
Resposta: 395

- Há também 102 répteis nesse zoológico. Quantos répteis, mamíferos e aves há ao todo? Calcule usando a estratégia de sua preferência e compare o resultado com o de um colega.
_____
Ao todo, nesse zoológico, há _____ répteis, mamíferos e aves.
PROFESSOR
Resposta: 497MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando composição e decomposição de números naturais (de até 4 algarismos).
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Atividade 1
Após a resolução de cada parte da atividade, verifique as respostas dos estudantes e solicite que comparem com um colega que tenha utilizado um método diferente, fazendo-os perceber que, independentemente do método utilizado para resolução, as respostas têm de ser iguais.
Peça aos estudantes que pensem em outras maneiras de calcular o resultado da operação envolvida (adição): por decomposição, pelo algoritmo usual, por estimativas e mentalmente.
Compare e discuta os diferentes procedimentos de cálculo com a turma.
Se julgar conveniente, antes que os estudantes completem o algoritmo usual, peça a um deles que faça na lousa a operação por decomposição. Há estudantes que iniciam o cálculo com o algarismo da ordem das centenas, depois com o das dezenas e por fim com o das unidades. A razão de se realizar o cálculo da direita para a esquerda ocorre pela necessidade de padronizar o procedimento no caso de a adição envolver reagrupamento.
BNCC em foco:
EF03MA02, EF03MA05
MP071
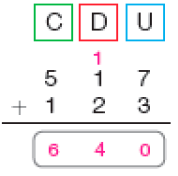
- Uma lanchonete encomendou 345 garrafas de suco de morango e 213 garrafas de suco de uva. Quantas garrafas de suco de morango foram encomendadas a mais que de uva?
Para descobrir, vamos subtrair 213 de 345.
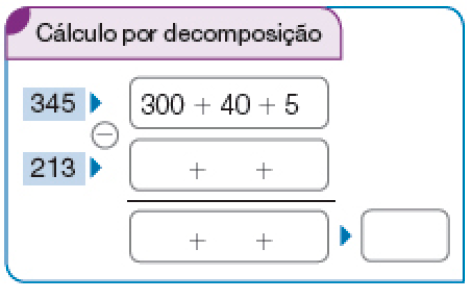
PROFESSOR
Resposta: 200 + 10 + 3PROFESSOR
100 + 30 + 2PROFESSOR
132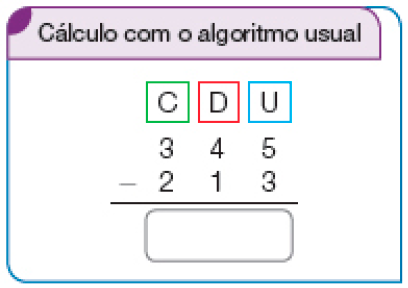
PROFESSOR
Resposta: 132
PROFESSOR
Resposta: 2, 3, 1Subtração - 345 − 213 = _____
PROFESSOR
Resposta: 132Foram encomendadas ______ garrafas de suco de morango a mais que de uva.
PROFESSOR
Resposta: 132- Para completar o pedido, a lanchonete encomendou também 396 garrafas de suco de laranja. Quantas garrafas de suco de laranja foram encomendadas a mais que de uva? Faça os cálculos usando a estratégia que preferir e compare o resultado com o de um colega.
Foram encomendadas _____ garrafas de suco de laranja a mais que de uva.
PROFESSOR
Resposta: 183MANUAL DO PROFESSOR
Atividade 2
De maneira semelhante à página anterior, após a resolução de cada parte da atividade, verifique as respostas dos estudantes e solicite que comparem com um colega que tenha utilizado um método diferente, fazendo-os perceber que, independentemente do método utilizado para resolução, as respostas têm de ser iguais.
Peça aos estudantes que pensem em outras maneiras de calcular o resultado da operação envolvida (subtração): por decomposição, pelo algoritmo usual, por estimativas e mentalmente.
Compare e discuta os diferentes procedimentos de cálculo com a turma.
Se julgar conveniente, antes que os estudantes completem o algoritmo usual, peça a um deles que faça na lousa a operação por decomposição. Há estudantes que iniciam o cálculo com o algarismo da ordem das centenas, depois com o das dezenas e por fim com o das unidades. A razão de se realizar o cálculo da direita para a esquerda ocorre pela necessidade de padronizar o procedimento no caso de a subtração envolver trocas.
BNCC em foco:
EF03MA02, EF03MA05
MP072
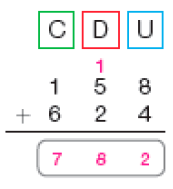
- Veja como Marcos encontrou o resultado da subtração 458 − 123.
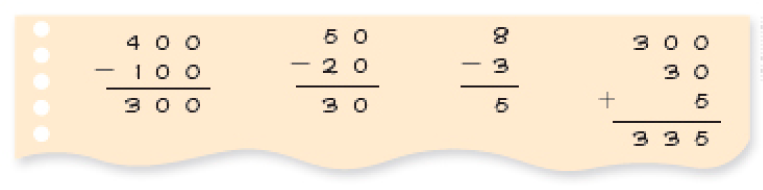


- Agora, explique para um
colega
a resolução de Marcos.
PROFESSOR
Resposta pessoal.
- Calcule o resultado de cada caso.
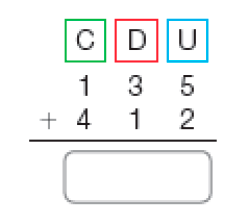
a)
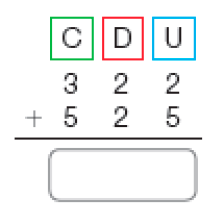
PROFESSOR
Resposta: 847b)
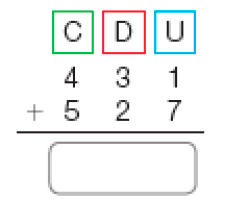
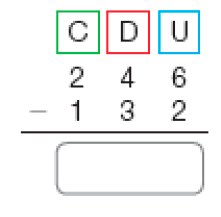
PROFESSOR
Resposta: 958c)
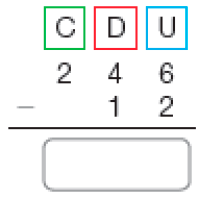
PROFESSOR
Resposta: 547d)
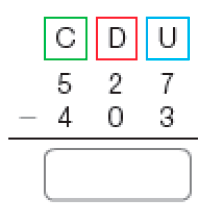
PROFESSOR
Resposta: 114e)
PROFESSOR
Resposta: 234f)
PROFESSOR
Resposta: 124- Juliana enganou-se ao encontrar o resultado de 13 + 112 + 30. Descubra o erro do cálculo de Juliana. Depois, no caderno, calcule o resultado correto.
Cálculo de Juliana

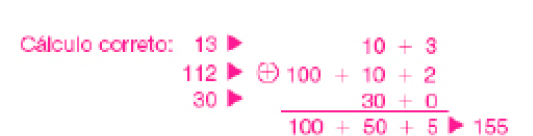
MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando composição e decomposição de números naturais (de até 4 algarismos).
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Atividade 3
Peça aos estudantes que observem a resolução feita por Marcos e depois a expliquem oralmente para um colega.
Exemplo de explicação: Primeiro, Marcos decompôs os números 458 e 123, observando o valor posicional de cada algarismo dos dois números:
458 = 400 + 50 + 8
123 = 100 + 20 + 3
Depois, ele fez as subtrações separadamente.
No caso das centenas: subtraiu 1 centena de 4 centenas (400 − 100 = 300). No caso das dezenas: subtraiu 2 dezenas de 5 dezenas (50 − 20). No caso das unidades: subtraiu 3 unidades de 8 unidades (8 − 3).
Então, no final, ele adicionou os três resultados: 300 + 30 + 5.
Atividade 4
Nessa atividade, os estudantes são incentivados a realizar as adições e subtrações por meio do algoritmo usual, em que os algarismos são adicionados ordem a ordem: unidades com unidades, dezenas com dezenas e centenas com centenas. É pertinente que efetuem mentalmente esses cálculos parciais.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05
Atividade 5
Situações de análise de erros, como a proposta aqui, possibilitam aos estudantes pensar no problema para além da simples resolução, já que a questão passa a ser identificar o erro, além de descobrir a resolução correta. Os estudantes devem perceber que o erro no cálculo de Juliana foi decompor o número 30 como 3 centenas, em vez de 3 dezenas e 0 unidade. Reforce a noção de que o valor posicional que o algarismo assume depende de sua posição no número.
MP073
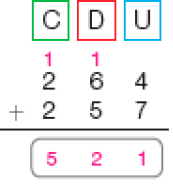
- Veja no esquema a seguir o circuito que Maiara percorre com a bicicleta.
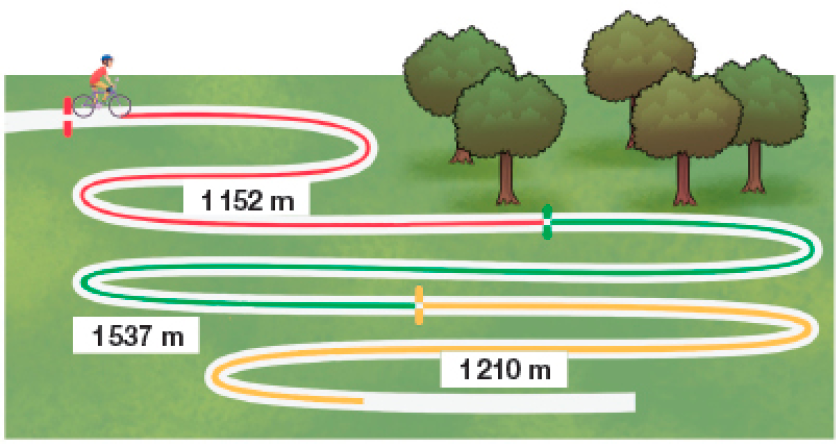
- Quantos metros ela
percorre
do início ao fim do circuito?
_____
Maiara percorre _____ metros do início ao fim do circuito.
PROFESSOR
Resposta: 3.899Boxe complementar:
Desafio
Com os algarismos 6, 7, 8 e 3, Diego forma o maior número possível. Vanessa usa os algarismos 3, 1, 2 e 5 e forma o menor número possível. Ambos usam os quatro algarismos que possuem sem repeti-los. Que número é obtido quando adicionamos os números formados por Diego e Vanessa?
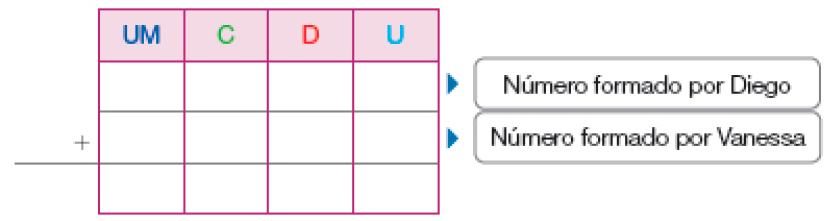
PROFESSOR
Resposta: UM: 8. C: 7. D: 6. U: 3. - Número formado por Diego.PROFESSOR
UM: 1. C: 2. D: 3. U: 5. - Número formado por Vanessa.PROFESSOR
UM: 9. C: 9. D: 9. U: 8. Total.Adicionando os dois números, formados por Diego e Vanessa, obtemos _____.
Resposta: 9.998
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 6
Disponibilize o Material Dourado para os estudantes usarem como apoio nos cálculos.
Nesta atividade, eles terão de recorrer ao esquema para saber quantos metros tem cada um dos três trechos que Maiara percorre com a bicicleta do início ao fim do percurso. Observe a estratégia usada pelos estudantes para efetuar a adição dos três números.
Desafio
Organize a turma em duplas para realizar esse desafio. Verifique as estratégias utilizadas pela dupla para obter o maior número formado pelos algarismos 6, 7, 8 e 3; quais as hipóteses levantadas e os argumentos validados. Se necessário, faça questionamentos como: “No algarismo das unidades de milhar desse número deve aparecer qual desses 4 algarismos para que ele seja o maior possível? Por quê?” (Espera-se que os estudantes reconheçam que, para ser o maior número, devem usar o algarismo 8.); “E nas centenas, qual desses algarismos deve aparecer?”(Espera-se que, desse modo, eles percebam que o número formado por Diego é 8.763.). Pensando de modo análogo, para obter o menor número com os algarismos 3, 1, 2 e 5, espera-se que os estudantes concluam que Vanessa formou o número 1.235.
Auxilie os estudantes a registrarem os números no quadro com os valores posicionais e incentive-os a fazerem os cálculos mentalmente para obter a soma em cada ordem, chegando a 9.998.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05; competência geral 2
MP074
Adição com reagrupamento: algumas estratégias
- Observe, abaixo, as promoções para o almoço.
-
Ivete
almoçou peixe grelhado e, de sobremesa, pediu uma fatia da
torta
de morango. Quanto
Ivete
gastou?
Para calcular quanto ela gastou, adicionamos 29 com 13.
-
Ivete
almoçou peixe grelhado e, de sobremesa, pediu uma fatia da
torta
de morango. Quanto
Ivete
gastou?

Cálculo com o Material Dourado
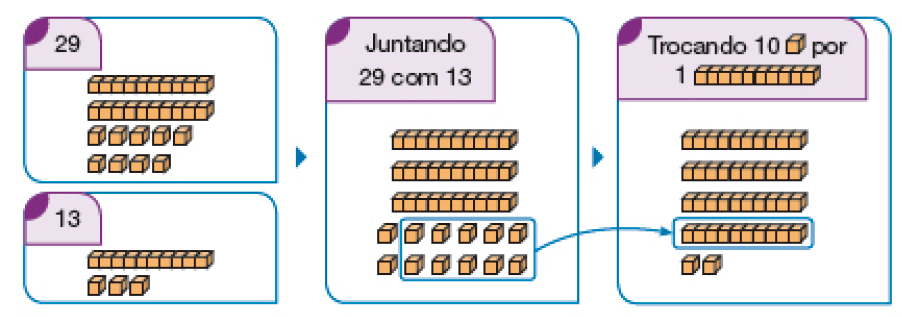
29 + 13 = _____
PROFESSOR
Resposta: 42Cálculo com o ábaco
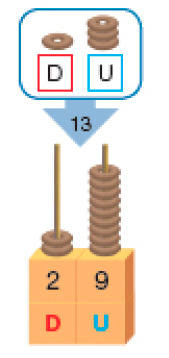
Temos de trocar 10 unidades por 1 dezena.
29 + 13 = _____
PROFESSOR
Resposta: 42Ao todo, Ivete gastou _____ reais nesse almoço.
PROFESSOR
Resposta: 42MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando composição e decomposição de números naturais (de até 4 algarismos).
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Atividade 1
Aprender os algoritmos de forma mecânica não representa uma real contribuição para o desenvolvimento do pensamento matemático. O que se defende não é o abandono dos algoritmos, mas a atribuição de significados para essas técnicas de cálculo. Nesse sentido, para evitar que os estudantes internalizem procedimentos mecânicos, sem significado, não recomendamos o uso da consagrada expressão “vai um” nem que o professor insista na decomposição.
Na situação apresentada com o Material Dourado, a adição dos cubinhos resulta em 12 unidades; desses cubinhos, 10 serão trocados por 1 barra, que, juntando-se com as 3 barras existentes, resultarão em 4 barras (4 dezenas). Portanto, o resultado da adição será 42.
O mesmo ocorre na situação do ábaco com o acréscimo das argolas. No entanto, com o ábaco retrata-se o valor posicional do nosso sistema de numeração, fato que não é possível verificar com o Material Dourado.
O trabalho com diferentes procedimentos de cálculo escrito possibilita aos estudantes a percepção das relações existentes entre eles e, com isso, o aperfeiçoamento das estratégias pessoais. Por exemplo, o uso do Material Dourado e da decomposição em uma mesma adição com reagrupamento possibilita que os estudantes percebam as relações entre os dois procedimentos.
Com o uso do Material Dourado, os estudantes percebem a troca de 10 cubinhos por 1 barra; no ábaco, percebem a troca de 10 argolas de um pino para 1 argola no pino vizinho à sua esquerda (reforçando a característica do valor posicional do nosso sistema de numeração).
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05
MP075
- Descubra quantos sorvetes Armando tinha no início do dia.

Cálculo por decomposição
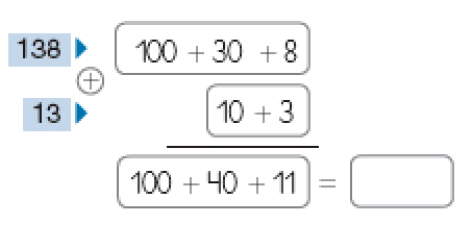
PROFESSOR
Resposta: 151Adição: 138 + 13 = _____
PROFESSOR
Resposta: 151Cálculo com o algoritmo usual
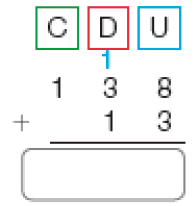
PROFESSOR
Resposta: 151- Primeiro adicionamos as unidades: 8 + 3 =
_____
PROFESSOR
Resposta: 11 - Trocamos 10 unidades por 1 dezena.
- Depois, adicionamos as dezenas: 1 + 3 + 1=
_____
PROFESSOR
Resposta: 5 - No final, adicionamos as centenas: 1 + 0 =
_____
PROFESSOR
Resposta: 1
Armando tinha _____ sorvetes no início do dia.
PROFESSOR
Resposta: 151


- Sueli quer calcular o resultado da adição 26 + 16 com uma calculadora, mas a tecla
 não está funcionando. Como ela pode encontrar o resultado dessa adição? Registre as teclas usadas e o resultado
obtido
no visor.
não está funcionando. Como ela pode encontrar o resultado dessa adição? Registre as teclas usadas e o resultado
obtido
no visor.
PROFESSOR
Exemplo de resposta: 25 + 1 + 15 + 1 = 42MANUAL DO PROFESSOR
Atividade 2
O algoritmo por decomposição é uma preparação para o uso do algoritmo usual, pois ele encaminha a adição em duas etapas. Na primeira, adicionam-se dezenas com dezenas e unidades com unidades (já que centena só há em um dos números), mesmo que o resultado de cada adição ultrapasse 9. Na segunda etapa, as unidades são reagrupadas em dezenas e unidades: 1 dezena e 1 unidade, que são adicionadas às 4 dezenas que já se tem, obtendo-se 1 centena, 5 dezenas e 1 unidade, que é igual a 151.
Incentive os estudantes a resolverem a questão de outras maneiras além da decomposição. É possível que alguns não usem o reagrupamento para obter a solução. Por exemplo, podem adicionar 140 unidades a 13 unidades, obtendo 153 unidades, e depois subtrair 2 unidades, o que resulta em 151. O uso de recursos como esse, para evitar o reagrupamento, é comum principalmente na realização de cálculo mental.
Proponha aos estudantes cálculos similares envolvendo adições com reagrupamento.
Atividade 3
A situação de uma calculadora sem o funcionamento da tecla 6 favorece a utilização de diferentes decomposições dos números 26 e 16, como:
25 + 1 + 15 + 1 = 42 ou 24 + 2 + 14 + 2 = 42
Problemas desse tipo mobilizam o raciocínio para a compreensão do funcionamento do sistema de numeração decimal e das propriedades relativas a ele. Sugira aos estudantes que comparem e discutam suas respostas com as de um colega.
Outra possibilidade é eles perceberem que podem gerar duas parcelas diferentes que produzam a mesma soma, como 27 + 15 = 42, compreendendo, assim, a ideia de igualdade para escrever sentenças com adições diferentes que resultem na mesma soma.
Ao realizarem cálculos por decomposição, os estudantes percebem a troca de 10 unidades por 1 dezena. Essa é a primeira etapa de trabalho que os levará a compreender que, toda vez que a adição dos algarismos de determinada ordem atinge 10, essa quantidade é trocada por uma única unidade da ordem imediatamente superior. Por exemplo, 10 unidades são trocadas por 1 dezena, 10 dezenas por 1 centena, 10 centenas por 1 unidade de milhar etc. (quando aprenderem ordens maiores).
A noção de compensação também é importante para os estudantes compreenderem que na composição ou na decomposição de números podem gerar adições com a mesma soma. Por exemplo, na impossibilidade de efetuar 26 + 16 na calculadora (atividade 3), pode-se adicionar 27 (26 + 1) a 15 (16 − 1), e obter a mesma soma.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05, EF03MA11
MP076
- Resolva.
- A massa de um urso-polar macho é 529 quilogramas, e a de uma fêmea é 297 quilogramas. Quantos quilogramas os dois têm juntos?
_____
PROFESSOR
Resposta: 826 quilogramas.

LEGENDA: Urso-polar no parque Yorkshire Wildlife, na Inglaterra, em 2021. FIM DA LEGENDA.
- O Parque Diversão deseja comprar novos equipamentos para aumentar o número de visitantes. Assim, foram realizadas entrevistas com crianças de 6 a 13 anos. Cada criança votou em um único brinquedo. Observe o gráfico.
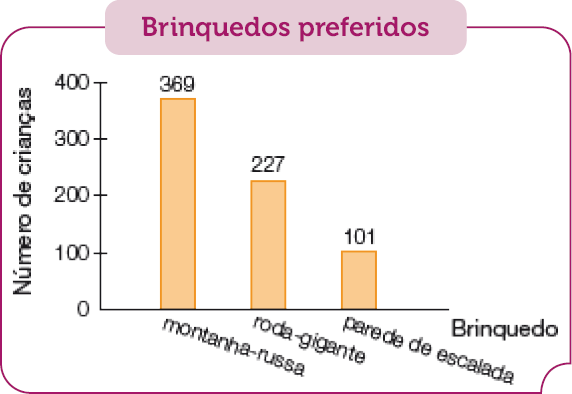
Fonte: Pesquisa feita pelo Parque Diversão. (jan. 2023)
- Quantas crianças foram entrevistadas no total?
_____
PROFESSOR
Resposta: 697 crianças.
- Qual é o brinquedo preferido das crianças entrevistadas?
_____
PROFESSOR
Resposta: Montanha-russa.
- Qual resposta apareceu com
menor
frequência nas entrevistas?
_____
PROFESSOR
Resposta: Parede de escalada.
MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando composição e decomposição de números naturais (de até 4 algarismos).
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Resolver problemas cujos dados estão apresentados em tabelas e em gráficos de colunas.
Atividade 4
Após a realização dos cálculos propostos, pergunte aos estudantes: “Vocês observaram que a quantidade adicionada às dezenas é sempre 1 (1 dezena) e às centenas também? Poderia ser 2, 3 ou mais? Por quê?”.
É importante os estudantes observarem que, tratando-se de uma adição de dois números, para o total de unidades e de dezenas, o máximo que se pode obter é 9 + 9, que equivale a 18, ou seja, sempre, no máximo, 1 dezena ou 1 centena será acrescentada.
Peça aos estudantes que estimem os resultados antes de calculá-los e sugira a eles que façam as adições também com o ábaco.
Atividade 5
Antes de realizarem o cálculo exato, peça aos estudantes que estimem o resultado. Uma proposta do ensino do cálculo consiste em desenvolver e sistematizar procedimentos de cálculo por estimativa e estratégias de verificação e controle de resultados. Ela decorre da larga aplicação desses procedimentos nas situações do dia a dia, nas quais respostas aproximadas são geralmente suficientes e nem sempre se dispõe de lápis e papel ou de calculadora.
O emprego do algoritmo usual da adição pode ser introduzido de maneira gradual, à medida que os estudantes trabalhem simultaneamente com outros modos de obter a soma. A vantagem desse algoritmo é a quantidade reduzida de etapas empregadas e, portanto, o menor tempo para obter a resposta. Entretanto, é importante considerar outras estratégias utilizadas pelos estudantes, desde que elas conduzam ao resultado correto e façam sentido para eles.
Com o tempo, é provável que as convenções sociais e a demanda por rapidez na execução façam-nos optar pelo algoritmo usual.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05, EF03MA26
MP077
- Observe a tabela abaixo e responda à questão.
Despesas mensais de Vânia
Tabela: equivalente textual a seguir.
|
Conta |
Valor |
|---|---|
|
Luz |
137 reais |
|
Aluguel |
738 reais |
|
Telefone |
84 reais |
Fonte: Dados fornecidos por Vânia em 2023.
- Qual é a despesa total de Vânia de acordo com os valores das contas mostradas na tabela?
_____
PROFESSOR
Resposta: 959 reais.
- João quer comprar um telefone celular e um tablet . Veja os modelos disponíveis e os preços. Em seguida, calcule o valor a ser pago em cada opção. Depois, responda às questões.
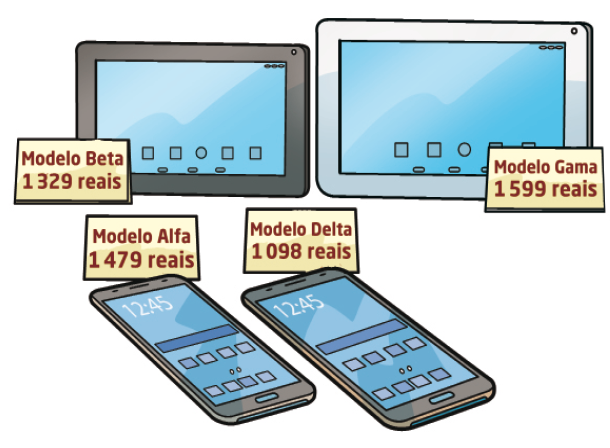
Alfa e Gama
_____
PROFESSOR
Exemplo de cálculos:
Alfa e Beta
_____
PROFESSOR
Exemplo de cálculos: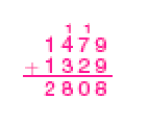
Delta e Gama
_____
PROFESSOR
Exemplo de cálculos:
Delta e Beta
_____
PROFESSOR
Exemplo de cálculos: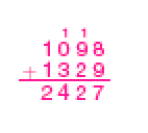
- Quantos reais, no máximo, João gastará?
_____
PROFESSOR
Resposta: Gastará, no máximo, 3 078 reais.
- E no mínimo?
_____
PROFESSOR
Resposta: Gastará, no mínimo, 2 427 reais.
MANUAL DO PROFESSOR
Atividade 6
O aspecto interessante da atividade é o uso do gráfico de colunas para a apresentação dos dados, que deverão ser localizados e interpretados pelos estudantes. Surge aqui a inter-relação das Unidades Temáticas Números e Probabilidade e estatística, favorecendo o reconhecimento de conexões entre diferentes áreas da Matemática.
Sugira aos estudantes que elaborem outra questão com as informações do gráfico e troquem o problema criado com um colega para a resolução.
Atividade 7
Deixe que os estudantes escolham o procedimento de sua preferência para efetuar a adição proposta. Escolha alguns deles para mostrar sua solução na lousa.
Atividade 8
Um aspecto interessante dessa atividade é a combinação de possibilidades de compra com avaliação de gastos.
Além disso, os estudantes terão de efetuar adições de números de 4 algarismos e poderão observar situações de dois ou três agrupamentos necessários.
Explore os procedimentos de cálculo pedindo aos estudantes que, antes de recorrerem ao algoritmo usual, calculem os resultados das adições por meio de cálculo mental, no ábaco ou usando outra estratégia de sua preferência, registrando os procedimentos e, depois, socializando-os com a turma.
O equilíbrio entre o uso de procedimentos convencionais, como o algoritmo usual, e o de procedimentos alternativos, como o cálculo mental e a decomposição, possibilita maior desenvolvimento do raciocínio matemático. Ao exercitarem os recursos convencionais, os estudantes se apropriam dos métodos socialmente estabelecidos e mais conhecidos de cálculo. Com as opções alternativas, eles desenvolvem o sentido de valor numérico, a ideia das relações entre as diversas ordens e a estrutura aditiva da escrita numérica.
BNCC em foco:
EF03MA02, EF03MA05
MP078
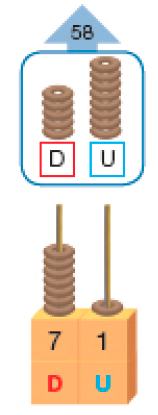
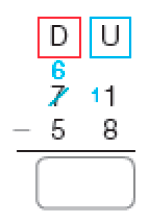
Subtração com trocas: algumas estratégias
- Em uma visita ao veterinário, Alex precisou pesar seu cachorro. Como Fiel não parava quieto, Alex subiu com ele na balança e, depois, subiu sozinho. Qual é a massa de Fiel?

Para descobrir a massa de Fiel, podemos subtrair 58 de 71.
Cálculo com o ábaco
Como não dá para tirar 8 unidades de 1 unidade, temos de trocar 1 dezena por 10 unidades.
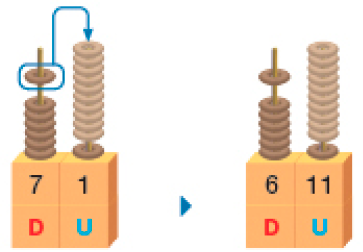
Subtraímos 8 unidades de 11 unidades e 5 dezenas de 6 dezenas.
PROFESSOR
Resposta: 13Cálculo com o Material Dourado
Subtração: 71 − 58 = _____
PROFESSOR
Resposta: 13MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando composição e decomposição de números naturais (de até 4 algarismos).
Construir e utilizar fatos básicos da subtração para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Atividade 1
O algoritmo da subtração com troca traz algumas dificuldades de compreensão, pois envolve subtrações pouco naturais.
Um exemplo é a subtração (71 − 58) dessa atividade. Como não é possível tirar 8 unidades de 1 unidade, alguns estudantes podem subtrair “de baixo para cima”, fazendo 8 − 1. Quando isso ocorre, é importante eles compreenderem que a quantidade 8 faz parte de 58, de modo que se deve subtrair 58 de 71, e não o contrário.
É essencial os estudantes compreenderem que o algoritmo é uma técnica que possibilita lidar com uma ordem de cada vez, e que essas ordens (dezenas e unidades) fazem parte de um todo (o número).
Os estudantes devem perceber que o algoritmo usual envolve trocas entre dezenas e unidades, por isso o uso do ábaco e do Material Dourado é tão importante.
Na subtração, assim como foi feito na adição, o algoritmo da decomposição pode ser entendido como preparação para o algoritmo usual.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05
MP079
Cálculo por decomposição

PROFESSOR
Resposta: 13Subtração: 71 - 58 = _____
PROFESSOR
Resposta: 13Cálculo com o algoritmo usual
PROFESSOR
Resposta: 13- Como não é possível subtrair 8 unidades de 1 unidade, trocamos 1 dezena por 10 unidades. Assim, ficamos com 6 dezenas e 11 unidades.
- Subtraímos as unidades: 11 − 8 =
_____
PROFESSOR
Resposta: 3 - Depois, subtraímos as dezenas: 6 − 5 =
_____
PROFESSOR
Resposta: 1
A massa de Fiel é _____ quilogramas.
PROFESSOR
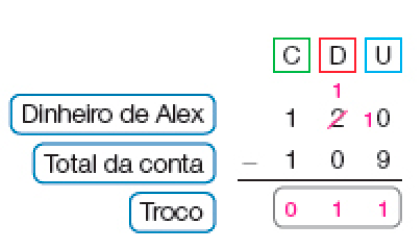
Resposta: 13- Alex gastou, ao todo, com a consulta ao veterinário e as vacinas, 109 reais. Ele pagou com uma cédula de 100 reais e uma de 20 reais. Quanto ele recebeu de troco?
- Como não é possível subtrair 9 unidades de 0 unidade, trocamos 1 dezena por 10 unidades.
- Subtraímos as unidades: 10 − 9 =
_____
PROFESSOR
Resposta: 1 - Em seguida, subtraímos as dezenas: 1 − 0 =
_____
PROFESSOR
Resposta: 1 - No final, subtraímos as centenas: 1 − 1 =
_____
PROFESSOR
Resposta: 0Alex recebeu _____ reais de troco.
PROFESSOR
Resposta: 11
MANUAL DO PROFESSOR
Atividade 2
A subtração com números de 3 algarismos pelo algoritmo usual envolve os mesmos passos que a subtração com números de 2 algarismos, tendo o acréscimo da ordem das centenas, o que pode envolver, além da troca de 1 dezena por 10 unidades, a troca de 1 centena por 10 dezenas. Explore essas igualdades com os estudantes, se necessário com o apoio do Material Dourado e do ábaco vertical. Incentive-os a apresentarem outros modos de resolução, pois isso amplia a compreensão do sistema de numeração decimal, do valor posicional dos algarismos nos números e da ideia de que uma quantidade não se altera com trocas entre dezenas e unidades ou entre centenas e dezenas.
Ao resolver um problema, é comum fazermos o registro escrito dos procedimentos empregados, pois ele nos ajuda tanto no encaminhamento da resolução quanto na correção de eventuais erros. Nesse ponto do aprendizado, é importante você analisar os registros feitos pelos estudantes, para verificar o domínio dos conhecimentos matemáticos que dão base ao cálculo escrito e, particularmente, à compreensão dos algoritmos.
Se possível, disponibilize para os estudantes ábacos verticais, pois esses instrumentos possibilitam a correspondência direta com o algoritmo usual, favorecendo a compreensão geral da subtração com troca. Em um ábaco, as trocas podem ser visualizadas quando, por exemplo, uma argola que representa 1 dezena é trocada por 10 argolas que representam unidades.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA05
MP080
- Veja como Marina e Carlos calcularam mentalmente o resultado de 63 − 26.


- Agora, calcule mentalmente o resultado em cada caso e registre sua estratégia no caderno.
- 71 − 28
PROFESSOR
Resposta: 43
- 50 − 24
PROFESSOR
Resposta: 26
- 62 − 15
PROFESSOR
Resposta: 47
- 83 − 36
PROFESSOR
Resposta: 47

- Jonas quer calcular o resultado de 64 − 28, mas a tecla
 de sua calculadora está quebrada. Como ele pode calcular esse resultado?
de sua calculadora está quebrada. Como ele pode calcular esse resultado?
PROFESSOR
Exemplo de resposta:PROFESSOR
Adicionando números ao 28 até completar 64.PROFESSOR
Por exemplo: 28 + 30 + 2 + 4 = 64PROFESSOR
30 + 2 + 4 = 36PROFESSOR
Então: 64 − 28 = 36- Em uma corrida de 850 metros, um atleta já percorreu 525 metros. Quantos metros ainda faltam para ele completar a corrida?
_____
Faltam _____ metros para o atleta completar a corrida.
PROFESSOR
Resposta: 325MANUAL DO PROFESSOR
Objetivos
Construir e utilizar fatos básicos da adição para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Resolver problemas cujos dados estão apresentados em gráfico de colunas.
Atividade 3
Essa é uma atividade de análise e aplicação de cálculo mental. Reforce aos estudantes a utilidade desse procedimento nas situações do dia a dia, quando nem sempre contamos com recursos de cálculo, como lápis, papel e calculadora.
Eles devem analisar os cálculos mentais de Marina e Carlos antes de calcularem e registrarem a estratégia utilizada.
Ressalte também o procedimento de compensação na subtração para obter diferentes sentenças de subtração que resultem na mesma diferença.
No item a, por exemplo, pode-se efetuar 70 − 27 (71 − 1 e 28 − 1) ou 73 − 30 (71 + 2 e 28 + 2) para obter o mesmo resultado que 71 − 28.
Atividade 4
Se não houver uma calculadora por grupo, em uma roda de conversa peça que exponham suas sugestões para que você as realize em uma calculadora.
Espera-se que os estudantes pensem em completar 28 para atingir 64. Assim, eles poderão usar adições e dispensar a tecla quebrada.
Incentive-os a usar uma estratégia na busca do número a ser adicionado. Por exemplo, eles podem pensar: “Como 60 = 30 + 30; 28 + 30 ainda não atinge 64: é um número possível”. Ao verem no visor da calculadora 58 (28 + 30 = 58), podem pensar: “58 + 2 = 60; então, 58 + 2 + 4 = 64”, e, assim, efetuarem: 28 + 30 + 2 + 4 = 64.
BNCC em foco:
EF03MA03, EF03MA05, EF03MA11
MP081
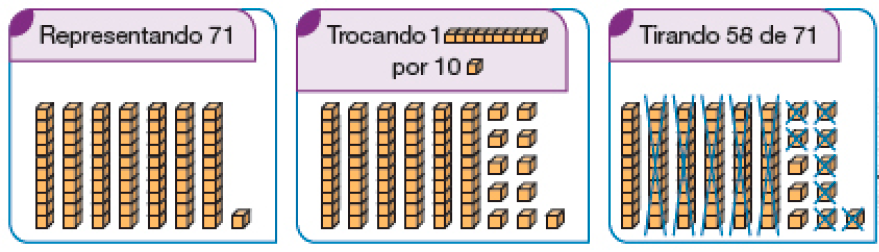
- Veja como foi feita a subtração 212 – 123 usando cédulas de 100 e de 10 reais e moedas de 1 real. Depois, complete.
1º. Representando 212.

_____ centenas, _____ dezena e _____ unidades
PROFESSOR
Resposta: 2, 1, 22º. Trocando 1 cédula de 100 reais por 10 cédulas de 10 reais e 1 cédula de 10 reais por 10 moedas de 1 real.

_____ centenas, _____ dezenas e _____ unidades
PROFESSOR
Resposta: 1, 10, 123º. Tirando 123 de 212.

_____ dezenas e _____ unidades
PROFESSOR
Resposta: 8, 9Subtração: 212 - 123 = _____
PROFESSOR
Resposta: 89- A quantidade de sofás produzidos, em 2022, pelas fábricas Pinho e Peroba é mostrada no gráfico abaixo.
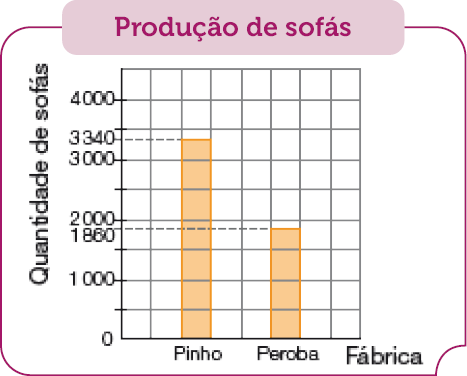
Fonte: Controle de produção das fábricas Pinho e Peroba em 2022.
Qual é a diferença entre a produção de sofás das duas fábricas?
_____
PROFESSOR
Resposta: 1.480 sofás.MANUAL DO PROFESSOR
Atividade 5
É possível que alguns estudantes pensem em completar a quantidade 525 até chegar a 850.
Nesse caso, eles podem fazer: 525 + 25 = 550 e depois 550 + 300 = 850, chegando a 25 + 300 = 325.
É relevante notar que a ideia de completar o subtraendo até igualar o minuendo é empregada em uma variação bastante conhecida do algoritmo usual. Nesse caso, a subtração na ordem das unidades é efetuada da seguinte maneira: de 5 para 10 faltam 5 unidades, como mostrado abaixo:
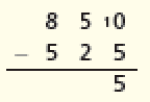
Em vez de subtrair 1 dezena do minuendo, riscando o algarismo 5 e escrevendo 4, aumenta-se 1 dezena no subtraendo, que passa a ser 3; então, de 3 (dezenas) para chegar a 5 (dezenas) faltam 2 (dezenas):
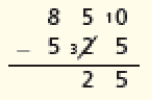
Finalmente, de 5 (centenas) para chegar a 8 (centenas) faltam 3 (centenas) e o resultado é igual a 325.
Atividade 6
A extensão do algoritmo da subtração aos casos em que há mais de uma troca exige que os estudantes coordenem a troca em duas ordens do minuendo, o que pode trazer alguma dificuldade. Por isso, use as cédulas e moedas previamente produzidas e acompanhe as trocas necessárias. Essa é uma estratégia muito comum, ao trabalhar com pagamento em espécie, empregada no dia a dia pelos operadores de caixa de lojas em geral.
BNCC em foco:
EF03MA05, EF03MA26
Atividade 7
Deixe à disposição dos estudantes material manipulável (por exemplo, Material Dourado e ábaco de pinos) como apoio para a realização dos cálculos.
Explore ainda mais a atividade perguntando: “Se a produção de sofás da fábrica Peroba aumentasse em 740 sofás, e a produção da fábrica Pinho diminuísse em 740 sofás, qual fábrica produziria a maior quantidade de sofás?”. (As duas fábricas produziriam a mesma quantidade: 2 600 sofás.)
MP082
Problemas

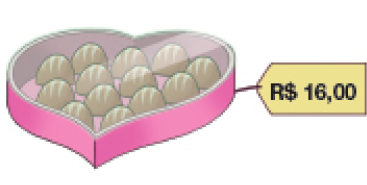
- Lucas tinha 20 reais e ganhou mais 5 reais de seu tio. Depois, com esse montante, comprou uma caixa de bombons, como a da figura ao lado. Quantos reais sobraram para Lucas?
_____
PROFESSOR
Resposta: Sobraram 9 reais.
- No sábado, Rosângela leu algumas páginas de um livro que tinha 56 páginas. No domingo, ela leu as páginas que faltavam desse livro.
- Se ela tivesse lido 20 páginas no sábado, quantas páginas ela leria no domingo para terminar o livro?
_____
PROFESSOR
Resposta: 36 páginas.
- Não é possível saber quantas páginas ela leu no sábado, mas é possível fazer suposições. Escreva 3 possibilidades.
_____
PROFESSOR
Exemplos de resposta: 18 páginas no sábado e 38 no domingo; 10 páginas no sábado e 46 no domingo; 28 páginas no sábado e 28 páginas no domingo.
- Se ela tivesse lido 20 páginas no sábado, quantas páginas ela leria no domingo para terminar o livro?
- Marcos está juntando dinheiro para comprar um brinquedo que custa 98 reais. Até ontem, ele tinha 32 reais. Hoje, seu irmão mais velho o presenteou com 30 reais em cédulas e 23 reais em moedas. Será que agora Marcos já tem a quantia suficiente para comprar o brinquedo? Explique.
_____
PROFESSOR
Resposta: Não, pois ainda faltam 13 reais.

- Mariana estava brincando de bater figurinhas. Ela começou o jogo com 32 figurinhas. Na primeira partida, ela ganhou 5, na segunda partida, perdeu 3 e, na última partida, perdeu mais 4. Com quantas figurinhas Mariana terminou o jogo?
_____
PROFESSOR
Resposta: Mariana terminou o jogo com 30 figurinhas.
MANUAL DO PROFESSOR
Objetivos
• Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
• Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
• Resolver problemas cujos dados estão apresentados em tabela.
Atividade 1
Os estudantes deverão calcular mentalmente o resultado de:
20 + 5 = 25 e 25 − 16 = 9.
Aproveite essa atividade para sugerir a eles que inventem um problema envolvendo adição e subtração. Por exemplo: 42 + 8 = 50 e 50 − 21 = 29.
Atividade 2
Para responder ao item a, os estudantes devem subtrair 20 de 56 da maneira que preferirem: cálculo mental, decomposição, algoritmo usual, representação na reta numérica ou contagem. É importante incentivá-los a socializar as diferentes estratégias de resolução para ampliar o repertório de resolução de problemas.
No item b, os estudantes devem perceber que basta escolher duas quantidades de páginas (uma para cada dia) que, adicionadas, resultem 56.
Atividade 3
Primeiro, os estudantes devem efetuar uma adição de três parcelas (32 + 30 + 23 = 85) para descobrir a quantia que Marcos tem; depois, efetuar uma subtração (98 − 85 = 13) para calcular a quantia que ainda falta para ele comprar o brinquedo: 13 reais.
BNCC em foco:
EF03MA05, EF03MA06
Os problemas apresentados exigem mais de um cálculo para a resolução. Na maioria deles, os estudantes precisam fazer uma adição e, em seguida, uma subtração.
A atividade 1 possibilita aos estudantes refletirem sobre o significado dos números e das operações apresentados e procurar contextualizá-los em uma situação-problema.
Aproveite a ocasião da atividade 2 para formular o problema de modo que tenham de pensar “de trás para a frente”. Por exemplo: “Rosângela leu as primeiras páginas de um livro em um dia; no dia seguinte ela leu 49 páginas, chegando à página 56 do livro. Quantas páginas Rosângela leu no primeiro dia? Quantas páginas ela leu no segundo dia a mais que no primeiro?”. (1º dia: 7 páginas (56 − 49); 2º dia: 42 páginas (49 − 7) a mais que no primeiro dia.)
MP083
- Dois potes estão cheios de sementes. Serão retiradas 138 sementes de cada um deles. Quantas sementes restarão nos dois potes juntos?

PROFESSOR
Exemplos de cálculo: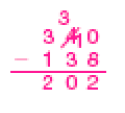
PROFESSOR
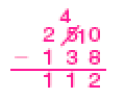
PROFESSOR
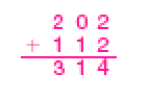
Restarão _____ sementes nos dois potes juntos.
PROFESSOR
Resposta: 314- Observe e complete a tabela abaixo, que mostra a população indígena de três municípios brasileiros. Depois, responda às questões.
População indígena, em alguns municípios, por domicílio – Brasil 2010
Tabela: equivalente textual a seguir.
|
Município |
Urbana |
Rural |
Total |
|---|---|---|---|
|
Barcelos |
1.370 |
6.997 |
_____ |
|
Boa Vista |
6.072 |
_____ |
8.550 |
|
Pesqueiro |
_____ |
5.287 |
9.335 |
Dados obtidos em: http://fdnc.io/eTS
PROFESSOR
Resposta: 4.048; 2.478; 8.367.- No município de Barcelos, quantos indígenas há a mais na área rural do que na área urbana?
_____
PROFESSOR
Resposta: 5.627 indígenas.
- Qual é a diferença entre a população indígena urbana e a rural, em Boa Vista?
_____
PROFESSOR
Resposta: 3.594 indígenas.
- Em qual dos municípios a população indígena total é maior?
_____
PROFESSOR
Resposta: Em Pesqueiro.

- Agora, invente outra questão que possa ser respondida com os dados da tabela e peça a um
colega
que a responda.
PROFESSOR
Resposta: Exemplo de questão: “Qual é a diferença entre a população indígena rural e urbana, em Pesqueiro?”. (1239 indígenas.)
MANUAL DO PROFESSOR
Atividade 4
Os estudantes podem efetuar cada operação na ordem em que elas aparecem: 32 + 5 = 37, 37 − 3 = 34 e 34 − 4 = 30, ou perceber que Mariana perdeu 2 figurinhas a mais do que ganhou e, assim, concluir que ela terminou o jogo com 2 figurinhas a menos do que tinha no início do jogo (32 − 2 = 30). Estimule a turma a utilizar o cálculo mental.
Atividade 5
Há mais de um modo possível de chegar à resposta. Por exemplo, os estudantes podem obter a quantidade total de bolinhas dos potes fazendo 340 + 250 = 590; depois, obter a quantidade total de bolinhas retiradas: 138 + 138 = 276; e, então, retirar essa quantidade de 590: 590 − 276 = 314.
Atividade 6
Retome com os estudantes a leitura de uma tabela de dupla entrada.
No item a, os estudantes devem comparar as populações indígenas rural e urbana do município de Barcelos, efetuando a subtração 6.997 − 1.370 = 627.
No item b, espera-se que eles associem a pergunta à subtração 6.072 − 478 = 3.594, que compara as populações urbana e rural do município de Boa Vista.
No item c, espera-se que os estudantes observem a coluna Total na tabela e comparem as três quantidades, observando que 9.335 é maior que 8.550 e 8.367; logo, Pesqueiro tem a maior população indígena ao todo.
Socialize e valide as questões inventadas e as resoluções com os estudantes.
BNCC em foco:
EF03MA05, EF03MA06, EF03MA26
Sugestão de leitura para o estudante
Livro
ROCHA, Ruth. Como se fosse dinheiro. Ilustrações de Mariana Massarani. São Paulo: Salamandra, 2010. (Série A turma da nossa rua).
Catapimba é um garoto legal. Amigo da turma toda, centroavante e secretário do Estrela-D’Alva Futebol Clube. Com ele o tempo só esquenta quando o Armandinho não apita o jogo direito. Nesse livro, o leitor vai descobrir a diferença entre uma bala e uma moeda, e que, quando alguém não quiser dar troco, vai saber que a coisa pode “dar bode”!
MP084
Compreender problemas
Para resolver
Fique atento a todas as informações nas ilustrações.
Problema 1
Davi tem 130 reais e quer comprar dois dos presentes anunciados no folheto abaixo.

- Quais são os dois presentes possíveis de Davi comprar?
PROFESSOR
Resposta: Exemplos de resposta: Bola e carrinho, bola e ursinho, carrinho e ursinho e carrinho e cavalinho.
- Se Davi comprar a bola e o carrinho, quantos reais vai gastar? E que quantia vai sobrar para ele?
PROFESSOR
Resposta: Exemplo de cálculos:PROFESSOR
41 + 23 = 64PROFESSOR
130 − 64 = 66PROFESSOR
Comprando a bola e o carrinho, Davi vai gastar 64 reais. Assim, sobrarão 66 reais.Problema 2
Pedro tem 42 bolinhas de gude e quer participar do campeonato anunciado no cartaz.

- Ele poderá formar uma dupla com Luís, que tem 32 bolinhas? E com Júlio, que tem 36 bolinhas?
PROFESSOR
Resposta: Pedro não pode formar dupla com Luís, porque juntos eles têm somente 74 bolinhas (42 + 32), mas pode formar dupla com Júlio (42 + 36 = 78).
- Juntos, Pedro e Júlio têm mais ou menos
bolinhas
de gude do que a quantidade mínima indicada no cartaz? Quantas a mais ou a menos?
PROFESSOR
Resposta: Pedro e Júlio têm mais bolinhas do que a quantidade mínima indicada no cartaz (78 > 75). Eles têm 3 bolinhas a mais.
MANUAL DO PROFESSOR
Objetivos
Utilizar diferentes procedimentos de cálculo mental ou escrito para resolver problemas envolvendo adição e subtração.
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Para resolver
Problema 1
Explore com os estudantes a leitura de anúncios publicitários. Você pode pedir, antecipadamente, que eles levem para a sala de aula alguns folhetos de propaganda, como os de ofertas de supermercados ou de lojas de departamentos. Depois de escolher alguns folhetos, faça perguntas como: “Qual é o produto mais barato? E o mais caro? Quantos produtos eu poderia comprar se tivesse ‘tantos’ reais?”.
Para o item a, os estudantes devem adicionar o preço de dois produtos de todas as maneiras possíveis e comparar com a quantia que Davi tem (130 reais) para saber quais ele pode comprar. Exemplos de resposta: carrinho e ursinho, carrinho e bola, carrinho e cavalinho, e ursinho e bola.
Para o item b, basta os estudantes considerarem os preços dos dois brinquedos citados e efetuarem os cálculos envolvidos.
Problema 2
Verifique se os estudantes compreendem a informação “no mínimo”, que aparece no cartaz. Espera-se que eles percebam que:
Pedro não pode formar dupla com Luís, porque juntos eles têm somente 74 bolinhas (42 + 32), mas pode formar dupla com Júlio (42 + 36 = 78).
Pedro e Júlio têm mais bolinhas do que a quantidade mínima indicada no cartaz, 78 > 75. Juntos eles têm 3 bolinhas a mais.
Tanto a resolução dos problemas quanto a análise de outras resoluções (na seção Para refletir) contribuem para os estudantes aprenderem a identificar os dados úteis na obtenção das respostas e para a tomada de decisões quanto às operações a realizar.
Em atividades do tipo do Problema 1, em que é preciso estudar possibilidades, ressalte para os estudantes que um facilitador desse estudo é ter uma estratégia para montar as possibilidades. Por exemplo: fixar um dos brinquedos e verificar todas as possibilidades de escolha entre os demais; depois, mudar o brinquedo fixado e fazer o mesmo procedimento sem considerar os brinquedos fixados anteriormente.
BNCC em foco:
EF03MA05, EF03MA06
MP085
Para refletir

- Para resolver o Problema 1, você usou todos os dados do folheto? Explique como você fez.
PROFESSOR
Resposta pessoal.
- No Problema 1, quais são os dois brinquedos que Davi pode comprar se quiser gastar o mínimo possível?
_____
PROFESSOR
Resposta: Os presentes serão o carrinho e a bola.
- Veja as afirmações que três estudantes fizeram sobre o Problema 1.
Miguel
Se comprar apenas o ursinho, Davi fica com 78 reais.
Valentina
Ao comprar a bola e o carrinho, Davi gasta 64 reais e fica com 66 reais.
Bruna
Para comprar o cavalinho e a bola, faltam 16 reais.
- As três afirmações são corretas?
_____
PROFESSOR
Resposta: Sim.
- Quem respondeu ao que o item b do problema perguntava?
_____
PROFESSOR
Resposta: Valentina.
- Contorne a conta abaixo que não foi necessária para resolver o Problema 2.
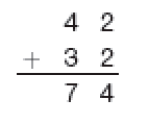
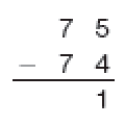
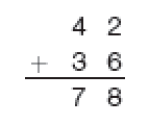
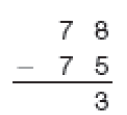
PROFESSOR
Resposta correta: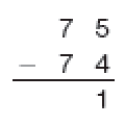
- Sobre o Problema 2, marque com um
X
as afirmações que complementam corretamente a sentença a seguir. Inicialmente, o total de
bolinhas
da dupla pode ser:
( ) menor que 75.
( ) igual a 75.
( ) maior que 75.
PROFESSOR
Respostas corretas: igual a 75 e maior que 75.
MANUAL DO PROFESSOR
Para refletir
Na atividade 1, os estudantes são levados a questionar a necessidade de usar todos os dados do folheto publicitário ilustrado. Nesse caso, espera-se que eles percebam que tiveram de utilizar todos os dados.
Na atividade 2, verifique se os estudantes compreendem que, para gastar o mínimo possível, basta escolher os dois brinquedos de menor valor: o carrinho e a bola.
Na atividade 3, os estudantes precisam interpretar as afirmações de Miguel, Valentina e Bruna, retomando as informações do Problema 1 (texto e ilustração), além de efetuar adições e subtrações. Espera-se que eles identifiquem as três afirmações como corretas e que a afirmação de Valentina é a resposta do item b, que eles já responderam ao resolverem esse problema.
Atividades como a 4 possibilitam aos estudantes ajustarem a compreensão a respeito de cada operação e da correspondência entre os valores apresentados e a questão a ser resolvida.
A atividade 5 propicia que se verifique o conhecimento apreendido pelos estudantes sobre a noção de “no mínimo 75 bolinhas” apresentada no Problema 2. Espera-se que eles percebam que, nesse caso, precisam ter 75 bolinhas ou mais (76, 77,78, ...). Desse modo, devem marcar com X as duas últimas afirmações: “igual a 75” e “maior que 75”.
BNCC em foco:
EF03MA05, EF03MA06
MP086
Matemática em textos
Leia
A nota fiscal
Ao realizarmos uma compra, devemos sempre receber um documento chamado nota fiscal. Nele, são informados o lugar e a data em que fizemos a compra, são apresentados os dados do consumidor, as informações sobre cada produto comprado e o total gasto.
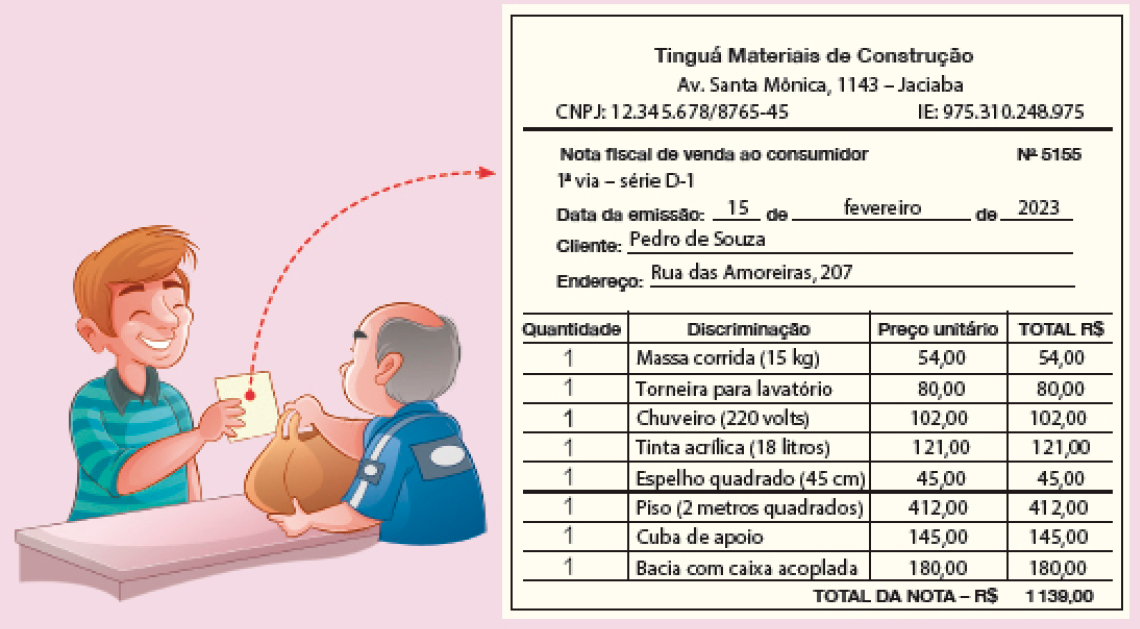
A nota fiscal é importante caso haja necessidade de troca ou o produto apresente algum defeito. A emissão da nota fiscal também é a garantia de que o lojista está pagando seus impostos. Veja o cupom fiscal que Pedro recebeu depois de fazer algumas compras.
Responda
- Qual é o nome e o endereço da loja de materiais para construção na qual a compra de Pedro foi realizada?
_____
PROFESSOR
Resposta: Tinguá Materiais de Construção, que fica na Avenida Santa Mônica, 1143, em Jaciaba.
- Quantos produtos diferentes foram comprados? Quantos reais Pedro gastou?
_____
PROFESSOR
Resposta: 8 produtos; 1.139 reais.
MANUAL DO PROFESSOR
Objetivo
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Leia
Discuta com a turma a importância da nota fiscal:
Para o estabelecimento comercial, é um registro dos produtos que foram vendidos, servindo para controlar o estoque e para calcular o total de vendas em determinado período.
Para o governo, possibilita a fiscalização dos estabelecimentos comerciais, servindo para verificar a correção no pagamento de impostos, que devem ser revertidos em benefício da população.
Para o consumidor, é um comprovante de que ele comprou determinado produto em um estabelecimento, de modo que, se houver necessidade de troca do produto, esse documento assegura seus direitos.
Responda
Nessas atividades, os estudantes deverão reconhecer os elementos presentes na nota fiscal apresentada.
Aproveite a atividade para pedir aos estudantes que imaginem uma reforma na própria casa, em que tenham de comprar alguns dos produtos listados na nota fiscal da atividade. Peça a eles que façam cálculos para saber quanto gastariam com esses produtos e depois comparem suas respostas. São muitas as possibilidades. Se julgar oportuno, escolha algumas duplas e peça que registrem na lousa sua resposta. Depois, pergunte à turma: “Todos chegaram a essa resposta? Ela está certa?”. É importante perceberem que muitos problemas de Matemática têm mais de uma solução.
BNCC em foco:
EF03MA06; competência específica 2
MP087
Analise

- Se Pedro tivesse pagado a compra com 6 cédulas de 200 reais, quantos reais ele teria recebido de troco?
_____
PROFESSOR
Resposta: 61 reais.
- Dois dias depois de Pedro, Vânia fez compras
nessa
loja de material para construção e encontrou os produtos com o mesmo preço.
- Complete a nota fiscal e descubra quanto ela gastou no total.
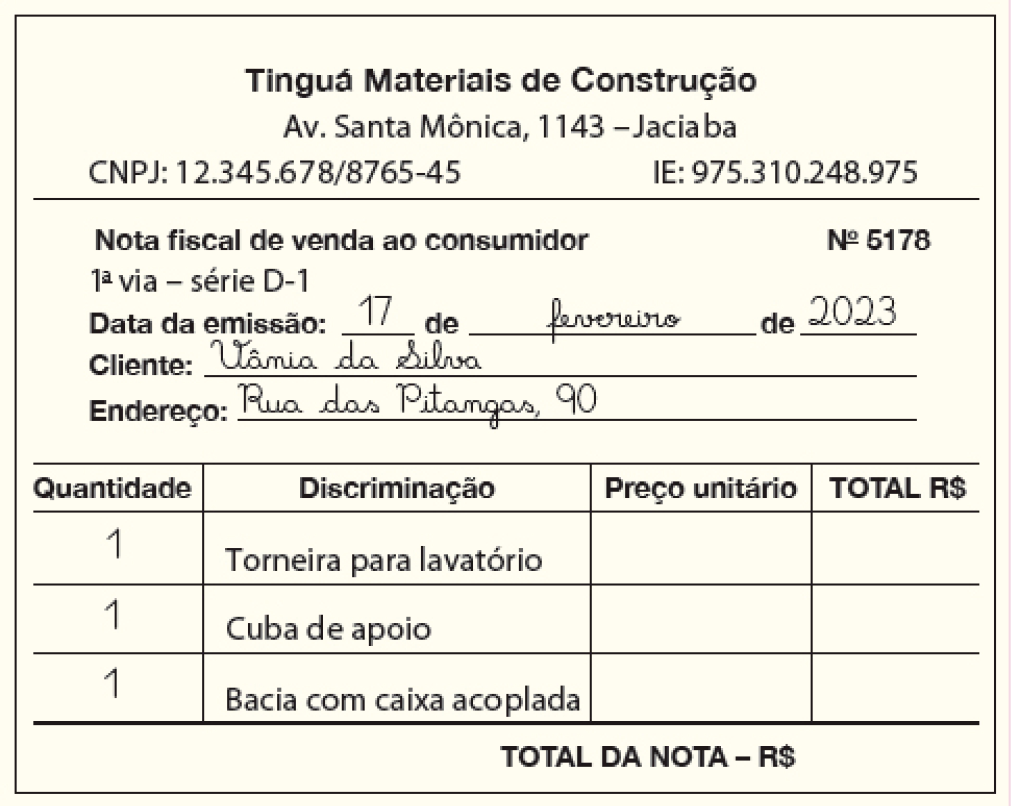
PROFESSOR
Resposta: 80,00; 80,00; 145,00; 145,00; 180,00; 180,00; 405,00.- Quantos reais Pedro gastou a mais que Vânia?
_____
PROFESSOR
Resposta: 734 reais.
Aplique


- Reúna-se com um
colega
e mostrem como Pedro poderia pagar a compra
dele
usando o
menor
número
possível de cédulas sem receber troco. Registre com um desenho.
PROFESSOR
Atenção professor: Espera-se que os estudantes desenhem 5 cédulas de 200 reais, 1 de 100 reais, 1 de 20 reais, 1 de 10 reais, 1 de 5 reais e 2 de 2 reais. Fim da observação.
MANUAL DO PROFESSOR
Analise
Observe se, com base na interpretação dos dados, os estudantes são capazes de responder às questões e preencher a nota fiscal. Sugira que peçam aos pais ou responsáveis notas fiscais e as levem para a sala de aula, anotando no caderno os dados que considerarem importantes.
Na atividade 1, espera-se que os estudantes façam uma adição para obter a quantia utilizada para pagar a compra (1.200 reais). Deixe à disposição dos estudantes o Material Dourado, caso necessitem de apoio para os cálculos.
Na atividade 2, os estudantes terão de recuperar no texto os valores necessários para o preenchimento da nota fiscal.
Aplique
Espera-se que os estudantes desenhem 5 cédulas de 200 reais, 1 cédula de 100 reais, 1 cédula de 20 reais, 1 cédula de 10 reais, 1 cédula de 5 reais e 2 cédulas de 2 reais.
BNCC em foco:
EF03MA06; competência específica 2
MP088
Compreender informações
Representar dados em gráfico de colunas
- A bibliotecária de uma escola fez uma pesquisa para saber o tipo de livro (romance, ficção, comédia, HQ, suspense e terror) mais procurado pelos estudantes nos últimos seis meses e colocou os dados obtidos em uma tabela. Depois, para visualizar melhor o resultado da pesquisa, montou um gráfico com os dados da tabela.


Complete o gráfico pintando as colunas de acordo com os dados da tabela e responda às questões.
Livros procurados nos últimos seis meses
Tabela: equivalente textual a seguir.
|
Tipo |
Quantidade de livros |
|---|---|
|
Romance |
100 |
|
Ficção |
250 |
|
Comédia |
200 |
|
HQ |
350 |
|
Suspense |
200 |
|
Terror |
150 |
Fonte: Biblioteca da escola. (dez. 2022)
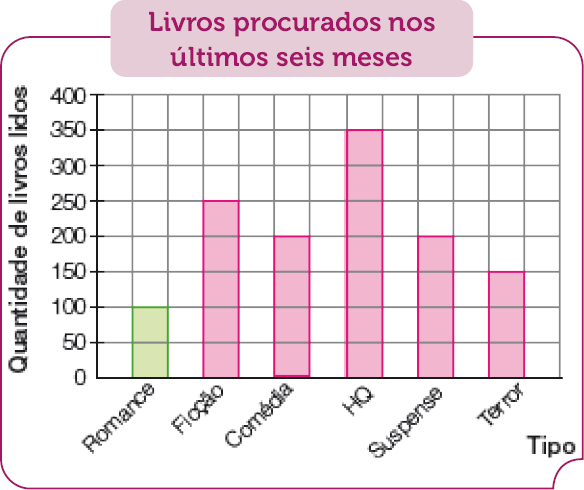
Fonte: Biblioteca da escola. (dez. 2022)
- Qual foi o tipo de livro mais procurado nos últimos seis meses? E o menos procurado?
_____
PROFESSOR
Resposta: HQ; romance.
- Quantos livros do tipo mais procurado foram emprestados a mais que os livros do tipo menos procurado?
_____
PROFESSOR
Resposta: 250 livros.
- Que tipos tiveram o mesmo
número
de livros procurados?
_____
PROFESSOR
Resposta: Comédia e suspense.
- É mais fácil responder às questões anteriores analisando o gráfico ou a tabela? Por quê?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivo
Organizar dados coletados em pesquisa utilizando tabelas e gráficos de colunas.
Atividade 1
Verifique se os estudantes fazem a leitura correta dos dados da tabela e se conseguem transpô-los para o gráfico. É importante observar se eles interpretam corretamente as informações do gráfico de colunas, tão usual nos meios de comunicação. Para isso, pode-se apresentar outros gráficos de colunas e solicitar a eles que interpretem ou elaborem questões que possam ser respondidas com base nos dados neles contidos.
Se julgar necessário, no item a, explique aos estudantes que o gênero mais procurado é o que apareceu com maior frequência na pesquisa, e o menos procurado, o que apareceu com menor frequência.
Explore a atividade perguntando aos estudantes: “Se o gênero romance tivesse sido escolhido por mais 50 pessoas, o que mudaria na tabela? E no gráfico?”. É importante que eles sejam capazes de perceber que as informações de gráficos e tabelas não são estáticas, isto é, se ocorre alguma alteração no conjunto de dados, as tabelas e os gráficos correspondentes também sofrem alteração.
A proposta do item d exige uma tomada de decisão sobre qual tipo de representação possibilita melhor compreensão das informações que correspondem às questões. É importante levar os estudantes à conclusão de que a escolha da forma que representará um conjunto de dados organizados depende do que se deseja investigar. Outro aspecto construtivo desse item é justificar a resposta.
MP089
- Fábio e seus amigos, em 2022, resgataram alguns animais que encontraram machucados no bairro onde vivem. Veja como esses animais estão bem agora.

Observação: As imagens não estão apresentadas em escala de tamanho. Cores fantasia. Fim da observação.
- Registre na tabela a quantidade animais resgatados.
Resgate de animais machucados
Tabela: equivalente textual a seguir.
|
Animais resgatados |
Coelho |
Pássaro |
Gato |
Cachorro |
|---|---|---|---|---|
|
Quantidade de animais |
2 |
_____ |
_____ |
_____ |
Fonte: Dados fornecidos por Fábio em 2022.
PROFESSOR
Resposta: Pássaro: 3; Gato: 5; Cachorro: 3.

- Represente no gráfico os dados da tabela pintando de acordo com as cores da legenda.
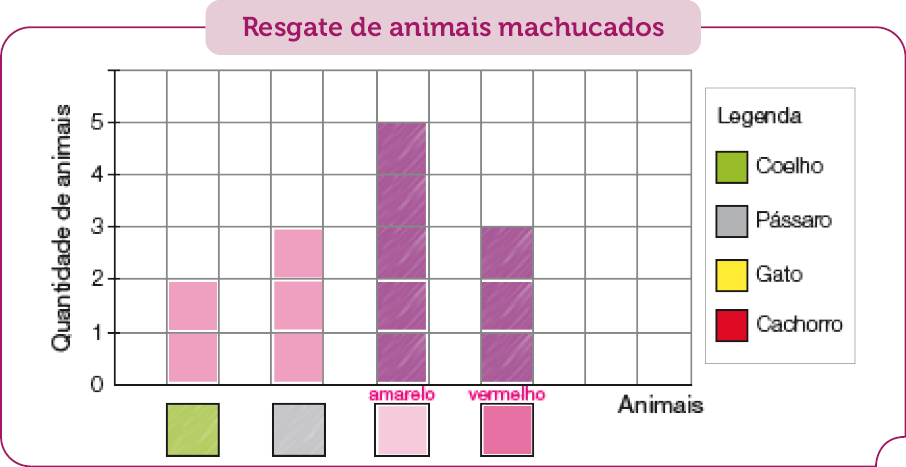
Fonte: Dados fornecidos por Fábio em 2022.

- No ano seguinte, 20 animais foram resgatados por Fábio e seus amigos. Quantos animais a mais foram resgatados em relação à quantidade do ano passado?
_____
PROFESSOR
Resposta: 7 animais a mais.
MANUAL DO PROFESSOR
Atividade 2
Nessa atividade, os estudantes recolhem animais que encontraram machucados, completam a tabela e representam suas quantidades em forma de gráfico de colunas. Verifique se alguma informação se perdeu durante as diferentes representações ou se existem dúvidas no momento de pintar os quadrinhos no gráfico de colunas.
BNCC em foco:
EF03MA26, EF03MA27; competência específica 4
MP090
O que você aprendeu
- Rafael comprou uma bicicleta que custa 599 reais, pagando 314 reais de entrada.

- Para saber quantos reais, aproximadamente, Rafael ainda tem de pagar, é mais adequado arredondar cada um dos números para a dezena mais próxima ou para a centena mais próxima?
PROFESSOR
Resposta pessoal.
- Quantos reais, aproximadamente, Rafael ainda tem de pagar? Faça uma estimativa.
_____
PROFESSOR
Resposta: Exemplo de estimativa: Aproximadamente, 300 reais.
- Para saber quantos reais, aproximadamente, Rafael ainda tem de pagar, é mais adequado arredondar cada um dos números para a dezena mais próxima ou para a centena mais próxima?
- Marisa trabalha fazendo aventais. Em outubro, ela fez 128 aventais, em novembro, fez 152 e, em dezembro, 199. Ao todo, quantos aventais Marisa cofeccionou?
_____
PROFESSOR
Resposta: 479 aventais.
- Faça os cálculos e ligue cada pessoa ao produto que ela comprou.
Coluna 1


Coluna 2


PROFESSOR
Resposta: Homem - rádio.PROFESSOR
Mulher - bicicleta.PROFESSOR
Exemplos de cálculos: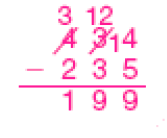 ;
; 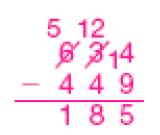


- Heitor tem 180 reais e pretende comprar os três produtos mostrados ao lado. O dinheiro que ele tem é suficiente para a compra que ele quer fazer? Por quê?
PROFESSOR
Resposta: Sim. Exemplo de explicação: Os três produtos juntos custam 160 reais, e Heitor tem mais do que essa quantia em dinheiro.
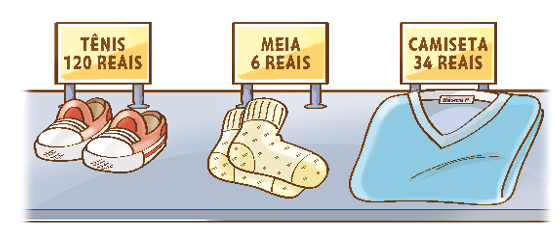
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Propicie conversas entre os estudantes a respeito das estratégias que usaram para resolver as atividades.
Atividade 1
Discuta com os estudantes a ideia de arredondamento, lembrando-os de que o resultado de uma operação com os números arredondados pode servir de parâmetro para validar a resposta de um cálculo exato. Por exemplo, digamos que um estudante tenha estimado que o resultado da adição 599 + 314 fosse, aproximadamente, 900. Se, no cálculo escrito (exato), ele se esquecer de adicionar as dezenas e obtiver o resultado 93, saberá que algum erro foi cometido no processo.
Comente com os estudantes que não há um modo único de fazer a aproximação. Por exemplo, o número 314 poderia ser aproximado para 310. Nesse caso, o resultado da adição seria 910. Sugira que façam a adição pelo algoritmo usual e, depois, comparem os resultados. Discuta com a turma os critérios de arredondamento que utilizaram e verifique com os estudantes a influência desse critério na diferença entre o valor real e o valor estimado.
Algumas propostas de resolução que podem surgir na atividade 3 são mostradas a seguir para a compra do rapaz, que se refere à subtração 434 − 235.
435 − 235 − 1 = 200 = 1 = 199
400 − 200 = 200
Atividade 2
Deixe à disposição dos estudantes materiais manipuláveis para apoio nos cálculos, como Material Dourado, ábaco de pinos etc.
Atividade 3
Antes de realizar a atividade, peça aos estudantes que obtenham a resposta sem o uso do algoritmo usual, para evidenciar a compreensão que eles têm do nosso sistema de numeração e para que possam apresentar as diferentes estratégias de resolução.
Atividade 4
Existem diferentes maneiras de realizar cálculos mentais. O importante é que os estudantes escolham a maneira que melhor se adapta a determinada situação, em razão dos números e das operações nela envolvidos. Nessa atividade, uma das maneiras de calcular o preço dos três produtos é primeiro adicionar 34 reais com 6 reais, obtendo o total de 40 reais, que será adicionado a 120 reais. Assim, tem-se:
34 + 6 = 40
40 + 120 = 160
180 > 160
BNCC em foco:
EF03MA05, EF03MA06
MP091
Avaliação processual
- O gráfico abaixo mostra o número de sobremesas servidas aos clientes de um restaurante em uma semana de abril.
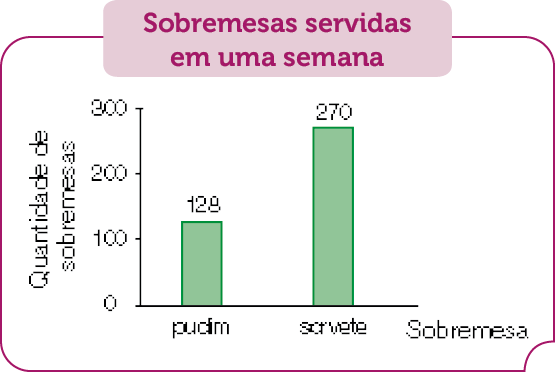
Fonte: Controle do restaurante. (abr. 2023)
- Qual sobremesa foi a mais servida?
_____
PROFESSOR
Resposta: Sorvete.

- Quantas sobremesas, aproximadamente, foram servidas
nessa
semana?
_____
PROFESSOR
Resposta: Foram servidas, aproximadamente, 400 sobremesas.

- Tânia queria calcular 81 − 34 com a calculadora, mas as teclas
 e
e  estavam com defeito. Então ela calculou 82 − 35, afirmando que obteria o mesmo resultado.
estavam com defeito. Então ela calculou 82 − 35, afirmando que obteria o mesmo resultado. 
- Tânia está certa? Por quê?
PROFESSOR
Resposta: Sim, pois acrescentou 1 unidade ao 81 e 1 unidade ao 34, mantendo a mesma diferença entre os números.
- Calcule o resultado das subtrações 82 − 35 e 81 − 34.
- Tânia está certa? Por quê?
PROFESSOR
Resposta: Exemplo de cálculos: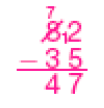
PROFESSOR
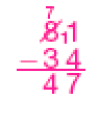
- Invente um problema para cada caso e escreva-o em seu caderno.
- O resultado do problema deve ser dado pela adição 38 + 57.
- O resultado do problema
deve
ser dado pela subtração 57 − 38.
PROFESSOR
Respostas pessoais.
Autoavaliação

- Identifico situações reais ou fictícias em que preciso utilizar cálculos de adição e subtração?
PROFESSOR
Resposta pessoal.
- Utilizo estratégias variadas de cálculo de adição e subtração?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 5
Aqui, os estudantes terão de ler as informações do gráfico. Para responder ao item a, podem observar as colunas e identificar a de maior altura ou observar a quantidade representada em cada coluna e comparar os números.
Atividade 6
Essa atividade, que envolve o uso de uma calculadora com teclas defeituosas, possibilita a reflexão sobre procedimentos alternativos para a descoberta de resultados. A situação apresenta uma estratégia que pode ser usada também no cálculo mental. Por exemplo, para calcular o resultado de 47 − 19, é mais fácil fazer mentalmente 48 − 20. Explore o uso dessa estratégia em outras atividades, ampliando assim a compreensão dos estudantes quanto à ideia de igualdade para escrever diferentes sentenças de subtração que resultem na mesma diferença.
Atividade 7
A atividade incentiva os estudantes a pensarem nos significados das operações que eles devem explorar e em como garantir que certa operação possibilite a resolução do problema criado.
No item b, cada estudante pode trocar os problemas criados com outro colega, para que este os resolva. Ao final, socialize enunciados e resoluções, fazendo uma correção coletiva.
Autoavaliação
Ao propor a primeira questão para os estudantes, peça que elenquem algumas das situações para além da resposta “sim” ou “não”. O exercício de resgatar situações de uso de adição e subtração fará os estudantes analisarem seus conhecimentos sobre o conteúdo.
Na segunda questão, é possível ampliar a discussão pedindo que expliquem algumas estratégias que empregam: o algoritmo usual, a decomposição e a estimativa. Também é pertinente que eles avaliem quais estratégias utilizam com maior ou menor frequência, a fim de problematizar o uso de novas estratégias nas próximas propostas.
Os estudantes devem sempre ser incentivados a usar diferentes tipos de cálculo. O recurso da calculadora é um deles, como na atividade 6. As atividades com calculadora adquirem significado quando possibilitam que o estudante seja colocado diante de desafios e o incentivam a explicitar, verbalmente ou por escrito, os procedimentos utilizados.
BNCC em foco:
EF03MA05, EF03MA06, EF03MA11, EF03MA26
MP092
Comentários para o professor
Conclusão da Unidade 2
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Identifica características do sistema de numeração decimal, empregando a composição e a decomposição de número natural de até quatro ordens? |
_____ |
_____ |
|
Constrói fatos básicos da adição e subtração utilizando-os no cálculo mental ou escrito? |
_____ |
_____ |
|
Representa e ordena números naturais na reta numérica utilizando-a na construção de fatos básicos da adição e da subtração? |
_____ |
_____ |
|
Desenvolve estratégias (decomposição e algoritmo usual) para efetuar cálculo mental e escrito e fazer estimativas nas adições com reagrupamento e subtração com trocas? |
_____ |
_____ |
|
Resolve problemas de adição e de subtração com os significados de juntar, acrescentar, separar, retirar, comparar e completar, empregando estratégias de cálculo exato ou aproximado, incluindo cálculo mental? |
_____ |
_____ |
|
Compreende a ideia de que podemos escrever diferentes adições ou subtrações que resultem na mesma soma ou diferença? |
_____ |
_____ |
|
Lê, interpreta e compara dados apresentados em tabelas de dupla entrada e gráficos de barras ou de colunas. |
_____ |
_____ |
|
Resolve problemas cujos dados são apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP093
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno . O professor pode fazer os ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: _____ |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |