MP094
Comentários para o professor
Introdução da Unidade 3
Assim como a abertura das outras Unidades, a desta traz a imagem de uma situação do cotidiano que apresenta várias informações, com possibilidade de serem exploradas, segundo a orientação do professor, no sentido de servir de ponte entre o que o estudante estudou no 2º ano e o que trabalhará nas páginas seguintes.
Nesta Unidade, predominam atividades que exploram habilidades da Unidade Temática Grandezas e medidas, com foco na leitura e no registro de medidas e intervalos de tempo, utilizando relógio (analógico e digital) para informar os horários de início e término de atividades e sua duração, e no estabelecimento da relação entre hora e minuto e entre minuto e segundo. O trabalho com medidas de tempo e leitura de relógio digital, realizado no 2º ano, será fundamental para o desenvolvimento das habilidades citadas.
Ainda na Unidade Temática Grandezas e medidas, problemas que envolvem a comparação e a equivalência de valores monetários do sistema brasileiro são retomados e aprofundados, em situações de compra, venda e troca, nesta Unidade.
A Unidade Temática Números é contemplada com atividades que buscam proporcionar ao estudante a oportunidade de empregar procedimentos de cálculo mental e escrito diversificados, inclusive os convencionais, para resolver problemas significativos envolvendo adição e subtração com números naturais. Essas atividades apoiam-se nos conhecimentos construídos ao longo do 2º ano e têm como objetivo promover sua ampliação, à medida que possibilitam aos estudantes superar o uso de estratégias pessoais ou convencionais na resolução e elaboração de problemas de adição e subtração, conduzindo-os para o uso de inusitadas estratégias.
Alguns problemas propostos exploram a habilidade dos estudantes quanto à resolução de problemas, cujos dados estão apresentados em tabelas de dupla entrada e em gráficos de barras ou de colunas. Portanto, a Unidade Temática Probabilidade e estatística também está contemplada nesta Unidade.
Cabe destacar a seção Compreender problemas, na qual, além de trabalhar conhecimentos sobre o sistema monetário brasileiro, propõe-se ao estudante uma reflexão sobre dados excessivos ou faltantes no enunciado de um problema.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.
Competência geral favorecida
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Minuto e segundo.
MP095
Sugestão de roteiro de aula – Minuto e segundo
1 ª parte – Atividade preparatória – Tempo sugerido: 10 minutos
Converse com a turma iniciando a aula com a seguinte pergunta aos estudantes: Já ouviram alguém falar a frase “É só 1 minutinho”? Se alguém responder “Sim”, peça para descreverem em qual situação isso ocorreu e se esse “1 minutinho” foi realmente um minutinho.
Proponha aos estudantes uma experiência simples: eles devem contar mentalmente do 1 ao 90, cada qual em um ritmo que considere ser, entre um número e o seguinte, o intervalo de 1 segundo. Antes de começarem, anuncie que irá cronometrar e que eles só devem interromper a contagem quando você avisar que já se passou 1 minuto, ou seja, 60 segundos. Nesse momento, cada um anota no caderno o número em que parou.Verifique, por mão levantada, quantos contaram menos, mais ou igual a 60. Repita essa experiência por, pelo menos, mais duas vezes. Verifique, junto com a turma, se os números em que pararam se aproximaram do 60 em relação à primeira experiência. O esperado é que sucessivas experiências os conduzam a uma mensuração do intervalo de 1 segundo, e, portanto, do intervalo de 1 minuto, mais próxima do tempo real.
2 ª parte – Atividades propostas – Tempo sugerido: 50 minutos
A primeira atividade deve ser conduzida com a participação livre e aberta dos estudantes. Agora que todos já mediram um intervalo de tempo em 1 minuto, podem estimar outros intervalos de tempo.
Avalie se, para a sua turma, é conveniente fazer as demais atividades individualmente ou em duplas. No segundo caso, convém formar duplas mesclando estudantes que já demonstraram desempenhos diferentes em termos de maior ou menor dificuldade, de sucesso ou de insucesso no aprendizado.
Este item da Unidade, Minuto e segundo, trabalha conceitos importantes e básicos para o acúmulo de conhecimentos futuros: a relação de igualdade entre 1 minuto e 60 segundos (atividade 2); a ideia de proporcionalidade da multiplicação (atividades 3 e 5); a ideia subtrativa da divisão (atividade 4); estimativa do tempo de duração de um evento cotidiano (atividade 6); a comparação de duas medidas de uma grandeza deve ser feita na mesma unidade de medida (atividade 7). Na perspectiva de uma avaliação formativa, acompanhe de perto, verifique e anote o desempenho dos estudantes – para posteriores providências em replanejamento próximo – verifique quais deles contemplam esses conhecimentos.
3 ª parte – Término – Tempo sugerido: 5 minutos
Providencie antecipadamente algum aparelho (celular, por exemplo) para reproduzir uma música relaxante. Antes de reproduzi-la, solicite que permaneçam de olhos fechados enquanto ouvem e contem quantos segundos ela dura. Ao final da música, cada um anota em seu caderno a quantidade de segundos passados na sua execução. Anuncie, então, a duração dessa música em segundo e parabenize os que acertaram ou que chegaram próximo dessa medida de tempo.
MP096
UNIDADE 3. Grandezas e medidas

MANUAL DO PROFESSOR
Objetivos da Unidade
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Escolher a unidade de tempo mais apropriada para cada situação.
Ler e registrar medidas e intervalos de tempo.
Ler horas em relógios digitais e em relógios analógicos.
Compreender a relação entre hora e minutos e entre minuto e segundos.
Resolver e elaborar problemas que envolvam valores monetários do sistema brasileiro.
Resolver problemas que exploram a busca de dados em textos, imagens e tabelas.
A Unidade explora unidades de medida de tempo (hora, minuto, segundo), bem como o sistema monetário brasileiro.
As situações-problema propostas possibilitam aos estudantes reconhecer horas e minutos em relógios analógicos e digitais, estimar resultados de medições e fazer comparações entre as unidades de medida.
Em uma roda de conversa, explore a ilustração da abertura da Unidade com perguntas para os estudantes. Por exemplo: “Quantos relógios há na cena?”
BNCC em foco:
EF03MA05, EF03MA22, EF03MA23, EF03MA24, EF03MA26
MP097
Boxe complementar
Para refletir...

Que horas o relógio da torre está marcando? _____
Resposta: 10 horas e 30 minutos

O atendimento diário dos pães artesanais será de quantas horas?
Resposta: 12 horas.
O relógio da banca de frutas está certo em relação ao relógio da torre? Por quê?
Resposta: Sim. Porque marcam a mesma hora.
Fim do complemento
MANUAL DO PROFESSOR
Para refletir…
Verifique se a turma tem dificuldade em responder à primeira pergunta e determinar a hora indicada no relógio da torre.
Se necessário, desenhe um relógio na lousa com números e ponteiros de hora e minuto, mudando inicialmente o ponteiro das horas e, depois, o dos minutos.
É possível que alguns estudantes respondam apenas 10 horas ou 10 horas e 6 minutos, pois, no ano anterior, estudaram somente a hora inteira e ainda podem não ter a noção do movimento dos ponteiros, que meia hora corresponde à metade do percurso do ponteiro dos minutos para 1 hora. Avalie a conveniência de retomar esta questão após as atividades da página 67.
Para responder à segunda questão, o estudante terá que consultar o cartaz e fazer o cálculo do período de atendimento, que começa às 10 horas e termina às 22 horas: 22 − 10 = 12. Portanto, a resposta é 12 horas.
MP098
Medindo o tempo
As horas nos relógios
- Observe as representações dos relógios.

O ponteiro menor aponta para o 3.
O ponteiro maior aponta para o 12.
São 3 horas.
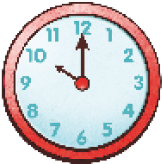
O ponteiro menor aponta para o 10.
O ponteiro maior aponta para o 12.
São 10 horas.
- Agora, escreva o horário que cada relógio marca.
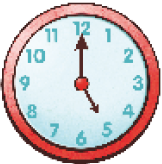
_____
PROFESSOR
Resposta: 5 horas
_____
PROFESSOR
Resposta: 9 horas
_____
PROFESSOR
Resposta: 11 horas- Desenhe os ponteiros dos relógios de acordo com a fala de cada criança.

MANUAL DO PROFESSOR
Objetivos
Ler horas em relógios digitais e em relógios analógicos.
Compreender a relação entre hora e minutos.
Atividade 1
Explore com os estudantes a função dos ponteiros para realizar a leitura de horários nos relógios analógicos (de ponteiros). Pergunte a eles por que os ponteiros não têm o mesmo comprimento.
Explique para os estudantes que, nos relógios de ponteiros representados na ilustração, o ponteiro menor indica a hora e o maior indica os minutos. Se julgar oportuno, comente com eles que há relógios com um ponteiro que indica os segundos.
Atividade 2
Nessa atividade, os estudantes são incentivados a representar as horas em relógio analógico.
BNCC em foco:
EF03MA23
MP099
Hora e meia hora
- Observe Rafael e Alice olhando as horas em dois momentos diferentes e complete.


- Agora, construa o relógio de ponteiros da página 247 para representar os horários indicados abaixo.
- 3 horas e 30 minutos
- 5 horas
- 4 horas e 30 minutos
- 6 horas e 30 minutos
- 7 horas
f) 10 horas e 30 minutos
- Complete com mais ou com menos em cada caso.
- Uma partida de futebol dura
_____
de 1 hora.
PROFESSOR
Resposta: mais
- Fritar um ovo demora
_____
de 1 hora.
PROFESSOR
Resposta: menos
- Escovar os dentes demora
_____
de 1 hora.
PROFESSOR
Resposta: menos
- Uma partida de futebol dura
_____
de 1 hora.
- Escreva a hora que cada representação de relógio marca.

_____
PROFESSOR
Resposta: 8 horas e 30 minutos.
_____
PROFESSOR
Resposta: 5 horas e 30 minutos.MANUAL DO PROFESSOR
Atividade 1
Oriente os estudantes a colocarem algum objeto para funcionar como eixo dos ponteiros, com a ajuda de um adulto. Sugestão: pedaço de palito de fósforo usado, palito de dente ou tampinha do final da carga de caneta esferográfica.
Reforce que, para fazer a leitura da hora em um relógio de ponteiros, é necessário observar a posição ocupada pelo ponteiro menor, que indica a hora. O ponteiro menor pode apontar exatamente para um número, indicando a hora, mas também pode apontar para uma posição entre dois números consecutivos; nesses casos, a hora indicada será a correspondente ao menor desses números.
Já o ponteiro maior indica os minutos. Como cada hora tem 60 minutos e há 12 números no visor do relógio, para descobrir a quantos minutos corresponde cada intervalo do relógio devemos fazer 60 ÷ 12 = 5, ou seja, entre dois números consecutivos, a diferença corresponde a 5 minutos. Alice vê o ponteiro menor apontar para uma posição entre os números 2 e 3, indicando 2 horas; e o ponteiro maior apontar para o número 6, portanto, 6 × 5 minutos = 30 minutos. Logo, o relógio está indicando 2 horas e 30 minutos. Assim, como 30 minutos equivalem a meia hora, podemos dizer duas horas e meia.
Atividade 2
A atividade possibilita aos estudantes trabalhar a estimativa de tempo tendo 1 hora como parâmetro. Peça a eles que deem mais exemplos de atividades que demoram:
menos de 1 hora (lavar as mãos, tomar um picolé, entre outras);
mais de 1 hora (período em que ficam na escola, período de sono durante a noite).
BNCC em foco:
EF03MA23
Atividade 3
A atividade possibilita aos estudantes ampliar o trabalho da leitura da hora em relógios de ponteiros com a escrita do horário representado em cada um deles. Observe se os estudantes fazem a leitura sem dificuldade. Por exemplo, no relógio com detalhe vermelho, o ponteiro menor aponta para uma posição entre os números 8 e 9, indicando 8 horas; o ponteiro maior está apontando para o número 6: 6 × 5 minutos = 30 minutos. Portanto, o relógio marca 8 horas e 30 minutos.
MP100
A hora e o minuto
- Observe como lemos as horas e os minutos em um relógio de ponteiros.
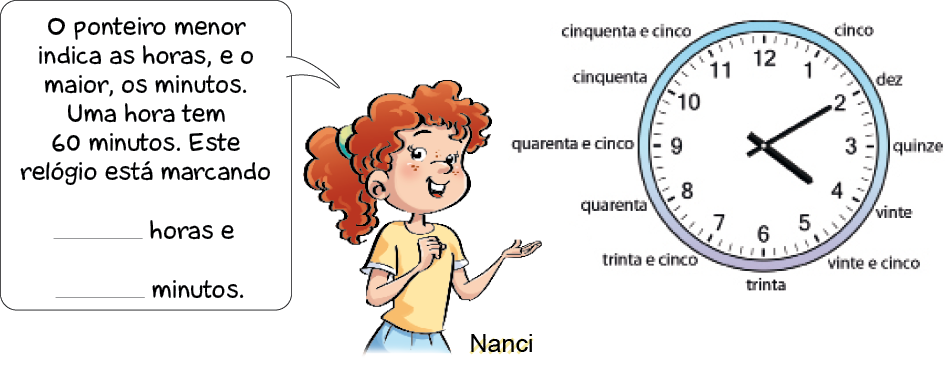
PROFESSOR
Resposta: 4 horas e 10 minutos.Em um relógio digital, as horas e os minutos são separados por dois-pontos. O número da esquerda indica as horas, e o número da direita indica os minutos.

O relógio de Cléber está marcando _____ horas e _____ minutos.
PROFESSOR
Resposta: 16, 10
Indicamos:
- 1 hora por 1 h
- 1 minuto por 1 min
60 minutos correspondem a 1 hora.
60 min = 1 h
MANUAL DO PROFESSOR
Objetivos
Ler horas em relógios digitais e em relógios analógicos.
Compreender a relação entre hora e minutos.
As atividades dessas páginas favorecem o reconhecimento das diferentes formas de registro de tempo entre relógios de ponteiros e relógios digitais.
Atividade 1
A atividade traz a representação de um relógio de ponteiros que destaca os intervalos a cada cinco minutos e explora o reconhecimento das diferentes formas de registro de tempo entre relógios digitais e relógios de ponteiros.
No relógio digital, o estudante vê o registro numericamente explícito da hora, além das 12 horas. Por exemplo: 16 horas e 10 minutos como 16:10.
Também vê a relação entre hora e minuto: 60 min = 1 h.
BNCC em foco:
EF03MA23
MP101
- Ricardo precisa ajustar o relógio digital de acordo com a hora mostrada pelo relógio analógico. Ajude-o a ajustar as horas escrevendo os números que o relógio digital deve marcar.

PROFESSOR
Resposta: 20:30- Escreva o horário que os relógios estão marcando em cada caso. Indique se é manhã ou noite.
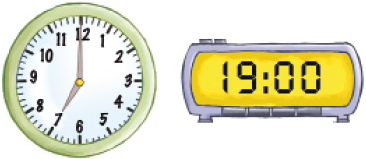
_____
PROFESSOR
Resposta: 7 horas da noite ou 19 horas.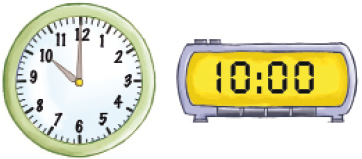
_____
PROFESSOR
Resposta: 10 horas da manhã.- Ligue os relógios que marcam a mesma hora.
Linha 1




Linha 2





PROFESSOR
Resposta: 1 - D; 2 - A e C; 3 - E; 4 - B.2.MANUAL DO PROFESSOR
Atividade 2
É importante os estudantes perceberem que, no relógio analógico, há a necessidade de o ponteiro menor dar duas voltas completas para indicar as horas anteriores ao meio-dia e as posteriores ao meio-dia, e assim completar as 24 horas do dia. Em alguns relógios digitais, a representação das horas continua após as 12 h, como 13 h, 14 h, 15 h, ... até as 24 h. Discuta a respeito de como saber, em um relógio digital que reinicia a indicação do horário após o meio-dia, se o horário indicado refere-se a horas anteriores ao meio-dia (AM) ou posteriores ao meio-dia (PM).
Verifique se os estudantes perceberam o contexto determinado pela ilustração da Lua aparecendo na janela a indicar o período noturno, fazendo com que a resposta, no mostrador do relógio digital, seja 20:30 e não 08:30.
Para ampliar a atividade 2, comente que os relógios de ponteiros foram inventados muito antes dos relógios digitais, existindo na forma atual (com ponteiros indicadores das horas e dos minutos) desde cerca do ano de 1 700. Já o relógio de pulso teve seus primeiros modelos criados no século XIX, principalmente para uso feminino. A adesão pelos homens está relacionada diretamente com um famoso brasileiro, Alberto Santos Dumont (1873-1932). Conta-se que, em razão de estar com as mãos constantemente ocupadas com os controles dos balões que costumava pilotar no início do século XX, em Paris, Santos Dumont pediu a seu amigo joalheiro Louis Cartier que construísse um modelo de pulso para ele. Atendido em seu pedido, passou a usar seu relógio de pulso com frequência, ajudando a popularizar a ideia, que rapidamente se disseminou.
BNCC em foco:
EF03MA23
Atividades 3 e 4
Sugira aos estudantes que, para resolver essas atividades, montem e usem o modelo de relógio de ponteiros fornecido no Material complementar.
Observe se eles percebem que a representação do segundo relógio de ponteiros da atividade 4 pode ser associada a duas representações de relógio digital.
Sugestão de atividade
Em dupla, um dos estudantes ajusta os ponteiros do relógio montado, indicando tratar-se de um horário anterior ou posterior ao meio-dia; o colega deve, então, registrar esse horário na forma digital. Depois, os integrantes da dupla podem se alternar.
MP102
- Para uma viagem de avião, Fabíola e sua irmã chegaram ao aeroporto às 16 horas e 15 minutos. De acordo com a previsão do voo, elas terão de aguardar por 1 hora e 10 minutos. Agora, responda.
- Qual é o horário previsto do voo?
_____
PROFESSOR
Resposta: 17 horas e 25 minutos.
- Devido ao mau tempo, o voo sofreu um atraso de 15 minutos.
Qual será o novo horário desse voo? _____
PROFESSOR
Resposta: 17 horas e 40 minutos.
- Qual é o horário previsto do voo?
_____
- Joana é professora de ginástica. Por dia, ela dá 4 aulas, uma após a outra. Cada aula dura 15 minutos.
- Complete o quadro de horários da professora Joana.

Tabela: equivalente textual a seguir.
|
1ª aula |
2ª aula |
3ª aula |
4ª aula |
||||
|---|---|---|---|---|---|---|---|
|
Início 18:00 |
Início 18:15 |
Início _____ |
Início _____ |
||||
|
Término 18:15 |
Término _____ |
Término _____ |
Término _____ |
||||
PROFESSOR
Resposta: 2ª aula - término: 18:30. 3ª aula - início: 18:30; término: 18:45. 4ª aula - início: 18:45; término: 19:00

- Agora, desenhe os ponteiros que estão faltando nos relógios abaixo.
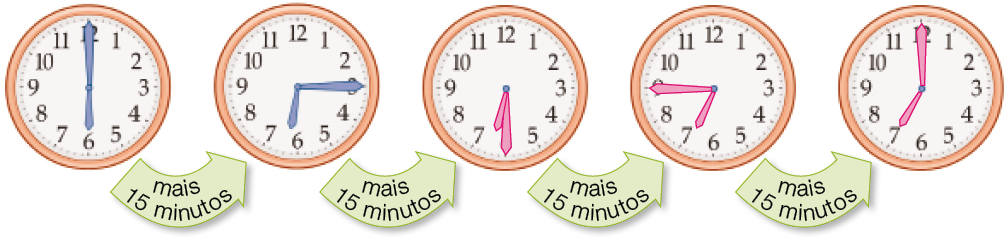
- Ernesto terminou de montar uma cerca de madeira às 10 horas e 45 minutos, após ter trabalhado por 1 hora e meia. A que horas Ernesto começou a montar a cerca?
_____
PROFESSOR
Resposta: Às 9 horas e 15 minutos.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental.
Ler e registrar medidas e intervalos de tempo.
Ler horas em relógios digitais e em relógios analógicos.
Compreender a relação entre hora e minutos.
Resolver problemas que exploram a busca de dados em textos e imagens.
Atividade 5
Os estudantes devem perceber que, para encontrar o novo horário, é necessário que eles adicionem o tempo de espera (1 hora e 10 minutos) ao tempo previsto de chegada (16 horas e 15 minutos). No item a, os estudantes podem adicionar 1 hora às 16 horas, e 10 minutos aos 15 minutos, obtendo17 horas e 25 minutos. No item b, basta que eles adicionem 15 minutos aos 25 minutos, obtendo 17 horas e 40 minutos.
Atividade 6
A atividade possibilita aos estudantes estabelecer relações entre horas e minutos (1 hora é o mesmo que 60 minutos). Peça a eles que observem o tempo de aula e o quadro. Se necessário, desenhe na lousa relógios indicando outros horários e peça a eles que indiquem esses horários.
Atividade 7
Para resolver a atividade, os estudantes podem determinar o horário do início da montagem da cerca subtraindo 1 hora de 10 horas e, depois, 30 minutos de 45 minutos, obtendo 9 horas e 15 minutos. Depois podem fazer a verificação da resposta adicionando a ela 1 hora e 15 minutos para obter o horário de término da construção da cerca.
BNCC em foco:
EF03MA05, EF03MA22, EF03MA23
MP103
- De outubro a fevereiro, costumava vigorar em alguns estados brasileiros o horário de verão. Nesses meses, as pessoas deveriam adiantar o relógio em 1 hora.
- Onde você mora teve horário de verão?
_____
PROFESSOR
Resposta pessoal.
- Imagine que no estado onde Nair mora vigore o horário de verão. Se o relógio
dela
marcar 15 horas neste momento, que horas seriam se o horário de verão não vigorasse no estado dela?
_____
PROFESSOR
Resposta: 14 horas.
- Quando o período do horário de verão terminava, o que as pessoas deviam fazer para ajustar o relógio?
_____
PROFESSOR
Resposta: Atrasar o relógio em 1 hora.
- Onde você mora teve horário de verão?
_____
- Registre sua
rotina
na agenda do celular ilustrada abaixo. Escreva algumas atividades que faz no período da manhã e no período da tarde. Escolha o dia da semana que quiser. Não se esqueça de marcar o horário de início e de término de cada atividade.
PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR
Atividade 8
Antes de realizar a atividade, verifique o que os estudantes sabem sobre o horário de verão.
Comente que a ideia de adiantar os relógios em uma hora, para melhor aproveitar a luz solar e economizar o consumo de luz artificial, foi colocada em prática pela primeira vez em 1907, na Inglaterra. Hoje, aproximadamente 30 países o utilizam em pelo menos parte de seu território. No Brasil, o horário de verão foi adotado em 1931, abrangendo todo o território nacional, mas houve vários anos em que não foi colocado em prática. Desde 1985, foi adotado novamente até 2018. A partir de 2019, mais uma vez deixou de ser adotado.
Atividade 9
Peça aos estudantes que escolham um dia da semana e anotem a data no espaço reservado. Depois, na frente dos horários indicados na agenda, eles devem registrar a atividade realizada. Questione-os sobre a duração de cada uma das atividades.
BNCC em foco:
EF03MA05, EF03MA22, EF03MA23
MP104
Minuto e segundo


- Debata as questões a seguir com os colegas.
- Em que situações você já mediu um intervalo de tempo em minutos? E em segundos?
- Você considera 1 minuto muito tempo ou pouco tempo? Por quê?
PROFESSOR
Respostas pessoais.
- Para esquentar seu lanche no micro-ondas, Júlia apertou a tecla correspondente a 1 minuto. Após 15 segundos, o aparelho indicava os segundos restantes, como mostra a ilustração abaixo.

- Por quantos segundos o lanche ainda vai esquentar?
_____
PROFESSOR
Resposta: 45 segundos.
- Por quantos segundos, ao todo, o lanche esquentará?
_____
PROFESSOR
Resposta: 60 segundos.
Indicamos 1 segundo por 1 s
1 minuto corresponde a 60 segundos.
1 min = 60 s
- Quanto tempo dura um intervalo de tempo se o ponteiro dos segundos der:
- 2 voltas?
_____
PROFESSOR
Resposta: 2 minutos ou 120 segundos.
- 3 voltas?
_____
PROFESSOR
Resposta: 3 minutos ou 180 segundos.
- meia-volta?
_____
PROFESSOR
Resposta: Meio minuto ou 30 segundos.
- 1 volta e meia?
_____
PROFESSOR
Resposta: 1 minuto e meio ou 90 segundos.
- 2 voltas?
_____

- Como saber, usando uma calculadora, quantos minutos e segundos correspondem a 132 segundos?
_____
PROFESSOR
Exemplo de resposta: Subtrair 60 de 132, obtendo 72, e, depois, subtrair 60 novamente, obtendo 12. Como o número 60 “coube” duas vezes em 132 e sobraram 12, a resposta é 2 minutos e 12 segundos.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Ler e registrar medidas e intervalos de tempo.
Compreender a relação entre hora e minutos e entre minuto e segundos.
Resolver problemas que exploram a busca de dados em textos, imagens e tabelas.
Atividade 1
A atividade busca o conhecimento prático que os estudantes adquirem no dia a dia a respeito de intervalos de tempo medidos em minutos e em segundos e, ao mesmo tempo, trabalha a capacidade deles de fazerem estimativas para tais intervalos.
Atividade 2
A situação apresentada, em que passados 15 segundos o marcador digital de tempo do micro-ondas indica que faltam 45 segundos para completar 1 minuto, possibilita aos estudantes concluir que 60 segundos é o mesmo que 1 minuto.
Atividade 3
A atividade explora a relação entre as voltas do ponteiro e os minutos e segundos. Mesmo que ainda não se torne consciente para o estudante, aqui ele vai tendo contato com fatos básicos sobre os números racionais.
Atividade 4
A atividade propõe o uso da calculadora para explorar o raciocínio dos estudantes. Como 1 minuto corresponde a 60 segundos, do número 132 eles devem subtrair 60 até quando for possível, e verificar que o número 60 coube 2 vezes: 132 − 60 = 72; 72 − 60 = 12. Portanto, 132 segundos correspondem a 2 minutos e 12 segundos.
BNCC em foco:
EF03MA05, EF03MA22
MP105

- Jaime analisou a vazão de uma torneira e descobriu que ela aberta despeja, em um balde, 1 litro de água a cada 15 segundos. Complete a tabela abaixo.
Vazão da torneira
Tabela: equivalente textual a seguir.
|
Tempo |
Número de litros |
|---|---|
|
15 segundos |
1 |
|
30 segundos |
_____ |
|
1 minuto |
_____ |
|
_____ |
12 |
|
_____ |
20 |
Fonte: Dados calculados por Jaime. (fev. 2023)
PROFESSOR
Resposta: Tempo: 3 minutos. Tempo: 5 minutos. Número de litros: 2. Número de litros: 4.
- Faça uma estimativa e escreva a duração do intervalo de tempo mais adequada à realização de cada atividade: 120 minutos, 5 minutos, 25 segundos ou 2 segundos.
Um atleta amador correr 100 metros.
_____
PROFESSOR
Resposta: 25 segundos.Abrir uma lata de refrigerante.
_____
PROFESSOR
Resposta: 2 segundos.Fazer um café.
_____
PROFESSOR
Resposta: 5 minutos.Assistir a um filme.
_____
PROFESSOR
Resposta: 120 minutos.- Observe as falas de Daniel e de Marcos.


- Faça como Marcos explicou a Daniel e descubra qual dos dois intervalos de tempo tem duração maior.
PROFESSOR
Resposta: 146 s
MANUAL DO PROFESSOR
Atividade 5
A atividade possibilita explorar a leitura e interpretação de tabela. Observe se os estudantes compreendem a proporcionalidade que deve ser mantida entre o tempo e a quantidade de litros. Por exemplo, ao dobrar a quantidade de segundos, a quantidade de litros de água escoada também dobra.
Para completar a tabela, os estudantes podem pensar que, se para cada 15 s a torneira despeja 1 litro de água, e 30 s correspondem a 15 s + 15 s, então 1 litro + 1 litro = 2 litros. Como 1 min corresponde a 60 s:
1 min = 60 s = 30 s + 30 s; então, 2 litros + 2 litros = 4 litros;
3 min = 60 s + 60 s + 60 s; então, 4 litros + 4 litros + + 4 litros = 12 litros;
5 min = 3 min + 1 min + 1 min; então, 12 litros + 4 litros + + 4 litros = 20 litros.
Atividade 6
Estimar o tempo necessário para a realização de algumas atividades é importante para o dia a dia dos estudantes. Uma estratégia que pode ser utilizada é eliminar os valores que seriam absurdos para determinada atividade, como fazer um café em 2 segundos,12 segundos ou 120 minutos.
Atividade 7
Verifique se os estudantes fazem a relação:
1 minuto = 60 segundos, 2 minutos = 60 segundos + 60 segundos = 120 segundos; como são 2 minutos e 16 segundos: 120 segundos + 16 segundos = 136 segundos.
Agora, basta comparar 136 segundos com 146 segundos (146 > 136).
Observe aos estudantes duas conclusões importantes:
para compararmos duas medidas, elas devem representar a mesma grandeza;
para compararmos duas medidas de uma mesma grandeza, elas devem ter a mesma unidade.
No caso da atividade, as medidas foram comparadas na unidade segundo.
BNCC em foco:
EF03MA22, EF03MA23
MP106
Sistema monetário brasileiro
- Você conhece a moeda e a cédula representadas abaixo?


- O que você consegue comprar com uma moeda ou com uma cédula dessas?
PROFESSOR
Resposta pessoal.
- Observe.

- Agora, ligue os quadros que contêm a mesma quantia.
Coluna 1



Coluna 2



PROFESSOR
Resposta: 1 – B, 2 – C, 3 – AMANUAL DO PROFESSOR
Objetivo
Resolver e elaborar problemas que envolvam valores monetários do sistema brasileiro.
Atividade 1
A atividade possibilita não apenas verificar se os estudantes conhecem a cédula de 2 reais e a moeda de 1 real, mas também observar a noção que eles têm do valor de compra de cada uma delas. Peça aos estudantes que compartilhem suas respostas com os colegas.
Atividade 2
A atividade propicia aos estudantes observar a equivalência de quantias iguais em quadros com moedas e cédulas de real. Verifique as estratégias utilizadas por eles e socialize-as com a turma.
BNCC em foco:
EF03MA24
MP107
- Veja a quantia que Paula ganhou dos pais dela. Em seguida, complete.
Ganhou da mãe:

Ganhou do pai:

Paula ganhou, no total, _____ reais.
PROFESSOR
Resposta: 7- Observe a quantia que Jonas tem.



- Elabore um problema com as informações dadas. Depois, troque-o com um
colega
para que ele
resolva
o seu e você
resolva
o dele.
_____
PROFESSOR
Resposta pessoal.

- Vanessa tem 22 moedas de 1 real e quer trocá-las por cédulas de 2 reais. Desenhe a quantidade de cédulas que ela vai receber.
_____
PROFESSOR
Resposta: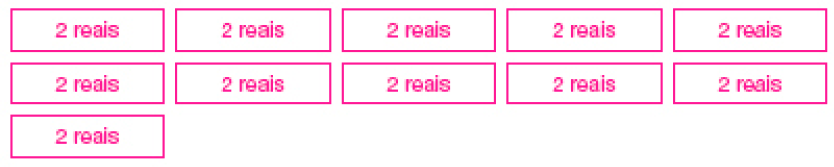
MANUAL DO PROFESSOR
Atividade 3
Na atividade, os estudantes terão de adicionar valores referentes a moedas e cédulas do sistema monetário brasileiro. A situação possibilita observar se os estudantes percebem que duas cédulas de 2 reais valem mais que três moedas de 1 real.
Atividade 4
Propicie a reflexão e discussão dos problemas elaborados pelos estudantes.
Atividade 5
Observe se os estudantes apresentam alguma dificuldade em verificar a equivalência de valores monetários do sistema brasileiro e fazer a representação das cédulas. Os estudantes devem entender que duas moedas de 1 real podem ser trocadas por uma cédula de 2 reais. Se necessário, trabalhe com material concreto.
BNCC em foco:
EF03MA05, EF03MA24
MP108
- Observe as cédulas de 5 e de 10 reais abaixo.


- Joana tem a quantia abaixo. Desenhe uma cédula para que a quantia total representada seja 10 reais.

PROFESSOR
Resposta:
Observação: As imagens não estão apresentadas em escala de tamanho. Cores fantasia. Fim da observação.

- Calcule e complete o quadro desenhando as cédulas e moedas necessárias para representar o troco em cada caso.
Tabela: equivalente textual a seguir.
|
Produto |
Pagou com |
Troco |
|---|---|---|
|
|
|
PROFESSORExemplo de resposta:PROFESSOR
|
|
|
|
PROFESSORExemplo de resposta:PROFESSOR
|
|
|
|
PROFESSORExemplo de resposta:PROFESSOR
|
|
|
|
PROFESSORExemplo de resposta:PROFESSOR
|
- Qual é o produto mais caro? E o mais barato?
_____
PROFESSOR
Resposta: Mais caro: barra de chocolate; mais barato: bombom.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Resolver e elaborar problemas que envolvam valores monetários do sistema brasileiro.
Resolver problemas que exploram a busca de dados em textos e imagens.
Atividade 6
A atividade explora o sistema monetário brasileiro trabalhando o reconhecimento das cédulas de 5 reais e de 10 reais e a equivalência de valores entre essas cédulas.
Atividade 7
Nessa atividade, os estudantes trabalham situações com compra, pagamento e troco. Valorize a representação das moedas e cédulas por desenhos. Explore a comparação de valores dos produtos.
BNCC em foco:
EF03MA05, EF03MA24
MP109
- Marcelo tem 20 cédulas de 2 reais, 15 moedas de 1 real e 3 cédulas de 5 reais. Ele quer trocar toda essa quantia por cédulas de 10 reais. Quantas cédulas de 10 reais ele terá depois da troca?
_____
Marcelo terá _____ cédulas de 10 reais.
PROFESSOR
Resposta: 7

- Observe o preço destes brinquedos. Depois, desenhe ao lado de cada um o menor número de cédulas de 10, 5 ou 2 reais necessárias para compor cada preço.
Tabela: equivalente textual a seguir.
|
|
|
|
|
|
|
|
|
Observação: As imagens não estão apresentadas em escala de tamanho. Cores fantasia. Fim da observação.
MANUAL DO PROFESSOR
Atividade 8
Verifique e discuta com a turma as estratégias usadas pelos estudantes. Amplie a atividade perguntando: “Marcelo poderia trocar a quantia que ele tem unicamente por cédulas de 20 reais?” (Não.).
Atividade 9
Nessa atividade, os estudantes devem decompor o preço de cada brinquedo usando apenas as cédulas de 10 reais, 5 reais ou 2 reais.
55 = 10 + 10 + 10 + 10 + 10 + 5
72 = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 2
98 = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 2 + 2 + 2 + 2
Outras decomposições podem aparecer; no entanto, é necessário que os estudantes percebam que a decomposição solicitada deve ter a menor quantidade de cédulas.
BNCC em foco:
EF03MA05, EF03MA24
MP110

Observação: As imagens não estão apresentadas em escala de tamanho. Cores fantasia. Fim da observação.
- Observe a ilustração acima e
resolva
as atividades.
- Ana foi à feira com a mãe dela. Veja o que elas compraram.

- Descubra se sobrou dinheiro das compras feitas na feira por Ana e sua mãe, sabendo que elas tinham 2 cédulas de 20 reais.
- Registre como você pensou.
PROFESSOR
Resposta: Exemplo de resposta:PROFESSOR
Compras: 7 + 10 + 5 + 5 = 27PROFESSOR
Dinheiro: 20 + 20 = 40PROFESSOR
27 é menor que 40; logo, sobrou dinheiro.MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Resolver e elaborar problemas que envolvam valores monetários do sistema brasileiro.
Resolver problemas que exploram a busca de dados em textos e imagens.
Atividades 10 e 11
Nessas atividades, os estudantes devem buscar os dados no texto e na ilustração da barraca de frutas da feira. Se necessário, lembre-os de que 1 dúzia corresponde a 12 unidades, e meia dúzia, a 6 unidades. Verifique e discuta as estratégias usadas pelos estudantes.
BNCC em foco:
EF03MA05, EF03MA24
MP111

- Ainda com base na ilustração acima,
resolva
as atividades.
- A família de Davi também foi à feira. Eles compraram 2 abacaxis e meia dúzia de mexericas. Quantos reais eles gastaram ao todo?
_____
PROFESSOR
Resposta: 14 reais.
- Com 1 cédula de 20 reais e 1 cédula de 10 reais, decida, em dupla, quais e quantas frutas você e seu
colega
podem comprar.
_____
- A família de Davi também foi à feira. Eles compraram 2 abacaxis e meia dúzia de mexericas. Quantos reais eles gastaram ao todo?
- Total gasto: _____ reais.
- Troco:
_____


- Verifique se alguma dupla gastou a mesma quantia que vocês e se escolheu as mesmas frutas.
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 11
Observe, por meio da atividade 11, se há indícios da compreensão ou não do estudante sobre proporcionalidade ao obter o preço de meia dúzia de bananas.
Incentive os estudantes a elaborarem um quadro com as frutas que podem ser compradas, como o do exemplo abaixo.
Tabela: equivalente textual a seguir.
|
Fruta |
Preço |
|---|---|
|
1 dúzia de bananas |
5 reais |
|
1 dúzia de laranjas |
5 reais |
|
1 dúzia de mexericas |
4 reais |
|
2 caixas de morangos |
10 reais |
|
1 abacaxi |
6 reais |
É importante que os estudantes percebam que 1 cédula de 20 reais e 1 cédula de 10 reais totalizam 30 reais. Sendo assim, o total não pode ultrapassar 30 reais. Compare e comente as respostas obtidas.
BNCC em foco:
EF03MA05, EF03MA24
MP112
Compreender problemas
Para resolver
Problema 1
Pedro economizou durante dois anos. Veja o dinheiro que ele tem.



- Quantas cédulas ele conseguiu juntar?
_____
PROFESSOR
Resposta: 24 cédulas.- Conte a um
colega
como você fez o cálculo.
PROFESSOR
Resposta pessoal.
- Qual é a quantia que Pedro possui?
_____
PROFESSOR
Resposta: 375 reais.
- Pedro quer comprar um micro-ondas de 500 reais. Falta ou sobra dinheiro? Quanto?
_____
PROFESSOR
Resposta: Faltam 125 reais.
- Conte a um
colega
como você fez o cálculo.
Problema 2
Um circo tem capacidade para um público de 2 600 pessoas, mas só metade compareceu ao último espetáculo. No setor B da plateia havia mais de 400 espectadores.

- Quantas pessoas compareceram ao último espetáculo desse circo?
_____
PROFESSOR
Resposta: 1.300 pessoas.
- Quantos lugares sobraram na
plateia
nesse espetáculo?
_____
PROFESSOR
Resposta: 1.300 lugares.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de adição e subtração, utilizando diferentes estratégias de cálculo, incluindo cálculo mental e estimativa.
Resolver e elaborar problemas que envolvam valores monetários do sistema brasileiro.
Resolver problemas que exploram a busca de dados em textos e imagens.
Nessa dupla de páginas, os problemas exploram a busca de dados em textos, falta ou excesso de informações e busca de dados fora do texto.
Para resolver
O Problema 1 requer que os estudantes contem quantas são as cédulas, qual é a quantia total, se com a quantia que Pedro tem é possível comprar um micro-ondas, explorando situações que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro em situações de compra.
No Problema 2, incentive os estudantes na leitura e interpretação das informações contidas no texto. É importante eles perceberem que nem todas as informações devem ser usadas para a resolução.
BNCC em foco:
EF03MA05, EF03MA24
MP113
Para refletir
- Quais operações podem ser usadas para resolver o item b do Problema 1 ? Escreva cada uma.
_____
PROFESSOR
Exemplo de resposta: Multiplicação e adição.PROFESSOR
5 × 50 = 250PROFESSOR
10 × 2 = 20PROFESSOR
4 × 20 = 80PROFESSOR
5 × 5 = 25PROFESSOR
250 + 20 + 80 + 25 = 375
- No Problema 1, quais cédulas de real não apareceram?
_____
PROFESSOR
Resposta: As cédulas de 200, de 100 e de 10 reais.
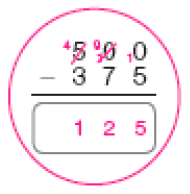
- Complete os cálculos e cerque com um linha aquele que foi usado na resolução do item c do Problema 1.
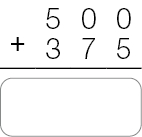
PROFESSOR
Resposta: 875PROFESSOR
- No Problema 2, existe alguma informação que não foi usada em sua resolução? Justifique sua resposta.
_____
PROFESSOR
Resposta: Sim, o fato de que no setor B da plateia havia mais de 400 espectadores.
- Qual é a quantidade exata de espectadores que estavam no setor B da plateia?
_____
PROFESSOR
Resposta: Não se sabe a quantidade exata, mas somente que eram mais de 400 pessoas.
MANUAL DO PROFESSOR
Para refletir
A questão 1 possibilita aos estudantes refletir sobre as estratégias utilizadas na resolução do problema.
Depois de os estudantes observarem as cédulas e moedas do sistema monetário brasileiro ao longo da Unidade, a questão 2 possibilita que eles verifiquem se reconhecem todas as cédulas para, desse modo, determinar quais não apareceram no Problema 1.
Na atividade 3, ao completarem os cálculos propostos na atividade, os estudantes terão a oportunidade de verificar a resposta e a resolução do item c do Problema 1.
A questão 4 é importante porque possibilita aos estudantes perceber que nem toda informação de um problema é necessária na sua resolução e que é fundamental realizar uma leitura atenta e analisar os dados.
A questão 5 mostra aos estudantes a existência de problemas em que não há dados suficientes para responder a uma pergunta.
BNCC em foco:
EF03MA05, EF03MA24
MP114
A Matemática me ajuda a ser
... um conhecedor de cédulas e moedas
Você já prestou atenção nas cédulas e moedas que usamos? No Brasil, o dinheiro tem valor em real.
As cédulas e moedas têm cores e tamanhos variados.
A história do dinheiro
Antes da existência do dinheiro, as pessoas trocavam os bens que tinham pelos produtos que queriam.
Mais de 2 mil anos atrás, surgiram as moedas.
Depois, apareceram as cédulas. Com elas, comprar e vender produtos ficou muito mais fácil.

Do que são feitas?
As cédulas são feitas de um tipo especial de papel, mais resistente e áspero que o papel comum. Mas é importante saber que não devemos rabiscá-las e que precisamos ter cuidado para não rasgá-las ou sujá-las.
Já as moedas são feitas de aço, que não enferruja, e duram mais tempo que as cédulas.

De onde vêm?
Quem fabrica cédulas e moedas é a Casa da Moeda do Brasil.
E quem decide quanto dinheiro vai ser fabricado é o Banco Central do Brasil. Produzir uma cédula de 10 reais custa mais ou menos 20 centavos de real.

Legenda: Produção de notas e moedas de real na Casa da Moeda do Brasil, no município do Rio de Janeiro, Rio de Janeiro, em 2017. Fim da legenda.

Legenda: Moedas comemorativas dos Jogos Olímpicos Rio 2016. Fim da legenda.
Dinheiro colecionável
Em datas comemorativas, a Casa da Moeda produz cédulas e moedas especiais. Elas podem ter cores, tamanhos e valores diferentes das cédulas e moedas comuns. São tão raras que algumas pessoas as colecionam.
Verdadeiras ou falsas?
Para saber se uma cédula é verdadeira, deve-se observar alguns detalhes. Uma lente de aumento permite notar números bem pequenos impressos nela. Se você colocar a cédula perto de uma lâmpada, vai achar a figura de um animal e outros números escondidos.

Fontes: Casa da Moeda do Brasil. Disponível em: http://fdnc.io/44U; Banco Central do Brasil. Disponível em: http://fdnc.io/eTT; CNN. Disponível em: http://fdnc.io/eTU. Acessos em: 12 fev. 2021.
Observação: As imagens não estão apresentadas em escala de tamanho. Fim da observação.
MANUAL DO PROFESSOR
Objetivo
Resolver e elaborar problemas que envolvam valores monetários do sistema brasileiro.
Antes de trabalhar a seção, questione os estudantes sobre o que sabem. “Como será que surgiu o dinheiro?”; “O que será que surgiu primeiro: a cédula ou a moeda?”; “De que material são feitas as cédulas e as moedas?”; “Onde as cédulas e as moedas são produzidas?”; “Como reconhecemos se uma cédula é verdadeira?”; “Você tem ou conhece alguém que tenha moedas especiais?”; “O que é ser um colecionador?”.
BNCC em foco:
EF03MA24; competência geral 1
Sugestão de trabalho interdisciplinar
O conteúdo da seção pode ser trabalhado de forma interdisciplinar com História, discutindo a prática do escambo antes da existência do dinheiro.
A aula a seguir pode ser um ponto de partida. PIMENTEL, Gilka Silva. O escambo e o sistema de troca. Portal do Professor. Disponível em: http://fdnc.io/eU2. Acesso em: 22 maio 2021.
MP115
Tome nota
Qual é o custo para produzir uma cédula de 10 reais?
_____
PROFESSOR
Resposta: Mais ou menos 20 centavos de real.Reflita

- Você conhece todas as cédulas e moedas brasileiras?
PROFESSOR
Resposta pessoal.
- Você tem alguma cédula ou moeda de data comemorativa? Conhece alguém que coleciona dinheiro brasileiro ou estrangeiro?
PROFESSOR
Resposta pessoal.
- Pesquise e escreva um item que pode ser comprado com 1 real e outro item que pode ser comprado com 50 reais.
_____
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Tome nota
Leia o texto com os estudantes e verifique se eles compreenderam as informações apresentadas antes de responderem à questão.
Reflita
Se julgar oportuno, para realizar a pesquisa, peça aos estudantes que considerem produtos vendidos em supermercados. Eles podem contar com a ajuda dos pais ou responsáveis.
BNCC em foco:
EF03MA24; competência geral 1
MP116
Compreender informações
Comparar e analisar dados
- Afonso tem uma criação de galinhas para produção de ovos. Ele anotou, semanalmente, as quantidades de ovos produzidos e de ovos vendidos. Observe as tabelas que Afonso elaborou com base nesses dados e, em seguida, faça o que se pede.
Ovos produzidos
Tabela: equivalente textual a seguir.
|
Período |
Quantidade |
|---|---|
|
1ª semana |
290 |
|
2ª semana |
310 |
|
3ª semana |
280 |
|
4ª semana |
300 |
Ovos vendidos
Tabela: equivalente textual a seguir.
|
Período |
Quantidade |
|---|---|
|
1ª semana |
270 |
|
2ª semana |
280 |
|
3ª semana |
260 |
|
4ª semana |
300 |
Fonte: Dados fornecidos por Afonso. (jan. 2023)
- Em qual período ocorreu a maior produção de ovos?
_____
PROFESSOR
Resposta: 2ª semana.
- Em qual período ocorreu a
menor
venda de ovos?
_____
PROFESSOR
Resposta: 3ª semana.
- Em qual período a quantidade de ovos vendidos foi igual à de ovos produzidos?
_____
PROFESSOR
Resposta: 4ª semana.
- De acordo com as informações acima, complete a tabela a seguir para mostrar a quantidade de ovos não vendidos em cada semana.
Ovos não vendidos
Tabela: equivalente textual a seguir.
|
Período |
Quantidade |
|---|---|
|
1ª semana |
_____ |
|
2ª semana |
_____ |
|
3ª semana |
_____ |
|
4ª semana |
_____ |
Fonte: Dados fornecidos por Afonso. (jan. 2023)
PROFESSOR
Resposta: 20, 30, 20, 0
MANUAL DO PROFESSOR
Objetivos
Resolver problemas cujos dados estão apresentados em tabelas.
Ler, interpretar e comparar dados apresentados em tabelas.
Organizar dados em tabelas, com e sem o uso de tecnologias digitais.
Atividade 1
Na atividade, os estudantes terão de fazer a leitura com compreensão das informações que constam das primeiras tabelas. As questões formuladas, ao serem respondidas, facilitam o entendimento de ambas.
Depois, eles devem comparar as duas tabelas apresentadas no enunciado do problema para completar a tabela do item d.
BNCC em foco:
EF03MA26
MP117

- Com base na tabela anterior, complete o gráfico que representa a quantidade de ovos não vendidos neste mês.
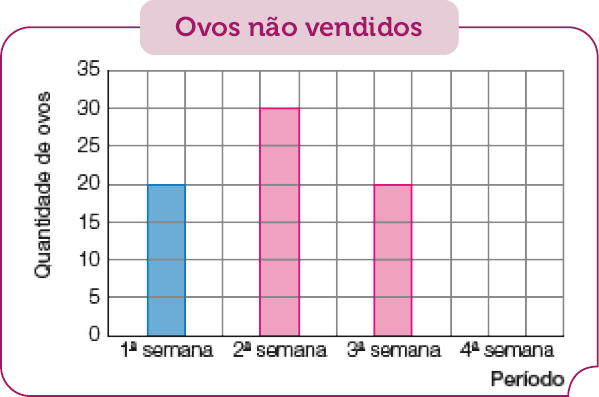
Fonte: Dados fornecidos por Afonso. (jan. 2023)
- Manoela digitou em uma planilha eletrônica as notas obtidas por ela em cada bimestre do 3º ano, em Língua Portuguesa e Matemática. Observe e, em seguida, responda às questões.
Tabela: equivalente textual a seguir.
|
A |
B |
C |
D |
E |
|
|---|---|---|---|---|---|
|
1 |
_____ |
Língua Portuguesa |
Matemática |
_____ |
_____ |
|
2 |
1 º bimestre |
6 |
7 |
_____ |
_____ |
|
3 |
2º bimestre |
6 |
6 |
_____ |
_____ |
|
4 |
3º bimestre |
7 |
8 |
_____ |
_____ |
|
5 |
4º bimestre |
9 |
8 |
_____ |
_____ |
|
6 |
_____ |
_____ |
_____ |
_____ |
_____ |
- Qual é a maior nota
obtida
por Manoela neste ano em Matemática? E em Língua Portuguesa?
_____
PROFESSOR
Resposta: 8; 9.
- Analisando essas informações, o que é possível afirmar em relação às notas de Manoela?
PROFESSOR
Resposta pessoal.
- Faça como ela e
organize
suas notas em uma tabela (no
caderno
ou em uma planilha eletrônica) para comparar as notas obtidas em Língua Portuguesa e Matemática.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
Após preencherem a tabela da atividade 1, os estudantes terão de completar o gráfico com as barras que correspondem à quantidade de ovos não vendidos em cada período. Verifique se os estudantes compreenderam que, na 4ª semana, não há barra porque a quantidade de ovos não vendidos é zero, ou seja, na 4ª semana, todos os ovos produzidos nela foram vendidos.
Atividade 3
No item c, incentive os estudantes a usarem uma planilha eletrônica para tabular suas notas.
Pergunte a eles sobre outras situações em que as tabelas ou planilhas eletrônicas podem ser úteis.
BNCC em foco:
EF03MA26
MP118
O que você aprendeu
- Raul, Isabela e Hugo usaram o computador por uma hora e meia no total, um após o outro, como mostra o quadro a seguir.
Tabela: equivalente textual a seguir.
|
Criança |
Tempo |
|---|---|
|
Raul |
meia hora |
|
Isabela |
25 minutos |
|
Hugo |
o tempo restante |
- Qual deles usou o computador por mais tempo?
_____
PROFESSOR
Resposta: Hugo.
- Cerque com uma linha o que podería comprar em cada caso com a quantia indicada, sem que sobrasse ou faltasse dinheiro.


PROFESSOR
Resposta: estojo; livro.

PROFESSOR
Resposta: vaso 6 reais e vaso 4 reais..Observação: Os objetos não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.
- Cristina acordou às 7 horas e chegou ao clube às 9 horas. Ela gastou 20 minutos para percorrer a distância de sua casa ao clube. Antes de sair de casa, ainda conseguiu fazer outras três atividades. Quais foram as atividades feitas por Cristina? Marque cada uma com um X .
( )

35 minutos
( )

50 minutos
( )

15 minutos
( )

55 minutos
PROFESSOR
Resposta: brincando com boneca; usando o computador; comendo.MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Se necessário, retome com os estudantes a relação entre hora e minuto: 1 hora corresponde a 60 minutos; meia hora, portanto, corresponde a 30 minutos. Espera-se que, após observar os dados da tabela, os estudantes concluam que: Raul usou por 30 minutos; Isabela, por 25 minutos; e Hugo, por 35 minutos (90 min − 30 min − 25 min = 35 min). Com base nesses valores, eles podem resolver a questão proposta.
Atividade 2
Espera-se que os estudantes compreendam o valor monetário do sistema brasileiro em situações de compra.
Com 1 cédula de 5 reais e 3 moedas de 1 real, temos 8 reais; por isso, é possível comprar um estojo de 3 reais e um caderno de 5 reais (3 reais + 5 reais = 8 reais) de modo que não haja troco.
E com uma cédula de 10 reais é possível comprar um vaso com flores amarelas de 6 reais e um vaso com flores rosa de 4 reais, totalizando 10 reais, de modo que também não haja troco.
Atividade 3
Espera-se que os estudantes percebam que, das 7 horas até as 9 horas, há um intervalo de 2 horas. Como 1 hora equivale a 60 minutos, então 2 horas correspondem a 120 minutos. Ao descontar os 20 minutos gastos no percurso, sobram 100 minutos (120 − 20 = 100).
Verifique se os estudantes percebem que:
35 minutos + 50 minutos + 15 minutos = 100 minutos
BNCC em foco:
EF03MA05, EF03MA22, EF03MA24
MP119
Avaliação processual
- Escreva o horário que o relógio indica em cada caso.
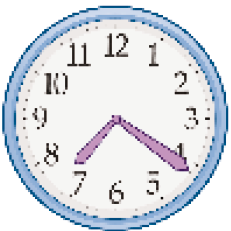
_____
PROFESSOR
Resposta: 7 horas e 21 minutos.
_____
PROFESSOR
Resposta: 9 horas e 44 minutos.
_____
PROFESSOR
Resposta: 2 horas e 7 minutos.- Complete a tabela com o
número
aproximado de horas que você gasta por dia em cada atividade.
Você pode incluir mais uma atividade à sua escolha.
Duração de algumas atividades
Tabela: equivalente textual a seguir.
|
Atividade |
Número aproximado de horas |
|---|---|
|
Dormir |
_____ |
|
Estudar |
_____ |
|
_____ |
_____ |
Fonte: Agenda do estudante.
PROFESSOR
Respostas pessoais.- Marcos tem 2 cédulas de 100 reais e 2 cédulas de 200 reais. Comprou um celular por 576 reais e só recebeu cédulas de troco. Que cédulas ele pode ter recebido?
_____
PROFESSOR
Exemplo de resposta: 2 cédulas de 2 reais e 1 cédula de 20 reais.
Autoavaliação

- Consigo fazer a leitura de horas em diferentes instrumentos e registros?
PROFESSOR
Resposta pessoal.
- Meus conhecimentos sobre o sistema monetário me permitem resolver situações de compra e venda de produtos ou serviços?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 4
Espera-se que os estudantes reconheçam e registrem o horário indicado em cada um dos relógios analógicos. Pode acontecer de alguns estudantes indicarem horários próximos, por exemplo: 7 horas e 20 minutos, 9 horas e 45 minutos e 2 horas e 8 minutos.
Se julgar necessário, retome algumas atividades trabalhadas ao longo da Unidade para relembrar como se leem as horas e os minutos em um relógio de ponteiros.
Atividade 5
Oriente os estudantes a preencher a tabela de acordo com as atividades listadas, que fazem parte do cotidiano deles, bem como as estimativas da quantidade de horas em cada uma delas.
Atividade 6
De acordo com os dados da atividade, Marcos tem 2 cédulas de 100 reais e 2 cédulas de 200 reais:
100 + 100 + 200 + 200 = = 600
O troco dele, em reais, é:
600 − 576 = 24
Respostas possíveis: 2 cédulas de 2 reais e 1 cédula de 20 reais; 2 cédulas de 10 reais e 2 cédulas de 2 reais; 4 cédulas de 5 reais e 2 cédulas de 2 reais; 12 cédulas de 2 reais; 7 cédulas de 2 reais e 2 cédulas de 5 reais; 7 cédulas de 2 reais e 1 cédula de 10 reais.
Autoavaliação
Na primeira questão, talvez seja necessário explicitar os instrumentos e registros, como a leitura das horas em relógio digital ou analógico e os registros em agendas ou anotações sobre organização do tempo. Espera-se que os estudantes analisem quanto já se apropriaram das medidas de tempo de modo que as reconheçam em diferentes registros e instrumentos.
Na segunda questão, os estudantes poderão avaliar seus conhecimentos sobre sistema monetário. Aprofunde a questão trazendo algumas ideias específicas, como o conceito de troco e a composição de valores com cédulas e moedas diferentes.
BNCC em foco:
EF03MA23, EF03MA24, EF03MA26
MP120
Comentários para o professor
Conclusão da Unidade 3
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Desenvolve estratégias (por decomposição, pelo algoritmo usual) de cálculo mental e escrito e usa de estimativas na adição com reagrupamento e na subtração com trocas? |
_____ |
_____ |
|
Faz corretamente, em relógio analógico e digital, a leitura e o registro de medida de tempo e de intervalos, ou seja, informa os horários de início e término de realização de uma atividade e sua duração? |
_____ |
_____ |
|
Faz a comparação de medidas de tempo com o reconhecimento de relações entre unidades de medida de tempo (hora e minuto; minuto e segundo)? |
_____ |
_____ |
|
Resolve problemas que envolvam o sistema monetário brasileiro? |
_____ |
_____ |
|
Lê, interpreta, compara dados e resolve problemas que envolvam dados organizados em tabelas de dupla entrada e em gráficos de barras ou de colunas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |












