MP144

Comentários para o professor:

Introdução da Unidade 5

Esta Unidade tem como foco tratar os conhecimentos a serem desenvolvidos na Unidade Temática Números, mais especificamente a operação multiplicação.

Assim como a abertura das outras Unidades, a desta traz a imagem lúdica de um jogo hipotético de trilha. Esse jogo apresenta várias informações com possibilidade de serem exploradas, segundo a orientação do professor, a fim de servir de ponte entre o que o estudante se ocupou nos estudos do 2 º ano e o que trabalhará nas páginas seguintes deste volume.

Algumas atividades retomam a construção e a utilização de fatos básicos da adição e da multiplicação para o cálculo mental e escrito, e outras diversificam e ampliam para a resolução e elaboração de problemas de multiplicação do tipo multiplicação por 2, 3, 4, 5 e 10, com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, o que demanda diferentes estratégias de cálculo e registros. Ressalta-se que as atividades desenvolvidas durante o 2 º ano já traziam problemas envolvendo multiplicação; no entanto, neste ano, acrescenta-se o número 10 como mais um fator a ser utilizado e inicia-se a ideia de proporcionalidade. Pretende-se que, ao longo do 4 º ano, os conhecimentos sejam ampliados, acrescentando-se de maneira mais sólida a proporcionalidade como mais um dos significados da multiplicação. Da mesma forma, em relação às estratégias de cálculo e registro para o próximo ano, serão incluídos o cálculo mental e, de maneira mais enfática, o uso de algoritmos tanto para a resolução dos problemas apresentados quanto para a resolução daqueles a serem elaborados pelos estudantes.

A Unidade Temática Álgebra é contemplada com atividades que trabalham a identificação e descrição de regularidades em sequências numéricas recursivas, resultantes da realização de adições ou subtrações sucessivas, por um mesmo número, visando descrever uma regra de formação da sequência e determinar elementos faltantes ou seguintes.

Algumas atividades também convidam os estudantes a desenvolverem as habilidades da Unidade Temática Probabilidade e estatística. Essas atividades trabalham a leitura, a interpretação e a representação de dados em tabelas de dupla entrada e gráficos de barras ou de colunas, envolvendo resultados de pesquisa, além de propor a coleta, a classificação e a organização de dados a serem representados por meio de tabelas e gráficos.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. De acordo com o conteúdo, as habilidades e os objetivos de aprendizagem que se pretende desenvolver nas seções, nos conteúdos apresentados e nas atividades, as possibilidades de dinâmicas em sala de aula variam e podem demandar uma organização individual, em duplas, em grupos ou coletivas. Além disso, elas requerem boas estratégias de gestão de tempo, de espaço, e um planejamento prévio detalhado. Também é preciso estabelecer uma série de combinados que devem ser respeitados por todos, para garantir que os objetivos sejam alcançados.

Competência específica favorecida

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

Sugestão de roteiro de aula

Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.

Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção Jogo desta Unidade.

Os jogos são recursos valiosos para o desenvolvimento simultâneo de habilidades matemáticas, motoras, sociais e éticas de estudantes em qualquer faixa etária. Sempre que a atividade demandar a fixação de prazo para ser realizada, o tempo sugerido desse prazo deve ser comunicado com antecedência.

MP145

Roteiro de aula – Jogo (pesquisa)

1 ª parte – Preparação – Tempo sugerido: 10 minutos

Solicite previamente aos estudantes a confecção dos 4 conjuntos de 10 cartas numeradas de 1 a 10 a serem usados no jogo para cada trio. Combine com os estudantes um padrão para as cartas para que elas não possam ser “adivinhadas” por alguma característica física, a não ser pelo número nela escrito. Assim, é importante que seja usado o mesmo tipo e cor de papel para as cartas, e que ele não seja fino, para melhor manuseio e não transparência. Combine, também, o tamanho que as cartas devem ter e o tamanho dos algarismos – eles devem ser visíveis.

Organize as carteiras de modo que os estudantes possam trabalhar em trios. Para a composição dos grupos, sugira escolhas livres, porém, fique atento e auxilie aqueles que estiverem com dificuldade em encontrar colegas para realizar a atividade. Após definidos os grupos, oriente-os a combinarem como farão o revezamento entre si para o papel de juiz.

Faça a leitura coletiva das regras do jogo e certifique-se de que elas foram compreendidas por todos. Avalie a necessidade de simular, junto com um dos grupos, um início de procedimento que sirva como exemplo e elimine possíveis dúvidas. Esta orientação é válida para os jogos em geral, portanto, pode ser adaptada para outras atividades semelhantes.

2 ª parte – Jogo – Tempo sugerido: 60 minutos

O tempo de cada rodada depende da dinâmica do grupo e, de certa forma, do acaso do jogo. É provável que o tempo seja diferente para as equipes. Por isso, convém estabelecer de antemão um teto que julgar adequado dentro da sua disponibilidade e programação. Porém, é importante que o tempo fixado seja suficiente para que cada elemento de todos os grupos experimente o papel de juiz.

Deixe-os jogar livremente, mas acompanhe as ações dos grupos para administrar impasses caso considere necessário.

3 ª parte – Questões sobre o jogo – Tempo sugerido: 20 minutos

A seguir, peça que retomem o livro e respondam individualmente às questões propostas que não tenham o ícone “oral” e, depois, que troquem os livros entre os elementos do grupo para socializarem as respostas.

Na sequência, dialogue com a turma sobre as questões 2, 4 e 5b, com o ícone “oral”. Explore e contraponha, se conflitantes, as respostas de um com as de outro, conforme elas forem surgindo. Este é um momento rico para a troca de entendimentos sobre a maneira de encarar os problemas propostos e a escolha de procedimentos e estratégias de cada um.

MP146

UNIDADE 5. Multiplicação

Ilustração. Galáxia em tons de roxo. No centro há crianças sorrindo sobre trilhas circulares. Em cada trilha há uma conta. Da esquerda para a direita: 2 x 30; 6 x 9; 24 x 2; 7 x 6; 9 x 4; 10 x 3; 8 x 3; 18 x 1; 4 x 3; 2 x 3. À direita, uma trilha com uma seta rosa em cima. Ao fundo, naves espaciais voando e sobre uma delas há uma placa com a pergunta: Qual é o resultado? Ao redor, Melissa, Caio e outras crianças estão observando e sorrindo.

MANUAL DO PROFESSOR

Objetivos da Unidade

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Reconhecer e efetuar multiplicações do tipo 2 vezes, 3 vezes, 4 vezes, 5 vezes,10 vezes.

Reconhecer que a ordem dos fatores não altera o produto.

Reconhecer que qualquer número multiplicado por um é o próprio número.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Identificar os termos de uma multiplicação.

Identificar regularidades em sequências ordenadas de números naturais e em multiplicações.

Resolver problemas que exploram a busca de dados em textos, imagens, tabelas e gráficos.

Ler, interpretar e comparar dados apresentados em tabelas de dupla entrada envolvendo resultados de pesquisa.

Realizar pesquisa, organizar os dados coletados em tabelas e representá-los em gráfico de barras.

A multiplicação associada aos significados da adição de parcelas iguais, da disposição retangular e da combinação de possibilidades sistematizadas é vista em situações-problema. A construção de listas de multiplicações possibilita observar regularidades e estabelecer relações entre os resultados de diferentes listas.

São dadas situações que envolvem a compreensão e o cálculo de multiplicações do tipo 2 vezes (dobro), 3 vezes (triplo), 4 vezes (quádruplo), 5 vezes (quíntuplo) e 10 vezes.

BNCC em foco:

EF03MA03, EF03MA07, EF03MA10, EF03MA26, EF03MA27, EF03MA28

MP147

Boxe complementar:

Para refletir...

Ícone: oral.

Este é um jogo de trilha. Quais poderiam ser as regras para os jogadores avançarem as casas?

PROFESSOR

Resposta pessoal.

Ícone: oral.

Você sabe resolver as multiplicações que estão na trilha?

PROFESSOR

Resposta pessoal.

Escolha uma multiplicação da trilha para encontrar o resultado.

_____

PROFESSOR

Resposta pessoal.

Ícone: oral.

Quais multiplicações você acha mais difíceis de resolver? E as mais fáceis?

PROFESSOR

Resposta pessoal.

Fim do complemento.

MANUAL DO PROFESSOR

Situações que envolvem, por exemplo, “2 vezes” e “vezes 2”, que apresentam o mesmo resultado, mas com significados distintos, possibilitam explorar as diferenças entre essas operações. Discuta com os estudantes o conceito: a ordem dos fatores não altera o produto 2 × 3 = 6 e 3 × 2 = 6, sem formalizar ou nomear a propriedade comutativa da multiplicação.

Para refletir…

Antes de iniciar a atividade, peça aos estudantes que observem a cena. Comente que as crianças que participam desse jogo de trilha acionam um controle que movimenta o dado eletrônico, que vai determinar quantas casas (de 1 a 6) a criança deve andar. Na casa em que ela parar, deve resolver a multiplicação proposta. Sugira que discutam entre si e elaborem as regras desse jogo de trilha. Para ajudá-los, faça perguntas como:

Qual é o objetivo do jogo? (Exemplos de respostas: Chegar ao final da trilha; ser o mais rápido a chegar ao final da trilha.)

Quem vence o jogo? (Exemplos de respostas: Vence quem acertar mais resultados das multiplicações; o que for mais rápido.)

Se errar a multiplicação, o que acontece? (Exemplos de respostas: Volta casa(s); passa a vez.)

Na segunda atividade, espera-se que os estudantes percebam que 18 × 1 é fácil, pois 1 é o elemento neutro da multiplicação, assim como 10 × 3, pois, ao multiplicar números naturais por 10, basta acrescentar um zero à direita ao fator diferente de 10. Explore o conceito: qualquer número multiplicado por 1 resulta nele mesmo, por exemplo: 18 × 1 = 1 × 18 = 18, sem formalizar ou nomear a propriedade do elemento neutro da multiplicação.

MP148

Situações de multiplicação

Observe a ilustração e responda às questões.

Ilustração. Quatro triciclos rosa com rodas pretas.

Acima, há quantos triciclos? _____

PROFESSOR
Resposta: 4 triciclos.

Quantas rodas há em cada triciclo? _____

PROFESSOR
Resposta: 3 rodas.

No total, há quantas rodas nesses triciclos? _____

PROFESSOR
Resposta: 12 rodas.

Represente a solução do problema com uma adição de quantidades iguais.
_____

PROFESSOR
Resposta: 3 + 3 + 3 + 3 = 12

Ângelo ganhou 5 pacotes de figurinhas. Em cada pacote, há 4 figurinhas. Quantas figurinhas Ângelo ganhou?
Ângelo ganhou _____ figurinhas.

PROFESSOR
Resposta: 20

Ilustração. Cinco pacotes e cada um tem quatro figurinhas dentro.

Represente a solução do problema por meio de uma adição de parcelas iguais. _____

PROFESSOR
Resposta: 4 + 4 + 4 + 4 + 4 = 20

Agora, represente-a por meio de uma multiplicação. _____

PROFESSOR
Resposta: 5 × 4 = 20

Escreva para cada figura uma multiplicação que represente o total de quadradinhos.
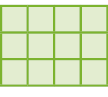
1. Multiplicação: _____
  
  PROFESSOR
  Resposta: 3 × 4 = 12 ou 4 × 3 = 12
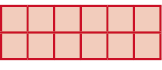
1. Multiplicação : _____
  
  PROFESSOR
  Resposta: 2 × 6 = 12 ou 6 × 2 = 12
1. O que se manteve constante nas multiplicações que você escreveu?
  
  PROFESSOR
  Atenção professor: Espera-se que os estudantes percebam que elas têm o mesmo resultado. Fim da observação.

MANUAL DO PROFESSOR

Objetivos

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Identificar os termos de uma multiplicação.

Resolver problemas que exploram a busca de dados em textos.

Identificar regularidades em sequências ordenadas de números naturais.

Atividades 1 e 2

Essas atividades exploram a multiplicação associada à adição de parcelas iguais. Com base nessa interpretação, definem-se papéis diferentes para o multiplicador (o número que indica quantas são as repetições) e para o multiplicando (o número que se repete), na tentativa de deixar claro que não é possível tomar um pelo outro. Crie oportunidades para explorar as estratégias de pensamento dos estudantes. É comum resolverem as situações iniciais de formação de um conceito por meio de desenhos.

Para ampliar a atividade 1, pergunte para os estudantes: “Por que esse brinquedo recebe o nome de triciclo?” (3 rodas – tri : três; ciclo : círculo ou roda). “E se fossem 4 bicicletas, quantas rodas seriam?” (8). Explore: bi = 2 e tri = 3.

Para ampliar atividade 2 , questione a turma: “E se Ângelo ganhasse 8 pacotes com 4 figurinhas?”(32); “E se, em cada pacote, houvesse 6 figurinhas, e ele ganhasse 5 pacotes?” (30). Ajude-os a perceber que, quando aumenta o número de pacotes de figurinhas, o número total de figurinhas também aumenta, e que isso também ocorre quando aumenta o número de figurinhas dentro de cada pacote.

BNCC em foco:

EF03MA03, EF03MA07

Atividade 3

Espera-se que os estudantes percebam que, em cada item, a quantidade total de quadradinhos é a mesma, independentemente da forma como foi calculada. A figura do item a, por exemplo, é formada por três linhas de quatro quadradinhos cada uma, ou, virando-se o livro em 90 graus, por quatro linhas de três quadradinhos cada uma. Em ambos os casos, o total de quadradinhos da figura é igual a 12.

MP149

Observe as representações das árvores abaixo.

Ilustração. Quatro colunas e duas fileiras de árvores.

Há quantas fileiras com 4 árvores? _____

PROFESSOR
Resposta: 2

Há quantas fileiras com 2 árvores? _____

PROFESSOR
Resposta: 4

Quantas árvores há no total? _____

PROFESSOR
Resposta: 8 árvores.

Escreva uma multiplicação com os números 2 e 4 cujo resultado seja o total de árvores. _____

PROFESSOR
Resposta: 4 × 2 = 8 ou 2 × 4 = 8

Compare a multiplicação que você escreveu com a de um colega. Vocês escreveram a mesma multiplicação?

PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que nessa situação é possível representar o total de árvores de duas maneiras: 4 × 2 = 8 ou 2 × 4 = 8. Fim da observação.

Invente um problema cuja resposta possa ser obtida pela adição “oito mais oito mais oito é igual a vinte e quatro” (8 + 8 + 8 = 24) ou a multiplicação “três vezes oito é igual a vinte e quatro” (3 × 8 = 24). Registre esse problema em seu caderno.

PROFESSOR
Resposta pessoal.

Observe a ilustração e complete o quadro.

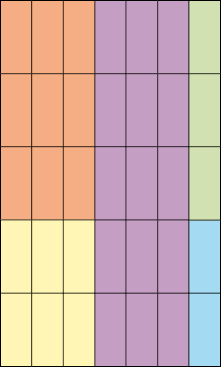
Ilustração. Figura composta por nove retângulos laranja, seis amarelos, quinze roxos, três verdes e dois azuis.

Tabela: equivalente textual a seguir.

Cor da figura	Número de retângulos pequenos que formam a figura	Multiplicação que representa o número de retângulos pequenos que formam a figura
Amarela	6	2 × 3 ou 3 × 2
Laranja	_____ PROFESSOR Resposta: 9	_____ PROFESSOR Resposta 3 × 3
Roxa	_____ PROFESSOR Resposta 15	_____ PROFESSOR Resposta 3 × 5 ou 5 × 3
Azul	_____ PROFESSOR Resposta 2	_____ PROFESSOR Resposta 2 × 1 ou 1 × 2
Verde	_____ PROFESSOR Resposta 3	_____ PROFESSOR Resposta 3 × 1 ou 1 × 3

MANUAL DO PROFESSOR

Atividade 4

Explore a ilustração para obter o total das árvores: 2 + 2 + 2 + 2 ou 4 × 2, que é igual a 8; 4 + 4 ou 2 × 4, que é igual a 8. Espera-se que os estudantes percebam que a quantidade total de árvores é a mesma, independentemente da maneira de calcular. A diferenciação entre os termos linha e coluna também é importante, embora se possa fazer a leitura da figura de qualquer posição. Sugira que os estudantes virem o livro 90 graus e observem a quantidade de linhas com duas árvores (4) e de colunas com quatro árvores (2).

Atividade 5

Verifique se o problema criado pelos estudantes possibilita o cálculo da multiplicação 3 × 8, e não de 8 × 3. Embora a propriedade comutativa da multiplicação garanta a igualdade dos resultados, os significados são diferentes (3 × 8 = 8 + 8 + 8 e 8 × 3 = 3 + 3 + 3 + 3 + 3 + + 3 + 3 + 3). Se julgar conveniente, sugira aos estudantes a representação por meio de desenhos e observe se eles fazem 3 grupos de 8, conforme a situação pede.

Atividade 6

A atividade possibilita a visualização da multiplicação na disposição retangular e sua articulação com o registro dos dados observados em um quadro. Para completar a segunda coluna, pode-se trabalhar com a contagem ou com o produto de linhas por colunas. Na terceira coluna, mostre que a ordem dos fatores não interfere no resultado da multiplicação (propriedade comutativa da multiplicação).

BNCC em foco:

EF03MA03, EF03MA07, EF03MA10

MP150

2 vezes ou o dobro

Mariana tem 3 bonecas em sua coleção. Gabi tem o dobro dessa quantidade de bonecas. Quantas bonecas Gabi tem?
Adição: 3 + 3 = _____

PROFESSOR
Resposta: 6

Multiplicação: 2 × 3 = _____

PROFESSOR
Resposta: 6

Gabi tem _____ bonecas.

PROFESSOR
Resposta: 6

Associe as quantidades iguais.

Linha 1

o dobro de 5

2 × 4

o dobro de 10

Linha 2

2 × 10

o dobro de 7

PROFESSOR

Resposta: o dobro de 5: 10

PROFESSOR

2 × 4: 8

PROFESSOR

14 - o dobro de 7

PROFESSOR

o dobro de 10: 2 × 10

Observe as canetas abaixo e, em seguida, faça o que se pede.

Ilustração. Seis canetas coloridas, lado a lado.

Se Cida tem o dobro dessa quantidade de canetas, quantas canetas ela tem? _____

PROFESSOR
Resposta: 12 canetas.

Escreva uma adição e uma multiplicação que representem a solução dessa situação.
Adição: _____

PROFESSOR
Resposta: 6 + 6 = 12

Multiplicação: _____

PROFESSOR
Resposta: 2 × 6 = 12

MANUAL DO PROFESSOR

Objetivos

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Reconhecer e efetuar multiplicações do tipo 2 vezes.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Resolver problemas que explorem a busca de dados em textos e imagens.

A multiplicação do tipo 2 vezes ou o dobro faz parte de práticas lúdicas, como a contagem de pontos em jogos. Habituá-los a situações que envolvam a compreensão e o cálculo de multiplicações fundamentais (dobro, triplo etc.) é um grande passo em direção à compreensão da noção de proporcionalidade.

Peça aos estudantes que deem exemplos do dobro de uma quantidade. Espera-se que relacionem a expressão o dobro com 2 vezes ou com adicionar duas quantidades iguais. Pergunte também se reconhecem algum tipo de regularidade nos resultados das multiplicações do tipo 2 vezes; talvez digam que os algarismos das unidades são sempre 2, 4, 6, 8 ou zero.

Atividades 1, 2 e 3

Essas atividades possibilitam a identificação de dobro em diferentes contextos: calcular o dobro de um número como duas vezes esse número; associar, com e sem apoio visual, as quantidades ao dobro.

BNCC em foco:

EF03MA03, EF03MA07

MP151

3 vezes ou o triplo

Leia e responda às questões.
1. Em um campeonato de futebol, o time de Fábio marcou 9 gols. O time de Cecília marcou o triplo de gols marcados pelo time de Fábio. Quantos gols marcou o time de Cecília? _____
  
  PROFESSOR
  Resposta: 27 gols.
1. Para ir ao trabalho, Marta caminha 4 quarteirões, e José percorre, de bicicleta, o triplo de quarteirões de Marta. Quantos quarteirões José percorre, de bicicleta, para chegar ao trabalho?
  _____
  
  PROFESSOR
  Resposta: 12 quarteirões.
1. Escreva uma adição e uma multiplicação que representem a solução de cada situação apresentada nos dois itens acima.
  _____
  
  PROFESSOR
  Resposta: a) Adição: 9 + 9 + 9 = 27; Multiplicação: 3 × 9 = 27
  
  _____
  
  PROFESSOR
  Resposta: b) Adição: 4 + 4 + 4 = 12; Multiplicação: 3 × 4 = 12

Ícone: mental.

Observe o gráfico e responda às questões.

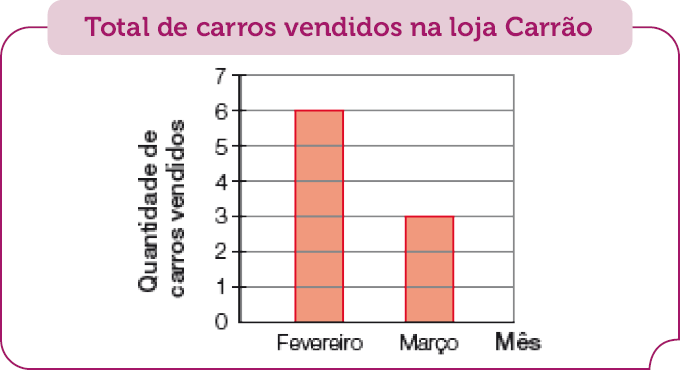
Gráfico de colunas. Total de carros vendidos na loja Carrão. No eixo vertical, a quantidade de carros vendidos e no eixo horizontal, o mês. Fevereiro: 6 carros; Março: 3 carros.

Fonte: Loja Carrão. (2023)

Qual foi o total de carros vendidos em fevereiro? _____

PROFESSOR
Resposta: 6 carros.

Se em abril a loja Carrão vendeu o triplo de carros que foram vendidos no mês de março, ela vendeu mais ou menos carros que em fevereiro? Quantos carros foram vendidos em abril? _____

PROFESSOR
Resposta: Mais; 9 carros.

MANUAL DO PROFESSOR

Objetivos

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Reconhecer e efetuar multiplicações do tipo 3 vezes.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Resolver problemas que explorem a busca de dados em textos e gráficos.

Atividade 1

No item a, discuta sobre as estratégias adotadas pelos estudantes e observe se conseguiram associar corretamente as expressões multiplicativas às correspondentes adições de parcelas iguais para representar cada situação. Depois da resolução, incentive a turma a formular novas questões com base nos dados da atividade. Por exemplo: “Quantos gols as duas equipes marcaram juntas nesse campeonato?”. (36)

Verifique, no item b, se a turma encontra com facilidade o triplo de quarteirões percorridos por José. Observe, no item c, se os estudantes conseguem associar corretamente as expressões multiplicativas com as correspondentes adições de parcelas iguais para representar a situação.

Atividade 2

A atividade possibilita reconhecer as quantidades na representação por meio de um gráfico de colunas. É possível trabalhar a leitura e a interpretação das informações do gráfico. Pergunte:

De que trata esse gráfico? (Da quantidade de carros vendidos na loja Carrão.)

Em que mês o número de carros vendidos na loja Carrão foi maior? (Fevereiro.)

Qual é a relação entre o número de carros vendidos em fevereiro e em março? (Espera-se que os estudantes percebam que em fevereiro foi vendido o dobro do número de carros vendidos em março.)

BNCC em foco:

EF03MA03, EF03MA07, EF03MA26

MP152

4 vezes ou o quádruplo

Andreia tem 8 anos. A idade da mãe dela é igual ao quádruplo (4 vezes) da idade de Andreia. Quantos anos tem a mãe de Andreia?
Adição: _____

PROFESSOR
Resposta: 8 + 8 + 8 + 8 = 32

Multiplicação: _____

PROFESSOR
Resposta: 4 × 8 = 32

A mãe de Andreia tem _____ anos.

PROFESSOR
Resposta: 32

Escreva o resultado de cada multiplicação que Sandra e Amanda fizeram na lousa. Depois, responda às questões.

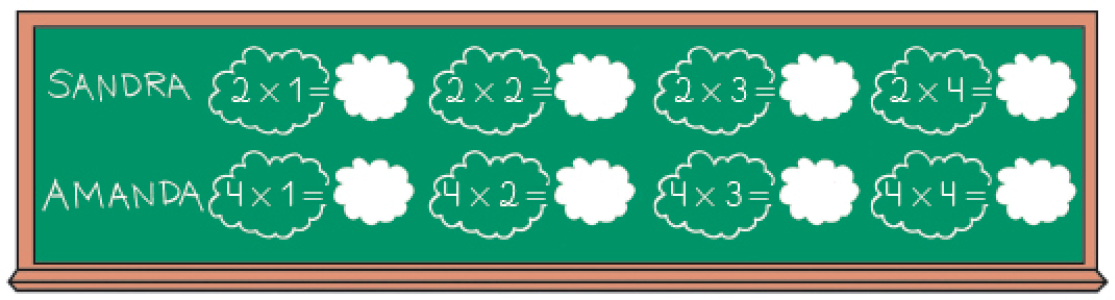
Ilustração. Lousa com as informações: Sandra: 2 x 1 = espaço para resposta, 2 x 2 = espaço para resposta, 2 x 3 = espaço para resposta, 2 x 4 = espaço para resposta, Amanda: 4 x 1 = espaço para resposta, 4 x 2 = espaço para resposta, 4 x 3 = espaço para resposta, 4 x 4 = espaço para resposta.

PROFESSOR

Resposta: 2, 4, 6, 8, 4, 8, 12, 16

Quais são os resultados em comum nas multiplicações de Sandra e Amanda? _____

PROFESSOR
Resposta: 4 e 8.

Quais são as multiplicações de Sandra e Amanda com esses resultados? _____

PROFESSOR
Resposta: Resultado 4: 2 × 2 = 4 (multiplicação de Sandra) e 4 × 1 = 4 (multiplicação de Amanda); Resultado 8: 2 × 4 = 8 (multiplicação de Sandra) e 4 × 2 = 8 (multiplicação de Amanda).

Observe os desenhos das caixas numeradas para descobrir a regra da sequência dos números delas. Depois, complete as caixas seguintes com números.

Ilustração. Dez caixas com números. Da esquerda para a direita: 4, 8, 12, 16, espaço para resposta, 24, espaço para resposta, espaço para resposta, espaço para resposta, 40.

PROFESSOR

Exemplo de resposta: 20, 28, 32, 36

MANUAL DO PROFESSOR

Objetivos

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Reconhecer e efetuar multiplicações do tipo 4 vezes.

Reconhecer que a ordem dos fatores não altera o produto.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Identificar regularidades em sequências ordenadas de números naturais.

Atividade 1

Os estudantes devem associar as expressões multiplicativas com as correspondentes adições de parcelas iguais.

Atividade 2

Sugira a produção de um quadro, conforme o que segue.

Quadro: equivalente textual a seguir.

2 vezes ou o dobro	4 vezes ou o quádruplo
2 × 1 = 2	4 × 1 = 4
2 × 2 = 4	4 × 2 = 8
2 × 3 = 6	4 × 3 = 12
2 × 4 = 8	4 × 4 = 16

Pergunte: “O que vocês observam nos resultados de cada linha?”. Diga que todo resultado de uma multiplicação de 4 vezes é o dobro de uma multiplicação de 2 vezes, pois 4 = 2 × 2.

Para ampliar a atividade 2, mostre que o fato de toda multiplicação de 4 vezes ser, também, resultado de uma multiplicação de 2 vezes não implica que a recíproca seja verdadeira. Mostre que algumas multiplicações de 2 vezes aparecem na de 4 vezes, outras não. Por exemplo: em 2 × 3 = 6, ressalte que 6 não é resultado de uma multiplicação do tipo 4 vezes com números naturais.

Além disso, explique que a memorização do quádruplo de alguns números é importante em usos sociais: 4 × 25 = 100 (o quádruplo de 25 unidades forma uma centena); 4 × 15 = 60 (o quádruplo de 15 minutos são 60 minutos ou 1 hora). A memorização deve ser obtida de forma gradual, e uma estratégia eficiente para isso são os jogos.

BNCC em foco:

EF03MA03, EF03MA07, EF03MA10

Atividade 3

Peça aos estudantes que escrevam os números que faltam nessa sequência.

MP153

5 vezes ou o quíntuplo

Resolva os problemas.
1. Por uma torneira aberta saem aproximadamente 3 litros de água por minuto. Quantos litros de água saem aproximadamente dessa torneira em 5 minutos? _____
  
  PROFESSOR
  Resposta: 15 litros.
1. O aniversário de Mara é daqui a 5 semanas. Quantos dias faltam para o aniversário dela? _____
  
  PROFESSOR
  Resposta: 35 dias.
1. Escreva uma adição e uma multiplicação que representem a solução de cada situação apresentada nos dois itens acima.
  _____
  
  PROFESSOR
  Resposta: a) Adição: 3 + 3 + 3 + 3 + 3 = 15; Multiplicação: 5 × 3 = 15.
  
  _____
  
  PROFESSOR
  Resposta: b) Adição: 7 + 7 + 7 + 7 + 7 = 35; Multiplicação: 5 × 7 = 35.

Ícone: mental.

Joana, Rita e Aline ganharam caixas para guardar suas pulseiras. Cada uma das meninas guardará 5 pulseiras em cada caixa. Joana tem 1 caixa. Rita tem 5 caixas. Aline tem o dobro da quantidade de caixas de Rita.

Quadro: equivalente textual a seguir.

Nome	Quantidade de caixas	Quantidade de pulseiras
Joana	_____ PROFESSOR Resposta: 1	_____ PROFESSOR Resposta: 5
Rita	_____ PROFESSOR Resposta: 5	_____ PROFESSOR Resposta: 25
Aline	_____ PROFESSOR Resposta: 10	_____ PROFESSOR Resposta: 50

Complete o quadro acima e descubra quem tem o quíntuplo (5 vezes) da quantidade de pulseiras de Joana.
_____

PROFESSOR
Resposta: Rita.

Ícone: mental.

Elza comprou 5 pacotes com 2 canetas em cada pacote para presentear seus sobrinhos. Sabendo que ela presenteou cada sobrinho com apenas uma caneta e não sobraram canetas, quantos sobrinhos Elza tem?
_____

PROFESSOR
Resposta: 10 sobrinhos.

MANUAL DO PROFESSOR

Objetivos

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Reconhecer e efetuar multiplicações do tipo 5 vezes.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

As regularidades nas multiplicações do tipo 5 vezes envolvem a repetição dos algarismos 5 e 0, na ordem das unidades, nos resultados. Esclareça que calcular 5 vezes um número é o mesmo que encontrar o quíntuplo desse número. Um modo de obter os resultados das multiplicações do tipo vezes 5 é associá-los aos números correspondentes aos minutos do mostrador de um relógio de ponteiros. Por exemplo, quando o ponteiro dos minutos aponta para 1, indica 5 minutos (1 × 5 = 5); quando aponta para 2, indica 10 minutos (2 × 5 = 10); e assim por diante.

Atividade 1

Observe a estratégia que os estudantes usaram para resolver a atividade e se a representação da multiplicação por adição de parcelas iguais ocorreu.

Atividade 2

Pergunte: “Se Aline ficasse com o triplo do número de caixas de Rita, quantas pulseiras Aline teria? Quantas pulseiras as três teriam no total?”. (75 pulseiras; 105 pulseiras.)

Atividade 3

Verifique e discuta a estratégia usada pelos estudantes. Se foi o cálculo do quíntuplo da quantidade de canetas (5 vezes 2) ou se usaram o apoio visual (desenhos). É um bom momento para dizer que existem diferentes estratégias para resolver um problema e que na Matemática isso é muito comum.

Os resultados das multiplicações do tipo 5 vezes também podem ser obtidos pelas multiplicações do tipo vezes 5 ou por meio de outras multiplicações. Por exemplo, para calcular 7 × 5 = 35, os estudantes podem fazer 2 × 5 = 10 e, usando a proporcionalidade, obter:

4 × 5 = 20

6 × 5 = 30

1 × 5 = 5

7 × 5 = 35

BNCC em foco:

EF03MA03, EF03MA07

MP154

10 vezes

Observe a ilustração e responda às questões.

Ilustração. Dez pratos sobre uma mesa. Em cada prato há seis brigadeiros.

Quantos brigadeiros há na mesa? _____

PROFESSOR
Resposta: 60 brigadeiros.

Escreva uma adição e uma multiplicação para representar a quantidade de brigadeiros dessa situação.
Adição: _____

PROFESSOR
Resposta: 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 + 6 = 60

Multiplicação: _____

PROFESSOR
Resposta: 10 × 6 = 60

Na aula de Arte, 10 crianças molharam uma das mãos na tinta e, em seguida, carimbaram uma vez em uma folha de cartolina.
1. Quantos dedos foram carimbados no total? _____
  
  PROFESSOR
  Resposta: 50 dedos.

Ilustração. Dez crianças com uniforme branco e vermelho estão ajoelhadas no chão e com as mãos sujas de tinta. Na frente de cada uma há um papel com a marca da mão. Ao redor há baldes de tinta.

Observação: Os objetos nesta página não estão apresentados em escala de tamanho. Fim da observação.

Ícone: mental.

Complete os quadros abaixo.

Ilustração. Uma bicicleta verde com duas rodas.

Quantas rodas?

Tabela: equivalente textual a seguir.

Quantidade de bicicletas	1	5	10
Quantidade de rodas	2	_____ PROFESSOR Resposta: 10	_____ PROFESSOR Resposta: 20

Ilustração. Um carrinho amarelo com quatro rodas.

Quantas rodas?

Tabela: equivalente textual a seguir.

Quantidade de carros	1	7	10
Quantidade de rodas	4	_____ PROFESSOR Resposta: 28	_____ PROFESSOR Resposta: 40

MANUAL DO PROFESSOR

Objetivos

Compreender a multiplicação associada ao significado de adição de parcelas iguais.

Reconhecer e efetuar multiplicações do tipo 10 vezes.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Identificar regularidades em sequências ordenadas de números naturais.

Resolver problemas que explorem a busca de dados em textos e imagens.

Os resultados das multiplicações do tipo 10 vezes podem ser associados: à contagem de dezenas inteiras; ao uso social das cédulas de 10 reais; à observação de regularidade, pois, ao número natural que está sendo multiplicado, sempre é acrescentado, à direita, o algarismo zero: 10 × 1 = 10, 10 × 2 = 20, ..., 10 × 9 = 90.

Atividade 1

Explore a leitura e a interpretação da ilustração: “Quantas bandejas há sobre a mesa? Em cada bandeja há quantos brigadeiros? Em todas as bandejas há a mesma quantidade de brigadeiros?”.

Atividade 2

Propicie a reflexão e a discussão da estratégia usada pelos estudantes para resolver a atividade. Se eles utilizaram a imagem para contar os dedos, se usaram a multiplicação associada à adição de parcelas iguais, se pensaram em 10 × 5 ou 5 × 10. Nesse caso, o raciocínio correto seria 10 × 5, e não o contrário.

Atividade 3

Na atividade, os estudantes podem usar o raciocínio proporcional para obter os resultados. No item a, por exemplo, se a quantidade de bicicletas é multiplicada por 5, a quantidade de rodas também será: 5 × 2 = 10.

Para determinar a quantidade de rodas de 10 bicicletas, eles podem fazer 10 × 2 = 20, ou perceber que 10 bicicletas são o dobro de 5 bicicletas, bastando dobrar a quantidade de rodas da coluna anterior: 2 × 10 = 20.

BNCC em foco:

EF03MA03, EF03MA07, EF03MA10

MP155

Calcule os resultados de cada lista de multiplicações.

5 × 0 = _____

PROFESSOR

Resposta: 0

5 × 1 = _____

PROFESSOR

Resposta: 5

5 × 2 = _____

PROFESSOR

Resposta: 10

5 × 3 = _____

PROFESSOR

Resposta: 15

5 × 4 = _____

PROFESSOR

Resposta: 20

5 × 5 = _____

PROFESSOR

Resposta: 25

5 × 6 = _____

PROFESSOR

Resposta: 30

5 × 7 = _____

PROFESSOR

Resposta: 35

5 × 8 = _____

PROFESSOR

Resposta: 40

5 × 9 = _____

PROFESSOR

Resposta: 45

5 × 1 = _____

PROFESSOR

Resposta: 50

10 × 0 = _____

PROFESSOR

Resposta: 0

10 × 1 = _____

PROFESSOR

Resposta: 10

10 × 2 = _____

PROFESSOR

Resposta: 20

10 × 3 = _____

PROFESSOR

Resposta: 30

10 × 4 = _____

PROFESSOR

Resposta: 40

10 × 5 = _____

PROFESSOR

Resposta: 50

10 × 6 = _____

PROFESSOR

Resposta: 60

10 × 70 = _____

PROFESSOR

Resposta: 70

10 × 80 = _____

PROFESSOR

Resposta: 80

10 × 90 = _____

PROFESSOR

Resposta: 90

10 × 10 = _____

PROFESSOR

Resposta: 100

Compare os resultados das multiplicações das duas listas. O que você observa?
_____

PROFESSOR
Exemplo de resposta: A lista de “10 vezes” tem os resultados dobrados em relação à lista de “5 vezes”.

Boxe complementar:

Desafio

Alessandra comprou uma mochila que custou 50 reais.

Alessandra pagou a mochila com cédulas de cinco reais. . Quantas cédulas dessa ela utilizou para pagar a mochila? _____

PROFESSOR

Resposta: 10 cédulas.

Se Alessandra pagasse a mochila com cédulas de dez reais , quantas cédulas ela utilizaria?

_____

PROFESSOR

Resposta: 5 cédulas.

CRÉDITO: FOTOS: BANCO CENTRAL DO BRASIL

Ilustração. Alessandra, mulher com vestido rosa está de costas e observando uma mochila na vitrine. Abaixo da mochila, placa com a informação: Mochila 50 reais.

CRÉDITO: MARCO CORTEZ

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 4

Os estudantes podem buscar as regularidades nas listas de multiplicação. Se julgar conveniente, sugira o uso de papel quadriculado (1 cm por 1 cm ou 0,5 cm por 0,5 cm) para representar cada multiplicação em uma disposição retangular.

Outra sugestão é o uso de material concreto para auxiliá-los a calcular os resultados das listas de multiplicação. Se necessário, retome a representação aditiva de uma multiplicação para justificar o fato de os resultados na lista de multiplicação 10 vezes serem o dobro de cada resultado correspondente na lista 5 vezes; por exemplo, para as multiplicações 5 × 4 e 10 × 4, temos:

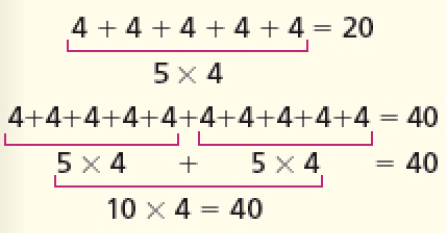
Esquema. 4 + 4 + 4 + 4 + 4 = 20 5 x 4 = 20. 4 + 4 + 4 + 4 + 4 = 5 x 4 4 + 4 + 4 + 4 + 4 = 5 x 4 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 40 5 x 4 + 5 x 4 = 40 10 x 4 = 40

Para ampliar a atividade 4, peça aos estudantes que comparem os resultados das multiplicações do tipo 10 vezes com os resultados das multiplicações do tipo 2 vezes e do tipo 5 vezes, e observem a relação entre elas: todo resultado de uma multiplicação do tipo 10 vezes pode ser obtido por uma multiplicação do tipo 2 vezes ou do tipo 5 vezes, pois 10 = 2 × 5. Por exemplo, 20 = 10 × 2, ou 20 = 2 × 10, ou 20 = 5 × 4.

Desafio

Os estudantes devem decompor o número 50 em parcelas iguais a 5 e em parcelas iguais a 10.

50 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 (dez cédulas de 5 reais);

50 = 10 + 10 + 10 + 10 + 10 (cinco cédulas de 10 reais).

BNCC em foco:

EF03MA03, EF03MA07, EF03MA10

MP156

2 vezes e vezes 2; 3 vezes e vezes 3...

Alice e Carlos ganharam bombons.
1. Veja como cada um agrupou os bombons para contá-los e escreva uma multiplicação para representar cada situação.

Alice fez assim:

Ilustração. Alice, menina com tranças e regata roxa, sorri e pensa: 5 mais 5 ou 2 vezes 5 são… Na frente dela há dez bombons sobre uma mesa. Os bombons estão divididos em dois grupos com cinco bombons cada.

Quantos bombons Alice ganhou? _____

PROFESSOR

Resposta: 10 bombons.

Multiplicação: _____

PROFESSOR

Resposta: 2 × 5 = 10

Carlos fez assim:

Ilustração. Carlos, menino ruivo com camiseta azul está com a mão direita sob o queixo. Ele pensa: 2 mais 2 mais 2 mais 2 mais 2 ou 5 vezes 2 são… Na frente dele há dez bombons sobre uma mesa. Os bombons estão divididos em cinco grupos com dois bombons cada.

Quantos bombons Carlos ganhou? _____

PROFESSOR

Resposta: 10 bombons.

Multiplicação: _____

PROFESSOR

Resposta: 5 × 2 = 10

Depois que cada um comeu 4 bombons, eles reorganizaram os que sobraram.

Bombons de Alice:

Ilustração. Três colunas e duas fileiras de bombons.

Sobraram quantos bombons para Alice? _____

PROFESSOR

Resposta: 6 bombons.

Multiplicação: _____

PROFESSOR

Resposta: 3 × 2 = 6

Bombons de Carlos:

Ilustração. Duas colunas e três fileiras de bombons.

Sobraram quantos bombons para Carlos? _____

PROFESSOR

Resposta: 6 bombons.

Multiplicação: _____

PROFESSOR

Resposta: 2 × 3 = 6

Quais das multiplicações anteriores têm o mesmo resultado?
_____

PROFESSOR
Resposta: 2 × 5 = 10 e 5 × 2 = 10; 3 × 2 = 6 e 2 × 3 = 6

MANUAL DO PROFESSOR

Objetivos

Reconhecer e efetuar multiplicações do tipo 2 vezes e 3 vezes.

Reconhecer que a ordem dos fatores não altera o produto.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Resolver problemas que explorem a busca de dados em textos e imagens.

O foco destas atividades é a exploração da propriedade comutativa da multiplicação. Os estudantes deverão perceber que, embora tenham o mesmo resultado, as multiplicações 2 × 5 e 5 × 2, por exemplo, têm significados diferentes. Nas atividades propostas, a análise é feita por meio da multiplicação em disposição retangular. Assim, a representação talvez seja a melhor maneira de explicar a equivalência sem induzir a erro, uma vez que, para uma mesma disposição retangular, é possível fazer número de linhas vezes número de colunas e vice-versa.

Atividade 1

A propriedade comutativa da multiplicação é apresentada por contagem e por comparação da quantidade de bombons dispostos em agrupamentos de 5 bombons (Alice) e de 2 bombons (Carlos). O objetivo é mostrar que os resultados de 2 × 5 e de 5 × 2 são iguais a 10. Depois de cada personagem comer os bombons, mostram-se os 6 bombons que restaram, organizados em duas disposições retangulares, o que favorece a verificação da igualdade: 3 × 2 = 2 × 3 = 6. Essa igualdade pode ser generalizada para quaisquer fatores, pois basta considerar como um dos fatores da multiplicação o número de linhas (fileiras horizontais) ou o número de colunas (fileiras verticais), como mostra a figura.

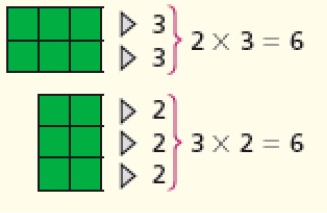
Ilustração. Retângulo composto por duas fileiras com três quadrados cada: 2 x 3 = 6. Abaixo, retângulo composto por três fileiras com dois quadrados cada: 3 x 2 = 6.

CRÉDITO: ADILSON SECCO

A propriedade comutativa da multiplicação facilita a memorização dos resultados das listas de multiplicações, pois o resultado da multiplicação do tipo 2 vezes (2 × 3 = 6) é o mesmo que o da multiplicação do tipo 3 vezes (3 × 2 = 6), de modo que basta memorizar o resultado de uma das multiplicações, o que reduz pela metade o número de resultados a lembrar. Para reforçar a assimilação da propriedade, sugira aos estudantes que façam outras multiplicações desse tipo, como: 4 × 5 e 5 × 4; 2 × 7 e 7 × 2; 1 × 5 e 5 × 1.

BNCC em foco:

EF03MA03, EF03MA07

MP157

Observe as ilustrações em disposição retangular e responda às questões.

Ilustração. Quatro colunas e duas fileiras de soldadinhos.

Quantos são os soldadinhos?
_____

PROFESSOR
Resposta: São 8 soldadinhos.

Represente a quantidade de soldadinhos por meio de duas multiplicações usando os números 2 e 4.
_____

PROFESSOR
Resposta: 4 × 2 = 8; 2 × 4 = 8

Ilustração. Cinco colunas e três fileiras de xícaras.

Quantas são as xícaras?
_____

PROFESSOR
Resposta: São 15 xícaras.

Represente a quantidade de xícaras por meio de duas multiplicações usando os números 3 e 5.
_____

PROFESSOR
Resposta: 3 × 5 = 15; 5 × 3 = 15

Observação: Os objetos nesta página não estão apresentados em escala de tamanho. Fim da observação.

Ícone: Desenho ou pintura.

Faça o que se pede.
1. Desenhe, numa disposição retangular, 12 bolinhas.

PROFESSOR

Resposta: Exemplos de desenho: Resposta: Ilustração. Doze bolinhas lado a lado. Abaixo, seis colunas e duas fileiras de bolinhas. Em seguida, quatro colunas e três fileiras de bolinhas.

Resposta: Ilustração. Doze bolinhas lado a lado. Abaixo, seis colunas e duas fileiras de bolinhas. Em seguida, quatro colunas e três fileiras de bolinhas.

Escreva multiplicações cujo resultado seja 12.
_____

PROFESSOR
Respostas possíveis: 12 × 1 = 12; 1 × 12 = 12; 3 × 4 = 12; 4 × 3 = 12; 2 × 6 = 12; 6 × 2 = 12

MANUAL DO PROFESSOR

Atividade 2

A atividade possibilita reforçar a propriedade comutativa da multiplicação explorando a representação dos seus elementos pela disposição retangular.

Atividade 3

Para a resolução da atividade, sugira aos estudantes que usem papel quadriculado. Para explorar a propriedade comutativa, peça que representem as multiplicações: 1 × 12, 12 × 1, 2 × 12, 12 × 2, 3 × 12, 12 × 3 etc.

Depois da resolução das atividades 2 e 3, apresente aos estudantes o quadro a seguir, que evidencia a comutatividade da multiplicação para diversos fatores. Vejamos, por exemplo, os números destacados no quadro, que correspondem aos resultados de 7 × 4 e 4 × 7 e de 6 × 9 e 9 × 6. Explique aos estudantes que, em decorrência da propriedade comutativa da multiplicação, esses resultados encontram-se dispostos simetricamente em relação à linha diagonal do quadro.

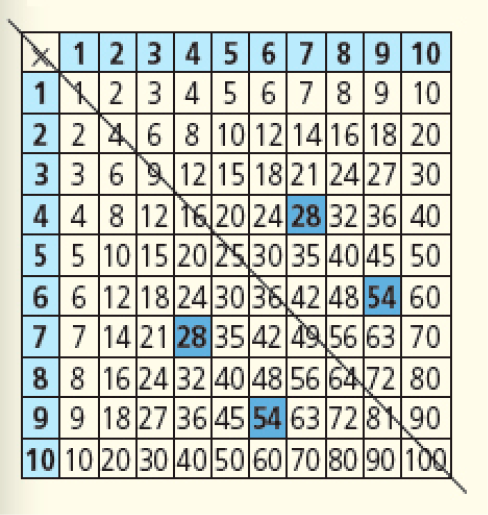
CRÉDITO: ADILSON SECCO

BNCC em foco:

EF03MA03, EF03MA07

MP158

Mais sobre multiplicação

Calcule o total de flores em cada ilustração e complete.
1. Quantas flores há nos vasos, no total?

Ilustração. Dois vasos com três flores rosas em cada um.

fator: 2 × fator: 3 = produto: _____

PROFESSOR

Resposta: 6

Há _____ flores no total.

PROFESSOR

Resposta: 6

Agora, quantas flores há no total?

Ilustração. Seis vasos com três flores rosas em cada um.

fator: _____ × fator: _____ = produto: _____

PROFESSOR

Resposta: 6 × 3 = 18

Há _____ flores no total.

PROFESSOR

Resposta: 18

Os números usados em uma multiplicação são chamados fatores. O resultado da multiplicação é chamado produto.

Ícone: mental.

Calcule o produto em cada ficha abaixo.

2 × 3 = _____

PROFESSOR

Resposta: 6

4 × 3 = _____

PROFESSOR

Resposta: 12

4 × 6 = _____

PROFESSOR

Resposta: 24

5 × 4 = _____

PROFESSOR

Resposta: 20

1 × 6 = _____

PROFESSOR

Resposta: 6

8 × 3 = _____

PROFESSOR

Resposta: 24

2 × 6 = _____

PROFESSOR

Resposta: 12

3 × 8 = _____

PROFESSOR

Resposta: 24

2 × 10 = _____

PROFESSOR

Resposta: 20

Ícone: oral.

O que você pode notar com o produto obtido nessas multiplicações?

PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que um mesmo produto pode ser obtido por meio da multiplicação de diferentes fatores. Fim da observação.

MANUAL DO PROFESSOR

Objetivos

Reconhecer e efetuar multiplicações do tipo 2 vezes, 3 vezes, 4 vezes, 5 vezes,10 vezes.

Reconhecer que a ordem dos fatores não altera o produto.

Reconhecer que qualquer número multiplicado por 1 é o próprio número.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Identificar os termos de uma multiplicação.

Identificar regularidades nas multiplicações dos números naturais.

Resolver problemas que exploram a busca de dados em textos.

Atividade 1

A atividade possibilita explorar os termos da multiplicação: fatores e produto. É importante os estudantes conhecerem a nomenclatura dos termos de uma operação, pois isso uniformiza e facilita a comunicação de conceitos matemáticos.

Atividade 2

Espera-se que os estudantes percebam que um mesmo produto pode ser obtido por meio da multiplicação de diferentes fatores. Por exemplo, 5 × 4 = 20 e 2 × 10 = 20.

BNCC em foco:

EF03MA03, EF03MA07

MP159

Ícone: mental.

Complete o quadro a seguir sabendo que:
- os números das casas pintadas de verde são os fatores das multiplicações;
  • o quadro deve ser completado com o produto de cada multiplicação.

Boxe complementar:

Dica

Atenção! Antes de completar o quadro de multiplicações, observe os exemplos.

Fim do complemento.

Tabela: equivalente textual a seguir.

×	2	3	4	5	6	7	8	9	10
2	4	_____ PROFESSOR Resposta: 6	_____ PROFESSOR Resposta: 8	_____ PROFESSOR Resposta: 10	_____ PROFESSOR Resposta: 12	_____ PROFESSOR Resposta: 14	_____ PROFESSOR Resposta: 16	18	20
3	_____ PROFESSOR Resposta: 6	9	_____ PROFESSOR Resposta: 12	_____ PROFESSOR Resposta: 15	_____ PROFESSOR Resposta: 18	_____ PROFESSOR Resposta: 21	_____ PROFESSOR Resposta: 24	_____ PROFESSOR Resposta: 27	_____ PROFESSOR Resposta: 30
4	_____ PROFESSOR Resposta: 8	_____ PROFESSOR Resposta: 12	_____ PROFESSOR Resposta: 16	_____ PROFESSOR Resposta: 20	_____ PROFESSOR Resposta: 24	_____ PROFESSOR Resposta: 28	_____ PROFESSOR Resposta: 32	_____ PROFESSOR Resposta: 36	_____ PROFESSOR Resposta: 40
5	10	_____ PROFESSOR Resposta: 15	_____ PROFESSOR Resposta: 20	_____ PROFESSOR Resposta: 25	_____ PROFESSOR Resposta: 30	_____ PROFESSOR Resposta: 35	_____ PROFESSOR Resposta: 40	_____ PROFESSOR Resposta: 45	_____ PROFESSOR Resposta: 50
6	_____ PROFESSOR Resposta: 12	_____ PROFESSOR Resposta: 18	_____ Resposta: 24	_____ PROFESSOR Resposta: 30	36	_____ PROFESSOR Resposta: 42	_____ PROFESSOR Resposta: 48	_____ PROFESSOR Resposta: 54	_____ PROFESSOR Resposta: 60
7	_____ PROFESSOR Resposta: 14	_____ PROFESSOR Resposta: 21	_____ PROFESSOR Resposta: 28	_____ PROFESSOR Resposta: 35	_____ PROFESSOR Resposta: 42	_____ PROFESSOR Resposta: 49	_____ PROFESSOR Resposta: 56	_____ PROFESSOR Resposta: 63	_____ PROFESSOR Resposta: 70
8	_____ PROFESSOR Resposta: 16	_____ PROFESSOR Resposta: 24	_____ PROFESSOR Resposta: 32	_____ PROFESSOR Resposta: 40	_____ PROFESSOR Resposta: 48	_____ PROFESSOR Resposta: 56	_____ PROFESSOR Resposta: 64	_____ PROFESSOR Resposta: 72	_____ PROFESSOR Resposta: 80
9	_____ PROFESSOR Resposta: 18	_____ PROFESSOR Resposta: 27	_____ PROFESSOR Resposta: 36	_____ PROFESSOR Resposta: 45	_____ PROFESSOR Resposta: 54	_____ PROFESSOR Resposta: 63	_____ PROFESSOR Resposta: 72	_____ PROFESSOR Resposta: 81	_____ PROFESSOR Resposta: 90
10	_____ PROFESSOR Resposta: 20	_____ PROFESSOR Resposta: 30	_____ PROFESSOR Resposta: 40	_____ PROFESSOR Resposta: 50	_____ PROFESSOR Resposta: 60	_____ PROFESSOR Resposta: 70	_____ PROFESSOR Resposta: 80	_____ PROFESSOR Resposta: 90	_____ PROFESSOR Resposta: 100

Ilustração. Um gato cinza está deitado sobre um muro e dormindo. Abaixo, um gato marrom está sorrindo.

Ícone: oral.

Responda à questão.
Sabendo que 8 × 5 é igual a 40, como você pode calcular 9 × 5?

PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que basta adicionar 40 a 5. Ou seja, 9 × 5 = 8 × 5 + 1 × 5 = 40 + 5 = 45. Fim da observação.

Ícone: mental.

Calcule o resultado de cada multiplicação.

0 × 5 = _____

PROFESSOR
Resposta: 0

0 × 31 = _____

PROFESSOR
Resposta: 0

8 × 0 = _____

PROFESSOR
Resposta: 0

0 × 9 = _____

PROFESSOR
Resposta: 0

4 × 0 = _____

PROFESSOR
Resposta: 0

) 4 × 1 = _____

PROFESSOR
Resposta: 4

5 × 1 = _____

PROFESSOR
Resposta: 5

7 × 1 = _____

PROFESSOR
Resposta: 7

) 1 × 8 = _____

PROFESSOR
Resposta: 8

Ícone: oral.

Ícone: dupla.

Você observou alguma regularidade nessas multiplicações? Explique a um colega o que você percebeu e ouça a explicação dele.

PROFESSOR

Atenção professor: Espera-se que os estudantes percebam que há regularidades nessas multiplicações. Nas multiplicações com dois fatores em que um deles é nulo, o produto é zero. No caso de um dos fatores ser o número 1, o produto é o outro fator. Fim da observação.

MANUAL DO PROFESSOR

Atividade 3

Sugira aos estudantes que reproduzam o quadro de multiplicações em uma cartolina e a recortem, de modo que possam consultá-lo para resolver as atividades que envolvam multiplicação. A constante consulta a essa tabela facilita a observação de regularidades e a memorização dos produtos mais utilizados.

Atividade 4

Observe as estratégias de pensamento dos estudantes. A atividade possibilita explorar a regularidade das multiplicações por 5 (se 8 × 5 é igual a 40; então, para encontrar 9 × 5, basta acrescentar 5) ou a leitura e a interpretação do quadro de multiplicações (olhar linha por coluna e coluna por linha, para que os estudantes percebam que a ordem dos fatores não interfere no produto).

Atividade 5

Incentive os estudantes a perceberem que, quando um dos fatores é zero, o produto será zero, e que, se um dos fatores é 1, o resultado será igual ao outro fator.

Inicie com:

5 × 0 = 0 + 0 + 0 + 0 + 0 = 0.

Para 0 × 5 ser igual a 5 × 0, ou seja, para continuar valendo a propriedade comutativa da multiplicação, devemos ter 0 × 5 = 0.

BNCC em foco:

EF03MA03, EF03MA07

MP160

Jogo: Pesquisa

Material: 4 conjuntos de 10 cartas numeradas de 1 a 10. As cartas podem ser confeccionadas pelos jogadores ou podem ser usadas as cartas numeradas de 2 a 10 e o ás de um baralho comum. Nesse caso, o ás substitui a carta de número 1.

Ícone: grupo.

Jogadores: 3

Regras:

Um jogador é escolhido para embaralhar as cartas e ser o juiz. Os outros dois jogadores sentam-se um de frente para o outro.
Depois de embaralhadas pelo juiz, as cartas são distribuídas igualmente entre os dois jogadores, que devem colocá-las à sua frente em montes virados para baixo.
O juiz diz: “Um, dois e já!”. Então, ao mesmo tempo, cada jogador pega a carta de cima de seu monte e a levanta sem olhá-la, de modo que apenas o juiz e o outro colega a vejam, colocando-a na altura da testa, por exemplo.
Depois, o juiz anuncia o resultado da multiplicação dos números das duas cartas.
Cada jogador deve descobrir o número da própria carta, que ele não pode ver.
Aquele que acertar primeiro o número da carta pega as duas cartas para si, formando um novo monte ao seu lado.
O jogo termina quando todas as cartas distribuídas tiverem acabado.
O vencedor será o jogador que tiver o maior número de cartas no fim do jogo.

Questões sobre o jogo

Qual é o maior produto que pode ser anunciado pelo juiz?
E o menor? _____

PROFESSOR
Resposta: 100; 1

MANUAL DO PROFESSOR

Objetivos

Reconhecer e efetuar multiplicações do tipo 2 vezes, 3 vezes, 4 vezes, 5 vezes, 10 vezes.

Reconhecer que a ordem dos fatores não altera o produto.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

O jogo envolve a descoberta de um “número escondido”. Na situação lúdica proposta, os estudantes podem experimentar a realização das multiplicações tratadas na unidade. Dependendo da estratégia que decidirem adotar para chegar ao resultado, poderão realizar tentativas de multiplicação de números naturais até obter o resultado.

O jogo pode ser usado como ferramenta de memorização dos resultados das listas de multiplicações: ele possibilita que, em um contexto lúdico e motivador, os estudantes recorram à memória ou reconstruam os resultados desses cálculos. Permita que joguem diversas vezes e que voltem a jogá-lo ao longo do ano letivo. Primeiro, realize uma partida simulada com um dos estudantes, para assegurar que compreenderam as regras e a dinâmica do jogo. Nesse momento, a velocidade na realização dos cálculos não é o mais importante. Por isso, pode-se sugerir aos estudantes que recorram a lápis e papel e, gradativamente, passem a usar apenas o cálculo mental.

Variações

A pressa com que os estudantes talvez queiram obter a resposta pode levá-los a enunciar muitos palpites para o número procurado sem a devida reflexão. Caso isso ocorra, sugira a criação de uma regra adicional, como limitar o número de tentativas de resposta para apenas duas ou três.

BNCC em foco:

EF03MA03, EF03MA07

Sugestão de atividade

Promova variações no jogo, como permitir que, em uma partida, sejam usados apenas números relacionados com as multiplicações do tipo vezes 2 e vezes 3 e, gradativamente, sejam incorporados outros números, a seu critério.

Outra variação é incluir a operação de adição: para descobrir o número de sua carta, os estudantes podem pensar no número que, adicionado ao do colega, resulta no número cantado pelo juiz.

MP161

Ícone: oral.

Qual estratégia ou cálculo você usou durante o jogo para descobrir o número de sua carta?

PROFESSOR

Resposta: Um exemplo de estratégia é tentar diversas multiplicações até acertar o número.

Qual é o número da carta cuja frente não se vê, em cada caso?

( )

Ilustração. Uma menina loira está segurando uma carta com o número 8 na testa. Na frente dela, uma menina ruiva está segurando uma carta sobre a testa. Entre elas, um menino com óculos sorri com o dedo indicador levantado e fala: Quarenta!

PROFESSOR

Resposta: 5

( )

Ilustração. A menina loira segura uma carta com o número 9 na testa. Na frente dela, a menina ruiva segura outra carta na testa. Entre elas, o menino diz: Trinta e seis!

PROFESSOR

Resposta: 4

Ícone: oral.

Se o outro jogador mostrar a carta com o número 4 e o juiz anunciar o produto 27, você consegue descobrir qual é sua carta? Por quê?

PROFESSOR

Resposta: Não. Exemplo de explicação: Porque não existe nenhum número nas cartas que, quando multiplicado por 4, tem como resultado 27. Certamente, o juiz se enganou.

Observe o que aconteceu em duas rodadas de um jogo.

Primeira rodada

Ilustração. Um menino ruivo está de costas e segurando uma carta na testa. Na frente dele, um menino com boné está segurando uma carta com o número 7 na testa. Entre eles, uma menina loira está sorrindo com o dedo indicador levantado. Ela fala: Vinte e um!

Segunda rodada

Ilustração. O menino ruivo está de costas e segurando a carta sobre a testa. Na frente dele, o menino com boné está segurando uma carta com o número 3 na testa. Entre eles, a menina loira fala: Vinte e um!

Qual é o número da carta escondida na primeira rodada? _____

PROFESSOR
Resposta: 3

É possível descobrir o número da carta escondida na segunda rodada sem fazer nenhum cálculo? Por quê?

PROFESSOR

Resposta: Sim. Exemplo de explicação: Porque 21 é o resultado de 7 × 3 e também de 3 × 7. O jogador pode memorizar o resultado anterior.

MANUAL DO PROFESSOR

Questões sobre o jogo

Na questão 1, espera-se que os estudantes percebam que, como o maior número é 10, o produto máximo é 100 (10 × 10) e o menor produto é 1 (1 × 1).

Nas questões 2 e 3, pode-se explorar o quadro de multiplicações para que os estudantes encontrem o outro fator ou recorrer à memorização dos resultados das listas de multiplicações.

Para chegar ao resultado 40, por exemplo, poderão realizar tentativas de multiplicação de números naturais por 8 até obter o resultado 40:

3 × 8 = 24 (3 é pouco);

4 × 8 = 32 (4 é pouco);

5 × 8 = 40 (5 é a resposta).

Na questão 4, a proposta é descobrir que o produto 27, com um dos fatores igual a 4, é uma situação impossível no jogo, uma vez que o número 27 não está na lista de resultados de multiplicações do tipo 4 vezes. É fundamental que, em situações escolares, sejam propostos problemas impossíveis, para que os estudantes tenham a oportunidade de trabalhar com esse tipo de análise, muito útil em situações cotidianas.

Na questão 5, explora-se a propriedade comutativa da multiplicação, possibilitando ao estudante observar que o resultado de 7 × 3 é o mesmo que o de 3 × 7. As estratégias de cálculo mental favorecem momentos ricos de exploração das propriedades numéricas (comutatividade, associatividade, elemento neutro, distributividade). No item b, peça aos estudantes que deem outros exemplos de jogadas em que isso pode ocorrer. Incentive-os a perceber que esses resultados sugerem que, em qualquer multiplicação, pode-se trocar a ordem dos fatores e o produto será o mesmo.

BNCC em foco:

EF03MA03, EF03MA07

MP162

Compreender problemas

Para resolver

Fique atento a todas as informações do texto e das tabelas a seguir.

Problema

Os pais de alguns estudantes compraram o material escolar de seus filhos na mesma papelaria. As tabelas abaixo mostram: o preço de cada material na papelaria escolhida e o que foi comprado pelos pais de cada um desses estudantes.

Custo do material

Tabela: equivalente textual a seguir.

Material	Preço (em real)
Caderno	8
Lápis	2
Caneta	3

Fonte: Preços da papelaria. (jan. 2023)

Quantidade de materiais comprados

Tabela: equivalente textual a seguir.

Material Estudante	Cadernos	Lápis	Canetas
Ângela	4	2	3
Luís	5	3	2
Sabrina	3	3	4

Material

Estudante

Cadernos

Lápis

Canetas

Ângela

Luís

Sabrina

Fonte: Compra dos pais. (jan. 2023)

Os pais de qual dos três estudantes citados acima tiveram o maior gasto com o material escolar? E os pais de qual estudante gastaram menos?
_____

Os pais de Luís tiveram o maior gasto (52 reais) e os pais de Sabrina tiveram o menor gasto (42 reais).

Converse com seus colegas e seu professor sobre como você pensou no item anterior.

PROFESSOR
Resposta pessoal.

Para refletir

Veja como os pais de Luís calcularam o total gasto com o material escolar.

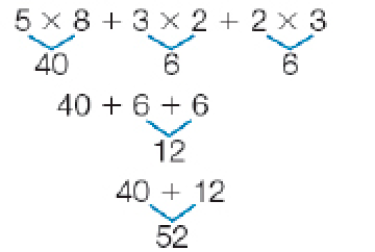
Esquema. 5 x 8 + 3 x 2 + 2 x 3 5 x 8 = 40 3 x 2 = 6 2 x 3 = 6 40 + 6 + 6 6 + 6 = 12 40 + 12 = 52

PROFESSOR

Exemplo de resposta: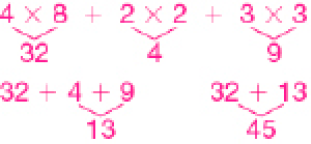 Esquema. 4 x 8 + 2 x 2 + 3 x 3 4 x 8 = 21 2 x 2 = 4 3 x 3 = 9 32 + 4 + 9 4 + 9 = 13 32 + 13 = 45

Essa resolução está correta?
_____

PROFESSOR
Resposta: Sim.

Faça como os pais de Luís para obter o gasto dos pais de Ângela.

MANUAL DO PROFESSOR

Objetivos

Reconhecer e efetuar multiplicações do tipo 2 vezes, 3 vezes, 4 vezes, 5 vezes, 10 vezes.

Construir e utilizar fatos básicos da multiplicação para o cálculo mental e escrito.

Resolver problemas que exploram a busca de dados em textos e tabelas.

Para resolver

Nessa seção, os estudantes terão de obter os dados do problema nos textos e nas tabelas que os complementam. Situações como as apresentadas aqui são comuns no dia a dia e evidenciam a relação entre a Matemática e o cotidiano, trazendo significado às atividades. Peça a alguns estudantes que comentem como realizaram os cálculos e que registrem na lousa essas operações.

Para refletir

Antes de começar a atividade, reproduza o esquema na lousa e discuta com os estudantes cada passo efetuado pelos pais de Luís. As questões dessa seção possibilitam pensar em outras soluções para os problemas apresentados em Para resolver, ou mesmo refletir sobre as próprias estratégias. Após a resolução das atividades, proponha novas questões, como: Faça como os pais de Luís para obter quanto os pais de Sabrina gastaram.

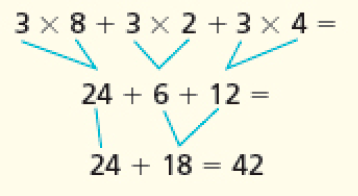
Esquema. 3 x 8 + 3 x 2 + 3 x 4 3 x 8 = 24 3 x 2 = 6 3 x 4 = 12 24 + 6 + 12 24 + 18 = 42

BNCC em foco:

EF03MA07, EF03MA26

Sugestão de leitura para o professor

Livro

SMOLE, Kátia Stocco; DINIZ, Maria Ignez. Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática. São Paulo: Artmed, 2001.

Destinado a professores das séries iniciais do Ensino Fundamental, o livro aborda o conceito de problema e a ampliação das habilidades tradicionais de resolver os cálculos e fornecer uma resposta em problemas matemáticos, bem como oferece ampla bibliografia e suporte teórico e prático para o uso da metodologia de resolução de problemas em sala de aula.

As autoras propõem uma metodologia de trabalho com a leitura de textos, a produção de significados no processo de resolução e a criação de problemas pelos estudantes.

MP163

A Matemática me ajuda a ser

... um praticante de esportes

Os esportes são jogos ou outras atividades que envolvem algum tipo de exercício físico, técnicas, táticas, estratégias e algumas regras. Por meio dos esportes aprendemos a lidar com os sentimentos de perda, frustração, ansiedade, além de exercitarmos a tolerância e o respeito ao próximo.

Conheça um dos vários esportes que você pode praticar.

Basquete

É um esporte coletivo, em que participam dez jogadores, cinco em cada time. Os objetivos do jogo são: fazer pontos, arremessando a bola na cesta da equipe adversária, e impedir que o adversário pontue. A pontuação varia. As cestas feitas de fora da área restritiva valem 3 pontos, as cestas feitas de dentro da área restritiva valem 2 pontos, e os lances livres valem apenas 1 ponto.

LEGENDA: Arremesso da bola à cesta. FIM DA LEGENDA.

Tome nota

O que podemos aprender com a prática de esportes?
_____

PROFESSOR
Resposta: Podemos aprender a lidar com os sentimentos de perda, frustração, ansiedade, além de exercitarmos a tolerância e o respeito ao próximo.

Em uma partida de basquete, o time de Júlio marcou 11 cestas de 3 pontos, 18 cestas de 2 pontos e 5 cestas de 1 ponto. Qual foi o total de pontos marcados pelo time de Júlio? _____

PROFESSOR
Resposta: 74 pontos.

Reflita

Ícone: oral.

Você pratica alguma modalidade esportiva? Qual esporte você gostaria de praticar? Por quê?

PROFESSOR

Respostas pessoais.

MANUAL DO PROFESSOR

Leia o texto com os estudantes, deixando-os comentar suas experiências com os esportes, os atletas que conhecem, seus ídolos em cada esporte, as preferências com relação a atividades físicas etc.

Tome nota

Aproveite as atividades 1 e 2 para a realização de interessantes trabalhos interdisciplinares com a disciplina Educação Física. Os estudantes podem pesquisar dados relativos a algumas das modalidades esportivas, seus recordes atuais, o número de medalhas de cada tipo conquistadas por alguns países nos Jogos Olímpicos, nos campeonatos mundiais e em outras competições. Com base nesses dados, podem construir gráficos de barras, além de formular perguntas para os colegas responderem.

Para ampliar o Tome nota, comente que a prática de atividades físicas é reconhecida como um dos mais importantes fatores para a saúde e o bem-estar físico e mental das pessoas. Em um modelo de sociedade urbano, com poucas áreas livres, e com a popularização dos jogos eletrônicos e da convivência social cada vez mais virtual, o incentivo à prática de esportes tem se tornado bastante importante. O contato com as diversas modalidades esportivas, o desenvolvimento da coordenação motora e outros aspectos agem como motivadores e despertam a curiosidade e o interesse. Nas situações-problema, os estudantes podem reconhecer as características do jogo, bem como elaborar possibilidades de pontuação e placar de jogo.

BNCC em foco:

EF03MA07

Reflita

Aproveite o contexto da atividade e comente que nos Jogos Paralímpicos participam atletas com algum tipo de deficiência física ou mental. Cada esporte tem um sistema próprio de classificação funcional do atleta. Se ele participa de mais de um esporte, recebe uma classificação para cada atividade. Os Jogos Paralímpicos têm sido realizados no mesmo ano que os Jogos Olímpicos e, desde 1988, em Seul, eles também têm sido sediados na mesma cidade. Nos Jogos Paralímpicos de 2016, realizados no Rio de Janeiro, o Brasil quebrou recordes históricos. Com o maior número de pódios do país em todas as edições, conquistou 14 medalhas de ouro, 29 de prata e 29 de bronze. O destaque foi Daniel Dias, que conquistou medalhas nas nove provas em que disputou, sendo 4 de ouro, 3 de prata e 2 de bronze.

MP164

Compreender informações

Como organizar dados de pesquisa

A nutricionista Carla fez uma pesquisa com algumas crianças a fim de descobrir se elas têm uma alimentação saudável, que envolve comer alimentos naturais como frutas, verduras e legumes.

Carla selecionou 9 crianças e verificou no período de uma semana quantas refeições saudáveis elas fizeram, considerando o almoço e o jantar. Os dados foram organizados na tabela a seguir.

Quantidade de refeições saudáveis

Tabela: equivalente textual a seguir.

Criança Refeição	Aline	Bianca	Diego	Flávio	Mário	Noeli	Paulo	Raísa	Túlio
Almoço	5	4	6	5	7	7	4	5	7
Jantar	7	4	4	6	3	7	6	5	5

Criança

Refeição

Aline

Bianca

Diego

Flávio

Mário

Noeli

Paulo

Raísa

Túlio

Almoço

Jantar

Fonte: Pesquisa da nutricionista Carla. (jun. 2023)

Qual criança fez mais refeições saudáveis nessa semana da pesquisa? Quantas foram as refeições? _____

PROFESSOR
Resposta: Noeli; 14 refeições.

Qual das crianças teve a menor quantidade de refeições saudáveis nesse período? Quantas foram? _____

PROFESSOR
Resposta: Bianca; 8 refeições.

De acordo com a tabela, complete o gráfico de barras duplas pintando as barras com as quantidades de refeições saudáveis no almoço e no jantar de cada criança.

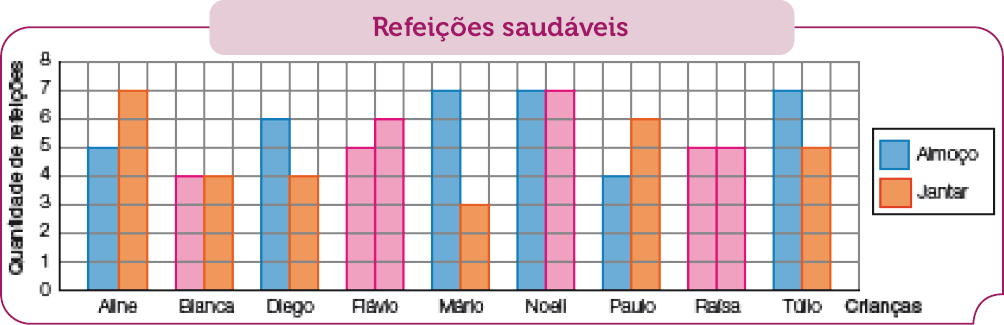
Gráfico de colunas. Refeições saudáveis. No eixo vertical, a quantidade de refeições e no eixo horizontal, as crianças. Aline: Almoço: 5. Jantar: 7. Bianca: Almoço: espaço para resposta. Resposta: 4. Jantar: 4. Diego: Almoço: 6. Jantar: 4. Flávio: Almoço: espaço para resposta. Resposta: 5. Jantar: espaço para resposta. Resposta: 6. Mário: Almoço: 7. Jantar: 3. Noeli: Almoço: 7. Jantar: espaço para resposta. Resposta: 7. Paulo: Almoço: 4. Jantar: 6. Raísa: Almoço: espaço para resposta. Resposta: 5. Jantar: espaço para resposta. Resposta: 5. Túlio: Almoço: 7. Jantar: 5.

Fonte: Pesquisa da nutricionista Carla. (jun. 2023)

Ícone: oral.

Você costuma fazer refeições saudáveis? Qual é a importância desse tipo de refeição?

PROFESSOR
Respostas pessoais.

MANUAL DO PROFESSOR

Objetivos

Resolver problemas cujos dados estão apresentados em tabela de dupla entrada e gráfico de barras.

Ler, interpretar e comparar dados apresentados em tabelas de dupla entrada envolvendo resultados de pesquisa.

Realizar pesquisa, organizar os dados coletados em tabelas e representá-los em gráfico de barras.

Atividade 1

Algumas perguntas podem ser feitas para ajudar os estudantes na leitura da tabela:

Quantas crianças participaram da pesquisa?

Quais são os nomes das crianças?

Quais refeições foram consideradas na pesquisa?

Quanto tempo durou a pesquisa?

No item c, peça aos estudantes que contem os quadrinhos de cada barra e comparem com o valor apresentado na tabela.

BNCC em foco:

EF03MA26, EF03MA27; competência específica 4

MP165

Durante todo o ano há produção de frutas no Brasil, mas a colheita delas é feita em determinados meses. Veja o quadro abaixo com os meses de colheita de algumas frutas.

Quadro: equivalente textual a seguir.

	Abacate	Ameixa	Caqui	Nectarina	Pera	Tangerina
Janeiro	X	X	_____	_____	X	_____
Fevereiro	X	X	X	_____	X	_____
Março	X	_____	X	_____	X	X
Abril	X	_____	X	_____	X	X
Maio	X	_____	X	_____	_____	X
Junho	X	_____	_____	_____	_____	X
Julho	X	_____	_____	_____	_____	X
Agosto	X	_____	_____	_____	_____	_____
Setembro	X	X	_____	X	_____	_____
Outubro	X	X	_____	X	_____	_____
Novembro	X	X	_____	X	_____	_____
Dezembro	X	X	_____	X	X	_____

Com os dados fornecidos no quadro, complete a tabela abaixo com a variedade de frutas que podem ser colhidas, ou seja, a quantidade de cada tipo de fruta colhida em cada mês.

Variedade de fruta colhida em cada mês

Quadro: equivalente textual a seguir.

Mês	Jan.	Fev.	Mar.	Abr.	Maio	Jun.	Jul.	Ago.	Set.	Out.	Nov.	Dez.
Variedade de frutas	3	_____	_____	4	_____	_____	_____	1	_____	_____	_____	_____

Dados obtidos em: http://fdnc.io/eTV. Acesso em: 12 fev. 2021.

PROFESSOR

Resposta: Fev. 4; Mar. 4; Maio 3; jun. 2; jul. 2; set. 3; out. 3; nov. 3; dez. 4.

Qual é o mês em que há menor variedade dessas frutas? _____

PROFESSOR
Resposta: Agosto.

Em quais meses há mais variedade dessas frutas?
_____

PROFESSOR
Resposta: Fevereiro, março, abril e dezembro.

Reúnam-se e façam uma pesquisa com todos os estudantes da sala sobre as refeições saudáveis (almoço e jantar) feitas na última semana. Organizem os dados coletados em tabelas e construam um gráfico de barras. Vocês podem usar uma planilha eletrônica ou uma malha quadriculada para auxiliar o trabalho.

PROFESSOR
Resposta variável.

MANUAL DO PROFESSOR

Atividade 2

Leia cada linha do quadro com os estudantes. Por exemplo: Em janeiro, há colheita de abacate, ameixa e pera; em fevereiro, há colheita de abacate, ameixa, caqui e pera; e assim por diante. Depois, peça a eles que completem a tabela do item a.

No item d, ajude os estudantes a realizarem a pesquisa supervisionando todas as etapas: coleta dos dados, organização dos dados em uma tabela e representação dos dados em um gráfico de barras.

No final da pesquisa, os dados obtidos podem ser comparados com os apresentados na atividade 1.

Se julgar oportuno, peça aos estudantes que elaborem questões que possam ser respondidas com os resultados da pesquisa.

BNCC em foco:

EF03MA27, EF03MA28; competência específica 4

MP166

O que você aprendeu

Escreva duas adições e duas multiplicações diferentes para representar o número de estudantes da sala de aula desenhada abaixo. Em seguida, complete com o total de estudantes que há nessa sala de aula.

Ilustração. Vista de cima de uma sala de aula. Há quatro colunas e cinco fileiras de alunos sentados em carteiras escolares.

PROFESSOR

Resposta: Adições:5 + 5 + 5 + 5 = 20, 4 + 4 + 4 + 4 + 4 = 20

PROFESSOR

Multiplicações:4 × 5 = 20, 5 × 4 = 20

Observação: Os elementos não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.

Nessa sala de aula, há _____ estudantes.

PROFESSOR
Resposta: 20

Ana, Dora e Válter foram à feira no último domingo para comprar ameixas. Complete o quadro com a quantia que cada um gastou, sabendo que todos pagaram o mesmo preço por quilograma.

Valor gasto na feira de domingo

Tabela: equivalente textual a seguir.

Cliente	Quantidade	Valor pago
Ana	2 quilogramas	8 reais
Dora	1 quilograma	_____ PROFESSOR Resposta: 4 reais
Válter	3 quilogramas	_____ PROFESSOR Resposta: 12 reais

Fonte: Lista de gastos de Ana, Dora e Válter. (ago. 2023)

MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um i nstrumento para avaliação formativa.

Propicie conversas entre os estudantes a respeito das estratégias que usaram para resolver as atividades.

Atividade 1

A atividade apresenta a multiplicação em disposição retangular. Explore a ilustração para obter o total de estudantes usando a multiplicação associada ao significado de adição de parcelas iguais. Espera-se que os estudantes percebam que a quantidade total de estudantes na ilustração é a mesma, independentemente da maneira de calcular.

Atividade 2

Espera-se que os estudantes percebam que a organização de dados em tabelas facilita o cálculo de multiplicações. Eles podem usar os resultados anteriores para obter os demais valores. Por exemplo, para saber o preço de 3 quilogramas, podem adicionar o preço pago por 2 quilogramas com o preço pago por 1 quilograma: 8 reais mais 4 reais, que é igual a 12 reais. Pergunte: “Qual é o preço de 4 quilogramas de ameixas?”. Para saber o preço de 4 quilogramas, os estudantes podem dobrar o valor pago por 2 quilogramas: 2 vezes 8 reais é igual a 16 reais.

BNCC em foco:

EF03MA03, EF03MA07

Sugestão de atividade

Calculadora

Peça aos estudantes que levem para a sala de aula uma calculadora simples e proponha as seguintes investigações:

Apertem as teclas Ilustração. Teclas: 3, x, 2, =, =, =. e observem os resultados obtidos no visor.

O que se pode concluir a respeito do uso da tecla Ilustração. Tecla =. ?

Que teclas devem ser apertadas para obter os resultados da lista de multiplicação do tipo vezes 5 (0 × 5, 1 × 5, 2 × 5, 3 × 5, ...)?

Nesse caso, eles podem perceber que, como a lista de multiplicação do tipo vezes 5 é o resultado de uma adição com parcelas iguais a 5, pode-se fazer:

Ilustração. Teclas: 0, +, 5, =, =, =.

CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO

MP167

Ícone: calculadora.

Ícone: Desenho ou pintura.

Uma calculadora está com a tecla quebrada.
Desenhe as teclas que você digitaria para calcular o resultado de 4 × 5.

PROFESSOR

Exemplo de resposta/desenho: Ilustração. Teclas: 3, x, 5, +, 5, =.

Tiago estudou 3 horas por dia em todos os dias da semana passada.
1. Quantas horas Tiago estudou na semana passada?
  _____
  
  PROFESSOR
  Resposta: 21 horas.
1. André, irmão de Tiago, estudou uma hora a menos por dia naquela semana. Quantas horas André estudou na semana passada?
  _____
  
  PROFESSOR
  Resposta: 14 horas.

Observe os quadros de números que Lucas e Ana fizeram.

Ilustração. Lucas. À frente, números de 1 a 18 ... Os números 3, 6, 9, 12, 15, 18 estão pintados de verde.

Ilustração. Ana. À frente, números de 1 a 18 ... Os números 6, 12, 18 estão pintados de laranja.

Os números 6, 12 e 18 foram pintados pelos dois. Se os quadros continuassem até o número 30, qual seria o próximo número em comum a ser pintado por eles? _____

PROFESSOR
Resposta: 24

Converse com os colegas sobre o que você observou na regularidade dos números pintados por Lucas e por Ana.

PROFESSOR
Atenção professor: É interessante que os estudantes percebam a regra que cada colega usou para escolher quais números pintar. Fim da observação.

Autoavaliação

Ícone: oral.

Consigo identificar diferentes ideias que envolvam o cálculo da multiplicação?

PROFESSOR
Resposta pessoal.
Utilizo fatos básicos da multiplicação para realizar outros cálculos?

PROFESSOR
Resposta pessoal.

MANUAL DO PROFESSOR

Atividade 3

Espera-se que o estudante perceba a regularidade nas multiplicações vezes 5. Assim, para obter o resultado de 4 × 5 é possível calcular 3 × 5 e acrescentar 5.

Atividade 4

Oriente os estudantes a explorarem a busca das informações no texto. Se necessário, lembre-os de que uma semana tem 7 dias.

Atividade 5

A atividade possibilita explorar as sequências numéricas para encontrar a regularidade das multiplicação 3 vezes ou vezes 3.

Autoavaliação

A primeira questão possibilita mostrar aos estudantes que a multiplicação pode ser utilizada em diferentes contextos, conforme foi trabalhado na Unidade. Explore a multiplicação associada aos significados como a adição de parcelas iguais e com a apresentação de seus elementos em disposição retangular. Se necessário, peça que observem as atividades da unidade.

Na segunda questão, os estudantes podem avaliar o quanto se apropriaram dos fatos básicos. Explique a eles que a memorização ou o reconhecimento de que 2 × 2 = 4, por exemplo, pode facilitar o cálculo de multiplicações de números maiores ou o cálculo de outras operações. É importante que os estudantes avaliem quanto utilizam fatos básicos como estratégia para outros cálculos.

BNCC em foco:

EF03MA03, EF03MA07, EF03MA10

MP168

Comentários para o professor

Conclusão da Unidade 5

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): ____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem	Desempenho	Observação
Constrói e aplica fatos básicos da adição e da multiplicação para realizar cálculo mental e escrito?	_____	_____
Resolve e elabora problemas de multiplicação (por 2, 3, 4, 5 e 10) com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, utilizando diferentes estratégias de cálculo e registros?	_____	_____
Reconhece regularidades em sequências numéricas recursivas e descreve as suas regras de formação identificando elementos ausentes ou seguintes?	_____	_____
Faz a leitura, a interpretação e a representação de dados em tabelas e gráficos de barras?	_____	_____
Lê, interpreta, compara dados e resolve problemas que envolvam dados organizados em tabelas de dupla entrada e em gráficos de barras ou de colunas?	_____	_____
Sabe pesquisar, coletar, organizar os dados em tabelas e construir gráfico de barras ou de colunas para representá-los?	_____	_____
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?	_____	_____
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?	_____	_____