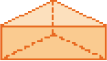
MP169
Introdução da Unidade 6
Nesta Unidade, predominam atividades que exploram habilidades a serem desenvolvidas na Unidade Temática Geometria, mais especificamente as que tratam de algumas figuras geométricas planas e não planas.
Nesse sentido, a abertura, cumprindo a função de estimular a leitura, a interpretação, a curiosidade intelectual, traz, no contexto de um centro de informações turísticas, imagens de uma maquete na qual são apresentados diversos exemplos de figuras geométricas, que possibilitam ao estudante relacioná-las com objetos do mundo físico, bem como nomeá-las.
As atividades que se seguem ao longo da Unidade não só reforçam o que podemos classificar como o primeiro nível do modelo de Van Hiele, sobre o desenvolvimento do pensamento geométrico, como propõem que os estudantes desenvolvam habilidades que os levem a descrever características de algumas figuras geométricas espaciais (prismas retos, pirâmides, cilindros, cones) e a relacionar essas figuras com as planificações de suas superfícies.
Com essa abordagem, pretende-se dar continuidade ao trabalho realizado no 2 º ano com as habilidades de classificar e comparar figuras planas (triângulo, quadrado, retângulo, trapézio e paralelogramo) em re lação a seus lados (quantidade, posições relativas e comprimento) e vértices.
Na Unidade, ainda há atividades que levam os estudantes a classificar e a comparar figuras planas em relação a seus lados e vértices e a reconhecer figuras congruentes usando sobreposições e desenhos em malhas quadriculadas. O estudo da congruência de figuras planas é um campo fértil, que será tratado nos anos seguintes com presença preponderante.
As habilidades da Unidade Temática Probabilidade e estatística também são trabalhadas em atividades cujos dados têm origem em pesquisas significativas e são apresentados por meio de tabelas de dupla entrada e gráficos de barras ou de colunas, contribuindo para a compreensão de aspectos da realidade sociocultural dos estudantes. Assim, o estudante também vai, paulatinamente, se apropriando de linguagem específica, que resulta em uma melhor comunicação.
Competências específicas favorecidas
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
MP170
UNIDADE 6. Geometria

MANUAL DO PROFESSOR
Objetivos da Unidade
Associar figuras geométricas não planas (cubo, paralelepípedo, pirâmide, cone, cilindro e esfera) a objetos do mundo físico.
Reconhecer e nomear figuras geométricas não planas.
Reconhecer as características de algumas figuras geométricas não planas.
Descrever características de algumas figuras geométricas não planas, relacionando-as com as planificações de sua superfície.
Identificar faces, arestas e vértices em figuras geométricas não planas.
Reconhecer e nomear figuras geométricas planas.
Associar figuras planas a partes planas de figuras geométricas não planas.
Identificar lados e vértices em figuras geométricas planas.
Classificar e comparar figuras planas em relação a seus lados (quantidade, posições relativas e comprimento) e vértices.
Reconhecer figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas.
Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas.
Ler, interpretar e comparar dados apresentados em tabelas de dupla entrada e gráficos de colunas.
Na abordagem de figuras geométricas não planas, apresentamos as características de um grupo especial – os prismas –, e exploramos outros tipos de figuras geométricas planas: pentágono, hexágono, paralelogramo e trapézio. Para explorar a cena de abertura, incentive os estudantes a observarem a ilustração, a descreverem o que lhes é familiar e a levantar hipóteses acerca da situação retratada.
BNCC em foco:
EF03MA13, EF03MA14, EF03MA15, EF03MA16, EF03MA26, EF03MA27
MP171
Boxe complementar:
Para refletir...
Diversos recursos são usados para divulgação, localização e preservação da memória de lugares. Maquetes, semelhantes àquilo que representam, fotografias e mapas possibilitam conhecermos um lugar.

Você já visitou um Centro de Informações Turísticas?
Já viu maquetes de lugares ou construções?
PROFESSOR
Respostas pessoais.Observe a maquete da página ao lado.

Quais partes da maquete lembram figuras geométricas? Que figuras são essas?
PROFESSOR
Respostas pessoais.Fim do complemento.
MANUAL DO PROFESSOR
Para refletir...
Os estudantes são incentivados a ler e a interpretar a ilustração que retrata um centro de informações turísticas, incluindo uma maquete. Verifique se eles entendem o significado da palavra maquete . Explique a eles que maquete é a representação tridimensional reduzida de uma obra de arquitetura ou engenharia.
Em uma roda de conversa, solicite aos estudantes que exponham suas respostas e, caso algum deles tenha visitado um centro turístico como esse, peça que conte aos colegas o que observou, se gostou, o que mais chamou a atenção etc.
Na segunda questão, os estudantes são convidados a expor o que percebem acerca das diferentes figuras geométricas que inspiraram as construções apresentadas na cena. Eles podem reconhecer, entre outras, as representações de:
cilindros, no alto do prédio;
pirâmides, em alguns telhados;
prismas em alguns edifícios;
cones, em algumas árvores;
esferas, nas luminárias dos postes;
pentágono, no espelho de água;
hexágonos, nos telhados do teatro e do coreto;
retângulos e quadrados, nas janelas.
MP172
Figuras geométricas
Observação: Os objetos desta página não estão apresentados em escala de tamanho. Fim da observação.
- Observe as imagens dos objetos abaixo e ligue cada objeto à figura geométrica que ele lembra.
Linha 1
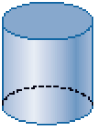
Cilindro

Cubo
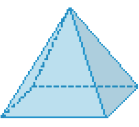
Pirâmide
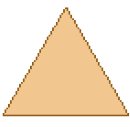
Triângulo
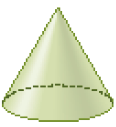
Cone

Círculo
Linha 2






PROFESSOR
Resposta: 1 – C; 2 – A; 3 – E; 4 – F; 5 – B; 6 – D.- Dos objetos acima, quais lembram figuras geométricas planas? E figuras geométricas não planas?
_____
PROFESSOR
Resposta: Objetos que lembram figuras planas: moeda e placa de trânsito.PROFESSOR
Objetos que lembram figuras não planas: dado, chapéu de aniversário, lata de milho e pirâmide de montar.
- Observe as peças do brinquedo de Gabriela.
A
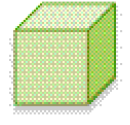
B

C

D
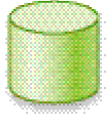
E


- Quais peças do brinquedo formam a peça que Gabriela montou?
_____
PROFESSOR
Resposta: A e C.
MANUAL DO PROFESSOR
Objetivos
Associar figuras geométricas não planas (cubo, paralelepípedo, pirâmide, cone, cilindro e esfera) a objetos do mundo físico.
Reconhecer e nomear figuras geométricas não planas.
Reconhecer e nomear algumas figuras geométricas planas.
Reconhecer as características de algumas figuras geométricas não planas.
Descrever características de algumas figuras geométricas não planas, relacionando-as com as planificações de sua superfície.
As figuras geométricas existem apenas como abstrações da mente, que associamos aos objetos que nos rodeiam. Por isso, dizemos que os objetos lembram ou se parecem com as figuras geométricas indicadas.
Atividade 1
A atividade trabalha a associação entre a forma de objetos variados e a forma de figuras geométricas (não planas ou planas). É possível que alguns estudantes identifiquem a moeda como uma figura não plana, por considerarem sua espessura. Questione-os sobre o que leva alguns a associar a moeda a uma figura plana, e outros, a uma figura não plana.
Atividade 2
É importante que os estudantes manipulem modelos de figuras geométricas não planas representados em três dimensões (em madeira, plástico, ou até mesmo embalagens). As informações coletadas em pesquisas mostram que o professor deve se preocupar sempre em conversar sobre os tipos de representação para que os estudantes consigam decodificar as imagens apresentadas.
BNCC em foco:
EF03MA13
MP173
Figuras geométricas não planas
Planificação
- Veja como Eduardo desmontou a caixa onde guarda alguns brinquedos.
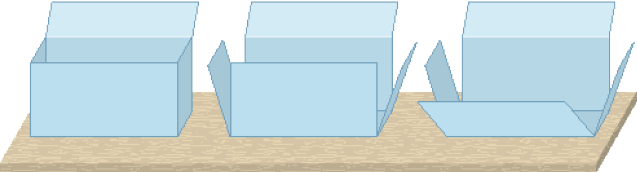
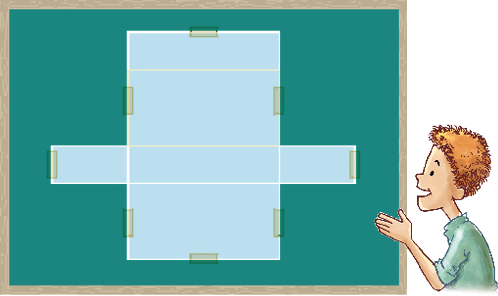
Quando a caixa estava completamente aberta, Eduardo esticou-a sobre a lousa e prendeu-a com fita adesiva, conforme mostrado ao lado.
Eduardo obteve a planificação da superfície da caixa de brinquedos.
- Agora, observe as representações de figuras geométricas não planas e ligue cada figura à planificação de sua superfície.
Linha 1



Linha 2
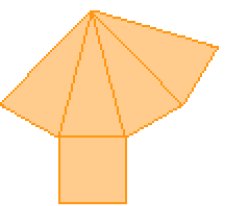
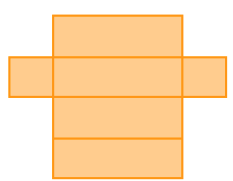
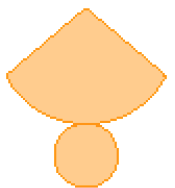
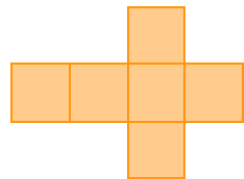
PROFESSOR
Resposta: 1 – D; 2 – C; 3 – A; 4 – B.MANUAL DO PROFESSOR
Objetivos
Reconhecer as características de algumas figuras geométricas não planas.
Descrever características de algumas figuras geométricas não planas, relacionando-as com as planificações de sua superfície.
Associar figuras geométricas não planas (cubo e paralelepípedo) a objetos do mundo físico.
Identificar faces, arestas e vértices em figuras geométricas não planas.
O estudo da planificação da superfície de modelos de figuras não planas possibilita aos estudantes associarem partes planas de figuras não planas com as figuras planas estudadas.
Esse estudo pode ser facilitado pela manipulação de objetos concretos. Na sala de aula, os estudantes poderão desmontar e recortar as abas de colagem de embalagens de papelão, com formas variadas e fáceis de serem desmontadas, de modo que obtenham as planificações dessas embalagens.
Atividade 1
Antes de iniciar os estudos de planificação, é importante providenciar embalagens vazias de papelão, como de creme dental, para serem desmontadas na sala de aula. Peça aos estudantes que levem tesoura com pontas arredondadas e fita adesiva para fazerem, na prática, o que Eduardo fez.
As representações de figuras não planas em uma folha de papel obedecem a algumas características que possibilitam identificá-las como tais. Por exemplo, a aplicação de um efeito de luz ou de uma textura sugere a ideia de tratar-se de uma figura não plana, assim como o uso da linha tracejada para indicar uma parte não visível da figura. Como tais características são convenções construídas e aceitas pelos leitores, é possível diferenciar figuras planas de figuras não planas.
O pesquisador francês Bernard Parzysz (1988) alerta que, ao transmitir uma mensagem, nesse caso a imagem de figuras não planas, quem codifica e quem decodifica deve conhecer essas convenções. Ele afirma que em toda representação há perda de informação. Por exemplo, a representação do cubo não possibilita a visualização de todas as suas faces. Assim, o professor deve auxiliar os estudantes a compreenderem essas convenções a fim de que fiquem claras e eles possam recorrer à imagem mental para perceberem os elementos “ocultos”.
BNCC em foco:
EF03MA14
MP174
- Observe Maria e sua caixa.

- Indique a
letra
da figura que representa o
molde
da caixa de Maria.
_____
PROFESSOR
Resposta: B
A

B
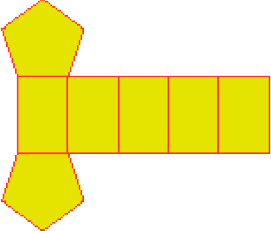
C
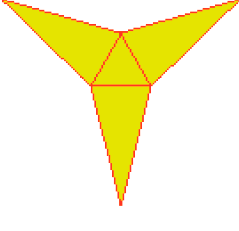
- Joana recortou as partes da planificação da superfície de um modelo de figura não plana. Observe.


- Usando todas essas partes, é possível montar o modelo de qual figura? Pinte-a.
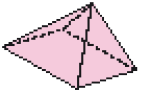
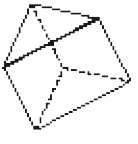

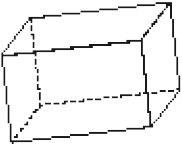
PROFESSOR
Resposta correta: a

- Se Joana recortasse as partes das planificações dos outros modelos que você não pintou, como elas seriam? Desenhe.
PROFESSOR
b)PROFESSOR
Resposta: Exemplos de desenhos:
PROFESSOR
c)PROFESSOR
Resposta: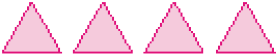
PROFESSOR
d)PROFESSOR
Resposta:
MANUAL DO PROFESSOR
Atividade 2
Os estudantes podem fazer o reconhecimento dessa planificação pela presença da figura plana de 5 lados que pode ser associada a uma das partes planas da caixa que Maria segura.
Atividade 3
Após a resolução, sugira aos estudantes que, em uma folha de cartolina, reproduzam as partes da planificação apresentadas no enunciado (quatro triângulos equiláteros e um quadrado cujo lado tem a mesma medida do lado do triângulo). Depois de recortar as figuras e montar o modelo da figura não plana, eles podem verificar se responderam corretamente.
Socialize os desenhos das partes das demais planificações para que os estudantes possam discutir semelhanças e diferenças entre elas.
BNCC em foco:
EF03MA14
MP175
Cubo e paralelepípedo
- Recorte os moldes do cubo e do paralelepípedo das páginas 243 e 241 no final do livro e monte os modelos dessas figuras.
- Observe as figuras geométricas não planas representadas abaixo.

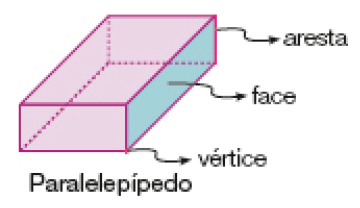
- Quantas arestas tem cada uma dessas figuras geométricas?
_____
PROFESSOR
Resposta: Ambas têm 12 arestas.
- Quantas faces tem cada uma dessas figuras geométricas?
_____
PROFESSOR
Resposta: Ambas têm 6 faces.
- Quantos vértices tem cada uma dessas figuras geométricas?
_____
PROFESSOR
Resposta: Ambas têm 8 vértices.
- Leia o que as crianças estão dizendo. Depois, marque com um X as imagens a seguir que lembram a forma de um cubo.

( )

( )

( )

( )

PROFESSOR
Respostas corretas: caixa de presente; cubo mágico.Observação: Os objetos não estão apresentados em escala de tamanho. Fim da observação.

- Agora, observe sua sala de aula e identifique objetos que lembram cubos ou paralelepípedos.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 1
Sempre que necessário, peça aos estudantes que manuseiem os modelos das figuras formadas com os moldes. Eles vão perceber, nessa manipulação, as peculiaridades de cada figura a respeito de vértices, arestas e faces, bem como as diferenças entre as faces do cubo e as faces do paralelepípedo.
Atividade 2
A manipulação dos modelos montados auxiliará os estudantes a contar a quantidade de vértices, de arestas e de faces de cada figura, o que evidenciará suas características comuns. Como o cubo e o paralelepípedo têm a mesma quantidade de faces, arestas e vértices, é provável que os estudantes perguntem por que são classificados com nomes diferentes. Peça a eles que observem que o cubo tem todas as faces com forma de quadrado, enquanto o paralelepípedo (não cúbico) tem algumas das faces com forma de retângulo. Explique a eles que o cubo é um paralelepípedo, mas com um nome especial, devido a uma característica específica: apresentar todas as faces quadradas.
Atividade 3
Verifique se os estudantes observam que a caixa de presente e o cubo mágico têm forma parecida com a de um cubo. Em seguida, pergunte com que figura geométrica os outros dois objetos apresentados se parecem. Espera-se que eles reconheçam que são modelos de paralelepípedos.
A segunda parte da atividade, em que os estudantes devem reconhecer objetos da sala de aula que parecem as figuras geométricas cubo e paralelepípedo (não cúbico), é uma maneira proveitosa de atribuir significados aos conteúdos geométricos.
É possível reconhecer as figuras geométricas cubo e paralelepípedo (não cúbico) em muitos objetos que fazem parte do cotidiano. Por isso, são as figuras geométricas não planas com as quais os estudantes têm mais familiaridade.
Leve para a sala de aula, por exemplo, uma caixa de sapato e uma caixa de presente que pareçam um paralelepípedo e um cubo, respectivamente, para que os estudantes as observem e manuseiem antes de realizarem as atividades.
BNCC em foco:
EF03MA13, EF03MA14
MP176
- Paula e Jair recortaram a planificação da superfície de um modelo de cubo de maneira que teve as seis faces separadas. Observe.
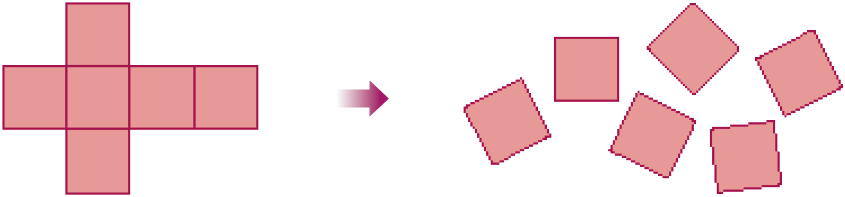
Paula, então, fez outra planificação do modelo de cubo:
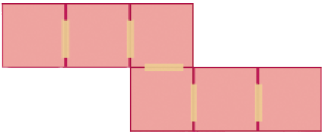
Jair não concordou com Paula e fez uma planificação diferente do modelo de cubo:



- Reúna-se com um colega para descobrir qual planificação possibilita montar um cubo.
PROFESSOR
Resposta: Apenas a planificação de Paula possibilita montar o cubo.Boxe complementar:
Desafio

Em cada uma das planificações da superfície de modelos de cubo, mostradas abaixo, foram destacadas duas linhas. Descubra em qual das planificações as duas linhas coincidirão quando o cubo for montado.
Resposta: C
A
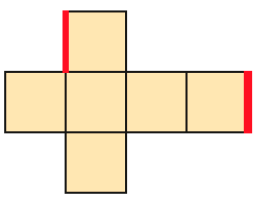
B
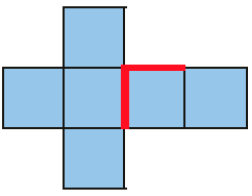
C
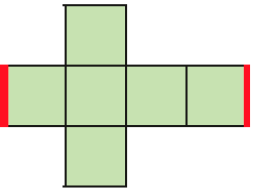
D
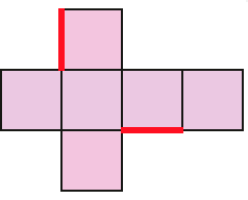
CRÉDITO: ADILSON SECCO
Como você pode verificar se sua resposta está certa?
PROFESSOR
Exemplo de resposta: Decalcando a planificação em uma cartolina, destacando as duas linhas, recortando a planificação e, então, montando o modelo de cubo.Fim do complemento.
MANUAL DO PROFESSOR
Objetivos
Descrever características de algumas figuras geométricas não planas, relacionando cada uma com a planificação de sua superfície.
Associar figuras geométricas não planas (prisma e pirâmide) a objetos do mundo físico.
Reconhecer e nomear figuras geométricas não planas.
Reconhecer as características de algumas figuras geométricas não planas.
Atividade 4
Sugira aos estudantes que recortem 6 quadrados de mesmo tamanho e testem as hipóteses de Paula e de Jair. Peça que investiguem outras possíveis planificações da superfície de modelos de cubo. Depois, pode-se fazer a socialização dos resultados.
É possível fazer a planificação de um cubo de 11 maneiras diferentes. Na atividade, apresentamos duas; a seguir, as outras nove.

CRÉDITO: ADILSON SECCO
Desafio
Um modo de abordar a situação é usar modelos desenhados em uma folha de papel, como os das ilustrações, e proceder às dobras das faces, verificando se as arestas coincidem. Também é possível analisar previamente com os estudantes a posição em que cada aresta ficará depois de dobradas as faces, valendo-se de um modelo de cubo montado.
BNCC em foco:
EF03MA14
Sugestão de leitura para o estudante
Livro
KING, Stephen Michael. O homem que amava caixas. Tradução de Gilda de Aquino. São Paulo: Brinque-Book, 1997.
Esse livro conta a história de um homem que era apaixonado por caixas e por seu filho. O problema era que ele não sabia como dizer ao filho que o amava. Com sua paixão por caixas, o pai construía castelos, aviões e todo tipo de objetos para divertir o menino. Seu amor pelo garoto se manifestava por meio das caixas, que eram usadas nas brincadeiras do filho.
MP177
Prismas
- Recorte os moldes de prismas das páginas 235 a 239 no final do livro e monte os modelos dessas figuras.
- Observe a barraca da ilustração.
- A barraca que Carlos montou se parece com uma figura geométrica. Marque com um X a representação dessa figura.
( )
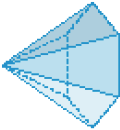
( )

PROFESSOR
Resposta correta: figura 2.

- Manipule os modelos de prisma que você montou e responda à questão.
- Quais características comuns você percebe entre esses modelos de figuras geométricas?
PROFESSOR
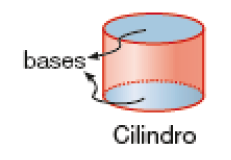
Exemplo de resposta: Nesses modelos de prisma, há faces retangulares em número igual ao número de lados das faces não retangulares.- Nos prismas representados abaixo, observe as faces laterais e as outras duas faces, que são chamadas de bases.
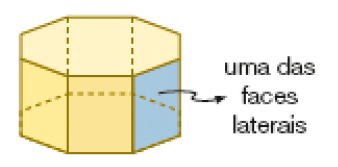
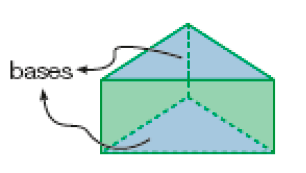
- As faces laterais desses prismas têm a forma de qual figura geométrica plana?
_____
PROFESSOR
Resposta: De um retângulo.
- Quantas faces laterais tem cada figura representada acima?
_____
PROFESSOR
Resposta: 8 faces laterais e 3 faces laterais.
- Quantas bases tem cada prisma?
_____
PROFESSOR
Resposta: Duas bases.
- Quais diferenças você
observa
entre esses prismas?
PROFESSOR
Atenção professor: Os estudantes podem observar, por exemplo, que o número de faces laterais e a forma das bases variam de um prisma para outro. Fim da observação.
MANUAL DO PROFESSOR
As atividades dessa página possibilitam a conceituação de prisma e de suas propriedades, como: o reconhecimento de duas faces idênticas (suas bases) e de faces laterais retangulares, e a compreensão das relações entre a quantidade de vértices e a quantidade de faces laterais nos prismas.
Explique aos estudantes que o cubo e o paralelepípedo também são tipos de prisma.
Atividades 1, 2 e 3
Sempre que necessário, sugira aos estudantes que manipulem as figuras formadas com as planificações. Eles vão perceber, nessa manipulação, as peculiaridades de cada figura em relação a vértices, arestas e faces. Também vão perceber as diferenças entre as faces dos prismas.
Peça aos estudantes que contem os vértices dos modelos de prismas apresentados e observem todas as suas faces. Em todos os modelos, espera-se que eles percebam a presença de duas faces idênticas. Informe que essas faces são denominadas bases do prisma e que as demais faces são chamadas de faces laterais. Solicite que contem a quantidade de faces laterais (que não são bases) e que comparem essa quantidade com a de vértices em cada modelo. Espera-se que os estudantes percebam que a quantidade de vértices é o dobro da de faces laterais de um prisma.
Na atividade 2, o contraponto com a figura da pirâmide é importante, pois alguns estudantes costumam confundir o prisma triangular com uma pirâmide. Se possível, disponibilize modelos desses dois tipos de figuras geométricas a eles.
Outra possibilidade de resposta para a atividade 3 é de que, nesses modelos de prisma, as bases são sempre faces idênticas e opostas entre si e podem ou não ser retangulares; já as faces laterais são sempre retangulares.
BNCC em foco:
EF03MA13, EF03MA14
Atividade 4
Incentive os estudantes a compararem as figuras apresentadas, estabelecendo diferenças e características comuns entre elas. Para os itens a, b e c, espera-se que eles observem que cada um desses prismas apresenta duas faces idênticas (mesma forma e tamanho), que são suas 2 bases, e que suas faces laterais têm a forma de retângulo. Além disso, devem observar que no prisma da esquerda há 8 faces laterais, e no da direita, 3 faces laterais. No item d, os estudantes podem observar, por exemplo, que a quantidade de faces laterais e a forma das bases variam de um prisma para outro.
Questione os estudantes sobre a relação da quantidade de faces laterais com a de vértices do prisma: a quantidade de faces laterais é igual à de vértices de uma das bases.
MP178
- Compare os objetos com as representações de prisma.
A

B

C

D

Representações de prisma

Prisma de base triangular
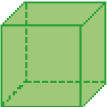
Cubo

Prisma de base hexagonal

Paralelepípedo
Observação: Os objetos não estão apresentados em escala de tamanho. Fim da observação.
- Escreva abaixo com qual representação de prisma cada objeto se parece.
A: _____
PROFESSOR
Resposta: Prisma de base hexagonal.B: _____
PROFESSOR
Resposta: Cubo.C: _____
PROFESSOR
Resposta: Paralelepípedo.D: _____
PROFESSOR
Resposta: Prisma de base triangular.
- Observe as representações de prisma e complete o quadro.
Tabela: equivalente textual a seguir.
|
Representações de prisma |
Número de vértices |
Número de arestas |
Número de bases |
Número de faces laterais |
|---|---|---|---|---|
|
|
6 |
_____ |
_____ |
_____ |
|
|
_____ |
_____ |
2 |
_____ |
|
|
_____ |
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Número de vértices: 10, 12; Número de arestas: 9, 15, 18; Número de bases: 2, 2; Númeor de faces laterais: 3, 5, 6.

- Compare o
número
de vértices com o
número
de faces laterais dessas representações de prisma e descubra uma regularidade.
PROFESSOR
Exemplo de resposta: O número de faces laterais é a metade do número de vértices.
MANUAL DO PROFESSOR
Objetivos
Associar figuras geométricas não planas (prismas, particularmente cubo e paralelepípedo, e pirâmide) a objetos do mundo físico.
Reconhecer e nomear figuras geométricas não planas.
Reconhecer as características de algumas figuras geométricas não planas.
Identificar faces, arestas e vértices em figuras geométricas não planas.
Atividade 5
A proposta de relacionar os objetos ilustrados com as representações dos diferentes prismas (retos) possibilita aos estudantes ampliar o olhar geométrico para as características de cada face.
Peça aos estudantes que observem em todas essas representações de prismas (retos) que as faces laterais são retangulares.
Atividade 6
Verifique se os estudantes contam corretamente vértices, arestas, bases e faces laterais em cada prisma. Para desenvolver essa habilidade, manipular modelos de figuras pode ajudar. Incentive-os a observarem as quantidades e procurarem por regularidades. Por exemplo, a quantidade de arestas é sempre o triplo da quantidade de faces laterais; a quantidade de vértices é o dobro da de faces laterais; a quantidade de arestas pode ser obtida pela adição da quantidade de faces laterais com a de vértices. É pertinente que os estudantes percebam que, ao adicionar a quantidade de bases (que é sempre 2) com a de faces laterais, obtemos o total de faces da figura, pois as bases também são faces.
Na faixa etária em que os estudantes estão, é importante que as nomenclaturas utilizadas socialmente na linguagem matemática sejam mais valorizadas, para que possam ampliar também as habilidades comunicativas.
BNCC em foco:
EF03MA13, EF03MA14
MP179
Pirâmides
- Recorte os moldes de pirâmide das páginas 227 a 233 no final do livro e monte os modelos dessas figuras.
- Kátia é artesã e faz embalagens de presente.

Observe as faces laterais e a outra face, que é chamada de base, das pirâmides representadas abaixo.
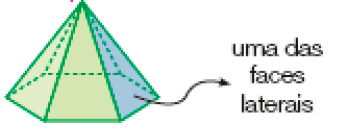
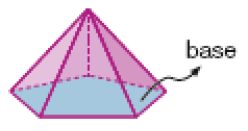
- As faces laterais dessas pirâmides lembram a forma de qual figura geométrica plana?
_____
PROFESSOR
Resposta: De um triângulo.
- Quantas bases tem cada pirâmide?
_____
PROFESSOR
Resposta: Uma base.
PROFESSOR
Atenção professor: Se necessário, os estudantes podem manipular os moldes montados anteriormente para ajudá-los na atividade. Fim da observação.- Observe as representações das pirâmides e complete o quadro.
Quadro: equivalente textual a seguir.
|
Representação de pirâmide |
|
|
|
|
|---|---|---|---|---|
|
Número de vértices |
4 |
_____ PROFESSORResposta: 5 |
_____ PROFESSORResposta: 6 |
_____ PROFESSORResposta: 7 |
|
Número total de faces |
4 |
_____ PROFESSORResposta: 5 |
_____ PROFESSORResposta: 6 |
_____ PROFESSORResposta: 7 |
|
Número de faces triangulares |
4 |
_____ PROFESSORResposta: 4 |
_____ PROFESSORResposta: 5 |
_____ PROFESSORResposta: 6 |
|
Número de arestas |
6 |
_____ PROFESSORResposta: 8 |
_____ PROFESSORResposta: 10 |
_____ PROFESSORResposta: 12 |
MANUAL DO PROFESSOR
A página explora a figura geométrica pirâmide, sua conceituação e suas propriedades, como: reconhecer que a pirâmide tem uma única base e um vértice fora da base e que as faces laterais são todas triangulares; perceber as relações entre a quantidade de vértices, de faces, de faces laterais e de arestas nas pirâmides.
Atividades 1 e 2
Sempre que necessário, peça aos estudantes que manipulem os modelos das figuras geométricas não planas, a fim de que percebam peculiaridades das figuras a respeito de vértices, arestas e faces. Também vão notar as diferenças entre as faces das pirâmides.
Pergunte aos estudantes: “Em que situações vocês já viram uma pirâmide?”. É possível que citem as famosas pirâmides egípcias, a pirâmide de vidro em frente ao Louvre ou alguns objetos decorativos com a forma de pirâmide.
Explore com a turma as ilustrações das embalagens e proponha uma discussão sobre características comuns e diferenças entre elas. Os estudantes podem levantar aspectos geométricos (formato das bases, por exemplo) ou não geométricos (cores e enfeites). É importante que percebam que todas as embalagens têm faces laterais triangulares.
Atividade 3
A manipulação de modelos concretos de pirâmides pode auxiliar os estudantes na percepção de seus elementos. Pergunte a eles: “Que regularidades vocês observam nas quantidades obtidas?”. Uma regularidade que pode ser observada é que a quantidade de vértices é igual à quantidade de faces.
BNCC em foco:
EF03MA13, EF03MA14
MP180
- Observe as figuras geométricas não planas representadas abaixo. Marque com um X as representações de pirâmide e cerque com uma linha as representações de prisma.
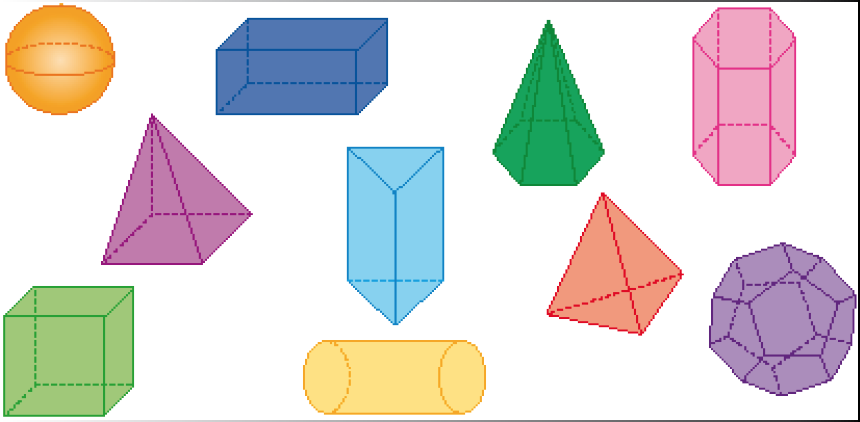
PROFESSOR
Resposta: representações de pirâmide: figura 3; figura 5; figura 7. Representações de prisma: figura 2; figura 4; figura 6; figura 8.- Lúcia montou três figuras que lembram pirâmides usando palitos e bolinhas de massa de modelar. Cada palito corresponde a uma aresta e cada bolinha corresponde a um vértice.


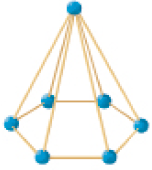
- Quantos
palitos
e quantas
bolinhas
ela usou, no total, para montar as três figuras que lembram pirâmides?
_____
PROFESSOR
Resposta: 30 palitos e 18 bolinhas.

- Laura girou a pirâmide várias vezes. Veja as diferentes posições em que ficou a pirâmide e pinte, com as cores corretas, as faces que estão em branco.

Pirâmide

Pirâmide em diferentes posições
Posição 1

PROFESSOR
Resposta: azulPosição 2

PROFESSOR
Resposta: verdePosição 3
PROFESSOR
Resposta: laranjaPosição 4

PROFESSOR
Resposta: laranjaMANUAL DO PROFESSOR
Objetivos
Reconhecer e descrever as características de algumas figuras geométricas não planas.
Identificar faces, arestas e vértices em figuras geométricas não planas.
Associar figuras geométricas não planas (cone, cilindro e esfer a) a objetos do mundo físico.
Reconhecer e nomear figuras geométricas não planas (cilindro, cone e esfera).
Atividade 4
Aproveite a atividade para comparar as representações de pirâmides e prismas. Peça aos estudantes que identifiquem características comuns e diferenças entre pirâmides e prismas. Eles podem empregar uma linguagem não formal, como: “As pirâmides têm um bico e os prismas não têm”. Espera-se que notem que as faces laterais das pirâmides são triângulos, e as dos prismas, retângulos. Outro aspecto é que os prismas têm duas bases, e as pirâmides, apenas uma. Além disso, as pirâmides possuem um vértice fora da base, e os prismas, não.
Atividade 5
A atividade possibilita aos estudantes perceberem que a base da pirâmide pode variar de forma (quadrado, pentágono, hexágono, ...), porém, as faces laterais serão sempre triangulares. Esse tipo de modelo também favorece a contagem das arestas e dos vértices.
Para a atividade, traga palitos de sorvete e massinhas e distribua aos estudantes, a fim de que reproduzam as montagens das pirâmides e que observem algumas características. Para auxiliá-los, faça perguntas, como: “Quantas faces laterais tem cada uma das pirâmides?” (1ª pirâmide: 4 faces laterais; 2ª pirâmide: 5 faces laterais; 3ª pirâmide: 6 faces laterais); “Qual é o formato das faces de cada pirâmide?”. (Todas são triangulares.)
BNCC em foco:
EF03MA14
Atividade 6
Se julgar conveniente, confeccione um modelo de pirâmide e pinte cada uma das faces de uma cor, conforme a atividade, para facilitar a visualização por parte dos estudantes.
Caso algum estudante considere o cilindro um prisma (por apresentar duas bases), esclareça que, nos prismas, as bases são figuras planas com lados retos e vértices (polígonos); no cilindro, as bases são circulares (não têm lados nem vértices).
MP181
Cilindro, cone e esfera
- Recorte os moldes de cone e cilindro das páginas 223 e 225 no final do livro e monte os modelos dessas figuras.
- Observe abaixo as representações de figuras geométricas e marque com um X as que são arredondadas.
( )
( )
( )

( )

( )
( )
PROFESSOR
Resposta: Respostas corretas: cone; esfera; cilindro.Essas figuras geométricas arredondadas recebem nomes especiais.


- Quais dessas figuras não têm arestas?
_____
PROFESSOR
Resposta: Cilindro, cone e esfera.
- Quais dessas figuras não têm vértices?
_____
PROFESSOR
Resposta: Esfera e cilindro.
- Qual dessas figuras tem apenas 1 vértice?
_____
PROFESSOR
Resposta: O cone.
- De qual figura geométrica não plana você se lembra quando observa cada uma destas imagens?

_____
PROFESSOR
Resposta: Esfera.
_____
PROFESSOR
Resposta: Cilindro.
_____
PROFESSOR
Resposta: Cone.
_____
PROFESSOR
Resposta: Cone.
_____
PROFESSOR
Resposta: Cilindro.
_____
PROFESSOR
Resposta: Cilindro.Observação: Os objetos não estão apresentados em escala de tamanho. Fim da observação.
MANUAL DO PROFESSOR
Atividades 1 e 2
Sempre que necessário, peça aos estudantes que manipulem as figuras formadas com os moldes das figuras geométricas não planas.
Depois que os estudantes montarem os modelos de cilindro e de cone, proponha uma roda de conversa para explorar a característica comum entre o cilindro, o cone e a esfera. Ressalte para a turma que os três têm a superfície arredondada e que, portanto, não têm arestas nem faces.
Peça aos estudantes que falem as diferenças que observam entre essas três representações. É possível que digam que:
a esfera não tem partes planas;
o cone tem uma parte plana circular, sua única base;
o cilindro tem duas partes planas circulares, que são suas duas bases.
Com a manipulação das figuras que acabaram de montar, os estudantes vão perceber que o cone tem um vértice e uma base, mas não tem aresta; o cilindro tem duas bases, mas não tem arestas nem vértices; e a esfera não tem arestas, nem vértices, nem bases.
Atividade 3
Sugira aos estudantes que, em grupos, pensem em objetos do cotidiano que lembram o cilindro, o cone e a esfera, e discutam as características de cada figura. É possível surgirem exemplos como: latas de alimentos, cestos de lixo e postes (parecem o cilindro); casquinha de sorvete e chapéu de festa de aniversário (parecem o cone); tipos variados de bolas e globo terrestre (parecem a esfera).
BNCC em foco:
EF03MA13, EF03MA14
MP182
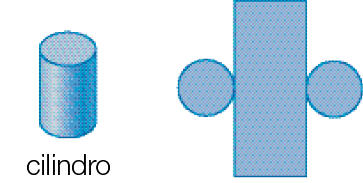
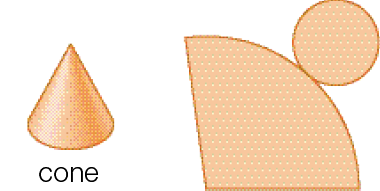
- Observe um modelo de cilindro e um modelo de cone e suas respectivas planificações das superfícies.
- A planificação do
modelo
de cilindro é formada pela representação de quais figuras geométricas planas?
_____
PROFESSOR
Resposta: Por um retângulo e dois círculos.
- A representação de qual figura plana faz parte da planificação tanto do
modelo
do cilindro como do
modelo
do cone?
_____
PROFESSOR
Resposta: Do círculo.
- Em cada cena, Mariana está segurando diante de Vítor um modelo de figura geométrica não plana.

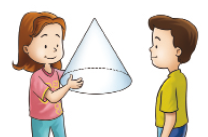
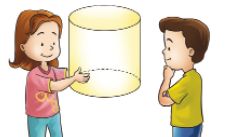
Observando cada um desses modelos, Vítor consegue representar a imagem que vê por meio de uma figura plana. Sabendo disso, complete.
Tabela: equivalente textual a seguir.
|
Imagem observada por Vítor |
|
|
|
|
Nome da figura geométrica não plana observada |
_____ PROFESSORResposta: esfera |
_____ PROFESSORResposta: cilindro |
_____ PROFESSORResposta: cone |


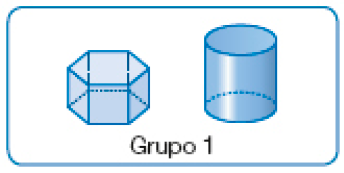
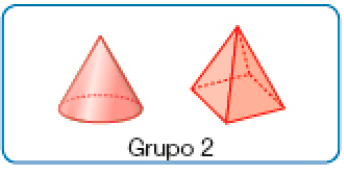
- Com um colega, compare as figuras em cada grupo e converse sobre o que há de parecido e de diferente entre essas figuras.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
Descrever características de algumas figuras geométricas não planas (cilindro e cone), relacionando-as com as planificações de sua superfície.
Reconhecer as características de algumas figuras geométricas não planas.
Associar figuras planas a partes planas de figuras geométricas não planas.
Reconhecer e nomear figuras geométricas planas.
Para o desenvolvimento desse tópico, peça antecipadamente aos estudantes que levem para a sala de aula embalagens diversas que se pareçam com as figuras não planas estudadas até aqui: cubo, paralelepípedo (não cúbico), prismas, pirâmides, cilindro, cone e esfera.
Atividade 4
A atividade possibilita aos estudantes observarem as planificações dos modelos de cone e de cilindro e identificarem suas partes comuns. Comente que a esfera não tem modelo planificado, pois não é possível planificar sua superfície sem deformá-la.
Atividade 5
A capacidade de perceber uma figura geométrica de diferentes pontos de vista é uma condição importante para a construção do pensamento geométrico. Na atividade, os estudantes devem identificar figuras planas observadas por Vítor nas figuras não planas apresentadas.
Atividade 6
Peça aos estudantes que, em duplas, manipulem os modelos de figuras não planas montados e observem semelhanças e diferenças. Depois, devem separá-las em dois grupos, de acordo com um critério definido pela dupla, e apresentar esses agrupamentos para os colegas descobrirem os critérios usados.
Cada dupla deve utilizar os próprios moldes para analisar os grupos de figuras. Exemplo de resposta:
Grupo 1: As duas figuras têm duas bases; uma figura tem superfície arredondada, e a outra, não.
Grupo 2: As duas figuras têm um vértice fora da base; a base do cone é um círculo, e a dessa pirâmide, um quadrado.
BNCC em foco:
EF03MA14
MP183
Figuras geométricas planas
- Camila apoiou embalagens sobre uma folha de papel e as contornou, obtendo algumas figuras. Depois, pintou o interior de cada uma delas. Observe as figuras obtidas por Camila.

Círculo

Triângulo

Retângulo

Pentágono

Quadrado

Hexágono
As figuras que Camila desenhou e pintou são representações de figuras geométricas planas.
- Agora, escreva o nome da figura ou das figuras geométricas planas que podem ser representadas após contornar uma das partes de cada embalagem abaixo.
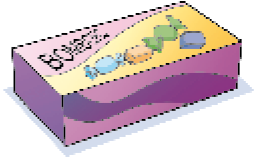
_____
PROFESSOR
Resposta: Retângulo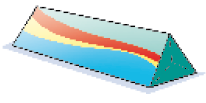
_____
PROFESSOR
Resposta: Triângulo ou retângulo
_____
PROFESSOR
Resposta: Quadrado
_____
PROFESSOR
Resposta: Pentágono ou retângulo
_____
PROFESSOR
Resposta: Círculo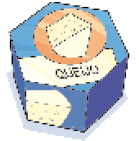
_____
PROFESSOR
Resposta: Retângulo ou hexágonoObservação: Os objetos não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.
MANUAL DO PROFESSOR
Objetivos
Reconhecer as características de algumas figuras geométricas não planas.
Associar figuras planas a partes planas de figuras geométricas não planas.
Reconhecer e nomear figuras geométricas planas.
Identificar lados e vértices em figuras geométricas planas.
Classificar e comparar figuras planas em relação a seus lados (quantidade, posições relativas e comprimento) e vértices.
As atividades propostas induzem os estudantes à conceituação de figuras geométricas planas a partir de figuras geométricas não planas. A exploração de modelos concretos favorece o relacionamento entre figuras geométricas planas e figuras geométricas não planas, tornando mais fácil a compreensão, por exemplo, de que um quadrado pode ser obtido da face de um modelo de cubo ou de uma de suas vistas. De acordo com o modelo de Van Hiele sobre o desenvolvimento do pensamento geométrico, elaborado pelo casal holandês, a aprendizagem da Geometria não depende de maturação ou da idade, mas da vivência com atividades adequadas. Segundo esse modelo, os estudantes passam por níveis sucessivos de compreensão:
Nível zero: reconhecem figuras por sua aparência como um todo, não por suas propriedades ou elementos, e são capazes de aprender um vocabulário geométrico, identificar formas e reproduzir figuras.
Nível um: identificam as características de uma figura e relacionam suas diferentes partes.
As atividades desenvolvidas na Unidade trabalham aspectos que fazem parte dos níveis zero e um de compreensão do modelo de Van Hiele. Os demais níveis do modelo não serão objeto de nosso estudo, porque são esperados de estudantes com maior grau de escolarização.
BNCC em foco:
EF03MA13, EF03MA15
Atividade 1
Na situação apresentada, os estudantes percebem que, ao contornar e depois pintar o interior:
das faces de paralelepípedos, obtêm quadrados e retângulos;
das bases de um cilindro, obtêm círculos;
das faces de um prisma de base triangular, obtêm triângulos e retângulos;
das faces de um cubo, obtêm quadrados.
MP184

- Pegue os modelos de cilindro, de cone e de cubo que você montou anteriormente e coloque-os apoiados em uma folha de papel sobre o tampo de uma mesa, como mostra a ilustração abaixo. Depois, contorne a base apoiada de cada modelo e responda às questões.
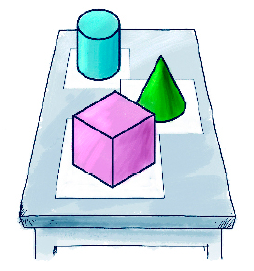
PROFESSOR
Resposta: Desenho do contorno da face apoiada de cada figura:PROFESSOR
 cilindro
cilindro PROFESSOR
 cone
cone PROFESSOR
 cubo
cubo - Quais desses
contornos
são possíveis de traçar com o auxílio de uma régua?
_____
PROFESSOR
Resposta: O contorno da base do cubo.
- Quais
contornos
não são possíveis de traçar com o auxílio de uma régua?
_____
PROFESSOR
Resposta: O contorno das bases do cilindro e do cone.
- Eugênio montou duas figuras geométricas planas por meio das representações de outras figuras planas. Ele usou a representação de dois triângulos e um quadrado.
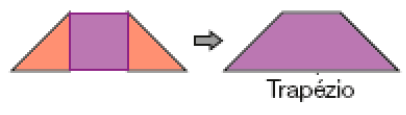
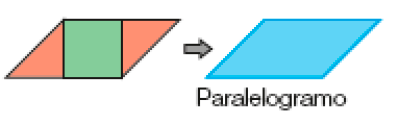

- Com essas representações, como devemos fazer para montar um retângulo? E um triângulo?
PROFESSOR
Exemplos de resposta: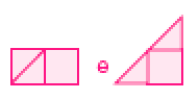
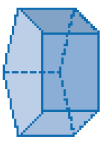
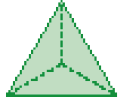
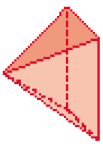
- Observe abaixo o contorno de cada uma das faces de um modelo de figura geométrica não plana.

- Qual das figuras geométricas abaixo representadas teve as faces
contornadas? _____
PROFESSOR
Resposta: D
Figuras geométricas não planas
A

B
C
D
MANUAL DO PROFESSOR
Atividade 2
Ao trabalhar com modelos concretos de cilindros, cones e cubos, os estudantes reproduzem o procedimento mostrado na atividade 1.
Contornando e depois pintando o interior:
da face de um modelo de cubo, obterão a figura plana quadrado;
das bases dos modelos de cilindro e de cone, obterão a figura plana círculo.
Os estudantes devem perceber que podemos traçar o contorno de uma face do modelo de cubo com uma régua, mas que não é possível traçar com régua o contorno das bases do modelo de cilindro ou do modelo de cone, pois são circulares. Entretanto, ao desenhar polígonos com quantidade crescente de lados, o contorno vai se aproximando ao de um círculo, mas jamais será igual a ele, pois é formado por segmentos de reta:

Hexágono (6 lados)

Decágono (10 lados)

CRÉDITO: ADILSON SECCO
Decágono (10 lados)
Atividade 3
Forneça modelos de triângulos e retângulos de modo que também seja possível compô-los, para que os estudantes vejam como ficam tais composições.
Atividade 4
Os estudantes precisam imaginar, nas representações planas, qual figura não plana elas podem formar. Eles podem usar os modelos de figuras não planas que já montaram e contornar suas faces, comparando-as com os contornos mostrados no livro. Isso pode ser feito depois de tentarem obter a resposta sem o uso dos modelos.
Observando a figura D, pode-se notar que 4 faces são triangulares e sua base é quadrada; por isso, ela é a figura não plana correspondente aos contornos de faces apresentados no enunciado.
Traga modelos do quadrado e dos triângulos para que os estudantes vivenciem as composições de Eugênio e observem características comuns e diferenças entre o trapézio e o paralelogramo.
Espera-se que os estudantes percebam que as figuras A e B têm algumas faces retangulares, portanto não são as figuras certas. Já a figura C tem todas as faces triangulares, de modo que também não é a figura certa.
BNCC em foco:
EF03MA14, EF03MA15
MP185
Lados e vértices
- Na aula de Geometria, a professora Clara fez um painel usando adesivos coloridos que representam figuras geométricas planas. Com uma caneta azul e uma régua, ela contornou os adesivos e, depois, colou um círculo de papel vermelho em cada “bico” dos adesivos.

- Para contornar um adesivo, a professora Clara fez um traço azul em cada um dos “lados” do adesivo. Quantos traços ela fez ao contornar um adesivo triangular?
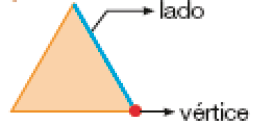
_____
PROFESSOR
Resposta: Três traços.
- Quantos círculos de papel vermelho deverão ser colados em um adesivo retangular?
_____
PROFESSOR
Resposta: Quatro círculos.
- Escreva abaixo o número de lados e o número de vértices da figura geométrica plana que cada adesivo a seguir lembra.
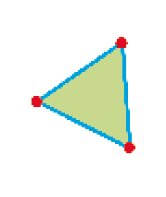
Triângulo
_____ lados
PROFESSOR
Resposta: 3_____ vértices
PROFESSOR
Resposta: 3
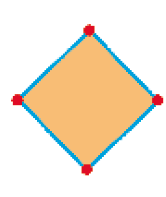
Quadrado
4 lados
4 vértices
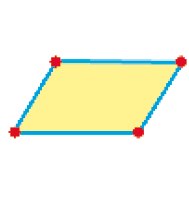
Paralelogramo
_____ lados
PROFESSOR
Resposta: 4_____ vértices
PROFESSOR
Resposta: 4
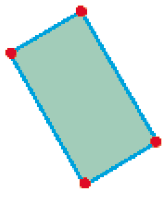
Retângulo
_____ lados
PROFESSOR
Resposta: 4_____ vértices
PROFESSOR
Resposta: 4
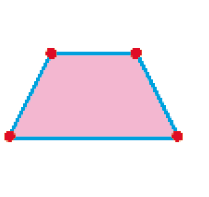
Trapézio
_____ lados
PROFESSOR
Resposta: 4_____ vértices
PROFESSOR
Resposta: 4

- Agora, descubra uma regularidade nos resultados obtidos.
PROFESSOR
Atenção professor: Espera-se que os estudantes observem, por exemplo, a igualdade entre o número de vértices e o número de lados. Fim da observação.MANUAL DO PROFESSOR
O trabalho de observação de regularidades em figuras geométricas planas possibilita a percepção de características comuns e diferenças entre elas. Dessa exploração, resultará o reconhecimento de diferentes figuras planas, como quadrados, pentágonos e triângulos. As atividades possibilitam compreender a importância do reconhecimento dos elementos lados e vértices (no caso de polígonos).
Identificar quantos lados a figura geométrica plana tem e observar a quantidade de vértices e de lados dessa figura garante a elaboração da propriedade de que a quantidade de lados e de vértices de um polígono é igual.
Atividade 1
Para explorar o uso dos termos lados e vértices, faça perguntas que levem os estudantes a observarem características, diferenças e similaridades entre diversas figuras planas. Por exemplo: “O que o quadrado e o retângulo têm em comum? E de diferente?”. Espera-se que eles observem que a quantidade de vértices e de lados do quadrado e do retângulo é a mesma. A diferença entre eles é o comprimento do lado : no quadrado, todos os lados têm mesmo comprimento; no retângulo apresentado na atividade, as medidas dos lados não são todas iguais (somente os lados opostos têm mesma medida). É importante ressaltar que, assim como os estudantes nessa faixa etária podem não perceber que o cubo é um tipo especial de paralelepípedo, também podem não reconhecer que o quadrado é um tipo especial de retângulo. Sugira que desenhem com régua outros adesivos como esses. Depois, peça a eles que contem quantos são os vértices e os lados das figuras geométricas correspondentes. Espera-se que observem que a quantidade de lados e a de vértices coincide.
BNCC em foco:
EF03MA15
MP186
Congruência
- Observe as cenas abaixo.
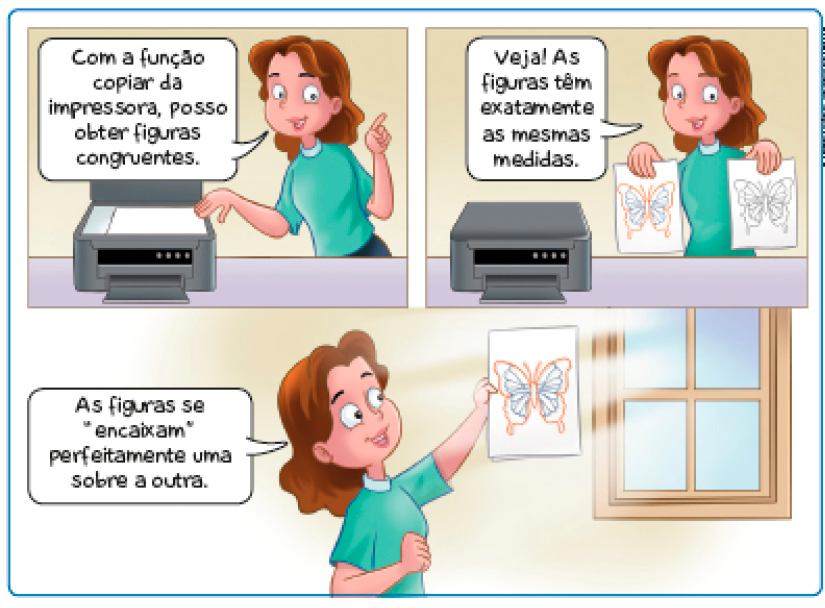
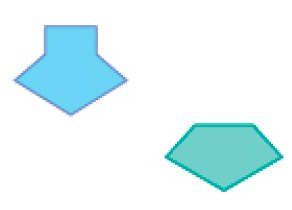
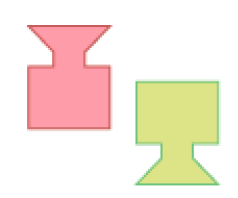
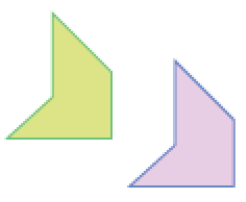
- Agora, marque com um X os pares de figuras que são congruentes.
( )
( )
( )
( )
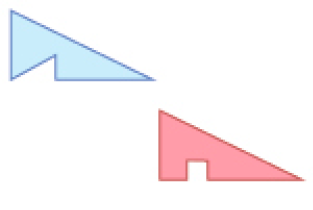
PROFESSOR
Respostas corretas: par 2; par 3.MANUAL DO PROFESSOR
Objetivo
Reconhecer figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas.
Nessas páginas, é explorada a ideia de congruência. O termo pode não fazer parte do vocabulário dos estudantes, sendo comum utilizarem “as figuras são iguais”. Entretanto, na Geometria, não se pode dizer que figuras são iguais, uma vez que elas são formadas por pontos diferentes. Desse modo, é possível dizer que duas figuras são congruentes quando são idênticas em forma e tamanho.
Atividade 1
Sugira aos estudantes que verifiquem a congruência das figuras reproduzindo-as em papel transparente e verificando quais delas são congruentes ou não. Ou seja, para serem congruentes, as duas figuras devem se encaixar perfeitamente uma sobre a outra.
BNCC em foco:
EF03MA16
MP187

- Desenhe na malha quadriculada o contorno de um polígono congruente ao polígono dado.
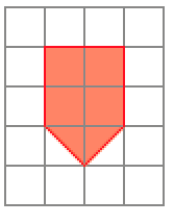
PROFESSOR
Resposta: Exemplo de desenhos: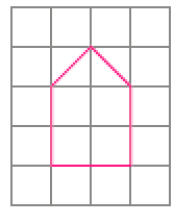
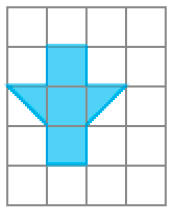
PROFESSOR
Resposta: Exemplo de desenhos: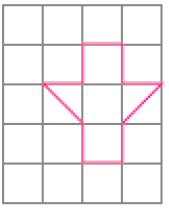
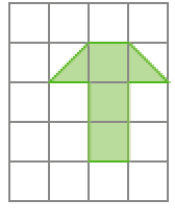
PROFESSOR
Resposta: Exemplo de desenhos: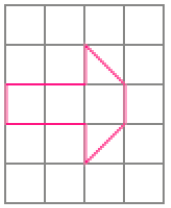
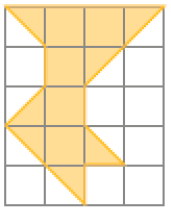
PROFESSOR
Resposta: Exemplo de desenhos: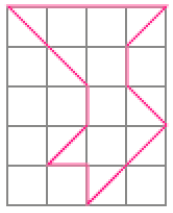

- Pinte da mesma cor os pares das representações de triângulos congruentes. Em seguida, converse com um colega para verificar se vocês marcaram os mesmos pares.
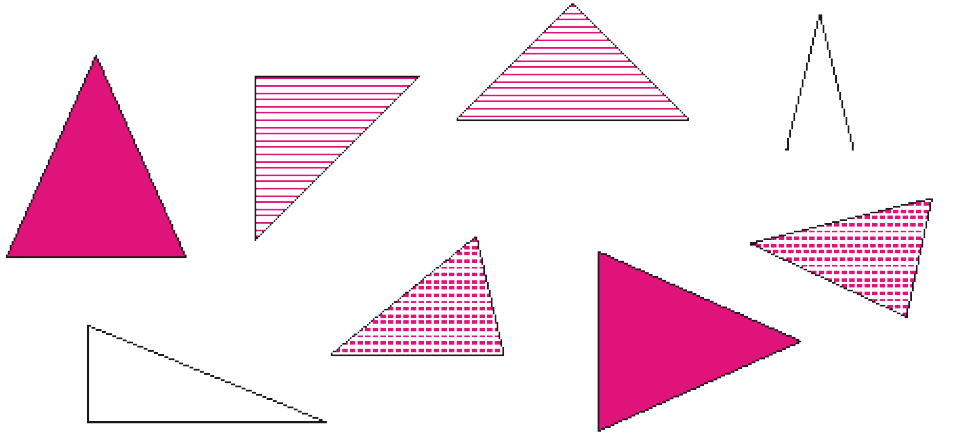
- Todas as representações de triângulo acima têm um par congruente?
_____
PROFESSOR
Resposta: Não.
MANUAL DO PROFESSOR
Atividade 2
A malha quadriculada é uma ferramenta interessante no trabalho de reprodução de representações de figuras congruentes. É importante que os estudantes percebam que as quadrículas podem ser contadas com o intuito de verificar se os tamanhos são iguais ou não. Além disso, a malha também possibilita observar se as figuras comparadas têm a mesma forma.
Se julgar oportuno, proponha uma atividade similar usando algum software gratuito de geometria dinâmica.
Atividade 3
É importante socializar as descobertas dos estudantes, pois alguns podem apresentar dificuldade na identificação dos triângulos congruentes devido aos diferentes posicionamentos das figuras. Permita que sobreponham uma folha de papel para decalcarem os triângulos e, depois, para recortá-los e verificarem quais deles se encaixam perfeitamente.
BNCC em foco:
EF03MA16
MP188
Matemática em textos
Leia
Um código para ajudar daltônicos
Você sabe o que significa ser daltônico? Quando uma pessoa é daltônica, ela tem dificuldade em diferenciar todas ou algumas cores. Por exemplo, alguns daltônicos confundem a cor vermelha com a cor verde.
Pensando nas dificuldades de um daltônico, o designer português Miguel Neiva criou um código que permite que pessoas daltônicas identifiquem as cores. O ColorADD, como é chamado, foi desenvolvido após oito anos de pesquisa.
O código é formado por pequenos símbolos que identificam as cores azul, amarela e vermelha. A união de dois símbolos representa cores, como verde-escuro, laranja e rosa (formadas pela união de duas ou mais cores).
As cores preta e branca são identificadas por pequenos quadrados. O quadrado que simboliza o preto é cheio; já o que representa o branco é vazio. Esses quadrados podem vir combinados aos símbolos das outras cores para identificar se são claras ou escuras.
Veja como são alguns símbolos nesse código:
Tabela: equivalente textual a seguir.
|
Nome da cor |
Cor |
Código |
|
Branco |
|
|
|
Preto |
|
|
|
Azul |
|
|
|
Vermelho |
|
|
|
Amarelo |
|
|
|
Verde-escuro |
|
|
|
Laranja |
|
|
|
Rosa |
|
|
FONTE: Informações obtidas em: http://fdnc.io/eTW. Acesso em: 26 jan. 2021.
MANUAL DO PROFESSOR
Objetivo
Reconhecer e comparar figuras planas.
No texto dessa seção, os estudantes entram em contato com um código utilizado por pessoas daltônicas, o ColorADD, em que pequenos símbolos representam as cores. Respeitando o texto original, o símbolo que representa a cor branca foi reproduzido na seção como um quadrado, embora consideramos que ele seja o contorno de uma figura próxima de um quadrado.
Do ponto de vista funcional, indivíduos com essa deficiência podem não conseguir realizar algumas tarefas, ou mesmo podem viver situações de risco quando dependem fortemente da leitura das cores, por exemplo, na compreensão de semáforos. Tendo isso em consideração, Neiva quis criar algo que aumentasse a autoestima e a segurança dos daltônicos.
BNCC em foco:
EF03MA15; competência específica 2
Sugestão de leitura para o estudante
Livro
PRADO, Ricardo Chaves. Uma cor só minha. Ilustrações de Anna Anjos. São Paulo: Moderna, 2011. (Coleção Girassol.)
Por conta de um jogo de boliche e umas meias com os pares trocados, Francisco descobriu que era daltônico. Aprendeu que via as cores de um jeito diferente, só seu. E naquele ano foram muitas descobertas, que podem ser acompanhadas nesse “diário de um daltônico”, contadas pelo próprio Francisco.
MP189
Responda
- Quantos anos demorou para que o código ColorADD
fosse
desenvolvido?
_____
PROFESSOR
Resposta: 8 anos.
- Marque com um X o símbolo que representa a cor vermelha:
( )

( )

( )

- Esse símbolo lembra qual figura geométrica?
_____
PROFESSOR
Resposta:
Analise
- Observe os símbolos no quadro da página anterior para completar com o nome das cores.
 vermelho +
vermelho +  amarelo =
amarelo = 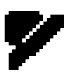 _____.
_____.
PROFESSOR
Resposta: laranja
 branco +
branco +  _____
=
_____
=  _____.
_____.
PROFESSOR
Resposta: vermelho, rosa

- Para obter a cor marrom, é necessário unir as cores vermelha, amarela e azul. Desenhe, no espaço ao lado, como seria o símbolo da cor marrom, de acordo com o código ColorADD.
PROFESSOR
Resposta:
Aplique

Forme grupo com 3 colegas e inventem um código para as cores azul, vermelha e amarela. Depois, seu professor vai orientá-los a representar com esse código as outras cores.
PROFESSOR
Resposta pessoal.MANUAL DO PROFESSOR
Responda
O ColorADD é um código formado por três símbolos que identificam as cores azul, amarela e vermelha e no qual as demais cores podem ser obtidas pela combinação desses símbolos, com exceção da preta e da branca, representadas por um quadrado cheio e um quadrado vazio, respectivamente.
Incentive os estudantes a buscarem as informações de que precisam no texto ou a mobilizarem seus conhecimentos construídos sobre figuras planas.
Para ampliar, pergunte: “Vocês acham que produtos como roupas e sapatos deveriam ter esse código? Por quê? Esse código deveria ser usado em locais como hospitais e metrô?”.
Analise
Escolha mais algumas cores e peça aos estudantes que as representem usando os símbolos do ColorADD. Aproveite para explorar um pouco mais esse tema. Promova uma discussão, fazendo perguntas como: “Vocês acham que a criação desse código foi importante para a vida das pessoas daltônicas? Por quê? Vocês conhecem pessoas daltônicas?”.Se houver algum estudante daltônico na sala, convide-o a contar suas experiências, caso ele queira, explicando, por exemplo, como faz para distinguir as cores quando não há esse código.
Aplique
Explique aos estudantes que, para obter algumas cores, são necessárias duas ou mais cores. Mostre as seguintes combinações:



CRÉDITO: ANDERSON DE ANDRADE PIMENTEL
Observando essas combinações, eles serão capazes de combinar os códigos que criaram para obter um código para as demais cores.
BNCC em foco:
EF03MA15; competência específica 2
MP190
Compreender informações
Interpretar tabelas de dupla entrada
- Na escola de Janaína, durante duas semanas, foram entrevistados 50 estudantes do 3 º ao 5 º ano como parte de um trabalho para ser apresentado na Mostra Cultural da escola com tema: Blogueiros do Brasil.

Para o trabalho a ser apresentado na Mostra, foram escolhidos 5 blogs com diferentes temas: alimentação, saúde, moda, esportes, curiosidades.
A coordenadora da Mostra fez uma tabela reunindo os votos de meninas e meninos sobre os temas dos blogs . Cada estudante escolheu apenas um tema de sua preferência.
Observe a tabela abaixo.
Preferência dos temas
Tabela: equivalente textual a seguir.
|
Gênero Tema |
Meninas |
Meninos |
|---|---|---|
|
Alimentação |
9 |
4 |
|
Saúde |
7 |
4 |
|
Moda |
8 |
2 |
|
Esportes |
5 |
6 |
|
Curiosidades |
3 |
2 |
Fonte: Coordenadora da Mostra Cultural. (mar. 2023)
- Quantas meninas participaram dessa pesquisa? E meninos?
_____
PROFESSOR
Resposta: 32 meninas; 18 meninos.
- Qual foi o tema mais votado, considerando os votos das meninas e dos meninos juntos? E o menos votado?
_____
PROFESSOR
Resposta: Alimentação; curiosidades.
MANUAL DO PROFESSOR
Objetivos
Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas.
Ler, interpretar e comparar dados apresentados em tabelas de dupla entrada e gráficos de colunas.
Atividade 1
A atividade explora a leitura e interpretação de tabela de dupla entrada. Leia com os estudantes a situação proposta para garantir que eles entendam todas as informações. Depois, peça que destaquem algumas informações da tabela. Explique que cada estudante votou em apenas um tema.
Do que a tabela trata? (Espera-se que os estudantes identifiquem que ela apresenta os temas escolhidos e a quantidade de votos recebidos, por meninas e por meninos.)
Entre os meninos, que tema foi mais votado? (Esportes.)
E entre as meninas? (Alimentação.)
Explique aos estudantes que a quantidade de votos que um tema recebeu determina a frequência com que cada tema apareceu. Pergunte:
Quantos estudantes votaram em Alimentação? Qual foi a frequência desse tema? (Espera-se que os estudantes percebam que o total de votos recebidos indica essa frequência. Como o tema Alimentação obteve 13 votos ao todo, esse valor é a sua frequência.)
Qual dos temas teve a maior frequência? E qual teve a menor? (Espera-se que os estudantes percebam que justamente foi Alimentação o tema mais frequente, e o menos frequente foi Curiosidades, com apenas 5 votos.)
BNCC em foco:
EF03MA26; competência específica 4
MP191
- O diretor de um grupo de teatro selecionou três peças com custos de produção próximos. Ele quer saber a opinião dos 30 integrantes do grupo para escolher a peça que vai produzir. Ele fez uma tabela com a opinião do grupo sobre a peça mais desejada quanto aos critérios: faixa etária do público e tema da peça.

Comparação dos critérios das peças de teatro
Tabela: equivalente textual a seguir.
|
Critério Peça |
Faixa etária do público |
Tema da peça |
|---|---|---|
|
A |
5 |
8 |
|
B |
16 |
12 |
|
C |
9 |
10 |
Fonte: Grupo de teatro. (mar. 2023)
- Em relação à faixa etária do público, qual peça teve a preferência do grupo de teatro?
_____
PROFESSOR
Resposta: Peça B.
- Considerando o tema da peça, a mais votada é a peça mais barata?
Qual é o custo de produção dela? _____
PROFESSOR
Resposta: Não; o custo de produção é 1.490 reais.
- Agora, complete o gráfico abaixo com as peças avaliadas pelos integrantes do grupo.
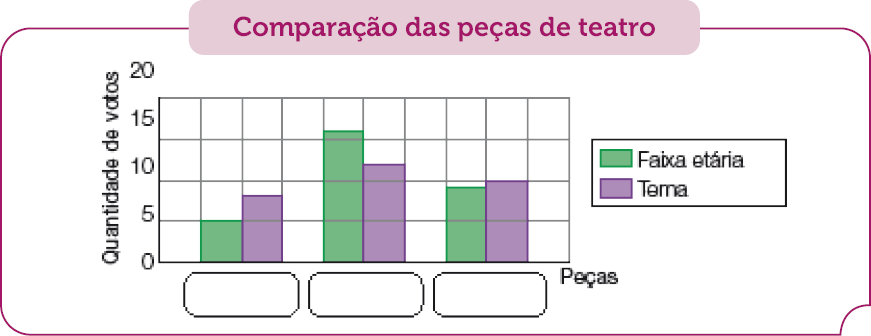
PROFESSOR
Resposta: A, B, CFonte: Grupo de teatro. (mar. 2023)

- Se você
fosse
esse diretor, considerando o valor e a opinião dos integrantes do grupo, qual peça de teatro escolheria?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
Para responder ao item a, os estudantes podem observar a informação direto na tabela: a peça B teve maior preferência em relação à faixa etária do público.
Para o item b, os estudantes precisam obter os totais e comparar os custos de produção:
Peça A: 5 + 8 = 13
13 votos; 1.450 reais;
Peça B: 16 + 12 = 28
28 votos; 1.490 reais;
Peça C: 9 + 10 = 19
19 votos; 1.550 reais.
Portanto, a peça mais votada foi a peça B, que não é a mais barata. O custo de produção da peça mais votada é 1.490 reais.
No item c, os estudantes devem perceber que cada par de colunas nas cores verde e roxa se refere a uma peça e, comparando com os valores da tabela, poderão identificar no gráfico que par representa cada peça.
Para o item d, promova uma discussão com as opiniões dos estudantes.
BNCC em foco:
EF03MA26, EF03MA27; competência específica 4
MP192
O que você aprendeu

- Pinte apenas as figuras não planas.


- Represente o
contorno
de duas figuras retangulares diferentes utilizando 10
palitos
de
fósforo
usados para cada uma. Depois, faça um desenho dessas figuras no espaço abaixo e responda às questões.
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que as duas figuras retangulares possíveis são: Fim da observação.
- O
número
de vértices de uma figura é diferente do
número
de vértices da outra figura?
_____
PROFESSOR
Resposta: Não.
- O
número
de lados de uma figura é diferente do
número
de lados da outra figura?
_____
PROFESSOR
Resposta: Não.
- O que há de diferente entre as duas figuras?
_____
PROFESSOR
Exemplo de resposta: A quantidade de palitos (medida) em cada lado das duas figuras.
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Propicie conversas entre os estudantes a respeito das estratégias que usaram para resolver as atividades.
Atividade 1
Verifique se os estudantes pintaram todas as figuras não planas. Depois de pintarem, peça que classifiquem as figuras como prismas ou pirâmides.
Atividade 2
Comente com os estudantes que nem todos os pontos de junção dos palitos são vértices, pois nem sempre estão nas extremidades dos lados.
No item c, um exemplo de resposta pode ser: A quantidade de palitos em cada lado das duas figuras.
No entanto, os estudantes podem afirmar que o “tamanho” das figuras é diferente, fazendo uma referência não formal à área das figuras. Com o objetivo de ilustrar que, nesse caso, a resposta também é válida, peça a eles que usem palitos para dividir a região interna de cada figura em quadrados de 1 palito de lado, e contem a quantidade de quadrados (unidade de área).
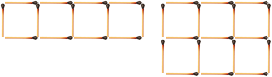
CRÉDITO: GEORGE TUTUMI
Observe que a figura da esquerda tem quatro unidades de área, enquanto a figura da direita tem seis unidades de área.
BNCC em foco:
EF03MA15
MP193
- Observe as pirâmides representadas e complete o quadro.
Quadro: equivalente textual a seguir.
|
Representação de pirâmide |
|
|
|
|---|---|---|---|
|
Número de vértices da face verde |
_____ PROFESSORResposta: 3 |
_____ PROFESSORResposta: 4 |
_____ PROFESSORResposta: 5 |
|
Número total de vértices |
_____ PROFESSORResposta: 4 |
_____ PROFESSORResposta: 5 |
_____ PROFESSORResposta: 6 |

- Desenhe e pinte um par de figuras congruentes que tenham 9 vértices cada uma.
PROFESSOR
Exemplo de desenhos:
- Uma figura em que a superfície tem apenas 1 base pentagonal e 5 faces laterais triangulares é uma figura geométrica plana ou não plana? Qual é o nome dessa figura geométrica?
_____
PROFESSOR
Resposta: É uma figura geométrica não plana; pirâmide de base pentagonal.
Autoavaliação

- Reconheço possibilidades de planificação da superfície de algumas figuras geométricas não planas?
PROFESSOR
Resposta pessoal.
- Consigo comparar características de figuras geométricas planas?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Espera-se que os estudantes identifiquem a face verde como a base de cada pirâmide. Explore o problema de modo que os estudantes discutam uma regularidade nos números obtidos e descubram que, nesse caso, o total de vértices é obtido acrescentando-se 1 unidade à quantidade de vértices da base (face verde). Isso acontece porque, nas pirâmides, os vértices estão na base, exceto um, que é o “encontro” das faces laterais.
Atividade 4
Na atividade, os estudantes poderão criar a representação de qualquer polígono, desde que tenha 9 vértices. Permita que utilizem régua e outras ferramentas para desenhar os polígonos congruentes.
Atividade 5
Promova uma discussão entre os estudantes para que cheguem a uma conclusão sobre o tipo de figura que a descrição cita. Espera-se que concluam ser uma pirâmide. Quando concluírem, peça que usem as pirâmides montadas anteriormente e decidam sobre qual é a pirâmide à qual a descrição faz referência. (Pirâmide de base pentagonal.)
Autoavaliação
Apresente as perguntas aos estudantes para que eles possam avaliar seus conhecimentos geométricos sobre figuras não planas e figuras planas.
Na primeira questão, é possível que os estudantes indiquem o reconhecimento de algumas planificações, especialmente as trabalhadas na Unidade. Incentive-os a verificar se conseguem identificar mais de um tipo de planificação para a mesma figura.
Na segunda questão, a comparação das características pode englobar quantidade de lados e de vértices, que auxiliam na classificação das figuras planas, além da ideia de congruência, explorada na Unidade.
BNCC em foco:
EF03MA14, EF03MA15, EF03MA16
MP194
Comentários para o professor
Conclusão da Unidade 6
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Reconhece e nomeia figuras geométricas não planas e suas características? |
_____ |
_____ |
|
Descreve características de algumas figuras geométricas não planas, relacionando-as com as planificações de sua superfície? |
_____ |
_____ |
|
Identifica faces, arestas e vértices em figuras geométricas não planas? |
_____ |
_____ |
|
Reconhece figuras geométricas planas e suas características? |
_____ |
_____ |
|
Reconhece figuras congruentes, usando sobreposição e desenhos em malhas quadriculadas ou triangulares? |
_____ |
_____ |
|
Faz leitura, interpretação e representação de dados em tabelas e gráficos de barras ou de colunas? |
_____ |
_____ |
|
Resolve problemas que envolvam dados organizados em tabelas de dupla entrada e em gráficos de barras ou de colunas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP195
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: _____ |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |