MP225
Introdução da Unidade 8
O tema reciclagem compõe a abertura desta Unidade, que oferece uma imagem em página dupla a ser explorada pelos estudantes, com a orientação do professor, iniciando, assim, uma primeira abordagem de conceitos matemáticos que serão aprofundados e ampliados.
Com base nos objetos de conhecimento vistos nas Unidades 1, 2 e 5, esta Unidade propõe situações-problema que exploram ideias da multiplicação e da divisão, consolidando o trabalho da Unidade Temática Números no 3º ano do Ensino Fundamental. Além de retomar atividades que exploram habilidades de identificar características do sistema de numeração decimal, por meio da composição e da decomposição de número natural de até quatro ordens; de construir e empregar fatos básicos da adição e da multiplicação para o cálculo mental ou escrito; de resolver problemas de multiplicação (por 2, 3, 4, 5 e 10) com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, utilizando diferentes estratégias de cálculo e registros; e atividades que exploram os significados de metade, terça parte, quarta parte, quinta parte e décima parte.
Pretende-se, com essa abordagem, preparar os estudantes para os conhecimentos a serem desenvolvidos no 4º ano, que abordam a resolução e elaboração de problemas de divisão, cujo divisor tenha no máximo dois algarismos envolvendo os significados de repartição equitativa e de medida com o uso de diferentes estratégias, entre elas, o cálculo por estimativas, o cálculo mental e os algoritmos.
A Unidade Temática Probabilidade e estatística também está contemplada, pois é mais uma vez explorada em problemas cujos dados estão apresentados em tabelas de dupla entrada e em gráficos de colunas ou de barras.
Competência geral favorecida
1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.
Competências específicas favorecidas
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
MP226
UNIDADE 8. Multiplicação e divisão

MANUAL DO PROFESSOR
Objetivos da Unidade
Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural de até 4 ordens.
Construir e utilizar fatos básicos da multiplicação para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de multiplicação com números naturais.
Resolver e elaborar problemas de multiplicação (por 2, 3, 4, 5 e 10) com o significado de adição de parcelas iguais, utilizando diferentes estratégias de cálculo e registros.
Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, com os significados de repartição equitativa e de medida, por meio de estratégias e registros pessoais.
Observar o resto de uma divisão e decidir se a divisão é exata ou não exata.
Reconhecer e nomear os termos de uma divisão.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de divisão com números naturais.
Identificar quando um número é par e quando ele é ímpar.
Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima parte.
Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada e em gráficos de barras.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA07, EF03MA08, EF03MA09, EF03MA26
MP227
Boxe complementar:
Para refletir...
Caio e Melissa visitaram um parque.
Observe a escada de pneus que dá acesso ao escorregador. Escreva uma multiplicação que indica a quantidade de pneus usados para montar essa escada. _____
PROFESSOR
Exemplo de resposta: 2 × 3 = 6Uma máquina troca embalagens por pontos.

Se uma pessoa já tem 10 latas de alumínio, quantas garrafas PET ela precisa para completar os pontos necessários para ganhar 1 bola?
PROFESSOR
Resposta: 10 garrafas PET.Fim do complemento.
MANUAL DO PROFESSOR
Esta Unidade retoma o estudo da multiplicação, ampliando as estratégias de cálculo, e apresenta a divisão e seus significados, desenvolvendo os conceitos tratados no 2º ano.
Explore a cena com os estudantes, incentivando-os a exporem suas opiniões sobre a imagem. Espera-se que eles percebam tratar-se de um parque com brinquedos para crianças. Depois, comente que esse é um parque que promove a reutilização e a reciclagem de materiais.
Verifique se os estudantes observam as informações do cartaz afixado na máquina de troca e no panfleto que o homem segura. Discuta com eles essas informações e registre-as na lousa.
Para refletir…
Espera-se que os estudantes associem a quantidade de pneus usados para montar a escada com as multiplicações 2 × 3 = 6 ou 3 × 2 = 6, observando a disposição retangular deles.
Na segunda questão, com as 10 latas de alumínio, essa pessoa já tem 40 pontos (10 × 4). Para atingir os 60 pontos, faltam 20. Como cada garrafa PET vale 2 pontos, os estudantes podem pensar “Que número vezes 2 dá 20?” ou “Quantos 2 cabem em 20?”, e assim obter 10 garrafas.
MP228
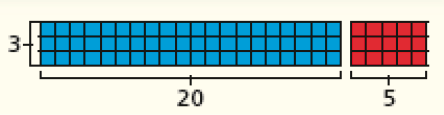
Multiplicação
- Veja abaixo a blusa e o vestido que estão na vitrine. Beatriz e Tânia pretendem comprar a blusa e querem saber o preço total que terão de pagar por ela.

- Observe como as duas calcularam o resultado de 4
X
22 e complete.
Beatriz fez o cálculo mentalmente.
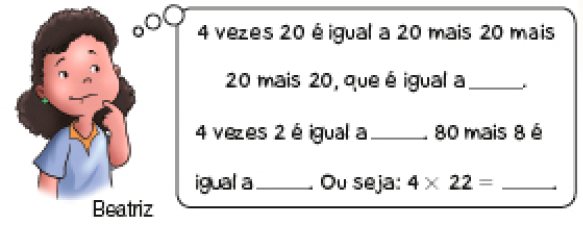
PROFESSOR
Resposta: 80, 8, 88, 88.Tânia calculou com o algoritmo usual.
1. Primeiro, Tânia calculou 4 vezes 2 unidades, que é igual a _____ unidades.
PROFESSOR
Resposta: 8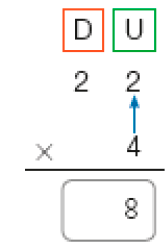

2. Em seguida, Tânia calculou 4 vezes 2 dezenas, que é igual a _____ dezenas.
PROFESSOR
Resposta: 8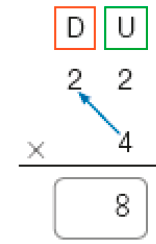
O preço total que elas terão de pagar pela blusa é _____ reais.
PROFESSOR
Resposta: 88- Agora, calcule o
preço
total do vestido.
PROFESSOR
Resposta: 96 reais.
MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural.
Construir e utilizar fatos básicos da multiplicação para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de multiplicação com números naturais.
As atividades dessas páginas iniciam a exploração de diferentes algoritmos da multiplicação, estabelecendo uma relação entre eles: o algoritmo usual, o algoritmo por decomposição e as estratégias de cálculo mental, de modo que os estudantes possam optar por aquele que faz mais sentido para eles. É importante incentivá-los a calcular o resultado de uma multiplicação por meio de diferentes estratégias.
Atividade 1
A atividade mostra a resolução da multiplicação 4 × 22 por meio do cálculo mental e do algoritmo usual.
É fundamental manter a linguagem adequada enquanto o algoritmo é aplicado. Os termos apresentados no livro evidenciam o valor posicional do algarismo em cada ordem. Por exemplo: “Tânia calculou pelo algoritmo usual. Primeiro ela calculou 4 vezes 2 unidades, que é igual a 8 unidades. Depois, calculou 4 vezes 2 dezenas, que é igual a 8 dezenas”. Quando se diz simplesmente 4 vezes 2 é igual a 8, o valor posicional não é destacado, e os estudantes podem tratar as diferentes ordens como “unidades”, o que mecaniza a operação de multiplicação, com prejuízo do significado.
Na atividade 1, se julgar adequado, apresente a mesma multiplicação pelo método da decomposição. Então, ao multiplicar 4 por 22, consideramos o número 22 decomposto em dezenas e unidades, e o número 4 multiplica cada uma dessas partes:
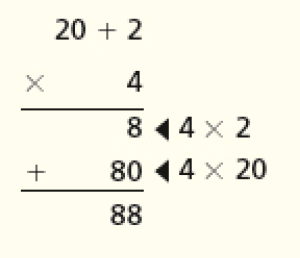
BNCC em foco:
EF03MA02, EF03MA03, EF03MA07
MP229
- Roberto
usa
diariamente 5 dúzias de ovos em sua confeitaria.
- Quantos ovos ele
usa
por dia?
A quantidade de ovos que Roberto usa é o resultado de 5 × 12.
Acompanhe a resolução e complete as lacunas.
- Quantos ovos ele
usa
por dia?
- Primeiro, decompomos o 12:
12 = 10 + 2

- Depois, fazemos 5 vezes 2 unidades, que é igual a 10 unidades.
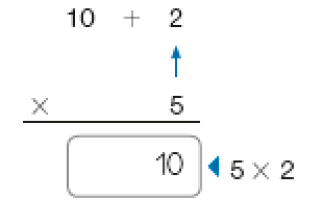
- Em seguida, fazemos 5 vezes 10 unidades, que é igual a 50 unidades.
Finalmente, adicionamos 10 a 50.
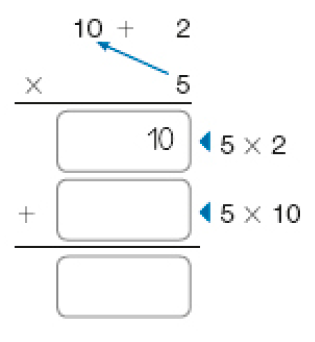
PROFESSOR
Resposta: 50, 50Roberto usa, diariamente, _____ ovos em sua confeitaria.
PROFESSOR
Resposta: 60- Quantos ovos ele
deve
reservar por semana?
_____
PROFESSOR
Resposta: 420 ovos.
- Há quantos lápis de cor em 4 caixas iguais a esta?

Há _____ lápis de cor em 4 caixas iguais a essa.
PROFESSOR
Resposta: 96MANUAL DO PROFESSOR
Atividade 2
Eis um exemplo de como a resolução da multiplicação por decomposição favorece a observação da propriedade distributiva da multiplicação em relação à adição, a qual fica menos evidente no algoritmo usual.
Aproveite a
ideia
de decomposição para discutir com os estudantes sua aplicação em problemas do tipo: “Pedro quer calcular o resultado da multiplicação 5 × 16 em uma calculadora, mas a tecla  está quebrada. Como ele pode resolver esse problema?”. Nesse caso, como a restrição é com o fator 5, ele pode ser decomposto em 4 + 1 ou em 3 + 2, e a multiplicação pode ser realizada destas maneiras:
está quebrada. Como ele pode resolver esse problema?”. Nesse caso, como a restrição é com o fator 5, ele pode ser decomposto em 4 + 1 ou em 3 + 2, e a multiplicação pode ser realizada destas maneiras:
CRÉDITO: ADILSON SECCO
5 × 16 = (4 + 1) × 16 = (4 × 16) + (1 × 16) = 64 + 16 = 80
5 × 16 = (3 + 2) × 16 = (3 × 16) + (2 × 16) = 48 + 32 = 80
Essa atividade possibilita aos estudantes perceberem que há várias maneiras de decompor um número e aplicar a propriedade distributiva da multiplicação em relação à adição.
Peça aos estudantes que comparem suas respostas, incentivando-os a perceber que, apesar de decompor o número 5 de diferentes maneiras, o resultado (ou produto) de 5 × 16 será sempre o mesmo.
Atividade 3
Nessa atividade, os estudantes terão a oportunidade de perceber uma situação do cotidiano em que eles podem utilizar a multiplicação. Espera-se que eles identifiquem a multiplicação 4 × 24 = 96.
Pergunte: “Como vocês resolveram o problema?”. Valorize as estratégias utilizadas pelos estudantes e incentive-os a calcular de mais de uma maneira. Por fim, peça que socializem as diferentes estratégias usadas.
BNCC em foco:
EF03MA02, EF03MA03, EF03MA07
MP230
- Tales tem 16 anos, e a idade de sua avó é quatro vezes a sua. Qual é a idade da avó de Tales?

Observação: Os elementos desta página não estão apresentados em escala de tamanho. Fim da observação.
A avó de Tales tem _____ anos.
PROFESSOR
Resposta: 64- Na casa de Alcides, há 3 estantes com 48 livros em cada uma. No total, quantos livros Alcides tem nas 3 estantes?

No total, Alcides tem livros _____ nas 3 estantes.
PROFESSOR
Resposta: 144- Sheila prepara salgados artesanais. Nas últimas duas semanas, ela fez 6 pacotes com 12 rissoles cada um.

- Quantos rissoles ela fez nessas duas semanas?
_____
PROFESSOR
Resposta: 72 rissoles.
- Se ela preparou metade na primeira semana, quantos fez na segunda semana?
_____
PROFESSOR
Resposta: 36 rissoles.
- Heitor é pintor e fez 9 reproduções da obra ilustrada a seguir, em que há apenas figuras geométricas planas. Quantas figuras geométricas planas há, ao todo, nas 9 reproduções?

Há, ao todo, _____ figuras geométricas.
PROFESSOR
Resposta: 99MANUAL DO PROFESSOR
Objetivos
Construir e utilizar fatos básicos da multiplicação para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de multiplicação com números naturais.
Resolver problemas de multiplicação (por 2, 3, 4, 5 e 10) com o significado de adição de parcelas iguais, utilizando diferentes estratégias de cálculo e registros.
É importante que os estudantes sejam incentivados a calcular o resultado das multiplicações por meio de diferentes estratégias.
Atividades 4, 5, 6 e 7
Essas atividades ampliam a exploração de situações com multiplicações. Sugira aos estudantes que utilizem as estratégias trabalhadas: decomposição ou algoritmo usual. Entretanto, caso surjam outras estratégias, é importante valorizá-las e solicitar a socialização para ampliar repertórios e avaliar a coerência da técnica empregada.
Para a realização das atividades, organize os estudantes em duplas e dê um tempo para que discutam cada questão. Cada dupla deve escolher uma das atividades para apresentar sua resolução na lousa, explicando a estratégia usada. Verifique se todas as atividades foram contempladas nessa escolha; se necessário, indique qual atividade cada dupla deve resolver.
Aproveite a atividade 7 para relembrar as figuras geométricas planas já estudadas. Incentive-os a nomear cada figura identificada na obra ilustrada.
Retome com a turma as questões que geraram mais dificuldades.
Na prática pedagógica, é comum que, depois do aprendizado do algoritmo usual, sejam abandonados os outros métodos de resolução. Contudo, a continuidade na exploração das diferentes formas de cálculo, além de possibilitar aos estudantes a escolha do algoritmo (aquele com o qual mais se identificam ou o mais propício para a situação), contribui para o desenvolvimento geral do raciocínio matemático, assim como para o cálculo mental e as estimativas. Oferecer aos estudantes a oportunidade de confrontar diferentes modos de resolução amplia o repertório de cálculo, agrega significado ao algoritmo usual, favorece a compreensão da estrutura de nosso sistema de numeração e valoriza o sentido numérico.
BNCC em foco:
EF03MA03, EF03MA07
MP231
Mais multiplicação
- Veja as duas maneiras que Felipe usou para calcular o triplo de 25 reais e complete as lacunas.
Cálculo por decomposição
- Primeiro, Felipe decompôs o 25:
25 = 20 + 5
- Em seguida, multiplicou 3 por 5 e, depois, 3 por 20.
- Finalmente, adicionou:
15 + 60 = _____
PROFESSOR
Resposta: 75
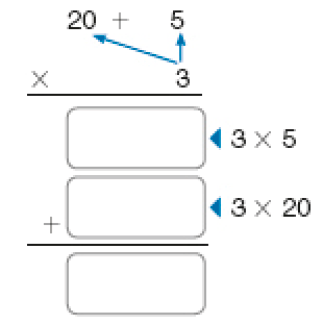
PROFESSOR
Resposta: 15, 60, 75Cálculo com o algoritmo usual
- Primeiro, Felipe multiplicou 3 pelas unidades.
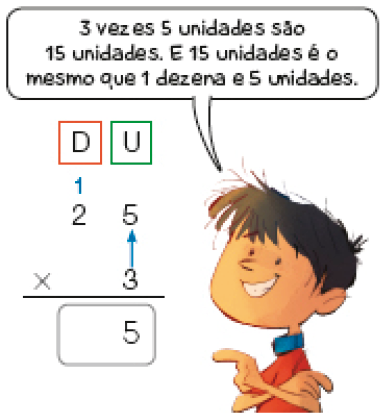
- Depois, multiplicou 3 pelas dezenas.

PROFESSOR
Atenção professor: 7 Fim da observação.Portanto, o triplo de 25 reais é _____ reais.
PROFESSOR
Resposta: 75MANUAL DO PROFESSOR
O método da decomposição evidencia o significado de cada etapa do algoritmo usual, o que favorece a compreensão da estrutura de nosso sistema de numeração e a aplicação da propriedade distributiva da multiplicação em relação à adição. Para esse aprendizado, é importante garantir que diferentes situações associadas à multiplicação sejam trabalhadas pelo método da decomposição.
Sugira aos estudantes que, nas atividades, calculem o resultado das multiplicações de mais de uma maneira: por decomposição e com o algoritmo usual, por exemplo.
Atividade 1
Verifique se os estudantes compreendem a correspondência entre o método por decomposição e o reagrupamento que é feito no algoritmo usual.
O reagrupamento ocorre quando em uma etapa o resultado da multiplicação de um fator pelo algarismo de uma das ordens resulta em um número igual ou superior a 10, o que exige a troca (ou reagrupamento). Na multiplicação apresentada (3 × 25), primeiro multiplicam-se 3 vezes 5 unidades, obtendo-se 15 unidades. Como 15 ultrapassa o número máximo permitido em qualquer ordem (até 9), deve ser realizado o reagrupamento, trocando-se 10 unidades por 1 dezena, que deve-se juntar às demais dezenas, restando 5 unidades. Depois, multiplicam-se 3 vezes 2 dezenas, o que resulta em 6 dezenas; adicionando 1 dezena do reagrupamento obtêm-se 7 dezenas, de modo que o resultado final é igual a 75.
Na atividade 1, se julgar adequado, explore a representação em malha quadriculada para que os estudantes reconheçam as etapas do algoritmo usual e do método da decomposição:

CRÉDITO: ADILSON SECCO
BNCC em foco:
EF03MA02, EF03MA03
MP232

- Veja como Cláudio calculou o resultado de 9 × 17 com uma calculadora que estava com a tecla
 quebrada.
quebrada.
1ª etapa

2ª etapa

- Agora, imagine que sua calculadora esteja com a tecla
 quebrada. Desenhe as teclas para:
quebrada. Desenhe as teclas para:
- calcular 5 × 36 usando as teclas
 e
e  ;
;
PROFESSOR
Resposta: Exemplo de desenho:PROFESSOR
1ª etapa:
PROFESSOR
2ª etapa:
- calcular 5 × 83 usando as teclas
 e
e  .
.
PROFESSOR
Resposta: Exemplo de desenho:PROFESSOR
1ª etapa:PROFESSOR

PROFESSOR
2ª etapa:PROFESSOR

MANUAL DO PROFESSOR
Objetivos
Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural.
Construir e utilizar fatos básicos da multiplicação para o cálculo mental ou escrito.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de multiplicação com números naturais.
Resolver problemas de multiplicação (por 2, 3, 4, 5 e 10) com o significado de adição de parcelas iguais, utilizando diferentes estratégias de cálculo e registros.
Atividade 2
Sugira aos estudantes que façam essa atividade em duplas. A obrigatoriedade de usar a tecla  no item a e a tecla
no item a e a tecla  no item b exige que os estudantes façam a decomposição de um dos fatores em cada multiplicação. No exemplo de desenhos do item a, repetimos as teclas 1, 4 e 4, e no exemplo de desenhos do item b, repetimos as teclas 4, 9 e 8, para destacar a 2ª etapa em ambos os casos. Essa repetição é, na maioria das calculadoras, desnecessária. Discuta com os estudantes essa questão.
no item b exige que os estudantes façam a decomposição de um dos fatores em cada multiplicação. No exemplo de desenhos do item a, repetimos as teclas 1, 4 e 4, e no exemplo de desenhos do item b, repetimos as teclas 4, 9 e 8, para destacar a 2ª etapa em ambos os casos. Essa repetição é, na maioria das calculadoras, desnecessária. Discuta com os estudantes essa questão.
CRÉDITO: ADILSON SECCO
A atividade explora a propriedade distributiva da multiplicação em relação à subtração quando sugere que 9 × 17 é o mesmo que 10 × 17 − 1 × 17 e é o mesmo que (10 − 1) × 17. A exigência do uso, em cada expressão, de uma multiplicação e adição ou subtração, garante a aplicação da ideia de distribuição.
Atividade 3
A atividade propicia aos estudantes conferir se fizeram boas estimativas e, eventualmente, ajustar suas estratégias de cálculo mental. Espera-se que eles arredondem os fatores de dois algarismos para a dezena inteira mais próxima.
BNCC em foco:
EF03MA03
MP233
- Observe a estimativa que João fez para descobrir quanto é 3 × 29.


- Faça uma estimativa do resultado de cada multiplicação abaixo. Depois, calcule o resultado exato com o algoritmo usual.
- 5 × 18
PROFESSOR
Exemplo de estimativa: 100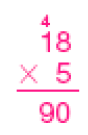
- 4 × 27
PROFESSOR
Exemplo de estimativa: 120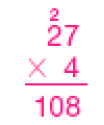
- 3 × 23
PROFESSOR
Exemplo de estimativa: 60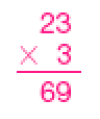
- 6 × 16
PROFESSOR
Exemplo de estimativa: 90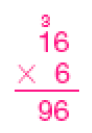
- Observe o gráfico que mostra os pontos feitos por Raquel no campeonato de basquete do ano passado.
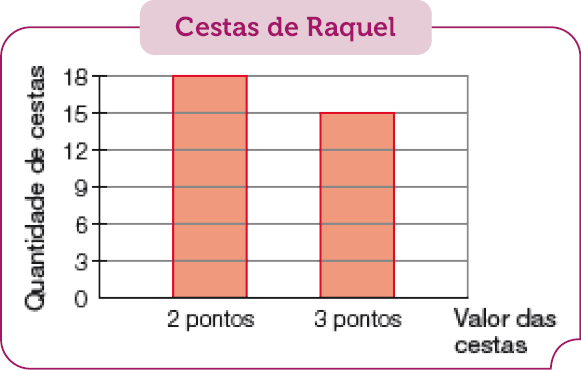
Fonte: Dados fornecidos pela jogadora. (2023)
- Quantos pontos Raquel fez no campeonato?
_____
PROFESSOR
Resposta: 81 pontos.
MANUAL DO PROFESSOR
Atividade 4
Na atividade, os estudantes trabalham a leitura e a interpretação de um gráfico de colunas com o intuito de obter os dados para calcular os pontos que Raquel fez com seus arremessos. Uma possibilidade de resolução é considerar que todos os arremessos sejam de 2 pontos, e, depois, adicionar 15 pontos, pois 15 deles são de 3 pontos (18 + 15 = 33; 33 × 2 = 66; 66 + 15 = 81), ou considerar que todos os arremessos sejam de 3 pontos e depois subtrair 18 pontos, já que 18 deles valem 2 pontos (18 + 15 = 33; 33 × 3 = 99; 99 – 18 = 81). Os estudantes também podem calcular a pontuação com os arremessos de 2 pontos (18 × 2 = 36), com os arremessos de 3 pontos (15 × 3 = 45) e adicionar os dois totais: 36 + 45 = 81. Observe as estratégias utilizadas nos cálculos pelos estudantes. Se necessário, deixe material manipulável à disposição deles (como o Material Dourado).
Sugestão de atividade
Maneiras de multiplicar
Peça aos estudantes que resolvam por decomposição e pelo algoritmo usual as seguintes multiplicações:
5 × 13
4 × 23
4 × 24
6 × 15
Se julgar oportuno, sugira que explorem as multiplicações na malha quadriculada.
Por exemplo, no caso de 5 × 13:
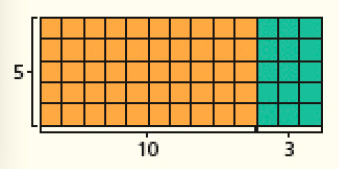
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF03MA03, EF03MA07, EF03MA26
Sugestão de leitura para o estudante
Livro
RAMOS, Luiza Faraco. Onde estão as multiplicações? São Paulo: Ática, 2021. (Coleção Turma da Matemática.)
O livro conta as aventuras de Adelaide e seus amigos, que tentam ajudar Binha a descobrir o que é multiplicar e em que situações a multiplicação pode ser usada. No decorrer da história, os personagens descobrem que a multiplicação não é somente coisa de escola, pois é utilizada em diversas situações do dia a dia. O livro traz ainda sugestões de jogos e atividades que podem ser realizados em sala de aula com diferentes materiais.
MP234
Situações de divisão
- Renato tem 18 figos para repartir igualmente entre 3 caixas. Cada caixa ficará com quantos figos?
_____
PROFESSOR
Resposta: 6 figos.
- Desenhe 3 sacolas e 9 bolinhas igualmente repartidas entre elas.
PROFESSOR
Exemplo de desenho:
- Agora, faça o que se pede.
- Escreva uma multiplicação que represente,
nessa
situação, o total de
bolinhas
nas sacolas.
_____
PROFESSOR
Resposta: 3 × 3 = 9
- Escreva uma divisão que represente,
nessa
situação, o
número
de
bolinhas em cada sacola. _____
PROFESSOR
Resposta: 9 ÷ 3 = 3
- Pinte de acordo com o que se pede em cada caso.
- A figura abaixo deve ser dividida em 3 partes de mesmo tamanho. Pinte cada uma dessas partes de uma cor.
PROFESSOR
Exemplo de pintura:
- A figura abaixo deve ser dividida em 4 partes de mesmo tamanho. Pinte cada uma dessas partes de uma cor.
PROFESSOR
Exemplo de pintura: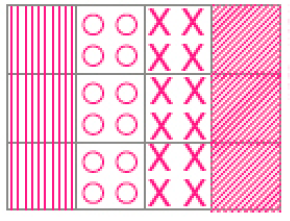
MANUAL DO PROFESSOR
Objetivo
Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, com o significado de repartição equitativa, por meio de estratégias e registros pessoais.
Atividade 1
A repartição em partes iguais envolve duas variáveis e uma relação constante entre elas. Na situação apresentada, as duas variáveis são a quantidade de figos (18) e a de caixas (3), envolvidas em uma relação constante: quantidade de figos para cada caixa. A dificuldade da divisão está em perceber qual é a relação constante. Os estudantes podem se valer de diferentes estratégias de resolução. Uma delas é a representação da situação com desenho. Eles podem, por exemplo, distribuir um figo por caixa, até completar a distribuição dos 18 figos, e depois contar os figos de cada caixa.
Se julgar oportuno, mostre aos estudantes a verificação do resultado por meio da multiplicação, isto é, raciocinando “de trás para a frente”.
Atividade 2
Assim como a multiplicação pode ser compreendida como uma adição de quantidades iguais, pode-se compreender a divisão como uma subtração de quantidades iguais. O problema pode ser resolvido colocando-se uma bolinha em cada uma das três sacolas:
9 − 3 = 6 (havia 9 bolinhas e foram distribuídas 3, restaram 6 bolinhas);
6 − 3 = 3 (das 6 bolinhas restantes, foram distribuídas 3, restaram 3 bolinhas);
3 − 3 = 0 (das 3 bolinhas restantes, todas foram distribuídas, não restaram bolinhas).
Como a distribuição foi feita três vezes, o resultado da divisão de 9 por 3 é 3.
Associar a divisão à ideia de repartir é, de modo geral, uma noção intuitiva para estudantes dessa faixa etária. Essa concepção intuitiva, no entanto, não inclui a ideia de divisão em partes iguais. É muito comum eles falarem em “repartir ao meio” como “dividir em duas partes”, mas não necessariamente iguais; daí a importância de se discutir esse aspecto conceitual.
BNCC em foco:
EF03MA08
MP235

- Quatro amigos foram a uma lanchonete e gastaram, abaixo, a quantia representada ao lado. Sabendo que a conta foi repartida igualmente entre eles, responda às questões.

- Quantos reais cada um pagou?
_____
PROFESSOR
Resposta: 11 reais.
- Escreva uma divisão que corresponda a essa situação.
_____ ÷ _____ = _____
PROFESSOR
Resposta: 44 ÷ 4 = 11
- Observe a tirinha. Depois responda às questões.

- Como deveria ser a divisão para que todas as crianças
recebessem
a mesma quantidade de sorvete?
_____
PROFESSOR
Resposta: 4 ÷ 4 = 1; um sorvete para cada criança.
- Você acha justa a divisão apresentada na tirinha? Por quê?
PROFESSOR
Resposta pessoal.
- Invente um problema que envolva os textos dos quadros abaixo e que possa ser resolvido com uma operação de divisão. Depois, peça a um
colega
que o resolva.
PROFESSOR
Resposta pessoal.7 dúzias de rosas
igualmente
4 vasos

MANUAL DO PROFESSOR
Atividade 3
Após a atividade, ofereça aos estudantes outros modelos de preenchimento em espaços quadriculados, mas nos quais não seja possível preencher todo o espaço, ou seja, em que a divisão não seja exata.
Uma possível ampliação dessa atividade é pedir aos estudantes que repartam a mesma figura dessa atividade em 5 partes de mesmo tamanho. Espera-se que eles percebam que um quadriculado de 4 por 3 totaliza 12 quadrinhos e que não é possível reparti-lo em 5 partes de mesmo tamanho (uma vez que o 12 não aparece nos agrupamentos de 5 em 5: 5, 10, 15 etc.).
Atividade 4
As cédulas e as moedas representadas também vão auxiliar os estudantes no processo de divisão, considerando que há exatamente 4 cédulas de 10 reais e 4 moedas de 1 real para uma repartição em 4 partes iguais.
Após a resolução, explore-a mudando a quantia em dinheiro disponível: 3 cédulas de 10 reais e 2 moedas de 1 real. Nesse caso, a quantidade de cédulas de cada valor não pode ser distribuída uma a uma. Uma possibilidade é trocar cada cédula de 10 reais por 10 moedas de 1 real. Isso pode ser indicado por 10 traços para cada cédula, formando 30 traços, que, adicionados aos 2 traços correspondentes às moedas de 1 real já existentes, resultam em 32 traços, os quais podem ser repartidos em 4 partes iguais:

CRÉDITO: ADILSON SECCO
32 ÷ 4 = 8
Atividade 5
Na atividade, os estudantes são incentivados a refletir sobre a diferença entre “repartir em partes iguais” e simplesmente “repartir”.
Em uma roda de conversa, peça aos estudantes que opinem sobre repartir de maneira justa ou não.
Atividade 6
Proponha aos estudantes que inventem mais problemas como esse com outras condições. Por exemplo, 7 dúzias de flores para serem distribuídas igualmente em 4 vasos.
(72 ÷ 4 = 18)
Após a resolução da atividade, peça aos estudantes que registrem seu problema (já reformulado, se for o caso) em uma tira de papel, que será guardada em uma “caixa de problemas”. Ao longo do estudo desta Unidade, sorteiam-se 2 ou 3 desses problemas para a turma resolver.
BNCC em foco:
EF03MA08
MP236
- Heloísa tem 20 laranjas para fazer bolos. Para cada receita, são necessárias 5 laranjas.
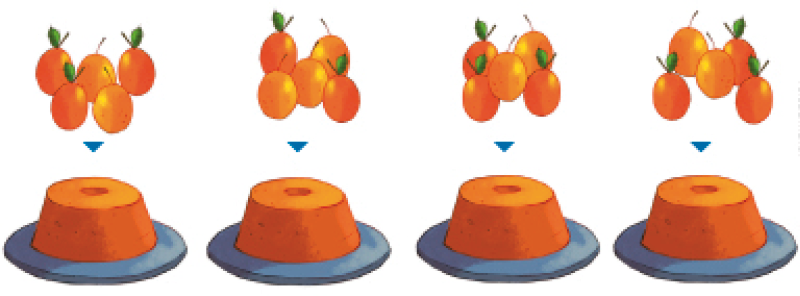
Observação: Os elementos não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.
Agora, responda.
- Quantos
bolos
Heloísa poderá fazer com essas 20 laranjas?
_____
PROFESSOR
Resposta: 4 bolos.
- Escreva a divisão que representa,
nessa
situação, o
número
de
bolos
que poderão ser feitos.
_____
PROFESSOR
Resposta: 20 ÷ 5 = 4

- Luciana tem 15 botões para pregar nas camisas. Ela precisa pregar 5 botões em cada camisa. Complete a ilustração desenhando as camisas e os botões que faltam.
PROFESSOR
Exemplo de desenho: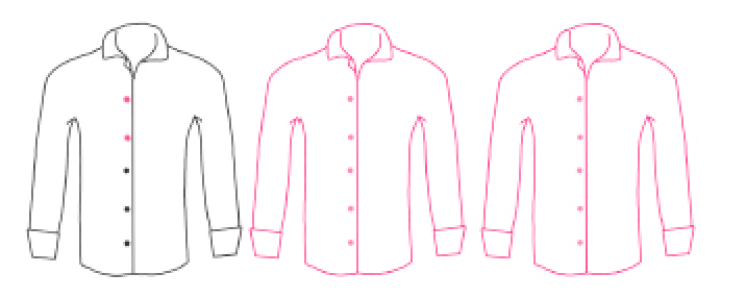
- Agora, responda às questões.
- Quantos grupos de 5
botões
é possível fazer com 15 botões?
_____
PROFESSOR
Resposta: 3
- Quantas camisas foram necessárias?
_____
PROFESSOR
Resposta: 3 camisas.
MANUAL DO PROFESSOR
Objetivo
Resolver problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, com o significado de medida, por meio de estratégias e registros pessoais.
Nessas páginas, as atividades desenvolvem situações de divisão com o significado de medida (quantas vezes uma quantidade cabe em outra), ideia na qual se apoia o algoritmo usual da divisão e que contribui para as estimativas no cálculo com divisões, e possibilitam ampliar a compreensão da relação entre a multiplicação e a divisão (exata), desenvolvendo a noção de operações inversas.
Atividade 7
Espera-se que os estudantes percebam que precisam descobrir quantos grupos de 5 laranjas é possível formar com 20 laranjas, ou seja, devem saber quantas vezes o 5 cabe em 20. Para isso, eles podem fazer a seguinte pergunta: “Que número vezes 5 resulta em 20?”, transformando o problema em uma situação de multiplicação: 4 × 5 = 20. Assim, os estudantes podem concluir que 5 cabe 4 vezes em 20, e, portanto, poderão ser feitos 4 bolos.
Atividade 8
Os estudantes devem identificar os dados do problema (quantos botões Luciana tem, quantos botões tem cada camisa) para desenhar os 2 botões na camisa já ilustrada e desenhar mais 2 camisas com 5 botões em cada uma. Eles devem relacionar esses dados aos termos da divisão 15 ÷ 5 = 3, ou seja, Luciana precisou de 3 camisas.
Atividade 9
É possível que os estudantes utilizem a multiplicação para resolver a situação. Por exemplo, para o item c, uma multiplicação do 5 que resulte em 30, ou seja: 6 × 5.
Peça aos estudantes que escrevam a divisão que está associada a cada situação. Espera-se que façam:
30 ÷ 2 = 15
30 ÷ 3 = 10
30 ÷ 5 = 6
30 ÷ 10 = 3
BNCC em foco:
EF03MA08
MP237
- A mãe de Sílvia fez 30 pulseiras para um evento beneficente. Sílvia vai ajudá-la a embalar as pulseiras. Ela tem embalagens para 2, 3, 5 ou 10 pulseiras.

- Se Sílvia embalar as pulseiras de 2 em 2, de quantas embalagens ela precisará? _____
PROFESSOR
Resposta: 15 embalagens.- Se ela embalar as pulseiras de 3 em 3, quantas embalagens serão necessárias? _____
PROFESSOR
Resposta: 10 embalagens.- Se escolher a embalagem para 5 pulseiras, de quantas embalagens ela precisará? _____
PROFESSOR
Resposta: 6 embalagens.- E se a escolha for por uma embalagem para 10 pulseiras, ela precisará de quantas embalagens? _____
PROFESSOR
Resposta: 3 embalagens.- Resolva os problemas.
- Quantas garrafas de 2 litros de água são necessárias para encher um recipiente de 20 litros?
PROFESSOR
Resposta: 10 garrafas.
- Quantos grupos de 6 pessoas podemos formar com 34 pessoas? Sobrarão pessoas? Se sobrarem, quantas?
PROFESSOR
Resposta: 5 grupos; sim, sobrarão 4 pessoas.
- Quantas garrafas de 2 litros de água são necessárias para encher um recipiente de 20 litros?
MANUAL DO PROFESSOR
Atividade 10
No item b, é proposta uma divisão não exata, adiantando o assunto do próximo tópico. Os estudantes podem começar a compreender que, quando o resto é diferente de zero (há sobras) em uma divisão, ela não é exata. Peça a eles que apresentem as estratégias que usaram para chegar à resposta; alguns estudantes podem desenhar 34 traços ou bolinhas na folha de papel, tentando agrupá-las de 6 em 6, como no esquema abaixo, e observar que sobram 4:

Outros podem simplesmente verificar que, na lista de multiplicações do 6, o resultado 34 não aparece, pois 5 × 6 = 30 e 6 × 6 = 36.
Sugestão de atividade
As figuras que cabem no esquema
Observe o esquema a seguir, que representa uma parede que será totalmente coberta por figuras formadas por 4 azulejos com formato quadrangular, conforme a figura (modelo) abaixo. Reparta o esquema da parede em figuras iguais ao modelo, de cores diferentes. Quantas dessas figuras serão usadas? (6 figuras.)
Exemplo de pintura:
Esquema da parede
Figura
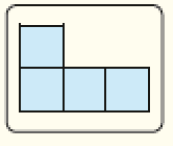
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
Sugestão de leitura para o professor
Artigo
MORO, Maria Lucia. Estruturas multiplicativas e tomada de consciência: repartir para dividir. Disponível em: http://fdnc.io/eU6. Acesso em: 12 fev. 2021.
O artigo aborda os níveis de tomada de consciência das relações envolvidas na operação de divisão, de acordo com as proposições dos pesquisadores Jean Piaget e Gérard Vergnaud. No estudo apresentado, desenvolvido com estudantes de 7 e 8 anos de idade de escolas públicas, foram trabalhadas tarefas de repartir coleções em quantidades iguais e a produção de notações adequadas a elas.
BNCC em foco:
EF03MA08
MP238
Divisão exata e divisão não exata
- Uma partida de basquete é disputada por times com 5 jogadores cada.
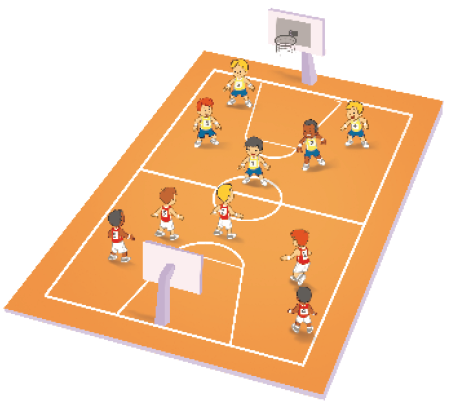
- Quantos times podem ser formados com 20 jogadores?
Sobram
jogadores? Quantos?
_____
PROFESSOR
Resposta: 4 times; não sobram jogadores.
- Se fossem 23 jogadores, quantos times de basquete poderiam ser formados? Sobrariam jogadores? Quantos?
_____
PROFESSOR
Resposta: 4 times; sim; sobrariam 3 jogadores.
- Leia o diálogo entre as crianças e responda às questões.

- A divisão de 18 por 3 é exata? Explique.
_____
PROFESSOR
Resposta: Sim. A divisão de 18 por 3 é exata porque o resto é zero.
- A divisão de 31 por 6 é exata?
_____
PROFESSOR
Resposta: Não. A divisão de 31 por 6 não é exata porque o resto é diferente de zero.
MANUAL DO PROFESSOR
Objetivos
Resolver problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, por meio de estratégias e registros pessoais.
Observar o resto de uma divisão e decidir se a divisão é exata ou não exata.
Atividade 1
Explore com os estudantes as diferentes possibilidades de resolução. Uma delas é representar os jogadores por desenhos e formar grupos de 5 jogadores.
Os estudantes também podem calcular com o auxílio de material manipulável. Por exemplo: os 23 jogadores do item b podem ser representados por 23 lápis. Ao repartir o total de lápis em grupos de 5, eles percebem facilmente que é possível formar 4 times e que sobram 3 jogadores.
Ressalte a diferença dessas situações de divisão: uma em que não há sobra de jogadores e a outra em que sobram 3.
Atividade 2
Explore com a turma as informações dos balões de fala. Peça aos estudantes que usem estratégias próprias para efetuar cada divisão. Incentive-os a fazer desenhos, um importante apoio na realização dos cálculos. É possível que alguns recorram à estratégia de contar em ordem decrescente a partir do número dado. Por exemplo:
No item a, em 18 ÷ 3, a contagem inicia em 17, em grupos de 3:
(17, 16, 15); (14, 13, 12), (11, 10, 9); (8, 7, 6); (5, 4 ,3); (2, 1, 0)
A contagem acabou em zero e não há sobra (resto zero): a divisão é exata.
No item b, em 31 ÷ 6, a contagem inicia em 30, em grupos de 6:
(30, 29, 28, 27, 26, 25); (24, 23, 22, 21, 20, 19); (18, 17, 16, 15, 14, 13); (12, 11, 10, 9, 8, 7); (6, 5, 4, 3, 2, 1)
A contagem acabou em 1, sobra 1 unidade: a divisão é não exata.
BNCC em foco:
EF03MA08
MP239

- Desenhe os peixinhos nos aquários, de acordo com o que a menina está dizendo. Depois, complete.
PROFESSOR
Exemplo de desenho:
Em cada aquário, ficarão _____ peixinhos.
PROFESSOR
Resposta: 4Divisão: 12 ÷ 3 = ______
PROFESSOR
Resposta: 4- Essa divisão é exata ou não exata? Por quê?
_____
PROFESSOR
Resposta: Exata, porque não sobra peixinho.
- Complete a tabela que Tiago fez e, depois, responda às questões.
Tiago gasta 4 reais de passagem de ônibus no trajeto de ida ao trabalho.
Gastos com transporte
Tabela: equivalente textual a seguir.
|
Número de trajetos feitos |
1 |
2 |
3 |
4 |
5 |
6 |
|---|---|---|---|---|---|---|
|
Quantia gasta (em real) |
4 |
8 |
12 |
16 |
20 |
24 |
PROFESSOR
Resposta: 8, 12, 16, 20, 24Fonte: Dados fornecidos por Tiago. (2023)
- Quantos desses
trajetos
Tiago poderá fazer com 26 reais?
Sobrará dinheiro? Quanto? _____
PROFESSOR
Resposta: Tiago poderá fazer 6 trajetos; sim, sobrarão 2 reais.
- Que divisão representa essa situação?
_____
PROFESSOR
Resposta: 26 ÷ 4 = 6 (resto 2).
- Lúcio tem uma
folha
de papel como mostra o
modelo
abaixo.

- É possível traçar linhas de 2 em 2 centímetros do início ao fim da folha?
_____
PROFESSOR
Resposta: Sim.
- E de 4 em 4 centímetros?
_____
PROFESSOR
Resposta: Não.PROFESSOR
Atenção professor: Peça aos estudantes que expliquem como pensaram para responder às questões. Fim da observação.
- É possível traçar linhas de 2 em 2 centímetros do início ao fim da folha?
MANUAL DO PROFESSOR
Atividade 3
Espera-se que os estudantes percebam que, distribuindo igualmente os 12 peixes entre os 3 aquários, obtêm-se 4 peixes em cada aquário e não sobra peixe. Desse modo, a divisão 12 ÷ 3 = 4 tem resto zero, o que indica que a divisão é exata.
Atividade 4
O uso da tabela favorece a percepção de proporcionalidade pela observação da regularidade: para cada aumento de 1 unidade no número de trajetos, aumentam-se 4 reais na quantia de dinheiro gasta, ou seja, a relação é de 1 para 4.
A tabela possibilita que os estudantes percebam que, para realizar 6 trajetos, são necessários 24 reais. Portanto, com 26 reais Tiago poderá fazer 6 trajetos e sobrarão 2 reais. Essa situação pode ser associada à seguinte divisão: 26 ÷ 4 = 6 (resto 2).
Atividade 5
Peça aos estudantes que expliquem como pensaram para responder às questões.
Proponha que discutam e experimentem algumas estratégias de resolução antes de fazerem as intervenções que julgar necessárias.
BNCC em foco:
EF03MA07, EF03MA08
MP240
Estratégias de cálculo
- Tamires tem 56 pingentes e quer fazer colares com 7 pingentes em cada um.
- Quantos colares ela poderá fazer?

1 colar :1 × _____ = _____ - _____ pingentes
PROFESSOR
Resposta: 7, 7, 72 colares: 2 × _____ = _____ - _____ pingentes
PROFESSOR
Resposta: 7, 14, 143 colares: 3 × _____ = _____ - _____ pingentes
PROFESSOR
Resposta: 7, 21, 21...
8 colares: _____ × _____ = _____ - _____ pingentes
PROFESSOR
Resposta: 8, 7, 56, 56Divisão na chave
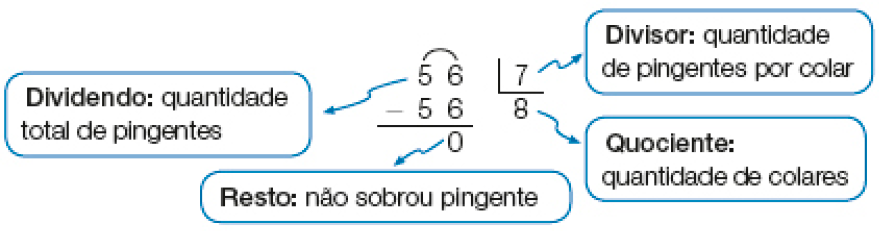
Tamires poderá fazer _____ colares.
PROFESSOR
Resposta: 8- Se a quantidade de pingentes em cada colar
fosse
9, quantos colares poderiam ser feitos? Sobrariam pingentes? Quantos?
_____
PROFESSOR
Resposta: Poderiam ser feitos 6 colares; sobrariam 2 pingentes.MANUAL DO PROFESSOR
Objetivos
Resolver problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero.
Reconhecer e nomear os termos de uma divisão.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de divisão com números naturais.
Nessas páginas inicia-se a representação da divisão na chave, preparando os estudantes para o algoritmo usual da divisão, e por estimativas.
Nas atividades dessas páginas, os estudantes têm a oportunidade de se apropriarem dos termos dessa operação e de reconhecerem regularidades entre esses termos.
Atividade 1
Na divisão de 56 por 7, a questão a ser respondida é: “Quantas vezes 7 cabe em 56?”. No item a, as multiplicações apresentadas no texto (1 × 7 = 7, 2 × 7 = 14, ..., 8 × 7 = 56) levam ao quociente da divisão (8) e ao resto zero.
Visualizar a subtração (56 − 56 = 0) na chave possibilita melhor compreensão do processo, sobretudo para os estudantes que têm dificuldade com o cálculo mental e se apoiam nos registros escritos.
Na chave, é importante apresentar o posicionamento dos termos na divisão: dividendo, divisor, quociente e resto.
No item b, os estudantes devem fazer a divisão de 56 por 9. E, para isso, responder à pergunta: “Quantas vezes 9 cabe em 56?”. Espera-se que eles concluam que poderiam ser feitos 6 colares e que sobrariam 2 pingentes.
BNCC em foco:
EF03MA08
MP241
- Veja dois cálculos diferentes para encontrar, por estimativas, o resultado da divisão de 96 por 6 e complete-os.
Cálculo de Ricardo
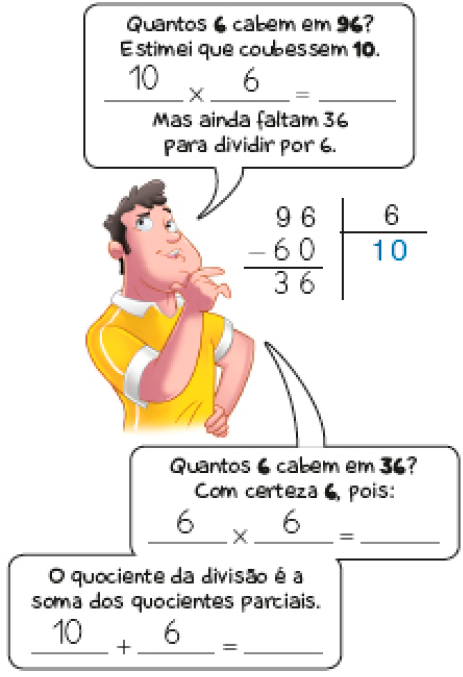
PROFESSOR
Resposta: 10 × 6 = 60PROFESSOR
6 × 6 = 36PROFESSOR
10 + 6 = 16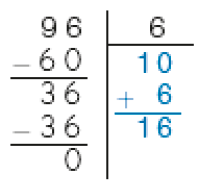
Cálculo de Rosa

PROFESSOR
Resposta: 12 × 6 = 72PROFESSOR
4 × 6 = 24PROFESSOR
12 + 4 = 16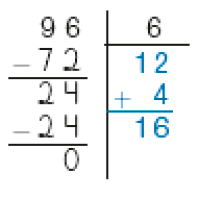
Portanto, os dois cálculos resultaram no quociente _____.
PROFESSOR
Resposta: 16MANUAL DO PROFESSOR
Atividade 2
Como a estimativa se apoia no cálculo mental, é importante comentar com os estudantes que é mais fácil usar dezenas inteiras ou multiplicações do tipo vezes 5 para as estimativas iniciais, pois esses resultados são mais fáceis de serem memorizados. Por exemplo, para a divisão apresentada na atividade (96 ÷ 6), eles podem estimar o quociente 10, uma vez que 10 × 6 = 60, menor que 96.
Peça aos estudantes que comparem a solução obtida com a de um colega e ressalte que há diferentes maneiras de realizar estimativas. Verifique se percebem que, apesar de as estimativas serem diferentes, se elas forem realizadas corretamente, os cálculos levarão ao mesmo quociente.
Para o bom desempenho na divisão por estimativas, é fundamental os estudantes compreenderem que a divisão corresponde a subtrações sucessivas.
A divisão por estimativas é um bom método para o entendimento do algoritmo usual da divisão e para a melhora do cálculo mental. O dividendo deve ser tomado como um número total e o quociente vai sendo obtido pela estimativa de quantas vezes o divisor cabe no dividendo.
No caso da atividade 2, o quociente 20 não seria uma estimativa possível, pois 20 × 6 = 120, que é maior que 96.
Fazer 12 × 6 = 72 para a primeira estimativa na divisão 96 ÷ 6 não é uma opção simples, pois os estudantes teriam de realizar mentalmente o cálculo da multiplicação.
BNCC em foco:
EF03MA08
MP242
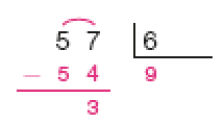
- Efetue cada divisão representada na chave. Depois, responda à questão.
PROFESSOR
Exemplo de respostas: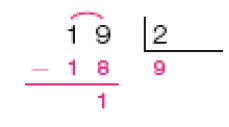
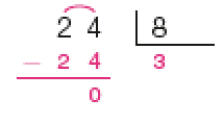
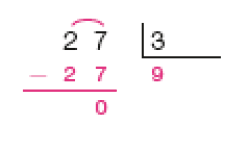
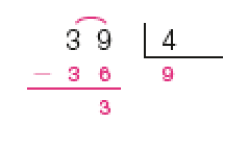
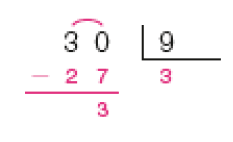
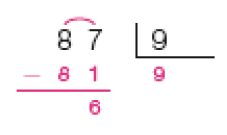
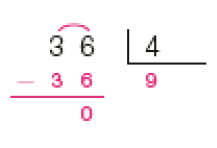
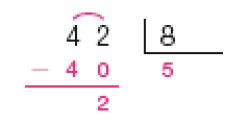


- Das divisões acima, quais têm resto igual a 3? Explique a um colega como você pensou para responder a essa questão.
PROFESSOR
Resposta: As divisões que têm resto igual a 3 são 39 ÷ 4, 57 ÷ 6 e 30 ÷ 9.

- Samuel quer comprar uma impressora como esta, pagando-a em 4 parcelas iguais. O valor de cada parcela será maior ou
menor
que 100 reais?
_____
PROFESSOR
Resposta: Maior.

MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, por meio de estratégias e registros pessoais.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de divisão com números naturais.
Atividade 3
Provavelmente os estudantes farão as divisões como na atividade 2. À medida que memorizam os resultados das multiplicações, os estudantes fazem os registros auxiliares menos detalhados. Por exemplo, na divisão 39 ÷ 4 (item d), os registros das multiplicações (1 × 4 = 4, 2 × 4 = 8, 3 × 4 = 12, …, 9 × 4 = 36) podem ser feitos fora da chave, para que se identifique o quociente 9. Como 39 − 36 = 3, o resto é igual a 3. É importante incentivar a turma a, antes de realizar os cálculos, estimar os possíveis quociente e resto de uma divisão. Como o resto deve ser sempre menor que o divisor, na divisão 39 ÷ 4 os restos possíveis seriam 0, 1, 2 e 3. Converse com os estudantes sobre isso. Observe se os estudantes confundem resto com quociente ou divisor.
Atividade 4
A questão aborda uma situação comum do dia a dia em que é importante fazer cálculos mentais para estimar o valor de uma parcela em uma compra. Pergunte: “Como vocês chegaram a essa resposta?”. Uma das possibilidades é observar que, como 4 × 100 = 400, ainda restam 12 unidades para dividir por 4, o que mostra que o valor de cada parcela será maior que 100. Como 12 ÷ 4 = 3, o quociente exato é obtido por 100 mais 3, ou seja, 103.
BNCC em foco:
EF03MA08
MP243
- Leia como Sérgio distribuiu 92 mangas em 4 caixas. Depois, responda às questões.

- Qual é a divisão que pode representar a distribuição feita por Sérgio?
_____
PROFESSOR
Resposta: 92 ÷ 4 = 23
- Faça estimativas e encontre o quociente de cada divisão.
- 76 ÷ 4 = _____
_____
PROFESSOR
Resposta: 19- 93 ÷ 3 = _____
_____
PROFESSOR
Resposta: 31- 85 ÷ 5 = _____
_____
PROFESSOR
Resposta: 17- 96 ÷ 4 = _____
_____
PROFESSOR
Resposta: 24


- Compare suas estimativas com as de um
colega
e confira se elas foram as mesmas.
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que fazer estimativas diferentes não altera o quociente final da divisão. Fim da observação.
MANUAL DO PROFESSOR
Atividade 5
Sugira aos estudantes que registrem na chave, como na atividade 2, as estimativas que Sérgio fez para dividir as 92 mangas em 4 caixas.
Atividade 6
É importante incentivar os estudantes a apresentar diferentes modos de resolver as divisões propostas. No item a, por exemplo, a divisão 76 ÷ 4 pode ser realizada de vários modos.Vejamos dois deles:
Começar estimando 10, pois 10 × 4 = 40; então restam 76 − 40 = 36. Como 9 × 4 = 36, o quociente estimado é 9. Portanto, o quociente da divisão 76 × 4 será 10 mais 9, ou seja, 19.
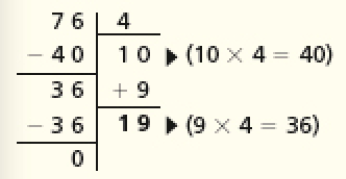
Começar estimando 20, pois 20 × 4 = 80, que é maior que o dividendo (76); esse valor não é registrado na representação na chave. Então, uma vez que a diferença entre o valor estimado (80) e o dividendo (76) é igual a 4, basta diminuir 1 unidade no valor estimado (20 − 1 = 19) para obter nova estimativa. Nesse caso, a estimativa registrada corresponde ao quociente da divisão.
BNCC em foco:
EF03MA08
MP244
Número par e número ímpar
- Faça o que se pede.
- Em cada caso, divida as bolinhas em 2 grupos com a mesma quantidade. Atenção: cada grupo deve ter a maior quantidade de bolinhas possível.
1º caso
PROFESSOR
Exemplo de agrupamentos:
2º caso
- Em qual dos casos foi possível formar 2 grupos com a mesma quantidade sem sobrarem bolinhas? Em qual dos casos sobrou 1 bolinha?
_____
PROFESSOR
Resposta: No 1º caso; no 2º caso.
- Na aula de Educação Física, a professora pediu aos estudantes que fizessem um exercício em duplas. Na turma, há 28 estudantes.
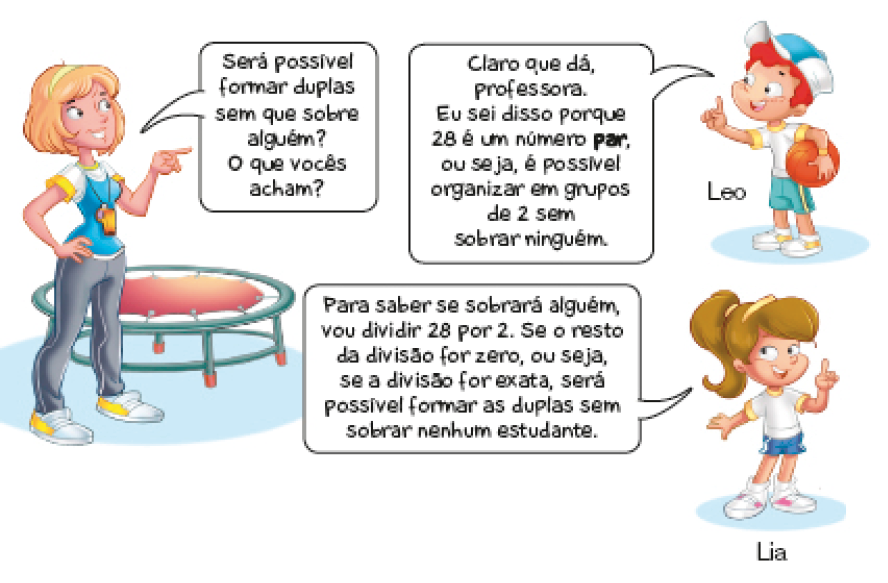
- Leo e Lia estão certos?
_____
PROFESSOR
Resposta: Sim.
- Quantas duplas serão formadas?
_____
PROFESSOR
Resposta: 14 duplas.
MANUAL DO PROFESSOR
Objetivos
Resolver problemas de divisão de um número natural por outro (até10), com resto zero e com resto diferente de zero, por meio de estratégias e registros pessoais.
Utilizar diferentes procedimentos de cálculo mental e escrito para resolver situações de divisão com números naturais.
Identificar quando um número é par e quando ele é ímpar.
Nessas páginas, explora-se o conceito de número par e de número ímpar com base na divisão de um número natural por 2. Por exemplo, em 36 ÷ 2, a divisão tem resto zero (é exata); como não há sobra, conclui-se que 36 é par. Em 37 ÷ 2, a divisão tem resto igual a 1 (é não exata); como há sobra de 1 unidade, conclui-se que 37 é ímpar.
Atividade 1
Nessa atividade, o 1º caso foi ilustrado com um número par de bolinhas, e o 2º caso, com um número ímpar. Espera-se que os estudantes percebam que foi possível dividir a quantidade par de bolinhas em duas partes iguais sem haver sobras; no grupo com quantidade ímpar de bolinhas, ao separá-las em duas partes iguais, sobrou 1 bolinha.
Atividade 2
Na situação proposta, os estudantes podem fazer a divisão de 28 por 2 pelo método que preferirem. Pode-se perguntar a eles: “Se sobrasse 1 estudante, a quantidade de estudantes seria par ou ímpar?”. Espera-se que eles concluam que, nesse caso, o número de estudantes seria ímpar.
Apresente para a turma outros números, para que os estudantes verifiquem se são pares ou ímpares.
BNCC em foco:
EF03MA08
MP245
- Descubra se o número é par ou ímpar.
-
37:_____
PROFESSOR
Resposta: Ímpar
- 62:
_____
PROFESSOR
Resposta: Par.
- 45:
_____
PROFESSOR
Resposta: Ímpar.
- 54:
_____
PROFESSOR
Resposta: Par.
- Observe a sequência de figuras. Depois, resolva o problema.
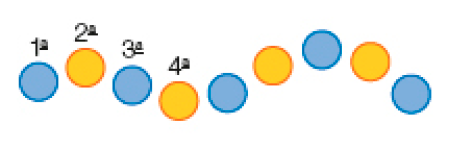
- Continuando com a mesma regra de alternar uma figura azul e uma figura amarela, qual será a cor da 12ª figura?
_____
PROFESSOR
Resposta: Amarela.
- Qual será a cor da 23ª figura?
_____
PROFESSOR
Resposta: Azul.
- As figuras de cor azul correspondem a números pares ou a números
ímpares? _____
PROFESSOR
Resposta: A números ímpares.
- E as figuras de cor amarela?
_____
PROFESSOR
Resposta: A números pares.
- Carolina brincava com uma moeda quando percebeu que, virando 2 vezes a moeda que inicialmente estava com a face coroa voltada para cima, essa moeda mostrava novamente a face coroa.

- Virando 3 vezes a moeda, que face ficaria voltada para cima?
_____
PROFESSOR
Resposta: Cara.
- E virando 10 vezes?
_____
PROFESSOR
Resposta: Coroa.
MANUAL DO PROFESSOR
Atividade 3
Deixe que os estudantes decidam que estratégia usar. Eles podem desenhar agrupamentos de 2 (como sugerido na atividade 2) ou dividir cada número por 2 (para verificar se a divisão é exata). Incentive-os a descobrir se cada número é par ou ímpar de diferentes maneiras.
Atividade 4
Reconhecer padrões e analisá-los por meio de conceitos matemáticos são importantes habilidades a serem desenvolvidas. Na atividade, a ideia de número par e de número ímpar está associada à disposição de figuras de cores que se alternam: as figuras de cor azul correspondem às posições ímpares, e as de cor amarela, às posições pares. Pergunte aos estudantes como eles descobriram a cor das figuras solicitadas na atividade. Observe se eles continuam a sequência até a posição solicitada ou se percebem que, ao descobrir se essa posição corresponde a um número par ou ímpar, podem determinar a cor da bolinha que ocupa essa posição.
Atividade 5
É pertinente que os estudantes verifiquem de maneira concreta a regularidade que se apresenta na movimentação de moeda sugerida nessa atividade. Para isso, proponha que, em duplas, façam experimentos com uma moeda de verdade, virando-a várias vezes e observando qual face fica voltada para cima. Espera-se que os estudantes percebam que ao virar a moeda um número par de vezes, a face que fica voltada para cima é a mesma do início, e que, ao virar a moeda um número ímpar de vezes, a face que fica voltada para cima é a oposta.
Incentive os estudantes a observarem as regularidades em sequências que possam ser associadas a números pares ou a números ímpares, como sugerem as atividades 4 e 5. Eles podem perceber que, se o algarismo das unidades é par (0, 2, 4, 6, 8), o número do qual faz parte também é par; se o algarismo das unidades é ímpar (1, 3, 5, 7, 9), o número do qual faz parte também é ímpar. Outra regularidade que os estudantes podem observar é a alternância de números pares e de números ímpares na sequência dos números naturais: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, e assim por diante. Essa observação possibilita verificar que tanto os números pares quanto os ímpares aparecem em acréscimos de 2 unidades a partir de um número par e de um número ímpar, respectivamente.
BNCC em foco:
EF03MA08
MP246
Jogo: Par ou ímpar?
Material: 2 dados numerados da página 217 e um quadro como o mostrado abaixo.
Tabela: equivalente textual a seguir.
|
Rodada |
Dado 1 |
Dado 2 |
Pontos |
|---|---|---|---|
|
1 |
_____ |
_____ |
_____ |
|
2 |
_____ |
_____ |
_____ |
|
3 |
_____ |
_____ |
_____ |
|
4 |
_____ |
_____ |
_____ |
|
5 |
_____ |
_____ |
_____ |
|
6 |
_____ |
_____ |
_____ |
|
TOTAL |
_____ |
Jogadores: 2
Regras:
- Os jogadores decidem quem começará o jogo.
- Cada jogador, na sua vez, lança os dados e anota no quadro o número sorteado em cada um dos dados.
- A verificação dos pontos a
serem
marcados é feita de acordo com os números sorteados nos dados e da seguinte maneira:
Tabela: equivalente textual a seguir.
|
Os números sorteados são |
O jogador marca |
|---|---|
|
um número par e um número ímpar |
1 ponto |
|
dois números pares |
2 pontos |
|
dois números ímpares |
3 pontos |
|
dois números iguais e pares |
4 pontos |
|
dois números iguais e ímpares |
5 pontos |
- Após 6 rodadas, o jogador deve adicionar os pontos obtidos.
- Vence quem conseguir o maior total de pontos.
- Caso os jogadores obtenham totais iguais, os dois ganham.
Questões sobre o jogo
- Quais são os números pares possíveis de
serem
sorteados nos dados?
_____
PROFESSOR
Resposta: 2, 4 e 6.
- Quais são os números ímpares que há em cada dado?
_____
PROFESSOR
Resposta: 1, 3 e 5.
MANUAL DO PROFESSOR
Objetivos
Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, por meio de estratégias e registros pessoais.
Identificar quando um número é par e quando ele é ímpar.
Organize os estudantes em duplas e auxilie-os na montagem dos dois dados, na leitura e na compreensão das regras. Incentive as duplas a inicialmente observarem os números nos dados. Pergunte: “Que faces contêm um número par? E um número ímpar?”. Peça que simulem situações com os dois dados que representem cada pontuação (considerando cada face em um dado). Por exemplo:
1 ponto: face 4 e face 1
2 pontos: face 4 e face 2
3 pontos: face 3 e face 1
4 pontos: face 2 e face 2
5 pontos: face 1 e face 1
Questões sobre o jogo
Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões propostas.
As questões 1, 2 e 3 tratam do reconhecimento direto de se os números das faces são pares ou ímpares. No item c da questão 3, os estudantes também devem aplicar a pontuação apresentada para verificar quem fez mais pontos na rodada.
As questões 4 e 5 propõem reflexões mais elaboradas sobre situações do jogo.
BNCC em foco:
EF03MA08
MP247
- Observe os dados lançados por Cássio e por Amanda em uma rodada do jogo.
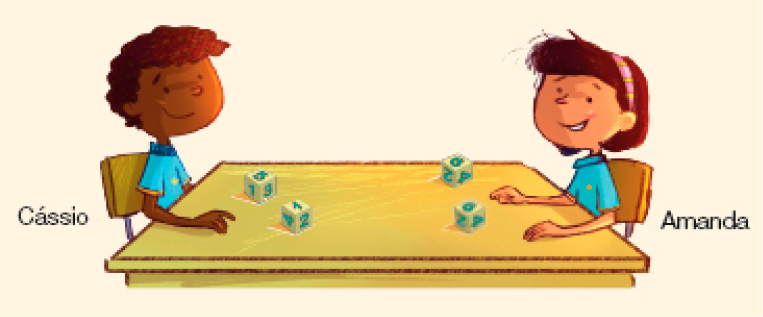
- Quais foram os números sorteados por Amanda? São números pares ou números ímpares?
_____
PROFESSOR
Resposta: 6 e 6; são dois números pares.
- Cássio sorteou que números? São números pares ou números ímpares?
_____
PROFESSOR
Resposta: 5 e 1; são dois números ímpares.
- Quem obteve o maior total de pontos
nessa
rodada?
_____
PROFESSOR
Resposta: Amanda.
- Imagine que você e seu
colega
estejam adicionando os pontos obtidos em uma partida. Seu
colega
já adicionou os
dele
e obteve, no total, 18 pontos. Se até a quinta rodada você obteve 12 pontos, ainda é possível que você ganhe essa partida do jogo? Por quê?
_____
PROFESSOR
Resposta: Não.PROFESSOR
Atenção professor: Exemplo de explicação: De acordo com as regras, um jogador pode marcar no máximo 5 pontos em cada rodada. Então, mesmo que eu tivesse marcado 5 pontos na sexta rodada, eu obteria, no total, 17 pontos. Fim da observação.
- Pensando nos pontos obtidos nas rodadas, é melhor que os números sorteados sejam: um
número
par e um
número
ímpar, dois números pares, dois números ímpares, dois números iguais e pares ou dois números iguais e ímpares? Por quê?
_____
PROFESSOR
Resposta: Dois números iguais e ímpares. Exemplo de explicação: São os números que, quando sorteados, fazem o jogador marcar mais pontos (5 pontos).
MANUAL DO PROFESSOR
Variações
Os jogadores de cada dupla sorteiam qual será o “par” e qual será o “ímpar”.
Cada jogador, na sua vez, lança os dados e multiplica o resultado das faces voltadas para cima. Se o resultado (produto) for par, o jogador “par” ganha 1 ponto; se o produto for ímpar, o jogador “ímpar” ganha 1 ponto. O jogo continua por 5 minutos. Quando você disser “parou!”, verifica-se quem fez mais pontos em cada dupla.
Após algumas rodadas, os estudantes perceberão que esse não é um jogo justo: o jogador “par” tem mais chance de vencer. Afinal, qualquer número, par ou ímpar, multiplicado por um número par terá produto par. Assim, as possibilidades são:
27 resultados pares:
1 × 2; 1 × 4; 1 × 6; 2 × 1; 2 × 2; 2 × 3; 2 × 4; 2 × 5; 2 × 6; 3 × 2; 3 × 4; 3 × 6; 4 × 1; 4 × 2; 4 × 3; 4 × 4; 4 × 5; 4 × 6; 5 × 2; 5 × 4; 5 × 6; 6 × 1; 6 × 2; 6 × 3; 6 × 4; 6 × 5; 6 × 6
9 resultados ímpares:
1 × 1; 1 × 3; 1 × 5; 3 × 1; 3 × 3; 3 × 5; 5 × 1; 5 × 3; 5 × 5
Essa variação do jogo, além de trabalhar com produtos pares e produtos ímpares, possibilita analisar o que é mais provável obter como produto de dois números (números pares e números ímpares).
BNCC em foco:
EF03MA08
MP248
Metade e terço


- Pinte, com a mesma cor, cada número e sua metade correspondente.

PROFESSOR
Resposta: 2040: verde, 1.620: azul, 2.460: laranja, 3.500: rosa, 4.680: cinza, 4.280: roxo.PROFESSOR
1.230: laranja, 1.750: rosa, 2.140: roxo, 2.340: cinza, 1.020: verde, 810: azul.- Leia e descubra quantos reais cada amigo de Ana tem.

Marcelo tem _____ reais e Bia tem _____ reais.
PROFESSOR
Resposta: 5, 10.- A altura de Alice é igual à terça parte da altura do pai dela. Sabendo disso, descubra e marque com X a medida da altura de Alice e do pai dela.
Medida da altura de Alice (em centímetro).
( ) 62
( ) 53
( ) 92
PROFESSOR
Resposta correta: 62.Medida da altura do pai de Alice (em centímetro).
( ) 179
( ) 186
( ) 184
PROFESSOR
Resposta correta: 186.MANUAL DO PROFESSOR
Objetivos
Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima partes.
Resolver problemas cujos dados estão apresentados em gráfico de colunas.
Atividade 1
Nessa atividade, os estudantes devem mobilizar seus conhecimentos sobre metade de um número e associá-lo com a divisão (exata) por 2. Antes de realizarem a atividade, sugira que separem 6 lápis com cores diferentes para auxiliá-los na pintura. Caso eles apresentem dificuldade, peça que realizem a atividade em duplas, para que possam compartilhar as estratégias utilizadas.
Atividade 2
Além dos conhecimentos sobre “metade”, os estudantes devem mobilizar o que já viram sobre a terça parte de um número e associá-la com a divisão (exata) por 3.
Atividade 3
Uma maneira de os estudantes descobrirem a relação entre os números da esquerda e os da direita é determinando a terça parte de todos os números que podem indicar a altura do pai de Alice e buscarem o resultado obtido. Desse modo, identificarão que a terça parte de 186 é 62.
BNCC em foco:
EF03MA09
MP249
Quarta parte, quinta parte e décima parte
- Artur tinha 12 figurinhas para colar em um álbum. Quantas figurinhas ele já colou nestas páginas?
Artur colou a quarta parte da quantidade de figurinhas que possui.
12 ÷ 4 = _____
PROFESSOR
Resposta: 3.A quarta parte de 12 é _____.
PROFESSOR
Resposta: 3.Artur já colou _____ figurinhas nessas páginas.
PROFESSOR
Resposta: 3.- O gráfico a seguir mostra o número de aparelhos eletrônicos comprados por uma rede de lojas. Sabendo que esses aparelhos devem ser distribuídos igualmente entre 4 lojas, responda às questões.
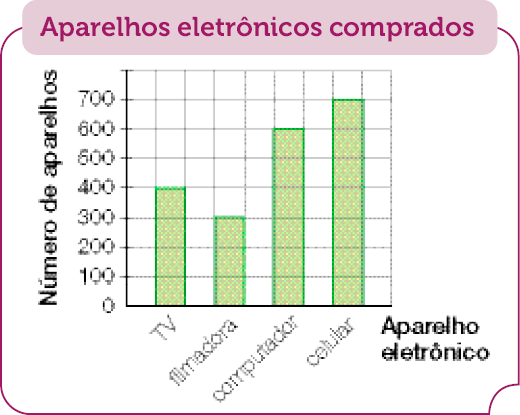
Fonte: Rede de lojas. (dez. 2023)
- Quantas TVs cada loja receberá?
_____
PROFESSOR
Resposta: 100 TVs.
- Quantos computadores cada loja receberá?
_____
PROFESSOR
Resposta: 150 computadores.
Boxe complementar:
Desafio

Nícolas resolveu as duas divisões a seguir usando uma calculadora.

CRÉDITO: SIDNEY MEIRELES
120 ÷ 2 = 60
120 ÷ 4 = 30

Como você pode explicar o fato de o resultado da segunda divisão ser a metade do primeiro, e não o dobro, já que 4 é o dobro de 2?
PROFESSOR
Resposta pessoal.Fim do complemento.
MANUAL DO PROFESSOR
Atividade 1
Espera-se que os estudantes percebam que o cálculo da quarta parte de uma quantidade está associado a repartir essa quantidade em 4 partes iguais e que cada uma dessas partes obtidas corresponde à quarta parte.
Os estudantes podem efetuar esse cálculo concretamente, repartindo em 4 partes iguais as figurinhas que cabem nessas páginas do álbum, cercando cada uma dessas partes com uma linha. Desse modo, poderão verificar que, em cada parte, ficarão 3 figurinhas, o que mostra que 3 figurinhas é a quarta parte de 12 figurinhas.
Atividade 2
A atividade explora a leitura e interpretação de um gráfico de colunas. Aproveite para sugerir aos estudantes que inventem outras perguntas envolvendo os dados desse gráfico.
Desafio
Uma possível explicação: apesar de 4 ser o dobro de 2, o quociente da divisão de um número por 4 não será o dobro do quociente desse mesmo número por 2. Na verdade, o quociente da divisão por 4 será a metade do quociente da divisão por 2, para um mesmo dividendo.
BNCC em foco:
EF03MA09, EF03MA26
MP250
- Observe as figuras e, em seguida, complete as lacunas.
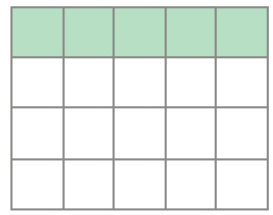
A quantidade de quadradinhos pintados representa a quarta parte do total de quadradinhos.
20 ÷ 4 = _____
PROFESSOR
Resposta: 5A quarta parte de 20 é _____.
PROFESSOR
Resposta: 5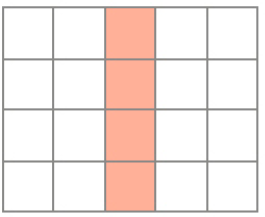
A quantidade de quadradinhos pintados representa a quinta parte do total de quadradinhos.
20 ÷ 5 = _____
PROFESSOR
Resposta: 4A quinta parte de 20 é _____.
PROFESSOR
Resposta: 4
A quantidade de quadradinhos pintados representa a décima parte do total de quadradinhos.
20 ÷ 10 = _____
PROFESSOR
Resposta: 2A décima parte de 20 é _____.
PROFESSOR
Resposta: 2- Para uma visita à Estação de Reciclagem da cidade, os 185 estudantes serão organizados em grupos com a mesma quantidade de estudantes em 5 ônibus. Cada ônibus viajará com quantos estudantes?
Cada ônibus viajará com _____ estudantes.
PROFESSOR
Resposta: 37- Laura foi ao banco e retirou 120 reais de sua conta-corrente. A metade dessa quantia ela usou para pagar a despesa no mercado. Com a quinta parte da quantia retirada, pagou a despesa na farmácia.
- Quantos reais Laura gastou no mercado?
_____
PROFESSOR
Resposta: 60 reais.
- Quantos reais Laura gastou na farmácia?
_____
PROFESSOR
Resposta: 24 reais.
- Quantos reais Laura gastou no mercado?
MANUAL DO PROFESSOR
Objetivos
Associar o quociente de uma divisão com resto zero de um número natural por 2, 3, 4, 5 e 10 às ideias de metade, terça, quarta, quinta e décima parte.
Resolver e elaborar problemas de divisão de um número natural por outro (até 10), com resto zero e com resto diferente de zero, por meio de estratégias e registros pessoais.
Para as atividades dessas páginas, disponibilize o Material Dourado para apoiar as estratégias desenvolvidas pelos estudantes.
Atividade 3
A possibilidade de contar a quantidade de quadrinhos de cada figura é um facilitador para os estudantes. Eles também poderão verificar geometricamente as relações apresentadas.
Atividade 4
Os estudantes podem representar o número 185 com as peças do Material Dourado (1 placa, 8 barrinhas e 5 cubinhos) e depois reparti-las igualmente em 5 partes. Desse modo, eles perceberão a necessidade de fazer as trocas: a placa por 10 barrinhas, que juntando-se às 8 resulta em 18 barrinhas. Distribuindo igualmente as 18 barrinhas em 5 partes, ficam 3 barrinhas em cada parte e sobram 3 barrinhas, que deverão ser trocadas por 30 cubinhos e acrescentados aos 5 cubinhos iniciais, obtendo-se 35 cubinhos.
Ao distribuir igualmente os 35 cubinhos nas 5 partes, ficam 7 cubinhos em cada parte e não há sobra. Assim, os estudantes verificam que cada parte ficou com 3 barrinhas e 7 cubinhos, ou seja, 37.
Atividade 5
Verifique se os estudantes percebem que devem encontrar a metade e a quinta parte partindo da quantia toda (120 reais).
Aproveite para explorar a atividade perguntando: “Qual foi o total gasto por Laura?” (84 reais); “Quanto sobrou de dinheiro para ela?” (36 reais).
BNCC em foco:
EF03MA08, EF03MA09
MP251
- A professora Tatiana vai distribuir 100 retalhos de tecido para 4 grupos de estudantes realizarem um trabalho, da seguinte maneira:
- O primeiro grupo receberá a quarta parte do total de retalhos.
- O segundo grupo receberá a quinta parte do total de retalhos.
- O terceiro grupo receberá a décima parte do total de retalhos.
- O quarto grupo receberá o restante dos retalhos.
Qual grupo receberá a maior quantidade de retalhos?
O _____ grupo receberá a maior quantidade de retalhos.
PROFESSOR
Resposta: quarto- Santiago preparou 18 sobremesas. Das sobremesas preparadas, um terço é de chocolate e metade é de baunilha.

- Quantas sobremesas de chocolate foram preparadas?
_____
PROFESSOR
Resposta: 6 sobremesas.
- Quantas sobremesas de baunilha foram preparadas?
_____
PROFESSOR
Resposta: 9 sobremesas.

- Calcule.
- a quinta parte de 50:
_____
PROFESSOR
Resposta: 10
- a quarta parte de 60:
_____
PROFESSOR
Resposta: 15
- a décima parte de 140:
_____
PROFESSOR
Resposta: 14
- a terça parte de 60:
_____
PROFESSOR
Resposta: 20
- a metade de 220 :
_____
PROFESSOR
Resposta: 110
- a quinta parte de 50:
_____
MANUAL DO PROFESSOR
Atividade 6
É importante verificar se os estudantes efetuam o cálculo das partes solicitadas sempre usando os 100 retalhos e observar as estratégias utilizadas para obter a quantidade de retalhos que o quarto grupo receberá. Espera-se que eles percebam que, depois de determinar as partes que receberão o primeiro, o segundo e o terceiro grupos, precisam adicionar o total de retalhos dos três grupos e retirar o total obtido dos 120 retalhos, para obter a quantidade de retalhos recebida pelo quarto grupo. Depois, devem comparar as quantidades recebidas por cada grupo e identificar a maior delas. Propicie aos estudantes o entendimento de cada uma dessas etapas.
Também é possível que alguns estudantes subtraiam do total cada quantidade apurada, etapa por etapa, em vez de fazer isso apenas ao final da distribuição.
Atividade 7
Além dos itens a e b, os estudantes podem calcular quantas sobremesas sobraram que não são de chocolate nem de baunilha.
Atividade 8
Essa atividade possibilita aos estudantes revisitar os conhecimentos construídos sobre o cálculo de partes de um número e identificar possíveis dúvidas. Proponha uma roda de conversa para que eles exponham as estratégias usadas e as dificuldades encontradas, de modo que possam ampliar seu repertório e ampliar e reorganizar seus conhecimentos sobre esse tema com troca de ideias com os colegas.
BNCC em foco:
EF03MA09
MP252
Matemática em textos
Leia
Dia da Consciência Negra

LEGENDA: Introduzida no Brasil como luta pelos africanos escravizados, a capoeira é hoje praticada como jogo e esporte. Roda de capoeira no município de Salvador, Bahia, em 2019. FIM DA LEGENDA.
Os africanos começaram a ser trazidos da África para o Brasil por volta de 1550. Durante quase 350 anos, a maior parte do trabalho no Brasil foi realizada por africanos escravizados.
Hoje, os negros e os pardos representam mais da metade da população de nosso país, e sua influência está presente na música, na dança, na língua, na culinária, no folclore etc.
Com tantas contribuições para a cultura brasileira, os negros passaram a valorizar mais sua identidade. Para preservar essa história tão importante, atualmente se comemora, em alguns municípios do Brasil, no dia 20 de novembro, o Dia da Consciência Negra. A data foi escolhida pois, no mesmo dia, em 1695, ocorreu a morte de Zumbi, o mais importante líder do quilombo dos Palmares.
O quilombo dos Palmares chegou a ter uma população de até 30 mil pessoas reunidas em terras do atual estado de Alagoas. Esse quilombo foi a mais forte e duradoura comunidade de escravizados fugidos da América. Nos quilombos, eles resistiam ao escravismo e lutavam pela liberdade. Palmares durou cerca de 100 anos.
MANUAL DO PROFESSOR
Objetivos
Associar o quociente de uma divisão com resto zero de um número natural por 2 à ideia de metade.
Interpretar texto e identificar informações contidas nele.
O texto trata de um assunto indispensável à compreensão da história de nosso país e da formação de nosso povo. Durante a leitura, explique aos estudantes que os quilombos eram aldeias dentro da mata formadas por negros escravizados que se rebelaram contra as péssimas condições de vida e a violência do trabalho escravo. Comente que ainda hoje existem comunidades remanescentes de quilombos em nosso país (seus habitantes são chamados quilombolas).
A discussão, do ponto de vista matemático, de assuntos de relevância social e cultural favorece uma educação matemática crítica.
BNCC em foco:
EF03MA09; competência geral 1; competência específica 2
Sugestão de trabalho interdisciplinar
O conteúdo dessa seção pode ser trabalhado de forma interdisciplinar:
com Língua Portuguesa: contribuições da cultura afro-brasileira para nossa língua, como
estudo do significado de algumas palavras derivadas dela;
com Educação Física: estudo das diversas modalidades de brincadeiras, jogos, danças e esportes relacionados com a cultura afro-brasileira;
com História: período escravagista;
com Geografia: estruturação das relações de trabalho.
MP253
Responda
- Quantos anos, aproximadamente, durou o quilombo dos Palmares?
_____
PROFESSOR
Resposta: Cerca de 100 anos.
- Em que data é comemorado o Dia da Consciência Negra?
_____
PROFESSOR
Resposta: 20 de novembro.
- Cite algumas contribuições que os negros
trouxeram
para a cultura do Brasil.
_____
PROFESSOR
Resposta: Sua influência está presente na música, na dança, na língua, na culinária, no folclore etc.
- Marque com um
X
a frase correta, de acordo com o texto.
( ) De cada 100 brasileiros, quase 50 são negros ou pardos.
( ) De cada 100 brasileiros, menos de 20 são negros ou pardos.
( ) De cada 100 brasileiros, mais de 50 são negros ou pardos.
PROFESSOR
Resposta correta: De cada 100 brasileiros, mais de 50 são negros ou pardos.
Analise

- Em sua opinião, qual é a mensagem transmitida na frase da imagem abaixo?

LEGENDA: Manifestantes durante protesto contra o racismo no Largo da Batata, no município de São Paulo, São Paulo, em 2020. FIM DA LEGENDA.
Aplique

- No dia 13 de maio de 1888, a escravidão foi abolida no Brasil. Contudo, até hoje acontecem situações de discriminação racial. O que você pensa sobre isso?


- Converse com seus colegas e diga se você já se sentiu discriminado em alguma situação. Presenciou algum fato que envolvesse discriminação?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Responda
Nas atividades 1, 2 e 3 trabalhamos dados apresentados no texto, oferecendo subsídios aos estudantes para que situem os fatos no tempo e compreendam as informações.
Na atividade 4, espera-se que os estudantes consigam interpretar a informação do texto, de que os negros e os pardos representam mais da metade da população e associá-la à frase correta: de cada 100 brasileiros, mais de 50 são negros ou pardos.
Analise
Converse com os estudantes sobre a frase na faixa e proponha uma roda de conversa sobre o assunto.
Aplique
As atividades propostas possibilitam aos estudantes discutir alguns aspectos relacionados à discriminação racial de modo que eles percebam a importância da construção de uma sociedade justa e solidária.
BNCC em foco:
EF03MA09; competência geral 1; competência específica 2
MP254
Compreender informações
Resolver problemas com base em gráficos e tabelas
- Olga irá reformar seu consultório odontológico e quer revestir parte da parede de alguns cômodos com pastilhas.
Preço das pastilhas
Tabela: equivalente textual a seguir.
|
Material |
Preço |
|---|---|
|
Vidro |
20 reais |
|
Mármore |
41 reais |
|
Porcelana |
49 reais |
Fonte: Tabela de preços de lojas de material de construção. (jan. 2023)
Ela foi a algumas lojas de material de construção e pesquisou os preços de pastilhas de 3 tipos de material. Observe a tabela ao lado com os melhores preços encontrados para cada tipo de material.
Os preços que Olga pesquisou são para placas de pastilhas de 30 cm por 30 cm, ou seja, peças quadradas.
Observe o gráfico abaixo, que mostra a quantidade de placas que Olga usará em cada cômodo.
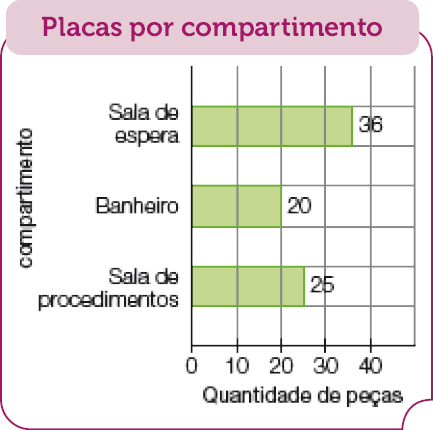
Fonte: Dados fornecidos por Olga. (jan. 2023)
- Ela quer usar pastilhas de mármore para revestir a sala de espera, mas o orçamento para esse cômodo é de 1.000 reais. Ela conseguirá usar o tipo de material que deseja? Por quê?
_____
PROFESSOR
Resposta: Não, pois o valor (1.476 reais) ultrapassa o orçamento.
- Para a sala de procedimentos o orçamento de Olga é de 1 500 reais. Qual é o tipo de material que ela pode escolher?
_____
PROFESSOR
Resposta: Qualquer um, pois todos estão dentro do orçamento (500 reais, 1.025 reais e 1.225 reais).
- Qual é o orçamento que Olga precisa ter para todos os compartimentos do consultório se quiser usar apenas pastilhas de porcelana?
_____
PROFESSOR
Resposta: 3.969 reais.
MANUAL DO PROFESSOR
Objetivo
Resolver problemas cujos dados estão apresentados em tabelas de dupla entrada e em gráficos de barras.
O foco dessas páginas é a interpretação de informações veiculadas por meio de tabelas de dupla entrada e de gráficos na resolução de problemas.
Atividade 1
Leia com a turma o enunciado, explore as informações da tabela de dupla entrada e analise o gráfico de barras. Pergunte: “Do que trata a tabela?” (A tabela apresenta o preço de cada placa de pastilhas de acordo com o tipo de material.); “E o gráfico?”. (O gráfico informa a quantidade de placas que serão usadas em cada espaço do consultório.)
Na atividade, os estudantes precisam combinar as informações da tabela e do gráfico para responder às questões.
No item a, devem observar que, pela tabela, cada placa de pastilhas de mármore custa 41 reais. O gráfico mostra que, na sala de espera, serão usadas 36 placas, o que daria 1.476 reais (36 × 41), superior aos 1.000 reais.
No item b, eles devem calcular os gastos considerando cada tipo de material e avaliar qual pode ser escolhido de acordo com o orçamento de 1.500 reais para a sala de procedimentos. Nesse caso, eles vão usar uma informação do gráfico combinada com todas as informações da tabela.
vidro: 25 × 20 reais = 500 reais
mármore: 25 × 41 reais = 1.025 reais
porcelana: 25 × 49 reais = 1.225 reais
No item c, os estudantes devem calcular o orçamento total para determinado material. Ou seja, eles terão de usar todas as informações do gráfico combinadas com uma informação da tabela (pastilhas de porcelana). E, por fim, devem adicionar os gastos em cada espaço do consultório.
sala de espera: 36 × 49 reais = 1.764 reais
No item c, os estudantes devem calcular o orçamento total para determinado material. Ou seja, eles terão de usar todas as informações do gráfico combinadas com uma informação da tabela (pastilhas de porcelana). E, por fim, devem adicionar os gastos em cada espaço do consultório.
sala de espera: 36 × 49 reais = 1.764 reais
banheiro: 20 × 49 reais = 980 reais
sala de procedimentos: 25 × 49 reais = = 1.225 reais
orçamento total: 1.764 + 980 + 1.225 = 3.969
Antes de propor a atividade, se possível, traga para a sala um jogo similar e com os estudantes organizados em duplas deixe que joguem um pouco. Pode-se usar palito de churrasco pintado com tinta spray. Esse tipo de atividade facilita a visualização dos estudantes.
BNCC em foco:
EF02MA26; competência específica 4
MP255
- Josefa e Ícaro estão jogando uma partida de pega-palitos. Nesse jogo há 25 varetas coloridas, sendo que: os
palitos
amarelos valem 5 pontos; os verdes valem 10 pontos; os azuis, 35 pontos; os vermelhos, 50 pontos; o único palito preto vale 100 pontos. A partida tem 3 rodadas.
Veja as tabelas que mostram a quantidade de palitos de cada cor que cada jogador pegou em duas rodadas.
Quantidade de palitos de Josefa
Tabela: equivalente textual a seguir.
|
Rodada Cor |
Primeira |
Segunda |
|---|---|---|
|
Amarelo |
6 |
3 |
|
Verde |
5 |
5 |
|
Azul |
5 |
4 |
|
Vermelho |
5 |
4 |
|
Preto |
1 |
0 |
Fonte: Palitos de Josefa.
Quantidade de palitos de Ícaro
Tabela: equivalente textual a seguir.
|
Rodada Cor |
Primeira |
Segunda |
|---|---|---|
|
Amarelo |
6 |
6 |
|
Verde |
2 |
5 |
|
Azul |
3 |
5 |
|
Vermelho |
4 |
4 |
|
Preto |
0 |
1 |
Fonte: Palitos de Ícaro.
- Qual é o total de pontos obtidos por Josefa nas duas rodadas? E o total de pontos de Ícaro?
_____
PROFESSOR
Resposta: Josefa: 1 010 pontos; Ícaro: 910 pontos
- Complete o gráfico abaixo.
Fonte: Dados obtidos no jogo.
PROFESSOR
Resposta: Segunda, primeira.- Ícaro precisa fazer, no mínimo, quantos pontos a mais que Josefa para totalizar mais pontos
nessa
partida?
_____
PROFESSOR
Resposta: No mínimo, 101 pontos.
MANUAL DO PROFESSOR
Atividade 2
Após soltar o maço de palitos sobre a mesa, um jogador pega cada palito por vez, sem mexer nos demais. Se mexer em outro palito, conta e registra os pontos relativos aos palitos já tirados e passa a vez. O maço com todos os palitos será solto novamente na mesa para o próximo jogador. Incentive os estudantes a organizarem a pontuação de cada cor de palito em um quadro.
Quadro: equivalente textual a seguir.
|
Cor |
Pontuação |
|---|---|
|
Amarela |
5 pontos |
|
Verde |
10 pontos |
|
Azul |
35 pontos |
|
Vermelha |
50 pontos |
|
Preta |
100 pontos |
Para responder às questões, os estudantes precisam interpretar as informações das duas tabelas de dupla entrada. É importante que eles compreendam todas as informações nelas apresentadas antes de iniciarem a atividade.
No item a, verifique as estratégias usadas pelos estudantes para calcular o total de pontos obtidos por Josefa e Ícaro nas duas rodadas: eles calculam o total de pontos de cada cor em cada rodada e adicionam os valores obtidos, ou obtêm o total de palitos de cada cor e depois aplicam a respectiva pontuação? Incentive-os a socializar seus procedimentos com os colegas. Nesse cálculo, eles devem observar e combinar as informações da tabela de cada jogador com a tabela de pontuação que montaram inicialmente.
No item b, explore o gráfico de barras duplas, destacando seus elementos. Explique a legenda relativa às cores das barras e como devem ser buscadas as informações nesse gráfico.
No item c, espera-se que os estudantes percebam que Ícaro deve fazer mais de 100 pontos a mais que Josefa, visto que a diferença atual de pontuação entre os dois jogadores é de 100 pontos.Apresentamos, a seguir, uma possível resolução para o item a da atividade 2.
Pontuação de Josefa
10 palitos amarelos: 10 × 5 = 50
18 palitos verdes: 18 × 10 = 180
8 palitos azuis: 8 × 35 = 280
8 palitos vermelhos: 8 × 50 = 400
1 palito preto: 1 × 100 = 100
Total: 50 + 180 + 280 + 400 + 100 = 1 010
Pontuação de Ícaro
14 palitos amarelos: 14 × 5 = 70
6 palitos verdes: 6 × 10 = 60
8 palitos azuis: 8 × 35 = 280
8 palitos vermelhos: 8 × 50 = 400
1 palito preto: 1 × 100 = 100
Total: 70 + 60 + 280 + 400 + 100 = 910
MP256
O que você aprendeu
- Paulo é dono de uma loja de enfeites. Em seu estoque, ele tem 4 caixas com 122 enfeites cada uma. Quantos enfeites Paulo tem no estoque?
_____
PROFESSOR
Resposta: 488 enfeites.
- Qual das promoções é mais vantajosa para comprar laranjas?

_____
PROFESSOR
Resposta: Nas duas promoções o preço da laranja é o mesmo.Observação: Os elementos desta página não estão apresentados em escala de tamanho. Cores fantasia. Fim da observação.
- Veja a quantia de dinheiro que Regina tem.

- Se Regina dividir igualmente essa quantia com sua irmã, com quantos reais cada uma ficará?
_____
PROFESSOR
Resposta: 117 reais.
- Qual é o
menor
número
que, ao dividirmos por 2 e por 3, terá resto igual a 1 em ambos os casos?
_____
PROFESSOR
Resposta: 7
- Em um carrinho de transporte do clube, cabem no máximo 5 cadeiras. José e seus colegas de trabalho têm de levar 76 cadeiras para o salão de festas. Qual é o
menor
número
de carrinhos de transporte de que eles precisarão para levar essas cadeiras em uma única viagem?
_____
PROFESSOR
Resposta: 16 carrinhos.
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Propicie c onversas entre os estudantes a respeito das estratégias que usaram para resolver as atividades.
Atividade 1
Verifique que método os estudantes usaram para obter o resultado. Peça que mostrem o raciocínio usado e discutam as diferentes estratégias.
Atividade 2
Deixe que os estudantes elaborem suas estratégias de resolução. Caso haja dificuldade na resolução, pergunte a eles quanto custam duas laranjas em cada uma das promoções. Eles devem concluir que, em ambas, 2 laranjas custam 1 real.
Atividade 3
Os estudantes poderão utilizar diferentes estratégias. Se eles usarem a estratégia de calcular a metade da quantia em cédulas e moedas, espera-se que percebam que terão de trocar 1 cédula de 10 reais por 2 cédulas de 5 reais ou por 10 moedas de 1 real.
Discuta com os estudantes o porquê de não adiantar trocar a cédula de 10 reais por 5 cédulas de 2 reais.
Atividade 4
Os estudantes podem resolver por tentativa e erro, iniciando por 3 (já que 2 é menor que 3 e a divisão de 2 por 3 não é possível no campo dos números naturais). Outra maneira é eles perceberem que esse número é ímpar, pois todo número par dividido por 2 tem resto zero. Daí, o menor número ímpar que dividido por 3 tem resto 1 é o 7 (pois 5 dividido por 3 tem resto 2). Então, realizam a divisão de 7 por 2 e confirmam o resultado.
BNCC em foco:
EF03MA07, EF03MA08
MP257
- Jairo tinha 50 reais quando comprou ingressos do parque para ele e seus amigos. O troco recebido por ele depois da compra foi de 5 reais. Ao todo quantos ingressos Jairo comprou?
_____
PROFESSOR
Resposta: 5 ingressos.

- João tinha alguns
botões
e distribuiu-os igualmente entre 3 caixinhas.

Qual poderia ser a quantidade de botões que João tinha se sobraram 2 botões?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que há mais de uma resposta possível: 5, 8, 11, 14, 17 etc. Fim da observação.
- Leia o diálogo a seguir.


- Agora, reúna-se com um
colega
e, juntos, respondam: a afirmação da menina está certa? Por quê?
_____
PROFESSOR
Resposta: Não.PROFESSOR
Atenção professor: Exemplo de explicação: O menino poderia ter ganhado 16, 18, 20, 22, 24, 26 ou 28 (números pares entre 15 e 30) bolinhas de gude. Fim da observação.
Autoavaliação

- Compreendo pelo menos duas estratégias diferentes para calcular divisões?
PROFESSOR
Resposta pessoal.
- Quais conteúdos deste ano ainda preciso estudar mais e quais já compreendo com facilidade?
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 5
Como a divisão de 76 por 5 tem quociente 15 (e resto 1), é possível que alguns estudantes respondam 15 carrinhos. Nesse caso, ressalte que a cadeira correspondente ao resto da divisão também deverá ser transportada, por isso será necessário mais um carrinho, totalizando 16.
Aproveite para perguntar: “Que outras quantidades de cadeiras poderiam ser transportadas em 16 carrinhos?”. Espera-se que os estudantes percebam que, adicionando 1, 2 ou 3 unidades ao resto da divisão, seriam suficientes os 16 carrinhos para transportá-las, assim como acrescentando 4 unidades, caso em que a divisão seria exata.
Portanto, as quantidades de cadeiras que poderiam ser transportadas em 16 carrinhos são: 76, 77, 78, 79 e 80.
Atividade 6
Para resolver esse problema, os estudantes podem primeiro observar que o dinheiro gasto com a compra de ingressos foi 45 reais (50 reais menos 5 reais) e daí determinar quantos ingressos de 9 reais podem ser comprados com essa quantia. Para isso, basta dividir 45 por 9, obtendo resultado igual a 5. Portanto, Jairo comprou 5 ingressos.
Atividade 7
Espera-se que os estudantes percebam que há mais de uma resposta possível: 5, 8, 11, 14, 17 etc.
O aspecto mais proveitoso de problemas desse tipo é levar os estudantes a pensarem nas operações que oferecem várias possibilidades de números que satisfaçam às condições do enunciado.
Atividade 8
Peça aos estudantes que expliquem o raciocínio que usaram para resolver a atividade.
Exemplo de explicação para a atividade 8: A afirmação da menina não está correta, porque o menino poderia ter ganhado 16, 18, 20, 22, 24, 26 ou 28 (números pares entre 15 e 30) bolinhas de gude.
BNCC em foco:
EF03MA07, EF03MA08
Autoavaliação
Para finalizar o trabalho do 3º ano, os estudantes poderão avaliar seus conhecimentos relativos às estratégias de cálculo de divisão.
A primeira questão aponta a necessidade do uso de pelo menos duas delas. Espera-se que eles avaliem quanto se apropriaram do cálculo por estimativa e do cálculo pelo algoritmo usual. Entretanto, os estudantes poderão apontar outras estratégias utilizadas por eles. Esse momento é importante tanto para eles quanto para você perceber como estão calculando divisões.
A última questão possibilita uma análise geral do ano, para que os estudantes possam concluir o trabalho com consciência de suas potencialidades e fragilidades para que, no ano seguinte, possam avançar ainda mais.
MP258
Comentários para o professor
Conclusão da Unidade 8
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Constrói e aplica fatos básicos da adição e da multiplicação para realizar cálculo mental e escrito? |
_____ |
_____ |
|
Resolve e elabora problemas de multiplicação (por 2, 3, 4, 5 e 10) com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, utilizando diferentes estratégias de cálculo e registros? |
_____ |
_____ |
|
Resolve e elabora problemas de multiplicação (por 2, 3, 4, 5 e 10) com os significados de adição de parcelas iguais e elementos apresentados em disposição retangular, utilizando diferentes estratégias de cálculo e registros? |
_____ |
_____ |
|
Resolve e elabora problemas de divisão de um número natural por outro (até 10) com os significados de repartição equitativa e de medida mediante estratégias e registros pessoais? |
_____ |
_____ |
|
Associa o resultado de uma divisão com resto zero de um número natural por 2, 3, 4, 5, 10 às ideias de metade, terça, quarta, quinta e décima partes? |
_____ |
_____ |
|
Lê, interpreta, compara dados e resolve problemas que envolvam dados organizados em tabelas de dupla entrada e em gráficos de barras ou de colunas? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP259
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: _____ |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |