MP034
Para começar
Olá! Vamos fazer estas atividades e descobrir o que você já sabe?
- Ao final de um jogo de boliche, Ana e Júlio montaram o quadro abaixo. Sabendo que a equipe 4 fez a metade dos pontos da equipe 1, ajude-os a preencher o que faltou, quando for possível. Depois, explique cada caso.
Quadro: equivalente textual a seguir.
|
1ª Rodada |
2ª Rodada |
3ª Rodada |
Total |
|
|---|---|---|---|---|
|
Equipe 1 |
12 |
13 |
15 |
_____ PROFESSORResposta: 40 |
|
Equipe 2 |
15 |
7 |
_____ PROFESSORResposta: 13 |
35 |
|
Equipe 3 |
_____ PROFESSORResposta: - |
15 |
8 |
20 |
|
Equipe 4 |
_____ PROFESSORResposta: - |
10 |
_____ PROFESSORResposta: - |
_____ PROFESSORResposta: 20 |
• Equipe 1: _____
PROFESSOR
Resposta: A equipe 1 terminou com 40 pontos (12 + 13 + 15 = 40).• Equipe 2: _____
PROFESSOR
Resposta: A equipe 2 fez 13 pontos na 3ª rodada, pois 35 − (15 + 7) = 13.• Equipe 3: _____
PROFESSOR
Resposta: Impossível responder com um número natural, pois o total é menor do que 15 + 8 = 23.• Equipe 4: _____
PROFESSOR
Resposta: O total de pontos foi 20, pois 20 = 40 ÷ 2.PROFESSOR
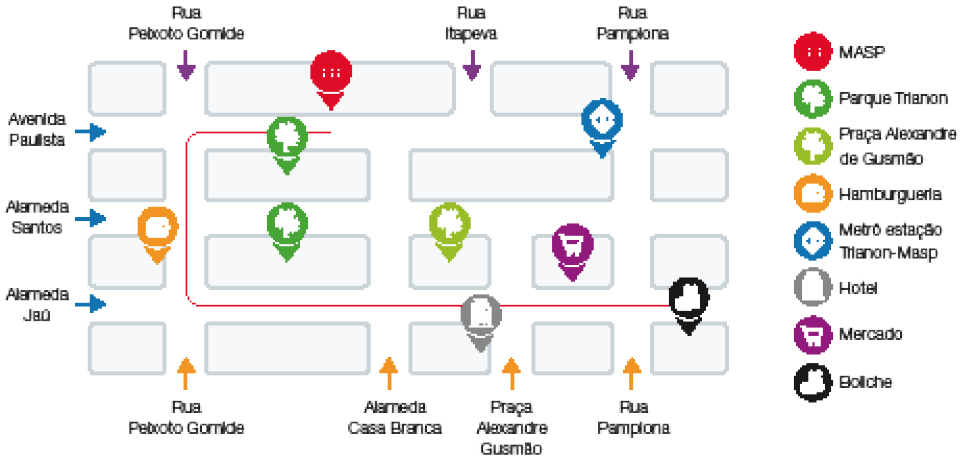
Há diversas possibilidades para a 1ª e a 3ª rodadas desde que a soma seja 10.- Os irmãos Ana e Júlio, de 10 e 12 anos, encontraram um mapa próximo ao MASP, um museu da cidade de São Paulo. Veja a seguir.
MANUAL DO PROFESSOR
As atividades propõem uma avaliação diagnóstica, sob a perspectiva da avaliação formativa. Faça a leitura com os estudantes, orientando-os a mobilizarem os conhecimentos que dominam.
São contempladas as Unidades Temáticas Números, Geometria, Álgebra, Grandezas e medidas e Probabilidade e estatística . Pretende-se verificar se os estudantes reconhecem números com 5 ordens, sua composição e decomposição, comparação entre o maior e o menor, ordenação e arredondamento até uma centena de milhar completa, além de procedimentos de cálculo mental, uso e aplicação das propriedades das operações e resolução de problemas do campo aditivo e multiplicativo; identificação de sequência recursiva; reconhecimento de ângulos retos, de paralelismo e de simetria de reflexão em figuras poligonais; medir intervalos de tempos; medir perímetros; identificação de eventos com maior ou menor chance de acontecer; análise de dados em tabela de dupla entrada, entre outros.
Comente com a turma que o objetivo é auxiliá-los a expressarem o que já sabem e destacar os conhecimentos que terão a oportunidade de aprender e de ampliar. As atividades podem ser lidas em grupo, porém cada estudante deve registrar sua resposta individualmente, da melhor maneira possível, auxiliando o professor a planejar e a rever seu trabalho para o ano letivo. Caso eles respondam oralmente, convém tomar nota das respostas.
Atividade 1
Para essa questão é importante observar se os estudantes compreendem a leitura dos dados na tabela e percebem a importância de resolver cada item para completar os dados que faltam.
Para os itens da questão, os estudantes serão estimulados a explicar matematicamente suas estratégias e resoluções, o que é importante para que eles também refaçam o percurso de aprendizagem (o que fizeram, como fizeram e por que fizeram). Além de calcular o total de pontos das três rodadas da equipe 1, devem explicar como chegaram ao resultado. Para a equipe 2, os estudantes devem calcular 15 + 7 obtendo 22 e adicionando a quantidade que precisam para chegar em 35 (+ 13) ou efetuar a subtração (35 − 22), obtendo 13. É importante perceber a estratégia usada e aceitar ambas as operações que estão no campo aditivo (adição e subtração), pois 35 = 15 + 7 + 13 e 35 − (15 + 7) = 13.
BNCC em foco na dupla de páginas:
EF04MA01, EF04MA03, EF04MA04, EF04MA05, EF04MA06, EF04MA07, EF04MA15, EF04MA16, EF04MA25, EF04MA27
MP035
- Trace no mapa o caminho do MASP ao boliche (com pontos de referência e direção). Depois, descreva-o.
_____
PROFESSOR
Resposta: Exemplo de resposta: Sair do MASP, virar à direita na Avenida Paulista; virar à esquerda e seguir na Rua Peixoto Gomide; virar à esquerda na Alameda Jaú e seguir em frente até chegar no boliche.
- O ingresso para crianças com até 12 anos custa 22 reais. O ingresso para adultos custa o dobro desse valor, mais 1 real. Quanto custa o ingresso para adultos? Explique escrevendo uma expressão numérica e calculando o seu valor.
_____
PROFESSOR
Resposta: 2 × 22 + 1 = 45. O ingresso para adultos custa 45 reais.
- Caso os irmãos fossem com a mãe ao MASP e depois ao boliche jogar por 1 hora, ao custo de 10 reais por hora por pessoa, quanto gastariam? Explique, escrevendo uma expressão numérica e calculando o seu valor.
_____
PROFESSOR
Resposta: Os três gastariam 119 reais (2 × 22 + 45 + 3 × 10).
- Observe na tabela a seguir os dados, em centímetro, dos lançamentos de dardos dos medalhistas nos Jogos Olímpicos de 2016, no Rio de Janeiro.
Lançamento de dardos Rio 2016 (medidas em cm)
Tabela: equivalente textual a seguir.
|
Medalha |
Atleta |
País |
1 |
2 |
3 |
4 |
5 |
Resultado |
|---|---|---|---|---|---|---|---|---|
|
Ouro |
Thomas Röhler |
Alemanha |
8.740 |
8.561 |
9.707 |
8 484 |
9 030 |
9.030 |
|
Prata |
Julius Yego |
Quênia |
8.824 |
— |
— |
— |
— |
8.824 |
|
Bronze |
Keshorn Walcott |
Trinidad e Tobago |
8.345 |
8.538 |
8.338 |
8 033 |
— |
8.538 |
Fonte dos dados: http://fdnc.io/eU7. Acesso em: 7 jun. 2021.
- Escreva, em ordem decrescente, os resultados da tentativa 1. Nesse caso, quem ganharia a medalha de ouro?
_____
PROFESSOR
Resposta: 8.824; 8.740; 8.345. Julius Yego.
- O recorde olímpico dessa modalidade tem a marca de 9.057 cm. Quanto faltou para o medalhista de ouro acima atingir esse recorde?
_____
PROFESSOR
Resposta: 27 cm.
- Quantos centímetros a mais ele deveria alcançar para garantir a medalha de ouro?
_____
PROFESSOR
Resposta: 207 (9.030 − 8.824 + 1)
- A massa do dardo de atletas masculinos adultos é 800 g, o dobro do dardo usado por atletas femininas infantis. Qual é a massa dos dardos dessas atletas?
_____
PROFESSOR
Resposta: 400 g.
MANUAL DO PROFESSOR
Para a equipe 3, precisarão observar que o total de pontos é menor do que a soma das parcelas escritas, o que torna impossível, dentro do campo dos números naturais, obter o valor da 1ª rodada. Os estudantes precisam mobilizar os conhecimentos sobre dobro/metade para obter o valor total da equipe 1 (20), pois (40 ÷ 2 = 20). Muitos podem fazer o cálculo mental ou registrar a operação inversa da divisão 40 = 2 × 20, ou mesmo optar pelo significado da multiplicação de adicionar parcelas iguais, registrando 40 = 20 + 20. Para a segunda parte da questão, os estudantes mobilizarão a propriedade comutativa da adição e trabalharão com várias possibilidades para determinar o total, desde que a soma das duas parcelas seja 10 (alguns exemplos 4 + 6 = 6 + 4 = 3 + 7 = 7 + 3 = 8 + 2 = 2 + 8 = 5 + 5).
Atividade 2
Os estudantes inicialmente devem compreender o mapa, observar as ruas e os pontos de referência presentes.
No item a, eles devem escolher um possível caminho para traçar o trajeto, descrever o caminho e apontar alguns pontos de referência e a direção a seguir. Diversas possibilidades podem ser aceitas.
No item b, eles devem traduzir as informações para a linguagem matemática. Para isso, basta escrever a expressão 2 × 22 + 1 = 45 e calcular o seu valor.
No item c, devem ampliar o que fizeram no item anterior traduzindo as informações para 2 × 22 + 45 + 3 × 10 e obter o gasto total de 119 reais.
Atividade 3
É importante observar se os estudantes compreendem a leitura dos dados na tabela e percebem a importância de resolver cada item selecionando e usando as informações pertinentes.
No item a, eles devem identificar a ordem dos valores da 1ª rodada d e lançamentos e concluir que, se a disputa terminasse ali, o medalhista de prata teria conquistado o ouro. Devem perceber que a determinação e o empenho do atleta alemão o fez ganhar, no 5º lançamento, o ouro olímpico.
No item b, verifica-se se os estudantes reconhecem a subtração com o significado de completar. Assim, 27 cm completam os 9.030 cm para chegar ao recorde de 9.057 cm.
No item c, o raciocínio é o mesmo, mas deve-se observar o acréscimo do 1 para garantir a superação, e não apenas o empate.
A leitura atenta é o que leva ao cálculo correto no item d: a massa dos dardos das atletas femininas infantis é a metade da massa dos dardos dos adultos masculinos, ou seja, 400 g.