MP036

Comentários para o professor:

Introdução da Unidade 1

A abertura da primeira Unidade, coerente com a proposta da coleção de dar continuidade à aprendizagem da etapa escolar anterior, propõe uma abordagem com observações e descobertas em uma imagem contextualizada, na qual se pode explorar o sistema de numeração decimal por meio de números de quatro algarismos, além de explorar grandezas e medidas.

Nesta Unidade, em que predomina a Unidade Temática Números, as atividades trabalham as habilidades que visam desenvolver a leitura, a escrita e a ordenação de números naturais até a ordem de dezena de milhar, estabelecendo relações entre os diferentes registros de um número. Nessa mesma perspectiva, destaca-se a relação entre os conhecimentos construídos nos anos anteriores do Ensino Fundamental e aqueles que são abordados nesse e no próximo ano do ciclo escolar. Por exemplo, a identificação das características do sistema de numeração decimal utilizando a composição e a decomposição de um número natural de até quatro ordens é ampliada, nesta série, para cinco ordens. Também é ampliado para cinco ordens o desenvolvimento da habilidade de mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potência de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculos.

O desenvolvimento das habilidades de leitura, escrita e ordenação de números naturais até a ordem de dezenas de milhar, assim como a resolução, com suporte de imagem e material manipulável, de problemas de contagem, como, por exemplo, a determinação do número de agrupamentos possíveis ao se combinar cada elemento de um conjunto com todos os elementos de outro, aplicando estratégias de registro pessoais, também será importante para o trabalho no 5º ano, momento em que os estudantes trabalharão com números até a ordem das centenas de milhar.

A Unidade Temática Álgebra é contemplada por meio da atividade que explora a regularidade da sequência formada por dezenas de milhar cheias.

Ao longo da Unidade também há problemas cujos dados estão apresentados em tabelas e gráficos de colunas, contemplando a Unidade Temática Probabilidade e estatística.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. As variáveis são muitas: dos conteúdos às habilidades e objetivos de aprendizagem.

Competência geral favorecida

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

Sugestão de roteiro de aula

Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.

Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado ao item Arredondamentos desta Unidade.

Roteiro de aula – Arredondamento 1 ª parte – Introdução – Tempo sugerido: 15 minutos

Inicie uma conversa com a turma comentando que, apesar de a Matemática ser chamada de Ciência exata, os conhecimentos adquiridos nessa área de estudos devem também ser úteis no dia a dia em situações que não requerem precisão.

MP037

Por exemplo, a administração da prefeitura de uma cidade registrou, nos quatro primeiros meses do ano, auxílio a 3.841, 3.438, 4.167 e 3.961 cidadãos do município. Ela precisa fazer uma previsão (orçamentária) de quanto vai gastar com esse tipo de auxílio para o restante do ano. Para isso, um cálculo estimativo da quantidade desses auxílios, dada a variação dessas quantidades, não convém ter valores exatos. Então, utiliza-se o arredondamento, ou seja, consideram-se números mais próximos desses, mas que terminem em 0 (dezena) ou 00 (centena) ou 000 (unidade de milhar) etc., conforme seja mais conveniente para a situação com a qual se trabalha. A forma arredondada do algarismo 0 parece ter dado o nome arredondamento a esse procedimento. No exemplo, os números podem ser arredondados para a:

• Dezena (10, 20, 30, 40, 50, 60, 70, 80, 90) mais próxima.

3.841 e 3.961 estão mais próximos de 3.840 e 3.960, respectivamente.

4.167 e 3.438 estão mais próximos de 4.170 e 3.440, respectivamente.

• Centena (100, 200, 300, 400, 500, 600, 700, 800, 900) mais próxima.

4.167 e 3.961 estão mais próximos de 4.200 e 4.000, respectivamente.

3.841 e 3.438 estão mais próximos de 3.800 e 3.400, respectivamente.

• Unidade de milhar (1.000, 2.000, 3.000, ..., 9.000).

3.841, 4.167 e 3.961 estão mais próximos de 4.000 do que de 3 000, então eles são arredondados para 4 000.

3.438 está mais próximo de 3.000 do que de 4.000, então ele é arredondado para 3.000.

Fica mais simples estimar a quantidade de auxílios necessários tendo como referência 4.000 e 3.000 do que aqueles números registrados.

Antes de passar às atividades, verifique se ainda há dúvidas sobre como obter o arredondamento de um número.

2 ª parte – Atividades do livro das páginas 26 a 28 – Tempo sugerido: 50 minutos

A seguir, faça uma leitura com a turma das atividades 1 e 2 e peça aos estudantes que completem a primeira e que respondam à segunda. Verifique e discuta possíveis dúvidas. Valide as resoluções corretas.

Em seguida, peça a eles que leiam as atividades 3, 4 e 5. Dê um tempo para que os estudantes as resolvam, percorrendo a sala para esclarecimentos individuais. Na atividade 5, após os estudantes explicarem em duplas as respectivas respostas, solicite a duas ou três duplas que falem para a turma e depois valide coletivamente as resoluções corretas.

Na sequência, solicite a eles que leiam e resolvam as atividades 6, 7 e 8. Para a atividade 7, é interessante que seja mostrado para a turma um mapa do Brasil e que sejam localizadas as cidades citadas na tabela. Percorra a sala de aula para possíveis atendimentos individuais, dando um tempo para que todos respondam a essas questões.

Finalize solicitando aos estudantes que arredondem cada distância da tabela para a centena mais próxima na atividade 7 e que, na atividade 8, arredondem o número escolhido para a dezena de milhar.

MP038

UNIDADE 1. Sistema de numeração decimal

Imagem: Ilustração. Uma menina com o número 1.927 na camiseta está correndo com os braços para cima e sorrindo. Atrás dela, Júlio com o número 7.291 está correndo. Em seguida, uma menina com o número 8.922 e um menino com o número 5.738 estão atravessando uma linha de chegada e acima deles há uma faixa com a informação: 18º CIRCUITO DE PRIMAVERA - CORRIDA DE 200 METROS. Ao lado há uma placa com o tempo: 08:54:31 - 200 METROS e uma ampulheta. Um homem está fotografando, um casal está sentado na grama e batendo palmas e outro casal está em pé e torcendo. Do outro lado há um pódio (VENCEDORES DA CORRIDA) com o 1º, 2º e 3º lugares. Ao lado, placa grande com a informação: 18º CIRCUITO DE PRIMAVERA - CORRIDA DE 200 METROS. E um homem está segurando uma sacola térmica com a informação: ÁGUA 500 ML – SUCO 250 ML. Em seguida, Sidney, Rosa, Ana e várias pessoas estão sentados em uma arquibancada e torcendo. Ao fundo, árvores e silhueta de prédios. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos da Unidade

Ler, escrever e ordenar números naturais (de até 5 algarismos).

Comparar números naturais (de até 5 algarismos).

Identificar características do sistema de numeração decimal, utilizando a composição e a decomposição de número natural de até cinco ordens.

Resolver problemas que envolvam a comparação e a equivalência de valores monetários do sistema brasileiro.

Representar números naturais (de até 5 algarismos) com o Material Dourado, no ábaco e no Quadro Valor de Lugar.

Representar números naturais na reta numérica.

Utilizar a reta numérica para a representação aproximada de números naturais.

BNCC em foco:

EF04MA01, EF04MA02, EF04MA08, EF04MA11, EF04MA27

MP039

Boxe Complementar

Para refletir...

Ao observar a capacidade da garrafinha de suco, você pode concluir que ela equivale à terça parte ou à metade da garrafinha de água?

_____

PROFESSOR Resposta: A capacidade da garrafinha de suco equivale à metade da capacidade do frasco de água.

Qual é o valor posicional do algarismo 7 nos números 1.927 e 7.291 nas camisetas dos corredores?

_____

PROFESSOR Resposta: No número 1.927, o algarismo 7 indica 7 unidades; no número 7.291, ele representa 7 unidades de milhar ou 7.000 unidades.

Fim do complememnto

MP040

Sistema de numeração indo-arábico

  1. Leia o texto e complete.

    O sistema de numeração que utilizamos é chamado indo-arábico. Ele tem esse nome porque foi desenvolvido pelos antigos indianos (povos que habitavam o vale do Rio Indo, onde hoje se localiza um país chamado Paquistão) e divulgado pelos árabes ao restante do mundo.

    1. Para representar os números nesse sistema, são usados 10 símbolos, chamados algarismos. Acredita-se que esse nome tenha sido dado em homenagem ao matemático árabe Abu Ja’far Muhammad ibn Musa Al-Khowarizmi.

      Os algarismos sofreram modificações ao longo do tempo, até ficarem no formato atual.

Imagem: Ilustração. À esquerda, um senhor com turbante e roupa laranja está sentado com as pernas cruzadas e na frente dele há três jarros com símbolos. Em seguida, uma ampulheta. No centro, um homem com pano na cabeça e roupa listrada está sorrindo e fechando um saco. Na frente dele há três sacos com símbolos sobre uma mesa. Em seguida, uma ampulheta. À direita, um homem com camisa e calça está empilhando caixas com números 4, 5, 6. Fim da imagem.

Os símbolos do sistema de numeração indo-arábico que chamamos de algarismos ou dígitos são: 0, 1, 2, 3, _____, _____, _____, _____, _____, _____.

PROFESSOR Resposta: 4, 5, 6, 7, 8, 9.

Com esses símbolos representamos qualquer número.

  1. O sistema de numeração indo-arábico é um sistema decimal, ou seja, os agrupamentos são feitos de 10 em 10.

    Veja abaixo, representados com o Material Dourado, alguns agrupamentos de 10 em 10 que podem ser feitos no sistema de numeração indo-arábico.

1 unidade

Imagem: Ilustração. Um cubinho dourado. Fim da imagem.

_____ unidade

PROFESSOR Resposta: 10
Imagem: Ilustração. Uma barra dourada composta por dez cubinhos. Fim da imagem.

1 dezena

_____ dezenas

PROFESSOR Resposta: 10
Imagem: Ilustração. Uma placa dourada composta por dez barras. Fim da imagem.

1 centena

_____ centenas

PROFESSOR Resposta: 10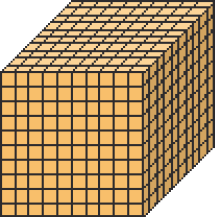
Imagem: Ilustração. Um cubo dourado composto por dez placas. Fim da imagem.

1 milhar

MANUAL DO PROFESSOR

Objetivos

Perceber regularidades e características do sistema de numeração decimal.

Estabelecer relações de maior e menor entre os números.

Atividade 1

No item a, comente com a turma que, de acordo com alguns historiadores, os dedos das mãos deram origem aos agrupamentos de 10 em 10. No sistema de numeração indo-arábico, os algarismos são associados à quantidade. Socialize a ordem dos algarismos com os estudantes e escreva na lousa números de vários algarismos para demonstrar que, com eles, podemos escrever qualquer número.

No item b, com o objetivo de facilitar a visualização, o Material Dourado é utilizado para representar os agrupamentos de 10 em 10 do sistema indo-arábico.

BNCC em foco:

EF04MA01

MP041

  1. Responda às questões.
    1. Qual é o maior número de um algarismo? _____
      PROFESSOR Resposta: 9
    1. Qual é o menor número de dois algarismos? _____
      PROFESSOR Resposta: 10
    1. Que números de dois algarismos podemos formar com os algarismos 1 e 8? _____
      PROFESSOR Resposta: 11, 18, 81 e 88.
    1. Qual é o maior número de três algarismos? _____
      PROFESSOR Resposta: 999
    1. Qual é o menor número de quatro algarismos? _____
      PROFESSOR Resposta: 1.000

Imagem: Ícone: mental. Fim da imagem.

  1. Responda às questões fazendo o cálculo mentalmente.
    1. Quantas moedas de Fotografia. Uma moeda de um real. formam Fotografia. Uma cédula de dez reais. ? _____
      PROFESSOR Resposta: 10 moedas de 1 real.
    1. Fotografia. Duas cédulas de duzentos reais. pode ser trocada por quantas cédulas de 10 reais? _____
      PROFESSOR Resposta: 40 cédulas.
    1. Fotografia. Uma cédula de cem reais e duas cédulas de dez reais. podem ser trocadas por quantas moedas de 1 real? _____
      PROFESSOR Resposta: 120 moedas.
    1. Quantas cédulas de Fotografia. Uma cédula de cem reais. formam 1.000 reais? _____
      PROFESSOR Resposta: 10 cédulas de 100 reais.
  1. Lúcia faz chaveiros artesanais.
    1. Se Lúcia fizer pacotes com 1 centena de chaveiros cada um, quantos pacotes ela fará com os chaveiros da figura abaixo?

      _____

      PROFESSOR Resposta: 10 pacotes.
Imagem: Ilustração. Lúcia, mulher com cabelo preso está com o braço apoiado em uma caixa grande com vários chaveiros coloridos dentro. Ao lado, placa com a informação: CONTÉM 1.000 CHAVEIROS. Fim da imagem.
  1. Se os pacotes que Lúcia fizer tiverem 1 dezena de chaveiros cada um, quantos pacotes ela fará com esses mesmos chaveiros?

    _____

    PROFESSOR Resposta: 100 pacotes.
MANUAL DO PROFESSOR

Atividade 2

Esta atividade permite verificar o entendimento dos estudantes em relação a algarismo e número. Explore mais a situação escrevendo na lousa três algarismos. Por exemplo, 7, 5 e 3. Em seguida, pergunte aos estudantes: “Quais números podem ser formados com esses algarismos sem repetir nenhum deles?” (753, 735, 573, 537, 375, 357.) “Quantos números puderam ser formados com esses três algarismos?” (6 números.).

Atividade 3

Trabalhar com cédulas e moedas é um interessante recurso didático para o estudo do nosso sistema de numeração. Se possível, produza com antecedência cédulas de 10 reais, de 100 reais e de 200 reais e moedas de 1 real para que os estudantes as manipulem. Isso também os auxilia na compreensão da troca de 10 unidades por 1 dezena, de 10 dezenas por 1 centena etc.

Atividade 4

Esta atividade explora a ideia de decomposição decimal. Peça aos estudantes que observem mais uma vez a ilustração do Material Dourado na atividade 1 e pergunte: “Quantos grupos de 100 cabem em 1.000?”. Socialize as respostas dos estudantes. Esses conceitos serão muito utilizados nas próximas Unidades.

Sugestões de leitura para o estudante

Livros

GUELLI, Oscar. Contando a História da Matemática. Jogando com a Matemática. São Paulo: Ática, 1999. v. 5.

Aborda o contexto histórico do surgimento do conhecimento matemático com situações e problemas propostos de maneira lúdica e divertida.

LAGO, Ângela. João Felizardo: o rei dos negócios. São Paulo: Cosac Naify, 2007.

O livro é uma releitura de um conto tradicional (uma das versões escritas é dos Irmãos Grimm). João recebe uma moeda de herança e, após uma série de trocas, percebe que a riqueza está no desprendimento e na simplicidade de um animal sossegado ou naquilo que os objetos e as coisas simbolizam. Com essa leitura, é possível discutir temas como aparência em contraposição à verdadeira essência ou as ideias de riqueza e de consumismo.

BNCC em foco:

EF04MA02, EF04MA08

MP042

Valor posicional

  1. Observe o número de quatro algarismos que cada criança escreveu e faça o que se pede.
Imagem: Ilustração. André, menino loiro com camiseta azul está sentado e escrevendo o número 4.328 em um papel. Fim da imagem.
  1. Qual é o valor de cada algarismo do número que André escreveu? Lembre que UM representa unidades de milhar, C, centenas, D, dezenas, e U, unidades.

Imagem: Quadro de ordens. UM: 4. C: 3. D: 2, U: 8. 4: espaço para resposta unidades de milhar ou espaço para resposta unidades. 3: espaço para resposta centenas ou espaço para resposta unidades. 2: duas dezenas ou 20 unidades. 8: 8 unidades Fim da imagem.

PROFESSOR Resposta: 3, 300, 4, 4.000.

4.328 = 4.000 + 300 + _____ + _____

PROFESSOR Resposta: 20, 8.

Lemos: Quatro mil _____ e _____ e _____.

PROFESSOR Resposta: trezentos e vinte e oito.
  1. Qual é o valor de cada algarismo do número que Clara escreveu?
Imagem: Ilustração. Clara, menina com cabelo preto e curto e camiseta azul está sentada e escrevendo o número 8.234 em um papel. Fim da imagem.
Imagem: Quadro de ordens. UM: 8. C: 2. D: 3, U: 4. 8: espaço para resposta unidades de milhar ou espaço para resposta unidades. 2: duas centenas ou 200 unidades. 3: espaço para resposta ou 20 espaço para resposta. 4: 4 unidades Fim da imagem.
PROFESSOR Resposta: 3, 30, 8, 8.000

8.234 = 8.000 + 200 + 30 + 4

PROFESSOR Resposta: 200 + 30 + 4

Lemos: Oito mil _____ e _____ e _____

PROFESSOR Resposta: duzentos e trinta e quatro.
  1. Os algarismos do número que Clara escreveu têm o mesmo valor no número de André? Escreva como você pensou para responder.

    _____

    PROFESSOR Resposta: Não.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que o valor de um algarismo em um número depende da posição que ele ocupa nesse número. Fim da observação.
MANUAL DO PROFESSOR

Objetivos

Identificar o valor posicional dos algarismos.

Explorar a decomposição dos números.

Reconhecer que todo número natural pode ser escrito por meio de adições de potências de dez.

Aproveite esse momento para comentar com os estudantes que, se não existisse um símbolo para a quantidade nula (o algarismo zero), a quantidade 2 centenas, 0 dezena e 3 unidades, por exemplo, teria de ser representada com um espaçamento vazio entre os algarismos das unidades e das centenas: 2 3, o que poderia gerar dúvidas a respeito do número representado. Números como duzentos e quarenta seriam ainda mais difíceis de registrar, pois, nesse caso, seria difícil representar o espaçamento indicativo da ordem vazia.

Atividade 1

Nesta atividade, os estudantes podem observar que, apesar de André e Clara usarem os mesmos algarismos (2, 3, 4 e 8), o valor posicional desses algarismos permitiu que formassem números diferentes. Pergunte para a turma: “Que outros números podem ser formados com esses mesmos algarismos?” (4.238, 4.283, 4.382, 4.823, 4.832, 8.243, 8.324, 8.342, 8 423, 8.432.).

BNCC em foco:

EF04MA01, EF04MA02

MP043

  1. Decomponha os números adicionando o valor posicional de cada algarismo.
    1. 543 = 500 + 40 + 3
    1. 2.489 = _____ + _____ + _____ + _____
      PROFESSOR Resposta: 2.000 + 400 + 80 + 9
    1. 5.847 = _____ + _____ + _____ + _____
      PROFESSOR Resposta: 5.000 + 800 + 40 + 7
    1. 8.166 = _____ + _____ + _____ + _____
      PROFESSOR Resposta: 8.000 + 100 + 60 + 6
  1. Escreva o valor de cada algarismo 3 no número e complete.
Imagem: Esquema. 3.333. 3: espaço para resposta unidades de milhar ou espaço para resposta unidades. 3: espaço para resposta centenas ou espaço para resposta unidades. 3: espaço para resposta dezenas ou espaço para resposta unidades. 3: 3 unidades Fim da imagem.
PROFESSOR Resposta: 3, 30, 3, 300, 3, 3.000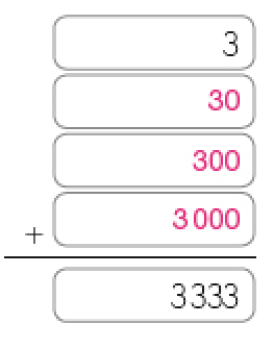
Imagem: Conta de adição na vertical. Na parte superior, o número 3. Em seguida, 30. Abaixo, 300. E em seguida, sinal de adição e o número 3.000. Abaixo, reta horizontal e o resultado 3.333. Fim da imagem.
  1. Escreva o número representado em cada ábaco. Depois, escreva por extenso o valor do algarismo 4 em cada número.
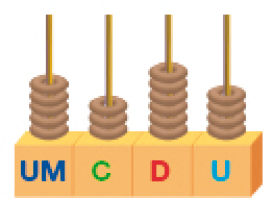
Imagem: Ilustração. Ábaco, base retangular com hastes de UM, C, D, U. Há cinco argolas em UM, três em C, seis em D e quatro em U. Fim da imagem.

_____ _____ _____ _____

PROFESSOR Resposta: 5.364

_____

PROFESSOR Resposta: quatro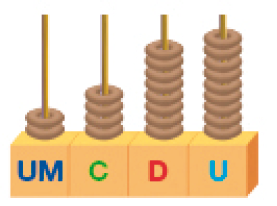
Imagem: Ilustração. Ábaco, base retangular com hastes de UM, C, D, U. Há duas argolas em UM, quatro em C, oito em D e nove em U. Fim da imagem.

_____ _____ _____ _____

PROFESSOR Resposta: 2.489

_____

PROFESSOR Resposta: quatrocentos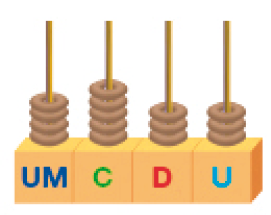
Imagem: Ilustração. Ábaco, base retangular com hastes de UM, C, D, U. Há quatro argolas em UM, cinco em C, três em D e três em U. Fim da imagem.

_____ _____ _____ _____

PROFESSOR Resposta: 4.533

_____

PROFESSOR Resposta: quatro mil

Boxe complementar:

Desafio

Vinícius prendeu sua bicicleta com um cadeado que tem uma senha de 4 algarismos. Ele lembra que:

Imagem: Ilustração. Vinícius, jovem com cabelo encaracolado está ajoelhado com a mão direita em um cadeado e a mão esquerda sobre a cabeça. Na frente dele, o cadeado está em volta de um poste e uma bicicleta. Fim da imagem.

CRÉDITO: MARINA ANTUNES E SILVA

o algarismo das centenas é o 4;

os outros 3 algarismos são o 2, o 5 e o 8.

Vinícius não sabe qual é a ordem correta em que esses algarismos aparecem. Então, ajude Vinícius e escreva todas as possíveis senhas do cadeado dele.

_____

Resposta: 2.458, 2.485, 5.428, 5.482, 8.425 e 8.452.

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 2

É importante que os estudantes percebam que o valor do algarismo depende da posição que ele ocupa em um número. Aproveite para explorar outras formas de decompor os números. Por exemplo, o número do item b.

2.489 = 2.489 unidades;

2.489 = 24 centenas, 8 dezenas e 9 unidades;

2.489 = 248 dezenas e 9 unidades;

2 .89 = 24 centenas e 89 unidades;

2.489 = 2 unidades de milhar, 48 dezenas e 9 unidades.

Atividade 3

É importante lembrar que o trabalho dos estudantes com o sistema posicional e com os agrupamentos de 10 em 10 não deve ser desenvolvido pela repetição mecânica de procedimentos, mas pela real compreensão dos processos envolvidos. Eles devem compreender o valor posicional na representação dos números porque, por exemplo, ao lidar com o número 90, precisam pensar que o algarismo 9 representa tanto 9 dezenas como 90 unidades.

Atividade 4

O ábaco é um excelente recurso auxiliar para a compreensão do valor posicional dos algarismos e a compreensão geral do nosso sistema de numeração. Se julgar oportuno, sugira aos estudantes que construam um ábaco usando uma placa de isopor, palitos de madeira sem pontas e contas ou argolas de plástico. Peça a eles que representem primeiro os números da atividade e depois outros números de quatro algarismos.

BNCC em foco:

EF04MA01, EF04MA02, EF04MA08Desafio

Espera-se que os estudantes percebam a posição do algarismo 4 na casa das centenas e possam permutar os algarismos restantes nas outras casas apresentando todas as combinações possíveis, sem alterar a posição do algarismo 4.

MP044

Problemas

  1. Observe o dinheiro de Daniel, depois responda às questões.
Imagem: Fotografia. Cinco cédulas de cem reais, oito cédulas de dez reais e três moedas de um real. Fim da imagem.
  1. Quantos reais Daniel tem? _____
    PROFESSOR Resposta: 583 reais.
  1. Como se lê essa quantia? _____
    PROFESSOR Resposta: Quinhentos e oitenta e três reais.
  1. Faça a decomposição do número que representa essa quantia, considerando a quantidade de cédulas e de moedas.

    583 = 5 × 100 + _____ × 10 + _____ × 1

    PROFESSOR Resposta: 8 ,3
  1. Observe os números nos quadros abaixo e classifique cada frase em V (verdadeira) ou F (falsa).

Quadro: equivalente textual a seguir.

A

1.783

Quadro: equivalente textual a seguir.

B

871

Quadro: equivalente textual a seguir.

C

7.318

Quadro: equivalente textual a seguir.

D

8 .731

( ) O valor do algarismo 7 no quadro A é setenta.

PROFESSOR Resposta: F

( ) O número do quadro D é o maior de todos.

PROFESSOR Resposta: V

( ) Ao decompor o número do quadro C, obtemos 7 × 100 + 3 × 10 + 18 × 1.

PROFESSOR Resposta: F

( ) O valor do algarismo 8 no quadro B é 8 centenas.

PROFESSOR Resposta: V
MANUAL DO PROFESSOR

Objetivos

Observar as regularidades referentes ao sistema de numeração decimal aplicadas a situações-problema no contexto da utilização do dinheiro.

Reconhecer que todo número natural pode ser escrito por meio de multiplicações de potências de dez.

Observar a decomposição das ordens decimais em diferentes situações.

Atividade 1

O foco desta atividade é o múltiplo uso social dos números. Inicialmente, retomam-se as aplicações para indicar determinada quantia de dinheiro. Para facilitar a prática das ações de agrupar de 10 em 10 e de trocar, em um sistema decimal, as atividades que trabalham com o sistema monetário são elaboradas apenas com moedas de 1 real e cédulas de 10 reais e de 100 reais.

Atividade 2

Peça aos estudantes que façam a decomposição dos números, por meio de adições e de multiplicações de potências de dez, para responderem às questões, e socialize as afirmações de modo que eles possam confrontá-las com as decomposições realizadas. Se julgar oportuno, proponha aos estudantes que corrijam as frases falsas. Assim:

O valor do algarismo 7 no quadro A é 700.

Ao decompor o número do quadro C, considerando o valor de cada algarismo, obtemos 7 × 1.000 + 3 × 100 + 1 × 10 + 8 × 1.

BNCC em foco:

EF04MA01, EF04MA02, EF04MA08

MP045

  1. Observe o número da placa abaixo. Se escrevermos o número 2 à esquerda do 4, o número aumentará em quantas unidades? _____
    PROFESSOR Resposta: Aumentará em 2.000 unidades.
Imagem: Ilustração. Placa com o número 458. Fim da imagem.
  1. Natália jogou 3 dados e, ordenando os valores obtidos, formou o maior número possível de 3 algarismos. Na sua vez, Carina fez a mesma coisa. Depois, elas compararam os números. Quem formou o maior número? Justifique.

    _____

    PROFESSOR Resposta: Carina, pois 543 é maior que 521.

Jogada de Natália

Imagem: Ilustração. Três dados sobre uma mesa com os números: 2, 5, 1. Fim da imagem.
PROFESSOR Resposta: 521

Jogada de Carina

Imagem: Ilustração. Três dados sobre uma mesa com os números: 4, 3, 5. Fim da imagem.
PROFESSOR Resposta: 543
  1. Componha cada número do quadro escrevendo-o com algarismos e por extenso.

Quadro: equivalente textual a seguir.

Número decomposto

Com algarismos

Por extenso

2 × 1.000 + 7 × 100 + 3 × 1

_____

_____

4.000 + 200 + 8

_____

_____

9 × 1.000 + 1 × 100 + 6 × 10

_____

_____

2.000 + 30 + 5

_____

_____

PROFESSOR Resposta: 2.703; Por extenso: Dois mil setecentos e três.
PROFESSOR 4.208; Por extenso: Quatro mil duzentos e oito.
PROFESSOR 9.160; Por extenso: Nove mil cento e sessenta.
PROFESSOR 2.035; Por extenso: Dois mil e trinta e cinco.

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Digite em uma calculadora o número formado por 3 milhares, 2 centenas, 4 dezenas e 1 unidade. Em seguida, aperte a tecla Ilustração. Tecla menos.e digite o menor número possível formado pelos algarismos 4, 3, 2 e 1.
    1. Os algarismos que você digitou no primeiro número são diferentes dos algarismos que você digitou no segundo número? O que muda de um número para o outro?

      _____

      PROFESSOR Resposta: Não.
      PROFESSOR Atenção professor: Espera-se que os estudantes percebam que o que muda é a posição dos algarismos em cada número. Fim da observação.
    1. Qual é o resultado dessa subtração que você fez na calculadora? _____
      PROFESSOR Resposta: 2 007

      Imagem: Ícone: Oral. Fim da imagem.

      Imagem: Ícone: Dupla. Fim da imagem.

    1. Quantas centenas e quantas dezenas há nesse número? Converse com um colega sobre isso.
      PROFESSOR Resposta: Nesse número há: 20 centenas e 7 unidades; 200 dezenas e 7 unidades.
MANUAL DO PROFESSOR

Atividade 3

Espera-se que os estudantes percebam que o algarismo 2 irá ocupar um lugar na casa dos milhares e, com isso, seu valor posicional representará 2 000 unidades. É interessante pedir a eles que escrevam outros números que podem ser formados acrescentando o algarismo 2 em outras posições: 4.258, 4.528, 4.582.

Os estudantes devem observar que, nesses casos, os números não aumentam o equivalente ao valor do algarismo 2 acrescentado, pois, em cada caso, já havia um algarismo ocupando a ordem em que ele foi colocado. Por exemplo, 458 transformou-se em 4.258, o acréscimo não foi de 200, e sim de 3.800.

Atividade 4

Verifique se os estudantes percebem que, para descobrir os números obtidos por Natália e Carina, os dois maiores algarismos que apareceram nos dados (5 e 2 para Natália e 5 e 4 para Carina) devem ocupar as ordens maiores, em ordem decrescente, da esquerda para a direita, de modo que Natália formou o número 521 e Carina, o número 543.

Atividade 5

Observe se os estudantes resolvem com facilidade a escrita de cada número decomposto com algarismos e por extenso.

Atividade 6

Espera-se que os estudantes sigam as orientações e digitem os números na calculadora nesta ordem:

3.241 − 1.234 = 2.007

Os estudantes devem perceber que os dois números são formados pelos mesmos algarismos (item a), mas o valor posicional desses algarismos nos dois números é diferente.

Em b, depois de seguirem as orientações, os estudantes obterão 2.007 como resultado.

Acompanhe as conversas das duplas sobre os questionamentos do item c. Verifique se conseguem perceber quantas são as dezenas e as centenas nesse número. Se julgar necessário, escreva o número 2.007 na lousa e destaque as duas ordens representadas pelo algarismo 0 (zero).

BNCC em foco:

EF04MA01, EF04MA02, EF04MA08

MP046

Dezena de milhar

  1. Em uma fábrica, os clipes de metal produzidos são colocados em uma caixa. Observe na imagem abaixo que, em cada caixa, há 1 000 unidades.
Imagem: Ilustração. Um homem com uniforme cinza está empurrando um carrinho com cinco caixas empilhadas em cima. Em cada caixa, a informação: CONTÉM 1.000 CLIPES. Na frente dele, um caminhão com a porta aberta. Fim da imagem.
  1. Em 2 caixas há quantos clipes de metal? E em 3 caixas? _____
    PROFESSOR Resposta: 2.000; 3.000.
  1. Em quantas caixas serão distribuídos igualmente 9.000 clipes de metal?

    _____

    PROFESSOR Resposta: Em 9 caixas.
  1. Em 10 dessas caixas há quantos clipes de metal? _____
    PROFESSOR Resposta: 10.000 clipes de metal.

1 dezena de milhar ou dez mil ou 10.000 unidades

  1. Escreva a quantidade que falta para completar 10.000 unidades (uma dezena de milhar) em cada caso.
  1. 9.000 folhas de sulfite.

    _____

    PROFESSOR Resposta: 1.000 folhas de sulfite.
Imagem: Ilustração. Várias folhas de sulfite empilhadas. Fim da imagem.
  1. 9.999 CDs. _____
    PROFESSOR Resposta: 1 CD.
Imagem: Ilustração. Vários CDs amontoados. Fim da imagem.
  1. 9.990 livros. _____
    PROFESSOR Resposta: 10 livros.
Imagem: Ilustração. Vários livros em uma prateleira. Fim da imagem.
  1. 9.900 canetas. _____
    PROFESSOR Resposta: 100 canetas.
Imagem: Ilustração. Várias canetas amontoadas. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos

Ler e escrever números naturais de até 5 algarismos.

Estabelecer relações entre os registros, numéricos e língua materna, de números de até 5 algarismos.

Reconhecer e descrever uma regra de formação de uma sequência numérica e determinar elementos faltantes ou seguintes.

Ler e interpretar dados numéricos.

Realizar cálculos que possibilitem reconhecer regularidades.

O estudo do valor posicional dos algarismos permite aos estudantes o reconhecimento de que, em nosso sistema de numeração, cada ordem corresponde a 10 vezes o valor da ordem imediatamente à direita no Quadro Valor de Lugar. Eles já viram que:

Quadro: equivalente textual a seguir

.10 - 1 dezena = 10 unidades

UM

C

D

U

1

0

1

0

0

1

0

0

0

100 - 1 centena = 10 dezenas = 100 unidades

1.000 - 1 unidade de milhar = 10 centenas = 1.000 unidades

Agora, os estudantes vão expandir a ideia para a dezena de milhar, compreendendo que:

1 dezena de milhar = 10 unidades de milhar = 10.000 unidades.

Atividade 1

A contagem de 1 em 1 ajuda a contar de 1.000 em 1.000. Os estudantes devem entender que, ao contar de 1.000 em 1.000, cada unidade de contagem incorpora mil unidades simples. Enfatize para a turma que 10 caixas com 1 000 clipes em cada uma poderiam ser trocadas por uma única caixa com 10.000 clipes, o que corresponderia a 1 dezena de milhar.

Atividade 2

As situações apresentadas nesta atividade permitem aos estudantes que percebam que os agrupamentos na casa das dezenas de milhar são compostos de unidades, dezenas, centenas e milhares.

BNCC em foco:

EF04MA01, EF04MA02

MP047

  1. Complete a sequência numérica e, em seguida, faça o que se pede.

10.000, 20.000, _____, 40.000, 50.000, _____, 70.000, _____, _____

PROFESSOR Resposta: 30.000, 60.000, 80.000, 90.000
  1. Escreva como lemos o último número dessa sequência:

    _____

    PROFESSOR Resposta: noventa mil
  1. O penúltimo número dessa sequência corresponde a _____ dezenas de milhar.
    PROFESSOR Resposta: 8
  1. Observe abaixo o extrato bancário da empresa de Ana e responda às questões.
Imagem: Ilustração. Papel com a informação: BANCO INVEST – EXTRATO CONTA-CORRENTE. AGÊNCIA: 0333. DATA: 22/02/2023. HORA: 15:32:53. CONTA: 33333-3. TIPO EMPRESA. DIA: 16. HISTÓRICO: SALDO ANTERIOR. ORIG: 16/01. VALOR: 14.475,93. FEVEREIRO/2019. DIA: 22. HISTÓRICO: DEPÓSITO. VALOR: 15.524,07. DIA: 22. HISTÓRICO: SALDO. VALOR: 30.000,00. Fim da imagem.
  1. Após conferir o extrato, Ana gastou vinte mil reais da conta bancária de sua empresa pagando a compra de móveis para o escritório. Com quantos reais a conta da empresa ficou?

    _____

    PROFESSOR Resposta: R$ 10.000,00 (dez mil reais)
  1. Em seguida, Ana depositou um cheque no valor de R$ 30.000,00. Qual passou a ser o saldo da conta da empresa de Ana?

    _____

    PROFESSOR Resposta: R$ 40.000,00 (quarenta mil reais)
  1. Complete o quadro com o resultado de cada adição e subtração.

Quadro: equivalente textual a seguir.

− 10.000

+ 10.000

40.000

30.000

50.000

50.000

_____

_____

60.000

_____

_____

70.000

_____

_____

80.000

_____

_____

PROFESSOR Resposta: 40.000; 60.000; 50.000; 70.000; 60.000; 80.000; 70.000; 90.000.
Imagem: Ilustração. Um menino ruivo está sorrindo e olhando para uma tabela. Ao seu lado, um cachorro branco o observa sentado. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 3

Proponha aos estudantes que eles contem de 10 em 10, de 100 em 100, de 1.000 em 1.000, de modo que percebam a regularidade presente no sistema de numeração decimal e a possibilidade de fazer agrupamentos também na casa das dezenas de milhar.

Atividade 4

Esta atividade explora a adição e a subtração de números formados por dezenas de milhar em um contexto de transações bancárias. Esclareça, em linguagem não formal, o significado dos termos que aparecem no texto: extrato é um documento em que são registradas as movimentações nos valores da conta bancária de uma pessoa ou de uma empresa, como retiradas (saques), depósitos ou transferências de valores em dinheiro ou cheque (entre contas) etc.; e saldo de uma conta bancária é o valor em dinheiro disponível àquele correntista ou, no caso de saldo negativo, o valor que ele está devendo ao banco.

Atividade 5

Após o preenchimento do quadro, peça aos estudantes que observem que, em todos os números, há quatro zeros, ou seja, todos têm a mesma ordem de grandeza, e apenas o primeiro dígito de cada um sofreu alteração ao ser efetuada a adição ou a subtração. Peça à turma que leia os números do quadro e as operações realizadas para obter cada resultado. Por exemplo:

40.000 − 10.000 = 30.000 (quarenta mil menos dez mil é igual a trinta mil).

BNCC em foco:

EF04MA02, EF04MA11

Sugestão de leitura para o professor

SMOLE, Katia Stocco; DINIZ, Maria Ignez. Materiais manipulativos para o ensino do sistema de numeração decimal. São Paulo: Penso, 2016. v. 1. (Coleção Mathemoteca)

O livro apresenta uma forma específica de ensino, que inclui o desenvolvimento da leitura e escrita em Matemática sob dois enfoques: a utilização de materiais manipulativos como recursos para favorecer a compreensão de conceitos matemáticos e a problemática como um arquivo de problemas diversificados para o desenvolvimento do raciocínio lógico e da habilidade de leitura de textos em problemas.

MP048

Números de cinco algarismos

  1. No site da revista eletrônica XYZ há uma informação sobre o número de visitantes por dia.
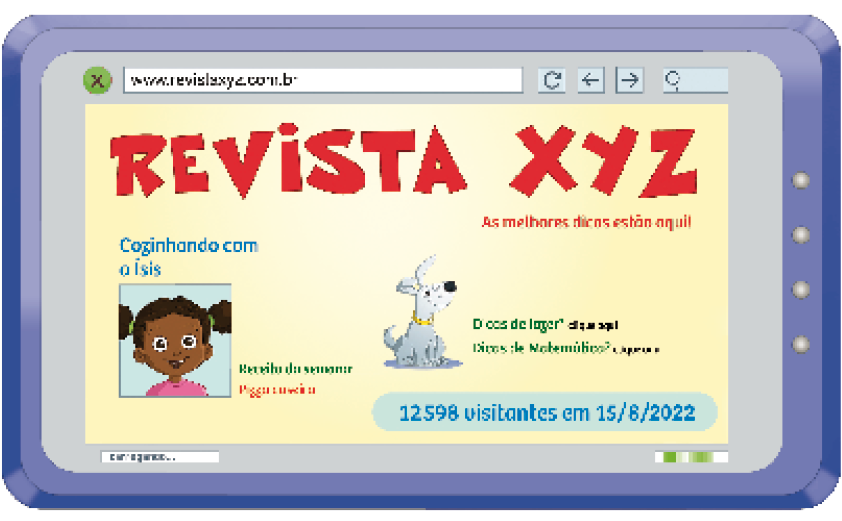
Imagem: Ilustração. Um tablet e na tela, a informação: REVISTA XYZ – As melhores dicas estão aqui! Cozinhando com a Ísis. Imagem de uma menina com cabelo encaracolado sorrindo. Receita da semana: Pizza caseira. Em seguida, imagem de um cachorro branco sentado e olhando para o lado. Dicas de lazer? Clique aqui. Dicas de Matemática? Clique aqui. 12.598 visitantes em 15/8/2022. Fim da imagem.
  1. Complete a decomposição desse número.
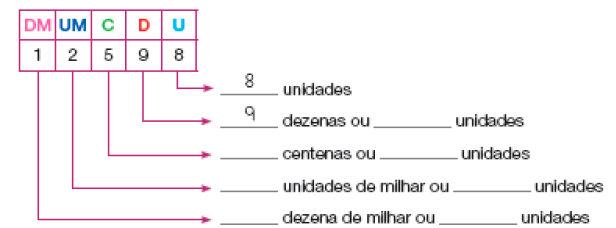
Imagem: Quadro de ordens. DM: 1. UM: 2. C: 5. D: 9 U: 8. 1: espaço para resposta dezenas de milhar ou espaço para resposta unidades. 2: espaço para resposta unidades de milhar ou espaço para resposta unidades. 5: espaço para resposta centenas ou espaço para resposta unidades. 9: 9 dezenas ou espaço para resposta ou espaço para resposta unidades. 8: 8 unidades Fim da imagem.

(DM significa dezenas de milhar)

PROFESSOR Resposta: 90, 5, 500, 2, 2.000, 1, 10.000

12.598 = _____ + _____ + _____ + _____ + _____

PROFESSOR Resposta: 10.000, 2.000, 500, 90, 8

Lemos: _____

PROFESSOR Resposta: Doze mil quinhentos e noventa e oito.
  1. O site de uma revista concorrente foi visitado em um mesmo dia por 3 dezenas de milhar, 4 unidades de milhar, 5 centenas e 12 unidades de pessoas. Escreva esse número com algarismos, depois registre o valor de seu algarismo 3.

    _____

    PROFESSOR Resposta: 34.512; trinta mil.
MANUAL DO PROFESSOR

Objetivos

• Reconhecer a escrita e a leitura de números de cinco algarismos.

• Realizar composição e reconhecer o valor posicional de um número de cinco algarismos.

• Resolver, com o suporte de imagem e de ábaco, problemas simples de contagem.

Atividade 1

Aproveite para fazer perguntas que envolvam outros números de cinco algarismos, como:

• Qual é o menor e qual é o maior número de cinco algarismos? (10.000 e 99.999, respectivamente.)

• Qual é o maior número de cinco algarismos distintos? (98.765.)

• Qual é o menor número de cinco algarismos distintos? (10.234.)

Peça aos estudantes que decomponham o número 12.598 de outras maneiras. Por exemplo, considerando multiplicações por potências de dez.

(12.598 = 1 × 10.000 +

+2 × 1.000 + 5 × 100 + 9 × 10 + 8 × 1)

BNCC em foco:

EF04MA01, EF04MA02

MP049

  1. Escreva com algarismos e por extenso o número que está representado em cada ábaco.
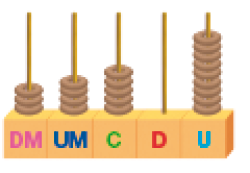
Imagem: Ilustração. Ábaco, base retangular com hastes de DM, UM, C, D, U. Há três argolas em DM, quatro em UM, cinco em C, zero em D e nove em U. Fim da imagem.

_____

PROFESSOR Resposta: 34.509
PROFESSOR Trinta e quatro mil quinhentos e nove.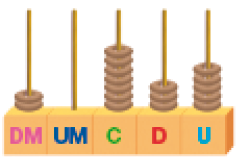
Imagem: Ilustração. Ábaco, base retangular com hastes de DM, UM, C, D, U. Há duas argolas em DM, zero em UM, sete em C, três em D e cinco em U. Fim da imagem.

_____

PROFESSOR Resposta: 20.735
PROFESSOR Vinte mil setecentos e trinta e cinco.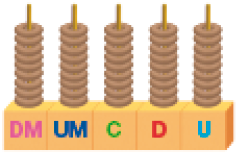
Imagem: Ilustração. Ábaco, base retangular com hastes de DM, UM, C, D, U. Há nove argolas em DM, nove em UM, nove em C, nove em D e nove em U. Fim da imagem.

_____

PROFESSOR Resposta: 99.999.
PROFESSOR Noventa e nove mil novecentos e noventa e nove.
  1. Observe quantas unidades vale cada ficha representada abaixo.
Imagem: Ilustração. Bola rosa (dez mil). Fim da imagem.

dez mil

Imagem: Ilustração. bola azul (mil). Fim da imagem.

mil

Imagem: Ilustração. bola laranja (cem). Fim da imagem.

cem

Imagem: Ilustração. bola amarela (dez). Fim da imagem.

dez

Imagem: Ilustração. bola verde (um). Fim da imagem.

um

Imagem: Ilustração. Duas bolas rosa, três bolas azuis, duas bolas laranja, quatro bolas amarelas e sete bolas verdes. Fim da imagem.

_____

PROFESSOR Resposta: 23.247 (vinte e três mil duzentos e quarenta e sete)
  1. Isadora, Alessandra e Gabriela foram à lousa escrever o número noventa mil trezentos e quarenta e dois.

    Qual delas o escreveu corretamente?

    _____

Imagem: Ilustração. Uma menina loira com cabelo preso está escrevendo em uma lousa: Isadora – 9.342. Uma menina com cabelo encaracolado e preso está escrevendo na lousa: Alessandra – 90.342. Uma menina com cabelo castanho está escrevendo na lousa: Gabriela – 93.042. Fim da imagem.
PROFESSOR Resposta: Alessandra.
MANUAL DO PROFESSOR

Atividade 2

Esta atividade explora a leitura, a escrita e o valor posicional de números de cinco algarismos no ábaco. Amplie-a, pedindo aos estudantes que escrevam o número que obteriam caso fosse desconsiderada a ordem com a quantidade nula nos dois primeiros itens. No item a, o número obtido seria 3.459; no item b, 2.735.

Atividade 3

Comente que a estrutura do nosso sistema de numeração permite a obtenção do número representado de forma direta. Por exemplo, o valor indicado pelas fichas pode ser determinado contando-se diretamente a quantidade de fichas de cada tipo e registrando-a com os algarismos 2, 3, 2, 4, 7, o que forma o número 23.247, ou adicionando-se:

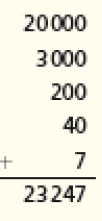
Imagem: Conta de adição na vertical. Na parte superior, o número 20.000. Abaixo, os números: 3.000, 200, 40, sinal de adição, 7. Em seguida, reta horizontal e o resultado: 23.247. Fim da imagem.

Atividade 4

É importante verificar como os estudantes realizam a escrita, por algarismos e por extenso, do número indicado. Observe se eles compreendem a ideia do valor posicional em números dessa grandeza, registrando os algarismos nas posições corretas. Os registros de Isadora e Gabriela apresentam erros comuns quando os estudantes não pensam no valor dos algarismos e escrevem um ou mais dos valores da maneira como os leem.

BNCC em foco:

EF04MA01, EF04MA02

MP050

Comparações

  1. Veja o esquema que Janaína fez para mostrar que 30 056 é menor que 31 120 e complete.
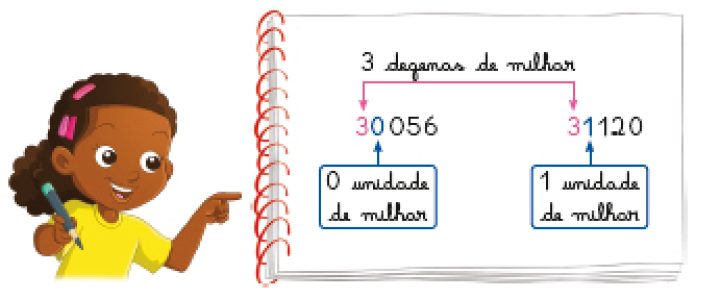
Imagem: Ilustração. Janaína, menina com cabelo encaracolado segura um lápis com a mão direita e aponta para o lado com a mão esquerda. Ao seu lado, um caderno com a informação: 30.056 (3 dezenas de milhar – 0 unidade de milhar). 31.120 (3 dezenas de milhar – 1 unidade de milhar). Fim da imagem.

Para saber qual é o número maior, Janaína comparou as ordens desses números.

Os dois números são da ordem de grandeza dezena de milhar.

Imagem: Ilustração. Caderno com a informação: 30.056 < 31.120. Fim da imagem.
  1. Complete com > (maior que) ou com < (menor que).
  1. 10.000 _____ 1.000
    PROFESSOR Resposta: >
  1. 13.401 _____ 13.291
    PROFESSOR Resposta: >
  1. 51.999 _____ 60.199
    PROFESSOR Resposta: <
  1. 24.009 _____ 24.100
    PROFESSOR Resposta: <
  1. 63.091 _____ 63.121
    PROFESSOR Resposta: <
  1. 21.212 _____ 21.211
    PROFESSOR Resposta: >
  1. 9.872 _____ 12.356
    PROFESSOR Resposta: <
  1. 94.789 _____ 96.234
    PROFESSOR Resposta: <
MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.

Comparar números naturais até a ordem de dezenas de milhar.

Organizar os números em determinada ordem (crescente ou decrescente).

Atividades 1 e 2

Ao fazerem comparações que envolvam somente números naturais, os estudantes têm a oportunidade de desenvolver estratégias apoiadas na lógica do nosso sistema de numeração. Veja algumas possibilidades de explicações para a comparação de pares de números:

3.600 é maior que 360, pois 3.600 tem mais algarismos que 360. Ou seja, o número 3 600 tem mais ordens que o 360 e, portanto, na sequência dos números naturais, 360 aparece antes de 3.600.

3.675 é maior que 3.670. Como os dois números têm a mesma quantidade de algarismos, pode-se comparar cada ordem começando pela maior: na 4ª ordem, os algarismos são iguais (3 e 3); na 3ª ordem, os algarismos são iguais (6 e 6); na 2ª ordem, os algarismos são iguais (7 e 7); finalmente, na 1ª ordem, como 5 é maior que 0, pode-se afirmar que 3.675 é maior que 3.670.

Incentive os estudantes a pensarem em outros pares de números (de mesma ordem de grandeza ou de ordens de grandeza diferentes) e trocar as propostas com os colegas, para a comparação entre os números.

BNCC em foco:

EF04MA01

MP051

  1. Responda às questões de acordo com o gráfico abaixo.
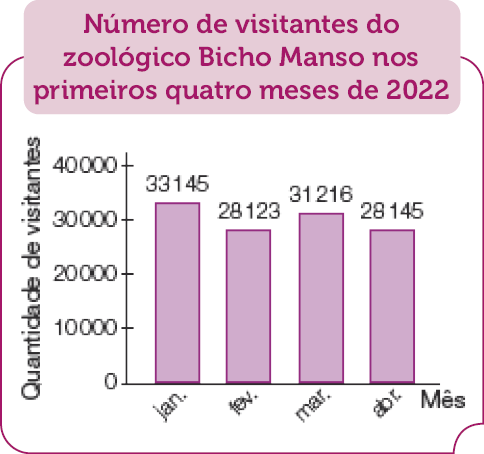
Imagem: Gráfico de colunas. Número de visitantes do zoológico Bicho Manso nos primeiros quatro meses de 2022. No eixo vertical, a quantidade de visitantes e no eixo horizontal, o mês. Jan.: 33.145. Fev.: 28.123. Mar.: 31.216. Abr.: 28.145. Fim da imagem.

Fonte: Zoológico Bicho Manso (2022).

  1. Carla foi ao zoológico Bicho Manso no mês mais movimentado dos primeiros quatro meses de 2022. Que mês foi esse?

    _____

    PROFESSOR Resposta: Janeiro.
  1. No mês de maio, o zoológico foi visitado por 28.101 pessoas. Esse mês foi mais ou menos movimentado que os quatro meses anteriores?

    _____

    PROFESSOR Resposta: Menos.
  1. Escreva em ordem crescente o número de visitantes dos meses de janeiro a maio de 2022. _____
    PROFESSOR Resposta: 28.101, 28.123, 28.145, 31.216, 33.145
  1. Observe a tabela com a população estimada de alguns municípios do Brasil em 2020, depois responda às questões.

População estimada de alguns municípios (2020)

Tabela: equivalente textual a seguir.

Município

População

Goiatuba (GO)

34.202

Barra (BA)

53.910

Eirunepé (AM)

35.700

Tupanciretã (RS)

24.068

Fonte: Instituto Brasileiro de Geografia e Estatística (IBGE). Disponível em: http://fdnc.io/eU8. Acesso em: 13 fev. 2021.

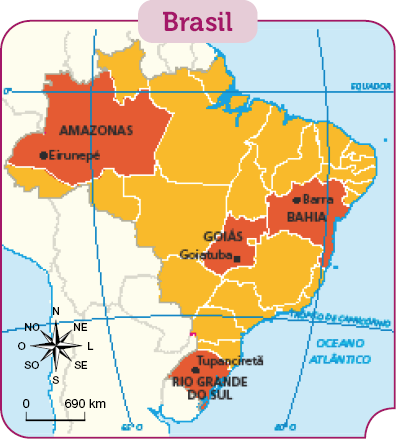
Imagem: Mapa. Brasil. Destaque para Eirunepé (Amazonas), Goiatuba (Goiás), Barra (Bahia) e Tupanciretã (Rio Grande do Sul). No canto inferior esquerdo, a rosa dos ventos e a escala. Fim da imagem.

Elaborado com base em: Atlas geográfico escolar. 6ª ed. Rio de Janeiro: IBGE, 2012. p. 90.

  1. Qual desses municípios tinha a maior população? E a menor?

    _____

    PROFESSOR Resposta: Maior: Barra, na Bahia; menor: Tupanciretã, no Rio Grande do Sul.
  1. Qual desses municípios tinha, aproximadamente, a metade da população de Barra? _____
    PROFESSOR Resposta: Tupanciretã.

    Imagem: Ícone: Dupla. Fim da imagem.

  1. Crie uma questão que possa ser respondida com os dados dessa tabela. Depois, peça a um colega que a responda.
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Para responder às questões, os estudantes devem ler e interpretar os valores indicados no gráfico de colunas. Espera-se que alguns deles percebam que também é possível fazer comparações entre a quantidade de visitantes que o zoológico recebeu em cada mês observando a altura de cada uma das colunas correspondentes no gráfico. Peça aos estudantes que expliquem como pensaram para responder às questões. É importante observar os comentários da turma sobre suas estratégias e verificar se elas são adequadas.

Atividade 4

Nesta atividade, os estudantes poderão observar e comparar a população de quatro municípios brasileiros. Estimule-os a dizer como pensaram para responder aos itens a e b.

Depois de verificar como a turma se organizou para a realização do item c, observe se as questões propostas podem ser respondidas com as informações fornecidas na tabela e no mapa e depois avalie as respostas dadas pelos colegas. Exemplos de questões que podem ser criadas pelos estudantes:

A população de Goiatuba é maior ou menor que a de Eirunepé? (Menor.)

O município de Tupanciretã está localizado em qual estado brasileiro? (Rio Grande do Sul.)

Qual é a ordem do algarismo 5 no número que representa a população de Barra? (Dezenas de milhar.)

BNCC em foco:

EF04MA01

MP052

Arredondamentos

  1. Observe o salário de algumas pessoas e a representação aproximada de cada valor em uma reta numérica.
Imagem: Ilustração. Quatro pessoas estão segurando papéis com as informações: Bernadete: 1.250 reais; Denílson: 820 reais; Helena: 2.120 reais; Válter: 880 reais. Fim da imagem.
Imagem: Ilustração. Reta numérica da esquerda para a direita: 800, 820, 880, 900, 1.000, 1.200, 1.250, 1.400, 2.100, 2.120. Fim da imagem.
  1. Qual dessas pessoas tem o salário mais próximo de 800 reais? E de 900 reais?

    _____

    PROFESSOR Resposta: Denílson; Válter.

    O arredondamento do número 820 para a centena mais próxima é 800.

    E o arredondamento do número 880 para a centena mais próxima é _____.

    PROFESSOR Resposta: 900
  1. Qual dessas pessoas tem o salário mais próximo de 1.000 reais?

    E de 2.000 reais? _____

    PROFESSOR Resposta: Bernadete; Helena.

    O arredondamento de 1.250 para a unidade de milhar mais próxima é _____.

    PROFESSOR Resposta: 1.000

    O arredondamento de 2.120 para a unidade de milhar mais próxima é _____.

    PROFESSOR Resposta: 2.000

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

  1. O quadro abaixo mostra o número de parafusos produzidos por uma fábrica durante três dias.

Quadro: equivalente textual a seguir.

Segunda-feira

Terça-feira

Quarta-feira

1.820

2.090

5.345

Podemos dizer que, nesses três dias, o total de parafusos produzidos foi de aproximadamente 9.000 unidades? Converse com o professor e os colegas.

MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.

Analisar os diferentes critérios que podem ser estabelecidos para os arredondamentos de números com três algarismos ou mais.

Realizar cálculos mentais aproximados para efetuar os arredondamentos.

Atividade 1

A representação na reta numérica possibilita a visualização geométrica para o arredondamento, auxiliando os estudantes a decidirem se ele deve ser feito “para mais” ou “para menos”. Esclareça que, no arredondamento, por exemplo, para a centena mais próxima, este será realizado “para mais” quando o algarismo da ordem das dezenas for igual a ou maior que 5, e “para menos” em caso contrário. Por exemplo, 820 deve ser arredondado para 800, pois o algarismo da ordem das dezenas é 2 (menor que 5) e 880 deve ser arredondado para 900, pois o algarismo da ordem das dezenas é 8 (maior que 5).

Atividade 2

Para responderem a essa questão, os estudantes deverão arredondar as quantidades correspondentes a cada dia para a unidade de milhar mais próxima. Caso tenham dificuldades, oriente-os.

BNCC em foco:

EF04MA01, EF04MA08, EF04MA11

MP053

  1. Localize de modo aproximado os números na reta numérica e responda.

    a) 23.035 e 28.653

Imagem: Ilustração. Reta numérica da esquerda para a direita: 20.000, 22.000, 24.000, 26.000, 28.000, 30.000. Resposta: 20.000, 22.000, 23.035, 24.000, 26.000, 28.000, 28.653, 30.000. Fim da imagem.
PROFESSOR Resposta: 23.035, 28.653
  1. 1.101 e 4.260
Imagem: Ilustração. Reta numérica da esquerda para a direita: 500, 1.000, 1.500, 2.000, 2.500, 3.000, 3.500, 4.000, 4.500, 5.000. Fim da imagem.
PROFESSOR Resposta: 1.101, 4.260
  1. Complete o quadro com os arredondamentos pedidos.

Quadro: equivalente textual a seguir.

Número

Para a dezena de milhar mais próxima

Para a unidade de milhar mais próxima

23.345

_____

_____

78.432

_____

_____

51.759

_____

_____

38.450

_____

_____

56.289

_____

_____

PROFESSOR Resposta: Para a dezena de milhar mais próxima: 20.000, 80.000, 50.000, 40.000, 60.000.
PROFESSOR Para a unidade de milhar mais próxima: 23.000, 78.000, 52.000, 38.000, 56.000.
  1. Descubra qual destes números é o mais próximo de 15.000.
    PROFESSOR Resposta: 15.008
Imagem: Ilustração. Papéis com os números: 15.300, 14.800, 15.008, 15.080. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 3

Esta atividade explora a representação do número como medida. Os estudantes têm a oportunidade de reconhecer, na reta numérica, a distância entre os números indicados e de identificar visualmente o arredondamento.

Amplie a atividade desenhando uma reta numérica na lousa com números diferentes dos apresentados no livro. Proponha aos estudantes arredondamentos “para mais” e “para menos” e peça a eles que façam a indicação na lousa. Socialize as estratégias individuais com a turma e pergunte se existem estratégias diferentes.

Sugira aos estudantes que façam arredondamentos de todas as ordens e incentive-os a perceberem que, quanto menor a ordem do arredondamento, mais próximo do número o arredondamento estará.

Atividade 4

A atividade permite verificar se os estudantes se apropriaram dos critérios para os arredondamentos dos números para a dezena de milhar mais próxima e para a unidade de milhar mais próxima.

Atividade 5

Nesta atividade, os estudantes devem buscar o melhor critério e a melhor estratégia para obterem o arredondamento mais perto de 15.000 e também observarem o valor posicional dos algarismos. Por exemplo, os números 15.008 e 15.080 têm os mesmos algarismos, mas a proximidade maior se dá pela posição do algarismo 8 na casa das unidades (15.008), e não na das dezenas (15.080).

BNCC em foco:

EF04MA01, EF04MA08, EF04MA11

MP054

  1. Faça a composição do número com as informações dos balões a seguir e escreva-o também por extenso.
Imagem: Ilustração. Quatro crianças estão segurando balões e dentro de cada um, a informação: 2 dezenas: espaço para resposta. 3 dezenas de milhar: espaço para resposta. 5 unidades: espaço para resposta. 6 centenas: espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 20, 30.000, 5, 600

_____

PROFESSOR Resposta: 30.000 + 600 + 20 + 5 = 30.625
Trinta mil seiscentos e vinte e cinco.
  1. Observe a tabela com as distâncias rodoviárias aproximadas entre algumas cidades brasileiras. Em seguida, responda às questões.

Distâncias entre cidades*

Tabela: equivalente textual a seguir.

De

Para

Distância em quilômetro

Porto Alegre (RS)

Goiânia (GO)

1.847

Rio Branco (A C)

Salvador (BA)

4.457

Fonte: Dados obtidos no site do Departamento Nacional de Infraestrutura de Transportes (DNIT). Disponível em: http://fdnc.io/eU9. Acesso em: 5 fev. 2021.

* A distância é calculada de centro a centro das cidades com os caminhos mais curtos, dando-se preferência a rodovias asfaltadas.

  1. Qual é a distância de Porto Alegre a Goiânia?

    _____

    PROFESSOR Resposta: 1.847 quilômetros.

    Imagem: Ícone: mental. Fim da imagem.

  1. Uma pessoa que sai de Rio Branco e vai para Salvador e depois volta para Rio Branco, fazendo o mesmo trajeto, percorre mais ou menos de 10.000 km?

    _____

    PROFESSOR Resposta: Menos.
  1. Escreva um número composto de cinco algarismos diferentes.

    _____

    PROFESSOR Exemplo de resposta: 52.687.
MANUAL DO PROFESSOR

Objetivos

Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.

Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.

Resolver problemas simples de contagem com o suporte de imagem e de ábaco.

Atividade 6

Espera-se que os estudantes percebam que as informações não estão organizadas em ordem quanto ao valor posicional de cada algarismo do número. Por isso, devem ordená-las ou simplesmente adicionar os valores indicados nos balões.

Atividade 7

Nesta atividade, espera-se que o estudante faça a leitura dos dados da tabela. No item b, espera-se que eles comparem 4.457 com a metade da dezena de milhar e façam a estimativa correta concluindo que o dobro de 4.457 é menor do que 10.000.

Atividade 8

Observe se os estudantes formam o número de cinco algarismos sem dificuldades.Verifique se eles escolheram algarismos ao acaso ou se a escolha revela alguma singularidade tal como o maior ou o menor número possível com algarismos diferentes, ou ainda, uma sequência do tipo 13.579.

BNCC em foco:

EF04MA01, EF04MA02, EF04MA08, EF04MA11

MP055

  1. Complete.

    a) 50.000 → Cinquenta mil ou 5 dezenas de milhar.

    b) 80.000 → _____ ou _____ dezenas de milhar.

    PROFESSOR Resposta: Oitenta mil, 8

    c) 90.000 → _____ ou _____ dezenas de milhar.

    PROFESSOR Resposta: Noventa mil, 9
  1. Em 2020, a população estimada do município de Capanema, no Pará, era de 69.431 habitantes, segundo o IBGE (Instituto Brasileiro de Geografia e Estatística).

    Escreva como se lê esse número e dê o valor de cada algarismo dele. Depois, represente esse número no ábaco.

    Lemos : _____

    PROFESSOR Resposta: Sessenta e nove mil quatrocentos e trinta e um.
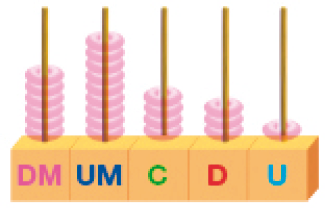
Imagem: Ilustração. Ábaco, base retangular com hastes de DM, UM, C, D, U. Há seis argolas em DM, nove em UM, quatro em C, três em D e um em U. Fim da imagem.
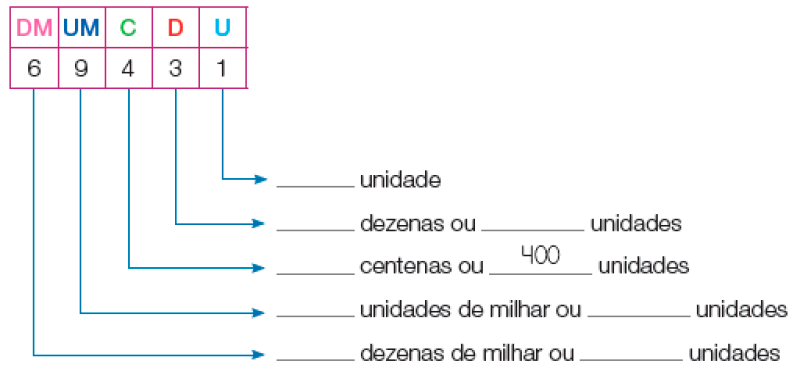
Imagem: Quadro de ordens. DM: 6. UM: 9. C: 4. D: 3 U: 1. 6: espaço para resposta dezenas de milhar ou espaço para resposta unidades. 9: espaço para resposta unidades de milhar ou espaço para resposta unidades. 4: espaço para resposta centenas ou 400 unidades. 3: espaço para resposta dezenas ou espaço para resposta unidades. 1: espaço para resposta unidade. Fim da imagem.
PROFESSOR Resposta: 1, 3, 30, 4, 9, 9.000, 6, 60.000
  1. Observe os números no quadro a seguir. Marque com um X a posição do algarismo 5 em cada um e escreva seu valor posicional.

Tabela: equivalente textual a seguir.

Número

DM

UM

C

D

U

Valor posicional

58.217

_____

_____

_____

_____

_____

_____

85.046

_____

_____

_____

_____

_____

_____

70.415

_____

_____

_____

_____

_____

_____

91.526

_____

_____

_____

_____

_____

_____

89.853

_____

_____

_____

_____

_____

_____

35.702

_____

_____

_____

_____

_____

_____

PROFESSOR Resposta: Número: 58.217; DM; 50.000.
PROFESSOR Número: 85.046; UM; 5.000.
PROFESSOR Número: 70.415; U; 5.
PROFESSOR Número: 91.526; C; 500.
PROFESSOR Número: 89.853; D; 50.
PROFESSOR Número: 35.702; UM; 5.000.
Imagem: Ilustração. Uma menina com cabelo castanho e preso está segurando um lápis atrás de uma tabela. Fim da imagem.
MANUAL DO PROFESSOR

Atividades 9 e 10

Nestas atividades, os estudantes devem relacionar a ordem da grandeza com a representação numérica, a escrita por extenso e a representação do número no ábaco.

Atividade 11

Verifique se os estudantes entendem como devem fazer a marcação no quadro para indicar a posição do algarismo 5 e em cada um dos números apresentados para determinar seu valor posicional.

BNCC em foco:

EF04MA01, EF04MA02

MP056

A Matemática me ajuda a ser

... um conhecedor de outra língua

Você já deve ter visto algumas pessoas se comunicando por meio de sinais com as mãos. Você sabe o que são esses sinais? Eles representam uma língua.

A Língua Brasileira de Sinais (Libras) é usada por alguns surdos do Brasil. Diferentemente de idiomas que são orais e auditivos, a Libras é visual e gestual, ou seja, uma língua pronunciada pelo corpo e interpretada pela visão.

Conheça o alfabeto da Libras.

Imagem: Fotografia. Alfabeto em Libras: Letra A: mão fechada com o dedo polegar para cima. Letra B: mão aberta com o dedo polegar fechado. Letra C: mão curvada. Letra Ç: mão curvada e balançando. Letra D: dedo indicador para cima e dedo polegar e do meio fechados. Letra E: dedos dobrados com a palma da mão aberta. Letra F: dedos esticados. Dedo indicador reto e dedo polegar por cima. Letra G: dedos dobrados. Dedo indicador e polegar para cima. Letra H: dedo indicador e do meio levantados, dedos anelar e mindinho dobrados e dedo polegar sobre os dedos dobrados. A mão vira para o lado. Letra I: dedos dobrados. Dedo mindinho para cima. Letra J: dedos dobrados. Dedo mindinho para cima. A mão balança de cima para baixo, fazendo uma curva. Letra K: dedo mindinho e anelar dobrados. Dedos do meio, indicador e polegar para cima. A mão faz movimento para cima. Letra L: dedo mindinho, anelar e do meio dobrados. Dedo indicador e polegar esticados. Letra M: dedo mindinho e polegar dobrados. Dedo anelar, do meio e indicador apontando para baixo. Letra N: dedo mindinho, anelar e polegar dobrados. Dedo do meio e indicador apontando para baixo. Letra O: dedos unidos e curvados. Letra P: dedo indicador, do meio e polegar esticados para frente. Letra Q: dedo indicador apontando para baixo. Letra R: dedo do meio e indicador esticados e cruzados. Letra S: dedos fechados com o polegar sobre eles. Letra T: dedo anelar e do meio levantados. Dedo indicador reto e polegar atrás dele. Letra U: dedo do meio e indicador levantados e unidos. Letra V: dedo do meio e indicador levantados e abertos. Letra W: dedo anelar, do meio e indicador levantados. A mão faz movimento para cima. Letra X: dedo indicador reto e curvado. A mão faz movimento para trás. Letra Y: dedo mindinho e polegar levantados. A mão faz movimento para cima. Letra Z: dedo indicador faz um Z no ar. Fim da imagem.

Os algarismos também podem ser representados em Libras.

Imagem: Fotografia. Números em Libras: Número 0: dedos unidos e curvados. Número 1: dedo polegar para cima. Número 2: dedo polegar para cima e indicador reto. Número 3: dedo anelar, do meio e indicador retos. Número 4: dedo mindinho, anelar, do meio e indicador retos. Número 5: dedo do meio e indicador dobrados e os outros dedos fechados. Número 6: polegar para cima e os outros dedos curvados. Número 7: indicador apontando para cima com o polegar ao lado. Número 8: mão fechada com o polegar sobre os dedos. Número 9: polegar para baixo e os outros dedos curvados. Fim da imagem.
MANUAL DO PROFESSOR

Objetivo

Resolver, com o suporte de imagem, problemas simples de contagem.

Nesta seção, os estudantes entram em contato com a Língua Brasileira de Sinais (Libras), língua visual-gestual usada por pessoas com deficiência auditiva em sua comunicação. Cada país possui sua própria língua de sinais, que sofre as influências da cultura nacional.

Os sinais dessa língua são formados pela combinação da forma e do movimento das mãos e do ponto no corpo ou no espaço em que esses sinais são feitos.

Ao usar a Libras, a expressão facial e/ou corporal é importante também, pois é por meio dela que ocorre a entonação.

Para conversar em Libras, é necessário conhecer os sinais e também sua estrutura gramatical.

Explore o texto com os estudantes e, com eles, represente cada letra do alfabeto e cada algarismo em Libras.

BNCC em foco na dupla de páginas:

EF04MA08; competência geral 4

MP057

Tome nota

  1. Para traduzir os números expressos em Libras com os algarismos do sistema de numeração indo-arábico, basta escrever os algarismos na ordem em que eles aparecem. Anote os números que estão representados em cada caso.
Imagem: Fotografia. Número 6: polegar para cima e os outros dedos curvados. Número 8: mão fechada com o polegar sobre os dedos. Número 2: dedo polegar para cima e indicador reto. Fim da imagem.

_____

PROFESSOR Resposta: 682
Imagem: Fotografia. Número 3: dedo anelar, do meio e indicador retos. Número 0: dedos unidos e curvados. Número 9: polegar para baixo e os outros dedos curvados. Fim da imagem.

_____

PROFESSOR Resposta: 309
Imagem: Fotografia. Número 5: dedo do meio e indicador dobrados e os outros dedos fechados. Número 1: dedo polegar para cima. Número 4: dedo mindinho, anelar, do meio e indicador retos. Fim da imagem.

_____

PROFESSOR Resposta: 514
Imagem: Fotografia. Número 7: indicador apontando para cima com o polegar ao lado. Número 5: dedo do meio e indicador dobrados e os outros dedos fechados. Número 8: mão fechada com o polegar sobre os dedos. Fim da imagem.

_____

PROFESSOR Resposta: 758

Imagem: Ícone: Oral. Fim da imagem.

Reflita

  1. Você já tinha ouvido falar sobre Libras? Conhece alguém que sabe usá-la?
    PROFESSOR Respostas pessoais.
  1. Além do alfabeto e dos algarismos, em Libras existem gestos para expressar palavras. Como você acha que é representada a palavra “amigo”? E a palavra “matemática”?

Imagem: Ícone: Dupla. Fim da imagem.

  1. Reúna-se com um colega e pesquisem como são representadas algumas palavras em Libras. Depois, tentem se comunicar por meio dos gestos que vocês aprenderam.
MANUAL DO PROFESSOR

Tome nota

Proponha que três estudantes se ofereçam para representar para a turma, em Libras, cada algarismo. Oriente-os a se posicionarem de modo que os colegas possam verificar se o número representado ficou correto.

Reflita

Estimule os estudantes a compartilharem as experiências com pessoas que usam a Libras; caso nenhum estudante conheça quem sabe usá-la, peça a eles que compartilhem como foi representar cada algarismo dos números.

Na segunda questão, chame alguns estudantes à frente da sala de aula para que mostrem como acreditam que as duas palavras são representadas com a Língua Brasileira de Sinais. Sugira a eles que “soletrem” a palavra, representando cada letra em Libras. Pergunte: “Como seria conversar soletrando cada letra de cada palavra?”. Espera-se que os estudantes percebam que as conversas ficariam mais fáceis com outro tipo de representação. Veja como representar “amigo” e “matemática” utilizando o Dicionário da Língua Brasileira de Sinais V3 – 2011.

Se julgar oportuno, na terceira questão, sugira aos estudantes que consultem o Dicionário da Língua Brasileira de Sinais V3 – 2011 para representarem as palavras escolhidas. Depois, proponha uma discussão sobre a pesquisa. Pergunte a eles: “Que dificuldades vocês encontraram para representar as palavras em Libras? Como vocês se sentiram?”. Se algum estudante for deficiente auditivo, peça a ele que compartilhe as dificuldades enfrentadas no dia a dia.

Aproveite a situação proposta e converse com os estudantes sobre atitudes sustentáveis e cidadãos educados e conscientes.

Sugestões para o professor

Dicionário da Língua Brasileira de Sinais, V3, 2011. Disponível em:

http://www.acessibilidadebrasil.org.br/libras_3/ . Acesso em: 27 fev. 2021.

Depois de digitar a palavra procurada, um vídeo mostra sua representação em Libras.

Repórter Visual. Disponível em: http://tvbrasil.ebc.com.br/visual . Acesso em: 27 fev. 2021.

O Repórter Visual é o primeiro telejornal diário com reportagens sobre a inclusão da pessoa com deficiência auditiva e também sobre notícias do Brasil e do mundo traduzidas para a Língua Brasileira de Sinais.

MP058

Compreender informações

Ler e interpretar informações em tabelas

1. A escola Mente e Corpo incentiva seus estudantes a praticarem atletismo e ginástica. Observe o registro que a escola fez do número de estudantes praticantes dessas duas modalidades esportivas nos últimos anos.

Número de estudantes praticantes de modalidades esportivas (2019-2022)

Tabela: equivalente textual a seguir.

Ano

Número de praticantes de atletismo

Número de praticantes de ginástica

2019

200

100

2020

300

200

2021

500

300

2022

600

600

Fonte: Escola Mente e Corpo (2022).

Imagem: Ilustração. Um menino com capacete está em um carrinho de rolimã e correndo em uma rua. Atrás dele há duas crianças correndo. Ao fundo, uma menina está se exercitando e atrás dela há uma construção grande. Fim da imagem.
  1. Em 2019, qual modalidade tinha mais praticantes?

    _____

    PROFESSOR Resposta: O atletismo.
  1. Em que ano a ginástica e o atletismo tiveram o mesmo número de praticantes?

    _____

    PROFESSOR Resposta: Em 2022.
  1. Qual modalidade teve maior aumento no número de praticantes de 2019 para 2022?

    _____

    PROFESSOR Resposta: A ginástica.
  1. Complete as frases a seguir de modo que se tornem afirmações verdadeiras sobre os dados da tabela.
    • De 2019 para 2022, o número de praticantes de atletismo aumentou em _____ praticantes.
      PROFESSOR Resposta: 400
    • Tanto o número de praticantes de atletismo quanto o de praticantes de ginástica sempre _____ de um ano para outro.
      PROFESSOR Resposta: aumentaram
    • Somente em 2022 o número de praticantes de ginástica se _____ ao número de praticantes de atletismo.
      PROFESSOR Resposta: igualou
    • Em 2019, o número de praticantes de atletismo era _____ do número de praticantes de ginástica.
      PROFESSOR Resposta: o dobro
MANUAL DO PROFESSOR

Objetivos

Ler e interpretar informações em tabelas.

Escrever afirmações com base na análise dos dados.

Nas atividades destas páginas, os estudantes analisarão informações organizadas em tabelas de dupla entrada com o objetivo de produzir afirmações sobre os dados apresentados.

Atividade 1

Comente que, em geral, uma tabela de dupla entrada é usada quando se pretende comparar dados de uma mesma categoria (no caso, número de praticantes de atletismo e de ginástica).

Os itens a, b e c têm como objetivo fazer com que os estudantes realizem uma leitura das informações contidas na tabela, identificando as respostas correspondentes. Para completar as frases no item d, os estudantes deverão fazer uma análise dos dados e interpretá-los. Se considerar adequado, peça a eles que escrevam mais uma afirmação que possa ser feita em relação a esses dados.

BNCC em foco:

EF04MA27

MP059

  1. No centro médico Cidade Alegre, é feito um controle semestral da quantidade de consultas médicas nas diferentes especialidades. As informações sobre os atendimentos de 2022, nas especialidades de ortopedia, cardiologia e oftalmologia, estão na tabela a seguir.
Imagem: Ilustração. À esquerda, pessoas estão sentadas em cadeiras. À direita, um homem está em pé, na frente de um balcão com duas recepcionistas sentadas. Acima deles há uma placa com a informação: RECEPÇÃO. No centro, uma médica está segurando um papel. Fim da imagem.

Número de consultas médicas em 2022

Tabela: equivalente textual a seguir.

Especialidade

Número de consultas

1 º semestre

2º semestre

Ortopedia

5.000

4.000

Cardiologia

5.000

8.000

Oftalmologia

12.000

12.000

Fonte: Centro médico Cidade Alegre (2022).

  1. Que especialidade teve aumento de consultas entre o 1º e o 2º semestres? E qual teve diminuição?

    _____

    PROFESSOR Resposta: A cardiologia. A ortopedia.
  1. Que especialidade se manteve estável no número de consultas nesse período?

    _____

    PROFESSOR Resposta: A oftalmologia.
  1. Quantas consultas foram realizadas nessas especialidades em 2022?

    _____

    PROFESSOR Resposta: 46.000 consultas.
  1. Em qual dessas especialidades o número de médicos especialistas deve ser maior? Por quê?

    _____

    PROFESSOR Resposta pessoal.
  1. Na sua opinião, a quantidade de médicos especialistas em ortopedia deve ser maior ou menor que a quantidade de médicos especialistas em cardiologia? Por quê?

    _____

    PROFESSOR Resposta pessoal.
  1. Escreva três afirmações que podem ser feitas em relação às informações contidas nessa tabela.

    _____

    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 2

Pergunte aos estudantes se eles sabem do que trata cada especialidade médica citada na atividade. Comente que a ortopedia trata dos ossos e dos músculos, a cardiologia trata das doenças do coração e a oftalmologia trata das doenças dos olhos.

Para responder ao item c, os estudantes devem perceber que é necessário adicionar todas as consultas que foram indicadas na tabela.

Para os itens d e e, não há resposta correta. Leve em consideração as argumentações dos estudantes para poder validá-las.

Aproveite para compartilhar com os estudantes as diferentes afirmações que forem apresentadas como respostas ao item f. É importante perceberem que é possível escrever afirmações diferentes das escritas por eles.

BNCC em foco:

EF04MA27

MP060

O que você aprendeu

  1. Escreva a ordem de grandeza dos números em cada caso.
Imagem: Ilustração. Placa com a informação: Número de dias de um ano. Fim da imagem.

_____

PROFESSOR Resposta: centena
Imagem: Ilustração. Placa com a informação: Número de metros de 1 quilômetro. Fim da imagem.

_____

PROFESSOR Resposta: unidade de milhar
Imagem: Ilustração. Placa com a informação: Número de dias de um mês. Fim da imagem.

_____

PROFESSOR Resposta: dezena
Imagem: Ilustração. Placa com a informação: Número de metros de 15 quilômetros. Fim da imagem.

_____

PROFESSOR Resposta: dezena de milhar
  1. A maratona é uma prova de corrida em que os atletas devem percorrer 42.195 metros.
Imagem: Fotografia. Várias mulheres com números nas regatas estão correndo em uma rua. Fim da imagem.

LEGENDA: Atletas participam da Maratona de Boston, nos Estados Unidos, em 2019. FIM DA LEGENDA.

  1. Represente esse número no quadro a seguir.

Quadro: equivalente textual a seguir.

Dezenas de milhar

Unidades de milhar

Centenas

Dezenas

Unidades

_____

_____

_____

_____

_____

PROFESSOR Resposta: 4 2 1 9 5.
  1. Decomponha esse número considerando o valor de cada um dos algarismos.

    _____

    PROFESSOR Resposta: 42.195 = 40.000 + 2.000 + 100 + 90 + 5
  1. Se você tivesse de arredondar esse número, para qual número arredondaria?

    _____

    PROFESSOR Resposta: Exemplo de arredondamento para a unidade de milhar mais próxima: 42.000.
  1. Marque V (verdadeira) ou F (falsa) para cada afirmação a seguir.
    1. ( ) 43.000 > 38.000
      PROFESSOR Resposta: V
    1. ( ) 24.387 < 24.598
      PROFESSOR Resposta: V
    1. ( ) 4.326 > 4.321
      PROFESSOR Resposta: V
    1. ( ) 12.025 < 12.018
      PROFESSOR Resposta: F
MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para a avaliação formativa.

Muitos dos conceitos/procedimentos desta Unidade vêm sendo construídos em séries anteriores. Aqui há a ampliação de números até a dezena de milhar. Caso algum estudante tenha dificuldade, faça a retomada desses conceitos/procedimentos.

Atividade 1

Oriente os estudantes a registrarem cada número antes de escreverem sua ordem de grandeza.

Atividade 2

Para responder ao item c, os estudantes podem adotar diferentes critérios para arredondar o número 42.195 (além do já indicado na atividade):

para a dezena mais próxima: 42.200;

para a centena mais próxima: 42.200;

para a dezena de milhar mais próxima: 40.000.

Atividade 3

Depois que os estudantes realizarem esta atividade, peça a eles que digam como pensaram para comparar os números e determinar qual deles é o maior. A troca de estratégias é importante para ampliar o repertório de resolução dos estudantes.

BNCC em foco:

EF04MA01, EF04MA02

MP061

  1. Observe a quantidade de votos que cada candidato recebeu em uma eleição e responda às questões.
Imagem: Ilustração. À esquerda, um homem loiro com camisa azul e abaixo, a informação: Jaime – 24.978 votos. No centro, uma mulher ruiva com cabelo ondulado e regata verde. Abaixo, a informação: Adriana – 89.987 votos. À direita, um homem com cabelo castanho e camiseta amarela. Abaixo, a informação: Marcos – 87.876 votos. Fim da imagem.
  1. Ordene os candidatos de acordo com a quantidade de votos recebidos, da maior quantidade para a menor.

    _____

    PROFESSOR Resposta: Adriana, Marcos e Jaime.
  1. De quantos votos a mais Marcos precisaria para vencer as eleições?

    _____

    PROFESSOR Resposta: 2.112 votos.
  1. Leia as dicas e descubra o número formado pelos algarismos abaixo.
Imagem: Ilustração. Flores coloridas com números dentro: Rosa (0), vermelho (7), laranja (5), lilás (2), verde (4), roxo (3). Fim da imagem.

Boxe complementar:

Dicas

  • É um número entre 50.000 e 60.000.
  • É um número ímpar.
  • O algarismo das dezenas é a metade do algarismo das centenas; quando adicionados, totalizam 6.
  • O algarismo das dezenas de milhar não é 7 nem 3.

Fim do complemento.

_____

PROFESSOR Respostas possíveis: 57.423; 53.427; 50.423; 50.427.

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 4

Nesta atividade, os estudantes terão de comparar a quantidade de votos recebida pelos três candidatos. Eles perceberão que Jaime foi quem recebeu a menor quantidade de votos, pois o algarismo da classe das dezenas de milhares é 2, enquanto o de Adriana e de Marcos é 8. Ao comparar o algarismo das unidades de milhar, os estudantes concluirão que Adriana venceu a eleição, pois o número que representa a quantidade de votos que ela recebeu tem nessa ordem o algarismo 9, que é maior que 7.

Atividade 5

Leia as dicas com os estudantes e escreva na lousa as hipóteses que forem surgindo. A primeira dica revela que o número tem 5 algarismos e está entre 50 000 e 60 000. Assim, esses dois números podem ser eliminados e já é possível saber que o 5 ocupará a dezena de milhar. Depois, os estudantes poderão pensar nas possibilidades de se obter soma 6 (6 + 0, 5 + 1, 4 + 2, 3 + 3) e descobrir em qual das opções uma parcela é a metade da outra (4 + 2), descobrindo os algarismos da dezena e da centena.

Tabela: equivalente textual a seguir.

DM

UM

C

D

U

5

4

2

Por fim, restam três algarismos (0, 3, 7) para completar o quadro nas ordens UM e U. Além disso, é importante lembrar que o algarismo zero não pode ocupar a ordem da unidade, pois o número é ímpar (segunda dica).

BNCC em foco:

EF04MA01, EF04MA02

Autoavaliação

A Unidade pode ser finalizada com os estudantes analisando como reconhecem e escrevem números envolvendo mais ordens. Caso seja necessário, coloque alguns números com até cinco algarismos na lousa para que eles possam perceber o quanto conseguem realizar as leituras e o que ainda precisam desenvolver.

A questão dos arredondamentos também é importante. Os estudantes deverão perceber se utilizam arredondamentos para realizar cálculos não exatos, compreendendo sua importância no cotidiano.

MP062

Comentários para o professor:

Conclusão da Unidade 1

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Consegue ler, escrever e comparar números naturais até a quinta ordem e estabelecer relações entre os registros numéricos (escritos ou com material manipulável) e língua materna?

_____

_____

Identifica características do sistema de numeração decimal, empregando a composição e a decomposição de número natural de até cinco ordens?

_____

_____

Utiliza características do sistema de numeração para resolução de problemas?

_____

_____

Estabelece a relação entre números naturais e pontos da reta numérica ordenando-os e também na construção de fatos da adição e da subtração, relacionando-os com deslocamentos?

_____

_____

Identifica regularidades em sequências numéricas resultantes de adições ou subtrações sucessivas?

_____

_____

Resolve problemas cujos dados são apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____