MP063

Introdução da Unidade 2

Esta Unidade tem como foco tratar os conhecimentos a serem desenvolvidos na Unidade Temática Números. Assim, a abertura traz, em página dupla, uma imagem próxima do cotidiano da criança na faixa etária do estudante do 4º ano do Ensino Fundamental, com informações a serem exploradas nas questões propostas na seção Para refletir....

Nesta Unidade, além de ampliar as habilidades na leitura, escrita e ordenação dos números naturais até a ordem de dezenas de milhar com o consequente aprofundamento na compreensão do sistema de numeração decimal – todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez – e nas estratégias de cálculo já trabalhadas na Unidade 1, explora-se o uso de diferentes procedimentos de cálculo mental, por estimativa e escrito na resolução de problemas que envolvam adição e subtração com números naturais, o uso da relação entre adição e subtração em estratégias de cálculos e o uso das propriedades das operações para desenvolver ainda mais estratégias de cálculo, ampliando os objetos de conhecimento da Unidade Temática Números.

Neste ano, há um aprofundamento dos problemas em relação aos do 3º ano, além de o campo numérico ter ampliado. Já no 5º ano, os Objetos de conhecimento desse tema serão ampliados — problemas de adição e subtração com números racionais cuja representação decimal é finita.

Nas atividades da Unidade Temática Álgebra explora-se o reconhecimento, por meio de investigações, e utilização, quando necessário, da calculadora, das relações inversas entre as operações de adição e de subtração, com o objetivo de aplicá-las na resolução de problemas. O trabalho que envolve essa habilidade de relacionar as operações contribuirá para o desenvolvimento de outras duas habilidades da Unidade:

• reconhecimento e demonstração, por meio de exemplos, que uma igualdade não se altera ao adicionar um mesmo número a seus dois termos ou ao subtrair um mesmo número de seus dois termos;

• determinação do número desconhecido que torna verdadeira uma igualdade que envolve as operações fundamentais com números naturais.

No 3º ano, os estudantes iniciaram o trabalho desse conteúdo com a compreensão da ideia de igualdade na escrita de diferentes sentenças de adições e subtrações. No 5º ano, os conhecimentos adquiridos no 4º ano contribuirão para a formação da noção de equivalência.

A Unidade Temática Probabilidade e estatística é contemplada em problemas que exploram a identificação, entre eventos aleatórios cotidianos, daqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis. No 3º ano, iniciou-se o trabalho com os conceitos de eventos aleatórios e de estimativa de chances. A habilidade assim desenvolvida também será explorada na Unidade 4, deste ano, e preparará para atividades de Probabilidade do 5º ano.

Competência geral favorecida

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

Competências específicas favorecidas

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

MP064

UNIDADE 2. Adição e subtração

Imagem: Ilustração. Vista de cima de um zoológico. À esquerda, uma gaiola gigante e dentro há várias araras coloridas. Na frente, um casal de idosos está tirando fotos. Em seguida, um homem está andando de mãos dadas com duas crianças. Abaixo há duas zebras em uma área com grama e árvores. Na frente delas, Sidney e Júlio e um senhor observam. Atrás deles há uma placa grande com a informação: VOCÊ SABIA? Neste zoológico há 216 espécies de aves, 102 espécies de mamíferos e 95 espécies de répteis. No centro, várias pessoas estão andando. À direita há várias tartarugas dentro de um lago. Em seguida, girafas atrás de um muro de madeira e ao lado, macacos dentro de uma gaiola gigante. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos da Unidade

Resolver e elaborar problemas envolvendo adição e subtração, utilizando estimativa, decomposição, algoritmos e cálculo mental.

Trabalhar, por meio de adições e subtrações, critérios de arredondamento de números para diferentes ordens.

Conceituar procedimentos relativos às propriedades associativa, comutativa e do elemento neutro da adição.

Formalizar a utilização de parênteses na organização de uma adição com três parcelas.

Explorar as operações de adição e subtração como operações inversas, por meio de situações envolvendo três números.

Reconhecer que uma igualdade não se altera quando se adiciona ou se subtrai um mesmo número a seus dois termos.

Resolver problemas identificando dados insuficientes.

Interpretar texto e identificar informações sobre prevenção ao contágio por coronavírus.

Identificar, entre eventos aleatórios, aqueles em que há maior chance de ocorrência, reconhecendo características de resultados mais prováveis.

Nas páginas de abertura, os estudantes podem observar a cena que retrata pessoas passeando em um zoológico. Peça a eles que contem se já foram ou não ao jardim zoológico; se foram, quais animais já viram. Pergunte quais animais estão retratados na ilustração e se eles sabem a que espécie cada um deles pertence. A arara é uma ave, a zebra, um mamífero, e a tartaruga, um réptil.

BNCC em foco:

EF04MA02, EF04MA03, EF04MA04, EF04MA05, EF04MA13, EF04MA14, EF04MA15, EF04MA26

MP065

Boxe complementar

Para refletir...

A família Silva foi a um zoológico.

Quantas espécies de aves e de répteis há nesse zoológico?

_____

PROFESSOR Resposta: 311 espécies.

Quantas espécies de aves e de répteis há a mais que mamíferos nesse zoológico?

_____

PROFESSOR Resposta: 209 espécies.

Até ontem, esse zoológico tinha 1.280 animais. Hoje, chegaram mais alguns, e o zoológico ficou com 1.430 animais. Quantos animais chegaram hoje?

_____

PROFESSOR Resposta: 150 animais.

Fim do complemento

MANUAL DO PROFESSOR

Para refletir...

Peça aos estudantes que leiam a placa com as informações sobre a quantidade de espécies de aves, mamíferos e répteis no zoológico para, em seguida, responderem às questões propostas.

O objetivo da questão é fazer os estudantes perceberem a relação entre a adição e a subtração. Permita a eles que discutam a questão proposta fazendo as intervenções necessárias.

MP066

Jogo: Número-alvo

Imagem: Ilustração. Um menino e uma menina estão sentados em volta de uma mesa. Cada um está segurando quatro cartas e na frente deles há uma carta com o número 7 sobre uma mesa e ao lado, um montinho de cartas viradas. Fim da imagem.

Materiais: 64 cartas numeradas de 0 a 15 (quatro de cada valor). As cartas podem ser confeccionadas em cartolina pelos jogadores.

Imagem: Ícone: Grupo. Fim da imagem.

Jogadores: 2, 3 ou 4.

Regras:

MANUAL DO PROFESSOR

Objetivo

Resolver problemas com números naturais envolvendo adição e subtração.

Ajude os estudantes na leitura e na compreensão das regras. Se necessário, simule com um ou dois estudantes o início de uma partida.

O jogo trabalha a composição de números por meio de adições e/ou de subtrações com os números disponíveis nas cartas, contribuindo para o desenvolvimento de habilidades de cálculo mental e de teste de possibilidades.

Alguns jogos com proposta similar resumem-se ao cálculo do resultado de uma adição ou subtração com números sorteados em dados ou cartas. Neste jogo, no entanto, os estudantes devem testar diversas possibilidades de cálculo para obter determinado resultado. Como os participantes jogam ao mesmo tempo para encontrar o número-alvo, todos estão sempre envolvidos e realizando cálculos mentais. Além de o desafio ser maior, os jogadores são incentivados a resolverem os problemas por meio de estratégias próprias, o que possibilita o surgimento, em algumas situações, de mais de um modo de resolução.

BNCC em foco:

EF04MA03; competências específicas 3 e 8

MP067

Questões sobre o jogo

  1. Observe as cartas de Sandra e descubra como ela pode obter o número-alvo.
Imagem: Ilustração. Sandra, menina ruiva com cabelo preso está sentada e de costas. Ela está segurando quatro cartas com os números: 11, 11, 4, 15. Na frente dela, Luciano, menino com cabelo castanho está segurando quatro cartas com uma sobrancelha levantada. Entre eles há um montinho de cartas viradas e uma carta com o número 0 sobre uma mesa. Fim da imagem.

_____

PROFESSOR Respostas possíveis: 11 − 11, 15 − 4 − 11 ou 11 + 4 − 15.
  1. Em uma rodada, o número-alvo era Ilustração. Carta: 13. . Sandra tinha as cartas mostradas abaixo. Como ela pôde obter o número-alvo usando somente duas cartas? E três cartas? E quatro cartas?

    _____

    PROFESSOR Resposta: Duas cartas: 6 + 7; três cartas: 6 + 7 + 0; quatro cartas: não é possível.
Imagem: Ilustração. Mão segurando quatro cartas com os números: 1, 6, 7, 0. Fim da imagem.
  1. Observe a jogada representada abaixo e faça o que se pede.
Imagem: Ilustração. Luciano está sentado de costas e segurando três cartas com os números: 1, 2, 3. Ele fala: Sandra, não vai dar para eu formar o número-alvo. Na frente dele, Sandra está segurando três cartas e sorrindo. Entre eles há um montinho de cartas viradas e uma carta com o número 15 sobre uma mesa. Fim da imagem.
MANUAL DO PROFESSOR

Questões sobre o jogo

Após os estudantes jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões, que auxiliam na compreensão de escolhas de possibilidades, na análise de riscos e na tomada de decisões.

As questões permitem que os estudantes estabeleçam estratégias que possam usar no decorrer do jogo, como a análise do maior ou do menor número que pode ser obtido com as cartas sorteadas.

Na questão 2, espera-se que os estudantes percebam que não é possível formar o número-alvo com quatro cartas.

Variações

Deixe os estudantes jogarem diversas vezes, para que se habituem às regras e aos números envolvidos nos cálculos. É possível que, após a realização de algumas partidas, queiram alterar as regras, como permitir o uso da multiplicação e da divisão, ou determinar um tempo a ser cronometrado para a realização de cada jogada, ou mudar os números que farão o papel de número-alvo (neste caso, peça a eles que verifiquem se o número escolhido pode ser obtido com as cartas disponíveis e com as operações permitidas no jogo).

BNCC em foco:

EF04MA03; competências específicas 3 e 8

MP068

Cálculo mental

  1. Veja como Carlos e Lígia calcularam mentalmente o resultado de 2 400 + 1 900.
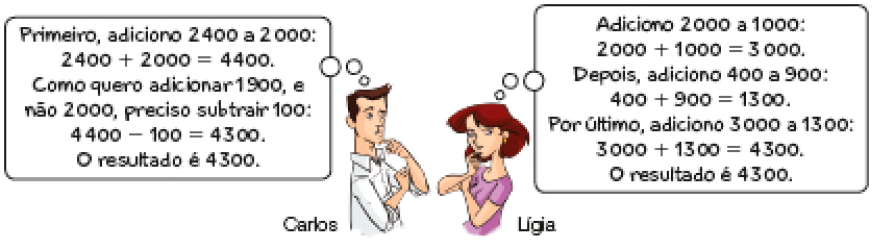
Imagem: Ilustração. Carlos, homem com cabelo castanho está com a mão esquerda sob o queixo. Ele olha para cima e pensa: Primeiro, adiciono 2.400 a 2.000: 2.400 + 2.000 = 4.400. Como quero adicionar 1.900, e não 2.000, preciso subtrair 100: 4.400 - 100 = 4.300. O resultado é 4.300. Na frente dele, Lígia, mulher com cabelo castanho-escuro está com a mão direita sob o queixo. Ela olha para o lado e pensa: Adiciono 2.000 a 1.000: 2.000 + 1.000 = 3.000. Depois, adiciono 400 a 900: 400 + 900 = 1.300. Por último, adiciono 3.000 a 1.300: 3.000 + 1.300 = 4.300. O resultado é 4.300. Fim da imagem.

Imagem: Ícone: Cálculo mental. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Observe as ilustrações e, depois, resolva o problema.
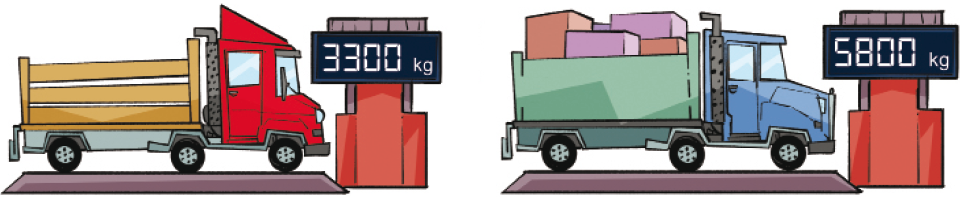
Imagem: Ilustração. Um caminhão vermelho está parado sobre uma balança com o peso: 3.300 kg. Ao lado, um caminhão azul está parado sobre uma balança com o peso: 5.800 kg. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

  1. Leia os dados da tabela abaixo para responder às questões.

População aproximada de municípios de Tocantins em 2020

Tabela: equivalente textual a seguir.

Município

Quantidade aproximada de habitantes

Araguatins

36.000

Guaraí

26.000

Dianópolis

22.000

Fonte: Instituto Brasileiro de Geografia e Estatística (IBGE). Disponível em: http://fdnc.io/eU8. Acesso em: 20 fev. 2021.

  1. Quantos habitantes havia a mais em Araguatins que em Dianópolis?

    _____

    PROFESSOR Resposta: 14.000 habitantes.
  1. Quantos habitantes havia, ao todo, nos três municípios?

    _____

    PROFESSOR Resposta: 84.000 habitantes.
MANUAL DO PROFESSOR

Objetivo

Resolver e elaborar problemas envolvendo adição e subtração, utilizando estimativa e cálculo mental.

Atividade 1

Sugira aos estudantes que busquem outras estratégias para fazer o cálculo proposto no enunciado compartilhando-as com a classe. Alguns cálculos possíveis são:

adicionar 2.400 com 1.000 e depois adicionar 900 ao resultado obtido:

(2.400 + 1.000 + 900) =

= 3.400 + 900 = 4.300;

adicionar 3.000 com 2.000, depois subtrair 600 e, em seguida, 100:

(3.000 + 2.000) − 600 − 100 = 5.000 − 600 − 100 = 4.300.

Lembre-os de que não há procedimentos melhores ou piores para o cálculo mental. O importante é colocar em prática os conhecimentos e as habilidades de cálculo e selecionar o procedimento com o qual se familiarizem mais.

Atividade 2

Nesta atividade, os estudantes devem comparar a soma das massas (leia o texto Medindo a massa, a seguir) dos dois caminhões com 9.000 quilogramas. No caso, a dificuldade do cálculo envolve a troca de 10 centenas por 1 unidade de milhar.

Eles podem calcular a soma 3.300 + 5.800 de diferentes maneiras:

adicionar 5.800 a 3.000 e, depois, adicionar 300:

(5.800 + 3.000) + 300 =

= 8.800 + 300 =

= 8.800 + 200 + 100 = 9 100;

adicionar 5.000 a 3.000 e 800 a 300 e, depois, adicionar os resultados parciais:

(5.000 + 3.000) + (800 + 300) =

= 8.000 + 1.100 = 9.100;

adicionar 6.000 a 3.300 e, depois, subtrair 200:

(6.000 + 3.300) − 200 =

= 9.300 − 200 = 9.100.

Discuta com a turma outras maneiras de calcular.

Atividade 3

Peça aos estudantes que compartilhem a estratégia usada no item a para determinar a subtração solicitada. Verifique se eles percebem que, para isso, podem usar as relações entre a adição e a subtração.

BNCC em foco:

EF04MA03, EF04MA05

MP069

  1. Veja como Marisa e Flávio calcularam o resultado da subtração 4.300 − 2.700. Depois, responda à questão.
Imagem: Ilustração. Marisa, mulher ruiva sorri e pensa: Primeiro, subtraio 3.000 de 4.300: 4.300 – 3.000 = 1.300. Como quero subtrair 2.700, e não 3.000, preciso acrescentar 300: 1.300 + 300 = 1.600. O resultado é igual a 1.600. Abaixo, Flávio, homem com cabelo castanho e óculos está com a mão esquerda sob o queixo. Ele pensa: Subtraio 2.000 de 4.300: 4.300 – 2.000 = 2.300. Depois, subtraio 300: 2.300 - 300 = 2.000. Então, subtraio 400: 2.000 - 400 = 1.600. O resultado é igual a 1.600. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

  1. Por que Marisa adicionou 300 a 1.300? E por que Flávio subtraiu 300 e depois 400? Converse com o professor e os colegas sobre essas questões.
    PROFESSOR Atenção professor: Espera-se que os estudantes compreendam que essas operações são justificadas por cálculos que estão implícitos. Eles devem perceber que Marisa adicionou 300 ao resultado porque 3.000 − 2.700 = 300, e que Flávio subtraiu 300 e depois 400 porque 300 + 400 = 700. Fim da observação.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Você efetuaria essa subtração de um modo diferente? Explique.
    PROFESSOR Resposta pessoal.

Imagem: Ícone: mental. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Observe no gráfico abaixo a quantidade de bicicletas produzidas pela empresa Pedalando no 1º trimestre de 2022 e responda às questões.
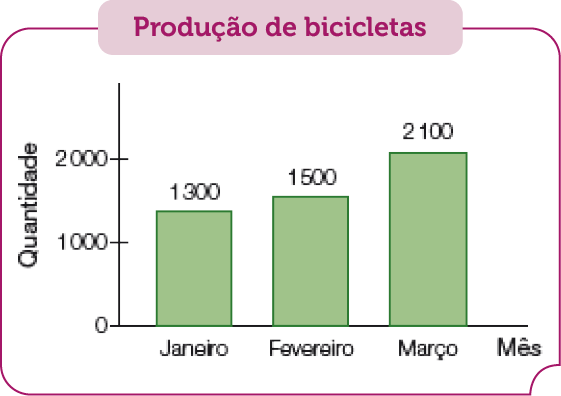
Imagem: Gráfico de colunas. Produção de bicicletas. No eixo vertical, a quantidade e no eixo horizontal, o mês. Janeiro: 1.300 bicicletas. Fevereiro: 1.500 bicicletas. Março: 2.100 bicicletas. Fim da imagem.

Fonte: Empresa Pedalando, 1º trimestre de 2022.

  1. Quantas bicicletas foram produzidas em fevereiro a mais que em janeiro?

    _____

    PROFESSOR Resposta: 200 bicicletas.
  1. Quantas bicicletas foram produzidas em março a mais que em janeiro?

    _____

    PROFESSOR Resposta: 800 bicicletas.
  1. Quantas bicicletas foram produzidas nesse trimestre?

    _____

    PROFESSOR Resposta: 4.900 bicicletas.
  1. Veja como Regina calculou mentalmente o resultado de uma subtração. Descubra a subtração que ela realizou e elabore, em seu caderno, um problema que seja resolvido por meio dessa subtração.
    PROFESSOR Resposta: Como 3.000 + 400 + 300 + 1 700 = 5.400, podemos representar a subtração que Regina realizou por 5.400 − 3.700 = 1.700.
    PROFESSOR Resposta pessoal para a elaboração do problema.
Imagem: Ilustração. Regina, mulher com cabelo encaracolado sorri com a mão esquerda virada para cima e fala: Primeiro, subtraí 3.000 de um número. Depois, subtraí 400 do resultado. Então, subtraí 300 e encontrei como resultado 1.700. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 4

No item b, incentive os estudantes a compartilharem com os colegas a estratégia utilizada, para que eles percebam que o cálculo mental pode ser feito de diferentes maneiras, como cada um achar mais conveniente. Ressalte que não existe maneira correta que seja considerada única.

Atividade 5

A representação gráfica das quantidades facilita o cálculo mental. Aproveite a atividade e faça outras perguntas, como: “Se a empresa quiser produzir um total de 10.000 bicicletas até o final do ano, quantas bicicletas ainda precisam ser produzidas?” (5.100 bicicletas.).

Atividade 6

Antes de resolver a questão proposta, apresente alguns exemplos para relembrar que a adição e a subtração são operações inversas. Em seguida, discuta as diferentes estratégias que eles empregaram. É importante compreenderem que subtrair 3.000 depois 400 e depois 300 é o mesmo que subtrair 3.700.

Se considerar adequado, solicite aos estudantes que compartilhem os problemas elaborados com os colegas e conversem sobre as diferentes situações-problema que possam ser resolvidas por meio dessa subtração.

BNCC em foco:

EF04MA03, EF04MA05; competências específicas 3 e 6

Medindo a massa

A expressão “medir a massa” é comumente utilizada para determinar o “peso” de algo. Conceitualmente, essa expressão está errada. De maneira simples, pode-se dizer que o peso de um corpo é a força resultante da atração da gravidade sobre esse corpo, e a massa é uma grandeza associada à inércia desse corpo, ou seja, dependendo da massa do corpo, haverá maior ou menor dificuldade de ser colocado em movimento ou de, uma vez em movimento, sofrer alteração em sua velocidade.

Nesta obra, procuramos evitar o uso da palavra peso, pois o que pretendemos dizer é massa, mesmo se usado o verbo pesar. Vale salientar que a compreensão dessa diferença é difícil para estudantes dessa faixa etária. Então, sugerimos que empregue o vocabulário correto e deixe os estudantes se apropriarem dele com o tempo.

MP070

Aproximações e estimativas

Imagem: Ícone: mental. Fim da imagem.
  1. Vítor quer comprar alguns materiais de construção para reformar sua casa. O gasto dele será 1.325 reais em azulejos, 1.988 reais em tintas e 2.180 reais em outros materiais.

    _____

    PROFESSOR Exemplo de resposta: Vítor pagará, aproximadamente, 5.500 reais.
Imagem: Ilustração. Vítor, homem com cabelo castanho e camiseta branca está com a mão direita virada para cima. Ele pergunta: Quantos reais pagarei, aproximadamente, na compra desses materiais? Fim da imagem.
  1. Cíntia quer saber o resultado aproximado de 6.460 + 2.110. Ajude-a a fazer esse cálculo respondendo às questões.
    1. Observe a reta numérica abaixo: 6.460 está mais próximo de 6.400 ou de 6.500?
      PROFESSOR Resposta: De 6.500.
Imagem: Ilustração. Reta numérica que vai de 6.400 a 6.500 alternando em 20. Da esquerda para a direita: 6.400, 6.420, 6.440, 6.460, 6.480, 6.500. Há um ponto sobre o número 6.460. Fim da imagem.
  1. Qual é a aproximação de 6.460 para a centena mais próxima? _____
    PROFESSOR Resposta: 6.500
  1. Qual é a aproximação de 2.110 para a centena mais próxima? _____
    PROFESSOR Resposta: 2.100
  1. Qual é o resultado aproximado de 6.460 + 2.110, considerando as respostas anteriores? _____
    PROFESSOR Resposta: 8.600

Imagem: Ícone: mental. Fim da imagem.

  1. Leia o que dizem Roberto e Fernando e responda à questão.
Imagem: Ilustração. Fernando, homem com cabelo preto e curto fala: Da minha cidade até a sua são 1.027 quilômetros, Roberto. Na frente dele, Roberto, homem com cabelo dividido no meio está com uma sobrancelha levantada e a mão direita virada para cima. Ele diz: Fernando, vou lhe ensinar um atalho e você vai percorrer apenas 724 quilômetros. Fim da imagem.
MANUAL DO PROFESSOR

Objetivo

Trabalhar, por meio de adições e subtrações, critérios de arredondamento de números para diferentes ordens.

Atividade 1

Explore esta atividade solicitando aos estudantes que compartilhem com a turma as estratégias usadas para obter a estimativa solicitada. Momentos como esse permitem observar maneiras diferentes de resolver uma mesma questão.

Atividade 2

Na situação apresentada, o arredondamento é feito para a centena mais próxima. A representação na reta numérica possibilita a visualização geométrica para o arredondamento, auxiliando os estudantes a decidirem se ele deve ser feito “para mais” ou “para menos”. Esclareça a eles que, no arredondamento para a centena mais próxima, este será realizado “para mais” quando o algarismo da ordem das dezenas do número for maior que ou igual a 5, e “para menos” em caso contrário. Por exemplo, 2.346 deverá ser arredondado para 2.300, pois o algarismo da ordem das dezenas é 4 (menor que 5), e 3.172 deverá ser arredondado para 3.200, pois o algarismo da ordem das dezenas é 7 (maior que 5).

Atividade 3

Depois que os estudantes fizerem a estimativa, pergunte se a sugestão de Roberto pode ajudar Fernando. Espera-se que eles percebam que 300 quilômetros a menos representam, entre outros, menos tempo de viagem, menos gasto de combustível e menor desgaste do veículo, desde que as estradas encontrem-se nas mesmas condições.

BNCC em foco:

EF04MA05; competência específica 3

Sugestão de atividade

Arredondamentos

Peça aos estudantes que se reúnam em duplas. Solicite a cada membro da dupla que escreva diversos números da ordem de grandeza unidade de milhar e troque com o colega, que deverá fazer o arredondamento para a centena mais próxima. Um estudante poderá escrever, por exemplo, os números abaixo.

2.725, 3.925, 6.830, 4.871, 7.984.

MP071

Imagem: Ícone: mental. Fim da imagem.

  1. Nádia quer comprar uma geladeira que custa 1.329 reais e um notebook que custa 2.198 reais. Fazendo uma estimativa, quanto ela gastará no total?

    _____

    PROFESSOR Resposta: Exemplo de estimativa: 3.500 reais.
Imagem: Ilustração. Nádia, mulher com cabelo volumoso, tiara e blusa vermelha está com a mão esquerda sob o queixo. Ela pensa em uma geladeira e um notebook. Fim da imagem.
  1. Observe no gráfico abaixo os dados de uma campanha beneficente realizada pela escola Aprender em janeiro de 2023. Depois, responda às questões.
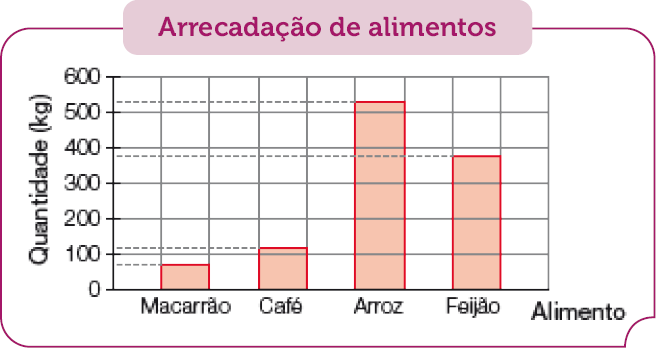
Imagem: Gráfico de colunas. Arrecadação de alimentos. No eixo vertical, a quantidade (kg) e no eixo horizontal, o alimento. Os dados são aproximados. Macarrão: 90 kg. Café: 110 kg. Arroz: 510 kg. Feijão: 390 kg. Fim da imagem.

Fonte: Escola Aprender, jan. 2023.

  1. Quantos quilogramas de alimentos, aproximadamente, foram arrecadados ao todo? _____
    PROFESSOR Exemplo de resposta: 1.100 quilogramas.
  1. Quantos quilogramas de arroz, aproximadamente, foram arrecadados a mais que de café?

    _____

    PROFESSOR Exemplo de resposta: 400 quilogramas.
  1. Observe a reta numérica abaixo e, em seguida, responda às questões.
Imagem: Ilustração. Reta numérica que vai de 3.800 a 4.100 alternando em 50. Da esquerda para a direita: 3.800, 3.850, A (perto de 3.850), 3.900, B (perto de 3.900), 3.950, C (perto de 3.950), D (perto de 4.000), 4.000, 4.050, 4.100. Fim da imagem.
  1. O número da posição D está mais próximo de qual número indicado na reta numérica? _____
    PROFESSOR Resposta: 4.000
  1. O número da posição B está mais próximo de 3.900 ou de 3.950? _____
    PROFESSOR Resposta: 3.900
  1. Qual letra representa um número que está mais próximo de 3.900 e está entre 3.950 e 4.000? _____
    PROFESSOR Resposta: C
  1. Qual número é maior que 3.800: o número da posição A ou o número da posição B? _____
    PROFESSOR Resposta: Ambos os números.
MANUAL DO PROFESSOR

Incentive-os a formularem questões, como as a seguir, e responder a elas, possibilitando que reflitam e desenvolvam estratégias para fazer arredondamentos.

2.725 está mais próximo de 2.700 ou de 2.800? (De 2.700.)

6.830 está mais próximo de 6.900 ou de 6.800? (De 6.800.)

A subtração 3 925 − 3 900 tem resultado maior ou menor que o da subtração 4.000 − 3.925? (Menor.)

Como ficaria a representação do número 7.984 na reta numérica? Esse número fica mais próximo de 8.000 ou de 7.900? (Mais próximo de 8.000.)

Atividade 4

Peça aos estudantes que, depois de terem feito as estimativas, realizem o cálculo exato e comparem os resultados obtidos:

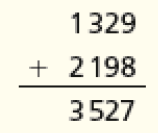
Imagem: Conta de adição na vertical. Na parte superior, o número 1.329. Em seguida, sinal de adição e o número 2.198. Abaixo, reta horizontal e o resultado: 3.527. Fim da imagem.

No caso, a diferença entre o valor aproximado que estamos considerando (3 500) e o resultado exato é de 27 reais. Explique aos estudantes que, considerando que o valor total é superior a 3 mil reais, essa diferença é pouco significativa.

Atividade 5

Ajude os estudantes a interpretarem os dados do gráfico e a relacioná-los com o arredondamento mais adequado. Explique que, como a escala do eixo vertical (correspondente à quantidade, em quilogramas, dos alimentos) é dada em centenas, o mais adequado é arredondar as quantidades para a centena mais próxima. Por exemplo, a massa de macarrão e a de café são, cada uma, cerca de 100 quilogramas (arredondando “para mais” e “para menos”, respectivamente); a massa de arroz está mais próxima de 500 do que de 600 quilogramas; já a massa de feijão pode ser arredondada para 400 quilogramas. Assim, para o item a, obtém-se:

100 kg + 100 kg + 500 kg + 400 kg = 1.100 kg; e para o item b, 500 kg − 100 kg = 400 kg.

Peça a eles que elaborem outras perguntas com base nos dados do gráfico, para que um colega responda.

Avalie a necessidade de esclarecer os estudantes sobre as linhas chamadas tracejadas, que indicam os valores (aproximados ou não) relativos ao eixo vertical.

Atividade 6

Amplie a atividade sugerindo a eles que façam outros questionamentos e troquem com um colega.

BNCC em foco:

EF04MA05; competências específicas 3 e 8

MP072

Cálculo por decomposição

  1. Na padaria de Tomás, foram produzidos 5.743 pães na semana passada e 6.587 pães nesta semana.

    Veja como Tomás calculou o total de pães produzidos nessas duas semanas.

Imagem: Ilustração. Tomás, homem com chapéu e avental brancos está segurando uma sacola com pães e fala: Fiz a decomposição de 5.743 em 5.000 + 700 + 40 + 3 e de 6.587 em 6.000 + 500 + 80 + 7. Então, adicionei 5.000 a 6.000, 700 a 500, 40 a 80 e 3 a 7. Agora, falta adicionar os resultados dessas adições. Fim da imagem.
Imagem: Ilustração. Caderno com a informação: Cálculo por decomposição: 5.743; 6.587. 5.000 + 6.000 = 11.000; 700 + 500 = 1.200; 40 + 80 = 120; 3 + 7 = 10. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

  1. Observe o esquema que Heitor elaborou para representar a disposição de quatro cidades e a tabela que ele construiu com os percursos.
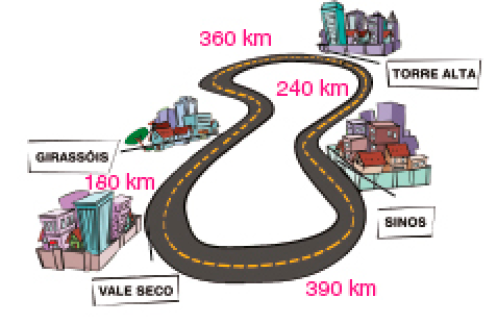
Imagem: Ilustração. No centro há uma pista circular. À esquerda, a cidade de Girassóis e abaixo, Vale Seco. À direita, Torre Alta e Sinos. Resposta: Girassóis, 180 km, Vale Seco, 390 km, Sinos, 240 km, Torre Alta, 360 km, Girassóis. Fim da imagem.

Percurso aproximado entre as cidades

Cidades

Percurso aproximado (em km)

Sinos a Vale Seco

390

Vale Seco a Girassóis

180

Torre Alta a Sinos

240

Girassóis a Torre Alta

360

Fonte: Esquema de Heitor (2023).

MANUAL DO PROFESSOR

Objetivos

Realizar adições e subtrações por decomposição com números de até cinco algarismos.

Usar a decomposição como estratégia de cálculo de adições e subtrações.

Atividade 1

Nesta atividade, os estudantes podem ampliar o uso do algoritmo usual da adição com o cálculo por decomposição, importante para que compreendam o processo de reagrupamento e, depois, o algoritmo usual, que emprega o reagrupamento de forma menos evidente.

Atividade 2

Esta atividade explora o cálculo por decomposição por meio da distância, em quilômetro, entre alguns municípios. Os estudantes devem pensar em estratégias de agrupamentos que resultem no menor percurso possível.

BNCC em foco:

EF04MA02, EF04MA03; competências específicas 2 e 6

MP073

  1. Lívia recebeu uma encomenda de 2.565 ímãs de geladeira e já entregou 1.742. Para saber quantos ímãs faltam para completar o total da encomenda, Lívia subtraiu, por decomposição, 1.742 de 2.565.

Cálculo por decomposição

Primeira decomposição:

Imagem: Conta de adição na vertical. Na parte superior, Primeira decomposição: 2.565: 2.000 + 500 + 60 + 5. Abaixo, sinal de subtração, 1.742: 1.000 + 700 + 40 + 2. Fim da imagem.
Imagem: Ilustração. Lívia, mulher com cabelo encaracolado sorri e fala: Como não dá para subtrair 700 de 500, fiz a segunda decomposição de 2.565. Fim da imagem.

Segunda decomposição:

Imagem: Conta de adição na vertical. Na parte inferior, Segunda decomposição: 2.565: 1.000 + 1.500 + 60 + 5. Abaixo, sinal de subtração, 1.742: 1.000 + 700 + 40 + 2. Em seguida, reta horizontal e o total: espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 800 + 20 + 3

Imagem: Ícone: Oral. Fim da imagem.

  1. Que mudança Lívia fez da primeira para a segunda decomposição de 2.565? Por que ela fez essa mudança? Converse com o professor e os colegas.
    PROFESSOR Resposta: A adição 2.000 + 500 da primeira decomposição, que é igual a 2.500, transformou-se em 1.000 + 1.500 na segunda decomposição. Exemplo de explicação: porque não dava para subtrair 700 unidades de 500 unidades, e com a mudança a subtração passou a ser 1.500 − 700.
  1. Quantos ímãs faltam para completar o total da encomenda? _____
    PROFESSOR Resposta: 823 ímãs.
  1. Calcule, usando decomposição.
  1. 3.932 + 2.611 = _____
    PROFESSOR Resposta: 6.543
  1. 8.629 − 6.435 = _____
    PROFESSOR Resposta: 2.194
  1. 47.895 − 23.960 = _____
    PROFESSOR Resposta: 23.935
  1. 23.256 + 7.620 = _____
    PROFESSOR Resposta: 30.876
  1. Em um mês, uma empresa recolheu 54.765 kg de papel para reciclagem. No mês seguinte, recolheu 51.584 kg. Qual foi a diferença entre as quantidades recolhidas de papel nesses 2 meses? _____
    PROFESSOR Resposta: 3.181 kg.
MANUAL DO PROFESSOR

Atividade 3

Esta proposta exige que os estudantes analisem a estratégia de decomposição que possibilita o cálculo da subtração. Assim, o processo de trocas não é entendido como um“passe de mágica”, pois decorre de uma necessidade justificável.

Dedique atenção especial à subtração, pois ela costuma oferecer mais dificuldade aos estudantes dessa faixa etária.

Atividade 4

Depois que os estudantes efetuarem as adições e as subtrações, pergunte a eles se poderiam fazer o cálculo 3.932 + 2.611, por exemplo, de outra maneira. Depois, peça que exponham para a classe a estratégia empregada. Uma maneira de fazer esse cálculo é adicionar 4.000 a 2.611, obtendo 6 611, e depois obter a diferença entre 4.000 e 3.932.

Para isso, eles podem completar 932 até chegar a 1.000: 932 + 8 = 940 e 940 + 60 = 1.000. Portanto, a diferença é igual a: 8 + 60 = 68.

A subtração 6.611 − 68, por sua vez, pode ser feita da seguinte forma: 6.611 − 11 = 6.600 e 6.600 − 57 = 6.543.

Atividade 5

Vamos considerar o seguinte cálculo por decomposição:

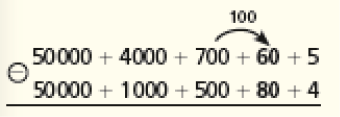
Imagem: Conta de adição na vertical. Na parte superior, a conta: 50.000 + 4.000 + 700 + 60 + 5. Entre 700 e 60, a indicação: 100. Abaixo, sinal de subtração e a conta: 50.000 + 1.000 + 500 + 80 + 4. Fim da imagem.

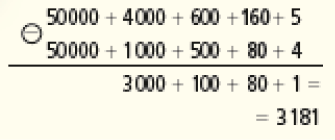
Por essa decomposição, observamos uma subtração que não é possível (60 − 80), de modo que é necessário subtrair 100 unidades de 700 (restando 600 unidades) e adicioná-las a 60, o que resulta em 160, como mostrado abaixo: Conta de adição na vertical. Na parte superior, a conta: 50.000 + 4.000 + 600 + 160 + 5. Abaixo, sinal de subtração e a conta: 50.000 + 1.000 + 500 + 80 + 4. Em seguida, reta horizontal e a conta: 3.000 + 100 + 80 + 1 = 3.181.

BNCC em foco:

EF04MA02, EF04MA03

MP074

Mais adição

  1. Veja duas maneiras de calcular o resultado de 7.467 + 1.709.

Cálculo com o ábaco

Representamos 7.467 no ábaco e adicionamos 1.709.

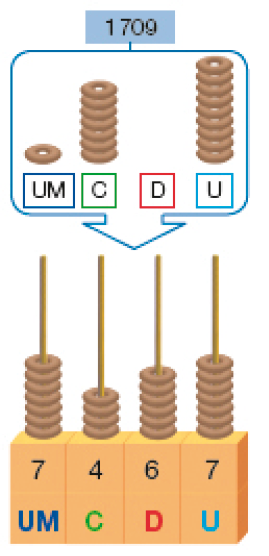
Imagem: Ilustração. Na parte superior, uma argola (UM), sete argolas (C), nenhuma argola (D), nove argolas (U). Em seguida, ábaco, base retangular com hastes de UM (7), C (4), D (6), U (7). Há sete argolas em UM, quatro em C, seis em D e sete em U. Fim da imagem.

Observe que foram obtidas 16 unidades e 11 centenas.

Trocamos 10 unidades por 1 dezena.

E trocamos 10 centenas por 1 unidade de milhar.

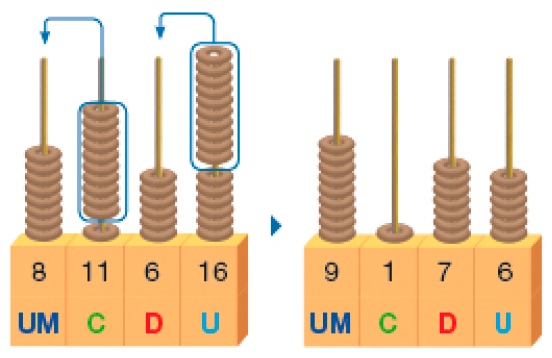
Imagem: Ilustração. Ábaco, base retangular com hastes de UM (8), C (11), D (6), U (16). Há oito argolas em UM, onze em C, seis em D e dezesseis em U. Há dez argolas agrupadas em U, que passam para D e dez argolas agrupadas em C, que passam para UM. Ao lado, seta para a direita, ábaco, base retangular com hastes de UM (9), C (1), D (7), U (6). Há nove argolas em UM, uma em C, sete em D e seis em U. Fim da imagem.

Cálculo com o algoritmo usual

O algoritmo usual segue a mesma sequência do cálculo com o ábaco. Observe:

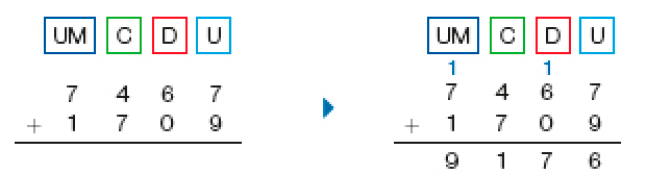
Imagem: Conta de adição na vertical. Acima, as siglas: UM, C, D, U. Em seguida, o número 7.467. Abaixo, sinal de adição e o número 1.709. Em seguida, reta horizontal. Seta para a direita. Acima, as siglas: UM, C, D, U. Em seguida, o número 7.467 (acima do número 7 e 6 há um número 1 pequeno). Abaixo, sinal de adição e o número 1.709. Em seguida, reta horizontal e o resultado: 9.176. Fim da imagem.

• Agora, calcule o resultado de 3.196 + 2.738. _____

PROFESSOR Resposta: 5.934
MANUAL DO PROFESSOR

Objetivo

Ampliar cálculo com o algoritmo usual da adição com reaprupamento.

Atividade 1

Esta atividade possibilita que os estudantes observem o cálculo da adição proposta com o ábaco e com o algoritmo usual.

Enfatize para a turma que o sistema de numeração que utilizamos é o decimal, pois os agrupamentos e reagrupamentos são feitos de 10 em 10.

Para a utilização do ábaco, precisamos compreender as regras básicas do sistema de numeração decimal e, em particular, a ideia de valor posicional: o mesmo algarismo pode representar valores diferentes dependendo da posição que ocupa no número. Por exemplo, o algarismo 1 representa, no número 10, uma dezena, já no número 100, representa uma centena. Essa mesma relação do valor com a posição do algarismo pode ser observada na representação dos números no ábaco.

BNCC em foco:

EF04MA03

MP075

  1. Determine os resultados.
  1. 4.287 + 2.534 = _____
    PROFESSOR Resposta: 6.821
  1. 5.287 + 316 = _____
    PROFESSOR Resposta: 5.603
  1. 43.684 + 15.719 = _____
    PROFESSOR Resposta: 59.403
  1. 35.094 + 9.728 = _____
    PROFESSOR Resposta: 44.822
  1. Complete o enunciado e, depois, responda à pergunta do problema usando os dados completados por você.

    Jair comprou um fogão por _____ reais e uma geladeira por _____ reais.

    PROFESSOR Exemplo de resposta: 900, 1.500

    Quanto Jair gastou na compra desses dois eletrodomésticos? _____

    PROFESSOR Resposta: 2.400 reais.

    Imagem: Ícone: Oral. Fim da imagem.

    • Compare as informações que você usou para completar o problema com as dos demais colegas da classe. Conversem sobre os valores atribuídos por vocês.
      PROFESSOR Atenção professor: Espera-se que os estudantes atribuam valores próximos dos reais. Fim da observação.

Boxe complementar:

Desafio

Joaquim precisa transportar as caixas mostradas abaixo. Porém, seu caminhão pode transportar, no máximo, 2 toneladas de carga por viagem.

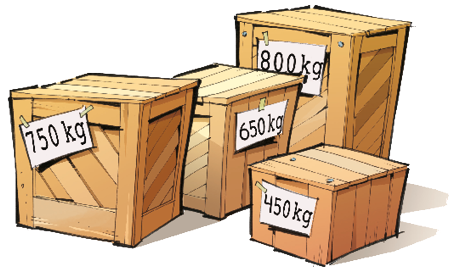
Imagem: Ilustração. Quatro caixas de madeira com tamanhos variados e placas com as informações: 750 kg, 650 kg, 800 kg, 450 kg. Fim da imagem.

CRÉDITO: MARCIO GUERRA

Joaquim poderá transportar em uma só viagem todas as caixas em seu caminhão, respeitando a carga máxima? Justifique sua resposta.

_____

PROFESSOR Resposta: Não, pois a soma das medidas das massas das caixas é maior que 2 t (2.650 kg > 2.000 kg).

Como Joaquim poderá fazer esse transporte?

_____

PROFESSOR Exemplo de resposta: Em duas viagens; na primeira, levaria as caixas de 750 kg, 800 kg e 450 kg; na segunda, levaria a caixa de 650 kg.

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 2

Nesta atividade, os estudantes poderão efetuar as adições e as subtrações e compartilhar com os colegas as estratégias usadas.

Atividade 3

Observe se os estudantes percebem que devem fazer uma estimativa do valor de cada eletrodoméstico para completar o enunciado. Socialize com a turma as respostas com a quantia, em reais, indicada para o fogão e para a geladeira. As diferentes estimativas devem ser consideradas, desde que não sejam extremamente absurdas. Caso considere necessário, converse com os estudantes sobre isso e solicite a eles que façam uma pesquisa na internet ou em panfletos de propaganda de lojas.

Desafio

Aproveite esse momento para comentar com os estudantes que alguns problemas apresentam mais de uma solução; depois, solicite a eles que compartilhem as diferentes soluções propostas.

Neste desafio, são explorados tanto o cálculo da adição por reagrupamento quanto a relação entre as unidades de medida de massa quilograma e tonelada. Se necessário, relembre que 1 tonelada equivale a 1.000 quilogramas.

A questão do item b mobiliza os estudantes a pensarem em estratégias de agrupamentos que possibilitem que toda a carga seja transportada.

BNCC em foco:

EF04MA03; competências específicas 2, 3 e 8

MP076

Mais subtração

  1. Veja duas maneiras de calcular o resultado de 7.142 − 3.516.

Cálculo com o ábaco

Representamos 7.142 no ábaco para subtrair 3.516.

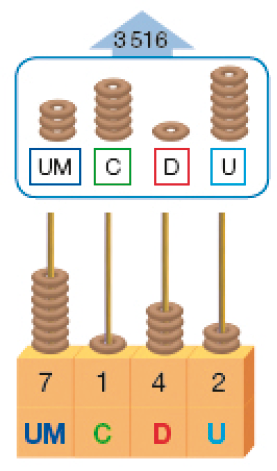
Imagem: Ilustração. Na parte superior, 3516, três argolas (UM), cinco argolas (C), uma argola (D), seis argolas (U). Em seguida, ábaco, base retangular com hastes de UM (7), C (1), D (4), U (2). Há sete argolas em UM, uma em C, quatro em D e duas em U. Fim da imagem.

Não dá para retirar 6 unidades de 2 unidades, nem 5 centenas de 1 centena.

Então, trocamos 1 dezena por 10 unidades e 1 milhar por 10 centenas.

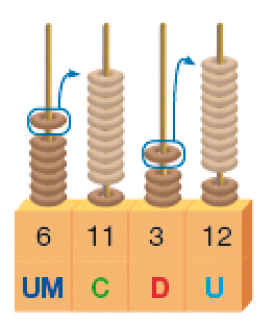
Imagem: Ilustração. Ábaco, base retangular com hastes de UM (6), C (11), D (3), U (12). Há seis argolas em UM, onze em C, três em D e doze em U. Há uma argola em UM, que passa para C e uma argola em D, que passa para U. Fim da imagem.

Subtraímos 6 unidades, 1 dezena, 5 centenas e 3 unidades de milhar.

Restam 3 unidades de milhar, 6 centenas, 2 dezenas e 6 unidades.

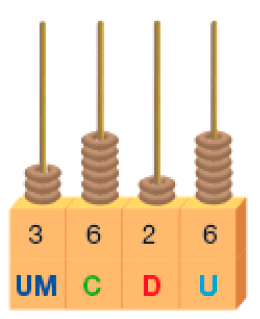
Imagem: Ilustração. ábaco, base retangular com hastes de UM (3), C (6), D (2), U (6). Há três argolas em UM, seis em C, duas em D e seis em U. Fim da imagem.

Cálculo com o algoritmo usual

O algoritmo usual segue a mesma sequência do cálculo com o ábaco. Observe:

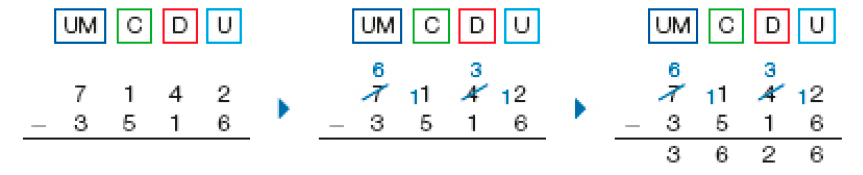
Imagem: Conta de subtração na vertical. Acima, as siglas: UM, C, D, U. Em seguida, o número 7.142. Abaixo, sinal de subtração e o número 3.516. Em seguida, reta horizontal. Seta para a direita. Acima, as siglas: UM, C, D, U. Em seguida, o número 7.142 (o número 7 está cortado com o número 6 pequeno em cima. Ao lado do número 1 há um número 1 pequeno. O número 4 está cortado com o número 3 pequeno acima. Ao lado do número 2 há um número 1 pequeno). Abaixo, sinal de subtração e o número 3.516. Em seguida, reta horizontal. Seta para a direita. Acima, as siglas: UM, C, D, U. Em seguida, o número 7.142 (o número 7 está cortado com o número 6 pequeno em cima. Ao lado do número 1 há um número 1 pequeno. O número 4 está cortado com o número 3 pequeno acima. Ao lado do número 2 há um número 1 pequeno). Abaixo, sinal de subtração e o número 3.516. Em seguida, reta horizontal e o resultado: 3.626. Fim da imagem.
  1. 5.269 − 3.735 = _____
    PROFESSOR Resposta: 1.534
  1. 2.987 − 849 = _____
    PROFESSOR Resposta: 2.138
  1. 5.605 − 4.742 = _____
    PROFESSOR Resposta: 863
  1. 9.876 − 3.210 = _____
    PROFESSOR Resposta: 6.666
MANUAL DO PROFESSOR

Objetivo

Ampliar a utilização do algoritmo usual da subtração.

Atividade 1

Nesta atividade, é possível dar significado ao algoritmo da subtração por meio da associação de seus diversos passos com as etapas dos procedimentos utilizados para efetuar essas operações no ábaco. A atividade também permite aprimorar a compreensão dos estudantes sobre as operações de adição e subtração.

Sugira a eles que, antes de resolver as subtrações, expliquem as duas maneiras de calcular o resultado da subtração 7.142 − 3 .516. Incentive-os a propor outros métodos de resolução.

Para números de quatro algarismos, em alguns casos, pode ser necessária a troca de 1 unidade de milhar por 10 centenas, como ocorreu na subtração 7.142 − 3.516. Realize, com os estudantes, cada etapa dessa subtração em um ábaco desenhado na lousa ou em um ábaco real. Peça a eles que sempre comparem os algarismos dos números envolvidos. Saber em que ordem será necessária a troca facilita a organização do cálculo. Acompanhe os passos realizados com o ábaco, repetindo-os com o algoritmo usual, para que os estudantes verifiquem a relação entre ambos e para que o algoritmo não seja um processo realizado mecanicamente, sem significado.

BNCC em foco:

EF04MA03

MP077

  1. Leia o diálogo entre Fernanda e Cláudia e responda à questão.
Imagem: Ilustração. Fernanda, mulher com cabelo encaracolado está com a mão esquerda virada para cima. Ela diz: No ano passado, arrecadamos 2.979 reais com o bazar beneficente. Na frente dela, Cláudia, mulher com cabelo preto está com as mãos na cintura. Ela responde: Neste ano, conseguimos 4.289 reais com o bazar. Fim da imagem.
  1. A tabela abaixo mostra a produção de leite na fazenda Pitangueiras nos meses de janeiro e fevereiro de 2023.

Produção de leite

Tabela: equivalente textual a seguir.

Mês

Número de litros

Janeiro

3.549

Fevereiro

5.826

Fonte: Fazenda Pitangueiras, (mar. 2023).

Imagem: Ilustração. Uma vaca malhada está atrás de um quadro. Fim da imagem.
  1. A produção de leite aumentou ou diminuiu de janeiro para fevereiro?

    _____

    PROFESSOR Resposta: Aumentou.
  1. Qual foi a diferença na produção de leite nesses dois meses? _____
    PROFESSOR Resposta: 2.277 litros.

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Rogério precisava calcular o resultado de 1.235 − 428 quando notou que a tecla 3 de sua calculadora estava quebrada. Para resolver esse problema, ele digitou primeiro o número 1.240 e subtraiu 5, obtendo no visor 1.235. Depois, subtraiu 428, chegando ao resultado 807.
    • Agora, imagine que você precisa calcular o resultado de 2.340 − 1.825 com uma calculadora que está com a tecla 0 quebrada. Como você faria? Qual é o resultado?
PROFESSOR Resposta pessoal. Exemplo de resposta: Digitaria primeiro o número 2.335 e adicionaria 5, obtendo no visor 2.340, e, então, subtrairia 1.825. Resultado: 515.
Imagem: Ilustração. Calculadora com o botão 0 quebrado. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 2

Aproveite a situação apresentada para perguntar o que os estudantes conhecem sobre “bazar beneficente”. Depois de ouvir as respostas, reforce a grafia correta do adjetivo beneficente.

Atividade 3

Para os estudantes responderem ao item a, basta compararem a ordem da unidade de milhar das duas quantidades apresentadas na tabela.

Para o item b, devem subtrair a quantidade de litros de leite produzidos em janeiro da produzida em fevereiro.

Atividade 4

Espera-se que os estudantes reflitam sobre as maneiras de utilizar a calculadora, considerando a impossibilidade de usar uma das teclas. Observe como eles resolvem e peça a alguns estudantes que compartilhem a estratégia com a turma, para permitir aos colegas ampliarem o repertório de resoluções.

Proponha novos desafios, alterando o número a ser exibido na calculadora e a tecla a ser inutilizada.

BNCC em foco:

EF04MA03

MP078

Termos da adição e termos da subtração

  1. A escola onde Deise estuda fez uma campanha a fim de arrecadar dinheiro para a reforma de uma casa de repouso.

    O 4º ano A arrecadou 1.675 reais, e o 4º ano B, 1.043 reais. Deise quer descobrir o total arrecadado pelas duas turmas do 4º ano.

Em uma adição, os números que estão sendo adicionados chamam-se parcelas. O resultado da adição chama-se soma ou total.

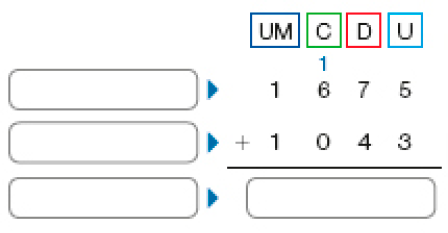
Imagem: Conta de adição na vertical. Acima, as siglas: UM, C, D, U. Em seguida, espaço para resposta: e o número 1.675 (acima do número 6 há um número 1 pequeno). Abaixo, sinal de adição, espaço para resposta e o número 1.043. Em seguida, reta horizontal, espaço para resposta e o resultado: espaço para resposta. Fim da imagem.
PROFESSOR Resposta: parcela, parcela
PROFESSOR soma ou total - 2.718
Imagem: Ilustração. Três jovens estão sorrindo. Na frente deles, um casal de idosos está na frente de uma porta aberta e sorrindo. Ao lado, placa com a informação: CASA DE REPOUSO. Fim da imagem.

O total arrecadado foi _____ reais.

PROFESSOR Resposta: 2.718
  1. O dono de uma livraria quer vender 9.665 livros em um semestre. Já se passaram três meses, e foram vendidos 4.073 livros. Para atingir o total de vendas desejado, ainda precisam ser vendidos quantos livros nos próximos três meses?

Em uma subtração, o número do qual se retira uma quantidade é chamado minuendo. A quantidade diminuída é chamada subtraendo, e o resultado da subtração chama-se resto ou diferença.

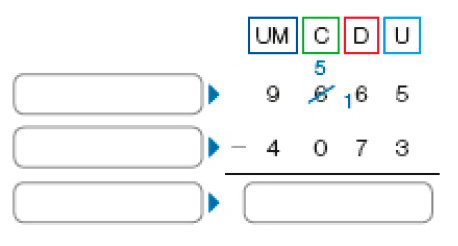
Imagem: Conta de subtração na vertical. Acima, as siglas: UM, C, D, U. Em seguida, espaço para resposta: e o número 9.665 (o número 6 está cortado com o número 5 pequeno em cima e ao lado do número 6 há o número 1 pequeno). Abaixo, sinal de subtração, espaço para resposta e o número 4.073. Em seguida, reta horizontal, espaço para resposta e o resultado: espaço para resposta. Fim da imagem.
PROFESSOR Resposta: minuendo - subtraendo - resto ou diferença - 5.592
MANUAL DO PROFESSOR

Objetivo

Ampliar a utilização dos algoritmos da adição e da subtração.

Conhecer os termos da adição e da subtração permite aos estudantes comunicarem com maior facilidade suas ideias e os resultados dessas operações. Contudo, não se deve dar ênfase exagerada à memorização, pois o uso constante é que trará familiaridade com esses termos. Comente com a turma que, apesar de no cotidiano muitas pessoas dizerem “fazer a soma” para indicar uma adição, o termo soma refere-se ao resultado de uma adição.

Atividade 1

Amplie a atividade pedindo aos estudantes que obtenham todas as somas possíveis de duas parcelas com os números 1.675, 1.043 e outro número qualquer, como 651. Espera-se que, nesse caso, cheguem a:

1.675 + 1.043 = 2.718;

1.675 + 651 = 2.326; e

1.043 + 651 = 1.694.

Antes de realizarem os cálculos, pergunte: “Qual adição apresentará a maior soma? E a menor?”.

Atividade 2

Da mesma maneira que os termos de uma adição, a nomenclatura usual dos termos de uma subtração tem por objetivo permitir a comunicação de procedimentos matemáticos e padronizar a linguagem. Entretanto, de modo diverso do que ocorre com os termos da adição, de uso mais comum nas práticas sociais, os da subtração são menos conhecidos, com exceção do termo diferença (ou resto). Enquanto os números adicionados são chamados de parcelas, já que na adição a ordem das parcelas não altera a soma, os números envolvidos na subtração recebem nomes diferentes, porque fazer 12 − 5 não é o mesmo que fazer 5 − 12.

BNCC em foco:

EF04MA05

MP079

Propriedades da adição

  1. Leia o que Flávia e Ricardo estão dizendo.
Imagem: Ilustração. Flávia, jovem com cabelo castanho e preso está com as mãos viradas para cima. Ela fala: Nas redes sociais, eu tinha 20 amigos e acrescentei 38. Ao lado, Ricardo, jovem com cabelo encaracolado está com a mão direita virada para cima. Ele fala: Nas redes sociais, eu tinha 38 amigos e acrescentei 20. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

PROFESSOR Resposta: Nenhum dos dois.
PROFESSOR Exemplo de explicação: Flávia e Ricardo ficaram com o mesmo número de amigos, 58.

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Use uma calculadora e descubra os resultados.
  1. 59 + 27 = _____
    PROFESSOR Resposta: 86
  1. 27 + 59 = _____
    PROFESSOR Resposta: 86
  1. 268 + 394 = _____
    PROFESSOR Resposta: 662
  1. 394 + 268 = _____
    PROFESSOR Resposta: 662
  1. 4.712 + 7.123 = _____
    PROFESSOR Resposta: 11.835
  1. ) 7.123 + 4.712 = _____
    PROFESSOR Resposta: 11.835

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

PROFESSOR Resposta: Adições com a mesma soma: a e b ; c e d ; e e f.
  1. Leia o que a professora está dizendo e depois responda à questão.
Imagem: Ilustração. A professora, mulher ruiva com óculos está com as mãos viradas para cima. Ela fala: Em qualquer adição, quando mudamos a ordem das parcelas, a soma não se altera. Esse fato é chamado de propriedade comutativa da adição. Fim da imagem.
  1. 140 + 30 = 30 + 140
  1. 100 + 80 + 90 = 180 + 90
  1. 420 + 0 = 0 + 420
  1. 230 + 360 + 140 = 230 + 500
PROFESSOR Resposta: A e C.
MANUAL DO PROFESSOR

Objetivos

Conceituar procedimentos relativos às propriedades associativa, comutativa e do elemento neutro da adição.

Formalizar a utilização de parênteses na organização de uma adição com três parcelas.

Um modo interessante de apresentar essa propriedade aos estudantes dessa faixa etária é pela representação geométrica dos números referentes às parcelas, como mostrado no esquema a seguir, em que se evidencia a igualdade das somas obtidas ao se alterar a ordem das parcelas.

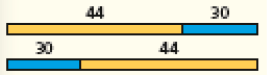
Imagem: Ilustração. Faixa comprida e amarela (44). Ao lado, faixa curta e azul (30). Abaixo, faixa curta e azul (30). Ao lado, faixa comprida e amarela (44). Fim da imagem.

CRÉDITO: ANDERSON DE ANDRADE PIMENTEL

Com o recurso da representação dos números como medidas, os estudantes podem visualizar a validade da propriedade comutativa da adição. Isso os ajudará a compreender que fazer 44 + 30 é o mesmo que fazer 30 + 44, uma vez que as duas operações conduzem à mesma medida final.

Atividade 1

Para que os estudantes visualizem que as parcelas são iguais, escreva na lousa quantos amigos cada um deles tinha e quantos amigos cada um adquiriu. Essa observação é um primeiro passo para que eles percebam a propriedade comutativa da adição.

Atividade 2

Com a calculadora, os estudantes poderão verificar as relações entre os itens que apresentam resultados iguais: alterando-se a ordem das parcelas, a soma continua a mesma.

Atividade 3

Esta atividade permite que, a partir das observações das atividades anteriores, os itens que representam a propriedade comutativa da adição sejam identificados.

BNCC em foco:

EF04MA05

Sugestão de leitura para o professor

Livro

SMOLE, Katia Stocco; DINIZ, Maria Ignez. Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática. São Paulo: Penso, 2001.

Esse livro propõe a discussão do lugar e do significado das competências e das habilidades no Ensino Fundamental, abordando as habilidades de ler, escrever e resolver problemas em Matemática.

MP080

  1. Substitua cada símbolo por um número, de modo que as sentenças fiquem verdadeiras.
    1. 74 + 28 = 28 + Ilustração. Círculo.
      PROFESSOR Resposta: Ilustração. Quadrado. = 74
    1. 542 + 195 = Ilustração. Quadrado. + 542
      PROFESSOR Resposta: Ilustração. Quadrado. = 195
    1. 95 + Ilustração. Círculo.= 61 + Ilustração. Retângulo.
      PROFESSOR Exemplos de resposta:
      PROFESSOR Ilustração. Pentágono.= 61 e Ilustração. Retângulo.= 95 ou
      PROFESSOR Ilustração. Pentágono.= 13 e Ilustração. Retângulo.= 47
    1. 45 + 38 = Ilustração. Trapézio. + Ilustração. Triângulo.
      PROFESSOR Exemplos de resposta:
      PROFESSOR Ilustração. Trapézio. = 38 e Ilustração. Triângulo.= 45 ou
      PROFESSOR Ilustração. Trapézio. = 57 e Ilustração. Triângulo.= 26
  1. Em um jogo eletrônico, Bia e Caio fizeram 18 pontos na 1ª etapa, 12 pontos na 2ª etapa e 27 pontos na 3ª etapa. Veja como cada um calculou o total de pontos:

Cálculo de Bia:

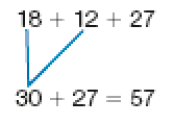
Imagem: Esquema. 18 + 12 + 27 18 + 12 = 30. 30 + 27 = 57. Fim da imagem.

Bia fez 18 mais 12 e obteve 30.

Depois, fez 30 mais 27, e o resultado foi 57.

Cálculo de Caio:

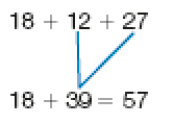
Imagem: Esquema. 18 + 12 + 27 12 + 27 = 39. 18 + 39 = 57. Fim da imagem.

Caio fez 12 mais 27 e obteve 39.

Depois, fez 39 mais 18, e o resultado foi 57.

Imagem: Ilustração. Uma mulher com cabelo preso e jaleco branco fala: Os parênteses indicam a adição que devemos fazer primeiro. Fim da imagem.

Esses cálculos podem ser representados assim:

Cálculo de Bia:

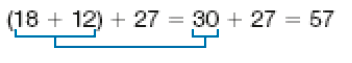
Imagem: Expressão. (18 + 12) + 27 = 30 + 27 = 57 (18 + 12) = 30 Fim da imagem.

Cálculo de Caio:

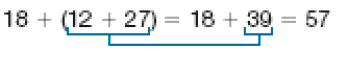
Imagem: Expressão. 18 + ( 12 + 27) = 18 + 39 = 57. ( 12 + 27) = 39. Fim da imagem.
  1. Em sua opinião, quem calculou o resultado dessa adição de uma maneira mais fácil?
    PROFESSOR Resposta pessoal.
  1. É possível resolver esse problema de um modo diferente de Bia e de Caio, usando uma adição também. Descreva essa adição a seguir.

    _____

    PROFESSOR Exemplo de resposta: (18 + 27) + 12 = 45 + 12 = 57
MANUAL DO PROFESSOR

Atividade 4

É interessante os estudantes perceberem que, nos itens c e d, há mais de uma resposta possível. Peça a alguns deles que exponham suas respostas para depois discuti-las com a turma. Solicite que observem, entre as respostas dadas, quais verificam a propriedade comutativa da adição.

Atividade 5

Nesta atividade, os estudantes têm a oportunidade de observar que a propriedade associativa da adição permite realizar a associação mais conveniente de parcelas em uma adição de mais de dois números. Percebem ainda que se trata de um recurso valioso para o cálculo de resultados, sobretudo quando há parcelas que completam dezenas inteiras. Por exemplo, a adição 18 + 12 + 27 pode ser realizada mais rapidamente se associarmos as parcelas 18 e 12, obtendo a dezena 30.

No item a, é provável que os estudantes digam que a associação feita por Bia facilita mais os cálculos, a não ser que Caio, para realizar 18 + 39, fizesse 18 + 40 − 1.

BNCC em foco:

EF04MA05; competência específica 6

MP081

  1. Calcule e registre o resultado das adições.
  1. ) 20 + (40 + 80) = _____
    PROFESSOR Resposta: 140
  1. (104 + 36) + 60 = _____
    PROFESSOR Resposta: 200
  1. ) ( 5 + 25) + 50 = _____
    PROFESSOR Resposta: 150
  1. ) 7 + (25 + 10) + 9 = _____
    PROFESSOR Resposta: 51
  1. ) 75 + (25 + 50) = _____
    PROFESSOR Resposta: 150
  1. ) ( + 25) + (10 + 9) = _____
    PROFESSOR Resposta: 51
  1. ) ( 0 + 40) + 80 = _____
    PROFESSOR Resposta: 140
  1. ) 104 + (36 + 60) = _____
    PROFESSOR Resposta: 200
Imagem: Ilustração. Um homem com cabelo castanho e óculos fala: Em qualquer adição, quando associamos as parcelas de maneiras diferentes, obtemos sempre o mesmo resultado. Chamamos esse fato de propriedade associativa da adição. Fim da imagem.
PROFESSOR Atenção professor: Espera-se que os estudantes percebam que esses resultados sugerem que, associando as parcelas de uma adição de maneiras diferentes, a soma não se altera. Fim da observação.

Imagem: Ícone: mental. Fim da imagem.

  1. Calcule mentalmente o resultado de cada adição. Depois, registre-os.
  1. 15 + 0 = _____
    PROFESSOR Resposta: 15
  1. 0 + 842 = _____
    PROFESSOR Resposta: 842
  1. 0 + 37 = _____
    PROFESSOR Resposta: 37
  1. 357 + 0 = _____
    PROFESSOR Resposta: 357
  1. 2.569 + 0 = _____
    PROFESSOR Resposta: 2.569
  1. ) 0 + 15.362 = _____
    PROFESSOR Resposta: 15.362

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

PROFESSOR Atenção professor: Espera-se que os estudantes percebam que esses resultados sugerem que, em uma adição de duas parcelas, quando uma delas é igual a zero, o resultado dessa adição é igual à outra parcela. Fim da observação.
  1. Cláudia joga handebol em uma equipe que realizou duas partidas em um fim de semana.

No sábado, o placar do jogo foi 4 a 0 para a equipe de Cláudia. No domingo, a equipe adversária venceu a equipe de Cláudia por 4 a 0. Represente com uma adição o total de gols de cada equipe nos dois jogos.

_____

PROFESSOR Resposta: Equipe de Cláudia: 4 + 0 = 4; equipe adversária: 0 + 4 = 4.
Imagem: Ilustração. Cláudia, mulher com cabelo castanho e comprido diz: Quando adicionamos zero a um número, o resultado será esse número. Por isso, dizemos que o zero é o elemento neutro da adição. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 6

Esta atividade trabalha a compreensão de que, em uma adição de mais de duas parcelas, fazer o cálculo de duas das parcelas antes das outras pode facilitar a obtenção do resultado.

Ao associar as parcelas, os estudantes entram em contato com outra propriedade da adição, a propriedade associativa, que é mais um recurso para a ampliação das estratégias e dos procedimentos de cálculo mental.

Observe se os estudantes consideram os parênteses para calcular o resultado das operações. Como os resultados das adições propostas nesta atividade podem ser obtidos com ou sem o uso dos parênteses, talvez alguns estudantes pensem que esses sinais sejam sempre dispensáveis. Entretanto, é importante que eles entendam que os parênteses indicam o que se faz primeiro em uma expressão. Comente que, em expressões numéricas que envolvem outras operações além da adição, não usar os parênteses pode levar a respostas erradas.

Atividade 7

Esta atividade apresenta aos estudantes adições em que uma das parcelas é zero. Observando todas as adições, os estudantes percebem que a adição com zero resulta no valor igual ao da outra parcela e que, portanto, o zero é o elemento neutro da adição.

Atividade 8

Esta atividade apresenta e fundamenta o elemento neutro da adição e contextualiza a propriedade por meio de uma situação-problema.

BNCC em foco:

EF04MA05; competência específica 2

MP082

Adição e subtração: operações inversas

Imagem: Ícone: Calculadora. Fim da imagem.
  1. Usando uma calculadora, calcule e registre o resultado em cada item.
  1. 28 + 19 = _____
    PROFESSOR Resposta: 47
  1. 47 − 28 = _____
    PROFESSOR Resposta: 19
  1. 47 − 19 = _____
    PROFESSOR Resposta: 28
  1. 68 + 56 = _____
    PROFESSOR Resposta: 124
  1. 124 − 68 = _____
    PROFESSOR Resposta: 56
  1. ) 124 − 56 = _____
    PROFESSOR Resposta: 68

Imagem: Ícone: Oral. Fim da imagem.

PROFESSOR Atenção professor: Espera-se que os estudantes percebam que, tanto no caso dos três primeiros quanto no dos três últimos itens, o maior dos três números é igual à soma dos outros dois números. Fim da observação.
  1. João tem 26 kg. Ele e Luís subiram juntos em uma balança que registrou 40 kg.
    1. Quantos quilogramas a balança registraria se apenas

      João descesse dela? _____

      PROFESSOR Resposta: 14 kg.
    1. E se apenas Luís descesse da balança? _____
      PROFESSOR Resposta: 26 kg.
  1. Leia o que Ricardo disse ao observar o esquema que mostra que a adição e a subtração são operações inversas.
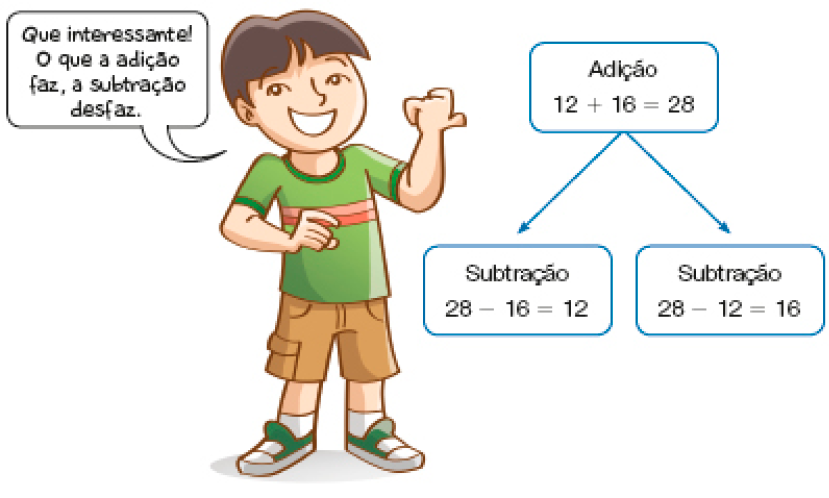
Imagem: Ilustração. Ricardo, menino com cabelo preto e curto aponta para o lado e fala: Que interessante! O que a adição faz, a subtração desfaz. Ao lado, na parte superior, a informação: Adição: 12 + 16 = 28. Abaixo, duas setas apontando para Subtração: 28 - 16 = 12; Subtração: 28 - 12 = 16. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

Explorar as operações de adição e subtração, como operações inversas, por meio de situações envolvendo três números.

Perceber as relações entre a adição e a subtração.

Reconhecer a importância do conceito de adição e subtração como operações inversas na conferência de resultados de cálculos com os algoritmos usuais.

As atividades destas páginas exploram as operações de adição e subtração como operações inversas. Pretende-se que, percebendo naturalmente as relações entre as duas operações, os estudantes consigam ampliar seu repertório de estratégias na resolução de problemas.

O aspecto mais interessante dessa sequência de atividades é a formulação na ordem inversa da que se trabalhou até o momento: os números envolvidos são apresentados, e os estudantes precisam descobrir quais operações conduzem aos resultados.

Eles também têm a oportunidade de reconhecer a importância do conceito de adição e subtração como operações inversas na conferência de resultados de cálculos realizados por algoritmos ou na calculadora. E ainda podem experimentar criar uma situação-problema que envolva adição e subtração.

Atividade 1

A realização dos cálculos permitirá que os estudantes observem também que, em cada bloco de três números, ao subtrair qualquer dos menores números do maior número, o resultado será igual ao outro número.

Atividade 2

Nesta atividade, os estudantes terão de perceber que, ao formularem na ordem inversa os números envolvidos, descobrirão os resultados.

Atividade 3

Esta atividade apresenta a propriedade da operação inversa de maneira empírica. Incentive a descoberta dos estudantes sem fundamentar a propriedade; isso fará com que eles se apropriem e signifiquem melhor os conceitos quando estes forem formalmente apresentados.

Observe que a fala do personagem Ricardo é intuitiva no sentido de que apresenta um conhecimento de maneira direta e imediata, sem ter embasamento conceitual.

BNCC em foco:

EF04MA04

MP083

  1. Observe como Fátima conferiu o resultado de 281 − 175.
Imagem: Ilustração. Fátima, menina com cabelo castanho e comprido, segura um giz e sorri. Ao seu lado, uma lousa com contas na vertical. À esquerda, conta de subtração na vertical. Na parte superior, o número 281 (o número 8 está riscado com o número 7 pequeno em cima e ao lado do número 1 há um número 1 pequeno). Em seguida, sinal de subtração e o número 175. Abaixo, reta horizontal e o resultado: 106. À direita, conta de adição na vertical. Na parte superior, o número 106 (acima do número 0 há um número 1 pequeno). Em seguida, sinal de adição e o número 175. Abaixo, reta horizontal e o resultado: 281. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Explique a um colega o raciocínio usado por Fátima.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que Fátima usou a adição como operação inversa da subtração. Fim da observação.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Agora, calcule o resultado de 362 − 184 e confira sua resposta.
PROFESSOR Resposta: Exemplo de cálculos: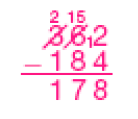
Conta de subtração na vertical. Na parte superior, o número 362 (o número 3 está riscado com o número 2 pequeno em cima. Ao lado, o número 6 está riscado com o número 15 pequeno em cima. Ao lado do número 2 há um número 1 pequeno). Em seguida, sinal de subtração e o número 184. Abaixo, reta horizontal e o resultado: 178.
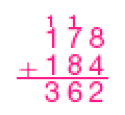
Conta de adição na vertical. Na parte superior, o número 178 (acima dos números 1 e 7 há um número 1 pequeno). Em seguida, sinal de adição e o número 184. Abaixo, reta horizontal e o resultado: 362.
ou
Conta de adição na vertical. Na parte superior, o número 184 (acima dos números 1 e 8 há um número 1 pequeno). Em seguida, sinal de adição e o número 178. Abaixo, reta horizontal e o resultado: 362.
  1. Leia o que as crianças estão falando após o jogo terminar.
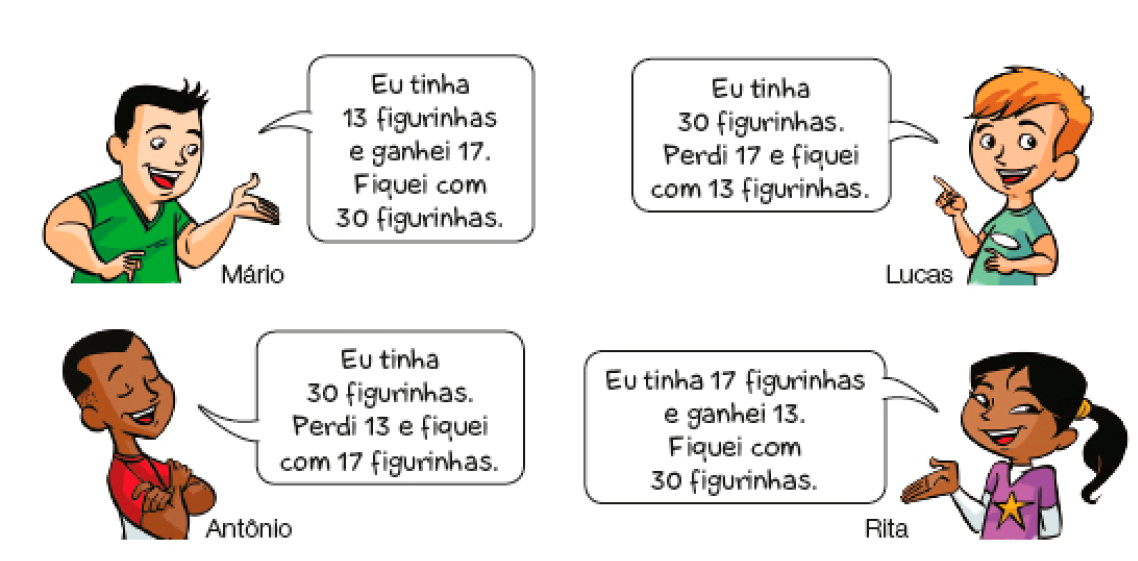
Imagem: Ilustração. Mário, menino com cabelo preto e curto fala: Eu tinha 13 figurinhas e ganhei 17. Fiquei com 30 figurinhas. Abaixo, Antônio, menino com cabelo preto e muito curto diz: Eu tinha 30 figurinhas. Perdi 13 e fiquei com 17 figurinhas. À direita, Lucas, menino loiro fala: Eu tinha 30 figurinhas. Perdi 17 e fiquei com 13 figurinhas. Abaixo, Rita, menina com cabelo preso diz: Eu tinha 17 figurinhas e ganhei 13. Fiquei com 30 figurinhas. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 4

Esta atividade permite aos estudantes reconhecerem a importância do conceito de adição e subtração como operações inversas na conferência de resultados de cálculos realizados por algoritmos ou na calculadora.

Atividade 5

Antes de os estudantes resolverem a questão, reproduza na lousa a figura abaixo e peça a eles que pensem em possíveis relações, expressas por adições ou subtrações, entre os dois grupos de bolinhas.

Imagem: Ilustração. À esquerda, cinco bolinhas verdes. À direita, três bolinhas verdes. Fim da imagem.

CRÉDITO: ADILSON SECCO

Considerando apenas a ilustração, há modos diferentes de relacionar os dois grupos de bolinhas:

adicionando 3 unidades a 5 unidades, obtém-se o total de 8 unidades: 5 + 3 = 8;

subtraindo 3 unidades de 8 unidades, restam 5 unidades: 8 − 3 = 5;

subtraindo 5 unidades de 8 unidades, restam 3 unidades: 8 − 5 = 3.

Como a figura não sugere qual ação deve ser executada, ambas as possibilidades são válidas, o que mostra a inversibilidade entre a adição e a subtração.

Essa relação deve ser percebida na leitura da atividade.

BNCC em foco:

EF04MA04; competência específica 2

MP084

  1. Os números 25, 35 e 60 podem ser relacionados por meio de duas adições e duas subtrações.
    • Escreva duas adições e duas subtrações usando os números 25, 35 e 60 em cada uma.

      _____

      PROFESSOR Resposta: 25 + 35 = 60; 35 + 25 = 60; 60 − 25 = 35; 60 − 35 = 25.
  1. Escreva duas adições e duas subtrações usando os números 15, 18 e 33 em cada uma.

    _____

    PROFESSOR Resposta: 18 + 15 = 33; 15 + 18 = 33; 33 − 15 = 18; 33 − 18 = 15.
  1. Roberta estava no 42º andar de um prédio. Ela desceu vários andares e chegou ao 18º andar.
    1. Quantos andares Roberta desceu? _____
      PROFESSOR Resposta: 24 andares.
    1. Como você pode conferir a resposta obtida? _____
      PROFESSOR Exemplo de explicação: fazendo 24 + 18 para verificar se o resultado é igual a 42.
      PROFESSOR É interessante que os estudantes descubram o resultado correto da adição.

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Flávio adicionou 2.789 com 1.316, obtendo a soma 4.005. Use uma calculadora para descobrir se esse resultado está certo sem usar a tecla Ilustração. Tecla: +. .

    Registre as teclas que você digitou.

PROFESSOR Exemplo de resposta: O resultado está errado, pois digitando Ilustração. Sequência de teclas com os números: 4 0 0 5 menos 1 3 1 6. igual.obtemos no visor Ilustração. Retângulo com o número 2689., e não 2.789.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Observe a reta numérica e invente duas questões relacionadas a ela: uma envolvendo adição, outra envolvendo subtração. Depois, peça a um colega que as resolva.
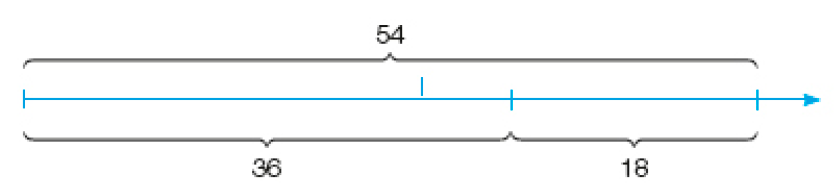
Imagem: Ilustração. Reta numérica com quatro pontos. Entre o primeiro e o quarto ponto, o número: 54. Entre o primeiro e o terceiro ponto, o número: 36. E entre o terceiro e quarto ponto, o número: 18. Fim da imagem.

_____

PROFESSOR Exemplo de questões:
PROFESSOR Subtração: Em um percurso de 54 metros, Marcos já percorreu 36. Quantos metros faltam para Marcos percorrer? Resposta: 18 metros.
PROFESSOR Adição: Ana e Cíntia colecionam selos. Ana tem 36 selos, e Cíntia, 18. Quantos selos elas têm juntas? Resposta: 54 selos.
MANUAL DO PROFESSOR

Atividade 6

A relação entre as operações adição e subtração pode ser explorada também por meio do recurso visual, como mostrado a seguir.

Imagem: Ilustração. À esquerda, dois quadrados azuis. À direita, cinco quadrados amarelos. Fim da imagem.

CRÉDITO: ADILSON SECCO

Com base na figura, podem ser escritas as igualdades 2 + 5 = 7; 5 + 2 = 7; 7 − 2 = 5 e 7 − 5 = 2. Comente que o uso de cada uma dessas formas de representar a situação depende do cálculo a ser efetuado. Por exemplo, se o problema pede que calculemos mentalmente a diferença entre 60 e 35, podemos retirar 35 de 60. Nesse caso, seria necessário contar 35 unidades em ordem decrescente, a partir de 60, ou subtrair 30 de 60 e, desse resultado, subtrair 5: 60 − 30 = 30, e depois: 29, 28, 27, 26, 25. Outra opção seria contar 25 unidades a partir de 35 até chegar a 60, ou fazer isso acrescentando dezenas inteiras e depois completando com as unidades necessárias: 35, 45, 55, e então 56, 57, 58, 59, 60. Usando a subtração, o cálculo realizado foi 60 − 35 = 25; no caso da adição, foi 35 + 25 = 60.

Atividades 7, 8 e 9

Aproveite estas atividades para reforçar a importância de verificar a solução de um cálculo ou de um problema. Incentive-os a desenvolver o hábito de fazer perguntas do tipo: “A resposta obtida está próxima do esperado para o problema?”; “Ela faz sentido considerando os dados do problema?”.

Atividade 10

É comum que os estudantes elaborem problemas com “números grandes” pensando que isso os torna mais difíceis. Nesses casos, chame a atenção deles para o fato de que “números grandes” não se associam necessariamente a raciocínios complexos, pois uma calculadora torna simples esse tipo de cálculo. Incentive-os a criarem situações com charadas, enigmas e perguntas criativas.

BNCC em foco:

EF04MA04, EF04MA13

MP085

Propriedades da igualdade

  1. Veja o experimento realizado por Camila.
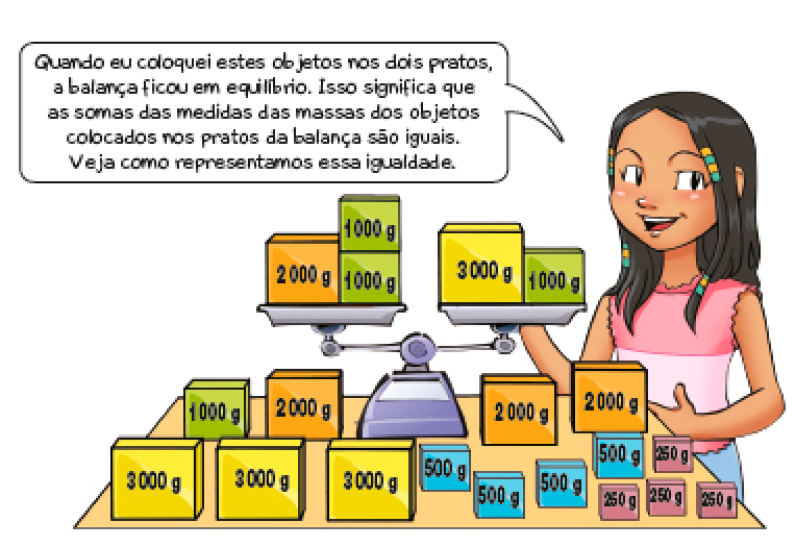
Imagem: Ilustração. Camila, jovem com cabelo preto e comprido diz: Quando eu coloquei estes objetos nos dois pratos, a balança ficou em equilíbrio. Isso significa que as somas das medidas das massas dos objetos colocados nos pratos da balança são iguais. Veja como representamos essa igualdade. Ao seu lado, uma balança de pratos. No prato à esquerda, um peso com 2.000 g e dois pesos com 1.000 g. No prato à direita, um peso com 3.000 g e um peso com 1.000 g. Na frente da balança há um peso com 1.000 g, três pesos com 2.000 g, três pesos com 3.000 g, quatro pesos com 500 g e quatro pesos com 250 g. Fim da imagem.

2.000 + 1.000 + 1.000 = 3.000 + 1.000

  1. Se Camila colocar um objeto de 2.000 g em cada um dos pratos da balança, ela continuará em equilíbrio? Justifique sua resposta.
    PROFESSOR Resposta: Sim.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que as novas medidas das massas continuarão iguais. Fim da observação.
  1. Escreva uma igualdade representando essa situação.

    _____

    PROFESSOR Resposta: 2.000 + 1.000 + 1.000 + 2.000 = 3.000 + 1.000 + 2.000

    Imagem: Ícone: Oral. Fim da imagem.

  1. E se Camila colocar um objeto de 250 g em um prato e um objeto de 500 g no outro prato? O que acontecerá?
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que ocorrerá um desequilíbrio, pois as somas das medidas das massas serão diferentes. Fim da observação.
  1. Indique um modo de Camila acrescentar dois objetos em cada prato e a balança continuar em equilíbrio.

    _____

    PROFESSOR Exemplos de resposta: Em cada prato, ela poderia acrescentar: 2 objetos de 500 g ou 2 objetos de 250 g.
MANUAL DO PROFESSOR

Objetivo

Reconhecer que uma igualdade não se altera quando se adiciona ou se subtrai um mesmo número a seus dois termos.

Atividade 1

Esta atividade utiliza uma ilustração de balança de dois pratos para explorar a noção de igualdade.

Espera-se que os estudantes percebam que, como a balança está em equilíbrio e com os dois pratos na mesma altura, porque a soma das massas dos dois pratos é 2 000 gramas, ao colocar a mesma massa em cada um dos pratos, a balança continuará em equilíbrio e com os dois pratos na mesma altura. O entendimento da igualdade é importante na construção e na compreensão de conceitos em Álgebra.

Se julgar oportuno, comente que a parte que fica antes do sinal de igual é denominada primeiro membro da igualdade e a parte que fica depois, segundo membro da igualdade.

BNCC em foco:

EF04MA04, EF04MA13

MP086

  1. Augusto ganhou 50 reais de sua mãe e 25 reais de seu tio. Já Antônio, seu irmão, ganhou 36 reais da mãe e 39 reais do tio.
    1. Com quantos reais cada um ficou?

      _____

      PROFESSOR Resposta: Ambos ficaram com a mesma quantia: 75 reais.
    1. Identifique a sentença que estabelece uma relação entre a quantia de Augusto e a de Antônio.

      ( ) 50 + 25 = 36 + 39

      ( ) 50 + 25 < 36 + 39

      ( ) 50 + 25 > 36 + 39

      PROFESSOR Resposta correta: 50 + 25 = 36 + 39
  1. Augusto gastou 13 reais do que ganhou comprando um brinquedo e 5 reais comprando um suco. Antônio gastou 11 reais com um sanduíche e 7 reais com uma revista em quadrinhos. Com quanto cada um ficou?

    _____

    PROFESSOR Resposta: Cada um deles ficou com 57 reais.
  1. Uma nova sentença que pode ser associada à relação entre as quantias que os irmãos ficaram é:

    ( ) 50 + 25 − 18 = 36 + 39 − 18

    ( ) 50 + 25 − 18 < 36 + 39 − 18

    ( ) 50 + 25 − 18 > 36 + 39 − 18

    PROFESSOR Resposta correta: 50 + 25 − 18 = 36 + 39 − 18
Imagem: Ilustração. Augusto, menino com cabelo preto está com a mão direita sob o queixo e olhando para o lado. Acima dele há um balão de pensamento com um carrinho e uma latinha. Ao lado, Antônio, menino com cabelo castanho sorri com a mão direita na cintura. Acima dele há um balão de pensamento com um lanche e uma revista. Fim da imagem.
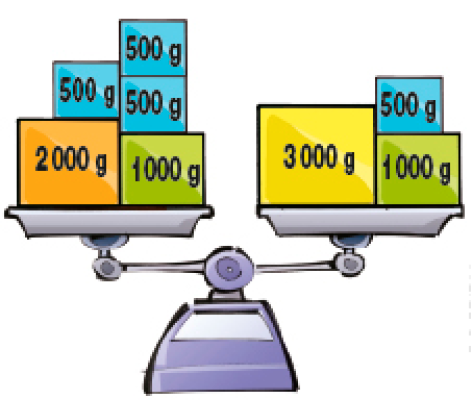
  1. A balança abaixo está em equilíbrio.

    Que objeto pode ser tirado de ambos os pratos de modo que a balança continue em equilíbrio?

    _____

    PROFESSOR Exemplos de resposta: tirar um objeto de 500 g de cada prato ou tirar um objeto de 1.000 g de cada prato.
Imagem: Ilustração. Uma balança de pratos. No prato à esquerda há um peso com 2.000g, um peso com 1.000 g e três pesos com 500 g. No prato à direita há um peso com 3.000 g, um peso com 1.000 g e um peso com 500 g. Fim da imagem.
MANUAL DO PROFESSOR

Atividades 2 e 3

Estas atividades exploram o fato de que, se duas operações matemáticas ou quantidades são iguais entre si, quando ambas têm a mesma quantidade de unidades, é caracterizada uma igualdade. Apresente outros exemplos:

15 + 15 + 15 = 45

10 + 10 + 5 = 15 + 10

18 − 2 − 4 − 1 = 19 − 8

Comente que, ao substituir qualquer uma das quantidades por uma operação matemática equivalente, a igualdade é mantida. Nas situações propostas, quando adicionamos ou subtraímos a mesma quantidade nos dois membros da igualdade, a igualdade foi mantida.

BNCC em foco:

EF04MA14; competência específica 2

MP087

  1. Veja como Reginaldo pensou para encontrar o número desconhecido em uma atividade proposta por sua professora.
Imagem: Ilustração. Reginaldo, jovem cadeirante e ruivo fala: Sei que o número desconhecido adicionado a 125 é igual a 130 + 5, ou seja, é igual a 135. Então, preciso descobrir que número devo adicionar a 125 para obter 135. Ao seu lado, uma lousa com a conta: 125 + círculo = 130 + 5. Fim da imagem.
  1. Sabendo que as igualdades a seguir são verdadeiras, que números devem substituir os símbolos Ilustração. Triângulo. , Ilustração. Losango. , Ilustração. Pentágono. e Ilustração. Círculo. nessas igualdades?
    1. 35 + Ilustração. Triângulo. = 27 + 8
    1. 123 − 56 = Ilustração. Losango. + 42
    1. 729 + Ilustração. Pentágono. = 879 − 20
    1. 1.455 − 365 = 850 + Ilustração. Círculo.

      Imagem: Ícone: Oral. Fim da imagem.

      Imagem: Ícone: Grupo. Fim da imagem.

      • Explique ao professor e aos colegas como você pensou para encontrar cada número.
        PROFESSOR Resposta pessoal.
PROFESSOR Resposta: Ilustração. Triângulo. = 0
PROFESSOR Ilustração. Losango. = 25
PROFESSOR Ilustração. Pentágono. = 130
PROFESSOR Ilustração. Círculo. = 240
  1. Larissa e Felipe estão conversando sobre a quantidade de cartas que cada um tem em sua coleção.
Imagem: Ilustração. Larissa, jovem loira fala: Com as cartas que conquistei hoje e com 63 que eu tenho em casa, ficamos com a mesma quantidade de cartas. Na frente dela, Felipe, jovem com cabelo castanho e ondulado responde: É verdade, hoje eu ganhei 26 cartas e tenho mais 58 em casa. Fim da imagem.
MANUAL DO PROFESSOR

Atividades 4 e 5

Sabendo que as igualdades são verdadeiras, os estudantes terão de descobrir o número que deve ser colocado no lugar de cada símbolo. Eles costumam gostar desse tipo de atividade.

Na atividade 5, peça a eles que compartilhem com a turma as estratégias que usaram para determinar cada número.

Atividade 6

Observe se os estudantes resolvem a atividade utilizando o que aprenderam nesta Unidade.

BNCC em foco:

EF04MA15

MP088

Compreender problemas

Para resolver

Leia atentamente os problemas e resolva-os em seu caderno.

Problema 1

No sítio de Paulo, há 5 vacas, 3 cavalos e algumas galinhas.

Quantos animais há ao todo nesse sítio?

Imagem: Ilustração. Três jovens com mochila nas costas estão andando em um corredor e sorrindo. Atrás deles, um homem com uniforme azul os observa com as mãos atrás das costas. Ao fundo, portas e uma seta para direita, indicando SALAS. Fim da imagem.

Problema 2

Em uma escola, há 5.000 estudantes no Ensino Fundamental, distribuídos em três períodos: manhã, tarde e noite. No período noturno, estudam 1.500 estudantes. Em que período há mais estudantes?

Para refletir

Imagem: Ícone: Oral. Fim da imagem.
  1. Foi possível resolver os dois problemas? Por quê?
    PROFESSOR Exemplo de resposta: Não. Porque faltam dados.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Para resolver o Problema 1, qual informação falta no enunciado?
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que falta no enunciado a informação sobre a quantidade de galinhas que há no sítio de Paulo. Fim da observação.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Qual dado falta para resolver o Problema 2?
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que falta o dado sobre o número de estudantes que estudam em pelo menos um dos períodos diurnos (manhã ou tarde). Fim da observação.
  1. Qual das informações a seguir permite resolver o Problema 2?

    ( ) Juntos, os estudantes do período da manhã e os estudantes do período da noite são, no total, 3.400 estudantes.

    ( ) Dos estudantes da tarde, a maioria é menina.

    ( ) São 3.500 estudantes que não estudam no período da noite.

    PROFESSOR Resposta correta: Juntos, os estudantes do período da manhã e os estudantes do período da noite são, no total, 3.400 estudantes.
  1. Faça o que se pede.
    1. Invente um dado para o Problema 1 de modo que ele tenha solução.
      PROFESSOR Exemplo de resposta: Dado: 10 galinhas.
      PROFESSOR Resposta: 18 animais.
    1. Elabore uma questão para o Problema 2 de modo que possa ser respondida apenas com os dados apresentados.
      PROFESSOR Exemplo de resposta: Questão: Quantos estudantes estudam nos outros dois períodos?
      PROFESSOR Resposta: 3.500 estudantes.
MANUAL DO PROFESSOR

Objetivos

Resolver problemas e identificar dados insuficientes.

Resolver e elaborar problemas de adição e subtração.

Nesta página, os problemas não fornecem dados suficientes para que possam ser solucionados. Observe se os estudantes percebem isso.

Para resolver Problemas 1 e 2

Os estudantes devem perceber que não há dados suficientes para resolver os dois problemas.

Para refletir Atividade 1

Incentive os estudantes na leitura e interpretação das informações contidas no texto. É importante que eles identifiquem que faltam dados para resolver os dois problemas.

Atividades 2 e 3

Na atividade 1, os estudantes observaram que faltavam dados. Agora, eles terão de identificar qual dado faltou para resolver cada problema.

Atividade 4

Das opções oferecidas, apenas uma informação permite aos estudantes resolver o Problema 2.

Peça aos estudantes que resolvam o Problema 2 após a escolha da informação. No período noturno, estudam 1.500 estudantes. Então no período da manhã, estudam 1.900 estudantes. Logo, no período da tarde, estudam 1.600 estudantes. Portanto, há mais estudantes no período da manhã. Peça a eles que comparem as respostas.

Atividade 5

Dê um tempo para que os estudantes façam o que é solicitado nos itens a e b. Em seguida, peça a eles que falem para os colegas como pensaram.

BNCC em foco:

EF04MA03; competências específicas 3 e 8

MP089

Matemática em textos

Leia

Observe os cartazes da campanha informativa sobre prevenção do coronavírus na sala de aula.

Imagem: Ilustração. Cartaz com a informação: CORONAVÍRUS – PREVENÇÃO NA SALA DE AULA. Desenho de um menino com máscara sobre o nariz e boca. PROFESSORES E ALUNOS – O uso da máscara é obrigatório. Se possível, associar com o protetor facial. Desenho de três carteiras escolares. Há um X na carteira do meio. ALUNOS – Mantenham distância. Intercalar o uso das cadeiras. Desenho de uma janela aberta. MANTER O AMBIENTE VENTILADO – Manter janelas abertas. Ligar ar condicionado somente se o mesmo for de janela. Caso contrário, manter desligado. Na parte inferior, logotipos e textos. À direita, cartaz com a informação: CORONAVÍRUS – DICAS GERAIS DE PREVENÇÃO. Desenho de um menino com máscara sobre o nariz e boca. USE MÁSCARA. Desenho de três pessoas. Há um X na pessoa do meio. EVITE AGLOMERAÇÕES. Desenho de uma mão segurando um borrifador. LIMPE COM FREQUÊNCIA OBJETOS PESSOAIS. Desenho de duas pessoas de frente e entre elas há uma seta (2 m). MANTENHA DISTÂNCIA. Desenho de duas mãos com sabão embaixo de uma torneira (Água e sabão). LAVE AS MÃOS COM FREQUÊNCIA. Desenho de duas mãos se cumprimentando. EVITE APERTO DE MÃOS. Na parte inferior, logotipos e textos. Fim da imagem.

Fonte: Ações na Pandemia – Biossegurança. Instituto de Química da Universidade Federal do Rio de Janeiro. Disponível em: http://fdnc.io/eUa. Acesso em: 22 fev. 2021.

Responda

  1. O que devemos fazer para evitar a contaminação pelo coronavírus?
    PROFESSOR Resposta: Usar máscara ao sair de casa; lavar as mãos com água e sabão frequentemente; limpar as mãos e os objetos de manuseio com álcool em gel; evitar aglomerações e aperto de mãos; manter distância; manter os ambientes ventilados.
  1. Cite outras medidas de prevenção que devemos praticar.
    PROFESSOR Resposta pessoal.

Analise

  1. Como se deve proceder para colocar ou tirar a máscara?
    PROFESSOR Atenção professor: Espera-se que os estudantes citem a lavagem das mãos antes de colocar a máscara; colocá-la de modo que cubra nariz, boca e queixo; retirá-la pelas alças laterais. Fim da observação.
  1. Faça uma pesquisa sobre algumas vacinas criadas para o enfrentamento da covid-19. Relate quais são os países onde elas foram elaboradas, quais são as instituições e/ou empresas responsáveis, qual é o tipo de vacina (vírus inativado, de vetor viral, genética, proteico subunitária).
    PROFESSOR Resposta pessoal.
  1. Em sua opinião, qual é a importância das campanhas de vacinação?
    PROFESSOR Resposta pessoal.

Aplique

Junte-se ao demais colegas e elaborem um cartaz sobre a importância das vacinas.

MANUAL DO PROFESSOR

Objetivo

Interpretar texto e identificar informações sobre prevenção de contágio por coronavírus.

Responda

Na atividade 2, deixe que os estudantes digam o que sabem a respeito e enfatize a importância de evitar aglomerações, ressaltando que o vírus é invisível e pode demorar a produzir sintomas ou nem produzi-los, de modo que não dá para saber quem está ou não contaminado.

Comente que estudos mostram que, mesmo depois que uma pessoa é considerada curada da covid, ela ainda pode ter sequelas, como problemas respiratórios e neurológicos, entre outros. Além disso, há casos constatados de reinfecção.

Analise

Na atividade 1, atente para que higienizem as mãos antes de pôr a máscara. Oriente também sobre a necessidade de trocar a máscara sempre que estiver úmida. Para isso, devem ter sempre dois saquinhos plásticos, um com as máscaras limpas e outro para transportar as máscaras usadas, caso não sejam descartáveis. Também é importante orientar que a máscara deve ser lavada após cada uso, e não ser reutilizada antes disso.

Na atividade 2, oriente os estudantes na pesquisa. Se possível, convide um médico ou enfermeiro para explicar as diferenças entre os tipos de vacinas quanto a produção, prazo para o começo do desenvolvimento de anticorpos, necessidade de reforço, índices de eficácia etc. Nesse caso, oriente-os a realizarem a pesquisa antes de ouvirem o profissional, de modo a fazerem perguntas que tragam aprofundamento ao debate, fugindo do senso comum, que nem sempre está correto.

Depois de ouvir as respostas dos estudantes sobre a atividade 3, comente que campanhas de vacinação são importantes porque têm como objetivo proteger a população contra as formas graves de infecção provocadas pelos vírus.

No caso das doenças respiratórias, como a covid e mesmo a influenza, elas podem ser transmitidas ao falar, tossir ou espirrar, e também pelo contato de objetos contaminados ou das mãos contaminadas com a boca, os olhos e o nariz, o que as torna muito contagiosas.

Aplique

Oriente os estudantes na confecção dos cartazes e exponha-os em área de grande circulação na escola, para que possam ser vistos por outros estudantes e pelos funcionários da escola.

BNCC em foco:

EF04MA03; competência geral 2; competências específicas 2 e 3

MP090

Compreender informações

Probabilidade

  1. Hélio foi a uma festa junina. Lá, há um jogo em que as crianças giram uma roleta colorida e recebem um prêmio de acordo com a cor indicada pelo ponteiro quando a roleta para.
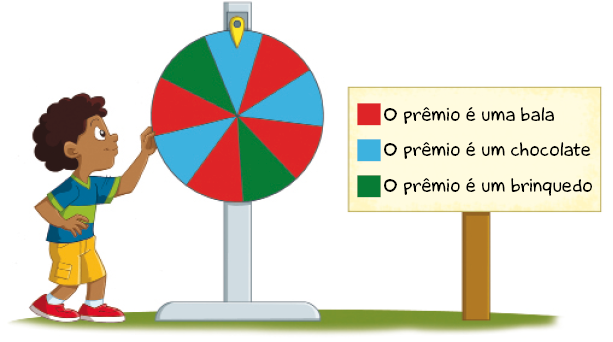
Imagem: Ilustração. Hélio, menino com cabelo encaracolado está com a mão sobre uma roleta colorida (há quatro partes vermelhas, três azuis e duas verdes). Ao lado, placa com a informação: Vermelho - O prêmio é uma bala; Azul - O prêmio é um chocolate; Verde - O prêmio é um brinquedo). Fim da imagem.
  1. Hélio girará a roleta. É possível saber que prêmio ele ganhará? Por quê?

    _____

    PROFESSOR Resposta: Não. Exemplo de justificativa: Porque é impossível prever para qual das três cores o ponteiro apontará quando a roleta parar.
  1. Que prêmio Hélio tem maior chance de ganhar? Por quê?

    _____

    PROFESSOR Resposta: A bala. Exemplo de justificativa: Porque a roleta tem mais partes de cor vermelha.
  1. Como você modificaria essa roleta para que a chance de ganhar cada prêmio fosse a mesma?

    _____

    PROFESSOR Resposta: Pintaria 3 partes de cada cor.
  1. Atribua os valores para dois dos eventos descritos a seguir. O valor zero deve ser atribuído ao evento que não tem chance de ocorrer, e o valor 1, para o evento que ocorrerá com certeza.

( ) Sortear uma bola azul em uma urna com 5 bolas azuis e 2 verdes.

( ) Sortear uma bola azul em uma urna com 7 bolas verdes.

PROFESSOR Resposta: 0

( ) Sortear uma bola azul em uma urna com 7 bolas azuis.

PROFESSOR Resposta: 1

( ) Sortear uma bola azul em uma urna com 5 bolas verdes e 2 azuis.

PROFESSOR Resposta: Sortear uma bola azul em uma urna com 5 bolas azuis e 2 verdes, porque há mais possibilidades de sortear uma bola azul.
MANUAL DO PROFESSOR

Objetivo

Identificar, entre eventos aleatórios, aqueles em que há maior chance de ocorrência, reconhecendo características de resultados mais prováveis.

Atividade 1

Observe se os estudantes compreendem que, quanto maior a área do círculo ocupada por determinada cor, maior será a chance de essa cor ser sorteada. Explique que um modo de expressar a medida da chance de ocorrência de um evento é pela comparação entre a quantidade de ocorrências favoráveis e o total de possibilidades.

Atividade 2

Nesta atividade, os estudantes terão dois momentos para observar e identificar a maior chance de ocorrência dos eventos. Peça a eles que compartilhem a estratégia usada para identificar o evento que não tem chance de ocorrer e o que ocorrerá com certeza. Depois, solicite aos estudantes que justifiquem como pensaram para escolher, entre os dois outros eventos, aquele com maior chance de ocorrer.

BNCC em foco:

EF04MA26

MP091

  1. Olívia e Renato estão sorteando bolinhas coloridas.
Imagem: Ilustração. Renato, homem com cabelo castanho está com um pano em volta dos olhos e com a mão dentro de uma caixa transparente. Dentro da caixa há quatro bolinhas vermelhas, três verdes, três azuis e uma amarela. Ao lado, Olívia, mulher loira com cabelo preso observa e sorri. Fim da imagem.
  1. Que cor de bola tem maior chance de ser sorteada? Por quê?

    _____

    PROFESSOR Resposta: Vermelha. Exemplo de justificativa: A quantidade de bolas dessa cor é maior que a das outras.
  1. Que cor de bola tem menor chance de ser sorteada? Por quê?

    _____

    PROFESSOR Resposta: Amarela. Exemplo de justificativa: A quantidade de bolas dessa cor é menor que a das outras.
  1. Que cores de bola têm a mesma chance de ser sorteadas? Por quê?

    _____

    PROFESSOR Resposta: As cores verde e azul. Exemplo de justificativa: O número de bolas verdes é igual ao de bolas azuis.
  1. O pai de Iolanda tem duas caixas como as ilustradas abaixo, ambas com bombons de morango (vermelhos) e de coco (azuis). Iolanda ganhará um desses bombons de acordo com as seguintes instruções:

    1º) Inicialmente, Iolanda deverá observar as caixas e escolher uma delas.

    2º) Depois, com os olhos fechados, terá de pegar um bombom da caixa escolhida.

Imagem: Ilustração. Caixa 1, com seis bombons vermelhos e dois azuis. Fim da imagem.
Imagem: Ilustração. Caixa 2, com seis bombons vermelhos e seis azuis. Fim da imagem.
MANUAL DO PROFESSOR

Atividades 3 e 4

É possível que alguns estudantes já tenham ouvido que determinado evento é provável, mas não confirmado. Esse tipo de informação gera uma dúvida muito comum: o fato de um evento classificado como provável não se concretizar significa que a informação a respeito de sua probabilidade estava errada? A resposta é não.

Um modo de verificar essa resposta é realizar várias vezes com os estudantes os experimentos apresentados nas atividades. Para isso, podem ser usados uma caixa qualquer e papéis coloridos, por exemplo.

Na atividade 3, peça a eles que observem atentamente as bolinhas coloridas da ilustração antes de responderem às questões.

Um exemplo de justificativa para a atividade 4 é de que a chance de, com os olhos fechados, pegar um bombom de morango na caixa 1 é maior que a de pegar na caixa 2, porque, na caixa 1, mais da metade dos bombons é de morango e, na caixa 2, a quantidade de bombons de morango é a mesma que a de bombons de coco.

BNCC em foco:

EF04MA26

MP092

O que você aprendeu

Imagem: Ícone: mental. Fim da imagem.
  1. Adriana fez algumas compras para sua casa. Qual foi, aproximadamente, o total pago por essas compras?

    _____

    PROFESSOR Exemplo de resposta:
    PROFESSOR Aproximadamente 2.700 reais.
Imagem: Ilustração. Papel com a informação: Compras da Adriana: 1 batedeira; Preço: 109 reais; Compras da Adriana: 1 jogo de sofá; Preço: 1.689 reais; Compras da Adriana: 1 TV de 29 polegadas; Preço: 899 reais. Fim da imagem.

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Com o auxílio de uma calculadora, descubra a regra para formar cada sequência e complete-as.
  1. 1.419, 1.476, 1.533, _____, _____
    PROFESSOR Exemplo de resposta: 1.590, 1.647.
    PROFESSOR Regra: adicionar 57 unidades ao termo anterior.
  1. 2.792, 2.623, 2.454, _____, _____
    PROFESSOR Exemplo de resposta: 2.285, 2.116
    PROFESSOR Regra: subtrair 169 unidades do termo anterior.
  1. _____, _____, 4.424, 4.619, 4.814
    PROFESSOR Exemplo de resposta: 4.034, 4.229
    PROFESSOR Regra: adicionar 195 unidades ao termo anterior.
  1. Amanda e Gabriel sorteavam cartões numerados de 0 a 9. Ela retirou de uma urna três cartões e formou com eles o maior número possível de três algarismos. Depois, Gabriel retirou outros três cartões de outra urna e formou com eles o menor número possível de três algarismos. Observe os cartões que eles sortearam e, depois, responda às questões.
Imagem: Ilustração. À esquerda, Amanda, jovem com cabelo encaracolado sorri e olha para três cartões sobre uma mesa. Nos cartões, os números: 1, 3, 7. Ao lado há uma urna. À direita, Gabriel, jovem com boné sorri e olha para três cartões sobre uma mesa. Nos cartões, os números: 9, 5, 4. Ao lado há uma urna. Fim da imagem.
  1. Quais foram os números formados por Amanda e por Gabriel?

    _____

    PROFESSOR Resposta: Amanda: 731; Gabriel: 459.
  1. Quantas unidades o número maior tem a mais que o menor?

    _____

    PROFESSOR Resposta: 272 unidades.
MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

Atividade 1

Os cálculos aproximados, muito comuns em situações do dia a dia, são um recurso valioso na tomada de decisões financeiras, como, por exemplo: se compensa ou não realizar determinada compra ou se a compra está dentro dos limites de gastos previstos no orçamento mensal.

No caso apresentado, como os números diferem da centena mais próxima em, no máximo, 11 reais (1.700 − 1.689), arredondar para a centena mais próxima é uma escolha adequada.

Assim, 109 reais podem ser arredondados para 100 reais; 1.689 reais, para 1.700 reais; e 899 reais, para 900 reais. Portanto, o valor total aproximado da compra de Adriana foi: 100 reais mais 1.700 reais mais 900 reais, que são 2.700 reais.

Atividade 2

Observe se os estudantes conseguem perceber cada uma das regras. Depois, peça a eles que contem para os colegas como conseguiram resolver o desafio.

Atividade 3

Para explorar a atividade, pergunte: “Se Amanda entregasse seus três cartões a Gabriel, qual seria o maior número que ele poderia formar com os seis algarismos?”. Espera-se que os estudantes, embora só tenham até aqui tratado de números de até 4 ordens, mobilizem os seus conhecimentos em situações similares em que, dados alguns algarismos, o maior número natural a ser formado com eles é escrito com esses algarismos em ordem decrescente de valor específico, e assim respondam 975.431.

BNCC em foco:

EF04MA03, EF04MA04

MP093

  1. Calcule os resultados.
  1. 3.748 + 5.276 = _____
    PROFESSOR Resposta: 9.024
  1. 7.106 + 2.582 = _____
    PROFESSOR Resposta: 9.688
  1. 4.638 − 1.276 = _____
    PROFESSOR Resposta: 3.362
  1. 2.812 − 935 = _____
    PROFESSOR Resposta: 1.877
  1. Considerando que a balança está em equilíbrio nas duas situações, responda à questão.
Imagem: Ilustração. 1ª situação: balança de pratos. No prato à esquerda, um cubo verde. No prato à direita, um peso com 2.127 g. Fim da imagem.
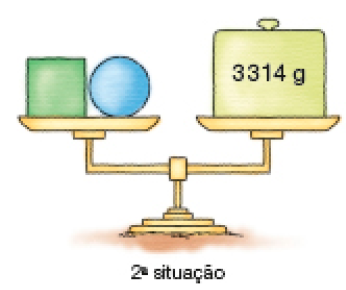
Imagem: Ilustração. 2ª situação: balança de pratos. No prato à esquerda, um cubo verde e uma esfera azul. No prato à direita, um peso com 3.314 g. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Escreva dois números quaisquer. Depois, peça a um colega que escreva um terceiro número que esteja relacionado a esses dois números por meio de uma adição.

    _____

    PROFESSOR Exemplo de resposta: números quaisquer: 12 e 5; terceiro número: 17.

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

• Compreendo informações de problemas e consigo escolher estratégias adequadas e eficientes para resolvê-los?

Imagem: Ícone: Oral. Fim da imagem.

• Utilizo composição e decomposição numérica em cálculos mentais e em algoritmos usuais da adição e da subtração?

PROFESSOR Respostas pessoais.
MANUAL DO PROFESSOR

Atividade 4

Depois que os estudantes resolverem as adições e as subtrações, reproduza-as na lousa para que eles possam observar eventuais enganos na resolução.

Atividade 5

Uma estratégia para discutir com os estudantes a resolução desta atividade é escrever na lousa algumas afirmações. Eles deverão identificar e justificar quais delas são verdadeiras. Lembre os estudantes de que as massas nos pratos são iguais quando a balança está em equilíbrio e com os pratos na mesma altura.

Observando somente a 1ª situação, é possível afirmar que o cubo tem mais de 2.000 g. (Verdadeira, o cubo tem exatamente 2.127 g.)

Observando somente a 2ª situação, podemos concluir que a massa da bola azul é maior que a massa do cubo. (Falsa, pois só é possível saber que as duas massas juntas resultam em 3.314 g.)

Pelas duas situações, é possível concluir que a bola azul tem massa menor que a do cubo. (Verdadeira, pois o cubo tem 2.127 g e, junto com a bola azul, tem 3.314 g, ou seja, a bola azul tem 1.187 g.)

Atividade 6

Solicite aos estudantes que escrevam a adição e a subtração relacionadas a esses números.

Autoavaliação

Na primeira questão, peça aos estudantes que relembrem como resolvem problemas matemáticos de adição e subtração e se as estratégias escolhidas ajudam a encontrar respostas. Aproveite para incentivar a ampliação de estratégias.

Na segunda questão, os estudantes deverão relacionar a ideia de composição e decomposição numérica com os procedimentos de cálculo, tanto mental como escrito. Eles deverão avaliar se no algoritmo, por exemplo, percebem as trocas quando decompõem os números, não realizando apenas processos mecânicos.

BNCC em foco:

EF04MA03, EF04MA14

MP094

Comentários para o professor:

Conclusão da Unidade 2

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Efetua cálculo de resultados de adições e de subtrações por meio de cálculo mental e escrito usando a decomposição como estratégia e também por meio do algoritmo usual?

_____

_____

Resolve e elabora problemas que envolvem significados da adição e da subtração?

_____

_____

Desenvolve estratégias diversificadas (decomposição e algoritmo usual) para efetuar cálculo mental e escrito e fazer estimativas e arredondamentos nas adições com reagrupamento e subtração com trocas?

_____

_____

Reconhece, por meio de investigações, com a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração, para aplicá-las na resolução de problemas?

_____

_____

Compreende e aplica as propriedades da adição para resolver problemas?

_____

_____

Compreende que uma igualdade não se altera quando se adiciona um mesmo número a seus dois termos ou quando se subtrai um mesmo número de seus dois termos?

_____

_____

Consegue determinar o número desconhecido que torna verdadeira uma igualdade que envolve as operações de adição e de subtração com números naturais?

_____

_____

Identifica, entre eventos aleatórios, aqueles em que há maior chance de ocorrência, reconhecendo características de resultados mais prováveis?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____

MP095

Sugestão de ficha de autoavaliação do estudante

O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.

Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.

Tabela: equivalente textual a seguir.

Autoavaliação

Nome:

Marque um X em sua resposta para cada pergunta.

Sim

Mais ou menos

Não

1. Presto atenção nas aulas?

_____

_____

_____

2. Pergunto ao professor quando não entendo?

_____

_____

_____

3. Sou participativo?

_____

_____

_____

4. Respeito meus colegas e procuro ajudá-los?

_____

_____

_____

5. Sou educado?

_____

_____

_____

6. Faço todas as atividades com capricho?

_____

_____

_____

7. Trago o material escolar necessário e cuido bem dele?

_____

_____

_____

8. Cuido dos materiais e do espaço físico da escola?

_____

_____

_____

9. Gosto de trabalhar em grupo?

_____

_____

_____

10. Respeito todos os meus colegas de turma, professores e funcionários?

_____

_____

_____