MP096
Comentários para o professor:
Introdução da Unidade 3
A abertura desta Unidade traz a cena de uma exposição de arte em que os estudantes podem observar imagens de objetos que lembram figuras geométricas não planas e figuras geométricas planas. O reconhecimento de elementos matemáticos em situações do mundo físico é fundamental para compreender conceitos básicos de Matemática.
Os estudos desta Unidade têm foco nos conhecimentos acerca da Unidade Temática Geometria. Aqui, as atividades propõem associações de representações de figuras geométricas não planas, como cones, cilindros, prismas e pirâmides às respectivas planificações de suas superfícies, analisando, nomeando e comparando seus atributos. Essa abordagem pauta-se no reconhecimento de que os estudantes já se apropriaram de algumas dessas ideias, uma vez que têm sido objeto de estudo desde o 1º ano do Ensino Fundamental. Particularmente, no 3º ano, em relação às figuras geométricas não planas, as atividades buscavam a associação de objetos do mundo físico às suas representações, bem como a descrição de suas características.
Então, no 4º ano, haverá um avanço, em relação aos conhecimentos adquiridos no 3º ano, pois, aqui, os estudantes vão nomear e comparar os atributos das figuras não planas. As habilidades desenvolvidas nesta Unidade serão retomadas e sistematizadas no 5º ano.
O conceito de ângulos (ideia de giro) é introduzido aos estudantes do 4º ano, tomando como ponto de partida atividades que envolvem localização e movimentação: representação de objetos e pontos de referência. São apresentadas diversas situações para a exploração das outras ideias de ângulos, além da identificação de ângulos em figuras poligonais. A habilidade de reconhecer ângulos retos e não retos (agudos e obtusos) em figuras poligonais com o uso de dobraduras e esquadros de papel, por comparação e sobreposição, é explorada em atividades práticas.
As atividades desenvolvidas nesta Unidade e os conceitos associados vão contribuir para o desenvolvimento de habilidades do 5º ano, tais como reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, além de desenhá-los, empregando material de desenho geométrico ou tecnologias digitais. Também serão suportes para obter o reconhecimento da congruência dos ângulos e da proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas e usando tecnologias digitais.
As atividades da Unidade Temática Probabilidade e estatística propostas nas Unidades 3 e 7 do 4º ano proporcionam aos estudantes o desenvolvimento de habilidades para analisar dados apresentados em tabelas simples ou de dupla entrada e em gráficos de colunas ou pictóricos, com base em informações das diferentes áreas do conhecimento. O trabalho que foi desenvolvido nos anos anteriores (leitura, interpretação e comparação de dados apresentados em gráficos e tabelas) será aplicado na pesquisa, organização de dados em tabelas e gráficos, interpretação e produção de texto com a síntese da análise. As atividades do 4º ano introduzirão situações mais complexas, que serão apresentadas no 5º ano.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. As variáveis são muitas: dos conteúdos às habilidades e objetivos de aprendizagem.
Competências gerais favorecidas
2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.
3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.
4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.
5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.
6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.
9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.
10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.
Competências específicas favorecidas
1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.
2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.
3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.
MP097
4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.
5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.
6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).
8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção Jogo desta Unidade.
Os jogos são recursos valiosos para o desenvolvimento simultâneo de habilidades matemáticas, motoras, sociais e éticas de estudantes nessa faixa etária. Sempre que a atividade demandar a fixação de prazo para ser realizada, o tempo sugerido desse prazo deve ser comunicado com antecedência.
Roteiro de aula – Jogo: O que é, o que é? 1 ª parte – Preparação – Tempo sugerido: 20 minutos
Organize as carteiras de modo que os estudantes possam trabalhar em trios ou quartetos. Para tal composição, sugira escolhas livres, porém, fique atento e auxilie aqueles que estiverem com dificuldade em encontrar um par para realizar a atividade.
Para obter as 28 cartas a serem usadas no jogo, oriente os estudantes a destacarem, com o auxílio de uma tesoura de ponta arredondada, a folha indicada na parte final do livro (Material complementar). Convém que ela seja colada em outro papel de maior consistência (cartolina ou papelão) antes de as cartas serem recortadas uma a uma. Para isso, solicite com antecedência que providenciem tesoura, cartolina e cola. Basta um jogo de cartas para cada grupo.
Faça a leitura coletiva das regras do jogo e certifique-se de que elas foram compreendidas por todos. Embora esse jogo proponha um procedimento simples, avalie a necessidade de simular, junto com um dos grupos, um início de procedimento que sirva como exemplo e elimine possíveis dúvidas. Esta orientação é válida para os jogos em geral, portanto pode ser adaptada para outras atividades semelhantes.
2 ª parte – Jogo – Tempo sugerido: 30 minutos
O tempo de cada rodada depende da habilidade e conhecimento dos elementos do grupo e, de certa maneira, do acaso do jogo. É provável que esses tempos sejam diferentes para as equipes. Por isso, convém estabelecer de antemão um teto que julgar adequado dentro da sua disponibilidade e programação.
Deixe-os jogar livremente, mas acompanhe as ações dos grupos para administrar impasses caso considere necessário.
3 ª parte – Questões sobre o Jogo – Tempo sugerido: 10 minutos
As questões propostas devem ser respondidas também em grupo e, muito provavelmente, elas estiveram presentes em algumas das passagens do jogo. É razoável supor que não haja dificuldade na resolução delas, mas é importante o acompanhamento de possíveis dúvidas.
Não é esperado que os estudantes apresentem respostas com rigor matemático. No entanto, avalie a conveniência de, após terem resolvido as questões, fazer algumas considerações. Por exemplo, na questão 3, caso apontem a porta da sala de aula como exemplo de retângulo, lembre-os da espessura da porta que a faria uma melhor representante de um prisma retangular (paralelepípedo reto-retângulo). Na questão 4, pergunte se os dois triângulos, base do prisma, podem ser diferentes ou se os três retângulos, quando sobrepostos, podem não coincidir.
Finalmente valide com a turma as respostas dadas às questões dessa seção.
MP098
UNIDADE 3. Geometria

MANUAL DO PROFESSOR
Objetivos da Unidade
Reconhecer e nomear figuras geométricas não planas.
Reconhecer e nomear figuras geométricas planas.
Identificar planificação de figuras geométricas não planas.
Identificar vértices, faces e arestas em figuras geométricas não planas.
Representar figuras geométricas planas e figuras geométricas não planas em malha quadriculada.
Desenvolver a noção de ângulo a partir de giros.
Identificar giros de uma volta, de meia-volta e de um quarto de volta.
Reconhecer ângulos retos e não retos em figuras poligonais.
Identificar lados, ângulos e vértices em polígonos.
Realizar pesquisa e agrupar dados em tabela.
Na cena de abertura desta Unidade, os estudantes podem observar situações em uma exposição de arte em que há objetos que lembram figuras geométricas não planas e figuras geométricas planas. O reconhecimento de elementos matemáticos em situações cotidianas é fundamental para compreender conceitos básicos de Matemática.
BNCC em foco:
EF04MA17, EF04MA18, EF04MA27, EF04MA28
MP099
Boxe Complementar
Para refletir...

A família Silva está visitando uma exposição de arte. Procure na cena objetos que lembrem figuras geométricas.
Resposta pessoal.

Que movimento Ana (menina de blusa vermelha e tiara) pode fazer para ficar de frente para a escultura com esferas?
Exemplo de resposta: Ana pode dar um giro de meia-volta.
Fim do Complemento
MANUAL DO PROFESSOR
Para refletir...
Na cena, há objetos que lembram figuras geométricas não planas – como cilindro, paralelepípedo, esfera e prisma – e, desconsiderada a espessura, objetos que lembram figuras geométricas planas – como retângulo, quadrado, triângulo e círculo. Comente que as figuras geométricas são criações matemáticas, por isso dizemos que os objetos lembram determinadas figuras geométricas. Jamais encontramos objetos do mundo físico com as mesmas características ideais dessas figuras matemáticas.
O objetivo da questão é levar os estudantes à ideia, ainda que intuitiva, de ângulo como giro. Para facilitar a compreensão desse conceito, a situação apresentada requer um giro de meia-volta, ideia que pode ser do conhecimento dos estudantes. Ajude-os perguntando em que situações costumam empregar expressões como “girar meia-volta”, “virar à direita” e “virar à esquerda”. É bastante provável que mencionem o contexto de algumas brincadeiras ou de explicações de trajetos – situações que envolvem mudanças de direção ou de sentido, um dos aspectos da ideia de ângulo.
MP100
Planificações

- Recorte as planificações das páginas 245 a 255, depois monte os moldes das figuras geométricas não planas.
- Observe a representação de embalagens desmontadas e responda à questão.
a)
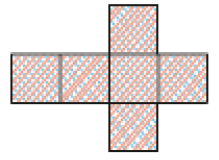
b)

c)
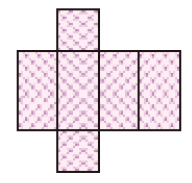
d)

e)
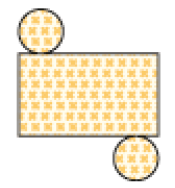
f)
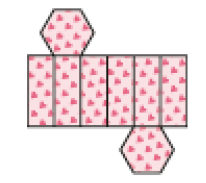
- Depois de montadas as figuras geométricas não planas abaixo, a qual planificação cada uma delas pode ser associada? Indique a letra correspondente.

LEGENDA: Cubo. FIM DA LEGENDA.
( )
PROFESSOR
Resposta: a
LEGENDA: Cilindro. FIM DA LEGENDA.
( )
PROFESSOR
Resposta: e
LEGENDA: Pirâmide de base quadrada. FIM DA LEGENDA.
( )
PROFESSOR
Resposta: d
LEGENDA: Cone. FIM DA LEGENDA.
( )
PROFESSOR
Resposta: b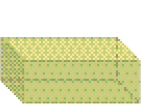
LEGENDA: Paralelepípedo. FIM DA LEGENDA.
( )
PROFESSOR
Resposta: c
LEGENDA: Prisma de base hexagonal. FIM DA LEGENDA.
( )
PROFESSOR
Resposta: f

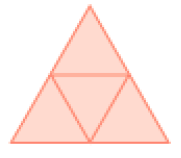
- Descubra a figura que Janice vai montar com as partes representadas abaixo.

PROFESSOR
Resposta: Prisma de base triangular.MANUAL DO PROFESSOR
Objetivo
Reconhecer e nomear figuras geométricas não planas.
Atividades 1 e 2
Ajude os estudantes na montagem dos moldes das figuras geométricas não planas. Eles precisam colar as planificações em um papel mais resistente, como uma cartolina, depois recortar novamente e montar os moldes.
O principal objetivo da atividade 1 é levar os estudantes a diferenciarem figuras geométricas planas de figuras geométricas não planas.
A atividade 2 permite ao estudante relacionar a planificação de uma figura geométrica não plana a sua representação. Os moldes da atividade 1 podem ser utilizados na realização desta atividade.
Atividade 3
Se julgar oportuno, reúna os estudantes em grupos e distribua para cada grupo um conjunto de figuras em cartolina, como as mostradas na atividade. Peça, então, que montem o modelo de figura com essas peças, para descobrir qual modelo de figura geométrica não plana foi montado por Janice. Faça isso com outras figuras não planas. As partes dessas figuras devem ser preparadas com antecedência, para serem distribuídas entre os estudantes.
BNCC em foco:
EF04MA17; competência específica 8
MP101
- Observe as ilustrações em cada item para responder às questões.
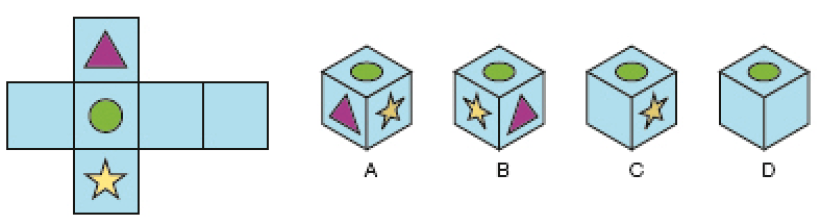
- Qual cubo representado corresponde à planificação?
_____
PROFESSOR
Resposta: C
- Qual cubo representado corresponde à planificação?
_____
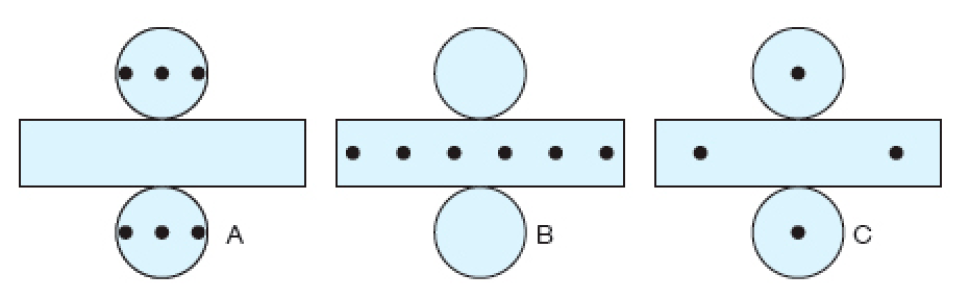
- Qual planificação corresponde ao objeto que lembra um cilindro feito de plástico transparente?
_____
PROFESSOR
Resposta: B

Objeto
- Abaixo estão representadas algumas planificações e algumas pirâmides.
A

B

C
D
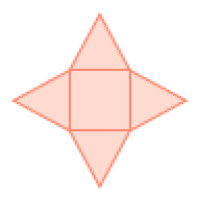
1

2

3

4
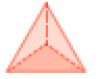
- Escreva a
letra
de cada planificação e o
número
da pirâmide correspondente.
_____
PROFESSOR
Resposta: A – 3; B – 1; C – 4; D – 2
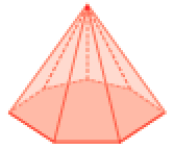
- Agora, observe a representação da pirâmide acima. Quantas partes teria a planificação da superfície dessa figura?
_____
PROFESSOR
Resposta: 8 partes.
MANUAL DO PROFESSOR
Atividade 4
Esta atividade explora a imagem mental entre uma planificação, com figuras geométricas em três de suas faces, e a correspondente figura geométrica não plana que resultará da montagem da planificação.
Para facilitar a identificação do cubo que corresponde à planificação mostrada, peça aos estudantes que imaginem que ele foi montado de modo que sua face superior seja aquela com o desenho de um círculo. Assim, a face com o desenho de um triângulo e a face com o desenho de uma estrela terão de ficar opostas uma à outra. Outro modo de os estudantes solucionarem o problema é construindo o modelo de um cubo em cartolina e desenhando as figuras em suas faces, como mostra a ilustração da atividade. Depois, peça a eles que verifiquem diretamente a disposição que corresponde à alternativa correta.
Na leitura do enunciado do item b, destaque a indicação de que o cilindro é feito com plástico transparente. Eles devem observar que os seis círculos pretos estão na superfície arredondada do cilindro, o que apenas a planificação B contempla.
Atividade 5
Espera-se que, nesta atividade, os estudantes percebam a regularidade existente entre a quantidade de lados da base e a quantidade de faces das pirâmides. As representações pretendem exemplificar que cada planificação é composta de uma base mais a quantidade de triângulos iguais à quantidade de lados da base.
No item b, verifique se os estudantes percebem que cada face lateral corresponde a uma aresta da base da pirâmide. Assim, como a base tem 7 lados, a planificação da sua superfície terá 8 partes.
BNCC em foco:
EF04MA17
MP102
Vértices, faces e arestas
- Cristiano e João estão montando estruturas conforme o modelo abaixo. Eles usam palitos e peças conectoras que se parecem com cubos. Já foram montadas 4 dessas estruturas.
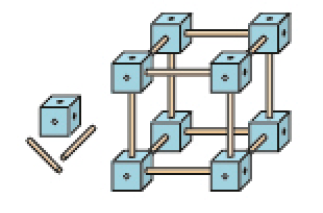
- Quantos
palitos
foram usados nessas 4 estruturas, no total?
_____
PROFESSOR
Resposta: 48 palitos.
- Quantas peças conectoras foram usadas nessas 4 estruturas, no total?
_____
PROFESSOR
Resposta: 32 peças.
- Observe as representações de figuras geométricas não planas e informações sobre elas. Depois, responda às questões.
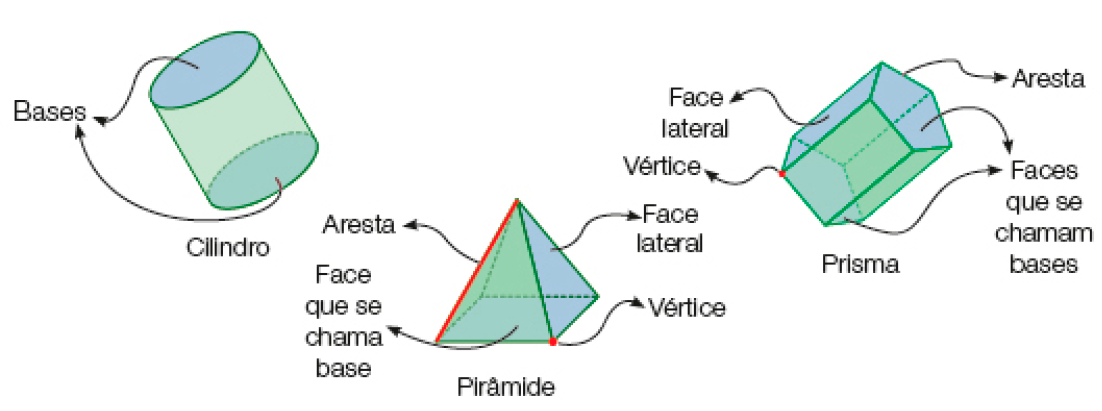
- A aresta fica no encontro de quantas faces?
_____
PROFESSOR
Resposta: De 2 faces.
- Em um prisma, o vértice fica no encontro de quantas arestas?
_____
PROFESSOR
Resposta: De 3 arestas.
- As faces laterais da pirâmide representada acima lembram qual figura geométrica plana?
_____
PROFESSOR
Resposta: Triângulo.
- As faces laterais do prisma representado acima lembram qual figura geométrica plana?
_____
PROFESSOR
Resposta: Retângulo.
- Quantas bases tem o prisma representado acima? E a pirâmide? E o cilindro?
_____
PROFESSOR
Resposta: Prisma: 2 bases; pirâmide: 1 base; cilindro: 2 bases.


- Reúna-se com um colega e conversem sobre uma maneira de descrever o cubo apresentando suas características.
PROFESSOR
Exemplo de resposta: É uma figura geométrica não plana com 6 faces, todas quadradas.MANUAL DO PROFESSOR
Objetivo
Identificar e contar os elementos (arestas, vértices e faces) de algumas figuras geométricas não planas e perceber as relações de quantidade desses elementos em cada figura.
Atividade 1
Modelos concretos de figuras geométricas não planas costumam atrair a atenção de estudantes dessa faixa etária. Durante a realização das atividades, disponibilize os modelos de figuras geométricas montados anteriormente para os estudantes manipularem e perceberem as propriedades das figuras geométricas correspondentes. Proponha a eles que reproduzam o modelo apresentado usando palitos de madeira sem pontas e conectores feitos com massinha de modelar. Usando esse material, outros modelos (convencionais ou não) podem ser construídos, de modo a explorar quantidades de vértices e arestas das figuras construídas. Antes da resolução das questões referentes às quatro estruturas montadas, explore com os estudantes as quantidades de palitos e peças conectoras da figura representada: doze palitos e oito peças conectoras.
Atividade 2
É importante os estudantes reconhecerem que os termos prismas e pirâmides designam classes de figuras, e não uma única figura, e que o nome completo de cada figura dessas classes dependerá de sua base: quando a base é um quadrado, por exemplo, temos um prisma ou uma pirâmide de base quadrada; quando a base é um pentágono, temos um prisma ou uma pirâmide de base pentagonal etc.
Depois da resolução, é interessante retomar a atividade anterior e perguntar aos estudantes quantos vértices, faces e arestas tem um cubo. Espera-se que respondam 8 vértices, 6 faces e 12 arestas. Verifique se eles percebem que o cubo e o paralelepípedo também são prismas.
Atividade 3
Comente com os estudantes que o modelo de cubo montado na atividade 1 pode ser manipulado para eles realizarem as descrições solicitadas.
BNCC em foco:
EF04MA17; competência geral 2; competência específica 8
MP103
- Observe as representações de figuras geométricas não planas e faça o que se pede.
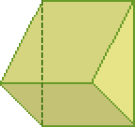
LEGENDA: Prisma de base triangular. FIM DA LEGENDA.

LEGENDA: Prisma de base pentagonal. FIM DA LEGENDA
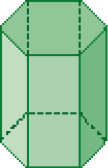
LEGENDA: Prisma de base hexagonal. FIM DA LEGENDA
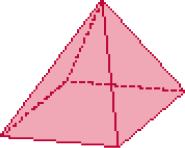
LEGENDA: Pirâmide de base quadrada. FIM DA LEGENDA
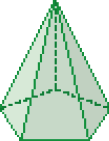
LEGENDA: Pirâmide de base pentagonal. FIM DA LEGENDA
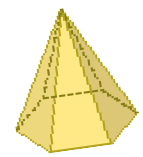
LEGENDA: Pirâmide de base hexagonal. FIM DA LEGENDA
- Complete o quadro abaixo.
Quadro: equivalente textual a seguir.
|
Figura geométrica não plana |
Número de vértices da base |
Número total de vértices |
|
Prisma de base triangular |
3 |
6 |
|
Prisma de base pentagonal |
_____ |
_____ |
|
Prisma de base hexagonal |
_____ |
_____ |
|
Pirâmide de base quadrada |
_____ |
_____ |
|
Pirâmide de base pentagonal |
_____ |
_____ |
|
Pirâmide de base hexagonal |
_____ |
_____ |
PROFESSOR
Resposta: Prisma de base pentagonal. 5,10.PROFESSOR
Prisma de base hexagonal. 6, 12.PROFESSOR
Pirâmide de base quadrada. 4, 5.PROFESSOR
Pirâmide de base pentagonal. 5, 6.PROFESSOR
Pirâmide de base hexagonal. 6, 7.


- Reúna-se com um
colega
e busquem regularidades sugeridas por esses números que você preencheu no quadro.
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que: o número total de vértices dos prismas é o dobro do número de vértices de uma de suas bases; o número total de vértices das pirâmides é o número de vértices da base mais uma unidade. Fim da observação.
- Em todas as faces retangulares do brinquedo de Geraldo há a mesma quantidade de buracos. Em cada uma das duas faces pentagonais há 1 buraco.

- Quantos buracos há ao todo no brinquedo?
_____
PROFESSOR
Resposta: 22 buracos.

- Faça um esquema para explicar como você descobriu quantos buracos há no brinquedo. Depois, você e seu
colega
comparam os esquemas que fizeram. Vocês pensaram da mesma maneira?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que o brinquedo lembra um prisma de base pentagonal. Fim da observação.
MANUAL DO PROFESSOR
Atividade 4
Deixe os estudantes manipularem os modelos de figuras geométricas montados anteriormente para ajudá-los a determinar com mais facilidade o número de vértices de cada uma. Depois de completarem o quadro, pergunte: “Qual a quantidade de vértices de um prisma de base heptagonal e de uma pirâmide de base heptagonal?” (Prisma: 14 vértices; pirâmide: 8 vértices). Se necessário, explique que uma figura geométrica plana heptagonal tem 7 lados e 7 vértices.
No item b, além das regularidades sugeridas sobre o número de vértices, podem ser observadas outras, como: nos prismas, o número de arestas é o triplo do número de vértices da base; nas pirâmides, o número de arestas é igual ao dobro do número de vértices da base.
Atividade 5
Os estudantes devem compreender que, para calcular o total de buracos do brinquedo com forma de prisma, é necessário determinar quantas são as faces com um buraco e quantas são as faces com quatro buracos.
Como um prisma tem duas bases (no caso, com um buraco em cada) e a quantidade de faces laterais é igual à quantidade de lados do polígono que corresponde às bases (no caso do pentágono, cinco lados), então o total de buracos é obtido pela adição: 2 (um buraco em cada uma das bases) + 20 (quatro buracos em cada uma das cinco faces laterais), ou seja, há 22 buracos no total.
Aproveite a questão para perguntar: “Quantas faces laterais tem essa figura geométrica? E quantas bases?” (5; 2).
BNCC em foco:
EF04MA17; competência geral 2; competências específicas 3 e 8
MP104
Jogo: O que é, o que é?

Material: Tabuleiro das páginas 238 e 239, 28 cartas das páginas 241 e 243, 4 marcadores de papel, de cores diferentes, para apostar em figuras.
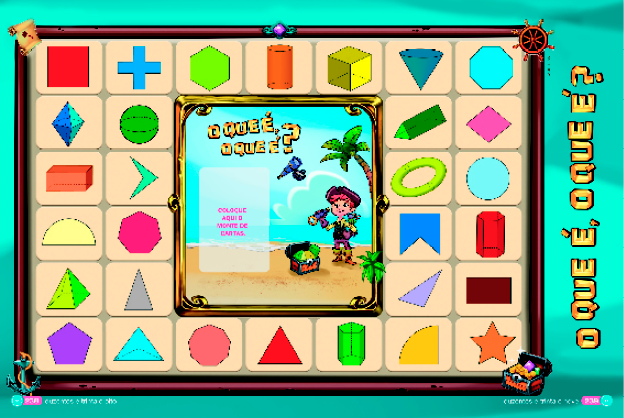
Jogadores: 3 ou 4.
Regras:
- As cartas devem ser embaralhadas e colocadas no centro do tabuleiro, com as informações voltadas para baixo.
- Sorteia-se quem vai ler a primeira carta retirada de cima do monte. Cada jogador segura seu marcador na mão, exceto quem fará a leitura.
- O jogador que está com a carta a lê em voz alta, para que todos o ouçam.
- Depois da leitura, os outros jogadores devem escolher no tabuleiro a figura que acham que foi descrita, colocando o seu marcador sobre ela. Uma mesma figura não pode ser escolhida por mais de um jogador. Um jogador pode decidir não escolher uma figura em uma jogada, mas não pode mudar sua escolha.
- O jogador que escolher a figura descrita ganha a carta para si. Caso nenhum jogador acerte a figura descrita, a carta deve ser colocada por último no monte.
- O próximo a pegar uma carta e descrevê-la é o jogador que está à esquerda de quem leu a carta por último.
- Ganha quem conseguir acumular 8 cartas primeiro.
MANUAL DO PROFESSOR
Objetivo
Reconhecer figuras geométricas planas e não planas por meio de suas características geométricas e relacioná-las às suas representações.
Ajude os estudantes na leitura e compreensão das regras.
O tabuleiro, que apresenta representações de figuras geométricas variadas, faz de O que é, o que é? um jogo muito criativo e atraente para os estudantes, pois exige que eles observem diversas características das figuras geométricas, distinguindo-as por aspectos relativos às características planas e não planas, à quantidade de lados etc. Essas ações simultâneas representam um desafio para eles, que devem verbalizar (linguagem oral) as características das figuras geométricas em uma estrutura de adivinhação (como a de jogos de “senha”). Pode-se iniciar o jogo de uma maneira mais simples, com você sorteando a primeira carta e fornecendo as características da figura geométrica, para os estudantes se habituarem ao tipo de linguagem matemática e se familiarizarem com o tabuleiro. Como as características apresentadas nas cartas descrevem uma única figura geométrica, é possível que mais de um componente do grupo escolha uma mesma figura geométrica na rodada. Caso isso ocorra, é preciso que os jogadores combinem entre si uma regra para resolver a situação, como estabelecer que o primeiro a escolher uma figura geométrica terá a prioridade.
As questões propostas auxiliam na identificação de características diferenciadoras entre as figuras geométricas representadas, o que permite aumentar e aprimorar o repertório dos estudantes em termos de linguagem matemática.
BNCC em foco:
EF04MA17; competências gerais 9 e 10; competência específica 8
MP105
Questões sobre o jogo
- Há quantas figuras geométricas planas representadas no tabuleiro? E quantas figuras geométricas não planas?
_____
PROFESSOR
Resposta: Há 18 figuras geométricas planas e 12 figuras geométricas não planas..

- Qual das figuras geométricas planas representadas no tabuleiro lembra uma das faces de um cubo? E qual das figuras representa uma das bases de um cilindro?
_____
PROFESSOR
Resposta: O quadrado; o círculo.
- O retângulo foi descrito na carta da seguinte maneira: “Uma cédula de dinheiro se parece comigo”. Você saberia descrevê-lo de outra maneira? Como?
_____
PROFESSOR
Exemplo de resposta: Sim; o contorno de uma lousa lembra meu contorno.
- Quais representações de figuras geométricas planas são necessárias para montar um
molde
de prisma de base triangular como o representado no tabuleiro?
_____
PROFESSOR
Resposta: Dois triângulos e três retângulos.

- Observe a situação de jogo acima, em que um jogador escolheu a figura indicada. Observe-a atentamente em seu tabuleiro. Qual é o nome dessa figura? Invente uma dica que poderia estar na carta correspondente a ela.
_____
PROFESSOR
Resposta: Cone. Alguns exemplos de dica: “Sou arredondado e tenho um ‘bico’”; “um chapéu de festa de aniversário se parece comigo”.
MANUAL DO PROFESSOR
Questões sobre o jogo
Questões 1 e 2
Aproveite para explorar com a turma outras características que descrevam uma mesma figura geométrica. Por exemplo, para descrever o cilindro: “Sou uma figura geométrica não plana, arredondada e tenho duas bases que lembram um círculo”. Pergunte também se, nas descrições das figuras geométricas, há mais informações que as necessárias. Por exemplo, na descrição de um quadrado, “Tenho quatro lados de mesma medida e ângulos retos, e sou uma face do cubo”, bastaria uma das frases; o recurso da redundância, nesse caso, tem o objetivo didático de oferecer a oportunidade de identificação de uma figura por diferentes modos.
Questão 3
Na exploração da descrição do retângulo, enfatize para os estudantes que se trata da superfície da cédula, pois ela como objeto possui espessura. Portanto, por menor que seja sua espessura, também poderia ser considerada semelhante a um paralelepípedo.
Questão 4
Espera-se que os estudantes respondam com facilidade a esta questão após a montagem e manipulação do modelo do prisma de base triangular.
Questão 5
Se julgar necessário, oriente os estudantes a observarem o tabuleiro do jogo para visualizarem melhor a figura indicada. É interessante propor que respondam a esta atividade em dupla e depois socializem as respostas, de modo a contribuir para aumentar o repertório de características das figuras. O mesmo trabalho pode ser feito com outras figuras representadas no tabuleiro.
BNCC em foco:
EF04MA17, EF04MA18; competência específica 8
Variações
Após a realização de algumas partidas, é possível que os estudantes queiram alterar as cartas com as figuras descritas. Nesse caso, incentive-os a preparar cartas com outras figuras e descrições, desenvolvendo habilidades de reconhecimento de figuras geométricas e de comunicação matemática.
MP106
Representando figuras geométricas

1. Desenhe na malha quadriculada de cada item, conforme as orientações.
a)

b)

- Agora, escreva o nome de cada figura desenhada.
_____
PROFESSOR
Resposta: Item a: quadrado; item b: triângulo.

- Na malha quadriculada abaixo, usando uma régua, ligue os pontos conforme a orientação. As linhas tracejadas representam as linhas que não vemos.Depois, pinte a figura formada e responda às questões.

- Qual é o nome da figura que você representou?
_____
PROFESSOR
Resposta: Paralelepípedo.
- Qual é o
número
de arestas e o
número
de vértices dessa figura?
_____
PROFESSOR
Resposta: Arestas: 12; vértices: 8.
MANUAL DO PROFESSOR
Objetivo
Representar, por meio de desenhos, figuras geométricas planas e não planas.
Nestas páginas, os estudantes aprendem a representar, por meio de desenhos, figuras geométricas planas e não planas. Eles têm também a oportunidade de perceber que o papel quadriculado é um importante aliado nessa representação, pois favorece a compreensão das características das figuras (como a quantidade de lados e a medida dos lados). Além disso, facilita a representação de arestas paralelas em perspectiva e a identificação de figuras demarcadas apenas por pontos. Explique que há outras formas de representar figuras não planas, como as técnicas de perspectiva, desenvolvidas desde o Renascimento, no século XV.
Atividade 1
Verifique se os estudantes resolvem com facilidade esta atividade ou precisam de algum tipo de ajuda.
Atividade 2
Esta atividade indica a sequência em que devem ser traçadas as arestas da figura. Aproveite para perguntar: “Quantas faces tem esse paralelepípedo? Se fossem traçados apenas A com B, A com D, B com C, B com F, C com D, C com G, D com H, G com F e G com H, todas as arestas e todos os vértices ficariam visíveis?” (Não; faltariam as representações das arestas A com E, E com F e E com H, respectivamente.). Essa dificuldade é superada com a indicação da fala da personagem “Ligue com uma linha tracejada: A com E ; E com F e H .”.
BNCC em foco:
EF04MA17
MP107
- Camila e Gustavo observaram as fotografias abaixo e fizeram alguns desenhos para representar as construções que aparecem nelas.

LEGENDA: Edifício em Brasília, Distrito Federal, em 2020. FIM DA LEGENDA.

LEGENDA: Museu do Louvre, em Paris, França, em 2019. FIM DA LEGENDA.

- Observe os desenhos de Camila e os de Gustavo. Qual das construções Camila pretendeu representar? E Gustavo?
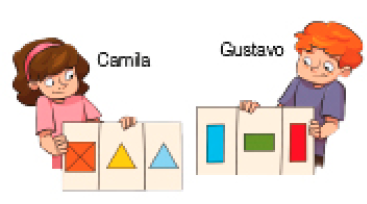
PROFESSOR
Resposta: Camila pretendeu representar a pirâmide do Museu do Louvre, e Gustavo, o edifício em Brasília.- Observe a representação de uma caixa desmontada e responda à questão.

- Se a caixa for montada e ficar apoiada na mesa sobre a parte azul, qual será a cor da parte que ficará oposta à parte apoiada na mesa?
_____
PROFESSOR
Resposta: Verde.
- Observe a imagem de uma lanterna chinesa abaixo.

- Qual figura geométrica não plana a
lanterna
lembra?
_____
PROFESSOR
Resposta: Uma esfera.
- Desenhe a figura plana que pode ser reconhecida na observação da imagem da
lanterna
acima.
_____
PROFESSOR
Resposta:
MANUAL DO PROFESSOR
Atividade 3
Pretende-se, nesta atividade, que os estudantes relacionem as faces com as construções apresentadas. Esclareça que as representações feitas por Camila e Gustavo são as projeções vistas de cima (superior), de frente (frontal) e de lado (lateral).
É interessante que eles sejam incentivados a observar características comuns e diferenças entre as figuras, assim como regularidades entre elas. Igual incentivo deve ser dado à formulação de hipóteses, processo mental que contribui para o desenvolvimento de habilidades geométricas importantes. Esclareça a eles que, quando se faz a representação em papel de figuras não planas, algumas características podem ser alteradas. Por exemplo, um retângulo que seja a base de um paralelepípedo é representado como um paralelogramo (não retângulo). Diga a eles que essas mudanças são necessárias para obter o efeito de profundidade da figura na representação em um plano.
Atividade 4
Para promover a reflexão dos estudantes, peça a eles que imaginem a caixa montada e digam quais são as cores das faces opostas desse cubo. Os estudantes podem comprovar as respostas fazendo o molde de um cubo com as cores da caixa desmontada representada na atividade.
Atividade 5
Espera-se que o estudante consiga diferenciar figura geométrica não plana de figura geométrica plana, podendo reconhecer o círculo ao observar a fotografia que lembra uma esfera.
BNCC em foco:
EF04MA17; competência geral 3; competência específica 4
MP108
Ideia de ângulos – giros
- Júlia está brincando com seus colegas. Nessa brincadeira, há momentos em que ela indica os colegas, sempre depois de indicar Clóvis.
Observe, abaixo, Júlia indicando Clóvis.
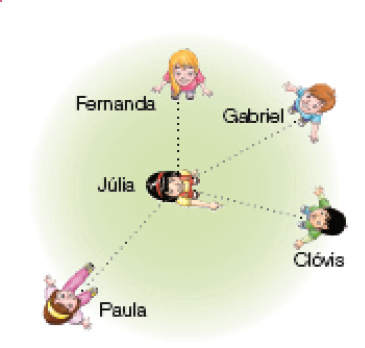
Depois de indicar Clóvis, Júlia indicou Gabriel, Fernanda e Paula, dando giros em torno de si mesma. Veja abaixo como foram os giros que Júlia deu.
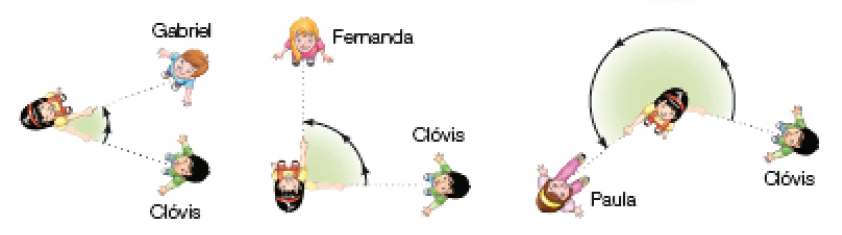

- O
menor
giro que Júlia deu foi para indicar quem? E o maior?
_____
PROFESSOR
Resposta: Gabriel; Paula.
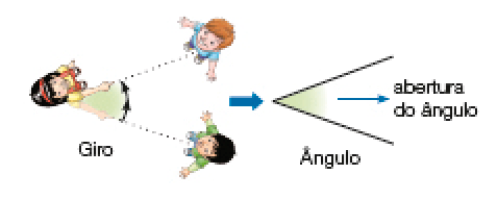
Um giro dá ideia de uma figura geométrica chamada ângulo.
Quanto maior o giro, maior a abertura do ângulo associado a ele.
- Observe os giros dados por Vanessa. Em seguida, responda.

- Dos três giros dados por Vanessa, qual foi o menor?
_____
PROFESSOR
Resposta: Giro 1.
MANUAL DO PROFESSOR
Objetivo
Identificar giros de uma volta, de meia-volta e de um quarto de volta.
Atividade 1
Leve os estudantes a um espaço aberto, como o pátio da escola, e desenhe no chão uma circunferência. Peça a eles que se dividam em grupos de cinco e se posicionem como na figura abaixo.
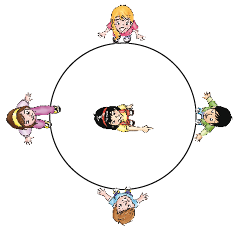
CRÉDITO: PAULO BORGES
Um estudante deve ficar no centro para realizar os giros de acordo com as indicações de outros. As orientações sempre devem tomar como referência a pessoa que se encontra no centro da circunferência e devem sugerir giros de uma volta , de meia-volta e de um quarto de volta para a esquerda e para a direita.
Explique que o giro de um quarto de volta é obtido quando se gira a metade de um giro de meia-volta ou a metade da metade de um giro de uma volta.
BNCC em foco:
EF04MA18
MP109
Outras ideias de ângulo
- Observe as imagens e o ângulo destacado em vermelho na lousa.
Observação: As imagens nesta página não foram representadas em escala de tamanho. Fim da observação.
PROFESSOR
Exemplos de resposta:



- Agora, destaque outros ângulos que você identificou nas imagens acima, pintando-os. Mostre-os a um colega.
- Observe as ilustrações e responda às questões.
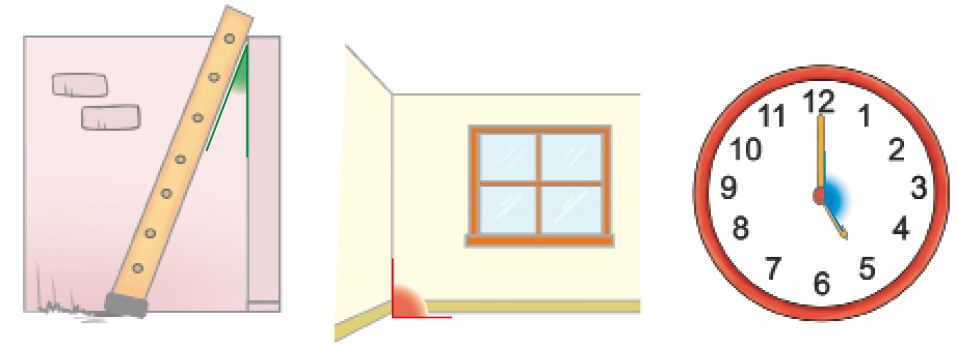
- O que foi destacado em cada uma das ilustrações?
_____
PROFESSOR
Resposta: Ângulos.
- Qual desses ângulos tem a maior abertura?
_____
PROFESSOR
Resposta: O destacado em azul.
- Qual desses ângulos tem a
menor
abertura?
_____
PROFESSOR
Resposta: O destacado em verde.
- Como você fez para descobrir?
PROFESSOR
Resposta pessoal.


- Cite três objetos ou situações em que podemos identificar um ângulo. Depois, no caderno, represente cada objeto ou situação com um desenho e destaque um ou mais ângulos.
PROFESSOR
Resposta e desenho pessoais.
MANUAL DO PROFESSOR
Objetivo
Observar e comparar ângulos levando em consideração a abertura de cada um.
Após a exploração da ideia de ângulo a partir de um movimento (giro), esta página trabalha a ideia de ângulo de um ponto de vista estático. Nas atividades desta página, os estudantes têm a oportunidade de identificar ângulos formados em figuras (atividade 1) e comparar aberturas de ângulos (atividade 2).
Atividade 1
Dê um tempo para os estudantes observarem as imagens e identificarem os ângulos em cada caso. O ângulo destacado na rampa, por exemplo, relaciona-se à inclinação dela.
Atividade 2
Para resolverem a atividade, os estudantes devem comparar os três ângulos destacados, levando em conta a abertura de cada um. As ilustrações destacam um ângulo agudo, um reto e um obtuso – classificações que serão introduzidas no próximo tópico.
O item d permite verificar se os estudantes identificam a abertura de cada ângulo destacado e se reconhecem a maior delas. Espera-se que eles percebam que a abertura do ângulo destacado na ilustração do relógio é visivelmente maior que a abertura dos ângulos destacados nas outras ilustrações e que a abertura do ângulo destacado na ilustração da escada é visivelmente menor.
Atividade 3
Verifique as respostas da turma e, depois de validá-las, peça aos estudantes que compartilhem com os colegas os exemplos que deram de onde os ângulos podem ser encontrados.
BNCC em foco:
EF04MA18; competência geral 4; competências específicas 2 e 6
Sugestão de atividade
Montagem de painel
Proponha aos estudantes que montem um painel com ilustrações ou fotografias de objetos que normalmente fazem movimentos de giro. Por exemplo, uma porta comum (movimento de abrir e fechar), um relógio de ponteiros, um velocímetro ou indicador de combustível de automóvel (giros de ponteiro). Outra opção é montar um painel com fotografias ou ilustrações de pessoas realizando atividades que envolvam a ideia de giro, como os movimentos de uma bailarina, de um patinador ou de um atleta em aparelho de ginástica.
MP110
Ângulo reto, ângulo agudo e ângulo obtuso
- Danilo pintou os quatro cantos de uma folha retangular. Depois, recortou a folha e juntou esses cantos.

Danilo pintou os quatro cantos.

Juntou os cantos.

Sobrepôs os cantos para comparar as medidas dos ângulos.
- Em cada um dos cantos pintados identificamos um ângulo. Esses ângulos têm a mesma abertura? Justifique.
_____
PROFESSOR
Resposta: Sim.PROFESSOR
Atenção professor: Espera-se que os estudantes justifiquem que, ao sobrepor os cantos da folha retangular, Danilo verificou que os quatro cantos têm a mesma medida. Fim da observação.
- Em cada um dos cantos da folha retangular de Danilo, identificamos um ângulo chamado ângulo reto, que pode ser associado a um giro de um quarto de volta.
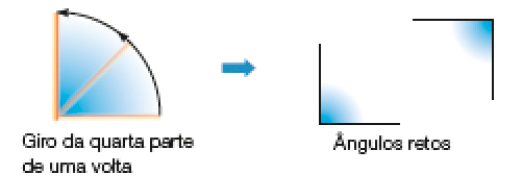
Qual das figuras abaixo tem um ângulo com a mesma abertura dos ângulos destacados na folha de Danilo? _____
PROFESSOR
Resposta: A figura C.
MANUAL DO PROFESSOR
Objetivo
Identificar ângulos retos, ângulos agudos e ângulos obtusos.
Nas atividades propostas, a distinção entre ângulos agudos e obtusos é feita tanto em situações em que a abertura dos ângulos é estática quanto por movimento giratório de um objeto em torno de um ponto central.
Atividade 1
Peça aos estudantes que reproduzam a atividade que Danilo fez. Primeiro, devem pintar os cantos da folha. Pergunte: “Vocês acham que os cantos pintados correspondem a um ângulo de mesma abertura?”. Espera-se que percebam que, independentemente do tamanho da mancha pintada, a abertura dos ângulos dos quatro cantos é a mesma.
Em seguida, peça aos estudantes que dobrem a folha duas vezes ao meio (uma no sentido do comprimento e outra no sentido da largura) e, abrindo a folha novamente, tracem as linhas marcadas pelas dobraduras. Eles devem, então, recortar a folha nessas linhas, obtendo quatro retângulos menores. Ao girar esses retângulos, juntando no centro os cantos pintados, como fez Danilo, os estudantes podem deduzir que a soma das medidas dos quatro ângulos completa a medida de um ângulo de uma volta.
Ao sobrepor os retângulos menores para comparar as aberturas dos quatro cantos, espera-se que os estudantes verifiquem, empiricamente, que as aberturas são iguais. Aproveite a situação para incentivá-los a perceberem que o ângulo reto pode ser associado a um giro de uma quarta parte de volta ou de um quarto de volta (aqui o estudante começa a ter contato com a expressão que designa uma fração).
BNCC em foco:
EF04MA18
MP111
- Observe como Danilo usou a abertura de um dos cantos da
folha
retangular (
 ) para comparar com a abertura de outros ângulos.
) para comparar com a abertura de outros ângulos.

- A abertura do ângulo formado pelo leque é maior ou
menor
que a abertura do ângulo reto?
_____
PROFESSOR
Resposta: Menor.
- E a abertura formada pelas lâminas da tesoura?
_____
PROFESSOR
Resposta: Maior.
O ângulo formado pelo leque é um exemplo de ângulo agudo, que pode ser associado a um giro menor que o da quarta parte de uma volta.

O ângulo formado pelas lâminas da tesoura é um exemplo de ângulo obtuso, que pode ser associado a um giro maior que o da quarta parte de uma volta e menor que o de meia-volta.


- Faça um desenho em uma
folha
à parte e destaque nele um ângulo reto, um ângulo agudo e um ângulo obtuso.
PROFESSOR
Resposta: Desenho pessoal.
MANUAL DO PROFESSOR
Atividade 2
Esta atividade possibilita o reconhecimento de ângulo agudo como aquele que tem abertura menor que a do ângulo reto, e de ângulo obtuso como aquele que tem abertura maior que a do ângulo reto e menor que a do ângulo de 180 graus. Conhecer essa classificação dos ângulos, bem como saber identificá-los, contribui para a descrição de percursos, para o reconhecimento das propriedades de figuras planas e para a denominação de movimentos giratórios.
O ângulo reto será a referência para a classificação de um ângulo como agudo ou obtuso, pois, além de facilmente identificável, ele é encontrado em diversas situações cotidianas. A comparação da abertura do ângulo reto com a de outro ângulo permite distinguir quando um ângulo é obtuso ou agudo, ou seja, quando a abertura é respectivamente maior ou menor que a do ângulo reto.
Atividade 3
Verifique os desenhos feitos pelos estudantes e pergunte: “É possível essa figura ser um triângulo?”. Eles podem experimentar desenhar diferentes triângulos até perceberem que não é possível um triângulo atender às condições do enunciado. O conceito que justifica esse fato somente será aprendido no decorrer da escolarização, mas experimentar a impossibilidade dessa construção é importante. Sabemos que a soma das medidas dos ângulos internos de qualquer triângulo é 180°. Se a figura precisa ter um ângulo reto (90°), as medidas dos outros dois ângulos somam 90°, ou seja, são dois ângulos agudos, o que não satisfaz à condição de haver um ângulo agudo e um ângulo obtuso. Portanto, a figura não pode ser um triângulo, mas pode ser, por exemplo, um trapézio retângulo.

CRÉDITO: ADILSON SECCO
BNCC em foco:
EF04MA18
MP112
- A que ângulo corresponde cada giro da caneta mostrada abaixo: ângulo reto, ângulo agudo ou ângulo obtuso?
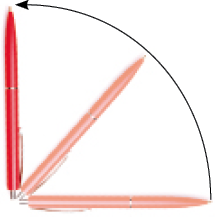
LEGENDA: Giro da quarta parte de uma volta. FIM DA LEGENDA.
_____
PROFESSOR
Resposta: Ângulo reto.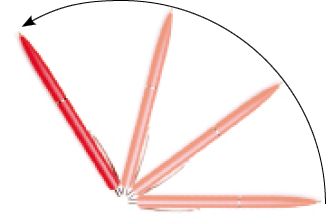
LEGENDA: Giro de mais da quarta parte de uma volta e menos de meia-volta. FIM DA LEGENDA.
_____
PROFESSOR
Resposta: Ângulo obtuso.
LEGENDA: Giro de menos da quarta parte de uma volta. FIM DA LEGENDA.
_____
PROFESSOR
Resposta: Ângulo agudo.Observação: As imagens nesta atividade não foram representadas em escala de tamanho. Fim da observação.
- Classifique cada um dos ângulos destacados em ângulo agudo, ângulo obtuso ou ângulo reto.
a)

_____
PROFESSOR
Resposta: Agudo.b)

_____
PROFESSOR
Resposta: Reto.c)
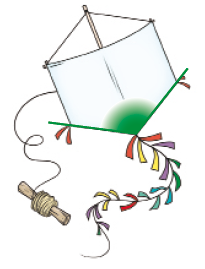
_____
PROFESSOR
Resposta: Obtuso.- Observe as figuras abaixo e descubra em qual delas encontramos exatamente dois ângulos retos.
_____
PROFESSOR
Resposta: Na figura c.
a)

PROFESSOR
Resposta: 4 ângulos retos.
b)

PROFESSOR
Resposta: 1 ângulo reto.
c)

PROFESSOR
Resposta: 2 ângulos retos.
d)
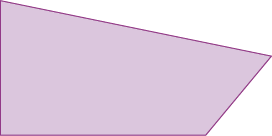
PROFESSOR
Resposta: 1 ângulo reto.
MANUAL DO PROFESSOR
Atividade 4
Aproveite a situação para classificar ângulos em agudo ou obtuso por meio da seguinte atividade: peça a um estudante que fique em uma posição qualquer à frente da classe e que escolha dois colegas, em relação aos quais será feita a classificação do ângulo. Ele deverá apontar, com o braço esticado, um dos colegas escolhidos e, em seguida, girar o braço até apontar para o outro colega. Os colegas deverão decidir se o ângulo associado ao giro dado é agudo ou obtuso. Se a abertura for próxima de um ângulo reto, eles poderão decidir mudar a posição de observação e repetir o procedimento ou usar algum objeto com ângulo reto para realizar a comparação, como um esquadro grande para lousa.
Atividade 5
Esta atividade apresenta alguns casos em que é possível reconhecer visualmente, de imediato, a classificação do ângulo destacado em agudo (vela do barco) ou obtuso entre as linhas de contorno da pipa.
O ângulo reto destacado na mesa, contudo, talvez gere dúvida; nesse caso, o canto reto de uma folha de papel, sobreposta à imagem, pode auxiliar na verificação.
Atividade 6
Os estudantes devem comparar os ângulos com a ajuda de um canto de uma folha retangular. É importante perceberem que, para ter certeza de que os ângulos são retos, precisam fazer a comparação por sobreposição.
BNCC em foco:
EF04MA18
Sugestão de leitura para o estudante
BRENMAN, Ian. A dobradura do samurai. Ilustrações de Fernando Vilela. São Paulo: Companhia das Letrinhas, 2005.
O livro relembra uma antiga lenda japonesa, segundo a qual quem dobrasse 1.000 tsurus teria seus desejos realizados. Nele, há um passo a passo que orienta as crianças a fazerem seus próprios tsurus.
MP113
Polígonos e ângulos
- Descubra e cerque com uma linha a figura “intrometida” em cada caso.
a)

PROFESSOR
Resposta correta: figura 5.b)

PROFESSOR
Resposta correta: figura 3.c)

PROFESSOR
Resposta correta: figura 3.- Todas as figuras a seguir são representações de polígonos. Para simplificar a linguagem, chamaremos as representações de polígonos apenas por polígonos. Repare que sempre podemos desenhar polígonos com uma régua.



- As figuras abaixo não são polígonos. Reúna-se com um
colega
para discutir o porquê disso.
PROFESSOR
Atenção professor: Espera-se que os estudantes observem que: a 1ª figura não é um polígono porque não pode ser desenhada com uma régua; a 2ª figura não é um polígono porque não é fechada; e a 3ª figura não é um polígono porque tem linhas que se cruzam.PROFESSOR
Avalie a conveniência de pedir aos estudantes que identifiquem, no tabuleiro das páginas 238 e 239 as figuras que representam polígonos. Fim da observação.

MANUAL DO PROFESSOR
Objetivos
Conceituar polígonos.
Reconhecer polígonos e seus principais elementos.
O objetivo das atividades com polígonos e ângulos é possibilitar aos estudantes, por meio de exemplos e contraexemplos, conceituar polígono – entendido neste livro como uma figura geométrica plana (superfície plana) que pode ser desenhada com uma régua e cujo contorno é fechado e formado por segmentos de reta que não se cruzam.
Atividade 1
Desenhe na lousa figuras geométricas planas conhecidas – como triângulos, quadrados, losangos, paralelogramos, trapézios, retângulos, pentágonos –, para que os estudantes as reconheçam como polígonos. É importante que eles justifiquem suas respostas. Ouça as justificativas para verificar se há coerência.
BNCC em foco:
EF04MA18; competência específica 4
Sugestão de atividade
Geoplanos
O geoplano é um recurso didático elaborado pelo matemático egípcio Caleb Gattegno (1911-1988).
Providencie alguns geoplanos e barbantes e reúna os estudantes em grupos. Depois, peça a eles que, usando barbante, representem alguns polígonos no geoplano.

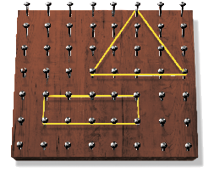
LEGENDA: Geoplanos 7 por 8 (um lado com 7 e outro com 8 pregos). FIM DA LEGENDA.
CRÉDITO: WAGNER WILLIAN
MP114
- Nos polígonos, podemos identificar ângulos internos, lados e vértices. De acordo com o número de lados, os polígonos recebem um nome.
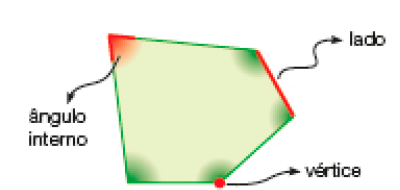
Triângulos
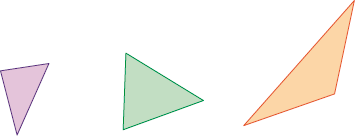
Pentágonos

Quadriláteros

Hexágonos

- Complete o quadro.
Quadro: equivalente textual a seguir.
|
Polígono |
Número de lados |
Número de ângulos internos |
Números de vértices |
|---|---|---|---|
|
Triângulo |
_____ |
_____ |
_____ |
|
Quadrilátero |
_____ |
_____ |
_____ |
|
Pentágono |
_____ |
_____ |
_____ |
|
Hexágono |
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Triângulo. 3. 3. 3.PROFESSOR
Quadrilátero. 4. 4. 4.PROFESSOR
Pentágono. 5. 5. 5.PROFESSOR
Hexágono. 6. 6. 6.

- Que regularidade é sugerida pelos números desse quadro?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que o número de lados de um polígono é igual ao número de ângulos internos e ao número de vértices. Fim da observação.
Boxe complementar:
Desafio
Represente o contorno de alguns polígonos usando um número determinado de palitos, sem deixar sobrar nenhum nem sobrepor dois ou mais palitos.
Com 6 palitos, represente um triângulo e depois um quadrilátero.
PROFESSOR
Exemplos de respostas:
Com 8 palitos, represente um pentágono.
PROFESSOR
Resposta:
Com 7 palitos, represente um hexágono.
PROFESSOR
Resposta:
CRÉDITO: ILUSTRAÇÕES: PAULO MANZI
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 2
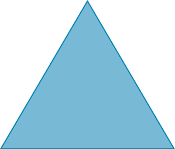
Quando se referem às figuras geométricas, os estudantes geralmente usam linguagem não formal, sem a preocupação com possíveis ambiguidades ou contradições. Por exemplo, eles podem se referir aos vértices de um polígono como “pontas” ou “bicos”. Os lados podem ser denominados “linhas”, e os ângulos, “aberturas”. Entretanto, à medida que os estudos avançam, é importante utilizarem a nomenclatura correta, para que possam comunicar com clareza suas ideias. Para a caracterização dos polígonos, é importante que sejam representados em posições diferentes das tradicionais, pois isso possibilita aos estudantes o entendimento de que sua classificação não depende da posição ou da orientação. Os triângulos, de modo geral, são apresentados com os três lados de mesma medida (triângulo equilátero) e na mesma posição.
CRÉDITO: ADILSON SECCO
Por esse motivo, o texto mostra polígonos com lados de medidas diferentes e em orientações não convencionais, para que os estudantes os reconheçam por meio de seus elementos e características principais.
Desafio
É importante que, no momento da construção, os estudantes relacionem a quantidade de lados e de ângulos do polígono solicitado e pensem como dividir o total de palitos na quantidade de lados. Por exemplo, quando se pede um quadrilátero com 6 palitos, se o estudante pensar em um quadrado, não conseguirá.
BNCC em foco:
EF04MA18; competência específica 4
MP115
- Com uma folha qualquer de papel, Lucas fez uma dobradura e construiu um esquadro de papel. Observe como ele fez:
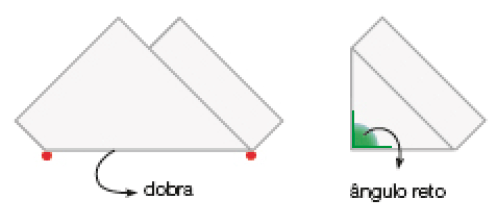

- Agora, faça um esquadro de papel como Lucas e descubra quais dos
polígonos abaixo têm pelo menos um ângulo reto. _____
PROFESSOR
Resposta: Figuras 1 e 3.
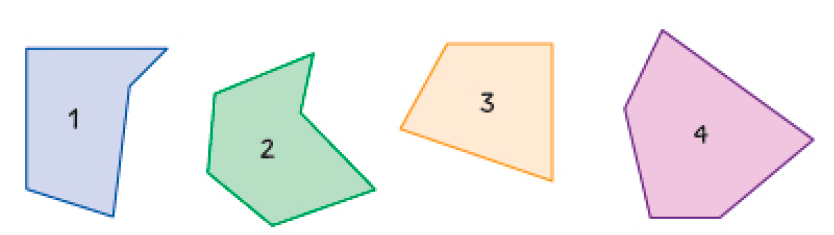
- Usando um software de geometria dinâmica, Luísa construiu um quadrado e alguns outros polígonos. Depois, sobrepondo um dos ângulos retos desse quadrado nos ângulos dos polígonos, verificou quais eram retos também.
- Construa um quadrado, com seus quatro ângulos retos, e alguns outros polígonos. Depois, tomando como exemplo um dos ângulos
retos
do seu quadrado, verifique se há algum ângulo reto nos polígonos que você desenhou.
PROFESSOR
Resposta variável.
MANUAL DO PROFESSOR
Atividade 3
Os estudantes devem comparar os ângulos com a ajuda do esquadro de papel construído. É importante perceberem que, para ter certeza de que os ângulos são retos, precisam fazer a comparação por sobreposição.
Atividade 4
Oriente os estudantes na construção dos polígonos, utilizando os comandos destacados na imagem. Para verificar quais ângulos são retos, eles devem arrastar o quadrado, sobrepondo-o aos demais polígonos, identificando, assim, os ângulos retos. Amplie a atividade pedindo a eles que identifiquem os ângulos agudos e obtusos em cada polígono.
BNCC em foco:
EF04MA18; competência geral 5; competências específicas 4 e 5
MP116
Matemática em textos
Leia
A Geometria nas obras de um artista brasileiro
O artista plástico Fortunato Ernesto Neto nasceu na cidade de Belém, capital do estado do Pará. Começou a pintar e desenhar na adolescência.
Caracterizadas por um estilo geométrico, suas obras retratam prédios, monumentos históricos, embarcações, garimpeiros, fauna, flora, ribeirinhos da região e o cotidiano em geral. Por exemplo, a tela reproduzida abaixo retrata um importante ponto turístico da cidade de Belém, o mercado Ver-o-Peso.
Nessa obra, Fortunato usou figuras geométricas, com o predomínio de triângulos.
Suas obras tiveram influência de importantes artistas como: Monet e Cézanne, no uso de cores fortes, e Pablo Picasso, no que se refere aos traços com linhas retas. No entanto, as obras de Fortunato foram desenvolvidas com identidade própria, caracterizada por uma variedade de cores fortes e contrastantes.

LEGENDA: Ver o Peso, de Fortunato Ernesto Neto, 2007, acrílica sobre tela, 80 cm × 60 cm. FIM DA LEGENDA.

LEGENDA: Mercado Ver-o-Peso, no município de Belém, Pará, em 2019. FIM DA LEGENDA.
MANUAL DO PROFESSOR
Objetivo
Relacionar a Geometria e as artes plásticas.
Apresente aos estudantes algumas informações sobre o artista Fortunato Ernesto Neto. A obra desse paraense revela a influência, entre outras, do estilo cubista de Picasso, no qual há nítida geometrização das formas e dos volumes do mundo real. Suas obras retratam o que ele observa à sua volta, o que faz parte da vida das pessoas que moram em Belém.
A Geometria é uma das ferramentas com as quais os artistas podem representar suas ideias sobre o mundo e transmiti-las para capturar o interesse do público, ainda que não use, em suas composições, figuras geométricas diretamente reconhecíveis, como triângulo, retângulo, círculo, entre outras.
Sugerimos levar um mapa para a sala de aula para que os estudantes localizem o estado do Pará e sua capital, Belém, e comparem sua localização com a do município onde estão. Leia o texto com a turma e, em seguida, pergunte aos estudantes se acharam a representação do mercado Ver-o-Peso parecida com sua aparência real. Explique a eles que nem sempre o artista tem por objetivo retratar um objeto como ele é de fato, podendo, às vezes, distorcê-lo e alterá-lo propositalmente para ressaltar características, transmitir sensações, emoções etc.
O texto “A Geometria nas obras de um artista brasileiro” menciona o nome de alguns pintores que podem não ser do conhecimento dos estudantes.
Se julgar oportuno, forneça informações sobre os artistas que influenciaram Fortunato Ernesto Neto.
Paul Cézanne (1839-1906), artista francês, inovou a pintura ao retratar o espaço com figuras planas. Sua personalidade tímida e irritadiça levou-o a isolar-se dos artistas importantes de seu tempo e a realizar obras diferentes das tendências da época.
Claude Monet (1840-1926), pintor francês, foi o mais famoso artista do Impressionismo, um movimento cuja ideia era retratar o aspecto efêmero da natureza e da vida usando técnicas de pincel que privilegiam os efeitos de luz e cor, deixando as linhas e os contornos pouco destacados.
BNCC em foco:
EF04MA18
MP117
Responda
- Onde nasceu Fortunato?
_____
PROFESSOR
Resposta: Nasceu em Belém, no Pará.
- Em que época da vida ele começou a pintar?
_____
PROFESSOR
Resposta: Começou a pintar na adolescência.
- O que Fortunato retrata em suas obras?
_____
PROFESSOR
Resposta: Prédios, monumentos históricos, embarcações, garimpeiros, fauna, flora, ribeirinhos da região e o cotidiano em geral.
- Que figura geométrica é predominante na obra Ver-o-Peso?
_____
PROFESSOR
Resposta: Triângulo.
Analise
Observe outra obra de Fortunato Ernesto Neto.

LEGENDA: Trabalhadores, de Fortunato Ernesto Neto, 2009, acrílica sobre tela, 80 cm × 60 cm. FIM DA LEGENDA.
Além dos triângulos, que outras figuras geométricas planas o artista usou nessa obra?
_____
PROFESSOR
Exemplo de resposta: Quadriláteros e pentágonos.Aplique

Agora, você é o artista. Usando figuras geométricas planas e cores fortes, faça um desenho bem bonito em seu caderno.
PROFESSOR
Resposta pessoal.MANUAL DO PROFESSOR
Pablo Picasso (1881-1973), pintor espanhol, é considerado um dos maiores gênios da pintura de todos os tempos. Sua pintura é representante do movimento cubista, em que a noção de profundidade é substituída pelo uso de figuras planas para retratar todas as partes de um objeto, ou seja, usam-se diversos planos ao mesmo tempo.
Responda Questões 1 a 4
O objetivo das questões é explorar a leitura e a interpretação das informações do texto.
Analise
Peça aos estudantes que destaquem um quadrilátero, um pentágono e um heptágono na obra do artista.
Aplique
Após os estudantes terminarem seu desenho, pode-se pedir que o mostrem a um colega para que ele identifique as formas geométricas usadas, classificando-as, no caso de polígonos, de acordo com o número de lados.
Outro aspecto que pode ser explorado é a identificação de ângulos nos desenhos. Peça aos estudantes que, se possível, identifiquem um ângulo reto, um ângulo agudo e um ângulo obtuso no desenho do colega.
Uma possibilidade interessante é pedir aos estudantes que façam seus desenhos em folhas avulsas, as quais podem ser reunidas em uma exposição na escola.
BNCC em foco:
EF04MA18; competência geral 6; competências específicas 1 e 2
MP118
Compreender informações
Agrupar dados de uma pesquisa em tabela
- Valmir realizou uma pesquisa com os clientes sobre preferência de livros. Observe as anotações que ele fez.
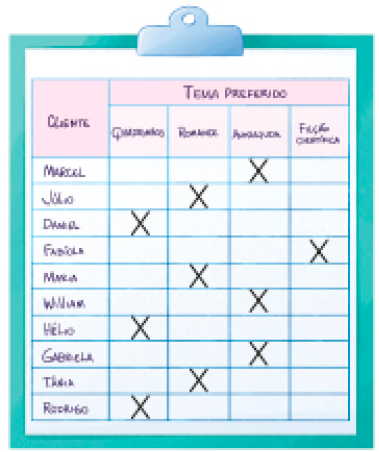
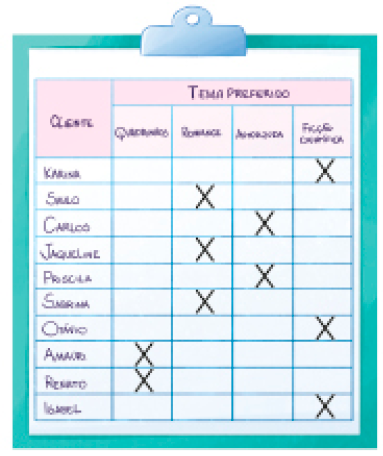
Depois de analisar os dados, Valmir contou a quantidade de pessoas que preferem cada tipo de livro e organizou as informações em uma tabela. Complete-a e depois responda às questões.
Pesquisa sobre preferência de livros
Tabela: equivalente textual a seguir.
|
Preferência |
Quantidade |
|---|---|
|
Quadrinhos |
_____ |
|
Romance |
_____ |
|
Autoajuda |
_____ |
|
Ficção científica |
_____ |
FONTE: Dados obtidos por Valmir (mar. 2023).
PROFESSOR
Resposta: Quadrinhos, 5.PROFESSOR
Romance, 6.PROFESSOR
Autoajuda, 5.PROFESSOR
Ficção científica, 4.
- Para saber quantas pessoas preferem cada tipo de livro é mais fácil consultar as anotações de Valmir ou a tabela?
- Em que outras situações você acha importante organizar os dados agrupando-os?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Objetivos
Agrupar dados em tabelas.
Realizar uma pesquisa envolvendo variáveis categóricas e numéricas.
Os estudantes já sabem que as tabelas são recursos importantes para organizar dados e resolver problemas. O objetivo destas atividades é incentivá-los a organizarem as informações apresentadas, agrupando-as para facilitar a leitura e a interpretação.
Atividade 1
O objetivo da atividade é apresentar aos estudantes dois modos de organizar os dados de uma mesma pesquisa para que eles possam, na atividade 2, organizar os dados de uma pesquisa realizada por eles.
No item b, é importante os estudantes perceberem que a necessidade de fazer agrupamentos deve-se, muitas vezes, ao fato de haver uma quantidade de dados muito grande, que dificilmente poderia ser analisada de maneira isolada.
Assim, eles podem compreender por que, nas tabelas, é interessante organizar os dados de modo que não fiquem dispersos.
BNCC em foco:
EF04MA27, EF04MA28; competência específica 4
MP119
- Agora, faça você uma pesquisa. Escolha 5 colegas de classe e 5 adultos da sua convivência. Pergunte a eles quantos livros eles já
leram
e anote o resultado nas tabelas a seguir.
PROFESSOR
Respostas pessoais.
Quantos livros meus colegas já leram
Tabela: equivalente textual a seguir.
|
Colega |
Quantidade de livros |
|---|---|
|
_____ |
_____ |
|
_____ |
_____ |
|
_____ |
_____ |
|
_____ |
_____ |
|
_____ |
_____ |
Quantos livros os adultos escolhidos já leram
Tabela: equivalente textual a seguir.
|
Pessoa escolhida |
Quantidade de livros |
|---|---|
|
_____ |
_____ |
|
_____ |
_____ |
|
_____ |
_____ |
|
_____ |
_____ |
|
_____ |
_____ |
Depois, organize as informações preenchidas nas tabelas acima em um gráfico de colunas, completando o esquema a seguir:
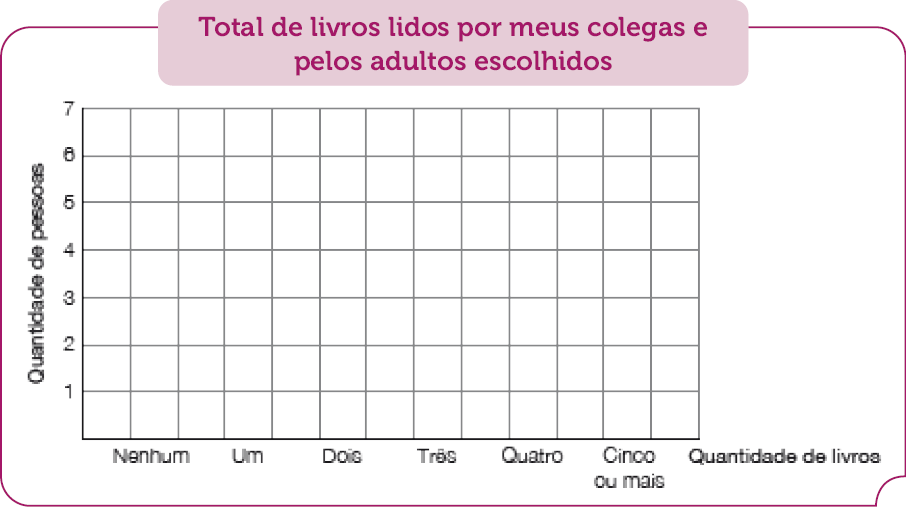
Fonte: _____
- Quantas pessoas pesquisadas leram três livros?
- Que colega ou adulto leu a maior quantidade de livros?
- Como você fez para responder a cada uma das perguntas anteriores?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que, dependendo da pergunta, as informações deverão ser obtidas em um dos meios de organização dos dados. Fim da observação.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, os estudantes deverão realizar uma pesquisa com cinco colegas e cinco adultos de seu convívio perguntando a quantidade de livros que eles já leram. Oriente-os a organizar as informações nas tabelas e depois no gráfico, considerando que cada quadrinho no gráfico corresponde a uma pessoa.
Após a organização dos dados, os estudantes responderão às perguntas. Eles devem perceber que a resposta do item a será obtida facilmente no gráfico e que a do item b só pode ser obtida por meio de uma das tabelas.
Antes de os estudantes realizarem a pesquisa, oriente-os a fazerem a abordagem de maneira educada, solicitando ao colega ou adulto escolhido que colabore com ele respondendo a uma pergunta de uma pesquisa. Oriente-os a reproduzirem as duas tabelas e tê-las em mãos para fazer as anotações necessárias ou, se preferirem, podem anotar as informações obtidas em um papel para, depois, passá-las para a respectiva tabela. Lembre-os de que as tabelas devem ter título, fonte e data das informações (no caso, pesquisa com cinco colegas da sala ou com adultos, escolhidos em dia, mês e ano tal).
Peça a um voluntário que inicie a abordagem a cinco colegas, represente os dados na tabela e, depois, preencha o esquema com quadrinhos coloridos para representar a quantidade de pessoas e de livros que leu. Como o esquema, depois de preenchido, transforma-se em um gráfico, lembre-os de que o gráfico também deve ter título, fonte com data e legenda com as cores dos quadrinhos.
BNCC em foco:
EF04MA27, EF04MA28
MP120
O que você aprendeu
- Observe as figuras e complete o quadro.

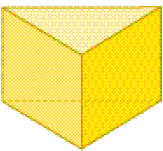
Tabela: equivalente textual a seguir.
|
Figura geométrica não plana |
Número de bases |
Número de faces laterais |
|---|---|---|
|
Pirâmide |
_____ |
_____ |
|
Prisma |
_____ |
_____ |
PROFESSOR
Resposta: Pirâmide: 1, 6.PROFESSOR
Prisma: 2, 3- Quais figuras geométricas planas podemos identificar nas faces laterais e nas bases do prisma? E na pirâmide?
_____
PROFESSOR
Resposta: Prisma: triângulo e retângulo; pirâmide: hexágono e triângulo.
- A representação de uma mesma figura em diferentes posições está escondida nos três desenhos a seguir.
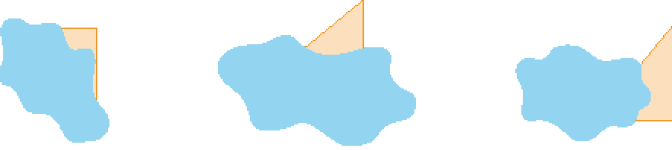
- Qual destas representações é a figura escondida?
_____
PROFESSOR
Resposta: C

- Responda às questões.
- Carlos deu um giro de uma volta em torno de si mesmo. Em que posição ele parou?
_____
PROFESSOR
Resposta: Ele parou na posição em que estava inicialmente.
- Amanda caminhava em linha reta por uma rua. Ao perceber que a rua não tinha saída, ela deu um giro de meia-volta e voltou no sentido contrário. Esse giro corresponde a quantos giros da quarta parte de uma volta?
_____
PROFESSOR
Resposta: Corresponde a dois giros de um quarto de volta.
- Viviane estava no pátio de sua escola quando deu um giro da quarta parte de uma volta e avistou sua amiga bem de frente para ela. Onde estava a amiga de Viviane?
_____
PROFESSOR
Resposta: Do lado direito ou do lado esquerdo de Viviane.
- Carlos deu um giro de uma volta em torno de si mesmo. Em que posição ele parou?
_____
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Os estudantes devem classificar as figuras como prisma ou pirâmide e determinar a quantidade de bases e faces laterais que cada uma possui.
Atividade 2
Explore esta atividade perguntando aos estudantes: “Caso tivéssemos apenas os dois primeiros desenhos, seria possível saber qual era a figura escondida? E se tivéssemos apenas os dois últimos desenhos? E se tivéssemos apenas o primeiro e o terceiro desenhos?”.
Atividade 3
Para resolver a questão, peça aos estudantes que realizem os giros descritos por Carlos, Amanda e Viviane.
Sugestão de atividade
Desenhando bandeiras
Os conteúdos desta Unidade poderão ser explorados em conjunto com a disciplina Geografia. Os estudantes podem ser divididos em grupos, e cada grupo representará um continente diferente. A partir dessa separação, proponha a eles que pesquisem cinco bandeiras dos países do continente selecionado e tragam-nas desenhadas em uma folha de papel sulfite. Entre as bandeiras que os estudantes trouxerem, selecione as que possuem imagens que tenham figuras geométricas planas, como triângulo, círculo, retângulo, quadrado, pentágono, hexágono etc. Os grupos poderão trocar as imagens entre si para que todos as identifiquem. Se for possível, escolha alguns dos países cuja bandeira tenha sido apresentada, localize-os no mapa e conte para a turma algumas curiosidades sobre essas nações.
BNCC em foco:
EF04MA17, EF04MA18; competência específica 6
MP121
- O ponteiro da balança serve para indicar a medida da massa de um objeto colocado sobre o prato.

- Quando um objeto de 25 quilogramas é colocado sobre o prato, o ponteiro forma com a linha imaginária que indica zero quilograma um ângulo reto, um ângulo agudo ou um ângulo obtuso?
_____
PROFESSOR
Resposta: Um ângulo reto.
- E se o objeto tiver 10 quilogramas? E se tiver 28 quilogramas?
_____
PROFESSOR
Resposta: Um ângulo agudo; um ângulo obtuso.
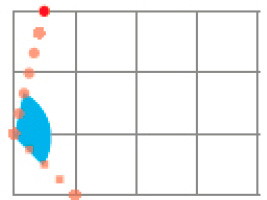
- Observe que em cada caso a trajetória da bolinha vermelha forma um ângulo. Classifique cada ângulo como: reto, agudo ou obtuso.
_____
PROFESSOR
Resposta: Obtuso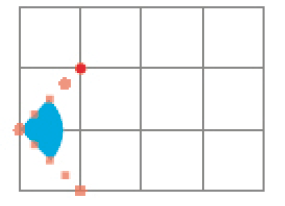
_____
PROFESSOR
Resposta: Reto.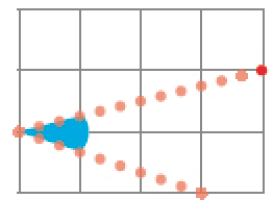
_____
PROFESSOR
Resposta: Agudo.Autoavaliação

- Consigo nomear e comparar figuras geométricas planas e não planas por meio de suas características?

- Compreendo a
ideia
de ângulo e reconheço-o em representações de figuras geométricas planas?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 4
Contextualize a atividade também com os ângulos formados pelos ponteiros de um relógio. Pergunte: “Qual é o menor ângulo formado pelos ponteiros de um relógio quando ele marca 3 horas?” (Ângulo reto, nesse caso). Os estudantes podem verificar que, antes das 3 horas, os ponteiros formam ângulos agudos; depois das 3 horas, formam ângulos obtusos.
Atividade 5
Para afirmar que o ângulo representado no item b é reto, sugira aos estudantes que comparem sua abertura com a de um dos cantos de uma folha de papel retangular.
Autoavaliação
Na primeira questão, os estudantes deverão avaliar o quanto reconhecem as características comuns e diferentes entre as figuras planas e não planas para que possam classificá-las.
Na segunda questão, poderão avaliar se o conceito de ângulo foi compreendido para além da ideia de giro, na identificação de ângulos dos polígonos e assim tornando-se mais uma característica para a classificação de figuras.
BNCC em foco:
EF04MA17, EF04MA18; competência específica 6
MP122
Comentários para o professor:
Conclusão da Unidade 3
Conceitos e habilidades desenvolvidos nesta unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Reconhece figuras geométricas planas e figuras geométricas não planas por meio de suas características? |
_____ |
_____ |
|
Identifica planificações da superfície de figuras geométricas não planas? |
_____ |
_____ |
|
Nomeia e identifica elementos de figuras geométricas não planas (vértices, faces e arestas) e de figuras planas poligonais (lados, ângulos e vértices)? |
_____ |
_____ |
|
Representa figuras geométricas planas e figuras geométricas não planas em malhas quadriculadas? |
_____ |
_____ |
|
Identifica ângulos de giros de uma volta, de meia-volta e de um quarto de volta? |
_____ |
_____ |
|
Reconhece ângulos agudo, reto e obtuso em figuras poligonais e em objetos do mundo físico? |
_____ |
_____ |
|
Realiza pesquisa envolvendo variáveis numéricas e organiza dados coletados por meio de tabelas e gráficos de colunas em diferentes áreas do conhecimento? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |