MP123

Introdução da Unidade 4

Esta Unidade tem como foco tratar os conhecimentos a serem desenvolvidos na Unidade Temática Números. Assim, a abertura traz, em página dupla, uma imagem próxima do cotidiano da criança na faixa etária do estudante do 4º ano do Ensino Fundamental com informações a serem exploradas nas questões propostas na seção Para refletir ... .

Com base nos objetos de conhecimento vistos na Unidade 2, esta Unidade propõe situações-problema que exploram ideias da multiplicação e da divisão, consolidando o trabalho da Unidade Temática Números.

Além de retomar as relações entre multiplicação e divisão e as propriedades das operações para ampliar e desenvolver estratégias de cálculo, agora, propõe-se aos estudantes resolver e elaborar problemas de multiplicação envolvendo diferentes significados da multiplicação (adição de parcelas iguais, organização retangular e proporcionalidade) e problemas de divisão cujo divisor tenha no máximo dois algarismos, envolvendo os significados de repartição equitativa e de medida, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

Pretende-se com essa abordagem preparar os estudantes para os conhecimentos a serem desenvolvidos no 5º ano, que abrangem a resolução e a elaboração de problemas envolvendo a multiplicação e a divisão em um campo numérico mais amplo (números racionais com representação decimal finita).

A Unidade Temática Álgebra contempla atividades que trabalham a identificação e a descrição de regularidades em sequências numéricas recursivas (sequência dos múltiplos), visando desenvolver a habilidade de identificar regularidades em sequências numéricas compostas por múltiplos de um número natural e, também, identificações de regularidades de grupos de números naturais para os quais as divisões por determinado número resultam em restos iguais. As relações entre as operações de multiplicação e divisão também serão utilizadas em problemas cuja estratégia de resolução é a investigação utilizando a calculadora quando necessário.

As atividades propostas no 4º ano serão fundamentais para o desenvolvimento de habilidades dos Objetos de conhecimento do 5º ano (Propriedade da igualdade e noção de equivalência, Grandezas diretamente proporcionais e Problemas envolvendo a partição de um todo em duas partes proporcionais).

Dentro da Unidade Temática Probabilidade e estatística, algumas atividades desta Unidade, em conjunto com as atividades da Unidade 2, contribuem para o desenvolvimento da habilidade de identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem o emprego de frações.

Competência geral favorecida

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

Competência específica favorecida

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

MP124

UNIDADE 4. Multiplicação e divisão

Imagem: Ilustração. À esquerda, uma mulher com avental está atrás de uma barraca com vasos azuis em cima. Ao seu lado há mais cinco vasos azuis no chão e uma senhora está com o dedo indicador levantado. Na frente delas há seis vasos grandes e amarelos e em cada um há doze rosas vermelhas. Ao lado há um homem e duas crianças. Ao fundo, uma mulher observa plantas em uma barraca. À direita, uma mulher olha para um menino, que segura um vaso com uma flor amarela e sorri. Ao lado, uma mulher cadeirante os observa. Atrás deles há vasos pequenos e amarelos com orquídeas rosa espalhados em caixas e prateleiras. Em seguida há onze vasos amarelos com orquídeas rosa em uma barraca coberta. Ao lado, um homem e uma menina estão com aventais e sorri. Ao fundo, plantas, árvores e morros. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos da Unidade

Compreender situações que envolvem a multiplicação.

Identificar as propriedades da multiplicação.

Desenvolver estratégias de cálculo.

Efetuar uma multiplicação com o algoritmo usual.

Compreender situações que envolvem a divisão.

Identificar divisão exata e divisão não exata.

Calcular o resultado de uma divisão por meio de estimativas e pelo algoritmo usual.

Explorar e compreender ideias relacionadas à divisão.

Relacionar multiplicação e divisão.

Identificar as possibilidades de ocorrência de um evento.

Nesta Unidade, são explorados os conceitos de multiplicação e divisão. São apresentadas diversas situações que exploram as ideias da multiplicação (proporcionalidade, adição de parcelas iguais, combinatória e organização retangular) e da divisão (repartir em partes iguais ou distribuir e quantas vezes cabe).

Nos tópicos aqui desenvolvidos, os estudantes têm oportunidade de: compreender a relação entre a divisão e a multiplicação; explorar situações que envolvem cálculo mental e as divisões exatas e não exatas; realizar divisões por estimativa e pelo algoritmo usual; atribuir significação ao algoritmo usual da divisão por meio dos conhecimentos sobre o funcionamento do nosso sistema de numeração.

BNCC em foco:

EF04MA03, EF04MA04, EF04MA05, EF04MA06, EF04MA07, EF04MA11, EF04MA12, EF04MA13, EF04MA26

MP125

Boxe complementar

Para refletir...

Conte quantas rosas há em cada vaso amarelo.

_____

PROFESSOR Resposta: Em cada vaso amarelo há 12 rosas.

Quantas rosas há nos seis vasos amarelos?

_____

PROFESSOR Resposta: No total há 72 rosas (6 × 12 ou 12 + 12 + 12 + 12 + 12 + 12).

Se eu comprar todos os vasos de orquídeas que estão na parte coberta da barraca e distribuir, igualmente, entre minhas 5 tias, quantos vasos cada tia receberá? Sobrará algum vaso?

_____

PROFESSOR Resposta: Há 11 vasos de orquídeas na barraca. Dividindo por 5, temos 2 e resto 1.
Cada tia receberá 2 vasos e sobrará 1 vaso.

Fim do complemento

MANUAL DO PROFESSOR

Para refletir...

Espera-se que os estudantes utilizem o pensamento multiplicativo e calculem, mentalmente, a quantidade de rosas (12, 24, 36, 48, 60, 72).

A questão explora a divisão não exata. Pergunte aos estudantes o que eles entendem quando sobra um resto na divisão. Os conhecimentos prévios deles sobre essa questão serão importantes no estudo desta Unidade.

MP126

Situações de multiplicação

Imagem: Ícone: mental. Fim da imagem.
  1. Cinco amigos foram a uma lanchonete. Cada um pediu um suco no valor de 3 reais e um sanduíche no valor de 5 reais.
    1. Quantos reais eles gastaram juntos com os sucos? _____
      PROFESSOR Resposta: 15 reais.
    1. E quanto eles gastaram juntos com os sanduíches? _____
      PROFESSOR Resposta: 25 reais.
  1. Observe a imagem do tabuleiro de damas abaixo.
Imagem: Ilustração. Um tabuleiro de damas com trinta e duas casas pretas e trinta e duas casa brancas. Fim da imagem.
  1. Quantas casas há ao todo nesse tabuleiro?

    _____

    PROFESSOR Resposta: 64 casas.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Como você fez para determinar o total de casas desse tabuleiro?
    PROFESSOR Resposta pessoal.

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Patrícia ganhou de presente uma boneca que vem acompanhada de 3 vestidos e 2 pares de sapatos. Pinte as possíveis combinações de 1 vestido e 1 par de sapatos com que Patrícia pode vestir a boneca.
PROFESSOR Resposta: rs: rosa
PROFESSOR vd: verde
PROFESSOR am: amarelo
PROFESSOR az: azul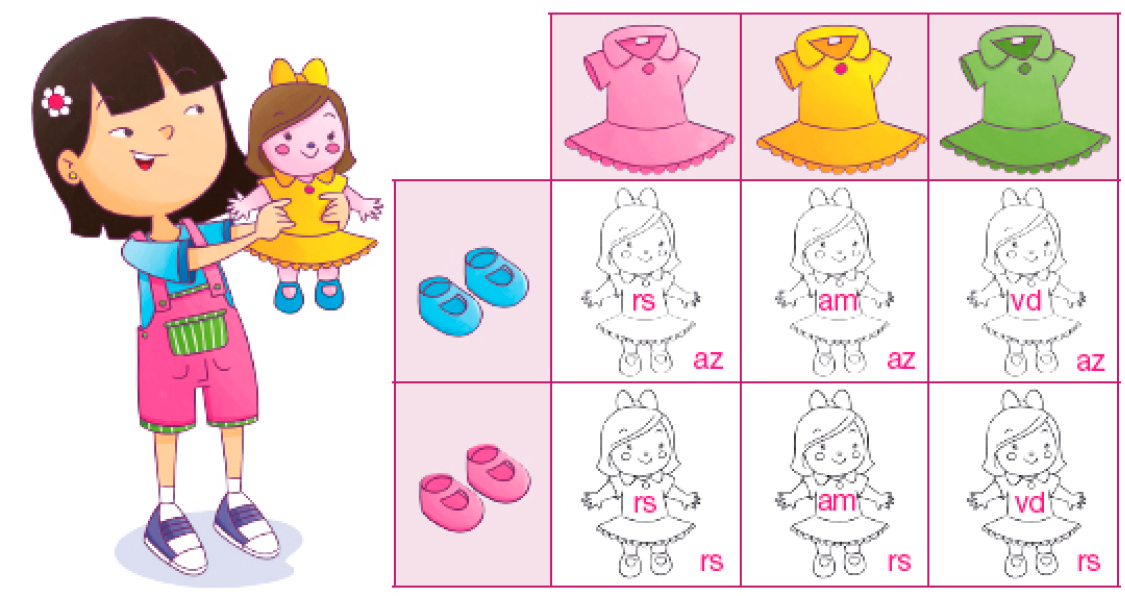
Imagem: Ilustração. Patrícia, menina com cabelo preto e curto sorri e segura uma boneca. À frente dela, tabela com ilustrações. Na parte superior: vestido rosa, vestido amarelo e vestido verde. Na lateral esquerda, sapatos azuis e sapatos rosa. Boneca em preto e branco. Resposta: Vestido rosa e sapatos azuis. Boneca em preto e branco. Resposta: Vestido amarelo e sapatos azuis. Boneca em preto e branco. Resposta: Vestido verde e sapatos azuis. Boneca em preto e branco. Resposta: Vestido rosa e sapatos rosa. Boneca em preto e branco. Resposta: Vestido amarelo e sapatos rosa. Boneca em preto e branco. Resposta: Vestido verde e sapatos rosa. Fim da imagem.
  1. De quantas formas é possível vestir a boneca de Patrícia? _____
    PROFESSOR Resposta: 6 formas.
  1. Que multiplicação está associada ao número de possibilidades para vestir a boneca de Patrícia com 1 vestido e 1 par de sapatos?

    Multiplicação: _____ × _____ = _____

    PROFESSOR Resposta: 3 × 2 = 6 ou 2 × 3 = 6
MANUAL DO PROFESSOR

Objetivos

Compreender situações que envolvem a multiplicação.

Efetuar multiplicações com dois fatores.

Observar a propriedade comutativa da multiplicação.

Atividade 1

A situação desta atividade permite aos estudantes fazerem a representação por meio de uma adição de parcelas iguais, que pode ser complementada com a observação da proporcionalidade existente (item a): se cada copo de suco custa 3 reais, cinco copos custarão 5 vezes 3 reais, ou seja, 15 reais. No item b, a adição de 5 parcelas iguais de 5 reais pode ser pensada na multiplicação 5 vezes 5 reais, ou seja, 25 reais.

Atividade 2

Aproveite esse momento e socialize com os estudantes os diferentes modos de obter essa quantidade, por meio de contagem, adição ou multiplicação (organização retangular).

Atividade 3

Para determinar quantas são as combinações possíveis, os estudantes devem usar o raciocínio multiplicativo, combinando três tipos de vestidos com dois tipos de sapatos, o que resulta em 6 maneiras possíveis

(3 × 2 = 6 ou 2 × 3 = 6).

BNCC em foco:

EF04MA06

MP127

  1. Observe a ilustração e responda às questões.

    Imagem: Ilustração. Três tortas e ao lado, placa com a informação: 3 TORTAS POR 10 REAIS. Fim da imagem.

    1. No sábado, Juliana vendeu 6 tortas como as representadas acima. Quantos reais ela recebeu?

      _____

      PROFESSOR Resposta: 20 reais.
    1. Ontem, Juliana vendeu 9 dessas tortas. Quantos reais ela recebeu? _____
      PROFESSOR Resposta: 30 reais.
    1. Se as tortas fossem vendidas por unidade, por qual valor Juliana poderia vender cada unidade? _____
      PROFESSOR Exemplo de resposta: 4 reais.
    1. Quanto Juliana teria arrecadado em cada dia, se ela tivesse vendido as tortas por unidade? Faça os cálculos de acordo com o valor atribuído por você.
      PROFESSOR Exemplo de resposta: Sábado: 24 reais (6 × 4); ontem: 36 reais (9 × 4).

Imagem: Ícone: mental. Fim da imagem.

  1. Leia o que Renata está dizendo e complete o quadro a seguir com as quantidades correspondentes.
Imagem: Ilustração. Renata, mulher com touca, luvas e avental está segurando uma escumadeira com pastel dentro de uma panela com óleo. Ela fala: 1 quilograma de massa rende 30 pastéis. Fim da imagem.

Quadro: equivalente textual a seguir.

Quantidade de quilogramas de massa

Quantidade de pastéis

1

30

2

_____

3

_____

4

_____

PROFESSOR Resposta: 60, 90, 120
Imagem: Ilustração. Cartela com a informação: COMPLETE E GANHE. Ao lado há quatro colunas e quatro fileiras de espaços para colar os selos. Fim da imagem.
  1. Para ganhar um brinde, Diana precisa completar a cartela de selos acima. Na cartela não há nenhum selo ainda. Quantos selos Diana precisa para completá-la?

Escreva a multiplicação cujo resultado seja o total de selos necessários para completar a cartela.

_____

PROFESSOR Resposta: 4 × 4 = 16; 16 selos.
MANUAL DO PROFESSOR

Atividade 4

Espera-se que, nesta atividade, os estudantes percebam que podem fazer agrupamentos a cada grupo de três tortas.

Como cada agrupamento custa 10 reais, para calcular o preço de seis tortas eles podem pensar que seis tortas correspondem a dois grupos de três tortas: 2 × 10 = 20, ou seja, 20 reais. Da mesma maneira, nove tortas correspondem a três agrupamentos: 3 × 10 reais = 30 reais.

Observe se os estudantes atribuem um preço compatível com o de uma unidade.

Atividade 5

Os estudantes podem usar diferentes estratégias para resolver esta atividade, como as dos exemplos a seguir.

Contar de 10 em 10, registrando os valores obtidos a cada 30 unidades: 40, 50, 60, 70, 80, 90, 100, 110, 120.

Adicionar 30 unidades a cada quantidade de pastéis de cada linha do quadro: 30 + 30 = 60; 60 + 30 = 90; 90 + 30 = 120.

A representação por meio de uma adição de parcelas iguais pode ser complementada com a observação da proporcionalidade existente: se cada quilograma de massa faz 30 pastéis, 2 quilogramas fazem 60 pastéis, 3 fazem 90.

Atividade 6

Esta atividade requer dos estudantes a resolução do problema por meio de uma multiplicação. Depois de realizada a atividade, peça aos estudantes que expliquem como pensaram para obter a multiplicação sugerida pela ilustração da cartela com 4 linhas e 4 colunas.

BNCC em foco:

EF04MA06

MP128

Imagem: Ícone: mental. Fim da imagem.

  1. No armário de materiais da escola, havia 1 pacote de cada objeto ilustrado abaixo. Cada pacote continha 6 unidades do objeto. Quantos objetos havia ao todo nesse armário?

    _____

    PROFESSOR Resposta: 24 objetos.
Imagem: Ilustração. Um lápis vermelho, uma caneta azul, uma borracha vermelha e um apontador verde. Fim da imagem.
  1. Diego foi a uma lanchonete que oferece diversas opções de vitaminas e lanches. Observe o cardápio e descubra quantas possibilidades Diego tem para escolher um tipo de vitamina e um tipo de lanche.
    PROFESSOR Resposta: 12 possibilidades.
Imagem: Ilustração. Cardápio aberto. À esquerda, as informações: VITAMINAS: - Simples: 3 reais; - Especial: 5 reais; - Mista: 4 reais; - Da casa: 3 reais. Ao redor, imagens de um abacaxi, um copo com suco e laranjas. À direita, as informações: LANCHES: - Misto: 3 reais; - Hambúrguer: 4 reais; - Natural: 5 reais. Ao redor, imagens de dois lanches e um hambúrguer. Fim da imagem.
  1. Para fazer 40 brigadeiros, Romildo usou 1 lata de leite condensado, 2 colheres (de sopa) de margarina e 3 colheres (de sopa) de chocolate em pó.
    1. Qual seria a quantidade usada de cada ingrediente para fazer 80 brigadeiros?

      _____

      PROFESSOR Resposta: 2 latas de leite condensado, 4 colheres (de sopa) de margarina e 6 colheres (de sopa) de chocolate em pó.

      Imagem: Ícone: Oral. Fim da imagem.

    1. Como você determinou a quantidade de cada ingrediente para fazer os 80 brigadeiros?
      PROFESSOR Resposta possível: Como 80 é o dobro de 40, é necessário dobrar a quantidade de cada ingrediente.
MANUAL DO PROFESSOR

Atividade 7

Nesta atividade, espera-se que os estudantes percebam a existência de 4 grupos de objetos, cada grupo com 6 unidades. Os estudantes podem resolver a situação com a adição de parcelas iguais, mas espera-se que eles calculem o total de objetos com a multiplicação: 6 × 4, totalizando assim 24 objetos.

Atividade 8

Nesta situação, em que aparece a ideia de combinação de possibilidades, eles podem fazer desenhos das possíveis combinações de cada tipo de vitamina com cada tipo de lanche, percebendo que é possível fazer 12 combinações.

Atividade 9

Nesta atividade, espera-se que os estudantes percebam a necessidade de manter a proporção da quantidade de todos os ingredientes da receita do brigadeiro. Registre na lousa a quantidade de cada um dos ingredientes que Romildo usou para fazer os 40 brigadeiros.

Os estudantes devem perceber que para fazer o dobro de brigadeiros será necessário dobrar a quantidade dos ingredientes, mantendo a proporção de todos os ingredientes para qualquer quantidade proposta.

BNCC em foco:

EF04MA06

Sugestão de atividade

Receita

Pode-se propor aos estudantes que preparem em conjunto uma receita (vitamina, salada de frutas, lanche natural etc.). Antes da atividade, é importante verificar se há algum estudante com algum tipo de restrição alimentar. Se necessário, faça adaptações à receita para que todos possam participar.

Pode-se trabalhar com essa atividade conceitos de outros componentes, como tipos de alimentos utilizados na receita (Ciências), origem/produção dos alimentos (Geografia) e o gênero de um texto de receita (Língua Portuguesa).

Apresente aos estudantes a receita escolhida. Analisem, em conjunto, as medidas e quantidades da receita, explorando os conceitos de Grandezas e medidas. Depois, proponha o cálculo das quantidades de ingredientes, mantendo a proporcionalidade da receita, para que o preparo seja suficiente para todos os estudantes da classe. Neste momento, trabalhe com quantidades inteiras de receitas (1 receita, 2 receitas, 3 receitas etc.).

MP129

Propriedades da multiplicação

Imagem: Ícone: Calculadora. Fim da imagem.
  1. Faça as multiplicações usando uma calculadora.
    1. 15 × 17 = _____
      PROFESSOR Resposta: 255
    1. 17 × 15 = _____
      PROFESSOR Resposta: 255
    1. 13 × 21 = _____
      PROFESSOR Resposta: 273
    1. 21 × 13 = _____
      PROFESSOR Resposta: 273
    1. 11 × 102 = _____
      PROFESSOR Resposta: 1.122
    1. ) 102 × 11 = _____
      PROFESSOR Resposta: 1.122
      • Você precisou fazer todas as multiplicações para descobrir o resultado? Justifique.

        _____

        PROFESSOR Atenção professor: Espera-se que os estudantes afirmem que não, pois, alterando a ordem dos fatores, o produto não muda. Fim da observação.
  1. Adriana quer saber quantos bombons há na caixa abaixo. Veja duas formas diferentes de calcular a quantidade de bombons que há na caixa.
Imagem: Ilustração. Vista de cima de uma caixa com quatro colunas e três linhas de bombons. Na primeira linha há quatro bombons vermelhos, na segunda, quatro verdes e na terceira, quatro amarelos. Fim da imagem.

Há 4 colunas com 3 bombons em cada uma.

Multiplicação: 4 × 3 = _____

PROFESSOR Resposta: 12

Fatores: 4 × 3; Produto: _____.

Há 3 linhas com 4 bombons em cada uma.

Multiplicação: 3 × 4 = _____

PROFESSOR Resposta: 12

Fatores: 3 × 4; Produto: _____

4 × 3 = 3 × 4

Na caixa, há _____ bombons.

PROFESSOR Resposta: 12
Imagem: Ilustração. Adriana, mulher com cabelo preso fala: Quando alteramos a ordem dos fatores em uma multiplicação, o produto não muda. Essa é a propriedade comutativa da multiplicação. Fim da imagem.
  1. Observe o que Leila está dizendo.

Imagem: Ícone: mental. Fim da imagem.

  1. Em que número Leila pensou?

    _____

    PROFESSOR Resposta: 30

    Imagem: Ícone: Oral. Fim da imagem.

  1. Explique como você descobriu esse resultado.
    PROFESSOR Resposta pessoal.
Imagem: Ilustração. Leila, mulher ruiva diz: Pensei em um número que é o resultado da multiplicação de 5 pelo dobro de 3. Fim da imagem.
MANUAL DO PROFESSOR

Para o preparo, converse com os estudantes sobre a importância da higiene na preparação dos alimentos e os cuidados necessários em uma cozinha (utensílios cortantes ou pontiagudos, utilização de equipamentos elétricos etc.). Lembre-se de que mesmo escolhendo uma receita que não necessita de aquecimento, a cozinha é um ambiente diferente da sala de aula, e precisa ter a supervisão de um adulto.

BNCC em foco:

EF04MA05

Objetivos

Representar e calcular o resultado de uma multiplicação com três fatores.

Observar as propriedades comutativa e associativa da multiplicação.

Observar que 1 é o elemento neutro da multiplicação.

Observar que zero é o elemento nulo da multiplicação.

Atividade 1

Espera-se que os estudantes percebam, intuitivamente, que invertendo a ordem dos fatores o produto não se altera.

Atividade 2

Na situação apresentada, os estudantes podem observar a propriedade comutativa da operação, percebendo que 4 × 3 e 3 × 4, embora tenham o mesmo produto e os mesmos fatores, traduzem ideias diferentes: a primeira multiplicação corresponde à adição de 4 parcelas iguais a 3; a segunda, à adição de 3 parcelas iguais a 4.

Pergunte aos estudantes: “O total de bombons da caixa corresponde a um fator ou ao produto? E o total de bombons de cada fileira?”. Espera-se que respondam produto e a um dos fatores, respectivamente.

O uso de uma linguagem convencional permite expressar, de modo simples e sem ambiguidades, ideias como a propriedade comutativa da multiplicação: “A ordem dos fatores não altera o produto”.

Atividade 3

Os estudantes devem perceber que, para resolver o enigma, é necessário determinar o dobro de 3 para, então, efetuar a multiplicação: 5 × 6 = 30.

MP130

  1. Complete o quadro abaixo com os resultados das multiplicações. Os números que estão dentro dos parênteses devem ser multiplicados primeiro. Na última linha, escolha três outros números.

Quadro: equivalente textual a seguir.

(2 × 3) × 4 = _____

2 × (3 × 4) = _____

(4 × 5) × 2 = _____

4 × (5 × 2) = _____

(5 × 2) × 3 = _____

5 × (2 × 3) = _____

(2 × 6) × 3 = _____

2 × (6 × 3) = _____

(_____ × _____) × _____ = _____

(_____ × _____) × _____ = _____

PROFESSOR Resposta: 24, 24, 40, 40, 30, 30, 36, 36
Imagem: Ilustração. Embalagem com doze garrafas de água, divididas em quatro colunas e três linhas. Fim da imagem.
  1. Catarina comprou duas embalagens de garrafas de água, como a da imagem acima. Ao todo, quantas garrafas ela comprou? Se em uma embalagem há 3 × 4 garrafas, então em duas embalagens há 2 × 3 × 4 garrafas. Essa multiplicação pode ser resolvida de, pelo menos, duas formas:
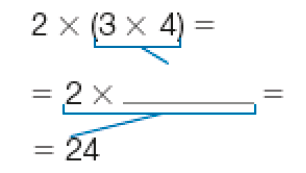
Imagem: Esquema. 2 x (3 x 4) =. = 2 x espaço apra resposta = 24 Fim da imagem.
PROFESSOR Resposta: 12

ou

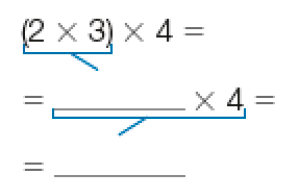
Imagem: Esquema. (2 x 3) x 4 =. = espaço apra resposta x 4. = espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 6, 24

2 × (3 × 4) = (2 × 3) × 4

Catarina comprou _____ garrafas.

PROFESSOR Resposta: 24
Imagem: Ilustração. Uma mulher com cabelo curto sorri com as mãos na cintura e fala: Quando associamos os fatores de uma multiplicação de modos diferentes, o resultado não muda. Chamamos esse fato de propriedade associativa da multiplicação. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

  1. Observe a ilustração abaixo e responda às questões.
Imagem: Ilustração. Uma caixa aberta e dentro há latas divididas em quatro colunas e seis linhas. Fim da imagem.
  1. Que multiplicação representa o número de latas nessa caixa?

    _____

    PROFESSOR Resposta: 4 × 6 = 24 ou 6 × 4 = 24
  1. Quantas latas cabem em 2 caixas iguais a essa? _____
    PROFESSOR Resposta: 48 latas.
  1. E em 4 caixas iguais a essa? _____
    PROFESSOR Resposta: 96 latas.
MANUAL DO PROFESSOR

Atividade 4

Esta atividade possibilita aos estudantes observarem que, ao associarem os fatores de uma multiplicação de maneiras diferentes, o resultado não muda.

Atividade 5

Na situação apresentada, os estudantes podem visualizar pelo menos duas formas de resolver a multiplicação. Antes de explorar a forma de resolvê-la, é importante que os estudantes percebam que a escrita matemática que caracteriza a situação é 2 × (3 × 4), pois são duas embalagens de quantidade 3 × 4. Entretanto, apesar de existir uma escrita matemática que melhor represente a situação, no caso da multiplicação a ordem de multiplicá-las não alterará o produto; assim, os estudantes podem escolher a estratégia que mais se aproxime de seu repertório com o intuito de encontrar resultados com mais rapidez.

Atividade 6

Peça aos estudantes que representem a quantidade de latas dos itens b e c por meio de uma multiplicação.

No item b: 2 × (4 × 6) = 48 ou 2 × (6 × 4) = 48

No item c: 4 × (4 × 6) = 96 ou 4 × (6 × 4) = 96

BNCC em foco:

EF04MA05

Sugestão de atividade

Proponha as situações a seguir para que os estudantes percebam os diferentes significados do cálculo ao fazerem diferentes associações dos fatores.

a) Em um bloco de apartamentos há 3 prédios. Cada prédio tem 10 apartamentos. Cada apartamento tem 5 janelas. Quantas janelas há em todos os prédios desse bloco? (3 × 10) × 5 ou 3 × (10 × 5)

b) Um pomar produz 5 caixas de morangos por semana. Em cada caixa, colocam-se 300 gramas de morangos. Considerando que um mês tem 4 semanas, quantos gramas de morangos esse pomar produz por mês? (5 × 300) × 4 ou (4 × 5) × 300 = 6.000. 6.000 gramas ou 6 quilogramas.

MP131

Imagem: Ícone: mental. Fim da imagem.

  1. Calcule mentalmente o resultado em cada caso.
    1. 1.050 × 0 = _____
      PROFESSOR Resposta: 0
    1. 1.050 × 1 = _____
      PROFESSOR Resposta: 1 050
    1. 654 × 0 = _____
      PROFESSOR Resposta: 0
    1. 654 × 1 = _____
      PROFESSOR Resposta: 654
    1. 365 × 0 = _____
      PROFESSOR Resposta: 0
    1. ) 365 × 1 = _____
      PROFESSOR Resposta: 365

      Imagem: Ícone: Oral. Fim da imagem.

      • O que acontece com o resultado quando multiplicamos um número qualquer por 1? E quando multiplicamos por zero? Converse com o professor e seus colegas.
        PROFESSOR Atenção professor: Espera-se que os estudantes percebam que, quando multiplicamos qualquer número por 1, o resultado será o próprio número, e que, quando multiplicamos por zero, o resultado será zero. Fim da observação.
  1. Amanda está construindo um jogo de tabuleiro. Em algumas casas desse jogo, o jogador deverá multiplicar os pontos obtidos por determinado número.

    Se um jogador tiver, por exemplo, 2 pontos e cair em uma casa com o comando “multiplicar por 2”, seus pontos passarão a ser iguais a 4, pois 2 × 2 = 4.

    1. Amanda quer que em uma dessas casas os pontos obtidos sejam transformados em zero. Qual deverá ser o comando para isso acontecer?

      _____

      PROFESSOR Resposta: Multiplicar por zero.
    1. E para que os pontos permaneçam o mesmo, qual deverá ser o comando?

      _____

      PROFESSOR Resposta: Multiplicar por 1.
Imagem: Ilustração. Um homem com cabelo encaracolado e óculos fala: Quando calculamos um número vezes 1 ou fazemos 1 vezes o número, o resultado é o próprio número. Dizemos que 1 é o elemento neutro da multiplicação. Quando multiplicamos qualquer número por zero, o resultado é sempre zero. Dizemos que zero é o elemento nulo da multiplicação. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 7

Ao efetuarem as multiplicações por 1 e por zero, os estudantes poderão perceber a regularidade que determina, respectivamente, o elemento neutro e o elemento nulo da multiplicação.

Atividade 8

Esta atividade permite observar se os estudantes se apropriaram, ainda que intuitivamente, de que, na multiplicação, o 1 é o elemento neutro, e o zero, o elemento nulo.

BNCC em foco:

EF04MA05

MP132

Estratégias de cálculo

Vezes 10, vezes 100 e vezes 1.000

Imagem: Ícone: Calculadora. Fim da imagem.
  1. Complete o quadro com os valores correspondentes e depois responda à questão.

Quadro: equivalente textual a seguir.

Imagem: Ilustração. Sinal de multiplicação. Fim da imagem.

10

100

1. 000

4

40

_____

_____

5

_____

_____

_____

7

_____

_____

_____

9

_____

_____

_____

PROFESSOR Resposta: Coluna 10: 50, 70, 90. Coluna 100. 400, 500, 700, 900. Coluna 1.000: 4.000, 5.000, 7.000, 9.000.
Imagem: Ilustração. Um menino com cabelo encaracolado está sentado e com a mão sobre uma calculadora. Ao seu lado há um papel e uma caneta. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  • O que você percebeu em relação aos resultados das multiplicações no quadro? Converse com o professor e os colegas.
    PROFESSOR Resposta: Os resultados sugerem que, quando multiplicamos um número por 10, o produto é esse número com 1 zero acrescentado à direita dele; quando se trata de um número vezes 100, acrescentam-se 2 zeros à direita dele; e, no caso do número vezes 1 000, acrescentam-se 3 zeros à direita dele.

    Imagem: Ícone: mental. Fim da imagem.

  1. Calcule mentalmente os resultados em cada caso. Antes de fazer as adições, efetue cada operação que está dentro dos parênteses.
    1. (8 × 100) + (5 × 10) = _____ + _____ = _____
      PROFESSOR Resposta: 800 + 50 = 850
    1. (5 × 100) + (7 × 10) = _____ + _____ = _____
      PROFESSOR Resposta: 500 + 70 = 570
    1. (4 × 1.000) + (6 × 100) + (9 × 10) = _____ + _____ + _____ = _____
      PROFESSOR Resposta: 4.000 + 600 + 90 = 4.690
  1. Em uma campanha beneficente realizada pela Escola Aprender, foram arrecadados diversos produtos enlatados, como mostra o gráfico abaixo.
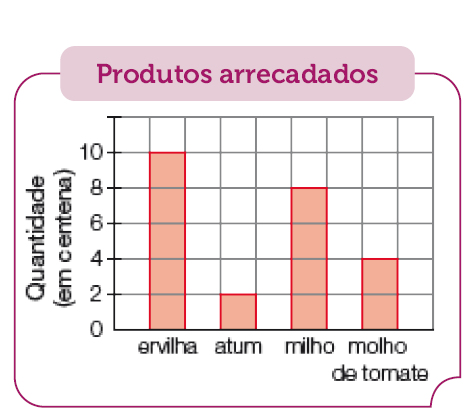
Imagem: Gráfico de colunas. Produtos arrecadados. No eixo vertical, a quantidade (em centena) e no eixo horizontal, o produto. Ervilha: 10; Atum: 2; Milho: 8; Molho de tomate: 4. Fim da imagem.

Fonte: Escola Aprender, 5 abr. 2023.

  1. Quantas latas de cada produto foram arrecadadas?

    Ervilha - _____

    PROFESSOR Resposta: 1.000 latas.

    Atum - _____

    PROFESSOR Resposta: 200 latas.

    Milho - _____

    PROFESSOR Resposta: 800 latas.

    Molho de tomate - _____

    PROFESSOR Resposta: 400 latas.
  1. Represente com uma única multiplicação o total de latas arrecadadas.

    _____

    PROFESSOR Resposta: 24 × 100 = 2.400
MANUAL DO PROFESSOR

Objetivos

Observar regularidades e calcular o resultado de multiplicações dos tipos vezes 10, vezes 100 e vezes 1.000.

Observar regularidades e calcular o resultado de multiplicações dos tipos vezes 20, vezes 30, vezes 40.

Representar uma multiplicação na reta numérica.

Atividade 1

Espera-se que percebam que, em multiplicações nas quais um dos fatores é 10, 100 ou 1.000, o resultado mantém o algarismo do outro fator acrescido da mesma quantidade de zeros à sua direita. Por exemplo, o resultado de 3 × 10 = 30 tem o primeiro algarismo igual ao fator 3 e é acrescido de um zero à sua direita. De modo similar, o resultado de 4 × 100 tem o primeiro algarismo igual a 4 e é acrescido de dois zeros à sua direita, formando-se o número 400.

Atividade 2

Espera-se que os estudantes percebam que a estratégia de cálculos vezes 10, vezes 100, vezes 1.000 facilita o cálculo mental.

Atividade 3

O objetivo desta atividade é os estudantes observarem a escala do eixo vertical do gráfico, no qual as cotas (quantidades) representam centenas, o que exige que multipliquem 100 pela cota correspondente à quantidade de produtos enlatados.

Aproveite para fazer outras perguntas com base no gráfico da atividade, como:

Quantas latas de milho foram arrecadadas a mais que latas de molho de tomate? (400.)

Quantas latas de atum precisariam ser arrecadadas para igualar com a quantidade de latas de ervilha? (800.)

BNCC em foco:

EF04MA06

MP133

Vezes 20, vezes 30, vezes 40...

  1. Para identificar seu material escolar, Talita comprou 3 cartelas com 20 etiquetas cada uma. Quantas etiquetas ela comprou no total?

    Complete a fala que explica como Talita calculou 3 vezes 20 mentalmente.

Imagem: Ilustração. Talita, menina com cabelo encaracolado, tiara e óculos fala: 3 vezes 20 é o mesmo que 3 vezes espaço para resposta dezenas, que são espaço para resposta dezenas. 6 dezenas é o mesmo que 6 vezes espaço para resposta. Então, o resultado é espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 2, 6, 10, 60

Talita comprou _____ etiquetas.

PROFESSOR Resposta: 60
  1. Complete os quadros. Depois, responda às questões.

Quadro I

4 × 20 = _____

PROFESSOR Resposta: 80

4 × 2 × 10 = _____

PROFESSOR Resposta: 80

Quadro II

5 × 30 = _____

PROFESSOR Resposta: 150

5 × 3 × 10 = _____

PROFESSOR Resposta: 150

Quadro III

6 × 40 = _____

PROFESSOR Resposta: 240

6 × 4 × 10 = _____

PROFESSOR Resposta: 240
  1. O que você observou nos resultados das multiplicações de cada quadro?

    _____

    PROFESSOR Resposta: Os resultados em cada quadro são iguais.
  1. Como você calcularia mentalmente o resultado de 8 × 60?

    _____

    PROFESSOR Exemplo de resposta: Calculando 8 vezes 6, que é igual a 48, e depois 48 vezes 10.
  1. Cícero trabalha em uma papelaria que cobra 20 centavos de real por fotocópia. Ele quer fazer um quadro informativo com o preço de diferentes quantidades de fotocópia para seus clientes. Ajude Cícero completando o quadro abaixo.

Quadro: equivalente textual a seguir.

Quantidade de fotocópias

Preço

1

20 centavos

2

_____

3

_____

4

_____

5

_____

PROFESSOR Resposta: 40 centavos; 60 centavos; 80 centavos; 1 real.
MANUAL DO PROFESSOR

Atividade 1

O objetivo desta atividade é explorar a multiplicação de 20 por meio de estratégias de cálculo mental.

O raciocínio de Talita pode ser acompanhado pela decomposição da multiplicação:

3 × 20 = 3 × 2 × 10 = 6 × 10.

A primeira passagem decompõe 20 em duas dezenas (2 × 10), enquanto a segunda passagem faz 3 × 2 dezenas = 6 dezenas (6 × 10).

Pergunte aos estudantes: “Quantas etiquetas Talita teria comprado se cada cartela tivesse 50 etiquetas?”.

Espera-se que observem que 50 é o mesmo que 5 dezenas e que 3 × 5 dezenas são 15 dezenas, ou que 15 × 10 é igual a 150.

Atividade 2

Discuta as respostas com a turma. Espera-se que os estudantes percebam que, em cada caso, o fator de dois algarismos pode ser decomposto em um fator menor que 10 e outro fator igual a 10. Por exemplo, a multiplicação 4 × 20 foi decomposta em 4 × 2 × 10.

Atividade 3

Alguns estudantes podem argumentar que basta pensar como se cada fotocópia custasse 2 centavos (no lugar de 20 centavos) e, depois, acrescentar zero ao resultado. Essa estratégia, embora correta, deve ser complementada de modo que se atribua mais sentido ao acréscimo de zero ao resultado. Na verdade, o que se fez foi pensar inicialmente em um valor correspondente a 1 décimo dos 20 centavos (2 centavos) e, depois, com os resultados registrados, pensar que o que se procurava eram valores iguais a 10 vezes os resultados obtidos, bastando então colocar um zero à direita do número. Outro ponto a destacar é que, na última linha da tabela, não é usual escrever 100 centavos, mas, sim, 1 real, uma vez que em nosso sistema monetário 100 centavos correspondem a 1 real.

BNCC em foco:

EF04MA06, EF04MA11

MP134

Multiplicação na reta numérica

  1. Leia e complete com as informações correspondentes.

    Tiago colocou 6 caixas lado a lado no corredor da casa dele. Cada caixa mede 40 centímetros de comprimento. Juntas, elas ocuparam todo o comprimento de uma parede. Qual é a medida do comprimento dessa parede?

    Essa medida pode ser obtida calculando 6 vezes 40 centímetros. Também podemos representar essa multiplicação em uma reta numérica, na qual os números sejam indicados de 40 em 40 centímetros.

Imagem: Ilustração. Seis caixas coloridas lado a lado. Da esquerda para a direita: verde-escuro, roxo, verde-claro, rosa, azul e laranja. Abaixo, reta numérica: 0, 40, 80, espaço para resposta, espaço para resposta, espaço para resposta, espaço para resposta Entre 0 e 40, a expressão: 1 x 40. Entre 0 e 80, a expressão: 2 x 40. Entre 0 e espaço para resposta, a expressão: 3 x 40. Entre 0 e espaço para resposta, a expressão: 4 x 40. Entre 0 e espaço para resposta, a expressão: 5 x 40. Entre 0 e espaço para resposta, a expressão: 6 x 40. Fim da imagem.
PROFESSOR Resposta: 120, 160, 200, 240

Esses números formam uma sequência cujo último número expressa a medida do comprimento total da parede, em centímetro.

Portanto, a medida do comprimento da parede é _____ centímetros.

PROFESSOR Resposta: 240
  1. Complete o esquema abaixo, que indica a distância aproximada, em quilômetro, entre Florianópolis e outras duas capitais brasileiras. Note que cada espaço do esquema tem o mesmo tamanho.
Imagem: Ilustração. Reta numérica com oito pontos, alternando em 100. À esquerda, 0 (Florianópolis), 100, 200, espaço para resposta (Curitiba), espaço para resposta, espaço para resposta, espaço para resposta, espaço para resposta (São Paulo). Fim da imagem.
PROFESSOR Resposta: 300, 400, 500, 600, 700
  1. Qual é a distância aproximada entre Florianópolis e Curitiba? _____
    PROFESSOR Resposta: 300 km
  1. Qual é a distância aproximada entre Florianópolis e São Paulo? _____
    PROFESSOR Resposta: 700 km
MANUAL DO PROFESSOR

Atividade 1

Esta atividade explora a reta numérica como suporte para a realização do cálculo de multiplicações, evidenciando a regularidade observável na reta numérica quando se fazem multiplicações. Isso contribui para que os estudantes tenham mais possibilidades de escolha na representação de multiplicações e também que tenham melhor compreensão das regularidades já observadas nas multiplicações em que um dos fatores é múltiplo de 100.

Atividade 2

Pode-se discutir com a turma o que significa, nesse caso, “distância aproximada”. Aqui, trata-se na verdade de arredondamentos para algum múltiplo de 100 – algo comum em algumas situações, especialmente para estimarmos uma distância e facilitar cálculos. Pergunte: “Qual é a distância aproximada entre Curitiba e São Paulo?” (400 quilômetros). Observe as estratégias de resolução dos estudantes. Veja se usam apenas as marcas das cidades de Curitiba e São Paulo ou se subtraem a distância de Florianópolis a Curitiba da distância entre Florianópolis e São Paulo.

BNCC em foco:

EF04MA06, EF04MA07, EF04MA11

Sugestão de atividade

Multiplicação

Peça aos estudantes que se reúnam em duplas e proponha que leiam as frases abaixo.

Nesta semana, ele já vendeu 16 caixas com 100 lápis em cada uma.

Quantos lápis foram vendidos ao todo?

Antônio é comerciante e na semana passada vendeu 18 caixas com 100 lápis em cada uma.Peça a eles que, em seguida, ordenem as frases no caderno e resolvam o problema usando a multiplicação por decomposição.

“Antônio é comerciante e na semana passada vendeu 18 caixas com 100 lápis em cada uma. Nesta semana, ele já vendeu 16 caixas com 100 lápis em cada uma. Quantos lápis foram vendidos ao todo?”.

Depois de resolverem, os estudantes deverão explicar como procederam para chegar ao resultado, de modo que possam ser identificadas possíveis diferenças de estratégias.

MP135

  1. Ronaldo alinhou 10 tijolos. Cada tijolo mede 30 centímetros de comprimento. Complete a reta numérica que representa essa situação com os números até o 10º tijolo.
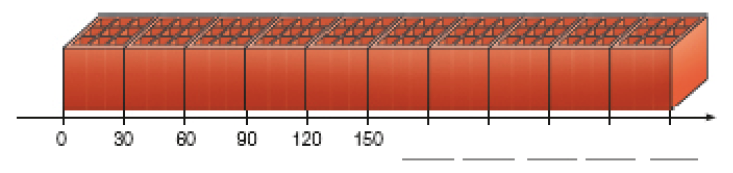
Imagem: Ilustração. Dez tijolos lado a lado. Abaixo, reta numérica: 0, 30, 60, 90, 120, 150, espaço para resposta, espaço para resposta, espaço para resposta, espaço para resposta, espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 180, 210, 240, 270, 300

Imagem: Ícone: mental. Fim da imagem.

  • Responda: qual é a medida do comprimento, em metro, desses 10 tijolos alinhados? _____
    PROFESSOR Resposta: 3 metros.
  1. Rita fez um caminho com pedras quadradas da entrada de sua casa até o portão de saída, como mostra o desenho abaixo.
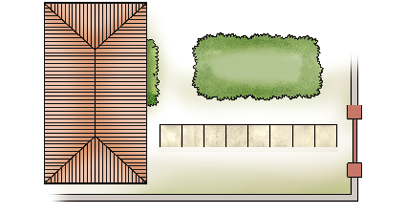
Imagem: Ilustração. Vista de cima de uma casa à esquerda. Na frente há oito pedras quadradas enfileiradas até o portão à direita. Ao lado, árvores. Fim da imagem.
  • Se cada pedra tem 60 centímetros de largura, quanto mede todo esse caminho?

    _____

    PROFESSOR Resposta: 480 centímetros ou 4 metros e 80 centímetros.
  1. O mapa abaixo mostra a distância em linha reta entre as cidades de Uruguaiana e Santa Cruz do Sul, no estado do Rio Grande do Sul. Leia o que Malu está dizendo e responda à questão feita por ela.
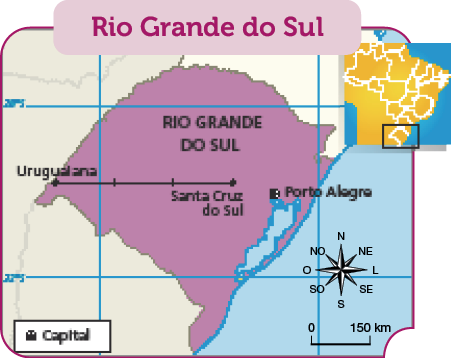
Imagem: Mapa. Rio Grande do Sul. Parte do mapa do Brasil com destaque para o Rio Grande do Sul. Entre Uruguaiana e Santa Cruz do Sul há uma reta numérica com três pontos. Ao lado, a capital: Porto Alegre. No canto inferior direito, a rosa dos ventos e a escala. No canto superior direito, mapa do Brasil com destaque para a região descrita. Fim da imagem.

FONTE: Elaborado com base em: IBGE. Atlas geográfico escolar. 7ª ed. Rio de Janeiro: IBGE, 2016.

Imagem: Ao lado do mapa, uma mulher com cabelo castanho pergunta: Cada um dos trechos indicados por (um ponto da reta numérica) corresponde a 150 quilômetros. Qual é a distância real entre Uruguaiana e Santa Cruz do Sul? Fim da imagem.

_____

PROFESSOR Resposta: 450 quilômetros.
PROFESSOR Como cada Ilustração. Um ponto da reta numérica. no mapa equivale a 150 quilômetros, deve-se calcular 3 × 150 quilômetros, que resulta em 450 quilômetros.
MANUAL DO PROFESSOR

Atividade 3

Para resolver esta atividade, é possível que os estudantes façam adições de 30 em 30. Verifique se eles observam que os números da reta numérica representam o comprimento em centímetro, e, no segundo item, é preciso converter esse comprimento em metro.

Atividade 4

Para resolver a situação proposta, os estudantes terão de observar a ilustração e considerar a quantidade de pedras para responder à questão. Eles devem considerar que todas as pedras têm os lados com medidas iguais para determinar a medida em centímetro ou em metro.

Atividade 5

Esclareça aos estudantes que a informação de que cada trecho (simbolizado por Ilustração. Um ponto da reta numérica.) corresponde a 150 quilômetros de distância. É o que se chama de escala do mapa. Nesse caso, a escala pode ser apresentada na forma 1 : 15.000.000, o que significa que cada 1 centímetro no mapa corresponde a 15.000.000 de centímetros na realidade. Verifique se eles percebem que, embora não tenham trabalhado com números tão grandes, podem recorrer à regularidade já observada na colocação de zeros, caso seja necessário fazer a conversão para a medida real de distâncias.

Para explorar a atividade, leve para a sala de aula um mapa do Brasil e um do seu estado e peça aos estudantes que, em duplas, escolham cidades separadas por um número exato de centímetros e determinem a distância, em quilômetros, entre elas. Se achar oportuno trabalhe, em conjunto, os conceitos de Cartografia.

BNCC em foco:

EF04MA06, EF04MA07, EF04MA11

MP136

Algoritmos da multiplicação

  1. Yuri organizou suas figurinhas em 5 grupos com 117 figurinhas cada um. Ao todo, quantas figurinhas Yuri tem?

    Complete o cálculo de 5 × 117 por decomposição para saber o número de figurinhas que Yuri tem.

Cálculo por decomposição

Imagem: Conta de multiplicação na vertical. Na parte superior: 117: 100 + 10 + 7. Abaixo, sinal de multiplicação e o número 5. Entre o número 5 e os números acima há uma seta. Em seguida, traço horizontal. Fim da imagem.
PROFESSOR Resposta: 500 + 50 + 35 = 585

Yuri tem _____ figurinhas.

PROFESSOR Resposta: 585
Imagem: Ilustração. Yuri, jovem com cabelo encaracolado segura uma carta. Na frente dele há cinco montes de cartas viradas para baixo sobre uma mesa. Fim da imagem.
  1. Juliana vai se hospedar em um hotel por 6 dias. O valor da diária é 132 reais. Quantos reais ela vai gastar com as diárias?
Imagem: Ilustração. Uma mulher está segurando uma caneta sobre um papel em um balcão. Ao seu lado, uma mulher a observa atrás do balcão. Ao fundo, um relógio e uma placa com a informação: HOTEL. Fim da imagem.

Complete o cálculo de 6 × 132 usando o algoritmo usual para saber quantos reais Juliana vai gastar.

Cálculo pelo algoritmo usual

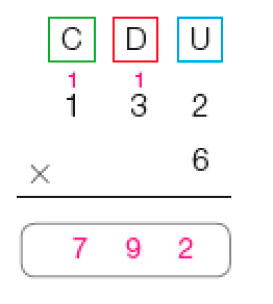
Imagem: Conta de multiplicação na vertical. Acima, as siglas: C, D, U. Abaixo, o número 132. Acima dos números 1 e 3 há um número 1 pequeno). Em seguida, sinal de multiplicação e o número 6. Abaixo, traço horizontal e o resultado: espaço para resposta. Fim da imagem.

• Primeiro, multiplicamos as unidades por 6.
6 vezes 2 unidades são 12 unidades, que é o mesmo que 1 dezena e 2 unidades.

• Em seguida, multiplicamos as dezenas por 6.6 vezes 3 dezenas são 18 dezenas.
18 dezenas mais 1 dezena são 19 dezenas, que é o mesmo que 1 centena mais 9 dezenas.

• Depois, multiplicamos as centenas por 6.
6 vezes 1 centena são 6 centenas. 6 centenas mais 1 centena são 7 centenas.

Juliana vai gastar _____ reais com as diárias.

PROFESSOR Resposta: 792
MANUAL DO PROFESSOR

Objetivo

Calcular o resultado de multiplicações por meio de decomposição e pelo algoritmo usual.

Atividade 1

O cálculo por decomposição facilita o entendimento do que acontece no sistema de numeração quando se realiza a multiplicação pelo algoritmo usual.

Na multiplicação por decomposição, os estudantes precisam reconhecer que o número 5 multiplica 100, 10 e 7, um dos fatores é, portanto, 5 e o outro fator é o número obtido pela adição 100 + 10 + 7.

Atividade 2

Dando continuidade ao trabalho com problemas que envolvem multiplicação, aqui os estudantes devem observar o modo de calcular o resultado exato com o uso do algoritmo usual.

Dê um tempo para os estudantes lerem e compreenderem o algoritmo usual da multiplicação. Sugira a eles que realizem o cálculo por decomposição e comparem o resultado com o do livro. É importante que percebam a relação entre as duas formas de resolução, observando que são estratégias de cálculo diferentes para uma mesma operação.

Decompomos 132: 132 = 100 + 30 + 2

Multiplicamos 2 por 6, 30 por 6 e 100 por 6.

Finalmente, fazemos a adição: 12 + 180 + 600 = 792 ou 12 + 100 + 80 + 600 = 792

Então, 6 × 132 = 792.

BNCC em foco:

EF04MA06

MP137

  1. Descubra a multiplicação que corresponde ao cálculo mental feito por Viviane.
Imagem: Ilustração. Viviane, jovem com cabelo ondulado fala: Primeiro calculei 3 vezes 100, que é igual a 300. Em seguida, fiz 3 vezes 20, que é igual a 60. Depois, calculei 3 vezes 3, que é igual a 9. Adicionei esses resultados e obtive 369. Fim da imagem.
PROFESSOR Resposta: 3 × 123 = 369
  1. Em um supermercado, há duas áreas usadas como estacionamento. Em cada uma, há 385 vagas para carros. Quantos carros são necessários para ocupar todas as vagas disponíveis?
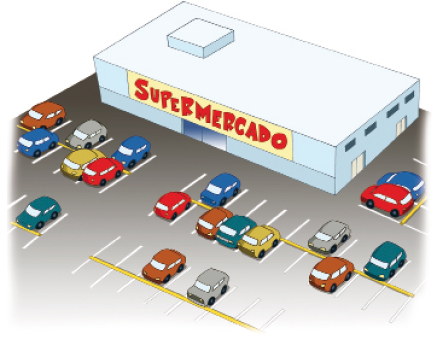
Imagem: Ilustração. Vista área de um supermercado. Ao lado há vários carros parados em um estacionamento. Fim da imagem.
PROFESSOR Exemplo de cálculo: Conta de multiplicação na vertical. Acima, o número 385 (Acima dos números 3 e 8 há um número 1 pequeno). Em seguida, sinal de multiplicação e o número 2. Abaixo, traço horizontal e o resultado: 770.

Para ocupar todas as vagas são necessários _____ carros.

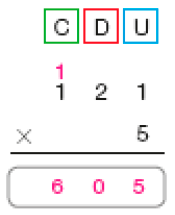
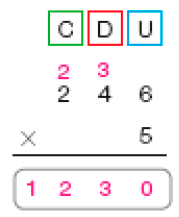
PROFESSOR Resposta: 770
  1. Calcule o resultado de cada multiplicação.

a)

Imagem: Conta de multiplicação na vertical. Acima, as siglas: C, D, U. Abaixo, o número 121 (Resposta: Acima do número 1 há um número 1 pequeno). Em seguida, sinal de multiplicação e o número 5. Abaixo, traço horizontal e o resultado: 605. Fim da imagem.

b)

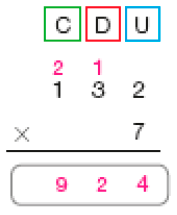
Imagem: Conta de multiplicação na vertical. Acima, as siglas: C, D, U. Abaixo, o número 132 (Resposta: Acima do número 1 há o número 2 pequeno e acima do número 3 há o número 1 pequeno). Em seguida, sinal de multiplicação e o número 7. Abaixo, traço horizontal e o resultado: 924. Fim da imagem.

c)

Imagem: Conta de multiplicação na vertical. Acima, as siglas: C, D, U. Abaixo, o número 371 (Resposta: Acima do número 3 há o número 2 pequeno). Em seguida, sinal de multiplicação e o número 4. Abaixo, traço horizontal e o resultado: 1.484. Fim da imagem.

d)

Imagem: Conta de multiplicação na vertical. Acima, as siglas: C, D, U. Abaixo, o número 246 (Resposta: Acima do número 2 há o número 2 pequeno e acima do número 4 há o número 3 pequeno). Em seguida, sinal de multiplicação e o número 5. Abaixo, traço horizontal e o resultado: 1.230. Fim da imagem.
  1. Aline quer enfeitar 6 toalhas com fita de seda. Para cada toalha ela usará 45 centímetros de fita. Quantos centímetros de fita de seda ela usará ao todo?

    _____

    PROFESSOR Resposta: 270 centímetros.
MANUAL DO PROFESSOR

Atividade 3

Nesta atividade, os estudantes acompanham as etapas de uma multiplicação por decomposição e têm de descobrir qual é a multiplicação correspondente. Assim, precisam reconhecer que o número 3 multiplica 100, 20 e 3 e que, portanto, um dos fatores é 3 e o outro fator é o número obtido pela adição: 100 + 20 + 3 = 123.

Atividade 4

Depois que os estudantes responderem à questão, valide as resoluções e socialize as estratégias utilizadas.

Atividade 5

Depois de os estudantes realizarem a atividade, peça a eles que efetuem os mesmos cálculos com uma calculadora, mas sem apertar a tecla correspondente ao fator de um algarismo. Por exemplo, a multiplicação do item a não pode ser feita apertando-se a tecla de número 5. Uma alternativa seria eles decomporem 5 em 4 + 1 e fazer: (4 × 121) + (1 × 121) =

= 484 + 121 = 605.

Essa estratégia facilitará a compreensão do algoritmo convencional da multiplicação com fatores com mais de um algarismo, que será estudado na página seguinte.

Atividade 6

Peça aos estudantes que expressem em metro e em centímetro a medida obtida (2 metros e 70 centímetros).

BNCC em foco:

EF04MA06

MP138

Multiplicação com fatores com mais de um algarismo

  1. No dia das crianças, a escola de Alice distribuiu 14 caixas com 12 marias-moles cada uma. Quantas marias-moles foram distribuídas?

    Para saber a quantidade de marias-moles podemos calcular o resultado de 14 × 12, completando o cálculo abaixo.

Imagem: Conta de multiplicação na vertical. Acima, as siglas: C, D, U. Abaixo, o número 12. Em seguida, sinal de multiplicação e o número 14. Abaixo, traço horizontal e o resultado: 48 (4 x 12). Em seguida, sinal de adição e o número 120 (10 x 12). Abaixo, traço horizontal e o resultado: espaço para Resposta: 168 (4 x 12) + (10 x 12). Fim da imagem.
PROFESSOR Resposta: 168
Imagem: Ilustração. Uma caixa com a informação: CONTÉM 12 UNIDADES. Ao lado, duas marias-moles brancas. Fim da imagem.

Foram distribuídas _____ marias-moles.

PROFESSOR Resposta: 168
  1. Os pais de Felipe compraram um tablet em 13 parcelas de 123 reais cada uma. Quanto custou o tablet .

    Para saber quanto custou o tablet, podemos calcular o resultado de 13 × 123, completando o cálculo abaixo.

Imagem: Ilustração. Um jovem com cabelo encaracolado está sorrindo e segurando um tablet. Fim da imagem.
Imagem: Conta de multiplicação na vertical. Acima, as siglas: UM, C, D, U. Abaixo, o número 123. Em seguida, sinal de multiplicação e o número 13. Abaixo, traço horizontal e o resultado: 369. Em seguida, sinal de adição e o número espaço para resposta. Abaixo, traço horizontal e o resultado: espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 1.230, 1.599

O tablet custou _____ reais.

PROFESSOR Resposta: 1.599
MANUAL DO PROFESSOR

Objetivo

Ampliar o uso do algoritmo usual para multiplicações que apresentem fatores com mais de um algarismo.

Atividade 1

A ampliação do algoritmo usual para multiplicações com fatores com mais de um algarismo traz uma diferença que pode oferecer alguma dificuldade aos estudantes.

É importante justificar para a turma todos os passos para obter o resultado de 14 × 12. Primeiro calculamos 4 vezes 12 e, depois, 10 vezes 12, ou seja, o fator 14 é decomposto em 4 + 10, e cada parte multiplica o outro fator da multiplicação.

Imagem: Conta de multiplicação na vertical. Acima, o número 12. Em seguida, sinal de multiplicação e o número 14. Abaixo, traço horizontal e o resultado: 48 (4 x 12). Em seguida, sinal de adição e o número 120 (10 x 12). Abaixo, traço horizontal e o resultado: 168. Fim da imagem.

Atividade 2

Depois que os estudantes terminarem, resolva a multiplicação na lousa pedindo a eles que digam o que você deve fazer, quais passos deve dar para efetuar a multiplicação.

BNCC em foco:

EF04MA06

MP139

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Usando uma calculadora, obtenha o resultado de 12 × 34 sem apertar a tecla Ilustração. Tecla: 2.. Registre os cálculos que você fez.
PROFESSOR Exemplos de resposta:
PROFESSOR • Imagem: Ilustração. Teclas: 1, 1, x, 3, 4, +, 3, 4, =. Visor: 408. Fim da imagem.
PROFESSOR • Imagem: Ilustração. Teclas: 1, 3, x, 3, 4, -, 3, 4, =. Visor: 408. Fim da imagem.
  1. O gráfico abaixo mostra a quantidade de pessoas que assistiram a um espetáculo no Teatro Verde em uma semana. O ingresso custa 10 reais para quem é estudante e 23 reais para não estudantes. Quantos reais foram arrecadados no total nessa semana?
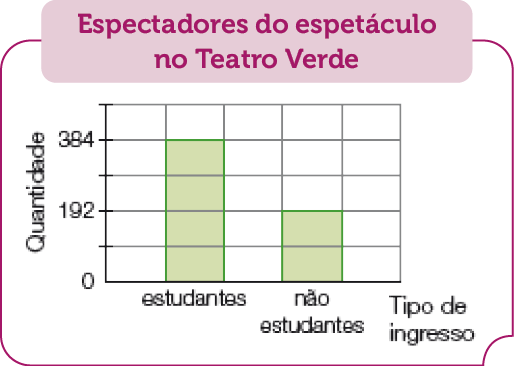
Imagem: Gráfico de colunas. Espectadores do espetáculo no Teatro Verde. No eixo vertical, a quantidade e no eixo horizontal, o tipo de ingresso. Estudantes: 384 espectadores. Não estudantes: 192 espectadores. Fim da imagem.

Fonte: Teatro Verde, semana de 9 mar. 2023.

PROFESSOR Exemplo de cálculo:
384 × 10 = 3.840
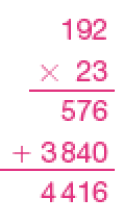
Conta de multiplicação na vertical. Acima, o número 192. Em seguida, sinal de multiplicação e o número 23. Abaixo, traço horizontal e o resultado: 576. Em seguida, sinal de adição e o número 3.840. Abaixo, traço horizontal e o resultado: 4.416.
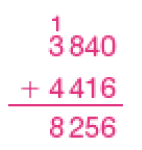
Conta de adição na vertical. Acima, o número 3.840 (acima do número 3 há o número 1 pequeno). Em seguida, sinal de adição e o número 4.416. Abaixo, traço horizontal e o resultado: 8.256.
8.256 reais.
  1. Veja como Beatriz calculou o resultado da multiplicação 24 × 22.
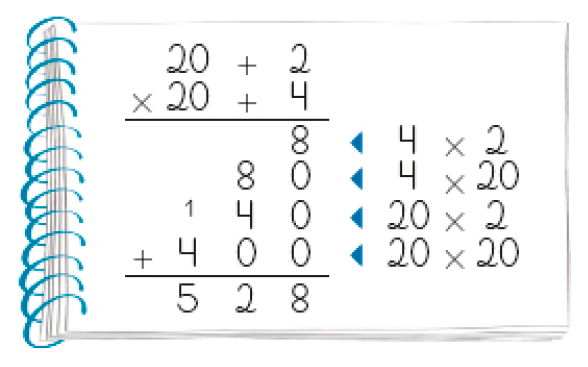
Imagem: Ilustração. Caderno com conta de multiplicação na vertical. Acima, o número 20 + 2. Em seguida, sinal de multiplicação e o número 20 + 4. Abaixo, traço horizontal e o resultado: 8 (4 x 2). Abaixo, o número 80 (4 x 20). Em seguida, o número 40 (20 x 2) - à esquerda, o número 1 pequeno. Em seguida, sinal de adição e o número 400. Abaixo, traço horizontal e o resultado: 528. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Elabore, em seu caderno, um problema envolvendo os números 363 e 25 que possa ser resolvido por meio de uma multiplicação. Depois, peça a um colega que o resolva.
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Nesta atividade, os estudantes têm a oportunidade de aplicar a propriedade distributiva na resolução do problema de calculadora com a tecla quebrada, pensando que 12 × 34 é o mesmo que, por exemplo, 11 × 34 + 34, porque 12 pode ser decomposto em 11 + 1; então:

(11 + 1) × 34 =

= 11 × 34 + 1 × 34 = 408.

Também podem decompor o número 12 em 10 + 2, já que a decomposição com dezenas inteiras lhes é mais familiar.

Atividade 4

Peça aos estudantes que observem o gráfico e pergunte:

Quantos estudantes assistiram ao espetáculo? (384.)

Quantos não eram estudantes? (192.)

Dê um tempo para os estudantes calcularem o total arrecadado com os ingressos. Depois, peça a eles que expliquem como pensaram para realizar esse cálculo.

Atividade 5

Uma maneira de realizar o cálculo é: 13 × 33 =

= (13 × 3) + (13 × 30) =

= 39 + 390 = 429.

Os estudantes podem calcular o resultado de 13 × 33 utilizando uma das estratégias já apresentadas até o momento ou utilizar uma estratégia própria. É importante socializar os diversos tipos de resolução para que os estudantes ampliem o repertório de cálculos.

Atividade 6

Peça aos estudantes que compartilhem os problemas criados com a turma e, depois, verifiquem se a resolução do colega está correta.

BNCC em foco:

EF04MA06

MP140

Situações de divisão

  1. Para a aula de Educação Física, a professora Luciana dividiu os estudantes em equipes e distribuiu 40 bambolês igualmente entre as equipes. Cada equipe recebeu 2 bambolês.

    Quantas equipes foram formadas para essa aula? _____

    PROFESSOR Resposta: 20 equipes.
  1. Veja como Ariane explicou a Felipe de que maneira ela pensou para obter o resultado de 54 dividido por 3.
Imagem: Ilustração. Ariane, jovem com cabelo preso fala: Eu subtraí 3 de 54, depois subtraí 3 do resultado obtido e, assim por diante, fui fazendo subtrações sucessivas até não sobrar nada. Depois, contei quantas vezes subtraí o número 3. Ao lado, Felipe, menino com cabelo curto responde: Entendi! O resultado da divisão é a quantidade de números 3 que você tirou de 54 até chegar em zero. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. O raciocínio de Ariane está correto? Justifique sua resposta.
    PROFESSOR Resposta: Sim.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que Ariane calculou o resultado da divisão de 54 por 3 verificando quantas vezes o número 3 cabe no número 54. Fim da observação.
  1. Qual foi o resultado encontrado por Ariane nessa divisão? _____
    PROFESSOR Resposta: 18

    Imagem: Ícone: Oral. Fim da imagem.

  1. Pense em outra maneira para fazer a divisão de 75 por 5 e escreva o resultado encontrado. Depois converse com o professor e os colegas sobre o modo como você fez essa divisão.
    PROFESSOR Resposta pessoal. O resultado da divisão é 15.
  1. Carla recebeu uma encomenda de 312 salgadinhos que serão entregues em 6 caixas. Em cada caixa, será colocada a mesma quantidade de salgadinhos e não haverá sobra. As caixas vão ficar completas. Veja como Carla fez para descobrir a quantidade de salgadinhos que ela deve colocar em cada caixa.
Imagem: Ilustração. Carla, mulher loira com cabelo curto fala: Para descobrir, dividi o número total de salgadinhos pelo número total de caixas. O resultado é a quantidade de salgadinhos que devo colocar em cada caixa. Fim da imagem.

Cada caixa foi entregue com quantos salgadinhos?

_____

PROFESSOR Resposta: 52 salgadinhos.
MANUAL DO PROFESSOR

Objetivo

Explorar situações que envolvem divisões.

As situações propostas permitem explorar a divisão ora como repartir em partes iguais, ora relacionada à ideia de quantas vezes cabe. É importante destacar que, apesar de os problemas propostos poderem ser resolvidos por meio de divisões, nada impede que os estudantes recorram a outras operações.

Peça a eles que expliquem como pensaram para responder às questões desta página e da página seguinte. É interessante questioná-los sobre como poderiam ter certeza de cada resposta.

Atividade 1

Como cada equipe precisará de dois bambolês e há 20 equipes, então serão necessários 40 bambolês (20 × 2 = 40). Incentive os estudantes a discutirem as estratégias pessoais.

Atividade 2

Para verificar se os estudantes compreendem o cálculo, peça a eles que resolvam uma divisão com subtrações sucessivas como a que Ariane fez. Por exemplo, 30 ÷ 5 = 6.

30 − 5 = 25

25 − 5 = 20

20 − 5 = 15

15 − 5 = 10

10 − 5 = 5

5 − 5 = 0

No item c, peça aos estudantes que contem como pensaram para fazer a divisão de 75 por 5 sem usar subtrações sucessivas.

Atividade 3

Neste momento, é importante os estudantes terem contato com diferentes descrições de cálculos da divisão. A expressão oral e escrita contribui para a compreensão do conceito. Estimule os estudantes a explicarem o raciocínio antes de fazerem o cálculo escrito.

BNCC em foco:

EF04MA07

MP141

  1. Um time de voleibol comprou 10 pares de meias por 80 reais, no total. Quanto foi pago por 5 desses pares de meias? _____
    PROFESSOR Resposta: 40 reais.
  1. Leia o que Alice está dizendo e responda à questão.
Imagem: Ilustração. Alice, jovem loira e cadeirante, segura um livro e fala: Todos os dias leio 20 páginas deste livro. Fim da imagem.
  1. Em um domingo, uma lanchonete vendeu 270 reais em sanduíches.
    1. Se cada sanduíche custa 9 reais, quantos sanduíches foram vendidos nesse dia? _____
      PROFESSOR Resposta: 30 sanduíches.
    1. Na segunda-feira, a venda de sanduíches foi metade da venda de domingo. Quantos sanduíches foram vendidos na segunda-feira? _____
      PROFESSOR Resposta: 15 sanduíches.
    1. Elabore uma pergunta envolvendo o número 25 e os dados do problema, para que seja resolvido por meio de uma divisão. Compartilhe sua pergunta com os colegas.

Boxe complementar:

Desafio

Imagem: Ícone: Dupla. Fim da imagem.

Reúna-se com um colega para resolver o problema a seguir. Quatro colegas ganharam algumas balas, que foram distribuídas igualmente entre eles, e sobraram 2 balas. Se havia menos de 20 balas, quantas balas eles ganharam para serem distribuídas?

Imagem: Ilustração. À esquerda, três jovens se entreolham e sorriem. À direita, um jovem segura uma sacola com a informação: BALAS. Fim da imagem.

CRÉDITO: MARCIO GUERRA

Atenção professor: Espera-se que os estudantes percebam que há mais de uma possibilidade de resposta: 6, 10, 14 ou 18 balas. Fim da observação.

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 4

Observe se os estudantes percebem que basta pensar que o valor dos 5 pares de meias corresponde à metade de 80 reais.

Atividade 5

Esta atividade pode ser resolvida por meio de multiplicações:

1 dia: 20 páginas;

2 dias: 2 vezes 20 páginas ou 40 páginas;

3 dias: 3 vezes 20 páginas ou 60 páginas;

4 dias: 4 vezes 20 páginas ou 80 páginas;

5 dias: 5 vezes 20 páginas ou 100 páginas.

Portanto, Alice levará 5 dias para ler o livro.

Essa resolução, embora mais longa, tem, nesse momento, maior significado para os estudantes quando confrontada com a resolução por meio de uma divisão.

Atividade 6

Peça aos estudantes que digam como pensaram para responder aos itens a e b. Depois, ouça com a turma as perguntas elaboradas no item c e valide-as.

Desafio

Esta atividade induz à análise do número de possibilidades. A resolução é ainda um grande desafio para os estudantes, que estão pouco habituados a problemas que admitem mais de uma solução. Um caminho possível é organizar os dados em um quadro, para melhor visualização das possibilidades.

Note que, em vez de fornecer a quantidade exata de balas, o enunciado informa que “havia menos de 20 balas”. Essa indeterminação abre espaço para mais de uma possibilidade de resposta. Como eram menos de 20 balas, podiam ser 19, 18 ou 17, até o valor 1. Porém, outras informações do enunciado permitem eliminar alguns valores:

BNCC em foco:

EF04MA07, EF04MA12

Tabela: equivalente textual a seguir.

Número de balas

19

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

Quantas balas cada colega recebe

4

4

4

4

3

3

3

3

2

2

2

2

1

1

1

1

0

0

0

Quantas balas sobram

3

2

1

0

3

2

1

0

3

2

1

0

3

2

1

0

3

2

1

Analisando o quadro, os estudantes podem perceber que há quatro possibilidades de resposta: 18, 14, 10 ou 6 (pois cada um dos quatro colegas ganhou, no mínimo, uma bala, e sobraram duas).

MP142

Divisão exata e não exata

  1. Ana quer distribuir 18 cerejas inteiras igualmente entre 3 bolos, sem que haja sobra.

    Para determinar a quantidade de cerejas que deve colocar em cada bolo, Ana calculou o resultado de 18 ÷ 3.

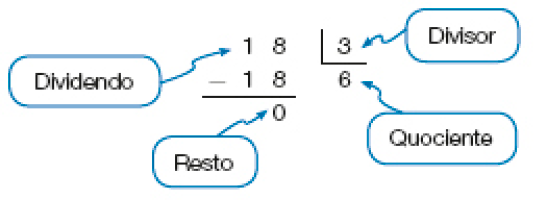
Imagem: Divisão na chave. À esquerda da chave, o dividendo: 18. À direita da chave, o divisor: 3. Abaixo do dividendo, sinal de subtração e o número 18. Em seguida, traço horizontal e resto: 0. Abaixo da chave, o quociente: 6. Fim da imagem.
Imagem: Ilustração. Ana, mulher ruiva com chapéu de cozinheira e avental fala: Quando o resto de uma divisão é zero, dizemos que a divisão é exata. Caso contrário, a divisão é não exata. Na frente dela há três bolos sobre uma mesa. Fim da imagem.

O resultado encontrado por Ana foi 6. Ela deve colocar 6 cerejas em cada bolo.

  1. Observe a ilustração e complete.
Imagem: Ilustração. Um jovem está com as mãos para cima e fala: Nossa turma de treino de basquete tem 28 integrantes. Na frente dele, uma jovem bate uma bola de basquete no chão e pergunta: Se montarmos times com 5 integrantes cada um, quantos times teremos? Fim da imagem.
PROFESSOR Exemplo de cálculo: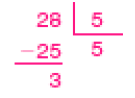 Divisão na chave. À esquerda da chave, o dividendo: 28. À direita da chave, o divisor: 5. Abaixo do dividendo, sinal de subtração e o número 25. Em seguida, traço horizontal e resto: 3. Abaixo da chave, o quociente: 5.

Teríamos _____ times, mas sobrariam _____ integrantes.

PROFESSOR Resposta: 5, 3

Imagem: Ícone: mental. Fim da imagem.

  1. Marlene tinha alguns ovos e colocou-os de 4 em 4 em algumas cestas. Sobraram 3 ovos. Marque com um X, entre os números a seguir, aquele que pode indicar o número de ovos que Marlene tinha.
Imagem: Ilustração. Quatro ovos sobre uma mesa e em cada um há um número: 21, 18, 17, 23. Fim da imagem.
PROFESSOR Resposta correta: 23.
PROFESSOR Atenção professor: Espera-se que os estudantes percebam que são 23 ovos, pois dessa forma Marlene teria dividido os ovos em 5 cestas com 4 ovos cada uma delas, e teriam sobrado 3 ovos: Fim da observação.
PROFESSOR Resposta: Expressão. 5 x 4 + 3 = 23 5 x 4 = 20.

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Objetivos

• Identificar divisões exatas e divisões não exatas.

• Decompor dividendo nas ordens das centenas, dezenas e unidades.

Atividade 1

O objetivo desta atividade é fazer com que os estudantes observem a divisão com resto zero e entendam que ela é classificada como divisão exata. Pergunte: “A divisão das 18 cerejas em 3 bolos é exata ou não exata? E a divisão de 20 cerejas em 3 bolos?”.

Atividade 2

Depois de os estudantes efetuarem a divisão e verificarem que sobrariam 3 estudantes, pergunte a eles que sugestão dariam para que todos os estudantes pudessem participar dos treinos de basquete, uma vez que os times são formados por 5 jogadores.

Atividade 3

Para resolver esta atividade, os estudantes podem realizar a divisão de cada um dos números por 4 e verificar qual dessas divisões tem resto igual a 3.

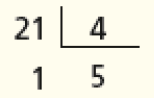
Imagem: Divisão na chave. À esquerda da chave, o dividendo: 21. À direita da chave, o divisor: 4. Abaixo do dividendo, o número 1. Abaixo da chave, o quociente: 5. Fim da imagem.

Imagem: Divisão na chave. À esquerda da chave, o dividendo: 18. À direita da chave, o divisor: 4. Abaixo do dividendo, o número 2. Abaixo da chave, o quociente: 4. Fim da imagem.

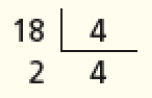
Imagem: Divisão na chave. À esquerda da chave, o dividendo: 17. À direita da chave, o divisor: 4. Abaixo do dividendo, o número 1. Abaixo da chave, o quociente: 4. Fim da imagem.

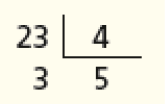
Imagem: Divisão na chave. À esquerda da chave, o dividendo: 23. À direita da chave, o divisor: 4. Abaixo do dividendo, o número 3. Abaixo da chave, o quociente: 5. Fim da imagem.

Dos números apresentados, o que pode indicar a quantidade de ovos que Marlene tinha é 23. É importante, contudo, comentar que, além desses números, há outras respostas para esse problema.

Se julgar oportuno, reproduza na lousa o quadro a seguir, em que o total de ovos é obtido multiplicando-se o número de ovos em cada cesta (4) pelo número de cestas e, depois, adicionando-se os 3 ovos restantes.

BNCC em foco:

EF04MA07, EF04MA12

Tabela: equivalente textual a seguir.

Número de cestas

Número de ovos em cada cesta

Total de ovos

1

4

(1 × 4) + 3 = 4 + 3 = 7

2

4

(2 × 4) + 3 = 8 + 3 = 11

3

4

(3 × 4) + 3 = 12 + 3 = 15

4

4

(4 × 4) + 3 = 16 + 3 = 19

...

4

...

MP143

Divisão por ordens

  1. A prefeitura de um município comprou 268 mudas de árvores frutíferas para distribuir igualmente entre 4 parques. Luís ficou encarregado de fazer a distribuição. Para saber quantas mudas seriam plantadas em cada parque, ele dividiu 268 por 4. Veja como Luís fez essa divisão.
Imagem: Ilustração. Cinco mudas de árvores. Fim da imagem.

268 ÷ 4

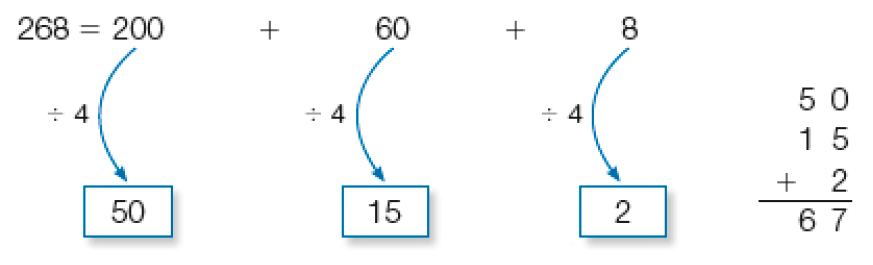
Imagem: Esquema. 268 = 200. dividido por 4 = 50. Mais. 60 dividido por 4 = 15 mmais 8 dividido por 4 = 2. Ao lado, conta de adição na vertical. Acima, o número 50. Em seguida, 15. Abaixo, sinal de adição e o número 2. Em seguida, traço horizontal e o resultado: 67. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Quantas mudas de árvores foram plantadas em cada parque?
    PROFESSOR Resposta: 67 mudas de árvores.

    Explique a um colega o cálculo que Luís fez.

    PROFESSOR Resposta pessoal.

    Imagem: Ícone: Dupla. Fim da imagem.

  1. No ano passado, 844 mudas de flores foram distribuídas igualmente entre esses parques. Quantas mudas de flores cada parque recebeu? Calcule e compare a resposta com a de seu colega.
    PROFESSOR Resposta: 211 mudas de flores.
  1. Complete a explicação de Regina.

    Regina explicou como fez para dividir 1.055 por 5.

Imagem: Ilustração. Uma jovem com cabelo preso aponta para frente e fala: Primeiro, dividi 1.000 por 5. O resultado foi espaço para resposta. Depois, dividi 50 por 5, e o resultado foi espaço para resposta. No fim, dividi espaço para resposta por 5, que é igual a espaço para resposta. Adicionei os quocientes parciais, e o resultado foi espaço para resposta. Fim da imagem.
PROFESSOR Resposta: 200, 10, 5, 1, 211.
MANUAL DO PROFESSOR

Objetivos

Decompor dividendo nas ordens das centenas, dezenas e unidades.

Efetuar divisões em que o divisor tenha um algarismo empregando o algoritmo usual.

Perceber a multiplicação como operação inversa da divisão.

Resolver problemas que envolvam a divisão empregando estratégias pessoais e convencionais.

As atividades destas páginas tratam da divisão pela decomposição do dividendo nas ordens das centenas, dezenas e unidades. A assimilação desse processo em relação à divisão contribui para o aprimoramento da compreensão do sistema de numeração decimal, além de ser uma preparação para o entendimento do algoritmo usual da divisão.

Atividade 1

Proponha aos estudantes que inventem um problema semelhante ao proposto e que o troquem com o de um colega, para a resolução e posterior discussão das respostas.

Atividade 2

Nesta atividade, ao acompanhar a explicação de Regina, os estudantes poderão observar a estratégia adotada por ela para efetuar a divisão e adicionar os quocientes parciais.

BNCC em foco:

EF04MA06, EF04MA07, EF04MA11

MP144

  1. Marque com um X somente as alternativas nas quais a frase apresenta informações verdadeiras.

( )

Imagem: Ilustração. Placa com a informação: O quociente da divisão 484 ÷ 4 é igual a: 100 + 20 + 1. Fim da imagem.

( )

Imagem: Ilustração. Placa com a informação: Dividindo 333 por 3, obtemos o resultado igual a: 1 + 1 + 1. Fim da imagem.

( )

Imagem: Ilustração. Placa com a informação: O quociente da divisão 848 ÷ 4 é igual a: 200 + 1 + 2. Fim da imagem.

( )

Imagem: Ilustração. Placa com a informação: Dividindo 999 por 3, obtemos o resultado igual a: 300 + 30 + 3. Fim da imagem.
PROFESSOR Respostas corretas: O quociente da divisão 484 ÷ 4 é igual a: 100 + 20 + 1
Dividindo 999 por 3, obtemos o resultado igual a: 300 + 30 + 3

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Calcule mentalmente o quociente e o resto de cada divisão.
    1. 693 ÷ 3
      PROFESSOR Resposta: Quociente: 231
      PROFESSOR Resto: 0
    1. 842 ÷ 2
      PROFESSOR Resposta: Quociente: 421
      PROFESSOR Resto: 0
    1. 489 ÷ 4
      PROFESSOR Resposta: Quociente: 122
      PROFESSOR Resto: 1
    1. 508 ÷ 5
      PROFESSOR Resposta: Quociente: 101
      PROFESSOR Resto: 3
  1. Observe a divisão que Luís fez.
Imagem: Ilustração. Caderno com as informações: 375 ÷ 3. 375 = 300 (÷ 3 = 100) + 70 (÷ 3 = 20 com resto 10) + adição na vertical: Na parte superior, o número 5. Abaixo, sinal de adição e o número 10 (Resposta: resto). Em seguida, traço horizontal e o resultado: 15 ÷ 3 = 5. Ao lado, conta de adição na vertical. Na parte superior, o número 100. Abaixo, o número 20 e em seguida, sinal de adição e o número 5. Abaixo, traço horizontal e o resultado: 125. 375 ÷ 3 = 125. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Agora, explique a um colega os cálculos de Luís.
    PROFESSOR Resposta pessoal.
  1. Calcule a divisão de 656 por 5 usando o mesmo procedimento de Luís. Qual foi o resultado encontrado?
    PROFESSOR Resposta: O resultado foi 131 com resto igual a 1.
MANUAL DO PROFESSOR

Atividade 3

Espera-se que a turma identifique as frases corretas. Erros nesta atividade podem indicar que ainda há estudantes que apresentam lacunas de aprendizagem em relação ao valor posicional do algarismo.

Atividade 4

Decompor o número e verificar se as partes são múltiplas do dividendo é uma estratégia que pode auxiliar os estudantes na resolução desta atividade.

Atividade 5

Espera-se que os estudantes percebam que Luís, ao dividir 70 por 3, obteve quociente parcial 20 e resto igual a 10, o qual, adicionado às 5 unidades, totaliza 15 unidades. Se julgar necessário, lembre-os de que podem escolher qualquer dos métodos de divisão para resolver o problema.

BNCC em foco:

EF04MA06, EF04MA07

MP145

Algoritmos da divisão

  1. Um livro tem 87 páginas distribuídas igualmente entre 3 capítulos. Quantas páginas tem cada capítulo desse livro?

    Veja como Mariana resolveu esse problema e complete com os valores correspondentes.

Imagem: Ilustração. Mariana, mulher com cabelo castanho fala: Para resolver esse problema, precisamos dividir 87 por 3. Fim da imagem.

Dividimos 8 dezenas por 3.

Obtemos 2 dezenas, e sobram 2 dezenas.

Imagem: Divisão na chave. À esquerda da chave, as siglas: D, U e o dividendo: 87. À direita da chave, o divisor: 3. Abaixo do dividendo, sinal de subtração e o número 6 (2 x 3 = 6). Em seguida, traço horizontal e resto: 2. Abaixo da chave, o quociente: 2 (D). Fim da imagem.

As 2 dezenas que restaram e as 7 unidades formam 27 unidades.

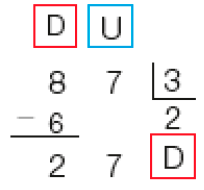
Imagem: Divisão na chave. À esquerda da chave, as siglas: D, U e o dividendo: 87. À direita da chave, o divisor: 3. Abaixo do dividendo, sinal de subtração e o número 6. Em seguida, traço horizontal e resto: 2 e ao lado, o número 7. Abaixo da chave, o quociente: 2 (D). Fim da imagem.

Dividimos 27 unidades por _____.

PROFESSOR Resposta: 3

Obtemos _____ unidades e sobra _____ unidade.

PROFESSOR Resposta: 9, 0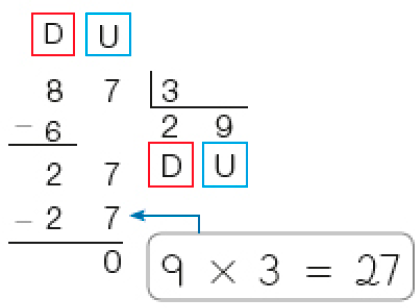
Imagem: Divisão na chave. À esquerda da chave, as siglas: D, U e o dividendo: 87. À direita da chave, o divisor: 3. Abaixo do dividendo, sinal de subtração e o número 6. Em seguida, traço horizontal e resto: 2 e ao lado, o número 7. Abaixo, sinal de subtração e o número 27 (9 x 3 = 27). Em seguida, traço horizontal e o resto: 0. Abaixo da chave, o quociente: 2 (D), 9 (U). Fim da imagem.

87 ÷ 3 = _____

PROFESSOR Resposta: 29

O quociente da divisão 87 ÷ 3 é _____, e o resto é _____.

PROFESSOR Resposta: 29, zero.

Então, cada um dos 3 capítulos do livro tem _____ páginas.

PROFESSOR Resposta: 29

Para ter certeza de que a divisão foi feita corretamente, podemos calcular (divisor × quociente + resto) e verificar se o resultado é igual ao dividendo, que nesse caso é o total de páginas do livro (87).

Imagem: Ilustração. Lousa com divisão na chave. À esquerda da chave, o dividendo: 87. À direita da chave, o divisor: 3. Abaixo do dividendo, o resto: 0. Abaixo da chave, o quociente: 29. Ao lado, conta de multiplicação na vertical. Na parte superior, o número 29 (acima do número 2 há o número 2 pequeno). Em seguida, sinal de multiplicação e o número 3. Abaixo, traço horizontal e o resultado: 87. 87 + 0 = 87. Fim da imagem.
  1. 69 ÷ 3
    PROFESSOR Resposta: Quociente: 23
    PROFESSOR Resto: 0
    PROFESSOR Verificação: 3 × 23 = 69 ou 23 × 3 = 69
  1. 76 ÷ 4
    PROFESSOR Resposta: Quociente: 19
    PROFESSOR Resto: 0
    PROFESSOR Verificação: 4 × 19 = 76 ou 19 × 4 = 76
  1. 86 ÷ 5
    PROFESSOR Resposta: Quociente: 17
    PROFESSOR Resto: 1
    PROFESSOR Verificação: 5 × 17 + 1 = 86 ou 17 × 5 + 1 = 86
MANUAL DO PROFESSOR

Como os estudantes já efetuaram divisões por estratégias variadas, a aprendizagem do algoritmo usual vem complementá-las e oferecer um procedimento de reconhecido uso social. Depois de conhecer os vários algoritmos e de compreender o funcionamento de cada um, os estudantes estarão mais capacitados para escolher o mais adequado à situação. Lembramos que é importante o aprendizado do algoritmo usual ser acompanhado da compreensão da estrutura do nosso sistema de numeração, que fundamenta as etapas do procedimento.

Um modo interessante de promover um melhor entendimento dos passos do algoritmo é usar a representação do dividendo como Material Dourado e executar as trocas e repartições com esse material em cada etapa do algoritmo.

Atividade 1

Verifique se os estudantes percebem que, para a verificação no item c, é necessário considerar o resto, pois precisam adicioná-lo ao quociente obtido na divisão.

BNCC em foco:

EF04MA06, EF04MA07

MP146

Jogo: Restou, ganhou!

Material: 36 cartas numeradas de 1 a 9 (4 cartas de cada algarismo), que devem ser confeccionadas em cartolina pelos jogadores, papel e lápis para anotações.

Imagem: Ícone: Grupo. Fim da imagem.

Jogadores: 2, 3 ou 4.

Regras:

Imagem: Ilustração. Quatro jovens estão sentados em círculo. Um deles está segurando uma caneta sobre um papel com uma conta de divisão na chave 24 dividido por 3 e 42 dividido por 3. Entre eles há três cartas com os números: 2 e 4 (dividendo) e 3 (divisor). Em volta há papéis e canetas. Fim da imagem.
MANUAL DO PROFESSOR

Objetivos

Ampliar estratégias de cálculo mental em divisão.

Explorar regularidades em divisões exatas e não exatas.

Analisar o resto de dezenas divididas por números naturais (de 1 a 9).

O aspecto mais interessante desse jogo é que o resto da divisão passa a ser importante para a marcação de pontos.

Assim, o hábito dos estudantes de desprezar o resto da divisão, por ele representar um “problema” na conta, passa a ter um sentido inverso no jogo, já que quem tem maior resto marca mais pontos.

Como não é usual a ênfase no resto do cálculo de uma divisão, deixe os estudantes jogarem diversas vezes, de modo que superem eventuais dificuldades iniciais.

Observe se reconhecem as estratégias mais adequadas às condições do jogo; se necessário, apresente alguns exemplos na lousa. Outro ponto forte desse jogo é requerer a tomada de decisão quanto à composição do número que será o dividendo: “Qual número oferecerá maior resto?”. Por exemplo, suponha que os algarismos escolhidos para o dividendo sejam 3 e 4 e que o algarismo do divisor seja 6. Os estudantes devem testar as divisões 34 ÷ 6 e 43 ÷ 6, verificando os restos obtidos (respectivamente 4 e 1), e assim optar pela primeira divisão. À medida que memorizam alguns resultados, sugira a eles que façam cálculos mentais para arriscar as estimativas. Assim, espera-se que tomem decisões acertadas sobre o dividendo que oferece maior resto, sem a necessidade de cálculos exatos.

Ajude os estudantes na leitura e compreensão das regras.

Após jogarem algumas vezes, proponha que, individualmente ou em duplas, respondam às questões.

BNCC em foco:

EF04MA07

Variações

Caso julgue oportuno, sugira que não se tenha a liberdade de escolher quais dos três algarismos apresentados em cada jogada fazem parte do dividendo e qual é o divisor. Deve-se então definir previamente, para cada partida, os montes que formarão o dividendo e o que formará o divisor. Outra modificação que pode ser feita nas regras é determinar o número de pontos que os jogadores devem atingir para vencer uma partida, em vez de encerrá-la ao término das cartas. Nesse caso, combine que deverão atingir exatamente o número de pontos determinado para a vitória, não podendo ultrapassá-lo. Assim, na última jogada deverão tentar obter o número exato de pontos que faltam para vencer a partida, e não necessariamente a divisão que apresentar o maior resto.

MP147

Questões sobre o jogo

  1. Em cada jogada, é bom obter resto zero para a divisão? Por quê?
    PROFESSOR Resposta: Não.
    PROFESSOR Atenção professor: Exemplo de explicação: Porque, quanto maior o resto, maior o número de pontos do jogador. Fim da observação.
Imagem: Ilustração. Um jovem com cabelo castanho comprido fala: 99 ÷ 9, 24 ÷ 6 e 49 ÷ 7. 45 ÷ 5 e 24 ÷ 4. Fim da imagem.
  1. Um jogador tirou as cartas Ilustração. Carta 4. e Ilustração. Carta 7. para o dividendo e a carta Ilustração. Carta 4. para o divisor. Em qual das duas situações, 47 ÷ 4 ou 74 ÷ 4, ele obterá maior resto?

    _____

    PROFESSOR Resposta: Fazendo 47 ÷ 4, o resto é 3; fazendo 74 ÷ 4, o resto é 2. Portanto, escolhendo a situação 47 ÷ 4, o jogador obterá maior resto.
  1. Qual é a maior pontuação que um jogador pode obter em uma jogada? Exemplifique uma combinação de cartas para essa situação. _____
    PROFESSOR Resposta: 8; exemplo de combinação: 17 ÷ 9
  1. Responda às questões.
    1. Na situação abaixo, a menina está feliz porque obteve a maior pontuação possível na jogada.

      Qual é o número da carta que está na mão esquerda da menina?

      _____

      PROFESSOR Resposta: A carta com o número 3 (pois tanto a divisão 35 ÷ 9 quanto a divisão 53 ÷ 9 têm resto 8).
Imagem: Ilustração. Dois jovens estão sentados e um deles está segurando uma carta com o número 5. Entre eles há uma carta virada com o número 9 e ao lado, duas cartas viradas para baixo (dividendo). Ao lado há papéis e lápis. Fim da imagem.
Imagem: Ilustração. Dois jovens ajoelhados. Entre eles há três montes de cartas. Duas estão viradas para baixo (dividendo) e uma virada para cima com o número 1. Ao lado há papéis e lápis. Fim da imagem.
MANUAL DO PROFESSOR

Questões sobre o jogo

Amplie a questão 1 solicitando aos estudantes que, em pequenos grupos, listem algumas divisões que podem aparecer no jogo que tenham resto zero. Depois, peça a eles que as socializem para ampliar a lista de divisões exatas, contribuindo para o repertório de cálculo.

Na questão 3, verifique quais estratégias os estudantes utilizarão para responder. Seria interessante que eles percebessem que não há necessidade de fazer cálculos, pois, sabendo que o maior divisor possível é o número 9, o resto não poderá passar de 8, já que qualquer número igual ou maior que 9 poderá continuar no processo de divisão.

Na questão 4, aproveite o item b para explorar outras regularidades nas divisões. Se possível, faça uma lista com as relações percebidas durante o jogo pelos estudantes.

BNCC em foco:

EF04MA07

MP148

Divisor com dois algarismos

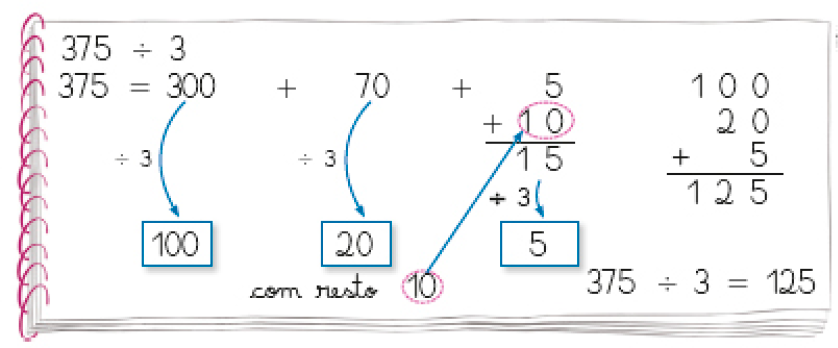
  1. Qual é o resultado da divisão 814 ÷ 13? Complete a resolução a seguir.

Como 8 centenas divididas por 13 não resultam em centena, dividimos 81 dezenas por _____.

PROFESSOR Resposta: 13
Imagem: Divisão na chave. À esquerda da chave, as siglas: C, D, U e o dividendo: 814. À direita da chave, o divisor: 13. Fim da imagem.

Dividindo 81 dezenas por _____, obtemos 6 dezenas e restam 3 dezenas.

3 dezenas e 4 unidades formam _____ unidades.

PROFESSOR Resposta: 13, 34
Imagem: Divisão na chave. À esquerda da chave, as siglas: C, D, U e o dividendo: 814. À direita da chave, o divisor: 13. Abaixo do dividendo, sinal de subtração e o número 78. Em seguida, traço horizontal e resto: 034. Abaixo da chave, o quociente: 6 (D). Fim da imagem.

Rascunho

1 × 13 = 13

2 × 13 = 26

3 × 13 = 39

Imagem: Conta de multiplicação na vertical. Na parte superior, o número 13 (acima do número 1, o número 2 pequeno). Em seguida, sinal de multiplicação e o número 7. Abaixo, traço horizontal e o resultado: 91. Fim da imagem.
Imagem: Conta de multiplicação na vertical. Na parte superior, o número 13 (acima do número 1, o número 1 pequeno). Em seguida, sinal de multiplicação e o número 6. Abaixo, traço horizontal e o resultado: 78. Fim da imagem.

Dividimos _____ unidades por _____.

PROFESSOR Resposta: 34, 13

Obtemos _____ unidades, e restam _____ unidades.

PROFESSOR Resposta: 2, 8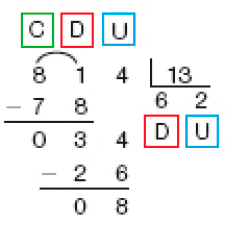
Imagem: Divisão na chave. À esquerda da chave, as siglas: C, D, U e o dividendo: 814. À direita da chave, o divisor: 13. Abaixo do dividendo, sinal de subtração e o número 78. Em seguida, traço horizontal e resto: 034. Abaixo, sinal de subtração e o número 26. Em seguida, traço horizontal e o resto: 08. Abaixo da chave, o quociente: 6 (D), 2 (U). Fim da imagem.

814 ÷ 13 = _____, e restam _____.

PROFESSOR Resposta: 62, 8
  1. Veja como Marina fez uma divisão por estimativas.
Imagem: Ilustração. Marina, menina com cabelo castanho e curto fala: Quantos 3 cabem em 192? Estimei que coubessem 60, pois 60 x 3 = 180, mas ainda restaram 12 para dividir por 3. Quantos 3 cabem em 12? Com certeza 4, pois: 4 x 3 = 12. O quociente dessa divisão é a soma dos quocientes parciais: 60 + 4 = 64. Fim da imagem.
  1. Qual foi a divisão feita por Marina? Qual foi o resultado dessa divisão?

    _____

    PROFESSOR Resposta: 192 ÷ 3; 64

    Imagem: Ícone: mental. Fim da imagem.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Faça como Marina e calcule o resultado da divisão 965 ÷ 7.
    PROFESSOR Resposta: Quociente: 137
    PROFESSOR Resto: 6
MANUAL DO PROFESSOR

Objetivos

Calcular o quociente de divisões com divisor de dois algarismos por meio do algoritmo usual.

Resolver problemas que envolvam a divisão empregando estratégias pessoais e convencionais.

Nestas páginas, o algoritmo usual da divisão tem sua compreensão ampliada para divisores com dois algarismos.

Atividade 1

Na divisão apresentada na situação, 814 ÷ 13, a divisão de 81 dezenas por 13 exige que se determine o número que deve multiplicar 13 para aproximar-se mais de 81, sem ultrapassá-lo. Isso exige algumas tentativas (mentais ou escritas) até que se verifique que 6 é o quociente procurado, pois 6 × 13 = 78.

Atividade 2

Aproveite a situação para perguntar: “O que ocorreria se Marina tivesse estimado 70 em sua primeira estimativa?”. Eles devem perceber que o resultado seria maior que 192, pois 70 × 3 = 210. Pergunte então como seria possível obter o resultado certo com base nessa estimativa. Espera-se que observem que, nesse caso, o resultado obtido seria 18 unidades maior que o valor dado (210 − 192 = 18); como 3 cabe 6 vezes em 18, basta subtrair 6 de 70, obtendo-se 64, que é o quociente da divisão 192 ÷ 3.

BNCC em foco:

EF04MA06, EF04MA07

MP149

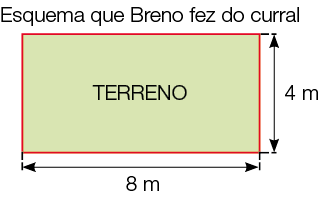
  1. Breno tem 264 m de arame para cercar um curral retangular. Veja o esquema abaixo. Com esse arame, é possível dar quantas voltas completas ao redor do curral?

    _____

    PROFESSOR Resposta: 11 voltas.
Imagem: Ilustração. Esquema que Breno fez do curral: um terreno com formato de retângulo com 4 m de largura e 8 m de comprimento. Fim da imagem.
  1. Observe o exemplo e determine o fator que falta em cada caso.
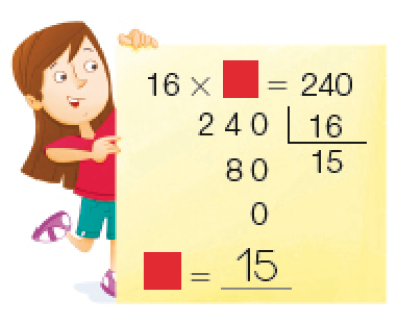
Imagem: Ilustração. Uma menina segura um papel com a conta: 16 x quadrado vermelho = 240. Divisão na chave. À esquerda da chave, o dividendo: 240. À direita da chave, o divisor: 16. Abaixo do dividendo, o número 80 e em seguida, o número 0. Abaixo da chave, o quociente: 15. Quadrado vermelho = 15. Fim da imagem.

45 × Ilustração. Quadrado verde.= 810

PROFESSOR Resposta: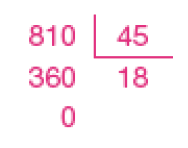 Divisão na chave. À esquerda da chave, o dividendo: 810. À direita da chave, o divisor: 45. Abaixo do dividendo, o número 360 e em seguida, o número 0. Abaixo da chave, o quociente: 18.

Ilustração. Quadrado verde.= _____

PROFESSOR Resposta: 18

31 × Ilustração. Quadrado roxo.= 6.541

PROFESSOR Resposta: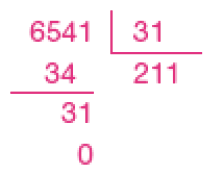 Divisão na chave. À esquerda da chave, o dividendo: 6.541. À direita da chave, o divisor: 31. Abaixo do dividendo, o número 34. Em seguida, traço horizontal e o número 31. Em seguida, o número 0. Abaixo da chave, o quociente: 211.

Ilustração. Quadrado roxo.= _____

PROFESSOR Resposta: 211

93 × Ilustração. Quadrado azul.= 6.417

PROFESSOR Resposta: Divisão na chave. À esquerda da chave, o dividendo: 6.417. À direita da chave, o divisor: 93. Abaixo do dividendo, o número 837. Em seguida, o número 0. Abaixo da chave, o quociente: 69.

Ilustração. Quadrado azul.= _____

PROFESSOR Resposta: 69
  1. Uma empresa de transportes dispõe de vários ônibus. Cada um acomoda 36 pessoas por viagem. Para realizar uma excursão que levará 457 estudantes, quantos ônibus, no mínimo, serão necessários?

    _____

    PROFESSOR Resposta: Serão necessários, no mínimo, 13 ônibus para realizar a excursão.
Imagem: Ilustração. Jovens em fila ao lado de um ônibus amarelo com a porta aberta. Ao fundo, árvores. Fim da imagem.
  1. Crie um problema que possa ser resolvido por meio de uma divisão exata e outro que possa ser resolvido por uma divisão não exata. Depois, peça a um colega que os resolva.

    _____

    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Nesta atividade, os estudantes precisam, primeiro, determinar quantos metros de arame são necessários para cercar o curral: 8 m + 4 m + 8 m + 4 m = 24 m.

Para saber quantas vezes 24 cabe em 264, é necessário calcular o resultado da divisão 264 ÷ 24, que tem quociente igual a 11.

Portanto, é possível dar 11 voltas no curral com o arame.

Atividade 4

Verifique se os estudantes percebem a relação entre divisão e multiplicação para obter o fator que deve ser determinado.

Atividade 5

Esta atividade exige a observação do resto da divisão. Como sobraram 25 pessoas, a quantidade de ônibus obtida na divisão (12) deverá ser acrescida de 1 unidade para transportar esses 25 passageiros, totalizando 13 ônibus, no mínimo.

Atividade 6

Verifique se os problemas criados estão de acordo com o que foi solicitado. Peça a cada estudante que leia os problemas para a turma. Depois, peça para quem resolveu o problema criado pelo colega dizer se conseguiu compreender o que foi solicitado e se resolveu sem dificuldade. Caso contrário, peça à turma que indique o que dificultou o entendimento, lembrando que a dificuldade pode estar tanto na formulação do problema como na sua interpretação.

BNCC em foco:

EF04MA06, EF04MA07, EF04MA13

MP150

Estimativas

  1. Marcos pretende comprar a lavadora de roupas representada abaixo, pagando o valor total em 4 parcelas iguais. Para saber quanto ele pagará em cada parcela, fez a seguinte estimativa.
Imagem: Ilustração. Um homem calvo pensa: Sei que 1.185 reais está próximo de 1.200 reais e que 1.200 ÷ 4 = 300. Portanto, pagarei aproximadamente 300 reais em cada prestação. Fim da imagem.
Imagem: Ilustração. Uma lavadora de roupas. Acima, placa com a informação: 1.185 reais. Fim da imagem.
  1. 5.483 ÷ 5 = _____
    PROFESSOR Resposta: Exemplo de resposta: 1.100
  1. 6.272 ÷ 3 = _____
    PROFESSOR Resposta: Exemplo de resposta: 2.100
  1. 4.813 ÷ 8 = _____
    PROFESSOR Resposta: Exemplo de resposta: 600
  1. 1.426 ÷ 7 = _____
    PROFESSOR Resposta: Exemplo de resposta: 200
  1. Catarina foi a uma loja comprar 6 camisetas, no valor de 47 reais, para presentear seus sobrinhos. Para saber se o dinheiro que levou era suficiente, ela fez o seguinte cálculo:
Imagem: Ilustração. Catarina, mulher loira olha para cima e pensa: Como 47 está próximo de 50, calculo 50 x 6, que resulta em 300. Como tenho 300 reais na bolsa, comprarei as camisetas. Fim da imagem.
  1. 883 × 5 = _____
    PROFESSOR Exemplo de resposta: 4.500
  1. 521 × 4 = _____
    PROFESSOR Resposta: 2.000
  1. 393 × 8 = _____
    PROFESSOR Resposta: 3.200
  1. 431 × 6 =_____
    PROFESSOR Resposta: 2.400
MANUAL DO PROFESSOR

Objetivo

Calcular o quociente de divisões por meio de estimativas.

A divisão por meio de estimativas contribui para que os estudantes adquiram confiança em seus procedimentos, uma vez que os passos da resolução respeitam as habilidades próprias de cada estudante e a compreensão que ele apresenta do processo.

A estimativa também permite o controle da razoabilidade do resultado obtido em uma divisão. Antes da resolução das questões, acompanhe com os estudantes o processo de estimativa apresentado nas ilustrações.

Atividade 1

Observe se os estudantes apresentam dificuldade na realização das estimativas. Explique que nem todos os colegas podem ter obtido os mesmos quocientes. Peça a eles que procurem observar qual centena é mais próxima do valor exato.

Atividade 2

Nesta atividade, a estimativa é em relação ao produto aproximado. Se julgar necessário, oriente-os a procurar a aproximação da centena mais próxima.

BNCC em foco:

EF04MA06, EF04MA07

MP151

  1. Letícia pagará 20 prestações de 77 reais pelos móveis que comprou. Quanto ela pagará aproximadamente por essa compra?
PROFESSOR Exemplo de resposta: 1.600 reais.
  1. Uma instituição de acolhimento precisa arrecadar, no mínimo, 2.745 reais para pagar a reforma do telhado. Para isso, venderá 100 toalhas que foram confeccionadas por voluntários.

    Para arrecadar a quantia necessária, qual deve ser aproximadamente o valor de venda de cada toalha? Justifique sua resposta.

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes concluam que o valor seja mais próximo de 28 reais do que de 27 reais, apesar de 2.745 estar mais próximo de 2.700 que de 2.800. Fim da observação.
Imagem: Ilustração. Toalhas coloridas dobradas e empilhadas. Fim da imagem.
  1. Escreva um problema em que o cálculo aproximado de um quociente ou de um produto seja suficiente para resolvê-lo.

    _____

    PROFESSOR Respostas pessoais.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Retome as operações realizadas nesta página e na página anterior, efetuando as operações indicadas com o auxílio de uma calculadora. Compare os resultados com os valores estimados por você e verifique se os valores estão próximos.
PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Comente a importância das estimativas em situações do dia a dia. Caso observe que os estudantes têm dificuldade em fazer a estimativa pelo fato de os dois fatores apresentarem dois algarismos, lembre-os de que um deles é o zero.

Atividade 4

Nesta atividade, verifique se os estudantes percebem que um dos fatores (100) tem dois zeros.

Atividade 5

Após a realização desta atividade, cada estudante deverá fazer a revisão do enunciado do problema criado e reescrevê-lo, fazendo as correções necessárias. Depois, selecione alguns problemas e transcreva-os na lousa para a resolução da classe.

Atividade 6

Acompanhe a realização da conferência dos resultados com a calculadora. Os resultados próximos do valor exato mostrarão que as aproximações foram adequadas.

BNCC em foco:

EF04MA06, EF04MA07

MP152

Relação entre multiplicação e divisão

  1. Observe os vasos com flores e, depois, responda às questões.
Imagem: Ilustração. Vaso rosa com seis flores vermelhas. Em seguida, vaso azul com seis flores rosa. Ao lado, vaso vermelho com seis flores amarelas. Em seguida, vaso verde com seis flores vermelhas. À direita, vaso roxo com seis flores brancas. Fim da imagem.
  1. Quantas flores há no total? Nessa situação, que multiplicação tem como resultado o número total de flores? _____
    PROFESSOR Resposta: 30 flores; 5 × 6 = 30
  1. Podemos dizer que as 30 flores estão divididas igualmente entre 5 vasos. Nessa situação, que divisão tem como resultado o número de flores de cada vaso? _____
    PROFESSOR Resposta: 30 ÷ 5 = 6
  1. Podemos dizer, também, que as 30 flores estão distribuídas em vasos com 6 flores cada um. Nessa situação, que divisão tem como resultado o número de vasos? _____
    PROFESSOR Resposta: 30 ÷ 6 = 5
    • Observe que os números 5, 6 e 30 podem ser relacionados por meio de duas multiplicações e de duas divisões.

      5 × 6 = 30

      6 × 5 = 30

      30 ÷ 6 = 5

      30 ÷ 5 = 6

PROFESSOR Resposta: A multiplicação 6 × 5 = 30 não representa a situação da atividade, mas relaciona os números 5, 6 e 30.
  1. Escreva duas multiplicações e duas divisões usando somente os três números em cada caso, sem repeti-los.
Imagem: Ilustração. Papel com os números: 2, 5 e 10. Fim da imagem.
PROFESSOR Resposta: 2 × 5 = 10 e 5 × 2 = 10;
PROFESSOR 10 ÷ 2 = 5 e 10 ÷ 5 = 2
Imagem: Ilustração. Papel com os números: 18, 6 e 3. Fim da imagem.
PROFESSOR Resposta: 3 × 6 = 18 e 6 × 3 = 18;
PROFESSOR 18 ÷ 3 = 6 e 18 ÷ 6 = 3
Imagem: Ilustração. Papel com os números: 20, 4 e 5. Fim da imagem.
PROFESSOR Resposta: 4 × 5 = 20 e 5 × 4 = 20;
PROFESSOR 20 ÷ 4 = 5 e 20 ÷ 5 = 4
MANUAL DO PROFESSOR

Objetivo

Compreender a relação entre multiplicação e divisão.

As atividades destas páginas buscam explicitar a relação entre as operações de multiplicação e divisão, mas sem as definir formalmente como operações inversas. Essa relação será trabalhada por meio de várias experiências (cálculos) que os estudantes farão com números e também pela comparação de diferentes resoluções para um mesmo problema. Como a intenção é fazer com que desenvolvam habilidades para resolver, da maneira que julgarem mais adequada, problemas que envolvam diferentes operações aritméticas, o estudo da relação entre multiplicação e divisão – tanto no aspecto numérico quanto no de significação – contribuirá para ampliar seus recursos de cálculo.

Atividade 1

Comente que a situação pode ser interpretada segundo duas diferentes ideias relacionadas com a divisão. Na hipótese do item b, sugere-se que as 30 flores estão divididas igualmente entre cinco vasos e pede-se a divisão correspondente: 30 ÷ 5 = 6; a ideia, então, é a de repartir em partes iguais. Na hipótese do item c, sugere-se que as 30 flores estão distribuídas em vasos com seis flores cada um e pede-se novamente a divisão correspondente: 30 ÷ 6 = 5; a ideia aqui é a de quantas vezes cabe.

Atividade 2

Peça aos estudantes que relacionem os pares de multiplicações e divisões entre si segundo as ideias associadas a essas operações. Por exemplo, no item b, se pensarmos na ideia da divisão de repartir em partes iguais, a divisão18 ÷ 3 = 6 (18 está repartido em 3 partes iguais) está relacionada com a multiplicação 3 × 6 = 18 (3 grupos com 6 unidades cada um), enquanto a divisão 18 ÷ 6 = 3 (18 está repartido em 6 partes iguais) está relacionada com a multiplicação 6 × 3 = 18 (6 grupos com 3 unidades cada um). Se, contudo, pensarmos na ideia de quantas vezes cabe, a divisão 18 ÷ 3 = 6 (3 cabe 6 vezes em 18) está relacionada com a multiplicação 6 × 3 = 18 (6 grupos com 3 unidades são 18 unidades), enquanto a divisão 18 ÷ 6 = 3 (6 cabe 3 vezes em 18) está relacionada com a multiplicação 3 × 6 = 18 (3 grupos com 6 unidades são 18 unidades).

BNCC em foco:

EF04MA04

MP153

  1. Veja os cálculos que Juliana fez para conferir uma divisão.
Imagem: Ilustração. Juliana, mulher com cabelo ondulado fala: Eu precisava saber quantos grupos de 4 pessoas poderiam ser formados com 36 pessoas. Então, dividi 36 por 4 e obtive o resultado 9, ou seja, 9 grupos. Para saber se minha divisão estava certa, fiz 4 vezes 9 e obtive 36. Então, tive certeza de ter calculado corretamente. Atrás dela, lousa com as contas: 36 ÷ 4 = 9; 4 x 9 = 36. Fim da imagem.
  1. 48 ÷ 6 = 8
    PROFESSOR Resposta: Certa, pois: 6 × 8 = 48 ou 8 × 6 = 48
  1. 36 ÷ 5 = 4
    PROFESSOR Resposta: Errada, pois: 4 × 5 = 20 ou 5 × 4 = 20, e não é igual a 36
  1. 45 ÷ 9 = 5
    PROFESSOR Resposta: Certa, pois: 9 × 5 = 45 ou 5 × 9 = 45
  1. 27 ÷ 3 = 8
    PROFESSOR Resposta: Errada, pois: 3 × 8 = 24 ou 8 × 3 = 24, e não é igual a 27
  1. 64 ÷ 8 = 8
    PROFESSOR Resposta: Certa, pois: 8 × 8 = 64
  1. ) 1.000 ÷ 10 = 100
    PROFESSOR Resposta: Certa, pois: 10 × 100 = 1 000 ou 100 × 10 = 1.000

Imagem: Ícone: Calculadora. Fim da imagem.

  1. Responda às questões.
    1. Tânia apertou as seguintes teclas na calculadora: Ilustração. Teclas: 8, 4, ?, 4, =. , e no visor apareceu 21.

      Que operação Tânia fez?

      PROFESSOR Resposta: 84 ÷ 4 = 21

      Imagem: Ícone: Desenho ou pintura. Fim da imagem.

    1. Tendo no visor 21, desenhe as teclas que Tânia deve apertar para que volte a aparecer 84.
      PROFESSOR Exemplo de resposta/desenho: Ilustração. Teclas: x, 4, =.
  1. Descubra o número em que cada criança pensou e escreva-os.
Imagem: Ilustração. Leandro, jovem com cabelo preto e curto fala: Pensei em um número e, depois, o multipliquei por 7. O resultado foi 63. Na frente dele, Marisa, jovem com cabelo castanho e comprido diz: Pensei em um número e o dividi por 4. Obtive como resultado 25. Fim da imagem.
PROFESSOR Resposta: Leandro: 9; Marisa: 100.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Atividade 3

Explorando a relação entre multiplicação e divisão, esta atividade apresenta a possibilidade de usar a multiplicação na verificação do resultado de uma divisão.

Em um caminho inverso, pode-se perguntar aos estudantes: “Qual é a divisão exata que pode ser verificada por meio da multiplicação 7 × 13 = 91?” (91 ÷ 13 = 7 ou 91 ÷ 7 = 13).

Atividade 4

Para a resolução do item b, é possível que alguns estudantes pensem em usar uma adição para obter o resultado 84, no caso, adicionando 63. Se isso acontecer, proponha a eles que resolvam novamente, mas agora recorrendo a uma multiplicação para chegar ao valor desejado. Espera-se que percebam que, multiplicando 21 por 4, obtemos 84.

Atividade 5

Esta atividade propõe um desafio interessante para os estudantes, que devem perceber que é necessário realizar a operação inversa para descobrir o número em que cada criança pensou.

BNCC em foco:

EF04MA04, EF04MA13

MP154

Compreender problemas

Para resolver

Problema 1

Para preparar um churrasco, Marcos comprou 5 kg de linguiça, 3 kg de picanha e 2 kg de coração de frango, no açougue perto de sua casa.

Observe na tabela o preço de cada produto. Quanto Marcos gastou no total?

_____

PROFESSOR Resposta: 200 reais.

Tabela de preços

Tabela: equivalente textual a seguir.

Produto

Preço do quilograma

Asa de frango

11 reais

Linguiça

12 reais

Coração de frango

16 reais

Contrafilé

20 reais

Picanha

36 reais

Fonte: Tabela de preços do açougue (maio 2023).

Imagem: Ilustração. Um homem com boné e avental está segurando um instrumento sobre uma churrasqueira com carnes. Ao seu lado há um prato e um rolo de papel sobre uma mesa. Fim da imagem.

Problema 2

Um prédio tem 21 andares, e cada andar tem 4 apartamentos. Todos os apartamentos têm 3 dormitórios e são habitados por 4 pessoas cada um.

Quantas pessoas moram nesse prédio?

_____

PROFESSOR Resposta: 336 pessoas.
Imagem: Ilustração. Um prédio amarelo e alto. Ao fundo, mais prédios e árvores. Fim da imagem.

Problema 3

Um recém-nascido tem aproximadamente 300 ossos e, à medida que vai crescendo, alguns ossos se juntam, formando um só osso. Os adultos têm 206 ossos, dos quais 27 estão em cada mão.

Qual é o total de ossos das duas mãos de 15 adultos?

_____

PROFESSOR Resposta: 810 ossos.
Imagem: Ilustração. Um esqueleto humano. Fim da imagem.
MANUAL DO PROFESSOR

Objetivo

Resolver e elaborar problemas envolvendo multiplicação.

Nesta dupla de páginas, os problemas trabalham com excesso de dados. Eles devem distinguir os dados necessários para a resolução dos problemas. É importante perceberem que, para classificar o uso de um dado, precisam analisar com atenção a questão formulada no problema.

Incentive-os a inventarem novas perguntas para cada problema, de modo que os dados desnecessários passem a ser usados na resolução.

Para resolver

Problema 1

Em cada caso, é necessário multiplicar a quantidade de cada tipo de carne pelo respectivo preço do quilograma. Assim, as informações do preço da asa de frango e do contrafilé não são relevantes para a resolução do problema.

Problema 2

Para determinar a quantidade de pessoas que moram no prédio, os estudantes precisam saber quantas pessoas moram em cada apartamento, quantos apartamentos há em cada andar e quantos andares tem o prédio. Não é necessário saber quantos dormitórios cada apartamento tem.

Problema 3

A quantidade de ossos em um adulto e em um recém-nascido é irrelevante para a resolução do problema. A informação necessária é somente a quantidade de ossos das mãos de um adulto para definir a quantidade de ossos das mãos de 15 adultos.

BNCC em foco:

EF04MA06

MP155

Para refletir

Imagem: Ícone: Oral. Fim da imagem.

1. Quais dados são necessários para responder à questão do Problema 1.

PROFESSOR Resposta: A massa da linguiça, da picanha e do coração de frango que Marcos comprou e o preço do quilograma da linguiça, da picanha e do coração de frango.
  1. Observe os cálculos registrados abaixo.

    5 × 12

    3 × 36

    2 × 16

    5 + 3 + 2

    2 × 20

    60 + 108 + 32

    3 × 11

    Quais dos cálculos acima são necessários para resolver o Problema 1? Circule-os.

    PROFESSOR Respostas corretas: 5 × 12, 3 × 36, 2 × 16, 60 + 108 + 32

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Você usou todos os dados do Problema 2 para resolvê-lo? Converse com um colega e verifiquem se há dados desnecessários no enunciado.
    PROFESSOR Resposta: Não.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que o dado desnecessário é o número de dormitórios que cada apartamento tem. Fim da observação.
  1. A professora Teresa pediu aos estudantes dela que reescrevessem o Problema 3 de modo que só permanecessem as informações necessárias para resolvê-lo. Veja como ficaram os enunciados de Joaquim e de Lucas.
    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que Joaquim apresentou um enunciado adequado. Fim da observação.
Imagem: Ilustração. Papel verde com o texto: Joaquim - Quando uma pessoa é adulta, tem 27 ossos em cada mão. Se contarmos os ossos das duas mãos de 15 adultos, quantos ossos serão? Fim da imagem.
Imagem: Ilustração. Papel amarelo com o texto: Lucas - Um recém-nascido tem aproximadamente 300 ossos e, à medida que vai crescendo, alguns ossos se juntam, formando um só osso. Se contarmos os ossos das duas mãos de 15 adultos, quantos ossos serão? Fim da imagem.
PROFESSOR Resposta: Lucas deixou uma informação desnecessária (um recém-nascido tem 300 ossos) e omitiu uma informação importante (um adulto tem 27 ossos em cada mão).

Imagem: Ícone: Oral. Fim da imagem.

Qual desses novos enunciados está adequado ao pedido da professora? Explique sua escolha.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Reúna-se com um colega e façam o que se pede.
    1. Inventem outros dados para o Problema 1 de modo que todas as informações da tabela sejam utilizadas para responder à questão do problema.
      PROFESSOR Exemplo de resposta: “Marcos comprou também 2 kg de asa de frango e 5 kg de contrafilé” (2 × 11 = 22; 5 × 20 = 100; Marcos gastou no total 322 reais, pois já tinha gastado 200 reais e agora gastou mais 122 reais).
    1. Com base nos dados do Problema 2, inventem outra questão de modo que a informação do número de dormitórios seja necessária.
      PROFESSOR Exemplo de resposta: “Quantos dormitórios há, no total, em cada andar do prédio?” (4 × 3 = 12; 12 dormitórios).
    1. Criem uma questão com base nos dados do Problema 3 de modo que a informação do número de ossos de um recém-nascido e a de um adulto sejam necessárias.
      PROFESSOR Exemplo de resposta: “Quantos ossos um recém-nascido tem a mais que um adulto?” (300 − 206 = 94; 94 ossos).
MANUAL DO PROFESSOR

Para refletir

Atividade 2

Esta atividade permite que os estudantes reflitam sobre o significado das operações apresentadas no contexto do problema, de modo que decidam quais delas correspondem à resolução da situação apresentada.

Um aspecto interessante é que as quatro operações necessárias para determinar o total que Marcos gastou estão separadas em diferentes quadros, o que torna a questão diferente do modelo comum de estabelecer alternativas em que a solução completa se encontra em apenas uma delas.

Atividade 5

A proposta da atividade é incentivar os estudantes a criarem uma nova pergunta para cada problema, de modo que o dado antes desnecessário se torne importante para a resolução. Essa ação exige a compreensão do motivo que fazia o dado ser desnecessário na situação anterior.

Para o problema 2, por exemplo, os estudantes podem perguntar: “Quantos dormitórios há nesse prédio?”, aproveitando a informação (desnecessária para a resolução da questão original) de que cada apartamento do prédio tem 3 dormitórios. Nesse caso, espera-se que façam 21 × 4 × 3 = 252 e respondam que no prédio há 252 dormitórios no total.

BNCC em foco:

EF04MA06

MP156

A Matemática me ajuda a ser

... uma pessoa que valoriza e respeita a cultura dos povos indígenas

Leia o relato abaixo, que descreve a Matemática usada por crianças da Escola do Diaurum, localizada no Parque Indígena do Xingu, no estado de Mato Grosso.

[...] Wenhoron Suyá nos avisa que há uma cerimônia de timbó perto da aldeia suyá. Ele convida Tarinu e outros colegas da escola para participar do evento. O grupo parte em seguida, levando consigo um carregamento de lanças, flechas, cestas, peneiras e farinha de mandioca. [...] A viagem foi um sucesso. O peixe é distribuído pelos Suyá a todos aqueles que vieram ao porto. [...]

[...] No dia seguinte, Wenhoron Suyá apresentou os números que ele coletou durante a expedição para os colegas de classe. Ele havia contado os peixes cuidadosamente (57 grandes, 98 médios e 168 pequenos). A partir dessas informações, vários [problemas] foram criados, com o intuito de praticar as quatro operações. [...]

[...] O primeiro [problema] a que nos dedicamos foi:

Ontem à noite peguei 10 peixes. Dei 3 para meu irmão. Quantos peixes tenho agora?

Tarinu Juruna explicou seu raciocínio:

“Fiquei com 13 peixes porque, quando eu dou alguma coisa para meu irmão, ele me paga de volta em dobro”.

Robtokti Suyá também obteve 13 como resposta:

“Eu dei 3 peixes para meu irmão, então 10 mais 3 é igual a 13”. [...]

“Quando os Suyá dão alguma coisa para alguém, isso não quer dizer que a gente fica com menos.” [...]

FERREIRA, Mariana Kawall Leal (org.). Ideias matemáticas de povos culturalmente distintos. São Paulo: Global, 2002. (Série Antropologia e educação). p. 55-56.

Imagem: Fotografia. Vista aérea de uma floresta. No centro há uma área com ocas em círculo. Ao fundo, um lago. Fim da imagem.

LEGENDA: Parque Indígena do Xingu, município de Querência, Mato Grosso, em 2018. FIM DA LEGENDA.

MANUAL DO PROFESSOR

Objetivo

Resolver problemas com números naturais envolvendo adição.

A Matemática dos povos indígenas é tema de estudo de diferentes pesquisadores da área de Educação Matemática. O texto selecionado para essa seção permite aos estudantes o contato com outras maneiras de pensar.

Leia em voz alta cada um dos trechos, para que os estudantes não se intimidem ao tentarem ler nomes diferentes dos usuais.

A valorização da Matemática produzida por diferentes culturas é importante para que os estudantes compreendam que esse é um saber que também pode ser estruturado “fora da escola”, sendo reinventado ao adquirir novos significados para quem dele se utiliza.

Complemente o texto sugerindo aos estudantes que se reúnam em grupos e façam pesquisas abordando a Matemática envolvida nas pinturas e no artesanato indígenas. Essas pesquisas permitirão que o professor trabalhe, por exemplo, com simetrias, ângulos e outros conceitos geométricos. Um modo interessante de conduzir a pesquisa é sugerir a cada grupo que pesquise um tema, como: artesanato, calendários (registro do tempo) ou trocas de produtos, para que se obtenham diversas informações, as quais podem ser apresentadas em mural ou painel para outras turmas.

BNCC em foco:

EF04MA03; competência geral 1; competência específica 1

MP157

Tome nota

Imagem: Ícone: Oral. Fim da imagem.
  1. Em que lugar se passam os acontecimentos relatados?
    PROFESSOR Resposta: No Parque Indígena do Xingu, no município de Querência, Mato Grosso.
  1. Quem são Wenhoron Suyá, Tarinu Juruna e Robtokti Suyá?

    _____

    PROFESSOR Resposta: Crianças indígenas.
  1. Quantos peixes, ao todo, foram pescados? _____
    PROFESSOR Resposta: 323 peixes.

Reflita

  1. Qual resultado é esperado para o problema relatado no texto usando nossa maneira de raciocinar? _____
    PROFESSOR Resposta: 7 peixes.
  1. Qual das histórias em quadrinhos representa o raciocínio usado por Tarinu na resolução do problema relatado no texto? _____
    PROFESSOR Resposta: b

a)

Imagem: Ilustração. À esquerda, um dia... um homem com cabelo encaracolado segura uma bandeja com peixes com a mão direita e com a mão esquerda estendida, ele segura três peixes. Na frente dele, um homem calvo está com as mãos estendidas. À direita, outro dia... o homem com cabelo encaracolado está sorrindo com as mãos estendidas. Na frente dele, o homem calvo está segurando três peixes. Fim da imagem.

b)

Imagem: Ilustração. À esquerda, um dia... um homem com cabelo encaracolado segura uma bandeja com peixes com a mão direita e com a mão esquerda estendida, ele segura três peixes. Na frente dele, um homem calvo está com as mãos estendidas. À direita, outro dia... o homem com cabelo encaracolado está sorrindo e segurando três peixes com a mão esquerda estendida. Na frente dele, o homem calvo está segurando três peixes com a mão esquerda e com a mão direita estendida. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Debata com seus colegas.
    PROFESSOR Respostas pessoais.
    1. O que você entende da afirmação de Robtokti Suyá: “Quando os Suyá dão alguma coisa para alguém, isto não quer dizer que a gente fica com menos”.
    1. Quando você dá alguma coisa para uma pessoa, você espera receber algo em troca?
MANUAL DO PROFESSOR

Tome nota

Se julgar oportuno, faça outras perguntas, como: “Wenhoron Suyá contou quantos peixes médios há a mais que peixes grandes? Quantos peixes pequenos foram contados a mais que médios? Quantos peixes ele ainda precisaria contar para obter 400 peixes?”. Espera-se que respondam 41, 70 e 77, respectivamente.

Reflita

O objetivo destas atividades é promover uma discussão sobre as diferentes maneiras de pensar e resolver um mesmo problema em culturas diferentes, o que não deve passar por questões de julgamento, de “certo” ou “errado”.

No item a da questão 3, que promove a discussão sobre a afirmação de Robtokti Suyá, “Quando os Suyá dão alguma coisa para alguém, isso não quer dizer que a gente fica com menos”, espera-se que os estudantes compreendam que essa afirmação não representa uma situação matemática, mas um modo de se relacionar com o outro, em que se valoriza a solidariedade, a amizade.

Aproveite para discutir a diferença dessa opinião de Robtokti Suyá em relação aos valores de nossa sociedade, com o objetivo de mostrar a diversidade de opiniões e de costumes. A questão do item b permite a discussão a respeito de solidariedade.

BNCC em foco:

EF04MA03; competência geral 1; competência específica 1

MP158

Compreender informações

Possibilidades

  1. Na escola em que Ana estuda, estão rifando uma bicicleta. A rifa tem 100 números, mas somente um será sorteado. Ana comprou 3 números dessa rifa, e Adriano, 4 números.
Imagem: Ilustração. Uma bicicleta amarela e vermelha. Fim da imagem.
  1. Há quantas possibilidades de sorteio nessa rifa?

    _____

    PROFESSOR Resposta: 100 possibilidades.
  1. Se Ana comprou 3 números, quantas possibilidades ela tem de ser sorteada?

    _____

    PROFESSOR Resposta: 3 possibilidades.
  1. Quantas possibilidades Adriano tem de ser sorteado?

    _____

    PROFESSOR Resposta: 4 possibilidades.
  1. Quem tem mais chance de ser sorteado, Ana ou Adriano? Justifique sua resposta.

    _____

    PROFESSOR Resposta: Adriano tem mais chance, pois 4 possibilidades é maior que 3 possibilidades.
  1. Uma pessoa que comprou 1 número dessa rifa terá mais ou menos chance de ser sorteada que Ana? Por quê?

    _____

    PROFESSOR Resposta: Terá menos chance, pois 1 possibilidade é menor que 3 possibilidades.
  1. Quantos números deveriam ser comprados para que se tenha certeza de ganhar a bicicleta? Justifique sua resposta.

    _____

    PROFESSOR Resposta: 100 números, pois para ter certeza é necessário ter todas as possibilidades de ser sorteado.
MANUAL DO PROFESSOR

Objetivo

Identificar em um experimento aleatório eventos que têm maiores chances de ocorrência.

O objetivo das atividades destas páginas é ampliar o conhecimento dos estudantes na compreensão da noção de probabilidade.

Atividade 1

Se possível, retrate a situação na sala de aula, para que os estudantes a vivenciem, dando mais significado ao aprendizado.

No item a, os estudantes devem compreender que qualquer dos 100 números pode ser sorteado, ou seja, ao todo há 100 resultados possíveis (100 possibilidades). Discuta com eles que, embora saibamos todos os resultados possíveis de sorteio, não podemos afirmar com certeza que número será sorteado nem quem será contemplado.

No item b, como Ana tem 3 desses 100 números, ela tem 3 possibilidades (em 100) de ganhar a bicicleta.

No item c, como Adriano tem 4 desses 100 números, ele tem 4 possibilidades em 100 de ser contemplado, 1 possibilidade a mais que Ana.

Nos itens d e e, os estudantes devem avaliar quem tem maior chance de ganhar a bicicleta: 3 em 100, 4 em 100 ou 1 em 100. Espera-se que reconheçam que a pessoa que tem a maior quantidade de números é a mais provável de ser contemplada. Discuta com eles o fato de que, se um evento tem maior chance de ocorrência, não significa que ele ocorrerá.

No item f, espera-se que os estudantes percebam que, para afirmar com certeza que certa pessoa ganhará a bicicleta, só há uma possibilidade: se ela tiver todos os números (evento certo), ou seja, 100 em 100.

BNCC em foco:

EF04MA26

MP159

  1. Raquel esqueceu a senha de sua conta bancária, que é composta de quatro dígitos. Ela lembra apenas que a senha é formada pelos números 6, 7, 8 e 9, mas não lembra a ordem em que eles devem ser digitados.
Imagem: Ilustração. Uma mulher com cabelo preso está na frente de uma caixa eletrônico. Fim da imagem.
  1. Complete a lista a seguir com as possibilidades de senha da conta bancária de Raquel.

    6.789, 7.689, 8.679, 9.678

    6.798, 7.698, 8.697, 9.687

    6.879, 7.869, 8.769, 9.768

    6.897, 7.896, 8.796, _____

    PROFESSOR Resposta: 9.786

    6.978, 7.968, _____, _____

    PROFESSOR Resposta: 8.967, 9.867

    6.987, 7.986, _____, _____

    PROFESSOR Resposta: 8.976, 9.876
  1. Há quantas possibilidades de formar a senha bancária com esses 4 números?

    _____

    PROFESSOR Resposta: 24 possibilidades.
  1. Se Raquel lembrar o primeiro número de sua senha, a chance de ela digitar a senha correta será maior ou menor? Justifique sua resposta.

    _____

    PROFESSOR Resposta: Maior, pois será uma possibilidade de senha correta em seis possibilidades totais.
  1. Raquel só pode digitar a senha incorreta em duas tentativas, pois na terceira digitação incorreta o cartão será bloqueado e ela não poderá movimentar sua conta. Se ela lembrar os dois primeiros números de sua senha, conseguirá movimentar a conta? Converse com o professor e os colegas.

    _____

    PROFESSOR Resposta: Sim, pois ela terá duas opções de senha e poderá digitar a senha incorreta uma única vez, sem bloquear seu cartão.
MANUAL DO PROFESSOR

Atividade 2

Inicialmente, na lousa, proponha aos estudantes que façam uma lista com as possibilidades de senhas a serem formadas com 6, 7, 8 e 9. Dê um tempo e verifique as estratégias que eles utilizam e se discutem entre si.

Apresente a lista do item a e peça que a completem. Peça que comparem a maneira de compor a lista no livro com sua própria lista e que observem similaridades e diferenças nos procedimentos utilizados.

Em uma roda de conversa, discuta com eles sobre a importância de escolher um método ao se fazer uma contagem com várias possibilidades. A organização das informações é importante para que não se repita ou que se esqueça de alguma dessas possibilidades.

No item b, peça aos estudantes que indiquem uma operação que possa representar a contagem que fizeram. Espera-se que surja alguma das multiplicações: 4 × 6 = 24 ou 6 × 4 = 24. No entanto, outros procedimentos devem também ser aceitos, como: 6 + 6 + 6 + 6 = 24.

No item c, explique que o fato de já se saber o primeiro número da senha correta exclui as demais senhas que não iniciem por esse número, reduzindo a quantidade de senhas possíveis, no caso, de 24 para 6 possibilidades. Por isso, a chance de ela digitar a senha correta na primeira tentativa é maior: vai de 1 em 24 para 1 em 6.

No item d, seguindo o mesmo raciocínio do item c, o fato de Raquel lembrar os dois primeiros números da senha correta reduz a quantidade de possibilidades para 2 senhas, o que garante que ela conseguirá digitar a senha correta com 2 tentativas. Espera-se que os estudantes observem que na lista que completaram no livro há apenas duas senhas de cada tipo que têm os dois primeiros números iguais.

Aproveite a atividade 2 e discuta com os estudantes a importância de escolher senhas seguras. Disponível em: http://fdnc.io/eUb. Acesso em: 11 jun. 2021.

Um guia mostra como criar e manter uma boa senha e também os principais riscos envolvidos em uma conta comprometida.

BNCC em foco:

EF04MA26

MP160

O que você aprendeu

  1. João fez dois mosaicos em uma malha quadriculada, mas acabou derrubando tinta branca em cima deles e manchou os dois.

Mosaico 1

Imagem: Ilustração. Retângulo com dez colunas e sete fileiras de quadradinhos coloridos. No centro há uma mancha branca. Fim da imagem.

Mosaico 2

Imagem: Ilustração. Retângulo com sete colunas e seis fileiras de quadradinhos coloridos. No centro há uma mancha branca. Fim da imagem.
  1. Quantos quadradinhos tinha o mosaico 1 antes de manchar?

    _____

    PROFESSOR Resposta: 70 quadradinhos.
  1. E o mosaico 2? _____
    PROFESSOR Resposta: 42 quadradinhos.
  1. Quantos quadradinhos o mosaico 1 tinha a mais que o mosaico 2?

    _____

    PROFESSOR Resposta: 28 quadradinhos.
  1. Em uma festa, todos os convidados beberam a mesma quantidade de copos de suco. Se Sílvia serviu 24 copos de suco para 12 convidados, quantos copos de suco ela serviu para outros 18 convidados? _____
    PROFESSOR Resposta: 36 copos de suco.

    3. Leia o que as meninas disseram e responda às questões.

Imagem: Ilustração. Sandra, menina com cabelo preso fala: Primeiro calculei 4 vezes 40 e, depois, calculei 4 vezes 3. Em seguida, adicionei os dois resultados. Na frente dela, Taís, menina com cabelo preto diz: Eu fiz primeiro 4 vezes 30 e, depois, 4 vezes 4. Então, adicionei os dois resultados. Fim da imagem.
  1. Invente um problema que possa ser resolvido por meio da multiplicação 13 × 15.

    Depois, peça a um colega que o resolva.

    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização dos conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

Atividade 1

A disposição retangular favorece a contagem dos quadradinhos nos mosaicos. No mosaico 1, tanto a multiplicação 7 × 10 como a 10 × 7 levam ao total de 70 quadradinhos.

No mosaico 2, tanto a multiplicação 6 × 7 como a 7 × 6 levam ao total de 42 quadradinhos.

Atividade 2

Espera-se nessa atividade que o estudante perceba que, se Sílvia serviu 24 copos de suco para 12 convidados, cada convidado bebeu 2 copos de suco (24 ÷ 12 = 2, ou 12 × 2 = 24).

Então, mantendo a mesma proporção, 18 × 2 = 36 copos de suco.

Atividade 3

Acompanhe as atividades criadas e verifique se satisfazem a condição exigida. Depois, valide a resolução de algumas delas.

Espera-se que o estudante perceba que, pela decomposição, o cálculo 34 × 4 pode ser realizado assim: 30 × 4 + 4 × 4 = 120 + 16 = 136.

Atividade 4

Explore com os estudantes as ideias da multiplicação envolvidas na elaboração do problema e verifique as estratégias de cálculo utilizadas para resolvê-lo.

BNCC em foco:

EF04MA06, EF04MA07

MP161

Imagem: Ícone: mental. Fim da imagem.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Faça estimativas e escreva um resultado aproximado para cada operação. Depois, compare seus resultados com os de um colega.
  1. 8 × 32
    PROFESSOR Resposta: Exemplo de estimativa: 240
  1. 15 × 31
    PROFESSOR Resposta: 450
  1. 238 ÷ 12
    PROFESSOR Resposta: 20
  1. 438 ÷ 11
    PROFESSOR Resposta: 40

Imagem: Ícone: Oral. Fim da imagem.

  1. André afirmou que 3 latinhas de 355 mL têm a mesma capacidade que uma garrafa de 1 L. André está certo? Por quê?
    PROFESSOR Resposta: André está errado, porque a capacidade de 3 latinhas é 1.065 mL, que é mais que 1 litro.
Imagem: Ilustração. André, menino com cabelo castanho-escuro e curto segura uma latinha sobre uma mesa, ao lado de uma garrafa e fala: Lembre-se de que 1 L é o mesmo que 1.000 mL. Fim da imagem.
  1. Complete o quadro e depois responda às questões.

Quadro: equivalente textual a seguir.

Fatores

Produto

11 e 13

_____

12 e 12

_____

15 e 17

_____

16 e 16

_____

PROFESSOR Resposta: 143, 144, 255, 256
  1. Comparando o resultado de 11 × 13 com o resultado de 12 × 12, o que você observa?

    _____

    PROFESSOR Resposta: A diferença dos produtos é 1.
  1. E o que você observa ao comparar o resultado de 15 × 17 com o de 16 × 16?

    _____

    PROFESSOR Atenção professor: Espera-se que os estudantes percebam que a diferença nos dois casos é 1 unidade. Fim da observação.

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 5

Incentive os estudantes a realizarem a divisão em cada caso por meio de estimativas, para que também desenvolvam habilidades de cálculo mental e comparem os resultados obtidos com cada método. Trabalhar com ambos os métodos possibilita estabelecer relações entre eles, e o repertório adquirido com o cálculo por estimativas auxilia no cálculo por meio do algoritmo usual.

Atividade 6

Nesta atividade, os estudantes podem observar a diferença entre o valor exato (1 L = 1 000 mL) e um valor correspondente a 3 latas de 355 mL. Nesse caso, o valor exato ultrapassa o valor aproximado em 65 mL, pois 3 vezes 355 mL são 1 065 mL, enquanto 1 L = 1 000 mL. Esclareça aos estudantes que, em algumas situações, a aproximação é suficiente como estimativa do valor exato, mas, em outras situações, a diferença entre a aproximação e o valor exato pode não ser aceitável.

Atividade 7

Espera-se que os estudantes percebam que a diferença nos dois casos é de 1 unidade.

Autoavaliação

Ao final da Unidade, é importante que os os estudantes compreendam os procedimentos de cálculos (evitando que os façam mecanicamente). Além disso, a compreensão da relação entre a multiplicação e a divisão ampliará o repertório operatório do estudante.

BNCC em foco:

EF04MA06, EF04MA07

MP162

Comentários para o professor:

Conclusão da Unidade 4

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Utiliza as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo?

_____

_____

Utiliza as propriedades das operações para desenvolver estratégias de cálculo?

_____

_____

Resolve e elabora problemas envolvendo diferentes significados da multiplicação empregando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos, com ou sem apoio da reta numérica?

_____

_____

Resolve e elabora problemas de divisão cujo divisor tenha no máximo dois algarismos, envolvendo diferentes significados de repartição equitativa e de medida empregando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos?

_____

_____

Identifica regularidades em sequências numéricas compostas por múltiplos de um número natural?

_____

_____

Reconhece, por meio de investigações, grupos de números naturais para os quais as divisões por determinado número resultam em restos iguais, identificando regularidades?

_____

_____

Reconhece, por meio de investigações com a calculadora, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas?

_____

_____

Identifica, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____

MP163

Sugestão de ficha de autoavaliação do estudante

O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.

Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.

Tabela: equivalente textual a seguir.

Autoavaliação

Nome:

Marque um X em sua resposta para cada pergunta.

Sim

Mais ou menos

Não

1. Presto atenção nas aulas?

_____

_____

_____

2. Pergunto ao professor quando não entendo?

_____

_____

_____

3. Sou participativo?

_____

_____

_____

4. Respeito meus colegas e procuro ajudá-los?

_____

_____

_____

5. Sou educado?

_____

_____

_____

6. Faço todas as atividades com capricho?

_____

_____

_____

7. Trago o material escolar necessário e cuido bem dele?

_____

_____

_____

8. Cuido dos materiais e do espaço físico da escola?

_____

_____

_____

9. Gosto de trabalhar em grupo?

_____

_____

_____

10. Respeito todos os meus colegas de turma, professores e funcionários?

_____

_____

_____