MP164
Comentários para o professor:
Introdução da Unidade 5
A abertura da Unidade apresenta uma cena em que a família limpa e organiza uma sala cujo espaço deve ser dimensionado para um bom aproveitamento do ambiente. Assim, questões como quantas estantes cabem ao longo de uma parede, ou qual é a altura da sala, permitem praticar cálculos de estimativa de medidas de comprimento e de área, além de explorar outros conteúdos trabalhados na Unidade.
Nesta Unidade, predominam atividades que exploram habilidades da Unidade Temática Grandezas e medidas, com foco em medidas e estimativas de comprimentos (incluindo perímetros), massas e capacidades, utilizando unidades de medidas padronizadas mais usuais.
O trabalho com medidas de comprimento realizado nos primeiros anos do Ensino Fundamental (em destaque, as atividades de medições utilizando as unidades de medida não padronizadas) será fundamental para o desenvolvimento dos conceitos tratados no 4º ano.
Inicia-se, neste ano, de forma mais sistematizada, a exploração da grandeza superfície. No 4º ano, são apresentadas atividades de medição, comparação e estimativa de áreas de figuras planas desenhadas em malha quadriculada, pela contagem de quadradinhos ou metade de quadradinho, reconhecendo que duas figuras com formatos diferentes podem ter a mesma medida de área. Essa abordagem será fundamental para a resolução de problemas envolvendo unidade de medida de área e recorrendo a transformações entre as unidades mais usuais em contextos socioculturais que serão exploradas no 5º ano.
Da mesma forma, nesta Unidade serão apresentadas situações envolvendo a grandeza temperatura, explorando contextos locais que utilizam a unidade de medida grau Celsius (° C), a comparação das temperaturas locais e de outras regiões e as temperaturas mínima e máxima de uma cidade. Esses conhecimentos também serão necessários no 5º ano, para a resolução de problemas envolvendo unidade de medida de temperatura.
Algumas atividades propostas propiciam o desenvolvimento de habilidades da Unidade Temática Probabilidade e estatística, na leitura e na elaboração de gráfico de colunas com as variações diárias de temperatura e na análise de dados apresentados em gráficos pictóricos.
Cada página deste livro propõe um novo desafio ao professor e aos estudantes. As variáveis são muitas: dos conteúdos às habilidades e objetivos de aprendizagem.
8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.
Sugestão de roteiro de aula
Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.
Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção Compreender problemas desta Unidade.
Roteiro de aula – Compreender problemas 1 ª parte – Introdução – Tempo sugerido: 25 minutos
Inicie uma conversa com a turma fazendo uma pergunta e um desdobramento dela:
• O que é um problema?
• Um problema e um exercício têm o mesmo significado?
Para marcar o foco da aula, registre na lousa a pergunta: “O que é um problema?”.
Passe a palavra para os estudantes e ouça com atenção as suas falas. Avalie a conveniência de registrar ou não, na lousa, algumas palavras-chave de possíveis respostas.
Após ouvir os estudantes, conduza a discussão para o entendimento que, de maneira geral, um problema existe quando propõe uma situação que gera uma dificuldade por insuficiência dos conhecimentos imediatos diante de um desafio. Um problema exige uma busca de estratégias que torne possível sua solução.
MP165
Um exercício pressupõe o conhecimento da teoria ou do assunto de que ele trata, a sua dificuldade é capilar, pode ficar restrita a algum detalhe que o diferencia de outros exercícios conhecidos. Por isso problema e exercício não têm o mesmo significado.
Registre na lousa outra pergunta:
• De início, o que é necessário para resolver um problema?
Novamente, após a manifestação dos estudantes, conduza a discussão para uma resposta um tanto óbvia: a primeira coisa necessária para resolver um problema é saber qual é o problema.
A seguir, proponha como sugestão alguns passos, com base nos ensinamentos de George Polya, que orientam a resolução de problemas. Convém registrar esses passos previamente em um cartaz para que eles fiquem disponíveis para as aulas futuras.
1) Compreender o enunciado do problema.
• O que o problema informa?
• O que o problema pergunta?
2) Planejar a resolução.
• Fazer um plano de resolução usando os conhecimentos sobre o assunto do problema.
3) Resolver o problema, isto é, realizar o plano de resolução.
4) Verificar a solução: confirmar se o resultado obtido está de acordo com os dados do problema.
Esclareça que essa é uma sugestão de abordagem que será assimilada aos poucos, conforme os estudantes forem resolvendo vários problemas.
Diga, então, que vamos ler as atividades propostas neste item do livro tentando, se possível, seguir os passos acima.
2 ª parte – Problema 1 – Tempo sugerido: 10 minutos
Leia com a classe o enunciado do problema 1. Peça a ajuda dos estudantes para escrever na lousa os passos de resolução sugeridos.
1. Dados do problema: Valdeci trabalha 7 dias e descansa 4. Iniciou o descanso em 27 de junho e reiniciou o trabalho em 1 º de julho.
Pergunta: Qual é o salário mensal de Valdeci?
2. Plano de resolução: procurar a relação entre os dias trabalhados e descansados com o salário.
3. Realizar o plano: Não é possível porque o enunciado não informa essa relação.
4. Verificação: Não há o que verificar.
Cada um desses passos tem sua importância. Diga que esse é apenas um auxílio para a resolução. Não é uma receita que fará o estudante acertar todos os exercícios.
A seguir, proponha um acréscimo ao enunciado do problema 1: Valdeci recebe 300 reais por dia trabalhado. Quanto recebeu em um mês em que trabalhou 21 dias?
Nova resolução na lousa.
1. Dados do problema: Valdeci trabalha 7 dias e descansa 4. Iniciou o descanso em 27 de junho, reiniciou o trabalho em 1 º de julho; recebe 300 reais por dia trabalhado.
Pergunta: Quanto recebeu por 21 dias trabalhados?
2. Plano de resolução: multiplicar 300 por 21.
3. Realizar o plano: 21 × 300 = 6.300
4. Verificação: 6.300 ÷ 21 = 300
Resposta: Valdeci recebeu 6.300 reais pelos 21 dias trabalhados.
3 ª parte – Problemas 2 e 3 e Para refletir – Tempo sugerido: 30 minutos
Solicite aos estudantes que, em duplas, resolvam os problemas 2 e 3 e que, depois, respondam às questões da seção Para refletir...
Acompanhe a resolução atendendo a eventuais dúvidas. Reserve 5 minutos para a validação dos problemas e das questões do Para refletir.
MP166
UNIDADE 5. Grandezas e medidas
Boxe Complementar
Para refletir...
Estime quantas estantes iguais à da cena é possível colocar entre a estante branca e o quadro de moldura amarela.
_____
PROFESSOR
Resposta: É possível colocar mais duas estantes.Quantos quadros brancos cabem na altura da parede?
_____
PROFESSOR
Resposta: Cabem dois quadros brancos.Se o quadro branco tem 1 m de altura por 80 cm de largura, então quais são as medidas da altura e da largura, aproximadamente, da parede vermelha?
_____
PROFESSOR
Resposta: 2 metros de altura e 480 centímetros de largura.Fim do Complemento
MANUAL DO PROFESSOR
Objetivos da Unidade
Medir comprimentos com unidades de medida padronizadas e não padronizadas.
Relacionar as unidades de medida de comprimento: quilômetro, metro, centímetro e milímetro.
Calcular o perímetro de uma figura plana.
Compreender a ideia de área.
Calcular a área de figuras planas representadas em malha quadriculada.
Empregar adequadamente a unidade de medida em centímetro quadrado.
Reconhecer que há problemas que não têm dados suficientes para serem resolvidos.
Construir e interpretar gráficos pictóricos.
Para refletir...
E sta cena de abertura apresenta um ambiente em que podem ser observados alguns brinquedos dentro de caixas e jogos em uma estante, que permitem explorar conteúdos trabalhados nesta Unidade.
Aproveite o contexto para trabalhar com a turma a habilidade de estimativa de medidas de comprimento.
Sugira aos estudantes que estimem a altura de um colega. Depois, com uma fita métrica ou uma trena, ajude-os a medir a altura dos colegas e verificar se as estimativas que fizeram estavam próximas das medidas reais.
Nesta seção, a ideia de área é abordada em uma situação em que, a partir das informações da altura e da largura do quadro branco, os estudantes poderão estimar a altura e a largura da parede vermelha. Remete-se, assim, à comparação entre medidas de superfícies.
Chame a atenção para a disposição das peças, de modo que os estudantes percebam a possibilidade de obter a quantidade de peças que podem ser colocadas por meio de raciocínio multiplicativo.
BNCC em foco:
EF04MA04, EF04MA20, EF04MA21, EF04MA22, EF04MA23, EF04MA24, EF04MA27
MP167

MANUAL DO PROFESSOR
Sugestão de atividade
Pesquisa
Sugira aos estudantes que, reunidos em grupos, pesquisem, em livros ou na internet, a origem e a história das medidas de comprimento. Depois, oriente-os a apresentarem os resultados dessa pesquisa para a classe.
MP168
Medidas de comprimento
Metro, centímetro e milímetro
- Pedro é mestre de obras e, em seu trabalho, faz muitas medições. Observe as imagens e complete.
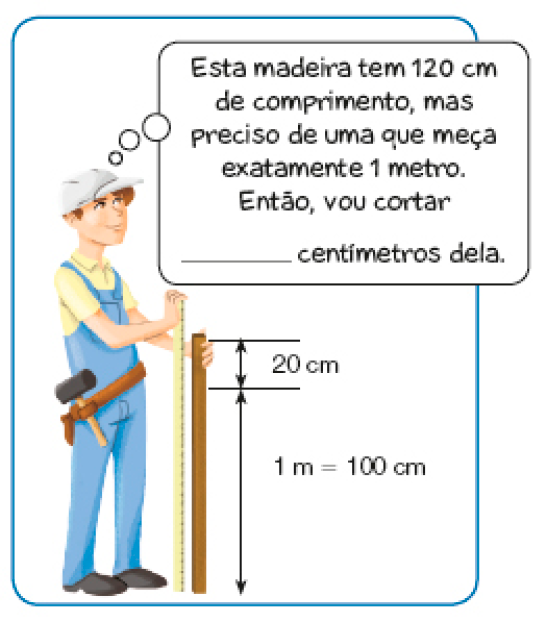
PROFESSOR
Resposta: 20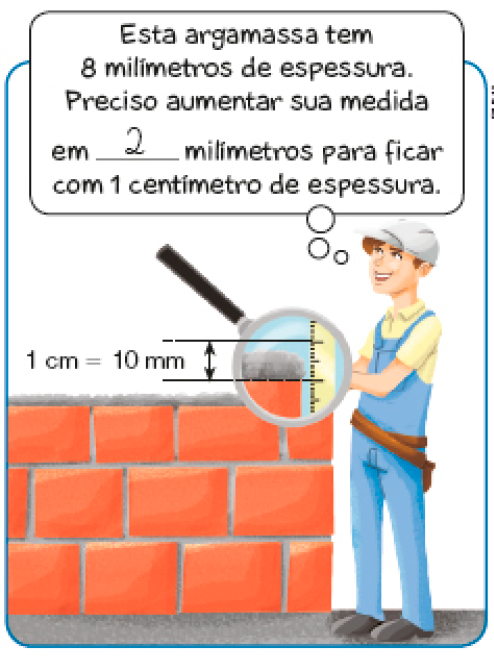
O metro, o centímetro e o milímetro são unidades usadas para medir _____.
PROFESSOR
Resposta: comprimentosUm metro corresponde a _____ centímetros.
PROFESSOR
Resposta: 100Um centímetro corresponde a _____ milímetros.
PROFESSOR
Resposta: 10_____ cm = 1 m
PROFESSOR
Resposta: 1001 cm = _____ mm
PROFESSOR
Resposta: 10Indicamos:
• 1 metro por 1 m
• 1 centímetro por 1 cm
• 1 milímetro por 1 mm
- Escreva o nome de um objeto cujo comprimento meça, aproximadamente, cada um dos valores a seguir. Para isso, faça estimativas para escolher os objetos.
- 2 metros. _____
- 15 centímetros. _____
- 1 metro e 20 centímetros. _____
- 4 metros.
_____
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Objetivos
Medir e estimar comprimentos utilizando as unidades de medida metro, centímetro e milímetro.
Realizar a conversão entre unidades de medida de comprimento metro, centímetro e milímetro.
Atividade 1
Com base no contexto de cada ilustração, espera-se que os estudantes estabeleçam relações entre unidades de medida de comprimento.
Se, de uma ripa de madeira de 120 cm de comprimento, é preciso retirar uma parte de 20 cm para obter 1 m, os estudantes podem deduzir que 1 m equivale a 120 cm menos 20 cm, ou seja, 100 cm.
Se, para obter uma argamassa de 1 cm de espessura, é necessário aumentar em 2 mm uma argamassa de 8 mm, é possível concluir que 1 cm equivale a 10 mm.
Reforce essas relações com os estudantes, disponibilizando uma trena, na qual fica mais fácil observar que a marca de 100 cm coincide com a marca de 1 m, assim como verificar que entre duas marcas sucessivas de centímetro há 10 espaços iguais a 1 mm. Pergunte: “Se 10 mm formam 1 cm e 100 cm formam 1 m, quantos milímetros formam 1 m?” (100 vezes 10 mm, que é igual a 1.000 mm).
Atividade 2
É interessante que, depois de escolherem os objetos, os estudantes os meçam, verificando as estimativas feitas. Proponha que compartilhem as respostas com os colegas.
BNCC em foco:
EF04MA20
MP169
- Observe as figuras e escreva a medida do comprimento de cada uma.
a)
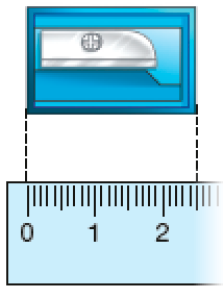
_____
PROFESSOR
Resposta: 25 milímetros ou 2 centímetros e 5 milímetros.b)
_____
PROFESSOR
Resposta: 30 milímetros ou 3 centímetros.c)
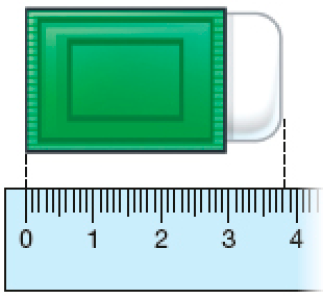
_____
PROFESSOR
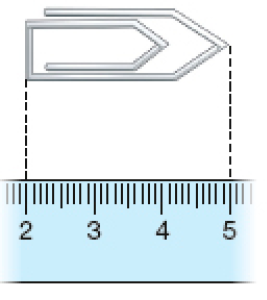
Resposta: 38 milímetros ou 3 centímetros e 8 milímetros.- Usando uma régua, meça o comprimento de cada figura.
a)

_____
PROFESSOR
Resposta: 30 milímetros ou 3 centímetros (30 mm ou 3 cm).b)

_____
PROFESSOR
Resposta: 20 milímetros ou 2 centímetros (20 mm ou 2 cm).

- Leia as falas e descubra a medida da altura de Carla.



A medida da altura de Carla é _____.
PROFESSOR
Resposta: 167 cm ou 1 m e 67 cm

- Responda às questões.
- Em que situação a diferença de 1 centímetro em uma medida de comprimento pode ser importante?
PROFESSOR
Exemplos de resposta: Na escolha de um parafuso ou no ajuste de uma peça de roupa.
- Em que situação a diferença de 1 metro em uma medida de comprimento pode não ser importante?
PROFESSOR
Exemplo de resposta: Na estimativa da distância entre duas cidades não vizinhas (sem limites comuns).
- Em que situação a diferença de 1 centímetro em uma medida de comprimento pode ser importante?
MANUAL DO PROFESSOR
Atividade 3
Dê atenção especial ao item b, pois alguns estudantes podem desconsiderar o fato de uma extremidade da figura estar na marca de 2 cm da régua, e não na marca zero. Caso tenham dificuldade em compreender que a medida é o resultado da subtração 5 cm menos 2 cm, que é igual a 3 cm, peça a eles que, no desenho do clipe no livro, contem quantos centímetros há da marca de 2 cm até a marca de 5 cm.
Atividade 4
Peça aos estudantes que discutam entre si as respostas obtidas para as medidas de comprimento da porca e do parafuso. É possível que tenham encontrado medidas diferentes, especialmente se não fizeram coincidir a marca correspondente ao zero da régua com a extremidade a ser medida. Esta é mais uma oportunidade para a discussão do uso correto da régua.
Atividade 5
Esta atividade exige interpretação e relacionamento dos dados apresentados na ilustração. A informação que permitirá o início dos cálculos para a obtenção da medida solicitada é fornecida por Carla: “Tatiana tem 1 m e 70 cm de altura”. Como Tatiana é 15 cm mais alta que Lúcia, para descobrir a altura de Lúcia basta calcular: 1 m e 70 cm menos 15 cm, que é igual a 1 m e 55 cm. Da mesma forma, como Lúcia é 12 cm mais baixa que Carla, para descobrir a altura de Carla basta adicionar 12 cm a 1 m e 55 cm, que é igual a 1 m e 67 cm.
Atividade 6
Nesta atividade, os estudantes devem pensar sobre quanto uma diferença de medida pode ser relativa, dependendo do contexto. Há casos em que uma diferença de 1 cm pode ser inaceitável, como no encaixe entre duas peças de uma máquina na qual não pode haver nenhuma folga, enquanto na medida de distância entre duas cidades, por exemplo, 1 m pode não ter importância.
BNCC em foco:
EF04MA20
MP170
Quilômetro e metro
- Faltam 50 metros para Vladimir completar a corrida de 1 quilômetro.
Ao final da corrida, Vladimir terá percorrido _____ metros ou 1 quilômetro.
PROFESSOR
Resposta: 1.000- Um quilômetro corresponde a
_____
metros.
PROFESSOR
Resposta: 1.000
- Um quilômetro corresponde a
_____
metros.

Indicamos: 1 quilômetro por 1 km
_____ m = 1 km
PROFESSOR
Resposta: 1.000- Faça estimativas e responda às questões.
- A distância de sua casa à escola em que você estuda é maior ou menor que 1 quilômetro? _____
- Escreva o nome de 2 lugares aos quais você costuma ir que ficam a uma distância de mais de 1 quilômetro de sua casa.
_____
PROFESSOR
Respostas pessoais.
- Francisco caminha todos os dias em volta de um parque retangular, conforme representado abaixo. Se em uma manhã ele deu 1 volta completa em torno do parque, a distância percorrida foi maior ou menor que 1 quilômetro? Justifique sua resposta.
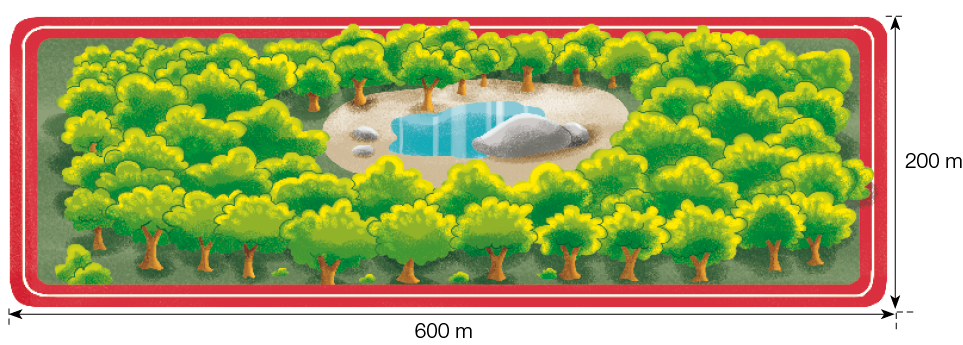
_____
PROFESSOR
Resposta: Maior que 1 quilômetro. Exemplo de justificativa: 1.600 metros é uma distância maior que 1.000 metros (1 quilômetro).MANUAL DO PROFESSOR
Objetivos
Medir e estimar comprimentos utilizando as unidades de medida quilômetro e metro.
Realizar a conversão entre unidades de medida de comprimento quilômetro e metro.
Atividade 1
Relembre à turma que uma unidade de medida padronizada muito usada para medir grandes distâncias é o quilômetro, que corresponde a 1.000 metros. Explorando o problema, pergunte: “Se Vladimir tivesse completado uma corrida de 15 quilômetros, quantos metros ele teria percorrido?” (15.000 metros).
Atividade 2
Para que os estudantes desenvolvam melhor a habilidade de estimativas de grandes distâncias, comente que, em geral, cada quarteirão corresponde a 100 metros. Então, peça a eles que pensem em quantos quarteirões eles precisam caminhar para ir de um lugar a outro e estimem se a distância é maior ou menor que 1 km.
Atividade 3
Nesta atividade, os estudantes precisam calcular, ainda que não dominem o conceito, o perímetro do parque que tem forma retangular – noção que será explorada mais explicitamente no próximo tópico.
Ajude-os a ampliar as referências de medidas de comprimento fazendo perguntas, por exemplo:
O que fica a 1 quilômetro da escola?
E a 5 quilômetros da escola?
Converse com os estudantes sobre as distâncias e os locais no entorno da escola. Considere a realidade local.
BNCC em foco na dupla de páginas:
EF04MA20
MP171

- Leia as falas e descubra quem percorreu a maior distância.

PROFESSOR
Resposta: 500 m
PROFESSOR
Resposta: 600 m
PROFESSOR
Resposta: 700 mQuem percorreu a maior distância foi _____.
PROFESSOR
Resposta: Pedro- Bianca e Alexandre percorriam trilhas diferentes e se encontraram em uma área de descanso. Leia o diálogo entre eles e, depois, responda às questões.

-
Qual deles percorreu a maior distância?
_____
PROFESSOR
Resposta: Alexandre.
-
Quantos metros um deles andou a mais que o outro?
_____
PROFESSOR
Resposta: Alexandre andou 80 metros a mais que Bianca.

- Faça uma estimativa e marque com um
X
a resposta correta.
A cada salto dado por um canguru, ele percorre pouco mais de 2 metros em uma linha reta horizontal. Se continuar saltando em frente sem sair dessa linha reta, quantos saltos serão necessários para que ele fique a uma distância de 1 quilômetro do ponto de partida?
( ) Mais de 500 saltos.
( ) Menos de 500 saltos.
PROFESSOR
Resposta correta: Menos de 500 saltos.
MANUAL DO PROFESSOR
Atividade 4
Depois que os estudantes realizarem esta atividade, peça-lhes que compartilhem com os colegas como pensaram para determinar quem percorreu a maior distância. Depois, pergunte: “É prático indicar a medida de grandes distâncias em metro? Por quê?”.
Espera-se que os estudantes compreendam que cada situação exige a unidade de medida de comprimento adequada.
Atividade 5
Veja dois modos possíveis de os estudantes resolverem o item a. Em um deles, podem manter em unidades mistas (quilômetro e metro) as distâncias percorridas por Bianca e adicionar as medidas, obtendo:
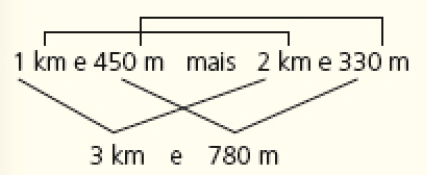
Como 3 km e 780 m é menor que 3 km e 860 m, pode-se concluir que Alexandre percorreu a maior distância. Outro modo de resolver é converter as medidas para metro e comparar os resultados:
Alexandre: 3.860 m.
Bianca: 1.450 m + 2.330 m = 3.780 m.
Como 3 780 m é menor que 3 860 m, Alexandre percorreu a maior distância.
No item b, basta calcular a diferença entre as distâncias percorridas por eles. Assim, já que as medidas em quilômetro são iguais, calcula-se apenas a diferença em metro: 860 m − 780 m = 80 m.
Atividade 6
Após a resolução, proponha aos estudantes uma nova leitura do enunciado, para mostrar que, mesmo fazendo cálculos corretos, a resposta não será exata, pois há uma informação imprecisa: “... percorre pouco mais de 2 metros...”. Isso não significa, porém, que a atividade não faz sentido. Pelo contrário, ela retrata de forma adequada uma situação real. Assim como no caso dos saltos do canguru, em muitas situações temos informações imprecisas, o que não nos impede de fazer uma ideia das grandezas envolvidas. É importante que os estudantes percebam que, se a distância percorrida a cada salto fosse exatamente igual a 2 metros, seriam necessários 500 saltos para ficar a uma distância de 1 quilômetro (1 000 metros) do ponto de partida, mas, como a distância é maior que 2 metros, será necessário um menor número de saltos.
MP172
Perímetro de uma figura
- Ivan deu uma volta ao redor do terreno da casa do tio dele. Quantos metros ele percorreu no total?

Perímetro é o comprimento do contorno de uma figura.
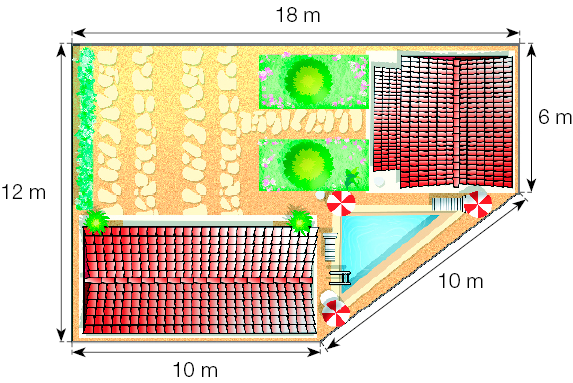
18 + 12 + _____ + _____ + _____ = _____
PROFESSOR
Resposta: 18 + 12 + 10 + 10 + 6 = 56No total, Ivan percorreu _____ metros.
PROFESSOR
Resposta: 56

- Calcule a medida do perímetro de cada figura.
a)
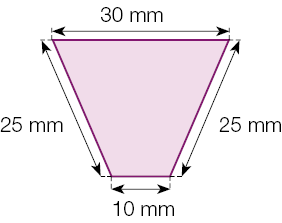
_____ milímetros
PROFESSOR
Resposta: 90b)
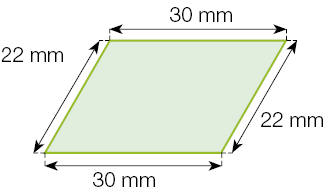
_____ milímetros
PROFESSOR
Resposta: 104c)
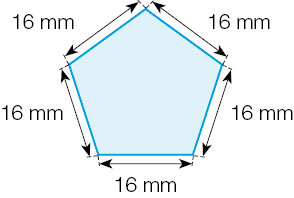
_____ milímetros
PROFESSOR
Resposta: 80

- Agora, desenhe um triângulo com uma régua. Depois, meça, em milímetro, cada um de seus lados e calcule a medida do perímetro desse triângulo.
_____
PROFESSOR
Resposta: Medida do perímetro do exemplo: 110 mm
PROFESSOR
Resposta: Exemplo de desenho:
MANUAL DO PROFESSOR
Objetivo
Explorar e calcular o perímetro de figuras.
Atividade 1
Explore a atividade perguntando: “Se o terreno da casa do tio de Ivan fosse retangular, com lados de medidas iguais a 11 metros e 7 metros, qual seria a medida da distância percorrida?” (36 metros).
Atividade 2
Salientamos que, nesta atividade, é muito importante o cuidado de não definir perímetro como a soma das medidas dos lados de uma figura, pois tal definição não se aplicaria a figuras como a circunferência, que não tem lados, mas pode ter seu perímetro calculado. Por isso, recomendamos que sempre se refira ao perímetro como a medida do comprimento do contorno de uma figura.
Atividade 3
Verifique se os estudantes consideram apenas o contorno de cada figura, e não o contorno de cada quadradinho.
Atividade 4
Nesta atividade, os estudantes aprendem uma maneira prática de obter o perímetro de figuras que não são formadas por segmentos de retas.
Peça a eles que deem exemplos de outras situações em que não poderiam medir o contorno desejado diretamente com uma régua. Por exemplo: a cintura de uma pessoa, o contorno de um desenho circular feito na lousa.
BNCC em foco:
EF04MA20
MP173
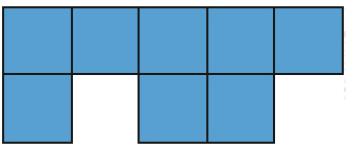
- Cada figura é formada por quadrinhos com lados que medem 1 cm de comprimento. Qual é a medida do perímetro de cada uma das figuras?
a)
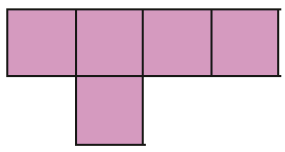
_____ cm
PROFESSOR
Resposta: 12b)
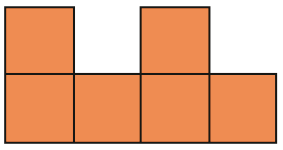
_____ cm
PROFESSOR
Resposta: 14c)
_____ cm
PROFESSOR
Resposta: 16- Veja como Márcio está medindo o perímetro do círculo azul usando barbante e régua.
Primeiro, ele contornou o círculo com um barbante.
Agora, está medindo o comprimento da parte do barbante que ele usou.

- Use o mesmo procedimento de Márcio para determinar a medida do perímetro aproximado do círculo verde abaixo.

A medida do perímetro do círculo verde é aproximadamente igual a:
( ) 15 cm
( ) 30 cm
( ) 25 cm
PROFESSOR
Resposta correta: 15 cm.- A medida do perímetro de um quadrado é 2 metros e 36 centímetros. Quantos centímetros mede cada lado desse quadrado?
PROFESSOR
Exemplos de cálculo:PROFESSOR
2 metros e 36 centímetros correspondem a 236 centímetros.PROFESSOR
236 cm ÷ 4 = 59 cmCada lado desse quadrado mede _____ centímetros.
PROFESSOR
Resposta: 59MANUAL DO PROFESSOR
Atividade 5
Esta atividade propõe o caminho inverso: da medida do perímetro de um quadrado, os estudantes devem deduzir a medida de seu lado. Eles podem calcular essa medida dividindo primeiramente por 4 a parte da medida do perímetro expressa em metro e, depois, a parte expressa em centímetro. Os estudantes podem transformar 2 metros em 200 centímetros e então dividir 200 por 4, obtendo 50 centímetros. Dividindo 36 centímetros por 4, o resultado é 9 centímetros. A medida do comprimento do lado do quadrado é, portanto, igual a 50 cm mais 9 cm, ou seja, 59 cm.
Sugestões de atividades
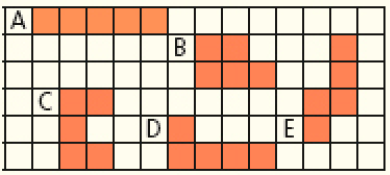
Brincando com pentaminós
Para explorar a noção de perímetro, proponha aos estudantes o traçado de alguns pentaminós, que são figuras formadas por cinco quadrados com lados de 1 cm de comprimento.
Peça a eles que desenhem, em uma folha de papel quadriculado, pentaminós com formatos diferentes e, depois, determinem o perímetro de cada um, como os propostos no exemplo abaixo.
(A: 12 cm; B: 10 cm; C: 12 cm; D: 12 cm; E: 12 cm.)
CRÉDITO: ADILSON SECCO
O quadro de Natália
Natália quer pintar um quadro em uma tela. Em qual das situações a seguir ela precisará saber o perímetro da tela? (Na situação 2.)
Natália vai comprar as tintas para pintar o quadro.
Natália vai comprar madeira para fazer a moldura do quadro.
Natália vai pendurar o quadro na parede da sala.
BNCC em foco:
EF04MA20
MP174
Ideia de área
- Observe os ladrilhos que Mateus está colocando no piso de sua cozinha.
Cabem 30 ladrilhos no piso da cozinha de Mateus.

Dizemos que a medida da área do piso corresponde a 30 ladrilhos. Cada ladrilho foi considerado uma unidade de medida de área.
unidade de medida: 
área do piso: 30 
- Qual é a medida da área de cada figura? A unidade de medida usada é o
 .
.
a)
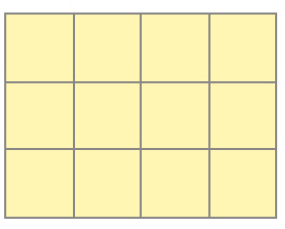
_____
PROFESSOR
Resposta: 12
b)
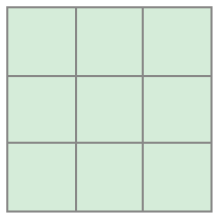
_____
PROFESSOR
Resposta: 9
c)
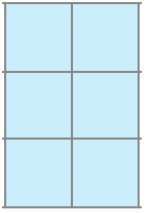
_____
PROFESSOR
Resposta: 6
- Observe a unidade de medida de área indicada em cada caso. Depois, calcule a medida da área de cada figura.
a)
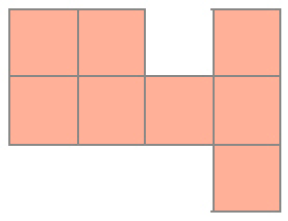
Unidade de medida: 
PROFESSOR
Resposta: 8
b)
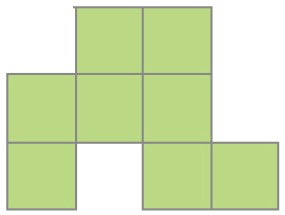
Unidade de medida: 
PROFESSOR
Resposta: 4
c)
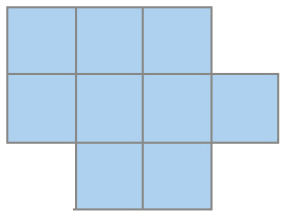
Unidade de medida: 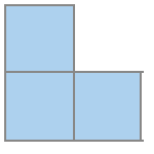
PROFESSOR
Resposta: 4
MANUAL DO PROFESSOR
Objetivos
Medir e comparar área de figuras geométricas planas desenhadas em malha quadriculada.
Reconhecer que duas figuras geométricas planas com formatos diferentes podem ter a mesma medida de área.
Atividade 1
Espera-se que os estudantes percebam que a medida da área de uma figura é o número de vezes que a unidade de medida cabe na superfície dela.
Atividade 2
Reforce a importância de ser observada a unidade de medida de cada uma das figuras para se determinar a respectiva medida da área.
Ampliação
Se achar conveniente, esclareça aos estudantes que há outras unidades de medida de superfície, como o hectare (medida agrária), ou uma unidade menos precisa, que é a da superfície de um campo de futebol como unidade de medida. Leve para classe reportagens que utilizam essas unidades de medida e oriente-os sobre a utilização da unidade de medida mais adequada em cada situação.
BNCC em foco:
EF04MA21
MP175
- Observe o esquema da fachada da casa abaixo e responda às questões.
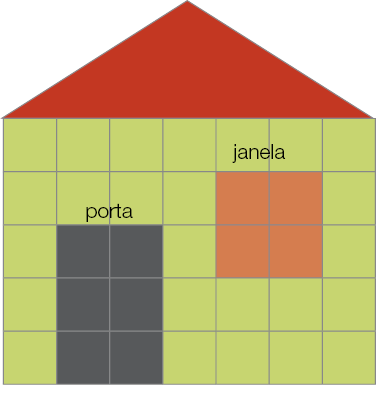
- A medida da área da parte verde da fachada da casa corresponde a quantos
 ?
_____
?
_____
PROFESSOR
Resposta: 25
- E a medida da área da porta?
_____
PROFESSOR
Resposta: 6
- E a medida da área da janela?
_____
PROFESSOR
Resposta: 4
- A área da porta e da janela juntas é maior ou
menor
que a área do restante da parede?
_____
PROFESSOR
Resposta: Menor.
- A medida da área da parte verde da fachada da casa corresponde a quantos

- Regina quer fazer 40 convites de aniversário retangulares, como mostra o desenho abaixo.
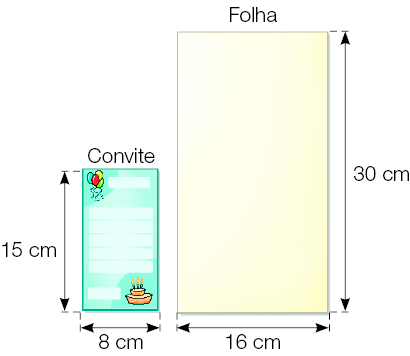
- Quantos convites ela pode fazer com cada folha?
_____
PROFESSOR
Resposta: 4 convites.
- De quantas
folhas
ela precisará para fazer os 40 convites?
_____
PROFESSOR
Resposta: 10 folhas.
- Quantos convites ela pode fazer com cada folha?
- Marque com um
X
a resposta certa.
Osvaldo está fazendo diversas reformas em seu sítio. Em qual destas situações ele não precisará saber a medida da área que corresponde à parte que será reformada?
( ) Colocar cerca em torno da plantação de laranjas.
( ) Colocar lajotas no piso da lavanderia.
( ) Pintar as paredes da casa.
PROFESSOR
Resposta correta: Colocar cerca em torno da plantação de laranjas.

- Na malha quadriculada abaixo, desenhe e pinte 3 figuras diferentes cuja área corresponda à medida 8
 .
.
PROFESSOR
Resposta: Exemplo de desenho: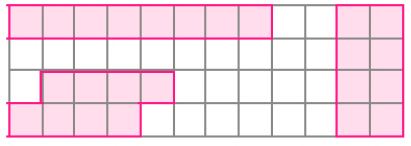
MANUAL DO PROFESSOR
Atividade 3
Verifique a estratégia usada pelos estudantes para determinar a medida da área solicitada no item a: se eles contam os quadrinhos verdes ou se multiplicam os quadrinhos verdes das colunas pelos das linhas e subtraem a quantidade de quadrinhos referente à porta e à janela.
Atividade 4
Para determinar o número de convites que podem ser confeccionados com uma folha de papel retangular, os estudantes devem perceber que as medidas dos lados da folha são números múltiplos de cada medida do convite. Se compararem o lado do convite de medida 8 cm com o lado da folha de medida 30 cm, haverá sobra de material; mas isso não ocorrerá se compararem o lado de medida 8 cm com o lado de medida 16 cm e, simultaneamente, o lado do convite de medida 15 cm com o lado da folha de medida 30 cm. Pergunte à turma: “Vocês conhecem outras situações em que é importante saber a medida da área de uma figura? Quais?”. Incentive os estudantes a discutirem os exemplos citados.
Atividade 5
Para a resolução dessa atividade, é essencial que os estudantes reconheçam a diferença entre os conceitos de área e de perímetro. Assim, terão condições de perceber que, para o revestimento de um piso com lajotas, é preciso saber a área desse piso; enquanto, para cercar um terreno, basta saber o perímetro desse terreno.
Atividade 6
Esta atividade possibilita reconhecer que figuras com formatos diferentes podem ter a mesma medida de área.
BNCC em foco:
EF04MA21
MP176
Área de figuras planas
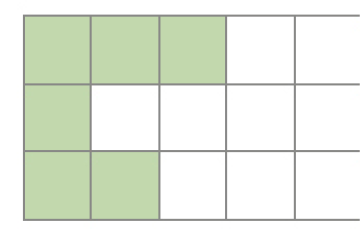
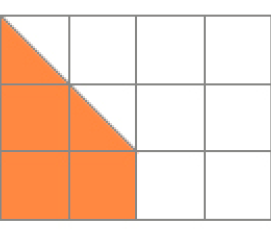
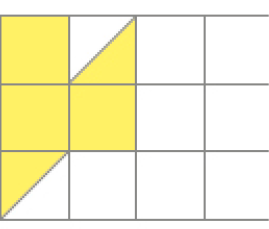
- Yara desenhou diversas figuras. Qual é a medida da área de cada uma das figuras desenhadas?
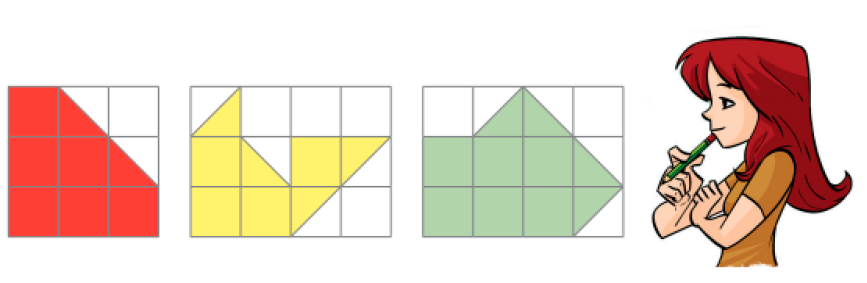
Yara observou que 1  com 1
com 1  formam 1
formam 1  . Então, concluiu que:
. Então, concluiu que:
Na figura vermelha, cabem
_____
 e
_____
e
_____
 .
.
PROFESSOR
Resposta: 6, 2A medida da área da figura vermelha é igual a
_____
 .
.
PROFESSOR
Resposta: 7Na figura amarela, cabem
_____
 e
_____
e
_____
 .
.
PROFESSOR
Resposta: 4, 4A medida da área da figura amarela é igual a
_____
 .
.
PROFESSOR
Resposta: 6Na figura verde, cabem
_____
 e
_____
e
_____
 .
.
PROFESSOR
Resposta: 6, 4A medida da área da figura verde é igual a
_____
 .
.
PROFESSOR
Resposta: 8- Determine a medida da área de cada figura a seguir.
a)
b)
c)
d)
_____

PROFESSOR
Resposta: 6
_____

PROFESSOR
Resposta: 4
_____

PROFESSOR
Resposta: 4
_____

PROFESSOR
Resposta: 6MANUAL DO PROFESSOR
Objetivo
Medir e comparar área de figuras planas em malha quadriculada.
Para estudantes dessa faixa etária, a ideia de área como grandeza adquire maior significado quando trabalham com situações em que é preciso preencher determinada superfície. Para tal finalidade, a malha quadriculada é um bom recurso, pois possibilita a representação de diversas figuras planas e a contagem das correspondentes unidades de área. Comente com os estudantes que as unidades de área poderiam ter a forma de retângulo, por exemplo, mas que, como o quadrado é uma figura simples e apresenta lados de mesma medida, é mais usado como unidade de medida. Outras formas, como o círculo, não são usadas por não permitirem pavimentar completamente o plano, ocorrendo então sobras ou faltas.
Atividade 1
Verifique se os estudantes compreendem a observação de Yara para conseguir determinar a área das figuras que ela fez. Para isso, peça-lhes que contem aos colegas como determinaram a área de cada uma das figuras.
Atividade 2
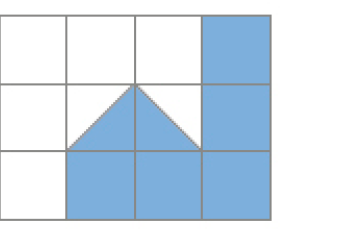
Para a resolução desta atividade, é essencial que os estudantes reconheçam a diferença entre os conceitos de área e de perímetro. Assim, terão condições de perceber que, para descobrirem quanto vale a área, precisam contar os quadrados no interior da figura e não seu contorno, e considerar que essas duas representações triangulares de mesma medida podem formar um quadrado.
BNCC em foco na dupla de páginas:
EF04MA21
MP177
- Observe as figuras.
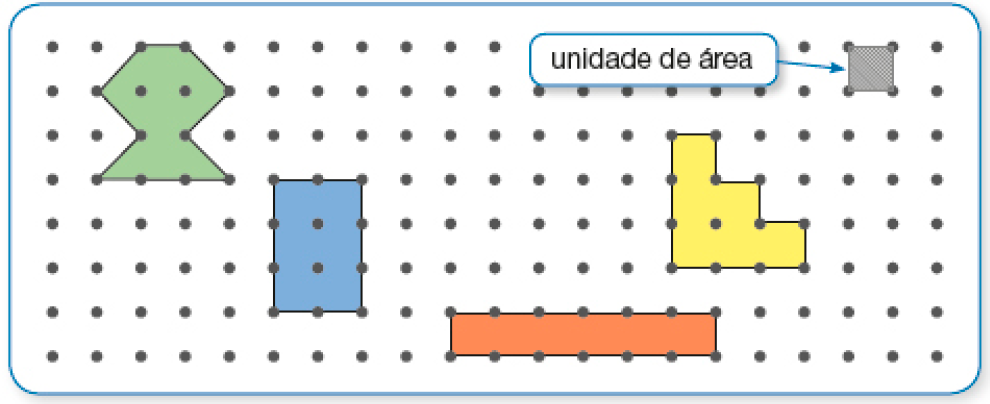
- Calcule a medida da área da:
- figura verde.
_____
PROFESSOR
Resposta: 6 unidades de área.
- figura amarela.
_____
PROFESSOR
Resposta: 6 unidades de área.
- figura azul.
_____
PROFESSOR
Resposta: 6 unidades de área.
- figura laranja.
_____
PROFESSOR
Resposta: 6 unidades de área.- Analisando as quatro figuras, o que você pode notar?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes notem que figuras diferentes podem ter áreas de mesma medida. Fim da observação.
- Analisando as quatro figuras, o que você pode notar?
- Na figura abaixo, a área de cada quadrado colorido é a metade da área do retângulo que está à
esquerda
dele. Se usarmos o quadrado amarelo como unidade de medida da área, qual será a medida da área da figura toda?
_____
PROFESSOR
Resposta: 16 quadrados amarelos.

- Catarina está fazendo um mosaico retangular com ladrilhos coloridos, todos de mesmo tamanho. Ela já colocou alguns ladrilhos, como mostra o esquema abaixo.
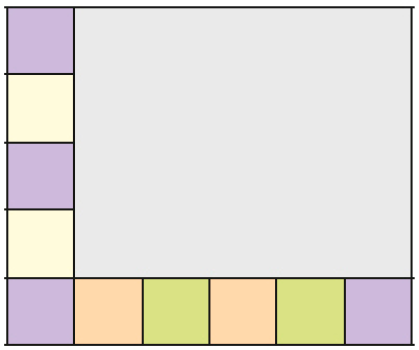
LEGENDA: Mosaico. FIM DA LEGENDA.
- Quantos ladrilhos ela usará para cobrir todo o mosaico?
_____
PROFESSOR
Resposta: 30 ladrilhos.
- Se em cada caixa há 12 ladrilhos, de quantas caixas Catarina precisará? Sobrarão ladrilhos? Se sobrarem, quantos?
_____
PROFESSOR
Resposta: De 3 caixas; sim; sobrarão 6 ladrilhos.
- Uma caixa de ladrilhos custa 63 reais. Qual foi o troco de Catarina ao comprar as caixas necessárias, se ela usou duas cédulas de 100 reais para pagar?
_____
PROFESSOR
Resposta: 11 reais.
- Quantos ladrilhos ela usará para cobrir todo o mosaico?
_____
MANUAL DO PROFESSOR
Atividade 3
Nesta atividade, os estudantes observam figuras geométricas planas representadas em malha pontilhada; por isso a contagem dos quadradinhos pode ser um pouco mais trabalhosa. Eles podem fazê-la visualizando cada quadradinho a partir de seus vértices. Se houver disponibilidade de material de apoio, explore a atividade em um geoplano.
Atividade 4
O aspecto mais interessante dessa atividade é possibilitar aos estudantes o reconhecimento de um padrão de medida que se repete: “metade” e “metade da metade”.
Uma possibilidade para resolver a questão proposta é os estudantes observarem que:
o quadrado azul tem mesma área que o quadrado amarelo: 1 unidade de área;
o retângulo menor (branco), ao lado desses dois quadrados, tem área igual à soma das áreas dos quadrados: 2 unidades de área;
o quadrado roxo tem área igual à soma das áreas dos dois quadrados e do retângulo branco: 4 unidades de área;
o retângulo maior (branco), à esquerda, tem área igual à soma das áreas das quatro figuras citadas acima: 8 unidades de área.
Portanto, a área total da figura é igual a 16 unidades de área, ou 16 quadrados amarelos.
Atividade 5
Nesta atividade, a situação apresentada não permite que os estudantes realizem a contagem dos quadradinhos, de modo que eles devem mobilizar seus conhecimentos para calcular essa quantidade. Espera-se que reconheçam o raciocínio multiplicativo como o modo mais prático de calcular o número de quadrados e, portanto, a área da figura, fazendo 5 × 6 = 30.
Sugestão de atividade
Formando superfícies no geoplano
Uma atividade interessante para a exploração da ideia de área é propor aos estudantes a construção, em um geoplano quadrangular (parecido com o da figura ao lado), de figuras geométricas planas com áreas predeterminadas por você. Por exemplo: “Construam no geoplano algumas figuras geométricas planas que tenham medida de superfície igual a 7 unidades de área”. Incentive os estudantes a construírem figuras com partes que dividam quadrados ao meio e compensem com outras metades. Estudantes dessa faixa etária costumam ser bem criativos e gostam de inventar figuras diversificadas.
CRÉDITO: ADILSON SECCO
MP178
Centímetro quadrado
- Flávia coleciona fotografias 3 × 4 de amigos dela. Ao todo, ela tem 10 fotografias, que serão coladas lado a lado, sem sobreposição, em um painel, como mostra a ilustração a seguir. Qual é a medida da área que Flávia vai ocupar no painel para colar todas as fotografias? Para saber, veja como ela fez.


O centímetro quadrado é uma unidade de medida de área correspondente a um quadrado cujos lados medem 1 centímetro.
Indicamos 1 centímetro quadrado por 1 cm².
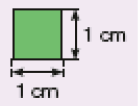
LEGENDA: A medida da área desse quadrado é 1 cm². FIM DA LEGENDA.

- Agora calcule a medida da área que Flávia vai ocupar no painel para colar as 10 fotografias.
_____
PROFESSOR
Resposta: 120 cm²

- Converse com os colegas.
- Em que situações você acha que é preciso calcular a medida de uma área em centímetro quadrado?
- Você conhece alguma outra unidade de medida de superfície? Se conhece, qual?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Objetivo
Explorar o centímetro quadrado como uma unidade de medida padronizada de superfície correspondente à área de um quadrado cujos lados medem 1 centímetro.
Atividade 1
Comente com a turma que, assim como eles estavam observando a área em malha quadriculada, aqui uma das fotografias também foi colocada em uma espécie de malha quadriculada, cada lado medindo 1 centímetro. Para determinar a área ocupada por dez fotografias, basta multiplicar os 12 centímetros quadrados de área de cada fotografia por 10.
Atividade 2
Os estudantes podem mencionar a superfície de uma folha de papel, a superfície do visor de uma calculadora, de uma tela de celular ou de computador. Comente que mesmo uma “grande” superfície, como uma quadra de basquete, pode ter a área expressa em centímetro quadrado, mas que essa unidade não seria a mais adequada, pois o número correspondente à medida seria muito elevado.
Verifique se eles identificam a simbologia (cm²) associada a essa unidade de medida.
É provável que, no item b, os estudantes respondam metro quadrado ou quilômetro quadrado por fazerem parte do cotidiano da maioria das pessoas. Se morarem em zona rural também podem citar acres ou hectares.
BNCC em foco:
EF04MA20, EF04MA21
MP179

- Pinte a próxima figura da sequência. Depois, determine a medida da área de cada uma delas e responda às perguntas.
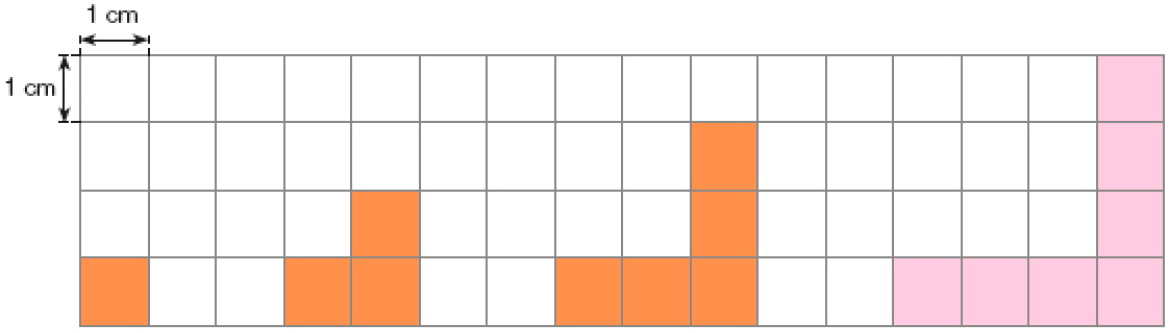
_____ cm²
PROFESSOR
Resposta: 1_____ cm²
PROFESSOR
Resposta: 3_____ cm²
PROFESSOR
Resposta: 5_____ cm²
PROFESSOR
Resposta: 7

- Quantos centímetros quadrados terá a próxima figura dessa sequência?
E a 7ª figura? _____
PROFESSOR
Resposta: 9 cm²; 13 cm²
- Juntando 2 retângulos azuis, sem ficar um sobre o outro, podemos compor figuras diferentes, como as mostradas abaixo.
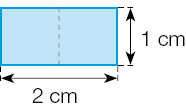
Figura 1

Figura 2

- Qual é a medida da área de cada uma dessas figuras?
_____
PROFESSOR
Resposta: Ambas têm área igual a 4 cm².
- Qual é a medida do perímetro de cada figura?
_____
PROFESSOR
Resposta: Figura 1: 10 cm; Figura 2: 8 cm.
Boxe complementar:
Desafio
Álvaro tinha uma chapa de madeira quadrangular, cujos lados mediam 2 cm de comprimento. Ele cortou a parte quadrada do centro e ficou apenas com a parte pintada de marrom mostrada na figura ao lado. Qual é a medida da área, em centímetro quadrado, da parte marrom que sobrou da chapa original?
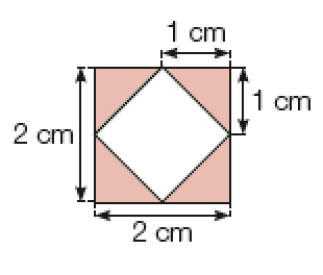
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
_____
PROFESSOR
Resposta: 2 cm²Fim do complemento.
MANUAL DO PROFESSOR
Atividade 3
Esta atividade explora uma sequência de quadrados com padrão. Peça aos estudantes que desenhem algumas das próximas figuras da sequência em papel quadriculado para descobrir o padrão a que a sequência obedece. Espera-se que observem que, nessa sequência, uma figura tem sempre dois quadradinhos a mais que a figura anterior. Como esses quadradinhos têm lados de 1 cm de comprimento, cada figura tem 2 cm² a mais de área que a figura anterior. Para determinar a área da 7ª figura, os estudantes podem desenhar as figuras até essa ordem ou observar a sequência de números do padrão:
1, 3, 5, 7, 9, 11, 13, ..., deduzindo então que a medida da área da 7ª figura é 13 cm². Peça-lhes que obtenham o perímetro das figuras dessa sequência e verifiquem se as medidas dos perímetros aumentam de acordo com um padrão.
Atividade 4
Após a resolução, pergunte aos estudantes: “Figuras diferentes podem ter áreas de medidas iguais?”. Espera-se que concluam que isso é possível.Pergunte se o mesmo vale em relação ao perímetro. Espera-se que percebam, por meio de exemplos, que a resposta é positiva. Incentive-os a observarem que podemos comparar perímetros de diferentes figuras e áreas de diferentes figuras. Não faz sentido, porém, comparar área com perímetro, pois as grandezas envolvidas são diferentes.
BNCC em foco:
EF04MA20, EF04MA21
Desafio
Os estudantes podem resolver o desafio reproduzindo a figura em uma malha quadriculada.
O cálculo de medida de áreas com o auxílio de malhas quadriculadas permite obter uma área aproximada, em que duas ou mais partes da figura formam, aproximadamente, um quadradinho de 1 cm² de área. Atividades dessa natureza contribuem para que os estudantes realizem cálculos aproximados de área, e não apenas cálculos exatos.
MP180
Medidas de temperatura
- No dia 10 de fevereiro de 2021, segundo o Instituto Nacional de Meteorologia, a temperatura da cidade do Rio de Janeiro variou de 19 °C a 31 °C. Observe a ilustração abaixo.

- Qual é a temperatura registrada no termômetro de rua?
_____
PROFESSOR
Resposta: 23 °C
Indicamos: 1 grau Celsius por 1 °C
- Leia a notícia abaixo.
Armazenamento é um dos maiores desafios da vacinação contra a Covid no DF
Exceto uma vacina produzida com RNA mensageiro (mRNA), que precisa ficar em temperatura de −70 ºC, as demais devem ser conservadas em temperatura de refrigeração, isto é, entre 2 ºC e 8 ºC.
MACHADO, Mariana. Correio Braziliense. 9 dez. 2020. Brasília – DF. Disponível em: http://fdnc.io/eUc. Acesso em: 24 fev. 2021.

- Escreva as medidas de temperatura indicadas na notícia. Qual delas representa a temperatura mais alta?
_____
PROFESSOR
Resposta: −70 °C, 2 °C e 8 °C. 8 °C.
MANUAL DO PROFESSOR
Objetivo
Reconhecer temperatura como grandeza e grau Celsius como unidade de medida a ela associada.
Atividades 1 e 2
Proponha aos estudantes que façam uma pesquisa sobre as temperaturas em diferentes regiões do Brasil. Peça relatos pessoais dos estudantes: se eles ou algum familiar conhecem regiões que são muito quentes ou muito frias.
Observe se os estudantes percebem que o número 70, embora seja o maior, refere-se à menor temperatura, já que é uma temperatura negativa. Essa pode ser uma boa maneira de introduzir o assunto números negativos, que ainda não foi apresentado a eles.
BNCC em foco:
EF04MA23, EF04MA24
MP181
- Responda às questões.
- Na sua cidade faz mais frio ou mais calor? _____
- Hoje está frio ou calor? _____
- Qual é a temperatura de hoje? _____
- Qual foi a
menor
temperatura registrada ontem em sua cidade? E a maior?
_____
PROFESSOR
Respostas pessoais.
- Vanessa tirou uma sobremesa do fogo, que estava com temperatura de 64 °C. Ela a colocou no freezer para resfriar. Sabe-se que a cada 5 minutos essa sobremesa perde a metade da temperatura. Ajude Vanessa a terminar de completar a tabela e, depois, responda à questão.
Temperatura da sobremesa
Tabela: equivalente textual a seguir.
|
Minutos transcorridos |
Temperatura (°C) |
|---|---|
|
0 |
64 |
|
5 |
32 |
|
10 |
_____ |
|
15 |
_____ |
|
_____ |
_____ |
Fonte: Dados obtidos por Vanessa (maio 2023).
PROFESSOR
Resposta: Minutos transcorridos: 20.PROFESSOR
Temperatura (º C): 16, 8, 4- Em quantos minutos a temperatura da sobremesa chegará a 2 °C?
_____
PROFESSOR
Resposta: Em 25 minutos.
- Qual deverá ser a temperatura da sobremesa em 30 minutos? E em 35 minutos?
_____
PROFESSOR
Resposta: 1 °C; metade de 1 °C abaixo de zero.
- Faça uma pesquisa e descubra as seis temperaturas mais altas e as mais baixas registradas em sua cidade até hoje. Depois, registre as temperaturas que você encontrou. Escreva as fontes da pesquisa.
PROFESSOR
Respostas pessoais.
Tabela: equivalente textual a seguir.
|
Temperaturas mais baixas |
|---|
|
_____ |
|
_____ |
|
_____ |
|
_____ |
|
_____ |
Tabela: equivalente textual a seguir.
|
Temperaturas mais altas |
|---|
|
_____ |
|
_____ |
|
_____ |
|
_____ |
|
_____ |
MANUAL DO PROFESSOR
Atividade 3
Como, em princípio, todos os estudantes da sala de aula moram na mesma cidade, ou nas imediações de onde a escola está localizada, espera-se que as respostas estejam de acordo com o clima e a temperatura locais.
Se achar conveniente, converse com os estudantes que “hoje está muito frio” ou “o calor está de rachar” são expressões do senso comum que usamos no dia a dia. Explore os conceitos de calor, sensação térmica e temperatura de maneira integrada com Ciências.
Atividade 4
Espera-se, nesta atividade, que o estudante perceba que a cada 5 minutos a sobremesa perde metade da temperatura. Mantendo a proporção, os estudantes chegam à temperatura de 2 °C em 25 minutos. Em 30 minutos, chega a 1° C e em 35 minutos à metade de 1° C.
Se julgar conveniente, proponha aos estudantes uma pesquisa sobre a existência ou não de temperatura ideal para armazenar alimentos na geladeira ou no congelador e quais cuidados devem ser tomados para evitar a proliferação de bactérias em variados tipos de alimento.
Atividade 5
Amplie a pesquisa, solicitando aos estudantes que pesquisem as temperaturas máxima e mínima de outros locais (do Brasil ou do exterior) de determinado dia.
BNCC em foco:
EF04MA23, EF04MA24
MP182
Temperatura máxima e temperatura mínima
- Observe as temperaturas máxima e mínima registradas em duas cidades pernambucanas em fevereiro de 2021.
Temperaturas máxima e mínima
Tabela: equivalente textual a seguir.
|
Cidade |
Temperatura máxima |
Temperatura mínima |
|---|---|---|
|
Recife |
31 °C |
22 °C |
|
Garanhuns |
32 °C |
17 °C |
Fonte: Inpe (Instituto Nacional de Pesquisas Espaciais). Disponível em: http://fdnc.io/eUd; http://fdnc.io/eUe. Acesso em: 24 fev. 2021.
- Qual foi a diferença entre as medidas das temperaturas máxima e mínima registradas em Recife? E em Garanhuns?
_____
PROFESSOR
Resposta: Em Recife, a diferença foi de 9 °C. Em Garanhuns, foi de 15 ºC.
- Leia o que o repórter do tempo está falando e, depois, complete o painel com a informação sobre as medidas das temperaturas máxima e a mínima.
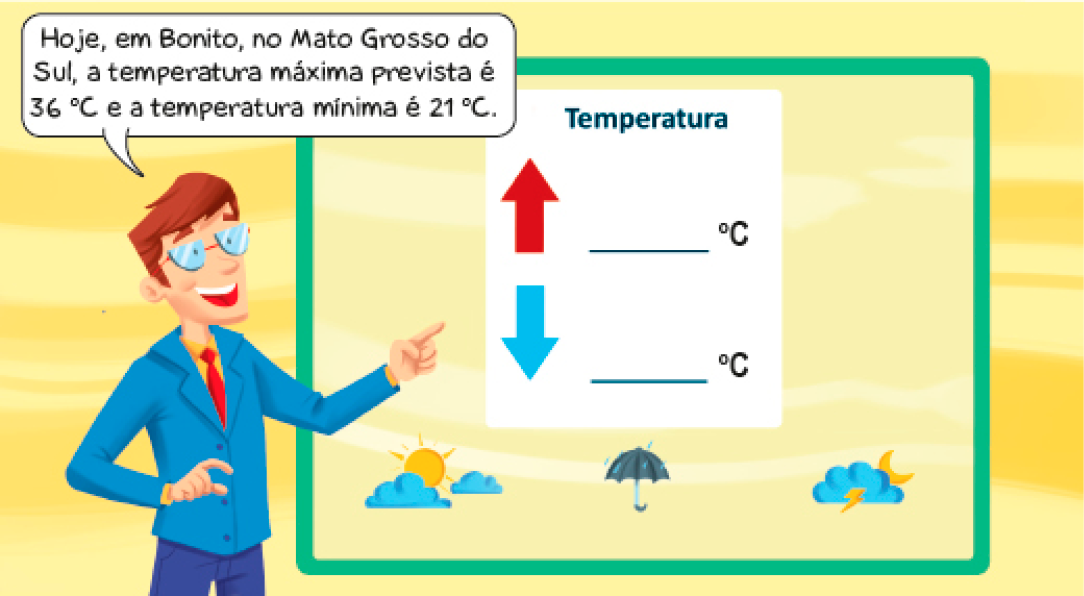
PROFESSOR
Resposta: 36 °CPROFESSOR
21 ºC- O que significam as setas no painel?
_____
PROFESSOR
Resposta: A seta vermelha para cima indica temperatura máxima e a seta azul para baixo indica a temperatura mínima.
MANUAL DO PROFESSOR
Objetivo
Observar e determinar as diferenças entre temperatura máxima e temperatura mínima.
Atividade 1
Nesta atividade, os estudantes entram em contato com a linguagem usual das previsões do tempo. Peça a eles que observem a tabela e digam se entendem as informações nela contidas. Comente com eles que a previsão indica que a temperatura pode variar entre a mínima e a máxima durante aquele dia.
Atividade 2
Nesta atividade, são utilizadas setas para indicar as temperaturas máxima e mínima. Espera-se que os estudantes identifiquem a temperatura máxima ao lado da seta com a ponta voltada para cima, e a mínima, com a ponta voltada para baixo.
BNCC em foco:
EF04MA23, EF04MA24
MP183
- Pesquise a previsão do tempo de sua cidade para a próxima semana. Depois, complete o quadro com a data e as temperaturas máxima e mínima.
Tabela: equivalente textual a seguir.
|
Dia da semana |
Data |
Temperatura máxima prevista |
Temperatura mínima prevista |
|---|---|---|---|
|
Domingo |
_____ |
_____ |
_____ |
|
Segunda-feira |
_____ |
_____ |
_____ |
|
Terça-feira |
_____ |
_____ |
_____ |
|
Quarta-feira |
_____ |
_____ |
_____ |
|
Quinta-feira |
_____ |
_____ |
_____ |
|
Sexta-feira |
_____ |
_____ |
_____ |
|
Sábado |
_____ |
_____ |
_____ |
PROFESSOR
Resposta pessoal.- Laís fez uma pesquisa sobre as temperaturas máxima e mínima registradas no mês de janeiro de 2023 de três cidades – Brasília, Chuí e Oiapoque. Ela escreveu o nome das cidades e as temperaturas em cartões, porém recortou os cartões e não sabe mais quais temperaturas correspondem a cada cidade. Leia as dicas e ligue cada cidade às medidas corretas.
Boxe complementar:
Dicas
- Chuí foi a cidade que registrou a maior diferença entre as medidas das temperaturas máxima e mínima em janeiro de 2023.
- Oiapoque foi a cidade que registrou a maior temperatura mínima entre as cidades pesquisadas por Laís.
Fim do complemento.
Linha 1



Linha 2



PROFESSOR
Resposta: Oiapoque - 31 °C/21 ºC.PROFESSOR
Chuí - 33 °C/14 °C.PROFESSOR
Brasília - 33 °C/16 °C.MANUAL DO PROFESSOR
Atividade 3
Oriente os estudantes a indicarem como obtiveram as informações com a previsão de temperaturas máxima e mínima durante a semana pesquisada. Pergunte a eles onde esses dados podem ser obtidos. Espera-se que saibam que esse tipo de previsão pode ser encontrado em celulares, jornais impressos e virtuais e em sites especializados em previsão de tempo e de temperatura.
Ampliação
Proponha aos estudantes que façam um gráfico de barras, inserindo os dados obtidos em uma planilha eletrônica. Nas páginas 202 e 203 do Livro do Estudante, há orientações sobre os procedimentos.
Atividade 4
Antes de os estudantes realizarem esta atividade, pergunte se eles sabem a localização de cada uma das três cidades. Se achar oportuno, mostre em um mapa a localização delas.
BNCC em foco:
EF04MA23, EF04MA24
MP184
Compreender problemas
Para resolver
Leia atentamente o enunciado dos problemas antes de resolvê-los.
Problema 1
Valdeci é caminhoneiro. Ele trabalha 7 dias e depois tem 4 dias de descanso. No dia 27 de junho, ele iniciou seu descanso de 4 dias e voltou a trabalhar no dia 1º de julho.
Qual é o salário mensal de Valdeci?
_____
PROFESSOR
Resposta: Não é possível calcular.
Problema 2
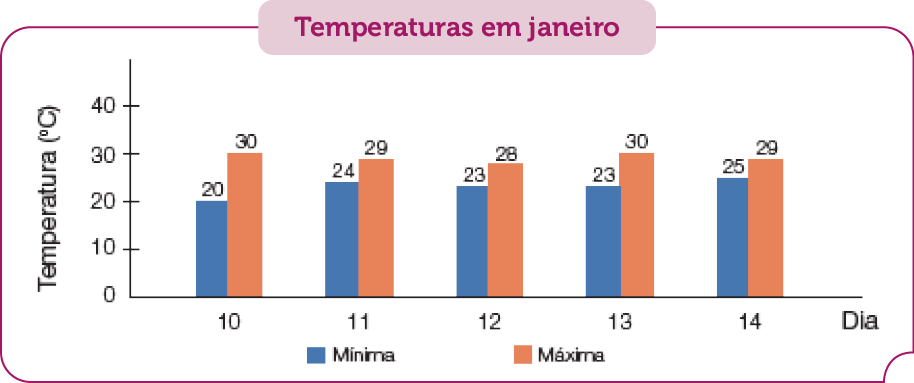
Observe o gráfico abaixo, que mostra as temperaturas mínima e máxima de alguns dias do mês de janeiro de 2023 na cidade onde Ana mora.
Fonte: Dados obtidos por Ana (jan. 2023).
Em qual dia Ana foi nadar? _____
PROFESSOR
Resposta: Não é possível responder.Problema 3
Mariana cortou 10 pedaços de barbante de diferentes tamanhos com o auxílio de régua e tesoura. O primeiro pedaço tinha 10 centímetros de comprimento; o segundo tinha 5 centímetros a mais que o primeiro; o terceiro tinha 5 centímetros a mais que o segundo, e assim por diante.
Quantos reais Mariana pagou por esses pedaços de barbante? _____
PROFESSOR
Resposta: Não é possível calcular.
MANUAL DO PROFESSOR
Objetivo
Explorar problemas que não têm dados suficientes para serem resolvidos.
Para resolver
O enunciado do Problema 1 não faz referência ao salário de Valdeci. No entanto, com os dados fornecidos, diversas questões podem ser criadas e respondidas. Algumas delas são analisadas na atividade 2 de Para refletir.
Nem o enunciado, nem o gráfico do Problema 2 fornecem dado algum relacionado à escolha de Ana quanto ao dia em que ela foi nadar. Portanto, não é possível deduzir que dia foi esse.
Como no Problema 3 não há dados sobre o preço do barbante, não é possível calcular a quantia gasta por Mariana.
BNCC em foco:
EF04MA23, EF04MA24
MP185
Para refletir
- Você conseguiu responder às questões dos problemas? Por quê?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que as questões não podem ser respondidas com os dados apresentados. Fim da observação.
- A professora pediu aos estudantes que inventassem uma questão adequada para o Problema 1. Veja o que eles escreveram.

- Qual é a resposta esperada para cada uma dessas questões?
_____
PROFESSOR
Resposta: Problema de Cecília: 8, 9, 10, 11, 19, 20, 21, 22, 30 e 31; problema de Roberta: 21 dias; problema de Lílian: junho, pois nesse mês Valdeci teve 12 dias de folga e, no mês de julho, 10 dias.
- Responda às questões que Yuri inventou para o Problema 2.
- Qual foi a maior medida de temperatura registrada? E a menor?
_____
PROFESSOR
Resposta: Maior medida de temperatura: 30 ºC; menor medida de temperatura: 20 ºC.
- Em qual dia houve maior variação da medida de temperatura?
_____
PROFESSOR
Resposta: Dia 10 de janeiro.
- Qual foi a maior medida de temperatura registrada? E a menor?
- Invente uma questão adequada para o Problema 3. Depois, peça a um
colega
que a responda.
_____
PROFESSOR
Resposta: Exemplo de resposta:PROFESSOR
Quantos centímetros de barbante Mariana usou no total?PROFESSOR
Ela usou 325 centímetros (3 metros e 25 centímetros).
MANUAL DO PROFESSOR
Para refletir
Atividade 1
Espera-se que os estudantes percebam que as questões não podem ser respondidas com os dados apresentados.
É importante que eles tenham contato com vários tipos de problema (com excesso de dados ou com falta de dados).
Atividade 2
Os estudantes poderão perceber que foi possível utilizar as informações do Problema 1 depois que inventaram questões que usassem os dados do problema.
Atividade 3
Os estudantes conseguirão responder às novas questões propostas com as informações do gráfico apresentado no Problema 2.
Atividade 4
Na primeira questão, observe se os estudantes inventam questões cuja resposta dependa realmente dos dados fornecidos no enunciado do problema. Na segunda, um exemplo de questão é: “Quantos centímetros de barbante Mariana usou para obter os 10 pedaços?”. Resposta: Ela usou o resultado da adição: 10 cm + 15 cm + 20 cm + 25 cm + 30 cm + 35 cm + 40 cm + 45 cm + 50 cm + 55 cm, ou seja, 325 cm.
BNCC em foco:
EF04MA04
Sugestão de leitura para o professor
Livro
SMOLE, Katia Stocco; DINIZ, Maria Ignez. Ler, escrever e resolver problemas: habilidades básicas para aprender Matemática. São Paulo: Penso, 2001.
Esse livro propõe a discussão do lugar e do significado das competências e das habilidades no Ensino Fundamental, abordando as habilidades de ler, escrever e resolver problemas em Matemática.
MP186
A Matemática me ajuda a ser
...uma pessoa que dorme bem
O sono é um processo muito importante para os seres vivos. Ele é responsável pela recuperação e manutenção do equilíbrio geral do nosso organismo, pela fixação da memória, pela regulação da temperatura corporal, entre outros benefícios.
Cada pessoa é única, assim como as necessidades de sono. Pesquisas relatam que crianças e adolescentes precisam de mais horas de sono que os adultos. O quadro abaixo apresenta o número de horas diárias de sono recomendadas de acordo com a idade.
Tabela: equivalente textual a seguir.
|
Idade |
Número de horas de sono recomendadas |
|---|---|
|
0 a 2 meses |
10 a 18 |
|
2 a 12 meses |
14 a 15 |
|
12 a 18 meses |
13 a 15 |
|
18 meses a 3 anos |
12 a 14 |
|
3 a 5 anos |
11 a 13 |
|
5 a 12 anos |
9 a 11 |
|
Adolescentes |
8 a 9 |
|
Adultos |
7 a 9 |
FONTE: Dados obtidos em: http://fdnc.io/eUf. Acesso em: 10 fev. 2021.

Tome nota
- Por que o sono é importante para os seres vivos?
_____
PROFESSOR
Resposta: Porque ele é responsável pela recuperação e manutenção do equilíbrio geral do nosso organismo, pela fixação da memória, pela regulação da temperatura corporal, entre outros benefícios.
- João tem 4 anos. Quantas horas de sono por dia são recomendáveis para ele?
_____
PROFESSOR
Resposta: De 11 a 13 horas.
MANUAL DO PROFESSOR
Objetivo
Analisar dados apresentados em texto e em tabela simples.
Tome nota Atividade 1
Espera-se que os estudantes localizem as informações solicitadas no texto.
Atividade 2
Nesta atividade, o estudante lerá dados da tabela.
BNCC em foco:
EF04MA22, EF04MA27; competência geral 8
MP187
Dicas para ter uma boa noite de sono:
- Tenha horários regulares para dormir e despertar.
- Organize um ambiente adequado para dormir: limpo, escuro, sem ruídos e confortável.
- Não coma muito, nem tome café ou refrigerantes próximo ao horário de dormir.
- Leia um livro ou ouça uma música relaxante antes de deitar.
- Se Pedro dorme 8 horas todos os dias, quantas horas ele dormirá em uma semana? E em 1 mês?
_____
PROFESSOR
Resposta: 56 horas; 240 horas.
PROFESSOR
Exemplos de cálculo:PROFESSOR
8 × 7 = 56PROFESSOR
8 × 30 = 240Reflita
- Quantas horas você costuma dormir por dia? Elas estão de acordo com as horas recomendadas para sua idade?
_____
PROFESSOR
Resposta pessoal.
- Por que você acha que crianças e adolescentes necessitam de mais horas de sono que os adultos?
_____
PROFESSOR
Resposta pessoal.
- Você já teve dificuldade para dormir? O que você faz quando não consegue dormir?
_____
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 3
Os estudantes podem determinar as horas de sono que Pedro dorme por semana multiplicando as 8 horas de sono por 7, e multiplicando esse resultado por 30 para determinar as horas de sono de Pedro durante 30 dias.
Reflita Atividades 1, 2 e 3
Verifique as respostas dos estudantes a esses questionamentos e peça a eles que compartilhem as respostas com os colegas, de modo que possam observar se as respostas são parecidas ou não.
BNCC em foco:
EF04MA22, EF04MA27; competência geral 8
MP188
Compreender informações
Construir e interpretar gráficos pictóricos
- No Centro Esportivo Municipal da cidade onde Felipe mora há 56 crianças que praticam natação, 36 que treinam futebol e 24 que fazem judô. Cada criança
pratica
apenas um esporte.
- Sabendo que cada
 corresponde a 4 crianças, complete o gráfico pictórico abaixo.
corresponde a 4 crianças, complete o gráfico pictórico abaixo.
- Sabendo que cada


Fonte: Centro Esportivo Municipal (maio 2023).

- Quantas
 você utilizou para indicar a quantidade de crianças que praticam futebol? Como você pensou para determinar essa quantidade?
você utilizou para indicar a quantidade de crianças que praticam futebol? Como você pensou para determinar essa quantidade? _____
PROFESSOR
Resposta: 9 . Exemplo de resposta: Dividi 36 por 4.
. Exemplo de resposta: Dividi 36 por 4.
- Identifique as afirmações corretas sobre os dados representados nesse gráfico.
( ) Mais de uma centena de crianças praticam um dos três esportes.
( ) O número de crianças que praticam natação é menor que o dobro de crianças que praticam judô.
( ) Podem ser formados 6 times de futebol de 6 crianças.
PROFESSOR
Respostas corretas: Mais de uma centena de crianças praticam um dos três esportes.PROFESSOR
Podem ser formados 6 times de futebol de 6 crianças.
- Escreva uma afirmação que pode ser feita sobre esses dados.
_____
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivos
Construir pictograma.
Interpretar dados em pictograma.
Escrever afirmações com base na análise dos dados.
Explique aos estudantes que o pictograma é um tipo de gráfico em que os dados são representados por figuras (ícones). Essas figuras podem se repetir em diferentes quantidades ou ter tamanhos proporcionais às quantidades representadas. Observe se eles identificam os ícones que formam os pictogramas dessas atividades e se os interpretam de maneira apropriada para analisar as informações apresentadas.
Atividade 1
No item b, para elaborar o pictograma, os estudantes deverão perceber que a quantidade de símbolos pictográficos deve aumentar proporcionalmente à quantidade de 4 praticantes. Por exemplo, o número de praticantes de natação é dado por 14 × 4 = 56, o número de praticantes de futebol, por 9 × 4 = 36, e o número de praticantes de judô, por 6 × 4 = 24.
Ao identificarem as afirmações corretas, no item c, os estudantes deverão analisar os dados organizados no pictograma. Essa análise será necessária para elaborarem uma afirmação em relação a esses dados, no item d.
Aproveite esse momento e solicite aos estudantes que compartilhem as diferentes afirmações que escreveram, para que todos da turma possam refletir sobre os dados organizados no pictograma.
BNCC em foco:
EF04MA27
MP189
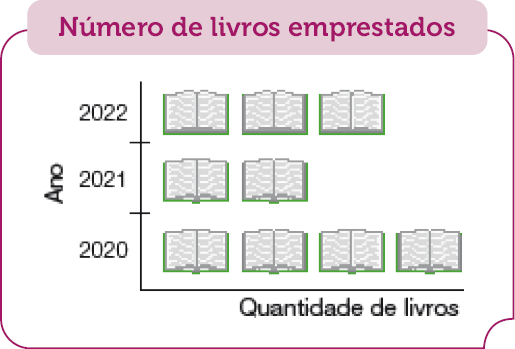
- O gráfico abaixo apresenta o número de livros emprestados da biblioteca municipal em um ano.

Fonte: Biblioteca municipal.
- Em qual ano foram emprestados mais livros?
_____
PROFESSOR
Resposta: No ano de 2020.
- Quantos livros foram emprestados no ano de 2020 a mais que no ano de 2021?
_____
PROFESSOR
Resposta: 2.000 livros.
- Quantos livros foram emprestados ao todo nos três anos?
_____
PROFESSOR
Resposta: 9.000 livros.
- Escreva duas afirmações que podem ser feitas em relação aos dados apresentados no gráfico.
_____
PROFESSOR
Resposta pessoal.
- Se cada
 representasse 500 livros emprestados, quantos desenhos como esse deveriam ser utilizados para indicar a quantidade de empréstimos em cada ano?
representasse 500 livros emprestados, quantos desenhos como esse deveriam ser utilizados para indicar a quantidade de empréstimos em cada ano? _____
PROFESSOR
Resposta: 2020: 8 desenhos; 2021: 4 desenhos; e 2022: 6 desenhos.
- No primeiro trimestre de 2023, foram emprestados 3.500 livros. Como você representaria essa informação no gráfico pictórico?
PROFESSOR
Atenção professor: O estudante pode considerar metade do ícone para representar 500 livros ou considerar que cada ícone represente uma quantidade diferente de 1 000 livros, por exemplo, 500 livros. Fim da observação.
MANUAL DO PROFESSOR
Atividade 2
A interpretação de dados estatísticos em um gráfico é mais bem explorada quando são feitas perguntas que permitam verificar se os estudantes compreendem que os gráficos servem para: elaborar hipóteses (por exemplo: “Por que em 2021 foram emprestados menos livros do que em 2020?”); comparar e relacionar os dados apresentados, como mostrado nas questões da atividade; prever tendências (por exemplo: “Se em 2023 a variação em relação a 2022 for a mesma, em quantidade, que a variação de 2020 para 2021, quantos livros serão emprestados em 2023?”). Promova uma discussão com a classe para que os estudantes percebam essas diversas possibilidades de aplicação dos dados apresentados. Incentive a análise, a argumentação e a expressão oral de opiniões.
BNCC em foco:
EF04MA27
Sugestão de atividade
Construção de pictograma
Proponha uma coleta de dados sobre a preferência de esportes entre os estudantes, de modo que seja possível a construção de um pictograma como o da atividade 1. Deixe os estudantes escolherem a relação entre a figura e a quantidade representada: se 1 figura representa 2 estudantes, ou 3 estudantes etc. Espera-se que eles percebam que a melhor escala depende de os dados serem todos números do tipo 2 vezes, ou 3 vezes etc.
MP190
O que você aprendeu
Avaliação processual
- Juliana apresenta um programa de previsão do tempo. Ela informou que hoje a temperatura máxima prevista é 28 ºC e que a previsão é que diminua 2 ºC a cada dia durante os próximos 8 dias, atingindo a temperatura mínima prevista para o mês.
Qual será a temperatura mínima nesse mês, se a previsão estiver correta?
_____
PROFESSOR
Exemplo de cálculo:PROFESSOR
2 × 8 = 16PROFESSOR
28 − 16 = 12Se a previsão estiver correta, a temperatura mínima será _____ °C nesse mês.
PROFESSOR
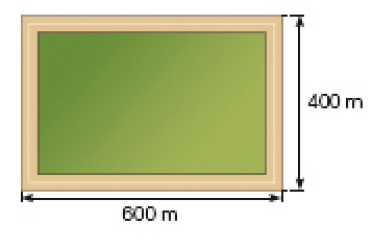
Resposta: 12- Veja abaixo a representação da pista retangular onde foi realizada uma corrida na qual Laura participou. Se ela deu 3 voltas
nessa
pista, qual foi a distância percorrida?
_____
PROFESSOR
Resposta: 6.000 m ou 6 km.
- Observe a planta da casa de Isadora e, depois, responda às questões.
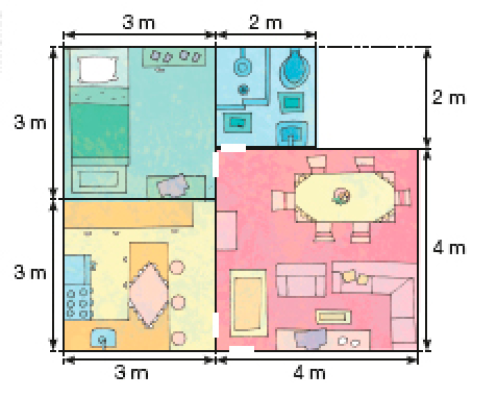
Na planta, cada metro está representado por 1 centímetro.
- Qual é a medida do perímetro da casa de Isadora?
_____
PROFESSOR
Resposta: 26 m
- Qual é o cômodo de maior área da casa?
_____
PROFESSOR
Resposta: A sala.
- E o de
menor
área?
_____
PROFESSOR
Resposta: O banheiro.
- Quantas vezes o cômodo de
menor
área cabe dentro do de maior área?
_____
PROFESSOR
Resposta: 4 vezes.
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Os estudantes podem construir uma tabela e registrar a temperatura dia a dia, ou verificar que a temperatura diminuirá 16 °C (2 × 8 = 16).
Atividade 2
Para resolver essa atividade, os estudantes precisam reconhecer que os lados opostos de um retângulo têm mesma medida. Assim, a pista de corrida tem dois “lados” de medida 600 metros e dois “lados” de medida 400 metros. Ou seja, uma volta completa pela pista corresponde a 2.000 m ou 2 km. Laura deu três voltas completas, ou seja, 3 vezes 2.000 m. Assim, foi de 6.000 m ou 6 km a distância percorrida por ela.
Atividade 3
Peça aos estudantes que reproduzam, em papel quadriculado, a planta apresentada, com o traçado de cada cômodo da casa de Isadora. Oriente-os a representarem cada 1 metro do esquema da casa pelo lado de 1 quadradinho do papel quadriculado. Depois, devem recortar cada cômodo, para verificar experimentalmente as respostas encontradas na atividade. Por exemplo, para saber que o cômodo de menor área cabe quatro vezes no cômodo de maior área, basta sobrepor o recorte menor no maior e observar as proporções.
BNCC em foco:
EF04MA20, EF04MA21, EF04MA23, EF04MA24
Sugestão de atividade
Medição
Os conteúdos estudados nesta Unidade poderão ser explorados com uma atividade prática de medição. Proponha aos estudantes que meçam os perímetros da quadra da escola e da sala de aula. Para isso, peça-lhes que levem para a aula uma fita métrica de casa. Com os dados que os estudantes encontraram, pode ser feita uma planta da quadra e da sala de aula, criando-se uma escala e transformando as medidas conforme essa escala. Outra atividade para explorar os conceitos da Unidade é levar para a sala de aula um mapa da cidade e pedir aos estudantes que analisem a escala utilizada no mapa e descubram, com base nesse dado, qual seria esse valor em outras unidades de medida. Após a observação desse mapa, pode-se pedir aos estudantes que representem a quadra onde moram com os valores em metro.
MP191
- Descubra a medida da área do quadrado maior da figura considerando o triângulo vermelho como a unidade de medida de área.
_____
PROFESSOR
Resposta: 4 triângulos vermelhos.

Boxe complementar:
Dica
O triângulo vermelho tem a mesma medida de área que o triângulo laranja.
Fim do complemento.
- Determine a medida da área, em centímetro quadrado, da figura em cada caso.
a)
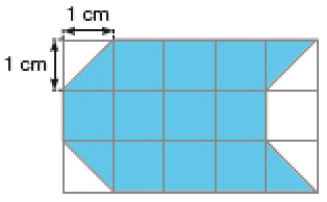
_____
PROFESSOR
Resposta: 12 cm²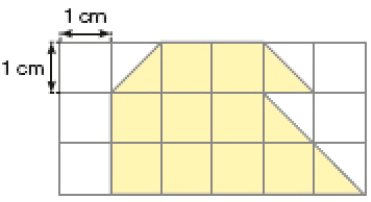
_____
PROFESSOR
Resposta: 11 cm²- Marque com um
X
a resposta correta.
Marcos quer saber quantos centímetros quadrados tem a folha que ele encontrou.
Ele a colocou sobre uma malha quadriculada e a desenhou.
Quantos centímetros quadrados, aproximadamente, tem a folha?
- ( ) 3 cm²
- ( ) 4 cm²
- ( ) 6 cm²
- ( ) 9
cm²
PROFESSOR
Resposta correta: 6 cm²
Autoavaliação

- Consigo perceber a relação de equivalência entre unidades de medida de comprimento?

- Compreendo a
ideia
de área e de perímetro?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 4
Incentive os estudantes a reproduzirem o Tangram para que possam representar a situação e, por meio da sobreposição de peças, concluir que a área do quadrado maior é igual à área de quatro triângulos vermelhos.
Atividade 5
Nesta atividade, os estudantes calculam a medida de uma superfície representada em malha quadriculada por meio de compensações de medidas, originadas de correspondências como “a metade de um quadrado (um triângulo) adicionada à metade de outro quadrado com lados de mesma medida (um triângulo) forma um novo quadrado, de medidas iguais aos quadrados originais”.
Atividade 6
Apesar de a folha estar sobre a malha quadriculada, os estudantes terão de fazer uma estimativa para determinar a área da folha, indicando a alternativa que mais se aproxima da medida real.
BNCC em foco:
EF04MA21
Autoavaliação
A primeira questão está relacionada às medidas de comprimento padronizadas. Os estudantes deverão analisar se conseguem perceber equivalências e fazer conversões, por exemplo, perceber que 100 centímetros equivalem a um metro.
Na segunda questão, os estudantes deverão perceber se não confundem as ideias de área e perímetro e, se possível, ampliando a questão, verificar se já conseguem mobilizar ferramentas para os cálculos.
MP192
Comentários para o professor:
Conclusão da Unidade 5
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue medir e estimar comprimentos (incluindo perímetros), utilizando unidades de medida padronizadas mais usuais? |
_____ |
_____ |
|
Consegue medir, comparar e estimar área de figuras planas desenhadas em malha quadriculada, pela contagem dos quadradinhos ou de suas metades, reconhecendo que duas figuras com formatos diferentes podem ter a mesma medida de área? |
_____ |
_____ |
|
Reconhece temperatura como grandeza e o grau Celsius como unidade de medida a ela associada? |
_____ |
_____ |
|
Registra as temperaturas máxima e mínima diárias e elabora gráficos de colunas com as variações diárias da temperatura? |
_____ |
_____ |
|
Interpreta e analisa dados apresentados em textos e em tabelas simples ou de dupla entrada? |
_____ |
_____ |
|
Constrói, analisa e interpreta gráficos de colunas ou pictóricos? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |