MP193
Comentários para o professor:
Introdução da Unidade 6
Esta Unidade tem como foco tratar os conhecimentos a serem desenvolvidos na Unidade Temática Números. Assim, a abertura traz, em página dupla, uma imagem próxima do cotidiano da criança na faixa etária do estudante do 4º ano do Ensino Fundamental com informações a serem exploradas nas questões propostas na seção Para refletir.
Os conhecimentos sobre frações e números na forma decimal, que compõem os estudos referentes à Unidade Temática Números, serão introduzidos nesta Unidade por meio de atividades que favorecem o reconhecimento das frações unitárias mais usuais, entre elas, e , como unidades de medida menores do que uma unidade, utilizando a reta numérica como recurso.
Em relação aos números na forma decimal, as atividades propostas pretendem promover o reconhecimento de que as regras do sistema de numeração decimal podem ser estendidas para a representação decimal de um número racional, conduzindo os estudantes a relacionarem décimos e centésimos com representações do sistema monetário brasileiro. Assim são apresentadas, além da já conhecida moeda de 1 real, outras moedas: 1 centavo (0,01 real), 5 centavos (0,05 real), 10 centavos (0,10 real), 25 centavos (0,25 real) e 50 centavos (0,50 real).
Cabe observar que os conhecimentos desenvolvidos, durante o 3º ano, acerca da comparação e da equivalência de valores do sistema monetário brasileiro são aportes necessários para as relações a serem estabelecidas entre eles e a representação decimal do número racional.
Várias atividades exploram as resoluções de problemas que envolvem o sistema monetário brasileiro, em contextos mais complexos dos que foram trabalhados no 3º ano, com situações de troco e desconto, enfatizando o consumo ético, consciente e responsável.
As atividades propostas, na perspectiva de que os estudantes se apropriem dos conhecimentos acima mencionados, envolvem também outras Unidades Temáticas, sobretudo Grandezas e medidas. Pretende-se, desta forma, garantir que os conhecimentos matemáticos não sejam apresentados de forma compartimentada e estanque, ao contrário, sejam compreendidos pelos estudantes a partir das conexões que se estabelecem entre conhecimentos relativos às diferentes Unidades Temáticas. Neste sentido, as atividades promovem o uso de medidas de comprimento, de massa, de capacidade e de tempo. Envolvem, também, conhecimentos acerca da Unidade Temática Probabilidade e estatística, por meio da leitura e da interpretação de dados apresentados em tabelas e em gráficos de barras e de colunas.
Cabe observar que os conteúdos tratados nesta Unidade se apresentam como suporte para aprendizagens da Unidade Temática Números e aplicações na Unidade Temática Grandezas e medidas no 5º ano.
MP194
UNIDADE 6. Frações e números na forma decimal

MANUAL DO PROFESSOR
Objetivos da Unidade
Reconhecer e representar partes menores que uma unidade com desenhos, frações e números na forma decimal.
Identificar, comparar e representar frações e números na forma decimal.
Reconhecer que as regras do sistema de numeração decimal podem ser estendidas para a representação decimal de um número racional.
Relacionar décimos e centésimos com a representação do nosso sistema monetário.
Expressar medidas por meio de números na forma decimal.
Resolver problemas que envolvam adição e subtração com frações.
Ler e interpretar dados em tabela e em gráfico de barras.
Esta Unidade explora números racionais representados na forma fracionária e na forma decimal.
É importante notar que, embora a principal ideia relacionada com a noção de fração – a de parte de um todo – seja bem explorada na Unidade, a representação numérica de uma fração representa um desafio para estudantes dessa faixa etária. Por isso, sugerimos que se dedique especial atenção à transposição das situações apresentadas em esquemas e, depois, dos esquemas em notação de frações.
A imagem da abertura apresenta uma cena em um posto de combustíveis.
BNCC em foco:
EF04MA09, EF04MA10, EF04MA20, EF04MA25, EF04MA27
MP195
Boxe complementar
Para refletir...
A família Silva foi viajar e parou para almoçar em um restaurante no posto de combustível da estrada.


O caminhão amarelo gastou metade dos 200 litros de diesel que cabem no tanque de combustível. Quantos litros de diesel restam no tanque?
PROFESSOR
Resposta: 100 litros.

Você compreende o significado de e de nos marcadores de combustível destacados nesta cena? Explique.
PROFESSOR
Resposta pessoal.Nesse restaurante, quantas moedas de 50 centavos são necessárias para comprar 1 picolé?
PROFESSOR
Resposta: 7 moedas.Fim do complemento
MANUAL DO PROFESSOR
Para refletir...
Antes de os estudantes resolverem as atividades, peça a eles que citem algumas situações em que usam expressões como meio e terço. Lembre-os do significado de termos como metade, terço, quarto etc. de uma quantidade e verifique se relacionam esses resultados com as frações , , etc. de uma mesma quantidade.
A primeira atividade requer dos estudantes um conhecimento familiar e muito frequente nas práticas diárias, que é a noção de metade como algo dividido em duas partes. Verifique se sabem que essas partes precisam ter a mesma medida.
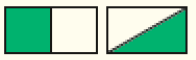
A atividade seguinte explora a comparação entre as frações e facilitada pelas ilustrações de marcadores de combustível. Em situações como esta, os estudantes percebem que o fato de 2 ser menor que 4 não significa que as frações em que esses números aparecem nos denominadores guardem a mesma relação, já que de um todo é maior que desse mesmo todo. Proponha a eles que representem quantidades fracionárias por meio de desenhos. Para isso, distribua duas folhas de papel sulfite por estudante e peça que encontrem maneiras de dividi-las em duas partes de mesmo tamanho (mesma área), pintando uma das partes. Sugira que considerem diferentes divisões do todo, como mostram as figuras abaixo.
CRÉDITO: ADILSON SECCO
Pergunte, então: “A parte pintada de verde em cada caso corresponde à mesma fração do todo?”. Espera-se que eles percebam que, em cada caso, a figura foi dividida em duas partes iguais e que a parte pintada corresponde a uma parte, ou seja, a da figura.
Se julgar oportuno, explique que diesel é um óleo derivado da destilação do petróleo bruto, usado como combustível.
MP196
Que números são estes?
- Observe as ilustrações e responda às questões.
- Flávia comeu ou a terça parte desta pizza, que foi dividida em pedaços de mesmo tamanho.

- Quantos pedaços ela comeu?
_____
PROFESSOR
Resposta: 1 pedaço.
- Giovana gastou ou a quarta parte da quantia abaixo fazendo compras na feira.

- Quantos reais ela gastou?
_____
PROFESSOR
Resposta: 50 reais.
- Veja, abaixo, a figura que Nara pintou.
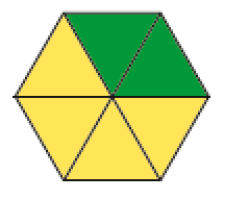
- Nara dividiu a figura em
_____
partes iguais e pintou
_____
partes de verde. Podemos dizer que 2 das 6 partes estão pintadas de verde ou, ainda, que dois sextos ou da figura foram pintados de verde.
PROFESSOR
Resposta: 6, 2

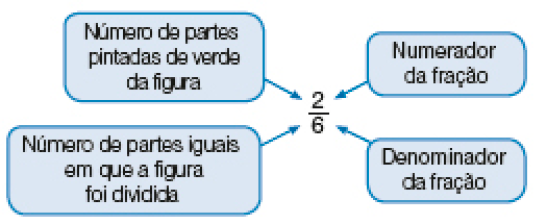
- Que fração representa as partes pintadas de amarelo da figura de Nara? Como lemos essa fração?
Fração: _____
PROFESSOR
Resposta:Lemos :_____
PROFESSOR
Resposta: Quatro sextos.MANUAL DO PROFESSOR
Objetivos
Reconhecer e representar partes do todo sob a forma de desenhos e de frações.
Identificar o numerador e o denominador em uma fração.
Nestas páginas, os estudantes trabalharão com situações variadas, e a representação da parte de um todo será feita por meio de desenhos, palavras ou símbolos numéricos.
Atividade 1
Esta atividade possibilita aos estudantes utilizar o significado das expressões: um terço ou terça parte, um quarto ou quarta parte. As imagens também colaboram para esse entendimento. No item b, é interessante observar que não é a cédula que será dividida, e sim a quantia que essa cédula representa (200 reais ÷ 4 = 50 reais).
Atividade 2
Esta atividade utiliza a representação de uma figura geométrica plana hexagonal, dividida em partes iguais, para explorar o total de partes da figura e as partes que foram pintadas por Nara. Isso permite aos estudantes se apropriarem do significado da “parte do todo” antes mesmo da apresentação do numerador e do denominador da fração.
Se julgar necessário, desenhe na lousa a figura ilustrada no livro. Pinte uma parte e pergunte: “Que fração representa essa parte pintada da figura?”. Pinte outra parte e pergunte: “E agora, que fração representa a parte pintada da figura? E se for pintada outra parte?”. Registre as respostas , , e pergunte: “O número que representa o total de partes da figura mudou ou permaneceu o mesmo? E os números que representam as partes pintadas?”.
BNCC em foco:
EF04MA09
MP197

- Pinte de cada figura e, depois, responda.
PROFESSOR
Exemplos de resposta: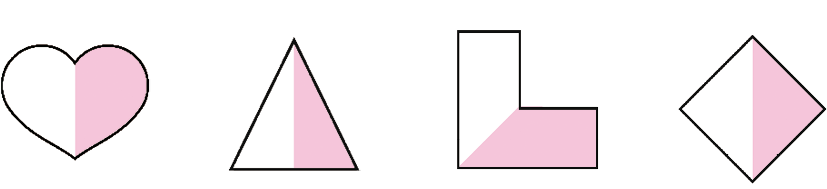
- Para pintar de cada figura, em quantas partes você dividiu cada uma? E quantas dessas partes pintou em cada uma delas?
_____
PROFESSOR
Resposta: 2; 1

- Compare suas pinturas com as de um colega. Elas são iguais?
PROFESSOR
Resposta pessoal.
- Veja como lemos algumas frações.
Tabela: equivalente textual a seguir.
|
|
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|---|
|
Um meio |
Dois terços |
Três quartos |
Quatro quintos |
Três sétimos |
Nove oitavos |
Cinco nonos |
Um décimo |
Sete doze avos |
- Agora, escreva como lemos as frações que representam a parte pintada de cada figura.
a)
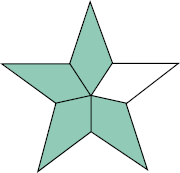
_____
PROFESSOR
Resposta: Quatro quintos.b)

_____
PROFESSOR
Resposta: Três oitavos.c)

_____
PROFESSOR
Resposta: Quatro nonos.- Escreva, para cada figura, a fração que representa a parte pintada. Depois, indique o numerador e o denominador e escreva como lemos cada fração.
a)

_____
PROFESSOR
Resposta:PROFESSOR
2 - NumeradorPROFESSOR
3 - DenominadorPROFESSOR
Dois terços.b)
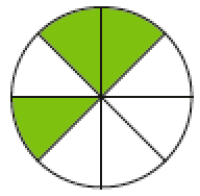
_____
PROFESSOR
Resposta:PROFESSOR
3 - NumeradorPROFESSOR
8 - DenominadorPROFESSOR
Três oitavos.c)

_____
PROFESSOR
Resposta:PROFESSOR
5 - NumeradorPROFESSOR
16 - DenominadorPROFESSOR
Cinco dezesseis avos.MANUAL DO PROFESSOR
Atividade 3
Verifique se os estudantes percebem que a fração apresentada corresponde à metade de cada figura. É preciso tomar cuidado para que realmente a metade da figura seja pintada e não se apresente apenas uma divisão em duas partes desiguais. No item b, aproveite para propor a discussão sobre as diferentes maneiras de dividir as figuras em duas partes iguais.
É interessante que os estudantes percebam as diversas maneiras como os colegas realizaram a pintura de de cada figura, constatando que a atividade pode ter várias respostas corretas.
Atividade 4
Trabalhe o significado dos termos de uma fração em cada caso. Pergunte: “O que significa o número 3 na fração quando dizemos de uma figura? E o número 5 na fração , ao falarmos de de uma figura?”. Espera-se que os estudantes respondam que o número 3 na fração indica o número de partes consideradas em uma figura dividida em 4 partes iguais e o número 5, na fração , o total de partes em que foi dividida a figura. Dê outros exemplos de leitura de frações envolvendo décimos, centésimos e milésimos. É interessante que os estudantes escrevam como lemos outras frações. Destaque que, quando o denominador é um número maior que 10, acrescentamos a palavra “avos” em sua leitura (exceto quando o denominador for igual a 100, 1.000 etc.).
Atividade 5
Peça aos estudantes que escrevam, também, uma fração que represente a parte não pintada de cada figura.
BNCC em foco:
EF04MA09
MP198
Situações com frações
- Por causa de uma obra, a polícia rodoviária interditou 3 das 4 faixas de um trecho de uma estrada. Que fração representa as partes interditadas nesse trecho? Você sabe como lemos essa fração? Escreva.
_____
PROFESSOR
Resposta: ; três quartos.

- Observe o desenho das maçãs na caixa e responda às questões.

- Quantas maçãs há na caixa?
_____
PROFESSOR
Resposta: 15 maçãs.
- Luciana usou (um terço) dessas maçãs para fazer uma torta. Quantas maçãs ela usou?
_____
PROFESSOR
Resposta: 5 maçãs.
- Quantas maçãs sobraram? Que fração das maçãs da caixa elas representam?
_____
PROFESSOR
Resposta: 10 maçãs; .

- Agora, converse com um
colega
sobre como cada um pensou para responder a essas questões.
PROFESSOR
Resposta pessoal.
- Quantas maçãs há na caixa?
_____
- Veja a coleção de carrinhos de Nelson e, depois, responda à questão.

- Nelson dará desses carrinhos para sua amiga Tânia. Quantos carrinhos ele dará para Tânia?
_____
PROFESSOR
Resposta: 5 carrinhos.
MANUAL DO PROFESSOR
Objetivos
Reconhecer e representar frações.
Resolver problemas que envolvam frações.
Atividade 1
Nesta atividade, os estudantes devem identificar que existem 3 faixas interditadas em 4 da estrada, relacionando assim com a fração (três de quatro).
Atividade 2
No item b, espera-se que os estudantes observem que devem formar 3 grupos de uma mesma quantidade de maçãs. Como na caixa da ilustração há 3 grupos com 5 maçãs, (um terço) dessas maçãs corresponde a 5 maçãs. Outro raciocínio possível é pensar que esta atividade trabalha com uma fração de quantidade cujo numerador é igual a 1, o que corresponde a efetuar a divisão da quantidade pelo número indicado no denominador da fração. Então, para obter de 15, basta dividir 15 por 3, obtendo 5.
Atividade 3
Seguindo a mesma linha de raciocínio da atividade anterior, os estudantes devem formar quatro grupos com uma mesma quantidade de carrinhos, ou seja, 4 grupos de 5 carrinhos cada. A ilustração sugere uma forma de fazer essa divisão, mas os estudantes precisam interpretar adequadamente a fração para decidirem como será feita essa divisão em grupos com a mesma quantidade de elementos. Para responder à questão, podem raciocinar da seguinte maneira: “Há 4 fileiras de 5 carrinhos cada uma. Então, 5 carrinhos correspondem a do total de carrinhos, ou seja, Nelson dará 5 carrinhos para Tânia”.
BNCC em foco:
EF04MA09
MP199
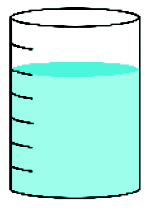
- Marque com um X o recipiente que está com de sua capacidade preenchidos com água.
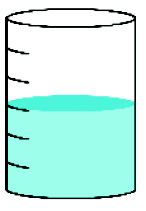
( )
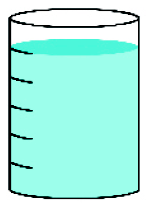
( )
( )
PROFESSOR
Resposta correta: recipiente 2.


- Calcule mentalmente e conte a um
colega
como você pensou para
obter
as respostas abaixo.
- Marta comprou 18 goiabas e usou dessas goiabas para fazer geleia. Quantas goiabas sobraram?
_____
PROFESSOR
Resposta: 6 goiabas.PROFESSOR
Resposta pessoal.
- Marta distribuiu igualmente a
geleia
de
goiaba
em 6
potes
de mesmo tamanho e deu para a irmã
dela
desses potes. Quantos
potes
de
geleia
a irmã de Marta ganhou?
_____
PROFESSOR
Resposta: 2 potes.
- Marta comprou 18 goiabas e usou dessas goiabas para fazer geleia. Quantas goiabas sobraram?
Boxe complementar:
Desafio
Ana, José e Diogo compraram 3 tortas de palmito, uma para cada um. As tortas eram iguais, mas cada um deles dividiu a torta de maneira diferente para comer. Descubra quem comeu a maior parte da torta. Justifique sua resposta.

CRÉDITO: FERNANDO VENTURA
_____
Resposta: Ana. Exemplo de justificativa: um pedaço de uma torta que foi dividida em 2 partes iguais é maior que um pedaço de uma torta que foi dividida em 4 partes iguais ou em 5 partes iguais.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 4
Nesta atividade, os estudantes devem observar as marcações de cada recipiente para determinar qual deles tem a capacidade solicitada. Ressalte que todos os recipientes têm a mesma capacidade e as marcas indicam divisões em partes iguais de capacidade.
Atividade 5
O objetivo desta atividade é promover a familiarização dos estudantes com situações em que são usadas frações.
Desenhe na lousa as 18 goiabas compradas por Marta e, junto com a turma, separe aquelas que serão usadas para fazer geleia e, depois, represente os 6 potes de geleia, separando-os de modo que os estudantes entendam quantos potes representam deles.
Desafio
Os estudantes podem fazer desenhos para resolver o problema. Exemplos de desenhos:
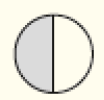
LEGENDA: Torta de Ana. FIM DA LEGENDA.
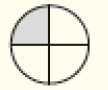
LEGENDA: Torta de José. FIM DA LEGENDA.
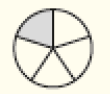
LEGENDA: Torta de Diogo. FIM DA LEGENDA.
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
BNCC em foco:
EF04MA09
MP200
Mais frações
- Observe o desenho de um estacionamento com 7 carros. O carro vermelho corresponde a que fração do total de carros? E os carros azuis? E os carros verdes?
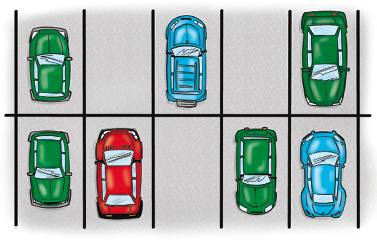
- Há
_____
carro vermelho entre os 7 carros do estacionamento. Esse carro vermelho corresponde a um sétimo ou do total de carros desse estacionamento.
PROFESSOR
Resposta: 1 - Há
_____
carros azuis entre os 7 carros do estacionamento. Esses carros azuis correspondem a
_____
ou do total de carros desse estacionamento.
PROFESSOR
Resposta: 2, dois sétimos - Há
_____
carros verdes entre os
_____
carros do estacionamento. Esses carros verdes correspondem a
_____
ou
_____
do total de carros desse estacionamento.
PROFESSOR
Resposta: 4, 7, quatro sétimos,
- Observe os cães e marque V para as frases verdadeiras e F para as falsas.

- ( ) 3 dos 8 cães são de cor caramelo.
PROFESSOR
Resposta: F
- ( ) Um nono dos cães está de coleira.
PROFESSOR
Resposta: V
- ( ) 5 dos 9 cães têm manchas pretas.
PROFESSOR
Resposta: V
- ( ) dos cães têm manchas pretas.
PROFESSOR
Resposta: F
MANUAL DO PROFESSOR
Objetivos
Reconhecer a fração como comparação entre parte e todo de uma quantidade.
Determinar a fração de um conjunto discreto.
Associar pontos da reta numérica a números fracionários.
Atividade 1
Para determinar as frações que expressam a quantidade de carros de cada cor em relação ao total de carros, os estudantes devem fazer a correspondência entre a quantidade de carros vermelhos, azuis ou verdes (1, 2 e 4, respectivamente) e a quantidade total de carros no estacionamento (7), e, então, expressar essa comparação na forma das frações: e respectivamente. Explore a atividade fazendo perguntas como:
“Se chegasse ao estacionamento mais um carro vermelho, a que fração do total de carros corresponderia a quantidade de carros vermelhos?” ( , dois oitavos ou 2 em 8 ou , um quarto ou 1 em 4).
E se fosse um carro azul, qual fração corresponderia aos carros vermelhos? ( um oitavo ou 1 em 8.).
Espera-se que os estudantes percebam que, no primeiro caso, são alteradas ambas as quantidades: tanto a relativa à parte (2 carros vermelhos) quanto à relativa ao todo (8 carros no total). Já no segundo caso, a quantidade relativa à parte se mantém (1 carro vermelho), mas a quantidade relativa ao todo se altera (8 carros no total).
Atividade 2
Proponha aos estudantes que corrijam as frases erradas. Uma correção possível seria responderem, no item a, que 4 em 9 cães são de cor caramelo e, no item d, que dos cães têm manchas pretas.
Peça a eles que leiam, em voz alta, cada uma das frações correspondentes aos agrupamentos de cães.
BNCC em foco:
EF04MA09
MP201
- Observe a quantidade de peixes do aquário e, depois, responda às questões.

- A fração representa os peixes de qual cor?
_____
PROFESSOR
Resposta: Da cor laranja.
- Que fração representa os peixes amarelos? E o peixe azul?
_____
PROFESSOR
Resposta:
- Que fração representa os peixes que não são laranja?
_____
PROFESSOR
Resposta:
- Veja o desenho da família de Heloísa e, depois, responda às questões.

- Quantas pessoas formam essa família?
_____
PROFESSOR
Resposta: 5 pessoas.
- Podemos dizer que 3 das 5 pessoas dessa família são crianças?
_____
PROFESSOR
Resposta: Sim.
- Escreva a fração que representa os adultos da família.
_____
PROFESSOR
Resposta: .
MANUAL DO PROFESSOR
Atividade 3
Esta atividade também apresenta a fração como comparação entre duas quantidades discretas (contáveis). O desafio encontra-se no fato de que os peixes do aquário não estão, em princípio, organizados.
Atividade 4
Esta atividade mobiliza os estudantes a pensarem em frases que resumem a cena observada e que utilizam a fração como um número representativo da quantidade que se deseja anunciar. É interessante abordar, de modo não formal, a adição de frações, fazendo perguntas como: “Juntando a fração correspondente às crianças da família com a fração correspondente aos adultos da família, que fração se obtém?”. Espera-se que os estudantes respondam , observando que essa fração corresponde ao inteiro, isto é, ao total de pessoas da família. Peça-lhes que desenhem sua família no caderno e representem com frações a quantidade de crianças e de adultos no desenho.
BNCC em foco:
EF04MA09
Sugestão de atividades
Brincando com tampinhas
Separe os estudantes em grupos e distribua 24 tampinhas de garrafas plásticas para cada grupo. Depois, pergunte quantas tampinhas, em relação ao total, correspondem a: e Espera-se que os estudantes respondam: 12, 8, 6, 4 e 2, respectivamente. Então, pergunte: “Qual dessas frações corresponde ao maior número de tampinhas?” ( ).
MP202
- Observe abaixo os passageiros em uma parte do avião e escreva uma frase relacionada à imagem na qual seja usada uma fração.
_____
PROFESSOR
Exemplo de resposta: As poltronas vazias correspondem a do total de poltronas dessa parte do avião.

- Felipe tinha 10 balas. Em cada 5 dessas balas, 2 eram de chocolate. Quantas balas de chocolate Felipe tinha?
_____
PROFESSOR
Resposta: 4 balas de chocolate.
- Raul ganhou 40
bolinhas
de gude. Em cada 10 dessas bolinhas, 4 eram verdes. Quantas
bolinhas
verdes Raul ganhou?
____
PROFESSOR
Resposta: 16 bolinhas verdes.

- Pinte cada barra conforme a legenda.
PROFESSOR
Exemplos de pinturas:-
 da barra
da barra  o restante da barra
o restante da barra

PROFESSOR
Resposta: vermelho, vermelho, vermelho, amarelo-
 da barra
da barra  o restante da barra
o restante da barra

PROFESSOR
Resposta: verde, verde, azul, azul, azul-
 da barra
da barra  o restante da barra
o restante da barra

PROFESSOR
Resposta: rosa, rosa, rosa, rosa, rosa, rosa, marrom, marrom-
 da barra
da barra  o restante da barra
o restante da barra

PROFESSOR
Resposta: laranja, laranja, laranja, laranja, laranja, laranja, laranja, lilás, lilás, lilásMANUAL DO PROFESSOR
Atividade 5
Espera-se que os estudantes relacionem a ideia com a noção de fração – a de parte de uma quantidade com a situação apresentada. Verifique e valide as frases que eles escreveram.
Atividade 6
Nesta atividade, os estudantes precisam reconhecer a quantidade total de balas de chocolate em relação ao todo, partindo de uma fração dessa quantidade. Sabendo que, quando o todo considerado é igual a 5 balas e há 2 balas de chocolate, pode-se deduzir que, quando o todo considerado é dobrado, para 10 balas, a quantidade de balas de chocolate também é dobrada, para 4 balas. Na questão proposta há uma comparação implícita entre as frações e que são equivalentes. Se julgar oportuno, proponha a eles que estabeleçam essa comparação para que verifiquem essa equivalência.
Atividade 7
Espera-se que os estudantes percebam que precisam conhecer o total de bolinhas de Raul para, assim, fazer, por exemplo, 4 agrupamentos e descobrir a quantidade de bolinhas verdes.
Atividade 8
Identificar a fração do inteiro que falta para completá-lo objetiva preparar os estudantes para o cálculo mental de adição e subtração com frações de mesmo denominador. Mostre, por exemplo, uma barra dividida em 12 partes iguais e peça aos estudantes que pintem da barra. Depois, pergunte: “Quanto falta para completar a pintura da barra? Como posso representar essa parte com uma fração? Como posso representar essa situação com uma adição com frações?”.
BNCC em foco:
EF04MA09
Números na forma de fração na reta numérica
Localizar um número na forma de fração na reta numérica pode ser usado como recurso visual para que os estudantes façam comparações entre duas frações.
Veja no exemplo abaixo como podemos relacionar várias frações e compará-las.


CRÉDITO: ADILSON SECCO
MP203
- Localize na reta numérica os números na forma de fração.
-

PROFESSOR
Resposta: , ,
PROFESSOR
Resposta: , ,- Compare a medida do comprimento do lápis com o comprimento das barras lilás e laranja. Em seguida, marque com um X as frases verdadeiras.

O lápis azul tem comprimento:
- ( ) maior que da barra lilás e menor que da barra laranja.
- ( ) maior que da barra lilás e menor que da barra laranja.
- ( ) menor que da barra lilás e maior que da barra laranja.
- ( )
menor
que da barra lilás e maior que da barra laranja.
PROFESSOR
Respostas corretas: maior que da barra lilás e menor que da barra laranja; enor que da barra lilás e maior que da barra laranja.
MANUAL DO PROFESSOR
Com essa representação, é possível trabalhar algumas estratégias que envolvem a comparação de duas frações. Repare que o recurso visual permite que os estudantes deem um significado para a situação. Por exemplo, eles podem ser levados a entender que é maior que porque quando o inteiro é dividido em quintos os intervalos ficam maiores do que quando ele é dividido em sextos. E, portanto, um comprimento que parta do zero e pare em tem medida maior que um comprimento que parta do zero e pare em .
Atividade 9
As retas numéricas desta atividade já têm as marcas em que os números na forma de fração serão localizados. No item a, o número (um quarto) pode ser localizado ao se perceber que o intervalo de 0 a 1 foi dividido em 4 partes iguais e que a primeira marca à direita do zero corresponde a um quarto. O mesmo raciocínio pode ser considerado para localizar . O número (meio) é facilmente localizado porque representa a metade. Vale a pena verificar se os estudantes notam que, no lugar de escrever para representar metade, eles poderiam escrever .
Atividade 10
Antes de os estudantes assinalarem as respostas corretas, oriente-os a localizarem as frações das barras, como mostramos a seguir.
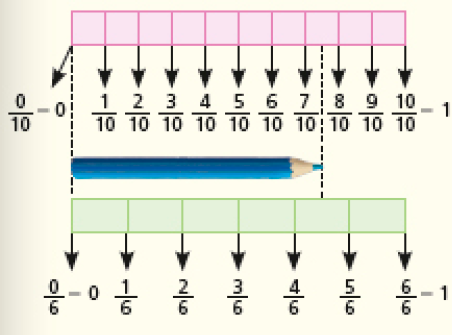
CRÉDITO: ADILSON SECCO
Com essas indicações, eles terão facilidade de reconhecer as respostas corretas, sem aplicar qualquer regra formal, tendo apenas o recurso visual. Crie outras situações de comparação usando a mesma figura. Peça aos estudantes que comparem, por exemplo, as frações e . Eles devem concluir que representam a mesma medida (metade da barra).
BNCC em foco:
EF04MA09
MP204
Frações e medidas
- Tadeu precisava
medir
a largura de um quadro, mas não tinha régua
nem
fita métrica. Então, ao usar um barbante para medir, ele percebeu que a medida da largura do quadro era igual à medida do comprimento de 2 barbantes mais um pedaço que ele não sabia bem de que tamanho era.
- Qual é a medida da largura desse quadro, considerando o barbante como unidade de medida?
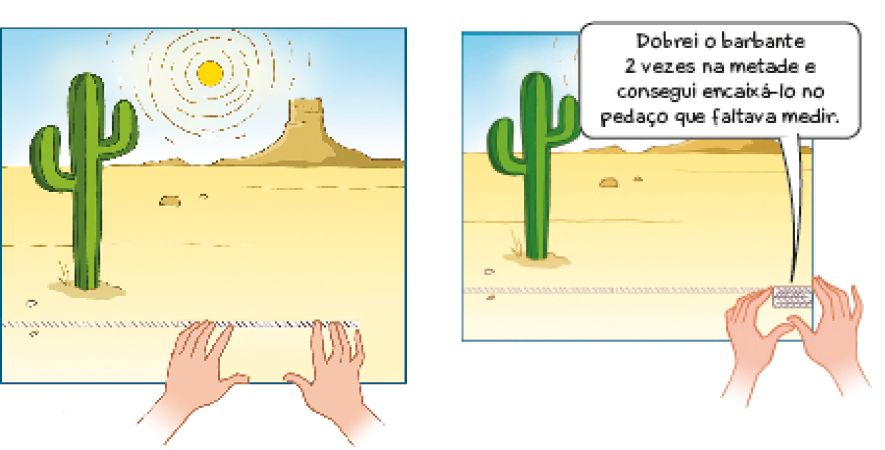
Então, a medida da largura desse quadro é igual a _____ barbantes e do barbante.
PROFESSOR
Resposta: 2- Observe os esquemas a seguir e descubra as medidas do comprimento da tira de papel azul e do comprimento da tira de papel amarelo usando os palitos como unidade de medida.
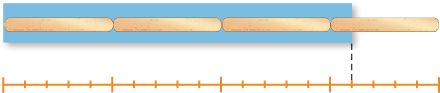
_____
PROFESSOR
Resposta: 3 palitos e do palito.b)
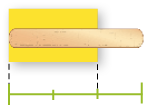
_____
PROFESSOR
Resposta: do palito.- Você demora mais ou menos de de hora para tomar banho?
_____
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Objetivo
Reconhecer e representar a fração de uma unidade de medida.
Atividade 1
Aproveite a situação de medição da largura de um quadro para comentar com a turma que o uso de medidas na forma de fração é mais comum em medidas dos chamados “sistemas imperiais” (como as unidades de medida polegada, milha e jarda), muito comuns em países como Estados Unidos e Inglaterra.
Atividade 2
No item a, os estudantes devem observar que 4 palitinhos ultrapassam a medida de comprimento da tira de papel azul, mas 3 palitinhos são insuficientes, de modo que a resposta será dada na forma de uma medida inteira e uma medida expressa na forma de fração. Já no item b, 1 palitinho ultrapassa a medida de comprimento da tira de papel amarela. Então, a resposta será dada por uma medida na forma de fração.
Atividade 3
Comente com os estudantes que a ideia de fração para representar intervalos de tempo em hora não ocorre com muita frequência em nossa língua, sendo mais comum a expressão meia hora. Metade de uma hora corresponde à metade ( ) de 60 minutos, ou seja, a 60 minutos divididos por 2, que são 30 minutos. Em alguns textos escritos, aparece a referência a “ de hora”, mas essa não é uma expressão usual. Os estudantes podem observar que de hora corresponde a de 60 minutos, ou seja, 60 minutos divididos por 4, que são 15 minutos. Podem também observar que de hora corresponde à metade da metade de 1 hora. Assim, metade da metade de 60 minutos são 15 minutos.
BNCC em foco:
EF04MA09
MP205
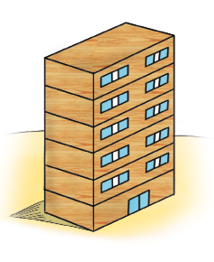
- Flávio montou um prédio de brinquedo com 6 peças de madeira de mesmo tamanho.
A que fração da medida da altura do prédio corresponde a altura de cada peça?
_____
PROFESSOR
Resposta: da medida da altura.
- Kauê precisou de 1 litro de tinta laranja para pintar a metade do muro representado abaixo. Agora, responda às questões.

- De que fração do litro de tinta Kauê precisou para pintar a parte azul do muro? E para pintar a parte verde?
_____
PROFESSOR
Resposta: litro (meio litro) para cada uma das partes.
- De quantos litros de tinta Kauê precisou para pintar o muro todo?
_____
PROFESSOR
Resposta: 2 litros.
- Leia o que diz Tarcísio e responda às questões.


- Para saber a medida da espessura de apenas 1
folha
desse papel, teríamos de dividir 1 centímetro em quantas partes?
_____
PROFESSOR
Resposta: 100 partes.
- Que fração do centímetro representa a medida da espessura de uma das
folhas
desse bloco?
_____
PROFESSOR
Resposta: do centímetro.
- Complete.
-
de uma hora equivale a
_____
minutos.
PROFESSOR
Resposta: 20
-
de um quilômetro equivalem a
_____
metros.
PROFESSOR
Resposta: 400
-
de um quilograma equivale a
_____
gramas.
PROFESSOR
Resposta: 500
MANUAL DO PROFESSOR
Atividade 4
Espera-se que os estudantes percebam que o prédio é composto por 6 peças e que cada uma delas representa desse prédio.
Atividade 5
Os estudantes devem compreender que, apesar de o muro estar dividido em 3 partes, cada uma não corresponde a do muro, pois essas partes não têm o mesmo tamanho (área). Pergunte: “A parte azul do muro corresponde a que fração do muro?” ( do muro.)
Atividade 7
Nesta atividade, os estudantes são incentivados a pensarem em representações inteiras de medidas representadas por frações, por exemplo: de hora como resultado da divisão 60 ÷ 3, ou pela representação geométrica de um círculo (mostrador de um relógio) dividido em 3 partes iguais, deduzindo que 20 minutos correspondem a de hora.
BNCC em foco:
EF04MA09
Sugestão de atividade
Criando frações
Proponha para a turma as questões a seguir.
Que fração da figura abaixo está pintada, da figura ou da figura? ( da figura.)

Que fração da figura a seguir está pintada, da figura ou da figura? ( da figura.)
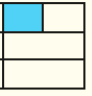
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
MP206
Números na forma decimal
Décimos
- Observe a ilustração e, depois, responda às questões.

- O comprimento do desenho do lápis é maior que 8 centímetros?
_____
PROFESSOR
Resposta: Sim.
- O comprimento do desenho do lápis é maior que 9 centímetros?
_____
PROFESSOR
Resposta: Não.
- Como você representaria a medida do comprimento do desenho do lápis?
PROFESSOR
Resposta pessoal.
- Luís está pintando um painel que foi dividido em 10 partes iguais. O painel todo representa um inteiro.
Cada parte corresponde a um décimo do painel.

: representação de 1 décimo em fração
0,1: representação de 1 décimo na forma decimal

- A quantidade de faixas pintadas corresponde a quantos décimos do painel em cada caso?
a)

_____
PROFESSOR
Resposta: 3 décimos do painel, do painel ou 0,3 do painel.b)

_____
PROFESSOR
Resposta: 6 décimos do painel, do painel ou 0,6 do painel.MANUAL DO PROFESSOR
Objetivos
Identificar, ler e representar pela escrita décimos, centésimos e milésimos de um todo na forma decimal.
Relacionar décimos, centésimos e milésimos com sua representação na forma de fração.
Comparar as representações nas formas de fração e decimal favorece a compreensão dos estudantes de que os números na forma decimal não representam um conceito diferente do envolvido pelas frações.
Atividade 1
Esta atividade apresenta a maneira mais imediata de os estudantes reconhecerem o décimo: pela observação da graduação na régua ilustrada para explorar o comprimento do lápis.
Converse com a turma sobre as diferentes formas de representação apresentadas. Eles poderão usar recursos gráficos, numéricos, a língua materna ou misturar as linguagens. Pode haver representações menos precisas que outras. Veja alguns exemplos:
8 e meio
8 e 6 mm
8 e
Atividade 2
Aqui, apenas uma das 10 partes em que o painel foi dividido está pintada, ou seja, foi pintado 1 décimo do painel, que pode ser representado por 0,1 ou por . É importante insistir na correspondência entre as duas representações da mesma quantidade, para que os estudantes entendam que 0,1 (representação na forma decimal) e (representação na forma de fração) são diferentes representações de um mesmo número, ou de uma mesma parte de um todo, e não dois números diferentes.
BNCC em foco:
EF04MA10
Sugestão de atividade
Problema
Ricardo tem uma barra de chocolate dividida em 10 partes iguais. Cada parte representa, então, um décimo do chocolate. Se ele comer 3 das partes desse chocolate, quantos décimos do chocolate sobrarão? (7 décimos do chocolate.)
MP207
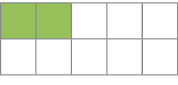
- Represente a parte pintada de cada figura com uma fração e na forma decimal.
a)
_____
PROFESSOR
Resposta: ; 0,2b)
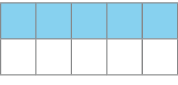
_____
PROFESSOR
Resposta: ; 0,5c)
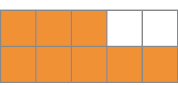
_____
PROFESSOR
Resposta: ; 0,8- Complete o quadro.
Quadro: equivalente textual a seguir.
|
Figura |
Representação com uma fração |
Representação na forma decimal |
Como lemos |
|---|---|---|---|
|
|
|
_____ |
três décimos |
|
|
_____ |
_____ |
_____ |
|
|
_____ |
_____ |
_____ |
PROFESSOR
Resposta: Representação com uma fração: ;PROFESSOR
Representação na forma decimal: 0,3; 0,5; 0,6.PROFESSOR
Como lemos: cinco décimos; seis décimos.- Mário é técnico da equipe de futebol Bons de Bola. Ele fez o gráfico abaixo com o número de gols marcados por seus jogadores em várias partidas.
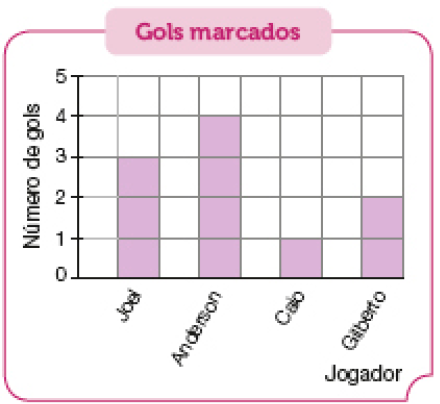
Fonte: Equipe Bons de Bola (maio 2023).
- Quantos gols foram marcados no total?
_____
PROFESSOR
Resposta: 10 gols.
- Que jogador fez quatro
décimos
dos gols da equipe?
_____
PROFESSOR
Resposta: Anderson.
- A quantidade de gols marcados por Joel corresponde a quantos
décimos
do total de gols marcados pela equipe Bons de Bola?
_____
PROFESSOR
Resposta: 3 décimos.

- Patrícia fez 0,7 de sua tarefa escolar. Ela fez mais ou menos que a metade da tarefa? Justifique sua resposta.
PROFESSOR
Resposta: Mais que a metade. Exemplo de justificativa: a metade da tarefa corresponde a 5 décimos ou 5 partes em 10.
MANUAL DO PROFESSOR
Atividade 3
Aqui, os estudantes devem expressar a parte pintada de cada uma das 3 figuras (todas divididas em 10 partes iguais) por meio de uma representação na forma de fração e de uma representação na forma decimal.
Verifique que frações os estudantes usaram para as representações solicitadas. Não desconsidere eventuais respostas com frações equivalentes às respostas dadas. Por exemplo: item a, item b, e item c, . Aproveite para pedir aos estudantes que representem na forma de fração e na forma decimal a parte não pintada de cada figura.
Atividade 4
Nesta atividade, além de estabelecer relações entre a representação gráfica de décimos (de um todo repartido em 10 partes de mesma área) e sua representação numérica (na forma de fração e na forma decimal), os estudantes começam a exercitar a escrita por extenso e a leitura dessas representações.
Atividade 5
Se julgar oportuno, peça aos estudantes que representem, por um número na forma de fração e por um número na forma decimal, a quantidade de gols que os outros jogadores marcaram em relação ao total de gols marcados.
Atividade 6
Esta atividade explora a comparação entre números na forma decimal. Caso os estudantes encontrem dificuldade para resolvê-la, proponha a eles que façam desenhos para representar a situação:
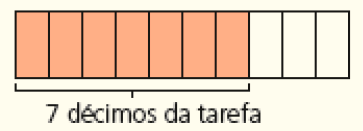
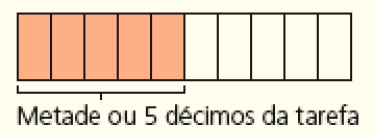
CRÉDITO: ADILSON SECCO
Comparando os desenhos, fica fácil constatar que 0,7 da tarefa é mais do que 0,5 da tarefa.
BNCC em foco:
EF04MA10
MP208
Centésimos
- Observe o tabuleiro de um jogo que é formado por 100 casas iguais.
Cada casa corresponde a um centésimo do tabuleiro.
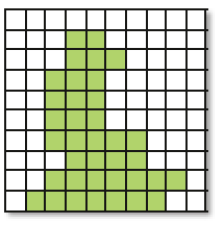
: representação de 1 centésimo com uma fração
0,01: representação de 1 centésimo na forma decimal

- As casas verdes correspondem a 37 centésimos do tabuleiro, que podem ser representados na forma de fração: ou na forma decimal:
_____
PROFESSOR
Resposta: 0,37
- As casas brancas correspondem a quantos centésimos do tabuleiro?
_____
PROFESSOR
Resposta: 63 centésimos, ou , ou 0,63 do tabuleiro.
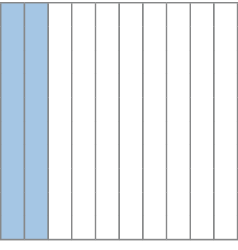
- Observe as figuras 1 e 2, de mesmo tamanho, e responda às questões.
- A parte pintada de azul da Figura 1 corresponde a quantos
décimos
da Figura 1 inteira?
_____
PROFESSOR
Resposta: 2 décimos da Figura 1.
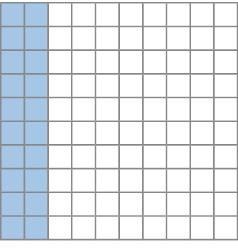
- A parte pintada de azul da Figura 2 corresponde a quantos centésimos da Figura 2 inteira?
_____
PROFESSOR
Resposta: 20 centésimos da Figura 2.
- A parte pintada de azul é maior na Figura 1 ou na Figura 2?
PROFESSOR
Resposta: Espera-se que os estudantes percebam que, nas duas figuras, as partes pintadas têm o mesmo tamanho.
Figura 1.

- Que parte de uma figura é maior: 0,2
dela
ou 0,20 dela?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que 0,2 de uma figura e 0,20 da mesma figura têm o mesmo tamanho: 0,2 = 0,20. Fim da observação.
Figura 2.
MANUAL DO PROFESSOR
Objetivos
Identificar, ler e representar pela escrita décimos, centésimos e milésimos de um todo na forma decimal.
Relacionar décimos, centésimos e milésimos com sua representação na forma de fração.
Atividade 1
Explique aos estudantes que, quando uma figura é repartida em 10 partes iguais, cada uma dessas partes corresponde a um décimo do total; de modo similar, quando há 100 partes iguais, cada parte corresponde a um centésimo do total. Assim, cada casa pintada da figura desta atividade representa uma das 100 casas do tabuleiro de jogo e pode ser representada tanto pela fração quanto pelo número na forma decimal 0,01.
Atividade 2
Para ampliar a atividade, considere as ilustrações e pergunte aos estudantes:
“Se, na figura 1, pintássemos mais uma parte (de mesmo tamanho que cada uma das partes destacadas na ilustração), quantos quadradinhos teríamos de pintar na figura 2 para que as partes pintadas das duas figuras continuassem com tamanhos iguais?” (Como seria pintado mais um décimo da figura 1, deveríamos pintar mais 10 centésimos da figura 2, ou seja, teríamos um total de 30 quadradinhos pintados na figura 2.)
“A quantas partes da figura 1 correspondem 90 quadradinhos da figura 2?” (A 9 partes da figura 1, pois 90 centésimos da figura 2 são equivalentes a 9 décimos da figura 1.)
A atividade 2 trabalha com uma das principais ideias relacionadas às representações dos números na forma decimal, já que possibilita aos estudantes reconhecerem que 0,2 e 0,20 são equivalentes. Esse reconhecimento é fundamental tanto no campo matemático quanto no social. Um exemplo são as práticas que envolvem uso de calculadora. Comente com a turma que é comum profissionais que trabalham com valores monetários, como os comerciantes, digitarem 
 para calcular o valor total de uma compra de 7 reais e 10 centavos e outra de 5 reais e 30 centavos, quando bastaria digitar
para calcular o valor total de uma compra de 7 reais e 10 centavos e outra de 5 reais e 30 centavos, quando bastaria digitar 
 .
.
CRÉDITO: ILUSTRAÇÕES: ADILSON SECCO
MP209
- Leia o que Ivan está dizendo sobre as casas amarelas na ilustração.


- Agora, escreva uma frase como a de Ivan para as casas verdes, outra para as azuis e outra para as vermelhas.
_____
PROFESSOR
Resposta: As casas verdes correspondem a quinze centésimos do total de casas. As casas azuis correspondem a trinta centésimos do total de casas. As casas vermelhas correspondem a cinquenta centésimos do total de casas.
- Represente as partes amarelas da figura abaixo com uma fração e na forma decimal. Faça o mesmo para as partes verdes, azuis, roxas e laranja.
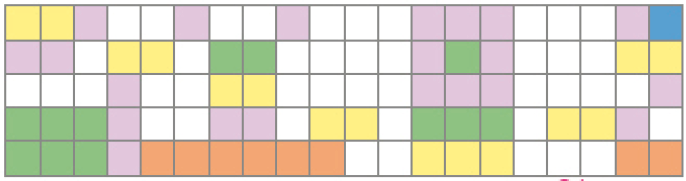
PROFESSOR
Resposta: Partes amarelas: ; 0,15;PROFESSOR
Partes verdes: ; 0,12;PROFESSOR
Partes azuis: ; 0,01;PROFESSOR
Partes roxas: ; 0,21;PROFESSOR
Partes laranja: ; 0,08.

- Agora, responda: as partes brancas representam mais ou menos que a metade da figura? Justifique sua resposta.
PROFESSOR
Resposta: Menos que a metade. Exemplo de justificativa: 0,43 é menor que 0,50.

- Aperte as teclas indicadas da calculadora e registre o resultado obtido em cada caso.
PROFESSOR
Resposta: Esclareça aos estudantes que tanto a tecla da calculadora como o ponto no visor indicam vírgula.
da calculadora como o ponto no visor indicam vírgula. a)

_____
PROFESSOR
Resposta: 0,03b)

_____
PROFESSOR
Resposta: 0,27- Usando a tecla de divisão
 , que teclas você
apertaria
para que no visor da calculadora aparecesse o resultado 0,45?
, que teclas você
apertaria
para que no visor da calculadora aparecesse o resultado 0,45?
PROFESSOR
Exemplo de resposta:
MANUAL DO PROFESSOR
Atividade 3
Ao observar a ilustração com 100 casinhas coloridas, os estudantes poderão determinar a quantidade de casinhas de cada cor e identificar a respectiva representação decimal para então escrever o texto indicando quantos centésimos cada cor de casinha representa.
Atividade 4
Nesta atividade, a partir de uma figura com 100 partes de medidas iguais, os estudantes terão de fazer a contagem das partes que compõem a figura nas cores amarela, verde, azul, roxa, laranja e branca. Depois da contagem, eles poderão identificar e registrar a representação de cada cor na forma de fração e na forma decimal. Para facilitar o registro de cada resposta, sugira aos estudantes que façam a representação em um quadro, como o sugerido abaixo.
Quadro: equivalente textual a seguir.
|
Cor das partes |
Representação na forma de fração |
Representação na forma decimal |
|---|---|---|
|
Amarela |
|
0,15 |
|
Verde |
|
0,12 |
|
Azul |
|
0,01 |
|
Roxa |
|
0,21 |
|
Laranja |
|
0,08 |
|
Branca |
|
0,43 |
Atividade 5
Após a resolução da atividade, pergunte aos estudantes se percebem alguma regularidade nas divisões de números inteiros por cem. Caso seja necessário, dê dicas sobre como contar a quantidade de casas após a vírgula e proponha outras divisões por 1.000, por 100 e por 10 que tenham como resultado números racionais.
BNCC em foco:
EF04MA10
Sugestão de atividade
Representando centésimos
Distribua aos estudantes pedaços de papel quadriculado, com 100 quadradinhos cada um, e peça-lhes que pintem a quantidade de quadradinhos que quiserem. Depois, darão o papel que pintaram a um colega, o qual deverá colá-lo no caderno e escrever ao lado a representação na forma de fração e a representação na forma decimal correspondentes à parte pintada.
MP210
Centavos de real

- Jéferson foi à padaria e comprou um pão doce. Ele pagou com 2 moedas de 50 centavos e não houve troco.
- Quantos centavos Jéferson pagou pelo pão doce?
PROFESSOR
Resposta: 100 centavos.
- Quantos centavos formam 1 real?
PROFESSOR
Resposta: 100 centavos.
- Quantos centavos Jéferson pagou pelo pão doce?
1 centavo de real é o mesmo que 1 centésimo de real.
Indicamos por: R$ 0,01

- Escreva como se representa cada quantia na forma decimal.
a)

_____
PROFESSOR
Resposta: R$ 0,03b)

_____
PROFESSOR
Resposta: R$ 0,05c)

_____
PROFESSOR
Resposta: R$ 0,10d)

_____
PROFESSOR
Resposta: R$ 0,25e)

_____
PROFESSOR
Resposta: R$ 0,50- )

_____
PROFESSOR
Resposta: R$ 0,11- Responda à questão de acordo com cada caso.
- Quantas moedas de 1 centavo de real são necessárias para formar a quantia indicada?
a)
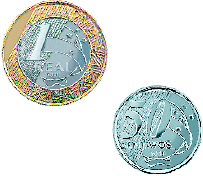
_____
PROFESSOR
Resposta: 150 moedas.b)
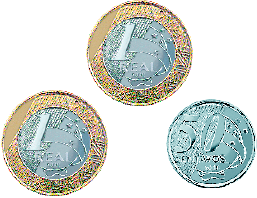
_____
PROFESSOR
Resposta: 250 moedas.c)
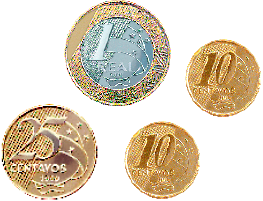
_____
PROFESSOR
Resposta: 145 moedas.MANUAL DO PROFESSOR
Objetivo
Observar a relação entre a ordem dos centésimos no sistema de numeração decimal e o centavo do real.
Atividade 1
A relação entre a ordem dos centésimos no sistema de numeração decimal e o centavo do real em nosso sistema monetário é mais uma aplicação de destaque da representação numérica decimal em práticas sociais do cotidiano.
Atividade 2
Esta atividade requer dos estudantes a representação na forma decimal de quantias de real apresentadas em 6 imagens.
Atividade 3
Após a resolução desta atividade, aproveite para discutir a pouca importância que se dá às moedas de 1 centavo de real ou até mesmo a dificuldade de encontrá-las. De modo geral, os valores que incluem centavos são arredondados nas práticas comerciais, pois dificilmente uma compra no valor de, por exemplo, R$ 12,97 será paga em dinheiro com exatidão. Pergunte à turma: “Quando vocês fazem uma compra de R$ 4,98, por exemplo, e pagam com uma cédula de R$ 5,00, vocês pedem troco?”. Encaminhe a discussão no sentido de mostrar aos estudantes que o troco é um direito de todos e, por isso, não deve haver vergonha nenhuma em pedi-lo. Explore a situação com outras perguntas, como: “Quantas moedas de 1 centavo são necessárias para formar a quantia de 2 reais? E a quantia de 1 real e 50 centavos?”. Espera-se que os estudantes respondam 200 moedas e 150 moedas, respectivamente. Converse com eles sobre a utilização dos décimos e dos centésimos em nosso sistema monetário. Por exemplo, 1 centavo equivale à centésima parte do real: = 0,01.
BNCC em foco:
EF04MA10, EF04MA25
MP211
- Leia o que Mariana está dizendo sobre o preço do chaveiro.

O número à esquerda da vírgula é a quantidade de unidades de real, e o número à direita da vírgula é a quantidade de centavos de real.
- Agora, escreva por extenso o preço de cada mercadoria.
a)

_____
PROFESSOR
Resposta: Sessenta e quatro reais e oitenta e sete centavos.b)

_____
PROFESSOR
Resposta: Cento e trinta e nove reais e oitenta centavos.c)

_____
PROFESSOR
Resposta: Quarenta e quatro reais e cinquenta e cinco centavos.d)

_____
PROFESSOR
Resposta: Setenta e oito reais e quarenta e nove centavos.Observação: Os elementos não estão em proporção. Fim da observação.

- Graziela foi a uma loja e comprou uma fivela. Observe o quadro e responda.
Quadro: equivalente textual a seguir.
|
Valor dado por Graziela |
Troco recebido por Graziela |
|---|---|
|
|
|
- Quanto Graziela pagou pela fivela?
_____
PROFESSOR
Resposta: R$ 1,25 (um real e vinte e cinco centavos).
- Qual teria sido o troco recebido por Graziela se ela tivesse pago a fivela com uma cédula de R$ 5,00?
_____
PROFESSOR
Resposta: R$ 3,75 (três reais e setenta e cinco centavos).
MANUAL DO PROFESSOR
Atividade 4
Considerando os preços apresentados nas ilustrações, amplie a atividade com perguntas como: “Comprei 1 teclado (item c) e paguei com uma cédula de R$ 50,00. De quanto foi meu troco?”; “Tenho R$ 20,00. Com esse dinheiro, é possível comprar um pendrive ?” (R$ 5,45; não, pois faltariam R$ 58,49).
Atividade 5
Os estudantes podem fazer os cálculos usando moedas como apoio, para juntar, tirar ou completar quantidades. As moedas podem ser apenas desenhadas ou recortadas em papel. Por exemplo, para saber quanto custou a fivela, podem usar a seguinte estratégia:

é o mesmo que

Então, retirando os R$ 0,75 de troco, restará o valor pago por Graziela:

CRÉDITO: FOTOS: BANCO CENTRAL DO BRASIL
Ou seja, 1 real e 25 centavos, ou R$ 1,25.
BNCC em foco:
EF04MA10, EF04MA25
MP212
Nosso sistema de numeração e os números na forma decimal
- Na última década, o Brasil conquistou quatro vezes o campeonato mundial de surfe com Gabriel Medina (2014 e 2018), Adriano de Souza (2015) e Ítalo Ferreira (2019).
Realizado pela Liga Mundial de Surfe (WSL), o Circuito Mundial (CT) é um campeonato de pontos corridos. De março a dezembro, os melhores surfistas do mundo disputam etapas em nove locais diferentes, como Austrália, Brasil, Fiji, África do Sul, Taiti, Estados Unidos, França, Portugal e Havaí.
Em 2019, pela primeira vez na história, dois brasileiros disputaram a final valendo o título mundial. O surfista Ítalo Ferreira, de Baía Formosa (RN), alcançou a nota 59,740 ao vencer a final do Pipe Masters, no Havaí, a última etapa do ano, contra Gabriel Medina, que terminou com 56,475. Registrando a nota 49,985, o sul africano Jordy Smith ficou em terceiro lugar.

LEGENDA: Ítalo Ferreira, surfista brasileiro, em Oahu, Havaí, em 2020. FIM DA LEGENDA.
- Complete o quadro abaixo com as notas de Gabriel Medina e de Jordy Smith.
Quadro: equivalente textual a seguir.
|
Parte inteira |
Parte decimal |
||||
|---|---|---|---|---|---|
|
D |
U |
d |
c |
m |
|
|
Ítalo Ferreira (BRA) |
5 |
9, |
7 |
4 |
0 |
|
Gabriel Medina (BRA) |
_____ |
_____ |
_____ |
_____ |
_____ |
|
Jordy Smith (SAF) |
_____ |
_____ |
_____ |
_____ |
_____ |
PROFESSOR
Resposta: D: 5, 4PROFESSOR
U: 6, 9,PROFESSOR
d: 4, 9,PROFESSOR
c: 7, 8PROFESSOR
m: 5, 5- Complete a decomposição da nota de Ítalo Ferreira.
5 9, 7 4 0
59: 59 inteiros ou 59
7: _____ décimos ou 0,7
PROFESSOR
Resposta: 74: _____ centésimos ou _____
PROFESSOR
Resposta: 4; 0,040: _____ milésimos ou 0,000
PROFESSOR
Resposta: 0
MANUAL DO PROFESSOR
Objetivo
Reconhecer que as regras do nosso sistema de numeração se mantêm quando aplicadas aos números escritos na forma decimal.
Atividade 1
Antes da resolução, retome o significado de valor posicional de um algarismo. Usando o Quadro Valor de Lugar, mostre que, à medida que um mesmo algarismo se desloca uma casa para a direita, seu valor é dividido por dez. Pergunte: “Que valor terá o algarismo 1 colocado na casa à direita da unidade?”. Espera-se que os estudantes percebam que, nesse caso, o algarismo 1 será a unidade dividida por 10, ou seja,1 décimo. Mostre que, para representar esse número na estrutura do nosso sistema de numeração, convencionou-se separar a ordem das unidades da ordem dos décimos por meio de uma vírgula:
Tabela: equivalente textual a seguir.
|
U |
d |
|
0, |
1 |
Explore a situação do item a sugerindo aos estudantes que façam a decomposição e escrevam como se lê a nota obtida por Ítalo Ferreira.
Após os estudantes preencherem o quadro, faça outras perguntas, como: “Que valor terá o algarismo 9 quando colocado na casa à direita dos décimos? E quando colocado na casa à direita dos centésimos?”. Espera-se que respondam 9 centésimos e 9 milésimos, respectivamente. O uso de um ábaco vertical que inclua as ordens de décimos, centésimos e milésimos pode facilitar o reconhecimento de similaridades entre as leituras de representação das quantidades decimais.
No item b, são exploradas as ordens do sistema de numeração tanto pela representação quanto pela decomposição nas casas decimais.
BNCC em foco:
EF04MA10
Sugestão de leitura para o professor
Artigo
CUNHA, Micheline Rizcallah Kanaan da; MAGINA, Sandra Maria Pinto. A medida e o número decimal: um estudo sobre a elaboração de conceito em crianças do nível fundamental. Disponível em: http://fdnc.io/eUg. Acesso em: 8 mar. 2021.
MP213
- Depois de pesquisar o preço de 1 litro de leite de quatro marcas vendidas no bairro, Dalva fez o gráfico a seguir.
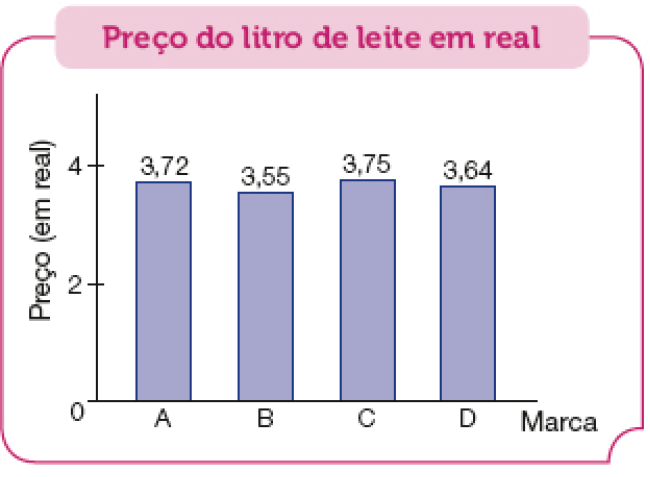
Fonte: Pesquisa de Dalva (maio 2023).
- Qual é a marca mais cara? E a mais barata?
_____
PROFESSOR
Resposta: A marca mais cara é a C; a marca mais barata é a B.
- Qual é a parte inteira de cada número?
_____
PROFESSOR
Resposta: 3
- Cada quadro em branco representa um número na reta numérica. Complete os quadros com o respectivo número da reta numérica.
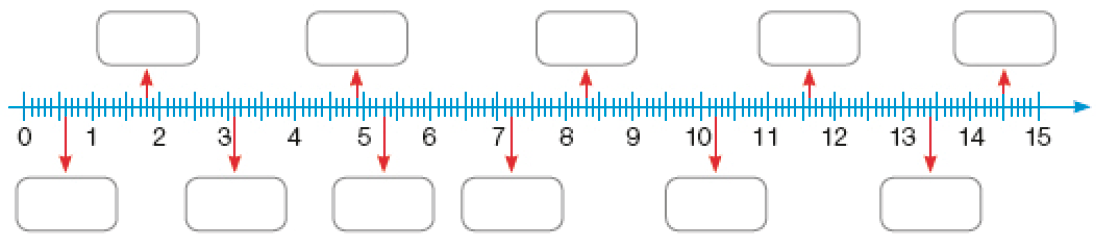
PROFESSOR
Resposta: 0,6; 1,8; 3,1; 4,9; 5,3; 7,2; 8,3; 10,2; 11,6; 13,4; 14,5- Escreva um
número
para cada caso.
- Número
menor
que 2 que tenha apenas um algarismo na parte decimal.
_____
PROFESSOR
Exemplo de resposta: 1,4.
- Número
menor
que 1 que tenha dois algarismos na parte decimal e que esses algarismos sejam iguais.
_____
PROFESSOR
Exemplo de resposta: 0,33.
- Número cuja parte inteira seja
menor
que 9, com três algarismos na parte decimal e que tenha o zero na posição dos centésimos.
_____
PROFESSOR
Exemplo de resposta: 5,304.
- Agora, compare suas respostas com as de alguns colegas e observe as diferenças.
PROFESSOR
Respostas variáveis.
- Agora, compare suas respostas com as de alguns colegas e observe as diferenças.
- Número
menor
que 2 que tenha apenas um algarismo na parte decimal.
- Qual é o valor do algarismo 6 em cada número?

_____
PROFESSOR
Resposta: 6 milésimos.-
b)

_____
PROFESSOR
Resposta: 6 inteiros.
-
c)

_____
PROFESSOR
Resposta: 6 centésimos.
-
d)

_____
PROFESSOR
Resposta: 6 décimos.
-
b)
MANUAL DO PROFESSOR
Esse artigo apresenta um estudo sobre a relação entre o conceito de número e o conceito de medida por meio de uma investigação das concepções de estudantes dos anos iniciais do Ensino Fundamental sobre os números decimais em diferentes contextos.
Atividade 2
Esta atividade explora a leitura e a interpretação de dados em gráfico de barras com números na forma decimal.
Atividade 3
Os estudantes devem perceber que, nessa representação de reta numérica, de um número para outro o segmento foi dividido em 10 partes iguais, cada parte representando 1 décimo (0,1).
Atividade 4
Discuta com os estudantes as várias respostas possíveis, todas envolvendo números maiores que zero.
No item a, o número pedido é do tipo __,__. Como deve ser menor que 2, há duas possibilidades para sua parte inteira: 0 ou 1. Quanto à parte decimal, pode ser qualquer algarismo: 0, 1, 2, …, 8, 9.
No item b, como o número pedido deve ser menor que 1, só há uma possibilidade para a parte inteira: 0. Como os dois dígitos da parte decimal devem ser iguais, há nove possibilidades: 0,11; 0,22; 0,33; 0,44; 0,55; 0,66; 0,77; 0,88; 0,99.
No item c, as possibilidades para a parte inteira são: 0, 1, 2, 3, 4, 5, 6, 7 e 8. Quanto à parte decimal, valem quaisquer combinações de algarismos para décimos e milésimos, mas o algarismo dos centésimos deve ser zero.
Atividade 5
Esta atividade reforça a noção de valor posicional, pois explora o valor numérico de um mesmo algarismo (6) em cada ordem decimal em estudo. Os estudantes podem dar respostas diferentes das mostradas; por exemplo, no item c, 60 milésimos, e no item d, 600 milésimos.
BNCC em foco:
EF04MA10
MP214
Medições


- Converse com seus colegas sobre as questões a seguir.
- A medida da altura de cada um de vocês é sempre um número inteiro de metro?
- A medida da massa de cada um de vocês é sempre um
número
inteiro de quilograma?
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que nos itens a e b as medidas, na maioria das vezes, são expressas por um número na forma decimal. Fim da observação.

- Descubra o que os números na forma decimal indicam em cada situação: medida de capacidade , medida de comprimento , medida de massa ou quantia em dinheiro.

PROFESSOR
Resposta: Quantia em dinheiro.
PROFESSOR
Resposta: Medida de massa.
PROFESSOR
Resposta: Medida de comprimento.
PROFESSOR
Resposta: Medida de capacidade.- Veja como Larissa e Bianca descobriram quantos gramas de bananas havia na balança.

- Qual é a massa em grama de um mamão de 0,340 kg?
_____
PROFESSOR
Resposta: 340 gramas.
- 1,5
kg
de feijão corresponde a quantos gramas de feijão?
_____
PROFESSOR
Resposta: 1.500 gramas.
MANUAL DO PROFESSOR
Objetivo
Compreender medidas (comprimento, massa e capacidade) representadas com números decimais.
Este tópico retoma o trabalho com medidas, já desenvolvido em outros momentos, para relacioná-las aos números escritos na forma decimal, uma vez que a maioria das medidas é assim representada.
Atividade 1
Se possível, leve algumas fitas métricas para a sala de aula e peça aos estudantes que, reunidos em grupos, meçam a altura dos colegas, anotando as medidas no caderno, na forma decimal e na escrita por extenso. Em relação à massa, caso não seja possível disponibilizar uma balança, antes de propor a atividade, peça aos estudantes que, como lição de casa, registrem suas massas.
Atividade 2
Esta atividade trabalha a associação entre representações decimais e medidas de comprimento, de massa, de capacidade e de quantias do nosso sistema monetário.
Esclareça aos estudantes que, muitas vezes, o ponto no número da indicação da balança representa a vírgula.
Atividade 3
Esta atividade exemplifica a conversão de medidas, o que possibilita trabalhar com as noções de décimos, centésimos e milésimos.
BNCC em foco:
EF04MA10, EF04MA20
Sugestões de atividades
Números decimais na calculadora
Peça aos estudantes que, reunidos em duplas e usando uma calculadora, realizem a seguinte atividade: um deles digita um número menor que 1 na forma decimal, podendo ter casas decimais até a ordem dos décimos, dos centésimos ou dos milésimos. Depois, entrega ao colega a calculadora com o número registrado no visor, para que ele descubra qual divisão pode resultar no número observado. Por exemplo: o número 0,3 (três décimos) pode ser obtido pela divisão 3 ÷ 10; o número 0,23 (vinte e três centésimos), pela divisão 23 ÷ 100; o número 0,529 (quinhentos e vinte e nove milésimos), pela divisão 529 ÷ 1.000.
MP215
- Use uma régua para medir o comprimento de cada traço em milímetro. Depois, expresse essa medida em centímetro. Lembre-se de que 1 centímetro é o mesmo que 10 milímetros.
a)

_____
PROFESSOR
Resposta: 53 milímetros; 5,3 centímetros.b)

_____
PROFESSOR
Resposta: 48 milímetros; 4,8 centímetros.- Leia algumas especificações técnicas (características) de um rádio e descubra qual esquema corresponde a esse rádio.
_____
PROFESSOR
Resposta: Esquema B.
Tabela: equivalente textual a seguir.
|
Especificações técnicas |
|
|---|---|
|
Altura |
127 milímetros |
|
Largura |
350 milímetros |
|
Profundidade |
117 milímetros |
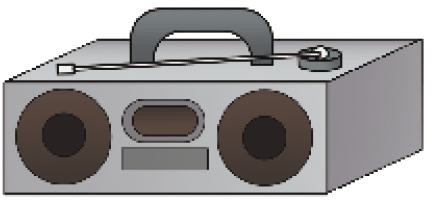
Esquema A
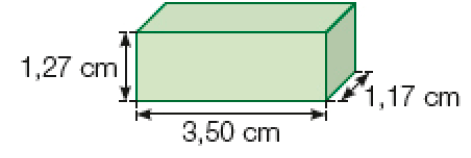
Esquema B

- Leia o texto, observe as imagens a seguir e responda às questões.


- Qual é a capacidade da garrafa de água em mililitro?
_____
PROFESSOR
Resposta: 1.500 mL
- A lata cheia contém quantos litros de suco?
_____
PROFESSOR
Resposta: 0,375 L
- Complete as frases com números na forma decimal.
- 15 centímetros é o mesmo que
_____
metro.
PROFESSOR
Resposta: 0,15
- 355 mililitros é o mesmo que
_____
litro.
PROFESSOR
Resposta: 0,355
- 400 gramas é o mesmo que
_____
quilograma.
PROFESSOR
Resposta: 0,400
- 15 centímetros é o mesmo que
_____
metro.
MANUAL DO PROFESSOR
Atividade 4
A própria régua é um recurso interessante para observar que cada centímetro corresponde a 10 milímetros e que, portanto, 1 milímetro é 1 décimo do centímetro. Por isso, 53 milímetros é o mesmo que 5,3 centímetros e 48 milímetros é o mesmo que 4,8 centímetros.
Recomendamos que sejam evitadas “regras” de conversão que não tenham significado para os estudantes, como “caminhar a vírgula para a esquerda (ou para a direita)”.
Atividade 5
Transformar medidas de uma unidade para outra pode trazer algumas dificuldades para estudantes dessa faixa etária. Observe se eles percebem que as unidades de medida relacionadas nesta atividade são o milímetro e o centímetro, cuja relação fica mais perceptível após a realização da atividade anterior (1 cm é o mesmo que 10 mm).
Atividades 6 e 7
Se julgar oportuno, lembre-os de que:
1 metro corresponde a 100 centímetros;
1 litro corresponde a 1.000 mililitros;
1 quilograma corresponde a 1.000 gramas.
BNCC em foco:
EF04MA10, EF04MA20
Lendo números na forma decimal
Divida a classe em duplas. Peça a cada estudante que escreva cinco números na forma decimal, com três casas decimais, para que o outro estudante da dupla leia em voz alta. Observe como eles leem os números cuja parte inteira é diferente de zero.
MP216
Compreender problemas
Para resolver
Problema 1
Veja os folhetos de promoções de um supermercado.

- Invente duas questões que possam ser respondidas com os dados apresentados nesses folhetos. Depois, responda às questões.
PROFESSOR
Respostas variáveis.
Problema 2
Raquel tirou algumas fotografias em seus 40 dias de férias. Veja algumas delas.

- Invente duas questões que possam ser respondidas com as informações das fotografias de Raquel. Depois, responda às questões.
PROFESSOR
Resposta variável.
MANUAL DO PROFESSOR
Objetivo
Elaborar problemas com base em dados apresentados em imagens.
A proposta destas atividades é trabalhar a formulação de questões com base em dados fornecidos em imagens. Vale notar que propostas de elaboração e escrita de problemas matemáticos não mobilizam apenas a criatividade. Para criar questões com significado, em contextos que incluam dados fornecidos, os estudantes precisam, antes de tudo, perceber as possíveis relações matemáticas entre esses dados, para só então escolherem questões que atendam a cada caso e deduzirem se as respectivas resoluções exigem uma ou mais etapas, assim como as operações matemáticas apropriadas para tal. Além disso, escrita e leitura são habilidades que precisam ser trabalhadas em todas as disciplinas, inclusive na Matemática.
Para resolver
Problema 1
Na parte da ilustração que mostra preços de leite em pó vendido em embalagens de mesma massa (800 g), os estudantes devem comparar os preços pagos no Nosso Mercado com os pagos na Loja X. Já na parte da ilustração das fitas adesivas de mesmo preço, devem comparar os diferentes comprimentos de fita oferecidos pelos estabelecimentos. Outras questões relacionadas com essas imagens são: “Qual é o preço pago por 100 g de leite em cada mercado? Qual é o preço de cada metro de fita adesiva na Loja X? E no Nosso Mercado?”.
Problema 2
Os estudantes devem observar o período de férias de Raquel e as anotações nas fotografias para que possam elaborar as duas questões.
BNCC em foco:
EF04MA09, EF04MA25
MP217
Para refletir
- Marque com um
X
as questões adequadas ao Problema 1. Depois, responda àquelas que você assinalou.
( ) Quantos reais o supermercado faturou com a venda de leite em pó e de fita adesiva?
( ) Quantas embalagens de leite em pó foram vendidas durante a promoção?
( ) Quantos metros mede o rolo de fita adesiva no Nosso Mercado?
( ) Qual é o preço da lata de leite em pó no Nosso Mercado?
PROFESSOR
Respostas corretas: Quantos metros mede o rolo de fita adesiva no Nosso Mercado?PROFESSOR
Qual é o preço da lata de leite em pó no Nosso Mercado?_____
PROFESSOR
Resposta: Fita adesiva no Nosso Mercado: 50 metros.PROFESSOR
Lata de leite em pó no Nosso Mercado: 6 reais.
- Um estudante leu o Problema 1 e fez as seguintes perguntas. Responda a cada uma delas.
- Quanto custam
 no Nosso Mercado?
_____
no Nosso Mercado?
_____
PROFESSOR
Resposta: 18 reais.
- No Nosso Mercado, em
 há quantos metros de fita adesiva?
_____
há quantos metros de fita adesiva?
_____
PROFESSOR
Resposta: 100 metros.
- De acordo com o anúncio, quanto custam
 na concorrência?
_____
na concorrência?
_____
PROFESSOR
Resposta: 16 reais.
- Quanto custam
- Usando as informações das imagens do Problema 2, responda às questões.
- Onde Raquel passou mais tempo: na casa da vovó Estela ou na chácara com seu primo Juarez?
_____
PROFESSOR
Resposta: Na chácara com seu primo Juarez.
- Em que cidade Raquel mora?
_____
PROFESSOR
Resposta: Impossível saber com base nos dados apresentados.
- Quantos dias Raquel ficou em Guarapari?
_____
PROFESSOR
Resposta: 20 dias.
- Quantos dias Raquel ficou no sítio onde ela mora?
_____
PROFESSOR
Resposta: 3 dias.
- Onde Raquel passou mais tempo: na casa da vovó Estela ou na chácara com seu primo Juarez?
_____
- Reúna-se com dois colegas e façam o que se pede.
Leia as questões que seus colegas inventaram para os dois problemas.
Verifique se a redação está adequada e, caso não esteja, sugira alterações.
Ouça seus colegas e faça os ajustes também em suas questões.
PROFESSOR
Respostas variáveis.
MANUAL DO PROFESSOR
Para refletir
Atividade 1
Os estudantes devem analisar a adequação das questões apresentadas levando em consideração os dados disponíveis na ilustração do Problema 1. A primeira pergunta (“Quantos reais o supermercado faturou com a venda de leite em pó e fita adesiva?”) não é adequada porque não foi fornecida a quantidade vendida de cada produto. A segunda pergunta (“Quantas embalagens de leite em pó foram vendidas durante a promoção?”) também não é adequada, porque essa informação não foi fornecida e não é possível obtê-la por meio dos dados apresentados. A terceira pergunta (“Quantos metros mede o rolo de fita adesiva no Nosso Mercado?”) pode ser respondida com base nos dados apresentados: de 40 metros é igual a 10 metros, portanto, o rolo de fita no Nosso Mercado mede 40 metros mais 10 metros, ou seja, 50 metros. A quarta pergunta (“Qual é o preço da lata de leite em pó no Nosso Mercado?”) pode ser respondida com base no preço da lata de leite na Loja X: de 12 reais é igual a 6 reais.
Atividade 2
Explore o raciocínio proporcional dos estudantes. Observe se eles percebem que o preço de 3 latas de leite na Loja X corresponde a 3 vezes 12 reais, ou seja, 36 reais, e, portanto, no Nosso Mercado, elas custam a metade de 36 reais, que é 18 reais.
Atividade 3
Esta atividade possibilita verificar se os estudantes consideraram todas as informações do Problema 2, fornecidas nas fotografias de Raquel, para responder às questões.
BNCC em foco:
EF04MA09, EF04MA25
Atividade 4
Quando são solicitados a analisarem questões que foram inventadas por colegas, os estudantes têm a oportunidade de julgar a coerência de ideias e a organização e clareza na expressão dessas ideias, assim como exercitar a troca de ideias e as capacidades de crítica e de argumentação.
MP218
A Matemática me ajuda a ser
... uma pessoa que se preocupa com o meio ambiente
Algumas vezes, as personagens de histórias em quadrinhos chamam a nossa atenção para assuntos muito importantes. Veja, por exemplo, estas tirinhas da Turma da Mônica e do Menino Maluquinho.
TURMA DA MÔNICA
Mauricio de Sousa

TURMA DA MÔNICA
Mauricio de Sousa

MENINO MALUQUINHO
Ziraldo

MANUAL DO PROFESSOR
Objetivo
Ler e interpretar histórias em quadrinhos que exploram situações sobre o meio ambiente.
A proposta desta dupla de páginas é levar os estudantes a refletirem sobre a degradação ambiental causada pelo ser humano. A linguagem escolhida para despertar a atenção para essas questões foi a das histórias em quadrinhos, que têm forte apelo junto aos estudantes.
Sugestão de atividade
Pesquisa
Peça aos estudantes que levem para a sala de aula recortes de revistas e jornais com matérias que abordem algum tipo de intervenção danosa do ser humano na natureza. Escolha então alguns deles para lerem o texto pesquisado em voz alta e discutirem com a classe os temas presentes nas matérias. Ajude-os perguntando o que determinada ação pode trazer como consequência, de que forma isso poderia ser mudado, quem poderia melhorar a situação etc.
BNCC em foco:
EF04MA09
MP219
Tome nota
- Na primeira tirinha, por que o Cebolinha ficou bravo?
_____
PROFESSOR
Exemplo de resposta: porque ele não conseguia pescar peixes.
- Na segunda tirinha, por que os peixes estão indo embora?
_____
PROFESSOR
Exemplo de resposta: porque o rio onde eles vivem está poluído.
- Do que trata a tirinha do Menino Maluquinho?
_____
PROFESSOR
Exemplo de resposta: poluição.
- O que há de parecido nas três tirinhas?
_____
PROFESSOR
Exemplo de resposta: as três tratam do tema poluição das águas.
Reflita

- Observe as imagens a seguir e responda.
PROFESSOR
Respostas pessoais.a)
MENINO MALUQUINHO
Ziraldo

Você também pediria socorro se estivesse na situação de Carol? Por quê?
b)

Você entraria no mar se visse a placa acima? Justifique sua resposta.

- Reúna-se com um
colega
e façam juntos, no caderno, uma lista de ações que poderiam ajudar a diminuir com a poluição de nosso planeta.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Tome nota
Pode-se relacionar na lousa todas as respostas da classe, promovendo uma discussão para aprofundar a compreensão que eles têm das tirinhas.
Atividade 1
Aproveite a questão para discutir as condições de saneamento básico. Comente que o saneamento inclui principalmente o abastecimento de água e o sistema de esgoto. Pode-se pedir aos estudantes que façam uma pesquisa para verificar tais condições em seu município.
Atividade 2
Comente que, na realidade, os peixes não conseguem ir embora do rio e muitos acabam morrendo por causa da poluição.
Amplie a discussão sobre a poluição da água enfatizando a importância desse recurso natural para a sobrevivência dos seres vivos. Converse sobre as consequências da poluição em mares e rios.
Atividade 3
Converse com a turma sobre a importância de não poluir as praias, colaborando com a limpeza e o adequado armazenamento do lixo produzido, e também sobre os perigos de entrar em águas impróprias: elas podem expor os banhistas a bactérias e vírus causadores de doenças.
Reflita
Espera-se que os estudantes listem ações e percebam que parte delas é simples e ajuda a diminuir a poluição (o descarte do lixo deve ser feito somente em locais adequados; reduzir a produção de lixo, fazendo reaproveitamentos e reúsos; consumir produtos com embalagens recicláveis etc.).
BNCC em foco:
EF04MA09
MP220
Compreender informações
Ler e interpretar tabela e gráfico de barras
- Após uma visita ao zoológico, o professor Fábio, do Colégio Imparare, fez uma pesquisa para saber o animal preferido dos estudantes das quatro salas do 4º ano. Todos os estudantes dessas salas foram ao zoológico e participaram da pesquisa. Cada estudante escolheu apenas um animal.
Animal preferido dos estudantes do 4º ano
Tabela: equivalente textual a seguir.
|
Animal |
Número de estudantes |
|---|---|
|
Serpente |
15 |
|
Elefante |
20 |
|
Macaco |
40 |
|
Girafa |
35 |
|
Tigre |
50 |
|
Camelo |
10 |
Fonte: Estudantes do 4º ano do Colégio Imparare (maio 2023).

- Qual foi o animal mais escolhido pelos estudantes do 4º ano?
_____
PROFESSOR
Resposta: Tigre.Quantos estudantes escolheram a girafa? _____
PROFESSOR
Resposta: 35 estudantes.
- Quantos estudantes há nas quatro salas do 4º ano dessa escola? Explique como você pensou para determinar essa quantidade.
_____
PROFESSOR
Resposta: 170 estudantes.
- Leia e complete com as informações corretas.
PROFESSOR
Resposta pessoal.Após todos escolherem o animal preferido, Fábio escreveu o seguinte texto:
Todos os _____ estudantes do 4º ano foram ao zoológico e escolheram o animal preferido. O _____ foi o animal preferido pela maioria dos estudantes, com _____ votos. Em segundo lugar foi _____ , com _____ votos e, em terceiro, _____, com _____ votos.
Além desses animais, os estudantes também escolheram _____ , _____e _____.
PROFESSOR
Resposta: 170; tigre; 50; o macaco; 40; a girafa; 35; o elefante; a serpente; o camelo.MANUAL DO PROFESSOR
Objetivos
Ler e interpretar dados em tabela e em gráfico de barras.
Escrever uma síntese sobre os dados apresentados.
Dados numéricos resultantes de pesquisas estatísticas podem ser organizados de várias maneiras, de acordo com o público a que se destinam e com o objetivo da veiculação de tais informações.
Tanto as tabelas quanto os gráficos são recursos muito comuns para apresentar dados. Nas aulas de Matemática do Ensino Fundamental, essas representações possibilitam muitos trabalhos e o desenvolvimento de diversas habilidades e conteúdos.
Atividade 1
A atividade tem como objetivo mostrar aos estudantes um modo de escrever um texto que sintetiza as informações presentes na tabela. Se considerar adequado, pergunte aos estudantes sobre as informações que eles consideram importantes e que poderiam ser acrescentadas a esse texto.
BNCC em foco:
EF04MA27
Sugestão de atividade
Coleta e análise de dados
Peça aos estudantes que pesquisem um tema de interesse comum e registrem suas preferências na lousa. O tema deve permitir que as preferências sejam expressas por diferentes categorias. Depois, eles devem organizar esses dados em uma tabela e transpô-los para um gráfico de barras horizontais, de modo que os resultados possam ser analisados visualmente.
Incentive a turma a inventar perguntas com base nos dados do gráfico e discutam as respostas dadas.
MP221
- A agência de viagens Voo Bom quer escolher uma cidade do país para montar um pacote promocional. Para isso, ela fez uma pesquisa com 1.400 pessoas. Veja alguns resultados da pesquisa.

- Observe o gráfico abaixo, que representa os dados da pesquisa, e complete-o com o nome das cidades e o número de pessoas que preferiram cada uma delas.
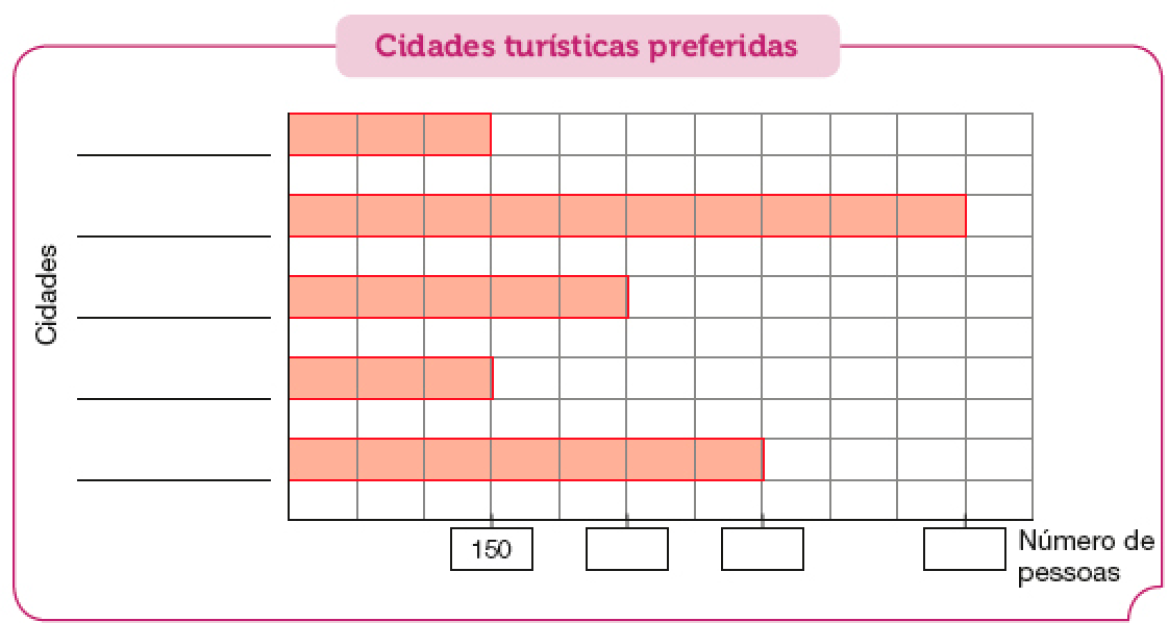
Fonte: pesquisa realizada pela agência de viagens Voo Bom (janeiro a março de 2023 ).
PROFESSOR
Resposta: Ouro Preto ou Manaus; Fortaleza; Maceió; Manaus ou Ouro Preto; Salvador.PROFESSOR
250; 350; 500.- Em sua opinião, qual cidade deveria ser escolhida pela agência de viagens para o pacote promocional?
_____
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 2
Nesta atividade, os estudantes devem completar o gráfico com as informações do resultado da pesquisa. Analise se eles respondem adequadamente às questões propostas. É importante conversar sobre a escala do gráfico; observe como fazem para determinar a quantidade de pessoas correspondente a cada retângulo. Talvez eles percebam que, por exemplo, se 3 retângulos pintados correspondem a 150 pessoas, então cada retângulo corresponde a 150 pessoas ÷ 3 = 50 pessoas.
No item b, a resposta é pessoal, mas deve ser justificada. Por exemplo, um estudante pode argumentar que a promoção deve ser feita para Ouro Preto (que tem a menor preferência, assim como Manaus), a fim de incentivar o turismo na região. Também pode ser dito que a promoção é mais interessante para Fortaleza, já que é o destino preferido e atrairá mais pessoas.
BNCC em foco:
EF04MA27
MP222
O que você aprendeu
Avaliação processual
- Tiago e Laura desenharam, cada um, uma figura e representaram a parte pintada dos desenhos de duas formas diferentes. Observe.

- As representações fracionárias e decimais das figuras desenhadas estão corretas? Justifique sua resposta.
_____
PROFESSOR
Exemplo de resposta: As representações fracionárias estão corretas. As representações decimais estão erradas; o correto seria 0,3 e 0,6.
- Sabe-se que de 100 pessoas que estão na fila de uma exposição tem menos de 15 anos de idade. Quantas são essas pessoas?
_____
PROFESSOR
Resposta: 50 pessoas.
- Camila e sua mãe foram ao cinema e ficaram de hora na fila para comprar ingressos. Quantos minutos elas ficaram na fila?
_____
PROFESSOR
Resposta: 20 minutos.


- O tanque de um carro, com capacidade para 40 litros de combustível, está com menos de de sua capacidade. Esse carro está com aproximadamente quantos litros de combustível?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes respondam que o carro está com menos de 10 litros de combustível, aproximadamente. Fim da observação.

- Agora, converse com um
colega
sobre como cada um pensou para resolver o problema.
PROFESSOR
Resposta pessoal.
- Agora, converse com um
colega
sobre como cada um pensou para resolver o problema.
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Nesta atividade, os estudantes precisam observar que a representação escrita na forma decimal não corresponde à representação na forma de fração. Três décimos na forma decimal se escreve 0,3, e seis décimos, 0,6.
Atividade 2
Espera-se que os estudantes já relacionem a fração à metade de um inteiro e percebam que a quantidade de pessoas com menos de 15 anos é igual a 50 pessoas.
Atividade 3
Nesta atividade, os estudantes são incentivados a pensarem em representações inteiras de medidas representadas por frações.
Atividade 4
Observando a ilustração, os estudantes devem perceber que o ponteiro indica a fração da capacidade total do tanque correspondente ao combustível disponível no tanque, e que de 0 a 1 há quatro partes iguais, ou seja, cada intervalo corresponde a (um quarto) da capacidade do tanque. A 1ª marca após a marca zero indica da capacidade, a 2ª marca indica ou metade da capacidade do tanque, a 3ª marca, e a últimamarca, ou seja, tanque cheio.
Como o tanque está com menos de de sua capacidade, ele tem menos de 10 litros (40 ÷ 4 = 10).
BNCC em foco:
EF04MA09, EF04MA10
MP223
- Observe as moedas a seguir.
Moedas de centavos de real

- Forme o valor em cada caso usando essas moedas.
- R$ 0,35 -
_____
PROFESSOR
Resposta: Exemplo de resposta: 1 moeda de R$ 0,25 e 1 moeda de R$ 0,10.
- R$ 0,76 -
_____
PROFESSOR
Resposta: Exemplo de resposta: 1 moeda de R$ 0,50, 1 moeda de R$ 0,25 e 1 moeda de R$ 0,01.
- R$ 0,98 -
_____
PROFESSOR
Resposta: Exemplo de resposta: 1 moeda de R$ 0,50, 1 moeda de R$ 0,25, 2 moedas de R$ 0,10 e 3 moedas de R$ 0,01.
- Cerque com uma linha a letra que corresponde à localização do número 1,56 na reta numérica em cada caso.
a)

PROFESSOR
Resposta: Ab)

PROFESSOR
Resposta: B- Janaína escreveu, na forma decimal, os números 15085 e 1538, mas se esqueceu de colocar a vírgula.
Coloque a vírgula nos números que Janaína escreveu sabendo que o algarismo 8 tem o mesmo valor posicional nos dois números e que o maior número é aquele que tem o algarismo 3.
_____
PROFESSOR
Resposta possível: 150,85 e 153,8
Autoavaliação

- Compreendo o uso de números escritos com uma fração apresentados nesta unidade?

- Identifico situações que permitem o uso de números na forma decimal?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 5
Espera-se que os estudantes possam relacionar centésimos e centavos do real. Pergunte: “De que outra forma é possível calcular essa quantia?”. Eles podem perceber que a quantia também pode ser obtida com outras combinações de moedas. Se julgar oportuno, proponha situações comerciais: “Preciso de 1 real para comprar uma borracha. Quantas moedas de R$ 0,25 são necessárias?”.
Atividade 6
Discuta com os estudantes como se pode comparar cada par de números sem o uso da reta numérica.
Atividade 7
Considerando as informações dadas, alguns números na forma decimal podem ser 150,85 e 153,8; 15,085 e 15,38; 1,5085 e 1,538 etc.
Autoavaliação
Na primeira questão, os estudantes deverão avaliar se compreendem o uso de representações fracionárias relacionado à ideia de parte e todo, trabalhada com ênfase no início da Unidade.
Na segunda questão, deverão verificar se já conseguem identificar situações do cotidiano em que números na forma decimal são comuns, como nas medidas de comprimento ou nos valores monetários.
BNCC em foco:
EF04MA10
MP224
Comentários para o professor:
Conclusão da Unidade 6
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Reconhece as frações unitárias mais usuais |
_____ |
_____ |
|
Lê, escreve e compreende o significado de fração, localização de frações em retas numéricas? |
_____ |
_____ |
|
Relaciona representações de frações com a de números na forma decimal? |
_____ |
_____ |
|
Reconhece que as regras do sistema de numeração decimal podem ser estendidas para a representação decimal de um número racional e relaciona décimos e centésimos com a representação do sistema monetário brasileiro? |
_____ |
_____ |
|
Faz uso correto de números na forma decimal no contexto de medidas e no sistema monetário brasileiro? |
_____ |
_____ |
|
Resolve e elabora problemas que envolvam situações de compra e venda e formas de pagamento, utilizando termos como troco e desconto, enfatizando o consumo ético, consciente e responsável? |
_____ |
_____ |
|
Lê, interpreta e compara dados apresentados em tabelas simples ou de dupla entrada e gráficos de barras ou de colunas? |
_____ |
_____ |
|
Consegue medir e estimar comprimentos, massas e capacidade utilizando unidades de medida padronizadas mais usuais? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP225
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |
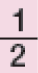
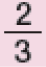
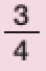

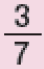
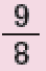

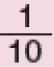
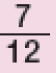
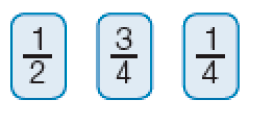

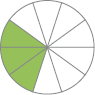
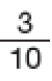
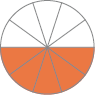
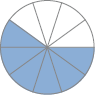
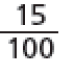
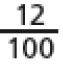
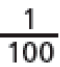
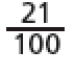
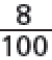
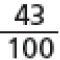
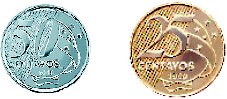
 ,
, 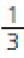 ,
, 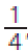 ,
, 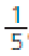 ,
, 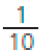 e
e 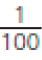 como unidades de medida
menores
do que uma unidade, utilizando a reta numérica como recurso?
como unidades de medida
menores
do que uma unidade, utilizando a reta numérica como recurso?