MP226

Comentários para o professor:

Introdução da Unidade 7

Em continuidade à abordagem da Unidade Temática Grandezas e medidas, tratada na Unidade 4 deste volume com medidas de comprimento, de área e de temperatura, temos aqui a complementação com os conteúdos das medidas das grandezas tempo, massa e capacidade.

De início, a abertura apresenta em página dupla uma situação própria do cotidiano escolar em que a cena de uma gincana proporciona, por meio de observação e descobertas, a exploração de diversos conceitos a serem aprofundados ao longo desta Unidade.

As atividades propostas nas páginas que se seguem visam à apropriação de conhecimentos relativos à leitura e ao registro de medidas e intervalos de tempo em horas, minutos e segundos, além da indicação de horários de início e término de realização de tarefas e sua duração. Importante observar que os aportes necessários para a abordagem desses conhecimentos encontram-se naqueles construídos no 3º ano.

Além da grandeza tempo, nesta Unidade são explorados contextos envolvendo as grandezas massa e capacidade em medir e estimar comprimentos, massas e capacidades, utilizando unidades de medidas padronizadas mais usuais, valorizando e respeitando a cultura local. A abordagem desses conteúdos também se pauta nos conhecimentos construídos no 3º ano sobre estimativa, medida e comparação de capacidade e de massa com o uso tanto de medidas não padronizadas quanto de padronizadas mais usuais, como litro, mililitro, quilograma e grama. As habilidades referentes à Unidade Temática Grandezas e medidas serão aplicadas, no 5º ano, nas resoluções e elaborações de problemas envolvendo grandezas e medidas.

Esta Unidade dará continuidade às habilidades da Unidade Temática Probabilidade e estatística iniciada na Unidade 3 deste volume. Os conhecimentos que foram desenvolvidos nos anos anteriores (leitura, interpretação e comparação de dados apresentados em gráficos e tabelas) serão aplicados na pesquisa, organização de dados em tabelas e gráficos, interpretação e produção de texto, com e sem uso de tecnologias digitais. As atividades do 4º ano introduzirão situações que se tornarão mais complexas quando reapresentadas no 5º ano.

Cada página deste livro propõe um novo desafio ao professor e aos estudantes. As variáveis são muitas: os conteúdos, as habilidades e os objetivos de aprendizagem.

Competências gerais favorecidas

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

Competência específica favorecida

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

Sugestão de roteiro de aula

Convém considerar que um planejamento de educação escolar tem variáveis que compõem as possibilidades múltiplas de uma aula, como se fossem composições de figuras geradas em um caleidoscópio, o que requer a administração apropriada de tempo, de espaço, de definição de grupos ou não, de materiais a serem utilizados e previamente elaborados.

Tendo em vista tais desafios, propomos um roteiro de aula que poderá servir de referência e contribuir com o trabalho do professor. Os roteiros apresentam orientações gerais para a condução das aulas de acordo com as atividades propostas e podem ser adaptados em função das características da turma e dos recursos disponíveis. Veja um exemplo de roteiro de aula relacionado à seção A Matemática me ajuda a ser... desta Unidade.

MP227

Roteiro de aula – A Matemática me ajuda a ser... um leitor de rótulos 1 ª parte – Introdução – Tempo sugerido: 15 minutos

Inicie a conversa com a turma com uma provocação: Nós comemos para viver ou vivemos para comer?

Se houver muitas falas opinativas a essa questão, alerte sobre a conveniência de serem breves, além de ser um de cada vez, para que os que queiram falar possam fazê-lo e ser ouvidos. É provável que não haja consenso, mas o importante é chamar a atenção para o tema alimentação. Anuncie que a aula terá a alimentação como tema.

Fale sobre a importância de uma alimentação saudável para evitarmos uma série de doenças, tais como desnutrição, obesidade, diabetes, hipertensão e outras. Informe aos estudantes que uma boa alimentação é aquela que garante todos os nutrientes de que o organismo necessita. Ela deve ter constância, quantidade, variedade, equilíbrio e qualidade dos alimentos consumidos.

Em geral, devemos dar preferência aos alimentos naturais. Mas também fazemos uso dos alimentos processados. Eles são feitos por indústrias, fiscalizadas e autorizadas por órgãos do governo, obrigadas a seguirem normas rígidas de higiene e qualidade estabelecidas por uma legislação que, entre outras coisas, exige transparência nas informações ao consumidor. Essas informações devem estar contidas nos rótulos das embalagens.

Porém, não basta as empresas cumprirem as obrigações legais se o consumidor não estiver atento às informações a respeito do que come. Então é indispensável nos informarmos pelo menos pela leitura dos rótulos.

2 ª parte – Leitura da seção – Tempo sugerido: 50 minutos

É muito importante que a turma tenha disponibilidade de dicionário (papel ou digital), se possível, um por grupo. O levantamento do vocabulário do texto, tal como a boa preparação de uma tela ou de uma parede é importante para possibilitar uma boa pintura, é fundamental para a compreensão da atividade.

Solicite aos estudantes que façam uma primeira leitura silenciosa de toda a seção. Sugerimos que a leitura seja feita em duplas ou trios. Estipule o tempo que considera necessário para a turma fazer essa leitura. A respeito das palavras que não conhecem, oriente os estudantes sobre como procurar o significado delas no dicionário e peça a eles que anotem no caderno cada palavra junto com o significado que melhor caiba no texto. Alerte-os de que nos rótulos há alguns termos e símbolos que eles só entenderão futuramente (kcal, kJ), portanto, não precisam se preocupar com eles.

Terminada a leitura dos estudantes, verifique as dúvidas de interpretação do texto e esclareça-as fazendo a sua leitura, em voz alta, do começo ao fim da seção.

Antes, explique, em particular, do modo mais simples possível, o significado do sinal %, símbolo de porcentagem. Por exemplo, no rótulo do biscoito, o sódio (sal de cozinha) aparece com 3% (lemos três por cento) na coluna VD (valores diários). Isso quer dizer que se dividirmos a quantidade de sal necessária à nossa alimentação diária em 100 partes, cada porção desses biscoitos corresponde a 3 dessas partes. Ou seja, 3% significa “3 em cada 100”.

Para os estudantes terem uma ideia melhor sobre a dimensão de 3%, leve para a aula uma folha de cartolina com o desenho de um quadriculado (o maior possível) de 10 linhas por 10 colunas, no qual estarão pintados apenas 3 quadradinhos (juntos ou separados).

3 ª parte – Tome nota e Reflita – Tempo sugerido 10 minutos

Agora que os estudantes já superaram as maiores dificuldades de entendimento do texto e da imagem da atividade, solicite a eles nova leitura, agora individual, e que respondam às perguntas do Tome nota e do Reflita.

Considere a possibilidade de pedir a elaboração de um trabalho em grupo com a confecção de cartazes sobre rótulos de alimentos processados com todas as informações de sua composição e imagens do produto. Depois, organize com os estudantes uma exposição com esses cartazes.

MP228

UNIDADE 7. Mais grandezas e medidas

Boxe complementar

Para refletir...

A classe de Ana está participando de uma gincana na escola.

Imagem: Ícone: Oral. Fim da imagem.

Cada equipe tem 2 minutos para completar todas as provas. Essa equipe já gastou 1 minuto e 17 segundos. Quanto tempo ainda resta a essa equipe?

PROFESSOR Resposta: 43 segundos.

Imagem: Ícone: Oral. Fim da imagem.

Na 3ª prova da gincana, se Ana puser na balança a peça que está segurando, conseguirá obter exatamente 1 quilograma? Justifique sua resposta.

PROFESSOR Resposta: 1.025 gramas; mais que 1 quilograma.

Fim do complemento

MANUAL DO PROFESSOR

Objetivos da Unidade

Compreender e relacionar as unidades de medida de tempo: dia, hora, minuto e segundo.

Compreender e relacionar as unidades de medida de tempo: milênio, século, década e ano.

Compreender e relacionar as unidades de medida de massa: tonelada, quilograma, grama e miligrama.

Compreender e relacionar as unidades de medida de capacidade: litro e mililitro.

Resolver problemas para os quais há mais de uma solução.

Realizar pesquisa e organizar dados em tabela e em gráfico de colunas utilizando o recurso da planilha eletrônica.

Ler e interpretar texto de embalagens de alimentos.

As situações apresentadas nestas páginas permitem explorar os conhecimentos dos estudantes a respeito de grandezas e medidas para responder às questões propostas.

Assim, antes de iniciar a exploração da cena, pergunte aos estudantes sobre as situações em que utilizam diferentes unidades de medida. Depois, peça a eles que descrevam a cena, indicando as unidades de medida que identificam nela.

Durante a descrição da cena, sugira aos estudantes que localizem cada personagem para retomar o vocabulário de orientação espacial.

BNCC em foco:

EF04MA20, EF04MA22, EF04MA27, EF04MA28

MP229

Imagem: Ilustração. Alunos com camiseta vermelha em uma quadra. À esquerda, placa com a informação: 1ª PROVA - ACERTE 5 CESTAS. Uma menina está jogando uma bola de basquete em uma cesta. Na frente dela há várias bolas de basquete. Em seguida, 2ª PROVA - COMPLETE O PERCURSO 2 VEZES. Um menino está correndo entre cones e atrás dele há um percurso com cordas e um tubo. Ao lado, 3ª PROVA - OBTENHA EXATAMENTE 1 QUILOGRAMA. Ana está segurando um peso de 150 gramas. Ao seu lado, um menino aponta para uma balança e sobre ela há dois pesos de 300 gramas, um peso de 150 gramas e um peso de 125 gramas. No visor, a indicação: 875 g. Atrás deles há pesos sobre um suporte: um peso com 150 gramas, um de 100 gramas, dois de 25 gramas, um de 300 gramas, um de 500 gramas e três de 125 gramas. Ao lado, o professor com boné está com um apito na boca e segurando um cronômetro. Ao fundo há crianças com camiseta verde observando e várias pessoas torcendo em uma arquibancada. Acima deles há um relógio indicando 00:01:17. Fim da imagem.
MANUAL DO PROFESSOR

Para refletir...

Na primeira questão, para saber quanto tempo a equipe de Ana ainda tem para completar o percurso, eles podem observar que 1 minuto é o mesmo que 60 segundos. Como o tempo que já passou é de 1 minuto e 17 segundos, faltam 43 segundos para a equipe completar 2 minutos.

Pergunte: “Em que situações costumamos calcular o tempo de duração de uma atividade?”. É importante incentivar os estudantes a apresentarem e discutirem suas respostas.

Oriente-os a fazerem uma estimativa para saber se Ana vai obter exatamente 1 kg ou não e, depois, a fazerem o cálculo para verificar se a estimativa foi boa ou não.

Como 1 kg corresponde a 1.000 g e o visor da balança apresenta o valor de 875 g, os estudantes podem concluir que faltam 125 g para completar 1.000 g (1.000 − 875 = 125). Portanto, ao colocar na balança a peça de 150 g, vai ultrapassar 1.000 g.

Aproveite para perguntar: “Seria possível obter exatamente 1 kg se só houvesse peças com 125 g?”. Podem ser usadas diversas estratégias para obter a resposta.

Uma possibilidade é adicionar parcelas iguais a 125 g, verificando se em algum momento o resultado é igual a 1.000 g: 125 g + 125 g + 125 g + 125 g + 125 g + 125 g + 125 g + 125 g = 1.000 g = 1 kg.

Portanto, 8 peças de 125 g têm 1 kg. Se julgar oportuno, peça aos estudantes que observem as peças disponíveis na gincana e identifiquem aquelas com as quais seria possível obter exatamente 1 quilograma sem usar peças com outra massa. Por exemplo: “Se só houvesse peças com 300 gramas, seria possível obter exatamente 1 quilograma? E se fossem peças com 150 gramas?”.

MP230

Medidas de tempo

Dia, hora e minuto

  1. Veja nos relógios das cenas abaixo a que horas Fabiana chegou ao hospital onde trabalha e a que horas ela saiu de lá em um dia da semana.
Imagem: Ilustração. À esquerda, Fabiana, mulher com cabelo castanho está entrando em um hospital. Ao lado, relógio de rua indicando 12:00. À direita, Fabiana está saindo do hospital, acenando e falando: ATÉ AMANHÃ! Ao lado, relógio na parede indicando 18:00. Atrás dela há pessoas acenando de trás de um balcão. Fim da imagem.
  1. Quantas horas Fabiana ficou no hospital nesse dia?

    _____

    PROFESSOR Resposta: 6 horas.
  1. Após quantos dias ela terá trabalhado o período de tempo em horas que equivale a 1 dia completo? _____
    PROFESSOR Resposta: 4 dias.

Indicamos 1 hora por: 1 h

1 dia = 24 h

  1. Na semana passada, de segunda a sábado, César dormiu da meia-noite às 6 horas da manhã. Quantas horas ele dormiu ao todo nesses dias?

    _____

    PROFESSOR Resposta: 36 horas.
    PROFESSOR Exemplo de cálculo: 6 × 6 = 36

    • Pinte o quadro que indica o período de tempo que César dormiu.

Menos de 1 dia.

1 dia e meio.

2 dias completos.

Mais de 2 dias completos

PROFESSOR Resposta correta: 1 dia e meio.

Imagem: Ícone: mental. Fim da imagem.

  1. Calcule mentalmente quantos dias estão representados em cada caso.
    1. 72 horas. _____
      PROFESSOR Resposta: 3 dias.
    1. 48 horas. _____
      PROFESSOR Resposta: 2 dias.
    1. 12 horas. _____
      PROFESSOR Resposta: Metade de 1 dia.
    1. 60 horas. _____
      PROFESSOR Resposta: 2 dias e meio.
MANUAL DO PROFESSOR

Objetivo

Compreender e relacionar as unidades de medida de tempo: dia, hora e minuto.

Atividade 1

Depois de os estudantes resolverem a atividade, faça perguntas como: “Quantos minutos tem um dia? E meio dia?”. Espera-se que observem que, como 1 dia tem 24 horas e cada hora tem 60 minutos, basta fazer 24 vezes 60 minutos, que são 1 440 minutos, para determinar o número de minutos em um dia. Para saber quantos minutos há em meio dia, basta dividir o resultado anterior por 2, obtendo 720 minutos.

Atividade 2

Os estudantes devem perceber que, da meia-noite às 6 horas da manhã, César dormiu 6 horas. Considerando que ele dormiu 6 horas de segunda-feira até sábado, que somam 6 dias, pode-se concluir que César dormiu 36 horas, que correspondem a 1 dia e meio.

Atividade 3

Espera-se que os estudantes não tenham dificuldade em realizar os cálculos mentalmente. Verifique, durante a realização desta atividade, se eles necessitam de seu auxílio.

BNCC em foco:

EF04MA22

Sugestão de atividade

Despertador

Hoje de manhã, o alarme do relógio de Rogério tocou pela primeira vez às 6 horas, mas ele só levantou depois das 7 horas. Como Rogério apertou a tecla de função soneca várias vezes, o relógio o despertava novamente a cada 9 minutos. Qual foi o último horário em que o relógio despertou Rogério antes das 7 horas da manhã? (6 h 54 min.).

MP231

  1. Renato vai assistir a uma comédia que acabou de estrear nos cinemas. Observe as cenas abaixo e responda às questões.
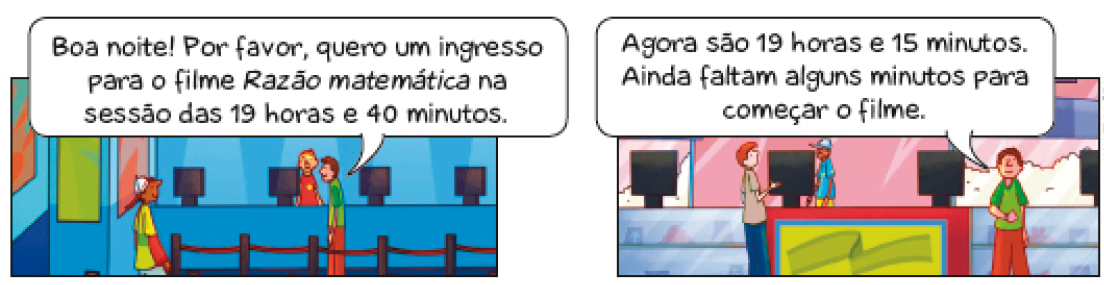
Imagem: Ilustração. À esquerda, Renato fala: Boa noite! Por favor, quero um ingresso para o filme Razão matemática na sessão das 19 horas e 40 minutos. Na frente dele há um balcão e um funcionário atrás de um computador. À direita, Renato olha para o relógio no pulso e diz: Agora são 19 horas e 15 minutos. Ainda faltam alguns minutos para começar o filme. Fim da imagem.
  1. Quantos minutos faltam para começar o filme? _____
    PROFESSOR Resposta: 25 minutos.
  1. Se a duração do filme é de 90 minutos, a que horas ele terminará?

    _____

    PROFESSOR Resposta: Às 21 horas e 10 minutos.

Indicamos 1 minuto por: 1 min

1 h = 60 min

  1. Uma partida de vôlei foi disputada em 4 sets, com intervalos de 5 minutos entre um set e outro.

Duração da partida de vôlei

Tabela: equivalente textual a seguir.

Set

Duração

1º

23 min

2º

19 min

3º

29 min

4º

31 min

Dados obtidos na partida de vôlei (nov. 2023).

Imagem: Ícone: mental. Fim da imagem.

  1. Quanto tempo durou a partida, incluindo os intervalos? _____
    PROFESSOR Resposta: 1 hora e 57 minutos ou 117 minutos.
  1. Qual foi o set que durou mais tempo? Esse tempo equivale a mais ou menos de meia hora? _____
    PROFESSOR Resposta: 4º set ; mais de meia hora.
  1. Escreva o horário registrado em cada relógio.

De dia

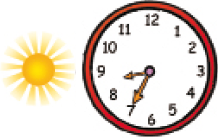
Imagem: Ilustração. Um sol e ao lado, relógio com o ponteiro pequeno entre os números 8 e 9 e o ponteiro grande sobre o número 7. Fim da imagem.

_____

PROFESSOR Resposta: 8 h 35 min

De noite

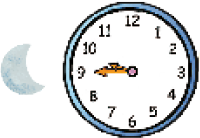
Imagem: Ilustração. Uma lua e ao lado, relógio com o ponteiro pequeno entre os números 9 e 10 e o ponteiro grande sobre o número 9. Fim da imagem.

_____

PROFESSOR Resposta: 21 h 45 min (ou 9 h 45 min da noite)

De dia

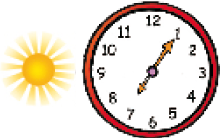
Imagem: Ilustração. Um sol e ao lado, relógio com o ponteiro pequeno no número 7 e o ponteiro grande sobre o número 1. Fim da imagem.

_____

PROFESSOR Resposta: 7 h 5 min

Imagem: Ícone: mental. Fim da imagem.

  1. Calcule mentalmente os minutos em cada caso.
  1. Duas horas. _____
    PROFESSOR Resposta: 120 min
  1. Meia hora. _____
    PROFESSOR Resposta: 30 min
  1. Um quarto de hora. _____
    PROFESSOR Resposta: 15 min
  1. Três horas. _____
    PROFESSOR Resposta: 180 min
MANUAL DO PROFESSOR

Atividade 4

Nesta atividade, os estudantes terão de determinar o tempo de duração de um intervalo até o início de um filme e a que horas terminará sua apresentação.

Eles estão familiarizados com esse tipo de situação, uma vez que familiares e eles próprios cumprem horários diariamente. Aproveite a situação para perguntar se há outras maneiras de alguém informar as horas. Desenhe na lousa um relógio de ponteiros que registra, por exemplo, 3 h 45 min e pergunte: “Qual é o horário registrado nesse relógio?”. Os estudantes podem responder: três horas e quarenta e cinco minutos, quinze horas e quarenta e cinco minutos, três e quarenta e cinco, faltam quinze minutos para as quatro horas ou quinze para as quatro.

Atividade 5

Espera-se que os estudantes percebam que o tempo total da partida de vôlei é o resultado da adição do tempo dos quatro sets, 102 minutos, com os 15 minutos de intervalo, ou seja, 102 minutos mais 15 minutos, que é igual a 117 minutos, ou 1 hora e 57 minutos.

Atividade 6

Observe se os estudantes determinam os horários registrados nos relógios analógicos com facilidade. Caso perceba que ainda precisam de ajuda, auxilie-os, apresentando outras situações como as propostas.

Atividade 7

Para os cálculos de variação de tempo, são indicadas as relações entre as unidades de medida de tempo. Um aspecto importante das atividades é trabalhar com medidas diferentes de meia hora ou de hora inteira, possibilitando aos estudantes melhor exploração das relações aprendidas.

BNCC em foco:

EF04MA22

Agenda semanal

Proponha aos estudantes a confecção de uma agenda semanal com o registro do horário em que eles costumam acordar, o tempo que eles gastam para escovar os dentes, tomar banho, se vestir, tomar café da manhã, ir para a escola, assistir às aulas, entre outras tarefas.

Sugira a eles que escolham algumas das atividades diárias e marquem, com o auxílio do relógio e pelo período de uma semana, o tempo gasto em cada uma. Depois, eles devem comparar, por meio de estimativas, todos os tempos registrados durante a semana. Após a realização dos registros semanais, pergunte à turma: “Em qual atividade diária vocês gastam mais tempo? Com o tempo que gastam nessas atividades, quanto do dia sobra para outras atividades? Em que dias da semana sua rotina é diferente da rotina dos outros dias?”.

MP232

Minuto e segundo

  1. Gisele quer esquentar seu lanche no forno de micro-ondas. Para isso, ela apertou a tecla correspondente a 1 minuto, e após 15 segundos o aparelho indicava os segundos restantes, como mostra a figura abaixo. Por quantos segundos, ao todo, o lanche esquentará?

    Após 15 segundos, ainda faltam 45 segundos para completar o tempo de 1 minuto de aquecimento.

    15 + 45 = _____

    PROFESSOR Resposta: 60

    1 minuto equivale a _____ segundos.

    PROFESSOR Resposta: 60

    O lanche esquentará por _____ segundos ao todo.

    PROFESSOR Resposta: 60
Imagem: Ilustração. Gisele, mulher ruiva com cabelo preso está sorrindo e apontando para um micro-ondas. No visor, o número 45. Fim da imagem.

Indicamos 1 segundo por: 1 s

1 min = 60 s

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

  1. Debata as questões a seguir com seus colegas.
    1. Em que situações você já mediu um intervalo de tempo em minuto? E em segundo?
    1. Você considera 1 minuto muito tempo ou pouco tempo? Por quê?
    1. No trânsito, o que podem significar alguns segundos? E 1 minuto?
      PROFESSOR Respostas pessoais.
  1. Um professor de ginástica pediu que cada exercício fosse repetido por determinado tempo. Por quanto tempo foi repetido cada exercício, se o ponteiro dos segundos deu:
    1. 2 voltas?

      _____

      PROFESSOR Resposta: 2 minutos ou 120 segundos.
    1. 3 voltas?

      _____

      PROFESSOR Resposta: 3 minutos ou 180 segundos.
    1. meia-volta?

      _____

      PROFESSOR Resposta: Meio minuto ou 30 segundos.
Imagem: Ilustração. Um homem ruivo aponta para um relógio e fala: A cada 1 minuto, o ponteiro vermelho, que é o dos segundos, dá uma volta completa. Ao lado, relógio com o ponteiro pequeno no número 2, o ponteiro grande no número 5 e o ponteiro vermelho no número 10. Abaixo, dois pesos. Fim da imagem.

Imagem: Ícone: Calculadora. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Como saber, usando uma calculadora, quantos minutos e segundos correspondem a 132 segundos?
    PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Objetivos

Reconhecer a relação entre as unidades de medida de tempo: minutos e segundos.

Estimar a duração de eventos.

Atividade 1

Esta atividade permite aos estudantes concluírem que 60 segundos equivalem a 1 minuto. Pergunte a eles: “Em que situações encontramos indicações de medida de tempo?”. Talvez sejam mencionados programas de computador que reproduzem músicas e que usam um indicador para o tempo de música que já passou e outro para o tempo restante; a adição desses dois tempos fornece o tempo total da faixa musical reproduzida.

Atividade 2

Esta atividade busca o conhecimento prático que os estudantes adquirem na vida diária a respeito de intervalos de tempo medidos em minutos e segundos, ao mesmo tempo que trabalha sua capacidade de estimativa para tais intervalos.

Aproveite a questão aberta, proposta no item c, para discutir com a turma a respeito de educação no trânsito: deveres e direitos de pedestres e de condutores de veículos.

Atividade 3

Incentive os estudantes a relacionarem minutos e segundos, compreendendo que 1 minuto corresponde a 60 segundos.

Atividade 4

Essa atividade propõe o uso da calculadora. A resolução se dá por meio de uma divisão, que, feita na calculadora, não conduz imediatamente ao resultado; por isso, a resposta ao problema sugere subtrações sucessivas. Exemplo de resposta: Subtrair 60 de 132, obtendo 72, e depois subtrair 60 novamente, obtendo 12. Como o número 60 “coube” duas vezes em 132 e sobraram 12, a resposta é 2 minutos e 12 segundos.

BNCC em foco:

EF04MA22

Sugestão de atividade

Cozinhando um ovo

Você quer cozinhar um ovo por 2 minutos. Entretanto, só possui dois relógios de areia (ampulhetas): um que marca 5 minutos e outro que marca 3 minutos. Como você pode cozinhar o ovo por 2 minutos exatos?

Exemplo de resposta: Vire as duas ampulhetas ao mesmo tempo. Quando toda a areia da ampulheta de 3 minutos tiver escoado, coloque o ovo para cozinhar e espere até que a areia da outra ampulheta (de 5 minutos) tenha escoado por completo. Se necessário, explique aos estudantes o que é uma ampulheta, se possível levando para a sala de aula um exemplar, para que façam melhor ideia desse artefato de medição de tempo.

MP233

Imagem: Ícone: mental. Fim da imagem.

  1. Complete o quadro a seguir, sabendo que uma torneira aberta fornece 1 litro de água a cada 15 segundos.

Quadro: equivalente textual a seguir.

Tempo

Número de litros

15 segundos

1

30 segundos

_____

1 minuto

_____

_____

12

_____

20

PROFESSOR Resposta: 3 minutos; 5 minutos, 2 litros, 4 litros.
Imagem: Ilustração. Um homem está segurando um balde embaixo de uma torneira aberta. Fim da imagem.

Imagem: Ícone: mental. Fim da imagem.

  1. Para fazer um desenho animado, são necessários 24 desenhos para cada 1 segundo de animação. Quantos desenhos são necessários para fazer 1 minuto de animação?

    São necessários _____ desenhos para fazer 1 minuto de animação.

    PROFESSOR Resposta: 1.440
  1. Faça uma estimativa e ligue cada ação ao tempo necessário para realizá-la.

Linha 1:

Um atleta correr 100 metros.

Piscar os olhos.

Fazer um café

Assistir a um filme.

Linha 2:

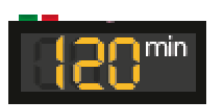
Imagem: Ilustração. Cronômetro indicando 120 min. Fim da imagem.
Imagem: Ilustração. Cronômetro indicando 5 min. Fim da imagem.
Imagem: Ilustração. Cronômetro indicando 1 s. Fim da imagem.
Imagem: Ilustração. Cronômetro indicando 12 s. Fim da imagem.
PROFESSOR Exemplo de resposta:
PROFESSOR Um atleta correr 100 metros - 12 s.
PROFESSOR Piscar os olhos - 1 s.
PROFESSOR Fazer um café - 5 min.
PROFESSOR Assistir a um filme - 120 min.
  1. Observe a conversa entre Daniel e Marcos.
Imagem: Ilustração. Um jovem ruivo pergunta: Marcos, como faço para descobrir qual intervalo de tempo é maior: 2 min e 16 s ou 146 s? Na frente dele, um jovem com cabelo encaracolado responde: Você pode transformar 2 min e 16 s em segundos e depois comparar os intervalos de tempo na mesma unidade de medida, o segundo. Fim da imagem.
MANUAL DO PROFESSOR

Atividade 5

Observe se os estudantes compreendem a proporcionalidade que deve ser mantida entre o tempo e o número de litros: quando a quantidade de segundos dobra, o número de litros de água escoada também dobra; quando a quantidade de segundos triplica, o número de litros triplica, e assim por diante. Incentive-os a buscarem diferentes estratégias de resolução. Peça-lhes que expliquem como chegaram aos resultados e que discutam seus procedimentos com a turma.

Atividade 6

Nesta atividade, espera-se que os estudantes percebam a relação de 24 desenhos por segundo e calculem 24 × 60 = 1 440, entendendo que 60 corresponde à quantidade de segundos por minuto.

Atividade 7

Estimar o tempo necessário para a realização de algumas atividades é uma habilidade importante a ser desenvolvida pelos estudantes e exige a vivência com algumas dessas atividades. Uma estratégia que pode ser adotada é eliminar os valores que seriam absurdos para determinada atividade, como 1 segundo, 12 segundos ou 120 minutos (2 horas) para fazer um café, obtendo a resposta desejada em cada caso.

Atividade 8

Depois de resolvida a situação, em uma roda de conversa com a turma, peça aos estudantes que digam se ficou mais fácil fazer a comparação dos dois valores na mesma unidade de tempo sabendo que 1 minuto equivale a 60 segundos.

BNCC em foco:

EF04MA22

Controlando o consumo de água

Proponha aos estudantes que, em casa, observem o tempo gasto em situações cotidianas que envolvem o uso de água (escovar os dentes, tomar banho, lavar louça etc.). Peça a eles que primeiro façam estimativas sobre essas medidas de tempo, para depois fazerem as medições com um instrumento apropriado (se possível, com um cronômetro, disponível na maioria dos telefones celulares). Oriente-os a montarem uma tabela para registrar, separadamente, as medidas estimadas e as medidas exatas. Aproveite para recordar a importância de economizar água, por exemplo, deixando a torneira fechada nos momentos das atividades em que a água não é usada ou evitando ao máximo o uso de mangueiras.

MP234

Milênio, século, década e ano

  1. Carla estava lendo o jornal e parou nesta página.
Imagem: Ilustração. Página de jornal com o texto: Acontece na cidade. Fábrica Áqua comemora uma década de liderança no ramo alimentício. Abaixo, foto de pessoas comemorando. Acima deles, placa com a informação: 10 ANOS NA LIDERANÇA. Ao fundo, uma fábrica grande e balões voando. Ao lado, o texto: Em 2023, houve a comemoração de um século da fundação do 1º clube esportivo da cidade. Abaixo, foto de pessoas sorrindo. Acima delas, uma faixa com a informação: 1923 - 2023 COMEMORAÇÃO DO CENTENÁRIO DO CLUBE 6 DE ABRIL. Na parte inferior, a informação: Exposição 1.000 anos de arte. Venha desvendar um milênio de mistérios na nova exposição do Museu de Arte. À esquerda, um globo terrestre e à direita, imagem de uma pintura. Fim da imagem.

A fábrica Áqua está na liderança do ramo alimentício há _____ década, que é o mesmo que _____ anos.

PROFESSOR Resposta: 1, 10

Em 2023, foi comemorado _____ século, ou _____ anos, da fundação do Clube 6 de Abril.

PROFESSOR Resposta: 1, 100

A nova exposição do Museu de Arte exibe itens de cerca de _____ milênio, que é o mesmo que _____ anos.

PROFESSOR Resposta: 1, 1.000

1 década = 10 anos

1 século = 100 anos

1 milênio = 1.000 anos

MANUAL DO PROFESSOR

Objetivo

Reconhecer a relação entre as unidades de medida de tempo: ano, década, século e milênio.

Em muitas situações de medição, as unidades de medida de tempo como hora, dia, minuto e segundo são adequadas, mas em outras – como calcular a idade de uma pessoa ou o tempo decorrido entre dois eventos históricos – elas já não convêm.

O objetivo das atividades destas páginas é favorecer o reconhecimento das relações entre as unidades de medida de tempo: ano, década, século e milênio.

Atividade 1

As unidades de medida de tempo trabalhadas relacionam-se da seguinte forma:

1 década são 10 anos;

1 século são 100 anos ou 10 décadas;

1 milênio são 1.000 anos ou 100 décadas ou 10 séculos.

BNCC em foco:

EF04MA22

MP235

Imagem: Ícone: Desenho ou pintura. Fim da imagem.

  1. Pinte da mesma cor as expressões equivalentes.
PROFESSOR Exemplos de resposta:
PROFESSOR az: azul
PROFESSOR am: amarelo
PROFESSOR ro: rosa
PROFESSOR vd: verde
PROFESSOR vm: vermelho

48 meses

PROFESSOR Resposta: az

3 séculos

PROFESSOR Resposta: vm

4 séculos

PROFESSOR Resposta: vd

10 décadas e 60 anos

PROFESSOR Resposta: ro

40 anos

PROFESSOR Resposta: am

40 décadas

PROFESSOR Resposta: vd

300 anos

PROFESSOR Resposta: vm

4 anos

PROFESSOR Resposta: az

400 anos

PROFESSOR Resposta: vd

4 décadas

PROFESSOR Resposta: am

29 décadas e 10 anos

PROFESSOR Resposta: vm

1 século e 6 décadas

PROFESSOR Resposta: ro
  1. Observe as fotografias e depois responda às questões.

Primeira transmissão de televisão, em 1925.

Imagem: Fotografia em preto e branco. Um homem com terno está ao lado de uma televisão grande e larga. Fim da imagem.

LEGENDA: John Baird ao lado de sua invenção, o 1º aparelho de televisão, no Science Museum, em 1926. FIM DA LEGENDA.

Invenção do automóvel a gasolina, em 1885.

Imagem: Fotografia. Automóvel com três rodas e de madeira. Fim da imagem.

LEGENDA: Modelo do 1º automóvel a gasolina, o Benz Patent Motorwagen. FIM DA LEGENDA.

Invenção do telefone, em 1876.

Imagem: Fotografia. Telefone de madeira com um objeto circular no meio e um rolo em cima. Fim da imagem.

LEGENDA: Reprodução do telefone de Graham Bell, de 1876. FIM DA LEGENDA.

  1. Qual desses acontecimentos é o mais antigo? E o mais recente?

    _____

    PROFESSOR Resposta: Acontecimento mais antigo: invenção do telefone;
    PROFESSOR acontecimento mais recente: 1ª transmissão de televisão.
  1. Quais desses acontecimentos têm mais de 1 século?

    _____

    PROFESSOR Resposta: A invenção do automóvel a gasolina e a do telefone. No último ano de uso previsto para este livro, a primeira transmissão de televisão pode ter mais de 1 século
  1. Quantas décadas, aproximadamente, separam o acontecimento mais antigo do mais recente? _____
    PROFESSOR Resposta: 5 décadas.
MANUAL DO PROFESSOR

Atividade 2

Nesta atividade, os estudantes deverão utilizar seus conhecimentos sobre conversões de medidas para pintar as medidas equivalentes. Para isso, é importante relembrar as informações apresentadas na página anterior e a composição de 12 meses para formar um ano. Os estudantes poderão recorrer à proporcionalidade para estabelecer as relações; por exemplo, se 1 ano equivale a 12 meses, a quantos meses vão equivaler 4 anos? (12 + 12 + 12 + 12 = 48 ou 4 × 12 = 48).

Atividade 3

É possível que alguns estudantes apresentem dificuldade ao inserirem as medidas de tempo em datas históricas, pois precisarão compará-las e operá-las. Assim, no momento de socialização, explicite cada etapa das estratégias que forem utilizadas. No item c, por exemplo, é possível registrar na lousa década por década, facilitando a visualização, para que percebam as aproximações:

Imagem: Ilustração. Reta numérica. 1876 + 1 década 1886 + 1 década 1896 + 1 década 1906 + 1 década 1916 + 1 década 1926. Fim da imagem.

Sugestão de leitura para o estudante

PORTO, Cristina. O diário escondido da Serafina. Ilustrações de Michele lacocca. São Paulo: Ática, 2021. (Coleção Serafina.)

Nesse volume da coleção, Serafina encontrou um esconderijo seguro para escrever seu diário, no qual registra inúmeros assuntos – seus sonhos, suas ideias originais, suas opiniões sobre os amigos, seus livros preferidos... O livro interage com o leitor trazendo uma surpresa a cada página, com ilustrações ocultas nas dobras, um calendário para o leitor marcar o aniversário de amigos e desenho para completar.

BNCC em foco:

EF04MA22

Sugestão de atividade

Pesquisa histórica

Proponha aos estudantes que, reunidos em grupos, pesquisem em livros ou na internet as datas de alguns acontecimentos importantes da História do Brasil ou do município em que moram. Depois, peça-lhes que elaborem uma tabela indicando há quantas décadas esses acontecimentos ocorreram. As tabelas podem ser trocadas entre os grupos, para que comparem as informações.

MP236

Medidas de massa

Tonelada, quilograma e grama

  1. Faça estimativas e cerque com uma linha o item que tem a maior massa em cada caso.
Imagem: Fotografia. Uma bola de tênis. Fim da imagem.

LEGENDA: Bola de tênis. FIM DA LEGENDA.

Imagem: Ilustração. uma bola de boliche. Fim da imagem.

LEGENDA: Bola de boliche. FIM DA LEGENDA.

PROFESSOR Resposta: bola de boliche.

b)

Imagem: Fotografia. Um balde. Fim da imagem.

LEGENDA: Balde. FIM DA LEGENDA.

Imagem: Ilustração. um ferro de passar roupas. Fim da imagem.

LEGENDA: Ferro de passar roupas. FIM DA LEGENDA.

PROFESSOR Resposta: ferro de passar roupas.

c)

Imagem: Fotografia. Um cacho de uvas. Fim da imagem.

LEGENDA: Cacho de uvas. FIM DA LEGENDA.

Imagem: Ilustração. uma melancia. Fim da imagem.

LEGENDA: Melancia. FIM DA LEGENDA.

PROFESSOR Resposta: melancia.

d)

Imagem: Fotografia. Uma fatia de bolo. Fim da imagem.

LEGENDA: Fatia de bolo. FIM DA LEGENDA.

Imagem: Ilustração. um balão de festa. Fim da imagem.

LEGENDA: Balão de festa. FIM DA LEGENDA.

PROFESSOR Resposta: fatia de bolo.
  1. Leia os diálogos e, depois, responda às questões.
Imagem: Ilustração. Um homem com boné e uniforme azul segura um papel com a mão estendida e fala: Foram entregues 500 quilogramas de café. Na frente dele, um homem com camisa sorri com a mão estendida e pensa: Puxa, meia tonelada de café! Ao fundo, um homem carrega sacas ao Ao lado, um homem com boné e avental segura um pegador e fala: Tem 800 gramas. Ao seu lado há uma sacola sobre uma balança indicando 800 g. Na frente dele há um balcão com pães. Um homem faz o número dois com os dedos e responde: Coloque mais 200 gramas, porque quero 1 quilograma. Fim da imagem.
  1. Meia tonelada corresponde a quantos quilogramas? E 1 tonelada?

    _____

    PROFESSOR Resposta: 500 quilogramas; 1.000 quilogramas.
  1. Quantos gramas formam 1 quilograma? _____
    PROFESSOR Resposta: 1.000 gramas.

O grama, o quilograma e a tonelada são unidades de medida de massa.

MANUAL DO PROFESSOR

Objetivos

Reconhecer a relação entre as unidades de medida de massa: tonelada, quilograma e grama.

Estimar a massa de objetos.

Atividade 1

Cada item apresenta duas fotografias, e os estudantes devem estimar a massa de cada objeto representado para poderem comparar e determinar aquele com a maior massa. O conhecimento de cada objeto representado permitirá aos estudantes fazerem essa estimativa.

Atividade 2

Considerando as informações apresentadas nos diálogos, os estudantes devem realizar cálculos simples para deduzir as relações entre grama, quilograma e tonelada. Do primeiro diálogo, devem deduzir que, se 500 quilogramas correspondem a meia tonelada, então 1 tonelada corresponde ao dobro de 500 quilogramas, ou seja, a 1.000 quilogramas. Pelas informações fornecidas no segundo diálogo, devem adicionar 800 gramas com 200 gramas para obter 1.000 gramas, ou seja, 1 quilograma. Aproveite para perguntar em que outras situações do cotidiano eles reconhecem o uso das unidades de medida massa, tonelada, quilograma e grama, incentivando a discussão.

BNCC em foco:

EF04MA20

Sugestão de atividade

Explorando a massa de alguns objetos

Peça aos estudantes que, reunidos em grupos, pesquisem, em folhetos publicitários, revistas ou na internet, a massa de alguns objetos comuns no dia a dia (geladeiras, televisores, automóveis etc.), registrando os dados obtidos. Depois, os grupos trocam o material pesquisado, para que façam estimativas das massas, escrevendo-as ao lado do nome de cada objeto. A seguir, o grupo que escolheu os objetos escreve a massa verdadeira de cada um, de modo que o grupo que fez as estimativas calcule a diferença entre elas e os valores reais. Essa é uma boa maneira de verificar a compreensão das unidades de medida estudadas e incentivar o desenvolvimento da capacidade de estimativa dos estudantes.

MP237

  1. Observe.
Imagem: Ilustração. Uma mulher com cabelo preso e óculos fala: Veja como indicamos as unidades de medida. Fim da imagem.

Indicamos:

  1. Qual é a unidade mais adequada para medir a massa em cada caso: tonelada, quilograma ou grama?
Imagem: Fotografia. Um gato cinza com manchas pretas. Fim da imagem.

_____

PROFESSOR Resposta: Quilograma.
  1. Trator
Imagem: Fotografia. Um trator verde. Fim da imagem.

_____

PROFESSOR Resposta: Tonelada.
  1. Menino
Imagem: Fotografia. Um menino com camiseta azul, calça e tênis. Fim da imagem.

_____

PROFESSOR Resposta: Quilograma.
Imagem: Fotografia. Uma maçã vermelha. Fim da imagem.

_____

PROFESSOR Resposta: Grama.

Observação: Os elementos não estão em proporção. Fim da observação.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

  1. Tente dizer para um colega a medida de sua massa em tonelada e a massa de um navio em quilograma.
    PROFESSOR Resposta: Respostas pessoais.
    • Em seguida, responda: foi fácil ou difícil dizer a quantidade dessas massas? Por quê?
      PROFESSOR Atenção professor: Espera-se que os estudantes percebam que é mais fácil expressar a medida da massa de um navio em tonelada e a de uma pessoa em quilograma. Fim da observação.
  1. Um caminhão transportará 6 toneladas de alimentos. A metade dessa carga é de feijão, 800 quilogramas são de milho, e o restante é de arroz.
    1. Quantos quilogramas de feijão o caminhão transportará? _____
      PROFESSOR Resposta: 3.000 quilogramas.
      PROFESSOR Exemplo de cálculo: 6.000 ꞉ 2 = 3.000
    1. E quantos quilogramas de arroz? _____
      PROFESSOR Resposta: 2.200 quilogramas.
      PROFESSOR Exemplo de cálculo: 3.000 − 800 = 2.200
MANUAL DO PROFESSOR

BNCC em foco:

EF04MA20

Atividade 3

Os estudantes podem sentir alguma dificuldade para realizar esta atividade, em razão de os números serem parecidos e de a colocação em ordem crescente exigir a conversão de unidades. Considerando as unidades tonelada, quilograma e grama, é interessante a transformação de tonelada e de grama em quilograma, por ser essa a unidade intermediária. Assim:

1.100 g = 1.000 g + 100 g = 1 kg + 100 g

1 t = 1.000 kg

Atividade 4

Depois de os estudantes indicarem a unidade mais adequada para expressar a massa em cada caso, podem organizá-los na ordem crescente de massa. Isso exigirá deles uma nova estimativa. Uma ordem possível é a seguinte: maçã, gato, menino e trator.

Atividade 5

Comente novamente com os estudantes que medir a massa é o que eles usualmente denominam pesar. No dia a dia, é comum o uso da palavra “peso” no lugar de “massa”, mas conceitualmente esse costume está errado. Peso não é o mesmo que massa.

Atividade 6

As informações fornecidas permitem aos estudantes determinarem a massa de todos os produtos transportados no caminhão. Das 6 toneladas, metade representa feijão, portanto 3 toneladas são de feijão, das 3 toneladas restantes, temos 800 quilogramas de milho, então sobram 2.200 quilogramas de arroz.

Porém, os estudantes devem observar que a unidade de medida solicitada no item a, por exemplo, é em quilograma. Portanto, é preciso fazer a correspondência de 6 toneladas com 6.000 quilogramas.

Comparando a massa das mochilas

Aproveite a discussão sobre medidas de massa e leve uma balança para a sala de aula para que os estudantes possam verificar a massa das mochilas que levam para a escola. Depois, construa um gráfico com as medidas encontradas e compare as massas. Caso julgue necessário, converse sobre o que há dentro de cada mochila, verificando se realmente é necessário carregar tudo que está lá. Explore também a massa dos objetos que precisam estar na mochila. Se houver tempo, peça aos estudantes que pesquisem sobre a massa que eles podem carregar sem prejudicar o corpo, especificamente a coluna.

MP238

Grama e miligrama

  1. Observe os preços praticados por uma empresa que presta serviços de envio e entrega de correspondências, em outubro de 2023, para o envio de carta comercial sem serviços adicionais. Depois, responda à questão.

Tabela: equivalente textual a seguir.

Massa (em grama)

Preço

Até 20

R$ 1,80

Mais de 20 até 50

R$ 2,55

Mais de 50 até 100

R$ 3,50

Mais de 100 até 150

R$ 4,25

Imagem: Ilustração. Uma caixa de correios. Fim da imagem.
PROFESSOR Exemplos de cálculo:
PROFESSOR 1,80 + 1,80 = 3,60
PROFESSOR 3,50 + 3,50 = 7,00
PROFESSOR 3,60 + 7,00 = 10,60

Imagem: Ícone: Oral. Fim da imagem.

Imagem: Ícone: Grupo. Fim da imagem.

  1. Converse com seus colegas.
    1. Vocês já ouviram falar em miligrama? Se ouviram, em que situação?
    1. Vocês sabem o que significa 1 miligrama?
      PROFESSOR Respostas pessoais.

Imagem: Ícone: mental. Fim da imagem.

  1. Leia o texto, observe a ilustração e responda às questões.

    Um farmacêutico estava verificando sua balança de precisão e, para sua satisfação, o aparelho estava em ordem. Então, ele colocou na balança dois comprimidos de 500 miligramas cada um.

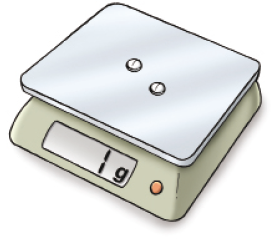
    Imagem: Ilustração. Dois comprimidos sobre uma balança. No visor, a indicação: 1 g. Fim da imagem.

    1. Quantos miligramas correspondem a 1 grama?

      _____

      PROFESSOR Resposta: 1.000 miligramas.
    1. Se ele tivesse colocado na balança 4 comprimidos de 500 miligramas cada um, que valor apareceria no visor? _____
      PROFESSOR Resposta: 2 g

Indicamos 1 miligrama por: 1 mg

1 g = 1.000 mg

MANUAL DO PROFESSOR

Objetivo

Reconhecer a relação entre as unidades de medida de massa: grama e miligrama.

Atividade 1

Esta atividade permite aos estudantes trabalharem com medidas de massa em uma situação que não envolve proporcionalidade. Peça-lhes que observem, no quadro, que alguns preços cobrados referem-se a todo um intervalo de massas.

Comente que cada carta deve ter sua massa medida e ter seu preço individual registrado com base nessa medida para depois determinar o preço total. Como a relação entre a massa das cartas e o preço pago por elas não é proporcional, o resultado obtido adicionando-se o preço pago pelo envio de cada carta separadamente não é o mesmo que ao se considerar a massa das 4 cartas juntas.

Atividade 2

Comente com os estudantes que a unidade de medida de massa miligrama é usada para massas muito pequenas, as quais as balanças comuns não são capazes de medir, sendo necessárias balanças de precisão fabricadas especialmente para essa finalidade.

Aproveite para falar sobre o prefixo mili -, que aparece em muitas palavras da nossa língua, como mililitro e milímetro, com o significado de “a milésima parte” (assim como centi - indica “a centésima parte” e deci -, “a décima parte”). Na palavra miligrama, esse prefixo sugere que a relação entre o grama e o miligrama é de 1 para 1000, ou seja, que 1 g corresponde a 1.000 mg. Para o item a, os estudantes podem citar o uso de miligrama na composição de medicamentos, xampus, leite em pó, achocolatados, entre outros.

Atividade 3

Esta atividade é proposta no contexto da atividade farmacêutica, no qual a unidade de medida miligrama é bastante empregada.

Explore a situação perguntando aos estudantes: “E se o farmacêutico tivesse colocado 5 comprimidos na balança, o que marcaria o visor?”. Espera-se que eles deduzam que apareceria um número na representação decimal (2,5 g), ou seja, 2 gramas e meio (2.500 miligramas).

BNCC em foco:

EF04MA20

MP239

  1. Escreva a quantos miligramas equivale a massa indicada em cada caso.
  1. 10 gramas: _____
    PROFESSOR Resposta: 10.000 miligramas.
  1. 0,5 grama: _____
    PROFESSOR Resposta: 500 miligramas.
  1. 3 grama: _____
    PROFESSOR Resposta: 3.000 miligramas.
  1. 8,25 gramas: _____
    PROFESSOR Resposta: 8.250 miligramas.
  1. 270 gramas: _____
    PROFESSOR Resposta: 270.000 miligramas.
  1. 19,05 gramas: _____
    PROFESSOR Resposta: 19.050 miligramas.

Imagem: Ícone: mental. Fim da imagem.

  1. Uma fábrica usa 5 mg de essência em pó na produção de cada frasco de perfume. Para produzir 1.000 frascos desse perfume, quantos gramas de essência em pó serão usados? _____
    PROFESSOR Resposta: 5 gramas.

Imagem: Ícone: mental. Fim da imagem.

  1. Observe a ilustração. Depois complete o quadro abaixo com a massa aproximada dos grãos de feijão.
Imagem: Ilustração. Um homem sorri e fala: Coloquei 400 grãos de feijão nesta balança. Ao seu lado há vários grãos de feijão sobre uma balança. No visor, a indicação: 100 g. Fim da imagem.

Tabela: equivalente textual a seguir.

Quantidade de grãos de feijão

Massa (em grama)

400

_____

200

_____

100

_____

PROFESSOR Resposta: 100; 50; 25.

Imagem: Ícone: Dupla. Fim da imagem.

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 4

Esta atividade propõe o desenvolvimento da noção de miligrama em situações em que a unidade é correlacionada ao grama, assim como a conversão entre essas unidades. Se julgar necessário, lembre à turma que 1 grama equivale a 1.000 miligramas.

Atividade 5

Incentive os estudantes a realizarem o cálculo mental da multiplicação por 1.000: 5 mg × 1.000 = 5.000 mg = 5 g.

Atividade 6

Os estudantes devem reconhecer uma regularidade nos dados do quadro, identificando a proporcionalidade entre as grandezas “quantidade de grãos de feijão” e “massa em grama”.

Antes da resolução, peça a eles que façam estimativas para responder, oralmente, às seguintes questões:

“Todos os grãos de feijão têm a mesma massa?” Exemplo de resposta: Não, mas como o tamanho não varia muito de um grão para outro, podemos considerar uma medida de massa média para cada grão.

“Quantos grãos de feijão há em um saco de 1 quilograma?” Resposta: Aproximadamente, 4.000 grãos.

Essas questões, embora evidenciem o caráter aproximado do procedimento apresentado, ajudam a ampliar o repertório de cálculos e estimativas dos estudantes.

BNCC em foco:

EF04MA20

Sugestão de atividade

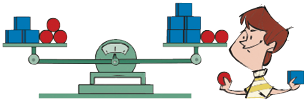
Desafio da balança

Apresente o seguinte desafio para os estudantes: A balança a seguir está em equilíbrio. Todas as bolinhas têm a mesma massa, e as caixinhas também são todas iguais e têm a mesma massa. A massa de uma bolinha corresponde à massa de quantas caixinhas? (2 caixinhas.)

Imagem: Ilustração. Um homem está segurando uma esfera vermelha e um cubo azul. Na frente dele há uma balança de pratos em equilíbrio. No prato à esquerda há três cubos e três esferas. No prato à direita há cinco cubos e duas esferas. Fim da imagem.

CRÉDITO: SIDNEY MEIRELES

MP240

Medidas de capacidade

Litro e mililitro

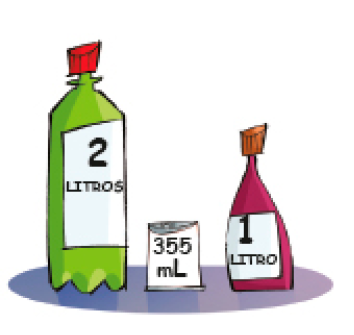
  1. Observe os rótulos das embalagens e responda às questões.
    1. Em qual das embalagens cabe maior quantidade de líquido? _____
      PROFESSOR Resposta: Na embalagem de 2 litros.

      Imagem: Ícone: mental. Fim da imagem.

    1. O conteúdo da garrafa de 1 litro pode encher completamente quantas latinhas iguais à mostrada abaixo: mais de 4 ou menos de 4?

      _____

      PROFESSOR Resposta: Menos de 4.
Imagem: Ilustração. Uma garrafa de 2 litros, uma latinha de 355 mL e uma garrafa de 1 litro. Fim da imagem.
  1. Jair foi ao supermercado para comprar uma embalagem com 2 litros de desinfetante, mas essa embalagem estava em falta. Então, ele comprou 4 embalagens de 500 mililitros, iguais à mostrada abaixo.
Imagem: Ilustração. Panfleto com a informação: DESINFETANTE 500 ML POR APENAS R$ 4,00. DESINFETANTE 2 L POR APENAS R$ 15,00. Ao lado, desenho de uma garrafa de 500 mL e um embalagem grande de 2 L. Fim da imagem.
  1. Quantos mililitros de desinfetante Jair comprou? Essa quantidade corresponde a quantos litros?

    _____

    PROFESSOR Resposta: 2.000 mililitros; 2 litros.
    PROFESSOR Exemplo de cálculo: 500 + 500 + 500 + 500 = 2.000
    PROFESSOR 2.000 mL = 2 L
  1. Quantos reais ele economizaria se tivesse comprado a embalagem com 2 litros de desinfetante?

    _____

    PROFESSOR Resposta: R$ 1,00
    PROFESSOR Exemplo de cálculo: 4 × 4 = 16
    PROFESSOR 16 − 15 = 1

Indicamos:

MANUAL DO PROFESSOR

Objetivo

Reconhecer a relação entre as unidades de medida de capacidade: litro e mililitro.

Atividade 1

Julgando oportuno, peça aos estudantes que observem o rótulo de produtos domésticos em que apareçam as unidades de medida litro (L ou ℓ) ou mililitro (mL ou mℓ), solicitando que não mexam em embalagens de produtos de limpeza. Eles podem, então, elaborar um problema com essas unidades de medida. Na sala de aula, peça-lhes que troquem o problema elaborado com o de um colega, para as resoluções e a posterior discussão das respostas. Anote na lousa alguns problemas que envolvam essas unidades de medida, os quais deverão ser resolvidos por todos juntos. Depois, esclareça eventuais dúvidas. A elaboração de problemas com base em informações de rótulos de produtos domésticos torna mais fácil a resolução das questões propostas nesta atividade.

Atividade 2

Comente que a situação apresentada se aplica ao cotidiano. Embalagens com maior massa ou maior capacidade geralmente são mais baratas que o equivalente em embalagens pequenas. No caso desta atividade, uma embalagem de 2 litros é R$ 1,00 mais barata que quatro embalagens de 500 mililitros, que formam os mesmos 2 litros.

BNCC em foco:

EF04MA20

MP241

  1. Faça estimativas e complete com a unidade de medida mais adequada em cada caso: L ou mL.
    1. A caixa-d’água de minha casa tem capacidade para 1.000 _____.
      PROFESSOR Resposta: L
    1. Na mamadeira, há 240 _____ de leite.
      PROFESSOR Resposta: mL
    1. A lata contém 18 _____ de tinta.
      PROFESSOR Resposta: L
    1. O pote plástico de guache contém 50 _____.
      PROFESSOR Resposta: mL
  1. Observe o gráfico.
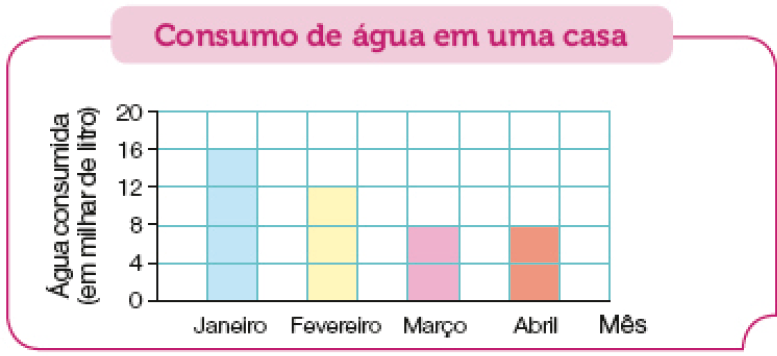
Imagem: Gráfico de colunas. Consumo de água em uma casa. No eixo vertical, a água consumida (em milhar de litro) e no eixo horizontal, o mês. Janeiro: 16 mil litros. Fevereiro: 12 mil litros. Março: 8 mil litros. Abril: 8 mil litros. Fim da imagem.

Fonte: Distribuidora de água (jan. a abr. 2023).

Boxe complementar:

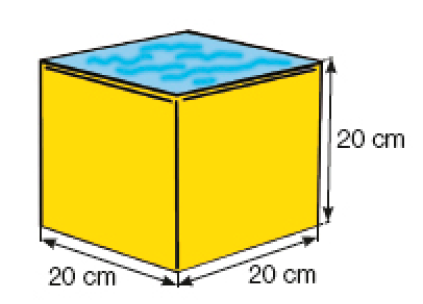
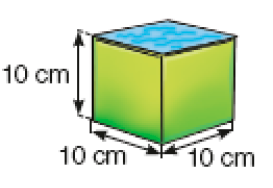
Desafio

Na embalagem cúbica verde cabem exatamente 1.000 mL de água.

Quantos litros de água cabem na embalagem cúbica amarela?

_____

Imagem: Ilustração. Uma embalagem cúbica amarela com 20 cm de altura, comprimento e profundidade. Fim da imagem.

Imagem: Ilustração. Uma caixa cúbica verde com 10 cm de altura, comprimento e profundidade. Fim da imagem.

CRÉDITO: PAULO BORGES

Resposta: 8 litros.

Fim do complemento.

MANUAL DO PROFESSOR

Atividade 3

Para auxiliar os estudantes na resolução desta atividade, leve para a sala de aula algumas embalagens de conteúdos líquidos (refrigerante, leite e suco, por exemplo), facilitando assim as estimativas de capacidade em mililitro e litro.

Atividade 4

O aspecto mais interessante desta atividade é trabalhar com as unidades de medida em estudo por meio da leitura e da interpretação dos dados fornecidos no gráfico. Amplie a atividade propondo aos estudantes o seguinte problema: “Sabendo que, em um banho de 5 minutos de duração, são gastos cerca de 9 litros de água, quantos litros de água serão necessários, aproximadamente, para um banho de 10 minutos de duração?”.

Espera-se que eles empreguem o raciocínio proporcional, percebendo que, se a duração do banho for dobrada (de 5 minutos para 10 minutos), a quantidade de água também dobrará (de 9 litros para 18 litros).

Desafio

Na embalagem cúbica amarela, “cabem” exatamente 8 embalagens cúbicas verdes. Então, na embalagem cúbica amarela cabem 8.000 mililitros de água. Como 1 litro é o mesmo que 1.000 mililitros, na embalagem cúbica amarela cabem 8 litros de água. É importante os estudantes perceberem que as medidas são dobradas, mas isso não significa que a capacidade seja dobrada, já que é preciso considerar o dobro em cada uma das três dimensões.

BNCC em foco:

EF04MA20

MP242

Compreender problemas

Para resolver

Problema 1

Catarina organizou uma exposição de fotografias que durou 3 dias. Para isso, precisou contratar 3 recepcionistas, Ofélia, Telma e Diego, que atenderiam os visitantes nos períodos da manhã e da tarde. Eles trabalharam nas seguintes condições:

Imagem: Ilustração. Uma mulher está sorrindo e segurando uma câmera fotográfica. Fim da imagem.

Complete o quadro que Catarina fez para organizar os horários dos recepcionistas.

Quadro: equivalente textual a seguir.

Dia

Quem trabalhará de manhã?

Quem trabalhará à tarde?

1 º dia

_____

Diego

2º dia

_____

_____

3º dia

_____

_____

PROFESSOR Resposta: Quem trabalhará de manhã? Ofélia; Telma; Diego.
PROFESSOR Quem trabalhará à tarde? Ofélia; Telma.
PROFESSOR Outra resposta possível:
PROFESSOR • 1º dia -Telma e Diego
PROFESSOR • 2º dia - Ofélia e Telma
PROFESSOR • 3º dia - Diego e Ofélia

Problema 2

Tiago fez suco para sua família. Ele precisou misturar 1 litro de água com o suco concentrado. Para medir 1 litro de água, ele só poderia usar 3 tipos diferentes de copo, como mostra a figura.

Como Tiago pôde medir exatamente 1 litro de água?

Imagem: Ilustração. Um homem com cabelo preto e curto está com a mão direita sob o queixo e com uma sobrancelha levantada. Na frente dele há três copos e uma jarra sobre uma mesa. Há um copo de 200 mL, um copo de 250 mL e outro copo de 300 mL. Fim da imagem.
PROFESSOR Respostas possíveis:
PROFESSOR • 5 copos de 200 mL.
PROFESSOR • 4 copos de 250 mL.
PROFESSOR • 2 copos de 300 mL e 2 copos de 200 mL.
PROFESSOR • 1 copo de 200 mL, 2 copos de 250 mL e 1 copo de 300 mL.
MANUAL DO PROFESSOR

Objetivos

Resolver problemas com mais de uma solução.

Elaborar problemas que envolvam medidas de tempo e de capacidade.

Para resolver Problema 1

Após a resolução, pergunte: “Que parte do quadro foi mais fácil de preencher? Como vocês podem conferir se a resposta obtida está correta?”.

Problema 2

Nesse problema, os estudantes precisam aplicar a relação entre litro e mililitro. É natural que, na resolução, eles:

tentem fazer uma combinação dos três tipos de copos: 200 mL, 250 mL e 300 mL;

encontrem apenas uma combinação possível, sem perceberem que existem outras.

BNCC em foco:

EF04MA20

MP243

Para refletir

Imagem: Ícone: Dupla. Fim da imagem.
Imagem: Ícone: Oral. Fim da imagem.
  1. Compare suas soluções para o Problema 1 e para o Problema 2 com as de um colega. Vocês obtiveram a mesma resposta para cada um dos problemas?
    PROFESSOR Resposta: É possível que os estudantes não tenham obtido a mesma resposta, pois tanto um como o outro problema apresentam mais de uma solução.
  1. Veja a solução que Lúcio encontrou para o Problema 1.

Tabela: equivalente textual a seguir.

Dia

Quem trabalhará de manhã?

Quem trabalhará à tarde?

1 º dia

Telma

Diego

2 º dia

Telma

Ofélia

3 º dia

Diego

Ofélia

  1. Qual dos estudantes apresentou uma solução possível para o Problema 2?
Imagem: Ilustração. Melina, menina com cabelo curto fala: Foi possível medir exatamente 1 litro de água usando 3 vezes o copo de 300 mL. Ao lado, Lucas, menino ruivo diz: Foi possível medir exatamente 1 litro de água usando apenas 1 vez o copo de 250 mL. Fim da imagem.

_____

PROFESSOR Resposta: Nenhum, pois ambas as soluções não resultam em 1 litro de água.
  1. Responda às questões.
    1. Como o Problema 1 pode ser alterado para que ele tenha uma única resposta?
    1. Como o Problema 2 pode ser alterado para que ele não tenha resposta?
      PROFESSOR Respostas pessoais.
MANUAL DO PROFESSOR

Para refletir Atividade 1

A comparação da própria solução com a de um colega ajuda os estudantes a perceberem que há mais de uma solução possível.

Se julgar oportuno, escreva na lousa uma solução e pergunte: “Alguém encontrou outra resposta? Como vocês fizeram para encontrá-la?”. Incentive a discussão das diferentes respostas.

Atividades 2 e 3

Estas atividades requerem que os estudantes analisem se uma resposta atendeu às condições estabelecidas. Esse tipo de problema propicia aos estudantes uma reflexão sobre a maneira como eles próprios devem resolver situações-problema.

Atividade 4

No item a, os estudantes poderão propor que se acrescente uma informação sobre outro recepcionista; por exemplo, afirmar que Telma trabalhou no 2º dia no período da manhã.

No item b, a questão poderia ser alterada para “Como é possível colocar exatamente 1 litro de água na jarra usando apenas o copo de 300 mL?”.

BNCC em foco:

EF04MA20

MP244

A Matemática me ajuda a ser

... um leitor de rótulos

Você sabe para que servem alguns dos nutrientes, como proteínas, gorduras e carboidratos, presentes em nossa alimentação?

Imagem: Fotografia. Uma embalagem de biscoitos ao lado de uma maçã. Na frente há uma pilha de biscoitos recheados e um copo com leite. Ao lado da embalagem, a informação: Porção - Fique atento! As informações nutricionais do rótulo se referem a uma porção do produto, e não a todo o conteúdo da embalagem. Nutrientes - Existem vários tipos de nutrientes; cada um tem sua função. Ter uma alimentação equilibrada significa ingerir os nutrientes sem exagerar nem deixar faltar nenhum. Na parte inferior, as informações: Carboidrato - Fornece energia para as células do corpo, principalmente para o cérebro. Ajuda no desenvolvimento do corpo. Gorduras - São as principais fontes de energia do corpo e ajudam na absorção de algumas vitaminas. Fibra alimentar - Contribui para uma boa digestão. Cálcio - Essencial na formação dos ossos e dos dentes. Proteína - É essencial para o fortalecimento dos músculos. Ferro - Previne a anemia e ajuda na circulação do sangue. Sódio - Regula a quantidade de líquidos do corpo. Vitaminas - Controlam o funcionamento do corpo e ajudam a prevenir doenças. Do outro lado da embalagem e ao lado dos biscoitos, as informações: 1 pacote (12 biscoitos) contém: 828 mg de cálcio - 83% da quantidade diária recomendada (desenho de um copo cheio de leite). 1 porção (3 biscoitos) contém: 207 mg de cálcio - 21% da quantidade diária recomendada (desenho de um copo com um pouco de leite). 1 biscoito contém: 69 mg de cálcio - 7% da quantidade diária recomendada (desenho de um copo com muito pouco leite). Sobre o copo, a informação: Atenção! Um pacote de biscoito pode ter quase toda a quantidade de cálcio de que precisamos consumir em um dia. Porém, o biscoito tem outros ingredientes que, em excesso, fazem mal à saúde. O ideal é complementar a dieta diária com outros alimentos ricos em cálcio, como brócolis, aveia, chia e linhaça. Um copo de 200 mL de leite integral, por exemplo, tem aproximadamente 250 mg de cálcio. Fim da imagem.

Fontes: Saiba como ler os rótulos de alimentos industrializados. Disponível em: http://fdnc.io/eMM. Acesso em: 11 mar. 2021.

MANUAL DO PROFESSOR

Objetivos

Utilizar conhecimentos matemáticos para explorar medidas e proporções.

Ler e interpretar infográfico.

Explore o infográfico com os estudantes destacando cada unidade de medida presente no pacote de biscoito. É importante comentar que todas as informações correspondem a apenas uma porção, portanto, se forem consumidos mais biscoitos, é necessário considerar o aumento de cada nutriente proporcionalmente.

Para explorar a ideia de proporcionalidade, proponha aos estudantes que observem a taxa percentual de cálcio com relação ao consumo diário, em 1 biscoito (7%), 3 biscoitos (21%) e 12 biscoitos (84%). Peça-lhes que encontrem alguma relação entre os números, por exemplo, a multiplicação de 7% de cálcio por quantidades de biscoito (7 × 3 = 21 e 7 × 12 = 84). Depois, se possível, faça perguntas como “Que taxa percentual de cálcio em relação à quantidade diária vou consumir se eu comer 5 biscoitos?” (35%, pois 7 × 5 = 35).

Aproveite o tema para discutir também conteúdos de outras áreas, como a funcionalidade de cada nutriente para o organismo.

BNCC em foco:

EF04MA20; competências gerais 2 e 7; competência específica 3

MP245

Tome nota

  1. Quantos biscoitos há em uma porção do pacote ilustrado na página anterior?

    _____

    PROFESSOR Resposta: 3 biscoitos.
  1. Entre os nutrientes citados, quais fornecem energia para nosso corpo?

    _____

    PROFESSOR Resposta: As gorduras e os carboidratos.

Reflita

Imagem: Ícone: Oral. Fim da imagem.

Você tem o hábito de observar os rótulos dos alimentos processados

que come? Considera sua alimentação saudável? _____

PROFESSOR Resposta pessoal.
MANUAL DO PROFESSOR

Tome nota Atividade 1

Para responder a esta pergunta, os estudantes precisarão apenas encontrar a informação já descrita no pacote de biscoitos.

Se possível, leve embalagens de diferentes produtos em que os estudantes possam identificar as porções.

Atividade 2

Sugira aos estudantes que releiam as informações sobre cada nutriente para responder a esta pergunta. Depois, amplie a atividade perguntando que outros alimentos têm grande quantidade de gordura e carboidrato.

Reflita

Relembre aos estudantes que uma alimentação saudável deve conter todos os nutrientes de forma equilibrada e de acordo com as necessidades individuais de cada pessoa.

Pode ser interessante permitir aos estudantes que falem sobre seus hábitos alimentares.

BNCC em foco:

EF04MA20; competências gerais 2 e 7; competência específica 3

MP246

Compreender informações

Organizar dados de uma pesquisa em planilhas eletrônicas

  1. Hélio quer fazer uma pesquisa com seus colegas de classe sobre o esporte preferido de cada um. Para isso, ele distribuiu entre eles a ficha representada a seguir.

Nome:

_____

Esporte preferido:

_____

Imagem: Ilustração. Uma menina com cabelo preso e uniforme vermelho está sorrindo e chutando uma bola de futebol. Fim da imagem.

Após receber todas as fichas preenchidas por seus colegas, Hélio organizou os dados em uma planilha eletrônica utilizando um computador.

Tabela: equivalente textual a seguir.

Ilustração. Seta para baixo.

A

B

C

1

Esporte

Total de votos

2

Futebol

10

3

Basquete

8

4

Natação

7

5

Judô

4

6

7

  1. Que informações Hélio colocou na coluna A dessa planilha?

    _____

    PROFESSOR Resposta: Quais foram os esportes escolhidos pelos colegas.
  1. E que informações ele colocou na coluna B?

    _____

    PROFESSOR Resposta: O total de colegas que escolheu cada esporte.
  1. Na linha 3, podemos identificar as informações correspondentes a qual esporte? _____
    PROFESSOR Resposta: Basquete.

    Imagem: Ícone: Oral. Fim da imagem.

  1. Que informação presente na ficha não foi representada na planilha eletrônica? Por que você acha que isso ocorreu?
    PROFESSOR Resposta: O nome do colega. Respostas pessoais.
  1. Construa, em uma malha quadriculada, um gráfico de colunas para representar as informações da pesquisa de Hélio. Não se esqueça de dar um título para o seu gráfico.
    PROFESSOR Respostas variáveis.
MANUAL DO PROFESSOR

Objetivos

Analisar dados apresentados em tabela (planilha eletrônica).

Organizar dados coletados em pesquisa utilizando tabelas e gráficos.

Atividade 1

Se possível, leve os estudantes à sala de informática para que possam utilizar uma planilha eletrônica e vivenciar a elaboração da tabela feita por Hélio. Caso a escola não ofereça essa possibilidade, leve um modelo de planilha eletrônica para apresentar para os estudantes, projetando-o na lousa.

Explique que cada quadrinho de uma planilha eletrônica se chama célula e que ela é indicada por uma letra (coluna) e por um número (linha). Explore com os estudantes os elementos da planilha que Hélio fez; por exemplo:

Na célula A1, Hélio colocou o título que indica os elementos da coluna A: Esporte

Na célula B1, ele colocou o título que indica os elementos da coluna B: Total de votos

Na coluna A, aparecem os esportes que foram citados nessa pesquisa.

Na linha 5, aparecem o esporte judô e a quantidade de votos que esse esporte recebeu, 4.

Dessa maneira, os estudantes responderão aos itens a, b e c com mais segurança.

No item d, espera-se que os estudantes verifiquem que na ficha aparece o nome do colega que a preencheu, mas essa informação não aparece na planilha. Deixe que eles exponham suas opiniões oralmente e verifique se percebem que cada voto representa 1 estudante.

No item e, distribua as folhas quadriculadas para que eles possam fazer o gráfico de colunas correspondente à planilha de Hélio.

BNCC em foco:

EF04MA27, EF04MA28

MP247

  1. Agora, faça uma pesquisa sobre o animal preferido de seus colegas. Para isso, veja as orientações a seguir:

√ Elabore uma ficha para que cada um de seus colegas indique o animal preferido.

√ Organize os dados em uma tabela ou em uma planilha eletrônica.

√ Construa um gráfico de barras com as informações obtidas.

  1. Que informações você colocou na ficha que seus colegas preencheram? Além do animal preferido, que outras informações você pode obter com os dados dessa ficha?

    _____

  1. Na tabela ou na planilha eletrônica, que informações você organizou em cada coluna?

    _____

  1. Ao construir seu gráfico, que informações você representou no eixo horizontal? E no eixo vertical?

    _____

    Imagem: Ícone: Dupla. Fim da imagem.

  1. Compare o gráfico que você construiu com o gráfico construído por outro colega. Há diferenças?

    _____

    Imagem: Ícone: Oral. Fim da imagem.

  1. Caso haja diferenças, por que você acha que isso ocorreu? Converse com o professor e os colegas.
  1. Escreva duas afirmações que podem ser feitas sobre os dados de sua pesquisa.

    _____

    PROFESSOR Respostas pessoais.
MANUAL DO PROFESSOR

Um possível gráfico é o sugerido abaixo.

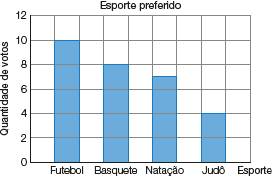
Imagem: Gráfico de colunas. Esporte preferido. No eixo vertical, a quantidade de votos e no eixo horizontal, o esporte. Futebol: 10 votos; Basquete: 8 votos; Natação: 7 votos; Judô: 4 votos. Fim da imagem.

Fonte: Colegas de Hélio (mar. 2017).

CRÉDITO: ERICSON GUILHERME LUCIANO

Depois de fazerem seus gráficos, peça aos estudantes que os mostrem e os comparem com os dos colegas. Pode-se fazer uma exposição.

Aproveite o momento e explore as informações do gráfico com os estudantes:

Qual foi o esporte mais votado? (O futebol.)

A quantidade de votos que cada esporte recebeu é a sua frequência (quantas vezes ele foi citado). Qual foi a frequência da natação? (7.)

Que esporte teve a menor frequência? (O judô.)

Atividade 2

Inicialmente, incentive os estudantes a organizarem as informações obtidas em uma tabela e, depois, se possível, transcrevam os dados para uma planilha eletrônica. Em seguida, mostre a eles como podem construir um gráfico de barras com base nessa planilha eletrônica, no computador. Se isso não for possível, distribua folhas quadriculadas para que eles possam elaborar o gráfico nessa malha quadriculada.

Explore a tabela e o gráfico junto com os estudantes, como sugerido na atividade 1.

BNCC em foco:

EF04MA28

MP248

O que você aprendeu

Avaliação processual

Imagem: Ícone: mental. Fim da imagem.
  1. Em 2 minutos e 30 segundos, Artur corre 500 metros de um percurso.

    Mantendo esse ritmo, em quanto tempo ele percorrerá 1 quilômetro?

    _____

    PROFESSOR Resposta: Em 5 minutos.
  1. Observe a reta numérica a seguir, que representa uma linha do tempo.
Imagem: Ilustração. Reta numérica (Ano): 1740 (A), 1800 (B), 1870 (C), 1940 (D). Fim da imagem.

Agora, responda às questões.

  1. Quantas décadas separam as datas (os anos) dos acontecimentos indicados pelas letras C e D?

    _____

    PROFESSOR Resposta: 7 décadas.
  1. Quais datas (anos) estão separadas na linha do tempo por 2 séculos?

    _____

    PROFESSOR Resposta: 1740 e 1940.
  1. Resolva os problemas a seguir.
    1. Ana tem 500 mL de água em um regador para distribuir igualmente entre seus 4 vasos de plantas. Quantos mililitros de água cada vaso receberá?

      _____

      PROFESSOR Resposta: 125 mL de água.
    1. Geraldo e sua família viajaram nas férias. Eles saíram de carro de Maceió no dia 21 de dezembro às 20 h e chegaram a São Paulo às 13 h 40 min do dia 23 de dezembro. Quanto tempo durou a viagem de Geraldo?

      _____

      PROFESSOR Resposta: 41 h 40 min

Imagem: Ícone: mental. Fim da imagem.

  1. Em cada caso, pinte as figuras que, juntas, completam exatamente 1 grama.
Imagem: Ilustração. Figuras ovais com os números: 3.000 mg, 300 mg, 600 mg, 250 mg, 100 mg. Resposta: 300 mg, 600 mg, 100 mg. Fim da imagem.
Imagem: Ilustração. Hexágonos com os números: 850 mg, 1.500 mg, 150 mg, 2.500 mg, 8.500 mg. Resposta: 850 mg, 150 mg. Fim da imagem.
MANUAL DO PROFESSOR

Objetivo

Retomar os conceitos estudados.

A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.

Atividade 1

Nesta atividade, trabalhamos medida e variação do tempo, relacionando tempo e distância percorrida. É importante os estudantes visualizarem que Artur corre 500 metros em dois minutos e meio, sendo assim, proporcionalmente dobrando o percurso (1 quilômetro), dobra o tempo, chegando a 5 minutos. A notação 2 minutos e 30 segundos não é explícita e os estudantes terão de perceber que equivale à metade de 5 minutos.

Atividade 2

Nesta atividade, trabalhamos a leitura de linha do tempo em diferentes séculos, em que os estudantes precisam resgatar os conceitos de décadas e séculos para resolver as questões propostas.

Atividade 3

Para responder ao item b, os estudantes precisam observar as datas de saída e de chegada da família de Geraldo no mês de dezembro:

das 20 h do dia 21 às 20 h do dia 22, são 24 horas;

das 20 h do dia 22 às 8 h do dia 23, são mais 12 horas;

das 8 h do dia 23 às 13 h do mesmo dia, são mais 5 horas;

das 13 h do dia 23 às 13 h e 40 min do mesmo dia, são mais 40 minutos.

Atividade 4

Esta atividade propõe trabalhar a adição de medidas de massa em miligrama de modo a completar 1 grama, reforçando a relação entre essas unidades de medida de massa.

BNCC em foco:

EF04MA20, EF04MA22

MP249

  1. Observe a ilustração, leia o texto e responda à questão.
Imagem: Ilustração. Um jarro de 1 litro, um copo largo e amarelo e um copo fino e azul. Fim da imagem.

No copo amarelo, cabe a mesma quantidade de água que em 2 copos azuis. Na jarra cabe a mesma quantidade de água que em 5 copos amarelos.

Imagem: Ícone: Dupla. Fim da imagem.

  1. Invente um problema com as informações abaixo. Depois, peça a um colega que o resolva.

Rosquinha de fubá

Rendimento: 10 rosquinhas

Imagem: Fotografia. Rosquinhas circulares em uma bandeja. Fim da imagem.

_____

PROFESSOR Resposta pessoal.
  1. Complete as frases.
    1. 50 anos correspondem a _____ século.
      PROFESSOR Resposta: meio
    1. Meio milênio equivale a _____ anos.
      PROFESSOR Resposta: 500
    1. _____ décadas correspondem a 1 século.
      PROFESSOR Resposta: 10
    1. _____ anos equivalem a 3 décadas.
      PROFESSOR Resposta: 30

Autoavaliação

Imagem: Ícone: Oral. Fim da imagem.

MANUAL DO PROFESSOR

Atividade 5

Nesta atividade, os estudantes devem perceber que, se na jarra cabe 1 litro, e essa é completada com 5 copos, então cada copo tem 200 mL. Se em 1 copo amarelo “cabem” 2 copos azuis, o copo azul tem a metade da capacidade do copo amarelo.

Assim, o copo azul tem capacidadede 100 mL.

Atividade 6

Algumas questões que podem ser elaboradas:

Qual das etapas é a mais demorada? (O tempo para assar.)

O preparo dessa receita exige mais ou menos de 1 hora? (Menos, pois são necessários cerca de 40 minutos.)

Atividade 7

Nesta atividade, os estudantes empregarão os conceitos de ano, década, século e milênio tratados na Unidade, fazendo correspondências e respondendo às questões.

Autoavaliação

Na primeira questão, os estudantes deverão avaliar se conseguem perceber equivalência em cada caso trabalhado na Unidade. Nas medidas de tempo, por exemplo, devem perceber que 1 hora equivale a 60 minutos, diferentemente das unidades de medida de massa e de capacidade, que se assemelham às equivalências das medidas de comprimento exploradas anteriormente.

Na segunda questão, eles deverão avaliar se têm utilizado os conhecimentos para além da realização de cálculos isolados. Por exemplo, para auxiliar na leitura e na interpretação de textos informativos.

BNCC em foco:

EF04MA20, EF04MA22

MP250

Comentários para o professor:

Conclusão da Unidade 7

Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.

Ficha de avaliação e acompanhamento da aprendizagem

Nome: _____

Ano/Turma: _____ Número: _____ Data: _____

Professor(a): _____

Legenda de Desempenho: S: Sim N: Não P: Parcialmente

Tabela: equivalente textual a seguir.

Objetivos de aprendizagem

Desempenho

Observação

Consegue ler e registrar medidas e intervalos de tempo em horas, minutos e segundos em situações relacionadas ao seu cotidiano, como informar os horários de início e término de realização de uma tarefa e sua duração?

_____

_____

Sabe medir e estimar comprimentos (incluindo perímetros), massas e capacidades, com o emprego de unidades de medida padronizadas mais usuais, valorizando e respeitando a cultura local?

_____

_____

Analisa dados apresentados em tabelas simples ou de dupla entrada e em gráficos de colunas ou pictóricos, com base em informações das diferentes áreas do conhecimento, e consegue produzir texto com a síntese de sua análise?

_____

_____

Realiza pesquisa e organiza os dados coletados por meio de tabelas e gráficos de colunas simples, com e sem uso de recurso da planilha eletrônica?

_____

_____

Faz leitura e análise de dados em rótulos?

_____

_____

Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo?

_____

_____

Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis?

_____

_____