MP251
Comentários para o professor:
Introdução da Unidade 8
A Unidade 8 tem como foco tratar os conhecimentos a serem desenvolvidos na Unidade Temática Geometria. Assim, a abertura traz, em página dupla, uma imagem com informações a serem exploradas nas questões propostas na seção Para refletir..., que estimulam o estudante a mobilizar os conhecimentos anteriores sobre ângulos associados à ideia de giro (de uma volta, de meia-volta e de um quarto de volta) e de paralelismo e perpendicularidade entre retas e segmentos de reta, mesmo que intuitivos.
Dando continuidade ao trabalho realizado no 3º ano, de movimentação de pessoas e objetos no espaço, incluindo mudanças de direção e sentido, com base em diferentes pontos de referência, esta Unidade busca descrever deslocamentos e localização de pessoas e de objetos no espaço, por meio de malhas quadriculadas e representações como desenhos, mapas, croquis, empregando termos como direita e esquerda, mudanças de direção e sentido, intersecção, transversais, paralelas e perpendiculares. Pretende-se, dessa forma, preparar os estudantes para o 5º ano, no qual vão utilizar e compreender diferentes representações para a localização de objetos no plano, como mapas, células em planilhas eletrônicas e coordenadas geográficas, a fim de desenvolverem as primeiras noções de coordenadas cartesianas; e interpretação, descrição e representação da localização ou movimentação de objetos no plano cartesiano (1º quadrante), utilizando as coordenadas cartesianas, indicando mudanças de direção e de sentido e giros.
Além disso, o conceito de simetria é iniciado nesta Unidade, com atividades que buscam desenvolver no estudante a habilidade de reconhecer simetria de reflexão em figuras e em pares de figuras geométricas planas e utilizá-la na construção de figuras congruentes, com o uso de malhas quadriculadas e de softwares de geometria. Tal desenvolvimento favorecerá, no 5º ano, o aprendizado de reconhecer a congruência dos ângulos e a proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas ou usando tecnologias digitais.
A Unidade Temática Probabilidade e estatística é mais uma vez contemplada com a exploração de problemas com dados apresentados em gráficos (nesta Unidade, são gráficos de barras duplas), em que os estudantes vão analisar os dados, e, ao final, produzir texto síntese.
MP252
UNIDADE 8. Mais Geometria

MANUAL DO PROFESSOR
Objetivos da Unidade
Elaborar, descrever e desenhar trajetos (ou caminhos) em malha quadriculada.
Ler e desenhar trajetos (ou caminhos) orientados em mapas.
Compreender a ideia de simetria e identificar eixos de simetria de figuras, caso existam.
Desenhar na malha quadriculada figuras que apresentam simetria.
Reconhecer e representar retas e segmentos de reta.
Classificar retas em paralelas ou concorrentes.
Resolver problemas envolvendo a montagem de figuras geométricas.
A abertura desta Unidade trabalha com ideias relacionadas à localização espacial. As atividades propostas mobilizam os conhecimentos anteriores da turma a respeito de ângulos associados a giros (de uma volta, de meia-volta e de um quarto de volta) e de paralelismo e perpendicularidade entre retas e segmentos de reta. Ainda que não tenham estudado formalmente essas últimas noções, os estudantes dessa idade já as adquiriram de modo intuitivo, em sua vivência social.
BNCC em foco:
EF04MA16, EF04MA19, EF04MA27
MP253
Boxe complementar
Para refletir...
As escolas de um bairro sempre desfilam no dia 7 de setembro.

O giro que as crianças da fanfarra têm de dar para ficar de frente para o palanque é de uma volta, de meia-volta ou de um quarto de volta?
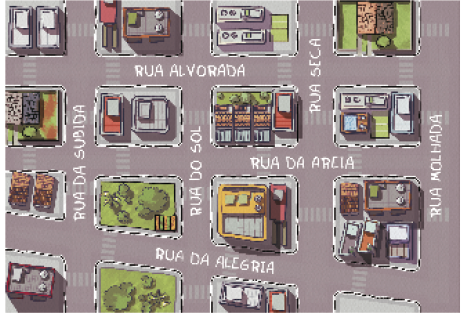
O desfile acontece em uma rua paralela à Rua da Areia.

Explique o que significam ruas paralelas.
PROFESSOR
Resposta pessoal.Observe o mapa. Em qual dessas ruas ocorreu o desfile?
PROFESSOR
Resposta: Rua Alvorada.Fim do complemento
MANUAL DO PROFESSOR
Para refletir...
No item a, comente que no dia 7 de setembro acontecem desfiles por todo o território brasileiro em comemoração à declaração da independência do Brasil, ocorrida em 7 de setembro de 1822. O mais famoso deles ocorre em Brasília, com a presença do presidente da República. Se julgar oportuno, peça aos estudantes que pesquisem o processo de independência do Brasil. Antes de responderem à questão, simule a situação na sala de aula, pedindo que deem giros e os classifiquem: de uma volta, de meia-volta etc. Pergunte: “O giro que as crianças da fanfarra têm de dar para ficar de frente para o palanque corresponde a um ângulo reto, agudo ou obtuso?” (Ângulo reto).
No item b, aproveite a primeira questão para observar o que os estudantes entendem por ruas paralelas. Por sua vivência social podem dizer, por exemplo, que ruas paralelas são ruas que não se cruzam. Para responder à segunda questão, precisam conhecer a ideia de paralelismo. Ajude-os apresentando exemplos de ruas paralelas no bairro onde a escola se situa. No mapa mostrado na cena, são exemplos de ruas paralelas: a Rua Alvorada e a Rua da Areia; a Rua Molhada, a Rua Seca, a Rua do Sol e a Rua da Subida. Apresente também exemplos de ruas que não são paralelas, como a Rua da Subida e a Rua da Alegria; a Rua da Areia e a Rua Seca.
MP254
Movimentação
Malha quadriculada
- Para chegar ao tesouro, Pedro fez o caminho mostrado na malha quadriculada ao lado. Ele partiu do ponto indicado em Início e, para os quatro primeiros movimentos, seguiu estas instruções:

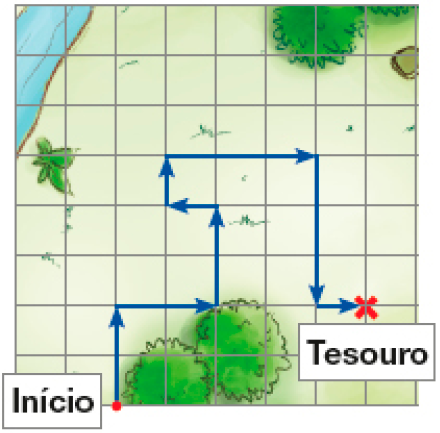

- Complete o trajeto de Pedro desenhando instruções que indiquem os outros quatro movimentos que ele fez até chegar ao tesouro.
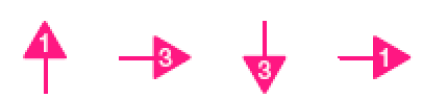
- Depois de cada movimento, para fazer o próximo, Pedro teve de dar um giro de uma volta, de meia-volta ou de um quarto de volta?
_____
PROFESSOR
Resposta: De um quarto de volta.
- Observe as instruções e marque com um X a resposta certa.
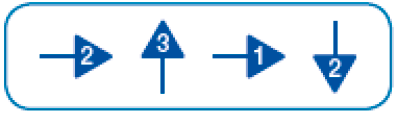
- Qual dos trajetos abaixo corresponde às instruções dadas?
( )
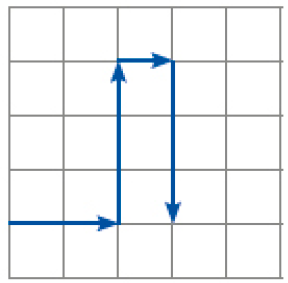
( )
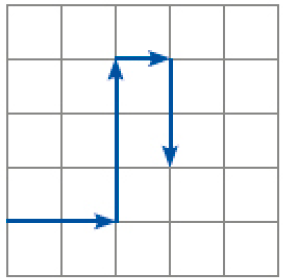
PROFESSOR
Resposta correta: imagem 2.MANUAL DO PROFESSOR
Objetivos
Elaborar, descrever e desenhar trajetos (ou caminhos) em malha quadriculada.
Ler e desenhar trajetos (ou caminhos) orientados em mapas.
Atividade 1
Os aspectos motores dos estudantes desenvolvem-se desde antes do seu nascimento, e cedo eles começam a lidar com o vocabulário relacionado à movimentação: para a frente, para trás, voltar, avançar, subir, descer etc. De posse dessas convenções da linguagem, locomovem-se e exploram o ambiente à sua volta; entretanto, o uso dessa linguagem e de símbolos associados à representação da movimentação realizada para percorrer um caminho exige intervenção. Na situação proposta, apresenta-se um caminho orientado por setas em uma malha quadriculada e, depois, alguns símbolos que correspondem a cada um dos movimentos possíveis nessa malha – para a movimentação e a descrição desses movimentos. É possível que alguns estudantes já tenham alguma familiaridade com situações desse tipo por manipularem joysticks de videogames ou usarem o controle remoto de carrinhos de brinquedo. Em ambos os casos, a movimentação orientada dos controles leva à movimentação do objeto no videogame ou do carrinho.
Atividade 2
Após a realização desta atividade, peça aos estudantes que descrevam oralmente a movimentação correta. Depois, oriente-os a escreverem, sem utilizar setas ou símbolos, essa mesma descrição no caderno.
BNCC em foco:
EF04MA16
Sugestão de atividade
O robô
Essa brincadeira pode ser realizada antes ou depois da abertura. Um voluntário, tendo os olhos vendados, deve assumir o papel de robô e seguir ordens dos colegas para ir para a frente ou para trás (número de passos) e virar à direita ou à esquerda, a fim de sair de um ponto de referência a outro – por exemplo, do fundo da sala até a frente. Nessa brincadeira, além de localizarem-se a partir do seu próprio corpo, os estudantes estimam a quantidade de passos e fazem previsões de sentido (as carteiras e os outros estudantes podem ser obstáculos no caminho do robô).
MP255

- Faça o que se pede.
- Invente um caminho na malha que comece no ponto vermelho e passe por todos os pontos verdes. Seu caminho deve ser feito sobre as linhas da malha.
PROFESSOR
Exemplo de resposta: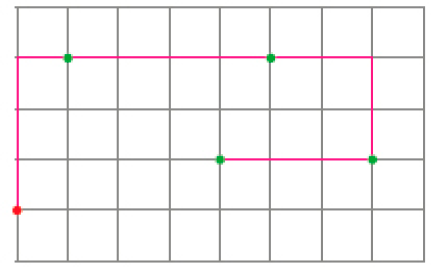
- Desenhe com setas as instruções do caminho que você inventou.
PROFESSOR
Resposta: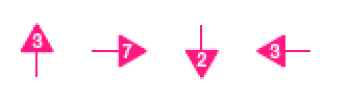

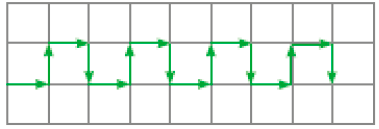
- O caminho representado na malha quadriculada abaixo é feito de 4 movimentos que se repetem. Quais são esses movimentos? Indique-os desenhando setas nos sentidos do percurso.
1º
PROFESSOR
Resposta:
2º
PROFESSOR
Resposta:
3º
PROFESSOR
Resposta:
4º
PROFESSOR
Resposta:


- Invente instruções de um trajeto e anote-as no caderno. Depois, entregue-o a um
colega
para que ele trace o trajeto em uma
folha
de papel quadriculado. Você também vai traçar o trajeto seguindo as instruções que seu
colega
inventar. As instruções podem ser indicadas por setas ou por outro código que vocês criarem.
PROFESSOR
Respostas variáveis.
MANUAL DO PROFESSOR
Atividade 3
Como existem vários caminhos possíveis, é importante socializar as diferentes formas de resolver o problema. Peça aos estudantes que comparem o caminho que inventaram com os caminhos traçados pelos colegas.
Pode-se promover uma discussão sobre qual foi o caminho mais longo e o mais curto inventado por eles.
Atividade 4
Nesta atividade, é interessante que os estudantes percebam a periodicidade do percurso apresentado.
Peça aos estudantes que observem o bloco que se repete e pergunte: “Quantas vezes esse bloco com os 4 movimentos aparece?” (4 vezes).
Atividade 5
Para realizar esta atividade, os estudantes precisarão de papel quadriculado.
Depois que todas as duplas concluírem os traçados, peça aos estudantes que comentem se as instruções do colega de dupla estavam fáceis de entender ou não. É importante eles perceberem a importância de informações claras, que permitam ao outro executar o que foi solicitado.
BNCC em foco:
EF04MA16
Sugestão de leitura para o professor
Livro
FILHO, Dirceu Zaleski. Matemática e arte. Rio de Janeiro: Autêntica, 2013.
Esse livro propõe a aproximação da Matemática com a Arte no ensino e justifica esta aproximação nas produções humanas desde a Antiguidade. Para isso, o autor apresenta recortes da história da Arte e da Matemática com ênfase nos possíveis ganhos com a conciliação das áreas. Deste modo, inclui nas discussões a presença da Matemática e da Arte na filosofia grega, no período da Idade Média, chegando ao período Moderno e à contemporaneidade. Picasso e Mondrian são alguns dos pintores destacados, que apresentam elementos ricos para a exploração da Geometria.
MP256
Reta e segmento de reta
- Observe as três tubulações (verde, azul e vermelha) que levam o hamster até a comida. Em seguida, responda à questão.
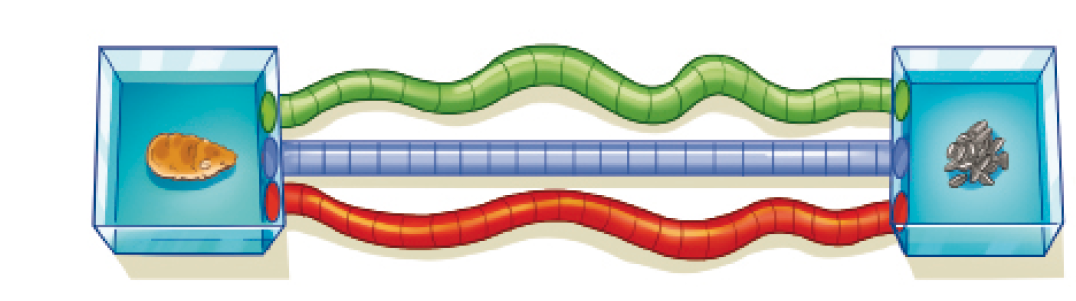
- Qual é a cor da tubulação que o hamster
deve
escolher para percorrer o caminho mais curto até a comida?
_____
PROFESSOR
Resposta: Tubulação azul.
- Observe os pontos marcados abaixo. Depois, ligue-os representando o caminho mais curto entre eles.

O caminho mais curto que une dois pontos é chamado de segmento de reta.
Veja como representamos um segmento de reta.

Os pontos A e B são as extremidades desse segmento de reta.
MANUAL DO PROFESSOR
Objetivos
Explorar a ideia de reta.
Explorar a ideia de segmento de reta.
Atividade 1
Vale notar que a definição de segmento de reta como o caminho mais curto que une dois pontos leva em consideração que tal deslocamento ocorra em uma superfície plana, pois, sobre uma superfície curva, a menor distância entre os pontos poderia não ser representada pela medida do comprimento de um segmento de reta.
Atividade 2
Comente que na indicação de segmentos de reta e reta (por exemplo: e respectivamente), o traço sobre as letras que designam as extremidades de um segmento de reta indica que ele tem começo e fim, enquanto a seta com ambas as pontas sobre as letras mostra que a reta se prolonga infinitamente em ambos os sentidos.
BNCC em foco:
EF04MA16
MP257
- Eduardo fez várias linhas coloridas.
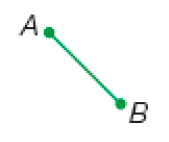
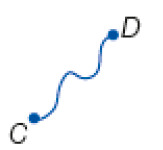


- Quais dessas linhas coloridas representam segmentos de reta?
_____
PROFESSOR
Resposta: A linha verde e a laranja.
- Quais são as extremidades desses segmentos?
_____
PROFESSOR
Resposta: Linha verde: A e B ; linha laranja: G e H.
- Leia o que Cláudio está dizendo e responda à questão.


- Você conhece algo que lembra uma reta? Dê exemplos.
PROFESSOR
Resposta pessoal.
- Observe a fotografia e as figuras. Em seguida, responda às questões.

LEGENDA: Trilhos de trem no município de Aguiarnópolis, Tocantins, em 2020. FIM DA LEGENDA.
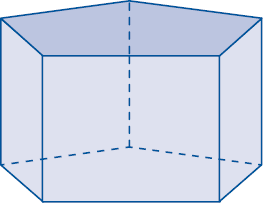
LEGENDA: Prisma. FIM DA LEGENDA.
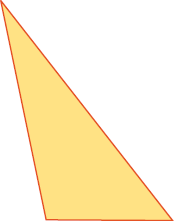
LEGENDA: Triângulo. FIM DA LEGENDA.
- Na fotografia, cada trilho de
ferro
lembra reta ou segmento de reta?
_____
PROFESSOR
Atenção professor: Espera-se que os estudantes associem cada trilho a uma reta. Fim da observação.
- As arestas do prisma são retas ou segmentos de reta?
_____
PROFESSOR
Resposta: Segmentos de reta.
- E os lados do triângulo?
_____
PROFESSOR
Segmentos de reta.
MANUAL DO PROFESSOR
Atividade 3
Aproveite para pedir aos estudantes que indiquem os segmentos que eles reconheceram na atividade: por exemplo, o segmento verde pode ser indicado por ou e o laranja, por ou . Solicite a eles que identifiquem em objetos da sala de aula linhas parecidas com segmentos de reta. Pode-se sugerir também que liguem, com pedaços de barbante, dois pontos quaisquer da sala de aula para fazer duas conexões – uma com “linha reta” e outra com “linha curva” – e depois comparem as medidas dos comprimentos dos dois barbantes.
Atividade 4
Nesta atividade, conceitua-se a reta como o prolongamento de um segmento de reta nos dois sentidos, indefinidamente. A fala da personagem explica que esse prolongamento “dá a ideia de reta”, e não que é uma reta. É importante garantir essa linguagem, para não induzir os estudantes a erros conceituais.
Atividade 5
As situações apresentadas possibilitam o reconhecimento de reta e segmento de reta e a diferenciação entre os dois elementos. A atividade incentiva os estudantes a associarem a reta ao trilho de uma estrada de ferro, que dá ideia de infinitude, e a reconhecerem segmentos de reta em uma figura geométrica não plana e em uma figura plana.
É interessante os estudantes observarem que as arestas de figuras não planas (poliedros) e os lados de figuras planas (polígonos) são segmentos de reta. O conceito de reta se apoia na abstração, uma vez que a ideia de infinito é um conceito matemático cuja existência não encontra comprovação no mundo físico. Por isso se fala que os trilhos de um trem “parecem com” ou “lembram” retas paralelas, mas não são, em si, retas paralelas. Notamos ainda que, para esse primeiro contato com essas noções elementares da Geometria, não se faz necessária a apresentação das nomenclaturas usuais. Por isso os segmentos de reta são aqui referidos apenas pela nomeação de suas extremidades por uma letra maiúscula do alfabeto.
BNCC em foco:
EF04MA16
MP258
Retas paralelas e retas concorrentes
- Observe o mapa e responda às questões.
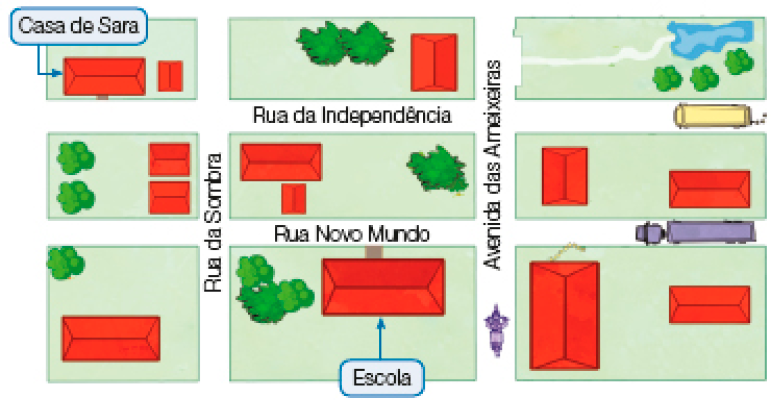
- Se o ônibus continuar andando pela Rua da Independência até a casa de Sara, e o caminhão continuar andando pela Rua Novo Mundo até a escola, eles se encontrarão?
_____
PROFESSOR
Resposta: Não.
- Se a motocicleta e o caminhão continuarem a seguir em frente, eles passarão por um mesmo cruzamento?
_____
PROFESSOR
Resposta: Sim.
As ruas que não se cruzam, mesmo que sejam prolongadas, dão ideia de retas paralelas, como as retas r e s representadas abaixo.

As ruas que se cruzam dão ideia de retas concorrentes, como as retas x e y representadas abaixo.
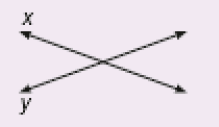
- A rua onde Sara mora é paralela à Avenida das Ameixeiras? Por quê?
_____
PROFESSOR
Resposta: Não, porque elas se cruzam.
MANUAL DO PROFESSOR
Objetivos
Explorar a ideia de retas paralelas.
Explorar a ideia de retas concorrentes.
As atividades deste tópico apresentam situações em que estão envolvidas as ideias de retas paralelas e retas concorrentes. Trabalhar essas ideias com os estudantes é importante tanto para os usos sociais, como a orientação em ruas, por exemplo, quanto para a ampliação do vocabulário matemático e a classificação de figuras geométricas de acordo com a existência ou não de lados opostos paralelos.
Atividade 1
Pergunte a eles que outras ruas representadas no mapa dão ideia de retas concorrentes e que outras dão ideia de retas paralelas. Os estudantes podem mencionar os pares de ruas: Rua da Sombra e Rua Novo Mundo, Avenida das Ameixeiras e Rua da Independência, Avenida das Ameixeiras e Rua Novo Mundo, no caso de ruas que dão ideia de retas concorrentes; e a Rua da Sombra e a Avenida das Ameixeiras, no caso de ruas que dão ideia de retas paralelas. Caso a localização da escola permita, questione-os sobre ruas próximas à rua da escola que deem ideia de retas paralelas e de retas concorrentes. Se julgar oportuno, comente uma curiosidade: o símbolo de igualdade em Matemática (=) foi criado pelo matemático inglês Robert Recorde (1510-1558). Para ele, nada era mais igual que um par de retas paralelas.
BNCC em foco:
EF04MA16
MP259
- Observe as representações das bandeiras abaixo. Escreva se as faixas brancas em cada bandeira lembram retas paralelas ou retas concorrentes.
a)

LEGENDA: Dinamarca. FIM DA LEGENDA.
_____
PROFESSOR
Resposta: Retas concorrentes.b)

LEGENDA: Cabo Verde. FIM DA LEGENDA.
_____
PROFESSOR
Resposta: Retas paralelas.- Observe as figuras. As retas r e s representadas em cada caso são paralelas ou concorrentes? Por quê?
a)

_____
PROFESSOR
Resposta: Retas concorrentes, porque elas se cruzam no prolongamento dos traçados.b)
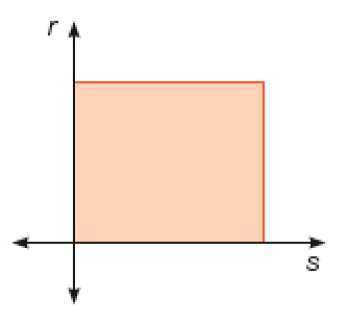
_____
PROFESSOR
Resposta: Retas concorrentes, porque elas se cruzam.c)
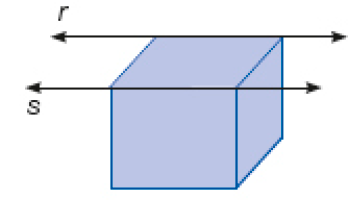
_____
PROFESSOR
Resposta: Retas paralelas, porque elas não se cruzam mesmo que se prolonguem.d)
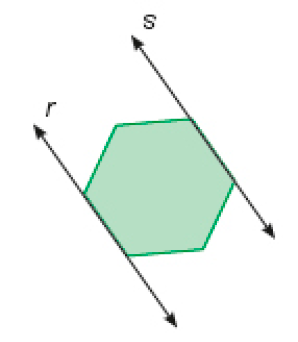
_____
PROFESSOR
Resposta: Retas paralelas, porque elas não se cruzam mesmo que se prolonguem.MANUAL DO PROFESSOR
Atividade 2
Esta atividade possibilita observar se os estudantes identificam retas paralelas e retas concorrentes nas imagens de bandeiras de 2 países. Sugira a eles que realizem uma pesquisa a respeito das bandeiras do Brasil, ou de outros países, obtendo informações sobre o significado de suas cores e formas.
Atividade 3
Aqui, os estudantes devem identificar pares de retas paralelas e de retas concorrentes de acordo com os conceitos apresentados e justificar as respostas. A variação de perspectiva é importante para os estudantes treinarem a aplicação dos conceitos em estudo a todo tipo de representação. A relação das retas como lados de um polígono também é importante de se ressaltar; por exemplo, no item b, a atividade apresenta retas concorrentes, mas também temos nesta representação dois pares de retas paralelas. Explore essas variações da atividade com os estudantes.
Sugestão de atividade
Construindo um mapa de ruas
É sempre produtivo relacionar os conteúdos trabalhados em sala de aula com o espaço de convívio dos estudantes. No caso do estudo de paralelismo e perpendicularidade de retas, você pode propor às crianças que construam um mapa das ruas próximas à escola, contendo as ruas principais e alguns pontos de referência. Para a composição do mapa, a classe pode ser dividida em grupos e, junto com o professor, fazer uma caminhada nas imediações, esboçando em papel quadriculado as principais partes do trajeto. Em sala de aula, os estudantes reorganizam as informações, formando o mapa com ruas paralelas e ruas transversais à rua da escola. Se necessário, ajude-os escrevendo algumas frases que correspondam ao espaço representado.
BNCC em foco:
EF04MA16
MP260
Retas perpendiculares
- Observe o mapa e, em seguida, faça o que se pede.
A linha tracejada representa o caminho que Juliana fez de sua casa ao mercado.
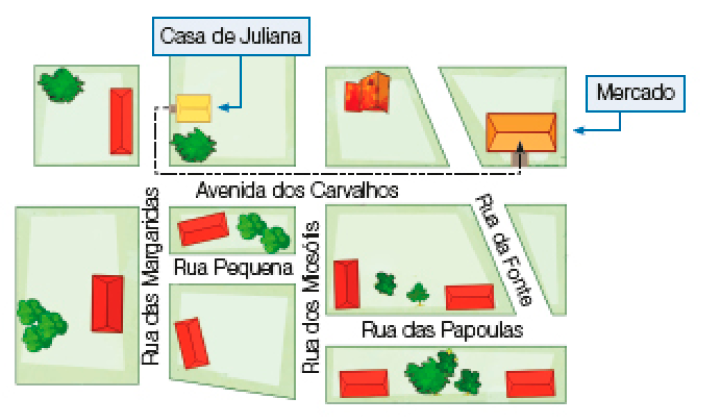
- Quando chegou à esquina da Avenida dos Carvalhos com a Rua das Margaridas, Juliana deu um giro à esquerda. Esse giro foi de uma volta, de meia-volta ou de um quarto de volta?
_____
PROFESSOR
Resposta: De um quarto de volta.
- A Avenida dos Carvalhos e a Rua das Margaridas lembram retas paralelas ou concorrentes? Por quê?
_____
PROFESSOR
Resposta: Retas concorrentes, porque elas se cruzam.
- Leia o que Juliana está falando. Depois faça o que se pede. No mapa acima, aponte com o dedo pares de ruas perpendiculares. Depois, registre um desses pares.
_____
PROFESSOR
Exemplo de resposta: Rua dos Miosótis e Avenida dos Carvalhos.

MANUAL DO PROFESSOR
Objetivo
Explorar o conceito de perpendicularidade.
É importante garantir que os estudantes compreendam que as retas perpendiculares são um caso particular de retas concorrentes. Assim, aproveite as atividades que apresentam mapas de ruas para esclarecer que a ideia de retas perpendiculares associa-se então à situação de duas ruas em que, caminhando por uma delas, precisamos dar um giro de de volta para caminharmos pela segunda rua. Eles devem perceber que a ideia de de volta está associada a um ângulo de medida 90 graus, ou seja, a um ângulo reto.
Atividade 1
No item b desta atividade, os estudantes têm oportunidade de exercitar o vocabulário adquirido no estudo dos conteúdos tratados até aqui: “ruas paralelas”, “ruas perpendiculares”, “ruas que se cruzam” etc. Aproveite para pedir a eles que pesquisem o mapa de uma cidade planejada – como Brasília, Teresina, Aracaju, Belo Horizonte, Goiânia e Palmas –, onde as ruas dão melhor ideia de paralelismo e perpendicularidade.
BNCC em foco:
EF04MA16
MP261
- Descreva a localização da rua de sua escola usando frases como: “Minha escola fica em uma rua paralela à Rua das Figueiras.”, “A rua da minha escola é perpendicular à Avenida das Rosas.” etc.
_____
PROFESSOR
Resposta pessoal.
- Observe as retas abaixo.
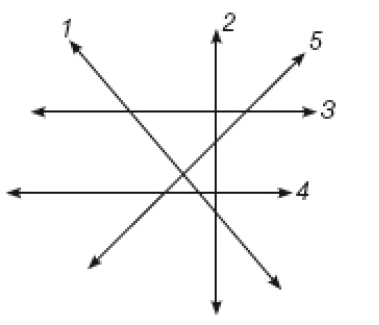
- Quais são os números das retas paralelas?
_____
PROFESSOR
Resposta: Retas 3 e 4.
- Cite um par de retas concorrentes.
_____
PROFESSOR
Exemplos de resposta: retas 2 e 5, retas 2 e 3.
- Cite um par de retas perpendiculares.
_____
PROFESSOR
Exemplos de resposta: retas 2 e 4, retas 1 e 5.
- Observe, em cada caso, as retas concorrentes e os ângulos destacados.
Figura 1
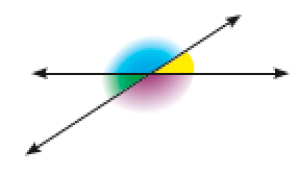
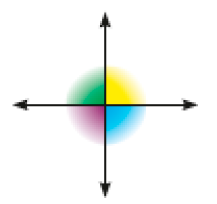
Figura 2
- Agora, pegue uma folha de papel sulfite e compare a abertura do ângulo do canto da folha (ângulo reto) com cada um dos ângulos destacados. Depois, complete os quadros abaixo.
Figura 1
Tabela: equivalente textual a seguir.
|
Cor da abertura do ângulo |
Ângulo reto, agudo ou obtuso? |
|---|---|
|
|
_____ |
|
|
_____ |
|
|
_____ |
|
|
_____ |
PROFESSOR
Resposta: Agudo; Obtuso; Obtuso; Agudo.Figura 2
Tabela: equivalente textual a seguir.
|
Cor da abertura do ângulo |
Ângulo reto, agudo ou obtuso? |
|
|
_____ |
|
|
_____ |
|
|
_____ |
|
|
_____ |
PROFESSOR
Resposta: Reto; Reto; Reto; Reto.- Se duas retas concorrentes formam quatro ângulos retos, elas são chamadas de retas perpendiculares. Quais das retas acima são perpendiculares: as retas da Figura 1 ou as retas da Figura 2?
_____
PROFESSOR
Resposta: Retas da Figura 2.
MANUAL DO PROFESSOR
Atividade 2
A ideia de perpendicularidade tem notável aplicação tanto nas situações cotidianas quanto em conteúdos matemáticos. Caso a localização da escola não permita a descrição solicitada, leve para a sala de aula um mapa de ruas e selecione um trecho dele para explorar os conceitos solicitados nesta atividade.
Atividade 3
Esta atividade trabalha com a identificação de retas paralelas, concorrentes e perpendiculares. Sugira aos estudantes que usem o canto reto de uma folha de papel sulfite para comparar a abertura dos ângulos formados pelas retas e classificá-las em perpendiculares ou não.
Atividade 4
Nesta atividade, os estudantes podem identificar duas retas perpendiculares como aquelas que formam quatro ângulos retos entre si. Para o item a, pergunte: “Qual é a medida de um ângulo reto?” (90 graus).
Peça a eles que, antes de comparar a abertura dos ângulos com o canto da folha de papel, estimem se têm abertura maior ou menor que a abertura do ângulo reto e, então, confiram as estimativas fazendo a comparação solicitada.
No item b, verifique se os estudantes percebem que todas as retas perpendiculares são concorrentes, mas nem todas as retas concorrentes são perpendiculares.
BNCC em foco:
EF04MA16
MP262
Simetria
- Gilda desenhou e recortou uma figura em uma folha de papel sulfite. Observe como ela fez.
1º

Gilda pegou uma folha de papel sulfite.
2°

Depois, ela dobrou a folha ao meio.
3°

Em seguida, desenhou a metade de uma figura na folha.
4°

Finalmente, Gilda recortou a figura nas linhas de seu contorno e desdobrou-a.
- Agora, marque com um X a figura que Gilda construiu.
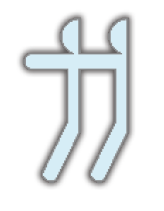
( )

( )

( )

( )
PROFESSOR
Resposta correta: figura 2Dizemos que a figura recortada apresenta simetria, pois tem duas partes que coincidem quando são dobradas uma sobre a outra.
A linha de dobra na folha representa o eixo de simetria da figura.
MANUAL DO PROFESSOR
Objetivo
Explorar o conceito de simetria e de reflexão.
No estudo da Geometria, o conceito de simetria é um dos que apresentam mais forte componente cultural, pois está presente desde os desenhos primitivos até as produções atuais, percorrendo toda a história em diversas expressões da criação humana, o que denota uma tendência permanente do ser humano na busca pelo equilíbrio nas formas. Na natureza, a simetria é observável em todas as esferas, desde a mineral (a forma dos cristais de quartzo, por exemplo) até a vegetal (formas de frutos, folhas e flores) e a animal (nos contornos coloridos da pele de alguns animais selvagens, por exemplo).
Atividade 1
Explore a atividade oferecendo aos estudantes uma folha de papel sulfite, ou de outro tipo que seja facilmente dobrável. Peça aos estudantes que dobrem a folha ao meio, desenhem o contorno de uma figura qualquer e depois a recortem, do mesmo modo como fez Gilda. Depois, peça-lhes que colem no caderno a figura obtida e tracem seu eixo de simetria. Outro modo de evidenciar a simetria em uma figura plana é pelo uso de um espelho posicionado ao longo do eixo de simetria. Por exemplo, um espelho colocado sobre a dobra da folha de Gilda mostraria a parte que falta da figura, que aparecerá após o recorte.
BNCC em foco:
EF04MA19
MP263

- Trace um eixo de simetria de cada figura. Use uma régua para auxiliar no traçado.
Observação: As imagens nesta atividade não foram representadas em escala de tamanho. Fim da observação.
a)
PROFESSOR
Exemplo de resposta.
b)

c)

d)

- A figura do quadro abaixo é uma das partes de uma figura que apresenta simetria. A linha verde é o eixo de simetria dela. Marque com um X a outra parte dessa figura.
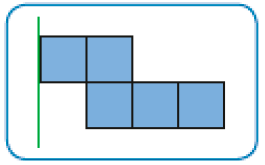
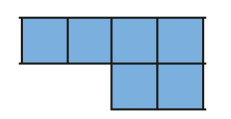
( )
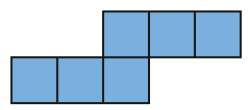
( )
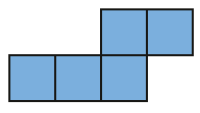
( )
PROFESSOR
Resposta correta: figura 3MANUAL DO PROFESSOR
Atividade 2
É importante considerar que a ideia de simetria trabalhada nestas páginas diz respeito a figuras planas, ou seja, desconsidera-se a dimensão de profundidade. Esclareça aos estudantes que o eixo de simetria não é apenas uma linha que divide a figura em duas partes; ele preserva a forma e o tamanho em cada lado da figura plana. Apresente algumas figuras geométricas planas para que os estudantes percebam que, em alguns casos, pode haver mais de um eixo de simetria. Por exemplo, no quadrado há quatro eixos de simetria.
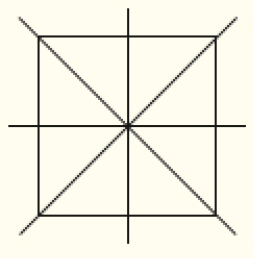
LEGENDA: 4 eixos de simetria. FIM DA LEGENDA.
CRÉDITO: ADILSON SECCO
Atividade 3
Esta atividade possibilita observar se os estudantes identificam a imagem que representa a simétrica da figura do quadro.
BNCC em foco:
EF04MA19
Sugestão de atividade
Pesquisa sobre simetria
Peça aos estudantes que levem para a sala de aula figuras recortadas de jornais ou revistas e investiguem, utilizando espelhos, os eixos de simetria delas. Grande parte dos logotipos ou logomarcas possui simetria de reflexão. Não se esqueça de orientar os estudantes a manusearem o espelho com cuidado, para não se cortarem.
MP264
- Ligue cada figura do lado esquerdo da página a uma figura do lado direito da página, de maneira que a figura geométrica formada por essas duas partes ligadas apresente simetria. A linha azul é um eixo de simetria.
a)

b)

- Agora, escreva o nome das figuras geométricas formadas.
_____
PROFESSOR
Resposta: Triângulo, trapézio.
- Marque um X a figura que apresenta simetria em relação ao eixo azul traçado.
( )
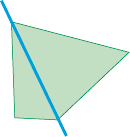
( )
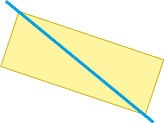
( )
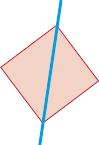
PROFESSOR
Resposta correta: figura 3.MANUAL DO PROFESSOR
Atividade 4
Verifique as estratégias usadas pelos estudantes para determinar a qual parte da figura geométrica com indicação de eixo de simetria é correspondente a outra representação. Depois de validar as respostas, peça aos estudantes que contem como fizeram para resolver a questão.
Atividade 5
Esta atividade explora a simetria de reflexão de diferentes modos. Lembre aos estudantes que uma figura apresenta simetria em relação a um eixo quando, ao “dobrá-la” nesse eixo de simetria, as duas partes da figura coincidem.
Pergunte aos estudantes que exemplos de simetria eles reconhecem no cotidiano. Como a simetria está presente em inúmeras situações (em fachadas de prédios e na pintura, por exemplo), é provável que eles apresentem muitas contribuições à discussão, que pode ser aprofundada com perguntas que levem a reconhecer os benefícios de uma figura simétrica. Por exemplo, pergunte o que achariam de um campo de futebol em que as partes de cada lado da linha do meio de campo fossem diferentes uma da outra. Nesse caso, a falta de simetria ofereceria condições diferentes às duas equipes.
BNCC em foco:
EF04MA19
Sugestão de vídeo
Simetria
Disponível em: http://fdnc.io/eUh. Acesso em: 11 mar. 2021.
Nesse vídeo, da série Arte e Matemática, apresenta-se a ideia de simetria nas mais diversas situações. Na Matemática, ela é abordada em curiosas relações numéricas e mesmo na Álgebra; na Física, é percebida na delicada simetria dos cristais. A ideia de simetria também é observada em manifestações artísticas, como na arquitetura (fachadas de catedrais em Minas Gerais), na pintura (em quadros de Vicente do Rego Monteiro e Rubem Valentin, entre outros), na dança (em coreografias) e na música (com relação ao ritmo que se repete no tempo, e mesmo nas composições de Johann Sebastian Bach).
MP265
Simetria na malha quadriculada
- Observe as figuras desenhadas nas malhas quadriculadas.
Figura 1
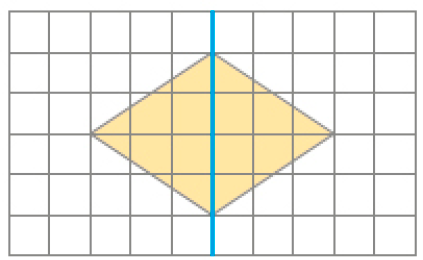
Figura 2
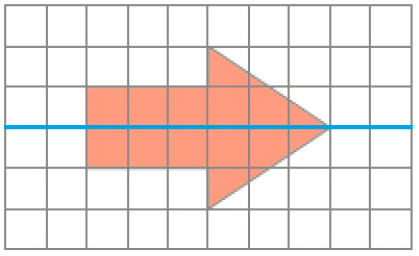
A parte da Figura 1 que está desenhada à direita do eixo de simetria tem a mesma forma e o mesmo tamanho da parte dessa figura que está desenhada à esquerda do eixo. O mesmo ocorre com as partes acima e abaixo do eixo de simetria da Figura 2.

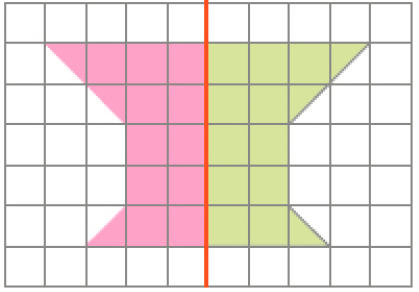
- Agora, complete as figuras abaixo, sabendo que o eixo de simetria é a linha laranja.
a)
b)
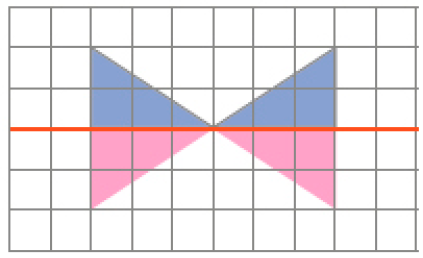

- Desenhe a outra parte para completar cada uma destas figuras, de modo que elas apresentem simetria em relação à linha azul. Se necessário, use uma régua.
a)
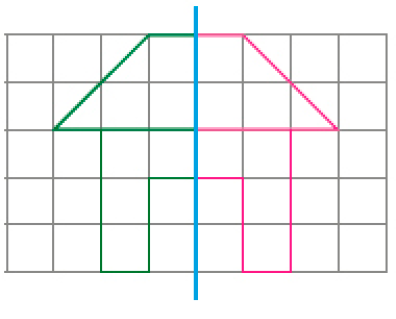
b)
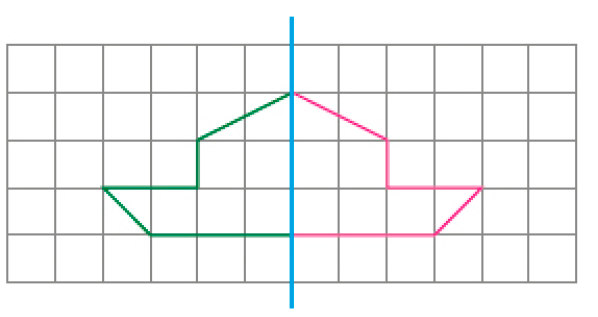
MANUAL DO PROFESSOR
Objetivo
• Explorar simetria de reflexão na malha quadriculada.
Atividades 1 e 2
Nestas atividades, os estudantes devem completar a figura a partir do eixo de simetria dado. Explore a ideia de reflexão com a turma. Se for possível, leve alguns espelhos para que os estudantes verifiquem suas respostas.
A malha quadriculada é um bom recurso para a exploração de figuras que apresentam simetria, em particular aquelas cujo contorno é formado por segmentos de reta. Ela facilita a repetição do contorno em atividades nas quais seja preciso completar a parte que falta em uma figura que apresenta simetria, seja por ela já oferecer as linhas retas da malha que servem de guia para o traçado, seja por auxiliar a contagem do número de lados dos quadrinhos desenhados.
Comente que, para que uma figura apresente simetria de reflexão, não basta cada uma de suas duas partes ter a mesma forma e o mesmo tamanho que a outra. Também é preciso que estejam na posição “refletida” em relação ao eixo de simetria. Por exemplo:
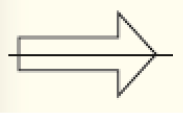
LEGENDA: Apresenta simetria de reflexão. FIM DA LEGENDA.
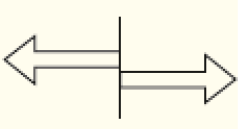
LEGENDA: Não apresenta simetria de reflexão. FIM DA LEGENDA.
CRÉDITO: ADILSON SECCO
BNCC em foco:
EF04MA19
MP266

- Complete as figuras abaixo, sabendo que o eixo de simetria é a linha azul.
a)
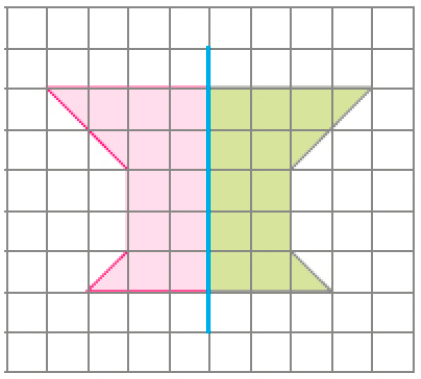
b)
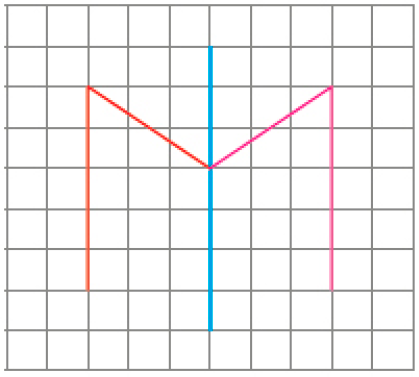
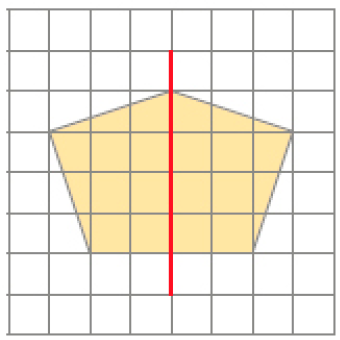
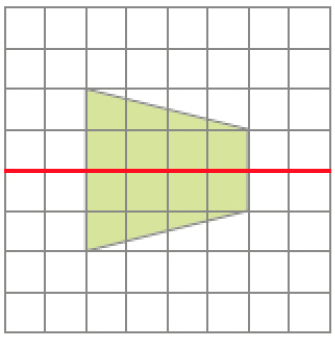
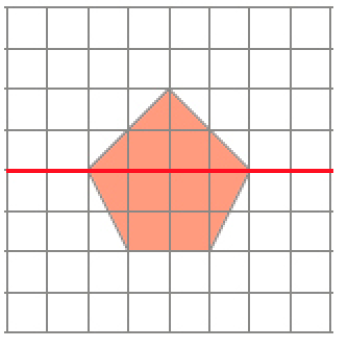
- Marque com um X as figuras que apresentam simetria em relação à linha vermelha.
( )
( )
( )
PROFESSOR
Respostas corretas: figura 1 e figura 2.

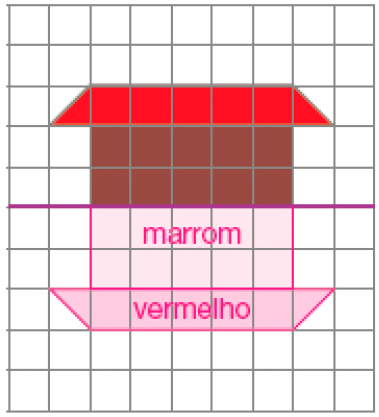
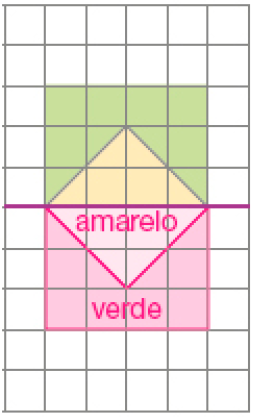
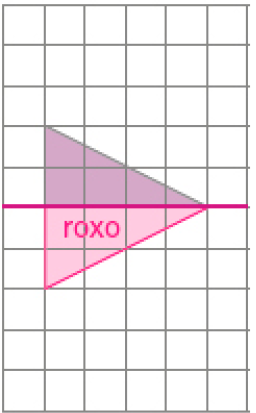
- Complete as figuras na malha quadriculada, sabendo que elas apresentam simetria em relação à linha roxa.
a)
b)
c)
MANUAL DO PROFESSOR
Atividade 3
Os estudantes devem completar a figura a partir do eixo de simetria dado (linha azul). Explore a ideia de reflexão com a turma. Se for possível, leve espelhos para que os estudantes verifiquem suas respostas.
Atividade 4
Verifique se os estudantes determinam com facilidade as figuras que representam simetria em relação ao eixo determinado.
Atividade 5
Esta atividade permite observar se os estudantes não realizam a atividade sem a devida compreensão do que é solicitado. Verifique se a turma toda completou as figuras pintando-as da mesma cor da outra parte.
BNCC em foco:
EF04MA19
MP267

- A letra V apresenta simetria em relação ao eixo azul traçado abaixo. Desenhe outras três letras que também apresentem simetria. Não se esqueça de desenhar o eixo de simetria.
PROFESSOR
Exemplos de desenhos: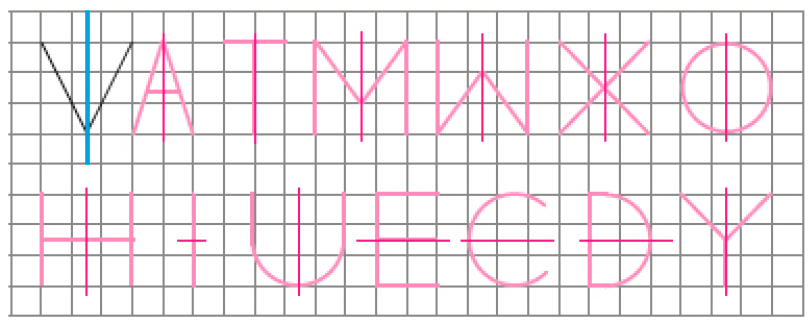


- Desenhe na malha quadriculada uma figura que apresente um ou mais eixos de simetria. Depois, troque seu livro com um colega, que deverá traçar os eixos de simetria em sua figura.
PROFESSOR
Resposta pessoal.
MANUAL DO PROFESSOR
Atividade 6
Nesta atividade, os estudantes reconhecem que algumas letras apresentam simetria em relação a um eixo. Sugira-lhes que usem folha quadriculada para escreverem palavras em que todas as letras tenham simetria, como OVO, BOI, BICO etc. Pergunte: “Quais letras do seu nome têm simetria?”. Depois, peça a cada estudante que tente representar essas letras em papel quadriculado.
Atividade 7
Nesta atividade, os estudantes podem usar a criatividade para a elaboração de um desenho que apresente simetria em relação a um ou mais eixos. Muitas figuras que apresentam simetria têm um forte apelo estético; nas artes, o uso dessas figuras é um recurso empregado com frequência. Se julgar oportuno, peça aos estudantes que façam uma pesquisa em livros e revistas e levem para a sala de aula algumas imagens de figuras que apresentam simetria.
BNCC em foco:
EF04MA19
MP268
Simétrica de uma figura
- Silvana pintou uma figura com guache e depois dobrou a folha ao meio com cuidado. Quando as duas partes da folha se tocaram, a tinta formou uma nova figura do outro lado da folha.


- Compare as figuras acima. O que você observou?
_____
PROFESSOR
Exemplo de resposta: As duas figuras têm o mesmo formato e o mesmo tamanho.
Cada uma dessas duas figuras é simétrica da outra em relação ao eixo de simetria representado pela linha de dobra da folha.
- Marque com um X os desenhos que mostram uma figura e sua simétrica em relação ao eixo azul.
( )
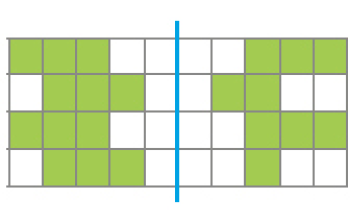
( )
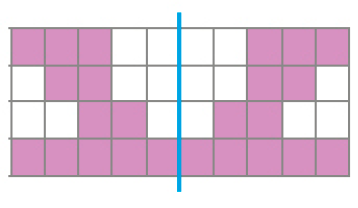
( )
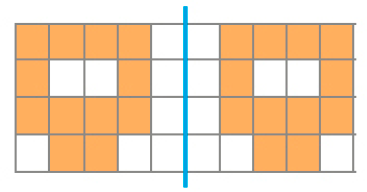
( )
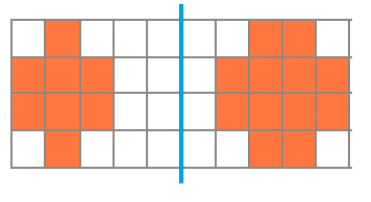
PROFESSOR
Respostas corretas: figura 2 e 3.MANUAL DO PROFESSOR
Objetivo
Explorar a ideia de simétrica de uma figura.
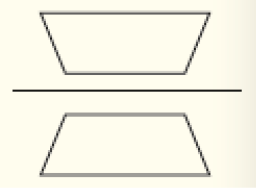
É comum falar em simetria de uma figura quando a ideia envolvida relaciona-se de fato com a ideia de simétrica de uma figura, e não de simetria na própria figura. A diferença entre os conceitos é que, no caso de simetria na própria figura (exemplo 1), o eixo de simetria está nela mesma, dividindo-a em duas partes iguais em forma e em tamanho (como ocorre com a figura de uma borboleta); no caso de uma figura simétrica de outra (exemplo 2), o eixo está fora da figura ou toca seu contorno.
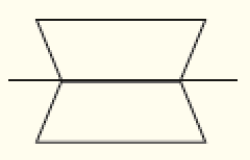
Exemplo 1
CRÉDITO: ADILSON SECCO
Exemplo 2
Atividade 1
Proponha aos estudantes a realização da mesma experiência de Silvana. É imprescindível que as figuras pintadas sejam bastante simples, para que se obtenha uma figura com pouca deformação. Assim como no caso da observação das figuras com simetria, o uso do espelho também pode ser um interessante recurso para a verificação da simétrica de uma figura.
Atividade 2
Espera-se que o estudante perceba que a atividade propõe que ele identifique figuras simétricas, embora a figura roxa apresente os dois tipos de simetria.
BNCC em foco:
EF04MA19
MP269

- Na imagem abaixo, a simétrica da figura do cachorro é sua imagem refletida no espelho.
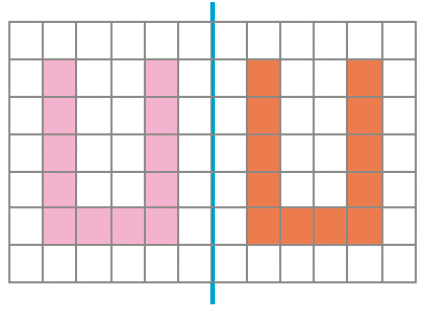
Imagine que há um espelho posicionado na linha azul em cada caso abaixo (como na imagem abaixo). Desenhe e pinte a simétrica das letras, ou seja, a imagem refletida no espelho.

a)
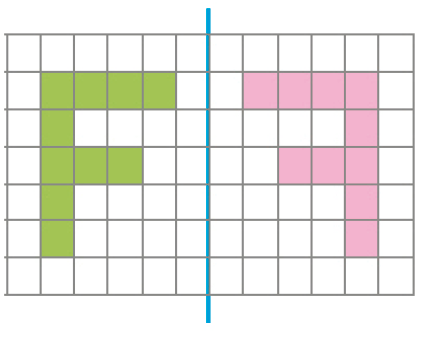
b)
- Em uma
folha
de papel sulfite, faça o que se pede.
- Dobre a folha em 4 partes iguais, como mostram as figuras.
1 ª dobra
2 ª dobra

- Desenhe um quadrado como o da figura abaixo e recorte-o usando uma tesoura com pontas arredondadas.
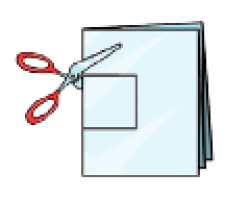

- Agora, desenhe como ficou a folha de papel após o recorte e trace com uma régua um eixo de simetria.
PROFESSOR
Exemplos de resposta: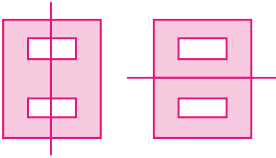
MANUAL DO PROFESSOR
Atividade 3
O uso de papel quadriculado nesta atividade facilita o desenho e a obtenção da simétrica das figuras apresentadas: a determinação da distância de cada ponto de uma figura e de sua simétrica em relação ao eixo dado pode ser feita pela contagem do número de lados de quadrinhos. Por exemplo, no item b, a simétrica da letra U deve estar à mesma distância, de um lado de quadrinho, da linha azul. Proponha aos estudantes que desenhem, em uma folha de papel quadriculado, outras letras do alfabeto. Se necessário, desenhe na lousa algumas letras e indique eixos em diferentes posições (horizontal, vertical) para a obtenção da simétrica da letra. Por exemplo:
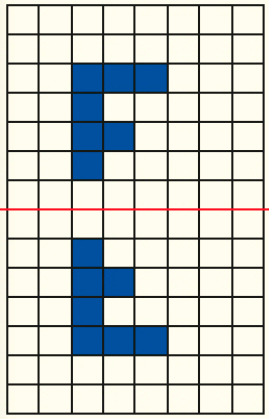
CRÉDITO: ADILSON SECCO
Atividade 4
Se julgar conveniente, peça aos estudantes que se reúnam em duplas para a utilização de tesoura com pontas arredondadas e régua, também necessárias para a realização desta atividade.
BNCC em foco:
EF04MA19
MP270
- André fez duas figuras na malha quadriculada, mas elas não são simétricas em relação à linha vermelha.


- Explique por que as figuras de André não ficaram simétricas.
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que, embora as figuras sejam congruentes, pontos que seriam simétricos não estão à mesma distância da linha vermelha. Fim da observação.
- Agora, utilize a malha quadriculada abaixo e faça o desenho de André de modo que as figuras sejam simétricas em relação à linha vermelha.
PROFESSOR
Resposta possível: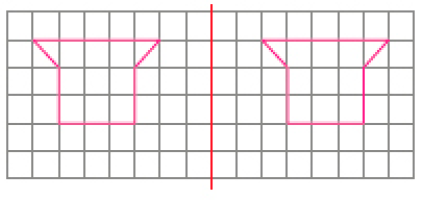
- Cerque com uma linha as figuras que são simétricas em relação à linha verde.



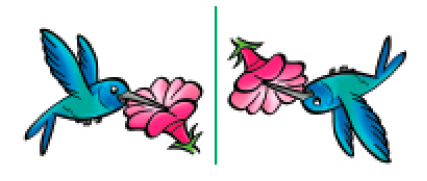
PROFESSOR
Respostas corretas: figura 2 e figura 3.MANUAL DO PROFESSOR
Atividade 5
Espera-se que os estudantes percebam que, embora as figuras sejam idênticas, a posição delas em relação ao eixo de simetria está diferente. É importante ressaltar que, nessa propriedade, a posição da figura em relação ao eixo de simetria é fundamental para determinar se elas são simétricas, não bastando as figuras serem idênticas. Se julgar necessário, pergunte: “Quantos quadrinhos separam a figura da esquerda do eixo de simetria? E a figura da direita?” (1; 2).
Atividade 6
Nesta atividade, é importante reforçar o conceito de reflexão com os estudantes, para que eles determinem quais figuras são simétricas.
Caso tenham dificuldade para visualizar a simetria, os estudantes podem posicionar um espelho sobre o eixo para facilitar a verificação. Recomende cuidado ao manusear o espelho. Seu uso permite também relacionar a ideia de simetria com a de referencial na descrição da localização ou do posicionamento de um objeto.
BNCC em foco:
EF04MA19
Sugestão de atividade
Objetos fotografados de diferentes pontos de vista
É possível explorar as imagens de vários objetos por meio de fotografias e perguntar aos estudantes se eles sabem dizer de que objeto se trata. Pode-se, por exemplo, fotografar uma escova de cabelo a partir do cabo, levar a imagem para os estudantes e questionar: “Alguém sabe dizer que objeto é esse?”. Algumas imagens são difíceis de serem identificadas, mas, de qualquer modo, esse tipo de atividade aguça a percepção e a observação dos objetos.
MP271
Mosaicos
- Caio e Melissa estão construindo mosaicos.

Mosaico de Melissa.
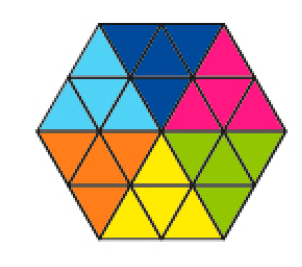
Mosaico de Caio.
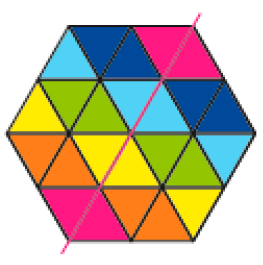
O mosaico que Caio construiu tem um eixo de simetria, já o mosaico de Melissa não tem eixo de simetria.

- Com uma régua, desenhe o eixo de simetria no mosaico que Caio fez.
Mosaico é uma composição formada pela repetição de figuras que cobrem uma superfície sem sobreposição. Um mosaico pode ter um, vários ou nenhum eixo de simetria.
- Os mosaicos abaixo apresentam simetria. Trace pelo menos um eixo de simetria em cada mosaico.
a)
PROFESSOR
Exemplos de respostas: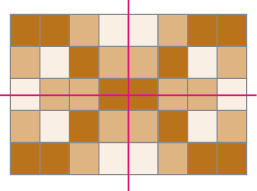
b)
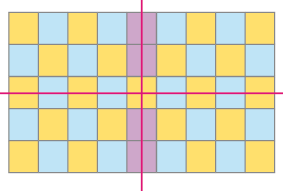
MANUAL DO PROFESSOR
Objetivo
Reconhecer padrões geométricos e conceitos de simetria em mosaicos.
Atividade 1
Na movimentação das peças, as crianças percebem que os encaixes dependem de características específicas das figuras, ampliando o olhar geométrico. Os trabalhos de Maurits Cornelis Escher (1898-1972) são reconhecidos mundialmente; seus mosaicos contam com precisão técnica e revelam conhecimentos matemáticos.
Além disso, a exploração desse conteúdo possibilita a aproximação entre diferentes disciplinas: Matemática, Arte e História. Explique aos estudantes que o mosaico é uma arte milenar, produzida por muitos povos em diferentes épocas. Na Antiguidade, eram empregados principalmente na criação de pavimentos e de paredes. Ainda hoje, o mosaico desperta muito interesse e tem grande uso na decoração, na tecelagem e na ornamentação arquitetônica.
Atividade 2
Espera-se que os estudantes observem que há mais de um eixo de simetria em cada figura. Caso nem todos percebam os eixos de simetria horizontal e vertical em cada figura, depois de validar as respostas, peça a eles que compartilhem suas respostas com os colegas.
BNCC em foco:
EF04MA19
MP272
- Marina está com a mãe dela em uma exposição de mosaicos.
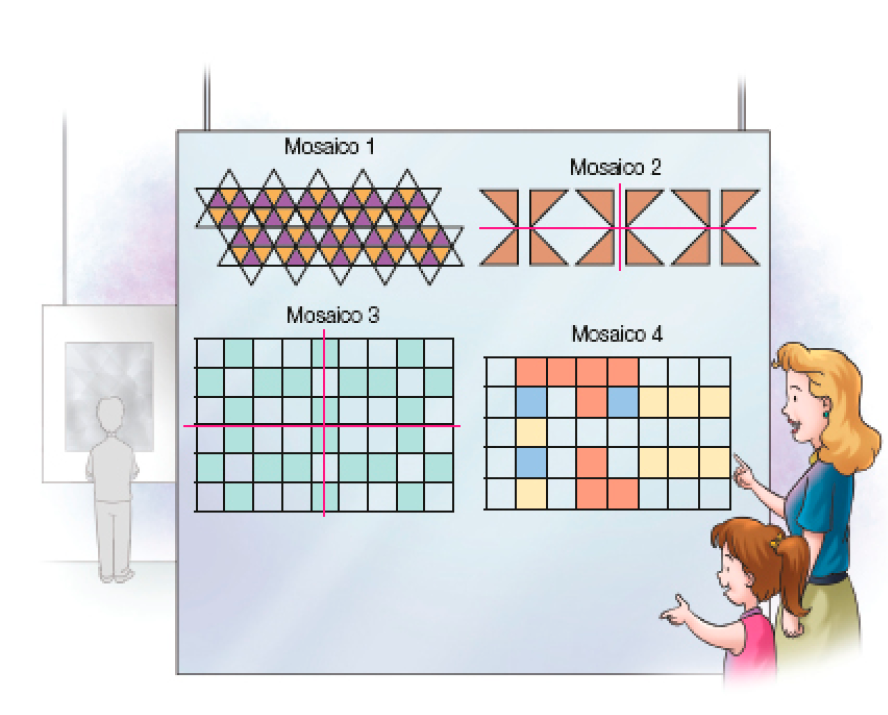
- Quais desses mosaicos apresentam uma sequência de figuras que formam um padrão?
PROFESSOR
Exemplo de resposta:_____
PROFESSOR
Resposta: Os mosaicos 1, 2 e 3.
- Qual desses mosaicos não apresenta padrão?
_____
PROFESSOR
Resposta: O mosaico 4.
- Trace, com uma régua, dois eixos de simetria nos mosaicos em que isso for possível.
Boxe complementar:
Importante
Um mosaico com padrão permite prosseguirmos desenhando e pintando as mesmas figuras, aumentando assim o mosaico.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 3
Nesta atividade é importante que os estudantes visualizem os eixos de simetria para determinarem o padrão em alguns casos.
Uma fonte de exploração de padrões geométricos são as produções indígenas. Nas pinturas corporais ou em cerâmicas, encontramos simetrias e construções que envolvem encaixes de figuras como os mosaicos. A arte marajoara, dos povos indígenas da Ilha de Marajó, é um exemplo. Além disso, resgatar e valorizar as produções indígenas é um modo de mostrar a diversidade cultural de nosso país.
Construção de um caleidoscópio
A construção pode ser feita em grupos, na sala de aula, com seu auxílio.
Material necessário:
3 espelhos de 20 cm de comprimento por 5 cm de largura;
miçangas ou continhas coloridas e bolinhas de papel crepom de várias cores;
fita-crepe para prender os espelhos e as bases;
papel-celofane, papel-manteiga, papel escuro e cartolina.
Primeiro, os estudantes constroem um prisma de base triangular, unindo com fita-crepe os 3 espelhos, com as faces espelhadas viradas para dentro.
Sobre a cartolina, colocam o prisma em pé e traçam o contorno de uma das bases (um triângulo equilátero de 5 cm de lado). Deixando em cada lado do triângulo uma borda de cerca de 0,5 cm, para dobrar e colar, recortam a cartolina. No centro do triângulo, fazem um orifício (como mostrado na figura a seguir), através do qual possam observar as imagens que se formarão. A seguir, revestem esse triângulo com plástico transparente, como se o orifício fosse a lente de uma máquina fotográfica.
Usando o triângulo de cartolina como molde, recortam mais dois triângulos: um de papel-celofane e outro de papel-manteiga. Fecham uma das extremidades do prisma com o triângulo de papel-celofane, colocam as miçangas ou continhas e os pedacinhos de papel colorido e, em seguida, colocam o triângulo de papel-manteiga. Fecham a outra extremidade do prisma com o triângulo de cartolina que tem um furo.
Por fim, encapam com o papel escuro todo o corpo do prisma. Pronto, o caleidoscópio está terminado! Encostando o olho na base que possui a “lente” e posicionando o caleidoscópio contra a luz, eles verão lindas imagens coloridas que se formam dentro dele e que, com movimentos de giro, transformam-se indefinidamente.

CRÉDITO: ILUSTRAÇÕES: GEORGE TUTUMI
BNCC em foco:
EF04MA19
MP273

- Pinte para completar os mosaicos sabendo que apresentam simetria em relação ao eixo azul.
PROFESSOR
Resposta: am: amarelo vm: vermelho vd: verde
a)
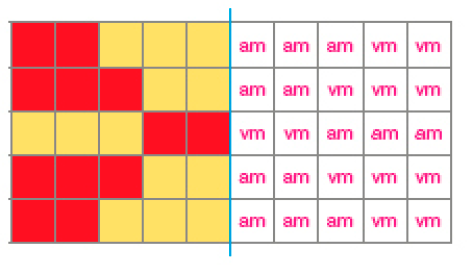
b)
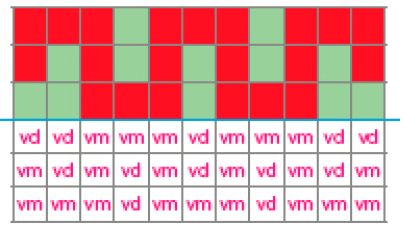

- Crie e desenhe um mosaico que apresente um padrão elaborado por você.
PROFESSOR
Resposta pessoal.


- Agora, peça a um
colega
que identifique o padrão que você elaborou e conte quantas vezes esse padrão se repete.
PROFESSOR
Atenção professor: A resposta vai depender do padrão elaborado pelo estudante. Fim da observação.
Boxe complementar:
Desafio

Pinte a figura abaixo com quatro cores diferentes e forme um mosaico.
Atenção!
As linhas pretas separam cores diferentes sempre.
O mosaico tem um eixo de simetria vertical e outro horizontal
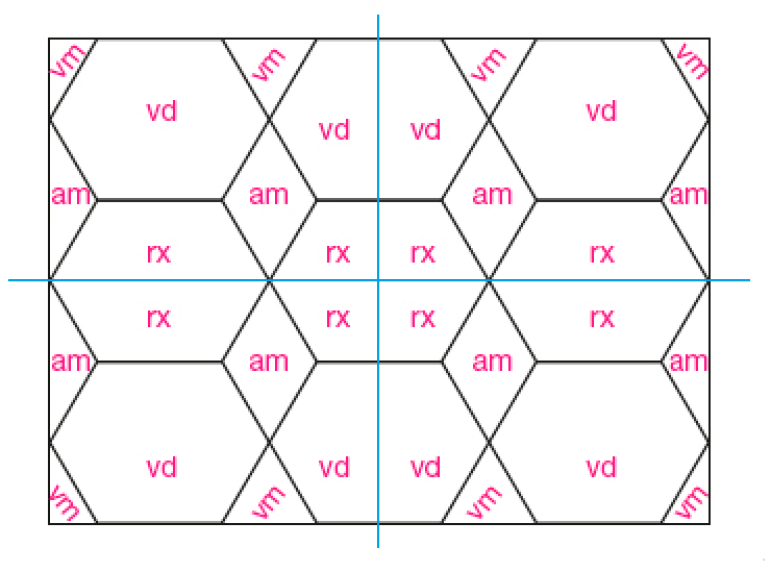 .
.
Exemplo de resposta: vm: vermelho; vd: verde; am: amarelo; rx: roxo.
Fim do complemento.
MANUAL DO PROFESSOR
Atividade 4
Nesta atividade, os estudantes devem aplicar os conceitos de simetria por reflexão, de modo que completem o mosaico. O exemplo do espelho é válido também nessa atividade, assim como pedir aos estudantes que imaginem o desenho dobrado no eixo de simetria e como ficariam as cores do outro lado desse eixo.
Atividade 5
Aproveite a atividade para sugerir aos estudantes uma pesquisa (em livros, revistas, jornais e internet) a respeito de artistas que costumam usar padrões em suas obras.
Desafio
O trabalho com mosaicos possibilita aliar os dois conceitos já trabalhados na Unidade: simetrias em figuras e padrões geométricos. Os mosaicos podem ser entendidos como obras de arte que, por meio de um padrão geométrico, formam figuras simétricas.
A aplicação desses conceitos está muito presente no desafio proposto. Chame a atenção dos estudantes para a presença de dois eixos de simetria, os quais precisam ser observados. Lembramos que o estudo de simetria e padrões em mosaicos é uma ótima oportunidade para estabelecer relações entre os componentes Matemática, Arte, História e Língua Portuguesa, favorecendo a discussão dos múltiplos aspectos relacionados ao tema.
BNCC em foco:
EF04MA19
Sugestão de atividade
Pesquisa sobre mosaicos
Divida os estudantes em grupos e sugira a cada grupo que pesquise um aspecto da arte dos mosaicos. No aspecto histórico, por exemplo, podem se concentrar nas características dos mosaicos produzidos por determinada civilização antiga. No artístico, podem produzir seus próprios mosaicos, para posterior exposição em mural. Com a ajuda da disciplina Língua Portuguesa, podem elaborar um texto coletivo sobre tudo o que aprenderam na pesquisa geral sobre mosaicos.
MP274
Compreender informações
Interpretar dados em gráfico de barras duplas
- Observe o gráfico que Rosana fez com base nos dados dos dois primeiros dias da campanha de doação de roupas de seu município.
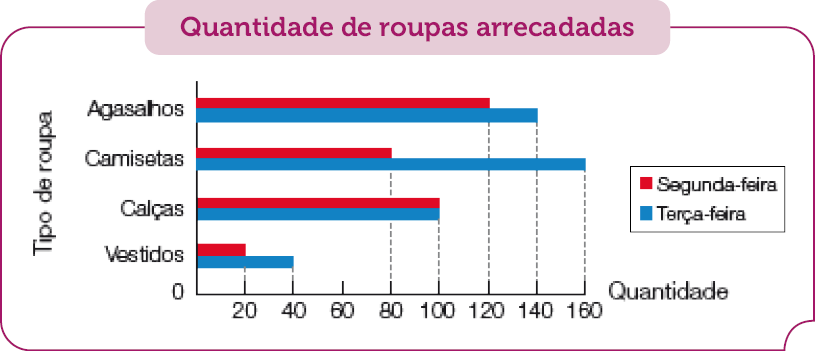
Fonte: Anotações de Rosana (jun. 2023).
- Agora, responda às questões.
- Qual foi o tema da pesquisa de Rosana?
_____
PROFESSOR
Resposta: Exemplo de resposta: Quantidade de peças arrecadadas em dois dias para uma campanha de doação de roupas.
- O que indicam as barras de cor vermelha? Como você descobriu isso?
_____
PROFESSOR
Resposta: Quantidade de roupas arrecadadas na segunda-feira. Espera-se que os estudantes observem a legenda e os eixos para essa conclusão.
- Qual foi o tipo de
roupa
que teve a mesma quantidade de peças arrecadadas na segunda-feira e na terça-feira?
_____
PROFESSOR
Resposta: Calças.
- Quais foram os tipos de
roupa
cuja quantidade arrecadada na terça-feira foi o dobro da quantidade arrecadada na segunda-feira?
_____
PROFESSOR
Resposta: Camisetas e vestidos.
- Como você descreveria uma comparação entre as arrecadações nesses dois dias a um
colega
que não tenha acesso a esse gráfico?
_____
PROFESSOR
Exemplo de resposta: Foram arrecadados em dois dias agasalhos, calças, camisetas e vestidos. Na terça-feira, foram arrecadadas mais peças do que na segunda-feira. O número de camisetas e de vestidos arrecadados na terça-feira foi o dobro do dia anterior e o de número de calças foi o mesmo. Foram arrecadados 20 agasalhos a mais na terça-feira do que na segunda-feira.
MANUAL DO PROFESSOR
Objetivos
Interpretar dados em gráficos de barras duplas.
Produzir texto com base na análise de dados apresentados em gráficos.
As atividades destas páginas trazem situações em que os dados estão organizados em gráficos de barras e de colunas duplas, tipo de representação muito útil no estabelecimento de comparações entre duas categorias.
É essencial os estudantes compreenderem que os dados em ambas as barras são indicados pela mesma grandeza do eixo correspondente. Ou seja, que não podemos fazer um gráfico desse tipo em que um dos dados se refira, por exemplo, a número de horas e outro dado, a uma quantia em reais. Também devem perceber que, nesse tipo de gráfico, é necessário algum tipo de legenda, para diferenciar as categorias representadas.
Atividade 1
Enriqueça a atividade pedindo aos estudantes que inventem uma questão com base nos dados do gráfico e, depois, troquem sua elaboração com a de um colega para resolução. Por exemplo, podem perguntar: “Quantas roupas foram arrecadadas ao todo na segunda-feira? E na terça-feira?”. Se julgar oportuno, com a autorização da escola, proponha uma campanha de arrecadação de roupas. Os estudantes podem construir um gráfico de barras duplas com o número de peças arrecadadas por turma de 4º ano. Depois, explore esse gráfico fazendo perguntas como: “Qual turma arrecadou mais roupas? Qual turma arrecadou menos roupas? Quantas peças a menos que a turma que mais arrecadou?”.
BNCC em foco:
EF04MA27
Sugestão de atividade
Construindo um gráfico de barras duplas
Reúna os estudantes em grupos de 5 ou 6 e, após uma breve discussão com cada grupo, eleja algumas personagens de desenho animado que farão parte da pesquisa da classe.
Essa prévia é importante para que não haja uma quantidade muito grande de personagens, o que pode dificultar a representação gráfica.
Depois de escolher as personagens, pergunte a cada estudante: “Qual dessas personagens é sua preferida?”. Com as respostas, a turma deve montar uma tabela que mostre a preferência dos meninos e das meninas e, depois, com base nos dados dessa tabela, construir um gráfico de barras duplas (vertical ou horizontal).
MP275
- Em uma cidade, o serviço de meteorologia registra a temperatura máxima e a mínima em cada mês do ano. Observe o gráfico com essas temperaturas nos primeiros seis meses do ano de 2023 e faça o que se pede.
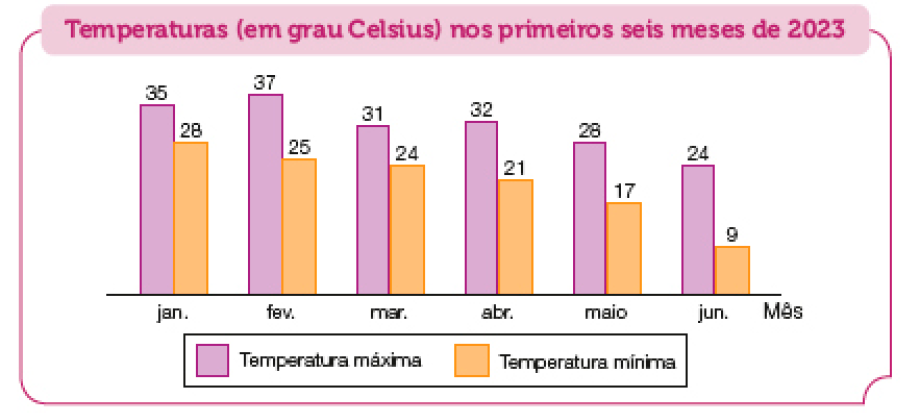
Fonte: Serviço de meteorologia (jul. 2023).
- Que mês teve a temperatura máxima mais alta?
_____
PROFESSOR
Resposta: Fevereiro.
- Que mês teve a temperatura mínima mais baixa?
_____
PROFESSOR
Resposta: Junho.
- Imagine que você é locutor de uma estação de rádio e está apresentando um programa no qual
deve
falar sobre o tempo
nessa
cidade.
Preencha o balão com o que você falaria nesse programa. Invente um nome para a cidade e para a estação de rádio.
PROFESSOR
Resposta pessoal.Seja criativo, pois você terá de prender a atenção dos ouvintes e transmitir todas as informações com clareza!
MANUAL DO PROFESSOR
Atividade 2
Explore mais a atividade fazendo perguntas como: “Em que mês a diferença entre a temperatura máxima e a mínima foi maior? E em que mês essa diferença foi menor?”. O item c permite explorar a proposta com os componentes Língua Portuguesa e Geografia, elaborando um texto que seja adequado a uma apresentação radiofônica e contenha informações relevantes, características do clima da cidade.
Um ponto importante a ressaltar é o fato de que os ouvintes da rádio não estão visualizando o gráfico que contém todos os dados relacionados às temperaturas da cidade, e, por isso, a comunicação tem de ser clara e objetiva. Aproveite e pergunte se eles costumam ouvir rádio (e o que ouvem), se eles já ouviram algum noticiário transmitido pelo rádio e as impressões que tiveram.
BNCC em foco:
EF04MA27
MP276
O que você aprendeu
Avaliação processual
- Observe a malha quadriculada e responda à questão.
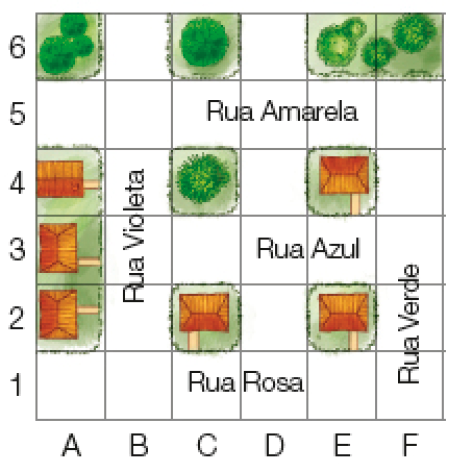
Adriano saiu da casa dele e seguiu estas indicações: virou à esquerda e seguiu em frente pela Rua Azul, depois entrou à direita na Rua Verde. Então, seguiu em frente até o final da rua.
- Qual é a localização da casa de Adriano?
_____
PROFESSOR
Resposta: E4
- Qual é a localização do lugar aonde ele chegou?
_____
PROFESSOR
Resposta: F1
- Cerque com uma linha o desenho que não apresenta simetria.

PROFESSOR
Resposta correta: casa verde.

- Pinte a simétrica da figura em relação ao eixo azul. Depois, pinte a simétrica da figura obtida em relação ao eixo verde.
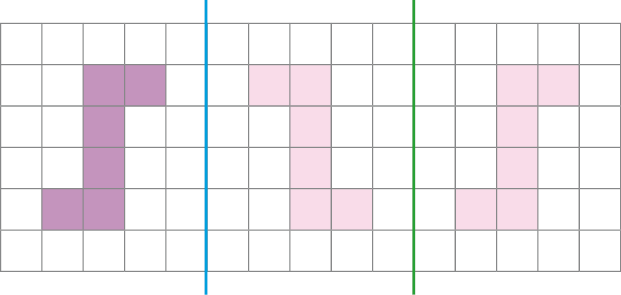


- Reúna-se com um
colega
e
conversem
sobre o que vocês observaram nessas figuras.
PROFESSOR
Atenção professor: Espera-se que os estudantes percebam que a terceira figura (simétrica da segunda) ocupa, na malha, a forma igual à da primeira figura. Fim da observação.
MANUAL DO PROFESSOR
Objetivo
Retomar os conceitos estudados.
A seção possibilita a sistematização de vários conceitos desenvolvidos ao longo da Unidade, além de ser um instrumento para avaliação formativa.
Atividade 1
Os estudantes devem perceber que, em primeiro lugar, precisam determinar a localização da casa de Adriano. Para isso, devem observar que, ao sair de sua casa, ele vira à esquerda e avança pela Rua Azul até cruzar com a Rua Verde. Isso permite determinar que Adriano mora na casa que se localiza em E4. Peça a eles que registrem o trajeto seguido por Adriano usando a simbologia composta de letra e número usada aqui. Espera-se que escrevam: E3, F3, F2 e F1.
Atividade 2
Para explorar mais a atividade, peça aos estudantes que desenhem o eixo de simetria nas figuras que não foram circuladas.
Atividade 3
Incentive os estudantes a perceberem que as três figuras têm mesma área e mesma forma. A figura central, que é simétrica da primeira (a figura fornecida), fica em posição invertida em relação à primeira. A última figura, simétrica da figura central, fica, por sua vez, em posição invertida em relação a esta, voltando, portanto, à posição da primeira figura. Explore essa ideia perguntando: “Se continuássemos a sequência de figuras, o que aconteceria em relação à posição delas?”.
BNCC em foco:
EF04MA16, EF04MA19
MP277

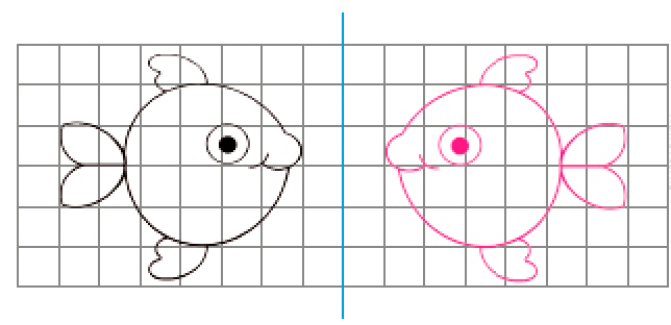
- Desenhe a simétrica da figura em relação ao eixo azul.
Boxe complementar:
Dica
Capriche, pois as linhas de contorno da figura são curvas!
Fim do complemento.

- Pinte cada mosaico seguindo o padrão que você identificar.
a)

b)


- Pense em um padrão para criar um mosaico na malha quadriculada abaixo.
PROFESSOR
Resposta: Desenho pessoal.
Autoavaliação

- Compreendi como, em uma malha, representar um percurso e a simétrica de uma figura?

- Quais conteúdos deste ano compreendo com facilidade e em quais ainda preciso de ajuda?
PROFESSOR
Respostas pessoais.
MANUAL DO PROFESSOR
Atividade 4
Esta atividade exige um pouco mais de empenho dos estudantes, pois as linhas a serem reproduzidas são todas curvas. O mais importante aqui não é a produção de desenhos perfeitos, mas o desenvolvimento da percepção de pontos simétricos em relação a uma figura dada. Avalie a conveniência de uma orientação prévia aos estudantes para identificarem, na malha, a posição de cada parte específica (olho, nariz, rabo etc.) do desenho dado e obterem a posição da parte simétrica em relação ao eixo azul.
Atividade 5
Verifique se os estudantes mantêm o padrão também em relação às cores. Peça a eles que especifiquem qual padrão adotaram. Se ele for coerente, aceite. Se julgar oportuno, peça-lhes que compartilhem suas respostas com os outros colegas.
Autoavaliação
Nesta unidade foram trabalhadas diferentes atividades em malha quadriculada. É importante que os estudantes percebam que esse recurso pode ser usado tanto para indicar percursos como para facilitar a elaboração e o reconhecimento de simetrias.
Na segunda questão, é possível propor uma reflexão sobre o ano todo, permitindo aos estudantes destacarem alguns dos conteúdos, compreendidos ou não, para que no ano posterior possam ampliar o trabalho.
BNCC em foco:
EF04MA19
MP278
Comentários para o professor:
Conclusão da Unidade 8
Conceitos e habilidades desenvolvidos nesta Unidade podem ser identificados por meio de uma planilha de avaliação da aprendizagem, como a que apresenta os principais objetivos, a seguir. O professor poderá copiá-la, fazendo os ajustes necessários, de acordo com sua prática pedagógica.
Ficha de avaliação e acompanhamento da aprendizagem
Nome: _____
Ano/Turma: _____ Número: _____ Data: _____
Professor(a): _____
Legenda de Desempenho: S: Sim N: Não P: Parcialmente
Tabela: equivalente textual a seguir.
|
Objetivos de aprendizagem |
Desempenho |
Observação |
|---|---|---|
|
Consegue fazer a leitura, a elaboração e a descrição de trajetos e movimentações em malhas quadriculadas? |
_____ |
_____ |
|
Consegue fazer a leitura, a elaboração e a descrição de trajetos em mapas? |
_____ |
_____ |
|
Tem a compreensão do significado de reta e segmento de reta? |
_____ |
_____ |
|
Tem a compreensão, com o uso de mapas, das relações entre retas: paralelas, concorrentes e perpendiculares? |
_____ |
_____ |
|
Consegue identificar eixos de simetria de uma figura? |
_____ |
_____ |
|
Explora a simetria em figuras apresentadas em malhas quadriculadas? |
_____ |
_____ |
|
Compreende a diferença entre figura que apresenta simetria e simétricas de uma figura? |
_____ |
_____ |
|
Analisa dados apresentados em tabelas simples ou de dupla entrada e em gráficos de barras e colunas duplas, com base em informações das diferentes áreas do conhecimento, e produz texto com a síntese de sua análise? |
_____ |
_____ |
|
Compreende e exercita o respeito às diferenças de opiniões e de propostas nos trabalhos em grupo? |
_____ |
_____ |
|
Nos trabalhos em grupo, elabora propostas e as defende com argumentos plausíveis? |
_____ |
_____ |
MP279
Continuação das orientações para o professor:
Sugestão de ficha de autoavaliação do estudante
O processo de avaliação formativa dos estudantes pode incluir seminários ou atividades orais; rodas de conversa ou debates; relatórios ou produções individuais; trabalhos ou atividades em grupo; autoavaliação; encenações e dramatizações; entre muitos outros instrumentos e estratégias.
Além da ficha de avaliação e acompanhamento da aprendizagem, fichas de autoavaliação, como a reproduzida a seguir, também podem ser aplicadas ao final do bimestre sugerido ou quando julgar oportuno. O professor pode fazer os ajustes de acordo com as necessidades da turma.
Tabela: equivalente textual a seguir.
|
Autoavaliação |
|||
|---|---|---|---|
|
Nome: |
|||
|
Marque um X em sua resposta para cada pergunta. |
Sim |
Mais ou menos |
Não |
|
1. Presto atenção nas aulas? |
_____ |
_____ |
_____ |
|
2. Pergunto ao professor quando não entendo? |
_____ |
_____ |
_____ |
|
3. Sou participativo? |
_____ |
_____ |
_____ |
|
4. Respeito meus colegas e procuro ajudá-los? |
_____ |
_____ |
_____ |
|
5. Sou educado? |
_____ |
_____ |
_____ |
|
6. Faço todas as atividades com capricho? |
_____ |
_____ |
_____ |
|
7. Trago o material escolar necessário e cuido bem dele? |
_____ |
_____ |
_____ |
|
8. Cuido dos materiais e do espaço físico da escola? |
_____ |
_____ |
_____ |
|
9. Gosto de trabalhar em grupo? |
_____ |
_____ |
_____ |
|
10. Respeito todos os meus colegas de turma, professores e funcionários? |
_____ |
_____ |
_____ |



