204
UNIDADE 7. Números na forma decimal

205
Boxe complementar
Para refletir...
Qual atleta chegou em terceiro lugar? Qual chegou em penúltimo lugar?
_____
Qual é a diferença entre o tempo do atleta que chegou em primeiro lugar e do que chegou em último?
_____
Fim do complemento
206
Décimos, centésimos e milésimos
- Conte quantas pessoas há na cena abaixo e complete as frases.

- Há _____ pessoas na cena.
- Cada pessoa corresponde a _____ décimo do total de pessoas.
- _____ décimo pode ser representado de duas formas:
- representação de 1 décimo com uma fração.
0,1 - representação de 1 décimo na forma decimal.
- Há _____ crianças na cena. Elas correspondem a _____ décimos do total de pessoas.
- _____ décimos podem ser representados com a fração: ou na forma decimal: _____.
- Um aparelho de som tem um mostrador da intensidade de volume que varia de 0 a 1. Quanto mais alto o som, mais partes vermelhas ficam visíveis no mostrador.
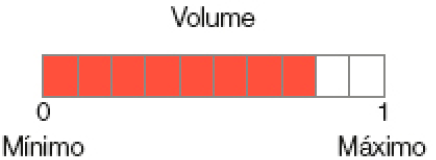
- A que fração do mostrador do aparelho de som corresponde cada parte em que ele está dividido?
_____
- Qual é a intensidade do volume registrado no mostrador desse aparelho?
_____
207
- Um painel luminoso é formado por uma placa com 100 lâmpadas coloridas, como mostra a figura abaixo. As lâmpadas vermelhas correspondem a que fração do total de lâmpadas?

As _____ lâmpadas vermelhas correspondem a _____ centésimos do total de lâmpadas. Podemos representar 66 centésimos de duas formas:
- representação de 66 centésimos com uma fração.
0,66 - representação de 66 centésimos na forma decimal.
- Agora, escreva a representação, na forma decimal, da parte das lâmpadas que são verdes. _____
- Complete o quadro abaixo.
Tabela: equivalente textual a seguir.
|
Animal |
Medida da altura em centímetro |
Medida da altura em metro |
|---|---|---|
|
Gato doméstico |
30 cm |
0,30 m |
|
Capivara |
50 cm |
_____ |
|
Leão |
_____ |
0,95 m |
|
Galinha |
35 cm |
_____ |


- Hugo quer comprar uma
paçoca
que custa R$ 0,35.
- Que combinação de moedas ele pode usar para pagar a
paçoca
sem que haja troco?
_____
- Se Hugo pagar com uma moeda de 1 real, quanto ele receberá de troco?
_____
- Se Hugo quiser comprar 10 paçocas para dividir com seus amigos, quantos reais ele gastará ao todo? _____
- Que combinação de moedas ele pode usar para pagar a
paçoca
sem que haja troco?
208
- Observe abaixo a quantidade de carne que Renata comprou.
Lembre-se de que 1 quilograma é o mesmo que 1.000 gramas (1 kg = 1.000 g).

- Que fração de 1 kg de carne Renata comprou? _____
- Quantos gramas de carne faltaram para Renata fazer essa torta? ______
- Veja como essa medida de massa pode ser representada de duas maneiras.

650 gramas correspondem a 650 milésimos de 1 quilograma.
- representação de 650 milésimos com uma fração.
0,650 - representação de 650 milésimos na forma decimal.
- Qual é a representação na forma decimal da fração de 1 kg de carne que Renata comprou? _____
- Represente com uma fração e na forma decimal a parte pintada de verde das figuras abaixo.
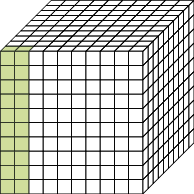
_____
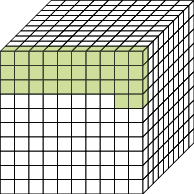
_____

- Com uma calculadora, faça os cálculos indicados e registre as respostas obtidas.



- Desenhe as teclas que você apertaria para obter no visor da calculadora, por meio de uma divisão por 1.000, o número 0,005 e o número 0,724.
209
Valor posicional
Em 2020, o piloto britânico Lewis Hamilton largou na 3ª posição na corrida do Grande Prêmio de Abu Dhabi, nos Emirados Árabes Unidos. O tempo da volta que lhe garantiu essa posição na largada foi de 95,332 segundos. Vamos escrever o valor de cada algarismo desse número.

LEGENDA: Grande Prêmio de Abu Dhabi, nos Emirados Árabes Unidos, em 2020. FIM DA LEGENDA.
Tabela: equivalente textual a seguir.
|
Parte inteira |
Parte decimal |
|||
|---|---|---|---|---|
|
D |
U |
d |
c |
m |
|
9 |
5, |
3 |
3 |
2 |
2: 2 milésimos
3: 3 centésimos
3: 3 décimos
5: 5 unidades
9: 9 dezenas
- Agora, observe o tempo das melhores voltas dos pilotos Max Verstappen e Valtteri Bottas na mesma corrida.
Tabela: equivalente textual a seguir.
|
Max Verstappen |
95,246 segundos |
|---|---|
|
Valtteri Bottas |
95,271 segundos |
- Registre o valor de cada algarismo desses números.
- Qual desses dois pilotos obteve o melhor tempo?
_____
210
Leitura de números na forma decimal
- Os números na forma decimal aparecem com frequência nos esportes.
Atletismo do Brasil nas Paralimpíadas 2016
O atleta brasileiro Petrúcio Ferreira dos Santos ganhou a medalha de ouro nos 100 metros rasos, categoria T47 do atletismo, além de bater o recorde mundial da prova, com 10,57 segundos.

LEGENDA: Prova final da Paralimpíada no Estádio Olímpico, Rio de Janeiro, em 2016. FIM DA LEGENDA.
Verônica Hipólito foi prata nos 100 metros da categoria T38. Apesar de ter se tornado a nova recordista nas semifinais, ela acabou ficando em 2º lugar na final, cronometrando 12,88 segundos.

LEGENDA: Pódio da cerimônia de premiação da Paralimpíada, no Estádio Olímpico, Rio de Janeiro, em 2016. FIM DA LEGENDA.
Para ler um número na forma decimal, observamos primeiro a parte inteira e depois a parte decimal. Veja como lemos o número que representa o tempo do atleta Petrúcio Ferreira dos Santos.
10,57
10 - parte inteira
57 - parte decimal
Lemos - dez inteiros e cinquenta e sete centésimos.
- Agora, escreva como se lê o número que representa o tempo de Verônica Hipólito. _____
- Escreva como lemos a medida indicada em cada caso.

_____

_____
211
- Complete o quadro.
Tabela: equivalente textual a seguir.
|
Número |
Como lemos |
|---|---|
|
0,4 |
_____ |
|
_____ |
catorze inteiros e trezentos e noventa e um milésimos |
|
0,084 |
_____ |
|
_____ |
um inteiro e duzentos e sete milésimos |
- Represente com um número na forma decimal a parte pintada de cada uma das figuras. Em seguida, escreva como lemos esses números.
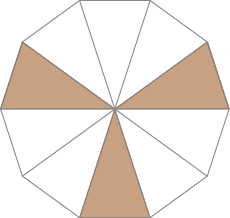
_____
_____
b)

_____
_____
c)
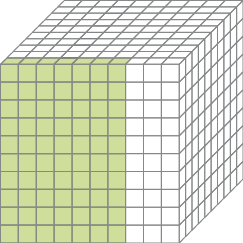
_____
_____
- Escreva por extenso a medida do comprimento do objeto em cada imagem.
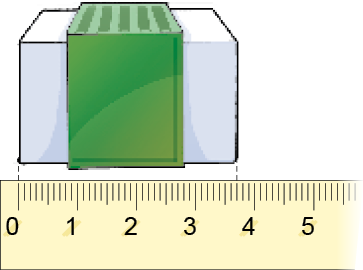
_____
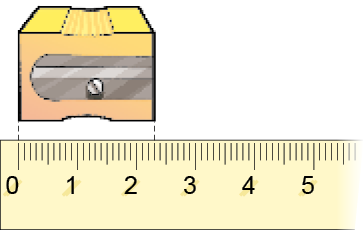
_____
212
Frações e números na forma decimal
- Observe que a metade de cada disco de cartolina representado abaixo está pintada de verde.

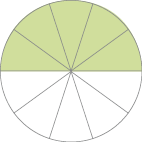
- O disco de cima foi dividido em 2 partes iguais. A parte verde pode ser representada por qual fração? _____
- O disco debaixo foi dividido em 10 partes iguais. A parte verde pode ser representada por qual fração com denominador igual a 10? E por qual número na forma decimal? _____
- Observe as três figuras de mesmo tamanho e faça o que se pede.
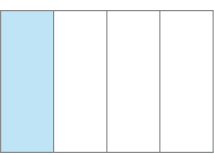
Figura I
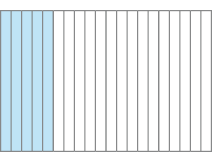
Figura II
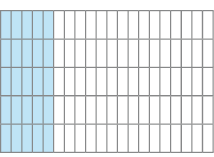
Figura III
- Em qual figura a parte pintada de azul é maior?
_____
- Escreva a fração que corresponde à parte pintada de azul em cada figura.
Figura I - _____
Figura II - _____
Figura III - _____
- Qual número na forma decimal corresponde à fração da parte pintada de azul da Figura III? _____

- Pinte da mesma cor os números que representam a mesma parte de um todo.
; 0,7; ; 0,07; ; 0,007.
213

- Pinte as partes de cada figura conforme solicitado.
- da figura de rosa

- da figura de verde

- 0,20 da figura de azul


- Raquel, Elaine e Osvaldo pintaram uma tela. Quantas partes dessa tela cada um deles pintou? Para descobrir, pinte você também na representação dessa tela abaixo.

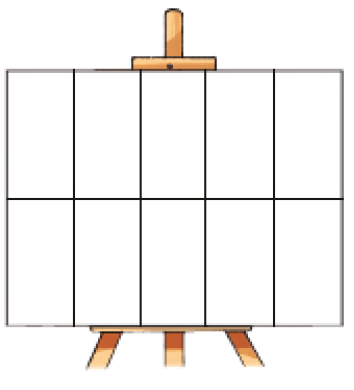
Raquel pintou _____ partes da tela, Elaine pintou _____ partes, e Osvaldo
pintou _____ partes.
- A balança indica a medida da massa em quilograma. Complete o visor da balança com o número, na forma decimal, que
deve
aparecer nele.


- Escreva a fração correspondente a cada número na forma decimal.
- 0,5 = _____
- 0,36 = _____
- 0,024 = _____
- 0,564 = _____
214
Comparação e ordenação de números na forma decimal
- Rebeca quer representar na reta numérica alguns números na forma decimal. Para isso, primeiro ela vai localizar a parte inteira e, depois, a parte decimal, dividindo em partes iguais o segmento que corresponde à unidade. Essa divisão depende da quantidade de casas decimais.
Para representar 2,3 na reta numérica, dividimos em 10 partes iguais o segmento localizado entre 2 e 3. Então, localizamos o número decimal.


- Para representar 2,34 na reta numérica, dividimos em 10 partes iguais o segmento localizado entre 2,3 e 2,4. Então, localizamos o número decimal. O segmento entre 2 e 3 ficará dividido em 100 partes iguais.

- Para representar 2,345 na reta numérica, dividimos em 10 partes iguais o segmento localizado entre 2,34 e 2,35. Então, localizamos o número decimal. O segmento entre 2 e 3 ficará dividido em 1 000 partes iguais.

- Quanto mais para a direita o
número
estiver na reta numérica, maior será esse número. Podemos compará-los utilizando os sinais < (menor que) ou > (maior que).
2,3 _____ 2,34 _____ 2,345
2,345 _____ 2,34 _____ 2,3
- Localize na reta numérica os números: 4,583 e 4,587.

215
- Ligue cada
número
decimal com sua representação na reta numérica.
Coluna 1
0,45
0,49
0,47
0,42
Coluna 2





- Usando a calculadora, aperte as teclas indicadas em cada caso e registre o número que aparecer no visor.





- Converse com um colega sobre o que esses resultados sugerem.
- Veja como Márcia comparou os números 1,2 e 1,135.

- Agora, compare os números utilizando os sinais < (menor que) ou > (maior que).
- 15,43 _____ 15,45
- 0,05 _____ 0,005
- 1,111 _____ 1,12
- 96,1 _____ 96,01
- Escreva os números abaixo na ordem decrescente.

_____ > _____ > _____ > _____ > _____
216
Adição e subtração com números na forma decimal
- Isabella vai comprar o micro-ondas e o fogão mostrados abaixo. Observe a imagem e responda às questões.
- Quantos reais Isabella gastará
nessa
compra?
Para descobrir, fazendo uma adição, adicionamos centésimos com centésimos e décimos com décimos. Depois, colocamos a vírgula do resultado debaixo das demais vírgulas.
- Quantos reais Isabella gastará
nessa
compra?


Isabella gastará nessa compra R$ _____ .
- Isabella pagará à vista e, por isso, terá um desconto de R$ 55,91. Nesse caso, quantos reais ela gastará?
Podemos descobrir fazendo uma subtração.

Nesse caso, Isabella gastará R$ _____ .
217
- Diana quer fazer a adição de 4,5 com 2,78. Veja como ela escreveu essa adição e responda às questões.


- Diana está fazendo uma afirmação correta? Justifique.
- Qual é o resultado dessa adição?
_____
- Analise as falas sobre as medidas das massas corporais e complete o quadro.

Quadro: equivalente textual a seguir.
|
Nome |
Medida de massa (kg) |
|
Diego |
_____ |
|
Giovana |
_____ |
|
Nara |
_____ |
|
Oscar |
_____ |

- Com a ajuda de um colega, elabore um problema com base no esquema abaixo. Depois, troque com outra dupla para que ela o resolva.
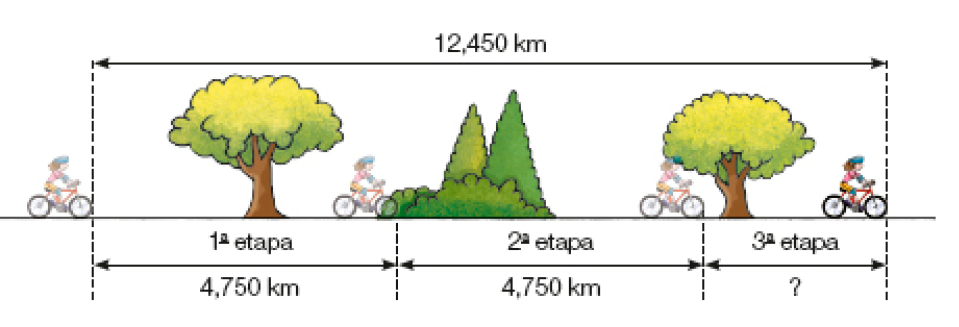
Observação: Os elementos nesta página não estão apresentados em escala de tamanho. Fim da observação.
218
Jogo: Jogo dos decimais
Material: Tabuleiro como modelo abaixo, 68 marcadores da página 259, dados da página 261 e um saco não transparente.
Jogadores: 2 a 4
Regras:
- Os marcadores devem ser colocados no saquinho.
- Cada jogador deve sortear 16 marcadores e organizá-los em uma das cartelas no tabuleiro, colocando cada marcador em uma casa, com os números virados para cima.
- Os jogadores decidem quem começará o jogo lançando um dos dados. O primeiro é aquele que tirar o maior número no dado.
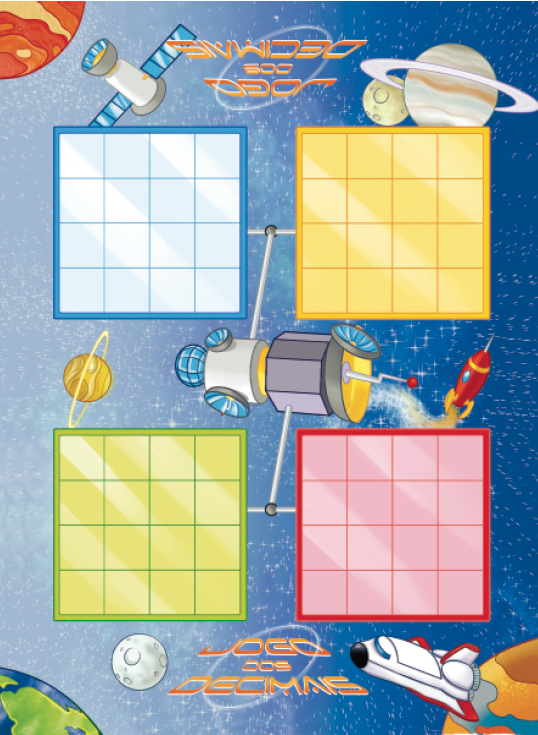
- Cada jogador, na sua vez, lança os 3 dados. Todos os jogadores que tiverem um marcador com o valor da soma dos números obtidos nos dados devem virá-lo para baixo.
- Atenção: se um jogador tiver dois marcadores com o valor da soma dos números obtidos nos dados, deverá virar para baixo apenas um marcador.
- Ganha quem virar primeiro os 4 marcadores de uma mesma fileira horizontal, vertical ou diagonal.

219
Questões sobre o jogo
- Responda.
- Qual é o menor valor que podemos obter com a adição dos dados? _____
- E qual é o maior valor? _____
- Escreva os valores nas faces dos dados em branco de forma que completem o valor de cada marcador.




- Nicole e Enzo estão jogando. Observe como estão as cartelas deles.

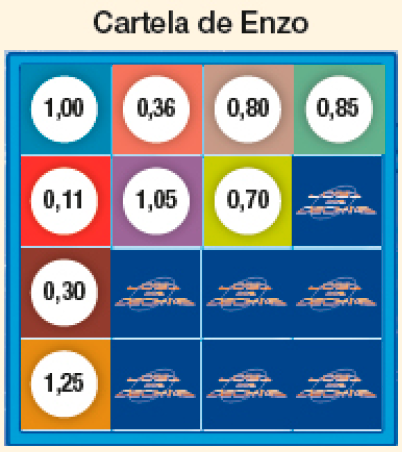
- Para Nicole vencer o jogo, qual valor ela
deve
tirar em cada dado?
_____
- E quais valores Enzo pode tirar nos dados para vencer?
_____
- Suponha que Nicole tenha jogado os dois primeiros dados e
obtido
0,50 e 0,50.
Quanto ela deve tirar no terceiro dado para virar um de seus marcadores, de forma que Enzo não vire nenhum dos seus? _____
220
Multiplicação com números na forma decimal

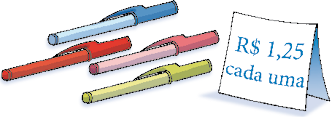
- Sueli comprou 4 canetas coloridas.
- Quanto ela pagou pelas canetas no total? _____
- De quanto foi o troco, se ela pagou com uma cédula de R$ 20,00? _____
- Sônia e Marília estão bordando juntas uma grande toalha e precisarão comprar 3 fitas coloridas, cada uma com 2,45 metros de comprimento. Quantos metros de fita elas precisarão comprar ao todo?
Vamos fazer uma adição para descobrir.

2,45 + 2,45 + 2,45 = 2,00 + 2,00 + 2,00 + 0,45 + 0,45 + 0,45 =
2,00 + 2,00 + 2,00: partes inteiras dos números
2,00 + 2,00 + 2,00: 6,00
0,45 + 0,45 + 0,45: partes decimais dos números
0,45 + 0,45 + 0,45: 1,35
6,00 + 1,35 = 7,35
Outra maneira de calcular é fazer a multiplicação 3 × 2,45.
Cálculo com o algoritmo usual
- Primeiro, calculamos 3 vezes 5 centésimos, obtendo 15 centésimos.
- Trocamos 10 centésimos por 1 décimo.
- Depois, fazemos 3 vezes 4 décimos, obtendo 12 décimos.
- 12 décimos mais 1 décimo são 13 décimos.
- Trocamos 10 décimos por 1 unidade.
- 3 vezes 2 unidades são 6 unidades.
- Acrescentando 1 unidade a 6 unidades, obtemos 7 unidades.
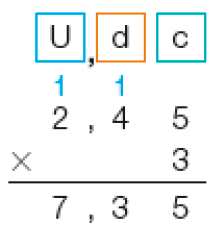
Portanto, Sônia e Marília precisarão comprar _____ metros de fita.
- Ao todo, quantos metros de fita elas teriam de comprar se precisassem de 4 fitas de 3,15 metros de comprimento cada uma?
_____
221
- Na escada abaixo, a medida da altura de cada degrau é 17,8 centímetros.

- Qual é a medida, em metro, da altura dessa escada de 4 degraus? _____
- Se essa escada tivesse 7 degraus, qual seria a medida da sua altura, em metro?
_____

- Calcule e registre suas respostas.
- 1,257 × 10 = _____
- 1,257 × 100 = _____
- 1,257 × 1.000 = _____
- 2,45 × 10 = _____
- 2,45 × 100 = _____
- 2,45 × 1.000 = _____


- Faça outras multiplicações como essas (com um dos fatores na forma decimal e o outro fator sendo 10, 100 ou 1.000). Troque ideias com seus colegas sobre o que esses resultados sugerem.

- Calcule mentalmente e registre suas respostas.
- Cléber tem a quantia indicada abaixo. Dez vezes essa quantia corresponde a quantos reais?
_____

- Quantos reais Ricardo gastará para abastecer seu caminhão com 100 litros de diesel?
_____

- Elabore um problema de multiplicação com base na ilustração. Em seguida, resolva-o.
_____

222
Quociente decimal
- Joana quer dividir igualmente entre 4 crianças a quantia abaixo.

- Quanto cada criança receberá?
_____


- Explique a um colega como você fez esse cálculo.

- Veja como Aline dividiu 81 por 2.

- Agora, calcule o resultado em cada caso.
- 17 ÷ 2 = _____
- 43 ÷ 2 = _____
- 21 ÷ 4 = _____
- Regina dividirá um barbante de 13 centímetros em 5 partes iguais.

- Cada parte terá mais de 2 centímetros de comprimento? _____
- Cada parte terá mais de 3 centímetros de comprimento?
_____


- Lembrando que 1 centímetro é o mesmo que 10 milímetros, como você pode obter o resultado dessa divisão? Converse com seus colegas a esse respeito.
- Com seu esqueite, Tainá deu 4 voltas em torno da praça perto de sua casa e percorreu 215 metros. Qual é a medida do perímetro dessa praça? _____
223
- Para fazer 4 varais na lavanderia de uma casa, será preciso dividir um rolo de varal de 11 metros de comprimento em 4 pedaços de mesmo comprimento.
Vamos dividir 11 por 4 para saber quantos metros terá cada varal.
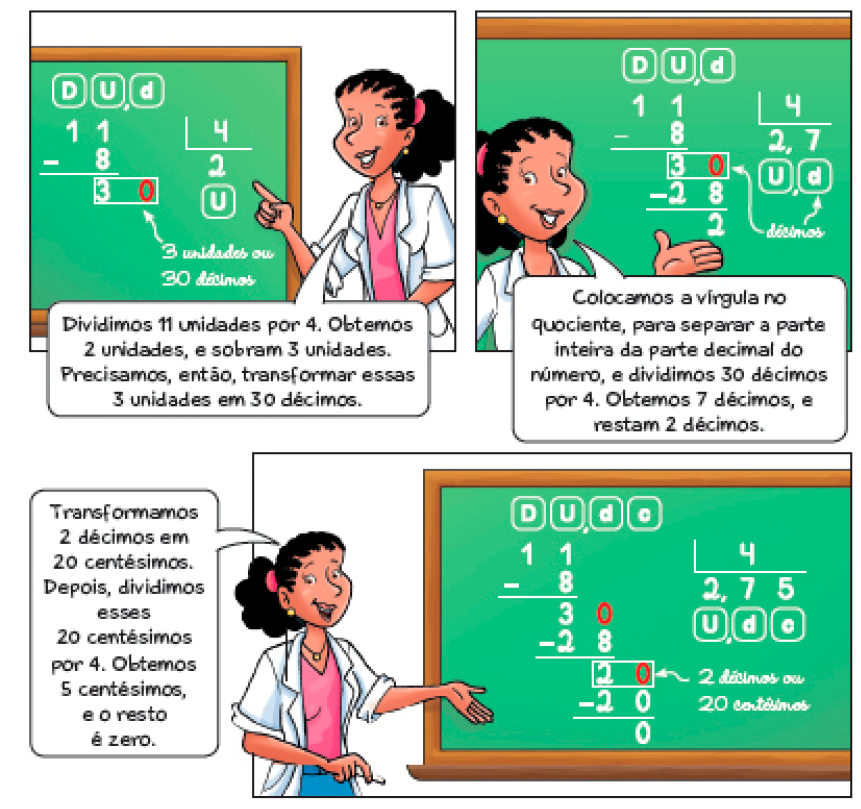
- Cada varal terá mais ou menos que 3 metros? _____
- Cada varal terá _____ metros e _____ centímetros.
- Calcule o resultado em cada caso.
- 45 ÷ 4
- 16 ÷ 5
- 21 ÷ 6
- 17 ÷ 8
- 9 ÷ 4
- 89 ÷ 8
- 39 ÷ 6
- 19 ÷ 8
224
Divisão com números na forma decimal

- Fernando decidiu comprar um computador em 6 prestações de mesmo valor.
- Faça uma estimativa sobre qual será, aproximadamente, o valor de cada prestação.
_____


- Conte para um colega como você pensou para fazer a estimativa.
- Faça uma estimativa sobre qual será, aproximadamente, o valor de cada prestação.

- Cristiano foi com R$ 15,00 à padaria. Chegando lá, ele comprou 3 doces de mesmo
preço
e recebeu R$ 1,50 de troco.
- Quanto Cristiano pagou pelos 3 doces?
_____

- Qual foi o
preço
de cada doce?
_____

- Explique a um colega como você resolveu esse problema.
- Quanto Cristiano pagou pelos 3 doces?
_____

- Viviane e 3 amigos foram a uma lanchonete e gastaram R$ 36,40. Na hora de pagar a conta, eles dividiram igualmente a despesa. Quantos reais cada um pagou?
Veja como Viviane fez a divisão de R$ 36,40 por 4.
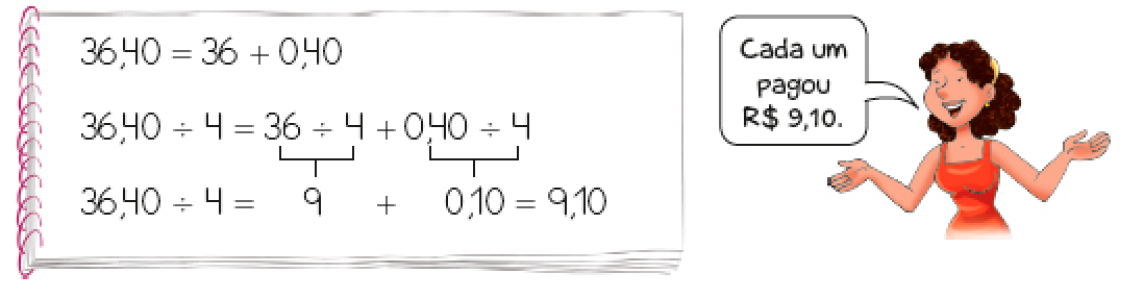
- Quanto cada um pagaria se a despesa tivesse sido de R$ 44,80? _____
- E se a despesa tivesse sido de R$ 49,60? _____
- Ana e 4 amigas compraram um pacote com 5
cadernos
por R$ 24,90. Em uma papelaria do bairro, um
caderno
igual a esses custaria R$ 7,70.
- Quantos reais cada uma pagou pelo caderno, se elas dividiram igualmente o valor do pacote com 5 unidades?
_____


- A compra foi vantajosa? Troque ideias com um colega sobre isso.
- Quantos reais cada uma pagou pelo caderno, se elas dividiram igualmente o valor do pacote com 5 unidades?
_____
225
- Roberto aproveitou uma liquidação para comprar bermudas e camisetas para dar de presente a seus sobrinhos. O valor total da compra foi de R$ 84,52. O pagamento será realizado em 4 prestações iguais sem acréscimo. Qual será o valor de cada prestação?
Cálculo com o algoritmo usual
1º
Dividimos 8 dezenas por 4, obtendo 2 dezenas. Depois, dividimos 4 unidades por 4. Obtemos 1 unidade, e não sobra resto.
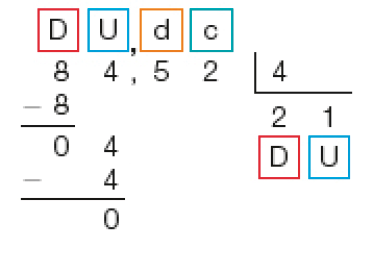
2°
Em seguida, dividimos 5 décimos por 4. Obtemos 1 décimo, e resta 1 décimo, que é o mesmo que 10 centésimos.
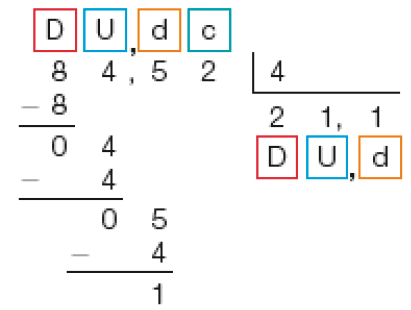
3°
Então, dividimos 12 centésimos por 4. Obtemos 3 centésimos, e o resto é zero.
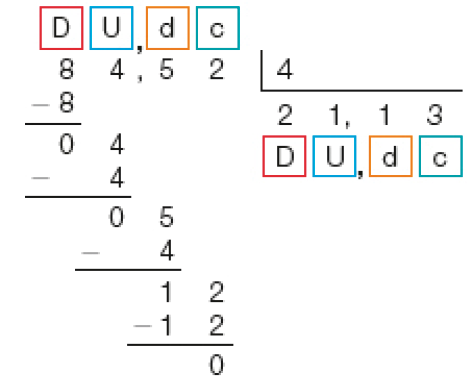

- Agora, calcule o resultado em cada caso.
- 36,60 ÷ 6
- 65,15 ÷ 5
- 72,56 ÷ 8
- 95,34 ÷ 3
- 77,76 ÷ 4
- 89,76 ÷ 3
226
- Reginaldo queria dividir 4 unidades em 10 partes iguais, em 100 partes iguais e em 1.000 partes iguais. Complete os quadros que ele fez e, em seguida, responda.
Quadro 1
Tabela: equivalente textual a seguir.
|
Número de unidades |
Número de décimos |
|---|---|
|
1 |
10 |
|
2 |
_____ |
|
3 |
_____ |
|
4 |
_____ |
Quadro 2
Tabela: equivalente textual a seguir.
|
Número de unidades |
Número de centésimos |
|---|---|
|
1 |
100 |
|
2 |
_____ |
|
3 |
_____ |
|
4 |
_____ |
Quadro 3
Tabela: equivalente textual a seguir.
|
Número de unidades |
Número de milésimos |
|---|---|
|
1 |
1.000 |
|
2 |
_____ |
|
3 |
_____ |
|
4 |
_____ |
- Quatro unidades é o mesmo que quantos décimos? E quantos centésimos? E quantos milésimos?
_____
- Quais das afirmações abaixo são corretas? _____
Dividir 4 unidades por 10 é equivalente a dividir 40 décimos por 10.
Dividir 4 unidades por 100 é equivalente a dividir 400 centésimos por 100.
Dividir 4 unidades por 1.000 é equivalente a dividir 4.000 milésimos por 1.000.
- De acordo com o item b, qual é o resultado de 4 ÷ 10? E de 4 ÷ 100? E de 4 ÷ 1.000? Escreva os resultados por extenso e na forma decimal. _____

- Faça os cálculos com a ajuda de uma calculadora e registre os resultados.
- 6 ÷ 10 = _____
- 6 ÷ 100 = _____
- 6 ÷ 1.000 = _____
- 3,5 ÷ 10 = _____
- 12,8 ÷ 100 = _____
- 345 ÷ 1.000 =
_____


- Ainda com a calculadora, faça várias outras divisões por 10, por 100 e por 1 000. Depois, converse com um colega sobre o que vocês observaram nos quocientes obtidos.
227

- Em uma campanha de arrecadação de alimentos feita em um município, foram arrecadados 350 quilogramas de arroz e 650 quilogramas de feijão para
serem
divididos igualmente entre 100 famílias de um município vizinho.
Quantos quilogramas de arroz cada família receberá? E de feijão?
_____
- Calcule o resultado da divisão da medida de massa da melancia, em cada caso.

- Divisão em 10 partes iguais. _____
- Divisão em 100 partes iguais. _____
- O diretor de uma empresa que fabrica sabonetes e desodorantes encomendou duas pesquisas com consumidores de seus produtos. O gráfico a seguir mostra a quantidade de consumidores entrevistados em cada pesquisa.
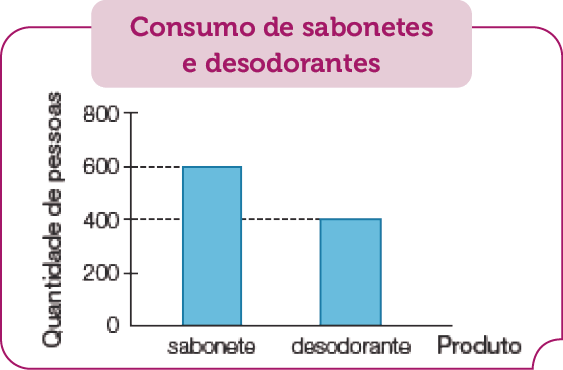
Fonte: Pesquisa da professora Ana (5 fev. 2023).
- Quantos consumidores foram entrevistados ao todo? _____
- Se dos entrevistados da pesquisa sobre o sabonete são mulheres, quantas mulheres participaram dessa pesquisa? _____

- Com um colega, elaborem um problema com base na ilustração abaixo que envolva a divisão. Depois, troquem-no com outra dupla para que ela o resolva.

228
Porcentagem
- Para saber quanto é 25% de 400 doces, Sílvia montou o quadro abaixo.
- Complete-o.

- Como você faria para calcular 10% de 400 com base no quadro de Sílvia?
- Complete-o.
Quadro: equivalente textual a seguir.
|
Taxa percentual de 400 |
Quantidade de doces |
|---|---|
|
100% ou 100 em cada 100 |
400 |
|
50% ou 50 em cada 100 |
_____ |
|
25% ou 25 em cada 100 |
_____ |
- Observe a situação.

- Agora, responda às questões.
- Qual é o valor do desconto na compra à vista? _____
- Quanto custarão à vista os brinquedos mencionados? _____
- Um site de viagens realizou uma pesquisa com 600 turistas sobre a preferência entre os três restaurantes de uma cidade. O gráfico seguinte mostra o resultado.
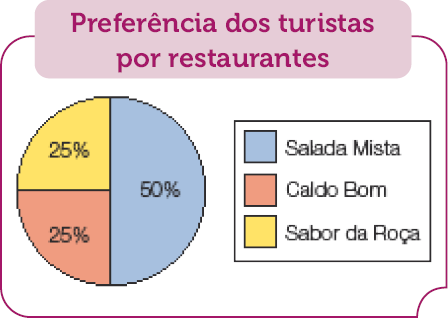
Fonte: Site de viagens (17 mar. 2023).
- Quantos turistas entrevistados disseram preferir o restaurante Salada Mista?
_____
- Quantas pessoas preferem o restaurante Caldo Bom? E o Sabor da Roça? _____
229
- O salário de Ana é composto de uma parte fixa de R$ 1 900,00 e uma parte variável de 3% do valor total de mercadorias que ela vende no mês.

1% de 8 000 é igual a de 8.000
8.000 ÷ 100 = 80
1% de 8.000 é igual a 80.
Então, 3% de R$ 8.000,00 é igual a 3 vezes R$ 80,00, ou seja, R$ 240,00.
Salário - R$ 1.900,00 mais R$ 240,00, ou seja: R$ 2.140,00
Para calcular 3% de 8.000, o gerente de Ana usou uma calculadora.
Sabendo que 3% = = 0,03, ele calculou essa porcentagem de duas maneiras.
Cálculo com o uso da tecla %

Cálculo sem o uso da tecla %

- Agora, calcule e registre no caderno a estratégia que você utilizou.
- 5% de 500
- 15% de 200
- 20% de 600
- 80% de 150
Boxe complementar:
Desafio
Na festa junina de uma escola, estavam presentes algumas pessoas, das quais 30 eram estudantes. As outras eram funcionários ou familiares de estudantes. Observe o gráfico e descubra quantas pessoas estavam presentes nessa festa junina.
_____
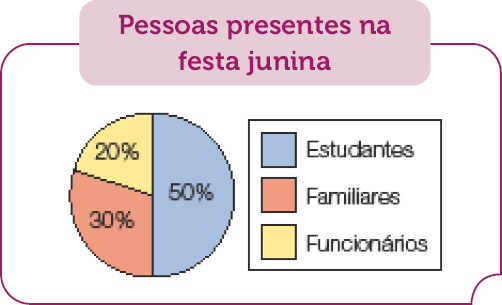
Fonte: Organizadora da festa junina (6 jun. 2023).
CRÉDITO: ADILSON SECCO
Fim do complemento.
230
A Matemática me ajuda a ser
…uma criança que não pratica bullying
Bullying é um termo em inglês que significa intimidar. Ocorre quando alguém ou um grupo maltrata repetidamente uma pessoa para que ela se sinta humilhada, desrespeitada e com medo.
O Instituto Brasileiro de Geografia e Estatística (IBGE) fez em 2015 uma pesquisa no Brasil sobre bullying com estudantes do 9º ano.
Porcentagem aproximada de estudantes, segundo a frequência com que se sentiram humilhados, no Brasil (em 2015)
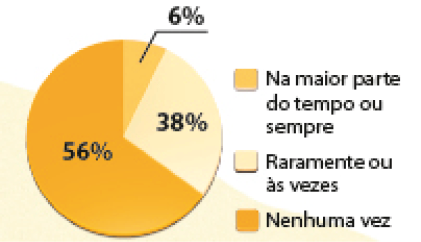
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/9oF. Acesso em: 13 mar. 2021.

Aproximadamente 20 em cada 100 estudantes entrevistados, ou seja, aproximadamente 20% deles, contaram ter esculachado, zoado, caçoado, mangado ou intimidado um colega a ponto de o magoar.
Veja como o problema do bullying em escolas atinge porcentagens próximas em todas as regiões do Brasil.
Porcentagem aproximada de estudantes que se sentiram humilhados por colegas por causa da cor ou da etnia, por região (em 2015)
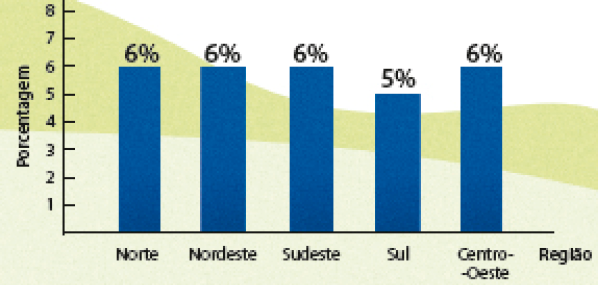
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/9oF. Acesso em: 17 maio 2021.


231
Nessa pesquisa realizada pelo IBGE, as causas das humilhações eram referentes a cor ou etnia, religião, aparência do rosto, aparência do corpo, orientação sexual, região de origem, entre outros motivos.

Porcentagem aproximada de estudantes que se sentiram humilhados por provocações devido à aparência do corpo, no Brasil (em 2015).
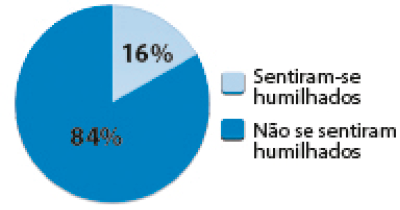
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/eUx. Acesso em 17 maio 2021.
Na pesquisa de 2015, também se perguntou se os estudantes estavam sendo legais uns com os outros.
Porcentagem aproximada de estudantes segundo a frequência com que os colegas os trataram bem e/ou foram prestativos, no Brasil (em 2015)
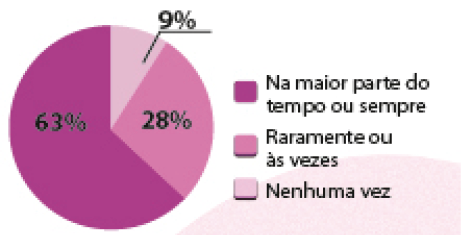
FONTE: Dados obtidos em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/eUx. Acesso em 17 maio 2021.

FONTE: Informações obtidas em: Pesquisa Nacional de Saúde do Escolar 2015. Rio de Janeiro: IBGE, 2015. Disponível em: http://fdnc.io/9oF. Acesso em: 26 fev. 2021.
Tome nota
- Em cada 100 estudantes entrevistados em 2015, aproximadamente quantos se sentiram humilhados raramente ou às vezes?
_____
- Na região do Brasil em que você mora, qual foi a porcentagem aproximada de estudantes que se sentiram humilhados por causa da cor ou da
etnia
em 2015?
_____
- Qual é a porcentagem aproximada de estudantes que se sentiram humilhados por provocações por causa da aparência do corpo segundo a pesquisa de 2015?
_____
- Segundo a pesquisa de 2015, aproximadamente quantos estudantes em cada 100 entrevistados declararam que os colegas os trataram bem e/ou foram prestativos na maior parte do tempo ou sempre? _____
Reflita


Converse com os colegas e o professor sobre as medidas que podem ser tomadas para combater o bullying na escola.
232
Compreender informações
Organizar dados coletados em gráficos de linha
- A rodoviária da cidade de Amarópolis registra todas as viagens que seus ônibus fazem. Observe na tabela a seguir quantas viagens foram feitas por mês no 1º semestre de 2023.
Quantidade de viagens feitas por mês
Tabela: equivalente textual a seguir.
|
Mês |
Quantidade de viagens |
|---|---|
|
Janeiro |
30 |
|
Fevereiro |
25 |
|
Março |
15 |
|
Abril |
20 |
|
Maio |
10 |
|
Junho |
5 |
Fonte: Rodoviária de Amarópolis (9 jul. 2023).

Esses dados podem ser apresentados em um gráfico de linha, no qual representamos por pontos a quantidade de viagens feitas em cada mês. Depois, para visualizar melhor a variação a cada mês, os pontos correspondentes a meses seguidos são ligados por uma linha reta.

Fonte: Rodoviária de Amarópolis (9 jul. 2023).
- Complete o gráfico de linha acima com as viagens que faltam de acordo com a tabela.
- Em qual mês foram feitas mais viagens? E menos viagens?
_____
- Nesse período, a quantidade de viagens só diminuiu? Justifique.
_____

- Você considera mais fácil visualizar a variação entre os dados observando a tabela ou o gráfico de linha? Justifique.
233
- Daniela registrou em sua agenda o
número
de horas de estudo em cada dia da semana passada.
- Complete o gráfico de linha a seguir de acordo com essas anotações.

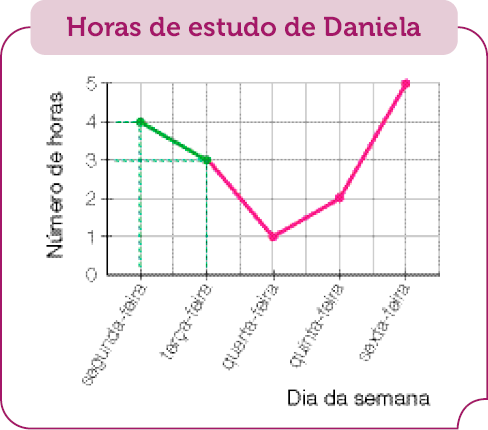
Fonte: Anotações de Daniela (11 ago. 2023).
- De segunda-feira para terça-feira, aumentou ou diminuiu a quantidade de horas de estudo? Quantas horas?
_____
- Ao longo dessa semana, qual foi o dia em que Daniela estudou menos tempo?
_____
- O gráfico abaixo mostra o valor obtido pelas exportações de brinquedos de uma indústria no período de 5 anos.
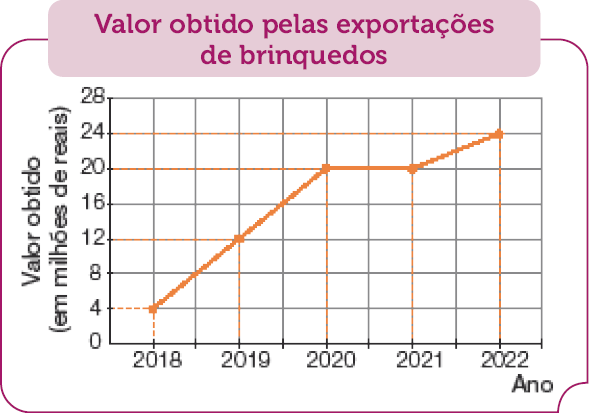
Fonte: Indústria de brinquedos (jan. 2023).
- De 2018 a 2022, o valor
obtido
sempre aumentou? Justifique.
_____

- Crie duas perguntas com base nos dados do gráfico e troque com um colega para respondê-las.
234
O que você aprendeu
Avaliação processual
- Bruna competiu em um campeonato juvenil de ginástica artística feminina. A pontuação obtida por ela em cada prova é mostrada no quadro a seguir.
Quadro: equivalente textual a seguir.
|
Prova |
Pontuação |
|---|---|
|
Salto sobre o cavalo |
12,435 |
|
Barras paralelas |
10,455 |
|
Trave |
12,250 |
|
Solo |
11,850 |
- Em qual
prova
Bruna obteve a maior pontuação? E a menor?
_____
- Qual é a diferença entre a maior e a
menor
pontuação
obtida
por ela?
_____
- Quantos pontos Bruna obteve no total?
_____
- O esquema representa os municípios de Trovoadas e de Calmaria. Nesse esquema, cada centímetro corresponde a 5,4 quilômetros.
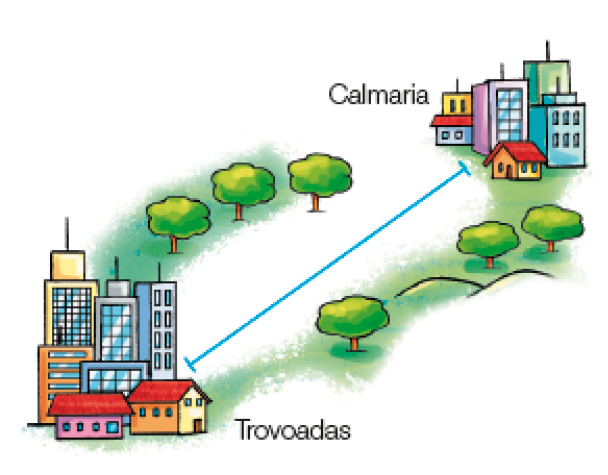
- Com uma régua, obtenha a medida da distância, em centímetros, que separa em linha reta esses dois municípios no esquema. _____
- Qual é a medida da distância entre esses dois municípios em quilômetros?
_____
- Escreva os números que completam os espaços indicados na reta numérica.


- Um
modelo
de pirâmide de base quadrada tem todas as arestas com comprimento de mesma medida. Se o perímetro de sua base
mede
38 centímetros, qual é a medida em centímetro do comprimento de cada aresta desse
modelo
de pirâmide?
_____
235

- Eduardo fez a divisão mostrada abaixo. Ele usou o algoritmo usual, mas cometeu um erro.

- Qual foi o erro de Eduardo?
- Qual é o resultado correto dessa divisão? _____
- Como você pode conferir se esse resultado está correto sem usar uma calculadora?
_____
- Ivan esqueceu-se de pagar uma conta no valor de R$ 230,00 até a data de vencimento. Por isso, ele teve de pagar 2% de multa sobre esse valor.
- Quanto Ivan teve de pagar de multa? _____
- Qual passou a ser o valor da conta? _____
- Ricardo foi a uma loja para comprar uma televisão que custa R$ 900,00, mas ele está indeciso sobre qual das duas formas de pagamento deve escolher.

- Se Ricardo pagar à vista, quanto custará a televisão? _____
- Se escolher a outra forma de pagamento, quanto ele pagará, no total, pela televisão? _____
- De quantos reais é a diferença entre os preços das duas formas de pagamento? _____
Autoavaliação

- Consigo representar um
número
com uma fração e na forma decimal?

- Consigo operar com números na forma decimal?